Входная контрольная по алгебре 9: Входная контрольная работа по алгебре 9 класс (с ответами) Макарычева скачать

Входная контрольная работа по математике 9 класс | Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс):

Входная контрольная работа

для учащихся 9 классов

МБОУ СОШ № 14 с.Кривенковское

Вариант 1.

1. Вычислить:       (-3 + 2)·(-8+ 7)
2. Найти значение выражения:
3. Решить уравнения:     х2- 4х+3=0
4. Решить неравенство: 3х + 4(-7 + 6х)≤-7х + 6
5. Упростить выражение:
6. Решить задачу:   В книге  два рассказа занимают 121 страницу. Число страниц первого рассказа составляет  от числа страниц второго рассказа. Сколько страниц занимает каждый рассказ?
7. Периметр квадрата равен 84. Найти площадь этого квадрата.
8. Средняя линия трапеции равна  25,5 , а меньшее основание равно 21. Найти большее основание трапеции.
9. Сумма двух углов в параллелограмме равна 80°. Найти один из оставшихся углов параллелограмма. Ответ дать в градусах.
10. Какие из следующих утверждений верны:

1)   У любой трапеции основания параллельны.

2)  Диагонали ромба равны.

3)  Медиана треугольника делит пополам угол, из  которого она проведена.

В ответ запишите номер верного утверждения.

Входная контрольная работа

для учащихся 9 классов

МБОУ СОШ № 14 с.Кривенковское

Вариант 2.

1. Вычислить:      1 ·(-) – (-2)·
2. Найти значение выражения:
3. Решить уравнение:    2х2-3х-2=0
4. Решить неравенство: -х — 8(2х-1) ≤ 3х — 9
5. Упростить выражение:
6. Решить задачу:    Учащиеся  младших классов составляют 45% всех учащихся школы. В более старших классах учатся остальные 385 учащихся. Сколько всего учащихся в школе?
7. Периметр квадрата равен 56. Найти площадь этого квадрата.
8. Средняя линия трапеции равна  23,   а меньшее основание равно 15.  Найти большее основание.
9. Один из углов параллелограмма больше другого на 52°. Найти больший угол. Ответ дать в градусах.
10. Какие из следующих утверждений верны:

1)  Средняя линия трапеции равна сумме её оснований.

2)  Диагонали ромба перпендикулярны.

3)  Площадь прямоугольника  равна квадрату суммы его сторон.

В ответ запишите номер верного утверждения.

Входная контрольная работа

для учащихся 9 классов

МБОУ СОШ № 14 с.Кривенковское

Вариант 3.

1. Вычислить:     · (-15,3 -24,3·)
2. Найти значение выражения:
3. Решить уравнение:   2х2 – 5х +2 = 0
4. Решить неравенство: 6х +10(7 + 5х) ≥-9х + 5
5. Упростить выражение:  
6. Решить задачу: В первый час машина проехала 12% всего пути, после чего ей осталось проехать 440 км. Какова длина всего пути?
7. Периметр квадрата равен  48. Найти площадь этого квадрата.
8. Средняя линия трапеции равна 11, а меньшее основание равно 5. Найти большее основание трапеции.
9. Один из углов параллелограмма больше другого на 62°. Найти больший угол. Ответ дать в градусах.
10. Какие из следующих утверждений верны:

1)  Смежные углы равны.

2)  Площадь параллелограмма равна половине произведения его оснований.

3) Средняя линия трапеции равна полусумме её оснований.

В ответ запишите номер верного утверждения.

 

Входная контрольная работа

для учащихся 9 классов

МБОУ СОШ № 14 с.Кривенковское

Вариант 4.

1. Вычислить:   1 : (- +  )
2. Найти значение выражения:
3. Решить уравнение:       7х2 – х – 8 =0
4. Решить неравенство: 2х + 4(-1 – 7х) ≥-х + 1
5. Упростить выражение:  
6. Решить задачу: Площадь двух комнат составляет 48 м2. Площадь одной комнаты составляет  от площади другой. Найти площадь каждой комнаты.
7. Периметр  квадрата равен 44. Найти площадь этого квадрата.
8. Средняя линия трапеции равна 7, а большее основание равно 10. Найти меньшее основание.
9. Сумма двух углов в параллелограмме равна 100°. Найти один из оставшихся углов параллелограмма. Ответ дать в градусах.
10. Какие из следующих утверждений верны:

1)  Сумма углов прямоугольного треугольника равна 90°

2) Площадь параллелограмма равна половине произведения его диагоналей.

3)  Вертикальные углы равны.

В ответ запишите номер верного утверждения.

Входная контрольная работа

для учащихся 9 классов

МБОУ СОШ № 14 с.Кривенковское

Вариант 5.

1. Вычислить:  (-24 + 13,8): 2
2. Найти значение выражения:
3. Решить уравнение:    6х2 + х – 7 = 0
4. Решить неравенство: 6х + 3(-5 – 8х)> 2х +4
5. Упростить выражение:  
6. Решить задачу:    В первый день путешествия туристы преодолели 7%  пути.   После этого им осталось пройти и проплыть 176,7 км. Каков путь туристов?
7. Периметр квадрата равен 60.Найти площадь этого квадрата.
8. Средняя линия трапеции равна  16, а меньшее основание равно 12. Найти большее основание.
9. Сумма двух углов в параллелограмме равна 120°. Найти один из оставшихся углов параллелограмма. Ответ дать в градусах.
10. Какие из следующих утверждений верны:

1)  Сумма смежных углов равна 180°.

2)  Средняя линия трапеции равна сумме её оснований.

3)  Площадь прямоугольного треугольника равна произведению длин его сторон.

В ответ запишите номер верного утверждения.

Ответы

к входной контрольной работе

для 9 класса

	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5
1		6,5	-24		-4
2	10,08	14,85	162,75	5,4	6,72
3	1 и 3	-0,5 и 2	0,5 и 2	1	-1 и 1
4	х ≤ 1	х≥0,85	х≥ -1	х ≤ -0,2	x
5
6	33 и 88	700	500	20 и 28	190
7	441	196	144	121	225
8	30	31	17	4	20
9	140	116	121	130	120
10	1	2	3	3	1

Входящая Контрольная Работа По Математике 9 Класс – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

Входящая Контрольная Работа По Математике 9 Класс

Опубликовано 20. 11.2016 — 9:03 — Кайибханова Анастасия Сергеевна
Входная контрольная работа предназначена для проведения в 9 классе. Данная работа проверяет качество усвоения знаний по основным темам, пройденным в 8 классе  по математике, учебник Алгебра 8 класс ,  авторы Ю.Н.Макарычев  , Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова.  В работе представлены 2 варианта заданий по шести различным темам (сложение и вычитание дробей, умножение и деление дробей, вычислите- корень квадратный, решите систему уравнений, решите неравенство, систему неравенств,найдите значение выражения содержащего корни квадратные) готовые к распечатке и бланк для проведения анализа работы.
1 Выполните сложение и вычитание дробей
2 Выполните умножение и деление дробей
 6 Вычислите координаты точки пересечения графиков
1    Выполните сложение и вычитание дробей
2 Выполните умножение и деление дробей
6 Вычислите координаты точки пересечения графиков
Итоги входной контрольной работы 9 класс. Дата проведения ________________________
Задание 1(а) Выполните сложение и вычитание дробей
Задание 1(б) Выполните сложение и вычитание дробей
Задание 2 (а) Выполните умножение и деление дробей
Задание 2 (б) Выполните умножение и деление дробей
Задание 3(а) Вычислите (корень квадратный, его свойства)
Задание 3(б) Вычислите (корень квадратный, его свойства)
Задание 4 (а) Решите  квадратное уравнение
Задание 4 (б) Решите неполное квадратное уравнение
Задание 4 (в) Решите систему уравнений
Задание 4 (г) Решите систему уравнений
Задание 5(а) Решите систему неравенств
Задание 6 Найдите координаты точки пересечения графиков
Задание 7 Найдите значение выражения, содержащего корни квадратные
Контрольная работа для учащихся 5 класса по математике к учебнику Н. Я. Виленкина по преемственности…
Входная контрольная работа проводится с целью определения уровня усвоения учащимися основных знаний и умений к началу обучения в 5 классе основной школы и рассчитана на один урок (40 минут).Работа сос…
Работа рассчитана на 40 минут урока. Контрольная работа включает задания трех уровней. В заданиях первого уровня ученикам следует выбрать букву правильного ответа. В заданиях второго и трет…
Работа рассчитана на 40 минут урока. Контрольная работа включает задания трех уровней. В заданиях первого уровня ученикам следует выбрать букву правильного ответа. В заданиях второго и трет…
Работа составлена с использованием материалов ГИА 9 класса…
Контрольная работа представлена в 4 вариантах. Удобен тем, что к нему есть ключ и пример анализа работы. Рекомендуется проводить в сентябре….

Контрольная работа по математике (входная) 9 класс
Входная контрольная работа по алгебре 9 класс
Входная контрольная работа по математике 9 класс .
Скачать | Аверсэв
Входная контрольная работа по математике 9 класс УМК…
Отчет По Практике Оренбург
Сочинение На Тему Хруцкий Цветы И Плоды
Тема Сочинения 15 3
Как Подготовиться К Сочинению 4 Класс
Жаһандану Мәселесі Эссе

Алгебра 9 Макарычев Контрольная 6 с ответами

Итоговая контрольная работа по алгебре с ответами для учащихся 9 класса по УМК Макарычев. Настоящая проверочная работа за год в 4-х вариантах является важным дополнением к учебнику Ю.Н.Макарычева и др. «Алгебра 9 класс». Цитаты из пособия «Контрольно-измерительные материалы (КИМ) по алгебре 9 класс / Глазков, Гаиашвили, Ахременкова» использованы в учебных целях. Алгебра 9 Макарычев Контрольная 6. Ответы на все 4 варианта адресованы родителям.

 

Алгебра 9 класс (Макарычев)

Итоговая контрольная работа

 

К-6. Вариант 1 (транскрипт)

1. На рисунке построен график функции y = f(x) с областью определения [–3; 5]. Найдите область значений этой функции.
2. Графики функций у = 1 – х² и у = –х – 1 пересекаются в точках А и В. Вычислите координаты точки В.
3. Решите систему уравнений
   { х + у = 2,
   { у² – х² = 12.
4. Решите неравенство (3 – 2х)/(х + 2) + 1 ≤ 0.
5. Дана геометрическая прогрессия –24; –12; –6;…. Найдите сумму первых пяти её членов.
6. В соревновании по метанию копья участвуют 4 спортсмена из Франции, 7 спортсменов из Швеции и 9 спортсменов из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.
7. Расстояние между двумя пунктами автомобиль должен был пройти за 3 ч. Первые 2 ч он ехал с намеченной скоростью, а затем увеличил ее на 10 км/ч, поэтому в конечный пункт приехал на 12 мин раньше, чем предполагал. Найдите расстояние между этими пунктами.
8. Упростите выражение (1/n – 1/m) : (m² – n²)/3mn и найдите его значение при m = √7 – 4 и n = 2 – √7.

Вариант 2

1. На рисунке построен график функции y = f(x) с областью определения [–4; 5]. Найдите область значений этой функции.
2. Графики функций у = х² – 3 и у = –х – 1 пересекаются в точках А и В. Вычислите координаты точки В.
3. Решите систему уравнений
   { х + у = 6,
   { x² – y² = 12
4. Решите неравенство (1 – 2х)/(х – 3) + 1 ≥ 0.
5. Дана геометрическая прогрессия –0,25; –1; – 4;…. Найдите сумму первых пяти её членов.
6. В среднем из 1000 авторучек, поступивших в продажу, 15 пишут плохо или не пишут. Найдите вероятность того, что одна случайно выбранная авторучка пишет хорошо.
7. Лодка проплыла за 3 часа по течению такое же расстояние, какое за 4 часа она проплыла против течения. Найдите расстояние, которое проплыла лодка вниз по течению, если собственная скорость лодки равна 14 км/ч.
8. Упростите выражение 2ху/(х² – у²) • (1/у – 1/х) и найдите его значение при х = √5 + 3 и у = 1 – √5.

---

 

Ответы на контрольную работу

 

---

Вы смотрели: Итоговая контрольная работа по алгебре с ответами для учащихся 9 класса по УМК Макарычев. Настоящая проверочная работа «Элементы комбинаторики и теории вероятностей» является важным дополнением к учебнику Ю.Н.Макарычева и др. «Алгебра 9 класс». Ответы адресованы родителям.

Вернуться к списку контрольных работ по алгебре в 9 классе (Макарычев)

 

входная контрольная работа по алгебре 9 класс макарычев

Рабочая программа по алгебре (9. Входная контрольная работа: 21-22. График. по алгебре: 9 класс к учебнику Ю.Н. Макарычев и др. Контрольные работы по алгебре 7. Контрольные работы по алгебре 7 класс по учебнику Ю.Н. Макарычев, Н. Г. Миндюк.. точка М (9; -25)? входная контрольная работа по алгебре 9 класс макарычев Работа всем! Зарабатывай в интернете от 200$ в день! Начни прямо сейчас! входная контрольная работа по алгебре 9 класс макарычев Рабочая программа по алгебре (9. Макарычев «Дидактические материалы по алгебре для 9 класса. входная контрольная работа. входная контрольная работа по алгебре 9 класс макарычев Заработок от 120$ в день! Работа в Интернете! Без вложений! Доступно для всех регионов России и СНГ! Контрольные работы в СПб! Контрольные на заказ от 1 дня, готовые от 15 минут. В офисе и online! входная контрольная работа по алгебре 9 класс макарычев Работа в компании «Мэри Кэй» Вакансия специально для женщин! Свободный график, возможно совмещение. входная контрольная работа по алгебре 9 класс макарычев Контрольные работы по алгебре для 9 — Контрольные работы по алгебре для 9 класса (Макарычев 2008 г) Контрольные работы … Контрольная работа! Зарабатывай в интернете от 140$ в день! Россия и СНГ! Входная контрольная работа по. Входная контрольная работа по алгебре 9 класс — на нашем сайте вы. Виленкин, Нелин, Макарычев … Скачать входная контрольная работа. Скачать входная контрольная работа по алгебре 9 класс макарычев 2 вариант — Сегодня .

.. Поиск кредита по всем банкам РФ Найти кредит до 30.000.000 на любые цели уже сейчас. Быстро, удобно, легко. Дидактические материалы по алгебре. Дидактические материалы по алгебре для 9 класса — Макарычев Ю.Н., контрольные работы входная контрольная работа по алгебре 9 класс макарычев Контрольные на заказ. СПБ Сделаем для Вас контрольную по любому предмету.Мин.сроки и цены.Офис центр входная контрольная работа по алгебре 9 класс макарычев Контрольные работы по алгебре по. Контрольные работы по алгебре по учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. входная контрольная работа по алгебре 9 класс макарычев контрольные работы по алгебре! Выполнение контрольных работ. Эксклюзивное написание. Скидки! входная контрольная работа по. … договор, гарантируем сдачу. входная контрольная работа по алгебре 9 класс макарычев ответы. входная контрольная работа по алгебре 9 класс макарычев контрольные работы по алгебре 9. контрольные работы по алгебре 9 класс макарычев. Скачать бесплатно Контрольные на 5, хорошие цены! Сжатые сроки от 1 дня.

Договор. 2 Офиса в Спб. Не плагиат. Работаем честно!

Входной срез по алгебре 9 класс ответы :: monutdahab

14.11.2016 07:21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ним для проведения промежуточной аттестации по русскому языку в 6,7, классах. Входной срез по алгебре 9 класс вариант 2 с ответами. Решить уравнение: Упростить выражение: Найти ОДЗ переменной в выражении:. Входной срез 9 классскачать. Административная контрольная за 1 полугодие, алгебра, 8 клскачать. Тест по математике за 3 четверть для учащихся 6 класса. Входная контрольная работа для 9 класса по алгебре проверяет знание. Учебное пособие для учителей.

Комментариев: 0. Отличные входные срезы для 11 класса. Беру себе. Хорошие задания вх. Среза по алгебре 9 кл. Он расчитан на 2 часа. К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Аркфункции, сам. Работа 11.

Клскачать. Дети с хорошей математической подготовкой справятся, конечно, гораздо раньше. Да, он рассчитан на 2 урока. Входной срез.9класс. Алимов. Вариант 1. Входной срез по алгебре 7 класс. Ответ дайте в градусах. Контрольная работа представлена с использованием заданий кимов ГИА 9 класса. С выбором ответа из четырех предложенных вариантов ученик должен выбрать только верный ответ. Входной срез по алгебре для учащихся 8 класса. Презентация по математике класс Производные. Обведите цифру, которая обозначает номер выбранного Вами ответа. Входной срез по алгебре. Входная контрольная работа по математике 9 класс. Предмет Класс Тема Тип контроля Форма контроля Время на выполнение работы Цель Планируемые образовательные результаты.

Входной контроль 9 класс Вариант 1. Инструкция по. Всего ответов: 79. Входной тест по математике 7 класстест. Входной срез по алгебре. Обведите цифру, которая обозначает номер выбранного Вами ответа. Функция определена на промежутке. При выполнении заданий 1 8 нужно указать ответы в. Входной срез.9 класс. Вариант 2. Вариант 1. Поделитесь материалом с коллегами.5. Доказать, что парабола и прямая имеют одну общую точку и найти координаты этой точки. Решить уравнение. Теляковского С. А.книга. Контрольные срезы по математике за первое полугодие с 5 по 9 классысрез. Алгебра и графика модуля. Скачать материал. В этом уравнении старший коэффициент равен единице. Предварительный просмотр: Входной срез.6 класс. Вариант 1. Тесты и ответы к.

 

Вместе с Входной срез по алгебре 9 класс ответы часто ищут

 

входной срез по алгебре 9 класс 2 вариант.

входной срез по алгебре 8 класс ответы.

входная контрольная работа по алгебре 9 класс ответы.

срез по алгебре 8 класс 2016.

входной срез по алгебре 10 класс.

контрольный срез по математике 9 класс ответы.

входной срез 8 класс 1 вариант ответы.

входная контрольная работа по алгебре 9 класс макарычев

 

Читайте также:

 

Упражнение 127 зеленина хохлова 3 класс

 

Решебник по английскому языку и.п агабекян 148 стр

 

Сборник диктантов для второго класса по программе школа

 

Проходная контрольна 9 класс — healthnsk.ru

Скачать проходная контрольна 9 класс PDF

ПРИЛОЖЕНИЕ К РАБОЧЕЙ ПРОГРАММЕ ПО МАТЕМАТИКЕ 7 КЛАСС. Контрольная работа №1 по теме: «Функции и их свойства. Квадратный трехчлен». Контрольная работа № 2 по теме: «Квадратичная функция. Степенная функция». Входная контрольная работа по алгебре 9 класс. Дидактический материал по алгебре для 9 класса содержит входную контрольную работу, Составленную в 4-х вариантах с разработанными критериями оценивания и ответами.

Решебник «Алгебра 9 Класс Дидактические материалы» (Авторы Ю.Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева) – это отличная помощь для школьников, учителей, а также родителей. В выпускном классе основной школы важно не допустить серьезных пробелов в знаниях, чтобы учащиеся отлично подготовились к экзаменам.

Подходит для всех. Здесь представлены готовые домашние работы, которые соответствуют ФГОС второго поколения. 9 класс. Контрольные работы по алгебре и геометрии для 9 класса. Ознакомительные версии (цитаты) из учебных пособий. К большинству контрольных работ даны ответы и решения. Для получения полных версий контрольных работ указаны ссылки на покупку пособий в интернет-магазине.

Алгебра 9 класс. УМК Мерзляк, Полонский, Якир — Дидактические материалы (6 контрольных, 2 варианта) УМК Мерзляк, Полонский, Якир — Буцко: Методическое пособие (6 контрольных, 4 варианта). Контрольные работы 9 класс» Александрова. Какие аспекты есть в пособии. В сборник вошло семь контрольных работ, в том числе и итоговая за весь курс.

Каждая из них предусматривает несколько уровней сложности, а проработка всех четырех вариантов поможет лучше узнать суть предмета. Детализированные решения в ГДЗ по алгебре 9 класс Александрова позволяют тщательно проработать все трудные аспекты. Для чего им надо пользоваться. Этот год становится для подростков поворотным: кто-то пойдет учиться в следующий класс, а некоторые и вовсе покинут школьные стены.

Контрольные работы по алгебре составлены к учебнику алгебры 9-гокласса Ю. Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С. Б. Суворовой, но могут быть использованы и при изучении алгебры по учебникам других авторов. Контрольная работа №1 Квадратный трехчлен.

Квадратичная функция. (Приложение 1). Контрольная работа №2 «Уравнения и неравенства с одной переменной» (Приложение 2). Контрольная работа № 3Системы уравнений с двумя переменными. (Приложение 3). Контрольная работа № 4 Арифметическая прогрессия. (Приложение 4). Контрольная работа №5 Геометрическая прогрессия (Приложение 5). Контрольная работ. Входная контрольная работа по алгебре 9 класс. Дидактический материал по алгебре для 9 класса содержит входную контрольную работу, Составленную в 4-х вариантах с разработанными критериями оценивания и ответами.

Алгебра 9 Макарычев Контрольные работы с ответами (4 варианта). Цитаты из пособия: «Алгебра. Дидактические материалы 9 класс / Ю.Н.

Макарычев, Н.Г. Миндюк, Л.Б. Крайнева — М.: Просвещение» использованы в учебных целях. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания. Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия.

rtf, fb2, PDF, djvu

Похожее:

Людина 21 століття презентація

Мерзляк геометрія 10 клас онлайн

Дитячі письменники презентація

Гдз решебник геометрія 9 клас єршова голобородько

Т. с.котик біологія 7 клас гдз

Географія 6 клас практичні роботи аксіома

Грушевський м с ілюстрована історія україни

Алгебра 9 Контрольные Мерзляк | Контроль-знаний.рф

Алгебра 9 Контрольные Мерзляк. Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Алгебра 9 класс. Дидактические материалы/ А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович и др. — М.: Вентана-Граф». Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник «Алгебра 9 класс» авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир системы УМК «Алгоритм успеха». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.

Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия (образец варианта № 1). Затем представлены ответы на оба варианта контрольной. При постоянном использовании данных контрольных работ рекомендуем КУПИТЬ книгу:  Мерзляк, Рабинович, Полонский: Алгебра. 9 класс. Дидактические материалы. ФГОС (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки учебного пособия.

Контрольные работы по алгебре

9 класс, УМК Мерзляк и др.

Выберите нужную вам контрольную работу:

 

Контрольная работа № 1 К-1 «Неравенства» Контрольная работа № 2 К-2 «Квадратичная функция, её график и свойства»

Контрольная работа № 3 К-3 «Решение квадратных неравенств. Системы уравнений с двумя переменными»

Контрольная работа № 4 К-4 «Элементы прикладной математики» Контрольная работа № 5 К-5 «Числовые последовательности» Контрольная работа № 6 К-6 Итоговая за 9 класс

---

Вернуться на страницу «Алгебра 9 класс. Все тесты и контрольные».

Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.

Другие контрольные работы по математике в 9 классе:

---

Вы смотрели страницу Алгебра 9 Контрольные Мерзляк. Цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Алгебра 9 класс. Дидактические материалы/ А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович и др. — М.: Вентана-Граф».

 

Введение в функции | Безграничная алгебра

Функции и их обозначения

Функция отображает набор входов на набор допустимых выходов. Каждому входу соответствует один и только один выход

Цели обучения

Соедините обозначение функций с обозначением уравнений и поймите критерии действительной функции

Основные выводы

Ключевые моменты

• Функции — это отношение между набором входов и набором выходов со свойством, что каждый вход сопоставляется ровно с одним выходом.
• Обычно функции называются одной буквой, например f .
• Функции можно представить как машину в коробке, открытой с двух сторон. Вы помещаете что-то в один конец коробки, это каким-то образом изменяется внутри коробки, а затем результат выскакивает из другого конца.
• Все функции являются отношениями, но не все отношения являются функциями.

Ключевые термины

• вывод : вывод — это результат или ответ функции.
• отношение : отношение — это связь между числами в одном наборе и числами в другом.
• функция : функция — это отношение, в котором каждый элемент ввода связан ровно с одним элементом вывода.

Функции

В математике функция — это отношение между набором входов и набором допустимых выходов. Функции обладают тем свойством, что каждый вход связан ровно с одним выходом.2 [/ latex], имеем упорядоченную пару [latex] (- 3, 9) [/ latex]. Если и вход, и выход являются действительными числами, то упорядоченную пару можно рассматривать как декартовы координаты точки на графике функции.

Еще одно часто используемое обозначение для функции — [latex] f: X \ rightarrow Y [/ latex], которое гласит, что [latex] f [/ latex] — это функция, отображающая значения из набора [latex] X [ / latex] на значения набора [latex] Y [/ latex].

Функционирует как машина

Функции часто описывают как машину в коробке, открытой с двух сторон.Вы помещаете что-то в один конец коробки, это изменяется внутри коробки, а затем результат выскакивает из другого конца. Функция — это машина внутри коробки, и она определяется тем, что она делает с тем, что вы в нее кладете.

Функциональная машина: Функция [latex] f [/ latex] принимает входные данные [latex] x [/ latex] и возвращает выходные данные [latex] f (x) [/ latex]. Одна метафора описывает функцию как «машину», которая для каждого ввода возвращает соответствующий вывод.

Допустим, у машины есть лезвие, которое разрезает все, что вы вставляете, на две части и отправляет одну половину этого объекта с другого конца.Если вы добавите банан, вы получите половину банана. Если вы положите яблоко, вы получите половину яблока.

Функция разделения фруктов пополам: Здесь показана функция, которая принимает фрукт на входе и выпускает половину фрукта на выходе.

Давайте определим функцию, чтобы взять то, что вы в нее положили, и разрезать пополам. То есть функция делит ввод на два. Если вы добавите [латекс] 2 [/ латекс], вы получите обратно [латекс] 1 [/ латекс]. Если вы положите [латекс] 57 [/ латекс], вы получите обратно [латекс] 28.5 [/ латекс]. Функциональная машина позволяет нам изменять выражения. В этом примере функция будет записана как:

[латекс] \ displaystyle f (x) = \ frac {1} {2} x [/ latex].

Функции как отношения

Функции также можно рассматривать как подмножество отношений. Отношение — это связь между значениями в одном наборе и значениями в другом. Другими словами, каждое число, которое вы вводите, связано с каждым числом, которое вы получаете. В функции каждый входной номер связан ровно с одним выходным номером. В отношении входной номер может быть связан с несколькими выходными номерами или без них.Это важный факт о функциях, который нельзя переоценить: каждый возможный вход функции должен иметь один и только один выход. Все функции являются отношениями, но не все отношения являются функциями.

Графическое представление функций

Графики обеспечивают визуальное представление функций, показывая взаимосвязь между входными и выходными значениями.

Цели обучения

Опишите взаимосвязь между графиками уравнений и графиками функций

Основные выводы

Ключевые моменты

• Функции имеют независимую переменную и зависимую переменную.Обычно [latex] x [/ latex] является независимой переменной, а [latex] y [/ latex] зависимой переменной.
• При выборе любого допустимого значения для независимой переменной зависимая переменная определяется функцией.
• Чтобы построить график функции, выберите некоторые значения для независимой переменной [latex] x [/ latex], вставьте их в функцию, чтобы получить набор упорядоченных пар [latex] (x, f (x)) [/ latex] , и нанесите их на график. Затем соедините точки так, чтобы они лучше всего соответствовали их расположению на графике.Убедитесь, что у вас достаточно очков.

Ключевые термины

• зависимая переменная : Зависимая переменная в уравнении или функции — это переменная, значение которой зависит от одной или нескольких независимых переменных в уравнении или функции.
• независимая переменная : Независимая переменная в уравнении или функции — это переменная, значение которой не зависит от какой-либо другой переменной в уравнении или функции.
• график : диаграмма, отображающая данные; в частности, тот, который показывает взаимосвязь между двумя или более величинами, измерениями или числами.

Независимые и зависимые переменные в функциональной нотации

Функции имеют независимую переменную и зависимую переменную. Когда мы смотрим на такую ​​функцию, как [latex] f (x) = \ frac {1} {2} x [/ latex], мы вызываем изменяемую переменную, в данном случае [latex] x [/ latex] , независимая переменная. Мы присваиваем значение функции переменной, в данном случае [latex] y [/ latex], которую мы называем зависимой переменной. Обозначение функции, [latex] f (x) [/ latex] читается как «[latex] f [/ latex] of [latex] x [/ latex]]», что означает «значение функции в [latex] x [ /латекс].”Поскольку выходная или зависимая переменная — [latex] y [/ latex], для обозначения функции часто [latex] f (x) [/ latex] рассматривается как [latex] y [/ latex]. Упорядоченные пары, обычно указываемые в линейных уравнениях как [latex] (x, y) [/ latex], в обозначениях функций теперь записываются как [latex] (x, f (x)) [/ latex].

Мы говорим, что [latex] x [/ latex] является независимым, потому что мы можем выбрать любое значение, для которого определена функция, в данном случае набор действительных чисел [latex] \ mathbb {R} [/ latex], в качестве входных данных. в функцию.Мы говорим, что результат присваивается зависимой переменной, поскольку он зависит от того, какое значение мы поместили в функцию.

Графические функции

Пример 1. Начнем с простой линейной функции:

[латекс] \ displaystyle f (x) = 5- \ frac {5} {2} x [/ latex].

Начните с построения графика, как если бы [latex] f (x) [/ latex] было линейным уравнением:

[латекс] \ displaystyle y = 5- \ frac {5} {2} x [/ latex]

Мы выбираем несколько значений для независимой переменной [latex] x [/ latex].Давайте выберем отрицательное значение, ноль и положительное значение:

.

[латекс] \ displaystyle x = -2, 0, 2 [/ латекс].

Затем подставьте эти значения в функцию для [latex] x [/ latex] и решите для [latex] f (x) [/ latex] (что означает то же, что и зависимая переменная [latex] y [/ latex] ): Получаем заказанные пары:

[латекс] \ displaystyle (-2,10), (0,5), (2,0) [/ латекс]

Это функция линии, так как наивысший показатель в функции — [латекс] 1 [/ латекс], поэтому просто соедините три точки. {3} -9x [/ латекс]. Степень функции равна 3, следовательно, это кубическая функция.

Тест вертикальной линии

Тест вертикальной линии используется для определения того, является ли кривая на плоскости [latex] xy [/ latex] функцией

Цели обучения

Объясните, почему тест вертикальной линии графически показывает, является ли кривая функцией

Основные выводы

Ключевые моменты

• Функция может иметь только один выход, [latex] y [/ latex], для каждого уникального входа, [latex] x [/ latex].Если какое-либо значение [latex] x [/ latex] в кривой связано с более чем одним значением [latex] y [/ latex], то кривая не представляет функцию.
• Если вертикальная линия пересекает кривую на плоскости [латекс] xy [/ latex] более одного раза, то для одного значения x кривая имеет более одного значения y , и кривая не представляет функция.

Ключевые термины

• функция : отношение, в котором каждый элемент ввода связан ровно с одним элементом вывода.
• Тест вертикальной линии : Визуальный тест, который определяет, является ли кривая функцией или нет, путем проверки количества значений [latex] y [/ latex], связанных с каждым значением [latex] x [/ latex], которое лежит на кривой.

В математике проверка вертикальной линии — это визуальный способ определить, является ли кривая графиком функции или нет. Напомним, что функция может иметь только один выход, [latex] y [/ latex], для каждого уникального входа, [latex] x [/ latex]. Если какое-либо значение [latex] x [/ latex] в кривой связано с более чем одним значением [latex] y [/ latex], то кривая не представляет функцию.

Если вертикальная линия пересекает кривую на плоскости [латекс] xy [/ latex] более одного раза, то для одного значения x кривая имеет более одного значения y , и кривая не представляет функция. Если все вертикальные линии
пересекают кривую не более одного раза, тогда кривая представляет функцию.

Тест вертикальной линии: Обратите внимание, что на верхнем графике одна вертикальная линия, проведенная там, где нанесены красные точки, пересекает кривую 3 раза.Таким образом, он не проходит проверку вертикальной линии и не представляет функцию. Любая вертикальная линия на нижнем графике проходит только один раз и, следовательно, проходит проверку вертикальной линии и, таким образом, представляет функцию.

Чтобы использовать тест вертикальной линии, возьмите линейку или другую линейку и проведите линию, параллельную оси [latex] y [/ latex], для любого выбранного значения [latex] x [/ latex]. Если нарисованная вами вертикальная линия пересекает график более одного раза для любого значения [latex] x [/ latex], то график не является графиком функции.Если, в качестве альтернативы, вертикальная линия пересекает график не более одного раза, независимо от того, где расположена вертикальная линия, тогда график является графиком функции. Например, кривая, представляющая собой любую прямую линию, отличную от вертикальной, будет графиком функции.

Пример

См. Три графика ниже: [латекс] (a) [/ латекс], [латекс] (b) [/ латекс] и [латекс] (c) [/ латекс]. Примените тест вертикальной линии, чтобы определить, какие графики представляют функции.

Применение теста вертикальной линии: Какие графики представляют функции?

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных на графиках [latex] (a) [/ latex] и [latex] (b) [/ latex]. Из этого можно сделать вывод, что эти два графика представляют функции. Третий график, [latex] (c) [/ latex], не представляет функцию, потому что не более чем [latex] x [/ latex] -значений, вертикальная линия будет пересекать график более чем в одной точке. Это показано на схеме ниже.

Не функция: Тест вертикальной линии показывает, что круг не является функцией. 3 — 1

— это функции, потому что каждое значение x дает другое значение y . В графических терминах функция — это отношение, в котором первые числа в упорядоченной паре имеют одно и только одно значение в качестве второго числа, другой части упорядоченной пары.

Проверка упорядоченных пар

Упорядоченная пара — это точка на графике координат x — y со значениями x и y. Например, (2, −2) — это упорядоченная пара с 2 в качестве значения x и −2 в качестве значения y .При наличии набора упорядоченных пар убедитесь, что ни одно значение x не имеет более одного парного значения y . Когда задан набор упорядоченных пар [(2, −2), (4, −5), (6, −8), (2, 0)], вы знаете, что это не функция, потому что x -Значение — в данном случае — 2, имеет более одного значения y . Однако этот набор упорядоченных пар [(−2, 4), (−1, 1), (0, 0), (1, 1), (2, 4)] является функцией, потому что y -value может иметь более одного соответствующего значения x .

Решение для Y

Относительно легко определить, является ли уравнение функцией, решив для y . Когда вам дается уравнение и конкретное значение для x , должно быть только одно соответствующее значение y для этого значения x . Например,

y = x + 1

— это функция, потому что y всегда будет на единицу больше x . Уравнения с показателями также могут быть функциями.2 = 9

имеет два возможных ответа (3 и −3).

Тест вертикальной линии

Определить, является ли отношение функцией на графике, относительно легко с помощью теста вертикальной линии. Если вертикальная линия пересекает отношение на графике только один раз во всех местах, отношение является функцией. Однако, если вертикальная линия пересекает отношение более одного раза, отношение не является функцией. При использовании теста вертикальной линии все линии, кроме вертикальных, являются функциями. Круги, квадраты и другие замкнутые формы не являются функциями, но параболические и экспоненциальные кривые — это функции.

Использование диаграммы ввода-вывода

Диаграмма ввода-вывода отображает вывод или результат для каждого ввода или исходного значения. Любая диаграмма ввода-вывода, где у входа есть два или более разных выхода, не является функцией. Например, если вы видите число 6 в двух разных входных пространствах, а результат — 3 в одном случае и 9 в другом, отношение не является функцией.Однако, если два разных входа имеют одинаковый выход, все еще возможно, что отношение является функцией, особенно если задействованы числа в квадрате.

3.1 Функции и обозначение функций — College Algebra

Цели обучения

В этом разделе вы:

• Определите, представляет ли отношение функцию.
• Найдите значение функции.
• Определить, является ли функция взаимно однозначной.
• Используйте тест вертикальной линии для определения функций.
• Изобразите функции, перечисленные в библиотеке функций.

Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения.

Определение того, представляет ли отношение функцию

Отношение — это набор упорядоченных пар.Набор первых компонентов каждой упорядоченной пары называется доменом , а набор вторых компонентов каждой упорядоченной пары называется диапазоном . Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.

{(1,2), (2,4), (3,6), (4,8), (5,10)} {(1,2), (2,4), (3,6), (4,8), (5,10)}

Домен: {1,2,3,4,5}. {1,2,3,4,5}. Диапазон: {2,4,6,8,10}. {2,4,6,8,10}.

Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой x.x. Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой y.y.

Функция ff — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене . Другими словами, значения x не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, {1,2,3,4,5}, {1,2,3,4,5 }, сочетается ровно с одним элементом в диапазоне, {2,4,6,8,10}.{2,4,6,8,10}.

Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами.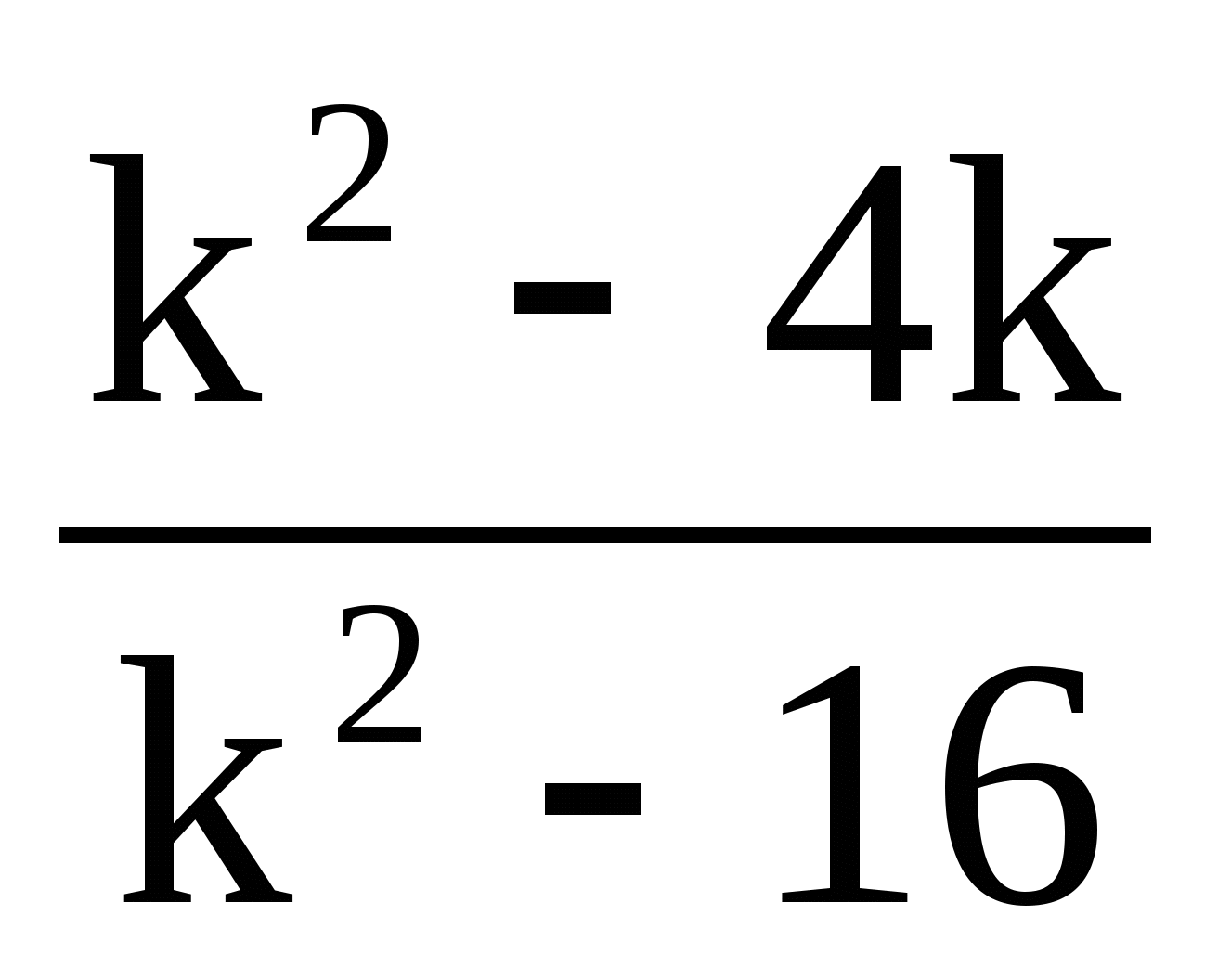 Это выглядело бы как

{(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5)} {(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5)}

Обратите внимание, что каждый элемент в домене, {четный, нечетный} {четный, нечетный} это , а не в паре с ровно одним элементом в диапазоне, {1,2,3,4,5}. {1,2,3,4,5}. Например, термин «нечетный» соответствует трем значениям из диапазона, {1,3,5} {1,3,5} а термин «даже» соответствует двум значениям из диапазона {2,4}.{2,4}. Это нарушает определение функции, поэтому это отношение не является функцией.

На рисунке 1 сравниваются отношения, которые являются функциями, а не функциями.

Рис. 1 (a) Это отношение является функцией, потому что каждый вход связан с одним выходом. Обратите внимание, что входные qq и rr дают выход n.n. (б) Эта связь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход qq связан с двумя разными выходами.

Функция

Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».

Входные значения составляют область, а выходные значения составляют диапазон.

Как к

Учитывая взаимосвязь между двумя величинами, определите, является ли взаимосвязь функцией.

1. Определите входные значения.
2. Определите выходные значения.
3. Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию.Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.

Пример 1

Определение того, являются ли прайс-листы меню функциями

Меню кофейни, показанное ниже, состоит из позиций и их цен.
Ⓐ Цена зависит от товара?
Ⓑ Товар зависит от цены?

Решение

ⓐ Начнем с рассмотрения ввода как пунктов меню. Выходные значения — это цены.

У каждого элемента в меню есть только одна цена, поэтому цена зависит от элемента.
ⓑ Два пункта меню имеют одинаковую цену. Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. Изображение ниже.

Следовательно, товар не зависит от цены.

Пример 2

Определение, являются ли правила оценки класса функциями

В конкретном математическом классе общая процентная оценка соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице 1 показано возможное правило присвоения баллов.

Процентное содержание	0–56	57–61	62–66	67–71	72–77	78–86	87–91	92–100
Средний балл	0,0	1,0	1. 5	2,0	2,5	3,0	3,5	4,0

Таблица 1

Решение

Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.

В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу.Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.

Попробуй # 1

Таблица 2 перечисляет пять величайших бейсболистов всех времен в порядке рангов.

Игрок	Рейтинг
Бэйб Рут	1
Уилли Мейс	2
Тай Кобб	3
Уолтер Джонсон	4
Хэнк Аарон	5

Таблица 2

1. ⓐРанг зависит от имени игрока?
2. ⓑ Является ли имя игрока функцией ранга?

Использование обозначения функций

Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли их понять и использовать, а иногда и чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями.

Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных hh на рост и аа для возраста. Буквы f, g, f, g и hh часто используются для обозначения функций точно так же, как мы используем x, y, x, y и zz для обозначения чисел и A, B, A, B, и CC для представления множеств.

Его fof a Мы называем функцию f; рост является функцией возраста.h = f (a) Мы используем круглые скобки для обозначения ввода функции. f (a) Мы называем функцию f; выражение читается как «fof a». his fof a Мы называем функцию f; высота является функцией возраста. h = f (a) Мы используем круглые скобки для обозначения входных данных функции. f (a) Назовем функцию f; выражение читается как «fof a».

Помните, мы можем использовать любую букву для названия функции; обозначение h (a) h (a) показывает нам, что hh зависит от a.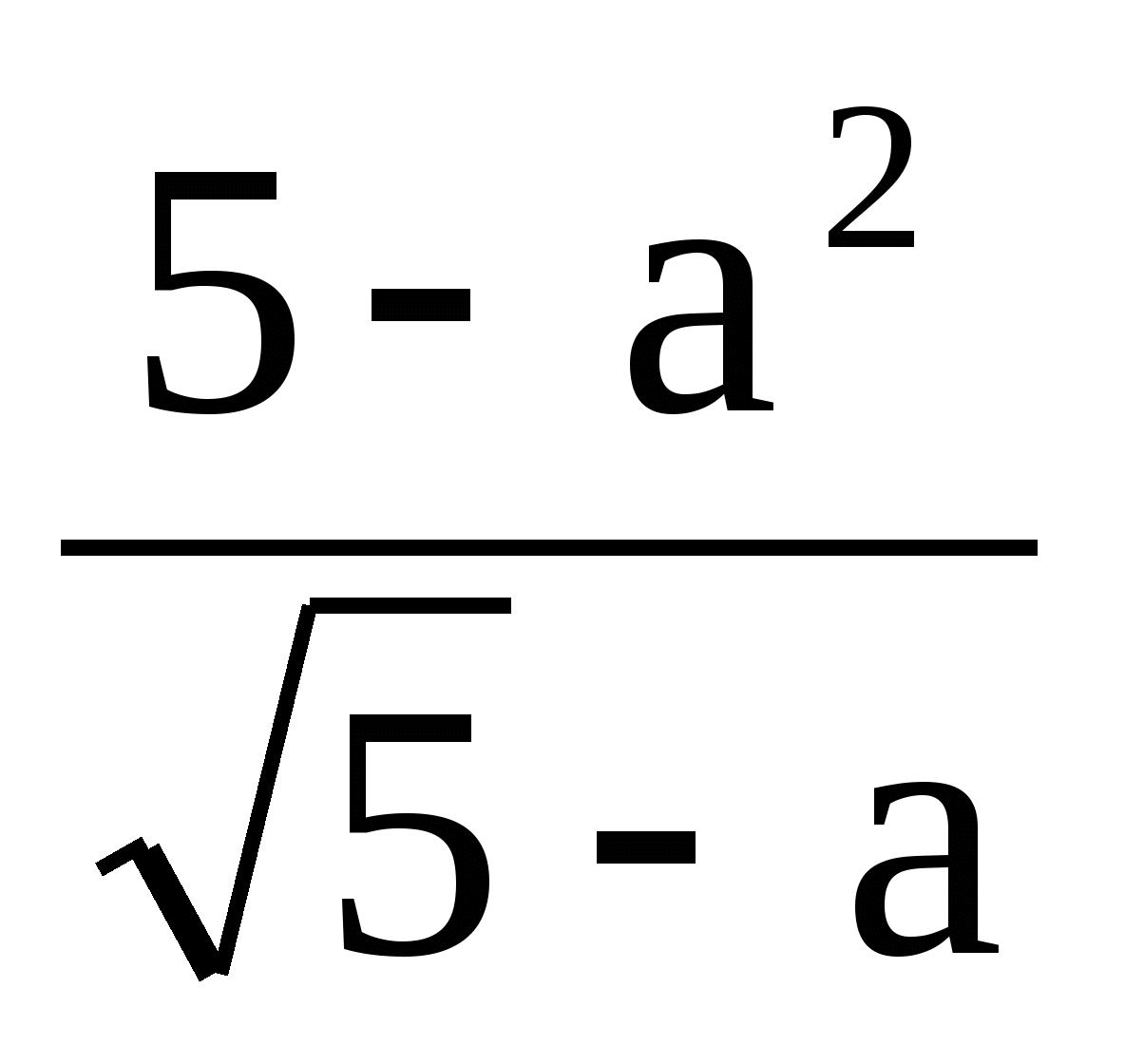 a. Значение aa необходимо поместить в функцию hh, чтобы получить результат. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.

Мы также можем дать алгебраическое выражение в качестве входных данных для функции. Например, f (a + b) f (a + b) означает «сначала сложите a и b , и результат будет входом для функции f ». Для получения правильного результата операции необходимо выполнять именно в таком порядке.

Обозначение функции

Запись y = f (x) y = f (x) определяет функцию с именем f.f. Это читается как «y» y является функцией x. X «. Буква xx представляет входное значение или независимую переменную.Буква y, y или f (x), f (x) представляет выходное значение или зависимую переменную.

Пример 3

Использование обозначения функций для дней в месяце

Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце. Предположим, что домен не включает високосные годы.

Решение

Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию f, f, мы запишем дни = f (месяц) дни = f (месяц) или d = f (m).d = f (м). Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.

Рисунок 2

Например, f (март) = 31, f (март) = 31, потому что в марте 31 день. Обозначение d = f (m) d = f (m) напоминает нам, что количество дней, dd (выход), зависит от названия месяца, мм (вход).

Анализ

Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.

Пример 4

Интерпретация обозначений функций

Функция N = f (y) N = f (y) дает количество полицейских, N, N, в городе в году y.y. Что означает f (2005) = 300f (2005) = 300?

Решение

Когда мы читаем f (2005) = 300, f (2005) = 300, мы видим, что входным годом является 2005. Значение выхода, количество полицейских (N), (N), равно 300.Помните, N = f (y). N = f (y). Выражение f (2005) = 300f (2005) = 300 говорит нам, что в 2005 году в городе было 300 полицейских.

Попробуй # 2

Используйте обозначение функции, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях d.d.

Q&A

Вместо обозначения, такого как y = f (x), y = f (x), можем ли мы использовать тот же символ для вывода, что и для функции, например y = y (x), y = y (x ), что означает: « y является функцией x ?»

Да, это часто делается, особенно в прикладных предметах, использующих высшую математику, таких как физика и инженерия. Однако при изучении самой математики нам нравится различать такие функции, как f, f, которые являются правилом или процедурой, и выходными данными yy, которые мы получаем, применяя ff к конкретному входу x.x. Вот почему мы обычно используем такие обозначения, как y = f (x), P = W (d), y = f (x), P = W (d) и т. Д.

Представление функций с помощью таблиц

Распространенным методом представления функций является таблица. Строки или столбцы таблицы отображают соответствующие входные и выходные значения. В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.

В таблице 3 перечислены входные числа каждого месяца (январь = 1, февраль = 2 и т. Д.) И выходное значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце ff, где D = f (m) D = f (m) определяет месяцы целым числом, а не именем.

Номер месяца, мм (ввод)	1	2	3	4	5	6	7	8	9	10	11	12
Дней в месяце, DD (выход)	31	28	31	30	31	30	31	31	30	31	30	31

Таблица 3

Таблица 4 определяет функцию Q = g (n). Q = g (n). Помните, что эта запись говорит нам, что gg — это имя функции, которая принимает вход nn и выдает на выходе Q .Q.

nn	1	2	3	4	5
QQ	8	6	7	6	8

Таблица 4

В таблице 5 показан возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.

Возраст в годах, а.о. (ввод)	5	5	6	7	8	9	10
Высота в дюймах, hh (на выходе)	40	42	44	47	50	52	54

Таблица 5

Как сделать

Учитывая таблицу входных и выходных значений, определите, представляет ли таблица функцию.

1. Определите входные и выходные значения.
2. Убедитесь, что каждое входное значение сопряжено только с одним выходным значением. Если это так, таблица представляет функцию.

Пример 5

Определение таблиц, представляющих функции

Какая таблица, таблица 6, таблица 7 или таблица 8, представляет функцию (если есть)?

Вход	Выход
–3	5
0	1
4	5

Таблица 7

Решение

Таблица 6 и Таблица 7 определяют функции. В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица 8 не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.

Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.

Функция, представленная в Таблице 6, может быть представлена ​​записью

f (2) = 1, f (5) = 3 и f (8) = 6f (2) = 1, f (5) = 3 и f (8) = 6

Аналогично, утверждения

g (−3) = 5, g (0) = 1 и g (4) = 5g (−3) = 5, g (0) = 1 и g (4) = 5

представляют функцию в таблице 7. .

Таблицу 8 нельзя выразить аналогичным образом, потому что она не представляет функцию.

Попробуй # 3

Представляет ли таблица 9 функцию?

Вход	Выход
1	10
2	100
3	1000

Таблица 9

Поиск входных и выходных значений функции

Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.

Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.

Вычисление функций в алгебраических формах

Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.Например, функция f (x) = 5−3x2f (x) = 5−3×2 может быть вычислена путем возведения входного значения в квадрат, умножения на 3 и последующего вычитания произведения из 5.

Как к

Учитывая формулу функции, оцените.

1. Замените входную переменную в формуле на указанное значение.
2. Рассчитайте результат.

Пример 6

Оценка функций при определенных значениях

Вычислить f (x) = x2 + 3x − 4f (x) = x2 + 3x − 4 в точке:

1. ⓐ 22
2. ⓑ aa
3. ⓒ а + га + ч
4. ⓓ Теперь оцените f (a + h) −f (a) hf (a + h) −f (a) h

Решение

Заменить xx в функции с каждым указанным значением.

1. ⓐ Поскольку входное значение представляет собой число 2, мы можем использовать простую алгебру для упрощения. f (2) = 22 + 3 (2) −4 = 4 + 6−4 = 6 f (2) = 22 + 3 (2) −4 = 4 + 6−4 = 6
2. ⓑ В данном случае вводимое значение представляет собой букву, поэтому мы не можем дальше упрощать ответ. f (a) = a2 + 3a − 4f (a) = a2 + 3a − 4
3. При входном значении a + h, a + h мы должны использовать свойство распределения. f (a + h) = (a + h) 2 + 3 (a + h) −4 = a2 + 2ah + h3 + 3a + 3h − 4f (a + h) = (a + h) 2 + 3 (a + h) −4 = a2 + 2ah + h3 + 3a + 3h − 4
4. ⓒ В этом случае мы применяем входные значения к функции более одного раза, а затем выполняем алгебраические операции над результатом. Мы уже обнаружили, что f (a + h) = a2 + 2ah + h3 + 3a + 3h − 4f (a + h) = a2 + 2ah + h3 + 3a + 3h − 4

   , и мы знаем, что

   f (a) = a2 + 3a − 4f (a) = a2 + 3a − 4

   Теперь объединим результаты и упростим.

   f (a + h) −f (a) h = (a2 + 2ah + h3 + 3a + 3h − 4) — (a2 + 3a − 4) h = 2ah + h3 + 3hh = h (2a + h + 3) hФактор h. = 2a + h + 3 Упростить. F (a + h) −f (a) h = (a2 + 2ah + h3 + 3a + 3h − 4) — (a2 + 3a − 4) h = 2ah + h3 + 3hh = h (2a + h + 3) hФактор h. = 2a + h + 3 Упростить.

Пример 7

Оценка функций

Учитывая функцию h (p) = p2 + 2p, h (p) = p2 + 2p, вычислить h (4) .h (4).

Решение

Чтобы оценить h (4), h (4), мы подставляем значение 4 для входной переменной pp в данной функции.

h (p) = p2 + 2ph (4) = (4) 2 + 2 (4) = 16 + 8 = 24 h (p) = p2 + 2ph (4) = (4) 2 + 2 (4) = 16 + 8 = 24

Следовательно, для входа 4 мы имеем выход 24.

Попробуй # 4

Учитывая функцию g (m) = m − 4, g (m) = m − 4, вычислите g (5). г (5).

Пример 8

Решение функций

Учитывая функцию h (p) = p2 + 2p, h (p) = p2 + 2p, решите относительно h (p) = 3. h (p) = 3.

Решение

h (p) = 3 p2 + 2p = 3 Подставим исходную функцию h (p) = p2 + 2p.p2 + 2p − 3 = 0 Вычтем по 3 с каждой стороны. (p + 3) (p − 1) = 0Factor. h (p) = 3 p2 + 2p = 3 Подставим исходную функцию h (p) = p2 + 2p.p2 + 2p − 3 = 0 Вычтем по 3 с каждой стороны. (p + 3) (p − 1) = 0Factor.

Если (p + 3) (p − 1) = 0, (p + 3) (p − 1) = 0, либо (p + 3) = 0 (p + 3) = 0, либо (p − 1) = 0 (p − 1) = 0 (или оба равны 0).Мы установим каждый коэффициент равным 0 и решим для каждого случая pp.

(p + 3) = 0, p = −3 (p − 1) = 0, p = 1 (p + 3) = 0, p = −3 (p − 1) = 0, p = 1

Это дает нам два решения. Выходной сигнал h (p) = 3h (p) = 3, когда на входе либо p = 1p = 1, либо p = −3.p = −3. Мы также можем проверить, построив график, как на рисунке 3. График проверяет, что h (1) = h (−3) = 3h (1) = h (−3) = 3 и h (4) = 24. h (4) = 24.

Рисунок 3

Попробуй # 5

Для функции g (m) = m − 4, g (m) = m − 4, решить g (m) = 2.g (m) = 2.

Вычисление функций, выраженных в формулах

Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнений.Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение 2n + 6p = 122n + 6p = 12 выражает функциональную связь между nn и п.п. Мы можем переписать его, чтобы решить, является ли pp функцией n.n.

Как к

Для функции в форме уравнения напишите ее алгебраическую формулу.

1. Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а с другой стороны как выражение, которое включает только входную переменную.
2. Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.

Пример 9

Нахождение уравнения функции

Выразите соотношение 2n + 6p = 122n + 6p = 12 как функцию p = f (n), p = f (n), если это возможно.

Решение

Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где pp является функцией n, n, что означает запись его как p = [expressioninvolvingn].р = [выражениеввольвинг].

2n + 6p = 126p = 12−2n Вычтите 2n с обеих сторон. P = 12−2n6 Разделите обе стороны на 6 и упростите. P = 126−2n6p = 2−13n2n + 6p = 126p = 12−2n Вычтите 2n с обеих сторон. P = 12− 2n6 Разделите обе части на 6 и упростите. P = 126−2n6p = 2−13n

Следовательно, pp как функция от nn записывается как

p = f (n) = 2−13np = f (n) = 2−13n

Анализ

Важно отметить, что не все отношения, выраженные уравнением, также можно выразить как функцию с формулой.

Пример 10

Выражение уравнения круга как функции

Представляет ли уравнение x2 + y2 = 1×2 + y2 = 1 функцию с xx на входе и yy на выходе? Если это так, выразите взаимосвязь как функцию y = f (x).у = f (х).

Решение

Сначала мы вычитаем x2x2 с обеих сторон.

Теперь мы пытаемся найти yy в этом уравнении.

y = ± 1 − x2 = + 1 − x2and −1 − x2y = ± 1 − x2 = + 1 − x2and −1 − x2

Мы получаем два выхода, соответствующие одному и тому же входу, поэтому это соотношение не может быть представлено как одна функция у = е (х). у = е (х).

Попробуй # 6

Если x − 8y3 = 0, x − 8y3 = 0, выразите yy как функцию от x.x.

Q&A

Существуют ли отношения, выраженные уравнением, которые действительно представляют функцию, но не могут быть представлены алгебраической формулой?

Да, такое бывает. Например, учитывая уравнение x = y + 2y, x = y + 2y, если мы хотим выразить yy как функцию от x, x, не существует простой алгебраической формулы, включающей только xx, равную y.y. Однако каждый xx определяет уникальное значение для y, y, и существуют математические процедуры, с помощью которых yy можно найти с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для yy как функции от x, x, даже если формулу нельзя записать явно.

Оценка функции, заданной в табличной форме

Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.

Функция, которая связывает тип домашнего животного с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу 10.

ПЭТ	Объем памяти в часах
Щенок	0,008
Взрослая собака	0,083
Кот	16
Золотая рыбка	2160
Бета-рыба	3600

Таблица 10

Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию P.P. Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца. Мы можем оценить функцию PP при входном значении «золотая рыбка». Мы бы написали P (золотая рыбка) = 2160.P (золотая рыбка) = 2160. Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции PP кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.

Как к

Для функции, представленной в виде таблицы, определите конкретные выходные и входные значения.

1. Найдите данный вход в строке (или столбце) входных значений.
2. Определите соответствующее выходное значение в паре с этим входным значением.
3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
4. Определите входное значение (я), соответствующее заданному выходному значению.

Пример 11

Оценка и решение табличной функции

с использованием таблицы 11,
Ⓐ Оцените g (3) .g (3).
Ⓑ Решите g (n) = 6.g (n) = 6.

nn	1	2	3	4	5
г (н) г (н)	8	6	7	6	8

Таблица 11

Решение

ⓐ Вычисление g (3) g (3) означает определение выходного значения функции gg для входного значения n = 3. п = 3. Выходное значение таблицы, соответствующее n = 3n = 3, равно 7, поэтому g (3) = 7.g (3) = 7.
Ⓑ Решение g (n) = 6g (n) = 6 означает определение входных значений n, n, которые производят выходное значение 6. В таблице 11 показаны два решения: 22 и 4.4.

nn	1	2	3	4	5
г (н) г (н)	8	6	7	6	8

Когда мы вводим 2 в функцию g, g, на выходе получаем 6. Когда мы вводим 4 в функцию g, g, наш результат также равен 6.

Поиск значений функций из графика

Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график. Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.

Пример 12

Чтение значений функций из графика

Учитывая график на рисунке 4,

ⓐ Оцените f (2).f (2).
Ⓑ Решите f (x) = 4. f (x) = 4.

Рисунок 4

Решение

ⓐ Чтобы оценить f (2), f (2), найдите точку на кривой, где x = 2, x = 2, затем прочтите координату y этой точки. Точка имеет координаты (2,1), (2,1), поэтому f (2) = 1. f (2) = 1. См. Рисунок 5.

Рисунок 5

Ⓑ Чтобы решить f (x) = 4, f (x) = 4, мы находим выходное значение 44 на вертикальной оси. Двигаясь горизонтально по линии y = 4, y = 4, мы обнаруживаем две точки кривой с выходным значением 4: 4: (−1,4) (- 1,4) и (3,4).(3,4). Эти точки представляют два решения f (x) = 4: f (x) = 4: −1−1 или 3.3. Это означает, что f (−1) = 4f (−1) = 4 и f (3) = 4, f (3) = 4, или когда на входе −1−1 или 3,3, на выходе будет 4,4. См. Рисунок 6.

Рисунок 6

Определение того, является ли функция взаимно однозначной

Некоторые функции имеют заданное выходное значение, которое соответствует двум или более входным значениям. Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.

Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице 12.

Буквенный класс	Средний балл
A	4,0
B	3.0
С	2,0
Д	1,0

Таблица 12

Эта система оценок представляет собой функцию «один к одному», поскольку каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.

Чтобы наглядно представить эту концепцию, давайте еще раз посмотрим на две простые функции, показанные на рис. 1 (a), и рис. 1, (b), .Функция в части (a) показывает взаимосвязь, которая не является взаимно однозначной, потому что оба входа qq и rr дают выход n.n. Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.

Индивидуальные встречи

Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.

Пример 13

Определение того, является ли отношение однозначной функцией

Является ли площадь круга функцией его радиуса? Если да, то функция взаимно однозначная?

Решение

Окружность радиуса rr имеет уникальную меру площади, равную A = πr2, A = πr2, поэтому для любого входа r, r существует только один выход A.A. Площадь является функцией радиуса r.r.

Если функция является взаимно однозначной, выходное значение, площадь, должно соответствовать уникальному входному значению, радиусу. Любая мера площади AA задается формулой A = πr2.A = πr2. Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: Aπ.Aπ. Таким образом, площадь круга однозначно зависит от радиуса круга.

Попробуй # 9

1. ⓐ Является ли остаток функцией номера банковского счета?
2. ⓑ Является ли номер банковского счета функцией баланса?
3. ⓒ Является ли баланс однозначной функцией номера банковского счета?

Попробуй # 10

Оцените следующее:

1. ⓐ Если каждая процентная оценка, полученная на курсе, соответствует одной буквенной оценке, является ли буквенная оценка функцией процентной оценки?
2. ⓑ Если да, то функция взаимно однозначная?

Использование теста вертикальной линии

Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика.Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений. Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.

Наиболее распространенные графики называют входное значение xx и выходное значение y, y, и мы говорим, что yy является функцией от x, x или y = f (x) y = f (x), когда функция называется f.f. График функции — это совокупность всех точек (x, y) (x, y) на плоскости, которая удовлетворяет уравнению y = f (x).у = f (х). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующее выходное значение. Например, черные точки на графике на рисунке 7 говорят нам, что f (0) = 2f (0) = 2 и f (6) = 1.f (6) = 1. Однако набор всех точек (x, y) (x, y), удовлетворяющих y = f (x) y = f (x), является кривой. Показанная кривая включает (0,2) (0,2) и (6,1) (6,1), потому что кривая проходит через эти точки.

Рисунок 7

Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, тогда график , а не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения. См. Рисунок 8.

Рисунок 8

Как к

Для графика используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.

1. Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
2. Если такая линия есть, определите, что график не представляет функцию.

Пример 14

Применение теста вертикальной линии

Какой из графиков на рисунке 9 представляет функцию y = f (x)? Y = f (x)?

Рисунок 9

Решение

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией.Обратите внимание, что любая вертикальная линия будет проходить только через одну точку из двух графиков, показанных в частях (a) и (b) рисунка 9. Из этого мы можем сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что при максимальном значении x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке 10.

Рисунок 10

Попробуй # 11

Представляет ли график на рисунке 11 функцию?

Рисунок 11

Использование теста горизонтальной линии

После того, как мы определили, что график определяет функцию, простой способ определить, является ли он взаимно однозначной функцией, — это использовать тест горизонтальной линии.Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.

Как к

Учитывая график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график функцию взаимно-однозначного соответствия.

1. Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
2. Если такая линия есть, определите, что функция не взаимно однозначна.

Пример 15

Применение теста горизонтальной линии

Рассмотрим функции, показанные на рисунке 9 (a) и рисунке 9 (b) . Являются ли какие-либо функции взаимно однозначными?

Решение

Функция на рисунке 9 (a) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке 12, пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.)

Рисунок 12

Функция на рисунке 9 (b) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.

Попробуй # 12

Является ли график на Рисунке 9 взаимно однозначным?

Определение базовых функций набора инструментов

В этом тексте мы исследуем функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем. Учимся читать, начинаем с алфавита.Изучая арифметику, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать xx в качестве входной переменной и y = f (x) y = f (x) в качестве выходной переменной.

Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги.Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную в Таблице 13.

3.1 Раздел Упражнения

Устный

1.

В чем разница между отношением и функцией?

2.

В чем разница между вводом и выводом функции?

3.

Почему тест с вертикальной линией говорит нам, представляет ли график отношения функцию?

4.

Как определить, является ли отношение взаимно-однозначной функцией?

5.

Почему тест горизонтальной линии говорит нам, является ли график функции взаимно однозначным?

Алгебраический

В следующих упражнениях определите, представляет ли отношение функцию.

6.

{(a, b), (c, d), (a, c)} {(a, b), (c, d), (a, c)}

7.

{(a, b), (b, c), (c, c)} {(a, b), (b, c), (c, c)}

Для следующих упражнений определите, представляет ли отношение yy как функцию от x.Икс.

Для следующих упражнений оцените f (−3), f (2), f (−a), — f (a), f (a + h). F (−3), f (2), f ( −a), — f (a), f (a + h).

28.

f (x) = — 5×2 + 2x − 1f (x) = — 5×2 + 2x − 1

30.

f (x) = 6x − 15x + 2f (x) = 6x − 15x + 2

31.

f (x) = | x − 1 | — | x + 1 | f (x) = | x − 1 | — | x + 1 |

32.

Учитывая функцию g (x) = 5 − x2, g (x) = 5 − x2, вычислим g (x + h) −g (x) h, h ≠ 0. G (x + h) −g (x ) h, h ≠ 0.

33.

Учитывая функцию g (x) = x2 + 2x, g (x) = x2 + 2x, вычислим g (x) −g (a) x − a, x ≠ ag (x) −g (a) x − a , x ≠ a.

34.

Для функции k (t) = 2t − 1: k (t) = 2t − 1:

1. ⓐ Оцените k (2) .k (2).
2. ⓑ Решить k (t) = 7. k (t) = 7.

35.

Для функции f (x) = 8−3x: f (x) = 8−3x:

1. ⓐ Вычислите f (−2) .f (−2).
2. ⓑ Решить f (x) = — 1. f (x) = — 1.

36.

Для функции p (c) = c2 + c: p (c) = c2 + c:

1. ⓐ Вычислите p (−3) .p (−3).
2. ⓑ Решите p (c) = 2.p (c) = 2.

37.

Для функции f (x) = x2−3x: f (x) = x2−3x:

1. ⓐ Оцените f (5).f (5).
2. ⓑ Решить f (x) = 4. f (x) = 4.

38.

Для функции f (x) = x + 2: f (x) = x + 2:

1. ⓐ Оцените f (7) .f (7).
2. ⓑ Решить f (x) = 4. f (x) = 4.

39.

Рассмотрим соотношение 3r + 2t = 18,3r + 2t = 18.

1. ⓐ Запишите соотношение как функцию r = f (t) .r = f (t).
2. ⓑ Вычислите f (−3) .f (−3).
3. ⓒ Решить f (t) = 2. f (t) = 2.

Графический

В следующих упражнениях используйте тест вертикальной линии, чтобы определить, какие графики показывают отношения, являющиеся функциями.

40. 42. 44. 46. 48. 50. 52.

Учитывая следующий график,

1. ⓐ Вычислить f (−1) .f (−1).
2. ⓑ Решить относительно f (x) = 3. f (x) = 3.

53.

Учитывая следующий график,

1. ⓐ Вычислить f (0) .f (0).
2. ⓑ Решить относительно f (x) = — 3. f (x) = — 3.

54.

Учитывая следующий график,

1. ⓐ Оцените f (4) .f (4).
2. ⓑ Решить относительно f (x) = 1. f (x) = 1.

Для следующих упражнений определите, является ли данный график взаимно однозначной функцией.

56. 58.

Numeric

В следующих упражнениях определите, представляет ли отношение функцию.

60.

{(−1, −1), (- 2, −2), (- 3, −3)} {(- 1, −1), (- 2, −2), (- 3, −3) }

61.

{(3,4), (4,5), (5,6)} {(3,4), (4,5), (5,6)}

62.

{(2,5), (7,11), (15,8), (7,9)} {(2,5), (7,11), (15,8), (7,9) }

Для следующих упражнений определите, представляет ли отношение, представленное в виде таблицы, yy как функцию от x.x.

Для следующих упражнений используйте функцию ff, представленную в таблице ниже.

хх	0	1	2	3	4	5	6	7	8	9
f (x) f (x)	74	28	1	53	56	3	36	45	14	47

Таблица 14

Для следующих упражнений оцените функцию ff при значениях f (−2), f (−1), f (0), f (1), f (−2), f (−1), f (0 ), f (1) и f (2).f (2).

70.

f (x) = 8×2−7x + 3f (x) = 8×2−7x + 3

72.

f (x) = x − 2x + 3f (x) = x − 2x + 3.

Для следующих упражнений вычислите выражения, заданные функциями f, g, f, g и h: h:

f (x) = 3x − 2f (x) = 3x − 2
g (x) = 5 − x2g (x) = 5 − x2
h (x) = — 2×2 + 3x − 1h (x) = — 2×2 + 3x − 1

74.

3f (1) −4g (−2) 3f (1) −4g (−2)

75.

f (73) −h (−2) f (73) −h (−2)

Технологии

Для следующих упражнений построим график y = x2y = x2 в заданной области.Определите соответствующий диапазон. Покажите каждый график.

Для следующих упражнений построим график y = x3y = x3 в заданной области. Определите соответствующий диапазон. Покажите каждый график.

Для следующих упражнений построим график y = xy = x в заданной области. Определите соответствующий диапазон. Покажите каждый график.

Для следующих упражнений построим график y = x3y = x3 в заданной области. Определите соответствующий диапазон. Покажите каждый график.

85.

[-0,001,0,001] [- 0,001,0,001]

86.

[-1000,1000] [- 1000,1000]

87.

[-1,000,000,1,000,000] [- 1,000,000,1,000,000]

Реальные приложения

88.

Количество мусора G, G, производимого городом с населением pp, определяется выражением G = f (p) .G = f (p). GG измеряется в тоннах в неделю, а pp — в тысячах человек.

1. ⓐ Город Тола с населением 40 000 человек производит 13 тонн мусора каждую неделю. Выразите эту информацию в терминах функции f.f.
2. ⓑ Объясните значение утверждения f (5) = 2.f (5) = 2.

89.

Количество кубических ярдов земли, D, D, необходимое для покрытия сада площадью aa квадратный фут, определяется как D = g (a) .D = g (a).

1. ⓐ Для сада площадью 5000 футов ² требуется 50 ярдов ³ земли. Выразите эту информацию в терминах функции g.g.
2. ⓑ Объясните значение утверждения g (100) = 1. g (100) = 1.

90.

Пусть f (t) f (t) будет количеством уток в озере через tt годы после 1990 года. Объясните значение каждого утверждения:

1. ⓐ f (5) = 30f (5) = 30
2. ⓑ f (10) = 40f (10) = 40

91.

Пусть h (t) h (t) будет высотой над землей в футах ракеты через tt секунд после запуска. Объясните значение каждого утверждения:

1. ⓐ ч (1) = 200 ч (1) = 200
2. ⓑ ч (2) = 350 ч (2) = 350

92.

Покажите, что функция f (x) = 3 (x − 5) 2 + 7f (x) = 3 (x − 5) 2 + 7 равна , а не взаимно однозначно.

1.1: Четыре способа представления функции

Цели обучения

• Определить, представляет ли отношение функцию.
• Найдите значение функции.
• Определить, является ли функция взаимно однозначной.
• Используйте тест вертикальной линии для определения функций.
• Изобразите функции, перечисленные в библиотеке функций.

Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования.В этом разделе мы разберем такие отношения.

Определение того, представляет ли отношение функцию

Отношение — это набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется областью, а набор вторых компонентов каждой упорядоченной пары называется диапазоном. Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.

\ [\ {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10) \} \ tag {1.1.1} \]

Домен \ (\ {1, 2, 3, 4, 5 \} \). Диапазон равен \ (\ {2, 4, 6, 8, 10 \} \).

Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой \ (x \). Каждое значение в диапазоне также называется выходным значением или зависимой переменной и часто обозначается строчной буквой \ (y \).

Функция \ (f \) — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене.Другими словами, никакие \ (x \) — значения не повторяются. Для нашего примера, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, {1, 2, 3, 4, 5}, связан ровно с одним элементом в диапазон, \ (\ {2, 4, 6, 8, 10 \} \).

Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Это будет выглядеть как

\ [\ mathrm {\ {(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5) \}} \ tag {1.1.2} \]

Обратите внимание, что каждый элемент в домене {четный, нечетный} не связан ровно с одним элементом в диапазоне \ (\ {1, 2, 3, 4, 5 \} \). Например, термин «нечетный» соответствует трем значениям из области \ (\ {1, 3, 5 \} \), а термин «четный» соответствует двум значениям из диапазона \ (\ {2, 4 \} \). Это нарушает определение функции, поэтому это отношение не является функцией.

На рисунке \ (\ PageIndex {1} \) сравниваются отношения, которые являются функциями, а не функциями.

Рисунок \ (\ PageIndex {1} \): (a) Это отношение является функцией, потому что каждый вход связан с одним выходом.Обратите внимание, что входные \ (q \) и \ (r \) оба дают выход \ (n \). (б) Эта связь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход \ (q \) связан с двумя разными выходами.

Функция

Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».

Входные значения составляют область , а выходные значения составляют диапазон .

Как сделать: учитывая связь между двумя величинами, определите, является ли связь функцией

1. Определите входные значения.
2. Определите выходные значения.
3. Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.

Пример \ (\ PageIndex {1} \): определение того, являются ли прайс-листы меню функциями

Меню кофейни, показанное на рисунке \ (\ PageIndex {2} \), состоит из предметов и их цен.

1. Цена зависит от товара?
2. Товар зависит от цены?
Рисунок \ (\ PageIndex {2} \): меню с ценами на пончики из кафе, где простой пончик стоит 1,49 доллара, а пончик с желе и шоколадный пончик — 1,99 доллара.

Решение

1. Давайте начнем с рассмотрения ввода как пунктов меню. Выходные значения — это цены. См. Рисунок \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \): меню с ценами на пончики из кафе, где простой пончик стоит 1 доллар.49, пончик с желе и шоколадный пончик — 1,99 доллара.

У каждого элемента в меню есть только одна цена, поэтому цена зависит от элемента.

1. Два пункта меню имеют одинаковую цену. Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. Рисунок \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \): Связь цен с пончиками.

Следовательно, товар не зависит от цены.

Пример \ (\ PageIndex {2} \): определение того, являются ли правила оценки класса функциями

В конкретном математическом классе общая процентная оценка соответствует среднему баллу. Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице \ (\ PageIndex {1} \) показано возможное правило назначения оценок.

Таблица \ (\ PageIndex {1} \): баллы класса.

Процентное содержание	0–56	57–61	62–66	67–71	72–77	78–86	87–91	92–100
Средний балл	0.0	1,0	1,5	2,0	2,5	3,0	3,5	4,0

Раствор

Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.

В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.

Упражнение \ (\ PageIndex {2} \)

Таблица \ (\ PageIndex {2} \) перечисляет пять величайших бейсболистов всех времен в порядке рангов.

Таблица \ (\ PageIndex {2} \): пять величайших бейсболистов.

Игрок	Рейтинг
Бэйб Рут	1
Вилли Мейс	2
Тай Кобб	3
Уолтер Джонсон	4
Хэнк Аарон	5

1. Является ли ранг функцией имени игрока?
2. Имя игрока зависит от ранга?

Ответьте на

Есть

Ответ б

да.(Примечание: если бы два игрока были разделены, скажем, за 4-е место, то имя не зависело бы от ранга.)

Использование обозначения функций

Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли их понять и использовать, а иногда и чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями.

Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных \ (h \) для роста и \ (a \) для возраста. Буквы \ (f \), \ (g \) и \ (h \) часто используются для обозначения функций точно так же, как мы используем \ (x \), \ (y \) и \ (z \) для обозначения числа и \ (A \), \ (B \) и \ (C \) для представления множеств.

\ [\ begin {array} {ll} h \ text {is} f \ text {of} a \; \; \; \; \; \; & \ text {Назовем функцию} f \ text {; высота является функцией возраста.} \\ h = f (a) & \ text {Мы используем круглые скобки для обозначения ввода функции.} \\ f (a) & \ text {Мы называем функцию} f \ text {; выражение читается как «} f \ text {of} a \ text {.»} \ end {array} \]

Помните, мы можем использовать любую букву для названия функции; обозначение \ (h (a) \) показывает нам, что \ (h \) зависит от \ (a \). Значение \ (a \) необходимо поместить в функцию \ (h \), чтобы получить результат. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.

Мы также можем дать алгебраическое выражение в качестве входных данных для функции.Например, \ (f (a + b) \) означает «сначала сложите \ (a \) и \ (b \), и результат будет входом для функции \ (f \)». Для получения правильного результата операции необходимо выполнять именно в таком порядке.

Обозначение функций

Запись \ (y = f (x) \) определяет функцию с именем \ (f \). Это читается как «\ (y \) является функцией \ (x \)». Буква \ (x \) представляет входное значение или независимую переменную. Буква \ (y \) или \ (f (x) \) представляет выходное значение или зависимую переменную.

Пример \ (\ PageIndex {3} \): использование обозначения функций для дней в месяце

Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце.

Решение

Использование обозначения функций для дней в месяце

Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце.

Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию \ (f \), мы напишем \ (\ text {days} = f (\ text {month}) \) или \ (d = f (m) \). Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.

Рисунок \ (\ PageIndex {5} \): функция \ (31 = f (январь) \), где 31 — результат, f — правило, а январь — вход.

Например, \ (f (\ text {March}) = 31 \), потому что в марте 31 день. Обозначение \ (d = f (m) \) напоминает нам, что количество дней, \ (d \) (выход), зависит от названия месяца \ (m \) (вход).

Анализ

Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.

Пример \ (\ PageIndex {3B} \): интерпретация обозначения функции

Функция \ (N = f (y) \) дает количество полицейских \ (N \) в городе в году \ (y \). Что означает \ (f (2005) = 300 \)?

Решение

Когда мы читаем \ (f (2005) = 300 \), мы видим, что входной год — 2005. Выходное значение, количество полицейских \ ((N) \), равно 300.Помните, \ (N = f (y) \). Утверждение \ (f (2005) = 300 \) говорит нам, что в 2005 году в городе было 300 полицейских.

Упражнение \ (\ PageIndex {3} \)

Используйте обозначение функции, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях \ (d \).

Ответ

\ (ш = е (г) \)

Вопросы и ответы

Вместо обозначения, такого как \ (y = f (x) \), можем ли мы использовать тот же символ для вывода, что и для функции, например \ (y = y (x) \), означающий «\ (y \) является функцией \ (x \)? »

Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, например физике и инженерии.Однако при изучении самой математики нам нравится проводить различие между такой функцией, как \ (f \) , которая является правилом или процедурой, и выходом y, который мы получаем, применяя \ (f \) к конкретному ввод \ (x \) . Вот почему мы обычно используем такие обозначения, как \ (y = f (x), P = W (d) \) и т. Д.

Представление функций с помощью таблиц

Общий метод представления функций — в виде таблицы. Строки или столбцы таблицы отображают соответствующие входные и выходные значения.В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.

Таблица \ (\ PageIndex {3} \) перечисляет входное число каждого месяца (\ (\ text {Январь} = 1 \), \ (\ text {Февраль} = 2 \) и т. Д.) И вывод значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце \ (f \), где \ (D = f (m) \) идентифицирует месяцы целым числом, а не именем.

Таблица \ (\ PageIndex {3} \): Месяцы и количество дней в месяце.

Номер месяца, \ (м \) (ввод)	1	2	3	4	5	6	7	8	9	10	11	12
Дней в месяце, \ (D \) (вывод)	31	28	31	30	31	30	31	31	30	31	30	31

Таблица \ (\ PageIndex {4} \) определяет функцию \ (Q = g (n) \). Помните, это обозначение говорит нам, что \ (g \) — это имя функции, которая принимает входные данные \ (n \) и дает результат \ (Q \).

Таблица \ (\ PageIndex {4} \): Функция \ (Q = g (n) \)

\ (п \)	1	2	3	4	5
\ (Q \)	8	6	7	6	8

Таблица \ (\ PageIndex {5} \) отображает возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Мы сразу видим, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.

Таблица \ (\ PageIndex {5} \): возраст детей и их рост.

Возраст в годах, \ (a \) (ввод)	5	5	6	7	8	9	10
Высота в дюймах, \ (h \) (выход)	40	42	44	47	50	52	54

Как: по таблице входных и выходных значений определить, представляет ли таблица функцию

1. Определите входные и выходные значения.
2. Убедитесь, что каждое входное значение сопряжено только с одним выходным значением. Если это так, таблица представляет функцию.

Пример \ (\ PageIndex {5} \): определение таблиц, представляющих функции

Какая таблица, Таблица \ (\ PageIndex {6} \), Таблица \ (\ PageIndex {7} \) или Таблица \ (\ PageIndex {8} \), представляет функцию (если есть)?

Таблица \ (\ PageIndex {6} \)

Ввод	Выход
2	1
5	3
8	6

Таблица \ (\ PageIndex {7} \)

Ввод	Выход
-3	5
0	1
4	5

Таблица \ (\ PageIndex {8} \)

Ввод	Выход
1	0
5	2
5	4

Раствор

Таблица \ (\ PageIndex {6} \) и Таблица \ (\ PageIndex {7} \) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица \ (\ PageIndex {8} \) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.

Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.

Функция, представленная таблицей \ (\ PageIndex {6} \), может быть представлена ​​записью

\ [f (2) = 1 \ text {,} f (5) = 3 \ text {и} f (8) = 6 \ nonumber \]

Аналогично выписки

\ [g (−3) = 5 \ text {,} g (0) = 1 \ text {и} g (4) = 5 \ nonumber \]

представляют функцию в таблице \ (\ PageIndex {7} \).

Таблица \ (\ PageIndex {8} \) не может быть выражена аналогичным образом, потому что она не представляет функцию.

Упражнение \ (\ PageIndex {5} \)

Представляет ли таблица \ (\ PageIndex {9} \) функцию?

Таблица \ (\ PageIndex {9} \)

Ввод	Выход
1	10
2	100
3	1000

Ответ

да

Поиск входных и выходных значений функции

Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию.Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.

Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем входные данные. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.

Вычисление функций в алгебраических формах

Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.2 + 2p − 3 = 0 & \ text {Вычтите по 3 с каждой стороны.} \\ (p + 3) (p − 1) = 0 & \ text {Factor.} \ End {array} \ nonumber \]

Если \ ((p + 3) (p − 1) = 0 \), либо \ ((p + 3) = 0 \), либо \ ((p − 1) = 0 \) (или оба они равны \ (0 \)). Мы установим каждый множитель равным \ (0 \) и решим относительно \ (p \) в каждом случае.

\ [(p + 3) = 0, \; р = −3 \ nonumber \]

\ [(p − 1) = 0, \, p = 1 \ nonumber \]

Это дает нам два решения. Выход \ (h (p) = 3 \), когда вход либо \ (p = 1 \), либо \ (p = −3 \). Мы также можем проверить, построив график, как на рисунке \ (\ PageIndex {6} \).2 + 2п \)

Упражнение \ (\ PageIndex {7} \)

Дана функция \ (g (m) = \ sqrt {m − 4} \), решить \ (g (m) = 2 \).

Ответ

\ (м = 8 \)

Вычисление функций, выраженных в формулах

Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения . Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме.Например, уравнение \ (2n + 6p = 12 \) выражает функциональную связь между \ (n \) и \ (p \). Мы можем переписать его, чтобы решить, является ли \ (p \) функцией \ (n \).

Как: Для данной функции в форме уравнения напишите ее алгебраическую формулу.

1. Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства, а другую сторону как выражение, которое включает только входную переменную.
2. Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.

Пример \ (\ PageIndex {8A} \): поиск уравнения функции

Выразите отношение \ (2n + 6p = 12 \) как функцию \ (p = f (n) \), если это возможно.

Решение

Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где \ (p \) является функцией \ (n \), что означает запись его как \ (p = [\ text {выражение с участием} п] \).

\ [\ begin {align *} 2n + 6p & = 12 \\ 6p & = 12−2n && \ text {Вычтите 2n с обеих сторон.} \\ p & = \ dfrac {12−2n} {6} & & \ text {Разделите обе стороны на 6 и упростите.} \\ p & = \ frac {12} {6} — \ frac {2n} {6} \\ p & = 2− \ frac {1} {3} n \ end {align *} \]

Следовательно, \ (p \) как функция от \ (n \) записывается как

\ [p = f (n) = 2− \ frac {1} {3} n \ nonumber \]

Анализ

Важно отметить, что не все отношения, выраженные уравнением, также можно выразить как функцию с формулой. 2 = 1 \) функцию с \ (x \) на входе и \ (y \) на выходе? Если это так, выразите отношение как функцию \ (y = f (x) \).y \), если мы хотим выразить y как функцию от x, не существует простой алгебраической формулы, включающей только \ (x \), которая равна \ (y \). Однако каждый \ (x \) определяет уникальное значение для \ (y \), и существуют математические процедуры, с помощью которых \ (y \) может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для \ (y \) как функции \ (x \), даже если формулу нельзя записать явно.

Оценка функции, заданной в табличной форме

Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.

Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы (Table \ (\ PageIndex {10} \)).

Таблица \ (\ PageIndex {10} \)

Память питомца	интервал в часах
Щенок	0,008
Взрослая собака	0.083
Кот	3
Золотая рыбка	2160
Бета-рыба	3600

Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию \ (P \). Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию \ (P \) при входном значении «золотая рыбка». Мы бы написали \ (P (золотая рыбка) = 2160 \). Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции P кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.

Как сделать: для данной функции, представленной в виде таблицы, определить конкретные выходные и входные значения

1.Найдите данный вход в строке (или столбце) входных значений.
2. Определите соответствующее выходное значение в паре с этим входным значением.
3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
4. Определите входные значения, соответствующие заданному выходному значению.

Пример \ (\ PageIndex {9} \): Вычисление и решение табличной функции

Использование таблицы \ (\ PageIndex {11} \),

а. Оцените \ (g (3) \).
г. Решите \ (g (n) = 6 \).

Таблица \ (\ PageIndex {11} \)

\ (п \)	1	2	3	4	5
\ (г (п) \)	8	6	7	6	8

Раствор

а.Вычисление \ (g (3) \) означает определение выходного значения функции \ (g \) для входного значения \ (n = 3 \). Выходное значение таблицы, соответствующее \ (n = 3 \), равно 7, поэтому \ (g (3) = 7 \).
г. Решение \ (g (n) = 6 \) означает определение входных значений n, которые производят выходное значение 6. Таблица \ (\ PageIndex {12} \) показывает два решения: 2 и 4.

Таблица \ (\ PageIndex {12} \)

\ (п \)	1	2	3	4	5
\ (г (п) \)	8	6	7	6	8

Когда мы вводим 2 в функцию \ (g \), на выходе получается 6.Когда мы вводим 4 в функцию \ (g \), наш результат также равен 6.

Упражнение \ (\ PageIndex {1} \)

Используя Table \ (\ PageIndex {12} \), вычислите \ (g (1) \).

Ответ

\ (г (1) = 8 \)

Поиск значений функций из графика

Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.

Пример \ (\ PageIndex {10} \): чтение значений функций из графика

Учитывая график на рисунке \ (\ PageIndex {7} \),

1. Вычислить \ (f (2) \).
2. Решите \ (f (x) = 4 \).
Рисунок \ (\ PageIndex {7} \): График положительной параболы с центром в \ ((1, 0) \).

Решение

Чтобы оценить \ (f (2) \), найдите точку на кривой, где \ (x = 2 \), затем прочтите координату y этой точки.Точка имеет координаты \ ((2,1) \), поэтому \ (f (2) = 1 \). См. Рисунок \ (\ PageIndex {8} \).

\ (\ PageIndex {8} \): график положительной параболы с центром в \ ((1, 0) \) с отмеченной точкой \ ((2, 1) \), где \ (f (2) = 1 \) .

Чтобы решить \ (f (x) = 4 \), мы находим выходное значение 4 на вертикальной оси. Двигаясь горизонтально по прямой \ (y = 4 \), мы обнаруживаем две точки кривой с выходным значением 4: \ ((- 1,4) \) и \ ((3,4) \). Эти точки представляют два решения \ (f (x) = 4 \): −1 или 3. Это означает \ (f (−1) = 4 \) и \ (f (3) = 4 \), или когда вход — -1 или 3, выход — 4.См. Рисунок \ (\ PageIndex {9} \).

Рисунок \ (\ PageIndex {9} \): График обращенной вверх параболы с вершиной в \ ((0,1) \) и помеченными точками в \ ((- 1, 4) \) и \ ((3 , 4) \). Прямая в точке \ (y = 4 \) пересекает параболу в отмеченных точках.

Упражнение \ (\ PageIndex {10} \)

Учитывая график на рисунке \ (\ PageIndex {7} \), решите \ (f (x) = 1 \).

Ответ

\ (x = 0 \) или \ (x = 2 \)

Определение того, является ли функция взаимно однозначной

Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям.Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.

Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице \ (\ PageIndex {13} \).

Таблица \ (\ PageIndex {13} \): буквенные оценки и десятичные эквиваленты.

Letter Grade	Средний балл
A	4,0
B	3,0
С	2,0
D	1,0

Эта система оценок представляет собой функцию «один-к-одному», потому что каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.

Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, изображенные на рисунках \ (\ PageIndex {1a} \) и \ (\ PageIndex {1b} \). Функция в части (a) показывает взаимосвязь, которая не является взаимно однозначной, потому что входы \ (q \) и \ (r \) оба дают выход \ (n \). Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.

Индивидуальные функции

Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.2 \). Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: \ (\ sqrt {\ frac {A} {\ pi}} \). Таким образом, площадь круга однозначно зависит от радиуса круга.

Упражнение \ (\ PageIndex {11A} \)

1. Является ли остаток функцией номера банковского счета?
2. Является ли номер банковского счета функцией баланса?
3. Является ли баланс однозначной функцией номера банковского счета?

Ответ

а.да, потому что на каждом банковском счете в любой момент времени имеется единый баланс;

г. нет, потому что несколько номеров банковских счетов могут иметь одинаковый баланс;

г. нет, потому что один и тот же выход может соответствовать более чем одному входу.

Упражнение \ (\ PageIndex {11B} \)

Оцените следующее:

1. Если каждая процентная оценка, полученная на курсе, соответствует одной буквенной оценке, является ли буквенная оценка функцией процентной оценки?
2. Если да, то функция взаимно однозначная?

Ответ

а.Да, буквенная оценка является функцией процентной оценки;
г. Нет, не один на один. Мы могли бы получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.

Использование теста вертикальной линии

Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.

Наиболее распространенные графики называют входное значение \ (x \) и выходное значение \ (y \), и мы говорим, что \ (y \) является функцией \ (x \), или \ (y = f (x) \), когда функция названа \ (f \). График функции — это совокупность всех точек \ ((x, y) \) на плоскости, которая удовлетворяет уравнению \ (y = f (x) \). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике на рисунке \ (\ PageIndex {10} \) говорят нам, что \ (f (0) = 2 \) и \ (f (6) = 1 \). Однако множество всех точек \ ((x, y) \), удовлетворяющих \ (y = f (x) \), является кривой. Показанная кривая включает \ ((0,2) \) и \ ((6,1) \), потому что кривая проходит через эти точки

. Рисунок \ (\ PageIndex {10} \): График многочлена.

Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, то график не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения.См. Рисунок \ (\ PageIndex {11} \) .

Рисунок \ (\ PageIndex {11} \): три графика, наглядно демонстрирующие, что является функцией, а что нет.

Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию

1. Проверьте график, чтобы убедиться, что какая-либо вертикальная линия пересекает кривую более одного раза.
2. Если такая линия есть, определите, что график не представляет функцию.

Пример \ (\ PageIndex {12} \): Применение теста вертикальной линии

Какой из графиков на рис. \ (\ PageIndex {12} \) представляет (ы) функцию \ (y = f (x) \)?

Рисунок \ (\ PageIndex {12} \): график полинома (a), наклонной вниз прямой (b) и круга (c).

Решение

Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) рисунка \ (\ PageIndex {12} \). Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что не более чем значений x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке \ (\ PageIndex {13} \).

Рисунок \ (\ PageIndex {13} \): График круга.

Упражнение \ (\ PageIndex {12} \)

Представляет ли график на рисунке \ (\ PageIndex {14} \) функцию?

Рисунок \ (\ PageIndex {14} \): График функции абсолютного значения.

Ответ

да

Использование теста горизонтальной линии

После того, как мы определили, что график определяет функцию, простой способ определить, является ли функция взаимно однозначной, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.

Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию

1. Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
2. Если такая линия есть, определите, что функция не взаимно однозначна.

Пример \ (\ PageIndex {13} \): применение теста горизонтальной линии

Рассмотрим функции, показанные на рисунке \ (\ PageIndex {12a} \) и рисунке \ (\ PageIndex {12b} \). Являются ли какие-либо функции взаимно однозначными?

Решение

Функция на рисунке \ (\ PageIndex {12a} \) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке \ (\ PageIndex {15} \), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.)

Рисунок \ (\ PageIndex {15} \): График многочлена с горизонтальной линией, пересекающей 2 точки

Функция на рисунке \ (\ PageIndex {12b} \) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.

Упражнение \ (\ PageIndex {13} \)

Является ли график, показанный на рисунке \ (\ PageIndex {13} \), взаимно однозначным?

Ответ

Нет, потому что он не проходит проверку горизонтальной линии.

В этом тексте мы будем исследовать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем.Учимся читать, начинаем с алфавита. Изучая арифметику, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать x как входную переменную и \ (y = f (x) \) как выходную переменную.

Мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования на протяжении всей этой книги. Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную в Таблице \ (\ PageIndex {14} \).

Ключевые уравнения

• Постоянная функция \ (f (x) = c \), где \ (c \) — постоянная
• Функция идентичности \ (f (x) = x \)
• Функция абсолютного значения \ (f (x) = | x | \)
• Квадратичная функция \ (f (x) = x ^ 2 \)
• Кубическая функция \ (f (x) = x ^ 3 \)
• Обратная функция \ (f (x) = \ dfrac {1} {x} \)
• Функция обратного квадрата \ (f (x) = \ frac {1} {x ^ 2} \)
• Функция квадратного корня \ (f (x) = \ sqrt {x} \)
• Корневая функция куба \ (f (x) = 3 \ sqrt {x} \)

Ключевые понятия

• Отношение — это набор упорядоченных пар.Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.
• Функциональная нотация — это сокращенный метод соотнесения ввода и вывода в форме \ (y = f (x) \).
• В табличной форме функция может быть представлена ​​строками или столбцами, которые относятся к входным и выходным значениям.
• Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно оценить, заменив входную переменную заданным значением.
• Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение.
• Алгебраическая форма функции может быть записана из уравнения.
• Входные и выходные значения функции можно определить по таблице.
• Связь входных значений с выходными значениями на графике — еще один способ оценить функцию.
• Функция взаимно однозначна, если каждое выходное значение соответствует только одному входному значению.
• График представляет функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке.
• График функции «один к одному» проходит проверку горизонтальной линии.

Глоссарий

зависимая переменная
выходная переменная

домен
набор всех возможных входных значений для отношения

функция
отношение, в котором каждое входное значение дает уникальное выходное значение

Проверка горизонтальной линии
Метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза

независимая переменная
входная переменная

ввод
каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция

однозначная функция
функция, для которой каждое значение вывода связано с уникальным значением ввода

вывод
каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию

диапазон
набор выходных значений, которые являются результатом входных значений в отношении

отношение
набор заказанных пар

Проверка вертикальной линии
Метод проверки того, представляет ли график функцию, путем определения того, пересекает ли вертикальная линия график не более одного раза

Авторы и авторство

Home — Math Nation Florida

Home — Math Nation Флорида

Комплексные интерактивные ресурсы по математике, соответствующие стандартам математики Флориды (MAFS) Университета Флориды для учащихся 6–8 классов по математике, алгебре 1, геометрии, алгебре 2 и выше.

КАК ЭТО РАБОТАЕТ?

Предыдущий слайд ◀ ︎ Следующий слайд ▶ ︎

• Динамическое видео

  Видео с динамическим содержанием, которые охватывают все, что нужно знать студентам Флориды, с примерами и практическими задачами, поставленными во Флориде, чтобы связать алгебру с повседневной жизнью студентов.Студенты могут выбирать между пятью разными репетиторами, которые преподают один и тот же материал по-разному и в разном темпе.

• Пользовательские книги

  Студенты могут получить рабочую тетрадь, дополняющую видео. Студенты могут писать в тетрадях и брать их домой для дополнительной практики!

• Инструмент для практики

  Инструмент для практики в конце каждого раздела видео позволяет студентам проверить свои знания, дает мгновенную обратную связь и предлагает ресурсы, которые устраняют пробелы в их понимании!

• Математические стены

  Интерактивная стена алгебры позволяет учащимся из Флориды, изучающим алгебру 1, геометрию и алгебру 2, получить дополнительную помощь от экспертов-исследователей, учителей и сверстников.

• Сотрудничество с учителями

  Учителя тоже могут сотрудничать! Область для учителей Math Nation предоставляет форум для совместной работы учителей, а также планы уроков и другие ресурсы, которые соответствуют видео и учебному пособию.

• Индивидуализированные инструменты для ремонта на рампе

  Учащиеся могут оценить свое понимание основных математических концепций и концепций предалгебры, используя адаптивные и индивидуализированные инструменты обзора по математике на рампе до 6-го класса и на рампе до алгебры 1.

Динамическое видео Пользовательские книги Инструмент для практики Математические Стены Сотрудничество с учителями Индивидуальные инструменты восстановления на рампе

Узнай, когда и где ты хочешь

Math Nation доступен онлайн 24/7.Если вам нужна помощь по математике на ходу, попробуйте бесплатное мобильное приложение Math Nation.


В прессе

Florida Daily —

Цифровая платформа Math Nation

UF расширяется, чтобы помочь большему количеству оценок с помощью Microsoft

Центр обучения Lastinger Университета Флориды объявил на прошлой неделе, что Microsoft U.S. выделил почти 1 миллион долларов на совершенствование своей цифровой платформы Math Nation, чтобы также обслуживать учеников начальных классов, готовящихся к средней школе. В ответ на быстрый переход к дистанционному обучению из-за COVID-19, платформа была сделана бесплатной для любой школы страны через […]

Подробнее

Новости Окичоби —

Math Nation доступна, поскольку школы готовятся к виртуальному обучению из-за COVID-19

ГАЙНСВИЛЛ — Поскольку наша страна принимает меры по минимизации распространения COVID-19, Math Nation, созданная Центром обучения и изучения Ластингера Университета Флориды, стремится поддерживать постоянный доступ к высококачественным портативным учебным материалам по математике для учителя и ученики.Поскольку семьи, школы и округа сталкиваются с трудными решениями относительно удержания учащихся […]

Подробнее

WCJB — 21 апреля 2020 г.

UF онлайн-обучение и учебная программа бесплатны

«Это время, когда многие из нас чувствуют себя беспомощными и неспособными что-либо делать. Способ показать, что мы заботимся, — это обычно показываться друг другу, а когда вы не можете появиться … предоставление этих ресурсов — это поддержка, которую мы можем предложить, чтобы помочь детям в это действительно сложное время.”

Подробнее Просмотреть всю прессу

 строка (1) "6"
строка (2) "fl"
 

В какую школу ты ходишь?

Если в вашей школе есть доступ к Math Nation, начните вводить текст и выберите свою школу ниже!

Школа не найдена.

Пожалуйста, напишите по электронной почте

(также можно скачать бесплатное мобильное приложение
выполнив поиск по запросу «Math Nation» в магазине приложений на телефоне / планшете)

×

Еще одна вещь!

Пожалуйста, введите ваше имя пользователя и пароль.

×

Еще одна вещь!

Чтобы войти в Math Nation, введите свой 7-значный ссылочный номер (идентификатор сотрудника) и свою фамилию.

Нужна помощь со входом?
Напишите по адресу [email protected] или позвоните по телефону 1-888-608-MATH.

×

Вы студент или учитель / администратор?

Ученик Учитель / Администратор

×

Добро пожаловать в Math Nation!

Math Nation — это динамический математический ресурс, финансируемый государством, который предоставляет учащимся бесплатные обучающие видео, рабочие тетради и интерактивные уроки.Настроить доступ легко и бесплатно! Кликните сюда, чтобы узнать больше.

Если в вашем школьном округе еще не настроен доступ к Math Nation, не волнуйтесь! Вы можете сразу изучить наши ресурсы.

×

учитель, гостевой логин

Пожалуйста, введите свое имя и адрес электронной почты, чтобы войти в систему в качестве гостя.

×

Войти как гость

Вы можете войти в систему как гость или вернуться, чтобы повторить попытку.

Если у вас есть вопросы о входе в систему, напишите нам на [email protected]

×

Добро пожаловать в Math Nation!

Чтобы продолжить, выберите вариант, который лучше всего описывает вас.

×

Количественное мышление

Формат для чтения с экрана

Инструкции для программы чтения с экрана

Раздел «Количественное мышление» Общего теста GRE ^® содержит четыре типа вопросов:

• Вопросы для количественного сравнения
• Вопросы с несколькими вариантами ответов — выберите один вариант ответа
• Вопросы с несколькими вариантами ответов — выберите один или несколько вариантов ответа
• Числовой ввод вопросов

Каждый вопрос появляется либо независимо как отдельный вопрос, либо как часть набора вопросов, называемого набором интерпретации данных.Все вопросы в наборе «Интерпретация данных» основаны на одних и тех же данных, представленных в таблицах, графиках или других отображениях данных. Ниже приведены описания, направления и образцы каждого типа вопросов.

Ознакомьтесь с разделом «Количественное мышление».

На этой странице представлен обзор типов вопросов, которые вы найдете в разделе «Количественное обоснование» Общего теста GRE. Примеры вопросов с пояснениями, обучающими видео, советами и общими советами см. В разделе «Подготовка к тесту количественного мышления».

Вопросы для количественного сравнения

Вопросы этого типа просят вас сравнить две величины — количество A и количество B — а затем определить, какое из четырех утверждений описывает сравнение.

Примеры вопросов

Указания: сравните количество A и количество B, используя дополнительную информацию, сосредоточенную над двумя величинами, если такая информация предоставлена, и выберите один из следующих четырех вариантов ответа.

1. Количество A больше.
2. Количество B больше.
3. Эти две величины равны.
4. Связь не может быть определена на основе предоставленной информации.

Символ, который встречается в вопросе более одного раза, имеет одинаковое значение на протяжении всего вопроса.

1. Кол-во A

   Кол-во В

   1. Количество A больше.
   2. Количество B больше.
   3. Эти две величины равны.
   4. Связь не может быть определена на основе предоставленной информации.

   Правильный ответ: A

   РГТУ — параллелограмм.

2. 1. Количество A больше.
   2. Количество B больше.
   3. Эти две величины равны.
   4. Связь не может быть определена на основе предоставленной информации.

   Правильный ответ: D

   Вопросы с несколькими вариантами ответов — выберите один вариант ответа

   Эти вопросы представляют собой вопросы с несколькими вариантами ответов, в которых вам предлагается выбрать только один вариант ответа из списка из пяти вариантов.

   Примеры вопросов

   Указания: выберите один вариант ответа.

1. На рисунке выше показан круг с центром C и радиусом 6. Какова сумма площадей двух заштрихованных областей?

   Правильный ответ: D

2. На рисунке выше показан график функции f, определенной для всех чисел x.Для какой из следующих функций g, определенных для всех чисел x, график g пересекает график f?

   Правильный ответ: E

   Вопросы с несколькими вариантами ответов — выберите один или несколько вариантов ответа

   Эти вопросы представляют собой вопросы с несколькими вариантами ответов, в которых вам предлагается выбрать один или несколько вариантов ответа из списка вариантов. Вопрос может указывать или не указывать количество вариантов выбора.

   Примеры вопросов

   Указания: выберите один или несколько вариантов ответа в соответствии с конкретными направлениями вопроса.

   Если в вопросе не указано, сколько вариантов ответа выбрать, выберите все подходящие варианты.

   Правильный ответ может быть как одним из вариантов, так и целым, в зависимости от вопроса.

   Кредит не начисляется, если вы не выберете все правильные варианты и никаких других.

   Если в вопросе указано, сколько вариантов ответа выбрать, выберите именно это количество вариантов.

1. Каждый сотрудник определенной компании находится в отделе X или Y, и в отделе X более чем в два раза больше сотрудников, чем в отделе Y. Средняя (среднеарифметическая) заработная плата составляет 25000 долларов для сотрудников отдела X и 35000 долларов. для сотрудников отдела Y. Какая из следующих сумм может быть средней заработной платой для всех сотрудников компании?

   Укажите все такие суммы.

   1. 26 000 долл. США
   2. 28 000 долл. США
   3. 29 000 долл. США
   4. 30 000 долл. США
   5. 31 000 долл. США
   6. 32 000 долл. США
   7. 34 000 долл. США

   Правильный ответ: A и B

2. Если f, g и h — положительные целые числа, такие что f является фактором g, а g является фактором h, какое из следующих утверждений должно быть верным?

   Укажите все такие утверждения.

   1. f — коэффициент
   2. f — коэффициент gh.
   3. f — коэффициент

   Правильный ответ: A, B и C

   Числовой ввод вопросов

   В вопросах этого типа вам предлагается ввести ответ в виде целого или десятичного числа в одно поле для ответа или ввести его в виде дроби в двух отдельных полях — одно для числителя и одно для знаменателя. В компьютерном тесте для ввода ответа используются компьютерная мышь и клавиатура.

   Примеры вопросов

   Указания: введите свой ответ в виде целого или десятичного числа, если есть одно поле для ответа, ИЛИ в виде дроби, если есть два отдельных поля — одно для числителя и одно для знаменателя.

   Все равнозначные формы правильного ответа, такие как 2,5 и 2,50, являются правильными. Дроби не нужно сокращать до наименьших значений, хотя вам может потребоваться уменьшить дробь, чтобы она уместилась в полях.

   Введите точный ответ, если вопрос не требует округления ответа.

1. Правильный ответ: 101

2. Университет принял 100 студентов, перешедших из других учебных заведений. Из этих студентов 34 переведены из двухгодичных общественных колледжей, 25 — из частных четырехгодичных учебных заведений, а остальные переведены из государственных четырехгодичных учебных заведений. Если два разных студента будут выбраны случайным образом из 100 студентов, какова вероятность того, что оба выбранных студента будут студентами, переведенными из двухгодичных общественных колледжей?

   Ответьте дробью.

   Правильный ответ: (или любая эквивалентная дробь).

   Наборы интерпретации данных

   вопросов по интерпретации данных сгруппированы вместе и относятся к одной и той же таблице, графику или другому представлению данных. Эти вопросы просят вас интерпретировать или анализировать предоставленные данные. Типы вопросов могут быть с множественным выбором (оба типа) или с числовым вводом.

   Примеры вопросов

   Указания: Вопросы с 1 по 3 основаны на следующих данных.

   Изменение месячной стоимости запасов в процентах *

   В таблице 3 столбца и 6 строк.

   Бизнес	Процентное изменение с апреля по май	Процентное изменение с мая по июнь
   G	6	8
   К	5
   M	2	12
   R	8
   В	14	0
   Z	2

   * Стоимость запасов определяется в конце каждого месяца.

1. Если стоимость запасов в Бизнесе К составляла 30 000 долларов в апреле, какова была стоимость запасов в Бизнесе К в июне?

   1. 22 500 долл. США
   2. 29 925 долларов США
   3. 30 000 долл. США
   4. 33 000 долл. США
   5. 33 075 долл. США

   Правильный ответ: B

2. В Бизнесе M стоимость запасов за май составляла какой процент от стоимости запасов за июнь?

   Ответьте с точностью до нуля.1 процент.

   %

   Правильный ответ: 89,3

3. Для какого из шести представленных предприятий процентное изменение стоимости товарно-материальных запасов с апреля по июнь было наибольшим?

   1. G
   2. К
   3. M
   4. R
   5. В

   Правильный ответ: A

   Указания: Вопросы с 4 по 6 основаны на следующих данных.

4. Примерно сколько человек заняты в производственном и транспортном секторе?

   1. 9 миллионов
   2. 12 миллионов
   3. 15 миллионов
   4. 18 миллионов
   5. 21 миллион

   Правильный ответ: E

5. Примерно какая часть рабочей силы в сфере общественного питания в сфере обслуживания состоит из членов профсоюзов?

   Правильный ответ: C

6. Что касается рабочей силы, соотношение количества членов профсоюзов к количеству нечленов такое же для сектора продаж, как и для защитной зоны обслуживания в сфере услуг.Что из перечисленного ближе всего к количеству лиц, не являющихся членами сектора продаж?

   1. 2,9 миллиона
   2. 3,6 миллиона
   3. 10,4 млн.
   4. 11,1 млн.
   5. 14,0 млн.

   Правильный ответ: A

Миссис Данна — Математика 8 / Алгебра 8

НЕДЕЛЯ 26.05 — 29.05

Те же задания, что и на прошлой неделе. Не повторяйте задание, если вам удалось его выполнить.Из-за наводнения занятия были приостановлены до вторника 26 мая. Я перепубликую тест в Google Классе.

Оставайтесь в безопасности!

НЕДЕЛЯ 5 / 18-5 / 22

ПРЕДАЛГЕБРА

Понедельник 18.05

Читать стр. 374 — 375 Точечные диаграммы Видео с точечной диаграммой есть 3, которые помогут с 9.1

Ссылка на викторину в классе Google должна быть доступна до 16:00 в четверг 21.05.

Четверг 21.05

Читать стр.380-381 Линия наилучшего соответствия (восходит к наклону линейных функций гл. 4)

Линия наиболее подходящего видео


Ссылка

Quizizz в классе Google должна быть доступна до 16:00 во вторник, 26 мая.

АЛГЕБРА

11,5 пошаговых ответов.

# 1-5


# 6-9


# 10-12


# 13


Понедельник 18.05

Читать стр. 582-584 Сложение и вычитание рациональных выражений Add & Subt.Крыса. Exp. Видео смотрите ролики со знакомыми и непохожими знаменателями.

Рабочий лист 11,6 Практика B

Не забудьте просто сфотографировать свою работу и отправить мне ее по электронной почте.

, четверг, 21 мая

Тест

Rational Expressions на викторине до вторника 26 мая до 16:00

Ссылка находится в гугл классе

АЛГЕБРА 11.5 ПОЛЕЗНЫЕ ВИДЕО

Видео с делительными полиномами


Другое видео


Неделя с 11.05 по 15.05

ПРЕДАЛГЕБРА

Я хотел бы, чтобы вы рассмотрели расширения, поиграв в игру в понедельник и четверг по 10 минут.Вот ссылка Преобразование гольфа. Если это не работает, просто преобразование гольфа в Google, это от Hooda Math.

Тогда задание ПОНЕДЕЛЬНИК — это тестовая викторина, которая должна пройти до 16:00 в четверг. 5/14 Находится в классе Google.

ЧЕТВЕРГ

Вы будете проходить тест на трансформацию в викторине, которую я опубликую в среду. в классе Google.

АЛГЕБРА

Читать стр. 576 — 577 делящих многочленов (это должно быть проще, чем 11.4)

Домашнее задание: 11.5 Практика A Я прилагаю рабочий лист, ключ для ответа и опубликую проблемы из Практики B позже, чтобы вам было легче, после того, как вы попробуете. Срок сдачи: до чт. 14.05 к 16:00.













Четверг задание — рассмотрение делящих многочленов. Я прилагаю лист с ответами, но работу нужно показать в меру ваших возможностей. Рабочий лист должен быть сдан до понедельника 18.05.




СН.11.4 ПОМОЩЬ !!!




4 мая, понедельник и 7 мая, четверг

ПРЕДАЛГЕБРА

Понедельник 5/4

Есть 2 новых раздела под P для проверки.

* Новые переводы: напишите правило и * Новые композиции преобразований конгруэнтности: нанесите графическое изображение на график Оба должны быть сданы в четверг, 7 мая, к 16:00. Умная оценка 85 или не менее 30 минут рабочего времени.

Четверг 7 мая

Смотрите первые 3 видео по ссылке.Общее время просмотра точек расширения, масштабного коэффициента расширения и расширяющихся форм составляет примерно 10:30 минут. Не стесняйтесь практиковать навыки на той же странице. Прочтите страницы 84 — 86.Ixl

Расстояния


Домашнее задание — ixl Section Q # 2 & # 3. Умная оценка 80 или 30 минут рабочего времени на каждую.

АЛГЕБРА

4 мая, понедельник и 7 мая, четверг

Понедельник 5/4

Прочтите страницы 570 — 571 Умножение и деление рациональных выражений.Вот ссылка на видео в помощь

Мульти. & Div. Крыса. Выражения. Первые 3 ссылки на видео на этой странице очень полезны. Вам пока не нужно указывать домен и диапазон, но это полезно на практике. Помните, что ваш знаменатель не может равняться нулю.

Тогда домашнее задание — это умный результат ixl Section GG # 4 на 80 или 45 минут рабочего времени. Срок сдачи: четверг, 7 июля, до 16:00.

Четверг 7 мая

Ваша домашняя работа — это повторение умножения и деления рациональных выражений.Вам ДЕЙСТВИТЕЛЬНО НЕ нужно распечатать эту страницу. Пожалуйста, выполните только 11.4 Практика A (Практика B — последняя страница).










Я прилагаю еще и ключ ответа. Показ работы принесет вам признание, а не только ответ. Загрузите рабочий лист на свой компьютер, и вы можете просто ввести свой ответ в текстовый документ, а затем отправить его мне по электронной почте для подтверждения.

№ 15 на листе — это № 15 по Практике Б, так что именно здесь вы найдете ответ.

Понедельник 27 апреля и четверг 30 апреля

ПРЕДАЛГЕБРА

Понедельник 27.04.

Практика размышлений IXL Раздел P # 11 и # 10 Срок сдачи до четверга (30.04) 16:00 Интеллектуальный счет 85 каждый

Четверг 30.04. Вращения Видео и практика при необходимости

Прочтите страницы 62-64 в учебнике, затем IXL Section P # 13 и # 12, которые должны быть выполнены к понедельнику (5/4) до 16:00

Умная оценка 80 или 35 минут работы

АЛГЕБРА

Понедельник 27.04.

Читать стр.552 — 554 Графические рациональные функции. Графическое изображение рационального видео На этой странице есть много ресурсов для понимания.

Затем ixl Section GG # 1 (довольно легко после просмотра асимптотической части видео), срок сдачи до четверга 30.04, 16:00 Интеллектуальный счет 80 или 45 минут работы

Четверг 30.04.

Читать страницы 562 -563 Упрощение рациональных выражений Упрощение видео Необходимо смотреть только первые 7:30 минут. Затем ixl Section GG # 3 Умная оценка 80 или 45 минут работы

Четверг

ПРЕДАЛГЕБРА

У меня было несколько вопросов от студентов о переводах, поэтому для следующего задания я посмотрю, не подойдет ли вам Khan Academy лучше.Щелкните ссылку Reflections # 1, и вы перейдете на сайт. Затем с левой стороны есть 8 вещей, связанных с видео. Смотрите и практикуйте первые 4.

Тогда ваше задание на сегодня в ixl — это разделы P № 9 и № 8 в указанном порядке. Срок сдачи: понедельник, 27 апреля

Отражения # 1


АЛГЕБРА

Было несколько вопросов по теореме Пифагора. Прилагаю ссылку из Академии Хана. Посмотрите видео или 2 с этой страницы, если вам это нужно.

Теорема Пифагора


Ваше задание в ixl — Раздел F # 18 & # 19 Срок сдачи: 27 апреля, понедельник

Понедельник 20.04 Мой офис часы. на этой неделе:

Вторник: 10-11 утра Среда: 1-2 дня Четверг: 2-3 Я все равно буду проверять электронную почту в течение дня.

Предварительная алгебра

Вот ваши задания на понедельник. Они должны быть сданы к четвергу с умным баллом не менее 80 .

Прочтите страницы 50 и 51 своего учебника о переводах рисунка. Видео, которое вы можете посмотреть, возможно, придется скопировать ссылку или нажать «развернуть окно» вверху. https://www.youtube.com/watch?v=dmydPJl8_4Y

Затем на ixl начните с раздела P и выполните пункты 6 и 7.

Алгебра

Вот ваши задания на понедельник. Они должны быть сданы к четвергу с умным баллом не менее 85 .

Прочтите страницы 522 и 523 в своем учебнике по теореме Пифагора.

Затем на ixl Section F # 16 и # 17.

Алгебра

Песня

Quadratic Formula — Google на YouTube, популярная версия, использует ласковую версию, чтобы помочь запомнить это.

Затем попрактикуйтесь в ixl Section BB # 11










гл. 9 Видео Вам, вероятно, придется скопировать ссылку и поместить в новое окно

Графики вершин и пересечений по оси x Вершины и пересечения по оси x


Завершение квадрата Завершение квадрата

Квадратичная формула и дискриминант Квадратичная формула и дискриминант

гл.8 Графики квадратичных видео https://www.youtube.com/watch?v=Cn1aFaxRyeU


ПРАКТИЧЕСКИЙ ТЕСТ PSAT АНГЛИЙСКИЙ И МАТЕМАТИЧЕСКИЙ







26.02.2020

В ПОНЕДЕЛЬНИК ДЛЯ ВСЕХ КЛАССОВ БУДУТ ПРОВЕРКА И ТЕСТ

ПОЖАЛУЙСТА, ПОЛУЧИТЕ ВСЕ МАТЕРИАЛЫ ДОМАШНИЙ ЧЕТВЕРГ ИЛИ ПЯТНИЦУ

20.02.2020

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Практика разложения многочленов

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Рабочий лист лабиринта объема * ДОПОЛНИТЕЛЬНЫЙ РАБОЧИЙ ЛИСТ КРЕДИТА *

19.02.2020

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Факторные полиномы при a> 1

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Сюжетные задачи с 3D-фигурами

18.02.2020

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Факторные полиномы

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

В классе измерительной деятельности

17.02.2020

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Решите многочлены в факторизованной форме

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Объем шара

12.02.2020

ВИКТОРИНА ПО АЛГЕБРЕ ЗАВТРА (ЧЕТВЕРГ)

Особые продукты

ВИКТОРИНА ПО АЛГЕБРЕ ЗАВТРА (ЧЕТВЕРГ)

Деятельность измерительных конусов и цилиндров

11.02.2020

АЛГЕБРА

Умножающие многочлены

ПРЕДАЛГЕБРА

Объем конусов

05.02.2020

АЛГЕБРА




7.1 Практика A

31.01.2020

АЛГЕБРА

ВИКТОРИНА НА 1 ЧАС ВО ВТОРНИК НА СЛЕДУЮЩЕЙ НЕДЕЛЕ

ВИКТОРИНА НА 6 ЧАС В СРЕДУ СЛЕДУЮЩЕЙ НЕДЕЛИ

Графические уравнения абсолютных значений

ПРЕДАЛГЕБРА

Популярная викторина по теореме Пифагора и квадратным корням

30.01.2020

АЛГЕБРА

Уравнения абсолютных значений

ПРЕДАЛГЕБРА

Теорема Пифагора

29.01.2020

АЛГЕБРА

Кусочные функции

ПРЕДАЛГЕБРА

Теорема Пифагора

28.01.2020

АЛГЕБРА

Кусочные функции

ПРЕДАЛГЕБРА

Квадратные корни

ЭКЗАМЕНЫ ДЛЯ ВСЕХ КЛАССОВ СРЕДА И ЧЕТВЕРГ

21.01.2020

АЛГЕБРА




ПРЕДАЛГЕБРА




ОБЗОР ЭКЗАМЕНА 20/21 И 21 января

13.01.2020

Все классы прошли тестирование AimsWeb сегодня










09.01.2020

АЛГЕБРА

Показательные функции

ПРЕДАЛГЕБРА

Обзор / рабочий день решения систем по устранению

08.01.2020

АЛГЕБРА

Деление на показатели

Отрицательная и нулевая экспоненты

ПРЕДАЛГЕБРА

Решить системы методом исключения (сложения / вычитания)

07.01.2020

АЛГЕБРА

Умножение на показатели

ПРЕДАЛГЕБРА

Решите системы, построив график

06.01.2020

АЛГЕБРА

Квадратные корни

ПРЕДАЛГЕБРА

Просмотр формы пересечения откоса

10.12.19

АЛГЕБРА

Практика на выбывание Pizzazz Pg.164 и 167

ПРЕДАЛГЕБРА

IXL

Y7 smart оценка 80

Y8 smart оценка 80

09.12.19

АЛГЕБРА

Решение систем умножением

Рабочий лист по математике

ПРЕДАЛГЕБРА

IXL

W12 Smart оценка 85

W14 смарт-оценка 85

Y6 smart оценка 80

06.12.19

АЛГЕБРА

Решите системы, используя исключение, добавляя и вычитая

Домашнее задание: рабочий лист Pizzazz стр.165

ПРЕДАЛГЕБРА

IXL — ВСЕ ДО КОНЦА ДНЯ СЕГОДНЯ!

Догоня:

W7, W8, W9, W11, Y1 и Y2

05.12.19

АЛГЕБРА

Просмотрите рабочий лист систем решения путем построения графиков и замены

ПРЕДАЛГЕБРА

IXL

W9 — умная оценка 85

W11 — умная оценка 80

Y2 — умная оценка 80

04.12.19

АЛГЕБРА

Решите системы, используя замену

ПРЕДАЛГЕБРА

Введение в IXL за каждые 10 баллов сверх установленного требования равняется 1 дополнительному кредитному баллу.

W7 — умная оценка 90

W8 — умная оценка 90

Y1 — умная оценка 80

03.12.19

АЛГЕБРА

Практикуйтесь в решении систем с помощью построения графиков

ПРЕДАЛГЕБРА

Тестовые поправки

02.12.19

ПРЕДАЛГЕБРА

Тестовые исправления должны быть сданы в среду в начале класса

АЛГЕБРА

Решение систем с помощью построения графиков

Домашнее задание: 4.1 Практика A

22.11.19

РАБОЧИЕ ЛИСТЫ ДЛЯ ВСЕХ КЛАССОВ ДЛЯ ТЕСТИРОВАНИЯ НА СЛЕДУЮЩИЙ ПОНЕДЕЛЬНИК И ВТОРНИК

21.11.19

РАБОЧИЕ ЛИСТЫ ДЛЯ ВСЕХ КЛАССОВ ДЛЯ ТЕСТА НА СЛЕДУЮЩИЙ ПОНЕДЕЛЬНИК И ВТОРНИК

20.11.19

ПРЕДАЛГЕБРА

Калькулятор практики

АЛГЕБРА

Построение графиков линейных неравенств

19.11.19

ПРЕДАЛГЕБРА

Написать линейное уравнение

АЛГЕБРА

сложные неравенства

18.11.19

ПРЕДАЛГЕБРА

Написать линейное уравнение

АЛГЕБРА

Многоступенчатые неравенства

15.11.19

Дополнительный урок алгебры




12.11.19

АЛГЕБРА

Положим сегодня и завтра

ПРЕДАЛГЕБРА

Задачи перехвата истории

Домашнее задание: Рабочий лист № 2 и № 5

Дополнительный кредит со сроком погашения завтра

11.11.19

АЛГЕБРА

Курсы пора заканчивать!

Отражение журнала и групповая оценка патта-патта

ПРЕДАЛГЕБРА

Рабочий лист «Убийство зомби»

Витраж с дополнительным баллом до среды

30.10.19

АЛГЕБРА

Окончательный проект, электронная таблица и рабочая страница должны быть выполнены

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Форма пересчета наклона

Домашнее задание: рабочий лист

29.10.19

АЛГЕБРА

Продолжение программы Putt-Putt (уравнения траектории мяча в четверг)

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Практический уклон

Домашнее задание: Рабочий лист

28.10.19

АЛГЕБРА

Продолжение программы Putt-Putt (уравнения траектории мяча в четверг)

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Нахождение откоса

Домашнее задание: Рабочий лист

21.10.19

АЛГЕБРА

Запущен проект Putt-Putt

Поле с препятствиями, блокираторами, ти и лункой должно быть завершено к началу занятий в среду.Включая все координатные точки.

ПРЕДАЛГЕБРА

Построение координатных точек

17.10.19

АЛГЕБРА

ТЕСТ

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Рабочий лист проверки параллельных и поперечных линий, углов треугольников и углов многоугольников

16.10.19

ТЕСТ АЛГЕБРЫ ЧЕТВЕРГ / ПЯТНИЦА

Обзор станции

для теста

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Углы полигонов

Домашнее задание: 3.3 Практика

15.10.19

ТЕСТ АЛГЕБРЫ ЧЕТВЕРГ / ПЯТНИЦА

Обзор станции

для теста

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Углы полигонов

1 0/14/19

ТЕСТ АЛГЕБРЫ ЧЕТВЕРГ / ПЯТНИЦА

Точечный откос

Домашнее задание: рабочий лист наклона

ПРЕДАЛГЕБРА ТЕСТ ПЯТНИЦА

Углы треугольников внутренние и внешние

Домашнее задание: рабочий лист «Треугольник»

11.10.19

1/2 ДНЯ ВСЕ КЛАССЫ

ПРОДИЖИ

10.10.19

АЛГЕБРА

Практикуется на калькуляторах

Домашнее задание: Рассказ Задачи 1-4

ПРЕДАЛГЕБРА

Рабочий день на параллельных и поперечных линиях

Домашнее задание: изложение 45 и 124

09.10.19

АЛГЕБРА

Написание линейных уравнений

Домашнее задание: 2.5 Практика

ПРЕДАЛГЕБРА

Танцевал в классе, без домашнего задания

08.10.19

АЛГЕБРА

Перехватывает Pizzazz Pg. 150 + графика

ПРЕДАЛГЕБРА

параллельные и поперечные линии

Домашнее задание: противоположное практике 71

07.10.19

АЛГЕБРА

Перехваты

Hmwk: только сторона листа пеликана 1-4

ПРЕДАЛГЕБРА

Параллельные и поперечные линии

Hmwk: только практика 71

04.10.19 ТЕСТ / ВИКТОРИНА ДЛЯ ВСЕХ КЛАССОВ

03.10.19 УЧЕБНАЯ ПРОГРАММА НОЧЬ 4:15 — 5:15

АЛГЕБРА Гл.2 ВИКТОРИНА ПЯТНИЦА

Дополнительная практика для викторины

P. 53 7-17 нечетные, 21, 22 P. 56 1-5 P. 57 7-11 P. 62 7-9,11,12 P. 63 25 P. 71 1-11, 14

Проект витража (40 ед.)

ПРЕДАЛГЕБРА CH. 1 ТЕСТ ПЯТНИЦА

Дополнительная практика для викторины, но сначала студентам необходимо попросить учебник

стр. 7 7-9,16,18,20,23,28 стр. 14 6,7,10,11,13 стр. 23-25 ​​6,7,10,11,16,21,22,37

Обзор станции

для теста Friday

02.10.19

ВИКТОРИНА ПО АЛГЕБРЕ ПЯТНИЦА

Параллель и перпендикуляр

Hmwk: 2.2 Практика

ПРЕДАЛГЕБРА CH. 1 ТЕСТ ПЯТНИЦА

Практические переменные с обеих сторон

25.09.19

АЛГЕБРА

Функции линейных уравнений и наклона

Без домашнего задания

ПРЕДАЛГЕБРА

Решение с переменными с обеих сторон

Домашнее задание: 1-12 рабочий лист

24.09.19

АЛГЕБРА

Отделка 2.1

ПРЕДАЛГЕБРА

Попрактикуйтесь в решении многоступенчатых уравнений

Домашнее задание: 1-24 листа без обведенных задач.

23.09.19

АЛГЕБРА

Построение графиков линейных функций с помощью таблиц

Домашнее задание: 2.1 Практика сторона 1

ПРЕДАЛГЕБРА

Решение многоступенчатых уравнений

домашнее задание: # 13-24 на обороте заметок

ВСЕ КЛАССЫ: ДОПОЛНИТЕЛЬНЫЙ КРЕДИТ НА КОРОБКУ ТКАНЕЙ (ТОЛЬКО 1 КОРОБКА НА ЧЕЛОВЕКА НА СЕМЕСТРА)


16.09.19

ВСЕ КЛАССЫ ПРОВЕРИЛИ ПРЕДВАРИТЕЛЬНЫЙ ТЕСТ СЕГОДНЯ БЕЗ ДОМАШНЕГО ЗАДАНИЯ

12.09.19

Викторина ВСЕ КЛАССЫ

11.09.19

АЛГЕБРА

Переменные с обеих сторон

Hmwk: Рабочий лист только 10 задач

ВИКТОРИНА ЗАВТРА

ПРЕДАЛГЕБРА

Оценка короткого цикла

Рабочий лист лабиринта

ВИКТОРИНА ЗАВТРА

10.09.19

ПРЕДАЛГЕБРА

Решите одношаговые уравнения

hmwk: Рабочий лист

ВИКТОРИНА ЧЕТВЕРГ

АЛГЕБРА

Вокруг комнаты активность

Hmwk: Рабочий лист

ВИКТОРИНА ЧЕТВЕРГ

09.09.19

АЛГЕБРА 1-Й ЧАС

Рабочий лист решения двухэтапных уравнений

ВИКТОРИНА ЧЕТВЕРГ

ПРЕДАЛГЕБРА 2-Й И 3-Й ЧАС

Упростите выражения и рабочий лист Pizzazz P.24

ВИКТОРИНА ЧЕТВЕРГ

ПЯТЫЙ ЧАС ПРЕДАЛГЕБРЫ И 6-Й ЧАС АЛГЕБРЫ

Aimsweb без домашнего задания

ВИКТОРИНА ЧЕТВЕРГ

06.09.19

АЛГЕБРА

Утренний урок сделал Aimsweb без домашнего задания

Дневное занятие (из-за отключения электричества) Решите домашнее задание из 2-х шаговых уравнений стр.

ПРЕДАЛГЕБРА

2-й и 3-й час не выполняли домашнее задание Aimsweb

5-часовой рабочий лист упрощенных выражений

05.09.19

АЛГЕБРА

Без домашнего задания

ПРЕДАЛГЕБРА

Рабочий лист упрощения выражений стр.16

Ссылки викторины за каждый час

1-й час Викторина

2-й час Викторина

3-й час Викторина

5-й час Викторина

6-й час Викторина

04.

No related posts.