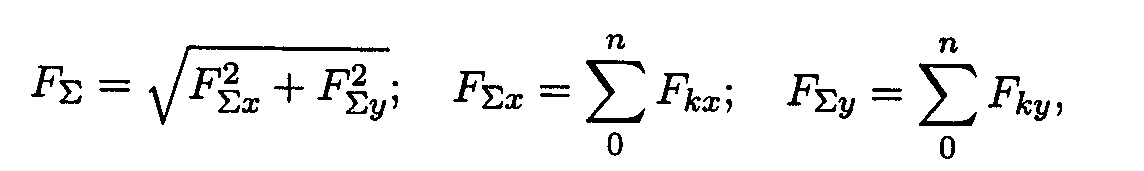
Задача 1. Шар силой тяжести 400 Н опирается на гладкую вертикальную стенку и удерживается в равновесии нитью АВ (рис. 21, схема I). Определить реакции нити и стенки. Как измелится натяжение нити и давление шара на стенку, если нить AB укоротить (удлинить)?
Задача 2. Шар силой тяжести 80 Н, лежащий на гладкой наклонной плоскости (рис. 21, схема 11), удерживается в равновесии нитью АВ. Определить реакции нити и плоскости. Как изменится натяжение нити и сила давления шара на наклонную плоскость, если укоротить нить AB?
Задача 3. Шар силой тяжести 100 11, лежащий на гладкой наклонной плоскости (рис. 21, схема III), удерживается в равновесии горизонтальной нитью АВ. Определить реакции нити и плоскости. Как изменится натяжение нити и сила давления шара на наклонную плоскость при увеличении наклона последней?
Задача 4. Шар силой тяжести 200 Н опирается на вертикальную гладкую стенку и гладкую плоскость, наклоненную к горизонту под углом α = 50° (рис. 21, схема IV)ю Определить реакции стенки и наклонной плоскости. Как изменятся силы давления шара на стенку и наклонную плоскость, если уменьшить угол α?
Задача 5. Шар силой тяжести 120 Н удерживается в равновесии двумя плоскостями, наклоненными к горизонту под углами α = 45° и β = 25° (рис. 21, схема V). Определить реакции наклонных плоскостей. Как станут изменяться силы давления шара на плоскости, если при неизменном угле α угол наклона β увеличивать до 45°?
Задача 6. Шар силой тяжести 150 Н опирается на гладкую наклонную плоскость и удерживается в равновесии нитью AB (рис.21, схема VI), которая образует с вертикалью угол α = 45°. Определить реакции нити и плоскости. При каком значении угла α сила давления шара на плоскость и натяжение нити численно равны друг другу?
Задача 7. Груз О удерживается в равновесии шарниром, закрепленным в точке В стержня 1 и динамометром 2, показание которого в заданном положении 485 Н (рис. 21, схема VII). Определить силу тяжести груза О и реакцию стержня 1. Каким образом следует изменить положение стержня I, чтобы он оказался сжатым, а не растянутым?
Задача 8. Определить, уравновешена ли система трех сил F1, F2 и F3 (рис. 21 , схема VIII). Если система не уравновешена, то чему равна и как направлена уравновешивающая сила F4?
Задача 9. Определить реакции стержней 1 и 2, удерживающих в равновесии груз G = 400 Н (рис. 21, схема IX). Изменятся ли реакции стержней, если длину стержня 1 уменьшить в два раза, не изменяя его положения относительно стержня 2?
Задача 10. Цилиндр силой тяжести 800 Н и диаметром 4 м опирается на ребра разновысоких стенок (рис. 21, схема X), расстояние между которыми 2,5 м. Определить реакции опор. Как изменятся эти реакции при одинаковой высоте стенок?
Задачи 11-12. Балка, шарнирно закрепленная в точке А и удерживаемая в горизонтальном положении стержнем ВС, нагружена, как показано на рис. 22, силой F и парой сил с моментом М, Определить реакции шарнира А и стержня ВС. Силой тяжести балки и стержня пренебречь. Числовые данные для своего варианта взять из табл. 2.
Задачи 21-22. На валу жестко закреплены шестерня 1 и колесо 2 (рис. 23, схема I к задаче 21 и схема II к задаче 22). Определить в положении равновесия вала реакции подшипников А к В, а также силы F2 и Fr2 =0,4F2, действующие на колесо, если F1 = 400 H, a Fr1 = O,4F1. Силой тяжести вала, шестерни и колеса пренебречь.
Задачи 23-25. На барабан, закрепленный на валу, действует груз G. Какую силу F следует приложить к рукоятке CD, чтобы удержать вал в равновесии в положении, показанном на рис. 23 (схема III к задаче 23, схема IV к задаче 24 и схема V к задаче 25). Определить также реакции подшипников А к В.
Задача 26. Однородная квадратная крышка ABCD люка может вращаться вокруг оси, проходящей через петли А и В. Горизонтальная веревка DE удерживает крышку в равновесии в положении, показанном на рис. 23 (схема IV). Определить реакции опор А и В, если сила тяжести крышки G = 48 Н.
Задача 27.Полка, нагруженная, как показано на рис. 23 (схема VII), силой тяжести G = 0,8 кН и могущая вращаться около оси, проходящей через петли А и В, удерживается в равновесии в горизонтальном положении стержнем DC, образующим с вертикалью угол 60°. Определить реакции петель А, В и стержня DC.
Задачи 28 – 29. На вал жестко насажены шкив 1 и колесо 2, нагруженные как показано на рис. 23 (схема VIII к задаче 28 и схема IX к задаче 29). Определить силы F2, Fr2 = 0,4F2, а также реакции опор А и В, если F1= 120 Н.
Задача 30. На вал жестко насажены шкивы 1 и 2, нагруженные, как показано на рис. 23 (схема X). Определить натяжения ветвей ремня шкива 2 (F2 и 2F2) и реакции опор А и В, если F1=150 Н.
Задачи 11 ...20. Балка, шарнирно закрепленная в точке А и удерживаемая в горизонтальном положении стержнем ВС, нагружена, как показано на рис. 22, силой Р, и парой сил с моментом М. Определить реакции шарнира А и стержня ВС. Силой тяжести балки и стержня пренебречь. Числовыё данные для своего варианта взять из табл. 2.
3адачи 21...30. Определить положение центра тяжести тонкой однородной пластинки, форма и размеры которой в мм заданы на рис. 23. Схему пластинки для задачи своего варианта взять из таблицы 3.
Задача 31. Точка, находящаяся в покое, начала прямолинейное движение с ускорением а=2 м/с2. Приобретя скорость V = 10 м/с, точка стала двигаться равномерно по дуге окружности радиуса R=8 м. Через 15 с равномерного движения точка внезапно остановилась. Определить: 1) путь, пройденный точкой за время ее, движения; 2 ) среднюю скорость на этом пути; 3) ускорение точки при движении но дуге окружности.
Задача 32. Шкив диаметром d имея угловую скорость ω=8 рад/с, начал вращаться равноускоренно и через 12 с его угловая скорость ω достигла значения 14 рад/с. Определить: 1) угловое ускорение шкива; 2 ) сколько оборотов успел сделать шкив за время равноускоренного движения.
Задача 33. Точка движется равномерно по дуге окружности радиуса r = 200 м. Пройдя 150 м за 10 с, точка стала двигаться равнозамедленно и остановилась через 40 с после начала равнозамедленного движения. Определить: 1) путь, пройденный точкой за все время движения; 2) ускорение точки в момент t = 24 с после начала равнозамедленного движения; 3) на каком расстоянии находилась точка в этот момент от места начала движения.
Задача 34. Тело при равнозамедленном вращении с угловым ускорением ε = —2 рад/с2 в течение 1,4 мин сделало 2100 оборотов. Определить: 1) угловую скорость тела в начале и в конце равнозамедленного вращения; 2 ) скорость и нормальное ускорение точек тела в момент t = 60 с после начала равнозамедленного вращения, если эти точки расположены на расстоянии r = 0,5 м от оси вращения тела.
Задача 35. Точка двигалась равномерно со скоростью 2 м/с в течение 10 с, а затем, получив ускорение, двигалась, равноускоренно еще 10 с, успев пройти за это все время (20 с) 90 м. С начала 91-го метра точка снова стала двигаться равномерно с той скоростью, которую приобрела к этому моменту. Через 10 с равномерного движения точка внезапно остановилась. Определить: 1) весь путь, пройденный точкой за 30 с; 2) ускорение точки в момент е = 15 с, считая от начала движения, если в этот момент движение происходит по дуге окружности радиуса г = 20 м.
Задача 36. Ротор при угловой скорости n0=720 об/мин начал равноускоренное вращение с угловым ускорением ε = 20 рад/с2. После 12 с равноускоренного вращения ротор в течение 420 с вращается равномерно. Определить; 1) угловую скорость равномерного вращения; 2) сколько оборотов совершил ротор за все рассмотренное в задаче время.
Задача 37. Точка двигалась раиномерно в течение 20 с и прошла путь 100 м. В начале 21-й секунды скорость точки внезапно возросла до 8 м/с, и с этой скоростью точка двигалась еще 20 с, а затем последовало равнозамедленное движение и через 20 с точка остановилась. Определить: 1) весь путь, пройденный точкой b построить графики перемещения, скорости и ускорения точки, считая движение точки прямолинейным.
Задача 38. В течение 15 с вращения вала происходило согласно уравнению φ = 20t + 0,5t3 (φ — в радианах, t — в секундах). Определить: 1) угловую скорость вала в момент t0 = 0 с и t1 = = 15 с; 2) угловое ускорение в эти же моменты; 3) сколько оборотов совершил вал за 15 с.
Задача 39. Точка начала прямолинейное движение из состоянии покоя с ускорением 0,8 м/с2. Через 15 с после начала движения точка стала двигаться ра внозамедленно и за последующие 20 с ее скорость уменьшилась до 6 м/с и с этой скоростью точка двигалась еще 20 с и остановилась. Написать уравнения, которым подчинялось движение точки на каждом этапе; построить графики перемещения, скорости н ускорения точки.
Задача 40. Движение точки по окружности радиуса r = 1 м подчиняется уравнению S = — 2t + 0,5×t2 ( S — в метрах, t — в секундах). Построить графики перемещения, скорости и касательного ускорения точки для первых шести секунд движения. На основании анализа графиков указать: в течение какого времени движение было ускоренным и в течение какого — замедленным, какой путь прошла точка за 6 с и успела ли она пройти окружность полностью.
Задача 41. Масса мотоциклиста вместе с мотоциклом — 280 кг. Когда мотоциклист проезжает по легкому мостику со скоростью 108 км/ч, то мостнк прогибается, образуя дугу радиусом 120 м. Определить максимальную силу давления, производимую мотоциклом на мостик.
Задача 42. К потолку вагона на тонкой нити подвешен груз, масса которого 1 кг. Определить, на какой угол α от вертикали отклонится нить при прямолинейном движении вагона с постоянным ускорением 5 м/с2. Каково при этом натяжение нити? Массой нити пренебречь.
Задача 43. Шарик, масса которого 0,5 кг, привязан к нити длиной 60 см и вращается вместе с ней в вертикальной плоскости с частотой 90 об/мин. Определить наибольшее натяжение нити, пренебрегая ее массой.
Задача 44. Человек, держащий в руке сумку с продуктами массой 12 кг, вошел в лифт. С какой силой действует сумка на руку человека в начале подъема лифта, если ускорение при этом постоянно и равно 6,2 м/с2?
Задача 45. Груз в 5 т, подзешенный на тросе длиной 4 м, совершает колебательное движение и при переходе через положение равновесия имеет скорость 1,6 м/с. Определить в этот момент натяжение троса. Массой троса и размерами груза пренебречь.
Задача 46. Груз массой 12 т, подвешенный на тросе, опускается вертикально вниз с ускорением 4,4 м/с2. Определить натяжение троса, пренебрегая его массой.
Задача 47. Шарик массой 0,8 кг привязан к нити, которая может выдержать натяжение не более 5 кН. При какой угловой скорости вращения в вертикальной плоскости нити с шариком возникает опасность ее разрыва, если длина нити 80 см. Массой нити пренебречь.
Задача 48. К потолку вагона на тонкой нити подвешен шарик массой 2 кг. При равноускоренном прямолинейном движении вагона нить отклоняется от вертикали на угол α = 15°. Определить ускорение вагона и натяжение нити. Массой нити пренебречь.
Задача 49. Какая максимальная сила прижимает летчика к креслу при выполнении фигуры высшего пилотажа «петля Нестерова», если масса летчика 80 кг, скорость самолета 150 км/ч, радиус траектории 180 м.
Задача 50. С какой скоростью мотоциклист должен проехать по выпуклому мостику, радиус кривизны которого 25 м, чтобы в самой верхней точке мостика сила давления мотоцикла на мостик была в два раза меньше его общей с мотоциклистом силы тяжести?
Задача 51. По ледяной дороге с подъемом под углом 12° к горизонту трактор тянет сани с грузом в 10 т со скоростью 9 км/ч. Коэффициент трения саней о дорогу 0,05. Определить развиваемую трактором мощность.
Задача 52. Каток массой 100 кг вкатывается по наклонной плоскости равномерно под действием постоянной силы F (рис. 24, схема 1), параллельной плоскости. Определить работу, совершаемую силой F при подъеме катка на высоту h = 4 м, если коэффициент трения качения fк = 0,25 см.
Задача 53. Станок приводится в движение ременной передачей от шкива, который получает вращение через редуктор от электродвигателя мощностью 2,4 кВт. Шкив диаметром 20 см вращается с частотой 180 об/мин, натяжение ведущем ветви ремня 1700 Н, ведомой 850 Н. Определить КПД передачи.
Задача 54. Определить общий КПД силовой передачи и гребного винта буксира, а также мощность вредных сопротивлений, если мощность на выходном валу двигателя 110 кВт при скорости 18 км/ч и общей силе полезного сопротивления движению 6 кН.
Задача 55. Тягач, развивая мощность 66 кВт, тянет по горизонтзльной ледяной дороге со скоростью 12 км/ч сани с грузом 25 т. Определить коэффициент трения между санями и дорогой. Какую работу совершает тягач на одном километре пути?
Задача 56. Двигатель мощностью 25 кВт, установленный на мотоцикле, сообщает ему на горизонтальном участке пути скорость 108 км/ч, а установленный на катере — скорость 10,5 м/с. Принимая КПД мотоцикла — 0,65 и катера — 0,15, определить полезные сопротивления движению в обоих случаях.
Задача 57. По вертикальным направляющим поднимается груз в 1,2 т со скоростью V = 0,5 м/с (рис. 24, схема II). Сила F, поднимающая груз, направлена под постоянным углом α = 15° к вертикали; коэффициент трения при движении груза по направляющим 0,35. Определить мощность, развиваемую при подъеме груза и КПД подъемника.
Задача 58, Каток диаметром 1,5 и н массой 2 т (рис. 24, схема III) равномерно катится под действием оилы F, направленной под углом α = 30° к горизонту. Определить работу силы F на пути 200 м, если коэффициент трения качения fк = 4 см.
Задача 59. На валу, вращающемся с постоянной частотой 750 об/мин, укреплены ведущие шкивы 1 я 2 ременных передач (рис. 24, схема IV). Натяжения в сбегающих ветвях соответственно равны F1= 1800 Н и F2 = 1500 Н. Определить работу, оовершаемую движущим моментом Мд за время 20 мин, и подводимую к валу мощность.
Задача. 60. Резиновую заглушку длиной b = 150 мм протаскивают сквозь трубу длиной 3Ь (рис. 24, схема V). Сила трения между внутренней поверхностью трубы и заглушкой пропорциональна поверхности их соприкосновения. Когда заглушка полностью находится в трубе, сила трення Ft = 200 Н. Определить работу силы треная при протаскивании заглушки сквозь трубу.
mehanika-sopromat.ru
Знать способы сложения двух сил и разложение силы на составляющие, геометрический и аналитический способы определения равнодействующей силы, условия равновесия плоской сходящейся системы сил.
Уметь определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси.
Расчетные формулы
Равнодействующая системы сил
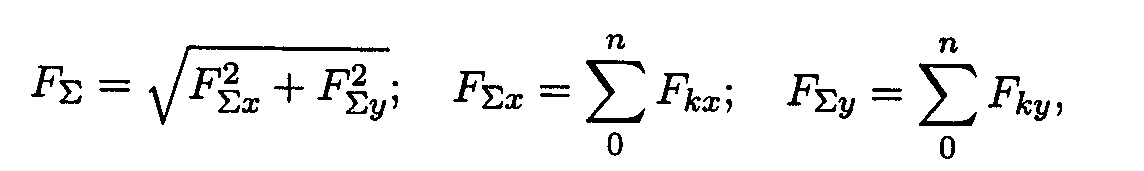
где PΣx, PΣy - проекции равнодействующей на оси координат; Pkx, Pky - проекции векторов-сил системы на оси координат.
 Где αΣх - угол равнодействующей с осьюОх.
Где αΣх - угол равнодействующей с осьюОх.
Условие равновесия

Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Пример 1.Определение равнодействующей системы сил
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П 1.1).
Дано: F1 = 10кН;F2 = 15кН;F3 = 12кН;F4 = 8кН;F5 = 8кН;
αl = 30˚; α2 = 60˚; α3= 120˚; α4 = 180˚; α5 = 300˚.
Решение
1. Определить равнодействующую аналитическим способом (рис. П 1.1а).






2. Определить равнодействующую графическим способом.

С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П l.l 6). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.

Результаты расчетов не должны отличаться более чем на 5 %:

Задание № 1
Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами.
Задание. Используя схему рис. П. 1.1а, определить равнодействующую системы сил.
| Параметр | Вариант | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| F1, кН | 12 | 8 | 20 | 3 | 6 | 8 | 20 | 12 | 8 | 3 |
| F2, кН | 8 | 12 | 5 | 6 | 12 | 12 | 5 | 8 | 12 | 6 |
| F3, кН | 6 | 2 | 10 | 12 | 15 | 2 | 10 | 6 | 2 | 12 |
| F4, кН | 4 | 10 | 15 | 15 | 3 | 10 | 15 | 4 | 10 | 15 |
| F5, кН | 10 | 6 | 10 | 9 | 18 | 6 | 10 | 10 | 6 | 9 |
| | 30 | О | О | 15 | О | 30 | 30 | 30 | О | О |
| | 45 | 45 | 60 | 45 | 15 | 45 | 45 | 45 | 60 | 60 |
| | О | 75 | 75 | 60 | 45 | О | О | О | 75 | 75 |
| | 60 | 30 | 150 | 120 | 150 | 60 | 60 | 60 | 50 | 15 |
| | 300 | 270 | 210 | 270 | 300 | 300 | 300 | 300 | 10 | 20 |
| Параметр | Вариант | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| F1, кН | 20 | 12 | 3 | 20 | 8 | 10 | 8 | 2 | 3 | 16 |
| F2, кН | 5 | 8 | 6 | 5 | 12 | 9 | 10 | 15 | 16 | 2 |
| F3, кН | 10 | 6 | 12 | 10 | 2 | 6 | 2 | 11 | 10 | 12 |
| F4, кН | 15 | 4 | 15 | 15 | 10 | 4 | 12 | 15 | 5 | 6 |
| F5, кН | 10 | 10 | 9 | 10 | 6 | 12 | 7 | 10 | 7 | 8 |
| | 15 | 30 | О | О | 30 | 30 | О | О | 15 | О |
| | 45 | 45 | 15 | 15 | 45 | 45 | 45 | 60 | 45 | 15 |
| | 60 | О | 45 | 45 | О | О | 75 | 75 | 60 | 45 |
| | 120 | 60 | 150 | 150 | 60 | 60 | 30 | 150 | 0 | 90 |
| | 270 | 300 | 300 | 300 | 300 | 300 | 270 | 210 | 270 | 30 |
| Параметр | Вариант | |||||||||
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| F1, кН | 8 | 2 | 13 | 9 | 3 | 4 | 6 | 2 | 20 | 8 |
| F2, кН | 15 | 15 | 7 | 14 | 16 | 15 | 18 | 6 | 5 | 12 |
| F3, кН | 13 | 14 | 15 | 16 | 17 | 20 | 1 | 2 | 3 | 2 |
| F4, кН | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | 10 |
| F5, кН | 9 | 10 | 11 | 20 | 19 | 18 | 15 | 12 | 13 | 6 |
| | 30 | 30 | 30 | О | О | 15 | 30 | О | О | 90 |
| | 45 | 45 | 45 | 60 | 60 | 0 | 45 | 15 | 15 | 45 |
| | О | О | О | 75 | 75 | 60 | О | 45 | 45 | 30 |
| | 60 | 60 | 60 | 150 | 150 | 120 | 60 | 150 | 150 | 85 |
| | 300 | 300 | 300 | 210 | 210 | 270 | 300 | 300 | 300 | 60 |
Пример 2. Решение задачи на равновесие аналитическим способом
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. Пl.2).

Решение.
1. Определяем вероятные направления реакций (рис. П1.2а).
Мысленно убираем стержень АВ, при этом стержень С В опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ - тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень С В поддерживает точку В снизу - реакция направлена вверх.
2. Освобождаем точку В от связи (рис. П1.2б).
3. Выберем направление осей координат, ось Ох совпадает с реакцией Rl.
4. Запишем уравнения равновесия точки В:

5. Из второго уравнения получаем:

Из первого уравнения получаем:

Вывод: стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.
Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.
В данном случае реакции направлены, верно.
Задание № 2
Условие равновесия плоской системы сходящихся сил в аналитической форме.
З адание.Определить реакции стержней АС и AD (рис. П l.3).
адание.Определить реакции стержней АС и AD (рис. П l.3).
| Параметры | Варианты. | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|
| 40 | 45 | 48 | 50 | 56 | 58 | 61 | 63 | 67 | 72 | 75 | 78 | 80 | 86 | 82 |
|
| 60 | 45 | 75 | 60 | 45 | 30 | 35 | 40 | 55 | 60 | 65 | 70 | 75 | 75 | 80 |
|
| 15 | 30 | 30 | 15 | 45 | 10 | 20 | 15 | 30 | 35 | 45 | 35 | 20 | 25 | 30 |
|
| 60 | 45 | 60 | 75 | 75 | 50 | 55 | 65 | 60 | 70 | 75 | 80 | 85 | 30 | 35 |
| Параметры | Варианты. | ||||||||||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|
| 45 | 48 | 50 | 56 | 58 | 61 | 63 | 67 | 72 | 75 | 78 | 86 | 45 | 30 | 35 |
|
| 60 | 45 | 30 | 75 | 45 | 40 | 55 | 60 | 35 | 30 | 50 | 60 | 65 | 45 | 20 |
|
| 15 | 45 | 10 | 30 | 35 | 45 | 20 | 25 | 30 | 20 | 15 | 35 | 20 | 10 | 40 |
|
| 70 | 75 | 80 | 55 | 55 | 65 | 40 | 45 | 60 | 80 | 90 | 35 | 85 | 30 | 35 |
Тест для самоконтроля:
Темы 1.1, 1.2. Статика.
Плоская сходящаяся система сил.
| Вопросы | Ответы | Код |
| 1. Определить проекции равнодействующей на ось Ох при F1 = 10кН; F2 = 20кН; F3 = 30кН. | Rx = 4,99kH | 1 |
| Rx = 7,89kH | 2 | |
| Rx = -3,18kH | 3 | |
| Rx =6,55kH | 4 | |
| 2. Определить величину равнодействующей силы по ее известным проекциям: Rx = 15 кН; Ry= 8,66 кН. | 23,66kH | 1 |
| 17,32kH | 2 | |
| 9,50kH | 3 | |
| 8,50kH | 4 | |
| 3. Как направлен вектор равнодействующей системы сил, если известно, что Rx = -4кН; Ry= 12кН? |
| 1 |
|
| 2 | |
|
| 3 | |
|
| 4 |
| Вопросы | Ответы | Код |
| 4. Груз находится в равновесии. Указать, какой из треугольников для шарнира В построен верно.
|
| 1 |
| 2 | ||
| 3 | ||
| 4 | ||
| 5. Груз F находится в равновесии. Указать, какая система уравнений равновесия для точки В верна.
|
| 1 |
|
| 2 | |
|
| 3 | |
| Верный ответ не приведен | 4 |
studfiles.net
Министерство образования и науки Донецкой Народной Республики
ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«КОМСОМОЛЬСКИЙ ИНДУСТРИАЛЬНЫЙ ТЕХНИКУМ»
Контрольная работа
по дисциплине «Техническая механика»
по разделу: «Теоретическая механика»
специальность 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)
Составила преподаватель: ____________ Винокурова Ю.Ю.
Рассмотрено на заседании цикловой комиссии электромеханических дисциплин
Председатель цикловой комиссии _______________Поляков Г.М.
«______» __________________2015 г
Пояснительная записка.
Целью изучения дисциплины «Техническая механика» являетсяформирование у студентов навыков решения инженерных задач и использования полученных результатов в профессиональной деятельности. Раздел дисциплины «Теоретическая механика» формирует необходимую базу знаний для изучения других технических дисциплин по профилю будущей профессиональной деятельности.
Варианты контрольных заданий охватывают весь объём материала в соответствии с разделом «Теоретическая механика». Задания равноценны по сложности и времени на их выполнение. Выполняя контрольную работу, студенты должны продемонстрировать умения правильно и четко излагать усвоенный материал. Для раскрытия сущности теоретических вопросов студентам необходимо изучить соответствующую литературу, рекомендованную в данной пояснительной записке.
Контрольная работа состоит из 18 вариантов заданий, выполняется на отдельных двойных листах со штампом техникума. В каждом варианте 2 теоретических вопроса и одна задача.
Каждое задание контрольной работы оценивается максимальным количеством баллов. За каждый правильный ответ на теоретический вопрос начисляется 1,5 балла, а за верное решение задачи начисляется 2 балла. За ошибки и недостатки при выполнении каждого задания оценка снижается. За грубую ошибку оценка за выполнение соответствующего задания, в зависимости от характера ошибок, снижается на 1,5 балла.
Студентам, которые не явились на контрольную работу без уважительной причины, выставляется оценка 2 (неудовлетворительно).
Рекомендованная литература:
Аркуша А.И. Техническая механика и сопротивление материалов: Учебник для машиностроительных специальностей техникумов / А. И. Аркуша. – 2-е изд., доп. . – М.: Высшая школа, 1989. – 352 с.
Никитин Е.М. Теоретическая механика для техникумов. М., 1969г., 432 с.
Сетков В.И.: Сборник задач для расчетно-графических работ по технической механике: Учеб. Пособие для техникумов. 2-е изд., доп. - М.: Стройиздат, 1989,-224 с.
Олофинская В.П. Техническая механика курс лекций с вариантами практических работ и тестовых заданий. М. Форум - ИНФРА-М. 2003г. 348стр. (электронная версия).
Оформление контрольной работы
Контрольная работа выполняется студентами на отдельных двоенных листах со штампом техникума.
На первой странице студент пишет:
Контрольная работа
по дисциплине: «Техническая механика»
по разделу: «Теоретическая механика»
студента группы ___________
____________________________________
(Фамилия, инициалы)
(число, месяц, год)
(№ варианта)
На каждой странице должны быть поля.
Выполнение контрольной работы должны начинать со второй страницы, на которую необходимо переписать условия задания, а потом давать на них ответ.
Ответы на отдельные вопросы задания разрешается давать в произвольном порядке, сохраняя нумерацию, которая дана в соответствующем варианте.
На выполнение контрольной работы отводится один академический час - 45 минут.
Пользоваться конспектами и учебниками не разрешается, за исключением [3].
Контрольная работы выполняется самостоятельно.
Критерии оценивания контрольной работы
по дисциплине: «Техническая механика»
по разделу: «Теоретическая механика»
Контрольная состоит из 18 вариантов, каждый из которых содержит 2 теоретических вопроса и одну задачу.
Каждое задание контрольной работы оценивается максимальным количеством баллов. За каждый правильный ответ на теоретический вопрос начисляется 1,5 балла, а за верное решение задачи начисляется 2 балла. За ошибки и недостатки при выполнении каждого задания оценка снижается. За грубую ошибку оценка за выполнение соответствующего задания, в зависимости от характера ошибок, снижается на 1,5 балла.
Если студент не пользуется соответствующей терминологией, либо ответ запутанный, непоследовательный, нелогичный, количество баллов снижается на 0,75 балла.
За неаккуратность, неряшливость, а также при большом количестве грамматических ошибок, оценка снижается на 0,1-0,3 балла.
Общая оценка за выполнение контрольной работы выставляется с учетом суммы баллов, набранных за выполнение всех заданий.
Общее оценивание контрольной работы:
При наличии существенных замечаний, а также при оценивании контрольной работы на 1-2 балла (неудовлетворительно), контрольная работы выполняется повторно, в установленный преподавателем период и задаётся на проверку.
Отчет о контрольной работе
по дисциплине: «Техническая механика»
Преподаватель: Винокурова Ю.Ю.
Общие сведения:
Тема работы: Теоретическая механика
Контрольная работа №1
Дата проведения « » _____ 20____г.
Группа _____________
Количество студентов в группе по списку____
Выполнили работу, студентов____
Отсутствуют студенты по причинам
Результаты выполнения работы: контрольную работу выполнили с оценками: «5» _______, «4» _______, «3» ______, «2» ______.
Успеваемость по результатам работы:
Общая ____________%;
Качество знаний______________%.
Краткий анализ контрольной работы (усвоение студентами группы темы, недостатки, которые имеют студенты в результате освоения темы):
Фамилии, инициалы студентов, которые получили неудовлетворительные оценки:
Краткая характеристика работы над материалом, в котором допущены ошибки:
Способы преподавателя по подготовке студентов к повторной сдаче контрольной работы:
Провести консультации, а потом индивидуальные занятия со студентами, которые сделали грубые ошибки и имели недоделки по изученному материалу.
Подпись преподавателя_______________Ю.Ю.Винокурова
Дата выполнения « » _____ 20____г.
Результаты контрольной работы изучены в цикловой комиссии, способы по повышению качества знаний студентов по результатам контрольной работы одобрены.
Глава цикловой комиссии________________________Г.М. Поляков.
Перечень вопросов, вынесенных на контрольную работу
Перечислить и объяснить основные виды опор балок и их реакции.
Начертить параллелепипед сил. Объяснить равнодействующую пространственную систему сходящихся сил.
Объяснить проекцию силы на координатные оси.
Охарактеризовать пару сил и равнодействующую пары сил.
Объяснить скорость движения точки и предоставить характеристику равномерного движения точки.
Объяснить теорему Вариньона для плоской системы сил.
Объяснить центр тяжести тела, как центр параллельных сил.
Объяснить аналитическое определение равнодействующей плоскости системы сходящихся сил (метод проекций).
Охарактеризовать поступательное движение твердого тела.
Охарактеризовать ускорение точки (полное, нормальное и касательное).
Охарактеризовать момент силы относительно оси и его знак.
Дать определение понятию главный вектор, главный момент плоскости системы сил.
Объяснить определение координат центра тяжести сложного сечения, состоящего из простых геометрических фигур.
Перечислить основные свойства пар. Объяснить понятие эквивалентности пар.
Охарактеризовать уравнения движения точки по заданной траектории.
Объяснить понятие вращательного движения твердого тела вокруг неподвижной оси.
Объяснить понятие момент пары. Охарактеризуйте правило знаков.
Охарактеризуйте скорость движения точки при неравномерном движении точки.
Объяснить разновидности связей и правила определения направления их реакций.
Объяснить классификацию нагрузок.
Объяснить понятие координаты центра тяжести однородного тела.
Объяснить понятие связи. Охарактеризовать реакции связей.
Охарактеризовать уравнение равновесия пространственной системы сходящихся сил.
Охарактеризовать законы динамики (четыре основные законы).
Объяснить определение равнодействующей двух сил, приложенных к точке.
Объяснить понятие плоская система сходящихся сил. Охарактеризовать аналитическую условие равновесия плоской системы сходящихся сил.
Объяснить определение центра тяжести сложного сечения, состоящего из стандартных профилей.
Объяснить положение центров тяжести простых геометрических фигур.
Охарактеризовать основное уравнение динамики.
Понятие силовой многоугольник. Охарактеризовать правило его построения.
Перечислить и объяснить способы задания движения точки.
Объяснить аналитические условия равновесия плоской системы сил.
Объяснить понятие балочные системы. Охарактеризовать разновидность опор и нагрузок.
Объяснить метод кинетостатики для материальной точки.
Охарактеризовать аксиомы статики.
Объяснить принцип Даламбера (метод кинетостатики).
| Контрольная работа №1 по дисциплине «Техническая механика» по разделу: «Теоретическая механика» Билет № 1
Определить положение центра тяжести сечения, составленного, из полос размером 120x10 мм, и швеллера № 12.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №2
Определить опорные реакции двухопорной балки.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №3
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №4
Определить координаты центра тяжести сечения фигуры. Показать положение центра тяжести на сечении.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 5
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №6
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 7
Определить координаты центра тяжести сечения фигуры. Показать положение центра тяжести на сечении.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №8
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 9
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №10
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 11
Определить координаты центра тяжести сечения фигуры. Показать положение центра тяжести на сечении.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №12
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 13
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №14
Определить координаты центра тяжести сечения фигуры. Показать положение центра тяжести на сечении.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 15
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №16
Определить координаты центра тяжести сечения фигуры. Показать положение центра тяжести на сечении.
Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет № 17
Определить опорные реакции двухопорной балки. Составил: преподаватель Ю.Ю. Винокурова. |
| Контрольная работа №1 По дисциплине «Техническая механика» По разделу: «Теоретическая механика» Билет №18
Определить координаты центра тяжести сечения фигуры. Показать положение центра тяжести на сечении.
Составил: преподаватель Ю.Ю. Винокурова. |
infourok.ru
Задача 4.1. Груз массой 18 кг, подвешенный на тросе, начали поднимать вертикально вверх. С какой силой необходимо потянуть за трос, чтобы через 0,5 с равноускоренного движения скорость груза достигла 1,4 м/с?
Задача 4.2. Груз массой 15 кг прикреплен к нити, которая рвется при натяжении в 280 Н. Можно ли с помощью этой нити поднять груз на высоту 0,8 м за 0,4 с, двигая его равноускоренно?
Задача 4.3. К потолку вагона на тонкой нити подвешен груз массой 0,2 кг. При трогании вагона с места нить с грузом отклонилась от вертикали на угол α=15°. Определить ускорение вагона и натяжение нити.
Задача 4.4. Шарик массой 1,8 кг, привязанный к нити длиной 120 см, вращается вместе с ней в вертикальной плоскости. При какой угловой скорости возникает опасность разрыва нити, если она может выдержать натяжение не более 30 Н?
Задача 4.5. На полке вагона, касаясь задней по ходу поезда стенки, лежит цилиндр массой 30кг. Начав двигаться равноускоренно, вагон за первые 5 с проходит 20м. С какой силой давит теперь цилиндр на горизонтальную полку и вертикальную стенку?
Задача 4.6. Шарик массой 1,5 кг привязан к нити, которую можно натягивать силой не более 300 Н. Какой длины нить можно взять, чтобы при вращении с шариком в вертикальной плоскости с частотой 170 об/мин она не порвалась?
Задача 4.7. Маневровый тепловоз трогает с места железнодорожный вагон, масса которого 40000 кг. За первые 40 с равноускоренного движения тепловоз с вагоном прошли расстояние 200 м. Определить натяжение стяжки между тепловозом и вагоном, если сила трения составляет 0,05 веса вагона.
Задача 4.8. Автомобиль, масса которого 1200 кг, проехал выпуклый мост длиной 50 м за 4 с. Радиус кривизны моста 100 м. С какой силой давит автомобиль на мост, проезжая его середину?
Задача 4.9. Какой постоянной силой нужно двигать стоящую на рельсах вагонетку, масса которой 200 кг, чтобы через 5 с после начала действия силы она приобрела скорость 1,4 м/с. Сопротивление трения считать постоянным и равным 0,02 веса вагонетки.
Задача 4.10. На нити длиной 120 см подвешен шарик, который, двигаясь по окружности в горизонтальной плоскости, заставляет нить описывать коническую поверхность, отклоняясь от вертикали на угол α = 40°. Определить вес шарика и скорость его движения, если нить натянута силой 50 Н.
Задача 5.1. Груз А массой 200 кг с помощью, наклонной плоскости с углом подъема α=30° поднят на высоту h=1,5 м силой, параллельной наклонной плоскости (рис. 4, схема I). При перемещении груза по наклонной плоскости коэффициент трения ƒ=0,4. Определить работу силы Р и КПД наклонной плоскости.
Задача 5.2. На шкив электродвигателя надета тормозная лента, один конец которой прикреплен к динамометру, а к другому прикреплена гиря в 1 кг (рис. 4, схема II). Когда двигатель включен, его шкив, диаметр которого d = 200 мм, вращается с частотой 1400 об/мин, а динамометр растянут силой 32 Н. Определить мощность двигателя. Какую работу совершил двигатель за 10 000 оборотов шкива?
Задача 5.3. Сваебойный молот делает 108 ударов в минуту. Масса ударной части 240 кг; высота подъема ударника 0,5 м; КПД молота 0,8. Определить мощность двигателя, приводящего в движение молот.
Задача 5.4. Шлифовальный камень диаметром 500 мм вращается с частотой 105 об/мин. Мощность, потребляемая при шлифовании, 1,4 кВт. Коэффициент трения шлифовального камня о деталь равен 0,28. С какой силой прижимает камень шлифуемую деталь?
Задача 5.5. Насос с двигателем мощностью в 2,5 кВт перекачивает воду, поднимая ее на высоту 7,5 м. КПД насоса 0,75. В течение какого времени насос перекачает 2000 м3 воды?
Задача 5.6. По наклонной плоскости с углом подъема α - 18° равномерно вкатывают каток массой 400 кг диаметром 0,5 м (рис. 4, схема III). Определить работу силы Р на пути t = 5 м и КПД наклонной плоскости, если коэффициент трения качения ƒк = 0,5 см.
Задача 5.7. Тело А массой 80кг равномерно передвинуто по горизонтальной плоскости силой Р на расстоянии 10 м за 50 с (рис. 4, схема IV). Определить работу силы Р и развиваемую мощность, если коэффициент трения ƒ=0,4.
Задача 5.8. При вращении шкива станка с помощью ременной передачи (рис. 4, схема V) натяжение ветвей ремня составляет T1 = 4 кН (ведущей) и Т2 = 2 кН (ведомой). Определить работу вращающего момента, приложенного к шкиву, за 1500 его оборотов. Какова мощность электродвигателя, приводящего шкив в движение, если КПД передачи 0,85, а работа продолжалась 4 мин?
Задача 5.9. Определить работу при перемещении кантованием из положения 1 в положение 2 (рис. 4, схема VI) ящика, масса которого 200 кг, а размеры показаны на рисунке. Каким должен быть коэффициент трения между полом АВ и ящиком, чтобы такая же работа была затрачена при перемещении его по полу горизонтальной силой.
Задача 5.10. Определить полезную мощность одноцилиндрового двигателя внутреннего сгорания, если среднее давление на поршень в течение всего хода 0,6 МПа, длина хода поршня 40 см, диаметр 22,5 см, число рабочих ходов в минуту 150 и коэффициент полезного действия 0,9.
mehanika-sopromat.ru
Задача 1
| Дано:
Найти: |
Рис. 1 |
Решение:
1. Решим задачу аналитически. Для этого рассмотрим равновесие шара 1. На него действует реакция N опорной поверхности А, перпендикулярная к этой поверхности; сила натяжения Т1 нити и вес Р1 шара 1 (рис. 2).

Рис. 2
Уравнения проекций всех сил, приложенных к шару 1, на оси координат имеют вид:
 :
:  (1)
(1)
 :
:  (2)
(2)
Из уравнения (1) находим силу натяжения Т1 нити:

Тогда из уравнения (2) определим реакцию N опорной поверхности:

Теперь рассмотрим равновесие шара 2. На него действуют только две силы: сила натяжения Т2 нити и вес Р2 этого шара (рис. 3).

Рис. 3
Поскольку в блоке Д трение отсутствует, получаем

2. Решим задачу графически. Строим силовой треугольник для шара 1. Сумма векторов сил, приложенных к телу, которое находится в равновесии, равна нулю, следовательно, треугольник, составленный из  ,
,  и
и  должен быть замкнут (рис. 4).
должен быть замкнут (рис. 4).

Рис. 4
Определим длины сторон силового треугольника по теореме синусов:



Тогда искомые силы равны:


Задача 2
| Дано:
Найти: |
Рис. 5 |
Решение
1. Рассмотрим равновесие балки АВ. На неё действует равнодействующая Q распределённой на отрезке ЕК нагрузки интенсивности q, приложенная в середине этого отрезка; составляющие XA и YA реакции неподвижного шарнира А; реакция RС стержня ВС, направленная вдоль этого стержня; нагрузка F, приложенная в точке К под углом  ; пара сил с моментом М (рис. 6).
; пара сил с моментом М (рис. 6).

Рис. 6
2. Равнодействующая распределенной нагрузки равна:

3. Записываем уравнение моментов сил, приложенных к балке АВ, относительно точки А:
 (3)
(3)
4. Уравнения проекций всех сил на оси координат имеют вид:
 :
:  , (4)
, (4)
 :
:  , (5)
, (5)
Из уравнения (3) находим реакцию RС стержня ВС:

По уравнению (4) вычисляем составляющую XA реакции неподвижного шарнира А:

С учетом этого, из уравнения (5) имеем:

Тогда реакция неподвижного шарнира А равна:

Задача 3
| Дано:
Найти: |
Рис. 7 |
Решение
Рассмотрим равновесие вала АВ. Силовая схема приведена на рис. 8.
Уравнения проекций сил на координатные оси имеют вид:
 :
:  , (6)
, (6)
 :
:  , (7)
, (7)

Рис. 8
Линии действия сил F1 , Fr2 XA и XB параллельны оси х, а линия действия силы ZA пересекает ось х, поэтому их моменты относительно этой оси равны нулю.
Аналогично линии действия сил Fr1 , Fr2 XA , XB , ZA и ZB пересекают ось у, поэтому их моменты относительно этой оси также равны нулю.
Относительно оси z расположены параллельно линии действия сил ZА , ZB Fr1 и F2 , а пересекает ось z линия действия силы XA , поэтому моменты этих сил относительно оси z равны нулю.
Записываем уравнения моментов всех сил системы относительно трёх осей:
 :
:  (8)
(8)
 :
:  (9)
(9)
 :
:  (10)
(10)
Из уравнения (4) получаем, что

Из уравнения (3) находим вертикальную составляющую реакции в точке В:

По уравнению (10), с учетом  , рассчитываем горизонтальную составляющую реакции в точке В:
, рассчитываем горизонтальную составляющую реакции в точке В:

Из уравнения (6) определяем горизонтальную составляющую реакции в точке А:

Из уравнения (7) имеем

Тогда реакции опор вала в точках А и В соответственно равны:


Задача 4
Решение
1. Поскольку маховик вращается равноускоренно, то точки на ободе маховика вращаются по закону:
 (11)
(11)
По условию задачи маховик в начальный момент находился в покое, следовательно,  и уравнение (11) можно переписать как
и уравнение (11) можно переписать как
 (12)
(12)
2. Определяем угловую скорость вращения точек обода маховика в момент времени  :
:

3. Находим угловое ускорение вращения маховика из уравнения (12):

4. Вычисляем угловую скорость вращения точек обода маховика в момент времени  :
:

5. Тогда частота вращения маховика в момент времени  равна:
равна:

6. По формуле Эйлера находим скорость точек обода маховика в момент времени  :
:

7. Определяем нормальное ускорение точек обода маховика в момент времени  :
:

8. Находим касательное ускорение точек обода маховика в момент времени  :
:

Задача 5
Решение
1. Работа силы F определяется по формуле:
 (13)
(13)
где  – перемещение груза.
– перемещение груза.
2. По условию задачи груз перемещается с постоянной скоростью, поэтому ускорение груза  .
.

Рис. 10
3. Выбираем систему координат, направляя ось х вдоль линии движения груза. Записываем уравнения движения груза под действием сил (рис. 10):
 :
:  (14)
(14)
 :
:  (15)
(15)
где  – сила трения скольжения.
– сила трения скольжения.
Выражаем из уравнения (14) реакцию  наклонной плоскости
наклонной плоскости

и подставляем в уравнение (15), получаем

Тогда работа силы F равна


4. Мощность, развиваемая за время перемещения  , определяется по формуле:
, определяется по формуле:

www.yurii.ru
1
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Ростовский государственный строительный университет»
Утверждено на заседании кафедры сопротивления материалов 30 ноября 2013 г.
ТЕХНИЧЕСКАЯ МЕХАНИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к контрольной работе для подготовки бакалавров заочного отделения направления 270800 «Строительство»
Ростов-на-Дону
2014

2
УДК 621.031
УДК 621.031
Техническая механика: методические указания к контрольной работе для подготовки бакалавров заочного отделения направления 270800 «Строительство». Ростов н/Д: Рост. гос. строит. ун-т,2014. - 24 с.
Предназначены для облегчения самостоятельной работы бакалавров заочной формы обучения при выполнении контрольной работы.
УДК 621.031
Составители: д-ртехн. наук, проф. Б.М. Языев, канд.физ.-мат.наук, доц. В.И. Авилкин
Редактор М.А. Цыганова Темплан 2014г., поз.
Подписано в печать 30.05.14. Формат 60х84/16 Бумага писчая. Ризограф. Уч.- изд. л. 1,0. Тираж 100 экз. Заказ
Редакционно-издательскийцентр Ростовского государственного строительного университета.
344022, Ростов-на-Дону,Социалистическая, 162.
3
©Ростовский государственный строительный университет,2014
Указания о порядке выполнения контрольной работы
Исходные данные для решения задач выбираются студентом из таблиц вариантов в соответствии с его личным шифром (номером зачетной книжки). Шифром считаются три последние цифры, например, если номер зачетной книжки – 27306, то учебным шифром будет 306. Каждая таблица вариантов разделена на три части. Для получения исходных данных надо выписать из таблицы три строки: первая строка отвечает первой цифре шифра; вторая строка отвечает второй (средней) цифре; и третья строка – последней (третьей) цифре шифра. Например, для номера зачетной книжки 27306, при решении первой задачи «Расчет статически определимой многопролетной балки», согласно табл. 1, получим следующие исходные данные:
l1 = 8 м;q = 1,8 кН/м;b = 1,9 м;l2 = 14 м;F = 3,2 кН, № сечения –3;
№схемы – 6;a = 2,1 м;c = 2,0 м;M = 1,1 кН м .
Взаголовке контрольной работы должны быть четко написаны: название дисциплины, фамилия, имя и отчество студента, наименование специальности, учебный шифр и точный почтовый адрес.
Контрольная работа выполняется в тетради обычного формата с полями для замечаний рецензента.
Перед решением каждой задачи необходимо выписать полностью ее условие с числовыми данными, составить аккуратный эскиз в масштабе и указать на нем в числах все величины, необходимые для расчета.
Решение должно сопровождаться объяснениями и чертежами.
После проверки контрольной работы студент должен исправить в ней отмеченные ошибки и выполнить все сделанные ему указания. Исправления должны быть вложены в соответствующие места отрецензированной работы.
4
ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ
Задача 1. Расчет статически определимой многопролетной балки
Для заданной схемы балки (рис.1) с размерами и нагрузкой,
определяемыми по табл. 1 требуется:
1.Построить эпюры изгибающих моментов(M) и поперечных сил (Q).
2.Построить линии влияния поперечной силы (Q) и изгибающего момента(M)
для заданного сечения, а также линию влияния одной опорной реакции (по выбору студента).
3.Определить по линиям влияния значения поперечной силы (Q), изгибающего момента(M) для заданного сечения и опорной реакции.
|
|
|
|
|
|
|
|
|
|
|
|
| Таблица 1 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| цифраПервая шифра | l1, | q, | b, | цифраВторая шифра | l2, |
| F, | сечения№ | цифраТретья шифра схемы№( ) | a, | c, |
| M, |
|
|
|
|
|
|
|
|
| ||||||||
|
| м | кН/м | м |
| м |
| кН |
|
| м | м |
| кН м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 | 10 | 1,2 | 1,0 | 1 | 8 |
| 3 | 1 | 1 | 1 | 1 |
| 2,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 14 | 2,0 | 0,8 | 2 | 7 |
| 2,5 | 2 | 2 | 1,2 | 2,2 |
| 2,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 | 8 | 1,8 | 1,9 | 3 | 9 |
| 6 | 3 | 3 | 2,0 | 1,4 |
| 2,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 | 12 | 3,0 | 1,4 | 4 | 6 |
| 2,8 | 4 | 4 | 2,2 | 1,6 |
| 2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 | 9 | 1,5 | 1,6 | 5 | 11 |
| 7 | 1 | 5 | 1,3 | 1,8 |
| 2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 6 | 11 | 2,5 | 2,1 | 6 | 10 |
| 3,3 | 2 | 6 | 2,1 | 2,0 |
| 1,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 7 | 7 | 1,4 | 1,2 | 7 | 12 |
| 5 | 3 | 7 | 1,4 | 1,1 |
| 2,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 8 | 6 | 0,8 | 1,8 | 8 | 15 |
| 8 | 4 | 8 | 1,9 | 1,3 |
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 9 | 5 | 1,0 | 1,5 | 9 | 14 |
| 4 | 1 | 9 | 1,5 | 1,5 |
| 2,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | 13 | 2,2 | 2,0 | 0 | 14 |
| 3,2 | 3 | 0 | 0,8 | 1,7 |
| 1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Замечание. | Для построения эпюры | M воспользоваться «поэтажной» схемой. | |||||||||||||
Ординаты эпюры моментов откладывать со стороны растянутых волокон.

5

6
Задача 2. Определение перемещений в статически определимой балке
Для заданной схемы балки (рис.2), с выбранными из табл.2 по шифру
данными, определить прогиб или угол поворота одного из сечений.
Замечание. Все перемещения следует определять по формуле Мора с использованием метода Верещагина. При перемножении эпюр, удобно использовать формулу перемножения прямолинейных эпюр (рис.3) [1]:
,
и прямолинейной на криволинейную (рис.4) [1]:

Первая цифра шифра
1
2
3
4
5
6
7
8
9
0
q, | l, |
кН/м | м |
|
|
1,0 | 10 |
|
|
1,2 | 8,0 |
|
|
1,6 | 9,6 |
|
|
2,0 | 12,0 |
|
|
2,4 | 12,4 |
|
|
2,8 | 13,0 |
|
|
3,0 | 14,0 |
|
|
3,6 | 15,0 |
|
|
5,0 | 16,0 |
|
|
4,0 | 18,0 |
|
|
Втораяцифра шифра | F, | сечения№ |
|
| |
| кН |
|
|
|
|
1 | 4,0 | 1 |
|
|
|
2 | 4,5 | 2 |
|
|
|
3 | 5,0 | 3 |
|
|
|
4 | 3,6 | 1 |
|
|
|
5 | 2,0 | 2 |
|
|
|
6 | 3,2 | 3 |
|
|
|
7 | 8,0 | 1 |
|
|
|
8 | 6,0 | 2 |
|
|
|
9 | 3,0 | 3 |
|
|
|
0 | 2,0 | 1 |
|
|
|
Третьяцифра шифра | схемы№( ) | Вид перемещения |
|
| |
|
|
|
1 |
| Прогиб |
|
|
|
2 |
| Прогиб |
|
|
|
3 |
| Прогиб |
|
|
|
4 |
| Прогиб |
|
|
|
5 |
| Прогиб |
|
|
|
6 |
| Угол поворота |
|
|
|
7 |
| Угол поворота |
|
|
|
8 |
| Угол поворота |
|
|
|
9 |
| Угол поворота |
|
|
|
0 |
| Угол поворота |
|
|
|
Замечание. Если нужно определить угол поворота в шарнире, то речь идет о повороте сечения основной балки примыкающей к шарниру.

8
Задача 3. Определение перемещений в статически определимой раме
Для заданной схемы статически определимой рамы (рис.5), с выбранными из табл.3 по шифру данными, определить горизонтальное перемещение или угол поворота одного из сечений.
|
|
|
|
|
|
|
|
|
|
|
|
| Таблица 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перваяцифра шифра | q, | l, | Втораяцифра | шифра | F, | h, | сечения№ | Третьяцифра шифра | схемы№( ) |
| I 2 |
| Вид перемещения |
|
|
|
|
|
|
| |||||||
| кН/м | м |
|
| кН | м |
|
|
|
| I1 | ||
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
| ||
1 | 1,0 | 9,0 |
| 1 | 9 | 6,0 | 1 | 1 |
| 1:2 | Угол поворота | ||
|
|
|
|
|
|
|
|
|
|
|
| ||
2 | 1,2 | 9,5 |
| 2 | 2 | 5,5 | 2 | 2 |
| 2:1 | Угол поворота | ||
|
|
|
|
|
|
|
|
|
|
|
| ||
3 | 1,5 | 8,0 |
| 3 | 5 | 5,0 | 1 | 3 |
| 1:3 | Угол поворота | ||
|
|
|
|
|
|
|
|
|
|
|
| ||
4 | 1,8 | 8,5 |
| 4 | 4 | 9,5 | 2 | 4 |
| 3:1 | Угол поворота | ||
|
|
|
|
|
|
|
|
|
|
|
| ||
5 | 2,0 | 5,0 |
| 5 | 3 | 9,0 | 1 | 5 |
| 2:3 | Угол поворота | ||
|
|
|
|
|
|
|
|
|
|
|
| ||
6 | 2,4 | 5,5 |
| 6 | 10 | 8,5 | 2 | 6 |
| 3:2 | Горизонтальное | ||
|
|
|
|
|
|
|
|
|
|
|
|
| перемещение |
7 | 3,0 | 6,0 |
| 7 | 7 | 8,0 | 1 | 7 |
| 3:5 | Горизонтальное | ||
|
|
|
|
|
|
|
|
|
|
|
|
| перемещение |
8 | 2,5 | 7,5 |
| 8 | 8 | 6,5 | 2 | 8 |
| 5:3 | Горизонтальное | ||
|
|
|
|
|
|
|
|
|
|
|
|
| перемещение |
9 | 3,2 | 6,2 |
| 9 | 1 | 10,0 | 1 | 9 |
| 3:4 | Горизонтальное | ||
|
|
|
|
|
|
|
|
|
|
|
|
| перемещение |
0 | 3,5 | 6,5 |
| 0 | 6 | 7,0 | 2 | 0 |
| 4:3 | Горизонтальное | ||
|
|
|
|
|
|
|
|
|
|
|
|
| перемещение |
Замечание. Поскольку в данной задаче жесткости отдельных стержней различны и заданы только их отношения, искомые перемещения должны быть выражены через или . При определении угла поворота в сечении 1 (задача№3), речь идет о повороте сечения слева от шарнира.

9
10
Задача 4. Построение эпюр внутренних усилий в статически
неопределимой раме
Для заданной схемы статически неопределимой рамы (рис.6), с
выбранными из табл.4 по шифру данными, требуется:
1.Установить степень статической неопределимости.
2.Выбрать основную систему
3.Написать каноническое уравнение.
4.Построить эпюры моментов от единичной силы и от внешней нагрузки и вычислить коэффициенты канонического уравнения.
5.Решить каноническое уравнение.
6.Построить эпюры внутренних усилий M, Q, N.
7.Проверить правильность построения эпюр.
|
|
|
|
|
| Таблица 4 | |
|
|
|
|
|
|
|
|
Первая | l, м | Вторая | h, м | F, | Третья | q, кH/м |
|
цифра |
| цифра |
| кH | цифра |
|
|
|
| шифра |
|
| |||
|
|
|
|
|
|
| |
шифра |
| шифра |
|
| (№ схемы) |
|
|
|
|
|
|
|
|
|
|
1 | 3,0 | 1 | 2,0 | 1,0 | 1 | 2,0 | 1:2 |
|
|
|
|
|
|
|
|
2 | 4,0 | 2 | 3,0 | 2,0 | 2 | 2,5 | 2:3 |
|
|
|
|
|
|
|
|
3 | 5,0 | 3 | 4,0 | 3,0 | 3 | 3,0 | 1:3 |
|
|
|
|
|
|
|
|
4 | 6,0 | 4 | 5,0 | 4,0 | 4 | 3,5 | 2:1 |
|
|
|
|
|
|
|
|
5 | 3,6 | 5 | 2,4 | 1,5 | 5 | 2,4 | 3:2 |
|
|
|
|
|
|
|
|
6 | 4,4 | 6 | 2,8 | 2,5 | 6 | 3,2 | 3:4 |
|
|
|
|
|
|
|
|
7 | 5,2 | 7 | 3,2 | 3,5 | 7 | 3,6 | 3:1 |
|
|
|
|
|
|
|
|
8 | 5,6 | 8 | 3,6 | 2,4 | 8 | 2,8 | 4:3 |
|
|
|
|
|
|
|
|
9 | 4,8 | 9 | 3,8 | 2,8 | 9 | 3,8 | 1:2 |
|
|
|
|
|
|
|
|
0 | 6,4 | 0 | 4,2 | 3,2 | 0 | 4,0 | 2:1 |
|
|
|
|
|
|
|
|
studfiles.net
Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет – УПИ»
Нижнетагильский технологический институт (филиал)
Нижнетагильский машиностроительный техникум
(Факультет среднего профессионального образования)
по специальности 150001 «Технология машиностроения»
Нижний Тагил
2007
Программа составлена в соответствии с Государственным образовательным стандартом среднего профессионального. Регистрационный номер ____________ от ________________
специальности _________________________________________________________________
_______________________________________________________________________________
и примерной программой, утвержденной ИПР СПО Минобразования РФ в 20 ___ г.
Программу составил: _____________________________________________________________
________________________________________________________________________________
Программа обсуждена и одобрена на заседании ЦК
«______» _______________ 200 г. Протокол № ____
Председатель ЦК ________________( )
Программа одобрена на заседании Методического совета НТМТ ФСПО
«______» _________________ 200 г. Протокол № ______
Председатель Методического совета
НТМТ ФСПО Л.А.Литвинов
Пояснительная записка. 4
Тематический план по дисциплине 5
Содержание учебной дисциплины. 7
Методические указания и контрольные задания для домашней контрольной работы. 18
Контрольная работа №1 18
Контрольная работа №2 37
Литература 59
Данное методическое пособие по дисциплине «Техническая механика» рекомендовано для специальности «Сварочное производство».
Изучение Технической механики позволяет сформировать базовые понятия и основы расчета машиностроительных конструкций, используемые в предметах специальных дисциплин, а так же общеучебные и специальные умения.
Техническая механика является той частью учебного процесса, которая связывает общеобразовательные предметы со спец. дисциплинами, даёт представление о многих процессах, протекающих в элементах конструкций в зависимости от материала, формы и внешних нагрузок. Отсюда вытекают основные дидактические задачи:
• Ознакомление с базовыми, фундаментальными теориями, законами, понятиями.
• Формирование умений делать умозаключения, анализировать причинно-следственные связи.
• Развитие логического мышления.
В данном методическом пособии приведены основные требование к уровню обучения, которые определяют обязательный минимальный уровень подготовки студентов по основному материалу.
При изучении курса «Техническая механика» студенты должны знать: о роли и месте знаний по дисциплине при освоении основной профессиональной образовательной программы по конкретной специальности и в сфере профессиональной деятельности техника.
При изучении курса «Техническая механика» студенты должны уметь: применять основные закономерности и способы расчета к различным видам конструкций.
| Наименование разделов и тем | Макс, учеб. нагрузка. | Количество аудиторных часов при заочной форме обучения | Самостоят, учеб. нагрузка. | ||
| Всего | В том числе | ||||
| Лаб. занятия | Прак. занятия | ||||
| Введение | 2 | 2 | |||
| Раздел 1. Теоретическая механика | 58 | 18 | 14 | 40 | |
| Статика | |||||
| Тема 1.1 Основные понятия и аксиомы статики | 4 | 2 | 2 | ||
| Тема 1.2 Плоская система сходящихся сил | 4 | 4 | 4 | ||
| Тема 1.3 Пара сил | 6 | 6 | |||
| Тема 1.4 Плоская система произвольно расположенных сил | 4 | 4 | 4 | ||
| Тема 1.5 Пространственная система сил | 4 | 4 | |||
| Тема 1.6 Центр тяжести | 6 | 4 | 2 | 2 | |
| Кинематика | |||||
| Тема 1.7 Основные понятия кинематики | 4 | 4 | |||
| Тема 1.8 Кинематика точки. Простейшие движения твердого тела | 8 | 2 | 2 | 6 | |
| Динамика | |||||
| Тема 1.9 Основные понятия и аксиомы динамики | 4 | 4 | |||
| Тема 1.10 Движение материальной точки. Метод кинетостатики | 8 | 2 | 2 | 6 | |
| Тема 1.11 Трение. Работа и мощность | 6 | 6 | |||
| Раздел 2. Сопротивление материалов | 114 | 18 | 14 | 96 | |
| Тема 2.1 Основные положения | 8 | 2 | 6 | ||
| Тема 2.2 Растяжение и сжатие | 16 | 2 | 2 | 14 | |
| 2Тема 2.3 Практические расчеты на срез и смятие | 12 | 12 | |||
| Тема 2.4 Геометрические характеристики плоских сечений | 8 | 2 | 2 | 6 | |
| Тема 2.5 Кручение | 18 | 2 | 2 | 16 | |
| Тема 2.6 Изгиб | 26 | 2 | 2 | 24 | |
| Тема 2.7Гипотезы прочности и их применение | 12 | 4 | 2 | 8 | |
| Тема 2.8 Устойчивость сжатых стержней | 8 | 2 | 2 | 6 | |
| Тема 2.9 Сопротивление усталости | 6 | 2 | 2 | 4 | |
| Раздел 3. Детали машин | 90 | 30 | 60 | ||
| Тема 3.1 Основные положения. Общие сведения о передачах | 4 | 4 | |||
| Тема 3.2 Фрикционные передачи | 4 | 4 | |||
| Тема 3.3 Ременные передачи | 4 | 4 | |||
| Тема 3.4 Зубчатые передачи | 6 | 6 | |||
| Тема 3.5 Цепные передачи | 8 | 8 | |||
| Тема 3.6 Червячные передачи | 8 | 8 | |||
| Тема 3.7 Муфты | 4 | 4 | |||
| Тема 3.8 Валы и оси. | 6 | 6 | |||
| Тема 3.9 Подшипники | 4 | 4 | |||
| Тема 3.10 Соединение деталей машин | 8 | 8 | |||
| Тема 3.11 Курсовое проектирование | 30 | 30 | |||
| Всего по дисциплине | 264 | 68 | 28 | 196 | |
studfiles.net