Контрольная работа «Свойства тригонометрических функций» для 10 класса
Контрольная работа №2 по теме «Тригонометрические функции, их графики и свойства»
Вариант 1 Часть 1. (каждое задание оценивается 1 балом) Найти область определения функции Найти множество значений функции Сравнить числа Найти наименьший положительный период функции Найти нули функции Часть 2. (каждое задание оценивается 2 баллами) Исследовать функцию на четность Найти наименьшее и наибольшее значение функции Часть 3. Построить график функции и найти все её свойства | Вариант 2 Часть 1. (каждое задание оценивается 1 балом) Найти область определения функции Найти множество значений функции Сравнить числа Найти наименьший положительный период функции Часть 2. (каждое задание оценивается 2 баллами) Исследовать функцию на четность Найти наименьшее и наибольшее значение функции Часть 3. (оценивается 3 баллами) Построить график функции и найти все её свойства |
Оценивание:
12 баллов – отметка 5
8-11 баллов – отметка 4
5-7 баллов – отметка 3
0-4 балла – отметка 2
Ершова Голобородько 9 класс самостоятельные и контрольные работы ГДЗ
Здесь представлены ответы к самостоятельным и контрольным работам по алгебре и геометрии 9 класс Ершова Голобородько. Вы можете смотреть и читать гдз онлайн (без скачивания) с компьютера и мобильных устройств.
Вы можете смотреть и читать гдз онлайн (без скачивания) с компьютера и мобильных устройств.
АЛГЕБРА
Квадратичная функция
С-1. Функции и их свойства 1 2 3 4 5
С-2. Квадратный трехчлен 1 2 3 4 5 6 7
С-3. График квадратичной функции 1 2 3 4 5 6 7 8 9
С-4*. Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа)
С-5. Решение квадратичных неравенств 1 2 3 4 5 6 7 8 9 10 11 12
С-6. Решение неравенств методом интервалов 1 2 3 4 5 6 7 8
К-2. Решение неравенств 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
Уравнения и системы уравнений
С-7. Решение целых уравнений 1 2 3 4 5 6 7 8 9 10 11
С-8*. Уравнения высших степеней: методы решения, задачи с параметрами (домашняя самостоятельная работа)
С-9. Решение систем уравнений второй степени 1 2 3 4 5 6 7
С-10.

С-11*. Системы рациональных уравнений (домашняя самостоятельная работа)
К-3. Целые уравнения и системы уравнений 1 2 3 4 5 6 7 8 9 10 11
Арифметическая и геометрическая прогрессии
С-12. Арифметическая прогрессия. Формула n-ого члена 1 2 3
С-13. Формула суммы п первых членов арифметической прогрессии 1 2 3 4
К-4. Арифметическая прогрессия 1 2 3 4 5 6
С-14. Геометрическая прогрессия. Формула n-ого члена 1 2 3 4
С-15. Формула суммы первых п членов геометрической прогрессии. 1 2 3 4
С-16*. Комбинированные задачи на прогрессии (домашняя самостоятельная работа)
Степень с рациональным показателем
С-17. Четные и нечетные функции. Функция У = *» 1 2 3
С-18. Корень n-ой степени и его свойства 1 2 3
С-19. Определение и свойства степени с дробным показателем 1 2 3
С-20.
 Преобразование степенных выражений с рациональными показателями 1 2
Преобразование степенных выражений с рациональными показателями 1 2 К-6. Степень с рациональным показателем 1 2 3 4 5
Тригонометрические выражения и их преобразования
С-21. Определение тригонометрических функций 1 2
С-22. Свойства тригонометрических функций. Радианная мера угла 1 2
С-24. Формулы приведения 1 2
К-7. Свойства тригонометрических функций. 1 2 3 4 5
С-25. Формулы сложения 1 2 3
С-26. Формулы двойного угла 1 2 3
С-27. Формулы суммы и разности тригонометрических функций 1 2
К-8. Формулы сложения и их следствия 1 2 3 4 5
С-28*. Дополнительные тригонометрические задачи (домашняя самостоятельная работа)
К-9. Годовая контрольная работа 1 2 3 4 5 6 7 8
ГЕОМЕТРИЯ (по Погорелову)
Подобие фигур
СП-1. Преобразование подобия и его свойства 1 2 3
СП-2.
СП-3. Подобие прямоугольных треугольников. 1 2 3 4 5 6
СП-4*. Подобие треугольников (домашняя самостоятельная работа)
КП-1. Подобие фигур 1 2 3 4 5 6 7
СП-5. Теорема о вписанных углах и ее следствия 1 2 3 4 5 6 7
СП-6*. Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)
Решение треугольников
СП-7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма 1 2 3 4 5 6 7
СП-8. Теорема синусов и ее следствия 1 2 3 4 5 6
КП-2. Решение треугольников 1 2 3 4 5 6 7
Многоугольники
СП-10. Выпуклый многоугольник 1 2 3 4 5
СП-11. Правильные многоугольники. 1 2 3 4 5 6
СП-12. Длина окружности. Радианная мера угла 1 2 3 4 5 6 7
КП-3. Многоугольники 1 2 3 4 5 6 7 8 9 10 11 12
Площади фигур
СП-13.
 Площадь прямоугольника, квадрата, параллелограмма 1 2 3 4 5 6 7 8 9 10
Площадь прямоугольника, квадрата, параллелограмма 1 2 3 4 5 6 7 8 9 10 СП-14. Площадь треугольника 1 2 3 4 5 6 7 8 9
СП-15. Площадь трапеции. Площадь четырехугольника 1 2 3 4 5 6 7 8 9 10 11
СП-17. Площади подобных фигур. Площадь круга и его частей 1 2 3 4 5 6
СП-18*. Площади фигур (домашняя самостоятельная работа)
КП-4. Площади фигур 1 2 3 4 5 6 7 8 9 10 11
КП-5. Годовая контрольная работа 1 2 3 4 5 6 7 8 9 10 11 12 13
ГЕОМЕТРИЯ (по Атанасяну)
Метод координат
СА-1. Координаты вектора 1 2 3 4 5
СА-2.Простейшие задачи в координатах 1 2 3 4 5 6
СА-3.Уравнение окружности 1 2 3 4 5 6 7
СА-4.Уравнение прямой 1 2 3 4
С-5*. Применение векторов и координат к решению задач (домашняя самостоятельная работа)
Соотношения между сторонами и углами треугольника.
 Скалярное произведение векторов
Скалярное произведение векторов СА-6.Синус, косинус, тангенс угла 1 2 3 4 5
СА-7.Теорема о площади треугольника. 1 2 3 4 5 6 7
Теорема синусов
СА-8.Теорема косинусов. Решение треугольников 1 2 3 4 5 6 7 8
СА-9.Скалярное произведение векторов 1 2 3 4 5 6 7
СА-10*. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа)
КА-2. Соотношение между сторонами и углами треугольника 1 2 3 4 5 6 7 8 9 10 11
СА-11. Правильные многоугольники 1 2 3 4 5 6
СА-12. Длина окружности, площадь круга, площадь кругового сектора 1 2 3 4 5 6 7 8 9
КА-3. Длина окружности и площадь круга 1 2 3 4 5 6 7 8 9
Движения
СА-13. Понятие движения 1 2 3 4 5
СА-14. Параллельный перенос и поворот 1 2 3
КА-4. Движение 1 2 3 4 5 6
КА-5. Годовая контрольная работа 1 2 3 4 5 6 7 8 9 10 11 12 13 14
▶▷▶ контрольная работа в 10 классе тригонометрические функции
▶▷▶ контрольная работа в 10 классе тригонометрические функции| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 08-11-2018 |
контрольная работа в 10 классе тригонометрические функции — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа №1 по теме » Тригонометрические функции» в znanioru/media/kontrolnaya_rabota_1_po_teme Cached Контрольная работа №1 по теме » Тригонометрические функции » в 11 классе , алгебра и начала Контрольная работа по теме «Тригонометрические функции, их infourokru/kontrolnaya-rabota-po-teme Cached Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления Контрольные работы по алгебре 10 класс, контрольные по mathematics-testscom/algebra- 10 -klass/ Cached Скачать: Контрольные работы по алгебре для 10 класса (pdf) Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса Контрольная Работа В 10 Классе Тригонометрические Функции — Image Results More Контрольная Работа В 10 Классе Тригонометрические Функции images Контрольная работа для 10 класса по алгебре по теме infourokru/kontrolnaya-rabota-dlya-klassa-po Cached Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления Подготовка к контрольной работе «Тригонометрические функции wwwuchmetru/library/material/154153 Cached Описание Контрольная работа представлена в 6 вариантах разной сложности, выполнена в программе MsOffice 2007, сохранена в MsOffice 2003 Контрольная работа по теме «Тригонометрические функции» pedportalnet/starshie-klassy/algebra/ Cached Контрольная работа по алгебре и началам анализа в 11 классе по теме » Тригонометрические Контрольная работа по теме «Тригонометрия» Алгебра 10 класс pedportalnet/starshie-klassy/algebra/ Cached Контрольная работа по теме «Тригонометрия» в 10 вариантах Алгебра 10 класс В работу Контрольная работа «Тригонометрические функции» — Математика easyenru//42- 1-0 -21388 Cached Контрольная работа состоит из 2-х вариантов В контрольной работе шесть заданий, рассчитана на 1 час для класса среднего уровня МАТЕМАТИКА В ШКОЛЕ — mathematics-testscom mathematics-testscom/matematika/ 10 -klass/ Контрольная работа по алгебре в 10 классе (Мордкович АГ) № 6 «Правила и формулы отыскания производных» КОНТРОЛЬНЫЕ, САМОСТОЯТЕЛЬНЫЕ, ДОМАШНИЕ ЗАДАНИЯ, ЗАДАЧИ, УРОКИ Контрольная работа по алгебре и началам анализа для 10 класса kopilkaurokovru/matematika/uroki/kontrol-naia Cached Контрольная работа по алгебре в 10 классе по теме « Тригонометрические формулы» Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 19,100 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- которые составлены в виде теста
- косинус
- 2
пожелания Все материалы проверены антив Скрыть 10 Алгебра 10 класс Контрольная работа № 3 по теме kopilkaurokovru › matematika/prochee…10…rabota…po… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 3 по теме: Тригонометрический функции Вариант 1 Постройте графики функций : у = sin x Просмотр содержимого документа «Алгебра 10 класс Контрольная работа № 3 по теме: « Тригонометрический функции »» Контрольная работа № 3 по теме: « Тригонометрический Читать ещё Контрольная работа № 3 по теме: Тригонометрический функции Вариант 1 Постройте графики функций : у = sin x ; y = cos 3x ; y = 3 sin (x ) ; y = cos + Решите Просмотр содержимого документа «Алгебра 10 класс Контрольная работа № 3 по теме: « Тригонометрический функции »» Контрольная работа № 3 по теме: « Тригонометрический функции » Вариант 1 Постройте графики функций Скрыть Контрольная работа № 2 Тригонометрические тождества e-osnovaru › PDF/osnova_3_26_4346pdf Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 1 Тригонометрические функции
которые составлены в виде теста
- размещенные на сайте
- smarter
- выполнена в программе MsOffice 2007
контрольная работа в 10 классе тригонометрические функции — Видео 20:36 Контрольная работа по тригонометрии 1 Valery Volkov YouTube — 7 окт 2015 г 8:51 Контрольная работа по тригонометрии 2 Valery Volkov YouTube — 7 окт 2015 г 7:10 Контрольная работа по тригонометрии №2 Valery Volkov YouTube — 7 окт 2015 г Все результаты Контрольная работа по теме «Тригонометрические функции, их › Математика Похожие Скачать: Контрольная работа по теме » Тригонометрические функции , их свойства и графики» алгебра 10 класс Контрольная работа в 10 классе по теме «Тригонометрические › Алгебра 7 мая 2018 г — Контрольная работа по теме « Тригонометрические функции » Вариант 1 Постройте схематично функции у = 2cosx Найдите область Контрольная работа по теме «Тригонометрические функции» › Алгебра Похожие Приложение Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 Найдите значение выражения: hello_html_m276b65d9 Контрольные работы по алгебре 10 класс, контрольные по Рейтинг: 5 — 12 голосов 4 апр 2017 г — Контрольная работа №1 «Определение тригонометрических функций » Вариант I 1 Вычислите функции: Контрольная работа по теме «Тригонометрические функции Контрольная работа по теме « Тригонометрические функции » — Тригонометрические функции — 1-е полугодие — Алгебра и начала анализа 10 класс Алгебра 10 класс Контрольная работа № 3 по теме 28 мар 2017 г — Контрольная работа № 3 по теме: Тригонометрический функции Вариант 1 Постройте графики функций: у = sin x ; y = cos 3x ; y = 3 sin [DOC] Контрольные работы по математике (алгебра) 10 класс Похожие Контрольные работы по математике (алгебра) 10 класс Демоверсия Контрольная работа №1 по теме «Определение тригонометрических функций » Контрольная работа по теме: Тригонометрические функции 10 gigabazaru/doc/149347html Похожие Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 Сравните с нулём Контрольная работа № 6 «Тригонометрические функции, их 15 апр 2016 г — Контрольная работа № 6 » Тригонометрические функции , их графики и свойства» 10 класс Алгебра Вариант 1Характеристика Контрольная работа по теме: Тригонометрические функции 10 класс 23 нояб 2011 г — Контрольная работа для учащихся 10 класса Состоит из 4 вариантов Контрольные работы по алгебре иначалам анализа 10 класс 20 нояб 2013 г — Контрольные работы по алгебре иначалам анализа 10 класс Максименко Определение тригонометрических функций Вариант 1 МАВ(С)ОУ «ЦО 1» Математика 10 класс Тригонометрия ЗАЧЁТ 1 класс Тригонометрия ЗАЧЁТ 1, 2 Таблицы, контрольные работы , зачёты выражения, тригонометрические функции формулы контрольные работы Картинки по запросу контрольная работа в 10 классе тригонометрические функции «cl»:3,»cr»:3,»ct»:3,»id»:»4c6Plmk18gv0ZM:»,»ml»:»600″:»bh»:90,»bw»:122,»oh»:328,»ou»:» «,»ow»:644,»pt»:»ds02infourokru/uploads/ex/03ad/00037294-9ae6f81a»,»rh»:»infourokru»,»rid»:»WN1PVkYIIq1yLM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcRfDNWB9rcFPK4iivhKYgCLyPRBJfLuQaoe37UYczpAGIUR8PIR8kB8pD8″,»tw»:177 «cb»:6,»cr»:6,»id»:»0C-lc-wY2eVBoM:»,»ml»:»600″:»bh»:90,»bw»:67,»oh»:725,»ou»:» «,»ow»:518,»pt»:»ds02infourokru/uploads/ex/03ad/00037294-9ae6f81a»,»rh»:»infourokru»,»rid»:»WN1PVkYIIq1yLM»,»rt»:0,»ru»:» «,»st»:»Инфоурок»,»th»:99,»tu»:» \u003dtbn:ANd9GcQudVbisiZotlcEiwYaWm_yWcF_3naNBkvHLAuIw6AuWuGJTkrsA9QxAIw»,»tw»:70 «cb»:3,»cl»:3,»cr»:3,»id»:»5yNrdI5lowagNM:»,»ml»:»600″:»bh»:90,»bw»:67,»oh»:384,»ou»:» «,»ow»:282,»pt»:»fs00infourokru/images/doc/2/1654/hello_html_m317″,»rh»:»infourokru»,»rid»:»vRfxsroUW2Ws1M»,»rt»:0,»ru»:» \u003d3512″,»sc»:1,»st»:»Инфоурок»,»th»:97,»tu»:» \u003dtbn:ANd9GcR9mZrdUbsGlmFTC2JCZ1NFo1Hpdqu4YOmRfm5_dB2b1v89M8rZKLmlbmo»,»tw»:71 «cr»:12,»id»:»aHLB_KPVMdU6jM:»,»ml»:»600″:»bh»:90,»bw»:82,»oh»:584,»ou»:» «,»ow»:530,»pt»:»ds02infourokru/uploads/ex/03ad/00037294-9ae6f81a»,»rh»:»infourokru»,»rid»:»WN1PVkYIIq1yLM»,»rt»:0,»ru»:» «,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcSPOcI1x16TuFGyKBOB7qFANMsL2xK3I-M08H690MQGrXDD4mdYHxy_YZ4″,»tw»:82 «id»:»sXKZM_2OIq72YM:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:1019,»ou»:» «,»ow»:1810,»pt»:»iytimgcom/vi/P1Ks0Y7zcvs/maxresdefaultjpg»,»rh»:»youtubecom»,»rid»:»GwZHv-UmUWHp_M»,»rt»:0,»ru»:» \u003dP1Ks0Y7zcvs»,»sc»:1,»st»:»YouTube»,»th»:90,»tu»:» \u003dtbn:ANd9GcQfRjODNFxsZ6unacUYYSQnhAPAx5jiBgUlJdFU_AS_wSyvGI7dNxE7JayM»,»tw»:160 «id»:»xpL9pWxRIy11SM:»,»ml»:»600″:»bh»:90,»bw»:122,»oh»:180,»ou»:» «,»ow»:464,»pt»:»fs00infourokru/images/doc/2/1654/hello_html_55d9″,»rh»:»infourokru»,»rid»:»vRfxsroUW2Ws1M»,»rt»:0,»ru»:» \u003d3512″,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcSpUpHkzeDz8NOsUF9VyMH8yVqDQ34XHkE6kTF-3Vn7_iGwn-hWJPwk0SE»,»tw»:232 Другие картинки по запросу «контрольная работа в 10 классе тригонометрические функции» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Сборник контрольных работ по алгебре, (10 класс) — Урокрф 22 нояб 2017 г — Контрольная работа № 2 по теме « Тригонометрические функции » Цель: проверить уровень усвоение ГОСО — умение находить Контрольная работа по алгебре и началам анализа за 1 — Урокрф 29 нояб 2017 г — Учебно-дидактические материалы по Алгебре для 10 класса по УМК знание свойств тригонометрических функций и их графиков Урок 29 Контрольная работа №1 unimathru › › Глава 1 Тригонометрические функции Похожие Алгебра 10 класс по учебнику АГ Мордковича и др Контрольная работа №1 знания и умение учащихся по теме « Тригонометрические функции » Контрольная работа по теме «Тригонометрические формулы», 10 › Контрольная работа 21 мая 2017 г — Cкачать: Контрольная работа по теме «Тригонометрические Урок по математике на тему » Тригонометрические функции «( 10 класс ) Подготовка к контрольной работе «Тригонометрические функции › › Алгебра › 11 класс 4 мая 2013 г — Контрольная работа по теме « Тригонометрические функции » Материалы Учебник Алгебра и начала анализа для 10 -11 класса алгебра 10 класс тригонометрические функции числового аргумента esareunioncom//algebra-10-klass-trigonometricheskie-funktsii-chislovogo-argumen Алгебра › 10 класс Урок по теме Тригонометрические функции числового 10 класс В 2 ч [DOC] Контрольная работа №1 Тригонометрические функции [DOC] Математика 10 кл базовый уровень pug-school2ucozru/Novyj_god/k/matematika_10_kl_bazovyj_urovendocx Похожие В 10 классе продолжаются и получают развитие содержательные линии: « Преобразование Сжатие и растяжение графиков тригонометрических функций 2309, 13, Контрольная работа № 1 по теме «Числовые функции », 1 Курс: АЛГЕБРА И НАЧАЛА АНАЛИЗА 10, : Контрольная работа Похожие АЛГЕБРА И НАЧАЛА АНАЛИЗА 10 Контрольная работа № 3 по теме « Тригонометрические функции и тождества Решение простейших тригонометрических уравнений» 1 Входное тестирование по алгебре для 10 классов Рабочая программа по математике 10-й класс открытыйурокрф/статьи/659923/ Рабочая программа по математике 10 -го класса ориентирована на использование Контрольная работа по теме « Тригонометрические функции », 1 [DOC] МОУ «Корниловская средняя школа» Рекомендована Утверждаю uchportfolioru/public_files/760453445doc Похожие автор: ЕВ Купцова — Похожие статьи Планирование для 10 класса по учебнику: Алгебра и начала анализа: Контрольная работа №2 по теме « Тригонометрические функции и их графики» [DOC] 10-11 класс ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО filesschool-collectioneduru/dlrstore/c3203a69-b8f6-a836-8fbd/69993doc Учебник для 10 -11 классов средней школы Соотношения между тригонометрическими функциями одного и того же угла Контрольная работа №2 [PDF] 10 класс алгебра (базовый уровень) 59428s003edusiteru/sveden/files/4624dde4-5847-447a-820b-cad3a8c50c74pdf АГ Мордкович Алгебра и начала анализа 10 -11 класс Учебник – М: алгоритмы построения графиков тригонометрических функций Уметь Тематика контрольных работ: Входная контрольная работа , «Числовые функции», [DOC] 10 класс wwwgeorg14edusiteru/DswMedia/rppoalgebre10-mordkovichdocx 10 — 11 класс : Контрольные работы для общеобразовательных учреждений Учебное пособие / А Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента Алгебра, 10 › › Алгебра › 10 класс › Тригонометрические функции Теоретические уроки, тесты и задания по предмету Тригонометрические функции числового аргумента, Тригонометрические функции , 10 класс , Контрольные работы по алгебре 10 класс wwwmatematika-proru/tests-for-algebra-grade-10html Похожие Контрольные работы по алгебре и началам анализа для 10 класса обеспечивают системный Тригонометрические функции , их график и свойства Печатные тесты по математике — 10 класс — Математика Материал можно использовать, как итоговую контрольную работу , так и переходным Тест «Обратные тригонометрические функции » в 4 — х вариантах Контрольная работа по теме «Тригонометрические функции», 10 Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 1 Найдите значение выражения: 1) ; 2) ; 3) ; 4) 0 2 Сравните с нулём Алгебра: 10 класс www56bitru/materials/algebra/10/ Перейти к разделу Глава 2 Тригонометрические функции [АГ Мордкович (базовый — Контрольная работа № 1 Тригонометрические функции контрольная работа по теме тригонометрические уравнения 10 wwwaspartnerru//kontrolnaia-rabota-po-teme-trigonometricheskie-uravneniia-10-k контрольная работа по теме тригонометрические уравнения 10 класс » Тригонометрические функции » infourokru/kontrolnaya-rabota-po-teme Cached Тригонометрические функции, уравнения и неравенства: Пособие windoweduru/catalog/pdf2txt/231/75231/55879 Похожие Тригонометрические функции , уравнения и неравенства: Пособие для довузовской подготовки, в школах и классах физико-математического 1 2 3 4 5 6 7 8 9 10 Контрольная работа № 1: Свойства тригонометрических Ответы@MailRu: контрольная работа по алгебре № 2 10 класс › Образование › Школы Похожие 1 ответ 5 нояб 2012 г — Пользователь Влад Байков задал вопрос в категории Школы и получил на него 1 ответ [DOC] Административная контрольная работа для 10 класса school38vrnru/images/users-files/admin/doc/trigonometriya_10adoc 10 класс Класс физико-математического профиля Материалы к уроку по Работа в парах Найдите все тригонометрические функции от угла , 2 и /2 [DOC] График контрольных точек по геометрии-10 класс(1 полугодие) Контрольная работа по теме: «Логарифмическая функция » 10 10 10 2701 402 1202 2 Тригонометрические формулы СР Поворот точки вокруг [DOC] Преобразование тригонометрических выражений — лицей сХлевное liceum-hlevnoe3dnru/rabprog/rabochaja_programma_algebra_10_klassdocx 10 класс : контрольные работы (профильный уровень) / ВИ Глизбург – М: Преобразование суммы тригонометрических функций в произведение Рабочая программа Алгебра 10 классdocx — Рабочая программа по Похожие Файл Рабочая программа Алгебра 10 класс docx для материала по дисциплинам Математика, в разделе тригонометрические функции , используя при необходимости справочные 11 Контрольная работа № 1 по теме Контрольная работа по алгебре и началам анализа Тема Похожие Вариант II Найти область определения функции Найти множество значений Контрольная работа по алгебре и началам анализа Тема: Тригонометрические функции (учебник алгебры и начал анализа 10 -11, авторов ШААлимова и др) Рабочая программа «Практикум по алгебре» в 10 а классе 10 класс — Блог учителя математики Евсейчика Юрия Владимировича 2002mathblogspotcom/p/10html Задачи для подготовки к контрольной работе по теме «Параллельность в рамках контрольной работы по теме » Тригонометрические функции » [PDF] Алгебра и начала анализа 10 класс ecolecousteauru/indexphp?option=com_docman&task=doc_download Похожие Календарно-тематическое планирование по алгебре 10 класс (см тригонометрических функций в произведение и формулы преобразования произведения При выполнении практической работы и контрольной работы : Решебник к сборнику самостоятельных работ по алгебре и 20 сент 2014 г — Контрольная работа М І Решебник к сборнику самостоятельных работ по алгебре и началам анализа для 10 класса Александровой ОНЛАЙН: 1 Тригонометрические функции углового аргумента С- 10 § 9 [PDF] МАВ(С)ОУ «ЦО№1» Математика 10 класс Тригонометрия ЗАЧЁТ zlat-centroschoolsiteru/DswMedia/10kltrigonompdf 10 класс Тригонометрия ЗАЧЁТ № 1, 2 Таблицы, контрольные работы , зачёты тригонометрические выражения, тригонометрические функции и [DOC] Тематическое планирование 10кл алгебра Профиль wwwisakovo-shkolaru/uchebnaya/196_322f3c4c1ae1f1dad51b935a81a0830f материала по алгебре и началам анализа в 10 классе 14, Контрольная работа № 1, 1 36, Тригонометрические функции углового аргумента, 1 Разработка урока алгебры «Графики тригонометрических функций pedsovetsu › Файлы для скачивания › Математика, алгебра, геометрия › К уроку Похожие 10 мар 2016 г — урока алгебры «Графики тригонометрических функций «; 10 класс В процессе работы учащиеся должны продемонстрировать не [DOC] АЛГЕБРА И НАЧАЛА АНАЛИЗА (Профильный уровень) 10 класс Контрольные работы для общеобразовательных учреждений 2-е изд Тригонометрические функции числового аргумента 1ч 21-22 23-24 25 [DOC] Знать s11006edu35ru/attachments/article/623/Математика%2010%20классdocx Рабочая программа по математике 10 класса составлена на основе и контрольные работы по алгебре и началам анализа для 10 -11 класса », Москва, Преобразования суммы тригонометрических функций в произведение и [PDF] Алгебра 10 класс Учебник: Алгебра и начала математического russchoolnyusanarodru/extern/10/al10dpdf Похожие Алгебра 10 класс Учебник: Преобразования суммы тригонометрических функций в произведение и выражений 2 Контрольная работа № 21 1 Алгебра — 10 класс Алгебра Тригонометрические функции Похожие Курс « 10 класс Алгебра Тригонометрические функции углового аргумента Формулы приведения» ориентирован на овладение обучаемыми скачать Вместе с контрольная работа в 10 классе тригонометрические функции часто ищут контрольная работа по теме тригонометрические функции 10 класс решение контрольная работа по теме тригонометрические функции 10 класс ответы контрольная работа по теме тригонометрические функции 11 класс контрольная работа по теме тригонометрические функции 11 класс ответы контрольная работа по теме тригонометрические функции 10 класс мордкович контрольная работа по теме тригонометрические формулы 10 класс ответы контрольная работа номер 1 тригонометрические функции 11 класс контрольная работа по алгебре 10 класс тригонометрические выражения Навигация по страницам 1 2 3 4 5 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Контрольная работа » Тригонометрические функции » 10 uchitelyacom › Алгебра › …-funkcii-10-klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 Контрольная работа по теме: Тригонометрические уравнения и неравенства 10 класс 1 вариант 1 Вычислите: arcsin Читать ещё Контрольная работа по теме: Тригонометрические функции 10 класс Вариант 1 1 Найдите значение выражения: 000 4590cos60sin2 tg 1) 132 Контрольная работа по теме: Тригонометрические уравнения и неравенства 10 класс 1 вариант 1 Вычислите: arcsin (2 3 ) + 2arctg(-1) 1) Скрыть 2 Контрольная работа по теме » Тригонометрические » infourokru › …rabota…trigonometricheskie-funkcii…i… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Инфоурок › Математика › Тесты › Контрольная работа по теме » Тригонометрические функции , их свойства и графики» (алгебра 10 класс ) Контрольная работа №3 Свойства и графики тригонометрических функций Читать ещё Инфоурок › Математика › Тесты › Контрольная работа по теме » Тригонометрические функции , их свойства и графики» (алгебра 10 класс ) Контрольная работа по теме » Тригонометрические функции , их свойства и графики» (алгебра 10 класс ) скачать материал библиотека материалов Контрольная работа №3 Свойства и графики тригонометрических функций Вариант 1 1 Постройте график функции : 2 Постройте график функции : 3 Найдите множество значений функции 4 Найдите наибольшее и наименьшее значение функции 5 Найдите наибольшее и наименьшее значение функции на отрезке 6 Построи Скрыть 3 Тест по алгебре ( 10 класс ) по теме: Контрольная работа nsportalru › …kontrolnaya…trigonometricheskie…10… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Контрольная работа по теме: Тригонометрические функции Вариант 3 Контрольная работа по теме » Тригонометрические уравнения» расчитана на 2 часа В ней есть задания базового уровня сложности, которые составлены в виде теста , и задания повышенного уровня сложности, пр Контрольная Читать ещё Контрольная работа по теме: Тригонометрические функции Вариант 3 Вычислите: а) ; б) в) г) Найдите заданную точку на числовой окружности: , ; -2,5; 140˚,90˚ Решите уравнение: а) б) Контрольная работа по теме » Тригонометрические уравнения» расчитана на 2 часа В ней есть задания базового уровня сложности, которые составлены в виде теста , и задания повышенного уровня сложности, пр Контрольная работа по алгебре «Показательная функция », 10 класс Контрольная работа по алгебре «Показательная функция », 10 класс , два варианта Контрольная работа по алгебре «Показательная функция », 10 класс Скрыть 4 Контрольная работа в 10 классе по теме infourokru › …v-klasse…trigonometricheskie-funkcii… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Инфоурок › Алгебра › Другие методич материалы › Контрольная работа в 10 классе по теме » Тригонометрические функции » Опишите свойства функции Контрольная работа по теме « Тригонометрические функции » Вариант 2 Постройте схематично график функции у = 0,5cosx Читать ещё Инфоурок › Алгебра › Другие методич материалы › Контрольная работа в 10 классе по теме » Тригонометрические функции » Контрольная работа в 10 классе по теме » Тригонометрические функции » скачать материал библиотека материалов Контрольная работа по теме « Тригонометрические функции » Вариант 1 Постройте схематично функции у = 2cosx Опишите свойства функции Контрольная работа по теме « Тригонометрические функции » Вариант 2 Постройте схематично график функции у = 0,5cosx Скрыть 5 Тест : Тригонометрические функции 10 класс nsportalru › …test-trigonometricheskie-funktsii-10… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа по теме: Тригонометрические функции 10 класс При подготовке к урокам часто возникает необходимость демонстрации графиков функций для повторения ранее пройденного, для пояснения решения той или иной задачи Очень много времени приходится тратить Зачётная работа Читать ещё Контрольная работа по теме: Тригонометрические функции 10 класс Контрольная работа для учащихся 10 класса Состоит из 4 вариантов Мини-исследование по теме «Преобразование графиков тригонометрических функций «, 10 класс Цель исследования — выяснить изменение графиков тригонометрических функций в зависимости от коэффициентов При подготовке к урокам часто возникает необходимость демонстрации графиков функций для повторения ранее пройденного, для пояснения решения той или иной задачи Очень много времени приходится тратить Зачётная работа по теме «Обратные тригонометрические функции » 10 класс Скрыть 6 Сборник контрольных работ по алгебре, ( 10 класс ) урокрф › 10 класс Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 2 по теме « Тригонометрические функции » Цель: проверить уровень усвоение ГОСО — умение находить период тригонометрических функций ; — уменияупрощать тригонометрические выражения с помощью основных формул тригонометрии ; — знание значений тригонометрических Читать ещё Контрольная работа № 2 по теме « Тригонометрические функции » Цель: проверить уровень усвоение ГОСО — умение находить период тригонометрических функций ; — уменияупрощать тригонометрические выражения с помощью основных формул тригонометрии ; — знание значений тригонометрических функций ; — умения строить графики тригонометрических функций ; — умения по графику определять свойства тригонометрических функций ; 1 Найдите наименьший положительный период функции 2 Вычислите значение выражения Скрыть 7 Контрольная работа по тригонометрии videourokinet › Разработки › kontrolnaya-rabota-po… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа содержит семь заданий в двух вариантах Сорокина Татьяна Викторовна 10 10 2014 Контрольная работа №2 « Тригонометрические функции » Вариант №1 В контрольной работе 7 заданий Читать ещё Контрольная работа содержит семь заданий в двух вариантах Сорокина Татьяна Викторовна 10 10 2014 Описание разработки В контрольной работе 7 заданий Критерий оценивания: «3» — верно выполнены 2 или 3 задания , «4» — верно выполнены 4 или 5 заданий , «5» — верно выполнены 6 или 7 заданий Весь материал — смотрите документ Содержимое разработки Контрольная работа №2 « Тригонометрические функции » Вариант №1 В контрольной работе 7 заданий Критерий оценивания: «3» — верно выполнены 2 или 3 задания , «4» — верно выполнены 4 или 5 заданий , «5» — верно выполнены 6 или 7 заданий Задание 1 Вычисл Скрыть 8 Контрольная работа в 10 классе Тригонометрические функции — смотрите картинки ЯндексКартинки › контрольная работа в 10 классе тригонометрические Пожаловаться Информация о сайте Ещё картинки 9 Контрольные работы по алгебре 10 класс mathematics-testscom › algebra-10…10…mordkovich Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра – 10 класс Контрольные работы с ответами к учебнику Мордковича АГ за 1, 2, 3, 4 четверти Контрольные на темы: «Определение тригонометрических функций «, «Свойства и графики тригонометрических функций » Читать ещё Алгебра – 10 класс Контрольные работы с ответами к учебнику Мордковича АГ за 1, 2, 3, 4 четверти Контрольные на темы: «Определение тригонометрических функций «, «Свойства и графики тригонометрических функций «, » Тригонометрические уравнения», » Тригонометрические функции сложения аргумента», «Правила и формулы отыскания производных», «Применение производной к исследованию функций » и др Дополнительные материалы по алгебре Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания Все материалы проверены антив Скрыть 10 Алгебра 10 класс Контрольная работа № 3 по теме kopilkaurokovru › matematika/prochee…10…rabota…po… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 3 по теме: Тригонометрический функции Вариант 1 Постройте графики функций : у = sin x Просмотр содержимого документа «Алгебра 10 класс Контрольная работа № 3 по теме: « Тригонометрический функции »» Контрольная работа № 3 по теме: « Тригонометрический Читать ещё Контрольная работа № 3 по теме: Тригонометрический функции Вариант 1 Постройте графики функций : у = sin x ; y = cos 3x ; y = 3 sin (x ) ; y = cos + Решите Просмотр содержимого документа «Алгебра 10 класс Контрольная работа № 3 по теме: « Тригонометрический функции »» Контрольная работа № 3 по теме: « Тригонометрический функции » Вариант 1 Постройте графики функций Скрыть Контрольная работа № 2 Тригонометрические тождества e-osnovaru › PDF/osnova_3_26_4346pdf Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 1 Тригонометрические функции , их свойства Содержание учебного материала Основные соотношения между тригонометрически -ми функциями одного аргумента Периодичность функций Читать ещё Контрольная работа № 1 Тригонометрические функции , их свойства Содержание учебного материала Радианная мера угла Синус, косинус, тангенс, котангенс угла Тригонометрические функции числового аргумента Основные соотношения между тригонометрически -ми функциями одного аргумента Периодичность функций Свойства и графики тригонометрических функций 8 Вариант 1 1 ° Вычислите: 2 Скрыть pdf Посмотреть Сохранить на ЯндексДиск Вместе с « контрольная работа в 10 классе тригонометрические функции » ищут: контрольные работы по математике 3 класс контрольная закупка контрольные работы итоговая контрольная работа по математике 6 класс готовые контрольные работы контрольные работы по математике 2 класс итоговая контрольная работа по алгебре 7 класс итоговая контрольная работа по математике 5 класс контрольные работы по математике 4 класс итоговая контрольная работа по математике 3 класс школа россии фгос 1 2 3 4 5 дальше Браузер Ускоряет загрузку файлов при медленном соединении 0+ Установить
Алгебра 9 Макарычев (угл) Контрольная 6 с ответами
Контрольная работа № 6 по алгебре с ответами для учащихся 9 класса с повышенным уровнем математической подготовки. Настоящая проверочная работа «Тригонометрические функции и их свойства» используется в комплекте с учебником «Алгебра 9 класс. Углубленное изучение» авторов: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистов. Алгебра 9 Макарычев (угл) Контрольная 6. Ответы адресованы родителям.
Настоящая проверочная работа «Тригонометрические функции и их свойства» используется в комплекте с учебником «Алгебра 9 класс. Углубленное изучение» авторов: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистов. Алгебра 9 Макарычев (угл) Контрольная 6. Ответы адресованы родителям.
Цитаты из пособия «Алгебра 9 класс. Дидактические материалы / И.Е. Феоктистов — М.: Мнемозина» использованы в учебных целях.
Алгебра 9 класс (угл.изуч.)
Контрольная работа № 6
Подготовительный вариант
- Найдите cos 2α и tg (α + π/4), если sin α = –1/√5, 3π/2 < α < 2π.
- Упростите выражение (cos α – cos 4α + cos 7α – cos 10α) : (sin α + sin 4α + sin 7α + sin 10α).
- Докажите тождество tg α + cos–1 α – 1 = (√2 sin α/2) : (sin (π/4 – α/2)).
- Пусть α, β и γ – углы треугольника. Докажите, что:
а) (sin α) / (sin β sin γ) = ctg β + ctg γ;
б) sin α + sin β + sin γ = 4 cos α/2 • cos β/2 • cos γ/2.
- Упростите выражение (sin 20 ° + 2 sin 40° – sin 100°) : √(1 – cos2 320°).
- Вычислите sin 18°.
Образец контрольной работы:
Ответы на контрольную работу № 6
Вы смотрели: Контрольная работа по алгебре с ответами (на все варианты) для учащихся 9 класса с повышенным уровнем математической подготовки «Тригонометрические функции и их свойства» по учебнику «Алгебра 9 класс. Углубленное изучение» авторов: Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешкова, И.Е. Феоктистов. Алгебра 9 Макарычев (угл) Контрольная 6. Ответы адресованы родителям.
Вернуться к списку контрольных работ по алгебре в 9 классе (Макарычев, угл.)
Тригонометрических функций
В тригонометрические соотношения также может рассматриваться как функция переменной, которая является мерой угла.
Эту угловую меру можно указать в
градусы
или же
радианы
.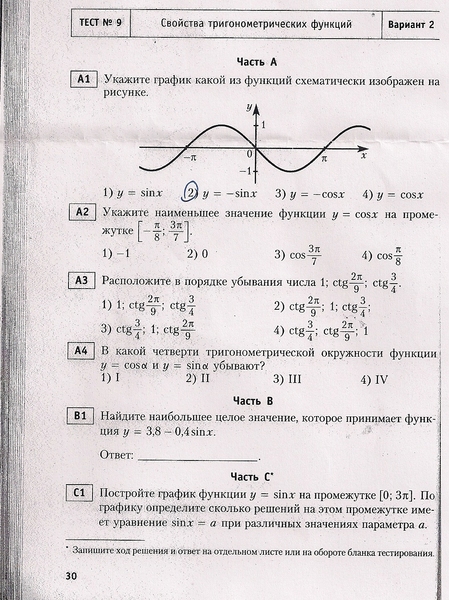
График синус функция выглядит так:
Обратите внимание, что домен функции у знак равно грех ( Икс ) ) — все действительные числа (синус определен для любой угловой меры), диапазон является — 1 ≤ у ≤ 1 .
График косинус функция выглядит так:
Область определения функции
у
знак равно
потому что
(
Икс
)
все действительные числа (косинус определяется для любой угловой меры), диапазон равен
—
1
≤
у
≤
1
.
График касательная функция выглядит так:
Область определения функции у знак равно загар ( Икс ) ) все действительные числа Кроме значения, где потому что ( Икс ) равно 0 , то есть значения π 2 + π п для всех целых чисел п .Диапазон касательной функции — это все действительные числа.
График функции секанса выглядит так:
Область определения функции
у
знак равно
сек
(
Икс
)
знак равно
1
потому что
(
Икс
)
снова все действительные числа, кроме значений, где
потому что
(
Икс
)
равно
0
, то есть значения
π
2
+
π
п
для всех целых чисел
п
. Диапазон функции:
у
≤
—
1
или же
у
≥
1
.
Диапазон функции:
у
≤
—
1
или же
у
≥
1
.
График функции косеканса выглядит так:
Область определения функции
у
знак равно
csc
(
Икс
)
знак равно
1
грех
(
Икс
)
это все действительные числа, кроме значений, где
грех
(
Икс
)
равно
0
, то есть значения
π
п
для всех целых чисел
п
.Диапазон функции:
у
≤
—
1
или же
у
≥
1
.
График функции котангенса выглядит так:
Область определения функции у знак равно детская кроватка ( Икс ) знак равно потому что ( Икс ) грех ( Икс ) это все действительные числа, кроме значений, где грех ( Икс ) равно 0 , то есть значения π п для всех целых чисел п .Диапазон функции — все действительные числа.
5.2: Свойства графиков тригонометрических функций
В разделе 5. 1 мы видели, как графики тригонометрических функций повторяются через каждые \ (2 \ pi \) радианы. В этом разделе мы обсудим это и другие свойства графиков, особенно для синусоидальных функций (синус и косинус).
1 мы видели, как графики тригонометрических функций повторяются через каждые \ (2 \ pi \) радианы. В этом разделе мы обсудим это и другие свойства графиков, особенно для синусоидальных функций (синус и косинус).
Во-первых, напомним, что область функции \ (f (x) \) — это набор всех чисел \ (x \), для которых функция определена.Например, область значений \ (f (x) = \ sin \; x \) — это набор всех действительных чисел, а область значений \ (f (x) = \ tan \; x \) — это набор все действительные числа, кроме \ (x = \ pm \, \ frac {\ pi} {2} \), \ (\ pm \, \ frac {3 \ pi} {2} \), \ (\ pm \, \ гидроразрыв {5 \ pi} {2} \), \ (… \). Диапазон функции \ (f (x) \) — это набор всех значений, которые \ (f (x) \) могут принимать в своей области. Например, диапазон \ (f (x) = \ sin \; x \) — это набор всех действительных чисел между \ (- 1 \) и \ (1 \) (т.е. интервал \ ([- 1, 1] \)), тогда как диапазон \ (f (x) = \ tan \; x \) — это набор всех действительных чисел, как мы можем видеть из их графиков.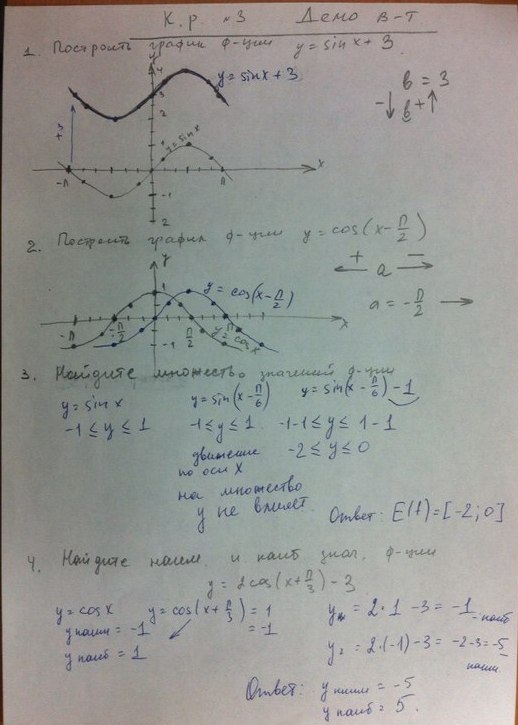
Функция \ (f (x) \) является периодической , если существует число \ (p> 0 \) такое, что \ (x + p \) находится в области \ (f (x) \) всякий раз, когда \ (x \) есть, и если выполняется следующее соотношение:
\ [\ label {уравнение: периодический} f (x + p) ~ = ~ f (x) \ quad \ text {для всех \ (x \)} \]
Может быть много чисел \ (p \), удовлетворяющих указанным выше требованиям. Если существует наименьшее такое число \ (p \), то мы называем это число периодом функции \ (f (x) \).
Пример \ (\ PageIndex {1} \)
Функции \ (\ sin \; x \), \ (\ cos \; x \), \ (\ csc \; x \) и \ (\ sec \; x \) имеют одинаковый период: \ (2 \ pi \) радиан.В разделе 5.1 мы видели, что графики \ (y = \ tan \; x \) и \ (y = \ cot \; x \) повторяются через каждые \ (2 \ pi \) радианы, но они также повторяются через каждые \ (\ пи \) радианы. Таким образом, функции \ (\ tan \; x \) и \ (\ cot \; x \) имеют период в \ (\ pi \) радиан.
Пример \ (\ PageIndex {2} \)
Какой период у \ (f (x) = \ sin \; 2x \, \)?
Решение
График \ (y = \ sin \; 2x \) показан на рисунке \ (\ PageIndex {1} \) вместе с графиком \ (y = \ sin \; x \) для сравнения по интервал \ ([0,2 \ pi] \).Обратите внимание, что \ (\ sin \; 2x \) « идет вдвое быстрее », чем \ (\ sin \; x \).
Рисунок \ (\ PageIndex {1} \): График \ (y = \ sin 2x \)Например, для \ (x \) от \ (0 \) до \ (\ frac {\ pi} {2} \), \ (\ sin \; x \) переходит от \ (0 \) к \ (1 \), но \ (\ sin \; 2x \) может переходить от \ (0 \) к \ (1 \) быстрее, чуть выше интервала \ ([0, \ frac {\ pi} {4}] \). В то время как \ (\ sin \; x \) требуется полный \ (2 \ pi \) радиан, чтобы пройти весь цикл (самая большая часть графика, которая не повторяется), \ (\ sin \; 2x \ ) проходит весь цикл всего в \ (\ pi \) радианах.Таким образом, период \ (\ sin \; 2x \) равен \ (\ pi \) радианам.
В приведенном выше примере использовался график \ (\ sin \; 2x \), но период можно найти аналитически. Поскольку \ (\ sin \; x \) имеет период \ (2 \ pi \), мы знаем, что \ (\ sin \; (x + 2 \ pi) = \ sin \; x \) для всех \ (x \ ). Поскольку \ (2x \) является числом для всех \ (x \), это, в частности, означает, что \ (\ sin \; (2x + 2 \ pi) = \ sin \; 2x \) для всех \ (x \) . Теперь определим \ (f (x) = \ sin \; 2x \). Тогда
Поскольку \ (\ sin \; x \) имеет период \ (2 \ pi \), мы знаем, что \ (\ sin \; (x + 2 \ pi) = \ sin \; x \) для всех \ (x \ ). Поскольку \ (2x \) является числом для всех \ (x \), это, в частности, означает, что \ (\ sin \; (2x + 2 \ pi) = \ sin \; 2x \) для всех \ (x \) . Теперь определим \ (f (x) = \ sin \; 2x \). Тогда
\ [\ nonumber \ begin {align *}
f (x + \ pi) ~ & = ~ \ sin \; 2 \, (x + \ pi) \\ \ nonumber
& = ~ \ sin \; (2x + 2 \ pi) \\ \ nonumber
& = ~ \ sin \; 2x \ quad \ text {(как мы показали выше)} \\ \ nonumber
& = ~ f (x)
\ end {align *} \]
для всех \ (x \), поэтому период \ (p \) для \ (\ sin \; 2x \) составляет не более \ (\ pi \) по нашему определению периода.Мы должны показать, что \ (p> 0 \) не может быть меньше \ (\ pi \). Для этого воспользуемся доказательством от противоречия . То есть предположим, что \ (0 Итак, предположим, что \ (0 \ [\ nonumber \ begin {align *} для всех \ (x \).Поскольку любое число \ (u \) может быть записано как \ (2x \) для некоторого \ (x \) (т.е. \ (u = 2 (u / 2) \)), это означает, что \ (\ sin \; u = \ sin \; (u + 2p) \) для всех действительных чисел \ (u \), и, следовательно, период \ (\ sin \; x \) равен наибольшему \ (2p \). Получили противоречие. Почему? Поскольку период \ (\ sin \; x \) равен \ (2 \ pi> 2p \). Следовательно, период \ (p \) числа \ (\ sin \; 2x \) не может быть меньше \ (\ pi \), поэтому период должен быть равен \ (\ pi \). Вышеупомянутое может показаться большой работой, чтобы доказать что-то, что было визуально очевидно из графика (и интуитивно очевидно благодаря идее «вдвое быстрее»). Для любого числа \ (\ omega> 0 \): \ [\ nonumber \ begin {alignat *} {4} Если \ (\ omega <0 \), используйте \ (\ sin \; (- A) = - \ sin \; A \) и \ (\ cos \; (- A) = \ cos \; A \ ) (е. Пример \ (\ PageIndex {3} \) Период \ (y = \ cos \; 3x \) равен \ (\ frac {2 \ pi} {3} \), а период \ (y = \ cos \; \ frac {1} {2} х \) равно \ (4 \ пи \). Графики обеих функций показаны на Рисунке 5.2.2: Мы знаем, что \ (\; — 1 \ le \ sin \; x \ le 1 \; \) и \ (\; — 1 \ le \ cos \; x \ le 1 \; \) для всех \ (x \). Таким образом, для константы \ (A \ ne 0 \) \ [\ nonumber для всех \ (x \).В этом случае мы называем \ (| A | \) амплитуду функций \ (y = A \, \ sin \; x \) и \ (y = A \, \ cos \; x \). В общем, амплитуда периодической кривой \ (f (x) \) составляет половину разницы наибольшего и наименьшего значений, которые может принимать \ (f (x) \): \ [\ nonumber Другими словами, амплитуда — это расстояние от верха или низа кривой до горизонтальной линии, которая делит кривую пополам, как на рисунке 5. Не все периодические кривые имеют амплитуду. Например, \ (\ tan \; x \) не имеет ни максимума, ни минимума, поэтому его амплитуда не определена. Аналогично, \ (\ cot \; x \), \ (\ csc \; x \) и \ (\ sec \; x \) не имеют амплитуды. Поскольку амплитуда включает вертикальные расстояния, она не влияет на период функции, и наоборот. Пример \ (\ PageIndex {4} \) Найдите амплитуду и период \ (y = 3 \, \ cos \; 2x \). Решение Амплитуда равна \ (| 3 | = 3 \), а период равен \ (\ frac {2 \ pi} {2} = \ pi \). График показан на Рисунке 5.2.4: Пример \ (\ PageIndex {5} \) Найдите амплитуду и период \ (y = 2 — 3 \, \ sin \; \ frac {2 \ pi} {3} x \). Решение Амплитуда \ (- 3 \, \ sin \; \ frac {2 \ pi} {3} x \) равна \ (| -3 | = 3 \). До сих пор в наших примерах мы могли довольно легко определять амплитуды синусоидальных кривых. Так будет не всегда. Пример \ (\ PageIndex {7} \) Найдите амплитуду и период \ (y = 3 \, \ sin \; x + 4 \, \ cos \; x \). Решение Иногда это называют комбинацией синусоидальной кривой , поскольку это сумма двух таких кривых. Период по-прежнему легко определить: поскольку \ (\ sin \; x \) и \ (\ cos \; x \) каждый повторяется каждые \ (2 \ pi \) радиан, то и комбинация \ (3 \, \ грех \; х + 4 \, \ соз \; х \). Из графика видно, что амплитуда равна \ (5 \), что может быть не сразу очевидно, просто взглянув на определение функции.Фактически, определение \ (y = 3 \, \ sin \; x + 4 \, \ cos \; x \) может соблазнить вас подумать, что амплитуда равна \ (7 \), поскольку наибольшее значение \ (3 \, \ sin \; x \) может быть равно \ (3 \), а наибольшее из возможных значений \ (4 \, \ cos \; x \) — это \ (4 \), так что наибольшая их сумма может быть равно \ (3 + 4 = 7 \). Однако \ (3 \, \ sin \; x \) никогда не может равняться \ (3 \) для того же \ (x \), которое делает \ (4 \, \ cos \; x \) равным \ (4 \ ) (Зачем?). Существует полезный метод (который мы обсудим далее в главе 6) для демонстрации того, что амплитуда \ (y = 3 \, \ sin \; x + 4 \, \ cos \; x \) равна \ (5 \ ).Пусть \ (\ theta \) будет углом, показанным в правом треугольнике \ [\ nonumber \ begin {align *} Таким образом, \ (| y | = | 5 \, \ sin \; (x + \ theta) | = | 5 | \, \ cdot \, | \ sin \; (x + \ theta) | \ le (5) (1) = 5 \), поэтому амплитуда \ (y = 3 \, \ sin \; x + 4 \, \ cos \; x \) равна \ (5 \). Как правило, комбинация синусов и косинусов будет иметь период, равный наименьшему общему кратному периодов добавляемых синусов и косинусов. В примере 5.9 \ (\ sin \; x \) и \ (\ cos \; x \) каждый имеет период \ (2 \ pi \), поэтому наименьшее общее кратное (которое всегда является целым числом , кратным ) равно \ (1 \, \ cdot \, 2 \ pi = 2 \ pi \). Пример \ (\ PageIndex {8} \) Найдите период \ (y = \ cos \; 6x + \ sin \; 4x \). Решение Период \ (\ cos \; 6x \) равен \ (\ frac {2 \ pi} {6} = \ frac {\ pi} {3} \), а период \ (\ sin \; 4x \) равно \ (\ frac {2 \ pi} {4} = \ frac {\ pi} {2} \). Наименьшее общее кратное для \ (\ frac {\ pi} {3} \) и \ (\ frac {\ pi} {2} \) равно \ (\ pi \): \ [\ nonumber \ begin {alignat *} {4} Таким образом, период \ (y = \ cos \; 6x + \ sin \; 4x \) равен \ (\ pi \). А как насчет амплитуды? К сожалению, мы не можем использовать технику из примера 5.9, так как мы не берем косинус и синус одного и того же угла; мы берем косинус \ (6x \), но синус \ (4x \). В этом случае из графика видно, что максимум близок к \ (2 \), а минимум близок к \ (- 2 \). В главе 6 мы опишем, как использовать программу численных вычислений, чтобы показать, что максимум и минимум равны \ (\ pm \, 1.2} \). Обратите внимание, что этот метод работает только в том случае, если угол \ (\ omega x \) одинаков как для синуса, так и для косинуса. Мы видели, как добавление константы к функции сдвигает весь график по вертикали. Теперь мы увидим, как сдвинуть весь график периодической кривой по горизонтали. Рассмотрим функцию вида \ (y = A \, \ sin \; \ omega x \), где \ (A \) и \ (\ omega \) ненулевые константы. Для простоты мы будем предполагать, что \ (A> 0 \) и \ (\ omega> 0 \) (в общем случае любой из них может быть отрицательным). Теперь рассмотрим функцию \ (y = A \, \ sin \; (\ omega x — \ phi) \), где \ (\ phi \) — некоторое постоянный. Амплитуда по-прежнему \ (A \), а период по-прежнему \ (\ frac {2 \ pi} {\ omega} \), поскольку \ (\ omega x — \ phi \) является линейной функцией \ (x \). Кроме того, мы знаем, что синусоидальная функция проходит весь цикл, когда ее угол изменяется от \ (0 \) до \ (2 \ pi \).Здесь мы берем синус угла \ (\ omega x — \ phi \). Так как \ (\ omega x — \ phi \) переходит от \ (0 \) к \ (2 \ pi \), полный цикл функции \ (y = A \, \ sin \; (\ omega x — \ phi) \) будет отслеживаться. Этот цикл начинается, когда \ [\ nonumber \ omega x — \ phi ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {\ phi} {\ omega} \] и заканчивается, когда \ [\ nonumber \ omega x — \ phi ~ = ~ 2 \ pi \ quad \ Rightarrow \ quad x ~ = ~ \ frac {2 \ pi} {\ omega} \; + \; \ frac {\ phi} { \ omega} ~. Таким образом, график \ (y = A \, \ sin \; (\ omega x — \ phi) \) — это просто график \ (y = A \, \ sin \; \ omega x \), сдвинутый по горизонтали by \ (\ frac {\ phi} {\ omega} \), как на рисунке 5.2.11. График смещается вправо, когда \ (\ phi> 0 \), и влево, когда \ (\ phi <0 \). Величина сдвига \ (\ frac {\ phi} {\ omega} \) называется фазовым сдвигом графика. Фазовый сдвиг определяется аналогично для других тригонометрических функций. Пример \ (\ PageIndex {9} \) Найдите амплитуду, период и фазовый сдвиг \ (y = 3 \, \ cos \; (2x — \ pi) \). Решение Амплитуда равна \ (3 \), период равен \ (\ frac {2 \ pi} {2} = \ pi \), а фазовый сдвиг равен \ (\ frac {\ pi} {2} \).График показан на Рисунке 5.2.12: Обратите внимание, что график такой же, как график \ (y = 3 \, \ cos \; 2x \), сдвинутый вправо на \ (\ frac {\ pi} {2} \), количество фазы сдвиг. Пример \ (\ PageIndex {10} \) Найдите амплитуду, период и фазовый сдвиг \ (y = -2 \, \ sin \; \ left (3x + \ frac {\ pi} {2} \ right) \). Решение Амплитуда равна \ (2 \), период равен \ (\ frac {2 \ pi} {3} \), а фазовый сдвиг равен \ (\ frac {- \ frac {\ pi} {2}} { 3} = — \ frac {\ pi} {6} \).\ circ \)) не в фазе, и \ (\ sin \; x \) будет сказано, что отставание \ (\ sin \; \ left (x — \ frac {\ pi} {6} \ right) \ ) на \ (\ frac {\ pi} {6} \) радиан, а \ (\ sin \; \ left (x — \ frac {\ pi} {6} \ right) \) ведет \ ( \ sin \; x \) на \ (\ frac {\ pi} {6} \) радиан. Периодические функции с одинаковым периодом и одинаковым фазовым сдвигом — это в фазе . Ниже приводится сводка свойств тригонометрических графиков: Для любых констант \ (A \ ne 0 \), \ (\ omega \ ne 0 \) и \ (\ phi \): В этом разделе вы: Пандус для инвалидных колясок, соответствующий стандартам Закона об американцах с ограниченными возможностями, должен образовывать угол с землей, касательная которого составляет 112112 или меньше, независимо от его длины. Касательная представляет собой отношение, поэтому это означает, что на каждый 1 дюйм подъема у рампы должен быть 12 дюймов пробега. Тригонометрические функции позволяют нам определять формы и пропорции объектов независимо от точных размеров. Чтобы определить остальные функции, мы еще раз нарисуем единичный круг с точкой (x, y) (x, y), соответствующей углу t, t, как показано на рисунке 1.Как и в случае с синусом и косинусом, мы можем использовать координаты (x, y) (x, y), чтобы найти другие функции. Рисунок 1 Первая функция, которую мы определим, — это касательная. Тангенс угла — это отношение значения y к значению x соответствующей точки на единичной окружности. На рисунке 1 тангенс угла tt равен yx, x ≠ 0.yx, x ≠ 0. Поскольку значение y равно синусу t, t, а значение x равно косинусу t, t, тангенс угла tt также может быть определен как sintcost, cost ≠ 0. Если tt — действительное число и (x, y) (x, y) — точка, в которой конечная сторона угла tt радиан пересекает единичный круг, то Точка (−32,12) (- 32,12) находится на единичной окружности, как показано на рисунке 2. Рисунок 2 Поскольку нам известны координаты (x, y) (x, y) точки на единичной окружности, обозначенной углом t, t, мы можем использовать эти координаты для нахождения шести функций:
sint = y = 12cost = x = −32tant = yx = 12−32 = 12 (−23) = — 13 = −33sect = 1x = 1−32 = −23 = −233csct = 1y = 112 = 2cott = xy = — 3212 = −32 (21) = — 3sint = y = 12cost = x = −32tant = yx = 12−32 = 12 (−23) = — 13 = −33sect = 1x = 1−32 = −23 = −233csct = 1у = 112 = 2котт = ху = −3212 = −32 (21) = — 3 Попробуй # 1 Точка (22, −22) (22, −22) находится на единичной окружности, как показано на рисунке 3.Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott. Рисунок 3 Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cottcott, когда t = π6. Ранее мы использовали свойства равносторонних треугольников, чтобы продемонстрировать, что sinπ6 = 12sinπ6 = 12 и cosπ6 = 32.cosπ6 = 32.Мы можем использовать эти значения и определения тангенса, секанса, косеканса и котангенса как функций синуса и косинуса, чтобы найти остальные значения функции. Попробуй # 2 Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cottcott, когда t = π3.t = π3. Поскольку мы знаем значения синуса и косинуса для общих углов первого квадранта, мы можем найти другие значения функций для этих углов, установив xx равным косинусу и yy равным синусу, а затем используя определения тангенса, секанс, косеканс и котангенс. Таблица 1 Мы можем оценивать тригонометрические функции углов вне первого квадранта, используя опорные углы, как мы уже делали с функциями синуса и косинуса. Чтобы помочь нам запомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера.Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который равен « A », и ll из шести тригонометрических функций положительны. В квадранте II « S mart» только s и его обратная функция, косеканс, положительны. Рисунок 4 Учитывая угол не в первом квадранте, используйте опорные углы, чтобы найти все шесть тригонометрических функций. Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −5π6. Угол между конечной стороной этого угла и осью x равен π6, π6, так что это опорный угол.Поскольку −5π6−5π6 находится в третьем квадранте, где и xx, и yy отрицательны, косинус, синус, секанс и косеканс будут отрицательными, а тангенс и котангенс будут положительными. Попробуй # 3 Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −7π4. − 7π4. Чтобы иметь возможность свободно использовать наши шесть тригонометрических функций как с положительными, так и с отрицательными угловыми входами, мы должны изучить, как каждая функция обрабатывает отрицательный вход. Рассмотрим функцию f (x) = x2, f (x) = x2, показанную на рисунке 5. График функции симметричен относительно оси y . На всем протяжении кривой любые две точки с противоположными значениями x имеют одинаковое значение функции. Это соответствует результату расчета: (4) 2 = (- 4) 2, (4) 2 = (- 4) 2, (−5) 2 = (5) 2, (- 5) 2 = (5) 2 ,
и так далее. Таким образом, f (x) = x2f (x) = x2 — четная функция, такая функция, что два противоположных входа имеют одинаковый выход.Это означает, что f (−x) = f (x) .f (−x) = f (x). Теперь рассмотрим функцию f (x) = x3, f (x) = x3, показанную на рисунке 6. График не симметричен относительно оси y . На всем протяжении графика любые две точки с противоположными значениями x также имеют противоположные значения y . Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичный круг с положительным и отрицательным углом, как на рисунке 7. Синус положительного угла равен y.y. Синус отрицательного угла — y . Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице 2. Рисунок 7 Таблица 2 Четная функция — это функция, в которой f (−x) = f (x). Нечетная функция — это функция, в которой f (−x) = — f (x) .f (−x) = — f (x). Косинус и секанс четные: Синус, тангенс, косеканс и котангенс нечетны: Если секанс угла tt равен 2, каков секанс угла −t? −t? Секанс — четная функция.Секущая угла равна секущей его противоположности. Таким образом, если секанс угла t равен 2, секанс −t − t также равен 2. Попробуй # 4 Если котангенс угла tt равен 3,3, то каков котангенс угла −t? −t? Мы исследовали ряд свойств тригонометрических функций. Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции могут быть связаны с функциями синуса и косинуса с помощью следующих основных соотношений: Поскольку нам известны значения синуса и косинуса для этих углов, мы можем использовать тождества для оценки других функций. ⓐ ⓑ Попробуй # 5 Оценить csc (7π6).csc (7π6). Упростите secttant.secttant. Мы можем упростить это, переписав обе функции в терминах синуса и косинуса. Показав, что secttantsecttant можно упростить до csct, csct, мы фактически установили новую идентичность. Попробуй # 6 Упростить (тант) (стоимость). (Тант) (стоимость). Мы можем использовать эти фундаментальные тождества для вывода альтернативных форм пифагорейской идентичности, cos2t + sin2t = 1.cos2t + sin2t = 1. Одна форма получается делением обеих частей на cos2t: cos2t: Другая форма получается делением обеих частей на sin2t: sin2t: Если cos (t) = 1213 cos (t) = 1213 и tt находится в квадранте IV, как показано на рисунке 8, найдите значения других пяти тригонометрических функций. Рисунок 8 Мы можем найти синус, используя тождество Пифагора, cos2t + sin2t = 1, cos2t + sin2t = 1, и оставшиеся функции, связав их с синусом и косинусом. Знак синуса зависит от значений y в квадранте, где расположен угол.Поскольку угол находится в квадранте IV, где значения y отрицательны, его синус отрицательный, −513. − 513. Остальные функции можно вычислить с помощью тождеств, связывающих их с синусом и косинусом. Если sec (t) = — 178sec (t) = — 178 и 0 Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция. Тригонометрические функции периодические. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или 2π, 2π,
приведет к одинаковым выводам для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты. Другие функции также могут быть периодическими.Например, продолжительность месяцев повторяется каждые четыре года. Если xx представляет собой продолжительность, измеряемую в годах, а f (x) f (x) представляет количество дней в феврале, тогда f (x + 4) = f (x). F (x + 4) = f ( Икс).
Этот образец повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и 4 годами ранее. Положительное число 4 — это наименьшее положительное число, которое удовлетворяет этому условию и называется периодом. Период PP повторяющейся функции ff — это число, представляющее интервал, такой что f (x + P) = f (x) f (x + P) = f (x) для любого значения x.x. Период функций косинуса, синуса, секанса и косеканса равен 2π.2π. Период функций касательной и котангенса равен π.π. Найдите значения шести тригонометрических функций угла tt по рисунку 9 . Рисунок 9 Найдите значения шести тригонометрических функций угла tt. Рисунок 10 Если sin (t) = — 32sin (t) = — 32 и cos (t) = 12, cos (t) = 12, найти sec (t), csc (t), tan (t), cot (t) .sec (t), csc (t), tan (t), cot (t). Если sin (t) = 22sin (t) = 22
и cos (t) = 22, cos (t) = 22, найти sec (t), csc (t), tan (t) и cot (t) .sec (t), csc (t), tan (t) ) И детская кроватка (t). Мы научились оценивать шесть тригонометрических функций для общих углов первого квадранта и использовать их в качестве опорных углов для углов в других квадрантах. Вычисление касательной функции с помощью научного калькулятора, в отличие от графического калькулятора или системы компьютерной алгебры, похоже на вычисление синуса или косинуса: введите значение и нажмите клавишу TAN. Для обратных функций может не быть каких-либо специальных клавиш с надписью CSC, SEC или COT.В этом случае функция должна быть вычислена как обратная величина синуса, косинуса или тангенса. Если нам нужно работать с градусами, а наш калькулятор или программное обеспечение не имеет режима градусов, мы можем ввести градусы, умноженные на коэффициент преобразования π180π180, чтобы преобразовать градусы в радианы. Чтобы найти секущую 30 °, 30 °, мы могли бы нажать или Для угла в радианах используйте научный калькулятор, чтобы найти косеканс. Если угол измеряется в радианах, используйте графическую утилиту / калькулятор, чтобы найти косеканс. Вычислите косеканс 5π7.5π7. Для научного калькулятора введите следующую информацию: Попробуй # 10 Вычислите котангенс −π8. − π8. Могут ли значения синуса и косинуса радианной меры когда-либо быть равными на интервале [0,2π), [0,2π)? Если да, то где? Каким должен быть косинус ππ градусов? Объясните свои рассуждения. Для любого угла в квадранте II, если бы вы знали синус угла, как бы вы могли определить косинус угла? Опишите секущую функцию. Тангенс и котангенс имеют период π.π.
Что это говорит нам о выходе этих функций? Для следующих упражнений найдите точное значение каждого выражения. В следующих упражнениях для оценки выражения используйте исходные углы. Если sint = 34, sint = 34 и tt находится в квадранте II, найдите costcost, sectsect, csctcsct, tanttant, cott.cott. Если cost = −13, cost = −13 и tt находится в квадранте III, найдите sint, sect, csct, tant, cott.sint, sect, csct, tant, cott. Если tant = 125, tant = 125 и 0≤t <π2,0≤t <π2, найдите sint, cost, sect, csct, sint, cost, sect, csct и cott.cott. Если sint = 32sint = 32 и cost = 12, cost = 12, найдите sect, csct, tant, sect, csct, tant и cott.коттеджи. Если sin40 ° ≈0,643 sin40 ° ≈0,643 а также cos40 ° ≈0,766 cos40 ° ≈0,766 найти sec40 °, csc40 °, tan40 °, sec40 °, csc40 °, tan40 °, а также cotand40 ° .cotand40 °. Если sint = 22, sint = 22, что такое sin (−t)? Sin (−t)? Если стоимость = 12, стоимость = 12, что такое cos (−t)? Cos (−t)? Если sect = 3.1, sect = 3.1, что такое sec (−t)? Sec (−t)? Если csct = 0,34, csct = 0,34, что такое csc (−t)? Csc (−t)? Если tant = −1,4, tant = −1,4, что такое tan (−t)? Tan (−t)? Если cott = 9,23, cott = 9,23, что такое детская кроватка (−t)? Cot (−t)? В следующих упражнениях используйте угол в единичной окружности, чтобы найти значение каждой из шести тригонометрических функций. Для выполнения следующих упражнений используйте графический калькулятор. Для следующих упражнений используйте личности, чтобы оценить выражение. Если tan (t) ≈2,7, tan (t) ≈2,7 и sin (t) ≈0,94, sin (t) ≈0,94, найти cos (t) .cos (t). Если tan (t) ≈1,3, tan (t) ≈1,3 и cos (t) ≈0,61, cos (t) ≈0,61, найти sin (t) . Если csc (t) ≈3,2, csc (t) ≈3,2 и cos (t) ≈0,95, cos (t) ≈0,95, найти tan (t) .tan (t). Если cot (t) ≈0,58, cot (t) ≈0,58 и cos (t) ≈0,5, cos (t) ≈0,5, найти csc (t) .csc (t). Определите, является ли функция f (x) = 2sinxcosxf (x) = 2sinxcosx четной, нечетной или ни одной из них. Определите, является ли функция f (x) = 3sin2xcosx + secxf (x) = 3sin2xcosx + secx четной, нечетной или ни одной из них. Определите, является ли функция f (x) = sinx − 2cos2xf (x) = sinx − 2cos2x четной, нечетной или ни одной из них. Определите, является ли функция f (x) = csc2x + secxf (x) = csc2x + secx четной, нечетной или ни одной из них. В следующих упражнениях используйте идентификаторы, чтобы упростить выражение. Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 15cos (1600d), h = 15cos (1600d), где hh представляет количество солнечных часов, а dd — день в году. Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 16cos (1500d), h = 16cos (1500d), где hh
представляет часы солнечного света, а dd
это день года.Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света 24 сентября, 267 -й день в году. Укажите период функции. Уравнение P = 20sin (2πt) + 100P = 20sin (2πt) +100 моделирует артериальное давление, P, P, где tt
представляет время в секундах. (а) Определите кровяное давление через 15 секунд. б) Какое максимальное и минимальное артериальное давление? Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 6, y = 2cosx + 6, где xx представляет угол поворота коленчатого вала.Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55 ° 0,55 °. Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 5, y = 2cosx + 5, где xx представляет угол поворота коленчатого вала. Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55 ° 0,55 °. Древнегреческие геометры считали углы только между 0 ° и 180 °, и они не считали ни прямой угол 180 °, ни вырожденный угол 0 ° углами. Рассмотрим единичный круг. Обозначьте его центр (0,0) как O, и обозначьте точку (1,0) на нем как A. Как движущаяся точка B движется по единичной окружности, начиная с A и двигаясь по против часовой стрелки, угол AOB как угол 0 ° и увеличивается.Когда B прошел весь путь по окружности и вернулся к A, , тогда угол AOB будет углом 360 °. Конечно, это тот же угол, что и угол 0 °, поэтому мы можем идентифицировать эти два угла. Поскольку B продолжает второй раз по кругу, мы получаем углы от 360 ° до 720 °. Это те же углы, которые мы видели в первый раз, но у нас есть разные названия. Например, прямой угол обозначается как 90 ° или 450 °. Если B начинается в той же точке A и движется по часовой стрелке, то мы получим отрицательные углы, или, точнее, названия в отрицательных градусах для тех же углов. Например, если вы пройдете четверть круга по часовой стрелке, угол AOB будет назван как –90 °. Конечно, это то же самое, что и угол 270 °. Итак, в общем, любой угол назван бесконечным множеством имен, но все они отличаются друг от друга на 360 °. cos ( θ + 360 °) = cos θ. Многие из современных приложений тригонометрии вытекают из использования тригонометрии в исчислении, особенно те приложения, которые имеют дело непосредственно с тригонометрическими функциями. cos ( θ + 2 π ) = cos θ. sin θ = cos ( π /2 — θ ) Мы видели это раньше, но теперь у нас есть это для любого угла θ. Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол заменяется его дополнением. Теперь мы готовы рассмотреть синус и косинус как функции. Синус — нечетная функция, а косинус — четная cos (- θ ) = cos θ. Эти факты вытекают из симметрии единичной окружности относительно оси x . Угол — t — тот же угол, что и t , за исключением того, что он находится с другой стороны оси x . Переворачивание точки ( x, y ) на другую сторону оси x превращается в ( x, –y ), поэтому координата y инвертируется, то есть синус инвертируется , но координата x осталась прежней, то есть косинус не изменился. Во-первых, заметим, что он периодичен с периодом 2 π . С геометрической точки зрения это означает, что если вы возьмете кривую и сдвинете ее 2 π влево или вправо, кривая вернется в исходное положение.Во-вторых, обратите внимание, что график находится в пределах одной единицы оси t . Мало что еще является очевидным, за исключением случаев, когда он увеличивается и уменьшается. Например, sin t увеличивается от 0 до π /2, поскольку координата y точки B увеличивается с увеличением угла AOB от 0 до π /2. Теперь давайте посмотрим на график косинуса. Опять же, возьмите горизонтальную ось за ось t , а теперь возьмите вертикальную ось за ось x и изобразите уравнение x = cos t. Обратите внимание, что он выглядит так же, как график sin t , за исключением того, что он сдвинут влево на π /2. Это из-за тождества cos t = sin ( π /2 + t ). Хотя мы раньше не сталкивались с этим тождеством, оно легко следует из уже рассмотренных: cos t = cos — t = sin ( π /2 — (- t )) = sin ( π /2 + т ). Вы также можете видеть, что тангенс имеет период π ; также есть вертикальные асимптоты через каждые π единиц слева и справа.Алгебраически эта периодичность выражается как tan ( t + π ) = tan t. График котангенса очень похож. Это сходство просто потому, что котангенс t является тангенсом дополнительного угла π — t. Как и следовало ожидать, график косеканса очень похож на график секанса. Как вы только что видели, запись для этих обратных тригонометрических функций уникальна. Мы используем показатель степени -1, чтобы сообщить нам, что мы имеем дело с обратной триггерной функцией. Это обозначение, которое вы чаще всего встретите в учебниках и в различных задачах триггера. И это, скорее всего, обозначение, которое вы будете использовать при написании своих задач. Но в тригонометрии у нас также есть формальные имена для этих функций. Мы называем функцию обратного синуса функцией арксинуса, функцию обратного косинуса функцией арккосинуса, а функцию арктангенса — функцией арктангенса.Хотя первые обозначения чаще встречаются в задачах, вы встретите эти формальные имена в математических дискуссиях. Итак, хорошо знать и то, и другое. Эти имена легко запомнить, если связать дугу с показателем -1. Все обратные тригонометрические функции начинаются с префикса arc- , за которым следует имя уже известной нам тригонометрической функции. Теперь вернемся к обычным триггерным функциям синуса, косинуса и тангенса. Красная линия — это график функции синуса , синяя линия — график функции косинуса , а фиолетовая линия — график функции тангенса .Что интересного вы заметили в этих графиках? Все эти графики периодически повторяются. Функция тангенса повторяет каждые пробелы пи, в то время как функции синуса и косинуса повторяются через каждые 2 пробела. Каждый раз, когда функция повторяется, мы получаем один и тот же выходной ответ. Поскольку эти функции повторяются, мы должны ограничить диапазон или выходные значения наших обратных триггерных функций. В противном случае мы бы каждый раз получали разные ответы. Ограничивая диапазон нашей обратной функции, мы находим главное или первичное значение нашей обратной функции.Это то, что происходит внутри вашего калькулятора всякий раз, когда вы выполняете функцию обратного триггера. Эти диапазоны не совсем соответствуют тому, как повторяются наши обычные триггерные функции.На этот раз у нас есть функция обратного косинуса, которая ограничена между 0 и пи. Функция обратного синуса ограничена диапазоном от -pi / 2 до pi / 2, включая эти точки. Функция обратной тангенса имеет такой же ограниченный диапазон, что и обратный синус, за исключением того, что две точки -pi / 2 и pi / 2 не включены. Что означают эти ограничения? Эти ограничения говорят вам, что ответ, который вы получите на калькуляторе, будет в этих пределах. И если вы рассчитываете вручную, эти пределы говорят вам, что ваш основной ответ также должен находиться в этом диапазоне.-1 (1) = пи / 2 . Это основной ответ, но на самом деле у нас есть ответы через каждые 2 пи. Мы можем включить все наши ответы, написав pi / 2 + 2 * pi * n , где n — количество пробелов, на которые ответ находится вне основного ответа. Поскольку наши обратные функции ограничены своим диапазоном, то же самое происходит и с нашей функцией, когда мы строим график. Вместо того, чтобы наши функции продолжались вечно, как наши графики синуса, косинуса и тангенса, наши графики арксинуса, арккосинуса и арктангенса показывают график только в пределах принятого ограниченного диапазона. На этом графике показана функция арксинуса , как красная линия, арккосинус , функция как синяя линия и арктангенс , функция как фиолетовая линия: Видите, как мы ограничили график каждой из этих функций? Если бы мы не ограничивали их, эти графики продолжали бы бесконечно повторяться снова и снова, как наши функции синуса, косинуса и тангенса. Давайте рассмотрим, что мы узнали. Обратные тригонометрические функции — это функции, обратные нашим тригонометрическим функциям. Наши триггерные функции — это наши обычные функции синуса, косинуса и тангенса. Есть два способа написать наши обратные функции. Мы можем называть их по имени. У нас есть арксинус, обратный синусу, арккосинус — арккосинус, а арктангенс — арктангенс. Мы также можем записать их, используя символ экспоненты -1. Эта обратная функция позволяет нам найти угол триггерной функции.-1 (1) . Мы оцениваем правую сторону, чтобы найти ответ. Мы можем использовать наш калькулятор, чтобы найти ответ. Если мы это сделаем, мы получим первичный ответ. Помните, что наши функции синуса и косинуса повторяются через каждые два пробела, а наша касательная функция повторяется через каждые два пробела. Поскольку наши обратные функции ограничены первичным ответом, каждая обратная функция также имеет ограниченный диапазон. Они следующие: Графики обратных функций также показывают этот ограниченный диапазон. По завершении этого урока у вас будет возможность: Тригонометрия — это раздел математики, который имеет дело с прямоугольными треугольниками и отношениями между их сторонами и углами.(Слово «триггер» связано со словом «треугольник», чтобы помочь вам запомнить.) Обычно в тесте ACT есть около 4-6 вопросов, касающихся тригонометрии (официальные инструкции по тестированию ACT говорят, что проблемы тригонометрии составляют 7% теста). Эта статья будет вашим исчерпывающим руководством по тригонометрии, которое вам нужно знать для ACT. Мы расскажем вам о значении тригонометрии, формулах и понимании, которые вам нужно знать, а также о том, как решать некоторые из самых сложных тригонометрических задач ACT. Тригонометрия изучает отношения между сторонами и углами прямоугольных треугольников. Соотношения между размерами сторон прямоугольного треугольника и размерами его углов постоянны, независимо от того, насколько большой или маленький треугольник. Некоторые из множества различных возможных типов прямоугольных треугольников. Если вы знаете размер одной стороны и один угол, отличный от 90 ° для прямоугольного треугольника, вы сможете определить остальные стороны и углы треугольника. $ c = √340 $ или $ c = 2√85 $ Но что, если у нас есть только одна длина стороны и мера одного из углов (не девяносто градусов)? Даже если у нас есть длина только одной стороны, мы все равно можем найти другие, используя тригонометрию, потому что у нас есть мера одного из острых углов. Итак, здесь мы могли бы сказать $ sin 34 ° = 12 / \ hypotenuse \ $ Итак, $ \ hypotenuse \ = 12 / {sin 34 °} $ Не волнуйтесь, если это еще не имеет для вас смысла! Мы разберем каждый шаг по мере продвижения в руководстве. (Примечание: чтобы найти фактическую величину угла в градусах с использованием двух длин сторон, вам нужно будет выполнить вычисление обратной функции (также называемой функцией «дуги»). Но НЕ БОЙТЕСЬ — ACT никогда не заставит вас Сделайте это! С точки зрения подготовки к математике ACT, поймите, что тест попросит вас вычислить только достаточно далеко, чтобы сказать, например, «$ Cosinex = 4/5 $». Мы находим эти меры, понимая отношение определенных сторон треугольника к их соответствующим углам. Это так называемые тригонометрические функции, и есть три, которые вы должны запомнить для ACT: синус, косинус и тангенс. Самый простой способ понять это — использовать мнемоническое устройство SOH, CAH, TOA , о котором мы поговорим чуть позже.> / P> Тригонометрия широко используется в навигации, а также для расчета высот и расстояний. (На случай, если вам интересно, нужен ли вам триггер в реальной жизни.) Вопросы по тригонометрии в ACT можно разделить на несколько категорий.Мы предоставили несколько реальных математических примеров ACT, чтобы продемонстрировать каждую концепцию. # 1: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла из заданной прямоугольной треугольной диаграммы. # 2: Нахождение синуса, косинуса или тангенса прямоугольного треугольника из задачи со словами. Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы составляет 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены? А.10 $ tan23 ° $ Б. 10 $ sin23 ° $ C. 10 $ cos23 ° $ D. $ cos {10/23} $ E. $ sin {10/23} # 3: Нахождение синуса, косинуса или тангенса (или, реже, косеканса, секанса или котангенса) угла от заданного sin, cos или tan и диапазона, в который попадает угол. Если $ tanΘ = 3/4 \ и 180 ° <Θ <270 ° $, что такое $ sinΘ $? A. $ 4/3 $ Б. $ -4 / 3 $ C. $ -3 / 4 $ Д.$ 3/5 $ -3 Э. $ / 5 # 4: Определение периода или амплитуды графика. Какова амплитуда графика? А. Б. 2 К. π Д. 2π E. 0 # 5: Закон синусов или закон косинусов. Для такого вопроса, , они дадут вам формулы закона синусов или закона косинусов , так что вам не нужно беспокоиться об их запоминании.Однако наличие формулы вам не очень поможет, если она вам покажется или звучит как тарабарщина. По мере того, как вы будете изучать это руководство, выполнять практические вопросы по математике ACT, которые мы предоставили, и знакомиться с языком тригонометрии, используемым в этих вопросах, их станет намного легче решать. Мы рассмотрим, как решить каждую из этих проблем, , но это даст вам представление о том, как будут выглядеть триггерные проблемы ACT в тесте. Помните эту знаменитую мнемонику? Это спасет вашу жизнь.Давайте пройдемся по каждому. Синус — это функция, в которой значение синуса (также называемого «грехом») угла тета можно найти, используя отношение стороны треугольника, противоположной углу тета, к гипотенузе треугольника. SOH : S дюйм $ Θ $ = O положительная сторона треугольника / H гипотенуза треугольника Итак, в этом треугольнике $ sinΘ = b / c $, потому что сторона, противоположная углу $ Θ $, равна b , а гипотенуза — c . Косинус — это функция, в которой значение косинуса (также называемого «$ cos $») угла тета ($ Θ $) можно найти, используя отношение стороны треугольника, примыкающей к углу $ Θ $ (т. Е. не гипотенуза) над гипотенузой треугольника. CAH : C os $ Θ $ = A djcenter сторона треугольника / H ypotenuse of треугольник Примечание: смежный означает, что сторона треугольника касается угла / помогает создать угол $ Θ $. В этом же треугольнике $ cosΘ = a / c $, потому что сторона, примыкающая к углу $ Θ $, равна a , а гипотенуза — c . Касательная — это функция, в которой значение тангенса (также называемого «тангенс») угла тета может быть найдено с помощью отношения стороны треугольника, противоположной углу тета, по соседней стороне треугольника к тета (что не является гипотенуза). TOA : T и $ $ = O противоположная сторона треугольника / A смежная сторона треугольника. В этом же треугольнике $ tanΘ = b / a $, потому что сторона, противоположная углу $ Θ $, равна b , а смежная сторона — a . Теперь, когда вы знакомы со своими мнемоническими устройствами, вы можете составлять вопросы в несколько этапов. Например, немного более сложный вопрос может выглядеть примерно так: Вам даны длины двух сторон треугольника, но для решения задачи требуется длина третьей стороны.2 = 21 $ $ x = √21 $ Теперь, когда у вас есть размер третьей стороны, вы можете найти $ tanB $. $ TanB = \ напротив / \ Соседний $ $ TanB = √21 / 2 $ Итак, ответ — франков, √21 долл. США / 2 долл. США Гипотенуза треугольника всегда остается неизменной, но противоположные или смежные стороны меняются в зависимости от угла фокусировки. Например, если вы пытаетесь найти $ sin $ угла $ γ $, вы должны использовать соотношение $ b / c $; если вы пытаетесь найти грех угла $ ξ $, вы должны использовать соотношение $ a / c $.2 = 44 $ $ x = √44 $ Теперь $ sin $ = $ \ Against / \ hypotenuse $, поэтому $ sinM = √44 / 12 $. Итак, ответ — K. Нет необходимости находить градусную меру (арксинус или обратный синус) угла M на вашем калькуляторе — это все, что вам нужно. Вам также может быть предоставлено значение угла и длины стороны знаменателя вашего соотношения. В этом случае управляйте уравнением, как алгебраическим уравнением, и умножайте противоположную сторону на знаменатель. $ sin Θ = \ напротив / \ гипотенуза $ $ гипотенуза $ * sinΘ = $ напротив Поскольку вас спрашивают о длине лодки до причала, а эта сторона составляет против под углом 52 °, вы знаете, что вам понадобится либо sin, либо tan (cos использует смежную и гипотенузу, а не противоположную). Вам также дается смежной длины , 30 миль, поэтому вы будете использовать tan. (Вы можете сказать, что эта сторона смежная, потому что сторона, противоположная углу 90 °, является гипотенузой, поэтому 30 миль должны быть еще одним катетом треугольника). $ tanΘ = \ напротив / \ рядом $ So $ tan52 ° = x / 30 $ 30 $ тан52 ° = x Итак, ответ — франков, длина лодки до причала 30 тангенциальных 52 °. И снова проблема со словом из ранее. Алекс подпирает лестницу к стене. Лестница составляет 23 ° от земли. Если длина лестницы составляет 10 футов, каково выражение для определения расстояния, на котором основание лестницы находится от стены? А. Б. 10 $ sin23 ° $ C. 10 $ cos23 ° $ D. $ cos10 / 23 $ E. $ sin10 / 23 $ Во-первых, нарисуйте свою картинку, чтобы легче было представить, о чем вас просят. Итак, $ cos23 ° = \ смежный / 10 $ (Почему 10? Длина лестницы 10 футов) Это становится 10 $ cos23 ° = \ смежный $ Итак, ответ: C , 10 $ cos23 ° $ Короткий ответ: нет, вас не попросят определить точную величину угла в градусах с помощью тригонометрии.2)} В зависимости от того, где расположен треугольник в двухмерном пространстве, значения sin, cos и tan будут отрицательными или положительными. В двухмерном пространстве четыре квадранта, разделенных по осям x и y. Как и в случае со значениями x и y, sin, cos и tan могут быть положительными или отрицательными в зависимости от квадранта, в котором находится треугольник / угол. Хороший способ запомнить это — использовать мнемоническую аббревиатуру ASTC — A ll S tudents T ake C hemistry — чтобы увидеть, какая из функций является положительной в зависимости от квадранта. Итак, A ll положительны в квадранте I, S in положительны в квадранте II, T an положительны в квадранте III, а C os положительны в квадранте IV Если $ tanΘ = 3/4 $ и $ 180 ° <Θ <270 ° $, что такое $ sinΘ $? A. $ 4/3 $ Б. $ −4 / 3 $ C. $ -3 / 4 $ D. $ 3/5 $ -3 Э. $ / 5 Чтобы решить эту проблему, сначала определите длины сторон треугольника, используя теорему Пифагора (или используя свои знания о 3-4-5 треугольниках).2 = 25 9000 долларов США 3 $ c = 5 Итак, наша гипотенуза равна 5. Мы знаем, что $ sin Θ = \ Against / \ hypotenuse $. Итак, $ sinΘ = 3/5 $. Но подождите! Мы еще не закончили. Поскольку они сказали нам, что $ Θ $ лежит между $ 180 ° $ и $ 270 ° $, мы знаем, что значение sin для $ Θ $ отрицательно. Согласно ASTC, только тангенс угла $ Θ $ будет положительным между 180 ° $ и 270 ° $. Итак, , наш окончательный ответ — евро, $ — 3/5 $ В редких случаях на ACT вас попросят указать одну из вторичных триггерных функций. Вы могли заметить, что они похожи на основные триггерные функции, которые вы изучили выше. Фактически, эти вторичные функции являются обратными (обратными) sin, cos и тангенсом. Чтобы помочь вам запомнить, что есть что, обратите внимание на третью букву каждого слова: Косеканс — величина, обратная синусу.$ Косеканс Θ = \ гипотенуза / \ напротив $ Секанс — величина, обратная косинусу. $ Секанс Θ = \ гипотенуза / \ смежный $ Котангенс — величина, обратная касательной. $ Котангенс Θ = \ смежный / \ противоположный $ Есть две формулы, которые время от времени будут появляться в ACT. Итак, мы имеем 1 + 1 = 2 Окончательный ответ: H , 2. $$ (sinΘ) / (cosΘ) = tanΘ $$ Это уравнение имеет логический смысл, если представить его в виде диаграммы. Допустим, у вас есть треугольник, который выглядит так $ Sin Θ $ будет 5 $ / 13 $. $ Cos Θ $ будет $ 12/13 $. $ Tan Θ $ будет 5 долларов США / 12%. Вы также можете сказать $ tanΘ = {sinΘ} / {cosΘ} = {5/14} / {12/13} = (5/13) (13/12) = 65/156 $ (вы также можете просто отменить обе 13s для упрощения) = 5 $ / 12 $ ACT не будет запрашивать у вас график триггерной функции, но вам нужно распознать, как каждая функция выглядит в виде графика. Синусоидальный график пересекает начало координат в виде волны. Это «нечетная» функция, потому что она не симметрична относительно оси y. График косинусов также «волнистый», но не пересекает начало координат. Он спускается после $ x = 0 $. Это может помочь вам вспомнить, что косинус убывает после x = 0, если подумать, что « co — это low » Косинус является «четной» функцией, потому что он симметричен относительно оси y.Это означает, что для всех значений $ x $ $ f (x) = f (-x) $. Например, на приведенном выше графике $ y = 0,7 $ как при $ x = 1 $ , так и при $ x = -1 $ Иногда все, что вам зададут, это определить, является ли график четным или нечетным, а также является ли график sin или cos. Вам будет легко понять это, если вы помните основные элементы тригонометрических графиков. Хотя вы можете понять этот вопрос из предоставленной информации, это займет гораздо меньше времени, если вы узнаете, что график является косинусным и, следовательно, четным. Касательный график выглядит совсем иначе, чем графики sin и cos — вам просто нужно уметь распознавать касательный график, когда вы его видите. ACT иногда просит вас найти период или амплитуду синусоидального или косинусного графика. Период графика — это расстояние по оси x, с которого график начинает повторяться.Найдите расстояние по оси x, на котором точка возвращается в исходное положение после завершения полного цикла . Период синусоидального графика здесь равен 2π. Он должен идти как вверх, так и вниз, прежде чем окончательно вернуться к $ y = 0 $. Период косинусного графика здесь также равен 2π. Он должен сначала спуститься, а затем снова подняться, чтобы вернуться в исходное положение при $ y = 1 $. Амплитуда графика — это его высота от оси x, расстояние между его наивысшим значением $ y $ и $ x = 0 $. Итак, чтобы использовать тот же график, что и выше: И синус, и косинус имеют амплитуду 1 (и, опять же, период 2π). Радианы — это еще один (более точный) способ измерения расстояния по окружности, а не в градусах. Вместо градусов радианы выражаются через π (и доли π). Если у вас есть полный круг, это 360 градусов. Это также 2π радиан. Почему 2π радиан? Что ж, придумайте формулу длины окружности. С = 2πr. Если ваш радиус равен 1, тогда ваша окружность равна 2π, что совпадает с вашей мерой в радианах. Окружность с радиусом 1 и центром в начале координат называется «единичной окружностью». Радианы удобно рассматривать, помещая их на единичный круг. Итак, если у вас есть полукруг, это 180 ° или π радиан. И так далее. 90 ° — это $ π / 2 $ радиан, 270 ° — $ (3π) / 2 $ радиан. Чтобы преобразовать градусы в радианы, проще всего использовать преобразование между 180 ° и π . Преобразовать 45 ° в радианы => $ (45) {π / 180} = π / 4 $ радиан Преобразовать $ (3π) / 4 $ радиан в градусы => $ {(3π) / 4} (180 / π) $ = 135 ° Итак, давайте рассмотрим, как разбить триггерный вопрос # 1: Определите, требует ли проблема тригонометрии. Вы можете сказать, что проблема потребует триггера, когда: # 2: Помните SOH, CAH, TOA. # 4 :. Вспомните, как выглядят графики синуса, косинуса и тангенса. И знайте, что: Период = горизонтальное расстояние Амплитуда = вертикальное расстояние # 5: Празднуйте, потому что вы ответили на триггерные вопросы ACT! Хотя проблемы тригонометрии могут показаться устрашающими, почти каждый вопрос о тригонометрии ACT может быть решен, если вы знаете основные элементы тригонометрии. Чтобы получить максимальную отдачу от подготовки к математике ACT, запомните эти три триггерные концепции: SOH, CAH, TOA, как управлять своими уравнениями и как распознавать графики функций. Если вы запомните их, вы обнаружите, что решаете практически все триггерные вопросы, которые ACT может бросить вам. Хотите больше математических стратегий и руководств ACT? Прочтите нашу статью по всем математическим темам, протестированным на ACT, чтобы убедиться, что вы их хорошо усвоили. Хотите получить высший балл по математике в ACT? Ознакомьтесь с нашей статьей о том, как набрать 36 баллов по математическому разделу ACT с помощью тестера ACT-Score. Чувствуете себя разбитым? Не знаю, с чего начать? Не ищите ничего, кроме наших статей о том, что считается хорошей, плохой или отличной оценкой ACT. Не знаете, в какие дни проводится ACT? Ознакомьтесь с нашим полным списком дат тестирования ACT, чтобы найти подходящие для вашего расписания. И если вы обнаружите, что у вас не хватает времени на математический раздел, посмотрите нашу статью о том, как перестать не хватать времени на математику ACT. Хотите улучшить свой результат SAT на 160 баллов? Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой тест SAT на 160 или более баллов. Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше. Воспользуйтесь нашей 5-дневной бесплатной пробной версией: Что делают тригонометрические личности на экзамене по математике? Поскольку математика имеет тенденцию опираться на предыдущие результаты, вы можете рассчитывать использовать все свои предыдущие математические знания при работе над задачами исчисления. Тригонометрия полезна при постановке задач с прямоугольными треугольниками. Прежде всего, вы должны быть знакомы с Unit Circle . Каждая точка ( x , y ) на окружности дает значение косинуса и синуса соответствующего угла. Например, найдите угол 2π / 3 (радианы). Основываясь на диаграмме единичного круга, вы знаете: Единичная окружность, которая отображает значения косинуса и синуса общих углов. К счастью, вам не нужно запоминать абсолютно все идентичности из класса Trig. Ниже приведен список того, что я считаю основными идентичностями. Факторные тождества полезны для повторного выражения триггерных функций в терминах sin и / или cos. Следующие правила предоставляют быстрые клавиши для работы с отрицательными входными данными. Возможно, самым известным и полезным уравнением во всей математике является теорема Пифагора. Если стороны прямоугольного треугольника равны a и b , а гипотенуза равна c , то: При применении к единичной окружности мы получаем три полезных тригонометрических тождества: Идентификаторы с половинным углом можно использовать для преобразования выражения в квадрате в форму, с которой легче работать. Поэтому, если синус-квадрат или косинус-квадрат появляются в интеграле, запомните эти тождества. Как видите, список основных триггерных идентификаторов не очень длинный. На самом деле, нужно запомнить всего несколько ключевых моментов. Теперь давайте посмотрим, как мы можем использовать эти тождества в реальных задачах исчисления AP. Найдите площадь заштрихованной области между y = sin x и линией y = 1/2. Мы знаем, что правильно настроенный интеграл поможет. Но каковы должны быть пределы интеграции? Сначала нам нужно решить sin x = 1/2. На основе единичной окружности есть два угла, под которыми значение синуса равно 1/2: π / 6 и 5π / 6. Следовательно, площадь заштрихованной области составляет: Обратите внимание, как мы также использовали единичный круг в конце для определения значений cos π / 6 и 5cos π / 6. Поначалу этот интеграл кажется невозможным! Однако при небольшом умелом манипулировании эта проблема превращается в более легкую. Сначала давайте перевыразим деление на cos 2 x как умножение на обратную величину, sec 2 x . Затем обратите внимание, что дополнительная секунда 2 x может быть исключена. Далее мы используем форму пифагорейской идентичности. Следовательно, мы можем переписать интеграл как: Обратите внимание на косинусы и секансы. Как мы знаем, эти две триггерные функции являются взаимными. Итак, точно так же, как 4 и 1/4 отменяются при умножении вместе, мы можем отменить два косинуса и секанс. Остается очень простой интеграл: Может показаться странным, что после всей этой работы окончательный ответ настолько тривиален.Но это часто имеет место при использовании тригонометрических тождеств для манипулирования проблемой. Создатели тестов действительно хорошо умеют создавать подобные проблемы. Опишите вектор-функцию (cos (- t ), sin (- t )), где 0 ≤ t ≤ 2π. (A) Круг, начерченный против часовой стрелки, начинающийся и заканчивающийся в (1, 0) (B) Круг, начерченный по часовой стрелке, начиная и заканчивающийся в (1, 0) (C) Круг, начерченный против часовой стрелки, начиная с ( 0, 1) (D) Круг, начерченный по часовой стрелке, начинается и заканчивается в (0, 1) Сначала подключите t = 0. (соз (-0), грех (-0)) = (соз (0), грех (0)) = (1, 0). Это немедленно исключает (C) и (D). Далее, самый простой способ определить правильное направление — использовать четные и нечетные свойства синуса и косинуса. cos (- t ) = cos ( t ). sin (- т ) = -sin ( т ). Следовательно, исходная векторная функция эквивалентна: (cos ( t ), -sin ( t )). Но этот новый путь является просто отражением исходного пути по оси x , потому что координата y была инвертирована. Если вы помните, что (cos ( t ), sin ( t )) очерчивает стандартный единичный круг против часовой стрелки, то (cos ( t ), -sin ( t )) выводит его из в другую сторону, то есть по часовой стрелке. Правильный ответ (B). Единственный способ продолжить это — использовать идентичности половинных углов. Давайте теперь разделим работу. Первый член тривиально прост. Но второй член требует замены. Пусть u = 8 x . Тогда du = 8 dx или, что эквивалентно, dx = (1/8) du . Сложив эти два результата вместе с основной проблемой, мы получим: Есть только несколько тригонометрических идентичностей, которые вы должны освоить для экзаменов AP Calculus.Вместе со знанием своего пути по единичной окружности убедитесь, что вы понимаете, когда и как использовать: Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT.
\ sin \; 2x ~ & = ~ f (x) \\ \ nonumber
& = ~ f (x + p) \ quad \ text {(поскольку \ (p \ ) — период \ (f (x) \))} \\ \ nonumber
& = ~ \ sin \; 2 (x + p) \\ \ nonumber
& = ~ \ sin \; (2x + 2p)
\ end {align *} \] К счастью, нам не нужно проделывать всю эту работу для каждой функции, поскольку аналогичный аргумент работает, когда \ (\ sin \; 2x \) заменяется на \ (\ sin \; \ omega x \) для любого положительного действительного числа. \ (\ omega \): вместо деления \ (2 \ pi \) на \ (2 \), чтобы получить период, разделите на \ (\ omega \). Этот аргумент работает и для других тригонометрических функций. Таким образом, получаем:
К счастью, нам не нужно проделывать всю эту работу для каждой функции, поскольку аналогичный аргумент работает, когда \ (\ sin \; 2x \) заменяется на \ (\ sin \; \ omega x \) для любого положительного действительного числа. \ (\ omega \): вместо деления \ (2 \ pi \) на \ (2 \), чтобы получить период, разделите на \ (\ omega \). Этот аргумент работает и для других тригонометрических функций. Таким образом, получаем:
\ sin \; \ omega x ~~ & \ text {имеет точку} ~~ \ frac {2 \ pi} {\ omega}
\ qquad \ quad & \ csc \; \ omega x ~~ & \ text {имеет точку} ~~ \ frac {2 \ pi} {\ omega} \\ \ nonumber
\ cos \; \ omega x ~~ & \ text {имеет точку} ~ ~ \ frac {2 \ pi} {\ omega}
\ qquad \ quad & \ sec \; \ omega x ~~ & \ text {имеет точку} ~~ \ frac {2 \ pi} {\ omega} \\ \ nonumber
\ tan \; \ omega x ~~ & \ text {имеет точку} ~~ \ frac {\ pi} {\ omega}
\ qquad \ quad & \ cot \; \ omega x ~~ & \ text {имеет точку} ~~ \ frac {\ pi} {\ omega}
\ end {alignat *} \] грамм. \ (\ sin \; (- 3x) = — \ sin \; 3x \)).
грамм. \ (\ sin \; (- 3x) = — \ sin \; 3x \)).
— | A | ~ \ le ~ A \, \ sin \; x ~ \ le ~ | A | \ quad \ text {and} \ quad
— | A | ~ \ le ~ A \, \ cos \; x ~ \ le ~ | A |
\]
\ text {Амплитуда \ (f (x) \)} ~ = ~ \ frac {\ text {(максимум \ (f (x) \))} ~ — ~ \ text {(минимум из \ (f (x) \))}} {2}
\] 2.3.
2.3. Добавление \ (2 \) к этой функции для получения функции \ (y = 2 — 3 \, \ sin \; \ frac {2 \ pi} {3} x \) не меняет амплитуду, даже если она меняет максимум и минимум.2) \) достигает максимального значения \ (2 \) и минимального значения \ (- 2 \). Таким образом, амплитуда действительно равна \ (2 \).
Добавление \ (2 \) к этой функции для получения функции \ (y = 2 — 3 \, \ sin \; \ frac {2 \ pi} {3} x \) не меняет амплитуду, даже если она меняет максимум и минимум.2) \) достигает максимального значения \ (2 \) и минимального значения \ (- 2 \). Таким образом, амплитуда действительно равна \ (2 \).
Примечание: эта кривая все еще синусоидальная, несмотря на то, что она не является периодической, поскольку общая форма все еще имеет форму «синусоидальной волны», хотя и с переменными периодами . Таким образом, \ (y = 3 \, \ sin \; x + 4 \, \ cos \; x \) имеет период \ (2 \ pi \). Мы можем видеть это на графике, показанном на Рисунке 5.2.7:
Таким образом, \ (y = 3 \, \ sin \; x + 4 \, \ cos \; x \) имеет период \ (2 \ pi \). Мы можем видеть это на графике, показанном на Рисунке 5.2.7:
на рисунке 5.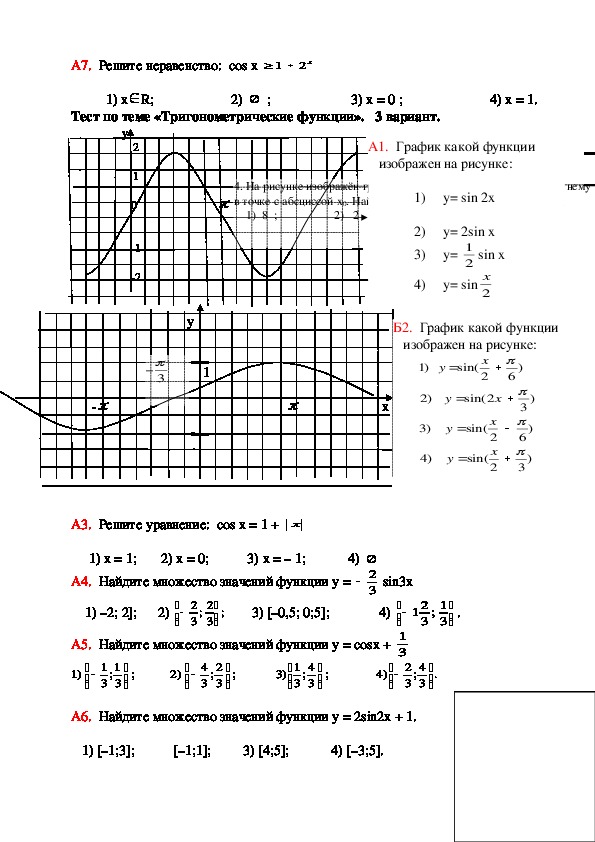 2.8. Затем \ (\ cos \; \ theta = \ frac {3} {5} \) и \ (\ sin \; \ theta = \ frac {4} {5} \). Мы можем использовать это следующим образом:
2.8. Затем \ (\ cos \; \ theta = \ frac {3} {5} \) и \ (\ sin \; \ theta = \ frac {4} {5} \). Мы можем использовать это следующим образом:
y ~ & = ~ 3 \, \ sin \; x ~ + ~ 4 \, \ cos \; x \\ \ nonumber
& = ~ 5 \, \ left ( \ tfrac {3} {5} \, \ sin \; x ~ + ~ \ tfrac {4} {5} \, \ cos \; x \ right) \\ \ nonumber
& = ~ 5 \, (\ cos \; \ theta \; \ sin \; x ~ + ~ \ sin \; \ theta \; \ cos \; x) \\ \ nonumber
& = ~ 5 \, \ sin \; (x + \ theta) \ quad \ text {(по формуле сложения синусов)}
\ end {align *} \]
1 \; \ cdot \; \ tfrac {\ pi} {3} ~ & = ~ \ tfrac {\ pi} {3} \ quad \ quad \ quad
& 1 \; & \ cdot \; \ tfrac {\ pi} {2} ~ & = ~ \ tfrac {\ pi} {2} \\ \ nonumber
2 \; \ cdot \; \ tfrac {\ pi} {3} ~ & = ~ \ tfrac {2 \ pi} {3} \ quad \ quad \ quad
& 2 \; & \ cdot \; \ tfrac {\ pi} {2} ~ & = ~ \ pi \\ \ nonumber
3 \; \ cdot \; \ tfrac {\ pi} {3} ~ & = ~ \ pi \ quad \ quad \ quad & {} & {} \\ \ nonumber
\ end {alignat *} \] Мы можем видеть это на его графике на Рисунке 5.2.9:
Мы можем видеть это на его графике на Рисунке 5.2.9: Тогда амплитуда равна \ (A \), а период равен \ (\ frac {2 \ pi} {\ omega} \). График представлен на Рисунке 5.2.10.
Тогда амплитуда равна \ (A \), а период равен \ (\ frac {2 \ pi} {\ omega} \). График представлен на Рисунке 5.2.10. \]
\]
Рисунок 5.2.12 \ (y = 3 \ cos (2x − π) \)
\ [\ nonumber \ begin {align *}
y = A \, \ sin \; (\ omega x — \ phi) ~~ & \ text {имеет амплитуду \ (| A | \), период \ (\ tfrac {2 \ pi} {\ omega} \) и сдвиг фазы
\ (\ tfrac {\ phi} {\ omega} \)} \\ \ nonumber
y = A \, \ cos \; (\ omega x — \ phi) ~~ & \ text {имеет амплитуду \ (| A | \), период \ (\ tfrac {2 \ pi} {\ omega} \) и сдвиг фазы
\ (\ tfrac {\ phi} {\ omega} \)} \\ \ nonumber
y = A \, \ tan \; (\ omega x — \ phi) ~~ & \ text {имеет неопределенные амплитуду, период \ (\ tfrac {\ pi} {\ omega} \) и сдвиг фазы
\ (\ tfrac {\ phi} {\ omega} \)} \\ \ nonumber
y = A \, \ csc \; (\ omega x — \ phi) ~~ & \ text {имеет неопределенную амплитуду, период \ (\ tfrac {2 \ pi} {\ omega} \ ) и сдвиг фазы
\ (\ tfrac {\ phi} {\ omega} \)} \\ \ nonumber
y = A \, \ sec \; (\ omega x — \ phi) ~~ & \ text {имеет неопределенная амплитуда, период \ (\ tfrac {2 \ pi} {\ omega} \) и сдвиг фазы
\ (\ tfrac {\ phi} {\ omega} \)} \\ \ nonumber
y = A \, \ cot \; (\ omega x — \ phi) ~~ & \ text {имеет неопределенную амплитуду, на iod \ (\ tfrac {\ pi} {\ omega} \) и сдвиг фазы
\ (\ tfrac {\ phi} {\ omega} \)}
\ end {align *} \] Авторы и авторство
5.
 3 Другие тригонометрические функции — Precalculus
3 Другие тригонометрические функции — Precalculus Цели обучения
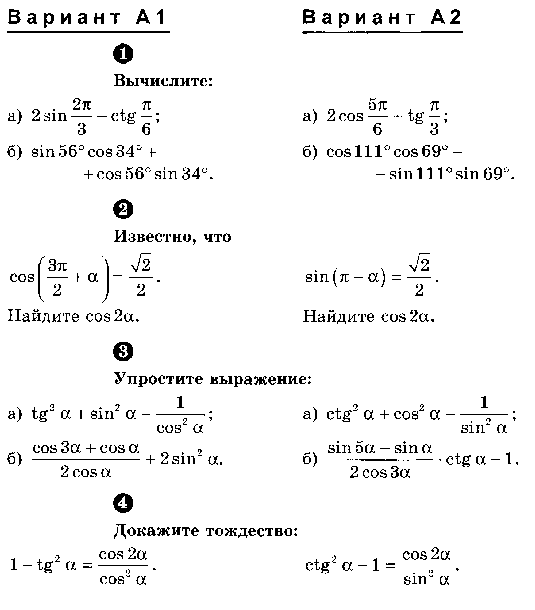 Мы уже определили функции синуса и косинуса угла.Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции.
Мы уже определили функции синуса и косинуса угла.Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции. Нахождение точных значений секанса, косеканса, тангенса и котангенса тригонометрических функций
 синткост, стоимость ≠ 0. Функция касательной обозначается как tan.tan. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили.
синткост, стоимость ≠ 0. Функция касательной обозначается как tan.tan. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили. Функции касания, секанса, косеканса и котангенса
Пример 1
Нахождение тригонометрических функций из точки единичной окружности
 Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott.
Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott. Решение
Пример 2
Нахождение тригонометрических функций угла
 t = π6.
t = π6. Решение
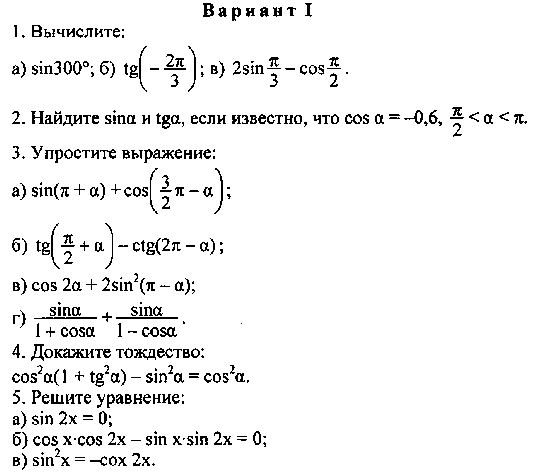 Результаты показаны в таблице 1.
Результаты показаны в таблице 1. Угол 00 π6, или 30 ° π6, или 30 ° π4, или 45 ° π4, или 45 ° π3, или 60 ° π3, или 60 ° π2, или 90 ° π2, или 90 ° Косинус 1 3232 2222 1212 0 Синус 0 1212 2222 3232 1 Касательная 0 3333 1 33 Неопределенный Секант 1 233233 22 2 Неопределенный Косеканс Неопределенный 2 22 233233 1 Котангенс Неопределенный 33 1 3333 0 Использование опорных углов для вычисления тангенса, секанса, косеканса и котангенса
 Процедура такая же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке 4 показано, какие функции в каком квадранте положительны.
Процедура такая же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке 4 показано, какие функции в каком квадранте положительны. В квадранте III, «установка T », только угол t и его обратная функция, котангенс, являются положительными.Наконец, в квадранте IV « C lass» только c осин и его реципрокная функция, секанс, положительны.
В квадранте III, «установка T », только угол t и его обратная функция, котангенс, являются положительными.Наконец, в квадранте IV « C lass» только c осин и его реципрокная функция, секанс, положительны. Как к
Пример 3
Использование опорных углов для поиска тригонометрических функций
 − 5π6.
− 5π6. Решение
Использование четных и нечетных тригонометрических функций
 Как выясняется, в этом отношении существует важное различие между функциями.
Как выясняется, в этом отношении существует важное различие между функциями. Итак, f (x) = x3f (x) = x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f (−x) = — f (x).f (−x) = — f (x).
Итак, f (x) = x3f (x) = x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f (−x) = — f (x).f (−x) = — f (x). sint = ysin (−t) = — ysint ≠ sin (−t) sint = ysin (−t) = — ysint ≠ sin (−t) стоимость = xcos (−t) = xcost = cos (−t) стоимость = xcos (−t) = xcost = cos (−t) tan (t) = yxtan (−t) = — yxtant ≠ tan (−t) tan (t) = yxtan (−t) = — yxtant ≠ tan (−t) sect = 1xsec (−t) = 1xsect = sec (−t) sect = 1xsec (−t) = 1xsect = sec (−t) csct = 1ycsc (−t) = 1 − ycsct ≠ csc (−t) csct = 1ycsc (−t) = 1 − ycsct ≠ csc (−t) cott = xycot (−t) = x − ycott ≠ cot (−t) cott = xycot (−t) = x − ycott ≠ cot (−t) Четные и нечетные тригонометрические функции
 f (−x) = f (x).
f (−x) = f (x). Пример 4
Использование четных и нечетных свойств тригонометрических функций
Решение
Распознавание и использование основных идентичностей
 Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности.Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены. Обычно идентичность может быть получена из определений и отношений, которые мы уже знаем. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности.Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены. Обычно идентичность может быть получена из определений и отношений, которые мы уже знаем. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса. Фундаментальные личности
Пример 5
Использование идентичностей для оценки тригонометрических функций
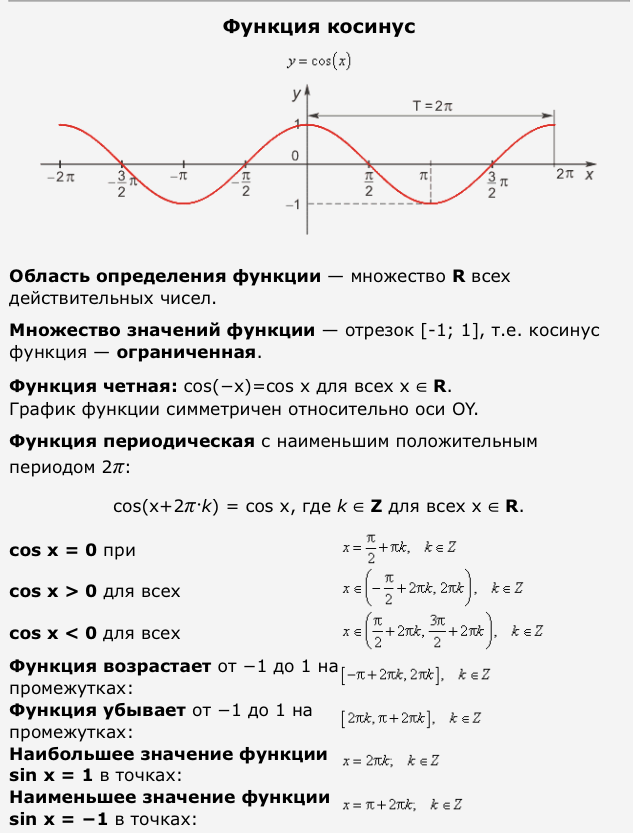 загар (45 °).
загар (45 °). Решение
tan (45 °) = sin (45 °) cos (45 °) = 2222 = 1tan (45 °) = sin (45 °) cos (45 °) = 2222 = 1
сек (5π6) = 1cos (5π6) = 1−32 = −23 = −233sec (5π6) = 1cos (5π6) = 1−32 = −23 = −233 Пример 6
Использование тождеств для упрощения тригонометрических выражений
Решение

Альтернативные формы пифагорейской идентичности
Альтернативные формы пифагорейской идентичности
1 + tan2t = sec2t1 + tan2t = sec2t
cot2t + 1 = csc2tcot2t + 1 = csc2t Пример 7
Использование тождеств для связи тригонометрических функций

Решение
Попробовать # 7
 Период — это самый короткий интервал, в течение которого функция завершает один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней.
Период — это самый короткий интервал, в течение которого функция завершает один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней. Период функции
Пример 8
Нахождение значений тригонометрических функций
Решение
sint = y = −32cost = x = −12tant = sintcost = −32−12 = 3sect = 1cost = 1−12 = −2csct = 1sint = 1−32 = −233cott = 1tant = 13 = 33sint = y = −32cost = x = −12tant = sintcost = −32−12 = 3sect = 1cost = 1−12 = −2csct = 1sint = 1−32 = −233cott = 1tant = 13 = 33 Попробовать # 8
 на основе рисунка 10 .
на основе рисунка 10 . Пример 9
Нахождение значения тригонометрических функций
Решение
sect = 1cost = 112 = 2csct = 1sint = 1−32−233tant = sintcost = −3212 = −3cott = 1tant = 1−3 = −33sect = 1cost = 112 = 2csct = 1sint = 1−32−233tant = sintcost = — 3212 = −3котт = 1тант = 1−3 = −33 Попробовать # 9
Вычисление тригонометрических функций с помощью калькулятора
 Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерное программное обеспечение. Если в калькуляторе есть режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем производить расчет.
Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерное программное обеспечение. Если в калькуляторе есть режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем производить расчет. How To

Как к
Пример 10
Оценка косеканса с использованием технологии
Решение
 279csc (5π7) ≈1,279
279csc (5π7) ≈1,279 5.3 Упражнения по разделам
Устные
1. Алгебраические


Графический
Технологии
Расширения
 sin (t).
sin (t). Реальные приложения
72. Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света 10 февраля, 42 -й день в году. Укажите период функции.
Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света 10 февраля, 42 -й день в году. Укажите период функции.
тригонометрических функций
тригонометрических функций Произвольные углы и единичная окружность
До сих пор мы использовали единичную окружность для определения тригонометрических функций для острых углов.В следующем разделе, где мы рассмотрим наклонные треугольники, нам понадобится нечто большее, чем острые углы. Некоторые наклонные треугольники являются тупыми, и нам нужно знать синус и косинус тупых углов. Пока мы делаем это, мы также должны определять триггерные функции для углов, превышающих 180 °, и для отрицательных углов. Сначала нам нужно четко определить, что это за углы. Эти частные случаи полезно не только рассматривать как углы, но также включать углы от 180 ° до 360 °, иногда называемые «углами отражения». С применением тригонометрии к предметам исчисления и дифференциальных уравнений, углы, превышающие 360 °, и отрицательные углы также стали приемлемыми.
Эти частные случаи полезно не только рассматривать как углы, но также включать углы от 180 ° до 360 °, иногда называемые «углами отражения». С применением тригонометрии к предметам исчисления и дифференциальных уравнений, углы, превышающие 360 °, и отрицательные углы также стали приемлемыми. Каждый раз по кругу мы получаем другое название угла.Таким образом, 90 °, 450 °, 810 ° и 1170 ° — это один и тот же угол.
Каждый раз по кругу мы получаем другое название угла.Таким образом, 90 °, 450 °, 810 ° и 1170 ° — это один и тот же угол. Синусы и косинусы произвольных углов
Теперь, когда мы указали произвольные углы, мы можем определить их синусы и косинусы. Пусть угол расположен так, чтобы его вершина находилась в центре единичной окружности O = (0,0), и пусть первая сторона угла расположена вдоль оси x . Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B , чтобы определить косинус угла и синус угла. В частности, координата x точки B является косинусом угла, а координата y точки B является синусом угла. Это определение расширяет определения синуса и косинуса, данные ранее для острых углов.
Мы используем координаты B , чтобы определить косинус угла и синус угла. В частности, координата x точки B является косинусом угла, а координата y точки B является синусом угла. Это определение расширяет определения синуса и косинуса, данные ранее для острых углов. Свойства синусов и косинусов, которые следуют из этого определения
Есть несколько свойств, которые мы можем легко вывести из этого определения.Некоторые из них обобщают тождества, которые мы уже видели для острых углов. Итак, мы должны использовать радиан, когда думаем о триггерах с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
Итак, мы должны использовать радиан, когда думаем о триггерах с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
 Например, f ( x ) = x 4 — 3 x 2 — 5.(Константа 5 равна 5 x 0 , а 0 — четное число.)
Например, f ( x ) = x 4 — 3 x 2 — 5.(Константа 5 равна 5 x 0 , а 0 — четное число.)
Графики функций синуса и косинуса
Давайте возьмем t как переменный угол. Вы можете думать о t как об угле и времени. Для людей хороший способ понять функцию — это посмотреть на ее график.Начнем с графика sin t. Возьмите горизонтальную ось за ось t (а не за ось x , как обычно), возьмите вертикальную ось за ось y и изобразите уравнение y = sin t . Похоже на это.
Графики тангенса и котангенса
График касательной функции имеет вертикальную асимптоту при x = π /2. Это потому, что касательная приближается к бесконечности, когда t приближается к π /2. (На самом деле, она приближается к минус бесконечности, поскольку t приближается к π /2 справа, как вы можете видеть на графике.
Графики функций секанса и косеканса
Секанс — это величина, обратная косинусу, и, поскольку косинус принимает только значения от –1 до 1, секанс принимает только значения выше 1 или ниже –1, как показано на графике.Также секанс имеет период 2 π . Свойства обратных тригонометрических функций — Видео и стенограмма урока
Обозначение
 Мы можем написать наши обратные триггерные функции так:
Мы можем написать наши обратные триггерные функции так: Ограниченный диапазон
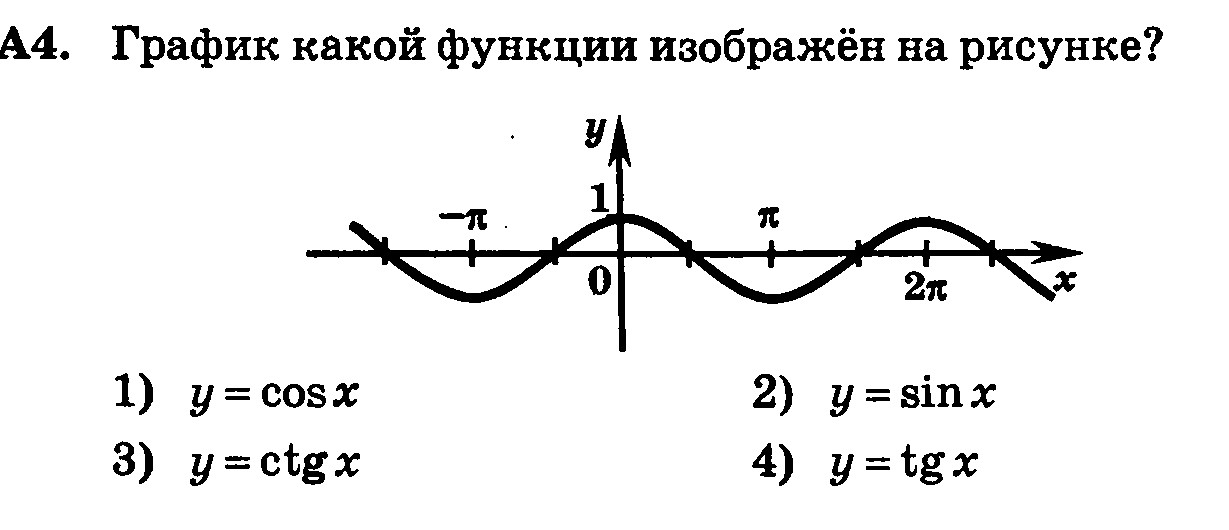 Вы помните их графики?
Вы помните их графики? Он дает вам ответ в допустимом диапазоне. Если бы мы не ограничивали наш диапазон, наш калькулятор не знал бы, какой ответ дать вам, поскольку ответы повторяются каждые 2pi для функций синуса и косинуса и pi для функции тангенса. Ниже приведены допустимые ограниченные диапазоны для наших обратных тригонометрических функций:
Он дает вам ответ в допустимом диапазоне. Если бы мы не ограничивали наш диапазон, наш калькулятор не знал бы, какой ответ дать вам, поскольку ответы повторяются каждые 2pi для функций синуса и косинуса и pi для функции тангенса. Ниже приведены допустимые ограниченные диапазоны для наших обратных тригонометрических функций: Обратная функция Диапазон y = arcsin x -pi / 2 <= y <= pi / 2 y = arccos x 0 <= y <= pi y = arctan x -pi / 2 
Графики

Резюме урока
Обратная функция Диапазон y = arcsin x -pi / 2 <= y <= pi / 2 y = arccos x 0 <= y <= pi y = arctan x -pi / 2  На этом графике функция арксинуса и показана красной линией, арккосинус — синей линией, а арктангенс — фиолетовой линией:
На этом графике функция арксинуса и показана красной линией, арккосинус — синей линией, а арктангенс — фиолетовой линией: Результаты обучения
ACT Тригонометрия: полное руководство
 На первый взгляд они могут показаться сложными, но большинство из них сводятся к нескольким простым концепциям.
На первый взгляд они могут показаться сложными, но большинство из них сводятся к нескольким простым концепциям. Что такое тригонометрия и как ее использовать?
 2 = 340 9000 долларов США 3
2 = 340 9000 долларов США 3 Вам никогда не придется находить действительную величину угла из х по АКТ.
Вам никогда не придется находить действительную величину угла из х по АКТ. Наиболее распространенные триггерные вопросы ACT

 1
1 SOH, CAH, TOA
SOH (синус)
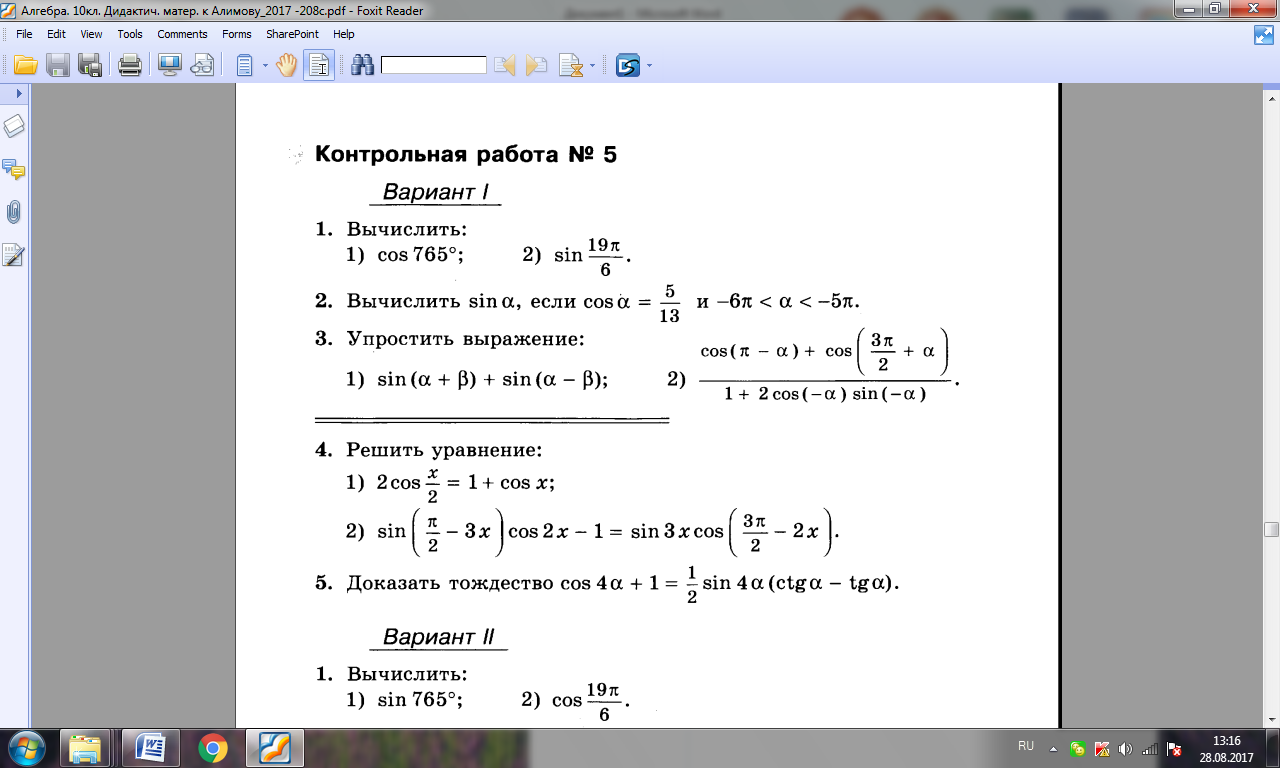
CAH (косинус)

TOA (касательная)

Какие стороны противоположны или смежны?

 10 $ загар23 ° $
10 $ загар23 ° $
Итак, расстояние между лестницей и землей составляет 23 ° $. Также мы работаем с длинами соседней стороны треугольника и гипотенузы. Это означает, что нам понадобится косинус, так как $ cosΘ = \ напротив / \ hypoteneuse $ Придется ли мне определять угол?
Когда Sin, Cos и Tan являются положительными или отрицательными?


Вторичные триггерные функции
 Это косеканс, секанс и котангенс. Они возникают не более чем по одному вопросу за тест.
Это косеканс, секанс и котангенс. Они возникают не более чем по одному вопросу за тест. Косеканс
Секант
Котангенс
Полезные формулы с Sin, Cos и Tan
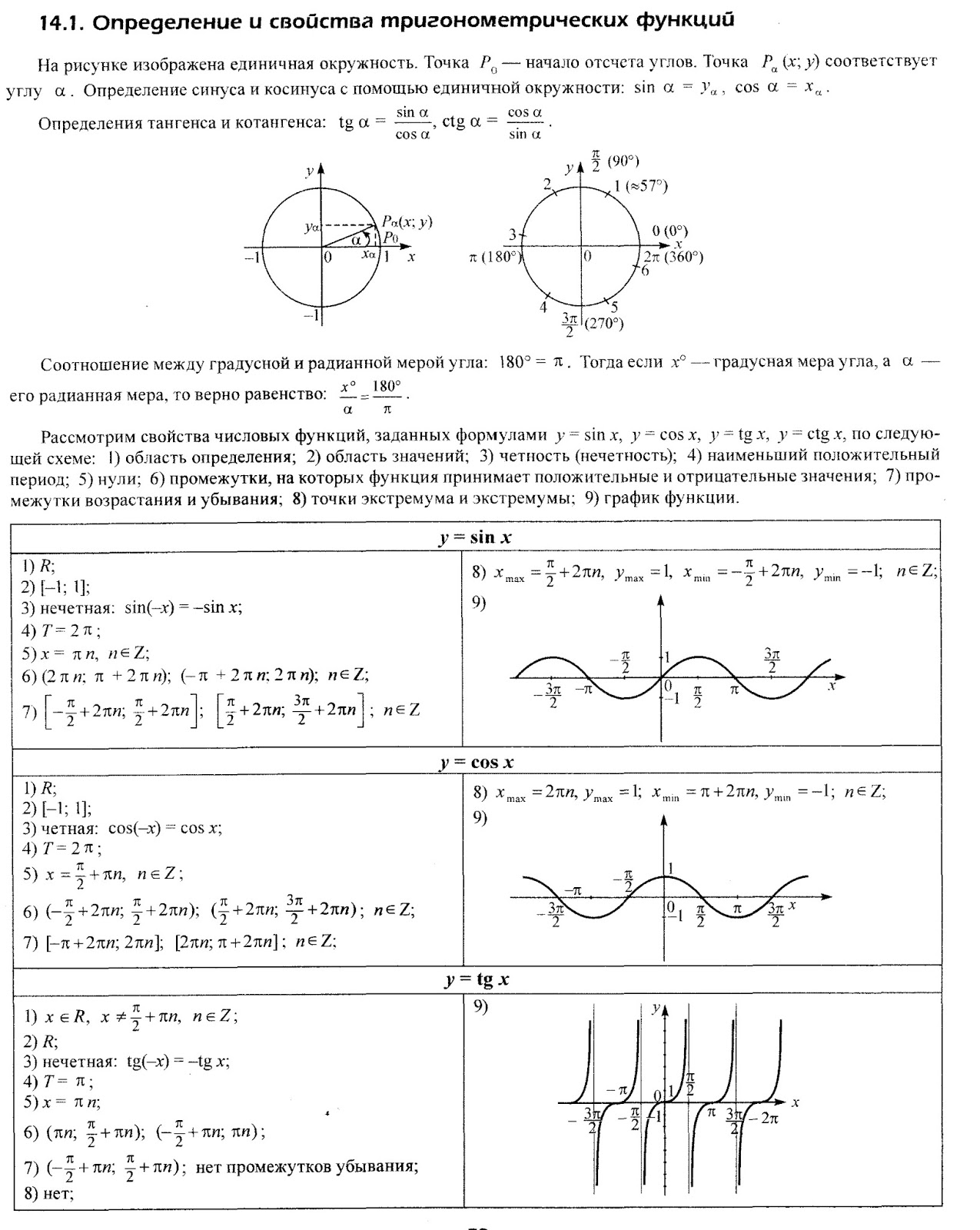 Если вы чувствуете, что не можете больше запоминать тригонометрию, не беспокойтесь об их запоминании — они могут ответить максимум на один вопрос за тест .2 {x}) $, что также равно 1.
Если вы чувствуете, что не можете больше запоминать тригонометрию, не беспокойтесь об их запоминании — они могут ответить максимум на один вопрос за тест .2 {x}) $, что также равно 1. Графические триггерные функции
Синус
 Он всегда возрастает после $ x = 0 $, после пересечения начала координат.
Он всегда возрастает после $ x = 0 $, после пересечения начала координат. Косинус
 А на ACT время ограничено и ценно.
А на ACT время ограничено и ценно. Касательная
Периоды и амплитуды
Период
Амплитуда

Радианы

Шаги к решению триггерного вопроса
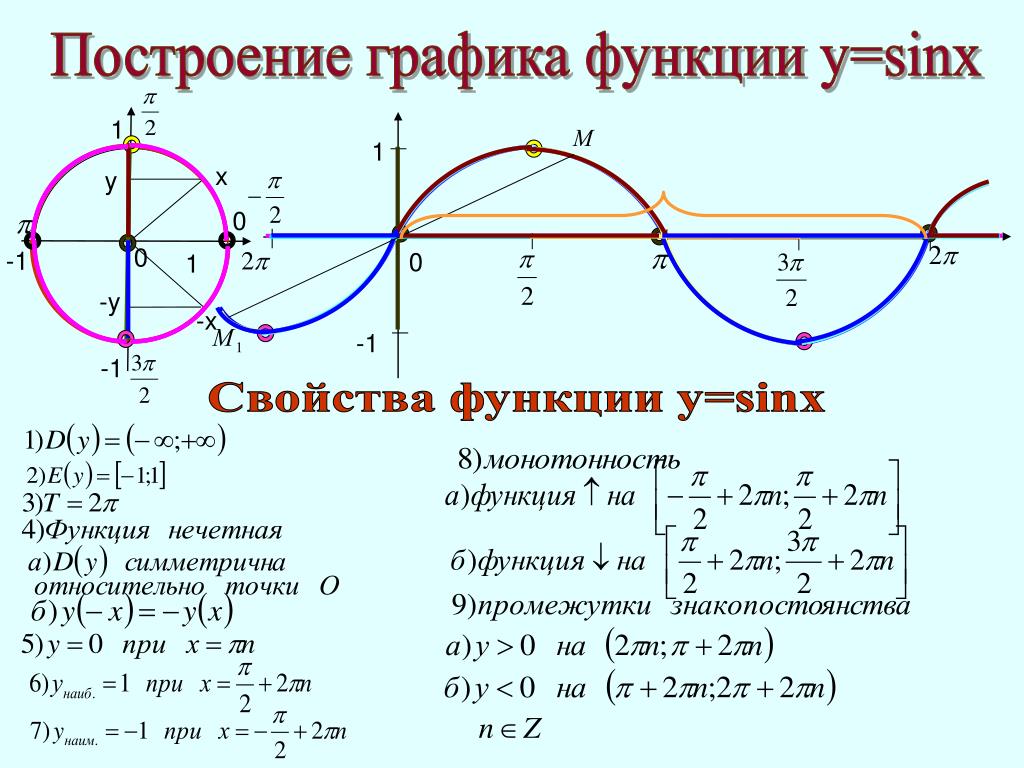 2 {Θ} и др.
2 {Θ} и др. Итоги
Что дальше?
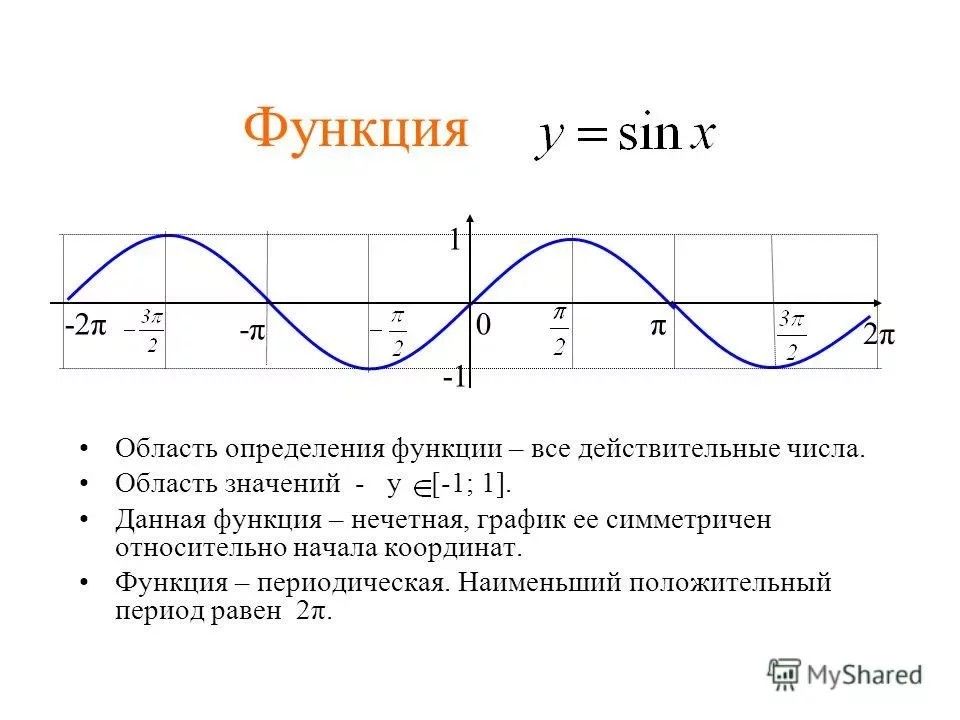 Вы знаете твердотельную геометрию ACT? Не забудьте освежить в памяти все, что вам нужно.
Вы знаете твердотельную геометрию ACT? Не забудьте освежить в памяти все, что вам нужно.
AP Calculus Review: Trigonometric Identities — Magoosh Blog
 Кроме того, тригонометрические тождества также помогают при определении пределов, производных и интегралов тригонометрических функций. В частности, эти тождества, кажется, чаще возникают при вычислении интегралов, особенно в разделах теста без калькулятора.
Кроме того, тригонометрические тождества также помогают при определении пределов, производных и интегралов тригонометрических функций. В частности, эти тождества, кажется, чаще возникают при вычислении интегралов, особенно в разделах теста без калькулятора. Unit Circle
Основные тригонометрические идентичности
1.Частные тождества
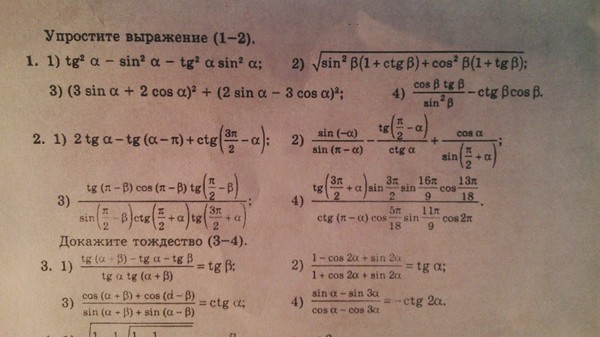
2. Свойства четных и нечетных
3. Тождества Пифагора
4.Идентичности с половинным углом
Примеры

Использование единичной окружности
Решение
Использование частных и пифагоровых тождеств
Решение

Использование четных и нечетных свойств
Решение

Использование идентичностей половинных углов
Решение
 Только будьте осторожны с 4 x внутри. Вам нужно будет умножить это на 2 в формуле.
Только будьте осторожны с 4 x внутри. Вам нужно будет умножить это на 2 в формуле. Резюме
Улучшите свой SAT или результат ACT, гарантированно. Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!


 (оценивается 3 баллами)
(оценивается 3 баллами)