
 ; 3) решений нет; 4);
; 3) решений нет; 4);  .
.Алгебра 8 класс. Контрольная работа № 4 по теме: «Квадратные уравнения».
Вариант № 1.
А 1.Укажите в квадратном уравнении х² + 3 – 5х = 0 коэффициент b.
1) 4. 2). 3. 3) - 5. 4) 1.
А 2. Решите уравнение х² + 6 = 0. 1). 5; 2) 
 ; 3) решений нет; 4);
; 3) решений нет; 4);  .
.
А 3. Найти корни уравнения (х + 1)² - 1 + 2х = 0. 1). нет решений. 2) 0; - 4; 3) 0; 4) 0; - 4.
А 4. Выделите квадрат двучлена в выражении х² + 6х + 8.
1). (х – 2)² + 3; 2) (х – 3)² +1; 3). (х + 3)² - 1; 4) ; (х – 6)² +9
А 5. Дискриминант уравнения 8х² – 9х + 3 = 0 равен 1) 49; 2) - 15; 3) -47; 4) 65.
А 6. Решите уравнение: 3х² + х – 4 = 0. 1) 4; - 3; 2) - 1;  ; 3) 1;
; 3) 1;  ; 4).
; 4). 
А 7. Имеет один корень уравнение
1) 4х² +4 х + 4 = 0; 2) 4х² -2 х + 0,25 = 0; 3) 9х² -6 х + 2 = 0; 4) 3х² - 1,5 х +5 = 0.
А 8. Если  - корни уравнения х² + pх + q = 0, то
- корни уравнения х² + pх + q = 0, то
1) p = 6, q = 5; 2) p = - 6, q = - 5; 3) p = - 5; q = - 6; 4) p = 5 , q = 6.
В 1. Один из корней уравнения х² + 8х + q = 0 равен 3. Найдите q.
В 2. Найдите разность большего и меньшего корней уравнения х² + 3х - 10 = 0.
С 1. Площадь прямоугольника 250 см². Одна сторона в 2,5 раза больше другой. Найдите большую сторону прямоугольника.
С 2. Разность корней квадратного уравнения х² +15х + q = 0 равна 3. Найдите q.
Вариант № 2.
А 1.Укажите в квадратном уравнении 7х – 5 - х² = 0 коэффициент а.
1) - 1. 2). 1. 3) 7. 4) - 5.
А 2. Решите уравнение (х – 2)(х + 2)= 4. 1). решений нет; 2) 2 ;
;  .; 3) 6 ; 4 ; 4) 0
.; 3) 6 ; 4 ; 4) 0
А 3. Найти корни уравнения - х² + 3 = 7х + 3 . 1). 0; - 7. 2) 7; 3) 0; 7; 4) нет решений
А 4. Выделите квадрат двучлена в выражении х² + 8х + 15.
1). (х + 4)² -1; 2) (х + 8)² - 16; 3). (х + 4)² + 1 ; 4) (х + 2)² + 4 ;
А 5. Дискриминант уравнения 7х² + 8х - 3 = 0 равен 1) 85; 2) - 20; 3) 148; 4) - 20.
А 6. Решите уравнение: 2х² + х – 3 = 0. 1) 3; - 2; 2) 1; 
 ; 3)
; 3)  ; 4)
; 4) 
А 7. Имеет два корня уравнение
1) 3х² +5х + 1 = 0; 2) 3х² -5 х + 3 = 0; 3) 2х² -2 х + 3 = 0 4) 7х² + х + 4 = 0;
А 8. Сумма и произведение корней уравнения х² - 3х - 5 = 0 равны
1) = 3,
= 3,  = - 5; 2)
= - 5; 2)  = 5;
= 5;  = - 3; 3)
= - 3; 3)  = - 3,
= - 3,  = - 5; 4)
= - 5; 4) = -5,
= -5,  = - 3.
= - 3.
В 1. Один из корней уравнения х² + рх + 24 = 0 равен 8. Найдите р.
В 2. Найдите разность большего и меньшего корней уравнения х² - х - 20 = 0.
С 1. Площадь прямоугольника 48 см². Одна его сторона составляет  другой. Найдите меньшую сторону прямоугольника.
другой. Найдите меньшую сторону прямоугольника.
С 2. Удвоенная разность корней квадратного уравнения х² -18х + q = 0 равна 8. Найдите q.
intolimp.org
Контрольная работа «Квадратное уравнение и его корни. Теорема Виета». Алгебра. 8 класс.
Вариант № 1.
А 1.Укажите в квадратном уравнении х² + 3 – 4х = 0 коэффициент b.
1) 1. 2). – 4. 3) 3. 4) 4.
А 2. Решите уравнение х² + 5 = 0. 1). решений нет; 2) 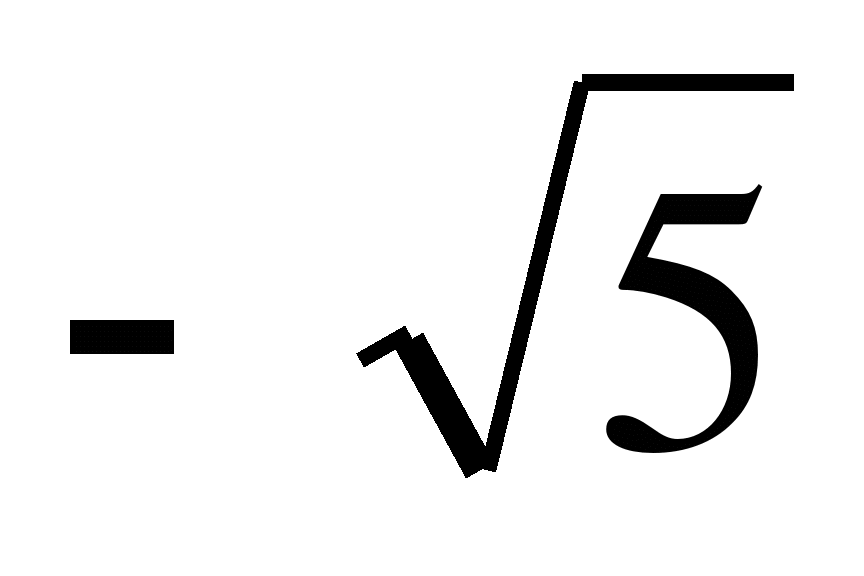 ; 3) 5; 4)
; 3) 5; 4) 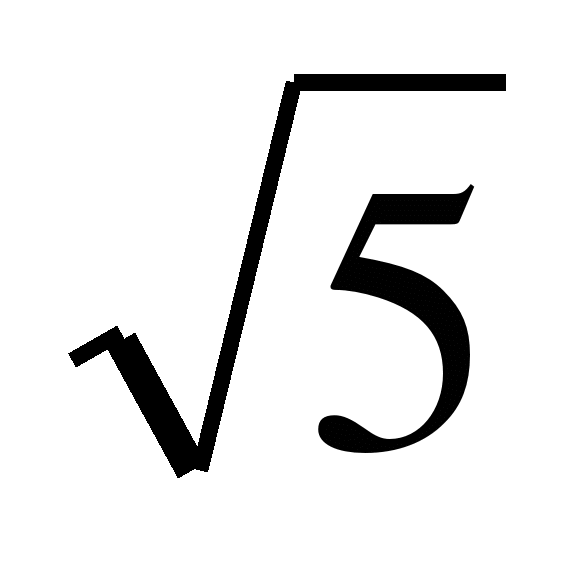 ;
; 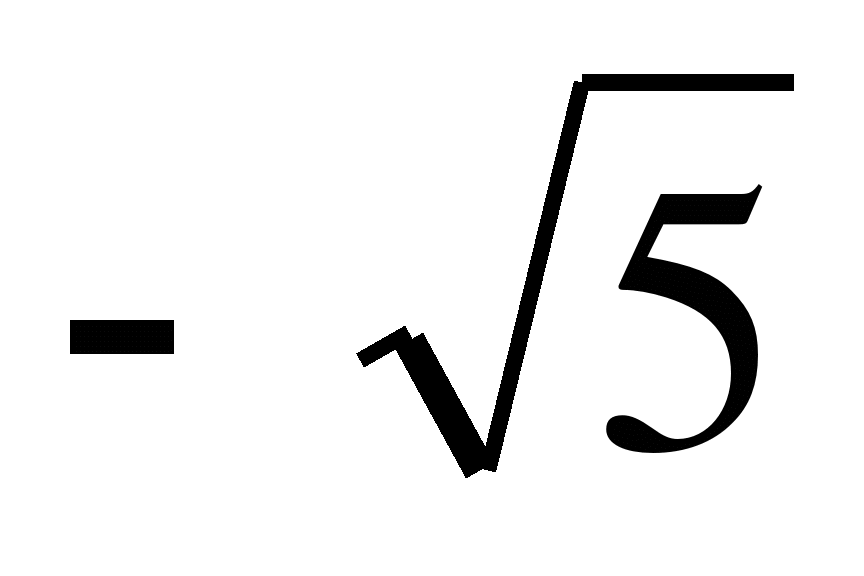 .
.
А 3. Дискриминант уравнения 8х² – 9х + 4 = 0 равен 1) – 47; 2) 65; 3) 49; 4) 17.
А 4. Решите уравнение: 3х² + х – 4 = 0. 1) 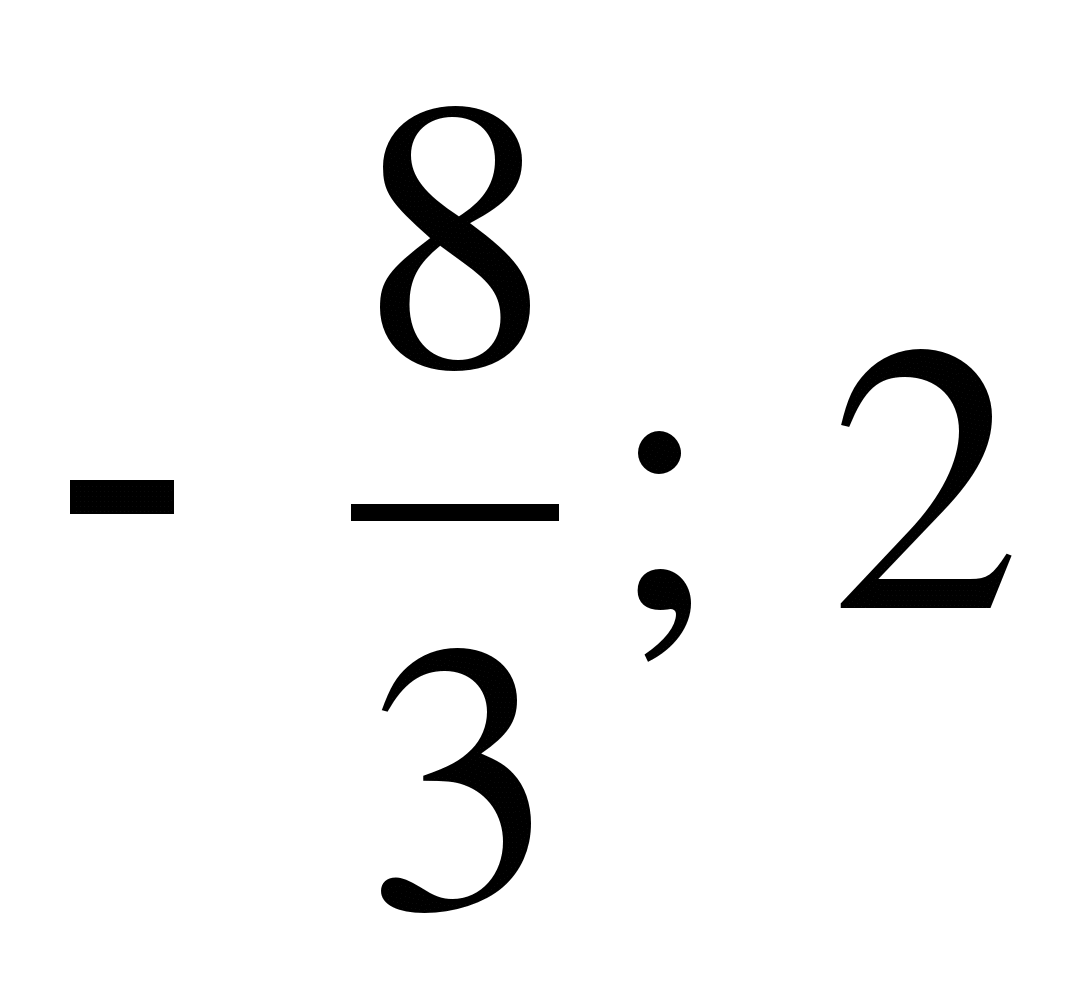 ; 2) 1;
; 2) 1; 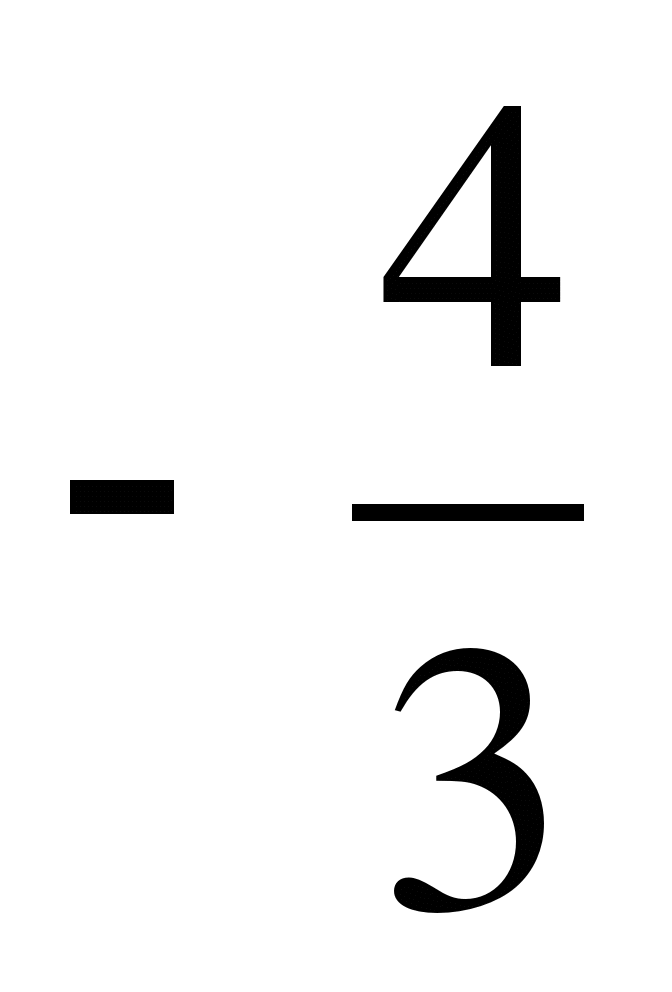 ; 3) - 1;
; 3) - 1; 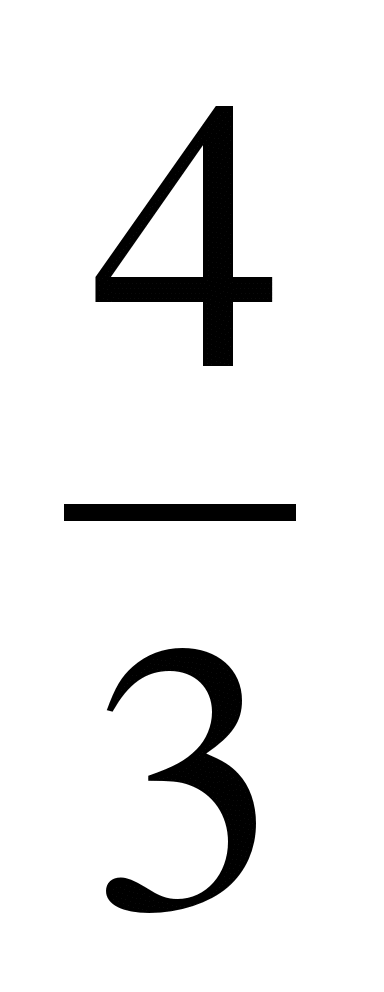 ; 4) 4; - 3.
; 4) 4; - 3.
А 5. Имеет один корень уравнение
1) 3х² - 1,5 х +5 = 0; 2) 4х² +4 х + 4 = 0; 3) 9х² -6 х + 2 = 0; 4) 4х² -2 х + 0,25 = 0.
А 6. Если 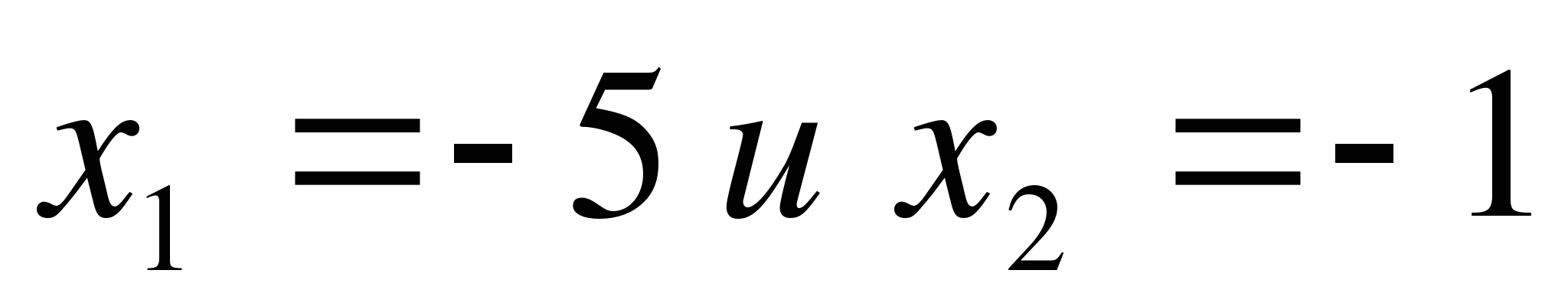 - корни уравнения х² + pх + q = 0, то
- корни уравнения х² + pх + q = 0, то
1) p = - 6, q = - 5; 2) p = 6, q = 5; 3) p = 5; q = 6; 4) p = - 5 , q = - 6.
В 1. Один из корней уравнения х² + 8х + q = 0 равен 3. Найдите q.
В 2. Найдите разность большего и меньшего корней уравнения х² + 3х - 10 = 0.
С 1. Площадь прямоугольника 250 см². Одна сторона в 2,5 раза больше другой. Найдите большую сторону прямоугольника.
Контрольная работа «Квадратное уравнение и его корни. Теорема Виета». Алгебра. 8 класс.
Вариант № 2.
А 1.Укажите в квадратном уравнении 7х – 5 - х² = 0 коэффициент а.
1) 1. 2). – 1. 3) - 5. 4) 7.
А 2. Решите уравнение (х – 2)(х + 2)= 4. 1). 6 ; 4 ; 2) решений нет ; 3) 0; 4) 2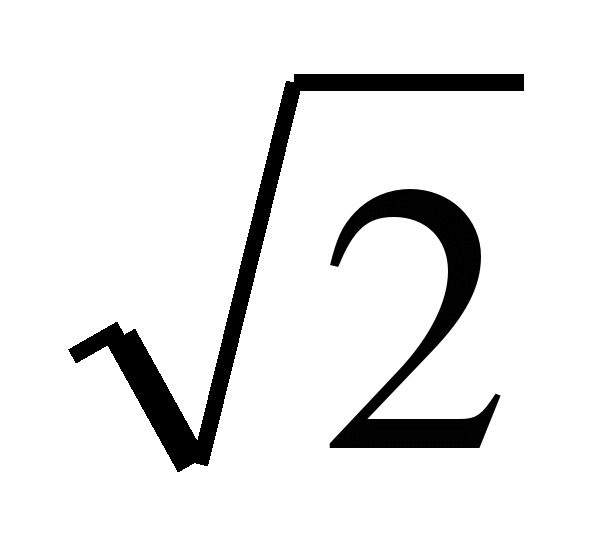 ;
; 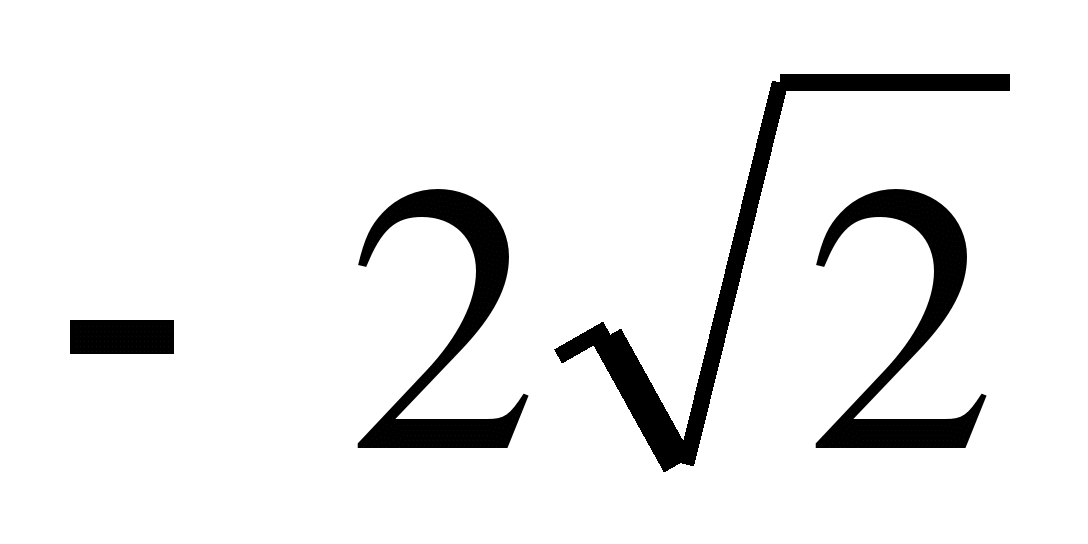 .
.
А 3. Дискриминант уравнения 7х² + 8х - 3 = 0 равен 1) – 20; 2) 85; 3) 43; 4) 148.
А 4. Решите уравнение: 2х² + х – 3 = 0. 1) 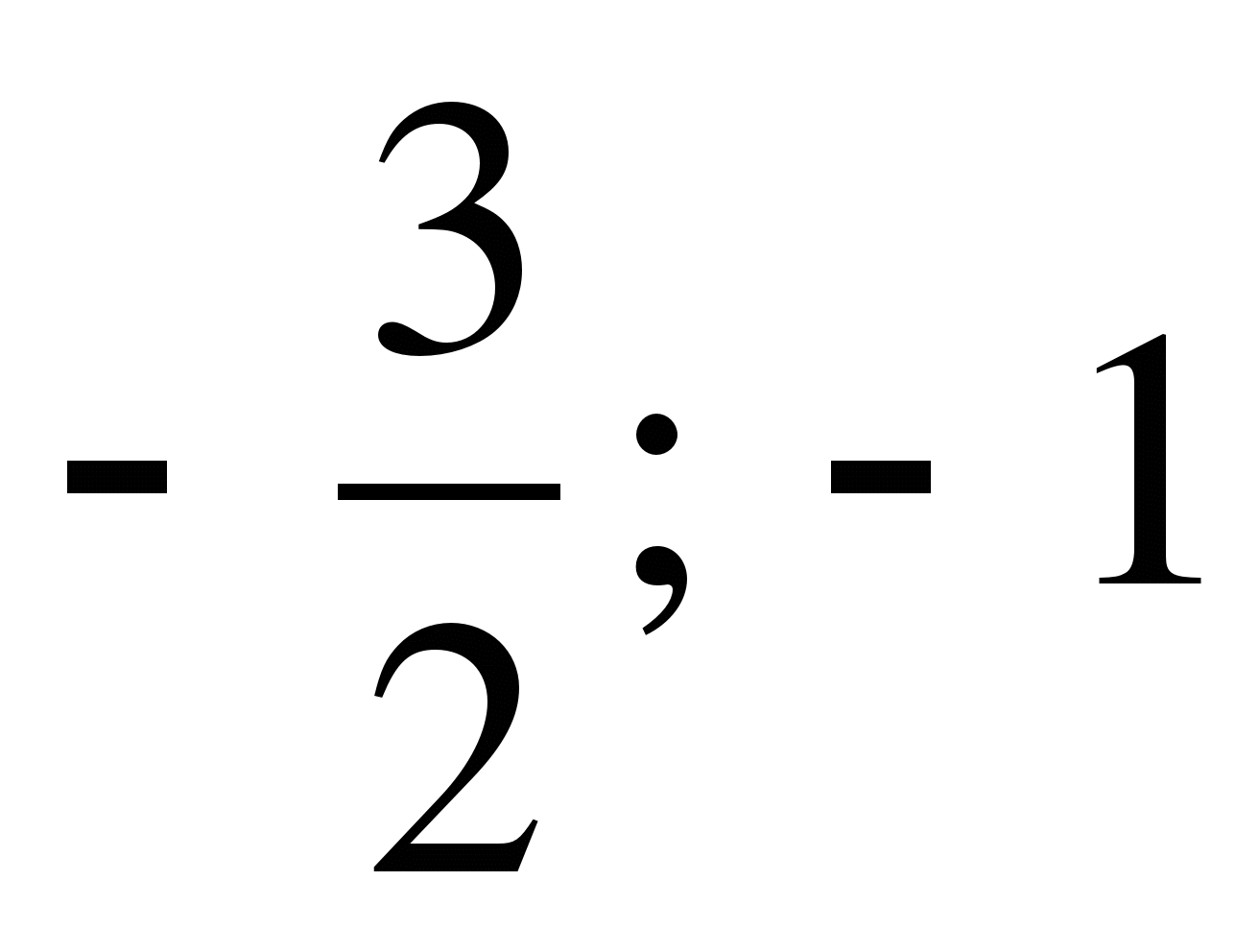 ; 2) 3;- 2
; 2) 3;- 2  ; 3)
; 3) 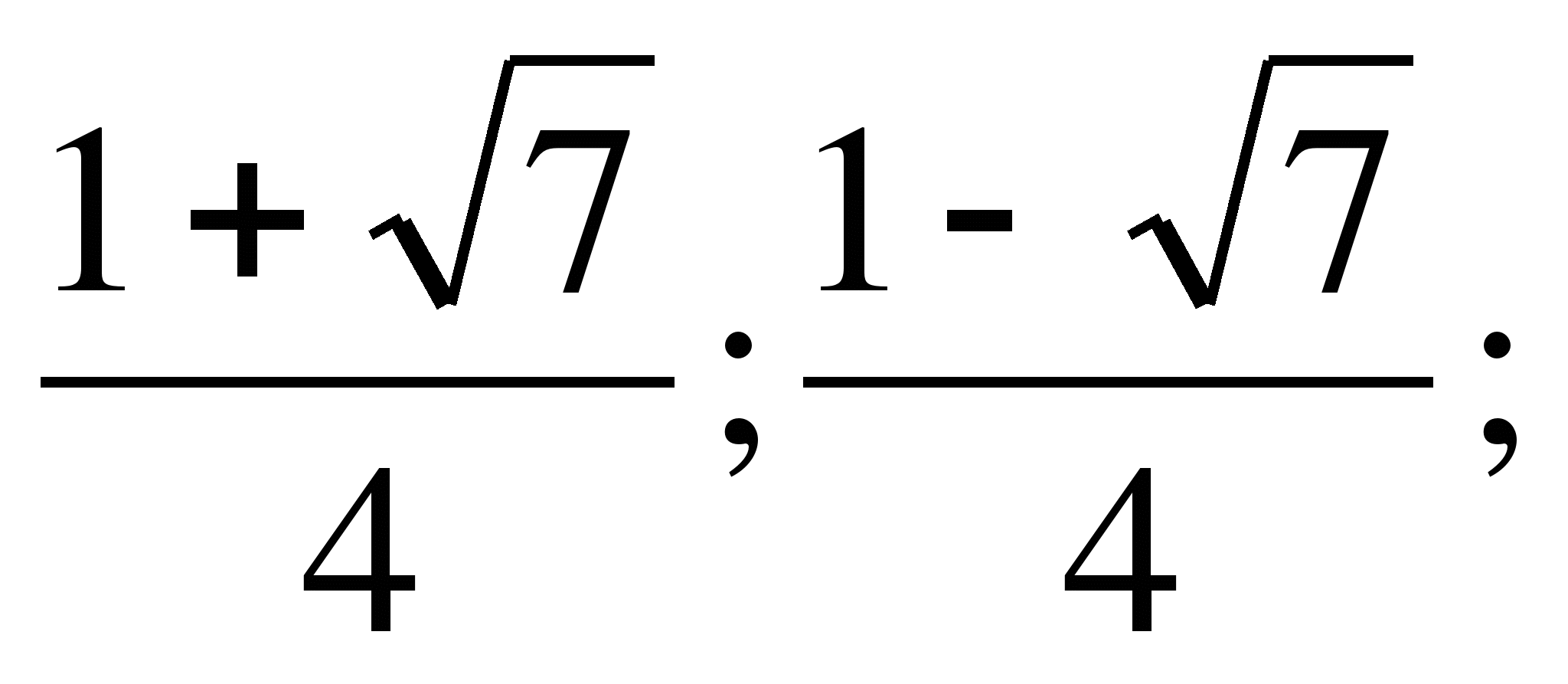 4) 1;
4) 1; 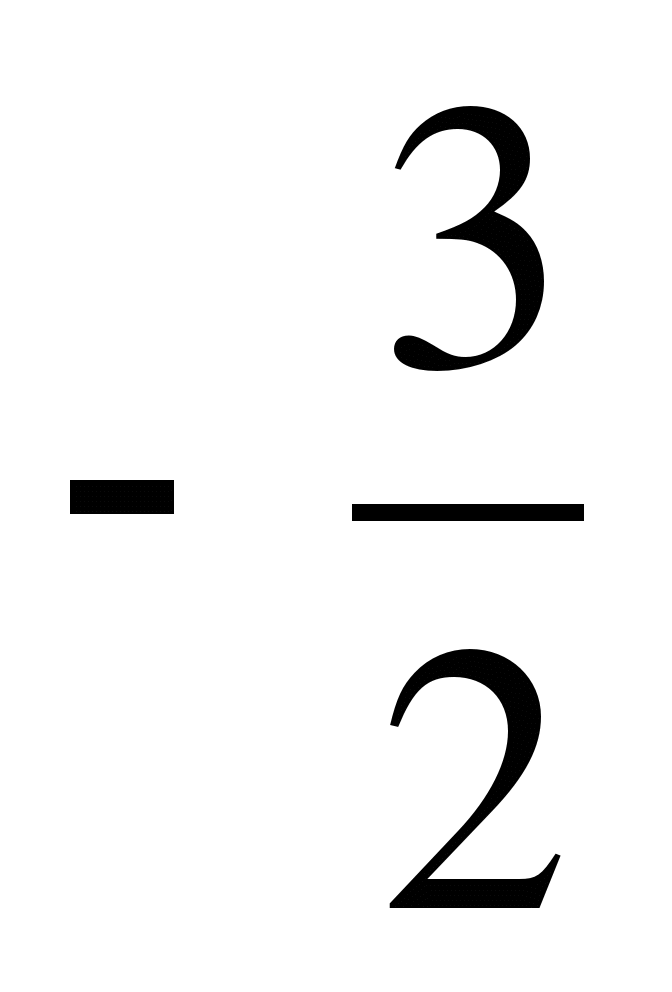
А 5. Имеет два корня уравнение
1) 7х² + х + 4 = 0; 2) 2х² -2 х + 3 = 0; 3) 3х² +5х + 1 = 0; 4) 3х² -5 х + 3 = 0.
А 6. Сумма и произведение корней уравнения х² - 3х - 5 = 0 равны
1)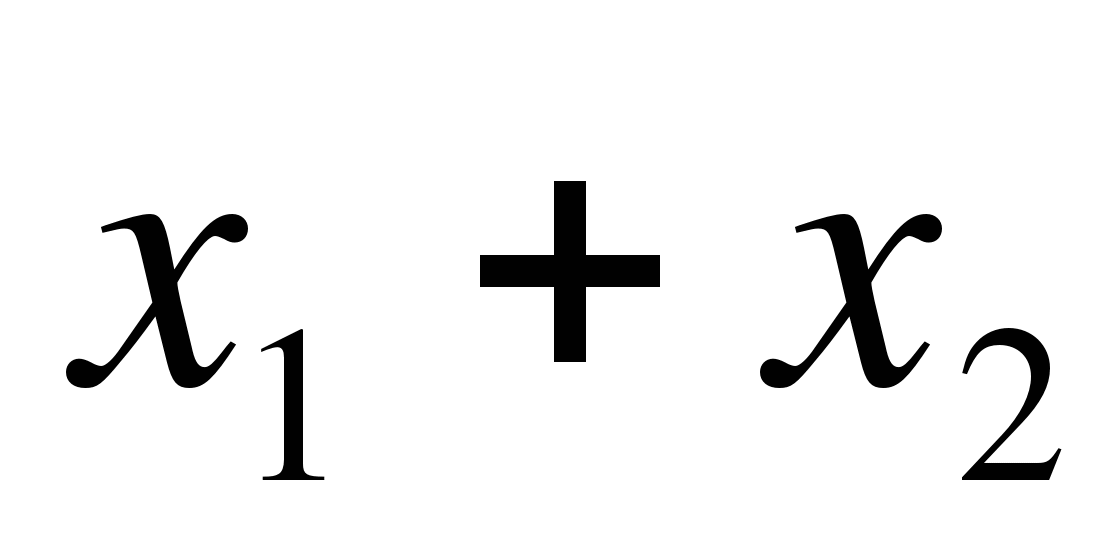 = - 3,
= - 3, 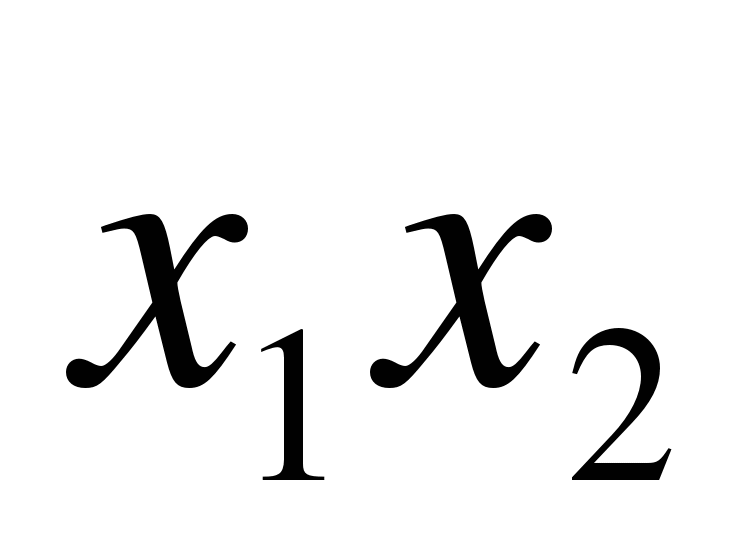 = - 5; 2)
= - 5; 2) 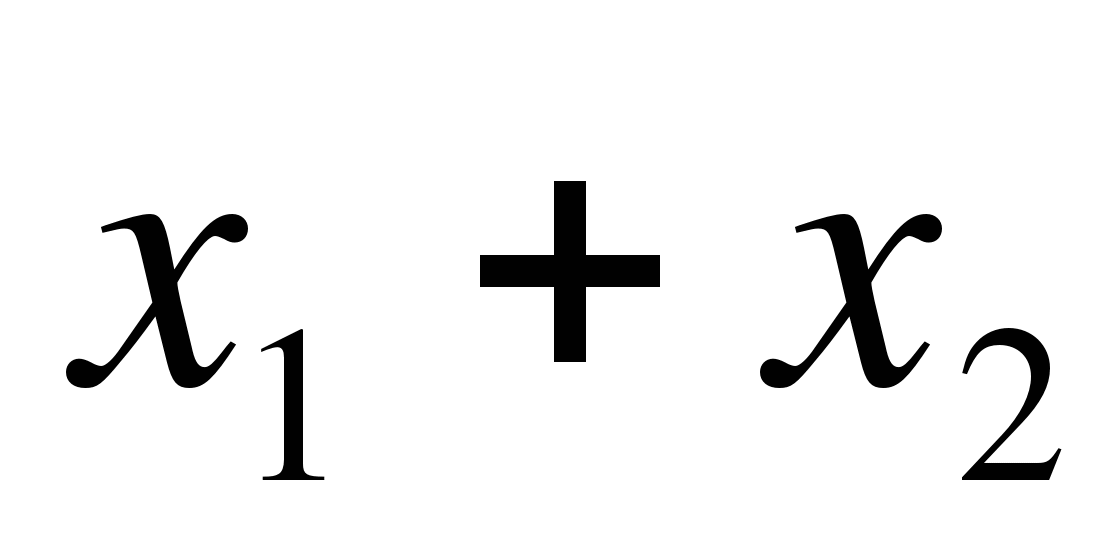 = - 5;
= - 5; 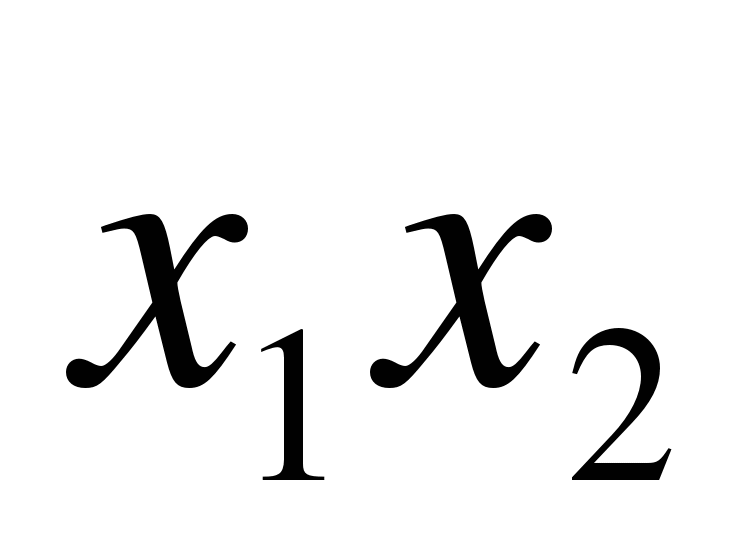 = - 3; 3)
= - 3; 3) 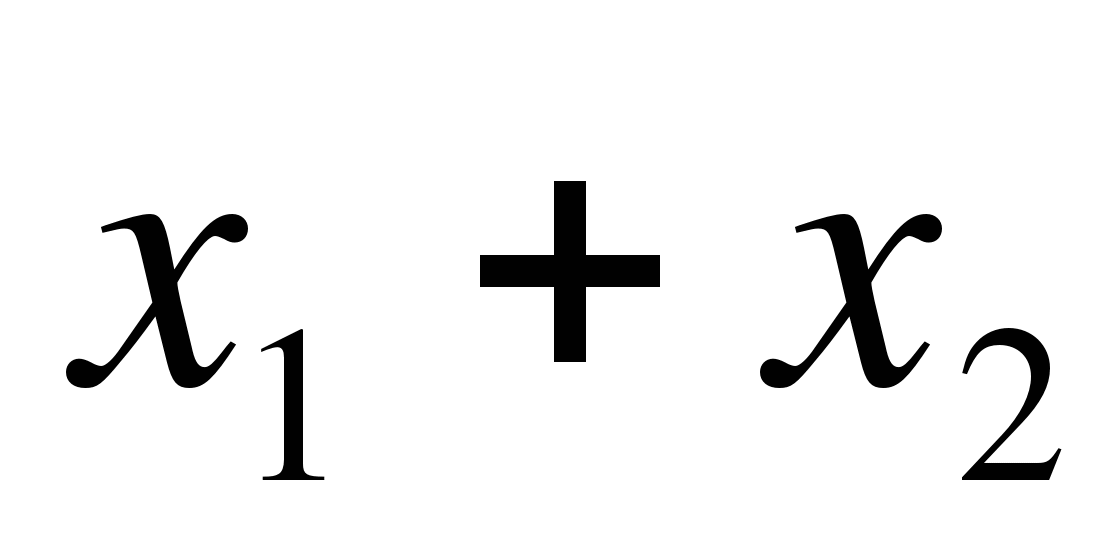 = 3,
= 3, 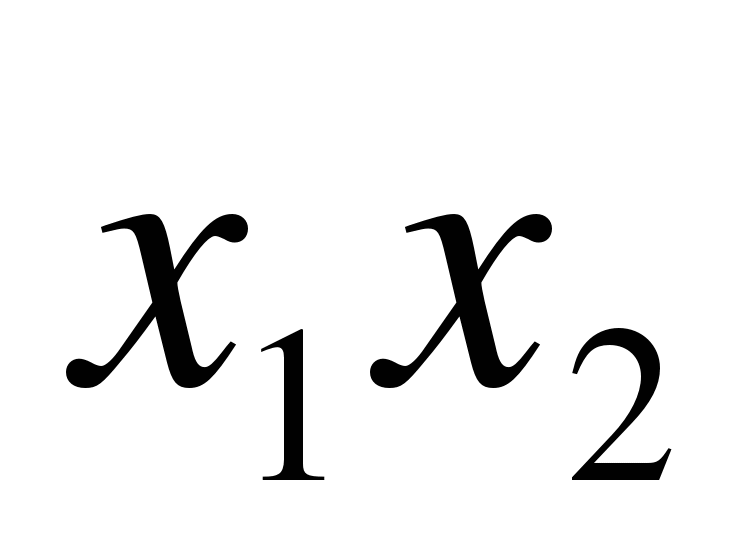 = - 5; 4)
= - 5; 4)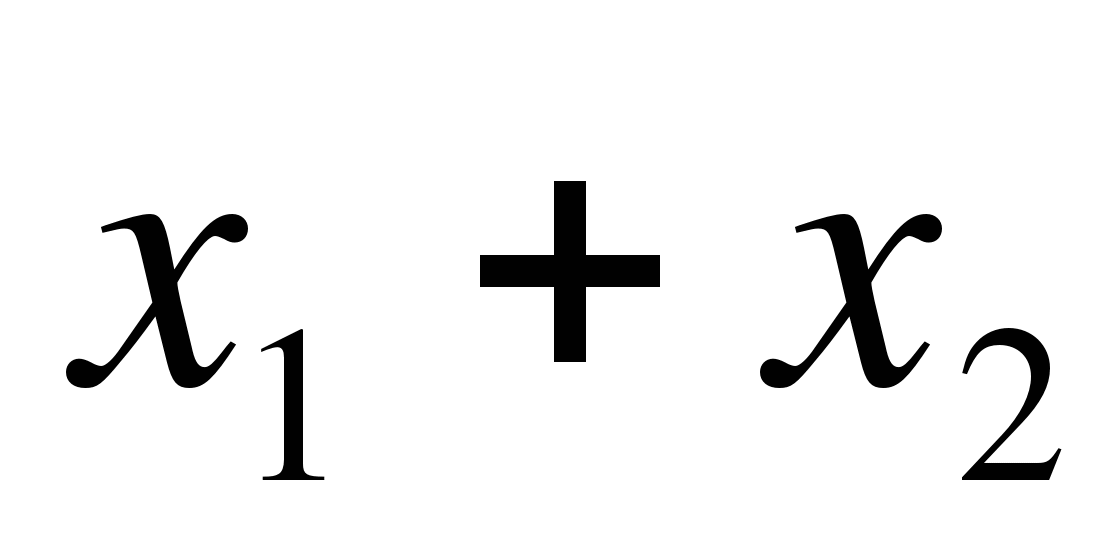 =5,
=5, 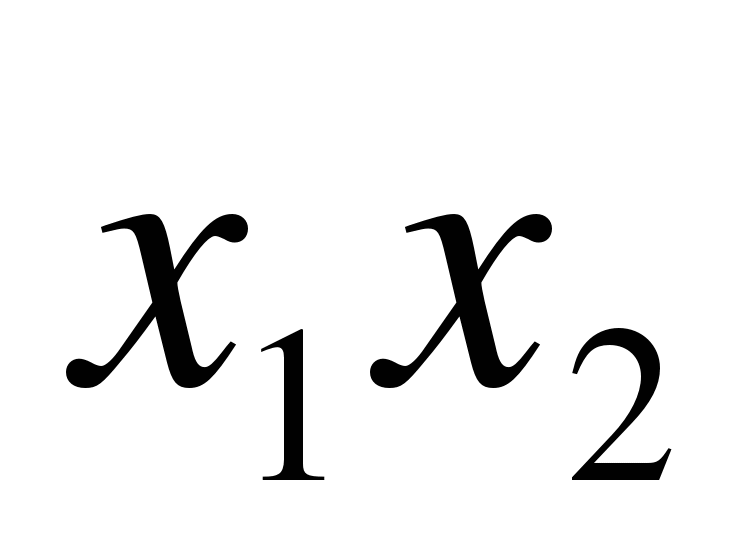 = - 3.
= - 3.
В 1. Один из корней уравнения х² + рх + 24 = 0 равен 8. Найдите р.
В 2. Найдите разность большего и меньшего корней уравнения х² - х - 20 = 0.
С 1. Площадь прямоугольника 48 см². Одна его сторона составляет 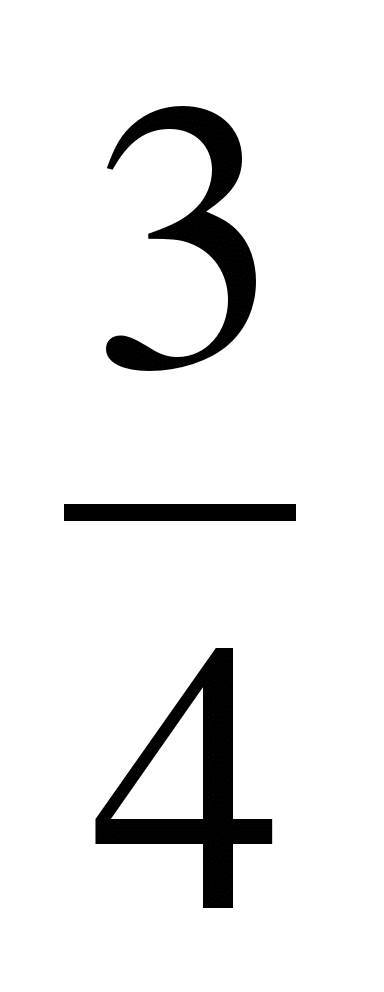 другой. Найдите меньшую сторону прямоугольника.
другой. Найдите меньшую сторону прямоугольника.
Контрольная работа «Квадратное уравнение и его корни. Теорема Виета». Алгебра. 8 класс.
Вариант № 3.
А 1.Укажите в квадратном уравнении х² + 3 – 4х = 0 коэффициент b.
1) 4. 2). 3. 3) - 4. 4) 1.
А 2. Решите уравнение х² + 5 = 0. 1). 5; 2) 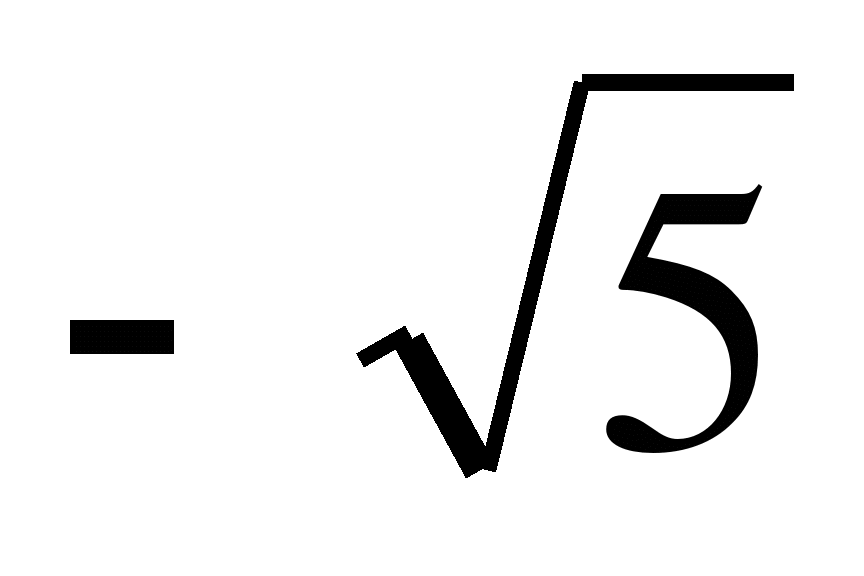
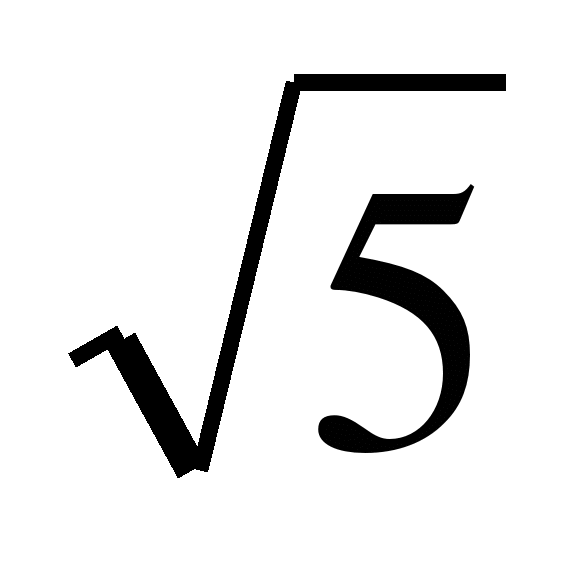 ; 3) решений нет; 4);
; 3) решений нет; 4); 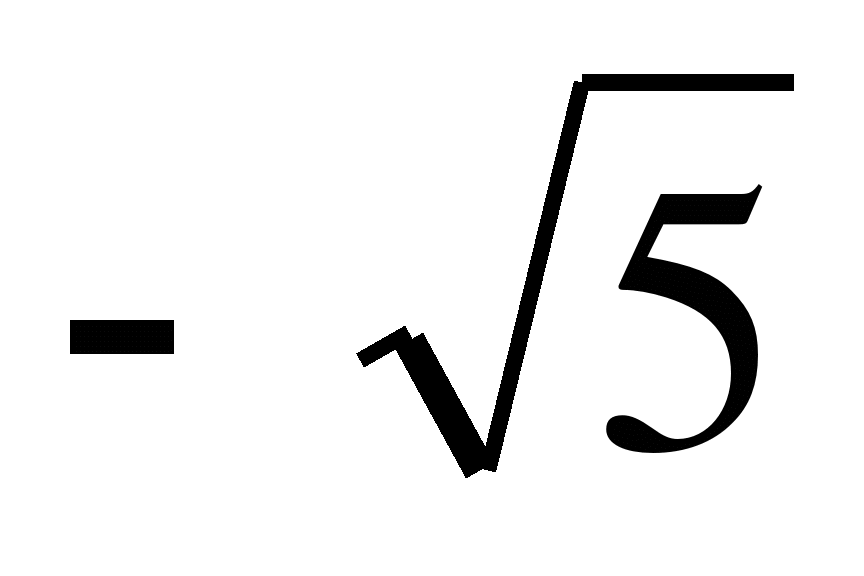 .
.
А 3. Дискриминант уравнения 8х² – 9х + 4 = 0 равен 1) 49; 2) 17; 3) -47; 4) 65.
А 4. Решите уравнение: 3х² + х – 4 = 0. 1) 4; - 3; 2) - 1; 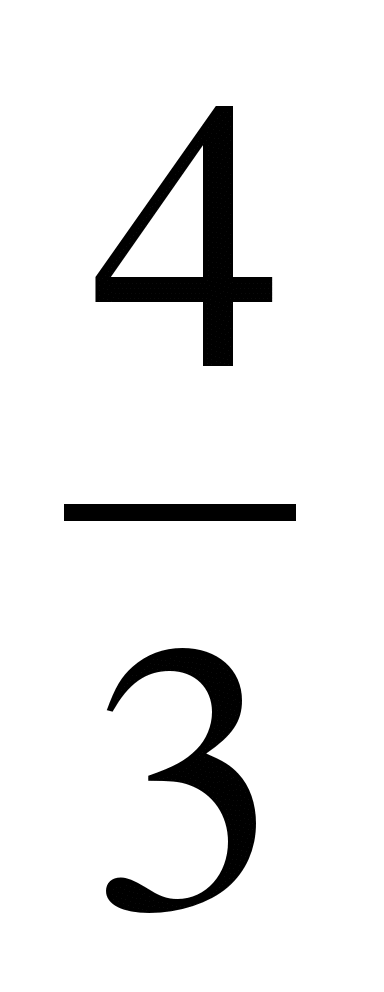 ; 3) 1;
; 3) 1; 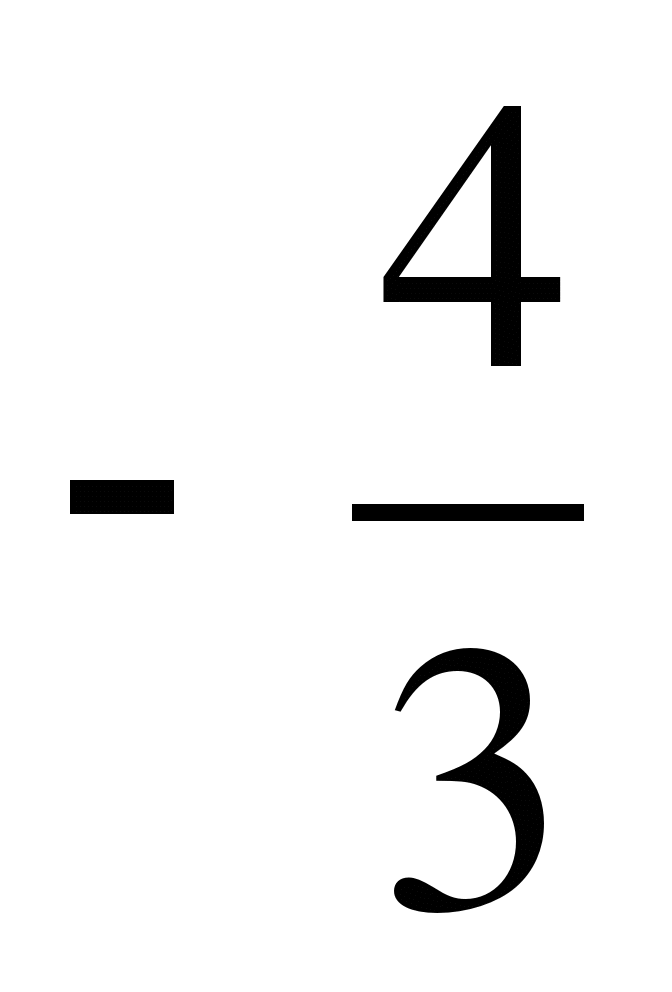 ; 4).
; 4). 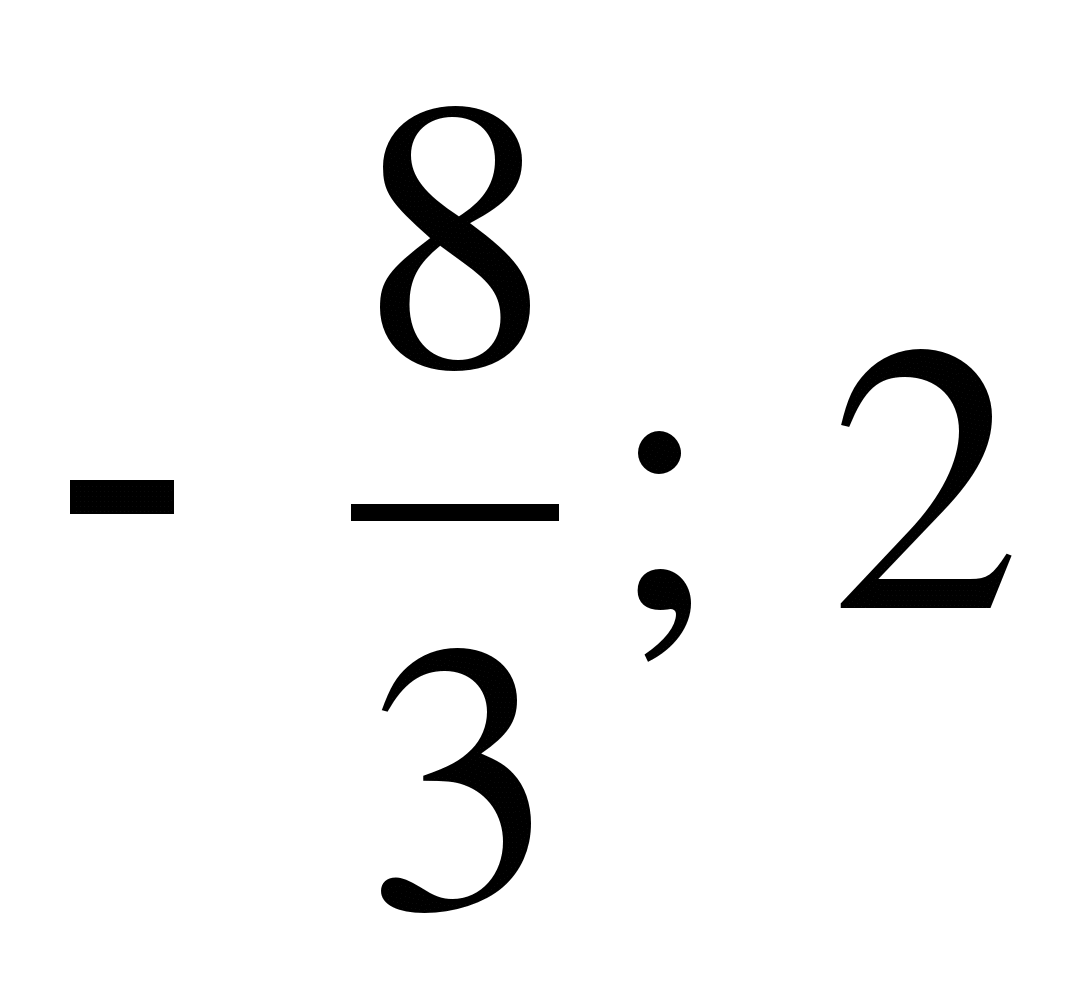
А 5. Имеет один корень уравнение
1) 4х² +4 х + 4 = 0; 2) 4х² -2 х + 0,25 = 0; 3) 9х² -6 х + 2 = 0; 4) 3х² - 1,5 х +5 = 0.
А 6. Если 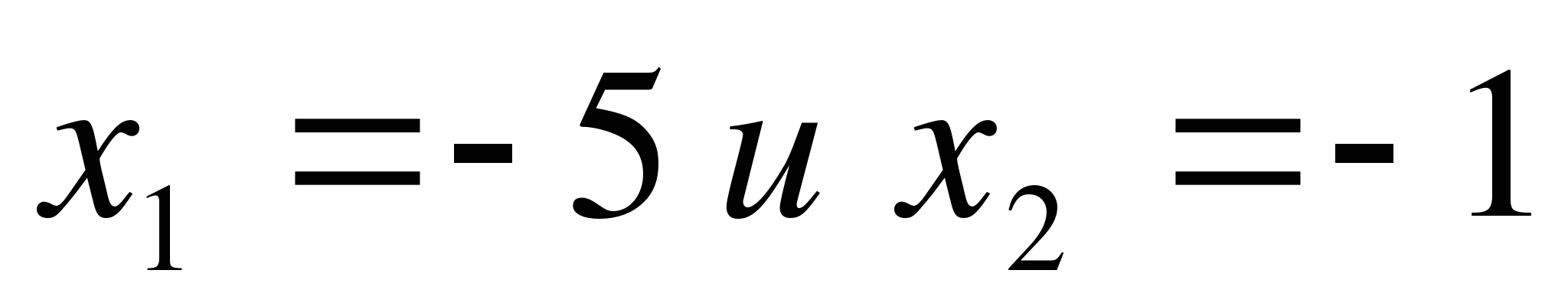 - корни уравнения х² + pх + q = 0, то
- корни уравнения х² + pх + q = 0, то
1) p = 6, q = 5; 2) p = - 6, q = - 5; 3) p = - 5; q = - 6; 4) p = 5 , q = 6.
В 1. Один из корней уравнения х² + 8х + q = 0 равен 3. Найдите q.
В 2. Найдите разность большего и меньшего корней уравнения х² + 3х - 10 = 0.
С 1. Площадь прямоугольника 250 см². Одна сторона в 2,5 раза больше другой. Найдите большую сторону прямоугольника.
Контрольная работа «Квадратное уравнение и его корни. Теорема Виета». Алгебра. 8 класс.
Вариант № 4.
А 1.Укажите в квадратном уравнении 7х – 5 - х² = 0 коэффициент а.
1) - 1. 2). 1. 3) 7. 4) - 5.
А 2. Решите уравнение (х – 2)(х + 2)= 4. 1). решений нет; 2) 2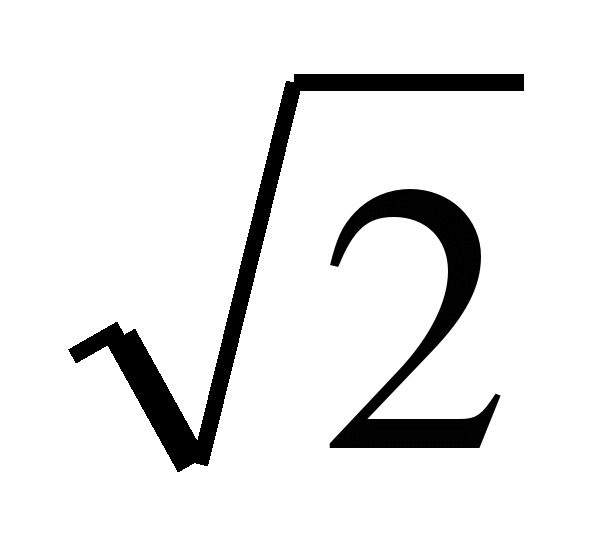 ;
; 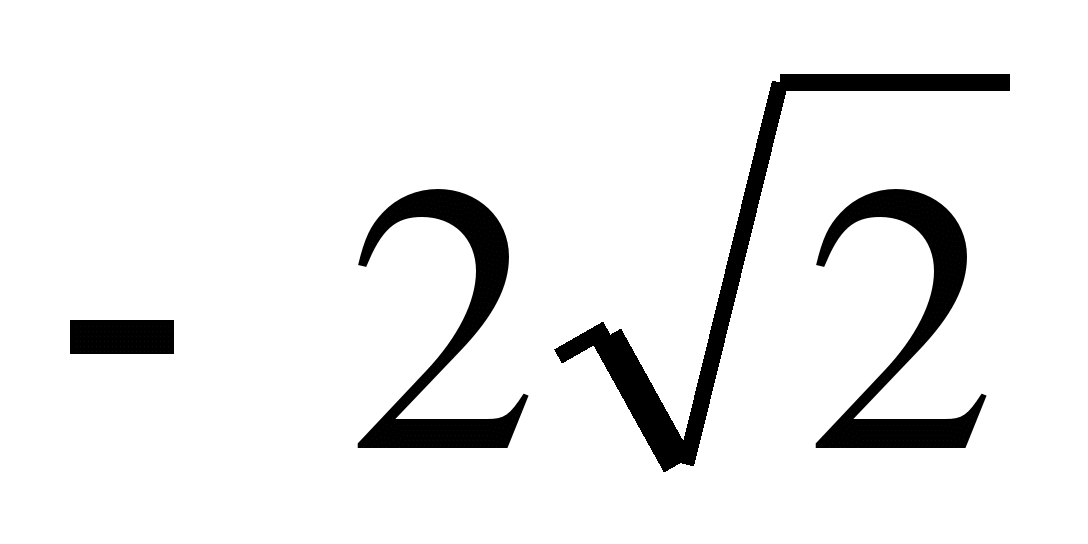 .; 3) 6 ; 4 ; 4) 0
.; 3) 6 ; 4 ; 4) 0
infourok.ru
Контрольная работа по алгебре «Квадратные уравнения»
Вариант 1.
Решите уравнение: а)3х2-8х+5=0
б) х2-2х+5=0
Решите неполные квадратные уравнения:
а) х2+5х=0 б) х2-9=0 в) 3х2+7=0
Решите квадратное уравнение с четным вторым коэффициентом: х2-24х+108=0
Решите квадратное уравнение, используя Теорему Виета: х2+9х+20=0
Решите задачу: Расстояние 30 км один из двух лыжников прошел на 20 минут быстрее другого. Скорость первого лыжника была на 3км/ч больше скорости второго. Какова была скорость каждого лыжника?
Контрольная работа по алгебре «Квадратные уравнения»
Вариант 2.
Решите уравнение: а) 4х2+10х-6=0
б) х2+3х+24=0
Решите неполные квадратные уравнения:
а) х2-12х=0 б) х2-64=0 в) 4х2+17=0
Решите квадратное уравнение с четным вторым коэффициентом: х2+26х-120=0
Решите квадратное уравнение, используя Теорему Виета: х2-15х+36=0
Решите задачу: Увеличив скорость на 10км/ч, поезд сократил на 1час время, затрачиваемое им на прохождение пути в 720 км. Найдите первоначальную скорость поезда.
Контрольная работа по алгебре «Квадратные уравнения»
Вариант 1.
Решите уравнение: а)3х2-8х+5=0
б) х2-2х+5=0
Решите неполные квадратные уравнения:
а) х2+5х=0 б) х2-9=0 в) 3х2+7=0
Решите квадратное уравнение с четным вторым коэффициентом: х2-24х+108=0
Решите квадратное уравнение, используя Теорему Виета: х2+9х+20=0
Решите задачу: Расстояние 30 км один из двух лыжников прошел на 20 минут быстрее другого. Скорость первого лыжника была на 3км/ч больше скорости второго. Какова была скорость каждого лыжника?
Контрольная работа по алгебре «Квадратные уравнения»
Вариант 2.
Решите уравнение: а) 4х2+10х-6=0
б) х2+3х+24=0
Решите неполные квадратные уравнения:
а) х2-12х=0 б) х2-64=0 в) 4х2+17=0
Решите квадратное уравнение с четным вторым коэффициентом: х2+26х-120=0
Решите квадратное уравнение, используя Теорему Виета: х2-15х+36=0
Решите задачу: Увеличив скорость на 10км/ч, поезд сократил на 1час время, затрачиваемое им на прохождение пути в 720 км. Найдите первоначальную скорость поезда.
Контрольная работа по алгебре «Квадратные уравнения»
Вариант 2.
Решите уравнение: а) 4х2+10х-6=0
б) х2+3х+24=0
Решите неполные квадратные уравнения:
а) х2-12х=0 б) х2-64=0 в) 4х2+17=0
Решите квадратное уравнение с четным вторым коэффициентом: х2+26х-120=0
Решите квадратное уравнение, используя Теорему Виета: х2-15х+36=0
Решите задачу: Увеличив скорость на 10км/ч, поезд сократил на 1час время, затрачиваемое им на прохождение пути в 720 км. Найдите первоначальную скорость поезда.
Контрольная работа по алгебре «Квадратные уравнения»
Вариант 1.
Решите уравнение: а)3х2-8х+5=0
б) х2-2х+5=0
Решите неполные квадратные уравнения:
а) х2+5х=0 б) х2-9=0 в) 3х2+7=0
Решите квадратное уравнение с четным вторым коэффициентом: х2-24х+108=0
Решите квадратное уравнение, используя Теорему Виета: х2+9х+20=0
Решите задачу: Расстояние 30 км один из двух лыжников прошел на 20 минут быстрее другого. Скорость первого лыжника была на 3км/ч больше скорости второго. Какова была скорость каждого лыжника?
infourok.ru
Проверочная работа
«Квадратные уравнения»
Вариант 1
1. Запишите общий вид квадратного уравнения.
2. Какие значения могут принимать а, в, с:
а) а, в, с- любые числа; в) а≠0, в≠0, с≠0;
б) а ≠0, в и с – некоторые числа; г) а=0, в≠0, с≠0.
3. Какое из уравнений является квадратным:
а) 2х-3+4х=0; б) 3(х3-4) – х2+5=0 в) х2 -4х +3=0; г) (2-х)(х2+6)=0
4. Укажите старший коэффициент квадратного уравнения 4х2+8х-5=0:
а) 4; б) -4; в) 8; г) -5.
5. После преобразований, уравнение 2- 3(х2-4)=х примет вид:
а) 2 – 3х2-12+х =0 в) -3х2+2х+12 =0
б) -3х2-х+14 =0; г) 3х2+х+10 =0
6. Сколько корней может иметь квадратное уравнение:
а) только 2 корня; в) может не иметь корней;
б) 1 или 2 корня; г) 1 или 2 или ни одного корня.
7. Какие из чисел являются корнями уравнения 2х2+3х-2=0:
а) -2; 0,5; б) 2; -0,5; в) 2; г) -0,5.
8. Решите квадратные уравнения:
а) 4х2+8х-5=0; в) 2х2-5х+7=0;
б) х2-4х+4=0; г) –2х2-5х-3=0.
9. Решите неполные квадратные уравнения:
а) 3х2+12х=0; б) 2х2-8=0; в) 3х2+27=0; г) 100х2-25=0.
10. Укажите приведённое квадратное уравнение:
а) 2 –х2+4х=0; б) 4х2+8х-5=0; в) -х2-5х+6=0; г) х2-5х+6=0.
11. Чему равна сумма и произведение корней уравнения х2+2х-15=0:
а) 2 и 15; б) -2 и -15; в) -2 и 15; г) 2 и -15.
12. Решите приведённое квадратное уравнение х2+2х-15=0, используя теорему Виета.
13. Установите соответствие между уравнениями и рациональными способами их решения:
А) по общей формуле; Б) по теореме Виета; В) по формуле для уравнения с чётным коэффициентом перед х.
1) х2+3х-1=0; 2) 2х2-7х+3=0; 3) х2+6х+8=0; 4) 7х2-20х+14=0.
А
Б
В
14. Составьте уравнение, корнями которого являются числа: 3 и 5
15. Решите квадратное уравнение 14у+у2+48=0 наиболее удобным способом.
Проверочная работа
«Квадратные уравнения»
Вариант 2
1. Запишите общий вид квадратного уравнения.
2. Какие значения могут принимать а, в, с:
а) а, в, с- некоторые числа; в) а≠0, в≠0, с≠0;
б) а =0, в и с – некоторые числа; г) а≠0, в и с – некоторые числа.
3. Какое из уравнений является квадратным:
а )х2 -4х +3=0; б) 3(х3-4) – х2+5=0 в) 2х-3+4х=0; г) (2-х)(х2+6)=0
4. Укажите старший коэффициент квадратного уравнения 4х2-8х+5=0:
а) - 4; б) 4; в)- 8; г) 5.
5. После преобразований, уравнение х +3(х2-4)= 2 примет вид:
а) 2 – 3х2-12+х =0 в) 3х2+х-14 =0
б) -3х2-2х+14 =0; г) 3х2+х+10 =0
6. Сколько корней может иметь квадратное уравнение:
а) только 1 корня; в) 1 или 2 или ни одного корня
б) 1 или 2 корня; г) не имеет корней.
7. Какие из чисел являются корнями уравнения 2х2+3х-2=0:
а) 2; -0,5; б) -2; 0,5; в) 2; г) -0,5.
8. Решите квадратные уравнения:
а) 4х2+4х+1=0; в) 2х2-7х+3=0;
б) х2-2х-8=0; г) 2х2-х+3=0.
9. Решите неполные квадратные уравнения:
а) 3х2+6х=0; б) 2х2-32=0; в) 2х2+18=0; г) 36х2-1=0.
10. Укажите приведённое квадратное уравнение:
а) 2 –х2+4х=0; б) 4х2+8х-5=0; в) -х2-5х+6=0; г) х2-5х+6=0.
11. Чему равна сумма и произведение корней уравнения х2+2х-15=0:
а) 2 и 15; б) -2 и -15; в) -2 и 15; г) 2 и -15.
12. Решите приведённое квадратное уравнение х2+2х-15=0, используя теорему Виета.
13. Установите соответствие между уравнениями и рациональными способами их решения:
А) по общей формуле; Б) по теореме Виета;
В) по формуле для уравнения с чётным коэффициентом перед х.
1) х2+3х-1=0; 2) 2х2-7х+3=0; 3) х2+6х+8=0; 4) 7х2-20х+14=0.
А
Б
В
14. Составьте уравнение, корнями которого являются числа: 3 и 5
15. Решите квадратное уравнение 14у+у2+48=0 наиболее удобным способом.
infourok.ru
Домашняя контрольная работа.
1. Восстановите квадратное уравнение, если его корнями являются числа:
1) 1 и 3 2) -2 и 5 3) 2 и -5 4) -1 и -3
2. Не решая квадратное уравнение, найдите сумму и произведение его корней:
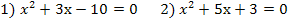

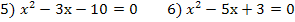

3. Решите неполное квадратное уравнение:



4. Решите квадратное уравнение по формуле:
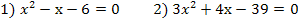


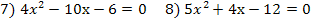

5. Дано 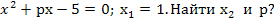
6. Дано 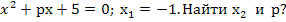
7. Найдите 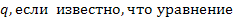
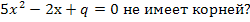
8. Найдите 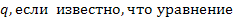
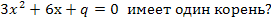
9. Найдите 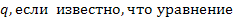
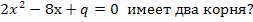
Домашняя контрольная работа.
1. Восстановите квадратное уравнение, если его корнями являются числа:
1) 1 и 3 2) -2 и 5 3) 2 и -5 4) -1 и -3
2. Не решая квадратное уравнение, найдите сумму и произведение его корней:
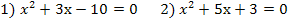

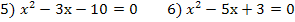

3. Решите неполное квадратное уравнение:



4. Решите квадратное уравнение по формуле:
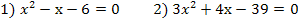


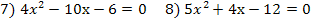

5. Дано 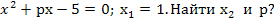
6. Дано 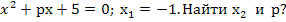
7. Найдите 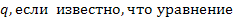
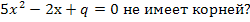
8. Найдите 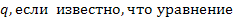
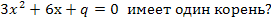
9. Найдите 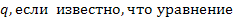
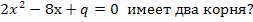
infourok.ru
7
Ф. И. ученика(цы)_____________________________________________ Дата__________________| № | Задания. Вариант 2 | ответ | Решение………………........... |
| 1 | Укажите полные квадратные уравнения
| абвгз | |
| 2 | Укажите неполные квадратные уравнения в задании 1 | деж | |
| 3 | Укажите приведённые квадратные уравнения в задании 1 | г | |
| 4 | Сколько корней имеет квадратное уравнение
| 1 | |
| 5 | Сколько корней имеет квадратное уравнение
| 0 | |
| 6 | Сколько корней имеет квадратное уравнение
| 2 | |
| 7 | Вычислите дискриминант уравнения
| 220 | |
| 8 | Вычислите корни уравнения | 0,2 и -3 | |
| 9 | Вычислите дискриминант уравнения | 28 | |
| 10 | Вычислите корни уравнения
| 3 и -1 | |
| 11 | Решите уравнение |
| |
| 12 | Вычислите корни уравнения | 0 и -8 | |
| 13 | Вычислите корни уравнения | ||
| 14 | Вычислите корни уравнения 2 | 0 и 7 | |
| 15 | Вычислите корни уравнения 2 | 1 и 1,5 | |
| 16 | Периметр прямоугольника равен 20. Найдите стороны прямоугольника, если площадь равна 24. | 6 и 4 | |
| 17 | В уравнении | 2 и 7 |
№
Задания. Вариант 3
Ответ……
Решение……………………….
1
Укажите полные квадратные уравнения
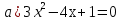 ;
; 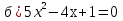 ;
;
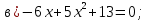
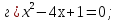
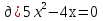 ;
; 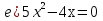 ;
; 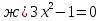 ;
; 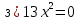 ;
;
2
Укажите неполные квадратные уравнения в задании 1
3
Укажите приведённые квадратные уравнения в задании 1
4
Сколько корней имеет квадратное уравнение
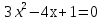
2
5
Сколько корней имеет квадратное уравнение
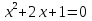
1
6
Сколько корней имеет квадратное уравнение
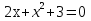
0
7
Вычислите дискриминант уравнения
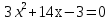
232
8
Вычислите корни уравнения 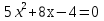
0,4 и -2
9
Вычислите дискриминант уравнения 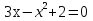
17
10
Вычислите корни уравнения 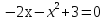
1 и -3
11
Решите уравнение 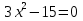
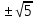
12
Вычислите корни уравнения 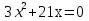
0 и -7
13
Вычислите корни уравнения 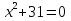
Корней
нет
14
Вычислите корни уравнения 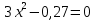
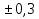
15
Вычислите корни уравнения 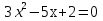
1 и 2\3
16
Периметр прямоугольника равен 20. Найдите стороны прямоугольника, если площадь равна 24.
4 и 6
17
В уравнении 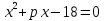 один корень равен -9. Найдите второй корень и коэффициент р.
один корень равен -9. Найдите второй корень и коэффициент р.
2 и 7
№
Задания. Вариант 4
Ответ……
Решение……………………….
1
Укажите полные квадратные уравнения
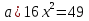 ;
; 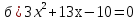 ;
; 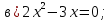
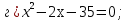
бг
2
Укажите неполные квадратные уравнения в задании 1
ав
3
Укажите приведённые квадратные уравнения в задании 1
г
4
Сколько корней имеет квадратное уравнение
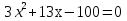
0
5
Сколько корней имеет квадратное уравнение
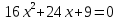
1
6
Сколько корней имеет квадратное уравнение
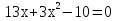
2
(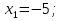
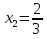 )
)
7
Вычислите дискриминант уравнения
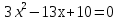
49
1 и 10\3
8
Вычислите корни уравнения 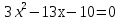
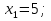
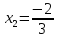
9
Вычислите дискриминант уравнения 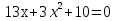
49
10
Вычислите корни уравнения 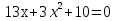
-1 и -10\3
11
Решите уравнение 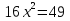
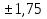
12
Вычислите корни уравнения 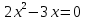
0 и 1,5
13
Вычислите корни уравнения 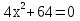
Корней
нет
14
Вычислите корни уравнения 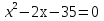
-5 и 7
15
Вычислите корни уравнения 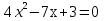
1 и 0,75
16
Периметр прямоугольника равен 30. Найдите стороны прямоугольника, если площадь равна 56.
8 и 7
17
В уравнении 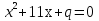 один корень равен -7. Найдите второй корень и коэффициент q.
один корень равен -7. Найдите второй корень и коэффициент q.
-4 и 28
№
Задания. Вариант 5
Ответ……
Решение……………………….
1
Укажите полные квадратные уравнения
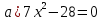 ;
; 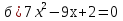 ;
;
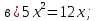
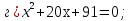
бг
2
Укажите неполные квадратные уравнения в задании 1
ав
3
Укажите приведённые квадратные уравнения в задании 1
г
4
Сколько корней имеет квадратное уравнение
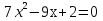
2
5
Сколько корней имеет квадратное уравнение
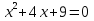
0
6
Сколько корней имеет квадратное уравнение
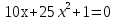
1
7
Вычислите дискриминант уравнения
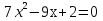
25
8
Вычислите корни уравнения 
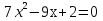
2\7 и 1
9
Вычислите дискриминант уравнения 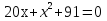
36
10
Вычислите корни уравнения 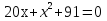
-7 и -13
11
Решите уравнение 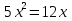
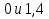
12
Вычислите корни уравнения 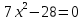
-2 и 2
13
Вычислите корни уравнения 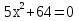
Корней
нет
14
Вычислите корни уравнения 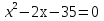
-5 и 7
15
Вычислите корни уравнения 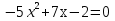
1 и 0,4
16
Периметр прямоугольника равен 26. Найдите стороны прямоугольника, если площадь равна 36.
9 и 4
17
В уравнении 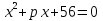 один корень равен -4. Найдите второй корень и коэффициент q.
один корень равен -4. Найдите второй корень и коэффициент q.
-14 и 28
№
Задания. Вариант 6
Ответ……
Решение……………………….
1
Укажите полные квадратные уравнения
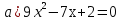 ;
; 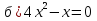 ;
;
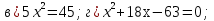
aг
2
Укажите неполные квадратные уравнения в задании 1
бв
3
Укажите приведённые квадратные уравнения в задании 1
г
4
Сколько корней имеет квадратное уравнение
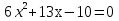
0
5
Сколько корней имеет квадратное уравнение
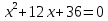
1
6
Сколько корней имеет квадратное уравнение
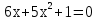
2
7
Вычислите дискриминант уравнения
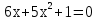
16
8
Вычислите корни уравнения
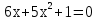
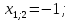
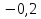
9
Вычислите дискриминант уравнения 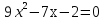
121
10
Вычислите корни уравнения
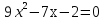
1 и -2\9
11
Решите уравнение 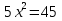
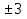
12
Вычислите корни уравнения

0 и 0,25
13
Вычислите корни уравнения
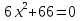
Корней
нет
14
Вычислите корни уравнения
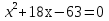
-21 и 3
15
Вычислите корни уравнения
-6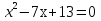
1 и -13\6
16
Периметр прямоугольника равен 22. Найдите стороны прямоугольника, если площадь равна 24.
8 и 3
17
В уравнении 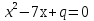 один корень равен 13. Найдите второй корень и коэффициент q.
один корень равен 13. Найдите второй корень и коэффициент q.
-6 и -78
Леново дом, рабочий стол,8 класс,дидактика,кв.урав. Страница 7
infourok.ru