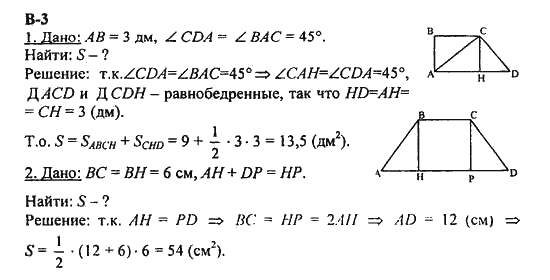Геометрия 8 Контрольные Атанасян (Зив)
Геометрия 8 Контрольные Атанасян (Зив)
Контрольные работы + Ответы
Геометрия 8 Контрольные Атанасян (Зив) — это цитаты контрольных работ из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.
Цитаты из пособия указаны в учебных и информационных целях. При постоянном использовании контрольных работ по геометрии в 8 классе рекомендуем купить книгу: Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение, в которой кроме контрольных работ есть еще 39 самостоятельных работ, математические диктанты и задачи повышенной трудности.
Для увеличения изображения — нажмите на картинку !
Чтобы скачать работу — нажмите на правую кнопку мыши и выберите «Сохранить изображение как …»
Контрольная работа № 1.

Четырехугольники
ОТВЕТЫ на Контрольную работу № 1
Контрольная работа № 2.
Площадь
ОТВЕТЫ на Контрольную работу № 2
Контрольная работа № 3.
Подобные треугольники
ОТВЕТЫ на Контрольную работу № 3
Контрольная работа № 4.
Применение подобия, решение прямоугольных треугольников
ОТВЕТЫ на Контрольную работу № 4
Контрольная работа № 5.
Окружность
ОТВЕТЫ на Контрольную работу № 5
Контрольная работа № 6.
Векторы
ОТВЕТЫ на Контрольную работу № 6
Контрольная работа № 7.
Итоговая работа за 8 класс
ОТВЕТЫ на Контрольную работу № 7
Вы смотрели страницу «Геометрия 8 Контрольные Атанасян (Зив)» — Контрольные работы из пособия для учащихся «Геометрия. Дидактические материалы. 8 класс / Б.Г. Зив, В.М. Мейлер — М.: Просвещение», которое используется в комплекте с учебником «Геометрия. 7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.
7-9 классы» авторов: Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева, Э.Г. Позняка, И.И. Юдиной, а также ответы на контрольные работы.
Контрольная работа по геометрии за 1 четверть. 8 класс. Атанасян
Вариант 1. 1.Диагонали прямоугольника ABCD пересекаются в точке О, угол АВО =36 градусов .Найдите угол АОD. 2.Найдите углы прямоугольной трапеции, если один из углов равен 20 градусов. 3.Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. 4.В равнобедренной трапеции сумма углов при большем основании равна 96 градусов. Найдите углы трапеции. 5. В ромбе МРКН с тупым углом К диагонали пересекаются в точке Е. Один из углов треугольника РКЕ равен 17градусов. | Вариант 2. 1.Диагонали прямоугольника MNKP пересекаются в точке О, угол MON равен 64градусов . Найдите угол OMP. 2.Найдите углы равнобокой трапеции, если один из её углов на 30 градусов больше другого. 3.Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. 4.В прямоугольной трапеции разность углов при одной из боковых сторон равна 48 градусов. Найдите углы трапеции. 5. Диагонали ромба ABCD пересекаются в точке О. Найдите углы ∆ АВО, если угол ВСD равен 110°. |
Вариант 3. 1.Диагонали прямоугольника MNKP пересекаются в точке О, угол MON равен 72градусов . 2. В равнобокой трапеции сумма углов при меньшем основании равна 210. Найдите углы трапеции. 3. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма .4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 52 градусов. Найдите углы трапеции. 5. Диагональ АС и сторона АВ образуют угол, в два раза больше, чем угол, образованной диагональю ВД со стороной АВ. Найти углы ромба. | Вариант 4. 1.Диагонали прямоугольника ABCD пересекаются в точке О, угол АОВ =72 градусов .Найдите угол АDО. 2.Найдите углы прямоугольной трапеции, если один из углов в два раза больше другого. 3.Стороны параллелограмма относятся как 4:5, а его периметр равен 72 см. Найдите стороны параллелограмма. 4.В равнобедренной трапеции сумма углов при большем основании равна в два раза больше суммы углов при меньшем основании. Найти углы трапеции. 5. В ромбе АВСD угол А=31°. Диагонали пересекаются в точке О. Найдите углы треугольника ВОС. |
Вариант 5 1.Диагонали прямоугольника KLMN пересекаются в точке О, угол KON =42 градусов .Найдите угол NOM. 2.Найдите углы прямоугольной трапеции, если один из углов в три раза меньше другого. 3.Стороны параллелограмма относятся как 3:7, а его периметр равен 40 см. Найдите стороны параллелограмма. 4.В равнобедренной трапеции сумма углов при большем основании равна 84 градусов. Найдите углы трапеции. 5.В ромбе KLMN, угол K в три раза меньше угла L, найдите угля ромба. | Вариант 6. 1.Диагонали прямоугольника АВСД пересекаются в точке О, угол АОВ равен 45 градусов . Найдите угол ВОС. 2.Найдите углы равнобокой трапеции, если угля при ее боковой стороне относятся как 2;4. 3.Периметр параллелограмма равен 60см. Одна из его сторон в 5 раз больше другой. Найти стороны параллелограмма 4.В прямоугольной трапеции разность углов при одной из боковых сторон относятся как 1:2. Найдите углы трапеции. 5. В ромбе АВСД, диагональ ВД, образует со стороной СД угол 56 градусов. Найти углы ромба |
Вариант 7. 1.Диагонали прямоугольника АВСД пересекаются в точке О, угол ДОС в два раза больше угла СОВ. Найдите эти углы. 2.Найдите углы равнобокой трапеции, если один из её углов на 25 градусов меньше другого.  Найти стороны параллелограмма, если одна из его сторон в 3 раза меньше другой, а их периметр равен 64см. Найти стороны параллелограмма, если одна из его сторон в 3 раза меньше другой, а их периметр равен 64см.4.В прямоугольной трапеции разность углов при одной из боковых сторон относятся как 5:1. Найдите углы трапеции. 5. В ромбе АВСД, диагональ АС образует со стороной АВ угол 45 градусов. Найдите угол АВД, и величину углов ромба. | Вариант 8 1.Диагонали прямоугольника KLMN пересекаются в точке О, угол MOL =15градусов .Найдите угол NOM. 2.Найдите углы прямоугольной трапеции, если один из углов равен 45 градусов. 3.Стороны параллелограмма относятся как 1:3, а его периметр равен 48 см. Найдите стороны параллелограмма. 4.В равнобедренной трапеции сумма углов при одном основании в два раза больше суммы углов при другом основании. Найти углы трапеции 5. Диагональ АС и сторона АВ образуют угол, в три раза меньбше, чем угол, образованной диагональю ВД со стороной АВ. |
Тест по геометрии. 8 класс
Тема: «Четырехугольники».
Вариант №1.
В заданиях 1 – 4 вставьте пропущенные слова.
1. *** называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков.
а) прямоугольник б) трапеция
в) ромб г) четырехугольник
2. Диагонали ромба являются *** его углов.
а) медианами б) высотами в) средними линиями г) биссектрисами
3. У параллелограмма противолежащие стороны равны, противолежащие *** равны.
а) вершины б) углы в) прямые г) отрезки
4. Ромб – это ***, у которого все стороны равны.
а) четырехугольник б) прямоугольник
в) квадрат г) параллелограмм
5. Найдите на рисунке параллелограмм.
а)
6. Назовите боковые стороны трапеции КМNЕ.
А) КЕ и МN Б) МN и ЕN В) КМ и NЕ Г) МN и МК
Тест по геометрии.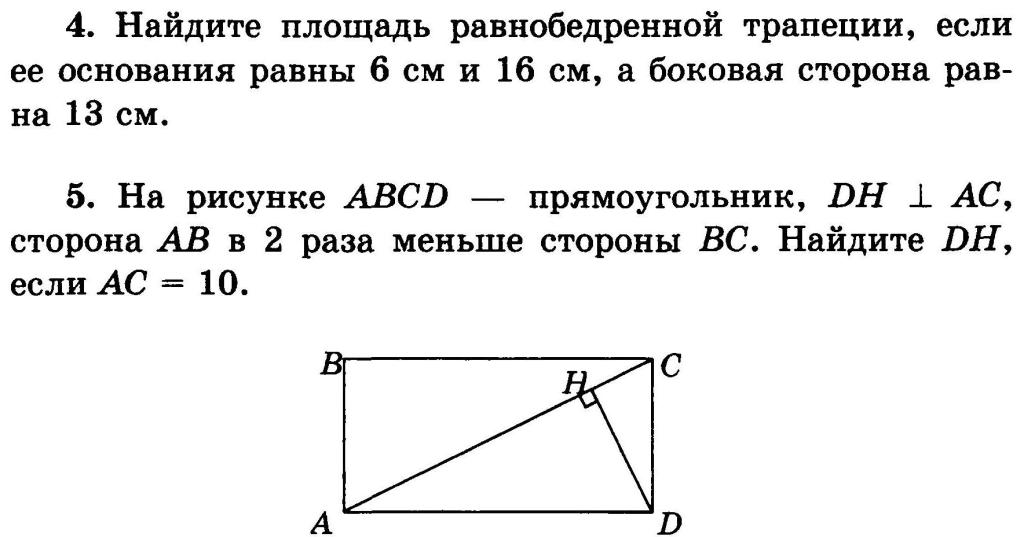 8 класс
8 класс
Тема: «Четырехугольники».
Вариант №2.
В заданиях 1-5 вставьте пропущенные.
1.Прямоугольник – это ***, у которого все углы прямые.
а) трапеция б) параллелограмм
в) ромб г) четырехугольник
2. *** называется четырехугольник, у которого только две противолежащие стороны параллельны.
а) прямоугольник б) трапеция
в) параллелограмм г) ромб
3. *** параллелограмма пересекаются и точкой пересечения делятся пополам.
а) вершины б) диагонали в) углы г) стороны
4. Диагонали *** равны.
а) четырехугольника б) прямоугольника
в) ромба г) трапеции
5. Найдите на рисунке трапецию.
а)
6. Назовите основания трапеции КМNЕ.
А) КЕ и МN Б) КМ и NЕ В) МN и ЕN Г) МN и МК
Контрольная работа № 1. Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. Найдите угол OMP. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. | |||||
Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2. | |||||
Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. Найдите площадь трапеции. | Контрольная работа № 2. Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. | |||||
Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. | |||||
Контрольная работа № 3. Г-8. Вариант-1. B № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D № 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2. | Контрольная работа №3. Г-8. Вариант-2. N № 1. Рисунок 1. P Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN. M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. | |||||
Контрольная работа № 3. Г-8. Вариант-3. № 1. Рисунок 1. D B Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD. Найти: а) DВ : АС; б) РАОС : РDBO ; в) SDBO: SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4. № 1. Рисунок 1. B Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. D E Доказать: DЕ ║АС. Найти: а) DЕ : АС; б) РABC : РDBE ; в) SDBE : SABC. № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН. | |||||
Контрольная работа № 4. Г-8. Вариант-1. № 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. № 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. Найдите ЕF, если сторона АС равна 15 см. № 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см, ВС = 5√3 см. № 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН. № 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см. | Контрольная работа №4. Г-8. Вариант-2. № 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника. № 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см. №3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см, КТ= 7 см. Найдите угол К и гипотенузу КР. № 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС. № 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. NK = 7 см. | |||||
Контрольная работа № 4. Г-8. Вариант-3. № 1. На стороне ВС треугольника АВС выбрана точка D так, что ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК. № 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см, СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ. № 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции. № 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см. № 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10, СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ. | Контрольная работа № 4. Вариант-4. № 1. На стороне АМ треугольника АВМ отмечена точка Н так, что АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и угол ВНМ. № 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см, NК =6√3 см, КD- медиана. Найдите угол КDN. № 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции. № 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника. № 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ. | |||||
Контрольная работа № 5. Г-8. Вариант-1. № 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12. Найдите ∟ВСА, ∟ВАС. B A 130O C № 3. Хорды MN и PK пересекаются точке E так, что ME =12 см, NE =3 см, PE=KE. Найдите PK. № 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника. | Контрольная работа № 5. Г-8. Вариант-2. № 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3. Найдите ∟ВОС, ∟АВС. A B 60O C O № 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см, ВF =16 см, СF=DF. Найдите CD. № 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. | |||||
Контрольная работа № 5. Г-8. Вариант-3. № 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника № 2. Точки А и В делят окружность с центром О на дуги АВМ и АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ. № 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. | Контрольная работа № 5. Г-8. Вариант-4. № 1. № 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН. № 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см, NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике основание равно 10 см, а высота, Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. | |||||
№ 1 | № 2 | № 3 | № 4 | № 5 | ||
Контрольная работа № 1. | Вариант-1 | ∟АОD=72 | 900 , 900, 1600, 200 | 5см, 10см, 5см, 10см | 480, 480, 1320, 1320 | DВ=6см |
Вариант-2 | ∟ОМР=32 | 750, 1050, 1050, 750 | 5см, 15см, 5см, 15см | 660, 1140, 900, 900 | АМ=3см | |
Вариант-3 | 10см, 15см, 10см, 15см | 800 | 450, 1350 450,1350 | AD=24см | AD=8см | |
Вариант-4 | 18см, 12см, 18см, 12см | 500 | 300, 300, 1500, 1500 | АВ= 7см | М1 М2 =6см | |
Контрольная работа № 2. | Вариант-1 | 24см2 | 10см, 24см2 | Р=4√41см, S= 40cм2 | S АВСК= 13,5см2 | — |
Вариант-2 | 24см2 | 5см, 30см2 | Р=4√61см, S= 60cм2 | S АВСD= 24√3см2 | — | |
Вариант-3 | 780cм2 | SABCD = 160cм2 | SABK =33,6см2, SCBK =50,4см2 | 6см | — | |
Вариант-4 | 154см2 | SABCD = 100cм2 | SKPT=36см2, SMPT =18см2 | 3см | — | |
Контрольная работа № 3. | Вариант-1 | а) 7,5; б) ; в) | 800, 600,400 | 5см | S = 5см2 | — |
Вариант-2 | а) 9; б) ; в) | AC=14см, ∟С=600 | 14см | 5см2 | — | |
Вариант-3 | а); б) ; в) | АВ=6см; АС= 16√3 | — | 10см | — | |
Вариант-4 | а) ; б) 3; в) | АС=4√5; ВD=8√5 | — | 20см | ||
Контрольная работа № 5. | Вариант-1 | 15см | ∟ВСА=550, ∟ВАС=600 | РЕ=6см, РК= 12см | АВ=16√3см, ВС= 16√2см | — |
Вариант-2 | 12см | ∟ВОС=1200, ∟АВС=450 | СF=8см, СD=16см | МN=12√3см; NК=12√2см | — | |
Вариант-3 | 6см, 8см, 10 см | ∟АМВ=600, ∟АВМ=900, ∟ АСВ=1050 | СD=21см, 19,5см | 3см, 6,25см | ||
Вариант-4 | 6см, 8см, 10см | ∟ЕКА=90, ∟ЕАН=670 30١, ∟ЕКН=1120 30١ | РК=16см, 9,5см | 3см, 7см |
Годовая контрольная работа по геометрии 8 класс
УТВЕРЖДАЮ:
Руководитель МО математики_______________
МБОУ «Лицей №2» г. Михайловск
Михайловск
«___» ____________ 2019 г.
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
по геометрии 2018-2019 уч.год 7 класс
Разработала:
Бережнова Н.Н.
учитель математики
Пояснительная записка
1.ВИД КОНТРОЛЯ– тестовая работа
2.СОДЕРЖАНИЕ КОНТРОЛЯ:
Проверяются следующие темы:
•Основные понятия планиметрии;
•площади многоугольников;
•касательные к окружности;
•центральные и вписанные углы;
•нахождение тригонометрических функций углов;
•подобные треугольники;
3. Цель: контроль освоения обучающимися образовательной программы, уровня сформированности следующих навыков по изученным темам: начальные геометрические сведения, треугольники, параллельные прямые, соотношения между сторонами и углами треугольника.
4. Работа ориен8класса.
5. Текст контрольной работы взят из учебно-методического пособия к учебнику Л.С.Атанасяна «Геометрия 7-9»: автор Н.Б. Мельникова «Контрольные работы по геометрии 8 класс». М.: «Экзамен», 2018.
М.: «Экзамен», 2018.
Контрольная работа представлена в двух вариантах и содержит 7 заданий.
На выполнение работы отводится 40 минут.
6. Критерии оценивания
За верное выполнение каждого задания – 1 балл
Максимальное количество баллов –7.
Критерии выставления оценок
№Количество балловШкольная оценка
1.6-7 «5»
2.4-5 «4»
3.2-3 «3»
4.Менее 2-х «2»
Годовая контрольная работа по геометрии 8 класс. Вариант 1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100. Найдите площадь трапеции, изображённой на рисунке. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма. Отрезок AB = 48 касается окружности радиуса 14 с центром O в точке B. Точка О — центр окружности, ∠AOB = 84° (см. рисунок). Найдите величину угла ACB (в градусах). Найдите тангенс угла B треугольникаABC, изображённого на рисунке. Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах). | Годовая контрольная работа по геометрии 8 класс. Вариант 2 1.Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85. 2. Найдите площадь трапеции, изображённой на рисунке. 3. Одна из сторон параллелограмма равна 20, а опущенная на нее высота равна 23. Найдите площадь параллелограмма. 4. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. 5. Точка О — центр окружности, ∠ACB = 24° (см. рисунок). Найдите величину угла AOB (в градусах). 6.Найдите тангенс угла С треугольника ABC , изображённого на рисунке. 7. На каком расстоянии от фонаря находится человек? |
|
Контрольная работа по геометрии 8 класс 1 вариант
а) Докажите, что AO : OC = BO : OD. б) Найдите AB, если OD=15 см, OB=9 см, CD=25 см.
2. Найдите отношение площадей треугольников ABC и KMN, если AB=8 см, BC=12 см, AC=16 см, KM=10 см, MN=15 см, NK=20 см. 3. Стороны треугольника равны 10 см, 17 см и 21 см. Периметр подобного ему треугольника равен 72 см. Найдите стороны второго треугольника.
|
Контрольная работа по геометрии 8 класс 2 вариант
а) Докажите, что AB : BM = CB : BN. б) Найдите MN, если AM=6 см, BM=8 см, AC=21 см. 2. Даны стороны треугольников PQR и ABC: PQ=16 см, QR=20 см, PR=28 см и AB=12 см, BC=15 см, AC=21 см, KM=10 см, MN=15 см, NK=20 см. Найдите отношение площадей этих треугольников. 3. Стороны треугольника относятся как 3:2:4. Периметр подобного треугольника равен 108 см. Найдите стороны второго треугольника.
|
Итоговая контрольная работа за курс 8 класса по математике (алгебра + геометрия)
Итоговая контрольная работа по математике за 8 класс
Вариант №1
Часть 1
Модуль «Алгебра»
А1 Укажите выражение, значение которого является наименьшим.
1. | 2. | 3. | 4. | 4 · 0,1 |
А2 Расположите в порядке возрастания числа: ; 3 ; 5,5.
1. | ; ; 5,5 | 2. | 5,5; | 3. | ; 5,5; | 4. | ; 5,5 |
А3 Найдите второй двучлен в разложении на множители квадратного трехчлена:
. А4 На одном из рисунков изображен график функции . Укажите номер этого рисунка. Варианты ответа: |
А5 Решите неравенство х+4≥4х-5 и укажите, на каком рисунке изображено множество его
решений.
Модуль «Геометрия»
А6 В прямоугольном треугольнике ВС = 8, соs∟В = 0,8 Найти АВ.
А7 В прямоугольном треугольнике один из катетов равен 10 см, а угол, лежащий напротив него, равен . Найдите площадь треугольника.
А8 Укажите номера верных утверждений:
Сумма двух противоположных углов параллелограмма равна 180°.
Если в четырехугольник можно вписать окружность и сумма длин двух его противоположных , сторон равна 200, а длина третьей стороны равна 60, то длина оставшийся стороны равна 140.
Около любого четырёхугольника можно описать окружность.
А9 Угол АОВ равен 63°.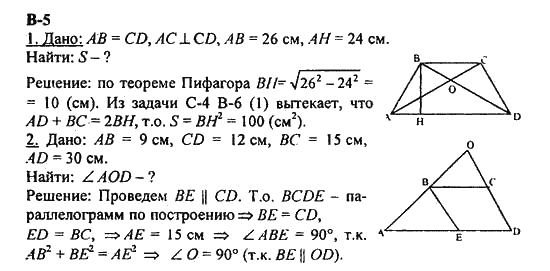 Найдите величину угла АСВ.
Найдите величину угла АСВ.
Часть 2
Модуль «Алгебра
В1. Решите уравнение .
В2. Вычислите .
В3. Решите неравенство:
В4. Решите задачу:
Катер прошел 40 км по течению реки и 6 км против течения, затратив на весь путь 3 ч. Найдите скорость катера в стоячей воде, если известно, что скорость течения равна 2 км/ч.
Часть 2
Модуль «Геометрия»
В5
Итоговая контрольная работа по геометрии 8 класс
Итоговая тестовая работа по геометрии 8 класс Подготовила: учитель математики МБОУ СОШ № 14 пос. Пятигорский Максимчук Людмила Владимировна Пояснительная записка Контрольная тестовая работа по геометрии предназначена для выходного контроля уровня знаний обучающихся 8х классов. Назначение работы – оценить уровень овладения обучающимися программным материалом по геометрии 8 класса. Курс геометрии изучается по учебнику «Геометрия 7 9» авторов Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк. Уроки геометрии проводятся 2 ч. в неделю, всего за год 70 ч. Тестовая часть работы направлена на проверку достижения уровня обязательной подготовки. Входящих в нее заданиях №1, 2, 3 необходимо из предложенных трех ответов выбрать один правильный и обвести кружком его номер. При решении заданий № 4 и № 5 требуется записать полученный краткий ответ. С помощью этих заданий проверяется умение владеть основными понятиями, знание алгоритмов при выполнении определенных действий, а также применение изученного в простейших практических ситуациях. Вторая часть задания № 6, 7, 8 и № 9, направлена на проверку повышенного уровня владения программным материалом. При выполнении этой части проверяется способность учащихся проанализировать условие, правильно выполнить чертеж к задаче, применять различные приемы рассуждений, грамотно обосновать свое решение. Система оценивания На выполнение работы отводится 45 мин. Первая часть выполняется в бланке с текстами заданий. В заданиях с выбором ответа ученик отмечает тот ответ, который считает верным; в заданиях с кратким ответом – вписывается ответ в отведенное место. Задания второй части выполняются на листах с выполненным чертежом и записью хода решения. Для оценивания результатов выполнения работы применяются отметки «2», «3», «4», «5». Задание первой части считается выполненным, если верно обведен номер ответа, или верно записан ответ. Задание второй части считается выполненным верно, если обучающийся выбрал правильный путь решения и получил верный ответ. правильно решено отметка 04 заданий «2» 5 6 заданий «3» 78 заданий «4» 9 заданий «5» Итоговая тестовая работа по геометрии. 8 класс В I А1. Периметр параллелограмма равен 24 см. Чему равна сумма двух соседних сторон? а) 16 см б) 12 см в) 18 см С А2. Найдите А, В, С ромба АВСD, если D = 70º. В D а) 110º, 70º, 110º б) 140º, 70º, 140º в) 55º, 70º, 55º А3. В треугольнике АВС угол С =900 АВ=25, sin a= 0,8. Найдите высоту СН Ответ:______________________ А4. Найдите периметр Δ FEK, образованный средними линиями Δ АВС, если АВ = 14cм, ВС = 16см, АС = 20см? В F E Ответ:________________ А K С А5. Для каждого из следующих утверждений выберите верное: 1)Любые две прямые имеют ровно одну общую точку; 2)Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны; 3)Вписанные углы, опирающиеся на одну и ту же хорду окружности равны. А6. Углы при основании трапеции равны 710 и 340. Остальные углы равны: 1) 340 и 710 2) 560 и 190 3)1050 и 750 4)1090 и 1460 ЧАСТЬ 2 В1. Боковая сторона равнобедренного треугольника АВС равна 29см, а высота составляет 21см. Чему равно основание АС этого треугольника? В2. Два острых угла прямоугольного треугольника относятся как 4:5. Найдите больший острый угол. Ответ дайте в градусах. В3. Колесо имеет 18 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. В4. Мальчик прошёл от дома по направлению на восток 560м. Затем повернул на север и прошёл 420 м. На каком расстоянии (в метрах) от дома оказался мальчик? Итоговая тестовая работа по геометрии. 8 класс В II А1. Сумма двух соседних сторон параллелограмма равна 10 см. Чему равен его периметр? а) 10 см б) 40 см в) 20 см N А2. Найдите М, N, К ромба МNКС, если С = 100º. М а) 80º,100º, 80º б) 130º, 100º, 130º в) 100º, 80º, 100º А3. В треугольнике АВС угол С =900 АВ=16 3 sin a= 0,5. Найдите высоту СН Ответ:______________________ А4. Найдите периметр Δ АВС, если средние линии его равны РD = 8cм, РК = 12см, DК = 10см? Р С В D Ответ:________________ А K А5. Для каждого из следующих утверждений выберите верное: К С 1)Диагонали Параллелограмма перпендикулярны; 2)Отношение площадей подобных треугольников равно квадрату коэффициента подобия; 3)Если дуга окружности составляет 800, то центральный угол, опирающийся на эту дугу равен 400. А6. Углы при основании трапеции равны 680 и 350. Остальные углы равны: 1) 350 и 710 2) 1000 и 1110 3)1120 и 1450 4)1090 и 1550 ЧАСТЬ 2 В1. Высота равнобедренного треугольника АВС равна 15см, длина основания АС равна 16 см. Чему равна боковая сторона этого треугольника? В2. Два острых угла прямоугольного треугольника относятся как 2:3. Найдите больший острый угол. Ответ дайте в градусах. В3. Колесо имеет 25 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. В4. Мальчик прошёл от дома по направлению на восток 400м. Затем повернул на север и прошёл 300м. На каком расстоянии (в метрах) от дома оказался мальчик? 2м8класс Ответы тестовой работы: № задания 1 вариант 2 вариант 1 б в 2 3 4 а 12 25 а 12 60 5 3 2 6 4 3 7 40 161 8 50 54 9 20 144 10 700 500 правильно решено отметка 04 заданий «2» 5 6 заданий «3» 78 заданий «4» 9 10 заданий «5» ИТОГОВАЯ контрольная работа по геометрии Дата_______________ Класс___________________ Фамилия______________________________ Имя__________________________________ Вариант_____________________________ № Ответ А1 А2 А3 А4 А5 А6 ИТОГОВАЯ контрольная работа по геометрии Дата_______________ Класс___________________ Фамилия______________________________ Имя__________________________________ Вариант_____________________________ № Ответ А1 А2 А3 А4 А5 А6 ИТОГОВАЯ контрольная работа по геометрии Дата_______________ Класс___________________ Фамилия______________________________ Имя__________________________________ Вариант_____________________________ № Ответ А1 А2 А3 А4 А5 А6 ИТОГОВАЯ контрольная работа по геометрии Дата_______________ Класс___________________ Фамилия______________________________ Имя__________________________________ Вариант_____________________________ № Ответ А1 А2 А3 А4 А5 А6 ИТОГОВАЯ контрольная работа по геометрии Дата_______________ Класс___________________ Фамилия______________________________ Имя__________________________________ Вариант_____________________________ № Ответ А1 А2 А3 А4 А5 А6
UnboundEd Mathematics Guide
Что входит в руководство по содержанию и как его использовать?
Получите ответы на все вопросы вашего Руководства по содержанию, в том числе о том, что входит в каждую часть и как их можно использовать в вашей роли в вашем учебном заведении.
Просмотреть ответы на часто задаваемые вопросы8.G.A | Понять соответствие и сходство с помощью физических моделей, прозрачностей,
или программное обеспечение для геометрии.
8.G.B | Поймите и примените теорему Пифагора.
Добро пожаловать в серию руководств по математике UnboundEd! Эти руководства предназначены для объяснения того, что новые высокие стандарты математики говорят о том, что учащиеся должны изучать в каждом классе, и что они означают для учебной программы и обучения. Это руководство, первое для 8-го класса, состоит из трех частей. Первая часть представляет собой «тур» по стандартам в первых двух кластерах области геометрии (касающихся конгруэнтности, сходства и теоремы Пифагора) с использованием свободно доступных онлайн-ресурсов, которые вы можете использовать или адаптировать для своего класса.Во второй части показано, как эти стандарты соотносятся с другими концепциями 8-го класса. А третья часть объясняет, где находятся совпадение, сходство и теорема Пифагора в процессе обучения от начальных классов до средней школы.
Соответствие и сходство
Стандарты для 8-го класса полны важных идей, так почему же начинать эту серию с соответствия и сходства? Во-первых, эти стандарты являются частью «основной работы» 8-х классов, а это означает, что они заслуживают большей части учебного времени в течение учебного года. 1 Приоритизация основной работы в течение года гарантирует, что этим стандартам будет уделено должное внимание. Конгруэнтность и сходство также необходимы учащимся для понимания других важных понятий в 8-м классе, в частности, наклона линии. (8.EE.B.6) Следовательно, работа с сопоставлением и подобием должна предшествовать линейным уравнениям, что является еще одной важной частью работы.
Конгруэнтность и сходство — также отличный способ начать год, потому что они предполагают «практический» подход через преобразования, что делает их доступными для любого ученика с базовым пониманием линий и углов.Более того, стандарты, связанные с конгруэнтностью и сходством, напрямую входят в стандарты геометрии средней школы (в частности, области совпадения и сходства и правильных треугольников), поэтому они важны для будущих успехов учащихся. Так что, если вам интересно, с чего начать год, конгруэнтность и сходство — надежная ставка.
В 8-м классе стандарты, касающиеся конгруэнтности и сходства, сгруппированы в один кластер (называемый 8.G.A, поскольку это первый набор геометрических стандартов в классе).Несмотря на то, что он содержит только пять стандартов, этому кластеру удается объединить ряд математических идей, в том числе три, которые не часто рассматриваются как связанные: конгруэнтность и сходство, преобразования и угловые отношения. Давайте посмотрим, что говорится в этих стандартах, а затем рассмотрим каждый из них более внимательно.
8.G.A | Поймите соответствие и сходство с помощью физических моделей, прозрачностей или программного обеспечения для работы с геометрией.
Порядок стандартов не указывает порядок, в котором они должны преподаваться.Стандарты — это лишь набор ожиданий относительно того, что студенты должны знать и уметь делать к концу каждого года; они не предписывают точную последовательность или учебный план. В этом случае имеет смысл сначала познакомить учащихся со свойствами отражений, перемещений и вращений (8.G.A.1), а затем использовать эти преобразования для установления концепции конгруэнтности (8.G.A.2). Исходя из этого, студенты должны быть готовы к расширению и концепции сходства (8.G.A.4). Решение задач с преобразованиями на координатной плоскости (8.G.A.3) можно интегрировать вместе с работой с этими первыми тремя стандартами, а применение преобразований (8.G.A.5) можно также обучать в сочетании с другой работой, или они могут быть сохранены напоследок.
Прежде чем мы начнем работать над этими стандартами, давайте ненадолго остановимся и рассмотрим, почему они так важны. В прошлом геометрия в классах K-8 была ориентирована на широкий круг тем, ни одна из которых не преподавалась очень глубоко. Студенты могли выучить термины «конгруэнтный» и «подобный» в очень общем виде (возможно, как «та же форма, тот же размер» и «та же форма, разный размер»), но это была степень их знакомства с этими двумя важными понятиями. .Преобразования рассматривались как совершенно отдельная идея — если они вообще рассматривались — с упором только на выполнение преобразований (а не на описание их свойств). С другой стороны, в старших классах геометрии много времени уделялось обучению критериям совпадения и сходства треугольников, которые плохо соотносились ни с чем, что ученики делали раньше. Однако теперь стандарты для 8-х классов и старших классов используют преобразования, чтобы помочь учащимся понять соответствие и сходство, и согласованы с их ожиданиями в отношении обучения учащихся.Их внимание сосредоточено не столько на выполнении преобразований, сколько на том, как они способствуют пониманию учащимися отношений между фигурами. Мы хотим, чтобы учащиеся не только могли изобразить, скажем, отражение прямоугольника над линией, но и объяснить, чем изображение этого прямоугольника похоже на оригинал или не похоже на него. Что мы знаем об изображении этого прямоугольника на основе того, что мы знаем об исходной фигуре и свойствах преобразований?
Отражения, переводы и вращения: основы
Прежде чем мы продолжим, давайте сделаем паузу и определим, что мы подразумеваем под отражением, перемещением и вращением.Эти идеи сложно описать словами, поэтому мы начнем с некоторых приблизительных определений, а затем рассмотрим несколько иллюстраций. 2
- Грубо говоря, отражение переносит фигуру (например, точку, линию, сегмент линии, многоугольник или круг) с одной стороны линии (называемой линией отражения) на другую сторону. Например, на диаграмме ниже △ ABC переводится в A’B’C ’за счет отражения поперек линии DE.
- Грубо говоря, перевод берет фигуру по определенному вектору.Например, на диаграмме ниже △ ABC теперь переводится в A’B’C ’путем перевода вдоль вектора DE.
- Грубо говоря, при вращении фигура вращается вокруг точки (называемой центром вращения) на фиксированный угол. В качестве последнего примера на диаграмме ниже △ ABC переводится в A’B’C ’поворотом на 90 ° по часовой стрелке.
- В совокупности эти три преобразования иногда называют основными жесткими движениями из-за того, как они «жестко» перемещают фигуру по плоскости, сохраняя длины сегментов и.(Позже в этом руководстве мы обсудим нежесткую трансформацию: расширение.)
Запоминание точного определения каждого преобразования не имеет значения. Лучше, если учащиеся попробуют каждое из преобразований, а затем разработают свои собственные определения, чтобы обработать свойства каждого из них. Поначалу следует ожидать таких слов, как «перевернуть», «скользить» и «повернуть». Однако они не охватывают все идеи, изложенные в стандарте, и студентам скоро придется пересмотреть их с более подробными сведениями.Все учащиеся должны уметь сказать, например, что отражение сохраняет расстояния по линиям и сегментам, а также меры углов. Они также должны заметить, что расстояние между каждой точкой на фигуре и линией отражения остается неизменным при отражении фигуры. На проработку всех трех жестких движений может потребоваться несколько дней — можно было бы сосредоточиться на одном в день, — но это время потрачено не зря, если учащиеся способны определить и четко сформулировать свойства каждой трансформации.
Понимание свойств отражений, сдвигов и вращений
Студенты должны начинать изучение конгруэнтности с практического опыта: пробовать на себе отражение, переводы и повороты и описывать свойства фигур при этих преобразованиях. (8.G.A.1) Лучшие инструменты для этого — прозрачные пластиковые пленки (для диапроекторов) или калька — могут показаться устаревшими, но они справляются со своей задачей. Существуют программные пакеты, которые позволяют учащимся легко экспериментировать с преобразованиями (GeoGebra — один из популярных продуктов, доступный бесплатно в Интернете), но многие учителя на собственном опыте считают, что для учащихся лучше сначала осязать все жесткие движения. .
Давайте взглянем на примерный план урока, чтобы увидеть, как может выглядеть введение одного типа трансформации. Этот план урока имеет дело с отражениями, но базовая структура будет работать так же хорошо, как для переводов, так и для поворотов.
8 класс, Модуль 2, Урок 4: Пример 1
Отражение поперек линии определяется с помощью следующего примера.
- Пусть 𝐿 — вертикальная линия, а and и 𝐴 — две точки, не лежащие на 𝐿, как показано ниже. Кроме того, пусть 𝑄 — точка на.(Черный прямоугольник обозначает границу бумаги.)
- Ниже приводится описание того, как отражение перемещает точки 𝑃, 𝑄 и 𝐴, используя прозрачность.
- Обведите красным цветом линию 𝐿 и три точки на прозрачной пленке. (Обязательно используйте прозрачную пленку того же размера, что и бумага.)
- Удерживая бумагу неподвижной, переверните прозрачную пленку поперек вертикальной линии (меняя местами левую и правую), удерживая вертикальную линию и точку 𝑄 поверх их черных изображений.
- Положение красных фигур на прозрачности теперь представляет собой отражение исходной фигуры. Отражение (𝑃) — это точка, представленная красной точкой слева от 𝐿, Отражение (𝐴) — это красная точка справа от 𝐿, а точка Отражение (𝑄) — это сама точка.
- Обратите внимание, что точка не изменяется из-за отражения.
8 класс, Модуль 2, Урок 4 Доступно на сайте engageny.org/resource/grade-8-mat Mathematics-module-2-topic-lesson-4; по состоянию на 29 мая 2015 г.Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
HideShow
Читая, имейте в виду, что этот урок является частью модуля, в котором для преобразований используется формальный язык и обозначения (включая обозначения функций). Стандарты не требуют обозначения функций в 8-м классе, и вы, возможно, не захотите знакомить учащихся с формальными терминами в первый день — это нормально. Что мы действительно хотим выделить, так это то, как этот урок знакомит студентов с концепцией отражения:
- Урок начинается с практического упражнения с прозрачными пленками.Учащиеся могут увидеть, как отражение определяет точки изображения, и, вероятно, сразу начнут замечать взаимосвязь между каждой точкой и ее изображением. Возможно, будет лучше, если их первая попытка будет не на координатной плоскости; правила построения графиков могут отвлекать студентов от изучения фундаментальных свойств отражений.
- Студенты пробуют еще несколько упражнений. На данный момент прозрачности еще не ожидается. Одно упражнение включает горизонтальную линию отражения, а другое включает фигуру с вершиной на линии отражения — оба хороших варианта для учащихся.
- В упражнениях 3-5 задаются важные вопросы, которые побуждают студентов сформулировать ключевые идеи стандарта. Их просят сравнить размеры углов и длины сегментов и заметить, что они совпадают. Это поможет им формализовать эти свойства на следующем этапе урока. (Эти идеи могут быть записаны на «якорной диаграмме», которая висит в классе для остальной части модуля.)
- Дополнительные примеры позволяют учащимся применять новые концепции.
Ожидайте, что студенты будут регулярно использовать свои прозрачные пленки в течение первых нескольких дней. В конце концов, они начнут развивать интуитивное ощущение того, как будет выглядеть каждое преобразование, и будут все меньше и меньше полагаться на прозрачность. Это «шестое чувство» того, как будет выглядеть изображение фигуры, — это то, к чему вы стремитесь, и оно позволит учащимся впоследствии представить себе решения всех видов проблем.
Сравнение
После того, как учащиеся изучат свойства каждого жесткого движения отдельно, они могут перейти к размышлениям о конгруэнтности и случаях, когда одна фигура переносится на другую с помощью последовательности жестких движений.(8.G.A.2) Оглядываясь на стандарт, мы видим, что он состоит из двух частей:
- Учащиеся должны понимать, что одна фигура соответствует другой, если одну можно сопоставить с другой серией жестких движений.
- Учащиеся должны уметь описывать последовательность жестких движений, которые переводят одну фигуру в другую.
Первая часть означает, что учащиеся должны разработать определение конгруэнтности, основанное на преобразованиях, и уметь объяснять, почему две фигуры совпадают, основываясь на свойствах жестких движений.(Обратите внимание, что это отличается от традиционного определения конгруэнтности «та же форма, тот же размер».) Вторая часть в значительной степени означает то, что она говорит: учащиеся должны уметь подробно описывать преобразования, которые переводят одну фигуру в другую. . Это задание представляет собой пример:
Конгруэнтных треугольников
Два треугольника на рисунке ниже совпадают:
- Задайте последовательность поворотов, перемещений и / или отражений, которые переводят 𝑃𝑅𝑄 в △ 𝐴𝐵𝐶.
- Можно ли показать сравнение в части (а), используя только сдвиги и вращения? Объяснять.
«Конгруэнтные треугольники» от Illustrative Mathematics под лицензией CC BY 4.0.
HideShow
Это задание носит учебный характер — это то, с чего начинается урок и приводит к новым идеям по мере его выполнения учащимися. Дайте его учащимся, когда они ознакомятся с жесткими движениями, и они быстро заметят, что ни одно преобразование не сделает этого — им придется использовать более одного.Поощряйте студентов быть точными в своих объяснениях. Если вы видите отражение, где должна быть линия отражения? Если вы видите перевод, по какому вектору? Может возникнуть большая дискуссия, когда студенты поделятся несколькими решениями проблемы.
После того, как учащиеся решат проблему, вы можете представить тот факт, что PQR точно отображается в ABC посредством перевода и отражения (или других, более сложных последовательностей), без пропусков или перекрытий. Поскольку они использовали только жесткие преобразования (которые не меняют меры углов или длину сегментов) для получения одной фигуры из другой, мы можем сказать, что они совпадают.С этого момента вы хотите, чтобы учащиеся использовали это определение конгруэнтности, и если их попросят продемонстрировать соответствие двух фигур, они должны будут делать это посредством преобразований.
Расстояния
Жесткие преобразования и их связь с конгруэнтностью потребуется некоторое время, чтобы закрепиться. Затем пришло время ввести понятие сходства, которое включает в себя еще одно дополнительное преобразование — расширение. (8.G.A.4) Как и выше, мы начнем с приблизительного определения, а затем поясним с помощью некоторых иллюстраций.Грубо говоря, растяжение — это преобразование фигуры (например, точки, линии, отрезка, многоугольника или окружности) в другую фигуру с определенным масштабным коэффициентом. При расширении расстояние между фиксированной точкой (называемой центром расширения) и расширяемым объектом становится длиннее или короче пропорционально масштабному коэффициенту. В приведенных ниже примерах показаны два расширения △ ABC с центром в точке P, одно с масштабным коэффициентом больше 1, а другое с масштабным коэффициентом меньше 1.
Как мы видим, в зависимости от масштабного коэффициента фигуры при растяжении можно преобразовать в изображения большего или меньшего размера.Это поднимает важный момент: «Расширение» имеет особое математическое значение, отличное от его значения в повседневном английском (где оно означает просто увеличение, а не сокращение). Студентам может потребоваться некоторое время, чтобы приспособиться к этому новому использованию знакомого слова, но просмотр примеров с масштабными коэффициентами различной величины поможет процессу.
Как и в случае с жесткими движениями, учащиеся должны иметь некоторый практический опыт с расширениями и должны использовать этот опыт для разработки все более точных определений расширения.Вы можете использовать прозрачные пленки для такого упражнения, но лучшими инструментами могут быть линейка или циркуль: учащиеся могут измерить расстояние от каждой точки фигуры до центральной точки. Затем они могут попытаться, например, умножить эти длины на коэффициент масштабирования 2, чтобы получить растяжение. (Точно так же они могут попробовать с коэффициентом масштабирования 1/2.) Этот план урока знакомит студентов с заданием, в котором это достигается с помощью компаса.
8 класс, Модуль 3, Урок 2: Пример 1
Вернитесь к предыдущей гипотезе или посмотрите наш список классов.Какие предположения оказались верными? Откуда вы знаете?
- Ответы могут отличаться в зависимости от предположений, сделанных классом. Учащиеся должны понять, что гипотеза о прямом отображении линии под растяжением верна.
Как вы думаете, что произойдет, если мы выберем другое место для центра или для точек 𝑃 и 𝑄?
- Точки 𝑂, 𝑃 и 𝑄 — произвольные точки. Это означает, что они могли быть где угодно в самолете. По этой причине результаты будут такими же; то есть расширение все равно будет давать линию, и линия будет параллельна оригиналу.
Посмотрите на рисунок еще раз и представьте, что с помощью нашей прозрачности мы переводим сегмент 𝑂𝑃 вдоль вектора 𝑂𝑃 в сегмент 𝑃𝑃 ’и переводим сегмент 𝑂𝑄 вдоль вектора 𝑂𝑄 в сегмент 𝑄𝑄‘. Обладая этой информацией, не могли бы вы сказать что-нибудь еще о строках 𝐿 и 𝐿 ’?
- Поскольку 𝑃 и 𝑄 являются произвольными точками на прямой and, а переводы отображают прямые в параллельные, когда вектор не параллелен исходной прямой или не является ее частью, мы можем сказать, что 𝐿 параллельна 𝐿 ’.
8 класс, Модуль 3, Урок 2 Доступно на сайте engageny.организация / ресурс / 8-й класс-модуль-математики 3-тема-урок-2; по состоянию на 29 мая 2015 г. Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
HideShow
Опять же, вы можете использовать любые имеющиеся у вас инструменты для подобного действия. Студенты могут использовать линейки для измерения расстояний от центра расширения или они могут использовать прозрачные пленки для отслеживания расстояний. В результате они развивают интуицию относительно того, как работают дилатации, и могут отвечать на множество дополнительных вопросов.Например, как изменение масштабного коэффициента влияет на изображение фигуры? Как перемещение центра расширения влияет на изображение фигуры? Что произойдет, если центр расширения находится внутри, на или за пределами фигуры? Что даст расширение с коэффициентом масштабирования 1? Любой из них может вызвать интересное обсуждение и помочь студентам лучше понять, как расширения ведут себя в различных условиях.
Сходство
Получив интуитивное представление о том, как работают расширения, учащиеся могут определять сходство и описывать серию преобразований подобия.(8.G.A.4) Как и в случае с конгруэнтностью, здесь преследуется двоякая цель; студенты должны:
- Поймите сходство с точки зрения жестких движений и расширений.
- Опишите последовательность преобразований подобия.
Можно начать с такой задачи:
Вы можете использовать это задание точно так же, как оно есть, или вы можете использовать его как учебное задание, чтобы представить идею подобия через жесткие движения и растяжения. В этом случае мы могли бы немного упростить вопрос: «Не могли бы вы сопоставить маленькую стрелку с большой, используя жесткие движения и растяжения? Поясните свой ответ.«Есть несколько способов сделать это, как показано в разделе решения задачи, и это возможность для обстоятельного обсуждения. После того, как будут разработаны несколько методов, вы можете объяснить учащимся, что они только что показали, что эти фигуры похожи, потому что мы смогли перенести одну фигуру на другую с помощью отражений, перемещений, вращений и растяжений. Это становится определением сходства. (Обратите внимание, что это отличается от определения сходства «та же форма, разный размер», с которым учащиеся могут быть знакомы.Дело не в том, что эти две фигуры связаны серией преобразований и похожи друг на друга; скорее, они похожи, потому что связаны серией трансформаций. Другими словами, как только мы установили последовательность преобразований, мы установили сходство.)
Соответствующие, похожие или оба?
Студентам важно понимать, что совпадение и сходство не исключают друг друга; это не тот случай, когда две фигуры — это одно, а не другое. Фактически, если две фигуры совпадают, они также похожи.Чтобы понять, почему, вспомните определение подобия: одна фигура похожа на другую, если она может быть получена последовательностью отражений, перемещений, вращений и расширений. Любое из рассмотренных выше преобразований конгруэнтности также подойдет под это определение — две задействованные фигуры будут конгруэнтными, но также будут соответствовать критериям подобия.
Переход к координатной плоскости
Первые встречи учащихся с каждым преобразованием (включая растяжения) не обязательно должны происходить в координатной плоскости.Фактически, введение каждого преобразования в «синтетический» контекст (без использования координат, как в приведенных выше примерах) часто позволяет студентам сосредоточиться на свойствах самих преобразований, не беспокоясь об условных обозначениях координатной плоскости. Это также хорошее напоминание о том, что вселенная преобразований — это гораздо больше, чем просто подмножество, которое мы можем описать с помощью целочисленных координат. (Студенты также склонны разрабатывать «правила» для выполнения преобразований в координатной плоскости — например, «переключать значения x и y» для поворота на 180 градусов — на этом не должно быть особого внимания в раннем обучении.Вспомните, как в нашем вводном плане урока по поворотам не было координатных сеток.)
Однако в какой-то момент учащиеся должны уметь работать с преобразованиями на координатной плоскости и четко описывать эффекты определенных преобразований, используя координаты. (8.G.A.3) По сути, этот стандарт заключается в том, чтобы взять все, что студенты узнали о преобразованиях в целом, и применить его к задачам на координатной плоскости. Разнообразие подразумеваемых здесь проблем огромно, и представить исчерпывающую выборку просто невозможно.Но давайте рассмотрим одно задание в качестве примера того, как ученики совершают прыжок на координатную плоскость:
Опять же, это только один пример, но давайте внимательно его рассмотрим. Помимо твердого понимания свойств преобразований и базового понимания координатной плоскости, учащиеся также должны быть знакомы с уравнениями горизонтальных линий. (Если вы еще не закончили свой год, ничего страшного; учащиеся все равно могут выполнять аналогичную задачу, включая отражение по оси абсцисс.) Если у них есть все это, они могут приступить к решению. Не нужно много времени, чтобы понять, что эта проблема устойчива к грубой силе; даже если бы лист миллиметровой бумаги размером 2 000 x 2 000 квадратных метров действительно существовал, потребовалась бы целая вечность, чтобы изобразить затронутую точку и отразить ее. Вместо этого им придется применить некоторые идеи об отражениях: в частности, что расстояние между точкой и линией отражения равно расстоянию между ее изображением и линией отражения. Студенты могут попробовать две стратегии:
- Попросите их создать грубый набросок координатной плоскости или части плоскости, чтобы помочь им визуализировать ситуацию.Тогда они смогут увидеть, что (1000, 2012) на 12 единиц выше y = 2000, поэтому отраженная точка будет на 12 единиц ниже y = 2000. Более того, отражение вообще не будет перемещать изображение влево или вправо. , поэтому координата x обеих точек будет одинаковой. Эти две подсказки позволят им собрать решение.
- Попросите их подумать о более простом случае, например, отразить точку (1, 10) над линией y = 8. Затем попросите их связать решение более простой проблемы с исходным вопросом.Цифры будут немного другими, но процесс останется прежним.
В обоих случаях студенты получают гибкое понимание того, как работают преобразования, и применяют это к определенным точкам и расстояниям на координатной плоскости.
Частные случаи сравнения: поперечины и треугольники
На первый взгляд последний стандарт в кластере 8.G.A может показаться неуместным. Как мы перешли от трансформаций к трансверсалиям? И какое отношение все это имеет к углам треугольника? Эти идеи — преобразования, трансверсалии и треугольники — долгое время рассматривались и преподавались как отдельные идеи.Но теперь все они понимаются как взаимосвязанные. (8.G.A.5) Чтобы увидеть, как преобразования связаны с трансверсалиями, давайте взглянем на этот урок:
8 класс, Модуль 2, Урок 12: Исследовательское задание 2
На рисунке ниже ‖ и 𝑚 — это поперечник. Измерьте углы 1–8 с помощью транспортира. Перечислите равные углы.
∠1 = ∠3 = ∠5 = ∠7 = и ∠2 = ∠4 = ∠6 = ∠8
а. Что вы обратили на меры ∠1 и 5? Как вы думаете, почему это так? (При необходимости используйте прозрачность.)
∠𝟏 и ∠𝟓 равны по размеру. Мы можем перенести ∠𝟏 вдоль вектора на прямой так, чтобы вершина ∠𝟏 отображалась на вершину. Переводы сохраняют угол, поэтому два угла будут совпадать.
г. Что вы заметили по меркам №3 и №7? Как вы думаете, почему это так? (При необходимости используйте прозрачность.) Существуют ли другие пары углов с таким же соотношением? Если да, перечислите их.
∠𝟑 и ∠𝟕 равны по размеру. Мы можем перенести ∠𝟑 вдоль вектора на прямой так, чтобы вершина ∠𝟑 отображалась на вершину.Переводы сохраняют угол, поэтому два угла будут совпадать. Другие пары углов с таким же соотношением — это ∠𝟒 и ∠𝟖, а также ∠𝟐 и ∠𝟔.
г. Что вы заметили в мерах №4 и №6? Как вы думаете, почему это так? (При необходимости используйте прозрачность.) Есть ли еще пара углов с такими же отношениями?
Меры ∠𝟒 и ∠𝟔 равны. Поворот на 𝟏𝟖𝟎 ° вокруг центра отобразит map в ∠𝟔. Вращения сохраняют угол, поэтому мы знаем, что и ∠𝟔 равны.∠𝟑 и ∠𝟓 имеют одинаковые отношения.
8 класс, Модуль 2, Урок 12 Доступно по адресу engageny.org/resource/grade-8-mat Mathematics-module-2-topic-c-lesson-12; по состоянию на 29 мая 2015 г. Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
HideShow
Как мы видим, ученики используют транспортир для измерения и определения отношений между углами. Затем они возвращаются к знакомому инструменту (прозрачности) из своей работы с преобразованиями, чтобы понять, почему существуют эти отношения.Последующее обсуждение особенно интересно: учащиеся должны заметить, как соотносятся соответствующие углы при переводе одного угла в другой. Точно так же альтернативные внутренние углы связаны поворотом одного угла на 180 градусов к другому. Фактически, это математическая основа идей, которые когда-то часто давались ученикам средней школы только как постулаты («альтернативные внутренние углы совпадают» и т. Д.). Потратив время на изучение причин, лежащих в основе этих угловых отношений, ученики с большей вероятностью запомнят их и в будущем будут использовать свои знания.
В прошлом еще одна идея, которую часто преподавали изолированно и давали студентам в качестве постулата, была сумма внутренних углов треугольника. Но после того, как учащиеся поймут углы, образованные трансверсалиями в свете трансформаций, они смогут объяснить, откуда взялась эта идея. Чтобы увидеть, как это сделать, давайте рассмотрим эту задачу.
Как объясняется в решении задачи, учащиеся могут развить неформальный аргумент, что a + b + c = 180, используя отношения альтернативных внутренних углов, чтобы установить, что три соседних угла на диаграмме имеют меры a, b и c, и что вместе эти три угла образуют прямой угол.Это непростой аргумент, но он не выходит за пределы досягаемости учащихся 8-го класса. Если ваши ученики имеют ограниченный опыт выполнения задач, требующих такого рода рассуждений и объяснений, могут быть полезны несколько эшафотов, которые помогут им полностью погрузиться в идеи. вовлеченный. Например, если у ваших учеников есть проблемы с измерениями углов, заданными как переменные, вы можете начать с треугольника с целыми числами углов. Вы также можете попросить их повторить ту же технику (удлинить одну сторону, а затем построить параллельную линию через противоположную вершину) на другом треугольнике с целочисленными углами, а затем перейти к «общему» треугольнику, показанному выше.А для второй части задания учащимся, не привыкшим объяснять свое мышление, может быть полезно начать с одного или двух предложений в начале своего ответа.
Последняя идея, которую студенты готовы объяснить с помощью преобразований, — это угловой критерий подобия треугольника. В этом задании учащиеся задают серию вопросов, призванных увести их от конкретного случая к более общему предложению.
Подобные треугольники II
Треугольники 𝐴𝐵𝐶 и 𝑃𝑄𝑅 ниже имеют две пары совпадающих углов, как показано на рисунке:
- Объясните, используя расширения, сдвиги, отражения и / или вращения, почему △ 𝑃𝑄𝑅 похоже на △ 𝐴𝐵𝐶.
- Углы 𝐶 и 𝑅 совпадают?
- Можете ли вы показать сходство частично без использования отражения? А как насчет использования дилатации? Объяснять.
- Предположим, что 𝐷𝐸𝐹 и 𝐾𝐿𝑀 — два треугольника с 𝑚 (∠𝐷) = 𝑚 (∠𝐾) и 𝑚 (∠𝐸) = 𝑚 (∠𝐿). Подобны ли треугольники 𝐷𝐸𝐹 и 𝐾𝐿𝑀?
«Подобные треугольники II» от Illustrative Mathematics под лицензией CC BY 4.0.
HideShow
Части (a), (b) и (c) этого задания основаны на понимании учащимися преобразований подобия.Затем часть (d) просит их, как и в двух предыдущих задачах, обобщить. Имея «общую» пару треугольников с двумя парами конгруэнтных углов, могут ли они показать сходство? Опять же, учащимся, не привыкшим объяснять свое мышление, могут понадобиться строительные леса. Им могут быть полезны некоторые возможные диаграммы DEF и KLM, чтобы увидеть, что точные преобразования не так важны, как тот факт, что некоторая последовательность жестких движений и растяжений приведет один треугольник к другому.Также могут быть полезны одно или два начала предложения. Как и в случае с любой из этих задач, цель состоит не в том, чтобы избавиться от необходимого обоснования, а в том, чтобы дать учащимся другой способ увидеть, о чем их просят подумать и объяснить.
Теорема Пифагора
Другая большая идея, дебютировавшая в геометрии 8-го класса, — это теорема Пифагора. Стандарты, связанные с теоремой Пифагора, также являются частью основной работы этой степени. Учитывая уравнения, с которыми студенты столкнутся при решении задач с теоремой Пифагора, такие как c2 = 25 и a2 = 17, может иметь смысл преподавать эти стандарты после того, как студенты освоят квадратные и кубические корни (8.EE.A.2) и работать с иррациональными числами. (8.NS.A.1) (Подробнее о взаимосвязи между стандартами в Части 2 этого руководства.) Однако независимо от того, как вы решите последовательность обучения, важно понимать, что ряд стандартов средней школы зависит от знания Теорема Пифагора, поэтому ученики обязательно должны получить это содержание в 8 классе.
Стандарты, связанные с теоремой Пифагора, сгруппированы в другой кластер (называемый 8.G.B, поскольку это второй кластер геометрических стандартов в 8-м классе).Давайте посмотрим, что они говорят.
8.G.B | Поймите и примените теорему Пифагора.
Опять же, порядок стандартов не указывает порядок, в котором они должны преподаваться. Но в этом случае имеет смысл начать с доказательства теоремы Пифагора (8.G.B.6), а затем перейти к решению различного рода задач (8.G.B.7 и 8.G.B.8).
Прежде чем мы начнем говорить о стандартах в этом кластере, давайте выделим две важные идеи в центр внимания.
- Теорема Пифагора гласит: если треугольник прямоугольный, длины катетов равны a и b, а длина гипотенузы равна c, тогда a2 + b2 = c2.
- Обратное к теореме Пифагора также верно: если треугольник имеет стороны длиной a, b и c и a2 + b2 = c2, то этот треугольник является прямоугольным.
В прошлом эта тема часто представлялась студентам, давая им формулу (названную выше: a2 + b2 = c2) и объясняя, что означают переменные.Затем инструкция вращалась вокруг относительно простых задач, в которых учащимся давали две стороны прямоугольного треугольника и они должны были найти третью. Такое решение проблем все еще происходит, но Стандарты начинают с того, что студентов просят объяснить доказательство теоремы Пифагора и ее обращения. (8.G.B.6) Поступая так, они узнают две важные вещи:
- Теорема Пифагора описывает отношения между сторонами прямоугольного треугольника (а не только формулу). Когда учащиеся понимают природу отношений и могут выразить их вербально (а также в алгебраических терминах), они готовы применять это в более широком диапазоне ситуаций и расширять свое обучение позже.
- Обращение теоремы Пифагора так же полезно, как и сама теорема. Студенты узнают, что они могут использовать теорему не только тогда, когда они знают, что у них есть прямоугольный треугольник, но и когда им нужно установить, что треугольник является прямоугольным.
Итак, откуда взялась теорема Пифагора? На самом деле существует много разных доказательств, некоторые из них более сложные, чем другие. Эти разные доказательства основаны на разных техниках и приводят разные причины того, что теорема Пифагора верна.В этом уроке используется доказательство «квадрат в квадрате» с использованием площади, начиная с этого:
8 класс, Модуль 2, Урок 15: Обсуждение
Первое доказательство теоремы Пифагора требует знания некоторых основных фактов о геометрии.
- Конгруэнтные треугольники имеют равные площади.
- Все соответствующие части равных треугольников равны.
- Теорема о сумме треугольника. (∠ сумма △)
- Для прямоугольных треугольников сумма двух углов, не являющихся прямыми, составляет 90 °.(∠ сумма рупий △)
Далее мы рассмотрим то, что называется квадратом внутри квадрата. Внешний квадрат имеет длину сторон (a + b), а внутренний квадрат — длину сторон c. Наша цель — показать, что + =
Для достижения этой цели мы сравниваем общую площадь внешнего квадрата с частями, из которых он состоит, то есть четырьмя треугольниками и меньшим внутренним квадратом.
8 класс, Модуль 2, Урок 15 Доступно по адресу engageny.org/resource/grade-8-mat Mathematics-module-2-topic-d-lesson-15; по состоянию на 29 мая 2015 г.Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
HideShow
Остальная часть доказательства, которую вы можете увидеть в плане урока, помогает студентам понять, что внутренняя фигура на самом деле является квадратом, а затем использует вычисление площади для вывода формулы. Если вы собираетесь использовать этот план урока, подумайте о том, какой объем поддержки вы хотите оказать — возможно, учащиеся смогут сами пройти через некоторые доказательства и закончить работу под вашим руководством, или, может быть, им нужно больше структуры.(Одно предупреждение: алгебра, задействованная в этом последнем вычислении, включает в себя умножение двух биномов, что не требуется до старшей школы. Возможно, вам придется помочь учащимся применить свойство распределения этим новым способом.) В любом случае они понимают что теорема Пифагора включает аспект области, который полезен для интерпретации определенных типов прикладных проблем.
Применение теоремы Пифагора для решения задач
Как только учащиеся поймут происхождение теоремы Пифагора, они перейдут к решению проблем.(8.G.B.7) Первоначально учащиеся могут решать задачи, содержащие только целые числа, чтобы сосредоточиться на интерпретации ситуации в терминах прямоугольного треугольника и выполнении точных вычислений. (Приведенный выше план урока включает несколько примеров этих задач вводного уровня.) Эта задача требует немного большего толкования.
Бег по футбольному полю
Во время игры плей-офф дивизиона 2005 года между «Денвер Бронкос» и «Патриотс Новой Англии» игрок «Бронко» Чемпион Бэйли перехватил Тома Брэди у линии ворот (см. B в кружке).Он пробежал мяч почти до другой линии ворот. Бен Уотсон из «Патриотов Новой Англии» (см. Обведенную букву W) погнался за Чемпом и выследил его прямо перед другой линией ворот.
На изображении ниже каждая метка равна одному ярду: обратите внимание, что поле имеет ширину 53 ярда.
- Как можно использовать диаграмму и теорему Пифагора, чтобы приблизительно определить, сколько ярдов пробежал Бен Ватсон, чтобы выследить Чемпа Бейли?
- Используйте теорему Пифагора, чтобы приблизительно определить, сколько ярдов пробежал Уотсон в этой пьесе.
- Какой игрок побежал дальше во время этой игры? Примерно на сколько ярдов больше?
«Бег по футбольному полю» от Illustrative Mathematics под лицензией CC BY 4.0.
HideShow
Студентам может потребоваться прочитать задачу несколько раз, чтобы понять, что представляет каждая часть диаграммы. И, как видите, некоторые оценки в порядке. Учитывая, что все поле составляет 100 ярдов в длину и 53 1/2 ярда в ширину, какова примерно длина сторон этого почти треугольника? Как только учащиеся смогут увидеть прямоугольный треугольник и его размеры, эта проблема станет очень решаемой.
Нахождение расстояний на координатной плоскости
Студенты также должны использовать теорему Пифагора для определения расстояний на координатной плоскости. (8.G.B.8) Это действительно конкретный вариант проблем, которые мы только что обсудили; студенты учатся интерпретировать две точки на координатной плоскости как определяющие гипотенузу прямоугольного треугольника. Эта проблема возникает из вводного урока по этой идее.
8 класс, модуль 7, урок 17: пример 1
Каково расстояние между двумя точками на координатной плоскости? Округлите свой ответ до десятого места.
8 класс, Модуль 7, Урок 17 Доступно на сайте engageny.org/resource/grade-8-mat Mathematics-module-7-topic-c-lesson-17; по состоянию на 29 мая 2015 г. Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
Прежде чем приступить к этой задаче, учащиеся сталкиваются с последовательностью вопросов, в которых они находят длины некоторых горизонтальных и вертикальных сегментов, понимая, что длина сегмента на координатной плоскости — это просто количество квадратов, которые он покрывает.Более того, они видят, что невозможно определить расстояние диагонального сегмента путем подсчета квадратов. Затем эта конкретная проблема представляется как вызов, и у студентов есть время, чтобы поработать над ней. (Скорее всего, когда они будут даны в контексте раздела по теореме Пифагора, ряд студентов подумают о применении своих новых знаний здесь. В идеале, студенты должны быть в состоянии объяснить своим сверстникам, как нарисовать прямоугольный треугольник из этих точек. и определите длину, о которой идет речь.)
После такой задачи ученики должны попрактиковаться в нахождении расстояния между точками в разных квадрантах координатной плоскости, а также расстояния между двумя точками, заданными в виде упорядоченных пар, а не нанесенными на плоскость.(Если вас интересует задача, которая может помочь им в этом, ознакомьтесь с разделом «Определение расстояния между точками» в «Иллюстративной математике». Комментарии и решения дают некоторые идеи о том, как ученики могут двигаться, чтобы найти расстояние между двумя конкретные пронумерованные точки на общий случай любых двух пар координат.)
Роль математических практик
Стандарты включают не только знания и навыки; они также признают необходимость для студентов заниматься некоторыми важными практиками математического мышления и общения.Эти «Математические практики» имеют свой собственный набор стандартов, которые содержат те же основные цели для классов K-12. 3 (Идея состоит в том, что учащиеся должны с годами развивать одни и те же мыслительные привычки все более изощренными способами.) Но вместо того, чтобы быть «просто еще одной вещью» для учителей, которую они могут использовать в своих классах, практики — это способы помочь учащимся прийти на глубокое концептуальное понимание, необходимое в каждом классе. Другими словами, практики помогают учащимся усвоить содержание.В таблице ниже приведены несколько примеров того, как математические практики могут помочь учащимся понять и применить концепции геометрии в 8-м классе.
Подкаст: важность математических практик с Эндрю Ченом и Питером Коу (начало 30:33, конец 43:39)
https://soundcloud.com/unboundedu/the-mat Mathematics-standards-and-shifts/s-tqwCA
Преобразования: связь с выражениями и уравнениями
Преобразования имеют решающее значение для понимания еще одной важной работы для 8-го класса: наклона. 4 Студенты сначала сталкиваются с наклоном через графики пропорциональных соотношений, понимая его как единичную скорость отношения. (Эта концепция впервые была разработана в 7-м классе.) Но почему же наклон линии постоянный? Этот вопрос часто остается незамеченным. Один из способов понимания — это применение подобия: каждая линия на координатной плоскости подразумевает любое количество похожих «наклонных треугольников» с пропорциональными сторонами. (8.EE.B.6) Это задание показывает один пример того, как студенты могут подойти к этой концепции.
Склоны между точками на прямой
Наклон между двумя точками вычисляется путем нахождения изменения значений y и деления на изменение значений x. Например, наклон между точками (7, -15) и (-8, 22) можно вычислить следующим образом:
- Разница значений y составляет -15-22 = -37.
- Разница в значениях x составляет 7 — (−8) = 15.
- Разделив эти две разницы, мы обнаружим, что наклон равен -.
Ева, Карл и Мария вычисляют наклон между парами точек на линии, показанной ниже.
Ева находит наклон между точками (0,0) и (3,2). Карл находит наклон между точками (3,2) и (6,4). Мария находит наклон между точками (3,2) и (9,6). Каждый из них нарисовал треугольник, чтобы помочь в расчетах (показано ниже).
- Какой студент нарисовал какой треугольник? Завершите расчет уклона для каждого ученика. Как можно геометрически интерпретировать различия в значениях x и y на изображениях, которые они нарисовали?
- Рассмотрим любые две точки (,) и (,) на линии, показанной выше.Нарисуйте треугольник, как треугольники, нарисованные Евой, Карлом и Марией. Какой наклон между этими двумя точками? Почему этот уклон должен быть таким же, как и уклон, рассчитанный тремя учениками?
«Уклоны между точками на линии» от Illustrative Mathematics под лицензией CC BY 4.0.
HideShow
Как отмечено в решении, треугольники в этом задании спроектированы таким образом, чтобы учащиеся могли легко определить их как похожие, используя серию жестких движений и расширений.Поскольку любой треугольник на прямой можно перевести в другой, больший или меньший, путем сдвига и растяжения, они должны быть похожими. Таким образом, учащиеся могут продемонстрировать, что наклон между любыми двумя точками на любой заданной линии будет одинаковым. (Это более дедуктивный и математически верный способ понять наклон линии, чем просто наблюдение того, что наклон между несколькими парами точек на одной конкретной прямой оказывается одинаковым.)
Теорема Пифагора: связь с выражениями и уравнениями и системой счисления
Теорема Пифагора тесно связана с работой в области системы счисления (NS) и выражений и уравнений (EE).Стандарты EE являются частью основной работы 8-го класса, в то время как стандарты NS определены как «вспомогательная» работа, поскольку они могут усилить и расширить основные темы.
В 8 классе стандарты NS знакомят учащихся с иррациональными числами (числами типа √2, которые не могут быть выражены дробями), (8.NS.A.1), а стандарты EE предоставляют учащимся простые уравнения, такие как x2 = 8 и y3 = 27, которые включают решение с квадратными и кубическими корнями. (8.EE.A.2) Поскольку применение теоремы Пифагора естественным образом порождает уравнения этого типа, решение задач в контексте прямоугольных треугольников представляет собой сходимость двух стандартов.Возьмем, к примеру, нашу задачу из стандарта 8.G.B.8 выше:
Когда ученики решают, они получают уравнение 22 + 62 = c2, и их решение выглядит примерно так:
22 + 62 = с2
4 + 36 = с2
40 = c2
√40 = с
Основываясь на стандарте 8.NS.A.1, ученик 8-го класса должен уметь сказать, что √40 — это число от 6 до 7, потому что 40 — это число от 36 (62) до 49 (72). Отсюда они могут сделать вывод, что оно меньше 6.5, потому что 40 ближе к 36, чем к 49, и, используя последовательные приближения, найдите, что это около 6,3. Оглядываясь назад на задачу, которая включает в себя расстояния в 2 единицы и 6 единиц для участков, это разумная длина, которую можно ожидать для гипотенузы.
Откуда берутся совпадение и сходство?
Хотя соответствие и сходство начинаются в 8-м классе, более фундаментальные геометрические концепции должны развиваться в начальных и средних классах. Еще в детском саду они начинают думать о длине и классификации форм.(K.G.A.2) Оценка 4 оказывается критически важной для работы с конгруэнтностью и сходством: понятие угловой меры определено (4.MD.C.5), как точки, линии, сегменты и лучи. (4.G.A.1) В 5 классе ученики изучают координатную плоскость и наносят точки в первом квадранте. (5.G.A.1) Затем в 6 классе учащиеся расширяют свои знания о системе счисления, включая отрицательные числа, тем самым раскрывая всю координатную плоскость. (6.NS.C.8) Работа на координатной плоскости продолжается в 7 классе, (7.RP.A.2), а учащиеся решают задачи с использованием масштабных чертежей. (7.G.A.1) Хотя эти задачи не требуют формального понимания сходства с точки зрения трансформаций, они дают студентам возможность работать с парами похожих фигур и масштабных коэффициентов.
Подкаст: важность согласованности с Эндрю Ченом и Питером Коу (начало 9:34, конец 26:19)
https://soundcloud.com/unboundedu/the-mat Mathematics-standards-and-shifts/s-tqwCA
Откуда взялась теорема Пифагора?
Теорема Пифагора также является новой для 8-го класса.Хотя он не требует длительного обучения, некоторые основные требования все же применяются:
- Учащимся нужно будет привыкнуть к экспоненциальной системе счисления с 6-го класса, чтобы понять алгебраическую формулу. (6.EE.A.1)
- Как отмечалось выше, учащимся необходим опыт решения уравнений для 6, 7 и 8 классов, чтобы решать задачи с помощью теоремы Пифагора. (6.EE.B.7, 7.EE.B.4, 8.EE.A.2)
- Как и преобразования, твердое понимание теоремы Пифагора опирается на элементарные геометрические понятия, такие как длина и угловая мера.(4.G.A.1)
Рекомендации для студентов, отстающих от
Если, переходя к разделу по конгруэнтности и сходству, вы знаете, что ваши ученики не имеют твердого представления об упомянутых выше идеях (или вообще не сталкивались с ними), что вы можете сделать? Непрактично (и даже не желательно) заново преподавать все, что ученики должны были выучить в 4–7 классах; в 8-м классе есть много нового материала, поэтому следует сосредоточить внимание на стандартах на уровне класса. В то же время есть стратегические способы свести «незавершенное обучение» к предыдущим оценкам в рамках единицы на соответствие.Вот несколько идей по адаптации вашей инструкции, чтобы восполнить пробелы.
- Если значительное число учащихся не полностью понимают углы или другие элементарные концепции, вы можете запланировать один или два урока, посвященных этим идеям, прежде чем приступить к преподаванию содержания на уровне своего класса. (Здесь могут быть полезны два урока для 4-го класса, один по измерению угла, а другой по различению длины и измерения угла.) Если вы считаете, что весь урок — это слишком много, вы можете спланировать короткий «мини-урок» или использовать некоторые задачи, связанные с этими идеями в качестве разминки для ваших первых нескольких уроков по конгруэнтности.
- Если значительное число студентов не имеют опыта работы с координатной плоскостью или еще не могут точно нанести точки, вы можете запланировать урок или серию разминок по этой идее, прежде чем начинать работу с преобразованиями на координатной плоскости. (Этот урок для 6-го класса по рисованию многоугольников на координатной плоскости может стать хорошим источником проблем для этого типа уроков.)
- Если значительное число учащихся не могут свободно определять и описывать геометрические фигуры (точки, линии, отрезки и т. Д.)), вы можете запланировать мини-урок или серию разминок, чтобы просмотреть их в течение первых нескольких дней модуля, включающего трансформации. (Этот урок для 4-го класса, который вводит только что упомянутые термины, содержит простое введение в эти идеи, и задачи, следующие за уроком, также могут быть полезны.)
Куда идут эти концепции?
Конгруэнтность и сходство долгое время были важными идеями в старшей школе, и, как объяснялось выше, преобразования сейчас являются центральными в понимании этих идей.Один из первых опытов школьников по геометрии — разработка точных определений жестких движений. (G-CO.A.4) Использование преобразований позволяет студентам устанавливать критерии конгруэнтности для треугольников (G-CO.B.8) и дает им инструмент для использования при доказательстве теорем. (G-CO.C) Когда учащиеся понимают конгруэнтность, они готовы решать задачи, связанные с конгруэнтными фигурами, (G.SRT.B.5) исследовать отношения внутри треугольников (G-C.A.2) и доказывать утверждения, используя координаты. (G-GPE.Б.4) В будущем они столкнутся с более специализированными приложениями конгруэнтности; Например, принцип Кавальери зависит от знания того, что означает совпадение поперечных сечений двух разных фигур. (G-GMD.A.1) Сходство включает в себя аналогичный процесс и ведет к изучению тригонометрии.G-SRT.C.9 Последняя ступень прогрессии показывает, как работа в 8 классе ведет в среднюю школу.
Если вы только что закончили это руководство, поздравляем! Надеюсь, он был информативным, и вы сможете вернуться к нему в качестве справочного материала при планировании уроков, создании модулей или оценке учебных материалов.Для получения дополнительных руководств из этой серии посетите нашу страницу с инструкциями по улучшению. Чтобы узнать больше о том, как вы можете использовать эти руководства в своей повседневной практике, посетите нашу страницу часто задаваемых вопросов. И если вам интересно узнать больше о конгруэнтности, сходстве и теореме Пифагора в 8-м классе, не забудьте эти ресурсы:
Партнеры по успеваемости учащихся: в центре внимания 8-й класс
Hung-Hsi Wu: обучение геометрии в соответствии с общими базовыми стандартами
EngageNY: 8 класс, материалы модуля 2 (соответствие)
EngageNY: 8 класс, материалы модуля 3 (сходство)
EngageNY: 8 класс, материалы модуля 7 (теорема Пифагора)
Иллюстративная математика 8 класс Задания
1.Что такое руководство по содержанию?
Работая с высокими академическими стандартами, мы часто слышим, как преподаватели спрашивают: «Как выглядит обучение в соответствии со стандартами?» Наши руководства по содержанию стремятся ответить на этот вопрос, предоставляя подробный обзор одного или нескольких групп математических стандартов за раз. Руководства по содержанию предназначены для каждого класса и предметной области, и есть руководства для каждого класса или курса, от детского сада до алгебры II. Если вы хотите узнать больше об обучении соотношениям и пропорциональным отношениям в 6 классе, например, в нашем соответствующем Руководстве по содержанию вы найдете исчерпывающее, но доступное объяснение этих стандартов, несколько примеров открытых образовательных ресурсов (OER), которые соответствуют стандартам, и конкретные предложения в поддержку обучения в 6-х классах соотношению и пропорциональному мышлению.
Наша цель при создании руководств по содержанию заключалась в том, чтобы предоставить занятым учителям практический и простой для чтения ресурс о том, что говорится в стандартах математики на уровне класса, а также примеры учебных материалов, которые поддерживают концептуальное понимание, решение проблем и т. и процедурные навыки и беглость для студентов.
Важно отметить, что руководства по содержанию не предназначены для использования в качестве учебной программы (или какого-либо документа, предназначенного для учащихся), руководства или исходного материала для мероприятий по подготовке к экзаменам или какого-либо инструмента оценки учителей.
2. Что в Руководстве по содержанию?
Каждое руководство по содержанию ориентировано на определенную группу стандартов. Большинство руководств по содержанию имеют одинаковую структуру из трех частей:
- Часть 1 разъясняет навыки и понимание учащихся, описанные в этой группе стандартов. Этот раздел иллюстрирует стандарты с использованием нескольких студенческих задач из свободно доступных онлайн-источников. Учителя могут использовать или адаптировать эти задания для своих учеников.
Часть 2 объясняет, как эта группа стандартов связана с другими стандартами того же класса.Мы подчеркиваем, как эти связи имеют значение для планирования и обучения и как согласованность внутри класса может улучшить доступ учащихся. Часть 2 также включает в себя несколько студенческих задач из свободно доступных онлайн-источников.
Часть 3 отслеживает отдельные этапы обучения, ведущие к содержанию уровня класса, обсуждаемому в конкретном Руководстве по содержанию. Это обсуждение переходит в серию конкретных и практических предложений о том, как учителя могут использовать прогрессии для обучения учащихся, которые могут быть не подготовлены к математике на уровне своего класса.Наконец, в Части 3 прослеживается переход к содержанию в более высоких классах.
3. Как я могу использовать руководства по содержанию?
учителей, прочитавших наши руководства по содержанию, говорят, что они видят преимущества для всех преподавателей. Вот несколько предложений о том, как разные преподаватели могут их использовать.
Учителя могут использовать руководства по математике по адресу:
- Повысьте или освежите свои знания о стандартах и ожиданиях в отношении того, что студенты должны знать к концу года.
- Адаптируйте уроки и разделы, используя соответствующие предварительные условия, для поддержки учащихся, отстающих от своего класса.
- Получите доступ к наилучшим доступным ООР по математике, чтобы использовать его для введения и / или закрепления концепций
- Убедитесь, что их учебная программа и / или единицы:
- Сосредоточьтесь на основной работе класса и соответствующей глубине каждого стандарта.
- Ориентируйтесь на соответствующие аспекты строгости — процедурные навыки и беглость, моделирование и применение, а также концептуальное понимание, описываемое стандартами.
- Помогите учащимся установить взаимосвязь между классами и учениками.
- Создайте или пересмотрите свои уроки и вопросы, чтобы сосредоточиться на важных концепциях стандартов.
Инструкторы и руководители школ могут использовать Руководства по математике по адресу:
- Обновите или расширите свои знания о стандартах и ожиданиях того, что студенты должны знать к концу года.
- Развивайте и сообщайте согласованные ожидания в отношении планирования уроков и обучения в соответствии со стандартами.
- Предоставьте ссылку при планировании и / или обсуждении обучения с учителями.
- Получите представление о том, как должны выглядеть инструкции и работа учащихся, чтобы соответствовать требованиям стандартов.
- Разработка и проектирование содержания и семинаров / семинаров по профессиональному развитию на основе стандартов.
- Стимулируйте содержательные, основанные на стандартах дискуссии между сотрудниками и повышайте уровень их знаний.
- Разрабатывать и / или пересматривать планы улучшения школы, чтобы поддерживать и включать содержание и практическое обучение и обучение.
4. Почему именно Руководства по содержанию?
Переход на более высокие стандарты привел к тому, что учителя по всей стране внесли существенные изменения в свое планирование и обучение, но только треть учителей считает, что они готовы помочь своим ученикам пройти более строгие экзамены, соответствующие стандартам (Kane et. др., 2016). Этого следовало ожидать, потому что новые высокие стандарты существенно отличаются от прежних стандартов. Стандарты требуют более глубокого понимания математического содержания, которое они преподают; различный прогресс в том, что учащимся необходимо выучить, в каком классе; а также различная педагогика, которая в равной степени подчеркивает концептуальное понимание учащимися, решение проблем и беглость процедур.
Однако поддержка учителей в обеспечении высоких стандартов в своих классах отстала. Исследования показывают, что подготовка учителей в США в настоящее время недостаточна для подготовки учителей к преподаванию требовательных новых стандартов (Центр исследований в области математики и естественнонаучного образования, 2010 г.). И хотя существуют некоторые ресурсы, которые «распаковывают» стандарты, немногие, если таковые имеются, объясняют, и иллюстрируют стандарты. «Распаковка» стандартов один за другим также может привести к разрозненному представлению, которое не учитывает структуру и последовательность стандартов.Создавая руководства по содержанию, мы стремились предоставить занятым учителям практичный, легкий для чтения ресурс, посвященный стандартам их класса и тому, как помочь всем учащимся усвоить их. Существует множество эмпирических доказательств того, что, когда учителя обладают как глубокими знаниями математического содержания, которое они преподают, так и педагогическими знаниями, которые помогают учащимся усвоить эти знания, их ученики усваивают больше (Baumert et. Al., 2010; Hill, Rowan and Ball , 2005; Rockoff et. Al., 2008). Имея в руках руководства по содержанию, мы надеемся, что учителя добьются большего успеха в помощи своим ученикам в достижении их готовности к поступлению в колледж и карьеры.
5. Какая связь между руководствами по содержанию и прогрессом?
Документы Progressions описывают развитие понимания математики от класса к классу. Они были основаны на исследованиях познавательного развития детей, а также логической структуры математики. Прогрессии объясняют, почему стандарты упорядочены именно так. Руководства по содержанию часто выделяют ключевые идеи из Прогрессов, но не добавляют новых стандартов и не меняют ожидания относительно того, что студенты должны знать и уметь; они стремятся объяснить и проиллюстрировать группу стандартов одновременно с использованием свободно доступных онлайн-источников.Хотя задачи и уроки OER в Руководствах по содержанию — это один из способов соответствовать стандартам уровня класса, они не единственное средство для этого.
6. Как отбирались ресурсы?
Мы выбрали типовые задания и уроки из свободно доступных онлайн-источников, таких как EngageNY, Illustrative Mathematics и Student Achievement Partners, чтобы проиллюстрировать стандарты. Эти источники выбраны потому, что они полностью соответствуют новым высоким стандартам, основанным на национальном обзоре учебных программ K-12, или созданы организациями, возглавляемыми авторами новых высоких стандартов.Кроме того, поскольку они являются открытыми образовательными ресурсами (ООР), они доступны для любого использования. Все материалы UnboundEd также являются OER, что является частью нашего стремления сделать высококачественный, согласованный контент доступным для всех преподавателей.
7. Почему Руководства по содержанию содержат лишь несколько стандартов? Где остальные стандарты?
В каждом руководстве по содержанию рассматривается подмножество стандартов оценки. Стандарты, рассматриваемые в первом наборе руководств по содержанию для каждой степени, обычно относятся к высокоприоритетному содержанию; эти стандарты также часто являются хорошим выбором для обучения в начале года.Более подробную информацию о выборе стандартов можно найти во введении к каждому Руководству по содержанию. Со временем мы разработаем дополнительные руководства по содержанию для каждого класса и обновим существующие. Мы планируем иметь четыре руководства по содержанию для каждого класса или курса, от детского сада до алгебры II. Справочники будут публиковаться волнами, каждая из которых будет состоять из одного справочника для каждого уровня. Мы планируем выпустить второй набор руководств по содержанию для каждого класса к концу 2016-17 учебного года.
8.Как я могу быть в курсе новых руководств по содержанию?
Если вы хотите получать обновления о контенте и событиях от UnboundEd, включая новые руководства по контенту, подпишитесь на анонсы UnboundEd здесь.
Поймите соответствие и сходство с помощью физических моделей, прозрачностей или программного обеспечения для работы с геометрией. Поймите и примените теорему Пифагора. Используйте аналогичные треугольники, чтобы объяснить, почему угол наклона m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b.Поймите соответствие и сходство с помощью физических моделей, прозрачностей или программного обеспечения для работы с геометрией. Поймите соответствие и сходство с помощью физических моделей, прозрачностей или программного обеспечения для работы с геометрией. Проверьте экспериментально свойства вращений, отражений и перемещений: Линии превращаются в линии, а сегменты линий — в сегменты одинаковой длины.Углы принимаются к углам той же меры. Параллельные линии переходят в параллельные. Поймите, что двухмерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; учитывая две совпадающие фигуры, опишите последовательность, демонстрирующую соответствие между ними.Опишите влияние расширений, перемещений, вращений и отражений на двумерные фигуры с помощью координат. Поймите, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и растяжений; для двух одинаковых двумерных фигур опишите последовательность, демонстрирующую сходство между ними.Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся, когда параллельные прямые пересекаются трансверсалью, и о критерии подобия треугольников угол-угол. Проверьте экспериментально свойства вращений, отражений и перемещений: Поймите, что двухмерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; учитывая две совпадающие фигуры, опишите последовательность, демонстрирующую соответствие между ними.Поймите, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и растяжений; для двух одинаковых двумерных фигур опишите последовательность, демонстрирующую сходство между ними. Опишите влияние расширений, перемещений, вращений и отражений на двумерные фигуры с помощью координат.Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся, когда параллельные прямые пересекаются трансверсалью, и о критерии подобия треугольников угол-угол. Проверьте экспериментально свойства вращений, отражений и перемещений: Поймите, что двухмерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; учитывая две совпадающие фигуры, опишите последовательность, демонстрирующую соответствие между ними.Поймите, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и растяжений; для двух одинаковых двумерных фигур опишите последовательность, демонстрирующую сходство между ними. Поймите, что двухмерная фигура похожа на другую, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и растяжений; для двух одинаковых двумерных фигур опишите последовательность, демонстрирующую сходство между ними.Опишите влияние расширений, перемещений, вращений и отражений на двумерные фигуры с помощью координат. Поймите соответствие и сходство с помощью физических моделей, прозрачностей или программного обеспечения для работы с геометрией. Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся, когда параллельные прямые пересекаются трансверсалью, и о критерии подобия треугольников угол-угол.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких полных квадратов и кубические корни из маленьких идеальных кубов. Знайте, что √2 иррационально. Знайте, что нерациональные числа называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показывают, что десятичное представление в конечном итоге повторяется, и преобразует десятичное представление, которое повторяется в конечном итоге, в рациональное число.Поймите и примените теорему Пифагора. Поймите и примените теорему Пифагора. Объясните доказательство теоремы Пифагора и ее обращения. Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальных и математических задачах в двух и трех измерениях.Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат. Объясните доказательство теоремы Пифагора и ее обращения. Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальных и математических задачах в двух и трех измерениях. Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.Объясните доказательство теоремы Пифагора и ее обращения. Примените теорему Пифагора для определения неизвестных длин сторон прямоугольных треугольников в реальных и математических задачах в двух и трех измерениях. Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат. Создавайте жизнеспособные аргументы и критикуйте рассуждения других.Ищите и используйте структуру. Рассуждайте абстрактно и количественно. Используйте аналогичные треугольники, чтобы объяснить, почему угол наклона m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b.Знайте, что нерациональные числа называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показывают, что десятичное представление в конечном итоге повторяется, и преобразует десятичное представление, которое повторяется в конечном итоге, в рациональное число. Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число.Вычислите квадратные корни из маленьких полных квадратов и кубические корни из маленьких идеальных кубов. Знайте, что √2 иррационально. Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат. Знайте, что нерациональные числа называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показывают, что десятичное представление в конечном итоге повторяется, и преобразует десятичное представление, которое повторяется в конечном итоге, в рациональное число.Правильно называйте фигуры независимо от их ориентации или общего размера. Распознавайте углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимайте концепции измерения углов: Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах.Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат с пересечением линий (начало координат), расположенным так, чтобы совпадать с 0 на каждой линии и заданной точкой на плоскости, расположенной с помощью упорядоченной пары числами, названными его координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, с условием, что имена двух осей и координаты соответствуют (e.g., ось x и координата x, ось y и координата y). Решайте реальные и математические задачи, отображая точки во всех четырех квадрантах координатной плоскости. Включите использование координат и абсолютного значения для нахождения расстояний между точками с одинаковой первой или одинаковой второй координатой. Признать и представить пропорциональные отношения между количествами. Решение проблем, связанных с масштабными чертежами геометрических фигур, включая вычисление фактических длин и площадей на основе масштабного чертежа и воспроизведение масштабного чертежа в другом масштабе.Напишите и оцените числовые выражения, включающие целочисленные показатели. Решайте реальные и математические проблемы, записывая и решая уравнения вида x + p = q и px = q для случаев, когда p, q и x являются неотрицательными рациональными числами. Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения проблем, рассуждая о величинах.Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x² = p и x³ = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких полных квадратов и кубические корни из маленьких идеальных кубов. Знайте, что √2 иррационально. Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах.Разработайте определения поворотов, отражений и перемещений в терминах углов, окружностей, перпендикулярных линий, параллельных линий и отрезков линий. Объясните, как критерии конгруэнтности треугольника (ASA, SAS и SSS) вытекают из определения конгруэнтности в терминах жестких движений. Докажите геометрические теоремы Используйте критерии конгруэнтности и подобия треугольников для решения задач и доказательства взаимосвязи в геометрических фигурах.Определите и опишите отношения между вписанными углами, радиусами и хордами. Используйте координаты, чтобы алгебраически доказать простые геометрические теоремы. Неформально аргументируйте формулы для длины окружности, площади круга, объема цилиндра, пирамиды и конуса.Рабочий лист постулата добавления сегментов, раскраска
Рабочие листы для печати на английском языке.Бесплатные загружаемые рабочие листы в формате PDF для учителей: загрузите и распечатайте раздаточные материалы, упражнения и викторины — ESL / K12. Распечатайте больше листов! 1. Выполните поиск упражнений в строке поиска выше 2. Перейдите на страницу 3. Используйте значок принтера для печати страницы.
Раскраски. Рабочие листы для печати по алфавиту для детей ясельного возраста и дошкольного возраста. Мгновенно загружайте более 200 распечатываемых раскрасок с алфавитом и рабочих листов для детей ясельного и дошкольного возраста, включая наши бесплатные прописные и строчные буквы.
Напишите постулат сложения сегментов для описанных пунктов.В следующих задачах предположим, что J находится между H и K. Используйте постулат сложения сегментов, чтобы найти x. Затем найдите длину каждого сегмента.
4) Как вы думаете, в чем разница между серединным перпендикуляром отрезка и биссектрисой отрезка. Нарисуйте диаграмму, чтобы показать разницу. 5) Найдите способ показать, что точки A = (-4, -1), B = (4, 3) и C = (8, 5) лежат на одной прямой.
Дополнительные задания с картинками, предназначенные для детей 4-7 лет, чтобы помочь им развлечься.Подсчет изображений и добавление рабочих листов. Дополнение на этом уровне концептуально. В этих бесплатных рабочих листах дети будут работать с добавлением идентичных элементов, а затем переходят к идентичным элементам, но разного цвета.
План интерактивного видеоурока по теме: Постулат сложения сегментов. Обзор упражнения: Постулат сложения сегментов с дробями: http Благодаря четырем приложениям, каждое из которых разработано для существующих занятий в классе, Spiral дает вам возможность проводить формирующую оценку всего, чему вы учите.
Эти рабочие листы сложения начинаются с прибавления чисел до 10, затем прибавляются до 20, а затем до 100 на уровне третьего класса. Когда дети достигают 4-го класса, они начинают учиться складывать десятичные дроби и денежные суммы, используя сложение столбцов. Приведенные ниже дополнительные листы помогут вашему ребенку …
Ознакомьтесь с нашей большой подборкой рабочих листов и печатных форм. Они совершенно бесплатны и удобны для использования в классе и дома!
TCR Advanced Disc 1+ PC (2021 г.) | Мужской гоночный велосипед
Тренировки, гонки, доведение до предела.Нападаете ли вы на поле или копаете глубоко в поисках нового PR, новый TCR Advanced Disc легче, жестче и быстрее благодаря стратегической форме аэродинамической трубы, увеличенному зазору шины и встроенной технологии дисковых тормозов.
Модернизированный с обновленной аэродинамической формой трубы в рулевой трубе, нижней трубе и вилке, а также увеличенный зазор для шин большего диаметра (до 32 мм) новый TCR Advanced Disc обеспечивает выдающуюся эффективность на дороге.Подседельный штырь Variant обеспечивает достаточную податливость, чтобы придать ему сбалансированное, настроенное на гонку ощущение на дороге. А благодаря интегрированной технологии дисковых тормозов, включая плоские крепления и 12-миллиметровые передние и задние сквозные оси, это всепогодная гоночная машина для любых условий, которая поможет вам оставаться в лидерах.
Ключевые факторы производительности
Лучшая в своем классе эффективность
Благодаря впечатляющему соотношению жесткости к весу и обновленной форме аэродинамической трубы, этот комплект рамы спроектирован так, чтобы предоставить гонщикам и гонщикам превосходные возможности для лазания, аэродинамическую эффективность и жесткость на спринте для победы в гонках.
Продвинутая аэродинамика
Именно здесь можно найти наиболее ощутимые преимущества TCR по сравнению с моделями предыдущего поколения. Каждая форма трубы была проанализирована, спроектирована и протестирована для создания общей конструкции со значительно меньшим сопротивлением при более широком диапазоне углов рыскания. В результате TCR становится быстрее, чем когда-либо, в спринтах и одиночных ситуациях.
Полный контроль
Встроенные дисковые тормоза обеспечивают плавное, мощное торможение и модуляцию для дополнительного контроля в изменчивых погодных и дорожных условиях. Плоские крепления и новые сквозные оси повышают жесткость и улучшают управляемость, а увеличенный зазор между рамой и вилкой позволяет устанавливать шины большего диаметра до 32 мм.
Все перечисленные характеристики могут быть изменены без предварительного уведомления.

 Найдите остальные углы этого треугольника и угол РМН.
Найдите остальные углы этого треугольника и угол РМН. Найдите угол OMP.
Найдите угол OMP.
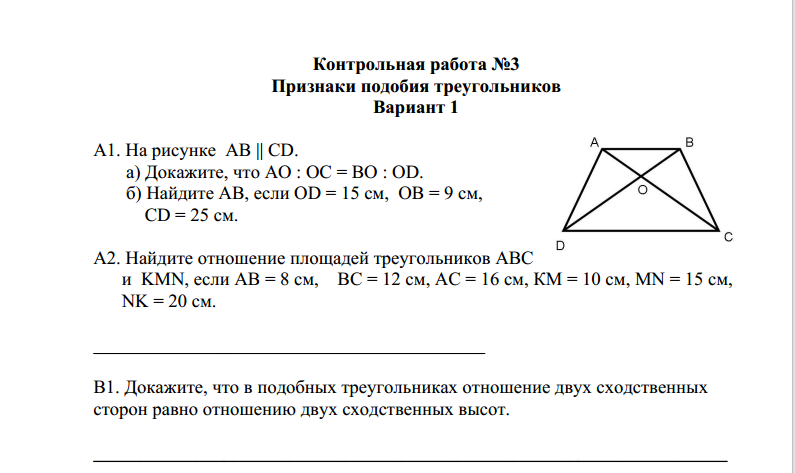
 Найти углы ромба.
Найти углы ромба. Г-8.
Г-8. Найдите стороны параллелограмма.
Найдите стороны параллелограмма.

 Г-8
Г-8 Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см.
Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см.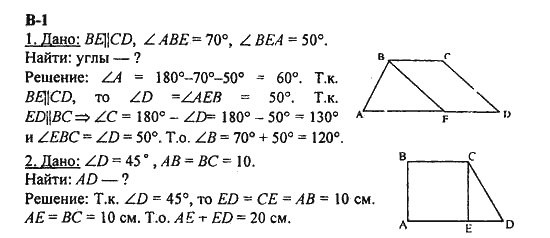 Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.

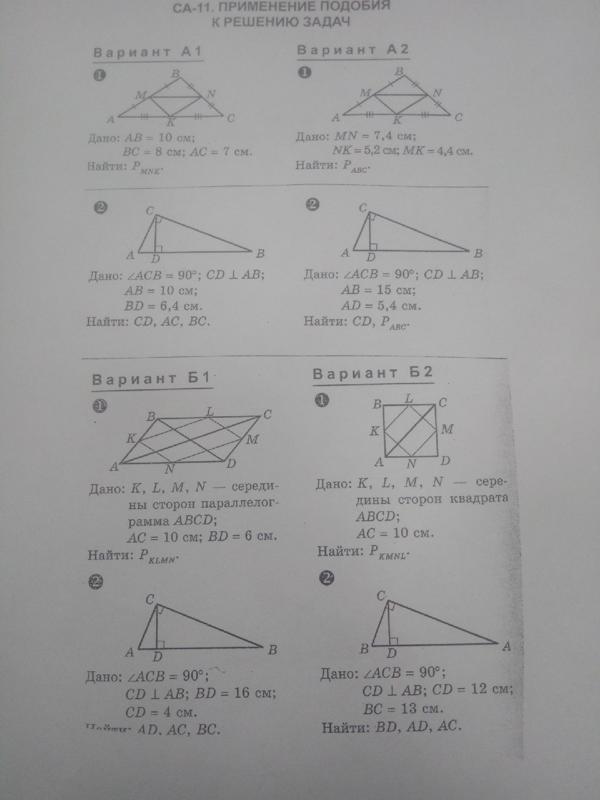 A C
A C Найдите угол В и гипотенузу АВ.
Найдите угол В и гипотенузу АВ. Найдите разность оснований трапеции, если
Найдите разность оснований трапеции, если Г-8.
Г-8. Найдите длины отрезков АС и АО, если АВ = 12 см.
Найдите длины отрезков АС и АО, если АВ = 12 см. Найдите стороны MN и NK треугольника.
Найдите стороны MN и NK треугольника. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см.
В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см.

 Окружность пересекает отрезок AO в точке D. Найдите AD.
Окружность пересекает отрезок AO в точке D. Найдите AD. Окружность пересекает отрезок AO в точке D. Найдите AD.
Окружность пересекает отрезок AO в точке D. Найдите AD.