1. В каких поведенческих особенностях индивида проявляется темперамент?
2. Какова сущность гуморального направления изучения темперамента?
3. Назовите основу темперамента в учении И. Павлова.
4. Что лежит в основе конституционального подхода к темпераменту?
5. Назовите различия между холериком и флегматиком по их отношению к работе и общению.
6. В чем вы усматриваете различия между сангвиником и меланхоликом по их отношению к работе и общению?
7. В чем заключаются особенности индивидуального подхода к лицам с ярко выраженными особенностями темперамента?
8. Раскройте содержание понятия характера?
9. Как соотносятся характер и темперамент?
10. Какие типологии характера вам известны?
11. Охарактеризуйте основные типы акцентуаций характера.
12. Как формируется характер?
13. Предложите свое определение способностей и сопоставьте его с прочитанным.
14. В чем заключается сущность понятия «склонность» и какова его связь с понятием способностей.
15. Одаренность, склонность, задатки, способности, гениальность – как различить и увязать эти понятия?
16. Охарактеризуйте основные виды способностей человека
17. Попытайтесь охарактеризовать собственные способности.
18. Как соотносятся понятия «интеллект» и «креативность»?
1. Психология управления как наука. Основные направления развития психологии управления
2. Процесс и система управления
3. Лидер и проблемы лидерства
4.Руководство и лидерство: общие и отличительные черты. Характеристика стилей управления
5.Психические требования, предъявляемые к руководителю
Вопросы для размышления.
1. Чем понятие «лидер» отличается от понятия «руководитель»?
2. С вашей точки зрения, лидером рождаются или становятся?
3. Какие особенности присущи авторитарному, демократическому, попустительскому стилю руководства?
4. Зависит ли эффективность руководства от возраста, пола, уровня образования?
5. Должны ли подчиненные боятся своего руководителя?
Задание 1. Представьте себя в роли руководителя. Как бы вы поступили в нижеописанных ситуациях? Объясните свое поведение. Продумайте возможные варианты.
Вы недавно назначены менеджером. Вы еще плохо знаете сотрудников фирмы, сотрудники еще не знают вас в лицо. Вы идете на совещание к генеральному директору. Проходите мимо курительной комнаты и замечаете двух сотрудников, которые курят и о чем-то оживленно беседуют. Возвращаясь с совещания, которое длилось один час, вы опять видите тех же сотрудников в курилке за беседой.
Вы начальник отдела. В отделе напряженная обстановка, срываются сроки выполнения работ. Не хватает сотрудников. Выезжая в командировку, вы случайно встречаете свою подчиненную – молодую женщину, которая уже две недели находится на больничном. Но вы находите ее в полном здравии. Она кого-то с нетерпением встречает в аэропорту.
Одна сотрудница высказывает другой претензии по поводу многочисленных и часто повторяющихся ошибок в работе. Вторая сотрудница принимает высказываемые претензии за оскорбление. Между ними возник конфликт.
Во время служебного совещания ваш подчиненный открыто критикует вашу деятельность.
Задание 2. Разделите нижеприведенные характеристики на две группы – слабые и высокие навыки руководства.
| Слабые навыки руководства | Высокие навыки руководства |
1) устанавливает дисциплину, если это требуется;
2) дает четкие указания;
3) избегает действий, связанных с наказанием;
4) редко делегирует полномочия;
5) не защищает собственную организацию;
6) не принимает во внимание того, что лежит в основе поведения подчиненных;
7) не стремится к ясности;
8) пренебрегает возможностью положительно отметить работу подчиненных;
9) приспосабливает стиль руководства к переменам;
10) пускает работу подчиненных на самотек;
11) развивает добрые отношения с окружающими;
12) регулярно анализирует работу подчиненных;
13) терпит минимальный вклад в работу;
14) устанавливает приемлемые отношения с «трудными» людьми;
15) устанавливает критерии успеха.
Задание 3. Вам предлагается набор типичных производственных ситуаций, каждая из которых имеет четыре варианта решения. Внимательно ознакомьтесь с содержанием ситуации, проанализируйте каждое решение и выберите тот вариант, который считаете наиболее правильным. Аргументируйте свой выбор.
Ситуация 1. Ваш непосредственный начальник, минуя вас, дает задание вашему подчиненному, который уже занят выполнением срочной работы. Вы и ваш начальник считаете свои задания неотложными. Выберите наиболее приемлемый вариант решения:
а) буду строго придерживаться субординации, не оспаривая решение начальника, предложу подчиненному отложить выполнение моего задания;
б) все зависит от того, насколько авторитетен в моих глазах начальник;
в) выражу свое несогласие с решением начальника, предупрежу его о том, что впредь в таких случаях буду отменять его задания, поручаемые подчиненному без предварительного согласования со мной. Совместно договоримся об очередности выполнения заданий;
г) в интересах дела отменю задание начальника, прикажу подчиненному продолжить начатую работу.
Ситуация 2. Между вашими подчиненными возник конфликт, который мешает им успешно работать. Каждый из них в отдельности обращался к вам с тем, чтобы вы приняли его сторону и разрешили конфликт. Ваша позиция:
а) мое дело – не допустить, чтобы они конфликтовали на работе, а решить сам конфликт – это их личное дело;
б) поручу разобраться в данной ситуации общественным организациям;
в) прежде всего мне надо разобраться в причинах конфликта и самому найти способ их примирить. Впоследствии обязательно привлеку общественность;
г) выясню, кто из членов коллектива служит авторитетом для конфликтующих, и буду воздействовать на них через этих людей.
Ситуация 3. Ваш подчиненный по причине недисциплинированности не выполнил задания в срок, хотя обещал сделать эту важную работу к намеченной дате. Ваша реакция:
а) сначала добиться выполнения задания, а затем уже поговорить наедине, если надо – наказать;
б) поговорить с ним наедине, выяснить и обсудить причину срыва, добиться выполнения работы, наказать в случае повторного нарушения вдвойне;
в) сначала поговорить с теми, кто больше знает о провинившемся, посоветоваться о том, какую форму воздействия применить к нему;
г) отменить задание, передать вопрос на решение администрации. В дальнейшем вести тщательный контроль за его работой, вовремя исправлять ошибки.
Ситуация 4. Вам предоставлена возможность назначить себе заместителя. Имеется несколько кандидатур. Каждый из претендентов отличается перечисленными ниже качествами. Выберите одного кандидата:
а) первый предпочитает избегать конфликтов с людьми, стремится, прежде всего, к тому, чтобы наладить доброжелательные отношения, создать в коллективе атмосферу взаимного доверия, дружеского расположения, что, однако, не всеми понимается правильно;
б) второй предпочитает в интересах дела идти на конфликт с людьми, не боится испортить личные отношения ради поставленной цели;
в) третий предпочитает строго придерживаться своих должностных прав и обязанностей, требует того же от вас и своих подчиненных, добивается четкого выполнения работы;
г) четвертый всегда сосредоточен на достижении своей цели, напорист в организационных вопросах, стремится добиться своего, не придает большого значения возникающим во взаимоотношениях с подчиненными недоразумениям и конфликтам.
Ситуация 5. Однажды вы услышали, что четверо руководителей спорят о том, как лучше обращаться с подчиненными. К какой из четырех точек зрения присоединитесь вы:
а) чтобы подчиненный хорошо работал, нужно подходить к нему индивидуально, учитывая его характер и темперамент, считаясь с его личностью, его интересами и потребностями;
б) все это мелочи, главное в оценке людей – их деловые качества, исполнительность. Каждый должен делать то, что ему положено;
в) успеха в руководстве можно добиться лишь в том случае, если подчиненные доверяют своему руководителю, любят его;
г) лучшие стимулы в работе – четкий приказ, приличная зарплата и своевременная премия.
studfiles.net
1. Какие утилиты используются для создания файла справки?
2. Какой из существующих способов создания справочной системы более перспективный?
3. Как изменить последовательность и иерархию разделов в оглавлении файла справки?
4. Рассмотрите самостоятельно создание окна поиска в справочной системе, скомпилированной из html-файлов.
5. Как в утилите HTML Help Workshop изменить картинки, отмечающие разделы справочной системы?
Цель: освоить технологию тестирования логики программ.
Оборудование: ПЭВМ IBM PC-AT.
Программные средства: ОС семейства Windows, среда Delphi 5.* (или выше).
Разработать по заданию преподавателя приложение, позволяющее решить одну из следующих задач:
Идентифицировать треугольник по трем сторонам (остроугольный, прямоугольный, тупоугольный, равносторонний, равнобедренный).
Идентифицировать четырехугольник по четырем сторонам (квадрат или ромб, прямоугольник, трапеция или обыкновенный четырехугольник).
Идентифицировать треугольник по двум сторонам и углу между ними (остроугольный, прямоугольный, тупоугольный, равносторонний, равнобедренный).
Определить, является ли заданное с клавиатуры шестизначное число четным, счастливым (сумма первых трех цифр равна сумме последних трех цифр) или делится на 13.
Идентифицировать треугольник по трем углам (остроугольный, прямоугольный, тупоугольный, равносторонний, равнобедренный).
Идентифицировать трапецию по двум сторонам и углу между ними (квадрат, равнобедренная, обыкновенная).
Выполнить тестирование логики полученной программы.
1. Получить вариант задания у преподавателя.
2. Подготовить вариант решения поставленной задачи в среде Delphi.
3. Выбрать метод тестирования и выполнить тестирование программы.
4. Продемонстрировать результаты работы преподавателю.
Тестирование программного обеспечения охватывает целый ряд видов деятельности, аналогичных последовательности процессов разработки программного обеспечения. В него входят: а) постановка задачи для теста; б) проектирование теста; в) написание тестов; г) тестирование тестов; д) выполнение тестов и е) изучение результатов тестирования.
Решающую роль играет проектирование тестов. Возможны разные подходы к проектированию тестов. Первый состоит в том, что тесты проектируются на основе внешних спецификаций программ и модулей, либо спецификаций сопряжения программы или модуля. Программа при этом рассматривается как черный ящик (стратегия "черного ящика"). Существо такого подхода – проверить соответствует ли программа внешним спецификациям. При этом логика модуля совершенно не принимается во внимание. Второй подход основан на анализе логики программы (стратегия "белого ящика"). Существо подхода – в проверке каждого пути, каждой ветви алгоритма. При этом внешняя спецификация во внимание не принимается.
Ни один из описанных подходов не является оптимальным. Из анализа существа первого подхода ясно, что его реализация сводится к проверке всех возможных комбинаций значений на входе программы. Тестирование любой программы для всех значений входных данных невозможно, так как их бесконечное множество, поэтому ограничиваются меньшим. При этом исходят из максимальной отдачи теста по сравнению с затратами на его создание. Она измеряется вероятностью того, что тест выявит ошибки, если они имеются в программе. Затраты измеряются временем и стоимостью подготовки, выполнения и проверки результатов теста.
Проанализируем теперь второй подход к тестированию. Даже если предположить, что выполнены тесты для всех путей программы, нельзя с полной уверенностью утверждать, что модуль не содержит ошибок. Очевидное основание этого утверждения состоит в том, что выполнение всех путей не гарантирует соответствия программы ее спецификациям. Допустим, если требовалось написать программу для вычисления кубического корня, а программа фактически вычисляет корень квадратный, то программа будет совершенно неправильной, даже если проверить все пути. Вторая проблема – отсутствующие пути. Если программа реализует спецификации не полностью (например, отсутствует такая специализированная функция, как проверка на отрицательное значение входных данных программы вычисления квадратного корня), никакое тестирование существующих путей не выявит такой ошибки. И, наконец, проблема зависимости результатов тестирования от входных данных. Путь может правильно выполняться для одних данных и неправильно для других. Например, если для определения равенства трёх чисел программируется выражение вида
IF (A+B+C)/3=A,
то оно будет верным не для всех значений A, B и C (ошибка возникает в том случае, когда из двух значений В или С одно больше, а другое на столько же меньше А). Если концентрировать внимание только на тестировании путей, нет гарантии, что эта ошибка будет выявлена.
Таким образом, полное тестирование программы невозможно. Тест для любой программы будет обязательно неполным, то есть тестирование не гарантирует полное отсутствие ошибок в программе. Стратегия проектирования тестов заключается в том, чтобы по возможности попытаться уменьшить эту неполноту. Тестирование по принципу "белого ящика" характеризуется степенью, какой тесты выполняют или покрывают логику (исходный текст программы).
Метод покрытия операторов.
Целью этого метода тестирования является выполнение каждого оператора программы хотя бы один раз.
Пример:

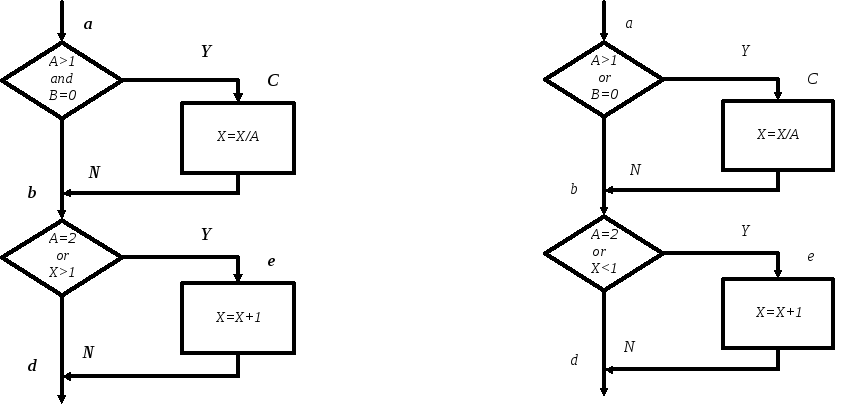
Рис. 12.1 Рис. 12.2
В этой программе можно выполнить каждый оператор, записав один единственный тест, который реализовал бы путь ace. То есть, если бы на входе было: А=2, В=0, Х=3, каждый оператор выполнился бы один раз. Но этот критерий на самом деле хуже, чем он кажется на первый взгляд. Пусть в первом условии вместо “and”“or” и во втором вместо “x>1”“x<1” (блок-схема правильной программы приведена на рис. 12.1, а неправильной – на рис. 12.2). Результаты тестирования приведены в табл. 12.1. Обратите внимание: ожидаемый результат определяется по алгоритму на рис. 12.1, а фактический – по алгоритму рис. 12.2, поскольку определяется чувствительность метода тестирования к ошибкам программирования. Как видно из этой таблицы, ни одна из внесенных в алгоритм ошибок не будет обнаружена.
Таблица 12.1 – Результат тестирования методом покрытия операторов
| Тест | Ожидаемый результат | Фактический результат | Результат тестирования |
| A=2, B=0, X=3 | X=2,5 | X=2,5 | неуспешно |
Метод покрытия решений (покрытия переходов)
Более сильный метод тестирования известен как покрытие решений (покрытие переходов). Согласно данному методу каждое направление перехода должно быть реализовано, по крайней мере, один раз.
Покрытие решений обычно удовлетворяет критерию покрытия операторов. Поскольку каждый оператор лежит на некотором пути, исходящем либо из оператора перехода, либо из точки входа программы, при выполнении каждого направления перехода каждый оператор должен быть выполнен.
Для программы приведенной на рис. 12.2 покрытие решений может быть выполнено двумя тестами, покрывающими пути {ace, abd}, либо {aсd, abe}. Пути {aсd, abe}покроим, выбрав следующие исходные данные: {A=3, B=0, X=3} и {A=2, B=1, X=1} (результаты тестирования – в табл. 12.2).
Таблица 12.2 – Результат тестирования методом покрытия решений
| Тест | Ожидаемый результат | Фактический результат | Результат тестирования |
| A=3, B=0, X=3 | X=1 | X=1 | неуспешно |
| А=2, В=1, Х=1 | Х=2 | Х=1,5 | успешно |
Метод покрытия условий
Лучшие результаты по сравнению с предыдущими может дать метод покрытия условий. В этом случае записывается число тестов, достаточное для того, чтобы все возможные результаты каждого условия в решении выполнялись по крайней мере один раз (табл. 12.3).
В предыдущем примере имеем четыре условия: {A>1, B=0}, {A=2, X>1}. Следовательно, требуется достаточное число тестов, такое, чтобы реализовать ситуации, где A>1, A1, B=0 и B0 в точке а и A=2, A2, X>1 и X1 в точке В. Тесты, удовлетворяющие критерию покрытия условий и соответствующие им пути, приведены ниже:
а) A=2, B=0, X=4 ace
б) A=1, B=1, X=0 abd
Таблица 12.3 – Результаты тестирования методом покрытия условий
| Тест | Ожидаемый результат | Фактический результат | Результат тестирования |
| A=2, B=0, X=4 | X=3 | X=3 | неуспешно |
| A=1, B=1, X=0 | X=0 | X=1 | успешно |
Критерий решений (условий)
Критерий покрытия решений/условий требует такого достаточного набора тестов, чтобы все возможные результаты каждого условия в решении выполнялись по крайней мере один раз, все результаты каждого решения выполнялись по крайней мере один раз и, кроме того, каждой точке входа передавалось управление по крайней мере один раз.
Два теста метода покрытия условий
а) A=2, B=0, X=4 ace
б) A=1, B=1, X=0 abd
отвечают и критерию покрытия решений/условий. Это является следствием того, что одни условия приведенных решений скрывают другие условия в этих решениях. Так, если условие А>1 будет ложным, транслятор может не проверять условия В=0, поскольку при любом результате условия В=0, результат решения ((А>1)&(В=0)) примет значение ложь. Следовательно, недостатком критерия покрытия решений/условий является невозможность его применения для выполнения всех результатов всех условий.
| Другая реализация рассматриваемого примера приведена на рис. 12.3. Многоусловные решения исходной программы разбиты на отдельные решения и переходы. Наиболее полное покрытие тестами в этом случае выполняется так, чтобы выполнялись все возможные результаты каждого простого решения. Для этого нужно покрыть пути HILP (тест А=2, В=0, Х=4), HIMKT (тест А=3, В=1, Х=0), HJKT (тест А=0, В=0, Х=0), HJKR (тест А=0, В=0, Х=2). Протестировав алгоритм на рис. 12.3, нетрудно убедиться в том, что критерии покрытия условий и критерии покрытия решений/условий недостаточно чувствительны к ошибкам в логических выражениях. |
Рис. 12.3 |
Метод комбинаторного покрытия условий
Критерием, который решает эти и некоторые другие проблемы, является комбинаторное покрытие условий. Он требует создания такого числа тестов, чтобы все возможные комбинации результатов условия в каждом решении выполнялись по крайней мере один раз. Набор тестов, удовлетворяющих критерию комбинаторного покрытия условий, удовлетворяет также и критериям покрытия решений, покрытия условий и покрытия решений/условий.
По этому критерию в рассматриваемом примере должны быть покрыты тестами следующие восемь комбинаций:
а) A>1, B=0;
б) A>1, B0;
в) A1, B=0;
г) А1, B0;
д) A=2, X>1;
е) A=2, X1;
ж) А2, X>1;
з) А2, X1.
Для того чтобы протестировать эти комбинации, необязательно использовать все 8 тестов. Фактически они могут быть покрыты четырьмя тестами (табл. 12.4):
- A=2, B=0, X=4 {покрывает а, д};
- A=2, B=1, X=1 {покрывает б, е};
- A=0,5, B=0, X=2 {покрывает в, ж};
- A=1, B=0, X=1 {покрывает г, з}.
Таблица 12.4 – Результаты тестирования методом комбинаторного покрытия условий
| Тест | Ожидаемый результат | Фактический результат | Результат тестирования |
| A=2, B=0, X=4 | X=3 | X=3 | неуспешно |
| A=2, B=1, X=1 | X=2 | X=1,5 | успешно |
| A=0,5 B=0, X=2 | X=3 | X=4 | успешно |
| A=1, B=0, X=1 | X=1 | X=1 | неуспешно |
studfiles.net
Что такое витамины? Для чего они нужны организму?
Что такое авитаминозы? Гиповитаминозы? Гипервитаминозы?
Каковы функции витамина А? Какие нарушения связаны с недостатком этого витамина в организме?
Для чего необходимы витамины группы В? Приведите примеры.
Как, по-вашему, можно предотвратить авитаминозы?
Запишите в тетради формулы витаминов А, С, В6.
Тема № 8. Минеральный обмен.
Минеральные (неорганические) вещества наряду с органическими – необходимые компоненты любой живой клетки, обеспечивающие процессы жизнедеятельности. Они поступают в организм в составе пищи и вместе с водой. Основную часть минеральных веществ составляет вода, хлориды Cl- ; сульфитыSO42- ; карбонатыCO32-; фосфатыPO43- ; натрияNa+; калияK+; магнияMg2+ ; кальцияCa2+. В небольших количествах (от 10-3до 10-6г.) для живого организма необходимы йод, бром, фтор, железо, медь, марганец, цинк, кобальт, молибден и др. так называемые микроэлементы.
Суточная потребность взрослого человека в минеральных веществах : вода – около 2 л; кальций – 0,81 г ; фосфор – 1 – 1,5 г ; натрий – 4-6 г ; калий – 2,5-5 г ;магний – 0,3-0,5 г ; железо – 15 мг ; цинк – 15 мг ;марганец – 5-10 мг ; хром – 0,2 мг ; медь – 2 мг ; кобальт – 0,1-0,2 мг ; молибден – 0,5 мг ; селен – 0,5 ; хлор – 5-7 г ; фтор – 0,5-1 мг ; йод – 0,1-0,2 мг .
Натрий, калий и хлор обеспечивают осмотические свойства, полную силу, полное равновесие между клеточным и межклеточным пространством, буферные системы организма.
Магний, кальций и фосфор входят в состав костей ; фтор – зубной ткани, йод – гормонов щитовидной железы, железо – крови, тканей печени и селезенки, цинк – в тканях поджелудочной железы и т.д.
Минеральные вещества в организме содержат в двух формах: в виде свободных ионов и в связанной (с белками, ферментами, витаминами) форме.
Минеральные соли принимают участие в регуляции проницаемости мембран, влияют на связывание воды белками. Выделение их из организма осуществляется через почки, кожу и кишечник.
Приборы и реактивы: пробирки, пробиркодержатели, никелевая (хромникелевая) проволока, горелка (спиртовая), метилоранж лакмус; 1% - ый растворFeCl3; насыщенный растворCa(Cl)2; 5% - ый растворMgSO4; 1% растворCuSO4; кристаллическийNaCl; кристаллическийKCl; 5% растворNa2CO3; 5% раствор концентрированного раствора аммиака ; 1% растворKSCN; 1- 2% раствор фенола; 2- 5% раствор молочной кислоты, 1% раствор AgNO3; 1% раствор BaCl2; 5- 7% раствор HCl ; раствор h4PO4; 5% раствор Na2CO3; раствор NaCl ; раствор MgSO4.
Качественные реакции на катионы
Катионы – положительно заряженные ионы в составе минеральных веществ.
Опыт 1. Обнаружение Na+.
На кончике хромникелевой проволоки помещают несколько кристаллов поваренной соли NaClи вносят в пламя горелки (спиртовки). Через некоторое время пламя окрашивается в желтый цвет, что свидетельствует о наличии ионовNa+.
Опыт 2. Обнаружение K +.
На кончике хромникелевой проволоки помещают несколько кристаллов хлорида калия KClи вносят в пламя горелки (спиртовки). Через некоторое время пламя окрашивается в фиолетовый цвет, что свидетельствует о наличии ионовK+.
Опыт 3 . Обнаружение Mg2+.
К 1- 2 мл раствора сульфата магния добавляют 1- 2 мл раствора Na2CO3. Появляется осадок карбоната магния белого цвета.
Опыт 4 . Обнаружение Ca2+.
К 1- 2 мл раствора гидроксида кальция добавляют 1- 2 мл раствора щавелевой кислоты h3C2O4. Появляется осадок оксалата кальция молочно- белого цвета:
Ca(OH)2 +h3C2O4→CaC2O4↓ +h3O
Опыт 5 . Обнаружение Cu2+.
К 1- 2 мл 1% раствора сульфата меди добавляют 1- 2 мл раствора аммиака. Образуется раствор ярко- синего цвета:
CuSO4+ 3Nh5OH→ [Сu(Nh4)4](OH)2+ (Nh5)2SO4+ 2h3O
Опыт 6 . Обнаружение Fe3+.
а) К 1- 2 мл 1% раствора хлорида железа добавляется к 1- 2 мл раствора роданида калия (или аммония). Сразу же появляется кроваво- красное окрашивание:
FeCl3+ 3KSCN→Fe(SCN)3Fe+ 3KCl
б) К 1- 2 мл раствора хлорида железа добавляют 1- 2 мл раствора фенола. Сразу же появляется фиолетовое окрашивание:
FeCl3+ 3C6H5OH→ (C6H5O)3Fe+ 3HCl
в) К 1- 2 мл раствора хлорида железа добавляют 1- 2 мл раствора молочной кислоты. Сразу же появляется лимонно- желтое окрашивание:
FeCl3+ 3Ch4–CHOH–COOH→ (Ch4CHOHCOOH)3Fe+ 3HCl
Опыт 7. Обнаружение H+.
К раствору щавелевой (или молочной) кислоты добавляется лакмус (или метилоранж). Сразу же появляется красное окрашивание.
Качественные реакции на анионы.
Анионы - отрицательно заряженные ионы в составе минеральных веществ.
Опыт 8. Обнаружение Cl -
К 1- 2 мл поваренной соли NaCl добавляют 1- 2 мл раствора серебра AgNO3. Выпадает белый творожистый осадок:
NaCl+AgNO3→NaNO3+AgCl↓
Опыт 9. Обнаружение SO4 2-:
К 1- 2 мл раствора сульфата магния MgSO4добавляют 1- 2 мл раствора хлорида бария BaCl2. Выпадает белый кристаллический осадок:
MgSO4+BaCl2→MgCl2+BaSO4↓
Опыт 10. Обнаружение PO43-:
К 1- 2 мл раствора фосфорной кислоты h4PO4добавляют 1- 2 мл раствора нитрата серебра AgNO3.Выпадает желто- оранжевый осадок:
h4PO4 + 3AgNO3→ 3HNO3 + Ag3PO4↓
Опыт 11. Обнаружение CO32-:
К 1- 2 мл раствора карбоната натрия Na2CO3добавляют 1- 2 мл раствора соляной кислоты HCl. Сразу же происходит выделение газа:
Na2CO3+ 2HCl→ 2NaCl+CO2↑ +h3O
Обнаружение минеральных веществ в продуктах питания.
Опыт 12.Несколько кристаллов пищевой соды помещают в пробирку и добавляют 1- 2 мл раствора HCl . Происходит выделение газа:
NaHCO3+HCl→NaCl+CO2↑ +h3O
Опыт 13.К 1- 2 мл минеральной воды добавляют 1- 2 мл раствора HCl. Происходит выделение газа:
CO32-+ 2H+ →CO2↑ +h3O
Опыт 14. К 1- 2 мл водопроводной воды добавляют 1- 2 мл роданида калия (или фенола). Происходит изменение окраски:
Fe3++ 3SCN- → Fe(SCN)3(красное окрашивание)
Fe3++ 3C6H5OH → (C6H5O)3Fe + 3H+(фиолетовое окрашивание)
Опыт 15.Небольшой кусочек сыра вымачивают в воде, а затем в воду добавляют 1 мл раствора серебра. Появляется помутнение осадка:
AgNO3+NaCl→AgCl↓ +NaNO3
Контрольные вопросы и задания:
Почему так необходимы минеральные вещества для организма?
Приведите качественные реакции на катионы Na+,Ca2+,Fe3+ и анионы
Cl -, CO32-.
3. Наличие какого химического соединения, входящего в состав сыра, можно доказать с помощью раствора серебра?
4. Допишите уравнения реакций:
а) Nа2СО3+ Н2SО4 →
б) АgNO3+HCl→
в) ВаСl2+Na2SO4 →
Тема № 9. Исследование особенностей химического строения мышц и механизма мышечного сокращения.
Цель: рассмотреть типы мышц и мышечных волокон и выяснить закономерности преобладания типа мышечных волокон в зависимости от направленности тренировочного процесса; выяснить особенности структурной организации и химического состава мышечных клеток; получить навык проведения экстракции веществ из природных объектов. А также обнаружения опытным путем белков и других биологически важных веществ, входящих в состав мышечной ткани.
Приборы и реактивы: пробирки, химические воронки, фильтровальная бумага, мышечная ткань, 10 % - ный раствор хлорида калия, дистиллированная вода, 10 % - ный раствор гидроксида натрия, 5 % - ный раствор сульфата меди, 5 % - ный раствор серной кислоты, раствор пикриновой кислоты, реактив Уффельмана.
Опыт 1. Получение экстракта мышц
Мышечную ткань залить водой, перемешать, настоять 5 минут, профильтровать в чистую пробирку (№1). Обработанные водой мышцы залить раствором хлорида калия, перемешать, настоять 5 минут, профильтровать в чистую пробирку (№2). Какие вещества мышц должны быть в водном и солевом фильтрате?
Опыт 2. Обнаружение саркоплазматических и структурных белков мышц
В пробирку наливают 2 мл водного экстракта и проводят биуретовую реакцию (к исследуемой жидкости добавляют 2 мл 10 % - ного раствора гидроксида натрия и 3 капли 5% - ного раствора сульфата меди). Какую окраску наблюдаете? О чем она свидетельствует?
В другую пробирку наливают 2 мл солевого экстракта и проводят биуретовую реакцию. Какую окраску наблюдаете? О чем она свидетельствует?
Опыт 3. Обнаружение креатина и креатинина
В две пробирки наливают по 1 мл водного фильтрата мышц. В первую пробирку добавляют 1 мл 5% - ного раствора серной кислоты и ставят в кипящую водяную баню на 30 минут. Это делают для того чтобы перевести креатин в креатинин.
tº
Креатин → креатинин
Вторую пробирку оставляют в штативе. Через 30 минут в первую пробирку помещают розовую лакмусовую бумажку и нейтрализуют жидкость 10% - ным раствором гидроксида натрия. Затем в обе пробирки наливают по 3 мл 10% - ного гидроксида натрия и по 5 – 8 капель пикриновой кислоты. Какая окраска появилась в первой и во второй пробирках? (Креатин дает с пикриновой кислотой оранжевую, а креатинин – красную окраску).
Опыт 4. Обнаружение молочной кислоты
Молочная кислоты дает с реактивом Уффельмана лимонно – желтое окрашивание вследствие образования лактата железа. В пробирку наливают 1 мл реактива Уффельмана и добавляют по каплям водный фильтрат. Какая появилась окраска, и о чем это свидетельствует? Напишите уравнения реакции образования лактата железа.
Контрольные вопросы и задания:
Как обнаружить в водном экстракте мышц белки?
Приведите реакцию обнаружения кретинина в водном экстракте мышц?
3. Напишите уравнения реакции образования лактата железа.
Рекомендуемая литература
Основная
Волков, Н.И. Биохимия мышечной деятельности / Н.И. Волков, Э.Н. Нессен, А.А. Осипенко, С.Н. Корсун. Киев: Олимпийская лит., 2000., 503.
Дубровский, В.И. Спортивная медицина / В.И. Дубровский. М. :: Владос, 2005. 528 с.
Николаев, А.Я. Биологическая химия / А.Я. Николаев. М.: Мед. Информ. Агенство, 2001. 496 с.
Михайлов. С.С. Спортивная биохимия / С.С. Михайлов. М.: Сов.спорт, 2004. 220 с.
Проскурина, И.К. Биохимия / И.К. Проскурина. М.: Владос, 2004. 236 с.
Дополнительная
Кушманова, О.Д. Руководство к лабораторным занятиям по биохимии / О.Д. Кушманова. М.: Медицина, 1983. 272 с.
Мирошникова, С.С. Динамическая биохимия. Биохимия физических упражнений: рабочая тетрадь / С.С. Мирошникова, В.А. Лиходеева, Н.В. Серединцева. Волгоград, 2007. 62 с.
Чуксеева, Т.П. Основы статической и динамической биохимии: учебное пособие / Т.П. Чуксеева, В.А. Лиходеева, Н.В. Серединцева. Волгоград, 1999. 116с.
Чуксеева, Т.П. Биохимия физических упражнений: учебное пособие / Т.П. Чуксеева, В.А. Лиходеева, Н.В. Серединцева. Волгоград, 1999. 153с.
Яковлев, Н.Н. Биохимия спорта / Н.Н. Яковлев. М.: Физкультура и спорт, 1974. 288 с.
Введение
Данное учебно-методическое пособие предназначено для студентов педагогических вузов направления подготовки 050100 «Педагогическое образование», профиль «Физическая культура и безопасность жизнедеятельности», изучающих курс «Основы биохимии спорта» и разработаны в соответствии с требованиями Государственного образовательного стандарта по указанному направлению.
Учебно – методическое пособие включает следующие темы курса «Основы биохимии спорта»: аминокислоты и белки, ферменты, углеводы, липиды, гормоны и витамины, минеральные вещества, а также материал по биохимии мышц. Особенностью данного практикума является включение в него лабораторных работ, не требующих дорогостоящего оборудования и реактивов. Тем не менее представленные общедоступные методики позволяют получить важную практическую информацию о биохимических процессах, происходящих в организме спортсмена. Химический эксперимент связан не только с проведением качественных реакций на те, или иные биологические вещества, что очень важно для обучающихся, но и с биохимическим анализом различных метаболитов в биологических жидкостях, например, в кожном экскрете, слюне. Такая тесная связь теории и практики, безусловно, повышает интерес студентов к изучаемой дисциплине, раскрывает важную роль биохимии как основы для изучения других дисциплин («Физиологии человека», «Физиологии физического воспитания и спорта»).
Также предусмотрены контрольные вопросы и задания по темам, решение которых способствует укреплению и углублению знаний студентов.
При оформлении в тетради лабораторной работы студент должен записать название темы и цель работы, из теоретической части выписать основные понятия, методику выполнения работы, выполнить опыты, отметить наблюдения, сделанные в ходе проведения опыта, (изменение окраски раствора, выпадение осадка), заполнить таблицы и сделать выводы, ответить на контрольные вопросы.
studfiles.net
1. Если в C++ не отключено декорирование имён, то какое имя будет помещено в объектный файл для функции int func(int x, double y) ?
2. В ассемблерных вставках нельзя использовать директиву OFFSET. А как ещё можно загрузить в регистр адрес переменной?
3. Каким образом процедура на ассемблере должна возвращать значение, чтобы из C++ её можно было вызывать как функцию?
4. Пусть в ассемблерном модуле стоит директива .model flat, stdcall, и вы не хотите её изменять. Каким образом вызывать процедуры этого модуля из C++?
5. Каким образом в используемом вами компиляторе C++ сгенерировать ассемблерный листинг результата компиляции программы?
6. Предложите несколько способов, которые можно использовать при оптимизации кода с целью ускорения его работы.
1. Решите на языке С++ задачу №37 из проверяющей системы (в ней требуется подсчитать количество простых чисел в диапазоне от 1 до n, где n не превышает 10 млн.) Ввод и вывод сделайте средствами C++, а само вычисление простых чисел выполните с помощью ассемблерной вставки. В качестве алгоритма рекомендуется использовать решето Эратосфена (изучалось в курсе «структуры и алгоритмы обработки данных»). Постарайтесь максимально эффективно реализовать данный участок кода.
2. Можно не только вызывать ассемблерные процедуры из языка высокого уровня, но и наоборот. В данной задаче вам предлагается запрограммировать такой пример.
Напишите ассемблерный модуль, содержащий процедуру BubbleSort для сортировки массива целых чисел методом пузырька. В качестве аргументов этой процедуре должен передаваться адрес массива, количество элементов в нём и адрес функции сравнения пар элементов.
Затем напишите на языке C++ функцию сравнения CmpFunc, которой передаётся два целых числа и она возвращает -1, если первое число меньше второго, 0, если они равны и +1, если первое число больше второго.
В функции main заполните массив случайными числами и вызовите процедуру BubbleSort, передав ей адрес массива, число элементов и адрес функции CmpFunc. Отсортированный массив выведите на консоль.
1. Перевод в двоичную систему и обратно. Как и целые, вещественные числа в памяти ЭВМ хранятся также в двоичной системе. Например, число 2.25 в двоичной системе выглядит как 10.01. Прежде чем изучать особенности машинного представления, рассмотрим перевод вещественных чисел в двоичную систему и обратно.
Целую часть числа мы переводить умеем (см. практ. работу 1), поэтому будем рассматривать лишь дробную часть. Проще всего перевести из двоичной системы в десятичную – нужно сложить те степени двойки, для которых в дробной части числа стоит единица. Например, 0.01001 = 2-2+2-5=0.28125
Для перевода из десятичной системы в двоичную рассмотрим два способа. Первый вариант – перебирать по очереди степени двойки - 2-1, 2-2, 2-3 и т.д. Каждую такую степень сравниваем с нашим числом. Если она больще, в ответ пишем ноль. Если меньше или равна, в ответ пишем 1 и вычитаем из нашего числа.
Для примера выполним перевод 0.59375. Вначале пробуем степень 2-1=0.5. Она не превышает числа, поэтому в ответ пишем 1 и вычитаем – остаётся 0.59375-0.5 = 0.09375. Теперь пробуем 2-2=0.25 – она больше 0.09375, поэтому в ответ просто пишем ноль. Следующая степень 2-3=0,125 получилась снова больше нашего числа - в ответ снова идёт ноль. Далее пробуем 2-4=0.0625 – она подходит, в ответ идёт 1, после вычитания остаётся 0,03125. Наконец, следующая степень 2-5 равна как раз 0,03125, поэтому в ответ идёт 1 и вычисление завершено. Ответ - 0.10011.
Примечание. Заметим, что многие числа, которые в виде десятичной дроби имеют конечную длину, в двоичной системе конечным числом цифр записать невозможно. Пример служит число 0.1 - для него вышеописанный алгоритм будет работать бесконечно долго. В таком случае при переводе просто ограничиваются некоторым количеством цифр в зависимости от того, какая точность нам требуется или сколько битов используется в машинном представлении.
Если при переводе в двоичную систему получается число бесконечной длины, и мы хотим найти период повторения цифр в дробной части, то можно использовать второй способ перевода [2]. Исходное число записывается в виде простой дроби, числитель и знаменатель переводятся в двоичную систему и выполняется деление столбиком. Если в процессе деления получим делимое, которое уже встречалось ранее, то период найден.
Для примера возьмём число 0.3. Его простая дробь выглядит как 3/10 или в двоичной системе как 11/1010. Производим деление столбиком:
11|1010
---------
0.01001
_1100
1010
_10000
1010
1100
Видим, что делимое 1100 повторилось – значит, дальше в ответе цифры тоже начнут повторяться. Период получился равным 1001, итоговое число можно записать как 0.0(1001), где период обозначается круглыми скобками.
Примечание. Возможно, в 21-м веке уже не все студенты помнят, как выполняется деление в столбик (в связи с повсеместным использованием калькуляторов и компьютеров). Данный материал выходит за рамки методических указаний, но его легко найти в сети Internet.
Одно и то же вещественное число можно записать по-разному. Например, 15.73 = 1.573*10 = 0.1573*102 = 1573*10-2. Вариант записи, в которой перед десятичной точкой стоит ровно одна ненулевая цифра, называется нормализованным представлением, а его получение - нормализацией. Для числа 15.73 нормализованным представлением будет 1.573 * 101, где 1.573 – мантисса, 1 – показатель степени (иногда еще его называют порядок).
Для двоичных чисел нормализация выполняется аналогично – например, число 1011.01101 после нормализации выглядит как 1.01101101 * 23. В памяти ЭВМ вещественные числа хранятся в основном в нормализованном виде (за некоторым исключением).
2. Представление в памяти ЭВМ. Рассмотрим теперь представление вещественных чисел в памяти ЭВМ [2]. В стандарте IEEE 754-1985 описаны 3 формата, их описание приведено в следующей таблице.
Таблица 3. Форматы вещественных чисел
| Формат | Описание |
| С одинарной точностью (в masm - REAL4, в С++ - float) | Длина 32 бита, из них слева направо: 1 бит – знак, 8 битов – показатель степени, 23 бита – дробная часть мантиссы. Диапазон примерно от 2-126 до 2127 (и отрицательные) |
| С двойной точностью (в masm - REAL8, в C++ - double) | Длина 64 бита, из них слева направо: 1 бит – знак, 11 битов – показатель степени, 52 бита – дробная часть мантиссы. Диапазон примерно от 2-1022 до 21023 (и отрицательные) |
| Расширенное с двойной точностью (в masm - REAL10, в C++ - long double) | Длина 80 бит, из них слева направо: 1 бит – знак, 16 битов – показатель степени, 63 бита – дробная часть мантиссы. Диапазон примерно от 2-16382 до 216383 (и отрицательные) |
Рассмотрим отдельно каждую часть представления числа. Бит знака равен 1, если число отрицательное, и 0, если положительное.
В поле мантиссы хранится только дробная часть, потому что для любого нормализованного двоичного числа цифра перед точкой – всегда единица. При хранении чисел в памяти для экономии места она опускается, но подразумевается при вычислениях. Следует помнить, что не любое вещественное число можно представить точно – разрядность мантиссы ограничена.
В поле показателя степени хранится показатель в виде 8-разрядного беззнакового целого числа, к которому прибавлено 127. Например, для числа 1.101*25 значение показателя равно 5+127=132, или в двоичном виде 10000100.
Для примера найдём представление с одинарной точностью числа 1101.101. Вначале выполним его нормализацию – получим 1.101101*23. Дробная часть мантиссы равна 101101, справа к ней допишем нули так, чтобы получилось 23 бита: 10110100000000000000000. В поле показателя степени будет 3+127=130, в двоичном виде это 10000010. Бит нуля равен 0. Итого получилось 01000001010110100000000000000000, или в более коротком шестнадцатеричном виде 415A0000.
Заметим, что не все вещественные числа можно представить в памяти ЭВМ в нормализованном виде. Если число очень близко к нулю, то в нормализованном варианте показатель степени может быть настолько большим, что не влезет в отведенное поле. Возьмём, например, число 101010*2127. В нормализованном виде оно превратится в 1.01010*2132, то есть в поле показателя степени должно быть 132+127=259. В значение с одинарной точностью такой показатель степени уже не поместится. Если в результате вычислений получилось такое число, оно будет сохранено в денормализованном виде, а в сопроцессоре возникнет ситуация потери точности (underflow). Особенности работы сопроцессора с такими числами выходят за рамки данных методических указаний.
В стандарте IEEE754-1985 представления вещественных чисел кроме собственно чисел, предусмотрено ещё несколько специальных значений [2] – они приведены в следующей таблице.
Таблица 4. Специальные значения в двоичных вещественных числах одинарной точности
| Значение | Знак, показатель, мантисса |
| Положительный ноль | 0 00000000 00000000000000000000000 |
| Отрицательный ноль | 1 00000000 00000000000000000000000 |
| Положительная бесконечность | 0 11111111 00000000000000000000000 |
| Отрицательная бесконечность | 1 11111111 00000000000000000000000 |
| Тихое NaN (QNaN) | x 11111111 1xxxxxxxxxxxxxxxxxxxxxx |
| Громкое NaN (SNaN) | x 11111111 0xxxxxxxxxxxxxxxxxxxxxx |
В таблице под символом x понимается любое значение (0 или 1). Для SNaN поле мантиссы должно содержать хотя бы одну единицу.
Значения бесконечностей можно сравнивать между собой и с другими числами, но при выполнении операций с ними может возникнуть переполнение (overflow).
Значение NaN является признаком нечислового значения. В некоторых математических библиотеках используется такой подход: если функция не может вычислить результат (например, корень из отрицательного числа), она не создаёт исключительную ситуацию, а просто возвращает NaN.
3. Работа с FPU. Рассмотрим теперь кратко применение сопроцессора для вычислений с вещественными числами.
Примечание. Вообще, название «сопроцессор» возникло вследствие того, что вначале это было действительно отдельное аппаратное устройство. В настоящее время он встраивается в центральный процессор, и всё чаще используется термин FPU (floating point unit – модуль вычисления с плавающей точкой).
В состав FPU входят 8 80-разрядных регистров R0-R7. Эти регистры организованы в виде стека, поэтому напрямую к ним обращаются редко – обычно используют относительные имена ST(0) – ST(7) или вообще применяют команды, не требующих указания регистров. Здесь ST(0) – вершина стека (один из 8 регистров), ST(1) – элемент в стеке перед ним и т.д.
Типичный пример вычисления выглядит так. В стек помещается операнд из памяти. Затем выполняется операция, где второй операнд указывается в её аргументе. Либо можно второй операнд также поместить в стек и затем выполнить операцию над обоими аргументами в стеке. После выполнения вычислений результат с вершины стека передаётся в память.
Рассмотрим команды, которые нам потребуются. Fld – поместить в стек вещественное число из памяти, fild – поместить в стек целое число из памяти (преобразовав в вещественное), fst – скопировать число с вершины стека в память, fstp - скопировать число с вершины стека в память и удалить из стека, fist - скопировать число с вершины стека в память в целочисленную ячейку, округлив до целого. Арифметические команды: fadd – сложение, fsub – вычитание, fdiv – деление, fmul - умножение и др.
Приведём пример вычисления суммы двух вещественных чисел.
include masm32rt.inc
.data
out_format BYTE "%f", 0
var_a REAL8 1.5
var_b REAL8 2.3
sum REAL8 ?
.code
main PROC
fld var_a ;поместить в стек
fadd var_b ;сложить
fst sum ;результат с вершины стека – в память
invoke crt_printf, ADDR out_format, sum
exit
main ENDP
end main
Рассмотрим теперь более сложный пример. Пусть надо вычислить значение выражения 3.1*(2.8+3.2). Сложное выражение удобно вначале перевести в обратную польскую (постфиксную) запись, где знак операции стоит не между аргументами, а после них (эта тема изучалась в курсе «Структуры и алгоритмы обработки данных»). Для данного примера получится 3.1 2.8 3.2 + *.
Затем идём слева направо по этому выражению и если встретим аргумент, то поместим его в стек, а если встретим операцию, то выполним её. Пример программы, где использовался данный подход:
include masm32rt.inc
.data
out_format BYTE "%f", 0
args REAL8 3.1, 2.8, 3.2
res REAL8 ?
.code
main PROC
fld args[0] ;аргумент в стек
fld args[1*TYPE args] ;аргумент в стек
fld args[2*TYPE args] ;аргумент в стек
fadd ;первая операция
fmul ; вторая операция
fst res ;результат из стека в память
invoke crt_printf, ADDR out_format, res
exit
main ENDP
end main
Рассмотрим теперь, как выполняется сравнение чисел. Для этого можно использовать команду fcom с одним аргументом – она вычитает из st(0) значение аргумента в памяти и выставляет соответствующие флаги FPU. Далее с помощью команды fstsw ax программа переписывает содержимое регистра состояния сопроцессора в регистр ax центрального процессора. Затем содержимое регистра ah переписывается в регистр флагов центрального процессора при помощи команды sahf. Биты кодов условий сопроцессора отображаются на регистр флагов центрального процессора таким образом, что для анализа кодов условий можно пользоваться командами условных переходов для беззнаковых целых чисел – ja, jb, jae и т.п. Пример кода:
fld varA ;загружаем в стек переменную varA
fcom varB ;сравниваем с переменной varB
fstsw ax ;переписываем флаги FPU в ax
sahf ;переписываем флаги из ah во flags
jb L1 ;если меньше, идём на метку
FPU поддерживает довольно большое число и других команд – например, fsqrt – вычисление квадратного корня, fsin – вычисление синуса, fabs – вычисление модуля числа. Полный перечень команд можно посмотреть в технической документации (например, на сайте www.intel.com), более подробные примеры – в учебниках из списка литературы.
studfiles.net