1 вариант
а)
б)
2 вариант
a)
б) 
3 вариант
а)
б)
4 вариант
а)
б)
5 вариант
а)
б)
6 вариант
а)
б)
7 вариант
а)
б)
8 вариант
а)
б)
9 вариант
а)
б)
10 вариант
а)
б)
Контрольная работа по алгебре и началам математического анализа
Тема «Производная функции и её применение»
2 курс системы НПО и 1 курс СПО
на базе основного образования
Контрольная работа по теме «Производная функции и её применение» ориентирована на учебник Ш.А.Алимова и др. «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и естественно-математического профилей.
Контрольная работа предназначена для самостоятельного выполнения вне аудитории.
Работа включает в себя 10 вариантов заданий одинакового уровня сложности. Вариант определяется последними цифрами номера зачетной книжки студента.
Работа выполняется студентом в отдельной тетради с соответствующим оформлением титульного листа. Оформление работы должно соответствовать «Единым требованиям оформления письменных работ по математике».
Правильное выполнение каждого задания оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 12. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Задание 1. Вычислить пределы
| а) | б) | |
| 2 вариант | a) | б) |
| 3 вариант | а) | б) |
| 4 вариант | а) | б) |
| 5 вариант | а) | б) |
| 6 вариант | а) | б) |
| 7 вариант | а) | б) |
| 8 вариант | а) | б) |
| 9 вариант | а) | б) |
| 10 вариант | а) | б) |
Задание 2. Найти точки разрыва графика функции:
1 вариант  2 вариант
2 вариант 
3 вариант  4 вариант
4 вариант 
5 вариант  6 вариант
6 вариант 
7 вариант  8 вариант
8 вариант 
9 вариант  10 вариант
10 вариант 
Задание 3. Найти главное приращение функции dy
1 вариант у = х2 + cos 3x – 5 2 вариант y = cos (1- x2)
3 вариант у = (1 – х2)5 4 вариант у = (2х2 – 5)3
5 вариант у =  6 вариант у =
6 вариант у = 
7 вариант у =  8 вариант у =
8 вариант у = 
9 вариант  10 вариант
10 вариант 
Задание 4. Найти вторую производную функции
1 вариант у =  2 вариант
2 вариант 
3 вариант  4 вариант
4 вариант 
5 вариант  6 вариант
6 вариант 
7 вариант  8 вариант
8 вариант 
9 вариант  10 вариант
10 вариант 
Задание 5. Найти производную по её определению (через предел)
1 вариант у = 2х2 – 3х 2 вариант у = 2х3
3 вариант у = х3 + х 4 вариант у = 5х2 - х
5 вариант у =  6 вариант у = 6 – х – х2
6 вариант у = 6 – х – х2
7 вариант у = 2 – х2 8 вариант у = х2 + 4х
9 вариант у = х2 – х 10 вариант у = х2 + 2х
Задание 6. Найти скорость и ускорение материальной точки в момент времени t
|
|
| |
| 2 вариант |
|
|
| 3 вариант |
|
|
| 4 вариант |
|
|
| 5 вариант |
|
|
| 6 вариант |
|
|
| 7 вариант |
|
|
| 8 вариант |
|
|
| 9 вариант |
|
|
| 10 вариант |
|
|
Задание 7. Найти производные, используя таблицу и правила дифференцирования
1 вариант а) y =  б) y =
б) y = 
в) y =  г) y =
г) y =  д) y =
д) y = 
2 вариант а) у =  б) у =
б) у = 
в) у =  г) у =
г) у =  д) у =
д) у = 

3 вариант а)  б)
б) 
в)  г)
г) д)
д) 
4 вариант а)  б)
б) 
в)  г)
г)  д)
д) 
5 вариант а)  б)
б) 
в)  г)
г)  д)
д) 
6 вариант а)  б)
б) 
в)  г)
г)  д)
д) 
7 вариант а)  б)
б) 
в) г)
г)
д) 
8 вариант а)  б)
б) 
в)  г)
г)  д)
д) 
9 вариант а)  б)
б) 
в)  г)
г)  д)
д) 
10 вариант а)  б)
б) 
в)  г)
г)  д)
д) 
Задание 8. Составить уравнение касательной к графику функции y = f(x) в точке х0
|
| X0 =1 | |
| 2 вариант |
| X0 = -1 |
| 3 вариант |
| X0 = 0 |
| 4 вариант |
| X0 = 2 |
| 5 вариант |
| X0 = 1 |
| 6 вариант |
| X0 = -2 |
| 7 вариант |
| X0 = 1 |
| 8 вариант |
| X0 = 2 |
| 9 вариант |
| X0 = 0 |
| 10 вариант |
| X0 = 1 |
Задание 9. Вычислить приближенно
| а) | б) (1,00012)3 | в) | |
| 2 вариант | а) | б) (2,0003)3 | в) |
| 3 вариант | а) | б) (0,997)4 | в) |
| 4 вариант | а) | б) (3.025)4 | в) |
| 5 вариант | а) | б) (1,9999)3 | в) |
| 6 вариант | а) | б) (0,989)3 | в) |
| 7 вариант | а) | б) (2,098)5 | в) |
| 8 вариант | а) | б) (2,005)4 | в) |
| 9 вариант | а) | б) (4,001)9 | в) |
| 10 вариант | а) | б) (4,0097)3 | в) |
Задание 10. Найти наибольшее и наименьшее значения функции y = f(x) на интервале [a; b] с помощью производной:
|
| [2; 2,5] | |
| 2 вариант |
| [-2; 1] |
| 3 вариант |
| [-4; 0] |
| 4 вариант |
| [-2; 0] |
| 5 вариант |
| [1; e] |
| 6 вариант |
| [0; 2] |
| 7 вариант |
| [-1; 1] |
| 8 вариант |
| [-1; 3] |
| 9 вариант |
| [0; 2] |
| 10 вариант |
| [0; 4] |
Задание 11. Составить уравнения асимптот к графику функции y = f(x)
1 вариант  2 вариант
2 вариант 
3 вариант  4 вариант
4 вариант 
5 вариант  6 вариант
6 вариант 
7 вариант  8 вариант
8 вариант 
9 вариант  10 вариант
10 вариант 
Задание 12. Исследовать свойства функции и построить график
|
|
| |
| 2 вариант |
|
|
| 3 вариант |
|
|
| 4 вариант |
|
|
| 5 вариант |
|
|
| 6 вариант |
|
|
| 7 вариант |
|
|
| 8 вариант |
|
|
| 9 вариант |
|
|
| 10 вариант |
|
|
globuss24.ru
Контрольная работа № 9 по теме «Производная функции»
Вариант 1Найдите производную функции:
а) 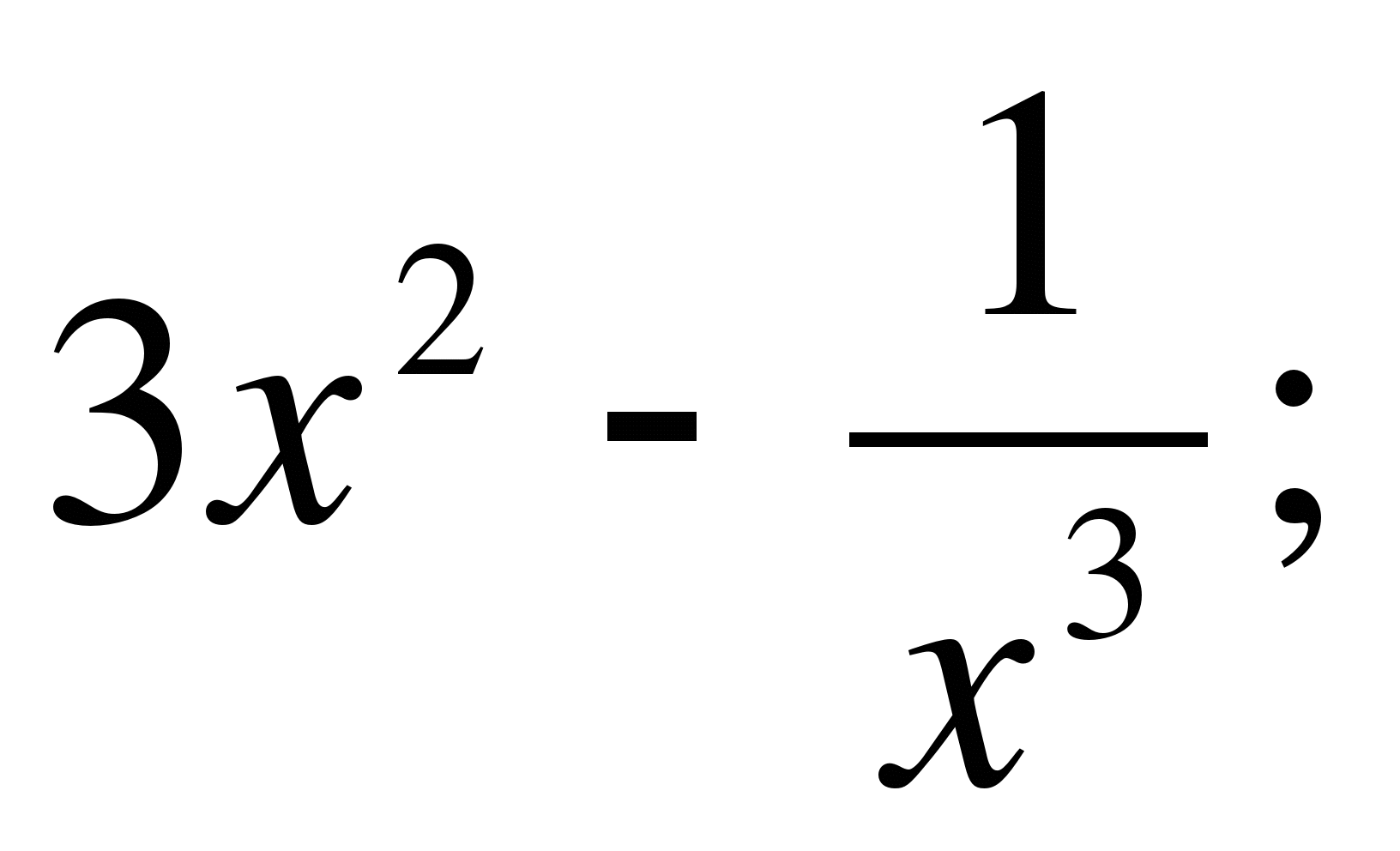 б)
б) 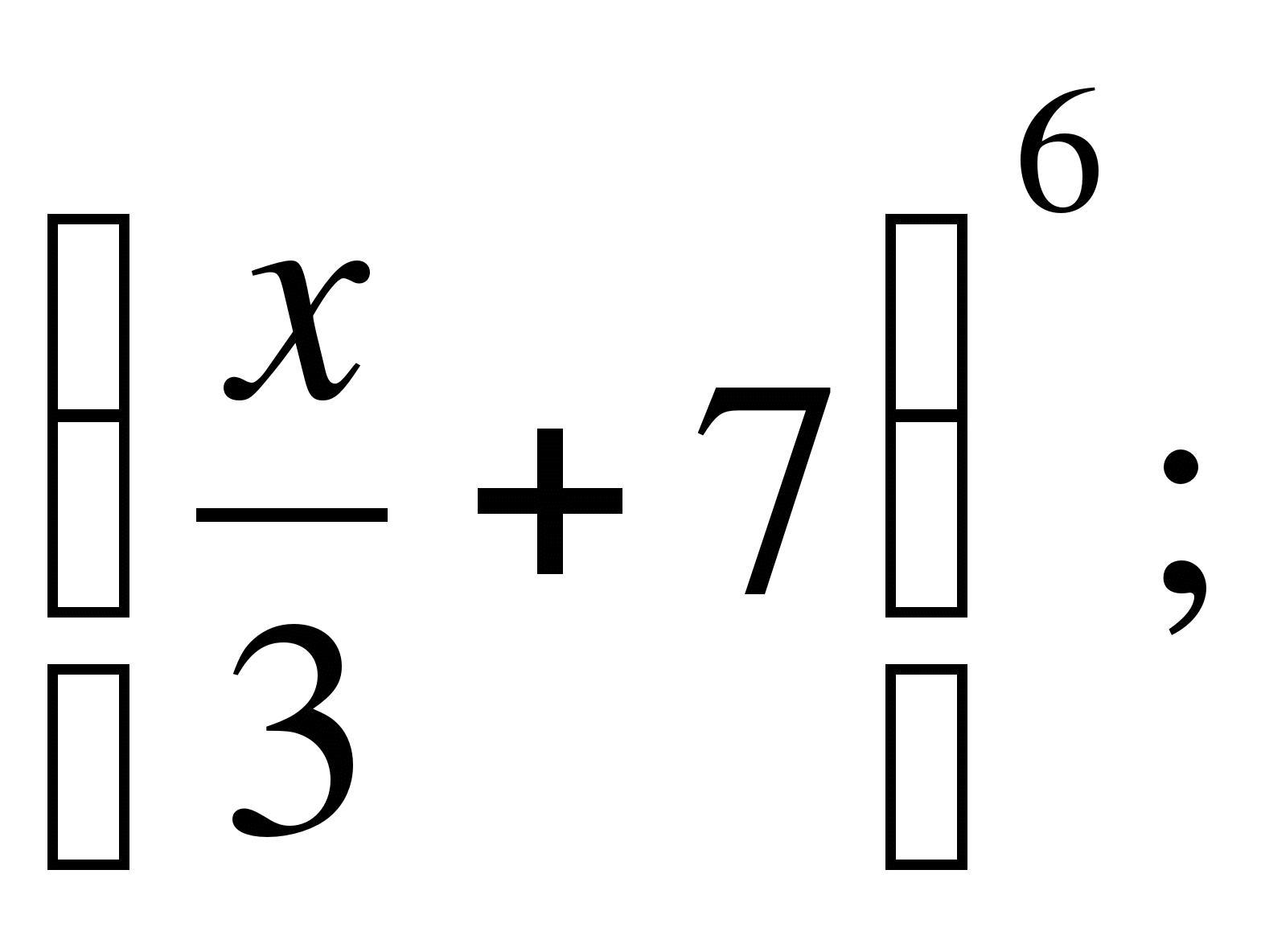 в)
в) 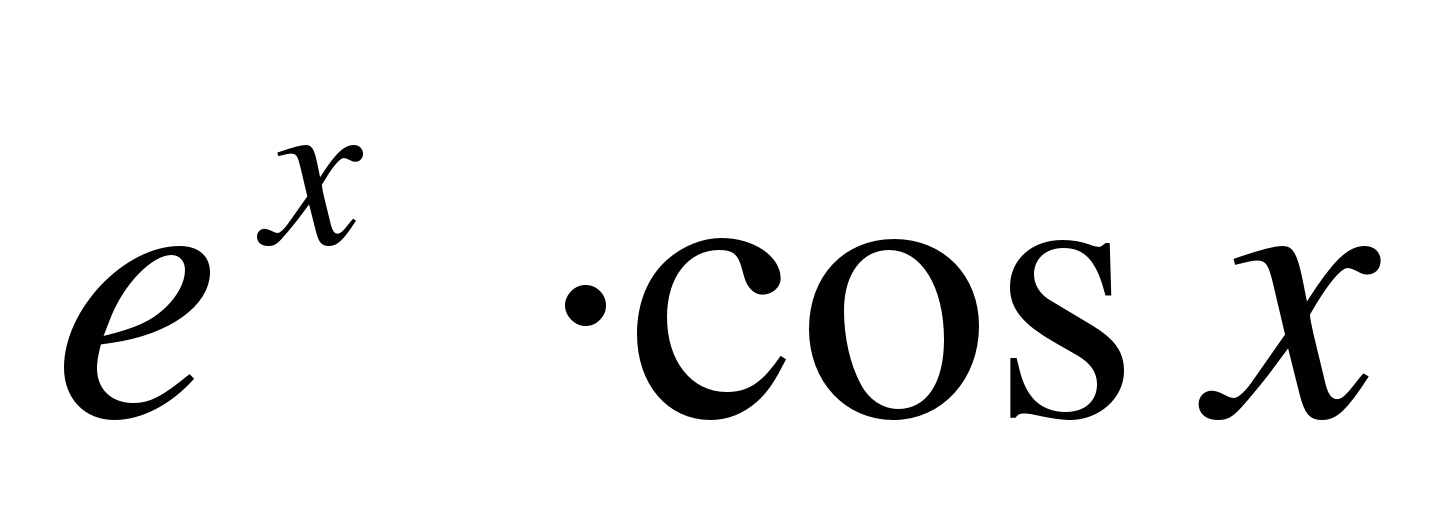
Найдите значение производной функции f(x) = 1 - 6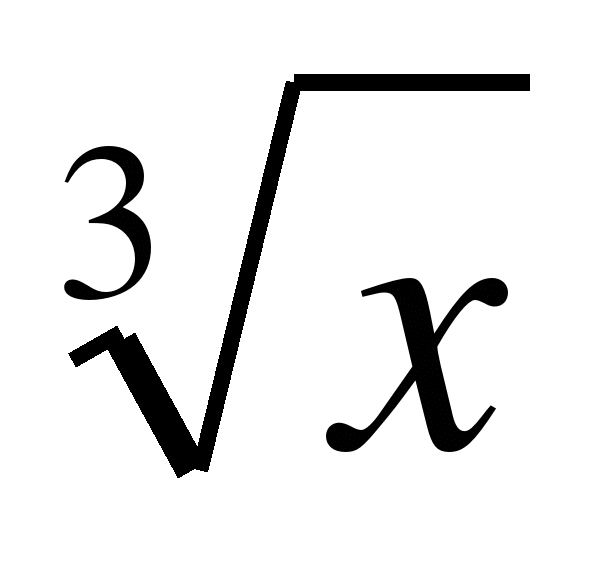 в точке
в точке 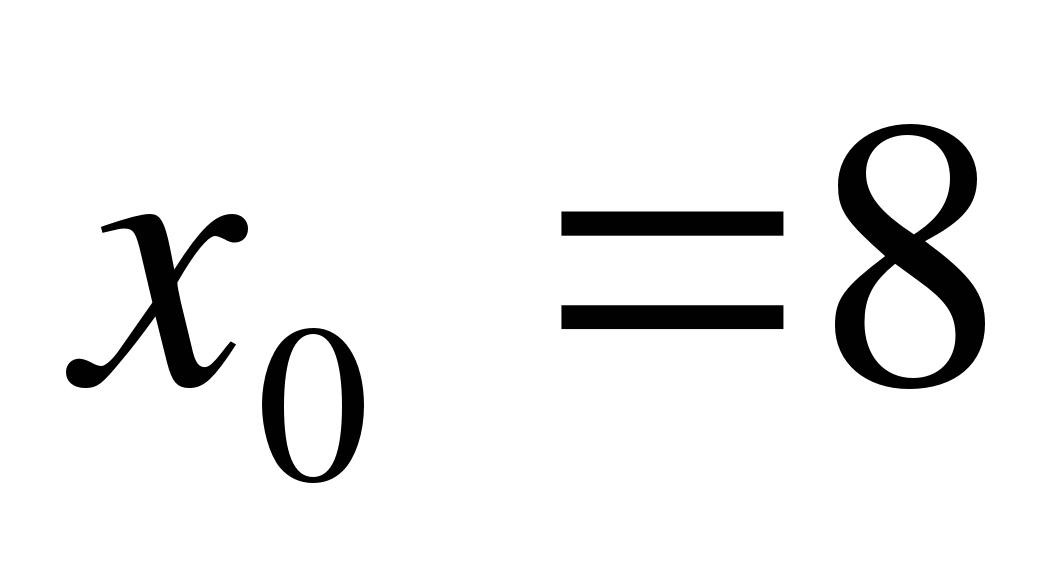 .
.
Запишите уравнение касательной к графику функции f(x) = sin x – 3x + 2 в точке 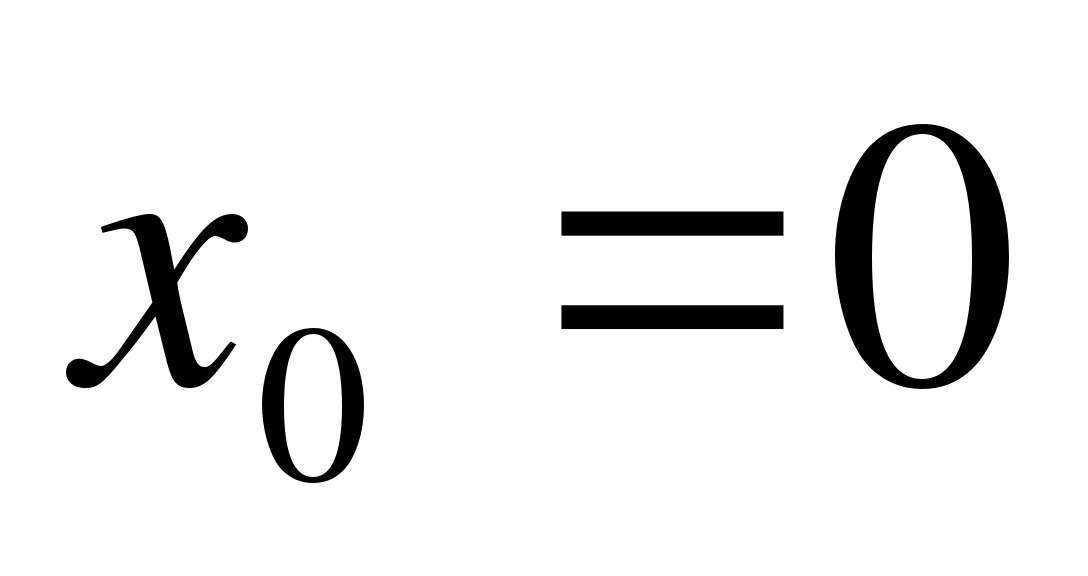 .
.
Найдите все значения х, при которых значения производной функции
f(x) = 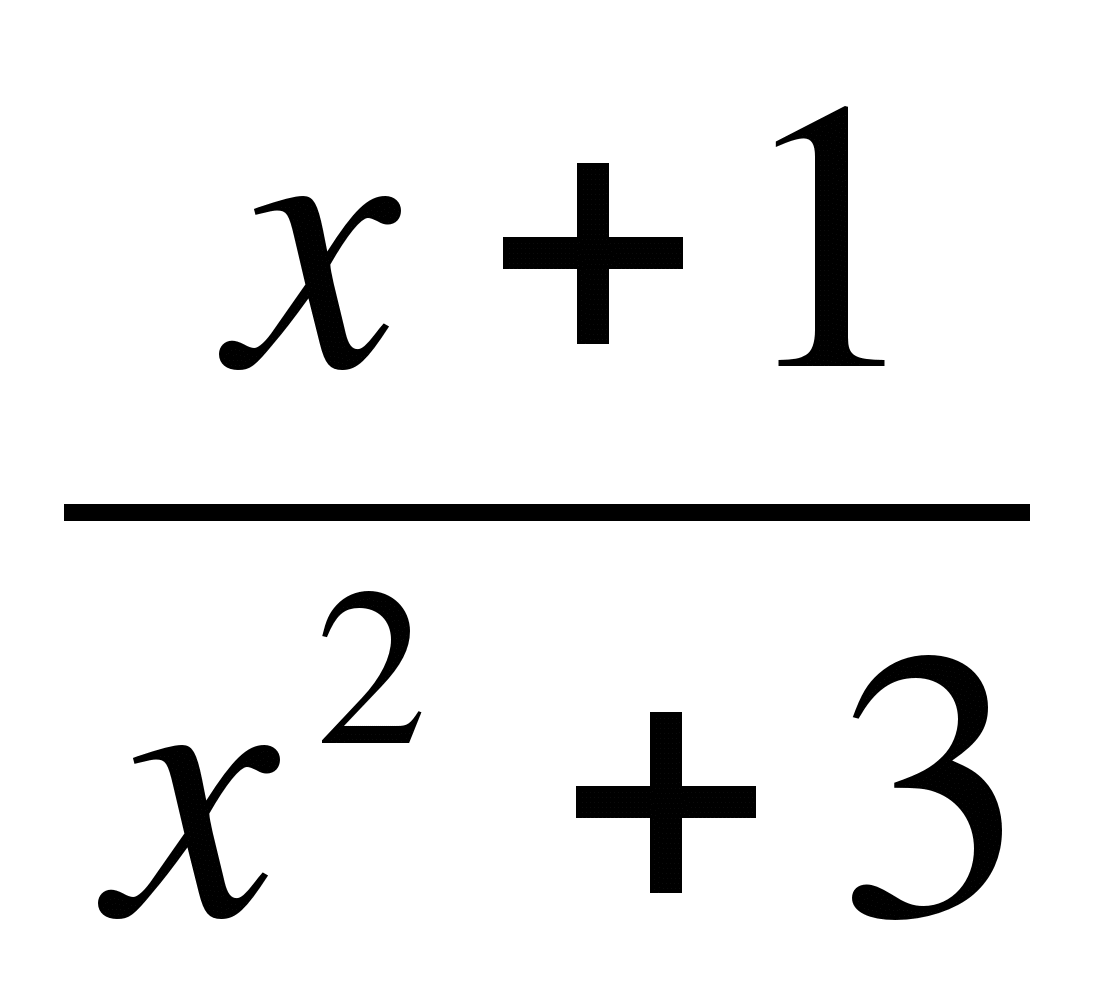 положительны.
положительны.
Найдите точки графика функции
f(x) = 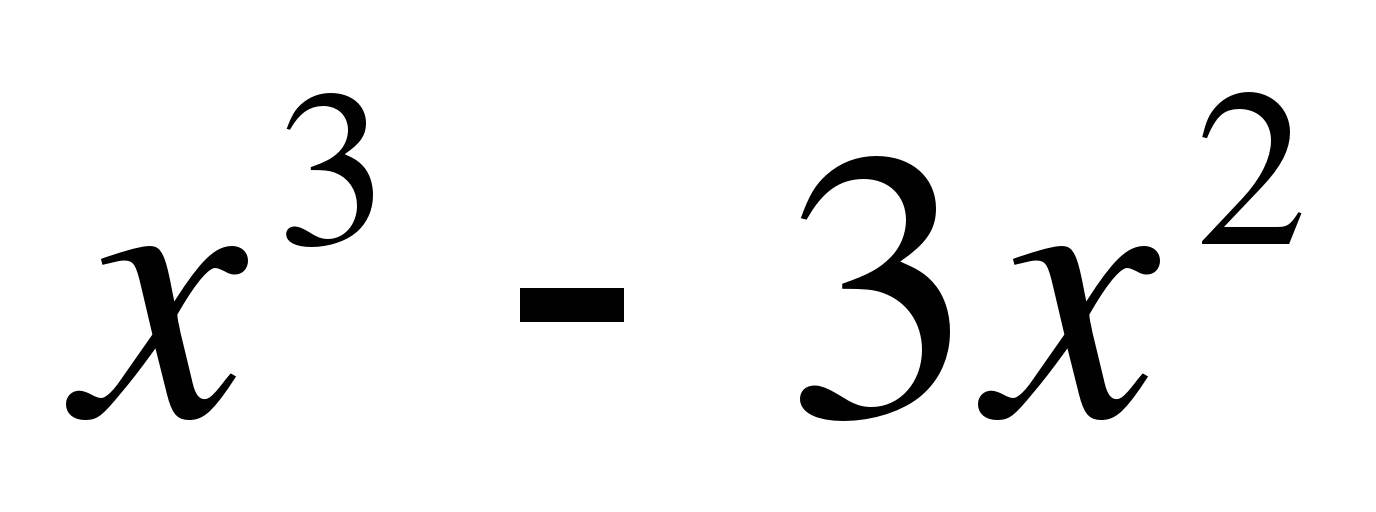 , в которых касательная к нему параллельна оси абсцисс.
, в которых касательная к нему параллельна оси абсцисс.
Вариант 2
Найдите производную функции:
а) 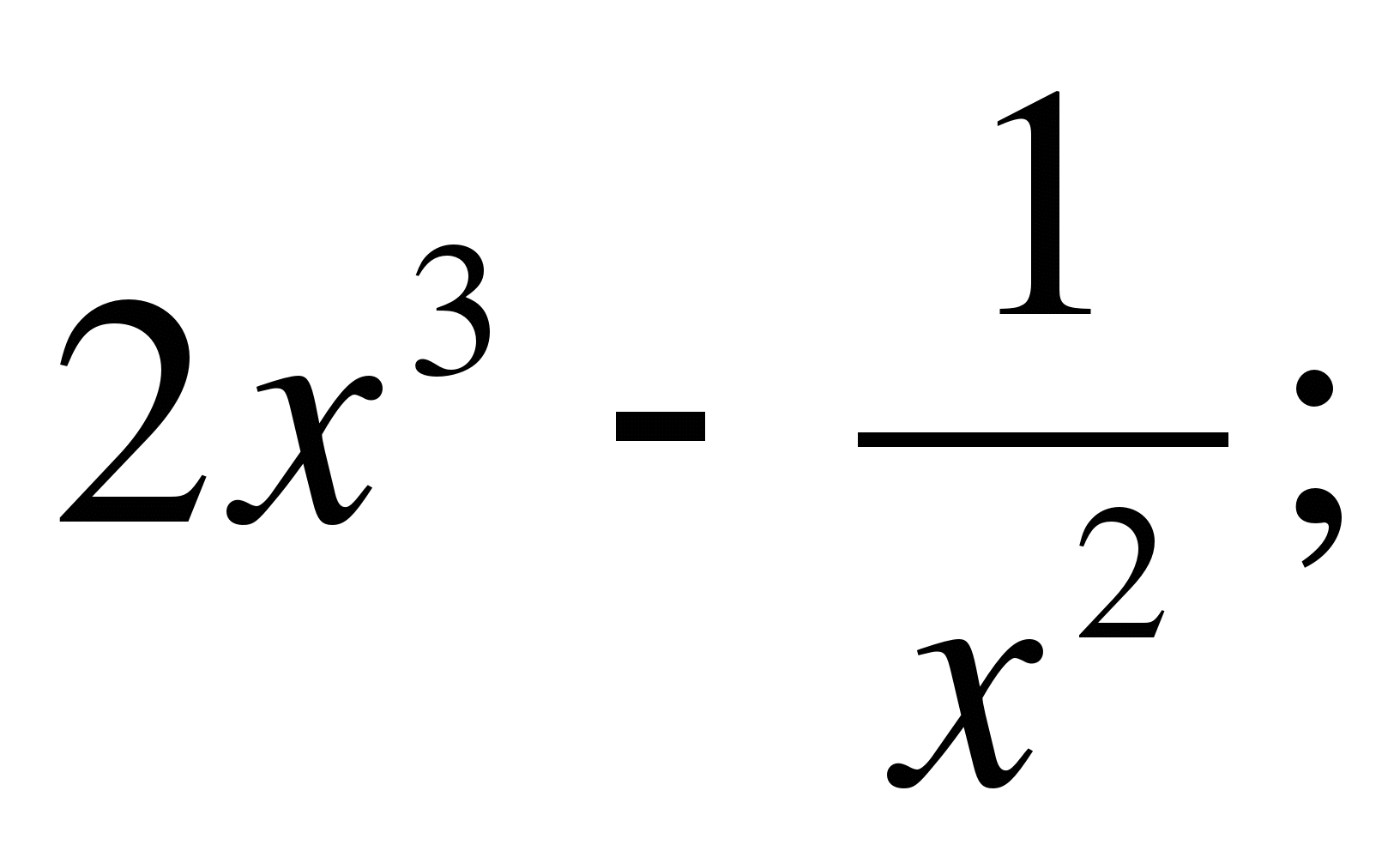 б)
б) 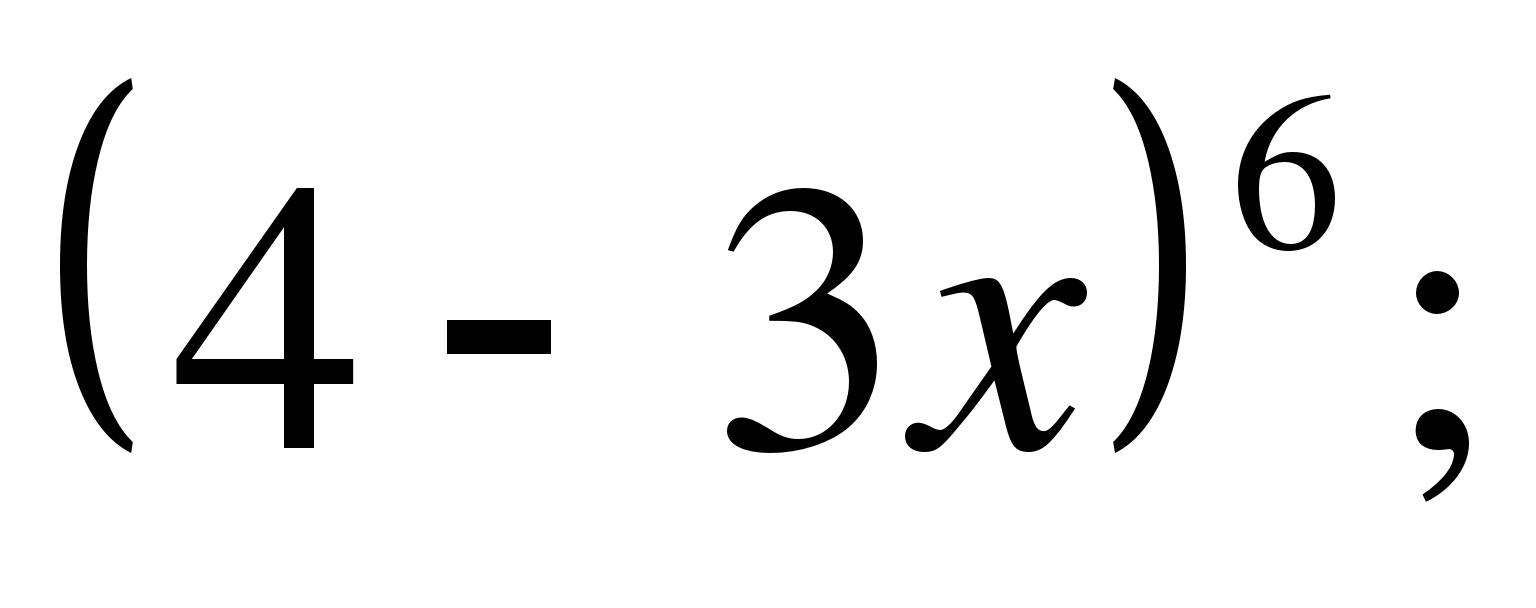 в)
в) 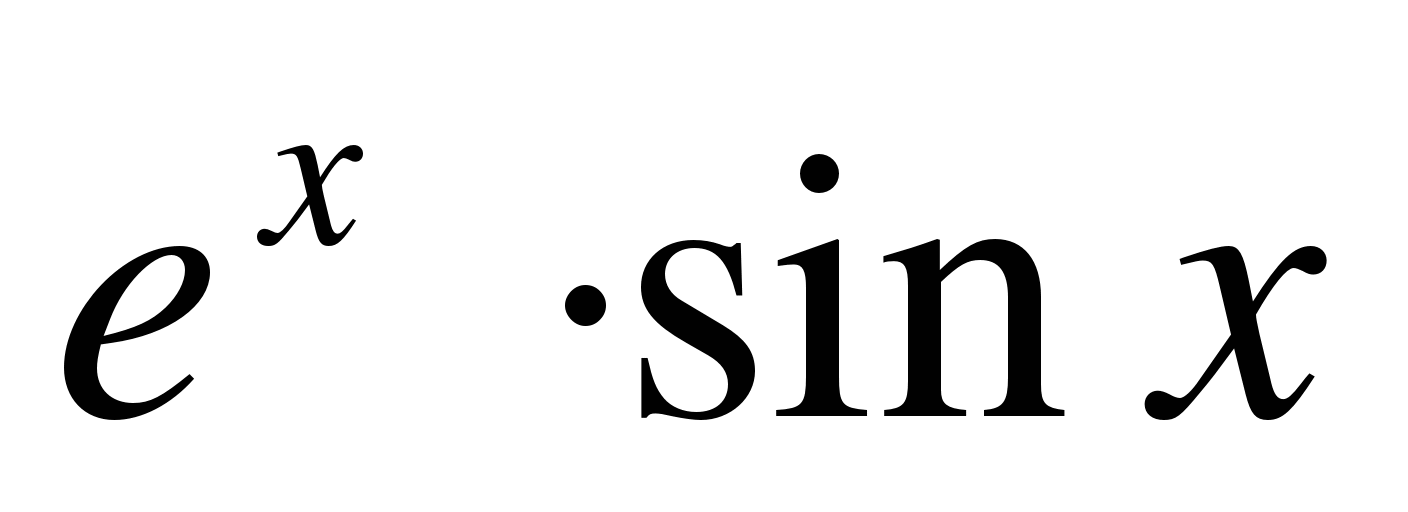
Найдите значение производной функции f(x) = 2-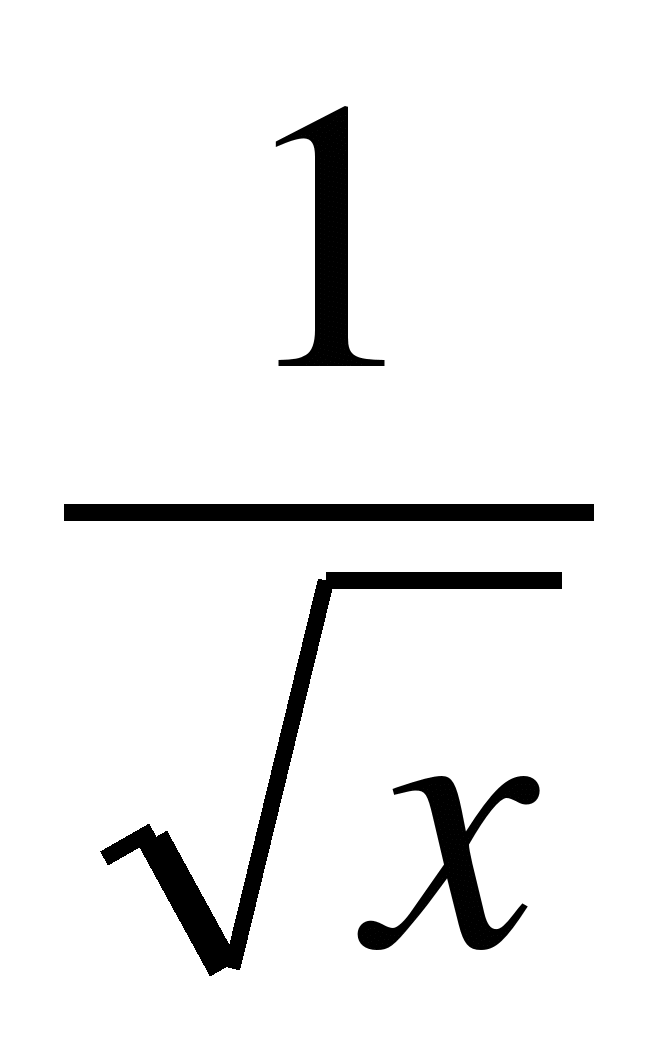 в точке
в точке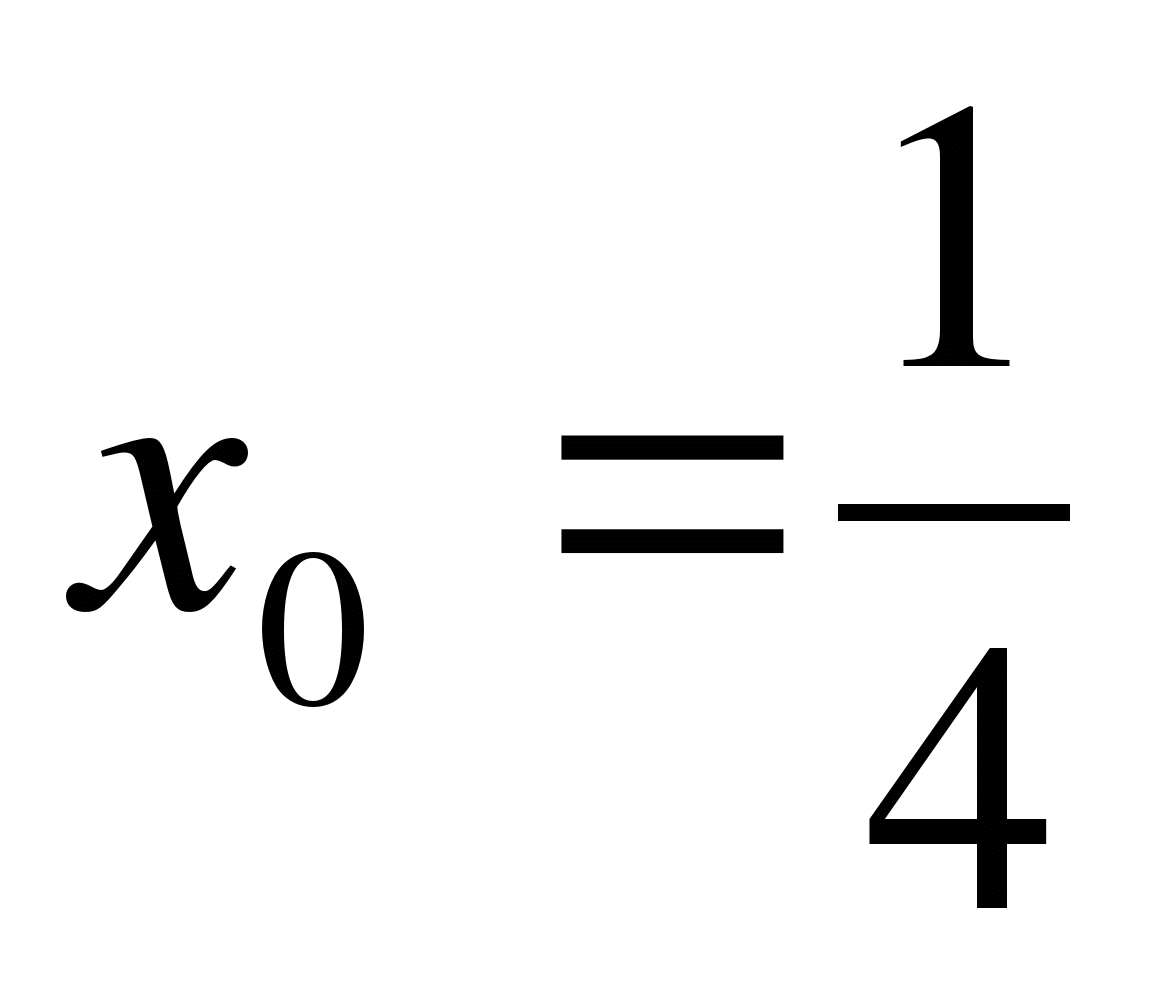 .
.
Запишите уравнение касательной к графику функции f(x) = 4х - sin x +1 в точке 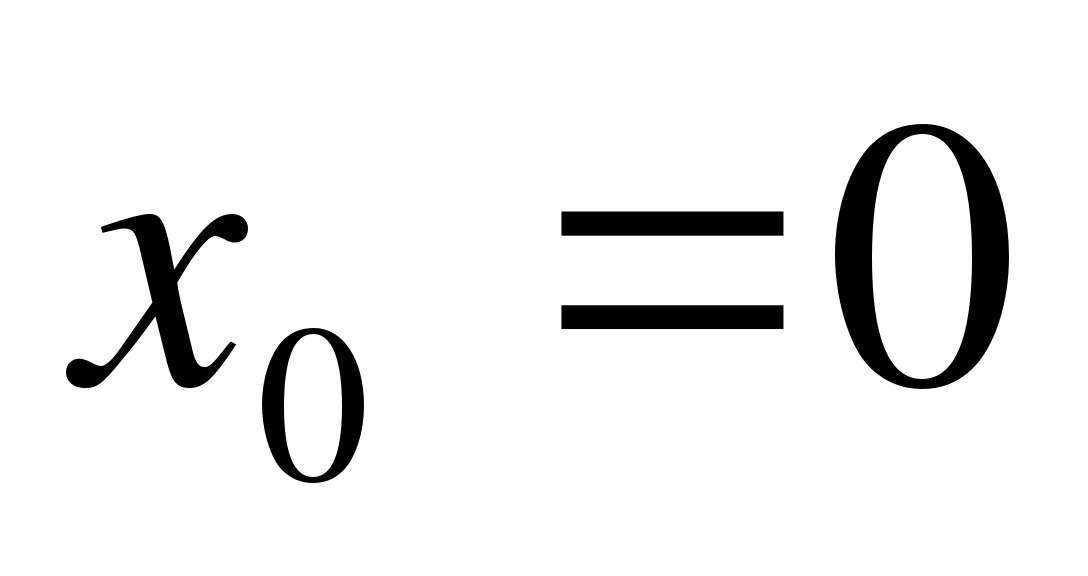 .
.
Найдите все значения х, при которых значения производной функции
f(x) = 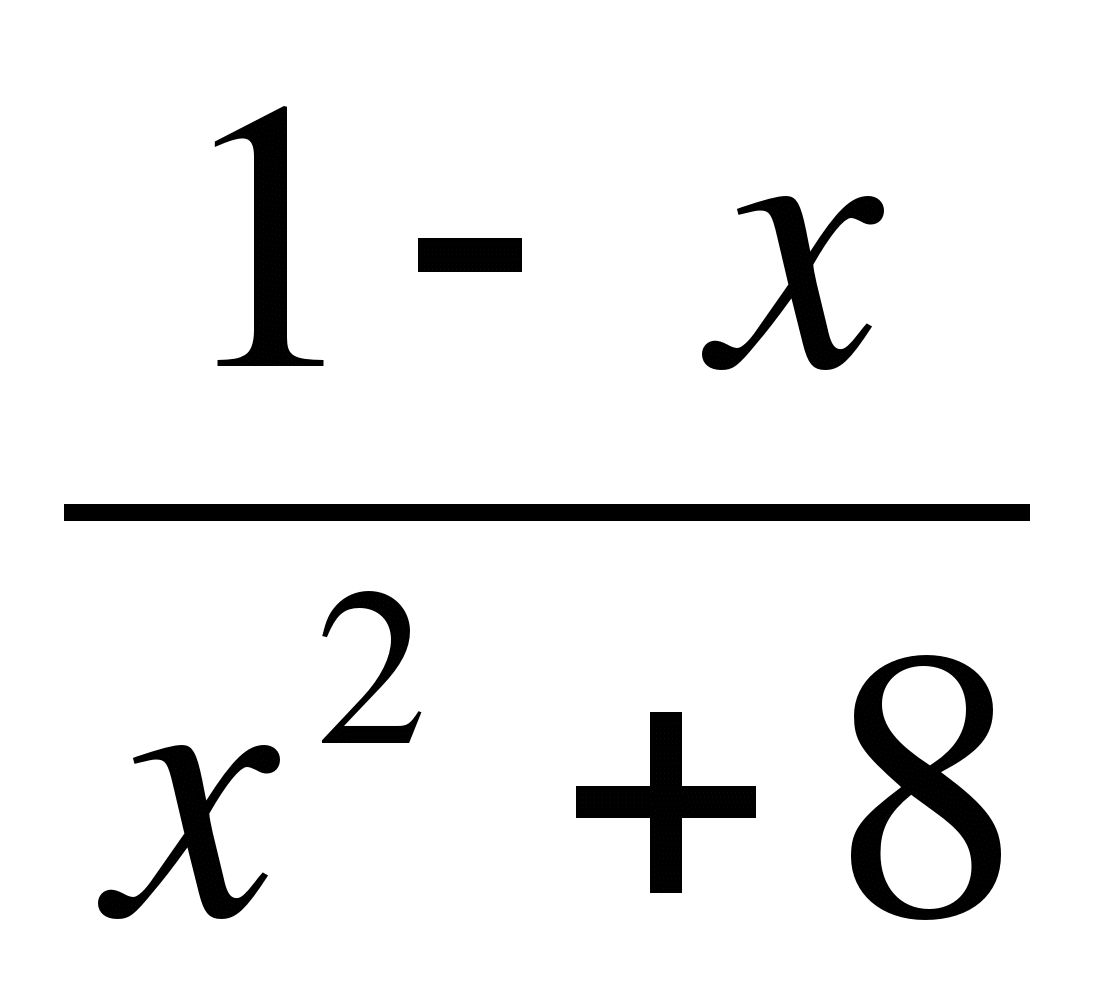 отрицательны.
отрицательны.
Найдите точки графика функции
f(x) = 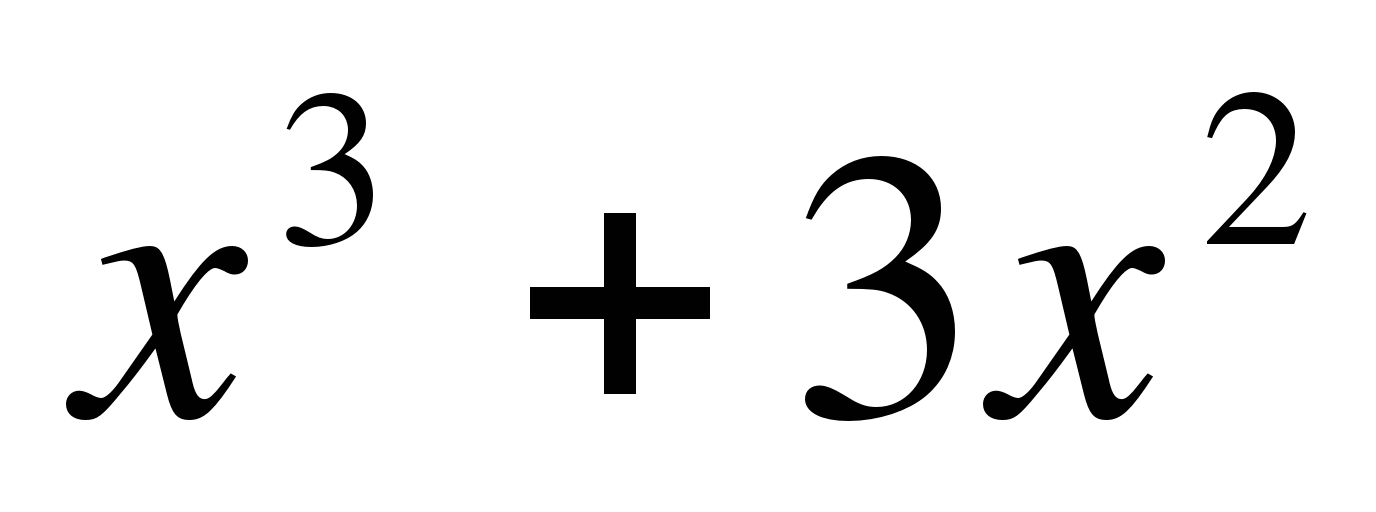 , в которых касательная к нему параллельна оси абсцисс.
, в которых касательная к нему параллельна оси абсцисс.
Контрольная работа № 9 по теме «Производная функции»
Вариант 1Найдите производную функции:
а) 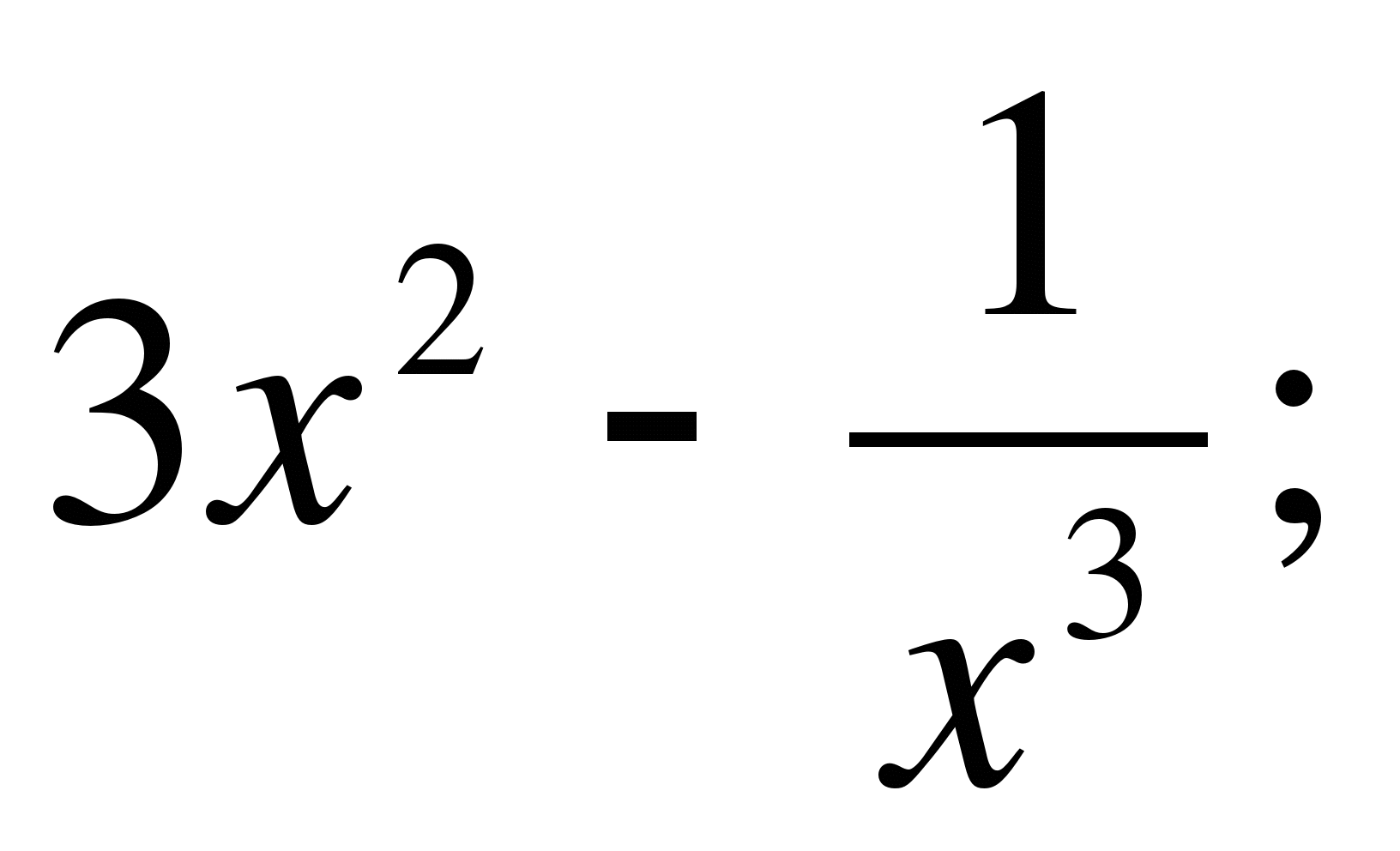 б)
б) 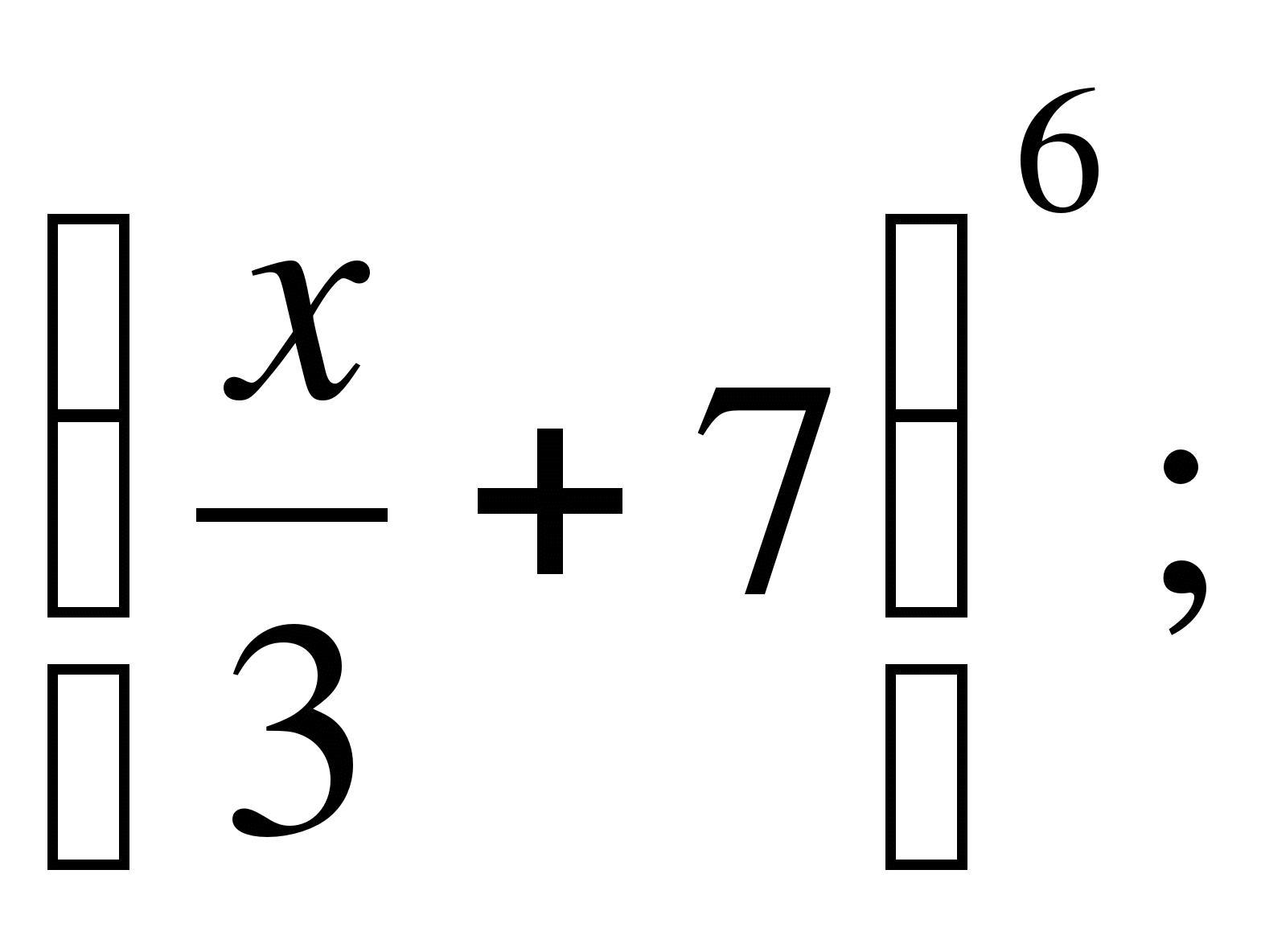 в)
в) 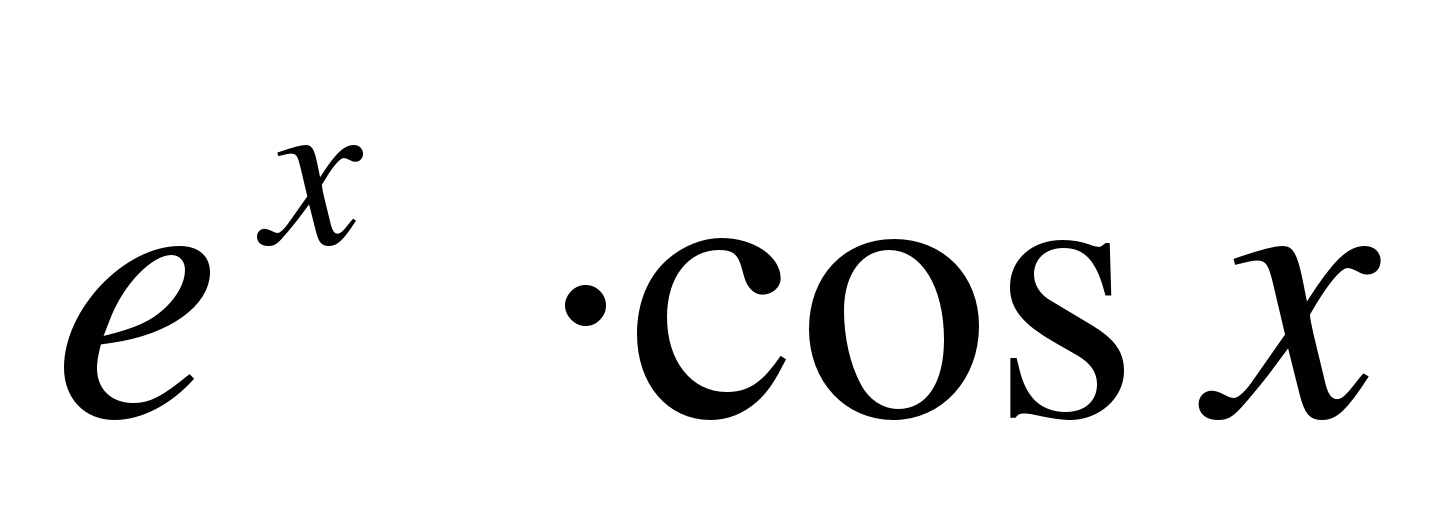
Найдите значение производной функции f(x) = 1 - 6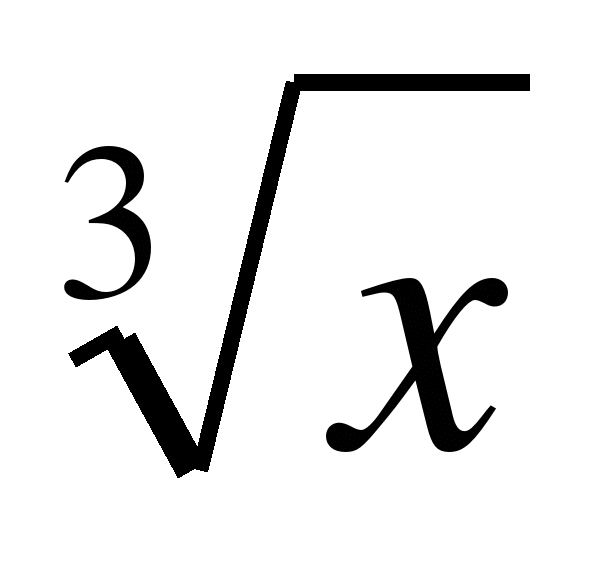 в точке
в точке 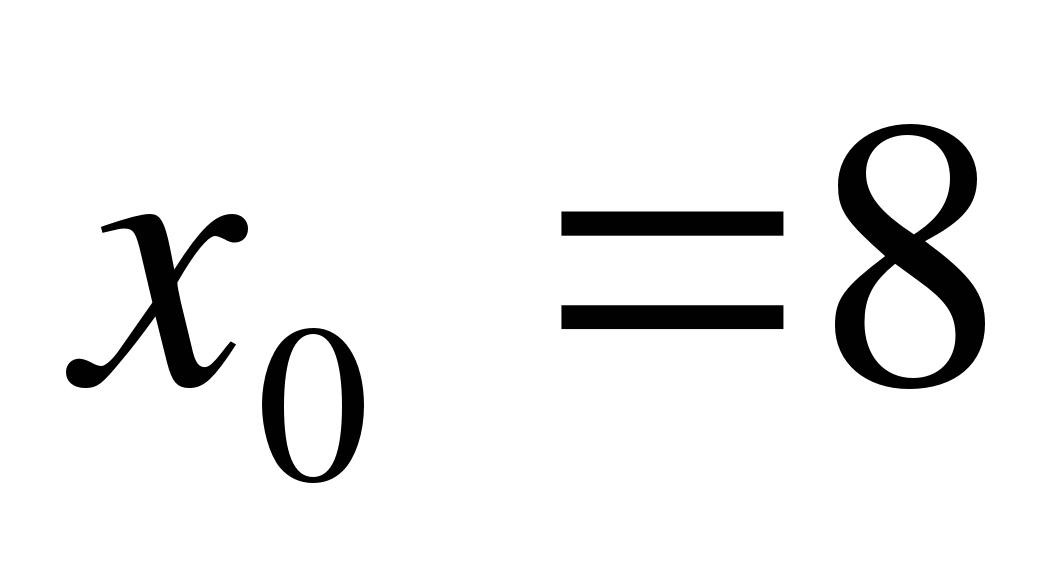 .
.
Запишите уравнение касательной к графику функции f(x) = sin x – 3x + 2 в точке 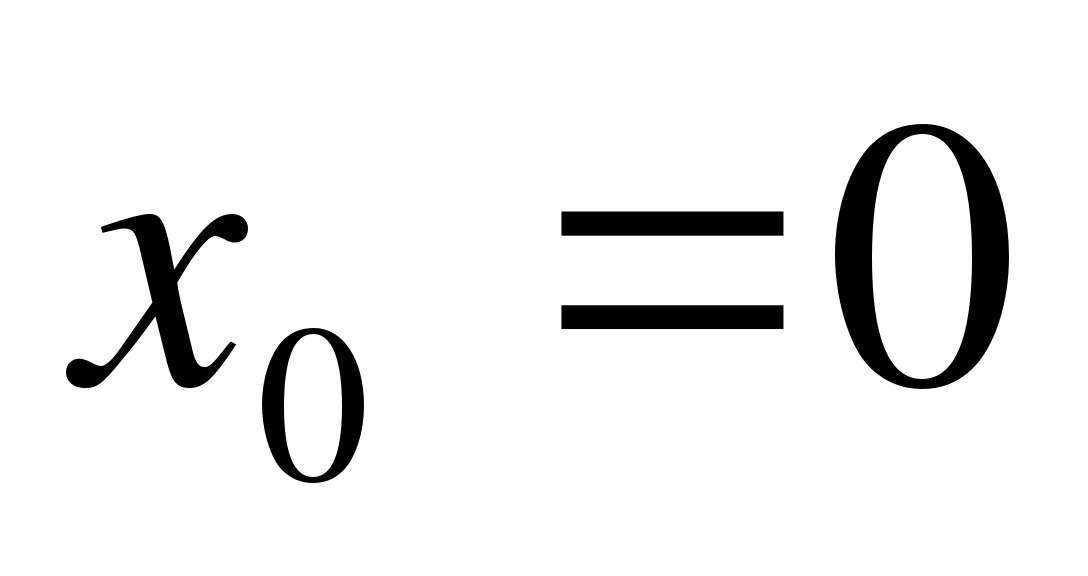 .
.
Найдите все значения х, при которых значения производной функции
f(x) = 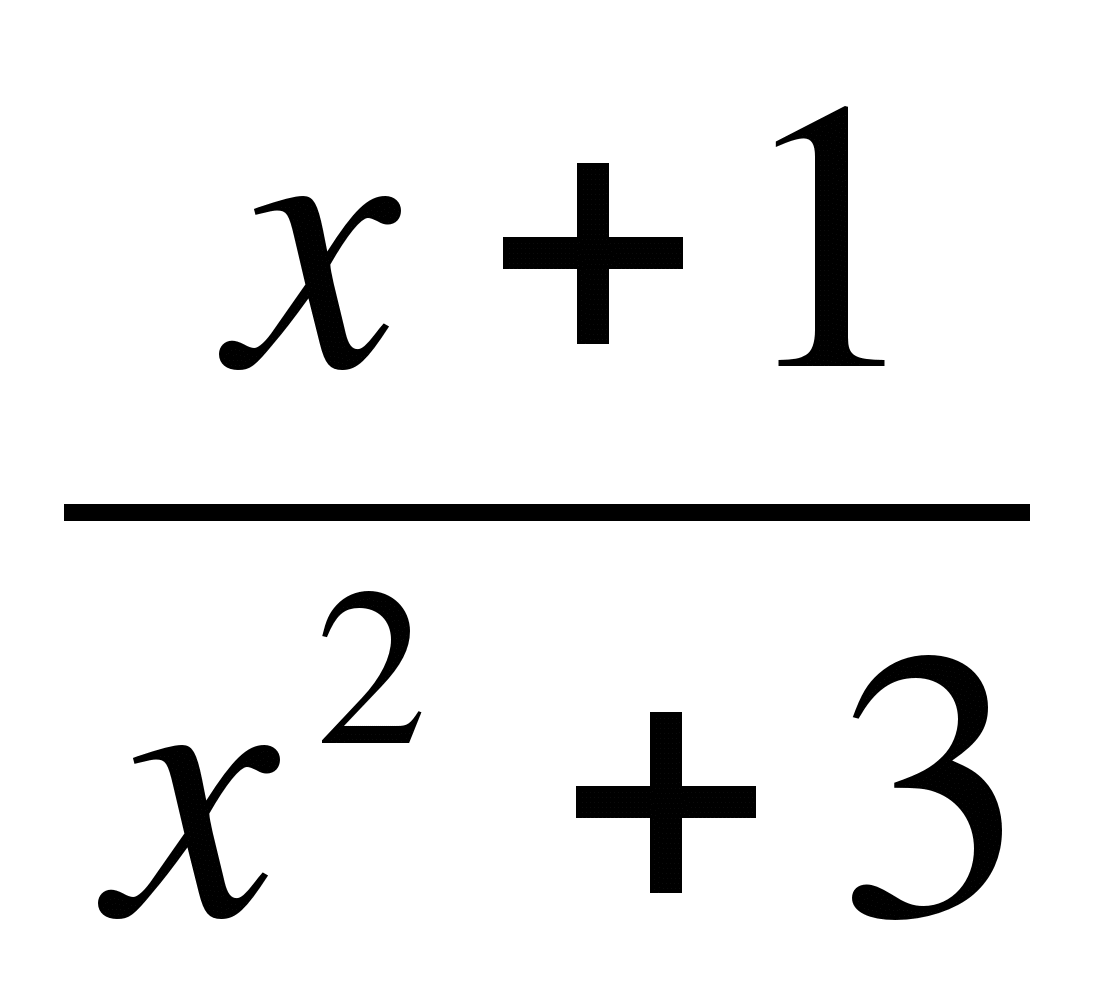 положительны.
положительны.
Найдите точки графика функции
f(x) = 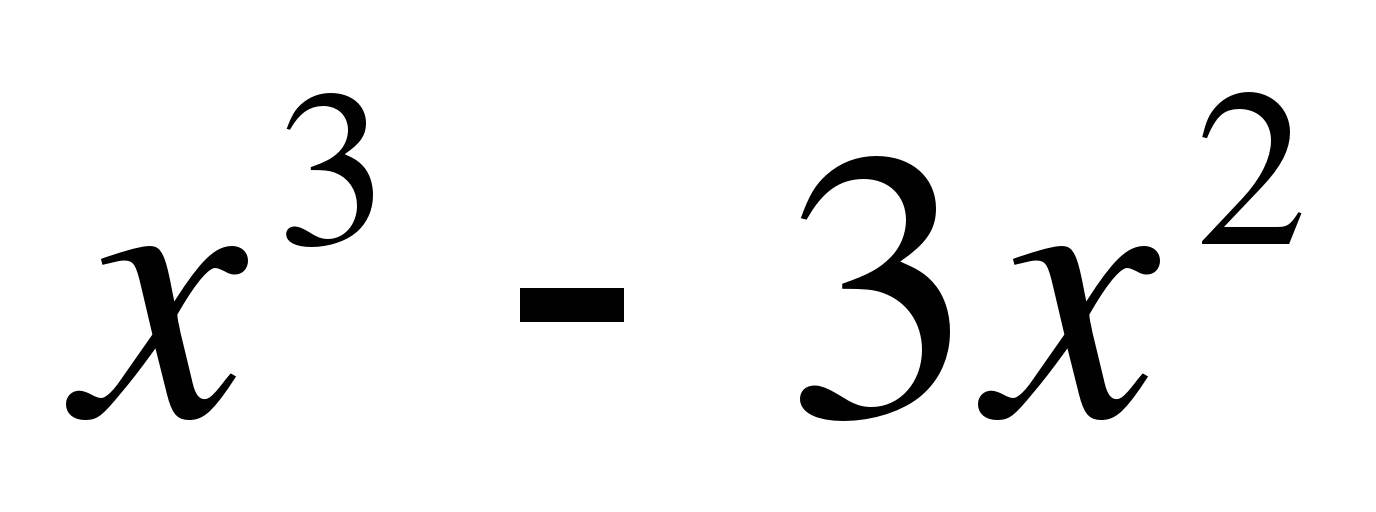 , в которых касательная к нему параллельна оси абсцисс.
, в которых касательная к нему параллельна оси абсцисс.
Вариант 2
Найдите производную функции:
а) 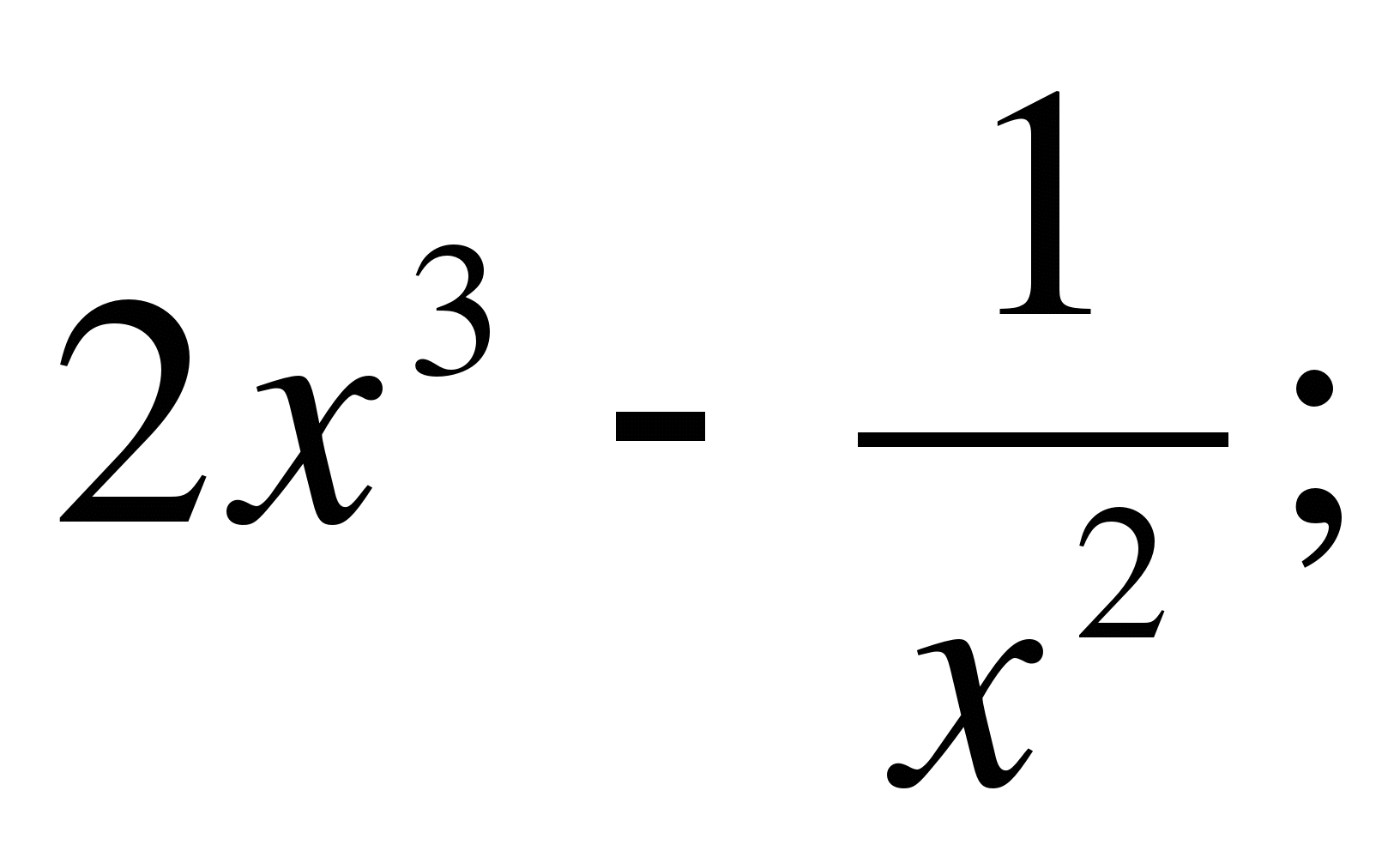 б)
б) 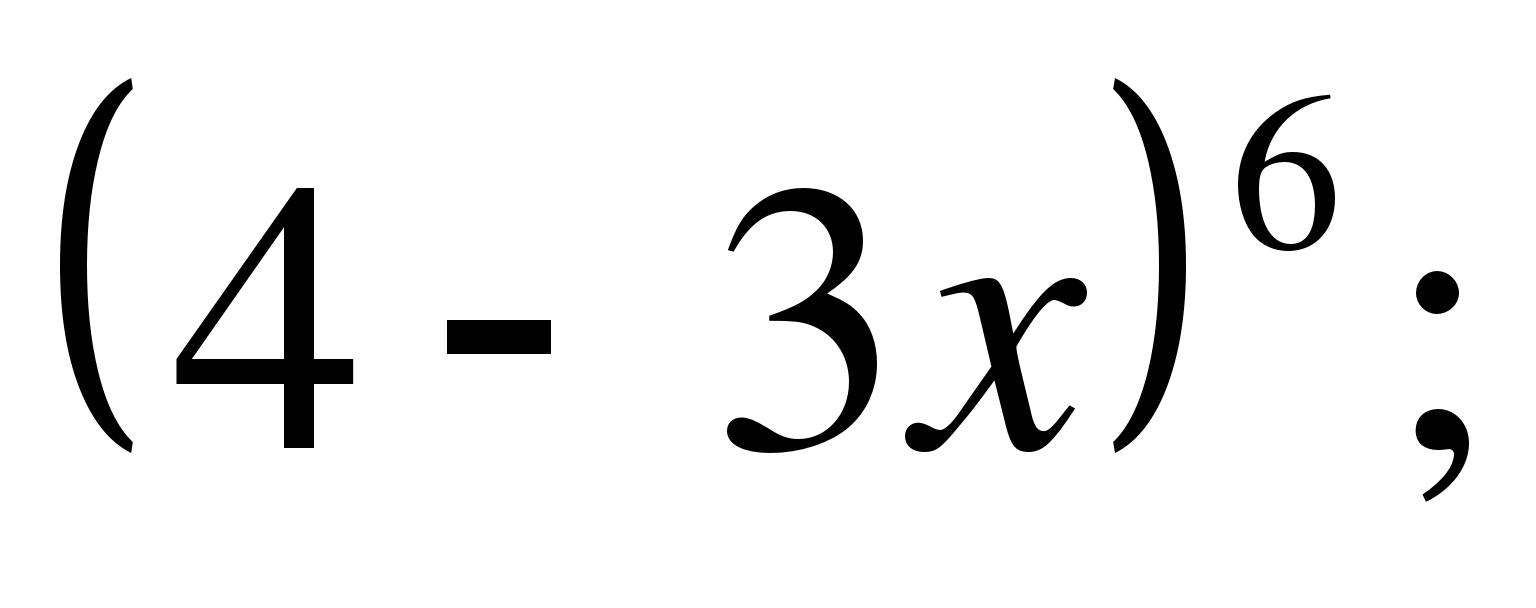 в)
в) 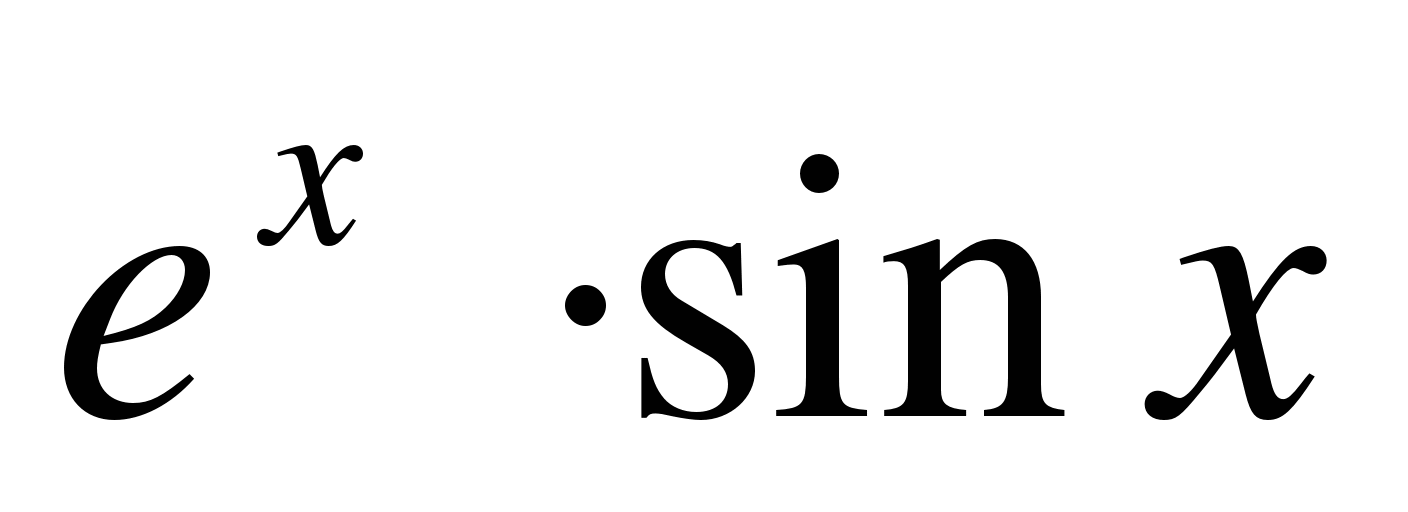
Найдите значение производной функции f(x) = 2-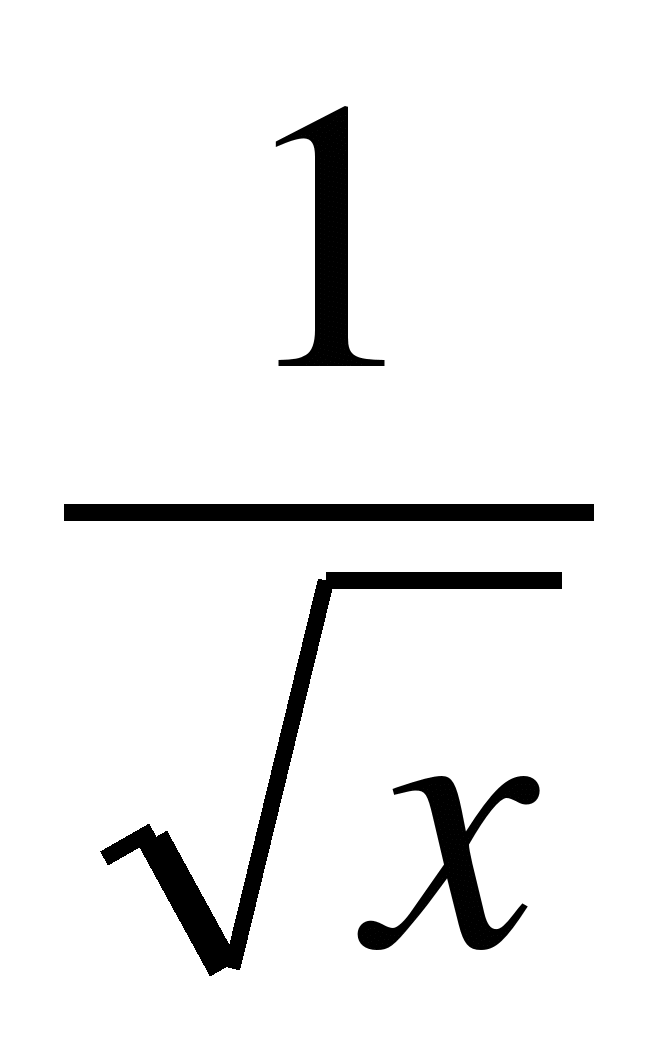 в точке
в точке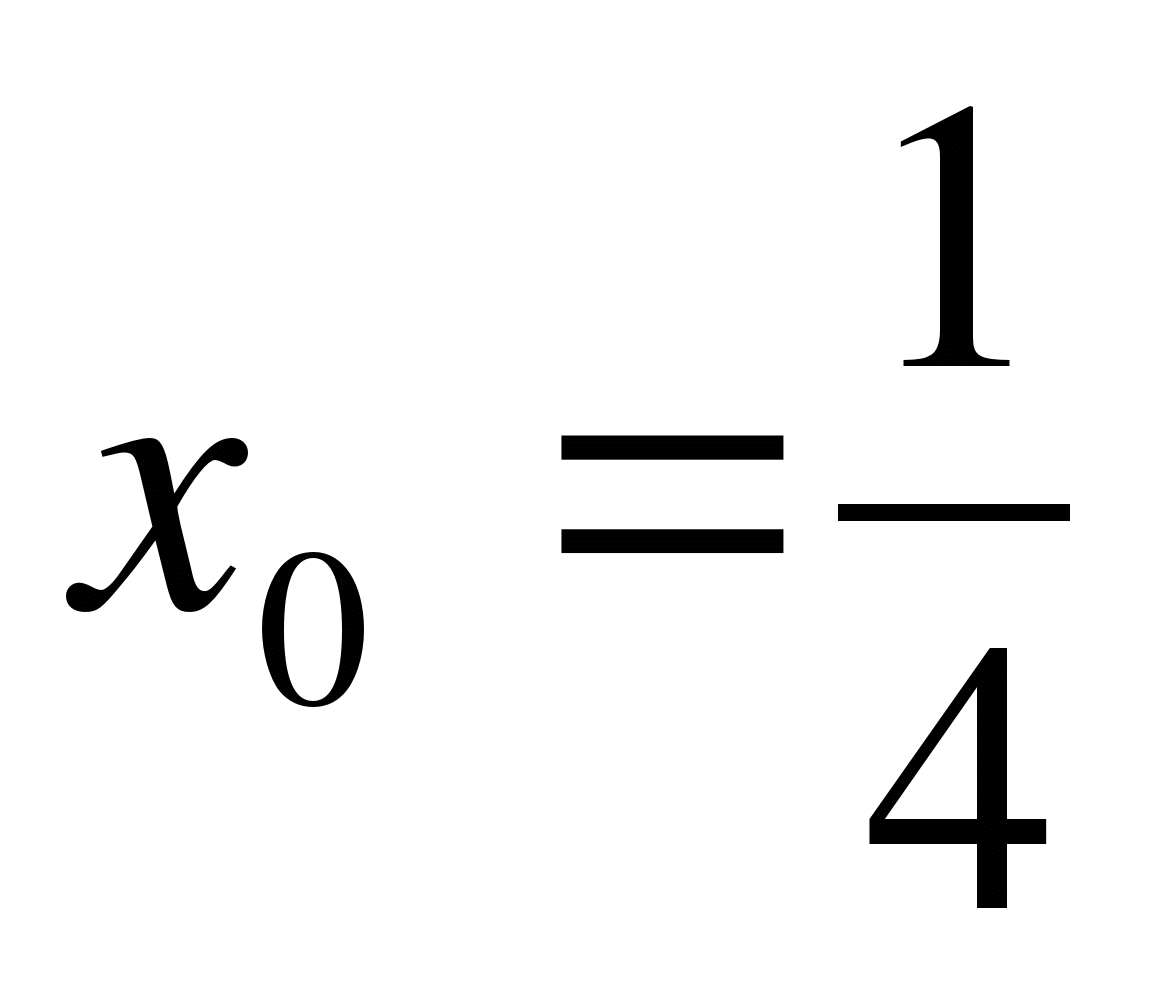 .
.
Запишите уравнение касательной к графику функции f(x) = 4х - sin x +1 в точке 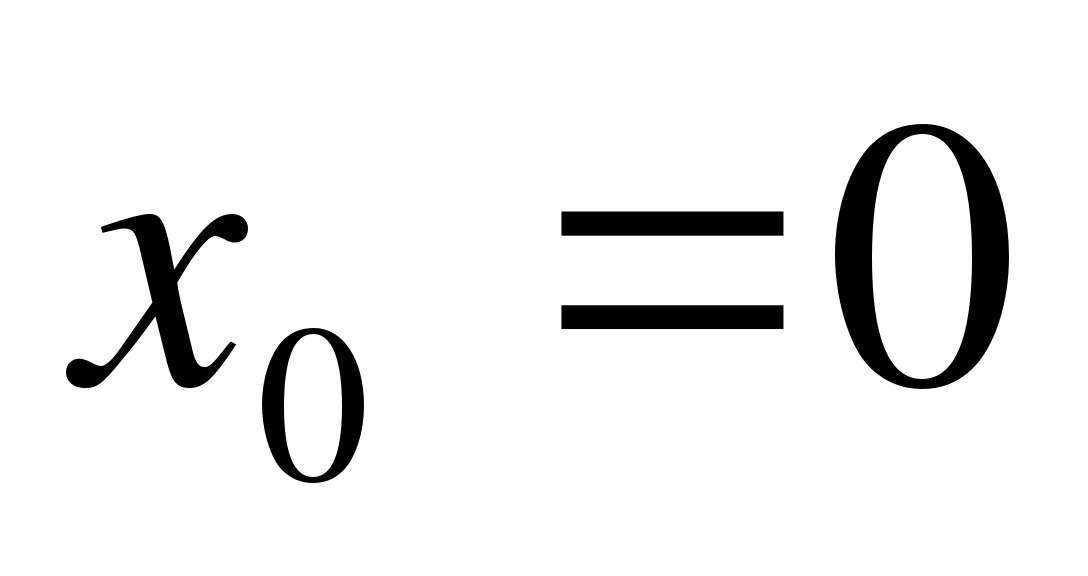 .
.
Найдите все значения х, при которых значения производной функции
f(x) = 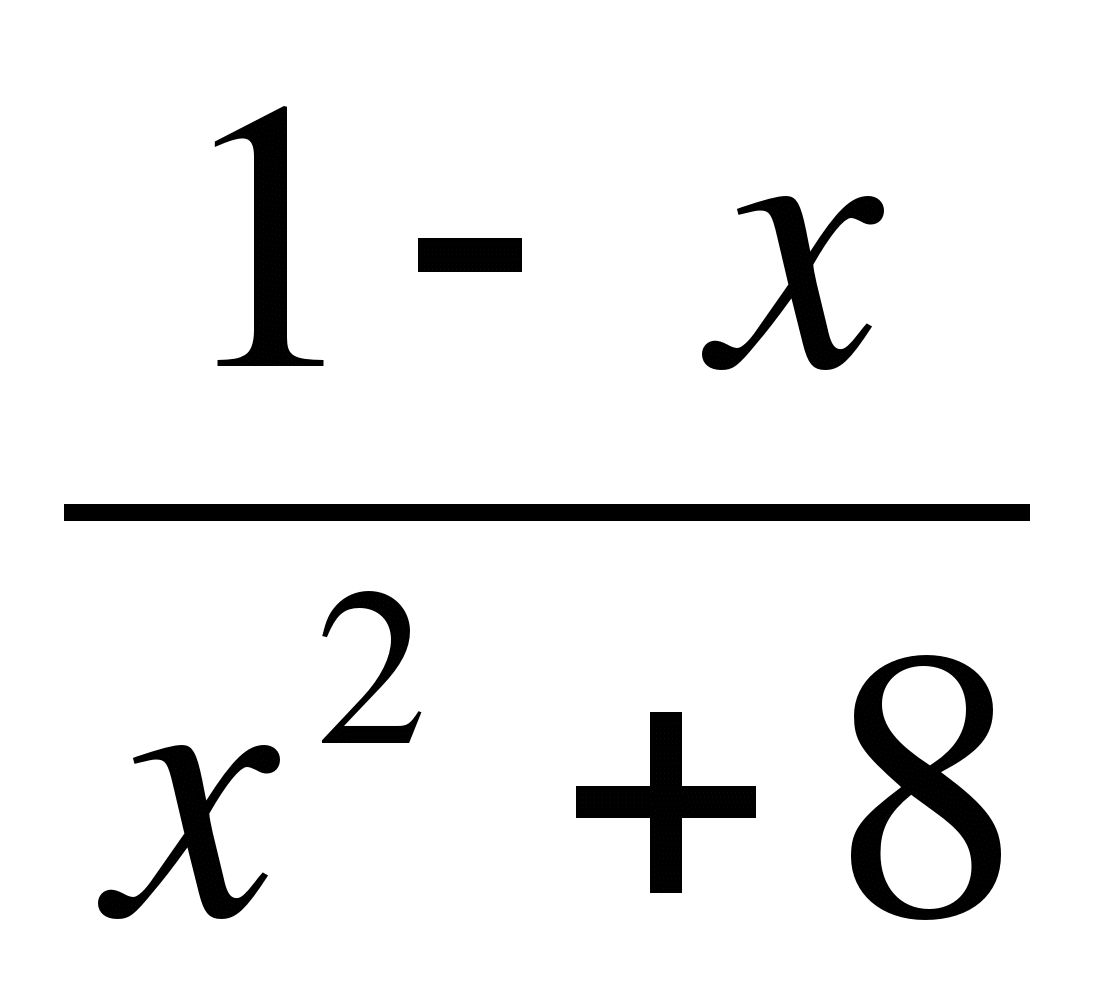 отрицательны.
отрицательны.
Найдите точки графика функции
f(x) = 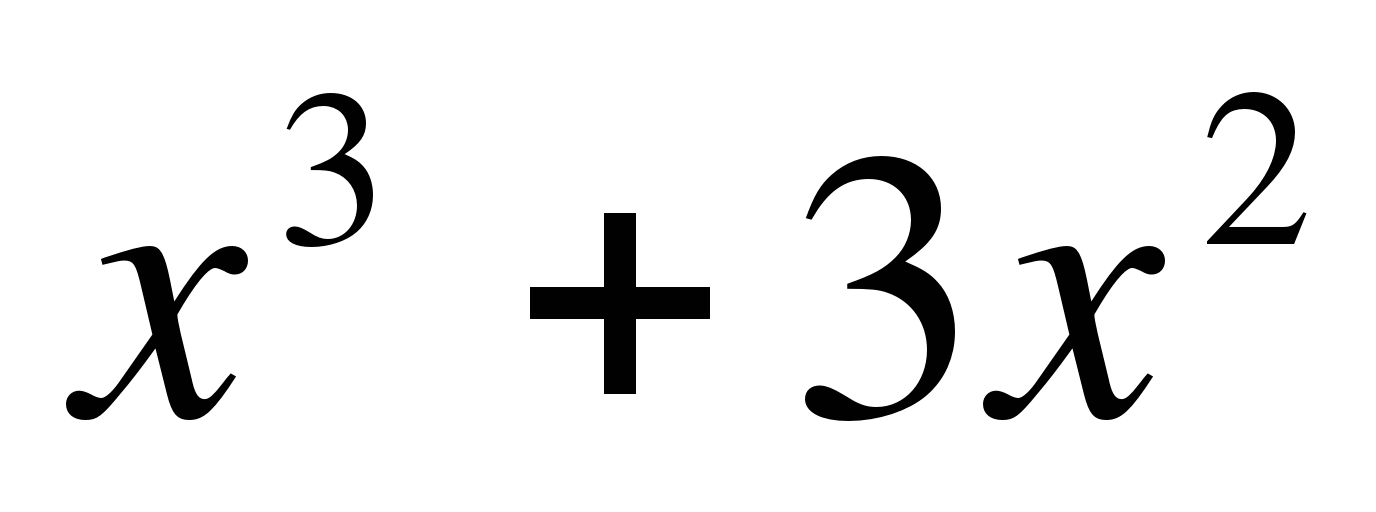 , в которых касательная к нему параллельна оси абсцисс.
, в которых касательная к нему параллельна оси абсцисс.
infourok.ru
Контрольная работа по алгебре и началам математического анализа
Тема «Производная функции и её применение»
2 курс системы НПО и 1 курс СПО
на базе основного образования
Контрольная работа по теме «Производная функции и её применение» ориентирована на учебник Ш.А.Алимова и др. «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и естественно-математического профилей.
Контрольная работа предназначена для самостоятельного выполнения вне аудитории.
Работа включает в себя 10 вариантов заданий одинакового уровня сложности. Вариант определяется последними цифрами номера зачетной книжки студента.
Работа выполняется студентом в отдельной тетради с соответствующим оформлением титульного листа. Оформление работы должно соответствовать «Единым требованиям оформления письменных работ по математике».
Правильное выполнение каждого задания оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 12. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Задание 1. Вычислить пределы
1 вариант
а)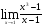
б)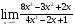
2 вариант
a)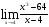
б) 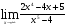
3 вариант
а)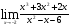
б)
4 вариант
а)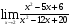
б)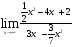
5 вариант
а)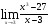
б)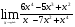
6 вариант
а)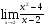
б)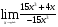
7 вариант
а)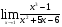
б)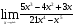
8 вариант
а)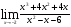
б)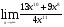
9 вариант
а)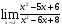
б)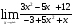
10 вариант
а)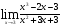
б)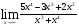
Задание 2. Найти точки разрыва графика функции:
1 вариант 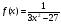 2 вариант
2 вариант 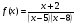
3 вариант 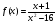 4 вариант
4 вариант 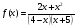
5 вариант 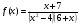 6 вариант
6 вариант 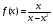
7 вариант 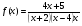 8 вариант
8 вариант 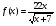
9 вариант 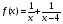 10 вариант
10 вариант 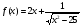
Задание 3. Найти главное приращение функции dy
1 вариант у = х2 + cos 3x – 5 2 вариант y = cos (1- x2)
3 вариант у = (1 – х2)5 4 вариант у = (2х2 – 5)3
5 вариант у = 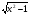 6 вариант у =
6 вариант у = 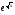
7 вариант у = 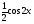 8 вариант у =
8 вариант у = 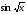
9 вариант 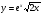 10 вариант
10 вариант 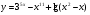
Задание 4. Найти вторую производную функции
1 вариант у = 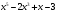 2 вариант
2 вариант 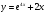
3 вариант 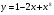 4 вариант
4 вариант 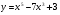
5 вариант 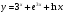 6 вариант
6 вариант 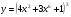
7 вариант 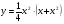 8 вариант
8 вариант 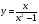
9 вариант 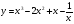 10 вариант
10 вариант 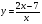
Задание 5. Найти производную по её определению (через предел)
1 вариант у = 2х2 – 3х 2 вариант у = 2х3
3 вариант у = х3 + х 4 вариант у = 5х2 - х
5 вариант у = 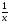 6 вариант у = 6 – х – х2
6 вариант у = 6 – х – х2
7 вариант у = 2 – х2 8 вариант у = х2 + 4х
9 вариант у = х2 – х 10 вариант у = х2 + 2х
Задание 6. Найти скорость и ускорение материальной точки в момент времени t
1 вариант
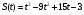
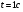
2 вариант

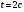
3 вариант
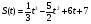
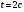
4 вариант
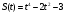
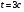
5 вариант
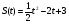
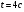
6 вариант
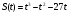
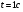
7 вариант
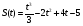
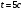
8 вариант
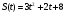
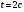
9 вариант
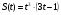
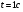
10 вариант
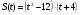
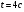
Задание 7. Найти производные, используя таблицу и правила дифференцирования
1 вариант а) y = 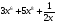 б) y =
б) y = 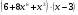
в) y = 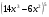 г) y =
г) y = 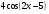 д) y =
д) y = 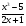
2 вариант а) у = 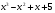 б) у =
б) у = 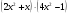
в) у = 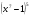 г) у =
г) у = 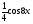 д) у =
д) у = 
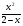
3 вариант а) 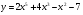 б)
б) 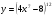
в) 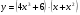 г)
г)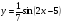 д)
д) 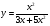
4 вариант а) 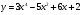 б)
б) 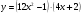
в) 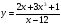 г)
г) 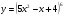 д)
д) 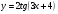
5 вариант а) 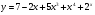 б)
б) 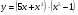
в) 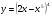 г)
г) 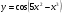 д)
д) 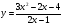
6 вариант а) 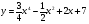 б)
б) 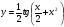
в) 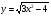 г)
г) 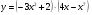 д)
д) 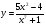
7 вариант а) 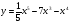 б)
б) 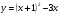
в)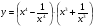 г)
г)
д) 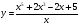
8 вариант а) 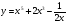 б)
б) 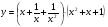
в) 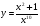 г)
г) 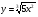 д)
д) 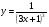
9 вариант а) 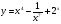 б)
б) 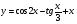
в) 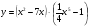 г)
г) 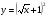 д)
д) 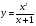
10 вариант а) 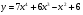 б)
б) 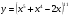
в) 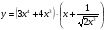 г)
г) 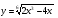 д)
д) 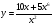
Задание 8. Составить уравнение касательной к графику функции y = f(x) в точке х0
1 вариант
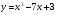
X0 =1
2 вариант
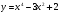
X0 = -1
3 вариант
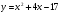
X0 = 0
4 вариант
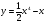
X0 = 2
5 вариант
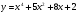
X0 = 1
6 вариант
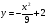
X0 = -2
7 вариант
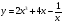
X0 = 1
8 вариант
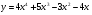
X0 = 2
9 вариант

X0 = 0
10 вариант
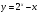
X0 = 1
Задание 9. Вычислить приближенно
1 вариант
а)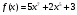 , х=2,0001
, х=2,0001
б) (1,00012)3
в) 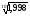
2 вариант
а)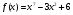 , х=3,999
, х=3,999
б) (2,0003)3
в) 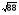
3 вариант
а)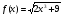 , х=3,012
, х=3,012
б) (0,997)4
в) 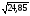
4 вариант
а)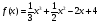 , х=1,099
, х=1,099
б) (3.025)4
в) 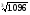
5 вариант
а)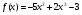 , х=1,1
, х=1,1
б) (1,9999)3
в) 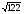
6 вариант
а)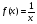 , х= 1,021
, х= 1,021
б) (0,989)3
в) 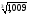
7 вариант
а)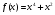 , х= - 2,002
, х= - 2,002
б) (2,098)5
в) 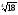
8 вариант
а)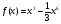 , х= 0,928
, х= 0,928
б) (2,005)4
в) 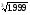
9 вариант
а)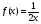 , х=2,0003
, х=2,0003
б) (4,001)9
в) 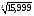
10 вариант
а)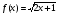 , х=0,0099
, х=0,0099
б) (4,0097)3
в) 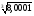
Задание 10. Найти наибольшее и наименьшее значения функции y = f(x) на интервале [a; b] с помощью производной:
1 вариант
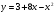
[2; 2,5]
2 вариант
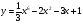
[-2; 1]
3 вариант
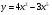
[-4; 0]
4 вариант
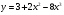
[-2; 0]
5 вариант
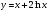
[1; e]
6 вариант

[0; 2]
7 вариант
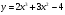
[-1; 1]
8 вариант
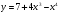
[-1; 3]
9 вариант
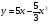
[0; 2]
10 вариант
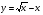
[0; 4]
Задание 11. Составить уравнения асимптот к графику функции y = f(x)
1 вариант 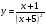 2 вариант
2 вариант 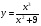
3 вариант 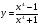 4 вариант
4 вариант 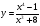
5 вариант 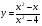 6 вариант
6 вариант 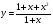
7 вариант 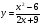 8 вариант
8 вариант 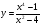
9 вариант 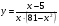 10 вариант
10 вариант 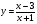
Задание 12. Исследовать свойства функции и построить график
1 вариант
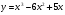

2 вариант
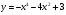
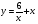
3 вариант
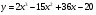
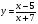
4 вариант
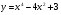

5 вариант
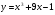
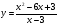
6 вариант
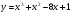
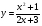
7 вариант
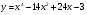
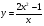
8 вариант
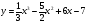
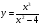
9 вариант
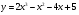
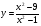
10 вариант
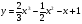
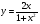
doc4web.ru