Материальная точка движется прямолинейно по закону 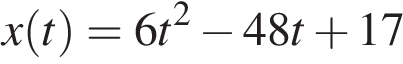 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9с.
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9с.
11 класс Алгебра и начала анализа Юрова Наталья Сергеевна
Контрольная работа по теме «Применение производной»
1 ВАРИАНТ
Физический смысл производной.
Материальная точка движется прямолинейно по закону 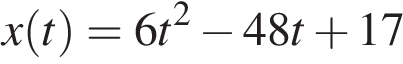 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9с.
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9с.
Геометрический смысл производной, касательная
Решение.
Найдем закон изменения скорости:
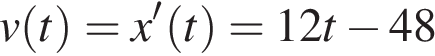 .
.
При t = 9 c имеем:
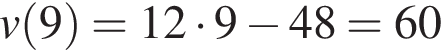 м/с.
м/с.
Ответ: 60.
Ответ: 60
119975
60
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой 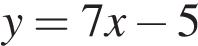 их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения
их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения  :
:
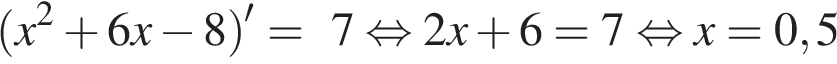 .
.
Ответ: 0,5.
Ответ: 0,5
27485
0,5
2. Прямая 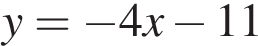 является касательной к графику функции
является касательной к графику функции 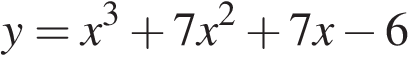 . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Решение.
Условие касания графика функции 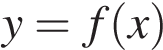 и прямой
и прямой 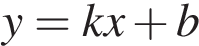 задаётся системой требований:
задаётся системой требований:
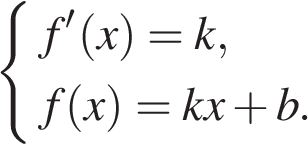
В нашем случае имеем:
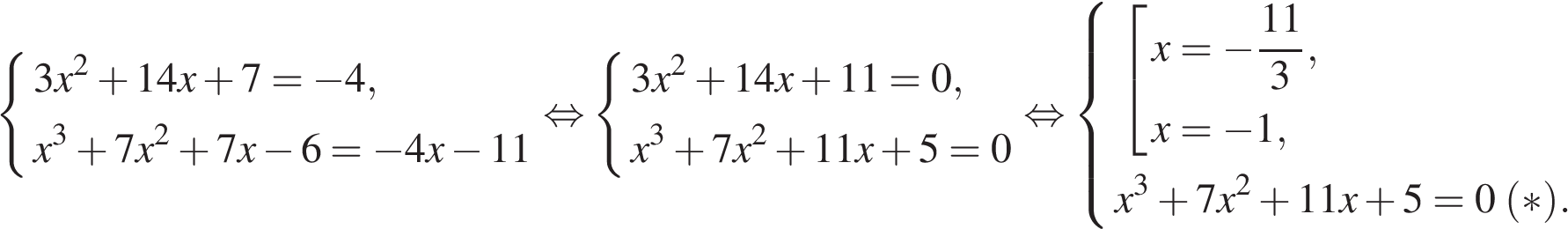
Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания −1.
Ответ: −1.
Ответ: -1
27486
-1
3. На рисунке 1 изображён график функции 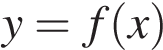 и восемь точек на оси абсцисс:
и восемь точек на оси абсцисс: 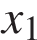 ,
, 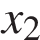 ,
, 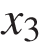 ,
,  ,
, 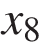 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 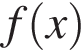 положительна?
положительна?
4. На рисунке 2 изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
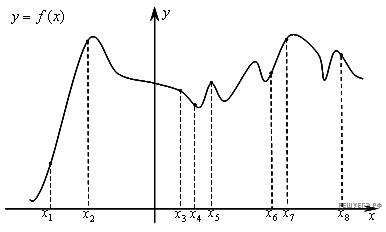
Рис.1
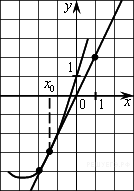
Рис.2
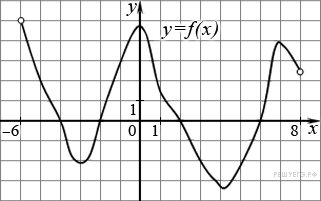
5. На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
Решение.
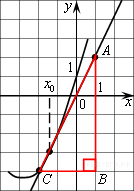 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен углу ACB:
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен углу ACB:
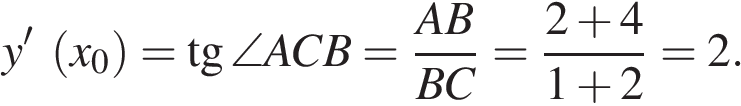
Ответ: 2.
Ответ: 2
Решение.
Положительным значениям производной соответствует интервалы, на которых функция  возрастает. На них лежат точки
возрастает. На них лежат точки  Таких точек 4.
Таких точек 4.
Ответ:4.
Ответ: 4
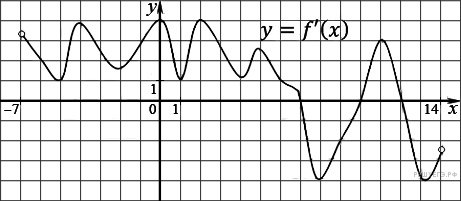
6. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].
Нахождение наибольшего и наименьшего значения функции
7. Найдите наименьшее значение функции 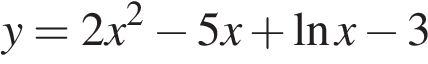 на отрезке
на отрезке 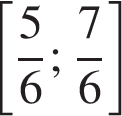
8. Найдите наибольшее значение функции  на отрезке
на отрезке 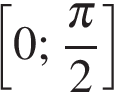 .
.
Решение.
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
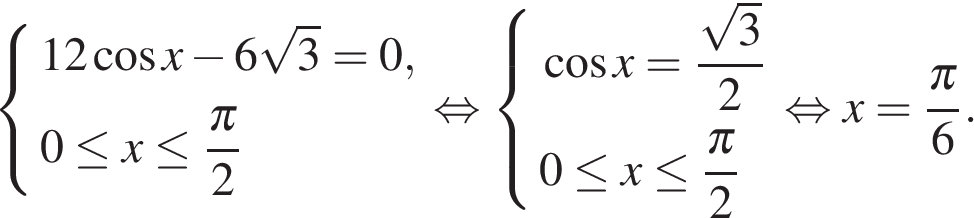
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
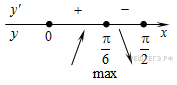
В точке 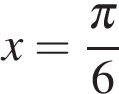 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
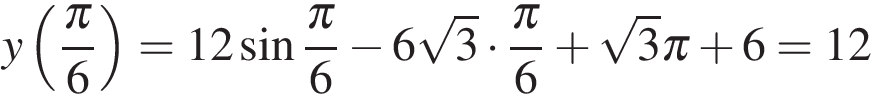 .
.
Ответ: 12.
Ответ: 12
77498
12
Решение.
Найдем производную заданной функции:
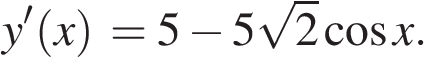
Найдем нули производной на заданном отрезке:
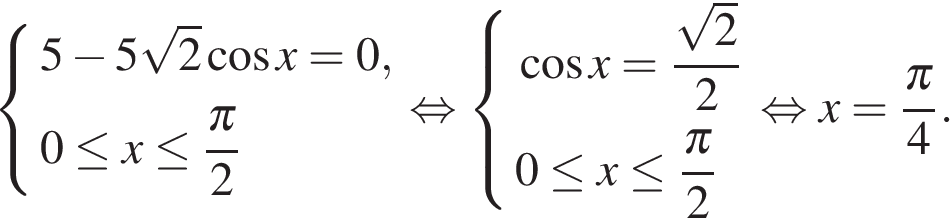
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
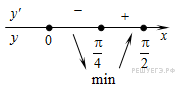
В точке 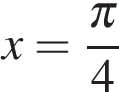 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
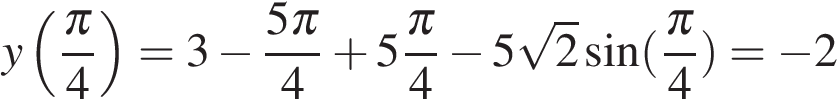 .
.
Ответ: −2.
Ответ: -2
9. Найдите точку максимума функции 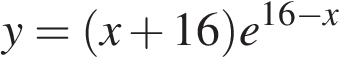 .
.
10. Найдите точку минимума функции 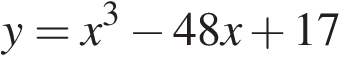 Решение.
Решение.
Найдем производную заданной функции:
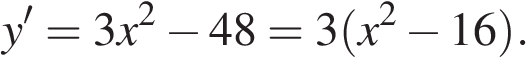
Найдем нули производной:
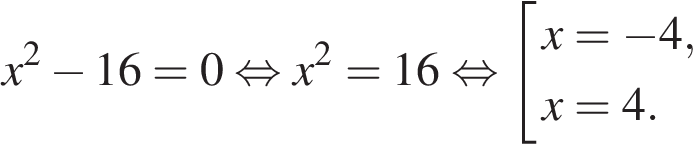
Определим знаки производной функции и изобразим на рисунке поведение функции:
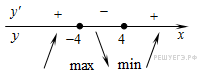
Искомая точка минимума 
Ответ: 4.
Ответ: 4
Контрольная работа по теме «Применение производной»
2 ВАРИАНТ
Физический смысл производной
1. Решение.
Найдем закон изменения скорости:
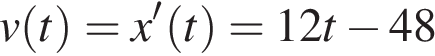 .
.
При t = 9 c имеем:
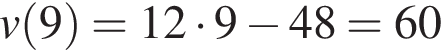 м/с.
м/с.
Ответ: 60.
Ответ: 60
119975
60
Материальная точка движется прямолинейно по закону 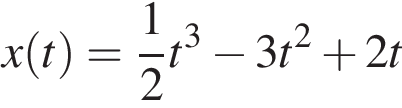 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
Геометрический смысл производной, касательная
Решение.
Условие касания графика функции 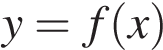 и прямой
и прямой 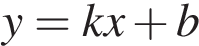 задаётся системой требований:
задаётся системой требований:
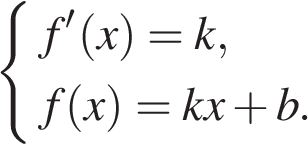
В нашем случае имеем:
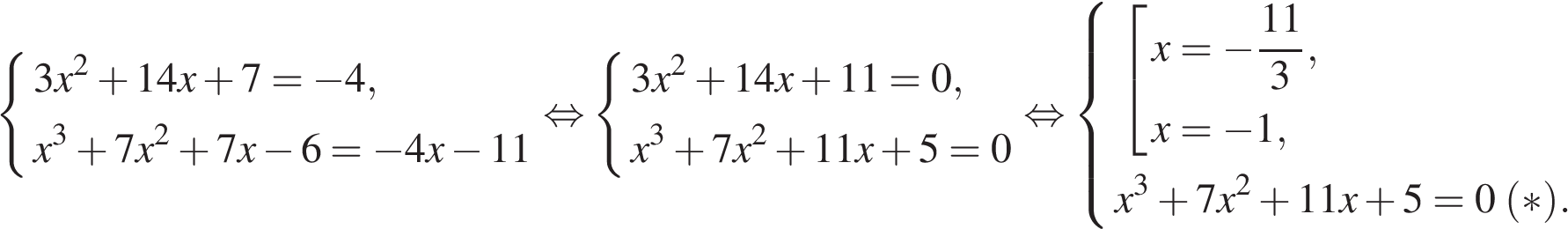
Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания −1.
Ответ: −1.
Ответ: -1
27486
-1
2. Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
Решение.
Прямая 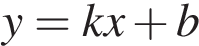 является касательной к графику функции
является касательной к графику функции 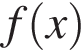 в точке
в точке 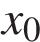 тогда и только тогда, когда одновременно
тогда и только тогда, когда одновременно  и
и 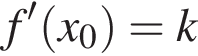 . В нашем случае имеем:
. В нашем случае имеем:
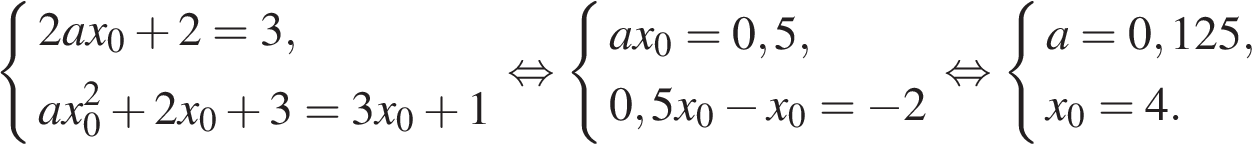
Искомое значение а равно 0,125.
Ответ: 0,125.
Приведем другое решение.
По смыслу задачи a ≠ 0, а значит, график заданной функции — парабола. Касательная к параболе (а также и к гиперболе) имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение ax2 + 2x + 3 = 3x + 1 имело единственно решение. Для этого дискриминант 1 − 8а уравнения ax2 − x + 2 = 0 должен быть равен нулю, откуда 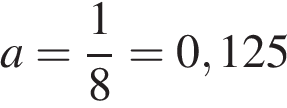 .
.
Ответ: 0,125
119972
0,125
Решение.
Найдем закон изменения скорости:
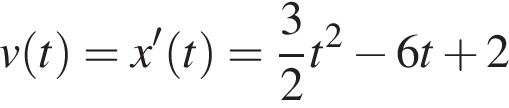 м/с.
м/с.
Тогда находим:
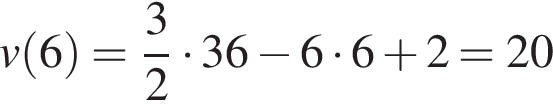 м/с.
м/с.
Ответ: 20.
Ответ: 20
119976
20
3. На рисунке изображён график функции 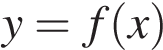 и двенадцать точек на оси абсцисс:
и двенадцать точек на оси абсцисс: 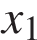 ,
, 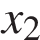 ,
, 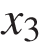 ,
,  ,
, 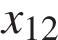 . В скольких из этих точек производная функции
. В скольких из этих точек производная функции 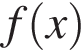 отрицательна?
отрицательна?
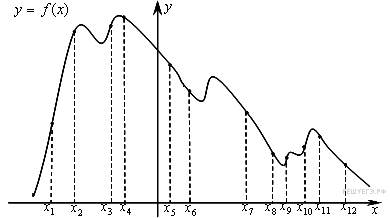
Решение.
Отрицательным значениям производной соответствуют интервалы, на которых функция 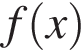 убывает. В этих интервалах лежат точки
убывает. В этих интервалах лежат точки 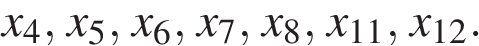 Таких точек 7.
Таких точек 7.
Ответ:7.
Ответ: 7
4. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение.
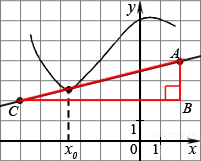 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; 4), B (2; 2), C (−6; 2). Угол наклона касательной к оси абсцисс будет равен углу ACB. Поэтому
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; 4), B (2; 2), C (−6; 2). Угол наклона касательной к оси абсцисс будет равен углу ACB. Поэтому
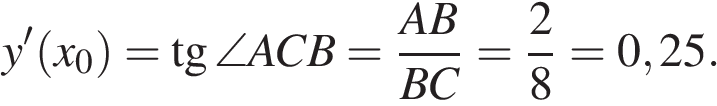
Ответ: 0,25.
Ответ: 0,25
На рисунке изображен график функции 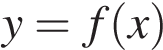 , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции
, определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции 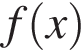 отрицательна
отрицательна
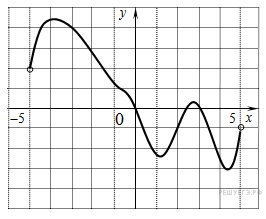
6. На рисунке изображен график производной функции f(x), определенной на интервале (−18; 6). Найдите количество точек минимума функции f(x) на отрезке [−13;1].
Нахождение наибольшего и наименьшего значения функции
7. Найдите наибольшее значение функции 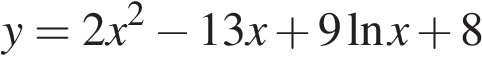 на отрезке
на отрезке 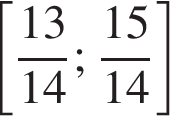 .
.
Решение.
Найдем производную заданной функции:
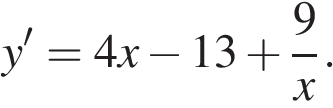
Найдем нули производной на заданном отрезке:
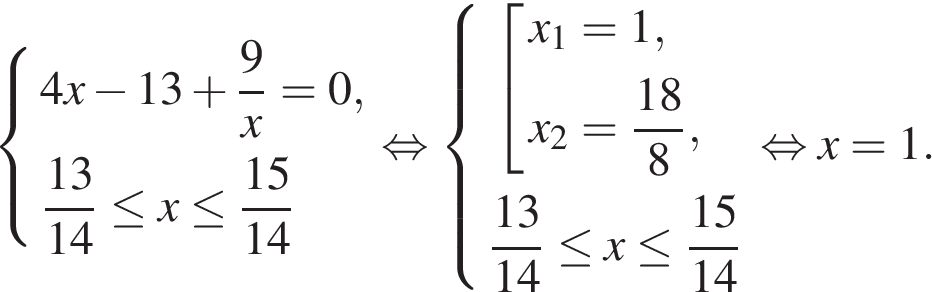
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
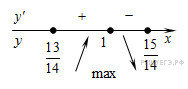
В точке  заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
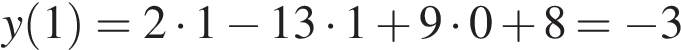 .
.
Ответ: −3.
Ответ: -3
8. Найдите наименьшее значение функции 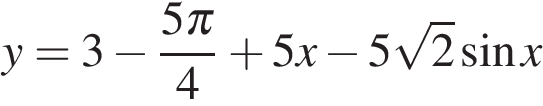 на отрезке
на отрезке 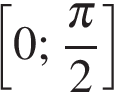 .
.
9. Найдите точку минимума функции  .
.
Решение.
Найдем производную заданной функции:
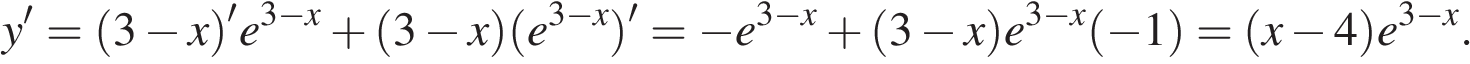
Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:
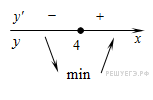
Искомая точка минимума  .
.
Ответ: 4.
Ответ: 4
26712
4
10. Найдите точку максимума функции 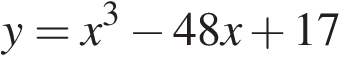 Решение. Найдем производную заданной функции:
Решение. Найдем производную заданной функции:
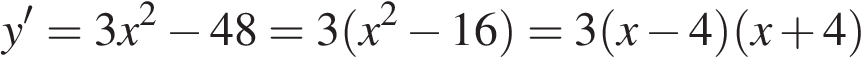
Найдем нули производной:
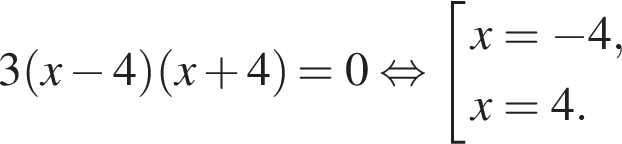
Определим знаки производной функции и изобразим на рисунке поведение функции:
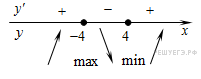
Искомая точка максимума 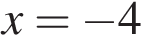 .
.
Ответ: −4.
Ответ: -4
77419
-4
Контрольная работа по теме «Применение производной»
3 ВАРИАНТ
Физический смысл производной
Материальная точка движется прямолинейно по закону 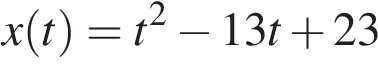 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Геометрический смысл производной, касательная
Прямая 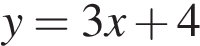 является касательной к графику функции
является касательной к графику функции 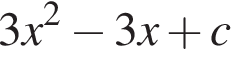 . Найдите
. Найдите  .
.
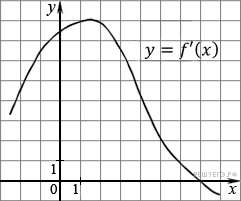
На рисунке изображен график производной функции 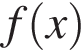 . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику 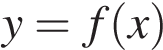 параллельна прямой
параллельна прямой 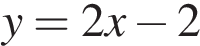 или совпадает с ней.
или совпадает с ней.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касател
Решение.
Условие касания графика функции 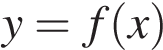 и прямой
и прямой 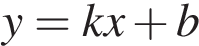 задаётся системой требований:
задаётся системой требований:
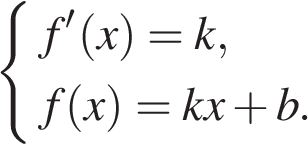
В нашем случае имеем:
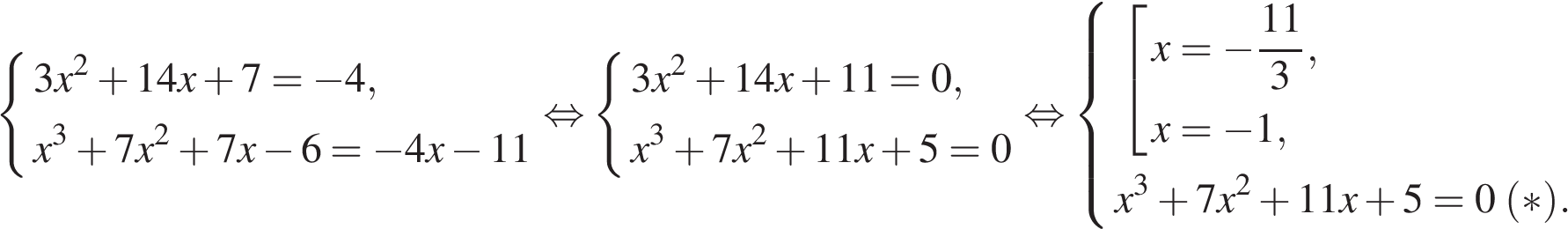
Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания −1.
Ответ: −1.
Ответ: -1
27486
-1
Решение.
Прямая 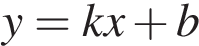 является касательной к графику функции
является касательной к графику функции  в точке
в точке  тогда и только тогда, когда одновременно
тогда и только тогда, когда одновременно  и
и 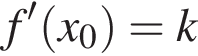 . В нашем случае имеем:
. В нашем случае имеем:
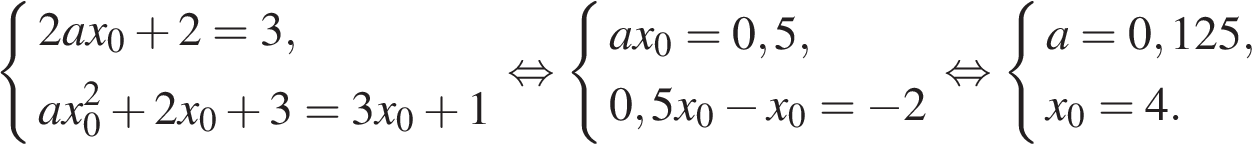
Искомое значение а равно 0,125.
Ответ: 0,125.
Приведем другое решение.
По смыслу задачи a ≠ 0, а значит, график заданной функции — парабола. Касательная к параболе (а также и к гиперболе) имеет с ней единственную общую точку. Поэтому необходимо и достаточно, чтобы уравнение ax2 + 2x + 3 = 3x + 1 имело единственно решение. Для этого дискриминант 1 − 8а уравнения ax2 − x + 2 = 0 должен быть равен нулю, откуда 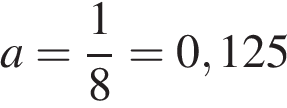 .
.
Ответ: 0,125
119972
0,125
4. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
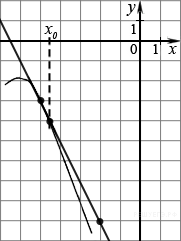 Решение.
Решение.
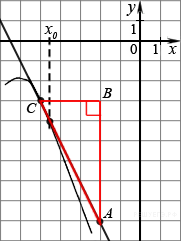 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−2; −9), B (−2; −3), C (−5; −3). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB. Поэтому
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−2; −9), B (−2; −3), C (−5; −3). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB. Поэтому
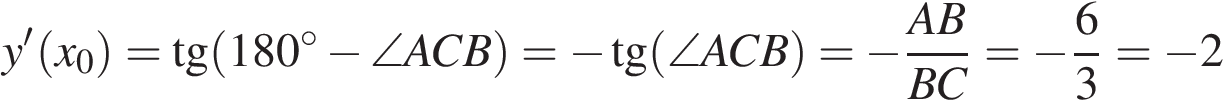 .
.
Ответ: −2.
Ответ: -2
Решение.
Условие касания графика функции  и прямой
и прямой  задаётся системой требований:
задаётся системой требований:
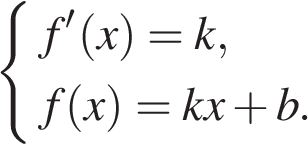
В нашем случае имеем:
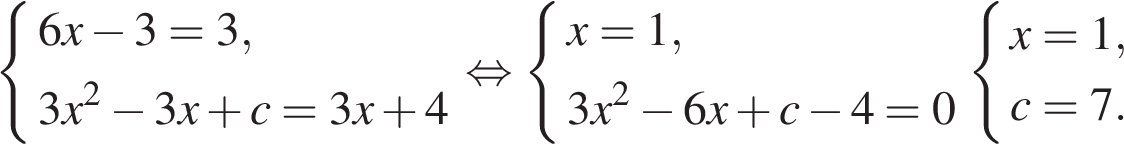
Ответ: 7.
Ответ: 7
119974
7
Решение.
Найдем закон изменения скорости:
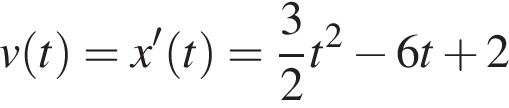 м/с.
м/с.
Тогда находим:
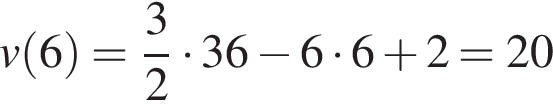 м/с.
м/с.
Ответ: 20.
Ответ: 20
119976
20
5. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
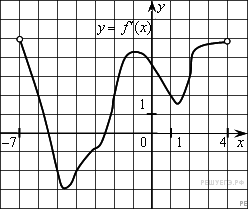
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].
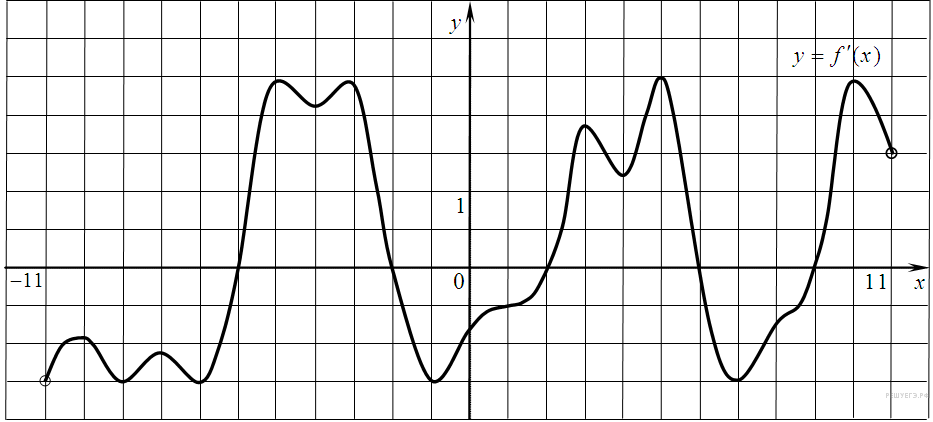
Нахождение наибольшего и наименьшего значения функции
Найдите наибольшее значение функции 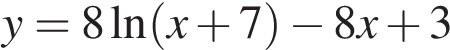 на отрезке
на отрезке 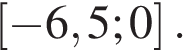
Решение.
Найдем производную заданной функции:
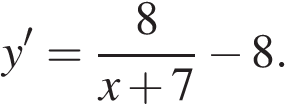
Найдем нули производной на заданном отрезке:
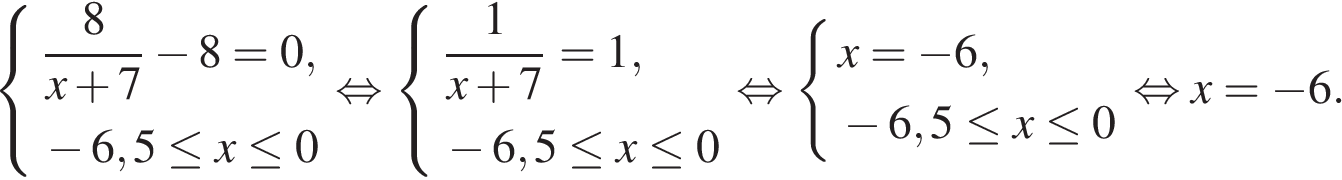
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
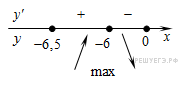
В точке 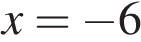 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
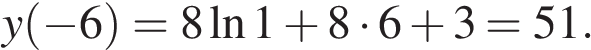
Ответ: 51.
Ответ: 51
Найдите наибольшее значение функции 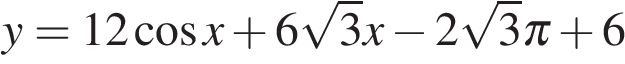 на отрезке
на отрезке 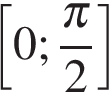 .
.
Решение.
Найдем производную заданной функции:
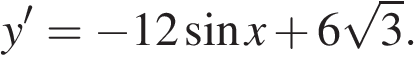
Найдем нули производной на заданном отрезке:
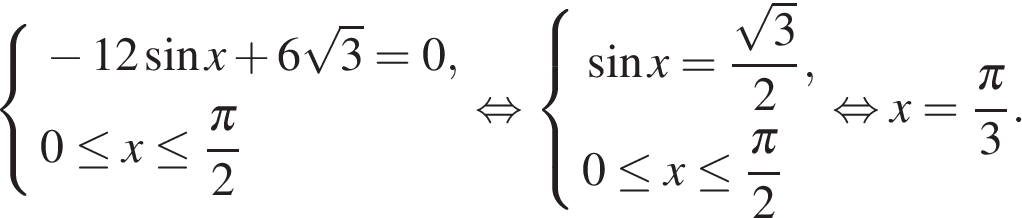
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
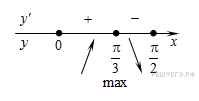
В точке 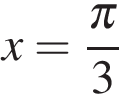 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
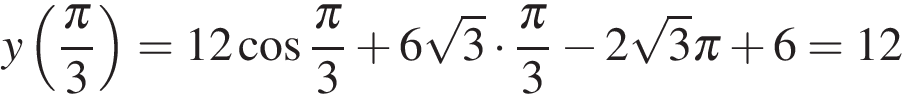 .
.
Ответ: 12.
Ответ: 12
9. Найдите точку максимума функции 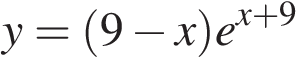 .
.
Решение.
Найдем производную заданной функции:
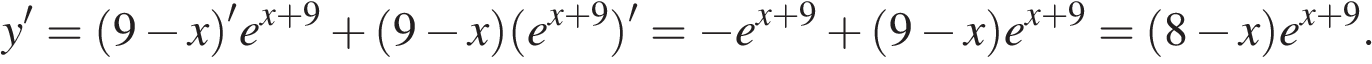
Найдем нули производной:

Определим знаки производной функции и изобразим на рисунке поведение функции:
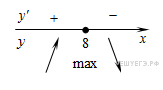 Искомая точка максимума
Искомая точка максимума  .
.
Ответ: 8.
Ответ: 8
26711
8
Решение.
Найдем производную заданной функции:
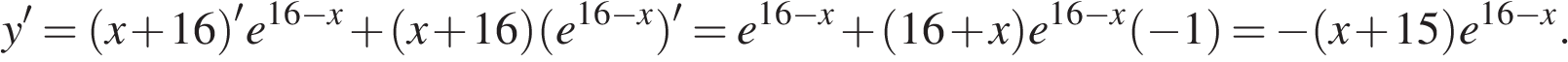
Найдем нули производной:
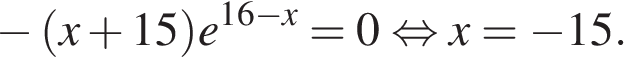
Определим знаки производной функции и изобразим на рисунке поведение функции:
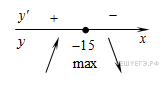
Искомая точка максимума 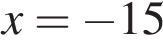 .
.
Ответ: −15.
Ответ: -15
Решение.
Найдем производную заданной функции:
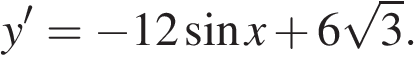
Найдем нули производной на заданном отрезке:
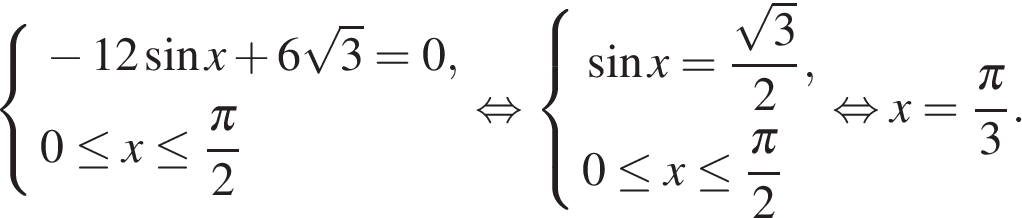
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
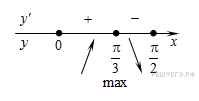
В точке 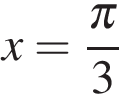 заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
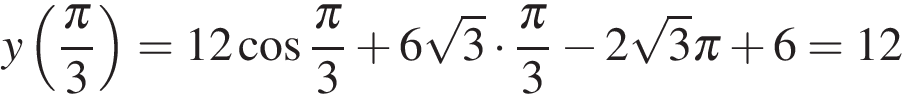 .
.
Ответ: 12.
Ответ: 12
Решение.
Найдем производную заданной функции:
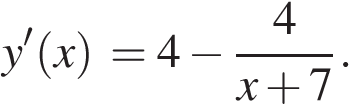
Найдем нули производной на заданном отрезке:
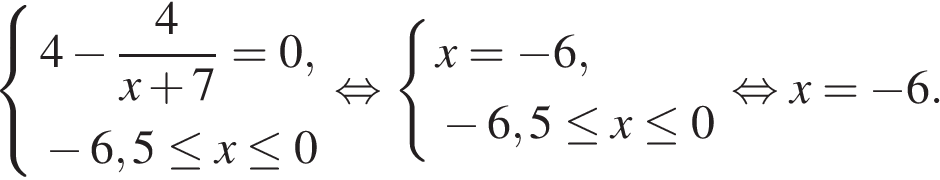
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
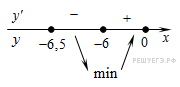
В точке 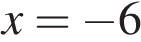 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
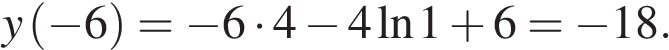
Ответ: −18.
Ответ: -18
Решение.
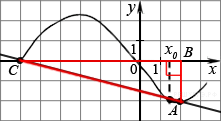 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
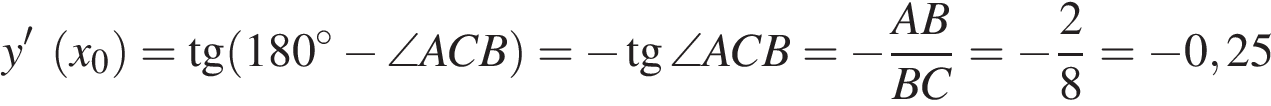 .
.
Ответ: − 0,25.
Ответ: -0,25
Решение.
Найдем производную заданной функции:
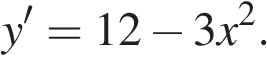
Найдем нули производной:
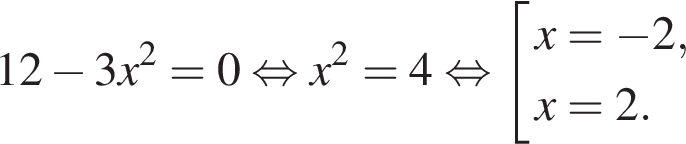
Определим знаки производной функции и изобразим на рисунке поведение функции:
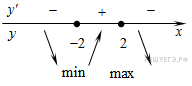
Искомая точка максимума 
Ответ: 2.
Ответ: 2
77435
2
10. Найдите точку минимума функции 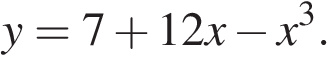 Решение. Найдем нули производной:
Решение. Найдем нули производной: 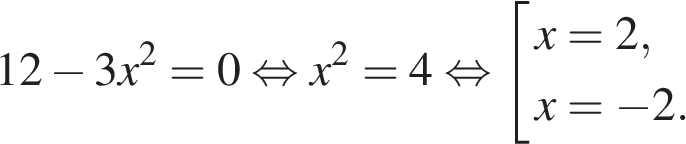
Определим знаки производной функции и изобразим на рисунке поведение функции:
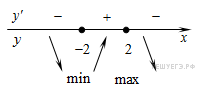
Искомая точка минимума 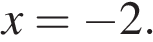
Ответ: −2.
Ответ: -2
Контрольная работа по теме «Применение производной»
4 ВАРИАНТ
Физический смысл производной
Решение.
Найдем закон изменения скорости:
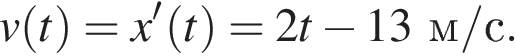
Чтобы найти, в какой момент времени 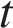 скорость была равна 3 м/с, решим уравнение:
скорость была равна 3 м/с, решим уравнение:
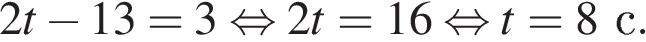
Ответ: 8.
Ответ: 8
119978
8
Материальная точка движется прямолинейно по закону 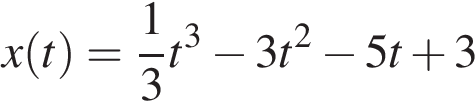 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Геометрический смысл производной, касательная
Решение.
Условие касания графика функции 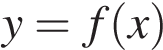 и прямой
и прямой 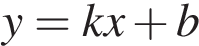 задаётся системой требований:
задаётся системой требований:
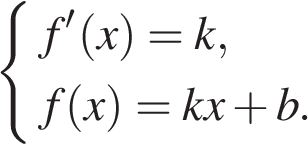
В нашем случае имеем:
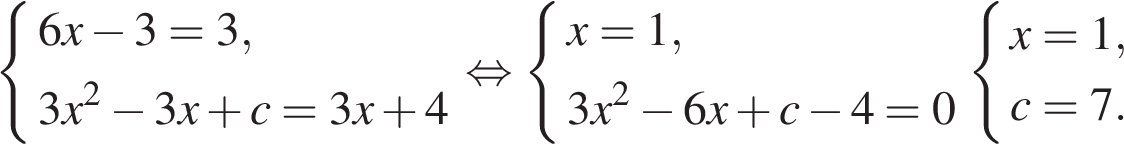
Ответ: 7.
Ответ: 7
119974
7
2. Прямая 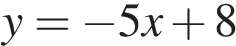 является касательной к графику функции
является касательной к графику функции 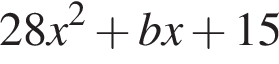 . Найдите
. Найдите 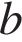 , учитывая, что абсцисса точки касания больше 0.
, учитывая, что абсцисса точки касания больше 0.
3. На рисунке изображен график производной функции 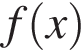 . Найдите абсциссу точки, в которой касательная к графику
. Найдите абсциссу точки, в которой касательная к графику 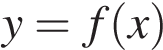 параллельна оси абсцисс или совпадает с ней.
параллельна оси абсцисс или совпадает с ней.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, она имеет вид  , и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка
, и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка 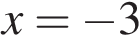 .
.
Ответ: -3.
Ответ: -3
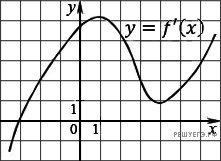
4. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
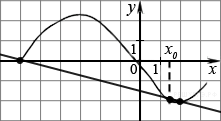
5. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

Нахождение наибольшего и наименьшего значения функции
Найдите наименьшее значение функции 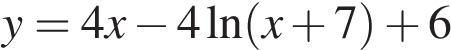 на отрезке
на отрезке 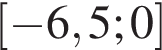 .
.
Найдите наибольшее значение функции 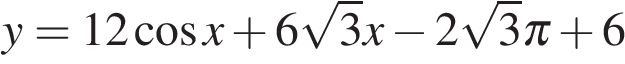 на отрезке
на отрезке 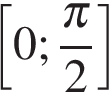 .
.
Найдите точку минимума функции 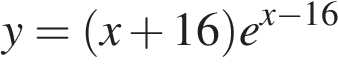 .
.
Найдите точку максимума функции 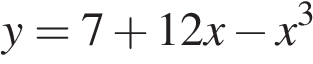 .
.
п. Саук – Дере МБОУ СОШ № 45 2015 - 2016 учебный год
infourok.ru
по теме «Исследование функции с помощью производной»
Вариант № 1
Часть А
1. Сколько интервалов убывания имеет функция f(х) = х3 – 3х?
А. 1. Б.2. В. 3. Г. Ни одного
2. Сколько критических точек имеет функция f(х) = х3 – 9х2 + 15х
А. 2. Б.1. В. 3. Г. Ни одной
3. Значение функции у = – х2 + 4х + 2 в точке максимума равно…
А. 0. Б.2. В. 6. Г.8.
4. Сумма абсцисс критических точек функции
f(х) = х3 + 12х2 + 21х – 6 равна…
А. – 1. Б.7. В. – 8. Г. – 7.
5. Точкой максимума функции f(х) = 16х3 + 81х2 – 21х – 2 является…
А. – 1. Б.3,5. В. – 3. Г. – 3,5.
Часть В.
1. Найдите тангенс угла наклона касательной к оси абсцисс, если касательная проведена через точку х₀графика функции у = f(х), где f(х) = х2 -3х + 1, х₀ =2
2. Найдите скорость точки в момент t0 = 4, если х(t) = t3 - 4t2
3. Найдите точку перегиба к графику функции у = х3 - 3х2 +1
Часть С.
1. Напишите уравнение касательной к графику функции f(х) = х3– 1 в точке с абсциссой х0 = - 1
2. Исследовать с помощью производной функцию и постройте график
а) f(х) = х3 – 3х2 – 9х
б) f(х) =
Вариант № 2
Часть А
1. Сколько интервалов возрастания имеет функция f(х) = х3 – 3х2?
А. 1. Б. Ни одного. В. 2. Г. 3
2. Сколько критических точек имеет функция f(х) = х3 – 6х2 + 9х
А. Ни одной. Б. 3. В. 1. Г. 2.
3. Значение функции у = 2х2 - 8х + 11 в точке минимума равно…
А. 0. Б.5. В. 2. Г.3.
4. Сумма абсцисс критических точек функции
f(х) = х3 - 3х2 - 9х – 4 равна…
А. – 1. Б.3. В. – 3. Г. – 2.
5. Точкой минимума функции f(х) = 16х3 -27х2 – х – 5 является…
А. 1. Б. . В. –. Г. –1 .
Часть В.
1. Найдите тангенс угла наклона касательной к оси абсцисс, если касательная проведена через точку х₀графика функции у = f(х), где f(х) = -х5-2х2 +2 , х₀ = -1
2. Найдите скорость точки в момент t0 = 4, если х(t) = t2 - t + 5
3. Найдите точку перегиба к графику функции у = - 3х3 +4,5х2 + 1
Часть С.
1. Напишите уравнение касательной к графику функции
f(х) = х3 - 2х + 1 в точке с абсциссой х0 = 2
2. Исследовать с помощью производной функцию и постройте график
а) f(х) = + х2 - 3х +1
б) f(х) =
Контрольная работа по теме «Производная»
1 вариант 2 вариант
1. Найдите производную функции. 1. Найдите производную функции.
а) а)
б) б)
в) в)
г) г)
д) д)
2. При движении тела по прямой расстояние S 2. При движении тела по прямой расстояние S
(в метрах) изменяется по закону S(t)=t2+t+2. (в метрах) изменяется по закону S(t)=0,5t2-4t+6
Через сколько секунд после начала движения Через сколько секунд после начала движения
Мгновенная скорость тела будет равна 5м/с? тело остановится?
3. Напишите уравнение касательной к графику 3. Напишите уравнение касательной к графику
графику функции f(x) в точке x=a. графику функции f(x) в точке x=a.
4. Найдите абсциссу точки, в которой касательная 4. Найдите абсциссу точки, в которой касательная
к графику ф-ции f(x) параллельна данной прямой. к графику ф-ции f(x) параллельна данной прямой.
5. При каких значениях аргумента скорость 5. При каких значениях аргумента скорость
изменения ф-ции y=f(x) равна скорости изменения ф-ции y=f(x) равна скорости
изменения ф-ции y=g(x). изменения ф-ции y=g(x).
6. Составьте уравнение касательной к графику 6. Составьте уравнение касательной к графику
ф-ции f(x) в точке x=a. ф-ции f(x) в точке x=a.
7*** Найдите точку пересечения касательных к графику функции , проведённых
через точки с абсциссами х=5, х= -5.
Контрольная работа по теме «Применение производной к исследованию функции»
1 ВАРИАНТ 2 ВАРИАНТ
1. Найдите критические, стационарные точки и 1. Найдите критические, стационарные точки и
точки экстремума функции. точки экстремума функции.
а) а)
б) б)
2. При каких значениях параметра р функция 2. При каких значениях параметра р функция
возрастает на всей убывает на всей
числовой прямой. числовой прямой.
3. Найдите множество значений функции 3. Найдите множество значений функции
4. Длина, ширина и высота прямоугольного 4. Площадь прямоугольного треугольника
параллелепипеда с квадратным основанием 8 см2 . Каким должны быть длины сторон
составляет в сумме 36 см. Чему равен наиболь- треугольника, чтобы сумма площадей
ший объём такого параллелепипеда? квадратов, построенных на его сторонах,
была наименьшей?
5. При каком значении параметра 5. При каком наименьшем значении параметра
р уравнение имеет три корня. n уравнение имеет ровно два
корня.
6. Построить график функции. 6. Построить график функции.
, если x0= 12. Составьте уравнение касательной к графику функции
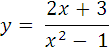
в точке x0= 2.
3. Определите промежутки монотонности функции:
а) y = 3x2– 6x + 1
б) y = x9 — 9x
4. Определите критические точки функции:
а) f(x) = x3– 9x
б) f(x) = - 
5. Найдите точки экстремума функции:
f(x) = 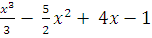
6. Найдите наименьшее и наибольшее значение функции на заданном отрезке:
f(x) = 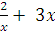 , [0,5 ; 3]
, [0,5 ; 3]
Контрольная работа по алгебре и началам анализа
для 10 класса по теме «Применение производной к исследованию функции»
Вариант № 2
1. Найдите угловой коэффициент касательной, проведённой к графику функции y = f(x) в точке с абсциссой x0, если:
f(x) =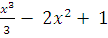 , если x0= 1
, если x0= 1
2. Составьте уравнение касательной к графику функции
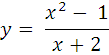
в точке x0= - 1.
3. Определите промежутки монотонности функции:
а) y = 2x2+ 4x — 1
б) y = x7— 7x
4. Определите критические точки функции:
а) f(x) = x2– 16x
б) f(x) = 
5. Найдите точки экстремума функции:
f(x) = 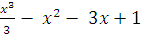
6. Найдите наименьшее и наибольшее значение функции на заданном отрезке:
f(x) = 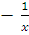 , [ -3 ; - 1]
, [ -3 ; - 1]
Урок в 10 классе по теме «Вычисление производных»
Найти производные функций
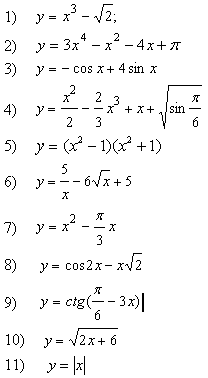
Решив эти примеры, вы расшифруете фамилию французского математика, который ввёл термин «производная»
1
I. f(x) = (4 – 3x)
II. f(x) =
III. f(x) =
IV. f(x) =
V. f(x) = cos2x + sin(x +)
1. f`'(x) = - 2sin2x + cos(x +)
2. f '(x) =
3. f '(x) =
4. f '(x) =
5. f '(x) = - 30(4 – 3x)
№
2
I. f(x) =
II. f(x) =
III. f(x) =
IV. f(x) = cos6x+sin4x
V. f(x) =
1. f`'(x) = - 6sin6x + 4cos4x
2. f '(x) = 63(9х-5)
3. f '(x) =
4. f '(x) = -15(4 - 1,5x)
5. f '(x) =
№
3
I. f(x) = (20x + 4)
II. f(x) = 4sin
III. f(x) = sin4xcos6x – cos4xsin6x
IV. f(x) =
VI. f(x) =
1. f`'(x) =
2. f '(x) = 420(20x + 4)
3. f '(x) =
4. f '(x) =
5. f '(x) = - 2cos2x
№
4
I. f(x) = sin5xcosx – cos5xsinx
II. f(x) =
III. f(x) =
IV. f(x) =
V. f(x) = cos4xcos5x - sin4xsin5x
1. f`'(x) = -
2. f '(x) =
3. f '(x) = -9sin9x
4. f '(x) = 4cos4x
5. f '(x) =
№
5
I. f(x) =
II. f(x) = cos(6 – 4x)
III. f(x) = (4x + 3)
IV. f(x) = sin7xsin5x + cos7xcos5x
V. f(x) = (9 -x) +
1. f`'(x) = - 2sin2x
2. f '(x) = -18x(9 -x)+
3. f '(x) = 36(4x + 3)
4. f '(x) =
5. f '(x) = 4sin(6 – 4x)
№
6
I. f(x) = cos4xcos2x - sin4xsin2x
II. f(x) = 34sinx
III. f(x) = ctg + 1
IV. f(x) =
V. f(x) = (3x – 4)
1. f`'(x) = -
2. f '(x) =
3. f '(x) = 18(3x – 4)
4. f '(x) = 34sin2x
5. f '(x) = - 6sin6x
№
7
I. f(x) = sin6xsin4x + cos6xcos4x
II. f(x) = (8x + 4)
III. f(x) =
IV. f(x) = 5sin( - )
V. f(x) =
1. f`'(x) = sin
2 f '(x) =
3. f '(x) = - 2sin2x
4. f '(x) = 48(8x + 4)
5. f '(x) = -
№
8
I. f(x) =
II. f(x) = sin5xcosx – cos5xsinx
III. f(x) = (5 – 3x)
IV. f(x) = 7 sinx
V. f(x) = (7x +3)
1. f '(x) = 7sin2x
2. f '(x) = 49(7x +3)
3. f '(x) = 4cos4x
4. f '(x) =
5. f '(x) = - 15(5 – 3x)
№
9
I. f(x) =
II. f(x) =
III. f(x) =
IV. f(x) = sinxcos2x + cosxsin2x
V. f(x) = (x- 2x + 5)
1. f '(x) = 3cos3x
2. f '(x) =
3. f '(x) = 6(x - 2x + 5)(3x - 4x)
4. f '(x) = -
5. f '(x) =
№
10
I. f(x) =
II. f(x) = (4х + 6)
III. f(x) = - 2sinsin
IV. f(x) =
V. f(x) =
1. f '(x) =
2. f '(x) = - 5sin5x + 2sin2x
3. f '(x) = 20(4х + 6)
4. f '(x) =
5. f '(x) =
№
11
I. f(x) = (7 – 8х)
II. f(x) =
III. f(x) = cos5x – sin2x
IV. f(x) = (7x + 3)
V. f(x) = 2sin( - )
1. f '(x) = 35(7x + 3)
2. f '(x) = - 5sin5x – 2cos2x
3. f '(x) =
4. f '(x) = - 144(7 – 8х)
5. f '(x) = cos( - )
№
12
I. f(x) = sinxcos2x + cosxsin2x
II. f(x) =
III. f(x) = (8 -2x)
IV. f(x) = cos - sin
V. f(x) = ()
1. f '(x) = 8(2x - 8)
2. f '(x) = - sin
3. f '(x) = -
4. f '(x) =
5. f '(x) = 3cos3x
№
13
I. f(x) = (4х + 2)
II. f(x) = cos(2x – π)
III. f(x) =
IV. f(x) =
V. f(x) = sin5xsin3x + cos5xcos3x
1. f '(x) =
2. f '(x) = 18(2х+4)
3. f '(x) = -2sin2x
4. f '(x) = 24(4х + 2)
5. f '(x) = sin2x
№
14
I. f(x) = (9x + 3)
II. f(x) =
III. f(x) =
IV. f(x) = 6 (х³+ 5х)
V. f(x) =
1. f '(x)= 18х²+30
2. f '(x) =
3. f '(x) =
4. f '(x) = 36(9x + 3)
5. f '(x) = -
№
15
I. f(x) = (5 – 4x)
II. f(x) =
III. f(x) =
IV. f(x) = - 5cos( - π)
V. f(x) =
1. f '(x) = - sin
2. f '(x) =
3. f '(x) =
4. f '(x) = 64(4x – 5)
5. f '(x) = -
№
16
I. f(x) = sin(2x + 40)
II. f(x) = ( 6x – 2)- (9x + 7)
III. f(x) = sin (8x + 3)
IV. f(x) =
V. f(x) = sin8xsin3x + cos8xcos3x
1. f '(x) = - 5sin5x
2. f '(x) =
3. f '(x) =8 cos(8х+3)
4. f '(x) = 14 sin(2x + 40)cos(2x + 40)
5. f '(x) = 90(6x – 2) + 72(9x + 7)
№
17
I. f(x) = 3sin( - )
II. f(x) = sin5xsin3x + cos5xcos3x
III. f(x) = 2cos
IV. f(x) =
V. f(x) =
1. f '(x) =
2. f '(x) = - 2sin2x
3. f '(x) = -
4. f '(x) = sin
5. f '(x) = - sin
№
18
I. f(x) = 4sin( - )
II. f(x) = sin8xsin3x + cos8xcos3x
III. f(x) =
IV. f(x) =
V. f(x) = 4cossin
1. f '(x) = -
2. f '(x) = cos
3. f '(x) =
4. f '(x) = sin
5.f '(x) = - 5sin5x
№
19
I. f(x) = 5sin( - π)
II. f(x) = sin5xsinx + cos5xcosx
III. f(x) =
IV. f(x) =
V. f(x) = 2cossin
1. f '(x) = - 4sin4x
2. f '(x) = -cos
3. f '(x) = -
4. f '(x) =
5. f '(x) = cos
№
20
I. f(x) = 6sin( - )
II. f(x) = sin9xsin2x + cos9xcos2x
III. f(x) =
IV. f(x) =
V. f(x) = 6sin
1. f '(x) = 3cos
2. f '(x) = -
3. f '(x) =
4. f '(x) = - 7sin7x
5. f '(x) = -2sin
Известно, что объем продукции у в течение рабочего дня представлен функцией 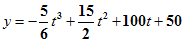 , t– время, ч.
, t– время, ч.
Может быть кто–нибудь знает, как вычислить производительность труда в течение каждого часа работы?
Производительность труда есть производная объема выпускаемой продукции.
СЛАЙД 9


1
2
3
4
1 вариант
б
в
а
г
2 вариант
в
г
б
а
Дополнительно
infourok.ru
Контрольная работа № 7 (1 час)
Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Вариант 1
1. Составьте уравнение касательной к графику функции 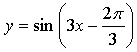 в точке
в точке 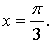
2. Составьте уравнения касательных к графику функции 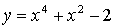 в точках его пересечения с осью абсцисс. Найдите точку ппересечения этих касательных.
в точках его пересечения с осью абсцисс. Найдите точку ппересечения этих касательных.
3. Исследуйте функцию 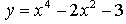 на монотонность и экстремумы и постройте её график.
на монотонность и экстремумы и постройте её график.
4. Найдите значение параметра а, при котором касательная к графику функции 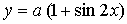 в точке с абсциссой
в точке с абсциссой 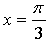 параллельна биссектрисе первой координатной четверти.
параллельна биссектрисе первой координатной четверти.
Вариант 2
1. Составьте уравнение касательной к графику функции 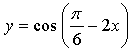 в точке
в точке 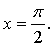
2. Составьте уравнения касательных к графику функции 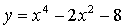 в точках его пересечения с осью абсцисс. Найдите точ-кку пересечения этих касательных.
в точках его пересечения с осью абсцисс. Найдите точ-кку пересечения этих касательных.
3. Исследуйте функцию 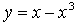 на монотонность и экстремумы и постройте её график.
на монотонность и экстремумы и постройте её график.
4. Найдите значение параметра а, при котором касательная к графику функции 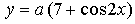 в точке с абсциссой
в точке с абсциссой 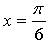 параллельна прямой
параллельна прямой 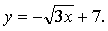
Вариант 3
1. Составьте уравнение касательной к графику функции 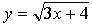 в точке х = 4.
в точке х = 4.
2. Составьте уравнения касательных к графику функции 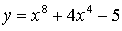 в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
3. Исследуйте функцию 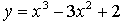 на монотонность и экстремумы и постройте её график.
на монотонность и экстремумы и постройте её график.
4. Найдите значение параметра а, при котором касательная к графику функции 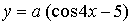 в точке с абсциссой
в точке с абсциссой 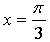 параллельна биссектрисе второй координатной четверти.
параллельна биссектрисе второй координатной четверти.
Вариант 4
1. Составьте уравнение касательной к графику функции 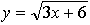 в точке х = 1.
в точке х = 1.
2. Составьте уравнения касательных к графику функции 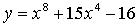 в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
3. Исследуйте функцию 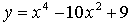 на монотонность и экстремумы и постройте её график.
на монотонность и экстремумы и постройте её график.
4. Найдите значение параметра а, при котором касательная к графику функции 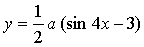 в точке с абсциссой
в точке с абсциссой 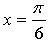 параллельна прямой
параллельна прямой 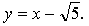
Решение вариантов контрольной работы
Вариант 1
1. 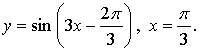
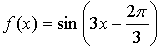
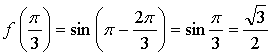
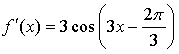
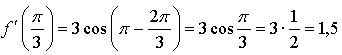
Уравнение касательной:
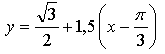
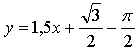
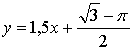
Ответ: 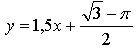
2. 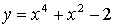
Найдем точки пересечения с осью 0х:
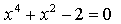
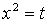
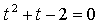
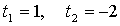
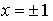
Составим уравнение касательной в точке х = 1:
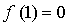
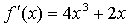
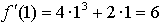
Получим, 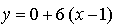
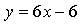
Составим уравнение касательной в точке х = –1:
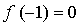
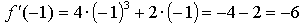
Получим 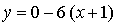
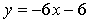
Найдем точку пересечения касательных:
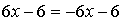
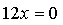
х = 0
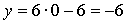
Ответ: 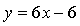 ,
, 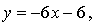 (0; –6).
(0; –6).
3. 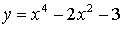
1) Область определения: 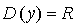
2) Чётность / нечётность:
 – чётная.
– чётная.
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
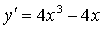
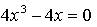
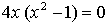
х = 0, х = 1
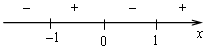
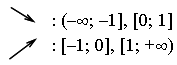
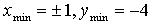
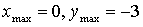
5) Контрольные точки:
4. 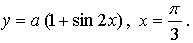
Биссектриса первой координатной четверти имеет уравнение у = х. Если касательная ей параллельна, то она имеет такой же угловой коэффициент, то есть k = 1.
Таким образом, нужно найти такое значение параметра а, при котором производная данной функции в точке 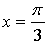 равна 1.
равна 1.
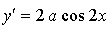
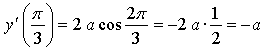
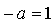
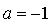
Ответ: 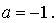
Вариант 2
1. 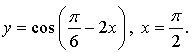
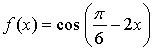
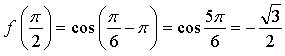
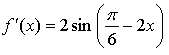
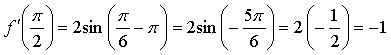
Уравнение касательной:
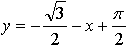
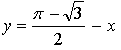
Ответ: 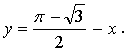
2. 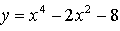
Найдем точки пересечения с осью 0х:
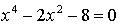
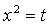
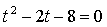
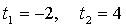
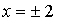
Составим уравнение касательной в точке х = 2:
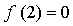
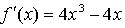
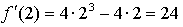
Получим 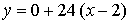
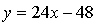
Составим уравнение касательной в точке х = –2:
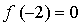
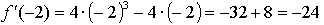
Получим 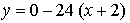
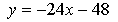
Найдем точку пересечения касательных:
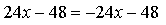
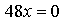
х = 0
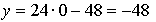
Ответ: 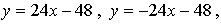 (0; –48).
(0; –48).
3. 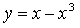
1) Область определения: 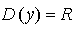
2) Чётность / нечётность:
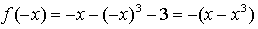 – нечётная.
– нечётная.
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
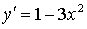
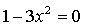
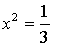
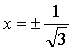
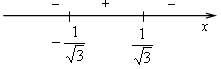
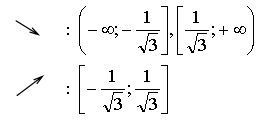
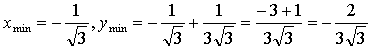
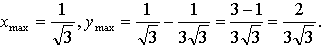
5) Контрольные точки:
Пересечение с осью 0х: 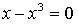
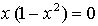
х = 0, х = 1
А (0; 0), В (1; 0), С (–1; 0).
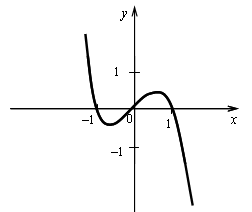
4. 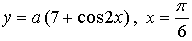
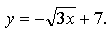
Если касательная параллельна прямой 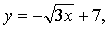 то она имеет такой же угловой коэффициент, то есть
то она имеет такой же угловой коэффициент, то есть 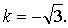 Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке
Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке 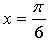 равна
равна 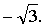
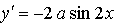
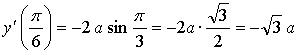
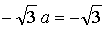
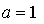
Ответ: 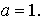
Вариант 3
1. 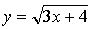 , х = 4.
, х = 4.
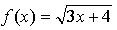
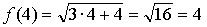
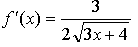
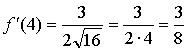
Уравнение касательной:
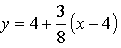
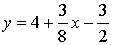
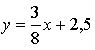
Ответ: 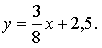
2. 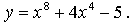
Найдем точки пересечения с осью 0х:
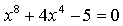
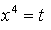
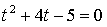
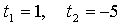
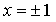
Составим уравнение касательной в точке х = 1:
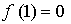
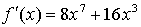
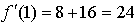
Получим 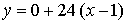
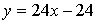
Составим уравнение касательной в точке х = –1:
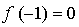
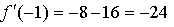
Получим 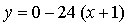
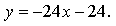
Найдем точку пересечения касательных:
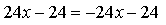
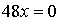
х = 0
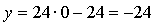
Ответ: 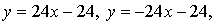 (0; –24).
(0; –24).
3. 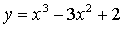
1) Область определения: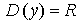
2) Чётность / нечётность:
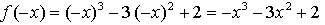 – ни чётная, ни нечётная.
– ни чётная, ни нечётная.
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
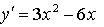
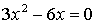
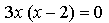
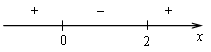
х = 0, х = 2
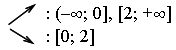
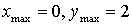
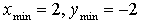
5) Контрольные точки:
4. 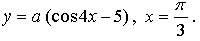
Биссектриса второй координатной четверти имеет уравнение у = –х. Если касательная ей параллельна, то она имеет такой же угловой коэффициент, то есть k = –1.
Таким образом, нужно найти такое значение параметра а, при котором производная данной функции в точке 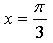 равна –1.
равна –1.
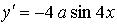
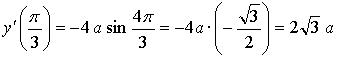
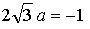
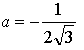
Ответ: 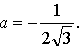
Вариант 4
1. 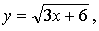 х = 1.
х = 1.
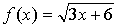
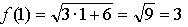
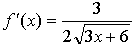
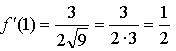
Уравнение касательной:
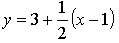
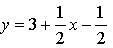
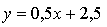
Ответ: 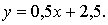
2. 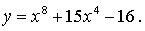
Найдем точки пересечения с осью 0х:
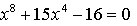
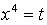
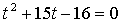
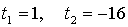
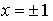
Составим уравнение касательной в точке х = 1:
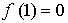
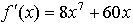
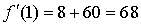
Получим 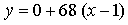
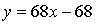
Составим уравнение касательной в точке х = –1:
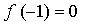
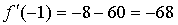
Получим 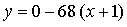
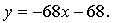
Найдем точку пересечения касательных:
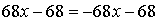
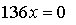
х = 0
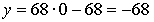
Ответ: 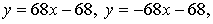 (0; –68).
(0; –68).
3. 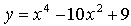 .
.
1) Область определения: 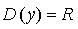
2) Чётность / нечётность:
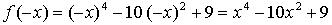 – чётная.
– чётная.
3) Асимптоты.
Асимптот нет.
4) Монотонность и экстремумы.
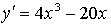
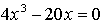
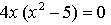
х = 0, х = 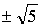
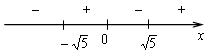
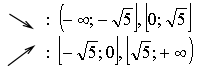
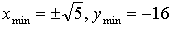
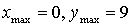
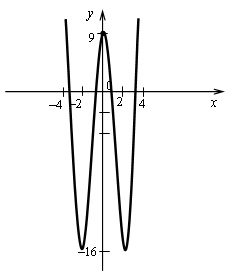
5) Контрольные точки:
4. 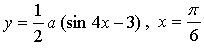
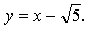
Если касательная параллельна прямой 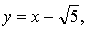 то она имеет такой же угловой коэффициент, то есть k = 1. Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке
то она имеет такой же угловой коэффициент, то есть k = 1. Значит, нужно найти такое же значение параметра а, при котором производная данной функции в точке 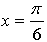 равна 1.
равна 1.
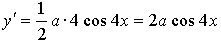
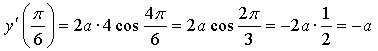
–а = 1
а = –1
Ответ: а = –1.
infourok.ru
КОНТРОЛЬНАЯ РАБОТА №10 по теме
«ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ПОСТРОЕНИЮ ГРАФИКОВ ФУНКЦИЙ»
1f(x) = 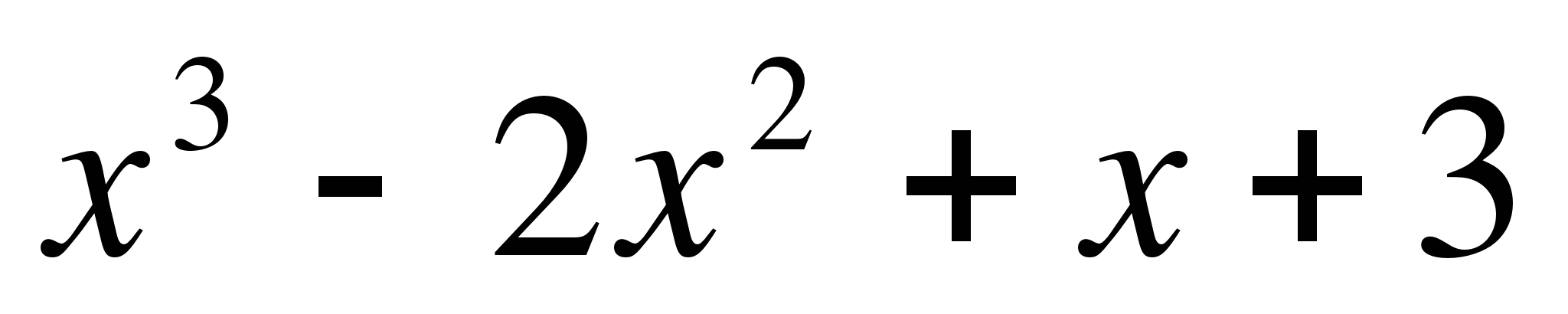 .
.
2. Найдите экстремумы функции:
а) f(x) = 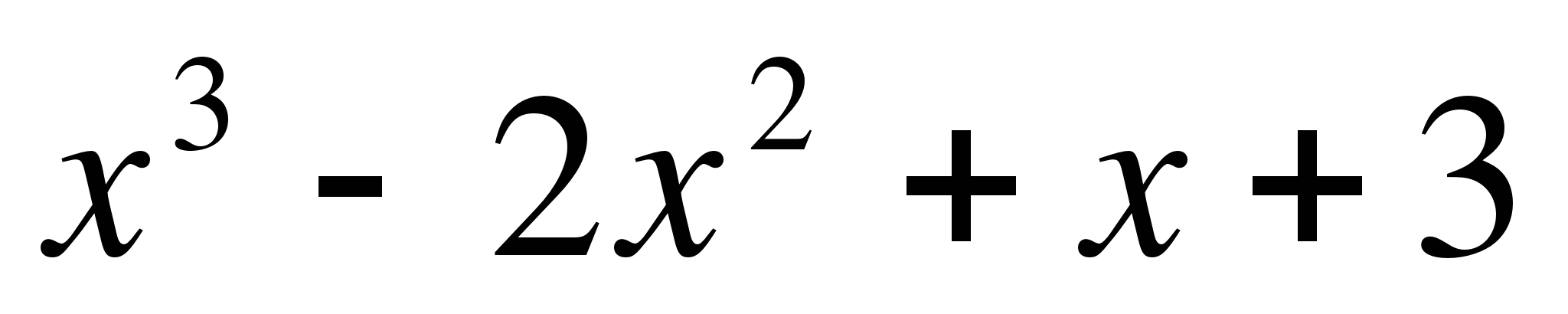 ;
;
б) f(x) = 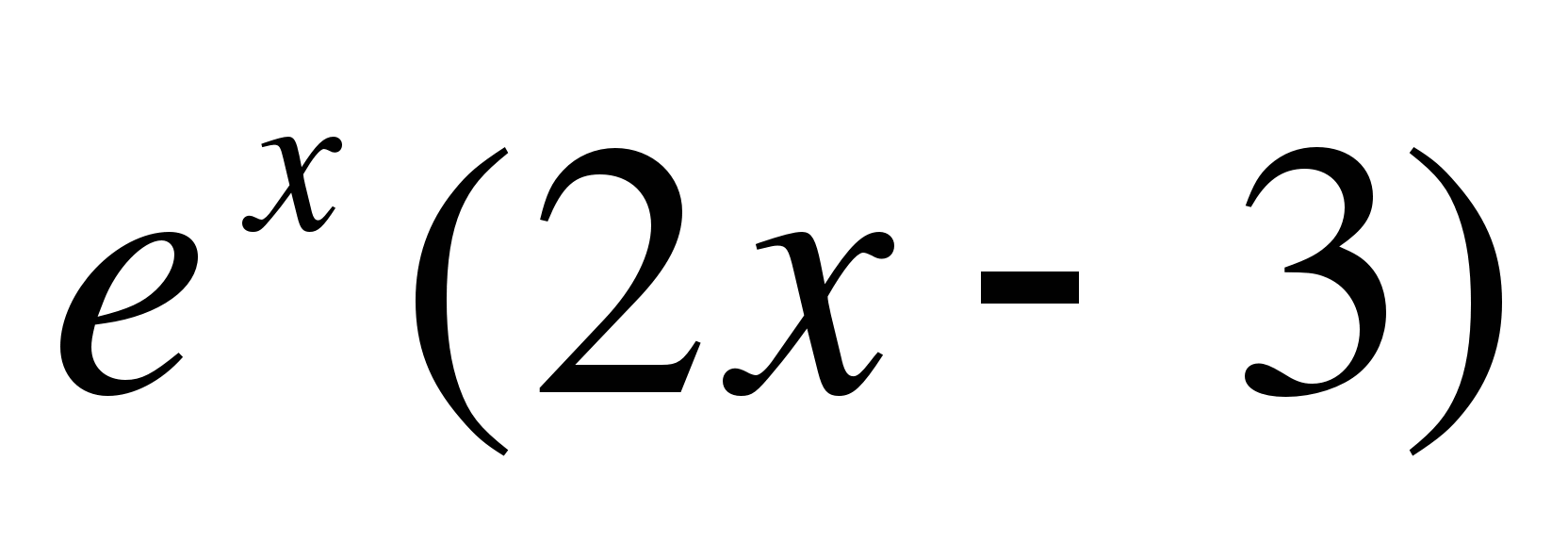 .
.
3. Найдите интервалы возрастания и
убывания функции
f(x) = 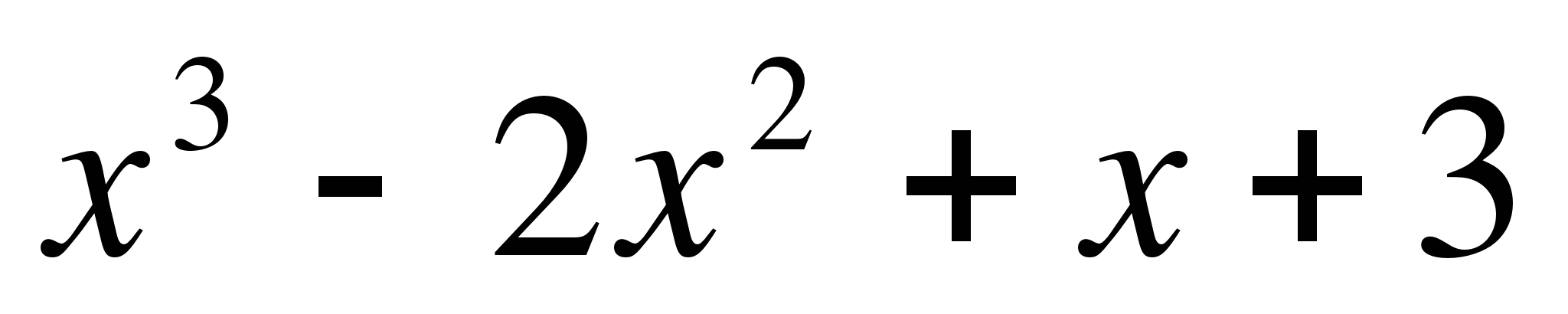 .
.
1. Найдите стационарные точки функции
f(x) = 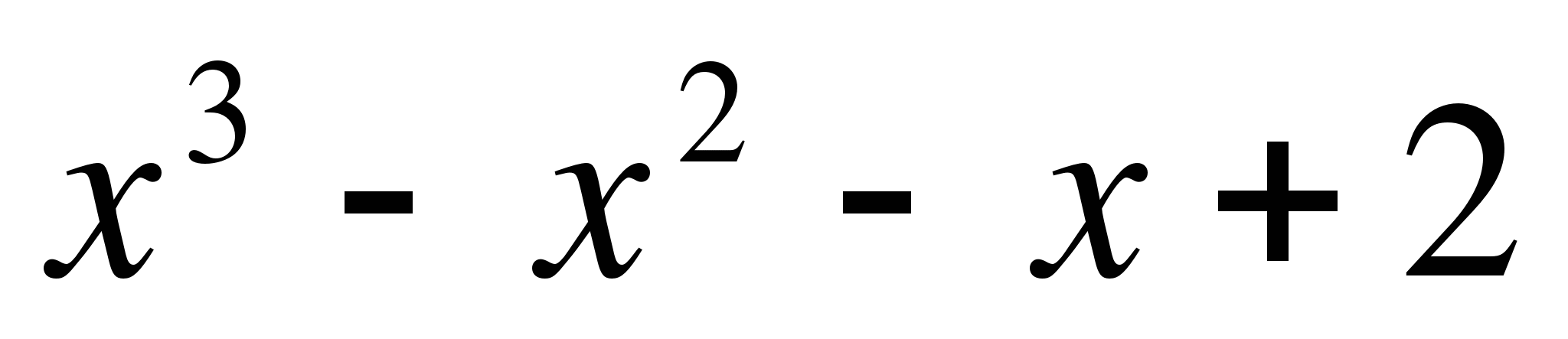 .
.
2. Найдите экстремумы функции:
а) f(x) = 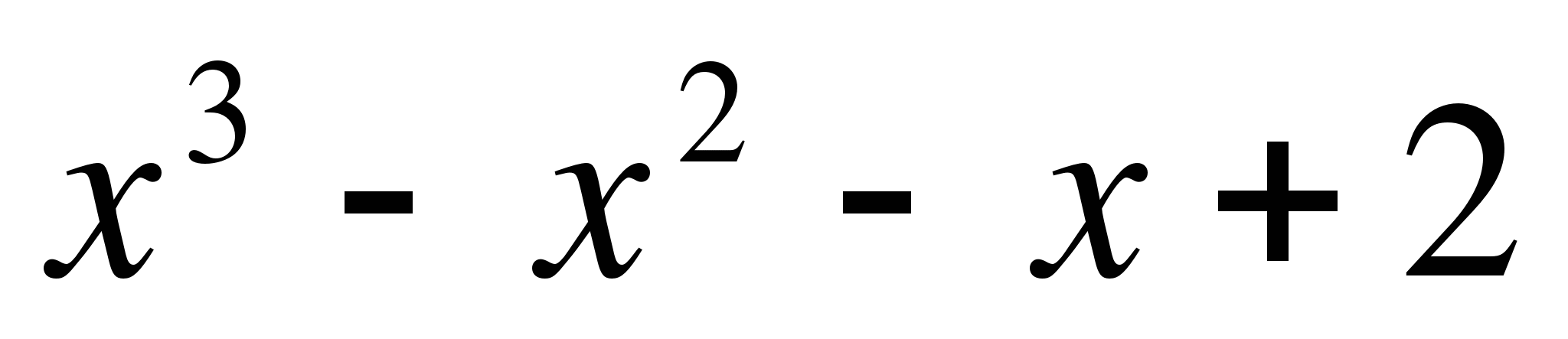 ;
;
б) f(x) = 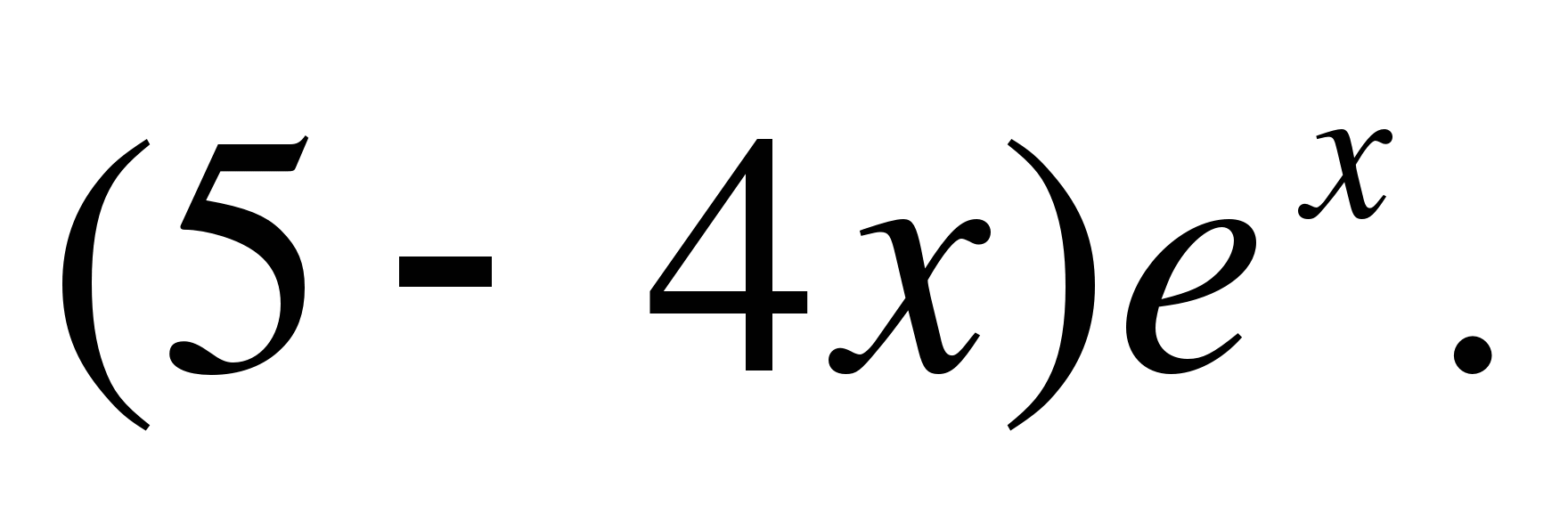 .
.
3. Найдите интервалы возрастания и
убывания функции
f(x) = 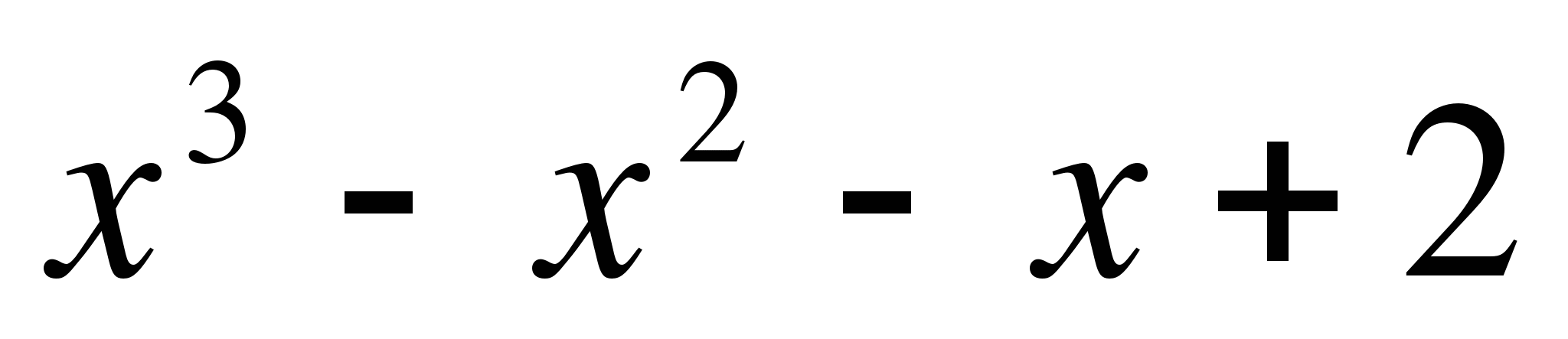 .
.
4. Найдите наибольшее и наименьшее
значения функции f(x) = 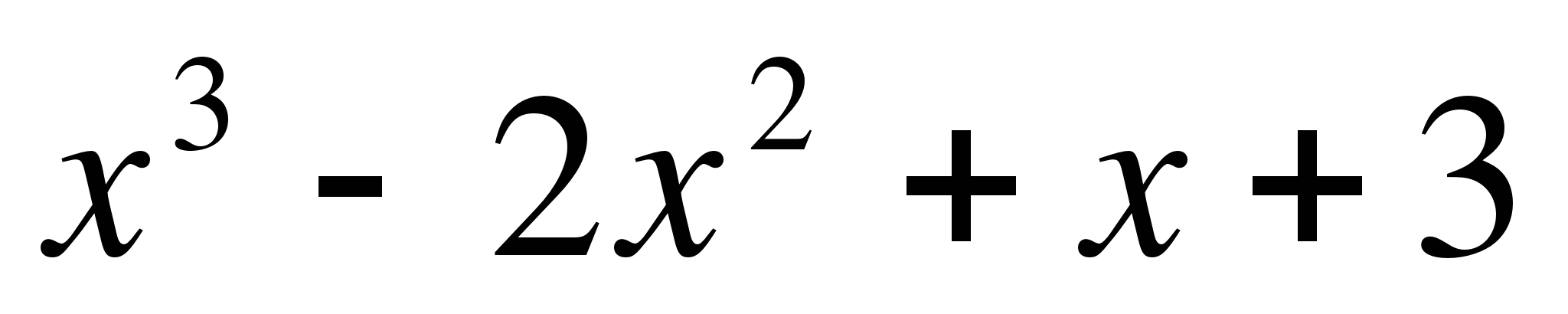
на отрезке 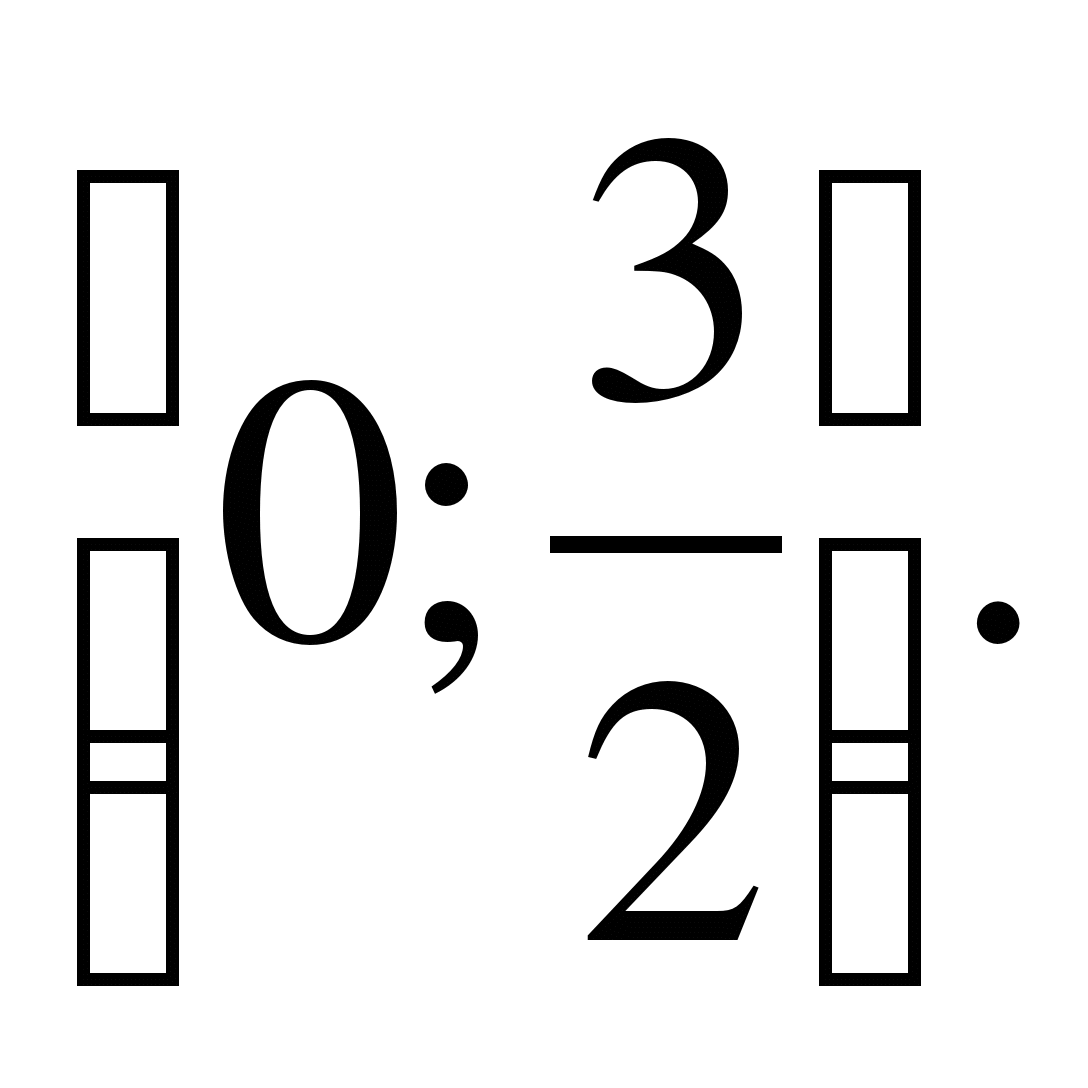
5. Постройте график функции
f(x) = 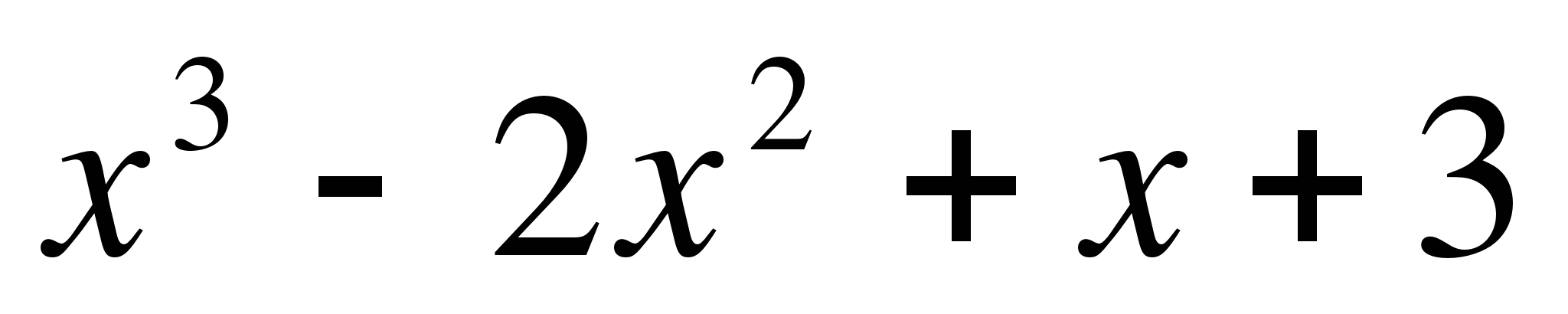 на отрезке
на отрезке 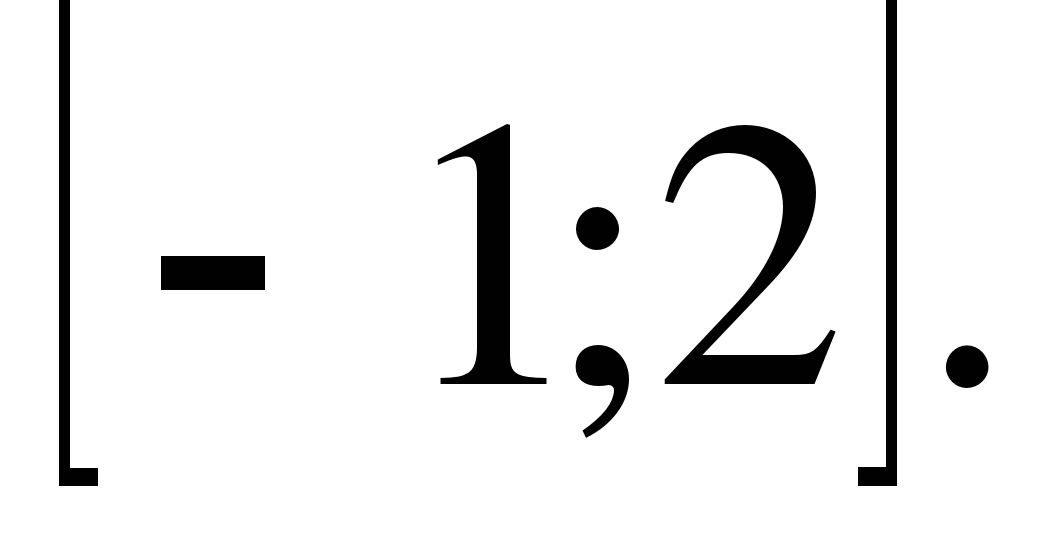
6. Среди прямоугольников, сумма длин
трех сторон у которых равна 20, найдите
прямоугольник наибольшей площади.
4. Найдите наибольшее и наименьшее
значения функции f(x) = 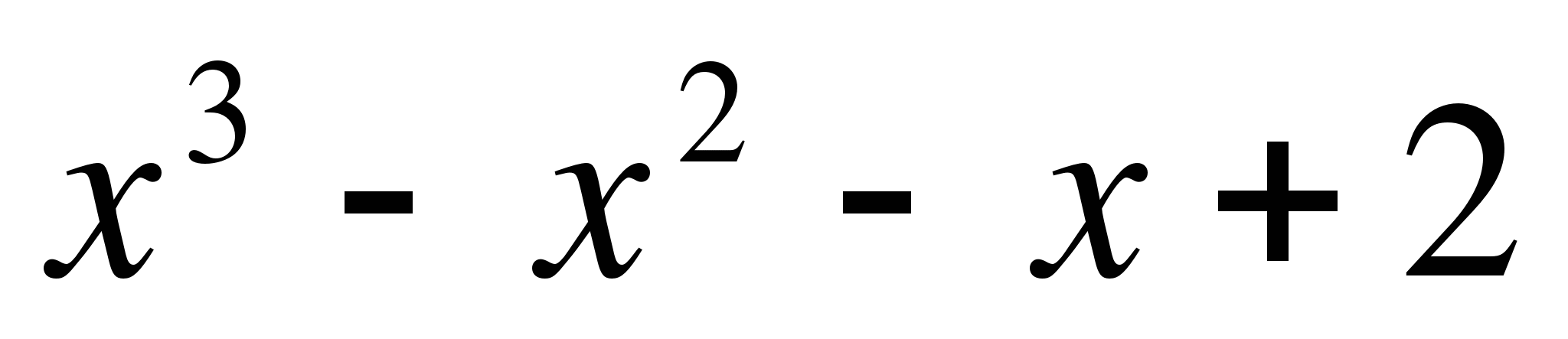
на отрезке 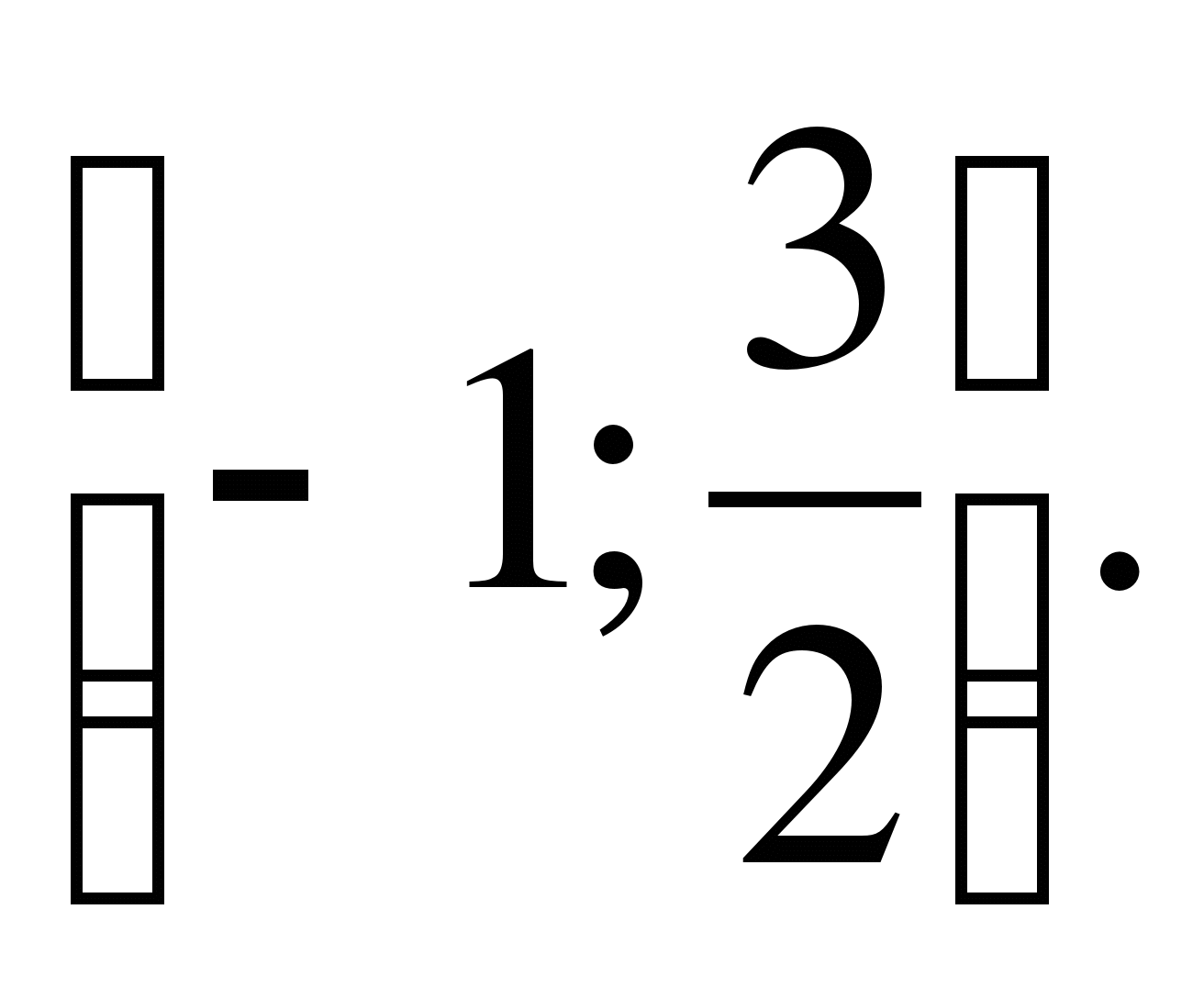
5. Постройте график функции
f(x) = 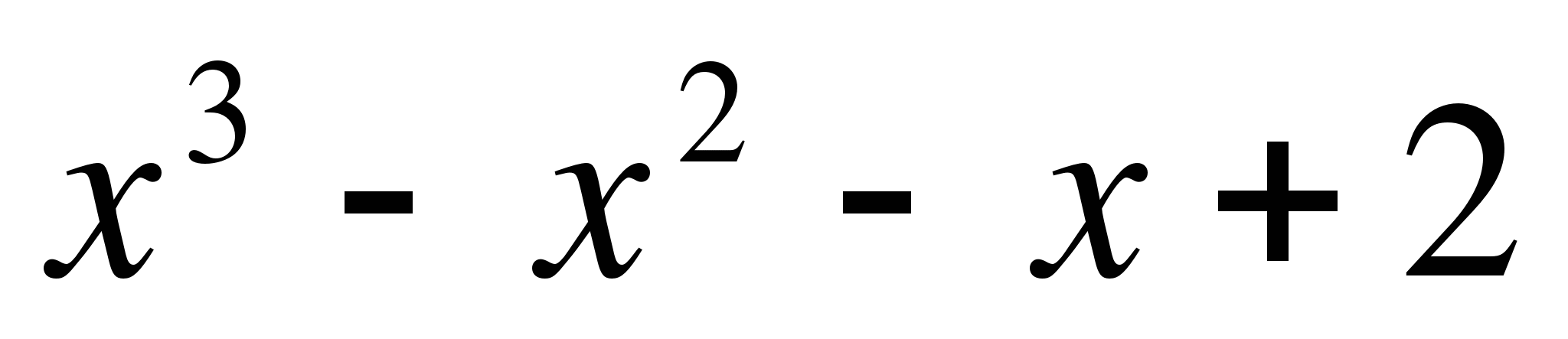 на отрезке
на отрезке 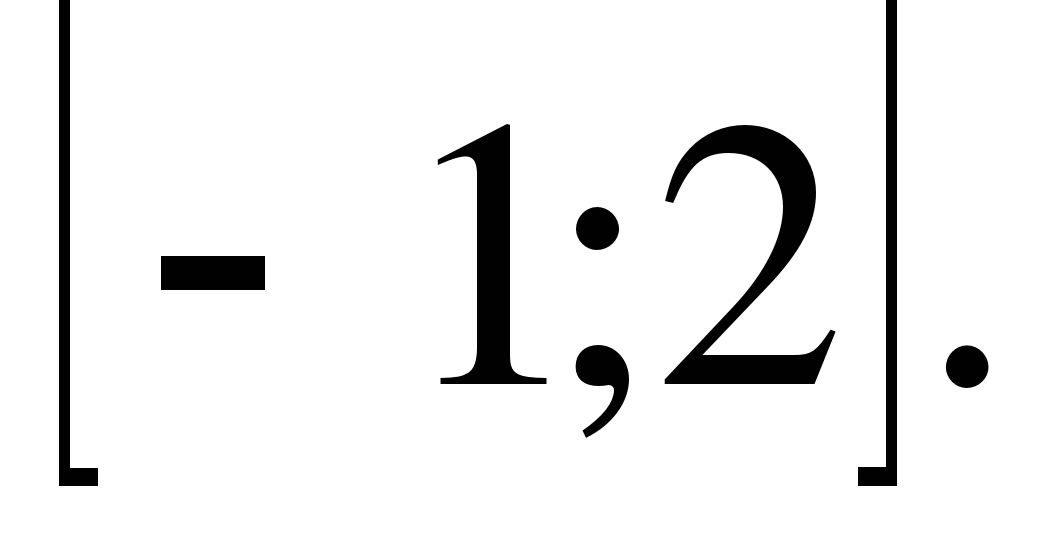
6. Найдите ромб с наибольшей площадью,
если известно, что сумма длин его
диагоналей равна 10.
КОНТРОЛЬНАЯ РАБОТА №10 по теме
«ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ПОСТРОЕНИЮ ГРАФИКОВ ФУНКЦИЙ»
1f(x) = 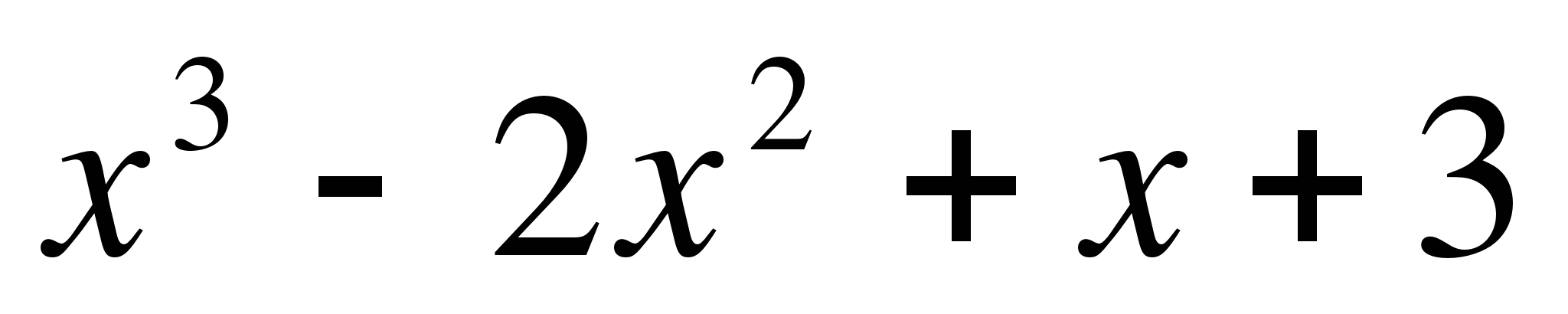 .
.
2. Найдите экстремумы функции:
а) f(x) = 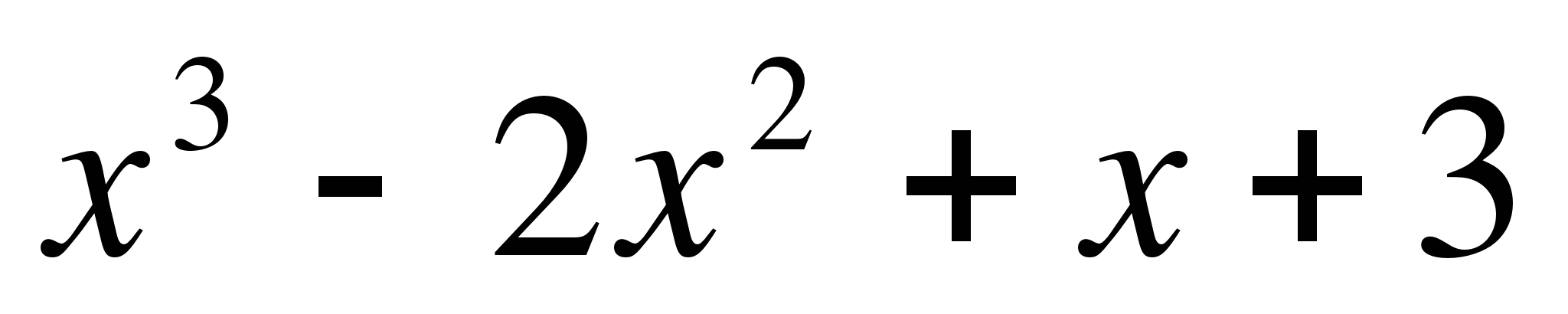 ;
;
б) f(x) = 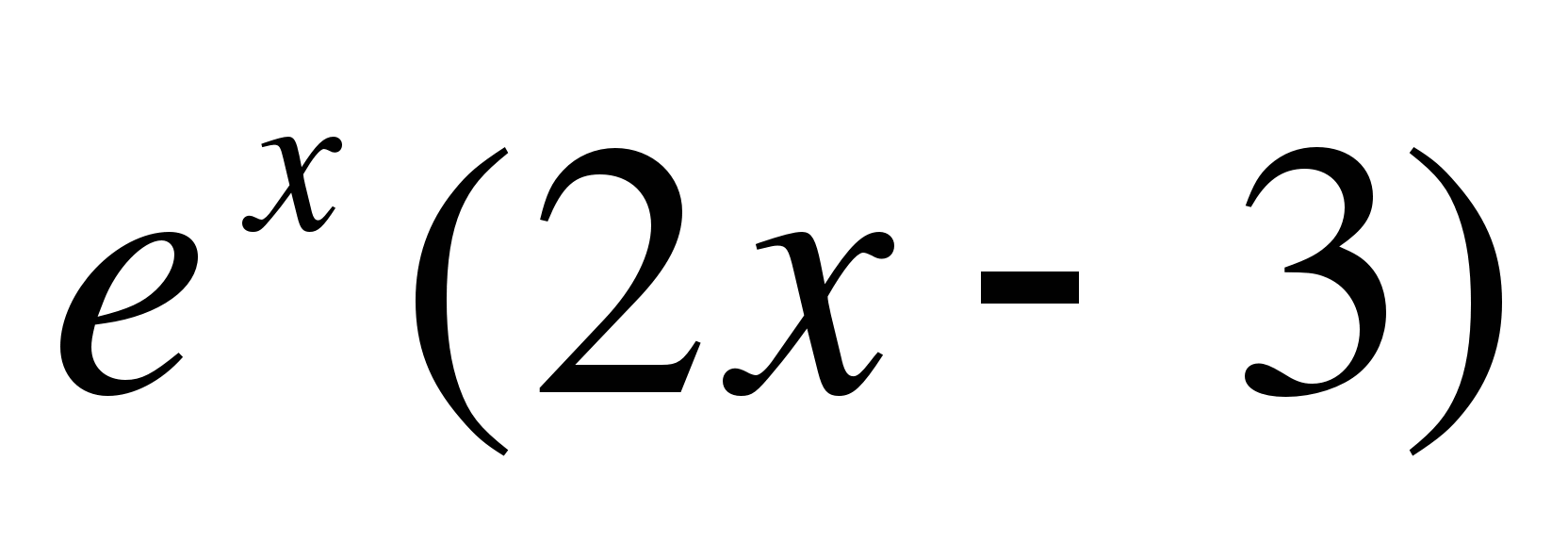 .
.
3. Найдите интервалы возрастания и
убывания функции
f(x) = 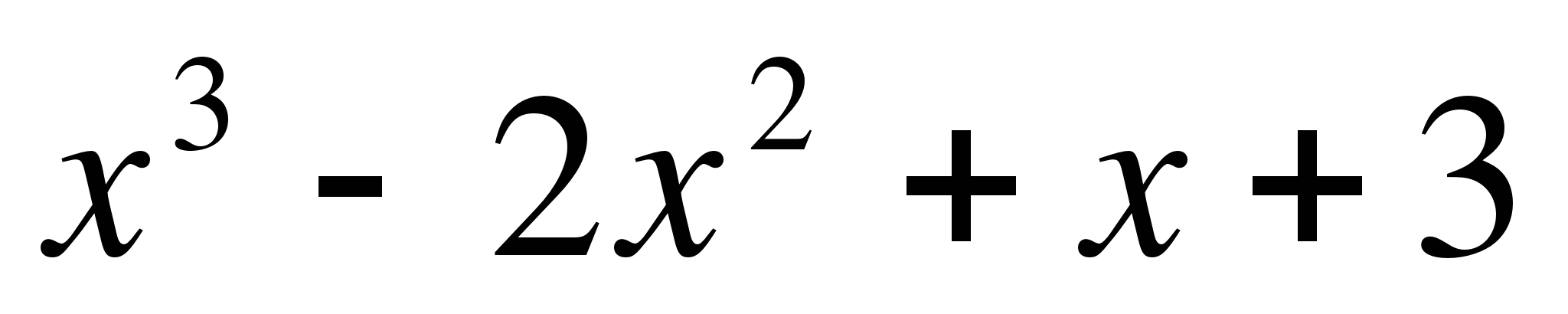 .
.
1. Найдите стационарные точки функции
f(x) = 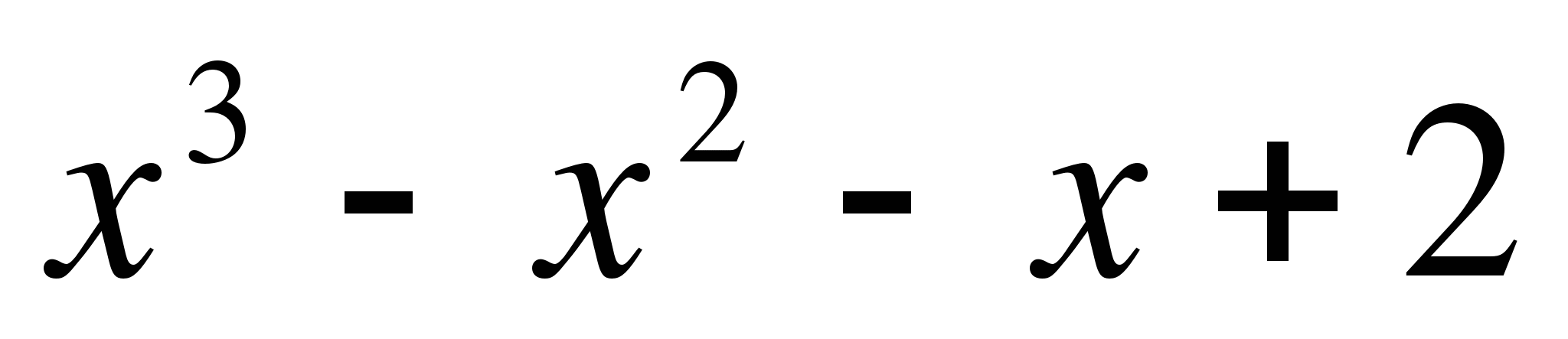 .
.
2. Найдите экстремумы функции:
а) f(x) = 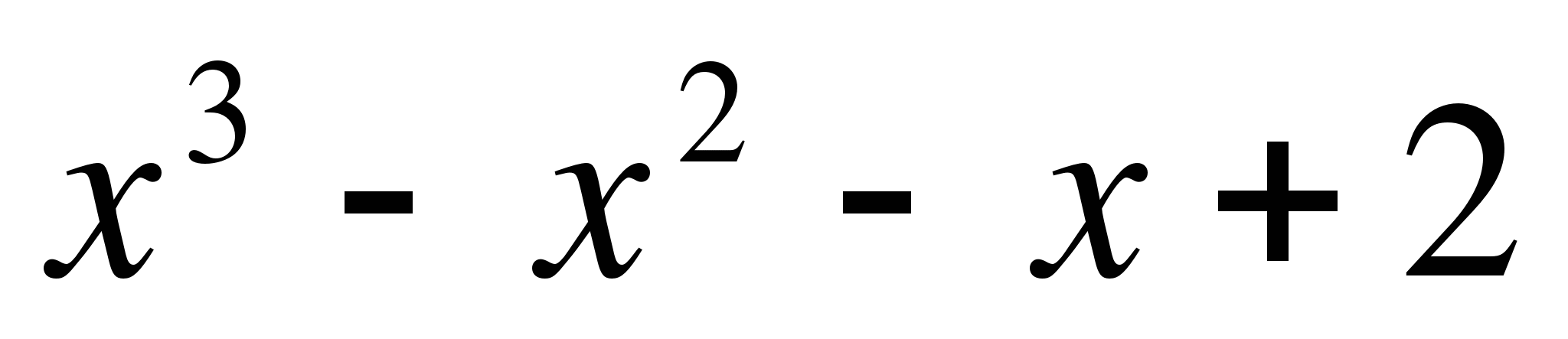 ;
;
б) f(x) = 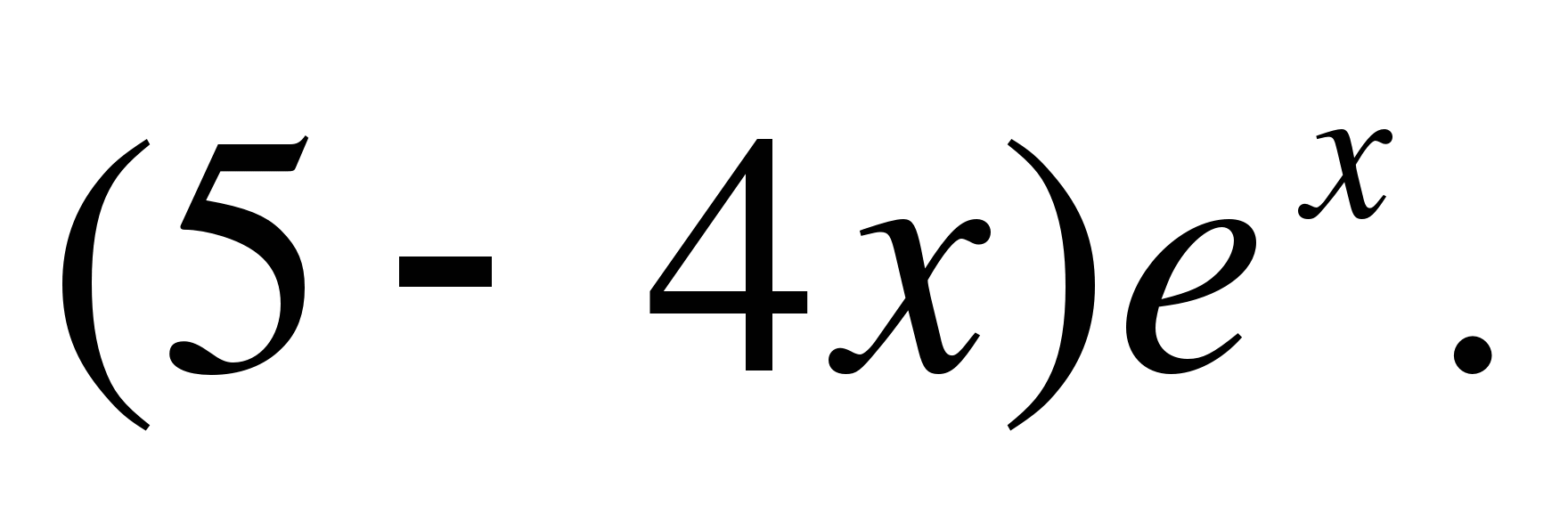 .
.
3. Найдите интервалы возрастания и
убывания функции
f(x) = 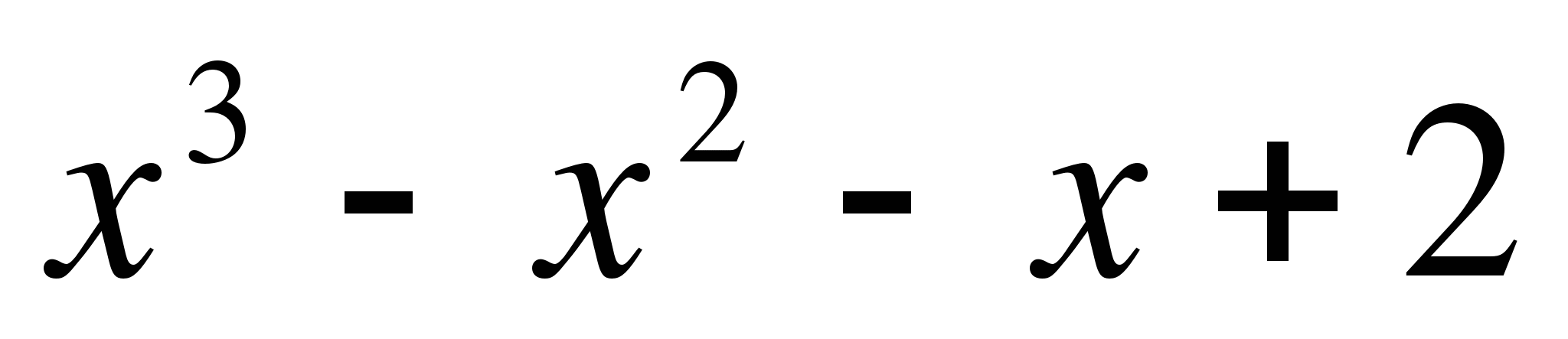 .
.
4. Найдите наибольшее и наименьшее
значения функции f(x) = 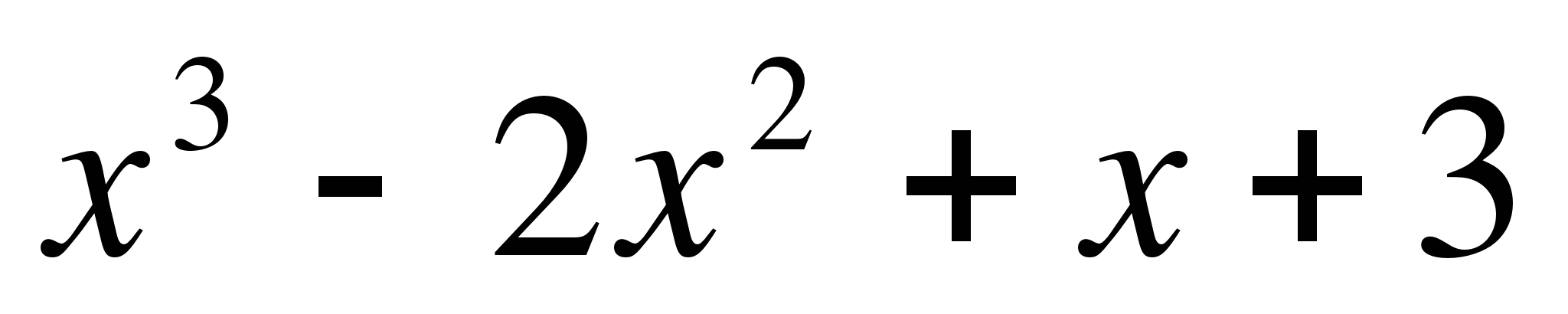
на отрезке 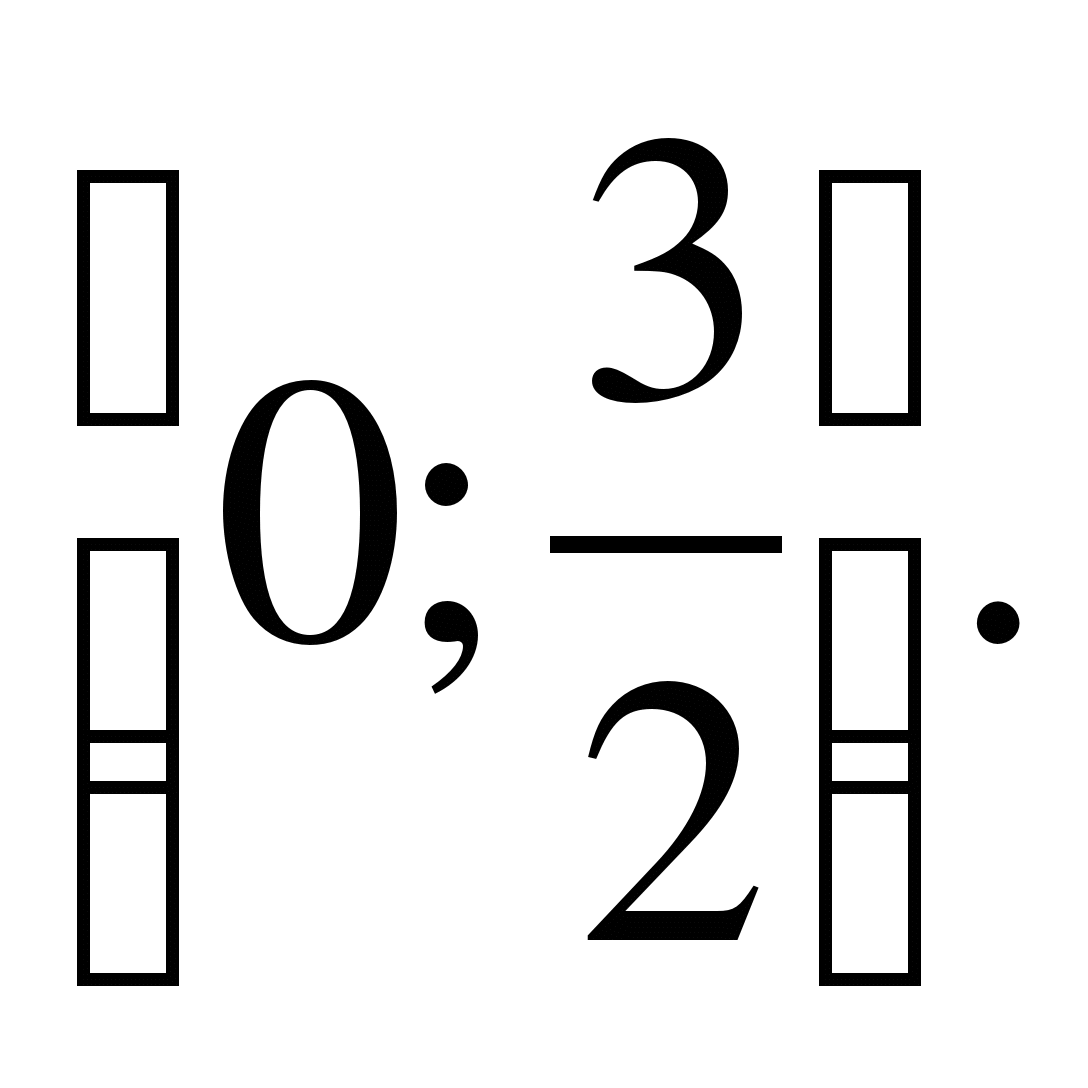
5. Постройте график функции
f(x) = 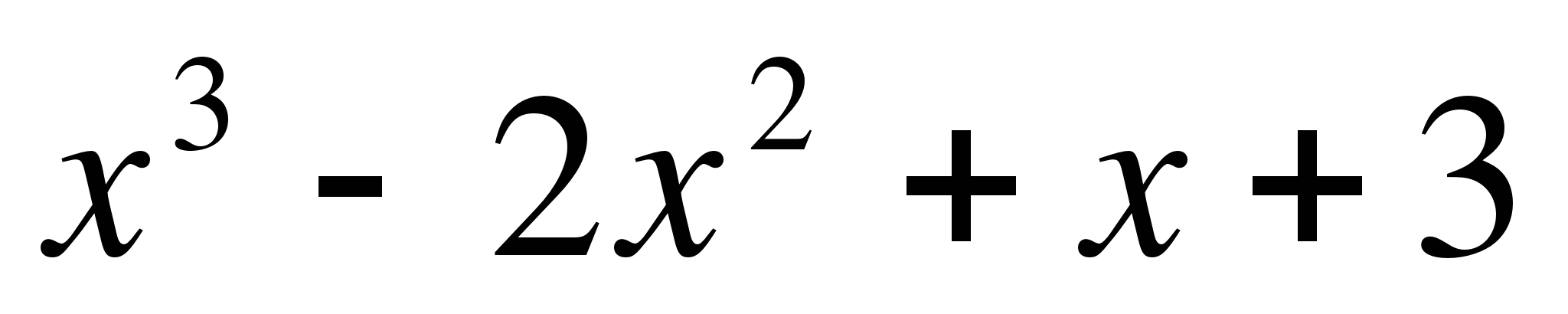 на отрезке
на отрезке 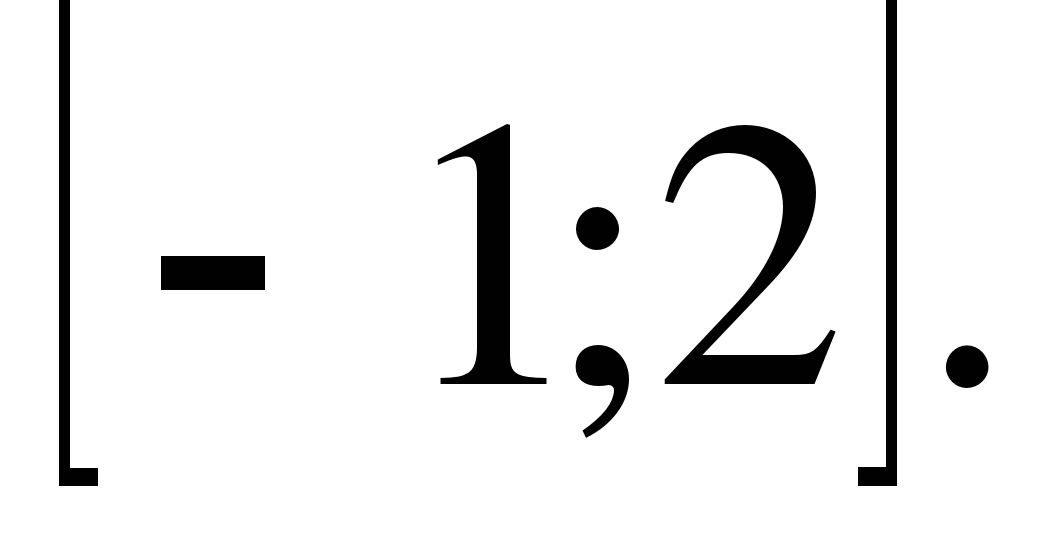
6. Среди прямоугольников, сумма длин
трех сторон у которых равна 20, найдите
прямоугольник наибольшей площади.
4. Найдите наибольшее и наименьшее
значения функции f(x) = 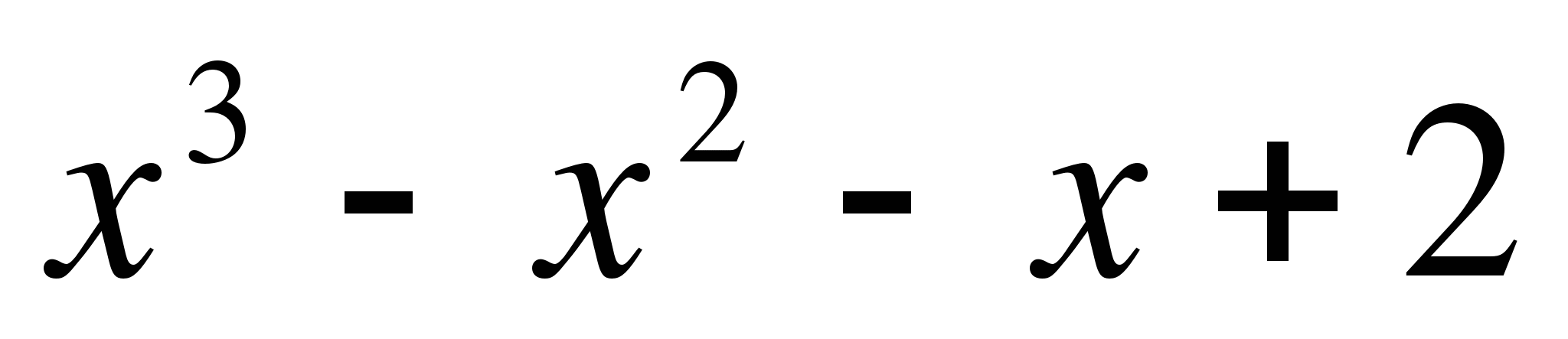
на отрезке 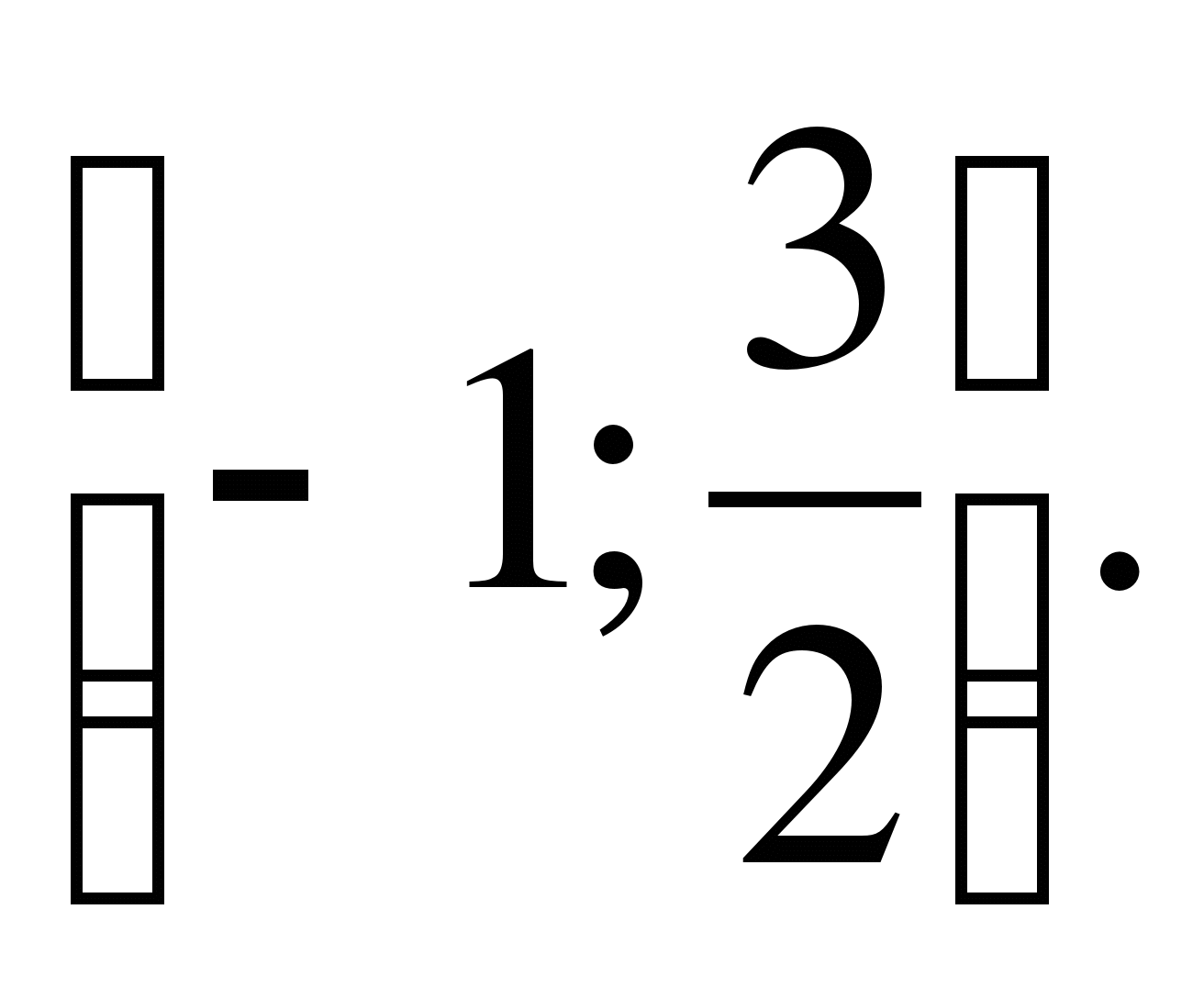
5. Постройте график функции
f(x) = 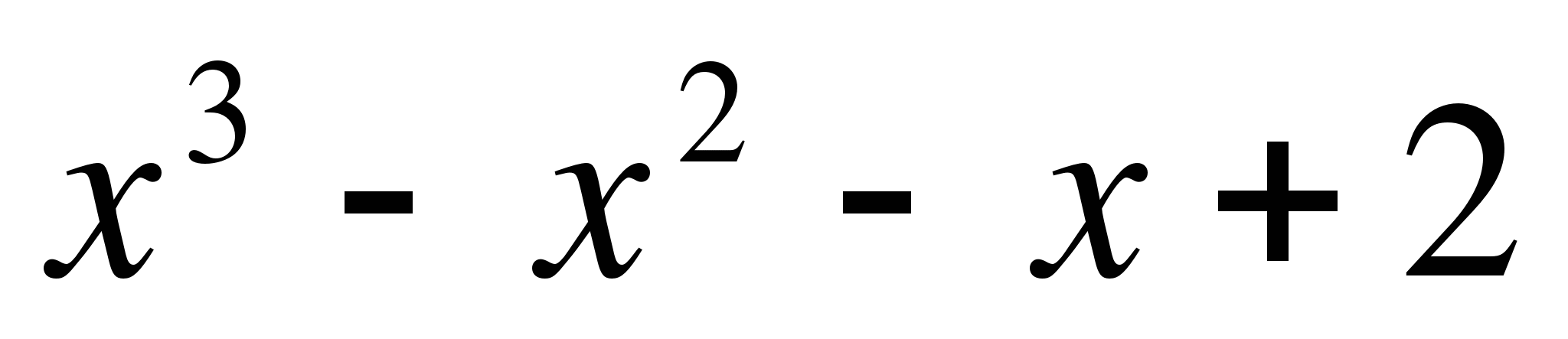 на отрезке
на отрезке 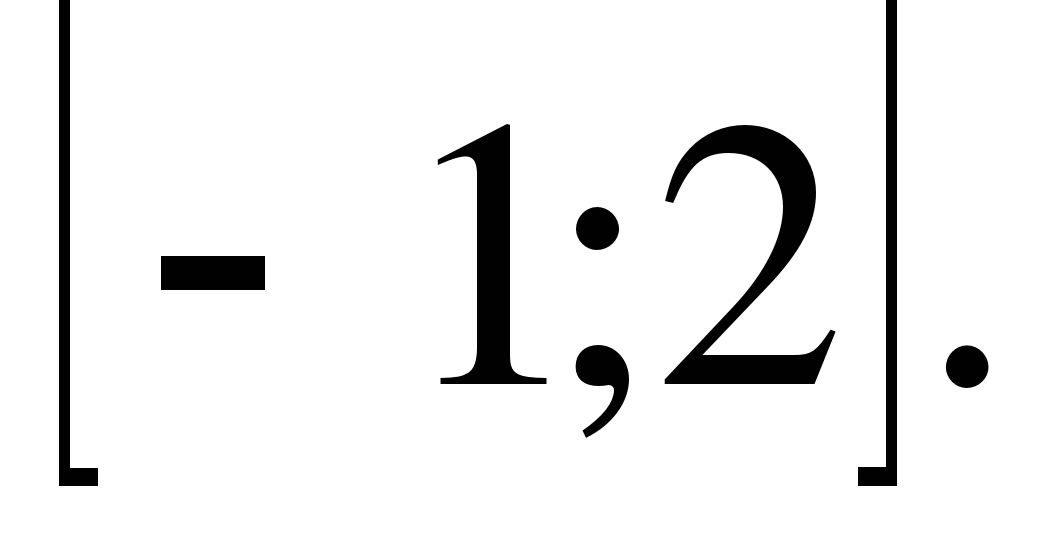
6. Найдите ромб с наибольшей площадью,
если известно, что сумма длин его
диагоналей равна 10.
infourok.ru
Министерство образования Ульяновской области
Областное государственное бюджетное образовательное
учреждение среднего профессионального образования
«Ульяновский электромеханический колледж»
Утверждаю
заместитель директора по учебной работе _________
« ______»________20_____г
Математика
Диагностические материалы контрольной работы
по теме «Производная и ее приложения»
для всех специальностей первого курса
Одобрено на заседании предметно – цикловой комиссии
математических и естественно - научных дисциплин
протокол № от «___» ____20__ г.
Председатель__________________
Разработал
Преподаватель
________Э.С.Статива
Ульяновск
1 Пояснительная записка
Контроль является одной из составляющих учебного процесса, и от его правильной организации на всех этапах обучения в конечном итоге зависит качество знаний студентов.
Контроль выполняет три функции:
- управляет процессом усвоения знаний, дает возможность увидеть ошибки, оценить результаты обучения, осуществить коррекцию знаний, умений и навыков;
- выполняет познавательную мотивацию и стимулирует творческую деятельность;
- является средством обучения и развития.
Структура каждого варианта заданий по форме приближена к структуре действующих форм итоговой проверки математической подготовки учащихся.
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Курс – для студентов первого курса всех специальностей
Форма проведения - контрольная работа
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 4 б
2 задание – 2 б
3 задание – 2 б
4 задание – 1 б
5 задание – 2 б
6 задание – 2 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 20-21 балл
«4» – 13-19 баллов
«3» – 10-12 баллов
«2» -набрано менее 12 баллов.
Контрольная работа по математике
по теме «Производная и ее приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 1.
Часть 1.
1.Найти производные следующих функций:
а) у = б) у =
в) у = г) у =
2.Найти значение производной функции в точке х0=0, если
3. Найти критические точки функции у = 7 + 12х -
4.Закон движения точки по прямой задается формулой , где t – время (в секундах), - отклонение точки в момент времени t (в метрах) от начального положения. Найти скорость и ускорение в момент времени t = 2 сек.
5.Определить промежутки монотонности функции у =
6. Используя данные таблицы, найти точку максимума функции у =
х(;-8 )
-8
( -8;0 )
0
( 0; +
+
0
-
0
+
Часть 2.
7. Составить и решить уравнение=, если .
8.Найти наибольшее и наименьшее значения функции у = х3-9х2+24х-1
на отрезке
9. Найти точки экстремума заданной функции и определить их характер
у =
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 4 б
2 задание – 2 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 1 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 20-21 балл
«4» – 13-19 баллов
«3» – 10-12 баллов
«2» -набрано менее 12 баллов.
Контрольная работа по математике
по теме «Производная и ее приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 2.
Часть 1.
1.Найти производные следующих функций:
а) у = - 3 б) у =
в) у = г) у =
2. Найти значение производной функции в точке х0= -1, если
3. Найти критические точки функции у = 3х3+2х2-7.
4.Закон движения точки по прямой задается формулой , где t – время (в секундах), - отклонение точки в момент времени t (в метрах) от начального положения. Найти скорость и ускорение в момент времени t = 3 сек.
5.Определить промежутки монотонности функции у =
6. Используя данные таблицы, найти точку максимума функции у =
х(;4 )
4
( 4;7)
7
( 7; +
-
0
+
0
-
Часть 2.
7. Составить и решить уравнение=, если .
8.Найти наибольшее и наименьшее значения функции у = х3+3х2-45х-2
на отрезке
9. Найти точки экстремума заданной функции и определить их характер
у =
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 4 б
2 задание – 2 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 1 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 20-21 балл
«4» – 13-19 баллов
«3» – 10-12 баллов
«2» -набрано менее 12 баллов.
Контрольная работа по математике
по теме «Производная и ее приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 3.
Часть 1.
1.Найти производные следующих функций:
а) у = 7 б) у =
в) у = г) у =
2.Найти значение производной функции в точке х0=1, если
3. Найти критические точки функции у = 8 +2-
4.Закон движения точки по прямой задается формулой , где t – время (в секундах), - отклонение точки в момент времени t (в метрах) от начального положения. Найти скорость и ускорение в момент времени t = 1 сек.
5.Определить промежутки монотонности функции у =
6. Используя данные таблицы, найти точку максимума функции у =
х(;-5)
-5
( -5;2)
2
( 2; +
-
0
+
0
-
Часть 2.
7. Составить и решить уравнение=, если .
8.Найти наибольшее и наименьшее значения функции у = х3-9х2+15х-3на отрезке
9. Найти точки экстремума заданной функции и определить их характер
у =
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 4 б
2 задание – 2 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 1 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 20-21 балл
«4» – 13-19 баллов
«3» – 10-12 баллов
«2» -набрано менее 12 баллов.
Контрольная работа по математике
по теме «Производная и ее приложения»
для студентов первого курса всех специальностей
Каждый вариант состоит из двух частей и содержит 9 заданий.
Часть 1 состоит из 6 заданий. Часть 2 состоит из 3 более сложных заданий. При выполнении заданий надо записать полное решение и полный ответ.
Вариант- 4.
Часть 1.
1.Найти производные следующих функций:
а) у = - б) у =
в) у = г) у =
2.Найти значение производной функции в точке х0= 2, если
3. Найти критические точки функции у = х4-8х2
4.Закон движения точки по прямой задается формулой , где t – время (в секундах), - отклонение точки в момент времени t (в метрах) от начального положения. Найти скорость и ускорение в момент времени t = 5 сек.
5.Определить промежутки монотонности функции у=
6. Используя данные таблицы, найти точку максимума функции у =
х(;0)
0
( 0;6)
6
( 6; +
+
0
-
0
+
Часть 2.
7. Составить и решить уравнение=, если .
8.Найти наибольшее и наименьшее значения функции у = х4-8х3+10х2+1
на отрезке
9. Найти точки экстремума заданной функции и определить их характер
у =
Время выполнения: 45 минут
Оценивание заданий: Часть 1. 1задание – 4 б
2 задание – 2 б
3 задание – 2 б
4 задание – 2 б
5 задание – 2 б
6 задание – 1 б
Часть 2. 7 задание – 3 б
8 задание – 3 б
9 задание – 3 б
Примечание: 1.Разрешается пользоваться справочниками и таблицами
Разрешается пользоваться МК
Отметка ставится только на основании правильных ответов; за ошибочные ответы баллы не снимаются
2 Критерии оценки
«5» - 20-21 балл
«4» – 13-19 баллов
«3» – 10-12 баллов
«2» -набрано менее 12 баллов.
infourok.ru