Главная » Контрольная » Контрольная работа по пределам

Контрольная работа по модулю "Понятия функции и пределов функций". Контрольная работа по пределам


контрольная работа №2 1 курс 1 семестр

1

Контрольная работа №2

Задание 67

Найдите пределы последовательностей.

а) б)

в)

Решение

а) Имеем неопределенность типа , чтобы избавиться от нее проведем преобразование выражения:

Разделим числитель и знаменатель на n3:

=

б) Имеем неопределенность типа , чтобы избавиться от нее проведем преобразование выражения:

Разделим числитель и знаменатель на n3:

в) Здесь имеет место неопределенность вида . Преобразуем выражение и воспользуемся вторым замечательным пределом.

Ответ: а) 0; б) ; в) е - 2

Задание 77

Найдите производную заданных функций:

а) б)

Решение

а)

Воспользуемся правилом дифференцирования сложных функций

(vn)' = n vn - 1 v ', где v = 2х3 + x в одном случае и v = - в другомслучае. Получаем:

Воспользуемся правилом дифференцирования сложной функций

(arctg u)′ = -, гдеu =. Получим

Воспользуемся правилом дифференцирования сложной функций

, где :

б)

Воспользуемся правилом дифференцирования сложной функций

, где в одном случае, и- в другом случае. Получим

Ответ: а) ; б)

Задание 87

Найдите предел функции :

1) не пользуясь правилом Лопиталя;

2) используя правило Лопиталя.

Решение

  1. При непосредственной подстановке в выражение значения x = 1 получаем неопределенность. Чтобы избавиться от нее, преобразуем выражение и воспользуемся первым замечательным пределом .

Введем замену переменной:

  1. x = t, x = 1 – t, ,t  0 при х  1.

  1. Так как имеем неопределенность, воспользуемся правилом Лопиталя:

Ответ : 

Задание 97

Дана функция .

1) вычислите все частные производные первого порядка;

2) найдите производную в точке М0 (2; 1; 1) по направлению вектора

;

3) найдите

Решение

1) Находим частные производные функции u= u(x,у):

2) Находим производную по направлению вектора :

Находим направляющие косинусы вектора :

cosα =

cosβ =

cosγ =

Находим значения частных производных в точке М0:

Находим производную по направлению вектора в точке М0 (2; 1; 1):

3) Находим градиент

Ответ: 1)

2) ; 3);

Задание 107

Дана функция . Вычислите значение ее частной производной четвертогопорядка в точке

Решение

Найдем частные производные:

Вычислим значение производной в точке:

Ответ: 36

Задание 107

Найдите неопределенные интегралы:

а) б)в)г)

Решение

а)Преобразуем подинтегральное выражение

Сделаем замену переменной: t = 2x, dt = 2dx, dx = dt/2.

Вернемся к переменной х:

б)

Найдем искомый интеграл методом замены переменной. Введем новую переменную t = sin5x. Тогда dt = 5cos5 dx, cos5 dx = dt/5 Имеем

Вернемся к переменной х:

в)

Применим метод интегрирования по частям, для чего воспользуемся формулой:

Положим u = =3х2 + 2х

Тогда = (3х2 + 2х )  =6x + 2; du = (6x + 2)dх = 2(3x + 1)

Повторным интегрированием по частям найдем интеграл .

3х + 1 = u, du 3dx

Тогда искомый интеграл

=

г)

Умножим числитель и знаменатель на сопряженное знаменателю выражение

:

Полученный интеграл представим в виде двух интегралов:

= ==

Аналогично найдем

= =

Получили

Ответ: а) ; б); в);

г)

studfiles.net

Практика24.Контрольная_работа_на_тему_Предел функции

Практика 24. Контрольная работа на тему "Предел функции\

24.1.Теоретическая часть

Вариант 1.

Сформулировать определения

1. lim f(x) = Aпо Гейне;

x!a

2.lim f(x) = 1 ïî Êîøè;

x!+1

3.f(x) ограниченная функция;

4.Критерий Коши существования предела функции в точке. Условие Коши.

Вариант 2.

Сформулировать определения

1.f(x) не имеет предела приx ! a по Гейне;

2.f(x) бесконечно малая функция приx ! 1 ïî Êîøè;

3.f(x) неубывающая функция;

4.sup f(x) = M.

x2X

Вариант 3.

Сформулировать определения

1.f(x) имеет предел приx ! +1 по Гейне;

2.f(x) бесконечно большая функция приx ! a 0 ïî Êîøè;

3.f(x) неограниченная на множествеD;

4.(x) = o ( (x)) ïðè x ! a.

Вариант 4. Сформулировать определения

1.lim f(x) = b 0 ïî Êîøè;

x!a+0

2.f(x) невозрастающая функция;

3.inf f(x) = m;

x2X

4. f(x) èg(x) функции одного порядка приx ! a.

О. А. Кузенков, Е. А. Рябова

2

 

 

24.2.Вариант 1.

Вычислить пределы:

 

 

 

 

2n p

 

 

 

 

 

;

1.

lim

 

4n2 1

 

 

 

 

 

 

 

 

 

 

 

 

n!1

 

 

pn2 + 3 n

2.

lim

 

 

n 10

 

 

3n+1 ;

n + 1

 

 

n!1

 

 

 

 

 

3.

lim

 

 

 

x2 2x + 1

 

 

x3 x2 x + 1

 

x!1+0

 

lim

p

 

p3

 

 

 

;

4.

cos x

cos x

 

 

 

 

 

 

 

x!0

 

 

 

sin2 x

 

 

 

 

 

5.

lim

tg( (1 + x=2))

:

 

 

x!0

 

 

ln(1 + x)

6. Нарисовать пример графика функции, удовлетворяющей предельному равенству

lim f(x) = 2 + 0:

x! 1

На рисунке отметить " и окрестности, дать определение по Коши.

7. Доказать по определению lim

2x

= 2 + 0:

1 + x

x! 1

 

О. А. Кузенков, Е. А. Рябова

3

 

 

24.3.Вариант 2.

Вычислить пределы:

pp

1.

lim

 

 

 

 

n2 + 1

 

n2 1

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n!1

 

 

pn2 + n n 1

 

 

 

 

 

 

n2

+ n

 

n

 

n!1

 

 

 

 

 

 

2n2

5n

 

 

2.

lim

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

sin x

 

 

 

 

 

 

3.

lim

 

 

 

1=(x a)

 

 

 

 

 

 

 

 

sin a

 

 

 

 

 

;

 

 

x!a

 

 

 

 

 

pp

4. lim

3 1 + 3x4 1 + x

;

 

 

 

x!+0

1 p1 x=2

5. lim

e4x1

x!0 sin( (x=2 + 1))

6. Нарисовать пример графика функции, удовлетворяющей предельному равенству

lim f(x) = 1 0:

x! 0

На рисунке отметить " и окрестности, дать определение по Коши.

7. Доказать по определению xlim0

2x = 1 0:

!

 

studfiles.net

Контрольная работа по модулью "Понятия функции и пределов функций"

Дата__________________________

ФИО__________________________

Вариант 1 Группа________________________

1. Переменная х называется -

  1. независимой переменной или аргументом

  2. функцией

  3. значением функции

  4. зависимой переменной функции

2. Какое из понятий лишнее?

a)монотонность b)четность и нечетность c)ограниченность d)независимость

3. Способы задания функции:

  1. табличный, аналитический, графический

  2. алгебраический, геометрический

  3. аналитический, не аналитический

  4. графический, не графический

4. Вычислите значение функции у = 3х - 5, если х = - 2.

a)1 b) -11 c) -1 d) 10

5. Как называется график функции у = 3х + 7?

a)парабола b)гипербола c)прямая d)косая

6. Найдите область определения функции у = 7/(2х +6) - 5

  1. множество всех чисел

  2. множество всех чисел, кроме 0

  3. множество всех чисел, кроме -3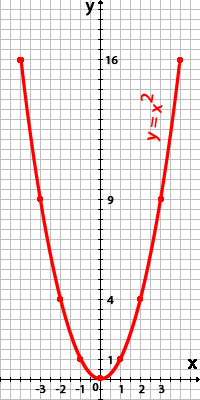hello_html_5b77e631.gif

  4. нет области определения

7. Как называется график функции у=х2

a) парабола

b) гипербола

c) прямая

d) горизонтальная

8. На какой из этих графиков показано горизонтальная асимптота графика функции у = f(х).

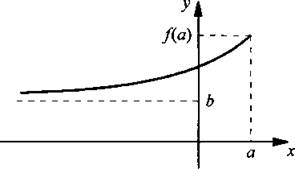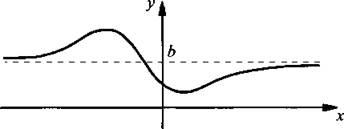
а а)hello_html_3906a3bb.jpgb)hello_html_2a897768.pngc) hello_html_124c8f91.pngd) hello_html_2991e1a.jpg

9. На какой из этих графиков показано вертикальная асимптота графика функции у = f(х).

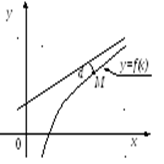а)hello_html_3906a3bb.jpgb)hello_html_2a897768.pngc) hello_html_124c8f91.pngd) hello_html_2991e1a.jpg

10. На какой из этих графиков показано наклонная асимптота графика функции у = f(х).

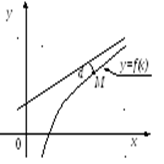а)hello_html_3906a3bb.jpgb)hello_html_2a897768.pngc) hello_html_124c8f91.pngd) hello_html_2991e1a.jpg

11. Переменная величина y называется числовой функцией переменной величины x, если …

  1. каждому возможному числовому значению величины y ставится в соответствие по какому-нибудь правилу или закону единственное числовое значение величины x

  2. каждому возможному числовому значению величины x ставится в соответствие по какому-нибудь правилу или закону единственное числовое значение величины y

  3. каждому возможному числовому значению величины x ставится в соответствие по какому-нибудь правилу или закону единственное числовое значение множества Х

  4. каждому возможному числовому значению величины у ставится в соответствие по какому-нибудь правилу или закону единственное числовое значение множества У

12.Произведение бесконечно большой и малой величин представляет собой…

  1. ситуацию неопределенности

  2. бесконечно малую величину

  3. ограниченную функцию

  4. бесконечно большую величину

13. Какое из понятий лишнее?

a)предел b)непрерывность c)асимптота d)дискриминант

14.Отметьте верные утверждения

  1. функция называется бесконечно малой величиной, если ее предел равен нулю

  2. односторонние пределы в одной и той же точке всегда равны друг другу

  3. разность бесконечно большой величины и ограниченной функции есть бесконечно малая величина

  4. если функция монотонна и ограничена, то она не имеет предел

15.Если функция f(x) является бесконечно большой величиной, то функция 1/f(x) является…

  1. бесконечно малой величиной

  2. не имеет предел

  3. бесконечно большой величиной

  4. никогда не имеет смысла

16.Предел произведения функций равен…

  1. бесконечно малой величине

  2. произведению пределов этих функций

  3. бесконечно большой величине

  4. это ситуация неопределенности

17.Предел частного двух функций равен…

  1. частному пределов этих функций

  2. бесконечно малой величине

  3. бесконечно большой величине

  4. это ситуация неопределенности

18.Если функция непрерывна в точке, то…

infourok.ru

Вычисление пределов

Санкт-Петербургское государственное образовательное учреждение среднего профессионального образования

Согласовано: Предметной (цикловой) комиссией Председатель ____________/_____________ (Подпись) (ФИО) «_____» __________200__г.

Утверждено:

Заместителем директора по УР

__________/______________/ (Подпись) (ФИО)  «____»________200___г.

Указания по проведению Специальность __080110, 080112, 080501__

Разработал преподаватель

_____________(___................. __) (Подпись) (ФИО) «_______» _________________200___г. Цель работы: 1. Формировать умения и навыки вычисления пределов 2.     Формировать умения и навыки самостоятельного умственного труда 3.     Прививать умения и навыки работы со справочным материалом 4. Определить уровень остаточных знаний студентов по данной теме Перечень справочной литературы : 1.     Богомолов Н.В. «Практические занятия по математике», М: Высшая школа, 2004 2.     Письменный Д. «Конспект лекций по высшей математике», ч.1., Москва, Айрис-Пресс, 2004 3.     Шипачев В.С. «Задачник по высшей математике», М: Высшая школа, 2003 4.     Выгодский М.Я. «Справочник по высшей математике», Росткнига, 2001 Краткие теоретические сведения: Предел последовательности Определение. Число  называется пределом последовательности , если для любого положительно  го числа найдется такое натуральное число , что при всех > выполняется неравенство Пишут: Графически это выглядит так: n-  Т.е. элемент  находится в - окрестности точки а. При этом последовательности  называется сходящейся, в противном случае – расходящейся. Основные свойства сходящихся последовательностей 1)Сходящаяся последовательность ограничена. 2)Пусть , , тогда а)  б)  в) 3)Если  и для всех  выполняется неравенства , то . 4) Если  и последовательность {уn} - ограниченная, то   Бесконечно большие и бесконечно малые функции Определение. Функция  называется бесконечно малой при , если Например: 1)  при  б. м. ф. т.к.  2)  при  б. м. ф. т. к Определение. Функция  называется бесконечно большой при , если ,  или Например,  есть б. б. Ф при ;  если б. б. ф. при  действительно  и Теорема (о связи между функций, ее приделом и бесконечно малой функцией). Если функция  имеет придел, равный , то ее можно представить как сумму числа  и бесконечно малой функции , т.е. если Теорема (обратная). Если функцию  можно представить в виде суммы числа А и б.м.ф. (x), то число А является пределом функции, т.е если , то Например, требуется вычислить . Представим числитель и знаменатель в виде суммы числа и б.м.ф. Функции  при  есть б.м.ф. таким образом Основные теоремы о пределах Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов: Теорема справедлива для алгебраической суммы любого конечного числа функций. Теорема 2. Функция может иметь только один предел при . Теорема 3. Предел произведения двух функций равен произведению их пределов: . Следствие 1. Постоянный множитель можно выносить за знак предела: Следствие 2. Предел степени с натуральным показателем равен той же степени предела: . Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю. Примеры: 1)== == === 2) = = 3) Первый замечательный предел Второй замечательный предел  или Примеры: Вычислить: 1) . 2) . 3) 4) ===№2. Найти пределы:    №3. Найти пределы: Порядок проведения работы: 1.                Используя теоретические сведения выполнить предложенное преподавателем задание 2.                Соответствующим образом оформить работу
Лист 1. Практическая работа по теме «Вычисление пределов» Выполнил:__________ (ФИО) группа:_____________ Проверил:__________ Оценка:____________ Лист 2. № примера Решение: Ответ:
Оформление работы:

www.coolreferat.com

Смотрите также