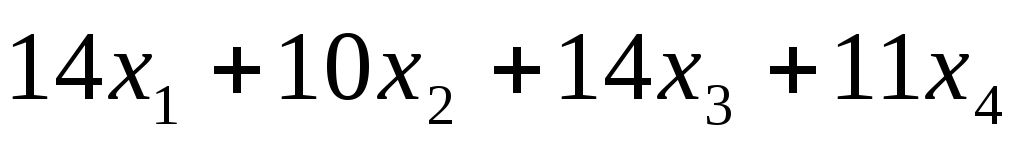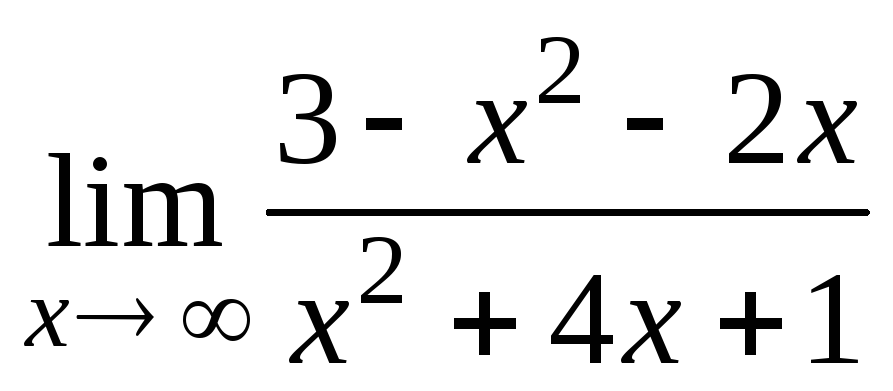Контрольная работа по теме "Комбинаторика". Контрольная работа по комбинаторике
Контрольная работа по комбинаторике
Контрольная работа по теме «Комбинаторика»
I вариант
Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков?
Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
Вычислить: 6! – 5!
II вариант
Сколькими способами могут встать в очередь в билетную кассу 3 человека?
Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
Сколькими способами один почтальон может разнести 7 писем по семи адресам.
Вычислите: 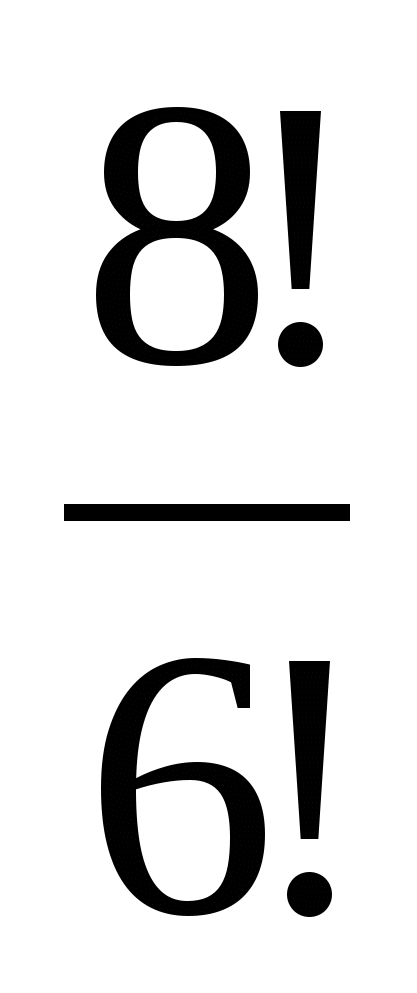
Ответы
№ задания
I вариант
II вариант
1
60480
6
2
3
1140
3
120
30
4
253
5040
5
600
56
Контрольная работа по теме «Комбинаторика»
I вариант
1. Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков?
2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
4. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
5. Вычислить: 6! – 5!
Контрольная работа по теме «Комбинаторика»
I вариант
1. Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков?
2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
4. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
5. Вычислить: 6! – 5!
Контрольная работа по теме «Комбинаторика»
II вариант
1. Сколькими способами могут встать в очередь в билетную кассу 3 человека?
2. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
4. Сколькими способами один почтальон может разнести 7 писем по семи адресам.
5. Вычислите: 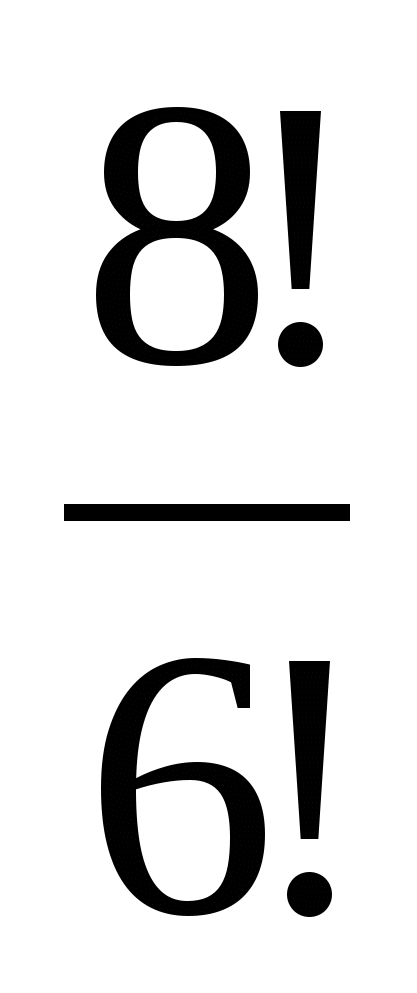
Контрольная работа по теме «Комбинаторика»
II вариант
1. Сколькими способами могут встать в очередь в билетную кассу 3 человека?
2. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
4. Сколькими способами один почтальон может разнести 7 писем по семи адресам.
5. Вычислите: 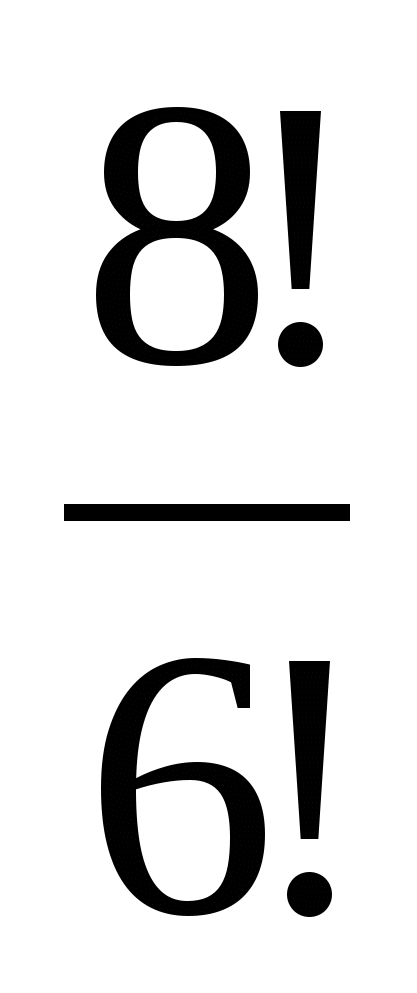
Контрольная работа по теме «Комбинаторика»
II вариант
1. Сколькими способами могут встать в очередь в билетную кассу 3 человека?
2. Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
4. Сколькими способами один почтальон может разнести 7 писем по семи адресам.
5. Вычислите: 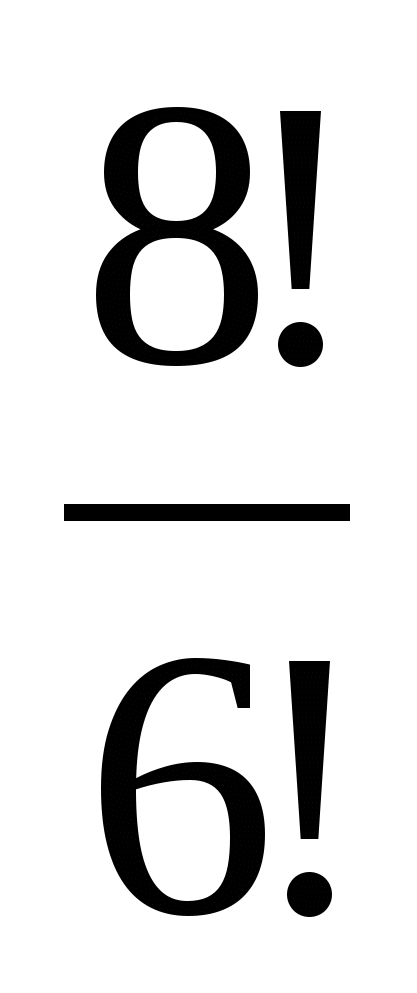
Контрольная работа по теме «Комбинаторика»
I вариант
1. Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков?
2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
3. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
4. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
5. Вычислить: 6! – 5!
infourok.ru
Домашняя контрольная работа по разделу 4 « Комбинаторика»
(номер варианта соответствует последней цифре номера в списке группы)
На день благодарения было решено подать жареную индейку. Для маринада можно использовать одну из четырех видов острых приправ или одну из двух видов пряных. Сколькими способами можно приготовить маринад?
В цветочный магазин завезли пять сортов роз, четыре сорта хризантем, герберы и два сорта лилий. Сколькими способами можно составить букет из этих цветов (каждый цветок может быть только одного сорта)?
В сериале «Зачарованные» Прю обладает двумя, а Пайпер и Фиби тремя волшебными силами, способными уничтожить демона. Сколькими способами они могут сделать это?
В магазине есть шесть фасонов кофт, подходящих к четырем фасонам брюк. Сколько можно составить костюмов?
Женщина в парикмахерской попросила сделать ей колорирование, соответствующее году огненной собаки. Ей предложили один из трех тонов красной краски и второй цвет на выбор из черного, темно-каштанового или светло-каштанового. Из скольких вариантов она может выбрать?
Новая фирма объявила набор сотрудников на конкурсной основе. На должность бухгалтера отобрали четыре человека, программиста – два человека, экономиста и юриста – три человека, секретаря – пять человек. Остальные должности определились однозначно. Сколькими способами можно набрать штат?
В торговой лавке продаются четыре вида матрешек, лапти трех размеров, шестнадцать видов брелоков с изображениями достопримечательностей России и стеклянный шар с мини-Кремлем внутри. Сколькими способами иностранный турист может выбрать себе один сувенир?
К кухонному гарнитуру можно подобрать семь видов обоев, четыре вида плитки и три цвета пластика. Сколькими способами можно сделать ремонт на кухне: а) используя один из материалов; б) сочетая обои и плитку; в) сочетая плитку и пластик?
В ресторане есть три сорта грибов и семь видов сыров. Сколькими способами можно приготовить жульен, если остальные ингредиенты неизменны?
К выпускному на те деньги, которые есть у Насти, на прокат можно взять либо один из двух наборов бижутерии, либо одно из трех колье, либо одну из пяти вечерних сумочек. Сколькими способами можно выбрать один аксессуар на Настины деньги?
Из 32 школьников 12 занимается волейболом, 15 - баскетболом, 8 - и волейболом, и баскетболом. Сколько учеников не занимается в этих секциях?
В классе 20 человек. На физкультуру в спортивный зал ходят 14 человек, а в спортивный зал и бассейн ходят 18 человек. Сколько человек ходят только в бассейн?
В аквариуме «Зимнего сада» живут 52 рыбки. 44 из них едят живой корм, 33 – сушеный, а 27 рыбок едят и тот, и другой корм. Остальные питаются свежими растениями. Сколько рыбок поглощают только свежие растения?
В школе плавания учатся 250 человек. Из них 170 человек плавают брасом, 92 человека – кролем, а 70 человек владеют и тем, и другим стилем. Сколько человек еще не умеют плавать?
В показе прет-а-порте коллекции «Gucci» участвовали 105 манекенщиц. 61 девушка была в зеленом, 52 – в красном, 55 – в белом; 42 манекенщицы были в зеленом и красном, 45 – в зеленом и белом, 40 – в красном и белом, 39 – в зеленом, красном и белом. Остальные – в синем. Сколько девушек были одеты в синее?
Из 120 студентов английский язык изучают 44 человека, немецкий – 50, французский – 49, английский и немецкий – 13 человек, английский и французский – 14, немецкий и французский – 12. Все три языка изучают 5 студентов. Сколько студентов изучают один язык? Сколько студентов не изучают ни одного языка?
В лыжной, хоккейной и конькобежной секциях занимаются 38 человек. Известно, что в лыжной секции занимается 21 человек, среди которых 3 человека занимались еще и в конькобежной секции, 6 человек еще в хоккейной секции и 1 человек занимался одновременно во всех трех. В конькобежной секции занимались 13 человек, среди которых 5 человек занимались одновременно в двух секциях. Сколько человек занималось в хоккейной секции?
Из 40 учащихся класса 32 занимаются в математическом кружке, 21 – в кружке «Умелые руки», а 15 – в обоих кружках. Сколько учащихся не занимаются ни в том, ни в другом кружке?
На турбазе отдыхало 60 человек. Из них 22 каталось на лыжах, 29 – на коньках, 30 – на санках. На лыжах и коньках – 10 человек, на лыжах и санках – 9 человек, на санках и коньках – 7 человек. Сколько человек не каталось вообще, если три человека каталось и на лыжах, и на санках, и на коньках?
Из 100 студентов 85 пересдают математический анализ, 45 – физику. Сколько человек пересдают оба предмета?
studfiles.net
Контрольная работа по теме "Комбинаторика"
Контрольная работа по теме «Комбинаторика»
1 вариант
Часть А
11. Элементами множества А = {x| xZ, -4 x 5} являются числа:
А) 0, 1, 2, 3, 4, 5
Б) 1, 2, 3, 4, 5
В) -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
2. . Определить какое из множеств является подмножеством
А = {10, 20, 30, 40, 50, 60}
a) {10} б) {10, 20, 30, 40, 50, 60, 70} в) {10, 15}
3. Какое из множеств определяет  , если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}
, если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}
a) {4, 5} б) {1, 2, 3, 4, 5} в) {1, 2, 3, 4, 5, 6, 7}
4. Какое из множеств определяет  , если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
, если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
а) {1, 3, 5, 7} б) {1, 2, 3, 4, 5, 7, 9} в) {1, 3}
5. На каком рисунке изображено объединение множеств А и В ( )?
)?

6. Дайте словесное описание множества {2,4,6,…,28,30}
Часть В
1.Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры: 1,2,и3?
2. Сколько различных четырёхбуквенных слов можно записать с помощью букв «т», «и», «в»?
3. Найти значение выражения: а)  б)
б) 
4. Сколько различных слов можно составить, переставляя местами буквы в слове «катет»?
5. Вычислить: А24, А84, С79, С919
Часть С
1.Решить относительно m уравнение: А3m=12m
2. На окружности отмечено 12 точек. Сколько различных треугольников с вершинами, выбранными из этих точек, можно построить?
3. Записать разложение бинома: (3х-2)4
4. Сколькими способами можно рассадить троих учащихся на имеющихся в классе 20 стульях?
Критерии оценки:
Часть «А» 1 балл, часть «В»-2 балла, часть «С»- 3балла
Оценка «3» ставиться за набранные 14-17 баллов
«4»-- за 19-21балл
«5»--- за 22-24 балла
Контрольная работа по теме «Комбинаторика»
2 вариант
Часть А
1. На координатной прямой изображено множество:

А) { x| xZ, -2 x 4}
Б) { x| xR, -2 x
В) { -2; -1; 0; 1; 2; 3; 4}
2. Определить какое из множеств является подмножеством
А = {5, 15, 25, 35, 45, 55}
a) {55} б) {5, 25, 50} в) {25, 55, 75}
3. Какое из множеств определяет  , если А = {2,4, 6, 8, 10}, B = {8, 10, 12, 14}
, если А = {2,4, 6, 8, 10}, B = {8, 10, 12, 14}
a) {2, 4, 6, 8, 10, 12, 14} б) {8, 10, 12, 14} в) {8, 10}
4. Какое из множеств определяет  , если A = {2,4, 6, 8, 10}, B = {2, 4, 8, 9}
, если A = {2,4, 6, 8, 10}, B = {2, 4, 8, 9}
а) {2, 4, 6, 8, 10} б) {2, 4, 8, 9} в) {2, 4, 8}
5. На каком рисунке изображено пересечение множеств А и В ( )?
)?
 6.Дайте словесное описание множества {2,4,6,38,40}
6.Дайте словесное описание множества {2,4,6,38,40}
Часть В
1.Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры: 4,5,6 и 7?
2. Сколько различных четырёхбуквенных слов можно записать с помощью букв «к» и «о»?
3. Найти значение выражения: а)  б)
б) 
4. Сколько различных слов можно составить, переставляя местами буквы в слове «задача»?
5. Вычислить: А35, А94, С610, С817
Часть С
1.Решить относительно m уравнение: А2m=56
2.На окружности отмечено 10 точек. Сколько различных выпуклых четырехугольников с вершинами, выбранными из этих точек, можно построить?
3. Записать разложение бинома: (2а -1)5
4. Сколько существует способов выбрать троих ученых из числа 12 сотрудников кафедры?
Критерии оценки:
Часть «А» 1 балл, часть «В»-2 балла, часть «С»- 3балла
Оценка «3» ставиться за набранные 14-17 баллов
«4»-- за 19-21балл
«5»--- за 22-24 балла
kopilkaurokov.ru
Контрольная работа но комбинаторике.
Контрольная работа по теме «Комбинаторные задачи»
Цели:
· Проверить знания, умения, навыки по всему курсу с помощью контрольной работы с разноуровневыми заданиями;
Оборудование: карточки с заданиями.
Ход урока
1. Сообщение темы и целей
2. Контрольная работа по вариантам
I вариант
Заполнить пропуски:
1. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются (комбинаторными).
2. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить способами. ( m ∙п)
3. Произведение всех чисел от 1 до n называется (факториалом)
4. Сочетаниями … из n элементов по т элементов называются соединения, каждое из которых состоит из m элементов, взятых из данных n элементов. (без повторений)
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
2. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
3. Сколькими способами можно расставить на полке 4 различные книги?
4. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
5. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
II вариант
Заполнить пропуски :
1. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются (комбинаторными).
2. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить способами. ( m ∙п)
3. Произведение всех чисел от 1 до nназывается (факториалом)
4. Сочетаниями … из n элементов по т элементов называются соединения, каждое из которых состоит из m элементов, взятых из данных n элементов. (без повторений)
Решить задачи:
1. Сколькими способами можно переставить 5 различных геометрических фигур?
2. Пять человек пожали друг другу руки. Сколько было рукопожатий?
3. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
4. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
5. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Ответы и решения
2. 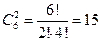
3. 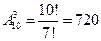
4. Pn =4!=24
5. Pn =5!=120
7. 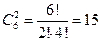
2. Pn =5!=120
3. 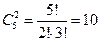
5. Рn =3!=6
6. Pn =5!=120
7. 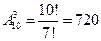
I вариант
Заполнить пропуски:
1. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются __________________
2. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать п способами, то выбор пары (А, В) в указанном порядке можно осуществить __________способами.
3. Произведение всех чисел от 1 до nназывается ________________
4. Сочетаниями _____________________ из n элементов по т элементов называются соединения, каждое из которых состоит из m элементов, взятых из данных n элементов.
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
infourok.ru
Контрольная работа по комбинаторике.
Подготовительный вариант
1)На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу  .
.

2). В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
3) Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
4) Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
5) В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
6)Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).
7) Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
8) Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.
1 вариант
1. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу  .
.

2. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 24 июля погода в Волшебной стране хорошая. Найдите вероятность того, что 27 июля в Волшебной стране будет отличная погода.
3. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
4. Чтобы поступить в институт на специальность «Международные отношения», абитуриент должен набрать на ЕГЭ не менее 67 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Менеджмент», нужно набрать не менее 67 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Т. получит не менее 67 баллов по математике, равна 0,6, по русскому языку — 0,5, по иностранному языку — 0,8 и по обществознанию — 0,9.
Найдите вероятность того, что Т. сможет поступить на одну из двух упомянутых специальностей.
5. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
6. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры.
7. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Вариант 2
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,8. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,03. Известно, что 45% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
3.В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
4. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может. На каждом разветвлении паук выбирает путь, по которому ещё не полз. Считая выбор дальнейшего пути случайным, определите, с какой вероятностью паук придёт к выходу  .
.

5. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 18 мая погода в Волшебной стране хорошая. Найдите вероятность того, что 21 мая в Волшебной стране будет отличная погода.
6. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25 этих стекол, вторая – 75
этих стекол, вторая – 75 . Первая фабрика выпускает 4
. Первая фабрика выпускает 4 бракованных стекол, а вторая – 2
бракованных стекол, а вторая – 2 . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
7. Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать на ЕГЭ не менее 79 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Таможенное дело», нужно набрать не менее 79 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Б. получит не менее 79 баллов по математике, равна 0,9, по русскому языку — 0,7, по иностранному языку — 0,8 и по обществознанию — 0,9.
Найдите вероятность того, что Б. сможет поступить на одну из двух упомянутых специальностей.
multiurok.ru
Контрольная работа по комбинаторике
Контрольная работа по комбинаторике.
Вариант 1
Вычислите  .
.
Вычислите 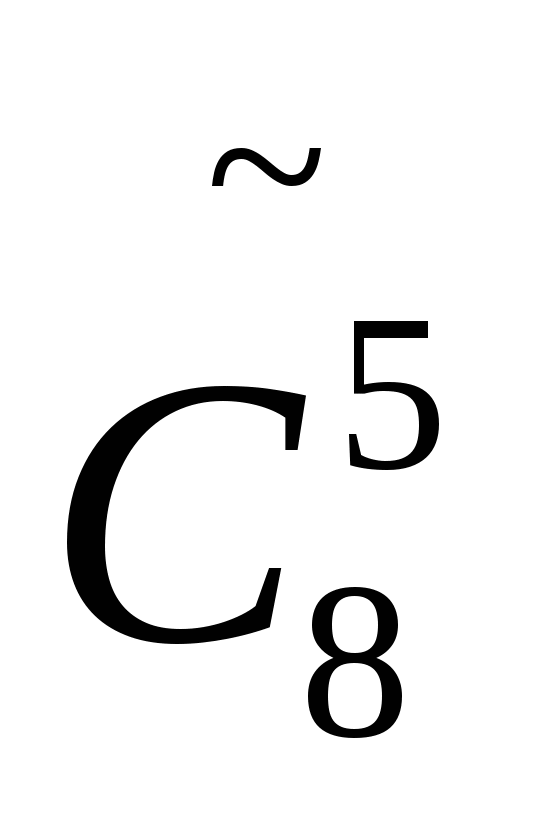 .
.
Девять лиц в этот обед сели как попало. Каждый следующий обед они решили пересаживаться на другое место. Сколько раз им придется обедать?
В чемпионате по футболу участвуют 16 команд. Сколько имеется вариантов распределения золотых, серебряных и бронзовых медалей?
Команда некоторой ЭВМ, записывается в виде набора из восьми цифровых знаков – нулей и единиц. Каково максимальное число различных команд?
Сколькими способами тренер баскетбольной команды может из десяти человек, включенных в заявку, составить стартовую пятерку? В баскетболе порядок, в котором тренер называет игроков, выходящих на площадку, роли не играет.
Сколькими способами можно 7 одинаковых предметов пронумеровать цифрами 2, 4, 6 и 8.
С помощью треугольника Паскаля найдите третий коэффициент в разложении многочлена 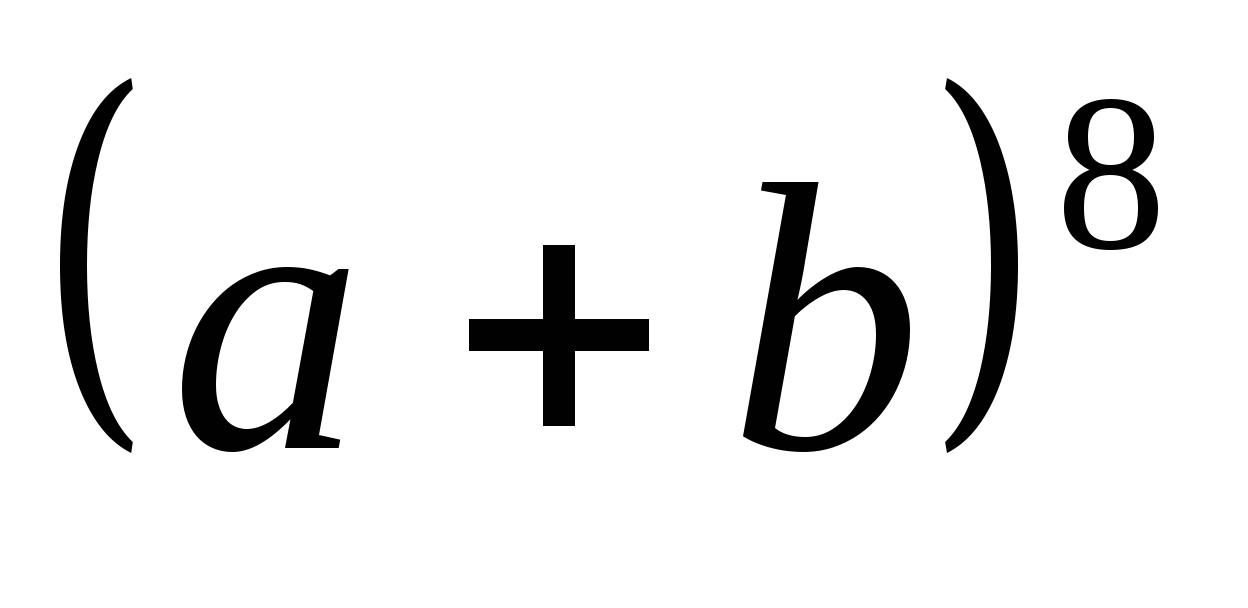 .
.
9. В разложении 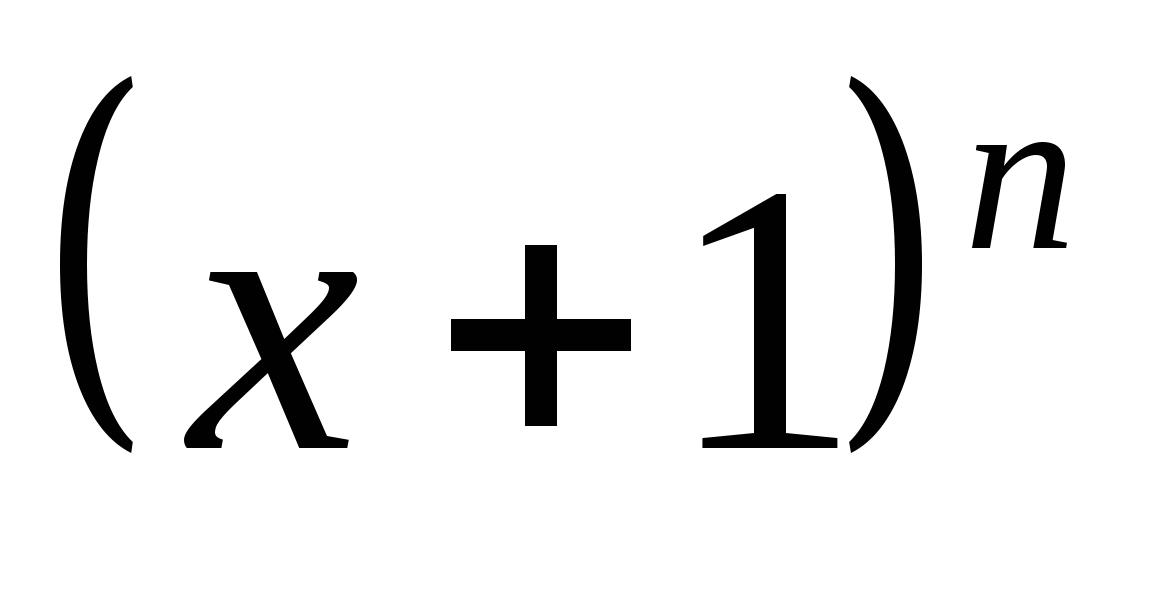 седьмой член равен 2,268. Найти значение
седьмой член равен 2,268. Найти значение  , если сумма биномиальных коэффициентов равна 512.
, если сумма биномиальных коэффициентов равна 512.
________________________________________________________________
Вариант 2
Вычислите  .
.
Вычислите  .
.
Сколькими способами можно рассадить 30 учеников в классе?
Сколько можно составить сигналов из 9 флажков различного цвета, взятых по 3?
Сколькими способами можно 7 различных предметов пронумеровать цифрами 1, 3, 5 и 7?
В алфавите племени 4 буквы. Сколько различных трехбуквенных слов может быть в словаре?
Сколькими способами можно 10 яблок разложить на 3 тарелки? Яблоки считаются одинаковыми.
С помощью треугольника Паскаля найдите четвертый коэффициент в разложении многочлена 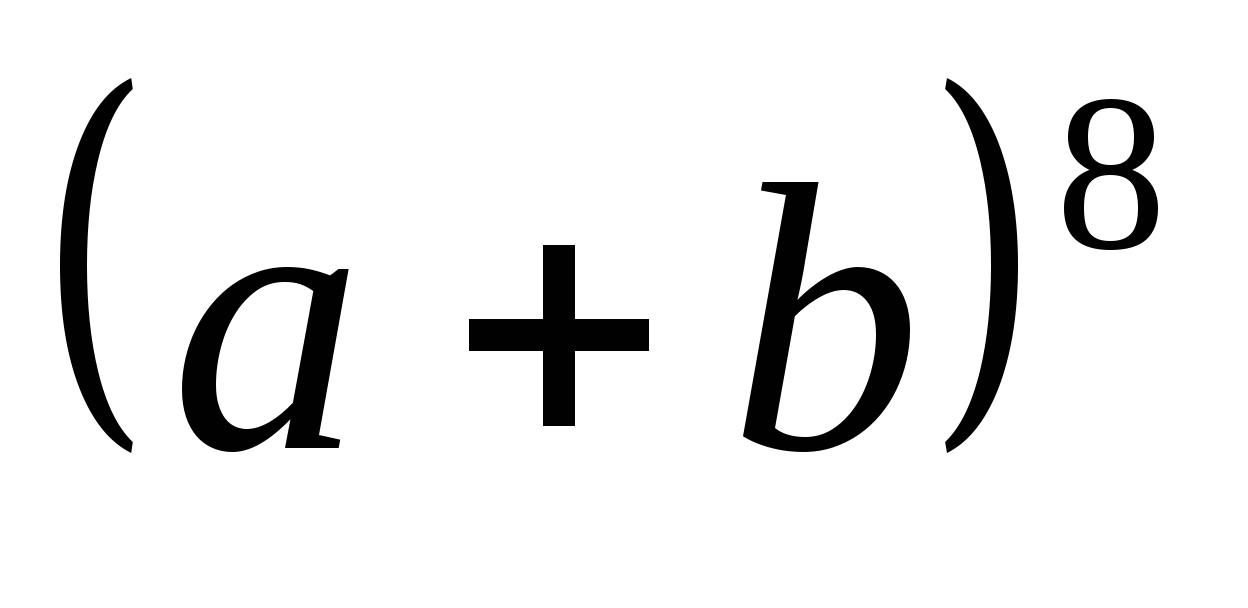 .
.
9. В разложении 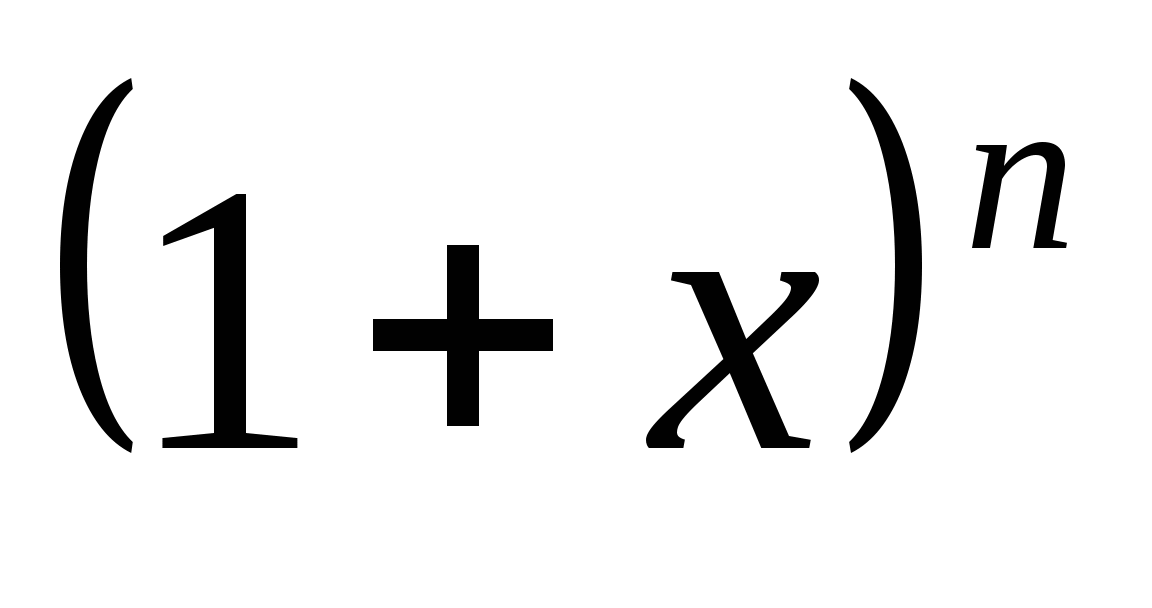 пятый член равен 0,336. Найти значение
пятый член равен 0,336. Найти значение 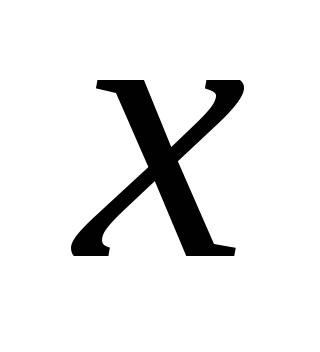 , если сумма биномиальных коэффициентов равна 1024.
, если сумма биномиальных коэффициентов равна 1024.
Вариант 3
Вычислите  .
.
Вычислите  .
.
Слово «игрушка» хотят зашифровать, переставляя в нем буквы. Сколькими способами это можно сделать?
Набирая номер телефона, абонент забыл последние 3 цифры и, помня лишь, что они различны, решил набрать все возможные варианты. Сколько существует таких комбинаций?
5. Бросают 4 игральные кости. Сколькими способами они могут раскрыться?
6. Сколькими способами из колоды в 36 карт можно выбрать 4 карты так, чтобы среди них не было ни одного туза?
Собрание, где присутствуют 30 человек, должно избрать одного делегата из 5 альтернативных кандидатур. Сколькими способами могут распределиться голоса, если каждый подает голос за одного и только одного претендента?
С помощью треугольника Паскаля найдите пятый коэффициент в разложении многочлена 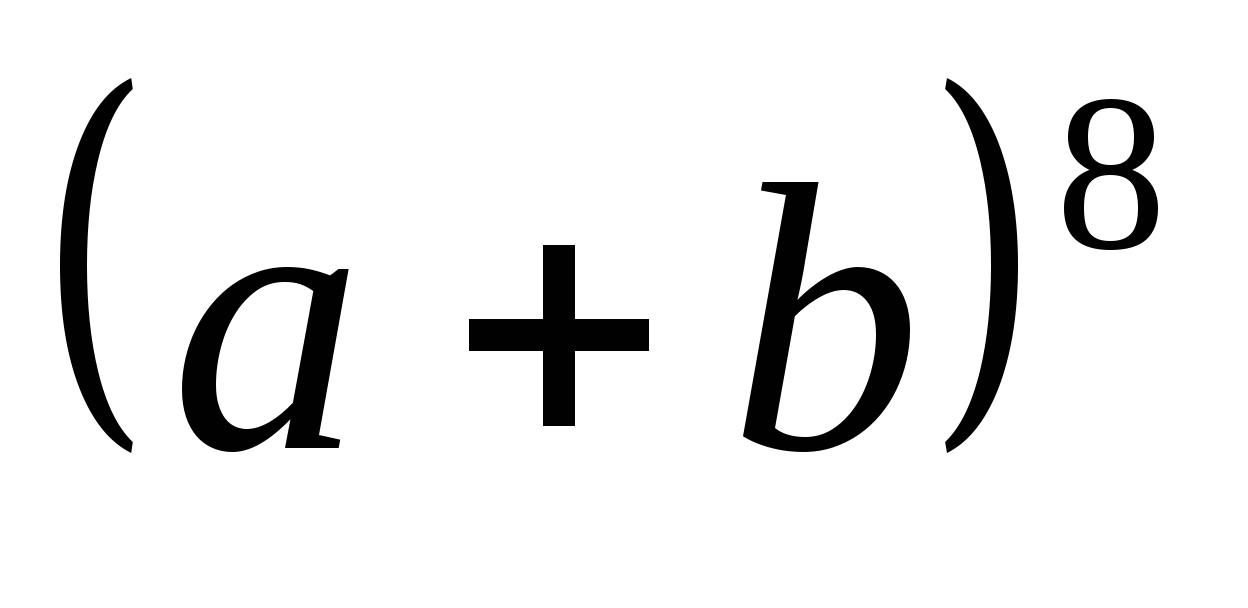 .
.
9. В разложении 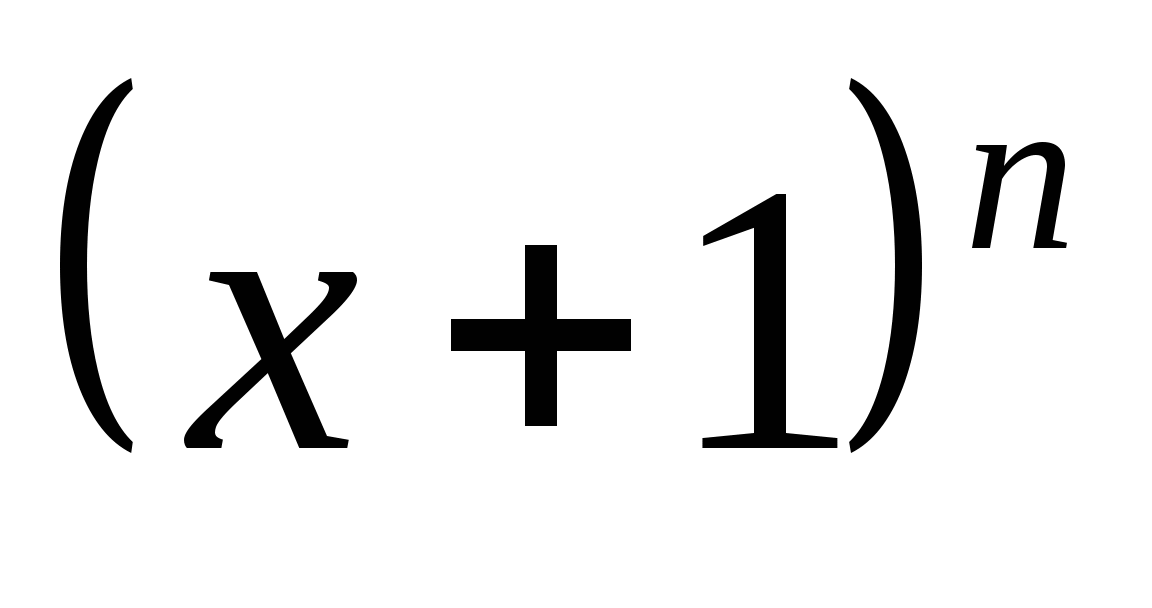 десятый член равен 27,5. Найти значение
десятый член равен 27,5. Найти значение 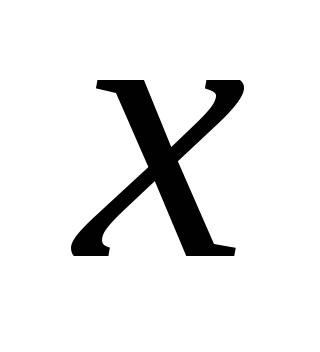 , если сумма биномиальных коэффициентов равна 4096.
, если сумма биномиальных коэффициентов равна 4096.
_______________________________________________________________
Вариант 4
Вычислите 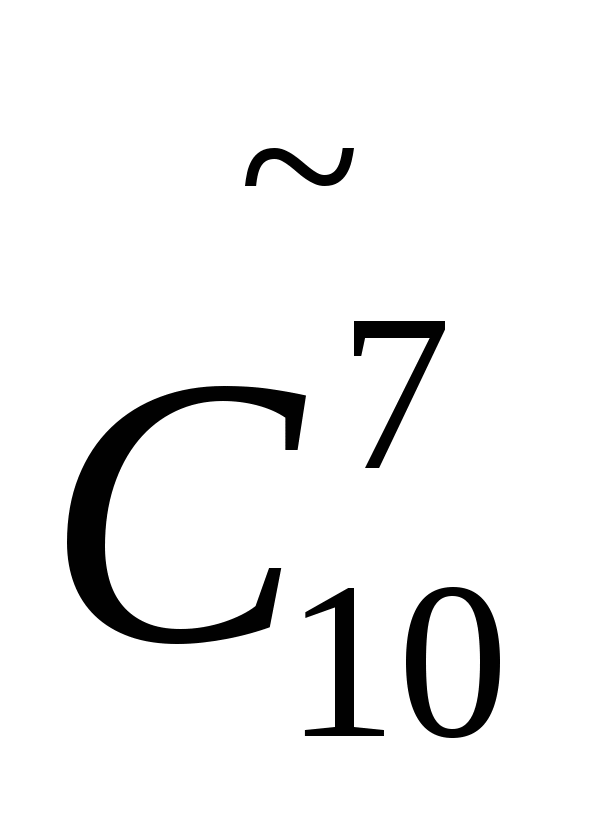 .
.
Вычислите  .
.
3. Сколько различных восьмизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7 и 8 так, чтобы каждая цифра повторялась 1 раз?
4. Сколькими способами тренер волейбольной команды может из десяти человек, включенных в заявку, составить стартовую шестерку? В волейболе порядок игроков на площадке фиксируется, и его изменение означает изменение стартовой шестерки.
5. Каждую клетку таблицы 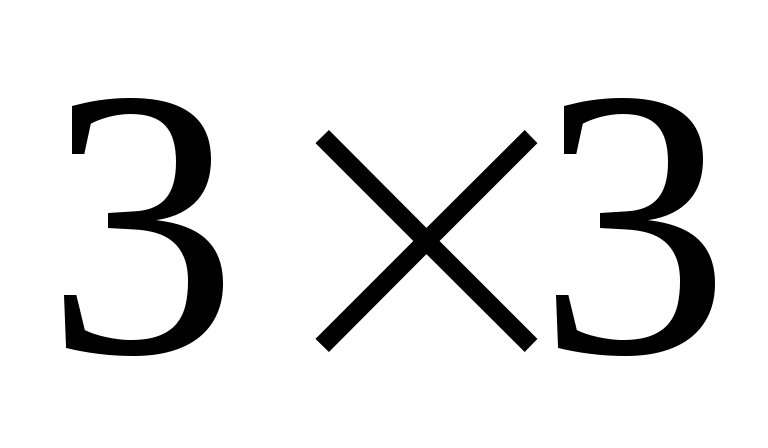 можно покрасить в синий или голубой цвет. Сколько существует способов окраски этой таблицы?
можно покрасить в синий или голубой цвет. Сколько существует способов окраски этой таблицы?
6. Из 12 солдат требуется назначить патруль в составе 8 солдат. Сколькими способами это можно сделать?
7. Сколькими способами учащиеся 9, 10 и 11 классов могут составить футбольную команду (11 человек) при условии участия в ней представителей каждого класса?
8. С помощью треугольника Паскаля найдите восьмой коэффициент в разложении многочлена 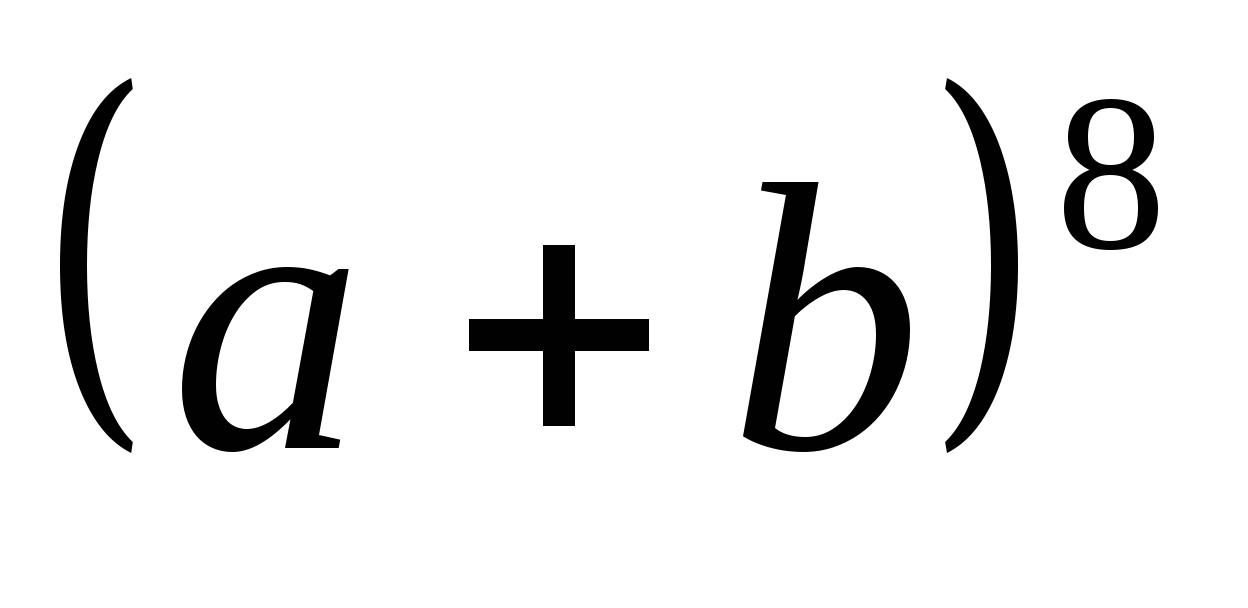 .
.
9. В разложении 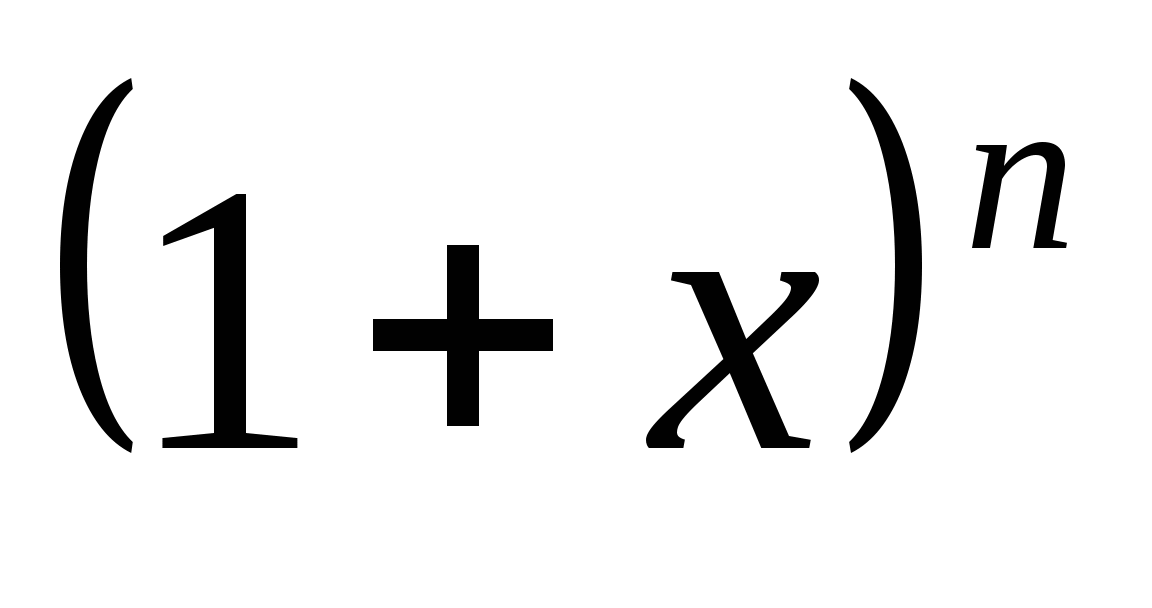 третий член равен 1,89. Найти значение
третий член равен 1,89. Найти значение  , если сумма биномиальных коэффициентов равна 128.
, если сумма биномиальных коэффициентов равна 128.
infourok.ru
Контрольная работа №5 "Комбинаторика"
Вариант 1
№
Сколькими способами?
Количество
баллов
1
В меню столовой имеется 3 первых и 5 вторых блюд. Сколькими способами можно выбрать обед из одного первого и одного второго блюда?
1
2
В меню столовой имеется 3 первых , 5 вторых и 4 третьих блюда. Сколькими способами можно выбрать обед из одного первого, одного второго и одного третьего блюда?
1
3
На прививку в медпункт пошли 8 учеников. Сколькими различными способами они могут встать в очередь в медицинский кабинет?
1
4
Сколько двузначных чисел можно составить, используя цифры 4,5 и 6?
1
5
Сколько двузначных чисел можно составить, используя цифры 4, 5 и 6 при условии, что они в записи числа не повторялись?
1
6
Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предметов?
1
7
Сколько шестизначных чисел можно составить, используя цифры 4, 5 и 6?
1
8
Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6 и 7, и при условии, что при записи числа используем каждую цифру только один раз.
1
9
Сколькими различными способами можно распределить между шестью лицами две разные путёвки в санатории?
1
10
Сколькими различными способами можно распределить две одинаковые путёвки между шестью лицами?
1
11
Сколько анаграмм можно составить из слова ТОР?
1
12
Сколько анаграмм можно составить из слова КОЛОБОК?
3
13
В классе 8 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
1
14
В вазе 8 конфет. Сколькими способами можно выбрать одну конфету?
1
15
В вазе 8 конфет. Сколькими способами можно выбрать пять конфет?
1
16
В вазе 8 конфет. Сколькими способами можно выбрать хотя бы одну конфету?
3
17
Восемь мячей раскладывают по двум коробкам. Сколькими способами это можно сделать?
3
18
На стол бросается игральный кубик. Какова вероятность исхода, что выпадет 7 очков?
1
19
На стол бросается два игральных кубика. Какова вероятность исхода, что выпадет 12 очков?
1
20
На стол бросается три игральных кубика. Какова вероятность исхода, что выпадет 12очков?
3
21
В случайном эксперименте симметричную монету бросают дважды. Найти вероятность события, что орел выпадет ровно один раз.
1
22
В случайном эксперименте симметричную монету бросают трижды. Найти вероятность события, что орел выпадет ровно один раз.
1
23
В случайном эксперименте симметричную монету бросают четырежды. Найти вероятность события, что орел выпадет ровно один раз.
1
Вариант 2
№
Сколькими способами?
Количество
баллов
1
У Даши 4 кофты – красная, жёлтая, синяя и зелёная – и 2 юбки – черная и белая. Сколькими способами она может себе составить костюм?
1
2
У Даши 4 кофты – красная, жёлтая, синяя и зелёная; 2 юбки – черная и белая и 3 шляпы – черная и красная. Сколькими способами она может себе составить костюм?
1
3
В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?
1
4
Сколько двузначных чисел можно составить, используя цифры 4,5,6 и 7?
1
5
Сколько двузначных чисел можно составить, используя цифры 4, 5, 6 и 7 при условии, что они в записи числа не повторялись?
infourok.ru
 , если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7}
, если А = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7} , если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
, если A = {1, 3, 5, 7, 9}, B={1, 2, 3, 4}
 б)
б) 

 б)
б) 
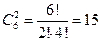
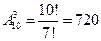
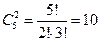
 .
.

 .
.
 .
.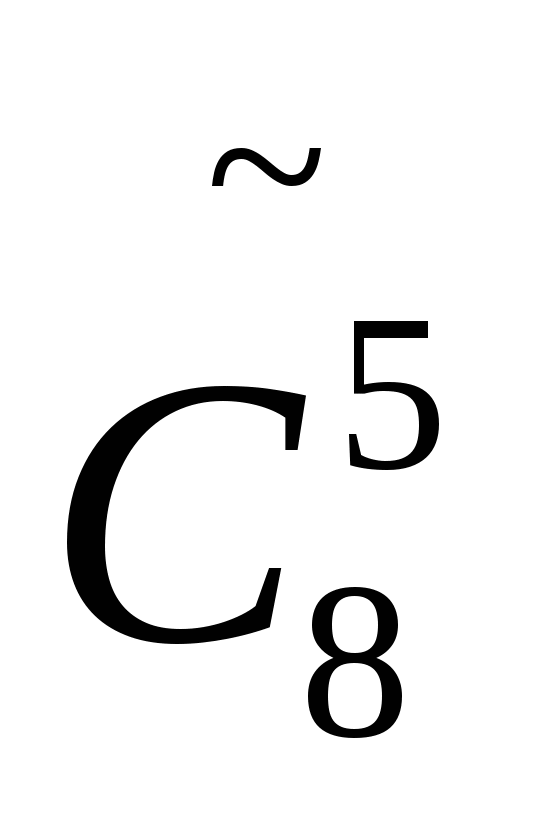 .
.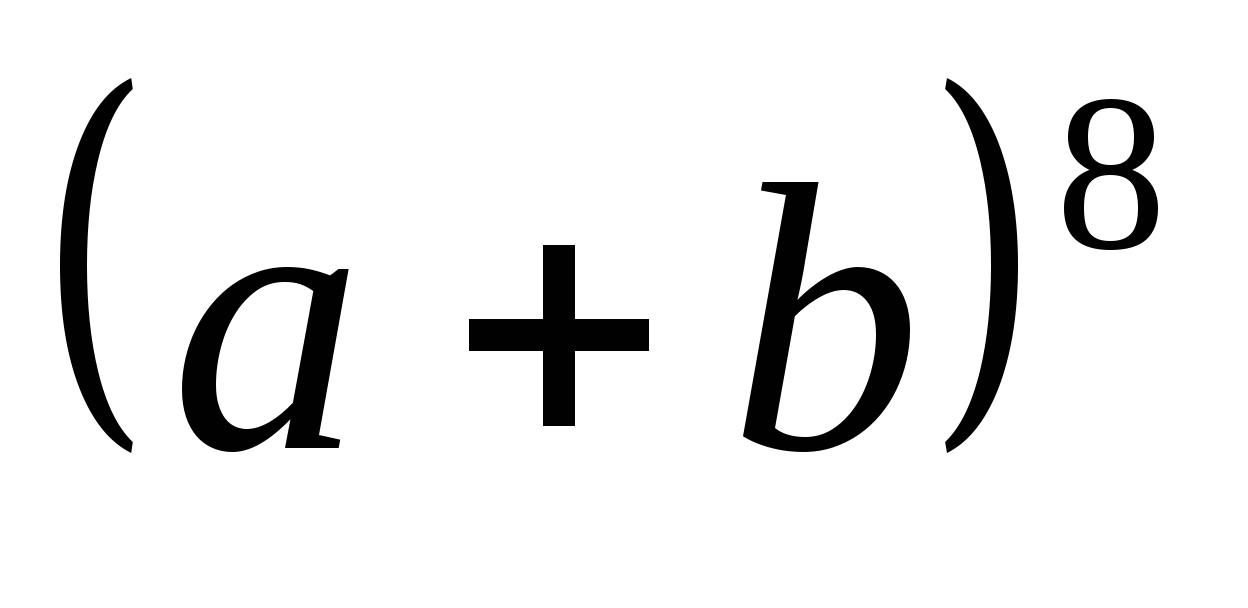 .
.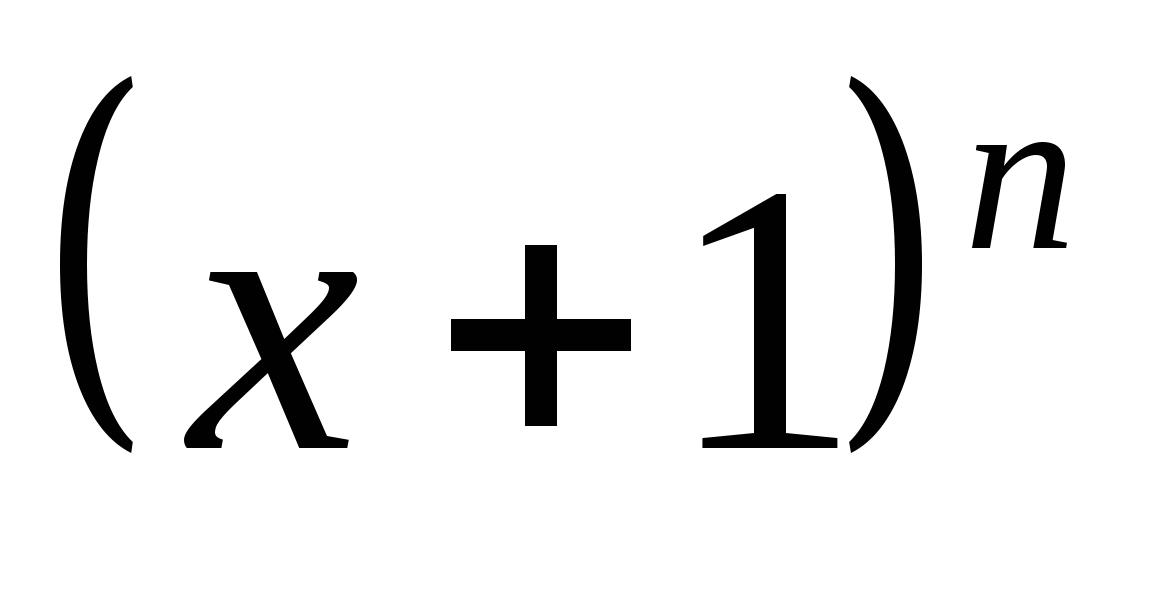 седьмой член равен 2,268. Найти значение
седьмой член равен 2,268. Найти значение 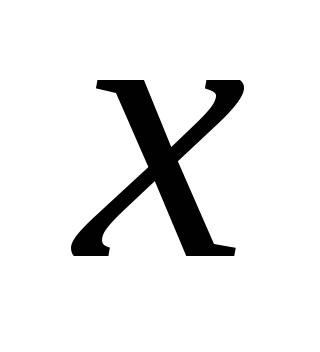 , если сумма биномиальных коэффициентов равна 512.
, если сумма биномиальных коэффициентов равна 512.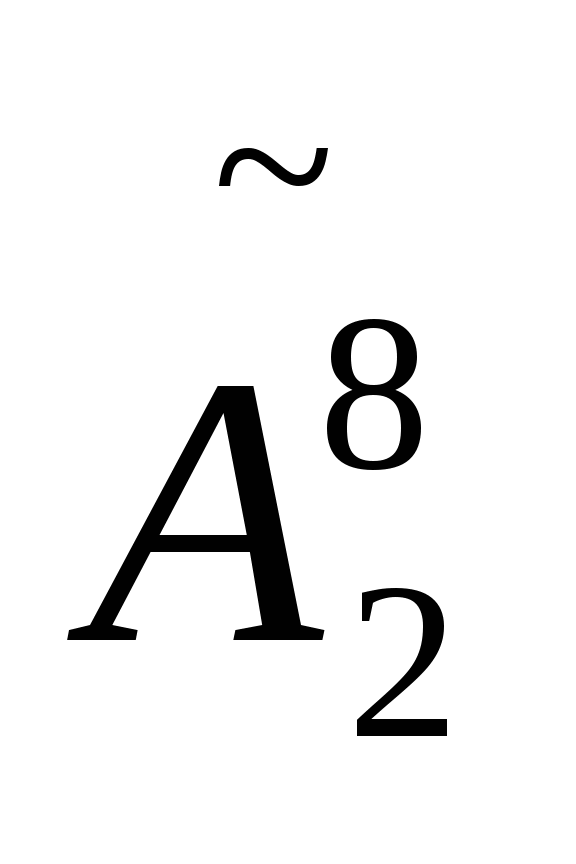 .
. .
.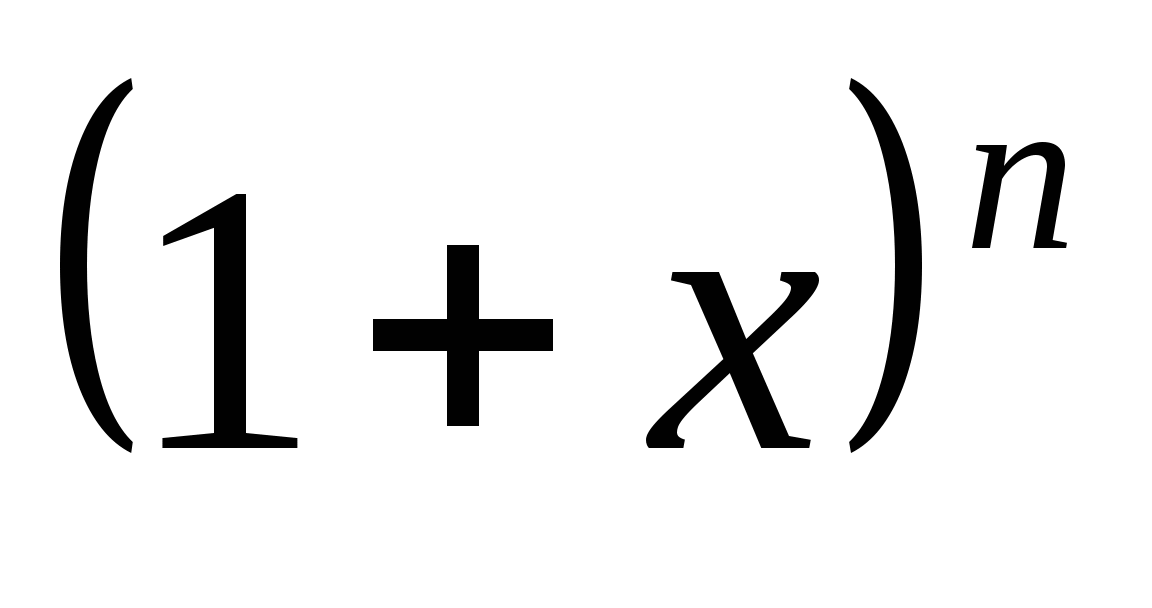 пятый член равен 0,336. Найти значение
пятый член равен 0,336. Найти значение  .
. .
.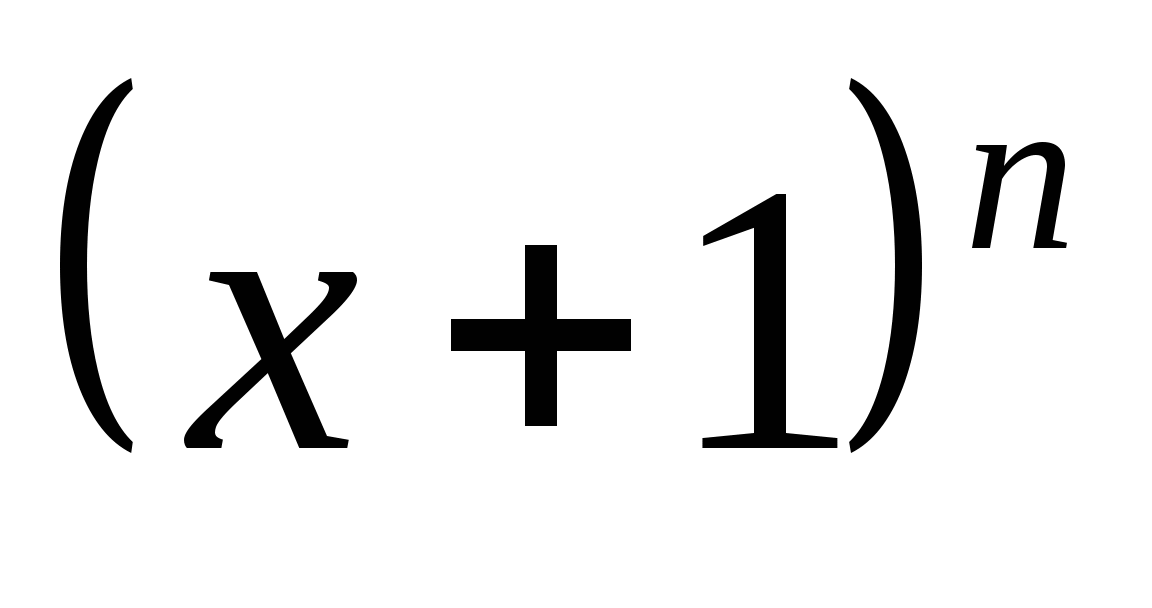 десятый член равен 27,5. Найти значение
десятый член равен 27,5. Найти значение 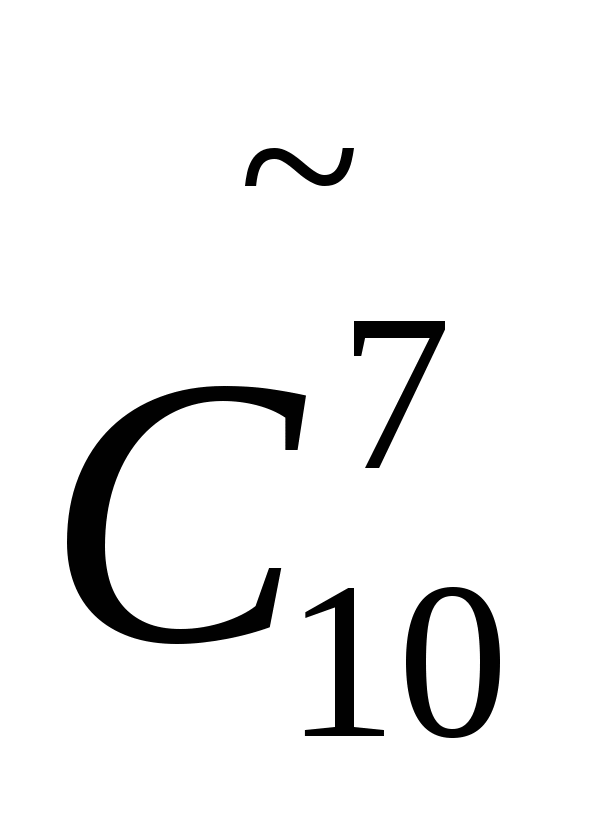 .
. .
.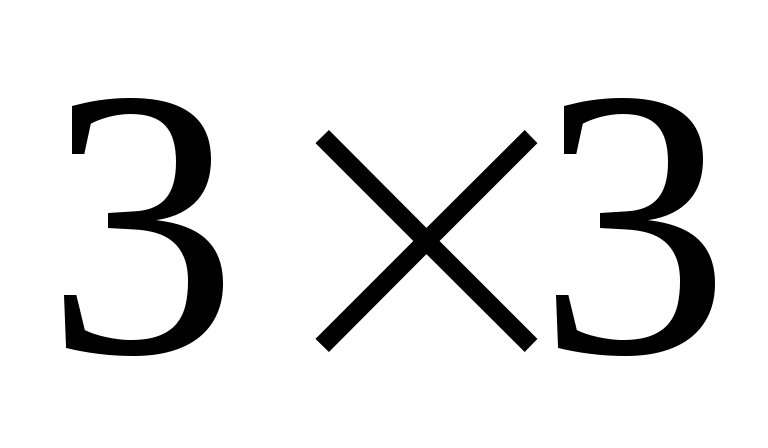 можно покрасить в синий или голубой цвет. Сколько существует способов окраски этой таблицы?
можно покрасить в синий или голубой цвет. Сколько существует способов окраски этой таблицы?