ГДЗ геометрия / Атанасян / контрольные работы / К-1 А1 алгебра 9 класс самостоятельные и контрольные работы Ершова, Голобородько
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Окружающий мир
- Технология
- 3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Музыка
- Литература
- Казахский язык
- 4 класс
- Математика
- Английский язык
Контрольно- измерительные материалы по геометрии
Контрольно-измерительные материалы
по геометрии 7 класс
по УМК Л.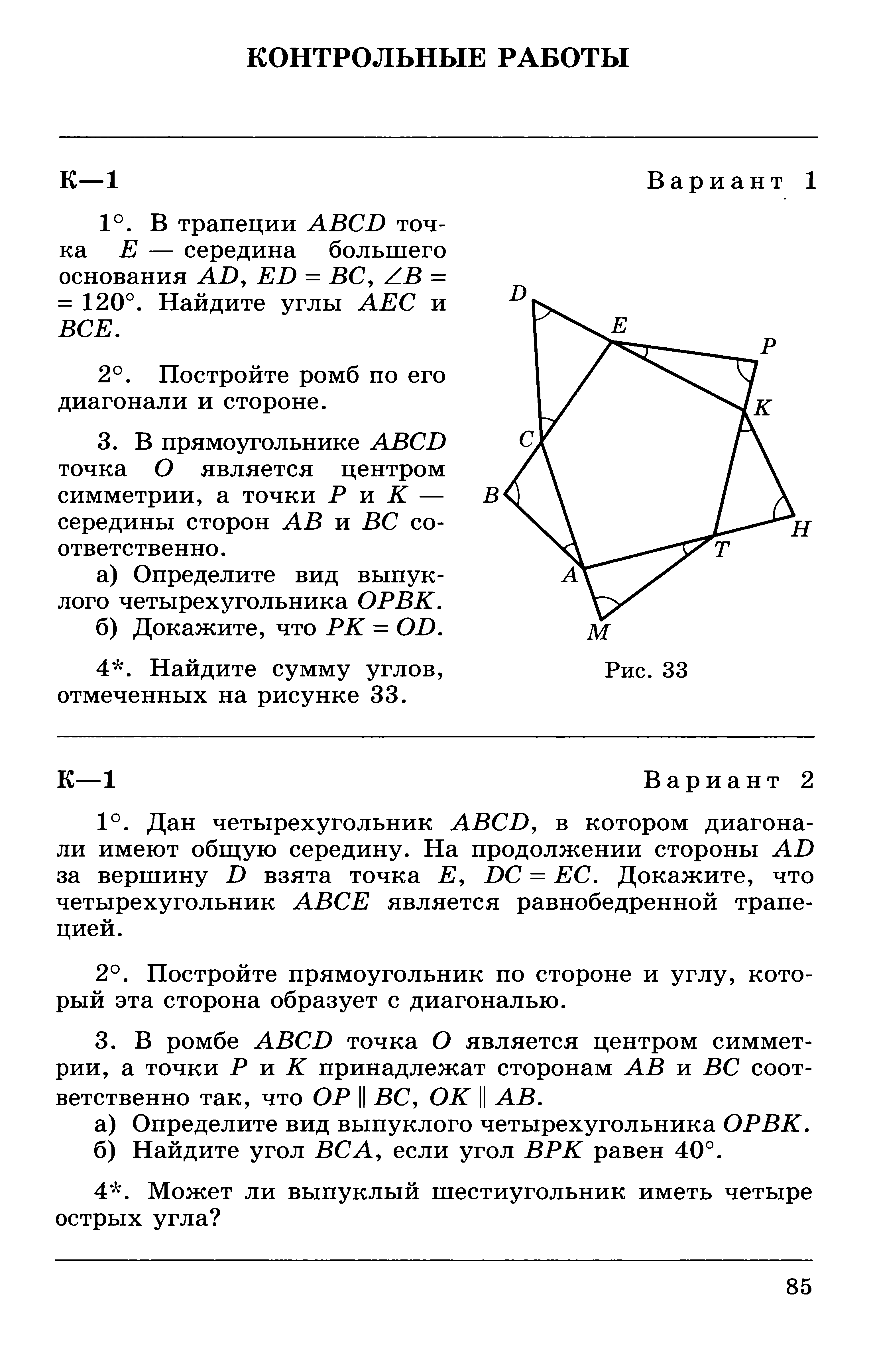 С. Атанасяна-7 класс
С. Атанасяна-7 класс
Контрольные работы представлены в различных вариантах (отдельные варианты для более подготовленных учащихся )
оценка «5» — правильное выполнение двух задач; (3 задание на дополнительную оценку)
Оценка «4» — имеются вычислительные ошибки, с их учетом дальнейшее решение правильное;
Оценка «3» — решение двух задач неполное, есть вычислительные ошибки;
Оценка «2» — нет решения ни одной задачи.
|
ТЕМА |
Контрольные работы- 5
|
|
1 четверть |
Контрольная работа №1 «Начальные геометрические сведения»
|
|
2 четверть |
Контрольная работа №2 «Треугольники»
|
|
3 четверть |
Контрольная работа №3 «Параллельные прямые»
|
|
4 четверть |
Контрольная работа №4 «Соотношения между сторонами и углами треугольника»
|
|
Контрольная работа №5 «Итоговая контрольная работа за курс 7 класса» |
I четверть
Цели: проверить знания, умение решать задачи и навыки учащихся по теме «Измерение отрезков. Измерение углов. Смежные и вертикальные углы».
Измерение углов. Смежные и вертикальные углы».
Вариант I
1. Три точки В, С и D лежат на одной прямой. Известно, что ВD =
= 17 см, DС = 25 см. Какой может быть длина отрезка ВС?
2. Сумма вертикальных углов МОЕ и DОС, образованных при пересечении прямых МС и DЕ, равна 204°. Найдите угол МОD.
3. С помощью транспортира начертите угол, равный 78°, и проведите биссектрису смежного с ним угла.
Вариант II
1. Три точки М, N и K лежат на одной прямой. Известно, что MN =
= 15 см, NK = 18 см. Каким может быть расстояние МК?
2. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108°. Найдите угол ВОD.
Найдите угол ВОD.
3. С помощью транспортира начертите угол, равный 132°, и проведите биссектрису одного из смежных с ним углов.
Вариант III
(для более подготовленных учащихся)
1. Лежат ли точки M, N и P на одной прямой, если MP = 12 см, MN =
= 5 см, PN = 8 см?
2. Найдите неразвернутые углы, образованные при пересечении двух прямых, если разность двух из них равна 37°.
|
3. На рисунке АВСD, луч ОЕ – биссектриса угла АОD. Найдите угол СОЕ. |
|
I I ЧЕТВЕРТь
КОНТРОЛЬНАЯ РАБОТА № 2
Цель: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.
Вариант I
1. На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что DАО = СВО.
2. Луч АD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что АDВ = АDС. Докажите, что АВ = АС.
3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
Вариант II
1. На рисунке 2 отрезки МЕ и РK точкой D делятся пополам. Докажите, что KМD = РЕD.
2. На сторонах угла Д отмечены точки М и K так, что DМ = DK. Точка Р лежит внутри угла D и РK = РМ. Докажите, что луч DР – биссектриса угла МDK.
Докажите, что луч DР – биссектриса угла МDK.
3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Вариант III
(для более подготовленных учащихся)
1. На рисунке 3 прямые АВ и СD пересекаются в точке Е, СЕ = ВЕ, С = В; АА1 и DD1 – биссектрисы треугольников АСЕ и DВЕ. Докажите, что АА1 = DD1.
2. На сторонах угла А отмечены точки В и С так, что АВ = АС. Точка М лежит внутри угла А и МВ = МС. На прямой АМ отмечена точка D так, что точка М лежит между точками А и D.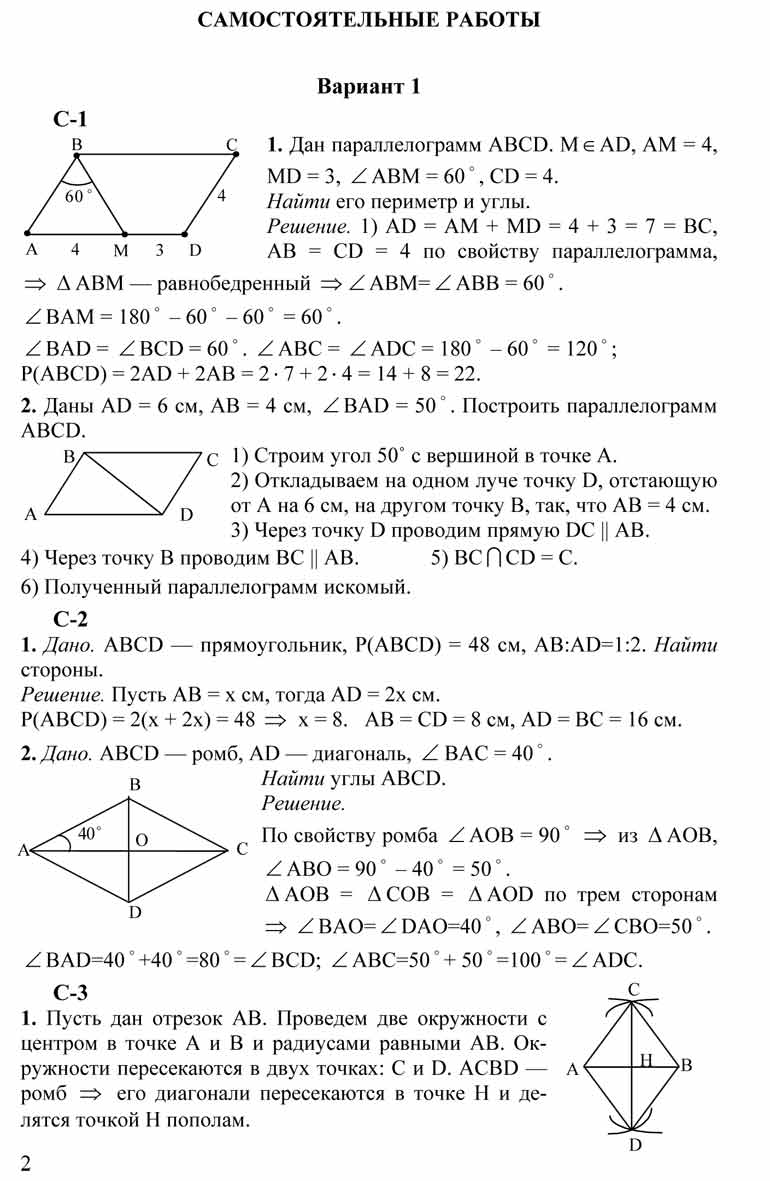 Докажите, что ВМD =
Докажите, что ВМD =
= СМD.
3. Начертите равнобедренный тупоугольный треугольник АВС с основанием ВС и с тупым углом А. С помощью циркуля и линейки проведите:
а) высоту треугольника АВС из вершины угла В;
б) медиану треугольника АВС к стороне АВ;
в) биссектрису треугольника АВС угла А.
Рис. 1 Рис. 2
Рис. 3
I I I четверть
КОНТРОЛЬНАЯ РАБОТА № 3
Цели: проверить знания, умения и навыки учащихся по теме «Параллельные прямые» и применение знаний к решению задач.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант III
(для более подготовленных учащихся)
1. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, пересекающая сторону АВ в точке Е так, что АЕ = ЕD. Найдите углы треугольника АЕD, если ВАС = 64°.
Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, пересекающая сторону АВ в точке Е так, что АЕ = ЕD. Найдите углы треугольника АЕD, если ВАС = 64°.
2. На рисунке 14 АС || ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка СD.
Вариант IV
(для более подготовленных учащихся)
1. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, пересекающая сторону DЕ в точке N так, что DN = MN. Найдите углы треугольника DMN, если СDЕ = 74°.
2. На рисунке 15 АВ || DС, АВ = DС. Докажите, что точка О – середина отрезков АС и ВD.
IV четверть
КОНТРОЛЬНАЯ РАБОТА № 4
Цели: проверить знания и умения учащихся в решении задач и применении изученного материала.
Вариант I
1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ > ДМ.
3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
Вариант II
1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.
2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что KР < МР.
3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Найдите стороны этого треугольника, если его периметр равен 77 см.
Вариант III
(для более подготовленных учащихся)
1. На рисунке 1 СВМ = АСF; РАВС = 34 см, ВС = 12 см. Найдите сторону АС треугольника АВС.
2. В треугольнике MNK K = 37°, М = 69°, NP – биссектриса треугольника. Докажите, что МР < РK.
3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника.
Вариант IV
(для более подготовленных учащихся)
1. На рисунке 2 ЕАМ = DВF; ВС = 17 см, РАВС = 45 см. Найдите сторону АВ треугольника АВС.
2. В треугольнике СDЕ Е = 76°, D = 66°, ЕK – биссектриса треугольника. Докажите, что KС > DK.
3. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника.
Рис. 1 Рис. 2
КОНТРОЛЬНАЯ РАБОТА № 5
Цели: проверить знания учащихся и их умение решать задачи; выяснить пробелы в знаниях учащихся с тем, чтобы их ликвидировать на уроках повторения.
Вариант I
1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОK = 9 см. Найдите расстояние от точки О до прямой MN.
2. Постройте прямоугольный треугольник по гипотенузе и острому углу.
*Дополнительное задание.
С помощью циркуля и линейки постройте угол, равный 150°.
Вариант II
1. В прямоугольном треугольнике DСЕ с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найдите расстояние от точки F до прямой DЕ.
2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
*Дополнительное задание.
С помощью циркуля и линейки постройте угол, равный 105°.
Вариант 3
1. В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОK = 12 см. Найдите расстояние от точки О до прямой MN.
2. Постройте прямоугольный треугольник по гипотенузе и острому углу.
*Дополнительное задание.
С помощью циркуля и линейки постройте угол, равный 135°.
Вариант 4
1. В прямоугольном треугольнике DСЕ с прямым углом С проведена биссектриса EF, причем FC = 11 см. Найдите расстояние от точки F до прямой DЕ.
2. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
*Дополнительное задание.
С помощью циркуля и линейки постройте угол, равный 105°.
Тесты по геометрии для 7-го класса онлайн
- Вход
- Тесты
- Опросы
- Кроссворды
- Диалоги
- Уроки
- Диалоги Уроки
- Онлайн тесты
- Геометрия
- 7 класс
-
Новый!
Окружность.Начальные сведения.
22.11.2020 32 0
Решебник по геометрии за 10‐11 класс контрольные работы Иченская М.А.
gdzguru.com Видеорешения решебники- 1 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Человек и мир
- Технология
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Французский язык
Контрольные работы по геометрии. 7 класс. Мельникова Н.Б. К учебнику Атанасяна Л.С. «Геометрия. 7
КОНТРОЛЬНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ.
7 КЛАСС.
МЕЛЬНИКОВА Н.Б.
к учебнику Атанасяна Л.С. и др. «Геометрия. 7 — 9 классы».
2009 г.
Скачать бесплатно пособие в формате PDF можно по ссылке ниже (кнопка).
Пособие «Контрольные работы по геометрии. 7 класс.» (Мельникова Н.Б.) предназначено для проверки знаний и умений учащихся по курсу геометрии 7 класса. Оно содержит проверочные работы по всем темам, изучающимся в 7 классе, и ориентировано на учебник Л.С.Атанасяна и др. «Геометрия. 7 — 9 классы.», рекомендованный Министерством образования и науки Российской Федерации и включенный в Федеральный перечень учебников.
Каждая проверочная работа дается в четырех вариантах. Кроме того, по каждой теме дается набор заданий для подготовки к контрольной работе. Каждый вариант включает задания трех видов: с выбором ответа, с кратким ответом и с развернутым ответом, что соответствует формам заданий, использующимся в настоящее время в экзаменационных работах ЕГЭ и в других современных видах испытаний учащихся.
Основная цель пособия — помочь учителю в организации тематического контроля знаний и умений учащихся.
К учебнику:
Содержание:
Предисловие
Тематика контрольных работ
Контрольные работы
Контрольная работа № 1
Начальные геометрические сведения
Контрольная работа № 2
Треугольники
Контрольная работа № 3
Параллельные прямые
Контрольная работа № 4
Соотношения между сторонами и углами треугольника
Контрольная работа № 5
Итоговая
Ответы к контрольным работам
| < Предыдущая | Следующая > |
|---|
PPT — Тест геометрии Ch. 1 Обзор презентации PowerPoint, скачать бесплатно
Geometry Test Ch. 1 Обзор
Инструкции • Примеры вопросов будут показаны на каждом слайде. • Попробуйте задать вопрос на бумаге для заметок. • Щелкните по экрану, и появится правильная работа и ответ.
Дайте другое имя плоскости T. (Любые 3 неколлинеарных точки. Пример: ABC) 2. Назовите точку, которая не содержится в линиях q или m.D 3. Назовите точку пересечения прямых q и n. CC • n D • E • F • B • A • qm T
Найдите значение переменной и VW, если V находится между U и Вт. UV = 4p -3 VW = 5p UW = 42 Переменная: UV + VW = UW 4p-3 + 5p = 42 9p — 3 = 42 9p = 45 p = 5 VW: VW = 5p 5 (5) 25
Найдите координаты средней точки с заданными конечными точками.A (-4, -4), B (-2,2) Средняя точка координаты X: = = = -3 Средняя точка координаты Y: = = = -1 Окончательный ответ: (-3, -1)
Найдите расстояние между конечными точками. G (5,2) H (-2, 8) Формула расстояния = = = = = ≈ 9,2
Чтобы ответить на вопросы, обратитесь к рисунку. • Назовите вершину угла 6. C • Назовите стороны угла 4. 3. Напишите другое имя для 7. ∠ABD или ∠ABE • Напишите другое имя для ∠9 E 4 9 DC 1 6 A 7 B
См. Рисунок. Назовите линейную пару. EX: ∠AFE и ∠ AFB Назовите пару вертикальных углов. EX: ∠EFD и ∠AFB Назовите угол, дополнительный к ∠AFB. EX: ∠ BFD Назовите пару дополнительных углов. ∠CFD и ∠DFE A E F B D C
Размеры двух дополнительных углов: (4r + 7) ° и (r — 2) °. Найдите меры переменной и углов. Дополнительный = 180 ° (4r +7) + (r — 2) = 180 5r + 5 = 180 5r = 175 r = 35 4r + 7 = 4 (35) + 7 = 147 ° r — 2 = 35-2 = 33 °
Два угла дополняют друг друга.Один угол на 26 градусов больше другого на градусов. Найдите размеры углов. Дополнительный = 90 ° A + B = 90 A = B + 26 (B + 26) + B = 90 2B + 26 = 90 2B = 64 B = 32 ° A = B +26 = 32 + 26 = 58 °
Назовите многоугольник по количеству сторон. Классифицируйте его как выпуклый или вогнутый и правильный или нерегулярный. Четырехугольник Выпуклый Правильный Десятиугольник Вогнутый Необычный
Найдите площадь и периметр каждой фигуры. A = ½ L x W A = ½ (3 x 4) = 6 м² P = сумма сторон Найдите третью сторону по теореме Пифагора.3² + 4² = c² c = 5 P = 3 + 4 + 5 = 12 м A = L x WA = 6,5 x 14 = 91 фут² P = 2L + 2W P = 2 (6,5) + 2 (14) P = 13 + 28 = 41 фут 3 м 6,5 футов 4 м 14 футов
Назовите каждую фигуру. 10 ярдов Прямоугольная призма Цилиндр 7 ярдов 3 дюйма 2 дюйма 5 дюймов
Укажите количество граней граней и вершин показанной фигуры . A B C F H G D E F = 6 V = 8 E = 12
| Метод | Объяснение |
| angleAndDistanceTo (other, {method}) | Возвращает кортеж угла и расстояния до другой точки, используя тип измерения. |
| граница () | Создает границу геометрии. |
| буфер (расстояние) | Создает многоугольник на заданном расстоянии от геометрии. |
| клип (конверт) | Создает пересечение геометрии и указанного экстента. |
| содержит (second_geometry, {отношение}) | Указывает, содержит ли базовая геометрия геометрию сравнения. содержит противоположность внутри. На этом рисунке показаны только отношения True. |
| convxHull () | Создает геометрию, которая является минимальным ограничивающим многоугольником, так что все внешние углы выпуклые. |
| крестов (second_geometry) | Указывает, пересекаются ли две геометрии в геометрии меньшего тип формы. Две полилинии пересекаются, если они имеют только общие точки, по крайней мере один из которых не является конечной точкой.Полилиния и многоугольник пересекаются, если они имеют общую полилинию или точку (для вертикальной линии) на внутренняя часть многоугольника, которая не эквивалентна всему полилиния. На этом рисунке показаны только отношения True. |
| разница (другое) | Создает геометрию, состоящую только из области, уникальной для базовая геометрия, но не часть другой геометрии. На следующем рисунке показаны результаты, когда красный многоугольник является исходной геометрией. |
| disjoint (second_geometry) | Указывает, не имеет ли базовая геометрия и геометрия сравнения общих точек. Два геометрии пересекаются, если disjoint возвращает False. На этом рисунке показаны только отношения True. |
| distanceTo (other) | Возвращает минимальное расстояние между двумя геометриями. Если геометрии пересекаются, минимальное расстояние равно 0. Обе геометрии должны иметь одинаковую проекцию. |
| равно (second_geometry) | Указывает, имеют ли базовая и сравнительная геометрия один и тот же тип формы и определяют тот же набор точек на плоскости. Это только двухмерное сравнение; Значения M и Z игнорируются. На этом рисунке показаны только отношения True. |
| getGeohash (precision) | Преобразует PointGeometry в координатах географической системы координат широты и долготы в строку геохеша с произвольной точностью в пределах ограничивающей рамки в сетке геохеша. |
| getPart ({index}) | Возвращает массив точечных объектов для определенной части геометрии или массив, содержащий несколько массивов, по одному для каждой части. Метод getPart эквивалентен индексации объекта; то есть obj.getPart (0) эквивалентно obj [0]. |
| пересечение (другое, измерение) | Создает геометрию, которая является геометрическим пересечением две входные геометрии. Для создавать разные типы фигур. Пересечение двух геометрических фигур одного и того же типа является геометрия, содержащая только области перекрытия между оригинальные геометрические формы. Для более быстрых результатов проверьте, не пересекаются ли две геометрии, прежде чем вызывать пересечение. |
| перекрытия (second_geometry) | Указывает, совпадает ли пересечение двух геометрий Тип формы как одна из входных геометрий и не эквивалентен ни одной из входных геометрий. На этом рисунке показаны только отношения True. |
| pointFromAngleAndDistance (angle, distance, {method}) | Возвращает точку под заданным углом в градусах и расстояние в единицах пространственной привязки геометрии с использованием указанного типа измерения. |
| projectAs (пространственная_ссылка, {трансформация_name}) | Проецирует геометрию и при необходимости применяет геотрансформацию. Для проецирования геометрия должна иметь пространственную привязку и не иметь UnknownCoordinateSystem. Новая система пространственной привязки, переданная методу, определяет выходную систему координат. Если какая-либо пространственная привязка неизвестна, координаты не будут изменены. Значения Z и меры не изменяются методом ProjectAs. |
| симметричный Различие (другое) | Конструкции геометрия, которая представляет собой объединение двух геометрий без пересечения этих геометрий. Две входные геометрии должны быть одного типа формы. |
| toCoordString (обозначение) | Преобразует PointGeometry в обозначение выбранной системы координат. |
| касаний (second_geometry) | Указывает, пересекаются ли границы геометрии. Две геометрии соприкасаются, когда пересечение геометрии не пусты, но пересечение их интерьеров пусто.Например, точка касается полилинии, только если точка совпадает с одной из конечных точек полилинии. На этом рисунке показаны только отношения True. |
| union (other) | Создает геометрию, которая является теоретико-множественным объединением входных геометрий. Две объединяемые геометрии должны быть одного типа формы. |
| в пределах (second_geometry, {ratio}) | Указывает, находится ли базовая геометрия в пределах геометрии сравнения. внутри — оператор, противоположный оператору contains. На этом рисунке показаны только отношения True. Базовая геометрия находится внутри сравниваемой геометрии, если базовая геометрия является пересечением геометрий, а пересечение их внутренних частей не пусто. внутри находится оператор Клементини, за исключением случая пустой базовой геометрии. |
Проверка геометрии Глава 1
- Ресурс исследования
- Исследовать
- Искусство и гуманитарные науки
- Бизнес
- Инженерная технология
- Иностранный язык
- История
- Математика
- Наука
- Социальная наука
Лучшие подкатегории
- Продвинутая математика
- Алгебра
- Основы математики
- Исчисление
- Геометрия
- Линейная алгебра
- Предалгебра
- Предварительный расчет
- Статистика и вероятность
- Тригонометрия
- другое →
Лучшие подкатегории
- Астрономия
- Астрофизика
- Биология
- Химия
- Науки о Земле
- Наука об окружающей среде
- Науки о здоровье
- Физика
- другое →
Лучшие подкатегории
- Антропология
- Закон
- Политология
- Психология
- Социология
- другое →
Лучшие подкатегории
- Бухгалтерский учет
- Экономика
- Финансы
- Менеджмент
- другое →
Лучшие подкатегории
- Аэрокосмическая техника
- Биоинженерия
- Химическая инженерия
- Гражданское строительство
- Компьютерные науки
- Электротехника
- Промышленное проектирование
- Машиностроение
- Веб-дизайн
- другое →
Лучшие подкатегории
- Архитектура
- Связь
- Английский
- Гендерные исследования
- Музыка
- Исполнительское искусство
- Философия
- Религиоведение
- Письмо
- другое →
Лучшие подкатегории
- Древняя история
- История Европы
- История США
- Всемирная история
