| 4 | -2 | 4 |
| = |
2 | 12 | |
1 | 2 | 2 | Вычислить определитель второго порядка всем |
1 вариант Вычислить определитель по первой строке | 2 вариант Вычислить определитель по первой строке | |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника | |
3 вариант Вычислить определитель по третьему столбцу | 4 вариант Вычислить определитель по третьему столбцу | |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника | |
5 вариант Вычислить определитель по правилу треугольника | 6 вариант Вычислить определитель по правилу треугольника | |
Вычислить определитель по второй строке | Вычислить определитель по второму столбцу | |
7 вариант Вычислить определитель по второй строке | 8 вариант Вычислить определитель по второму столбцу | |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника | Оценка уровня подготовки |
Балл (оценка) | Вербальный аналог | |
90-100 | 5 | отлично |
80-89 | 4 | хорошо |
70-79 | 3 | удовлетворительно |
менее 70 | 2 | неудовлетворительно |
Вычислить определитель матрицы
Г., Задулина С.В. Под редакцией В.А. Гусева Математика. – М.: Образовательно-издательский центр «Академия», 20124.1.1 Матрицы и определители. Основные понятия
Исторически понятия матрицы и определителя появились в связи с изучением систем линейных уравнений. Мы же начнем изучение линейной алгебры с этих двух понятий, а затем покажем, каким образом можно использовать матричный аппарат для решения других задач.
Определение.
Матрицей размера называется прямоугольная таблица, составленная из чисел ( строк, столбцов).
Обозначаются матрицы
, ,
Или кратко: , или одной буквой, например .
В частности, когда , матрица состоит из одной строки и называется матрицей – строкой. Если же , а , то получаем одностолбцовую матрицу, которую называют матрицей-столбцом.
Числа называются элементами матрицы.
Вообще, элементы матрицы могут быть произвольной природы, однако в данном разделе рассматриваются числовые матрицы.
Если , то матрицу называют квадратной матрицей порядка .
Определение. Перестановку чисел , когда большее число стоит раньше (левее) меньшего, назовем инверсией или беспорядком.
Число инверсий в перестановке обозначается .
Например, (Слагаемые в сумме показывают, сколько инверсий образуют числа в исходной перестановке).
Определение. Определителем Квадратной матрицы -го порядка называется алгебраическая сумма слагаемых, в каждом из которых сомножителей, взятых по одному и только по одному из каждой строки и каждого столбца, причем каждое слагаемое имеет множитель , где – число инверсий в перестановке верхних индексов (индексов строк), – число инверсий в перестановке нижних индексов (индексов столбцов).
Число называется порядком определителя.
Для обозначения определителя используются символы:
Замечание 1. Определитель – число, поэтому, когда говорят о строках и столбцах определителя, то под этим понимают строки и столбцы соответствующей матрицы.
Замечание 2. Если верхние (нижние) индексы расположить в порядке возрастания (что достигается перестановкой сомножителей), то для определения знака каждого слагаемого в определителе достаточно сосчитать число инверсий только среди нижних (верхних) индексов.
Пример 1. Какое из слагаемых: a) , b) , c) , d) входит в качестве слагаемого в определитель 4-го порядка и с каким знаком?
Решение. Произведения b) и d) не могут войти в качестве слагаемых в определитель 4-го порядка, так как в b) присутствуют два элемента из второго столбца (должно быть по одному), а из четвертого столбца нет ни одного элемента; произведение d) имеет пять сомножителей, а у определителя 4-ого порядка четыре cтроки и четыре столбца.
Два других произведения входят в качестве слагаемого в определитель 4-ого порядка, так как каждая строка и каждый столбец представлены единственным элементом, причем а) входит со знаком плюс, а с) со знаком минус. Действительно, расположим, допустим, нижние индексы по порядку , и сосчитаем , . Перед слагаемым а) будет множитель , а перед с) множитель , которые и определяют знак.
Можно было бы не наводить порядок среди индексов, тогда для слагаемого а) нужно сосчитать , и поставить перед ним знак , для слагаемого с) считаем , и ставим знак .
Пример 2. Выбрать значения и так, чтобы произведение входило в определитель пятого порядка со знаком минус.
Решение. По верхним индексам видим, что в произведении первая, третья и пятая строки представлены каждая своим элементом, а вторая и четвертая – нет. Следовательно, и должны принимать значения или . Имеется две возможности: 1) , или 2) , . Исследуем знак слагаемого в каждой ситуации.
Для этого расположим индексы столбцов по порядку и найдем , . Итак, исследуемое слагаемое войдет в определитель пятого порядка со знаком минус, если положить , .
Определение. Матрица , полученная из матрицы заменой строк столбцами с теми же номерами и наоборот, называется транспонированной по отношению к .
.
Определители обладают рядом свойств, которые лежат в основе практических способов их вычисления.
Свойство 1. Определитель квадратной транспонированной матрицы равен определителю исходной матрицы.
Отсюда следует, что строки и столбцы определителя равноправны, т. е. любое свойство определителя, доказанное для строк, справедливо и для столбцов и наоборот.
Свойство 2. При перестановке любых двух строк определитель меняет знак.
Свойство 3. Определитель, имеющий две одинаковые строки, равен нулю.
Свойство 4. Общий множитель всех элементов некоторой строки определителя можно выносить за знак определителя.
Свойство 5. Определитель, содержащий две пропорциональные строки, равен нулю.
Свойство 6. Если все элементы некоторой строки определителя равны нулю, то определитель равен нулю.
Свойство 7. Определитель не изменится, если к элементам одной из его строк прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
| < Предыдущая | Следующая > |
|---|
Практическая работа для студентов 2 курса колледжа » Действия над матрицами»
Практическая работа № 1
на тему
«Матрицы и операции над ними»
Технологическая карта урока: «Практическое занятие»:
Урок __по дисциплине______________«Математика»___________
Тема___ Практическое занятие № 1 Дата___________________
Матрицы.
Сложение, транспонирование, умножение на число
Преподаватель _Мамошкина Юлия Владиславовна________
|
1. |
Организационный этап. |
Приветствие включение в деловой ритм, создание рабочей атмосферы подготовка к работе оформление титульного листа |
|
2. |
Постановка цели и задач урока. Мотивация учебной деятельности учащихся. |
Активация знания учащихся создание проблемной ситуации построение проекта выхода надо -могу-хочу |
|
3. |
Актуализация знаний. |
Определение типичных недостатков индивидуальные затруднения актуализация изученного включение в систему знаний и повторений |
|
4. |
Выявление знаний умений и навыков, проверка уровня сформированных математических умений. |
Выполнение практических заданий с использованием конспекта и консультацией преподавателя по образцу самостоятельное выполнение задания |
|
Практическая работа в 6 вариантах состоит из 4 разделов: |
||
|
-5- заданий на составление матриц по описанию, -4 -задания на сложение матриц -3 -задания на транспонирование матриц -1-задание на линейную комбинацию матриц |
||
|
5. |
Информация о домашнем задании, инструктаж по его выполнению |
Оформление работы, вариант соседа |
|
6. |
Рефлексия (подведение итогов занятия) |
Фиксация изученного на уроке. соотношение с целью, план |
Т.1. Элементы линейной и векторной алгебры
Теоретические основы дисциплины
Матрицы и операции над ними. Умножение матриц
Определители второго и третьего порядка, их свойства и методы вычисления. Миноры. Алгебраические дополнения. Разложение определителя по элементам строки или столбца Матрицы и действия с ними.
Обратная матрица. Нахождение обратной матрицы
Система линейных алгебраических уравнений Решение систем линейных алгебраических уравнений методом Крамера.
Решение систем линейных алгебраических уравнений матричным методом
Решение системы линейных уравнений методом Гаусса
Задание № 1 Матрицы и операции над ними
Прямоугольная таблица чисел вида:
|
𝑎11 𝑎21
|
𝑎12 … . 𝑎22 … .
|
𝑎1𝑚 𝑎2𝑚
|
𝑎
31 𝑎.
32 …. 𝑎3𝑚 … … … … . … … …(𝑎𝑛1 𝑎𝑛2 …. 𝑎𝑛𝑚) Называется матрицей.
𝑎𝑖𝑗 -действительные числа называемые элементы матрицы .
i-строки j- столбцы
m×n-размерность матрицы
Матрица все элементы которой равны 0- нулевая матрица
Если m=n матрица называется квадратной.
𝑎11
𝑎 …. 𝑎33Упорядочная совокупность элементов 22… .
( …. 𝑎𝑛𝑛)
называется главной диагональю квадратной матрицы.
Квадратная матрица называется диагональной если ее элементы находящийся на главной диагонали не равны 0 а все остальные =0.
Единичной называется диагональная матрица у которой все элементы главной диагонали =1.
Две матрицы называются равными (А=В) если они имеют одинаковые размеры и их соответствующие элементы равны
Сумма матриц А и В одинакового размера матрица С того же размера причем:
с𝑖𝑗 = 𝑎𝑖𝑗 + 𝑏𝑖𝑗
Умножение матрицы на число Произведением матрицы А на число к≠0 называется матрица каждый элемент которой получен умножением
соответствующего элемента А на число к≠0
Транспонирование матриц замена строк матрицы на столбцы.
Симметрическая матрица – квадратная матрица у которой элементы симметричные относительно главной диагонали, равны.
ПРИМЕР
1 2 1 3
Дано: А=( ) В=( )
4 5 0 5
Найти: 2А-В𝑇
1 2 2 4
Решение: 2А=2 ( ) = ( )
4 5 8 10
В𝑇 = (1 0 ) 2А-В𝑇 = (2 4 ) − (1 0 ) = (1 4)
3 5 8 10 3 5 5 5
Практическая работа №1 -Ω
На тему: «Операции над матрицами»
1.%202.bmp)
Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 2×3
2. Квадратную матрицу содержащую 4 строки
3. Симметричную матрицу содержащую 3 столбца
4. Диагональную матрицу 4×4
5. Единичную матрицу содержащую 2 строки
2. Выполнить возможные линейные операции над матрицами:
1 5 2 4 7 1
1. (4 5 2) +(5 8 4) =
6 2 4 3 3 5
2.
3.
4. (1 4) + (4 1) =
2 0 2 6
5. (1 5) + (5)
4
3. Транспонировать матрицу:
4 5
1. (4 8)
2 3
2. (1 4 7)
2 5 1
3. (3 2 6)
5 1 4
4. Выполнить действие 2А+3В-ЕТ 3ET+AT-2B
1 2 4 2 4 1 5 4 6
А=(5 4 1) В=(5 3 6) Е=(2 4 5)
6 2 4 1 2 3 4 1 5
Практическая работа №1 ¥— На тему: «Операции над матрицами »
1.
Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 3×4
2. Квадратную матрицу содержащую 5 строки
3. Симметричную матрицу содержащую 2 столбца
4. Диагональную матрицу 6×6
5. Единичную матрицу содержащую 3 строки
2. Выполнить возможные линейные операции над матрицами:
2 5 1 2 3 1
1. (4 4 2)+(4 8 4) =
9 2 4 3 1 5
2.
3. (3 5 5) ∗ 2 =
4. (7 1) + (5 3) =
4 5 4 6
5. (4 1) +
3
( )
3
3. Транспонировать матрицу:
2 7
1. (5 1)
3 4
2.
(4 0 5)
3. (1)
5
4. Выполнить действие 2А+3В-Ет 3ET+AT-2B
1 2 4 3 1 4 4 1 1
А=(1 5 1) В=(0 3 2) Е=(7 2 5)
6 2 2 1 2 3 3 1 8
Практическая работа №1 —£—
На тему: «Операции над матрицами »
1.
Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 2×5
2. Квадратную матрицу содержащую 2 строки
3. Симметричную матрицу содержащую 4 столбца
4. Диагональную матрицу 2×2
5. Единичную матрицу содержащую 5 строки
2. Выполнить возможные линейные операции над матрицами:
1 5 2 4 2 1
1. (8 3 8)+(4 5 4) =
4 2 4 3 1 2
2.
|
|
|
|
3.
|
2 7) ∗ 3 = |
|
7 |
1 5 3 |
(14. ( ) + ( ) =
4 5 4 6
5. (6 2) (5)
1
1. (1 5 4)
5 2 6
5 4
2. (2 6)
3 2
3.
(4 7)
5 6
4. Выполнить действие А-2В+Ет 3Ат+Е-3Вт
8 3 1 0 2 4 0 1 1
А=(0 5 6) В=(0 5 7) Е(4 2 5)
9 3 8 1 0 3 6 1 8
Практическая работа 1 Вариант —¿— На тему: «Операции над матрицами »
1. Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 4×1
2. Квадратную матрицу содержащую 3 строки
3.
Симметричную матрицу содержащую 2 столбца
4. Диагональную матрицу 5×5
5. Единичную матрицу содержащую 3 столбца 2. Выполнить линейные операции над матрицами:
0 5 1 5 4 2
1. (8 4 5)+(0 2 3) =
7 1 4 3 5 2
2.
|
|
|
|
3. (0
|
8 2) ∗ 4 = |
|
5 |
3 4 1 |
4.
( ) + ( ) =
2 1 0 9
5. (4 1) (7)
0
3. Транспонировать матрицу:
1. (2 0 0)
5 1 1
0 7
2. (1 3)
3 2
3. (2 4)
1 0
4. Выполнить действие А-2В+Ет 2Ат+Е-3Вт
1 2 1 8 3 2 0 5 9
А=(7 0 6) В=(0 1 7) Е= (5 4 5)
1 2 0 9 0 4 6 0 8
Практическая работа №1 Вариант — Þ-
На тему: «Операции над матрицами »
1.
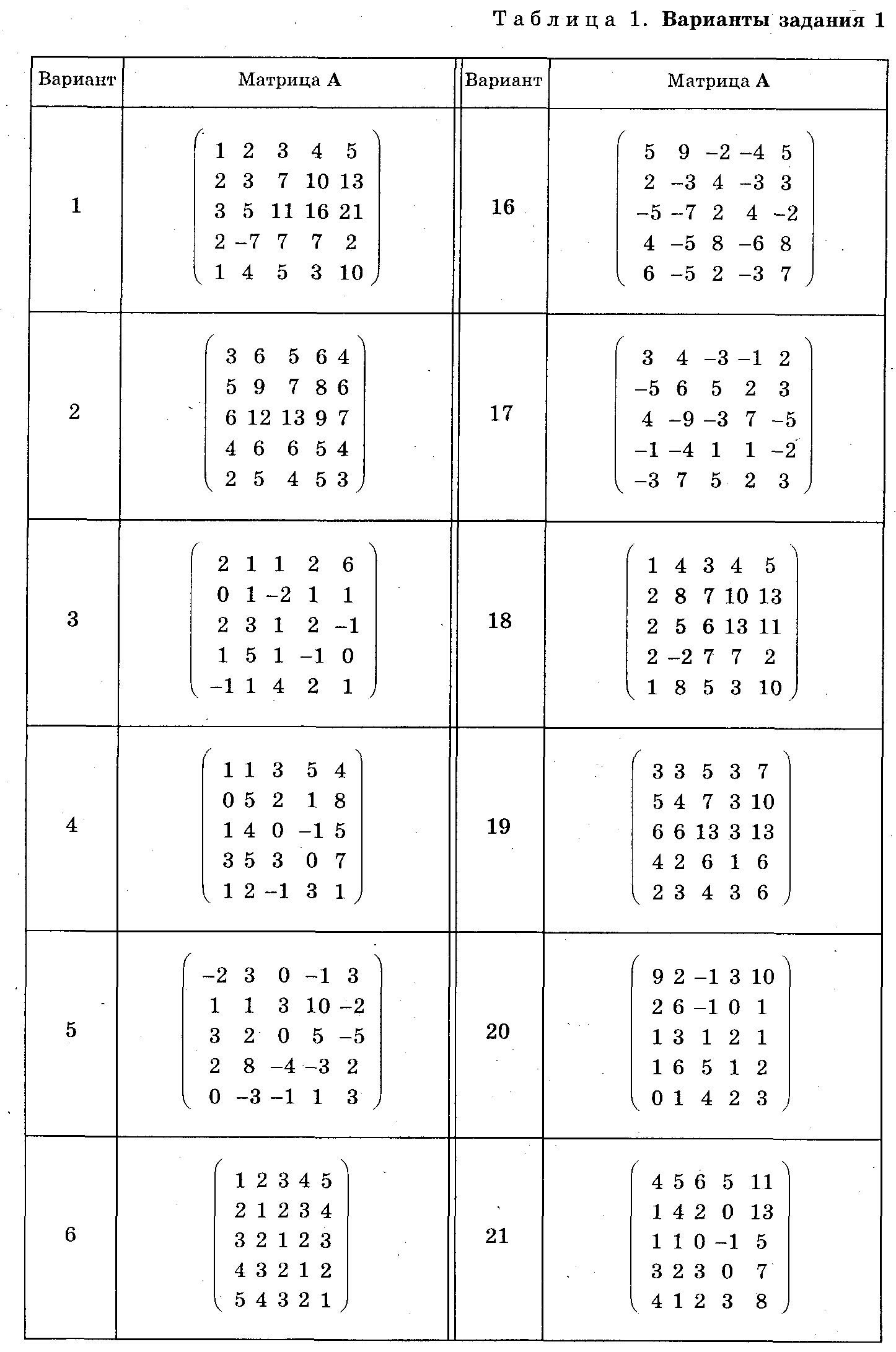Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 1×1
2. Квадратную матрицу содержащую 4 строки
3. Симметричную матрицу содержащую 3 столбца
4. Диагональную матрицу 4×4
5. Единичную матрицу содержащую 2 столбца 2. Выполнить линейные операции над матрицами:
0 2 1 4 1 4
1. (8 4 4)+(0 3 1) =
1 0 7 3 6 2
2.
|
|
|
|
3.
|
7 4) ∗ 3 = |
|
0 |
2 8 1 |
(14. ( ) + ( ) =
4 1 8 4
5. (9 0) (5)
1
3. Транспонировать матрицу:
1. (7 2 3)
4 5 1
4 1
2.
(0 8)
3 0
3. (5 4)
0 2
4. Выполнить действие А-2В+Ет, 3ET+AT-2B
5 1 5 5 8 2 3 4 1
А=(9 5 7) В=(0 5 7) Е= (1 6 5)
1 1 0 9 1 6 9 0 5
Практическая работа №1 Вариант — ð — На тему: «Операции над матрицами »
1.
Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 3×1
2. Квадратную матрицу содержащую 2 строки
3. Симметричную матрицу содержащую 5 столбцов
4. Диагональную матрицу 5×5
5. Единичную матрицу содержащую 4 столбца 2. Выполнить линейные операции над матрицами:
0 1 1 1 1 4
1. (8 0 4)+(0 1 1) =
1 0 1 3 0 2
2.
|
|
|
|
3.
|
2 1) ∗ 3 = |
|
1 |
22 10 1 |
(54. ( ) + ( ) =
8 1 0 6
5. (2 5 7 0) +
5
4
( )
11
1
3. Транспонировать матрицу:
1. (5 7 0)
5 4 2 2.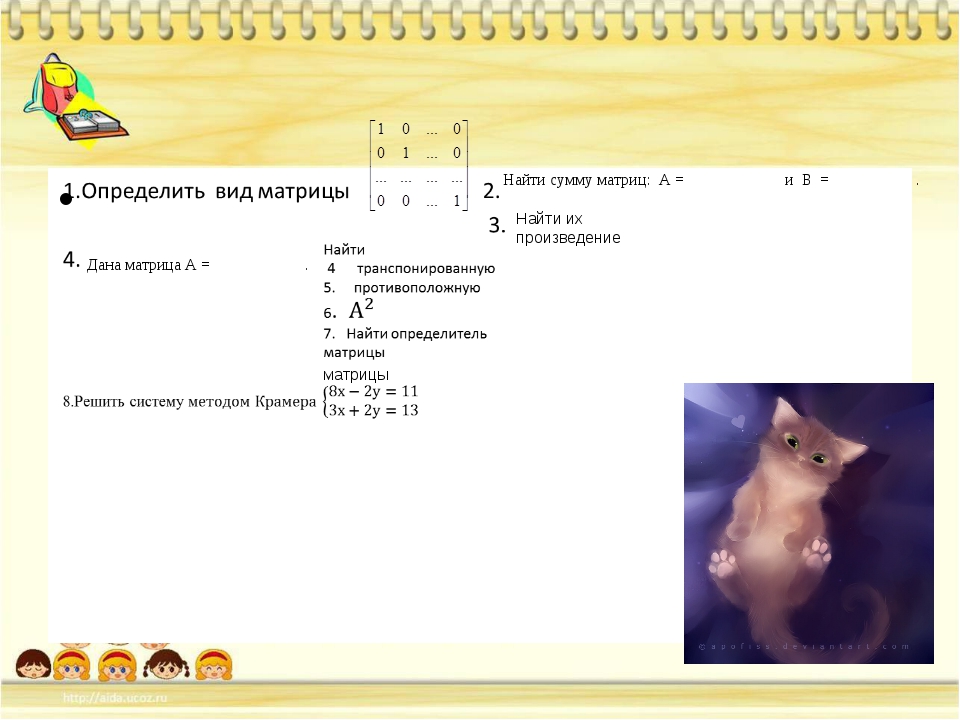
(3 7 8)
5 4 1
3. (2 4 1)
8 6 3
4. Выполнить действие А-2В+Ет . 3Ат+2Е-Вт
5 4 1 5 4 1
А=(2 3 5) В=(2 6 2) Е= (4 5 1)
2 3 0
2 6 8 1 3 2
Практическая работа №1 Вариант — æ — На тему: «Операции над матрицами »
1.
Из цифр: 1,2,3,4,5,6,7,8,9,0 составить:
1. Матрицу 1×5
2. Квадратную матрицу содержащую 3 строки
3. Симметричную матрицу содержащую 6 столбцов
4. Диагональную матрицу 7×7
5. Единичную матрицу содержащую 5 столбцов
2. Выполнить линейные операции над матрицами:
1 2 5 0 1 2
1. (4 6 5)+(4 5 6) =
4 1 2 2 3 1
1 4
2. (5 2) ∗ 3 =
1 4
3.
(1 1 1) ∗ 11 =
4. (0 1) + (1 11) =
9 2 0 16
52
5. (12 51 72 0) (1141 )
10
3. Транспонировать матрицу: 1
1. (2)
5
2. (2 5 4)
1 3 8
3. (5 4)
1 2
4. Выполнить действие 4А-3В+Ет 2Ат+Е-3Вт
5 4 1 5 2 1 11 2 1
А=(2 3 6) В=(4 1 2) Е= ( 2 1 2)
5 12 5 3 6 9 1 3 5
Ответы к практической работе «Операции над матрицами»
|
|
¿ |
£ |
|
|
¥ |
|
|
|
|
Ω |
|||||||||||||||||||||||
|
1 |
|
1
|
𝟏 𝟐 𝟑 ( 𝟐 |
𝟒 |
𝟓 ) |
𝟏 (𝟐 𝟑 |
𝟐 |
|
𝟑 |
𝟒 ) |
( |
|
|||||||||||||||||||||
|
2 |
1 (2 3 |
) |
(𝟏) 𝟐 |
|
|
𝟏 𝟐 𝟑 𝟒 (𝟓 |
𝟐 |
𝟑 |
𝟒 |
𝟓 |
) |
𝟏 𝟐 ( 𝟑 𝟒 |
𝟐 𝟑 |
𝟒 ) |
|||||||||||||||||||
|
3 |
|
1 ( 6 |
6 ) 5 |
𝟏 𝟏 ( 𝟒 𝟐 𝟕 𝟓 |
𝟒 𝟐 𝟔 |
𝟕 𝟓 ) 𝟔 |
|
𝟒 ( 𝟖 |
|
𝟖 ) 𝟑 |
|
|
𝟐 |
𝟏 𝟐 𝟓 |
|
|
|||||||||||||||||
|
4 |
2 0 0 0 (0 |
0 5 0 0 0 |
0 0 2 0 0 |
0 0 0 4 0 |
0 0 0 0 7) |
|
𝟐 ( 𝟎 |
𝟎 𝟑 |
) |
|
𝟏 𝟐 𝟑 𝟒 𝟓 (𝟔 |
𝟎 𝟐 𝟎 𝟎 𝟎 𝟎 |
𝟎 𝟎 𝟑 𝟎 𝟎 𝟎 |
|
𝟎 𝟎 𝟎 𝟒 𝟎 𝟎 |
𝟎 𝟎 𝟎 𝟎 𝟓 𝟎 |
𝟎 𝟎 𝟎
𝟎 𝟎 𝟔) |
𝟏 𝟎 ( 𝟎 𝟎 |
𝟎 𝟒 𝟎 𝟎 |
𝟎 𝟎 𝟕 𝟎 |
𝟎 𝟎 ) 𝟎 𝟖 |
||||||||||||
|
5 |
1 (0 0 |
0 1 0 |
0 0) 1 |
𝟏 𝟎 𝟎 𝟎 (𝟎 |
𝟎 𝟏 𝟎 𝟎 𝟎 |
𝟎 𝟎 𝟏 𝟎 𝟎 |
𝟎 𝟎 𝟎 𝟏 𝟎 |
𝟎 𝟎 𝟎 𝟎 𝟏) |
𝟏 𝟎 (𝟎 𝟏 𝟎 𝟎 |
𝟎 𝟎) 𝟏 |
|
|
𝟏 𝟎 ( ) 𝟎 𝟏 |
|
|||||||||||||||||||
|
1 |
5 (8 10 |
9 6 6 |
3 8) 6 |
𝟓 (𝟏𝟐 𝟕 |
𝟕 𝟖 𝟑 |
𝟑 𝟏𝟐) 𝟔 |
𝟒 (𝟖 𝟏𝟐 |
𝟖 𝟏𝟐 𝟑 |
𝟐 𝟔) 𝟗 |
𝟓 (𝟗 𝟗 |
𝟏𝟐 𝟏𝟑 𝟓 |
𝟑 𝟔) 𝟗 |
|||||||||||||||||||||
|
2 |
2 ( 10 |
10 2 |
4 ) 0 |
𝟐𝟎 ( 𝟏𝟔 |
𝟑𝟔 𝟒 |
𝟏𝟐 ) 𝟖 |
𝟑 ( 𝟏𝟐 |
𝟏𝟓 𝟔 |
𝟗 ) 𝟏𝟐 |
𝟑 ( 𝟐𝟒 |
𝟏𝟐 𝟔 |
𝟏𝟓 ) 𝟏𝟐 |
|||||||||||||||||||||
|
3 |
(0 32 |
8) |
(𝟑 𝟔 𝟐𝟏)
|
(𝟔 𝟏𝟎 |
𝟏𝟎) |
𝟐 (𝟖) 𝟒 |
|||||||||||||||||||||||||||
|
4 |
9 ( 2 |
4 ) 10 |
𝟏𝟐 𝟒 ( ) 𝟖 𝟏𝟏 |
𝟏𝟐 𝟒 ( ) 𝟖 𝟏𝟏 |
𝟓 ( 𝟒 |
𝟓 ) 𝟔 |
|||||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
2 (0 0 |
5 1) 1 |
𝟏 𝟓 (𝟓 𝟐) 𝟒 𝟔 |
𝟐 𝟓 𝟑 ( ) 𝟕 𝟏 𝟒 |
𝟒 𝟒 𝟐 ( ) 𝟓 𝟖 𝟑 |
||||||||||||||||||||||||||||
|
2 |
0 ( 7 |
1 3 ) 3 2 |
𝟓 ( 𝟒 |
𝟐 𝟑 ) 𝟔 𝟐 |
𝟒 (𝟎) 𝟓 |
|
𝟏 (𝟒) 𝟕 |
||||||||||||||||||||||||||
|
3 |
2 ( 4 |
1 ) 0 |
𝟒 ( 𝟕 |
𝟓 ) 𝟔 |
|
(𝟏 𝟓) |
𝟐 (𝟓 𝟏 |
𝟑 𝟐 𝟔 |
𝟓 𝟏) 𝟒 |
||||||||||||||||||||||||
|
1 |
−𝟏𝟓 (𝟏𝟐 −𝟖 |
𝟏 𝟐 𝟕 |
𝟑 −𝟖) 𝟎 |
𝟖 (𝟏 𝟖 |
𝟑 −𝟑 𝟖 |
−𝟏 −𝟕) 𝟏𝟎 |
𝟕 (𝟏 𝟏𝟒 |
𝟎 𝟏𝟕 𝟏𝟕 𝟕) 𝟓 𝟓 |
𝟑 (𝟐𝟏 𝟗 |
𝟏𝟒 𝟏𝟑 𝟓 |
𝟕 𝟏𝟗) 𝟏𝟐 |
||||||||||||||||||||||
|
2 |
−𝟐𝟐 𝟏𝟗 ( 𝟎 𝟏 𝟐 −𝟗 |
−𝟏𝟔 𝟗 ) −𝟒 |
𝟐𝟒 (𝟕 −𝟑 |
𝟏 𝟐 −𝟐 |
𝟐𝟓 𝟏𝟒) 𝟐𝟐 |
𝟕 (𝟓 𝟓 |
𝟐𝟎 𝟕 𝟓 𝟏) 𝟏𝟐 𝟐𝟎 |
𝟏𝟐 (𝟒 𝟐𝟎 |
𝟐 𝟏𝟎 𝟏𝟐 |
𝟏𝟕 −𝟕) 𝟏𝟑 |
|||||||||||||||||||||||
Ответы к практической работе «Операции над матрицами»
|
|
Þ |
|
|
|
|
ð |
|
|
|
æ |
|
||||
|
1 |
(5)
|
|
|
|
|
|
( |
) |
|
(1 |
2 |
3 |
4 |
|
5) |
|
2 |
( |
|
|
) |
|
|
|
|
|
|
|
|
|||
|
3 |
|
1 (2 3 |
2 5 8 |
3 8) 7 |
|
|
( |
) |
|
4 1
2 3 5 (6 |
1 2 4 1 1 1 |
2 4 8 8 5 2 |
3 1 8 7 5 4 |
5 1 5 5 9 0 |
6 1
2
4 0 1) |
|
4 |
2 0 ( 0 0 |
0 5 0 0 |
0 0 4 0 |
0 0 ) 0 8 |
|
𝟏 0 0 0 (0 |
0 𝟓 0 0 0 |
0 0 0 0 0 0 𝟒 0 0 0 𝟕 0 0 0 𝟏) |
2 0 0 1 0 0 0 0 0 0 0 0 0 0 |
0 0 7 0 0 0 0 |
0 0 0 1 0 0 0 |
0 0 0 0 5 0 0 |
0 0 0 0 0 0 0 0 0 0 1 0 0 1 |
||
|
5 |
1 ( 0 |
|
0 ) 1 |
|
𝟏 0 ( 0 0 |
0 𝟏 0 0 |
0 0 𝟏 0 |
0 0 ) 0 𝟏 |
1 0 0 0 (0 |
0 1 0 0 0 |
0 0 1 0 0 |
0 0 0 1 0 |
0 0 0 0 1) |
|||||
|
1 |
4 (8 4 |
3 7 6 |
5 5) 9 |
|
𝟏 (𝟖 𝟒 |
|
𝟐 𝟏 𝟎 |
𝟓 𝟓) 𝟑 |
|
𝟏 (𝟖 𝟔 |
𝟑 𝟕 𝟏𝟏 𝟏𝟏) 𝟒 𝟑 |
|||||||
|
2 |
15 ( 12 |
6 27 ) 21 0 |
|
5. 8
|
8 12 ) 10 0 |
|
𝟑 𝟏𝟐 (𝟏𝟓 𝟔) 𝟑 𝟏𝟐 |
|||||||||||
|
3 |
(3 21 12) |
|
(15 |
6 3) |
|
𝟏𝟏 𝟏𝟏 𝟏𝟏 |
||||||||||||
|
4 |
8 ( 12 |
3 ) 5 |
|
11 ( 8 |
23 ) 7 |
|
𝟏 ( 𝟗 |
𝟏𝟐 ) 𝟏𝟖 |
||||||||||
|
5 |
|
|
|
|
|
|
|
|
||||||||||
|
1 |
𝟕 (𝟐 𝟑 |
𝟒 𝟓) 𝟏 |
|
( |
𝟓 𝟕) 𝟎 |
|
(𝟏 |
𝟐 𝟓) |
||||||||||
|
2 |
𝟒 ( 𝟏 |
𝟎 𝟑 ) 𝟖 𝟎 |
|
𝟓 (𝟒 𝟐 |
𝟑 𝟕 𝟖 |
𝟓 𝟒) 𝟏 |
|
𝟐 (𝟓 𝟒 |
𝟏 𝟑) 𝟖 |
|||||||||
|
3 |
𝟓 ( 𝟒 |
𝟎 ) 𝟐 |
|
𝟐 (𝟒 𝟏 |
𝟖 𝟔) 𝟑 |
|
𝟓 𝟒 |
𝟏
𝟐 |
|
|||||||||
|
1 |
−𝟐 −𝟏𝟒 𝟏𝟎 (𝟏𝟑 𝟏 −𝟕) −𝟏𝟔 𝟒 −𝟕 |
|
−𝟐 −𝟏𝟒 (𝟏𝟑 𝟏 −𝟏𝟔 𝟒 |
𝟏𝟎 −𝟕) −𝟕 |
|
𝟏𝟔 (−𝟐 𝟏𝟐 |
𝟏𝟐 𝟏𝟎 𝟑𝟐 |
𝟐 𝟐𝟏) −𝟐 |
||||||||||
|
2 |
𝟑 𝟑𝟏 −𝟐𝟑 (−𝟐𝟎 𝟔 𝟓 ) 𝟏𝟖 𝟎 −𝟏𝟑 |
|
𝟏𝟎 𝟒 (𝟖 𝟑 𝟐 𝟏𝟑 |
𝟓 𝟏𝟔) 𝟐𝟐 |
|
𝟔 (𝟒 𝟎 |
−𝟔 𝟒 𝟗 |
𝟐 𝟖) 𝟏𝟐 |
||||||||||
(4
Тест «Определители и матрицы»
«Математика – это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями»
Юджин Вигнер, американский физик и математик (1902-1995)
Часть I.
Выберите один правильный ответ.
1. Раздел математики, изучающий определители и матрицы называется:
а) алгеброй
б) линейной алгеброй
в) высшей математикой
г) линейным программированием
2. Определитель – это:
а) число
б) матрица
в) таблица чисел
г) вектор
3. Чему не может быть равен определитель:
а) нулю
б) отрицательному значению
в) дробному значению
г) бесконечности
4. Порядок определителя – это:
а) диапазон значений его элементов
б) значение определителя
в) число его строк и столбцов
г) сумма индексов последнего элемента последней строки
5. Минор определителя – это:
а) сумма элементов главной диагонали
б) произведение элементов главной диагонали
в) другой определитель, полученный из данного вычеркиванием строки и столбца
г) алгебраическое дополнение элемента определителя
6.
Алгебраическое дополнение каждого элемента равно:
а) минору этого элемента, взятому с противоположным знаком
б) минору этого элемента, взятому со своим знаком
в) минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, нечетно, и с обратным знаком, если — четно
г) минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит данный элемент, четно, и с обратным знаком, если — нечетно
7. Разложением определителя по элементам строки называется:
а) нахождение определителя как суммы произведений элементов строки на их алгебраические дополнения
б) нахождение определителя как суммы произведений элементов столбца на их алгебраические дополнения
в) нахождение определителя как суммы произведений элементов строки на миноры этих элементов
г) нахождение определителя как суммы произведений элементов столбца на миноры этих элементов
8.
Матрица – это:
а) прямоугольная таблица чисел
б) определитель
в) отличный от нуля минор
г) неопределяемое понятие
9. Порядок может быть только у матрицы следующего вида:
а) прямоугольной
б) квадратной
в) матрицы-строки
г) любой
10. Диагональной называется матрица, у которой:
а) все элементы вне главной диагонали равны нулю
б) все элементы главной диагонали равны нулю
в) все элементы главной диагонали равны единице
г) все элементы на главной и побочной диагоналях равны нулю
11. Присоединённой матрицей к квадратной матрице может являться:
а) матрица того же порядка
б) матрица, определитель которой равен определителю данной матрицы
в) матрица порядка на один меньше, чем у данной матрицы
г) такая матрица, что произведение их определителей равно единице
12.
Чтобы вычислить произведение матрицы на число, нужно:
а) умножить элементы главной диагонали на это число
б) умножить элементы первой строки на это число
в) умножить элементы первого столбца на это число
г) умножить каждый элемент на это число
13. При умножении матрицы на единичную матрицу будет получена:
а) исходная матрица
б) транспортированная матрица
в) обратная матрица
г) единичная матрица
14. Операция умножения матриц не обладает свойством:
а) ассоциативности
б) коммутативности
в) дистрибутивности
15. Система линейных уравнений называется совместной, если она:
а) имеет единственное решение
б) не имеет решений
в) имеет бесконечное множество решений
г) имеет хотя бы одно решение
16. При решении систем уравнений методом Гаусса нельзя:
а) удалять равные или пропорциональные строки кроме одной
б) любую строку умножать или делить на некоторое число
в) переставлять местами строки
г) умножать любой столбец на некоторое число
17.
Если при решении системы уравнений методом Крамера все определители равны нулю, то:
а) система имеет единственное решение
б) система имеет ненулевые решения
в) система имеет бесконечное множество решений
г) система не имеет решений
18. Методом обратной матрицы может быть решена:
а) любая система линейных уравнений
б) система линейных уравнений, имеющая квадратную матрицу
в) система линейных уравнений, имеющая квадратную невырожденную матрицу
г) система как линейных, так и нелинейных уравнений
19. Для решения систем линейных уравнений методом Крамера в MS Excel ее главный и вспомогательные определители вычисляют с использованием функции:
а) МОБР
б) МОПРЕД
в) МУЛЬТИНОМ
г) МУМНОЖ
20. В MathCAD для нахождения определителя используют оператор Determinant на панели инструментов:
а) Calculator
б) Calculus
в) Matrix
г) Evaluation
Часть II.
Выберите несколько правильных ответов.
1. Свойства определителей:
а) определитель транспонированной матрицы равен определителю исходной матрицы
б) определитель обратной матрицы равен определителю исходной матрицы
в) умножение всех элементов строки или столбца определителя на некоторое число равносильно умножению определителя на это же число
г) если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный
д) если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю
е) если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен единице
ж) если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю
з) определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали
и) если все элементы k-ой строки (столбца) определителя представлены в виде сумм ak j + bk j, то определитель можно представить в виде произведения двух определителей
к) определитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и то же число
л) определитель произведения двух квадратных матриц равен произведению определителей этих матриц
2.
К элементарным преобразованиям матриц относятся:
а) перестановка строк
б) умножение любой строки на число, отличное от нуля
в) прибавление к одной из строк любой другой строки, умноженной на любое число
г) приписывание к данной матрице единичной матрицы
д) умножение любой строки матрицы на другую строку
е) замена строк матрицы ее столбцами
3. К арифметическим действиям над матрицами относятся:
а) нахождение обратной матрицы
б) нахождение транспортированной матрицы
в) сумма матриц
г) произведение матрицы на число
д) произведение матриц
е) деление матриц
Часть III. Каждому элементу первого столбца поставьте в соответствие один или несколько элементов второго столбца.
1. Виды матриц.
Виды матриц: | Характеристики: |
1. | А. число строк матрицы совпадает с числом столбцов |
2. вырожденная | Б. матрица, составленная из алгебраических дополнений элементов данной матрицы, разделенных на величину определителя исходной матрицы |
3. квадратная | В. получена из данной матрицы заменой строк столбцами с соответствующим номером |
4. диагональная | Г. определитель матрицы равен нулю |
5. единичная | Д. не имеет обратной матрицы |
6. транспортированная | Е. |
| Ж. на главной диагонали стоят некоторые числа, а остальные элементы — нули |
| З. на главной диагонали стоят единицы, а остальные элементы — нули |
| И. является частным случаем диагональной матрицы |
| К. имеет определитель |
обратная
равна произведению исходной и обратной матриц2. Методы решения систем линейных уравнений.
Методы: | Характеристики: |
1. метод Гаусса | А. |
2. метод Крамера | Б. метод последовательного исключения неизвестных, приведение матрицы системы к ступенчатому виду |
3. матричный метод | В. неизвестные вычисляются как отношение определителей, полученных из определителя системы заменой соответствующих столбцов на столбец свободных членов, к определителю системы уравнений |
| Г. подходит для произвольной системы линейных уравнений |
| Д. подходит только для систем линейных уравнений, у которых число уравнений равно числу неизвестных |
| Е. |
матрица-столбец неизвестных вычисляется как произведении обратной матрицы на матрицу-столбец свободных членов
матрица системы должна быть невырожденной
Тест в интерактивной форме:
С выбором 1 ответа
Пазл «Классификация матриц»
СтратегииКак решать задачи IQ с матрицами воронов
В этом уроке вам будет предоставлено следующее:
- Объяснение того, что такое матрицы IQ-тестов и как они используются
- Учебное пособие по стратегиям решения задач расширенного теста матриц Ворона с примерами
- Ссылка на оригинальный тест Raven Progressive Matrices — чтобы вы могли проверить себя
- Ссылки на дополнительные ресурсы по тестированию матриц
Матрицы IQ Tests
Матричный тест — это невербальный IQ-тест «культурной ярмарки» с несколькими вариантами ответов, который измеряет ваш подвижный интеллект (Gf) — вашу способность рассуждать и решать проблемы.Плавный интеллект — это ключевой компонент вашего общего интеллекта.
В каждом тестовом задании испытуемого просят определить недостающий элемент, завершающий набор фигур.
Паттерны представлены в виде матрицы 4 × 4, 3 × 3 или 2 × 2, что и дает название тесту. Здесь показан пример теста матриц с сайта Smart-kit.com.
Благодаря простоте использования и интерпретации, а также независимости от языка и навыков чтения и письма, матричные тесты имеют широкое практическое применение — в качестве меры интеллекта среди населения в целом как для взрослых, так и для детей, для соискателей в качестве психометрического показателя. тест, для поступающих в вооруженные силы, и для оценки клинических (e.грамм. Аутизм) населения.
Стратегии, чтобы получить высокий балл в матричном тесте
Каждый тест Raven имеет одинаковый формат: матрица 3 x 3, в которой отсутствует правый нижний элемент, и ее необходимо выбрать из 8 альтернатив.
Решение проблем типов матриц Raven по существу требует выяснения лежащих в основе правил , которые объясняют последовательность форм.
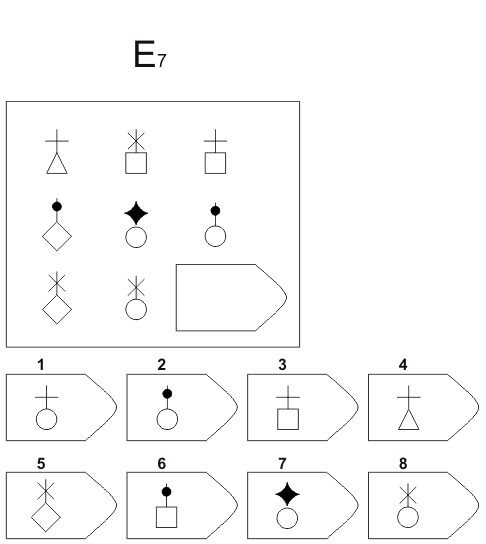
Вот пример, который нужно выяснить:
Правильный ответ — 5.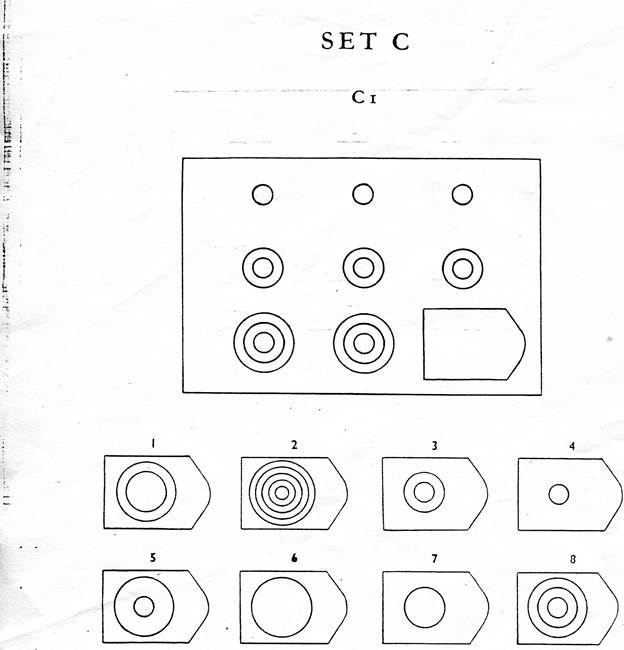
Вариации записей в строках и столбцах этой задачи можно объяснить тремя правилами.
1. Каждая строка содержит 3 фигуры (треугольник, квадрат, ромб).
2. В каждой строке по 3 полосы (черная, полосатая, прозрачная).
3. Ориентация каждой полосы одинакова в строке, но меняется от строки к строке (вертикальная, горизонтальная, диагональная).
Из этих 3 правил можно вывести ответ (5).
5 правил решения проблем с матрицами (расширенный тест матриц)
Джон Рэйвен разработал все задачи для своего теста расширенных матриц, основанных на пяти основных типах правил.Каждая проблема может иметь комбинации разных правил или разных экземпляров одного и того же правила.
Для эффективного решения задач расширенного теста матриц Ворона вам будет полезно изучить некоторые правила.
Это правила:
1. Константа подряд. Это «правило 3» в приведенном выше примере матрицы — ориентация полосы одинакова в каждой строке, но изменяется вниз по столбцу.
2. Количественная прогрессия. Увеличение или уменьшение между соседними записями по размеру, положению или количеству. Пример этого правила показан ниже:
Правильный ответ: 3. Количество черных квадратов в каждой записи увеличивается в верхней строке с 1 до 2 до 3. Аналогичным образом количество черных квадратов в первом столбце уменьшается с 3 до 2 до 1.
3. Сложение или вычитание цифр. Цифра из одного столбца добавляется или вычитается из другого столбца для получения третьего.Пример приведен ниже:
Правильный ответ 8
4. Распределение 3 значений. В каждой строке всегда присутствуют три значения категории, например форма. Два примера этого правила показаны в первой матрице, которую мы рассмотрели выше. Каждая строка содержит 3 фигуры (треугольник, квадрат, ромб), а каждая строка — 3 полосы (черная, полосатая, прозрачная).
5.
Распределение 2 значений. Два значения категории, такие как форма, всегда присутствуют в каждой строке, но третье значение равно нулю / не имеет значения.Пример этого приведен ниже.
Правильный ответ — 5. Каждый элемент фигуры (горизонтальная линия, вертикальная линия, V-образная форма) встречается два раза в каждой строке.
Поиск соответствующих элементов
В задачах с более чем одним правилом решатель должен выяснить, какие элементы головоломки подчиняются одному и тому же правилу — это можно назвать «поиском соответствия».
Пример проблемы соответствия показан ниже:
Правильный ответ — 5.Выяснение того, что соответствует тому, требует, чтобы вы сформировали в уме гипотез и проверили их. Гипотеза — это воображаемое объяснение или предсказание, которое необходимо проверить.
В приведенном выше примере одна гипотеза состоит в том, что одно правило применяется к стержням, другое правило применяется к темным кривым, а другое правило применяется к прямым линиям.
Хотя верно, что в каждом столбце есть по две формы каждого типа, эта гипотеза не объясняет количество различных элементов.Нужна еще одна гипотеза. Ориентация (вертикальная или горизонтальная) может быть основой правил, необходимых для решения этой проблемы. В каждом ряду всегда 1, 2 и 3 горизонтальных элемента и 1,2 и 3 вертикальных элемента. В дополнение к этому, 1,2 и 3 элемента каждой формы распределены по трем рядам.
Дополнительные учебные ресурсы
Тест прогрессивных матриц Равена (стандартный) — оригинал можно взять здесь. Плата составляет 20 евро. Это действительный IQ-тест, и по сравнению с другими профессионально проводимыми IQ-тестами он не требует больших затрат.Это не тест Advanced Progressive Matrices.
Альтернативных матриц тестов, основанных на тесте Равена и использующих аналогичные принципы, можно найти здесь (текст на итальянском языке). Чтобы получить результаты после прохождения любого теста, вам необходимо указать свой возраст в соответствующем поле и затем нажать «IQ».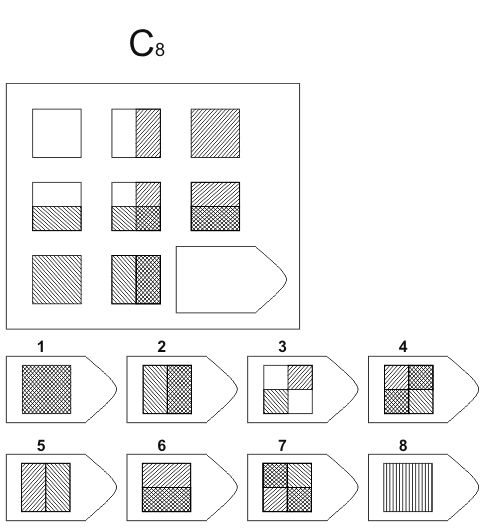
Smart-kit.com Матрицы Тестовые пазлы. Здесь есть что попробовать.
Для тестов матриц (например, расширенных прогрессивных матриц Raven) вы можете потренироваться на этом форуме здесь. Или стратегии ментальной модели.
Тест матриц SimilarMinds — набрано.
Приложение i3 Mindware, основанное на фактических данных, предназначенное для повышения показателей IQ и тестов по матрицам.
Подпишитесь на бесплатные электронные книги по матричным тестам IQ и увеличению IQ
матриц Raven | 25 практических тестов
Основная причина, по которой вам следует потренироваться в режиме онлайн для прохождения теста Raven’s IQ перед фактической оценкой, заключается в том, что вы хотите максимизировать свои шансы на успешную сдачу теста с оптимальным баллом.Распространенное заблуждение, что человек не может улучшить свои результаты на тестах IQ. Научно подтверждено, что правильная аналитическая и рефлексивная тренировка может значительно улучшить ваши результаты на прогрессивных матрицах Raven.
Тем более, что эффект от тренировок не зависит ни от возраста, ни от пола.
Пара быстрых тренировок имеет краткосрочный положительный эффект на результаты вашего теста Raven’s Test. Знание типов шаблонов и характеристик важно для аналитического увеличения скорости обработки и способности быстро отвечать на вопросы.Важно отметить, что у прогрессивных матриц Raven есть ограничение по времени. Поэтому практика и повторение имеют решающее значение.
Кроме того, полезно размышлять над ответами и решениями и учиться на своих ошибках, чтобы снизить вероятность повторения их снова. Помните, практика ведет к совершенству. Вы увидите, что благодаря практике ваша производительность улучшится. Ознакомление с психометрическими тестами — первый шаг к успеху. Практикуясь, вы получите четкое представление о том, что это за тесты, как они выглядят, что они измеряют и каковы будут условия тестирования.
Assessment-Training.com — это популярная платформа для практики сертификации, обучения тестированию / проверке профессиональных навыков и подготовки заявлений о приеме на работу.
Мы предлагаем индивидуальные подготовительные пакеты с тестами в том же стиле, что и настоящие тесты прогрессивных матриц Raven.
В дополнение к тому факту, что все наши практические тесты содержат отработанные решения и объяснение того, как получить правильный ответ, мы предлагаем вам уникальную персональную систему отслеживания прогресса .
Эта система прогресса поможет вам отслеживать ваш прогресс и даст подробный обзор ваших выступлений. Это поможет вам определить ваши сильные и слабые стороны и даст представление о ваших областях развития. Инструмент прогресса отслеживает ваши результаты, время тестирования и общий прогресс.
Мы предлагаем вам инструменты, которые помогут уменьшить беспокойство и убедиться, что вы получите максимальную отдачу от себя в день сертификации, оценочного теста или собеседования при приеме на работу! Исследования среди наших пользователей показали, что благодаря практике ваши результаты могут улучшиться до 80% .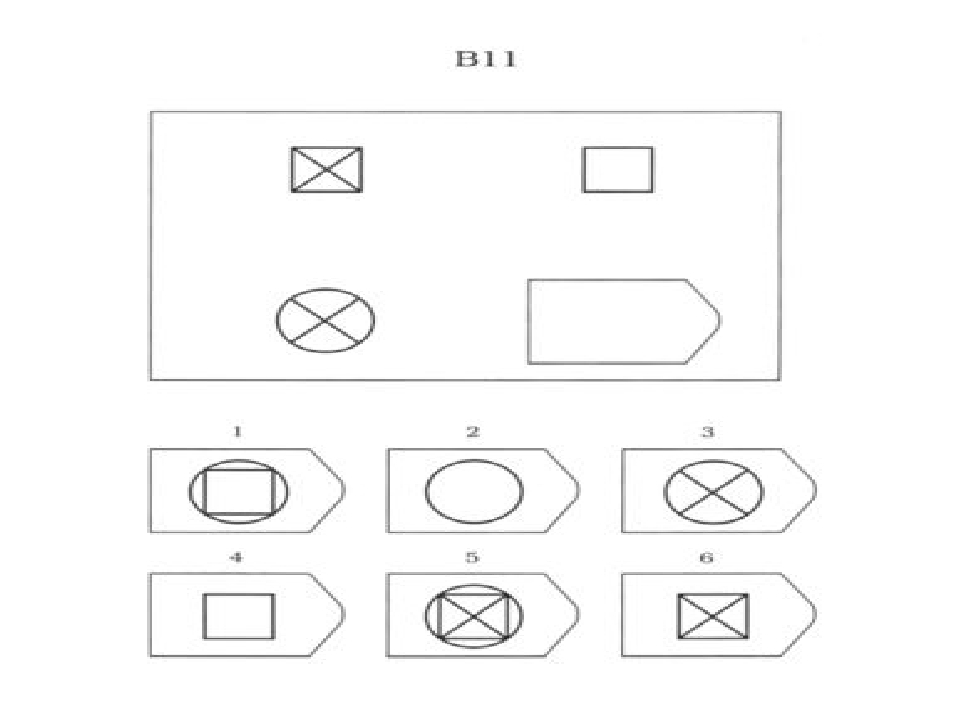
Более 96% наших клиентов порекомендовали бы Assessment-Training для практики.
Начните обучение прямо сейчас и получите немедленный доступ к тестам и практике 24/7 на вашем компьютере, телефоне или планшете!
Тест прогрессивных матриц— Nibcode Solutions
Тест прогрессивных матриц, созданный доктором Джоном С. Рэйвеном в 1938 году, представляет собой тест абстрактного мышления для измерения общего интеллекта, интеллектуальных способностей и общих умственных способностей.Это культурно справедливый (уровень образования не имеет решающего значения для реализации), невербальный (применяется ко всем, независимо от языка, образования и вербальных способностей), интересный и легкий тест.
Этот тест измеряет ключевой компонент интеллекта: развивающую способность или способность извлекать и понимать информацию из сложной ситуации, способность воспринимать и способность определять отношения. Это стандартизированный тест интеллекта, который состоит из визуально представленных задач, похожих на геометрические аналогии, в которых матрица геометрических фигур представлена без одной пропущенной записи, и правильная пропущенная запись должна быть выбрана из набора вариантов ответов.
Тест состоит из 60 задач, сгруппированных в пять наборов по двенадцать задач, которые упорядочены по сложности:
- Первые серии требуют точности в различении.
- Вторая серия посложнее, так как охватывает аналогии, перестановки и переделки модели.
- Последние серии представляют собой логические отношения.
Для обучения работе с этим типом тестов мы предоставляем 12 анкет, аналогичных тесту Ворона, одна из которых совпадает с ним.В каждой анкете 60 вопросов, на которые нужно ответить за 40 минут.
Каждая геометрическая фигура представляет собой матрицу системы мышления. Чтобы найти матрицу мышления, включенную в каждую фигуру, вы должны использовать свои аналогичные рассуждения, восприятие и способность абстрагироваться. Заполнение матрицы выполняется путем множественного выбора из 6 или 8 возможных ответов.
На приведенном выше рисунке показан пример одной из этих проблем. Третий рисунок каждой строки можно сделать, наложив два предыдущих рисунка, но стирая общие линии.
Исходя из этих рассуждений, можно сделать вывод, что выходом является вариант 8.
Если хотите, в режиме обучения вы можете увидеть решение, нажав на кнопку, расположенную в правом верхнем углу каждого вопроса. Иногда предоставляется дополнительная информация об используемой логике.
Анкетыне могут быть выбраны, они будут выходить постоянно и периодически, когда вы запрашиваете тест.
Примеры и объяснения тестов прогрессивных матриц Raven
Автор статьи: Dr.Эдвин ван Тиль, обновлено 3 июля 2020 г.
Матрицы Ворона — это тест невербальных способностей, используемый для оценки абстрактных рассуждений. Тест является прогрессивным в том смысле, что вопросы усложняются по мере прохождения теста. Задача состоит в том, чтобы определить недостающий элемент в шаблоне, который обычно представлен в виде матрицы, отсюда и название матрицы Равена.
Тесты были первоначально разработаны Джоном К. Рэйвеном в 1936 г. 1 и в настоящее время лицензированы Pearson PLC.
Вот пример используемого формата.
Вопрос в стиле теста прогрессивных матриц Равена. В этой матрице 3 X 3 восемь шаблонов, недостающий должен быть определен из восьми вариантов ответа. В этом примере существует «правило» того, как паттерны меняются слева направо и сверху вниз. Вы видите правильный ответ?
Учитывая невербальность теста, он также считается форматом, который снижает культурные предубеждения. Вы можете бесплатно пройти восемь вопросов по матрицам Raven, например, по тесту, если хотите.Это очень популярный тест для оценки подвижного интеллекта в группах.
Есть три формы, предназначенные для респондентов разного уровня подготовки. Тесты можно проводить в возрасте от пяти лет и до пожилого возраста. Вот эти три теста:
Стандартные прогрессивные матрицы Raven
Это оригинальный тест, опубликованный в 1938 году. Все вопросы представляли собой черные узоры на белом фоне. Всего было 60 вопросов, распределенных по пяти блокам, в каждом из которых задания были представлены с возрастающей (прогрессивной) сложностью.
Цветные прогрессивные матрицы Raven
Эти матрицы были разработаны для людей с ограниченными способностями из-за возраста (старые, молодые) или умственно отсталых. Он содержит два первых набора из стандартных матриц с дополнительным набором из 12 элементов, вставленных между ними. Однако вопросы в основном были представлены на цветном фоне, чтобы сделать их визуально стимулирующими.
Расширенные прогрессивные матрицы Raven
Расширенная форма матриц дополнительных элементов (48), представленных как один набор из 12 (набор I), а другой из 36 (набор II).Пункты представлены черным цветом на белом фоне, как и в стандартной версии, и также становится все труднее на протяжении всего теста. Эти предметы подходят взрослым и подросткам с интеллектом выше среднего. Вы можете пройти бесплатный тест на логическое мышление, чтобы понять, о чем этот тест. Если вам нужно подготовиться к аттестации, вы можете использовать наш обширный пакет практики логического мышления
В 1998 году были созданы и опубликованы «параллельные» формы стандартных и цветных прогрессивных матриц.
Это стало необходимым, поскольку матрицы Ворона стали слишком известными, то есть правильные ответы можно было легко найти до прохождения теста. Кроме того, была опубликована пересмотренная версия стандартного теста под названием SPM — Standard Progressive Matrices Plus — с более сложными элементами, заменяющими некоторые из параллельных. Благодаря этим психометрическим характеристикам эта версия лучше дифференцируется среди респондентов.
1 Рэйвен, Дж. К. (1936). Психологические тесты, используемые в генетических исследованиях: Показатели родственных особей на тестах, в основном образовательных и в основном репродуктивных. Диссертация на степень магистра, Лондонский университет .
Матричный продукт — линейная алгебра
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Матрица фигур — невербальные вопросы и ответы
Почему матрица фигур невербального рассуждения?
В этом разделе вы можете выучить и попрактиковаться в вопросах невербального мышления на основе «Матрицы фигур» и улучшить свои навыки, чтобы пройти собеседование, конкурсный экзамен и различные вступительные испытания (CAT, GATE, GRE, MAT, банковский экзамен, железнодорожный экзамен).
и т.п.) с полной уверенностью.
Где я могу получить вопросы и ответы о невербальной матрице рисунков с пояснениями?
IndiaBIX предоставляет вам множество полностью решенных вопросов о невербальном мышлении (матрица рисунков) и ответов с пояснениями. Решенные примеры с подробным описанием ответов, даны пояснения, которые легко понять. Все студенты, первокурсники могут загрузить вопросы викторины по невербальной матрице логических рассуждений с ответами в виде файлов PDF и электронных книг.
Где я могу получить вопросы и ответы на собеседовании с невербальной матрицей логического мышления (объективный тип, множественный выбор)?
Здесь вы можете найти вопросы и ответы по матрице невербальных логических фигур объективного типа для собеседований и вступительных экзаменов. Также предусмотрены вопросы с множественным выбором и вопросы истинного или ложного типа.
Как решить проблемы с Матрицей невербальных рассуждений?
Вы можете легко решить все виды вопросов невербального мышления, основанные на Матрице фигур, практикуя упражнения объективного типа, приведенные ниже, а также получите быстрые методы для решения задач Матрицы невербальных рассуждений.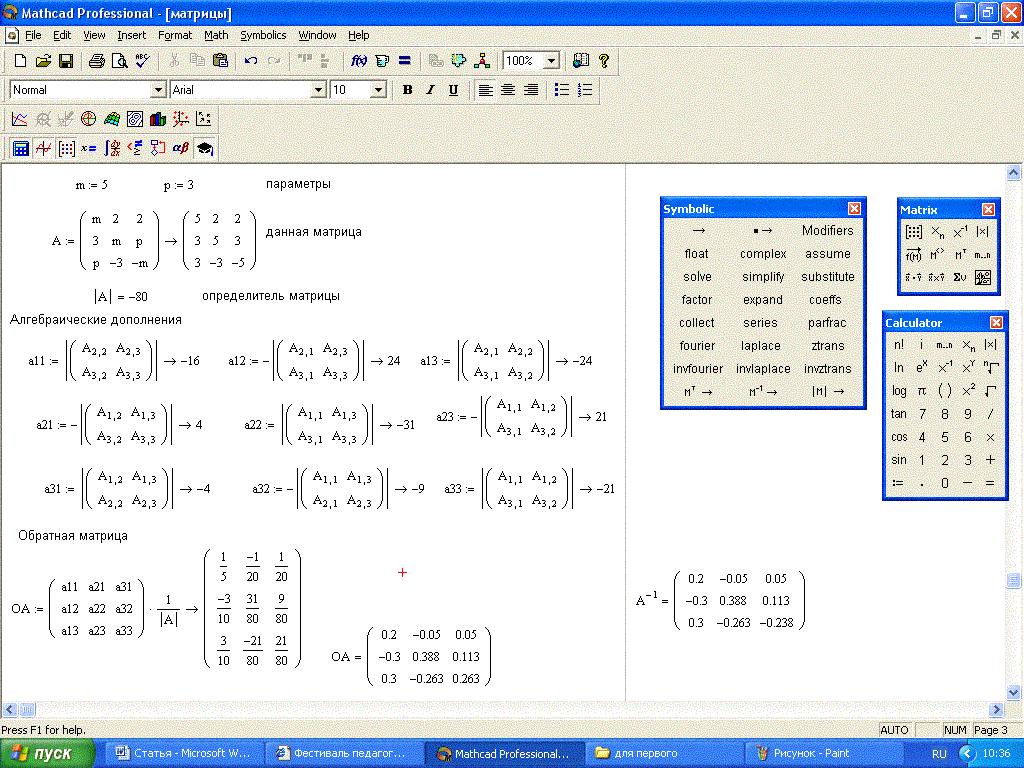
Упражнение :: Матрица фигур — Раздел 1
В каждом из следующих вопросов выясните, какая из цифр (1), (2), (3) и (4) завершает матрицу цифр?
Как использовать вопросы матричного типа — чем мы можем вам помочь?
Чтобы добавить матричный вопрос, перейдите в «Курсы», нажмите на название курса и отредактируйте соответствующий «Тестовый блок» (если у вас его еще нет, перейдите в «Добавить контент» -> «Добавить тест». ).В разделе «Вопросы» нажмите «Добавить вопрос» и в раскрывающемся списке «Тип» выберите «Матрица».
По умолчанию ваш новый вопрос матрицы будет состоять из 2 строк и 2 столбцов.
Нажмите кнопку «плюс» (+) (1) , чтобы добавить больше строк и столбцов.
Каждый раз, когда вы это делаете, добавляются и строка, и столбец. Если вам нужно больше столбцов, чем строк, или наоборот, нажимайте кнопку «плюс» (+), пока не достигнете желаемого числа. Затем заполните только обязательные поля, а остальные оставьте пустыми.
Примечание: Нажмите «Создать матрицу» (2) в любое время, когда вы захотите просмотреть изменения, внесенные в вашу сетку .
В настройках «Режим подсчета баллов» вы можете определить, что считается одним правильным или неправильным ответом в балле пользователя, отдельным флажком («Полная матрица») или целой строкой («На каждую строку матрицы»). (3 ) .
Например:
1) Матричный вопрос ниже настроен на режим подсчета очков «Полная матрица».Он состоит из 4 строк, 3 столбцов, 12 флажков и 6 правильных ответов. Возможных ответов — 12, что соответствует количеству флажков. Один неверный флажок стоит пользователю 1/12 или 8,33% от общей суммы баллов.
2) Матричный вопрос ниже настроен на режим расчета баллов «По строкам матрицы». Он состоит из 4 строк, 3 столбцов, 12 флажков и 6 правильных ответов. Возможные ответы в каждой строке: 3. Один неправильный флажок стоит пользователю целую строку, что соответствует 1/4 или 25% от общей суммы баллов.
В то время как 2 или 3 ошибки в одной строке имеют одинаковый вес в результатах, 2 неправильных флажка в 2 разных строках будут стоить пользователю 50% общей оценки.
В настройках «Режим ответа» вы можете определить, могут ли пользователи устанавливать только один («Один флажок в строке») или несколько флажков («Многие флажки в строке») в каждой строке. (4) . В случае «Один флажок на строку», если пользователи уже установили флажок и пытаются выбрать другой в той же строке, система автоматически удаляет первый выбор.В случае «Многие флажки в строке» флажки представлены в виде переключателей.
Примечание: Для настройки функций «Связанный модуль», «Сложность модуля», «Секунды до завершения», «Объяснение» и «Связанный навык» перейдите в раздел «Дополнительные настройки».