Контрольная работа квадратные корни 8 класс: Контрольная работа по алгебре на тему «Квадратные корни» (8 класс)

Алгебра 8 Макарычев КР-3 Вариант 4

Контрольная работа по алгебре в 8 классе КР-3 В-4

Алгебра 8 Макарычев КР-3 Вариант 4. Задания, решения и ответы на контрольную работу «Арифметический квадратный корень. Свойства арифметического квадратного корня» из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение». Представленные ниже контрольная работа в 2-х вариантах ориентирована на учебник «Алгебра 8» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки учебного пособия.

---

Алгебра 8 класс (Макарычев)
Контрольная работа № 3. Вариант 4

§ 5. Арифметический квадратный корень. § 6. Свойства арифметического квадратного корня.

К-3. Вариант 4 (транскрипт заданий)

1. Вычислите: а) 1/6 √144 + 1/3 √0,81; б) 2,1 + 1,3 √[81/169]; в) (0,4 √5)².
2. Найдите значение выражения: а) √[225 • 0,04]; б) √28 • √63; в) √48 / √3;   г) √[2⁶ • 7²].
3. Решите уравнение: а) x² = 0,09; б) х² = 92.
4. Упростите выражение: а) 1/7 x² √[49x⁶], где х ≥ 0; б) –5y⁶ √[1/(81y¹⁰)], где y < 0.
5. Укажите две последовательные десятичные дроби с одним знаком после запятой, между которыми заключено число √56.
6. При каких значениях переменной у имеет смысл выражение 2/(√y + 3) ?

 

ОТВЕТЫ на контрольную работу

КР-3. Ответы на Вариант 4.

№ 1. а) 2,3;   б) 3;   в) 0,8.

№ 2. а) 3;   б) 42;   в) 4;   г) 56.
№ 3. а) –0,3;  0,3;   б) –√92; √92.
№ 4. а) –х⁵;   б) 5у/9.
№ 5. 7,4 и 7,5.
№ 6. x ∈ [0; +∞).

Смотреть РЕШЕНИЯ заданий Варианта 4

 

---

Алгебра 8 Макарычев КР-3 Вариант 4. Контрольная работа по алгебре 8 класс (УМК Макарычев). Задания, решения и ответы на контрольную работу № 2 из учебного пособия: «Алгебра 8 класс. Дидактические материалы/ Жохов, Макарычев, Миндюк — М.:Просвещение».

Другие варианты:  КР-3 Вариант 1 КР-3 Вариант 2 КР-3 Вариант 3

Вернуться к Списку контрольных работ Алгебра 8 Макарычев (авт. В.И.Жохов и др.)

Авторская контрольная работа по алгебре 8 класс на тему «Квадратные корни»

Тема контрольной работы: «Квадратные корни»

Цель контрольной работы: проверка знаний учащихся и умения решать задания по теме «Квадратные корни».

Рекомендации по переводу первичных баллов в отметки по пятибалльной шкале

КР_№2_А8                    Вариант №1	КР_№2_А8             Вариант №2
1. Найти значение числового выражения	1.Найти значение числового выражения
2.Избавьтесь от иррациональности в выражении	2.Избавьтесь от иррациональности в выражении
А)        Б)	А)        Б)
3.Сравните числа	3. Сравните числа
4.Вынесите множитель из-под знака корня	4.Вынесите множитель из-под знака корня
5.Внесите множитель под знак корня	5.Внесите множитель под знак корня
6. Избавьтесь от модуля	6. Избавьтесь от модуля
7.Вычислите значения квадратного корня	7.Вычислите значения квадратного корня
КР_№2_А8                    Вариант №1	КР_№2_А8                    Вариант №2
1. Найти значение числового выражения	1.Найти значение числового выражения
2.Избавьтесь от иррациональности в выражении	2.Избавьтесь от иррациональности в выражении
А)        Б)	А)        Б)
3.Сравните числа	3. Сравните числа
4.Вынесите множитель из-под знака корня	4.Вынесите множитель из-под знака корня
5.Внесите множитель под знак корня	5.Внесите множитель под знак корня
6. Избавьтесь от модуля	6. Избавьтесь от модуля
7.Вычислите значения квадратного корня	7.Вычислите значения квадратного корня
КР_№2_А8                    Вариант №1	КР_№2_А8                    Вариант №2
1. Найти значение числового выражения	1.Найти значение числового выражения
2.Избавьтесь от иррациональности в выражении	2.Избавьтесь от иррациональности в выражении
А)        Б)	А)        Б)
3.Сравните числа	3. Сравните числа
4.Вынесите множитель из-под знака корня	4.Вынесите множитель из-под знака корня
5.Внесите множитель под знак корня	5.Внесите множитель под знак корня
6. Избавьтесь от модуля	6. Избавьтесь от модуля
7.Вычислите значения квадратного корня	7.Вычислите значения квадратного корня

Контрольная работа по алгебре для 8 класса по теме Квадратные корни в 8-и вариантах

КР – 4 Вариант 1
1.Упростите выражение:
а) 72+2218-98 б) (23+12)3 в) 23(3-475)-332. 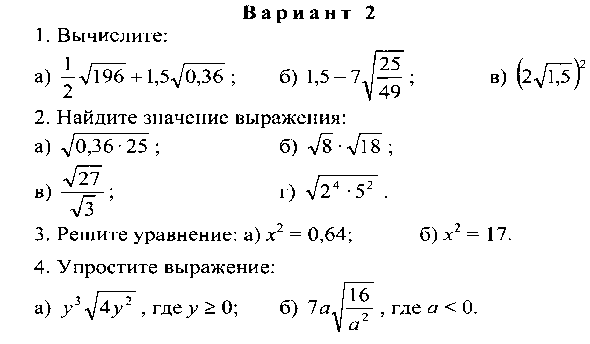Сравните: 1232 и 15753. Сократите дробь: а) 15-53-15 б) a-3a3a-94. Освободитесь от иррациональности в знаменателе: а) 5224 б) 3313-25. Докажите, что значение выражения есть число рациональное 311-2-311+2КР – 4 Вариант 2
1.Упростите выражение:
а) 73+2248-75 б) (32+18)2 в) 25(3-480)-352. Сравните: 1372 и 14803. Сократите дробь: а) 10-25-10 б) d-4d3d-124. Освободитесь от иррациональности в знаменателе: а) 5315 б) 513+35. Докажите, что значение выражения есть число рациональное 27-2-27+2КР – 4 Вариант 3
1.Упростите выражение:
а) 75+1980-45 б) (32+32)2 в) 22(3-550)-322. Сравните: 1432 и 15503. Сократите дробь: а) 14-27-14 б) c-5c3c-154. Освободитесь от иррациональности в знаменателе: а) 7298 б) 65-265 Докажите, что значение выражения есть число рациональное 513-2-513+2КР – 4 Вариант 4
1. Упростите выражение:
а) 73+1948-75 б) (33+12)3 в) 23(4-575)-832. Сравните: 1480 и 15753. Сократите дробь: а) 15-35-15 б) 3a-9a-3a4. Освободитесь от иррациональности в знаменателе: а) 5222 б) 2711-25. Докажите, что значение выражения есть число рациональное 417-3-417+3КР – 4 Вариант 5
1.Упростите выражение:
а) 73+1948-75 б) (33+12)3в) 25(3-480)-352. Сравните: 1480 и 15753. Сократите дробь: а) 15-53-15 б) a-3a3a-94. Освободитесь от иррациональности в знаменателе: а) 7298 б) 65-265. Докажите, что значение выражения есть число рациональное 417-3-417+3КР – 4 Вариант 6
1.Упростите выражение:
а) 72+2218-98 б) (23+12)3в) 22(3-550)-322. Сравните: 1372 и 14803. Сократите дробь: а) 10-25-10 б) d-4d3d-124. Освободитесь от иррациональности в знаменателе: а) 5224 б) 3313-25. Докажите, что значение выражения есть число рациональное 513-2-513+2КР – 4 Вариант 7
1.Упростите выражение:
а) 75+1980-45 б) (32+32)2в) 23(3-475)-332. Сравните: 1432 и 15503. Сократите дробь: а) 15-35-15 б) 3a-9a-3a4. Освободитесь от иррациональности в знаменателе: а) 5315 б) 513+35. Докажите, что значение выражения
311-2-311+2есть число рациональное. КР – 4 Вариант 8
1.Упростите выражение:
а) 73+2248-75 б) (32+18)2в) 23(4-575)-832. Сравните: 1232 и 15753. Сократите дробь: а) 14-27-14 б) c-5c3c-154. Освободитесь от иррациональности в знаменателе: а) 5222 б) 2711-25. Докажите, что значение выражения
27-2-27+2есть число рациональное.

Квадратные корни

Государственное общеобразовательное учреждение

лицей № 150

Калининского района Санкт-Петербурга

Открытый урок.

Тема: «Квадратные корни».

Предмет: алгебра.

Класс: 8

Автор разработки: учитель математики

Мангуш Мария Юрьевна

Санкт-Петербург

2018

Оглавление.

Методическая разработка урока «Квадратные корни».
1.Цель и задачи урока	с.3
2.Содержание учебного материала урока	с.4
3. Этапы урока	с.5-8
Методическое обеспечение и методические аспекты организации урока.
1 Используемые технологии.	с.9
2. Информационно-содержательная насыщенность урок	с.9
3.Оборудование.	с.9
4. Дидактические материалы	с.9
5.Оформление	с.9
Итоги урока.
1. Рефлексия учителя по итогам урока.	с.10
Приложения	с.11-12

Методическая разработка урока: «Арифметические квадратные корни».

Цель занятия: стимулировать интерес к изучению математики.

Задачи урока:

Образовательные:

1) приобщить учащихся к разнообразным формам и методам повторения материала;

2)систематизировать и обобщить знания учащихся по теме:

«Арифметические квадратные корни»;

3) развивать вычислительные навыки учащихся

Развивающие:

1) развивать навыки реализации теоретических знаний в практической деятельности.

2) продолжить развивать у учащихся умения осуществлять поиск информации по теме, анализировать, делать выводы по данному материалу

3) применять знания в незнакомой и несколько изменённой ситуации

Воспитательные:

1) способствовать развитию таких качеств личности, как: внимательность, толерантность, способность к эффективному общению;

2)способствовать развитию общей культуры и культуры поведения

Побудительные, организующие:

1)способствовать формированию у учащихся активной позиции в процессе обучения;

2)способствовать формированию таких жизненных установок личности как: динамизм, сотрудничество, ответственность

План проведения урока.

1 Определение темы, цели урока ,планирование деятельности

2..Закрепление и обобщение изученного материала:

а) выделение главного, обобщение, систематизация информации;

б) выбор формы преобразования информации;

в) принятие решений и осознание ответственности при принятии решения

4.Вывод по теме урока: на основе самооценки и оценки другими учащимися

Основные формы преобразования информации, используемые на уроке

1) решение заданий по карточке

2) суждение, определение, рассуждение, объяснение.

Содержание урока.

Содержание учебного материала

Формируемые и используемые учебные действия

1. Освобождение от иррациональности в знаменателе дроби; 2. Преобразования выражений, содержащих корни; 3. Формулы сокращенного умножения; 4. Выражение в формуле одной переменной через другие 5. Вычисление квадратных корней

Регулятивные УУД 1. Определять цель, тему в учебной деятельности 2.Выдвигать версии 3.Планировать учебную деятельность 4.Выбирать формы преобразования информации 5.Оценивать степень и способ деятельности и достижения цели в учебной ситуации 6. Самостоятельно исправлять ошибки Коммуникативные УУД 1.Излагать свое мнение(в монологе, диалоге),аргументируя его, подтверждая фактами Личностные УУД 1.Вырабатывать собственные мировоззренческие позиции Познавательные УУД 1.Систематизировать информацию. 2.Выделять главное и обобщать информацию.

Ход занятия (этапы урока)

Первый этап Организационный. Подготовка учащихся к урочной деятельности.

Деятельность учителя	Деятельность учащихся
Вступительное слово учителя о форме урока	Слушают вступительное слово учителя о форме урока

Второй этап. Определение темы урока, выдвижение гипотез, планирование собственной деятельности

Регулятивные УУД

1. Выдвигать версии.

2.. Планировать деятельность в учебной ситуации.

3. Оценивать степень и способы достижения цели в учебной ситуации.

Познавательные УУД

1. Анализировать

2. Определять понятия.

3. Обобщать, делать выводы.

Коммуникативные УУД

1. Умение работать в группах

2. Излагать своё мнение, аргументируя его.

3. Создавать устные и письменные тексты.

4. Использовать речевые средства в соответствии с ситуацией общения.

Личностные УУД

1. Оценивать свои и чужие поступки.

Деятельность учителя	Деятельность учащихся
Предлагает прослушать куплет песни «Я теряю корни» группы «Корни» и определить тему, которой будет посвящен урок	Слушают фрагмент песни «Я теряю корни» группы «Корни» и высказывают версии о теме урока
Если первая попытка не увенчалась успехом, на доске появляется картинка дерева с корнями.	Догадываются о теме урока

Третий этап Актуализация знаний.

Регулятивные УУД

1. Выдвигать версии.

2.. Планировать деятельность в учебной ситуации.

3. Оценивать степень и способы достижения цели в учебной ситуации.

Познавательные УУД

1. Находить достоверную информацию в разных источниках

2. Анализировать

3. Определять понятия.

4. Обобщать, делать выводы.

Коммуникативные УУД

1. Умение работать в группах

2. Излагать своё мнение, аргументируя его.

3. Создавать устные и письменные тексты.

4. Использовать речевые средства в соответствии с ситуацией общения.

Личностные УУД

1. Оценивать свои и чужие поступки.

Деятельность учителя	Деятельность учащихся
Предлагает в устной работе найти ошибки и исправить их	Находят, исправляют, проговаривают правила
Сообщает условия работы (в парах и сменных парах): предлагаются карточки с типовыми заданиями по данной теме. Дается время на самостоятельное решение заданий. Далее по сигналу взаимопроверка. Далее смена в парах, обмен своими заданиями, самопроверка, проверка, выставление оценок.	Слушают
Предлагает выполнить задание по алгебре согласно карточкам (см. приложение 1)	Выполняют задание по математике «Артиллерийская подготовка» согласно карточкам (см. приложение 1) Проверяют свою работу, в дальнейшем работу одноклассника, оценивают. Меняются парами согласно инструкции учителя.
Проведение физминутки. Опрос учащихся о выполнении заданий.	Отвечают.

Дает новую инструкцию по выполнению нового задания (с последующим контролем учителя)

Выполняют индивидуальные задания согласно карточкам.

Четвертый этап Домашнее задание

Деятельность учителя	Деятельность учащихся
Предлагает учащимся выполнить тест из учебника	Записывают домашнее задание

Пятый этап Подведение итогов. Рефлексия

Коммуникативные УУД

1. Излагать своё мнение, аргументируя его.

Личностные УУД

1. Оценивать свои и чужие поступки.

Деятельность учителя	Деятельность учащихся
Предлагает учащимся оценить по 5-балльной системе свою работу на уроке.	Учащиеся оценивают свою работу по 5-балльной системе
Учитель предлагает учащимся выразить свое отношение к теме урока; учебному материалу; форме закрепления материала; своему эмоциональному состоянию: 1-й вариант: заполнение анкеты (см. приложение 8) 2-й вариант. Учащиеся, поднимают над головой карточку с заранее нарисованными смайликами: грустный, если тема не была для них актуальна, и урок не удался (голубой цвет карточки) или веселый, если все удалось (розовый цвет карточки). смайлики заранее разложены на партах.	1-й вариант: заполняют анкеты. 2-й вариант. Учащиеся поднимают над головой заранее нарисованные смайлики: грустный, если тема не была для них актуальна (голубой цвет карточки), и урок, на их взгляд, не удался или веселый, если удался (розовый цвет карточки).

Методические обеспечение урока и методическое аспекты организации урока.

Используемые технологии.

Название технологии	Место используемых технологий в уроке
Коммуникативно-диалоговые технологии	Работа в парах
НИТИ (новые информационные технологии и Интернет)	Работа с презентацией (в течение урока). При существующей возможности работа учащихся с материалами сайтов Интернета. Использование мобильного класса (по возможности)
Технология оценки уровня успешности	Оценивать степень и способы достижения цели в учебной ситуации на основе самооценки и взаимооценки, самостоятельноисправлять ошибки. В течение всего урока

Информационно-содержательная насыщенность урока.

Работа с различными источниками информации: слайдами презентации, Интернет-ресурсами.

Оборудование.

1)Мультимедиапроектор,

2)Экран или интерактивная доска

3) Компьютер с выходом в Интернет..

4) Мобильный класс.

Дидактические материалы.

Раздаточный материал (см. приложение 1 )

Оформление урока.

Презентации учителя (см. приложение на диске)

Прогнозируемые результаты.

После изучения темы учащиеся должны:

1) уметь проводить вычисления с квадратными корнями, избавляться от иррациональности в знаменателе, работать с формулами, упрощать выражения.

2)принимать индивидуальные и коллективные решения.

Рефлексия учителя.

Занятие соответствует современным требованиям, предъявляемым к ФГОС

1)тема занятия, цели и задачи определяются совместно с учащимися.

2)формы организации деятельности – работа в группах

3) на уроке создается атмосфера сопричастности и интереса учащихся к изучаемому материалу.

4)рационально использована наглядность, дидактический материал и технические средства обучения.

5)занятие способствует формированию гражданской позиции учащихся.

6)выбраны наиболее оптимальные технологии обучения, позволяющие обеспечить познавательную активность, сочетать различные формы коллективной и индивидуальной работы и максимальную самостоятельность учащихся в процессе учения.

7) на уроке создаются условия для формирования и развития УУД (регулятивных, коммуникативных, познавательных и личностных).

Приложения

Приложение 1.

Работа в группах и сменных группах

Карточка 1.

Избавьтесь от иррациональности в знаменателе

Карточка 2.

Преобразуйте выражение, используя формулы сокращенного умножения

Карточка 3.

Упростите выражение

Карточка 4.

Из формулы выразите переменную

Карточка 5.

Найдите значение выражения

_{Индивидуальная работа}

а) для «слабых»Тест «Квадратный корень»

Известно, что . Какое из следующих равенств верно?

Расстояние , которое пролетает тело при свободном падении, вычисляется по формуле где -ускорение свободного падения, — время падения. Выразите из этой формулы время .

Найдите значение выражения

Какое из следующих выражений не равно

Упростите выражение

б)для подготовленных

Освободитесь от иррациональности в знаменателе

Докажите, что верно равенство

Приложение2.Анкета для рефлексии.

На уроке я работал (а)	Активно	Пассивно
Своей работой на уроке я	Доволен	не доволен
Урок мне показался	Коротким	Длинным
За урок я	Устал	Не устал
Мое настроение	Стало лучше	Стало хуже
Материал урока мне	Понятен	Не понятен
	Интересен	Не интересен
	Полезен	Бесполезен

MCQ Квадраты и квадратные корни класса 8 с ответами Скачать PDF

Вышеупомянутые NCERT CBSE и KVS MCQ для квадратов и квадратного корня класса 8 помогут вам повысить свои оценки, поскольку на экзаменах появляются вопросы с несколькими вариантами ответов. Эти MCQ CBSE NCERT Class 8 Square and Square Roots были разработаны опытными преподавателями StudiesToday.com для учащихся 8 класса.

Преимущества CBSE NCERT MCQ для квадратов и квадратного корня класса 8

a) MCQ NCERT CBSE KVS для квадратов и квадратного корня класса 8 помогут детям укрепить свои представления и улучшить оценки на тестах и ​​экзаменах.

b) Эти вопросы с несколькими вариантами ответов для класса 8 «Квадраты и квадратные корни» помогут улучшить аналитические навыки и навыки декодирования сложных задач.

c) Ежедневная практика различных MCQ по различным предметам поможет развить глубокое понимание каждой темы, которую вы будете помнить до даты экзамена

d) Вы также сможете правильно пересматривать все главы, посвященные квадратам и квадратным корням, и сохранять время во время ваших классных тестов и экзаменов.

Распечатать бесплатные MCQ в формате PDF CBSE Класс 8 Квадраты и квадратные корни разработаны школьными учителями в StudiesToday. com. Мы предоставляем самые эксклюзивные бесплатные печатные MCQ из базы данных в соответствии со стандартами CBSE NCERT и KVS. Все MCQ были тщательно разработаны для всех типов студентов, вы можете загрузить в формате PDF CBSE Class 8 Squares and Square Roots Банк вопросов MCQ по главам с ответами и использовать их для дальнейшего изучения. Вам также следует внимательно ознакомиться с учебной программой для класса 8 «Квадраты и квадратные корни» и загрузить MCQ по каждой изучаемой вами теме. Это очень поможет в выявлении всех ошибок в вашем понимании темы.Ежедневно выполняйте MCQ по классификации CBSE для оценки 10 квадратов и квадратного корня, чтобы получить более высокие баллы на экзамене.

Щелкните по ссылкам ниже для NCERT Class 8 Squares and Square Roots , чтобы загрузить последние решенные образцы документов CBSE (NCERT), вопросники за прошлый год (за последние десять лет) с решениями, рабочие листы для печати в формате pdf для Class 8 Squares and Square Roots NCERT Books и решения NCERT для квадратов и квадратного корня класса 8 NCERT , основанные на учебной программе и руководящих принципах, выпущенных CBSE и NCERT.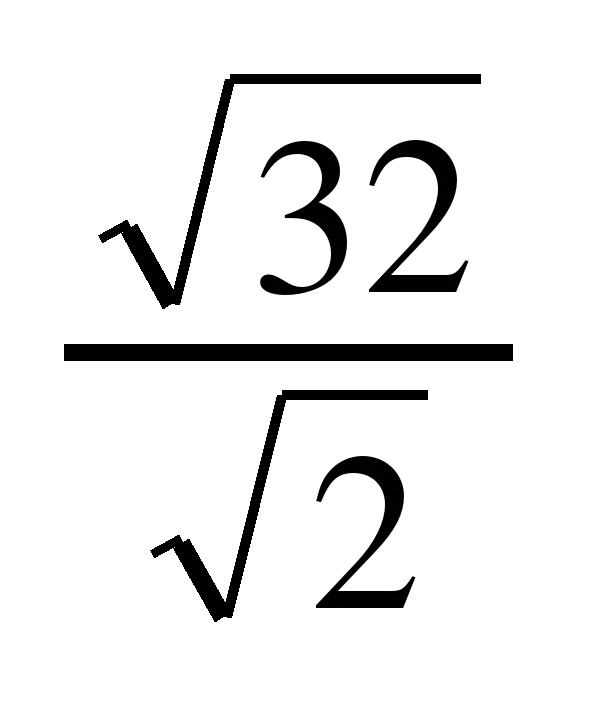 Учебный материал для NCERT для квадратов и квадратных корней класса 8 был подготовлен опытными учителями ведущих школ Индии и доступен для бесплатной загрузки

Квадратные корни и радикалы | Ресурсы Wyzant

Квадратный корень определяется как число, которое при умножении само на себя дает действительное неотрицательное число, называемое квадратом.

Квадратный корень лучше всего определить, используя геометрию, где, учитывая квадрат (который является четырехсторонним многоугольником, все стороны которого равны) квадратный корень определяется как длина диагонали этого квадрата (диагональ — это линия, проведенная из одной вершины / угла в противоположную вершину квадрата).

Радикал — это корень числа. Квадратный корень — это радикал. Корни могут быть квадратными корни, кубические корни, корни четвертой степени и так далее.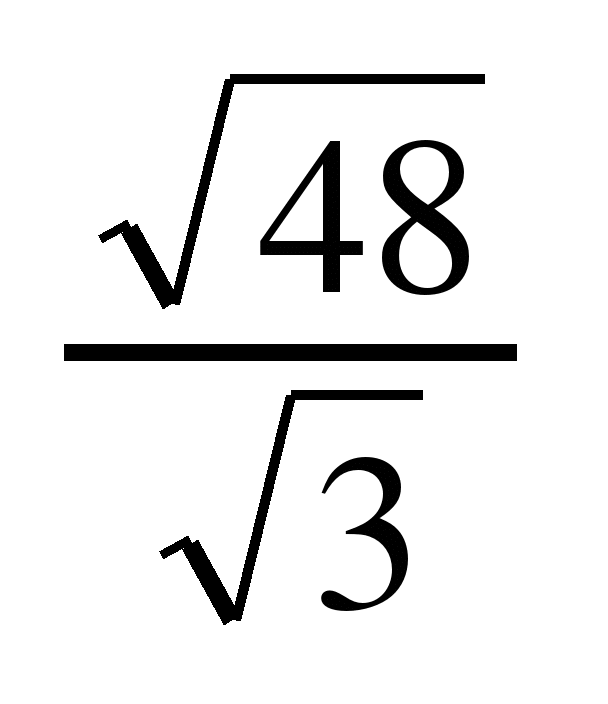

Квадратный корень обычно отображается как

.

где известен как радикальный знак и известен как подкоренное выражение.

Квадратный корень из числа также можно представить как

и радикал как

где мы говорим, что выше, мы находим n-й корень из x .За Подробнее о приведенных выше обозначениях см. в разделе экспоненты.

Радикал также можно представить как

Квадратный корень также представлен как

.

Кубический корень как

Корень четвертой степени как

Каждый квадрат имеет два квадратных корня; один положительный, а другой отрицательный. Это показано как:

который записывается как

Это можно доказать следующим образом. Рассмотрим число, a

но также

Введение в квадратные корни

Рассмотрим √x.Это читается как «квадратный корень из x». В этом конкретном термине x называется основанием квадратного корня.

Базовые квадратные корни не имеют числа, записанного в корне, и считаются вторым корнем в основании. Итак, при вычислении квадратного корня из x мы хотим знать, какое еще число, умноженное само на себя два раза, даст x.

Например:

√9 = 3, потому что 3 x 3 = 9.

√25 = 5, потому что 5 x 5 = 25.

√16 = 4, потому что 4 x 4 = 16.

Распространенная ошибка при вычислении квадратных корней — деление основания на два. Например, в последнем примере ученик может сказать, что √16 = 8, потому что 16/2 = 8. Будьте осторожны! Нахождение квадратного корня — это не деление на 2, а скорее то, какое число , умноженное на само , даст нашу основу.

До сих пор во всех примерах использовались полные квадраты или числа, для которых существует точный целочисленный квадратный корень. Это не всегда так. Мы легко можем оценить ценность такой проблемы.

Например:

√20

Эта база не является идеальным квадратом.Если мы введем этот член в калькулятор, мы получим иррациональное число, которое нужно будет округлить.

Однако нам не нужен калькулятор, чтобы получить достаточно хорошее предположение для значения этого выражения. Рассмотрим:

√16 = 4

√25 = 5

16
Наш ответ должен быть между 4 и 5, потому что наша база находится между точными квадратами 16 и 25.

ПРАКТИЧЕСКИЕ ПРОБЛЕМЫ

1. Рассмотрим термин √36.

а. Какая база?

г. Какой ответ?

2. Рассмотрим член √43.

а. Какая база?

г. Оцените ответ.

3. Эндрю решил задачу с квадратными корнями. Его работа показана ниже:

√100 + √64 = 50 + 32 = 82

Объясните, что Андрей сделал не так.

ОТВЕТЫ НА ПРОБЛЕМЫ ПРАКТИКИ

1.a. База — 36. 1.b. √36 = 6, потому что 6 x 6 = 36.

2.a. База 43.

2.b. Поскольку число 43 не является точным квадратом, оцените ответ на основе полных квадратов непосредственно перед и после 43.36 — это полный квадрат перед 43, а √36 = 6. 49 — это полный квадрат после 43, а √49 = 7. Итак, √43 должно быть между 6 и 7.

3. Андрей находит число, которое дает основание при умножении на два, а не само по себе. Мы не можем разделить на два при нахождении квадратного корня. Вместо этого:

√100 = 10, потому что 10 x 10 = 100

√64 = 8, потому что 8 x 8 = 64

Итак, √100 + √64 = 10 + 8 = 18

Калькулятор квадратного корня

Графический калькулятор Texas Instruments TI-84 Plus

Чтобы извлечь квадратный корень из числа, нажмите [2ND] (дополнительная функциональная клавиша), а затем [ √ & nbsp ] (клавиша с символом корня, которая используется для извлечения квадратного корня из числа), затем число, из которого вы хотите найти квадратный корень, а затем клавишу [ENTER].

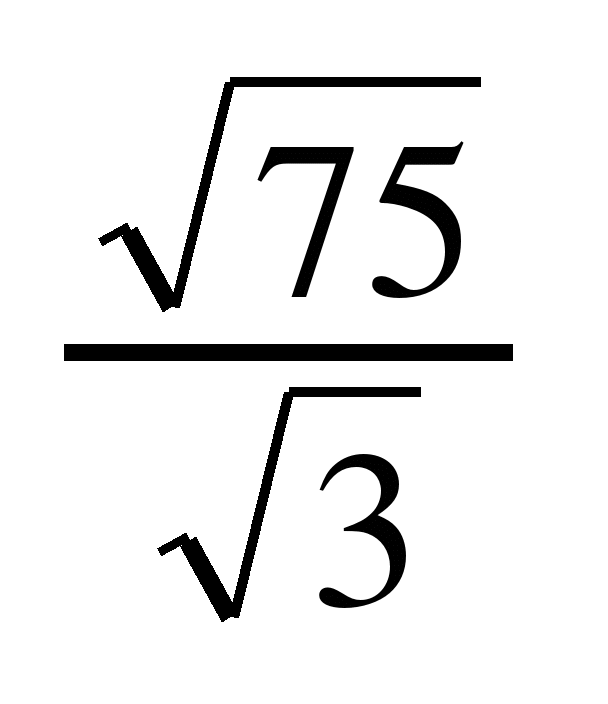
Пример :
Чтобы найти квадратный корень из 2, нажмите:
[2ND] [ √ ] 2 [ENTER]
Это даст вам ответ: 1.414213562, если все сделано правильно.

(Примечание: этот же метод также работает с калькуляторами TI-83 и TI-81)

График :
Чтобы построить график функции квадратного корня y = √x
Нажмите [Y =] [2ND] [ √ & nbsp ] [X, T, O, n] [GRAPH]

Используйте клавишу [Trace] и клавиши со стрелками, чтобы отслеживать и отображать значения на графике.

(Чтобы увидеть, как выглядит график на этом калькуляторе, нажмите кнопку «Показать график» под изображением калькулятора на этой странице.)

Плюсы:
Его можно использовать на многих вступительных экзаменах в колледж (проверьте критерии экзамена).

Это популярный калькулятор. (Если вам нужна помощь, вероятность найти того, кто умеет ею пользоваться, выше).

На дисплее отображается семь строк ввода / вывода. Можно просматривать и проверять длинные уравнения. (Это приятное преимущество графических калькуляторов по сравнению с научными калькуляторами, которые могут иметь только однострочный дисплей.) Еще одно преимущество большого дисплея — вы можете сравнить свой текущий ответ с прошлыми ответами, которые все еще отображаются на экране. Это часто может помочь вам обнаружить ошибку ввода, которая в противном случае могла бы остаться незамеченной.

Минусы:
Он крупнее научного калькулятора.
Он стоит примерно на 85 долларов больше, чем научный калькулятор.

Цена:
Лучшая цена для этого калькулятора на 9-2-2014 составляет около 94 долларов США.

Графический калькулятор Casio (FX-9750GII)

Чтобы извлечь квадратный корень из числа, нажмите [SHIFT], а затем [ √ ] (радикальный символ находится над клавишей x ² ), затем число, из которого вы хотите найти квадратный корень, а затем клавишу [EXE].

Пример :
Чтобы найти квадратный корень из 2, нажмите:
[СДВИГ] [ √ & nbsp ] 2 [EXE]
Это даст вам ответ: 1. 414213562, если введен правильно.

График :
Чтобы построить график функции квадратного корня y = √x
Нажмите [MENU], выберите Graph, [EXE]
[СДВИГ] [ √ & nbsp ] [X, O, T] [EXE] [F6]
Используйте клавишу [F6] для переключения между экраном графика и экраном уравнения.

Используйте клавишу [F1] и клавиши со стрелками для отслеживания и отображения значений на графике.

(Чтобы увидеть этот график, нажмите кнопку «Показать график» под изображением калькулятора на этой странице.)

Плюсы:
Стоимость составляет половину стоимости калькулятора ТИ-84.
Он немного меньше калькулятора ТИ-84.
Его можно использовать на многих вступительных экзаменах в колледж (проверьте критерии экзамена).
На дисплее отображается семь строк ввода / вывода.

Минусы:
Он не так популярен, как калькулятор ТИ-84. (Если у вас есть вопрос о том, как пользоваться калькулятором, найти кого-нибудь, кто поможет, может быть сложнее. )

Цена:
Лучшая цена на 2 сентября 2014 года составляет около 42,74 доллара США.

PPT — Презентация PowerPoint «Квадраты и квадратные корни», скачать бесплатно

примечания Квадраты и квадратные корни ЧАСТЬ I: Идеальные квадраты ОПРЕДЕЛЕНИЕ: квадрат целого числа

Квадратное число • Также называется « полный квадрат »• Число, являющееся квадратом целого числа (может быть представлено расположением объектов в квадрате.)

Квадратные числа

примечания Квадратные числа • 1 x 1 = 1 • 2 x 2 = 4 • 3 x 3 = 9 • 4 x 4 = 16

примечания Квадрат Числа • 1 x 1 = 1 • 2 x 2 = 4 • 3 x 3 = 9 • 4 x 4 = 16 Задание: у вас есть 2 минуты! В своих заметках: вычислите полные квадраты до 152…

нот квадратных чисел • 9 x 9 = 81 • 10 x 10 = 100 • 11 x 11 = 121 • 12 x 12 = 144 • 13 x 13 = 169 • 14 x 14 = 196 • 15 x 15 = 225 • 1 x 1 = 1 • 2 x 2 = 4 • 3 x 3 = 9 • 4 x 4 = 16 • 5 x 5 = 25 • 6 x 6 = 36 • 7 x 7 = 49 • 8 x 8 = 64

SLATE Задание: у вас есть 5 секунд… возьмите белую доску , маркер и ластик. ИСПОЛЬЗУЙТЕ ЗАМЕЧАНИЯ, ЧТОБЫ ПОМОЧЬ ВАМ • 16 • 15 • 146 • 300 • 324 • 729 Определите следующие числа как точные квадраты или нет. Если это идеальный квадрат, покажите ОСНОВНОЙ квадрат (во 2-й степени). Пример: 9 ЯВЛЯЕТСЯ точным квадратом, потому что он равен 3²

Задание: Определите следующие числа как полные квадраты или нет. • 16 = 4 x 4 • 15 • 146 • 300 • 324 = 18 x 18 • 729 = 27 x 27

примечания Квадраты и квадратные корни ЧАСТЬ II: Квадратный корень ОПРЕДЕЛЕНИЕ: длина стороны квадрата с площадью, равной заданному числу. РАДИКАЛЬНЫЙ ЗНАК √: используется для представления квадратного корня

Квадратные числа • Одно из свойств полного квадрата состоит в том, что он может быть представлен квадратным массивом.• Каждый маленький квадрат в показанном массиве имеет длину стороны 1 см. • У большого квадрата длина стороны 4 см. 4 см 4 см 16 см2

Квадратные числа • Большой квадрат имеет площадь 4 см x 4 см = 16 см2. • Число 4 называется квадратным корнем из 16. • Запишем: 4 = 16 4 см 4 см 16 см2

примечания Квадратный корень • Число, которое при умножении на само дает другое число. • Пример: 5 — квадратный корень из 25. 5 = 25

нот Нахождение квадратного корня • Быстрые шаги: найдите… 64 • ШАГ 1: ДУМАЙТЕ… Какой # во второй степени РАВНО # внутри корня ? ___ ² = 64 • ШАГ 2. Дважды проверьте свой ответ с умножением.Умножьте BASE X BASE. 8 X 8 = 64, поэтому квадратный корень из 64 = 8

примечания Поиск квадратного корня • Практическое руководство: найдите квадратный корень из 100 100 • Мы знаем, что 10² = 100 Итак, квадратный корень из 100 = 10

Поиск квадратного корня У вас есть 3 секунды: белая доска, маркер, ластик • Задание: найдите квадратный корень из 144 144 • Мы знаем, что 12² = 144 Итак, квадратный корень из 100 = 12

Поиск Квадратные корни • Упражнение: Найдите квадратный корень из 121 121 • Мы знаем, что 11² = 121 Итак, квадратный корень из 121 = 11

Поиск квадратного корня • Задание: Найдите квадратный корень из 169 169 • Мы знаем что 13² = 169 Таким образом, квадратный корень из 169 = 13

примечания Нахождение квадратного корня из чисел больше 200 • Задание: Найдите квадратный корень из 256 256 ШАГ 1: РАЗБИРАЙТЕ БОЛЬШЕЕ # НА МЕНЬКИЕ РАДИКАЛЫ = 4 x 64 ШАГ 2: НАЙДИТЕ КВАДРАТНЫЙ КОРЕНЬ КАЖДЫЙ РАДИКАЛ = 2 x 8 ШАГ 3: УМНОЖЕНИЕ ДВУХ #S = 16

заметок Поиск квадратного корня чисел больше 200 • Задание: Найдите квадратный корень из 10000 ШАГ 1: РАЗБИРАЙТЕ БОЛЬШЕЕ # НА МЕНЬШИЕ РАДИКАЛЫ ИДЕАЛЬНЫХ КВАДРАТОВ 10000 = 100x 100 ШАГ 2: НАЙДИТЕ КВАДРАТНЫЙ КОРН КАЖДОГО РАДИКАЛА = 10 x 10 ШАГ 3: УМНОЖИТЬ ДВА #S = 100

заметок БЫСТРЫЙ ЗАПИСЬ: Краткое изложение обучения Друг только что позвонил вам и спросил , «Что мы узнали сегодня на уроке математики?» (Ваш ответ… У ВАС ЕСТЬ 2 МИНУТЫ НА ЗАПИСЬ… используйте ключевой словарь)

ДОМАШНИЕ РАБОТЫ 5-6 PW (1-28 все)

примечания Квадраты и квадратные корни Оценка квадратного корня НЕИАЛЬНЫЙ КВАДРАТ — #, которое в квадрате не является целым #. Пример: 6 — не идеальный квадрат, потому что √6 является ДЕСЯТИЧНЫМ числом

Оценка квадратного корня 25 =?

Оценка квадратного корня 25 = 5

Оценка квадратного корня 49 =?

Оценка квадратного корня 49 = 7

Оценка квадратного корня 27 =?

Оценка квадратного корня 27 =? Поскольку 27 не является точным квадратом, мы должны использовать другой метод для вычисления квадратного корня.

примечания Оценка квадратного корня • Не все числа являются точными квадратами. • Не каждое число имеет целое число для квадратного корня. • Мы должны вычислять квадратные корни для чисел между полными квадратами.

примечания Оценка квадратного корня • Чтобы вычислить квадратный корень из несовершенного квадрата ШАГ 1: Поместите значения соседних точных квадратов на числовую линию. ШАГ 2: Интерполируйте между точками, чтобы оценить их с точностью до десятых.

примечания Оценка квадратного корня • Пример: 27 Каковы идеальные квадраты на каждой стороне числа 27? 5 6 √25 √36

Оценка квадратного корня • Пример: 27 половина 5 6 √25 30 35 √36 27 Оценка 27 = 5,2

Оценка квадратного корня • Пример: 27 • Оценка: 27 = 5.2 • Проверить: (5.2) (5.2) = 27,04

КЛАСС СТРАНИЦА 302 — 1,3,6,8,9,11,13 СТРАНИЦА 303 — 16,17,20,22,23,24 , 26 По завершении: заполните страницу 50, чтобы подготовиться к тесту.(-3/4) [/ math] [math] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ «Шаг 8:» \ \ \ [/ math] [math ] 1/729 [/ math]

Правильно ли работает Кори? Если нет, то какой шаг неверен и почему?

1. Да, его работа верна, и таков его окончательный ответ.

   No related posts.