Контрольная работа корень степени n: Контрольная работа «Корень степени n»

Контрольная работа №2. «Корень степени n»

Алгебра 10 класс 18.11.2019

Контрольная работа № 2

Корень степени n

Вариант 1

Вычислите

Избавиться от иррациональности в знаменателе

Найдите значение выражения .

Вынести множитель за знак корня: а) б) , если х<0.

Найдите значение выражения при .

Алгебра 10 класс 18.11.2019

Контрольная работа № 2

Корень степени n

Вариант 2

Вычислите

Найдите значение выражения при .

Избавиться от иррациональности в знаменателе

Внести множитель под знак корня: а) ; б) mn,если m<0.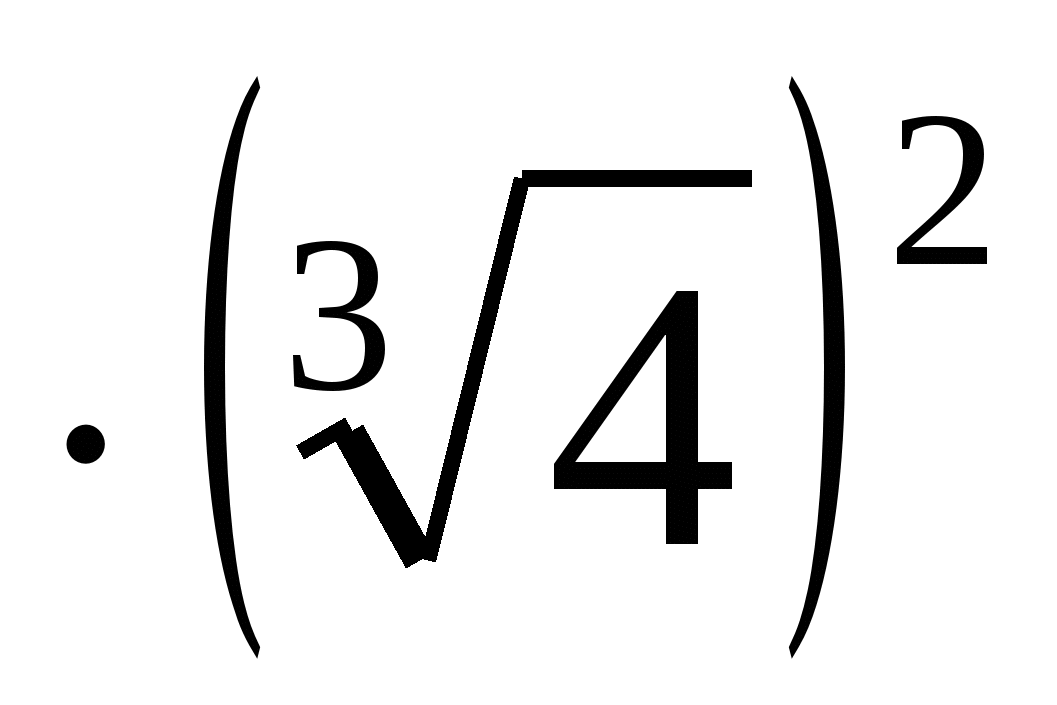

Найдите значение выражения: .

Алгебра 10 класс 18.11.2019

Контрольная работа № 2

Корень степени n

Вариант 3

Вычислите

Найдите значение выражения при .

Избавиться от иррациональности в знаменателе:

Внести множитель под знак корня: а) ; б) m2 n, если m<0.

Найдите значение выражения:

Алгебра 10 класс 18.11.2019

Контрольная работа № 2

Корень степени n

Вариант 4

Вычислите

Найдите значение выражения при .

Избавиться от иррациональности в знаменателе:

Внести множитель под знак корня: а) ; б) m3 n2, если n<0.

Найдите значение выражения: .

Контрольная работа по теме Степени и корни

Контрольная работа №2
по теме: «Степени и корни. Степенная функция»
Цель работы: прооверить уровень ГОСО
— знания определение корня п-й степени и его свойства
— знания определения арифметического корня п-й степени
знания определения степени с рациональным и иррациональным показателем и их свойства;
умения преобразовывать рациональные и иррациональные выражения
умения вычислять арифметический корень п-й степении и степень с рациональным показателем
Вариант 1
Часть 1
Задания с выбором одного правильного ответа
1. Выполните действия:
A) ; B) ; C) ; D) ; E) .
2. Вычислите:
A) ; B) 6; C) 5,5; D) ; E) 8.
3. Упростите выражение:
A) 1; B) 2; C) 0,7; D) ; E) .
4. Найдите значение выражения: при
A) 2; B) ; C) ; D) 4; E) 16.
5. Упростите выражение:
A) ; B) ; C) ; D) ; E) .
Часть 2
Задания, требующие краткого ответа
Вычислите: .
Найдите значение выражения:
Часть 3
Задание, требующее развернутого ответа
Найдите значение выражения при m = — 5

Вариант 2
Часть 1
Задания с выбором одного правильного ответа
1. Выполните действия:
A) ; B) ; C) ; D) ; E) .
2. Вычислите:
A) ; B) 8,5; C) 10; D) 12; E) 9.
3. Упростите выражение:
A) 1,6; B) 9; C) ; D) ; E) .
4. Найдите значение выражения: при
A) 4,5; B) ; C) ; D) 9; E) .
5. Найдите значение выражения:

A) -460; B) -100; C) 260; D) -250; E) 350.
Часть 2
Задания, требующие краткого ответа
1. Вычислите:
Найдите значение выражения:
Часть 3
Задание, требующее развернутого ответа
Найдите значение выражения при а = 16, в = 9

Критерии оценивания
I вариант
№ задания Ответ Баллы Дополнительная информация
1. 1 A 1 1.2 B 1 1.3 E 1 1.4 D 1 1.5 B 1 2.1 21 2.2 -4 1 3 m12+1m12-1-m12-1m12+1m322-12m12=m12+12-m12-12m-1∙m2-12m12=m+2m12+1-m+2m12-1m-1∙m-1m+12m12=4m12m+12m12=2m+12-5+1=2∙-4=-81

1
1
1
[4] Балл выставляется за знание свойств корня n-ой степени из действительного числа.
Балл выставляется за применение формул сокращенного выражения.
Балл выставляется за умения преобразовывать рациональные выражения.
Балл выставляется за нахождение значения буквенного выражения.
II вариант
№ задания Ответ Баллы Дополнительная информация
1.1 D 1 1.2 D 1 1.3 E 1 1.4 C 1 1.5 E 1 2.1 3 1 2.2 10 1 3 a14a14-b14-b14a14+b14÷a-b4a-4a12b12==a12+a14b14-a14b14+b12a12-b12÷a-b4a12a12-b12==a12+b12a12-b12∙4a12a12-b12a12-b12a12+b12==4a12a12-b124∙16121612-912=4∙44-3=161
1
1
1
[4] Балл выставляется за знание свойств корня n-ой степени из действительного числа.
Балл выставляется за применение формул сокращенного выражения.
Балл выставляется за умения преобразовывать рациональные выражения.
Балл выставляется за нахождение значения буквенного выражения.
Шкала перевода баллов в оценку
Процент выполнения 0-49% 50-69% 70-89% 90-100%
Баллы 0-4 5-6 7-8 9-10
Оценка 2 3 4 5

Приложенные файлы

• 25412
  Размер файла: 78 kB Загрузок: 0

Урок по алгебре «Свойства корней степени n» (9-й класс)

Тип урока:

совершенствование умений и навыков.

Характеристика темы: Преподавание ведётся по учебнику “Алгебра 9” Никольского С.М. для общеобразовательных учреждений. На данную тему отводится 3 часа. Это третий урок.

Дидактическая цель урока: Научить применять полученные знания при решении различных задач, в том числе повышенного уровня сложности, стимулировать учащихся к овладению рациональными приемами и методами решения.

Образовательная цель урока: Обеспечить в ходе урока закрепление материала о свойствах корней степени n и применение этих свойств при выполнении упражнений.

Развивающая цель урока: Развивать логическое мышление, память, познавательный интерес, продолжать формирование математической речи учащихся.

Воспитательная цель урока: Воспитывать интерес к математике как учебному предмету через современные технологии преподавания, приучать к умению выслушивать других, умению общаться, прививать аккуратность и трудолюбие.

Формы работы организации познавательной деятельности: фронтальная, индивидуальная.

Оборудование.

• Компьютеры.
• Программа компьютерного тестирования Knowing (представляет собой удобную программу для тестирования с возможностью составления тестов и автоматической оценки результатов тестирования).

Ход урока.

1. Организационный момент.

2. Актуализация прежних знаний.

1) Какие из следующих записей не имеют смысла?

; ; ;

2) При каких значениях переменной а выражение имеет смысл?

3) Вычислите:

4) Проверка домашнего задания.

3. Формирование умений и навыков.

Упростить выражение

Решение.

Преобразуем знаменатель дроби:

 – это неполный квадрат суммы чисел 3 и . Чтобы избавиться от иррациональности в знаменателе дроби, умножим ее числитель и знаменатель на разность этих чисел:

Упростить выражение
 и найти его значение при х=
Решение.

Так как х≥0 ( в противном случае выражение  не имеет смысла), то .

Тогда

Найти значение выражения
 при х=.

Решение.

Преобразуем данное выражение при х( в противном случае данное выражение не имеет смысла):

При заданных значениях х и у имеем

.

Значит,

а) Вынести множитель из-под знака корня  при условии, что х0.

б) Внести множитель под знак корня 3учто у.

Решение.

а) Так как х0 по условию, а у (в противном случае выражение не имеет смысла), то  =

б) Так как у по условию, а хне имеет смысла выражение , то

3у

4. Самостоятельная работа (компьютерное тестирование).

Приложение 1.

Приложение 2.

5. Подведение итогов урока.

6. Домашее задание.

П. 4.6, №553, 555.

7. Использованная литература.

1. С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. Алгебра 9 класс – М.: Просвещение, 2009 г
2. М.К. Потапов, А.В. Шевкин. Дидактические материалы для 9 класса – М.: Просвещение, 2008 г
3. Воробьева Е.А. Алгебра. 9 класс. Проверочные работы с элементами тестирования. – Саратов: Лицей, 2008
4. Воробьева Е. А. Алгебра. 9 класс: В 2 ч. – Саратов: Лицей, 2008
5. Капитонова Т.А. Алгебра. 9 класс: Проверочные и контрольные работы. – Саратов: Лицей, 2006

Свойства корня n-й степени. Преобразование иррациональных выражений. Алгебра, 11 класс: уроки, тесты, задания.

1.	Корень из произведения, десятичные дроби и целые числа Сложность: лёгкое	2
2.	Корень из произведения, целые числа и обыкновенные дроби Сложность: лёгкое	3
3.	Корень из частного, обыкновенные дроби Сложность: лёгкое	2
4.	Корень из произведения Сложность: лёгкое	4
5.	Корень из корня Сложность: лёгкое	1
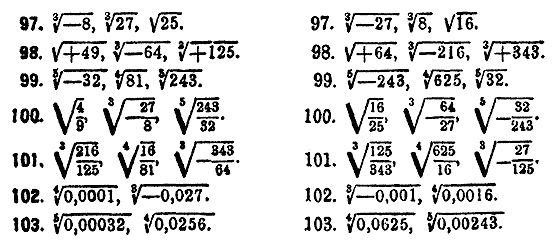
6.	Извлечение корня из степени Сложность: лёгкое	3
7.	Показатели корня Сложность: лёгкое	2
8.	Корни с разными показателями Сложность: лёгкое	2
9.	Корень из произведения степеней, корень в степени (целые числа) Сложность: среднее	3
10.	Корень из дроби Сложность: среднее	5
11.	Произведение корней Сложность: среднее	4
12.	Частное корней Сложность: среднее	3
13.	Произведение корня из произведения степеней и корня из степени Сложность: среднее	5
14.	Корень из частного степеней Сложность: среднее	3
15.	Корень из степени Сложность: среднее	4
16.	Сравнение корней Сложность: среднее	3
17.	Произведение корней с разными показателями Сложность: среднее	3
18.	Частное корней с разными показателями Сложность: среднее	3
19.	Произведение корней с разными показателями из произведений степеней Сложность: среднее	6
20.	Степень произведения (число и корень) Сложность: среднее	6
21.	Степень произведения (одночлен и корень) Сложность: среднее	4
22.	Корень из произведения степеней (десятичные дроби) Сложность: среднее	4
23.	Уравнение Сложность: сложное	5
24.	Уравнение, сводимое к квадратному (метод введения новой переменной) Сложность: сложное	5
25.	Уравнение, сводимое к квадратному (полное) Сложность: сложное	8

Алгебра 9 Макарычев К-2 В-3

Контрольная работа по алгебре в 9 классе «Квадратичная функция и её график. Степенная функция. Корень n-й степени» с ответами и решениями. Алгебра 9 Макарычев К-2 В-3.

Алгебра 9 класс (Макарычев)

Контрольная работа № 2. Вариант 3

§ 3. Квадратичная функция и её график. § 4. Степенная функция. Корень

n-й степени.

КР-2. Вариант 3 (транскрипт заданий)

1. Постройте график функции у = х² – 4х – 5. Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = 3;
в) нули функции; промежутки, в которых у > 0 и в которых у < 0;
г) промежуток, в котором функция возрастает.

2. Найдите наименьшее значение функции у = х² + 2х – 24.

3. Найдите область значений функции у = х² – 2х – 8, где х ∈ [–1; 3].

4. Не выполняя построения, определите, пересекаются ли парабола у = х²/3 и прямая у = 6х – 15. Если точки пересечения существуют, то найдите их координаты.

5. Найдите значение выражения ³√[–4 ¹⁷/₂₇] + 6 ⁴√[3 ¹³/₈₁].

---

Алгебра 9 Макарычев К-2 В-3 ОТВЕТЫ:

КР-2. Ответы на Вариант 3.

№2. –25.
№3. [–9;–5].
№4. Пересекаются в точках (3; 3) и (15; 75).
№5. 6 ¹/₃.

Смотреть РЕШЕНИЯ заданий Варианта 3 в тетради

Алгебра 9 Макарычев К-2 В-3. Контрольная работа по алгебре 9 класс «Квадратичная функция и её график. Степенная функция. Корень n-й степени» с ответами и решениями.
Другие варианты: К-2 Вариант 1   К-2 Вариант 2   К-2 Вариант 4

В учебных целях использованы цитаты из пособия:

«Алгебра. Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение». Представленная контрольная работа ориентирована на УМК Макарычева. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.

Список контрольных работ по алгебре в 9 классе для УМК Макарычев (Оглавление) \ infty \ dfrac1n \) расходится, поскольку члены \ (\ {1 / n \} \) недостаточно быстро приближаются к 0. »

Сравнительные тесты предыдущего раздела определяют сходимость путем сравнения членов ряда с членами другого ряда, сходимость которого известна. В этом разделе представлены тесты отношения и корня, которые определяют сходимость путем анализа членов ряда, чтобы увидеть, приближаются ли они к 0 «достаточно быстро».

Тест соотношения

теорема 68: проверка соотношения

Пусть \ (\ {a_n \} \) будет положительной последовательностью, где \ (\ lim \ limits_ {n \ to \ infty} \ dfrac {a_ {n + 1}} {a_n} = L \).\ infty a_n \) расходится.

Если \ (L = 1 \), тест соотношения не дает результатов.

Теорема 64 позволяет нам применять тест отношения к рядам, где \ (\ {a_n \} \) положительно для всех, кроме конечного числа членов. n} {n!} \).2} \).

Тест отношения не эффективен, если члены ряда только содержат алгебраические функции (например, многочлены). Это наиболее эффективно, когда члены содержат некоторые факториалы или экспоненты. Предыдущий пример также укрепляет нашу развивающуюся интуицию: факториалы доминируют над экспонентами, которые доминируют над алгебраическими функциями, которые доминируют над логарифмическими функциями. В Части 1 примера факториал в знаменателе преобладал над экспонентой в числителе, в результате чего ряды сходились.В Части 2 экспонента в числителе преобладала над алгебраической функцией в знаменателе, в результате чего ряды расходились.

Несмотря на то, что мы использовали факториалы в предыдущих разделах, мы не исследовали их подробно, и, вероятно, еще нет сильного интуитивного ощущения того, как они себя ведут. Следующий пример дает больше практики с факториалами.

Пример \ (\ PageIndex {2} \): применение теста соотношения

Определите сходимость \ (\ sum \ limits_ {n = 1} ^ \ infty \ dfrac {n! N!} {(2n)!} \).

Решение

Прежде чем мы начнем, обязательно обратите внимание на разницу между \ ((2n)! \) И \ (2n! \). Когда \ (n = 4 \), первое будет \ (8! = 8 \ cdot7 \ cdot \ ldots \ cdot 2 \ cdot1 = 40,320 \), а второе — \ (2 (4 \ cdot3 \ cdot2 \ cdot1) = 48 \).

Применение теста соотношения:

\ [\ begin {align *}
\ lim \ limits_ {n \ to \ infty} \ dfrac {(n + 1)! (N + 1)! / \ Big (2 (n + 1) \ big)! } {n! n! / (2n)!} & = \ lim \ limits_ {n \ to \ infty} \ dfrac {(n + 1)! (n + 1)! (2n)!} {n! n! (2n + 2)!} \\
\ text {Отметив, что \ ((2n + 2)! = (2n + 2) \ cdot (2n + 1) \ cdot (2n)! \), Мы имеем} & \ \
& = \ lim \ limits_ {n \ to \ infty} \ dfrac {(n + 1) (n + 1)} {(2n + 2) (2n + 1)} \\
& = 1/4.2} = 2 \).
Поскольку это больше единицы, мы заключаем, что ряд расходится.

Каждый из тестов, с которыми мы столкнулись до сих пор, требовал, чтобы мы проанализировали серии из положительных последовательностей. Следующий раздел ослабляет это ограничение, рассматривая чередующийся ряд , , где в базовой последовательности есть члены, которые чередуются между положительными и отрицательными значениями.

Авторы и авторство

• Грегори Хартман (Военный институт Вирджинии).Свой вклад внесли Трой Симерс и Димплекумар Чалишаджар из VMI и Брайан Хайнольд из Университета Маунт-Сент-Мэри. Этот контент защищен авторским правом Creative Commons Attribution — Noncommercial (BY-NC) License. http://www.apexcalculus.com/

Тесты соотношения

и корня — том исчисления 2

Цели обучения

• Используйте тест отношения для определения абсолютной сходимости ряда.
• Используйте корневой тест для определения абсолютной сходимости ряда.
• Опишите стратегию проверки сходимости заданного ряда.

В этом разделе мы докажем два последних теста сходимости серий: тест отношения и тест корня. Эти тесты особенно хороши, потому что они не требуют от нас поиска сопоставимой серии. Тест отношения будет особенно полезен при обсуждении степенных рядов в следующей главе.

На протяжении всей этой главы мы видели, что ни один тест сходимости не работает для всех рядов. Поэтому в конце этого раздела мы обсудим стратегию выбора того, какой тест сходимости использовать для данного ряда.

Тест соотношения

Рассмотрим ряд. Из нашего предыдущего обсуждения и примеров мы знаем, что это не является достаточным условием для сходимости ряда. Не только нам нужно, но и нужно достаточно быстро. Например, рассмотрим серию и серию Мы знаем это и Однако сходится только серия. Ряд расходится, потому что члены в последовательности не приближаются к нулю достаточно быстро, поскольку здесь мы вводим тест отношения, который обеспечивает способ измерения того, насколько быстро члены ряда приближаются к нулю.

Проба

Позвольте быть серией с ненулевыми членами.

Начнем с доказательства части i. В этом случае, поскольку существует такое, что Пусть По определению предела последовательности существует такое целое число, что

Следовательно,

и, таким образом,

Начиная с геометрической серии

сходится. Учитывая приведенные выше неравенства, мы можем применить сравнительный тест и сделать вывод, что серия

сходится. Следовательно, с

где — конечная сумма и сходится, заключаем, что сходится.

По части ii.

Так как существует такое, что Let По определению предела последовательности, существует такое целое число, что

Следовательно,

и, таким образом,

Начиная с геометрической серии

расходится. Применяя сравнительный тест, делаем вывод, что серия

расходится, и поэтому расходится ряд.

По части iii. мы показываем, что тест не предоставляет никакой информации, если, рассматривая Для любого действительного числа

Однако мы знаем, что если расходится, тогда как сходится, если

□

Тест отношения особенно полезен для рядов, члены которых содержат факториалы или экспоненты, где соотношение членов упрощает выражение. Тест отношения удобен тем, что не требует от нас поиска сравнительного ряда. Недостатком является то, что тест иногда не дает никакой информации о сходимости.

Использование теста соотношения

Для каждого из следующих рядов используйте тест отношения, чтобы определить, сходится ли ряд или расходится.

Используйте тест отношения, чтобы определить, сходится ли ряд или расходится.

Подсказка

Оценить

Корневой тест

Подход корневого теста аналогичен подходу теста отношения. Рассмотрим ряд, такой, что для некоторого действительного числа Тогда для достаточно большого, Следовательно, мы можем аппроксимировать, написав

Выражение в правой части представляет собой геометрический ряд. Как и в случае теста отношения, ряд сходится абсолютно, если и ряд расходится, если тест не предоставляет никакой информации. Например, для любой серии p мы видим, что

Чтобы оценить этот предел, мы используем функцию натурального логарифма. При этом мы видим, что

Используя правило Л’Опиталя, следует, что и, следовательно, для всех. Однако мы знаем, что серия p сходится только тогда, когда и расходится, если

Корневой тест полезен для рядов, члены которых включают экспоненты. В частности, для ряда, члены которого удовлетворяют тогда, и нам нужно только оценить

Используйте корневой тест, чтобы определить, сходится ли ряд или расходится.

Подсказка

Оцените по правилу L’Hôpital.

Выбор теста сходимости

На данный момент у нас есть длинный список тестов сходимости. Однако не все тесты можно использовать для всех серий. Получив серию, мы должны определить, какой тест лучше всего использовать. Вот стратегия поиска лучшего теста для применения.

Использование тестов сходимости

Для каждой из следующих серий определите, какой тест сходимости лучше всего использовать, и объясните, почему. Затем определите, сходится ли ряд или расходится.Если ряд является чередующимся рядом, определите, сходится ли он абсолютно, сходится условно или расходится.

1. Шаг 1. Серия не является геометрической или геометрической.
   Шаг 2. Серии не чередуются.
   Шаг 3. При больших значениях аппроксимируем ряд выражением
   

   
   Следовательно, кажется разумным применить сравнительный тест или предельный сравнительный тест, используя серию. Используя предельный сравнительный тест, мы видим, что
   

   
   Поскольку ряды расходятся, расходится и этот ряд.

2. Шаг 1. Серия не знакомая серия.
   Шаг 2. Серии чередуются. Поскольку нас интересует абсолютная сходимость, рассмотрим серию
   

   
   Шаг 3. Серия не похожа на серию p или геометрическую серию.
   Шаг 4. Поскольку каждый член содержит факториал, примените тест отношения. Мы видим, что
   

   
   Следовательно, этот ряд сходится, и мы заключаем, что исходный ряд сходится абсолютно, а значит, сходится.

3. Шаг 1. Сериал не знакомый сериал.
   Шаг 2. Это не чередующаяся серия.
   Шаг 3. Нет очевидной серии, с которой можно было бы сравнивать эту серию.
   Шаг 4. Факториала нет. Питание есть, но для рут-теста ситуация не идеальная.
   Шаг 5. Чтобы применить тест дивергенции, мы вычисляем, что
   

   
   Следовательно, по тесту дивергенции ряд расходится.

4. Шаг 1. Эта серия не знакомая серия.
   Шаг 2. Это не чередующаяся серия.
   Шаг 3. Нет очевидной серии, с которой можно было бы сравнивать эту серию.
   Шаг 4. Поскольку каждый член является степенью, мы можем применить корневой тест. С
   г.

   
   по корневому тесту, мы заключаем, что ряд сходится.

Для серии определите, какой тест сходимости лучше всего использовать, и объясните, почему.

Тест сравнения, потому что для всех положительных целых чисел также можно использовать тест сравнения пределов.

Подсказка

Серия аналогична геометрической серии

В (рисунок) мы суммируем тесты сходимости и когда каждый из них может быть применен. Обратите внимание, что хотя сравнительный тест, предельный сравнительный тест и интегральный тест требуют, чтобы ряд содержал неотрицательные члены, при наличии отрицательных членов эти тесты могут применяться для проверки абсолютной сходимости.

Используйте тест отношения, чтобы определить, сходится ли, где указано в следующих задачах.Укажите, является ли тест на соотношение безрезультатным.

сходится.

сходится.

сходится.

сходится.

Ratio test безрезультатен.

сходится.

Используйте корневой тест, чтобы определить, сходится ли, где следующее.

Дивергенты.

сходится.

сходится.

сходится.

по правилам L’Hôpital. Сходится.

В следующих упражнениях используйте либо тест отношения, либо тест корня, чтобы определить, сходится ли ряд с заданными членами, или укажите, является ли тест неубедительным.

Сходит по критерию соотношения.

Сходит по корневому тесту.

Отклоняется по корневому тесту.

Используйте тест отношения, чтобы определить, сходится ли он, или укажите, является ли тест отношения безрезультатным.

Используйте тесты сравнения корня и предела, чтобы определить, сходится ли.

В следующих упражнениях используйте соответствующий тест, чтобы определить, сходится ли ряд.

Абсолютно сходится по сравнению с

по пределу

Серия

расходится.

( Подсказка:

Сроки не стремятся к нулю: с

сходится по сравнению с геометрическим рядом.

( Подсказка:

Следующие ряды сходятся по критерию соотношения.Используйте суммирование по частям, чтобы найти сумму данного ряда.

Член k -й член каждого из следующих рядов имеет коэффициент. Найдите диапазон, для которого проверка отношения подразумевает, что ряд сходится.

Существует ли сходящееся число?

Let Для каких действительных чисел сходится?

Все действительные числа по критерию соотношения.

Предположим, что для каких значений должны сходиться?

Предположим, что для каких значений гарантированно сходятся?

Для каких значений, если они есть, сходится? ( Подсказка:

Предположим, что для всех Можете ли вы сделать вывод, что сходится?

Пусть где — наибольшее целое число, меньшее или равное Определить, сходится ли и обосновать свой ответ.

Следующие расширенные упражнения используют обобщенный тест отношения для определения сходимости некоторых рядов, возникающих в конкретных приложениях, когда тесты в этой главе, включая тест отношения и корень, недостаточно эффективны для определения их сходимости.Тест утверждает, что if then сходится, а if then расходится.

Упражнения для повторения главы

Верно или неверно? Обоснуйте свой ответ доказательством или контрпримером.

Если то сходится.

Если то расходится.

Если сходится, значит сходится.

Если сходится, значит сходится.

Является ли последовательность ограниченной, монотонной, сходящейся или расходящейся? Если он сходится, найдите предел.

неограниченный, немонотонный, расходящийся

ограниченный, монотонный, сходящийся,

неограниченный, немонотонный, расходящийся

Ряд сходится или расходится?

Ряд сходится или расходится? Если сходится, является ли оно абсолютно сходящимся?

сходится, но не совсем

Оценить

Легенда из Индии гласит, что математик изобрел шахматы для короля. Королю настолько понравилась игра, что он позволил математику потребовать любую плату. Математик попросил одно зерно риса для первого квадрата на шахматной доске, два зерна риса для второго квадрата на шахматной доске и так далее. Найдите точное выражение для общей суммы платежа (в зернах риса), запрошенной математиком. Если предположить, что в фунте есть зерна риса, а в тонне — фунты, сколько тонн риса попытался получить математик?

Следующие задачи рассматривают простую модель популяции комнатной мухи, которую можно представить с помощью рекурсивной формулы, где — популяция комнатных мух в поколении, а — среднее количество потомков на одну комнатную муху, которые доживают до следующего поколения.Предположим, что начальное население —

человек.

Найдите выражение для и Что оно физически представляет?

При каких значениях ряды будут сходиться и расходиться? К чему сходится ряд?

5.6 Тесты соотношения и корня — Объем исчисления 2

Тест дивергенции Для любого ряда ∑n = 1∞an, ∑n = 1∞an вычислим limn → ∞an. limn → ∞an.	Если limn → ∞an = 0, limn → ∞an = 0, проверка не дает результатов.	Этот тест не может доказать сходимость ряда.
	Если limn → ∞an ≠ 0, limn → ∞an ≠ 0, ряд расходится.
Геометрическая серия ∑n = 1∞arn − 1∑n = 1∞arn − 1	Если | r | <1, | r | <1, ряд сходится к а / (1 — г). а / (1 — г).	Любой геометрический ряд можно переиндексировать и записать в виде a + ar + ar2 + ⋯, a + ar + ar2 + ⋯, где aa — начальный член, а rr — отношение.
	Если | r | ≥1, | r | ≥1, ряд расходится.
p -Серия ∑n = 1∞1np∑n = 1∞1np	Если p> 1, p> 1, ряд сходится.	При p = 1, p = 1 имеем гармонический ряд ∑n = 1∞1 / n.n = 1∞1 / n.
	Если p≤1, p≤1, ряд расходится.
Сравнительный тест Для ∑n = 1∞an∑n = 1∞an с неотрицательными членами сравните с известным рядом ∑n = 1∞bn.∑n = 1∞bn.	Если an≤bnan≤bn для всех n≥Nn≥N и ∑n = 1∞bn∑n = 1∞bn сходится, то ∑n = 1∞an∑n = 1∞an сходится.	Обычно используется для серии, аналогичной геометрической или pp-серии. Иногда бывает сложно найти подходящую серию.
	Если an≥bnan≥bn для всех n≥Nn≥N и ∑n = 1∞bn∑n = 1∞bn расходится, то ∑n = 1∞an∑n = 1∞an расходится.
Сравнительный тест предельных значений Для ∑n = 1∞an∑n = 1∞an с положительными членами сравните с рядом ∑n = 1∞bn∑n = 1∞bn, оценив L = limn → ∞anbn. L = limn → ∞anbn.	Если LL — вещественное число и L ≠ 0, L ≠ 0, то ∑n = 1∞an∑n = 1∞an и ∑n = 1∞bn∑n = 1∞bn сходятся или расходятся.	Обычно используется для серии, аналогичной геометрической или pp-серии. Часто применять проще, чем сравнительный тест.
	Если L = 0L = 0 и ∑n = 1∞bn∑n = 1∞bn сходится, то ∑n = 1∞an∑n = 1∞an сходится.
	Если L = ∞L = ∞ и ∑n = 1∞bn∑n = 1∞bn расходится, то ∑n = 1∞an∑n = 1∞an расходится.
Интегральный тест Если существует положительная непрерывная убывающая функция ff такая, что an = f (n) an = f (n) для всех n≥N, n≥N, вычислить ∫N∞f (x) dx.∫N∞f (x) dx.	∫N∞f (x) dx∫N∞f (x) dx и ∑n = 1∞an∑n = 1∞ оба сходятся или оба расходятся.	Только для тех серий, для которых можно легко интегрировать соответствующую функцию ff.
Переменная серия ∑n = 1∞ (−1) n + 1bnor∑n = 1∞ (−1) nbn∑n = 1∞ (−1) n + 1bnor∑n = 1∞ (−1) nbn	Если bn + 1≤bnbn + 1≤bn для всех n≥1n≥1 и bn → 0, bn → 0, то ряд сходится.	Применяется только к чередующимся сериям.
Тест соотношения Для любого ряда ∑n = 1∞an∑n = 1∞an с ненулевыми членами положим ρ = limn → ∞ | an + 1an |.ρ = limn → ∞ | an + 1an |.	Если 0≤ρ <1,0≤ρ <1, ряд абсолютно сходится.	Часто используется для рядов, включающих факториалы или экспоненты.
	Если ρ> 1 или ρ = ∞, ρ> 1 или ρ = ∞, ряд расходится.
	Если ρ = 1, ρ = 1, проверка не дает результатов.
Корневой тест Для любого ряда ∑n = 1∞an, ∑n = 1∞an пусть ρ = limn → ∞ | an | n. ρ = limn → ∞ | an | n.	Если 0≤ρ <1,0≤ρ <1, ряд абсолютно сходится.	Часто используется для серий, где | an | = bnn. | An | = bnn.
	Если ρ> 1 или ρ = ∞, ρ> 1 или ρ = ∞, ряд расходится.
	Если ρ = 1, ρ = 1, проверка не дает результатов.

AP Calculus BC Review: Ratio and Root Tests — Magoosh Blog

Ratio и Root Tests — незаменимые инструменты для определения, сходится ли ряд или расходится. Эти тесты также играют большую роль в определении радиуса и интервала сходимости для ряда функций.

В этой статье мы обсудим, как работают Ratio и Root Tests. Кроме того, вы увидите несколько примеров из экзамена AP Calculus BC.

Тесты соотношения и корня

И тест отношения, и тесты корня в основном сравнивают, насколько близок ваш ряд к геометрическому ряду.

Напомним, что геометрический ряд — это ряд, в котором члены имеют общее отношение .

Тест на сходимость геометрического ряда очень прост.Пусть r будет обычным отношением.

• Если | r | <1, то геометрический ряд сходится.
• Если | r | ≥ 1, то геометрический ряд расходится.

Площадь фракталов, таких как Снежинка Коха, может быть найдена путем вычисления сходящегося геометрического ряда.

Тест соотношения

Теперь предположим, что у вас есть общая бесконечная серия, подобная приведенной ниже.

Обычная серия не имеет общего отношения.Другими словами, если вы разделите a _{n + 1} на a _n , полученные значения будут зависеть от n . (В случае геометрического ряда a _{n + 1} / a _n = ar ^{n + 1} / ( ar ⁿ ) = r , что является константа.)

Итак, чтобы обойти тот факт, что не существует общего отношения к , мы просто берем предел. Затем мы будем использовать это предельное значение, чтобы решить, сходится наш ряд или нет.

Фактически, тест соотношения определяет абсолютную сходимость . (Для получения дополнительной информации см .: AP Calculus BC Review: Absolute and Conditional Convergence.)

Тест соотношения. Пусть

.

• Если L <1, то ряд абсолютно сходится.
• Если L > 1, то ряд расходится.
• Однако, если L = 1, тогда проверка соотношения не дает результатов . (И тогда потребуются другие тесты, чтобы определить, сходится ли этот ряд или расходится.)

Корневой тест

Корневой тест также служит для выявления общего потенциального отношения, но делает это другим способом. На этот раз мы берем n корень -й степени общего члена, а затем позволяем n уходить в бесконечность.

Однако неравенство осталось прежним. Нам все еще нужно проверить, является ли предел меньше, больше или равен 1.

Корневой тест. Пусть

.

• Если L <1, то ряд абсолютно сходится.
• Если L > 1, то ряд расходится.
• Однако, если L = 1, тогда проверка соотношения не дает результатов . (А затем потребуются другие тесты, чтобы определить, сходится ли этот ряд или расходится.)

Итак, как корень n -й степени может извлекать информацию о потенциальном общем соотношении? Давайте посмотрим, как ведет себя предел, когда у вас есть геометрический ряд: Σ ar ⁿ .

Предел L = | r |, что является общим коэффициентом! (Ну, технически это абсолютное значение обычного отношения, но достаточно близко.)

Три полезных предела для корневого теста

Может быть сложно справиться с ограничением n корнем -й степени некоторого количества. Следующие три свойства сделают вашу жизнь намного проще:

Радиус схождения

Тесты отношения и корня могут помочь найти радиус сходимости для ряда функций.Вот как это работает:

1. Установите лимит L с учетом общих условий, как указано выше.
2. Если L = 0, то радиус сходимости бесконечен ( R = ∞).
3. Если L = ∞, то радиус равен нулю ( R = 0).
4. В противном случае, если L ненулевое и конечное значение, установите неравенство L <1 и найдите выражение | x — c |. Числовое значение, которое отображается в правой части неравенства, равно R .

Примеры

A Числовой ряд

Определите, сходится или расходится следующий ряд.

Ваша интуиция может вас обмануть

Когда дело доходит до последовательностей и серий, часто наша интуиция может вводить в заблуждение. Например, если вы выпишете первые три члена этой серии, вы получите:

Для n = 0 имеем 3 (0!) / (0 ² + 1) = 3 (1) / 1 = 3.

Тогда для n = 1 имеем 3 (1!) / (1 ² + 1) = 3 (1) / 2 = 1.5.

А для n = 2 значение равно 3 (2!) / (2 ² + 1) = 3 (2) / 5 = 1,2.

Кажется, что термины просто убывают по мере увеличения n , не так ли? Но на самом деле сроки меняются и через некоторое время начинают увеличиваться!

Удивленный кот удивлен.

Для n = 3 имеем 3 (3!) / (3 ² + 1) = 3 (6) / 10 = 1,8.

Тогда для n = 4, член будет 3 (4!) / (4 ² + 1) = 3 (24) / 17 = 4. 235.

Фактически, сами члены становятся неограниченными при n → ∞. Уже одно это говорит о том, что серия расходится (если вы можете это доказать).

Но давайте посмотрим, как работает Ratio или Root Test в этом случае.

Решение

Обычно, когда в общем термине есть факториалы, тест отношения легче применять, чем тест корня.

Теперь, потому что предел больше 1 — и действительно, насколько больше 1 вы можете получить, чем бесконечность !? — делаем вывод, что этот ряд расходится.

Когда тесты не проходят

Определите, сходится или расходится чередующийся гармонический ряд.

Решение

Вы можете выбрать Ratio или Root Test. Я устрою для вас тест на соотношение.

На этот раз предел равен 1. Это означает, что тест соотношения не дает результатов. Вместо этого попробуйте Root Test — вы получите тот же результат.

Итак, что нам теперь делать?

Вам придется выбрать другой тест на сходимость. Я бы порекомендовал тест чередующихся серий (AST), потому что, в конце концов, эта серия чередующихся.

Рассматривая абсолютное значение общего члена, 1/ n , мы видим, что оно действительно уменьшается до нуля (как n → ∞). Следовательно, согласно AST, знакопеременный гармонический ряд сходится.

Определение радиуса схождения

Найдите радиус сходимости следующего ряда.

Решение

Этот просто просит рут-теста!

Поскольку предел не был ни 0, ни бесконечностью, мы должны установить выражение меньше 1 и решить.

Последняя строка дает две части информации. Оба являются производными от общего шаблона, | x — c | < R , где c — центр, а R — радиус схождения.

• Радиус схождения R = 1/3.
• Центр степенного ряда — c = -2/3.

Гарантированно повысьте свой результат по SAT или ACT. Начните 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep уже сегодня!

Между прочим, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!

О Шоне Олте

Шон получил докторскую степень по математике в Университете штата Огайо в 2008 году (Go Bucks !!). В 2002 году он получил степень бакалавра математики и информатику в Оберлинском колледже. Кроме того, Шон получил степень бакалавра искусств. из Консерватории Оберлина в том же году по специальности «музыкальная композиция». Шон по-прежнему любит музыку — почти так же сильно, как математику! — и он (думает, что) может играть на пианино, гитаре и басу. Шон обучал и обучал студентов математике около десяти лет и надеется, что его опыт поможет вам добиться успеха!

корней

А квадратный корень ряда б , написано б , является решением уравнения Икс 2 знак равно б .

Пример: 49 знак равно 7 , потому что 7 2 знак равно 49 .

Аналогичным образом кубический корень ряда б , написано б 3 , является решением уравнения Икс 3 знак равно б .

Пример: 64 3 знак равно 4 , потому что 4 3 знак равно 64 .

В более общем плане п th корень б , написано б п , это число Икс что удовлетворяет Икс п знак равно б .

В п th root также можно записать в виде дробной экспоненты:

б п знак равно б 1 п

Когда п th корень существует, а сколько их?

Если вы работаете только в системе счисления, тогда

• Если п четное целое число, п th корень б существует всякий раз, когда б положительный ; и для всех б .
• Если п нечетное целое число, п th корень б существует для всех б

Примеры:

— 81 год 4 не настоящее число.

— 32 5 знак равно — 2

Если вы работаете в комплексная система счисления , тогда все становится еще сложнее.

Здесь каждый номер имеет 2 квадратные корни, 3 кубические корни, 4 четвертые корни, 5 пятый корень и т. д.

Например, 4 корни четвертой степени числа 81 год являются 3 , — 3 , 3 я и — 3 я . Потому что:

3 4 знак равно 81 год ( — 3 ) 4 знак равно 81 год ( 3 я ) 4 знак равно 3 4 я 4 знак равно 81 год ( — 3 я ) 4 знак равно ( — 3 ) 4 я 4 знак равно 81 год

корень | математика | Britannica

Корень , в математике решение уравнения, обычно выражаемое числом или алгебраической формулой.

В IX веке арабские писатели обычно называли один из равных множителей числа джадхр («корень»), а их средневековые европейские переводчики использовали латинское слово radix (от которого происходит прилагательное , радикал ). . Если a — положительное действительное число, а n — положительное целое число, существует уникальное положительное действительное число x такое, что x ⁿ = a . Это число — (главный) n корень -й степени из a — записывается как ⁿ Квадратный корень из √ a или a ^{1/ n} .Целое число n называется индексом корня. Для n = 2 корень называется квадратным корнем и записывается как квадратный корень из √ a . Корень ³ Квадратный корень из √ a называется кубическим корнем из a . Если a отрицательное значение и n нечетное, уникальный отрицательный корень n -й степени из a называется главным. Например, главный кубический корень из –27 равен –3.

Если целое число (положительное целое) имеет рациональный корень n -й степени — i.е., которое можно записать в виде обыкновенной дроби — тогда этот корень должен быть целым числом. Таким образом, 5 не имеет рационального квадратного корня, потому что 2 ² меньше 5 и 3 ² больше 5. Точно n комплексных чисел удовлетворяют уравнению x ⁿ = 1, и они равны называется комплексом n -го корня из единицы. Если правильный многоугольник из n сторон вписан в единичный круг с центром в начале координат, так что одна вершина лежит на положительной половине оси x , радиусы вершин — это векторы, представляющие комплекс n n -е корни единства.Если корень, вектор которого составляет наименьший положительный угол с положительным направлением оси x , обозначен греческой буквой омега, ω, то ω, ω ² , ω ³ ,…, ω _ⁿ = 1 составляют все n -й корень из единицы. Например, ω = — ¹ / ₂ + ^{Квадратный корень из √ −3} / ₂ , ω ² = — ¹ / ₂ — ^{Квадратный корень из √ −3} / ₂ и ω ³ = 1 — все кубические корни из единицы.Любой корень, обозначаемый греческой буквой эпсилон, ε, который имеет свойство ε, ε ² ,…, ε ⁿ = 1 давать все n -й корень из единицы, называется примитивным. Очевидно, проблема нахождения корней n -й степени из единицы эквивалентна задаче вписания правильного многоугольника из n сторон в круг. Для каждого целого числа n корни n -й степени из единицы могут быть определены в терминах рациональных чисел с помощью рациональных операций и радикалов; но их можно построить с помощью линейки и циркуля (т.е., определяется в терминах обычных операций арифметики и вычисления квадратного корня), только если n является произведением различных простых чисел в форме 2 ^h + 1, или 2 ^k раз, таких как product или имеет вид 2 ^k . Если a — комплексное число, а не 0, уравнение x ⁿ = a имеет ровно n корней , и все корни n th из a являются произведениями любого из них. этих корней на n -го корня из единицы.

Член корень был перенесен из уравнения x ⁿ = a во все полиномиальные уравнения. Таким образом, решение уравнения f ( x ) = a ₀ x ⁿ + a ₁ x ^{n — + 1} +… a _{n — 1} x + a _n = 0, где a ₀ ≠ 0, называется корнем уравнения.Если коэффициенты лежат в комплексном поле, уравнение n -й степени имеет точно n (не обязательно различных) комплексных корней. Если коэффициенты действительны и n нечетно, значит, существует действительный корень.