Контрольная работа №1 (Корень n-й степени. Степенные функции) Вариант 1
а) б) в) г) д) 2. Упростите выражение: а) б) в) г) д) 3. Постройте график функции 4. Расположите в порядке возрастания 5. Упростите выражение | Контрольная работа №1 (Корень n-й степени. Степенные функции) Вариант 2
а) б) в) г) д) 2. Упростите выражение: а) б) в) г) д) 3. Постройте график функции 4. , , 5. Упростите выражение | Контрольная работа №1 (Корень n-й степени. Степенные функции) Вариант 1
а) б) в) г) д) 2. Упростите выражение: а) б) в) г) д) 3. Постройте график функции 4. Расположите в порядке возрастания 5. Упростите выражение | Контрольная работа №1 (Корень n-й степени. Степенные функции) Вариант 2
а) б) в) г) д) 2. Упростите выражение: а) б) в) г) д) 3. Постройте график функции 4. Расположите в порядке возрастания , , 5. |
Контрольная работа «Корень степени n»
Урок в 10 классе
Контрольная работа №2 .
Тема. «Корень n-ой степени».
Цель: выявить уровень усвоения учащимися темы «Корень степени n.», развивать навыки самостоятельной учебной деятельности, воспитывать культуру письменной математической речи.
Ход урока.
Оргмомент.
Инструкция по выполнению контрольной работы.
Контрольная работа состоит из двух частей – обязательной и дополнительной. Обязательная часть включает в себя 8 заданий базового уровня, дополнительная – 1 задание повышенного уровня сложности.
Время выполнения контрольной работы – 45 минут.
Предлагается 4 варианта контрольной работы.
Шкала оценок
Уровень Количество правильно выполненных заданий
заданий Для получения Для получения Для получения Для получения
отметки «2» отметки «3» отметки «4» отметки «5»
Базовый Менее 4 Не менее 5 Не менее 6 Не менее 7
Повышенный — — 1 1
Выполнение контрольной работы.

Итог урока.
Вариант 1
Верно ли равенство:
а) =2; б) =-3 б) =4 г) =-5
Найдите значение выражения: а) ; б)
в) ; г)
Избавиться от иррациональности в знаменателе
Упростите выражение: а) ; б) ; в)
Найти область допустимых значений выражения а) ; б)
Расположите в порядке возрастания
Вынести множитель за знак корня: а) б) , если х<0.
Решить уравнение: а) х3 =-216; б)
_______________________________________________________________________
Найдите значение выражения .
Вариант 2
1. Верно ли равенство: а) =-3; б) =4; в) =5 г)=-6
Найдите значение выражения а) ; б)
в), г)
3. Избавиться от иррациональности в знаменателе
4.
Найдите область допустимых значений выражения: а) ; б)
Расположите в порядке возрастания , ,
Решить уравнение: а) х3 =-216; б)
Внести множитель под знак корня: а) ; б) mn,если m<0.
________________________________________________________________________
Найдите значение выражения:
Вариант 3
Верно ли равенство: а) =-4; б) ) =5 ; в) =6 ; г)=-7
Найдите значение выражения: а) :; б); в),
г)
Избавиться от иррациональности в знаменателе:
Упростить выражение: а) ; б) б) в)
Найдите область допустимых значений: а) ; б)
Расположить в порядке убывания: , ,
Внести множитель под знак корня: а) ; б) m2n,если m<0.
Решить уравнение: а) х3 =-125; б)
_______________________________________________________________________________
Найдите значение выражения:
Вариант 4
Верно ли равенство: а) =-5; б) ) =6 ; в) =-7 г)=8
Найдите значение выражения: а)
г)
Избавиться от иррациональности в знаменателе:
Упростить выражение: а) ; б)в)
Найдите область допустимых значений: а) ; б)
Расположить в порядке убывания: , ,
Внести множитель под знак корня: а) ; б) m3n2,если n<0.

Решить уравнение: а) х3 =-64; б)
_______________________________________________________________________________
Найдите значение выражения:
Контрольная работа №2. «Корень степени n»
Алгебра 10 класс 18.11.2019
Контрольная работа № 2
Корень степени n
Вариант 1
Вычислите
Избавиться от иррациональности в знаменателе
Найдите значение выражения .
Вынести множитель за знак корня: а) б) , если х<0.
Найдите значение выражения при .
Алгебра 10 класс 18.11.2019
Контрольная работа № 2
Корень степени n
Вариант 2
Вычислите
Найдите значение выражения при .
Избавиться от иррациональности в знаменателе
Внести множитель под знак корня: а) ; б) mn,если m<0.
Найдите значение выражения: .
Алгебра 10 класс 18.11.2019
Контрольная работа № 2
Корень степени n
Вариант 3
Вычислите
Найдите значение выражения при .
Избавиться от иррациональности в знаменателе:
Внести множитель под знак корня: а) ; б) m2 n, если m<0.
Найдите значение выражения:
Алгебра 10 класс 18.11.2019
Контрольная работа № 2
Корень степени n
Вариант 4
Вычислите
Найдите значение выражения при .
Избавиться от иррациональности в знаменателе:
Внести множитель под знак корня: а) ; б) m3 n2, если n<0.
Найдите значение выражения: .
Алгебра 9 Макарычев К-2 В-3
Алгебра 9 класс (Макарычев)
Контрольная работа № 2. Вариант 3
§ 3. Квадратичная функция и её график. § 4. Степенная функция. Корень n-й степени.
КР-2. Вариант 3 (транскрипт заданий)
1. Постройте график функции у = х2 – 4х – 5. Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = 3;
в) нули функции; промежутки, в которых у > 0 и в которых у < 0;
г) промежуток, в котором функция возрастает.
2. Найдите наименьшее значение функции у = х2 + 2х – 24.
3. Найдите область значений функции у = х2 – 2х – 8, где х ∈ [–1; 3].
4. Не выполняя построения, определите, пересекаются ли парабола у = х2/3 и прямая у = 6х – 15. Если точки пересечения существуют, то найдите их координаты.
5. Найдите значение выражения 3√[–4 17/27] + 6 4√[3 13/81].
Алгебра 9 Макарычев К-2 В-3 ОТВЕТЫ:
КР-2. Ответы на Вариант 3.
№2. –25.
№3. [–9;–5].
№4. Пересекаются в точках (3; 3) и (15; 75).
№5. 6 1/3.
Смотреть РЕШЕНИЯ заданий Варианта 3 в тетради
Алгебра 9 Макарычев К-2 В-3. Контрольная работа по алгебре 9 класс «Квадратичная функция и её график. Степенная функция. Корень
Другие варианты: К-2 Вариант 1 К-2 Вариант 2 К-2 Вариант 4
В учебных целях использованы цитаты из пособия: «Алгебра. Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение». Представленная контрольная работа ориентирована на УМК Макарычева. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.
Дидактические материалы 9 класс / Макарычев, Миндюк, Крайнева — М.: Просвещение». Представленная контрольная работа ориентирована на УМК Макарычева. Ответы адресованы родителям, которые смогут проконтролировать правильность выполнения заданий. Цитаты представлены в учебных целях, а также для ознакомления и покупки указанного учебного пособия.
Список контрольных работ по алгебре в 9 классе для УМК Макарычев (Оглавление)
Контрольная работа по математике (Степенная функция. Корень n-й степени.) для 9-го класса от учителей Цумадинского района в 2018 году
Ответы
Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 184 | 62 | Загрузок |
|---|---|---|---|
| Добавил | Гость | 15. 09.2019 09.2019 | Дата |
| День | Воскресенье | 00:56 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: Сайт Ассоциации учителей математики Цумадинского района
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено.
Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Справочные материалы
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Контрольная работа по математике (Корень n-ой степени) для 11-го класса от Учительского портала в 2010 году
Ответы
Ответы к заданиям
(при их наличии) доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 101 | 45 | Загрузок |
|---|---|---|---|
| Добавил | Гость | 14.12.2019 | Дата |
| День | Суббота | 16:30 |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: учительский портал Учителя.ком
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Справочные материалы
Загрузка формул. ..
..
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Калькулятор корня
Калькулятор квадратного корня
Калькулятор кубического корня
Калькулятор общего корня
Калькулятор связанных показателей | Научный калькулятор | Log Calculator
В математике, общий корень или корень n th числа a — это другое число b , которое при умножении на себя n раз равно a . В формате уравнения:
n √a = b
б н = а
Оценка корня
Некоторые общие корни включают квадратный корень, где n = 2, и кубический корень, где n = 3.Вычисление квадратных корней и корней n th довольно сложно. Это требует оценки, проб и ошибок. Существуют более точные и эффективные способы вычисления квадратных корней, но ниже приведен метод, который не требует глубокого понимания более сложных математических концепций. Для расчета √a:
Для расчета √a:
- Оценить число b
- Разделите a на b . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение b и c и использование результата в качестве нового предположения
- Повторите шаг два
| EX: | Найти √27 до 3 знаков после запятой |
| Предположение: 5.125 27 ÷ 5,125 = 5,268 (5,125 + 5,268) / 2 = 5,197 27 ÷ 5,197 = 5,195 (5,195 + 5,197) / 2 = 5,196 27 ÷ 5,196 = 5,196 |
Оценка n th Корень
Вычисление корней n th можно выполнить с помощью аналогичного метода с изменениями для работы с n .Вычисление квадратного корня полностью вручную утомительно. Оценить более высокие корни n th , даже если использовать калькулятор для промежуточных шагов, значительно утомительнее. Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n th . Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета n √a:
Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n th . Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета n √a:
- Оценить число b
- Разделите a на b n-1 .Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение: [b × (n-1) + c] / n
- Повторите шаг два
| EX: | Найти 8 √15 до 3 знаков после запятой |
| Предположение: 1.432 15 ÷ 1,4327 = 1,405 (1,432 × 7 + 1,405) / 8 = 1,388 15 ÷ 1,388 7 = 1,403 (1,403 × 7 + 1,388) / 8 = 1.402 |
Тогда должно быть ясно, что дальнейшие вычисления приведут к числу, округляемому до 1,403, в результате чего 1,403 будет окончательной оценкой с точностью до 3 знаков после запятой.
ROOTS AND EXPONENTS: РЕШАЕМЫЕ УПРАЖНЕНИЯ: SYMPLIFY ROOTS: ELEMENTAL AND HIGH SCHOOL
Содержимое этой страницы:
Введение
Корни как полномочия, свойства полномочий, важное свойство, произведение и соотношение корней
Решенные упражнения: упрощающие выражения с корнями
Введение
Степень является выражением этого типа
a b = a · a · · · a · a
Это выражение представляет собой результат умножения основания на , на , само по себе столько раз, сколько указывает показатель , b .Мы читаем это как « a в степени b ».
На этой странице мы увидим случаи, когда показатель степени, b , является дробью. n = a $$
n = a $$
Другими словами, n -й корень числа a число b , которое в степени n равно a (Итак, b n = a ).
Число n называется степенью корня и называется подкоренным элементом и корня.
Давайте посмотрим на некоторые частные случаи:
Корень степени n = 2 известен как корень квадратный .
Пример:
Квадратный корень из 9 равен 3, потому что 3 в степени двойки равно 9.
$$ \ sqrt {9} = 3 $$
Корень степени n = 3 известен как кубический корень .
Пример:
Кубический корень из -8 равен -2, потому что -2 в степени трех равняется -8.
$$ \ sqrt [3] {- 8} = -2 $$
Важно: Нет корней с четной степенью
(2, 4, 6, 8 . .) отрицательных чисел
(это комплексные числа), но там
являются корнями отрицательных чисел, если степень
нечетное число.
.) отрицательных чисел
(это комплексные числа), но там
являются корнями отрицательных чисел, если степень
нечетное число.
СВОЙСТВА ДАННЫХ | ||
| Товар | Мощность | |
| Частное | Отрицательная экспонента | |
| Обратный | Обратное обратное | |
Важное свойство
Вероятно, мы будем использовать чаще всего следующее свойство:
$$ a ^ \ frac {b} {c} = \ sqrt [c] {a ^ b} $$
Произведение и соотношение корней
Произведение двух корней с одинаковым степень — это корень (той же степени) произведения подкоренных выражений, это,
$$ \ sqrt [n] {a} \ cdot \ sqrt [n] {b} = \ sqrt [n] {a \ cdot b} $$
То же самое и с частным:
$$ \ frac {\ sqrt [n] {a}} {\ sqrt [n] {b}} = \ sqrt [n] {\ frac {a} {b}} $$
Упростите выражения с дробными показателями
Упражнение 1
Показать решение
У нас есть квадратный корень, записанный в виде степени. Мощность составляет:
Мощность составляет:
Мы знаем, что квадратный корень из 9 равен 3, но мы можем записать 9 как 9 = 3 2 , чтобы лучше понять, как исчезает квадратный корень (это то, что мы будем делать с более сложными выражениями):
Упражнение 2
Показать решение
Пишем власть в виде корня.Поскольку знаменатель показатель степени равен 4, это четвертый корень степени (корень четвертой степени):
Обратите внимание, что числитель 3 остается показателем степени подкоренного выражения.
Мы не можем удалить термин из корня, потому что
это корень четвертой степени, и для этого
подкоренное выражение должно иметь показатель больше
или равно 4.
Упражнение 3
Показать решение
Мы можем записать квадратный корень в виде степени для работы с показателем степени:
Теперь применим свойства степеней: у нас есть степень степени, поэтому мы умножаем показатели:
Запишем степень в виде корня (четвертая степень):
Мы выразили подкоренное выражение как продукт, который нужно увидеть есть фактор, который мы можем извлечь из выражение.Поскольку это четвертый корень, мы можем написать 5 для каждого 5 4 мы имеем в подкоренном выражении:
Мы не можем дальше упрощать выражение.
Упражнение 4
Показать решение
Помните, что продукт корни с одинаковой степенью — это корень с такой же степенью продукт подкормки:
Потому что у нас в числителе корень и знаменатель (в той же степени) мы можем запишите их как один корень:
Примечание: : шаг выше обусловлен свойствами степеней, потому что
Теперь мы можем упростить дробь подкоренного выражения:
В связи с тем, что у нас 1 в числитель и его квадратный корень равен 1, мы собираемся снова написать два корня:
Вычисляем куб частного:
Наконец, математики не любят корни в знаменатель, поэтому умножаем в числителе и знаменатель по корню, чтобы он оставался в числителе:
Упражнение 5
Показать решение
Запишем корень двенадцатой степени как степень:
Мы упростили дробь экспоненты. Теперь запишем подкоренное выражение (49) в виде степени: 49 = 7 2 .
Теперь запишем подкоренное выражение (49) в виде степени: 49 = 7 2 .
Упражнение 6
Показать решение
Это упражнение может показаться сложным, потому что в корнях есть корни, но единственное нам нужно написать квадрат корни как силы и применять свойства of powers (мощность мощности):
Упражнение 7
Показать решение
Мы пишем 72 как сила для применения свойств:
Запишем дробную экспоненту как кубический корень, и мы сможем извлечь множитель:
Обратите внимание: поскольку это куб
корень (третья степень), мы можем извлечь 3
от подкоренного выражения для каждого 3 3 .
Упражнение 8
Показать решение
Запишем корни степенями:
Теперь мы запишем 4 как степень, 4 = 2 2 , чтобы иметь возможность упростить:
Упражнение 9
Показать решение
Мы записываем числа и корни в экспоненциальной форме, чтобы применить свойства:
Следовательно
Упражнение 10
Показать решение
Мы запишем корни в виде степеней (один — куб, а другой — квадрат), а 9 — как 9 = 3 2
Теперь умножаем все показатели (степень степени):
Наконец, упростим дроби в показателях степени:
Мы можем извлечь множитель:
Как обычно, мы удалим корень из знаменателя.
Поскольку это кубический корень, мы должны умножить его дважды в числителе и в знаменателе, чтобы он исчез:
Упражнение 11
Показать решение
Прежде всего, потому что мы иметь дробь в степени минус единицы, мы пишем обратное, чтобы экспонента исчезла:
Теперь, поскольку все корни квадратные, мы можем их умножить:
Упростим дробь:
А теперь немного поработаем, чтобы избегаем корня в знаменателе: разделяем корни
Умножаем и делим на корень 2:
Упражнение 12
Показать решение
Выражение довольно пугающее, но все, что нам нужно сделать, это записать все корни как степени:
Обратите внимание, что мы записали все показатели только за один шаг.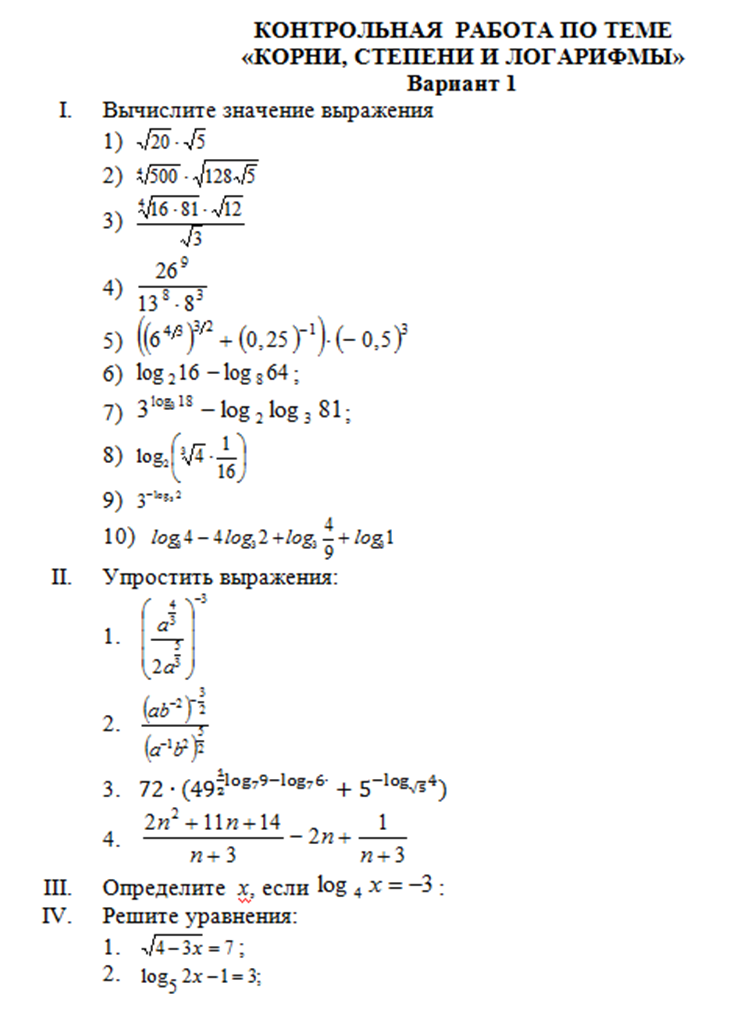
Упрощаем показатель степени:
Упражнение 13
Показать решение
У нас есть корень отрицательного числа, но поскольку это куб корень (неравномерная степень), он существует.
Запишем кубический корень в виде степени:
Умножаем показатели (степень степени):
Обратите внимание, что мы можем удалить отрицательный знак, потому что (-5) 2 = 5 2
Упражнение 14
Показать решение
Запишем пять корней как степени:
Умножаем показатели (степень степени):
Дробь равна 1.
Следовательно,
Упражнение 15
Показать решение
Мы можем извлечь 4 как общий множитель в подкоренном выражении:
4 оставляет квадратный корень как 2 (потому что это 2 2 ):
Нам нужно понять, что подкоренное выражение является результатом биномиальной теоремы Ньютона (квадрат вычитания):
Наконец, корень исключает квадрат
Важно: На самом деле, когда мы отменяем квадратный корень с число в квадрате нам нужно написать абсолютное значение
Это связано с тем, что если значение x делает полином x — 3 отрицательное, (когда x <3 ), тогда степень двойки составляет
подкоренное выражение положительное и, следовательно, квадратный корень существует и является
положительное число. Но, если мы не записываем число как
абсолютное значение, когда мы исключаем корень,
получаем отрицательное число и, как следствие, ложное равенство.
Но, если мы не записываем число как
абсолютное значение, когда мы исключаем корень,
получаем отрицательное число и, как следствие, ложное равенство.
Давайте посмотрим на пример:
Предположим, что x = 0 . Затем
Но
Однако, если мы запишем абсолютное значение, мы получим
Matesfacil.com
компании J. Llopis под лицензией
творческий
Международная лицензия Commons Attribution-NonCommercial 4.0.
| msg272638 — (просмотр) | Автор: Стивен Д’Апрано (steven. daprano) * daprano) * | Дата: 2016-08-14 02:26 | |
|---|---|---|---|
Впервые сообщил Мартин Пантер здесь: http: // ошибки.python.org/issue27181#msg272488 Боюсь, я недостаточно знаю о PowerPC, чтобы предложить исправление, кроме ослабления теста на этой платформе. | |||
| msg272639 — (просмотр) | Автор: Стивен Д’Апрано (steven.daprano) * | Дата: 2016-08-14 02:27 | |
Тесты сборщика Power PC завершаются неудачно: http://buildbot.python.org/all/builders/PPC64LE%20Fedora%203.x/builds/1476/steps/test/logs/stdio ================================================== ==================== ОТКАЗ: testExactPowers (test.test_statistics.Test_Nth_Root) (i = 29, n = 11) -------------------------------------------------- -------------------- Отслеживание (последний вызов последний): Файл "/home/shager/cpython-buildarea/3.x.edelsohn-fedora-ppc64le/build/Lib/test/test_statistics. | |||
| msg272643 — (просмотр) | Автор: Раймонд Хеттингер (rhettinger) * | Дата: 2016-08-14 03:16 | |
Вы не можете ничего лучше, чем посоветоваться с дядей Тимми. | |||
| msg272649 — (просмотр) | Автор: Мартин Пантер (martin. panter) * panter) * | Дата: 2016-08-14 06:02 | |
Проблема более распространена, чем просто Power PC. Такие же сбои (+/- 29) наблюдаются и у трех сборочных роботов s390x. Есть несколько сбоев testExactPowers (Negatives) на
http://buildbot.python.org/all/builders/x86%20Tiger%203.x/builds/11140/steps/test/logs/stdio
Первый - это
AssertionError: 9.000000000000002! = 9
Немного другой сбой происходит с сборщиками AMD64 Free BSD и Open Indiana:
http://buildbot.python.org/all/builders/AMD64%20OpenIndiana%203.x/builds/11077/steps/test/logs/stdio
================================================== ====================
ОТКАЗ: testFraction (test.test_statistics.Test_Nth_Root)
-------------------------------------------------- --------------------
Отслеживание (последний вызов последний):
Файл "/ export / home / buildbot / 64bits / 3.x.cea-indiana-amd64 / build / Lib / test / test_statistics.py ", строка 1247, в testFraction
self. | |||
| msg272658 — (просмотр) | Автор: Марк Дикинсон (mark.dickinson) * | Дата: 2016-08-14 08:29 | |
Стивен: не могли бы вы объяснить, почему вы думаете, что ваш код * должен * давать точные результаты для точных степеней? Есть ли у вас анализ ошибок, который говорит о том, что так должно быть? Одна из проблем здесь в том, что функции libm pow сильно различаются по качеству, поэтому любой алгоритм, который зависит от ** или математики.pow будет трудно что-либо доказать. Думаю, просто надо ослабить тесты: рассчитывать на идеальный результат в этом случае неразумно. | |||
| msg272663 — (просмотр) | Автор: Стивен Д’Апрано (steven.daprano) * | Дата: 2016-08-14 10:44 | |
В воскресенье, 14 августа 2016 г., в 08:29:39 +0000, Марк Дикинсон написал: > Стивен: вы можете объяснить, почему вы думаете, что ваш код * должен * давать > точные результаты для точных мощностей? У вас есть анализ ошибок, > говорит, что так должно быть? Никакого анализа ошибок, только экспериментальные результаты.> Одна из проблем заключается в том, что функции libm pow сильно различаются по качеству, поэтому > любой алгоритм, который зависит от ** или math.pow, будет сложно > что-нибудь доказывать. pow () - это только отправная точка. Более ранняя версия функции началось с первоначального предположения x как корня n-й степени x, но это было очень медленно, а иногда не сходит в разумные сроки. От переключившись на первоначальное предположение, вычисленное с помощью pow (), я сократил количество итераций до гораздо меньшего числа.Поскольку я не беспокоюсь о сверхбыстости, функция корня n-й степени проходит следующие шаги: - используйте y = pow (x, 1 / n) для первоначального предположения; - если y ** n == x, вернуть y; - улучшить предположение с помощью «алгоритма корня N-й степени»; - если через некоторое время это не сходится, вернуть y; - наконец, сравните эпсилон абс (y ** n - x) для первоначального предположения и улучшенная версия, возвращающая то, что дает меньший эпсилон. Поэтому я уверен, что nth_root () никогда не должен быть хуже pow (). > Думаю, надо просто ослабить тесты: неразумно > Ожидайте идеального результата в этом случае.Ладно. Я ослаблю тесты. | |||
| msg272664 — (просмотр) | Автор: Марк Дикинсон (mark.dickinson) * | Дата: 2016-08-14 10:48 | |
> - если y ** n == x, вернуть y; Но вот проблема: вы снова используете libm pow в этом тесте, поэтому результат True не дает точной информации о том, насколько y близок к n-му корню x (и результат теста может отличаться от платформы к платформе). | |||
| msg272665 — (просмотр) | Автор: Марк Дикинсон (mark.dickinson) * | Дата: 2016-08-14 10:52 | |
> - наконец, сравните эпсилоны абс (y ** n - x) для первоначального предположения > и улучшенная версия, возвращающая то, что дает меньший эпсилон. > > Я уверен, что nth_root () никогда не должен быть хуже pow (). То же самое и здесь: это не настоящие ошибки; они приближения к ошибкам, так как вычисления эпсилонов зависят от (а) обычного округления с плавающей запятой и, что более важно, (б) точности вычисления `y ** n`.Вполне возможно, что значение, дающее меньший эпсилон, на самом деле является худшим из двух приближений. | |||
| msg272667 — (просмотр) | Автор: Стивен Д’Апрано (steven.daprano) * | Дата: 14.08.2016 11:50 | |
В воскресенье, 14 августа 2016 г., в 10:52:42 +0000, Марк Дикинсон написал: > То же самое и здесь: это не настоящие ошибки; они приближения > к ошибкам, так как вычисления эпсилонов зависят от (a) > обычное округление с плавающей запятой и, что более важно (б) > точность вычисления `y ** n`.Вполне возможно, что > значение, дающее меньший эпсилон, на самом деле худшее из двух > приближения. Назовем два вычисленных корня y и w, где y порождается pow () и w - это "улучшенная" версия, а фактическая истинная математический корень - r (который может оказаться между числами с плавающей запятой). Вы говорите, что может оказаться, что abs (y ** n - x) | |||
| msg272668 — (просмотр) | Автор: Марк Дикинсон (mark.dickinson) * | Дата: 2016-08-14 12:05 | |
> Что еще я могу сделать? Поскольку я имею дело только с целочисленными степенями, я должен > попробовать использовать мой собственный ipow (y, n) для тестирования? Я ожидал, что умножение квадрата и умножения будет менее точным, чем математика.pow, как правило, просто из-за количества задействованных операций с плавающей запятой. Но я не думаю, что здесь есть настоящая проблема, если вы не ожидаете получения сверхточных (например, правильно или точно округленных) результатов; Тестирование с точностью до 10 мкл или около того, вероятно, будет достаточно хорошим. Если вам нужен действительный корень n-й степени с правильным округлением только для целей тестирования, конечно, можно создать его с помощью целочисленной арифметики, но более простой альтернативой может быть просто использование функции MPFR «mpfr_root» (в оболочке gmpy2) для генерации тестовых значений. | |||
| msg272670 — (просмотр) | Автор: Стивен Д’Апрано (steven.daprano) * | Дата: 2016-08-14 12:34 | |
В воскресенье, 14 августа 2016 г., в 12:05:37 +0000, Марк Дикинсон написал: > Но я не думаю, что здесь есть настоящая проблема, пока вы не > рассчитывать на получение сверхточных (например, правильно округленных > или точно округленные) результаты; тестирование, результаты которого точны > в пределах 10 мкл, вероятно, достаточно.Спасибо за совет, Марк. Это определенно показало мою наивность, когда дело касается чисел с плавающей запятой :-( Я думал, что IEEE 754 должен положить конец подобного рода перекрестным различия платформ. Если бы это была триггерная функция, я бы не стал так удивлен, но я не ожидал, что pow () будет так отличаться. Однажды я начал получать точные результаты на моей машине, я думал, что все будут вижу то же самое. | |||
| msg272672 — (просмотр) | Автор: Марк Дикинсон (марка.Дикинсон) * | Дата: 14.08.2016 13:34 | |
> Я думал, что IEEE 754 должен положить конец подобным межплатформенным различиям. Возможно, однажды. (Хотя я не задерживаю дыхание.) IEEE 754-2008 действительно * рекомендует * (но не * требует *) правильно округленные реализации всех обычных трансцендентных и степенных функций (включая корень n-й степени). И если бы все следовали этим рекомендациям, то да, правильное округление означало бы, что эти межплатформенные различия уйдут в прошлое.Однако я не вижу, чтобы это произошло в ближайшее время: написать реализацию журнала (например), которая доказуемо правильно округлена для всех возможных входных данных, намного сложнее, чем написать реализацию, которая просто «почти всегда» правильно округляет (например, доказуемо точная до 0,53 мкл вместо 0,5 мкл), и последнего будет достаточно в подавляющем большинстве контекстов. Переход от «почти всегда правильно округлено» к «правильно округленному» не окажет большого влияния на общую точность многоступенчатого числового алгоритма, поэтому все, что вы покупаете (за исключением вероятного снижения времени работы), - это перекрестный воспроизводимость платформы, и не совсем ясно, насколько полезна кроссплатформенная воспроизводимость как самостоятельная цель.В целом, это не похоже на хороший компромисс. Особенно сложно правильно округлить функцию pow, не в последнюю очередь из-за ее двух входов. По крайней мере, для трансцендентных функций с одним входом есть некоторая (возможно, отдаленная) надежда провести исчерпывающее тестирование 18 миллионов миллионов миллионов возможных входов с двойной точностью; для функции, принимающей два входа, это совершенно невозможно. Вы можете взглянуть на CRlibm [1], чтобы увидеть усилия в направлении правильного округления libm; AFAIK он не получил широкого распространения, и его функция pow все еще работает.[1] http://lipforge.ens-lyon.fr/www/crlibm/ | |||
| msg272713 — (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 2016-08-15 03:44 | |
Мета-примечание: одна итерация метода Ньютона вообще, грубо говоря, удваивает количество «хороших битов» в начальном приближении. Для плавающего корня n-й степени это была бы удивительно плохая библиотека libm pow (), которая не получила более половины ведущих битов в pow (x, 1 / n) правильно.Таким образом, одной итерации Ньютона, если она выполняется с бесконечной точностью, должно быть достаточно, чтобы все биты были "правильными" (что означает ненамного хуже, чем ошибка 0,5 ulp при преобразовании обратно в число с плавающей запятой). Так что, если вы выполняете более одной итерации Newton, вы просто боретесь с шумом с плавающей запятой. Это иллюзия - на самом деле ничего не становится лучше, разве что случайно. Это предполагает один подход для удвоений (в C - то же, что и для Python с плавающей запятой): получить приближение pow ().Подайте его в конструктор fractions.Fraction (). Сделайте одну итерацию по Ньютону, используя тип Fraction. Затем используйте `float ()`, чтобы преобразовать результат в число с плавающей точкой. Я считаю, что это лучшее, что вы можете сделать без реальной работы ;-) | |||
| msg272782 — (просмотр) | Автор: Марк Дикинсон (mark.dickinson) * | Дата: 2016-08-15 17:11 | |
Ради удовольствия, вот рецепт правильно округленной операции корня n-й степени для положительных конечных чисел с плавающей запятой.Я не предлагаю использовать это в бизнес-логике: скорее всего, это слишком медленно (особенно для больших n), но может быть использовано в тестах. Логика итерации Ньютона в floor_nroot следует из этого ответа на вопрос о переполнении стека: http://stackoverflow.com/a/35276426
из математического импорта frexp, ldexp
def floor_nroot (x, n):
"" "Для положительных целых чисел x, n вернуть нижний предел корня n-й степени из x." ""
# Первоначальное предположение: здесь мы используем наименьшую степень двойки, превышающую n-ю
# корень.Но подойдет любое значение, большее или равное целевому результату.
a = 1 << - (- x.bit_length () // n)
в то время как True:
d = x // a ** (n-1)
если a <= d:
вернуть
a = ((n-1) * a + d) // n
def nroot (x, n):
"" "
Правильно округленный корень n-й степени (n> = 2) из x для конечного положительного числа с плавающей запятой x.
"" "
если нет (x> 0 и n> = 2):
поднять ValueError ("x должно быть положительным; n должно быть не менее 2")
m, e = frexp (x)
rootm = floor_nroot (int (m * 2 ** 53) << (53 * n + (e-1)% n - 52), n)
return ldexp (rootm + rootm% 2, (e-1) // n - 53) | |||
| msg272784 - (просмотр) | Автор: Марк Дикинсон (марка.Дикинсон) * | Дата: 2016-08-15 17:19 | |
> для положительных конечных чисел с плавающей запятой ... конечно, при условии, что формат IEEE 754 binary64. | |||
| msg272806 - (просмотр) | Автор: Нед Дейли (ned.deily) * | Дата: 2016-08-15 23:01 | |
Поскольку test_NTh_Root дает сбой на очень многих различных платформах buildbot и по-разному, я отмечаю это как «средство блокировки выпуска».Было бы очень полезно решить эту проблему до версии 3.6.0b1 в следующем месяце. Предлагаем проверить выходные данные результатов тестирования различных ведомых устройств 3x build, чтобы убедиться, что все случаи рассмотрены. https://www.python.org/dev/buildbot/ | |||
| msg272871 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 16.08.2016 18:00 | |
Спасибо, Марк! Я разработал алгоритм floor_nroot много лет назад, но упустил связь с неравенством AM-GM.В результате, вместо того, чтобы быть легким, доказательство правильности оказалось болью, растянувшейся на страницы. Рад видеть, насколько очевидным это может быть!
К вашему сведению, это было мое "дешевое" предложение:
из фракций импортных фракций
def rootn (x, n):
g = Дробь (x ** (1.0 / n))
g = ((n-1) * g + Дробь (x) / g ** (n-1)) / n
возвратный поплавок (г)
Ради интереса я прогнал это и ваш `nroot` над несколькими миллионами случайных случаев с` x` в форме
ldexp (случайный (), рандомный (-500, 501))
и `n` в randrange (2, 501).Они всегда давали один и тот же результат, который отличался от «x ** (1 / n)» примерно в четверти случаев. В среднем nroot занимал примерно в 3,7 раза больше времени.
Но сокращение диапазона `n` до randrange (1, 100) более чем в половине случаев (общий) результат отличался от` x ** (1 / n) `, а` nroot` был значительно быстрее.
Мораль истории: ничего не вижу ;-) | |||
| msg272902 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 2016-08-17 05:17 | |
Заметим, что floor_nroot можно значительно ускорить, если дать ему лучшее начальное предположение.В контексте `nroot` последний _could_ передает ʻint (x ** (1 / n))` как отличное начальное предположение. В отсутствие какой-либо помощи эта версия выясняет это сама; необязательный аргумент ʻa = None` (для предоставления начального предположения, если требуется) имеет смысл.
def floor_nroot (x, n):
"" "Для положительных целых чисел x, n вернуть нижний предел корня n-й степени из x." ""
bl = x.bit_length ()
если bl <= 1000:
a = int (с плавающей запятой (x) ** (1.0 / n))
еще:
xhi = x >> (bl - 53)
# х ~ = xhi * 2 ** (bl-53)
# х ** (1 / n) ~ = xhi ** (1 / n) * 2 ** ((bl-53) / n)
# Пусть (bl-53) / n = w + f, где w - целая часть.# 2 ** (w + f) тогда 2 ** w * 2 ** f, где 2 ** w - сдвиг.
а = xhi ** (1,0 / п)
t = (bl - 53) / n
w = int (t)
а * = 2,0 ** (т - ш)
m, e = frexp (а)
а = целое (м * 2 ** 53)
е + = ш - 53
если e> = 0:
а << = е
еще:
а >> = -е
# Угадай 1 может быть ужасно медленным, с тех пор следующее
# предположение приблизительно равно x / n.Так заставьте первое предположение
# быть не менее 2. Если он слишком велик, хорошо, он будет
# сразу уменьшите до 1.
а = макс (а, 2)
a = ((n-1) * a + x // a ** (n-1)) // n
в то время как True:
d = x // a ** (n-1)
если a <= d:
вернуть
a = ((n-1) * a + d) // n
Я еще не нашел случая в контексте `nroot`, где он не выходит при первом тесте ʻif a <= d:`.Конечно, вы можете вызвать столько итераций, сколько захотите, передав `x` с намного более чем 53« значащими »битами (большие` x`, переданные `nroot`, в основном представляют собой длинные строки из завершающих 0 битов). | |||
| msg272911 - (просмотр) | Автор: СТИННЕР Виктор (встиннер) * | Дата: 17.08.2016 08:31 | |
"Ради забавы, вот рецепт правильной операции с корнем n-й степени для положительных конечных чисел с плавающей запятой.Я не предлагаю использовать это в бизнес-логике: это, вероятно, слишком медленно (особенно для больших n), но может быть использовано в тестах ». Я не очень хорошо знаю модуль статистики, но похоже, что он не использует напрямую числа с плавающей запятой, а скорее тип чисел более высокого уровня, чтобы попытаться уменьшить ошибки округления. Для меня математический модуль - это тонкая оболочка математических функций библиотеки C, за исключением нескольких функций, специфичных для Python, таких как math.factorial. Но модуль статистики находится на более высоком уровне.Может, стоит провести грань между точностью и скоростью. Например, объясните в модуле статистики, что модуль предназначен для точности? Извините, если я совершенно не понял дизайн модуля статистики :-) | |||
| msg272912 - (просмотр) | Автор: СТИННЕР Виктор (встиннер) * | Дата: 17.08.2016 08:39 | |
По поводу компромисса, можно ли добавить возможность выбора качества точности? Например, флаг для выбора между «быстрым корнем n-й степени» или «точным корнем n-й степени».В Python уже есть два вида чисел: десятичные и числа с плавающей запятой. Может быть, «флаг» должен быть типом входных чисел, десятичным или плавающим? Я спрашиваю, потому что несколько лет назад я смотрел http://lipforge.ens-lyon.fr/www/crlibm/, и такая библиотека предназначена для точности, а не для скорости. crlibm основан на библиотеке scslib, которая составляет число, используя несколько чисел с плавающей запятой, чтобы получить лучшую точность. Чтобы получить правильное округление, crlibm требует больше итераций цикла и больше операций с числами с плавающей запятой, поэтому, как и ожидалось, он работает медленнее.К вашему сведению, моя старая статья в блоге (на французском!): Http://www.haypocalc.com/blog/index.php/2009/02/20/188-bibliotheque-mathematique-arrondi-exact-crlibm | |||
| msg272914 - (просмотр) | Автор: СТИННЕР Виктор (встиннер) * | Дата: 2016-08-17 08:56 | |
Просто хочу поделиться своим небольшим опытом с округлением чисел.
В последние годы я работал над API для преобразования меток времени между числами с плавающей запятой и целыми числами, частным «PyTime C API»:
https: // haypo.github.io/pytime.html
Вначале я использовал различные числа с плавающей запятой, которые отлично смотрятся в десятичном формате. Но вскоре у меня возникли проблемы с округлением на различных сборочных роботах. После многих лет борьбы с компиляторами и попыток написать полный набор тестов я решил использовать только числа, которые могут быть сохранены точно в IEEE 754:
если use_float:
# числа с точным представлением в IEEE 754 (основание 2)
для pow2 в (3, 7, 10, 15):
нс = 2.0 ** (-pow2)
ns_timestamps.extend ((- нс, нс))
Если вам интересно, посмотрите классы CPyTimeTestCase, TestCPyTime и TestOldPyTime в Lib / test / test_time.py.
В конце я решил заново реализовать каждую функцию преобразования на чистом Python, используя decimal.Decimal, и сравнить результат с реализацией C. Это делает модульные тесты короче и проще. | |||
| msg272929 - (просмотр) | Автор: Марк Дикинсон (марка.Дикинсон) * | Дата: 2016-08-17 12:31 | |
Виктор: под «слишком медленно» я действительно * действительно * имею в виду слишком медленно. :-) floor_nroot выполняет арифметические операции с целыми числами длиной примерно 54 * n. Для малых n это нормально, но если кто-то попытается взять среднее геометрическое из списка из 50000 значений (что, как мне кажется, должно быть вполне разумным вариантом использования), floor_nroot будет тогда пытаться выполнять вычисления с многомиллионными -битовые целые числа.В частности, операция ʻa ** (n-1) `была бы убийцей для больших` n`. | |||
| msg272948 - (просмотр) | Автор: СТИННЕР Виктор (встиннер) * | Дата: 17.08.2016 14:19 | |
> floor_nroot выполняет арифметические операции с целыми числами длиной примерно 54 * n. О, я вижу. Но, возможно, Decimal достаточно быстро для таких гигантских чисел, поскольку мы можно контролировать точность? | |||
| msg273753 - (просмотр) | Автор: Тим Петерс (тим.Питерс) * | Дата: 27.08.2016 02:49 | |
Меня не волнует правильное округление здесь, но, например, немного смущает, что
>>> 64 ** (1/3)
3,99999999999999996
Что вы можете видеть или не видеть на своем поле, в зависимости от вашей платформы pow (), но что вы «должны» видеть: 1/3 - это не треть, это двоичное приближение, которое немного меньше 1/3, поэтому 64 к этой мощности должно быть меньше 4.
Есть две практические проблемы с 'nroot', обе уже отмечены: (1) Его очень дешевое начальное предположение происходит за счет необходимости нескольких итераций, чтобы получить хорошее предположение до 54 бит.Это можно отремонтировать, и уже показали, как. (2) Чем больше n, тем больше битов требуется. Как заметил Марк, при n = 50000 мы выполняем арифметику с многомиллионными битами. Это присуще - и медленно.
Моя простая функция fractions.Fraction тоже страдает от второй проблемы, но работает еще медленнее для больших n.
Но если вы откажетесь от гарантированно правильного округления, это действительно довольно просто: как я отмечал ранее, одна итерация Ньютона примерно удваивает количество "хороших битов", поэтому _ любой_ способ получить эффект дополнительной точности за одну итерацию будет получить результат, достаточно хороший для всех практических целей.Обратите внимание, что граница ошибки строго меньше 1 ulp достаточно, чтобы гарантировать получение точного результата всякий раз, когда точный результат представим.
Вот один из способов использования того, что десятичный модуль имеет регулируемую точность:
импорт десятичной дроби
def rootn (x, n):
c = decimal.getcontext ()
oldprec = c.prec
пытаться:
c.prec = 40
g = десятичный. десятичный (x ** (1.0 / n))
g = ((n-1) * g + десятичный.Десятичный (x) / g ** (n-1)) / n
возвратный поплавок (г)
наконец-то:
c.prec = oldprec
Теперь использование памяти остается тривиальным, независимо от n. Я еще не нашел случая, когда результат отличался бы от правильно округленного `nroot ()`, но не очень старался. И, например, даже при относительно скромном n = 5000 это более чем в 500 раз быстрее, чем `nroot` (модифицированный для использования масштабированного x ** (1 / n) в качестве отличного начального предположения, так что он тоже всегда выходит после его первого шага Ньютона).При n = 50000 это более чем в 15000 раз быстрее.
Однако для n меньше примерно 70 `nroot` работает быстрее. Несмотря на это, для меня это достаточно быстро.
Примечание: на случай путаницы, `rootn (64.0, 3)` возвращает ровно 4.0 _ не обязательно потому, что он "более точен", чем pow () в этом поле, а потому, что он видит точные 3 вместо приближения к 1 / 3 pow () видит. Это приближение идеально подходит для получения начального предположения (64 ** (1/3)) почти до 53 бит. Настоящее улучшение происходит от шага Ньютона с использованием _exactly_ 3.Тем не менее, я видел редкие случаи, когда этот (и `nroot`) давал лучший результат, чем платформа pow () даже для n = 2 (где 1 / n _is_ точно представимо). | |||
| msg273759 - (просмотр) | Автор: Сергей Сторчака (serhiy.storchaka) * | Дата: 27.08.2016 05:03 | |
Что делать, если использовать pow () с точно представленной степенью на этапе аппроксимации?
def rootn (x, n):
г = х ** (1.0 / п)
m = 1 << (n-1) .bit_length ()
если n! = m:
г = (х * г ** (м-п)) ** (1,0 / м)
вернуть г
Возможно, потребуется несколько итераций, потому что он сходится медленнее, чем приближение Ньютона. Но каждый шаг может быть быстрее. | |||
| msg273760 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 2016-08-27 05:44 | |
Сергей, я не знаю, о чем ты там думаешь, да и код мне не понятен.Например, рассмотрим n = 2. Тогда m == n, так что вы принимаете начальное предположение `g = x ** (1.0 / n)`. Но, как я уже сказал, есть случаи, когда это не дает лучшего результата, в то время как другие алгоритмы дают. Например, на этом ящике: >>> сергей (7.073208563506701e + 46, 2) 2.6595504438733062e + 23 >>> pow (7.073208563506701e + 46, 0.5) # точно так же, как ваш код 2.6595504438733062e + 23 >>> nroot (7.073208563506701e + 46, 2) # наилучший результат 2.6595504438733066e + 23 >>> импорт математики >>> math.sqrt (7.073208563506701e + 46) # также достигается sqrt () 2.6595504438733066e + 23 По общему принципу, вы не можете ожидать, что добьетесь большего успеха, чем простой pow (), если не сделаете _something_, что даст эффект использования более 53 бит мантиссы - если только платформа pow () действительно ужасна. Многократное использование pow () бесполезно; выполнение шагов Ньютона _в_ родной точности с плавающей запятой (C double) бесполезно; даже некоторая форма «двоичного поиска» бесполезна, потому что простое вычисление g ** n (с исходной точностью) приводит к ошибкам округления, более серьезным, чем с самого начала pow ().Пока вы придерживаетесь собственной точности, вы боретесь с ошибками округления, по крайней мере, так же плохо, как и с начальными ошибками округления, которые вы пытаетесь исправить. Нет никаких априорных причин даже надеяться, что итерации сойдутся. | |||
| msg273804 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 28.08.2016 04:01 | |
Добавление еще одной версии последнего кода, быстрее за счет сокращения количества используемых дополнительных цифр и за счет использования «обычных» низкоуровневых трюков со скоростью CPython.Я не утверждаю, что оно всегда правильно округлено - хотя я не нашел конкретного случая, когда это не так. Я утверждаю, что он вернет точный результат всякий раз, когда точный результат может быть представлен в виде числа с плавающей запятой.
Я также утверждаю, что он «достаточно быстрый» - эта версия на моем компьютере обеспечивает от 50 до 100 тысяч корней в секунду, в значительной степени независимо от `n`.
импорт десятичной дроби
c = десятичный.DefaultContext.copy ()
c.prec = 25
def rootn (x, n,
D = десятичный.Десятичный,
pow = c.power,
mul = c. умножить,
добавить = c.add,
div = c.divide):
г = D (х ** (1,0 / п))
п1 = D (п-1)
g = div (добавить (mul (n1, g),
div (D (x), pow (g, n1))),
п)
возвратный поплавок (г)
дель десятичный, c | |||
| msg273822 - (просмотр) | Автор: СТИННЕР Виктор (встиннер) * | Дата: 28.08.2016 13:11 | |
Hum, "g = D (x ** (1.0 / n)) "вычисляет число с плавающей запятой, а затем преобразует его в десятичное число, верно? Можем ли мы добавить комментарии, чтобы объяснить, почему вы начинаете с float, compute десятичный и закончить с плавающей точкой? А может быть, еще и алгоритм задокументировать? | |||
| msg273826 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 28.08.2016 15:42 | |
Виктор, рад добавить комментарии, но только если есть достаточный интерес к его использованию.В контексте этого отчета о проблеме действительно важно, чтобы Марк это понимал, и он уже понимает ;-) Например, оно начинается с float `**`, потому что это, безусловно, самый быстрый способ получить очень хорошее приближение. Затем он переключается на Decimal, чтобы выполнить шаг Ньютона с точностью больше, чем с плавающей запятой, что необходимо для поглощения ошибок округления на промежуточных шагах. Затем он снова округляется до числа с плавающей точкой, потому что это необходимо - это функция «плавать внутрь, плавать наружу». По той же причине, e.g., что функция Mark `nroot` преобразует числа с плавающей запятой в потенциально гигантские целые числа для своего шага (ов) Ньютона, а моя другая функция` fractions.Fraction` преобразует числа с плавающей точкой в потенциально гигантские рациональные числа. "Потенциально гигантский" может быть необходим для обеспечения всегда правильного округления окончательного результата, но не обязательно, чтобы гарантировать <1 ошибку ulp в конечном результате. | |||
| msg273827 - (просмотр) | Автор: Стивен Д'Апрано (steven.daprano) * | Дата: 2016-08-28 16:08 | |
Это действительно открыло глаза, и я просто хотел написать вам записку что я внимательно слежу за этой веткой.Моя первоочередная задача - получить все тесты, проходящие до беты 1 на 2016-09-12, даже если (как кажется вероятно), что означает ослабление тестов, а затем вернуться и посмотреть, может подтянуть его снова позже. Еще не проверял, но уже успел упростить nth_root, следуя совету Тима, что более одной итерации Метод Ньютона - пустая трата времени. Благодарность! Кто-нибудь может здесь прокомментировать мои рассуждения? Я начинаю с предположения о корне, используя г = pow (х, 1.0 / н). Затем я проверяю, если r ** n == x, если это так, я делаю вывод, что r является либо точным корнем, либо настолько близким к представлению, как число с плавающей запятой, и просто верните его, не беспокоясь ни об одной итерации. Разумно? Или я должен всегда запускать одну итерацию Newton и верить, что она хуже не будет? | |||
| msg273829 - (просмотр) | Автор: Сергей Сторчака (serhiy.storchaka) * | Дата: 28.08.2016 16:27 | |
Разве последующая реализация не будет быстрее?
импорт десятичной дроби
c = десятичный.DefaultContext.copy ()
c.prec = 25
def rootn (x, n,
D = десятичный. Десятичный,
sub = c.subtract,
mul = c. умножить,
log = c.ln):
г = х ** (1,0 / п)
g + = float (sub (log (D (x)), mul (log (D (g)), D (n)))) * g / n
вернуть г
дель десятичный, c | |||
| msg273833 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 28.08.2016 17:49 | |
Это умно, Сергей! Откуда это? Это не метод Ньютона, но, похоже, он также обладает квадратичной сходимостью.Что касается скорости, почему вы спрашиваете? Вы должны уметь рассчитывать время, да? На моем ящике он примерно в 6 раз медленнее, чем последний опубликованный мной код. Я предполагаю (но не знаю), потому что + - * / имеют тривиальную стоимость по сравнению с power () и ln (), и ваш код использует два ln (), в то время как последний опубликованный мной код использует только одну power (). Кроме того, мой power () имеет точный целочисленный показатель степени, который - по каким-либо причинам - работает намного быстрее, чем использование нецелого десятичного показателя. Именно по последней причине я не предлагал просто выполнить `return float (D (x) ** (D (1) / n))` (намного медленнее).Или, может быть, это «платформенная вещь». К вашему сведению, я использую выпущенный Python 3.5.2 на 64-битной Win 10 Pro. | |||
| msg273834 - (просмотр) | Автор: Тим Петерс (tim.peters) * | Дата: 2016-08-28 18:08 | |
Стивен, вы, конечно, _can_ ;-) сначала проверите, действительно ли `r ** n == x`, но можете ли вы доказать, что` r` является наилучшим возможным результатом, если это правда? Навскидку, не могу. Я сомневаюсь в этом, потому что это редко кажется _бы_ истиной (менее чем в 1% случайных тестовых случаев, которые я пробовал).Дорогой тест, который редко бывает верным, в целом замедляет работу, а не ускоряет ее.
Что касается того, не ухудшит ли положение шаг Ньютона, для этого нужно увидеть точный код, который вы используете. Существует множество математически эквивалентных способов кодирования «шага Ньютона», которые имеют различное числовое поведение. Если по какой-то непостижимой (для меня) причине вы решили придерживаться собственной точности, то, вообще говоря, лучший способ выполнить «шаг исправления» с числовой точки зрения - это закодировать его в форме:
r + = коррекция # где "коррекция" мала по сравнению с "r"
Кодирование шага Ньютона здесь как, e.g., `r = ((n-1) * r + x / r ** (n-1)) / n` при собственной точности было бы по существу бесполезным: в последних нескольких битах результата обнаруживаются множественные ошибки округления, но последние несколько бит - единственные, которые мы пытаемся исправить.
Когда «коррекция» мала по сравнению с «r» в «r + = коррекция», ошибки округления при вычислении «коррекции» проявляются в последних нескольких битах коррекции, которые далеки от последних нескольких битов «r». (_because_ `Correction` мала по сравнению с` r`). Так что такой способ написания _может_ быть полезным. | |||
| msg273843 - (просмотр) | Автор: СТИННЕР Виктор (встиннер) * | Дата: 2016-08-28 21:35 | |
Тим Петерс: «Виктор, счастлив | |||
Ошибка | Wyzant Resources
Авторизоваться зарегистрироватьсяНайдите репетитора
Поиск репетиторов Запросить репетитора Онлайн-репетиторствоКак это работает
Для студентов Для высшего образования часто задаваемые вопросы Что говорят клиентыресурсов
Спросите эксперта Поиск вопросов Задайте вопрос Уроки Блог WyzantСтать репетитором
Применить сейчас О репетиторстве Найти работу репетитора Как это работает для репетиторов часто задаваемые вопросыО нас
Насчет нас Наша команда Карьера Свяжитесь с нами Авторизоваться зарегистрироватьсяНайти репетитора
Поиск репетиторов Запросить репетитора Онлайн-репетиторствоКак это работает
Для студентов
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Банкноты более 7.1 нет настоящих корней четвертой степени Поиск корней энной степени
Презентация на тему: «В заметках по 7.1 нет настоящих корней четвертой степени. Поиск корней n-й степени» - стенограмма презентации:
1 Примечания Более 7.1 нет действительных корней 4-й степени Поиск корней n-й степени
Найдите указанный действительный корень (-и) n-й степени числа.нет настоящих 4-х корней
2 Примечания к 7.1. Поиск корней n-й степени
Найдите указанный действительный корень (-и) n-й степени числа.
3 Примечания по поводу 7.1 Оценка выражений с помощью рациональных экспонентов
Вычислите выражение без использования калькулятора.
4 Примечания более 7.1 Вычисление выражений с помощью рациональных экспонентов
Вычислите выражение без использования калькулятора.
5 Примечания к 7.1 Аппроксимация корня с помощью калькулятора
Вычислите выражение с помощью калькулятора. Результат округляется до двух десятичных знаков.
6 Примечания более 7.1 Аппроксимация корня с помощью калькулятора
Вычислите выражение с помощью калькулятора. Результат округляется до двух десятичных знаков.
7 Примечания к 7.1 Решение уравнений с использованием корней n-й степени
Решите уравнение. При необходимости округлите ответ до двух десятичных знаков.

 Расположите в порядке возрастания
Расположите в порядке возрастания Упростите выражение
Упростите выражение py", строка 1216, в testExactPowers
self.assertEqual (self.nroot (x, n), я)
AssertionError: 29.000000000000004! = 29
================================================== ====================
ОТКАЗ: testExactPowersNegatives (test.test_statistics.Test_Nth_Root) (i = -29, n = 11)
-------------------------------------------------- --------------------
Отслеживание (последний вызов последний):
Файл "/home/shager/cpython-buildarea/3.x.edelsohn-fedora-ppc64le/build/Lib/test/test_statistics.py", строка 1228, в testExactPowersNegatives
self.assertEqual (self.nroot (x, n), я)
AssertionError: -29.000000000000004! = -29
py", строка 1216, в testExactPowers
self.assertEqual (self.nroot (x, n), я)
AssertionError: 29.000000000000004! = 29
================================================== ====================
ОТКАЗ: testExactPowersNegatives (test.test_statistics.Test_Nth_Root) (i = -29, n = 11)
-------------------------------------------------- --------------------
Отслеживание (последний вызов последний):
Файл "/home/shager/cpython-buildarea/3.x.edelsohn-fedora-ppc64le/build/Lib/test/test_statistics.py", строка 1228, в testExactPowersNegatives
self.assertEqual (self.nroot (x, n), я)
AssertionError: -29.000000000000004! = -29  assertEqual (self.nroot (x ** 12, 12), float (x))
AssertionError: 1.1866666666666665! = 1.1866666666666668
assertEqual (self.nroot (x ** 12, 12), float (x))
AssertionError: 1.1866666666666665! = 1.1866666666666668