Контрольная работа геометрия 11 класс векторы: Учебно-методический материал по геометрии (11 класс) на тему: Контрольная работа по геометрии 11 класс по теме «Координаты точки. Координаты вектора «

Учебно-методический материал по геометрии (11 класс) на тему: Контрольная работа по геометрии 11 класс по теме «Координаты точки. Координаты вектора «

Вариант 1 1.        Даны векторы {–3; 1; 4} и {2; –2; 1}. Найдите координаты вектора  =  + . 2.        Даны векторы {8; –4; 2}, {0; –3; –2} и {2; 0; 1}. Найдите координаты вектора . 3.        Найдите значения т и п, при которых векторы {т; –2; 3} и {–8; 4; п} будут коллинеарными.

Вариант 2 1.        Даны векторы {–2; 2; 2} и {1; –1; 4}. Найдите координаты вектора  =  – . 2.        Даны векторы {3; 2; 0}, {9; 0; 3} и {2; –5; 4}. Найдите координаты вектора . 3.        Найдите значения т и п, при которых векторы {–3; 2; п} и {т; –6; –3} будут коллинеарными.

4. Даны векторы {2; –5; –2}, {–4; 3; –2}. а)        Будут ли коллинеарными векторы  и  ? б)        Вычислите . 5.        А(4; 7; –4), В(–4; 5; –3), С(2; –1; 3). Найдите координаты вершины D параллелограмма ABCD. 6. Докажите, что ABCD — квадрат, если А(–2; 1; –2), В(0; –2; 4), С(3; 4; 6),D(1; 7; 0).

4.        Даны векторы {4; –3; –4}, {–2; 4; –3}. а)        Будут ли коллинеарными векторы  и  ? б)        Вычислите . 5.        А(3; 8; –2), В(–4; 5; –1), С(2; –1; 1).Найдите координаты вершины D параллелограмма ABCD. 6. Докажите, что ABCD — ромб, если  А(11; 3; 5),         В(5; 3; –7), С(–5; –5; –11), D(1; –5; 1).

7*.  Вершины треугольника АВС имеют координаты                               А(2; 1; -8), В(1; -5; 0), С(8;1; -4). ☻ Докажите, что треугольник АВС равнобедренный. ☻ Найдите длину средней линии  треугольника, параллельной его основанию

7*.  Вершины треугольника АВС имеют координаты                               А(-1; 5; 3), В(-3; 7; -5), С(3;1; -5). ☻ Докажите, что треугольник АВС равнобедренный. ☻ Найдите длину средней линии  треугольника, параллельной его основанию

Контрольные работы по геометрии по теме «Векторы в пространстве» 11 класс

11 класс Контрольная работа по теме « Векторы в пространстве» вариант 1

1. Какому из указанных векторов равен вектор (1; 2;3)?

А) (2; 3; 1) Б) (3;1;2) В) (1;2;3) Г) (1;3;2)

2. Найдите скалярное произведение векторов (-1; 3; -2) и (0; -1; 5)

А) -14; Б) -13; В) 0; Г) 7; Д) 4.

3. При каких значениях n векторы (1;-1; n) и (n; 1; n) коллинеарны?

А) ни при каких; Б) при n=-1; В) при n=1; Г) при n=1.

Часть 2

4. Вычислите длину вектора = 2+ 3, если (1;1;-1), (2; 0; 0).

5. При каком значении р векторы (3; р; -1) и (р; -2; 5) взаимно перпендикулярны?

6. Разложите вектор (5; -17; 11) по векторам (3; -2; 0), (-2; 4; 1) и (-1; -3; 4)

Часть 3

4. Найдите градусную меру угла φ между векторами = 3+ и = + 2, где и — единичные и взаимно перпендикулярные векторы.

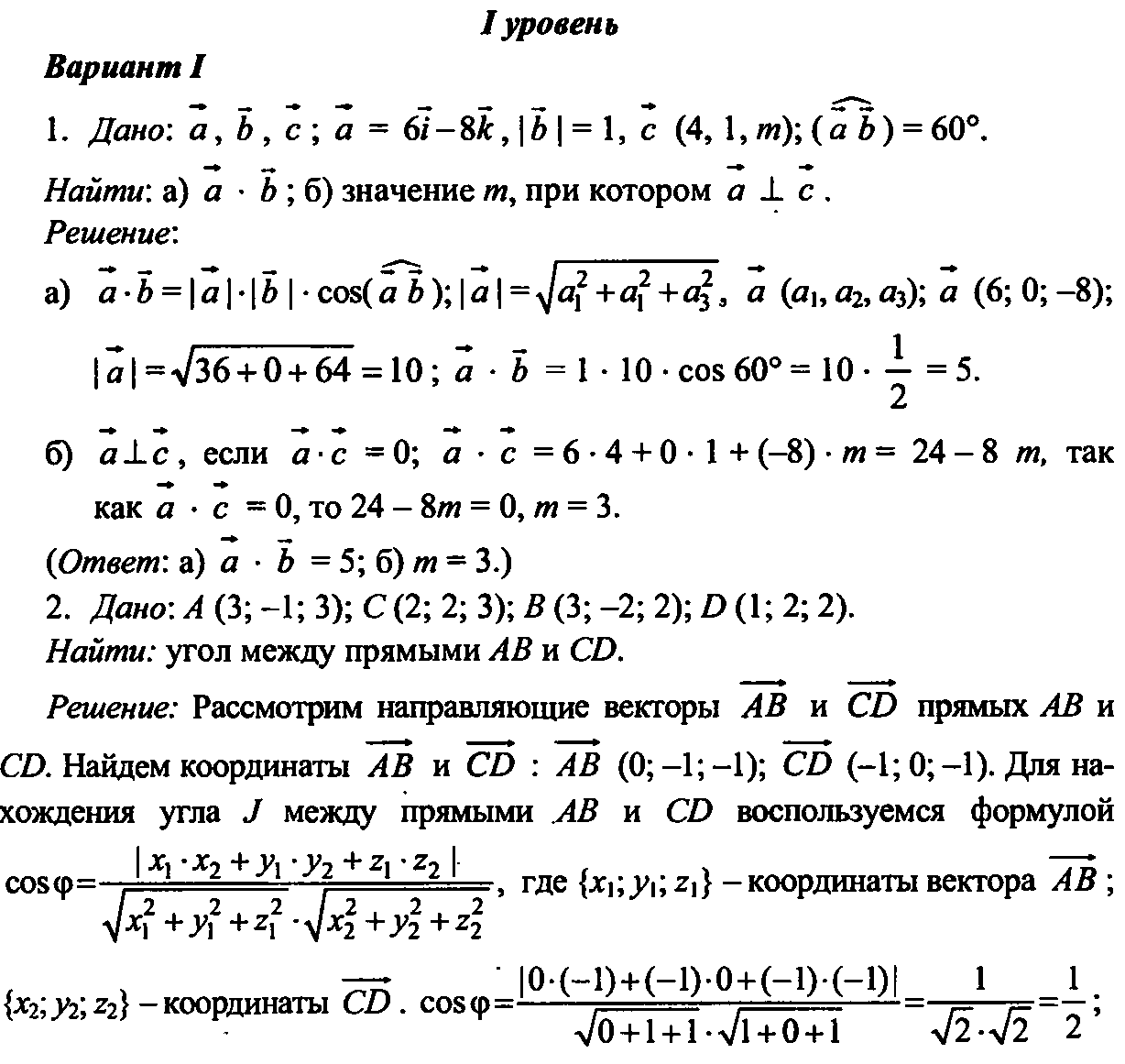
11 класс Контрольная работа по теме « Векторы в пространстве» вариант 2

1. Какому из указанных векторов равен вектор (3; 1;2)?

А) (2; 3; 1) Б) (3;1;2) В) (1;2;3) Г) (1;3;2)

2. Найдите координаты вектора , если А(-3;-2; -1), В(-1; 2; 3), С(0; -1; -2)

А) (0; -5; -7) Б) (-2; 1; 3) В) (-3; 1; 2)

Г) (2; -1; -3) Д) (0; 5; 7)

3. При каких значениях n векторы (2; 1; n) и (n; 1; n) перпендикулярны?

А) ни при каких; Б) при n=-1; В) при n=1; Г) при n=1.

Часть 2

4. При каких значениях n и m векторы (-1; 4; -2) и (-3; m; n) коллинеарны?

5. Дан треугольник АВС: А(0;1;-1), В(1;-1;2) и С(3;1;0). Найти косинус угла А треугольника АВС

6. Разложите вектор (1; 4; 3) по векторам (1; -1; 0), (0; 1; 1) и

(1; 0; -1)

Часть 3

4. Вычислите длину вектора = — 2, если = 2, =1, а угол между векторами и равен 60⁰ .

11 класс. Векторы в пространстве вариант 3

1. Вычислите координаты вектора , если А(2;3;1), В(1;0;2)

А) (1;3;-1) Б) (;;) В) (-1;-3;1) Г) другой ответ

2. Найдите скалярное произведение векторов (4; -3; 1) и (-2; 1; -1)

А) -24; Б) -12; В) 0; Г) -1; Д) -10.

3. Вычислите длину вектора = — 2, если (-1;2;-2)

А) Б) 3 В) 1 Г) 6 Д) другой ответ

Часть 2

4.При каких значениях n и m векторы (-2;8; -4) и (-6; m; n) коллинеарны?

5. Разложите вектор (11; -4; 11) по векторам (1; 2; 3), (2; -1; 1) и (3; -5; 2)

6. Дан треугольник АВС: А(2; 1; 7), В(-1; 1; 3) и С(-8; 1; 2). Найти внутренний угол при вершине В.

Часть 3

7.Угол между векторами и равен 60;, , причем длины векторов , и равны 1. Найдите скалярное произве-дение (-2)2+).

11 класс. Векторы в пространстве вариант 4

1. Вычислите координаты вектора , если А(-2;4;1), В(1;0;-2)

А) (3;-4;-3) Б) (-; 2; -) В) (-1;4;-1) Г) другой ответ

2. Какому из указанных векторов равен вектор (4; 2;3)?

А) (2; 3; 4) Б) (3;4;2) В) (4;2;3) Г) (4;3;2))

3. Являются ли векторы (8;-4;3) и (-4;2;-) коллинеарными?

А) да Б) нет В) невозможно определить

Часть 2

4. Вычислите длину вектора = 2+ 3, если(3;1;0), (0;1;-1).

5. Дан треугольник АВС: А(-1; -2; 4), В(-4; -2; 0) и С(3; -2; 1). Найти внутренний угол при вершине В.

6. Разложите вектор (4; 0; -7) по векторам (1; 2; -3), (0; 3; 1) и (2; 5; 2)

Часть 3

4. Векторы , и — единичные; и образуют угол 60

   0, а вектор перпендикулярен им. Найдите длину вектора + +.

Контрольная работа по геометрии на тему «Векторы.Скалярное произведение векторов» (11 класс)

Вариант 1		Вариант 2
1	Даны векторы и , причем Найти .	1	Даны векторы и , причем Найти .
2	Найдите угол между прямыми АВ и СD, если А(3,-1,3), В(3,-2,2), С(2,2,3), D(1,2,2).	2	Найдите угол между прямыми АВ и СD, если А(1,1,2), В(0,1,1), С(2,-2,2), D(2,-3,1).
3	Вершины треугольника АВС имеют координаты А(-2,0,1), В(-1,2,3), С(8,-4,9). Найдите координаты вектора , если ВМ – медиана треугольника АВС.	3	Вершины треугольника АВС имеют координаты А(-1,2,3), В(1,0,4), С(3,-2,1). Найдите координаты вектора , если АМ – медиана треугольника АВС.
4	Вычислите скалярное произведение векторов если	4	Вычислите скалярное произведение векторов если
5	Найдите координаты точек, в которые переходят точки А(2; 4; 8), В (4; — 3; 10), С(11; -7; -5) при: а) центральной симметрии относительно начала координат; б) осевой симметрии относительно координатных осей; в) зеркальной симметрии относительно координат.	5
Вариант 1		Вариант 2
1	Даны векторы и , причем Найти .	1	Даны векторы и , причем Найти .
2	Найдите угол между прямыми АВ и СD, если А(3,-1,3), В(3,-2,2), С(2,2,3), D(1,2,2).	2	Найдите угол между прямыми АВ и СD, если А(1,1,2), В(0,1,1), С(2,-2,2), D(2,-3,1).
3	Вершины треугольника АВС имеют координаты А(-2,0,1), В(-1,2,3), С(8,-4,9). Найдите координаты вектора , если ВМ – медиана треугольника АВС.	3	Вершины треугольника АВС имеют координаты А(-1,2,3), В(1,0,4), С(3,-2,1). Найдите координаты вектора , если АМ – медиана треугольника АВС.
4	Вычислите скалярное произведение векторов если	4	Вычислите скалярное произведение векторов если
5	Найдите координаты точек, в которые переходят точки А(2; 4; 8), В (4; — 3; 10), С(11; -7; -5) при: а) центральной симметрии относительно начала координат; б) осевой симметрии относительно координатных осей; в) зеркальной симметрии относительно координат.	5	С(9; 0; -4) при: а) центральной симметрии относительно начала координат; б) осевой симметрии относительно координатных осей; в) зеркальной симметрии относительно координат.

Диагностическая контрольная работа по геометрии, (11 класс)

Диагностическая контрольная работа по геометрии 11 класс

Цель: проверить уровень усвоения ГОСО по темам «Параллельность прямых и плоскостей в пространстве», « «Перпендикулярность в пространстве», «Координаты вектора в пространстве»:

— знание взаимного расположения прямых и плоскостей в пространстве;

— знание и умение применять свойство параллельности прямых, параллельности прямой и плоскости;

— знание и умение применять свойство перпендикулярных прямой и плоскости;

— знание и умение применять при решении задач понятия перпендикуляр и наклонная, расстояние от точки до плоскости;

-знать и уметь применять признаки подобия треугольников и теорему Пифагора;

— умение находить расстояние между точками, заданными в координатной виде;

— умение находить угол между векторами.

Содержание контрольной работы

Вариант 1 1.Длины сторон прямоугольника 8см и 6см.Через точку О пересечения его диагоналей проведена прямая ОК перпендикулярная его плоскости. Найдите расстояние от точки К до вершин прямоугольника, если ОК=12см. 2.Плоскость  пересекает стороны АВ и ВС треугольника АВС в точках М и К соответственно и параллельна стороне АС. Найдите длину отрезка МК, если АС=12см, а ВМ  АМ=3  1. 3. Даны точки: А(2; –8; 1), В(–7; 10; –8), С(–8; 0; –10), D( –9; 8; 7).  Найдите: а) угол между векторами и ; б) расстояние между серединами отрезков AB и CD. 4 .Из точки к плоскости проведены две наклонные, равные 17 см и 15 см. проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных.

Вариант 2 1. Длина стороны ромба ABCD1 0см.Длина диагонали BD равна 16 см. Через точку О пересечения его диагоналей проведена прямая ОК перпендикулярная его плоскости. Найдите расстояние от точки К до вершин ромба, если ОК= 6см. 2.Плоскость  пересекает стороны DF и EF треугольника DEF в точках K и P соответственно и параллельна стороне DE. Найдите длину стороны DE треугольника, если DE-KP=4см, FK  KD=2  1. 3. Даны точки: А(5; 0; 1), В(0; –1; 2), С(3; 0; 1), D(–2; –1; 2). Найдите: а) угол между векторами и б) расстояние между серединами отрезков AB и CD. 4. Из точки к плоскости проведены две наклонные, одна из которых на 6 см длиннее другой. Проекции наклонных равны 17 см и 7 см. Найдите длины наклонных.

 

Распределение заданий по содержанию и уровню сложности. Технологическая матрица.

Содержательные линии	Воспроизведение	Применение	Интеграция	%
Перпендикулярность прямой и плоскости	№1			20%
Параллельность прямых и плоскостей в пространстве.	№2			20%
Метод координат в пространстве		№3 (а) №3 (б)		40%
Перпендикуляр, наклонная и её проекция			№4	20%
	40%	40%	20%	100%

Критерии оценивания по проверяемым элементам.

№ задания	тема	Проверяемые элементы	Кол-во баллов	итого
1	Перпендикулярность прямой и плоскости	Построение чертежа по условию задачи Перпендикулярность прямой и плоскости Свойство диагоналей прямоугольника и ромба Теорема Пифагора Оформление решения задания	1 1 1 1 1	5
2	Параллельность прямых и плоскостей в пространстве.	Построение чертежа по условию задачи Признак подобия треугольников Оформление решения задания	1 2 2	5
3	Векторы в пространстве	Нахождение координат вектора по координатам его начала и конца Нахождение длины вектора по его координатам Нахождение угла между векторами Нахождение координат середины отрезка по координатам его концов Нахождение длины отрезка	1 1 1 1 1	5
4	Перпендикуляр, наклонная и её проекция	Понятие наклонная и её проекция Теорема Пифагора Составление уравнения по условию задачи Оформление решения задания	1 1 2 1	5

Критерий оценивания

1-9 баллов – «2»

10-13 баллов – «3»

14-18 баллов – «4»

19-20 баллов – «5»

Векторы в пространстве 11 класс

Контрольная работа по теме: «Векторы в пространстве» вариант 1 Справедливо ли утверждение: А) любые два противоположно направленных вектора не коллинеарны: Б) вектор это отрезок имеющий направление; В) любые два коллинеарных вектора соноправленны; Г) длина вектора это модуль данного вектора; Д) равенство векторов это когда векторы коллинеарны и равна их длина; Е) если a↑↓b и b↑↓c, то a ↑↓ c. 2. Запишите сочетательное свойство сложения 3. Что такое разность векторов 4.Запишите свойства умножения вектора на число 5. Запишите признак компланарности векторов 6. Сформулируйте теорему о разложении вектора по трем не компланарным 7. Упростите выражение: a)FK+MQ + KP + AM + QK + PF; б) AD+MP + EK – EP – MD. 8. Дан параллелепипед ABCDA1B1C1D1. Изобразите на рисунке векторы, равные: 1) В1С1 + АВ + СС1 + В1А; 2) DC – CB1. 9.В тетраэдре DABC М – точка пересечения медиан грани BDC, Е – середина АС. Разложите вектор EM по векторам AC,AB и AD. 1 0. Даны три неколлинеарных вектора a,b и c. Найдите значения р и g, при которых векторы m = pa+gb +8c и n = a + pb + gc коллинеарны. 11. В тетраэдре DABC точки М и Н – середины соответственно ребер АD и ВС. Докажите, используя векторы, что прямыеАВ,НМ и DC параллельны одной плоскости.

Контрольная работа по теме: «Векторы в пространстве» вариант 2 Справедливо ли утверждение: А) любые два противоположно направленных вектора коллинеарны: Б) вектор это направленный отрезок; В) любые два не коллинеарных вектора соноправленны; Г) длина вектора это расстояние между началом и концом вектора; Д) любые два соноправленных вектора равны; Е) если a↑↓b и b↑↓c, то a ↑↑ c. 2. Запишите переместительное свойство сложения 3. Запишите формулу разности векторов, через сумму векторов 4.Запишите свойства умножения вектора на число 5. Запишите обратный признак компланарности векторов 6. Сформулируйте теорему о разложении вектора по трем не компланарным 7.Упроститевыражение: a) KM+ DF + AC + FK + CD + CA + MP; б) AC — BC –PM –AP + BM. 8. Дан параллелепипед ABCDA1B1C1D1. Изобразите на рисунке векторы, равные: 1) AC1 + DA1+ B1B + BA; 2) BA –B1C1. 9. В тетраэдре DABC точка Е – середина ребра AD, а М – точка пересечения медиан грани BDC. Разложите вектор EM по векторам AC,AB и AD. 1 0. Даны три неколлинеарных вектора a,b и c. Найдите значения р и g, при которых векторы m = pa+gb +8c и n = a + pb + gc коллинеарны. 11. В тетраэдре DABC точки M и N – середины АВ и CD соответственно. Докажите, что середины отрезков МС,MD,NA и NB являются вершинами параллелограмма.

Контрольные работы по геометрии 11 класс

Геометрия 11 класс

Контрольная работа № 1 по теме:
«Координаты точки и координаты вектора»

Вариант 1

1. Найдите координаты вектора , если А (5;-1; 3), В (2;-2; 4).

2. Даны векторы (3; 1;-2) и (1; 4;-3). Найдите .

3. Изобразите систему координат Охуz и постройте точку А (1;-2;-4). Найдите расстояния от этой точки до координатных плоскостей.

Вариант 2

1. Найдите координаты вектора , если С (6; 3;-2), D (2; 4;-5).

2. Даны вектора (5;-1; 2) и (3; 2;-4). Найдите .

3. Изобразите систему координат Охуz и постройте точку В (-2;-3; 4). Найдите расстояния от этой точки до координатных плоскостей.

Геометрия 11 класс

Контрольная работа № 1 по теме:
«Координаты точки и координаты вектора»

Вариант 1

1. Найдите координаты вектора , если А (5;-1; 3), В (2;-2; 4).

2. Даны векторы (3; 1;-2) и (1; 4;-3). Найдите .

3. Изобразите систему координат

   Охуz и постройте точку А (1;-2;-4). Найдите расстояния от этой точки до координатных плоскостей.

Вариант 2

1. Найдите координаты вектора , если С (6; 3;-2), D (2; 4;-5).

2. Даны вектора (5;-1; 2) и (3; 2;-4). Найдите .

3. Изобразите систему координат Охуz и постройте точку В (-2;-3; 4). Найдите расстояния от этой точки до координатных плоскостей.

Геометрия 11 класс

Контрольная работа № 2 по теме:

«Метод координат в пространстве»

Вариант 1

4. Вычислите скалярное произведение векторов , если

5. Дан куб АВСДА₁В₁С₁Д₁. Найдите угол между прямыми АД₁ и ВМ, где М – середина ребра ДД₁.

6. При движении прямая b отображается на прямую b₁, а плоскость  — на плоскость 1 и b׀׀₁. Докажите, что b₁׀׀_1.

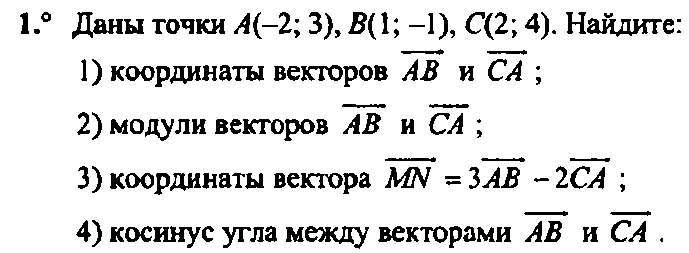
Вариант 2

1. Вычислите скалярное произведение векторов , если

2. Дан куб АВСДА₁В₁С₁Д₁. Найдите угол между прямыми АС и ДС₁.

3. При движении прямая а отображается на прямую а₁, а плоскость  — на плоскость ₁ и а. Докажите, что а₁_1.

Геометрия 11 класс

Контрольная работа № 2 по теме:
«Метод координат в пространстве»

Вариант 1

1. Вычислите скалярное произведение векторов , если

2. Дан куб АВСДА₁В₁

   С₁Д₁. Найдите угол между прямыми АД₁ и ВМ, где М – середина ребра ДД₁.

3. При движении прямая b отображается на прямую b₁, а плоскость  — на плоскость 1 и b׀׀₁. Докажите, что b₁׀׀_1.

Вариант 2

1. Вычислите скалярное произведение векторов , если

2. Дан куб АВСДА₁В₁С₁Д₁. Найдите угол между прямыми АС и ДС₁.

3. При движении прямая

   а отображается на прямую а₁, а плоскость  — на плоскость ₁ и а. Докажите, что а₁_1.

Контрольная работа №2 по теме: «Метод координат».

Вариант 1

1. С(-3,2,-4). Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.

2. Известны координаты вершин треугольника С(-2;3;1), Д(2;-4;3), Е(-2;-3;1). ДК – медиана треугольника. Найдите ДК.

3. При параллельном переносе точка А (-3;4;6) переходит в точку А₁ (2;-4;5).

   Найдите сумму координат точки В₁, в которую при этом параллельном переносе переходит точка В(-2;-4;1).

4. Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).

Вариант 2

1. А(3,-2,-4). Найдите сумму расстояний от точки А до оси Оу и точки А до плоскости Оxz.

2. Известны координаты вершин треугольника А(2;-1;-3), В(-3;5;2), С(-2;3;-5). ВМ – медиана треугольника. Найдите ВМ.

3. При параллельном переносе точка М (-3;2;-5) переходит в точку М

   1 (1;-3;-2). Найдите сумму координат точки К₁, в которую при этом параллельном переносе переходит точка К(1;-2;-5).

4. Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).

Контрольная работа №2 по теме: «Метод координат».

Вариант 1

1. С(-3,2,-4). Найдите сумму расстояний от точки С до оси Ох и точки С до плоскости Оуz.

2. Известны координаты вершин треугольника С(-2;3;1), Д(2;-4;3), Е(-2;-3;1). ДК – медиана треугольника. Найдите ДК.

3. При параллельном переносе точка А (-3;4;6) переходит в точку А₁ (2;-4;5). Найдите сумму координат точки В₁, в которую при этом параллельном переносе переходит точка В(-2;-4;1).

4. Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).

Вариант 2

1. А(3,-2,-4). Найдите сумму расстояний от точки А до оси Оу и точки А до плоскости Оxz.

2. Известны координаты вершин треугольника А(2;-1;-3), В(-3;5;2), С(-2;3;-5). ВМ – медиана треугольника. Найдите ВМ.

3. При параллельном переносе точка М (-3;2;-5) переходит в точку М₁ (1;-3;-2). Найдите сумму координат точки К₁, в которую при этом параллельном переносе переходит точка К(1;-2;-5).

4. Найдите площадь треугольника АВС, если А (3;0;0), В(0;-4;0), С(0;0;1).

Геометрия 11 класс

Контрольная работа № 3 по теме:
«Цилиндр, конус и шар»

Вариант 1

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см

   2. Найдите площадь поверхности цилиндра.

2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120. Найдите:
   а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30;
   б)площадь боковой поверхности конуса.

3. Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите длину линии пересечения сферы с этой плоскостью.

Вариант 2

1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30. Найдите:
   а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60;
   б) площадь боковой поверхности конуса.

3. Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите площадь сечения шара этой плоскостью.

Геометрия 11 класс

Контрольная работа № 3 по теме:
«Цилиндр, конус и шар»

Вариант 1

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16 см². Найдите площадь поверхности цилиндра.

2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120. Найдите:
   а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30;
   б)площадь боковой поверхности конуса.

3. Диаметр шара равен 2т. Через конец диаметра проведена плоскость под углом 45 к нему. Найдите длину линии пересечения сферы с этой плоскостью.

Вариант 2

1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.

2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30. Найдите:
   а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60;
   б) площадь боковой поверхности конуса.

3. Диаметр шара равен 4т. Через конец диаметра проведена плоскость под углом 30 к нему. Найдите площадь сечения шара этой плоскостью.

Геометрия 11 класс

Контрольная работа № 4 по теме:
«Объемы тел»

Вариант 1

1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60. Найдите объем пирамиды.

2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45. Найдите объем цилиндра.

Вариант 2

1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60. Найдите объем пирамиды.

2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45. Найдите объем конуса.

Геометрия 11 класс

Контрольная работа № 4 по теме:
«Объемы тел»

Вариант 1

1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен 60. Найдите объем пирамиды.

2. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45. Найдите объем цилиндра.

Вариант 2

1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол в 60. Найдите объем пирамиды.

2. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 30. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 45. Найдите объем конуса.

Геометрия 11 класс

Контрольная работа № 5 по теме:
«Объем шара и площадь сферы»

Вариант 1

3. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60. Найдите отношение объемов конуса и шара.

4. Объем цилиндра равен 96 см³, площадь его осевого сечения 48 см². Найдите площадь сферы, описанной около цилиндра.

Вариант 2

3. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.

4. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.

Геометрия 11 класс

Контрольная работа № 5 по теме:
«Объем шара и площадь сферы»

Вариант 1

1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60. Найдите отношение объемов конуса и шара.

2. Объем цилиндра равен 96 см³, площадь его осевого сечения 48 см². Найдите площадь сферы, описанной около цилиндра.

Вариант 2

1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.

2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.

Геометрия 11 класс

Итоговая контрольная работа

Вариант 1

1. В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро -5. Найдите:

1. площадь боковой поверхности пирамиды;

2. объем пирамиды;

3. угол наклона боковой грани к плоскости основания;

4. скалярное произведение векторов ;

5. площадь описанной около пирамиды сферы;

6. угол между ВD и плоскостью DMC.

Вариант 2

1. В правильной треугольной пирамиде МАВС сторона основания равна , а боковое ребро -5. Найдите:

1. площадь боковой поверхности пирамиды;

2. объем пирамиды;

3. угол наклона боковой грани к плоскости основания;

4. скалярное произведение векторов , где Е – середина ВС;

5. объем вписанного в пирамиду шара;

6. угол между стороной основания и плоскостью боковой грани.

Геометрия 11 класс

Итоговая контрольная работа

Вариант 1

1. В правильной четырехугольной пирамиде МАВСD сторона основания равна 6, а боковое ребро -5. Найдите:

1. площадь боковой поверхности пирамиды;

2. объем пирамиды;

3. угол наклона боковой грани к плоскости основания;

4. скалярное произведение векторов ;

5. площадь описанной около пирамиды сферы;

6. угол между ВD и плоскостью DMC.

Вариант 2

1. В правильной треугольной пирамиде МАВС сторона основания равна , а боковое ребро -5. Найдите:

1. площадь боковой поверхности пирамиды;

2. объем пирамиды;

3. угол наклона боковой грани к плоскости основания;

4. скалярное произведение векторов , где Е – середина ВС;

5. объем вписанного в пирамиду шара;

6. угол между стороной основания и плоскостью боковой грани.

IGCSE 11 и 12 классы по математике Заметки, советы и руководство по изучению математики

В этой статье представлены заметки по математике для 11 и 12 классов IGCSE. Вы получите доступ к заметкам об изучении математики, советам по учебе и инструкциям по редактированию, которые также доступны для загрузки в формате PDF.

Заметки по математике для 11 и 12 классов IGCSE

Заметки по математике 11 и 12 классов по IGCSE — Логическая алгебра

Заметки по математике для 11 и 12 классов IGCSE — Ежедневные коды

IGCSE 11 и 12 классы Примечания к изучению математики — Анализ критического пути

Примечания к изучению математики 11 и 12 классов IGCSE — Уравнение различия 1

Примечания к исследованию математики 11 и 12 классов IGCSE — Уравнение различия 2

Примечания к изучению математики 11 и 12 классов IGCSE — Перечисление

Примечания к изучению математики 11 и 12 классов IGCSE — Графики

Примечания к изучению математики 11 и 12 классов IGCSE — Неравенства

Примечания к исследованию математики 11 и 12 классов IGCSE — Линейное программирование

Изучение математики 11 и 12 классов IGCSE Примечания — Логика

Примечания к изучению математики IGCSE 11 и 12 классов — Сетевые потоки

Глава 11: Векторы и геометрия пространства

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

8604

\ (\ newcommand {\ vecs} [1] {\ overset {\ scriptstyle \ rightharpoonup} {\ mathbf {# 1}}} \) \ (\ newcommand {\ vecd} [1] {\ overset {- \! — \! \ rightharpoonup} {\ vphantom {a} \ smash {# 1}}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \ ) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ kernel} {\ mathrm {null} \,} \) \ (\ newcommand {\ range} {\ mathrm {диапазон } \,} \) \ (\ newcommand {\ RealPart} {\ mathrm {Re}} \) \ (\ newcommand {\ ImaginaryPart} {\ mathrm {Im}} \) \ (\ newcommand {\ Argument} {\ mathrm {Arg}} \) \ (\ newcommand {\ norm} [1] {\ | # 1 \ |} \) \ (\ newcommand {\ inner} [2] {\ langle # 1, # 2 \ rangle} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \) \ (\ newcommand {\ Span} {\ mathrm {span} } \) \ (\ newcommand {\ kernel} {\ mathrm {null} \,} \) \ (\ newcommand {\ range} {\ mathrm {range} \,} \) \ (\ newcommand {\ RealPart} { \ mathrm {Re}} \) \ (\ newcommand {\ ImaginaryPart} {\ mathrm {Im}} \) \ (\ newcommand {\ Argument} {\ mathrm {Arg}} \) \ (\ newcommand {\ norm} [1] {\ | # 1 \ |} \) \ (\ newco mmand {\ inner} [2] {\ langle # 1, # 2 \ rangle} \) \ (\ newcommand {\ Span} {\ mathrm {span}} \)

1. Участники

• 11.1: Векторы в плоскости

  Некоторые величины, такие как или сила, определяются как размером (также называемым величиной), так и направлением. Величина, имеющая величину и направление, называется вектором.

• 11.2: Векторы в пространстве

  Векторы — полезные инструменты для решения двумерных задач. Однако жизнь существует в трех измерениях. Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства.

• 11.3: Точечное произведение

  Скалярное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, встречаются ли два вектора под прямым углом.

• 11.4: Перекрестное произведение

  В этом разделе мы разрабатываем операцию, называемую перекрестным произведением, которая позволяет нам найти вектор, ортогональный двум заданным векторам.Расчет крутящего момента — важное применение перекрестных произведений, и мы рассмотрим крутящий момент более подробно позже в этом разделе.

• 11.5: Уравнения линий и плоскостей в пространстве

  Чтобы написать уравнение для линии, мы должны знать две точки на линии, или мы должны знать направление линии и хотя бы одну точку через который проходит линия. В двух измерениях мы используем понятие уклона для описания ориентации или направления линии. В трех измерениях мы описываем направление линии, используя вектор, параллельный линии.В этом разделе мы исследуем, как использовать уравнения для описания линий и плоскостей в пространстве.

• 11.6: Квадрические поверхности

  Мы изучали векторы и векторные операции в трехмерном пространстве, и мы разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями, для изучения множества других поверхностей, которые можно изобразить в трехмерной системе координат.

• 11.7: Цилиндрические и сферические координаты

  Декартова система координат обеспечивает простой способ описания местоположения точек в пространстве. Однако некоторые поверхности сложно смоделировать с помощью уравнений, основанных на декартовой системе. Как следует из названия, цилиндрические координаты полезны при решении задач, связанных с цилиндрами. Точно так же сферические координаты полезны для решения задач, связанных со сферами.

• Глава 11 Упражнения на повторение

Участники

• Гилберт Стрэнг (Массачусетский технологический институт) и Эдвин «Джед» Херман (Харви Мадд) со многими авторами. Этот контент OpenStax находится под лицензией CC-BY-SA-NC 4.0. Загрузите бесплатно с http://cnx.org.

1. К началу
2. • Содержание
   • 11.1: Векторы на плоскости

1. Нет рекомендуемых статей.

1. Вид товара

   Глава

   .

   Встроенный CalcPlot3D?

   да

   укрытие

   решений

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   На этой странице нет тегов.

Геометрия первого класса

Добро пожаловать на страницу с рабочими листами по математике для первого класса по геометрии саламандр.

Здесь вы найдете ряд бесплатных печатных листов геометрии, которые помогут вашему ребенку выучить свои двухмерные и трехмерные фигуры.

На этой веб-странице вы найдете наш ассортимент рабочих листов по геометрии для 1-го класса для детей.

Существует ряд листов с геометрией для печати, включая идентификационные 2d и 3d формы в разной ориентации и рисование 2d фигур.

Использование этих листов поможет вашему ребенку:

• определение и подсчет сторон и углов;
• идентификация открытых и закрытых форм;
• распознавать набор двухмерных фигур — квадраты, прямоугольники, круги и треугольники;
• распознавать различные трехмерные формы — сферы, конусы, кубы, кубоиды и пирамиды;
• нарисуйте набор двухмерных фигур.

Следующие ниже листы включают нумерацию и подсчет углов ряда двумерных фигур.

Следующие листы включают нумерацию и подсчет сторон диапазона двухмерных фигур.

На следующих листах подсчитываются стороны и углы двухмерных фигур.

Следующие ниже листы включают идентификацию открытых или закрытых форм.

Второй лист также включает в себя изменение открытой формы на закрытую.

Почему бы не взглянуть на наши рабочие листы произвольной формы для детского сада?

Эта веб-страница посвящена идентификации двухмерных фигур.

На листах исследуются квадраты, прямоугольники, круги и треугольники, а также совпадают одинаковые формы.

Существуют также рабочие листы для обведения фигур, которые помогут вашему ребенку научиться называть двумерные формы и попрактиковаться в их отслеживании, чтобы улучшить свои мелкие моторики.

Есть раздел рабочих листов форм для дошкольников, которые находятся на очень базовом уровне, и раздел рабочих листов детских садов с более широким диапазоном. форм в разной ориентации.

Приходите и посмотрите наши рабочие листы по геометрии для второго класса.

Здесь вы найдете ряд листов с 2-мя и 3-мя фигурами, которые помогут Помогите ребенку понять геометрию на втором уровне класса.

Эти листы более сложны, чем те, что представлены на этой странице.

На каждом листе есть ответы.

Взгляните на еще несколько наших рабочих листов, похожих на эти.

Здесь вы найдете подборку листов для печати 2d и 3d форм.

Каждый лист доступен в цветном или черно-белом цвете, с маркировкой или без нее.

Использование этих листов поможет вашему ребенку:

• распознает и назовет диапазон 2D и 3D форм;
• распознает правильные и неправильные формы.

Здесь вы найдете наш ассортимент бесплатных 2D-форм 1-го класса.Следующие печатные формы содержат изображения общих 2D-форм. используется в геометрии первого класса, которую должен знать ваш ребенок.

Использование этих листов поможет вашему ребенку:

• знать свойства различных 2D и 3D фигур;
• распознавать разные типы треугольников, прямоугольников и квадратов;

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле комментариев Facebook внизу каждой страницы.

Общая базовая учебная программа (9781608408399) :: Домашнее задание и ответы :: Slader

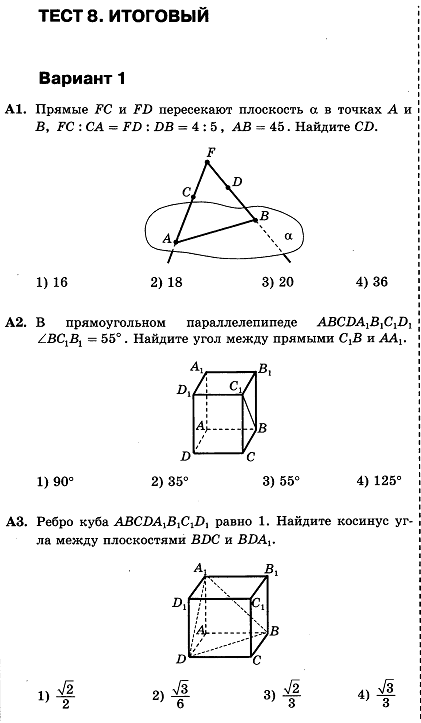
1.1	Точки, линии и плоскости	Упражнения	стр.8
1,2	Измерение и построение сегментов	Упражнения	с.16
1,3	Использование формул средней точки и расстояния	Упражнения	стр.24
		Викторина	стр.28
1,4	Периметр и площадь в координатной плоскости	Упражнения	с.34
1,5	Измерение и построение углов	Упражнения	стр.43
1,6	Описание пар углов	Упражнения	с.52
		Обзор главы	с. No related posts. Leave a Reply Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт