Контрольная работа по геометрии «Векторы в пространстве»
Вариант №1
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, противоположно направленные вектору и имеющие такую же длину. 1) и 2) и 3) и 4) и
2. Дан параллелепипед ABCD A1B1C1D1 . Упростите сумму . Укажите полученный вектор. 1) ; 2) 3) 4)
3. Вектор разложен по трем некомпланарным векторам Найдите разложение вектора по векторам и. 1) 2) 3) 4)
4. В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите ||. 1)22 2)16 3)8 4)24
5. Дан куб ABCD A1B1C1D1 с ребром, равным a. Точка Е и АЕ:Е = 1: 2, точка F C1 и CF : FC1 = 2 : 3. Разложите вектор по векторам и и найдите его длину.
Вариант №2
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, противоположно направленные вектору и имеющие такую же длину.
2. В тетраэдре АВСD: =8. Найдите величину . 1) 1; 2) 2; 3)8; 4)11
3. Упростите выражение: 3(2 3) + 5( ) 2()
4. В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите ||.
5. Ребро куба ABCD A1B1C1D1 равно 3. Найдите величины: +| и
Вариант №3
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, coнаправленные вектору и имеющие такую же длину. 1) и 2) и 3) и 4) и
3. Дан куб ABCD A1B1C1D1 с ребром, равным a. Вычислите. 1) 3 a; 2) 2 a; 3) a; 4) a
4. Вектор разложен по трем некомпланарным векторам Найдите разложение вектора по векторам и. 1) 2) 3) 4)
5. Векторы и некомпланарны, точка К лежит в плоскости треугольника АВС. Найдите значение числа х, если .
Найдите значение числа х, если .
Вариант №4
2. Дан параллелепипед ABCD A1B1C1D1 .
1. В параллелепипеде ABCD A1B1C1D1 укажите векторы, coнаправленные вектору и имеющие такую же длину. 1) и 2) и 3) и 4) и
3. Дан куб ABCD A1B1C1D1 с ребром, равным b. Вычислите. 1) 3b; 2) 2 b; 3) b; 4) b
4. В пирамиде SАВС все ребра равны, апофема равна 18 Точка Е и АЕ:ЕS = 2:1, точка FAB и BF : FA = 1:2. Найдите |EF|.
5. Дан куб ABCD A1B1C1D1 с ребром, равным
Геометрия 10-й класс — Контрольная работа
Геометрия
10-й класс.
УЧЕБНИК:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г.
“Геометрия 10 — 11”
(М.: Просвещение, 1992 и последующие издания)
Примерное поурочное планирование
(2 часа в неделю, всего 68 часов)
Тема | Кол-во часов | Примечание (изменения, которые планирует учитель) | ||
Введение (2ч.) | ||||
Параллельность прямых и плоскостей (19ч.) | ||||
Параллельность прямых, прямой и плоскости. Контролирующая самостоятельная работа. | 3 | |||
 | 1 | |||
Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Контролирующая самостоятельная работа. | 3 | |||
Решение задач. | 1 | |||
Контрольная работа №1. | 1 | |||
Параллельность плоскостей. Контролирующая самостоятельная работа. | 3 | |||
Зачет №2. | 1 | |||
Тетраэдр
и параллелепипед. | 5 | |||
Контрольная работа №2. | 1 | |||
Перпендикулярность прямых и плоскостей (16ч.) | ||||
Перпендикулярность прямой и плоскости. | 4 | |||
Перпендикуляр и наклонные. Угол между прямой и плоскостью. Контролирующая самостоятельная работа. | 4 | |||
Зачет №3. | 1 | |||
Двугранный
угол. | 4 | |||
Решение задач. | ||||
Контрольная работа №3. | 1 | |||
Многогранники (16ч.) | ||||
Понятие многогранника. Призма. Контролирующая самостоятельная работа. | 4 | |||
Пирамида. Контролирующая самостоятельная работа. | 5 | |||
Правильные
многогранники. | 2 | |||
Зачет №4. | 1 | |||
Решение задач. | 3 | |||
Контрольная работа №4. | 1 | |||
Векторы в пространстве (11ч.) | ||||
Понятие вектора в пространстве. | 2 | |||
Сложение
и вычитание векторов. Умножение вектора
на число. | 2 | |||
Компланарные векторы. Контролирующая самостоятельная работа. | 3 | |||
Зачет №5. | 1 | |||
Решение задач. | 2 | |||
Контрольная работа №5. | 1 | |||
Итоговое повторение (4ч.) | ||||
КОНТРОЛЬНЫЕ, САМОСТЯТЕЛЬНЫЕ РАБОТЫ И ЗАЧЕТЫ
ГЕОМЕТРИЯ10-й КЛАСС
Глава
I.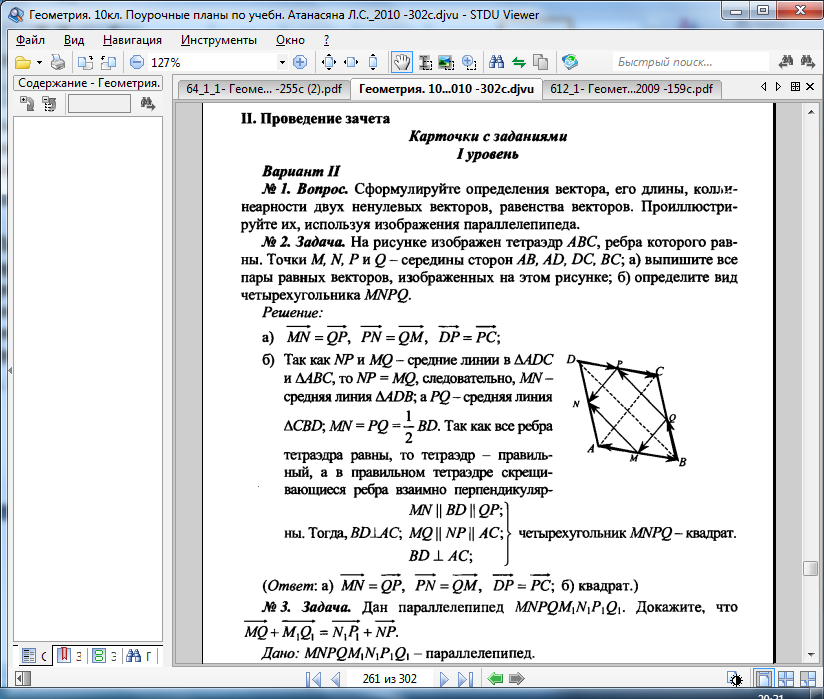 Параллельность прямых и
плоскостей
Параллельность прямых и
плоскостей
Контролирующая самостоятельная работа к § 1
I вариант Задания № 23, 28 из учебника.
II вариант Задания № 24, 27 из учебника.
Зачет № 1
Образцы карточек к зачету
Карточка 1
1. Сформулируйте аксиомы А1 — А3, разъясните их смысл.
2. Сформулируйте и докажите признак параллельности прямой и плоскости.
3.
Вершины B и С треугольника AВС лежат в плоскости
,
а вершина А не лежит в этой плоскости. Прямая а параллельна прямой АС и
пересекает сторону АВ в точке М так,
что AM : MB =3 : 4. а) Докажите, что прямая а пересекает плоскость
.
б) Найдите сторону AC,
если длина отрезка прямой а от точки М до
плоскости равна 7 см.
Карточка 2
1. Опишите все случаи взаимного расположения прямой и плоскости.
2. Сформулируйте и докажите теорему о плоскости, проходящей через две пересекающиеся прямые.
3. На сторонах АВ и АС треугольника AВС взяты соответственно точки Р и T; РТ = 4 см, АР : РВ =1 : 3. Плоскость проходит через точки Р и T и параллельна отрезку ВС. а) Докажите, что отрезки РТ и ВС параллельны, б) Найдите отрезок ВС.
Контролирующая самостоятельная работа к § 2I вариант
Задание № 45 из учебника.
II вариант
Задание № 46 из учебника.
Контрольная работа № 1
I вариант
1.
Середины сторон CD и BD треугольника BCD лежат в плоскости
,
а сторона ВС не лежит в этой плоскости: Докажите, что
прямая ВС и
плоскость параллельны.
2. Точки А, В, С и D не лежат в одной плоскости. Докажите, что любые три из них не лежат на одной прямой.
3. Прямая КМ параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости AВС. Выясните взаимное расположение прямых КМ и AВ и найдите угол между ними, если AВС = 110°.
II вариант
1. Середины сторон CD и АВ параллелограмма ABCD лежат в плоскости , а сторона ВС не лежит в этой плоскости. Докажите, что прямая AD и плоскость параллельны.
2. Точки А, В, С и D не лежат в одной плоскости. Докажите, что любые три из них являются вершинами треугольника.
3.
Прямая КМ параллельна стороне ВС треугольника AВС и не лежит в плоскости АВС. Выясните взаимное
расположение прямых КМ и АВ и найдите
угол между ними, если АВС
= 105°.
Контролирующая самостоятельная работа к § 3
I вариант
1. Отрезки АВ, AC, AD не лежат в одной плоскости. Точки К, М, N — соответственно их середины, а) Докажите, что плоскости BCD и KMN параллельны, б) Найдите площадь треугольника BCD, если площадь треугольника KMN равна 36 м2.
2. Задача 63 (а) из учебника.
II вариант
1.
Три прямые, проходящие через точку М и не лежащие в одной
плоскости, пересекают одну из параллельных
плоскостей в точках А, В и С, а вторую — в точках A1, B1, C1. а) Докажите, что
треугольники АВС и A1B1C1 подобны, б) Найдите АВ : А1В1, если МС = CC1.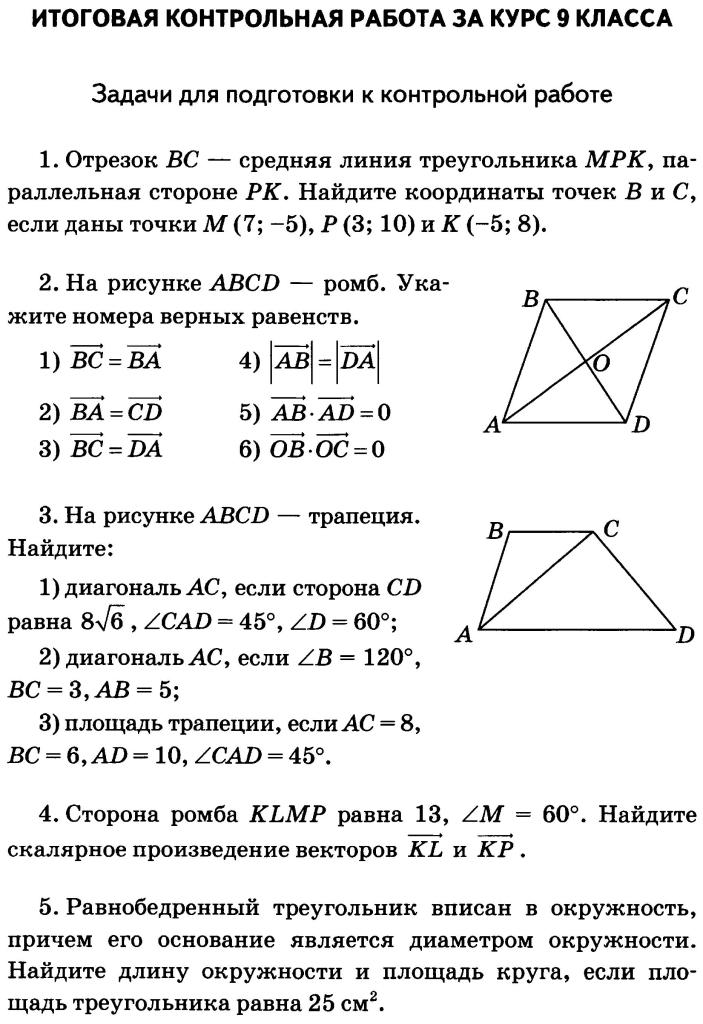
2. Задание № 63 (б) из учебника.
Зачет № 2
Образцы карточек к зачету
Карточка 1
1. Сформулируйте определение скрещивающихся прямых.
2. Сформулируйте и докажите признак параллельности двух плоскостей.
3. Через вершины треугольника АВС проведены параллельные прямые, пересекающие плоскость , параллельную плоскости АВС, соответственно в точках А1, B1 и С1 Найдите стороны треугольника A1B1C1, если АВ = 5 см, АС = 4 см, ВАС = 60°.
Карточка 2
1. Перечислите все случаи взаимного расположения двух прямых.
2.
Сформулируйте и докажите теорему об
отрезках параллельных прямых, заключенных
между двумя параллельными плоскостями.
3. Даны треугольник АОВ и параллелограмм ABCD, не лежащие в одной плоскости. Найдите угол между прямыми АО и CD, если ОАВ = 130°.
Контрольная работа № 2
I вариант
1. В тетраэдре ABCD точки М, К и Р— середины ребер АВ, BD и ВС. Докажите, что плоскость МКР параллельна плоскости ACD, и найдите площадь треугольника МКР, если площадь треугольника ACD равна 48 см2.
2. Дан параллелепипед ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра АВ параллельно плоскости ACC1.
3.
Верно ли утверждение, что прямая, лежащая
в одной из двух параллельных плоскостей,
параллельна второй плоскости? Ответ
обоснуйте.
II вариант
1. В тетраэдре ABCD точки М, К и Р— середины ребер AD, BD и DC. Докажите, что плоскость МКР параллельна плоскости ABС, и найдите площадь треугольника AВС, если площадь треугольника МКР равна 48 см2.
2. Дан параллелепипед ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра AВ параллельно плоскости DBB1.
3. Прямые а и b расположены соответственно в параллельных плоскостях и . Верно ли, что эти прямые не имеют общих точек? Ответ обоснуйте.
Глава II. Перпендикулярность прямых и плоскостей
Контролирующая самостоятельная работа к § 2I вариант
Задания
№ 141, 149, 158 из учебника.
II вариант
Задания № 198, 154, 157 из учебника.
Зачет № 3
Образцы карточек к зачету
Карточка 1
1. Сформулируйте определение угла между прямой и плоскостью.
2. Сформулируйте и докажите теорему о трех перпендикулярах.
3. Из точки A, удаленной на расстояние 5 см от плоскости, проведены к этой плоскости наклонные AВ и AС под углом 30° к плоскости. Найдите угол между наклонными, если ВС = 10 см.
Карточка 2
1. Объясните, что такое перпендикуляр и наклонная, проведенные из точки к плоскости, основание перпендикуляра, основание и проекция наклонной.
2. Сформулируйте и докажите признак перпендикулярности прямой и плоскости.
3.
Через вершину А правильного треугольника AВС проведена прямая AM, перпендикулярная к его плоскости. Найдите расстояние от точки М до стороны ВС,
если АВ = 4 см, AM = 2 см.
Найдите расстояние от точки М до стороны ВС,
если АВ = 4 см, AM = 2 см.
I вариант
Задания № 171, 189 (а), 193 (б), 196 (а) из учебника.
II вариант
Задания № 172, 189 (б), 193 (а), 196 (б) из учебника.
Контрольная работа № 3
I вариант
1. Через вершину К треугольника МКР проведена прямая KN, перпендикулярная к плоскости треугольника. Известно, что KN = 15см, МК = КР = 10 см, МР = 12 см. Найдите расстояние от точки N до прямой МР.
2.Дан
прямоугольный параллелепипед ABCDA1B1C1D1.
Найдите двугранный угол B1ADB, если AС = 6 м, AВ1 = 4
м, ABCD — квадрат.
II вариант
1. Через вершину прямого угла С в равнобедренном треугольнике CDE проведена прямая СA, перпендикулярная к плоскости треугольника. Известно, что СA = 35 дм, CD = 12 дм. Найдите расстояние от точки A до прямой DE.
2. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Найдите двугранный угол ADCA1,
если AС=13 см, DC =5 см, AA1 = 12 см.
Глава III. Многогранники
Контролирующая самостоятельная работа к § 1I вариант
1.
Основание прямой призмы — ромб со
стороной 12 см и углом 60°. Меньшая
диагональ параллелепипеда равна 13 см.
Найдите площадь: а) боковой поверхности
призмы; б) полной поверхности призмы;
в) диагонального сечения, содержащего
меньшую диагональ призмы.
II вариант
Основание прямой призмы — ромб с меньшей диагональю 5 см и углом 120°. Меньшая диагональ параллелепипеда образует угол 45° с плоскостью основания. Найдите площадь: а) боковой поверхности призмы; б) полной поверхности призмы; в) диагонального сечения, содержащего меньшую диагональ призмы.
Контролирующая самостоятельная работа к § 2I вариант
Задания № 250, 257 из учебника.
II вариант
Задания № 251, 258 из учебника.
Зачет № 4
Образцы карточек к зачету
Карточка 1
1. Какая призма называется: а) прямой, б) наклонной, в) правильной?
2. Сформулируйте и докажите теорему о площади боковой поверхности правильной пирамиды.
3.
Докажите, что прямая, проходящая через
середины двух противоположных ребер
правильного тетраэдра, перпендикулярна
к ним. Найдите длину отрезка, соединяющего
середины противоположных ребер
правильного тетраэдра, если ребро
тетраэдра равно 1 м.
Найдите длину отрезка, соединяющего
середины противоположных ребер
правильного тетраэдра, если ребро
тетраэдра равно 1 м.
Карточка 2
1. Какие точки называются симметричными относительно плоскости? Приведите пример многогранника, имеющего плоскость симметрии.
2. Сформулируйте и докажите теорему о площади боковой поверхности прямой призмы.
3. В правильной треугольной пирамиде высота равна стороне основания. Найдите угол между боковым ребром и плоскостью основания.
Контрольная работа № 4
I вариант
1.
Основанием прямой призмы ABCDA1B1C1D1 является параллелограмм ABCD со сторонами
6 дм и 12 дм и углом, равным 60°. Диагональ B1D призмы образует с плоскостью
основания угол в 30°. Найдите площадь
боковой поверхности призмы.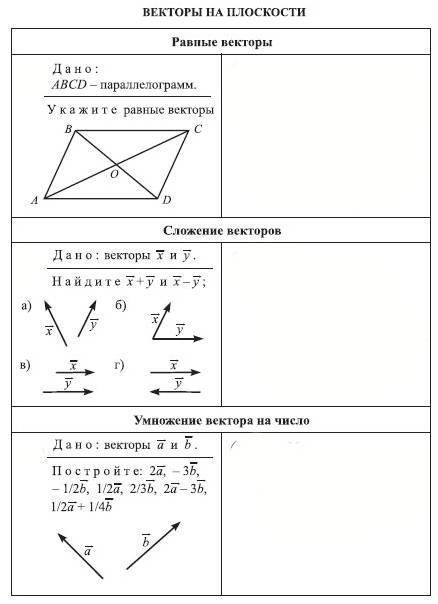
2. Сторона основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45°. Найдите площадь полной поверхности пирамиды.
II вариант
1. Основанием прямой призмы ABCD A1B1C1D1 является параллелограмм ABCD со сторонами 4 см и 4 см и углом, равным 30°. Диагональ AC1 призмы образует с плоскостью основания угол в 60°. Найдите площадь боковой поверхности призмы.
2. Высота основания правильной треугольной пирамиды равна 3 см, а угол между боковой гранью и основанием пирамиды равен 45°. Найдите площадь полной поверхности пирамиды.
Глава IV. Векторы в пространстве
Контролирующая самостоятельная работа к § 2I вариант
Задания
№ 335 (в), 336 (б), 337 (в), 339 (б), 351 (а), 382 (а, в).
II вариант
Задания № 335 (г), 336 (в), 337 (б), 339 (а), 351 (б), 382 (б, г).
Контролирующая самостоятельная работа к § 3I вариант
Задания № 358 (б), 382 (а, г), 388 (б), 393 (а).
II вариант
Задания № 358 (в), 382 (б, в), 388 (а), 393 (б).
Зачет № 5
Образцы карточек к зачету
Карточка 1
1. Объясните правила треугольника и параллелограмма сложения двух векторов. Докажите, что сумма двух векторов не зависит от выбора точки, от которой откладывается первый вектор.
2. Дан параллелепипед ABCDA1B1C1D1, . Найдите вектор с началом и концом в вершинах параллелепипеда, равный сумме векторов и .
3.
Даны параллелограмм ABCD и произвольная точка O пространства. Докажите, что
Докажите, что
.
Карточка 2
1. Что значит разложить вектор по трем некомпланарным векторам? Сформулируйте и докажите теорему о разложении вектора по трем некомпланарным векторам.
2. Упростите выражение: .
3. Даны четыре произвольные точки пространства А, В, С и D. Докажите, что .
Контрольная работа № 5
I вариант
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах
параллелепипеда, равный: а) , б) .
2. Дан тетраэдр DABC. Точка М — середина ребра ВС, точка N—середина отрезка DM.
Выразите вектор через векторы и .
3.
В параллелепипеде ABCDA1B1C1D1 медианы треугольника ABD пересекаются в точке Р.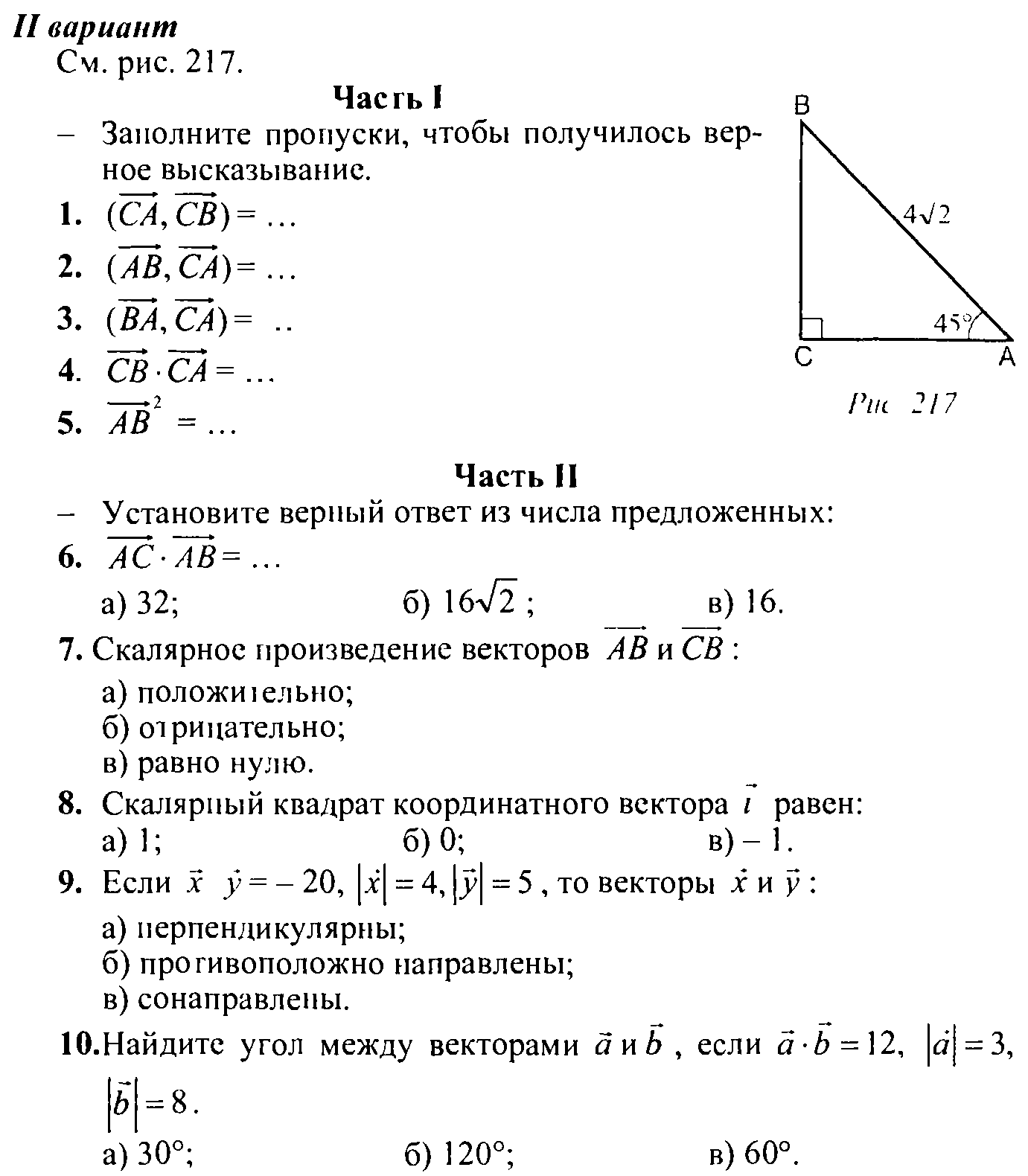
Разложите вектор по векторам .
II вариант
1. Дан параллелепипед ABCDA1B1C1D1. Укажите вектор с началом и концом в вершинах параллелепипеда, равный: а) , б) .
2. Дан тетраэдр DABC. Медианы треугольника BDC пересекаются в точке Р, точка К—
середина отрезка АР. Выразите вектор через векторы .
3. В параллелепипеде ABCDA1B1C1D1 точка O лежит на отрезке B1D1, причем В1О : OD1 = 2 : 1. Разложите вектор по векторам .
Контрольная работа по теме «Векторы»
Контрольная работа по теме «Векторы» 10 класс
1. Распределение задач по уровням сложности соответствует современной классификации уровней владения знаниями:
Распределение задач по уровням сложности соответствует современной классификации уровней владения знаниями:
задания части А – вопросы, тестовые задания в которых преобладает
Узнавание. Для правильного решения учащийся должен сопоставить собственные знания с информацией, содержащейся в вопросе ,которые являются самыми легкими и выполняемыми, так как даже учащиеся, уделяющие недостаточное внимание домашней подготовке, находят в своей памяти образ информации, соответствующий вопросу.
Воспроизведение. Этот уровень требует от учащихся восстановления имеющейся в памяти информации. Задания такого типа требуют от тестируемого закончить определение, сопоставить формулу и ее словесное прочтение и т. д.
задания части В – задачи в 1 – 2 действия, в которых предполагается использование выученных формул, законов, определений из данной темы. Такие задачи в большом количестве рассматриваются на уроках применения знаний, повторения и обобщения.
задания части С – задачи, требующие применения знаний по данной теме в измененной ситуации. Для решения задач данного типа кроме знаний из текущей темы, учащийся должен применить знания их других разделов физики, математические знания, сведения из других смежных наук.
2. Соответствие №задания, уровня и необходимых знаний и умений
№ задания | Уровень | необходимые знания и умения |
А1 А2 А3 А4 А5 | узнавание материала вопросы с выбором ответа | Коллинеарность и компланарность векторов Равные векторы формулы нахождение длины вектора сложения векторов умножение вектора на число скалярное произведение векторов |
А6 | применение знаний | Вычисление длины вектора |
А7 | воспроизведение знаний | Вычисление координат вектора полученного при сложении векторов и умножении вектора на число |
В1 | применение знаний | Вычисление неизвестной координаты вектора исходя из коллинеарности векторов при известной длине вектора |
В2 | применение знаний | Вычисление угла между векторами |
С | применение знаний | Разложение вектора Нахождение высот и медиан треугольника Задачи на доказательство |
Подбор заданий.
- http://uztest.ru/simulator
Программа для составления контрольных работ http://www.google.com/search ?client=opera&rls=ru&hl=ru&ie=UTF-8&oe=UTF-8&
Вариант 1 | |
1. | |
2. | |
3. | |
4. | |
Вариант 2 | |
1. | |
2. | |
3. | |
4. | |
Вариант 3 | |
1. | |
2. | |
3. | |
4. | |
Вариант 4 | |
1. | |
2. | |
3. | |
4. | |
Вариант 5 | |
1. | |
2. | |
3. | |
4. | |
Вариант 6 | |
1. | |
2. | |
3. | |
4. | |
Вариант 1 | |
1. | |
2. | |
3. | |
4. | |
Вариант 2 | |
1. | |
2. | |
3. | |
4. | |
Вариант 3 | |
1. | |
2. | |
3. | |
4. | |
Вариант 4 | |
1. | |
2. | |
3. | |
4. | |
Вариант 5 | |
1. | |
2. | |
3. | |
4. | |
Вариант 6 | |
1. | |
2. | |
3. | |
4. | |
Вариант 7 | |
1. | |
2. | |
3. | |
4. | |
Вариант 8 | |
1. | |
2. | |
3. | |
4. | |
Вариант 9 | |
1. | |
2. | |
3. | |
4. | |
Контрольная работа по математике (геометрия) 10 класс по теме «Векторы» | План-конспект урока по математике (10 класс) на тему:
Контрольная работа по геометрии 10 класс «Векторы»
Вариант №1
1. Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти: а) координаты векторов АВ и СД.
Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти: а) координаты векторов АВ и СД.
Б) 2 – в) косинус угла между векторами АВ и СД.
2. При каком значении п векторы и будут перпендикулярны, если А(1;0;1), В(-2;3;0), С(4;6;п), Д(п;6;-8).
3. Даны точки с координатами Р(4;-1;2), К(3;0;-1), М(1;-6;8). Найдите координаты точки С, чтобы вектора РК и МС были равны.
Контрольная работа по геометрии 10 класс «Векторы»
Вариант №2
1. Даны точки А(3;0;-2), В(4;2;-2), С(5;-6;3), Д(2;5;-4). Найти: а) координаты векторов АВ и СД.
Б) 5 – в) косинус угла между векторами АВ и СД.
2. При каком значении п векторы и будут перпендикулярны, если А(2;0;2), В(-3;4;0), С(5;7;п), Д(п;4;-3).
3. Даны точки с координатами Р(5;-2;3), К(4;1;-2), М(2;-5;7). Найдите координаты точки С, чтобы вектора РК и МС были равны.
Контрольная работа по геометрии 10 класс «Векторы»
Вариант №1
1. Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти: а) координаты векторов АВ и СД.
Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти: а) координаты векторов АВ и СД.
Б) 2 – в) косинус угла между векторами АВ и СД.
2. При каком значении п векторы и будут перпендикулярны, если А(1;0;1), В(-2;3;0), С(4;6;п), Д(п;6;-8).
3. Даны точки с координатами Р(4;-1;2), К(3;0;-1), М(1;-6;8). Найдите координаты точки С, чтобы вектора РК и МС были равны.
Контрольная работа по геометрии 10 класс «Векторы»
Вариант №2
1. Даны точки А(3;0;-2), В(4;2;-2), С(5;-6;3), Д(2;5;-4). Найти: а) координаты векторов АВ и СД.
Б) 5 – в) косинус угла между векторами АВ и СД.
2. При каком значении п векторы и будут перпендикулярны, если А(2;0;2), В(-3;4;0), С(5;7;п), Д(п;4;-3).
3. Даны точки с координатами Р(5;-2;3), К(4;1;-2), М(2;-5;7). Найдите координаты точки С, чтобы вектора РК и МС были равны.
Контрольная работа по геометрии 10 класс «Векторы»
Вариант №1
1. Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти: а) координаты векторов АВ и СД.
Даны точки А(2;0;-1), В(3;1;-2), С(4;-7;2), Д(1;4;-5). Найти: а) координаты векторов АВ и СД.
Б) 2 – в) косинус угла между векторами АВ и СД.
2. При каком значении п векторы и будут перпендикулярны, если А(1;0;1), В(-2;3;0), С(4;6;п), Д(п;6;-8).
3. Даны точки с координатами Р(4;-1;2), К(3;0;-1), М(1;-6;8). Найдите координаты точки С, чтобы вектора РК и МС были равны.
Контрольная работа по геометрии 10 класс «Векторы»
Вариант №2
1. Даны точки А(3;0;-2), В(4;2;-2), С(5;-6;3), Д(2;5;-4). Найти: а) координаты векторов АВ и СД.
Б) 5 – в) косинус угла между векторами АВ и СД.
2. При каком значении п векторы и будут перпендикулярны, если А(2;0;2), В(-3;4;0), С(5;7;п), Д(п;4;-3).
3. Даны точки с координатами Р(5;-2;3), К(4;1;-2), М(2;-5;7). Найдите координаты точки С, чтобы вектора РК и МС были равны.
Вариант 1
| Вариант 2
|
Вариант 1
| Вариант 2
|
Вариант 1
| Вариант 2
|
Поурочные разработки по геометрии 10 класс
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА
Введение. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ
АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ
Урок 1. Предмет стереометрии. Аксиомы стереометрии
Урок 2. Некоторые следствия из аксиом
Урок 3. Решение задач на применение аксиом стереометрии и их следствий
Урок 4. Решение задач на применение аксиом стереометрии и их следствий
Урок 5. Решение задач на применение аксиом стереометрии и их следствий. Самостоятельная работа
Глава I. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
§ 1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ
Урок 6. Параллельные прямые в пространстве
Урок 7. Параллельность прямой и плоскости
Урок 8. Решение задач по теме «Параллельность прямой и плоскости»
Урок 9. Решение задач по теме «Параллельность прямой и плоскости»
Урок 10. Решение задач по теме «Параллельность прямой и плоскости»
§ 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ
Урок 11. Скрещивающиеся прямые
Урок 12. Углы с сонаправленными сторонами. Угол между прямыми
Урок 13. Решение задач по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми»
Угол между двумя прямыми»
Урок 14. Решение задач по теме «Параллельность прямых и плоскостей»
Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»
§ 3. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Урок 16. Параллельные плоскости
Урок 17. Свойства параллельных плоскостей
§ 4. ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД
Урок 18. Тетраэдр
Урок 19. Параллелепипед
Урок 20. Задачи на построение сечений
Урок 21. Задачи на построение сечений
Урок 22. Закрепление свойств параллелепипеда
Урок 23. Контрольная работа № 1
Урок 24. Зачет № 1
Глава II. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
§ 1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Урок 25. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости
Урок 26. Признак перпендикулярности прямой и плоскости
Урок 27. Теорема о прямой, перпендикулярной к плоскости
Урок 28. Решение задач на перпендикулярность прямой и плоскости
Урок 29. Решение задач на перпендикулярность прямой и плоскости
Решение задач на перпендикулярность прямой и плоскости
Урок 30. Решение задач на перпендикулярность прямой и плоскости
§ 2. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Урок 31. Расстояние от точки до плоскости. Теорема о трех перпендикулярах
Урок 32. Угол между прямой и плоскостью
Урок 33. Повторение теории. Решение задач на применение теоремы о трех перпендикулярах (ТПП), на угол между прямой и плоскостью
Урок 34. Решение задач на применение ТТП, на угол между прямой и плоскостью
Урок 35. Повторение (решение задач на теорему о 3-х перпендикулярах)
Урок 36. Угол между прямой и плоскостью (повторение)
§ 3. ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Урок 37. Двугранный угол
Урок 38. Признак перпендикулярности двух плоскостей
Урок 39. Прямоугольный параллелепипед
Урок 40. Решение задач на свойства прямоугольного параллелепипеда
Урок 41. Перпендикулярность прямых и плоскостей (повторение)
Урок 42. Решение задач
Решение задач
Урок 43. Контрольная работа по теме «Перпендикулярность прямых и плоскости»
Урок 44. Зачет № 2
Глава III. МНОГОГРАННИКИ
§ 1. ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА
Урок 45. Понятие многогранника
Урок 46. Призма. Площадь поверхности призмы
Урок 47. Повторение теории, решение задач на вычисление площади поверхности призмы
Урок 48. Решение задач на вычисление площади поверхности призмы
§ 2. ПИРАМИДА
Урок 49. Пирамида
Урок 50. Правильная пирамида
Урок 51. Решение задач по теме «Пирамида»
Урок 52. Решение задач по теме «Пирамида». Самостоятельная работа
Урок 53. Усеченная пирамида. Площади поверхности усеченной пирамиды
§ 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Урок 54. Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников
Урок 55. Контрольная работе № 3.1 по теме «Многогранники»
Урок 56. Зачет № 3 по теме «Многогранники. Площадь поверхности призмы, пирамиды»
Глава IV. ВЕКТОРЫ В ПРОСТРАНСТВЕ
ВЕКТОРЫ В ПРОСТРАНСТВЕ
§ 1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ
Урок 57. Понятие векторов. Равенство векторов
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
Урок 58. Сложение и вычитание векторов. Сумма нескольких векторов
Урок 59. Умножение вектора на число
§ 3. КОМПЛАНАРНЫЕ ВЕКТОРЫ
Урок 60. Компланарные векторы. Правило параллелепипеда
Урок 61. Разложение вектора по трем некомпланарным векторам
Урок 62. Зачет по теме «Векторы в пространстве»
ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ
Урок 63. Итоговое повторение. Аксиомы стереометрии и их следствия
Урок 64. Параллельность прямых и плоскостей
Урок 65. Повторение (теорема о трех перпендикулярах, угол между прямой и плоскостью)
Урок 66. Контрольная работа № 5
Урок 67. Повторение. Векторы в пространстве, их применение к решению задач
Урок 68. Заключительный урок-беседа по курсу геометрии
ПРИЛОЖЕНИЯ
Приложение 1. Контрольные и самостоятельные работы
Контрольные и самостоятельные работы
Урок 5. Самостоятельная работа
Урок 9. Самостоятельная работа обучающего характера
Урок 10. Проверочная самостоятельная работа
Урок 14. Работа по карточкам
Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»
Урок 17. Самостоятельная работа
Урок 23. Контрольная работа № 1
Урок 30. Самостоятельная работа
Урок 53. Тест
Урок 55. Контрольная работа № 3.1 по теме «Многогранники»
Урок 63. Теоретический тест с последующей самопроверкой
Урок 66. Контрольная работа № 5
Урок 67. Мини-тест по теории
Приложение 2. Плакаты № 1, 2, 3, 4, рекомендуемые к урокам № 51, 52, 53
Контрольная работа № 1 по теме «Координаты и векторы в пространстве» (11 класс, Мерзляк А.Г. и др.)
Контрольная работа № 1 по теме «Координаты и векторы в пространстве»
Вариант 1
1. Точка A — середина отрезка MK. Найдите координаты точки A и длину отрезка MK, если M (5; −2; 1), K (3; 4; −3).
2. Точки A и B симметричны относительно точки C. Найдите координаты точки B, если A (−3; 5; −7), C (6; 2; −1).
3. Даны векторы (3; −2; −1) и (1; 2; 4). Найдите:
1) координаты вектора ;
2) косинус угла между векторами и .
4. Даны векторы (2; −6; 8) и (−1; k; −4). При каком значении k векторы и :
1) коллинеарны;
2) перпендикулярны?
5. Составьте уравнение плоскости, проходящей через точку A и перпендикулярной прямой AB, если A (1; 2; −3), B (4; 8; −6).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали C1D его грани отметили точку M так, что DM : MC1 = 5 : 3.
1) Выразите вектор через векторы , и .
2) Найдите модуль вектора .
Вариант 2
1. Точка M — середина отрезка AB. Найдите координаты точки M и длину отрезка AB, если A (6; −5; 2), B (−4; 3; 10).
2. Точки M и K симметричны относительно точки D. Найдите координаты точки K, если M (4; −6; 3), D (−2; 1; 5).
3. Даны векторы (2; −1; 3) и (−1; 2; 5). Найдите:
1) координаты вектора ;
2) косинус угла между векторами и .
4. Даны векторы (5; −4; 6) и (15; −12; p). При каком значении p векторы и :
1) коллинеарны;
2) перпендикулярны?
5. Составьте уравнение плоскости, проходящей через точку B и перпендикулярной прямой BC, если B (3; −2; 4), C (−2; 8; 19).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AD1 его грани отметили точку E так, что AE : ED1 = 2 : 7.
1) Выразите вектор через векторы , и .
2) Найдите модуль вектора .
Вариант 3
1. Точка K — середина отрезка CD. Найдите координаты точки K и длину отрезка CD, если C (−3; 4; −1), D (1; −2; 3).
2. Точки E и F симметричны относительно точки P. Найдите координаты точки F, если E (0; −8; 4), P (−4; 2; 2).
3. Даны векторы (2; 0; −3) и (1; −2; −1). Найдите:
1) координаты вектора ;
2) косинус угла между векторами и .
4. Даны векторы (−20; 10; −15) и (a; −2; 3). При каком значении a векторы и :
1) коллинеарны;
2) перпендикулярны?
5. Составьте уравнение плоскости, проходящей через точку C и перпендикулярной прямой CD, если C (4; 1; −1), D (7; −2; 5).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали A1B его грани отметили точку K так, что A1K : KB = 4 : 3.
1) Выразите вектор через векторы , и .
2) Найдите модуль вектора .
Вариант 4
1. Точка D — середина отрезка FK. Найдите координаты точки D и длину отрезка FK, если F (6; −3; 2), K (4; 1; 4).
2. Точки B и C симметричны относительно точки M. Найдите координаты точки B, если C (9; −5; 6), M (3; 0; −2).
3. Даны векторы (4; −1; 2) и (−2; 1; 0). Найдите:
1) координаты вектора ;
2) косинус угла между векторами и .
4. Даны векторы (1; −2; 3) и (7; m; 21). При каком значении m векторы и :
1) коллинеарны;
2) перпендикулярны?
5. Составьте уравнение плоскости, проходящей через точку D и перпендикулярной прямой DM, если D (−3; 20; −4), M (9; 24; 16).
6. Дан куб ABCDA1B1C1D1, ребро которого равно 1 см. На диагонали AC его грани отметили точку F так, что AF : FC = 3 : 7.
1) Выразите вектор через векторы , и .
2) Найдите модуль вектора .
Введение в векторы и скаляры | Векторы и скаляры
20.1 Введение в векторы и скаляры (ESAGH)
Мы ежедневно соприкасаемся со многими физическими величинами в мире природы. Например, такие вещи, как время, масса, вес, сила и электрический заряд, являются физическими величинами, с которыми мы все знакомы. Мы знаем, что время идет и физические объекты имеют массу. Вещи имеют вес из-за силы тяжести. Мы прикладываем силу, когда открываем двери, ходим по улице и пинаем мячи.Мы испытываем электрический заряд напрямую от статического электричества зимой и от всего, что работает на электричестве.
В природе существует множество физических величин, и мы можем разделить их на две большие группы, называемые векторами и скалярами .
Скаляры и векторы (ESAGI)
Скаляры — это физические величины, которые имеют только числовое значение или размер (величину). Скаляр говорит вам , сколько там чего-то.
- Скалярная
Скаляр — это физическая величина, имеющая только величину (размер).
Например, человек покупает кадку с маргарином, на которой указана масса \ (\ text {500} \) \ (\ text {g} \). Масса кадки маргарина — величина скалярная. Для его описания требуется только одно число, в данном случае \ (\ text {500} \) \ (\ text {g} \).
Векторы отличаются, потому что это физические величины, имеющие размер и направление a. Вектор говорит вам , сколько чего-то есть и , в каком направлении он находится.{-1} $} \) (это величина), и мы знаем, куда он идет — на восток (это направление). Эти две величины, скорость и направление автомобиля (величина и направление) вместе образуют вектор, который мы называем скоростью.
Примеры скалярных величин:
масса имеет только значение, без направления
электрический заряд имеет только значение, без направления
Примеры векторных величин:
сила имеет значение и направление.Вы толкаете или тянете что-то с некоторой силой (величиной) в определенном направлении
вес имеет значение и направление. Ваш вес пропорционален вашей массе (величине) и всегда направлен к центру Земли.
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.
Зарегистрируйтесь здесьВекторы и скаляры
Упражнение 20.1Классифицируйте следующие элементы как векторы или скаляры
длина
сила
направление
высота
время
скорость
температура
скаляр
вектор
скаляр
скаляр
скаляр
скаляр
скаляр
Векторное представление (ESAGJ)
Векторы отличаются от скаляров и должны иметь свои собственные обозначения.Есть много способов записать символ вектора. В этой книге векторы будут обозначаться символами со стрелкой, указывающей вправо над ней. Например, \ (\ vec {F} \), \ (\ vec {W} \) и \ (\ vec {v} \) представляют векторов силы, веса и скорости, что означает, что оба они имеют величину и направление.
Иногда нужна просто величина вектора. В этом случае стрелка опускается. Для случая вектора силы:
Общие сведения о скалярных и векторных величинах
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Изучение использования множественных представлений для обучения векторов в 10 классе по физическим наукам
Абстрактные
Целью данной статьи было изучить использование множественного представления подход в качестве стратегии обучения для улучшения понимания учащимися векторов в 10 класс Физические науки.Исследование также хотело рассмотреть подход MR. через призму учащихся. Выборка, состоящая из 45 учеников 10 класса из Всего в исследовании приняли участие 160 учащихся 10-х классов физических наук. Оба количественные и качественные данные были собраны и проанализированы. Учащиеся были первыми прошли предварительный тест для установления их первоначального понимания векторов. Этот предварительный тест был с последующим вмешательством в форме урока. Урок проводился по порядку познакомить учащихся с обучением через множественные представления.Затем был проведен посттест вводится для определения воздействия вмешательства. Чтобы собрать и количественно оценить восприятие учащимися использования множественных представлений в преподавании и обучении векторов в 10-х классах учащихся физических наук раздали анкеты полный. Последним шагом было собеседование с учащимися для триангуляции результатов три инструмента. Исследование показало, что учащиеся боролись с понимание векторов в их традиционных уроках разговорной речи и их восприятие векторов было отрицательным.Исследование также показало, что множественные Представления могут улучшить понимание и развить позитивное восприятие учащихся к преподаванию и изучению векторов. Это улучшение происходит только если несколько представлений используются правильно. Исследование также выяснило, что когда Множественные представления используются неправильно, это ограничивает более глубокое понимание учащиеся. По результатам исследования был сделан ряд рекомендаций. Некоторые из них заключались в том, что при обучении следует использовать несколько представлений. векторов, и советники по предметам и учителя должны быть должным образом подготовлены использование нескольких представлений.Учебники по физическим наукам должны быть разработаны для размещения нескольких представлений.
Вопросы и решения по математике для 10 класса
Консорциум Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя множество вопросов, усовершенствованных с помощью новых технологий.
Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Таблицы соответствия, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнение / числовое значение, Расширенный составной ответ, Короткий ответ и многие другие.
Эта страница содержит несколько примеров вопросов, а также ссылки на практические тесты по математике для 10 класса, которые дают вам представление о вопросах, которые ваши ученики, вероятно, увидят на тесте. После каждого типового вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, придется учитывать в отношении навыков, процессов и информации, которые должны знать ваши ученики.
Домен: оценка 10 >> Число и количество — система вещественных чисел
Пример вопроса: Оценить 9 150/300
- 18
- 9
- 3
- 81
Ответ Объяснение: 9 150/300 = 9 1/2 = квадратный корень из 9 = 3.В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени может быть уменьшен, поэтому сначала мы должны уменьшить его. Показатель 150/300 = 1/2. Таким образом, проблема становится 9 в степени 1/2. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, который равен 3. В числителе 1, поэтому мы возводим 3 в 1-ю степень и получаем 3.
Стандарты: HSN.RN.A.1
Нажмите здесь, чтобы попрактиковаться: Число и количество — система действительных чисел Вопросы по математике 10-го класса
Домен: Оценка 10 >> Количество и количество — Количество
Пример вопроса: Перепишите x 1/2 в радикальной форме.
- √x
- √x 2
- 1 / √x
- -√x
Ответ Объяснение: В задаче с рациональным показателем числитель указывает степень, а знаменатель — корень. Поскольку проблема в том, что x 1/2 , знаменатель равен 2, что означает, что мы должны извлечь квадратный корень, а числитель равен 1, поэтому мы возведем его в первую степень, иначе экспоненты не будет, поскольку показатель степени 1 редко бывает использовал. Это делает ответ квадратным корнем из x, записанным как √x.
Стандарты: HSN.RN.A.1
Нажмите здесь, чтобы попрактиковаться: Число и количество 10-го класса — вопросы о количестве
Область: уровень 10 >> Число и количество — комплексная система счисления
Пример вопроса: Полное упрощение i (7 − i)
- 7i − i 2
- 1 + 7i
- 6i
- −1 + 7i
Объяснение ответа: i (7 − i) = i * 7 − i * i = 7i − i 2 = 7i — (- 1) = 7i + 1 = 1 + 7i
Начните с использования распределительного метода.Теперь упростим −i 2 = 1 по определению. Теперь переставьте и поместите реальную часть первой, а воображаемую — последней, чтобы она выглядела так: a + bi.
Стандарты: HSN.CN.A.2
Нажмите здесь, чтобы попрактиковаться: Математические числа и количество для 10 класса — вопросы по комплексной системе счисления
Домен: Оценка 10 >> Число и количество — векторные и матричные количества
Пример вопроса: Вектор в стандартной форме имеет компоненты.Какая начальная точка?
- (0, 0)
- (3, 10)
- (6, 20)
- Недостаточно информации
Объяснение ответа: Поскольку вектор находится в стандартном положении, мы знаем, что начальная точка — это (0, 0) или начало координат.
Стандарты: HSN.VM.A.2
Нажмите здесь, чтобы попрактиковаться: Число и количество — Вопросы о векторных и матричных величинах для 10-го класса по математике
Область: 10 класс >> Алгебра — видение структуры в выражениях
Пример вопроса: Какое выражение эквивалентно 9x 2 — 16y 2 ?
- (3x — 4 года) (3x — 4 года)
- (3x + 4 года) (3x + 4 года)
- (3x + 4 года) (3x — 4 года)
- (3–4 года) 2
Ответ Объяснение: Студент должен понять, что выражение — это разница двух полных квадратов
Стандарты: HSA.SSE.A.2
Щелкните здесь, чтобы попрактиковаться: Алгебра — определение структуры выражений Вопросы для 10 класса по математике
Область: 10 класс >> Алгебра — арифметика с многочленами и рациональными выражениями
Пример вопроса: Вычислить f (x) = — a 3 + 6a − 7 при a = — 1 и сформулировать остаток.
- -14
- -12
- 14
- 12
Объяснение ответа: Студент должен подставить — 1 в функцию следующим образом — (- 1) 3 +6 (−1) −7 = −12 и найти значение, чтобы получить остаток
Стандарты: HSA.APR.B.2
Щелкните здесь, чтобы попрактиковаться: Алгебра — Арифметика с многочленами и рациональными выражениями Вопросы для 10 класса по математике
Область: 10 класс >> Алгебра — Создание уравнений
Пример вопроса: Соотношение персонала и гостей на гала-вечере было 3: 5. Всего в бальном зале присутствовало 576 человек. Сколько гостей было на гала-вечере?
- 276
- 300
- 360
- 216
Объяснение ответа: Установите соотношение гостей к общему количеству людей, 8/5 = x / 576.Решить крестным умножением. 8x = 2880. Разделите обе части на 8. Итак, x = 360.
Стандарты: HSA.CED.A.3
Нажмите здесь, чтобы попрактиковаться: Алгебра — Создание уравнений Вопросы для 10 класса по математике
Область: 10 класс >> Алгебра — Рассуждение с помощью уравнений и неравенств
Пример вопроса: Решите квадратичный x 2 + 10x = −25.
- -10
- 10
- 5
- -5
Ответ Объяснение: Эту проблему можно легко решить, переставив уравнение так, чтобы оно решалось для нуля, а затем разложив на множители, как показано:
х 2 + 10х = -25
х 2 + 10х + 25 = 0
(х + 5) (х + 5) = 0
Поскольку оба фактора абсолютно одинаковы, у вас будет только одно решение этой проблемы.
х + 5 = 0
х = −5
Стандарты: HSA.REI.B.4
Нажмите здесь, чтобы попрактиковаться: Алгебра — Рассуждение с помощью уравнений и неравенств Вопросы для 10 класса по математике
Домен: Уровень 10 >> Функции — Функции интерпретации
Пример вопроса: Какой график может представлять график f (x) = sin (x)?
Ответ Пояснение: График функции sin всегда выглядит как волна.Единственная функция, которая может быть функцией sin, — это D.
.Стандарты: HSF.IF.C.7
Нажмите здесь, чтобы попрактиковаться: Функции — вопросы по интерпретации функций для 10-го класса по математике
Домен: Уровень 10 >> Функции — Функции построения
Пример вопроса: Опишите, как можно получить график g (x) = x 3 -5, сдвигая f (x) = x 3 + 2.
- Сдвиг вправо 7 шт.
- Сдвиг влево 7 шт.
- Сдвиг на 7 единиц
- Сдвиг вниз на 7 единиц
Объяснение ответа: Единственное, что изменилось в двух уравнениях, — это точка пересечения по оси Y, которая управляет вертикальным смещением (вверх или вниз).Чтобы получить график g (x) путем сдвига графика f (x), вы должны сдвинуть f (x) вниз на 7 единиц, чтобы изменить значение от +2 до -5.
Стандарты: HSF.BF.B.3
Нажмите здесь, чтобы попрактиковаться: Функции — Вопросы по построению функций для 10-го класса по математике
Домен: Уровень 10 >> Функции — Функции интерпретации
Пример вопроса: Решите 3 x = 12, используя логарифмическую форму.
- x = ln12 / ln3
- x = ln (4)
- x = ln (9)
- Ни один из этих
Ответ Объяснение:
Решите, используя журналы следующим образом:
3 x = 12
x = log (основание 3) 12
x = ln12 / ln3
Стандарты: HSF.LE.A.4
Нажмите здесь, чтобы попрактиковаться: Функции — вопросы по интерпретации функций для 10-го класса по математике
Домен: Уровень 10 >> Функции — тригонометрические функции
Пример вопроса: На единичном круге видно, что tan (5π / 4) = 1. Какое значение cos (5π / 4)?
- −√2 / 2
- undefined
- √2 / 2
- -1
Объяснение ответа:
Тригонометрическое отношение косинуса — это отношение длины соседней стороны к длине гипотенузы.Длина соседней стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, которая соответствует этому углу. Тригонометрическое отношение касательной — это длина противоположной стороны, деленная на длину соседней стороны. Длина противоположной стороны — это значение y в точке на единичной окружности, а длина соседней стороны — это значение x в точке на единичной окружности.Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение тангенциального отношения любого угла в единичной окружности — это отношение yx от точки на единичной окружности, которая соответствует этому углу. В этом вопросе tan (5π / 4) = 1. Это отношение берется из точки (−2 / √2, −2 / √2), которая соответствует углу с мерой 5π / 4 радиан. Таким образом, используя информацию выше, значение cos (5π4) совпадает со значением x в точке (−2 / √2, −2 / √2). Следовательно, значение cos (5π / 4) = −2 / √2.
Стандарты: HSF.TF.A.2
Нажмите здесь, чтобы попрактиковаться: Функции — Вопросы по тригонометрическим функциям для 10-го класса по математике
Домен: оценка 10 >> Геометрия — сравнение
Пример вопроса: Какими будут координаты точки S после применения следующего правила: (x + 3, y -2)?
- (1, -4)
- (-2, -2)
- (2, -2)
- (3, -2)
Ответ Объяснение: Ответ: B
Объяснение: Данное правило преобразования заключается в переводе точки на 3 единицы вправо и на 2 единицы вниз, как показано на следующей диаграмме:
Стандарты:
Нажмите здесь, чтобы попрактиковаться: Геометрия — вопросы на соответствие для 10 класса по математике
Область: уровень 10 >> Геометрия — подобие, прямоугольные треугольники и тригонометрия
Пример вопроса: По какому свойству углы BAX и TSX могут быть сочтены совпадающими?
- Соответствующие углы
- Вертикальные углы
- Альтернативные внутренние углы
- Конгруэнтные углы
Ответ Объяснение: Ответ: A
Хотя это равные углы, вопрос задает свойство.Так как они находятся в соответствующих местах с поперечиной (AX), правильный ответ — A
.Стандарты: HSG.SRT.A.3
Щелкните здесь, чтобы попрактиковаться: Геометрия — подобие, прямоугольные треугольники и тригонометрические вопросы для 10 класса по математике
Домен: уровень 10 >> Геометрия — круги
Пример вопроса: Каково правило перевода и масштабный коэффициент расширения как Окружность F → Окружность F ‘?
- (х, у) → 1/4 (х, у + 10)
- (х, у) → 4 (х, у + 10)
- (х, у) → 1/4 (х + 10, у)
- (х, у) → 1/4 (х, у-10)
Объяснение ответа: Исходная окружность F имеет центр в точке (−5, −6) с радиусом 4 единицы.Смещенный / расширенный круг F ’имеет центр в точке (-5,4) с радиусом 1 единицы. Это означает, что центр был переведен на 10 единиц. В качестве преобразования этот перенос записывается как (x, y) → (x, y + 10). Круг F также был расширен в 1/4 раза, потому что радиус был уменьшен с 4 единиц до 1 единицы. В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Объединяя перенос и расширение, получаем правило (x, y) → 1/4 (x, y + 10).
Стандарты:
Нажмите здесь, чтобы попрактиковаться: Геометрия — Круги Вопросы для 10 класса по математике
Область: Уровень 10 >> Геометрия — Выражение геометрических свойств с помощью уравнений
Пример вопроса: Какое значение на числовой прямой на рисунке ниже делит сегмент EF на две части с соотношением их длин 3: 1?
- -5
- -3
- -2
- -1
Объяснение ответа: Точка E находится в -7 на числовой прямой на рисунке, а точка F находится в 1.Таким образом, длина сегмента EF равна 8. Чтобы разделить сегмент на две части с соотношением их длин 3: 1, измените соотношение на 3x: 1x, чтобы разрешить изменение положения на числовой прямой. Затем установите сумму двух частей равной 8 и решите относительно x. 3x + 1x = 8; 4x = 8; x = 2. Теперь, когда вы знаете, что x = 2, найдите 3x, что равно 6. Найдите значение на числовой прямой, прибавив 6 к положению точки E. −7 + 6 = -1. Значение на числовой прямой, которая делит сегмент EF в соотношении 3: 1, равно -1.
Стандарты: HSG.GPE.B.6
Щелкните здесь, чтобы попрактиковаться: Геометрия — Выражение геометрических свойств с помощью уравнений Вопросы для 10 класса по математике
Область: уровень 10 >> Геометрия — геометрические измерения и размеры
Пример вопроса: Каков объем призмы, показанной ниже?
- 1350 см 3
- 1350 см
- 675 см 3
- 675 см
Объяснение ответа: Используйте формулу объема пирамиды:
В = 1/2.a.c.h
В данном случае длина 15 см, длина основания 10 см, а высота 9 см. Следовательно:
V = 1 / 2.15.10.9 = 675 см 3
Стандарты: HSG.GMD.A.3
Нажмите здесь, чтобы попрактиковаться: Геометрия — геометрические измерения и вопросы о размерах для 10-го класса по математике
Область: Уровень 10 >> Геометрия — Моделирование с помощью геометрии
Пример вопроса: Компания отправляет сферические пресс-папье в кубических ящиках.Окружность пресс-папье составляет 9π см. Если коробка подходит к сфере точно так, чтобы стороны сферы касались коробки, каков объем самой маленькой коробки, которую компания может использовать для доставки.
- 81 см 3
- 81 π см 3
- 729 см 3
- 1009 π см 3
Объяснение ответа:
Обратите внимание, что диаметр сферы будет таким же, как и сторона кубической коробки.Используя значение окружности, можно определить диаметр пресс-папье.
C = πd9π
cm = πd9
cm = d
Поскольку диаметр равен по мере сторонам {\ dots}
V = s 3
V = (9 см) 3
V = 729 см 3
Стандарты: HSG.MG.A.3
Нажмите здесь, чтобы попрактиковаться: Геометрия — моделирование с помощью вопросов по геометрии для 10-го класса по математике
Область: 10 класс >> Статистика и вероятность — интерпретация категориальных и количественных данных
Пример вопроса: Учитывая приведенный ниже график разброса, какой тип функции выражает корреляцию между двумя переменными?
- Линейный
- Экспоненциальная
- Квадратичная
- Полярный
Объяснение ответа: Обратите внимание, что тренд графика (красный) между точками данных образует линию.
Стандарты: HSS.ID.A.4
Щелкните здесь, чтобы попрактиковаться: Статистика и вероятности — Интерпретация категориальных и количественных данных Вопросы для 10 класса по математике
Область: 10 класс >> Статистика и вероятность — делать выводы и обосновывать выводы
Пример вопроса: В рамках исследовательского проекта о поведении домашних животных была выбрана случайная выборка из 400 кошек. Исследование показало, что 60% кошек предпочитают спать в доме.Курица была любимой едой 35% этих кошек. Исследование также показало, что 85% кошек, которые предпочитали спать вне дома, имели другое любимое блюдо. Сколько кошек в выборке больше всего любили курицу и предпочитали спать внутри?
- 84
- 56
- 160
- 156
Объяснение ответа: Если в выборке 400 кошек и 60% кошек предпочли спать в помещении, то 400,0,60 = 240 кошек предпочли спать в помещении и 160 кошек предпочли спать на улице.Далее, если любимым блюдом 35% кошек, которые предпочитали спать внутри, была курица, то 240.0.35 = 84 кошки в выборке предпочли спать внутри и выбрали курицу в качестве своего любимого блюда.
Стандарты: HSS.IC.B.6
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — делать выводы и обосновывать выводы Вопросы для 10-го класса по математике
Область: оценка 10 >> Статистика и вероятность — условная вероятность и правила вероятности
Пример вопроса: В студенческом совете есть одна предстоящая вакансия.В школе проводятся выборы, и у нее есть восемь равновероятных кандидатов. Класс AP Statistics хочет смоделировать результаты выборов, поэтому учащиеся должны выбрать подходящий метод моделирования. Они намерены провести испытания с симуляцией. Какой из этих методов будет наиболее подходящим?
- Покрутите колесо с восемью равными промежутками
- Подбросить монету восемь раз за каждые выборы
- Бросьте кости
- Бросить четыре кубика
Объяснение ответа: В вопросе указано, что существует восемь равновероятных кандидатов.Это означает, что каждый кандидат имеет одинаковые шансы на победу на выборах. Только вращающееся колесо с восемью равными ячейками могло смоделировать эту ситуацию, потому что колесо имеет равные шансы приземлиться на каждую ячейку.
Стандарты: HSS.IC.A.1
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — условная вероятность и правила вероятностных вопросов для 10-го класса по математике
Область: оценка 10 >> Статистика и вероятность — использование вероятности для принятия решений
Пример вопроса:
Используя приведенную выше диаграмму Венна, найдите P (C или E).
- 1/3
- 7/24
- 5/24
- Ни один из этих
Объяснение ответа: Просто посчитайте точки данных в кругах C и E. Их 8 из 24 общих точек данных, и, уменьшив, мы получим 8/24 = 1/3.
Стандарты: HSS.CP.B.7
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы для 10 класса по математике
Область: оценка 10 >> Статистика и вероятность — использование вероятности для принятия решений
Пример вопроса: Статистик работает в Sweet Shop USA, и ему была поставлена задача выяснить, какова вероятность того, что неисправность машины для приготовления помадки приведет к испорчению всей партии помадки в процессе.Каждая неисправность машины обходится компании в 250 долларов. Статистик рассчитывает вероятность того, что 1 из 20 партий фаджа будет потеряна из-за неисправности машины. Какова ожидаемая стоимость этих потерь за один месяц, если компания производит 20 партий помадки каждый день?
- $ 3750
- 150 000 долл. США
- $ 7500
- $ 375
Объяснение ответа: Поскольку в большинстве месяцев 30 дней, мы предположим, что в месяце 30 дней. Мы можем использовать E (x) = x1p1 + x2p2 +… + xipi или просто вычислить следующим образом
E (X) =.05 * 250 * 30 = 375
Стандарты: HSS.MD.A.4
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность — использование вероятности для принятия решений Вопросы для 10 класса по математике
Обновление … Ċ 1.3 Темпы изменений.pdf(273k) Michael Cammock, 7 февраля 2021 г., 18:32 Ċ Michael Cammock, 7 февраля 2021 г., 18:32 Michael Cammock, 31 марта 2018 г. 11:16 AM Ċ Michael Cammock, 13 апреля 2018 г., 12:01 Ċ Michael Cammock, 15 апреля 2018 г. 13:47 Ċ Michael Cammock, 16 апреля 2018 г., 8:26 Ċ Michael Cammock, 19 апреля 2018 г., 12:12 Ċ Michael Cammock, 18 апреля 2018 г., 13:51 Ċ Michael Cammock, 30 апреля 2018 г., 11:32 AM Ċ Michael Cammock, 2 мая, 2018, 14:18 Michael Cammock, 21 мая 2018 г., 7:46 Michael Cammock, 9 0005 22 мая 2018 г. 13:16 Ċ Michael Cammock, 23 мая 2018 г., 17:01 Ċ Michael Cammock, 21 мая 2019 г., 10:05 Ċ Michael Cammock, 4 июня 2018 г., 14:50 Ċ Michael Cammock, 5 июня 2018 г., 15:22 Ċ Michael Cammock, 6 июня, 2018, 16:50 Ċ Michael Cammock, 4 июня 2019 г., 13:57 Ċ Michael Cammock, 5 июня 2019 г., 15:53 Ċ Algebraic dot продукт.pdf(134k) Michael Cammock, 24 мая 2018 г., 16:49 Ċ Michael Cammock, 8 апреля 2020 г., 7:33 AM Ċ Приложения Dot и Cross Products .pdf(361k) Michael Cammock, 23 мая 2019 г., 17:02 Ċ Таблица формул вычислений и векторов.pdf(139k) Michael Cammock, 16 июня 2019 г., 5 : 52 AM Ċ Примечания к классу Concavity.pdf(383k) Michael Cammock, 2 апреля 2019 г., 18:52 Ċ Michael Cammock, 22 мая 2019 г., 2:51 PM 5 Michael Cammock, 18 февраля 2020 г., 12:19 Ċ Michael Cammock, 2 марта 2020 г., 12:46 Ċ Michael Cammock, февраля 12, 2020, 11:00 Ċ День 5 — Примеры вопросов викторины 2018.pdf(200k) Michael Cammock, 3 апреля 2018 г., 13:54 Ċ Day 5 Continuity.pdf(491k) Michael Cammock, 8 февраля 2021 г., 13:07 Ċ Заметки о занятиях в день 5.pdf(221k) Michael Cammock, 5 марта 2020 г., 11:23 AM Ċ Michael Cammock, 21 марта 2019 г., 11:59 AM Ċ Michael Cammock, 22 апреля 2018 г., 11:13 Ċ DerivativesRules2.pdf(23k) Michael Cammock, 24 февраля 2020 г., 11:33 AM Ċ Michael Cammock, 4 апреля 2020 г., 18:30 Ċ Michael Cammock, 17 июня 2019 г., 7:56 Ċ Finding Extreme.pdf(163k) Michael Cammock, 19 апреля 2018 г., 13:38 Ċ Michael Cammock, 28 мая, 2019, 12:14 Ċ Linear Combinations.pdf(296k) Michael Cammock, 13 мая 2018 г., 17:07 Ċ Решения для практических экзаменов MCV4U.pdf(527k) Майкл Каммок, 12 июня 2018 г., 10:16 Майкл Каммок, 26 марта 2021 г., 15:23 Ċ Практический экзамен-Calculus.pdf( 248k) Michael Cammock, 12 июня 2019 г., 7:33 AM Ċ Prerequisite Knowledge.pdf(646k) Michael Cammock, 29 января 2020 г., 18:28 Ċ Michael Cammock, 24 февраля 2019 г., 11:21 Ċ Свойства векторов.pdf(195k) Michael Cammock, 3 мая 2018 г., 13:59 Ċ Michael Cammock, 20 февраля 2020 г., 12:19 Ċ Michael Cammock, 6 мая 2019 г., 16:29 Michael Cammock, 7 мая 2019 г., 10:13 Ċ SOLUTIONS — Prerequisite Skills.pdf(228k) Michael Cammock, фев 1 января 2019 г., 11:43 Ċ Примеры ответов на викторину.pdf(168k) Michael Cammock, 4 апреля 2018 г., 6:51 Ċ Сумма и различия векторов. pdf(253k) Michael Cammock, 1 мая 2018 г., 4: 32 PM Ċ TestReview-Answers.pdf(2032 КБ) Майкл Каммок, 27 мая 2019 г., 16:25 Ċ TestReview2019.pdf(195 КБ) Майкл Каммок 4 мая 27 января 2019 г., 5:34Ċ Набор задач БЛОКА 3 — 2018.pdf(208k) Michael Cammock, 19 марта 2018 г., 12:05 Ċ Ежедневный план Unit 1 — с критериями успеха — февраль 2019.pdf(202k) Michael Cammock, февраля 3, 2019, 9:15 AM Ċ Unit 1 Test Review-Answers.pdf(1932k) Michael Cammock, 14 февраля 2021, 19:39 Ċ Unit 1 Test Review.pdf(219k) Michael Cammock, 14 февраля 2021 г., 19:39 Ċ Набор задач 1 и 2 — 2018.pdf(168k) Michael Cammock, 21 февраля 2018 г., 8:40 Ċ Набор задач 1 и 2 — 2020.pdf(167k) Michael Cammock, 21 февраля 2020 г. , 10:10 AM Ċ Unit 2 Daily Outline.pdf(40k) Michael Cammock, 11 февраля 2020 г., 9:28 AM Ċ Unit 3 Daily Outline March 2020.pdf(20k ) Michael Cammock, 28 февраля 2020 г., 10:33 Ċ Ежедневный план блока 4 — с критериями успеха — март 2020 г.pdf(152k) Michael Cammock, 12 марта 2020 г., 5:26 AM Ċ Ежедневный план блока 5 — с критериями успеха — апрель 2018 г.pdf(146k) Michael Cammock, апр. 13, 2018, 11:58 Ċ Ежедневный план блока 5 — с критериями успеха — апрель 2020.pdf(144k) Michael Cammock, 20 апреля 2020 г., 9:07 Ċ Unit 6 Daily Outline April 20178.pdf(144k) Michael Cammock, 30 апреля 2018 г., 11:35 Ċ Unit 6 Daily Outline May 2020.pdf(172k) Michael Cammock, 13 мая 2020 г., 12:12 Ċ Unit 7 Daily Outline May 2018.pdf(76k) Michael Cammock, 21 мая 2018 г., 7 : 50 AM Ċ Unit 8 Daily Outline 2018.pdf(56k) Michael Cammock, 4 июня 2018 г., 14:51 Ċ Vectors in 2 space and 3 space.pdf(238k ) Michael Cammock, 5 мая 2019 г., 17:23 Ċ некоторые проблемы оптимизации 2018.pdf(47k) Michael Cammock, 13 марта 2018 г., 12:26 |
Learnhive | Cambridge IGCSE Mathematics Vectors
Learnhive | Cambridge IGCSE Mathematics Vectors — уроки, упражнения и практические тестыВход в систему Learnhive
Выберите приложение Learnhive
×— Выберите свой класс / класс —LKGUKG12345678910 — Выберите свой класс / класс —LKGUKG12345678
Learnhive Зарегистрироваться
ИЛИ
Заполните форму ниже
Доска:
— Выберите свой Совет по образованию — CBSE (Индия) ICSE (Индия) Совет штата Махараштра (Индия) Совет штата Тамилнад (Индия) Совет штата Карнатака (Индия) Общие основные стандарты IGCSE (США)
Класс / Оценка:
— Выберите свой класс / сорт —
×Математика / Векторы
Величины, которые имеют только величину, называются скалярами.
Пример: скорость
Величины, которые имеют как величину, так и направление, называются векторами.
Пример: скорость, смещение
Изучите различные свойства векторов и различные операции над векторами
- Темы
- Темы
- Векторы
- Представление векторов
- Сложение и вычитание векторов
- Вектор в форме компонента
- Скалярное умножение
Индия CBSE
Индия ICSE
Общее ядро США
IGCSE
Индия Махараштра
Индия Тамилнад
Индия Карнатака
Тысячи учеников используют Learnhive, чтобы осваивать концепции и продвигаться в школе с нашим БЕСПЛАТНЫМ контентом.Зарегистрируйтесь, чтобы получать индивидуальные уроки и упражнения.
Какие проблемы решает Learnhive?
Мои дети не справляются с темпами изучения тем в классе
Наша система обучения помогает вашим детям учиться в удобном для них темпе. Они могут повторять уроки сколько угодно раз.
Мой ребенок хочет изучать только некоторые предметы
Мы делаем обучение увлекательным и увлекательным, чтобы повысить уровень интереса вашего ребенка.С Learnhive вашему ребенку понравится изучать любой предмет.
Мои дети делают глупые ошибки на школьных тестах
Когда дети недостаточно тренировались, они склонны совершать глупые ошибки. Learnhive предлагает большое количество упражнений, которые помогут им уменьшить эти ошибки.
Свяжитесь с нами
Поставьте нам лайк на Facebook и получите еженедельный доступ к упражнениям.
2.2 Скорость и скорость — физика
Задачи обучения раздела
К концу этого раздела вы сможете делать следующее:
- Рассчитать среднюю скорость объекта
- Связать смещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, руководство лаборатории физики средней школы рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Раздел Основные термины
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителя
Поддержка учителя
В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.
[BL] [OL] Перед тем, как студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто используются как синонимы в повседневной жизни, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, — это его скорость. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость является скаляром, потому что у нее есть величина, но не направление. Поскольку скорость — это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Единицей времени в системе СИ является секунда (с), а единицей скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v avg , представляет собой пройденное расстояние, разделенное на время, в течение которого происходит движение.
vavg = distancetimevavg = distancetimeВы, конечно, можете изменить уравнение для решения либо расстояния, либо времени
время = distancevavg.time = distancevavg. distance = vavg × timedistance = vavg × timeПредположим, например, что автомобиль проезжает 150 километров за 3 секунды.2 часа. Его средняя скорость за поездку —
. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени — это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.
Teacher Support
Teacher Support
[OL] [AL] Предупредите учащихся, что средняя скорость не всегда равна средней начальной и конечной скорости объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км — со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.
[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на повседневном языке часто называют просто скоростью.Подчеркните важность в науке использования правильной терминологии, чтобы избежать путаницы и правильно передавать идеи.
Рисунок 2.8 За 30 минут до магазина туда и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода туда и обратно равно нулю, потому что не было чистого изменения положения.
Рабочий пример
Расчет средней скорости
Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?
Стратегия
Мы знаем расстояние, которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / сОбсуждение
Средняя скорость — это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды — это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
8.Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?
- 40 м / с
- -40 м / с
- 0,03 м / с
- 8,5 м / с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?
- 146 с
- 0.01 с
- 2,50 мин.
- 287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость — это смещение, деленное на время, в течение которого смещение происходит.
vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления в течение определенного интервала времени оказывает большее влияние на скорость и скорость.
Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или отступил, прежде чем он добрался до задней части самолета. Чтобы получить больше деталей, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направляющегося к задней части самолета, показаны более мелкие отрезки его поездки.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.
Watch Physics
Расчет средней скорости или скорости
В этом видео рассматриваются векторы и скаляры и описывается, как рассчитать среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.
Проверка захвата
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
Поддержка учителей
Поддержка учителей
Это видео хорошо подчеркивает разницу между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Прежде чем ученики посмотрят видео, укажите, что преподаватель использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является обычным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.
Рабочий пример
Расчет средней скорости
Студент перемещается на 304 м к северу за 180 с. Какова была средняя скорость ученика?
Стратегия
Мы знаем, что смещение составляет 304 м к северу, а время — 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.
Решение
vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны включить в ответ направление и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с — только двух, поэтому частное должно состоять только из двух значащих цифр.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.
Поддержка учителей
Поддержка учителей
Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные вычисления. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда носить с собой одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение для смещения, когда известны средняя скорость и время
Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток2,2
Обсуждение
Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.
Советы для успеха
Размерный анализ — хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица компенсирует, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны смещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?
Стратегия
Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.
Решение
vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с2,3
Обсуждение
Здесь нам снова пришлось использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
10.Дальнобойщик проезжает по прямой трассе 0,25 ч со смещением 16 км к югу.Какова средняя скорость дальнобойщика?
- 4 км / ч север
- 4 км / ч юг
- 64 км / ч север
- 64 км / ч юг
Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?
- 42 м запад
- 6 м запад
- 6 м восток
- 42 м на восток
Virtual Physics
The Walking Man
В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графическом отображении движения далее в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость — отрицательным. Затем посмотрите, сможете ли вы сделать обратное.
Проверка захвата
Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Человек движется от 0 слева от 0
- Человек движется от 0 справа от 0
Поддержка учителей
Поддержка учителей
Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Introduction . Вкладку Charts можно использовать после того, как студенты узнают о графическом движении позже в этой главе.
Проверьте свое понимание
12.Два бегуна движутся по одному и тому же прямому пути. Они начинаются в одно и то же время и заканчиваются в одно и то же время, но на полпути у них разные мгновенные скорости. Могут ли они иметь одинаковую среднюю скорость для поездки?
- Да, потому что средняя скорость зависит от чистого или полного смещения.
- Да, потому что средняя скорость зависит от общего пройденного расстояния.
- Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
- Нет, потому что мгновенные скорости бегунов должны оставаться такими же на полпути, но могут быть разными в другом месте.
Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?
- Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
- Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. Оба варианта одинаковы, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.
Может ли средняя скорость быть отрицательной?
- Да, в случаях, когда чистое смещение отрицательное.
- Да, если тело постоянно меняет направление во время движения.
- Нет, средняя скорость описывает только величину, а не направление движения.
- Нет, средняя скорость описывает только величину в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте вопросы Проверьте свое понимание , чтобы оценить, насколько учащиеся достигли целей обучения по разделам. Если учащиеся не справляются с какой-либо конкретной целью, Check Your Understanding поможет определить, кто из них и направит их к соответствующему содержанию.


 Перпендикулярность плоскостей.
Контролирующая самостоятельная
работа.
Перпендикулярность плоскостей.
Контролирующая самостоятельная
работа.
 Контролирующая самостоятельная
работа.
Контролирующая самостоятельная
работа.
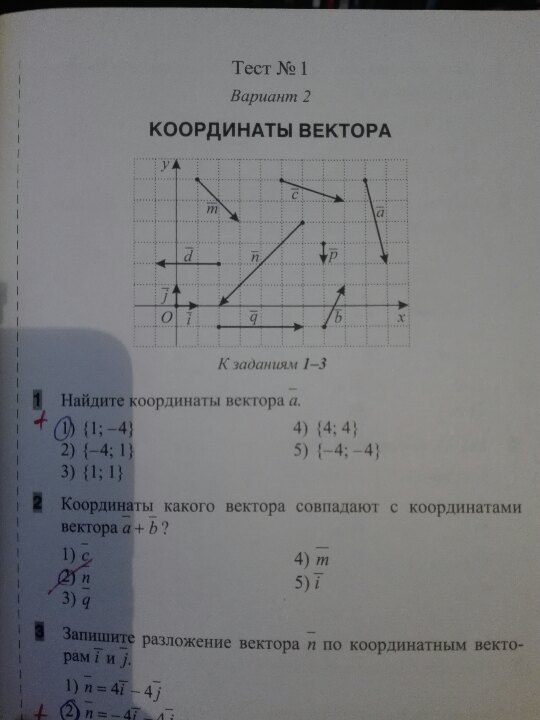




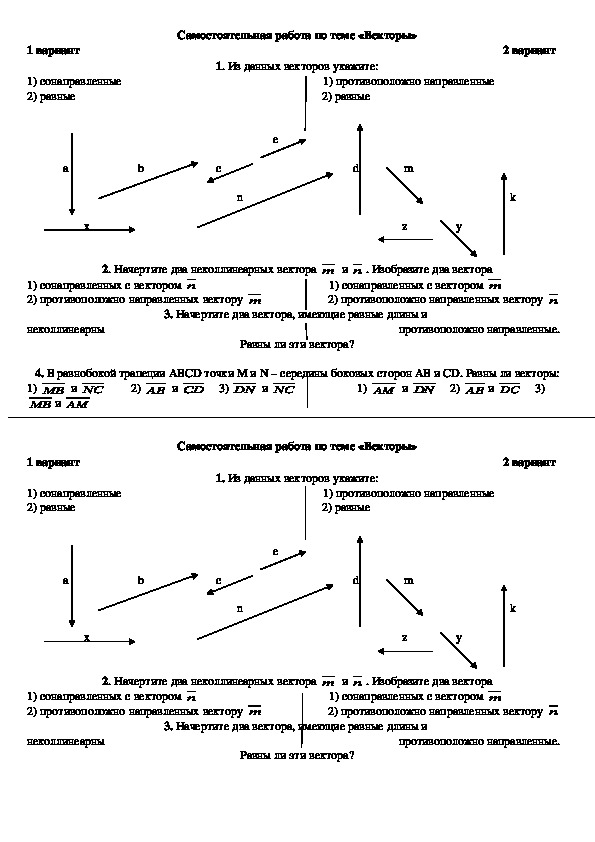
 2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны.
2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны. 2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны.
2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны. 2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны.
2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны.