Решение задач контрольной работы по теории вероятностей. Контрольная по теории вероятности
Решение задач контрольной работы по теории вероятностей
 Время от времени посетители сайта, узнав, что я являюсь действующим сотрудником МПГУ (Московского Педагогического Государственного Университета) и непосредственно связан с преподаванием физики в этом вузе, задают мне вопрос, занимаюсь ли я решением контрольных работ для студентов. Иногда этот вопрос звучит в более «мягкой» форме, а именно, осуществляю ли я помощь в выполнении контрольных работ по физике и математике для студентов вузов. Как бы то ни было, смысл остается тем же. Отвечаю вам на этот вопрос, уважаемые читатели.
Время от времени посетители сайта, узнав, что я являюсь действующим сотрудником МПГУ (Московского Педагогического Государственного Университета) и непосредственно связан с преподаванием физики в этом вузе, задают мне вопрос, занимаюсь ли я решением контрольных работ для студентов. Иногда этот вопрос звучит в более «мягкой» форме, а именно, осуществляю ли я помощь в выполнении контрольных работ по физике и математике для студентов вузов. Как бы то ни было, смысл остается тем же. Отвечаю вам на этот вопрос, уважаемые читатели.
Я являюсь действующим репетитором по физике и математике в Москве и занимаюсь в основном подготовкой школьников к сдаче ГИА и ЕГЭ по физике и математике. Однако, иногда (в случае наличия свободного времени) из интереса к вузовскому курсу математики я могу помочь студентам при выполнении контрольных работ по физике и математике (конкретно, по общей физике, классической механике и электродинамике, алгебре и геометрии, математическому анализу, теории вероятностей и математической статистике). Решил сегодня поделиться с вами одной из последних контрольных работ по дисциплине «Теория вероятностей» для II курса Московского отделения Всероссийского Заочного Финансово-Экономического Института (ВЗФЭИ).
Задача 1. Из 40 вопросов курса высшей математики студент знает 32. На экзамене ему случайным образом предлагаются два вопроса. Какова вероятность того, что студент ответит правильно: - хотя бы на один вопрос;
- на оба вопроса?
Решение. Более подробно о решении элементарных задач по теории вероятностей читайте в статье «Задачи на вероятность из ЕГЭ». Под случайным событием в данной задаче понимается получение студентом двух вопросов на экзамене. Вопросы повторяться не могут и порядок их следования в билете не важен. Тогда общее число возможных исходов данного события определяется число сочетаний из 40 элементов по 2 и вычисляется по формуле:
![Rendered by QuickLaTeX.com \[ C_{40}^2 = \frac{40!}{2!\cdot (40-2)!} = \frac{39\cdot 40}{2} = 780. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-048dcdd963e24c7f0914ae3a7b50be86_l3.png)
а) Рассчитаем вероятность того, что студенту попадется в билете два вопроса из тех, которые он не знает. Вновь имеем дело с сочетаниями 8 элементов по 2, число которых определяется по формуле:
![Rendered by QuickLaTeX.com \[ C_8^2=\frac{8!}{2!\cdot (8-2)!} = \frac{7\cdot 8}{2} = 28. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0f81a8cbccea79d78000a1ea06fc1cd2_l3.png)
Тогда вероятность такого события равна 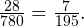 Тогда вероятность противоположного события, заключающегося в том, что студенту попадется хотя бы один вопрос, который он знает, равна:
Тогда вероятность противоположного события, заключающегося в том, что студенту попадется хотя бы один вопрос, который он знает, равна: 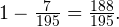
б) Ищем теперь вероятность того, что студенту попадутся оба вопроса из тех, что он знает. Имеем дело с сочетаниями из 32 элементов по 2, число которых определяется по формуле:
![Rendered by QuickLaTeX.com \[ C_{32}^2 = \frac{32!}{2!\cdot (32-2)!} = \frac{31\cdot 32}{2} = 496. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-12a3133b7b3e4fd718e81ff10a886f41_l3.png)
Тогда вероятность этого события равна 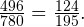
Задача 2. При высаживании рассады помидоров только 80% приживаются. Найти вероятность того, что из 6 высаженных кустов приживутся не менее 5?
Решение. Искомую вероятность ищем по формуле Бернулли. Вероятность того, что событие наступит 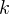 раз в
раз в 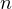 независимых испытаниях равна
независимых испытаниях равна 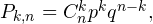 здесь
здесь 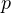 — вероятность наступления отдельного события (в нашем случае
— вероятность наступления отдельного события (в нашем случае 
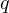 — вероятность того, что это событие не наступит в единичном исследовании (в нашем случае
— вероятность того, что это событие не наступит в единичном исследовании (в нашем случае  Ищем вероятность того, что приживется 5 или 6 кустов, то есть искомая вероятность равна:
Ищем вероятность того, что приживется 5 или 6 кустов, то есть искомая вероятность равна:
![Rendered by QuickLaTeX.com \[ P_{5,6}+P_{6,6} = C_6^5\cdot 0,8^5\cdot 0,2^{6-5}+C_6^6\cdot 0,8^6\cdot 0,2^{6-6} = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f61eb86b58cee1caa39346f75e078b49_l3.png)
![Rendered by QuickLaTeX.com \[ =6\cdot 0,32768\cdot 0,2+0,262144 = 0,65536. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8447981b9b8bc2417aa50010f3be60da_l3.png)
Задача 3. Человек, проходящий мимо киоска, покупает газету с вероятностью 0,2. Найти вероятность того, что среди 400 человек, прошедших мимо киоска в течение часа: - купят газету 90 человек;
- не купят газету от 300 до 340 человек (включительно).
Решение.
а) Имеем 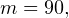
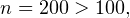
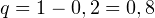 , тогда
, тогда 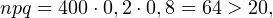 следовательно в расчетах можно использовать локальную и интегральную теоремы Муавра-Лапласа.
следовательно в расчетах можно использовать локальную и интегральную теоремы Муавра-Лапласа.
![Rendered by QuickLaTeX.com \[ x_m = \frac{m-n\cdot p}{\sqrt{npq}} = \frac{90-0,2\cdot 400}{\sqrt{400\cdot 0,2\cdot 0,8}} = 1,25. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-75995a827e502815d836cf672057b25f_l3.png)
![Rendered by QuickLaTeX.com \[ f(x_m) = f(1,25) = 0,1826. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8fdc12b62b166252929f4850eb7a8a4b_l3.png)
Искомая вероятность равна:
![Rendered by QuickLaTeX.com \[ P_{400}(90) = \frac{1}{\sqrt{npq}}\cdot f(x_m) = \frac{1}{8}\cdot 0,1826 = 0,0228. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-16748bde51f89edf9f70baae0e56fa0d_l3.png)
б) Ищем вероятность того, что газеты не купят, поэтому в данном случае 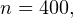
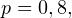
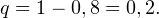 Получаем тогда:
Получаем тогда:
![Rendered by QuickLaTeX.com \[ x_1 = \frac{a-np}{\sqrt{npq}} = \frac{300-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}} = -2,5 \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ec35da10570cf9fed184637f0bb9b2f8_l3.png)
![Rendered by QuickLaTeX.com \[ x_2 = \frac{b-np}{\sqrt{npq}} = \frac{340-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}} = 2,5. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c256a7284f4c0ae0f3fe90828da35b94_l3.png)
Тогда получаем, что искомая вероятность равна (см. таблицу значений функции Лапласа):
![Rendered by QuickLaTeX.com \[ p = \frac{1}{2}\left[\Phi(2,5)-\Phi(-2,5)\right] = \Phi(2,5) = 0,98758. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9fcd19d2dbae5fe0c4c1a12bf9ed537a_l3.png)
Задача 4. Пульт охраны связан с тремя охраняемыми объектами. Вероятность поступления сигнала с этих объектов составляет соответственно 0,2, 0,3 и 0,6. Составить закон распределения случайной величины: числа объектов с которых поступит сигнал. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Введем обозначения 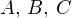 — события, заключающиеся в поступлении сигналов с первого, второго и третьего объектов соответственно. Тогда:
— события, заключающиеся в поступлении сигналов с первого, второго и третьего объектов соответственно. Тогда:
![Rendered by QuickLaTeX.com \[ P(0) = P(\overline{A}\,\overline{B}\,\overline{C}) = 0,8\cdot 0,7\cdot 0,4 = 0,224; \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-581f2f2c8fd9de4857d3cbd8ce86f5ea_l3.png)
![Rendered by QuickLaTeX.com \[ P(1) = P(A\overline{B}\,\overline{C}+\overline{A}B\overline{C}+\overline{A}\,\overline{B}C) = 0,2\cdot 0,7\cdot 0,4+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f2e5c34553f5236907574ab1b40d232c_l3.png)
![Rendered by QuickLaTeX.com \[ +0,8\cdot 0,3\cdot 0,4+0,8\cdot 0,7\cdot 0,6 = 0,488; \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f8a15550fd8950148bc9e7d6d67a00a1_l3.png)
![Rendered by QuickLaTeX.com \[ P(2) = P(AB\overline{C}+A\overline{B}C+\overline{A}BC) = 0,2\cdot 0,3\cdot 0,4+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-316f01123d56f704aaa40db910a75290_l3.png)
![Rendered by QuickLaTeX.com \[ +0,2\cdot 0,7\cdot 0,6+0,8\cdot 0,3\cdot 0,6 = 0,252. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-00b92a73226e5ca2baf5d3a5de4286bd_l3.png)
![Rendered by QuickLaTeX.com \[ P(3) = P(ABC) = 0,2\cdot 0,3\cdot 0,6 = 0,036. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a1452e310ada656aa30edb01ae643726_l3.png)
Контроль: 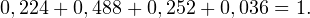
Закон распределения тогда принимает вид:
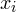 | 0 | 1 | 2 | 3 |
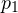 | 0,224 | 0,488 | 0,252 | 0,036 |
Математическое ожидание вычисляем по формуле:
![Rendered by QuickLaTeX.com \[ M(X) = \sum^{4}_{i=1} {x_ip_i}=0\cdot 0,224+1\cdot 0,488+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ce01ec24386249f05e7c4e7f3bb8568e_l3.png)
![Rendered by QuickLaTeX.com \[ +2\cdot 0,252+3\cdot 0,036 = 1,1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-354f230e20d6d0f7ddc0321221c7215f_l3.png)
Дисперсию вычисляем по формуле:
![Rendered by QuickLaTeX.com \[ D(X) = M\left(X^2\right) - \left[M(X)\right]^2=\sum^{4}_{i=1}{x^2_ip_i}-\left[M(X)\right]^2 = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2976d9b810bc080a402644049a69d994_l3.png)
![Rendered by QuickLaTeX.com \[ = 0^2\cdot 0,224+1^2\cdot 0,488+2^2\cdot 0,252+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e32c60dd9cb35ca33d1794555570898_l3.png)
![Rendered by QuickLaTeX.com \[ +3^2\cdot 0,036 - 1,1^2 = 0,61. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d04ecd6df01c9055e17adb059c5f3108_l3.png)
Решение.
а) В соответствии с основным свойством плотности вероятности, несобственный интеграл от плотности вероятности в пределах от 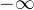 до
до 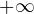 равен единице, то есть в нашем случае получаем:
равен единице, то есть в нашем случае получаем:
![Rendered by QuickLaTeX.com \[ \int\limits_{-\mathcal{1}}^{+\mathcal{1}} \varphi (x) \,dx = \int\limits_1^b \frac{1}{4}\,dx = \frac{1}{4}(b-1) = 1\Rightarrow b = 5. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a75b4572d358b230ad74b0828443f746_l3.png)
Итак, функция плотности вероятности случайной величины 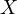 имеет вид:
имеет вид:
![Rendered by QuickLaTeX.com \[ \varphi(x) = \begin{cases} 0,\, x<1, \\ \frac{1}{4},\, 1\leqslant x\leqslant 5, \\ 0, x>5.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4fa2396b42f48c8260c9000bb38a08f9_l3.png)
б) Математическое ожидание непрерывной случайной величины определяется в нашем случае по формуле:
![Rendered by QuickLaTeX.com \[ M(X) = \int\limits_{-\mathcal{1}}^{+\mathcal{1}} x\cdot \varphi (x) \,dx = \int\limits_1^5 \frac{1}{4}x\, dx = \Bigl. \frac{x^2}{8} \Bigr|_1^5 = 3. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2552f3f2b86657821112ccc742e34f02_l3.png)
Дисперсия непрерывной случайной величины вычисляется в данном случае по формуле:
![Rendered by QuickLaTeX.com \[ D(X) = \int\limits_{-\mathcal{1}}^{+\mathcal{1}} x^2\cdot \varphi (x) \,dx - \left[M(X)\right]^2 = \int\limits_1^5 \frac{1}{4}x^2\, dx - 3^2= \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-635d9b33892f7d84de279acccb04989f_l3.png)
![Rendered by QuickLaTeX.com \[ =\Bigl. \frac{x^3}{12} \Bigr|_1^5 - 9 = \frac{125}{12}-\frac{1}{12} - 9 = \frac{31}{3}-9=\frac{4}{3}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1368ac740d5366954a6d20240c86018f_l3.png)
в) Функция распределения связана с плотностью вероятности следующим образом:
![Rendered by QuickLaTeX.com \[ F(x) = \int\limits_{-\mathcal{1}}^x \varphi (x) \,dx. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bd4780c5b881ddfebb6058cbe235b0b2_l3.png)
Интегрируя, получаем:
![Rendered by QuickLaTeX.com \[ F(x) = \begin{cases}0,\, x<1, \\ \frac{1}{4}x-\frac{1}{4},\, 1\leqslant x\leqslant 5, \\ 1,\, x>5. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bffbd0018f1900288aa6cc46078718dd_l3.png)
С помощью неравенства Чебышева оценим, что случайная величина принимает значения, находящиеся в промежутке ![Rendered by QuickLaTeX.com [1,5;4,5]:](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-976e7a3280c2cff12c53d38d91e8fd0b_l3.png)
![Rendered by QuickLaTeX.com \[ P(|x-a|\leqslant \varepsilon)\geqslant 1-\frac{D(X)}{\varepsilon^2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d6194bf1d6c59d011ea889d294f3547a_l3.png)
В нашем случае получаем:
![Rendered by QuickLaTeX.com \[ P(|x-3|\leqslant 1,5) \geqslant 1-\frac{\left(\frac{4}{3}\right)^2}{1,5^2} = \frac{17}{81}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-90c29f07d68e6c01178a488d1b078b3a_l3.png)
Это означает, что вероятность того, что наша случайная величина примет значение, находящееся в промежутке ![Rendered by QuickLaTeX.com [1,5;4,5]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-877ee616efaa4f89e3a85aa184029f38_l3.png) ограничена снизу значением
ограничена снизу значением 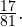
Оценим теперь эту же вероятность с помощью функции распределения:
![Rendered by QuickLaTeX.com \[ P = F(4,5)-F(1,5) = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-19904f196d7140286a6222a569560d4d_l3.png)
![Rendered by QuickLaTeX.com \[ =\frac{1}{4}\cdot 4,5-\frac{1}{4}-\left(\frac{1}{4}\cdot 1,5-\frac{1}{4}\right)=0,75. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f0ed769b2cac3d77132a873729e87ad7_l3.png)
Полученные значения не совпадают, поскольку неравенство Чебышева дает лишь нижнюю оценку вероятности случайного события, а не точное значение этой вероятности.
Репетитор по физике и математикеСергей ВалерьевичЧитать @Sergey_V_S
Один шанс на миллион выпадает десять раз из десяти!© Девиз оптимистов
Оптимизм — это недостаток информации.© Фаина Георгиевна Раневская
yourtutor.info
Контрольная работа№1 - Теория вероятностей и математическая статистика
Министерство образования Республики Беларусь
Учреждение образования
«Белорусский Государственный университет
информатики и радиоэлектроники»
Факультет непрерывного и дистанционного обучения
КОНТРОЛЬНАЯ РАБОТА №1
по дисциплине
Теория вероятностей и математическая статистика
Вариант № 5
Выполнил студент
Группа
Дата 2011-04-20
2011
Задача 1(3).
Подбрасываются две игральные кости. Определить вероятность того, что сумма выпавших чисел превышает 10.
Решение.
Равновозможными элементарными исходами здесь являются пары (x, y), где x и y принимают значения: 1,2,3,4,5,6. Таким образом, общее число элементарных исходов равно n = 6 * 6 = 36.
Событию А благоприятствуют пары (5;6), (6;6), (6;5), число которых равно m = 3.
Следовательно, Р(А) = m/n = 3/36 = 0,83+
Задача 2(39)
Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5, 6 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5 q6=0,6 . Найти вероятность того, что сигнал пройдет со входа на выход.

1 2 3
Решение.
Аi – работает i-ый элемент;
 - не работает i-ый элемент
- не работает i-ый элемент

 =
=
=(0,9*0,7+0,8*0,6-0,9*0,8*0,7*0,6)*(0,5+0,4-0,5*0,4)=0,5653+
Задача 3(27)
Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором - 10 белых и 10 черных шаров, в третьем - 20 черных шаров. Из каждого ящика вынули шар. Затем из этих трех шаров наугад взяли один шар. Вычислить вероятность того, что шар белый.
Решение.
А = {вынутый шар - белый};
Вi = {шар вынули из i-го ящика};
p(B1)=20/60=1/3; p(B2)=1/3; p(B3)=1/3 .
p(A/B1)=1; p(A/B2)=1/2; p(B3)=0 .
По формуле полной вероятности
p(A)=p(B1)*p(A/B1)+p(B2)*p(A/B2)+p(B3)*p(A/B3)=
=1/3 * 1 + 1/3 * 1/2 + 1/3 * 0 =0.5
Задача 4(21)
Монету подбрасывают восемь раз. Какова вероятность того, что она четыре раза упадет гербом вверх?
Решение.
Вероятность выпадения монеты гербом вверх p=1/2. По формуле Бернулли

n=8, k=4, p=1/2, q=1 - p=1/2
 +
+
Задача 5(7)
Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таблице). Найти p отмеченные *. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Таблица. 5.1
| Вариант | x1 | x2 | x3 | x4 | x5 | p1 | p2 | p3 | p4 | p5 |
| 5.7 | -5 | -2 | 0 | 1 | 2 | 0,5 | 0,1 | 0,1 | 0,2 | 0,1 |
Решение.
Математическое ожидание:

Дисперсия
 Определяем функцию распределения
Определяем функцию распределения






Строим график:

+
Задача 6(22)
Случайная величина Х задана плотностью вероятности


Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал .
.
| Вариант |  x,c) x,c)
| a | B | | |
| 6.22 | c x10 | -1 | 1 | -0,5 | 0,5 |
Решение.

Константу с вычислим исходя из условия нормировки




Математическое ожидание:

Дисперсия:

Функция распределения:

Вероятность попадания в интервал (-0,5; 0,5) будет:

+
Задача 7(11)
Случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).
| Вариант | 
| a | b |
| 7.11 | 
| -4 | 6 |
Решение.
Так как X равномерно распределено на интервале [-4; 6], то ее плотность вероятности:

Строим график величины y=2x в интервале [-4; 6] и в зависимости от числа k обратных функций выделим следующие интервалы для y:
[ -∞; -8] k=0
-∞; -8] k=0
[-8; 12] k=1
[12; +∞] k=0
Для интервалов (-∞; -8) и (12; -∞) g(y)=0
Для интервалов [-∞; 12] g(y)=y/2
Тогда получаем

+
Задача 8(31)
Двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рисунке области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:


Вычислить коэффициент корреляции между величинами X и Y.

Вариант | x1 | x2 | x3 | x4 | x5 | x6 | y1 | y2 |
| 8.31 | 0 | 0 | 0 | 1 | 1 | 2 | 1 | 2 |

Решение.
Плотность вероятности будет

Определим С:

Так как имеем симметричную фигуру, то mx=my; Дx=Ду;



Коэффициент корреляции

Задача 9(9)
Вычислить математическое ожидание и дисперсию величин U и V, а так же определить их коэффициент корреляции  :
:

 .
.
Конкретные значения коэффициентов  и числовые характеристики случайных величин
и числовые характеристики случайных величин приведены в таблице
приведены в таблице
Таблица
| Вариант | a0 | a1 | a2 | b0 | b1 | b2 | m1 | m2 | m3 | D1 | D2 | D3 | K12 | K23 | K13 |
| 9.9 | -1 | 7 | 1 | -9 | -7 | -3 | 0 | 5 | 1 | 4 | 16 | 4 | 4 | 4 | 0 |


Вычислим математические ожидания U и V:
mU=-1+7 m1+ m2=4;
mV=-9-7 m2-3 m3=-47;
Вычислим дисперсии U и V:


Вычислим корреляционный момент KUV




Тогда 
Величина RUV будет:
 +
+
studfiles.net
Контрольная работа по теории вероятности
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Уральский государственный экономический университет» в г. Березники
Кафедра экономики
Контрольная работа
по дисциплине: «Теория вероятностей»
Вариант №2
Выполнил:
студент 1 курса, группы БЭС-12
Григорьев М.А.
Проверил:
К.ф.-м.н., профессор
Кобзев Виктор Николаевич
Березники
2013
Вариант №2
Задание №1
В первой урне находятся 17 белых и 3 черных шаров, во второй урне – 4 белых и 4 черных шаров. Из первой урны во вторую переложили 2 шара, а затем из второй урны извлекли один шар.
Найти вероятность того что этот шар белый.
Решение:
Мы провели 3 опыта:
Из 1-ой урны во 2-ую переложили 1 шар
Из 1-ой урны во 2-ую переложили 1 шар
Из 2-ой урны извлекли 1 шар
Следовательно, дерево вероятностей содержит 3 уровня вершин и 2 возможных варианта исхода. Составим дерево вероятностей.
| Достаем 1-ый шар из 1-ой урны |
| Белый  | Черный  |
| 2-ой шар из 1-ой урны | 2-ой шар из 1-ой урны |
| Белый  | Черный  | Белый  | Черный  |
| Шар из 2 урны | Шар из 2 урны | Шар из 2 урны | Шар из 2 урны |
| Белый  | Черный  | Белый  | Черный  | Белый  | Черный  | Белый  | Черный  |
| Б Б Б | Б Б Ч | Б Ч Б | Б Ч Ч | Ч Б Б | Ч Б Ч | Ч Ч Б | Ч Ч Ч |
Всего 8 возможных путей, выбираем вероятности при которых шар извлеченный из 2 урны шар будет белым.
Вероятность того что шар извлеченный из 2 урны будет белый равна:

Задание №2
На заводах A и B изготавливают 90% и 10% всех деталей. Из прошлых данных известно, что 30% деталей завода А и 10% деталей завода В оказываются бракованными. Случайно выбранная деталь оказалась бракованной. Какова вероятность того, что она изготовлена на заводе А?
Решение:
Проводим 2 опыта:
Случайно выбираем завод
Случайно выбираем деталь
Составим дерево вероятностей.
| Выбран завод |
| А  | В  |
| Брак  | Не брак  | Брак  | Не брак  |
| 
| 
| 
| 
|
Найдем процент брака на заводах А и В:

Найдем процент брака на заводе А:

Вероятность того, что бракованную деталь изготовили на заводе А будет равна:

Задание №3
Вероятность поражения стрелком мишени при одном выстреле равна  . Найти вероятность того что при
. Найти вероятность того что при выстрелах мишень будет поражена не менее
выстрелах мишень будет поражена не менее раз.
раз.
Решение:
Найдем вероятность поражения стрелком мишени используя интегральную теорему Лапласа.

 =
=





Задание №4
Среднее число самолетов, прибывающих в аэропорт за 1 минуту, равно  . Найти вероятность того, что за время
. Найти вероятность того, что за время минуты прибудут:
минуты прибудут:
 самолетов
самолетов
не менее  самолетов
самолетов
Поток предполагается простейшим.
Решение:



События  и
и
 противоположные.
противоположные.
Поэтому сумма их вероятностей равна 1.



Тогда,



Задание №5
Произведено  независимых испытаний. В каждом из них вероятность появления события А равна
независимых испытаний. В каждом из них вероятность появления события А равна . Найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа
. Найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа .
.
Решение:



Где Ф функция Лапласа.
Задание №6
Дискретная случайная величина принимает значения  с вероятностями
с вероятностями .
.
Найти ее математическое ожидание и дисперсию.
Решение:
Для определения математического ожидания и дисперсии дискретной СВ Х заполним таблицу.
| 
| 
| 
| 
| 
|
| 4 | 0,4 | 1,6 | 16 | 6,4 |
| 7 | 0,5 | 3,5 | 49 | 24,5 |
| 1 | 0,1 | 0,1 | 1 | 0,1 |
| Сумма | 1 | 5,2 | 66 | 31 |


Задание №7
Плотность распределения вероятностей непрерывной случайной величины Х имеет вид, показанный на графике. Найти неизвестное число m, функцию распределения F(x), математическое ожидание М(х) и дисперсию D(x).

Решение:
 свойство функции f(x)
свойство функции f(x)

(геометрический смысл определенного интеграла)


На участке 1  и на участке 4
и на участке 4
На участке 2  это отрезок прямойAB. Проходящей через точки
это отрезок прямойAB. Проходящей через точки  , тогда
, тогда

Следовательно 
На участке 3  графикf(x) это отрезок прямой СВ. Проходящей через точки
графикf(x) это отрезок прямой СВ. Проходящей через точки  , тогда
, тогда

Следовательно 

Найдем функцию распределения F(x). Известно, что 
Воспользуемся геометрическим смыслом определенного интеграла.
Если  , то
, то и площадь под кривой равна 0.
и площадь под кривой равна 0.
Если  , то
, то
Если  , то
, то

Координаты точек М(х;0) и N(х;f(х)) . Тогда
. Тогда

Если  , то
, то


Координаты точек 
Тогда


Математическое ожидание:



Дисперсия:


Задание №8
Плотность распределения вероятностей нормально распределенной случайной величины Х имеет вид

Найти неизвестно число  , математическое ожиданиеM(X), дисперсию D(X),
, математическое ожиданиеM(X), дисперсию D(X),
вероятность выполнения неравенства  и
и .
.
Решение:
Выделим полный квадрат в выражении:


Следовательно, из нормального закона распределения вероятностей:

Следовательно





 и
и 

Это стандартное отклонение.




studfiles.net
Контрольная по теории вероятности
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ИНСТИТУТ ВЫСОКИХ ТЕХНОЛОГИЙ
Факультет заочного и послевузовского обучения
КОНТРОЛЬНАЯ РАБОТА №1
По дисциплине: "Теория вероятностей и элементы математической статистики"
Воронеж 200 4 г.
Вариант – 9.
Задача № 1.
№№ 1-20. Техническое устройство, состоящее из трех узлов, работало в течение некоторого времени t. За это время первый узел оказывается неисправным с вероятностью р1 , второй – с вероятностью р2 , третий – с вероятностью р3 . Найти вероятность того, что за время работы: а) все узлы оставались исправными; б) все узлы вышли из строя; в) только один узел стал неисправным; г) хотя бы один узел стал неисправным (см. исходные данные в таблице).
p 1 =0,4 p2 =0,6 p3 =0,9
Решение:
Пусть событие А означает, что первый узел оказался неисправным, В оказался неисправным второй узел и С – оказался неисправным третий узел, тогда
 - первый узел был исправен в промежуток времени t ,
- первый узел был исправен в промежуток времени t ,  - был исправен второй узел,
- был исправен второй узел,  - был исправен третий узел.
- был исправен третий узел. а) Пусть событие D означает, что все узлы оставались исправными, тогда
 . Поэтому , учитывая независимость событий
. Поэтому , учитывая независимость событий  ,
,  и
и  , по теореме умножения вероятностей имеем:
, по теореме умножения вероятностей имеем: 
б) Пусть событие Е – все узлы вышли из строя, тогда:

в) Пусть событие F – только один узел стал неисправным, тогда:

События
 несовместные. Поэтому, применяя теорему сложения вероятностей несовместимых событий, получим:
несовместные. Поэтому, применяя теорему сложения вероятностей несовместимых событий, получим: 


г) Пусть событие D1 – хотя бы один узел стал неисправным, тогда:

 .
. Задача № 2
№39. По линии связи могут быть переданы символы А, В, С. Вероятность передачи символа А равна 0,5; символа В – 0,3; символа С – 0,2. Вероятности искажения при передаче символов А, В, С равны соответственно 0,01; 0,03; 0,07. Установлено, что сигнал из двух символов принят без искажения. Чему равна вероятность, что передавался сигнал АВ?
Решение:
Пусть событие А – передача символа А, событие В – передача символа В, событие С – передача символа С, событие
 - искажение при передаче символа А, событие
- искажение при передаче символа А, событие  и
и  - искажения при передаче символов В и С соответственно.
- искажения при передаче символов В и С соответственно. По условию вероятности этих событий равны:
 ,
, 
 ,
,  ,
,  ,
, 
Если события
 ,
,  и
и  - искажения при передаче символов, то события
- искажения при передаче символов, то события  ,
,  и
и  - отсутствие искажений при передаче. Их вероятности:
- отсутствие искажений при передаче. Их вероятности: 
Обозначим через D событие, состоящее в том, что были переданы два символа без искажений.
Можно выдвинуть следующие гипотезы:
Н1 – переданы символы АА,
Н2 – символы АВ,
Н3 – символы ВА,
Н4 – символы АС,
Н5 – символы СА,
Н6 – символы ВВ,
Н7 – символы ВС,
Н8 – символы СВ,
Н9 – символы СС.
Вероятности этих гипотез:









Условные вероятности события D если имела место одна из гипотез будут:


По формуле Бейеса вычислим условную вероятность
 с учетом появления события Р :
с учетом появления события Р : 

Задача № 3
№№ 41-60. Найти вероятность того, что в п независимых испытаниях событие появится: а) ровно k раз; б) не менее k раз; в) не более k раз; г) хотя бы один раз, если в каждом испытании вероятность появления этого события равна р (см. исходные данные в таблице).
Решение:
Так как число испытаний невелико, то для вычисления искомой вероятности воспользуемся формулой Бернулли:
 , где
, где 
число сочетаний из п элементов по k , q=1- p . В рассматриваемом случае:
а) вероятность появления события ровно 4 раза в 5 испытаниях:

б) вероятность появления события не менее 4 раз в 5 испытаниях:

в) вероятность появления события не более 4 раз в 5 испытаниях:

г) вероятность появления события хотя бы один раз в 5 испытаниях:

Задача № 4
№№ 61-80. Дана плотность распределения f( x) случайной величины Х. Найти параметр а, функцию распределения случайной величины, математическое ожидание М[Х], дисперсию D[ X], вероятность выполнения неравенства х1 < x< x2 , построить график функции распределения F( x).

Решение:
Для определения параметра а воспользуемся основным свойством плотности распределения:
 , так как при
, так как при  плотность распределения равна нулю, то интеграл примет вид:
плотность распределения равна нулю, то интеграл примет вид:  или
или  , откуда
, откуда  ;
; 
Функция распределения связана с функцией плотности соотношением:

Откуда получим:

mirznanii.com
Контрольная работа по теме «Теория вероятности»
Контрольная работа по теме «Теория вероятности» Вариант 1 1. В фирме такси в данный момент свободно 15 машин: 4 желтых, 6 белых и 5 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Результат округлите до сотых. 2. Из множества натуральных чисел от 5 до 15 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3 без остатка? 3. За круглый стол на 6 стульев в случайном порядке рассаживаются 4 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом. 4. Николай Иванов регистрируется на посадку в самолет. Всего в самолете 300 мест, из них для пассажиров высокого роста удобны только 10 мест возле запасных выходов и 20 мест за перегородками, разделяющими салоны. Найдите вероятность того, что Николаю достанется удобное место при регистрации, если он высокого роста. 5. На семинар приехали 3 ученых из Норвегии, 4 из России и 8 из Испании. Порядок докладов определяется жеребьевкой. Найдите вероятность того, что девятым окажется доклад ученого из России. Ответ округлите до сотых. 6. В классе 24 учащихся, среди них два друга — Радим и Евгений. Класс случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Радим и Евгений окажутся в одной группе. 7. Конкурс исполнителей проводится 1 неделю. Всего заявлено 45 выступлений - по одному от каждой, участвующей, страны. В первый день 9 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Ответ округлите до сотых. | Контрольная работа по теме «Теория вероятности» Вариант 2 1. В фирме такси в наличии 50 легковых автомобилей. 27 из них красные с черными надписями, остальные – белые с синими надписями. Найдите вероятность того, что на случайный вызов приедет белая машина с синими надписями. 2. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет больше 2, но меньше 7? 3. Настя, Аня, Дима и Олег бросили жребий – кому сегодня дежурить. Найдите вероятность того, что дежурить будет Олег. 4. Группу туристов из 40 человек забрасывают вертолетом на остров по 5 человек за рейс. Вертолет забирает туристов в случайном порядке.. Найдите вероятность, что туристка Марина полетит первым рейсом вертолета 5. На семинар приехали 4 ученых из Франции, 3 из Болгарии и еще 2 из Франции. Порядок докладов определяется жеребьевкой. Найдите вероятность того, что восьмым окажется доклад ученого из Франции. Ответ округлите до десятых. 6. Научная конференция проводится в 4 дня. Всего запланировано 60 докладов — в первый день 18 докладов, остальные распределены поровну между остальными тремя днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Результат округлите до сотых. 7. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 146 бадминтонистов, среди которых 7 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Результат округлите до сотых. | Контрольная работа по теме «Теория вероятности» Вариант 3 1. На экзамен по математике вынесено 70 вопросов. Вадим не выучил 10 из них. Какова вероятность, что ему попадется не выученный вопрос? Ответ округлите до сотых. 2. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 5, но не дойдя до отметки 10 часов. Результат округлите до сотых. 3. Профсоюз закупил 40 призов на школьный художественный конкурс. Из них 14 блокнотов и 26 коробок карандашей. Подарки распределяются случайным образом. Найдите вероятность того, что Ане достанется коробка карандашей. 4. В экзаменационном сборнике задач по механике 30 билетов, в 5 из них встречается вопрос по законам Ньютона. Какова вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по законам Ньютона. Ответ округлите до сотых. 5. На соревнованиях «Мистер Олимпия» участвуют: 6 бодибилдеров из США, 4 бодибилдера из Канады, 8 бодибилдеров из Франции и 3 бодибилдера из Германии. Порядок, в котором выступают бодибилдеры, определяется жребием. Найдите вероятность того, что бодибилдер, который выступает последним, окажется из США. Ответ округлите до сотых. 6. В чемпионате мира участвуют 35 команд, одна из которых США. С помощью жребия их нужно разделить на пять групп по семь команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда США окажется в первой группе? 7. В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что решка не выпадет ни разу. Результат округлите до сотых. | Контрольная работа по теме «Теория вероятности» Вариант 4 1. На экзамене 55 вопросов, Коля не выучил 9 из них. Найдите вероятность того, что ему попадется выученный вопрос. Результат округлите до сотых. 2. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет четной? 3. Процент брака при производстве стекла составляет 2%. Какова вероятность купить бракованное стекло? 4. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 14 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России? Результат округлите до сотых. 5. На чемпионате по стрельбе из лука выступают 15 спортсменов, среди них 7 стрелков из России и 8 стрелков из Малайзии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что седьмым будет выступать стрелок из России. Ответ округлите до сотых. 6. В среднем из 750 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. Ответ округлите до тысячных. 7. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А = «сумма очков равна 9»? | Контрольная работа по теме «Теория вероятности» Вариант 5 1. На тарелке 16 пирожных: 7 шоколадных, 5 клубничных и 4 со сливочным кремом. Коля наугад берет пирожное. Какова вероятность, что оно окажется клубничным? Ответ округлите до сотых. 2. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет меньше 5? 3. В кармане у Коли было четыре конфеты: «Грильяж», «Коровка», «Ласточка» и «Пчелка», а также ключи от квартиры. Вынимая ключи, Коля случайно выронил одну конфету. Какова вероятность, что потерялась конфета «Ласточка»? 4. В экзаменационном сборнике задач по биологии всего 70 билетов, в 13 из них встречается вопрос по неклеточным формам жизни. Определите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по неклеточным формам жизни. Ответ округлите до сотых. 5. На мировом чемпионате, по легкой атлетике, участвуют 35 спортсменов: 10 из России, 8 из Канады, остальные - из Китая. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Китая. Ответ округлите до сотых. 6. Фабрика выпускает сумки. В среднем на 150 качественных сумок приходится семь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. 7. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 14 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России? Результат округлите до сотых. | infourok.ru
 Время от времени посетители сайта, узнав, что я являюсь действующим сотрудником МПГУ (Московского Педагогического Государственного Университета) и непосредственно связан с преподаванием физики в этом вузе, задают мне вопрос, занимаюсь ли я решением контрольных работ для студентов. Иногда этот вопрос звучит в более «мягкой» форме, а именно, осуществляю ли я помощь в выполнении контрольных работ по физике и математике для студентов вузов. Как бы то ни было, смысл остается тем же. Отвечаю вам на этот вопрос, уважаемые читатели.
Время от времени посетители сайта, узнав, что я являюсь действующим сотрудником МПГУ (Московского Педагогического Государственного Университета) и непосредственно связан с преподаванием физики в этом вузе, задают мне вопрос, занимаюсь ли я решением контрольных работ для студентов. Иногда этот вопрос звучит в более «мягкой» форме, а именно, осуществляю ли я помощь в выполнении контрольных работ по физике и математике для студентов вузов. Как бы то ни было, смысл остается тем же. Отвечаю вам на этот вопрос, уважаемые читатели.![Rendered by QuickLaTeX.com \[ C_{40}^2 = \frac{40!}{2!\cdot (40-2)!} = \frac{39\cdot 40}{2} = 780. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-048dcdd963e24c7f0914ae3a7b50be86_l3.png)
![Rendered by QuickLaTeX.com \[ C_8^2=\frac{8!}{2!\cdot (8-2)!} = \frac{7\cdot 8}{2} = 28. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0f81a8cbccea79d78000a1ea06fc1cd2_l3.png)
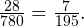 Тогда вероятность противоположного события, заключающегося в том, что студенту попадется хотя бы один вопрос, который он знает, равна:
Тогда вероятность противоположного события, заключающегося в том, что студенту попадется хотя бы один вопрос, который он знает, равна: 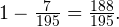
![Rendered by QuickLaTeX.com \[ C_{32}^2 = \frac{32!}{2!\cdot (32-2)!} = \frac{31\cdot 32}{2} = 496. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-12a3133b7b3e4fd718e81ff10a886f41_l3.png)
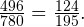
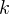 раз в
раз в 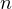 независимых испытаниях равна
независимых испытаниях равна 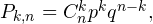 здесь
здесь 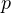 — вероятность наступления отдельного события (в нашем случае
— вероятность наступления отдельного события (в нашем случае 
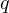 — вероятность того, что это событие не наступит в единичном исследовании (в нашем случае
— вероятность того, что это событие не наступит в единичном исследовании (в нашем случае  Ищем вероятность того, что приживется 5 или 6 кустов, то есть искомая вероятность равна:
Ищем вероятность того, что приживется 5 или 6 кустов, то есть искомая вероятность равна:![Rendered by QuickLaTeX.com \[ P_{5,6}+P_{6,6} = C_6^5\cdot 0,8^5\cdot 0,2^{6-5}+C_6^6\cdot 0,8^6\cdot 0,2^{6-6} = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f61eb86b58cee1caa39346f75e078b49_l3.png)
![Rendered by QuickLaTeX.com \[ =6\cdot 0,32768\cdot 0,2+0,262144 = 0,65536. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8447981b9b8bc2417aa50010f3be60da_l3.png)
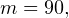
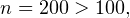
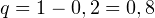 , тогда
, тогда 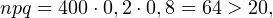 следовательно в расчетах можно использовать локальную и интегральную теоремы Муавра-Лапласа.
следовательно в расчетах можно использовать локальную и интегральную теоремы Муавра-Лапласа.![Rendered by QuickLaTeX.com \[ x_m = \frac{m-n\cdot p}{\sqrt{npq}} = \frac{90-0,2\cdot 400}{\sqrt{400\cdot 0,2\cdot 0,8}} = 1,25. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-75995a827e502815d836cf672057b25f_l3.png)
![Rendered by QuickLaTeX.com \[ f(x_m) = f(1,25) = 0,1826. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8fdc12b62b166252929f4850eb7a8a4b_l3.png)
![Rendered by QuickLaTeX.com \[ P_{400}(90) = \frac{1}{\sqrt{npq}}\cdot f(x_m) = \frac{1}{8}\cdot 0,1826 = 0,0228. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-16748bde51f89edf9f70baae0e56fa0d_l3.png)
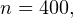
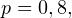
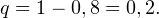 Получаем тогда:
Получаем тогда:![Rendered by QuickLaTeX.com \[ x_1 = \frac{a-np}{\sqrt{npq}} = \frac{300-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}} = -2,5 \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ec35da10570cf9fed184637f0bb9b2f8_l3.png)
![Rendered by QuickLaTeX.com \[ x_2 = \frac{b-np}{\sqrt{npq}} = \frac{340-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}} = 2,5. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c256a7284f4c0ae0f3fe90828da35b94_l3.png)
![Rendered by QuickLaTeX.com \[ p = \frac{1}{2}\left[\Phi(2,5)-\Phi(-2,5)\right] = \Phi(2,5) = 0,98758. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9fcd19d2dbae5fe0c4c1a12bf9ed537a_l3.png)
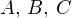 — события, заключающиеся в поступлении сигналов с первого, второго и третьего объектов соответственно. Тогда:
— события, заключающиеся в поступлении сигналов с первого, второго и третьего объектов соответственно. Тогда:![Rendered by QuickLaTeX.com \[ P(0) = P(\overline{A}\,\overline{B}\,\overline{C}) = 0,8\cdot 0,7\cdot 0,4 = 0,224; \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-581f2f2c8fd9de4857d3cbd8ce86f5ea_l3.png)
![Rendered by QuickLaTeX.com \[ P(1) = P(A\overline{B}\,\overline{C}+\overline{A}B\overline{C}+\overline{A}\,\overline{B}C) = 0,2\cdot 0,7\cdot 0,4+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f2e5c34553f5236907574ab1b40d232c_l3.png)
![Rendered by QuickLaTeX.com \[ +0,8\cdot 0,3\cdot 0,4+0,8\cdot 0,7\cdot 0,6 = 0,488; \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f8a15550fd8950148bc9e7d6d67a00a1_l3.png)
![Rendered by QuickLaTeX.com \[ P(2) = P(AB\overline{C}+A\overline{B}C+\overline{A}BC) = 0,2\cdot 0,3\cdot 0,4+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-316f01123d56f704aaa40db910a75290_l3.png)
![Rendered by QuickLaTeX.com \[ +0,2\cdot 0,7\cdot 0,6+0,8\cdot 0,3\cdot 0,6 = 0,252. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-00b92a73226e5ca2baf5d3a5de4286bd_l3.png)
![Rendered by QuickLaTeX.com \[ P(3) = P(ABC) = 0,2\cdot 0,3\cdot 0,6 = 0,036. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a1452e310ada656aa30edb01ae643726_l3.png)
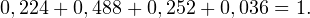
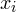
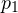
![Rendered by QuickLaTeX.com \[ M(X) = \sum^{4}_{i=1} {x_ip_i}=0\cdot 0,224+1\cdot 0,488+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-ce01ec24386249f05e7c4e7f3bb8568e_l3.png)
![Rendered by QuickLaTeX.com \[ +2\cdot 0,252+3\cdot 0,036 = 1,1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-354f230e20d6d0f7ddc0321221c7215f_l3.png)
![Rendered by QuickLaTeX.com \[ D(X) = M\left(X^2\right) - \left[M(X)\right]^2=\sum^{4}_{i=1}{x^2_ip_i}-\left[M(X)\right]^2 = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2976d9b810bc080a402644049a69d994_l3.png)
![Rendered by QuickLaTeX.com \[ = 0^2\cdot 0,224+1^2\cdot 0,488+2^2\cdot 0,252+ \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e32c60dd9cb35ca33d1794555570898_l3.png)
![Rendered by QuickLaTeX.com \[ +3^2\cdot 0,036 - 1,1^2 = 0,61. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d04ecd6df01c9055e17adb059c5f3108_l3.png)
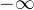 до
до 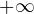 равен единице, то есть в нашем случае получаем:
равен единице, то есть в нашем случае получаем:![Rendered by QuickLaTeX.com \[ \int\limits_{-\mathcal{1}}^{+\mathcal{1}} \varphi (x) \,dx = \int\limits_1^b \frac{1}{4}\,dx = \frac{1}{4}(b-1) = 1\Rightarrow b = 5. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a75b4572d358b230ad74b0828443f746_l3.png)
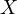 имеет вид:
имеет вид:![Rendered by QuickLaTeX.com \[ \varphi(x) = \begin{cases} 0,\, x<1, \\ \frac{1}{4},\, 1\leqslant x\leqslant 5, \\ 0, x>5.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4fa2396b42f48c8260c9000bb38a08f9_l3.png)
![Rendered by QuickLaTeX.com \[ M(X) = \int\limits_{-\mathcal{1}}^{+\mathcal{1}} x\cdot \varphi (x) \,dx = \int\limits_1^5 \frac{1}{4}x\, dx = \Bigl. \frac{x^2}{8} \Bigr|_1^5 = 3. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2552f3f2b86657821112ccc742e34f02_l3.png)
![Rendered by QuickLaTeX.com \[ D(X) = \int\limits_{-\mathcal{1}}^{+\mathcal{1}} x^2\cdot \varphi (x) \,dx - \left[M(X)\right]^2 = \int\limits_1^5 \frac{1}{4}x^2\, dx - 3^2= \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-635d9b33892f7d84de279acccb04989f_l3.png)
![Rendered by QuickLaTeX.com \[ =\Bigl. \frac{x^3}{12} \Bigr|_1^5 - 9 = \frac{125}{12}-\frac{1}{12} - 9 = \frac{31}{3}-9=\frac{4}{3}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1368ac740d5366954a6d20240c86018f_l3.png)
![Rendered by QuickLaTeX.com \[ F(x) = \int\limits_{-\mathcal{1}}^x \varphi (x) \,dx. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bd4780c5b881ddfebb6058cbe235b0b2_l3.png)
![Rendered by QuickLaTeX.com \[ F(x) = \begin{cases}0,\, x<1, \\ \frac{1}{4}x-\frac{1}{4},\, 1\leqslant x\leqslant 5, \\ 1,\, x>5. \end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-bffbd0018f1900288aa6cc46078718dd_l3.png)
![Rendered by QuickLaTeX.com [1,5;4,5]:](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-976e7a3280c2cff12c53d38d91e8fd0b_l3.png)
![Rendered by QuickLaTeX.com \[ P(|x-a|\leqslant \varepsilon)\geqslant 1-\frac{D(X)}{\varepsilon^2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-d6194bf1d6c59d011ea889d294f3547a_l3.png)
![Rendered by QuickLaTeX.com \[ P(|x-3|\leqslant 1,5) \geqslant 1-\frac{\left(\frac{4}{3}\right)^2}{1,5^2} = \frac{17}{81}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-90c29f07d68e6c01178a488d1b078b3a_l3.png)
![Rendered by QuickLaTeX.com [1,5;4,5]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-877ee616efaa4f89e3a85aa184029f38_l3.png) ограничена снизу значением
ограничена снизу значением 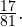
![Rendered by QuickLaTeX.com \[ P = F(4,5)-F(1,5) = \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-19904f196d7140286a6222a569560d4d_l3.png)
![Rendered by QuickLaTeX.com \[ =\frac{1}{4}\cdot 4,5-\frac{1}{4}-\left(\frac{1}{4}\cdot 1,5-\frac{1}{4}\right)=0,75. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-f0ed769b2cac3d77132a873729e87ad7_l3.png)

 - не работает i-ый элемент
- не работает i-ый элемент
 =
=
 +
+
 Определяем функцию распределения
Определяем функцию распределения








 .
. x,c)
x,c)











 -∞; -8] k=0
-∞; -8] k=0 










 :
:
 .
. и числовые характеристики случайных величин
и числовые характеристики случайных величин приведены в таблице
приведены в таблице








 +
+



























 . Найти вероятность того что при
. Найти вероятность того что при выстрелах мишень будет поражена не менее
выстрелах мишень будет поражена не менее раз.
раз.
 =
=




 . Найти вероятность того, что за время
. Найти вероятность того, что за время минуты прибудут:
минуты прибудут: самолетов
самолетов самолетов
самолетов


 и
и противоположные.
противоположные.





 независимых испытаний. В каждом из них вероятность появления события А равна
независимых испытаний. В каждом из них вероятность появления события А равна . Найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа
. Найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит заданного числа .
.


 с вероятностями
с вероятностями .
.







 свойство функции f(x)
свойство функции f(x)


 и на участке 4
и на участке 4
 это отрезок прямойAB. Проходящей через точки
это отрезок прямойAB. Проходящей через точки  , тогда
, тогда

 графикf(x) это отрезок прямой СВ. Проходящей через точки
графикf(x) это отрезок прямой СВ. Проходящей через точки  , тогда
, тогда



 , то
, то и площадь под кривой равна 0.
и площадь под кривой равна 0. , то
, то
 , то
, то

 . Тогда
. Тогда
 , то
, то











 , математическое ожиданиеM(X), дисперсию D(X),
, математическое ожиданиеM(X), дисперсию D(X), и
и .
.







 и
и 





 - первый узел был исправен в промежуток времени t ,
- первый узел был исправен в промежуток времени t ,  - был исправен второй узел,
- был исправен второй узел,  - был исправен третий узел.
- был исправен третий узел.  . Поэтому , учитывая независимость событий
. Поэтому , учитывая независимость событий 


 несовместные. Поэтому, применяя теорему сложения вероятностей несовместимых событий, получим:
несовместные. Поэтому, применяя теорему сложения вероятностей несовместимых событий, получим: 



 .
.  - искажение при передаче символа А, событие
- искажение при передаче символа А, событие  и
и  - искажения при передаче символов В и С соответственно.
- искажения при передаче символов В и С соответственно.  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  и
и  - отсутствие искажений при передаче. Их вероятности:
- отсутствие искажений при передаче. Их вероятности: 











 с учетом появления события Р :
с учетом появления события Р : 

 , где
, где 





 , так как при
, так как при  плотность распределения равна нулю, то интеграл примет вид:
плотность распределения равна нулю, то интеграл примет вид:  или
или  , откуда
, откуда  ;
;