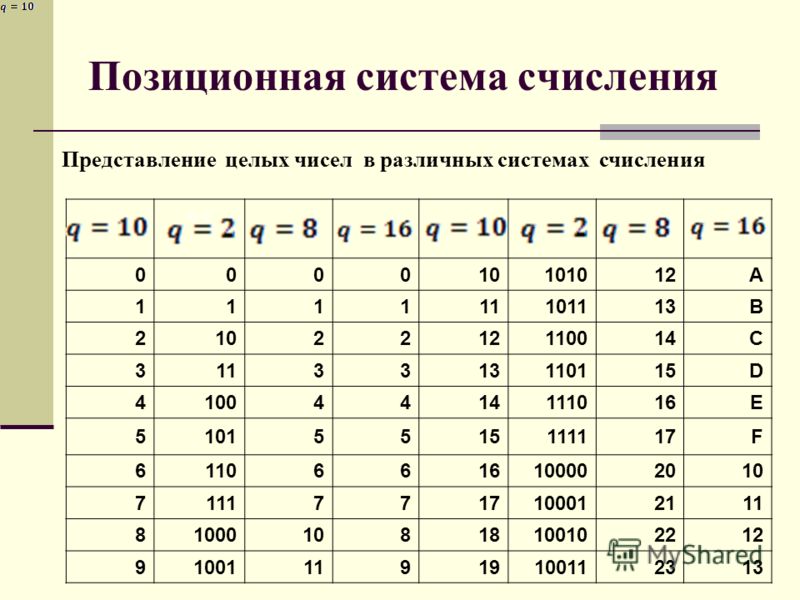
Контрольная работа по теме «Системы счисления» 8 класс
Контрольная работа №1
по теме «Системы счисления» (8 класс)
Вариант 1.
Часть А.
Задание 1. Тестовые вопросы. Определите один правильный ответ. За каждый правильный ответ 1 балл.
Совокупность знаков, с помощью которых записываются числа, называется:Алфавитом системы счисления
Системой счисления
Цифрами системы счисления
Основанием системы счисления
Система счисления – это:
Знаковая система, в которой приняты определенные правила чтения и записи чисел
Знаки, с помощью которых записываются числа
Совокупность знаков, с помощью которых записываются числа
Ничего неправильно
Число 301011 может существовать в системах счисления с основаниями:
2 и 4 c) 4 и 8
4 и 3 d) 2 и 10
В классе 110010% девочек и 10102 мальчиков.
Сколько учеников в классе.
40 b) 30 c)20 d) 10
Сколько единиц в двоичном представлении десятичного числа 15?
1 b) 2 c) 3 d) 4
Ячейка памяти компьютера состоит из однородных элементов, называемых:
Коэффициентами c) Цифрами
Разрядами d) кодами
Количество разрядов, занимаемых однобайтовым числом, равно
64 b) 32 c) 16 d) 8
Положительное число, представленное в 8-разрядном прямом коде:
11111001 c) 1001000
11110110 d) 00000001
Отрицательные числа хранятся в компьютере в :
прямом коде b) обратном коде c) дополнительном коде
В знаковый разряд ячейки для положительных чисел заносится:
1 b) 0 c) + d) —
В компьютере используются системы счисления:
Двоичная, четверичная, десятичная
Двоичная, восьмеричная и шестнадцатеричная
Восьмеричная и шестнадцатеричная
Двоичная и десятичная
Восьмеричная система счисления имеет следующий алфавит:
0,1,2,3,4,5,6,7
0,1,2,3,4,5,6,7,8
1,2,3,4,5,6,7,8,
0,1,8.
Простейшая и самая древняя система счисления:
Унарная
Позиционная
Непозиционная
Система счисления называется НЕпозиционной, если:
значение цифры (ее «вес») зависит от ее позиции в записи числа, в которой она стоит
значение цифры (ее «вес») не зависит от ее позиции в записи числа, в которой она стоит
Найдите НЕправильное утверждение:
Основанием позиционной системы счисления может служить любое натуральное число
В непозиционной системе счисления любое число может быть представлено в развернутой форме
Двоичные числа представляются в компьютере с помощью простых технических устройств с двумя устойчивыми состояниями (триггеры)
Обмен информацией между компьютерными устройствами осуществляется путем передачи двоичных кодов
Часть В.
За каждый правильный ответ с решением 1 балл.
Задание 2. Представьте в развернутой форме следующие числа:
10011,012 b) 17702,558.
Задание 3. Переведите числа из 10-й системы счисления в 2-ую:
Задание 4. Переведите числа из 2-й системы счисления в 10-ую:
100012 b) 10101,12.
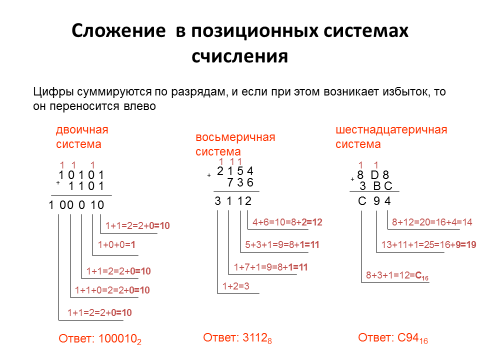
Задание 5. Выполните арифметические операции над двоичными числами:
110101+10101 b) 110011-11101 c) 101*10
Задание 6. Представьте в однобайтовой ячейке целое положительное и отрицательное число: +14 и -14.
Задание 7.
Найдите значение x, для которого верно следующее равенство: 23
Контрольная работа №1
по теме «Системы счисления» (8 класс)
Вариант 2.
Часть А.
Задание 1. Тестовые вопросы. Определите один правильный ответ. За каждый правильный ответ 1 балл.
Простейшая и самая древняя система счисления:Непозиционная b) Позиционная c) Унарная
Система счисления называется позиционной, если:
значение цифры (ее «вес») не зависит от позиции в записи числа, в которой она стоит
значение цифры (ее «вес») зависит от позиции в записи числа, в которой она стоит
Найдите НЕправильное утверждение:
Двоичные числа представляются в компьютере с помощью простых технических устройств с двумя устойчивыми состояниями (триггеры)
Обмен информацией между компьютерными устройствами осуществляется путем передачи троичных кодов
Основанием позиционной системы счисления может служить любое натуральное число
В позиционной системе счисления любое число может быть представлено в развернутой форме
Положительные числа хранятся в компьютере в :
прямом коде b) обратном коде c) дополнительном коде
Ячейка памяти компьютера состоит из однородных элементов, называемых:
Разрядами c) кодами
Коэффициентами d) Цифрами
Отрицательное число, представленное в 8-разрядном прямом коде:
01111001 c) 10010000
01110110 d) 00000001
Количество разрядов, занимаемых двухбайтовым числом, равно
8 b) 16 c) 32 d) 64
В знаковый разряд ячейки для отрицательных чисел заносится:
+ b) – c) 1 d) 0
Знаки, с помощью которых записываются числа, называется:
Цифрами системы счисления
Основанием системы счисления
Алфавитом системы счисления
Системой счисления
Система счисления – это:
Совокупность знаков, с помощью которых записываются числа
Знаки, с помощью которых записываются числа
Знаковая система, в которой приняты определенные правила чтения и записи чисел
Ничего неправильно
В классе 1010% девочек и 1100102 мальчиков.
Сколько учеников в классе.
10 c) 20
30 d) 40
Сколько единиц в двоичном представлении десятичного числа 15?
4 b) 3 c) 2 d) 1
Вещественные числа представляются в компьютере в :
естественной форме
развернутой форме
экспоненциальной форме с нормализованной мантиссой
виде обыкновенной дроби
Число 301011 может существовать в системах счисления с основаниями:
2 и 4 c) 4 и 3
2 и 10 d) 4 и 8
Шестнадцатеричная система счисления имеет следующий алфавит:
0,1, A, B, C, D, E, F
1,2,3,4,5,6,7,8,
0,1,2,3,4,5,6,7,8,9,A,B, C, D, E, F
0,1,2,3,4,5,6,7,8,9,10,A,B, C, D, E, F
Часть В
За каждый правильный ответ с решением 1 балл.
Задание 2.
101101,012 b) 567102,718.
Задание 3. Переведите числа из 10-й системы счисления в 2-ую:
1610 b) 2910.
Задание 4. Переведите числа из 2-й системы счисления в 10-ую:
111012 b) 11000,12.
Задание 5. Выполните арифметические операции над двоичными числами:
1010101+100111 b) 11001-1101 c) 110*11
Задание 6. Представьте в однобайтовой ячейке целое положительное и отрицательное число: +12 и -12.
Задание 7. Найдите значение x, для которого верно следующее равенство:
15 x=910.
Учебно-методический материал по информатике и икт (8 класс): Контрольная работа по теме «Система счисления»
Контрольная работа по теме: «Системы счисления»
Контрольная работа составлена так, что первые три задания направлены на проверку освоения требований базового уровня и содержит задания, выполняемые по аналогии с теми, что рассматривались на уроках. Четвертое и пятое задания – повышенного уровня. Они дают возможность достигать более высоких образовательных результатов, продвигаться к хорошим и отличным отметкам, выбирать нестандартные решения, выходить за рамки опорных знаний по предмету.
Вариант 1
Задание 1. Переведите в десятичную систему счисления:
а) 1458;
б) 111012;
Задание 2. Переведите из 10-ой системы счисления в двоичную, восьмеричную и шестнадцатеричную:
645 10
Задание 3. Выполните действия в двоичной системе счисления.
а) 10101+1111
б) 10001*11
Задание 4. Восстановите неизвестные цифры, обозначенные знаком вопроса, в следующих примерах на сложение и вычитание, определив вначале, в какой системе изображены числа.
а) 2?21 б) 5?55
+123? +?327
?203 ?16?4
Задание 5. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:
1) 1100 ? 11 ? 100 = 100000;
2) 1100 ? 10 ? 10 = 100;
Вариант 2
Задание 1. Переведите в десятичную систему счисления:
а) 1258;
б) 110012;
Задание 2. Переведите из 10-ой системы счисления в двоичную, восьмеричную и шестнадцатеричную:
428 10
Задание 3. Выполните действия в двоичной системе счисления.
а) 11101+1101
б) 1011*11
Задание 4. Восстановите неизвестные цифры, обозначенные знаком вопроса, в следующих примерах на сложение и вычитание, определив вначале, в какой системе изображены числа.
а) 21?02 б) 4?5
+?1212 -136
?2?021 ?56
Задание 5. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:
1) 1100 ? 10 ? 10 = 110000;
2) 1100 ? 10 ? 10 = 1011;
Ответы:
Вариант 1
Задание 1.
а) 10110
б) 29 10
Задание 2.
10100001012, 12058, 28516
Задание 3.
а) 1010102
б) 1100112
Задание 4.
а) 2421 +1232= 4203, 5-ричная с/с
б) 5255 +4327 =11604, 8-ричная с/с
Задание 5.
- 12*3- 4=32
- 12 :2- 2=4
Вариант 2
Задание 1.
а) 8510
б) 2010
Задание 2.
1101011002, 6548, 1AC6
Задание 3.
а) 1010102
б) 1000012
Задание 4.
а) 21102 +21212 =120021, 3-ичная с/с
б) 425 -136 256, 7-ричная с/с
Задание 5.
- 12*2*2=48
- 12-2:2=11
Контрольная работа «Система Счисления» 8 класс
8 класс
I вариант
1.
Переведи числа из восьмеричной в десятичную систему счисления
А) 103
Б)147
2. Переведите числа в восьмеричную системы счисления:
А) 2910;
Б) 9910.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 11110;
Б) 9510;
4. Переведите числа в десятичную системы счисления:
А) 1D16
5. Переведите из двоичной системы счисления в десятичную
А)11010112
II вариант
1.
Переведи числа из восьмеричной в десятичную систему счисления
А) 1208
Б) 1138;
2. Переведите числа в восьмеричную системы счисления:
А) 2410;
Б) 8910.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 8510;
Б) 9910
4 Переведите в шестнадцатеричную систему счисления.
А) 15610
5. Переведите из двоичной системы счисления в десятичную
А) 1000012
III вариант
1.
. Переведи числа из восьмеричной в десятичную систему счисления
А) 2018
Б) 1178;
2. Переведите числа в восьмеричную системы счисления:
А) 5510;
Б) 11110.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 6410;
Б) 10010;
4. Переведите в шестнадцатеричную систему счисления
А) 33310 ;
5. Переведите из двоичной системы счисления в десятичную
А)111002
IV вариант
1.
Переведи числа из восьмеричной в десятичную систему счисления
А) 338
Б) 1238
2. Переведите числа в восьмеричную системы счисления:
А) 8710;
Б) 17710.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 4710;
Б) 11010;
4. Переведите в шестнадцатеричную систему счисления
А)25310;
5. Переведите из двоичной системы счисления в десятичную
А) 10111110012;
V вариант
1.
Переведи числа из восьмеричной в десятичную систему счисления
А)1748;
Г) 338
2. Переведите числа в восьмеричную системы счисления:;
А) 7910;
б) 18510.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 6710;
Б) 7310;
4. Переведите в шестнадцатеричную систему счисления
А) 25210.
5. Переведите из двоичной системы счисления в десятичную
А) 101011110102;
I вариант
1.
Переведи числа из восьмеричной в десятичную систему счисления
А) 103
Б)147
2. Переведите числа в восьмеричную системы счисления:
А) 2910;
Б) 9910.
3. Переведите числа из десятичной системы счисления в двоичную:
А) 11110;
Б) 9510;
4. Переведите числа в десятичную системы счисления:
А) 1D16
5. Переведите из двоичной системы счисления в десятичную
А)11010112
«Математические основы информатики. Система счисления и элементы алгебры логики», 8 класс
Система счисления и элементы алгебры логики», 8 классПояснительная записка
К контрольной работе по теме: «Математические основы информатики. Система счисления и элементы алгебры логики» 8 класс
по предмету Информатика и ИКТ
Контрольная работа составлена на основе учебника «Информатика» и рабочей тетради для 8 класса авторов Босовой Л. Л., Босовой А. Ю. – М.: Бином. Лаборатория знаний, 2014 г. и требований федерального образовательного стандарта по Информатике для 8 класса. Контрольная работа состоит из 2 вариантов по 7 заданий в каждом, которые включают в себя задания на решение логических задач, составление таблиц истинности, перевод из одной СС в другую. Каждое задание оценивается в 2 балла.
В конце контрольной работы находится ключ для проверки.
Критерии оценивания:
— каждый правильный ответ оценивается в 2 балла;
— оценка «5» — 14 – 16 баллов, «4» -10-13 баллов, «3» — 6-9 баллов.
Контрольная работа по теме: «Математические основы информатики. Система счисления и элементы алгебры логики» 8 класс, 1 вариант.
- Переведите число 178 из десятичной системы счисления в троичную.
- Переведите число 4А1 из шестнадцатиричной системы счисления в десятичную.
- Переведите смешанное двоичное число 100010,0111 в десятичную систему счисления.
- Представьте число 49(в десятичной сс) в восьмиразрядном формате.
- Найдите основание х системы счисления, если 22х=810
- Постройте таблицу истинности следующих выражений:
А) .
Б) .
7. Решите логическую задачу:
В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что у одного из нас белые, у другого черные, а у третьего рыжие волосы, но ни у кого цвет волос не соответствует фамилии», – заметил черноволосый. «Ты прав», – сказал Белов. Какого цвета волосы у художника.
Контрольная работа по теме: «Математические основы информатики.
Система счисления и элементы алгебры логики» 8 класс, 2 вариант.
- Переведите число 189 из десятичной системы счисления в троичную.
- Переведите число 5С3 из шестнадцатиричной системы счисления в десятичную.
- Переведите смешанное двоичное число 1100101,1101 в десятичную систему счисления.
- Представьте число 67(в десятичной сс) в восьмиразрядном формате.
- Найдите основание х системы счисления, если 27х=2310
- Постройте таблицу истинности следующих выражений:
А) .
Б) .
7. Решите логическую задачу:
Пятеро одноклассников: Аня, Саша, Лена, Вася и Миша стали победителями школьных олимпиад по истории, математике, информатике, литературе и географии. Известно, что: 1) победитель олимпиады по информатике учит Аню и Сашу работе на компьютере, 2) Лена и Вася тоже заинтересовались информатикой, 3) Саша всегда побаивался истории, 4) Лена, Саша и победитель олимпиады по литературе занимаются плаванием, 5) Саша и Лена поздравили победителя олимпиады по математике, 6) Аня сожалеет о том, что у нее остается мало времени на литературу.
Кто оказался победителем олимпиады по математике?
Ответы к контрольной работе
1. 20121
2. 1185
3. 34,4375
4. 00110001
5. Х=3
6. А) F2=1011111 Б)f4=11111111
7. Чёрные
Ответы 2 вариант:
1. 21000
2. 1475
3. 101,8125
4. 01000011
5. Х=8
6. А)F3= 11111111 Б)f1=00111111
7. Аня
Проверочная работа по теме «Двоичная системы счисления»
Двоичная система счисления
Вид работы: проверочная работа
Автор: Шевченко Е.А.
Предмет: информатика
аудитория: 8 класс
Описание: данная работа может быть использована в качестве текущего, тематического контроля и направлена на закрепление и коррекцию знаний, умений, полученных в процессе изучения данной темы. Учащимся предлагается шесть вариантов проверочной работы. Каждый вариант состоит из одного теоретического вопроса на проверку знаний о системах счисления, их видах и пяти практических заданий для проверки навыков перевода чисел из десятичной системы счисления в двоичную и наоборот.
Каждое задание оценивается в один балл.
Цель: отработка умений осуществлять перевод чисел их десятичной системы счисления и наоборот
Задачи: сформировать навыки по переводу чисел из десятичной системы счисления и наоборот; выявить качество и уровень овладения знаниями и умениями по теме «Двоичная система счисления»; развитие навыков индивидуальное практической деятельности; развитие познавательного интереса и внимания учащихся, умение оценивать правильность выполнения задания
Ожидаемые результаты:
умение давать определения основным понятиям систем счисления;
формирование устойчивых навыков перевода из десятичной системы счисления в двоичную и наоборот;
умение действовать по заданному алгоритму, оценивать правильность выполнения задания;
формирование ответственного отношения к обучению;
Вариант 1
1 Как называется количество символов в алфавите позиционной системы счисления?
2 Запишите числа в двоичной системе счисления: 27 38
3 Запишите числа в десятичной системе счисления: 11102 101102
4 Сколько единиц в двоичной записи числа 12
Вариант 2
1 Значение цифры не зависит от ее положения в числе в _____________ системе счисления
2 Запишите числа в двоичной системе счисления: 24 41
3 Запишите числа в десятичной системе счисления: 10112 101112
4 Сколько значащих нулей в двоичной записи числа 13
Вариант 3
1 Система счисления в которой для записи любых чисел используется два символа -это _____________ система счисления
2 Запишите числа в двоичной системе счисления: 22 37
3 Запишите числа в десятичной системе счисления: 11012 100112
4 Сколько единиц в двоичной записи числа 14
Вариант 4
1 Десятичная система счисления — это _____________ система счисления
2 Запишите числа в двоичной системе счисления: 26 42
3 Запишите числа в десятичной системе счисления: 11002 110012
4 Сколько значащих нулей в двоичной записи числа 11
Вариант 5
1 Система счисления в которой для записи любых чисел используется всего один символ -это _____________ система счисления
2 Запишите числа в двоичной системе счисления: 25 43
3 Запишите числа в десятичной системе счисления: 10012 110112
4 Сколько единиц в двоичной записи числа 13
Вариант 6
1 Значение цифры зависит от ее положения в числе в _____________ системе счисления
2 Запишите числа в двоичной системе счисления: 21 33
3 Запишите числа в десятичной системе счисления: 11112 100102
4 Сколько значащих нулей в двоичной записи числа 14
Урок 04. компьютерные системы счисления. контрольная работа — Информатика — 8 класс
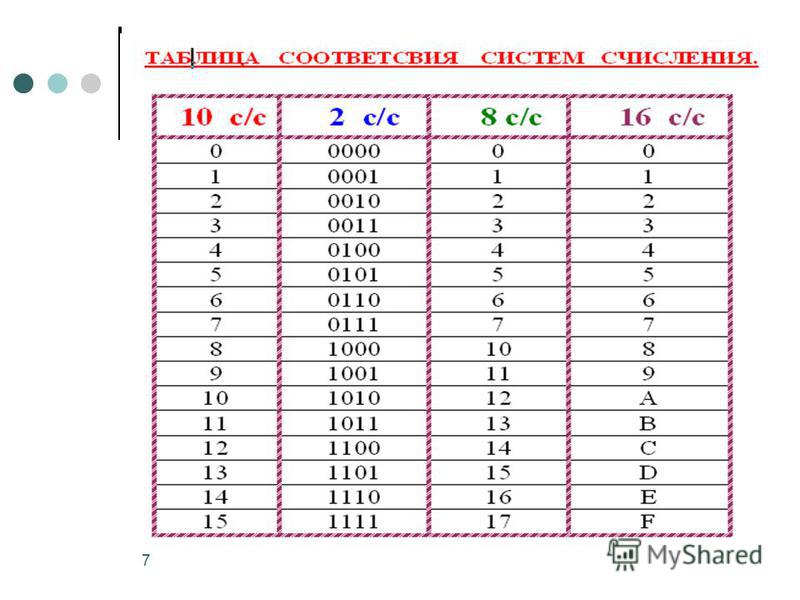
компьютерные системы счисления. контрольная работа — Информатика — 8 классДля начала рассмотрим алфавиты восьмеричной и шестнадцатеричной систем счисления, т. е. цифры, с помощью которых мы будем записывать числа в этих системах счисления.
Восьмеричные числа записываются с помощью восьми цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Алфавит шестнадцатеричной системы счисления состоит из десяти цифр и шести букв латинского алфавита: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Как и в десятичной системе, восьмеричное или шестнадцатеричное число можно записать в развёрнутом виде, т. е. представить как сумму произведений составляющих его цифр и соответствующих степеней основания системы счисления: восемь или шестнадцать.
Например, развёрнутая форма записи восьмеричного числа 167 будет такой: 1678 = 1×82 + 6×81 + 7×80
И ещё один пример с шестнадцатеричным числом: 5FC16=5 × 162+ F×161+C×160
Вернёмся к развёрнутой записи восьмеричного числа.
Если вычислить значение этого выражения, то будет найден десятичный эквивалент этого числа.
Вернёмся к развёрнутой записи шестнадцатеричного числа. Каждая буква в алфавите шестнадцатеричной системы счисления имеет числовой эквивалент.
Если в развёрнутой записи заменить буквы их числовыми эквивалентами и вычислить значение выражения, то получится значение числа в десятичной системе счисления.
5FC16= 5×162+ F×161 +C×160 = 5×162+ 15×161 + 12 = 1280 + 240 + 12 = 153210.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока частное не станет равным нулю.
Например, нужно десятичное число 571 перевести в восьмеричную систему счисления. Разделим 571 на 8.Неполное частное 71 и остаток 3. Продолжим деление. 71 делим на 8. Неполное частное 8, остаток 7. При делении 8 на 8 получается частное 1, а остаток равен 0.
Разделим 1 на 8. Неполное частное 0, а остаток 1.
Мы получили неполное частное 0, следовательно можем записать результат. Для этого записываем остатки от последнего к первому.
57110 = 10738.
Аналогично осуществляется перевод из десятичной системы счисления в шестнадцатеричную. Выполняется последовательное деление на 16.
Переведём десятичное число 467 в шестнадцатеричную систему счисления.
Разделим 461 на 16. Неполное частное 28 и остаток 13. Продолжим деление. 28 делим на 16. Неполное частное 1, остаток 12. Разделим 1 на 8. Неполное частное 0, а остаток 1. Мы получили неполное частное 0, следовательно, можем записать результат, выписывая остатки от последнего к первому.
Если остаток –двузначное число, то его надо заменить соответствующей буквой.
A | B | C | D | E | F |
10 | 11 | 12 | 13 | 14 | 15 |
Получаем: 46110 = 1CD16
Итак, сегодня вы узнали, что к компьютерным системам счисления кроме двоичной относятся также восьмеричная и шестнадцатеричная системы счисления.
Познакомились с алфавитами этих систем счисления, рассмотрели правила записи чисел. Узнали правила перевода чисел из десятичной системы счисления в восьмеричную или шестнадцатеричную. А так же научились переводить восьмеричные и шестнадцатеричные числа в десятичную систему счисления. Закрепите полученные знания на практике, выполнив упражнения.
Что такое тест когнитивных способностей (CogAT)?
Что такое CogAT?
Посмотрите это короткое видео, чтобы узнать все, что вам нужно знать о тесте CogAT:
Тест на познавательные способности (CogAT) — это тест с несколькими вариантами ответов, предназначенный для оценки академических и одаренных способностей ребенка.
CogAT Form 7 , наиболее распространенная версия теста, измеряет когнитивное развитие и навыки решения проблем.Тест состоит из трех разделов, называемых батареями:
Эти элементы можно проводить по отдельности или вместе, в зависимости от школы, проводящей тест.
CogAT выдается учащимся классов K-12. Всего существует десять уровней CogAT. Число, присвоенное каждому уровню, соответствует возрастному уровню, которому он назначен. Например, уровень 9 предназначен для учащихся примерно 9 лет и обычно предоставляется учащимся 3-го класса.Уровни тестирования для формы 7 CogAT и уровень, к которому они обычно назначаются, следующие:
Форма CogAT 7 уровней
| Уровень | Оценка |
|---|---|
| 5/6 | К |
| 7 | 1-й |
| 8 | 2-я |
| 9 | 3-й |
| 10 | 4-я |
| 11 | 5-я |
| 12 | 6-й |
| 13/14 | 7-8 места |
| 15/16 | 9-10 |
| 17/18 | 11–12 |
Батареи CogAT Form 7
Устный
- Изображение / Словесные аналогии: уясните взаимосвязь между двумя понятиями (представленными либо через изображения, либо через слова, в зависимости от возраста ученика).
- Завершение предложения: Завершите предложения, услышав или прочитав их.
- Картинная / словесная классификация: классифицируйте данное понятие на основе его отношения к другим данным понятиям (представленным через изображения или слова, в зависимости от возраста учащегося).
Количественный
- Числовые аналогии: Определите взаимосвязь между двумя математическими понятиями на основе другой данной пары понятий.
- Числовой ряд: Завершите ряд чисел, выведя базовый образец.
- Картинная / словесная классификация: классифицируйте данное математическое понятие на основе его отношения к другим данным понятиям.
Невербальный
- Классификация фигур: выберите фигуру / фигуру, которая больше всего подходит для данной категории.
- Матрицы фигур: в матрице 2X2 определите взаимосвязь между двумя верхними квадратами и примените ее к двум нижним квадратам.
- Фальцовка бумаги: Определите конечный результат при сгибании перфорированной бумаги определенным образом.
Нормы и баллы CogAT
CogAT использует два типа норм при оценке тестов: возрастных норм и оценок .
Возрастные нормы сравнивают успеваемость учащегося по сравнению с другими детьми того же возраста. Эти нормы составляют от 4 лет 11 месяцев до 18 лет. Студенты группируются с интервалом в один месяц.
Нормы оценок сравнивают успеваемость учащегося по сравнению с другими детьми того же класса.
Баллы CogAT рассчитываются следующим образом:
- Во-первых, общий балл рассчитывается путем подсчета общего количества вопросов, на которые даны правильные ответы. Затем
- необработанные баллы конвертируются в баллы по универсальной шкале (USS) для каждой из трех батарей, которые затем используются для расчета стандартного возрастного балла (SAS), процентильного ранга и оценки станина.
- Используя эти оценки, наряду с анализом закономерностей, присутствующих в оценке учащегося, учащемуся дается профиль оценки.
Подробнее о подсчете баллов CogAT.
CogAT Form 7 Language Adjustments
CogAT Form 7 доступна для студентов, не говорящих по-английски, из-за ее невербального формата. Основная причина изменений между уровнями начальной школы Form 6 и Form 7 заключалась в том, чтобы принять учеников, изучающих английский язык (ELL), студентов. Начальные уровни формы 7 (5 / 6-8) теперь почти полностью состоят из невербальных вопросов.
Единственный раздел, требующий языковых навыков, — это дополнительный раздел Sentence Completion , который доступен как на английском, так и на испанском языках.Инструкции для всех уровней предлагаются на английском или испанском языках.
Как оформляется форма 7 CogAT?
Время проведения теста может варьироваться в зависимости от того, сколько времени требуется наблюдателю для проведения теста.
Студентам обычно предоставляется от 30-45 минут на батарею. С учетом времени администрирования требуется от двух до трех часов, для полной зарядки всех трех батарей. Всего в CogAT имеется от 118 до 176 вопросов , в зависимости от уровня.
Порядок проведения теста зависит от класса вашего ребенка, школы и формы CogAT, которую он / она сдает. Вот что мы делаем знаем об администрировании CogAT Form 7:
- Ваш ребенок, скорее всего, будет проходить тест с небольшой группой учеников (не более 20)
- Батарейки часто используются вместе
- В некоторых школах используются только определенные батареи CogAT, поэтому важно точно выяснить, какие батареи Cog AT будет брать ваш ребенок.
- Тест CogAT можно пройти онлайн или на бумаге.
Другие формы CogAT
CogAT Screening Form Test
Скрининговая форма CogAT — это сокращенная версия теста CogAT, состоящая из раздела аналогий для каждой батареи.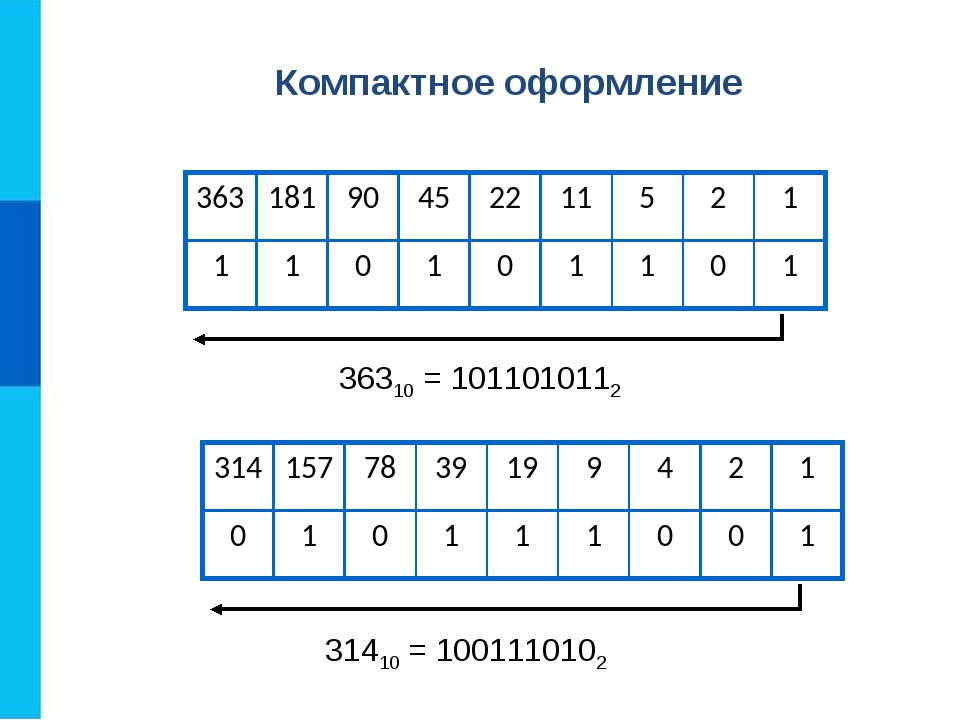
Тест позволяет эффективно оценить навыки учащегося, так как его выполнение занимает всего 30 минут. Он идеально подходит как для студентов, чей родной язык не английский, так и для студентов, испытывающих трудности с чтением.Узнайте больше о форме отбора CogAT.
Форма 8 CogAT
Форма 8 CogAT используется вместе с формой 7 CogAT, чтобы обеспечить максимально справедливую оценку учащегося. Важно подчеркнуть, что форма CogAT Form 8 идентична форме CogAT Form 7 как по формату, так и по темам, так что, готовясь к CogAT Form 7, вы также готовитесь к CogAT Form 8. Узнайте больше о форме CogAT 8.
Форма CogAT 6
Форма CogAT Form 6 , предшествующая форма CogAT Form 7 , все еще может использоваться в некоторых школах.Важно знать разницу между этими двумя вариантами теста и тем, который будет проходить ваш ребенок.
Одно из основных различий между формой Form 6 и Form 7 — количество вопросов в каждом тесте.
В следующей таблице показаны изменения количества вопросов на каждом уровне формы Form 6 и формы Form 7 :
| 5/6 | 7 | 8 | 9 | 10-18 | |
|---|---|---|---|---|---|
| CogAT 6 | 120 | 132 | 144 | 190 | 190 |
| CogAT 7 | 118 | 136 | 154 | 170 | 176 ‘ |
Уровни тестирования в CogAT Form 7 отличаются от того, как были разделены уровни тестирования в CogAT Form 6 и других предыдущих изданиях.Подобно существующей системе уровней, уровни CogAT Form 6 не соответствуют строго уровню класса. Уровни K – 2 предназначены для учащихся от детского сада до второго класса, а уровни A – H предназначены для учащихся классов 3–12 .
Тем не менее, хорошо успевающий второклассник может сдать , уровень A , а низко успевающий ученик третьего класса может пройти уровень 2. Эта гибкая система позволяет проводить более конкретное и целенаправленное тестирование для каждого ученика.
Формат также изменился с Form 6 на Form 7 . В Form 6 формат для начальных уровней (K – 2) отличался от более высоких уровней. В Форме 7 формат практически одинаков для всех уровней. См. Таблицу ниже для разбивки батарей и подтестов на каждом уровне.
Батареи CogAT Form 6 (первичные уровни)
| Аккумулятор | Субтесты |
|---|---|
| Устный | Устный словарь |
| Устное рассуждение | |
| Количественный | Концепции отношений |
| Количественные концепции | |
| Невербальный | Матрицы |
| Рисунок Классификация |
Первичные уровни — это уровни K-2 в форме 6 , соответствующие уровням 5 / 6-8 в форме 7 .
CogAT Form 7 Примеры вопросов
TestPrep-Online Совет разработчика: Подумайте о правиле, которое описывает сходство между изображениями в верхнем ряду. Если вам трудно придумать правило, просмотрите варианты ответов, чтобы увидеть, есть ли среди них фигура с особыми характеристиками. Например, вы можете обнаружить, что только один вариант ответа окрашен определенным образом.Подробнее CogAT Levels 5-6 Примеры вопросов и советов!
Подробнее CogAT Level 7 Примеры вопросов и советов!
Подробнее CogAT Level 8 Примеры вопросов и советов!
TestPrep-Online Совет разработчика: Хорошая стратегия для вопросов по аналогии — начать с составления короткого простого предложения, соединяющего два слова в первой аналогии.Например: «Пародия сатирическая». Затем вы можете заменить слова из второй аналогии, чтобы избежать вариантов ответа.Подробнее CogAT Level 9 Примеры вопросов и советов!
Подробнее CogAT Level 10 Примеры вопросов и советов!
| Пример вопроса: форма 7 CogAT, уровень 11, класс 5 |
Какое число будет следующим в серии? 50 54 41 45 32? A) 42B) 40 C) 38 D) 36 |
Ответ и объяснение ▼ | ▲ Правильный ответ — 36. В этой серии шаблон выглядит следующим образом: сначала добавляется 4 , затем вычитается 13 , затем добавляется 4 , затем вычитается 13 и так далее. Шаблон следующий: + 4-13 + 4-13 … Последние два числа в этой серии: 45 и 32 . 32 меньше 45 на 13 , поэтому следующий номер в серии должен быть больше 32 на 4 . 32 + 4 = 36 . В качестве альтернативы мы можем рассматривать паттерн как комбинацию двух отдельных паттернов, которые чередуются. Один образец ( нечетных членов ) представляет собой серию чисел, которые уменьшаются на 9, а другой образец ( четных членов ) — это еще один ряд, который уменьшается на 9. Образец следующий: 50 54 41 45 32 .. Нам не хватает шестого числа, которое является четным членом, поэтому оно должно быть меньше последнего четного члена (четвертого числа) на 9 . |
Четвертое число — 45 , поэтому: 45-9 = 36 . Следовательно, 36 — правильный ответ.Подробнее CogAT Level 11 Примеры вопросов и советов!
Подробнее CogAT Level 12 Примеры вопросов и советов!
Как подготовиться к CogAT
Сегодня конкуренция за одаренные программы достигла рекордного уровня. Правильно подготовив своего ребенка к предстоящему экзамену CogAT, вы можете значительно повысить его или шансы на участие в программе, на которую вы оба наблюдаете. Чтобы помочь вам подготовиться как можно лучше, TestPrep-Online предлагает комплексные учебные пакеты с учетом возраста, чтобы ваш ребенок мог учиться, прогрессировать и преуспевать в каждом разделе CogAT.
Наши пакеты включают практические тесты, а также дополнительные примеры вопросов, учебные пособия и пояснения. Начните подготовку к тестированию CogAT сегодня .Начните подготовку с нашими тренировочными пакетами CogAT прямо сейчас!
В Канаде или Великобритании? Ознакомьтесь с нашей информацией о CCAT и CAT4!CCAT, CogAT и другие товарные знаки являются собственностью соответствующих владельцев товарных знаков. Ни один из владельцев товарных знаков не связан с TestPrep-Online или этим веб-сайтом.
Двоичная система счисления
Основное различие между двоичной системой счисления и нашей знакомой системой счисления по основанию 10 состоит в том, что группировка выполняется группами по 2 вместо 10.
Например, чтобы представить 24 в базе 10 с помощью палочек, вы можете использовать две группы по десять и четыре, как показано ниже.
Но нужно помнить кое-что важное, и это ключ к пониманию этого урока!
- Цифры 0,1,2,3,4,5,6,7,8,9 используются для представления всех возможных чисел. Обратите внимание, что основание 10 состоит из 10 цифр
- В зависимости от того, насколько велико число, мы составляем группы из десяти, сотен, тысяч, десяти тысяч и т. Д. (Это степень 10: 10 1 = 10, 10 2 = 100, 10 3 = 1000)
- Если число меньше 10, например 8 и 9, создавать группы не нужно. И это число будет занимать единичное значение .
- Если число больше 9 и меньше 100, например 10, 55 и 98, необходимо создать группы из десяти.Группы по десять человек будут занимать десятичное значение.
- Если число больше 99 и меньше 1000, например 100, 255 и 999, необходимо создать группы по сотне. Группы сотен будут занимать разрядное значение сотен.
- И так далее …
Обратите внимание, что основание 10 состоит из 10 цифр Так как число больше 99, пришлось сделать группы по сто десять.
Обратите внимание также, как группы из сотен помещаются в разряд сотен, а группы из десяти помещаются в разряд десятков.
Аналогичным образом двоичная система счисления имеет собственное разрядное значение.
- Цифры 0,1 используются для представления всех возможных чисел в двоичной системе счисления. Обратите внимание, что основание 2 состоит из 2 цифр для представления всех возможных чисел.
- В зависимости от размера числа мы составляем группы по 2, 4, 8, 16, 32 и т. Д… (Это степень 2: 2 1 = 2, 2 2 = 4, 2 3 = 8)
- Если число меньше 2, например 1, создавать группы не нужно. И это число будет занимать первое место со значением . Это значение разряда соответствует разряду единиц в базе 10
- Фактически, это 1 одно и то же в двоичной системе счисления и системе с основанием 10.
- Если число больше 1 и меньше 4, например 2 и 3, необходимо создать группу из двух человек. Группа из двух человек займет второе место со значением . Вы также можете назвать это «двухзначным» значением
- Если число больше 3 и меньше 8, например 4 и 7, необходимо создать группу из четырех человек. Группа из четырех человек займет третье место со значением . Вы также можете назвать это «четырехзначным» значением
- Если число больше 7 и меньше 16, например 8, 11 и 14, необходимо создать группу из восьми человек. Группа из восьми будет занимать четвертое место , значение .Вы также можете назвать это «восьмеркой».
- Если число больше 15 и меньше 32, например 16, 21 и 30, необходимо создать группу из шестнадцати человек. Группа из шестнадцати человек займет пятое место со значением . Вы также можете назвать это «шестнадцатиместным» значением.
- Если число больше 31 и меньше 64, например 32, 45 и 63, необходимо создать группу из тридцати двух. Группа из тридцати двух человек займет шестое место со значением . Вы также можете назвать это «тридцатью двумя» позициями.
- И так далее …
Группа из двух человек займет второе место со значением . Вы также можете назвать это «двухзначным» значением
Вы также можете назвать это «тридцатью двумя» позициями.Ну, это означает, что мы можем создать только 1 группу, а не 2, а не 3
Так как мы используем только 0 и 1 для представления чисел , записать двоичные числа с помощью числа 2 будет невозможно.
Теперь переведем 25 в двоичную систему счисления
Обратите внимание, что нет групп из двух и четырех.В результате поставьте нули на второе место и на третье место.
Как выполняется группировка в двоичной системе счисления. Как преобразовать из базы 10 в базу 2
Группа с n-го места на первое. Это означает, что вы должны сначала создать группу с максимально возможной степенью 2
. Например, я пытаюсь преобразовать 45 в двоичную систему счисления.
Спросите себя. Какая наибольшая степень 2 меньше 45?
2 6 = 64,2 5 = 32.
Таким образом, наибольшая степень 2 меньше 45 составляет 2 5 = 32
Поскольку 32 идет на шестом месте, поместите 1 на шестое место . Затем попытайтесь выяснить, что раньше входит в разряд.
45-32 = 13
Спросите себя. Какая наибольшая степень 2 меньше 13?
2 4 = 16. 2 3 = 8. Таким образом, наибольшая степень двойки меньше 13 равна 2 3 = 8
Поскольку 8 идет на четвертом месте, поместите 1 на четвертое место . .Затем попытайтесь выяснить, что раньше входит в разряд.
13-8 = 5
Спросите себя. Какая максимальная степень 2 меньше 5?
2 3 = 8. 2 2 = 4. Таким образом, наибольшая степень 2 меньше 5 равна 2 2 = 4
Поскольку 4 идет на третьем месте, поместите 1 на третье место . . Затем попытайтесь выяснить, что раньше входит в разряд.
5-4 = 1 и 1 переходит на первое место .
Обратите внимание, что вы ничего не ставите на пятое и второе места, поэтому в этих местах идут нули
Следовательно, 45, преобразованное в двоичную систему счисления, будет 101101
Вы также можете написать 45 десять или 101101 два
Будьте очень внимательны при чтении 101101 двух ! 101101 2 читается один ноль один один ноль один основание 2
Введение в физику
18 ноя, 20 13:20
Первоклассное введение в физику.
Универсальный ресурс для глубокого понимания важных концепций физикиПодробнее
Универсальный ресурс для глубокого понимания важных концепций физикиНовые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
Система счисления PDF
Система счисления
Для Все учебные материалы по предметам — Щелкните здесь
Система счисления
Если основание или основание системы счисления — «r», то числа, представленные в этой системе счисления, находятся в диапазоне от нуля до r-1.Общее количество чисел в этой системе счисления — «r». Итак, мы получим различные системы счисления, выбирая значения системы счисления больше или равные двум.
В этой главе давайте обсудим популярные системы счисления и способы представления числа в соответствующей системе счисления.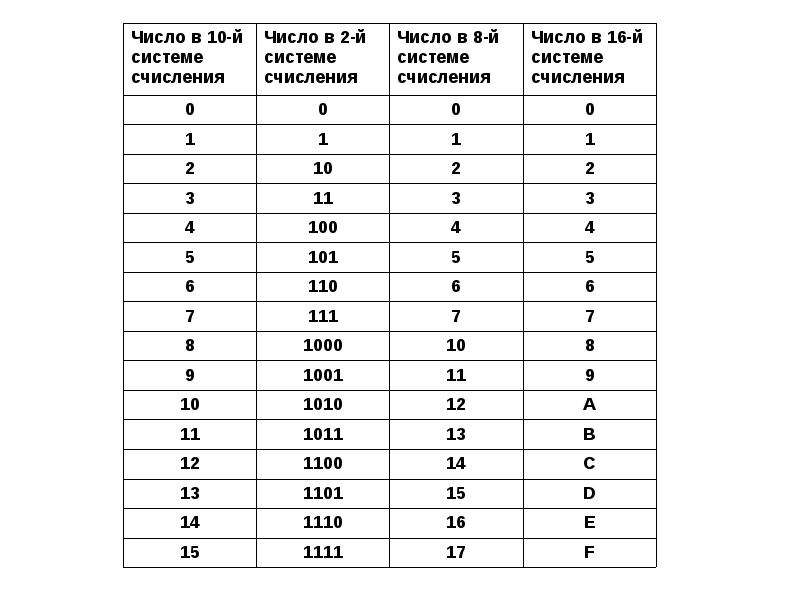
Наиболее часто используются следующие системы счисления.
- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
Десятичная система счисления
Основание или основание десятичной системы счисления — 10 .Итак, в этой системе счисления используются числа от 0 до 9. Часть числа, которая находится слева от десятичной точки , называется целой частью. Точно так же часть числа, которая находится справа от десятичной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от десятичной точки, имеющие веса 10 0 , 10 1 , 10 2 , 10 3 и так далее. Аналогично, последовательные позиции справа от десятичной точки имеют веса 10 -1 , 10 -2 , 10 -3 и так далее.Это означает, что каждая позиция имеет определенный вес, который составляет степень основания 10
.
Пример
Рассмотрим десятичное число 1358,246 . Целая часть этого числа — 1358, дробная часть — 0,246. Цифры 8, 5, 3 и 1 имеют веса 100, 101, 10 2 и 10 3 соответственно. Точно так же цифры 2, 4 и 6 имеют веса 10 -1 , 10 -2 и 10 -3 соответственно.
Математически , мы можем записать это как
1358.246 = (1 × 10 3 ) + (3 × 10 2 ) + (5 × 10 1 ) + (8 × 10 0 ) + (2 × 10 -1 ) +
(4 × 10 -2 ) + (6 × 10 -3 )
После упрощения членов правой части мы получим десятичное число, которое находится в левой части.
Двоичная система счисления
Все цифровые схемы и системы используют эту двоичную систему счисления. Основание или основание этой системы счисления — 2 .Итак, в этой системе счисления используются числа 0 и 1.
Часть числа, которая находится слева от двоичной точки , называется целой частью. Точно так же часть числа, которая находится справа от двоичной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от двоичной точки, имеющие веса 2 0 , 2 1 , 2 2 , 2 3 и так далее. Точно так же последовательные позиции справа от двоичной точки имеют веса 2 -1 , 2 -2 , 2 -3 и так далее.Это означает, что каждая позиция имеет определенный вес, который равен степени от основания 2 .
Пример
Рассмотрим двоичное число 1101.011 . Целая часть этого числа — 1101, а дробная часть — 0,011. Цифры 1, 0, 1 и 1 целой части имеют веса 2 0 , 2 1 , 2 2 , 2 3 соответственно. Точно так же цифры 0, 1 и 1 дробной части имеют веса 2 -1 , 2 -2 , 2 -3 соответственно.
Математически , мы можем записать это как
1101.011 = (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) + (0 × 2 -1 ) +
(1 × 2 -2 ) + (1 × 2 -3 )
После упрощения членов правой части мы получим десятичное число, которое является эквивалентом двоичного числа в левой части.
Восьмеричная система счисления
Основание или основание восьмеричной системы счисления — это 8 .Итак, в этой системе счисления используются числа от 0 до 7. Часть числа, которая находится слева от восьмеричной точки , называется целой частью. Точно так же часть числа, которая находится справа от восьмеричной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от восьмеричной точки, имеющие веса 8 0 , 8 1 , 8 2 , 8 3 и так далее.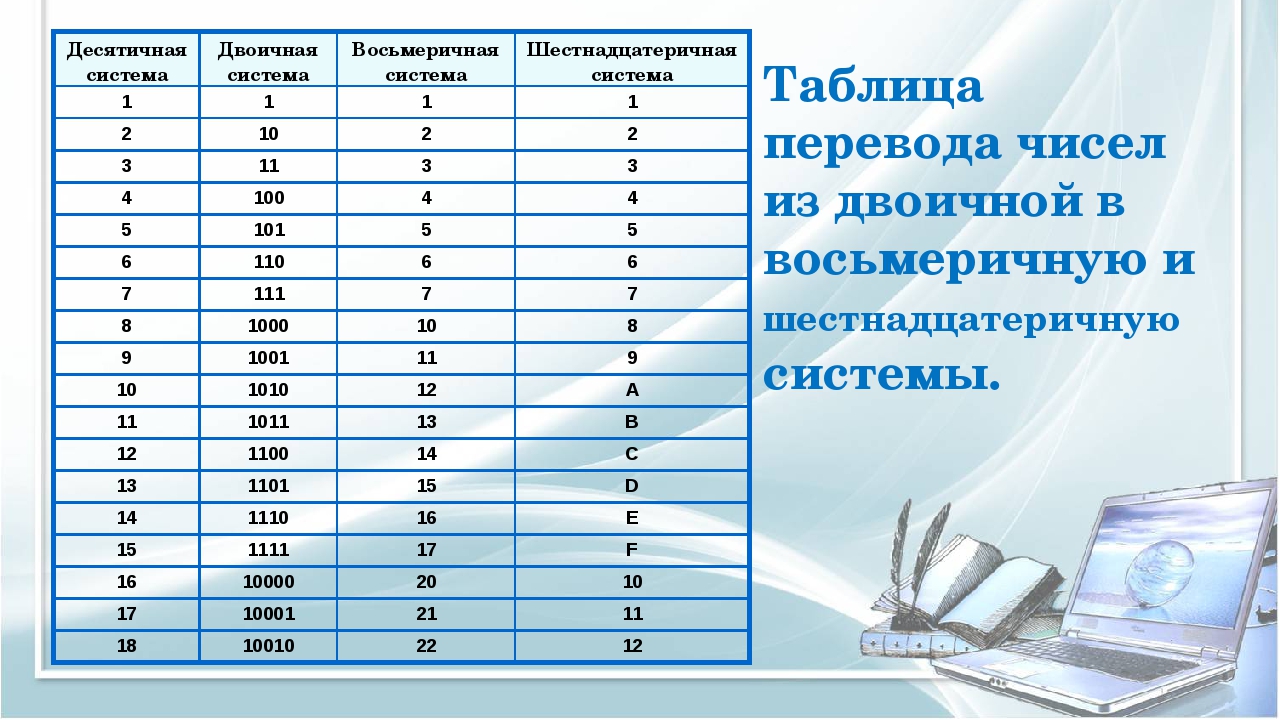
Точно так же последовательные позиции справа от восьмеричной точки имеют веса 8 -1 , 8 -2 , 8 -3 и так далее.Это означает, что каждая позиция имеет определенный вес, который равен степени от основания 8 .
Пример
Рассмотрим восьмеричное число 1457.236 . Целая часть этого числа — 1457, а дробная часть — 0,236. Цифры 7, 5, 4 и 1 имеют веса 8 0 , 8 1 , 8 2 и 8 3 соответственно. Точно так же цифры 2, 3 и 6 имеют веса 8 -1 , 8 -2 , 8 -3 соответственно.
Математически , мы можем записать это как
1457,236 = (1 × 8 3 ) + (4 × 8 2 ) + (5 × 8 1 ) + (7 × 8 0 ) + (2 × 8 -1 ) +
(3 × 8 -2 ) + (6 × 8 -3 )
После упрощения членов правой части мы получим десятичное число, которое является эквивалентом восьмеричного числа в левой части.
Шестнадцатеричная система счисления
Основание или основание шестнадцатеричной системы счисления — это 16 .Итак, в этой системе счисления используются числа от 0 до 9 и буквы от A до F. Десятичный эквивалент шестнадцатеричных цифр от A до F — от 10 до 15.
Часть числа, которая находится слева от шестнадцатеричной точки , называется целой частью. Точно так же часть числа, которая находится справа от десятичной шестнадцатеричной точки, называется дробной частью.
В этой системе счисления последовательные позиции слева от шестнадцатеричной десятичной точки, имеющие веса 16 0 , 16 1 , 16 2 , 16 3 и так далее.Точно так же последовательные позиции справа от десятичной шестнадцатеричной точки имеют веса 16 -1 , 16 -2 , 16 -3 и так далее. Это означает, что каждая позиция имеет определенный вес, который равен степени от основания 16 .
Пример
Рассмотрим шестнадцатеричное число 1A05.2C4 . Целая часть этого числа — 1A05, а дробная часть — 0,2C4. Цифры 5, 0, A и 1 имеют веса 16 0 , 16 1 , 16 2 и 16 3 соответственно.Точно так же цифры 2, C и 4 имеют веса 16 -1 , 16 -2 и 16 -3 соответственно.
Математически , мы можем записать это как
1A05.2C4 = (1 × 16 3 ) + (10 × 16 2 ) + (0 × 16 1 ) + (5 × 16 0 ) + (2 × 16 -1 ) + (12 × 16 -2 ) + (4 × 16 -3 )
После упрощения членов правой части мы получим десятичное число, которое является эквивалентом шестнадцатеричного числа в левой части.
Загрузить PDF
Вернуться к Примечаниям по микроэлектронике
оценок и преобразование оценок | theCrag
Введение в скалолазание Стили снаряжения маршрута Система оценок почти такая же старая, как и само восхождение.
Присвоение сложности восхождению кажется не менее важным, чем описание его другими характеристическими параметрами, такими как длина, защита или тип скалы. Системы оценок изначально разрабатывались в ограниченных географических районах, что несколько упрощало сравнение восхождений, развивалась с течением времени и постоянно расширялась по мере того, как альпинистам удается преодолевать все более сложные подъемы.Например, теперь называемая система оценок UIAA имеет высшую оценку VI (шесть), что означает, что всему, что сложнее, чем VI, просто присваивался VI, пока она не была окончательно открыта в конце 1970-х.
Даже сегодня многие системы оценок привязаны к определенным географическим регионам, иногда к зонам восхождения (например, Саксонии, Фаунтинбло), в основном к странам (Южная Африка, Бразилия, Франция и т. Д.) Или даже на континентах (Ewbanks, YDS), а иногда они экспортируются. и зарекомендовали себя в различных областях, благодаря чему одни системы оценок стали более распространенными, чем другие.
Большинство систем оценок относятся к определенному стилю. Существуют системы оценок для боулдеринга, системы оценок для спортивного лазания, системы оценок для вспомогательного лазания и так далее, но даже системы оценок для одного и того же стиля не всегда хорошо сочетаются друг с другом. Причина в том, что ширина оценок по определенной шкале несопоставима или что оценки не являются линейными по всей шкале.
Для вас, как для скалолаза, это означает, что иногда может быть довольно сложно точно преобразовать конкретный уровень из одной системы оценок в другую; для нас, как глобального поставщика информации и услуг, сложно отображать всю информацию об оценках в контексте, в котором пользователь хочет ее видеть, и точно использовать ее для целей оценки и ранжирования.
Вместе со скалолазным сообществом theCrag разработал и продолжает развивать всесторонний и интуитивно понятный охват оценок в системе. Поэтому мы приветствуем отзывы об оценках и новых разработках в этой области.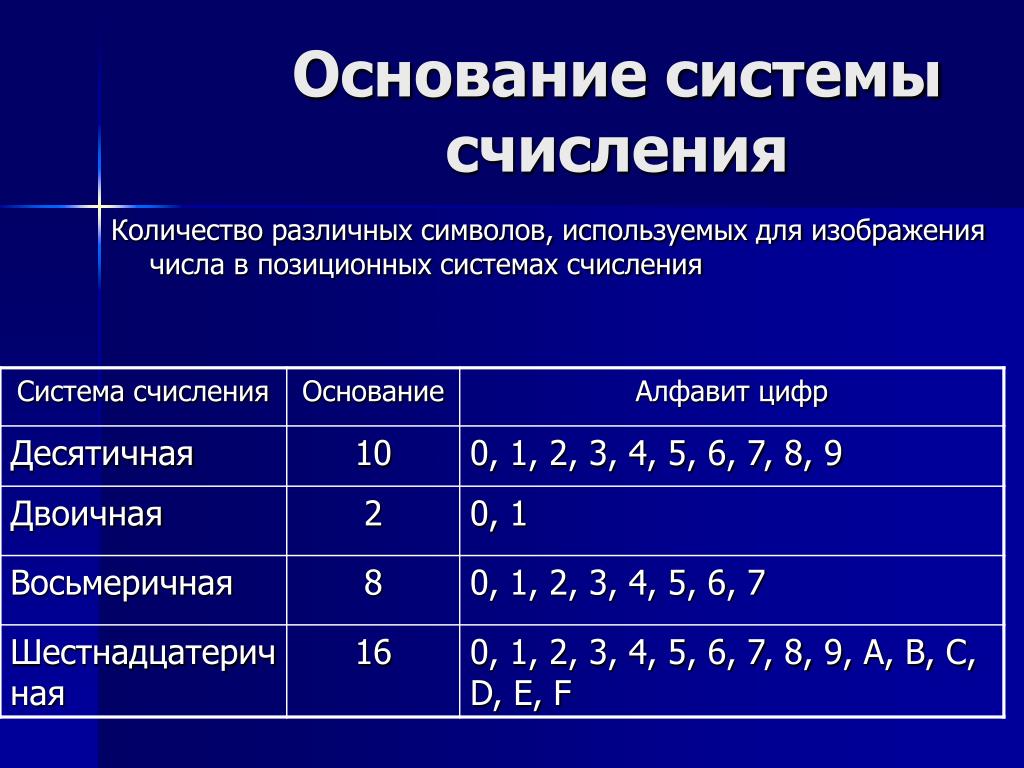
Однако, чтобы это было полезно для сообщества в целом, мы рекомендуем вам вносить предложения и критику в наш список проблем, чтобы все сообщество могло внести конструктивный вклад.
theCrag автоматически преобразует оценки между различными системами оценок в соответствии с приведенными ниже таблицами.theCrag делает это с помощью открытой и детализированной внутренней системы преобразования оценок с более чем 500 уровнями оценок, позволяющими отразить тонкости большинства известных систем оценок и их преобразование друг в друга.
Если у вас есть учетная запись на Crag, вы можете установить предпочитаемую систему оценок для основных стилей снаряжения на странице своего профиля, что позволит вам просматривать любую зону лазания по всему миру в системе оценок, к которой вы наиболее привыкли. Вы также можете просто преобразовать одну оценку, используя интерактивный конвертер оценок, представленный ниже.
Интерактивный конвертер оценок Назад к содержанию
Контекст оценок:
AU: Австралийский (Юбанкс .
..)
BRZ: бразильский
FB: Фонтенбло
FIN: финский
FR: французский
HK: Гонконг
NWG: норвежский
POL: Польский
SA: Южная Африка
SWE: шведский
SX: саксонский
UIAA: UIAA
Великобритания: британский
США: американец (YDS …)
Стиль шестерни: Помощь Альпийский Боулдер Глубоководное соло Ледяной Спорт Верхняя веревка Trad Траверс Неизвестно Via Ferrata
Ваш ввод:
Преобразовать в систему оценок: — Альпийский лед Annot B-Scale Ewbanks B-шкала Шкала Дерева Джошуа P-шкала S-шкала V-шкала Бразилия Технический Бразилия Генерал Класс Фонтенбло Перемещение шрифта Финский французкий язык Смешанный рок / лед Шкала NCCS норвежский язык Старый Южноафриканский Польский Южноафриканский Феррата Шалл Шотландская зима Шотландский зимний технический Шведский Саксонский МАА Британский прил.British Tech. Феррата Френч Феррата Нум Ледяная вода YDS
Преобразованный сорт:
Системы традиционного и спортивного класса Назад к содержанию
Начинающий Средний Опытный Эксперт Элитный | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 18 19 20 21 22 23 24 25 26 27 28 29 30 30 3435 36 37 38 39 | 5. Leave a Reply
|
