Контрольная работа № 1 «Параллелограмм» Вариант 1 1. Один из углов параллелограмма равен 55⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 64 см, а одна из его сторон больше другой стороны на 4 см. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол BАD равен 80⁰. Найдите углы треугольника CОD. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 5 см. Найдите периметр прямоугольника. | Контрольная работа № 1 «Параллелограмм» Вариант 2 1. Один из углов параллелограмма равен 138⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 3 см, а одна из его сторон больше другой стороны в 2 раза. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол АDС равен 110⁰. Найдите углы треугольника АОВ. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 6 см. Найдите периметр прямоугольника. | Контрольная работа № 1 «Параллелограмм» Вариант 1 1. Один из углов параллелограмма равен 55⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 64 см, а одна из его сторон больше другой стороны на 4 см. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол BАD равен 80⁰. Найдите углы треугольника CОD. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 5 см. | Контрольная работа № 1 «Параллелограмм» Вариант 2 1. Один из углов параллелограмма равен 138⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 3 см, а одна из его сторон больше другой стороны в 2 раза. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол АDС равен 110⁰. Найдите углы треугольника АОВ. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 6 см. Найдите периметр прямоугольника. | Контрольная работа № 1 «Параллелограмм» Вариант 1 1. Один из углов параллелограмма равен 55⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 64 см, а одна из его сторон больше другой стороны на 4 см. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол BАD равен 80⁰. Найдите углы треугольника CОD. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 5 см. Найдите периметр прямоугольника. | Контрольная работа № 1 «Параллелограмм» Вариант 2 1. Один из углов параллелограмма равен 138⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 3 см, а одна из его сторон больше другой стороны в 2 раза. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол АDС равен 110⁰. Найдите углы треугольника АОВ. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 6 см. Найдите периметр прямоугольника. | Контрольная работа № 1 «Параллелограмм» Вариант 1 1. 2. Периметр параллелограмма равен 64 см, а одна из его сторон больше другой стороны на 4 см. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол BАD равен 80⁰. Найдите углы треугольника CОD. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 5 см. Найдите периметр прямоугольника. | Контрольная работа № 1 «Параллелограмм» Вариант 2 1. Один из углов параллелограмма равен 138⁰. Найдите остальные углы параллелограмма. 2. Периметр параллелограмма равен 3 см, а одна из его сторон больше другой стороны в 2 раза. Найдите стороны параллелограмма. 3. В ромбе ABCD, где О – точка пересечения диагоналей BD и AC, а угол АDС равен 110⁰. Найдите углы треугольника АОВ. 4. Биссектриса угла прямоугольника делит его сторону на две части, каждая из которых равна 6 см. Найдите периметр прямоугольника. |
К-1 В-1 Геометрия 8 Мерзляк
Контрольная работа по геометрии в 8 классе № 1 «Параллелограмм и его виды» с ответами и решениями в 2-х вариантах. К-1 В-1 Геометрия 8 Мерзляк. Дидактические материалы для школьников, учителей и родителей.
Вернуться к Списку контрольных работ по геометрии в 8 классе (Мерзляк).
Геометрия 8 класс (УМК Мерзляк)
Контрольная работа № 1. Вариант № 1
К-1 «Параллелограмм и его виды» (транскрипт заданий)
1. Одна из сторон параллелограмма в 5 раз больше другой, а его периметр равен 36 см. Найдите стороны параллелограмма.
2. В прямоугольнике АВСD диагонали пересекаются в точке О, АD = 14 см, ВD = 18 см. Найдите периметр треугольника ВОС.
3. Сторона ромба образует с одной из его диагоналей угол 68°. Найдите углы ромба.
Найдите углы ромба.
4. На диагонали АС параллелограмма АВСD отметили точки Р и К так, что АР = СК (точка Р лежит между точками А и К). Докажите, что ∠АDР = ∠СВК.
5. В параллелограмме АВСD биссектриса угла D пересекает сторону АВ в точке Р. Отрезок АР меньше отрезка ВР в 6 раз. Найдите периметр параллелограмма, если АВ = 14 см.
6. Прямая, пересекающая диагональ ВD параллелограмма АВСD в точке Е, пересекает его стороны АВ и СD в точках М и К соответственно, причем МЕ = КЕ. Докажите, что четырехугольник ВКDМ – параллелограмм.
К-1 В-1 Геометрия 8 Мерзляк.
Решения и ответы
Ответы на контрольную работу:
№ 1. АВ = 3 см; ВС = 15 см.
АВ = 3 см; ВС = 15 см.
№ 2. Р = 32 см.
№ 3. ∠А = 136°; ∠В = 44°.
№ 4. См.решение.
№ 5. Р = 32 см.
№ 6. См.решение.
Смотреть РЕШЕНИЯ заданий в тетради
Вы смотрели: Контрольная работа по геометрии в 8 классе № 1 «Параллелограмм и его виды» (УМК Мерзляк): задания, решения и ответы на нее. Перейти к другому варианту этой контрольной: КР-01. Вариант 2
Вернуться к Списку контрольных работ по геометрии в 8 классе (Мерзляк).
Цитаты из учебного пособия «Геометрия. Дидактические материалы. 8 класс ФГОС» (авт. А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир, изд-во «Вентана-Граф» использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Решения и ОТВЕТЫ на контрольную работу (нет в пособии) адресованы родителям для проверки знаний учащихся.
Геометрия 8 Контрольные Мерзляк | Контроль-знаний.рф
Геометрия 8 Контрольные Мерзляк
Геометрия 8 Контрольные Мерзляк — это цитаты контрольных работ и ответы на задачи контрольных работ из учебного пособия: «Геометрия: дидактические материалы 8 класс: пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович и др. / М.: Вентана-Граф, 2018». Представленные ниже контрольные работы в 2-х вариантах ориентированы на учебник «Геометрия 8 класс» авторов А.Г. Мерзляк, В.Б. Полонский, М.С.Якир системы УМК «Алгоритм успеха». Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Нажмите на необходимую вам тему контрольной работы. В начале указана цитата (материал контрольной работы) из вышеуказанного учебного пособия. Каждая цитата представлена в форме удобной для проверки знаний (на одной странице). Затем представлены ответы на оба варианта контрольной. При постоянном использовании данных контрольных работ (в 4-х вариантах) рекомендуем
Затем представлены ответы на оба варианта контрольной. При постоянном использовании данных контрольных работ (в 4-х вариантах) рекомендуем
КОНТРОЛЬНАЯ РАБОТА 1.
Чтобы скачать контрольную нажмите на картинку правой кнопкой мыши и выберите «Сохранить изображение как…»
ОТВЕТЫ на контрольную работу № 1.
КР-01. Вариант 1.
№ 1. Ответ: 9 см, 15 см.
№ 2. Ответ: 25 см.
№ 3. Ответ: 36° и 54°.
№ 5. Р = 42 см.
КР-01. Вариант 2.
№ 1. Ответ: 3 см, 15 см.
№ 2. Ответ: 32 см.
№ 3. Ответ: 136° и 44°.
№ 5. Р = 32 см.
КОНТРОЛЬНАЯ РАБОТА 2.
ОТВЕТЫ на контрольную работу № 2.
КР-02. Вариант 1.
№ 1. Р = 12+18+20 = 50 (см)
№ 2. Ответ: 24 см, 40 см.
№ 3. Р = 38 (см)
№ 5. Ответ: 121°, 59°, 80°, 100°.
№ 6. Р = 42 (см).
КР-02. Вариант 2.
№ 1. Р = 7+6+5 = 18 (см)
№ 2. Ответ: 32 см, 56 см.
№ 3. Р = 36 (см)
№ 4. Р = 8+8+8+10 = 34 (см)
№ 5. Ответ: 82°, 112°, 68°, 98°.
№ 6. Р = 14 (см).
КОНТРОЛЬНАЯ РАБОТА 3.
ОТВЕТЫ на контрольную работу № 3
Вариант 1.
Вариант 2.
[/vc_tta_section][vc_tta_section title=»Контрольная работа № 4. » tab_id=»1529172743670-592f63c8-a03b»]
КОНТРОЛЬНАЯ РАБОТА 4.
ОТВЕТЫ на контрольную работу № 4
Вариант 1.
Вариант 2.
[/vc_tta_section][vc_tta_section title=»Контрольная работа № 5. » tab_id=»1529172744840-e3f18ff7-6ac0″]
КОНТРОЛЬНАЯ РАБОТА 5.
ОТВЕТЫ на контрольную работу № 5
Вариант 1.
Вариант 2.
[/vc_tta_section][vc_tta_section title=»Контрольная работа № 6. » tab_id=»1529172746709-9820a8f0-98b2″]
КОНТРОЛЬНАЯ РАБОТА 6.
ОТВЕТЫ на контрольную работу № 6
Вариант 1.
Вариант 2.
[/vc_tta_section][vc_tta_section title=»Контрольная работа № 7.

КОНТРОЛЬНАЯ РАБОТА 7 (ИТОГОВАЯ).
ОТВЕТЫ на контрольную работу № 7
Вариант 1.
№ 1. Ответ: 103°, 103°, 77°, 77°.
№ 2. Ответ: 15 см.
№ 3. Ответ: 26 см.
№ 4. Ответ: 128√2 см2.
№ 5. Ответ: 22,5 см.
Вариант 2.
№ 1. Ответ: 74°, 106°, 74°, 106°.
№ 2. Ответ: 4,5 см.
№ 3. Ответ: 10√3 см.
№ 4. Ответ: 45√15 см2.
№ 5. Ответ: 14,5 см.
Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.
Другие контрольные работы по математике в 8 классе:
Контрольная работа № 1. Г-8. Вариант-1 № 1. Диагонали прямоугольника ABCD пересекаются в точке О, ∟АВО=360. Найдите угол AOD. № 2. Найдите углы прямоугольной трапеции, если один из его углов равен 200. № 3. Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма. № 4. В равнобедренной трапеции сумма углов при большем основании равна 960. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, АМ = 4 см. Найдите длину диагонали АD. | Контрольная работа № 1. Г-8. Вариант-2. № 1. Диагонали прямоугольника MNKP пересекаются в точке О, ∟MОN=640. № 2. Найдите углы равнобедренной трапеции, если один из его углов на 300 больше другого. № 3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма. № 4. В прямоугольной трапеции разность углов при одной из боковых сторон равна 480. Найдите углы трапеции. № 5*. Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 300, длина диагонали АС равна 6 см. Найдите AМ, если точка М лежит на продолжении стороны AD. | |||||
Контрольная работа № 1. Г-8. Вариант-3. № 1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма. № 2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4: 5. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон. № 4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∟ADB = ∟BDC = 300. Найдите длину АD, если периметр трапеции равен 60 см. № 5*. В параллелограмме ABCD биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М 1М2 = 8см. Найдите AD. | Контрольная работа № 1. Г – 8. Вариант – 4. 1. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма. № 2. Угол между диагоналями прямоугольника равен 800. Найдите угол между диагональю и меньшей стороной прямоугольника. № 3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма. № 4. № 5*. В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и ВСD пересекаются в точке М. На прямых АВ и СD взяты точки К и Р так, что А –В – К, D – C – P. Биссектрисы углов КВС и ВСР пересекаются в точке М 2. Найдите М1М2. | |||||
Контрольная работа № 2. Г-8 Вариант-1. № 1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. № 2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь этого треугольника. № 3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см. № 4*. В прямоугольной трапеции АВСК большая боковая сторона равна 3√2 см, угол К равен 450, а высота СН делит основание АК пополам. | Контрольная работа № 2. Г-8 Вариант-2. № 1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника. № 2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь этого треугольника. № 3. Диагонали ромба равны 10 и 12 см. Найдите его площадь и периметр. № 4*. В прямоугольной трапеции АВСD большая боковая сторона равна 8 см, угол А равен 600, а высота ВН делит основание АD пополам. Найдите площадь трапеции. | |||||
Контрольная работа № 2. Г-8 Вариант-3. № 1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 300. Найдите площадь параллелограмма. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если А= 24 см, ВС = 16 см, ∟А= 45, ∟D=90 0. № 3. Дан треугольник АВС. На стороне АС отмечена точка К так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см. № 4*. Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон. | Контрольная работа № 2. Г-8 Вариант-4. № 1.Высота ВК, проведенная к стороне АD параллелограмма АВСD, делит эту сторону на два отрезка АК = 7 см, КD = 15 см. Найдите площадь параллелограмма, если ∟А =450. № 2. Вычислите площадь трапеции АВСD с основаниями АD и ВС, если ВС = 13 см, АD = 27 см, СD = 10см, ∟D = 300. № 3. Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ= 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см. № 4*. В равностороннем треугольнике большая сторона составляет 75% суммы двух других. | |||||
Контрольная работа № 3. Г-8. Вариант-1. B № 1. Рисунок 1 Дано: ∟А = ∟В, СО = 4, DО = 6, АО = 5. С Найти: а) ОВ; б) АС : ВD; в) SAOC : SBOD. А О D № 2. В треугольнике АВС АВ = 4 см, ВС= 7 см, АС = 6 см, а в треугольнике МNК МК = 8 см, МN =12 см, КN = 14 см. Найдите углы треугольника МNК, если ∟А = 80, ∟В = 600. № 3. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ║АС, ВМ : АМ = 1: 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, А = 12 см, ВС = 4 см. | Контрольная работа №3. Г-8. Вариант-2. N № 1. Рисунок 1. P Дано: РЕ ║NК, МР = 8, МN = 12, МЕ = 6. Найти: а) МК; б) РЕ : NК; в) SМЕР : SMKN. M E K № 2. В ∆АВС АВ = 12 см, ВС = 18 см, ∟В = 700,а в ∆ МNК MN = 6 cм, NК = 9 см, ∟N= 700. Найдите сторону АС и угол С треугольника АВС, если МК = 7 см, ∟К = 600. № 3. Отрезки АВ и СD пересекаются в точке О так, что ∟АСО = =∟ВDО, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника ВОD равен 21 см. № 4*. В трапеции АВСD (АD и ВС основания) диагонали пересекаются в точке О, SAOD= 32 см2, S BOC = 8 см2. Найдите меньшее основание трапеции, если большее из них равно 10 см. | |||||
Контрольная работа № 3. Вариант-3. № 1. Рисунок 1. D B Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, ОD = 6,3 см. O Доказать: АС ║ВD. Найти: а) DВ : АС; б) РАОС : РDBO ; в) SDBO: SAOC A C № 2. Диагонали ромба АВСD пересекаются в точке О, ВD = 16 см. На стороне АВ взята точка К так, что ОК ┴ АВ и ОК = 4√3 см. Найдите сторону ромба и второю диагональ. № 3. В выпуклом четырехугольнике АВСD АВ = 9 см, ВС = 8 см, СD = 16 см, АD = 6 см, ВD = 12 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике МNК с основанием МК, равным 10 см, МN= NК = 20 см. На стороне NК лежит точка А так, что АК : АN= 1 : 3. Найдите АМ. | Контрольная работа № 3. Г-8. Вариант-4. № 1. Рисунок 1. B Дано: ВD = 3,1 см, ВЕ = 4,2 см, ВА = 9,3 см, ВС = 12,6 см. Доказать: DЕ ║АС. Найти: а) DЕ : АС; б) РABC : РDBE ; в) SDBE : SABC. A C № 2. Диагонали ромба АВСD пересекаются в точке О. На стороне АВ взята точка К так, что ОК ┴ АВ, АК = 2 см, ВК = 8 см. Найдите диагонали ромба. № 3. АВСD – выпуклый четырёхугольник, АВ = 6 см, ВС = 9 см, СD = 10 см, DА = 25 см, АС = 15 см. Докажите, что АВСD – трапеция. № 4*. В равнобедренном треугольнике АВС АВ = ВС = 40 см, АС = 20 см. На стороне ВС отмечена точка Н так, что ВН : НС = 3 : 1. Найдите АН. | |||||
Контрольная работа № 4. Г-8. Вариант-1. № 1. Средние линии треугольника относятся как 2: 2: 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. № 2. Медианы треугольника АВС пересекаются в точке О. Через точку О проведена прямая, параллельная стороне АС пересекающая стороны АВ и ВС в точках Е и F соответственно. № 3. В прямоугольном треугольнике АВС (∟С= 900) АС = 5 см, ВС = 5√3 см. Найдите угол В и гипотенузу АВ. № 4. В треугольнике АВС ∟А =α, ∟С =β, сторона ВС = 7 см, ВН-высота. Найдите АН. № 5. В трапеции АВСD продолжения боковых сторон пересекаются в точке К, причем точка В-середина отрезка АК. Найдите сумму оснований трапеции, если АD = 12 см. | Контрольная работа №4. Г-8. Вариант-2. № 1. Средние линии треугольника относятся как 4: 5: 6, а периметр треугольника, образованного средними линиями, равен 30 см. Найдите средние линии треугольника. № 2. Медианы треугольника MNK пересекаются в точке О. Через точку О проведена прямая, параллельная стороне MK пересекающая стороны MN и NK в точках A и B соответственно. Найдите MK, если длина отрезка АB равна 12 см. №3. В прямоугольном треугольнике РКТ (∟Т= 900), РТ = 7√3 см, КТ= 7 см. № 4. В треугольнике АВС ∟А =α, ∟С =β , высота ВН равна 4 см. Найдите АС. № 5. В трапеции MNKP продолжения боковых сторон пересекаются в точке E, причем EK=KP. Найдите разность оснований трапеции, если NK = 7 см. | |||||
Контрольная работа № 4. Г-8. Вариант-3. № 1. На стороне ВС треугольника АВС выбрана точка D так, что ВD: DС = 3:2, точка К – середина отрезка АВ, точка F–середина отрезка АD, КF =6 см, ∟АDС=1000. Найдите ВС и ∟АFК. № 2. В прямоугольном треугольнике АВС ∟С= 900, АС = 4 см, СВ = 4√3 см, СМ –медиана. Найдите угол ВСМ. № 3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α . Найдите периметр и площадь трапеции. № 4.В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА =13 см, ОВ = 10 см. № 5. В трапеции АВС (ВС ║АD) АВ ┴ ВD, ВD =2√5 , AD =2√10, СЕ – высота треугольника ВСD, а tg∟ECD= 3. Найдите ВЕ. | Контрольная работа № 4. Г-8. Вариант-4. № 1. На стороне АМ треугольника АВМ отмечена точка Н так, что АН: НЬ = 4:7; точка С – середина стороны АВ, точка О –середина стороны отрезка ВН, АМ = 22 см, ∟ВОС = 1050. Найдите СО и угол ВНМ. № 2. В прямоугольном треугольнике MNK ∟K= 90, KM = 6см, NК =6√3 см, КD- медиана. Найдите угол КDN. № 3. В равнобедренной трапеции боковая сторона равна 6 см, меньшее основание 10 см, а меньший угол α . Найдите площадь трапеции. № 4. В прямоугольном треугольнике АВС (∟С =900) медианы пересекаются в точке О, ОВ = 10 см, ВС = 12 см. Найдите гипотенузу треугольника. № 5. В трапеции АВСD ∟А =90, АС= 6√2, ВС=6, DЕ –высота треугольника АСD, tg∟ACD= 2. Найдите СЕ. | |||||
Контрольная работа № 5. Вариант-1. № 1. АВ и АС- отрезки касательных, проведенных к окружности радиуса 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕВС = 11 : 12. Найдите ∟ВСА, ∟ВАС. B A 130O C № 3. Хорды MN и PK пересекаются точке E так, что ME =12 см, NE =3 см, PE=KE. Найдите PK. № 4.Окружность с центром в точке О радиусом 16 см описана около треугольника ABC так, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BC треугольника. | Контрольная работа № 5. Г-8. Вариант-2. № 1. MN и MK-отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MN и MK, если МО= 13 см. № 2. Рисунок 1. Дано: ᵕАВ : ᵕАС = 5 : 3. Найдите ∟ВОС, ∟АВС. A B 60O C O № 3. Хорды АВ и СD пересекаются точке F так, что АF =4 см, ВF =16 см, СF=DF. № 4.Окружность с центром в точке О радиусом 12 см описана около треугольника MNK так, что ∟MON=1200, ∟NOK=900. Найдите стороны MN и NK треугольника. | |||||
Контрольная работа № 5. Г-8. Вариант-3. № 1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см,4 см,5 см. Определите вид треугольника № 2. Точки А и В делят окружность с центром О на дуги АВМ и АСВ так, что дуга АСВ на 600 меньше дуги АМВ. АМ- диаметр окружности. Найдите углы АМВ, АВМ, АСВ. № 3. Хорды АВ и СD пересекаются в точке Е так, что АЕ=3 см, ВЕ=36 см, СЕ: DЕ =3:4. Найдите СD и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. | Контрольная работа № 5. Г-8. Вариант-4. № 1. В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см. № 2.Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 900 меньше дуги ЕАН, ЕА- диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН. № 3. Хорды МN и РК пересекаются в точке А так, что МА= 3 см, NА= 16 см, РА: КА= 1: 3. Найдите РК и наименьшее значение радиуса этой окружности. № 4. В равнобедренном треугольнике основание равно 10 см, а высота, Проведенная к ней, 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. | |||||
№ 1 | № 2 | № 3 | № 4 | № 5 | ||
Контрольная работа № 1. | Вариант-1 | ∟АОD=72 | 900 , 900, 1600, 200 | 5см, 10см, 5см, 10см | 480, 480, 1320, 1320 | DВ=6см |
Вариант-2 | ∟ОМР=32 | 750, 1050, 1050, 750 | 5см, 15см, 5см, 15см | 660, 1140, 900, 900 | АМ=3см | |
Вариант-3 | 10см, 15см, 10см, 15см | 800 | 450, 1350 450,1350 | AD=24см | AD=8см | |
Вариант-4 | 18см, 12см, 18см, 12см | 500 | 300, 300, 1500, 1500 | АВ= 7см | М1 М2 =6см | |
Контрольная работа № 2. | Вариант-1 | 24см2 | 10см, 24см2 | Р=4√41см, S= 40cм2 | S АВСК= 13,5см2 | — |
Вариант-2 | 24см2 | 5см, 30см2 | Р=4√61см, S= 60cм2 | S АВСD= 24√3см2 | — | |
Вариант-3 | 780cм2 | SABCD = 160cм2 | SABK =33,6см2, SCBK =50,4см2 | 6см | — | |
Вариант-4 | 154см2 | SABCD = 100cм2 | SKPT=36см2, SMPT =18см2 | 3см | — | |
Контрольная работа № 3. | Вариант-1 | а) 7,5; б) ; в) | 800, 600,400 | 5см | S = 5см2 | — |
Вариант-2 | а) 9; б) ; в) | AC=14см, ∟С=600 | 14см | 5см2 | — | |
Вариант-3 | а); б) ; в) | АВ=6см; АС= 16√3 | — | 10см | — | |
Вариант-4 | а) ; б) 3; в) | АС=4√5; ВD=8√5 | — | 20см | ||
Контрольная работа № 5. | Вариант-1 | 15см | ∟ВСА=550, ∟ВАС=600 | РЕ=6см, РК= 12см | АВ=16√3см, ВС= 16√2см | — |
Вариант-2 | 12см | ∟ВОС=1200, ∟АВС=450 | СF=8см, СD=16см | МN=12√3см; NК=12√2см | — | |
Вариант-3 | 6см, 8см, 10 см | ∟АМВ=600, ∟АВМ=900, ∟ АСВ=1050 | СD=21см, 19,5см | 3см, 6,25см | ||
Вариант-4 | 6см, 8см, 10см | ∟ЕКА=90, ∟ЕАН=670 30١, ∟ЕКН=1120 30١ | РК=16см, 9,5см | 3см, 7см |
Контрольная работа по геометрии 8 класс на тему «Четырехугольники»
Автор Maria На чтение 10 мин. Опубликовано
Контрольная работа № 1
I Уровень (обязательный уровень).
Вариант 1
1. Диагонали прямоугольника АВСД пересекаются в точке О. найдите угол между диагоналями, если АВО=44.
2. В параллелограмме KMNP проведена биссектриса угла MKP, которая пересекает сторону MN в точке Е.
а) Докажите, что треугольник KME равнобедренный.
б) Найдите сторону KP, если ME=12см, а периметр параллелограмма равен 68 см.
Вариант 2
1. Диагонали ромба KMNP пересекается в точке О. Найдите углы треугольника КОМ, если угол MNP равен 80.
2. На стороне ВС параллелограмма АВСД взята точка М так, что АВ=ВМ.
а) Докажите, что АМ – биссектриса угла ВАД.
II Уровень (средний уровень сложности)
Вариант 1
1. Периметр параллелограмма 50см одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.
2. Найдите углы между диагоналями прямоугольника, если каждый из них делит угол прямоугольника в отношении 4:5.
3. В трапеции АВСД диагональ ВД перпендикулярна боковой стороне АВ, АДВ=ВДС=30. Найдите длину АД, если периметр трапеции равен 60см.
4*. В параллелограмме АВСД биссектрисы углов АВС и ВСД пересекаются в точке М1. На прямых АВ и СД взяты точки К и Р так, что А-В-К, Д-С-Р. биссектрисы углов КВС и ВСР пересекаются в точке М2, М1 М2=8см. найдите АД.
Вариант 2.
1. Периметр параллелограмма 60 см. одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.
2. Угол, между диагоналями прямоугольника равен 80. Найдите угол между диагональю и меньшей стороной прямоугольника.
3. В трапеции АВСД диагональ АС перпендикулярна боковой стороне СД и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, Д=60.
4*. В параллелограмме АВСД АД=6см. биссектрисы углов АВС и ВСД пересекаются в точке М1. На прямых АВ и СД взяты точки К и Р так, что А-В-К, Д-С-Р. Биссектрисы углов КВС и ВСР пересекаются в точке М2. Найдите М1 М2.
III Уровень (сложный)
Вариант 1
1. В равнобедренной трапеции длина боковой стороны 2d, длины оснований 5d и 7d. Найдите углы трапеции.
2. В ромбе АВСД биссектриса угла ДСА перпендикулярна стороне АД. Найдите углы ромба.
3. Внутри квадрата АВСД выбрана точка М так, что треугольник АМД – равносторонний. Найдите угол АМВ.
4*. Биссектриса угла С параллелограмма АВСД пересекает сторону АД в точке М и продолжение стороны АВ за точку А в точке N. Найдите периметр параллелограмма, если АN=4см, ДМ=3см.
Вариант 2.
1. В равнобедренной трапеции боковая сторона равна меньшему основанию, а диагональ перпендикуляра боковой стороне. Найдите углы трапеции.
3. Внутри квадрата АВСД выбрана точка N так, что треугольник ВNС равносторонний. Найдите угол NАД.
4*. В параллелограмме АВСД биссектриса угла А пересекает сторону ВС в точке F и продолжение стороны СД за точку – в точке Е. Найдите периметр параллелограмма, если ВF=2см, ЕС=3см.
Контрольная работа № 2
1 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 40 см, а сторона АВ больше ВС на 4 см.
2. Найти углы параллелограмма АВСД, если известно, что угол А больше угла В в 3 раза.
3. Найти углы равнобедренной трапеции, если один из них равен 75º.
5. В четырехугольнике АВСД: АВ=СД, Докажите, что АВСД – параллелограмм.
6. В ромбе АВСД угол А равен . Диагонали ромба пересекаются в точке О. Найти углы треугольника ВОС.
2 вариант.
1. Найти стороны параллелограмма АВСД, если его периметр равен 54 см, а сторона АВ больше ВС в 2 раза.
2. Найти углы параллелограмма АВСД, если известно, что угол А меньше угла В на
3. Найти углы прямоугольной трапеции, если больший из них равен 120º.
4. Найти диагонали прямоугольника АВСД, если , АД=6 см.
5. В четырехугольнике сумма углов, прилежащих к каждой из двух смежных сторон, равна . Докажите, что АВСД – параллелограмм.
Контрольная работа № 3
1 Вариант
1. Диагонали прямоугольника АВСД пересекаются в точке О, угол АВО равен 36. Найдите угол АОД. (3 б.)
2. Найдите углы прямоугольной трапеции, если один из ее углов равен 20.(2 б. )
3. Диагонали ромба КМНР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МНР равен 80.(4 б.)
4. В равнобокой трапеции сумма углов при большем основании равна 96. Найдите углы трапеции.(4 б.)
5. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.(5 б.)
6. В параллелограмме КМНР проведена биссектриса угла МКР, которая пересекает сторону МН в точке Е. а) Докажите, что треугольник КМЕ равнобедренный. б) найдите периметр КМНР, если МЕ = 10 см, ЕН = 6 см.( 8 б.)
критерии оценки
« 3 » — 5 – 8 баллов
« 4 » — 9 – 10 баллов
« 5 » — 12 – 13 баллов
более 14 баллов – дополнительная оценка.
2 вариант
1. Диагонали прямоугольника МНКР пересекаются в точке О, угол МОН равен 64
Найдите угол ОМР. (3 б.)
2. Найдите углы равнобокой трапеции, если один из ее углов равен 70.(2 б. )
3. Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол ВОА, если угол АОВ равен 65.(4 б.)
4. В равнобокой трапеции сумма углов при меньшем основании равна 210. Найдите углы трапеции.(4 б.)
5. Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.(5 б.)
6. На стороне ВС параллелограмма АВСД взята точка М так, что АВ = ВМ . а) Докажите, что АМ – биссектриса угла ВАД. б) найдите периметр параллелограмма, если СД = 8 см, СМ = 6 см.( 8 б.)
критерии оценки
« 3 » — 5 – 8 баллов
« 4 » — 9 – 10 баллов
« 5 » — 12 – 13 баллов
более 14 баллов – дополнительная оценка.
Контрольная работа № 4
I уровень сложности
Вариант 1
Диагонали прямоугольника ABCD пересекается в точке О, ∠ABO = 36°. Найдите угол AOD.
Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.
Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма.
В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.
* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, AM = 4 см. Найдите длину диагонали BD ромба, если точка М лежит на стороне AD.
Вариант 2
Диагонали прямоугольника MNKP пересекаются в точке О, ∠MON = 64°. Найдите угол ОМР.
Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго.
Стороны параллелограмма относятся как 3 : 1, а его периметр равен 40 см. Найдите стороны параллелограмма.
В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции.
* Высота ВМ, проведенная из вершины угла ромба ABCD образует со стороной АВ угол 30°, длина диагонали АС равна 6 см. Найдите AM, если точка М лежит на продолжении стороны AD.
II уровень сложности
Вариант 1
Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.
Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4 : 5.
Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон.
В трапеции ABCD диагональ BD перпендикулярна боковой стороне АВ, ∠ADB = ∠BDC = 30°. Найдите длину AD, если периметр трапеции 60 см.
* В параллелограмме ABCD биссектрисы углов АВС и BCD пересекаются в точке M1. На прямых АВ и CD взяты точки К и Р так, что А – В – К, D – С – Р. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М1М2 = 8 см. Найдите AD.
Вариант 2
Периметр параллелограмма 60 см. Одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.
Угол между диагоналями прямоугольника равен 80°. Найдите угол между диагональю и меньшей стороной прямоугольника.
Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна половине неперпендикулярной к ней стороны параллелограмма.
В трапеции ABCD диагональ АС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∠D = 60°.
* В параллелограмме ABCD AD = 6 см. Биссектрисы углов АВС и BCD пересекаются в точке M1. На прямых АВ и CD взяты точки К и Р так, что А – В – К, D – С – Р. Биссектрисы углов КВС и ВСР пересекаются в точке М2. Найдите М1М2.
III уровень сложности
Вариант 1
В равнобокой трапеции длина боковой стороны 2d, длины оснований 5d и 7d. Найдите углы трапеции.
В параллелограмме ABCD известно, что ∠А = 60°, АВ = 10, AD = 16. Найдите расстояния от вершин В и D до биссектрисы ∠BCD.
В ромбе ABCD биссектриса угла DCA перпендикулярна стороне AD. Найдите углы ромба.
Внутри квадрата ABCD выбрана точка М так, что треугольник AMD равносторонний. Найдите угол AMВ.
* Биссектриса угла С параллелограмма ABCD пересекает сторону AD в точке М и на продолжении стороны АВ за точку А в точке N. Найдите периметр параллелограмма, если AN = 4, DM = 3.
Вариант 2
В равнобокой трапеции боковая сторона равна меньшему основанию, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.
В параллелограмме KMNP угол М равен 120°, КМ = 8, КР = 10. Найдите расстояния от вершин М и Р до биссектрисы угла МКР.
Высота ромба делит его сторону пополам. Найдите углы ромба.
Внутри квадрата ABCD выбрана точка N так, что треугольник BNC равносторонний. Найдите угол NAD.
* В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке F и на продолжении стороны CD за точку С в точке Е. Найдите периметр параллелограмма, если BF = 2 см, ЕС = 3 см.
Критерии оценивания результатов контрольной работы
оценка «5» — правильно решены три задачи;
оценка «4» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
оценка «3» — правильно решена одна задача;
оценка «2» — все задачи решены неправильно.
За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.
Контрольная работа № 5
Вариант I
1. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите угол между диагоналями, если ∠ABO = 30°.
2. В параллелограмме KMNP проведена биссектриса угла МКР, которая пересекает сторону MN в точке Е.
а) Докажите, что треугольник КМЕ равнобедренный.
б) Найдите сторону КP, если ME = 10 см, а периметр параллелограмма равен 52 см.
Вариант II
1. Диагонали ромба KMNP пересекаются в точке О. Найдите углы треугольника КОМ, если ∠MNP = 80°.
2. На стороне ВС параллелограмма ABCD взята точка Мтак, что АВ = ВМ.
а) Докажите, что AM — биссектриса угла BAD.
б) Найдите периметр параллелограмма, если CD = 8 см, СМ = 4 см.
Вариант III
1. Через вершину С прямоугольника ABCD проведена прямая, параллельная диагонали BD и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найдите периметр четырехугольника ACMN, если диагональ BD равна 8 см.
2. Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Луч DM пересекает прямую АВ в точке N. Найдите периметр параллелограмма ABСD, если AN = 10 см
Контрольная работа №1. Четырехугольники. 8 класс Вариант 1 1. На сторонах РК и МН параллелограмма МРКН взяты точки А и В соответственно, МР=РВ=АК, МРВ = 60°. Найдите углы параллелограмма и сравните отрезки ВМ и АН. 2. В прямоугольной трапеции острый угол и угол, который составляет меньшая диагональ с меньшим основанием равны по 60°. Найдите отношение оснований. 3. В ромбе АВСD О – точка пересечения диагоналей, ОМ, ОК, ОЕ – перпендикуляры, опущенные на стороны АВ, ВС, СD соответственно. Докажите, что ОМ=ОК, и найдите сумму углов МОВ и СОЕ. 4. В треугольнике АВС В=90°, АВ=ВС. На сторонах АВ и ВС взяты точки М и Р, а на стороне АС – точки К и Н так, что четырехугольник МРНК является квадратом, МР=а. Найдите АС. | Контрольная работа №1. Четырехугольники. 8 класс Вариант 2 1. На сторонах ВС и АD параллелограмма АВСD взяты точки M и K, АВ=ВМ=КD, АМВ = 30°. Найдите углы параллелограмма и сравните отрезки АМ и СК. 2. В прямоугольной трапеции диагональ перпендикулярна к боковой стороне, острый угол равен 45°. Найдите отношение оснований. 3. В ромбе МРНК диагонали пересекаются в точке О.На сторонах МК, КН, РН взяты точки А, В, С соответственно, АК=КВ=РС. Докажите, что ОА=ОВ, и найдите сумму углов РОС и МОА. 4. В треугольнике МРК М=90°, МР=МК. На сторонах МР, РК, МК отмечены точки А, В, С соответственно так, что четырехугольник МАВС является квадратом, АС=а. Найдите РК. |
уроков геометрии в 8 классе
Четырехугольник — замкнутая плоскость фигура ограничена четырьмя отрезками прямых. Например, цифра ABCD показана вот четырехугольник.
Отрезок, проведенный из одной вершины четырехугольник к противоположной вершине называется диагональю четырехугольник. Например, AC — это диагональ четырехугольник ABCD , а так — BD . четырехугольник ABCD-правильный При именовании четырехугольника его вершины должны быть в последовательный порядок (на основе из рисунка выше)
Уголки: (можно назвать одной буквой)
угол A / DAB
угол B / ABC
угол C / BCD
угол D / CDA
Типы четырехугольников
Есть особые виды четырехугольника:
Свойства четырехугольника
- Четыре стороны (края)
- Четыре вершины (углы)
- В сумме внутренние углы составляют 360 градусов :
Прямоугольник
| означает «прямой угол» | ||
| а также | показать равные стороны | |
Прямоугольник — это четырехсторонняя форма, каждый угол которой является прямым (90 °).
Также противоположных сторон параллельны и равной длины.
Ромб
Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину.
Также противоположные стороны параллельны и равны противоположные углы.
Еще один интересный момент: диагонали (пунктирные линии на втором рисунке) пересекаются посередине под прямым углом. Другими словами, они «рассекают» друг друга пополам под прямым углом.
Площадь
| означает «прямой угол» | ||
| показать равные стороны | ||
У квадрата равные стороны, и каждый угол — прямой угол (90 °)
Также противоположные стороны параллельны.
Квадрат также соответствует определению прямоугольника (все углы равны 90 °) и ромба (все стороны равной длины).
Параллелограмм
У параллелограмма противоположные стороны параллельны и равны по длине. Также равны противоположные углы (углы «а» одинаковы, а углы «b» одинаковы).
ПРИМЕЧАНИЕ: квадраты, прямоугольники и ромбы — это параллелограммы!
Пример:
Параллелограмм с:
это квадрат ! |
Трапеция (Великобритания: Trapezium)
Трапеция | Равнобедренная трапеция |
Трапеция (в Великобритании ее называют трапецией) имеет пару параллельных противоположных сторон.
Она называется равнобедренной трапецией , если стороны, которые не параллельны, равны по длине и оба угла, идущие с параллельной стороны, равны, как показано.
А трапеция (UK: trapezoid) — четырехугольник без параллельных сторон:
| Трапеция | Трапеция | |
| США: | пара параллельных сторон | НЕТ параллельных сторон |
| Великобритания: | НЕТ параллельных сторон | пара параллельных сторон |
Воздушный змей
Эй, похоже на воздушного змея.У него две пары сторон. Каждая пара состоит из смежных сторон равной длины. На стыке пар углы равны. Диагонали (пунктирные линии) пересекаются под прямым углом, и одна из диагоналей делит пополам (делит пополам) другую. Сумма внутренних углов
Сумма внутренних углов
Докажите, что сумма углов a четырехугольник равен 360º.
Следовательно, сумма углов четырехугольника равна 360º.
Применение свойств углов в четырехугольниках
Доказанные теоремы можно использовать для доказательства других теорем.Их также можно использовать, чтобы найти значения местоимений в задаче.Найдите значение местоимения x в сопроводительная диаграмма. Обоснуйте свой ответ. Найдите значение каждого местоимения в кайт показан здесь. Обоснуйте свои ответы. Найдите значение каждого местоимения в сопроводительная диаграмма. Обоснуйте свои ответы.
8 класс Математика Геометрия: Урок 2
Геометрия 2D-форм
Название: Геометрия двумерных фигур Ответьте на следующие вопросы в своей классной тетради: 1.Дайте определения каждой из следующих форм и нарисуйте каждую из них: а) равносторонний треугольник б) равнобедренный
ПодробнееОценка угловых мер
1 Оценка угловых мер Сравните и оцените угловые меры. Вам понадобится транспортир. 1. Оцените размер каждого угла. а) в) Вы можете оценить размер угла, сравнив его с углом
ПодробнееГлоссарий по алгебре и геометрии.Угол 90
lgebra Геометрия Глоссарий 1) острый угол угол меньше 90 острый угол 90 угол 2) острый треугольник треугольник, все углы которого меньше 90 3) смежные углы, углы, имеющие общий отрезок Пример:
Подробнее39 Симметрия плоских фигур
39 Симметрия плоских фигур В этом разделе нас интересуют симметричные свойства плоских фигур.Под симметрией плоской фигуры мы понимаем движение плоскости, которое перемещает фигуру так, что
ПодробнееСловарь форм от YR до Y6
Словарь форм с YR по Y6. Указания. Термины в этом словаре взяты из буклета «Математический словарь», выпущенного Национальной стратегией счисления. Детям нужно понимать и использовать
Подробнее2006 Геометрия Форма A Страница 1
2006 Форма Геометрии Страница 1 1.Гипотенуза прямоугольного треугольника имеет длину 12 дюймов, а один из острых углов составляет 30 градусов. Длина более короткой части должна быть: () 4 3 дюйма () 6 3 дюйма () 5 дюймов
Подробнее11.3 Кривые, многоугольники и симметрия
11.3 Кривые, многоугольники и симметрия Простое определение многоугольников Форма является простой, если она не пересекает себя, за исключением, возможно, конечных точек. Замкнутое Определение Фигура закрывается, если концы встречаются.Многоугольник
ПодробнееПримечания к формам и рисункам
Задача 1.1 Определения: правильные многоугольники — многоугольники, у которых все длины сторон и углы имеют одинаковые грани измерения — также называемые стороной мозаики фигуры — покрывающие плоскую поверхность с
ПодробнееОтрезки, лучи и линии
ГЛАВНАЯ ССЫЛКА Сегменты линии, лучи и семейство линий Примечание Помогите ребенку сопоставить каждое имя, указанное ниже, с правильным рисунком линии, луча или сегмента линии.Затем понаблюдайте, как ваш ребенок рисует линейкой
. ПодробнееПлощадь. Обзор области. Определить: Площадь:
Определить: Область: Обзор области Воздушный змей: Параллелограмм: Прямоугольник: Ромб: Квадрат: Трапеция: Постулаты / Теоремы: У каждой закрытой области есть область. Если замкнутые фигуры совпадают, то их площади равны.
ПодробнееГеометрия и измерения
Студент сможет: Геометрия и измерение 1.Продемонстрировать понимание принципов геометрии и измерений и операций с использованием измерений. Использовать американскую систему измерения для
. Подробнееповерхности, 569-571, 576-577, 578-581 треугольника, 548 Ассоциативное свойство сложения, 12, 331 умножения, 18, 433
Абсолютное значение и арифметика, 730-733 определены, 730 Острый угол, 477 Острый треугольник, 497 Дополнение, 12 Дополнительное ассоциативное свойство, (см. Коммутативное свойство), переносящее, 11, 92 коммутативное свойство
ПодробнееЛестница прогресса геометрии
Лестница прогресса в геометрии Математика имеет смысл Основание Цели на конец года стр. 2 Математика имеет смысл 1 2 Цели в конце блока стр. 3 Математика имеет смысл 3 4 Цели в конце блока стр. 4 Математика дает
ПодробнееДорогие семьи 4-х классов,
Дорогие семьи 4-х классов! В течение следующих нескольких недель наш класс будет изучать геометрию.В ходе повседневной деятельности мы будем исследовать взаимосвязь между плоскими двухмерными фигурами и твердыми трехмерными фигурами
. ПодробнееE XPLORING ЧЕТВЕРТЫЕ
E XPLORING QUADRILATERALS E 1 Состояние геометрии Цель 9: использовать геометрические методы для анализа, категоризации и заключения о точках, линиях, плоскостях и пространстве. Заявление о целях: Действия в этом
ПодробнееКраткая справочная электронная книга
Этот файл распространяется БЕСПЛАТНО издателем Quick Reference Handbooks и автором.Электронная книга «Краткий справочник» Щелкните «Содержание» или «Указатель» на левой панели, чтобы выбрать тему. Математические факты перечислены
ПодробнееКлассификация треугольников урока 1
Классификация Урок 1 острый угол congruent scalene Классификация СЛОВАРЬ прямой угол равнобедренный Диаграмма Венна тупой угол равносторонний Вы классифицируете многие вещи вокруг себя. Например, вы можете выбрать
Подробнее9 Площадь, периметр и объем
9 Площадь, периметр и объем 9.1 Двумерные фигуры В следующей таблице приведены названия некоторых двухмерных фигур. В этом разделе мы рассмотрим свойства некоторых из этих фигур. Прямоугольник Все углы прямые
ПодробнееПримечания к геометрии ПЕРИМЕТР И ПЛОЩАДЬ
Периметр и площадь Страница 1 из 57 ПЕРИМЕТР И ПЛОЩАДЬ Цели: После завершения этого раздела вы должны быть в состоянии сделать следующее: Вычислить площадь заданных геометрических фигур.Рассчитать периметр
ПодробнееДомыслы. Глава 2. Глава 3
Гипотезы Глава 2 Гипотеза о линейных парах C-1 Если два угла образуют линейную пару, то сумма углов составляет 180. (Урок 2.5) C-2 Гипотеза о вертикальных углах Если два угла вертикальны
ПодробнееКлассификация четырехугольников
1 классификация Четырехугольников Определите и отсортируйте четырехугольники.1. Какой из этих параллелограммов? ,, четырехугольник представляет собой замкнутую форму с 4 прямыми сторонами. трапеция имеет ровно 1 пару параллельных сторон.
Подробнее43 Периметр и Площадь
43 Периметр и площадь Периметры фигур встречаются в реальных жизненных ситуациях. Например, кто-то может захотеть узнать, какой длины забор будет окружать прямоугольное поле. В этом разделе мы изучим
ПодробнееУрок 9.1 Теорема Пифагора
Урок 9.1. Теорема Пифагора. Дайте все ответы, округленные до ближайшей 0,1 единицы. 1. а. п. a 75 см 14 см p 6 7 см 8 см 1 см 4 6 4. rea 9 дюймов 5. Найдите площадь. 6. Найдите координаты h и радиус
ПодробнееДроби в действии! Дон Джесси
Дроби в действии! Dawn Jesse Fractions In Action Dawn Jesse Fractions In Action — это интерактивное занятие, состоящее из прямого обучения, совместного обучения и основанное на запросах.Как ученики
ПодробнееG3-33 Строительные пирамиды
G3-33 Строительство пирамид Цель: Учащиеся будут строить каркасы пирамид и описывать свойства пирамид. Требуемые предварительные знания: многоугольники: треугольники, четырехугольники, пятиугольники, шестиугольники Словарь:
ПодробнееМЕНСУРАЦИЯ. Определение
МЕНСУРАЦИЯ Определение 1.Измерение: это раздел математики, который занимается вопросами длины линий, площадей поверхностей и объемов твердых тел. 2. Измерение плоскости: это касается сторон, периметров
ПодробнееСветящаяся в темноте геометрия
Большая идея: светящаяся в темноте геометрия На этой неделе вы будете делать геометрические фигуры из светящихся палочек. Дети попробуют треугольники и четырехугольники всех размеров и форм, а затем выложат палочки из мистического
. ПодробнееПериметр.14 футов. 5 футов. 11 футов.
Периметр Периметр геометрической фигуры — это расстояние вокруг фигуры. Периметр можно рассматривать как обход фигуры, отслеживая пройденное расстояние. Чтобы определить
ПодробнееКоврики для задания 2 для 8-го класса
8-й класс Задача 2 Коврики Задача учащегося Основная идея 4 Геометрия и размеры Найдите периметры фигур.Используйте теорему Пифагора, чтобы найти длины сторон. Примените соответствующие методы, инструменты и формулы для определения
Подробнее12 Площадь и объем поверхности
12 Площадь поверхности и объем 12.1 Трехмерные фигуры 12.2 Площадь поверхности призм и цилиндров 12.3 Площадь поверхности пирамид и конусов 12.4 Объемы призм и цилиндров 12.5 Объемы пирамид
ПодробнееPPT — Геометрия Раздел 6-2B Доказательство того, что четырехугольники являются параллелограммами Страница 423 Будьте готовы к оценке 6-2A Презентация PowerPoint
Геометрия Раздел 6-2B Доказательство четырехугольников — это параллелограммов Страница 423 Будьте готовы к оценке 6-2A
Ответы для 6-2A • 13 • 44 • 135o • 122o • 98o • Диагонали делятся пополам • Противоположные стороны конгруэнтны • Последовательные углы являются дополнительными • Противоположные углы конгруэнтны • a.ZW YX, ZY WX (2 очка) b. ZW @ YX, ZY @ WX (2 очка) c. W&X, X&Y, Y&Z, Z&W (4 очка) d. ÐZWX @ ÐXYZ, ÐWXY @ ÐYZW (2 балла)
Ответы на 6-2A продолж. • 11. (6,5), (2,5), (4, -1) (3 балла) • 10 баллов. (Порядок может быть другим, спросите, есть ли у вас вопрос.) • ABCD — параллелограмм — Учитывая • Нарисуйте AC 2 балла. определить линию • AB DC def. параллелограмма • AD BC def параллелограмма • ÐDAC @ ÐBCA alt. внутр. углы конгруэнтны • ÐACD @ ÐBAC alt.внутр. углы совпадают • AC @ AC Reflexive • DADC @DCBA ASA • AB @ CD CPCTC • BC @ AD CPCTC 32 точки. возможно
ШКАЛА СОРТА — 32 ВОЗМОЖНАЯ 31,5 — 98% 24,5 — 77% 31 — 97% 24 — 75% 30,5 — 95% 23,5 — 73% 30 — 94% 23 — 72% 29,5 — 92% 22,5 — 70% 29 — 91% 22 — 69% 28,5 — 89% 21,5 — 67% 28 — 88% 21 — 66% 27,5 — 86% 20,5 — 64% 27 — 84% 20 — 63% 26,5 — 83% 19,5 — 61% 26 — 81% 19 — 59% 25,5 — 80% 18,5 — 58% 25 — 78% 18 — 56% 4
Параллелограммы: Вы можете быть уверены, что четырехугольник является параллелограммом, если обе пары противоположных сторон параллельно.(определение параллелограмма) Четырехугольник — это параллелограмм…… если обе пары противоположных сторон параллельны. Стр.425… если обе пары противоположных углов совпадают. … Если обе пары противоположных сторон совпадают. … Если последовательные углы являются дополнительными. … Если диагонали пересекают друг друга.
Попробовать: Это параллелограмм? Обосновать ответ. Да, противоположные стороны совпадают. Pg.424
Попробовать: Это параллелограмм? Обосновать ответ.Да, диагонали делят друг друга пополам. Pg.424
Попробовать: Это параллелограмм? Обосновать ответ. Да, последовательные углы являются дополнительными. Pg.424
Попробовать: Это параллелограмм? Обосновать ответ. Может быть. ОБА набора противоположных сторон должны быть параллельны. Pg.424
Упражнения: Если AE @ EC и DE @ EB, это параллелограмм? Обосновать ответ. # 4 Pg.425 Да, диагонали делят друг друга пополам.
Упражнения: Если ÐADC @ ÐABC, это параллелограмм? Обосновать ответ. # 5 Pg.425 Возможно. Должно быть 2 набора совпадающих противоположных углов.
Упражнения: Если AB @ CD и AD @ BC, является ли это параллелограммом? Обосновать ответ. # 6 Pg.425 Да, противоположные стороны совпадают.
Упражнения: Если ABCD и AD BC, является ли это параллелограммом? Обосновать ответ. # 7 Pg.425 Да, противоположные стороны параллельны.
Упражнения: Какие значения x и y гарантируют, что четырехугольник является параллелограммом. Обосновать ответ. # 10 Pg.426 Противоположные стороны совпадают. 4x = 20 5y = 40 y = 8 x = 5
Упражнения: Какие значения для x и y гарантируют, что четырехугольник является параллелограммом. Обосновать ответ. # 11 Pg.426 Альтернативные внутренние углы совпадают. 3x + 6 = 27 8y = 64 y = 8 3x = 21 x = 7
Упражнения: Какие значения x и y гарантируют, что четырехугольник является параллелограммом.Обосновать ответ. # 12 Pg.426 Противоположные углы совпадают Последовательные углы являются дополнительными 5 (20) + y = 125 5x + y + 4x — y = 180 9x = 180 100 + y = 125 x = 20 y = 25
# 15 Pg.426 mn Дано Ð1 @ Ð2 Дано Ð1 @ Ð3 Alt. Int. Бs @. Ð3 @ Ð2 Переходное свойство p q Если соответствующие углы, образованные поперечным разрезом 2 прямых, совпадают, то прямые параллельны.
Домашнее задание: Практика 6-2B (Обязательно объясните, даже если вы скажете «нет».)
Рабочий лист параллелограммов для 10 класса
Поиск Поиск образовательных ресурсовПоиск
Меню- Войти в систему Попробуйте бесплатно
- Обнаружить
- Откройте для себя ресурсы Искать в проверенных образовательных ресурсах по ключевому слову, предмету, оценке, типу и т. Д.
- Менеджер учебной программы (Мои ресурсы) Управление сохраненными и загруженными ресурсами и папками Для доступа к Менеджеру учебной программы Войти в систему или Присоединяйся сейчас
- Просмотр каталога ресурсов Просматривайте образовательные ресурсы по предметам и темам
- Учебный календарь Изучите ресурсы учебной программы по дате
- Статьи по планированию уроков Своевременные и вдохновляющие идеи обучения, которые вы можете применить в своем классе
- Решения
- Издание для учителей Сэкономьте время на планировании уроков, изучив нашу библиотеку отзывов преподавателей о более чем 550 000 открытых образовательных ресурсов (OER).
- Исследователь обучения Универсальный репозиторий учебных объектов и платформа для управления учебными планами, которая объединяет библиотеку отзывов преподавателей Lesson Planet для открытых образовательных ресурсов с материалами округа и материалами издателей, лицензированными округом.
- Сеть обучения PD Комплексное онлайн-решение edtech PD для школ и округов. Педагоги получают цифровые значки, подтверждающие их знания, навыки и опыт.
- Около
- Наша история
- Часто задаваемые вопросы
- Отзывы
- Свяжитесь с нами
- Ценообразование
- Войти в систему
- Попробуйте бесплатно
- Поделиться через фейсбук
- Твитнуть этот ресурс
- Закрепить этот ресурс
- Ссылка на сайт
Куратор и рецензирование
Планета уроков
Подробная информация о ресурсе


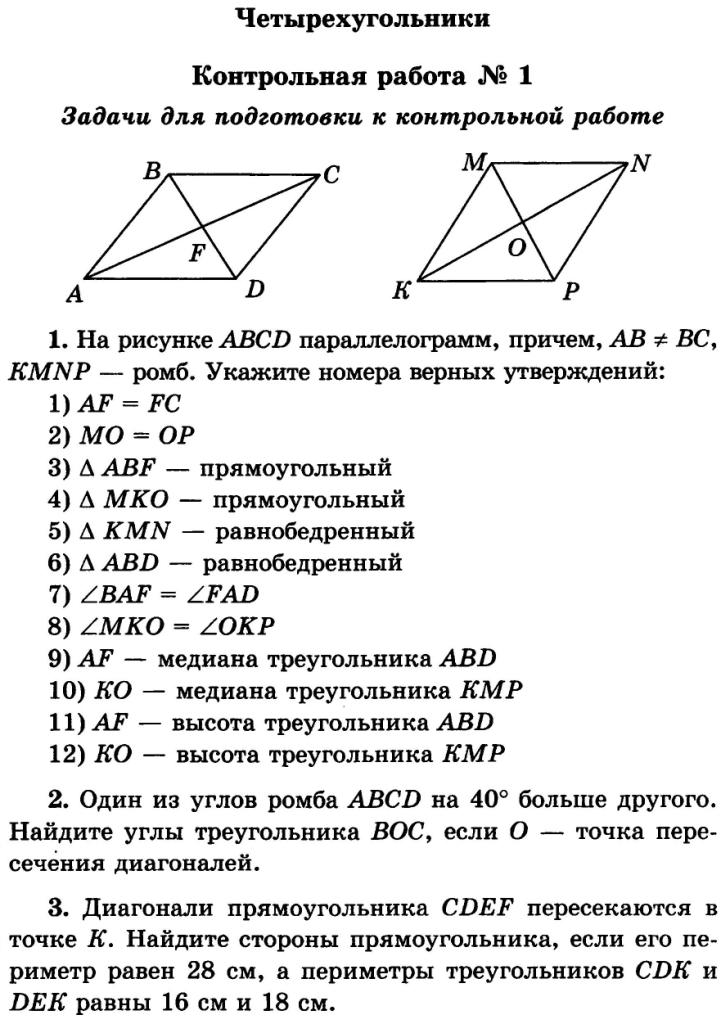 Найдите периметр прямоугольника.
Найдите периметр прямоугольника. Найдите стороны параллелограмма.
Найдите стороны параллелограмма. Один из углов параллелограмма равен 55⁰. Найдите остальные углы параллелограмма.
Один из углов параллелограмма равен 55⁰. Найдите остальные углы параллелограмма.
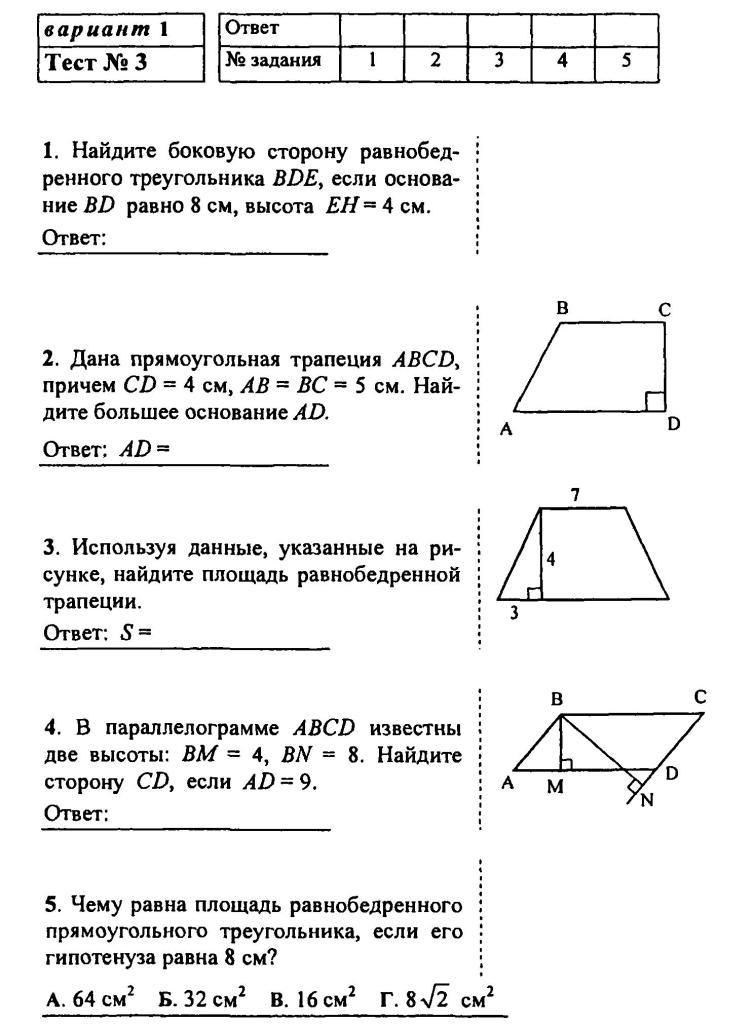 Найдите угол OMP.
Найдите угол OMP.
 В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600.
В трапеции ABCD диагональ AС перпендикулярна боковой стороне CD и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, ∟D = 600. Найдите площадь трапеции.
Найдите площадь трапеции.
 Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.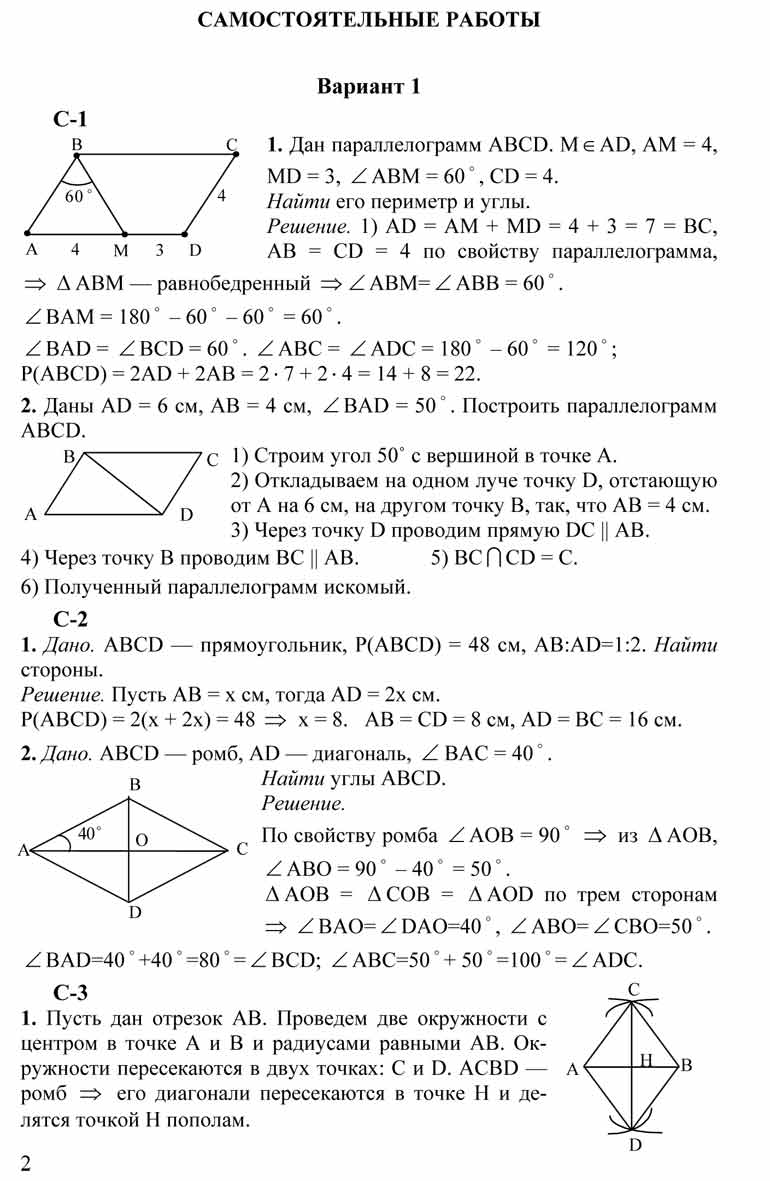 Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2.
Найдите площадь треугольника ВОС, если площадь треугольника АОD равна 45 см2. Г-8.
Г-8. D E
D E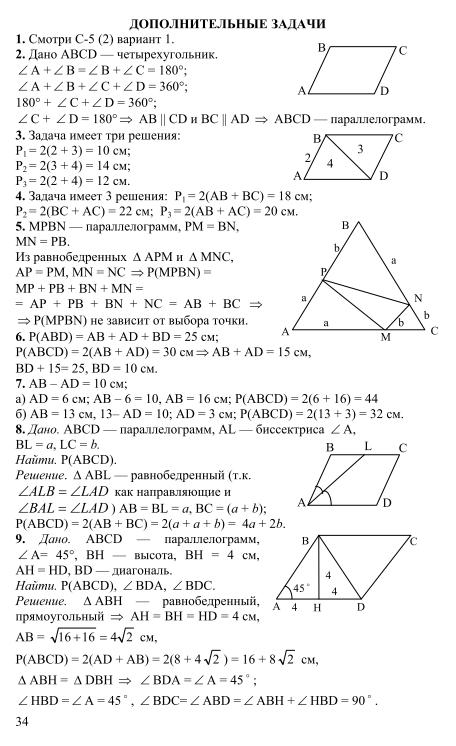 Найдите ЕF, если сторона АС равна 15 см.
Найдите ЕF, если сторона АС равна 15 см. Найдите угол К и гипотенузу КР.
Найдите угол К и гипотенузу КР.
 Г-8.
Г-8. Найдите CD.
Найдите CD.