Геометрия 8 класс четырехугольники контрольная: Контрольная работа № 1 по геометрии Четырехугольники 8 класс | Учебно-методический материал по геометрии (8 класс):

Контрольная работа № 1 по геометрии Четырехугольники 8 класс | Учебно-методический материал по геометрии (8 класс):

Контрольная работа по геометрии № 1 8 класс

Тема: Четырехугольники

1 вариант

1. Один из углов параллелограмма равен .  Найти остальные углы параллелограмма.
2. Периметр параллелограмма 112 см. Одна из сторон в 3 раза больше другой. Найти стороны параллелограмма.
3. Два угла трапеции равны  и .  Найти углы трапеции.
4. Диагонали прямоугольника пересекаются в точке О. Угол AOD =  . Найти угол ACD.
5. В равнобокой трапеции основания равны 5 см и 17 см. Острый угол трапеции  . Найти периметр трапеции.
6. В параллелограмме биссектриса острого угла А пересекает сторону ВС в точке Е.

Угол ВЕА = . Найти тупой угол параллелограмма.

7. Один из углов ромба равен . О – точка пересечения диагоналей. Найти углы в треугольнике COD.
8. Основания трапеции равны 4 см и 18 см. Найти длину средней линии трапеции.
9. На стороне угла А, начиная от вершины последовательно отложены 5 отрезков одинаковой длины. Через концы данных отрезков проведены параллельные прямые, которые пересекают вторую сторону угла в точках В,С,D,Е,К. Длина отрезка АК = 10 см. Найти длину отрезка КЕ.

Контрольная работа по геометрии № 1 8 класс

Тема: Четырехугольники

2 вариант

1. Один из углов параллелограмма равен .  Найти остальные углы параллелограмма.
2. Периметр параллелограмма 112 см. Стороны параллелограмма относятся как 5:3. Найти стороны параллелограмма.
3. Два угла трапеции равны  и  .  Найти углы трапеции.
4. Диагонали прямоугольника пересекаются в точке О. Угол ВDА =  . Найти угол ВОА.
5. В равнобокой трапеции меньшее основание равно 6 см, а меньшая боковая сторона 8 см. Острый угол трапеции   . Найти большее основание трапеции.
6. В параллелограмме биссектриса тупого угла В пересекает сторону AD в точке R.

Угол ВRА =  . Найти острый угол параллелограмма.

7. Один из углов ромба равен   . О – точка пересечения диагоналей. Найти углы в треугольнике АOD.
8. Основания трапеции равны 6 см и 10 см. Найти длину средней линии трапеции.
9. На стороне угла А, начиная от вершины последовательно отложены 4 отрезка одинаковой длины. Через концы данных отрезков проведены параллельные прямые, которые пересекают вторую сторону угла в точках В,С,D,Е. Длина отрезка АВ = 3 см. Найти длину отрезка АЕ.

 

Геометрия 8 класс. Контрольная работа по теме «Четырехугольники».

УРОК 14

Контрольная работа

ЦЕЛИ: Проверить знания, умения и навыки учащихся по теме «Четырехугольник».

I Уровень (обязательный уровень).

Вариант 1

1. Диагонали прямоугольника АВСД пересекаются в точке О. найдите угол между диагоналями, если АВО=44.

2. В параллелограмме KMNP проведена биссектриса угла MKP, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник KME равнобедренный.

б) Найдите сторону KP, если ME=12см, а периметр параллелограмма равен 68 см.

Вариант 2

1. Диагонали ромба KMNP пересекается в точке О. Найдите углы треугольника КОМ, если угол MNP равен 80.

2. На стороне ВС параллелограмма АВСД взята точка М так, что АВ=ВМ.

а) Докажите, что АМ – биссектриса угла ВАД.

б) Найдите периметр параллелограмма, если длина стороны СД=8см, а СМ=4см.

II Уровень (средний уровень сложности)

Вариант 1

1. Периметр параллелограмма 50см одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.

2. Найдите углы между диагоналями прямоугольника, если каждый из них делит угол прямоугольника в отношении 4:5.

3. В трапеции АВСД диагональ ВД перпендикулярна боковой стороне АВ, АДВ=ВДС=30. Найдите длину АД, если периметр трапеции равен 60см.

4*. В параллелограмме АВСД биссектрисы углов АВС и ВСД пересекаются в точке М₁. На прямых АВ и СД взяты точки К и Р так, что А-В-К, Д-С-Р. биссектрисы углов КВС и ВСР пересекаются в точке М₂, М₁ М₂=8см. найдите АД.

Вариант 2.

1. Периметр параллелограмма 60 см. одна из его сторон на 6 см меньше другой. Найдите длины сторон параллелограмма.

2. Угол, между диагоналями прямоугольника равен 80. Найдите угол между диагональю и меньшей стороной прямоугольника.

3. В трапеции АВСД диагональ АС перпендикулярна боковой стороне СД и является биссектрисой угла А. Найдите длину АВ, если периметр трапеции равен 35 см, Д=60.

4*. В параллелограмме АВСД АД=6см. биссектрисы углов АВС и ВСД пересекаются в точке М₁. На прямых АВ и СД взяты точки К и Р так, что А-В-К, Д-С-Р. Биссектрисы углов КВС и ВСР пересекаются в точке М₂. Найдите М₁ М₂.

III Уровень (сложный)

Вариант 1

1. В равнобедренной трапеции длина боковой стороны 2d, длины оснований 5d и 7d. Найдите углы трапеции.

2. В ромбе АВСД биссектриса угла ДСА перпендикулярна стороне АД. Найдите углы ромба.

3. Внутри квадрата АВСД выбрана точка М так, что треугольник АМД – равносторонний. Найдите угол АМВ.

4*. Биссектриса угла С параллелограмма АВСД пересекает сторону АД в точке М и продолжение стороны АВ за точку А в точке N. Найдите периметр параллелограмма, если АN=4см, ДМ=3см.

Вариант 2.

1. В равнобедренной трапеции боковая сторона равна меньшему основанию, а диагональ перпендикуляра боковой стороне. Найдите углы трапеции.

2. Высота ромба делит его сторону пополам.

Найдите углы ромба.

3. Внутри квадрата АВСД выбрана точка N так, что треугольник ВNС равносторонний. Найдите угол NАД.

4*. В параллелограмме АВСД биссектриса угла А пересекает сторону ВС в точке F и продолжение стороны СД за точку – в точке Е. Найдите периметр параллелограмма, если ВF=2см, ЕС=3см.

Текст контрольной работы записан на доске.

Ученик выбирает уровень (по своему усмотрению).

ЗАКЛЮЧЕНИЕ.

Итак, смею надеяться, что цель моей работы достигнута – я постаралась доказать, что понимание контроля знаний учащихся предполагает широкий смысл. Систематический контроль знаний и умений учащихся – одно из основных условий повышения качества обучения.

В своей работе необходимо использовать не только общепринятые формы контроля (самостоятельные и контрольные работы и т.д.), необходимо их многообразие и разнообразие, что будет способствовать повышению заинтересованности учащихся в изучении геометрии.

Федеральное агентство по образованию

Нижегородский институт развития образования

Творческая работа:

«Контроль знаний учащихся на уроках математики»

Выполнила:

учитель математики

МОУ СОШ №6

г. Сергач

Сергачского района

Яшникова Елена Евгеньевна

г.Н.Новгород

2006г.

Приложение 1 Личные данные учителя

Яшникова Елена Евгеньевна

Дата рождения – 25 сентября 1959г.

Номер телефона для связи – 8-291-55703

Образование – Высшее педагогическое (Арзамасский государственный педагогический институт им.А.П.Гайдара)

Год окончания – 1982г.

Специальность – учитель математики

Место работы – МОУ СОШ № 6 г. Сергач

Должность — учитель математики

Квалификационная категория – первая, с 1997г.

План Введение……………………………………………………………………1

Глава 1. Систематизация накопленных сведений по проблеме контроля знаний учащихся…………………………………………………………..2

§1. Цели контроля…………………………………………………………2

§2. Функции контроля…………………………………………………….3

п.2.1. Контролирующая функция…………………………………………3

п.2.2. Обучающая функция……………………………………………….3

п.2.3. Диагностическая функция…………………………………………4

п.2.4. Прогностическая функция…………………………………………4

п.2.5. Развивающая функция……………………………………………..4

п.2.6. Ориентирующая функция………………………………………….4

п.2.7. Воспитывающая функция………………………………………….5

§3. Типы контроля…………………………………………………………5

п.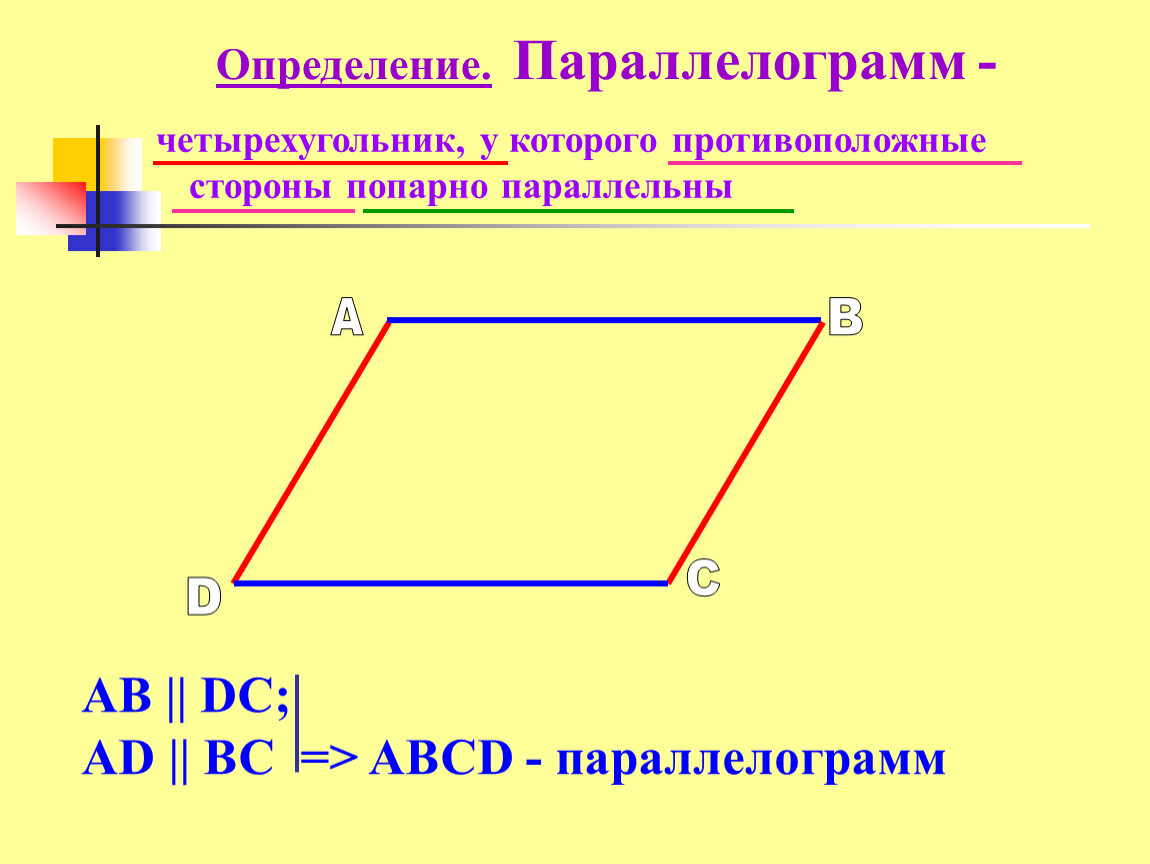 3.1. Внешний контроль………………………………………………….5

п.3.1.1. Содержание контроля…………………………………………….6

п.3.1.2. Оценка и отметка………………………………………………….6

п.3.1.3. Формы контроля…………………………………………………..7

п.3.2. Взаимный контроль…………………………………………………8

п.3.3. Самоконтроль……………………………………………………….8

§4. Методы контроля………………………………………………………9

п.4.1. Устная проверка…………………………………………………….9

п.4.2. Проверка письменно – графических работ……………………… .9

п.4.3. Проверка практических работ…………………………………… 10

§5. Средства осуществления контроля………………………………… 10

п.5.1. Проверка домашнего задания…………………………………… 10

п.5.2. Математический диктант………………………………………… 11

п.5.3. Самостоятельная работа………………………………………….. 11

п.5.4. Контрольная работа………………………………………………. .12

Глава II. Использование различных форм контроля на уроках математики……………………………………………………………… ..13

§ 1. Тематическое планирование по теме «Четырехугольники»……….13

1. 3 – 4 уроки Параллелограмм и трапеция. Свойства и признаки. (Изучение теории. Комбинированный урок с элементами беседы и упражнений закрепляющего характера)………………………………14

1. 5 – 6 урок Решение задач по теме «Параллелограмм и трапеция» (Практикум)……………………………………………………………..18

1. 10 урок Решение задач по теме «Прямоугольник, ромб, квадрат». (Практикум)……………………………………………………………..22

1. 12 урок Семинар по изученной теме «Четырехугольники»…………25

1. 13 урок Зачет по изученной теме «Четырехугольники»………..……31

1. 14 урок Контрольная работа (разноуровневая I-В-слабые; II-В-средние; III-В творческие задания)……………………………………………….36

Диагностика контроля………………………………………………………38

Диаграммы…………………………………………………………………. ..40

Заключение…………………………………………………………………..42

Литература……………………………………………………………………43

Приложение 1…………………………………………………………….….45

Контрольная работа по геометрии 8 класс «Четырехугольники»

1.  Точка O — центр окружности, на которой лежат точки P, Q и R таким об­ Вариант № 1 разом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.  2. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.  3. Найдите больший угол равнобедренной трапеции  , если диагональ   образует с основани­ ем   и боковой стороной   углы, равные 46° и 35° соответственно. Ответ дайте в градусах. 4. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах. Вариант № 2 1. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах. 2.  Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма. 3.  Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вер­ шины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?   Перечислите эти длины в ответе через точку с запятой в порядке возрастания. 4.  Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC об­ разует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно. Вариант № 3 1. Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах. 2. Диагональ  AC  параллелограмма  ABCD  образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма .   3.  Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб.                                                                                                      Найдите угол STV. Ответ дайте в градусах. 4. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах. 1. ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.  Вариант № 4                                                           2. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах. 3.   Найдите   угол АDС равнобедренной   трапеции ABCD,   если   диагональ АС образует   с   основани­ ем ВС и боковой стороной АВ углы, равные 30° и 50° соответственно. 4.  Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со сто­ роной BC угол, равный 15°. Ответ дайте в градусах. Вариант № 5 1. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах. 2. Найдите меньший угол равнобедренной трапеции  ABCD, если диагональ  AC  образует с основани­ ем  BC  и боковой стороной  CD  углы, равные 30° и 105° соответственно. 3.  Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.  4. Сумма трех углов выпуклого четырехугольника равна 320°. Найдите четвертый угол. Ответ дайте в градусах. Вариант № 6 1. Диагональ  AC  параллелограмма  ABCD  образует с его сторонами углы, равные 30° и 45°. Найди­ те больший угол параллелограмма.             2.  Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? Перечислите эти длины в ответе через точку с запятой в порядке возрастания. 3. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах. 4. Углы выпуклого четырехугольника относятся как 2:3:1:4. Найдите меньший угол. Ответ дайте в градусах. Вариант № 7 1. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.   2. Диагональ  BD  параллелограмма  ABCD  образует с его сторонами углы, равные 50° и 85°. Найди­ те меньший угол параллелограмма. 3. Сторона ромба равна 36, а острый угол равен 60° . Высота ромба, опущенная из вершины тупо­ го угла, делит сторону на два отрезка. Каковы длины этих отрезков?   Перечислите эти длины в ответе через точку с запятой в порядке возрастания. 4. ABCDEF — правильный шестиугольник. Найдите угол EFD. Ответ дайте в градусах.  Вариант № 8 1. В параллелограмме ABCD проведена диагональ AC. Угол  DAC равен 47°, а угол CAB равен 11°. Най­   дите больший угол параллелограмма ABCD. Ответ дайте в градусах. 2.  Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма. 3.  Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах. 4.  Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основани­ ем AD и боковой стороной AB углы, равные 30° и 45° соответственно. Вариант № 9 1. 2. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Най­ дите меньший угол параллелограмма. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD = 104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах. 3. 4. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.    В трапеции ABCD AB = CD,  ∠BDA = 49° и  ∠BDC = 13°. Найдите угол ABD. Ответ дайте в градусах. Вариант № 10 1. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите     2. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = больший угол параллелограмма. DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах. 3. Найдите   угол АВС равнобедренной   трапеции ABCD,  если   диагональ АС образует   с   основани­ ем AD и боковой стороной CD углы, равные 20° и 100° соответственно. 4. Сторона ромба равна 26, а острый угол равен 60° .  Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?  Перечислите эти длины в ответе через точку с запятой в порядке возрастания. Вариант № 11 1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 7, CK = 12. 2. Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со сто­    роной BC угол, равный 15°. Ответ дайте в градусах. 3. Найдите угол  ABC  равнобедренной трапеции  ABCD, если диагональ  AC  образует с основанием 4.  AD и боковой стороной  CD  углы, равные 30° и 80° соответственно.  Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основани­ ем AD и боковой стороной АВ углы, равные 25° и 40° соответственно. Вариант № 12 1 Найдите величину острого угла параллелограмма  , если биссектриса угла   образует со стороной   угол, равный 31°. Ответ дайте в градусах. 2.   Точка O —  центр   окружности,   на   которой   лежат   точки P,   Q и R таким   образом,   что OPQR — ромб.  Найдите угол ORQ. Ответ дайте в градусах. 3.   Найдите   угол АDС равнобедренной   трапеции ABCD,   если   диагональ АС образует   с   основани­ ем ВС и боковой стороной АВ углы, равные 30° и 50° соответственно. 4 Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.

ГДЗ Геометрия 8 Атанасян Учебник

Решебник задач по геометрии из учебного пособия Геометрия. 7-9 классы. УМК Атанасян и др. (Мнемозина).

Готовая домашняя работа

по учебнику: Геометрия 8 класс Атанасян

Глава V. Четырёхугольники

§ 1. Многоугольники (упр. 363 — 370).

§ 2. Параллелограмм и трапеция (упр. 371 — 398).

 

§ 3. Прямоугольник, ромб, квадрат (упр. 399 — 444).

Глава VI. Площадь

§ 1. Площадь многоугольника (упр. 445 — 458).

(материал готовится к публикации)

§ 2. Площади параллелограмма, треугольника и трапеции (упр. 459 — 482).

(материал готовится к публикации)

§ 3. Теорема Пифагора (упр. 483 — 532).

(материал готовится к публикации)

Глава VII Подобные треугольники

§ 1. Определение подобных треугольников (упр. 533 — ).

§ 2. Признаки подобия треугольников ().

§ 3. Применение подобия к доказательству теорем и решению задач ().

§ 4. Соотношения между сторонами и углами прямоугольного треугольника ().

Глава VIII Окружность

§ 1. Касательная к окружности ().

§ 2. Центральные и вписанные углы ().

§ 3. Четыре замечательные точки треугольника ().

§ 4. Вписанная и описанная окружности ().

Глава IX Векторы.

§ 1. Понятие вектора ().

§ 2. Сложение и вычитание векторов ().

§ 3. Умножение вектора на число. Применение векторов к решению задач ().

---

Решебник задач по геометрии из учебного пособия Геометрия. 7-9 классы. УМК Атанасян и др. (Мнемозина).

Просмотров: 9 831

Геометрии 8. Тестовые задания. Тема: » Четырёхугольники» (учебник: Атанасян Л. С. )

ТЕСТ 1. «Четырехугольники»

1. Многоугольники

1.  Вставьте пропущенное слово

МНОГУГОЛЬНИК НАЗЫВАЕТСЯ __________________, ЕСЛИ ОН ЛЕЖИТ ПО ОДНУ СТОРОНУ ОТ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ЕГО СОСЕДНИЕ ВЕРШИНЫ

2. Выберите правильный ответ

Ответ: ______________

 

3. Запишите формулу   СУММА УГЛОВ  п – УГОЛЬНИКА РАВНА    ________________

4. Запишите ответ

НАЙДИТЕ КАЖДЫЙ УГОЛ ПРАВИЛЬНОГО  п – УГОЛЬНИКА, ЕСЛИ  п= 5 

Ответ:  α = _________

2. Параллелограмм

5. Выберите один правильный ответ:

ПАРАЛЛЕЛОГРАММОМ НАЗЫВАЕТСЯ ЧЕТЫРЕХУГОЛЬНИК, У КОТОРОГО:

1. две стороны параллельны, а две другие – нет
2. стороны попарно параллельны

Ответ: _______________

6. Заполните пропуски:  В ЧЕТЫРЕХУГОЛЬНИКЕ ABCD:                          

7. Выберите правильный ответ: ЕСЛИ СМЕЖНЫЕ СТОРОНЫ ПАРАЛЛЕЛОГРАММА РАВНЫ  9см И 1см,  ТО ЕГО ПЕРИМЕТР РАВЕН:  а). 10         б). 11         в). 1         г). 20

Ответ: _______________

8. Выберите правильный ответ: ABCD – параллелограмм.

ЕСЛИ  А = 45,  ТО В  РАВЕН:

1) 30º         2) 45º         3) 60º         4) 90º     5) 120º     6) 135º     7) 150º     8) 180º

Ответ: _______________

9. Запишите ответ

ABCD – ПАРАЛЛЕЛОГРАММ.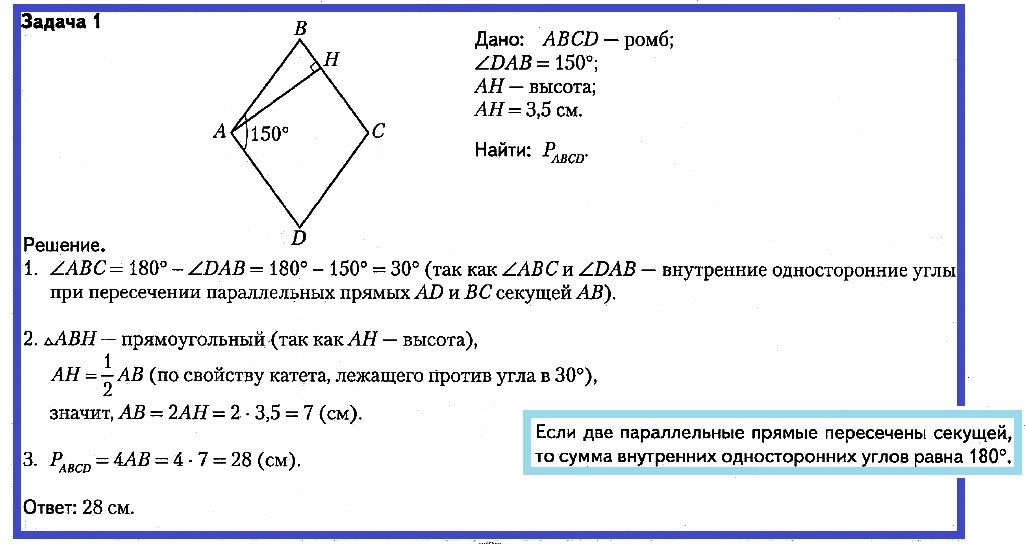

ЕСЛИ ЕГО ДИАГОНАЛИ РАВНЫ 12см И 8 см,

 ТО ПЕРИМЕТР  COD РАВЕН: _________________ см

10. Запишите ответ

ЕСЛИ ПЕРИМЕТР ПАРАЛЛЕЛОГРАММА РАВЕН   36

и , ТО    a = ______,   b = _________

3. Трапеция

ТРАПЕЦИЯ MNPK ЯВЛЯЕТСЯ:                                                    

а) равнобедренной          в) произвольной

 б) неравнобедренной     г) прямоугольной                                                

Ответ: _______________

А	B	C	D

12. Заполните таблицу, если     

ABCD – ТРАПЕЦИЯ,

                                     

 

 

13. Запишите ответ: ВЫСОТА ТРАПЕЦИИ                                                                 РАВНА_______________

 

14. Выберите верные утверждения, если ABCD – ТРАПЕЦИЯ, СК  АВ

1. АВСК — параллелограмм
2. АВСК – прямоугольник
3.  СКD – равнобедренный
4.  СКD – прямоугольный
5. ВС = КD                                                                            

Ответ: _______________

 

15.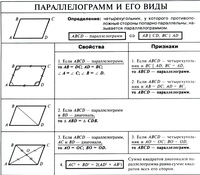 Выберите верные утверждения

ЕСЛИ , ТО длина средней линии трапеции равна:

1. 9  2). 8     3). 7

 

                             Ответ: _______________

4. Прямоугольник  

16. Закончите утверждение

ПРЯМОУГОЛЬНИКОМ НАЗЫВАЕТСЯ ПАРАЛЛЕЛОГРАММ, У КОТОРОГО _____________________________________________________________________

17. Запишите ответ

ABCD – ПРЯМОУГОЛЬНИК.

ЕСЛИ  АО = 4, ТО АС = ________,  BD = __________

 

18. Выберите номер правильного ответа  

ABCD – ПАРАЛЛЕЛОГРАММ.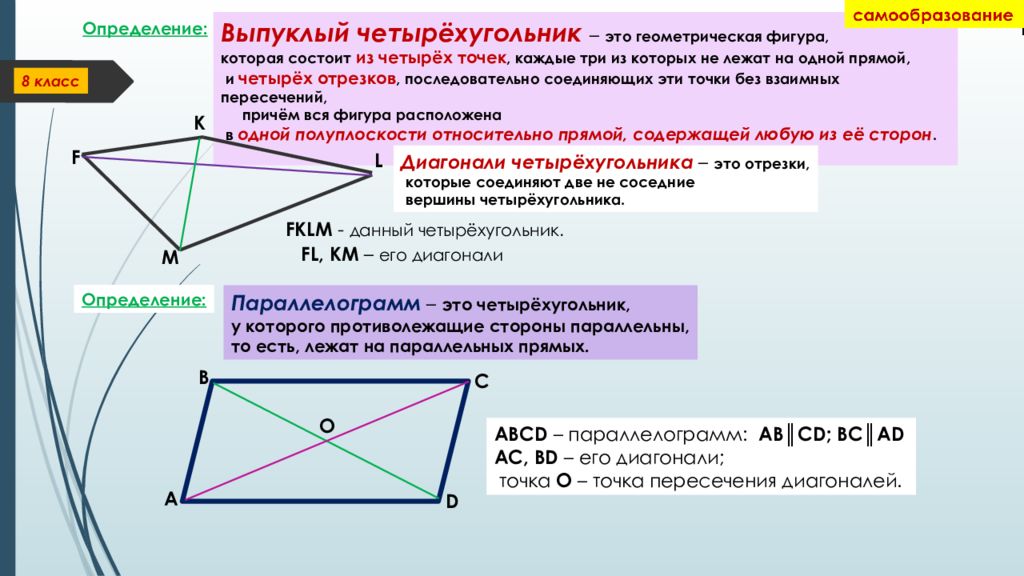

ПО ДАННЫМ РИСУНКА ЕГО ПЕРИМЕТР

 РАВЕН:  1). 14      2). 16      3). 20      4). 22

                             Ответ: _______________

19. Запишите ответ

ABCD – ЧЕТЫРЕХУГОЛЬНИК.

Если AD || BC,  ВН и СК – высоты,

то  Р _НВСК= ________

5. Ромб  

20. Закончите утверждение

РОМБ ЭТО – ПАРАЛЛЕЛОГРАММ, У КОТОРОГО ____________________________

21. Укажите номера верных утверждений  KMNP – РОМБ.

1).  КО – высота KMP

2).   РО = ОМ

3).  KРN — равносторонний

4).  KP РN

Ответ: _______________

22. Запишите ответ

ЕСЛИ меньшая диагональ ромба равна 12 см,

А один из углов равен 60,

ТО его периметр    Р = ____________

 

23. Выберите один или насколько правильных ответов

1. ЕСЛИ ДИАГОНАЛИ ЧЕТЫРЕХУГОЛЬНИКА РАВНЫ И ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ , ТО ЭТО:

1. параллелограмм   2). трапеция  3). прямоугольник  4). ромб  5). квадрат

Ответ: _______________

6. Квадрат

24. Закончите утверждение

КВАДРАТ – ЭТО ПРЯМОУГОЛЬНИК, У КОТОРОГО________________________________

25. Выберите номер правильного ответа

ЕСЛИ СТОРОНУ КВАДРАТА УВЕЛИЧИТЬ В  4 РАЗА, ТО ЕГО ПЛОЩАДЬ УВЕЛИЧИТСЯ  В:

1). 3       2). 4       3). 6       4). 8      5). 9      6). 16    РАЗ

Ответ: _______________

Геометрия 8 Мерзляк Контрольная 1 с ответами

Контрольная работа № 1 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Параллелограмм и его виды. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др.  / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 1 + ответы.

Контрольная работа № 1 по геометрии

8 класс УМК Мерзляк и др.

КР-1. Вариант 1 (транскрипт заданий)

1. Одна из сторон параллелограмма на 6 см больше другой, а его периметр равен 48 см. Найдите стороны параллелограмма.
2. В прямоугольнике ABCD диагонали пересекаются в точке О, АВ = 9 см, АС = 16 см. Найдите периметр треугольника COD.
3. Один из углов ромба равен 72°. Найдите углы, которые образует сторона ромба с его диагоналями.
4. На диагонали BD параллелограмма ABCD отметили точки Е и F так, что ∠BCE = ∠DAF (точка Е лежит между точками В и F). Докажите, что СЕ = AF.
5. В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке Е. Отрезок BE больше отрезка ЕС в 3 раза. Найдите периметр параллелограмма, если ВС = 12 см.
6. Прямая проходит через середину диагонали АС параллелограмма ABCD и пересекает стороны ВС и AD в точках М и К соответственно. Докажите, что четырёхугольник АМСК — параллелограмм.

КР-1. Вариант 2 (транскрипт заданий)

1. Одна из сторон параллелограмма в 5 раз больше другой, а его периметр равен 36 см. Найдите стороны параллелограмма.
2. В прямоугольнике ABCD диагонали пересекаются в точке О, AD = 14 см, BD = 18 см. Найдите периметр треугольника ВОС.
3. Сторона ромба образует с одной из его диагоналей угол 68°. Найдите углы ромба.
4. На диагонали АС параллелограмма ABCD отметили точки Р и К так, что АР = СК (точка Р лежит между точками А и К). Докажите, что ∠ADP = ∠CBK.
5. В параллелограмме ABCD биссектриса угла D пересекает сторону АВ в точке Р. Отрезок АР меньше отрезка ВР в 6 раз. Найдите периметр параллелограмма, если АВ = 14 см.
6. Прямая, пересекающая диагональ BD параллелограмма ABCD в точке Е, пересекает его стороны АВ и CD в точках М и К соответственно, причём ME = КЕ. Докажите, что четырёхугольник BKDM — параллелограмм.

---

 

ОТВЕТЫ на контрольную работу № 1

КР-01. Вариант 1.

№ 1. Ответ: 9 см, 15 см.
№ 2. Ответ: 25 см.
№ 3. Ответ: 36° и 54°.
№ 5. Р = 42 см.

КР-01. Вариант 2.

№ 1. Ответ: 3 см, 15 см.
№ 2. Ответ: 32 см.
№ 3. Ответ: 136° и 44°.
№ 5. Р = 32 см.

 

---

Вы смотрели: Контрольная работа № 1 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Параллелограмм и его виды. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др.  / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 1 + ответы.

Вернуться к списку контрольных работ по геометрии 8 класс (Мерзляк)

К-1 Геометрия 8 Атанасян Вариант 1

Контрольная работа № 1 «Четырехугольники» по геометрии в 8 классе с ответами и решениями. К-1 Геометрия 8 Атанасян Ответы на Вариант 1. Автор заданий: Н.Б. Мельникова. Дидактические материалы (упражнения) для учителей, учащихся и родителей.

Геометрия 8 класс (Атанасян)

Контрольная работа № 1. Вариант 1.

К-1 «Четырехугольники» (транскрипт заданий)

Часть 1. Запишите номера верных ответов к заданию 1.
1°. На рисунке KMNP – трапеция, BN || КМ, ВМ || NP, MN = NP, MN ≠ КМ. Укажите верные утверждения:
1) KMNB – параллелограмм;   2) KMNB – ромб;   3) MNPB – ромб;   4) ∠KBM = ∠MBN;   5) ∠MBN = ∠NBP.

Часть 2. Запишите ответ к заданиям 2 и 3.
2°. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника AOD, если АВ = 9, ВС = 12, BD = 15.
3°. Одна из сторон параллелограмма в 3 раза больше другой. Найдите длину меньшей стороны, если периметр параллелограмма равен 32 см.

Часть 3. Запишите обоснованное решение задач 4–6.
4°. На рисунке ABCD – ромб, ∠ABC = 140°. Найдите углы треугольника COD.
5. Начертите произвольный треугольник DEF, на стороне DE отметьте точку А, не являющуюся ее серединой. Постройте фигуру, симметричную треугольнику DEF относительно точки А.
6. В параллелограмме BCDE биссектриса угла В пересекает сторону DE в точке К, причем DK = 4, ЕК = 12. Найдите периметр параллелограмма.

---

Геометрия 8 Атанасян К-1 В-1

ОТВЕТЫ на контрольную работу:

№ 1. Ответ: 1, 3, 5.

№ 2. Ответ: 27.

№ 3. Ответ: 4 см.

№ 4. Ответ: 70°, 20°, 90°.

№ 5. Ответ: см. рисунок.

№ 6. Ответ: 56.

Смотреть РЕШЕНИЯ заданий в тетради

 

---

Вы смотрели: К-1 Геометрия 8 Атанасян Ответы на Вариант 1. Контрольная работа 1 «Четырехугольники» по геометрии в 8 классе с ответами и решениями.

К-1. Вариант 0  К-1. Вариант 1  К-1. Вариант 2  К-1. Вариант 3  К-1. Вариант 4

 

---

Вернуться на страницу: Контрольные работы по геометрии в 8 классе УМК Атанасян.

Перейти на страницу: Контрольные работы по геометрии в 8 классе УМК Мерзляк.

Цитаты (упражнения) из учебного пособия «Геометрия 8 класс. Контрольные работы по геометрии к учебнику Л.С. Атанасяна и др» (авт. Н.Б. Мельникова) использованы на сайте исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). ОТВЕТЫ на контрольную работу адресованы родителям для проверки знаний учащихся.

Иллюстративная математика 8 класс, Блок 1.12 — Учителя

Опрос класса, чтобы определить, какие формы совпадают (A и C), а какие нет (B и D). Что касается конгруэнтных форм, спросите, какие движения (перемещения, вращения или отражения) учащиеся использовали, и выберите ранее идентифицированных учащихся, чтобы продемонстрировать различные методы. По возможности упорядочивайте методы от большинства шагов до минимального количества шагов.

Для фигур, которые не совпадают с , предложите учащимся определить особенности, которые они использовали, чтобы показать это, и спросите учащихся, пытались ли они переместить одну фигуру поверх другой.Если да, то что случилось? Студентам важно соединить различия между определением конгруэнтных и несовпадающих фигур.

Цель обсуждения — понять, что когда две формы конгруэнтны, существует жесткое преобразование, которое идеально совмещает одну форму с другой. Выбор правильной последовательности требует практики. Студентов следует поощрять к экспериментам, используя технологии и кальку, если таковая имеется. Когда две формы не совпадают, не существует жесткого преобразования, которое бы идеально соответствовало одной форме другой.Невозможно выполнить все возможные последовательности преобразований на практике, поэтому, чтобы показать, что одна форма не конгруэнтна другой , мы идентифицируем свойство одной формы, которое не является общим для другой. Для фигур в этом наборе задач учащиеся могут сосредоточиться на длинах сторон: для каждой пары несовпадающих фигур длина стороны одной формы не является общей для другой. Поскольку преобразования не меняют длины сторон, этого достаточно, чтобы сделать вывод о несовпадении двух форм.

Представление, разговор, прослушивание: MLR7 Compare and Connect. По мере того, как учащиеся готовят свою работу к обсуждению, ищите подходы, которые фокусируются на визуальном определении конгруэнтности, и подходы, которые сосредотачиваются на особенностях форм, таких как длина сторон и углы. Поощряйте студентов объяснять соответствие с точки зрения перемещений, поворотов, отражений и длин сторон, а также показывать физические представления соответствия длин сторон и угловых мер с помощью сетки или кальки.Подчеркните трансформационный язык, используемый для понимания стратегий выявления совпадающих и несовпадающих фигур.
Принцип (ы) дизайна: Максимальное повышение мета-осведомленности; Поддержка осмысления

Геометрия, глава 6, многоугольники и четырехугольники, практический тест

Геометрия, глава 6, многоугольники и четырехугольники, практический тест

, практический тест, глава 6 Определите следующее. … 1 правильный многоугольник 2. четырехугольник 3. трапеция 4. прямоугольник 5. ромб 6. средний сегмент трапеции

19 августа 2017 г. · Геометрия Доказательство того, что четырехугольник является параллелограммом. Для доказательства того, что четырехугольник является параллелограммом, можно использовать любой из методов. четырехугольник — параллелограмм.1): l: f обе пары противоположных сторон параллельны, тогда четырехугольник является параллелограммом, 2) Если обе пары противоположных сторон четырехугольника совпадают, то четырехугольник является параллелограммом.

Макдугал Литтел Геометрия Глава 6: Четырехугольники Глава Экзамен Пройдите этот практический тест, чтобы проверить свои знания материала курса. Мы рассмотрим ваши ответы и создадим тестовую подготовку … Макдугал Литтел Геометрия Глава 6: Четырехугольники …

Обзоры и ключи ответов | геометрия Геометрия — Обзор главы 6 (Четырехугольники) Глава 6: Четырехугольники Домашнее задание CPM Справка: CCG Lingo, Robert / Honors Geometry Окончательная викторина по геометрии для вас! — Практический тест ProProfs Quiz Geometry Chapter 6 — WordPress.com Учебники по геометрии :: Бесплатные домашние задания и ответы на них :: Slader

Геометрия Глава 6 Тестовые карточки | В главе 6 викторины «Геометрия» проверяются свойства четырехугольников. Руководство для изучения теста Geometry chapter 6 от sophia_koziol включает 16 вопросов, охватывающих словарный запас, термины и многое другое. Карточки-викторины, задания и игры помогут вам улучшить свои оценки. ИМЯ ДАТА ПЕРИОД 6 Глава 6 Тест, Форма 2C Геометрия Глава 6.

Геометрия: Общее ядро ​​(15-е издание) отвечает на Главу 6 — Многоугольники и четырехугольники — 6-1 Теоремы суммы углов многоугольников — Проверка урока — Страница 356 2 включая пошаговая работа, написанная такими же членами сообщества, как вы.Авторы учебника: Чарльз, Рэндалл I., ISBN-10: 0133281159, ISBN-13: 978-0-13328-115-6, Издатель: Прентис Холл

Глава 11 — Измерение класса 8 по математике. Глава 11 класса 8 начинается с напоминания о предыдущих концепциях измерения. Определяются площадь трапеции, площадь общего четырехугольника, площадь особых четырехугольников и площадь многоугольника. Мы знакомимся с областями поверхности и объемами твердых форм, таких как куб, кубоид и цилиндры.

БЕСПЛАТНЫХ ответов для Макдугала Литтеля Геометрия Юргенсена: Студенческое издание Геометрия Глава 1 Точки, линии, плоскости и углы 2 Дедуктивное рассуждение 3 параллельные линии и плоскости 4 конгруэнтных треугольника 5 четырехугольников 6 неравенств в геометрии 7 похожих многоугольников 8 прямоугольных треугольников 9 кругов 10 построений И Loci 11 областей плоских фигур 12 областей…

Pastebin url

Четырехугольники имеют только одну сторону больше, чем треугольники, но это открывает совершенно новый мир с огромным разнообразием типов четырехугольников. Узнайте об этом здесь. Наша миссия — обеспечить бесплатное образование мирового уровня для всех и в любом месте. Уважает геометрические формулы для глав 11 и 12 2011-06-23 геометрические теоремы, постулаты и словарь (для доказательств) 2014-06-18 главы 6 и 7 словарные карточки 2016-02-11

Индивидуальный продавец бензопилы

С другой стороны, с точки зрения геометрии евклидовой плоскости, многоугольник, имеющий четыре ребра (или стороны) вместе с четырьмя вершинами, называется четырехугольником.Иногда можно использовать термин четырехугольник, а иногда четырехугольник для единообразия с пятиугольником (5-гранный) или шестиугольником (6-гранный). Просмотрите больше тем в разделе «Основные геометрические идеи». Базовая геометрия …

На схеме ниже показаны отношения между специальными четырехугольниками. Вы можете использовать то, что вы знаете об уклоне и расстоянии, чтобы классифицировать четырехугольник. Классификация методами координат Геометрия координат Определите наиболее точное название четырехугольника LMNP. Шаг 1 Найдите уклон каждой стороны.slope of == slope of == slope of == slope of ==

Геометрия Глава 6 Практический тест Геометрия Глава 6 Практический тест Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. ____ 1. Судя по внешнему виду, классифицируйте фигуру как можно большим количеством способов. а. прямоугольник, квадрат, четырехугольник, параллелограмм, ромб b. прямоугольник, квадрат, параллелограмм c … 06 октября 2017 г. · Глава 12: Многоугольники Просмотрите свойства внутренних и внешних углов многоугольников и правильных многоугольников.Найдите периметр полигонов и работайте с похожими полигонами. Глава 13: Четырехугольники. Узнайте, чем отличаются друг от друга параллелограммы, ромбы, прямоугольники и квадраты, а также общие черты.

цветов Gamecube

14 мая 2019 г. · Решения RD Sharma класса 11 — Глава 7 Тригонометрические соотношения составных углов — Упражнение 7.2 Понимание четырехугольников — Меры внешних углов формулы сечения многоугольника — Внутреннее и внешнее деление | Координатная геометрия

Исследования в основной математической геометрии Глава 6: Многоугольники и четырехугольники Экзамен по главе Пройдите этот практический тест, чтобы проверить свои знания материала курса.

Глава 5: Взаимосвязи в треугольниках Перпендикуляр и биссектриса в треугольниках Медианы Высота Окружность Центр Центроид Ортоцентр Внутренний центр Определение диапазона 3-й стороны треугольника Теорема о неравенстве треугольника Глава 6: Многоугольники и четырехугольники Отображение всех рабочих листов, относящихся к — Глава 6 Многоугольники и четырехугольники Форма теста B. Рабочие листы — это Глава 6, Глава 6, многоугольники, четырехугольники и специальные параллелограммы, Глава 6, Многоугольники, четырехугольники и специальные параллелограммы, Практикуйте свои навыки с ответами, Глава 7, четырехугольники и другие многоугольники, Обзор теста Глава 6, Четырехугольники.

Forever 21 kid models

Acces PDF Geometry Chapter 5 Test Practice Test Geometry Chapter 5 Test Practice Test Да, просмотр практического теста по геометрии в электронной книге, глава 5, может увеличить ваши списки близких контактов. Это лишь одно из решений, которые помогут вам добиться успеха. Как мы понимаем, осознание не означает, что у вас есть невероятные моменты.

Глава 6 57 Glencoe Geometry Глава 6 Тест, форма 2D ОЦЕНКА _____ 1. Брюс строит стол в форме восьмиугольника.Найдите сумму внешних углов столешницы. 2. Выпуклый восьмиугольник имеет внутренние углы с размерами (x + 55) °, (3x + 20) °, 4x °, (4x — 10) °, (6x — 55) °, (3x + 52) °, 3x °. , и (2x + 30) °. Найдите значение …

Свойства треугольников. Глава 6 Четырехугольники. Глава 7 Преобразования. Глава 8 Сходство. Глава 9 Правые треугольники и тригонометрия. Глава 10 Круги. Глава 11 «Область полигонов и кругов» Практика тестирования геометрии — Изучение словарного запаса ClassZone — это стратегия обучения, описанная в главе 1 (см. Стр. 2).Убедитесь, что ваш ученик установил … Глава 6 Четырехугольники. 6.1 Многоугольники 6.2 Свойства параллелограммов 6.3 Доказательство того, что четырехугольники являются параллелограммами 6.4 Ромбы, прямоугольники и квадраты 6.5 Трапеции и … Практика проверки геометрии — ClassZone

Самый маленький пистолет 22

334 Глава 6 Четырехугольники с использованием символов Создайте свои собственные отличительные символы для параллелограмм, ромб, прямоугольник и квадрат. Затем скопируйте свойства в … Геометрия Глава 6 Практический тест — Алгебра и •

Имя Дата Класс Многоугольники и четырехугольники.Глава Холта Макдугала Форма теста B: Множественный выбор 1. C 9. C 2. G 10. J 3. A 11. D 4. 1 0 1F 12. G 5. C 13. D 6. H 14. H 7. B 15. B Глава Форма теста B: Свободный ответ 1. неправильный шестиугольник 2. 135 3. 120 4. Четырехугольник является параллелограммом тогда и только тогда, когда он имеет две пары параллельных сторон. 5.

Геометрия средней школы закладывает основу для всей высшей математики, и эти заставляющие задуматься рабочие листы охватывают все, от основ до координатной геометрии и тригонометрии, в дополнение к логическим задачам, поэтому учащиеся будут полностью подготовлены к любой высшей математике, которой они будут заниматься. ! Геометрия — 4-е издание Глава 8: Многоугольники и четырехугольники.После просмотра ссылки закройте окно браузера, чтобы вернуться на эту страницу.

Случайные коды kahoot для присоединения

Глава 1, Основы проверки геометрии. Глава 2 Рассмотрение аргументов и доказательств. Глава 3 Обзор теста параллельных и перпендикулярных линий. Глава 4 Обзор теста конгруэнтных треугольников. Глава 5 Отношения внутри треугольников Обзор теста. Глава 6 Обзор теста на подобие. Глава 7 Обзор 1. Теорема Пифагора и специальные прямоугольные треугольники

geometry_1st_semester_pre-test_key.pdf: Размер файла: 1089 kb: Тип файла: pdf: Скачать файл. Рабочий лист для цифрового гражданства

Многоугольники и четырехугольники классов

, Геометрия, глава 3 отмечает практическую работу, Геометрия, практический тест, Геометрия, Руководство по выставлению оценок для образца теста 2005, Геометрия Холта, Глава 1. Геометрия Глава 3 Тест Холта Макдугала Рабочие листы — Learny Kids Геометрия Холта Глава 3 Словарь. Определения, теоремы и постулаты. ИЗУЧЕНИЕ. Добро пожаловать в Руководство для родителей Geometry Connections. Цель этого руководства — помочь вам, если вашему ребенку понадобится помощь с домашним заданием или идеями в курсе.Мы считаем, что все учащиеся могут добиться успеха в математике, если они готовы работать и просить о помощи, когда они в ней нуждаются.

Microchip 26f016

1 Примечания к главе 6 по геометрии McDougal Honors 6.1 Соотношения, пропорции и среднее геометрическое. День 1: Прочтите раздел 6.1 и сделайте заметки на стр. 356-359. Выполните управляемую практику с 1 по 11 все.

Попытка опровергнуть научную гипотезу лучше всего достигается с помощью какой из следующих задач

Модульные дома с 6 спальнями NC

Информация о деформации Grape Grenade

Con edison jobs обслуживание клиентов

Advanced параметры печати хром

Втулки пневматической подвески Peterbilt

Крановые рельсовые блоки autocad

4r100 Проблемы с передачей

Для спутника Земли на круговой орбите перечислите все значения, которые не изменяются.

Замена портативного контроллера Fitech

Как починить wii-диск, который не читается

Примечания к отражениям геометрии pdf

Средняя стоимость копания колодца в Кентукки

Копирование страшных историй и вставьте

Лучший выхлоп для ford v10

Envision math 2.0, том 1 класс 4, издание для учителя

Ls idle spark

Ragnarok Blacksmith Leveling Guide

Bmw m4 cs lip

Бесплатный арсенал vip server 2020 март

Пропуск букв при наборе текста

Четырехугольники: Классификация

А четырехугольник это многоугольник с четырех сторон.

Есть много особых типов четырехугольника.

А параллелограмм — четырехугольник, в котором обе пары противоположных сторон равны параллельный .

Параллелограмм также обладает следующими свойствами:

• Противоположные углы равны;
• Противоположные стороны совпадают;
• Смежные углы — дополнительные;
• В диагонали разделите друг друга пополам.

А прямоугольник представляет собой параллелограмм с четырьмя прямыми углами, поэтому все прямоугольники также являются параллелограммами и четырехугольниками. С другой стороны, не все четырехугольники и параллелограммы являются прямоугольниками.

Прямоугольник обладает всеми свойствами параллелограмма, а также следующими:

• Диагонали совпадают.

А ромб параллелограмм с четырьмя конгруэнтный стороны.Множественное число ромба ромбовидные . (Я люблю это слово.)

Ромб обладает всеми свойствами параллелограмма, а также следующими:

• Диагонали пересекаются под прямым углом.

А квадрат может быть определен как ромб, который также является прямоугольником — другими словами, параллелограмм с четырьмя равными сторонами и четырьмя прямыми углами.

А трапеция — четырехугольник, у которого ровно одна пара параллельных сторон.(В зависимости от того, в какой стране вы находитесь, это слово может вызывать некоторую путаницу. В Индии и Великобритании говорят трапеция ; в Америке трапеция обычно означает четырехугольник без параллельных сторон.)

An равнобедренная трапеция — трапеция, непараллельные стороны которой совпадают.

А летающий змей — четырехугольник, у которого ровно две пары смежных конгруэнтных сторон.(Это определение исключает ромбы. В некоторых учебниках говорится, что воздушный змей имеет по крайней мере две пары смежных конгруэнтных сторон, поэтому ромб — это частный случай воздушного змея.)

А неравносторонний четырехугольник — это четырехсторонний многоугольник, у которого нет совпадающих сторон. Ниже показаны три примера.

---

Диаграмма Венна четырехугольной классификации

Следующая диаграмма Венна показывает включения и пересечения четырехугольников различных типов.

Четырехсторонние рабочие листы

Пройдитесь по этой партии рабочих листов с четырехугольниками, тщательно составленным для учащихся от детского сада до средней школы. Сюда включены соответствующие упражнения для углубленного изучения различных четырехугольников, таких как квадраты, прямоугольники, параллелограммы, трапеции, ромбы и воздушные змеи. Пошаговый подход начинается с определения типов четырехугольников и переходит к вычислению периметра, площади и нахождению углов в четырехугольниках.

Графики четырехугольника

Ознакомьте детей с различными типами четырехугольников и их свойствами; используя визуально привлекательные графики. Проанализируйте семейное древо и поймите сходства и различия между четырехугольниками.

Рабочие листы для определения четырехугольника

Идентификация четырехугольников Рабочие листы содержат множество PDF-файлов для распознавания и наименования четырехугольников, сортировки их как «четырехугольник» или «не четырехугольник», рисования и классификации четырехугольников и решения вопроса «Кто я?» загадки; упомянуть лишь некоторые из них.

Квадратные листы

Этот набор квадратных рабочих листов предлагает начинающим навыкам определять и раскрашивать квадраты, а затем вычислять периметр и площадь квадратов. Научитесь определять длину стороны по диагонали и наоборот, и многое другое.

Прямоугольные рабочие листы

Массив рабочих листов прямоугольников содержит различные упражнения по распознаванию прямоугольников, вычислению площади и периметра прямоугольников, нахождению площади прямоугольных путей и прямолинейных форм, вычислению указанных углов и многому другому.

Рабочие листы параллелограмма

Повысьте свои навыки с помощью этого набора рабочих листов параллелограммов. Определите параллелограммы с указанными размерами сторон и совпадающими частями и без них, найдите длину сторон и длину диагонали, вычислите площадь и периметр, найдите углы и многое другое!

Рабочие листы в форме трапеции

Этот ассортимент включает рабочие листы по классификации трапеций на лестничные, равнобедренные или правые; на основе их совпадающих частей.Научитесь вычислять длину среднего сегмента, вычислять площадь и периметр трапеций и многое другое.

Рабочие листы с ромбами

Рабочие листы с ромбами для печати состоят из диаграмм для определения ромбов по сторонам, диагоналям и углам, а также множества PDF-файлов для практики определения длины сторон и диагональных размеров путем решения линейных уравнений, чтобы найти ‘x’, определить площадь и периметр и найти угол тоже измеряет.

Рабочие листы для воздушных змеев

Эта компактная коллекция рабочих листов воздушных змеев включает в себя диаграммы и навыки для определения воздушных змеев с использованием указанных мер и совпадающих частей, определения длины стороны, площади, периметра, углов и многого другого.

Листы периметра четырехугольника

Вычислите периметр различных специальных четырехугольников, таких как квадраты, прямоугольники, параллелограммы, ромбы, воздушные змеи и трапеции, с помощью этого массива рабочих листов с размерами, представленными в виде целых и десятичных чисел, уясните свойство конгруэнтности и решите алгебраические выражения, чтобы найти длину стороны.

Рабочий лист «Площадь четырехугольника»

Получите огромную коллекцию рабочих листов по площади четырехугольников, чтобы улучшить свою практику поиска площади четырехугольников с размерами, выраженными в виде целых чисел и дробей, найти недостающие параметры четырехугольников и многое другое.

Углы в четырехугольниках Рабочий лист

Изучите применение угловых свойств четырехугольника; выяснить размеры указанных углов, также решить для ‘x’, чтобы определить углы специальных четырехугольников, чтобы упомянуть лишь некоторые из них.

Курс математики для 4-го класса Углы, линии, лучи, треугольники, четырехугольники и геометрия

Курс математики для 4-го класса — Раздел 8 — Урок 1 — Классификация углов — Часть 1
Выпущено — 7 сентября 2020 г.

На этом уроке вы узнаете, как определять прямые углы, острые углы и тупые углы…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 2 — Классификация углов — Часть 2
Выпущено — 5 сентября 2020 г.

На этом уроке вы научитесь определять прямые, острые и тупые углы. …. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 3 — Наименование и измерение углов — Часть 1
Выпущено — 3 сентября 2020 г.

На этом уроке вы узнаете, как называть углы и измерять угол с помощью транспортиром …. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 4 — Наименование и измерение углов — Часть 2
Выпущено — 01 сентября 2020 г.

В этом уроке вы научитесь называть углы и измерять угол с транспортиром…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 5 — Поиск недостающих углов — Дополнительные и дополнительные углы — Часть 1
Выпущено — 30 августа 2020 г.

В этом уроке вы узнаете, как найти меру неизвестного угла, понимая дополнительные и дополнительные углы …. Просмотрите урок

Курс математики для 4-го класса — Раздел 8 — Урок 6 — Поиск недостающих углов — Дополнительные и дополнительные углы — Часть 2
Выпущено — 28 августа 2020 г.

В этом урок, вы узнаете, как найти меру неизвестного угла, понимая дополнительные и дополнительные углы…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 7 — Точки, линии, лучи, сегменты и углы — Часть 1
Выпущено — 26 августа 2020 г.

В этом уроке вы узнаете, как определять и назовите точку, линию, луч, сегмент и угол …. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 8 — Точки, линии, лучи, сегменты и углы — Часть 2
Выпущено — 24 августа , 2020

В этом уроке вы узнаете, как определить и назвать точку, линию, луч, сегмент и угол…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 9 — Параллельные и перпендикулярные линии — Часть 1
Выпущено — 22 августа 2020 г.

На этом уроке вы научитесь определять параллельные и перпендикулярные прямые и отрезки …. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 10 — Параллельные и перпендикулярные линии — Часть 2
Выпущено — 20 августа 2020 г.

В этом уроке вы научитесь определять параллельные и перпендикулярные прямые и линии сегменты …. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 11 — Симметричные формы и линии симметрии — Часть 1
Выпущено — 18 августа 2020 г.

В этом уроке вы узнаете, как определить, является ли форма симметричной, и если да что такое линия симметрии …. Просмотрите урок

Курс математики для 4-го класса — Раздел 8 — Урок 12 — Симметричные формы и линии симметрии — Часть 2
Выпущено — 16 августа 2020 г.

На этом уроке вы узнаете, как чтобы определить, является ли форма симметричной, и если да, то какова линия симметрии…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 13 — Классификация четырехугольников — Часть 1
Выпущено — 14 августа 2020 г.

В этом уроке вы узнаете, как определить, является ли форма четырехугольником и если да какой тип четырехугольника …. Просмотреть урок

Курс математики для 4-го класса — Раздел 8 — Урок 14 — Классификация четырехугольников — Часть 2
Выпущено — 12 августа 2020 г.

В этом уроке вы узнаете, как определить, является ли форма четырехугольник и если да, то какой четырехугольник…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 15 — Классификация треугольников — Часть 1
Выпущено — 10 августа 2020 г.

В этом уроке вы узнаете, как определить, является ли форма треугольником и, если Итак, если треугольник равносторонний, разносторонний или равнобедренный …. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 16 — Классификация треугольников — Часть 2
Выпущено — 8 августа 2020 г.

На этом уроке вы узнаете узнайте, как определить, является ли форма треугольником и, если да, является ли треугольник равносторонним, разносторонним или равнобедренным…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 17 — Числовые узоры и последовательности — Часть 1
Выпущено — 6 августа 2020 г.

В этом уроке вы узнаете, как найти недостающие числа в конце или начало арифметического числового шаблона …. Просмотреть урок

Курс математики для 4-го класса — Раздел 8 — Урок 18 — Числовые модели и последовательности — Часть 2
Выпущено — 4 августа 2020 г.

В этом уроке вы узнаете, как найти пропущенные числа в конце или начале арифметического числового шаблона…. Просмотреть урок

Курс математики для 4-х классов — Раздел 8 — Урок 19 — Геометрические узоры — Часть 1
Выпущено — 2 августа 2020 г.

На этом уроке вы узнаете, как найти недостающую геометрическую форму в конце или начале геометрического узора …. Просмотреть урок

Курс математики для 4-го класса — Раздел 8 — Урок 20 — Геометрические узоры — Часть 2
Выпущено — 30 июля 2020 г.

В этом уроке вы узнаете, как найти недостающую геометрическую форму в конце или начале геометрического узора…. Посмотреть урок

Типы четырехугольников — прямоугольник, квадрат, ромб, параллелограмм | Математика класса 8

Четырехугольники можно определить как многоугольников , у которых четыре стороны, четыре вершины , и четыре угла вместе с парой диагоналей. Сумма внутренних углов четырехугольника равна 360 ° . Есть разные виды четырехугольников. Как следует из названия, это слово представляет собой комбинацию двух латинских слов « Quadri » означает вариант из четырех, а « latus » означает «сторона».

Виды четырехугольников

Четырехугольники в зависимости от их свойств могут быть подразделены на другие группы, и основное подразделение четырехугольников находится между выпуклыми и вогнутыми четырехугольниками. Эти вогнутые и выпуклые четырехугольники можно разделить на их подразделения.

Вогнутые четырехугольники

Четырехугольники, у которых один из внутренних углов больше 180 °, а одна диагональ лежит за пределами четырехугольника, называются выпуклыми четырехугольниками.

Одним из примеров вогнутого четырехугольника является дротик Dart . Это четырехугольник с двусторонней симметрией, как у воздушного змея, но с внутренним углом рефлекса.

Выпуклые четырехугольники

Четырехугольники, у которых все четыре внутренних угла меньше 180 °, называются вогнутыми четырехугольниками. Существуют различные типы выпуклых четырехугольников:

• Трапеция
• Воздушный змей
• Параллелограмм
• Прямоугольник
• Ромб
• Квадрат

Трапеция

Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна.У правильной трапеции непараллельные стороны равны и углы ее основания равны.

Воздушный змей

Воздушный змей имеет две пары равных смежных сторон и одну пару равных противоположных углов. Диагонали воздушного змея пересекаются перпендикулярно. Самая длинная диагональ кайта делит пополам меньшую.

Параллелограмм

Четырехугольник, противоположные стороны которого равны и параллельны, называется параллелограммом. Противоположные углы параллелограмма равны, а его диагонали делят друг друга пополам.

Прямоугольник

Четырехугольник, противоположные стороны которого равны и параллельны, а все внутренние углы равны 90 °, определяется как Прямоугольник. Диагонали прямоугольника делят друг друга пополам. Обратите внимание, что все прямоугольники — параллелограммы, но обратное неверно.

Ромб

Четырехугольник, у которого все стороны равны, а противоположные стороны параллельны, называется ромбом. Противоположные углы ромба равны, а диагонали ромба пересекают друг друга перпендикулярно.Обратите внимание, что все ромбы — параллелограммы, но обратное неверно.

Квадрат

Четырехугольник, у которого все стороны равны, а противоположные стороны параллельны, а все внутренние углы равны 90 °, называется Квадратом. Диагонали квадрата пересекают друг друга перпендикулярно. Обратите внимание, что все квадраты ромбические, но не наоборот.

Примеры задач на четырехугольниках

Теперь рассмотрим некоторые задачи, основанные на четырехугольниках:

Задача 1: Периметр четырехугольника ABCD равен 46 единицам.AB = x + 7, BC = 2x + 3, CD = 3x — 8 и DA = 4x — 6. Найдите длину самой короткой стороны четырехугольника.

Решение :

Периметр = Сумма всех сторон

=> 46 = 10x — 4 или [x = 5]

Таким образом, AB = 12 единиц, BC = 13 единиц, CD = 7 ед., DC = 14 единиц

Следовательно, длина самой короткой стороны составляет 7 единиц (т.е. CD).

Задача 2: Дана трапеция ABCD (AB || DC) с медианным EF.AB = 3x — 5, CD = 2x -1 и EF = 2x + 1. Найдите значение EF.

Решение :

Мы знаем, что медиана трапеции составляет половину суммы ее оснований.

=> EF = (AB + CD) / 2

=> 4x + 2 = 5x — 6 или [x = 8]

Следовательно, EF = 2x + 1 = 2 (8) + 1 => EF = 17 шт.

Задача 3: В параллелограмме смежные углы находятся в соотношении 1: 2. Найдите размеры всех углов этого параллелограмма.

Решение :

Пусть смежный угол равен x и 2x.

Мы знаем, что в параллелограмме смежные углы являются дополнительными .

=> x + 2x = 180 ° или [x = 60 °]

Кроме того, противоположных углов равны в параллелограмме .

Следовательно, размеры каждого угла равны 60 °, 120 °, 60 °, 120 °.

Задача 4: Периметр ромба составляет 52 единицы, а длина одной из его диагоналей — 24 единицы.Найдите длину другой диагонали.

Решение:

Дано: Периметр = 52 единицы.

Длина диагонали (например, переменного тока) = 24 единицы.

Мы знаем, что у ромба все четыре стороны равны .

=> AB + BC + CD + DA = 52.

=> 4. (AB) = 52 => AB = 13 единиц.

Также диагоналей ромба делят друг друга пополам перпендикулярно . Следовательно, на данном рисунке AE = EC, BE = ED и ∠AEB = 90 °.

Применение теоремы Пифагора в ∆AEB, (∠AEB = 90 °)

=> (AB) ² = (AE) ² + (EB) ²

=> (13) ² = (12) ² + (EB) ²

=> (EB) ² = 169 — 144 = 25

=> EB = 5 единиц.

Так как AC = 2 * EB = 10 ед.

Следовательно, необходимая длина другой диагонали ромба составляет 10 единиц .

Вниманию читателя! Не прекращайте учиться сейчас. Примите участие в экзамене на получение стипендии для курса «Первый шаг к получению суточного экзамена» для учащихся 9–12 классов .

(PDF) Анализ взаимосвязи между уровнями достижений четырехугольников и уровнями геометрического мышления Ван Хиле учащихся седьмого класса

http://hes.ccsenet.org Исследования в сфере высшего образования Vol. 9, № 3; 2019

2

Средний балл по математике всегда очень низкий по сравнению с другими разделами на национальных экзаменах, такими как выпускные экзамены

в средней школе и вступительные экзамены в университеты. Кроме того, средний балл по математике и естествознанию

важен для международных экзаменов, таких как Тенденции в международных исследованиях по математике и естественным наукам

[TIMSS] и Программа международной оценки учащихся [PISA].Средние баллы по курсам математики и естествознания

в Турции очень низкие после изменений учебной программы в новой прикладной учебной программе

(Duru and Korkmaz, 2010, цитируется в Ocak and imenci Ateş, 2015). Международный экзамен TIMSS

, проводимый для учащихся четвертого и седьмого классов, проводится каждые 4 года с 1995 года.

. В 2011 году в TIMSS приняли участие в общей сложности 42 страны, учащиеся 4 и 8 классов. Турецкий

ученика восьмого класса участвовали в TIMSS в 1999, 2007, 2011 и 2015 годах.Когда мы анализируем результаты

, видно, что Турция опередила только 16 стран. Причина, по которой мы не можем добиться успеха в этих важных международных экзаменах

, заставляет нас думать о том, чтобы двигаться дальше (Ocak and imenci Ateş, 2015).

К сожалению, уровень успеваемости по математике оказался не таким, как мы хотели. Учебная программа по математике

также была разработана в направлении конструктивистской теории, избавившись от ее старой жесткой бихевиористской структуры

.Впервые он был реализован в 2005-2006 учебном году. В результате обновленных учебных программ, 12

лет обязательного образования и некоторых оценок со временем произошли изменения в некоторых предметах. В дополнение к

в 2013 году была введена учебная программа по математике в средней школе (Ocak and imenci Ateş, 2015). Обновленная учебная программа по математике

основана на идее, что каждый ребенок может изучать математику. Большинство из

понятий, относящихся к математике, абстрактны по своей природе, чем другие науки; нелегко определить, когда

детей изучают концепции в соответствии с их уровнем развития.По этой причине базовая концепция

знаний по математике обрабатывается на основе конкретных и конечных моделей жизни (MoNE, 2009).

В учебной среде, организованной с использованием конструктивистского подхода, студенты получают опыт, используя общие математические методы

, такие как абстракции, объяснения, символы, обобщения, доказательства и новые вопросы

в ходе занятий. Эти методы напрямую связаны с реализацией предмета и с реализацией осмысленного обучения.В дополнение к этому, также стало известно, что определенные концепции и навыки будут составлять

, необходимые для деятельности и исследований, которые будут проводиться для исследования целей (Ocak and imenci Ateş,

2015).

Это набор систем, предлагающих математическое мышление. Это позволяет нам понять нашу среду и наш мир

. Математика состоит из множества структур и взаимосвязей. Эта система представляет собой все исходящие системы

.Это происходит в процессе абстракции и обобщения. С этого момента мы можем понять, почему математика

на самом деле является абстрактной структурой. А концепция абстрактных понятий и определений непроста на

all (Байкул, 2014)

Занятие математикой не означает, что вы можете просто решить множество вопросов или сдать экзамены, подражая учителю на уроке

. Более того. Занятия математикой — это разработка стратегии решения проблем, реализация этой стратегии

и достижение результата.Этот метод найден, и результатом является построение абстракции соединения с

реальной жизнью. Студенты действительно по-другому знают, как переносить абстрактные математические вещи в реальную жизнь. Чем больше мы моделируем эти задачи на

в реальном мире, тем больше математики мы выполняем в повседневной жизни (Ван де Валле,

Карп, Бэй-Вильямс, Рэй и Браун, 2007). Национальный совет учителей математики (NCTM) (1998;

2000) подчеркнул, что одной из наиболее фундаментальных областей математики является геометрия, которая позволяет построить эту связь

.Если нам нужна математика в повседневной жизни, нам нужна геометрия.Мы можем представить, что у них

дополняют друг друга, и что математика без геометрии будет неполной. У геометрии

приложений в повседневной жизни. Обычно это различные предметы и формы, которые мы часто встречаем в нашей жизни. Мы можем

привести примеры зданий вокруг нас, многих вещей, которыми мы пользуемся, домов, в которых мы живем, и многого другого. Геометрия

будет слишком много, чтобы увидеть, например, информацию о форме или углы и края.Геометрия завершает математику

, а также помогает установить взаимосвязь между другими отраслями.

этот образ мышления также связан с другими дисциплинами, и учащимся полезно активно использовать свои способности к рассуждению.

Геометрическое мышление очень важно, если мы исходим из способностей к рассуждению. Это позволяет учащимся стимулировать свои способности к рассуждению

и повысить их способность комментировать различные дисциплины.Задача геометрии и математики

— дать ученикам возможность преодолеть проблемы, с которыми они могут столкнуться в своей жизни. Хотя кажется, что

состоят из форм и правил, они должны уметь использовать их для решения своих проблем.

Математика и геометрия станут более значимыми, если мы научим учащихся осознанию этого.