Контрольные работы по геометрии 10 класс УМК Атанасян. Геометрия 10 класс контрольные
Сборник контрольных работ по геометрии, (10 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
10 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
Контрольная работа №1 10 класс.
Тема: «Аксиомы и их следствия».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач аксиомы стереометрии и их следствия;
- умение оформлять рисунки по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1.Могут ли две различных плоскости иметь три общие точки, не лежащие на одной прямой? 2.Прямая а лежит в плоскости α. Плоскость β пересекает плоскость α по прямой b. Известно, что прямая a пересекает плоскость β в точке b. Где лежит точка b ? 3.Прямые a, b и c, не лежащие в одной плоскости, проходят через одну и ту же точку. Сколько различных плоскостей можно провести через эти прямые, взятые по две. 4.Точки A, B и прямая CD не лежат в одной плоскости. Каково взаимное расположение прямых CD и AB ? 5.Две соседние вершины и точка пересечения диагоналей квадрата лежат в плоскости α. Докажите, что и две других вершины квадрата лежат в этой же плоскости. |
| II вариант. |
| 1. Плоскости α и β пересекаются по прямой а . Прямая b лежащая в плоскости β, пересекает плоскость α в точке А. Где лежит точка А ? 2.Прямая AB и точки С и D не лежат в одной плоскости. Докажите, что прямые AB и CD пересекаются. 3.Плоскости α и β пересекаются по прямой AB. Плоскости β и γ по прямой BC, а плоскости α и γ по прямой АС. Докажите, что A, B, C лежат на одной прямой. 4.Даны точки А и В. Доказать, что существуют такие точки C и D, что четыре точки A, B, C, D не лежат в одной плоскости. 5.Сторона АВ и диагональ BD прямоугольника ABCD лежат в плоскости α. Докажите, что и вершина С этого прямоугольника лежит в этой же плоскости. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Аксиомы стереометрии | №1,2 | №3,4 | | 80% |
| Прямоугольник. Признаки и свойства | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 3 балла |
| Логичность обоснования. | 1 балл |
| Запись решения. | 1 балл |
| 2 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 3 балла |
| Логичность обоснования. | 1 балл |
| Запись решения. | 1 балл |
| 3 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 5 баллов |
| Логичность обоснования. | 2 балла |
| Запись решения. | 2 балла |
| 4 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 5 баллов |
| Логичность обоснования. | 2 балла |
| Запись решения. | 2 балла |
| 5 | Задача на применение аксиом. | Построение чертежа по условию задачи. | 1 балл | 5 баллов |
| Логичность обоснования. | 2 балла |
| Запись решения. | 2 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 балла – «4»
20-21 балл – «5»
Контрольная работа №2 10 класс.
Тема: «Параллельность прямых, прямой и плоскости, плоскостей».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач определения и признаки параллельных прямых, параллельных прямой и плоскости, плоскостей;
- умение оформлять рисунки по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Известно, что точки A, B, C, D лежат в одной плоскости. Определите, могут ли прямые AB и CD: а) быть параллельными; ;б) пересекаться в) быть скрещивающимися. 2. Через сторону AD четырехугольника ABCD проведена плоскость α. Известно, что BCA = CAD. Докажите, что BC параллельно α. 3.Квадрат ABCD и трапеция BEFC не лежат в одной плоскости. Точки M и N середины отрезков BE и FC соответственно. а) докажите, что MN параллельно AD б) найдите MN, если AD=10 см, EF=6 см. 4. На стороне AD параллелограмма ABCD выбрана точка А1 так, что DA1=4 см. Плоскость, параллельная диагонали АС, проходит через точку А1 и пересекает сторону CD в точке С1.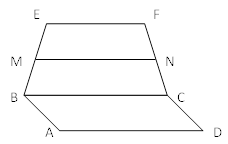 а) Докажите подобие треугольников C1DA1 и ABC б) Найдите АС, если ВС=10 см, А1С1=6см. 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите А2В2 и АА2, если А1В1=18, АА1=24, АА2=⅔А1А2. |
| II вариант. |
| 1. Известно, что точки A, B, C, D не лежат в одной плоскости. Определите, могут ли прямые AB и CD: а) быть параллельными; б) пересекаться; в) быть скрещивающимися. 2.Через сторону AD четырехугольника ABCD проведена плоскость α. Известно, что ABC + DAB = 180º .Докажите, что BC параллельно α. 3. Треугольник BEC и прямоугольник ABCD не лежат в одной плоскости. Точки M и N середины отрезков BE и EC соответственно. а) докажите, что AD параллельно MN б) найдите AD, если MN=5 см. 4. На стороне ВС параллелограмма ABCD выбрана точка С1 так, что С1В=3 см.Плоскость параллельная диагонали АС, проходит через С1 и пересекает сторону АВ в точке А1. а) Докажите подобие треугольников ADС и C1ВA1  б) Найдите АD, если А1С1=4 см, АС=12см. 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите АА2 и АВ2, если А1А2=2, А1А=12, АВ1=5. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Расположение прямых в пространстве | №1 | № 3 | | 40% |
| Расположение прямой и плоскости | №2 | № 4 | | 40% |
| Параллельные плоскости | | | № 5 | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Расположение прямых в пространстве. | Знание определения. | 1 балл | 3 балла |
| Логическое обоснование ответа. | 2 балла |
| 2 | Расположение прямой и плоскости. | Знание признака параллельности прямой и плоскости. | 1 балл | 3 балла |
| Оформление решения задачи. | 2 балла |
| 3 | Расположение прямых в пространстве. | Знание признака параллельности прямых. | 1 балл | 5 баллов |
| Свойство средней линии. | 2 балла |
| Оформление решения задачи. | 2 балла |
| 4 | Расположение прямой и плоскости. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Свойства прямой параллельной плоскости. | 1 балл |
| Подобие треугольников. | 1 балл |
| Оформление решения задачи. | 2 балла |
| 5 | Свойства параллельных плоскостей. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Подобие треугольников. | 2 балла |
| Оформление решения задачи. | 2 балла |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №3 10 класс.
Тема: «Параллельность плоскостей».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач определение, признаки и свойства параллельных плоскостей;
- знания и умения применять при решении задач свойства параллельного проектирования;
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1С и С1С не лежащие в плоскости параллелограмма. Докажите параллельность плоскостей А1АВ и С1СD. 2. Основания трапеции параллельны некоторой плоскости. Верно ли, что боковые стороны трапеции так же параллельны этой плоскости? Ответ объясните. 3. Постройте проекцию квадрата ABCD, зная проекции его вершин А, В и точки пересечения диагоналей О, точки А1, В1 и О1. 4. Параллельные прямые а и b пересекают одну из двух параллельных плоскостей в точках А1 и В1, а другую в точках А2 и В2 соответственно. а) Докажите, что А1В1 параллельно А2В2 б) Найдите А2А1В1, если А1А2В2=140ᴼ 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите А2В2 и АА2, если А1В1=18, АА1=24, АА2=⅔А1А2. |
| II вариант. |
| 1. Через вершины А и С параллелограмма ABCD проведены параллельные прямые А1С и С1С не лежащие в плоскости параллелограмма. Докажите параллельность плоскостей А1АD и C1CB. 2. Боковые стороны трапеции параллельны некоторой плоскости. Верно ли, что основания трапеции так же параллельны этой плоскости? Ответ объясните. 3. Постройте проекцию правильного треугольника АВС, зная проекции его вершины А и середины К, М сторон АВ и ВС, точки А1, К1 и М1. 4. Параллельные прямые а и b пересекают одну из двух параллельных плоскостей в точках А1 и В1, а другую в точках А2 и В2 соответственно. а) Докажите, что А1В1 равно А2В2 б) Найдите В1В2А2, если В1А1А2=50ᴼ 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите АА2 и АВ2, если А1А2=2, А1А=12, АВ1=5. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Параллельные плоскости | №1,2 | №4 | №5 | 80% |
| Параллельное проектирование | | №3 | | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Признак параллельности плоскостей | Выполнение чертежа по условию задачи | 1 балл | 3 балла |
| Применение признака параллельности плоскостей | 1 балл |
| Оформление решения задачи | 1 балл |
| 2 | Признак параллельности плоскостей | Применение признака параллельности плоскостей | 1 балл | 3 балла |
| Оформление решения задачи | 2 балла |
| 3 | Параллельное проектирование | Знание и применение свойств параллельного проектирования | 3 балла | 5 баллов |
| Выполнение построения | 1 балл |
| Оформление решения задачи | 1 балл |
| 4 | Свойства параллельных плоскостей | Выполнение чертежа по условию задачи | 1 балл | 5 баллов |
| Применение свойств параллельных плоскостей | 1 балл |
| Свойство углов | 1 балл |
| Оформление решения задачи | 2 балла |
| 5 | Квадрат. Признаки и свойства | Выполнение чертежа по условию задачи | 2 балла | 5 баллов |
| Подобие треугольников | 2 балла |
| Оформление решения задачи | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №4 10 класс.
Тема: «Перпендикулярность прямых, прямой и плоскости».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач определение, признаки и свойства перпендикулярных прямых, прямой и плоскости;
-знания и умения применять при решении задач теорему о трех перпендикулярах;
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Дано: АВ ┴ α, CD ┴ α, AB=CD.Определить вид четырехугольника ABCD. 
2. Дан куб ABCDA1B1C1D1. Докажите что: AD ┴ (DCC1). 3. Из точки S к плоскости α проведены перпендикуляр SO и наклонные SA и SB. Найдите SB, если SA=20 см, АО=16 см, ОВ=5см. 4. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояния от точки S до вершин прямоугольника, если расстояние от точки S до плоскости АВС равно 24 см, АВ=12 см, ВС=16 см. 5. Из точки к плоскости прямоугольного треугольника с катетами 15 и 20 см проведен перпендикуляр длинной 16 см. Основание перпендикуляра, вершина прямого угла треугольника. Найдите расстояние от данной точки до гипотенузы. |
| II вариант. |
| 1.Дано: ABCD параллелограмм  АВ ┴ α, АС=8. Найти BD 2. Дан куб ABCDA1B1C1D1. Докажите что: BB1 ┴ (ABC). 3. Из точки S к плоскости α проведены перпендикуляр SO и наклонные SA и SB. Найдите АО, если SB=17 см, ОВ=15 см, SA=10 см. 4. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояние от точки S до плоскости прямоугольника, если стороны прямоугольника 6 и 8 см, а SA=13 см. 5. Из точки, к плоскости треугольника со сторонами 13 см, 14 см, 15 См проведен перпендикуляр, основание которого вершина угла противоположная стороне 14 см. Расстояние от данной точки до этой стороны равно 20 см. Найдите расстояние от точки, до плоскости треугольника. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Перпендикулярные прямые | №1 | | | 20% |
| Перпендикулярные прямая и плоскость | № 2 | | | 20% |
| Перпендикуляр и наклонная | | №3, 4 | | 40% |
| Теорема о трех перпендикулярах | | | №5 | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Свойства перпен-дикулярных прямых. | Применение свойств прямых перпендикулярных плоскости. | 2 балла | 3 балла |
| Оформление решения задачи. | 1 балл |
| 2 | Признак перпендикулярности прямой и плоскости. | Применение признака перпендикулярности. | 1 балл | 3 балла |
| Оформление решения задачи. | 2 балла |
| 3 | Перпендикуляр и наклонная. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 3 балла |
| 4 | Перпендикуляр и наклонная. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Применение свойства точки равноудаленной от вершин прямоугольника. | 1 балл |
| Вычисление. | 1 балл |
| Оформление решения задачи | 2 балла |
| 5 | Теорема о трех перпендикулярах. | Выполнение чертежа по условию задачи. | 2 балла | 5 баллов |
| Знание и применение ТТП. | 2 балла |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №5 10 класс.
Тема: «Перпендикулярность плоскостей».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач определение, признаки и свойства перпендикулярных плоскостей;
-умения определять расстояние между скрещивающимися прямыми, углы между плоскостями
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Прямая SA проходит через вершину прямоугольника ABCD и перпендикулярна его сторонам АВ и AD. Докажите перпендикулярность плоскостей: SAD и АВС. 2. Ребро куба ABCDA1B1C1D1 равно 4. Найдите расстояние между прямыми АВ и СС1. 3. Плоскости равнобедренных треугольников ABD и АВС с общим основанием перпендикулярны. Найдите CD, если AD= см, АВ=6 см, АСВ=60ᴼ. см, АВ=6 см, АСВ=60ᴼ. 4. Перпендикулярные плоскости α и β пересекаются по прямой L. Отрезки ОА и ОВ лежащие на плоскостях α и β соответственно, перпендикулярны прямой L, а их общий конец – точка О лежит на прямой L. Найдите АВ, если ОА=20 см, ОВ:АВ=12:13 5. Через вершину В равнобедренного треугольника АВС проведена плоскость, параллельная основанию АС. Найдите углы наклона боковых сторон к этой плоскости, если основание АС=12 см и удалено от данной плоскости на 5 см, а площадь треугольника равна 48 см2. |
| II вариант. |
| 1. Прямая SA проходит через вершину прямоугольника ABCD и перпендикулярна его сторонам АВ и AD. Докажите перпендикулярность плоскостей: SAB и АВС. 2. Ребро куба ABCDA1B1C1D1 равно 4. Найдите расстояние между прямыми СС1 и В1D1. 3.Плоскости равнобедренных треугольников ABD и АВС с общим основанием перпендикулярны. Найдите CD, если AD=10 см, AВ=16 см, САВ=45ᴼ. 4. Перпендикулярные плоскости α и β пересекаются по прямой L. Отрезки ОА и ОВ лежащие на плоскостях α и β соответственно, перпендикулярны прямой L, а их общий конец – точка О лежит на прямой L. Найдите АВ и ОВ, если АВ=40 см, ОА:ОВ=3:4 5. Через вершину А ромба ABCD проведена плоскость, параллельная диагонали BD. Найдите углы наклона сторон АВ и AD к этой плоскости, если диагональ BD равна 16 см и удалена от данной плоскости на 5 см, а площадь ромба равна 96 см2. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Перпендикулярные плоскости | №1 | №3,4 | | 60% |
| Расстояние между скрещивающимися прямыми | №2 | | | 20% |
| Угол между прямой и плоскостью | | | №5 | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Признак перпендикулярности плоскостей | Выполнение чертежа по условию задачи | 1 балл | 3 балла |
| Применение признака перпендикулярности плоскостей | 1 балл |
| Оформление решения задачи | 1 балл |
| 2 | Расстояние между скрещивающимися прямыми | Определение расстояние между скрещивающимися прямыми | 1 балл | 3 балла |
| Оформление решения задачи | 2 балла |
| 3 | Перпендикулярные плоскости | Знание и применение свойств перпендикулярных плоскостей | 2 балла | 5 баллов |
| Выполнение построения | 1 балл |
| Оформление решения задачи | 2 балла |
| 4 | Свойства параллельных плоскостей | Выполнение чертежа по условию задачи | 1 балл | 5 баллов |
| Применение свойств параллельных плоскостей | 1 балл |
| Составление уравнения | 1 балл |
| Оформление решения задачи | 2 балла |
| 5 | Угол между прямой и плоскостью | Выполнение чертежа по условию задачи | 2 балла | 5 баллов |
| Нахождение углов | 2 балла |
| Оформление решения задачи | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №6 10 класс.
Тема: «Координаты и векторы в пространстве».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач формул нахождения середины отрезка, расстояние между точками
- знания и умения применять при решении задач нахождение координат и модуля вектора, условия перпендикулярности и коллинеарности векторов, скалярное произведение векторов;
- умение оформлять решение задачи.
| I вариант. |
| 1.Найдите координаты точек, симметричных точке А ( 7 ; -3 ; 1 ): а) плоскости XZ, б) оси Y, в) начала координат. 2.Дан треугольник АВС с вершинами А (11; -2;- 9) , В(2;6;-4), С (8;-6;-8) а) найдите координаты середины отрезка ВС, б) найдите координаты и модуль вектора ВС, в) найдите вектор АВ + BC, г) докажите перпендикулярность векторов AB и AC. 3. Дан вектор а (2; 1; -2) а) известно, что а = EF. Найдите координаты точки Е, если F (4;-1;-2) б) Найдите значения m и n, при которых векторы a и b коллинеарны, если b (-4; m; n) в) Найдите координаты и модуль вектора с, если с = 2а 4. Даны векторы a(-3; 0; 4) и b(1; -2; 2) а) Найдите вектор 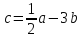
б) Найдите (a + b)(a – b) в) Найдите косинус угла между векторами a и b 5. Докажите, что четырехугольник параллелограмм, и найдите его центр симметрии, если А(-2;-4;1), В(-5;-6;-1), С(4;10;3), Р(7;12;5). |
| II вариант. |
| 1. Найдите координаты точек, симметричных точке: В (2 ; 4 ; -5): а) плоскости XY, б) оси Х, в) начала координат 2. Дан треугольник АВС с вершинами А (11; -2; - 9) , В(2;6;-4), С (14; 2; -10) а) найдите координаты середины отрезка ВС, б) найдите координаты и модуль вектора ВС, в) найдите вектор АВ + BC; г) докажите перпендикулярность векторов AB и AC 3. Дан вектор а (2; 1; -2) а) известно, что а = EF. Найдите координаты точки F, если E (2;0;3) б) Найдите значения m и n, при которых векторы a и b коллинеарны, если b (m; n; -4) в) Найдите координаты и модуль вектора с, если с = -3а 4. Даны векторы a(-2; -2; 1) и b(0; -4; 3) а) Найдите вектор 
б) Найдите (a + b) (a – b) в) Найдите косинус угла между векторами a и b 5.Докажите, что четырехугольник параллелограмм, и найдите его центр симметрии, если А(-1;4;3), В(-3;6;-5), С(3;0;-5), Р(5;-2;3) |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Преобразование симметрии | №1 | | | 20 % |
| Координаты в пространстве | №2 | | | 20 % |
| Векторы в пространстве | | №3, №4 | №5 | 60% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Координаты в пространстве. | Координаты точек симметричных относительно координатной плоскости | 1 балл | 3 балла |
| Координаты точек симметричных относительно координатной оси | 1 балл |
| Координаты точек симметричных относительно начала координат | 1 балл |
| 2 | Координаты и векторы. | Координаты середины отрезка | 1 балл | 5 баллов |
| Координаты и модуль вектора | 1 балл |
| Координаты суммы векторов | 1 балл |
| Условие перпендикулярности векторов | 1 балл |
| Оформление решения задачи | 1 балл |
| 3 | Координаты и векторы. | Координаты начала вектора | 1 балл | 5 баллов |
| Условие коллинеарности | 1 балл |
| Координаты вектора | 1 балл |
| Модуль вектора | 1 балл |
| Оформление решения задачи | 1 балл |
| 4 | Координаты и векторы. | Координаты вектора | 1 балл | 5 баллов |
| Скалярное произведение векторов | 1 балл |
| Нахождение косинуса | 2 балла |
| Оформление решения задачи | 1 балл |
| 5 | Координаты и векторы. | Применение признаков параллелограмма | 2 балла | 5 баллов |
| Нахождение центра симметрии | 2 балла |
| Оформление решения задачи | 1 балл |
Критерии оценивания:
1-11 баллов – «2»
12-16 баллов – «3»
17-21 балл – «4»
22-23 баллов – «5»
.
xn--j1ahfl.xn--p1ai
Контрольные работы по геометрии (10 класс)
Контрольная работа по геометрии. 10 кл.
Параллельность прямых.
Параллельность прямой и плоскости
Вариант 1
1. Параллелограмм ABCD и треугольник ВСК не лежат в одной плоскости. М и Р – середины сторон ВК и СК. Как взаимно расположены AD и МР?
2. Плоскость α параллельна стороне МР треугольника
МРК и пересекает две другие стороны треугольника в точках М1 и Р1, МР = 27 см, ММ1 : М1 К = 5:4. Найти М1Р1
3. Дан куб АВСDА1В1С1D1. Как взаимно расположены
а) ВС и А1D1 б) ВВ1 и АВС
ВВ1 и В1С1 С1D1 и АВС
СС1 и АD DD1 и DCC1
в) Найти угол между прямыми СС1 и АD,
между прямыми А1С1 и DС.
4. Прямая р не лежит в плоскости квадрата ABCD и параллельна диагонали АС. Как взаимно расположены
р и BD? Найти угол между этими прямыми.
Контрольная работа по геометрии. 10 кл.
Параллельность прямых.
Параллельность прямой и плоскости
Вариант 2
1. Параллелограмм ABCD и трапеция ВСКЕ не лежат в одной плоскости. М и Р – середины сторон ВЕ и СК. Как взаимно расположены AD и МР?
2. Плоскость α параллельна стороне МР треугольника
МРК и пересекает две другие стороны треугольника в точках М1 и Р1, МР = 24 см, ММ1 : М1 К = 5:3. Найти М1Р1
3. Дан куб АВСDА1В1С1D1. Как взаимно расположены
а) ВС и В1С1 б) DD1 и АВВ1
ВВ1 и А1В1 С1D1 и А1В1С1
СС1 и АВ ВС и DCC1
в) Найти угол между прямыми ВВ1 и АD,
между прямыми АВ и DС1.
4. Прямая р не лежит в плоскости ромба ABCD и параллельна диагонали BD. Как взаимно расположены
р и АС? Найти угол между этими прямыми.
Контрольная работа по геометрии. 10 кл.
Параллельность плоскостей.
Тетраэдр и параллелепипед
Вариант 1
1. Прямые a и b лежат соответственно в параллельных плоскостях α и β. Как они могут быть взаимно расположены? Сделайте рисунок для каждого возможного случая.
2. Параллельные плоскости α и β пересекают стороны угла ВАС: сторону АВ - соответственно в точках А1 и А2, сторону АС - в точках В1 и В2. Найти В1В2 , если
АА1 = 6 см, А1А2 = 9 см, АВ1 = 8 см.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки D, В1 и точку M, являющуюся серединой ребра СС1. Вычислите периметр сечения, если АВ = 10 см, АD = 12 см, АА1 = 16 см.
4. Изобразите тетраэдр DABC и отметьте точку M – середину ребра DC, и точку N – середину отрезка DМ. Постройте сечение тетраэдра плоскостью, проходящей через точку N и параллельной плоскости АМВ.
Контрольная работа по геометрии. 10 кл.
Параллельность плоскостей.
Тетраэдр и параллелепипед
Вариант 2
1. Прямые a и b лежат соответственно в параллельных плоскостях α и β. Как они могут быть взаимно расположены? Сделайте рисунок для каждого возможного случая.
2. Параллельные плоскости α и β пересекают стороны угла ВАС: сторону АВ - соответственно в точках А1 и А2, сторону АС - в точках В1 и В2. Найти В1В2 , если
АА1 = 4 см, А1А2 = 20 см, АВ1 = 6 см.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки D, В1 и точку M, являющуюся серединой ребра СС1. Вычислите периметр сечения, если АВ = 14 см, АD = 10 см, АА1 = 18 см.
4. Изобразите тетраэдр DABC и отметьте точку M – середину ребра DC, и точку К – середину отрезка МС. Постройте сечение тетраэдра плоскостью, проходящей через точку К и параллельной плоскости АМВ.
Контрольная работа по геометрии. 10 кл.
Перпендикулярность прямых и плоскостей
Вариант 1
Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найти расстояние от этой точки до прямой АС и до плоскости α, если АВ=6 см, ВАС=120º и двугранный угол ВАСВ1 равен 30º.
Плоскости α и ß перпендикулярны. Прямая а – линия их пересечения. В плоскости α лежит точка А, а в плоскости ß – точка В, так что расстояния от них до прямой а равны соответственно 4 и 5 см. Найти АВ, если расстояние между основаниями перпендикуляров, проведенных из точек А и В к прямой а, равно 2√2 см.
Через вершину тупого угла В ромба АВСD к его плоскости проведен перпендикуляр ВК, длина которого равна 4 см. Найти расстояние от К до CD, если АВ=16 см, А=45º
Сумма площадей всех граней прямоугольного параллелепипеда равна 2124 см2, а его измерения пропорциональны числам 5, 6 и 8. Найти диагональ параллелепипеда.
Контрольная работа геометрии. 10 кл.
Перпендикулярность прямых и плоскостей
Вариант 2
Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найти расстояние от этой точки до прямой АС и до плоскости α, если АВ=12 см, ВАС=150º и двугранный угол ВАСВ1 равен 60º.
Плоскости α и ß перпендикулярны. Прямая а – линия их пересечения. В плоскости α лежит точка А, а в плоскости ß – точка В, так что расстояния от них до прямой а равны соответственно 6 и 7 см. Найти расстояние между основаниями перпендикуляров, проведенных из точек А и В к прямой а, если АВ равно √110 см.
Через вершину прямого угла С прямоугольного треугольника АВС к его плоскости проведен перпендикуляр СК, длина которого равна 9,6 см. Найти расстояние от К до АВ, если АС=12 см,
ВС=9 см.
Сумма площадей всех граней прямоугольного параллелепипеда равна 3050 см2, а его измерения пропорциональны числам 3, 4 и 7. Найти диагональ параллелепипеда.
Годовая контрольная работа по геометрии. 10 кл.
Вариант 1
1. Дан параллелепипед АВСDА1В1С1D1, АВ=4 см, АD=7 см, АА1=10 см. М – середина АА1. Построить сечение параллелепипеда плоскостью В1МD, найти периметр сечения.
2. Через вершину прямого угла С прямоугольного треугольника АВС к его плоскости проведен перпендикуляр СК, длина которого равна 8 см. Найти расстояние от К до АВ, если АС=15 см, ВС= 20см.
3. Дана правильная треугольная призма АВСА1В1С1. Сторона основания 8 см, диагональ боковой грани 17 см. Найти площадь полной поверхности призмы.
4. Высота правильной четырехугольной пирамиды РАВСD равна 12 см, радиус окружности, описанной около основания 9√2 см. Найти площадь полной поверхности пирамиды.
5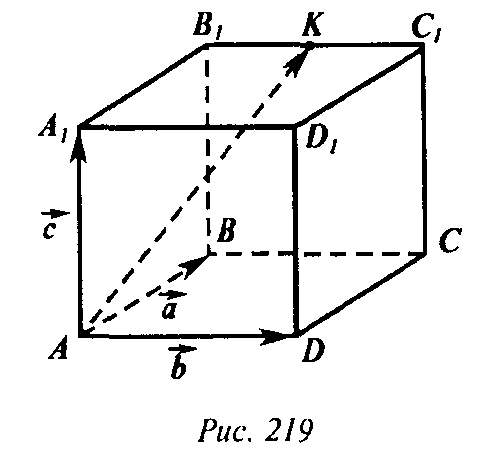 .
.
Дан параллелепипед, К – середина ребра В1С1. Выразить через векторы ā, b, с векторы
АВ, В1К, СА, С1А, АК, ВD, А1D.
Годовая контрольная работа по геометрии. 10 кл.
Вариант 2
1. Дан параллелепипед АВСDА1В1С1D1, АВ=5 см, АD=6 см, АА1=8 см. М – середина АА1. Построить сечение параллелепипеда плоскостью В1МD, найти периметр сечения.
2. Через вершину прямого угла С прямоугольного треугольника АВС к его плоскости проведен перпендикуляр СК, длина которого равна 9,6 см. Найти расстояние от К до АВ, если АС=9 см, ВС=12 см.
3. Дана правильная треугольная призма АВСА1В1С1. Сторона основания 10 см, диагональ боковой грани 26 см. Найти площадь полной поверхности призмы.
4. Высота правильной четырехугольной пирамиды РАВСD равна 6 см, радиус окружности, описанной около основания 8√2 см. Найти площадь полной поверхности пирамиды.
5 .
.
Дан параллелепипед, К –середина ребра В1С1. Выразить через векторы ā, b, с векторы АА1, КС1, АС, С1А, АК, DВ, А1В.
infourok.ru
Контрольные работы по геометрии 10 класс. УМК Л.С. Атанасян и др.
КОНТРОЛЬНЫЕ РАБОТЫ
ПО ГЕОМЕТРИИ
10 КЛАСС
УЧЕБНИК АТАНАСЯН Л.С.
Контрольная работа № 1
Тема: Параллельность прямых и плоскостей
Вариант I
1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а) Каково взаимное положение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если  АВС = 150°? Поясните.
АВС = 150°? Поясните.
2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
Контрольная работа № 1
Тема: Параллельность прямых и плоскостей
Вариант II
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых РK и АВ?
б) Чему равен угол между прямыми РK и АВ, если  АВС = 40° и
АВС = 40° и  ВСА = 80°? Поясните.
ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е  CD, K
CD, K  DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа № 2
Тема: Параллельность плоскостей. Тетраэдр и параллелепипед.
Вариант I
1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1и А2соответственно, прямая m – в точках В1и В2. Найдите длину отрезка А2В2, если А1В1= 12 см, В1О : ОВ2= 3 : 4.
3. Изобразите параллелепипед ABCDA1B1C1D1и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
Контрольная работа № 2
Тема: Параллельность плоскостей. Тетраэдр и параллелепипед.
Вариант II
1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1и А2соответственно, прямая m – в точках В1и В2. Найдите длину отрезка А1В1, если А2В2= 15 см, ОВ1: ОВ2= 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K  DA, АK : KD = 1 : 3.
DA, АK : KD = 1 : 3.
Контрольная работа № 3
Тема: Перпендикулярность прямых и плоскостей
Вариант I
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии  от точки D.
от точки D.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM,М  α.
α.
infourok.ru
Контрольные работы по геометрии 10 класс
Примерные материалы контрольных работ
Геометрия 10 класс (А.В.Погорелов)
Вариант 1
1. Точки К, М, Р, Т не лежат в одной плоскости. Могут ли прямые КМ и РТ пересекаться?
Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1,В1,М1 соответственно. Найдите длину отрезка ММ1, если АА1 = 13 м, ВВ1 = 7 м, причем отрезок АВ не пересекает плоскость α.
Точка Р не лежит в плоскости трапеции АВСD с основаниями АD и ВС. Докажите, что прямая, проходящая через середины отрезков РВ и РС, параллельна средней линии трапеции.
Вариант 2
Прямые EN и KM не лежат на одной плоскости. Могут ли прямые ЕМ и NК пересекаться? (Ответ обоснуйте.)
Через точки А, В и середину М отрезка АВ проведеныпараллельные прямые, пересекающие некоторую плоскость α в точках А1, В1? М1 соответственно. Найдите длину отрезка ММ1, если АА1 = 3 м, ВВ1 = 17 м, причем отрезок АВ не пересекает плоскость α.
3. Точка Е не лежит в плоскости параллелограмма АВСD. Докажите, что прямая, проходящая через середины отрезков ЕА и ЕВ, параллельна стороне СD.
Вариант1
Плоскости α и β параллельны, причем плоскость а α пересекает некоторую прямую а. Докажите, что и плоскость β пересекает прямую а.
Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, ВС, СD. Докажите, что плоскость КМР параллельна прямым АС и ВD.
3. Даны две параллельные плоскости и не лежащая между ними точка Р. Две прямые, проходящие через точку Р, пересекают ближнюю к точке Р плоскость в точках А1 и А2, а дальнюю — в точках В1 и В2 соответственно. Найдите длину отрезка В1В2, если А1А2 = 6 см и РА1 : А1В1= 3:2.
4. Постройте проекцию квадрата АВСD, зная проекции его вершин А, В и точки пересечения диагоналей О: точки а1, В1 и О1.
Вариант 2
1. Прямые а и b параллельны, причем прямая а пересекает некоторую плоскость α. Докажите, что и прямая b пересекает плоскость α.
Точки А, В, С, D не лежат в одной плоскости, точки К, М, Р — середины отрезков АВ, АС, АD. Докажите, что плоскости КМР и ВСD параллельны.
Даны две параллельные плоскости и не лежащая междуними точка Р. Две прямые, проходящие через точку Р, пересекают ближнюю к точке Р плоскость в точках А1 и А2, а дальнюю — в точках B1 и В2 соответственно. Найдите длину отрезка В1В2, если А1А2 = 10 см и РА1 : А1В1 = 2:3.
Постройте проекцию правильного треугольника, знаяпроекции его вершины А и середин К, М сторон АВ и ВС: точки А1, К1 и М1.
Вариант 1
1. Концы отрезка АВ, не пересекающего плоскость, удалены от нее на расстояния 2,4 м и 7,6 м. Найдите расстояние от середины М отрезка АВ до этой плоскости.
Перекладина длиной 5 м своими концами лежит на двух вертикальных столбах высотой 3 м и 6 м. Каково расстояние между основаниями столбов?
Из точки к плоскости проведены две наклонные, равные 17 см и 15 см. Проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных.
Из вершины равностороннего треугольника АВС восставлен перпендикуляр АD к плоскости треугольника. Чему равно расстояние от точки D до прямой ВС, если АD = 1 дм, ВС = 8 дм?
Вариант 2
Точка А лежит в плоскости, точка В — на расстоянии 12,5 м от нее. Найдите расстояние от плоскости до точки М, делящей отрезок АВ в отношении АМ : МВ = 2:3.
Какой длины нужно взять перекладину, чтобы ее можно было положить концами на две вертикальные опоры высотой 4 м и 8 м, поставленные на расстоянии 3 м одна от другой?
Из точки к плоскости проведены две наклонные, одна из которых на 6 см длиннее другой. Проекции наклонных равны 17 см и 7 см. Найдите наклонные.
Из вершины квадрата АВСD восставлен перпендикуляр АЕ к плоскости квадрата. Чему равно расстояние от точки Е до прямой ВD, если АЕ = 2 дм, АВ = 8 дм?
Вариант 1
Даны точки А (0; 0; 2) и В (1; 1; -2), О — начало координат.
На оси у найдите точку М (0; у; 0), равноудаленную от точек А и В.
В плоскости ху найдите точку С (х; у; 0), такую, чтобы векторы АС и ВО были коллинеарными.
При каком значении х вектор ν(х; 2; 1) будет перпендикулярен вектору АВ?
Вариант 2
Даны точки А (0; -2; 0) и В (1; 2; -.1), О — начало координат.
1. На оси z найдите точку М (0; 0; z), равноудаленную от точек А и В.
2. Найдите точку С (х; у; z), такую, чтобы векторы СО и АВ были равными.
3. При каком значении х вектор ν (х; 1; 2) будет перпендикулярен вектору ВА?
infourok.ru
Контрольные работы по геометрии 10 класс
Итоговая контрольная работа.
I вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков DA и
DB, параллельна плоскости АВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 10см и
имеет проекцию длиной 8см. Найдите длину
второй наклонной, если она образует с данной
плоскостью угол 30 .
.
3. SC – перпендикуляр к плоскости
прямоугольного треугольника АВС
(В = 90 ). Найдите расстояние от точки S до
). Найдите расстояние от точки S до
прямой АВ, если АС = 13см, АВ = 5см,
SC = 16см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если
А – середина отрезка ВD. Сравните модули
векторов  и
и  , если С(1;5;-2)
, если С(1;5;-2)
I вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков DA и
DB, параллельна плоскости АВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 10см и
имеет проекцию длиной 8см. Найдите длину
второй наклонной, если она образует с данной
плоскостью угол 30 .
.
3. SC – перпендикуляр к плоскости
прямоугольного треугольника АВС
(В = 90 ). Найдите расстояние от точки S до
). Найдите расстояние от точки S до
прямой АВ, если АС = 13см, АВ = 5см,
SC = 16см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если
А – середина отрезка ВD. Сравните модули
векторов  и
и  , если С(1;5;-2)
, если С(1;5;-2)
II вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков AВ и
АС, параллельна плоскости DВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 16см и
образует с данной плоскостью угол 30 .
.
Найдите длину второй наклонной, если ее
проекция на данную плоскость равна 6см.
3. SА – перпендикуляр к плоскости
прямоугольника АВСD. Найдите его длину,
если АВ = 5см, если ВD = 13см, а точка S
удалена от прямой СD на 15см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если В –
середина отрезка АD. Сравните модули
векторов  и
и  , если С(-4;3;2)
, если С(-4;3;2)
II вариант
1.Точки А, В, С, и D не лежат в одной
плоскости. Докажите, что прямая,
проходящая через середины отрезков AВ и
АС, параллельна плоскости DВС.
2. Из точки к плоскости проведены две
наклонные. Одна из наклонных равна 16см и
образует с данной плоскостью угол 30 .
.
Найдите длину второй наклонной, если ее
проекция на данную плоскость равна 6см.
3. SА – перпендикуляр к плоскости
прямоугольника АВСD. Найдите его длину,
если АВ = 5см, если ВD = 13см, а точка S
удалена от прямой СD на 15см.
4. Даны координаты точки А(3;-1;2) и В(2;1;-4).
Найдите координаты точки D, если В –
середина отрезка АD. Сравните модули
векторов  и
и  , если С(-4;3;2)
, если С(-4;3;2)
kopilkaurokov.ru
Контрольные работы по геометрии (10 класс, УМК Атанасяна, 4 шт.)
1 вариант
1). Основание АD трапеции АВСD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а). Каково взаимное расположение прямых
ЕF и АВ?
б). Чему равен угол между прямыми ЕF и АВ,
если АВС = 1500?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, в котором диагонали АС и ВD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а). Выполните рисунок к задаче;
б). Докажите, что полученный четырех –
угольник – ромб.
|
2 вариант
1). Треугольники АВС и АDС лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина DС.
а). Каково взаимное расположение прямых
РК и АВ?
б). Чему равен угол между прямыми РК и
АВ, если АВС = 400 и ВСА = 80?
Ответ обоснуйте.
2). Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно, Е СD, К D, DА : ЕС = 1 : 2, DК : КА = 1 : 2.
а). Выполните рисунок к задаче;
б). докажите, что четырехугольник МNЕК –
трапеция.
|
1 вариант
1). Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3). Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
|
2 вариант
1). Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а). Параллельными;
б). Скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2). Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3). Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
|
1 вариант
1). Диагональ куба равна 6 см. Найдите:
а). Ребро куба;
б). Косинус угла между диагональю куба и
плоскостью одной из его граней.
2). Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.
а). Найдите расстояние от точки С до плоскости α;
б). Покажите на рисунке линейный угол двугранного угла DABM, М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
|
2 вариант
1). Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна см, а его измерения относятся как 1:1:2. Найдите:
а). Измерения параллелепипеда;
б). Синус угла между диагональю параллеле –
пипеда и плоскостью его основания.
2). Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.
а). Найдите расстояние от точки С до плоскости α.
б). Покажите на рисунке линейный угол
двугранного угла BADM, М α.
в). Найдите синус угла между плоскостью
квадрата и плоскостью α.
|
1 вариант
1). Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
|
2 вариант
1). Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2). Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а). меньшую высоту параллелограмма;
б). угол между плоскостью АВС1 и плоскостью основания;
в). площадь боковой поверхности параллелепипеда;
г). площадь поверхности параллелепипеда.
|
uchkopilka.ru
Контрольные работы по геометрии 10 класс УМК Атанасян
1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если  АВС = 150°? Поясните. АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. | 2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если  АВС = 40° и АВС = 40° и  ВСА = 80°? Поясните. ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е  CD, K CD, K  DA, DE : EC = 1 : 2, DK : KA = 1 : 2. DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. | 1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. | 2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K  DA, АK : KD = 1 : 3. DA, АK : KD = 1 : 3. | 1 вариант 1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии  от точки D. от точки D. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM,М  α. α. в) найдите синус угла между плоскостью ромба и плоскостью α | 2 вариант 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2  см, а его измерения см, а его измерения относятся как 1 : 1 : 2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии  от точки В. от точки В. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM,М  α. α. в) Найдите синус угла между плоскостью квадрата и плоскостью α. | 1 вариант 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда | 2 вариант 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a  и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. | multiurok.ru






 см, АВ=6 см, АСВ=60ᴼ.
см, АВ=6 см, АСВ=60ᴼ. 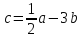

 .
. АВС = 150°? Поясните.
АВС = 150°? Поясните. CD, K
CD, K  от точки D.
от точки D. .
. и
и  , если С(1;5;-2)
, если С(1;5;-2) АВС = 150°? Поясните.
АВС = 150°? Поясните. CD, K
CD, K  от точки D.
от точки D.