Контрольная работа по алгебре «Производная функции» 11 класс
Контрольная работа №1 по теме: «Производная функции»
Вариант №1.
1. Найдите производную функции:
а) f(x)=2+7
б) f(x)=3sin x – cos x + tg x
в) f(x)=(3x4+1)(2x3-3)
г) f(x)=
д) f(x)=
2. Решите неравенство f ´(x)>0, если f(x)=2x3+6x2
3. Напишите уравнение касательной, проведенной к графику функции f
4. Тело движется по закону х(t)=2t2-8t+7. Определите момент времени, когда скорость тела равна нулю.
Контрольная работа №1 по теме: «Производная функции»
Вариант №2.
1. Найдите производную функции:
а) f(x)=5-4
б)
в) f(x)=(2x3+1)(4x4—2)
г) f(x)=
д) f(x)=
2. Решите неравенство f ´(x)<0, если f(x)=4x3-6x
3. Напишите уравнение касательной, проведенной к графику функции f(x)=x2-3x+1 в точке х=2.
Напишите уравнение касательной, проведенной к графику функции f(x)=x2-3x+1 в точке х=2.
4. Тело движется по закону х(t)=3t2-12t+8. Определите момент времени, когда скорость тела равна нулю.
Контрольная работа по теме «Производная»
2020-2021 Контрольная работа №4 11 класс
по теме «Производная»
Вариант 1
1º.Найти производную функции:
1) ; 2) ; 3) ; 4) ; 5) .
2º.Найдите значение производной функции в точке = 3.
3º.Точка двигается по закону. (s — в метрах).
а)º Найдите её скорость в момент времени t = 1 с.
б) В какой момент времени ускорение будет равно 11 .
4. Решите уравнение , если .
5. Решить неравенство , если
6. Найти производную функции .
2020-2021 Контрольная работа №4 11 класс
по теме «Производная»
Вариант 2
1º.Найти производную функции:
1) ; 2) ; 3) ; 4) ; 5) .
2º.Найдите значение производной функции в точке = 5.
3º. Точка двигается по закону. (s — в метрах).
а)º Найдите её скорость в момент времени t = 2 с.
б) В какой момент времени ускорение будет равно 21 .
4. Решите уравнение , если .
5. Решить неравенство , если
6. Найти производную функции .
2020-2021 Контрольная работа №4 11 класс
по теме «Производная»
Вариант 1
1º. Найти производную функции:
Найти производную функции:
1) ; 2) ; 3) ; 4) ; 5) .
2º.Найдите значение производной функции в точке = 3.
3º.Точка двигается по закону. (s — в метрах).
а)º Найдите её скорость в момент времени t = 1 с.
б) В какой момент времени ускорение будет равно 11 .
4. Решите уравнение , если .
5. Решить неравенство , если
6. Найти производную функции .
2020-2021 Контрольная работа №4 11 класс
по теме «Производная»
Вариант 2
1º.Найти производную функции:
1) ; 2) ; 3) ; 4) ; 5) .
2º.Найдите значение производной функции в точке = 5.
3º. Точка двигается по закону. (s — в метрах).
а)º Найдите её скорость в момент времени t = 2 с.
б) В какой момент времени ускорение будет равно 21 .
4. Решите уравнение , если .
5. Решить неравенство , если
6. Найти производную функции .
Найти производную функции .
Контрольная работа по алгебре и началам анализа вариант № 1
При выполнении заданий А1 – А8 в бланке ответов №1 под номером выполняемого задания поставьте знак «х», в клеточку, номер которой соответствует номеру выбранного вами ответа.
А1. Вычислите .
А2. Вычислите .
 Определите, сколько часов
температура воздуха была выше 12°С.
Определите, сколько часов
температура воздуха была выше 12°С.А5. Укажите область определения функции .
А6. Укажите множество значений функции .
А7. Решите уравнение .
А8. Найдите производную функции .
Ответом на задание В1-В2 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать в бланк ответов №1 справа от номера задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами.
В1. Найдите значение выражения , если , .
В2. Функция определена на всей числовой прямой и
является периодической с периодом 5. На
рисунке изображен график этой функции
при .
Сколько корней имеет уравнение на отрезке ?
На
рисунке изображен график этой функции
при .
Сколько корней имеет уравнение на отрезке ?
Для записи ответа на задание С1 используйте обратную сторону бланка ответов №1. Запишите сначала условие задания, а затем обоснованное решение.
С1. Найдите множество значений функции , которая задана на множестве решений неравенства .
Контрольная работа по алгебре и началам анализа вариант № 2
При выполнении заданий А1 – А8 в бланке ответов №1 под номером выполняемого задания поставьте знак «х», в клеточку, номер которой соответствует номеру выбранного вами ответа.
А1. Вычислите .
А2. Найдите значение выражения , если .
А3. Укажите график нечетной функции.
 На
рисунке показано изменение расстояния при движении
автобуса между населенными пунктами.
Укажите промежуток времени с наибольшей
скоростью движения.
На
рисунке показано изменение расстояния при движении
автобуса между населенными пунктами.
Укажите промежуток времени с наибольшей
скоростью движения.А5. Укажите область определения функции .
А6. Укажите множество значений функции .
А8. Найдите производную функции .
Ответом на задание В1-В2 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать в бланк ответов №1 справа от номера задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами.
В1. Найдите значение выражения , если , .
В2. Функция определена на всей числовой прямой и
является периодической с периодом 5. На
рисунке изображен график этой функции
при .
Найдите сумму корней уравнения на отрезке .
Функция определена на всей числовой прямой и
является периодической с периодом 5. На
рисунке изображен график этой функции
при .
Найдите сумму корней уравнения на отрезке .
Для записи ответа на задание С1 используйте обратную сторону бланка ответов №1. Запишите сначала условие задания, а затем обоснованное решение.
С1. Найдите значение функции в точке минимума.
Самостоятельные и контрольные работы по алгебре и началам анализа для
Предлагаемое пособие в первую очередь предназначено для учителей и учащихся, работающих по двухуровневому учебнику «Нелин Е.П., Лазарев В.А. Алгебра и начала математического анализа. 11 класс: базовый и профильный уровни» (издательство «Илекса»), но может использоваться и при работе по другим учебникам алгебры и начал математического анализа, особенно при подготовке учащихся к решению заданий ЕГЭ и ГИА.
1.
 Сборник содержит полный набор самостоятельных и контрольных работ по всему курсу алгебры и начал математического анализа 11 класса, как базового, так и профильного уровней.
Сборник содержит полный набор самостоятельных и контрольных работ по всему курсу алгебры и начал математического анализа 11 класса, как базового, так и профильного уровней.Контрольные работы рассчитаны на один урок, самостоятельные работы — на 25—40 минут, в зависимости от темы и уровня подготовки учащихся.
 Эти задания могут в полном объеме или частично предлагаться учащимся в качестве зачетных, а также использоваться как дополнительные задания для проведения контрольных работ. По усмотрению учителя выполнение нескольких или даже одного такого задания может оцениваться отличной оценкой.
Эти задания могут в полном объеме или частично предлагаться учащимся в качестве зачетных, а также использоваться как дополнительные задания для проведения контрольных работ. По усмотрению учителя выполнение нескольких или даже одного такого задания может оцениваться отличной оценкой.Ответы к контрольным и домашним самостоятельным работам приводятся в конце книги.
СОДЕРЖАНИЕ
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ 5
С-1. Понятие предела функции в точке. Метод интервалов решения неравенств 5
С-2. Вычисление пределов числовых последовательностей и функций. Непрерывность функции 7
С-3. Асимптоты графика функции 9
С-4. Определение производной. Простейшие правила вычисления производных 12
С-5. Производные элементарных и сложных функций 15
С-6. Геометрический и механический смысл производной 18
С-7*. Дополнительные задачи на нахождение асимптот графика функции (домашняя самостоятельная работа) 22
K-l(KII-l). Производная 23
С-8. Исследование функции на монотонность и экстремумы 27
0-9. Исследование показательных, логарифмических и степенных функций на монотонность и экстремумы 29
Исследование показательных, логарифмических и степенных функций на монотонность и экстремумы 29
С-10*. Построение графиков функций с помощью производной (домашняя практическая работа) 31
С-11. Нахождение наибольшего и наименьшего значений функции 32
С-12*. Избранные задачи дифференциального исчисления (домашняя самостоятельная работа) 35
К-2 (КП-2) Применение производной 36
С-13. Производные обратных тригонометрических функций. Доказательство тождеств с помощью производной 39
С-14. Выпуклость и точки перегиба функции. Расширенная схема исследования функции 40
С-15. Применение производной к решению уравнений и неравенств и к доказательству неравенств 41
(КП-3). Применение производной к решению уравнений и неравенств 43
ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ 45
С-16. Первообразная. Вычисление первообразных 45
С-17. Определенный интеграл. Вычисление площадей плоских фигур 48
С-18. Применение первообразной и интеграла 50
С-19*. Избранные задачи интегрального исчисления (домашняя самостоятельная работа) 53
К-3 (КП-4). Первообразная и интеграл 57
Первообразная и интеграл 57
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИКИ 61
С-20. Основные формулы комбинаторики. Простейшие комбинаторные задачи 61
С-21. Комбинаторные задачи. Правило суммы и правило произведения 64
С-22. Бином Ньютона. Свойства биномиальных коэффициентов 66
С-23*. Дополнительные задачи по комбинаторике (домашняя самостоятельная работа) 68
С-24. Классическая вероятность. Использование формул комбинаторики при вычислении вероятности 70
С-25. Теоремы сложения и умножения вероятностей 72
С-26. Статистическое определение вероятности. Геометрическое определение вероятности 75
С-27. Вероятность осуществления хотя бы одного из независимых событий. Схема Бернулли 78
С-28. Понятие о статистике. Генеральная совокупность и выборка. Числовые характеристики рядов данных 80
К-4 (КП-5) Комбинаторика, вероятность, статистика 83
КОМПЛЕКСНЫЕ ЧИСЛА 87
С-29. Понятие комплексного числа. Действия с комплексными числами в алгебраической форме 87
С-30. Модуль и аргумент комплексного числа. Геометрическое изображение комплексных чисел 90
Модуль и аргумент комплексного числа. Геометрическое изображение комплексных чисел 90
С-31. Тригонометрическая форма комплексного числа 93
С-32*. Дополнительные задачи с комплексными числами (домашняя самостоятельная работа) 96
К-5 (КП-6). Комплексные числа 97
СИСТЕМАТИЗАЦИЯ И ОБОБЩЕНИЕ СВЕДЕНИЙ ОБ УРАВНЕНИЯХ, НЕРАВЕНСТВАХ И ИХ СИСТЕМАХ 101
С-33. Методы решения уравнений, неравенств и их систем 101
С-34. Задачи с параметрами 104
К-6 (КП-7). Обобщение сведений о решении уравнений, неравенств и их систем 105
К-7 (КП-8). Итоговое повторение курса алгебры и начал анализа 108
ОТВЕТЫ 112
Ответы к контрольным работам 112
Ответы к домашним самостоятельным работам 120
ЛИТЕРАТУРА 136
ПРИЛОЖЕНИЕ. Ориентировочное тематическое планирование курса алгебры и начал математического анализа в 11 классе по учебнику Нелина Е.П., Лазарева В.А. (и распределение самостоятельных и контрольных работ) 137
Пособие содержит самостоятельные и контрольные работы к двухуровневому учебнику «Алгебра и начала математического анализа. 11 класс: базовый и профильный уровни» Е.П. Нелина, В. А. Лазарева. Пособие также можно использовать при работе по любому учебнику и для самообразования, например, при подготовке к решению заданий ЕГЭ. Предлагаемые работы состоят из 6 вариантов трех уровней сложности и предназначены для организации дифференцированной самостоятельной работы учащихся.
11 класс: базовый и профильный уровни» Е.П. Нелина, В. А. Лазарева. Пособие также можно использовать при работе по любому учебнику и для самообразования, например, при подготовке к решению заданий ЕГЭ. Предлагаемые работы состоят из 6 вариантов трех уровней сложности и предназначены для организации дифференцированной самостоятельной работы учащихся.
«Контрольная работа по алгебре в формате ЕГЭ». 10–11-е классы
Данная контрольная работа предназначена для подготовки к Единому государственному экзамену, организации и проведению итогового повторения, диагностики проблемных зон в знаниях старшеклассников и последующей коррекции.
Контрольная работа написана в соответствии с утвержденными демоверсией и спецификацией ЕГЭ по математике. Работа позволяет проверить навыки решения задач, качество усвоения материала, выстроить индивидуальные траектории повторения и эффективно подготовиться к сдаче ЕГЭ.
Эту работу можно провести и в 10-ом классе, как
итоговую после изучения тем: “Показательная и
логарифмическая функции”, “Степени и корни”,
“Основные тригонометрические формулы”.
Вариант 1.
А. Решить уравнение:
- =27
- =
- =5
- =2
- =5
Б. Дано: =-,
Найти:
а)
б) tg a.
В. Найти значение выражения:
- .
- 34
С.1. Решите уравнение14 и укажите корень принадлежащий отрезку
С.2. Упростить выражение и найти его значение при a =.
Вариант 2.
А. Решить уравнение:
- =125
- (=
- =2
- =2
- =2
Б. Дано: =-
Найти:
а)
б) tg a.
В. Найти значение выражения:
- .
- -46
- 1
С.1. Решите уравнение и укажите корень принадлежащий отрезку
С.2. Упростить выражение и найти его значение при a =.
Литература.
1. Алгебра и начала математического анализа.10-11 классы. Задачник. А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова, Т.Г.Мишустина, П.В.Семенов, Е.Е.Тульчинская. Издательство “Мнемозина”. Москва 2012.
2. ЕГЭ. Математика. Типовые Экзаменационные варианты. Под редакцией И.В.Ященко.36 вариантов. Издательство “Национальное образование”. Москва 2015.
Одиннадцатый класс (11 класс) Вопросы о функциях и взаимосвязях для тестов и рабочих листов
Вы можете создавать печатные тесты и рабочие листы из этих 11 класс Функции и отношения вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом. Затем нажмите кнопку добавить выбранные вопросы к кнопке теста перед переходом на другую страницу.
Затем нажмите кнопку добавить выбранные вопросы к кнопке теста перед переходом на другую страницу.
- [математика] {(- 5,1), (0, -3), (-2, 1), (10,11), (7, 1)} [/ математика]
- [математика] {(9, 3), (6, 2), (3, 2), (3, 1), (6, -2)} [/ математика]
- [математика] {(4, 9), (5, 3), (-2, 0), (5, 4), (8, 1)} [/ математика]
- Все отношения — это функции.

- Ни одно из отношений не является функциями.
- Домен и диапазон — это действительные числа.
- Домен — это все действительные числа меньше нуля, а диапазон — все действительные числа.
- Домен — это все действительные числа, а диапазон — все действительные числа, равные или меньшие нуля.

- Ни один из вышеперечисленных.
- {1, 2, 3}
- {5, 6, 7}
- {1, 2, 3, 5, 6, 7}
- {1, 7}
- [математика] {(0, 1), (1, 0), (2, 1), (3, 1), (4, 2)} [/ математика]
- [математика] {(7, 4), (4, 9), (-3, 1), (1, 7), (2, 8)} [/ математика]
- [математика] {(1, 4), (3, 2), (5, 2), (1, -8), (6, 7)} [/ математика]
- Все вышеперечисленное — это функции.

- Ни одно из вышеперечисленных не является функциями.
Функции 11-го класса — ОБЗОР ЭКЗАМЕНА
MCR3U 1 Обзор экзамена Полиномы Полином — это алгебраическое выражение с действительными коэффициентами и неотрицательным целым
Просмотры 88 Загрузки 9 Размер файла 246KB
Отчет DMCA / Copyright
СКАЧАТЬ ФАЙЛ
Рекомендовать историиПредварительный просмотр цитирования
MCR3U
1
Exam Review
Полиномы Полином — это алгебраическое выражение с действительными коэффициентами и неотрицательными целыми показателями. Многочлен с 1 членом называется мономом 7 x. Многочлен с двумя членами называется двучленом 3 x 2 — 9. Многочлен с 3 членами называется трехчленом 3 x 2 + 7 x — 9. Степень полинома определяется значением наивысшего показателя переменной в полиноме. например 3 x 2 + 7 x — 9, степень равна 2. Для многочленов с одной переменной, если степень равна 0, то она называется константой. Если степень равна 1, то она называется линейной. Если степень равна 2, то она называется квадратичной.Если степень равна 3, то она называется кубической. Мы можем складывать и вычитать многочлены, собирая одинаковые члены. например Упрощать. Отрицательный знак перед скобками 5 x 4 — x 2 — 2 — x 4 — 2 x 3 + 3x 2 — 5 применяется к каждому члену в скобках.
Многочлен с 1 членом называется мономом 7 x. Многочлен с двумя членами называется двучленом 3 x 2 — 9. Многочлен с 3 членами называется трехчленом 3 x 2 + 7 x — 9. Степень полинома определяется значением наивысшего показателя переменной в полиноме. например 3 x 2 + 7 x — 9, степень равна 2. Для многочленов с одной переменной, если степень равна 0, то она называется константой. Если степень равна 1, то она называется линейной. Если степень равна 2, то она называется квадратичной.Если степень равна 3, то она называется кубической. Мы можем складывать и вычитать многочлены, собирая одинаковые члены. например Упрощать. Отрицательный знак перед скобками 5 x 4 — x 2 — 2 — x 4 — 2 x 3 + 3x 2 — 5 применяется к каждому члену в скобках.
(
) (
)
= 5x — x — 2 — x + 2 x — 3x + 5 4
2
4
3
2
То есть каждый член умножается на –1.
= 5 x 4 — x 4 + 2 x 3 — x 2 — 3x 2 — 2 + 5 = 4 x 4 + 2 x3 — 4 x 2 + 3 Чтобы умножить многочлены, умножьте каждый член первого многочлена на каждый член во-вторых. например Расширяйте и упрощайте.
например Расширяйте и упрощайте.
(x
2
) (
)
+ 4 x2 — 2x + 3
= x 4 — 2 x 3 + 3x 2 + 4 x 2-8 x + 12 = x 4 — 2 x 3 + 7 x 2 — 8 x + 12 Факторинговые многочлены. Раскрытие означает запись произведения многочленов в виде суммы или разности членов. Фактор означает записать сумму или разность членов как произведение многочленов. Факторинг — это операция, обратная расширению. Развертывание
(2 x + 3) (3x — 7) = 6 x 2 — 5 x — 21 Факторинговое произведение многочленов
Сумма или разность условий
MCR3U
2
Обзор экзамена
Типы факторинг: общие факторы: факторы, общие для каждого термина.например Фактор, каждый член делится на. 35m3n3 — 21m 2 n 2 + 56m 2 n
(
= 7 m 2 n 5mn 2 — 3n + 8
)
Фактор по группировке: сгруппируйте термины для помощи в процессе факторинга. 1 + 6x + 9×2 — идеальный вариант, например. Фактор, группа 4mx — 4nx и квадратный трехчлен A: 4mx + ny — 4nx — my ny — my, множитель каждый B: 1+ 6x + 9×2 — 4 y2 группа Разница квадратов = 4mx — 4nx + ny — my = (1 + 3 x) 2 — 4 y 2 = 4 x (m — n) + y (n — m) Вспомните n — m = — (m — n) = [(1 + 3 x) + 2 y] [(1 + 3 x) — 2 y] = 4 x (m — n) — y (m — n) = (1 + 3 x + 2 y) (1 + 3 x — 2 y) Общий множитель = (4 x — y) (m — n) Факторизация ax 2 + bx + c Найдите произведение ac. Найдите два числа, которые умножаются на ac и прибавляются к b. например Фактор, A: y 2 + 9 y + 14 B: 3x 2-7 xy — 6 y 2 Произведение = 14 = 2 (7) = y + 7 y + 2 y + 14 Sum = 9 = 2 + 7 = y ( y + 7) + 2 (y + 7) = (y + 2) (y + 7) 2
Найдите два числа, которые умножаются на ac и прибавляются к b. например Фактор, A: y 2 + 9 y + 14 B: 3x 2-7 xy — 6 y 2 Произведение = 14 = 2 (7) = y + 7 y + 2 y + 14 Sum = 9 = 2 + 7 = y ( y + 7) + 2 (y + 7) = (y + 2) (y + 7) 2
= 3 x — 9 xy + 2 xy — 6 y = 3 x (x — 3 y) + 2 y ( x — 3 y) = (3 x + 2 y) (x — 3 y) 2
2
Произведение = 3 (–6) = –18 = –9 (2) Сумма = — 7 = –9 + 2 Разложите средний член — 7xy на –9xy + 2xy. Фактор по группировке.
Иногда многочлены можно разложить на множители с помощью специальных шаблонов.Полный квадрат трехчлена, например Множитель, A: 4 p 2 + 12 p + 9 = (2 p + 3) 2
a 2 + 2ab + b 2 = (a + b) (a + b) B: 100 x 2 — 80 xy + 16 y 2 = 4 (25 x 2 — 20 xy + 4 y 2) = 4 (5 x — 2 y) (5 x — 2 y)
a 2 — b 2 = (a + b) (a — b) Разность квадратов 9 x 2 — 4 y 2 = (3 x + 2 y) (3 x — 2 y) например. Фактор, о чем следует подумать при факторинге: • Есть ли общий фактор? • Могу ли я фактор по группировке? • Есть ли какие-то особые узоры? • Проверьте, могу ли я множить x 2 + bx + c? • Проверьте, могу ли я множить ax 2 + bx + c?
или a 2 — 2ab + b 2 = (a — b) (a — b)
MCR3U
3
Exam Review
Рациональные выражения Для полиномов F и G рациональное выражение формируется, когда e. грамм.
грамм.
3x + 7 21x + 14 x + 9
F, G ≠ 0. G
2
Упрощение рациональных выражений, например Упростите и укажите ограничения. m2 — 9 (m + 3) (m — 3) = 2 m + 6m + 9 (m + 3) (m + 3) (m + 3) (m — 3) = (m + 3) (m + 3) ) m − 3 =, m ≠ −3 m + 3
Разложите на множители числитель и знаменатель. Обратите внимание на ограничения. Упрощать. Укажите ограничения.
Умножение и деление рациональных выражений, например Упростите и укажите ограничения. x2 — 9 x2 — 4x + 3 B: 2 ÷ 2 x2 + 7 xx 2 + 3x + 2 A: 2 × x + 5x + 4 x + 5x + 4 x — 1 x 2 + 14 x + 49 (x + 3 ) (x — 3) (x — 1) (x — 3) Фактор.Фактор. = ÷ x (x + 7) (x + 1) (x + 2) Обратите внимание на ограничения. = × (x + 4) (x + 1) (x + 4) (x + 1) Обратите внимание на ограничения. (x + 1) (x — 1) (x + 7) (x + 7) (x + 3) (x — 3) (x + 4) (x + 1) Инвертировать и умножать. = × x (x + 7) (x + 1) (x + 2) Упростить. = × (x + 4) (x + 1) (x — 1) (x — 3) Обратите внимание на любые новые ограничения. (x + 1) (x — 1) (x + 7) (x + 7) (x + 3) (x — 3) (x + 4) (x + 1) = × x (x + 2) Государственные ограничения . Упрощать. =, x ≠ ± 1, — 7 (x + 4) (x + 1) (x — 1) (x — 3) (x — 1) (x + 7) (x + 3) =, x ≠ −4 , ± 1, 3 Ограничения по состоянию.(x — 1) Сложение и вычитание рациональных выражений, например Упростите и укажите ограничения. 3 5 Фактор. A: 2 + Обратите внимание на ограничения. x −4 x + 2 Упростите, если возможно. 3 5 = + (x — 2) (x + 2) x + 2 Найдите ЖК-дисплей. 3 5 (x — 2) Запишите все члены = + (x — 2) (x + 2) (x + 2) (x — 2) с помощью ЖК-дисплея. 3 + 5 x — 10 = Добавить. (x + 2) (x — 2) 5x — 7 =, x ≠ ± 2 Ограничения по состоянию. (x + 2) (x — 2)
Упрощать. =, x ≠ ± 1, — 7 (x + 4) (x + 1) (x — 1) (x — 3) (x — 1) (x + 7) (x + 3) =, x ≠ −4 , ± 1, 3 Ограничения по состоянию.(x — 1) Сложение и вычитание рациональных выражений, например Упростите и укажите ограничения. 3 5 Фактор. A: 2 + Обратите внимание на ограничения. x −4 x + 2 Упростите, если возможно. 3 5 = + (x — 2) (x + 2) x + 2 Найдите ЖК-дисплей. 3 5 (x — 2) Запишите все члены = + (x — 2) (x + 2) (x + 2) (x — 2) с помощью ЖК-дисплея. 3 + 5 x — 10 = Добавить. (x + 2) (x — 2) 5x — 7 =, x ≠ ± 2 Ограничения по состоянию. (x + 2) (x — 2)
Коэффициент. Обратите внимание на ограничения. Если возможно, упростите.
2 3 — x — xy xy — y 2 2 3 Найдите LCD. = — Запишите все члены x (x — y) y (x — y) с помощью ЖК-дисплея.2y 3x = — xy (x — y) xy (x — y) Вычесть. 2 y — 3x =, x ≠ 0, y, y ≠ 0 Ограничения по состояниям. xy (x — y)
B:
2
Обратите внимание, что после сложения или вычитания числитель может быть факторизован на множители и дальнейшее упрощение выражения.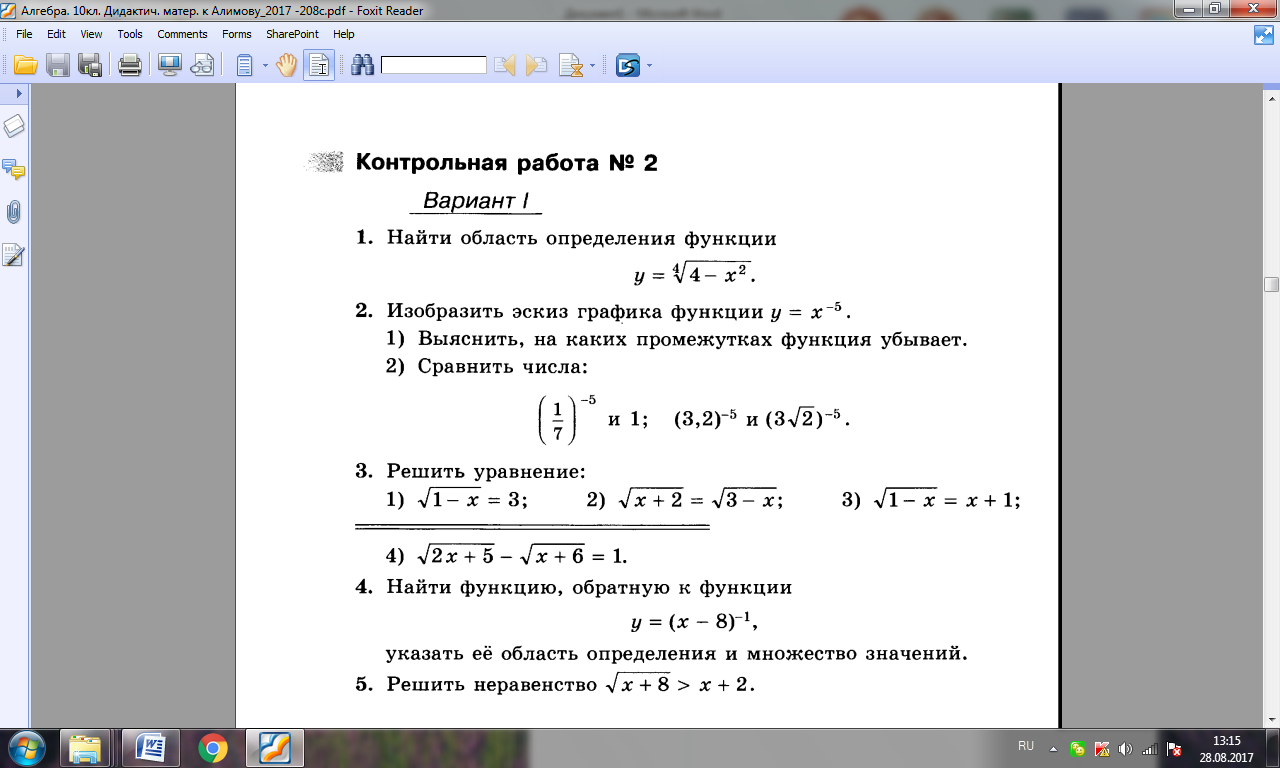 Всегда сокращайте ответ до минимума.
Всегда сокращайте ответ до минимума.
MCR3U
4
Обзор экзамена
Радикалы напр.
n
a,
называется радикальным знаком, n — индексом радикала, а a называется подкоренным выражением.
3 называется радикалом порядка 2.
3
5, 2 5, — 3 5
Подобные радикалы:
8 — радикал порядка 3. В отличие от радикалов:
5, 3 5 , 3
Такой же порядок, как подкоренные группы
Целые радикалы:
Другой порядок
8, 16, 29
Разные подкоренные группы
Смешанные радикалы: 4 2, 2 3, 5 7 Радикал в простейшей форме соответствует следующему условия: Для радикала порядка n подкоренное выражение не имеет множителя n-й степени целого числа.Непростая форма
Подкоренное выражение не содержит дробей. 3 3 2 = × 2 2 2
8 = 4 × 2
=
= 2 × 2 2
= 2 2
=
Простейшая форма
6 22
Подкрепленное выражение не содержит множителей с отрицательными экспоненты. 1 a −1 = a
1 a −1 = a
=
1 a × aa
=
a a2
6 22
6 = 2
Простейшая форма
a = a
Индекс радикала должен иметь вид как можно меньше.4
32 =
32
= 3 Простейшая форма
Простейшая форма
Сложение и вычитание радикалов Чтобы добавить или вычесть радикалы, вы добавляете или вычитаете коэффициенты каждого радикала. например Упрощать. 2 12 — 5 27 + 3 40 = 2 4 × 3 — 5 9 × 3 + 3 4 × 10
(
) () (
= 2 2 3 — 5 3 3 + 3 2 10 = 4 3 — 15 3 + 6 10
)
Выразите каждый радикал в простейшей форме.
Собирать как радикалы. Сложить и вычесть.
= −11 3 + 6 10 Умножение радикалов a × b = ab, a ≥ 0, b ≥ 0, например Упрощать. 2 +2 3 2 −3 3 =
(
) (
) (2) (2) — (2) (3 3) + (2 3) (2) — (2 3) (3 3) = 2 — 3 6 + 2 6 — 6 (3) = 2 — 18 — 3 6 + 2 6 = −16 — 6
Используйте свойство распределения, чтобы развернуть
Коэффициенты умножения вместе. Умножьте подкоренные выражения вместе.
Умножьте подкоренные выражения вместе.
Соберите похожие термины. Выразите в простейшей форме.
MCR3U
5
Exam Review
Конъюгаты
(a
Противоположные знаки
)
(
)
b + c d и a b — c d называются конъюгатами.
Те же термины
Те же термины
При умножении конъюгатов результатом является рациональное выражение (без радикалов). например Найдите товар.
(
5 +3 2
) (
) () (2
5 −3 2 = 5–3 2 = 5–9 (2) = 5–18 = −13
)
2
Деление радикалов a = b
a, a, b∈ R, a ≥ 0, b ≥ 0 b
например Упрощать. 2 10 + 3 30 2 10 3 30 = + 5 5 5 = 2
10 30 +3 5 5
= 2 2 +3 6 Простое факторизация Разложите число на простые множители, используя метод древовидной диаграммы.
180
например,
3
60 6 2
10 3
2
5
Правило экспоненты Правило Факторная мощность продукта
Описание am × an = a m + nam ÷ an = am − n
Мощность a частное
an a =, b ≠ 0 bn b a0 = 1 1 a −m = m, a ≠ 0 a
Ноль как показатель степени Отрицательные показатели Рациональные показатели
(a)
мин
Пример 4 2 × 45 = 47 54 ÷ 52 = 52
(3)
2 4
= am × n
n
m
an = n am =
(a) n
5
= 38 5
3 3 = 5 4 4 70 = 1 1 9 −2 = 2 9 м
4
27 3 = 3 27 4 =
(
3
27
)
4
MCR3U e. грамм. Оценивать.
грамм. Оценивать.
(3
0
+3
)
например Упрощать.
= (1 + 9)
2 −2
−2
= 10 1 = 2 10 1 = 100
−2
b3 −3 2a
Следуйте порядок действий. Сначала оцените скобки.
9 x − 2 = 73 + 8 9 x −2 = 9 2
−2
=
b3 (−2) (2a −3) −2
b −6 2 −2 a −3 ( −2) 2 2 b −6 = a6 4 = 6 6 ab =
Решение экспоненциальных уравнений e.грамм. Решите для x. 9 x − 2-8 = 73 Прибавляем 8 к обеим сторонам. 9 x − 2 = 81
6
Обзор экзамена
x − 2 = 2 x = 2 + 2 x = 4
Упростите.
Примечание LS и RS — это степени 9, поэтому перепишите их как степени, используя одну и ту же базу.
Степень частного.
Мощность продукта.
Когда основания совпадают, приравняйте экспоненты. Решите для x.
LS = 9 x − 2-8 RS = 73 = 9 4− 2-8 = 81-8 = 73 = RS
Не забудьте проверить свое решение!
x = 4 проверки
Функции Отношение — это отношение между двумя наборами. Отношения можно описать с помощью: уравнения; диаграммы со стрелками; графика 2 gy = 3x — 7 8 -1 0 7 в словах 6 -3 «выход на три больше, чем вход» 3 -5 набор упорядоченных пар {(1, 2 ), (0, 3), (4, 8)} 2
Отношения можно описать с помощью: уравнения; диаграммы со стрелками; графика 2 gy = 3x — 7 8 -1 0 7 в словах 6 -3 «выход на три больше, чем вход» 3 -5 набор упорядоченных пар {(1, 2 ), (0, 3), (4, 8)} 2
-2
таблица xy 1 2 2 3 3 4 4 3
обозначение функции f (x) = x 2 — 3 x Область определения отношение — это набор возможных входных значений (значений x). Диапазон — это набор возможных выходных значений (значений y). например Укажите домен и диапазон. A: {(1, 2), (0, 3), (4, 8)} B: Домен = {0, 1, 4} Диапазон = {2, 3, 8}
4
2
Ищу на графике видно, что y не опускается ниже 0.Таким образом, Domain = R Range =
C: y = x — 5 Какое значение x сделает x — 5 = 0? x = 5 Подкоренное выражение не может быть меньше нуля, поэтому Domain = {x | x ≥ 5, x ∈ R} Диапазон = {y | y ≥ 0, y ∈ R}
MCR3U
7
Exam Review
Функция — это особый тип отношения, в котором каждый элемент домена соответствует ровно одному элементу диапазона. y = x — 7 и y = x 2 + 15 являются примерами функций. y = ± x не является функцией, потому что для каждого значения x есть два значения y.Тест вертикальной линии используется для определения того, является ли график отношения функцией. Если вертикальная линия может быть проведена по всей длине графика и никогда не касается более одной точки за раз, то отношение является функцией. например A: B: Линия проходит больше, чем через одну точку, поэтому эта вертикальная линия отношения не проходит тест вертикальной линии. Это тест, поэтому это не функция. функция. 4
y = x — 7 и y = x 2 + 15 являются примерами функций. y = ± x не является функцией, потому что для каждого значения x есть два значения y.Тест вертикальной линии используется для определения того, является ли график отношения функцией. Если вертикальная линия может быть проведена по всей длине графика и никогда не касается более одной точки за раз, то отношение является функцией. например A: B: Линия проходит больше, чем через одну точку, поэтому эта вертикальная линия отношения не проходит тест вертикальной линии. Это тест, поэтому это не функция. функция. 4
4
2
2
Обратные функции Обратный, f −1, отношения, f, отображает каждый выход исходного отношения обратно в соответствующее входное значение.Область обратного значения — это диапазон функции, а диапазон обратного значения — это область определения функции. То есть, если (a, b) ∈ f, то (b, a) ∈ f −1. График y = f −1 (x) является отражением графика y = f (x) в прямой y = x. например Дано f (x) =
3x — 1. 5
5
Вычислите f (−3). 3 (−3) — 1 Заменить все 5 x на –3. Оценивать. — 9 −1 f (−3) = 5-10 f (−3) = 5 f (−3) = −2 f (−3) =
Определите f −1 (x). 3x — 1 y = 3x — 1 Записываем f (x) как y = 5 5 3y −1 Поменяем местами x и y.x = Решить относительно y. 5 5x = 3 y — 1 3 y = 5x + 1 5x + 1 y = 3 5x + 1 ∴ f −1 (x) = 3
Вычислить 3 f (2) + 1 3 (2) — 1 3 f (2) + 1 = 3 +1 5 6 — 1 = 3 +1 5 5 = 3 + 1 5 = 3 (1) + 1 3 f (2) + 1 = 4
Вы хотите найти значение выражения 3 f (2) + 1. Вы не решаете
f (2).
Вычислить f −1 (2) 5x + 1 3 5 (2) +1 f −1 (2) = 3 10 + 1 = 3 11 f −1 (2) = 3 f −1 (x) =
Если вы еще не определили f −1 (x), сделайте это.Используя f −1 (x), замените все x на 2. Оцените.
MCR3U
8
Обзор экзамена
например Нарисуйте график обратной функции y = f (x). 4
4
4
−1
2
2
Отразите график в линии y = x.
Проведите линию y = x.
y = f (x)
y = f (x)
2
-2
-2
-2
-4
-4
-4
Обратная функция не обязательно будет функцией.Если вы хотите, чтобы обратная функция также была функцией, вам, возможно, придется ограничить домен или диапазон исходной функции. В приведенном выше примере обратное будет функцией, только если мы ограничим область до {x | x ≥ 0, x ∈ R} или {x | x ≤ 0, x ∈ R}. Преобразования функций Чтобы построить график y = af [k (x — p)] + q из графика y = f (x), рассмотрим: a — определяет вертикальное растяжение. График y = f (x) растянут по вертикали в a раз. Если 0, график сдвигается вправо на p единиц.Если p 0, график сдвинется вверх на q единиц. Если q
При применении преобразований к графику, растяжки и отражения должны применяться перед любыми переводами. например График y = f (x) преобразуется в y = 3 f (2 x — 4). Опишите преобразования. Во-первых, фактор в скобках для определения значений k и p. y = 3 f (2 (x — 2)) a = 3, k = 2, p = 2 Есть вертикальный участок 3. 1 Горизонтальный участок. 2 График сместится на 2 единицы вправо.
1 Горизонтальный участок. 2 График сместится на 2 единицы вправо.
2
e.грамм. Учитывая график y = f (x), нарисуйте график y = 2 f (- (x — 2)) + 1
-2
y = f (x)
4
4
Растянуть по вертикали в 2 раза.
Отражение по оси ординат.
2
2
-2
-2
-4
-4
4
2
-2
-4
4
Сдвиг вправо на 2.
Сдвиг вверх на 1. 2-2
Это график y = 2 f (- (x — 2)) + 1
-4
-4
4
Квадратичные функции
2
График квадратичной функции f (x) = ax 2 + bx + c представляет собой параболу.Когда a> 0, парабола раскрывается. Когда
a> 0
минимум
-5
5
максимум -2
Форма вершины: f (x) = a (x — h) + k a 0, есть 2 нуля. Для определения нулей из стандартной формы используйте формулу корней квадратного уравнения. Для ax 2 + bx + c = 0 используйте x =
— b ± b 2 — 4ac, чтобы найти x. 2a
2a
Взаимные функции Обратная функция функции f определяется как
1 1. Чтобы помочь вам построить график y =, вы должны f (x) f
использовать следующее: 1 будет, где f (x) = 0 f (x) 1 1 По мере увеличения f (x) уменьшается.По мере уменьшения f (x) увеличивается. е (х) е (х) 1 1> 0. Для f (x) 0, f (x) f (x) 1 График y = всегда проходит через точки, где f (x) = 1 или f (x) = −1. f (x) Возможно, вам будет полезно сначала нарисовать график y = f (x), прежде чем строить обратную величину. Вертикальные асимптоты y =
4
1, например, Нарисуйте график y = 2. x — 4x Посмотрите на функцию f (x) = x 2 — 4 x. Факторизуйте это. е (х) = х (х — 4). Нули равны x = 0 и x = 4. Вертикальные асимптоты будут при x = 0 и x = 4.Вы можете нарисовать график f (x) = x 2 — 4 x, чтобы увидеть, где функция увеличивается и уменьшается, где f (x) = 1 или –1. Используйте информацию выше, чтобы сделать набросок обратного.
2
y = x 2 — 4x 5
-2
-4
4
2
y = 5
-2
-4
Вертикальные асимптоты
1 x — 4x
Экспоненциальные функции f (x) = 2x
f (x) = 2x-2 + 3
6
Как правило, экспоненциальная функция определяется уравнением y = ax или f (x) = ax, a> 0, x ∈ R. Преобразования применяются к экспоненциальным функциям так же, как и ко всем другим функциям.
Преобразования применяются к экспоненциальным функциям так же, как и ко всем другим функциям.
4
2
6
4
2
Экспоненциальный рост и распад Рост населения и радиоактивный распад можно моделировать с помощью экспоненциальных функций. Рост: N (t) = N (2) 0
td
t
N 0 — начальное количество
ч Распад: N (t) = N 0 1 2
N 0 — начальная сумма
t — истекшее время d — период удвоения N (t) — сумма в момент времени t Сложный процент Расчет будущей суммы: A = P (1 + i) n Расчет текущей суммы: P = A (1 + i) — n
t — прошедшее время h — период полураспада N (t) — количество в момент времени t
A — будущая сумма P — текущая (начальная) сумма i — процентная ставка за период конверсии n — количество периодов конверсии
Тригонометрия Для прямоугольного треугольника мы можем использовать следующие отношения. Первичные тригонометрические отношения yxy sin θ = cosθ = tan θ = rrx Взаимные тригонометрические отношения r 1 x 1 r 1 csc θ = = cot θ = = secθ = = y sin θ y tan θ x cosθ Тригонометрия косинусоидальных треугольников abc = = sin A sin B sin C Может использоваться, если вы знаете закон косинуса ASA, AAS, SSA a 2 = b 2 + c 2 — 2bc cos A Можно использовать, если вы знаете SSS , SAS 9 0007
r y x
A b
C
c
a
B
Когда вы знаете SSA, это считается неоднозначным случаем.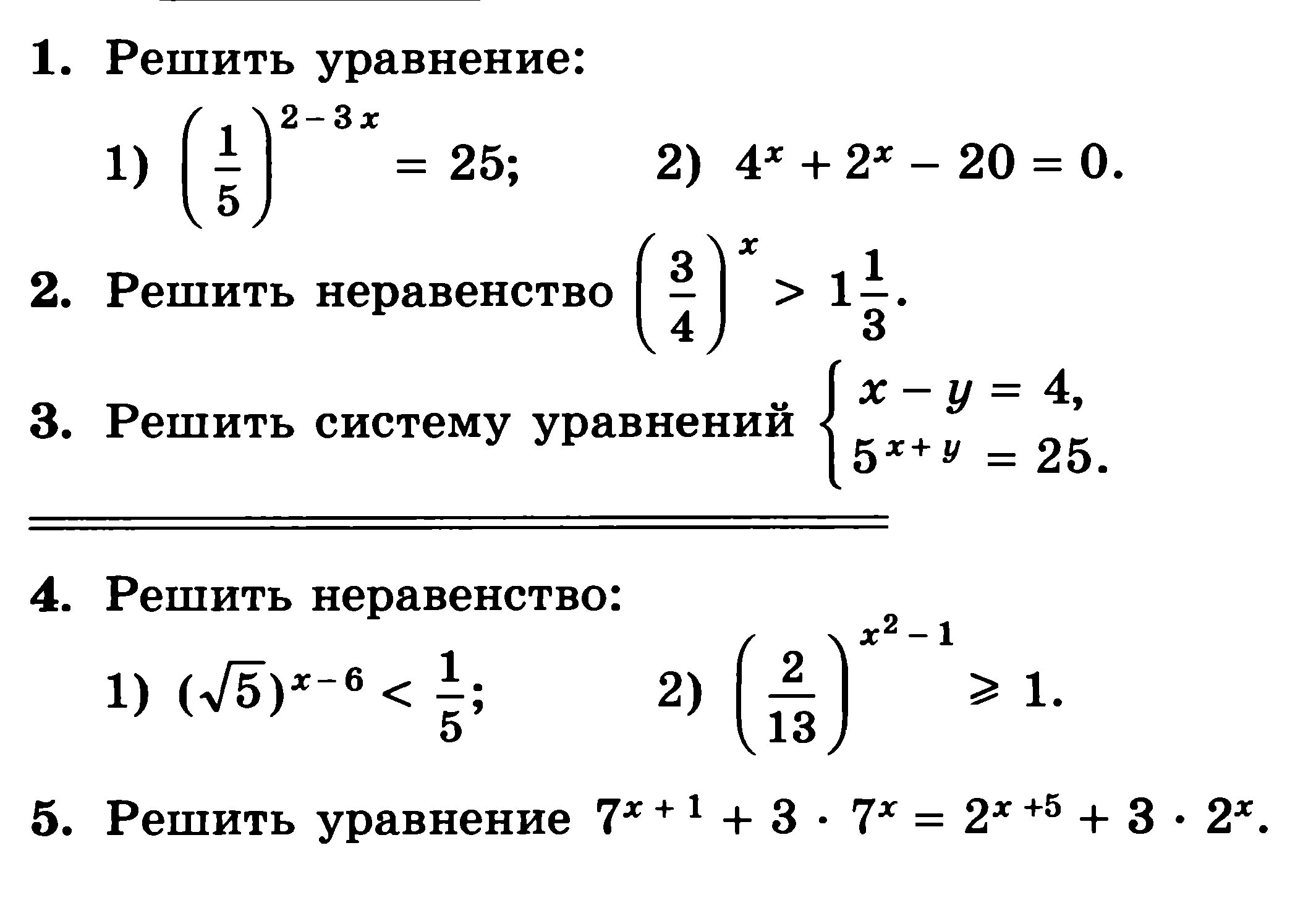 Угол
Угол
Условия
∠A 90
Число треугольников 0 1 2 0
ab sin A a≤ba> b
C
b
ab sinA
C A
C
C
b
1
B
a
A
B
Тригонометрическая идентичность Коэффициент идентичности: tan θ =
Пифагорейская идентичность: sin 2 θ + cos 2 θ2 eg = 1 9 Подтвердите личность. sin 2 θ + 2 cos 2 θ — 1 = cos 2 θ Работаем с каждой стороной отдельно.LS = sin 2 θ + 2 cos 2 θ — 1 = sin 2 θ + cos 2 θ + cos 2 θ — 1 = 1 + cos 2 θ — 1
sin θ cosθ
Ищите частное или тождество Пифагора. Возможно, вам потребуется факторизовать, упростить или разделить термины. Когда вы закончите, напишите заключительное заявление.
Поскольку LS = RS, то sin 2 θ + 2 cos 2 θ — 1 = cos 2 θ истинно для всех значений θ.
= cos 2 θ = RS
Периодические функции Периодическая функция имеет повторяющийся образец. Цикл — это наименьший полный повторяющийся узор. Ось кривой — это горизонтальная линия, которая находится посередине между максимальным и минимальным значениями графика. Уравнение: максимальное значение + минимальное значение y =. 2
Ось кривой — это горизонтальная линия, которая находится посередине между максимальным и минимальным значениями графика. Уравнение: максимальное значение + минимальное значение y =. 2
Период — это длина цикла. Амплитуда — это величина вертикального расстояния от оси кривой до максимального или минимального значения. Уравнение: максимальное значение — минимальное значение a = 2
Тригонометрические функции Графики y = sin θ, y = cosθ и y = tan θ показаны ниже. y = sin θ y = tan θ 1
y = sin θ
0.5
50
100
150
200
250
300
350
-0,5
Период = 360˚ Амплитуда = 1 Нули = 0˚, 180˚, 360˚…
-1
y = cosθ
1
y = cosθ
0,5
50-0,5
100
150
200
250
300
350
Период = 360 90˚, 270˚…
-1
Преобразования тригонометрических функций
5
50
100
150
200
250
300
-5
y = tg ˚ Нули = 0˚, 180˚, 360˚… Вертикальные асимптоты = 90˚, 270˚…
350
Преобразования применяются к триггерным функциям так же, как и к любой другой функции. Графики y = a sin k (θ + b) + d и y = a cos k (θ + b) + d являются преобразованиями графиков y = sin θ и y = cos θ соответственно. Значение a определяет вертикальное растяжение, называемое амплитудой. Он также сообщает, отражается ли кривая по оси θ. Значение k определяет горизонтальное растяжение. График растянут в
Графики y = a sin k (θ + b) + d и y = a cos k (θ + b) + d являются преобразованиями графиков y = sin θ и y = cos θ соответственно. Значение a определяет вертикальное растяжение, называемое амплитудой. Он также сообщает, отражается ли кривая по оси θ. Значение k определяет горизонтальное растяжение. График растянут в
1 раз. Мы можем использовать k
это значение, чтобы определить период преобразования y = sin θ или y = cos θ. 360 180 y = sin k θ y = cos k θ y = tan k θ Период или равен, k> 0.Период k> 0. k k Значение b определяет горизонтальный сдвиг, известный как фазовый сдвиг. Значение d определяет вертикальный перенос. y = d — уравнение оси кривой. например например 1 y = cos 2θ + 1 y = sin θ + 45 2
(
g (x) = cos (2⋅x) +1
2
)
1
1,5 0,5
g ( x) = 0,5 sin (x + 45)
1
0,5
50
50
100
150
200
250
300
350
400 (
f) = cos (x)
150
200
250
300
350
-0. 5
5
-0,5
-1
100
-1
f (x) = sin (x)
400
| Название экзамена | Источник требований | Контент протестирован | Цель теста | Необходимое время * | График ** | Распределение результатов |
| Краткое описание подростковой депрессии (BSAD) | Дивизия | Психическое здоровье и благополучие | Для выявления симптомов депрессии | Прибл.10 минут | 23 августа — 17 декабря | Включено в постоянное общение с родителями / опекунами об успеваемости в классе |
| Инвентарь по математике | Дивизия ТОЛЬКО для студентов, изучающих курс алгебры 1 или алгебры 1, часть 1 | Математика | Для определения текущего уровня математических навыков развития и отслеживания роста | Прибл. 45 минут 45 минут | авг.С 30 по 29 октября 6 декабря — 28 января 9 мая — 10 июня | Передано родителям / опекунам в течение прибл. 1 месяц после закрытия окна оценки |
| Диагностика записи NoRedInk | Дивизия | Письмо | Для отслеживания прогресса в развитии навыков письма и грамматики | Прибл. 30 минут | 4 октября — 12 ноября фев.2–25 февраля | Включено в постоянную коммуникацию с родителями / опекунами |
| Оценка на основе результатов (PBA) для подтвержденного кредита, выданного на местном уровне (LAVC) | Государство ТОЛЬКО для студентов, обучающихся на курсах социальных исследований с подтвержденным кредитом | История | Для измерения знания стандартов курса и дисциплинарных навыков | Прибл.2-4 часа | 18 октября — 27 мая | Включено в сообщение об успеваемости родителям / опекунам в рамках выпускных классов |
| Предварительный SAT (PSAT) | Дивизия | Чтение, логические рассуждения, математика | Для измерения готовности к продвинутым курсам и права на получение национальной стипендии за заслуги | Прибл. 3 часа 3 часа | 13 октября | Доступно через учетную запись Совета колледжей для учащихся и включена в текущую информацию об успеваемости для родителей / опекунов |
| Инвентарь для чтения | Дивизия ТОЛЬКО для студентов, обучающихся на курсах повышения грамотности | Чтение | Для определения текущего уровня развития навыков чтения и отслеживания роста | Прибл.45 минут | 30 августа — 29 октября 6 декабря — 28 января 9 мая — 10 июня | Передано родителям / опекунам в течение прибл. 1 месяц после закрытия окна оценки |
| Проверка социально-эмоционального обучения (SEL) | Дивизия | Социально-эмоциональные навыки обучения | Для измерения развития социально-эмоционального обучения, отношений и благополучия | Прибл.20 минут | 12 октября — 22 октября 25 января — 11 февраля 25 апреля — 13 мая | Включено в постоянную коммуникацию с родителями / опекунами |
| Тесты по стандартам обучения (SOL) | Государство ТОЛЬКО для зачисленных на курс SOL, которым нужен тест на участие в федеральном округе или подтвержденный кредит для окончания | Письмо, чтение, математика, естественные науки | Для измерения уровня знаний стандартов содержания курса для государственной и федеральной ответственности | Прибл. 2 часа по предмету 2 часа по предмету | Расписание на основе требований курса и окончания 6 декабря — 14 января 7 марта — 23 марта (только написание) 25 апреля — 27 мая | Передано родителям / опекунам в течение прибл. 2 месяца после закрытия окна оценки |
| Программа альтернативной оценки штата Вирджиния (VAAP) | Государство ТОЛЬКО для студентов, обучающихся по адаптированной программе | Чтение, математика | Для измерения знаний о согласованных стандартах подотчетности на уровне штата и на федеральном уровне | TBD | янв.5 к 4 июня | Передано родителям / опекунам к началу следующего учебного года |
| ДОСТУП WIDA для ELLS | Государство ТОЛЬКО для изучающих английский язык | Чтение, письмо, устная речь, аудирование | Для измерения ежегодного уровня владения английским языком и прогресса в соответствии с федеральным законом | Прибл. 5 часов 5 часов | 18 января — 18 марта | Передано родителям / опекунам к началу следующего учебного года |
| WIDA Screener | Государство ТОЛЬКО для потенциальных изучающих английский язык | Чтение, письмо, устная речь, аудирование | Чтобы определить право на получение услуг для изучающих английский язык в соответствии с федеральным законом | Прибл.90 минут | В течение 14 дней после поступления из-за пределов государственных школ Вирджинии | Передано родителям / опекунам в течение прибл. 1 месяц |
| Рабочие клавиши | Дивизия ТОЛЬКО для студентов, обучающихся на английском языке 11, которые не прошли тест SOL и нуждаются в подтвержденном зачете для выпуска | Чтение, письмо | Для измерения способности применять знания о содержании к реальной ситуации | Прибл.30-45 минут на предмет | 31 мая — 9 июня | Включено в постоянную коммуникацию с родителями / опекунами |
5.
 3 Гиперболические функции | Функции
3 Гиперболические функции | ФункцииТеперь рассмотрим гиперболические функции вида \ (y = \ frac {a} {x + p} + q \) и эффекты параметр \ (p \).
Эффект \ (p \) — горизонтальный сдвиг, потому что все точки перемещаются на одинаковое расстояние в в том же направлении (весь график скользит влево или вправо).
Значение \ (p \) также влияет на вертикальную асимптоту, линию \ (x = -p \).
Эффект \ (q \) — вертикальный сдвиг. Значение \ (q \) также влияет на горизонтальное асимптоты, прямая \ (y = q \).
Значение \ (a \) влияет на форму графика и его положение на декартовой плоскости.
Знакомство с характеристиками
Для функций общего вида: \ (f (x) = y = \ frac {a} {x + p} + q \):
Домен и диапазон
Домен \ (\ {x: x \ in \ mathbb {R}, x \ ne -p \} \). Если \ (x = -p \), доминатор
равна нулю, а функция не определена.
Если \ (x = -p \), доминатор
равна нулю, а функция не определена.
Мы видим, что \ [y = \ frac {a} {x + p} + q \] можно переписать как: \ [y-q = \ frac {a} {x + p} \] Если \ (x \ ne -p \), то: \ begin {align *} \ влево (у-д \ вправо) \ влево (х + р \ вправо) & = а \\ х + р & = \ гидроразрыва {а} {у-д} \ end {выровнять *} Следовательно, диапазон равен \ (\ {y: y \ in \ mathbb {R}, y \ ne q \} \).
Эти ограничения на область определения и диапазон определяют вертикальную асимптоту \ (x = -p \)
и горизонтальная асимптота \ (y = q \).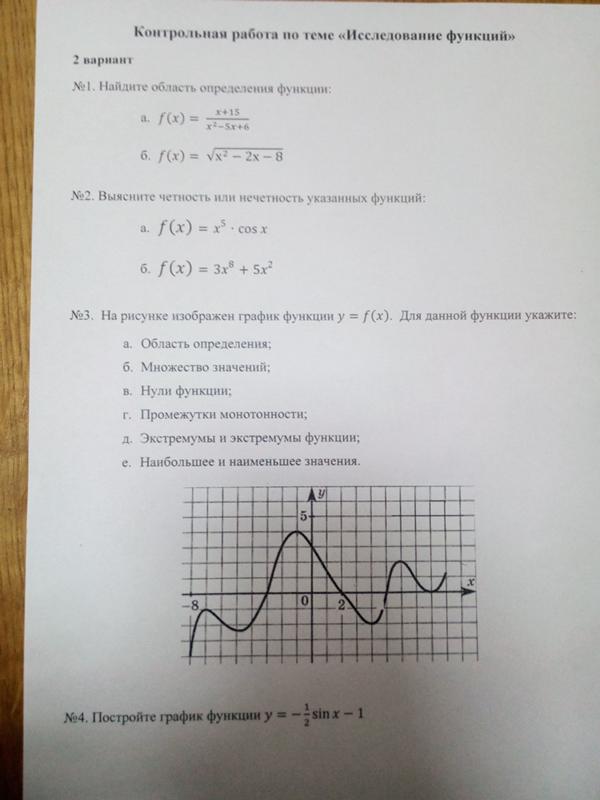
Рабочий пример 9: Домен и диапазон
Определите домен и диапазон для \ (g (x) = \ frac {2} {x + 1} + 2 \).
Определить домен
Домен \ (\ {x: x \ in \ mathbb {R}, x \ ne -1 \} \), поскольку \ (g (x) \) не определено для \ (x = -1 \).
Определить диапазон
Пусть \ (g (x) = y \):
\ begin {align *}
y & = \ frac {2} {x + 1} + 2 \\
y — 2 & = \ frac {2} {x + 1} \\
(у-2) (х + 1) & = 2 \\
х + 1 & = \ frac {2} {y-2}
\ end {выровнять *}
Следовательно, диапазон равен \ (\ {g (x): g (x) \ in \ mathbb {R}, g (x) \ ne 2
\} \).
Домен и диапазон
Учебное упражнение 5.10\ begin {align *} \ text {Домен:} & \ left \ {x: x \ in \ mathbb {R}, x \ neq 0 \ right \} \\ \ text {Диапазон:} & \ left \ {y: y \ in \ mathbb {R}, y \ neq 1 \ вправо \} \ end {выровнять *}
\ (g (x) = \ frac {8} {x — 8} +4 \)
\ begin {align *} \ text {Домен:} & \ left \ {x: x \ in \ mathbb {R}, x \ neq 8 \ right \} \\ \ text {Диапазон:} & \ left \ {y: y \ in \ mathbb {R}, y \ neq 4 \ вправо \} \ end {выровнять *}
\ (y = — \ frac {4} {x + 1} -3 \)
\ begin {align *} \ text {Домен:} & \ left \ {x: x \ in \ mathbb {R}, x \ neq -1 \ right \} \\ \ text {Диапазон:} & \ left \ {y: y \ in \ mathbb {R}, y \ neq -3 \ вправо \} \ end {выровнять *}
\ (x = \ frac {2} {3 — y} + 5 \)
\ begin {align *} x & = \ frac {2} {3 — y} + 5 \\ х -5 & = \ frac {2} {3 — y} \\ (х -5) (3 — у) & = 2 \\ 3 — y & = \ frac {2} {3x — 5} \\ — y & = \ frac {2} {x — 5} — 3 \\ \ поэтому y & = — \ frac {2} {x — 5} + 3 \\ \ text {Домен:} & \ left \ {x: x \ in \ mathbb {R}, x \ neq 5 \ right \} \\ \ text {Диапазон:} & \ left \ {y: y \ in \ mathbb {R}, y \ neq 3 \ вправо \} \ end {выровнять *}
\ begin {align *} (у — 2) (х + 2) & = 3 \\ y — 2 & = \ frac {3} {x + 2} \\ \ поэтому y & = \ frac {3} {x + 2} + 2 \\ \ text {Домен:} & \ left \ {x: x \ in \ mathbb {R}, x \ neq -2 \ right \} \\ \ text {Диапазон:} & \ left \ {y: y \ in \ mathbb {R}, y \ neq 2 \ вправо \} \ end {выровнять *}
Перехваты
\ (y \) — перехват:
Для вычисления точки пересечения \ (y \) положим \ (x = 0 \). Например, \ (y \) — перехватчик
\ (g (x) = \ frac {2} {x + 1} + 2 \) определяется установкой \ (x = 0 \):
\ begin {align *}
g (x) & = \ frac {2} {x + 1} + 2 \\
g (0) & = \ frac {2} {0 + 1} + 2 \\
& = 2 + 2 \\
& = 4
\ end {выровнять *}
Это дает точку \ ((0; 4) \).
Например, \ (y \) — перехватчик
\ (g (x) = \ frac {2} {x + 1} + 2 \) определяется установкой \ (x = 0 \):
\ begin {align *}
g (x) & = \ frac {2} {x + 1} + 2 \\
g (0) & = \ frac {2} {0 + 1} + 2 \\
& = 2 + 2 \\
& = 4
\ end {выровнять *}
Это дает точку \ ((0; 4) \).
\ (x \) — точка перехвата:
Для вычисления точки пересечения \ (x \) положим \ (y = 0 \). Например, \ (x \) — перехватчик
\ (g (x) = \ frac {2} {x + 1} + 2 \) определяется установкой \ (y = 0 \):
\ begin {align *}
g (x) & = \ frac {2} {x + 1} + 2 \\
0 & = \ frac {2} {x + 1} + 2 \\
-2 & = \ frac {2} {x + 1} \\
-2 (х + 1) & = 2 \\
-2x — 2 & = 2 \\
-2x & = 4 \\
х & = -2
\ end {выровнять *}
Это дает точку \ ((- 2; 0) \).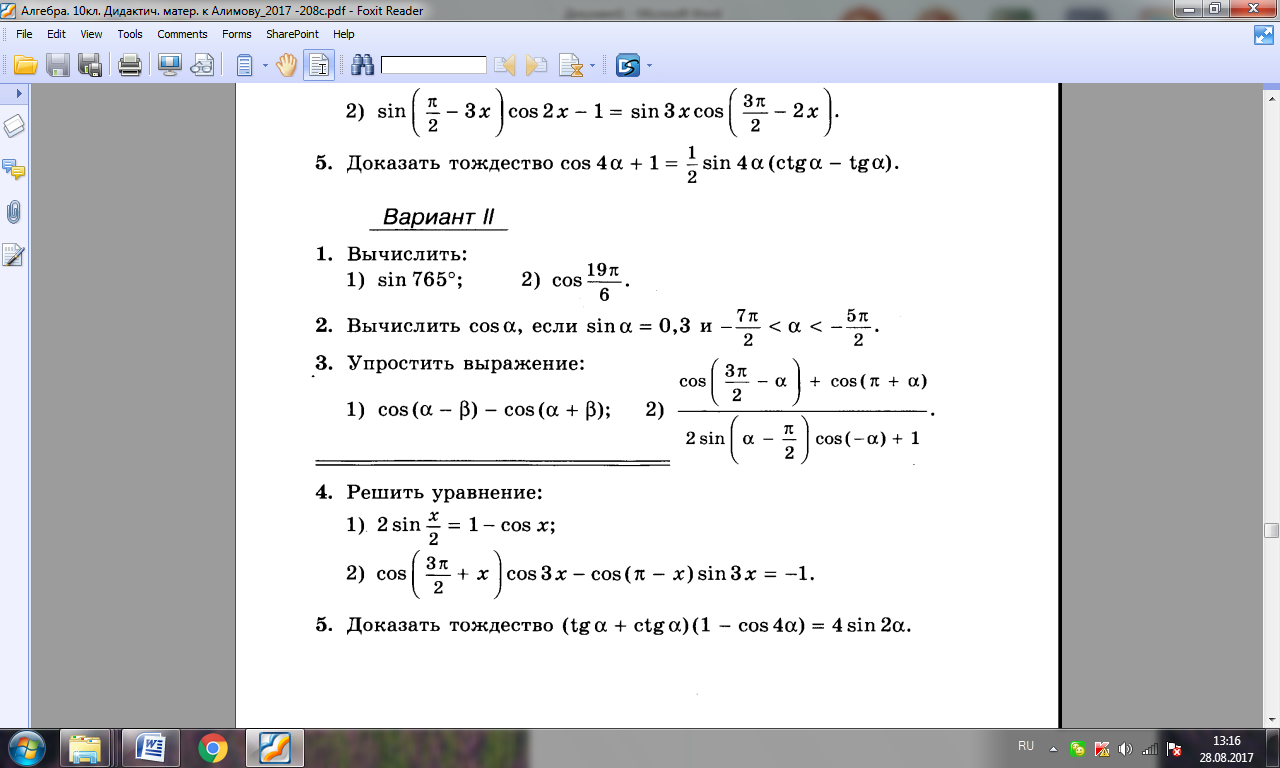
Перехваты
Учебное упражнение 5.11\ (f (x) = \ frac {1} {x + 4} — 2 \)
\ begin {align *} f (x) & = \ frac {1} {x + 4} — 2 \\ \ text {Let} x & = 0 \\ f (0) & = \ frac {1} {4} — 2 \\ \ поэтому y_ \ text {int} & = (0; -1 \ frac {3} {4}) \\ \ text {Let} y & = 0 \\ 0 & = \ frac {1} {x + 4} — 2 \\ 2 & = \ frac {1} {x + 4} \\ 2 (х + 4) & = 1 \\ 2х + 8 & = 1 \\ 2x & = -7 \\ \ поэтому x & = — \ frac {7} {2} \\ \ поэтому x_ \ text {int} & = \ left (-3 \ frac {1} {2}; 0 \Правильно) \ end {выровнять *}
\ (g (x) = — \ frac {5} {x} + 2 \)
\ begin {align *} g (x) & = — \ frac {5} {x} + 2 \\ \ text {Let} x & = 0 \\ \ поэтому g (x) & \ text {не определено} \\ \ поэтому \ text {no} & x- \ text {intercepts} \\ \ text {Let} y & = 0 \\ 0 & = — \ frac {5} {x} + 2 \\ -2 & = — \ frac {5} {x} \\ 2x & = 5 \\ \ поэтому x & = \ frac {5} {2} \\ \ поэтому x_ \ text {int} & = \ left (\ frac {5} {2}; 0 \Правильно) \ end {выровнять *}
\ (j (x) = \ frac {2} {x — 1} + 3 \)
\ begin {align *} j (x) & = \ frac {2} {x — 1} + 3 \\ \ text {Let} x & = 0 \\ j (0) & = \ frac {2} {- 1} + 3 \\ & = 1 \\ \ поэтому y_ \ text {int} & = (0; 1) \\ \ text {Let} y & = 0 \\ 0 & = \ frac {2} {x — 1} + 3 \\ -3 & = \ frac {2} {x — 1} \\ -3 (х-1) & = 2 \\ -3x + 3 & = 2 \\ -3x & = -1 \\ \ поэтому x & = \ frac {1} {3} \\ \ поэтому x_ \ text {int} & = \ left (\ frac {1} {3}; 0 \Правильно) \ end {выровнять *}
\ (h (x) = \ frac {3} {6 — x} + 1 \)
\ begin {align *} h (x) & = \ frac {3} {6 — x} + 1 \\ \ text {Let} x & = 0 \\ h (0) & = \ frac {3} {6} + 1 \\ & = \ frac {3} {2} \\ \ поэтому y_ \ text {int} & = \ left (0; \ frac {3} {2} \Правильно) \\ \ text {Let} y & = 0 \\ 0 & = \ frac {3} {6 — x} + 1 \\ -1 & = \ frac {3} {6 — x} \\ — (6 — х) & = 3 \\ -6 + х & = 3 \\ -3x & = -1 \\ \ поэтому x & = \ frac {1} {3} \\ \ поэтому x_ \ text {int} & = \ left (\ frac {1} {3}; 0 \Правильно) \ end {выровнять *}
\ (k (x) = \ frac {5} {x + 2} — \ frac {1} {2} \)
\ begin {align *} k (x) & = \ frac {5} {x + 2} — \ frac {1} {2} \\ \ text {Let} x & = 0 \\ k (0) & = \ frac {5} {2} — \ frac {1} {2} \\ & = 2 \\ \ поэтому y_ \ text {int} & = \ left (0; 2 \ right) \\ \ text {Let} y & = 0 \\ 0 & = \ frac {5} {x + 2} — \ frac {1} {2} \\ \ frac {1} {2} & = \ frac {5} {x + 2} \\ х + 2 & = 5 (2) \\ х & = 10-2 \\ \ поэтому x & = 8 \\ \ поэтому x_ \ text {int} & = \ left (8; 0 \ right) \ end {выровнять *}
Асимптоты
Есть две асимптоты для функций вида \ (y = \ frac {a} {x + p} + q \).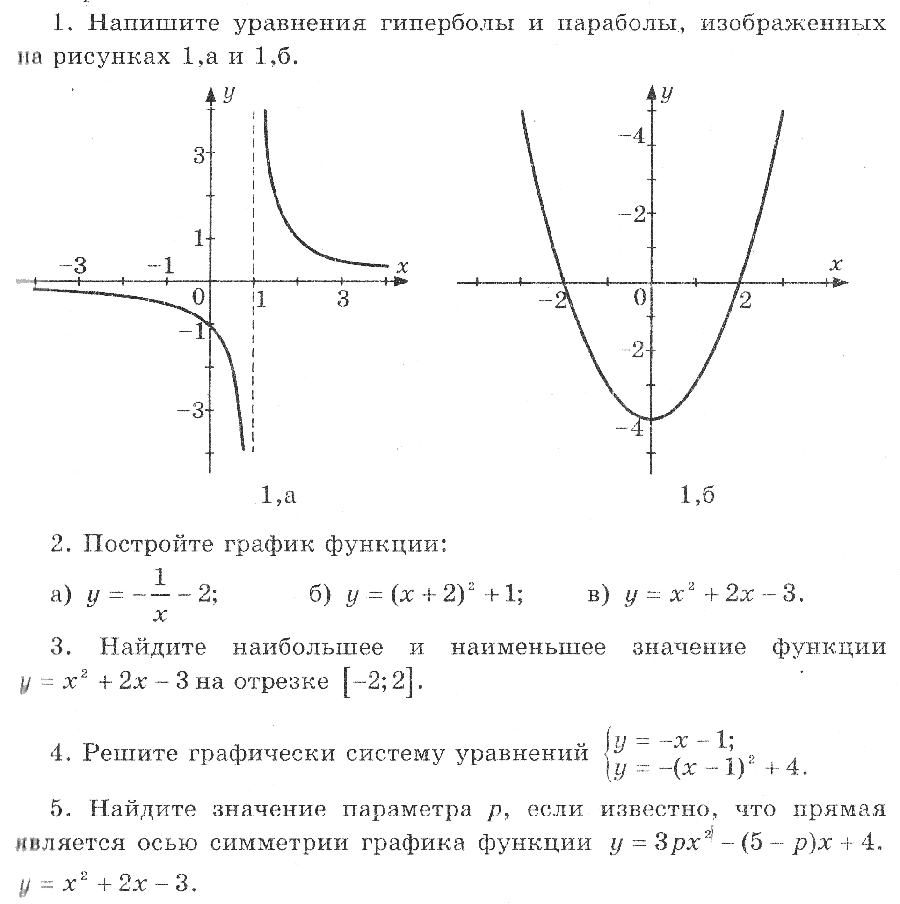 В
асимптоты указывают значения \ (x \), для которых функция не существует.
Другими словами, значения, исключенные из домена и диапазона. В
горизонтальная асимптота — это прямая \ (y = q \), а вертикальная асимптота — это прямая
\ (х = -р \).
В
асимптоты указывают значения \ (x \), для которых функция не существует.
Другими словами, значения, исключенные из домена и диапазона. В
горизонтальная асимптота — это прямая \ (y = q \), а вертикальная асимптота — это прямая
\ (х = -р \).
Асимптоты
Учебное упражнение 5.12\ (y = \ frac {1} {x + 4} — 2 \)
\ begin {align *} \ text {Вертикальная асимптота:} y & = -2 \\ \ text {Горизонтальная асимптота:} x & = -4 \ end {выровнять *}
\ begin {align *} \ text {Вертикальная асимптота:} y & = 0 \\ \ text {Горизонтальная асимптота:} x & = 0 \ end {выровнять *}
\ (y = \ frac {3} {2 -x} + 1 \)
\ begin {align *} y & = \ frac {3} {2 -x} + 1 \\ & = \ frac {3} {- (x — 2)} + 1 \\ & = — \ frac {3} {x — 2} + 1 \\ \ text {Вертикальная асимптота:} y & = 1 \\ \ text {Горизонтальная асимптота:} x & = 2 \ end {выровнять *}
\ begin {align *} \ text {Вертикальная асимптота:} y & = -8 \\ \ text {Горизонтальная асимптота:} x & = 0 \ end {выровнять *}
\ begin {align *} \ text {Вертикальная асимптота:} y & = 0 \\ \ text {Горизонтальная асимптота:} x & = 2 \ end {выровнять *}
Оси симметрии
Есть две линии, относительно которых гипербола симметрична.
Для стандартной гиперболы \ (y = \ frac {1} {x} \) мы видим, что если мы заменим \ (x \ Rightarrow y \) и \ (y \ Rightarrow x \), получаем \ (y = \ frac {1} {x} \). Сходным образом, если мы заменим \ (x \ Rightarrow -y \) и \ (y \ Rightarrow -x \), функция остается такой же. Следовательно, функция симметрична относительно прямых \ (y = х \) и \ (у = -х \).
Для сдвинутой гиперболы \ (y = \ frac {a} {x + p} + q \) оси симметрии пересекаются в точке \ ((- p; q) \).
Для определения осей симметрии определим две прямые \ (y_1 = m_1x +
c_1 \) и \ (y_2 = m_2x + c_2 \). Для стандартной и сдвинутой гиперболической
функция, градиент одной из линий симметрии равен \ (\ text {1} \), а
градиент другой линии симметрии равен \ (- \ text {1} \). Оси симметрии
перпендикулярны друг другу и произведение их градиентов равно
\(-\текст 1}\). Поэтому положим \ (y_1 = x + c_1 \) и \ (y_2 = -x + c_2 \). Мы
затем подставляем \ ((- p; q) \), точку пересечения осей симметрии,
в оба уравнения, чтобы определить значения \ (c_1 \) и \ (c_2 \).
Оси симметрии
перпендикулярны друг другу и произведение их градиентов равно
\(-\текст 1}\). Поэтому положим \ (y_1 = x + c_1 \) и \ (y_2 = -x + c_2 \). Мы
затем подставляем \ ((- p; q) \), точку пересечения осей симметрии,
в оба уравнения, чтобы определить значения \ (c_1 \) и \ (c_2 \).
Рабочий пример 10: Оси симметрии
Определите оси симметрии для \ (y = \ frac {2} {x + 1} — 2 \).
Определите точку пересечения \ ((- p; q) \)
Из уравнения видно, что \ (p = 1 \) и \ (q = -2 \). Итак, топоры
симметрии пересекаются в точке \ ((- 1; -2) \).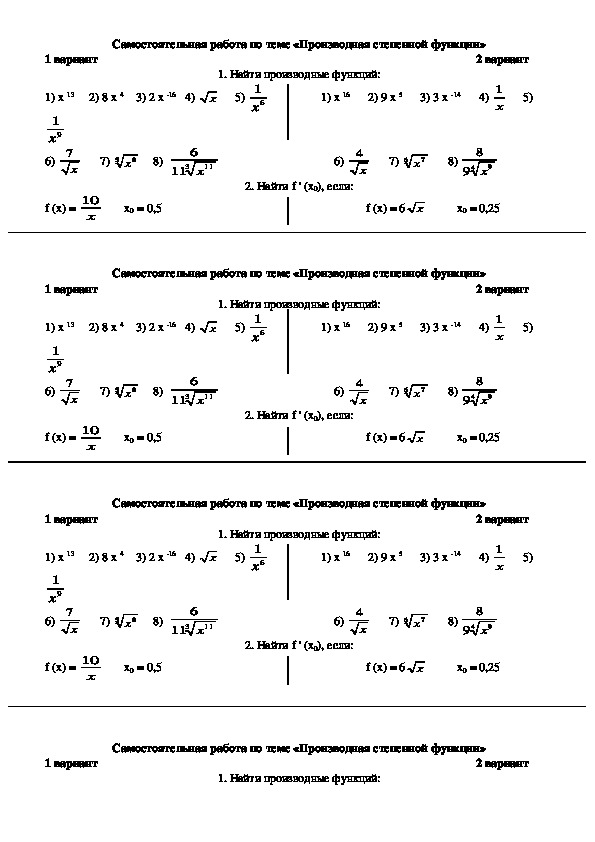
Определите два уравнения прямой линии
\ begin {align *} y_1 & = x + c_1 \\ y_2 & = -x + c_2 \ end {align *}
Решите относительно \ (c_1 \) и \ (c_2 \)
Используйте \ ((- 1; -2) \), чтобы найти \ (c_1 \):
\ begin {align *} y_1 & = x + c_1 \\ -2 & = -1 + c_1 \\ -1 & = c_1 \ end {выровнять *}Используйте \ ((- 1; -2) \), чтобы найти \ (c_2 \):
\ begin {align *} y_2 & = -x + c_2 \\ -2 & = — (- 1) + c_2 \\ -3 & = c_2 \ end {выровнять *}Напишите окончательный ответ
Оси симметрии для \ (y = \ frac {2} {x + 1} — 2 \) — это прямые \ begin {align *} у_1 & = х — 1 \\ y_2 & = -x — 3 \ end {align *}
временный текстОси симметрии
Учебное упражнение 5. 13
13\ (f (x) = \ frac {2} {x} \)
\ (g (x) = \ frac {2} {x} + 1 \)
\ (f (x) = — \ frac {3} {x} \)
\ (g (x) = — \ frac {3} {x + 1} \)
\ (f (x) = \ frac {5} {x} \)
\ (g (x) = \ frac {5} {x — 1} — 1 \)
Гипербола вида \ (k (x) = \ frac {a} {x + p} + q \)
проходит через точку \ ((4; 3) \).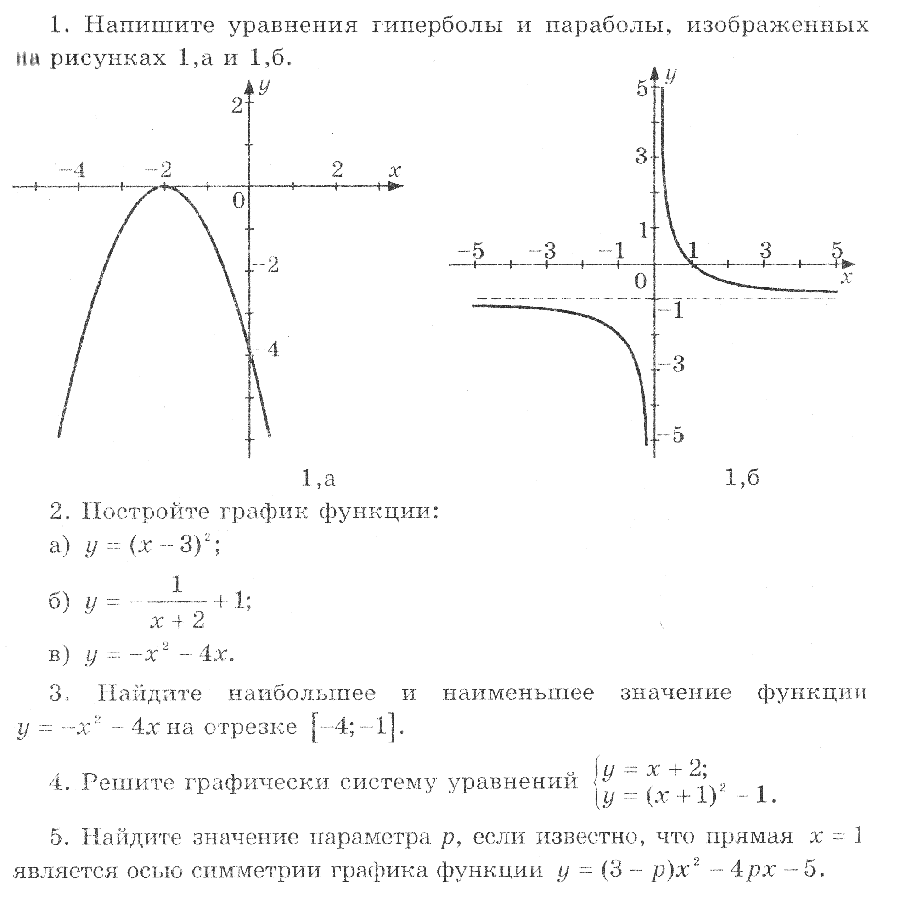 Если топоры
симметрии пересекаются в \ ((- 1; 2) \), определить
уравнение \ (k (x) \).
Если топоры
симметрии пересекаются в \ ((- 1; 2) \), определить
уравнение \ (k (x) \).
Набросок графов вида \ (f (x) = \ frac {a} {x + p} + q \)
Чтобы нарисовать графики функций вида \ (f (x) = \ frac {a} {x + p} + q \), нам понадобится для расчета пяти характеристик:
квадранта
асимптоты
\ (y \) — перехват
\ (x \) — перехватить
домен и диапазон
Рабочий пример 11: Построение гиперболы
Нарисуйте график \ (y = \ frac {2} {x + 1} + 2 \). Обозначить
точки пересечения, асимптоты и оси симметрии. Укажите домен
и диапазон функции.
Обозначить
точки пересечения, асимптоты и оси симметрии. Укажите домен
и диапазон функции.
Изучите уравнение вида \ (y = \ frac {a} {x + p} + д \)
Заметим, что \ (a> 0 \), поэтому график будет лежать в первый и третий квадранты.
Определить асимптоты
Из уравнения мы знаем, что \ (p = 1 \) и \ (q = 2 \).
Следовательно, горизонтальная асимптота — это прямая \ (y = 2 \) и
вертикальная асимптота — это прямая \ (x = -1 \).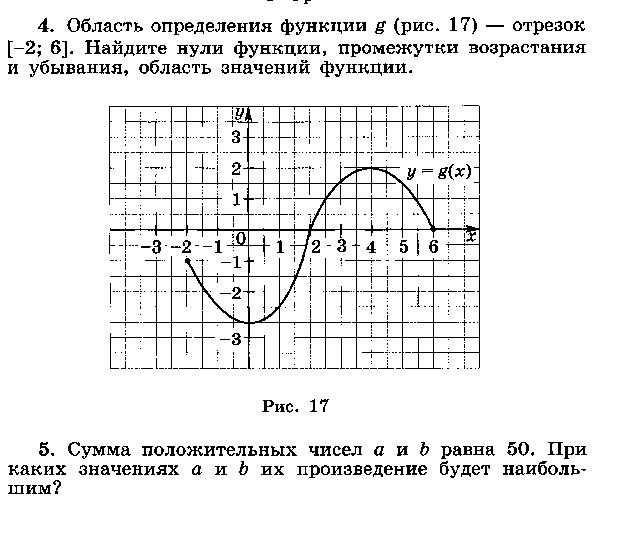
Определите точку пересечения \ (y \)
Перехват \ (y \) — получается, если \ (x = 0 \): \ begin {align *} y & = \ frac {2} {0 + 1} + 2 \\ & = 4 \ end {выровнять *} Это дает точку \ ((0; 4) \).
Определите точку пересечения \ (x \)
Перехватчик \ (x \) получается, если \ (y = 0 \):
\ begin {align *}
0 & = \ frac {2} {x + 1} + 2 \\
-2 & = \ frac {2} {x + 1} \\
-2 (х +1) & = 2 \\
-2x -2 & = 2 \\
-2x & = 4 \\
х & = -2
\ end {выровнять *}
Это дает точку \ ((- 2; 0) \).
Определить оси симметрии
Использование \ ((- 1; 2) \) для решения относительно \ (c_1 \):
\ begin {align *}
y_1 & = x + c_1 \\
2 & = -1 + c_1 \\
3 & = c_1
\ end {выровнять *}
\ begin {align *}
y_2 & = -x + c_2 \\
2 & = — (- 1) + c_2 \\
1 & = c_2
\ end {выровнять *}
Следовательно, оси симметрии — это \ (y = x + 3 \) и \ (y = -x +
1 \).
Постройте точки и начертите график
Укажите домен и диапазон
Домен: \ (\ {x: x \ in \ mathbb {R}, x \ ne -1 \} \)
Диапазон: \ (\ {y: y \ in \ mathbb {R}, y \ ne 2 \} \)
Рабочий пример 12: Построение гиперболы
Используйте горизонтальный и вертикальный сдвиги, чтобы нарисовать график \ (f (x) = \ frac {1} {x — 2} + 3 \).
Изучите уравнение вида \ (y = \ frac {a} {x + p} + д \)
Заметим, что \ (a> 0 \), поэтому график будет лежать в
первый и третий квадранты.
Набросок стандартной гиперболы \ (y = \ frac {1} {x} \)
Начните с наброска стандартной гиперболы \ (g (x) = \ frac {1} {x} \).
Вертикальная асимптота \ (x = 0 \), а горизонтальная асимптота \ (у = 0 \).
Определить вертикальный сдвиг
Из уравнения видно, что \ (q = 3 \), что означает, что \ (g (x) \) должен сдвинул \ (\ text {3} \) единицы вверх.
Горизонтальная асимптота также сдвинута на \ (\ text {3} \) единицы до \ (y
= 3 \).
Определить горизонтальный сдвиг
Из уравнения видно, что \ (p = -2 \), что означает, что \ (g (x) \) должен сдвинуты \ (\ text {2} \) единицы вправо.
Вертикальная асимптота также сдвинута на \ (\ text {2} \) единиц в сторону Правильно.
Определите точку пересечения \ (y \)
Перехват \ (y \) — получается, если \ (x = 0 \):
\ begin {align *}
y & = \ frac {1} {0–2} + 3 \\
& = 2 \ frac {1} {2}
\ end {выровнять *}
Это дает точку \ ((0; 2 \ frac {1} {2}) \).
Определите точку пересечения \ (x \)
Перехватчик \ (x \) получается, если \ (y = 0 \):
\ begin {align *}
0 & = \ frac {1} {x — 2} + 3 \\
-3 & = \ frac {1} {x -2} \\
-3 (х — 2) & = 1 \\
-3x + 6 & = 1 \\
-3x & = -5 \\
х & = \ гидроразрыв {5} {3}
\ end {выровнять *}
Это дает точку \ ((\ frac {5} {3}; 0) \).
Определить домен и диапазон
Домен: \ (\ {x: x \ in \ mathbb {R}, x \ ne 2 \} \)
Диапазон: \ (\ {y: y \ in \ mathbb {R}, y \ ne 3 \} \)
Рабочий пример 13: Нахождение уравнения гиперболы из график
Используйте график ниже, чтобы определить значения \ (a \), \ (p \) и \ (q \) для \ (y = \ frac {a} {x + p} + q \).
Изучите график и выведите знак \ (a \)
Мы замечаем, что график лежит во втором и четвертом квадрантах,
поэтому \ (a <0 \).
Определить асимптоты
Из графика мы видим, что вертикальная асимптота равна \ (x = -1 \), поэтому \ (p = 1 \).Горизонтальная асимптота равна \ (y = 3 \), и поэтому \ (q = 3 \). \ [y = \ frac {a} {x + 1} + 3 \]
Определите значение \ (a \)
Для определения значения \ (a \) подставляем точку на графике, а именно \ ((0; 0) \): \ begin {align *} y & = \ frac {a} {x + 1} + 3 \\ 0 & = \ frac {a} {0 + 1} + 3 \\ \ поэтому -3 & = a \ end {align *}
Напишите окончательный ответ
\ [y = — \ frac {3} {x + 1} + 3 \] временный текстПостроение графиков
Учебное упражнение 5. 14
14Дан график гиперболы вида \ (y = \ frac {1} {x + p} + q \), определить значения \ (p \) и \ (q \).
\ begin {align *} y & = \ frac {1} {x + p} + q \\ \ text {Из графика} \ quad p & = 2 \\ q & = -1 \\ \ поэтому y & = \ frac {1} {x + 2} — 1 \ end {выровнять *}
Дан набросок функции вида \ (y =
\ frac {a} {x + p} + q \), определить значения
\ (а \), \ (р \) и \ (д \).
\ begin {align *} y & = \ frac {a} {x + p} + q \\ \ text {Из графика} \ quad p & = 0 \\ q & = 2 \\ \ поэтому y & = \ frac {a} {x} + 2 \\ \ text {Subst.} (2; 0) \ quad 0 & = \ frac {a} {2} + 2 \\ -2 & = \ frac {a} {2} \\ -2 (2) & = а \\ \ поэтому a & = -4 \\ у & = — \ frac {4} {x} + 2 \ end {выровнять *}
Нарисуйте график \ (f (x) = — \ frac {3} {x} \),
\ (х> 0 \).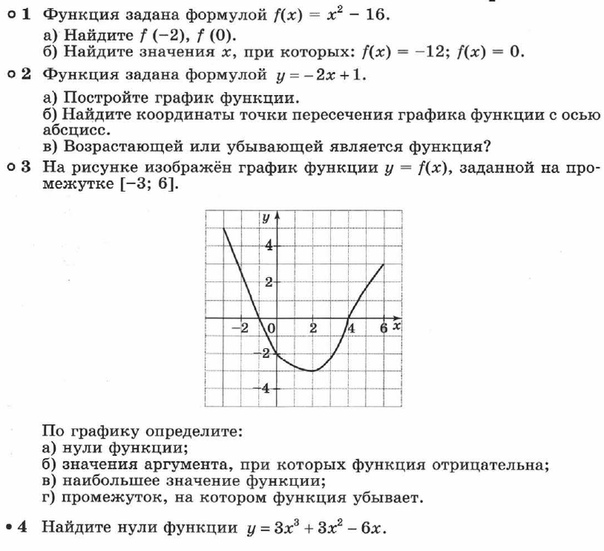
Определите средний градиент графика между \ (x = 1 \) и \ (x = 3 \).
\ begin {align *} \ text {Средний градиент} & = \ frac {f (3) — f (1)} {3 — 1} \\ & = \ dfrac {- \ frac {3} {3} — \ left (- \ frac {3} {1} \ right)} {3-1} \\ & = \ dfrac {-1 +3} {2} \\ & = \ dfrac {2} {2} \\ & = 1 \ end {выровнять *} Средний градиент между \ (x = 1 \) и \ (x = 3 \)
есть \ (1 \).
Градиент на \ ((\ frac {1} {2}; — 6) \) меньше чем или больше среднего градиент между \ (x = 1 \) и \ (x = 3 \)? Проиллюстрируйте это на своем графике.
\ begin {align *} \ text {Средний градиент} & = \ frac {f (a + h) — f (a)} {(a + h) — a} \\ & = \ dfrac {- \ frac {3} {a + h} — \ left ( — \ frac {3} {a} \ right)} {(a + h) -a} \\ & = \ dfrac {- \ frac {3} {a + h} + \ frac {3} {a}} {h} \\ & = \ dfrac {\ frac {-3 (a) + 3 (a + h)} {a (a + h)}} {h} \\ & = \ dfrac {\ frac {-3a + 3a + 3h} {a ^ 2 + ah}} {h} \\ & = \ dfrac {\ frac {3h} {a ^ 2 + ah}} {h} \\ & = \ frac {3h} {a ^ 2 + ah} \ times \ frac {1} {h} \\ & = \ frac {3} {a ^ 2 + ah} \\ \ поэтому \ text {At} (\ frac {1} {2}; -6) \ qquad a & = \ frac {1} {2} \\ \ поэтому \ text {And} \ qquad h & = 0 \\ \ поэтому \ text {Средний градиент} & = \ frac {3} {\ left (\ frac {1} {2} \ right) ^ 2 + \ frac {1} {2} (0)} \\ & = 3 \ times \ frac {4} {1} \\ & = 12 \ end {выровнять *} Средний градиент в \ ((\ frac {1} {2}; — 6) \) равен
больше среднего градиента
между \ (x = 1 \) и \ (x = 3 \).
| День | Раздел | Тема | Практика |
| 1 | 3.1 | U3D1_S Отношения функций D & R U3D1_T Отношения функций D _ R Видео Академии Хана: Что такое функция? Видео Академии Хана: Сфера функции Видео Академии Хана: диапазон функций | U3D1_S Рабочий лист Отношения функций D & R U3D1 Рабочий лист Решения Функции Отношения D & R |
| 2 | 3,1 3,2 | Построение графиков и определение свойств корневой функции и обратной функции U3D2_S Разминка D&R U3D2_S Базовый класс 11 Графики U3D2_T Графики взаимных и корневых функций | Мастер, отображающий «корневую функцию», «обратную функцию» (и асимптоты), «функцию абсолютного значения», «квадратичную функцию» и линии. U3D2_S_parent_functions_summary_table U3D2 полная таблица parent_functions_summary_table |
| 3 | 3,3 | U3D3_S Вертикальный и горизонтальный перевод U3D3_T Вертикальный _ горизонтальный перевод
| с. 189-192 № 1,2,3,4i, 5 (без проверки), 7, 15, 16, 10, 13, 17 U3D3 Учебник HW Solutions U3D3_S Дополнительная практика 1 Обозначение функций и перевод U3D3 Дополнительная практика 2 Обозначение функций U3D3 Extra Practice 1 SOLUTIONS Обозначение функций и перевод U3D3 Дополнительная практика 2 Решения Обозначение функции |
4
| 3.4 | U3D4_S Отражение функций U3D4_T Отражение функций Видео Академии Хана: сдвиги и отражение корневой функции Академия Хана: определение трансформаций | с. Учебник U3D4 HW Solutions U3D4_S Контрольный опрос U3D4_Review-for-Quiz-Solutions 2017 F MCR3UI_Unit 3_Quiz |
| 5 | 3.5 | ВИКТОРИНА !! U3D5_S ИНВЕРСИЯ U3D5_T ИНВЕРСИРУЕТ Академия Хана: Введение в инверсии | с. 215 # 3а, 5-все U3D5_Textbook HW Solutions |
6 | 3,5 | U3D6_S INVERSES продолжение U3D6_T ИНВЕРСИЯ продолжение | с. 215 # 10ii, v, 12, 13cg, 14iv, vi, 15b, 22, 23 U3D6 Учебник HW Solutions.pdf |
| 7 | 3,6 | U3D7_S Преобразования с растяжками U3D7_T Преобразования с растяжками Видео Академии Хана | с. «шансы» означают a, c, e, g и т. Д. U3D7 Учебник HW Solutionss.pdf U3D7_S Раздаточный материал для дополнительного домашнего задания 1 U3D7_S Раздаточный материал для дополнительного домашнего задания 2 U3D7 Решения для дополнительного домашнего задания 1 и 2 |
| 8 | 3.7 | U3D8_S Объединение преобразований U3D8_T Объединение преобразований U3D8_T Например, 2 (b) Комбинирование преобразований более подробное объяснение | с. 240 # 7 (шансы), 8-9 (шансы, эскиз по одному с каждого), 14 U3D8 Учебник HW Solutions U3D8_S_Дополнительные практики Комбинации преобразований U3D8 Решения для дополнительной практики Комбинации преобразований |
| 9 | U3D9_S Обзор УРОК Обзор | Раздаточный материал для обзора функций U3D9_S Обзор функций U3D9 Раздаточные материалы См. U3D9_S ДОПОЛНИТЕЛЬНЫЙ РАБОЧИЙ ЛИСТ U3D9_Extra Review Решения для рабочего листа Extra Review можно найти в учебнике: стр.246–256 U3D9 Учебник HW Solutions | |
| | | ДОПОЛНИТЕЛЬНАЯ ПРАКТИКА:mcr3ui старый тест 1 mcr3ui-old test-1 -решения mcr3ui старый тест 2 mcr3ui старый тест 2 решения |
Практические тесты по исчислению 1
Пройдите бесплатный диагностический тест Varsity Learning Tools для Calculus 1, чтобы определить, какой академический концепции, которые вы понимаете, а какие требуют вашего постоянного внимания.Каждая проблема Calculus 1 привязана к основной, основной концепции, которая проходит тестирование. Результаты диагностического теста Calculus 1 показывают, как вы выполняли каждую часть теста. Затем вы можете использовать результаты для создания индивидуального учебного плана, основанного на вашей конкретной области потребностей.
КурсыCalculus I предоставляют студентам углубленное введение в основные концепции пределов, производных и интегралов, основываясь на предварительном понимании этих концепций, которое студенты получили на курсах Pre-Calculus при подготовке их к более сложному материалу Calculus II, Исчисление II и дифференциальные уравнения.Курсы исчисления часто необходимы студентам, чтобы иметь возможность заниматься не только этими курсами математики более высокого уровня, но и продвинутым материалом по естественным наукам. Если вы планируете получить специализацию в области математики, естественных наук или любой другой количественной области, изучение математики до поступления в колледж может быть настоящим благом, поскольку курсы математики в старших классах часто изучают материал в несколько более медленном темпе, чем университетские курсы, поэтому необходимо убедиться, что учащиеся полностью понять каждую концепцию, прежде чем двигаться дальше. Нужны ли вам лучшие преподаватели математического анализа в Нью-Йорке, преподаватели математического анализа в Чикаго или лучшие преподаватели математического анализа в Лос-Анджелесе, работа с профессионалом может вывести ваше обучение на новый уровень.
Материал, преподаваемый на курсах «Исчисление I», можно разбить на три основные категории: пределы, производные и интегралы; однако большинство курсов по исчислению I начинаются с обзора основных характеристик функций, отображаемых на координатной плоскости, включая непрерывность, асимптоты, а также абсолютные и локальные экстремумы. При рассмотрении этих концепций учащихся могут попросить найти наклон линии или уклона в точке.
Углубляясь в понятие пределов функций, курсы исчисления обычно начинаются с процесса вычисления и оценки простых пределов и переходят к введению понятий асимптот и непрерывности, вычисления пределов до бесконечности и других сложностей.
Обсуждение производных — основная часть каждого курса Calculus I. Студенты знакомятся с производными посредством обсуждения определения производной, предельного определения производной и дифференциальных уравнений, чтобы укрепить концептуальное понимание производных производных. Крайне важно, чтобы учащиеся полностью понимали, что представляют собой производные по мере их продвижения в исчислении I, поскольку вскоре их просят применить эти знания, вычисляя производные в точке и функции, а также вторые производные.Их также учат правилу цепочки. Студентам также предлагается построить графики производных и вторых производных, а также линейные аппроксимации производных. По мере увеличения знаний учащихся о производных, Calculus I вводит концепции увеличения и уменьшения интервалов, вогнутости и выпуклости, точек перегиба и полей наклона. Студентам также предлагается использовать теорему о среднем значении. Учитываются конкретные производные, такие как производные логарифмов, показателей степени, суммы, частные, произведения и тригонометрические функции, а также неявное дифференцирование.
Последняя основная тема каждого курса «Исчисление I» — интегралы. Интегралы вводятся, говоря об определении интеграла, интегральных обозначений, определенных интегралов и сумм Римана. После подробного ознакомления с понятием интеграла студенты изучают фундаментальную теорему исчисления, как получить интеграл от функции и как построить график интегралов. Вероятно, возникнут все более сложные проблемы, поскольку студентов просят взять интеграл от более сложных функций, таких как суммы, частные и произведения, логарифмы, показатели и тригонометрические функции.Varsity Tutors предлагает такие ресурсы, как бесплатные диагностические тесты Calculus 1, чтобы помочь вам в самостоятельном обучении, или вы можете выбрать репетитора Calculus 1.
Из всех математических курсов, которые студенты могут пройти в старших классах школы, Calculus I получил репутацию заведомо сложного. Если вы в настоящее время участвуете в курсе Calculus I и вам нужно пройти повторение или подготовиться к экзамену, или вы изучаете более продвинутый курс математики и вам нужно пересмотреть фундаментальные концепции, преподаваемые в Calculus I, используйте бесплатные практические тесты Calculus I от Varsity Tutors, чтобы освежите свои знания в области исчисления I.Каждый бесплатный практический тест «Исчисление I» содержит дюжину задач «Исчисление I» и ответы с несколькими вариантами ответов. Вы получите подробные результаты после выполнения каждого из них, а также доступ к пошаговым объяснениям того, как прийти к правильному ответу для каждой проблемы. Если вы обнаружите, что вам нужно сосредоточиться на задачах, относящихся к одной конкретной теме, такой как Фундаментальная теорема исчисления, вы можете сделать это, поскольку задачи организованы в практические тесты по концепции. В дополнение к практическим тестам по исчислению 1 и обучению по математическому анализу 1 вы также можете рассмотреть возможность использования некоторых из наших карточек по исчислению 1.
Вы также можете попробовать один из бесплатных полных практических тестов по исчислению I, в которых вам задают вопросы по всему спектру тем, с которыми вы столкнетесь в ходе курса. Полные практические тесты — отличный способ попрактиковаться в проверке своих навыков. Когда вы завершите тест, вам будет показан ваш результат с подробным объяснением правильного ответа на каждый вопрос и ссылками на дополнительные упражнения для проверки. Эти бесплатные практические онлайн-тесты также могут помочь вам составить индивидуальное учебное пособие по исчислению.Показав вам, на каких концепциях вам следует сосредоточиться, вы сможете упростить свой обзор. После ознакомления с некоторыми другими инструментами обучения вы можете отслеживать свой рост, пройдя еще один практический тест «Исчисление I полной длины».
Используя разнообразные бесплатные ресурсы по исчислению, которые предлагает веб-сайт инструментов обучения Varsity Tutors, вы можете победить свой страх перед математикой и направить нервозность на изучение, чтобы полностью овладеть предметом.
Наши совершенно бесплатные практические тесты Calculus 1 — идеальный способ освежить свои навыки.Брать один из наших многочисленных практических тестов Calculus 1 для ответов на часто задаваемые вопросы. Ты получат невероятно подробные результаты подсчета очков в конце вашего практического теста Calculus 1, чтобы поможет вам определить свои сильные и слабые стороны. Выберите один из наших практических тестов Calculus 1 прямо сейчас и начнем!
Практические тесты по концепции
clep_calculus-functionsвопросов : 40
Сложность теста :
Среднее затраченное время : 1 час 21 минута
clep_calculus-дифференциал-функциивопросов : 40
Сложность теста :
Среднее затраченное время : 22 минуты
clep_calculus-midpoint-riemann-суммыВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 49 секунд
clep_calculus-как-найти-середину-суммы РиманаВопросы : 2
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-другие-дифференциальные-функциивопросов : 40
Сложность теста :
Среднее затраченное время : 42 минуты
clep_calculus-как-найти-дифференциальные-функциивопросов : 40
Сложность теста :
Среднее затраченное время : 1 час 53 минуты
clep_calculus-уравнениеВопросы : 13
Сложность теста :
Среднее затраченное время : 7 минут
clep_calculus-дифференциальные-уравненияВопросы : 6
Сложность теста :
Среднее затраченное время : 5 минут
clep_calculus-графики-дифференциальные-уравненияВопросы : 2
Сложность теста :
Среднее затраченное время : 51 минута
clep_calculus-local-maximumВопросы : 3
Сложность теста :
Среднее затраченное время : 2 минуты 22 секунды
clep_calculus-как-найти-локальный-максимум-по-графику-дифференциальным-уравнениямВопросы : 3
Сложность теста :
Среднее затраченное время : 5 минут
clep_calculus-local-minimumВопросы : 2
Сложность теста :
clep_calculus-как-найти-локальный-минимум-по-графику-дифференциальным-уравнениямВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 8 секунд
clep_calculus-другое-графическое-дифференциальные-уравненияВопросы : 1
Сложность теста :
clep_calculus-как-граф-дифференциальные-уравненияВопросы : 1
Сложность теста :
Среднее затраченное время : 47 секунд
clep_calculus-решения-дифференциальные-уравненияВопросы : 6
Сложность теста :
Среднее затраченное время : 10 минут
clep_calculus-как-найти-решения-дифференциальных-уравненийВопросы : 6
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-написание-уравненийВопросы : 7
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-интегральные-выраженияВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 42 секунды
clep_calculus-как-найти-интегральные-выраженияВопросы : 2
Сложность теста :
Среднее затраченное время : 8 минут
clep_calculus-другое-написание-уравненийВопросы : 7
Сложность теста :
Среднее затраченное время : 23 минуты
clep_calculus-как-писать-уравненияВопросы : 7
Сложность теста :
Среднее затраченное время : 8 минут
clep_calculus-графики-функцииВопросы : 7
Сложность теста :
Среднее затраченное время : 9 минут
clep_calculus-areaВопросы : 5
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-How-to-Graph-Функции-ПлощадьВопросы : 5
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-кривыеВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 7 секунд
clep_calculus-local-maximumВопросы : 2
Сложность теста :
Среднее затраченное время : 2 часа 45 минут
clep_calculus-как-найти-локальный-максимум-график-функции-кривыхВопросы : 2
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-local-minimumВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 42 секунды
clep_calculus-как-найти-локальный-минимум-график-функции-кривыхВопросы : 2
Сложность теста :
Среднее затраченное время : 1 минута 53 секунды
clep_calculus-другие-кривыеВопросы : 3
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-How-to-Graph-Функции-КривыеВопросы : 3
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-intervalВопросы : 1
Сложность теста :
Среднее затраченное время : 2 минуты 17 секунд
clep_calculus-вогнутые-вниз-интервалыВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 10 секунд
clep_calculus-как-найти-вогнутые-вниз-интервалы-по-графическим-функциямВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 17 секунд
clep_calculus-continuous-on-the-intervalВопросы : 2
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-how-to-find-continuous-on-the-interval-by-graphing-functionsВопросы : 2
Сложность теста :
Среднее затраченное время : 21 секунда
clep_calculus-уменьшение-интервалыВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 45 секунд
clep_calculus-как-найти-уменьшающие-интервалы-по-графическим-функциямВопросы : 2
Сложность теста :
Среднее затраченное время : 6 минут
clep_calculus-возрастающие интервалыВопросы : 1
Сложность теста :
Среднее затраченное время : 52 секунды
clep_calculus-как-найти-увеличивающие-интервалы-по-графическим-функциямВопросы : 1
Сложность теста :
Среднее затраченное время : 1 мин 29 сек
clep_calculus-relative-extremumВопросы : 2
Сложность теста :
Среднее затраченное время : 1 минута 52 секунды
clep_calculus-relative-maximumВопросы : 2
Сложность теста :
Среднее затраченное время : 1 минута 23 секунды
clep_calculus-how-to-find-relative-maximum-on-the-interval-by-graphing-functionsВопросы : 2
Сложность теста :
Среднее затраченное время : 1 мин 26 сек
clep_calculus-relative-minimumВопросы : 1
Сложность теста :
Среднее затраченное время : 1 час 24 минуты
clep_calculus-how-to-find-relative-minimum-on-the-interval-by-graphing-functionsВопросы : 1
Сложность теста :
clep_calculus-трапециевидное-приближениеВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 6 секунд
clep_calculus-как-найти-трапециевидную-аппроксимацию-графиком-функциямиВопросы : 2
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-linesВопросы : 3
Сложность теста :
Среднее затраченное время : 1 минута 5 секунд
clep_calculus-уравнение-линииВопросы : 2
Сложность теста :
Среднее затраченное время : 1 мин 47 сек
clep_calculus-как-найти-уравнение-линии-графика-функцийВопросы : 2
Сложность теста :
Среднее затраченное время : 1 минута 22 секунды
clep_calculus-length-of-lineВопросы : 2
Сложность теста :
Среднее затраченное время : 1 минута 46 секунд
clep_calculus-how-to-find-length-of-line-by-graphing-functionsВопросы : 2
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-slopeВопросы : 1
Сложность теста :
Среднее затраченное время : 57 секунд
clep_calculus-how-to-find-slope-by-graphing-functionsВопросы : 1
Сложность теста :
Среднее затраченное время : 2 минуты 6 секунд
clep_calculus-pointsВопросы : 1
Сложность теста :
Среднее затраченное время : 2 мин 31 сек
clep_calculus-descriptioning-pointsВопросы : 2
Сложность теста :
Среднее затраченное время : 1 мин. 20 сек.
clep_calculus-how-to-describe-points-by-graphing-functionsВопросы : 2
Сложность теста :
clep_calculus-other-pointsВопросы : 1
Сложность теста :
Среднее затраченное время : 2 минуты 58 секунд
clep_calculus-How-to-Graph-Функции-ТочкиВопросы : 1
Сложность теста :
Среднее затраченное время : 1 мин 26 сек
clep_calculus-points-of-inflectionВопросы : 2
Сложность теста :
Среднее затраченное время : 1 минута 5 секунд
clep_calculus-how-to-graph-functions-of-points-of-перегибВопросы : 2
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-значение-функцийВопросы : 9
Сложность теста :
Среднее затраченное время : 17 минут
clep_calculus-как-найти-значение-функцийВопросы : 9
Сложность теста :
Среднее затраченное время : 19 минут
clep_calculus-rateВопросы : 5
Сложность теста :
Среднее затраченное время : 54 минуты
clep_calculus-приближение-скоростиВопросы : 2
Сложность теста :
Среднее затраченное время : 5 минут
clep_calculus-как-найти-приближение-скоростиВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 58 секунд
clep_calculus-константа-пропорциональностиВопросы : 3
Сложность теста :
Среднее затраченное время : 1 минута 41 секунда
clep_calculus-как-найти-константа-пропорциональности-скоростиВопросы : 3
Сложность теста :
Среднее затраченное время : 2 минуты 18 секунд
clep_calculus-дифференцируемая-ставкаВопросы : 2
Сложность теста :
Среднее затраченное время : 17 секунд
clep_calculus-как-найти-дифференцируемый-скоростиВопросы : 2
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-модели прогнозированияВопросы : 2
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-как-найти-модели-предсказанияВопросы : 2
Сложность теста :
Среднее затраченное время : 2 минуты 3 секунды
clep_calculus-rate-of-changeВопросы : 1
Сложность теста :
Среднее затраченное время : 2 минуты 7 секунд
clep_calculus-как-найти-скорость-измененияВопросы : 1
Сложность теста :
Среднее затраченное время : 1 минута 54 секунды
clep_calculus-rate-of-flowВопросы : 1
Сложность теста :
Среднее затраченное время : 1 минута 2 секунды
clep_calculus-как-найти-скорость-потокаВопросы : 1
Сложность теста :
Среднее затраченное время : 1 мин 38 сек
clep_calculus-solution-for-timeВопросы : 3
Сложность теста :
Среднее затраченное время : 2 минуты 51 секунда
clep_calculus-как-решить-за-времяВопросы : 3
Сложность теста :
Среднее затраченное время : 7 минут
clep_calculus-регионыВопросы : 12
Сложность теста :
Среднее затраченное время : 55 минут
clep_calculus-areaВопросы : 10
Сложность теста :
Среднее затраченное время : 44 минуты
clep_calculus-как-найти-область-в-регионеВопросы : 10
Сложность теста :
Среднее затраченное время : 18 минут
clep_calculus-volumeВопросы : 2
Сложность теста :
Среднее затраченное время : 17 минут
clep_calculus-как-найти-объем-областиВопросы : 2
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-пространственное исчислениевопросов : 25
Сложность теста :
Среднее затраченное время : 46 минут
clep_calculus-ускорениеВопросы : 11
Сложность теста :
Среднее затраченное время : 21 минута
clep_calculus-как-найти-ускорениеВопросы : 11
Сложность теста :
Среднее затраченное время : 13 минут
clep_calculus-distanceВопросы : 3
Сложность теста :
Среднее затраченное время : 5 минут
clep_calculus-как-найти-расстояниеВопросы : 3
Сложность теста :
Среднее затраченное время : 3 минуты
clep_calculus-positionВопросы : 4
Сложность теста :
Среднее затраченное время : 6 минут
clep_calculus-как-найти-позициюВопросы : 4
Сложность теста :
Среднее затраченное время : 4 минуты
clep_calculus-velocityВопросы : 7
Сложность теста :
Среднее затраченное время : 6 минут
clep_calculus-как-найти-скоростьВопросы : 7
Сложность теста :
Среднее затраченное время : 4 минуты
Когда мне следует сдавать SAT в первый раз?
Если бы на этот вопрос был универсальный ответ, этот блог был бы одним простым предложением по длине.Тем не менее, решение о том, когда сдавать первый экзамен SAT, зависит от контекста, и получение правильного ответа для — требует учета ряда важных факторов. Далее следует исследование переменных, которые должны взвесить все подростки и родители, в том числе:
- Когда предлагается SAT
- Когда большинство студентов впервые сдают SAT
- Сроки ваших курсов, особенно математики
- У вас достаточно времени на учебу?
- Политика получения высшего балла и выбора баллов в ваших будущих колледжах
- Планирование экзаменов AP
- Причины сдать SAT рано
Начнем с того, что посмотрим на месяцы, в которые предлагается SAT.
Когда предлагается SAT?В настоящее время SAT предлагается семь раз в год: август, октябрь, ноябрь, декабрь, март, май и июнь.
Когда большинство студентов впервые сдают SAT?Наиболее типичное первое плавание происходит осенью или весной младшего года обучения. Для большинства подростков это будут два наиболее разумных варианта; тем не менее, у некоторых могут быть законные причины рассмотреть вопрос о прохождении теста на втором курсе (подробнее об этом позже).Как бы то ни было, College Board, организация, которая создает и проводит SAT, рекомендует вариант B — дождаться весны 11 -го класса , чтобы пройти тест впервые.
Вот последовательности PSAT / SAT, которые подавляющее большинство старшеклассников выбирают для изучения:
Вариант А: Падение 11-го класса испытательного путиPSAT: Осенью 10 класса
СБ №1: Осенний 11 класс
СБ №2: Весна 11 класса
СБ №3 (при необходимости): Лето или осень 12 класса
Вариант B: Пружина 11-го класса испытательного путиPSAT: Падение 10 класса и / или падение 11 класса
СБ №1: Осенний 11 класс
СБ №2: Весна 11 класса
СБ №3 (при необходимости): Лето, осень или зима 12 класса
Независимо от того, какой путь вы выберете, у вас всегда будет возможность пройти тест SAT в четвертый раз, если это абсолютно необходимо.Даже если вы подадите раннее решение или заблаговременно предпримете меры, вы все равно можете пройти еще один SAT в декабре старшего года, так как результаты обычно публикуются до даты, когда многие школы принимают решение об ED / EA.
Согласование SAT с учебной работой в средней школеЭто одно из самых важных соображений для учеников 11-х классов при определении того, когда лучше сдать экзамен SAT. Учтите, что SAT измеряет ваши способности в трех основных областях математики, а также в категории «Дополнительные темы».Их:
- Сердце алгебры (19 вопросов): линейные уравнения, системы уравнений и линейные отношения.
- Решение проблем и анализ данных (17 вопросов): Соотношения, пропорции, проценты, анализ графиков, понимание количественных данных.
- Passport to Advanced Math (16 вопросов): квадратные уравнения и уравнения высшего порядка, манипулирование полиномами, более сложные уравнения или функции.
- Дополнительные темы по математике (6 вопросов): Геометрические понятия, основы тригонометрии, арифметика комплексных чисел.
Итак, что из всего этого можно сделать? По сути, учащиеся должны хотя бы приблизиться к изучению геометрии и алгебры II, чтобы полностью подготовиться как к SAT, так и к ACT. Если вы изучаете алгебру II в младших классах, вы можете подождать до конца весны, чтобы начать свое путешествие по стандартизированному тестированию.
Сколько времени мне нужно на учебу?Среди пожилых людей, повторно сдавших SAT, 55% отметили повышение своих баллов; среднее улучшение на 40 баллов.Лишь 4% участников повторного тестирования видят, что их оценка по чтению или математике подскочила на 100+ баллов. Однако цифры намного более обнадеживают для тех, кто учится, чем для тех, кто не учится, и это не обязательно означает, что нужно платить сотни или тысячи долларов за индивидуальное обучение или модные классы SAT. Фактически, исследование, опубликованное в этом году Советом колледжей, показало, что всего 20 часов целенаправленной практики в Академии Хана (которая полностью бесплатна) привели к среднему приросту баллов на 115 баллов.
Если вы сможете выкроить достаточно времени для подготовки к экзамену летом после второго года обучения, и к августу вы сдадите практические тесты, то, возможно, вы будете готовы к осеннему экзамену SAT.Если вам нужно больше времени (рождественские каникулы, весенние каникулы и т. Д.), То дождаться весны может быть более выгодным.
Воспользуйтесь преимуществом SuperscoringБольшинство американских колледжей получают оценку SAT (полный список — здесь). Это означает, что они возьмут ваши самые высокие баллы по чтению и математике из нескольких экзаменов. Эта политика дает большое преимущество тем, кто проходит тест несколько раз. Если в ваших будущих колледжах действует политика высшего балла, вы можете записаться на любое количество экзаменов без каких-либо последствий.
Некоторые из примечательных учебных заведений, которые НЕ получают супер-оценку: все школы в системе Калифорнийского университета, Мичиганский университет, штат Пенсильвания, Юта-Остин и Университет Висконсина.
Предлагают ли колледжи, в которые я подаю заявление, программу Score Choice? Политика«Выбор баллов» позволяет вам сообщать только те баллы SAT, которыми вы хотите поделиться с потенциальными колледжами, исключая риск единственной низкой оценки. Подавляющее большинство школ имеют такую политику (за исключением школ Карнеги-Меллона, Джорджтауна, Стэнфорда, Йельского университета и Калифорнийского университета).Чтобы просмотреть полный список, нажмите здесь.
Могу ли я пройти несколько курсов AP на первом курсе?Если вы участвуете в нескольких тестах AP в младших классах, то с начала до середины мая уже будет адское время, наполненное интенсивной подготовительной работой и сдачей экзаменов. Студентам в этой ситуации целесообразно впервые сдать SAT осенью младшего года обучения, либо в марте или апреле, чтобы избежать перегрузки по стандартизированному тестированию при проведении тестов AP. Обычно это хорошо работает для таких людей, потому что те, кто на треке AP, как правило, покрывают подавляющее большинство предметов математики к этому моменту.
Причины сдать SAT до младшего годаСуществует ряд причин, по которым учащийся может отказаться от традиционного графика SAT и сдать экзамен в качестве первокурсника, второкурсника или даже, в некоторых крайне редких случаях, ученика средней школы. К ним относятся:
1) Учащиеся математики с продвинутым уровнем, которые уже изучили основы геометрии и алгебры, необходимые для успешной сдачи экзамена SAT до 11 -го класса . Для некоторых материал, рассматриваемый в разделе SAT по математике, может быть самым свежим в их памяти в начале их школьной карьеры.
2) Студенты, которые чувствуют, что они на 100% готовы к экзамену, и знают, что следующий год (ваш первый год) будет забит шестью курсами AP (и последующими экзаменами) и множеством трудоемких внеклассных занятий.



 Понимание исследований предметной области и диапазона функций на данный момент.
Понимание исследований предметной области и диапазона функций на данный момент. 203 # 1c, 2abc, 3, 5, 7, 10
203 # 1c, 2abc, 3, 5, 7, 10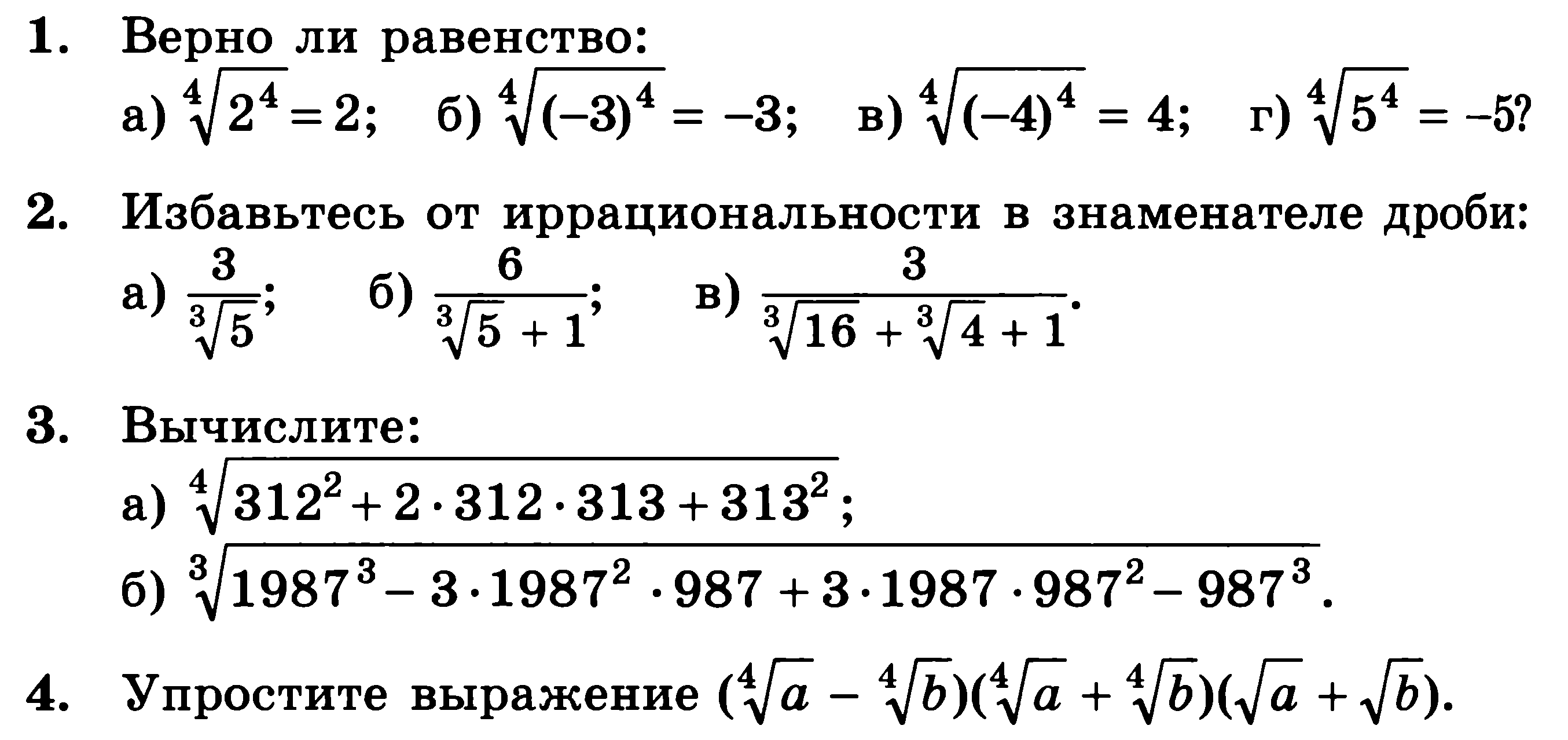 229 # 3, 4ii, 5 (шансы), 6 (шансы), 7, 11 (шансы)
229 # 3, 4ii, 5 (шансы), 6 (шансы), 7, 11 (шансы) Ниже старые тесты
Ниже старые тесты