Контрольные работы по геометрии с ответами к учебнику Атанасяна Л.С. за 1, 2, 3, 4 четверти
Дата публикации: .
Контрольные на темы: «Аксиомы стереометрии. Взаимное расположение прямой и плоскости», «Перпендикулярность прямых и плоскостей», «Многогранники» и др.
Контрольная работа №1
Аксиомы стереометрии. Взаимное расположение прямой и плоскостиВариант I
Часть А
1) Прямые a и b скрещивающиеся. Прямая с параллельна прямой b. Могут ли прямые а и с пересекаться?
2) Плоскость α проходит через верхнее основание трапеции АВСD. Докажите, что любая прямая, лежащая в плоскости α и параллельная прямой ВС, параллельна прямой АD. Точки М и N — середины боковых сторон. Найдите АD, если BC=8, MN=12.
3) Прямая FА проходит через вершину параллелограмма АВСD и не лежит в плоскости параллелограмма.
а) Докажите, что FA и CD скрещивающиеся.
б) Чему равен угол между прямыми FA и CD, если угол FAB равен 30 градусов?
Часть Б
1) Прямая а параллельна плоскости α, прямая b также параллельна плоскости α. Могут ли а и b:
а) Быть параллельными?
б) Пересекаться?
в) Быть скрещивающимися прямыми?
2) Точка М лежит вне плоскости параллелограмма АВСD.
а) Докажите, что средние линии треугольников MAD и MBC параллельны.
б) Найдите эти средние линии, если боковая сторона параллелограмма равна 5, а его высота равная 4 и делит сторону, к которой проведена, пополам.
3) Через вершину С квадрата АВСD, проходит прямая СК, не лежащая в плоскости квадрата.
а) Докажите, что СК и АD скрещивающиеся.
б) Чему равен угол между СК и АD. Угол СВК равен 45 градусов, угол СКВ равен 75 градусов?
Часть В
1) Две плоскости пересекаются по прямой L. Прямые L и A скрещивающиеся, прямые L и В параллельны. Могут ли прямые А и В:
а) Лежать в одной из плоскостей?
б) Лежать в разных плоскостях?
в) Пересекать эти плоскости?
В случае утвердительного ответа укажите взаимное расположение прямых L и A.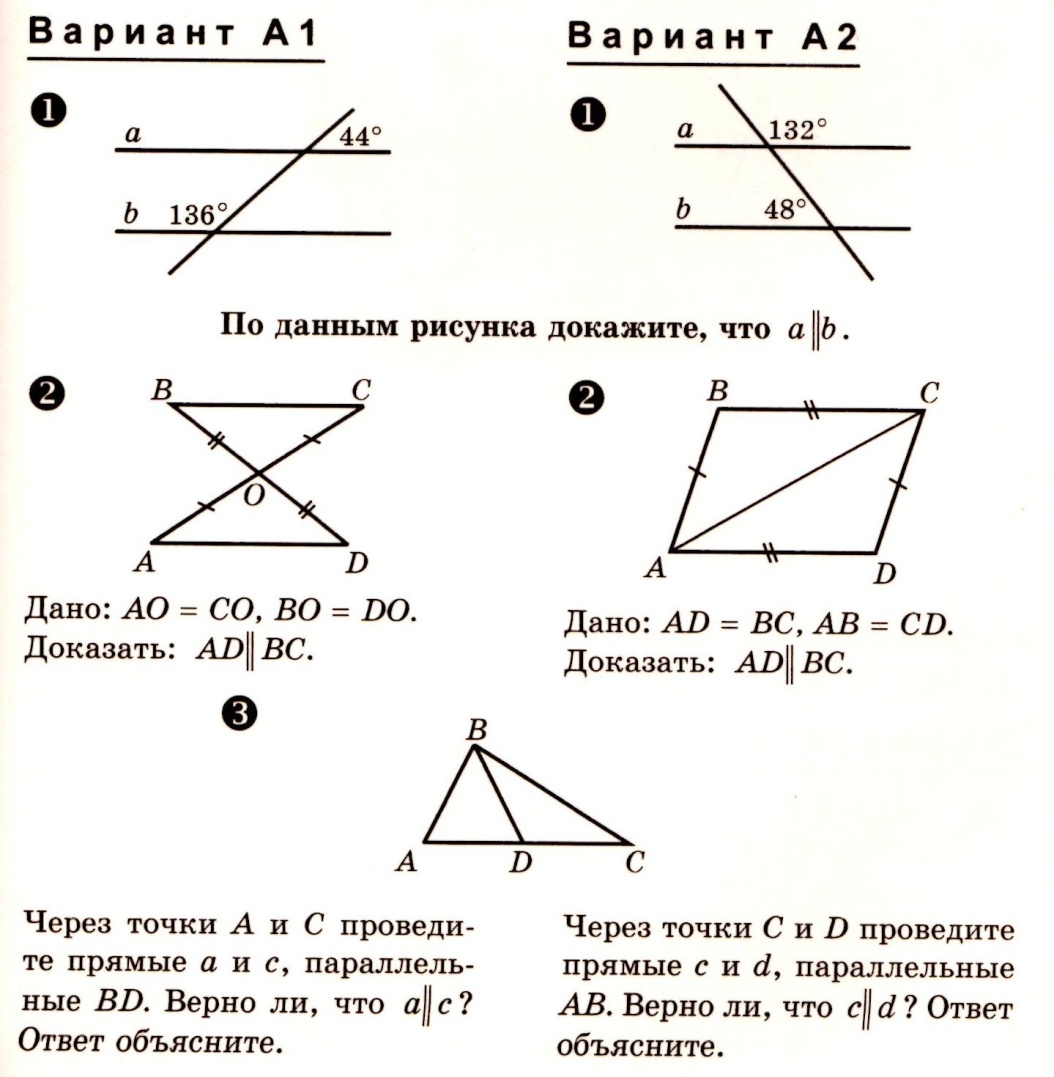
2) Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно. BN:NC=5:8. MB:AB=5:13.
а) Докажите, что АС || α.
б) Найдите MN, если АС=26.
3) Точки А, В, С и D не лежат в одной плоскости. Найдите угол между прямыми АС и BD, если АС=16, ВD=20. Расстояние между серединами AD и ВС равно 6.
Вариант II
Часть А
1) Прямые a и b параллельны. Прямая с скрещивающиеся с прямой b. Могут ли прямые b и с быть параллельны?
2) Плоскость α проходит через нижнее основание трапеции АВСD, докажите что любая прямая лежащая в плоскости α и параллельная прямой ВС, параллельна прямой АD. Точки М и N — это середины боковых сторон. Найдите ВС, если AD=24, MN=18.
3) Прямая GА проходит через вершину трапеции АВСD и не лежит в ее плоскости.
а) Докажите, что GА и ВC скрещивающиеся.
б) Чему равен угол между прямыми GА и ВC, если угол GAD равен 70 градусов?
Часть Б
1) Прямая а пересекает плоскость α, прямая b также пересекает плоскости α. Могут ли а и b:
Могут ли а и b:
а) Быть параллельными?
б) Пересекаться?
в) Быть скрещивающимися прямыми?
2) Треугольник АВС и трапеция KMNP имеют общую среднюю линию EF, MN||EF, EF||BC.
а) Докажите, что ВС|| KP.
б) Найдите KP и MN, если ВС=24. КР:MN = 8:3.
3) Точка F лежит вне плоскости трапеции ABCD.
а) Докажите, что AF и BC скрещивающиеся.
б) Чему равен угол между AF и BC, если угол AFD равен 70 градусов, угол FDA равен 40 градусов?
Часть В
1) Две плоскости пересекаются по прямой L. Прямые L и A скрещивающиеся, прямые L и В скрещивающиеся. Могут ли прямые А и В:
б) Лежать в разных плоскостях?
в) Пересекать эти плоскости?
В случае утвердительного ответа укажите взаимное расположение прямых L и A.
2) Плоскость α проходит через сторону АВ треугольника АВС. Прямая пересекает стороны ВС и АС в точках M и N соответственно. МС:ВC=6:13 NC:AN=6:7.
а) Докажите, что MN || α.
б) Найдите MN, если АС=39.
3) Точки А, В, С и D не лежат в одной плоскости. Найдите угол между прямыми АС и BD, если АС=10, ВD=10. Расстояние между серединами AD и ВС равно 5.
Ответы на контрольную работу №1
Контрольная работа №2
Перпендикулярность прямых и плоскостейВариант I
Часть А
1) Отрезок КС – перпендикуляр к плоскости треугольника АВС, КВ перпендикулярно АВ.
а) Докажите, что треугольник АВС прямоугольный.
б) Докажите перпендикулярность плоскостей КАС и АВС.
в) Чему равен КВ, если АС=14, ВС=6. Угол КВС равен 45 градусам.
2) Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки А до плоскости α, если АВ=5, $АС=2\sqrt{23}$, а двугранный угол между плоскостью треугольника и плоскостью α равен 60 градусам.
3) Из точки А к плоскости α проведены наклонные АВ и АС, образующие с плоскость угол 60 градусов. ВС=АС=6. Найдите АВ.
Часть Б
1) Отрезок КА – перпендикуляр к плоскости АВС. Точка М — середина ВС. КМ перпендикулярно ВС. АВ=ВС
Точка М — середина ВС. КМ перпендикулярно ВС. АВ=ВС
а) Докажите, что треугольник АВС — равносторонний.
б) Докажите перпендикулярность плоскостей КВС и КАМ.
в) Найдите площадь треугольника АВС, если ВК=8, $КА=\sqrt{39}$, ВС=6.
2) Точка S удалена от вершин правильного треугольника на $\sqrt{33\frac{3}{4}}$ см. Найдите двугранный угол SABC, если АВ=9.
3) Прямая АВ – ребро двугранного угла, равного 90 градусов. Прямые $АА_{1}$ и $ВВ_{1}$ принадлежат разным граням данного угла. $АА_{1}||ВВ_{1}$, $ВВ_{1}$ перпендикулярно АВ. Докажите, что прямые $АА_{1}$ и $ВВ_{1}$ скрещивающиеся. Найдите угол между этими прямыми.
Часть В
1) Точка О лежит на биссектрисе угла АВС, равного 60 градусов, отрезок DO перпендикулярен плоскости АВС. АВ=АС.
а) Докажите, что точка D равноудалена от точек А и С.
б) Докажите перпендикулярность плоскостей DAC и DOВ.
в) Найдите DB, если АС=12 и DO=8.
2) Равнобедренные треугольники АВС и АДС имеют общее основание АС, двугранный угол ВАСД — прямой. Найдите двугранный угол ДСВА, если угол АСД равен 45 градусов, а угол САВ равен 60 градусов.
Найдите двугранный угол ДСВА, если угол АСД равен 45 градусов, а угол САВ равен 60 градусов.
3) В кубе $АВСДА_{1}В_{1}С_{1}Д_{1}$ постройте и найдите линейный угол между плоскостями сечений $АВ_{1}С_{1}Д$ и $А_{1}Д_{1}СВ$.
Вариант II
Часть А
1) Отрезок КС – перпендикуляр к плоскости треугольника АВС, КВ перпендикулярно АВ.
а) Докажите, что треугольник АВС — прямоугольный.
б) Докажите перпендикулярность плоскостей КАС и АВС.
в) Найдите КВ, если АС=16, ВС=8. Угол КВС равен 45 градусам.
2) Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки А до плоскости α, если АВ=20, АС=25, а двугранный угол между плоскостью треугольника и плоскостью α равен 45 градусам.
3) Из точки А к плоскости α проведены наклонные АВ и АС и перпендикуляр АО. Наклонные образуют с этой плоскостью углы равные 60 градусам. Найдите ВС, если ВС=ВО, ОС=8.
Часть Б
1) Отрезок КА – перпендикуляр к плоскости прямоугольника АВСД. Точка О — пересечение АС и ВД. КО перпендикулярно ВД.
Точка О — пересечение АС и ВД. КО перпендикулярно ВД.
а) Докажите, что АВСД — квадрат.
б) Перпендикулярность плоскостей КВД и КОА.
в) Найдите площадь прямоугольника АВСД, если КО=5, КА=3, угол ВКД равен 90 градусам.
2) Точка S удалена от вершин правильного треугольника на $\sqrt{48} см$. Найдите двугранный угол SABC, если АВ=12.
Часть В
1) Отрезок ДО – перпендикуляр к плоскости угла АВС, равного 90 градусам. Точка О лежит внутри угла, а точка Д равноудалена от его сторон.
а) Докажите, что прямая ВО делит угол АВС пополам.
б) Докажите перпендикулярность плоскостей DAC и DOВ.
в) Найдите DО, если АС=12 и DВ=16.
2) Равнобедренный треугольник АДС с углом Д равным 90 градусам, и равносторонний треугольник АВС имеют общее основание АС.
а) Найдите все углы между прямыми проведенными к вершинам треугольника АВС и этой плоскостью.
б) Найдите углы треугольника образованного высотами треугольников АВС и АДС, опущенными к стороне АС.
3) В кубе $АВСДА_{1}В_{1}С_{1}Д_{1}$ постройте и найдите линейный угол между плоскостями сечений $С_{1}Д_{1}АВ$ и $ДСВ_{1}А_{1}$.
Ответы на контрольную работу №2
Контрольная работа №3
МногогранникиВариант I
Часть А
1) Основание прямой призмы – прямоугольный треугольник с гипотенузой 5см и катетом 4см. Найдите площадь боковой поверхности, если грань содержащая наименьший катет – квадрат.
2) Боковое ребро правильной четырехугольной пирамиды равно 8см, и образует угол 30 градусов с плоскостью основания.
а) Найдите высоту пирамиды.
б) Найдите площадь боковой поверхности.
3) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АВ и делящее его в отношении 1:3, и проходящей параллельно ребру ВС. Найдите площадь сечения.
Найдите площадь сечения.
Часть Б
1) Основание прямого параллелепипеда – ромб с диагоналями 48 и 20 см. Большая диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов. Найдите площадь полной поверхности.
2) Основание пирамиды — правильный треугольник с площадью равной $16\sqrt{3}$. Две боковые грани перпендикулярны плоскости основания, а третья наклонена к ней под углом 45 градусов.
а) Найдите длину ребер пирамиды.
б) Найдите площадь боковой поверхности.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечение куба плоскостью, проходящей через прямую $АД_{1}$ и середину ВС. Найдите площадь сечения.
Часть В
1) Основание прямой призмы — прямоугольный треугольник с катетами 12 и 9 см. Найдите площадь боковой поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро — квадрат.
2) Основание пирамиды – ромб с меньшей диагональю d и тупым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площадь боковой поверхности пирамиды.
Найдите площадь боковой поверхности пирамиды.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечения куба плоскостью, проходящей через середины ребер $АА_{1}$, АД, $А_{1}В_{1}$.
Вариант II
Часть А
1) Основание прямой призмы – прямоугольный треугольник с гипотенузой 5см и катетом 12см. Найдите площадь боковой поверхности, если грань содержащая больший катет – квадрат.
2) Высота правильной четырехугольной пирамиды равна 6 см, а боковое ребро образует угол 45 градусов с плоскостью основания.
а) Найдите длину бокового ребра пирамиды.
б) Найдите площадь боковой поверхности.
3) Ребро правильного тетраэдра равно а. Постройте сечение плоскостью, проходящей через ребро АС и делящее его в отношении 1:2, и проходящей параллельно ребру АВ. Найдите площадь сечения.
Часть Б
1) Основание прямого параллелепипеда – ромб с большей диагональю 30 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов и равна $24\sqrt{2}$. Найдите площадь полной поверхности.
2) Основание пирамиды — равнобедренный прямоугольный треугольник с гипотенузой равной $6\sqrt{2}$. Две боковые грани, содержащие катеты, перпендикулярны плоскости основания, а третья наклонена к ней под углом 30 градусов.
а) Найдите длину ребер пирамиды.
б) Найдите площадь боковой поверхности.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечение куба плоскостью, проходящей через точку В и середину ДА, параллельно $А_{1}Д$. Найдите площадь сечения.
Часть В
1) Основание прямой призмы — равнобедренный треугольник с боковой стороной 26 см и основанием 20 см. Найдите площадь боковой поверхности призмы, если ее наименьшее сечение, проходящее через боковое ребро — квадрат.
2) Основание пирамиды – ромб с боковой стороной равной а и острым углом α. Все двугранные углы при основании пирамиды равны β. Найдите площадь боковой поверхности пирамиды.
3) Ребро куба $АВСДА_{1}В_{1}С_{1}Д_{1}$ равно а. Постройте сечения куба плоскостью, проходящей через середины ребер АВ, $ДД_{1}$, $В_{1}С_{1}$.
Ответы на контрольную работу №3
Ответы на контрольную работу №1
Вариант I
Часть А
1. Да, если лежат в одной плоскости.
2. 16.
3. 30 см.
Часть Б
1.
2. 3.
3. 60.
Часть В
1.
2. 10.
3. 90.
Вариант II
Часть А
1. Нет.
2. 12.
3. 70.
Часть Б
1.
2. КР=32; MN=12.
3. 70.
Часть В
1.
2. 18.
3. 60.
Ответы на контрольную работу №2
Вариант I
Часть А
1. $\sqrt{116}$.
2. 6.
3. 6.
Часть Б
1. 12.
2. 45.
3. 90.
Часть В
1. 16.
2. 60.
3. 90.
Вариант II
Часть А
1. 4$\sqrt{10}$
2. $7,5\sqrt{2}$.
3. 8.
Часть Б
1. 32.
2. 60.
Часть В
1. 8.
2. а) 45, 45, 30; б) 30,60,90.
3. 90.
Ответы на контрольную работу №3
Вариант I
Часть А
1.2\sqrt{3}}{4}$.
1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. | 2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. | 1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. | 2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3. | 1 вариант 1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM, в) найдите синус угла между плоскостью ромба и плоскостью α | 2 вариант 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM, в) Найдите синус угла между плоскостью квадрата и плоскостью α. | 1 вариант 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда | 2 вариант 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. |
1 вариант 1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно. а) Каково взаимное положение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните. 2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками. а) Выполните рисунок к задаче. б) Докажите, что полученный четырехугольник есть ромб. | 2 вариант 1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC. а) Каково взаимное положение прямых РK и АВ? б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните. 2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2. а) Выполните рисунок к задаче. б) Докажите, что четырехугольник MNEK есть трапеция. | 1 вариант 1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4. 3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1. | 2 вариант 1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися? Сделайте рисунок для каждого возможного случая. 2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5. 3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3. | 1 вариант 1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. 2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла DABM, в) найдите синус угла между плоскостью ромба и плоскостью α | 2 вариант 1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите: а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания. 2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В. а) Найдите расстояние от точки С до плоскости α. б) Покажите на рисунке линейный угол двугранного угла BADM, в) Найдите синус угла между плоскостью квадрата и плоскостью α. | 1 вариант 1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите: а) высоту ромба; б) высоту параллелепипеда; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда | 2 вариант 1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды. 2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите: а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания; в) площадь боковой поверхности параллелепипеда; г) площадь поверхности параллелепипеда. |
Сборник контрольных работ по геометрии, (10 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
10 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
Контрольная работа №1 10 класс.
Тема: «Аксиомы и их следствия».
Цель: проверить уровень усвоения ГОСО:
— знания и умения применять при решении задач аксиомы стереометрии и их следствия;
— умение оформлять рисунки по условию задачи;
— умение оформлять решение задачи.
I вариант. |
1.Могут ли две различных плоскости иметь три общие точки, не лежащие на одной прямой? 2.Прямая а лежит в плоскости α. Плоскость β пересекает плоскость α по прямой b. Известно, что прямая a пересекает плоскость β в точке b. Где лежит точка b ? 3.Прямые a, b и c, не лежащие в одной плоскости, проходят через одну и ту же точку. Сколько различных плоскостей можно провести через эти прямые, взятые по две. 4.Точки A, B и прямая CD не лежат в одной плоскости. Каково взаимное расположение прямых CD и AB ? 5.Две соседние вершины и точка пересечения диагоналей квадрата лежат в плоскости α. Докажите, что и две других вершины квадрата лежат в этой же плоскости. |
II вариант. |
1. Плоскости α и β пересекаются по прямой а . Прямая b лежащая в плоскости β, пересекает плоскость α в точке А. Где лежит точка А ? 2.Прямая AB и точки С и D не лежат в одной плоскости. Докажите, что прямые AB и CD пересекаются. 3.Плоскости α и β пересекаются по прямой AB. Плоскости β и γ по прямой BC, а плоскости α и γ по прямой АС. Докажите, что A, B, C лежат на одной прямой. 4.Даны точки А и В. Доказать, что существуют такие точки C и D, что четыре точки A, B, C, D не лежат в одной плоскости. 5.Сторона АВ и диагональ BD прямоугольника ABCD ле |
ГДЗ по Геометрии 10 класс самостоятельные и контрольные работы Ершова
Авторы: Ершова А.П., Голобородько В.В..
Математика у многих школьников вызывает трудности, поэтому советуем использовать ГДЗ по геометрии 10 класс самостоятельные и контрольные работы Ершова. Особенно сложно становится в последние годы обучения, когда нужно готовиться к экзаменам. С этой целью и создали сборники. Здесь содержатся все знания, требуемые для учеников. Решение заданий предоставляется в понятной форме. Каждое упражнение классифицируется по номеру и уроку для удобства поиска. Все составляется в соответствии с ФГОС. Учитывается рабочая программа для разных учебных заведений, распределяя материал по уровням сложности.
Особенности сборника по геометрии за 10 класс, самостоятельные и контрольные работы от Ершовой
Школьники зачастую жалуются на большую загруженность при посещении школы. Необходимо выполнять большое количество действий, изучать дисциплины. По ним задаются упражнения на каждый урок. Самостоятельно разобраться во всем без помощи посторонних достаточно сложно.
Решебник – это специальное пособие, которое содержит в себе правильные ответы на все вопросы. Теперь подготовка к занятиям становится более простой. Достаточно просто решить задачу, посмотреть ее номер, открыть и проверить себя. В результате будут выявлены ошибки, что поможет с их устранением в будущем. Такая форма контроля уже давно пользуется широкой популярностью. Это также удобный инструмент для преподавателей, позволяющий заниматься составлением рабочей программы, планов, методических указаний. ГДЗ – учебник, содержащий все необходимые материалы для улучшения успеваемости учеников. Вся тематика распределяется по разделам геометрии: простые геометрические фигуры, стереометрия, объемные фигуры, решение заданий по формулам. Среди преимуществ:
- изучение информации самостоятельно;
- просмотр верных ответов онлайн;
- готовиться к тестам, проверочным работам;
- широкий спектр задач разной степени сложности;
- воспитание дисциплины;
- улучшение оценок и общей успеваемости.
Справочник по геометрии для 10 класса, самостоятельные и контрольные работы (авторы: Ершова А.П., Голобородько В.В.) поможет ребенку подготовиться к предстоящим экзаменам. В нем содержатся примеры, понятное описание и объяснение всех алгоритмов. Теперь процесс обучения в школе станет немного проще и продуктивнее.
Рабочая программа учебного предмета «Математика» 10 класс по учебникам Мордкович и Атанасян
Муниципальное бюджетное общеобразовательное учреждение
«Кадетская школа имени генерал-майора милиции В.А.Архипова»
города Чебоксары Чувашской Республики
Утверждаю
Директор МБОУ «Кадетская школа» г. Чебоксары
_________ С.В.Иванова
Приказ №105-О
«26» августа 2020 года
Рабочая программа учебного предмета
«Математика»
Уровень образования: среднее общее образование
Классы: 10 класс
Срок реализации программы: 2020-2021 учебный год
Ф.И.О. учителя: Самуилова А. Н.
Принята
на заседании ШМО учителей
_________________________ МБОУ «Кадетская школа»
г. Чебоксары
Протокол № 1
26 августа 2020 г.
г. Чебоксары, 2020
Планируемые результаты освоения учебного предмета, курса.
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
- систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
- расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
- развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.
Цели.
Изучение математики в старшей школе на базовом уровне направлено на достижение:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественно-научных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
- воспитание средствами математики культуры личности: отношение к математике как к части общечеловеческой культуры; знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного процесса.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
- построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
- выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
- самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
- проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
- самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе основного общего образования на изучение алгебры в 10 классе отводится 85 часов и геометрии 51 час.
Личностные, метапредметные и предметные результаты освоения содержания
курса алгебры и геометрии 10 класса
Личностные результаты:
- воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных ученых в развитие мировой науки;
- формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;
- ответственное отношение к обучению, готовность и способность к саморазвитию на протяжении всей жизни; сознательное отношение к непрерывному образованию как к условию успешной профессиональной и общественной деятельности;
- осознанный выбор будущей профессиональной деятельности на базе ориентировки в мире профессий и профессиональных предпочтений; отношений к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду, развитие опыта участия в социально значимом труде;
- умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;
- умение управлять своей познавательной деятельностью;
- умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
- критичность мышлени, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
- умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в учебе;
- умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
- умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания;
- владение навыками познавательной, учебно-исследовательской и проектной деятельности;
- формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
- умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы;
- формирование компетентности в области использования информационно-коммуникационных технологий;
- умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
- умение находить в различных источниках информацию, необходимую для решения математических задач, и представлять ее в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;
- умение понимать и использовать математические средства наглядности (графики, таблицы, схемы) для иллюстрации, интерпретации, аргументации;
- умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
- понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
- осознание значения математики для повседневной жизни человека;
- представление о математической науке как сфере математической деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
- умения описывать явления реального мира на математическом языке; представления о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющим описывать и изучать разные процессы и явления;
- представление об основных понятиях, идеях и методах алгебры и математического анализа;
- представление о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умение находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
- владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
- практически значимые математические умения и навыки, их применение к решению задач, предполагающие умения:
- выполнять вычисления с действительными и комплексными числами;
- решать рациональные, иррациональные, показательные, степенные и тригонометрические уравнения, неравенства, системы уравнений и неравенств;
- решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений и неравенств;
- использовать алгебраический язык для описания предметов окружающего мира и создание соответствующих математических моделей;
- выполнять тождественные преобразования рациональных, иррациональных, степенных, показательных и тригонометрических выражений;
- выполнять операции над множествами;
- исследовать функции с помощью производной и стоить их график;
- вычислять площади фигур и объемы тел с помощью определенного интеграла;
- проводить вычисления статистических характеристик, вычислять приближенные вычисления;
- решать комбинаторные задачи
- владение навыками использования компьютерных программ при решении математических задач.
Содержание учебного предмета, курса.
Содержание курса алгебры 10 класса включает следующие тематические блоки:
|
№ |
Тема |
Количество часов |
Контрольных работ |
|
1 |
Числовые функции
|
5 |
1 |
|
2 |
Тригонометрические функции
|
21 |
1 |
|
3 |
Тригонометрические уравнения
|
11 |
1 |
|
4 |
Преобразование тригонометрических выражений |
18 |
1 |
|
5 |
Производная и ее применение |
30 |
1 |
|
|
Итого |
85ч |
5 |
Содержание курса геометрии 10 класса включает следующие тематические блоки:
|
№ п/п |
Тема |
Количество часов |
В том числе |
|
Контрольные работы |
|||
|
1. |
Введение. Аксиомы стереометрии |
3 |
|
|
2. |
Параллельность прямых и плоскостей |
16 |
2 |
|
3 |
Перпендикулярность прямых и плоскостей |
17 |
1 |
|
4 |
Многогранники |
12 |
1 |
|
6 |
Повторение |
3 |
|
|
|
Итого |
51 |
4 |
Календарно-тематическое планирование
(по учебнику А. Г. Мордковича «Алгебра 10 класс» 2,5 часа в неделю, 85 ч. за год)
|
№ урока |
Наименование темы |
Кол-во часов |
|
|
Числовые функции (5 ч ) |
|
|
1-2 |
Определение числовой функции и способы её задания |
2 |
|
3 |
Свойства функции |
1 |
|
4 |
Обратная функция |
1 |
|
5 |
Входная контрольная работа |
1 |
|
Тригонометрические функции (21ч). |
||
|
6 |
Числовая окружность |
1 |
|
7 |
Числовая окружность на координатной плоскости |
1 |
|
8-10 |
Синус, косинус. Тангенс, котангенс |
3 |
|
11-12 |
Тригонометрические функции числового аргумента |
2 |
|
13 |
Тригонометрические функции углового аргумента |
1 |
|
14-15 |
Формулы приведения |
2 |
|
16-17 |
Функции , ее свойства и графики |
2 |
|
18-19 |
Функции , ее свойства и графики |
2 |
|
20 |
Периодичность функций у=sinx, y=cosx |
1 |
|
21-23 |
Преобразование графиков тригонометрических функций |
3 |
|
24-25 |
Функции , , их свойства и графики |
2 |
|
26 |
Контрольная работа № 1 |
1 |
|
Тригонометрические уравнения (11 ч) |
||
|
27-28 |
Арккосинус. Решение уравнения cost=a |
2 |
|
29-30 |
Арксинус. Решение уравнения sint=a |
2 |
|
31-32 |
Арктангенс и арккотангенс. Решение уравнений tgx=a, ctgx=a |
2 |
|
33-36 |
Решение тригонометрических уравнений. |
4 |
|
37 |
Контрольная работа № 2 |
1 |
|
Преобразование тригонометрических выражений (18ч). |
||
|
38-40 |
Синуса и косинуса суммы и разности аргумента |
3 |
|
41-42 |
Тангенс суммы и разности аргумента |
2 |
|
43-47 |
Формулы двойного угла и формулы понижения степени |
5 |
|
48-52 |
Преобразование сумм тригонометрических функций в произведение |
5 |
|
53-54 |
Преобразование произведения тригонометрических функций в сумму |
2 |
|
55 |
Контрольная работа № 3 |
1 |
|
Производная (30ч) |
||
|
56-58 |
Предел числовой последовательности и функции |
3 |
|
59-60 |
Сумма бесконечной геометрической последовательности |
2 |
|
61-64 |
Предел функции |
4 |
|
65-66 |
Определение производной |
2 |
|
67-70 |
Вычисление производной |
4 |
|
71-74 |
Уравнение касательной к графику функции |
4 |
|
75-78 |
Исследование функций на монотонность и экстремумы |
4 |
|
79-80 |
Построение графиков функций |
2 |
|
81-83 |
Нахождение наибольших и наименьших значений функции |
3 |
|
84 |
Контрольная работа № 4 |
1 |
|
85 |
Итоговая контрольная работа |
1 |
Календарно – тематическое планирование
(по учебнику Л. С. Атанасьяна «Геометрия. 10-11 класс », 1,5 часа в неделю, всего 51 ч в год)
|
№ урока |
Наименование разделов и тем |
Кол- во |
|
Введение(3) |
||
|
1 |
Предмет стереометрии. Аксиомы стереометрии |
1 |
|
2 |
Некоторые следствия из аксиом |
1 |
|
3 |
Решение задач на применение аксиом стереометрии и их следствий |
1 |
|
Параллельность прямых и плоскостей(16) |
||
|
4 |
Параллельные прямые в пространстве |
1 |
|
5 |
Параллельность прямой и плоскости |
1 |
|
6 |
Решение задач по теме «Параллельность прямой и плоскости» |
1 |
|
7 |
Решение задач по теме «Параллельность прямой и плоскости» |
1 |
|
8 |
Скрещивающиеся прямые |
1 |
|
9 |
Углы с сонаправленными сторонами. Угол между прямыми |
1 |
|
10 |
Решение задач по теме «Параллельность прямых и плоскостей» |
1 |
|
11 |
Контрольная работа № 1 «Параллельность прямых» |
1 |
|
12 |
Параллельные плоскости |
1 |
|
13 |
Свойства параллельных плоскостей |
1 |
|
14 |
Тетраэдр |
1 |
|
15 |
Параллелепипед |
1 |
|
16 |
Параллелепипед |
1 |
|
17 |
Задачи на построение сечений |
1 |
|
18 |
Контрольная работа № 2 «Параллельность плоскостей» |
1 |
|
19 |
Зачет № 1 «Параллельность прямых и плоскостей» |
1 |
|
Перпендикулярность прямых и плоскостей(17) |
||
|
20 |
Перпендикулярность прямой и плоскости |
1 |
|
21 |
Параллельные прямые, перпендикулярные к плоскости |
1 |
|
22 |
Признак перпендикулярности прямой и плоскости |
1 |
|
23 |
Теорема о прямой, перпендикулярной к плоскости |
1 |
|
24 |
Решение задач по теме «Теорема о прямой , перпендикулярной к плоскости» |
1 |
|
25 |
Расстояние от точки до плоскости |
1 |
|
26 |
Теорема о трех перпендикулярах |
1 |
|
27 |
Теорема о трех перпендикулярах |
1 |
|
28 |
Решение задач по теме «Теорема о трех перпендикулярах» |
1 |
|
29 |
Угол между прямой и плоскостью |
1 |
|
30 |
Угол между прямой и плоскостью |
1 |
|
31 |
Двугранный угол |
1 |
|
32 |
Признак перпендикулярности двух плоскостей |
1 |
|
33 |
Прямоугольный параллелепипед |
1 |
|
34 |
Решение задач по теме «Прямоугольный параллелепипед» |
1 |
|
35 |
Контрольная работа № 3 «Перпендикулярность прямых и плоскостей» |
1 |
|
36 |
Зачет № 2 «Перпендикулярность прямых и плоскостей» |
1 |
|
Многогранники (12) |
||
|
37 |
Понятие многогранника |
1 |
|
38 |
Призма. Площадь боковой поверхности |
1 |
|
39 |
Призма. Площадь боковой поверхности. Решение задач. |
1 |
|
40 |
Пирамида |
1 |
|
41 |
Пирамида правильная |
1 |
|
42 |
Пирамида. Площадь поверхности |
1 |
|
43 |
Пирамида. Усеченная пирамида |
1 |
|
44 |
Правильные многогранники. Симметрия в пространстве |
1 |
|
45 |
Понятие правильного многогранника |
1 |
|
46 |
Понятие правильного многогранника. Виды. Элементы симметрии правильных многогранников |
1 |
|
47 |
Контрольная работа № 4 «Многогранники» |
1 |
|
48 |
Зачет № 3 «Многогранники»
|
1 |
|
Повторение(3 часа) |
||
|
49 |
Аксиомы стереометрии и их следствия. |
1 |
|
50 |
Параллельность прямых и плоскостей. |
1 |
|
51 |
Перпендикулярность прямых и плоскостей. |
1 |
Приложение. Контрольные работы по алгебре.
|
Контрольная работа № 1 |
|
|
1 вариант
1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5).
2). Найти D(у), если:
3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции
4). Для заданной функции найти обратную:
|
2 вариант
1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5).
2). Найти D(у), если:
3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции
4). Для заданной функции найти обратную:
|
|
Контрольная работа № 2 |
|
|
1 вариант
1). Вычислите:
2). Упростите:
3). Известно, что: . Вычислить .
4). Решите уравнение: .
5). Докажите тождество: .
|
2 вариант
1). Вычислите:
2). Упростите:
3). Известно, что: . Вычислить .
4). Решите уравнение: .
5). Докажите тождество: .
|
|
Контрольная работа № 3 |
|
|
1 вариант
1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке .
2). Упростить выражение:
3). Исследуйте функцию на четность:
4). Постройте график функции:
5). Известно, что . Докажите, что .
|
2 вариант
1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке .
2). Упростить выражение:
3). Исследуйте функцию на четность:
4). Постройте график функции:
5). Известно, что . Докажите, что .
|
|
Контрольная работа № 4 |
|
|
1 вариант
1). Решить уравнение:
2). Найти корни уравнения на отрезке .
3). Решить уравнение:
4). Найти корни уравнения , принадлежащие отрезку .
|
2 вариант
1). Решить уравнение:
2). Найти корни уравнения на отрезке .
3). Решить уравнение:
4). Найти корни уравнения , принадлежащие отрезку .
|
|
Контрольная работа № 5 |
|
|
1 вариант
1). Вычислить:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение а).
5). Зная, что и , найти . |
2 вариант
1). Вычислите:
2). Упростить выражение:
3). Доказать тождество:
4). Решить уравнение а).
5). Зная, что и , найти .
|
|
Контрольная работа № 6 |
|
|
1 вариант
1). Найдите производную функции: а). ; б). ; в). ; г). ; д). .
2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1.
3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с.
4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке .
|
2 вариант
1). Найдите производную функции: а). ; б). ; в). ; г). ; д). .
2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1.
3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с.
4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке .
|
|
Контрольная работа № 7 ( итоговая ) |
|
|
1 вариант
1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осью Ох угол 600. 2). Решите уравнение:
3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
2 вариант
1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение:
3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции .
|
Контрольные работы по геометрии.
Контрольная работа № 1
Тема «Параллельность прямых и плоскостей »
Вариант 1
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых РK и АВ?
б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок к задаче.
б)* Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа № 2
Тема «Параллельность прямых и плоскостей »
Вариант 1
- Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
- Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно,
прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см,
В1О : ОВ2 = 3 : 4.
3.* Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
Контрольная работа № 2
Тема «Параллельность прямых и плоскостей »
Вариант 2
- Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть: а) параллельными; б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
- Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно,
прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см,
ОВ1 : ОВ2 = 3 : 5.
3.* Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что
K DA, АK : KD = 1 : 3.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM,
М α.
в)* найдите синус угла между плоскостью ромба и плоскостью α
Контрольная работа № 3
Тема «Перпендикулярность прямых и плоскостей »
Вариант 2
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ
параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания.
|
2. |
Сторона |
квадрата |
ABCD равна а. Через |
сторону |
AD проведена |
плоскость α на |
|
|||
|
|
|
a |
|
|
|
|
|
|
|
|
|
расстоянии |
2 |
от точки В. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
а) Найдите расстояние от точки С до плоскости α. |
|
|
|
|
||||||
|
б) |
Покажите |
на |
рисунке |
линейный |
угол |
двугранного |
угла |
BADM, |
|
|
|
М |
|
|
|
|
|
|
|
|
|
|
|
α. |
|
|
|
|
|
|
|
|
|
|
в)* Найдите синус угла между плоскостью квадрата и плоскостью α.
Контрольная работа № 4
Тема «Многогранники »
Вариант 1
- Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
- Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба; б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда; г)* площадь поверхности параллелепипеда
Контрольная работа № 4
Тема «Многогранники »
Вариант 2
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны a
и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма; б) угол между плоскостью АВС1 и плоскостью основания;
в) площадь боковой поверхности параллелепипеда; г)* площадь поверхности параллелепипеда.
Геометрия. 10 класс. Самостоятельные работы. Учебное пособие для общеобразовательных организаций. УМК Атанасяна. ФГОС
Иченская М.А.
Аннотация
Учебное пособие представляет собой сборник самостоятельных работ к учебнику «Геометрия. 10-11 классы» Л.С. Атанасана и др. К каждой теме учебника дано 4 варианта самостоятельных работ, оформленных в виде разрезных карточек. Пособие адресовано учащимся, учителям математики и студентам педвузов.
Дополнительная информация
| Регион (Город/Страна где издана): | Москва |
| Год публикации: | 2018 |
| Тираж: | 3000 |
| Страниц: | 64 |
| Формат: | 70×90/16 |
| Ширина издания: | 170 |
| Высота издания: | 215 |
| Вес в гр.: | 79 |
| Язык публикации: | Русский |
| Тип обложки: | Мягкий / Полужесткий переплет |
| Цвета обложки: | Коричневый, Зелёный |
| Возраст от: | 12 |
| Полный список лиц указанных в издании: | Иченская М.А. |
Как найти в магазине
Нет отзывов о товаре
С этим товаром покупают
Популярные книги автора
MCAS 2013 Практический тест по математике для 10 класса
% PDF-1.6 % 353 0 объект > / ViewerPreferences> / Metadata 1901 0 R / Pages 349 0 R / OpenAction 858 0 R / StructTreeRoot 131 0 R / Type / Catalog / Lang (EN) / PageLabels 346 0 R >> эндобдж 1901 0 объект > поток 2012-09-20T10: 34: 13-04: 002012-09-20T12: 08: 54-04: 002012-09-20T12: 08: 54-04: 00Adobe InDesign CS4 (6.0.5)
8B636E2E111B2F5D5DD8B0482742012-08-09T12: 03: 04-04: 00Adobe InDesign 6.0 /
Оценка окислительной деструкции N-метилпирролидона (NMP) в процессах изготовления микроэлектроники с использованием многоплатформенного аналитического подхода
Во время строительства записывающих головок коррозия металлических элементов и последующее осаждение побочных продуктов коррозии наблюдались.Предыдущие исследования показали, что использование N-метилпирролидона (NMP) может быть одним из факторов. В этом исследовании мы сообщаем об использовании нового многоплатформенного аналитического подхода, включающего pH, жидкостную хроматографию / УФ-детектирование (ЖХ / УФ), оптическую эмиссионную спектроскопию с индуктивно связанной плазмой (ИСП-ОЭС) и ЖХ / масс-спектрометрию (ЖХ / МС. ), чтобы продемонстрировать, что условия реакции, имитирующие общие процессы удаления фоторезиста, могут вызвать окисление NMP во время процесса фотолитографии.Впервые мы подтвердили, что окисление NMP снижает pH, способствуя растворению переходных металлов, осажденных на подложках пластин, во время процессов после маскирования и перед отрывом при производстве микроэлектроники. Это отрицательно сказывается на характеристиках микроэлектронного устройства. Кроме того, было показано, что при выполнении процесса в инертной атмосфере окисление NMP было подавлено, а pH стабилизирован, что указывает на доступную модификацию стадии запуска фотолитографии для повышения качества записывающих головок.Это новое исследование предоставило ключевые данные, которые могут оказать существенное влияние на проектирование, оптимизацию и контроль текущего и будущего производственного процесса. Приведенные здесь результаты предполагают включение pH в качестве ключевой входной переменной процесса (KPIV) при разработке новых процессов удаления фоторезиста.
1. Введение
Изготовление полупроводниковых устройств — это процесс, используемый для создания интегральных схем, присутствующих в электрических и электронных устройствах [1]. Процесс изготовления, показанный на рисунке 1, начинается с пластины из полупроводникового материала и включает в себя последовательность этапов фотографической и химической обработки, во время которых электронные схемы постепенно создаются на пластине-подложке [2].Современные полупроводники могут содержать миллиарды транзисторов на слое кремния размером в квадратный сантиметр, поэтому производство должно строго контролироваться и осуществляться с большой точностью для достижения характеристик на наномасштабе [3].
Производство полупроводников зависит от использования процессов фотолитографии [4], в которых используются химические составы в специализированных производственных инструментах, которые формируют интегральные схемы с шириной линии, которая может составлять всего десять нанометров или меньше.
На литографию приходится более одной трети общих производственных затрат при изготовлении микроэлектроники [5], поскольку на этой стадии часто возникают дефекты [6]. Однако дефекты, возникающие в результате химических явлений, происходящих в химикатах для удаления фоторезиста и фоторезиста, изучены меньше.
Составы фоторезиста обычно состоят из пяти или более отдельных химических компонентов, включая полимерную смолу, чувствительное к излучению соединение и растворитель [6], которые должны работать вместе, чтобы получить световое изображение и очертить желаемый рисунок интегральной схемы на поверхности. поверхность пластины [2].Этап полосы фоторезиста должен выполняться таким образом, чтобы полностью и равномерно удалить остаточный фоторезист, без неблагоприятного воздействия на поверхности материалов, составляющих нижележащую пластинчатую подложку [7, 8]. Один из методов удаления фоторезиста и нижних антибликовых покрытий (BARC) включает использование жидкого N-метилпирролидона (NMP) в качестве растворителя. NMP медленно окисляется воздухом и очень гигроскопичен [9]. Однако было показано, что NMP окисляется в присутствии переходных металлов в нетропосферных условиях с помощью хорошо известных каталитических механизмов [9–12], а также в присутствии УФ-излучения и гидроксильных радикальных инициаторов [13].
Во время предыдущих исследований инженеров по фотолитографии компании Seagate Technology были обнаружены проблемы, связанные с колебаниями сопротивления магниторезистивных записывающих головок (MRR) (дополнительный рисунок 1), что привело к тому, что привод не мог считывать сервоприводы жесткого диска. СМИ. Анализ технологического процесса фотолитографии показал, что проблема была результатом коррозии элементов переходного металла на стопке контактных считывающих устройств, происходящей во время процесса снятия фоторезиста (неопубликованные данные).В данном случае рассматриваемым химическим веществом был NMP, который, как известно, растворяет некоторые переходные металлы [13]. Существуют различные гипотезы относительно потенциальных механизмов действия этого химического вещества, которые в конечном итоге приводят к разрушению важнейших компонентов записывающей головки.
Рейст и Джордж [14] предоставили ценные сведения о механизме растворения меди в водных условиях. В своем исследовании они обнаружили, что присутствие молекулярного кислорода (O 2 ) позволило сформировать поверхностный слой CuO, который защищает лежащую под ним металлическую медь.Однако в присутствии протонного раствора ионы H + обладают высоким сродством к кислородному компоненту поверхностного слоя оксида меди (II), и поэтому два эквивалента протонов легко соединяются с кислородом поверхностного оксида с образованием генерируют воду и сольватированные ионы Cu (II + ). Это обнажает находящуюся под ним металлическую медь, позволяя протекать дальнейшему процессу окисления-растворения. Основываясь на этой и другой работе [15], относящейся к влиянию системного pH на растворение металла, мы выдвигаем гипотезу, что, хотя сам NMP имеет достаточно щелочной pH, воздействие химического вещества на пластины незавершенного производства (WIP) может инициировать химическое превращение, которое действует, чтобы сольватировать переходные металлы на поверхности пластины, одновременно снижая pH системы, тем самым ускоряя процесс растворения и / или процесс разложения NMP.
Здесь мы сообщаем о разработке и применении нового мультиплатформенного аналитического подхода, который сочетает в себе использование методов pH, ЖХ / УФ, ИСП-ОЭС и ЖХ / МС для оценки путей окислительной деградации NMP и мониторинга его развития в рамках фотолитографического подъема. вне процессов.
2. Материалы и методы
2.1. Химические вещества
N-Метилпирролидон (степень чистоты для ВЭЖХ, ≥99%), N-метилсукцинимид (99%), 1- (2-гидроксиметил) -2-пирролидон (98%), 2-пирролидон (≥99%), сукцинимид ( 99.1%), N-гидроксиметилпирролидон (синтезирован НИОКР — данные о чистоте отсутствуют), гексагидрат хлорида кобальта (II) (98%) и муравьиная кислота (98% об. / Об.) Были получены через Sigma Aldrich, Хаверхилл, Великобритания. Водный раствор нитрата серебра (0,02 М, ≥99%) был получен через VWR Chemicals, Lutterworth, UK. Цеолит натрия Y-52 был получен через Honeywell Fluka, Кембридж, Великобритания. Кислород (99,999%), азот (99,999%), ацетонитрил (степень чистоты для ВЭЖХ, ≥99%), вода MiliQ (проводимость 18 Ом), метанол (степень чистоты для ВЭЖХ, ≥99%), буферный раствор pH 10 (pH 10 ± 0.01 при 25 ° C, 0,1 M) и буферный раствор pH 7 (pH 7 ± 0,04 при 25 ° C, 0,1 M) были получены через Schlötter, Co. Kildare, Ирландия. Дейтерированная вода: Cambridge Laboratories, INC. Лот № 6K-328, Кембридж, Великобритания. Стандартные растворы элементов ICP-OES были получены через Thermo Scientific, Altrincham, UK.
2.2. Анализ pH
Анализ pH проводили с использованием электрода EasyClean Solvotrode (Metrohm UK) с электролитом сравнения LiCl в этаноле (1 M) и прибором 716 DMS Titrino (Metrohm UK).Данные pH анализировали с помощью Tiamo 2.4 (Metrohm UK).
2.3. Анализ методом оптической эмиссионной спектроскопии с индуктивно связанной плазмой (ICP-OES)
Анализ ICP-OES проводили с использованием прибора iCAP 7400 ICP-OES (Thermo Fisher Scientific). Перед анализом образцы NMP растворяли в деионизированной воде (10% об. / Об.). Условия плазмы были следующими: мощность РЧ: 1250 Вт, поток вспомогательного газа: 0,5 л / мин, поток охлаждающего газа: 12 л / мин, поток газа распылителя: 0,5 л / мин, давление газа распылителя: 270 кПа.Спектры анализировали с использованием Qtegra ISDS (Thermo Fisher Scientific).
2.4. Калибровка оптической эмиссионной спектроскопии с индуктивно связанной плазмой (ICP-OES)
Прибор iCAP 7400 ICP-OES был откалиброван по следующим элементам: алюминий, мышьяк, кобальт, хром, медь, железо, галлий, никель, платина и кремний. Рабочий стандарт с высокой концентрацией (10 мг / л) был приготовлен растворением соответствующего элементного стандарта (1 мл) в концентрированной HNO 3 (2 мл), кислотные растворы были объединены и полученный раствор был разбавлен до 100 мл деионизированным раствором. вода.Рабочий стандарт низкой концентрации (0,1 мг / л) получали растворением аликвоты рабочего стандарта высокой концентрации (1 мл) в концентрированной HNO 3 (2 мл), затем полученный раствор разбавляли до 100 мл деионизированной водой. . Затем прибор был откалиброван с использованием стандартных растворов на основе NMP (таблица S1).
2,5. Получение Y-цеолита кобальт-натрия
Кобальтовый материал на цеолитной основе был приготовлен, как описано ранее [10]. Гексагидрат хлорида кобальта (II) (2 × 10 -2 моль) добавляли в коническую колбу на 500 мл, содержащую деионизированную воду (200 мл) и снабженную магнитной мешалкой.В реакционную колбу добавляли Y-цеолит натрия (10 г) и реакционную смесь оставляли перемешиваться при 70 ° C в течение 24 часов. Полученное твердое вещество розового цвета отфильтровывали под вакуумом и промывали деионизированной водой до тех пор, пока не перестанет обнаруживаться хлорид при добавлении раствора нитрата серебра (0,1 н.). Затем твердое вещество сушили в вакууме в течение 48 часов при 150 ° C в вакуумном сушильном шкафу с получением бледно-пурпурного / синего твердого вещества (8,8329 г). Затем высушенное твердое вещество переносили в вакуумный эксикатор и давали ему охладиться до комнатной температуры в вакууме, после чего оно было готово к использованию.
2.6. Каталитическое окисление NMP в кислороде
Методика основана на предыдущей работе [16]. В трехгорлую круглодонную колбу (RBF), оборудованную магнитной мешалкой, как показано на (Рисунок S2), добавляли N-метилпирролидон (50 мл). Трехходовой сепаратор с баллоном, заполненным кислородом, прикрепленным к одному соплу, и вакуумной линией, установленной к другому, был вставлен в центральное отверстие колбы, в то время как два других отверстия были закрыты стеклянными пробками — все отверстия были закрыты. с вакуумной смазкой и парафильмом.В реакционную колбу добавляли сухой кобальт-натриевый цеолит Y-52 (0,2629 г), получая светло-голубую гетерогенную смесь. Из реакционного сосуда откачивали воздух и трижды продували кислородом (99,999%), затем помещали в водяную баню с температурой, поддерживаемой между 75 ° C и 80 ° C, и оставляли для перемешивания в течение приблизительно 164 часов. В ходе реакции отмечали множественные изменения цвета, которые записывались в следующем порядке: светло-синий, мутно-зеленый, светло-коричневый и темно-коричневый / черный. В конце реакции твердый катализатор не выделялся.Ежедневные образцы реакционной смеси (1 мл) экстрагировали и переносили пипеткой в 250-мл химический стакан, содержащий деионизированную воду (99 мл), и перемешивали. Аликвоту полученного водного раствора (1,5 мл) подвергали анализу ЖХ-УФ и ЖХ / МС. После отбора образцов систему вакуумировали и трижды продували газообразным кислородом.
2.7. Каталитическое окисление NMP в атмосфере азота (контроль)
Реакцию проводили в тех же условиях, что описаны ранее в разделе 2.6 за исключением того, что одно сопло трехгорлового RBF было заполнено азотом (99,999%) вместо кислорода.
2,8. Анализ методом жидкостной хроматографии / ультрафиолетового обнаружения (ЖХ / УФ)
Стандарты готовили следующим образом: 1 мл стандартного раствора (1 М) переносили в мерную колбу на 100 мл, добавляли 90 мл воды, перемешивали на вортексе в течение 5 секунд и доводят до объема водой до получения 0,01 М раствора. ЖХ-УФ-анализ проводили с использованием Thermo Fisher Scientific Dionex Ultimate 3000 RSLC (Thermo Fisher Scientific, США) в градиентном режиме.Температуру колонки устанавливали на 40 ° C, а УФ-детектор устанавливали на 230 нм. Подвижные фазы были следующими: A: вода, B: ацетонитрил с объемом впрыска 10 мкл л, и система ЖХ работала в градиентном режиме (таблица S2). Thermo Scientific Acclaim RSLC 120 C18 2,2 мкм мкм 120 Å 3,0 × 100 мм (Thermo Fisher Scientific, США) использовали в качестве колонки для ЖХ. Все данные ЖХ-УФ обрабатывали с использованием программного обеспечения Thermo Scientific Chromeleon 7.2 CDS (Thermo Fisher Scientific, США).
2.9. Анализ жидкостной хроматографии / масс-спектрометрии (ЖХ / МС)
Жидкостная хроматография / масс-спектрометрический анализ проводился с использованием Micro-LC Dionex RLSC nano Ultimate 3000, адаптированного с микропотоком, соединенным с LTQ-XL-Orbitrap XL (Thermo Fisher Scientific) масс-спектрометр. Был использован тот же градиент, что и в таблице S1, за исключением добавления кислотного модификатора (муравьиная кислота 0,01% (об. / Об.)) Как к подвижным фазам, так и к колонке для микроЖХ Acclaim RSLC 120 C18 2,2 мкм м 120 Å1,0 × 50 мм (Thermo Fisher Scientific) использовали при постоянном расходе 45 мк л / мин.Ионизация осуществлялась электрораспылением (ESI) в режиме положительных ионов в диапазоне масс 50–200 Да. Условия ESI были следующими: напряжение ионного распыления: 4,6 (В), температура капилляров: 280 ° C, поток газа в оболочке: 20 (произв. Ед.), Поток вспомогательного газа: 8 (усл. Ед.), Энергия столкновения (для диссоциации, вызванной столкновением (CID), MSn ) режим линейного нарастания от 15 до 50 (В) и режим массового разрешения IT-FT: 30 000 разрешающей способности (RP). Масс-спектры обрабатывали с помощью Xcalibur версии 2.2 (Thermo Fisher Scientific).
2.10. Анализ дейтериевого обмена
Анализ дейтериевого обмена проводили с использованием той же платформы ЖХ, что и в разделе 2.8. D 2 O + 0,01% муравьиной кислоты (об. / Об.) Использовали в качестве подвижной фазы A.
3. Результаты и обсуждение
3.1. Оценка изменения pH NMP в стандартных рабочих условиях
Стабильность pH NMP, используемого в процессе фотолитографии, сначала наблюдалась в течение периода времени при стандартных рабочих условиях, в которых химическое вещество подвергается воздействию воздуха. Значение pH оставалось почти постоянным в диапазоне от 10,39 до 9,69 в течение 144 часов. Через 168 часов NMP подвергали воздействию 328 незавершенных пластин (WIP) в течение 48 часов при 80 ° C, что привело к быстрому изменению pH с 9.От 69 до 6,82 (рисунок 2 (а)). Учитывая наблюдаемую стабильность pH NMP при стандартной рабочей температуре 80 ° C, можно сделать вывод, что изменение pH было результатом неизвестного взаимодействия между NMP и материалами на пластине, такими как непрореагировавший фоторезист или переходные металлы из построенные электромагнитные элементы.
3.2. Анализ ICP-OES NMP в инертных условиях эксплуатации
Растворение элементов с поверхности пластин WIP во время процесса фотолитографии было подтверждено с помощью анализа ICP-OES для наблюдения за изменением содержания элементов в NMP в течение его срока службы. в процессе изготовления (рис. 2 (б)).
В течение примерно трех месяцев наблюдалось устойчивое увеличение концентрации кобальта, растворенного в NMP, в то время как концентрация остальных исследованных элементов увеличивалась лишь относительно незначительно за тот же период. PH NMP во время этого эксперимента показал немедленное быстрое снижение с pH 11,28 до 7,10 в течение периода 144 часов в процессе изготовления с последующим более медленным снижением до pH 5,65 после периода 552 часов. После этого начального периода быстрого снижения pH система стала более стабильной с относительно низкой скоростью снижения pH в течение оставшейся части срока службы NMP в процессе изготовления с минимумом pH 4.83 наблюдается через 2328 ч. На основании этих результатов существует четкая корреляция между сродством к растворению кобальта и pH NMP. Высокие уровни кобальта наблюдались в растворителе после воздействия на 15000 пластин WIP, в то время как было показано, что pH NMP быстро снижается за относительно короткий период инициирования. Это снижение pH в корреляции с повышенной концентрацией переходных металлов, растворенных в NMP с течением времени, согласуется с консенсусом в современной литературе о том, что кислая среда способствует растворению переходных металлов [17, 18].Более того, хотя скорость растворения кобальта, по-видимому, преобладает по сравнению с другими металлами, отслеживаемыми с помощью анализа ICP-OES, в настоящее время нет понимания роли чисто органической среды в механизме растворения таких металлов; таким образом, причина предпочтительной сольватации кобальта неизвестна. Однако кинетика и механизм растворения кобальта широко изучались в кислых водных средах и в присутствии органических добавок [19–21]. В таких кислых водных условиях растворение кобальта и других переходных металлов происходит за счет взаимодействия центров оксида металла с ионами H + и / или парами анионов H — с органическими добавками, ускоряющими процесс за счет образования комплексов с центрами металла.Это комбинированное исследование с использованием анализа ICP-OES и измерения pH позволило глубже понять источник подкисления в системе. Учитывая, что в этих испытаниях ICP-OES / pH использовался азотный покров, эффекты воздействия с воздуха, такие как чрезмерное количество воды и содержание CO 2 [14], можно не учитывать; следовательно, подкисление химической среды было чисто феноменом взаимодействия NMP-пластина.
3.3. pH-анализ деградации NMP в присутствии кобальта
При значительном количестве кобальта, растворенного NMP во время экспериментов ICP-OES, затем был использован мелкомасштабный мониторинг для наблюдения за ролью кобальта в снижении pH NMP.Чтобы избежать воздействия других материалов пластины WIP, кобальт был суспендирован на стандартной подложке из цеолита Y ионообменного типа и помещен в NMP в стандартных рабочих условиях для фотолитографии в присутствии как богатой кислородом, так и богатой азотом сред. В условиях, богатых кислородом, наблюдался период быстрого снижения pH в течение первых 44 часов с падением pH системы с 8,95 до 4,48. За этим последовал непрерывный период снижения pH, но с гораздо меньшей скоростью с минимумом pH 3.47 наблюдается через 164 ч. Для сравнения, в условиях, богатых азотом, этот начальный период быстрого снижения pH практически исчез с падением pH с 8,06 до 6,71 в течение первых 44 часов. Кроме того, pH NMP в условиях, богатых азотом, оставался стабильным в диапазоне pH от 6,8 до 6,4 до конца периода реакции (рис. 2 (c)). Следовательно, можно видеть, что в богатой кислородом среде pH NMP быстро снижается до кислого pH за короткий период времени. Напротив, когда та же система была насыщена азотом, первоначальное быстрое снижение pH NMP было почти устранено.Кроме того, скорость снижения pH значительно подавлялась NMP со стабилизированным pH в слабокислом диапазоне pH от 6,8 до 6,4. Это также наблюдалось в экспериментах ICP-OES, проводившихся до начала фотолитографии, в которых pH NMP, использованного на этом этапе изготовления, оставался стабильным в течение нескольких месяцев, достигая минимального значения pH 4,83 примерно через три месяца и воздействия 15000 пластин WIP. Затем был сделан вывод, что кислород играет решающую роль в разложении NMP, приводящем к наблюдаемому кислому раствору, что побудило использовать методы ЖХ / УФ и ЖХ / МС для оценки механизма подкисления на молекулярном уровне.
3.4. Оценка каталитического окисления с помощью LC / UV
После воздействия цеолита Co-Na Y-52 NMP в основном разложился до относительного времени удерживания (RRT) 0,92 (10,5%), NMS (15%) и RRT 1,16 (11,4%). ) и другие второстепенные продукты разложения при RRT 0,27 (2,5%), RRT 1,52 (2,1) и RRT 1,82 (1,5%), как показано на рисунке 3 (b). Разложение было существенно подавлено в атмосфере азота с RRT 0,92 (~ 4,3%) и NMS (2,8%), являющимися основным продуктом разложения, как показано на Фигуре 3 (c). Идентичность NMS была подтверждена с использованием продуктов разложения NMP и смеси стандартных растворов технологических примесей, как показано на рисунке 3 (f).Сводка профиля примесей представлена в таблице 1.
| |||||||||||||||||||||||||||||||||||||||||||
RT: время удерживания Ncc, RRT: отн. . | |||||||||||||||||||||||||||||||||||||||||||
Основываясь на предыдущей литературе Паттона и Драго [10], мы предположили, что продукты окислительной деградации NMP были источником наблюдаемого снижения pH, при котором кобальт мог взаимодействовать с молекулярным кислородом в триплетном состоянии в системе с образованием реактивного металл-пероксогруппы. Эти реакционноспособные частицы могут быть источником радикального окислительного механизма класса IV с NMP [11, 12] из-за восприимчивости α -углеродного положения лактамных соединений к отщеплению водорода [10, 22–24].Чтобы проверить эту гипотезу, мы использовали LC / -UV для количественной оценки изменений уровней NMP во время его воздействия кобальтом в условиях мелкомасштабной реакции. Наш аналитический метод был разработан для обнаружения и количественной оценки известных примесей / продуктов разложения NMP, включая NMS, как указано различными авторами [10, 15-17], а также сукцинимид и пирролидин-2-он (2P), которые наблюдались с помощью Friesen et al. [25]. Профили ЖК, представленные на рисунке 3, показывают, что только NMS наблюдалась в исследуемых экспериментальных условиях (рисунок 3 (b)).Образование NMS наблюдалось в предыдущих исследованиях [15-17] и согласуется с окислительным путем, описанным Драго [12]. Этот рисунок также показывает, что неидентифицированные (неизвестные) продукты разложения (RRT 0,92 и RRT 1,16) образовывались в больших количествах. При замене газообразного кислорода инертным азотом (рис. 3 (c)) реакция окислительного разложения была значительно подавлена, показывая, что основные продукты разложения (RRT 0,92) и NMS были обнаружены при более низкой концентрации по сравнению с окислением с помощью кислорода.Предлагаемая хроматографическая платформа является подходящим методом определения стабильности, поскольку все известные технологические примеси и основные продукты разложения хорошо разделены.
3.5. Масс-спектрометрическая характеристика
Чтобы охарактеризовать неизвестные продукты разложения, на обоих образцах был проведен масс-спектрометрический анализ. В таблице 2 приведены все полученные данные МС, включая точные измерения массы, фрагментацию и анализ дейтериевого обмена.
На основании полученных данных (рисунки 4 и 5) были предложены возможные структуры, а также предложен путь химического разложения, как показано на рисунке 6. Чтобы идентифицировать как можно больше продуктов реакции, как ESI-MS, так и MS / МС-эксперименты проводились в режимах положительных ионов с диапазоном сканирования 50–250 Да. NMP был обнаружен в режиме положительных ионов на высоте м / z 100,0759 Да с точностью измерения массы 1,0 ppm (рисунок 4 (b)). MS 2 родительского на 100.07 Da показал основной дочерний ион на m / z 58 Da и второстепенный ион-продукт на m / z 72 Da (Рисунок 4 (b)). Одним из основных продуктов разложения, идентифицированных при ЖХ-УФ, был N-метилсукцинимид (НМС) (RRT 0,63) (рис. 3 (а)), это было подтверждено ЖХ / МС в режиме положительных ионов при м / z = 114,0552 Да с погрешностью по массе 2,1 ppm (рис. 4 (c)), главный дочерний ион на высоте м / z = 86 Да, и никаких обменных протонов не наблюдалось (рис. 4 (c)).Идентификация также была подтверждена с помощью стандарта. Основной продукт разложения при RRT 0,92 показал родительский ион при m / z 116,0708 Да и ион-продукт при m / z 73 Да (рис. 4 (d)). В обзоре Von Sonntag и Schuchmann [26] показано, что при окислении органических соединений в водной фазе может происходить одновременное образование гидроксикарбонильных и дикарбоновых соединений. Более того, Friesen et al. [25] также наблюдали одновременное образование NMS (дикарбонила) и 5-гидрокси-N-метилпирролидона (5-HNMP).Таким образом, образование 5-HNMP было предложено для неизвестного продукта разложения при RRT 0,92 на основании точности определения массы (1,46 ppm), хорошего согласия с моделями фрагментации (потеря CH 2 CO) и данных анализа обмена дейтерия в виде одного протона наблюдалось. Идентификация также была подтверждена с помощью стандарта. Что касается RRT 1.16, наблюдалась такая же моноизотопная протонированная масса, что и NMS ( m / z 114.0553 Да) (Рисунок 5 (a)). Аткинсон [27] показал, что 1-формил-2-пирролидон (FP) является важным первичным продуктом реакции окисления NMP в газовой фазе.Моноизотопная молекулярная масса FP составляет 113,0471 Да (точность определения массы 2,7 ppm), что соответствует молекулярной массе NMS. Анализ MS 2 выявил образование одного доминирующего дочернего иона при m / z 98 Да. FP не имеется в продаже и не может быть подтвержден с помощью стандарта. Основной путь фрагментации FP включает потерю воды. Такая фрагментация приводит к образованию главного дочернего иона на m / z = 98 Да, таким образом подтверждая «предварительную» идентичность FP.Следовательно, вероятно, что FP может быть неидентифицированным первичным продуктом реакции, обнаруженным в LC-UV при RRT 1,16. Образование соединения, обнаруженное на высоте м / z 118,0865 Да (RRT 0,27), может соответствовать гидролизу NMP до N-метил-4-аминобутановой кислоты (NM4ABA) в остаточной воде, содержащейся в NMP (Рисунок 4 (а)). Присутствие предложенной молекулы было предположено Zegota et al. [28] и подтверждено дальнейшими исследованиями [29]. Наконец, Драго и Райли [30] охарактеризовали NM4ABA во время окисления N-алкиламидов в водной фазе.К сожалению, коммерческие стандарты NM4ABA недоступны; следовательно, идентификация была основана исключительно на данных MS. Два протона, способных обмениваться дейтерием, наблюдались вместе с дочерними ионами при m / z = 100 и 88 Да, соответственно, и точность определения массы 2,2 ppm. Следовательно, вероятно, что пик при RRT 0,27 Да соответствует NM4ABA. Другие незначительные примеси, наблюдаемые при RRT 1,33, RRT 1,52 и RRT 1,82, показали путь окислительного разложения и не наблюдались в атмосфере азота.Поскольку идентификация незначительных примесей не является основной целью данного исследования, стандартное подтверждение не проводилось. RRT 1.82 был предложен как N-этилпирролидон (NEP), хорошо известная технологическая примесь. Протонированная моноизотопная ( м / z 114,0915 Да) масса согласовывалась с предложенной структурой с точностью определения массы 1,8 ppm (рисунок 5 (b)). MS 2 показала основной фрагмент на высоте м / z 100, соответствующий потере CH 3 . Эксперименты по обмену дейтерия дополнительно подтвердили предложенную структуру, поскольку обменных протонов не наблюдалось.Предлагаемый NEP следует путем окислительной деградации с образованием RRT 1,33 (разделенный пик) 1- (2-гидроксиэтил) -2-пирролидона (2-AP) на м / z 128,0710 Да (Рисунок 5 (d)) и RRT 1,52 (1-ацетил-2-пирролидон, 2-NEP) на м / z 130,0867 Да (рисунок 5 (c)). Обе деградации показали хорошую точность определения массы по сравнению с предложенными структурами (3,02 и 3,73 частей на миллион, соответственно). Фрагментация показала потерю CO (28 Да) для RRT 1,33 и потерю воды (18 Да) для RRT 1.52, а обменные протоны дополнительно подтвердили предложенные структуры. 3,6. Предлагаемые химические механизмы разложенияНа основании идентифицированных продуктов реакции мы предлагаем механизм окисления / гидролиза NMP в неводной фазе в условиях кислорода и кобальт-натриевый Y-цеолитный катализатор (рисунок 6 (а)) в качестве основного разложения. путь. Это окисление частично останавливается с помощью инертной атмосферы. Реакция может протекать тремя разными путями (рис. 6 (а)).Путь I: Атака OH . радикалов протекает через отрыв водорода от группы CH 2 , смежной с аминогруппой NMP [17]. Это приводит к образованию алкильного радикала, который реагирует с растворенным кислородом с образованием пероксирадикала. По аналогии с поведением в водной фазе других пероксирадикалов [25, 27], этот радикал может само реагировать с образованием тетроксида, который быстро разлагается до NMS. Путь II: Атака OH . радикалов происходит посредством отщепления водорода от метильной группы NMP.Этот путь приводит к образованию другого алкильного радикала, который затем реагирует с растворенным кислородом с образованием пероксирадикала. Этот пероксирадикал может само реагировать с образованием тетроксида, который быстро разлагается, что приводит к образованию FP. Анализ LC-UV подтвердил важность этого пути, поскольку FP составлял 11,4% деградации NMP. Этот второй путь ранее упоминался Friesen et al. [25] только кратко, и насколько нам известно, наше исследование является первым экспериментальным доказательством этого пути.Путь III: этот путь является более умозрительным, чем пути I и II. Аналогичный путь был ранее идентифицирован Horikoshi et al. [31–33], которые провели ОН-окисление 2P в водной фазе в присутствии твердой фазы TiO 2 . В наших условиях, т.е. в отсутствие частиц, этого пути не было. Однако этот путь следует учитывать в реальных тропосферных условиях, поскольку в водных каплях присутствуют частицы твердой фазы различного происхождения. Это происходит по механизму раскрытия кольца, что приводит к образованию NM4ABA.Мы также предложили путь разложения незначительных примесей (рис. 6 (б)). Химия разложения в этом случае была аналогична предложенной для пути II. 4. ЗаключениеЭто исследование подтвердило нашу гипотезу о том, что окисление NMP присутствует в процессе фотолитографии в текущих рабочих условиях удаления фоторезиста. Впервые pH NMP отслеживался на всем пути окислительного разложения NMP как в производственных, так и в экспериментальных процессах.Было продемонстрировано, что окисление коррелирует со снижением pH и что его можно остановить с помощью инертной атмосферы азота. Подкисление химической среды во время стадии отрыва коррелировало с растворением слоев переходного металла, осажденных на поверхности подложки пластины перед стадией отрыва. Мы определили pH как ключевую входную переменную процесса (KPIV) в фотолитографии и предлагаем внедрить строгие процессы для измерения и контроля pH NMP, чтобы избежать нежелательных коррозионных дефектов в конструкции пластины.Использование этого нового многоплатформенного аналитического подхода будет большим преимуществом для инженеров-технологов при оценке проблемных областей на начальной стадии фотолитографии. Следовательно, это исследование имеет значение для разработки процессов изготовления микроэлектроники, оптимизации критических этапов сборки пластины и демонстрирует необходимость большего контроля в отношении качества, стабильности и устойчивости промышленно приемлемых материалов, используемых в процессе фотолитографии. Аббревиатуры
Доступность данныхНеобработанные данные ЖХ / УФ, ИСП-ОЭС и ЖХ / МС, использованные для подтверждения результатов этого исследования, можно получить у соответствующего автора по запросу. Конфликт интересовВсе авторы заявили об отсутствии конфликта интересов. БлагодарностиАвторы благодарны техническому персоналу Центра масс-спектрометрии Ольстерского университета, который предоставил экспертные знания, которые во многом помогли исследованию. Эта работа была поддержана Seagate Technology PLC, Лондондерри, Великобритания. Дополнительные материалыРисунок S1: анализ сфокусированным ионным пучком (FIB) стека контактного считывателя, погруженного в NMP через 400, 980 и 1800 секунд, с использованием FEI FIB200TEM. Рисунок S2: экспериментальный план, используемый для каталитического окисления NMP в кислороде. По материалам Victor et al., 2015. Таблица S1: Составы калибровочных стандартных растворов ICP-OES. Таблица S2: Профиль градиента ЖХ / УФ и ЖХ / МС. (Дополнительные материалы) Анализ продуктивного поведения учащихся при обучении с использованием немедленной корректирующей обратной связи в смешанной среде обучения… • Начальный словарь / таксономия для успеваемости — Оценка зачисления — Удержание курса / отсев — Оценка за курс — Диапазон оценок за курс (например, AC, DF) — Успешен / не пройден курс — Оценка за экзамен -GPA -Оценка — Сохранение программы / отсев — Неуказанная успеваемость -Не применимо -Другое [7, 22, 46, 47, 62, 63, 71-73, 83, 87, 89, 94, 104, 107, 147, 149, 166, 172, 173, 177, 184, 186, 206, 208, 215, 218, 220, 231, 232, 244, 279, 296, 299, 315, 319, 327, 329, 337, 341, 358, 359, 373, 374, 407, 411, 424] Экзамен / Оценка или балл по окончании теста [9,10,21,24,33,35,52,59, 67, 68,77,80,81,85,90,96,109,114,116,127,136,152,162,163,169,193,195,199,202,205,214,217,224,233,238,241,270,274,275,277,384,224,233,238,241,270,274,275,277,384,246,360,360 или курс, курс, курс, курс [1] 14, 19, 21, 26, 27, 33, 34, 52, 57, 60, 64, 67-69, 74, 75, 78, 86, 93, 103, 105, 115, 118, 119, 122, 126- 128, 133, 138, 141, 142, 144, 146, 158, 159, 171, 173-175, 183, 187, 197, 200, 203, 210, 237, 238, 240, 248, 250, 268, 272, 273, 285, 286, 292, 303, 304 [52,54,59,60,65,82,92,105,106,123,124,127,143,151,165,179,187,188,195,209,216,223,228,239,242,251,256,264,286,309,310,352,364,365,376,383,389,395,399,408,415,16,75,16,75 или 3,89,395,399,408,415,16,75,16,75,15 , 97.100.101.117.125.132.134.187.199.229.234.245.247.271.276.280.281.288.290.294.295.298.300.328.334.342.343.367.371.392.410] курс удерживания / Выпадение [42,74,91,153,172,178,192,196,212,213,218,220,225,257,261,262,388,398,403,422] ГПД, или средний балл Диапазон (включая CGPA, SGPA) [4, 12, 28-32, 36, 37, 64, 66, 73, 113, 129, 135, 137 , 140, 149, 167, 181, 189, 206, 211, 218, 240, 249, 255, 263, 265, 266, 268, 291, 297, 322, 325, 339, 344, 345, 366, 385, 390 , 402, 405, 413] Диапазон оценок курса (e.g., AB / CF, прошел / не прошел) [17, 20, 38, 52, 58, 61, 77, 95, 108, 110, 111, 121, 126, 130, 139, 172, 174, 182, 194, 207, 222, 226, 227, 238, 254, 257, 258, 260, 267, 278, 289, 293, 316, 317, 323, 331, 332, 361, 363, 370, 379-381, 386, 402, 403, 406, 418, 421] Приобретение знаний [23,156,164,192,201,270,401,419] □ Определите факторы, используемые для прогнозирования. Опишите их так подробно, чтобы их понял читатель, не знакомый с вашим конкретным контекстом. … Развитие исследований в области математического образования% PDF-1.4 % 1 0 объект > эндобдж 5 0 obj > эндобдж 2 0 obj > эндобдж 3 0 obj > эндобдж 4 0 obj > поток Изменены следствия теоремы.Теорема Чевы и измененная. Зачем все это нужноКласс: 9 Задачи урока:
Задачи урока:
Тип урока: урок по обобщению и систематизации знаний. Оборудование: карточки для коллективной работы на уроке по данной теме, индивидуальные карточки для самостоятельной работы, компьютер, мультимедийный проектор, экран. На занятияхI этап. Организационный момент (1 мин.)Учитель разъясняет тему и цель урока. Этап II. Обновление базовых знаний и навыков (10 мин.)Учитель: На уроке мы вспоминаем теоремы Менелая и Чевы, чтобы успешно перейти к решению задач.Давайте вместе с вами посмотрим на экран. Для какой теоремы дана эта цифра? (Теорема Менелая). Постарайтесь четко сформулировать теорему. Рисунок 1 Пусть точка A 1 лежит на стороне BC треугольника ABC, точка C 1 — на стороне AB, точка B 1 — на продолжении стороны AC за точку C. Точки A 1, B 1 и C 1 лежат на одной прямой, если и только если выполняется равенство Учитель: Давайте вместе посмотрим на следующий рисунок. Сформулируйте теорему для этого рисунка. Линия AD пересекает две стороны и является продолжением третьей стороны треугольника BMC. По теореме Менелая Линия MB пересекает две стороны и является продолжением третьей стороны треугольника ADC. По теореме Менелая Учитель: Какой теореме соответствует цифра? (Теорема Чевы). Сформулируйте теорему. Пусть в треугольнике ABC точка A 1 лежит на стороне BC, точка B 1 — на стороне AC, точка C 1 — на стороне AB.Отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство III этап. Решать проблемы. (22 мин.)Класс делится на 3 команды, каждая из которых получает карточку с двумя разными задачами. Дается время на решение, затем на экране отображается … Используя готовые чертежи задач, представители команд поочередно объясняют свое решение. Каждое объяснение сопровождается обсуждением, ответами на вопросы и проверкой правильности решения на экране.В обсуждении принимают участие все члены команды. Чем активнее команда, тем выше ее оценивают при подведении итогов. Карточка 1. 1. В треугольнике ABC на стороне BC берется точка N так, чтобы NC = 3BN; на продолжении стороны AC за точку A берется точка M так, чтобы MA = AC. Прямая MN пересекает сторону AB в точке F. Найдите отношение .2. Докажите, что медианы треугольника пересекаются в одной точке. Решение 1 По условию задачи MA = AC, NC = 3BN.Пусть MA = AC = b, BN = k, NC = 3k. Прямая MN пересекает две стороны треугольника ABC и продолжение третьей. По теореме Менелая Ответ: Проба 2 Пусть AM 1, BM 2, CM 3 — медианы треугольника ABC. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что Тогда по (обратной) теореме Чевы отрезки AM 1, BM 2 и CM 3 пересекаются в одной точке. У нас: Итак, доказано, что медианы треугольника пересекаются в одной точке. Карточка 2. 1. На стороне PQ треугольника PQR берется точка N, а на стороне PR — точка L, а NQ = LR. Пересечение отрезков QL и NR делит QL в соотношении m: n, считая от точки Q. Найдите 2. Докажите, что биссектрисы треугольника пересекаются в одной точке. Решение 1 По условию NQ = LR, Пусть NA = LR = a, QF = км, LF = kn.Линия NR пересекает две стороны треугольника PQL и продолжение третьей. По теореме Менелая Ответ: Проба 2 Покажем, что Тогда по (обратной) теореме Чевы AL 1, BL 2, CL 3 пересекаются в одной точке. По свойству биссектрис треугольника Почленно умножая полученные равенства, получаем Для биссектрис треугольника выполняется равенство Чевы, следовательно, они пересекаются в одной точке. Карточка 3. 1. В треугольнике ABC AD — это медиана, точка O — это середина медианы. Прямая BO пересекает сторону AC в точке K. В каком отношении точка K делит AC, считая от точки A? 2. Докажите, что если окружность вписана в треугольник, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке. Решение 1 Пусть BD = DC = a, AO = OD = m.Линия BK пересекает две стороны и является продолжением третьей стороны треугольника АЦП. По теореме Менелая Ответ: Проба 2 Пусть A 1, B 1 и C 1 — точки касания вписанной окружности треугольника ABC. Чтобы доказать, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы: Используя свойство касательных, проведенных к окружности из одной точки, введем обозначения: C 1 B = BA 1 = x, AC 1 = CB 1 = y, BA 1 = AC 1 = z. Равенство Чевы выполняется, что означает, что биссектрисы треугольника пересекаются в одной точке. IV этап. Решение задач (самостоятельная работа) (8 мин.)Учитель: Работа команд окончена и теперь мы приступим к самостоятельной работе над индивидуальными карточками по 2 вариантам. Материалы к уроку для самостоятельной работы студентов Вариант 1. В треугольнике ABC, площадь которого равна 6, на стороне AB берется точка K, разделив эту сторону в соотношении AK: BK = 2: 3, а на стороне AB сторона AC — точка L, делящая AC в соотношении AL: LC = 5: 3.Точка Q пересечения прямых SK и BL удалена от линии AB на некоторое расстояние. Найдите длину стороны AB. (Ответ: 4.) Вариант 2. На стороне переменного тока в треугольнике ABC берется точка K. АК = 1, КС = 3. Со стороны АВ берется точка L. AL: LВ = 2: 3, Q — точка пересечения прямых BK и CL. Найти длину высоты треугольника ABC, выпавшего из вершины B. (ответ: 1.5.) Работы переданы на проверку учителю. Этап V. Подведение итогов (2 мин.)Ошибки проанализированы, оригинальные ответы и комментарии отмечены. Подведены итоги работы каждой команды и выставлены оценки. VI этап. Домашнее задание (1 мин.)Домашнее задание состоит из задач № 11, 12 с. 289-290, № 10, с. 301. Заключительное слово преподавателя (1 мин.).Сегодня вы услышали математические речи друг друга и оценили свои способности. В будущем мы будем применять такие обсуждения, чтобы лучше понять предмет.Аргументы на уроке дружили с фактами, а теория — с практикой. Спасибо вам всем. Литература:
ТЕОРЕМА ЧЕВЫ И МЕНЕЛЫ Теорема Чевы Большинство замечательных точек треугольника можно получить, используя следующую процедуру. Пусть существует какое-то правило, по которому мы можем выбрать некоторую точку A 1 , на стороне BC (или ее продолжении) треугольника ABC (например, выберите середину этой стороны).Затем строим аналогичные точки B 1, C 1 на двух других сторонах треугольника (в нашем примере еще две середины сторон). Если правило выбора выполнено успешно, то прямые AA 1, BB 1, CC 1 пересекаются в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачный, так как медианы треугольника пересекаются в точках один пункт). Я хотел бы иметь какой-нибудь общий метод, который позволяет по положению точек на сторонах треугольника определять, пересекаются ли соответствующие тройки прямых в одной точке или нет. Универсальное условие, которое «закрыло» эту проблему, было найдено в 1678 году итальянским инженером Джованни Чева . Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжения), называются шевианами, если они пересекаются в одной точке. Есть два варианта расположения шевианов. В одном варианте осуществления точка пересечения является внутренним, а концы шевианов лежат на сторонах треугольника.Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. Рисунки). Теорема 3. ( Прямая теорема Чевы) В произвольном треугольнике ABC на сторонах BC, CA, AB или их продолжениях берутся точки A соответственно 1 , ИН 1 , ИЗ 1 такие, что прямые AA 1 , BB 1 , SS 1 пересекаются в некоторой общей точке, затем . Обоснование: есть несколько оригинальных доказательств теоремы Чевы; мы рассмотрим доказательство, основанное на двукратном применении теоремы Менелая. Впервые выпишем соотношение теоремы Менелая для треугольника ABB 1 и секущей CC 1 (точка пересечения шевиана обозначена Z): , г. и второй раз для треугольника B 1 BC и секанс AA 1 : . Умножая эти два отношения и делая необходимые сокращения, мы получаем соотношение, содержащееся в формулировке теоремы. Теорема 4. (обратная теорема Чевы) . Если для выбранных по сторонам треугольника ABC или их продолжения точек А 1 , ИН 1 и С 1 Чева Состояние выполнено: , г. затем прямо AA 1 , г. BB 1 и CC 1 пересекаются в одной точке . Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая. Рассмотрим примеры применения прямой и обратной теорем Чевы. Пример 3. Докажите, что медианы треугольника пересекаются в одной точке. Решение. Рассмотрим отношение для вершин треугольника и середин его сторон. Очевидно, что в каждой дроби в числителе и знаменателе есть равные отрезки, поэтому все эти дроби равны единице.Следовательно, соотношение Чевы выполняется, следовательно, по обратной теореме медианы пересекаются в одной точке. Теорема (теорема Шевы) … Пусть точки лежат на сторонах и треугольнике соответственно. Пусть отрезки и пересекаются в одной точке. Затем (обойти треугольник по часовой стрелке). Доказательства. Обозначим через точку пересечения отрезков прямой и … Опустим от точек и перпендикуляров к прямой, прежде чем пересекать ее в точках и соответственно (см. Рисунок). Поскольку треугольники и имеют общую сторону, то их площади называются высотами, проведенными к этой стороне, то есть: Последнее равенство верно, поскольку прямоугольные треугольники и имеют одинаковый острый угол. Аналогично получаем и Умножим эти три равенства: q.E.D. О медианах: 1. Поместите единичные массы в вершины треугольника ABC. Кстати, сразу следует, что они делятся перекрестком в соотношении 2: 1.Поскольку масса центра масс точек A и B равна 2, а масса точки C равна 1, следовательно, общий центр масс согласно теореме о пропорции будет делить медианное значение в соотношении 2/1. Большое спасибо, четко сказано, думаю, будет не лишним представить документ методами массовой геометрии, например: 2. Теорема ЧевыОтрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется cheviana … Таким образом, если в треугольнике ABC Х , Y и Z — точки лежащие по бокам BC , CA , AB соответственно сегменты AX , BY , CZ являются чевианцами.Этот термин происходит от имени итальянского математика Джованни Чева, который опубликовал следующую очень полезную теорему в 1678 году: Теорема 1,21. Если три шевиана AX, BY, CZ (по одной из каждой вершины) треугольника ABC конкурируют, то | BX || XC | · | CY || YA | · | AZ || ZB | = 1 . Когда мы говорим, что три линии (или сегмента) конкурентоспособны , то имеется в виду, что все они проходят через одну точку, которую мы обозначим P … Чтобы доказать теорему Чевы, напомним, что площади треугольников одинаковой высоты пропорциональны основаниям треугольников. Ссылаясь на рисунок 3, мы имеем: | BX || XC | = SABXSAXC = SPBXSPXC = SABX − SPBXSAXC − SPXC = SABPSCAP. Аналогично | CY || YA | = SBCPSABP, | AZ || ZB | = SCAPSBCP. Теперь, если мы их умножим, мы получим | BX || XC | · | CY || YA | · | AZ || ZB | = SABPSCAP · SBCPSABP · SCAPSBCP = 1 . Верна и обратная теорема к этой теореме: Теорема 1.22. Если три чевиана AX, BY, CZ удовлетворяют соотношению | BX || XC | · | CY || YA | · | AZ || ZB | = 1 , то они конкурентоспособны . Чтобы показать это, предположим, что первые два Чевиана пересекаются в точке P , как и прежде, и третья шевиана, проходящая через точку P , составит CZ ′ … Тогда по теореме 1.21 | BX || XC | · | CY || YA | · | AZ ′ || Z′B | = 1 . А по предположению | BX || XC | · | CY || YA | · | AZ || ZB | = 1 . Следовательно, | AZ || ZB | = | AZ ′ || Z′B | , точка Z ′ совпадает с точкой Z , и мы доказали, что отрезки AX , BY и CZ соревновательные (стр. 54 и, стр. 48, 317). Теорема Менелая или теорема о полном четырехугольнике известна со времен Древней Греции. Свое название он получил в честь своего автора — древнегреческого математика и астронома Менелай Александрийский (ок.100 г. н.э.). Эта теорема очень красивая и простая, но, к сожалению, в современном школьном курсе ей не уделяется должного внимания. А между тем во многих случаях он помогает очень легко и изящно решать довольно сложные геометрические задачи. Теорема 1 (теорема Менелая) … Пусть ∆ABC пересекает прямая, которая не параллельна стороне AB и пересекает две ее стороны AC и BC в точках F и E соответственно, а прямая AB в точка D (рис.1) , , затем A F FC * CE EB * BD DA = 1 Примечание. Чтобы легко запомнить эту формулу, вы можете использовать следующее правило: двигайтесь по контуру треугольника от вершины к точке пересечения с прямой линией и от точки пересечения к следующей вершине. Доказательства. Из вершин A, B, C треугольника проведите соответственно три параллельные линии, пока они не пересекутся с секущей линией. Получаем три пары одинаковых треугольников (знак сходства в двух углах). Подобие треугольников влечет следующие равенства А теперь умножаем полученные данные на равенства: Теорема доказана. Чтобы ощутить всю красоту этой теоремы, попробуем решить предложенную ниже геометрическую задачу двумя способами: с помощью вспомогательной конструкции и с помощью теорем Менелая . Цель 1. В ∆ABC биссектриса AD делит сторону BC в соотношении 2: 1. В каком соотношении медиана CE делит эту биссектрису? Решение. Использование вспомогательной конструкции: Пусть S — точка пересечения биссектрисы AD и медианы CE.Построим ∆ASB до параллелограмма ASBK. (рис.2) Очевидно SE = EK, так как пересечение параллелограмма делит диагонали пополам. Рассмотрим теперь треугольники ∆CBK и ∆CDS. Нетрудно заметить, что они похожи (признак сходства в двух углах: и как внутренние односторонние углы с параллельными прямыми AD и KB и секущей CB). Подобие треугольника подразумевает следующее: Используя условие, получаем: CB CD = CD + DB CD = CD + 2CD CB = 3CD CD = 3 Теперь обратите внимание, что KB = AS, как противоположные стороны параллелограмма.Тогда AS SD = KB SD = CB CD = 3 Использование теоремы Менелая. Рассмотрим ∆ABD и применим к нему теорему Менелая (прямая, проходящая через точки C, S, E, является секущей): BE EA * AS SD * DC CB = 1 По условию теоремы у нас BE / EA = 1, так как CE — медиана, а DC / CB = 1/3, как мы рассчитали ранее. 1 * АС СД * 1 3 = 1 Отсюда получаем AS / SD = 3 На первый взгляд оба решения достаточно компактны и примерно равноценны.Однако идея дополнительной конструкции для школьников часто оказывается очень сложной и совсем не очевидной, тогда как, зная теорему Менелая, ему нужно только правильно ее применить. Рассмотрим другую задачу, в которой теорема Менелая работает очень элегантно. Цель 2. На сторонах AB и BC ∆ABC даны точки M и N соответственно такие, что выполняются следующие равенства AM MB = CN NA = 1 2 В каком соотношении точка пересечения S отрезков BN и CM делит каждый из этих отрезков (рис.3)? Решение. Рассмотрим ∆ABN. Применим теорему Менелая для этого треугольника (прямая, проходящая через точки M, S, C, является секущей) AM MB * BC SN * CN CA = 1 Из условия задачи имеем: AM MB = 1 2 NC CA = NC CN + NA = NC CN + 2NC = NC 3 NC = 1 3 Подставляем эти результаты и получаем: 1 2 * БС СН * 1 3 = 1 Отсюда BS / SN = 6.И, следовательно, точка S пересечения отрезков BN и CM делит отрезок BN в соотношении 6: 1. Рассмотрим ∆ACM. Применим теорему Менелая для этого треугольника (прямая, проходящая через точки N, S, B, является секущей): AN NC * CS SM * MB BA = 1 Из постановки задачи имеем: AN NC = 2 МБ BA = MB BM + MA = 2MA 2MA + MA = 2MB 3MA = 2 3 Подставляем эти результаты и получаем: 2 * КС СМ * 2 3 = 1 Отсюда CS / SM = 3/4 Это означает, что точка S пересечения отрезков BN и CM делит отрезок CM в соотношении 3: 4. Верна и обратная теорема Менелая. Часто это бывает даже полезнее. Это особенно хорошо работает в задачах доказательства. Часто с его помощью красиво, легко и быстро решаются даже олимпиадные задачи. Теорема 2 (обратная теорема Менелая). Пусть дан треугольник ABC и точки D, E, F принадлежат прямым BC, AC, AB соответственно (обратите внимание, что они могут лежать как на сторонах треугольника ABC, так и на их продолжениях) (рис. 4) . Тогда если AF FC * CE EB * BD DA = 1 то точки D, E, F лежат на одной прямой. Доказательства. Докажем теорему от противного. Предположим, что соотношение из условий теоремы выполнено, но точка F не лежит на прямой DE (рис. 5). Обозначим точку пересечения прямых DE и AB буквой O. Теперь применим теорему Менелая и получим: AE EC * CD DB * BO OA = 1 Но, с другой стороны, равенство BF FA = BO OA не может быть выполнен. Следовательно, соотношение из условий теоремы не может быть выполнено. Получили противоречие. Теорема доказана. Сайт, при полном или частичном копировании материала ссылка на источник обязательна. А.В. Шевкин ФМС № 2007 Теоремы Чевы и Менелая на экзамене Подробная статья «Вокруг теорем Шевы и Менелая» опубликована на нашем сайте в разделе СТАТЬИ.Он адресован учителям математики и старшеклассникам, которые заинтересованы в хороших знаниях математики. Вы можете вернуться к нему, если хотите разобраться в проблеме более подробно. В этой заметке мы предоставим краткую информацию из указанной статьи и проанализируем решения задач из сборника для подготовки к ЕГЭ-2016. Теорема Чевы Дан треугольник ABC и на его сторонах AB , BC и AC отмечены точки C 1, A 1 и B 1 соответственно (рис.1). a) Если отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке, то б) Если равенство (1) верно, то отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке. На рисунке 1 показан случай, когда отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке внутри треугольника. Это так называемый случай внутренней точки. Теорема Чевы также верна в случае внешней точки, когда одна из точек И 1, B 1 или ОТ 1 принадлежит стороне треугольника, а две другие принадлежат продолжениям треугольника. стороны треугольника.В этом случае точка пересечения отрезков AA 1, BB 1 и CC 1 лежит вне треугольника (рис. 2). Как вспомнить равноправие Чевы? Обратим внимание на технику запоминания равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении пересечения вершин треугольника ABC , начиная с точки A … Из точки A переходим в точку B , встречаем точку ИЗ 1, записываем дробь Обратите внимание, что любой отрезок, соединяющий вершину треугольника с любой точкой прямой, содержащей противоположную сторону треугольника, называется cheviana . Рассмотрим несколько способов доказательства утверждения а) теоремы Чевы для случая внутренней точки. Для доказательства теоремы Чевы необходимо доказать утверждение а) любым из предложенных ниже методов, а также доказать утверждение б).Доказательство утверждения б) проводится после первого способа доказательства утверждения а). Доказательства теоремы Чевы для случая внешней точки аналогичны. Доказательство утверждения а) теоремы Чевы с использованием теоремы о пропорциональных отрезках Пусть три чевиана A A 1, B B 1 и C C 1 пересекаются в точке Z внутри треугольника ABC . Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) на отношения отрезков, лежащих на одной прямой. Через точку IN проведите прямую линию, параллельную шевиане SS 1. Прямой AA 1 пересекает построенную линию в точке M , и прямая, проходящая через точку C и параллель AA 1, — в точке T … Через точки И и ИЗ проведем прямые параллельные чевианы BB 1. Они пересекут линию VM в точках N и R соответственно (рис.3). P по теореме о пропорциональных отрезках, имеем: , г. Тогда равенства . В параллелограммах ZСTM и ZCRB отрезки TM , СZ и ВR равны противоположным сторонам параллелограмма. Значит, . При доказательстве утверждения б) мы используем следующее утверждение. Рисунок: 3 Лемма 1. Если точки ОТ 1 и ОТ 2 делят отрезок AB внутренним (или внешним) способом в одном и том же отношении, считая от одной и той же точки, то эти точки совпадают. Докажем лемму для случая, когда точки ОТ 1 и ОТ 2 делят отрезок AB внутренне одинаково: Доказательства. Из равенства Доказательство леммы для случая, когда точки ОТ 1 и ОТ 2 делят отрезок AB внешне, проводится аналогично. Доказательство части б) теоремы Чевы Пусть теперь выполняется равенство (1). Докажем, что отрезки AA 1, BB 1 и CC 1 пересекаются в одной точке. Пусть чевианы AA 1 и BB 1 пересекаются в точке Z , проведем через эту точку отрезок CC 2 ( ИЗ 2 лежит на отрезке AB ).Тогда на основании утверждения а) получаем правильное равенство . (2) И сравнивая равенства (1) и (2), мы заключаем, что Можно доказать, что процедура записи равенства (1) не зависит от того, в какой точке и в каком направлении пересекаются вершины треугольника. Упражнение 1. Найдите длину сегмента И N на Рисунке 4, где показаны длины других сегментов. Ответ. 8. Задача 2. Chevians AM , BN , CK пересекаются в одной точке внутри треугольника ABC … Найдите отношение Ответ. P Приведем доказательство теоремы Чевы из статьи. Идея доказательства состоит в том, чтобы заменить отношения отрезков из равенства (1) на отношения отрезков, лежащих на параллельных прямых. Пусть прямые A A 1, B B 1, C C 1 пересекаются в точке O внутри треугольника ABC (рис.5). Поперек вершины ОТ треугольника ABC проведите прямую, параллельную AB , и точки ее пересечения с прямыми A A 1, B B 1 обозначают соответственно A 2, В 2. Из подобия двух пар треугольников CB 2 B 1 и ABB 1, BAA 1 и CA 2 A 1, рис.пять имеем равенства , г. Из подобия треугольников BC 1 O и B 2 CO , A ОТ 1 O и A 2 CO имеем равенства . (4) P Умножая равенства (3) и (4), получаем равенство (1). Утверждение а) теоремы Чевы доказано. Рассмотрим доказательства утверждения а) теоремы Чевы с использованием площадей для внутренней точки.Это изложено в книге А.Г. Мякишева и опирается на утверждения, которые мы сформулируем в виде задач 3 и 4 . Задача 3. Отношение площадей двух треугольников с общей вершиной и оснований, лежащих на одной прямой, равно отношению длин этих оснований. Докажите это утверждение. Задача 4. Докажите, что если Пусть отрезки AA 1, BB 1 и CC 1 пересекаются в точке Z (рис.6), затем , г. И из равенств (5) и второй постановки задачи 4 следует, что , , то есть равенство (1) выполняется, как и требуется. Утверждение а) теоремы Чевы доказано. Задание 15. Пусть Чевианы пересекаются в одной точке внутри треугольника и разделят его на 6 треугольников, площади которых равны S 1, S 2, S 3, S 4, S 5, S 6 (рис.7). Докажи это. Рисунок: 7 Задача 6. Найдите площадь S треугольник CNZ (площади остальных треугольников показаны на рисунке 8). Ответ. 15. Задача 7. Найдите площадь S треугольника CNO , если площадь треугольника AND NO равна 10 и Ответ. 30. Задача 8. Найдите площадь S треугольника CNO , если площадь треугольника AND BC равна 88 и, Раствор R. Так как, то обозначим Как Итак, Назначение 9 . В треугольнике ABC точки K и L принадлежат соответственно сторонам AB и B C . Ответ. 1,75. Теорема Т Менелая Дан треугольник ABC и на его сторонах AC и CB отмечены точки B 1 и A 1 соответственно, а на продолжении стороны AB точка обозначена C 1 (рис.11). a) Если точки И 1, B 1 и ИЗ 1 лежат на одной прямой, то . (6) б) Если равенство (7) верно, то точки И 1, B 1 и ИЗ 1 коллинеарны. Рис.11 Как помнить о равенстве Менелая? Способ запоминания равенства (6) такой же, как и для равенства (1). Вершины треугольника в каждом отношении и сами отношения записываются в направлении обхода вершин треугольника ABC — сверху вниз, проходя через точки деления (внутренние или внешние). Задача 10. Докажите, что запись равенства (6) из любой вершины треугольника в любом направлении дает тот же результат. Для доказательства теоремы Менелая необходимо доказать утверждение а) любым из предложенных ниже методов, а также доказать утверждение б). Доказательство утверждения б) проводится после первого способа доказательства утверждения а). Доказательство утверждения а) с помощью теоремы о пропорциональных интервалах I путь. а) Идея доказательства состоит в замене соотношений длин отрезков в равенстве (6) на отношения длин отрезков, лежащих на одной прямой. Пусть точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Через точку C проведем прямую l , параллельную прямой AND 1 B 1, она пересекает линию AB в точке M (рис.12). R По теореме о пропорциональных отрезках имеем: Тогда верны равенства Доказательство утверждения б) теоремы Менелая Пусть теперь равенство (6) выполнено, докажем, что точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Пусть прямые AB, и AND 1 B 1 пересекаются в точке ОТ 2 (рис.13). Поскольку точки И 1 B 1 и ИЗ 2 лежат на одной прямой, то по утверждению а) теоремы Менелая Сравнивая равенства (6) и (7), получаем , г. Последнее равенство верно только при условии Утверждение б) теоремы Менелая доказано.Рис.13 Доказательство утверждения а) с использованием подобия треугольников Идея доказательства состоит в том, чтобы заменить отношения длин отрезков из равенства (6) на отношения длин отрезков, лежащих на параллельных прямых. Пусть точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Из точек A , B и C проведите перпендикуляры AA 0, B B 0 и SS 0 к этой прямой (рис.14). R Из подобия трех пар треугольников AA 0 B 1 и CC 0 B 1, CC 0 A 1 и BB 0 A 1, C 1 B 0 B и C 1 A 0 A (под двумя углами) имеем правильные равенства , г. умножая их, получаем: . Утверждение а) теоремы Менелая доказано. Подтверждение утверждения a) с использованием областей Идея доказательства состоит в замене отношения длин отрезков из равенства (7) на отношение площадей треугольников. Пусть точки И 1, B 1 и ИЗ 1 лежат на одной прямой. Соедините точки C и C 1. Обозначим площади треугольников S 1, S 2, S 3, S 4, S 5 (рис.15). Тогда равенства , г. Умножая равенства (8), получаем: Утверждение а) теоремы Менелая доказано. R Точно так же, как теорема Шевы остается верной, если точка пересечения хевианов находится вне треугольника, теорема Менелая остается верной, если секущая пересекает только продолжения сторон треугольника. В этом случае можно говорить о пересечении сторон треугольника во внешних точках. Доказательство утверждения а) для случая внешних точек P секущая устье пересекает стороны треугольника ABC во внешних точках, т. Е. Пересекает продолжения сторон AB , BC и AC в точках C 1, A 1 и B 1 соответственно, и эти точки лежат на одной прямой (рис. 16). По теореме о пропорциональных отрезках имеем: и. Тогда равенства верны Утверждение а) теоремы Менелая доказано. Рис шестнадцать Отметим, что приведенное выше доказательство совпадает с доказательством теоремы Менелая для случая, когда секущая пересекает две стороны треугольника во внутренних точках и одну — во внешней. Доказательство утверждения б) теоремы Менелая для случая внешних точек аналогично приведенному выше доказательству. Задания 11. В треугольнике ABC точки И 1, IN 1 лежат соответственно на сторонах Sun и A FROM . P — точка пересечения отрезков AA 1 и BB 1 . Решение. Обозначим , , откуда следует, что … Фиг.17 Ответ. . Задания 12 (МГУ, заочная подготовка). В треугольнике ABC , площадь 6, сбоку AB точка взята TO , разделяет эту сторону относительно Решение. От точек R и ОТ опускаем перпендикуляры PR и CM на прямой AB … Обозначим Из подобия треугольников TO MC и TO RP (в двух углах) получаем, что Теперь, зная длину высоты, удерживаемой на стороне AB треугольника ABC , и площадь этого треугольника, вычисляем длину стороны: Ответ. 4. Задания 13. Три окружности с центрами И , IN , ИЗ , , чьи радиусы связаны как Решение. Обозначим По теореме Менелая для треугольника BCY и секущей OX имеем: Ответ. . Задание 14 (ЕГЭ-2016). Точки IN 1 и ОТ AS и AB треугольник ABC и AB 1: B 1 ОТ = а) Докажите, что линия АО половинки сбоку вс. AB 1 OC 1 на площадь треугольника ABC , если известно, что AB 1: B 1 ОТ = 1: 4. Решение. а) Пусть прямая АО пересекает сторону BC в точке A 1 (рис.20). По теореме Шевы имеем: . (9) Как AB 1: B 1 ИЗ = AS 1: ИЗ 1 B , то равенство (9) означает, что б) Пусть площадь треугольника AB 1 O равно S . Как AB 1: B 1 ИЗ CB 1 O равняется 4 S , а площадь треугольника AOC равно 5 S … Тогда площадь треугольника AOB также 5 S , так как треугольники AOB и AOC имеют общее основание AO , а их вершины B и C равноудалены от прямой AO … При этом площадь треугольника AOC 1 равна S , as AS 1: ИЗ 1 B = 1: 4. Тогда площадь треугольника ABB 1 равна 6 S … Поскольку AB 1: B 1 ОТ = 1: 4, то площадь треугольника CB 1 O равна 24 S , а площадь треугольника ABC равно 30 S … Теперь находим отношение площадей четырехугольника AB 1 OC 1 (2 S ) на площадь треугольника ABC (30 S ), он равен 1:15. Ответ. 1:15. Задание 15 (ЕГЭ-2016). Точки IN 1 и FROM 1 лежат на сторонах соответственно AS и AB треугольника ABC и AB 1: B 1 FROM = а) Докажите, что линия АО половинки стороны вс. б) Найдите отношение площади четырехугольника AB 1 OC 1 к площади треугольника ABC , если известно, что AB 1: B 1 ИЗ = 1: 3. Ответ. 1:10. Задания 1 6 (ЕГЭ-2016). На отрезке BD взято точка ОТ … Биссектриса BL ABC с фундаментом Sun BLD с фундаментом BD . а) Докажите, что треугольник DCL равнобедренный. б) Известно, что cos а) Докажите, что треугольник DCL равнобедренный. б) Известно, что cos ABC =.В каком отношении прямая DL разделяет сторону AB ? Ответ. 4:21. Литература 1. Смирнова И.М., Смирнов В.А. Замечательные точки и линии треугольника. М .: Математика, 2006, № 17. .2. Мякишев А.Г. Элементы геометрии треугольника. (Серия «Библиотека« Математическое образование »). М .: МЦНМО, 2002. — 32 с. .3. Геометрия. Дополнительные главы к учебнику для 8-х классов: Учебное пособие для учащихся школ и классов с углубленным изучением / Л.С. Атанасян, В.Ф. Бутузов, С. Кадомцев и др. — М .: Вита-Пресс, 2005. — 208 с. 4. Эрдниев П., Манцаев Н. Теоремы Чевы и Менелая. М .: Квант, 1990, № 3. С. 56–59. 5. Шарыгин И.Ф. Теоремы Чевы и Менелая. М .: Квант, 1976, № 11. С. 22–30. 6. Вавилов В.В. Медианы и средние линии треугольника. М .: Математика, 2006, № 1. .7. Ефремов Дм. Новая геометрия треугольника. Одесса, 1902. — 334 с. 8. Математика.50 вариантов типовых тестовых заданий / И.В. Ященко, М.А.Волькевич, И. Высоцкий и другие; изд. И.В. Ященко. — М .: Издательство «Экзамен», 2016. — 247 с. Математика — 10 класс Мендель Виктор Васильевич, декан факультета естественных наук, математики и информационных технологий ДВГГУ ТЕОРИИ ЧЕВЫ И МЕНЕЛАЙ Особое место в планиметрии занимают две замечательные теоремы: теорема Чевы и теорема Менелая. Эти теоремы не входят в базовую программу школьного курса геометрии, но их изучение (и применение) рекомендуется всем, кто интересуется математикой немного больше, чем это возможно в рамках школьной программы… Чем интересны эти теоремы? Во-первых, отметим, что при решении геометрических задач продуктивно сочетаются два подхода: — один основан на определении базовой конструкции (например: треугольник — круг; треугольник — секущая; треугольник — три прямые. проходящий через его вершины и пересекающийся в одной точке; четырехугольник с двумя параллельными сторонами и т. д.), а второй — метод опорных задач (простых геометрических задач, к которым сводится процесс решения сложной задачи).Итак, теоремы Менелая и Шевы относятся к числу наиболее распространенных построений: первая рассматривает треугольник, стороны или продолжения сторон которого пересекаются некоторой прямой (секущей), вторая — треугольником и тремя прямые, проходящие через его вершины, пересекающиеся в одной точке. Теорема Менелая Эта теорема, в которой наблюдаются (вместе с обратными) соотношениями, показаны отрезки, паттерн, соединяющий вершины треугольника и точки пересечения секущей со сторонами (продолжениями сторон) треугольника.На рисунках показаны два возможных случая расположения треугольника и секущей. В первом случае секущая пересекает две стороны треугольника и продолжение третьей, во втором — продолжение всех трех сторон треугольника. Теорема 1. (Менелай). Пусть ABC пересекает прямая, которая не параллельна стороне AB и пересекает две ее стороны AC и BC соответственно в точках B1 и A1, а прямая AB в точке C1, тогда AB1 CA1 BC1 1. B1C A1B C1 A Теорема 2.(обратная теореме Менелая). Пусть точки A1, B1, C1 в треугольнике ABC принадлежат прямым BC, AC, AB соответственно, тогда если AB1 CA1 BC1 1 B1C A1B C1 A, то точки A1, B1, C1 лежать на одной прямой. Доказательство первой теоремы можно провести следующим образом: перпендикуляры из всех вершин треугольника опускаются на секущую. В результате получились три пары одинаковых прямоугольных треугольников. Соотношения отрезков, фигурирующие в формулировке теоремы, заменяются соотношениями перпендикуляров, соответствующих им по подобию.Получается, что каждый отрезок — перпендикуляр в дробях будет присутствовать дважды: один раз в одной дроби в числителе, второй раз в другой дроби, в знаменателе. Таким образом, произведение всех этих соотношений будет равно единице. Обратная теорема доказывается от противного. Предполагается, что в условиях теоремы 2 точки A1, B1, C1 не лежат на одной прямой. Тогда прямая A1B1 пересекает сторону AB в точке C2, отличной от точки C1. В этом случае в силу теоремы 1 для точек A1, B1, C2 будет выполнено то же соотношение, что и для точек A1, B1, C1.Отсюда следует, что точки C1 и C2 будут делить отрезок AB в одинаковом соотношении. Тогда эти точки совпадают — мы получили противоречие. Рассмотрим примеры приложений теоремы Менелая. Пример 1. Докажите, что медианы треугольника в точке пересечения делятся в соотношении 2: 1, считая от вершины. Решение. Запишем соотношение, полученное в теореме Менелая для треугольника ABMb и прямой McM (C): AM c BM M bC 1. M c B MM b CA Первая дробь в этом произведении, очевидно, равна 1 , а третье второе отношение равно 1.Следовательно, 2 2: 1, как и положено. Пример 2. Секущая пересекает продолжение стороны AC треугольника ABC в точке B1, так что точка C является серединой отрезка AB1. Этот секанс делит сторону AB пополам. Найдите, в каком отношении он разделяет сторону BC? Решение. Запишем для треугольника и секанса произведение трех соотношений из теоремы Менелая: AB1 CA1 BC1 1. B1C A1B C1 A Из условий задачи следует, что первое отношение равно единице, а третье — 1, 2, поэтому второе отношение равно 2, т.е.е. То есть секущая делит сторону BC в соотношении 2: 1. Следующий пример применения теоремы Менелая мы встретим, когда будем рассматривать доказательство теоремы Шевы. Теорема Чевы Большинство замечательных точек треугольника можно получить с помощью следующей процедуры. Пусть существует какое-то правило, по которому мы можем выбрать некоторую точку A1 на стороне BC (или ее продолжении) треугольника ABC (например, выбрать середину этой стороны). Затем построим аналогичные точки B1, C1 на двух других сторонах треугольника (в нашем примере еще две середины сторон).Если правило выбора выполнено успешно, то прямые AA1, BB1, CC1 пересекаются в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачный, так как медианы треугольника пересекаются в одной точке) . Я хотел бы иметь какой-то общий метод, который позволяет по положению точек на сторонах треугольника определять, пересекаются ли соответствующие тройки прямых в одной точке или нет. Универсальное условие, которое «закрыло» эту проблему, было найдено в 1678 году итальянским инженером Джованни Чева.Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжениях), называются шевианами, если они пересекаются в одной точке. Есть два варианта расположения чевианов. В одном варианте осуществления точка пересечения является внутренней, а концы шевианов лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного шевиана лежит сбоку, а два других имеют концы на продолжениях сторон (см. Рисунки).Теорема 3. (Прямая теорема Шевы) В произвольном треугольнике ABC на сторонах BC, CA, AB или их продолжениях выбираются точки A1, B1, C1 соответственно, такие, что прямые AA1, BB1, CC1 пересекаются в некоторых общих точках. точка, то BA1 CB1 AC1 1 CA1 AB1 BC1. Доказательство: существует несколько оригинальных доказательств теоремы Шевы, мы рассмотрим доказательство, основанное на двукратном применении теоремы Менелая. Впервые запишем связь теоремы Менелая для треугольника ABB1 и секущей CC1 (обозначим точку пересечения хевианов через Z): AC1 BZ B1C 1, C1B ZB1 CA и второй раз для треугольника B1BC и секущая AA1: B1Z BA1 CA 1.ZB A1C AB1 Умножая эти два отношения и делая необходимые сокращения, получаем соотношение, содержащееся в формулировке теоремы. Теорема 4. (обратная теорема Чевы). Если для точек A1, B1 и C1, выбранных на сторонах треугольника ABC или их продолжений, выполняется условие Чевы: BA1 CB1 AC1 1 CA1 AB1 BC1, то прямые AA1, BB1 и CC1 пересекаются в одной точке. Доказательство этой теоремы проводится от противного, как и доказательство теоремы Менелая. Рассмотрим примеры применения прямой и обратной теорем Чевы.Пример 3. Докажите, что медианы треугольника пересекаются в одной точке. Решение. Рассмотрим отношение AC1 BA1 CB1 C1B A1C B1 A для вершин треугольника и середин его сторон. Очевидно, что в каждой дроби в числителе и знаменателе есть равные отрезки, поэтому все эти дроби равны единице. Следовательно, соотношение Чевы выполняется, следовательно, по обратной теореме медианы пересекаются в одной точке. Задания для самостоятельного решения Предлагаемые здесь задания — это тест №1 для учащихся 9 класса.Решите эти задачи, запишите решения в отдельную (не относящуюся к физике и информатике) тетрадь. Укажите на обложке следующую информацию о себе: 1. Фамилия, имя, класс, профиль класса (например: Пупкин Василий, 9 класс, математический) 2. Почтовый индекс, адрес проживания, e-mail (если есть), телефон ( дом или мобильный) 3. Информация о школе (например: МБОУ №1, поселок Бикин) 4. Фамилия, имя учителя математики (например: учитель математики Петрова М.И.) Рекомендуется решить не менее четырех задач.М 9.1.1. Может ли секущая из теоремы Менелая разрезать стороны треугольника (или их продолжения) на отрезки длины: а) 3, 3, 5, 7,10, 14; в) 3, 5, 6, 7, 7, 10, Если такие варианты возможны, приведите примеры. Сегменты могут быть в разном порядке. M 9.1.2. Могут ли внутренние шевианы треугольника делить его стороны на отрезки: а) 3, 3, 5, 7,10, 14; в) 3, 5, 6, 7, 7, 10, Если такие варианты возможны, приведите примеры. Сегменты могут идти в разном порядке. Подсказка: придумывая примеры, не забывайте проверять неравенство треугольника.M 9.1.3. Используя обратную теорему Шевы, докажите, что: а) биссектрисы треугольника пересекаются в одной точке; б) отрезки, соединяющие вершины треугольника с точками на противоположных сторонах, в которых эти стороны касаются вписанной окружности, пересекаются в одной точке. Направления: а) запомните, в каком отношении биссектриса делит противоположную сторону; б) использовать то свойство, что отрезки двух касательных, проведенных из одной точки в определенную окружность, равны. М 9.1.4. Завершите доказательство теоремы Менелая, начатое в первой части статьи.M 9.1.5. Докажите, что высоты треугольника пересекаются в одной точке, используя обратную теорему Чевы. М 9.1.6. Докажите теорему Симпсона: из произвольной точки M, взятой на окружности, описанной вокруг треугольника ABC, опускаются перпендикуляры к сторонам или продолжениям сторон треугольника, докажите, что основания этих перпендикуляров лежат на одной прямой. Подсказка: используйте обратную теорему Менелая. Попробуйте выразить длину отрезков линии, используемых во взаимосвязях, через длины перпендикуляров, проведенных к их точке M.Также полезно запомнить свойства углов вписанного четырехугольника. Таблица 10.9 Перпендикулярность прямого и плоского решения. Перпендикулярная прямая и плоскость, характеристика и условия перпендикулярности прямой и плоскостиПрямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку пересечения этой прямой и плоскости. На рисунке 131 показана прямая A в перпендикулярной плоскости a. Т.2.9. Если прямая пересекающаяся плоскость перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, она перпендикулярна плоскости. Эта теорема называется признаком перпендикулярности прямого и плоского или теоремой о двух перпендикулярах. На рисунке 132 показана прямая A, перпендикулярная прямой с прямой, проходящая через точку пересечения плоскости A и прямой A и лежащая в плоскости.Можно утверждать, что. Следующие две теоремы относятся к взаимосвязи между параллельностью и перпендикулярностью прямых и плоскостей. Т.2.10. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна другой. Т. 2.11. Два прямых, перпендикулярных одной плоскости, параллельных. На рисунке 133 показана такая прямая A, а также плоскость A, которые упоминаются в теоремах 2.10 и 2.11. Угол между прямой и плоскостью называется углом между этой прямой и ее проекцией на плоскость. На рисунке 134 показаны плоскость A и прямая a, которые пересекает. Direct A есть прямая проекция A на плоскость a. Тогда угол — это угол между прямой А и плоскостью а. Угол между параллельной прямой и плоскостью считается равным дуулу, а угол между перпендикулярной прямой и плоскостью составляет 90 °. Поскольку прямая А, ее проекция А на плоскость А и перпендикуляр к плоскости А в точке ее пересечения с прямой А лежат в одной плоскости, угол между прямой и плоскостью дополняет до 90 ° угла между этой прямой и прямой. перпендикулярно плоскости. Пример. Длина 10 см пересекает плоскость, а его концы находятся на расстоянии 3 и 2 см от плоскости. Найдите угол между этим отрезком и плоскостью. М .: 2014. — 80 с. Пособие оформлено в виде таблиц и содержит более 350 заданий. Задания каждой таблицы соответствуют определенной теме учебного года по геометрии 10-11 классов и расположены внутри таблицы в порядке возрастания сложности. Учитель математики, работающий в старшей школе, знает, как сложно научить учеников наглядно и правильно рисовать стереометрические задания. Из-за отсутствия пространственного воображения задача стереометра, к которой рисунок нужно выполнить самостоятельно, часто становится для школьника невыносимой. Именно поэтому использование готовых чертежей в стереометрических задачах значительно увеличивает количество рассматриваемого материала, повышает его эффективность. Предлагаемое пособие является дополнительным сборником заданий по геометрии для учащихся классов общеобразовательной школы и ориентировано на учебник А.В.Погорелова «Геометрия 7-11». Это продолжение аналогичного пособия для учеников 7-9 классов. Формат: PDF. (2014, 80с.) Размер: 1,2 МБ Watch, скачать: drive.google ; РГОСТ. Формат: djvu. (2006, 80с.) Размер: 1,3 МБ Загрузить: drive.google Содержание 6.1 Определение перпендикулярности прямой и плоскости Идея прямого, а точнее, о отрезках, перпендикулярных плоскостях, дает вертикально стоящие полюса (они перпендикулярны поверхности земли), натянутый шнур на на которых висит светильник (перпендикулярно потолку), ножки стола (они перпендикулярны полу).Вертикальная дверь двери перпендикулярна полу, а нижний край двери, прилегающий к полу, перпендикулярен джаматику во всех положениях двери (рис. 73, а). Это свойство определяется перпендикулярностью прямой и плоскости. Определение. Прямая называется перпендикулярной плоскостью, если она пересекает эту плоскость и перпендикулярна любой прямой в этой плоскости, проходящей через точку пересечения (рис. 73, б). Рис. 73. Также говорят, что плоскости перпендикулярны прямым или что они взаимно перпендикулярны.Для взаимно перпендикулярных прямой A и плоскости применяется обозначение A ⊥ α или α ⊥ a. Вырез или балка перпендикулярна плоскости, если она лежит на прямой линии, перпендикулярной этой плоскости. Если отрезок перпендикулярен плоскости и его конец лежит в этой плоскости, то он называется перпендикулярным к этой плоскости. 6.2 Перпендикулярно и наклонно Сегмент, имеющий одну общую точку плоскости, является концом сегмента, но не перпендикулярно этой плоскости, называется наклонной плоскостью. Пусть из одной точки A, не лежащей в плоскости A, проведен перпендикуляр AB и наклонный динамик (рис. 74). Отрезок самолета называется проекцией наклонного динамика на плоскость α. Рис. 74. Короче перпендикуляр av наклонным динамиком, т.е. av Это можно сказать так: перпендикуляр AB из точки A на плоскости α является самым коротким из отрезков, соединяющих точку A с точки плоскости α. Свойство перпендикуляра быть самым коротким отрезком является характерным свойством.Это означает, что верно и обратное утверждение: если AV — кратчайший отрезок от точки A до плоскости α, то AB перпендикулярна плоскости α. Доказательства. Докажем это методом от скверны. Предположим, что av перпендикулярно α. Затем через точку на плоскости α проходит прямая A, не перпендикулярная AB (рис. 75). Спускаемся с перпендикуляра am на прямой a. В прямоугольном треугольнике AVM Carthew AM без гипотенузы AV: am Рис.75. Длина перпендикуляра, опущенная от самой высокой точки объекта на его основании, измеряет высоту объекта. Таким образом, высотой пирамиды называется длина перпендикуляра, опущенного от вершины пирамиды к плоскости ее основания, а также самого перпендикуляра (на рисунке 76, A, B — разрез РО) . Рис. 76. 6.3 О величине перпендикуляра Перпендикуляр к плоскости играет очень важную роль и, кроме того, он самый короткий среди всех отрезков от этой точки до точек плоскости.Поясним его значение. Положение плоскости в пространстве можно задать, указав непосредственно обновленную и точку, в которой она пересекает эту прямую. Самым важным свойством перпендикуляра является то, что плоскость расположена симметрично относительно него. Что это значит? Все лучи, лежащие в этой плоскости, образуют с ней равные углы — прямые, а для наклонных это не так (рис. 77, а). При вращении вокруг перпендикуляра плоскость совмещается сама с собой: колесо необходимо прибить к оси так, чтобы его плоскость была перпендикулярна оси.Прямоугольник со стороной, перпендикулярной плоскости, вы можете вращать вокруг этой стороны, а другая сторона будет скользить по плоскости. Это хорошо видно на правой двери. Если ее край не вертикальный, дверь не открывается свободно и ушибает пол. Рис. 77. На примерах из физики можно отметить, что давление жидкости или газа на стенку сосуда направлено перпендикулярно стенке, а также давление груза на стенку. опора направлена перпендикулярно ей (рис.77, б и 78, а). Рис. 78. Перпендикуляр к поверхности проявляется в законах отражения и преломления света. Таким образом, закон отражения гласит: «Луч падает и луч отражается в одной плоскости с перпендикуляром к поверхности зеркала в точке падения и образуют с ним равные углы». «Угол падения» и «угол отражения» — это углы между указанным перпендикуляром и падающим и отраженным лучом (рис.78, б). Но главная ценность перпендикуляра — это его роль в технике и во всей нашей жизни. Можно сказать, в окружении перпендикуляров: ножки стола перпендикулярны полу, край шкафа перпендикулярен стене и т. Д. Вертикаль перпендикулярна горизонтальной плоскости. Вертикаль проверяется отвесом (см. Фото). Перпендикулярность играет важную роль в строительстве: межслойные перекрытия укладываются перпендикулярно колоннам каркаса здания. Как мы видим далее, параллельность плоскостей связана с наличием общего перпендикуляра. Перпендикулярность и параллельность прямых и плоскостей — существенный элемент в строительстве, поэтому учение о перпендикулярах и параллелях можно назвать основами «строительной геометрии». Вопросы для самоконтроля
Внимание! Предварительный просмотр слайдов используется исключительно в информационных целях и может не дать представление обо всех возможностях презентации.Если вам интересна эта работа, пожалуйста, скачайте полную версию. Класс: 10. Базовый учебник: Геометрия 10-11: Базовый и профильный уровни / Л.С. Атанасян, Дт.- М .: Просвещение, 2009. К уроку прилагается презентация, тест, сделанный в Microsoft Excel для компьютерной проверки знаний студентов ( Приложение 1, ), образовательный модуль Федерального центра информационных и образовательных ресурсов ( Приложение 2.), состоящий из 5 заданий разного уровня сложности. Все задачи этого модуля параметризованы, что позволяет формировать индивидуальные задачи. Задачи предназначены для проверки решения задач по признаку прямой и плоской перпендикулярности. Для работы с обучающим модулем необходимо установить специальную программу, она находится в Приложении 3. . В презентации к уроку идет самостоятельная работа по изучаемой теме. Таким образом, количество предлагаемого материала является избыточным, что позволяет его дозировать, варьируя в зависимости от уровня подготовки класса. Тип урока: урок творческого использования знаний. Форма проведения: Мастерская решения ключевых задач. Затраченное время: 45 минут. Расположение в разделе : 4 урок. Цели: Обучение:
Разработка:
Образовательный:
Методы: частичный поиск, исследование. Формы организации: фронтальная, групповая, индивидуальная, самостоятельная работа. Оборудование: компьютерный класс, мультимедийный проектор, экран, компьютерная презентация по теме, тест (Приложение 1), карточки для самостоятельной работы (слайд 9), карточки с вопросами теории, EOR с практическим параметризованным заданием (Приложение 2) . На занятияхОрганизационный момент — проверка готовности класса к уроку. I. Мотивационно-оценочная часть.1. Актуализация знаний. — Сегодня мы продолжаем работу над темой «Перпендикулярность прямого и плоского». На последних уроках мы «открыли» определение прямого, перпендикулярного к плоскости признака перпендикулярности прямого и плоского, разобрали простейшие задачи. В качестве домашнего задания каждый из вас получил лист с вопросами теории, вам было предложено подготовить ответы на эти вопросы. Проверьте, как вы справились с этой задачей. Есть фронтальный осмотр. (слайды 6-8).
Подведены итоги устной работы, оценены отзывы студентов. 2. Формирование учебного задания. Сегодня мы продолжим формировать умение применять известные утверждения в задачах для доказательства и при решении типовых задач. 1. Следующий этап работы — вызывают к доске двух учеников для самостоятельной работы над карточками, с остальными учениками идет фасадная работа по готовым рисункам. Карточки для индивидуальной работы: Заданий для устной работы над готовыми рисунками:
— Ребята, в задачах 4-6 речь идет о наклонной плоскости.Как вы думаете, что я имею в виду? Есть ли аналогия с концепциями перпендикуляра и наклона прямой, изучаемыми в планиметрии? Студентам предлагается изучить презентации на слайде 10 и решить эти задачи. 2. Работа в паре — задачи решаются по готовым чертежам. Решения обсуждаются. Ответы оцениваются отдельными студентами. Следующий этап занятия — выполнение практического задания на компьютере, работающем с EOR. III. Светоотражающая оценочная часть.1. Итоговая работа Урок представляет собой контрольную работу в тестовой форме. Подведены итоги занятия, выставлены сметы. 2. Домашнее задание: № 130, 131, 145, 148. (Примечание: используйте знак перпендикулярности прямой и плоскости). Задания и упражнения по готовым рисункам, 10-11 классы, геометрия, Рабинович Э. М., 2006. Оглавление Скачайте бесплатно электронную книгу в удобном формате, смотрите и читайте: Скачать PDF. МЕТОДОЛОГИЯ ОБУЧЕНИЯ «ТРИГОНОМЕТРИИ» НА АНГЛИЙСКОМ языке мақаласыСагындык В ВИДЕ. МЕТОДОЛОГИЯ ПРЕПОДАВАНИЯ «ТРИГОНОМЕТРИЯ» В АНГЛИЙСКИЙ Новая эра дает нам много возможностей. процветание науки и Информация; каждый человек сможет достичь вершины познания.Чтобы соответствовать требованиям времени, мы должны стремиться вперед. И, конечно, это продвижение не может без новых знаний. В свою очередь, мы получаем знания от книга. Поскольку из 10 миллионов книг которые издаются в мире, 85% публикуются на английском языке и 80% связей между компьютером и человеком на английском языке мы будем необходимо знать международный язык, который откроет все двери для мир знаний. Теперь все доступно. Например, человек может все заказать дома; даже ты можешь сделать покупки за покупками не выходя из дома.Все равно не будем уметь перечислить все возможности Интернета, которые подлежат современный человек. Обучение выгодно сторона Интернета. Сегодня дистанционное обучение может позволить себе каждый через Интернет. Новые технологии позволяют людям объединяться и делиться их опыт, находясь на большом расстоянии друг от друга. Из этого можно понять, что современный мир мужчине, стремясь к новым навыкам, знаниям, везде есть возможности учиться.Если у вас есть доступ в Интернет, то вы можете самостоятельно выучить язык Мир. В нашей стране с 2016-2017 учебного года предмет английского изучается с первого класса. А также в в будущем планируется введение трехъязычного обучение в школах Казахстана. В свою очередь, возникает вопрос: насколько сложно детям будет изучать математику на английском языке, который является одним из сложных предметов для учеников в школа. Математика в Английский для школьников — это только сложная задача на первых порах взгляд, но с этим справится каждый ребенок! Математика на английском языке развивает не только логическое мышление школьников, расширяет словарный запас, учит думать по-английски, но также дает детям умение анализировать различные жизненные ситуации.Знание математики — это важно и полезно, но научить этому вдвойне эффективнее на английском. Секция «Тригонометрия» школьного курса математики — самый сложно для студентов. Одна из причин этого — недостаточное количество программных часов, посвященных изучению этого раздел, а также поверхностное изложение некоторых важных вопросы, связанные с решением тригонометрических уравнений, подбор и изучение корней, решение тригонометрических неравенства.Учитывая все это, мы предлагаем электронные образовательные и методическое проектирование школы по теме «Тригонометрия». Мы создали электронный учебник, ориентированный на расширение базового уровня знания школьников по математике; это предметно-ориентированный и дает студентам возможность познакомиться с интересные, нестандартные вопросы тригонометрии, с очень общие методы решения тригонометрических задач, чтобы проверить их способности по математике на английском языке.Вопросы, рассмотренные в курс выходит за рамки обязательного содержания. На В то же время они вплотную примыкают к основному блюду. Следовательно, это учебник будет способствовать совершенствованию и оформлению наиболее важные математические знания и навыки, предоставляемые школой учебный план, поможет оценить ваши способности в математика. Мы рассмотрели четыре основных разделы: І. Тригонометрический функции. ІІ.Тригонометрический выражения. ІІІ.Тригонометрические уравнения и системы уравнений. ІV. Тригонометрический неравенства. С помощью из нашего электронный дизайн студенты могут самостоятельно изучите лекции по этим разделам и изучите примеры для решения задания для самостоятельной работы. Помимо основных разделов в учебник, студенты могут познакомиться с терминологией на курс «Тригонометрия», пройти итоговое тестирование по материалам а также у каждого студента есть возможность изучить история тригонометрии и применения тригонометрии в человеческая жизнь. Слово «тригонометрия» означает от древнегреческого τρίγωνον — «треугольник» и μετρέω «мера», то есть измерение треугольников. Работа с другими предметные дисциплины, использование ИКТ и понимание математики Вот некоторые из новаторских подходов, применяемых школами для улучшения изучение математики. В частности, ряд мероприятия, представленные в тематических исследованиях, включают идеи о том, как студенты могут применить свои знания по тригонометрии в 3-х измерениях.Руководство содержит рекомендации о том, как спланировать увлекательное обучение. опыта и некоторые стратегии для разработки и работы с богатыми математическая деятельность. Электронный учебные аспекты тригонометрии, часто используемые в области инженерное дело. Они включают использование тригонометрических соотношений, Теорема Пифагора и правила синусов и косинусов. Всесторонний примечания с четкими описаниями для каждого ресурса, вместе с соответствующими диаграммами и примерами. Студенты, желающие проанализировать и закрепить свои знания и понимание тригонометрия найдет их полезными, поскольку каждая тема включает отбор вопросов для заполнения, на которые даются ответы при условии. Логика и организация математического мозга помогает решать задачи и каждая страница электронного учебника посвящена тригонометрия, показывающая, почему это полезно и что вы можете сделать с Это. Вы обнаружите, что использование тригонометрии в следующие области, которые обычно преподаются на вводных курсах наук о Земле классы и многие другие:
Номер ссылки
Leave a Reply
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
