3.11 Трехфазные цепи.
Трехфазные цепи являются частным случаем многофазных систем , под которымипонимают совокупность нескольких нагрузок и источников питания, имеющих одинаковую частоту и смещенных по фазе на некоторый угол друг относительно друга . Каждая пара источник-нагрузка может рассматриваться как отдельная цепь и называется фазой системы .
Если отдельные фазы системы не соединены между собой электрически (рис. 1 а)), то такую систему называют несвязанной . Несвязанная система не обладает никакими особыми свойствами, и если между фазами отсутствует и магнитная связь, то такая совокупность цепей вообще не может рассматриваться как многофазная.
Соединение фаз системы между собой (рис. 1б)) придает ей особые качества, благодаря которым многофазные системы ( в особенности трехфазные) получили исключительное распространение в области передачи и преобразования электрической энергии. Одним из очевидных преимуществ связанной системы (рис. 1) является сокращение с шести до четырех числа проводников, соединяющих источники с нагрузкой. При благоприятных обстоятельствах это число может быть уменьшено до трех. В дальнейшем мы отметим целый ряд других преимуществ, которым обладают связанные системы.
Любая многофазная система может быть симметричной и несимметричной. Симметрия системы определяется симметрией ЭДС, напряжений и токов. Под симметричной многофазной системой ЭДС, напряжений или токов понимают совокупность соответствующих величин, имеющих одинаковые амплитуды и смещенных по фазе на угол 2 p /m по отношению друг к другу, где m — число фаз системы . Если для обозначения фаз трехфазной системы использовать первые буквы латинского алфавита, то симметричную систему ЭДС можно записать в виде
Аналогичные выражения можно написать и для токов и падений напряжения в симметричной трехфазной системе.
Основное свойство симметричных многофазных систем заключается в том, что сумма мгновенных значений величин образующих систему в каждый момент времени равна нулю. Для изображений величин образующих систему это свойство означает равенство нулю суммы фазных векторов . В справедливости этого утверждения легко убедиться на примере трехфазной системы, если в области изображений сложить числа в скобках в правой части выражений (1).
Многофазная система симметрична только тогда, когда в ней симметричны ЭДС, токи и напряжения. Если принять равными нулю внутренние сопротивления источников питания или включить их значения в сопротивления нагрузки, то условие симметрии системы сводится к симметрии ЭДС и равенству комплексных сопротивлений нагрузки. Это условие для трехфазной системы записывается в виде
В дальнейшем мы будем считать, что источники питания являются источниками ЭДС и использовать условия симметрии системы в виде выражений (1) и (2).
В многофазные системы объединяют источники ЭДС и нагрузки. Для обеспечения правильного соотношения сдвига фаз при соединения или связывании системы в общем случае необходимо определить выводы элементов, по отношению к которым выполняются условия (1). Они называются начало и конец фазы источника или нагрузки. Для источников многофазной системы принято за положительное направление действия ЭДС от начала к концу.
На электрических схемах, если это необходимо, начало и конец обозначают буквами латинского алфавита. На рис. 1 а) начала элементов соответствуют индексам XYZ, а концы — ABC. В дальнейшем мы будем использовать строчные буквы для нагрузки, а прописные для источников ЭДС.
Существуют два способа связывания элементов в многофазную систему — соединение звездой и соединение многоугольником. Звезда это такое соединение, в котором начала всех элементов объединены в один узел, называемый нейтральной точкой . Подключение к системе при этом осуществляется концами элементов (рис. 2 а)). Многоугольник это соединение, в котором все элементы объединены в замкнутый контур так, что у соседних элементов соединены между собой начало и конец . С системой многоугольник соединяется в точках соединения элементов. Частным случаем многоугольника является треугольник рис. 2 б).
Источники питания и нагрузки в многофазных системах в общем случае могут быть связаны разными способами.
При анализе многофазных систем вводится ряд понятий, необходимых для описания процессов. Проводники, соединяющие между собой источники и нагрузку, называются линейными проводами , а проводник соединяющий нейтральные точки источников и нагрузки — нейтральным проводом .
Электродвижущие силы источников многофазной системы (eA, E A, EA, eB, E B, EB, eC, E C, EC ), напряжения на их выводах (uA, U A, UA, uB, U B, UB, uC, U C, UC ) и протекающие по ним токи (iA, I A, IA, iB, I B, IB, iC, I C, IC ) называются фазными . Напряжения между линейными проводами (U AB, UAB, U BC, Uac, U CA, UCA ) называются линейными .
Связь линейных напряжений с фазными можно установить через разность потенциалов линейных проводов рис. 1 б) как uAB = uAN + uNB = uAN -uBN = uA -uB или в символической форме
U AB = U A -U B; U BC = U B -U C ; U CA = U C -U A . | (3) |
Построим векторную диаграмму для симметричной трехфазной системы фазных и линейных напряжений (рис. 3). В теории трехфазных цепей принято направлять вещественную ось координатной системы вертикально вверх.
Каждый из векторов линейных напряжений представляет собой сумму одинаковых по модулю векторов фазных напряжений (U ф = UA = UB =UC ), смещенных на угол 60°. Поэтому линейные напряжения также образуют симметричную систему и модули их векторов (U л = UAB = UBC =UCA ) можно определить как .
Выражения (3) справедливы как для симметричной системы, так и для несимметричной. Из них следует, что векторы линейных напряжений соединяют между собой концы фазных (вектор U CA рис. 3). Следовательно, при любых фазных напряжениях они образуют замкнутый треугольник и их сумма всегда равна нулю . Это легко подтвердить аналитически сложением выражений (3) — U AB + U BC + U CA = U A -U B + U B -U C + U C -U A = 0.
Тот факт, что геометрически векторы линейных напряжений соединяют концы векторов фазных, позволяет сделать заключение о том, что любой произвольной системе линейных напряжений соответствует бесчисленное множество фазных . Это подтверждается тем, что для создания фазной системы векторов при заданной линейной, достаточно произвольно указать на комплексной плоскости нейтральную точку и из нее провести фазные векторы в точки соединения многоугольника линейных векторов.
Из уравнений Кирхгофа для узлов a, b и c нагрузки соединенной треугольником (рис. 2 б)) можно представить комплексные линейные токи через фазные в виде
| I A = I ab -I ca; I B = I bc -I ab; I C = I ca -I bc . | (4) |
В случае симметрии токов IA = IB = IC = I л и Iab = Ibc = Ica = I ф, поэтому для них будет справедливо такое же соотношение, как для линейных и фазных напряжений в симметричной системе при соединении звездой, т.е . Кроме того, их сумма в каждый момент времени будет равна нулю, что непосредственно следует из суммирования выражений (4).
Перейдем теперь к рассмотрению конкретных соединений трехфазных цепей.
Пусть фазы источника и нагрузки соединены звездой с нейтральным проводом (рис. 4а)). При таком соединении нагрузка подключена к фазам источника и U A = U a, U B = U b и U C = U c., а I A = I a, I B = I b и I C = I c. Отсюда по закону Ома токи в фазах нагрузки равны
I a = U A /Z a; I b = U B /Z b и I c = U C /Z c . | (5) |
Ток в нейтральном проводе можно определить по закону Кирхгофа для нейтральной точки нагрузки. Он равен
Выражения (5) и (6) справедливы всегда, но в симметричной системе Z a = Z b = Z c = Z , поэтомуI N =I a +I b +I c = U A /Z a +U B /Z b +U C /Z c = (U A +U B +U C )/Z = 0, т.к. по условию симметрии U A +U B +U C =0. Следовательно, в симметричной системе ток нейтрального провода равен нулю и сам провод может отсутствовать. В этом случае связанная трехфазная система будет передавать по трем проводам такую же мощность, как несвязанная по шести. На практике нейтральный провод в системах передачи электроэнергии сохраняют, т.к. его наличие позволяет получать у потребителя два значения напряжения — фазное и линейное (127/220 В, 220/380 В и т.д.). Однако сечение нейтрального провода обычно существенно меньше, чем у линейных проводов, т.к. по нему протекает только ток, создаваемый асимметрией системы.
При симметричной нагрузке токи во всех фазах одинаковы и смещены по отношению друг к другу на 120°. Их модули или действующие значения можно определить как I = U ф /Z .
Векторные диаграммы для симметричной и несимметричной нагрузки в системе с нейтральным проводом приведены на рис. 4 б) и в).
При отсутствии нейтрального провода сумма токов в фазах нагрузки равна нулю I a +I b +I c =0. В случае симметричной нагрузки режим работы системы не отличается от режима в системе с нейтральным проводом.
При несимметричной нагрузке между нейтральными точками источника и нагрузки возникает падение напряжения. Его можно определить по методу двух узлов, перестроив для наглядности схему рис. 5 а). В традиционном для теории электрических цепей начертании она будет иметь вид рис. 5 б). Отсюда
где Y a =1/Z a, Y b =1/Z b, Y c =1/Z c — комплексные проводимости фаз нагрузки.
Напряжение U nN представляет собой разность потенциалов между нейтральными точками источника и нагрузки. По схеме рис. 5 б) его можно представить также через разности фазных напряжений источника и нагрузки U nN = U A -U a = U B -U b = U C -U c. Отсюда фазные напряжения нагрузки
| U a = U A -U nN; U b = U B -U nN; U c = U C -U nN . | (8) |
Токи в фазах нагрузки можно определить по закону Ома
| I a = U a /Z a; I b = U b /Z b; I c = U c /Z c . | (9) |
Векторные диаграммы для симметричной и несимметричной нагрузки приведены на рис. 6. Диаграммы симметричного режима (рис. 6 а)) ничем не отличаются от диаграмм в системе с нулевым проводом.
Диаграммы несимметричного режима (рис. 6 б)) иллюстрируют возможность существования множества систем фазных напряжений для любой системы линейных. Здесь системе линейных напряжений U AB U BC U CA соответствуют две системы фазных. Фазные напряжения источника U A U B U C и фазные напряжения нагрузки U a U b U c. .
В трехфазных цепях нагрузка и источник могут быть соединены по-разному. В частности нагрузка, соединенная треугольником, может быть подключена к сети, в которой источник питания соединен звездой (рис. 7 а)).
При этом фазы нагрузки оказываются подключенными на линейные напряжения
U ab = U AB; U bc =U BC; U ca = U CA .
Токи в фазах можно найти по закону Ома
I ab = U ab /Z ab; I bc = U bc /Z bc ;
I ca = U ca /Z ca ,
а линейные токи из уравнений Кирхгофа для узлов треугольника нагрузки
| I A = I ab -I ca; I B = I bc -I ab; I C = I ca -I bc . | (10) |
Векторы фазных токов нагрузки на диаграммах для большей наглядности принято строить относительно соответствующих фазных напряжений. На рис. 7 б) векторные диаграммы построены для случая симметричной нагрузки. Как и следовало ожидать, векторы фазных и линейных токов образуют симметричные трехфазные системы.
На рис. 7 в) построена векторная диаграмма для случая разных типов нагрузки в фазах. В фазе ab нагрузка чисто резистивная, а в фазах bc и ca индуктивная и емкостная. В соответствии с характером нагрузки, вектор I ab совпадает по направлению с вектором U ab; вектор I bc отстает, а вектор I ca опережает на 90° соответствующие векторы напряжений. После построения векторов фазных токов можно по выражениям (10) построить векторы линейных токов I A, I B и I C .
Трехфазная цепь является совокупностью трех однофазных цепей, поэтому ее мощность может быть определена как сумма мощностей отдельных фаз.
При соединении звездой активная мощность системы будет равна
P = P a + P b + P c = U a I a cosja + U b I b cosjb + U c I c cosjc = =I a 2R a + I b 2R b + I c 2R c , | (11) |
а реактивная
Q = Q a + Q b + Q c = U a I a sinja + U b I b sinjb + U c I c sinjc = =I a 2X a + I b 2X b + I c 2X c . | (12) |
Если нагрузка соединена треугольником, то активная и реактивная мощности будут равны
P = P ab + P bc + P ca = U ab I ab cosjab + U bc I bc cosjbc + U ca I ca cosjca = =I ab 2R ab + I bc 2R bc + I ca 2R ca , | (13) |
Q = Q ab + Q bc + Q ca = U ab I ab sinjab + U bc I bc sinjbc + U ca I ca sinjca = =I ab 2X ab + I bc 2X bc + I ca 2X ca . | (14) |
Полную мощность можно определить из треугольника мощностей как
Следует обратить внимание на то, что полная мощность трехфазной цепи не является суммой полных мощностей фаз .
При симметричной нагрузке мощности всех фаз одинаковы, поэтому полная мощность и ее составляющие для соединения звездой будут равны
При соединении нагрузки треугольником
Из выражений (16) и (17) следует, что полная мощность трехфазной сети и ее составляющие при симметричной нагрузке могут быть определены по линейным токам и напряжениям независимо от схемы соединения .
Понятие потенциала или разности потенциалов u позволяет определить работу, совершаемую электрическим полем при перемещении элементарного электрического заряда dq, как dA = udq. В то же время, электрический ток равен i = dq /dt. Отсюда dA = ui dt, следовательно, скорость совершения работы, т.е. мощность в данный момент времени или мгновенная мощность равна
где u и i — мгновенные значения напряжения и тока.
Величины тока и напряжения, входящие в выражение (1), являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной и для ее оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период T работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т.е.
Пусть u =U m sinwt и I m sin(wt -j ), тогда средняя мощность будет равна
т.к. интеграл второго слагаемого равен нулю. Величина cos jназывается коэффициентом мощности .
Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока I и напряжения U, но и от разности фаз j между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению UI. При сдвиге фаз между током и напряжением в ± 90° средняя мощность равна нулю. Максимальные значения напряжения и тока любой электрической машины определяются ее конструкцией, а максимальная мощность, которую они могут развивать — произведением этих величин. Если электрическая цепь построена нерационально, т.е. сдвиг фаз j имеет значительную величину, то источник электрической энергии и нагрузка не могут работать на полную мощность. Поэтому в любой системе источник-нагрузка существует т.н. "проблема cos j ", которая заключается в требовании возможного приближения cosj к единице.
Выражение (3) можно представить также с помощью понятий активных составляющих тока I а и напряжения U а в виде
| P = UI cosj = U (I cosj ) = UI а = I (U cosj ) = IU а . | (4) |
Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как I а =U /R или U а =IR, выражение (4) можно записать также в форме
Среднюю мощность P называют также активной мощностью и измеряют в ваттах [Вт].
Выделим подинтегральную функцию выражения (3)
Отсюда следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей UI cosj равной средней или активной мощности.
При cosj = 1 (j = 0), т.е. для цепи, обладающей чисто резистивным сопротивлением
Временные диаграммы, соответствующие этому случаю приведены на рис. 1 а).
Положительные значения мгновенной мощности соответствуют поступлению энергии от источника в электрическую цепь. Следовательно, при резистивной нагрузке вся энергия поступающая от источника преобразуется в ней в тепло .
При cosj = 0 (j = ±p /2), т.е. для чисто реактивной цепи
Временные диаграммы, соответствующие чисто индуктивной и чисто емкостной нагрузке приведены на рис. 1 б) и г). Из выражений (8) и временных диаграмм следует, что мощность колеблется относительно оси абсцисс с двойной частотой, изменяя свой знак каждые четверть периода. Это означает, что в течение четверти периода (p > 0) энергия поступает в электрическую цепь от источника и запасается в магнитном или электрическом поле, а в течение следующей четверти (p < 0) она целиком возвращается из цепи в источник. Так как площади, ограниченные участками с положительной мощностью и с отрицательной одинаковы, то средняя мощность отдаваемая источником нагрузке равна нулю и в цепи не происходит преобразования энергии.
В общем случае произвольной нагрузки 1 > cosj > 0 ( 1< |j | < p /2) и
Как следует из временных диаграмм рис. 1 в), большую часть периода мощность потребляется нагрузкой (p > 0), но существуют также интервалы времени, когда энергия запасенная в магнитных и электрических полях нагрузки возвращается в источник. Участки с положительным значением p независимо от характера реактивной составляющей нагрузки всегда больше участков с отрицательным значением, поэтому средняя мощность P положительна. Это означает, что в электрической цепи преобладает процесс преобразования электрической энергии в тепло или механическую работу .
Рассмотрим энергетические процессы в последовательном соединении rLC (рис. 2). Падение напряжения на входе цепи уравновешивается суммой падений напряжения на элементах u =ur +uL +uC. Мгновенная мощность в цепи равна
Пусть напряжение и ток на входе равны u =U m sinwt и I m sin(wt -j ). Тогда падения напряжения на элементах будут ur = rI m sin(wt -j ), uL = wLI m sin(wt -j +p /2) = xL I m sin(wt -j +p /2), uC = I m sin(wt -j -p /2)/(w C) = xC I m sin(wt -j -p /2). Подставляя эти выражения в (9), получим
Уравнение (10) в левой и правой частях имеет постоянную и переменную составляющие. Постоянная составляющая представляет собой активную или среднюю мощность. Второе слагаемое в правой части это переменная составляющая активной мощности с амплитудой равной P = UI cosj. Третье слагаемое правой части также является переменной составляющей мгновенной мощности, но эта составляющая находится в квадратуре с переменной составляющей активной мощности и имеет амплитуду Q = UI sinj. Эту величину называют реактивной мощностью . Она равна среднему за четверть периода значению энергии, которой источник обменивается с магнитным и электрическим полями нагрузки. Реактивная мощность не преобразуется в тепло или другие виды энергии , т.к. ее среднее значение за период равно нулю.
Реактивную мощность также можно представить через реактивные составляющие тока или напряжения
| Q = UI sinj = U (I sinj ) = UI р = I (U sinj ) = IU р . | (11) |
В отличие от всегда положительной активной мощности, реактивная мощность положительна при j > 0 и отрицательна при j < 0 .
Из условия равенства переменных составляющих левой и правой частей уравнения (10) можно найти связь между P, Q и S = UI в виде
Величина S называется полной или кажущейся мощностью . Из выражения (12) следует, что полную мощность можно представить гипотенузой прямоугольного треугольника с углом j, катетами которого являются активная и реактивная мощности.
Таким образом, полная мощность это максимально возможная активная мощность, т.е. мощность, выделяющаяся в чисто резистивной нагрузке (cosj = 0). Именно эта мощность указывается в паспортных данных электрических машин и аппаратов.
Реактивные составляющие токов и напряжений можно представить через активные и реактивные составляющие комплексного сопротивления, тогда для составляющих мощности
P = UI а = I 2R = U аI = U 2 /R = U 2G ; Q = UI р = I 2X = U рI = U 2 /X = U 2B ; S = UI = I 2Z = U 2 /Z = U 2Y. | (13) |
Треугольник мощностей можно описать также с помощью комплексных чисел и изобразить векторами на комплексной плоскости в виде
где S — комплексная полная мощность, — сопряженный комплексный ток.
Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4) и (11)), треугольник мощностей можно построить в двух вариантах (рис. 3 а) и б)). В первом случае активная и реактивная составляющие полной мощности выражаются через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I .
Очевидно, что все виды мощности имеют одинаковую размерность, поэтому для их отличия от активной мощности, измеряемой в ваттах [Вт], для полной мощности введена единица, называемая вольт-амперы [ВА], а для реактивной мощности — вольт-амперы реактивные [ВАр]
Выражение для активной мощности P = UI cosj позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.
Для этого на вход цепи включают приборы по схеме рис. 4 и по их показаниям определяют коэффициент мощности в виде
,
где W, V и A — показания соответственно ваттметра, вольтметра и амперметра действующих значений. Из этого выражения можно также определить угол сдвига фаз j между током и напряжением на входе двухполюсника.
·Обзорные статьи
·Промо-статьи
·Презентации
·Качество электроэнергии
·Учебные пособия по электротехники для самостоятельного изучения
·Рефераты по электротехнике и радиоэлектронике
Учебное пособие по курсу электротехники Электрические микромашины. Курс лекций Общая Электротехника. Учебное пособие Сборник лекций по теоретическим основам электротехники
Карта сайта
www.ronl.ru
Федеральное агентство по образованию ГОУ ВПО "Уральский государственный технический университет – УПИ"
Электротехника: Трехфазные электрические цепи
Учебное пособие
В.С. Проскуряков, С.В. Соболев, Н.В. Хрулькова Кафедра "Электротехника и электротехнологические системы"
Екатеринбург 2007
2
Оглавление
1.Основные понятия и определения
2.Получение трехфазной системы ЭДС.
3.Способы соединения фаз в трехфазной цепи.
4.Напряжения трехфазного источника.
5.Классификация приемников в трехфазной цепи.
6.Расчет трехфазной цепи при соединении фаз приемника «Звездой»
7.Значение нейтрального провода
8.Расчет трехфазной цепи при соединении фаз приемника «треугольником»
9.Мощность трехфазной цепи
3
Трехфазные электрические цепи.
1. Основные понятия и определения
Трехфазная цепь – это совокупность трех электрических цепей, в которых
действуют синусоидальные ЭДС, одинаковые | по амплитуде и частоте, | ||
сдвинутые по фазе одна от другой на угол | 2π | =120° и создаваемые общим | |
3 |
| ||
|
|
| |
источником энергии.
Каждую отдельную цепь, входящую в трехфазную цепь принято называть фазой.
Таким образом, термин "фаза" имеет в электротехнике два значения: первое – аргумент синусоидально изменяющейся величины, второе – часть многофазной системы электрических цепей.
Трехфазная цепь является частным случаем многофазных систем переменного тока.
Широкое распространение трехфазных цепей объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями:
•экономичность производства и передачи энергии по сравнению с однофазными цепями;
•возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя;
•возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.
Каждая фаза трехфазной цепи имеет стандартное наименование:
первая фаза – фаза "А"; вторая фаза – фаза "В"; третья фаза – фаза "С".
Начала и концы каждой фазы также имеют стандартные обозначения. Начала первой, второй и третьей фаз обозначаются соответственно А, В, С, а концы фаз – X, Y, Z.
Основными элементами трехфазной цепи являются: трехфазный генератор, преобразующий механическую энергию в электрическую; линии электропередач; приемники (потребители), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания).
4
2. Получение трехфазной системы ЭДС.
Трехфазный генератор создает одновременно три ЭДС, одинаковые по величине и отличающиеся по фазе на 1200.
Получение трехфазной системы ЭДС основано на принципе электромагнитной индукции, используемом в трехфазном генераторе. Трехфазный генератор представляет собой синхронную электрическую машину. Простейшая конструкция такого генератора изображена на рис. 3.1.
Рис. 3.1. Схема устройства трехфазного генератора
На статоре 1 генератора размещается трехфазная обмотка 2. Каждая фаза трехфазной обмотки статора представляет собой совокупность нескольких катушек с определенным количеством витков, расположенных в пазах статора. На рис. 3.1 каждая фаза условно изображена одним витком. Три фазы обмотки статора генератора повернуты в пространстве друг относительно друга на 1/3 часть окружности, т.е. магнитные оси фаз повернуты в пространстве на угол
23π =120°. Начала фаз обозначены буквами A, B и C, а концы – X, Y, Z.
Ротор 3 генератора представляет собой постоянный электромагнит, возбуждаемый постоянным током обмотки возбуждения 4. Ротор создает постоянное магнитное поле, силовые линии которого показаны на рис.3.1 пунктиром. При работе генератора это магнитное поле вращается вместе с ротором.
5
При вращении ротора турбиной с постоянной скоростью происходит пересечение проводников обмотки статора с силовыми линиями магнитного поля. При этом в каждой фазе индуктируется синусоидальная ЭДС.
Величина этой ЭДС определяется интенсивностью магнитного поля ротора и количеством витков в обмотке.
Частота этой ЭДС определяется частотой вращения ротора.
Поскольку все фазы обмотки статора одинаковы (имеют одинаковое количество витков) и взаимодействуют с одним и тем же магнитным полем вращающегося ротора, то ЭДС всех фаз имеют одинаковую амплитуду Em и частотуω.
| 2π | Но, так | как магнитные оси фаз в | пространстве повернуты на | угол | ||||||||
| =120°, начальные фазы их ЭДС отличаются на угол | 2π | . |
| |||||||||
3 |
|
| |||||||||||
|
|
|
|
|
|
| 3 |
|
| ||||
|
| Примем начальную фазу ЭДС фазы А, равной нулю, то есть ψеА = 0 | , | ||||||||||
| тогда | eA = Em sinωt. | (3.1) | ||||||||||
ЭДС фазы В отстает от ЭДС фазы А на |
| 2π |
|
|
|
|
| ||||||
|
|
| : |
|
|
|
|
| |||||
3 |
|
|
|
|
|
| |||||||
|
|
|
| 2π | = Em sin(ωt −120). |
| |||||||
|
|
| eB = Em sin ωt− |
|
|
| (3.2) | ||||||
|
|
|
|
| |||||||||
|
|
|
|
| 3 |
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| 2π |
| |||
ЭДС фазы С отстает от ЭДС фазы В еще на |
| : |
|
|
| ||||||||
3 |
|
|
| ||||||||||
|
|
|
| 4π | = Em sin(ωt −240). |
| |||||||
|
|
| eС = Em sin ωt− |
|
|
|
| (3.3) | |||||
|
|
|
|
|
| ||||||||
|
|
|
|
| 3 |
|
|
|
|
| |||
Действующее значение ЭДС всех фаз одинаковы:
E | A | = E | B | = E | = | Em= E | . | (3.4) |
|
| C |
| 2 | ||||
|
|
|
|
|
|
|
|
Трехфазная симметричная система ЭДС может изображаться тригонометрическими функциями, функциями комплексного переменного, графиками на временных диаграммах, векторами на векторных диаграммах.
Аналитическое изображение тригонометрическими функциями приведено в (3.1) – (3.3).
6
В комплексном виде ЭДС фаз изображаются их комплексными действующими значениями:
& | j0 | 0 | & | = Ee | − j120 | 0 | & | − j2400 |
|
|
|
| (3.5) | ||||
EA = Ee |
|
| = E; EB |
|
| ; EC = Ee |
Графики мгновенных значений трехфазной симметричной системы ЭДС на временной диаграмме показаны на рис. 3.2. Они представляют из себя три синусоиды, сдвинутые друг относительно друга на 1/3 часть периода.
Рис. 3.2. Графики мгновенных значений трехфазной симметричной системы ЭДС.
На векторной диаграмме ЭДС фаз изображаются векторами одинаковой длины, повернутыми друг относительно друга на угол 120° (рис.3.3а).
Рис. 3.3. Векторные диаграммы ЭДС трехфазных симметричных систем. (а – прямая последовательность фаз; б – обратная последовательность фаз).
7
Так как ЭДС индуктированные в обмотках статора имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на один и тот же угол 120°, полученная трехфазная система ЭДС является симметричной.
Следует отметить, что чередование во времени фазных ЭДС зависит от направления вращения ротора генератора относительно трехфазной обмотки статора. При вращении ротора по часовой стрелке, как показано на рис.3.1, полученная симметричная трехфазная система ЭДС имеет прямое чередование (А – В – С) (рис.3.3а). При вращении ротора против часовой стрелки образуется также симметричная трехфазная система ЭДС. Однако чередование фазных ЭДС во времени изменится. Такое чередование называетсяобратным (А – С – В) (рис.3.3б).
Чередование фазных ЭДС важно учитывать при анализе трехфазных цепей и устройств. Например, последовательность фаз определяет направление вращения трехфазных двигателей, и т.п. Для практического определения последовательности фаз используются специальные приборы – фазоуказатели.
По умолчанию при построении трехфазных цепей и их анализе принимается прямое чередование фазных ЭДС трехфазного источника.
На схемах обмотку статора генератора изображают как показано на рис. 3.4а с использованием принятых обозначений начал и концов фаз.
На схеме замещения трехфазный источник представлен тремя идеальными источниками ЭДС (рис.3.4б)
Рис. 3.4. Условное изображение обмотки статора генератора.
За условное положительное направление ЭДС в каждой фазе принимают направление от конца фазы к началу.
3. Способы соединения фаз в трехфазной цепи.
Для построения трехфазной цепи к каждой фазе трехфазного источника присоединяется отдельный приемник электроэнергии, либо одна фаза трехфазного приемника.
8
Рис.3.5 Схема несвязанной трехфазной цепи.
Здесь трехфазный источник представлен тремя идеальными источниками ЭДС E&A , E&B , E&C . Три фазы приемника представлены условно идеальными
элементами с полными комплексными сопротивлениями Z a ,Z b ,Z c . Каждая фаза приемника подсоединяется к соответствующей фазе источника, как показано на рис. 3.5. При этом образуются три электрические цепи, объединенные конструктивно одним трехфазным источником, т.е. трехфазная цепь. В этой цепи три фазы объединены лишь конструктивно и не имеют между собой электрической связи (электрически не связаны между собой). Такая цепь называется несвязанной трехфазной цепью и практически не используется.
На практике три фазы трехфазной цепи соединены между собой (электрически связаны).
Существуют различные способы соединения фаз трехфазных источников и трехфазных потребителей электроэнергии. Наиболее распространенными являются соединения "звезда" и "треугольник". При этом способ соединения фаз источников и фаз потребителей в трехфазных системах могут быть различными. Фазы источника обычно соединены "звездой", фазы потребителей соединяются либо "звездой", либо "треугольником".
При соединении фаз обмотки генератора (или трансформатора) "звездой" их концы X,Y иZ соединяют в одну общую точкуN, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников x, y, z также соединяют в одну точкуn (нейтральная точка приемника). Такое соединение называется соединение "звезда".
9
Рис. 3.6. Схема соединения фаз источника и приемника в звезду.
Провода A-a,B-b иC-c,соединяющие начала фаз генератора и приемника, называются линейными проводами (линейный провод А, линейный провод В, линейный провод С). ПроводN-n,соединяющий точкуN генератора с точкойn приемника, называют нейтральным проводом.
Здесь по–прежнемукаждая фаза представляет собой электрическую цепь, в которой приемник подключен к соответствующей фазе источника посредством нейтрального провода и одного из линейных проводов (пунктир на рис.3.6). Однако, в отличие от несвязанной трехфазной цепи, в линии передачи используется меньшее количество проводов. Это определяет одно из преимуществ трехфазных цепей – экономичность передачи энергии.
При соединении фаз трехфазного источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началомВ второй фазы, конецY второй фазы – с началомС третьей фазы, конец третьей фазыZ – c началом первой фазыА. НачалаА,В иС фаз подключаются с помощью трех проводов к трем фазам приемника, также соединенным способом "треугольник".
Рис. 3.7. Схема соединения фаз источника и приемника в треугольник
10
Здесь также каждая фаза представляет собой электрическую цепь, в которой приемник подключен к соответствующей фазе источника посредством двух линейных проводов (пунктир на рис.3.7). Однако в линии передачи используется еще меньшее количество проводов. Это делает передачу электроэнергии еще более экономичной
При способе соединения "треугольник" фазы приемника именуют двумя символами в соответствии с линейными проводами, к которым данная фаза подключена: фаза "ab", фаза "bc", фаза "ca". Параметры фаз обозначают
соответствующими индексами: Z ab ,Z bc ,Z ca
4. Напряжения трехфазного источника.
Трехфазный источник, соединенный способом "звезда", создает две трехфазные системы напряжения разной величины. При этом различают фазные напряжения и линейные напряжения.
На рис.3.8 показана схема замещения трехфазного источника, соединенного "звездой" и присоединенного к линии электропередачи.
Рис.3.8. Схема замещения трехфазного источника
Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (U&A , U&B , U&C ). За условно
положительные направления фазных напряжений принимают направления от начала к концу фаз.
Линейное напряжение (UЛ) – напряжение между линейными проводами или между началами фаз (U&AB , U&BC , U&CA ). Условно положительные
направления линейных напряжений приняты от точек соответствующих первому индексу, к точкам соответствующим второму индексу (то есть, от точек с более высоким потенциалом к точкам с более низким) (рис. 3.8).
studfiles.net
Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.
Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.
Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o.
Рис. 3. Схема трёхфазного генератора.
В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.
eА = Еm· sinωt eB = Еm· sin(ωt – 1200) eC = Еm· sin(ωt + 1200)
Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю:
На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы - последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу.
Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.
3.1.1 Соединение в звезду. Схема, определения.
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 4.
Рис. 4. Трехфазная цепь, соединенная звездой
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника N и приемника N' называют нейтральным (нулевым) проводом.
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.
Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах - линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами:
Iл = Iф.
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений:
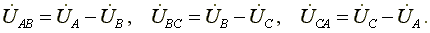
или
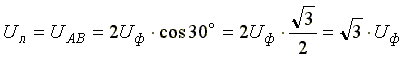
При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.
studfiles.net
Трехфазные электрические цепи раздел Электротехника, Теория / ТОЭ / Лекция N 16. Трехфаз....
| Теория / ТОЭ / Лекция N 16. Трехфазные электрические цепи. |
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой,т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на  эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на рад. (см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
- экономичность передачи электроэнергии на большие расстояния;
- самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
- возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
- уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенноститрехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
Система ЭДС (напряжений, токов и т.д.) называется симметричной,если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол  . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3.
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4). Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными.Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б). Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.
Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной. Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звездуи в … Линейнымназывается провод, соединяющий начала фаз обмотки генератора и … Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным(на рис. 6 показан пунктиром).… Для симметричной системы ЭДС имеем . Литература
Контрольные вопросы и задачи
|
Лекция N17
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в… Если к симметричной трехфазной цепи приложена симметричная трехфазная система… Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз можно… При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при… ; ; . По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:Литература
Контрольные вопросы и задачи
; 
; 
; 
. Линейное напряжение равно 380 В. Определить ток в нейтральном проводе.
Ответ: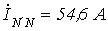 
.
; 
. Остальные параметры те же. Определить ток в нейтральном проводе.
Ответ: 
.
Определить фазные напряжения на нагрузке.
Ответ: 
; 
; 
.
Определить фазные напряжения на нагрузке.
Ответ: 
; 
; 
.
Лекция N 18
Несимметричные режимы в простейших характерных случаях (короткое замыкание и холостой ход) могут быть проанализированы на основе построения… Рассмотрим режимы обрыва и короткого замыкания фазы при соединении в звезду… . Активная мощность генератора, определяемая как среднее за период значение… . 1. Четырехпроводная система, несимметричный режим. Представленная на рис. 8 схема называется схемой трех ваттметров.Литература
Контрольные вопросы и задачи
Ответ: 
.
Ответ: в два раза.
Ответ: 
.
соединена в звезду. Линейное напряжение 
. Определить показание ваттметра.
Ответ: 
.
. Определить показания ваттметров.
Ответ: 
.
Лекция N 19
Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их… Симметричную систему прямой последовательности образуют (см. рис. 1,а) три… . Тогда с учетом (4) , (7) ,Обратной
и нулевой
Литература
Контрольные вопросы и задачи
, если 
, 
. Ответ: 
.
. Ответ: 
; 
.
и 
. Определить действующие значения токов в фазах двигателя, если его сопротивления прямой и обратной последовательностей соответственно равны: 
; 
. Нейтральный провод отсутствует. Ответ: 
; 
; 
.
Лекция N 20
В тех случаях, когда трехфазная цепь в целом симметрична, а несимметрия носит локальный характер (местное короткое замыкание или обрыв фазы,… При мысленном устранении несимметрии (несимметричного участка) для оставшейся… В отдельности рассчитываются входные сопротивления симметричной цепи для различных последовательностей, которая… Для фазных напряжений имеем (15) Учитывая, что комплекс, сопряженный , равен и наоборот, для сопряженных… Подставляя (15) и (16) в (14), после соответствующих преобразований получимЛитература
Контрольные вопросы и задачи
и 
в цепи на рис. 3, если фазная ЭДС 
, а сопротивления прямой и обратной последовательностей равны: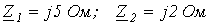 
. Ответ: 
.
, а сопротивления прямой и обратной последовательностей 
. Ответ: 
.
allrefers.ru
Элементы трёхфазных цепей переменного тока.
Генераторы, линии передачи электроэнергии, электродвигатели оказываются технически более совершенными, и в конечном итоге более выгодными экономически, если они построены на принципах трёхфазных цепей переменного тока.
Создание в 1889г. выдающимся русским учёным Михаилом Осиповичем Доливо-Добровольским (1862 г – 1919 г) связанной трёхфазной цепи переменного тока явилось важным событием в истории электротехники. (Он же изобрёл и асинхронный двигатель АД).
Трёхфазная электрическая цепь является упорядоченным электрическим соединителем трёх источников переменного напряжения (или тока), имеющих постоянную разность временных фаз, и трёх потребителей (или трёх групп потребителей) электроэнергии.
Каждая ветвь трёхфазной цепи называется фазой.
Упорядоченность трёхфазной цепи проявляется в том, что в фазах источником обеспечивается … примерное равенство амплитуд напряжений, а также амплитуд токов. Это достигается конструкцией генераторов и выравниванием сопротивлений фаз потребителей.
Для получения трёхфазного тока на электростанциях применяют специальные трёхфазные генераторы, имеющие три обмотки, сдвинутые относительно друг друга и поэтому дающие три ЭДС с фазовым сдвигом 1200 между собой.
Наличие двух различных напряжений является одним из достоинств трёхфазного тока.
рис.8.2. Графики а) и векторная диаграмма б) фазных и одного линейного напряжения
Каждая фаза имеет начало и конец. Начало фаз принято обозначать латинскими буквами A, B, C, а концы – буквами X, Y, Z (для генератора), малыми буквами a, b, c (начала), x, y, z (концы) – для потребителя
Практически используются две схемы симметричных соединений трёх фаз: звезда (рис.8.3а), когда соединяются вместе концы всех обмоток X, Y, Z, и треугольник (рис.8.3б), когда соединяются начало одной обмотки с концом другой в последовательности A – Z, B – X, C – Y.
Фазы генератора:
Начала и концы фаз обозначаются соответственно:
A – X, B – Y, C – Z.
Фазы потребителя:
Начала и концы фаз обозначаются соответственно:
a – x, b – y, c – z.
рис.8.3.
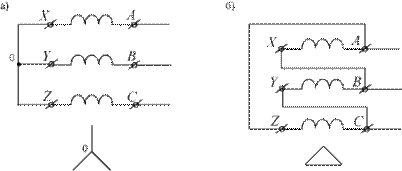
рис.8.4.
Фазы трёхфазного генератора (источника) соединяются либо звездой (соединение точек X, Y, Z), либо треугольником (соединение A – Z, B – X, C – Y). Фазы трёхфазного потребителя обозначаются малыми буквами (x, y, z; a, b, c).
Варианты схем соединений фаз источников и приёмников
И П
рис.8.5.
1 – «треугольник» — «треугольник»
2 – «треугольник» — «звезда»
3 – «звезда» — «треугольник»
4 – «звезда» — «звезда».
Трёхпроводная линия соединяет начала соответствующих фаз источника и приёмника ( A – a, B – b, C – c).
Участки цепи A – a, B – b, C – c называются фазами линии.
Возможны любые сочетания схем соединений у источника «И» и приёмника «П» (рис.8.5.). В цепях с соединением «звезда» — «звезда» используется также четвёртая линия, соединяющая нуль источника (соединение X, Y, Z) и нуль приёмника (соединение x, y, z). Эта соединительная нейтраль называется нейтральным (нулевым) проводом.
В трёхфазной цепи возможно включение отдельных однофазных потребителей (или их сочетаний) на фазы линии и на одну фазу и нулевой провод (рис.8.6.).
рис.8.6.
Провода, соединяющие фазы генератора и приёмника, называются – линейными, а токи в них линейными токами ( 
). Напряжение этих токов условно принято указывать от генератора к приёмнику, также как направление ЭДС ( 
) от концов фаз к их началам. Напряжения между началами и концами фаз генератора называются фазными и обозначаются 
. Напряжения между началами фаз генератора называются линейными и обозначаются 
.
Фазными токами называются токи, протекающие по фазам, причём у источников их положительные направления принимаются от конца фазы к её началу ( 
), а у приёмников – в противоположном направлении ( 
).
Мгновенные значения токов генератора описываются уравнениями:
refac.ru
. Определить комплексы остальных фазных и линейных токов. 