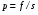, где p - степень вероятности, c - общее число возможных вариантов, f - количество благоприятных вариантов. В случае с монетой мы имеем соотношение 1 к 2 т.к. число сторон равно 2, а возможность выпадения орла или решки не превышает единицы [1].Азартные игры привлекают людей уже очень давно, ведь выигрыш и проигрыш зависит от везения, случая и немного от умения игрока играть. Азартные игры бывают разнообразные – баккара, рулетка, очко, штос, лотерея, спортивные пари и все ставки в тотализаторе и другие, но всех их объединяет теория вероятности выигрыша и проигрыша.
Игра в рулетку
Основной элемент. Предвидеть случайность
Теория вероятности в азартных играх проявила себя еще в XVII веке, благодаря Шевалье де Меру. Он придумал заключать пари с наибольшей вероятностью выигрыша, просчитав все варианты, он сначала выигрывал и из-за того, что с ним никто больше не хотел заключать пари, просчитал другой, как он думал выигрышный вариант. Он думал, что он будет выигрышным, как и первый, но немного просчитался. Чтобы понять, где он совершил ошибку, он обратился к математику Блезу Паскалю. Так, благодаря Шевалье и его теории вероятности в азартных играх, возникла новая наука. Многие ученые пытались просчитать разные возможности выигрыша и проигрыша в игре.
На грани безумия. Невероятная вероятность.
Теория вероятности в азартных играх берет во внимание несколько категорий:
Если рассмотреть теорию вероятности в лотереи, то можно применить такую формулу:
n*(n-1)*(n-2)*…*(n-(m-1))/ m*(m-1)*(m-2)*…*1
n – общее количество шариков;m – количество, которое нужно угадать.
В лотереи из 49 шаров, где нужно угадать 6 шаров, расчет будет выглядеть так:
49 * 48 * 47 * 46 * 45 * 44 / 6 * 5 * 4 * 3 * 2 * 1 = 13 983 816
13 983 816 – число, степени уверенности в выигрыше.
Игральные кубики
Для разных азартных игр, теория вероятности будет разная. Бросая игральный кубик, у игрока вероятность выигрыша составляет 16,66%, то есть возможность, что выпадет необходимая комбинация — 1, делится на число возможных комбинаций — 6:
1 / 6 = 16,66 %.
Такое событие, как выигрыш может быть: случайным, невозможным или достоверным.
Достоверное событие – событие, которое произойдет в любом случае если соблюдать все условия, для его совершения. Играя в кости, рано или поздно выиграешь.
Случайное – случайный выигрыш, например, когда человек начал играть и сам того не ожидая, сразу же выиграл.
Невозможное событие – когда возможность выигрыша равна 0.
Яков Бернулли, исследуя теорию вероятности выигрыша, установил, что чем больше количество испытаний, количество одних или других событий будет стремиться к вероятности, умноженной на количество этих испытаний. Этот закон срабатывает, если в одну игру сыграть примерно 10000 раз. Этот закон он установил бросая монетку.
В случае с азартными играми этот закон действует также Игрок при огромном количестве игр выиграет столько же сколько и проиграет.
Если человек будет бросать кубик 6000 раз, а сумма ставки — 1 $, то он выиграет:
1 / 6 * 6000 * 5$ = 5000$ и проиграет также 5000$, ведь 5 / 6 * 6000 * 1 = 5000$.
Для того чтобы закон больших чисел начал работать – нужно верить в результат и проявлять усердие в игре. Все в мире выравнивается, в том числе и результат игры, но бывают случаи, когда закон не действует из-за везения или невезения человека.
Вероятность выигрыша в игре можно рассчитать, но расчеты – еще не гарантия того, что человек выиграет. Если рассмотреть игру в рулетку, то вероятность выигрыша 1 / 38, но сыграв 38 раз человек может и не выиграть вовсе. В этом случае человек задумывается о том, что удача отвернулась от него.
В мире существует огромное количество азартных игр, и вероятность выигрыша у них совершенно разные. Все зависит от количества выигрышных комбинаций. Количества игроков, везения, суммы ставок.
Для того чтобы увеличить выигрыш можно играть по-разному. Одни играют много, но на маленькие суммы, другие играют мало, но по крупному. Считается, что увеличить количество денег проще, если играть мало, но делать большие ставки – тогда выигрыш максимальный. Если сыграть в рулетку выбрав цвет или четность, то вероятность выигрыша будет примерно 48 %. Играя с большими ставками вероятность, выиграть огромные деньги увеличивается. Вероятность выигрыша в некоторых играх зависит от везения, но в некоторых вероятность можно увеличить благодаря возможности выбора – карточные игры.
Играя в блекджек или покер, человек может выиграть или проиграть, сделав неправильный выбор. Выигрыш в таких играх зависит не только от теории вероятности, но и от мастерства игрока и его умения держать эмоции под контролем .
Играем в карты
Играя в азартные игры, люди, которые впервые столкнулись с игрой и теорией вероятности выигрыша, очень часто совершают одну и ту же ошибку – гонятся за выигрышем, каждый раз ставят на разные числа, цвета. В таком случае возможность выигрыша постоянно уменьшается. Если ставить на одно и то же, то теория вероятности сработает рано или поздно. Если игрок умеет играть, он соблюдая свою стратегию игры, может длительное время играть в минус, но в конечном результате выйти в плюс.
Азартные игры – это всегда интересно, но играя нужно постоянно трезво оценивать свои возможности на выигрыш или проигрыш. Удача – очень часто изменчива и если следовать за принципами теории вероятности, то выиграв несколько раз, потом можно все проиграть, если не остановиться. Бывали случаи, когда бедные люди выигрывали за несколько часов миллионы и проигрывали их в тот же день, оставаясь с тем, с чем пришли. А другие выигрывали и вовремя останавливались, что давало возможность полностью поменять свою жизнь к лучшему.
Теория вероятности в азартной игре может помочь выиграть, но если человек все хорошо продумает, просчитает и останется верным выбранной стратегии. В любом случае всегда есть возможность выигрыша и возможность проигрыша в азартной игре, но если накапливать знания и умения играть, то в некоторых случаях это дает возможность увеличить шансы на выигрыш.
Почему математики не тратят время на лотереи
www.13min.ru
Слайд 1
в азартных играх Кортунов Роман 11аСлайд 2
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях. Самые ранние работы учёных в области теории вероятностей относятся к XVII веку.
Слайд 3
Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей. Важный вклад в теорию вероятностей внёс Якоб Бернулли: он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
Слайд 4
В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышёв, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.
Слайд 5
В начале XVII века к великому Галилею явился приятель, который захотел получить разъяснение по следующему поводу. Играя в три кости, он заметил, что число 10, как сумма очков на трех костях, появляется чаще чем число 9. «Как же так, – спрашивал игрок, – ведь как в случае девятки, так и в случае десятки эти числа набираются одинаковым числом способов, а именно шестью?» Приятель был формально прав. Разбираясь в этом противоречии, Галилей решил одну из первых задач комбинаторики – основного инструмента расчетов вероятностей .
Слайд 6
Часто приходиться составлять из конечного числа элементов различные комбинации и производить подсчет числа всех возможных комбинаций, составленных по некоторому правилу. Такие задачи получили название комбинаторных, а раздел математики , занимающийся их решением, называется комбинаторикой.
Слайд 7
К началу XX в. Комбинаторика считалась законченной частью математики. Давно сложилась принятая специфическая терминология (перестановки, сочетания, размещения и т.д.).. В XX в.комбинаторику стали воспринимать как первую главу теории множеств, занимающуюся конечными множествами (их подмножествами, отображениями друг на друга и т.п.), что содействовало более последовательной классификации комбинаторных задач.
Слайд 8
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Слайд 9
Колмогоров Андрей Николаевич (1903-87), российский математик, основатель научных школ по теории вероятностей и теории функций, академик АН СССР (1939), Герой Социалистического Труда (1963). Фундаментальные труды по теории функций, математической логике, топологии, дифференциальным уравнениям, функциональному анализу и особенно по теории вероятностей (аксиоматическое обоснование, теория случайных процессов) и теории информации. Ленинская премия (1965), Государственная премия СССР (1941).
Слайд 10
Если тысячи и миллионы опытов, поставленных в одних и тех же условиях, всегда приводят к определенному событию (выпущенное из руки яблоко падает на землю), то событие называется достоверным. А коль скоро миллионы опытов показывают, что некоторый их исход никогда не наблюдается (монета, брошенная на стол, никогда не останавливается на ребре), то такие события называются невозможными.
Слайд 11
Несомненно каждому из нас случалось рассуждать о «вероятности» наступления того или иного события, говорить, что какое-либо событие «наиболее вероятно», «мало вероятно» и т.п.
Слайд 12
Слово «азарт» приобрело в русском языке новый смысл. Это перевод французского слова hazard, что означает « случай ». Так что азартные игры – это игры, построенные на случае, что звучит уже вполне научно и респектабельно.
Слайд 13
На заре человечества появились азартные игры. Их история начинается с игральных костей. Изобретение этого развлечения, источника радостей и несчастий, приписывается и индийцам, и египтянам, и грекам в лице Паламеда .
Слайд 14
Проигрыши и выигрыши чередуются случайно, и, в конце концов, обязательно встретится то, что называют «полосой везения» или «полосой невезения». Эти полосы могут быть настолько затяжными, что у партнера победнее будут выкачаны все деньги.
Слайд 15
Есть лишь одно обстоятельство, которое нарушает равенство игроков, сражающихся в такие игры как игральные кости. То есть в игры, где игрокам ничего не надо решать, ибо игрой не предусмотрен выбор (за исключением выбора: играть или отказаться). Этим обстоятельством является количество денег .
Слайд 16
Нетрудно видеть, что шансы на стороне того игрока, у которого их больше.
Слайд 17
Можно ли выиграть в рулетку? Нет ничего невозможного. Представьте, что вы хотите выиграть в орлянку. Неважно сколько, допустим, $1. Можете ли вы выиграть наверняка? Ответ: в реальной жизни – да, можете, но при соблюдении двух условий: 1. Если примут ваши правила игры. 2. Если у вас есть значительный капитал, позволяющий играть по определённой системе.
Слайд 18
Какова вероятность того, что орёл не выпадет никогда? Давайте посчитаем. Вероятность того, что орёл не выпадет первым же броском, составляет 1/2. Вероятность того, что орёл не выпадет ни первым, ни вторым броском – (1/2)2 или 1/4. Дальше вероятность уменьшается в геометрической прогрессии. Из трёх бросков – 1/8, из четырёх – 1/16... из десяти – 1/1024.
Слайд 19
С рулеткой дело обстоит точно так же, если вы ставите на так называемые равные шансы: красное-чёрное, чёт-нечет, больше-меньше. Разница лишь в том, что вероятность выпадения каждого из этих шансов составляет чуть меньше половины – не 1/2, а 18/37 (за счёт того, что на рулетке есть zero ).
Слайд 20
ВСЯ БЕДА ЗАКЛЮЧАЕТСЯ В ТОМ, ЧТО НАМ С ВАМИ НЕ ДАДУТ ПРИМЕНИТЬ НА ПРАКТИКЕ СТОЛЬ БЛЕСТЯЩИЙ СПОСОБ ОБОГАЩЕНИЯ!!! Игорное заведение имеет простой способ не допустить превращения игры в скачку со ставками, где игрок был бы практически «обречён» на выигрыш.
Слайд 21
Особо популярными были и остаются игровые автоматы. Но здесь дело обстоит немного сложнее. Выпадение чисел основано на теории вероятности, но за это отвечает программа . Ясное дело, что, как бы ни старался игрок, он все равно останется в проигрыше. Однако это вовсе не значит, что автомат нельзя обмануть. Это всего лишь программа. А любую программу можно либо обойти, либо сломать.
Слайд 22
Работа любого игрового автомата, вне зависимости от способа реализации игровых услуг, целиком и полностью подчинена определенному алгоритму.
Слайд 23
В истории игорного бизнеса надолго остался один из способов ограбления слотов, известный как «засечка времени активизации диска». Его было трудно обнаружить, так как отсутствовали внешние признаки вмешательства в нормальную работу механизма. Среди умельцев было множество никак не связанных между собой групп, научившихся стабильно выигрывать у «одноруких бандитов».
Слайд 24
Суть открытия «темп – бойз » состояла в том, что если дёргать рукоятку слот – машины в определённое время ( с точностью до секунды ), то аппарат повторяет только что выпавшую комбинацию. Казино тогда были оснащены исключительно механическими слот – машинами, а у них был один существенный недостаток: роль ГСЧ выполнял сам набор барабанов, надетых на одну ось.
Слайд 25
Как выиграть в карты? Скорее всего, вопрос поставлен немного те так. Лучше будет задаться вопросом - как не проиграть в карты? Многие считают, что в карты выигрывать постоянно невозможно, в конечном итоге проигрыш все-равно наступит. И это так, но если систематически выигрывать большие суммы, а потом проиграть одну маленькую, то проигрыш не будет казаться разорительным.
Слайд 26
Большую роль играет соперник. Как выиграть в карты у профессионального шулера, знает только такой же шулер. А вот, как выиграть в карты у дилера казино? - это уже вопрос другой. Возьмем, к примеру, карточную игру Блэкджек . Математические шансы выигрыша игрока немного превышают шансы казино. Но, почему-то казино, практически, всегда выигрывает.
Слайд 27
Существенным моментом, который может помешать Вам выиграть в карты, является размер ставок. Для каждой игры он различается. Ставка должна рассчитываться из суммы вашего бюджета. Если Вы играете в Блэкджек и Ваш бюджет равен 1500$, то оптимальная ставка будет 100$. Для Семикарточного стад покера - 50$. А вот для пятикарточного покера 50$ будет маловато.
Слайд 28
Чтобы часто выигрывать в карты нельзя играть долгий период времени, обязательно нужно делать перерывы в игре. Сейчас объясню, почему. В начале у Вас имеется определенная сумма для игры, когда Вы проигрываете или выигрываете эта сумма, то убавляется, то прибавляется, т. е. то в плюс, то в минус.
Слайд 29
По традиции, испокон веков местом, где делались спортивные ставки, был ипподром. Но только лишь в XIX веке самые разные виды спорта начали становиться предметом тотализатора. Вскоре практика показала, что ставить можно на всё, что бегает, прыгает, ездит и летает. Тогда же зародилась профессия букмекера — профессионального спорщика. первую официальную букмекерскую контору в мире открыли в середине 19 века в Лондоне Левиафан Дэвис и Фред Суинделл . Здесь джентльмены встречались пообщаться, посмотреть на лошадиные бега и сделать спортивные ставки на выигрыш.
Слайд 30
Если, скажем, вероятность натолкнуться на соответствующую информацию в течение одного дня равна одной сотой, то через сто дней 37 процентов населения, так сказать, омываемого этим потоком информации, так и не столкнется с этой рекламой, другие 37 процентов встретятся с упоминанием о рекламируемом предмете 1 раз, 18 процентов – два раза, 6 процентов – три раза и т.д. Эти числа дает распределение Пуассона.
Слайд 31
Эффективным средством повышения действенности рекламы является повышение усвоения информации. Реклама должна быть не только привлекательной, но и информативной. В случае, когда полученная посредством рекламы информация не обманывает надежд покупателя, вы получаете постоянных клиентов.
Слайд 32
Таким образом, огромное число факторов делает совершенно непредсказуемым результат выброса костей, изготовленных без жульничества. А рассуждения о том, что вот если бы была возможность разместить кости в кубке в положении, фиксируемом с микронной точностью, да если бы еще направление выбрасывания костей можно было бы установить с точностью тысячных долей углового градуса, да, кроме того, силу броска измерить с точностью до миллионных долей грамма... вот тогда можно было бы предсказать результат, и случай был бы с позором изгнан из этого опыта, – есть абсолютно пустой разговор. Ведь постоянство условий, при которых протекает явление или ставится опыт, есть практическое понятие. А условия проведения двух испытаний одинаковы лишь в том случае, если мы не можем установить различий между ними.
Слайд 33
Выводы делать только вам .
nsportal.ru
Костюков Е.А.,
11класс МБОУ «Лицей №1», г. Чистополь
Научный руководитель: Семина М.А.,
доцент кафедры ЕНД
Чистопольского Филиала «Восток»
КНИТУ-КАИ им. А.Н. Туполева
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ В АЗАРТНЫХ ИГРАХ
И. Гете
В нашу жизнь властно вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов, и даже сводки погоды сообщают о том, что завтра ожидается дождь с вероятностью 40%.
В жизни человека много интересных и необычных занятий. Можно заниматься экстремальным спортом, ходить в кино, играть в компьютерные игры. Но такое времяпровождение – однообразно. Есть занятие, которое начинается всегда одинаково, но одинакового завершения не имеет никогда. Это – азартные игры.
Азарт (фр. - hasard - случай, риск, от арабского аз-захр – игральная кость) является основной причиной увлеченности чем-либо, а когда в игре от тебя ничего не зависит, это уравнивает шансы всех играющих.
Что же такое азартная игра? Большинство считает, что это игра на деньги (до того, как я занялся исследованием Теории вероятностей, я тоже так считал), это не совсем так. На деньги можно играть и в теннис, и в шахматы. Теннисисты и шахматисты получают большие гонорары за выигрыши в турнирах, но в них главную роль играет все же мастерство, а вот любая игра в карты – азартная игра. Почему? Потому, что в ней главную роль играет случай – от него зависит, какие именно карты окажутся у партнеров. Правда, и в картежной игре умение игрока значит много. Но есть игры, в которых от игроков уже не требуется никакого умения, а все зависит от случая. Например, игра в «орлянку», когда подбрасывают монету и в зависимости от того, какой стороной она упала, определяется победитель. Или другая игра, где властвует случай, - игра в кости.
Актуальность проблемы. Моя тема актуальна, так как математика соприкасается с обыденной жизнью гораздо теснее, чем этому учат традиционно в школе. Уивер Уоррен пишет: «Теория вероятностей и статистика - две важные области, неразрывно связанные с нашей повседневной деятельностью. Мир промышленности, страховые компании в большей степени являются должниками вероятностных законов. Сама физика имеет существенно вероятностную природу; такова же в основе своей биология. Между тем, несмотря на эту важность, универсальный характер теории вероятностей и статистики всё еще не стал общепринятым. Лотереи, азартные игры, выборные кампании, страховые компании и т.п. Как предсказать результат?.. Какую позицию выбрать?..» Для ответа на эти вопросы я и решил заняться этим исследованием.
В качестве объектов изучения выступают различные азартные игры, на основе которых вводятся основные понятия теории вероятностей.
В работе проводится анализ реальных, исторических и современных азартных игр. Общим является способ их решения.
Предмет исследования: задачи об азартных играх.
Цель: привести примеры использования теории вероятностей в различных играх; продемонстрировать возможности теории вероятностей при решении определенных жизненных задач.
Гипотеза: большинство считают, что предугадать результат азартных игр, в которых властвует случай, невозможно. Это не так. Математическое ожидание выигрыша - величина, которая поможет нам определить, справедлива ли та или иная игра, и выгодно ли нам в нее играть.
ПЕРВОНАЧАЛЬНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
В курсе теории вероятностей рассматриваются математические модели случайных событий. Понятие события является первоначальным.
Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет.
Испытание – любое действие, которое может привести к одному или нескольким результатам.
При осуществлении каждого испытания мы получаем его исходы – конечный результат испытания.
Пример 1. Бросают игральную кость – испытание. Возможные исходы: выпало 1 очко; выпало 2 очка; выпало 3 очка; выпало 4 очка; выпало 5 очков; выпало 6 очков.
Теория вероятности разделяет события на:
1) невероятные (выбросить семь очков, имея одну кость) - вероятность такого события равна нулю;
2) неизбежные (после броска кости одна из граней будет верхней) - вероятность равна единице;
3) вероятные (при первом же броске выпадет шестёрка) - вероятность лежит в пределах от нуля до единицы.
В январе 1963 года английский актёр Шон О' Коннери в трёх партиях подряд выиграл в рулетку около 30000 долларов. Все три раза он ставил на номер 17.
Шансы выпадения одного и того же числа три раза подряд составляют 1 к 46656.
Знание основ теории вероятности поможет оценить свои шансы на выигрыш и адекватность приза риску.
Вероятность события, основанного на чистой случайности, определяется формулой 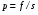, где p - степень вероятности, c - общее число возможных вариантов, f - количество благоприятных вариантов. В случае с монетой мы имеем соотношение 1 к 2 т.к. число сторон равно 2, а возможность выпадения орла или решки не превышает единицы [1].
Вероятность события - это число случаев благоприятного исхода данного события в сравнении с общим количеством возможных исходов, при условии, что вероятность наступления любого из них абсолютно одинакова.
Для более сложных расчётов используются правило сложения и правило умножения вероятностей.
Вероятность наступления в некоторой операции какого-либо одного (безразлично какого именно) из результатов равна сумме вероятностей этих результатов, если каждые два из них несовместимы между собой.
Пример 2. Пусть мы поставили в рулетку с 36 секторами на 15 и 28 и теперь хотим узнать, какова вероятность выигрыша.
Очевидно, что вероятность угадывания одного числа - 1/36, вероятность угадывания другого числа тоже 1/36. Значит, вероятность угадывания одного из двух чисел - 1/18:
.
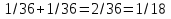Несовместимы - не могут наблюдаться в одной и той же единичной операции: 15 и 28 не могут выпасть одновременно.
В основе всех рассматриваемых в данной задаче операций лежит некоторая определенная совокупность условий К, которые предполагаются выполненными для всех операций. Если при вычислении какой-либо вероятности никаких иных условий, кроме совокупности К, не налагается, то такую вероятность мы назовем безусловной; условной же будет называться вероятность, вычисленная в предположении, что кроме общей для всех операций совокупности условий К, выполняются еще те или другие, точно оговоренные дополнительные условия.
Правило умножения: вероятность совместного наступления двух событий равна произведению вероятности первого события на условную вероятность второго, вычисленную в предположении, что первое событие состоялось.
ВИДЫ АЗАРТНЫХ ИГР
Игры со «сгорающими» очками
Идея рассмотрения игр со «сгорающими» очками возникла по аналогии с карточной игрой в «21 очко», когда есть желание набрать максимальное число очков на извлекаемых из колоды картах, но есть и опасность «сгорания» очков, если получаемая сумма окажется больше 21 очка.
Под играми со сгорающими очками будем понимать игры, в которых участники по очереди проводят какие – либо опыты сериями и могут добровольно передать ход другому игроку после определённого числа испытаний или, набрав то или иное число очков в данной серии, или ход передаётся принуждённо, когда очки серии «сгорели» при определённом исходе испытания. Игра прекращается после проведения одинаково числа серий у участников. Побеждает тот, у которого в результате получается наибольшая сумма очков во всех сериях.
Возможны два подхода к рассмотрению таких игр:
Рулетка
Рулетка – самая старая из существующих игр в казино. Её изобретение приписывали Блезу Паскалю, итальянскому математику Дону Паскуале и некоторым другим. В любом случае колесо рулетки впервые появилось в Париже в 1765 году.
Играть в рулетку очень просто. Колесо вращается, а затем маленький шар бросается в канавку в противоположном направлении движению колеса. В результате шар попадает в углубление в одном из секторов колеса. Естественно, мы предполагаем, что колесо правильное, то есть попадание шара в любой из секторов колеса равновероятно.
Существует несколько различных разновидностей рулетки. Наиболее известные – это американская рулетка (рулетка Лас – Вегаса) и европейская рулетка (рулетка Монте – Карло).
Американская рулетка
Колесо американской рулетки имеет 38 секторов, пронумерованные, как 00, 0, и 1 – 36. Секторы 0, 00 зелёные; секторы 1, 3, 5, 7, 9 ,13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35 красные; секторы 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36 чёрные.
Если не считать 0 и 00, секторы на колесе рулетки чередуются между красным и чёрным. Такой странный порядок чисел на колесе предназначен для того, чтобы большие и маленькие числа, так же как чётные и нечётные числа, имели тенденцию чередоваться.
Ставки
Как и азартные игры в кости, рулетка популярна в казино из-за богатого разнообразия ставок.
Вот ставки, которые используются в казино:
Прямая ставка или ставка на число – является ставкой на единственное число и оплачивается в случае выигрыш 35:1, т.е. при выпадении выбранного вами числа выигрыш равен 35 единицам, в других случаях вы поигрываете одну единицу (ставку).
Ставка на 2 числа является ставкой на два смежных числа в таблице на столе рулетки. Фишка ставится на черту, разделяющую два номера. Выигрыш оплачивается как 17:1, если выпадает любое из выбранных чисел.
Ставка на 3 числа (или ставка на строку C) является ставкой на три числа в вертикальной строке таблицы. Фишка ставится на вертикальную черту, ограничивающую ряд справа. Выигрыш оплачивается как 11:1, если при одном вращении колеса рулетки выпадет одно из трёх чисел.
Ставка на 4 числа (D) является ставкой на четыре числа, которые образуют квадрат на столе рулетки. Фишка ставится на угол между четырьмя номерами. Выигрыш оплачивается как 8:1, если при одном вращении колеса рулетки выпадает одно из 4 чисел.
Ставка на 5 чисел (E) является ставкой на числа 0, 00, 1, 2, 3. Выигрыш оплачивается как 6:1, если при одном вращении колеса рулетки выпадет одно из 5 чисел.
Ставка на 6 чисел (F) является ставкой на шесть чисел в двух смежных строках. Выигрыш оплачивается как 5:1, если выпадает одно из выбранных чисел.
Ставка на 12 чисел. Ставки на 12 чисел могут быть сделаны несколькими способами. Ставка на столбец (G) делается на любой из трёх столбцов, расположенных горизонтально на столе. Фишка ставится на поле возле выбранной колонки.
Другие ставки на 12 чисел (H) – первая дюжина (1 – 12), средняя дюжина (13 – 24) и последняя дюжина (25 – 36). Ставки на 12 чисел
оплачиваются как 2:1, если выпадает одно из выбранных чисел. Ставка на 12 чисел проигрывает, если выпадает 0 или 00.
Ставки на 18 чисел. Ставка на цвет (I) является ставкой на красное или чёрное. Ставка на чёт – нечёт (K) является ставкой на чётные числа от 1 до 36 или на нечётные числа от 1 до 36. Малая ставка (J) является ставкой на числа 1 – 18, и большая ставка является ставкой на числа от 19 до 36. Ставки на 18 чисел оплачиваются 1:1, если при одном вращении колеса рулетки выпадает одно из выбранных чисел. Ставка на 18 чисел на 18 чисел проигрывает, если выпадает 0 или 00.
Интересно: есть ли в американской рулетке ставки, более выгодные для игрока? Чтобы ответить на этот вопрос, надо определить математическое ожидание для каждой ставки. Как это сделать? Для примера хочу решить несколько задач на определение ожидаемого выигрыша.
Пример 3. Определить величину ожидаемого выигрыша при единичной ставке на число в американской рулетке.
Решение.
Случайная величина X={величина выигрыша}.
Составим закон распределения случайной величины X для данной ставки [3].
Таблица 1
X
-1
35
P (X)
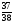
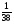
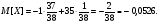
Так как полученное число меньше ноля, но не намного, то это игра является несправедливой лишь немного.
Пример 4. Определить величину ожидаемого выигрыша при единичной ставке на 2 числа в американской рулетке.
Решение.
Эта задача подобна предыдущей. Тут также необходимо составит закон распределения случайной величины для данной ставки и затем найти её математическое ожидание.
Таблица 2
X
-1
17
P (X)
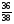
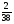
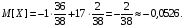
Эта игра, как и предыдущая, является лишь немного несправедливой. А вообще, если проверить, математическое ожидание любой ставки в американской рулетке будет везде одинаково и будет всегда равно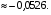 
Сам собой напрашивается вопрос: «Интересно, а чему равно математическое ожидание в европейской рулетке и одинаково ли оно для всех ставок?»
Давайте вместе попробуем ответить на него, но сначала разберёмся в основных принципах европейской рулетки.
Европейская рулетка (рулетка Монте – Карло)
Колесо рулетки Монте - Карло имеет 37 секторов, в отличие от американской рулетки содержит только один зеленые сектор – «0».
Правила игры и ставки в основном совпадают с правилами и ставками американской рулетки, но есть несколько различий. При игре в европейскую рулетку, когда делается ставка на 18 чисел (на красное / чёрное, на чёт / нечёт, на меньшее или большее), при выпадении сектора «0» (zero) в различных казино могут быть предложены различные варианта продолжения игры.
Рассмотрим некоторые из них.
1. Правило «LaPartage». В этом случае игрок теряет половину своей ставки.
2. Правило «EnPrison». В этом случае ставки не сгорают, а попадают в «тюрьму» на игровом столе до следующего розыгрыша числа. Если же ставка, находящаяся в «тюрьме» при следующем броске шарика выигрывает, она возвращается игроку без выплаты выигрыша, если же ставка проигрывает, или выпадает «0», ставка теряется.
3. Сложная «Тюрьма». В этом случае, так же как и в предыдущем, ставка помещается в «тюрьму». Если ставка сыграет на следующем броске, то она возвращается игроку, а если ставка не сыграет, то она проигрывается. Если же выпадает «0» и при следующем броске, то ставку помещают в «двойную тюрьму». Когда ставка находиться в «двойной тюрьме» и выигрывает, то она возвращается в простую «тюрьму», и игра продолжается, как прежде. Если ставка, находящаяся в «двойной тюрьме», не сыграла или выпал «0», то ставка проигрывается.
Теперь, чтобы ответить на наш вопрос, решим пары задач на определение математического ожидания выигрыша игрока при различных ставках.
Пример 5. При игре в европейскую рулетку игрок поставил на «красное». Найти математическое ожидание выигрыша игрока, если казино придерживается правила «LaPartage».
Решение.
Случайная величина X={величина выигрыша без учёта ставки}.
Составим граф распределения случайной величины Х и вычислим по нему математическое ожидание [3].
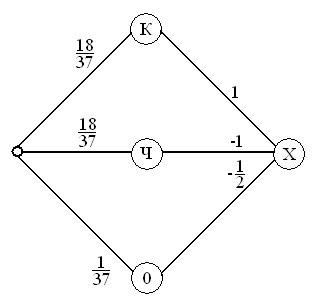
Рис. 1
Таким образом, это игра является несправедливой, но лишь немного.
Пример 6. При игре в европейскую рулетку игрок поставил на число 17. Необходимо найти математическое ожидание выигрыша игрока.
Решение.
Случайная величина X={величина выигрыша}.
Составим закон распределения случайной величины для данной ставки.
X
-1
35
P (X)
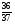
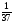
Таблица 3
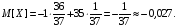
Таким образом, при игре в европейскую рулетку ожидаемые величины выигрышей для различных ставок различаются, но всегда
являются отрицательными для игроков.
Я показал, что при игре в американскую рулетку математические ожидания выигрыша для всех ставок одинаковы. А при игре в европейскую рулетку – различны. На основе сделанного исследования я советую: чтобы меньше проиграть, нужно ставить ставку с наибольшим математическим ожиданием. В европейской рулетке это ставки на 18 чисел. «А какую же ставку выбрать при игре в американскую рулетку?»
Реальный средний выигрыш будет приближаться к ожидаемому, если играть достаточно долго (в идеале бесконечно). При ограниченном числе игр результаты могут значительно отличаться от ожидаемых как в ту (выигрыш), так и в другую (проигрыш) сторону. Кроме математического ожидания, важными характеристиками случайных величин являются дисперсия и среднеквадратическое отклонение, которые показывают, насколько результат единичного испытания может отличаться от ожидаемого. Чем выше дисперсия, тем больше возможные отклонения.
ЗАКЛЮЧЕНИЕ
Приведенные в работе задачи раскрывают широкий круг задач на виды азартных игр, решаемых при помощи понятий теории вероятностей, повышают интерес к изучаемой теме. Подобранные задачи с решениями можно использовать при изучении тем теории вероятностей в старших классах.
Список литературы
Антипов И.Н. Избранные вопросы математики / И.Н. Антипов - М: Просвещение, 1979. - 191 стр.
Глеман М., Варга Т. Вероятность в играх и развлечениях. – М.: Просвещение, 1979 - 176 с.
Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. – М.: Наука, 1985 - 86 с.
infourok.ru
История азартных игр как фактор развития теории вероятностей
Семенова Н.И., кандидат технических наук,
доцент кафедры высшей математики СПбГЛТУ,
старший методист ГБОУ средняя школа 16, Санкт-Петербург
Читая ежегодно в курсе высшей математики лекции по комбинаторике и теории вероятностей, преподавателю технического ВУЗа приходится отвечать на ряд вопросов, связанных с историей этих разделов науки. И в первую очередь возникает настоятельная необходимость рассказать об истории азартных игр, давших толчок к развитию вычислений и доказательству ряда утверждений, на которых основываются указанные разделы.
Толковый словарь русского языка под редакцией С.И.Ожегова предлагает следующее определение: «Азартные игры – игры, в ходе которых ставки постоянно возрастают, а выигрыш зависит от случая». Поскольку теория вероятностей изучает закономерности возникновения случайных явлений, то неудивительно, что азартные игры явились некой основой для ее развития. Комбинаторика же имеет благодатную почву для решения задач на вычисление количества «благоприятных» комбинаций при игре в карты, кости и домино.
Приведенный ниже материал позволит преподавателю подготовиться к лекции по теме «История азартных игр как фактор развития теории вероятностей» или использовать отдельные его фрагменты на практических занятиях.
План лекции:
1. Родина игральных карт –Индия или Китай.
2. Проникновение карточных игр в Европу. Первая фабричная колода карт. Карточные масти.
3. Появление карт в России.
4. Карты – модель общества. Знаменитые игроки.
5. Кости как орудие состязания в меткости.
6. Родина игральных костей. Изобретатели игры в кости.
7. Кости в жизни великих людей.
8. Запрет на азартные игры.
9. Божественное участие в игре в кости.
10. Происхождение и философский смысл игры «домино».
11.Теория вероятностей применительно к игре в кости.
12. Формирование комбинаторики и теории вероятностей как самостоятельных разделов науки.
1.Среди исследователей карточных игр до сих пор идут споры по поводу страны, в которой впервые появились карты.
Некоторые историки утверждают, что цветные китайские плитки, датируемые Iвеком н.э., хранящиеся в собрании Бостонского музея, стали в свое время прообразом игральных карт. В словаре Чинг-Цзе, с которым европейцы познакомились в 1678 году, есть сведения, что игральные карты имели всеобщее распространение в Китае еще в 1120 году. В те давние времена карты представляли собой длинные и узкие пластинки, маркированные цифрами от 1 до 13. Они содержали четыре масти, каждая из которых символизировала время года. В колоде было 52 листа, по количеству недель в году.
Родиной первых карт с изображением фигур, по одному из предположений, является Индия. Древние индийские карты имели вид маленьких кружков, сделанных из лакированной клеенки. В них было 8 мастей, или армий, отличительным признаком которых являлись различные эмблемы и цвета. В каждой масти было 12 карт, таким образом, колода состояла из 96 листов. Масть имела своего короля и визиря, остальные фигуры представляли солдат и пешек с различной нумерацией.
Однако некоторые исследователи не согласны с подобным предположением. Они утверждают, что Индия не могла быть родиной карт, так как рисунок на них был выполнен в персидском стиле, а сам принцип игры больше соответствовал шахматам.
2.Ряд исследователей связывает появление карт с жителями «страны Сарацин», то есть с арабами. В результате Крестовых походов, совершаемых на Ближний Восток, игральные карты проникли в Европу. Первое документальное доказательство огромной популярности карточных игр в Европе относится к 1254 году, когда король Франции Людовик Святой издал указ, запрещающий играть в карты. Тех же, кто ослушается, велено было сечь кнутом.
Карточные игры покорили практически все страны Европы. Широко распространившись, вскоре они стали запрещаться властями. Поскольку люди были подвержены суевериям, они усмотрели в картах связь с нечистой силой.
Д. Гоффман, немецкий исследователь истории карт, указал на один из европейских законодательных актов, датированный 23 мая 1376 года. Это распоряжение городских властей Флоренции о запрещении «наиббе» – карточной игры, которая получила широкое распространение среди жителей города.
Известно, что еще во времена Колумба европейцы, создав свои первые поселения на острове Сан-Доминго, играли в карты, которые изготавливали из пальмовых листьев. Спустя несколько лет в разных странах Европы появились картонажные фабрики, где производились карты.
Родиной европейских карт считают Францию, где в одной из провинций и появилась первая фабричная колода, называвшаяся «тарот». Колода состояла из четырех мастей, которые имели следующие названия: мечи, жезлы, деньги и чаши. В каждой масти было четырнадцать карт: десять карт с цифрами и четыре с картинками, на которых были изображены король, королева, рыцарь и оруженосец (или паж). Всего в колоде было 56 карт.
Позже масти приобрели другие названия: лопаты (пики), сердца (черви), дубинки (трефы), бриллианты (бубны). В скором времени такие карты распространились по всей Европе.
Еще древние историки отмечали, что карты служат не только средством развлечений, но и символизируют общественное и государственное устройство с его королями, королевами и вассалами. Черви олицетворяют священнослужителей; бубны являются символом буржуа, потому что напоминают камни их домов; пики, служившие оружием офицерства, представляют дворянство; трефы обозначают крестьян.
3.В Россию карты попали из Германии, скорее всего через Украину. Еще запорожские казаки коротали свое свободное время за игрой в карты. При царе Алексее Михайловиче, отце Петра I, карточные игры распространились даже среди простолюдинов.
Со временем карточная символика, заимствованная у немцев, была изменена. Пики, например, переименовали в вины, поскольку они символизировали виноградный лист. А трефы в то время называли желудями.
О появлении карт в России написано в одной из статей Соборного Уложения 1649 года. В ней рассказывается и об их запрещении: ослушавшихся игроков надлежало «бить кнутом и рубить им руки и пальцы».
Позднее, во времена царствования Елизаветы, в 1761 году был издан указ, в котором игры делились на запрещенные и разрешенные. К запрещенным относились азартные игры, к разрешенным – коммерческие. Изменялись и меры наказания. При Петре III, например, практиковался денежный штраф. Но применялся он только к тем, кто делал ставки на очень большие суммы или играл в долг.
4.В XVIII—XIXвеках карты стали своеобразной моделью общества. Они привлекали людей не только надеждами на выигрыш, но и сулили успех, удачу, власть. Выигрыш для честного игрока был не самоцелью. Люди играли в карты, чтобы вызвать ощущение риска, внести в повседневную жизнь разнообразие и непредсказуемость.
На кон ставили лошадей и коляски, драгоценности, имения и крепостных, иногда и собственную жизнь. Случались и совсем необычные ставки: в 1802 году известный московский кутила и картежник А.Н.Голицын проиграл графу Л.К.Разумовскому свою жену.
Известный композитор XIXвека А.А.Алябьев, автор знаменитого романса «Соловей», был страстным картежником. Играя как-то с князем М., он с обычной ему ловкостью и быстротой тасовал карты. Князь обвинил партнера в использовании нечестных приемов. Алябьев в гневе ударил обидчика по голове и случайно его убил, за что был сослан на каторгу.
Среди литераторов тоже были азартные игроки. Про баснописца И.А.Крылова, члена Английского карточного клуба в Санкт-Петербурге, говорили, что мелом на сукне он пишет чаще, чем пером на бумаге. Суеверный поэт Н.А.Некрасов, играя в карты, всегда следовал приметам, но это не спасло его от серьезного заболевания, вызванного сидением бессонными ночами за игорным столом. Н.В.Гоголь блестяще разбирался в карточной терминологии и шулерских хитростях, что демонстрирует его пьеса «Игроки».
Несмотря на государственные указы о запрещенных играх, карточные игры приобрели широкий размах во времена царствования Александра I. Как говорил А.С.Пушкин, все эти указы лишь пополняли череду «бесчисленных пустых мер, принимаемых ежедневно».По всей России возникали все новые и новые игорные дома, куда стекалось местное дворянство. Особенно много их было на Петергофской дороге, которая славилась своими трактирами. Проезжавшие по ней на перекладных иногда надолго задерживались на промежуточных станциях, где играли в карты от зари до зари. Иногда карт накапливалось столько, что их собирали лопатами и вывозили возами.
5.Игра в кости известна с давних времен. Однако раньше вместо выточенных из различных материалов шестигранных кубиков использовались зубы бобра, обломки рогов оленя, косточки различных фруктов, морские раковины, грубо обработанные куски дерева. Археологи также находят астрагалы (кости животных, по которым древние люди предсказывали будущее), использовавшиеся не по своему прямому назначению.
Если самыми первыми играми были соревнования в силе и ловкости, то через некоторое время популярностью стали пользоваться состязания в меткости. Где как не здесь самое место случайности?!
Метали в цель в основном камни и обломки костей животных, и следующей ступенью развития игры в кости стало изобретение новых правил и условий, предусматривающих бросок не в далеко отстоящую мишень, а прямо перед собой, а также нанесение на грани кости обозначений и раскрашивание самих граней в различные цвета. Самослово «азарт» переводится с арабского как «трудный», так называли редко выпадавшие комбинации костей.
Первой настольной игрой с использованием костей стал триктрак, по сути своей явившийся прародителем абсолютно всех настольных игр. Подражая скачкам и остальным соревнованиям на скорость, триктрак позволял игрокам делать фишками ходы, количество которых совпадало с выпавшим обозначением на грани кости.
6.Родина игральных костей и первых правил самой игры вполне точно определена: это Азия. Здесь их использовали в качестве вспомогательного средства для игры в триктрак.
Прообразы современных игральных костей найдены в Египте, и датируются они примерно 2000 годом до н.э. Сходство определяется правильной кубической формой и количественной разметкой (на грани нарисованы точки, а не число или картинка). Попадающие под ту же характеристику кости были обнаружены и при раскопках на территории Китая. На данный момент им порядка 2600 лет.
Дальнейшее распространение игр с использованием нескольких кубиков с точками несомненно: за несколько сотен лет увлечение стало практически повальным. Свидетельством тому служат находки костей из бронзы, фарфора, оникса, гипса, горного хрусталя, агата и других материалов, что говорит о переходе игры из состояния, в котором ею увлечены единицы, в состояние, когда нет ни одного человека, не слышавшего о ней и хотя бы раз в жизни не попробовавшего сыграть.
Однако имени изобретателя игры в кости до сих пор не знает никто. Если следовать выводам, сделанным Геродотом, получается, что идея игры в кости была впервые воплощена в жизнь во времена правления царя Атиса такой народностью, как лидийцы. В то же самое время Софокл в своих сочинениях упоминает о некоем воине. Звали данную личность Паламедом, и его маркированные кубики впервые увидели свет во время осады Трои. По всей видимости, нападающим было очень скучно...
Даже Евангелие не обошлось без упоминания об игре в кости! Достаточно открыть страницы, на которых описывается распятие Христа, как в глаза бросается эпизод, в котором римские легионеры разыгрывают одежды Спасителя.
7.В жизни великих людей кости занимали не последнее место.
Любовь к игре римского императора Клавдия, даже в поездках не расстававшегося с парой кубиков, стала поводом для того, чтобы драматург Сенека написал одну из своих замечательных сатир, где Клавдий описан сидящим в аду и пытающимся метнуть кости посредством стакана с отсутствующим дном.
Калигула, также занимая высокий пост императора, нередко пользовался своим высоким положением для оплаты долгов, «заработанных» на игре в кости. Надо заметить, что довольно часто эти долги составляли весь капитал правителя.
Фортуна редко поворачивалась к Калигуле лицом, и для того, чтобы пополнить казну, императору приходилось забирать состояния других богатых римлян. Для этого правитель арестовывал и казнил богачей, приписывая им в последствии многие грехи, основным из которых была измена родине. Как следствие, все имущество патрициев, включая жен и прислугу (они также свободно проигрывались в кости), плавно перекочевывало в руки азартного императора.
8.Любителей погреметь кубиками сначала в кружке, а затем – на столе (камне, доске, земле или любой другой ровной поверхности) преследовала длинная рука закона. Правда, в некоторых странах это занятие наказуемо и до сих пор, однако порицание и небольшой штраф не идут ни в какое сравнение с тем, что было несколько сотен лет назад. В Древнем Риме IIIвека до н.э. попавшихся с поличным игроков лишали определенного количества денег, наказывали плетьми, предавали общественному осмеянию. В последнем случае давала о себе знать необузданная фантазия правителей. Игрока могли макнуть в смолу, а затем в перья, после чего носить в таком виде по городу. Его могли замуровать в стену, чтобы все тело было с одной стороны, а ступни – с другой, а рядом повесить длинное гусиное перо: желающих послушать здоровый смех всегда находилось изрядное количество.
При прочих негативных моментах игроки все равно находились, а сама игра расширяла территории своего распространения, цвела и благоухала: даже те чиновники, что занимались составлением соответствующих законов, не раз были замечены играющими, а в глазах иxгорел лихорадочный огонь азарта.
Постановления церковных соборов, поучения святых отшельников полны грозных запретов азартных игр. Мусульманские ученые писали про игру в нарды, в которой передвижения фишек определяются броском костей: «Как же отвратительно для мудрого стать рабом двух камней до такой степени, что он вручает свое достояние и свою землю в их руки, и они приказывают ему и запрещают, а он подчиняется их руководству больше, чем подчиняется верблюд, когда его ведет маленькая девочка».
Но ничто не помогало, и в любом городе можно было наблюдать картину, описанную в «Божественной комедии» Данте:
Когда кончается игра в три кости,
То проигравший снова их берет,
И мечет их один в унылой злости;
Другого провожает весь народ...
9.В кости играли герои знаменитых древнеиндийских эпосов, причем в ряде случаев данное развлечение заставляло игроков прибегать к помощи колдунов, нереальных зверей и птиц, а также прикладывать максимум усилий для того, чтобы остаться в живых.
Один из персонажей «Махабхараты», сев играть в кости, заколдованные злым духом, проиграл все свое царство. Пришлось ему принять облик путешественника и отправиться странствовать. Однако не тут-то было! Волшебные игральные кости превратились в птиц, догнали игрока-неудачника и отобрали у того практически всю одежду.
Что же тогда сделал любитель покидать кубики? Он не нашел иного выхода, как научиться всем премудростям игры в кости, чем и занялся. По прошествии нескольких лет он вернулся из странствий и снова сел за игровой стол: отыграть царство обратно не составило никакого труда.
В Индии считали, что кости могут лишить всего, что имеет человек, в один миг, но если игрок – профессионал, то кости смогут стать его выходом из любой ситуации.
До современного человека доходят также мифы и легенды, имеющие своей целью показать Божественное участие в игре в кости. Древние германцы, например, посредством костей выясняли свою судьбу, которую таким образом определял Бог. Проигрывая все до своей последней древнегерманской копейки, играющий ставил на кон одежду, а когда оказывался уже и без нее, то не находил другого выхода, кроме как выручить денег на очередную (а для многих – последнюю) ставку посредством продажи сопернику самого себя. Следует заметить, что ни о каком сопротивлении в тот момент, когда новоиспеченный раб подвергался перевозу на другое место жительства, и речи не могло идти! Действительно, если такова воля Бога и человеку предопределено быть рабом, то почему он должен сопротивляться? Во-первых, бесполезно, а во-вторых, игра-то культовая... О том же упоминает и Тацит в своем трактате «О происхождении германцев и местоположении Германии».
10.Некоторые исследователи считают, что появление домино связано с игральными костями. Об этом говорят таблички, найденные при раскопках древних городов. Человек делал их тогда из костей животных и использовал как предмет игры, чтобы занять себя в свободное время.
Изобретение домино нередко приписывается монахам доминиканского ордена. В качестве доказательства приводится черный цвет плащей и капюшонов, которые они носили. К тому же само слово «домино» имеет общий корень со словом «dominus». В переводе с латинского это означает «господствующий». Такой молитвой открывается месса в католическом приходе: «Господь да пребудет с вами» («Dominusvobiscum»).
Имеется также версия, согласно которой родиной домино является Китай. Примерным временем его появления называют XIIвек. В тот период костяшки служили, по-видимому, только для магических обрядов или гадания. Но и сейчас в Индии и других странах Востока с помощью домино раскрывают перед человеком его судьбу.
На Востоке сейчас известно около пятидесяти видов этой игры. Они носят названия, имеющие поэтическую окраску, например, «прыжок газели», «гвоздики в тумане» и др. Есть домино, где кости выкрашены в разные цвета.
Европа узнала домино после того, как эту игру привез из дальних стран знаменитый путешественник Марко Поло. Она сразу же стала пользоваться большой популярностью у европейцев. Распространившись в Италии и Франции, к концу XVIIIвека игра достигла границ Англии.
Существует предположение, что домино представляет собой модель мироздания. В нем зашифрован закон, универсальность которого заключается в гармонии внешнего мира (макрокосмоса) и внутреннего мира человека (микрокосмоса). Об этом говорят цифры, помещенные на гранях костей – их ровно 7, что символизирует наше бытие и Вселенную, содержащую семь структур.
11.В XVIвеке к игре в кости была впервые применена теория вероятности. Джероламо Кардано, итальянский ученый, целитель, математик, философ и изобретатель, и сам не брезгуя развлечься парой партий в кости, решил составить таблицу наиболее часто и до минимума редко выпадающих комбинаций. Он не стал сутки напролет сидеть за столом и бросать кубики, записывая каждый результат: этим до него занимались игроки несколько столетий. Кардано решил рассчитать эти значения математически, принимая в расчет одинаковую возможность быть верхней для каждой из шести граней кости.
В XVIIвеке одним из самых азартных игроков в кости был шевалье де Мере, непрерывно изобретавший новые виды состязаний. Например, он предложил, что будет бросать четыре кости и брать выигрыш лишь в случае, когда хотя бы одна из них откроется на шести. Однако вскоре его партнеры отказались от участия в такой игре – шевалье чаще выигрывал, чем проигрывал. Тогда де Мере придумал новый вариант – он бросал несколько раз пару костей и брал выигрыш, если хотя бы раз выпадали две шестерки. Надо было лишь определить, сколько следует сделать бросков, чтобы игра была ему столь же выгодна, как и первая. Шевалье решил, что надо бросать кости 24 раза, но опыт не подтвердил надежд де Мере – теперь он стал чаще проигрывать, чем выигрывать.
Другой проблемой для де Мере была задача о разделе ставки: пусть «матч» ведется до шести выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а другой – 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив.
Де Мере обратился за разъяснениями к двум крупнейшим математикам Франции XVIIвека – Блезу Паскалю и Пьеру Ферма. Разбираясь в этих и других задачах, поставленных перед ними де Мере, они сформулировали и доказали первые теоремы комбинаторики и теории вероятностей. А задачу о разделе ставки Паскаль решил в общем случае, когда одному игроку остается до выигрыша rпартий, а второму sпартий. Другое решение задачи дал Ферма.
12.Работы Блеза Паскаля и Пьера Ферма ознаменовали рождение двух новых ветвей математической науки – комбинаторики и теории вероятностей. Если до них комбинаторные проблемы лишь затрагивались в общих трудах по астрологии, логике и математике, а большей частью относились к области математических развлечений, то уже в 1666 г. Готфрид Вильгельм Лейбниц публикует «Диссертацию о комбинаторном искусстве», в которой впервые появляется сам термин «комбинаторный». Титульный лист книги двадцатилетнего автора, имевшего уже ученую степень бакалавра... юриспруденции, обещал приложения ко всем областям науки: к силлогизмам, смешению цветов и стихосложению, к логике, геометрии, военному искусству, грамматике, юриспруденции, медицине и теологии.
Лейбниц считал, что комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным расположением, в то время как обычная математика занимается большим и малым, единицей и многим, целым и частью. Иными словами, под комбинаторикой Лейбниц понимал примерно тот раздел науки, что сейчас называется дискретной математикой. К области комбинаторики Лейбниц относил и «универсальную характеристику» – математику суждений, т.е. прообраз нынешней математической логики.
В 1713 г. племянник Якоба Бернулли Николай опубликовал часть второй книги своего дяди «Arsconjectandi» («Искусство предположений»), в которой, например, указывались формулы для числа размещений из п элементов по k.
Замечательные достижения в области комбинаторики принадлежат одному из величайших математиков XVIIIвека Леонарду Эйлеру, швейцарцу, прожившему почти всю жизнь в России, где он был членом Петербургской академии наук.
После работ Паскаля и Ферма, Лейбница и Эйлера можно было уже говорить о комбинаторике как о самостоятельной ветви математики, тесно связанной с такими областями науки, как теория вероятностей, учение о рядах и многими другими.
Использованная литература:
1. Азартные игры: энциклопедия./ Ред.-сост. Брехова Н.Г., Бойков Е.К., Мохова Л.Н. – М.: АСТ, 2002. – 528 с.
2. Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.:ФИМА, МЦНМО, 2006.
3. Майстров Л.Е. Теория вероятностей. Исторический очерк. М.: Наука, 1967.
4. Ожегов С.И., Шведова Н.Ю. Толковый словарь русского языка. – 4 изд. – М.: Азбуковник, 1999.
ext.spb.ru
www.ronl.ru
