WinNavigator

Frigate

Norton Commander

WinNC

Dos Navigator

Servant Salamander

Turbo Browser

Winamp, Skins, Plugins

Необходимые Утилиты

Текстовые редакторы

Юмор

File managers and best utilites

Сила (физическая величина). Реферат сила в механике

Реферат Сила (в механике)

скачать

Реферат на тему:

План:

1 История понятия
2 Ньютоновская механика
- 2.1 Первый закон Ньютона
- 2.2 Второй закон Ньютона
- 2.3 Третий закон Ньютона
3 Фундаментальные взаимодействия
- 3.1 Гравитация
- 3.2 Электромагнитное взаимодействие
  - 3.2.1 Электростатическое поле (поле неподвижных зарядов)
  - 3.2.2 Электромагнитное поле (поле постоянных токов)
- 3.3 Сильное взаимодействие
- 3.4 Слабое взаимодействие
4 Производные виды сил
5 Равнодействующая

Введение

Классическая механика

$\vec{F} = \frac{\mathrm{d}}{\mathrm{d}t}(m \vec{v})$ Второй закон Ньютона

История… Фундаментальные понятия

Пространство · Время · Масса · СилаЭнергия · Импульс

Формулировки

Ньютоновская механикаЛагранжева механикаГамильтонова механикаФормализм Гамильтона — Якоби

Разделы

Прикладная механикаНебесная механикаМеханика сплошных средГеометрическая оптикаСтатистическая механика

Учёные

Галилей · Кеплер · НьютонЭйлер · Лаплас · Д’АламберЛагранж · Гамильтон · Коши

См. также «Физический портал»

Объединяет все силы то, что они вызывают ускоренное движение массивных тел и возникновение в этих телах деформаций.

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.[1]

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами.В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы). [2].

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе.

При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями.[3][4][5][6]

С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.[3] Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия.[7]

Размерность силы — LMT−2, единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.

1. История понятия

Понятие силы использовали ещё ученые античности в своих работах о статике и движении. Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед.[8] Представления Аристотеля о силе, связанные с фундаментальными несоответствиями, просуществовали в течение нескольких столетий. Эти несоответствия устранил в XVII в. Исаак Ньютон, используя для описания силы математические методы. Механика Ньютона оставалась общепринятой на протяжении почти трехсот лет.[5] К началу XX в. Альберт Эйнштейн в теории относительности показал, что ньютоновская механика верна лишь в при сравнительно небольших скоростях движения и массах тел в системе, уточнив тем самым основные положения кинематики и динамики и описав некоторые новые свойства пространства-времени.

2. Ньютоновская механика

Исаак Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (знаменитые законы Ньютона).[5][9]

2.1. Первый закон Ньютона

Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.[9] Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.[10]

Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скоростью и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга.

2.2. Второй закон Ньютона

Хотя второй закон Ньютона традиционно записывают в виде: $\scriptstyle{\vec{F}=m\vec{a}}$ , сам Ньютон записывал его несколько иначе

Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.

$\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t},$

где $\vec{p}$ − импульс материальной точки, $\vec{F}$ − суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки.[9]

По определению импульса:

$\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t} = \frac{\mathrm{d}\left(m\vec{v}\right)}{\mathrm{d}t},$

где − масса, $\vec{v}$ − скорость.

По правилу нахождения производной произведения:

$\vec{F} = m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} + \vec{v}\frac{\mathrm{d}m}{\mathrm{d}t}.$

Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид:

$\vec{F} = m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}.$

Учитывая определение ускорения точки, второй закон Ньютона принимает вид:

$\vec{F} =m\vec{a}.$

Считается, что это «вторая самая известная формула в физике»[11], хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна .

Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.

2.3. Третий закон Ньютона

Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2.[12] Математически закон записывается так:

$\vec{F}_{1,2}=-\vec{F}_{2,1}.$

Этот закон означает, что силы всегда возникают парами «действие-противодействие».[9] Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:

$\vec{F}_{1,2}+\vec{F}_{\mathrm{2,1}}=0.$

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.[3]

3. Фундаментальные взаимодействия

Все силы в природе основаны на четырех типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные − между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.

Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется берущей из античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».

Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящими через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово сила, заменяя его словом взаимодействие.[13]

Каждый вид взаимодействия обусловлен обменом соответствующих переносчиков взаимодействия: гравитационное − обменом гравитонов (существование не подтверждено экспериментально), электромагнитное − виртуальных фотонов, слабое − векторных бозонов, сильное − глюонов (и на больших расстояниях — мезонов). В настоящее время электромагнитное и слабое взаимодействия объединены в более фундаментальное электрослабое взаимодействие. Делаются попытки объединения всех четырех фундаментальных взаимодействие в одно (так называемая теория великого объединения).

Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к этим четырем фундаментальным взаимодействиям. Например, трение − это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули,[14] который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решетки вещества удерживаться около положения равновесия.[3].

Однако на практике оказывается не только нецелесообразной, но и просто невозможной по условиям задачи подобная детализация рассмотрения вопроса о действии сил.

3.1. Гравитация

Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Исааком Ньютоном в его труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчете, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел[15]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой , прямо пропорциональной произведению масс ( ~m_1 и ~m_2 ) и обратно пропорциональной квадрату расстояния между ними:

$F=G\frac{m_1 m_2}{R^2}.$

Здесь − гравитационная постоянная[16], значение которой впервые получил в своих опытах Генри Кавендиш. Используя данный закон, можно получить формулы для расчета силы тяготения тел произвольной формы. Теория тяготения Ньютона хорошо описывает движение планет Солнечной системы и многих других небесных тел. Однако, в ее основе лежит концепция дальнодействия, противоречащая теории относительности. Поэтому классическая теория тяготения неприменима для описания движения тел, перемещающихся со скоростью, близкой к скорости света, гравитационных полей чрезвычайно массивных объектов (например, черных дыр), а также переменных полей тяготения, создаваемых движущимися телами, на больших расстояниях от них[17].

Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривленным траекториям в трехмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырехмерном пространстве-времени, в котором время в разных точках течет по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе[3].

3.2. Электромагнитное взаимодействие

3.2.1. Электростатическое поле (поле неподвижных зарядов)

Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью C. Однако, исходя из требований практики, основанных на удобствах измерения, вместо заряда нередко стал использоваться электрический ток с размерностью I, причём I = CT − 1. Единицей измерения величины заряда является кулон, а силы тока ампер.

Поскольку заряд, как таковой, не существует независимо от несущего его тела, то электрическое взаимодействие тел проявляется в виде той же рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух «точечных зарядов» в вакууме используется закон Кулона:

$\vec{F}= \frac{1}{4 \pi \varepsilon \varepsilon_0} \frac{q_{1}q_{2}}{r^3} \vec{r},$

где $\vec{r}$ — расстояние между зарядами, а $\varepsilon_0$ ≈ 8.854187817·10−12 Ф/м. В однородном (изотропном) веществе в этой системе сила взаимодействия уменьшается в ε раз, где ε — диэлектрическая постоянная среды.

Направление силы совпадает с линией, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым бы перемещалась лишённая массы заряжённая частица. Эти линии начинаются на одном и заканчиваются на другом зарядах.

3.2.2. Электромагнитное поле (поле постоянных токов)

Существование магнитного поля было известно ещё в средние века китайцам, использовавшим «любящий камень» — магнит, в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.

Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.

Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.

Ампер высказал гипотезу, признаваемую в физике, как модель процесса возникновения магнитного поля, заключающуюся в существовании в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.

Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции $\vec{B}$ , лежащим в плоскости, расположенной перпендикулярно по отношению к направлению движения заряда.

Единицей измерения магнитной индукции является тесла: 1 Тл = 1 Т кг с−2 А−2Количественно задача была решена Ампером, измерявшим силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.

Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга описывается законом Кулона. Однако заряды, находящиеся в движении относительно друг друга создают магнитные поля, посредством которых созданные движением зарядов токов в общем случае приходят в состояние силового взаимодействия.

Принципиальным отличием силы, возникающей при относительном движении зарядов от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сил взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.

В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обех токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.

Закон взаимодействия токов используется для эталонирования постоянного электрического тока.

3.3. Сильное взаимодействие

Сильное взаимодействие -- короткодействующие силы между адронами и кварками. В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающее отталкивание, благодаря этому атомные ядра не «схлопываются».

Внутри самих адронов сильное взаимодействие удерживает вместе кварки -- составные части адронов. Квантами сильного поля являются глюоны. Каждый кварк имеет один из трёх «цветовых» зарядов, каждый глюон состоит из пары «цвет»-«антицвет». Глюоны связывают кварки в т.н. «конфайнмент», из-за которого на данный момент свободные кварки в эксперименте не наблюдались. При отдалении кварков друг от друга энергия глюонных связей возрастает, а не уменьшается как при ядерном взаимодействии. Затратив много энергии (столкнув адроны в ускорителе) можно разорвать кварк-глюонную связь, но при этом происходит выброс струи новых адронов. Впрочем, свободные кварки могут существовать в космосе: если какому-то кварку удалось избежать конфайнмента во время Большого взрыва, то вероятность аннигилировать с соответствующим антикварком или превратиться в бесцветный адрон для такого кварка исчезающе мала.

3.4. Слабое взаимодействие

Слабое взаимодействие -- фундаментальное короткодействующее взаимодействие. Радиус действия 10−18 м. Симметрично относительно комбинации пространственной инверсии и зарядового сопряжения. В слабом взаимодействии участвуют все фундаментальные фермионы (лептоны и кварки). Это единственное взаимодействие, в котором участвуют нейтрино (не считая гравитации, пренебрежимо малой в лабораторных условиях), чем объясняется колоссальная проникающая способность этих частиц. Слабое взаимодействие позволяет лептонам, кваркам и их античастицам обмениваться энергией, массой, электрическим зарядом и квантовыми числами — то есть превращаться друг в друга. Одно из проявлений -- бета-распад.

4. Производные виды сил

Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила упругости направлена противоположно смещению, перпендикулярно поверхности. Вектор силы противоположен направлению смещения молекул.

Сила трения — сила, возникающая при относительном движении твёрдых тел и противодействующая этому движению. Относится к диссипативным силам. Сила трения имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы трения направлен противоположно вектору скорости.

Сила сопротивления среды — сила, возникающая при движении твёрдого тела в жидкой или газообразной среде. Относится к диссипативным силам. Сила сопротивления имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы сопротивления направлен противоположно вектору скорости.

Сила нормальной реакции опоры — сила упругости, действующая со стороны опоры на тело. Направлена перпендикулярно к поверхности опоры.

Силы поверхностного натяжения — силы, возникающие на поверхности фазового раздела. Имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила натяжения направлена по касательной к поверхности раздела фаз; возникает вследствие нескомпенсированного притяжения молекул, находящихся на границе раздела фаз, молекулами, находящимися не на границе раздела фаз.

Осмотическое давление

Силы Ван-дер-Ваальса — электромагнитные межмолекулярные силы, возникающие при поляризации молекул и образовании диполей. Ван-дер-Ваальсовы силы быстро убывают с увеличением расстояния.

Сила инерции — фиктивная сила, вводимая в неинерциальных системах отсчёта для того, чтобы в них выполнялся второй закон Ньютона. В частности, в системе отсчёта, связанной с равноускоренно движущимся телом сила инерции направлена противоположно ускорению. Из полной силы инерции могут быть для удобства выделены центробежная сила и сила Кориолиса.

5. Равнодействующая

При расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей. Это геометрическая сумма всех сил, действующих на тело. При этом действие каждой силы не зависит от действия других, то есть каждая сила сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил (принцип суперпозиции).

Источники

Григорьев В. И., Мякишев Г. Я. — «Силы в природе»
Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6

Примечания

Glossary - eobglossary.gsfc.nasa.gov/Library/glossary.php3?mode=alpha&seg=f&segend=h. Earth Observatory. NASA. — «Сила — любой внешний фактор, который вызывает изменение в движении свободного тела или возникновение внутренних напряжений в зафиксированном теле.» (англ.)
Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
↑ 12345Lectures on Physics, Vol 1. — Addison-Wesley, 1963. (англ.)
An introduction to mechanics. — McGraw-Hill. (англ.)
↑ 123University Physics, Sears, Young & Zemansky, pp. 18-38 (англ.)
Хайкин С. Э.Силы инерции и невесомость. Изд-во «Наука» М.,1967, с илл.
Weinberg, S. Dreams of a Final Theory. — Vintage Books USA, 1994. — ISBN 0-679-74408-8 (англ.)
Heath,T.L. The Works of Archimedes (1897) - www.archive.org/details/worksofarchimede029517mbp. Archive.org. (англ.)
↑ 1234Newton, I. The Principia Mathematical Principles of Natural Philosophy. — University of California Press, 1999. — ISBN 0-520-08817-4 (англ.)
Мултановский В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 80−81.
Принято не подчёркивать специально, что в такой формулировке Второй закон Ньютона годится только для наблюдателя, имеющего достаточные основания считать, что он находится в инерциальной системе отсчёта, из которой он и наблюдает движущееся под действием силы тело. Если же он сам находится в системе отсчёта, связанной с ускоряемым телом, в которой оно для него неподвижно, то в этой ситуации Второй закон Ньютона принимает вид: F − ma = 0 . Или F − F(i) = 0 , где F(i) есть сила инерции, действующей на ускоряемое тело, уравновешивающая по Третьему закону Ньютона действующее на него силу, что является причиной неподвижности этого тела в рассматриваемой неинерциальной системе отсчёта. Сила инерции фиктивна в том смысле, что причиной её возникновения не являются, в конечном итоге, ни силы гравитации, ни силы электромагнитного происхождения. Она появляется исключительно из-за неинерциальности движения системы наблюдателя.
Henderson, Tom Lesson 4: Newton's Third Law of Motion - www.glenbrook.k12.il.us/gbssci/phys/Class/newtlaws/u2l4a.html. The Physics Classroom (1996-2007). (англ.)
Капра, Фритьоф ДАО ФИЗИКИ. СПб.,"ОРИС"*"ЯНА-ПРИНТ". 1994 г. 304 с. ISBN 5-88436-021-5
Nave, R Pauli Exclusion Principle - hyperphysics.phy-astr.gsu.edu/hbase/pauli.html. HyperPhysics***** Quantum Physics. (англ.)
University Physics, Sears, Young & Zemansky, pp. 59−82 (англ.)
Sir Isaac Newton: The Universal Law of Gravitation - csep10.phys.utk.edu/astr161/lect/history/newtongrav.html. Astronomy 161 The Solar System. (англ.)
Статья И. Д. Новикова Физический энциклопедический словарь. — М.: Советская энциклопедия, 1984. — С. 772−775.

www.wreferat.baza-referat.ru

Реферат Механическая сила

скачать

Реферат на тему:

План:

1 История понятия
2 Ньютоновская механика
- 2.1 Первый закон Ньютона
- 2.2 Второй закон Ньютона
- 2.3 Третий закон Ньютона
3 Фундаментальные взаимодействия
- 3.1 Гравитация
- 3.2 Электромагнитное взаимодействие
  - 3.2.1 Электростатическое поле (поле неподвижных зарядов)
  - 3.2.2 Электромагнитное поле (поле постоянных токов)
- 3.3 Сильное взаимодействие
- 3.4 Слабое взаимодействие
4 Производные виды сил
5 Равнодействующая

Введение

Классическая механика

$\vec{F} = \frac{\mathrm{d}}{\mathrm{d}t}(m \vec{v})$ Второй закон Ньютона

История… Фундаментальные понятия

Пространство · Время · Масса · СилаЭнергия · Импульс

Формулировки

Ньютоновская механикаЛагранжева механикаГамильтонова механикаФормализм Гамильтона — Якоби

Разделы

Прикладная механикаНебесная механикаМеханика сплошных средГеометрическая оптикаСтатистическая механика

Учёные

Галилей · Кеплер · НьютонЭйлер · Лаплас · Д’АламберЛагранж · Гамильтон · Коши

См. также «Физический портал»

1. История понятия

2. Ньютоновская механика

2.1. Первый закон Ньютона

2.2. Второй закон Ньютона

$\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t},$

По определению импульса:

$\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t} = \frac{\mathrm{d}\left(m\vec{v}\right)}{\mathrm{d}t},$

где − масса, $\vec{v}$ − скорость.

По правилу нахождения производной произведения:

$\vec{F} = m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t} + \vec{v}\frac{\mathrm{d}m}{\mathrm{d}t}.$

$\vec{F} = m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}.$

Учитывая определение ускорения точки, второй закон Ньютона принимает вид:

$\vec{F} =m\vec{a}.$

2.3. Третий закон Ньютона

$\vec{F}_{1,2}=-\vec{F}_{2,1}.$

$\vec{F}_{1,2}+\vec{F}_{\mathrm{2,1}}=0.$

3. Фундаментальные взаимодействия

3.1. Гравитация

$F=G\frac{m_1 m_2}{R^2}.$

3.2. Электромагнитное взаимодействие

3.2.1. Электростатическое поле (поле неподвижных зарядов)

$\vec{F}= \frac{1}{4 \pi \varepsilon \varepsilon_0} \frac{q_{1}q_{2}}{r^3} \vec{r},$

3.2.2. Электромагнитное поле (поле постоянных токов)

Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.

Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.

Закон взаимодействия токов используется для эталонирования постоянного электрического тока.

3.3. Сильное взаимодействие

3.4. Слабое взаимодействие

4. Производные виды сил

Осмотическое давление

5. Равнодействующая

Источники

Григорьев В. И., Мякишев Г. Я. — «Силы в природе»
Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6

Примечания

Glossary - eobglossary.gsfc.nasa.gov/Library/glossary.php3?mode=alpha&seg=f&segend=h. Earth Observatory. NASA. — «Сила — любой внешний фактор, который вызывает изменение в движении свободного тела или возникновение внутренних напряжений в зафиксированном теле.» (англ.)
Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
↑ 12345Lectures on Physics, Vol 1. — Addison-Wesley, 1963. (англ.)
An introduction to mechanics. — McGraw-Hill. (англ.)
↑ 123University Physics, Sears, Young & Zemansky, pp. 18-38 (англ.)
Хайкин С. Э.Силы инерции и невесомость. Изд-во «Наука» М.,1967, с илл.
Weinberg, S. Dreams of a Final Theory. — Vintage Books USA, 1994. — ISBN 0-679-74408-8 (англ.)
Heath,T.L. The Works of Archimedes (1897) - www.archive.org/details/worksofarchimede029517mbp. Archive.org. (англ.)
↑ 1234Newton, I. The Principia Mathematical Principles of Natural Philosophy. — University of California Press, 1999. — ISBN 0-520-08817-4 (англ.)
Мултановский В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 80−81.
Принято не подчёркивать специально, что в такой формулировке Второй закон Ньютона годится только для наблюдателя, имеющего достаточные основания считать, что он находится в инерциальной системе отсчёта, из которой он и наблюдает движущееся под действием силы тело. Если же он сам находится в системе отсчёта, связанной с ускоряемым телом, в которой оно для него неподвижно, то в этой ситуации Второй закон Ньютона принимает вид: F − ma = 0 . Или F − F(i) = 0 , где F(i) есть сила инерции, действующей на ускоряемое тело, уравновешивающая по Третьему закону Ньютона действующее на него силу, что является причиной неподвижности этого тела в рассматриваемой неинерциальной системе отсчёта. Сила инерции фиктивна в том смысле, что причиной её возникновения не являются, в конечном итоге, ни силы гравитации, ни силы электромагнитного происхождения. Она появляется исключительно из-за неинерциальности движения системы наблюдателя.
Henderson, Tom Lesson 4: Newton's Third Law of Motion - www.glenbrook.k12.il.us/gbssci/phys/Class/newtlaws/u2l4a.html. The Physics Classroom (1996-2007). (англ.)
Капра, Фритьоф ДАО ФИЗИКИ. СПб.,"ОРИС"*"ЯНА-ПРИНТ". 1994 г. 304 с. ISBN 5-88436-021-5
Nave, R Pauli Exclusion Principle - hyperphysics.phy-astr.gsu.edu/hbase/pauli.html. HyperPhysics***** Quantum Physics. (англ.)
University Physics, Sears, Young & Zemansky, pp. 59−82 (англ.)
Sir Isaac Newton: The Universal Law of Gravitation - csep10.phys.utk.edu/astr161/lect/history/newtongrav.html. Astronomy 161 The Solar System. (англ.)
Статья И. Д. Новикова Физический энциклопедический словарь. — М.: Советская энциклопедия, 1984. — С. 772−775.

www.wreferat.baza-referat.ru

§ 12. Силы в механике

Силы тяготения (гравитационные силы).

В системе отсчета связанной с Землей, на всякое тело массой m действует сила: , называемая силой тяжести – сила, с которой тело притягивается с Землей. Под действием силы притяжения к Земле все тела падают с одинаковым ускорением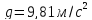, называемым ускорением свободного падения.

Весом тела – называется сила, с которой тело вследствие тяготения к Земле действует на опору или натягивает нить подвеса.

Сила тяжести действует всегда, а вес проявляется лишь тогда, когда на тело кроме силы тяжести действуют другие силы. Сила тяжести равна весу тела только в том случае, когда ускорение тела относительно Земли равно нулю. В противном случае , где- ускорение тела с опорой относительно Земли. Если тело свободно движется в поле силы тяготения, тои вес равен нулю, т.е. тело будет невесомым.

Невесомость - это состояние тела, при котором оно движется только под действием силы тяжести.

Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией.

Упругая сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия:

где – радиус-вектор, характеризующий смещение частицы из положения равновесия,- упругость. Примером такой силы является сила упругости деформации пружины при растяжении или сжатии.

Сила трения скольжения возникает при скольжении данного тела по поверхности другого:

где k – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей; N - сила нормального давления, прижимающая трущиеся поверхности друг другу.

Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого.

§ 13. Энергия. Работа и мощность

Энергия –это универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и т.д.

Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.

Рисунок 13.1

Если рассматриваемая сила постоянна, а тело, к которому она приложена, движется поступательно и прямолинейно, то работой, совершаемой силойпри прохождении телом пути, называют величину

где а - угол между силой и направлением движения тела.

Рисунок 13.2

Работа - скалярная величина. Если вектор силы и вектор перемещений образуют острый угол, т.е. , то, если, то, т.е. сила, действующая перпендикулярно к перемещению тела, работы не совершает.

В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.13.2). Выделим элементарный участок пути dS, на котором силу можно считать постоянной, и перемещение прямолинейным. Элементарная работа на этом участке равна

Полная работа на пути определяется интегралом

Единица работы – джоуль (Дж) – работа совершаемая силой 1Н на пути 1м: 1Дж-1Нс.

Рисунок 13.3

Силу , действующую на материальную точку, называют консервативной или потенциальной, если работа , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:

Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории, например 1-a-2-b-1, работа консервативной силы равна нулю.

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности. Мощность равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.

Единица мощности - ватт (Вт): 1 Вт – мощность, при которой за время 1с совершается работа 1 Дж:=1Вт=1Дж/с.

studfiles.net

Виды взаимодействий и силы в механике

Количество просмотров публикации Виды взаимодействий и силы в механике - 543

Второй закон Ньютона занимает в механике очень важное место. Это связано с тем, что уравнение

представляет собой дифференциальное уравнение относительно функции . Решение этого уравнения дает решение основной задачи механики – определения положения тела в любой момент времени. Но это можно сделать только в том случае, в случае если известны все силы, действующие на тело. По этой причине изучение различных взаимодействий физических объектов является одной из главных задач физики.

В современной науке выделяют 4 типа взаимодействий. Два из них, которые рассматриваются в механике, называются гравитационное и электромагнитное. Им соответствуют силы, которые нельзя свести к более простым, и в связи с этим они называются фундаментальными. Сила гравитационного взаимодействия (фундаментальная сила) описывается законом всемирного тяготения:

. (2.5)

Здесь G – постоянная всемирного тяготения, m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними. В законе всемирного тяготения масса выступает мерой тяготения тел и принято называть гравитационной массой. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, мы уже знаем 2 определения массы: с одной стороны – это мера инерции, а с другой стороны, масса – мера тяготения тел.

Вторая, фундаментальная сила, которая описывает взаимодействие между двумя точечными зарядами, подчиняется закону Кулона:

. (2.6)

Гравитационные взаимодействия. О законе Кулона мы будем говорить позже. Сейчас же скажем несколько слов о законе всемирного тяготения. Видно, что величина силы пропорциональна массам взаимодействующих тел. В случае если мы возьмём 2 тела с массами, к примеру, в 100 (кг), и пусть расстояние между этими телами 1 (м), то они будут взаимодействовать с силой, которая равна 6,67·10-7(Н).[3] Такая маленькая сила не способна даже сдвинуть с места эти два тела. При этом если взаимодействующие тела обладают гигантской массой – к примеру, звезда и планета͵ то величина силы будет очень большой. Именно сила всемирного тяготения является тем архитектором, который управляет структурой нашей Вселенной. Именно сила всемирного тяготения определяет взаимное расположение галактик, звезд и планетных систем.

Мы все живем на теле с огромной массой – на планете Земля. Человек и любой другой предмет массы m притягиваются к Земле вследствие закона всемирного тяготения. Эту силу притяжения к Земле мы называем силой тяжести и рассчитываем по формуле , которая является ничем иным как следствием закона всемирного тяготения. Следовательно,

. (2.7)

Здесь g – ускорение свободного падения, M – масса Земли, а R=RЗ+h – расстояние от центра Земли до тела массы m (рис. 2.2).

Рисунок 2.2 – Закон всемирного тяготения

Из уравнения (2.7) находим, что

. (2.8)

То есть, в общем случае ускорение свободного падения зависит от высоты тела над поверхностью Земли. Так как в большинстве практически важных случаев выполняется условие (RЗ = 6,4·10 6(м) = 6400 (км) !), то в формуле (2.8) можно пренебречь h, и формула для g примет вид

. (2.9)

Все величины в формуле (2.9) - ϶ᴛᴏ константы. Следовательно, ускорение свободного падения не зависит от массы падающего тела, то есть для всех тел одинаково![4] После несложных вычислений получим g = 9,81 (м/с2). Направлена сила тяжести к центру Земли, именно это направление мы принимаем как вертикальное и определяем с помощью подвеса.

Электромагнитные взаимодействия. Электромагнитные взаимодействия в механических явлениях проявляются как силы упругости, которые появляются при деформации тел. Деформация - ϶ᴛᴏ изменение размеров или формы тела под воздействием других тел. Как известно из курса школьной физики, все тела состоят из электрических зарядов. При деформации тел изменяются расстояния между зарядами, а это, в свою очередь, приводит к нарушению равновесия между силами притяжения и отталкивания между зарядами. При растяжении тела преобладают силы притяжения между зарядами и тело ʼʼсопротивляетсяʼʼ растяжению, аналогично, при сжатии преобладают силы отталкивания.

В наиболее простых случаях, к примеру деформации пружины, силу упругости можно рассчитать с помощью закона Гука:

,(2.10)

где x – смещение конца пружины из положения равновесия. Знак “–” показывает, что направление силы обратно направлению смещения. Коэффициент k принято называть жесткостью и определяется экспериментально. Рассмотрим некоторые проявления сил упругости.

Силы реакции опоры и натяжения подвеса. Рассмотрим тело на опоре или подвесе (рис. 2.3).

Рисунок 2.3 – Силы реакции опоры и натяжения подвеса

Как мы уже знаем, на наше тело действует сила тяжести , под действием которой тело стремится двигаться к центру Земли. При этом ʼʼстремленииʼʼ двигаться тело деформирует опору или подвес. В результате деформации появляется сила упругости, действующая на тело. В случае тела на опоре эту силу называют силой реакции опоры, а в случае тела на подвесе – силой натяжения подвеса.

Вес тела. Весом тела называют силу, с которой тело действует на опору или подвес. При взаимодействии тела с опорой или подвесом деформируется и само тело, что приводит к появлению силы упругости, действующей на опору или подвес.

Силы веса и реакции опоры связаны между собой согласно третьему закону Ньютона: . Аналогичное равенство имеет место и для тела на подвесе. Вес тела очень часто путают с силой тяжести из-за того, что в случае неподвижного тела эти силы оказываются равными по величине. Но это две разные силы: сила тяжести является гравитационной силой (взаимодействуют тело и Земля), в то время как вес тела - ϶ᴛᴏ сила упругости (взаимодействуют тело и опора). Сила тяжести действует на тело, а вес – на опору (или подвес), на которой (-ом) находится это тело. Вместе с тем, вес тела оказывается зависящим от условий, в которых находится тело, в частности, он зависит от ускорения, с которым движется рассматриваемое тело (рис. 2.4).

Рисунок 2.4 – Вес тела

И ещё одна сила, с которой имеют дело в механике – сила трения. Мы будем иметь дело с внешним трением - ϶ᴛᴏ трение между соприкасающимися поверхностями движущихся относительно друг друга тел. Сила трения тоже сводится к взаимодействию между атомами двух тел в местах контакта соприкасающихся тел, то есть, в конечном счёте, – к силам электромагнитного происхождения. Трение между поверхностями двух тел при отсутствии прослойки газа или жидкости между ними принято называть сухим трением. Сухое трение ещё делят на трение скольжения и трения качения. Последнее обычно много меньше первого. Различают трение скольжения и трение покоя. Сила трения покоя обычно меньше силы трения скольжения. Сила трения скольжения описывается выражением

, (2.11)

где N – сила нормального давления, которая прижимает трущиеся поверхности друг к другу, m – коэффициент трения. Сила трения всегда направлена противоположно вектору скорости.

referatwork.ru

Силы в механике — реферат

где p0 – добавочное давление, обусловленное силами межмолекулярного притяжения, которые быстро уменьшаются с увеличением расстояния между частицами; S – площадь контакта между телами; fист – истинный коэффициент трения скольжения.

Трение играет большую роль в природе и технике, однако в некоторых случаях силы трения оказывают вредное воздействие и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку, которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга, а скользят лишь отдельные слои жидкости. Таким образом, внешнее трение твёрдых тел заменяется значительно меньшим внутренним трением жидкости.

Радикальным способом уменьшения силы трения является замена трения скольжения трением качения. Сила трения качения определяется по закону, установленному Кулоном:

Fтр=fx*N/r,

где r- радиус катящегося тела; fx- коэффициент трения качения, имеющий размерность dimfx=L.

Закон сохранения импульса.

Это фундаментальный закон природы, который носит универсальный характер. Он справедлив не только в классической физике, хотя и получен как следствие законов Ньютона. Эксперименты показывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики).

Закон сохранения импульса является следствием определённого свойства симметрии пространства. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого её физические свойства не изменяются.

Для вывода закона сохранения импульса нужно рассмотреть некоторые понятия. Механическая система-это совокупность материальных точек, рассматриваемых как единое целое. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой. Если механическая система состоит из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, равны и противоположно направлены, то есть геометрическая сумма внутренних сил равна нулю:

dp/dt=F1+F2+…+Fn,

где p=∑mivi-импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической суме внешних сил, действующих на систему.

В случае отсутствия внешних сил

dp/dt=∑d/dt(mivi)=0, т.е. p=∑mivi =const

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Заключение

Основной раздел классической механики составляют законы Ньютона, сформулированные в 1687 году. Они являются незыблемым фундаментом научного познания и позволяют решить многие задачи механики, а также записать уравнения движения для любой механической системы. Законы Ньютона играют исключительную роль в механике и являются обобщением результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов. Важно понимать, что эти законы имеют ограниченную область применения.

Сегодня мы постоянно пользуемся творениями великого учёного. Можно утверждать, что на всей физике лежал индивидуальный отпечаток его мысли, наука без него развивалась бы иначе.

Литература

Кибец И.Н., Кибец В.И. Физика: Справочник - Харьков: Фолио; Ростов н/Д: Феникс, 1997.-479с.
Трофимова Т.И. Курс физики: Учебное пособие для вузов – М: Высшая школа, 2003. – 542с.

turboreferat.ru

Силы в механике

Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях.

Название силы	Природа взаимодействия	Формула для расчета силы	Зависимость силы от расстояния или относительной скорости	Зависит ли сила от массы взаимодействующих тел	Как направлена сила
Сила тяготения	гравитационная		Является функцией расстояния между взаимодействующими телами	Прямо пропорциональна массам взаимодействующих тел	Вдоль прямой, соединяющей взаимодействующие тела
Сила упругости	электромагнитная		Является функцией расстояния (зависит от деформации)	Не зависит	Противоположно направлению перемещения частиц при деформации
Сила трения а)сухого б)жидкого	электромагнитная		Является функцией скорости относительного движения	Не зависит	Противоположно направлению вектора скорости