ФГБОУ ВО «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ М. Е. ЕВСЕВЬЕВА»
Факультет физико-математический
Кафедра информатики и вычислительной техники
ФРАКТАЛЬНАЯ ГРАФИКА В СПЕЦИАЛЬНЫХ ПРОГРАММНЫХ СРЕДСТВАХ
Реферат выполнила
студентка 5 курса группы МДИ-113 Тимошина Светлана
Направление подготовки 050100 «Педагогическое образование».
Профили подготовки «Математика» и «Информатика».
Реферат проверила ______________________ Т. В. Кормилицина
Саранск 2017
Содержание
Введение………………………………………………………………………...…31. Общие сведения о фракталах и фрактальной графике…......………..…….3-5
2. Специальные программные средства..........………..………………..….…5-13
Заключение……………………………………………………….……………...13
Список использованной литературы…………………………………………...14
Введение
На сегодняшний день Фрактальная графика является второй по росту популярности из четырёх видов компьютерной графики.
Так же есть Растровая и Векторная. Одна – для создания фотореалистичных изображений; Другая – для создания сложных геометрических объектов; и Трёхмерная – как отдельный вид от предыдущих для создания объёмных зрительно-подобных изображений и объектов.
Фрактальные изображения применяются в самых разных сферах, начиная от создания обычных текстур и фоновых изображений и кончая фантастическими ландшафтами для компьютерных игр или книжных иллюстраций. Создаются фрактальные изображения путем математических расчетов. Базовым элементом фрактальной графики является сама математическая формула - это означает, что никаких объектов в памяти компьютера не хранится, и изображение строится исключительно на основе уравнений. Таинство фрактального изображения не кроется лишь в одной удачной формуле. Не менее важны и иные аспекты. Например, цветовая настройка, фильтры трансформации и др. Существует очень много программ по созданию фрактальных изображений. Эти программы имеют свои достоинства и недостатки. С развитием технологий количество программ увеличивается, а их качество и возможности улучшаются.
Общие сведения о фракталах и фрактальной графике
Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
Фрактальная графика, как и векторная, основана на математических вычислениях. Базовыми элементами фрактальной графики являются сами математические формулы, описывающие линии и линейные поверхности, то есть никаких объектов в памяти ЭВМ не хранится и изображение строится исключительно по формулам (уравнениям).
Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Одним из первых описал динамические фракталы в 1918 году французский математик Гастон Жюлиа в своем объемном труде в несколько сотен страниц. Но в нем отсутствовали какие-либо изображения. Компьютеры сделали видимым то, что не могло быть изображено во времена Жюлиа. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Квазифрактал отличается от идеальных абстрактных фракталов неполнотой и неточностью повторений структуры. Большинство встречающихся в природе фракталоподобных структур (границы облаков, линия берега, деревья, листья растений, кораллы, …) являются квазифракталами, поскольку на некотором малом масштабе фрактальная структура исчезает. Природные структуры не могут быть идеальными фракталами из-за ограничений, накладываемых размерами живой клетки и, в конечном итоге, размерами молекул.
Мультифрактал — комплексный фрактал, который может детерминироваться не одним единственным алгоритмом построения, а несколькими последовательно сменяющими друг друга алгоритмами. Каждый из них генерирует паттерн со своей фрактальной размерностью. Для описания мультифрактала вычисляют мультифрактальный спектр включающий в себя ряд фрактальных размерностей присущих элементам данного мультифрактала.
Предфрактал — это самоподобная геометрическая фигура, каждый фрагмент которой повторяется в упрощённом виде при уменьшении масштаба конечное число раз. Количество уровней масштаба, на которых наблюдается подобие, называется порядком предфрактала. При порядке, стремящемся к бесконечности, предфрактал переходит в фрактал.
Фрактальный подход нашел широкое применение во многих областях компьютерной графики, науки и искусства.
Фрактальная графика не является, строго говоря, частью векторной графики, поскольку широко использует и растровые объекты. Фракталы широко используются в растровых (AdobePhotoshop) и векторных (CorelDraw) редакторах и трехмерной (CorelBryce) графике.
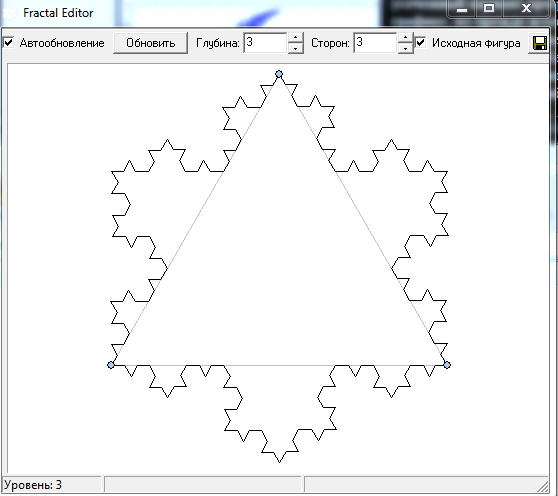
1. Программа Fractal Editor
Знакомство с основами фрактальной графики лучше всего начать с пакета Fractal Editor. Этот редактор (созданный фирмой Fractal Design, а теперь принадлежащий Corel) фактически представляет собой усеченный вариант программы Painter. Это отличная программа для обучения не только компьютерной графике, но прежде всего азам рисования. Малый объем требуемой памяти (для его установки необходимо всего 10 Мбайт), а также простой интерфейс, доступный даже ребенку, позволяют использовать его в школьной программе.
2. Программа Ultra Fractal
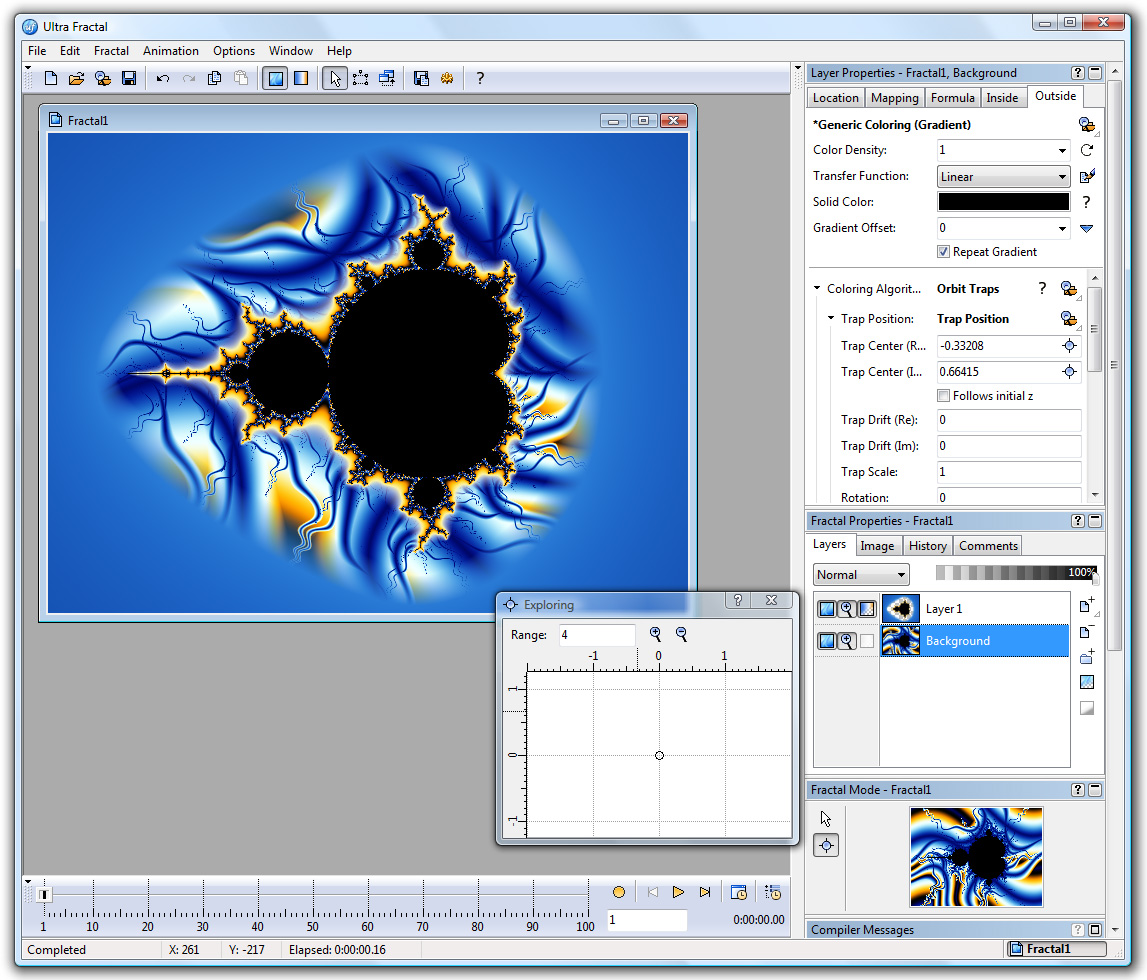Ultra Fractal - лучшее решение для создания уникальных фрактальных изображений профессионального качества. Пакет отличается дружественным интерфейсом, многие элементы которого напоминают интерфейс Photoshop (что упрощает изучение), и сопровождается невероятно подробной и прекрасно иллюстрированной документацией с серией туториалов, в которых поэтапно рассматриваются все аспекты работы с программой. Ultra Fractal представлен двумя редакциями: Standard Edition и расширенной Animation Edition, возможности которой позволяют не только генерировать фрактальные изображения, но и создавать анимацию на их основе. Созданные изображения можно визуализировать в высоком разрешении, пригодном для полиграфии, и сохранить в собственном формате программы или в одном из популярных фрактальных форматов. Визуализированные изображения также могут быть экспортированы в один из растровых графических форматов (jpg, bmp, png и psd), а готовые фрактальные анимации - в AVI-формат. Принцип создания фрактальных изображений достаточно традиционен, самое простое - воспользоваться одной из прилагаемых в поставке формул (сориентироваться относительно возможного вида генерируемого по выбранной формуле изображения поможет встроенный браузер), а затем подредактировать параметры формулы желаемым образом. А если эксперимент оказался неудачен, то последние действия легко отменить. Готовых фрактальных формул очень много, и число их может быть расширено путем скачивания новых формул с сайта программы. Подготовленные пользователи могут попытать счастья и в создании собственной формулы, для чего в пакете имеется встроенный текстовый редактор с поддержкой базовых шаблонов, основанных на стандартных конструкциях языка программирования фрактальных формул. Однако не стоит думать, что таинство фрактального изображения кроется лишь в удачной формуле. Не менее важны и иные аспекты. Например, цветовая настройка, предполагающая выбор варианта окраски и точную настройку ее параметров. Настройка цвета реализована на уровне солидных графических пакетов, например градиенты можно создавать и настраивать самостоятельно, корректируя множество параметров, включая полупрозрачность, и сохранять их в библиотеке для дальнейшего использования. Применение слоев с возможностью изменения режимов их смешивания и корректировкой полупрозрачности позволяет генерировать многослойные фракталы и за счет наложения фрактальных изображений друг на друга добиваться уникальных эффектов. Использование масок непрозрачности обеспечивает маскирование определенных областей изображения. Фильтры трансформации позволяют выполнять в отношении выделенных фрагментов изображения разнообразные преобразования: масштабировать, зеркально отражать, обрезать по шаблону, искажать посредством завихрения или ряби, размножать по принципу калейдоскопа и т.д.
3. Программа Fractal Explorer
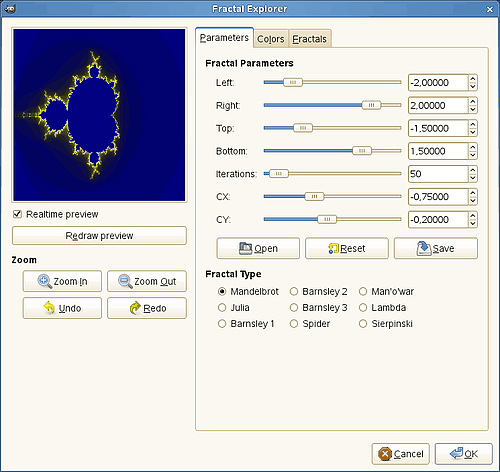Fractal Explorer - программа для создания изображений фракталов и трехмерных аттракторов с достаточно впечатляющими возможностями. Имеет интуитивно понятный классический интерфейс, который может быть настроен в соответствии с пользовательскими предпочтениями, и поддерживает стандартные форматы фрактальных изображений (*.frp; *.frs; *.fri; *.fro; *.fr3, *.fr4 и др.). Готовые фрактальные изображения сохраняются в формате *.frs и могут быть экспортированы в один из растровых графических форматов (jpg, bmp, png и gif), а фрактальные анимации сохраняются как AVI-файлы. Генерация фракталов возможна двумя способами - на основе базовых фрактальных изображений, построенных по входящим в поставку формулам, или с нуля. Первый вариант позволяет получить интересные результаты сравнительно просто, ведь выбрать подходящую формулу несложно, тем более что удобный файловый браузер позволит оценить качество фрактала из базы еще до создания на его основе фрактального изображения. У полученного таким путем фрактального изображения можно сменить цветовую палитру, добавить к нему фоновое изображение и определить режим смешивания фрактального и фонового слоев, а также степень прозрачности фрактального слоя. Затем можно будет подвергнуть фрактальное изображение трансформации, при необходимости масштабировать, определить размеры изображения и провести рендеринг. Создание изображения с нуля гораздо сложнее и предполагает выбор одного из двух способов. Можно выбрать тип фрактала почти из 150 вариантов. А затем уже перейти к изменению разнообразных параметров: настройке палитры, фона и пр. А можно попробовать создать свою пользовательскую формулу, воспользовавшись встроенным компилятором. Перед рендерингом готового изображения может потребоваться проведение автоматической коррекции цветового баланса и/или ручной коррекции яркости, контрастности и насыщенности. 4. Программа ChaosPro
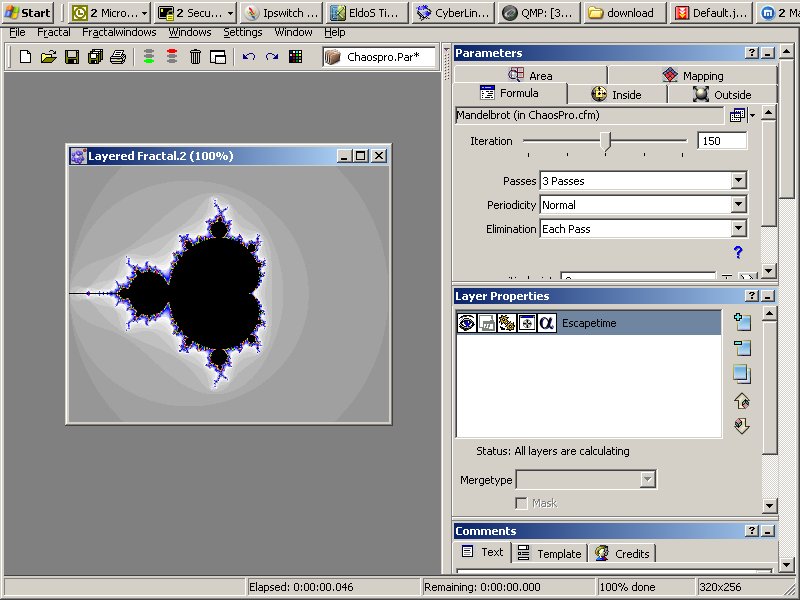ChaosPro - один из лучших бесплатных генераторов фрактальных изображений, с помощью которого нетрудно создать бесконечное множество удивительных по красоте фрактальных изображений. Программа имеет очень простой и удобный интерфейс и наряду с возможностью автоматического построения фракталов позволяет полностью управлять данным процессом за счет изменения большого количества настроек (число итераций, цветовая палитра, степень размытия, особенности проецирования, размер изображения и др.). Кроме того, создаваемые изображения могут быть многослойными (режимом смешивания слоев можно управлять) и к ним можно применить целую серию фильтров. Все накладываемые на строящиеся фракталы изменения тут же отражаются в окне просмотра. Созданные фракталы могут быть сохранены в собственном формате программы, либо в одном из основных фрактальных типов благодаря наличию встроенного компилятора. Или экспортированы в растровые изображения или 3D-объекты (если предварительно было получено трехмерное представление фрактала). В списке возможностей программы:
точная цветовая настройка, обеспечивающая плавные градиентные переходы цветов друг в друга;
одновременное построение нескольких фракталов в разных окнах;
возможность создания анимации на основе фрактальных изображений с определением ключевых анимационных фаз, которые могут отличаться по любому изменяемому параметру: углам поворота и вращения, цветовым параметрам и пр.;
создание трехмерных представлений фракталов на основе обычных двумерных изображений;
поддержка многих стандартных форматов фрактальных изображений, изображения в которых могут быть импортированы и отредактированы в среде ChaosPro.
5. Программа Apophysis
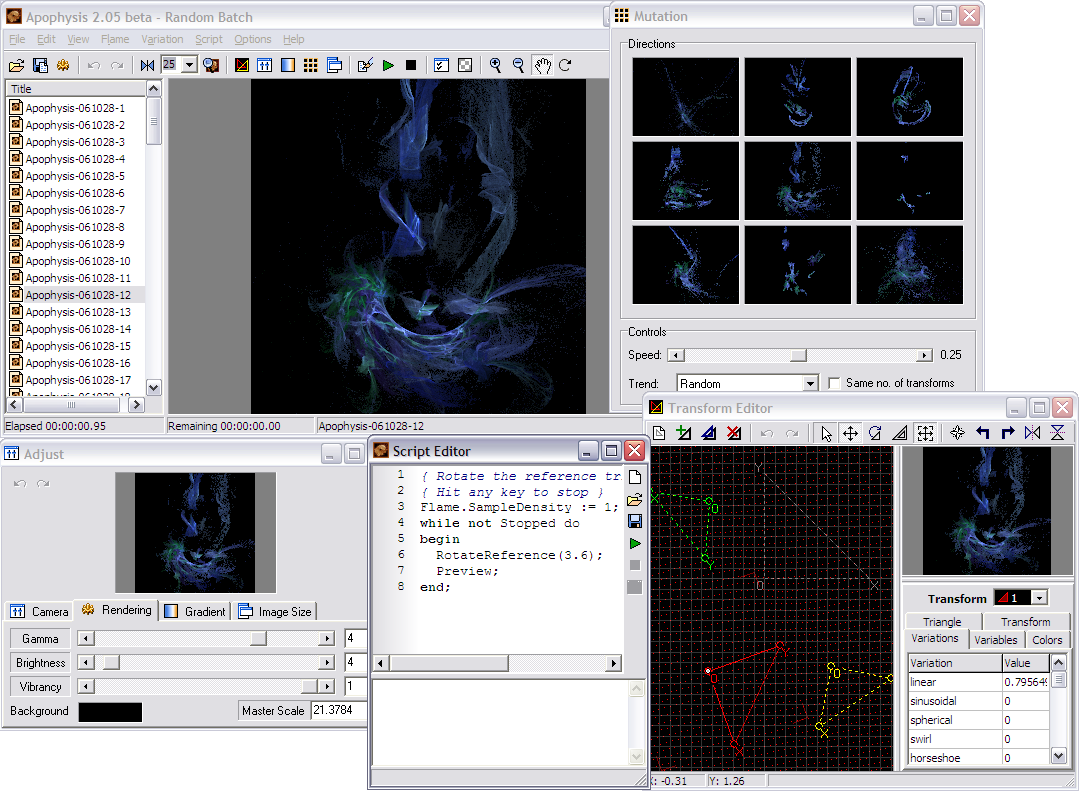Apophysis - интересный инструмент для генерации фракталов на основе базовых фрактальных формул. Созданные по готовым формулам фракталы можно редактировать и неузнаваемо изменять, регулируя разнообразные параметры. Так, например, в редакторе их можно трансформировать, либо изменив лежащие в основе фракталов треугольники, либо применив понравившийся метод преобразования: волнообразное искажение, перспективу, размытие по Гауссу и др. Затем стоит поэкспериментировать с цветами, выбрав один из базовых вариантов градиентной заливки. Список встроенных заливок достаточно внушителен, и при необходимости можно автоматически подобрать наиболее подходящую заливку к имеющемуся растровому изображению, что актуально, например, при создании фрактального фона в том же стиле, что и иные изображения некоего проекта. При необходимости несложно подрегулировать гамму и яркость, изменить фон, масштабировать фрактальный объект и уточнить его расположение на фоне. Можно также подвергнуть результат разнообразным мутациям в нужном стиле. По окончании следует задать размеры конечного фрактального изображения и записать его визуализированный вариант в виде графического файла (jpg, bmp, png).
6. Программа Mystica
Mystica - универсальный генератор уникальных фантастических двумерных и трехмерных изображений и текстур, которые в дальнейшем можно использовать в разных проектах, например в качестве реальных текстур для Web-страниц, фонов Рабочего стола или фантастических фоновых изображений, которые могут быть задействованы, например, при оформлении детских книг. Пакет отличается нестандартным и достаточно сложным интерфейсом и может работать в двух режимах: Sample (ориентирован на новичков и содержит минимум настроек) и Expert (предназначен для профессионалов). Создаваемые изображения могут иметь любой размер и затем экспортироваться в популярные графические 2D-форматы. Прямо из окна программы их можно отправить по электронной почте, опубликовать в Html-галерее или создать на их основе видеоролик в форматах divx, mpeg4 и др. Встроенный трехмерный движок программы может быть использован при создании трехмерных сцен для компьютерных игр, например фантастических фонов и ландшафтов. Генерация изображений осуществляется на основе заложенных в пакете фрактальных формул, а система подготовки изображения многоуровневая и включает очень подробную настройку цветов, возможность простейших трансформаций генерируемых элементов и массу прочих преобразований. В их числе применение фильтров, изменение освещения, корректировка цветовой гаммы, яркости и контрастности, изменение использованного при генерации материала, добавление к изображению "хаотических" структур и пр.
Заключение
Данный вид графики незаменим при создании таких сложных повторяющихся объектов, состоящих из самоподобных частей, как облака, горы, вода и т.д. Фактически, благодаря фракталу, найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Позволим заметить, что кроме графики, так же есть и живопись, и музыка. Все они построены на технологии фрактала.
Бесспорными достоинствами фрактала являются:
Малый размер исполняемого файла при большом изображении.
Бесконечная масштабируемость и увеличение сложности картинки.
Незаменимость в построении сложных фигур, состоящих из однотипных элементов (облака, вода и т.д.).
Относительная легкость в создании сложных композиций.
Фотореалистичность.
Недостатки:
Все вычисления делаются компьютером, чем сложнее изображение, тем больше загруженность ЦП и ОЗУ.
Неосвоенность технологии.
Плохое распространение и поддержка различными системами.
Небольшой спектр создания объектов изображений.
Ограниченность материнских математических фигур.
В общем то, как всегда. У всего есть достоинства и недостатки. Графика тем более грешит и тем, и тем.
Литература
Мандельброт, Б. Фрактальная геометрия природы / Б. Мандельборт.−
М.: «Институт компьютерных исследований», 2002.
Федер, Е. Фракталы / Е. Федер. − М: «Мир», 1991.
Шредер, М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая / М. Шредер.−Ижевск: «РХД», 2001.
www.metod-kopilka.ru
Реферат на тему:
Множество Мандельброта — классический образец фрактала
Фрактал (лат. fractus — дробленый, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.
Фрактальная форма подвида цветной капусты (Brassica cauliflora)
Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба[1].
Фрактал — самоподобное множество нецелой размерности[1].
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Начиная с конца XIX века, в математике появляются примеры самоподобных объектов с патологическими с точки зрения классического анализа свойствами. К ним можно отнести следующие:
Построение кривой Коха
Существует простая рекурсивная процедура получения фрактальных кривых на плоскости. Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую. На рисунке справа приведены три первых шага этой процедуры для кривой Коха.
Примерами таких кривых служат:
Свойство самоподобия можно математически строго выразить следующим образом. Пусть — сжимающие отображения плоскости. Рассмотрим следующее отображение на множестве всех компактных (замкнутых и ограниченных) подмножеств плоскости:
Можно показать, что отображение Ψ является сжимающим отображением на множестве компактов с метрикой Хаусдорфа. Следовательно, по теореме Банаха, это отображение имеет единственную неподвижную точку. Эта неподвижная точка и будет нашим фракталом.
Рекурсивная процедура получения фрактальных кривых, описанная выше, является частным случаем данной конструкции. В ней все отображения — отображения подобия, а n — число звеньев генератора.
Для треугольника Серпинского n = 3 и отображения ψ1, ψ2, ψ3 — гомотетии с центрами в вершинах правильного треугольника и коэффициентом 1/2. Легко видеть, что треугольник Серпинского переходит в себя при отображении Ψ.
В случае, когда отображения ψi — преобразования подобия с коэффициентами ri > 0, размерность s фрактала (при некоторых дополнительных технических условиях) может быть вычислена как решение уравнения . Так, для треугольника Серпинского получаем s = ln3 / ln2.
По той же теореме Банаха, начав с любого компактного множества и применяя к нему итерации отображения Ψ, мы получим последовательность компактов, сходящихся (в смысле метрики Хаусдорфа) к нашему фракталу.
Множество Жюлиа́
Фракталы естественным образом возникают при изучении нелинейных динамических систем. Наиболее изучен случай, когда динамическая система задаётся итерациями многочлена или голоморфной функции комплексной переменной на плоскости. Первые исследования в этой области относятся к началу XX века и связаны с именами Фату и Жюлиа.
Пусть F(z) — многочлен, z0 — комплексное число и рассмотрим следующую последовательность:
.
Нас интересует поведение этой последовательности при . Эта последовательность может:
Множества значений z0, для которых последовательность демонстрирует один конкретный тип поведения, а также множества точек бифуркации между различными типами, часто обладают фрактальными свойствами.
Так, множество Жюлиа на картинке справа — множество точек бифуркации для многочлена F(z) = z2 + c, то есть тех значений z0, для которых поведение последовательности zn может резко меняться при сколь угодно малых изменениях z0.
Другой вариант получения фрактальных множеств — введение параметра в многочлен F(z) и рассмотрение множества тех значений параметра, при которых последовательность zn демонстрирует определённое поведение при фиксированном z0. Так, множество Мандельброта — это множество всех , при которых zn для F(z) = z2 + c и z0 = 0 не стремится к бесконечности.
Ещё один известный пример такого рода — бассейны Ньютона.
Популярно создание красивых графических образов на основе комплексной динамики путём раскрашивания точек плоскости в зависимости от поведения соответствующих динамических систем. Например, для дополнения множества Мандельброта можно раскрасить точки в зависимости от скорости стремления zn к бесконечности (определяемой, скажем, как наименьший номер n, при котором | zn | превысит фиксированную большую величину A).
Биоморфы — фракталы, построенные на основе комплексной динамики и напоминающие живые организмы.
Рандомизированный фрактал на основе множества Жюлиа
Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов:
Фрактальная монотипия, или стохатипия — направления в изобразительном искусстве, заключающиеся в получении изображения случайного фрактала.
Вид спереди на трахею и бронхи
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста:
В структурных фракталах схема текста потенциально фрактальна:
В семантических и нарративных фракталах автор рассказывает о бесконечном подобии части целому:
Фрактальные антенны
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.
Фрактальное дерево
Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.
Ещё одно фрактальное дерево
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).
Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.
wreferat.baza-referat.ru
Рис. 1− Пример фрактального объекта
В переводе с английского “фрактальный” означает состоящий из частиц, частей. Такими поверхностями называют класс нерегулярных геометрических форм, задаваемых вероятностным способом на основе исходного описания низкого уровня. Закон дробления линии (поверхности) подбирается опытным путем по критерию визуального согласования синтезируемого (моделируемого) изображения с реальным объектом, изображение которого стремятся получить.
Таким способом строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие ландшафты и трехмерные объекты. Наиболее часто фрактальные поверхности используют для моделирования горных ландшафтов. Горный массив (рис. 1) предварительно, очень приближенно, описывают полигональной поверхностью, составленной из плоских четырехугольников. Далее каждый четырехугольник разбивается с помощью случайной функции на четыре фигуры меньших размеров, при этом все фигуры вероятностным образом сдвигаются относительно исходной плоскости, сохраняя для каждой фигуры по одной общей вершине с исходным четырехугольником. Деление продолжается до достижения желаемого уровня изрезанности поверхности. Удаляются скрытые поверхности и закрашиваются сгенерированные четырехугольники. Изображения, созданные на основе фрактальных поверхностей, только статистически идентичны реальным объектам.
Фрактальный подход нашел широкое применение во многих областях компьютерной графики, науки и искусства.
Фрактальная графика не является, строго говоря, частью векторной графики, поскольку широко использует и растровые объекты. Фракталы широко используются в растровых (AdobePhotoshop) и векторных (CorelDraw) редакторах и трехмерной (CorelBryce) графике.
Работа со средствами компьютерной графики предполагает использование при создании графической информации (рисунков, чертежей, иллюстраций) разнообразных графических пакетов растровой и векторной графики (PhotoShop,CorelDraw,bCad,AutoCad, Компас и др.). Все эти пакеты работают в соответствующих форматах, позволяющих не только сохранить созданную информацию, экспортировать ее в другие пакеты, но и импортировать графическую информацию других пакетов. В компьютерной графике применяется большое количество форматов, но лишь небольшая их часть стала стандартом де-факто и применяется в подавляющем множестве программ. Разнообразие в подходах (алгоритмах) и средствах в решении традиционных задач компьютерной графики приводит к несовместимости выходных данных. Как правило, несовместимые форматы выходных файлов имеют векторные, растровые, трехмерные изображения, хотя существуют форматы файлов, позволяющие хранить данные разных классов. Многие приложения ориентированы на задачи с собственными специфическими форматами, но стремление интегрироваться в общую информационную структуру, вынуждает их использовать специальные приемы, фильтры или экспортировать изображение в стандартный обменный формат.
TIFF (Tagget Image File Format) предназначен для хранения растровых изображений высокого качества (расширение файла .TIF) в графических пакетах, работающих MS-DOS, PC IBM, Unix, Macintosh платформах. Широта использования этого формата объясняется его возможностями: поддержка множества цветовых моделей, наличие восьмибитного альфа-канала3, сохранение обтравочных контуров, различные алгоритмы сжатия без потери информации. Формат обеспечен поддержкой со стороны большинства графических, верстальных и дизайнерских, растровых и векторных программ. Цветовые модели GIF CMYK и Pantone, поддерживаемые TIFF, обеспечивают верную цветопередачу при выводе изображений на полиграфическую печать; допускает запись в файл цветовой профиль ICC. Последние версии TIFF поддерживают несколько алгоритмов сжатия изображения: LZW – без потери информации; ZIP –без потери информации, JPED -- с частичной потерей информацией.Универсальным принято считать метод сжатия LZW, обеспечивающий меньший размер выходного файла. Формат широко используется для хранения и обмена графической информацией между различными графическими платформами.
infourok.ru
Содержание
1. Виды компьютерной графики
2. Векторная графика
3. Растровая графика и пиксел
4. Фрактальная графика
5. Программное обеспечение
Список литературы
1. Виды компьютерной графики
Различают три вида компьютерной графики. Это растровая графика, векторная графика и фрактальная графика. Они отличаются принципами формирования изображения при отображении на экране монитора или при печати на бумаге. В растровой графике изображение представляется в виде набора окрашенных точек. Такой метод представления изображения называют растровым. Растровую графику применяют при разработке электронных (мультимедийных) и полиграфических изданий. Иллюстрации, выполненные средствами растровой графики, редко создают вручную с помощью компьютерных программ. Чаще всего для этой цели используют отсканированные иллюстрации, подготовленные художниками, или фотографии. В последнее время для ввода растровых изображений в компьютер нашли широкое применение цифровые фото- и видеокамеры.
Большинство графических редакторов, предназначенных для работы с растровыми иллюстрациями, ориентированы не столько на создание изображений, сколько на их обработку. В Интернете пока применяются только растровые иллюстрации. Векторный метод – это метод представления изображения в виде совокупности отрезков и дуг и т.д. В данном случае вектор – это набор данных, характеризующих какой-либо объект. Программные средства для работы с векторной графикой предназначены в первую очередь для создания иллюстраций и в меньшей степени для их обработки. Такие средства широко используют в рекламных агентствах, дизайнерских бюро, редакциях и издательствах. Оформительские работы, основанные на применении шрифтов и простейших геометрических элементов, решаются средствами векторной графики много проще.
Растровое изображение строится из множества пикселей. Векторное изображение описывается в виде последовательности команд. Растровые рисунки эффективно используются для представления реальных образов.
Векторная графика не позволяет получать изображения фотографического качества.
При масштабировании и вращении растровых картинок возникают искажения.
Векторные изображения могут быть легко преобразованы без потери качества.
Растровые рисунки могут быть легко напечатаны на принтерах. Векторные рисунки иногда не печатаются или выглядят на бумаге не так, как хотелось бы. Программные средства для работы с фрактальной графикой предназначены для автоматической генерации изображений путем математических расчетов. Создание фрактальной художественной композиции состоит не в рисовании или оформлении, а в программировании. Фрактальная графика, как и векторная — вычисляемая, но отличается от неё тем, что никакие объекты в памяти компьютера не хранятся. Изображение строится по уравнению (или по системе уравнений), поэтому ничего, кроме формулы, хранить не надо. Изменив коэффициенты в уравнении, можно получить совершенно другую картину. Способность фрактальной графики моделировать образы живой природы вычислительным путем часто используют для автоматической генерации необычных иллюстраций.
2. Векторная графика
В отличие от растровой графики в векторной графике изображение строится с помощью математических описаний объектов, окружностей и линий. Хотя на первый взгляд это может показаться сложнее, чем использование растровых массивов, но для некоторых видов изображений использование математических описаний является более простым способом. Ключевым моментом векторной графики является то, что она использует комбинацию компьютерных команд и математических формул для объекта. Это позволяет компьютерным устройствам вычислять и помещать в нужном месте реальные точки при рисовании этих объектов. Такая особенность векторной графики дает ей ряд преимуществ перед растровой графикой, но в тоже время является причиной ее недостатков. Векторную графику часто называют объектно-ориентированной графикой или чертежной графикой. Простые объекты, такие как окружности, линии, сферы, кубы и тому подобное называется примитивами, и используются при создании более сложных объектов. В векторной графике объекты создаются путем комбинации различных объектов. Для создания объектов примитивов используются простые описания. Прямая линия, дуги, окружности, эллипсы и области однотонного или изменяющегося света – это двухмерные рисунки, используемые для создания детализированных изображений. В трехмерной компьютерной графике для создания сложных рисунков могут использоваться такие элементы как сферы, кубы. Команды, описывающие векторные объекты большинству пользователей возможно никогда не придется увидеть. Определять, как описывать объекты будет компьютерная программа, которая используется для подготовки векторных объектов. Для создания векторных рисунков необходимо использовать один из многочисленных иллюстрационных пакетов. Достоинство векторной графики в том, что описание является простым и занимает мало памяти компьютера. Однако недостатком является то, что детальный векторный объект может оказаться слишком сложным, он может напечататься не в том виде, в каком ожидает пользователь или не напечатается вообще, если принтер неправильно интерпретирует или не понимает векторные команды. Программы векторной графики способны создавать растровые изображения в качестве одного из типов объектов. Это возможно потому, что растровый рисунок просто набор инструкций для компьютера, и так как инструкции эти очень просты, то векторная графика способна воспринимать растровые изображения наравне с остальными объектами, хотя можно поместить растровые изображения в виде объекта векторном формате, но не удается отредактировать и изменить в нем отдельные пиксели.
ASCII – компьютерный код для представления цифровых символов. Существует всего 256 возможных двухзначных шестнадцатеричных кодов, поэтому ASCII содержит 256 символов по одному на любое значение кода. Иногда векторные форматы представляют выбор способа кодирования данных в файле. Двоичное кодирование использует минимум один знак 0 и 1 для записи данных, тогда как ASCII кодирование применяет минимум восемь 0 и 1 для записи любого элемента данных. Выбор двоичного кодирования вместо ASCII влияет на размер файла изображения только в том случае, если файл содержит данные растрового рисунка. Если заполнить данное растровое изображение в виде кодов ASCII, то размер файла увеличится в два, а то и три раза.
Различные векторные форматы обладают различными цветовыми возможностями. Простейшие форматы, которые могут не содержать вообще никакой информации о цвете, используют цвет по умолчанию тех устройств, на которые они выводятся, другие форматы способны сохранять данные о полном тридцати двух битном цвете. Какую бы цветовую модель не применял бы векторный формат, на размер файла он не влияет, кроме тех случаев, когда файл содержит растровые образы. В обычных векторных объектах значение цвета относится ко всему объекту в целом. Цвет объекта хранится в виде части его векторного описания. Некоторые векторные файлы могут создать растровый эскиз изображений хранящихся в них. Эти растровые картинки, иногда называемые краткими описаниями изображений, обычно представляют собой эскизы векторных рисунков в целом. Краткое описание изображения, особенно полезно в ситуациях, когда вы не хотите открывать весь файл, чтобы посмотреть, что в нем хранится или когда вы не можете видеть векторный рисунок во время его использования. Первая ситуация возникает, когда вам необходимо найти файл с помощью одной из многих специально разработанных для этого программ. Для облегчения поиска нужного векторного файла такие программы могут считывать растровый эскиз изображения и другие характеристики, например, векторный формат, время создания, битовую глубину изображения и так далее. Вторая ситуация возникает, когда в каком-либо издательском пакете помещается на страницу векторный рисунок. Изображение, которое вы увидите, будет растровым эскизом настоящего векторного рисунка, у которого нельзя изменить размер, обрезать или как-то иначе обработать изображение. За эскизы изображения приходится расплачиваться памятью, т.к. эскизы – это растровая версия рисунков, а растровые данные используют много памяти компьютера.
Достоинства векторной графики.
Самая сильная сторона векторной графики в том, что она использует все преимущества разрешающей способности любого устройства вывода. Это позволяет изменять размеры векторного рисунка без потери его качества. Векторные команды просто сообщают устройству вывода, что необходимо нарисовать объект заданного размера, используя столько точек сколько возможно. Другими словами, чем больше точек сможет использовать устройство вывода для создания объекта, тем лучше он будет выглядеть. Растровый формат файла точно определяет, сколько необходимо создать пикселей и это количество изменяется вместе с разрешающей способностью устройства вывода. Вместо этого происходит одно из двух либо при увеличении разрешающей способности, размер растровой окружности уменьшается, так как уменьшается размер точки составляющих пиксель; либо размер окружности остается одинаковым, но принтеры с высокой разрешающей способностью используют больше точек для любого пикселя. Векторная графика обладает еще одним важным преимуществом, здесь можно редактировать отдельные части рисунка не оказывая влияния на остальные, например, если нужно сделать больше или меньше только один объект на некотором изображении, необходимо просто выбрать его и осуществить задуманное. Объекты на рисунке могут перекрываться без всякого воздействия друг на друга. Векторное изображение, не содержащее растровых объектов, занимает относительно не большое место в памяти компьютера. Даже очень детализированные векторные рисунки, состоящие из 1000 объектов, редко превышают несколько сотен килобайт.
Недостатки векторной графики.
Природа избегает прямых линий. К сожалению, они являются основными компонентами векторных рисунков. До недавнего времени это означало, что уделом векторной графики были изображения, которые никогда не старались выглядеть естественно, например, двухмерные чертежи и круговые диаграммы, созданные специальными программами САПР, двух и трех мерные технические иллюстрации, стилизованные рисунки и значки, состоящие из прямых линий и областей, закрашенных однотонным цветом. Векторные рисунки состоят из различных команд посылаемых от компьютера к устройствам вывода (принтеру). Принтеры содержат свои собственные микропроцессоры, которые интерпретируют эти команды и пытаются их перевести в точки на листе бумаги. Иногда из-за проблем связи между двумя процессорами принтер не может распечатать отдельные детали рисунков. В зависимости от типов принтера случаются проблемы, и у вас может оказаться чистый лист бумаги, частично напечатанный рисунок или сообщение об ошибке.
3. Растровая графика и пиксель
Компьютерная индустрия породила сотни новых и необычных терминов, пытаясь объяснить, что такое компьютер и как он работает. Термин растровая графика достаточно очевиден, если усвоить понятия, относящиеся к растровым изображениям. Растровые изображения напоминают лист клетчатой бумаги, на котором любая клетка закрашена либо черным, либо белым цветом, образуя в совокупности рисунок. Пиксел – основной элемент растровых изображений. Именно из таких элементов состоит растровое изображение. В цифровом мире компьютерных изображений термином пиксель обозначают несколько разных понятий. Это может быть отдельная точка экрана компьютера, отдельная точка напечатанная на лазерном принтере или отдельный элемент растрового изображения. Эти понятия не одно и тоже, поэтому чтобы избежать путаницы следует называть их следующим образом: видео пиксель при ссылке на изображение экрана компьютера; точка при ссылке на отдельную точку, создаваемую лазерным принтером. Существует коэффициент прямоугольности изображения, который введен специально для изображения количества пикселей матрицы рисунка по горизонтали и по вертикали.
Возвращаясь к аналогии с листом бумаги можно заметить, что любой растровый рисунок имеет определенное количество пикселей в горизонтальных и вертикальных рядах. Существуют следующие коэффициенты прямоугольности для экранов: 320х200, 320х240, 600х400, 640х480, 800х600 и др. Этот коэффициент часто называют размером изображения. Произведение этих двух чисел дает общее количество пикселей изображения. Существует также такое понятие как коэффициент прямоугольности пикселей. В отличие от коэффициента прямоугольности изображения он относится к реальным размерам видео пиксель и является отношением реальной ширины к реальной высоте. Данный коэффициент зависит от размера дисплея и текущего разрешения, и поэтому на разных компьютерных системах принимает различные значения. Цвет любого пикселя растрового изображения запоминается в компьютере с помощью комбинации битов. Чем больше битов для этого используется, тем больше оттенков цветов можно получить. Число битов, используемых компьютером для любого пикселя, называется битовой глубиной пикселя. Наиболее простое растровое изображение состоит из пикселей имеющих только два возможных цвета черный и белый, и поэтому изображения, состоящие из пикселей этого вида, называются однобитовыми изображениями. Число доступных цветов или градаций серого цвета равно 2 в степени равной количеству битов в пикселе.
--PAGE_BREAK--Цвета, описываемые 24 битами, обеспечивают более 16 миллионов доступных цветов и их часто называют естественными цветами. Растровые изображения обладают множеством характеристик, которые должны быть организованы и фиксированы компьютером. Размеры изображения и расположение пикселей в нем это две основных характеристики, которые файл растровых изображений должен сохранить, чтобы создать картинку. Даже если испорчена информация о цвете любого пиксель и любых других характеристиках компьютер все равно сможет воссоздать версию рисунка, если будет знать, как расположены все его пиксели. Пиксель сам по себе не обладает никаким размером, он всего лишь область памяти компьютера, хранящая информацию о цвете, поэтому коэффициент прямоугольности изображения не соответствует никакой реальной размерности. Зная только коэффициент прямоугольности изображения с некоторой разрешающей способностью можно определить настоящие размеры рисунка. Поскольку размеры изображения хранятся отдельно, пиксель запоминаются один за другим, как обычный блок данных. Компьютеру не приходится сохранять отдельные позиции, он всего лишь создает сетку по размерам заданным коэффициентом прямоугольности изображения, а затем заполняет ее пиксель за пикселей. Это самый простой способ хранения данного растрового изображения, но не самый эффективный с точки зрения использования компьютерного времени и памяти. Более эффективный способ состоит в том, чтобы сохранить только количество черных и белых пикселей в любой строке. Этот метод сжимает данные, которые используют растровые изображения. В этом случае они занимают меньше памяти компьютера.
4. Фрактальная графика
Среди всех картинок, которые может создавать компьютер, лишь немногие могут поспорить с фрактальными изображениями, когда идет речь о подлинной красоте. У большинства из нас слово «фрактал» вызывает в памяти цветные завитушки, формирующие сложный, тонкий и составной узор. Но на самом деле этот термин имеет гораздо более широкий смысл. Фрактал — объект, обладающий бесконечной сложностью, позволяющий рассмотреть столько же своих деталей вблизи, как и издалека. Земля – классический пример фрактального объекта. Из космоса она выглядит как шаp. Если приближаться к ней, мы обнаружим океаны, континенты, побережья и цепи гор. Будем рассматривать горы ближе – станут видны еще более мелкие детали: кусочек земли на поверхности горы в своем масштабе столь же сложный и неровный, как сама гора. И даже еще более сильное увеличение покажет крошечные частички грунта, каждая из которых сама является фрактальным объектом.
Компьютеры дают возможность строить модели таких бесконечно детализированных структур. Есть много методов создания фрактальных изображений на компьютере. Два профессора математики из Технологического института штата Джоржия разработали широко используемый метод, известный как Cистемы Итерируемых Функций (СИФ). С помощью этого метода создаются реалистичные изображения природных объектов, таких, например, как листья папоротника, деревья, при этом неоднократно применяются преобразования, которые двигают, изменяют в размере и вращают части изображения. В СИФ используется самоподобие, которое есть у творений природы, и объект моделируется как композиция множества мельчайших копий самого себя. Фрактальные изображения с многоцветными завитушками относятся обычно к разряду так называемых фракталов с временным порогом, которые изображаются точками на комплексной плоскости с цветами, отражающими время, требуемое для того, чтобы орбита данной точки перешла («перебежала») определенную границу. Комплексная плоскость — как координатная плоскость с осями x и y. По паре координат точка строится на комплексной плоскости так же, как и точка на плоскости Oxy, но числа имеют другой, необычный смысл: они обладают мнимой компонентой, называемой i, которая равна квадратному корню из -1. (Вот почему i — мнимая единица — в действительности корень из -1 не существует). Это искажает обычные правила математики, так что такие общепринятые операции как умножение двух чисел, дают необычные результаты.
Наиболее известный фрактал, множество Мандельброта – фрактал с временным порогом. Для каждой точки на экране компьютер считает координаты серии точек, определяющих мнимый путь, называемый орбитой. Точки, чьи орбиты никогда не выходят за пределы мнимого цилиндра, расположенного в начале координат комплексной плоскости, считаются элементами множества Мандельброта и обычно закрашиваются черным. Точки, чьи орбиты выходят за пределы цилиндра, раскрашиваются в соответствии с быстротой «убегания»: пиксель, чья орбита покидает цилиндр, например, на шестой итерации, можно раскрасить голубым, a тот — орбите которого требуется для этого семь итераций — красным. В результате на изображении получим множество Мандельброта и его окружение с «нестабильными» областями фрактала — областями, для которых малые изменения формулы ведут к большой разнице в орбитальном поведении. Это характеризуется густотой закраски рисунка. Меняя формулу для подсчета орбит, получим другие, такие же экзотические фракталы с временным порогом. Бесконечно детализированная структура множества Мандельброта становится «ясной», когда вы увеличиваете произвольную область. Неважно, сколь маленький участок вы рассматриваете: рисунок, который вы увидите, будет одинаково сложным. Почему? Потому что в двумерной плоскости, на которой строится множество Мандельброта, любая область содержит бесконечное число точек. Когда вы выбираете область для отображения, компьютер точкам из области ставит в соответствие точки на экране. И каждая точка, выбранная как угодно близко к другой, имеет свою характеристическую орбиту, порождающую соответствующий цветовой узор.
Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.
Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале.
В центре фрактальной фигуры находится её простейший элемент — равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.
Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом, можно описать и такой графический элемент, как прямую. Изменяя и комбинирую окраску фрактальных фигур можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также, составлять из полученных фигур «фрактальную композицию». Фрактальная графика, также как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется.
Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы. Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект»; «Фрактальная прямая»; «Фрактальная композиция»; «Объект-родитель» и «Объект наследник». Следует обратить Ваше внимание на то, что фрактальная компьютерная графика, как вид компьютерной графики двадцать первого века получила широкое распространение не так давно. Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать такие композиционные приёмы как, горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение?
Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную структуру. Это свойство фрактального объекта может быть удачно использовано при составлении декоративной композиции или для создания орнамент. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу. С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной графике найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные.
Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.
Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ.
Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.
5. Программное обеспечение
Растровую графику применяют при разработке электронных (мультимедийных) и полиграфических изданий. Иллюстрации, выполненные средствами растровой графики, редко создают вручную с помощью компьютерных программ. Чаще для этой цели используют сканируют иллюстрации, подготовленные художником на бумаге, или фотографии. В последнее время для ввода растровых изображений в компьютер нашли широкое применение цифровые фото- и видеокамеры. Соответственно, большинство графических редакторов, предназначенных для работы с растровыми иллюстрациями, ориентированы не столько на создание изображений, сколько на их обработку. В Интернет пока применяются только растровые иллюстрации. Программные средства для работы с векторной графикой наоборот предназначены, в первую очередь, для создания иллюстраций и в меньшей степени для их обработки. Такие средства широко используют в рекламных агентствах, дизайнерских бюро, редакциях и издательствах. Оформительские работы, основанные на применении шрифтов и простейших геометрических элементов, решаются средствами векторной графики намного проще. Существуют примеры высокохудожественных произведений, созданных средствами векторной графики, но они скорее исключение, чем правило, поскольку художественная подготовка иллюстраций средствами векторной графики чрезвычайно сложна.
Программные средства для работы с фрактальной графикой предназначены для автоматической генерации изображений путем математических расчетов. Создание фрактальной художественной композиции состоит не в рисовании или оформлении, а в программировании. Фрактальную графику редко применяют для создания печатных или электронных документов, но ее часто используют в развлекательных программах.
Список литературы
Джеф Проузис. Как работает компьютерная графика. – СПб.: Питер, 2008. – 654 с.
Жвалевский А., Гурская И, Гурский Ю. Компьютерная графика: Photoshop CS3, CorelDRAW X3, Illustrator CS3. Трюки и эффекты. – СПб.: Питер, 2008. – 992 с.
Божко А., Жук Д.М., Маничев В.Б. Компьютерная графика. Гриф УМО ВУЗов России. – М.: Издательство «МГТУ им. Баумана», 2007. – 392 с.
Вишневская Л. Компьютерная графика для школьников. – М.: Новое знание, 2007. – 160 с.
Летин А., Пашковский И., Летина О. Компьютерная графика. Гриф МО РФ. – М.: Форум, 2007. – 256 с.
Сергеев А., Кущенко С. Основы компьютерной графики. Adobe Photoshop и CorelDRAW – два в одном. Самоучитель. – М.: Диалектика, 2007. – 544 с.
Андреев О.Ю., Музыченко В.Л. Самоучитель компьютерной графики. Учебное пособие. – М.: Триумф, 2007. – 432 с.
www.ronl.ru
Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.
Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского "fractus" и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале. 
В центре фрактальной фигуры находится её простейший элемент — равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.
Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом можно описать и такой графический элемент как прямая.
Изменяя и комбинирую окраску фрактальных фигур, можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также составлять из полученных фигур «фрактальную композицию». Фрактальная графика, так же как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений ничего, кроме формулы, хранить не требуется.
Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.
Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект», «Фрактальная прямая», «Фрактальная композиция», «Объект-родитель» и «Объект наследник».
Следует обратить внимание на то, что фрактальная компьютерная графика как вид компьютерной графики двадцать первого века получила широкое распространение не так давно.
Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать множество приёмов: горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение? Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную композицию. Это свойство фрактального объекта может быть удачно использовано для создания орнамента или декоративной композиции. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически, благодаря фрактальной графике, найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.
Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ.
Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например, Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.
esate.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (МАМИ)»
(УНИВЕРСИТЕТ МАШИНОСТРОЕНИЯ)
Кафедра «Стандартизация, метрология и сертификация»
Дисциплина «Основы фрактального анализа»
Реферат
Тема «Фракталы. Фрактальная графика»
Выполнил:
Студент Мальцев А.А.
Группа 5-МС-6
Преподаватель:
Вячеславова О.Ф.
Москва 2013
Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видов компьютерной графики.
Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видов компьютерной графики.
Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.
Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале.
В центре фрактальной фигуры находится её простейший элемент — равносторонний треугольник, который получил название «фрактальный». Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.
Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом, можно описать и такой графический элемент, как прямую.
Изменяя и комбинирую окраску фрактальных фигур можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также, составлять из полученных фигур «фрактальную композицию». Фрактальная графика, также как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется.
Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.
Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект»; «Фрактальная прямая»; «Фрактальная композиция»; «Объект-родитель» и «Объект наследник». Следует обратить Ваше внимание на то, что фрактальная компьютерная графика, как вид компьютерной графики двадцать первого века получила широкое распространение не так давно.
Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать такие композиционные приёмы как, горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение? Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную структуру. Это свойство фрактального объекта может быть удачно использовано при составлении декоративной композиции или для создания орнамента. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу.
С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной графике найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.
Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ.
Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.
ИСПОЛЬЗОВАНИЕ ФРАКТАЛЬНОЙ ГРАФИКИ В ИНТЕРЬЕРЕ
Особая тема – использование фрактальной графики в интерьере. Здесь возможности, не побоюсь этого слова, безграничны. Поскольку фрактальная картина печатается типографским способом, она может быть любого размера, напечатана на любом материале, включая баннерную ткань или полимерную пленку, что позволяет украшать фракталами например кухню, ванную или сауну. Фракталы можно использовать в прихожей, холле, спальне, столовой, кабинете руководителя или комнате отдыха для сотрудников. Можно украсить фракталом внешнюю стену коттеджа. Фрактал можно вписывать в любой интерьер, предварительно идеально выверив по цвету, размеру и ритму с общим дизайном помещения. Предложение. Вы можете заказать любой фрактал, представленный на этом сайте для своих интерьеров. Если вы предварительно вышлете фотографии места, которое предполагается украсить фрактальной картиной, можно сделать дизайн-проект, чтобы вы имели наглядное представление о том, как это будет выглядеть в действительности. На любой картине можно поменять цвет, чтобы она лучше согласовалась с цветом ваших обоев, штор, стен и т.д., а так же найти оптимальный размер для вашего помещения. Материал, на котором печатается фрактальная картина подбирается в зависимости от помещения, в котором она будет висеть. Для гостинной - ткань, для ванной - пленка и т.п. Рама может быть любой: дерево, пластик, металл. Эти картины не портятся со временем, поэтому их не нужно закрывать стеклом. Если вы сами нарисуете фрактальную картину, которую захотите повесить у себя дома, я могк помочь ее напечатать и оформить. Что еще рассказать о фрактальных картинах? Поскольку они по определению находятся в гармонии с природой, они смогут гармонизировать и помещение, в котором висят. Только здесь есть одно «но». Если вы добрый, наполненный любовью, человек, фрактал усилит доброту, а если вы завистливый и корыстный - фрактал может усилить именно эти качества. Так что загляните в себя прежде, чем украшать свое жилище столь непростыми картинами.
ИНТЕГРАЦИЯ ДЕТЕРМИНИРОВАННЫХ ФРАКТАЛОВ И ХАОС
Из рассмотренных примеров детерминистских фракталов можно увидеть, что они не проявляют никакого хаотического поведения и что они на самом деле очень даже предсказуемы. Как известно, теория хаоса использует фрактал для того, чтобы воссоздать или найти закономерности с целью предсказания поведения многих систем в природе, таких как, например, проблема миграции птиц. Теперь давайте посмотрим, как это в действительности происходит. Используя фрактал, называемый Деревом Пифагора, не рассматриваемого здесь (который, кстати, не изобретен Пифагором и никак не связан с теоремой Пифагора) и Броуновского движения (которое хаотично), давайте попытаемся сделать имитацию реального дерева. Упорядочение листьев и веток на дереве довольно сложно и случайно и, вероятно не является чем-то достаточно простым, что может эмулировать короткая программа из 12 строк. Для начала нужно сгенерировать Дерево Пифагора (слева). Результат напоминает те старые детсадовские рисунки… Так что давайте сделаем ствол толще. На этой стадии Броуновское движение не используется. Вместо этого, каждый отрезок линии теперь стал линией симметрии прямоугольника, который становится стволом, и веток снаружи. Но результат все еще выглядит слишком формальным и упорядоченным. Дерево еще не смотрится как живое. Попробуем применить некоторые из тех знаний в области детерминированных фракталов, которые мы только что приобрели. Теперь можно использовать Броуновское движение для создания некоторой случайной беспорядочности, которая изменяет числа, округляя их до двух разрядов. В оригинале были использованы 39 разрядные десятичные числа. Результат (слева) не выглядит как дерево. Вместо этого, он выглядит как хитроумный рыболовный крючок! Может быть округление до 2 разрядов было слишком уж много? Снова применяем Броуновское движение, округленное на этот раз до 7 разрядов. Результат по-прежнему выглядит как рыболовный крючок, но на этот раз в форме логарифмической спирали! Так как левая сторона (содержащая все нечетные числа) не производит эффект крючка, случайные беспорядочности, произведенные Броуновским движением применяются дважды ко всем числам с левой стороны и только один раз к числам справа. Может быть этого будет достаточно чтобы исключить или уменьшить эффект логарифмической спирали. Итак, числа округляются до 24 разрядов. На этот раз, результат — приятно выглядящая компьютеризированная хаотическая эмуляция реального дерева.
КРИВАЯ КОХА
Кривая Коха один из самых типичных детерминированных фракталов. Она была изобретена в девятнадцатом веке немецким математиком по имени Хельге фон Кох, который, изучая работы Георга Контора и Карла Вейерштрассе, натолкнулся на описания некоторых странных кривых с необычным поведением. Инициатор — прямая линия. Генератор — равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова. В своем исследовании, Мандельброт много экспериментировал с кривыми Коха, и получил фигуры такие как Острова Коха, Кресты Коха, Снежинки Коха и даже трехмерные представления кривой Коха, используя тетраэдр и прибавляя меньшие по размерам тетраэдры к каждой его грани. Кривая Коха имеет размерность ln4/ln3 = 1.261859507. Крест Коха — это один из вариантов кривой Коха, изобретенный Мандельбротом. Вместо отрезка прямой, он использовал в качестве инициатора квадрат или прямоугольник. Так как в этом фрактале использован та же самая идея что и в оригинальной кривой Коха, его фрактальная размерность такая же: ln4/ln3 = 1.261859507.
СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ
Рандомизированный фрактал на основе множества Жюлиа Природные объекты часто имеют фрактальную форму. Для их моделирования могут применяться стохастические (случайные) фракталы. Примеры стохастических фракталов: траектория броуновского движения на плоскости и в пространстве; граница траектории броуновского движения на плоскости. В 2001 году Лоулер, Шрамм и Вернер доказали предположение Мандельборта о том, что её размерность равна 4/3. эволюции Шрамма-Лёвнера — конформно-инвариантные фрактальные кривые, возникающие в критических двумерных моделях статистической механики, например в модели Изинга и перколяции. различные виды рандомизированных фракталов, то есть фракталов, полученных с помощью рекурсивной процедуры, в которую на каждом шаге введён случайный параметр. Плазма — пример использования такого фрактала в компьютерной графике. Фрактальная монотипия, или стохатипия — направления в изобразительном искусстве, состоящие в получении изображения случайного фрактала.
РЕШЕТКА СЕРПИНСКОГО
Это один из фракталов, с которыми экспериментировал Мандельброт, когда разрабатывал концепции фрактальных размерностей и итераций. Треугольники, сформированные соединением средних точек большего треугольника вырезаны из главного треугольника, образовывая треугольник, с большим количеством дырочек. В этом случае инициатор — большой треугольник а шаблон — операция вырезания треугольников, подобных большему. Так же можно получить и трехмерную версию треугольника, используя обыкновенный тетраэдр и вырезая маленькие тетраэдры. Размерность такого фрактала ln3/ln2 = 1.584962501. Чтобы получить ковер Серпинского, возьмем квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. В конце концов образуется плоская фрактальная сетка, не имеющая площади, но с бесконечными связями. В своей пространственной форме, губка Серпинского преобразуется в систему сквозных форм, в которой каждый сквозной элемент постоянно заменяется себе подобным. Эта структура очень похожа на разрез костной ткани. Когда-нибудь такие повторяющиеся структуры станут элементом строительных конструкций. Их статика и динамика, считает Мандельброт, заслуживает пристального изучения.
yaneuch.ru
На сегодняшний день Фрактальная графика является второй по росту популярности из четырёх видов компьютерной графики (далее КГр).
Так же есть Растровая и Векторная. Одна – для создания фотореалистичных изображений; Другая – для создания сложных геометрических объектов; и Трёхмерная – как отдельный вид от предыдущих для создания объёмных зрительно-подобных изображений и объектов.
Фрактал – основа Фрактальной графики, это математически построенная фигура, являющаяся частью точной её копии в разы большей, чем одна часть. В свою очередь, большая фигура является частью еще большей.
Чтобы было лучше понять, представьте треугольник, состоящий из трёх треугольников, каждый из которых состоит из 3-х меньших и т.д. Таким образом получается матрёшка, где одна копия встроена в большую копию. Но это не значит, что всё изображение будет однообразным. Далее из таких треугольников, можно состряпать куда более сложную композицию, походящую на естественный объект встречающийся в повседневной жизни. Процесс наследования можно продолжать до бесконечности, без увеличения размера файла.
Посему мы не могли не заметить, как сильно схожи Фрактальная и Векторная графики. Обе имеют в своей базе данных файла информацию о математической формуле или системе формул, задающих очертания фигуры и конечных её размерах.
Для тех, кто изучает данный вид компьютерной графики с научной точки зрения, будет не лишним знать о существовании ряда базовых понятий этой сферы:
«Фрактальный треугольник», «Фрактальная фигура», «Фрактальный объект», «Фрактальная прямая», «Фрактальная композиция», «Объект-родитель», «Объект наследник».
В связи с недавней распространенностью этого формата КГр, на сегодняшний день существует достаточно мало теоретической базы в плане терминологий и практической в плане создания больших или иных элементов.
Сейчас трудно недооценить возможности и важность фракталов в создании реалистичных изображений. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, с возможностью осуществления множества различных приемов: горизонтали и вертикали, диагональные направления, симметрию и асимметрию и т.д. Из-за малой истории и плохой распространенности, очень мало людей, в том числе программистов, аниматоров и простых художников в мире действительно хорошо знакомы и умеют обращаться с Фрактальной графикой на должном уровне. Её пока что не практикуют в университетах. В школьной программе о ней не упоминается ни слова. А ведь сейчас это самый перспективный вид графики, даже перспективнее трёхмерной.
Фракталом можно делать большее. Структура фрактала похожа на составляющие кристалла, снежинки. Тем самым на выходе мы получаем некую невиданную доселе композицию цвета и форм. И всё из-за одной(2-3) нехитрых формул, изменив переменные которой, можно кардинально изменить само изображение.
Данный вид графики незаменим при создании таких сложных повторяющихся объектов, состоящих из самоподобных частей, как облака, горы, вода и т.д. Фактически, благодаря фракталу, найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Позволим заметить, что акромя графики, так же есть и живопись, и музыка. Все они построены на технологии фрактала.
Бесспорными достоинствами фрактала являются:
Недостатки:
В общем то, как всегда. У всего есть достоинства и недостатки. Графика тем более грешит и тем, и тем.
smartappliance.ru
