Главная »
Реферат »
Позиционные и непозиционные системы счисления реферат
Позиционные и непозиционные системы счисления. Позиционные и непозиционные системы счисления реферат
Лекция - Позиционные и непозиционные системы счисления
Системы счисления принято делить на два класса: непозиционные и позиционные.
В непозиционных СС от положения (позиции) цифры в записи не зависит величина, которую она обозначает. Характерным примером такой системы счисления является римская СС.
Например, в римской СС число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Например:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
Такие системы счисления используются редко, т.к. не приспособлены для вычислений.
На практике наибольшее распространение получили позиционные системы счисления.
Позиционная система счисления– система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. В каждой позиционной системе счисления имеется основание. Любое число записывается в виде последовательности из цифр основания. Количество цифр основания равно самому основанию. Основание показывает, во сколько раз вес каждой цифры меньше веса цифры, стоящей в старшем соседнем разряде.
Некоторые позиционные системы счисления
Таблица 3.1
| Основание | Система счисления | Знаки |
| Двоичная | 0,1 |
| Троичная | 0,1,2 |
| Четвертичная | 0,1,2,3 |
| Пятиричная | 0,1,2,3,4 |
| Восьмиричная | 0,1,2,3,4,5,6,7 |
| Десятиричная | 0,1,2,3,4,5,6,7,8,9 |
| Двенадцатиричная | 0,1,2,3,4,5,6,7,8,9, А, В |
| Шестнадцатиричная | 0,1,2,3,4,5,6,7,8,9, А, В,D,E,F |
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также называется десятичной. Называются они так потому, что каждое число можно составить из набора цифр содержащего 10 символов (цифр) –0123456789.
Возьмём, к примеру, число 246. Его запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство:
246 = 200 + 40 + 6 = 2 * 102 + 4 * 101 + 6 * 100
Здесь знаками равенства отделены три способа записи одного и того же числа. Для нас наиболее интересна третья форма записи: 2 * 102 + 4 * 101 + 6 * 100. Она построена следующим образом:
В нашем числе три цифры. Старшая цифра «2» имеет номер 3. Так вот она умножается на 10 во второй степени. Следующая цифра «4» имеет порядковый номер 2 и умножается на 10 в первой степени. Уже видно, что цифры умножаются на десять в степени на единицу меньше порядкового номера цифры.
При этом пользуются следующим алгоритмом:
1) цифра в каждой позиции умножается на основание в степени на 1 меньшую, чем номер позиции;
2) полученные таким образом значения складываются.
Например:
12310 = 1*102+2*101+3*100;
1023.2810=1*103+0*102+2*101+3*100+2*10-1+8*10-2
В других системам счисления такой перевод будет выглядеть следующим образом:
1238 = 1х82+2х81+3х80=8310;
1012 = 1х22+0х21+1х20=510;
1Е316 = 1х162+14х161+3х160=48310.
Здесь индекс числа служит указанием на основание системы счисления. Назовем основанием системы счисления число, равное мощности множества (т.е. количеству элементов множества) различных символов, допустимых в каждой позиции числа.
Десятичная система счисления является однородной. Это означает, что одних и тех же символов достаточно для изображения любого числа. Но в повседневной жизни мы пользуемся и неоднородными системами счисления, и системами счисления с другим основанием. Пример тому – неметрические системы единиц (1 пуд=40 фунтов), система счета времени (1 минута = 60 секунд).
В дальнейшем мы будем рассматривать однородные позиционные системы счисления.
Обозначим через p основание системы счисления. Тогда веса позиций числа могут быть представлены следующим образом:
Таким образом, любое число X в позиционной системе счисления с основанием p можно представить в следующей развернутой форме записи:
,
или
,
где,
p – основание системы счисления;
m – количество позиций или разрядов, отведенное для изображения целой части числа;
s – количество разрядов, отведенное для изображения дробной части числа;
n=m+s – общее количество разрядов в числе,
ai – любой допустимый символ в разряде (т.е. должен принадлежать множеству {0,1,…,p-1}).
Заметим, что число, равное основанию системы счисления, в самой системе счисления записывается в виде:
pp=10p
В компьютерных науках наибольшее распространение получила не десятичная, а системы счисления с основанием, кратным 2 – двоичная, восьмеричная, шестнадцатеричная.
В двоичной системе счисления допустимыми символами являются только 0 и 1, а само число может быть представлено в виде последовательности нулей и единиц.
Например:
110100102=1*27+1*26+0*25+1*24+0*23+0*22+1*21+0*20=16210
В восьмеричной системе счисления допустимыми символами являются 0,1,…7.
Например:
2428=2*82+4*81+2*80=16210
В шестнадцатеричной системе допустимыми символами являются 0,1,…9,A,B,C,D,E,F.
Например:
A216=10*161+2*160=16210
www.ronl.ru
Позиционные и непозиционные системы счисления
 Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной 
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.  Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Системой счисления называется совокупность приемов и правил представления чисел с помощью цифровых знаков.
Непозиционной называется такая система счисления, в которой значение любой цифры не зависит от положения (позиции) в ряду цифр, изображающих это число.
Например, в числе ХХХ, записанном в римской системе счисления, каждый разряд означает 10 единиц.
Задача 1. Записать числа в римской нумерации: а) 193; б) 564; в) 2708.
Решение: а) 193 - это сто (С) + девяносто, т.е. сто без десятка (ХС) + три (III). Следовательно, 193 запишется как СХСIII.
б) 564 - это пятьсот (D) + пятьдесят (L) + десять (Х) + четыре (IV), т.е. число 564 запишется как DLХIV.
в) 2708 - это две тысячи (ММ) + плюс пятьсот (D) + сто (С) + сто (С) + пять (V) + три (III). Следовательно, число 2708 записывается так: ММDCCVIII.
Позиционной называется такая система счисления, в которой значение любой цифры зависит от ее положения (позиции) в ряду цифр, изображающих это число.
Например, цифра 3 в числе 723, записанном в десятичной системе счисления, означает три единицы, а в числе 325 – три сотни. К позиционным СС можно отнести шестидесятиричную вавилонскую и десятичную системы счисления.
Под основанием системы счисления понимается определенное постоянное для данной системы счисления отношение единиц соседних разрядов.
Основанием системы счисления может быть любое натуральное число большее 1.
Система счисления с основанием равным 1 называется унарной.
Для записи чисел в позиционной системе счисления используются цифры, количество которых соответствует основанию системы.
Десятичная система счисления, запись чисел в ней
В практике установилась десятичная система счисления. Как известно, в десятичной СС для записи чисел используются 10 знаков (цифр): 1,2,3,4,5,6,7,8,9,0. Из них образуются конечные последовательности, которые являются краткими записями чисел. Например, последовательность 3745 является краткой записью числа  . .
Определение 4.Десятичной записью натурального числа xназывается его представление в виде:
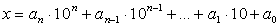 , ,
где коэффициенты an, an-1, …, a1, a0 принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и 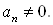
Сумму  в краткой форме принято записывать последовательностью цифр с чертой наверху, чтобы отличать от произведения чисел: в краткой форме принято записывать последовательностью цифр с чертой наверху, чтобы отличать от произведения чисел:
 . .
Так как понятие числа и его записи нетождественны, то существование и единственность десятичной записи натуральной записи надо доказывать.
Теорема 1. Любое натуральное число х можно представить в виде:
 (1) (1)
где коэффициенты an, an-1, …, a1, a0 принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
и такая запись единственная.
Десятичная запись числа позволяет просто решать вопрос о том, какое из них меньше.
Теорема 2. Пусть х и у – натуральные числа, запись которых дана в десятичной системе счисления:

 . .
Тогда число х меньше числа у, если выполнено одно из условий:
а) n<m;
б) n = m, но an<bn;
в) n = m, an= bn, …, ak = bk, но ak-1<bk-1.
Пример: 1) если х = 345, а у = 4678, то х<y, так как первое число трехзначное, а второе – четырехзначное.
2) если х = 345, а у = 467, то x<y, так как в первом из двух значений трехзначных чисел меньше сотен.
3) Если х = 3456, а у = 3467, то x<y, так как, несмотря на то что в каждом из четырехзначных чисел число тысяч и сотен одинаковое, десятков в числе х меньше, чем в числе у.
Разряды
Если натуральное число х представлено в виде  , то числа 1, 10, 102, …, 10n называют разрядными единицамисоответственно первого, второго, …, n+1 разряда, причем 10 единиц одного разряда составляют одну единицу следующего высшего разряда, т.е. отношение соседних разрядов равно 10 – основанию системы счисления. , то числа 1, 10, 102, …, 10n называют разрядными единицамисоответственно первого, второго, …, n+1 разряда, причем 10 единиц одного разряда составляют одну единицу следующего высшего разряда, т.е. отношение соседних разрядов равно 10 – основанию системы счисления.
Три первых разряда в записи числа соединяют одну группу и называют первым классом, или классом единиц. В первый класс входят единицы, десятки и сотни.
Четвертый, пятый и шестой разряды в записи числа образуют второй класс – класс тысяч. Затем следует третий класс – класс миллионов, состоящий тоже из трех разрядов: седьмого, восьмого и девятого, т.е. из единиц миллионов, десятков миллионов и сотен миллионов.
Последующие три разряда также образуют новый класс и т.д. выделение классов единиц, тысяч, миллионов и т.д. создает удобства для записи и прочтения чисел.
В десятичной СС всем числам можно дать название (имя). это достигается следующим образом: имеются названия первых 10 чисел, затем из них в соответствии с определением десятичной записи и путем прибавления еще немногих слов образуются названия последующих чисел. Так числа второго десятка, представляемые в виде  , образуются из соединения первых десяти названий и несколько измененного слова десять ("дцать"): , образуются из соединения первых десяти названий и несколько измененного слова десять ("дцать"):
одиннадцать - один на десять;
двенадцать - два на десять и т.д.
Может быть естественнее было бы говорить "два и десять", но наши предки предпочли говорить "два на десять", что и сохранилось в речи.
Слово "двадцать" обозначает два десятка. Продолжая счет, получим название чисел третьего, четвертого, пятого, шестого и т.д. десятков. Только в трех случаях появляются новые слова: сорок, девяносто и сто. Десять десятков называют сотней. Название чисел второй сотни составляются из слова "сто" и названий чисел первого и последующих десятков. Отсчитав новую сотню, будем иметь две сотни, которые для краткости называют "двести".Затем получим особые названия: триста, четыреста, пятьсот, и т.д. до тех пор, пока не отсчитаем 10 сотен, которые носят название тысяча. После отсчета тысячи тысяч получим число, имеющее наименование миллион (106). Далее считаем миллионами до тех пор, пока не дойдем до тысячи миллионов, данное число носит название - миллиард (109). Миллион миллионов называется биллионом(1012). Затем получим триллион (1015), потом квадриллион (1018) и т.д.
Таким образом, чтобы назвать все натуральные числа в пределах миллиарда, потребовалось только 16 различных слов: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, сорок, девяносто, сто, тысяча, миллион, миллиард. Остальные названия чисел (в пределах миллиарда) образуются из основных.
| megapredmet.ru
Позиционные и непозиционные системы счисления
Количество просмотров публикации Позиционные и непозиционные системы счисления - 645
Системы счисления принято делить на два класса: непозиционные и позиционные.
В непозиционных СС от положения (позиции) цифры в записи не зависит величина, которую она обозначает. Характерным примером такой системы счисления является римская СС.
К примеру, в римской СС число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. В случае если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
К примеру:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
Такие системы счисления используются редко, т.к. не приспособлены для вычислений.
На практике наибольшее распространение получили позиционные системы счисления.
Позиционная система счисления– система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. Размещено на реф.рфВ каждой позиционной системе счисления имеется основание. Любое число записывается в виде последовательности из цифр основания. Количество цифр основания равно самому основанию. Основание показывает, во сколько раз вес каждой цифры меньше веса цифры, стоящей в старшем соседнем разряде.
Некоторые позиционные системы счисления
Таблица 3.1
| Основание
| Система счисления
| Знаки
|
|
| Двоичная
| 0,1
|
|
| Троичная
| 0,1,2
|
|
| Четвертичная
| 0,1,2,3
|
|
| Пятиричная
| 0,1,2,3,4
|
|
| Восьмиричная
| 0,1,2,3,4,5,6,7
|
|
| Десятиричная
| 0,1,2,3,4,5,6,7,8,9
|
|
| Двенадцатиричная
| 0,1,2,3,4,5,6,7,8,9,А,В
|
|
| Шестнадцатиричная
| 0,1,2,3,4,5,6,7,8,9,А,В,D,E,F
|
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также принято называть десятичной. Называются они так потому, что каждое число можно составить из набора цифр содержащего 10 символов (цифр) –0123456789.
Возьмём, к примеру, число 246. Его запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство:
246 = 200 + 40 + 6 = 2 * 102 + 4 * 101 + 6 * 100
Здесь знаками равенства отделены три способа записи одного и того же числа. Стоит сказать, что для нас наиболее интересна третья форма записи: 2 * 102 + 4 * 101 + 6 * 100 . Она построена следующим образом:
В нашем числе три цифры. Старшая цифра "2" имеет номер 3. Так вот она умножается на 10 во второй степени. Следующая цифра "4" имеет порядковый номер 2 и умножается на 10 в первой степени. Уже видно, что цифры умножаются на десять в степени на единицу меньше порядкового номера цифры.
При этом пользуются следующим алгоритмом:
1) цифра в каждой позиции умножается на основание в степени на 1 меньшую, чем номер позиции;
2) полученные таким образом значения складываются.
К примеру:
12310 = 1*102+2*101+3*100;
1023.2810=1*103+0*102+2*101+3*100+2*10-1+8*10-2
В других системам счисления такой перевод будет выглядеть следующим образом:
1238 = 1х82+2х81+3х80=8310;
1012 = 1х22+0х21+1х20=510;
1Е316 = 1х162+14х161+3х160=48310.
Здесь индекс числа служит указанием на основание системы счисления. Назовем основанием системы счисления число, равное мощности множества (ᴛ.ᴇ. количеству элементов множества) различных символов, допустимых в каждой позиции числа.
Десятичная система счисления является однородной. Это означает, что одних и тех же символов достаточно для изображения любого числа. Но в повседневной жизни мы пользуемся и неоднородными системами счисления, и системами счисления с другим основанием. Пример тому – неметрические системы единиц (1 пуд=40 фунтов), система счета времени (1 минута = 60 секунд).
В дальнейшем мы будем рассматривать однородные позиционные системы счисления.
Обозначим через p основание системы счисления. Тогда веса позиций числа бывают представлены следующим образом:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, любое число X в позиционной системе счисления с основанием p можно представить в следующей развернутой форме записи:
 ,
,
или
 ,
,
где,
p – основание системы счисления;
m – количество позиций или разрядов, отведенное для изображения целой части числа;
s – количество разрядов, отведенное для изображения дробной части числа;
n=m+s – общее количество разрядов в числе,
ai – любой допустимый символ в разряде (ᴛ.ᴇ. должен принадлежать множеству {0,1,…,p-1}).
Заметим, что число, равное основанию системы счисления, в самой системе счисления записывается в виде:
pp=10p
В компьютерных науках наибольшее распространение получила не десятичная, а системы счисления с основанием, кратным 2 – двоичная, восьмеричная, шестнадцатеричная.
В двоичной системе счисления допустимыми символами являются только 0 и 1, а само число должна быть представлено в виде последовательности нулей и единиц.
К примеру:
110100102=1*27+1*26+0*25+1*24+0*23+0*22+1*21+0*20=16210
В восьмеричной системе счисления допустимыми символами являются 0,1,…7.
К примеру:
2428=2*82+4*81+2*80=16210
В шестнадцатеричной системе допустимыми символами являются 0,1,…9,A,B,C,D,E,F.
К примеру:
A216=10*161+2*160=16210
referatwork.ru
Позиционные и непозиционные системы счисления, реферат — allRefers.ru
Позиционные и непозиционные системы счисления - раздел Компьютеры, Математика в компьютере
Конструкция вычислительных машин и программирование на них тесно связаны с системами счисления. Система счисления – это совокупность приемов наименования и записи чисел. Условные знаки, применяемые при записи чисел, называются цифрами.
Все системы счисления делятся на две группы: позиционные и непозиционные. Непозиционной называется такая система, у которой количественное значение цифры зависит от ее начертания и не зависит от положения, т.е. каждый знак всегда изображает одно и то же число. Примером такой системы счисления может служить римская система счисления. В этой системе запись различных целых чисел производится с помощью следующих цифр:
I V X C D M и т.д.
1 5 10 50 100 1000
Для записи больших цифр в римской системе введенных знаков будет не хватать, и нужны новые. И сколько бы мы их не вводили, всегда можно придумать число, которое уже введенными знаками изобразить трудно. Римская система счисления не используется в вычислениях. Ее применяют обычно для обозначения месяцев, веков, глав и т. п. Большинство систем счисления относятся к позиционным. В них значение каждой цифры изменяется в зависимости от места (позиции), на котором она находится. Общепринятой системой счисления является десятичная позиционная система, берущая свое начало от счета на пальцах. Она была изобретена в Индии, затем заимствована арабами и уже через арабские страны пришла в Европу.
В различные исторические периоды человек использовал позиционные системы счисления, отличные от десятичной. Так, в Древнем Вавилоне (2000 лет до н. э.) применялась шестидесятичная система счисления. Эта система счисления применяется до сих пор при измерении углов, времени, а именно: остатки ее мы находим в делении часа на 60 минут, а минуты на 60 секунд, круга на 360 градусов, т.е. 6 раз по 60. Возникновение шестидесятичной системы счисления связано со слиянием в одно государство двух древних народов – сумерийцев и аккадян. Во вновь образованном государстве остались в ходу единицы веса, используемые ранее тем и другим народами, причем одна из этих единиц была приблизительно в 60 раз больше другой.
Кроме шестидесятичной системы употреблялась также и две-надцатиричная, следами которой является сохранившийся обычай считать некоторые предметы дюжинами.
Число 12 люди считают магическим с тех пор, когда они научились считать. На нем построены системы измерения и летосчисления, по нему ориентируются календари, оно входит во многие пословицы.
Каждый знает: год делится на 12 месяцев. Но, кроме того, существуют 12 апостолов, 12 знаков зодиака и 12 разбойников. Изучавшие математику называют 12 «поцелуйным числом третьего измерения». Если вокруг шара расположить еще 12 шаров того же диаметра, то каждый из них математически «поцелуется» с центральным, то есть коснется его в одной точке.
Почему число 12 играет такую роль в истории нашей цивилизации? Одна из наиболее важных причин – календарь, дающий возможность рационально разделить год на составные части. Это связано с полнолунием, которое мы наблюдаем на небе 12 раз в году. К тому же и круг с помощью циркуля и линейки можно разделить на 6 (а тем самым на 12) равных частей. Использование числа 12 в качестве базового значительно облегчало счет.
Даже античные жители Израиля, упрямо признававшие из 12 заповедей только 10, не могли полностью освободится от магии дюжины. У мудрого Иакова было 12 сыновей, которые стали основателями 12 колен Израиля. Иисус Навин в знак благодарности за удачную переправу через Иордан велел воздвигнуть там 12 каменных глыб. Купель Соломона окружали 12 бронзовых быков, а на груди у главного священника сверкало 12 драгоценных камней. В свою очередь, у Иисуса было 12 верных слуг. В Апокалипсисе от Иоанна у небесного Иерусалима 12 ворот. Он стоит на 12 камнях, на которых высечены имена 12 апостолов. Римские законы были записаны на 12 бронзовых дощечках. Со времен Древнего Рима повелось назначать 12 присяжных при судебных разбирательствах.
Древние китайцы, наблюдавшие за ночным небом, тоже делили год на 12 лун и создали соответствующую астрологию. Больше других европейцев к числу 12 оказались привержены англичане, с большим трудом перешедшие за десятичную систему, да и то не во всем. И только древние германцы, жившие в лесах и мало смотревшие в небо, в меньшей степени уверовали в магию дюжины. Хотя и в немецком языке само это слово появилось не случайно. И, наконец, 12 занимает почетное место в играх, например, в лото. Словом, счастливым числом его считают вполне заслуженно.
Встречались, например, в древнем Китае, пятеричная система счисления. У населявших американский континент народностей – ацтеков и майя была распространена двадцатеричная система счисления. Кроме названных систем, цивилизации известны и другие.
Чтобы различать, в какой системе счисления записано число, рядом с числом в виде индекса (в десятичной системе) указывается основание системы счисления. Например, 25710 – записано в десятичной системе счисления, а 2578 – в восьмеричной. Указание основания опускается в тех случаях, когда основание используемой системы не вызывает сомнений.
Принцип построения позиционных систем проще всего проиллюстрировать на примере десятичной системы счисления. В этой системе для записи любых чисел используется десять различных символов (цифр): 0,1,2,...,9. С помощью одной цифры можно изобразить самое большее число – 9. Число на единицу большее, чем 9, уже записывается двумя цифрами – 10. Затем младший разряд возрастет до максимальной цифры (число 19). После чего добавляется единица к следующему разряду, а в младшем разряде снова 0 (20) и т.д. Дойдя до числа 99, т.е., имея в обоих разрядах максимальную цифру, мы записываем 1 в новом, более старшем разряде, а в обоих младших – нули (100). Точно такую же процедуру можно использовать и для случая, когда количество используемых цифр меньше десяти.
Итак, введя для числа «десять» обозначение «10», мы не ввели никаких новых символов (цифр), а использовали уже имеющиеся. Однако введением этого обозначения сделан важный шаг в построении системы счисления, а именно: значение каждой из цифр поставлено в зависимость от того места, где она стоит в изображении числа.
Пример. В записи числа 141,14 единица, стоящая слева на первом месте, означает количество сотен; единица, стоящая перед запятой, – количество единиц; а единица, стоящая после запятой, – количество десятых долей, содержащихся в числе. Последовательность цифр 141,14 представляет собой сокращенную запись выражения:
141,14 = 1·100+4·10+1+1:10+4:100.
Количество различных цифр, используемых в позиционной системе счисления для изображения произвольных чисел, называется основанием системы счисления. Основанием десятичной системы счисления является число десять. То есть в десятичной системе для записи числа употребляются десять цифр: 0,1,......, 9; а в пятеричной системе счисления достаточно пяти цифр: 0,1,2,3,4. Основание пятеричной системы счисления число пять – изобразится в ней как «10», поскольку оно является единицей следующего (второго) разряда. Так будет в любой системе счисления: основание системы счисления в любой системе записывается как 10. Позиции, на которых в последовательности стоят цифры, перенумерованы. Эти позиции называются разрядами числа. Каждой цифре рассмотренной последовательности приписано определенное значение. Цифра, стоящая в некотором разряде, имеет значение большее того, которое она бы имела в разряде с номером, меньшим на единицу, во столько раз, каково основание системы счисления. Цифра, стоящая в нулевом разряде, имеет своим значением соответствующее число из основания.
Умножение числа на основание системы счисления сводится к переносу запятой на один разряд вправо, а деление на основание системы – к переносу запятой на один разряд влево.
Последовательность цифр обозначает число, равное сумме значений ее цифр. В соответствии со сказанным, например, последовательность десятичных цифр 257 можно представить так:
257 = 200+50+7.
Любое число в позиционной, в том числе и в десятичной системе, записывается в виде последовательности цифр, разделенных запятой на целую и дробную части. Такая запись числа есть сокращенная запись. Возьмем, например, число А = 627,3. В развернутом виде оно запишется так:
А10 = 6·102+2·101+7·100+3·10-1.
Аналогичным образом представится десятичная запись произвольного числа в десятичной системе:
аn·10n+аn-1·10n-1+...+а0·100+а-1·10-1+...,
где а – одна из цифр 0,1,2,.....,9.
В двоичной системе счисления любое положительное число можно записать аналогично:
А2=аn·2n+...+а0·20+а-1·2-1+...+а-m·2-m,
где а – принимает значения 0 или 1.
Запись произвольного числа А в позиционной системе c данным основанием p будет выглядеть так:
Аp=аn·pn+...+a0·p0+a-1·p-1+...+а-m·p-m.
Как и в десятичной системе, число Аp можно записать в сокращенном виде:
Аp=anan-1...a1а0,a-1...a-m.
Эта последовательность цифр и будет являться изображением числа А в p-ичной системе счисления.
Если Аp – число, записанное в p-ичной системе счисления, тогда под преобразованием этого числа в q-ичную систему понимают запись числа А последовательностью цифр q-ичной системы.
Подводя итоги, можно сказать, что позиционная система счисления – это способ представления чисел, при котором вклад, вносимый каждой цифрой зависит от ее численного значения и разряда, который она занимает в числе. Обычно этот вклад определяется как произведение значения цифры на некоторое число, определяемое разрядом, – вес разряда. Позиционная система счисления с заданным основанием – это позиционная система, в которой веса являются степенями некоторого числа – основания.
В первых ЭВМ вначале применялась десятичная система счисления (например, в ЭНИАК). Впоследствии стали применять двоичную систему счисления.
allrefers.ru


 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. .
.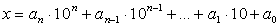 ,
,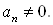
 в краткой форме принято записывать последовательностью цифр с чертой наверху, чтобы отличать от произведения чисел:
в краткой форме принято записывать последовательностью цифр с чертой наверху, чтобы отличать от произведения чисел: .
. (1)
(1)
 .
. , образуются из соединения первых десяти названий и несколько измененного слова десять ("дцать"):
, образуются из соединения первых десяти названий и несколько измененного слова десять ("дцать"):