|
|
|
|
 Far Far |
 WinNavigator WinNavigator |
 Frigate Frigate |
 Norton
Commander Norton
Commander |
 WinNC WinNC |
 Dos
Navigator Dos
Navigator |
 Servant
Salamander Servant
Salamander |
 Turbo
Browser Turbo
Browser |
|
|
 Winamp,
Skins, Plugins Winamp,
Skins, Plugins |
 Необходимые
Утилиты Необходимые
Утилиты |
 Текстовые
редакторы Текстовые
редакторы |
 Юмор Юмор |
|
|
|
File managers and best utilites |
Показательные уравнения и неравенства. Показательные уравнения реферат
Показательные уравнения | Бесплатные курсовые, рефераты и дипломные работы
Показательными принято называть уравнения, в которых неизвестное входит только в показатели степеней при постоянных основаниях. Простейшим показательным уравнением является уравнение вида
 . (1)
. (1)
Его решением при  , является
, является  .
.
Некоторые показательные уравнения приводятся к виду (1) с помощью равенств:

Многие показательные уравнения решаются методом приведения обеих частей к одному основанию.
Пример 1. Решить уравнение  .
.
Решение. Поскольку  , то
, то

Ответ:  .
.
…
При решении простейших показательных уравнений используется преобразование, состоящее в вынесении общего множителя за скобки.
Пример 2. Решить уравнение  .
.
Решение. Вынося в левой части уравнения выражение  за скобки, получаем
за скобки, получаем

Ответ: 
Уравнение вида
 (2)
(2)
может быть решено при помощи логарифмирования обеих частей (это возможно, так как обе части уравнения положительны).
Логарифмируя, получаем уравнение  , равносильное уравнению (2).
, равносильное уравнению (2).
Пример 3. Решить уравнение  .
.
Решение. Обе части положительны, поэтому можно прологарифмировать его по основанию 5. Получим уравнение
 ,
,
равносильное исходному. Таким образом,
 .
.
Ответ:  .
.
Если показательное уравнение имеет вид
 (3)
(3)
то его решение заменой  сводится к решению уравнения вида
сводится к решению уравнения вида
 ,
,
где  – корни уравнения
– корни уравнения  .
.
Пример 4. Решить уравнение  .
.
Решение. Обозначая  , получаем квадратное уравнение
, получаем квадратное уравнение
 ,
,
корнями которого будут  .
.
Таким образом, решение данного уравнения свелось к решению уравнений  .
.
Второе уравнение решений не имеет, так как  при всех допустимых значениях
при всех допустимых значениях  . Из одного уравнения следует другое
. Из одного уравнения следует другое

Проверкой убеждаемся, что эти корни удовлетворяют исходному уравнению.
Ответ: 
Показательные уравнения, основания степеней которых являются последовательными членами геометрической прогрессии, а показатели степеней одинаковы, делением на любой из крайних членов приводятся к уравнениям вида (3).
Пример 5. Решить уравнение  .
.
Решение. Разделим обе части уравнения на  . Имеем
. Имеем
 .
.
Обозначая  , получаем уравнение
, получаем уравнение  , корнями которого будут
, корнями которого будут  .
.
Таким образом, решение уравнения сводится к решению двух простейших показательных уравнений  .
.
Ответ:  .
.
Пример 6. Решить уравнение  .
.
Решение.Область допустимых значений данного уравнения состоит из всех натуральных чисел, больших 1.
Разделив обе части уравнения на  и положив
и положив  , получим уравнение
, получим уравнение  , корни которого
, корни которого  .
.
Таким образом, решение уравнения сводится к решению двух уравнений  , которые решений не имеют.
, которые решений не имеют.
Ответ: нет решений.
Уравнения вида
 (4)
(4)
с множеством допустимых значений, определяемых условием  , логарифмированием обеих частей приводятся к эквивалентному уравнению
, логарифмированием обеих частей приводятся к эквивалентному уравнению
 . (5)
. (5)
Последнее уравнение эквивалентно двум уравнениям:
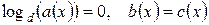 . (6)
. (6)
Пример 7. Решить уравнение  .
.
Решение. Множество допустимых значений неизвестного данного уравнения  . Логарифмируя обе части уравнения по основанию 3 и приводя подобные члены, получаем
. Логарифмируя обе части уравнения по основанию 3 и приводя подобные члены, получаем  , которое эквивалентно двум уравнениям:
, которое эквивалентно двум уравнениям:
 .
.
Ответ:  .
.
refac.ru
Показательно-степенные уравнения и неравенства - Дипломная работа
белгородский государственный университет
КАФЕДРА алгебры, теории чисел и геометрии
Тема работы: Показательно-степенные уравнения и неравенства.
Дипломная работа студента физико-математического факультета
Научный руководитель:
______________________________
Рецензент : _______________________________
________________________
Белгород. 2006 г.
Содержание.
Введение 3Тема I.Анализ литературы по теме исследования.Тема II.Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств.I.1.Степенная функция и ее свойства.I.2.Показательная функция и ее свойства.Тема III.Решение показательно-степенных уравнений, алгоритм и примеры.Тема IV.Решение показательно-степенных неравенств, план решения и примеры.Тема V.Опыт проведения занятий со школьниками по теме: Решение показательно-степенных уравнений и неравенств.V.1.Обучающий материал.V.2.Задачи для самостоятельного решения.Заключение. Выводы и предложения.Список используемой литературы.Приложения Введение.
…радость видеть и понимать…
А.Эйнштейн.
В этой работе я попыталась передать свой опыт работы учителем математики, передать хоть в какой-то степени свое отношение к ее преподаванию человеческому делу, в котором удивительным образом переплетаются и математическая наука, и педагогика, и дидактика, и психология, и даже философия.
Мне довелось работать с малышами и выпускниками, с детьми, стоящими на полюсах интеллектуального развития: теми, кто состоял на учете у психиатра и кто действительно интересовался математикой
Мне довелось решать множество методических задач. Я попытаюсь рассказать о тех из них, которые мне удалось решить. Но еще больше не удалось, да и в тех, что вроде бы решены, появляются новые вопросы.
Но еще важнее самого опыта учительские размышления и сомнения: а почему он именно такой, этот опыт?
И лето нынче на дворе иное, и разворот образования стал поинтереснее. Под юпитерами нынче не поиски мифической оптимальной системы обучения всех и всему, а сам ребенок. Но тогда с необходимостью и учитель.
В школьном курсе алгебры и начал анализа, 10 11 класс, при сдаче ЕГЭ за курс средней школы и на вступительных экзаменах в ВУЗы встречаются уравнения и неравенства, содержащее неизвестное в основании и показатели степени это показательно-степенные уравнения и неравенства.
В школе им мало уделяется внимания, в учебниках практически нет заданий на эту тему. Однако, овладение методикой их решения, мне кажется, очень полезным: оно повышает умственные и творческие способности учащихся, перед нами открываются совершенно новые горизонты. При решении задач ученики приобретают первые навыки исследовательской работы, обогащается их математическая культура, развиваются способности к логическому мышлению. У школьников формируются такие качества личности как целеустремленность, целеполагание, самостоятельность, которые будут полезны им в дальнейшей жизни. А также происходит повторение, расширение и глубокое усвоение учебного материала.
Работать над данной темой дипломного исследования я начала еще с написания курсовой. В ходе, которой я глубже изучила и проанализировала математическую литературу по этой теме, выявила наиболее подходящий метод решения показательно-степенных уравнений и неравенств.
Он заключается в том, что помимо общепринятого подхода при решении показательно-степенных уравнений (основание берется больше 0) и при решении тех же неравенств (основание берется больше 1 или больше 0, но меньше 1), рассматриваются еще и случаи, когда основания отрицательны, равны 0 и 1.
Анализ письменных экзаменационных работ учащихся показывает, что неосвещенность вопроса об отрицательном значении аргумента показательно-степенной функции в школьных учебниках, вызывает у них ряд трудностей и ведет к появлению ошибок. А также у них возникают проблемы на этапе систематизации полученных результатов, где могут в силу перехода к уравнению следствию или неравенству следствию, появиться посторонние корни. С целью устранения ошибок мы используем проверку по исходному уравнению или неравенству и алгоритм решения показательно-степенных уравнений, либо план решения показательно-степенных неравенств.
Чтобы учащиеся смогли успешно сдать выпускные и вступительные экзамены, я считаю, необходимо уделять больше внимания решению показательно-степенных уравнений и неравенств на учебных занятиях, либо дополнительно на факультативах и кружках.
Таким образом тема, моей дипломной работы определена следующим образом: Показательно-степенные уравнения и неравенства.
Целями настоящей работы являются:
- Проанализировать литературу по данной теме.
- Дать полный анализ решения показательно-степенных уравнений и неравенств.
- Привести достаточное число примеров по данной теме разнообразных типов.
- Проверить на урочных, факультативных и кружковых занятиях как будет восприниматься предлагаемые приемы решения показательно-степенных уравнений и неравенств. Дать соответствующие рекомендации к изучению этой темы.
Предметом нашего исследования является разр
www.studsell.com
Показательные уравнения и неравенства — Курсовая
Введение 3Γлава 1. Функции и их свойства, используемые при решении показательных уравнений и неравенств 51.1. Показательные функции, уравнения 51.2. Показательные неравенства 7Γлава 2. Решение показательных уравнений и неравенств 82.1. Решение показательных уравнений, алгоритм и примеры 82.2. Решение показательных неравенств, план решения и примеры 12Γлава 3. Занятие со школьниками по теме: «Решение показательных уравнений и неравенств». 16Заключение 24Список литературы 25
1. Авербух Б.Г., Рубинштейн А.И. Об определении степени и решении уравнений и неравенств, содержащих показательно степенную функцию.//Математика в школе. – 1996. -№2. - с.29-33.2. Алгебра и начала анализа: Учебник для 10-11 классов общеобразовательных учреждений: Колмагоров А.Н., Абрамов А.М., Дудинцын Ю.П. и др.; Под редакцией Колмагорова А.Н. – 12-е изд. – М.: Просвещение, 2002.3. Белоненко Т.В., Васильев А.Е., Васильева Н.И., Крымская .Д. Сборник конкурсных задач по математике. – СПб.: Спецлитература, 2008.4. Василенко Ю.К. Тождества, уравнения, неравенства: Пособие для повышения квалификации учителей математики. – Белаидит. Белгород, 2003.5. Василюк Л.И., Куваева Л.А. Математика для абитуриентов: Справочник в экзаменационных вопросах и ответах. – Мн. Амалфея, 2009.6. Дорофеев Г.В., Потапов М.К., Розов Н.Х. Математика для поступающих в ВУЗы. – М.: Дрофа, 2000.7. Дудинцын Ю.П., Смирнова В.К. Содержание и анализ письменных экзаменационных работ по алгебре и началам анализа: Пособие для учителя. – М.: Просвещение, 2005.8. Единый государственный экзамен: Математика: Контрольно-измерительные материалы./ Денищева Л.О., Бойченко Е.М., Глазков6 под редакцией Ковалевой Г.С; М-во образования Российской Федерацию – М.: Просвещение, 2003.9. Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. – 2-е изд. - М.: Просвещение, 2008.10. Математика. Методические указания по подготовке к вступительным экзаменам./ СПбГИТМО. – СПб., 2000.11. Нараленков М.И. Вступительные экзамены по математике. Алгебра: как решать задачи: Учебно-практическое пособие. – М.: Экзамен, 2008.12. Норин А.В. Сборник задач по математике для поступающих в ВУЗы: Учебное пособие. – Спб.: Питер, 2003.13. Потапов М.К., Олейник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике: Справочное пособие. – 2-е изд. – М.: Физмалит, 2005.14. Потапов М.К., Александров А.В., Пасиченко П.И. Алгебра и начала анализа. Современный курс для поступающих в ВУЗы. – М.: Экзамен, 1998.15. Симонов А.Я., Бакаев Д.С., Элельман А.Г. Система тренировочных задач и упражнений по математике. – М.: Просвещение, 1991.16. Сканави М.И. Сборник задач по математике для поступающих в ВУЗы. - М.: Просвещение, 1988.17. Цыпкин А.Г., Пинский А.И. Справочник пособие по методам решения задач по математике для средней школы. – М.: Наука. ГРФМЛ, 2005.18. Черкасов О.Ю., Якушев А.Г. Математика. Интенсивный курс подготовки к экзаменам. – М.: Рольф, 2007.19. Шарыгин И.Ф. Математика. Для поступающих в ВУЗы: Учебное пособие. – 4-е изд. –М.: Дрофа, 2002.20. Шарыгин И.Ф., Голубев В.И. Решение задач: Учебное пособие для 11 класса общеобразовательных учреждений. – 2-е изд. – М.: Просвещение, 2005.21. Якушева Е.В., Попов А.В., Черкасов О.Ю., Якушев А.Г. Экзаменационные вопросы и ответы. Алгебра и начало анализа 9 и 11 выпускные классы: Учебное пособие.- М.: АСТ-Пресс, 2000.
| Тема: | Показательные уравнения и неравенства |
| Артикул: | 1200942 |
| Дата написания: | 25.05.2009 |
| Тип работы: | Курсовая работа |
| Предмет: | Теория и методика обучения математике |
| ВУЗ: | ТГГПУ |
| Научный: | - |
| Оригинальность: | Антиплагиат.ВУЗ — 71% |
| Количество страниц: | 26 |
| Особенности: | - |
a-center.ru
Показательные уравнения | Бесплатные курсовые, рефераты и дипломные работы
Функция вида  , где а – положительное число, не равное единице, называется показательной. Свойства показательной функции:
, где а – положительное число, не равное единице, называется показательной. Свойства показательной функции:
1)область определения – множество всех действительных чисел, 
2) область значений – множество всех положительных чисел, 
3) если 
4) если 
5)  тогда и только тогда, когда
тогда и только тогда, когда 
6)  , если
, если 
График показательной функции приведен на рис. 4.1.
|
|

Рис. 4.1. График показательной функции.
Уравнения, содержащие переменную в показателе степени, называются показательными.
Уравнения вида  где
где 
равносильны уравнению  Если
Если  то решением являются все значения х, принадлежащие одновременно областям определения функций f (x) и g (x). Аналогично в случае а = 0,
то решением являются все значения х, принадлежащие одновременно областям определения функций f (x) и g (x). Аналогично в случае а = 0, 
Пример 1. Решить уравнение: 
Решение.  поэтому уравнение можно записать в виде:
поэтому уравнение можно записать в виде:



Ответ: x = 6.
Уравнения вида  можно, заменив
можно, заменив  свести к квадратному (или линейному при А = 0) уравнению:
свести к квадратному (или линейному при А = 0) уравнению: 
Пример 2. Решить уравнение : 
Решение. 
Обозначим  тогда
тогда



По теореме Виета 
 не удовлетворяет условию
не удовлетворяет условию  поэтому у = 25.
поэтому у = 25.
 откуда х = 2.
откуда х = 2.
Ответ: х = 2.
Пример 3. Решить уравнение: 
Решение. 
Обозначим  тогда
тогда 
По теореме Виета 
Если  то
то 
если  то
то 
Ответ:  или
или 
Уравнения вида  делением на b2х приводят к виду:
делением на b2х приводят к виду:
 а затем заменой
а затем заменой  сводят к квадратному уравнению
сводят к квадратному уравнению 
Пример 4. Решить уравнение :

Решение . 
Разделим почленно уравнение на 92х:

Обозначим  тогда
тогда
 ,
,

Если y = 1, то  если
если 
то 
Ответ:  или
или 
Пример 5. Решить уравнение:

Решение. Поскольку  то
то  . Следовательно, если обозначить
. Следовательно, если обозначить  то исходное уравнение примет вид
то исходное уравнение примет вид  .
.
Уравнение  имеет два корня
имеет два корня
 и
и  .
.
При  , получим уравнение,
, получим уравнение,

или  , откуда
, откуда  , х = 4.
, х = 4.
Если  ,то получим уравнение,
,то получим уравнение,



Ответ: х = 4, х = –4.
Пример 6. Решите уравнение:

Решение. Примеры аналогичного типа предлагаются в вариантах ЕГЭ в разделе С. Поэтому решение должно быть достаточно подробным с указанием всех переходных моментов. Перепишем уравнение в виде
 преобразуем
преобразуем  и введем замену
и введем замену  и
и  Теперь уравнение примет вид
Теперь уравнение примет вид 
Такие уравнения называются однородными и всегда имеют нулевые решения  причём если
причём если  то и
то и  .
.
В силу замены, которую мы произвели,  и
и  поэтому можно почленно разделить уравнение либо на а2, либо на b2. Разделим на b2 и получим:
поэтому можно почленно разделить уравнение либо на а2, либо на b2. Разделим на b2 и получим:  .
.
Пусть  , тогда
, тогда  ,
,  ,
,  .
.
Если  , то
, то  ,
,  и
и  ,
,
откуда  ,
,  ,
,  ,
,  .
.
Если  ,то
,то  ,
,  и
и 
или  , откуда
, откуда 

Ответ: 
Замечание. В вариантах ЕГЭ иногда требуют пояснить переход от равенства  к равенству
к равенству  непрерывностью и монотонностью показательной функции.
непрерывностью и монотонностью показательной функции.
Пример 7. Решить уравнение:

Решение. Выражение в правой части  может принимать значения либо 1, либо (–1). Левая часть уравнения представляет собой квадрат некоторого действительного числа, поэтому не может принимать отрицательных значений. Следовательно, и правая часть уравнения неотрицательна.
может принимать значения либо 1, либо (–1). Левая часть уравнения представляет собой квадрат некоторого действительного числа, поэтому не может принимать отрицательных значений. Следовательно, и правая часть уравнения неотрицательна.
В силу этих рассуждений  откуда
откуда  Обозначим
Обозначим  тогда
тогда  или
или 

Значение  не удовлетворяет условию
не удовлетворяет условию  поэтому
поэтому 
Заменив  получим квадратное уравнение
получим квадратное уравнение 
Если  то
то 
Если  , то
, то 

Ответ: 
refac.ru
|
|
..:::Счетчики:::.. |
|
|
|
|
|
|
|
|




