Опубликовать ОпубликоватьРеферат на тему:
Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек (атомов), которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с центрами молекул.
В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решётке могут присутствовать дополнительные трансляции, называемые решётками Браве. В трёхмерных решётках бывают гранецентрированная (F), объёмноцентрированная (I), базоцентрированная (A, B или C), примитивная (P) и ромбоэдрическая (R) решётки Браве. Примитивная система трансляций состоит из множества векторов (a, b, c), во все остальные входят одна или несколько дополнительных трансляций. Так, в объёмноцентрированную систему трансляций Браве входит четыре вектора (a, b, c, ½(a+b+c)), в гранецентрированную — шесть (a, b, c, ½(a+b), ½(b+c), ½(a+c)). Базоцентрированные системы трансляций содержат по четыре вектора: A включает вектора (a, b, c, ½(b+c)), B — вектора (a, b, c, ½(a+c)), а C — (a, b, c, ½(a+b)), центрируя одну из граней элементарного объёма. В системе трансляций Браве R дополнительные трансляции возникают только при выборе гексагональной элементарной ячейки и в этом случае в систему трансляций R входят вектора (a, b, c, 1/3(a+b+c), —1/3(a+b+c)).
Гранецентрированная
Объёмноцентрированная
Базоцентрированная
Сингонии:
Категории: Научные классификации, Физика твёрдого тела, Кристаллография, Химическая связь.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
Содержание:
Как мы знаем, все материальные вещества могут пребывать в трех базовых состояниях: жидком, твердом, и газообразном. Правда есть еще состояние плазмы, которое ученые считают ни много ни мало четвертым состоянием вещества, но наша статья не о плазме. Твердое состояние вещества потому твердое, так как имеет особую кристаллическую структуру, частицы которой находятся в определенном и четко заданном порядке, создавая, таким образом, кристаллическую решетку. Строение кристаллической решетки состоит из повторяющихся одинаковых элементарных ячеек: атомов, молекул, ионов, других элементарных частиц, связанных между собой различными узлами.
В зависимости от частиц кристаллической решетки существует четырнадцать типов оной, приведем наиболее популярные из них:
Далее более подробно опишем все типы кристаллической решетки.
Главной особенностью строения кристаллической решетки ионов являются противоположные электрические заряды, собственно, ионов, вследствие чего образуется электромагнитное поле, определяющее свойства веществ, имеющих ионную кристаллическую решетку. А это тугоплавкость, твердость, плотность и возможность проводить электрический ток. Характерным примером ионной кристаллической решетки может быть поваренная соль.
Вещества с атомной кристаллической решеткой, как правило, имеют в своих узлах, состоящих собственно из атомов сильные ковалентные связи. Ковалентная связь происходит, когда два одинаковых атома делятся друг с другом по-братски электронами, образуя, таким образом, общую пару электронов для соседних атомов. Из-за этого ковалентные связи сильно и равномерно связывают атомы в строгом порядке – пожалуй, это самая характерная черта строения атомной кристаллической решетки. Химические элементы с подобными связями могут похвастаться своей твердостью, высокой температурой плавления. Атомную кристаллическую решетку имеют такие химические элементы как алмаз, кремний, германий, бор.
Молекулярный тип кристаллической решетки характеризуется наличием устойчивых и плотноупакованных молекул. Они располагаются в узлах кристаллической решетки. В этих узлах они удерживаются такими себе вандервальсовыми силами, которые в десять раз слабее сил ионного взаимодействия. Ярким примером молекулярной кристаллической решетки является лед – твердое вещество, имеющее однако свойство переходить в жидкое – связи между молекулами кристаллической решетки совсем слабенькие.
Тип связи металлической кристаллической решетки гибче и пластичнее ионной, хотя внешне они весьма похожи. Отличительной особенностью ее является наличие положительно заряженных катионов (ионов метала) в узлах решетки. Между узлами живут электроны, участвующие в создании электрического поля, эти электроны еще называются электрическим газом. Наличие такой структуры металлической кристаллической решетки объясняет ее свойства: механическую прочность, тепло и электропроводность, плавкость.
И в завершение подробное видео пояснения о свойствах кристаллических решеток.
www.poznavayka.org
ОпубликоватьРеферат на тему:
Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек (атомов), которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с центрами молекул.
В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решётке могут присутствовать дополнительные трансляции, называемые решётками Браве. В трёхмерных решётках бывают гранецентрированная (F), объёмноцентрированная (I), базоцентрированная (A, B или C), примитивная (P) и ромбоэдрическая (R) решётки Браве. Примитивная система трансляций состоит из множества векторов (a, b, c), во все остальные входят одна или несколько дополнительных трансляций. Так, в объёмноцентрированную систему трансляций Браве входит четыре вектора (a, b, c, ½(a+b+c)), в гранецентрированную — шесть (a, b, c, ½(a+b), ½(b+c), ½(a+c)). Базоцентрированные системы трансляций содержат по четыре вектора: A включает вектора (a, b, c, ½(b+c)), B — вектора (a, b, c, ½(a+c)), а C — (a, b, c, ½(a+b)), центрируя одну из граней элементарного объёма. В системе трансляций Браве R дополнительные трансляции возникают только при выборе гексагональной элементарной ячейки и в этом случае в систему трансляций R входят вектора (a, b, c, 1/3(a+b+c), —1/3(a+b+c)).
Гранецентрированная
Объёмноцентрированная
Базоцентрированная
Сингонии:
Категории: Научные классификации, Физика твёрдого тела, Кристаллография, Химическая связь.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
ОпубликоватьРеферат на тему:
Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек (атомов), которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с центрами молекул.
В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решётке могут присутствовать дополнительные трансляции, называемые решётками Браве. В трёхмерных решётках бывают гранецентрированная (F), объёмноцентрированная (I), базоцентрированная (A, B или C), примитивная (P) и ромбоэдрическая (R) решётки Браве. Примитивная система трансляций состоит из множества векторов (a, b, c), во все остальные входят одна или несколько дополнительных трансляций. Так, в объёмноцентрированную систему трансляций Браве входит четыре вектора (a, b, c, ½(a+b+c)), в гранецентрированную — шесть (a, b, c, ½(a+b), ½(b+c), ½(a+c)). Базоцентрированные системы трансляций содержат по четыре вектора: A включает вектора (a, b, c, ½(b+c)), B — вектора (a, b, c, ½(a+c)), а C — (a, b, c, ½(a+b)), центрируя одну из граней элементарного объёма. В системе трансляций Браве R дополнительные трансляции возникают только при выборе гексагональной элементарной ячейки и в этом случае в систему трансляций R входят вектора (a, b, c, 1/3(a+b+c), —1/3(a+b+c)).
Гранецентрированная
Объёмноцентрированная
Базоцентрированная
Сингонии:
Категории: Научные классификации, Физика твёрдого тела, Кристаллография, Химическая связь.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
ОпубликоватьРеферат на тему:
Кристалли́ческая решётка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек (атомов), которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит к её параллельному переносу и совмещению. Для удобства анализа обычно точки решётки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с центрами молекул.
В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решётке могут присутствовать дополнительные трансляции, называемые решётками Браве. В трёхмерных решётках бывают гранецентрированная (F), объёмноцентрированная (I), базоцентрированная (A, B или C), примитивная (P) и ромбоэдрическая (R) решётки Браве. Примитивная система трансляций состоит из множества векторов (a, b, c), во все остальные входят одна или несколько дополнительных трансляций. Так, в объёмноцентрированную систему трансляций Браве входит четыре вектора (a, b, c, ½(a+b+c)), в гранецентрированную — шесть (a, b, c, ½(a+b), ½(b+c), ½(a+c)). Базоцентрированные системы трансляций содержат по четыре вектора: A включает вектора (a, b, c, ½(b+c)), B — вектора (a, b, c, ½(a+c)), а C — (a, b, c, ½(a+b)), центрируя одну из граней элементарного объёма. В системе трансляций Браве R дополнительные трансляции возникают только при выборе гексагональной элементарной ячейки и в этом случае в систему трансляций R входят вектора (a, b, c, 1/3(a+b+c), —1/3(a+b+c)).
Гранецентрированная
Объёмноцентрированная
Базоцентрированная
Сингонии:
Категории: Научные классификации, Физика твёрдого тела, Кристаллография, Химическая связь.
Текст доступен по лицензии Creative Commons Attribution-ShareAlike.wreferat.baza-referat.ru
Свойства материалов зависят главным образом от их структуры и состава.
По структуре все твёрдые тела делятся на кристаллические и аморфные. В аморфных телах атомы и молекулы располагаются беспорядочно, что и делает структуру материала бесформенной. Аморфные вещества можно рассматривать как застывшие вязкие жидкости, которые различаются степенью подвижности. Эти тела при нагреве переходят в жидкое состояние, при этом температура, приводящая к размягчению материала, может быть очень небольшой. При охлаждении процесс идёт в обратном направлении.
В отличие от аморфных в кристаллических телах атомы расположены с определенной для каждого материала закономерностью. Такие тела при нагреве остаются твёрдыми, т.е. сохраняют приданную им форму до вполне высокой температуры (температуры плавления), после которой переходят в жидкое состояние. При охлаждении процесс идёт в обратном направлении.
Все твёрдые металлы и сплавы имеют кристаллическое строение. Основу структуры материала составляет кристаллическая решётка. Особенность расположения атомов в решётке, плотность насыщения ими решётки, междуатомные расстояния во многом определяют совокупность свойств, характерных для разных металлов, и отличают их от неметаллов. В металлах и сплавах междуатомные расстояния значительно меньше, чем в неметаллах, поэтому плотность металлов и сплавов намного больше, чем неметаллов.
Наиболее распространённые металлы имеют кристаллические решётки следующих типов: объёмноцентрированную кубическую, гранецентрированную кубическую и гексагональную плотноупакованную.
Большинство веществ в твердом состоянии имеет кристаллическое строение. В этом легко убедится, расколов кусок твердого вещества и рассмотрев полученный излом. Обычно на изломе (например, у сахара, серы) хорошо заметны мелкие кристаллики определенной формы.
Такие вещества называются кристаллическими. Исследованием с помощью рентгеновских лучей было доказано, что кристаллические твердые вещества характеризуются строго закономерным расположением составляющих их частиц.
Расположение этих частиц (атомов, ионов или молекул) напоминает строение обыкновенной решетки с чередующимися узлами. Отсюда возникло название «кристаллическая решетка».
Она отражает внутреннее строение кристаллического вещества. Исходя из основных типов химической связи, различают ионные, атомные, молекулярные и металлические кристаллические решетки.
Типичным представителем вещества с молекулярной кристаллической решеткой является лед, в узлах которого находятся полярные молекулы. Молекулярные кристаллические решетки - это такие решетки, в узлах которых находятся молекулы, как полярные, так и неполярные. Между молекулами, связь сравнительно слабая. Вещества с молекулярной решеткой менее прочные, чем вещества с ионной решеткой. Поэтому они имеют низкие температуры плавления и почти не проводят электрический ток.
К веществам с молекулярными кристаллическими решетками относятся инертные газы, углекислый газ, водород, галогены и др.
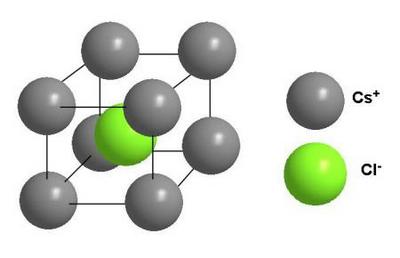
Типичным представителем веществ с ионной кристаллической решеткой являются соли. Например, ионная решетка, присущая солям галогеноводородных кислот, характеризуются правильным чередованием противоположено заряженных ионов. Хлорид натрия представляет собой кубическую решетку, где в углах ее расположены поочередно ионы Na+ и Cl- . Здесь нельзя выделить отдельную молекулу соли. Весь кристалл представляет собой как бы гигантскую молекулу NaCl. Силы связи между ионами в таком кристалле достаточно велики, поэтому вещества с ионной решеткой обладают сравнительно большой твердостью и высокой температурой плавления, хорошо растворяются в воде и плохо в органических жидкостях. Так, температура плавления хлорида натрия – 801оС. Растворы и расплавы веществ с ионной решеткой неплохо проводят электрический ток.
Атомные кристаллические решетки характерны для таких простых веществ как бор В, углерод С, кремний Si и другие. В узлах атомов кристаллических решеток находятся отдельные атомы, связанные между собой ковалентными связями. Представителем веществ с атомной кристаллической решеткой является алмаз, который состоит из атомов углерода. В алмазе каждый атом углерода связан ковалентной связью с четырьмя соседними атомами. То же вещество, имеющее такую же решетку из атомов углерода, называется графитом. Различие между алмазом и графитом заключается в формах кристаллов. Кристаллы атомов алмаза имеют октаэдрическую форму , а кристаллы графита - призматическую . Поэтому они различаются и свойствами. Например, твердость алмаза превышает твердость всех веществ. Это позволяет применять алмазы для бурения горных пород и для механической обработки различных твердых сплавов. Кристаллическая решетка графита состоит из плоских, параллельных друг к другу атомных слоев. В слоях связь между атомами углерода очень прочная, но слои между собой связаны непрочно . Благодаря слабым связям между слоями графита они могут легко скользить относительно друг друга, поэтому он обладает способностью отслаиваться чешуйками. Именно это свойство графита использует для изготовления карандашных грифелей. Атомные кристаллические решетки образуют не только простые, но и некоторые сложные вещества. Например, обычный речной песок SiO2.
3
student.zoomru.ru
СОДЕРЖАНИЕ
Введение. 2
Глава 1. Колебания кристаллической решетки. 3
1.1.Одномерная цепочка с одним атомом в ячейке. 4
1.2.Одномерная цепочка с двумя атомами в примитивной ячейке. 11
1.3. Трехмерный кристалл. 13
Глава 2. Фононы. Фононный газ. 16
Глава 3. Акустическая и оптическая ветки колебаний.19
Решение со знаком ''минус''19
Решение со знаком ''плюс''.22
Глава 4. Энергия колебаний и теплоемкость кристаллической решетки. 26
4.1. Модель Эйнштейна. 27
4.2. Модель Дебая. 27
Выводы… 34
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ… 35
Одной из важных и сложных задач теории твердого тела является расчет теплоемкости и теплопроводности твердого тела. Для твердых тел в рамках классической механики были получены значения теплоемкости, которые лишь приблизительно были равны реальным значениям теплоемкости при нормальных температурах. При повышенных температурах и при температурах следующих к абсолютному нулю значения теплоемкости оказались зависимы от температуры, чего классическая теория объяснить не могла. Лишь использование квантовой теории смогло объяснить эту зависимость.
Для нахождения величин теплоемкости и теплопроводности твердых кристаллических тел в широком температурном диапазоне вводят понятие фононов – квазичастиц, которые распространяются в твердом теле.
К данной работе мы рассмотрим явления колебаний кристаллической решетки, которые и являются фононами и их виды в зависимости от строения вещества. Также рассмотрим процессы рассеивания с участием акустических и оптических фононов.
Кристаллическая структура – равновесное состояние системы атомов, отвечающее минимуму потенциальной энергии. В состоянии покоя сумма сил, действующих на каждый атом кристалла со стороны других атомов, равна нулю.
Если вывести эту систему из положения равновесия, в кристалле возникнут сложные колебания. Эти колебания, в частности, всегда имеются при конечной температуре, когда кристаллическая структура обладает определенной (тепловой) энергией, то есть не находится в состоянии статического равновесия.
Рассмотрим колебания решетки в рамках классической механики.
При смещении атома относительно других атомов кристалла возникает сила, стремящаяся вернуть его в равновесное положение. Если смещения невелики, мы можем разложить зависимость силы от смещений в ряд и ограничится линейными по смещениям членами. Тогда колебания кристаллической решетки будут линейными, то есть будут описываться системой линейных дифференциальных уравнений.
Такая система уравнений обладает важным свойством: если есть несколько решений, то их сумма также является решением и сумма двух возможных колебаний – тоже колебание.
Эта система может быть решена, если известна зависимость силы, действующей на атом, от его смещения, а основные характеристики линейных колебаний могут быть предсказаны на основании одних только свойств симметрии кристалла.
Чтобы показать главные черты линейных колебаний кристаллической решетки, мы рассмотрим простейший случай одномерного кристалла – одномерную цепочку атомов.
Рассмотрим одномерную периодическую цепочку атомов – одномерный кристалл с одним атомом в элементарной ячейке. Пусть период этой цепочки равен a. Тогда в состоянии равновесия координата n -го атома цепочки xn равна na.
Рис. 1.1. Одномерная цепочка с одним атомом в элементарной ячейке.
Обозначим через un смещение n -го атома из положения равновесия. Будем считать, что атомы взаимодействуют только с ближайшими соседями. Сила, с которой (n +1)–й атом действует на n -й зависит от разности смещений этих двух атомов un +1 –un. При небольших смещениях эту силу можно считать пропорциональной разности смещений: Fn ,n +1 = γ (un +1 –un ), где γ – коэффициент пропорциональности. Удобно представить, что атомы связаны друг с другом пружинками с жесткостью γ.
На рис.1.1 пружинка между n -м и n +1 -м атомами растянута, так что она действует на n -й атом в положительном направлении. Растянутая пружинка между n –1-м и n -м атомом действует на n -й атом в отрицательном направлении: Fn ,n –1 = –γ (xn –xn –1 ).
Запишем закон Ньютона для n -го атома цепочки:
(1).
Первое слагаемое в правой части – сила, действующая на n -й атом со стороны n +1-го атома, второе – сила, действующая со стороны n –1-го атома.
После упрощения получим:
(2).
Система таких уравнений, записанных для каждого атома, полностью описывает колебания цепочки.
Если рассматривать только длинноволновые колебания, т. е. колебания с длиной волны много большей периода цепочки a, то можно заменить разность un +1 –un на (∂ un /∂ x )a, а величину, стоящую в правой части (2) – на γ a 2 (∂2u /∂ x 2 ). В результате получим волновое уравнение:
(3).
Решением которого являются волны u = A exp(ikx –iω t ) с линейным законом дисперсии ω = |k | (звуковые волны). Здесь — скорость звука: . Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.
Будем искать колебания, зависящие от времени по гармоническому закону: un = Cn e –iω t (5).
Здесь ω – частота колебаний, одна и та же для всех атомов (такие колебания называются гармоническими). Cn – комплексная амплитуда колебаний n -го атома. Напомним, что колебания описывает вещественная часть уравнения (5), но технически удобно пользоваться комплексным решением.
Такая подстановка – стандартный метод решения линейных систем уравнений с постоянными коэффициентами. В силу линейности уравнений, колебание с произвольной временной зависимостью может быть разложено в интеграл (ряд) Фурье по гармоническим колебаниям.
Изуравнения (2) для амплитуды Cn получаем уравнение:
(6).
Эти уравнения образуют бесконечную систему линейных уравнений. Если применить к цепочке граничные условия Борна-Кармана, то система будет конечной. (Заметим, что условия Борна-Кармана в одномерном случае эквивалентны тому, что цепочка достаточно большой длины L замкнута в кольцо). Тогда, приравняв определитель нулю, можно найти частоты колебаний, а затем, решив систему уравнений для каждой из найденных частот – соответствующие амплитуды.
Но мы поступим иначе. Будем искать решение в виде плоской волны:
(7).
Подставив это выражение в (6), получим:
(8)
Разделим последнее уравнение на exp(ikxn ) и воспользуемся тем, что xn +1 = xn +a, xn –1 = xn –a: –M ω 2 = γ (eika +e –ika –2) (9).
Таким образом, подстановка в виде плоской волны оказалась верной: мы избавились от номера атома n и получили уравнение, связывающее ω и k, то есть уравнение, определяющее закон дисперсии волн.
Поскольку: (10), то (11).
Мы получаем закон дисперсии для упругих колебаний одномерной цепочки: (12).
Итак, мы пришли к выводу, что смещения атомов при колебании одномерной цепочки описываются плоской гармонической волной:
(13).
Точнее, колебания представляют собой произвольную сумму таких волн. Здесь φ – фаза комплексной амплитуды A: A = |A |exp(iφ ). Смещение – вещественная величина, которая описывается вещественной частью комплексной плоской гармонической волны, что явно записано в (13). В дальнейшем, при описании вещественных колебаний комплексной плоской волной, будем для краткости опускать обозначение вещественной части.
Волновой вектор k в плоской волне (13) может, вообще говоря, быть любым. Но вследствие дискретности цепочки (xn может принимать лишь дискретный набор значений na ) плоские волны, волновые вектора которых отличаются друг от друга на произвольный вектор обратной решетки 2π l /a, описывают одно и то же колебание. (Здесь l — любое целое число).
Действительно, так как xn = na, т:
(14).
Поэтому достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна –π /a <k <π /a. Крайние значения волнового вектора ±π /a соответствуют одному и тому же колебанию с минимальной длиной волны λ = 2π /k = 2a. При такой длине волны соседние атомы цепочки движутся в противофазе. Интуитивно ясно, что короче длина волны быть уже не может.
График зависимости ω (k ) для одномерной цепочки с одним атомом в примитивной ячейке изображен на рис. 1.2.
| Рис. 1.2. Закон дисперсии колебаний цепочки с одним атомом в примитивной ячейке. |
Обсудим теперь особенности закона дисперсии (12).
Важным его свойством является то, что частота волн, распространяющихся по цепочке, ограничена частотой . Чтобы оценить эту частоту, надо знать порядок величины постоянной γ.
Посмотрим на размерность γ. Сила F равна произведению γ на смещение u, поэтому:
(15).
Характерная длина, межатомное расстояние a, имеет порядок 1A = 10–8 cм. Характерная энергия – энергия, которую приобретает атом при смещении на расстояние порядка a. Ее можно оценить как энергию химической связи, которая по порядку величины равна 10 эВ. Таким образом:
(16).
В качестве массы для оценки можно подставить величину 10Mp, где Mp ≈ 1,67· 10–27 кг – масса протона.
Для ωmax получаем:
(17).
Найдем длину волны электромагнитного излучения такой частоты:
(18).
Электромагнитные волны с такой длиной принадлежат инфракрасному диапазону.
При ka /2<<1, когда длина волны λ = 2π /k много больше a, sin(ka /2)≈ ka /2, поэтому:
(19).
Таким образом, длинноволновые колебания – это звуковые волны с линейным законом дисперсии ω = |k |. Выше мы уже получали такой результат, заменив точное уравнение цепочки (2) волновым уравнением (3). Это и неудивительно: длинные волны ''не чувствуют'' дискретной структуры цепочки, цепочка ведет себя как непрерывная упругая среда. По этой причине скорость звука зависит только от макроскопических характеристик цепочки: линейной плотности, M /a, и упругой постоянной цепочки γ a – коэффициента пропорциональности между относительным удлинением цепочки и возникающей при этом силой натяжения:
(20).
Рассмотренные нами колебания одномерной цепочки называют акустическими, поскольку при k → 0 (λ →∞) они соответствуют звуковым волнам.
Ниже мы увидим, что в цепочке с двумя (и более) атомами в элементарной ячейке наряду с акустическими могут распространяться волны другого типа.
При квантовомеханическом описании каждому колебанию соответствует квазичастица с импульсом p = ħ k и энергией . Квазичастицы, соответствующие упругим колебаниям кристаллической решетки называются фононами. Фононы, соответствующие акустическим колебаниям, также называются акустическими.
Оценим максимальную энергию акустического фонона в одномерной цепочке:
(21)
Экспериментальные значения ħωmax в реальных кристаллах составляют 30 ч 40 мэВ.
Эта величина намного меньше большинства характерных электронных энергий (~ 1 эВ) и близка к тепловой энергии при комнатной температуре (kT ≈ 0.025эВ, здесь k – постоянная Больцмана).
Исследуем теперь колебания цепочки, элементарная ячейка которой состоит из двух атомов с разными массами: M 1 и M 2, для определенности положим M 1 <M 2. Период цепочки (расстояние между узлами ее решетки Браве) как и прежде обозначим через a (рис. 3). Для простоты будем считать, что ''пружинки'' соединяющие атомы имеют одинаковую жесткость γ.
| Рис. 1. 3. Одномерная цепочка с двумя атомами в примитивной ячейке и ее решетка Браве. |
Запишем закон Ньютона для двух атомов n -й ячейки:
(22).
Здесь un и vn – смещения соответственно маленького и большого атома n -й ячейки из положения равновесия.
Будем, как и в случае цепочки с одним атомом в примитивной ячейке, искать решение в виде плоской гармонической волны:
(23).
Амплитуды колебаний маленького и большого атомов A и B в общем случае разные как по абсолютной величине, так и по фазе.
После подстановки (23) в (22) получим линейную однородную систему уравнений для A и B:
–M 1ω 2A = γ (Beika +B –2A )
–M 2ω 2B = γ (A +Ae –ika –2B ) (24).
Перепишем ее в стандартном виде:
(25)
Такая система имеет решения лишь в том случае, когда ее определитель равен нулю. Приравнивая нулю определитель (25) получим уравнение, связывающее ω и k, т. е. дисперсионное уравнение:
M 1M 2ω 4 – 2γ (M 1 +M 2 )ω 2 +2γ 2 (1–cos ka ) = 0 (26).
Это уравнение удобно переписать, использую приведенную массу атомов примитивной ячейки μ:
(27).
(28)
Его решения имеют вид:
(29)
или (30).
Величина 4μ 2 /(M 1M 2 ) при любых M 1, M 2 не превосходит единицы, поэтому подкоренное выражение всегда неотрицательно.
Мы рассмотрели колебания в одномерной цепочке. Подобным образом могут быть описаны и колебания решетки трехмерного кристалла.
Предположим, что примитивная ячейка кристалла состоит из l атомов. Каждый атом ячейки будем обозначать индексом s, этот индекс принимает l различных значений. Любой атом кристалла однозначно определяется радиус-вектором , задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).
Смещение атомов при колебаниях решетки является линейной комбинацией плоских гармонических волн (точнее, их вещественных частей): (40).
Частота колебаний одинакова для всех атомов кристалла. Амплитуда колебаний зависит от типа атома (индекса s ), тоесть одинакова для всех однотипных атомов. Направление вектора амплитуды может, вообще говоря, быть каким угодно.
Индекс j обозначает ветвь колебаний. Волновой вектор и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости и являются непрерывными функциями.
Если примитивная ячейка кристалла содержит l атомов, то число ветвей равно 3l. Таким образом, каждому значению волнового вектора соответствуют 3l разных колебаний.
Три из этих ветвей – акустические, в предельном случае длинных волн их частота пропорциональна длине волнового вектора ω = |k |. Однако скорость звука зависит от направления распространения волны, то есть от направления вектора . В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.
Остальные 3l –3 ветвей – оптические, при их частота отлична от нуля.
По направлению амплитуды относительно волнового вектора акустические колебания можно разделить на продольное и два поперечных. Как правило, скорость звука у продольного колебания больше, чем у поперечных.
У кристаллов со структурой алмаза или цинковой обманки примитивная ячейка содержит 2 атома. Соответственно, кроме трех акустических, эти кристаллы обладают тремя оптическими ветвями колебаний, из которых также можно выделить продольную и две поперечных ветви.
Как и в одномерном случае, волновые вектора, отличающиеся друг от друга на вектор обратной решетки, соответствуют одному и тому же колебанию. По этой причине достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна.
Количество разрешенных волновых векторов в зоне Бриллюэна равно N = V /v 0– числу примитивных ячеек в нормировочном объеме кристалла V = L 3 (v 0– объем примитивной ячейки). Действительно, плотность разрешенных волновых векторов в обратном пространстве равна V /(2π )3, т. е. в объеме обратного пространства Δ 3k содержится Δ 3k · V /(2π )3 разрешенных волновых векторов. Объем зоны Бриллюэна – объем примитивной ячейки обратной решетки — равен (2π )3 /v 0, и для числа разрешенных состояний получаем (2π )3 /v 0· V /(2π )3 = V /v 0= N.
Число ветвей — 3l, поэтому полное число колебаний равно 3lN — утроенному числу атомов кристалла в объеме L 3, т. е. числу степеней свободы механической системы.
Колебаниям решетки, согласно квантовой механике, можно сопоставить квазичастицы – фононы. Каждому колебанию соответствует одно состояние фонона с импульсом и энергией .
Минимальная порция энергии которую может поглотить или испустить кристаллическая решетка при тепловых колебаниях соответствует на этом рисунке переходу с одного энергетического уровня на другой равна и называется фононом.
Таким образом между светом и тепловыми колебаниями кристаллической решетки можно провести аналогию – упругие волны рассматриваются как распространение неких квазиупругих частиц – фононов.
Р. Паерлс в 1929 году ввел в теорию Дебая квантовые (фононные) явления и показал, что тепловое сопротивление решетки обусловлено взаимодействием фононов. Фонон, в отличии от обычных частиц, может существовать лишь в некоторой среде, которая пребывает в состоянии теплового возбуждения. Нельзя вообразить фонон, который распространялся бы в вакууме, поскольку он описывает квантовый характер тепловых колебаний решетки и навечно замкнут в кристалле. Корпускулярный аспект малых колебаний атомов решетки кристалла приводит к понятию фонона, и распространение упругих тепловых волн в кристалле можно рассматривать как перенесение фононов.
Фононы являются бозе-частицами: число фононов, соответствующих определенному колебанию (число фононов одном состоянии), может быть сколь угодно большим. В состоянии термодинамического равновесия среднее число фононов njk ветви j с волновым вектором зависит только от энергии фонона (частоты колебания):
(31).
Здесь k – постоянная Больцмана. С точки зрения квантовой (да и классической) механики, нормальные колебания решетки ведут себя как набор независимых гармонических осцилляторов. Роль координаты осциллятора играет при этом амплитуда колебания, число фононов является уровнем энергии осциллятора.
На каждое колебание приходится средняя энергия . Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна . Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.
При высоких температурах, kb T >> ħω, число фононов пропорционально температуре: (32).
Средняя энергия колебания при этом равна kT. Это известный результат классической статистической механики для средней энергии гармонического осциллятора. Таким образом, пока температура превосходит энергию фонона, квантовые эффекты не играют роли.
Они играют существенную роль при низких температурах. Если k T << ħω, то среднее число фононов экспоненциально мало:
(33).
Можно сказать, что колебания, частота которых превосходит величину kT /ħ, ''вымерзают''. Энергия колебания не может быть меньше энергии одного фонона ħωjk а энергия фонона много больше характерной тепловой энергии kT, поэтому такие колебания практически не возбуждаются.
Итак, для каждого волнового вектора k, согласно уравнения (30) существуют две частоты ω, удовлетворяющие дисперсионному уравнению. Точнее, есть две непрерывные функции ω (k ), которые отличаются знаком перед корнем. Говорят, что существуют две ветви колебаний.
Исследуем обе ветви.
Напомним, что волновые вектора, отличающиеся на вектор обратной решки, описывают одно и то же колебания. (Вследствие этого функция ω (k ) периодична с периодом обратной решетки 2π /a, а в трехмерном случае обладает трансляционной симметрией обратной решетки). Поэтому мы считаем, что волновой вектор лежит в пределах первой зоны Бриллюэна: –π /a <k <π /a.
В точке k = 0:
(34).
На границе зоны Бриллюэна:
(35)
При ka << 1 (длинные волны):
(36)
Или другими словами:
(37)
Мы видим, что в длинноволновом пределе закон дисперсии этой ветви линеен, то есть, как и в случае цепочки с одним атомом в примитивной ячейке, описывает акустические колебания. По этой причине вся ветвь (решение со знаком ''–'') называется акустической (рис.3.1).
| Рис. 3.1. Закон дисперсии колебаний цепочки с двумя атомами в примитивной ячейке. |
Выражение для скорости звука имеет такой же вид, что и соответствующее выражение для цепочки с одним атомом в ячейке (20) и зависит от тех же макроскопических характеристик: линейной плотности и упругой постоянной цепочки:
(38).
Линейная плотность двухатомной цепочки равна (M 1 +M 2 )/a, а упругая постоянная — γ · a /2 (так как длина одной пружинки в наших обозначениях равна a /2).
Это и неудивительно. Мы уже видели, изучая цепочку с одним атомом в примитивной ячейке, что длинноволновые акустические колебания можно получить, рассматривая цепочку, как непрерывную упругую среду. Атомы ячейки при таких колебаниях движутся вместе, как единое целое, поэтому структура примитивной ячейки не играет роли, а важны лишь макроскопические, усредненные характеристики цепочки.
То, что атомы ячейки при длинноволновых акустических колебаниях движутся вместе, можно получить и непосредственно, решив систему (25). Эта система разрешима, когда ее определитель равен нулю, а определитель равен нулю, когда ω и k связаны законом дисперсии. При этом уравнения системы уже не являются независимыми, и мы можем взять любое из них, чтобы найти отношение амплитуд A и B.
Из первого уравнения системы (25) получаем:
(39),
откуда в пределе длинноволновых акустических колебаний (k → 0, ω = s |k |→ 0) следует B /A → 1, т. е. A = B: атомы движутся в фазе с одинаковыми амплитудами.
| Рис. 3.2. Амплитуды атомов цепочки в случае длинноволновых акустических колебаний. |
Отметим также, что на границе зоны Бриллюэна групповая скорость ∂ω /∂ k равна нулю. Это утверждение справедливо для обеих ветвей колебаний.
В точке k = 0:
(40)
На границе зоны Бриллюэна:
(41)
Групповая скорость этой ветви ∂ω /∂ k равна нулю как на границе зоны Бриллюэна, так и при k = 0.
Эта ветвь целиком лежит выше акустической ветви: ее минимальная частота больше максимальной частоты акустических колебаний . Таким образом, в цепочке могут распространяться волны в частотами от 0 до и от до . Интервал частот является ''запрещенной зоной'': волн с такими частотами не существует. Относительная ширина этого интервала тем больше, чем больше отношение масс M 2 /M 1.
Чтобы понять, что представляют собой длинноволновые колебания этой ветви, найдем отношение амплитуд колебаний B /A при k = 0 с помощью (36):
(42)
Мы видим, что атомы в каждой ячейке движутся в противофазе, то сближаясь, то удаляясь друг от друга, причем одновременно во всех ячейках (если k = 0). Амплитуда движения легкого атома больше амплитуды тяжелого в M 2 /M 1 раз, т. е. центр тяжести ячейки остается на месте.
| Рис. 3.3. Амплитуды атомов цепочки в случае длинноволновых оптических колебаний. |
Если атомы заряжены, то при колебаниях такого типа каждая ячейка представляет собой переменный дипольный момент. Дипольные моменты взаимодействуют с электромагнитным полем, и колебания легко возбуждаются электромагнитными волнами соответствующих частот. В связи с этим, вся ветвь колебаний называется оптической.
При длинноволновых акустических колебаниях атомы ячейки движутся в фазе и никакого дипольного момента не возникает. Поэтому акустические колебания с электромагнитным полем взаимодействуют слабо.
Энергия длинноволнового оптического фонона имеет тот же порядок величины, что и энергия фонона акустического колебания с максимальной частотой, которую мы оценили в 0,05 эВ. Энергии оптических фононов большинства полупроводниковых кристаллов лежат в диапазоне 0,03ч 0,1 эВ.
Посмотрим теперь, как колеблются атомы, когда длина волны минимальна, т. е. когда волновой вектор лежит на границе зоны Бриллюэна.
В случае акустических колебаний ω 2 = 2γ /M 2, коэффициент при B во втором уравнении системы (25) обращается в ноль, откуда следует что A = 0.
В случае оптических колебаний ω 2 = 2γ /M 1, и из первого уравнения (25) следует что B = 0.
Таким образом, при k = π /a в случае акустических волн колеблются тяжелые атомы, а легкие неподвижны, в случае оптических, наоборот: колеблются легкие, тяжелые стоят на месте.
Обобщим теперь полученные результаты. Нетрудно показать, что если примитивная ячейка одномерной цепочки содержит l атомов, то спектр колебаний состоит из l ветвей, одна из которых акустическая, а остальные – оптические.
Мы рассматривали бесконечную цепочку, не накладывая никаких ограничений на длины волн упругих колебаний. В результате, мы пришли к выводу, что в цепочке могут распространяться колебания с любыми волновыми векторами, лежащими в первой зоне Бриллюэна. (Было показано, что из-за дискретности цепочки волновые вектора, отличающиеся на произвольный вектор обратной решетки, описывают одни и те же колебания. Поэтому можно брать волновой вектор из любой зоны Бриллюэна. Естественней всего описывать колебание наименьшим волновым вектором, т.е. вектором из первой зоны Бриллюна.)
Чтобы иметь дело не с непрерывным, а с дискретным набором волновых векторов, можно потребовать, чтобы отклонение атомов от равновесия было периодической функцией: u (xn ) = u (xn +L ). Иными словами — поставить граничные условия Борна-Кармана. Период L должен быть кратен постоянной решетки цепочки.
Условиям Борна-Кармана удовлетворяют только гармонические колебания с ''разрешенными'' волновыми векторами kn = 2π n /L. Нетрудно подсчитать, что в зоне Бриллюэна размещается L /a разрешенных волновых векторов, т. е. ровно столько, сколько примитивных ячеек укладывается на длине L. (Волновым векторам –π /a и π /a соответствует одно и то же колебание и поэтому считаем эти два значения за одно). Мы уже упоминали выше об этом свойстве зоны Бриллюэна.
Так как колебание однозначно определяется волновым вектором и ветвью, то различных колебаний столько, сколько атомов содержит цепочка. Это общее свойство линейных колебательных систем: количество независимых колебаний (нормальных мод) равно числу степеней свободы системы.
Энергию колебаний и теплоемкость решетки будем рассчитывать для единичного объема кристалла, т. е. положим нормировочный объем равным единице: V = L 3 = 1.
Чтобы вычислить среднюю энергию колебаний кристаллической решетки, нужно просуммировать среднюю энергию всех типов колебаний (всех состояний фононов):
(43).
Проще всего это сделать при высоких температурах, когда для частот всех колебаний выполняется неравенство ħωjk << kT (классический предел). Тогда средняя энергия, приходящаяся на каждое колебание, равна kB T, всего колебаний 3lN = 3lN, для полной энергии E получаем:
(44).
Так как N – число примитивных ячеек кристалла в единице объема, то N = 1/v 0, где v 0– объем примитивной ячейки.
Теплоемкость решетки при высоких температурах постоянна (закон Дюлонга и Пти): CV = 3lNk (45).
При невысоких температурах все сложнее. Чтобы точно вычислить энергию решетки, то есть сосчитать сумму (45), необходимо знать дисперсионные зависимости для всех ветвей колебаний. И даже при условии, что зависимости эти известны, аналитическое выражение для энергии получить практически невозможно.
Поэтому для нахождения энергии и теплоемкости решетки применяют различные приближения.
В модели Эйнштейна предполагается, что частоты всех фононов одинаковы: ωjk = ω 1 (46).
Тогда для энергии получаем:
(47).
При высоких температурах, kB T >>ħω 1, эта зависимость приводит к выражению (45) для энергии и закону Дюлонга и Пти (46) для теплоемкости.
При низких температурах, kT <<ħω 1, энергия колебаний и теплоемкость экспоненциально уменьшаются:
Модель Эйнштейна хорошо описывает вклад в энергию и теплоемкость оптических ветвей фононов, у которых частота слабо зависит от волнового вектора и ее можно считать постоянной. Чтобы учесть только оптические ветви, частоту которых мы полагаем равной ω 1, нужно вместо 3l писать число этих ветвей. В общем случае, частоты разных оптических ветвей могут сильно отличаться друг от друга и их вклад в энергию и теплоемкость нужно учитывать отдельно.
Опыт показывает, что теплоемкость действительно падает с уменьшением температуры, но не экспоненциально, а пропорционально T 3. Дело в том, что при любых, сколь угодно низких температурах в кристалле найдутся колебания, энергия фонона которых меньше kB T. Это – длинноволновые акустические колебания. Именно такие колебания, точнее те из них, частота которых меньше kB T /ħ, вносят основной вклад в энергию при низких температурах. Колебания с большими частотами (оптические и более коротковолновые акустические) ''заморожены'': фононов этих колебаний экспоненциально мало.
Сделаем простую оценку. Вклад в энергию вносят фононы, энергия которых меньше kT. Пусть скорость звука j -й акустической ветви равна j и не зависит от направления волнового вектора: ω = j |k |. Тогда вклад в энергию дают колебания с волновыми векторами, меньшими kmax = kB T /(ħ j ). Плотность разрешенных значений волновых векторов в k -пространстве кристалла равна V /(2π )3, поэтому внутри сферы радиуса kmax содержится разрешенных значений волновых векторов. Это число колебаний одной акустической ветви, вносящих существенный вклад в энергию. На каждое такое колебание приходится энергия порядка kT. Для энергии колебаний одной акустической ветви получаем:
(50).
Так как мы вычисляем энергию и теплоемкость единицы объема кристалла, то в (50) мы положили V = 1.
Таким образом, вклад одной акустической ветви в теплоемкость пропорционален T 3:
(51).
Чтобы получить полную энергию и теплоемкость, надо сложить вклады от трех акустических ветвей:
(52),
где через j обозначена скорости звука j -й акустической ветви.
Мы сделали достаточно грубую оценку, поэтому к численным коэффициентам в последних двух выражениях не стоит относиться серьезно. Тем не менее, эта оценка дает правильную зависимость энергии и теплоемкости от температуры и скорости звука.
Посчитаем теперь энергию решетки при низких температурах более аккуратно.
Формула (44) имеет вид суммы по различным колебаниям (различным состояниям фононов) определенной величины, которая зависит только от энергии фонона:
Такие суммы встречаются довольно часто. Так как f зависит только от энергии фонона, то от суммы по состояниям можно перейти к интегралу по энергии:
(54).
Здесь — плотность состояний фононов. Напомним, что — это число состояний квазичастиц (фононов) в единице объема с энергиями от до , то есть число различных колебаний с такими энергиями.
Суммарная плотность состояний складывается из плотности состояний разных ветвей: ; плотность состояний ветви определяется ее законом дисперсии . Аналитически получить законы дисперсии и плотности состояний фононов реальных кристаллов практически невозможно.
Однако при низких температурах энергия и теплоемкость определяются длинноволновыми акустическими фононами. Плотность состояний акустических фононов нам известна, мы получили ее в качестве примера, когда вводили само понятие плотности состояний . Если для j -й акустической ветви ω = j |k |, то:
(55).
Плотность состояний длинноволновых колебаний всех акустических ветвей получается суммированием по трем акустическим ветвям:
(56), где — ''усредненная'' скорость звука:
(57).
Линейный закон дисперсии ω = |k | и соответствующая плотность состояний верны только для малых k. При больших значениях волнового вектора закон дисперсии и плотность состояний имеют более сложный вид.
Однако при низких температурах вклад в энергию и теплоемкость вносят как раз только длинноволновые фононы, а при высоких температурах вид плотности состояний не важен, так как в этом случае на каждое колебание приходится энергия kT. Чтобы получить выражение, которое давало бы правильные предельные зависимости при низких и высоких температурах, Дебай предложил считать, что закон дисперсии ω = |k | выполняется и при больших k. Максимальное значение волнового вектора kD при этом выбирается так, чтобы в шаре радиуса kD содержалось столько разрешенных значений волновых векторов, сколько их содержится в зоне Бриллюэна, N = 1/v 0. Иными словами, объем этого шара должен быть равен объему зоны Бриллюэна (2π )3 /v 0, откуда
(58).
Таким образом, сохраняя число акустических колебаний, мы заменяем первую зону Бриллюэна сферой, а реальный закон дисперсии – линейным. Фонон с волновым вектором kD имеет энергию . Соответствующая температура:
(59), называется температурой Дебая.
В таком приближении мы можем вычислить вклад акустических ветвей в энергию и теплоемкость решетки:
При низких температурах, T <<θ, верхний предел интеграла много больше единицы. Благодаря экспоненте в знаменателе интеграл сходится очень быстро, что позволяет положить верхний предел равным бесконечности. Значение такого интеграла известно: (61).
Для энергии акустических колебаний при низких температурах получаем:
(62)
Откудаследует, что теплоемкость решетки при низких температурах пропорциональна T 3:
(63).
При высоких температурах, T >>θ, верхний предел интегрирования мал, поэтому можно считать, что exp(x )–1≈ x, таким образом:
(64).
Тогда: E = 3NkT и CV = 3Nk .
Это закон Дюлонга и Пти, только вместо полного числа колебаний 3lN стоит число колебаний акустических ветвей 3N. (При высоких температурах на каждое колебание приходится средняя энергия kT, полное число акустических колебаний равно 3N, поэтому вклад акустических ветвей в энергию равен 3NkT ).
В пределе низких и высоких температур модель Дебая дает точные значения для вклада акустических ветвей в энергию и теплоемкость. В области же промежуточных температур, T ~θ, эта модель лишь аппроксимирует реальную зависимость энергии и теплоемкости от температуры.
Температура Дебая разделяет две температурные области. В области низких температур на энергию и теплоемкость решетки сильное влияние оказывают квантовые эффекты (''вымерзание'' высокочастотных колебаний). В области высоких температур эти эффекты не существенны, и теплоемкость может быть вычислена в классическом приближении. Для большинства кристаллов температура Дебая лежит в интервале от 100 до 300K.
Чтобы получить полную энергию и теплоемкость кристаллической решетки, надо к вкладу акустических колебаний прибавить вклад оптических ветвей, для которого хорошим приближением является модель Эйнштейна. Этот вклад пренебрежимо мал при низких температурах. При высоких температурах вклады всех ветвей в энергию и теплоемкость равны.
В данной работе были рассмотрены явления колебаний кристаллической решетки твердого тела и поставлено в соответствие рассмотренным колебаниям квазичастицы – фононы. Для одномерных цепочек атомов проведен математический анализ колебаний и рассмотрен оптическую и акустическую составляющую колебаний. Оптические и акустические фононы отвечают за различные свойства кристаллов. Оптические колебания (фононы) играют основную роль в процессах поглощения взаимодействия света с кристаллом. В частности поглощение инфракрасного излучения ионными кристаллами обусловлено именно оптическими колебаниями решетки.
Акустические колебания играют основную роль в определении тепловых свойств кристаллов – теплоемкости, теплопроводности, теплового расширения.
В качестве примера рассмотрено нахождение теплоемкости тел при различных температурах и вклад оптических и акустических колебаний в величину теплоемкости при различных температурах.
1. Ансельм А. И. Введение в теорию полупроводников. – М.: Мир, 1965. – 588 с.
2. Басс Ф. Г. Электроны и фононы в ограниченных полупроводниках. – М.: Наука, 1984. – 287 с.
3. Дущенко В. П., Кучерук И. М. Общая физика. – К.: Высшая школа, 1995. – 430 с.
4. Епифанов Г. И. Физические основы микроэлектроники. М.: Советское радио, 1971, 374 с.
5. Зисман Г. А., Тодес О. М. Курс общей физики. В 3 т. – М.: Наука, 1995. – 343 с.
6. Кухлинг Х. Справочник по физике: Пер. с нем. – М.: Мир, 1983. – 520 с.
7. Случинская И. А. Основы материаловедения и технологи полупроводников. М.: Либрус, 2002, 376 с.
8. Харрисон У. Теория твёрдого тела. – М.: Мир. – 1978. – 616 с.
9. Шалимова К. В. Физика полупроводников. М.: Энергия, 1976, 417 с.
10. Яворский Б. М., Детлаф А. А. Справочник по физике. – М.: Наука, 1982. – 846 с.
www.ronl.ru
