Геометрическая прогрессия. Геометрическая прогрессия реферат

Геометрическая прогрессия

РЕФЕРАТ

по теме:

ГЕОМЕТРИЧЕСКАЯ

ПРОГРЕССИЯ

работу выполнил:

студент Ставропольского

Государственного Университета

IV курса, Физ-Мат Факультета,

отделения МИИТ, гр. ”Б”

Неботов Виталий Дмитриевич

Ставрополь 1997 г.

СОДЕРЖАНИЕ :

Стр.

1. Вступительное слово....................................................................................3

2. Определение геометрической прогрессии..................................................3

3. Свойства геометрической прогрессии.........................................................3

4. Сумма геометрической прогрессии.............................................................4

5. Заключение....................................................................................................5

6. Список использованной литературы............................................................6

Геометрическая прогрессия играет большую и важную роль не только в школьном курсе алгебры, но и (как я мог убедится) в дальнейшем обучении в высших учебных заведениях. Важность этого на первый взгляд небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения, в частности он часто применяется в теории рядов, рассматриваемой на II-III курсах университета. Поэтому мне кажется крайне важным дать здесь полное описание этого курса, дабы внимательный читатель мог повторить уже известный ему (надеюсь - прим. автора) из школьного курса материал, или даже почерпнуть много нового и интересного.

Прежде всего необходимо дать определение геометрической прогрессии, ибо не определившись о предмете разговора невозможно продолжать сам разговор. Итак: числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и тоже не равное нулю число, называется геометрической прогрессией.

Внесу некоторую ясность в данное выше определение: во-первых, мы требуем от первого члена неравенства нулю для того, что при умножении его на любое число мы в результате снова получим ноль, для третьего члена опять ноль, и так далее. Получается последовательность нулей, которая не попадает под данное выше определение геометрической прогрессии и не будет являться предметом нашего дальнейшего рассмотрения.

Во-вторых, число на которое умножаются члены прогрессии опять же не должно быть равно нулю, по вышеизложенным причинам.

В-третьих, предоставляю возможность вдумчивому читателю самому найти ответ на вопрос, почему мы умножаем все члены прогрессии на одно и тоже число, а не, скажем, на разные. Ответ не так прост, как может показаться вначале.

Далее, из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. b2:b1 = b3:b2 = ... = bn:bn-1 = bn+1:bn = ... . Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.

Несколько слов необходимо сказать и о способах задания геометрической прогрессии. Для того чтобы задать геометрическую прогрессию (bn), достаточно знать ее первый член b1 и знаменатель q. Например, условиями b1 = 2, q = -5 (q < 0) задается геометрическая прогрессия 2, -10, 50, -250, ... . Эта прогрессия не является ни возрастающей ни убывающей последовательностью.

Следует заметить, что: последовательность называется возрастающей (убывающей) если каждый последующий член последовательности больше (меньше) предыдущего.

Таким образом, если q > 0 (q1), то прогрессия является монотонной последовательностью. Пусть, например, b1 = -3, q = 4, тогда геометрическая прогрессия -3, -12, -48, -192, ... есть монотонно убывающая последовательность.

Однако, если q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.

Любая геометрическая прогрессия обладает определенным характеристическим свойством. Это свойство является следствием самого правила задания геометрической прогрессии: последовательность (bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.

Пользуясь этим свойством можно находить любой член геометрической прогрессии если известны два рядом стоящие.

Для нахождения n-ного члена геометрической прогрессии есть еще одна формула. Для того чтобы найти любой член геометрической прогрессии необходимо, чтобы она была задана, т. е. были известны значения b1 и q:

Так как геометрическая прогрессия это числовая последовательность, то мы можем найти ее сумму. Для нахождения суммы геометрической прогрессии применяют следующую формулу:

Если в данную формулу подставить вместо bn его выражение в виде b1qn-1, то получим еще одну формулу для вычисления суммы геометрической прогрессии:

У геометрической прогрессии есть еще одно свойство, а именно: из определения знаменателя геометрической прогрессии следует, что b1bn = b2bn-1 = ..., т. е. произведение членов, равно отстоящих от концов прогрессии, есть величина постоянная.

Наконец, нельзя не коснуться такого важного с научной точки зрения понятия, как бесконечной геометрической прогрессии при . Здесь наиболее важным понятием является понятие суммы бесконечной геометрической прогрессии: пусть (xn) - геометрическая прогрессия со знаменателем q, где Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию, называется предел суммыn первых ее членов при .

Найти эту сумму можно по следующей формуле:

Заканчивая описание геометрической прогрессии хочется лишний раз повторить, что за видимой простотой геометрической прогрессии скрывается большой прикладной потенциал этого раздела алгебры.

Список использованной литературы:

1. В. С. Крамор, Повторяем и систематизируем школьный курс

алгебры и начал анализа, Москва, Просвещение, 1990 г.

2. С. А. Теляковский, Алгебра, учебник для 8 класса средней школы,

Москва, Просвещение, 1987 г.

3. Личные заметки и наблюдения автора.

studfiles.net

Реферат Геометрическая прогрессия

Опубликовать скачать

Реферат на тему:

План:

1 Примеры
2 Свойства

Введение

Геометри́ческая прогре́ссия — последовательность чисел $b_1,\ b_2,\ b_3,\ \ldots$ (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число $q \quad$ (знаменатель прогрессии), где $b_1\not=0$ , $q\not=0$ : $b_1,\ b_2=b_1q,\ b_3=b_2q,\ \ldots,\ b_n=b_{n-1}q$ [1].

Любой член геометрической прогрессии может быть вычислен по формуле:

$b_n=b_1q^{n-1} \quad$

Если b1 > 0 и q > 1, прогрессия является возрастающей последовательностью, если 0 < q < 1, — убывающей последовательностью, а при q < 0 — знакопеременной

Своё название прогрессия получила по своему характеристическому свойству:

$|b_{n}| = \sqrt{b_{n-1} b_{n+1}},$

то есть каждый член равен среднему геометрическому его соседей.

1. Примеры

2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½
π,π,π,π — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0)

2. Свойства

Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию

Доказательство

Пусть wn — последовательность : $w_n = \log_pb_n\$

$\forall n>1\quad \frac{w_{n-1} + w_{n+1}}{2} = \frac{\log_pb_{n-1} + \log_pb_{n+1}}{2} = \frac{\log_pb_1q^{n-2} + \log_pb_1q^{n}}{2} =$ $= \frac{\log_p(b_1^2q^{2n-2})}{2} = \frac{2\cdot \log_pb_1q^{n-1}}{2} = \log_pb_n = w_n\$ Полученное соотношение является характеристическим для арифметической прогрессии.

$b_{n}^2 = b_{n-i} b_{n+i}, i < n$

Доказательство

$b_n^2 = b_nb_n = b_1q^{n - 1}b_1q^{n - 1} = b_1q^{n - 1 - i}b_1q^{n - 1 + i} = b_{n - i}b_{n + i}$

Произведение первых n членов геометрической прогрессии можно рассчитать по формуле: $P_{n} = (b_1\cdot b_n)^\frac{n}{2}$ ,

Доказательство

$P_n = \prod_{i=1}^nb_i = \prod_{i=1}^nb_1q^{i-1} = b_1^n\prod_{i=1}^nq^{i-1} = b_1^{\frac{n}{2}}b_1^{\frac{n}{2}}q^{\frac{n(0 + (n - 1))}{2}} = (b_1b_1q^{n-1})^{\frac{n}{2}} = (b_1b_n)^{\frac{n}{2}}$

Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле: $P_{k,n} = \frac{P_{n}}{P_{k-1}}$

Доказательство

$P_{k,n} = \prod_{i=k}^nb_i = \frac{\prod_{i=1}^nb_i}{\prod_{j=1}^{k-1}b_j} = \frac{P_n}{P_{k-1}}$

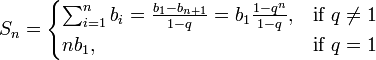
Сумма n первых членов геометрической прогрессии: $S_n = \begin{cases} \sum_{i=1}^n b_i = \frac{b_1-b_{n+1}}{1-q}=b_1\frac{1-q^n}{1-q}, & \mbox{if } q \ne 1 \\ nb_1, & \mbox{if } q = 1 \end{cases}$

Доказательство

Примечания

Геометрическая прогрессия - mathematics.ru/courses/function/content/chapter1/section1/paragraph5/theory.html на mathematics.ru

скачатьДанный реферат составлен на основе статьи из русской Википедии. Синхронизация выполнена 11.07.11 23:00:03Похожие рефераты: Прогрессия, Арифметическая прогрессия, Экспоненциальная прогрессия, Геометрическая абстракция, Геометрическая керамика, Тор (геометрическая фигура), Геометрическая фигура, Геометрическая черепаха, Геометрическая форма.

Категории: Арифметика.

Текст доступен по лицензии Creative Commons Attribution-ShareAlike.

wreferat.baza-referat.ru

Реферат - Геометрическая прогрессия - Рефераты на репетирем.ру

Ставропольский Государственный Университет

РЕФЕРАТ

по теме:

ГЕОМЕТРИЧЕСКАЯ

ПРОГРЕССИЯ

работу выполнил:

студент Ставропольского

Государственного Университета

IV курса, Физ-Мат Факультета,

отделения МИИТ, гр. ”Б”

Неботов Виталий Дмитриевич

Ставрополь 1997 г.

СОДЕРЖАНИЕ :

Стр.

1. Вступительное слово....................................................................................3

2. Определение геометрической прогрессии..................................................3

3. Свойства геометрической прогрессии.........................................................3

4. Сумма геометрической прогрессии.............................................................4

5. Заключение....................................................................................................5

6. Список использованной литературы............................................................6

Таким образом, если q > 0 (q 1), то прогрессия является монотонной последовательностью. Пусть, например, b1 = -3, q = 4, тогда геометрическая прогрессия -3, -12, -48, -192, ... есть монотонно убывающая последовательность.

Наконец, нельзя не коснуться такого важного с научной точки зрения понятия, как бесконечной геометрической прогрессии при . Здесь наиболее важным понятием является понятие суммы бесконечной геометрической прогрессии: пусть (xn) - геометрическая прогрессия со знаменателем q, где Суммой бесконечной геометрической прогрессии, знаменатель которой удовлетворяет условию , называется предел суммы n первых ее членов при .

Найти эту сумму можно по следующей формуле:

Список использованной литературы:

1. В. С. Крамор, Повторяем и систематизируем школьный курс

алгебры и начал анализа, Москва, Просвещение, 1990 г.

2. С. А. Теляковский, Алгебра, учебник для 8 класса средней школы,

Москва, Просвещение, 1987 г.

3. Личные заметки и наблюдения автора.

referat.store

Арифметическая и геометрическая прогрессии | Учеба-Легко.РФ

Числовая последовательность. Арифметическая прогрессия.

Разность прогрессии. Геометрическая прогрессия. Знаменатель

прогрессии. Бесконечно убывающая геометрическая прогрессия.

Обращение периодической десятичной дроби в обыкновенную.

Последовательности. Рассмотрим ряд натуральных чисел:

1, 2, 3, … , n – 1, n , … .

Если заменить каждое число n в этом ряду некоторым числом un , следуя некоторому закону, мы получим новый ряд чисел:

u1 , u2 , u3 , …, u n - 1 , u n , … ,

называемый числовой последовательностью. Число un называется общим членом числовой последовательности.

П р и м е р ы числовых последовательностей:

2, 4, 6, 8, 10, … , 2n, … ;

1, 4, 9, 16, 25, … , n² , … ;

1, 1/2, 1/3, 1/4, 1/5, … , 1/n , … .

Арифметическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d , называется арифметической прогрессией. Число d называется разностью прогрессии. Любой член арифметической прогрессии вычисляется по формуле:

an = a1 + d ( n – 1 ) .

Сумма n первых членов арифметической прогрессии вычисляется как:

П р и м е р . Найти сумму первых ста нечётных чисел.

Р е ш е н и е . Применим последнюю формулу. Здесь a1 = 1, d = 2 . Тогда

Геометрическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q , называется геометрической

прогрессией. Число q называется знаменателем прогрессии. Любой член геометрической прогрессии вычисляется по формуле:

bn = b1 q n - 1 .

Сумма n первых членов геометрической прогрессии вычисляется как:

Бесконечно убывающая геометрическая прогрессия. Это геометрическая прогрессия, у которой | q | < 1 . Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии, а именно: это число, к

которому неограниченно приближается сумма n первых членов рассматриваемой прогрессии при неограниченном возрастании числа n. Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:

П р и м е р . Найти сумму членов бесконечно убывающей геометрической прогрессии:

Р е ш е н и е . Применим последнюю формулу. Здесь b1 = 1, q = 1/2. Тогда:

Обращение периодической десятичной дроби в обыкновенную. Предположим, мы хотим обратить периодическую десятичную дробь 0.(3) вобыкновенную. Рассмотрим эту десятичную дробь в следующем виде:

Это бесконечно убывающая геометрическая прогрессия, первый член которой равен 3/10, а разность q = 1/10. В соответствии с выше приведенной формулой эта сумма равна:

Таким образом, 0.(3) = 1/3.

uclg.ru

Геометрическая прогрессия. Геометрическая прогрессия реферат