1.Что представляет собой ветвь электрической цепи?
2. Что представляет собой узел электрической цепи?
3. Что представляет собой контур электрической цепи?
а. участок цепи вдоль которого проходит один и тот же ток и который состоит из последовательно соединенных элементов;
б. это место соединения трех и более ветвей;
в. это любой замкнутый путь который можно обойти, перемещаясь по нескольким ее ветвям;
3.Сформулируйте 1 закон Кирхгофа.
а. в любом замкнутом электрическом контуре алгебраическая сумма э.д.с. равна алгебраической сумме напряжений на резисторах, входящих в этот контур;
б. в узлах цепи заряды не могут возникать;
в. в любом узле электрической цепи сумма притекающих токов равна сумме утекающих токов;
г. в узлах цепи заряды не могут накапливаться;
4.Укажите формулу 1 закона Кирхгофа.
а. Σ U = 0; б. Σ R = 0; в. Σ E = 0; г. Σ I = 0
5.Какое следствие вытекает из 1 закона Кирхгофа?
а. в любом замкнутом электрическом контуре алгебраическая сумма э.д.с. равна алгебраической сумме напряжений на резисторах, входящих в этот контур;
б. в узлах цепи заряды не могут возникать и длительно накапливаться;
в. в любом узле электрической цепи сумма притекающих токов равна сумме утекающих токов;
г. в узлах цепи заряды не могут накапливаться;
6. Сформулируйте 2 закон Кирхгофа.
а. в любом замкнутом электрическом контуре алгебраическая сумма э.д.с. равна алгебраической сумме напряжений на резисторах, входящих в этот контур;
б. в узлах цепи заряды не могут возникать;
в. в любом узле электрической цепи сумма притекающих токов равна сумме утекающих токов;
г. в узлах цепи заряды не могут накапливаться;
7. Какое следствие вытекает из 2 закона Кирхгофа?
а. в любом замкнутом электрическом контуре алгебраическая сумма э.д.с. равна алгебраической сумме напряжений на резисторах, входящих в этот контур;
б. потенциал любой точки цепи однозначно определяется ее положением в цепи;
в. в любом узле электрической цепи сумма притекающих токов равна сумме утекающих токов;
г. в узлах цепи заряды не могут накапливаться;
8.Укажите формулу 2 закона Кирхгофа.
а. Σ U = Σ I r; б. Σ R = ρ s ⁄ ℓ; в. Σ E = 0; г. Σ I = 0.
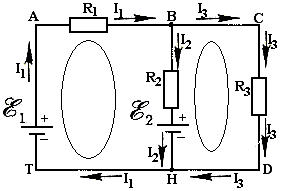
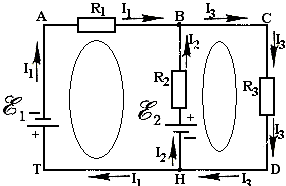
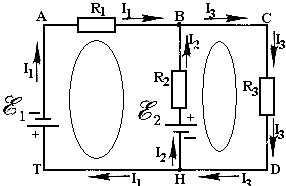
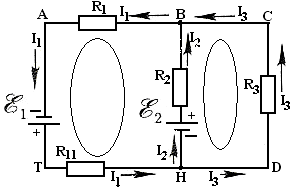
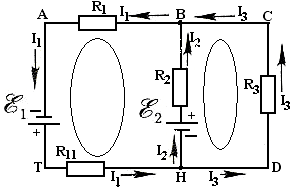
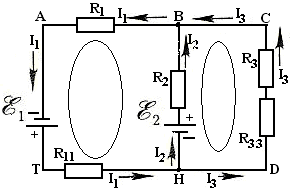
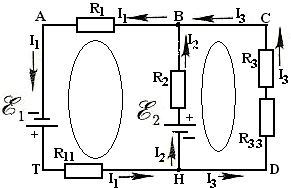
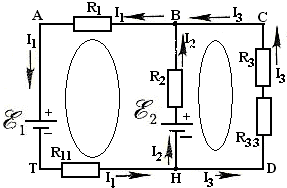
9.Определите количество ветвей, узлов, контуров в указанной цепи:
а. ветви- 3; узел – 2; контур – 3;
r1r2 б. ветви- 2; узел – 3; контур – 1;
в. ветви- 4; узел – 2; контур – 2;
Е1 r3 Е2 г. ветви- 5; узел – 2; контур – 4;
10.Каково применение законов Кирхгофа?
а. для расчета простых цепей; б. для расчета сложных цепей; в. для расчета магнитных цепей;
infourok.ru
1
2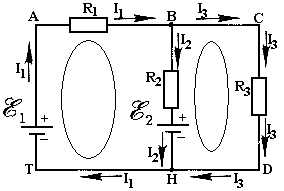
3
4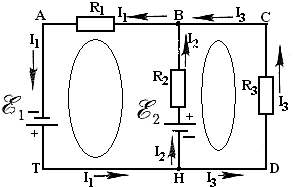 
7
10
5
8
11
6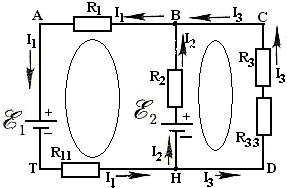
9
1. Дана электрическая цепь постоянного тока. Необходимо найти эквивалентное сопротивление RЭКВИВ.
Для этого на параллельно соединенных резисторах R3 и R4 найдем их общее сопротивление: их произведение разделим на их сумму:
R34 = (R3 ∙ R4) / (R3 + R4)
Затем точно также на параллельных участках R6 и R7 найдем их общее сопротивление
R67 = (R6 ∙ R7) / (R6 + R7)
Резисторы R2 и R34 соединены последовательно, значит, их надо сложить:
R2+ R34 = R234
Резисторы R234 и R5 соединены параллельно. Поэтому (как для двух параллельных) их произведение разделим на их сумму:
R2345 = (R234 ∙ R5) / (R234 + R5)
Получаем, что резистор R1 и эквивалентно рассчитанные участки сопротивлениями R2345 и R67 соединены последовательно, их сложим и найдем полное сопротивление, т. е. эквивалентное сопротивление всей цепи:
RЭКВИВ = R1 + R2345 + R67
2. Зная напряжение (или ток), подведенное к цепи, найдем ток (или напряжение) цепи из закона Ома для участка цепи. U = I∙ R или I = U / R
3. Т. к. участки с сопротивлениями R1, R2345 и R67 соединены последовательно, то ток на этих участках одинаков:
I1 = I2345 = I67 = I
Значит, можем найти напряжение на этих же участках, умножив ток (ток одинаков на последовательных участках цепи!) на сопротивления участков.
U1 = I1∙ R1
U2345 = I1∙ R2345 = U234 = U5, т. к. на параллельных участках цепи напряжение одинаково.
U67 = I1∙ R67 = U6 = U7 , т. к. на параллельных участках цепи напряжение одинаково.
Зная напряжения на резисторе R5 и участке R234, найдем токи на них: I5 = U5 / R5 ; I234 = U234 / R234
Аналогично (заметьте, напряжение на них одинаково, но сопротивление разное, поэтому и токи разные!): I6 = U6 / R6; I7 = U7 / R7
Проверка: А) должно быть, чтобы сумма токов I6 и I7 равно току I67 на этом участке с сопротивлением R67, согласно первому закону Кирхгофа. I67 = I6 + I7
Б) должно быть, чтобы сумма токов I234 и I5 равно току I2345 на этом участке с сопротивлением R2345, т. е. I2345 = I234 + I5
Но токи на последовательно соединенных участках R2 и R34 цепи одинаковы,
т. е. ток I2 равен току на I34, но I34 = I3 + I4. Запишем это:I2 = I34 = I3 + I4
5. Напряжения на последовательно соединенных участках R2 и R34 цепи равно сумме напряжений
U234 = U2 + U34 . Но U34 = U3 = U4
Зная ток I2 на R2, найдем напряжение U2 на нем U2 = I2∙ R2
Также, зная ток I34, найдем напряжение U34 на участке U34 = I34∙ R34
Проверка. Должно быть, что напряжения U34 = U3 = U4 , т. к. напряжение на параллельных участках одинаково. Отсюда найдем из закона Ома токи на резисторах R3 и R4.
6. Остается найти мощности на всей цепи и на отдельных участках по любой из известных формул мощности: Рi = Ii ∙ Ui или Рi = Ii2 ∙ Ri
Задача решена в общем виде.
studfiles.net
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра: «Средства связи и информационная безопасность»
Лабораторная работа по дисциплине «Основы теории цепей»
Тема: Законы Кирхгофа, принцип наложения и эквивалентного источника энергии.
Работа в среде MicroCAP
Омск 2009 г.
1) Первый закон Кирхгофа
Построим электрическую схему согласно рисунку
 | Е1 – 5 вольт Е2 – 9 вольт R1 – 3 кОма R2 – 5 кОма R3 – 10 кОма R4 – 1 кОма R5 – 0,8 кОма R6 – 7 кОма f – потенциал = 0 |
Проанализируем токи протекающие на сопротивлениях подходящие к точке « а »
Выберем Analysis (Alt+A) -> DC… или просто нажав - (Alt+3)
! Не забудьте включить AutoScaleRange !
Далее нажмите на кнопке Run
На появившемся графике посмотрим значение в точке «5в» т.к. в значении Range мы оставили значение по умолчанию, нам показывается диапазон до 10в. любым удобным способом (можно просто подвести курсор мышки к значению 5в., но более точно и удобно будет если выбрать Go to X и в вести значение 5 т.к. в нашем случае по значению «Х» откладывается напряжение.
 |
Повторим замеры и снимем значение токов для сопротивлений R1, R3, R4, R5
Значения даны в миллиамперах.
По первому закону Кирхгофа сумма сходящихся токов в точке « а » должна нам дать нулевой результат. Проверим это:
Что и требовалось доказать (проверить).
Формулировка первого закона Кирхгофа :
Алгебраическая сумма мгновенных значений токов, сходящихся в узле, равна нулю. Одно из направлений токов при этом (например, к узлу) считается положительным.
2) Второй закон Кирхгофа
Формулировка второго закона Кирхгофа :
В любом замкнутом контуре электрической цепи алгебраическая сумма мгновенных значений ЭДС равна алгебраической сумме падений напряжений на пассивных элементах.
Проверим это сложив все значения напряжений. Для этого снова выберем Analysis (Alt+A) -> DC…, но уже будем снимать значения напряжений во потенциалах точек a..f
В среде MicroCAP ранее при построении схемы можно просто включить «показать узлы» Node Numbers тогда на схеме покажутся все узлы, в нашем случае мне удобнее было переименовать узлы согласно схеме. Это можно сделать двойным щелчком на узле, при этом появится форма в которой номерному узлы присваиваем «имя». На примере, номерному узлу 2 по умолчанию, было присвоено имя « а ». Это гораздо облегчает при рассмотрении схемы без дополнительных перестроений.
При замерах так же можно пользоваться горячими клавишами F9 – вернуться к выбору измеряемых параметров, F3 – закрыть анализ, Alt+Tab – переход к схеме и обратно к графику и другими стандартными комбинациями, что облегчает работу. (Более подробно можно всё прочитать в помощи F1 – словарь Вам в помощь)
Получаем данные (значения в вольтах):
| a | b | c | d | e | f |
| 0.788 | - 0.594 | 4.406 | 2.103 | 9.000 | 0.000 |
И проверим второй закон Кирхгофа по более подходящей нам формулировке:
Алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю.
Найдём напряжения и сложим их, направление возьмём по часовой стрелке. Тогда получим, что Ufa + Uab + Ubc + Ucd + Ude + Uef = 0
 | Ufa = f – a = - 0.788 Uab = a – b = 1.382 Ubc = b – c = - 5.000 Ucd = c – в = 2.303 Ude = в – e = - 6.897 Uef = e – f = 9.000 -0.788 + 1.382 + (-5) + + 2.303 + (-6.897) + 9 = 0 |
3) Формулировка теоремы наложения
Мгновенное значение тока или напряжения в любой ветви линейной электрической цепи от нескольких источников энергии, действующих в цепи, может быть найдено алгебраическим суммированием мгновенных значений токов или напряжений, от источников энергии, взятых в отдельности.
При использовании для анализа теоремы наложения последовательно исключаются все источники энергии, кроме одного (ветви с источником тока размыкаются, а идеальные источники напряжения замыкаются перемычками).
Проверку проведу на примере I(R4).
| При двух источниках в цепи, E1 и E2 ток I(R4) = 1,315 мА |
 | При одном источнике в цепи, E1 ток I`(R4) = 0,462 мА |
 | При одном источнике в цепи, E2 ток I``(R4) = 0,853 мА ! При замере нужно выбрать E2 и смотреть данные на уровне 9 вольт ! |
I`(R4) + I``(R4) = 0.462 + 0.853 = 1.315 что равно значению I(R4).
4) Формулировка теоремы об эквивалентном источнике энергии
Для определения тока или напряжений в произвольной ветви электрической цепи оставшаяся часть может быть заменена эквивалентным источником ЭДС (
) с последовательным сопротивлением (
) или эквивалентным источником тока (
) с параллельным сопротивлением (). Параметры эквивалентных источников энергии определяются как:
, (4.1)
, (4.2)
, (4.3)
где индексом "
", "
" означают режимы холостого хода и короткого замыкания на клеммах, к которым подключена анализируемая ветвь.
 | Отключим ветвь с резистором R3 и замерим Uхх которое будет равно Uda или что тоже самое U(R4). ! Замер между потенциалами d-a можно выполнить указав непосредственно V(d)-V(a) ! И в итоге получаем Uхх = 1.419 в. Подключим цепь с R3 и установив его значение = 0 Ом замерим ток, этот ток I(R3) = 1.779 мА будет током Iкз Найдём Rвн которое будет равно Uхх /Iкз Rвн = 1.419/1.799*10-3 = 797.6 Ом |
Теперь зная напряжение холостого хода ( Uхх = 1.419 в ) и внутренне сопротивление (Rвн = 797.6 Ом) я могу найти ток который будет протекать в цепи при подключении R3 = 10 кОм. Который можно найти по формуле I = Uхх / (Rвн + R3) = 0.131 мА.
Восстановим цепь и проверим значение I(R3)
При проверке получим I(R3) = 0.131 мА. Что и требовалось доказать.
закон кирхгоф наложение эквивалентный
Вывод: На практике, с работой в программе MicroCAP, я убедился в выполнении основных законов Кирхгофа, принципа наложения и эквивалентного источника энергии, что доказывает не их неопровержимое выполнение, а выполнение их на программном уровне. Этой проверка показывает, что можно пользоваться расчётами программ и применять их на практике. Это облегчает и ускоряет проверку и разработку электрических схем.
www.yurii.ru
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
ЭЛЕКТРОТЕХНИКА
И ЭЛЕКТРОНИКА
Методические указания и контрольные задания для студентов заочной формы обучения специальностей не электроэнергетического профиля
Электротехника и электроника. Программа, методические указания и контрольные задания. Составили Макарьева И.П., Гаврилова Ю. В. - Иркутск: Изд-во ИрГТУ, 2008. – 43 с.
Издательство
Иркутского государственного технического университета
Требования к оформлению контрольной работы
1. Расчетно-графическую работу выполняют в отдельной тетради. На обложке должны быть указаны факультет и номер группы, фамилия, инициалы и шифр студента. Номер варианта контрольных задач определяется по последней цифре учебного шифра студента. Например, если учебный шифр 12167, то студент выполняет вариант 7.
4. Буквенные обозначения и единицы электрических величин:
Сопротивление резистивное (активное) R, Ом.
Сопротивление реактивное индуктивное ХL, Ом.
Сопротивление реактивное емкостное ХC, Ом.
Сопротивление полное Z, Ом.
Емкость С, Ф (Фарад).
Индуктивность L, Гн (Генри).
Электродвижущая сила (ЭДС) Е, В (Вольт).
Напряжение U, В (Вольт).
Ток I, А (Ампер).
Мощность активная Р, Вт (Ватт).
Мощность реактивная Q, ВАр (Вольт-Ампер реактивный).
Мощность полная S, В А (Вольт-Ампер).
Магнитный поток Ф, Вб (Вебер).
Частота f, Гц (Герц).
Угловая частота w, рад/с (радиан на секунду).
7. Векторные диаграммы строят в масштабе, который указывается таким образом: mU=…В/мм, mI=… А/ мм.
8. В конце контрольной работы ставят дату ее выполнения и подпись.
Линейные цепи постоянного тока
Основные понятия, определения и законы электрических цепей
Электрической цепью называют совокупность устройств и объектов, образующих путь для электрического тока.
Электрическая схема – графическое изображение электрической цепи, составленное из условных обозначений её элементов и показывающее способы соединения этих элементов.
Ветвь электрической цепи – участок цепи, ток которого имеет одно и тоже значение и направление.
Узел – место соединения трех и более ветвей.
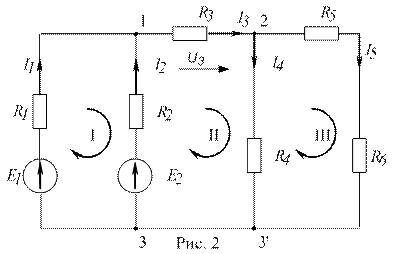
Различают понятия геометрического и потенциального узлов. Геометрические узлы 3 и 3' (рис. 2), имеющие одинаковые потенциалы, являются одним потенциальным узлом. На рис. 2 четыре геометрических и три потенциальных узла.
Контур – любой замкнутый путь, проходящий, через несколько ветвей и узлов разветвленной электрической цепи.
Основными законами электротехники являются закон Ома и законы Кирхгофа. Необходимо различать закон Ома для участка цепи (1), не содержащего ЭДС:
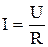или 
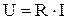(1)
Например, для ветви 1-2
(см. рис. 2):
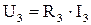- называют напряжением или падением напряжения на резисторе 
,
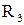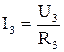– ток в резисторе.
Закон Ома для участка цепи, содержащего ЭДС, который называют обобщенным законом Ома:
.
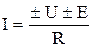Первый закон Кирхгофа относится к узлам электрической цепи: алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю.
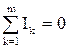, (2)
где m – число ветвей, подключенных к узлу.
Направления токов выбирают произвольно.
В уравнениях по первому закону Кирхгофа токи, направленные к узлу, берут, как правило, со знаком «плюс», а токи, направленные от узла, – со знаком «минус».
Например, для узла 2 (см. рис. 2) в соответствии с первым законом Кирхгофа (2):
,
.
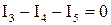Второй закон Кирхгофа относится к замкнутым контурам электрической цепи: алгебраическая сумма падений напряжений на всех элементах любого замкнутого контура равна алгебраической сумме ЭДС этого контура.
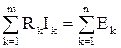, (3)
где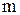 
– число элементов с сопротивлением 
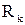в контуре;
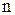– число источников ЭДС в контуре.
Использование законов Кирхгофа для расчета сложных электрических цепей
Для определения токов в ветвях электрической цепи используют следующие правила:
1. Выбираются произвольно условно – положительные направления токов в ветвях, которые фиксируются стрелкой. Знаки ответов покажут правильны ли они.
2. Определяется число неизвестных токов по числу ветвей –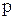 
.
3. Определяется число узлов q и для любых узлов цепи записываются, (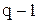 
) уравнений по первому закону Кирхгофа (2).
4. Недостающие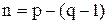 
уравнений записываются по второму закону Кирхгофа (3)для n независимых контуров. Независимым называют контур, в который входит хотя бы одна новая ветвь.
5. Произвольно выбираются направления обхода контуров, например, по ходу часовой стрелки (см. рис. 2).
6. При составлении уравнений со знаком «плюс» записываются слагаемые, в которых ток и ЭДС имеют направления, совпадающие с направлением обхода контура, и со знаком «минус» если их направления противоположны обходу контура.
7. Решается система уравнений относительно токов в ветвях. Если обнаруживается отрицательное значение тока, то это говорит о том, что действительное направление противоположно условно выбранному. Истинное направление тока показывается на схеме.
megapredmet.ru
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра: «Средства связи и информационная безопасность»
Лабораторная работа по дисциплине «Основы теории цепей»
Тема: Законы Кирхгофа, принцип наложения и эквивалентного источника энергии.
Работа в среде MicroCAP
Омск 2009 г.
Первый закон Кирхгофа
Построим электрическую схему согласно рисунку
|
| Е1 – 5 вольт Е2 – 9 вольт R1 – 3 кОма R2 – 5 кОма R3 – 10 кОма R4 – 1 кОма R5 – 0,8 кОма R6 – 7 кОма f – потенциал = 0 |
Проанализируем токи протекающие на сопротивлениях подходящие к точке « а »
Выберем Analysis (Alt+A) -> DC… или просто нажав - (Alt+3)
! Не забудьте включить Auto Scale Range !
Далее нажмите на кнопке Run
На появившемся графике посмотрим значение в точке «5в» т.к. в значении Range мы оставили значение по умолчанию, нам показывается диапазон до 10в. любым удобным способом (можно просто подвести курсор мышки к значению 5в., но более точно и удобно будет если выбрать Go to X и в вести значение 5 т.к. в нашем случае по значению «Х» откладывается напряжение.
|
|
Повторим замеры и снимем значение токов для сопротивлений R1, R3, R4, R5
Значения даны в миллиамперах.
По первому закону Кирхгофа сумма сходящихся токов в точке « а » должна нам дать нулевой результат. Проверим это:
Что и требовалось доказать (проверить).
Формулировка первого закона Кирхгофа:
Алгебраическая сумма мгновенных значений токов, сходящихся в узле, равна нулю. Одно из направлений токов при этом (например, к узлу) считается положительным.
Второй закон Кирхгофа
Формулировка второго закона Кирхгофа:
В любом замкнутом контуре электрической цепи алгебраическая сумма мгновенных значений ЭДС равна алгебраической сумме падений напряжений на пассивных элементах.
Проверим это сложив все значения напряжений. Для этого снова выберем Analysis (Alt+A) -> DC…, но уже будем снимать значения напряжений во потенциалах точек a..f
В среде MicroCAP ранее при построении схемы можно просто включить «показать узлы» Node Numbers тогда на схеме покажутся все узлы, в нашем случае мне удобнее было переименовать узлы согласно схеме. Это можно сделать двойным щелчком на узле, при этом появится форма в которой номерному узлы присваиваем «имя». На примере, номерному узлу 2 по умолчанию, было присвоено имя « а ». Это гораздо облегчает при рассмотрении схемы без дополнительных перестроений.
При замерах так же можно пользоваться горячими клавишами F9 – вернуться к выбору измеряемых параметров, F3 – закрыть анализ, Alt+Tab – переход к схеме и обратно к графику и другими стандартными комбинациями, что облегчает работу. (Более подробно можно всё прочитать в помощи F1 – словарь Вам в помощь)
Получаем данные (значения в вольтах):
| a | b | c | d | e | f |
| 0.788 | - 0.594 | 4.406 | 2.103 | 9.000 | 0.000 |
И проверим второй закон Кирхгофа по более подходящей нам формулировке:
Алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю.
Найдём напряжения и сложим их, направление возьмём по часовой стрелке. Тогда получим, что Ufa + Uab + Ubc + Ucd + Ude + Uef = 0
|
| Ufa = f – a = - 0.788 Uab = a – b = 1.382 Ubc = b – c = - 5.000 Ucd = c – d = 2.303 Ude = d – e = - 6.897 Uef = e – f = 9.000 -0.788 + 1.382 + (-5) + + 2.303 + (-6.897) + 9 = 0 |
Формулировка теоремы наложения
Мгновенное значение тока или напряжения в любой ветви линейной электрической цепи от нескольких источников энергии, действующих в цепи, может быть найдено алгебраическим суммированием мгновенных значений токов или напряжений, от источников энергии, взятых в отдельности.
При использовании для анализа теоремы наложения последовательно исключаются все источники энергии, кроме одного (ветви с источником тока размыкаются, а идеальные источники напряжения замыкаются перемычками).
Проверку проведу на примере I(R4).
|
| При двух источниках в цепи, E1 и E2 ток I(R4) = 1,315 мА |
|
| При одном источнике в цепи, E1 ток I`(R4) = 0,462 мА |
|
| При одном источнике в цепи, E2 ток I``(R4) = 0,853 мА ! При замере нужно выбрать E2 и смотреть данные на уровне 9 вольт ! |
I`(R4) + I``(R4) = 0.462 + 0.853 = 1.315 что равно значению I(R4).
Формулировка теоремы об эквивалентном источнике энергии
Для определения тока или напряжений в произвольной ветви электрической цепи оставшаяся часть может быть заменена эквивалентным источником ЭДС (
) с последовательным сопротивлением (
) или эквивалентным источником тока (
) с параллельным сопротивлением (). Параметры эквивалентных источников энергии определяются как:
, (4.1)
, (4.2)
, (4.3)
где индексом "
", "
" означают режимы холостого хода и короткого замыкания на клеммах, к которым подключена анализируемая ветвь.
|
| Отключим ветвь с резистором R3 и замерим Uхх которое будет равно Uda или что тоже самое U(R4). ! Замер между потенциалами d-a можно выполнить указав непосредственно V(d)-V(a) ! И в итоге получаем Uхх = 1.419 в. Подключим цепь с R3 и установив его значение = 0 Ом замерим ток, этот ток I(R3) = 1.779 мА будет током Iкз Найдём Rвн которое будет равно Uхх/Iкз Rвн = 1.419/1.799*10-3 = 797.6 Ом |
Теперь зная напряжение холостого хода ( Uхх = 1.419 в ) и внутренне сопротивление (Rвн = 797.6 Ом) я могу найти ток который будет протекать в цепи при подключении R3 = 10 кОм. Который можно найти по формуле I = Uхх / (Rвн + R3) = 0.131 мА.
Восстановим цепь и проверим значение I(R3)
При проверке получим I(R3) = 0.131 мА. Что и требовалось доказать.
закон кирхгоф наложение эквивалентный
Вывод: На практике, с работой в программе MicroCAP, я убедился в выполнении основных законов Кирхгофа, принципа наложения и эквивалентного источника энергии, что доказывает не их неопровержимое выполнение, а выполнение их на программном уровне. Этой проверка показывает, что можно пользоваться расчётами программ и применять их на практике. Это облегчает и ускоряет проверку и разработку электрических схем.
topref.ru
Согласно первого закона Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю
∑I = 0.
Поскольку речь идет об алгебраической сумме ∑I, необходимо учитывать знаки слагаемых токов. Входящие в узел токи принято считать положительными, выходящие – отрицательными. Для узла "а" (рис. 2.5) имеем
I1 + I2 - I3 = 0.
Согласно второго закона Кирхгофа алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах контура
∑E = ∑R·I.
Для составления уравнения по второму закону Кирхгофа произвольно выбирают направление обхода контура. Принято ЭДС, токи и напряжения считать положительными, если они совпадают по направлению с направлением обхода контура, а если не совпадают – отрицательными. При обходе контура E1, E2, R2, R1 электрической цепи (рис. 2.5) по часовой стрелке имеем
E1 - E2 = R1·I1 - R2I2.
При расчётах сложных электрических цепей применяют формулы последовательного (смотреть пункт 2.1), параллельного, смешанного соединения элементов, а также преобразования "треугольника" в "звезду" и обратно. Рассмотрим эти соотношения.
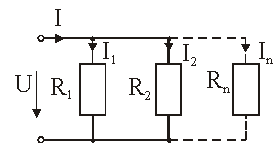Рис. 2.6. – Параллельное соединение элементов
При таком соединении элементов общее сопротивление определяется выражением
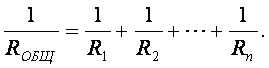
При двух сопротивлениях, соединенных параллельно
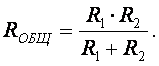
Если R1 = R2 = … Rn, то
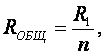
где п – число параллельно соединенных элементов.
Смешанным соединением называют сочетание последовательного и параллельного соединений резисторов.
При смешанном соединении элементов для эквивалентного преобразования пользуются методом последовательных эквивалентных преобразований, т.е. последовательно преобразуются участки цепи, имеющие простое (только последовательное, или только параллельное) соединение элементов.
Поясним это на конкретном примере расчета электрической цепи (рис.1.3).
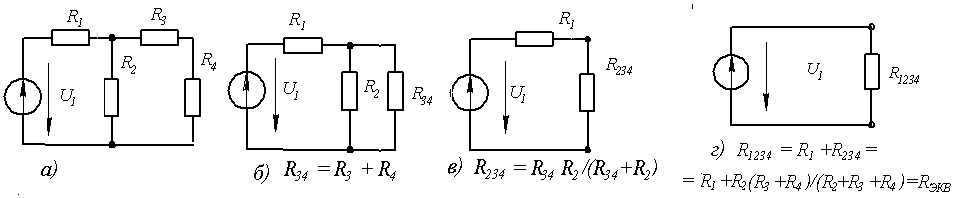
Рис.1.3. Смешанное соединение элементов.
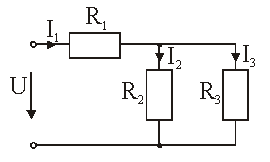Рис. 2.7. – Смешанное соединение элементов
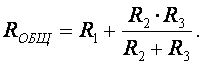
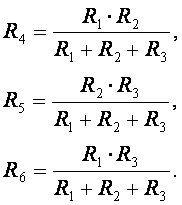
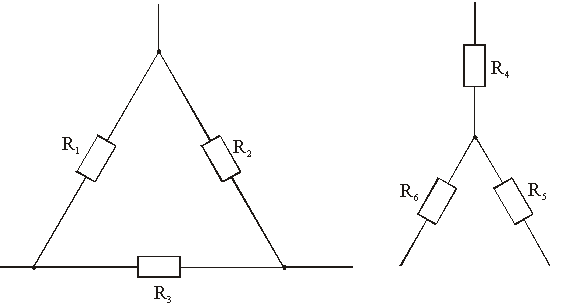Рис. 2.8. – Соединение сопротивлений в "треугольник" и "звезду"
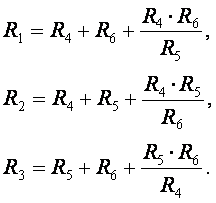
При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС, сопротивления элементов электрической цепи. Задача расчета электрической цепи сводится к определению токов в ветвях. По найденным токам можно рассчитать напряжения на элементах цепи, мощность отдельных элементов и электрической цепи в целом, мощность источников, сечения проводников.
Для расчета электрических цепей с одним источником энергии применяется метод эквивалентных преобразований, заключающийся в постепенном преобразовании и замене последовательно и параллельно соединенных элементов эквивалентными. Всю группу элементов цепи заменяют одним эквивалентным. Преобразования начинают в ветвях, наиболее удалённых от источника. Затем в преобразованной (предельно простой) цепи по закону Ома определяют ток. Полученные в процессе преобразования расчетные схемы позволяют определить токи во всех остальных ветвях.
Пример 1: Рассчитать эквивалентное сопротивление цепи Rэкв и, токи в каждом резисторе.
Дано: R1 = 3 Ом; R2 = 2 Ом; R3 = 5 Ом; R4 = 10 Ом; E = 50 В.
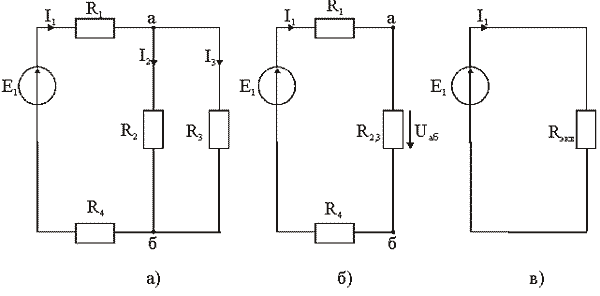Рис. 2.9 - Пример эквивалентных преобразований: а) схема электрической цепи до преобразования; б) расчетная схема после первого преобразования; в) - расчетная схема после второго (окончательного) преобразования
Определить токи в ветвях схемы, представленной на рис. 2.9, а.
Выбираем направления токов в ветвях. Преобразуем параллельно соединенные резисторы R2 и R3, заменяя их эквивалентным элементом R2, 3
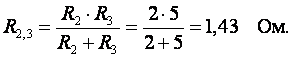
Расчетная схема после первого преобразования показана на рис. 2.9, б.
Проводим второе преобразование. Для этого последовательно соединенные резисторы R1, R2, 3, R4 заменяем одним эквивалентным RЭКВ.
RЭКВ = R1 + R2, 3 + R4 = 3 + 1,43 + 10 = 14,43 Ом.
Теперь исходная схема сведена к простейшей, показанной на рис. 2.9, в, в которой
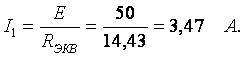
Для определения токов I2 и I3, необходимо определить напряжение Uаб, рис. 2.9, а, которое рассчитываем по рис. 2.9, б
Uаб = R2, 3·I1 = 1,43·3,47 = 4,96 В.
Возвращаясь к схеме рис 2.9, а, получим
Для проверки правильности расчета токов составляем баланс мощности. Мощность, вырабатываемая всеми источниками энергии в цепи, должна быть равна мощности, потребляемой всеми приёмниками электрической энергии (нагрузкой). Относительная погрешность расчета не должна превышать одного процента.
Мощность, вырабатываемая источником ЭДС
РИ = Е·I1 = 50·3,47 = 173,5 Вт.
Мощность, потребляемая нагрузкой
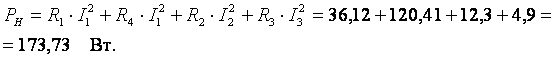
Погрешность баланса мощности
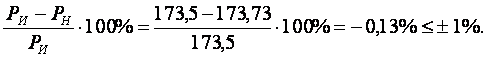
Если баланс сходится с допустимой погрешностью, то расчет токов выполнен верно.
Пример выполнения задачи 1.
Для электрической цепи постоянного тока, приведенной на рис. 4:
1. Рассчитать эквивалентное сопротивление цепи.
2. Рассчитать ток в каждом резисторе.
3. Проверить выполнение первого закона Кирхгофа во всех узлах схемы и второго Закона Киhхгофа для одного из контуров.
4. Определить мощности, рассеиваемые на резисторах схемы.
5. Проверить выполнение баланса мощностей
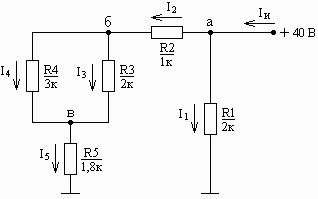
Рис. 4. Электрическая цепь постоянного тока
1. Расчет эквивалентного сопротивления цепи проводим методом последовательных эквивалентных преобразований..
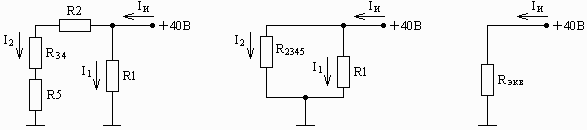
а) б) в)
Рис. 5. "Этапы эквивалентного преодразования электрической цепи
Эквивалентное сопротивление ветвей R3 и R4 соединенных параллельно определяем по формуле:
,
.
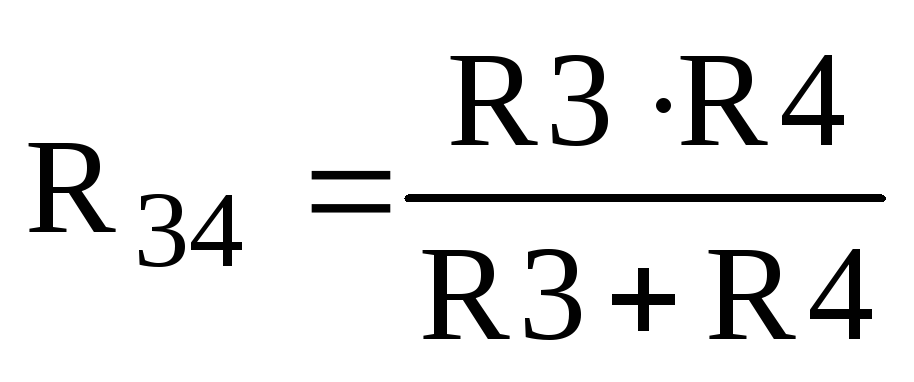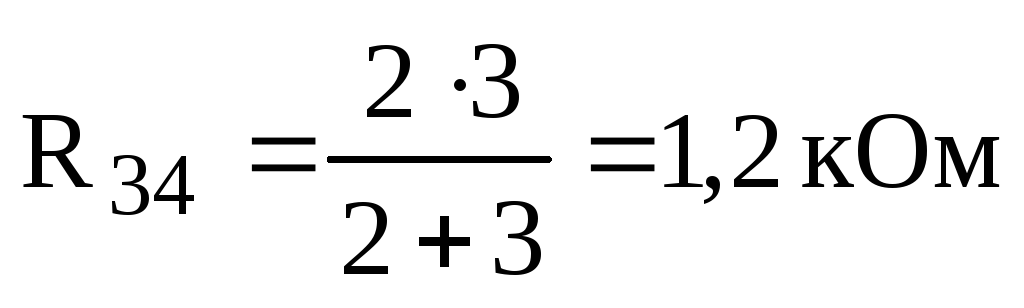Эквивалентное сопротивление элементов R2, R34 и R5, соединенных последовательно находим по формуле:
,
.
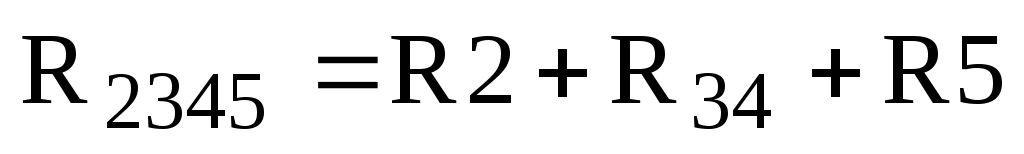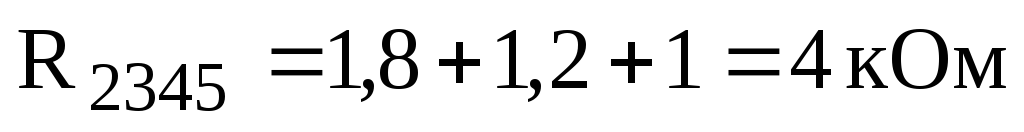Эквивалентное сопротивление всей цепи (R2345 и R1 -соединены параллельно):
,
.
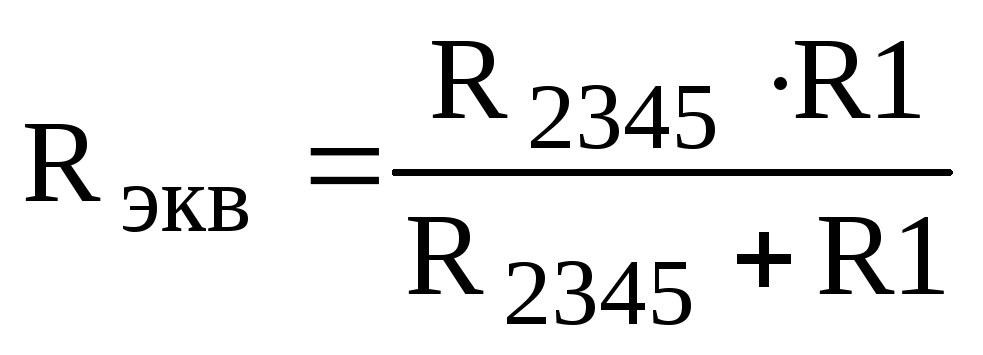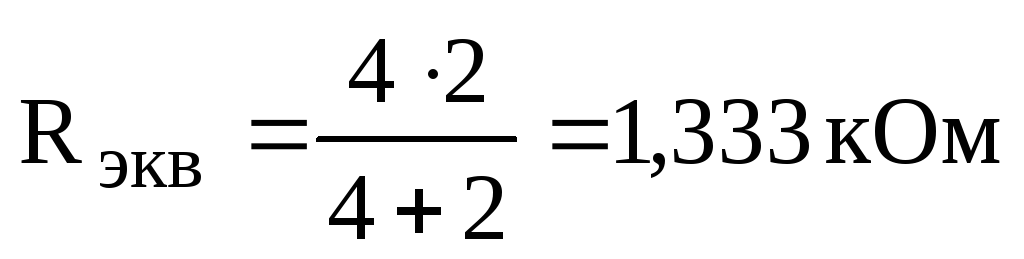2. Рассчитаем токи во всех ветвях.
Ток, потребляемый цепью от источника питания:
,
.
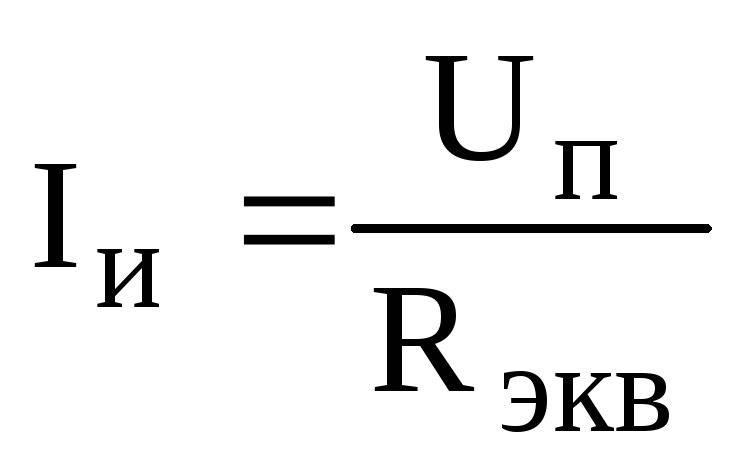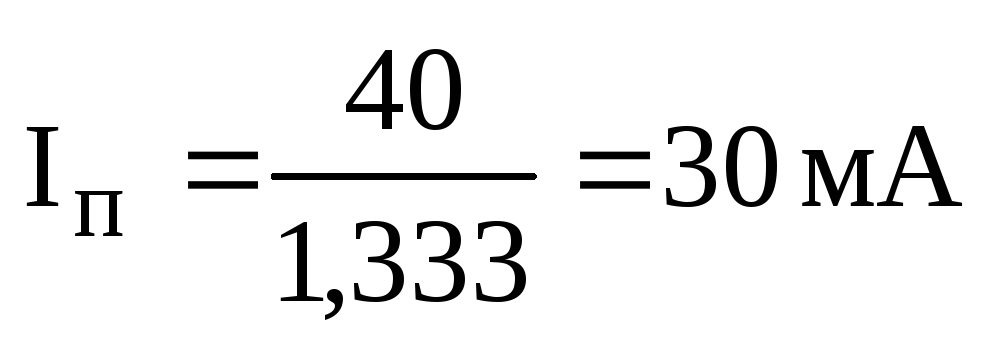Ток в ветви R1:
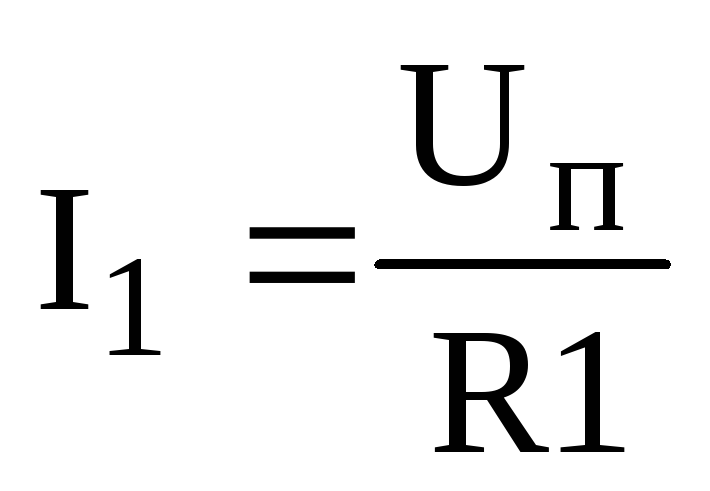
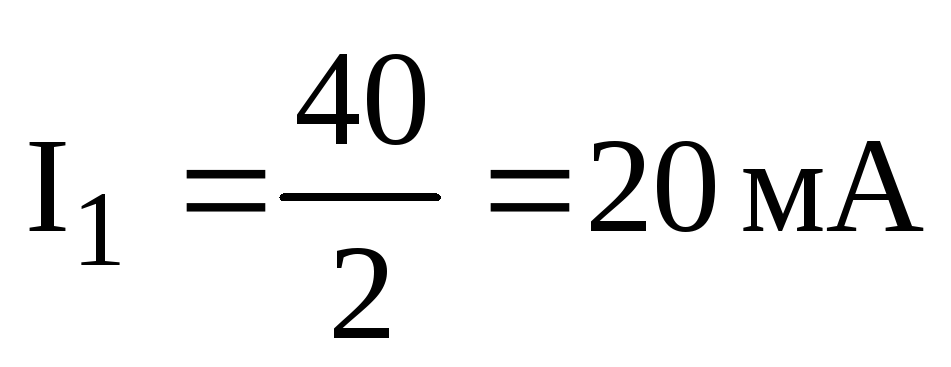
Ток в ветви R2345:
,
.
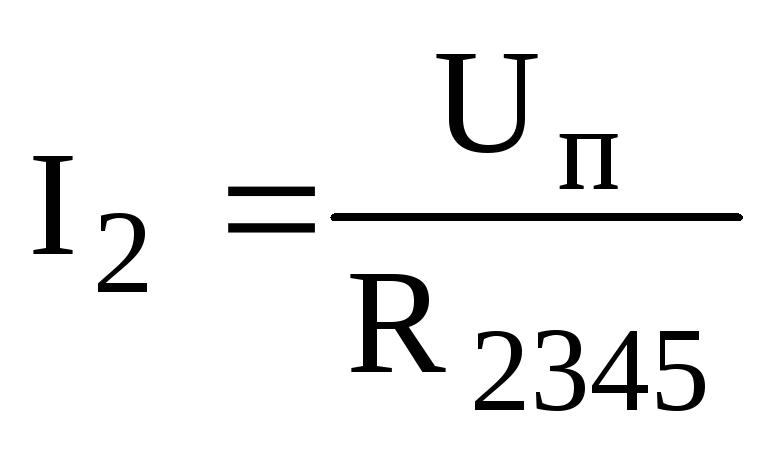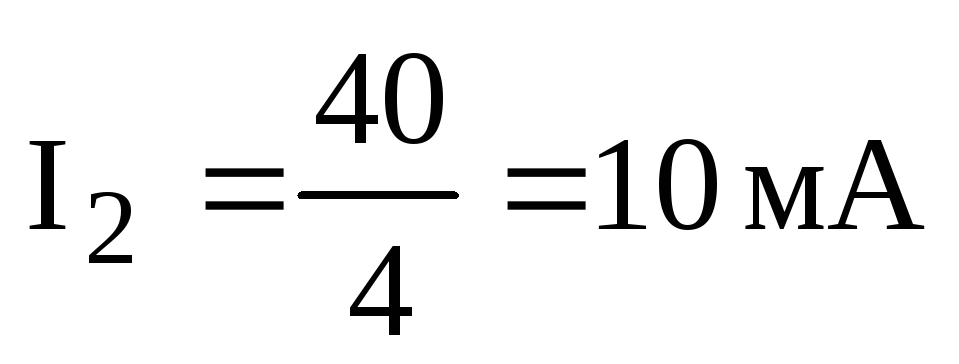Определяем потенциал узла «б»:
,
.
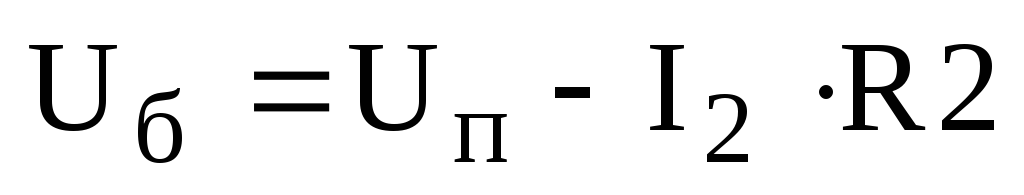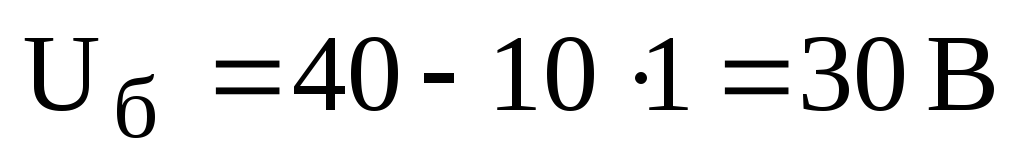Определяем потенциал узла «в»:
.
Очевидно, что I5 = I2, откуда
.
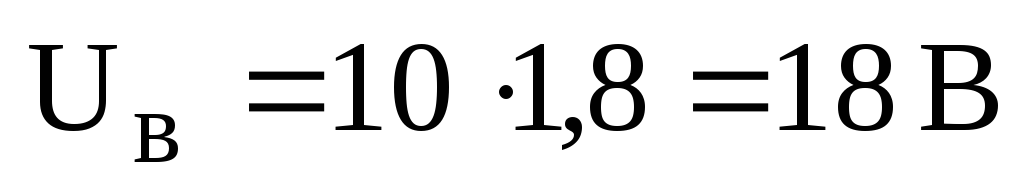Определяем разность потенциалов между узлами «б» и «в»:
,
.
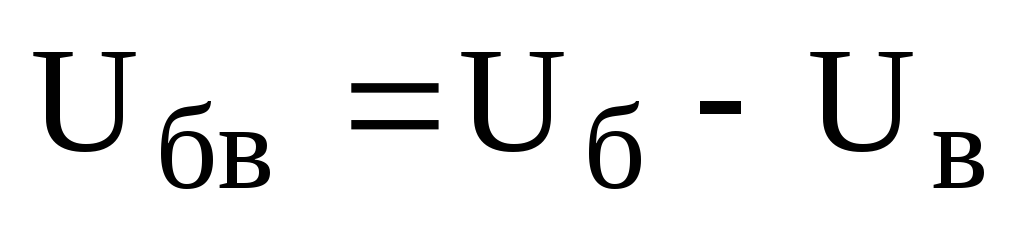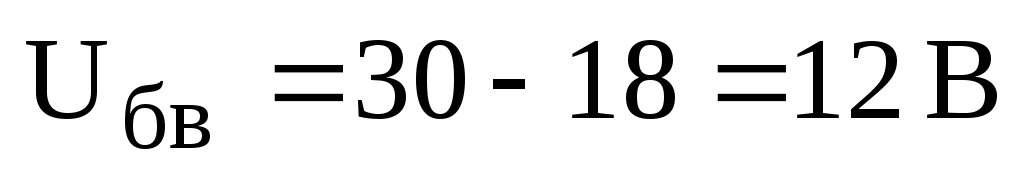Определяем токи в ветвях R3 и R4:
,
;
,
.
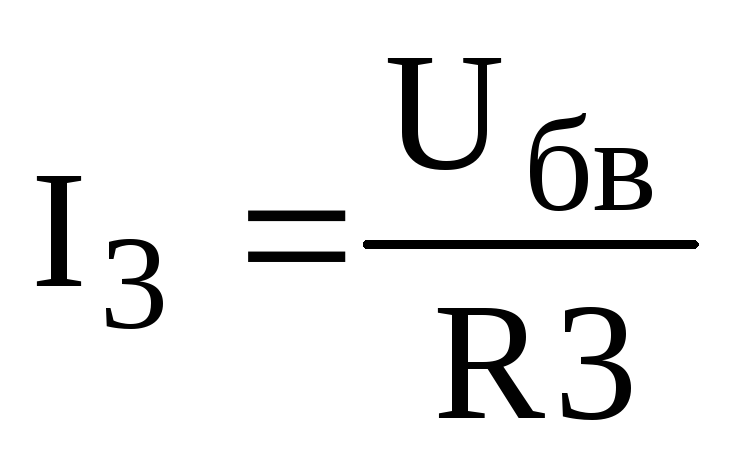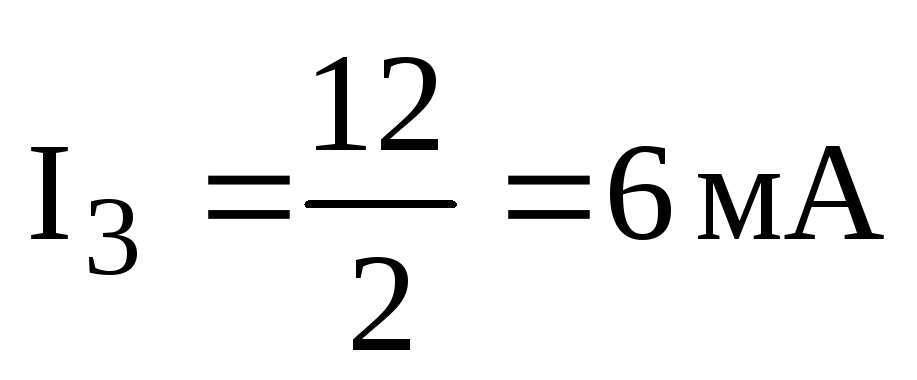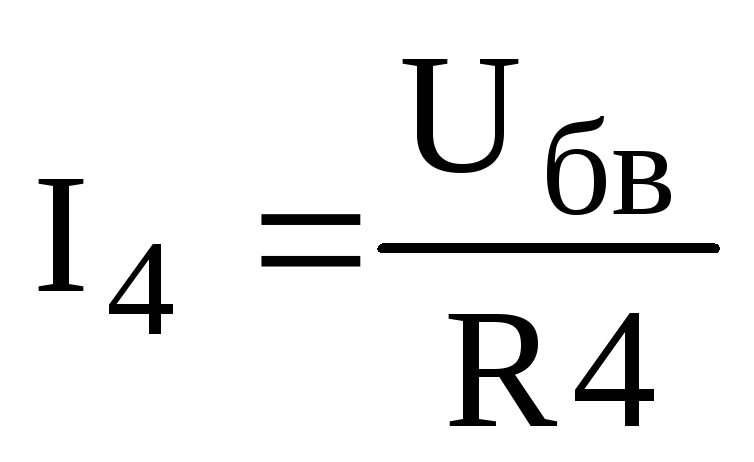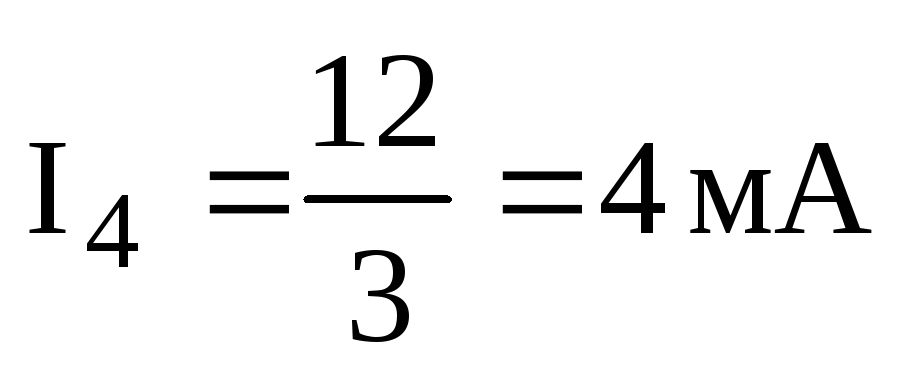3. Проверяем выполнение первого закона Кирхгофа для токов в узлах.
Для узла «а»: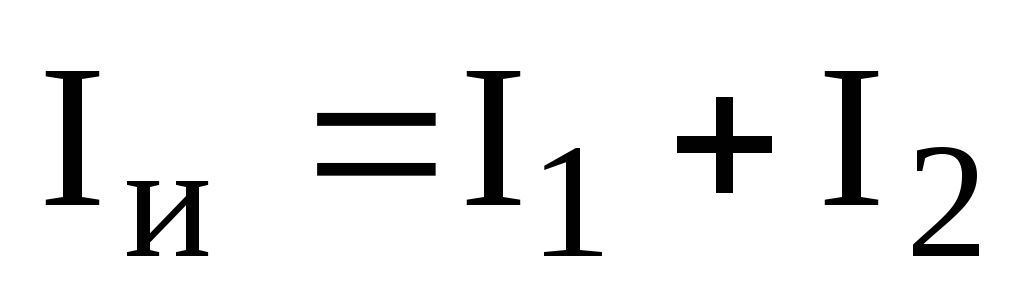 
,
.
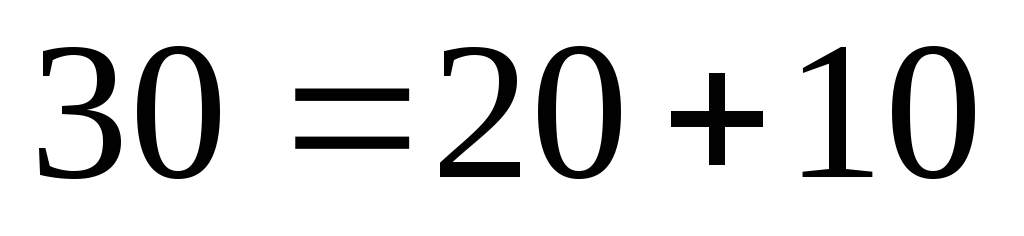Для узла «б»: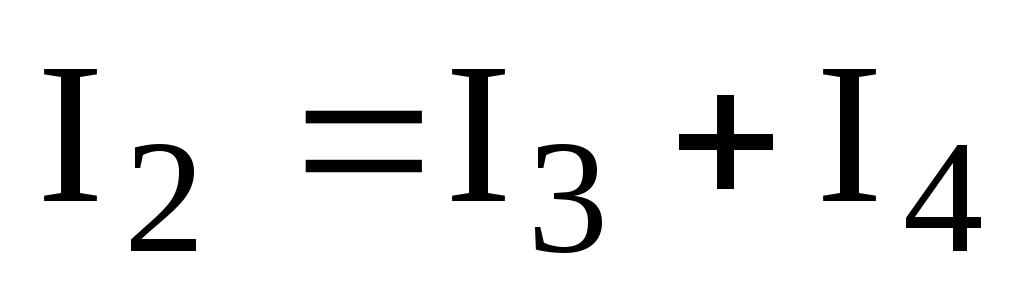 
,
.
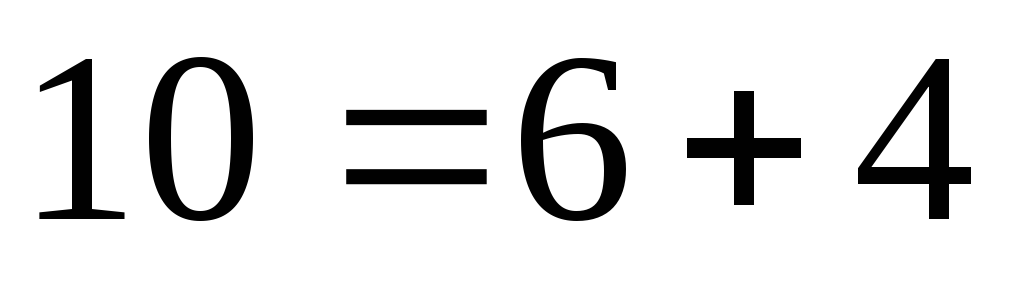Для узла «в»: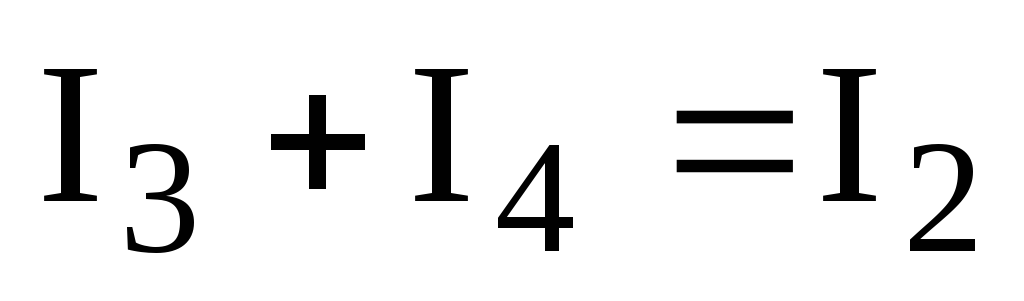 
,
.
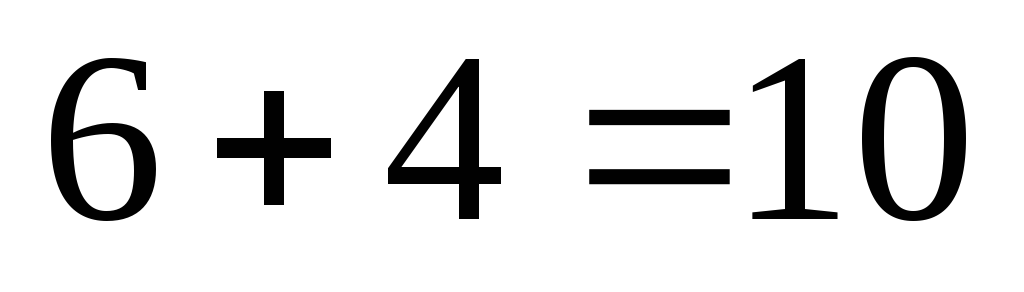Проверяем выполнение второго закона Кирхгофа для контура R5, R3, R2, R1:
,
,
.
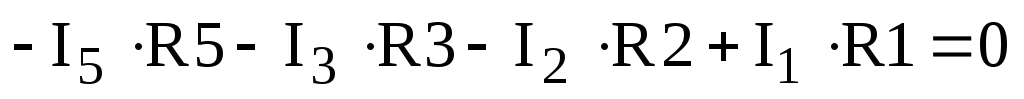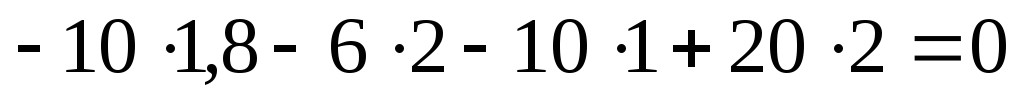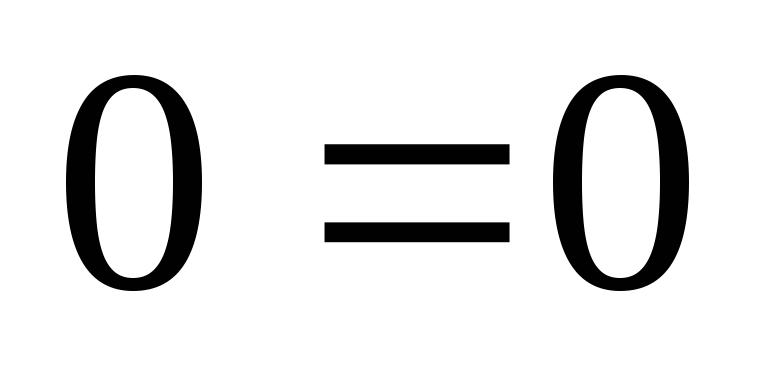4. Определяем мощности, рассеиваемые на резисторах:
,
;
,
;
,
;
,
;
,
.
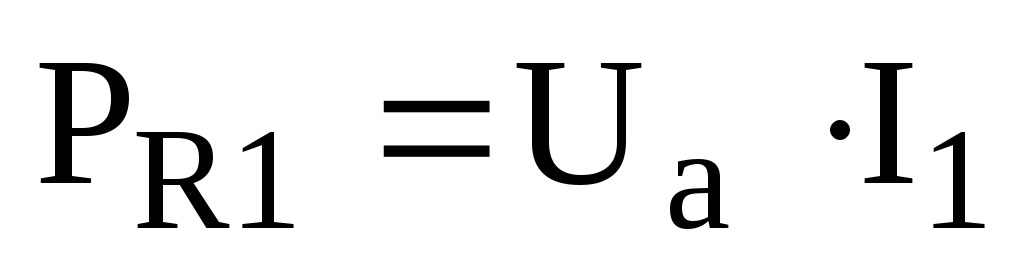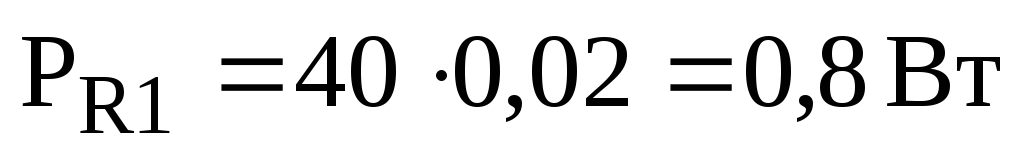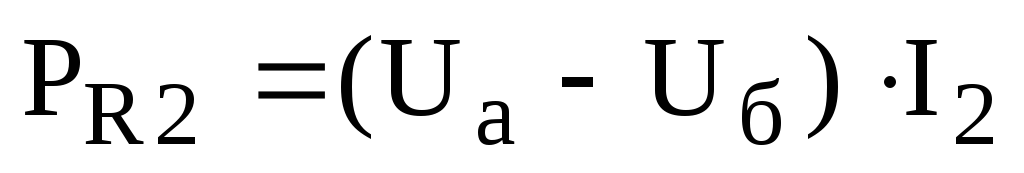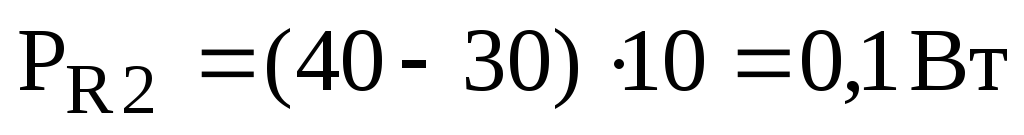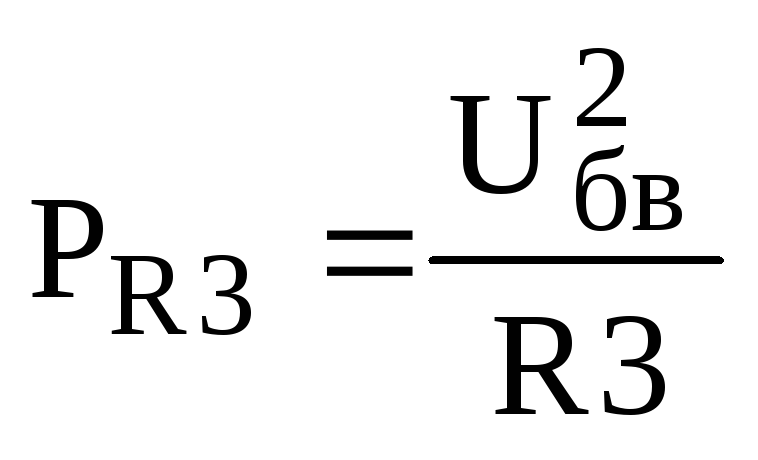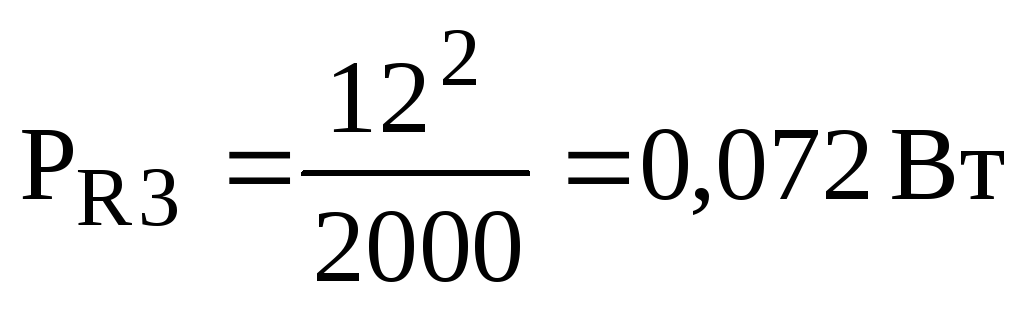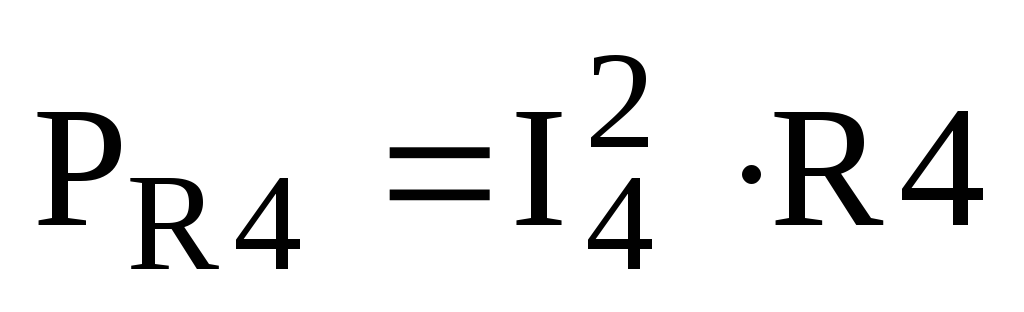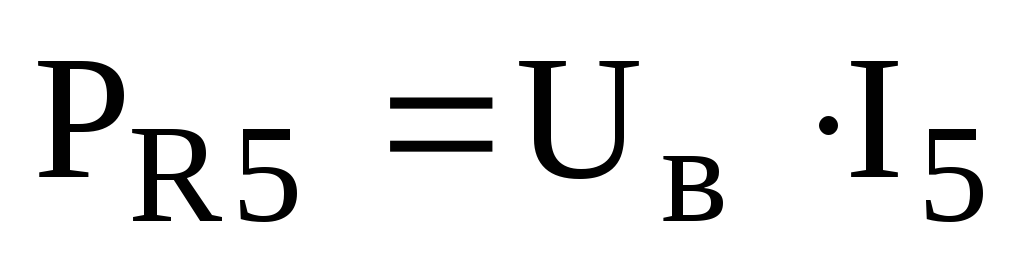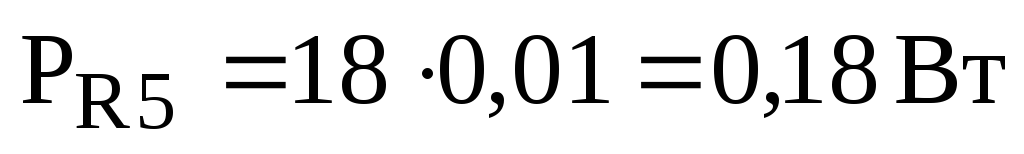5. Проверяем выполнение баланса мощностей.
Мощность, потребляемая цепью от источника питания:
,
.
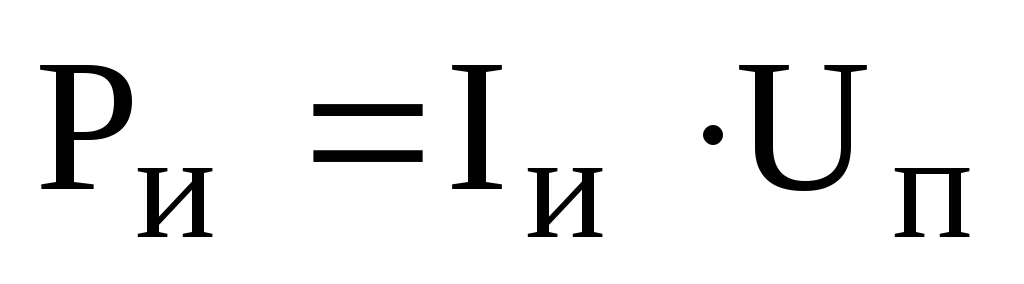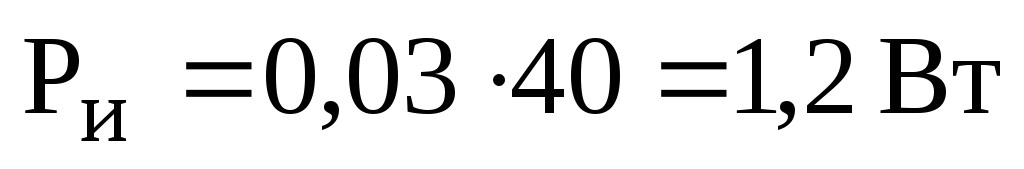Составляем уравнение для проверки баланса мощностей:
,
,
.
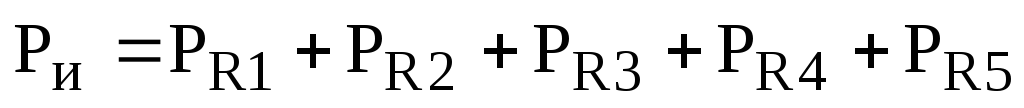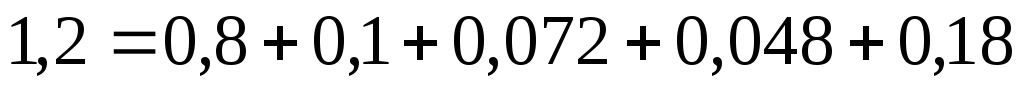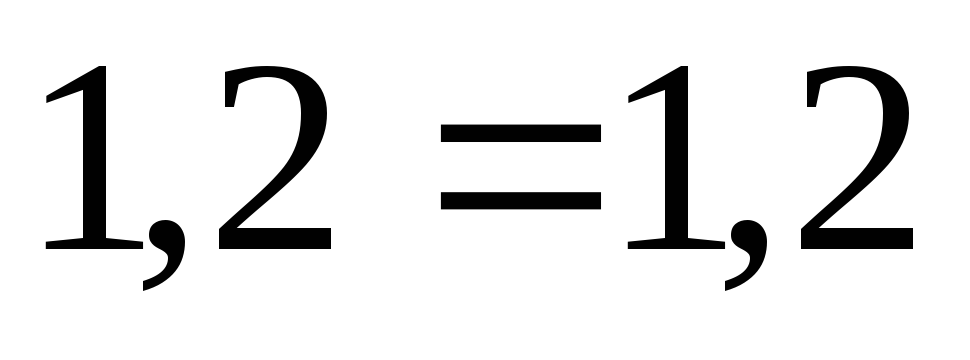Баланс мощностей выполняется.
Методические указания к выполнению задания 2.
Методы расчета цепей постоянного (переменного) тока
Под расчетом цепи, в общем случае, понимают нахождение токов во всех ветвях схемы.
Основные методы расчета:
1. Метод токов ветвей.
2.Метод контурных токов.
3. Метод узловых напряжений.
4. Метод наложения.
5. Метод эквивалентных преобразований
Метод токов ветвей
В общем случае токи сложной электрической цепи могут быть определены в результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа. Для однозначного нахождения всех токов необходимо составить в уравнений, где в- число ветвей схемы (без источников тока).
Последовательность расчета следующая:
1. Проводят топологический анализ схемы.
1.1. обозначают токи во всех ветвях (I1, I2, …,Iв), произвольно выбирают их положительное направление и обозначают на схеме стрелками;
1.2. подсчитывают общее число узлов у и определяют число независимых узлов Nу=у-1 и показывают их на схеме;
1.3. подсчитывают число независимых контуров Nk = в-у+1, и показывают их на схеме дугой.
2. По первому закону Кирхгофа для независимых узлов и по второму закону Кирхгофа для независимых контуров относительно токов ветвей записывают уравнения. После приведения подобных членов они сводятся к системе линейных алгебраических уравнений (ЛАУ)
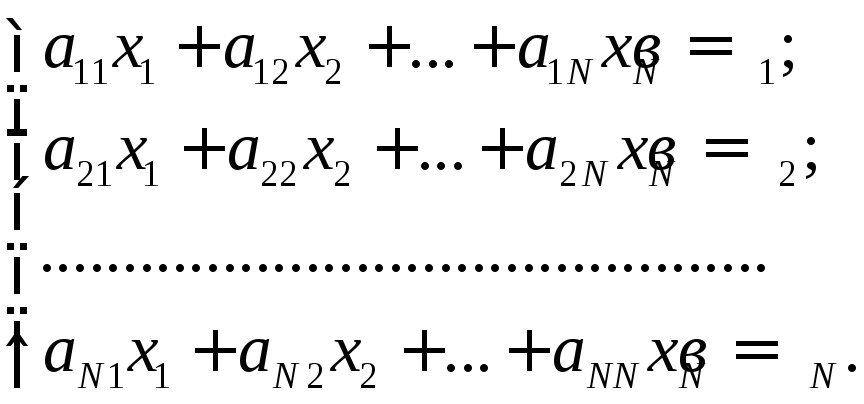
где xi =Ii– искомые токи ветвей; aji – постоянные коэффициенты, зависящие от параметров пассивных элементов схемы; вi – постоянные величины, зависящие от параметров активных элементов схемы.
3. Решая систему из в уравнений относительно токов, по методу Крамера находят токи во всех ветвях схемы:
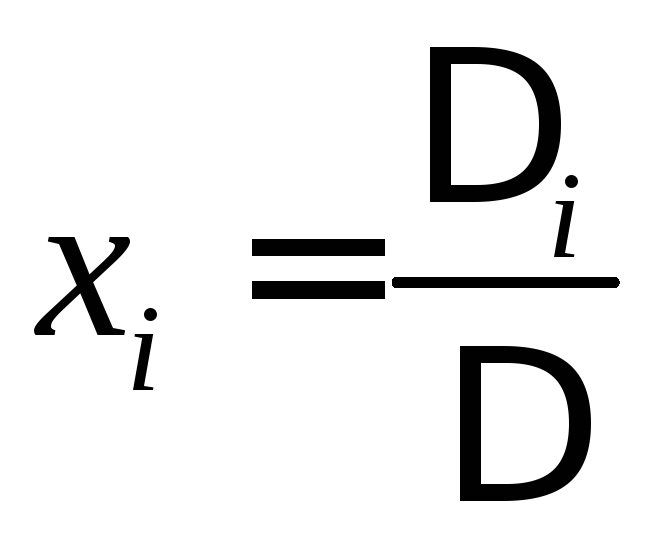
где D – главный определитель системы; Di – определитель, получается из главного D путем замены i-го столбца на столбец свободных членов вi.
Если значения некоторых токов отрицательные, то действительные направления их будут противоположны первоначально выбранным направлениям. I1
Пример 1. Для электрической цепи рис. 1.1 n = 2, m = 3, и расчет токов цепи осуществляется путем решения следующей системы уравнений
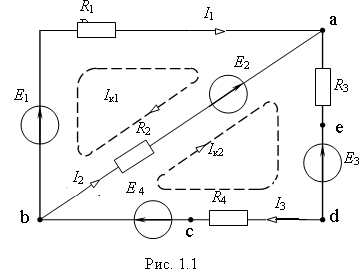
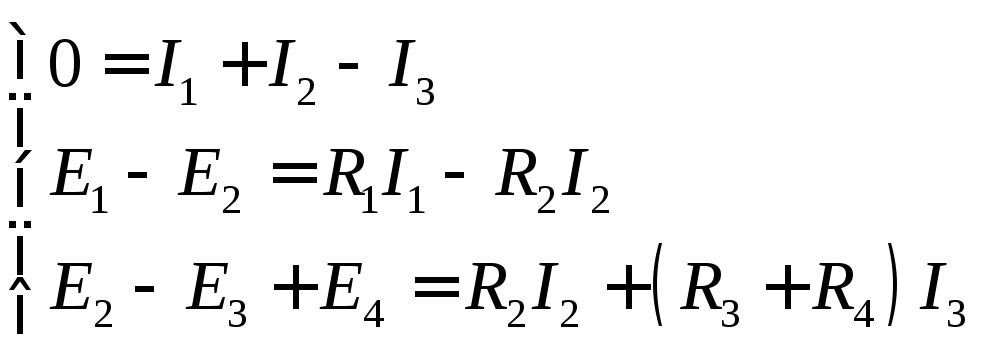
studfiles.net
