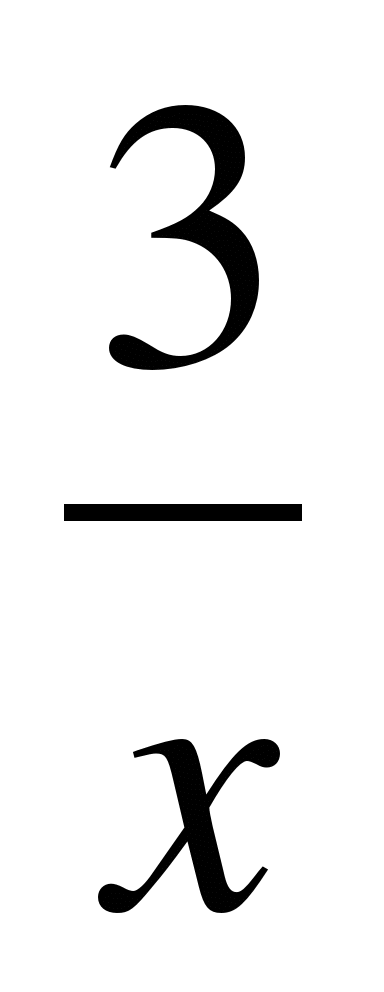Главная » Контрольная » Производная 11 класс контрольная

Урок алгебры 11 класс , контрольная работа по теме"Применение производной". Производная 11 класс контрольная


Урок алгебры 11 класс , контрольная работа по теме"Применение производной"

Контрольная работа № 3.

«Применение производной к исследованию функций».

Вариант 1.

А1. Определить интервалы возрастания и убывания функции у = 3х3- 9х.

А2. Найти точки экстремума функции f(x) = 12х –3х2+ 2х3.

А3. Найти наибольшее значение функции f(x) = х3+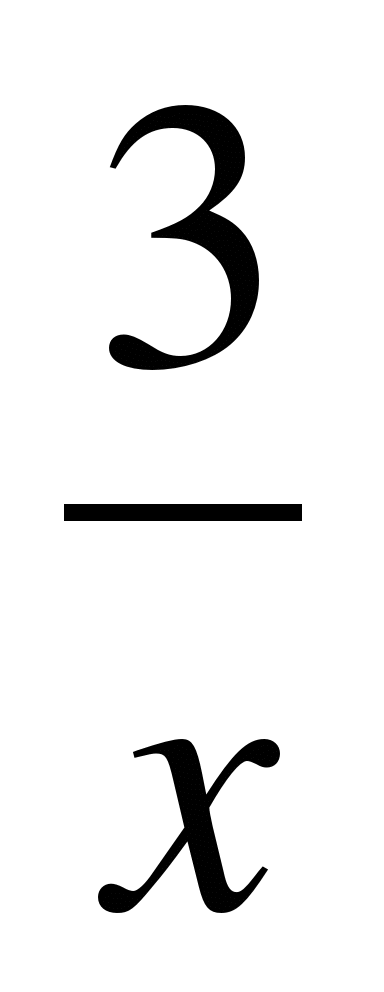hello_html_46bfa79c.gif на отрезке [0,5; 2].

А4. Построить график функции у = х4–2х2+2.

В1. Исследовать функцию у = 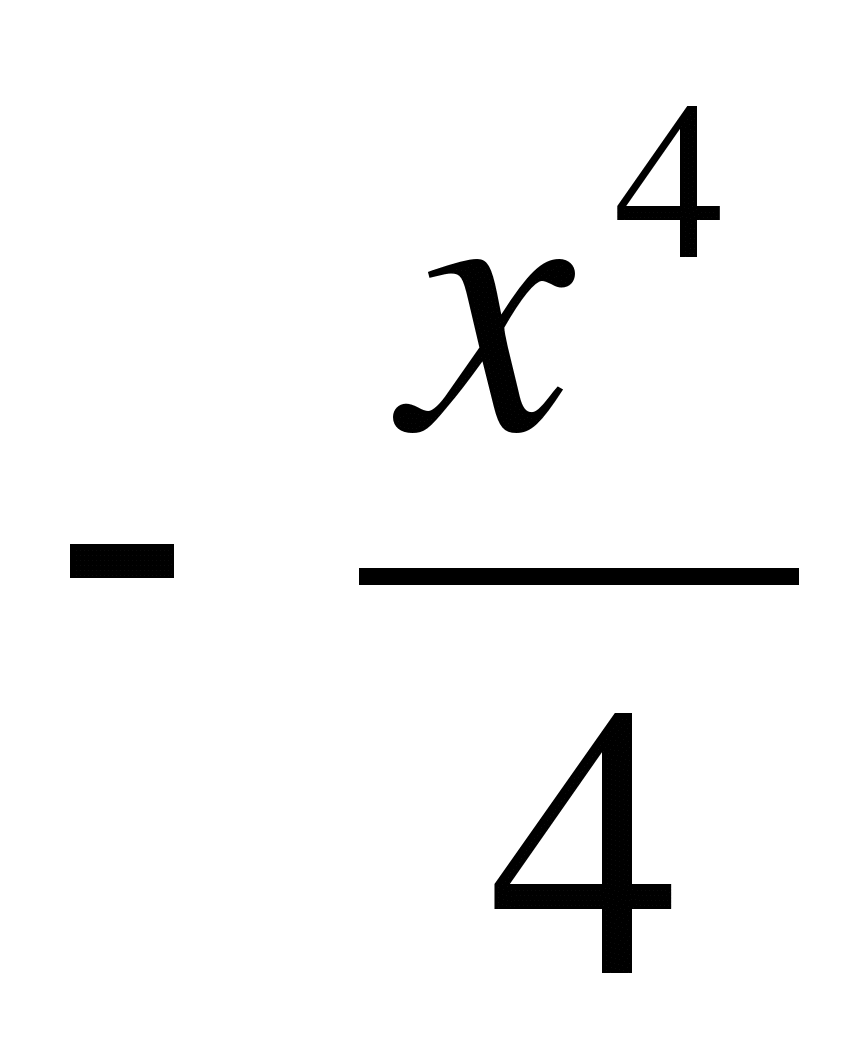hello_html_7023756d.gif + х2и построить ее график.

В2. Исследовать функцию у = 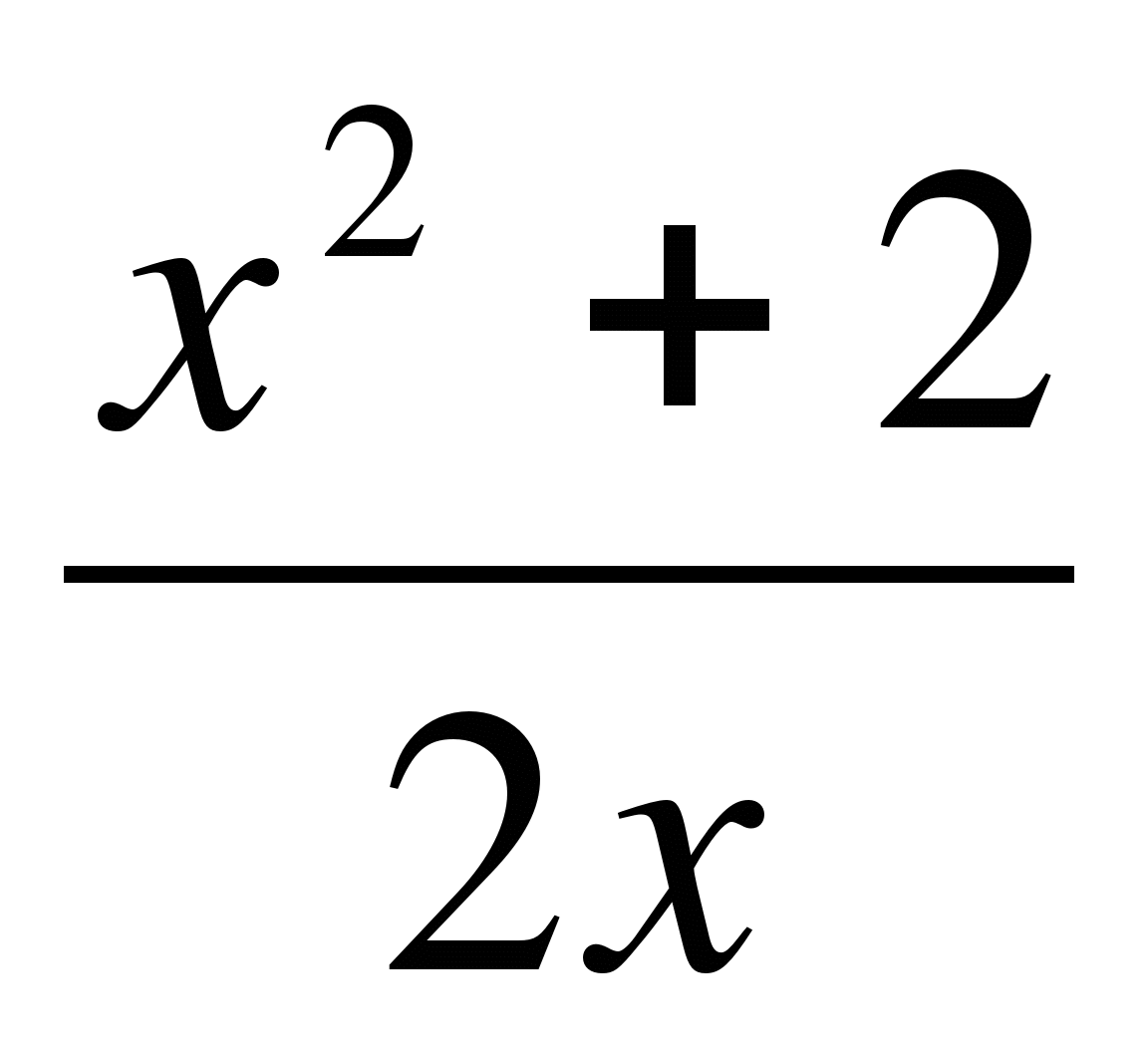hello_html_m67b8508b.gif и построить ее график.

C1. Найти наибольшее и наименьшее значение функции 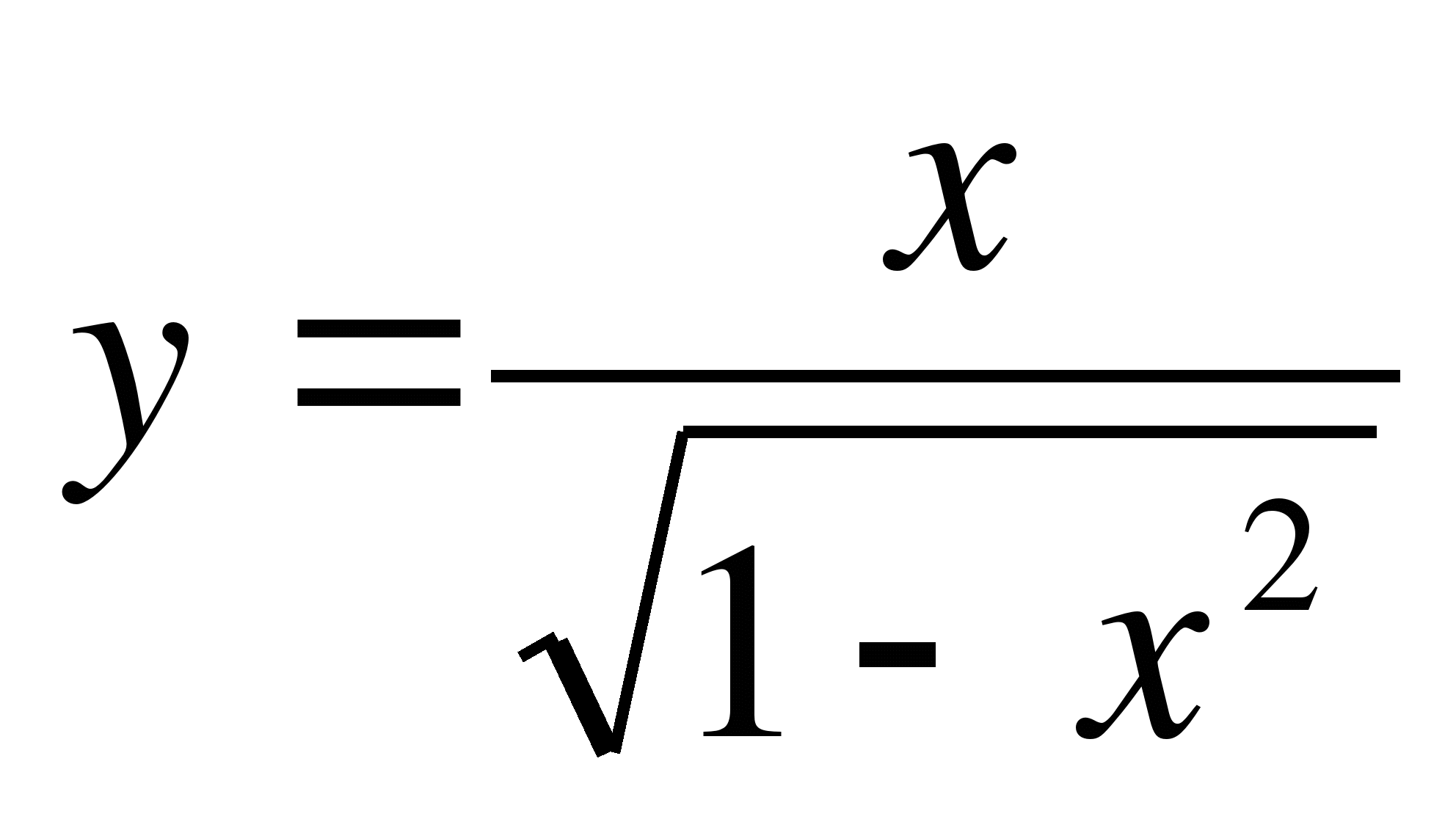hello_html_mf25f3c3.gif на отрезке [0; 1].

С2. Периметр осевого сечения цилиндра 6 дм. При каком радиусе основания цилиндра площадь его боковой поверхности будет наибольшей?

Нормы оценок: «3» - любые 3А, «4» - 2А + 1В, «5» - 1А + 1В +1С.

________________________________________________________________

Контрольная работа № 3.

«Применение производной к исследованию функций».

Вариант 2.

А1. Определить интервалы возрастания и убывания функции у = х3–24х.

А2. Найти точки экстремума функции f(x) = х4–4х3.

А3. Найти наибольшее значение функции f(x)=х3-3х2+ 2 на отрезке [-2; 3].

А4. Построить график функции у = -х4+8х2–16 .

В1. Исследовать функцию у = х4–0,5 х2и построить ее график.

В2. Исследовать функцию у = 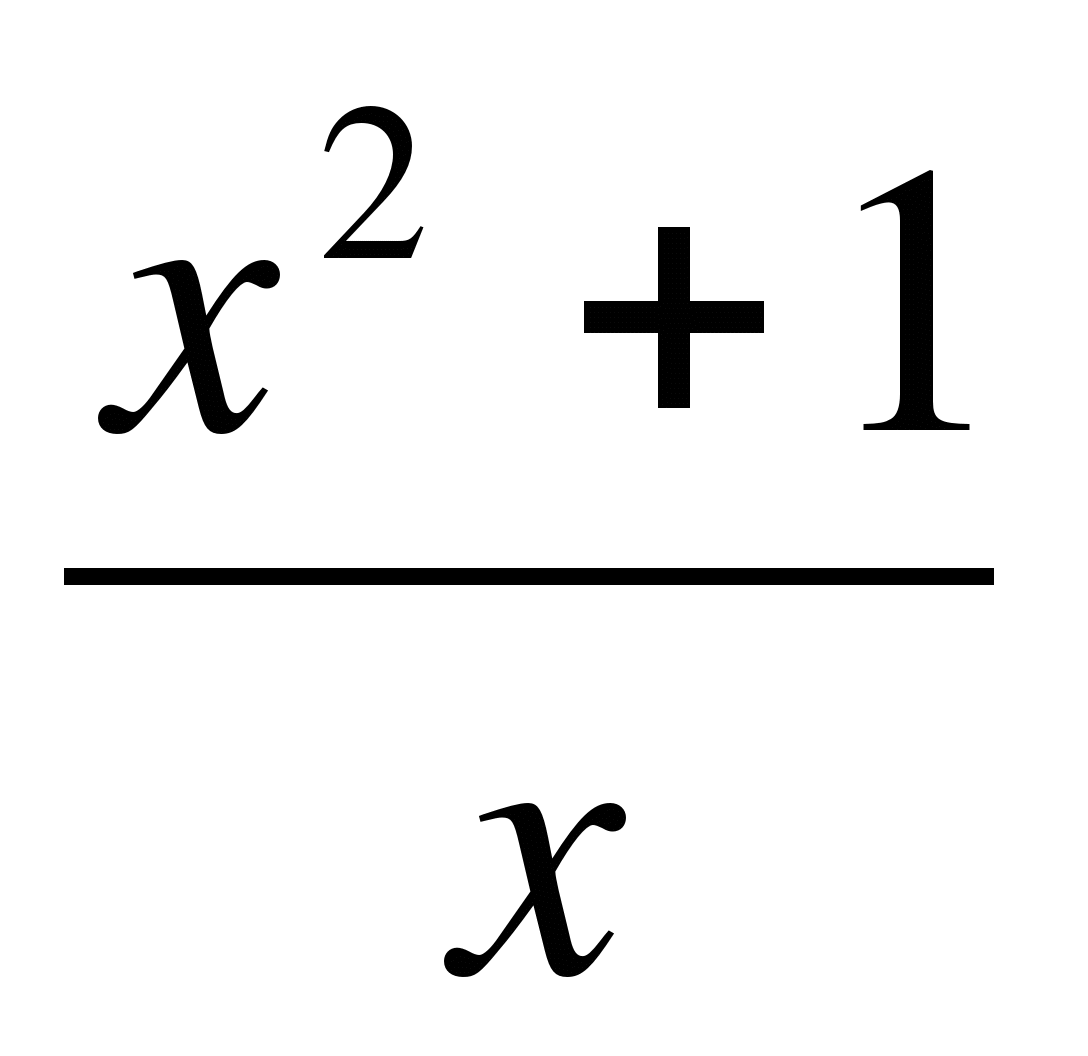hello_html_m429c4acf.gif и построить ее график.

C1. Найти наибольшее и наименьшее значение функции

f(x) = х2(2х –3) –12(3х –2) на отрезке [-3; 6].

С2. Периметр осевого сечения цилиндра 6 дм. При каком радиусе основания цилиндра площадь его боковой поверхности будет наибольшей?

Нормы оценок: «3» - любые 3А, «4» - 2А + 1В, «5» - 1А + 1В +1С.

Контрольная работа № 3.

«Применение производной к исследованию функций».

Вариант 3.

А1. Определить интервалы возрастания и убывания функции у = 12х2–2х3.

А2. Найти точки экстремума функции f(x) = х3–27х

А3. Найти минимальное значение функции f(x) = х3-3х2на отрезке [1; 3].

А4. Построить график функции у = х4-8х2+16 .

В1. Исследовать функцию у = -х4+8 х2-9 и построить ее график.

В2. Исследовать функцию у = 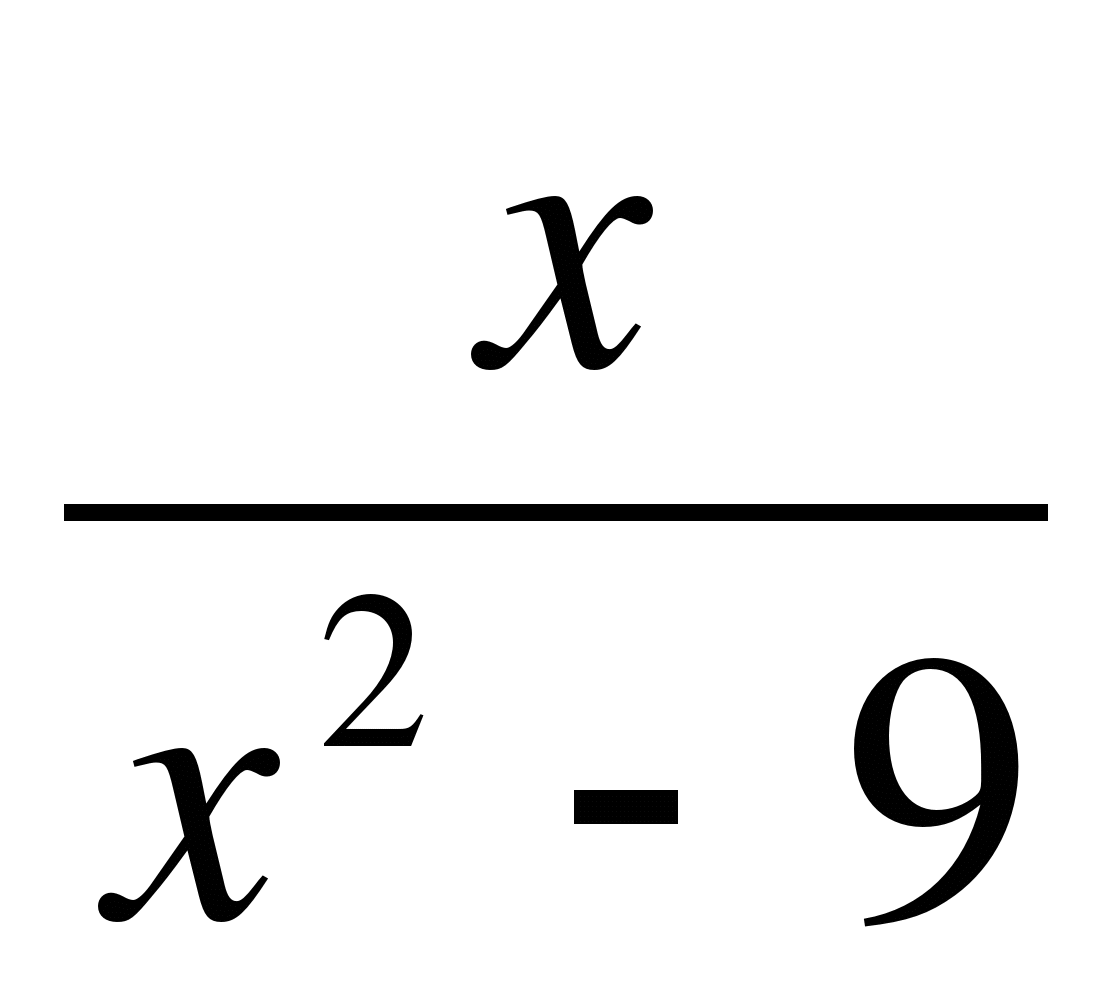hello_html_6c92031b.gif и построить ее график.

C1. Найти максимум функции f(x) = 15х4+20х3–24х5.

С2. Периметр осевого сечения цилиндра 6 дм. При каком радиусе основания цилиндра площадь его боковой поверхности будет наибольшей?

Нормы оценок: «3» - любые 3А, «4» - 2А + 1В, «5» - 1А + 1В +1С.

__________________________________________________________________

Контрольная работа № 3.

«Применение производной к исследованию функций».

Вариант 4.

А1. Определить интервалы возрастания и убывания функции у = 75х2–2х3.

А2. Найти точки экстремума функции f(x) = х3–6х2.

А3. Найти максимальное значение функции х3–5х2+5 на отрезке [-1; 1].

А4. Построить график функции у = -х4+8х2–16 .

В1. Исследовать функцию у = -х4+0,5 х2и построить ее график.

В2. Исследовать функцию у = 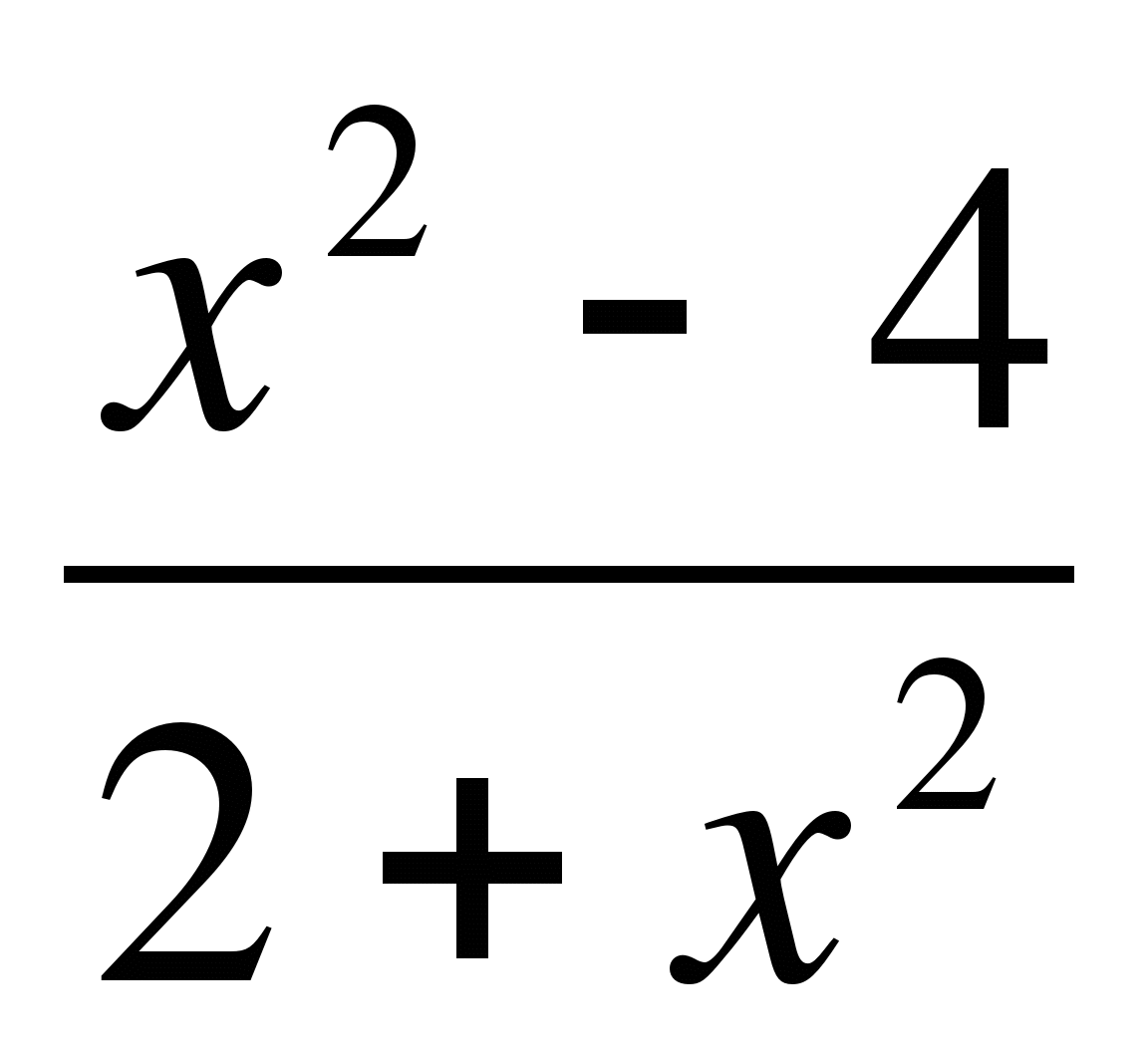hello_html_m7266d9cb.gif и построить ее график.

C1. Найти максимум функции f(x) = 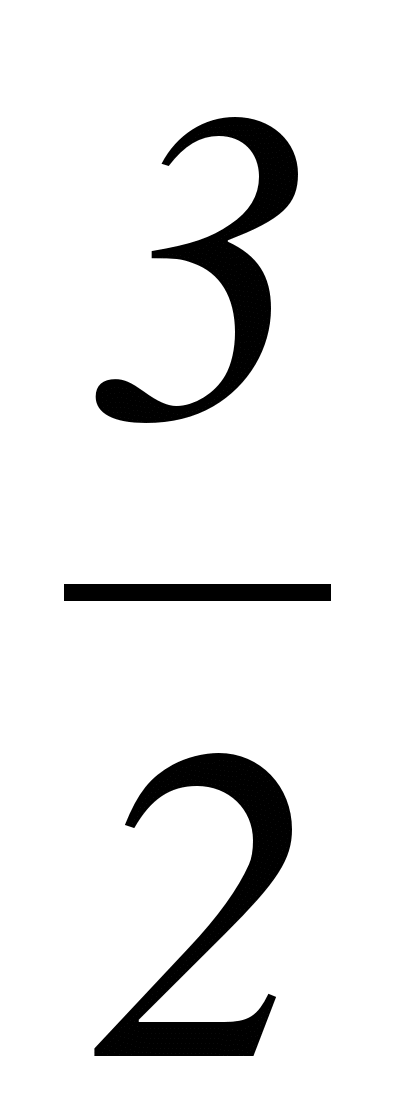hello_html_23eeeadb.gifх4–2х3–6х2+7. С2. Периметр осевого сечения цилиндра 6 дм. При каком радиусе основания цилиндра площадь его боковой поверхности будет наибольшей?

Нормы оценок: «3» - любые 3А, «4» - 2А + 1В, «5» - 1А + 1В +1С.

infourok.ru

Контрольная работа по алгебре 11 класс "Геометрический смысл производной"

Министерство образования и науки Российской Федерации

Муниципальное казенное общеобразовательное учреждение

«Средняя общеобразовательная школа № 2»

623281,Свердловская область, г. Ревда, ул. Павла Зыкина, 18

Тел. (34397) 3-25-88, 3-25-45. Факс: (34397) 3-25-47. Е-mail: [email protected]

ИНН 6627008779; ОГРН 1026601643848; КПП 662701001; ОКПО 44650710

Контрольная работа 11 класс

на тему «Производная. Геометрический смысл производной»

УМК Ш.А.Алимов «Алгебра и начала анализа»

Составил: Главатских Надежда Вилегановна,

учитель математики

МКОУ «СОШ №2»

Ревда, Свердловская обл.

Цель: проверить уровень усвоение материала по данной теме, в частности усвоение правил дифференцирования, геометрического смысла производной, составления уравнения касательной к графику в заданной точке.

К.Р. «Производная степенной функции» В1 А11

  1. Найти производную функции.

Функция

Производная

Функция

Производная

а)f(x) =

2х5+х7- 128

г)f(x) =

=ln (4x+3)

б)f(x) =

7х -3+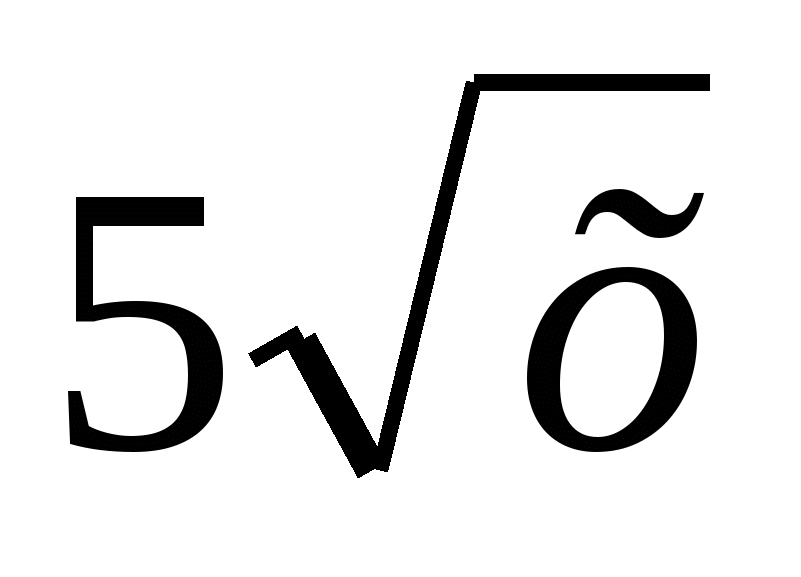hello_html_m4a719b2e.gif

д)f(x) =

=ех(2х+5)

в)f(x) =

sin(6-2x)

е)f(x) =

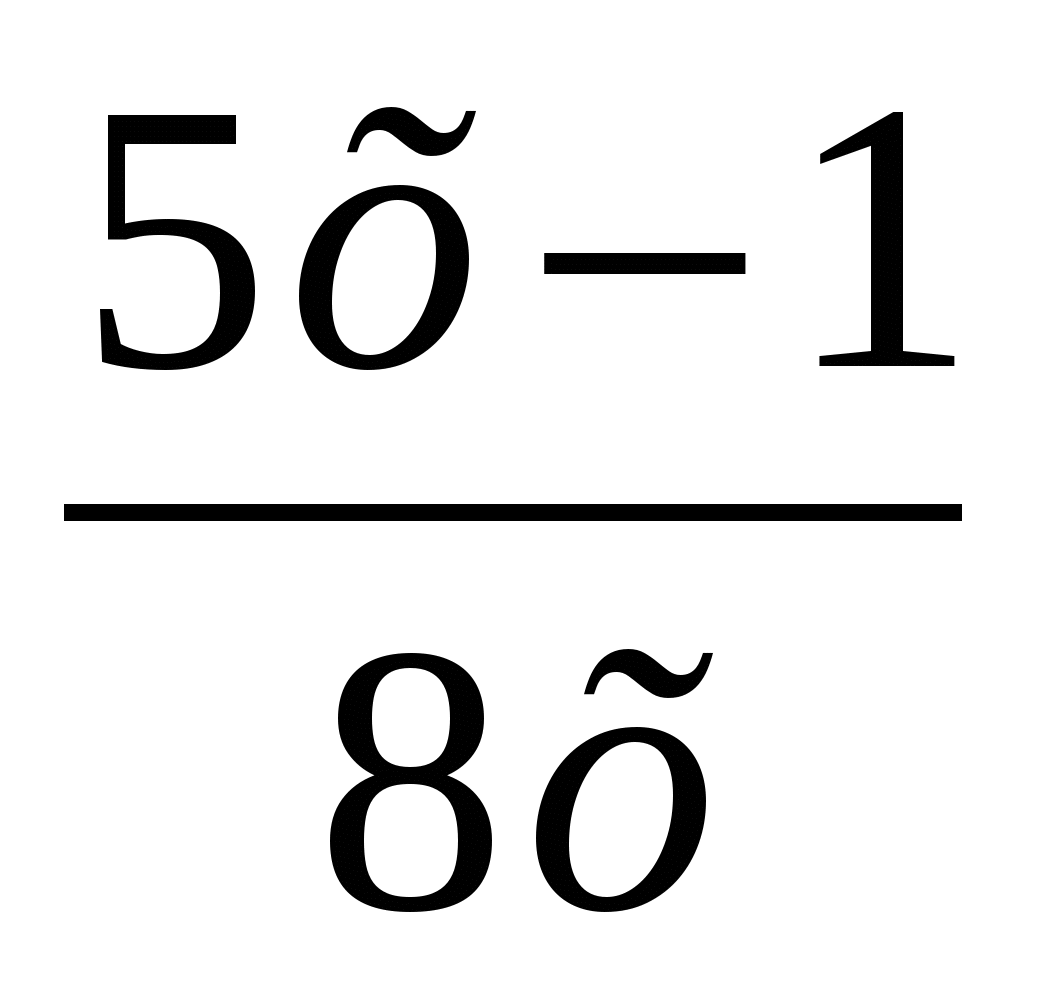
=hello_html_52dbc2d4.gif

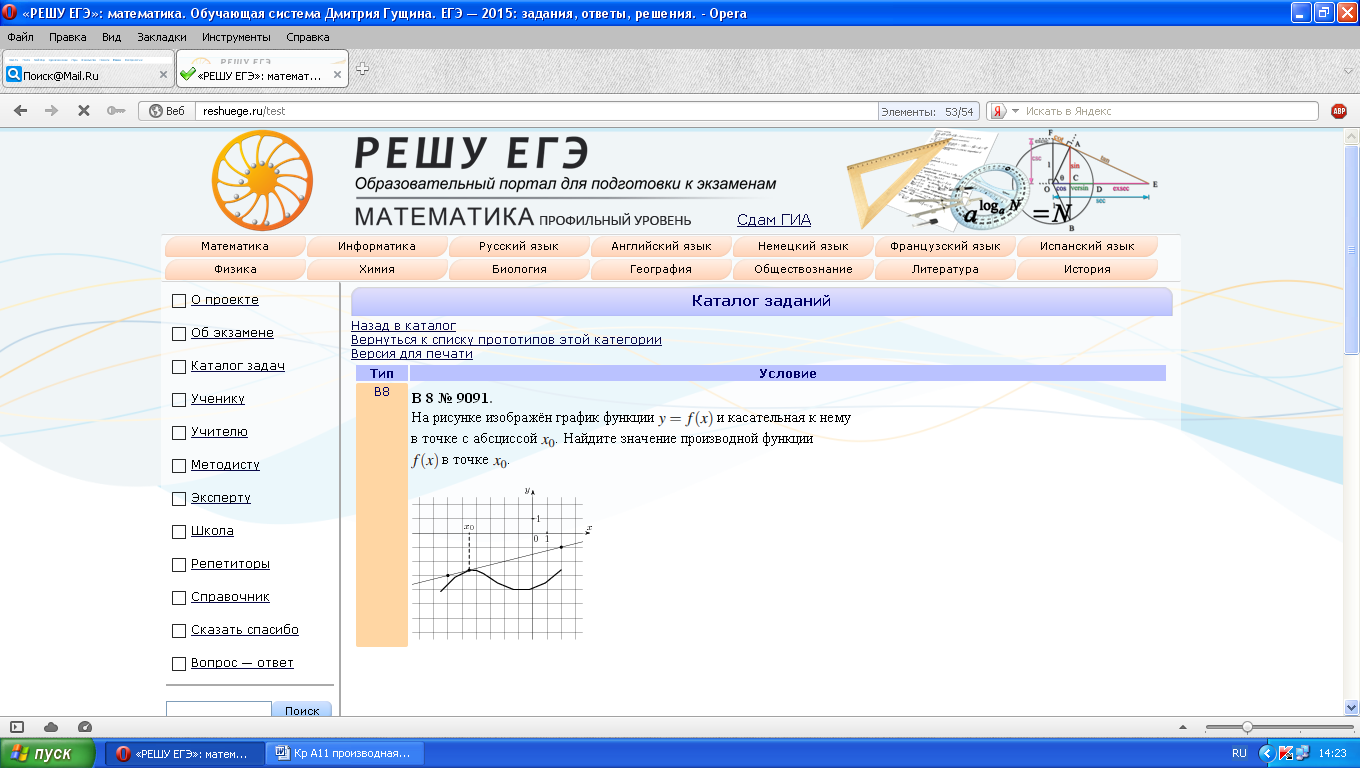
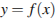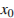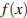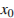  1. На ри­сун­ке изоб­ражён гра­фик функ­ции hello_html_m6f8f94dd.pngи ка­са­тель­ная к нему в точке с абс­цис­сой hello_html_m3261c831.png. Най­ди­те зна­че­ние про­из­вод­ной функ­ции hello_html_m36610309.pngв точке hello_html_m3261c831.png.

hello_html_6ff12b25.png

hello_html_m40c0cae3.png

  1. Найти значение производной в точке х0:

f(x) = 8х3 + 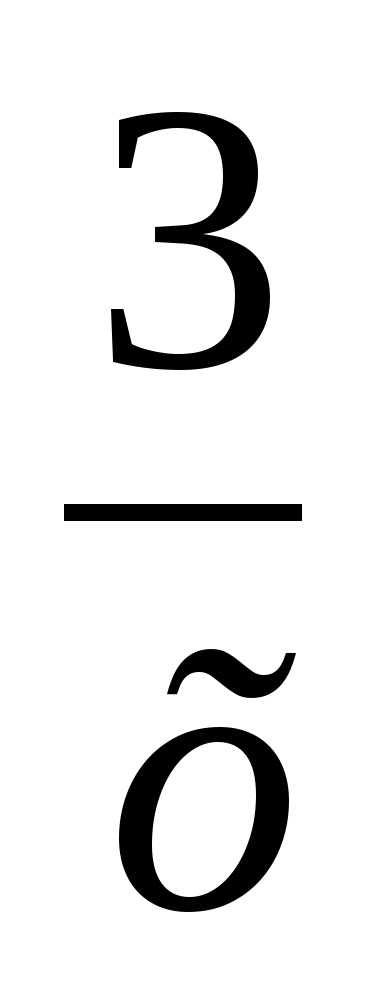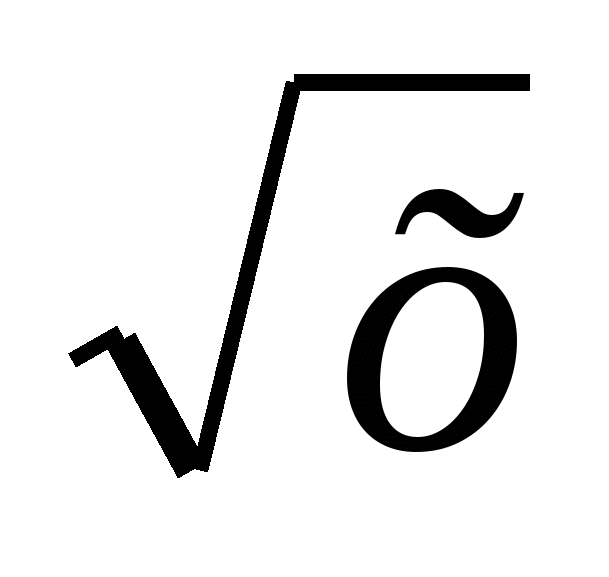hello_html_63b47fe4.gif - hello_html_652737e1.gif +67, х0 = 1

  1. Найти, при каких значениях х производная равна нулю; положительна; отрицательна.

f(x) = х3 – 3х2

  1. Записать уравнение касательной для функции в точке х0

f(x) = 2х2 + 3х + 1, х0 = -3

К.Р. «Производная степенной функции» В2 А11

  1. Найти производную функции.

Функция

Производная

Функция

Производная

а)f(x) =

х6+3х4+ 1,5

г)f(x) =

=ln (4-5х)

б)f(x) =

2х -2+4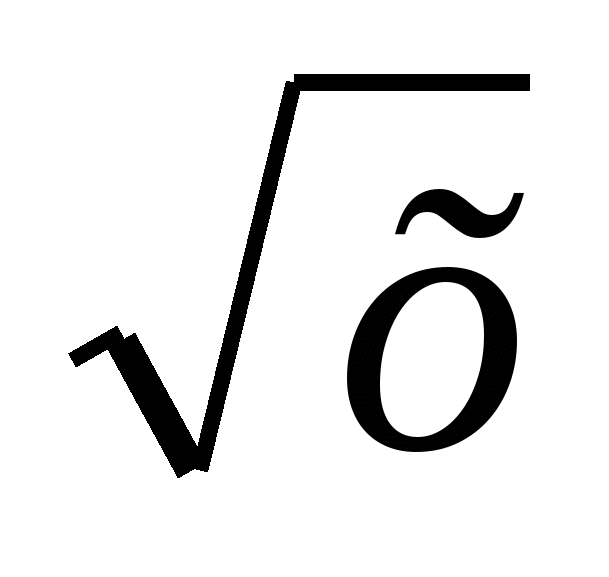hello_html_652737e1.gif

д)f(x) =

=ех(6х-2)

в)f(x) =

cos(3x+8)

е)f(x) =

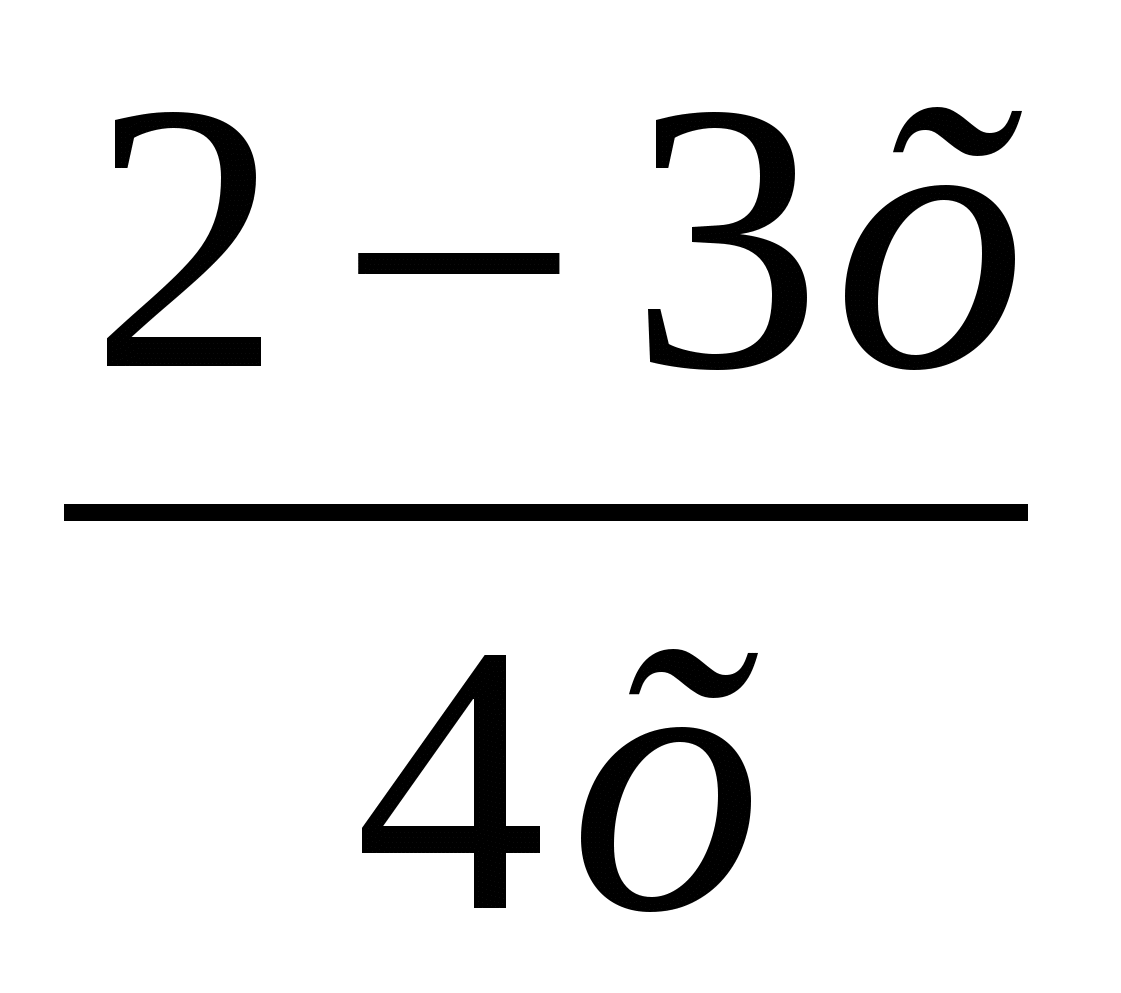
=hello_html_6c29c63d.gif

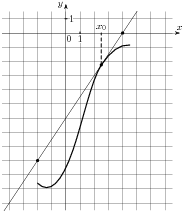
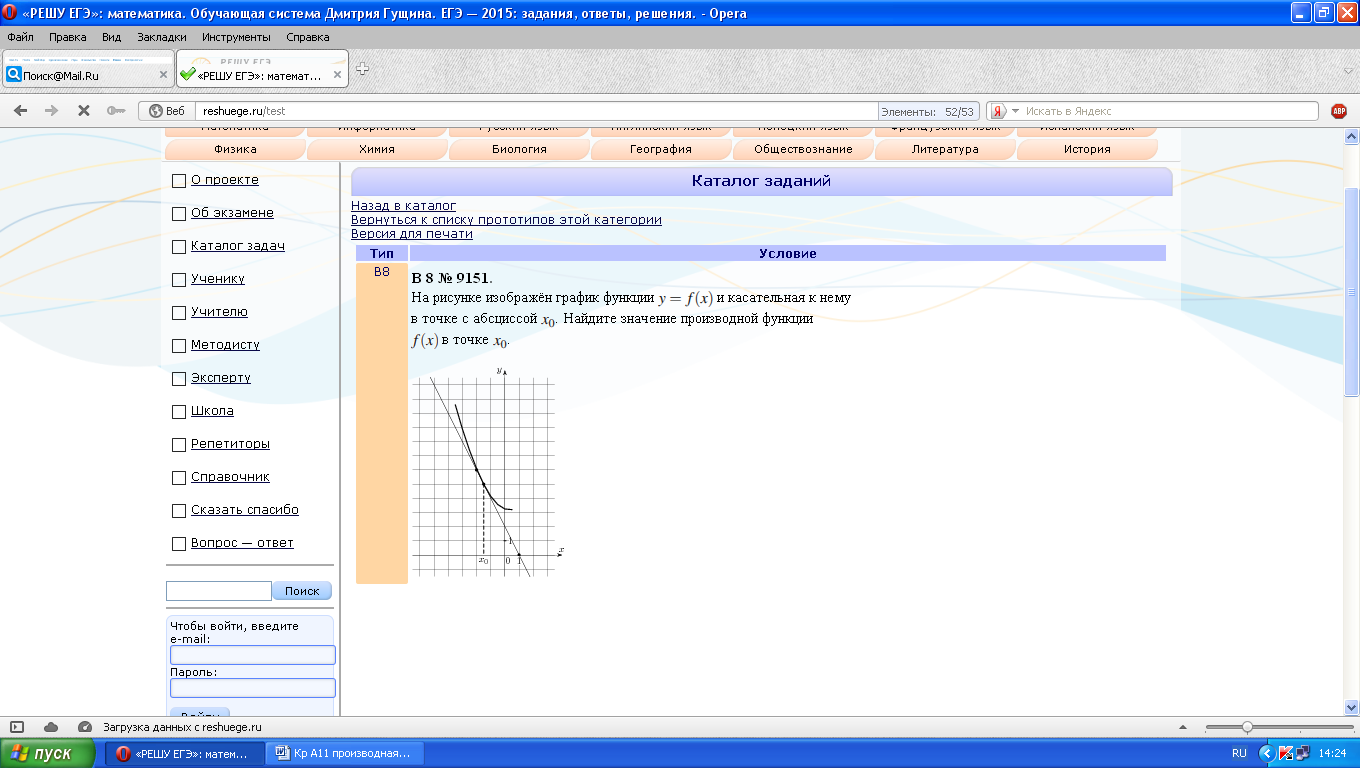
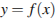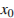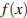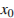  1. На ри­сун­ке изоб­ражён гра­фик функ­ции hello_html_m6f8f94dd.pngи ка­са­тель­ная к нему в точке с абс­цис­сой hello_html_m3261c831.png. Най­ди­те зна­че­ние про­из­вод­ной функ­ции hello_html_m36610309.pngв точке hello_html_m3261c831.png.

hello_html_44b018c3.png

hello_html_39694c24.png

  1. Найти значение производной в точке х0

f(x) = 5х3 + 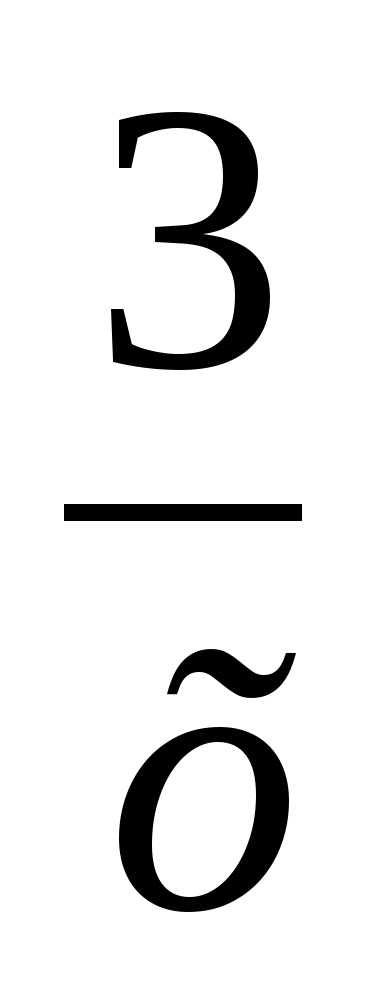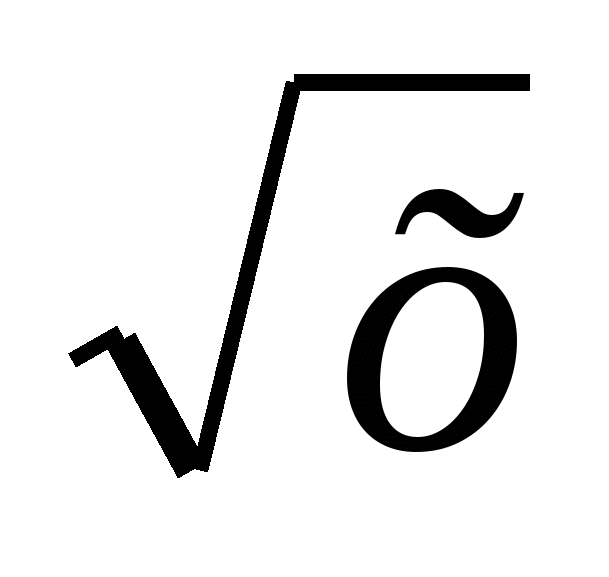hello_html_63b47fe4.gif - hello_html_652737e1.gif - 16, х0 = 1

  1. Найти, при каких значениях х производная равна нулю; положительна; отрицательна.

f(x) = х3 + 2х2

  1. Записать уравнение касательной для функции в точке х0

f(x) = 2х2 -5х + 6, х0 = -2

К.Р. «Производная степенной функции» В3 А11

  1. Найти производную функции.

Функция

Производная

Функция

Производная

а)f(x) =

2х5+4х4+ 2,9

г)f(x) =

=ln (1-2х)

б)f(x) =

3х -2+8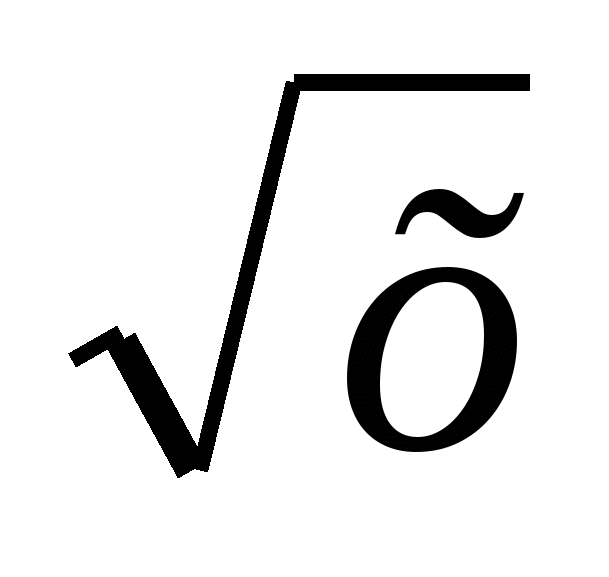hello_html_652737e1.gif

д)f(x) =

=ех(4х-2)

в)f(x) =

cos(7x-3)

е)f(x) =

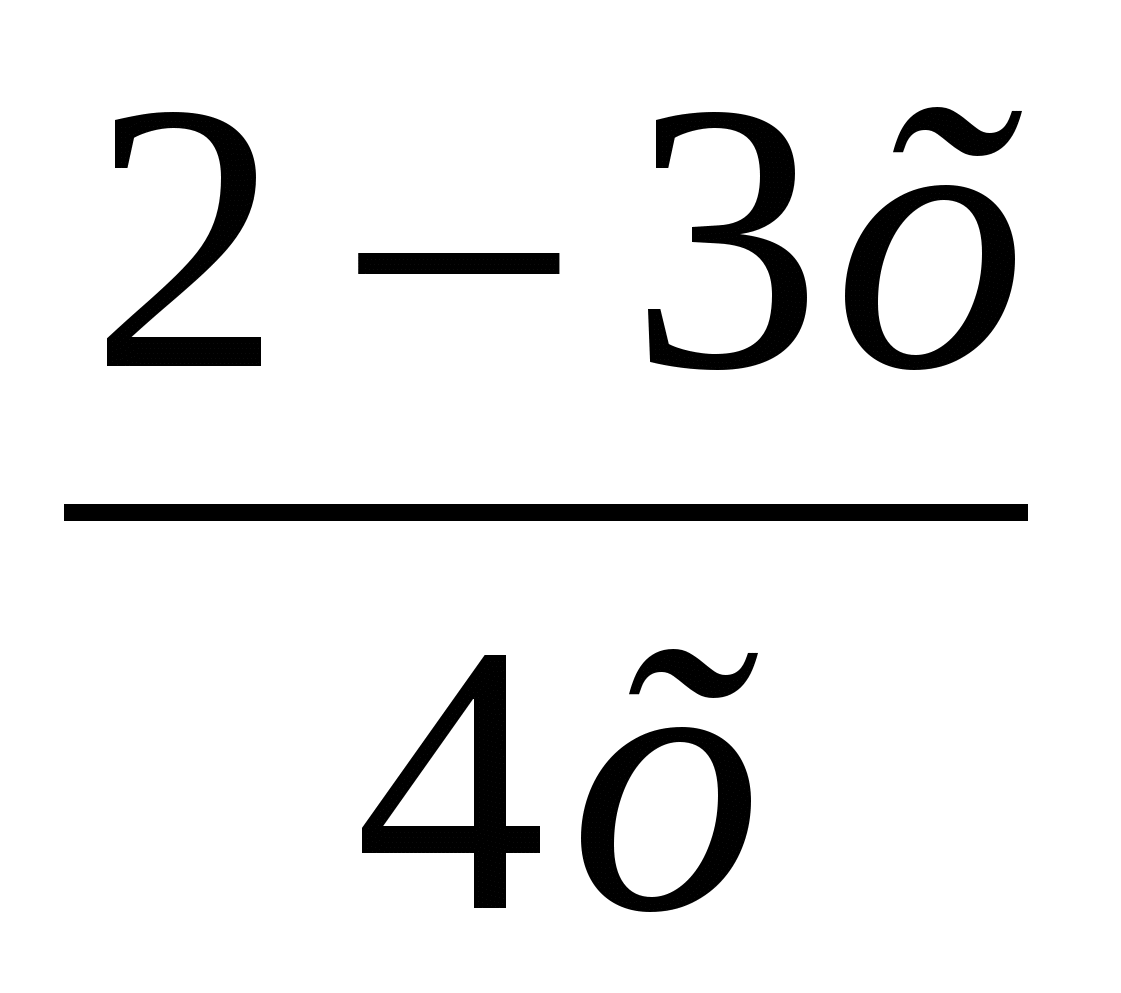
=hello_html_6c29c63d.gif

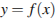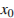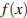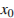  1. На ри­сун­ке изоб­ражён гра­фик функ­ции hello_html_m6f8f94dd.pngи ка­са­тель­ная к нему в точке с абс­цис­сой hello_html_m3261c831.png. Най­ди­те зна­че­ние про­из­вод­ной функ­ции hello_html_m36610309.pngв точке hello_html_m3261c831.png.

hello_html_m988556c.png

hello_html_79eb1171.png

  1. Найти значение производной в точке х0

f(x) = 2х3 + 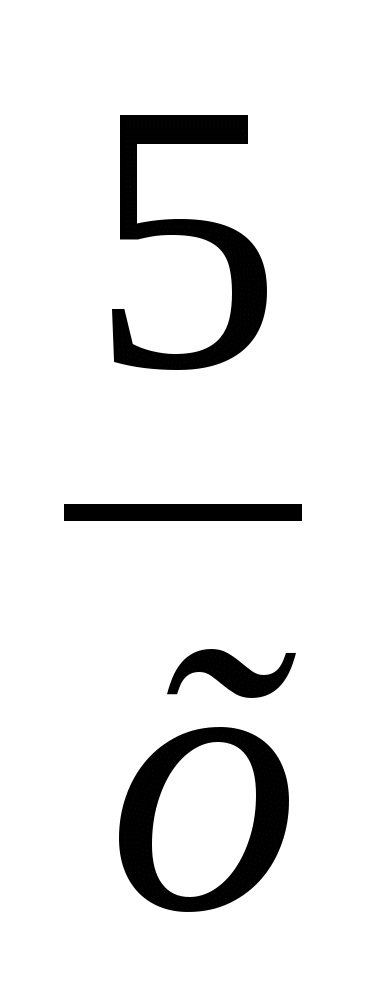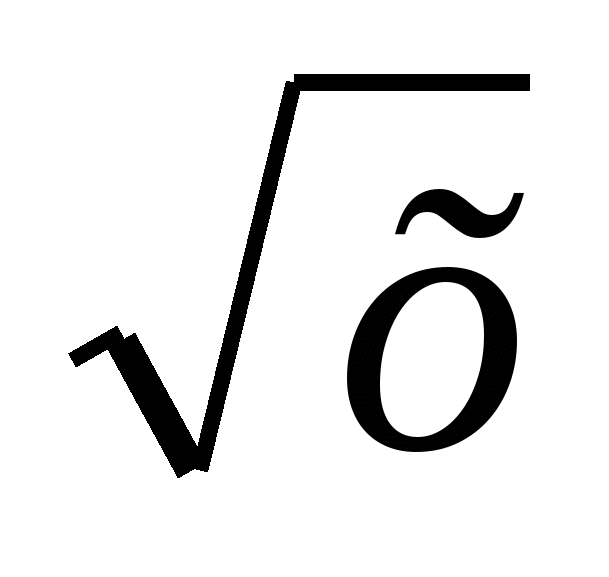hello_html_m43ade748.gif - hello_html_652737e1.gif + 24, х0 = 1

  1. Найти, при каких значениях х производная равна нулю; положительна; отрицательна.

f(x) = 2х3 - 4х2

  1. Записать уравнение касательной для функции в точке х0

f(x) = 7х2 + 3х - 4, х0 = -2

К.Р. «Производная степенной функции» В4 А11

  1. Найти производную функции.

Функция

Производная

Функция

Производная

а)f(x) =

9х2+7х3+ 9

г)f(x) =

=ln (5-4х)

б)f(x) =

2х -2+2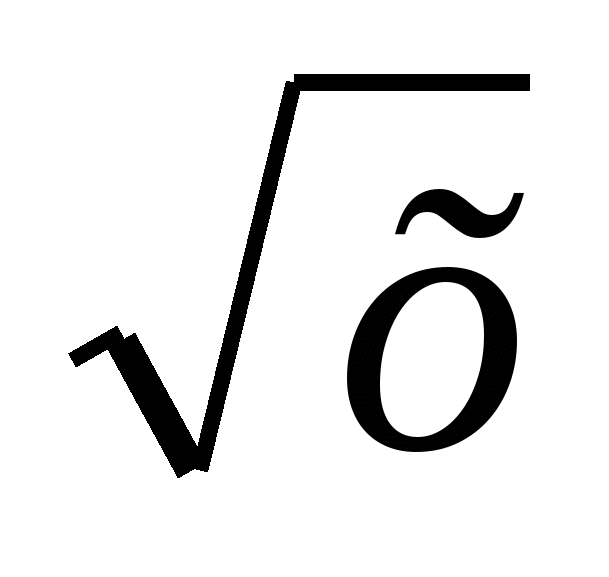hello_html_652737e1.gif

д)f(x) =

=ех(3х-1)

в)f(x) =

cos(6x-7)

е)f(x) =

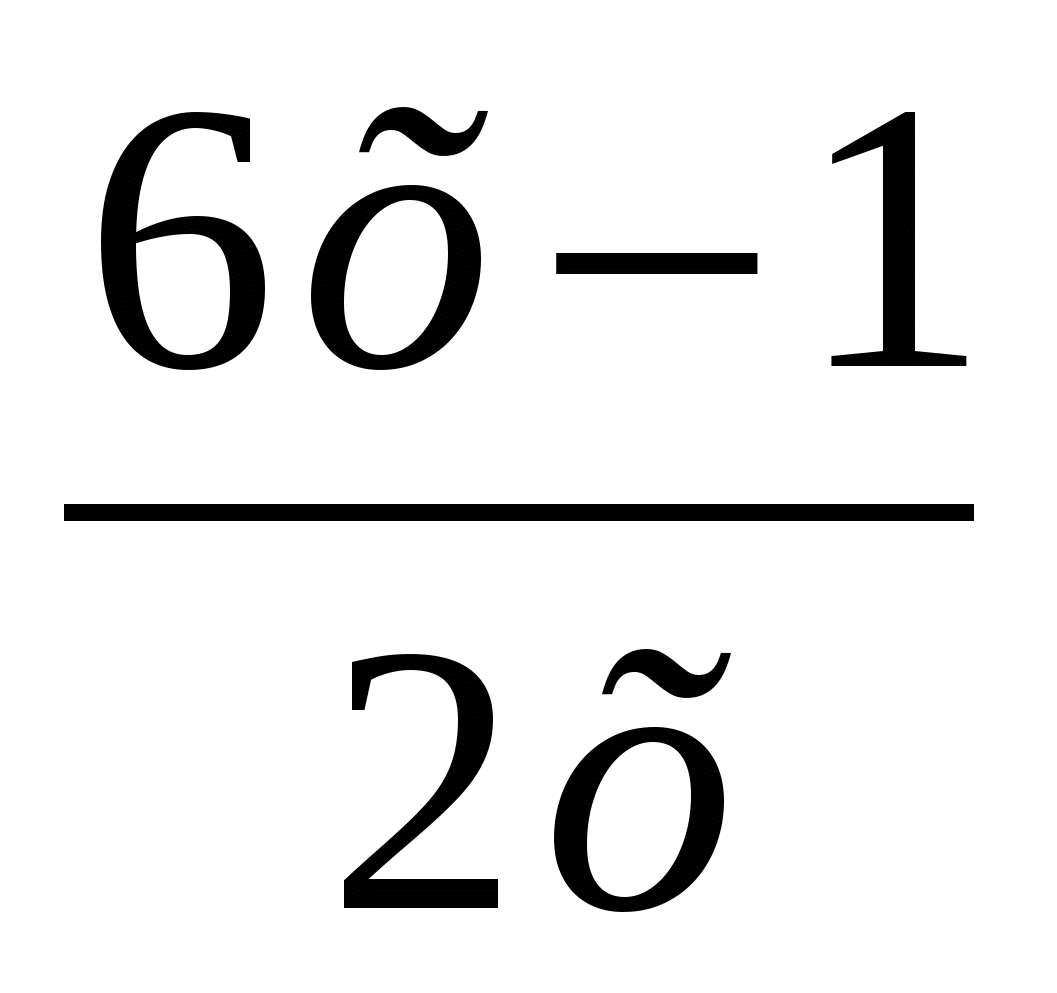
=hello_html_725e3f9a.gif

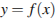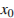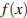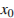  1. На ри­сун­ке изоб­ражён гра­фик функ­ции hello_html_m6f8f94dd.pngи ка­са­тель­ная к нему в точке с абс­цис­сой hello_html_m3261c831.png. Най­ди­те зна­че­ние про­из­вод­ной функ­ции hello_html_m36610309.pngв точке hello_html_m3261c831.png.

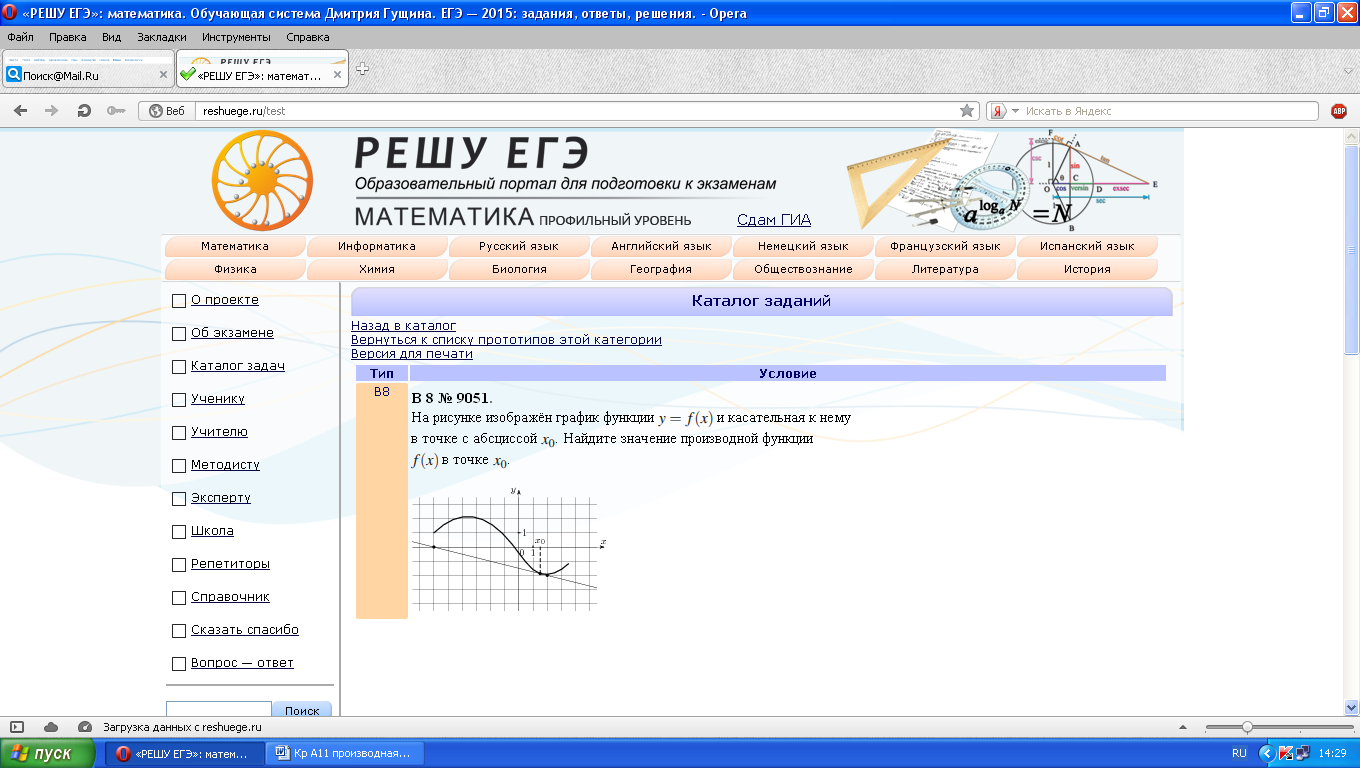
hello_html_7a39ead5.png

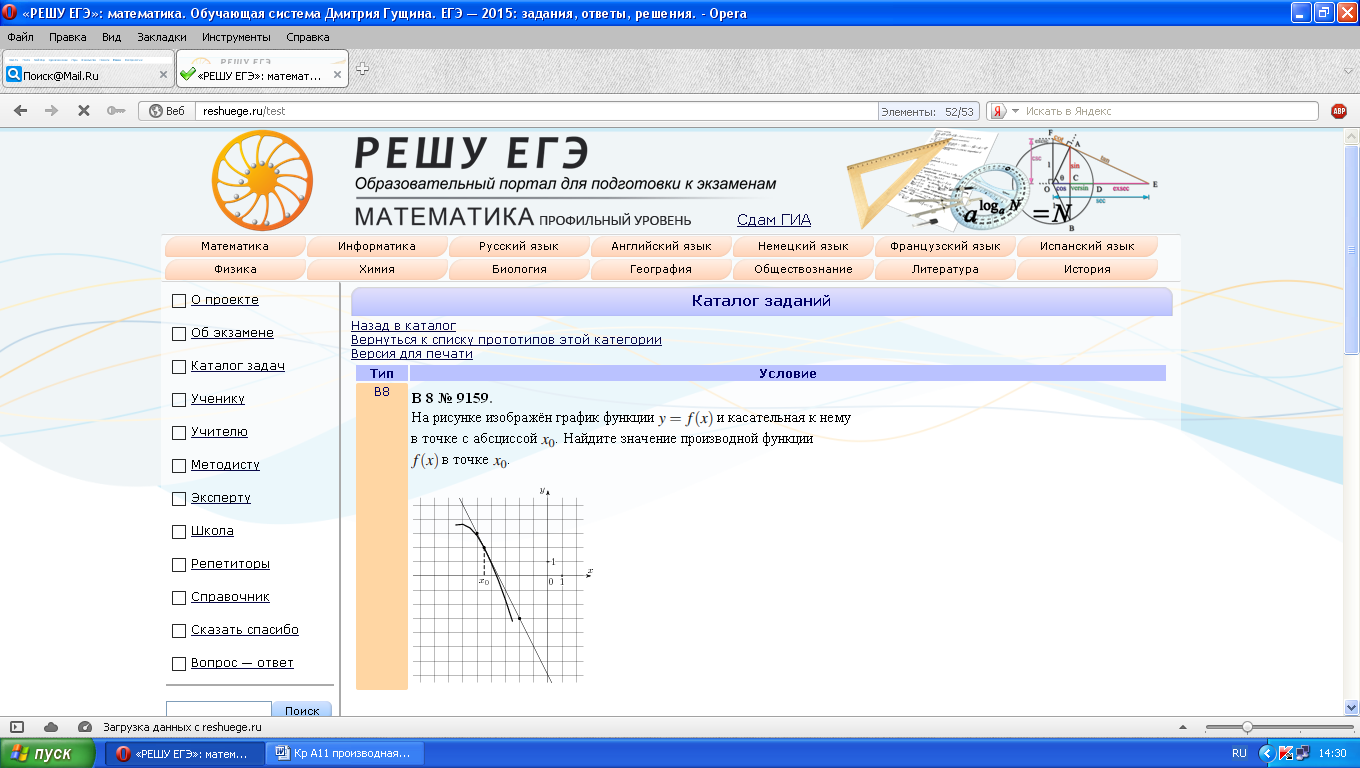
hello_html_7fdae128.png

  1. Найти значение производной в точке х0

f(x) = х3 + 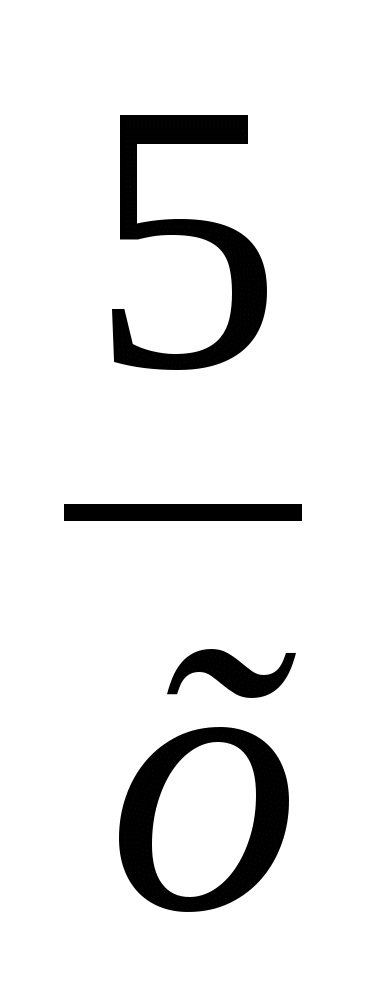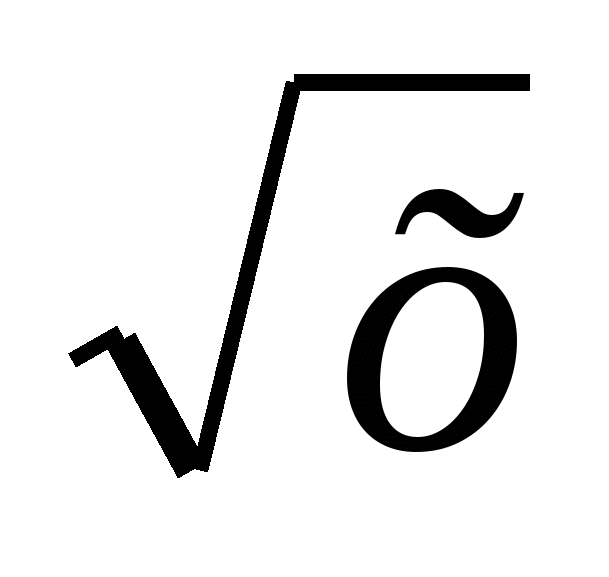hello_html_m43ade748.gif - hello_html_652737e1.gif - 5,4, х0 = 1

  1. Найти, при каких значениях х производная равна нулю; положительна; отрицательна.

f(x) = 5х3 - 2х2

  1. Записать уравнение касательной для функции в точке х0

f(x) = х2 + 5х - 11, х0 = -3

infourok.ru

Контрольная работа для 11 класса по теме "Производная"

Контрольная работа № 2 по теме «Производная».

Вариант – 1.

Часть первая.

1. Найти производную функции:

1) у = – а) у = – б) у = х2 – х

в) у = х3 – х2 г) у = 3х2 – 2х.

2) у = 0,5 х2 + 7х – 4 а) у = х + 3 б) у = х + 7

в) у = х3 + 7 г) у = х3 + 3.

3) у = (3х + 1)5 а) у = 3(3х + 1)5 б) у = 5(3х + 1)4

в) у = 15(3х + 1)4 г) у = 8(3х + 1)4.

4) у = + 3х4 а) у = + 7х3 б) у = +

в) у = + 7х3 г) у = + 12х3.

5) у = + а) у = + б) у = – + 4

в) у = 0 г) у = 4.

6) у = а) у = б) у =

в) у = г) у = ..

7) у = а) у = б) у = ( + )

в) у = ( – ) г) у = х.

8) у = а) у = б) у = –

в) у = г) у = – .

9) у = х а) у = 1 б) у = х + 1

в) у = + 1 г) у = х + 1.

10) у = а) у = – б) у = –

в) у = г) у = .

11) у = 5 а) у = б) у =

в) у = г) у = .

12) у = а) у = (х – 1) б) у =

в) у = г) у = .

Часть вторая.

1. Найти производную функции:

1) у = х5 – 3х3 + х2 – 1 2) у =

3) у = 4) у = х

2. Вычислить значение производной данной функции

у = – в точке х0 = .

3. Решить уравнение у (х) = 0, если:

1) у = (х + 4)2 (х – 9)2;

2) у = 0,5 – 0,25;

3) у = .

4. Решить неравенство у (х) + h(x) 0, если у(х) = 2х3 + 12х2,

h(х) = 9х2 + 72х.

Контрольная работа № 2 по теме «Производная».

Вариант – 2.

Часть первая.

1. Найти производную функции:

1) у = – а) у = – б) у = х3 – х2

в) у = х4 – х3 г) у = 4х3 – 3х2.

2) у = 0,5 х2 – 6х + 5 а) у = х – 6 б) у = х – 1

в) у = х3 – 1 г) у = х3 – 6.

3) у = (4х – 3)7 а) у = 28(4х – 3)6 б) у = 7(4х – 3)6

в) у = 21(4х – 3)6 г) у = 4(4х – 3)7.

4) у = 2 + х3 а) у = + 3х2 б) у = + 3x2

в) у = + г) у = + .

5) у = – а) у = 1 б) у = – –

в) у = 0 г) у = – 3.

6) у = а) у = б) у =

в) у = г) у = ..

7) у = а) у = б) у =

в) у = ( + ) г) у = ( + )

8) у = а) у = б) у = –

в) у = г) у = – .

9) у = х2 а) у = х + х б) у = 2х + х

в) у =2х + 1 г) у = х + 1.

10) у = а) у = – б) у = –

в) у = г) у = .

11) у = 4 а) у = б) у =

в) у = г) у = .

12) у = а) у = (х – 1) б) у =

в) у = г) у = .

Часть вторая.

1. Найти производную функции:

1) у = 3х7 – 6х6 – 4х3 + 5х2 + 17 2) у =

3) у = 4) у = х

2. Вычислить значение производной данной функции

у = + в точке х0 = .

3. Решить уравнение у (х) = 0, если:

1) у = (х + 7)2 (х – 8)2;

2) у = 4 + 2;

3) у = .

4. Решить неравенство у (х) – h(x) 0, если у(х) = 2х3 – 36х,

h(х) = 15х2 – 49.

Контрольная работа № 3 по теме «Применения производной».

Вариант – 1.

Часть первая.

1. Тело движется по закону s(t) = 2 + 20t – 5t2(м). В момент времени t = 1 c скорость равна …

а) 12 м/с б) 30 м/с в) 10 м/с г) другой ответ.

2. Угловой коэффициент касательной к графику функции у = в точке = равен …

а) 1 б) – 1 в) 0 г) другой ответ.

3. Критические точки функции у = – 0,5х равны …

а) 1 б) 1 в) 1; 0 г) другой ответ.

4. Функция у = – х2 + 2х – 3 убывает на промежутке …

а) (– ; + ) б) (– ; 1) в) 1; + ) г) другой ответ.

5. Функция у = 5х2 – 3х + 1 возрастает на промежутке …

а) (– ; 0,3 б) ( ; + ) в) 0,3; + ) г) – 0,3; 0,3.

6. Функция у = х3 – 6х2 имеет точки экстремумов …

а) = 4; = 0 б) = 0; = 4

в) = – 4; = 0 г) другой ответ.

7. Наибольшее и наименьшее значения функции

у = х3 – 4х на промежутке 0; 3 равны …

а) 5 ; 0 б) 5 ; 0 в) 0; – 5 г) 4; 1.

Часть вторая.

1. Тело движется по закону s(t) = 2t2 – 3t + 1 (м). Найти скорость тела в момент времени t = 3 c.

2. Найти экстремумы функции у = .

3. Найти промежутки возрастания и убывания функции

у = – х2 + 2х – 3.

4. Написать уравнение касательной к графику функции

у = х2 – 3х + 5, которая параллельна прямой у = 3х + 2.

5. Найти наибольшее и наименьшее значения функции

у = х + на промежутке 1; 3.

6. Исследовать функцию у = х3 – 3х и построить ее график.

Контрольная работа № 3 по теме «Применения производной».

Вариант – 2.

Часть первая.

1. Тело движется по закону s(t) = 3t2 + t3(м). В момент времени t = 1 c скорость равна …

а) 4 м/с б) 9 м/с в) 12 м/с г) другой ответ.

2. Угловой коэффициент касательной к графику функции у = в точке = равен …

а) 1 б) 0 в) – 1 г) другой ответ.

3. Критические точки функции у = + равны …

а) 2; 0 б) 2 в) 2 г) другой ответ.

4. Функция у = х2 – х убывает на промежутке …

а) (– ; + ) б) – 0,5; 0,5 в) (– ; – 0,5 г) (– ; 0,5.

5. Функция у = х2 – 2х + 3 возрастает на промежутке …

а) (– ; + ) б) 1; + ) в) (– ; 1) г) другой ответ.

6. Функция у = 2х3 – 3х2 имеет точки экстремумов …

а) = 0; = 1 б) = 1; = 0

в) = 0; = – 1 г) другой ответ.

7. Наибольшее и наименьшее значения функции

у = – х3 + х на промежутке – 2; 0 равны …

а) – ; – 1 б) ; – в) – ; – 2 г) ; .

Часть вторая.

1. Тело движется по закону s(t) = 3t2 – 2t + 4 (м). Найти скорость тела в момент времени t = 2 c.

2. Найти экстремумы функции у = .

3. Найти промежутки возрастания и убывания функции

у = х2 – 2х + 3.

4. Написать уравнение касательной к графику функции

у = х2 – 4х + 7, которая параллельна прямой у = 2х – 8.

5. Найти наибольшее и наименьшее значения функции

у = – х – на промежутке 1; 4.

6. Исследовать функцию у = х3 + х2 и построить ее график.

multiurok.ru

Проверочные (зачётные) работы для учащихся 10-11 классов по теме " Производная. Геометрический смысл производной. Исследование функции с помощью производной"

Проверочная работа по теме :

«Производная. Геометрический и механический смысл производной .Исследование функции с помощью

производной.»

Данная работы составлена в 4-х вариантах и предназначена для выполнения зачётных работ для учащихся как после окончания изучения темы , так и в процессе повторения и подготовки выпускников к сдаче ЕГЭ по математике.

Работа может быть использована для выполнения в класса и дома.

Каждый вариант состоит из 2-х частей :

1 часть - геометрический и механический смысл производной;

2 часть - исследование функций с помощью производной по

графику производной , физический смысл производной.

ВАРИАНТ 1

Часть 1.

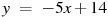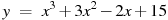1.1 Прямая hello_html_2f22566d.pngявляется касательной к графику функции hello_html_1a04983f.png. Найдите абсциссу точки касания.

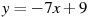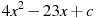1.2 Прямая hello_html_m39d41129.pngявляется касательной к графику функции hello_html_56233407.png. Найдите c.

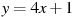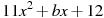1.3 Прямая hello_html_1299914f.pngявляется касательной к графику функции hello_html_e3d9bbf.png. Найдите b, учитывая, что абсцисса точки касания меньше 0.

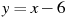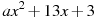1.4 Прямая hello_html_5e742a3e.pngявляется касательной к графику функции hello_html_5d385fbc.png. Найдите a.

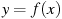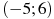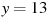1.5 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_306d3938.png. Найдите количество точек, в которых касательная к графику функции параллельна прямой hello_html_5333265b.png.

hello_html_29c18c.png

1.6 На рисунке изображены график функции 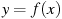hello_html_30b342ca.pngи касательная к нему в точке с абсциссой hello_html_m3f9dbcc.png. Найдите значение производной функции hello_html_4d830c3.pngв точке hello_html_m3f9dbcc.png.

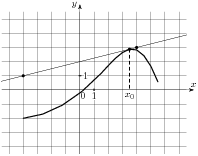
hello_html_m5e090e88.png

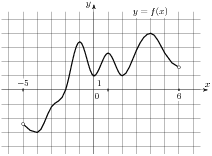
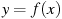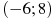1.7..На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_4aaed623.png. Найдите количество точек, в которых производная функции hello_html_4d830c3.pngравна 0 .

hello_html_4b64520e.png

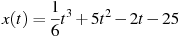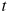1.8 Материальная точка движется прямолинейно по закону hello_html_m4c8ad83d.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 20 м/с?

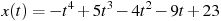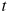1.9 Материальная точка движется прямолинейно по закону hello_html_m673cd701.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени 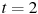hello_html_m91e7a3b.pngс.

Часть 2.

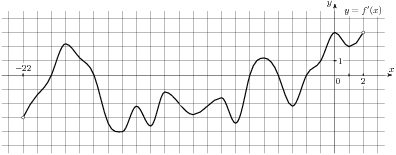
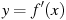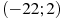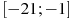2.1 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m35020d35.png. Найдите количество точек экстремума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_2472a6e1.png.

hello_html_34717181.png

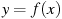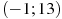2.2 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m2f9acc5f.png. Найдите сумму точек экстремума функции hello_html_4d830c3.png.

hello_html_m1ec17323.png

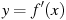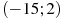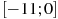2.3 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_13221f97.png. Найдите количество точек максимума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_3a5fa79f.png.

hello_html_m464176e5.png

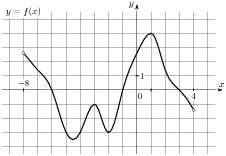
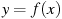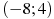2.4 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m1fdf58f7.png. Определите количество целых точек, в которых производная функции положительна.

hello_html_m6aad7b34.png

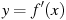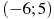2.5 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_1a39015c.png. В какой точке отрезка 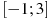hello_html_5172fb26.pngфункция hello_html_4d830c3.pngпринимает наибольшее значение?

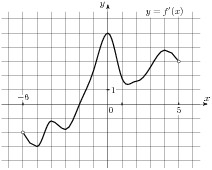
hello_html_7e266956.png

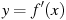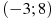2.6 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_126270e8.png. Найдите промежутки возрастания функции hello_html_4d830c3.png. В ответе укажите сумму целых точек, входящих в эти промежутки.

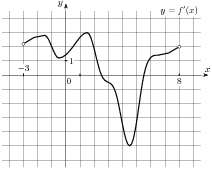
hello_html_5665ea8b.png

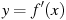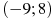2.7 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_7db3bb8f.png. Найдите промежутки убывания функции hello_html_4d830c3.png. В ответе укажите длину наибольшего из них.

hello_html_m2c50bddf.png

ВАРИАНТ 2

Часть 1.

1.1 Прямая 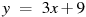hello_html_m2c973fd6.pngявляется касательной к графику функции hello_html_3376889e.png. Найдите абсциссу точки касания.

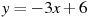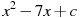1,2 Прямая hello_html_m22e79347.pngявляется касательной к графику функции hello_html_5348c59.png. Найдите c.

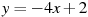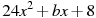1.3 Прямая hello_html_m2d8262ca.pngявляется касательной к графику функции hello_html_m74acfa05.png. Найдите b, учитывая, что абсцисса точки касания больше 0.

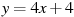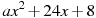1.4 .Прямая hello_html_m76b86ade.pngявляется касательной к графику функции hello_html_460d7e06.png. Найдите a.

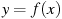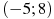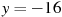1.5 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_739cafc7.png. Найдите количество точек, в которых касательная к графику функции параллельна прямой hello_html_m546dae7c.png.

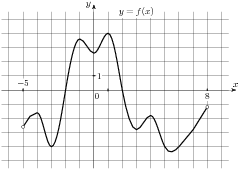
hello_html_m694dcdbd.png

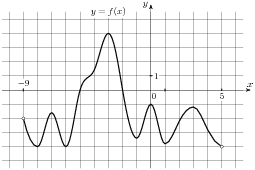
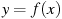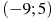1.6 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_2d246cf0.png. Найдите количество точек, в которых производная функции hello_html_4d830c3.pngравна 0 .

hello_html_66f4ce76.png

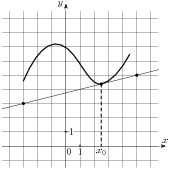
1.7. На рисунке изображены график функции 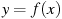hello_html_30b342ca.pngи касательная к нему в точке с абсциссой hello_html_m3f9dbcc.png. Найдите значение производной функции hello_html_4d830c3.pngв точке hello_html_m3f9dbcc.png.

hello_html_9dbbb8b.png

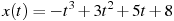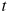1.8 Материальная точка движется прямолинейно по закону hello_html_m22d83ab3.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 8 м/с?

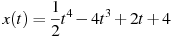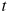1.9 Материальная точка движется прямолинейно по закону hello_html_24f7fdc.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени 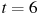hello_html_m5131a6f8.pngс.

Часть 2.

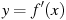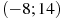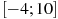2.1 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_5e13f1a.png. Найдите количество точек экстремума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_119f6d9b.png.

hello_html_3ee217a4.png

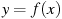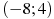2.2 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m1fdf58f7.png. Найдите сумму точек экстремума функции hello_html_4d830c3.png.

hello_html_m5f0ea7c4.png

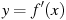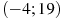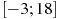2.3 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_1b17e7c5.png. Найдите количество точек максимума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_ma2dd0f0.png.

hello_html_m66e73018.png

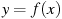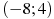2.4 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m1fdf58f7.png. Определите количество целых точек, в которых производная функции положительна.

hello_html_m6aad7b34.png

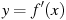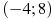2.5 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m6dfa436e.png. Найдите промежутки убывания функции hello_html_4d830c3.png. В ответе укажите сумму целых точек, входящих в эти промежутки.

hello_html_mf8eeb90.png

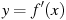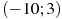2.6 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m2ce6ede0.png. В какой точке отрезка 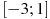hello_html_52930ec1.pngфункция hello_html_4d830c3.pngпринимает наименьшее значение?

hello_html_m18f32b21.png

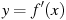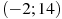2.7 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m1c1fe477.png. Найдите промежутки убывания функции hello_html_4d830c3.png. В ответе укажите длину наибольшего из них.

hello_html_57d27596.png

ВАРИАНТ 3

Часть 1.

1.1 Прямая 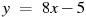hello_html_2c1a5a9b.pngпараллельна касательной к графику функции 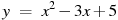hello_html_35a5fd04.png. Найдите абсциссу точки касания

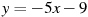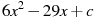1.2 Прямая hello_html_m54da2eb6.pngявляется касательной к графику функции hello_html_7652e0a1.png. Найдите c.

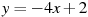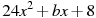1.3 Прямая hello_html_m2d8262ca.pngявляется касательной к графику функции hello_html_m74acfa05.png. Найдите b, учитывая, что абсцисса точки касания больше 0.

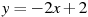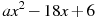1.4 Прямая hello_html_m3d1b6ac3.pngявляется касательной к графику функции hello_html_m75c2607c.png. Найдите a.

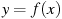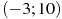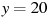1.5 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m289fb558.png. Найдите количество точек, в которых касательная к графику функции параллельна прямой hello_html_m492f4031.png.

hello_html_2becdc76.png

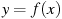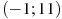1.6 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m37fa9fdf.png. Найдите количество точек, в которых производная функции hello_html_4d830c3.pngравна 0 .

hello_html_58f627f6.png

1.7 На рисунке изображены график функции 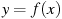hello_html_30b342ca.pngи касательная к нему в точке с абсциссой hello_html_m3f9dbcc.png. Найдите значение производной функции hello_html_4d830c3.pngв точке hello_html_m3f9dbcc.png.

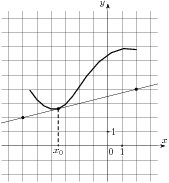
hello_html_m2100b084.png

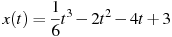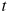1.8 Материальная точка движется прямолинейно по закону hello_html_2c688e69.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 38 м/с?

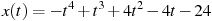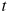1.9 Материальная точка движется прямолинейно по закону hello_html_m545da7dc.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени 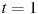hello_html_m14e5383.pngс.

Часть 2.

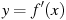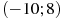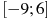2.1 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_4a8933c4.png. Найдите количество точек максимума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_7ceb7ca8.png.

hello_html_m83f042c.png

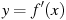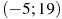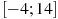2.2 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m301ea8b6.png. Найдите количество точек экстремума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_m32ad2fe2.png.

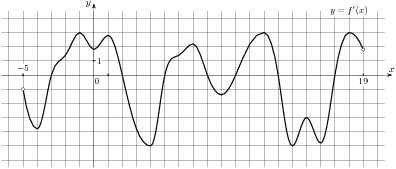
hello_html_m518b4415.png

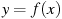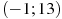2.3 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m2f9acc5f.png. Найдите сумму точек экстремума функции hello_html_4d830c3.png.

hello_html_m1ec17323.png

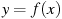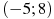2.4 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_739cafc7.png. Определите количество целых точек, в которых производная функции отрицательна.

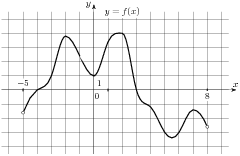
hello_html_m28d32d21.png

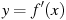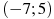2.5 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_me59aed2.png. Найдите промежутки убывания функции hello_html_4d830c3.png. В ответе укажите сумму целых точек, входящих в эти промежутки.

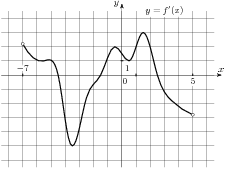
hello_html_m29425ee6.png

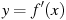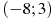2.6 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_406e069f.png. В какой точке отрезка 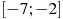hello_html_5f642a7f.pngфункция hello_html_4d830c3.pngпринимает наименьшее значение?

hello_html_e517e50.png

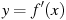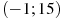2.7 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m7c4a1b90.png. Найдите промежутки возрастания функции hello_html_4d830c3.png. В ответе укажите длину наибольшего из них.

hello_html_1ea90e92.png

ВАРИАНТ 4

Часть 1.

1.1 Прямая 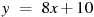hello_html_m47c62a73.pngпараллельна касательной к графику функции 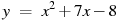hello_html_38cbb69c.png. Найдите абсциссу точки касания.

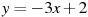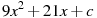1.2 Прямая hello_html_5ad534e0.pngявляется касательной к графику функции hello_html_1acd6c91.png. Найдите c.

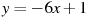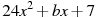1.3 Прямая hello_html_5b32baa8.pngявляется касательной к графику функции hello_html_3b1db0c3.png. Найдите b, учитывая, что абсцисса точки касания меньше 0.

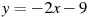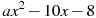1.4 Прямая hello_html_35472028.pngявляется касательной к графику функции hello_html_1cfc98cc.png. Найдите a.

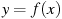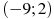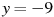1.5 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_7e5a30bf.png. Найдите количество точек, в которых касательная к графику функции параллельна прямой hello_html_m4591acd5.png.

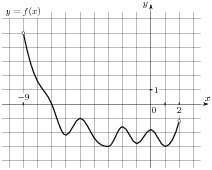
hello_html_m39d0ee63.png

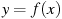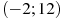1.6 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m74cb8863.png. Найдите количество точек, в которых производная функции hello_html_4d830c3.pngравна 0 .

hello_html_m7aeb64f4.png

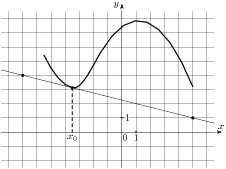
1.7 На рисунке изображены график функции 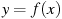hello_html_30b342ca.pngи касательная к нему в точке с абсциссой hello_html_m3f9dbcc.png. Найдите значение производной функции hello_html_4d830c3.pngв точке hello_html_m3f9dbcc.png.

hello_html_7f6d399e.png

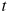1.8 Материальная точка движется прямолинейно по закону hello_html_m157c2335.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?

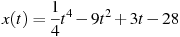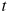1.9 Материальная точка движется прямолинейно по закону hello_html_3984d0df.png, где hello_html_m70662fb5.png — расстояние от точки отсчета в метрах, hello_html_74e3654b.png — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени 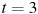hello_html_m75c585b2.pngс.

Часть2.

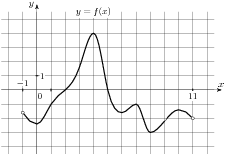
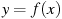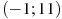2.1 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m37fa9fdf.png. Найдите сумму точек экстремума функции hello_html_4d830c3.png.

hello_html_m221f7106.png

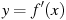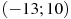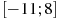2.2 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m56fff8a6.png. Найдите количество точек экстремума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_33929d79.png.

hello_html_m53102d00.png

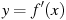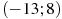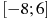2.3 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m423589f9.png. Найдите количество точек максимума функции hello_html_4d830c3.png, принадлежащих отрезку hello_html_62d0da87.png.

hello_html_m52d02a4d.png

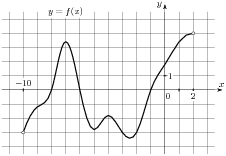
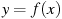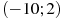2.4 На рисунке изображен график функции hello_html_30b342ca.png, определенной на интервале hello_html_m3a78f9f8.png. Определите количество целых точек, в которых производная функции отрицательна.

hello_html_m10b42d1f.png

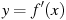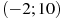2.5 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m65963c6d.png. Найдите промежутки возрастания функции hello_html_4d830c3.png. В ответе укажите сумму целых точек, входящих в эти промежутки.

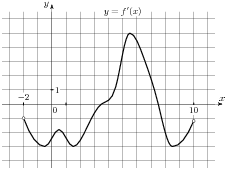
hello_html_m487e4ef7.png

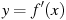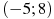2.6 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_739cafc7.png. В какой точке отрезка 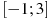hello_html_5172fb26.pngфункция hello_html_4d830c3.pngпринимает наибольшее значение?

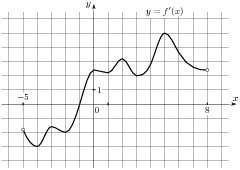
hello_html_181984f7.png

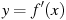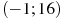2.7 На рисунке изображен график hello_html_m74a1e876.png — производной функции hello_html_4d830c3.png, определенной на интервале hello_html_m266c17d1.png. Найдите промежутки возрастания функции hello_html_4d830c3.png. В ответе укажите длину наибольшего из них.

hello_html_m2ecbfb6b.png

infourok.ru

Смотрите также