Контрольные работы по начертательной геометрии составлены с учетом требований государственного образовательного стандарта высшего профессионального образования к минимуму содержания и уровню подготовки выпускников технических специальностей. Контрольные работы №1, 2 выполняются студентом во втором семестре.
Контрольная работа №1
Контрольная работа №1 состоит из 5 задач.
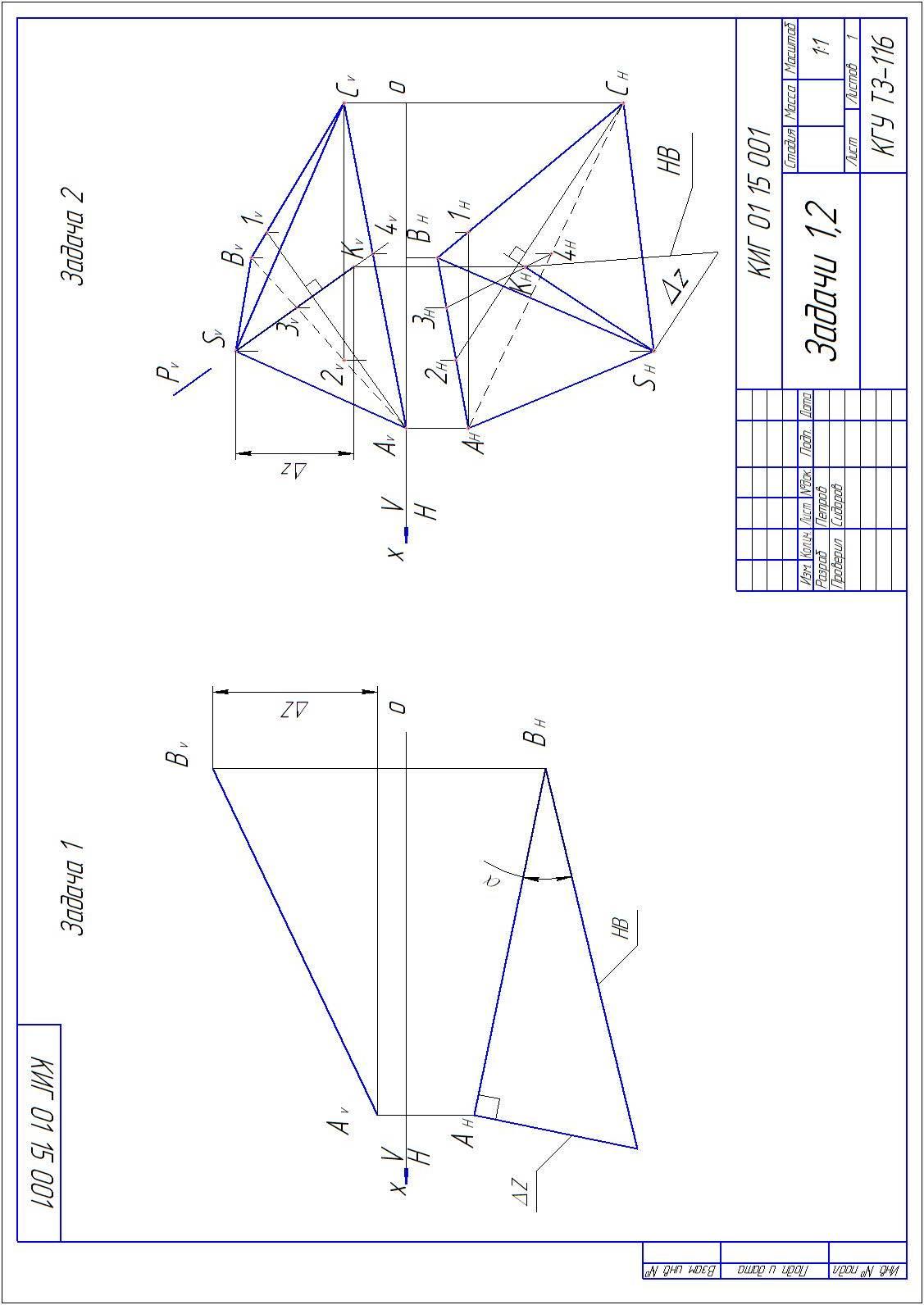
Задача 1
Построить проекции отрезка прямой. Данные выбираются из таблицы 1.
Методические указания
Задача решается способом прямоугольного треугольника.
Следует вспомнить построение прямоугольного треугольника, у которого гипотенуза является натуральной величиной отрезка, один из катетов – это проекция отрезка на какую-либо плоскость, а другой катет – это разница расстояний концов отрезка (DZ или DY) до этой плоскости. Также следует помнить, что в прямоугольном треугольнике против катета DZ лежит угол a, а против катета DY лежит угол b. Пример решения задачи приведен на рисунке 4.
Таблица 1
| № варианта | Условие задачи |
| 0 | Определить натуральную величину отрезка АВ и угол его наклона к плоскости проекций Н. Точка А имеет координаты ( 120, 60, 50), а точка В лежит на оси Х на расстоянии 20 мм от профильной плоскости проекций. |
| 1 | Построить горизонтальную проекцию отрезка прямой [MN] с натуральной величиной, равной 120 мм. Точка М лежит на оси Y на расстоянии 10 мм от плоскости V, а точка N имеет координаты (130, ? , 25). |
| 2 | Построить горизонтальную проекцию отрезка [AB], проходящего через точку А(5, 15, 10), с углом наклона 30º к плоскости V. Точка В расположена на расстоянии 30 мм от плоскости Н и 130 мм от плоскости W. |
| 3 | Определить натуральную величину отрезка прямой [NK] и углы его наклона к плоскостям проекций H и V. Точка N расположена на плоскости V на расстоянии 25 мм от плоскости Н и 20 мм от плоскости W, а точка К имеет координаты (125, 40, 55). |
Продолжение таблицы 1
| 4 | Построить фронтальную проекцию отрезка прямой [CD] с углом наклона 35º к плоскости проекций Н. Точка D расположена на расстоянии 50 мм от плоскости V и 110 мм от плоскости W, а точка С расположена на оси Z на расстоянии 15 мм от плоскости Н. |
| 5 | Построить горизонтальную проекцию отрезка прямой [NC] с углом 30º к плоскости V, если точка С имеет координаты (125, ?, 30), а точка N расположена на оси Z на расстоянии 10 мм от плоскости Н. |
| 6 | Определить натуральную величину отрезка [CK] и углы его наклона к плоскостям проекций H и V. Точка С расположена на оси Х на расстоянии 25 мм от плоскости проекций W, а точка К имеет координаты (130, 40, 40). |
| 7 | Построить фронтальную проекцию отрезка [BC], проходящего через точку К, с углом наклона 25º к плоскости Н по заданной горизонтальной проекции этого отрезка: В(120, 5, ?), С(0, 20, ?). Точка К расположена на расстоянии 30 мм от горизонтальной плоскости проекций и 10 мм от профильной плоскости проекций. |
| 8 | Построить горизонтальную проекцию отрезка прямой [CK] с углом наклона 30º к фронтальной плоскости проекций. Точка С имеет координаты (90, 20, 10), а точка К расположена на расстоянии 30 мм от горизонтальной плоскости проекций и 5 мм от профильной плоскости проекций. |
| 9 | Определить натуральную величину отрезка [MN] и углы его наклона к плоскостям проекций H и V. Точка М имеет координаты (120, 60, 60), а точка N расположена на оси Z на расстоянии 20 мм от плоскости Н. |
| 10 | Построить фронтальную проекцию отрезка прямой [NC] с натуральной величиной, равной 135 мм. Точка N расположена на плоскости V на расстоянии 20 мм от плоскости Н и 135 мм от плоскости W, а для точки С дана горизонтальная проекция с координатами: Х= 15, Y= 10. |
| 11 | Построить горизонтальную проекцию отрезка прямой [NK] с углом наклона 25º к плоскости V. Точка К имеет координаты (100, ?, 65), а точка N расположена на оси Z на расстоянии 10 мм от плоскости Н. |
| 12 | Построить фронтальную проекцию отрезка прямой [AB] с натуральной величиной, равной 120 мм. Точка А расположена на оси Х на расстоянии 130 мм от плоскости W, а точка В имеет координаты (25, 30, ?). |
| 13 | Построить фронтальную проекцию отрезка прямой [CD] с углом наклона 30º к плоскости Н. Точка С расположена на оси Y на расстоянии 15 мм от плоскости V, а точка D имеет координаты (120, 50, ?). |
| 14 | Построить горизонтальную проекцию отрезка прямой [АC] с углом наклона 30º к плоскости V. Точка А имеет координаты (100, ?, 40), а точка С расположена на оси Х на расстоянии 15 мм от плоскости W. |
| 15 | Определить натуральную величину отрезка прямой [EM] и углы его наклона к плоскостям V и H. Точка Е имеет координаты (105, 35, 50), а точка М расположена на оси Y на расстоянии 10 мм от плоскости V. |
| 16 | Построить фронтальную проекцию отрезка прямой [КМ] с углом наклона 30º к плоскости Н. Точка М имеет координаты (10,10,5). Точка К расположена на расстоянии 50 мм от плоскости V и 100 мм от плоскости W. |
| 17 | Построить горизонтальную проекцию отрезка прямой [АВ] с натуральной величиной 110 мм. Точка А расположена на расстоянии 15 мм от плоскости Н и 10 мм от плоскости W. Точка В имеет координаты (100, 15, 55). |
| 18 | Определить натуральную величину отрезка прямой [CD]. Точка С имеет координаты (115, 55, 30), а точка D расположена на оси Х на расстоянии 10 мм от плоскости W. |
Рисунок 4
Задача 2
Определить высоту пирамиды. Основание пирамиды – треугольник АВС. Точка S – вершина пирамиды. Исходные данные взять из таблицы 2.
Задачу следует решать, не используя способы преобразования проекций.
Определить видимость ребер пирамиды, считая, что грани непрозрачны.
Методические указания
При решении этой задачи без преобразования проекций студент должен продемонстрировать знание основных определений и теорем начертательной геометрии.
Видимость ребер пирамиды определяется с помощью конкурирующих точек. Следует вспомнить из школьной программы определение перпендикулярности прямой к плоскости.
Необходимо уметь строить главные линии плоскости – горизонталь, фронталь.
Для построения проекций высоты пирамиды студент должен уметь использовать теорему о прямом угле.
Чтобы найти основание высоты пирамиды, следует использовать алгоритм нахождения точки пересечения прямой с плоскостью.
Натуральную величину высоты пирамиды определить способом прямоугольного треугольника.
Пример решения задачи 2 приведен на рисунке 4
Таблица 2
| № вар. | A | B | C | S | ||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | |
| 0 | ||||||||||||
| 1 | 20 | 10 | 40 | 80 | 50 | 0 | 40 | 0 | 70 | 35 | 65 | 10 |
| 2 | 15 | 40 | 10 | 80 | 0 | 10 | 45 | 60 | 35 | 50 | 35 | 65 |
| 3 | 80 | 10 | 40 | 25 | 70 | 60 | 10 | 25 | 15 | 60 | 60 | 0 |
| 4 | 70 | 40 | 10 | 25 | 40 | 40 | 10 | 0 | 0 | 55 | 10 | 55 |
| 5 | 20 | 20 | 40 | 80 | 50 | 10 | 55 | 80 | 65 | 70 | 10 | 55 |
| 6 | 20 | 50 | 10 | 90 | 65 | 40 | 100 | 20 | 0 | 50 | 0 | 50 |
| 7 | 100 | 40 | 75 | 5 | 10 | 40 | 70 | 60 | 10 | 35 | 55 | 75 |
| 8 | 30 | 50 | 5 | 90 | 50 | 25 | 10 | 15 | 40 | 40 | 90 | 65 |
| 9 | 35 | 0 | 50 | 80 | 20 | 35 | 10 | 25 | 10 | 50 | 65 | 80 |
| 10 | 95 | 10 | 55 | 15 | 15 | 40 | 50 | 40 | 85 | 70 | 75 | 10 |
| 11 | 30 | 0 | 50 | 100 | 25 | 40 | 10 | 40 | 15 | 50 | 70 | 60 |
| 12 | 20 | 50 | 0 | 90 | 35 | 20 | 10 | 20 | 40 | 50 | 60 | 80 |
| 13 | 60 | 45 | 15 | 5 | 30 | 35 | 85 | 0 | 45 | 60 | 85 | 70 |
| 14 | 15 | 30 | 60 | 95 | 10 | 20 | 70 | 50 | 0 | 80 | 70 | 50 |
| 15 | 20 | 30 | 60 | 80 | 10 | 15 | 40 | 55 | 15 | 90 | 65 | 60 |
| 16 | 90 | 50 | 40 | 20 | 10 | 20 | 20 | 40 | 60 | 55 | 0 | 75 |
| 17 | 0 | 25 | 15 | 85 | 10 | 35 | 35 | 50 | 60 | 70 | 40 | 0 |
| 18 | 60 | 60 | 30 | 20 | 20 | 10 | 35 | 0 | 50 | 0 | 60 | 55 |
Задача 3
Построить линию пересечения двух треугольников АВС и DEK. Определить видимость сторон треугольников в проекциях.
Определить натуральную величину треугольника АВС способом плоскопараллельного перемещения. Данные для своего варианта взять из таблицы 3.
Методические указания к решению задачи
В левой половине листа формата А3 намечается ось Х, и строятся по координатам проекции двух треугольников. Линию пересечения треугольников строят по двум точкам, принадлежащим этой линии. Эти точки можно найти, дважды решив задачу на пересечение стороны одного треугольника с плоскостью другого, используя вспомогательные секущие проецирующие плоскости. В задаче 2 было подобное решение, когда определялась точка пересечения высоты пирамиды с её основанием. Проецирующие плоскости можно проводить через любые стороны треугольников, но следует подобрать эти плоскости таким образом, чтобы точка пересечения стороны одного треугольника с другим треугольником оказалась внутри формата.
Способом конкурирующих точек определяется видимость сторон треугольников на каждой проекции.
Для определения натуральной величины треугольника АВС следует использовать способ плоскопараллельного перемещения. Сначала треугольник АВС приводится в положение проецирующей плоскости. Для этого используется горизонталь или фронталь плоскости. В приведенном примере использована горизонталь А-1. Далее вращением вокруг проецирующей прямой треугольник АВС переводят в такое положение, когда он становится параллельным плоскости проекций Н (А´V В´V С ´V || Х ). На плоскости Н проекция треугольника А´н В´н С´н будет натуральной величиной.
Пример решения задачи 3 приведен на рисунке 5
Таблица 3
| № ва- риан- та | А | В | С | D | E | K | ||||||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | x | y | z | x | y | z | |
| 0 | 20 | 10 | 40 | 85 | 80 | 110 | 135 | 50 | 45 | 65 | 85 | 20 | 0 | 35 | 110 | 120 | 0 | 80 |
| 1 | 20 | 40 | 10 | 80 | 110 | 80 | 135 | 45 | 50 | 60 | 20 | 80 | 0 | 105 | 30 | 35 | 80 | 0 |
| 2 | 115 | 10 | 40 | 50 | 80 | 110 | 0 | 50 | 45 | 65 | 85 | 20 | 95 | 35 | 110 | 15 | 0 | 75 |
| 3 | 110 | 40 | 10 | 50 | 105 | 80 | 0 | 45 | 50 | 70 | 20 | 85 | 95 | 110 | 35 | 10 | 80 | 0 |
| 4 | 20 | 10 | 40 | 85 | 80 | 110 | 125 | 50 | 50 | 70 | 85 | 20 | 0 | 35 | 110 | 115 | 10 | 75 |
| 5 | 15 | 45 | 10 | 85 | 110 | 80 | 135 | 45 | 55 | 70 | 20 | 80 | 0 | 110 | 30 | 120 | 80 | 0 |
| 6 | 120 | 40 | 75 | 50 | 105 | 10 | 0 | 50 | 40 | 95 | 20 | 0 | 70 | 110 | 50 | 20 | 80 | 85 |
| 7 | 115 | 35 | 70 | 55 | 110 | 5 | 0 | 45 | 40 | 90 | 25 | 0 | 70 | 105 | 45 | 15 | 80 | 85 |
| 8 | 15 | 75 | 40 | 80 | 5 | 100 | 130 | 40 | 45 | 0 | 20 | 0 | 45 | 110 | 120 | 115 | 85 | 80 |
| 9 | 20 | 15 | 90 | 85 | 80 | 25 | 130 | 50 | 80 | 75 | 85 | 95 | 0 | 30 | 15 | 120 | 0 | 50 |
| 10 | 15 | 10 | 85 | 80 | 80 | 20 | 130 | 50 | 75 | 70 | 80 | 90 | 0 | 35 | 20 | 110 | 0 | 45 |
| 11 | 120 | 90 | 10 | 50 | 20 | 75 | 0 | 80 | 45 | 70 | 95 | 85 | 90 | 30 | 20 | 15 | 0 | 50 |
| 12 | 115 | 90 | 10 | 50 | 25 | 80 | 0 | 80 | 45 | 65 | 95 | 80 | 95 | 20 | 35 | 5 | 50 | 0 |
| 13 | 15 | 90 | 10 | 85 | 25 | 80 | 135 | 85 | 50 | 65 | 95 | 85 | 0 | 20 | 35 | 120 | 55 | 0 |
| 14 | 20 | 10 | 85 | 85 | 80 | 25 | 130 | 50 | 80 | 70 | 85 | 95 | 0 | 35 | 20 | 120 | 0 | 50 |
| 15 | 115 | 75 | 40 | 50 | 5 | 105 | 0 | 35 | 45 | 95 | 0 | 20 | 70 | 50 | 110 | 15 | 85 | 80 |
| 16 | 15 | 40 | 75 | 80 | 115 | 5 | 135 | 45 | 40 | 65 | 20 | 0 | 0 | 110 | 45 | 120 | 75 | 85 |
| 17 | 20 | 10 | 90 | 85 | 75 | 25 | 135 | 50 | 85 | 65 | 85 | 95 | 0 | 35 | 20 | 115 | 0 | 50 |
| 18 | 10 | 85 | 10 | 80 | 25 | 75 | 130 | 80 | 50 | 85 | 0 | 20 | 0 | 20 | 30 | 120 | 50 | 0 |
Задача 4
Определить расстояние между ребрами пирамиды АВ и SC. Данные для своего варианта взять из таблицы 2.
Методические указания к решению задачи
Задача решается способом замены плоскостей проекций. Ребра пирамиды АВ и SC являются скрещивающимися прямыми. Для определения кратчайшего расстояния между этими ребрами достаточно одно из ребер спроецировать в точку. Тогда перпендикуляр, опущенный из полученной точки на проекцию второго ребра, будет натуральной величиной расстояния между ребрами. Если ребра АВ и SC – прямые общего положения, то потребуется две замены плоскостей проекций. После первой замены одно из ребер проецируется в натуральную величину, второй заменой плоскостей проекций это ребро следует сделать проецирующим.
Пример решения задачи 4 приведен на рисунке 6.
Задача 5
Определить натуральную величину угла при вершине С основания пирамиды – грани АВС способом вращения вокруг линии уровня. Четный вариант – решить задачу вращением вокруг горизонтали, нечетный вариант – решить задачу вращением вокруг фронтали. Данные для своего варианта взять из таблицы 2.
Методические указания к решению задачи
В треугольнике АВС строится линия уровня. Вращение треугольника выполняется на той проекции, на которой линия уровня проецируется в натуральную величину. Следует помнить правило, что при вращении каждая точка фигуры описывает дугу окружности, плоскость которой перпендикулярна оси вращения. Натуральную величину радиуса вращения определить способом прямоугольного треугольника.
Пример решения задачи 5 приведен на рисунке 6.
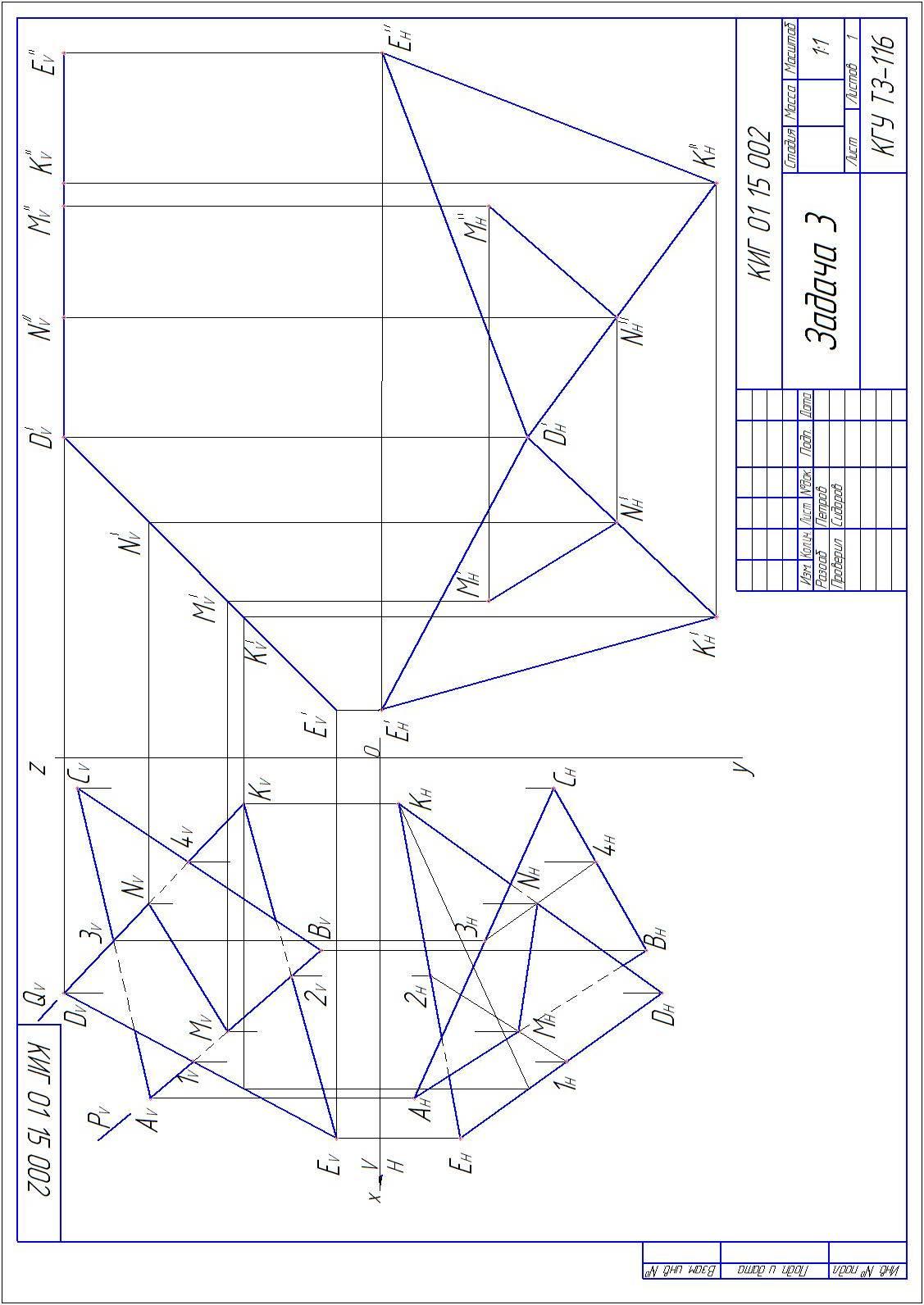
Рисунок 5
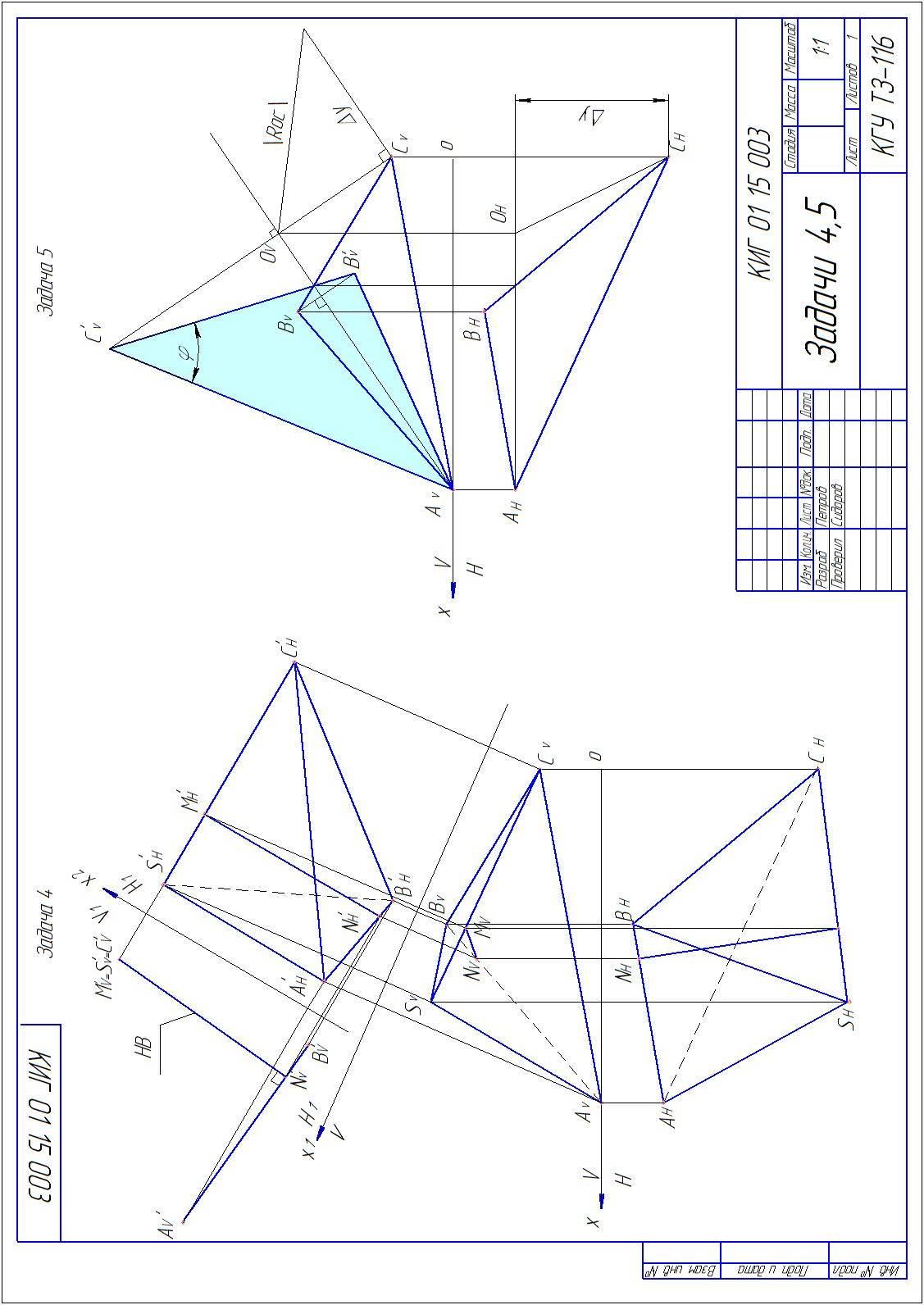
Рисунок 6
Контрольная работа №2
Контрольная работа №2 состоит из 5 задач.
Задача 6
По фронтальной проекции сферы со сквозным вырезом построить горизонтальную и профильную проекции сферы. Сквозное отверстие треугольной формы. Данные для своего варианта взять из таблицы 4.
Таблица 4
| № вари-анта | О (центр сферы) | R (радиус сферы) | A | B | C | ||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | ||
| 0 | 80 | 65 | 60 | 45 | 116 | - | 86 | 43 | - | 86 | 66 | - | 26 |
| 1 | 72 | 60 | 55 | 43 | 75 | - | 90 | 45 | - | 25 | 105 | - | 45 |
| 2 | 75 | 65 | 65 | 50 | 44 | - | 95 | 44 | - | 25 | 95 | - | 25 |
| 3 | 80 | 80 | 70 | 48 | 118 | - | 99 | 41 | - | 41 | 118 | - | 41 |
| 4 | 70 | 63 | 58 | 42 | 70 | - | 90 | 40 | - | 38 | 100 | - | 38 |
| 5 | 80 | 65 | 60 | 45 | 110 | - | 70 | 55 | - | 90 | 70 | - | 25 |
| 6 | 70 | 63 | 58 | 42 | 95 | - | 85 | 35 | - | 58 | 62 | - | 20 |
| 7 | 80 | 80 | 70 | 48 | 80 | - | 118 | 56 | - | 28 | 128 | - | 70 |
| 8 | 75 | 65 | 65 | 50 | 55 | - | 100 | 105 | - | 30 | 105 | - | 100 |
| 9 | 72 | 60 | 55 | 43 | 95 | - | 85 | 40 | - | 30 | 95 | - | 30 |
| 10 | 80 | 80 | 70 | 48 | 80 | - | 110 | 40 | - | 50 | 120 | - | 50 |
| 11 | 80 | 65 | 60 | 45 | 80 | - | 105 | 37 | - | 44 | 122 | - | 44 |
| 12 | 75 | 65 | 65 | 50 | 105 | - | 100 | 45 | - | 100 | 75 | - | 25 |
| 13 | 70 | 63 | 58 | 42 | 101 | - | 30 | 48 | - | 90 | 48 | - | 30 |
| 14 | 72 | 60 | 55 | 43 | 45 | - | 85 | 72 | - | 12 | 108 | - | 55 |
| 15 | 80 | 80 | 70 | 48 | 55 | - | 102 | 55 | - | 38 | 115 | - | 70 |
| 16 | 70 | 63 | 58 | 42 | 97 | - | 85 | 45 | - | 85 | 45 | - | 30 |
| 17 | 80 | 65 | 60 | 45 | 105 | - | 90 | 40 | - | 60 | 105 | - | 30 |
| 18 | 75 | 65 | 65 | 50 | 110 | - | 35 | 40 | - | 35 | 75 | - | 90 |
Методические указания к решению задачи
Намечаются оси координат с началом координат в центре листа. Строятся проекции сферы заданного радиуса R с центром в точке О. Определяются по заданным координатам проекции точек А, В, С – вершин сквозного выреза. Строится треугольник – вырожденная проекция линии сквозного отверстия.
Вначале следует построить проекцию выреза на горизонтальной плоскости проекций, а затем строится проекция выреза на профильной плоскости проекций.
Необходимо определить характер линий, получаемых от сечения сферы плоскостями сквозного отверстия. По существу, как сферу не разрезай плоскостью, в сечении всегда будет получаться окружность либо ее часть. Вопрос в том, как смотреть на эту окружность. Если смотреть вдоль окружности, то увидим прямую линию, если смотреть перпендикулярно плоскости окружности, то получим окружность в натуральную величину, если смотреть на окружность под углом, отличным от нуля и 90º, то увидим эллипс. Анализируя, таким образом, плоскости выреза, представленного на рисунке 7 делаем вывод, что на плоскость проекций Н в прямую линию будет проецироваться плоскость по линии АС. Эта же плоскость на W будет проецироваться в дугу окружности. Плоскость по линии ВС на плоскость Н будет проецироваться в дугу окружности, и на плоскость W она будет проецироваться в прямую линию. Только часть выреза по линии АВ будет проецироваться на плоскости Н и W в виде дуги эллипса. Чтобы построить дугу эллипса, следует отметить на линии АВ ряд точек, найти проекции этих точек на плоскости Н и соединить их плавной кривой с помощью лекало. На линии АВ точки 2 и 3 являются границами видимости для плоскостей W и Н соответственно. Проекции этих точек, а также точек А и 5 определяются по линиям связи без дополнительных построений на плоскости Н. Проекции остальных точек на плоскости Н определяются одним и тем же способом – через построение параллелей, проходящих через эти точки. В качестве примера построена параллель через точку 1V. На плоскости Н строится проекция параллели в виде окружности и на ней определяются проекции точек 1Н и 1'Н.
Для построения проекций точек выреза на плоскости W вначале проводят линии связи от точек с плоскости V. Перенос проекций точек на W осуществляется измерением координат Y этих точек. За начало отсчета удобно принять горизонтальную ось сферы на плоскости Н, а на плоскости W координаты Y откладывают от вертикальной оси вдоль линии связи.
Пример решения задачи 6 приведен на рисунке 7.
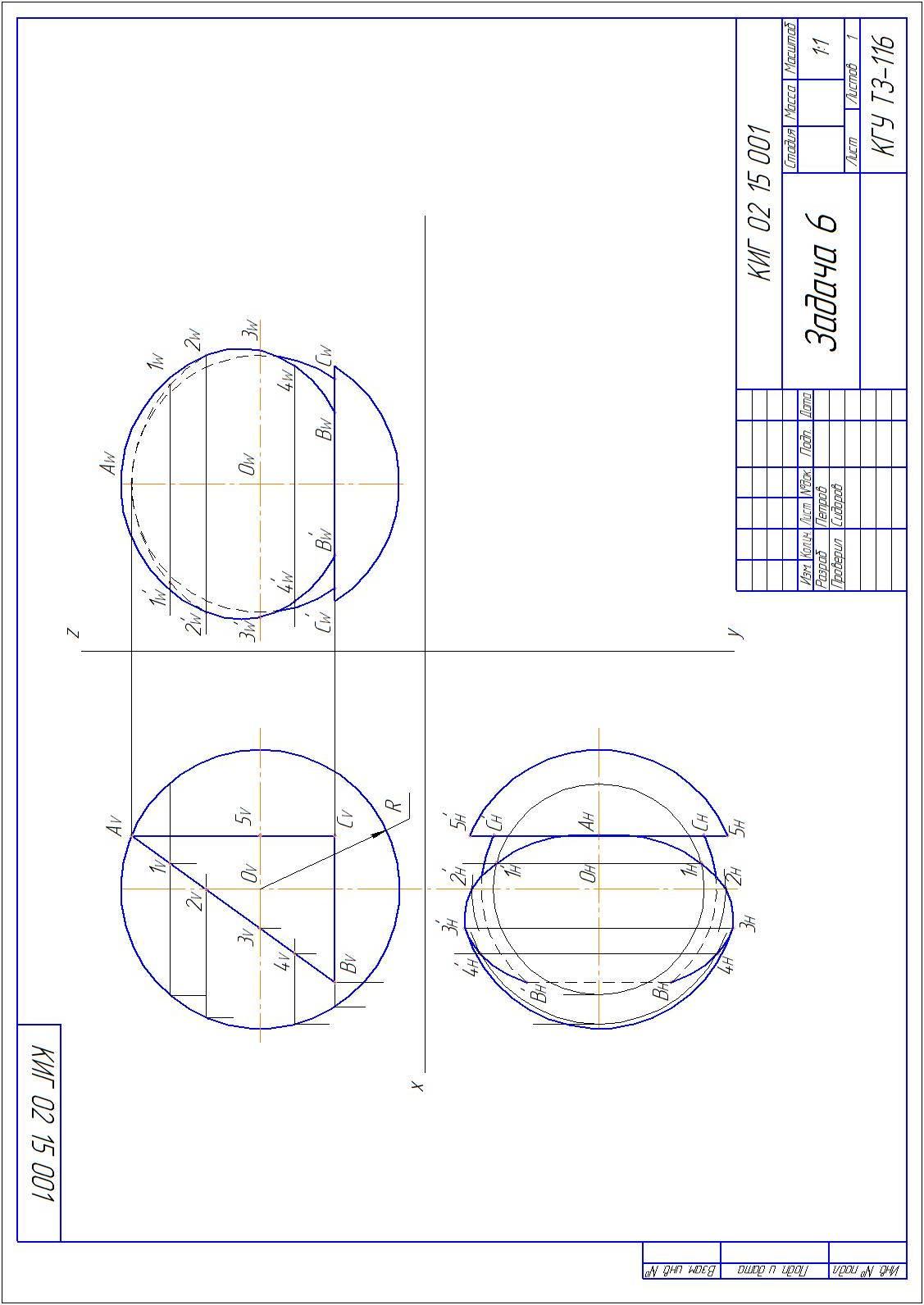
Рисунок 7
Задача 7
Построить линию пересечения конуса вращения плоскостью АВС общего положения. Данные для своего варианта взять из таблицы 5.
Таблица 5
| № вари-анта | К | А | В | С | R | H | ||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | |||
| 0 | 80 | 70 | 0 | 40 | 25 | 60 | 12 | 50 | 60 | 85 | 125 | 0 | 45 | 102 |
| 1 | 80 | 70 | 0 | 40 | 25 | 62 | 15 | 48 | 62 | 86 | 125 | 8 | 45 | 97 |
| 2 | 85 | 68 | 0 | 40 | 30 | 64 | 16 | 45 | 64 | 85 | 140 | 8 | 46 | 97 |
| 3 | 85 | 68 | 0 | 44 | 28 | 66 | 15 | 46 | 66 | 85 | 138 | 19 | 46 | 96 |
| 4 | 85 | 70 | 0 | 44 | 28 | 68 | 15 | 46 | 68 | 86 | 138 | 10 | 46 | 96 |
| 5 | 85 | 70 | 0 | 45 | 26 | 70 | 16 | 48 | 70 | 88 | 142 | 8 | 46 | 95 |
| 6 | 85 | 70 | 0 | 48 | 26 | 68 | 16 | 48 | 68 | 90 | 142 | 8 | 42 | 95 |
| 7 | 86 | 64 | 0 | 46 | 26 | 70 | 14 | 50 | 70 | 90 | 140 | 6 | 42 | 98 |
| 8 | 86 | 64 | 0 | 44 | 28 | 65 | 14 | 50 | 65 | 88 | 140 | 4 | 44 | 98 |
| 9 | 86 | 64 | 0 | 44 | 30 | 65 | 14 | 52 | 65 | 88 | 136 | 4 | 44 | 100 |
| 10 | 80 | 68 | 0 | 46 | 28 | 60 | 10 | 48 | 60 | 80 | 126 | 0 | 45 | 98 |
| 11 | 80 | 72 | 0 | 46 | 30 | 62 | 82 | 125 | 10 | 10 | 50 | 62 | 45 | 100 |
| 12 | 78 | 72 | 0 | 10 | 50 | 62 | 46 | 30 | 62 | 82 | 125 | 10 | 45 | 100 |
| 13 | 82 | 68 | 0 | 49 | 30 | 66 | 12 | 48 | 66 | 84 | 130 | 5 | 44 | 102 |
| 14 | 82 | 65 | 0 | 45 | 32 | 62 | 15 | 48 | 62 | 84 | 135 | 0 | 42 | 100 |
| 15 | 78 | 72 | 0 | 82 | 125 | 10 | 10 | 50 | 62 | 46 | 30 | 62 | 45 | 100 |
| 16 | 84 | 64 | 0 | 45 | 30 | 66 | 10 | 52 | 66 | 85 | 136 | 5 | 44 | 102 |
| 17 | 80 | 70 | 0 | 10 | 50 | 62 | 82 | 125 | 10 | 46 | 30 | 62 | 45 | 100 |
| 18 | 82 | 68 | 0 | 48 | 28 | 65 | 10 | 52 | 65 | 84 | 128 | 6 | 43 | 98 |
Методические указания к решению задачи
В левой половине листа формата А3 намечаются оси координат и из таблицы 5 согласно своему варианту берутся величины, которыми задаются поверхность конуса вращения и плоскость АВС. Здесь: К – точка основания конуса, А, В, С – координаты трех точек секущей плоскости, R – радиус конуса, Н – высота конуса.
Плоскость общего положения АВС следует перевести в проецирующую плоскость способом замены плоскостей проекций. Новая ось Х1 строится перпендикулярно горизонтальной проекции горизонтали. Конус и плоскость АВС проецируются на новую плоскость V1. Теперь сечение на конусе от плоскости АВС и сама плоскость АВС сливаются в одну линию. Отмечают характерные точки сечения (точки 1'V и 6'V) и ряд промежуточных точек.
На плоскости проекций Н проекции точек сечения определяются с помощью параллелей, затем плавной кривой эти точки соединяются.
Из точек сечения на плоскости проекций Н строят линии связи перпендикулярно оси Х и от этой оси вдоль линий связи откладывают расстояния, измеренные от оси Х1 до проекций точек сечения на плоскости V1. Определяют видимость линии сечения на плоскости проекций V.
Пример решения задачи 7 приведен на рисунке 8.
Задача 8 Построить линию пересечения двух тел. Данные для своего варианта взять из таблицы 6.
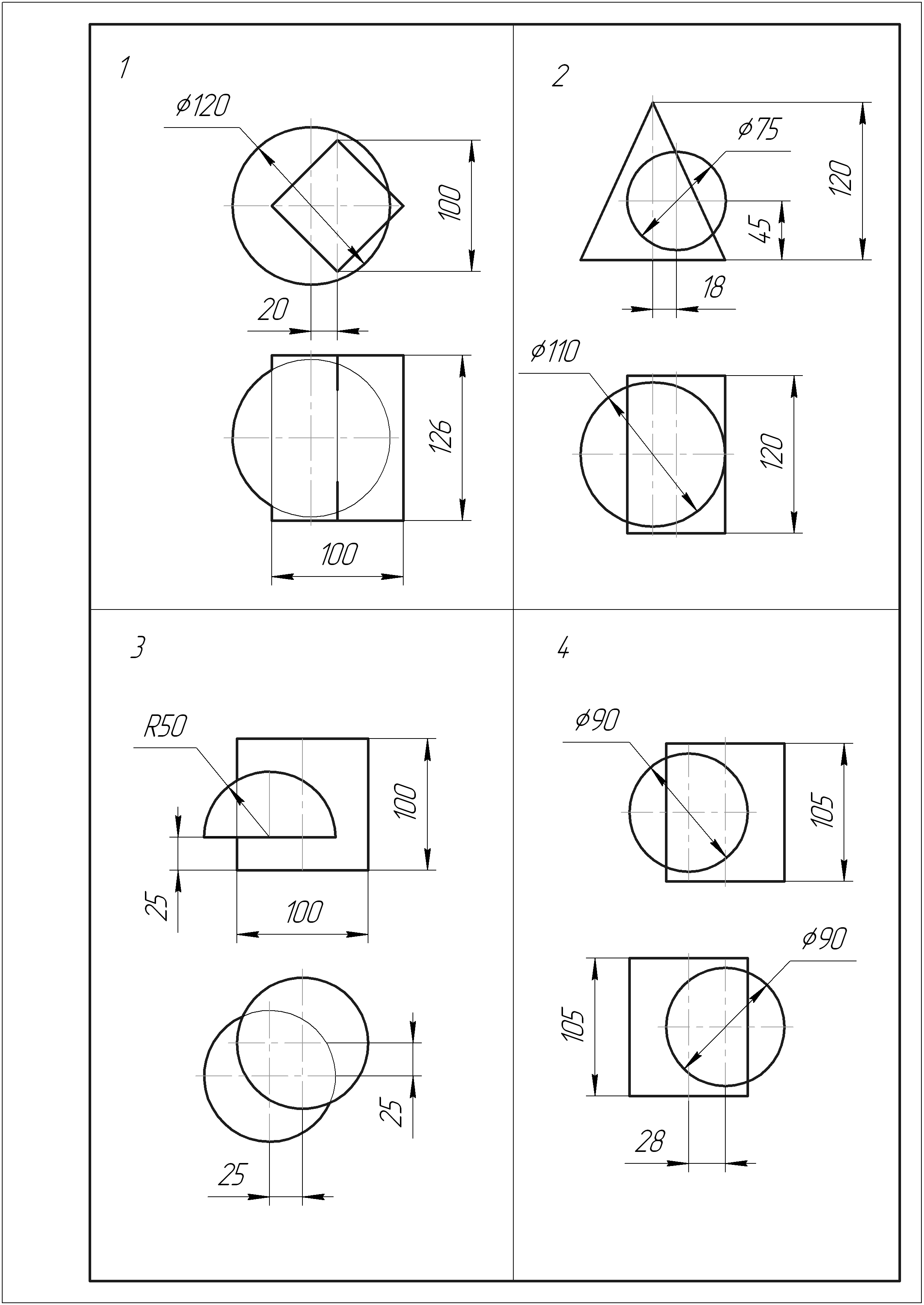Таблица 6
Продолжение таблицы 6
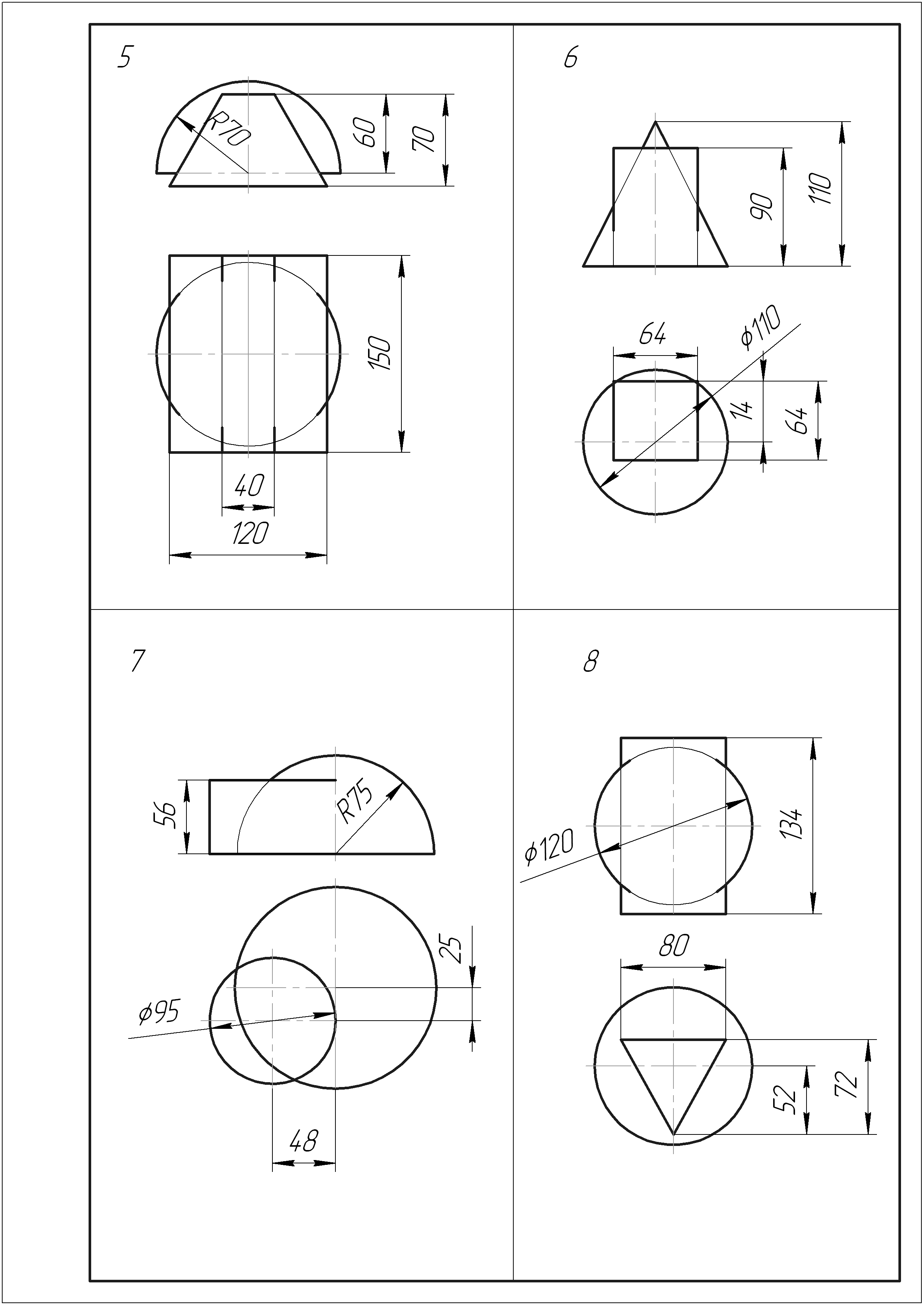
Продолжение таблицы 6
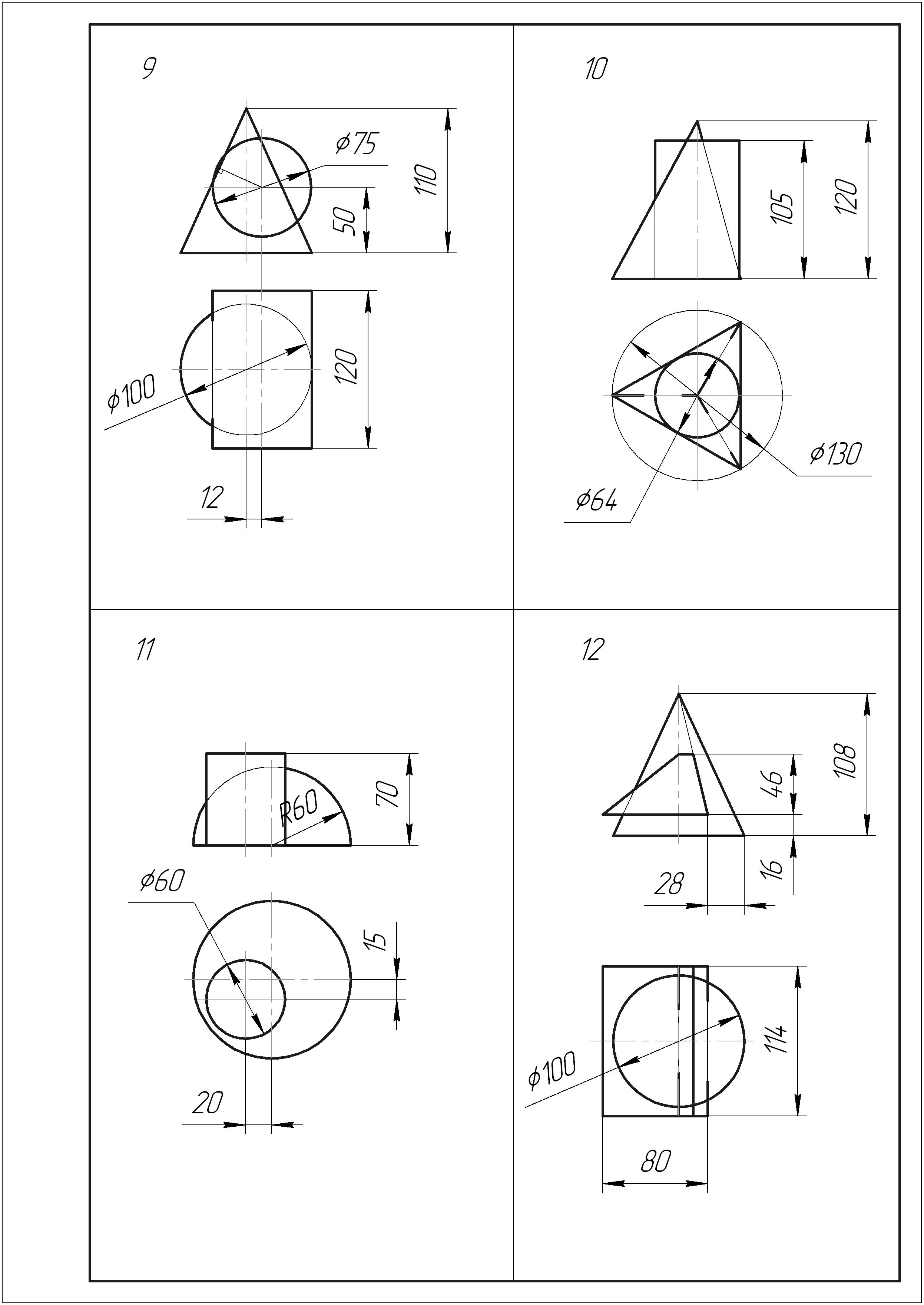
Продолжение таблицы 6
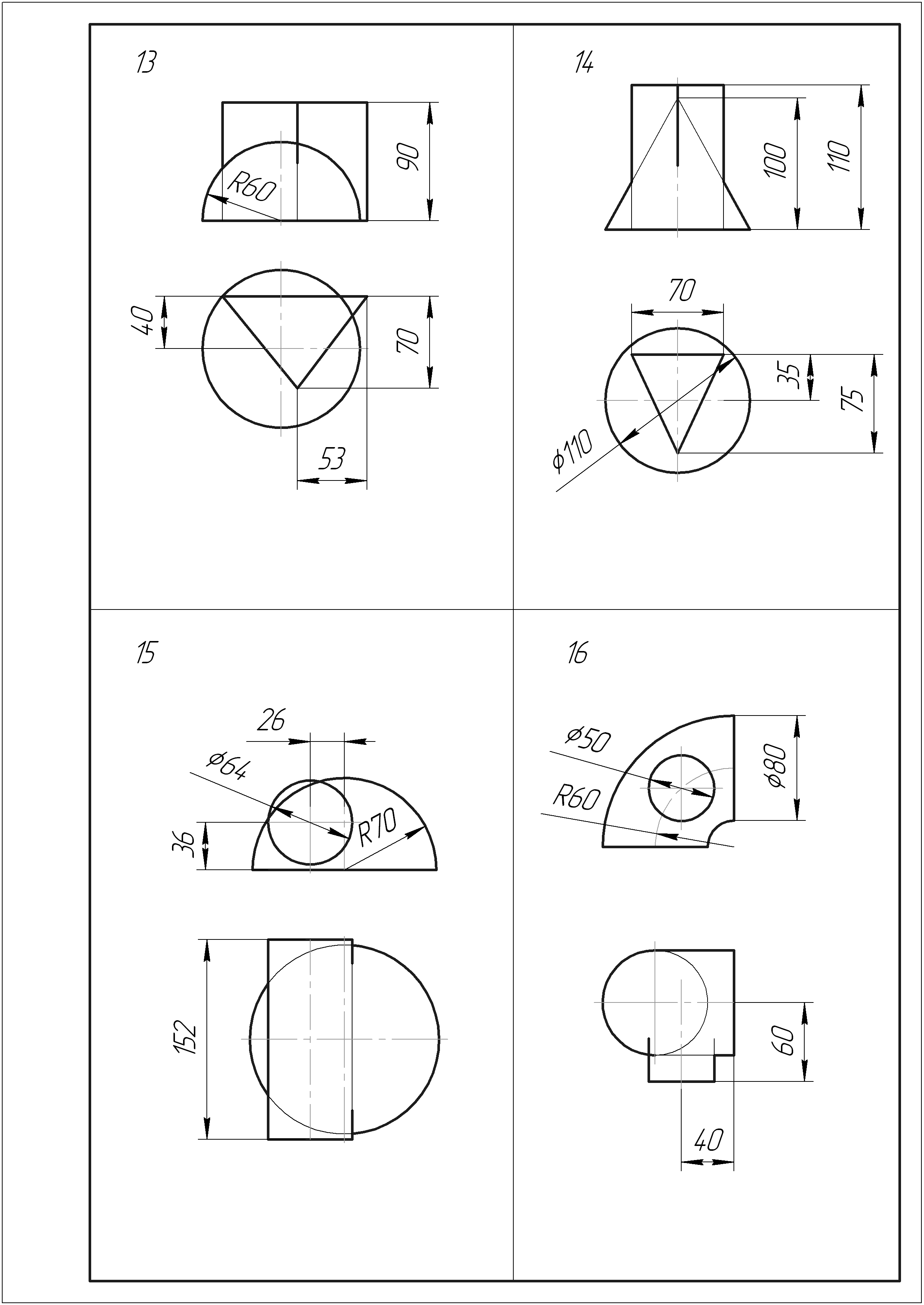
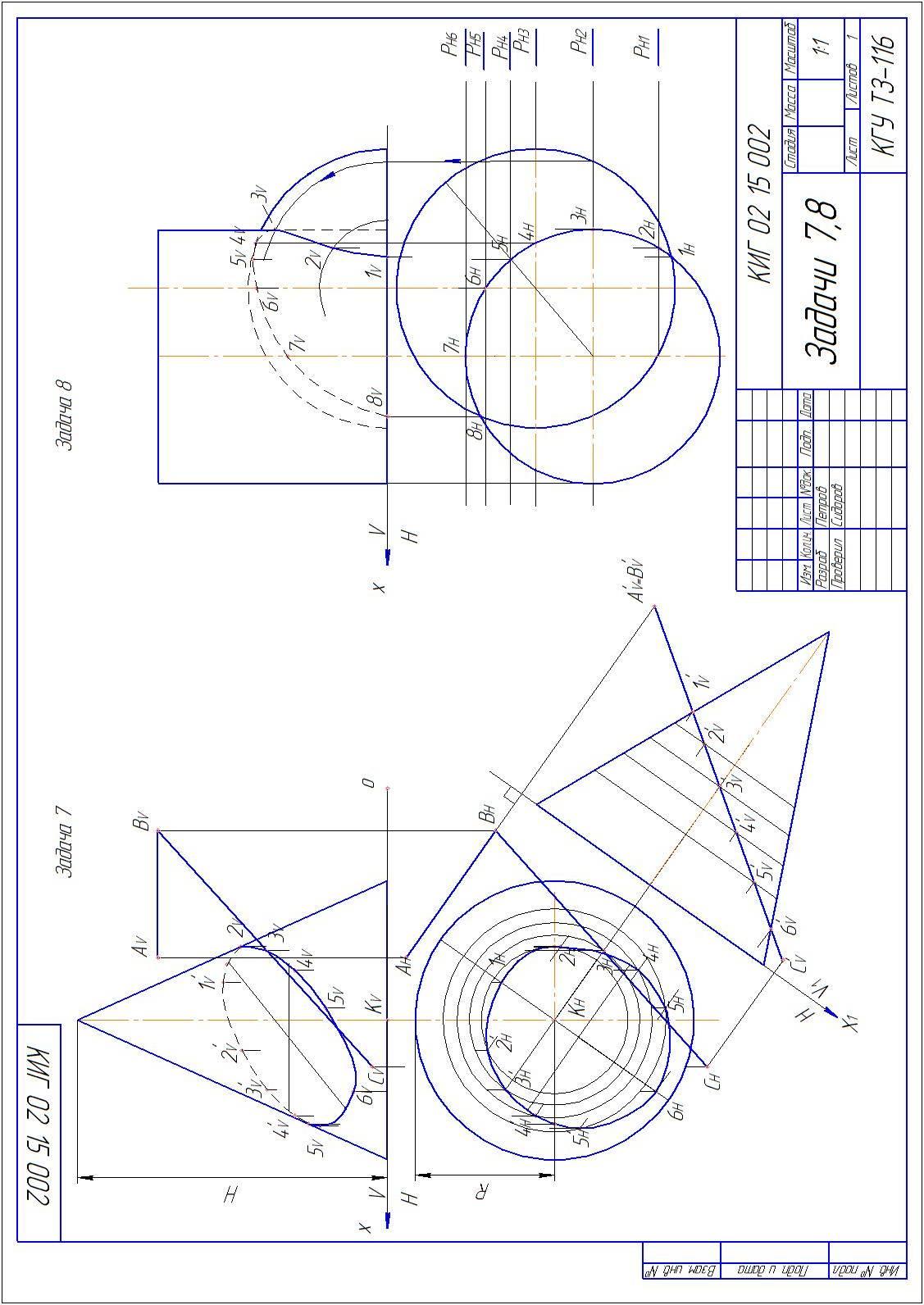
Рисунок 8
Методические указания к решению задачи
В общем виде эта задача решается способом вспомогательных секущих плоскостей. Линия пересечения поверхностей строится по точкам. Для определения точек на этой линии следует подобрать вспомогательные секущие плоскости таким образом, чтобы в сечениях на одном и втором теле получались простые линии – прямые, окружности. Чаще всего в качестве вспомогательных плоскостей используют плоскости уровня.
Вначале определяют характерные точки. В приведенном примере на рисунке 8 самые низшие точки – точки 1, 8; самая верхняя точка – точка 5; точка на границе видимости – точка 3. Количество промежуточных вспомогательных плоскостей для построения точек линии пересечения тел выбирается самостоятельно и определяется точностью построения линии и насыщенностью чертежа дополнительными построениями.
От сечения вспомогательными плоскостями РН1 – РН5 на поверхности полусферы будут получаться дуги окружностей, а на поверхности цилиндра – прямые линии. Плоскость РН6 касается крайней образующей цилиндра и проекция линии касания на плоскости V совпадает с проекцией оси цилиндра.
На рисунке 8 показано, как была найдена проекция точки 3V, лежащей на границе видимости.
На плоскости проекций Н верхняя точка сечения - точка 5Н определяется с помощью линии, соединяющей точки пересечения осей цилиндра и полусферы.
Задача 9
Построить линию пересечения поверхностей вращения способом вспомогательных концентрических сфер. Данные для своего варианта взять из таблицы 7.
Методические указания к решению задачи
Способ вспомогательных концентрических сфер применяется если:
- обе поверхности – поверхности вращения;
- оси поверхностей пересекаются;
- общая плоскость симметрии тел параллельна какой-либо плоскости проекций.
В левой половине листа формата А3 намечаются оси координат и строятся по размерам проекции тел согласно своему варианту из таблицы 7.
Линия пересечения двух тел строится по точкам. Проекции точек этой линии определяются с помощью концентрических сфер, которые строятся из точки пересечения осей тел. С каждым из тел сфера пересекается по окружности. На плоскости проекций V эти окружности проецируются в прямые линии. Точки пересечения окружностей и будут являться общими точками для двух тел.
Сфера наименьшего диаметра должна вписаться в большее из тел и пересекать образующие меньшего тела. На рисунке 9 наименьшая сфера вписана в конус.
Сфера наибольшего радиуса не должна выходить за наиболее удаленную точку пересечения тел. Характерные точки – верхняя и нижняя точки сечения (точки АV и ВV) определяются по пересечению фронтальных меридианов конуса и цилиндра. Следовательно, сфера наибольшего радиуса не должна выходить за точку ВV .
Промежуточные сферы строятся произвольными радиусами и должны располагаться между наименьшей и наибольшей вспомогательными сферами.
Проекция линии пересечения тел на плоскости Н строится по точкам с использованием параллелей.
Таблица 7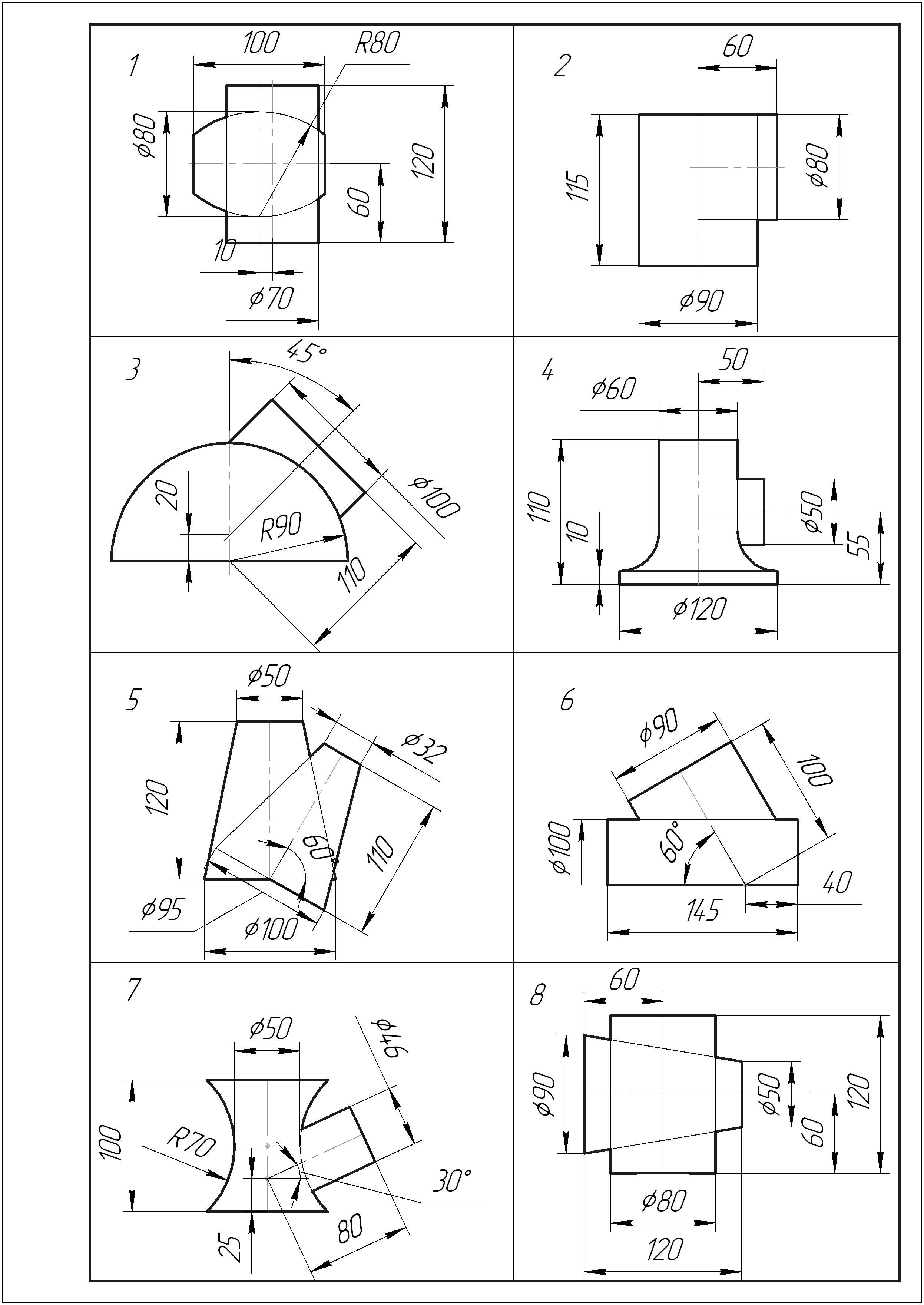 
Продолжение таблицы 7
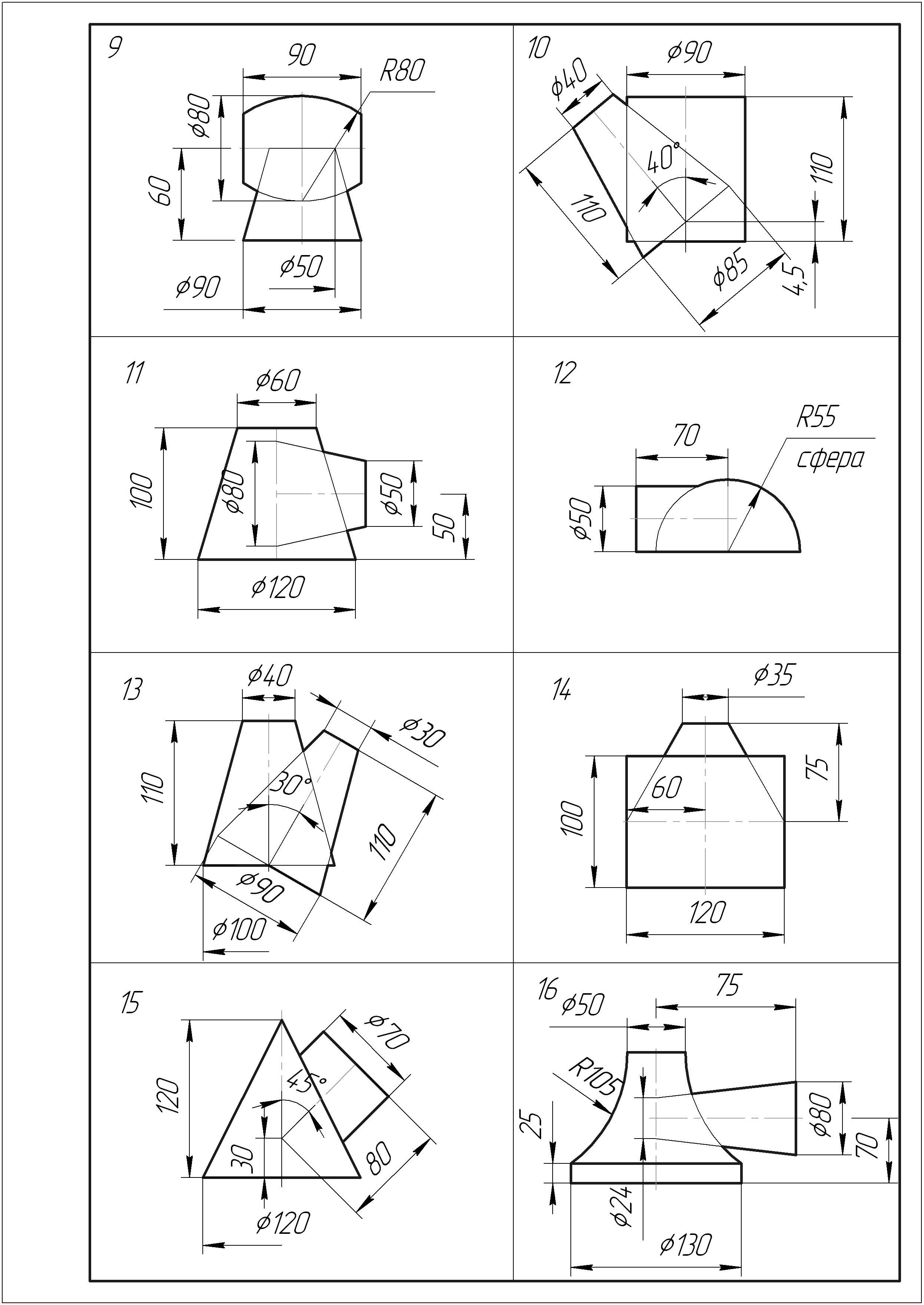
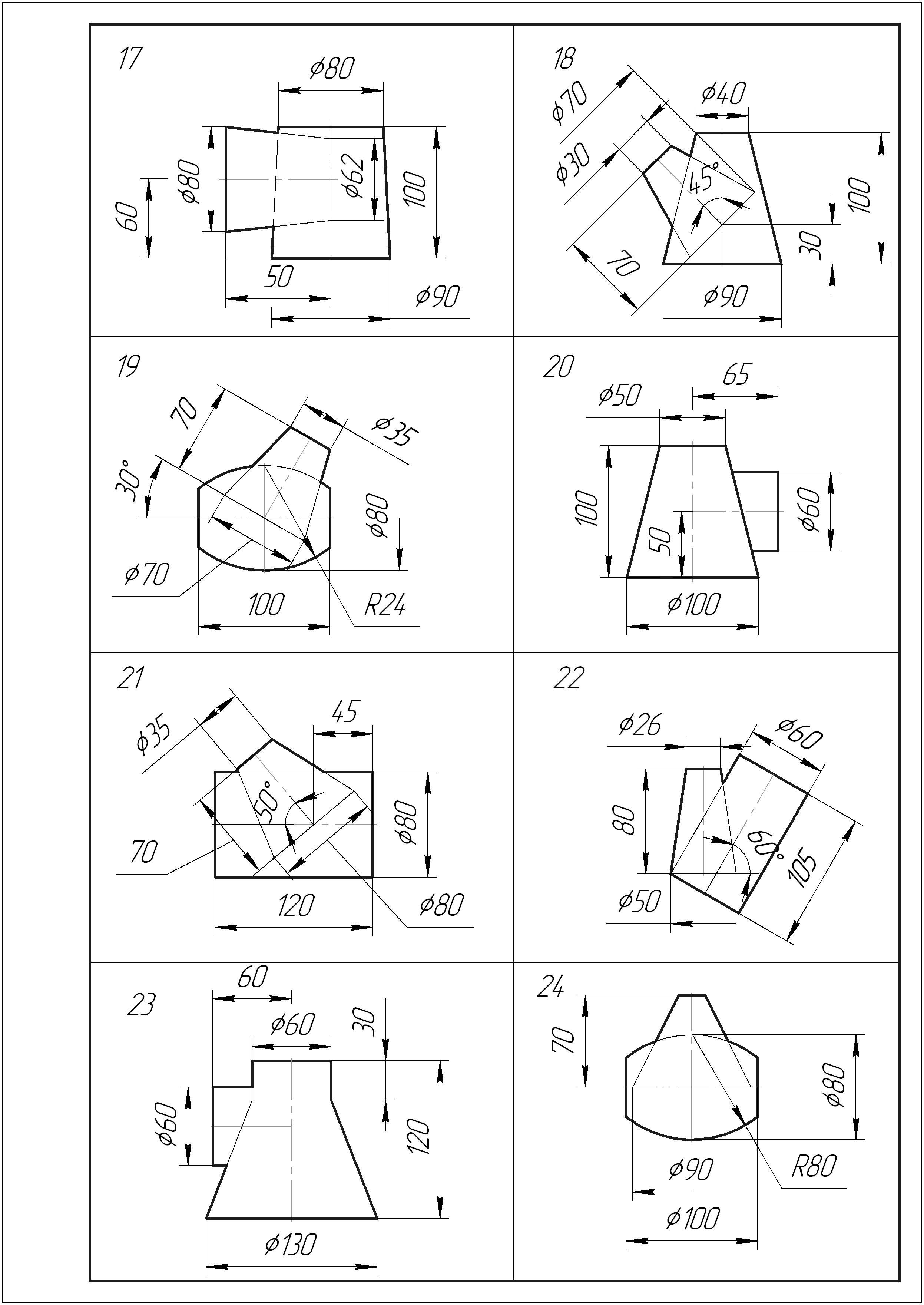
Пример решения задачи 9 приведен на рисунке 9.
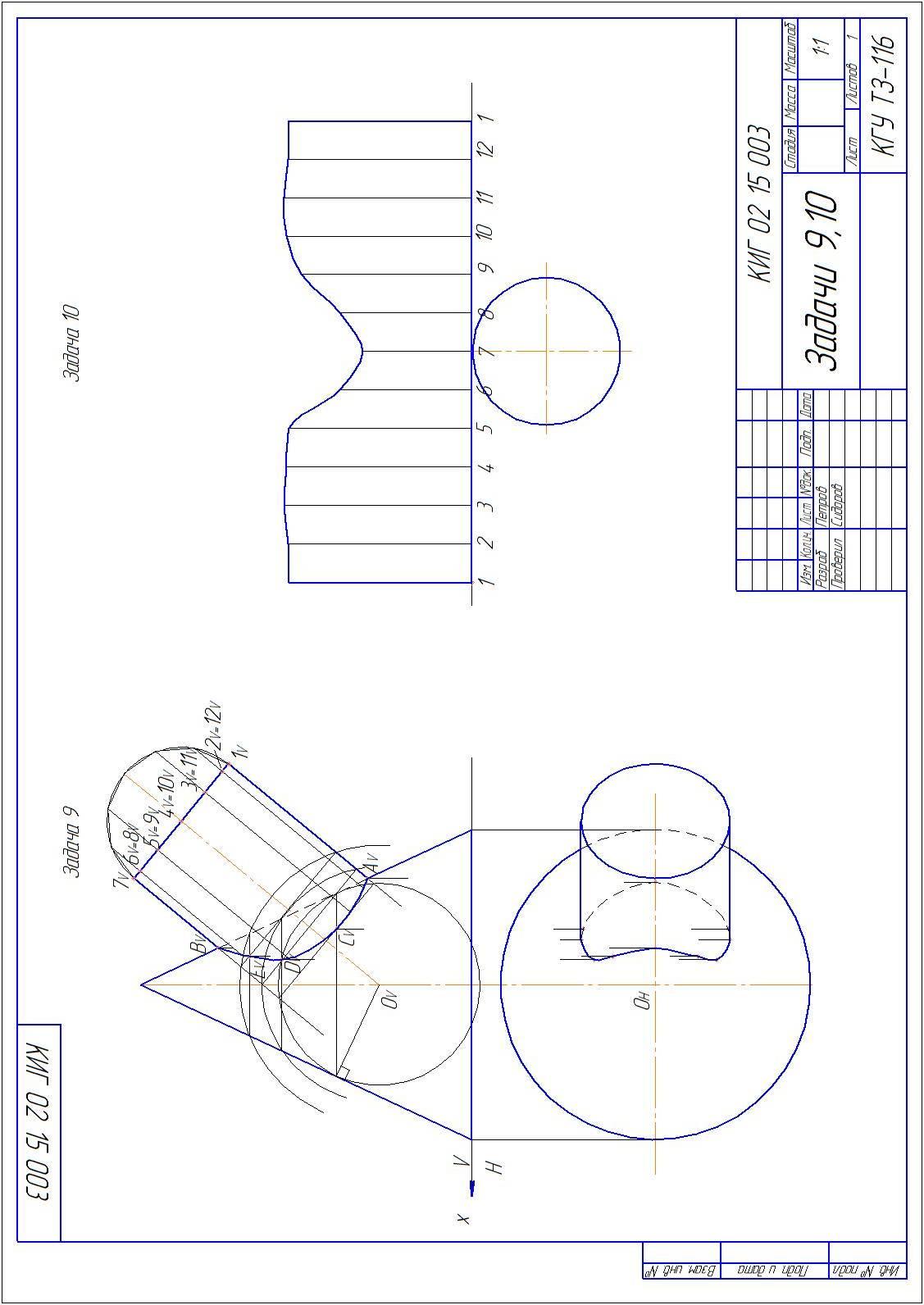
Рисунок 9
Задача 10
Построить развертку боковой поверхности одного из тел из задачи 9.
Методические указания к решению задачи
Поверхность вращения аппроксимируется гранной поверхностью – призмой или пирамидой. На рисунке 9 выполнена развертка цилиндра.
Подготовительные действия выполняются в задаче 9. В поверхность цилиндра вписывают 12 – гранную призму. Для этого на плоскости проекций V на верхнем основании цилиндра строят половину окружности, которую циркулем делят на 6 равных частей. Строят проекции боковых ребер призмы от верхнего основания до линии пересечения тел. На свободной части листа формата А3 строят горизонтальную линию. Отмечают на этой линии точку 1 и откладывают вправо от этой точки двенадцать раз величину ребра основания грани призмы (на дуге полуокружности это длина хорды между соседними точками). Вверх от полученных точек откладывают длины ребер боковых граней призмы (расстояния от верхнего основания призмы до линии пересечения тел). Соединяя точки на концах ребер плавной линией, получают приблизительную развертку боковой поверхности цилиндра.
Если строить развертку конуса, то следует иметь в виду, что только крайние ребра вписанной пирамиды проецируются на плоскость V в натуральную величину. Для определения длин остальных ребер следует прибегнуть к способу вращения вокруг проецирующей оси.
Иванов Вадим Валентинович
studfiles.net
Правила оформления контрольных работ
Контрольные работы выполняется на листах чертежной бумаги формата А3 (297 х 420 мм) с помощью чертежных инструментов, с обводкой тушью и отмывкой плоскостей, теней. Эпюры в графическом отношении должны удовлетворять требованиям ГОСТов по оформлению чертежей.
Для качественного графического выполнения контрольных работ следует придерживаться следующих рекомендаций:
Линии чертежа должны быть следующей толщины:
видимых контуров 1,0мм – 0,8 мм;
невидимых контуров 0,5 - 0,4 мм;
осевых линий и линий вспомогательных построений 0,15-0,2 мм.
Все подписи на эпюрах выполнять архитектурным шрифтом высотой 10 мм, например:
Основную надпись расположить согласно данному образцу.
Контрольная работа 1 состоит из двух эпюров: эпюра 1 (на позиционные и метрические задачи), эпюра 2 (на пересечение многогранников).
С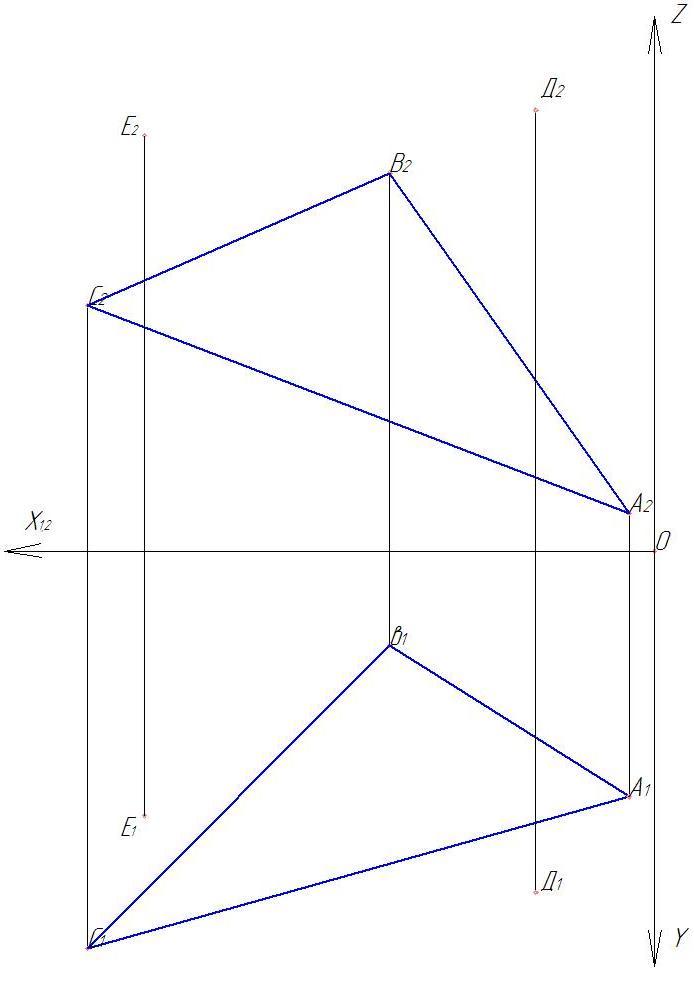
одержание эпюра.
Дано: плоскость треугольника АВС и точки D и E, требуется:
задача 1 – определить расстояние от точки D до плоскости, заданной треугольником АВС;
задача 2 – построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от неё на 50 мм.;
задача 3 – через прямую DE провести плоскость, перпендикулярную треугольнику АВС, построить линию пересечения этих двух плоскостей, определить видимость.
Указания к выполнению эпюра. Данные для выполнения эпюра взять из таблицы в соответствии с вариантом. Координаты точек даны в мм. Задачи 1 и 2 можно совместить на одном чертеже. Точку Е построить только для задачи 3.
Образец выполнения задания представлен на рисунке 9.
(выбор варианта по последней цифре зачетной книжке (студенческого билета)
| Вариант | Координаты точек | х | y | z |
| 0 | А | 140 | 50 | 40 |
| B | 70 | 20 | 110 | |
| C | 90 | 130 | 10 | |
| D | 130 | 20 | 0 | |
| E | 20 | 50 | 120 | |
| Вариант | Координаты точек | х | y | z |
| 1 | А | 150 | 40 | 80 |
| B | 80 | 120 | 120 | |
| C | 20 | 80 | 40 | |
| D | 20 | 20 | 130 | |
| E | 150 | 80 | 60 | |
| Вариант | Координаты точек | х | y | z |
| 2 | А | 160 | 90 | 100 |
| B | 90 | 20 | 10 | |
| C | 30 | 130 | 100 | |
| D | 130 | 130 | 10 | |
| E | 20 | 30 | 110 | |
| Вариант | Координаты точек | х | y | z |
| 3 | А | 160 | 60 | 30 |
| B | 110 | 0 | 140 | |
| C | 30 | 10 | 90 | |
| D | 150 | 110 | 80 | |
| E | 20 | 10 | 10 | |
| Вариант | Координаты точек | х | y | z |
| 4 | А | 150 | 130 | 60 |
| B | 180 | 30 | 100 | |
| C | 40 | 120 | 20 | |
| D | 140 | 130 | 120 | |
| E | 30 | 40 | 20 | |
| Вариант | Координаты точек | х | y | z |
| 5 | А | 190 | 90 | 120 |
| B | 20 | 30 | 80 | |
| C | 130 | 150 | 10 | |
| D | 30 | 140 | 130 | |
| E | 180 | 70 | 80 | |
| Вариант | Координаты точек | х | y | z |
| 6 | А | 150 | 60 | 20 |
| B | 60 | 30 | 130 | |
| C | 20 | 140 | 60 | |
| D | 120 | 120 | 120 | |
| E | 130 | 10 | 20 | |
| Вариант | Координаты точек | х | y | z |
| 7 | А | 170 | 40 | 30 |
| B | 120 | 0 | 160 | |
| C | 40 | 90 | 70 | |
| D | 180 | 130 | 130 | |
| E | 10 | 30 | 130 | |
| Вариант | Координаты точек | х | y | z |
| 8 | А | 120 | 130 | 40 |
| B | 90 | 40 | 100 | |
| C | 10 | 20 | 20 | |
| D | 40 | 140 | 120 | |
| E | 60 | 10 | 10 | |
| Вариант | Координаты точек | х | y | z |
| 9 | А | 170 | 80 | 20 |
| B | 80 | 20 | 20 | |
| C | 30 | 120 | 120 | |
| D | 150 | 20 | 120 | |
| E | 20 | 50 | 60 |
studfiles.net
Начертательная геометрия
Учебно-методическое пособие
по выполнению контрольных работ
для студентов-бакалавров профиля подготовки
«Архитектурное проектирование» и «Проектирование городской среды».
Направление подготовки 270100 «Архитектура»
Астрахань – 2011
Учебно-методическое пособие рекомендовано для студентов бакалавров профиля подготовки «Архитектурное проектирование» и «Проектирование городской среды». Направление подготовки 270100 «Архитектура».
Содержит методические указания и задания к контрольным работам по начертательной геометрии, а также пояснения и примерные решения заданий, необходимые для понимания и самостоятельного выполнения контрольных работ. – Астрахань, 2011– с.
Утверждено на заседании кафедры НГиГ
Протокол № __ от ____ ________2011г.
Согласовано с УМО АИСИ
«____»__________20____
Рекомендовано к рассмотрению на методсовете направления «Строительство» АИСИ
Протокол №___ от «___»__________20_____
Утверждено на РИС АИСИ
Протокол №___ от «___»__________20_____
Составитель: Качуровская Наталья Михайловна, кандидат педагогических наук, доцент кафедры НГиГ
Рецензенты:
Козлова Ирина Алексеевна, кандидат технических наук, доцент кафедры «Начертательная геометрия» Астраханского государственного технического университета
Кокарев Александр Михайлович, кандидат технических наук, зав. кафедрой «Промышленное и гражданское строительство»
© Качуровская Н.М.
© ГАОУ АО ВПО «Астраханский инженерно-строительный институт»
СОДЕРЖАНИЕ
стр.
| Введение………………………………………………………… | |
| Контрольная работа №1……………........................................... Эпюр 1. Точка, прямая, плоскость................................................ | |
| Эпюр 2. Пересечение многогранных поверхностей (пример 1)..... |
ВВЕДЕНИЕ
Учебно-практическое пособие предназначено для студентов изучающих дисциплину «Начертательная геометрия», обучающихся по профилю подготовки «Архитектурное проектирование» и «Проектирование городской среды» направления подготовки 270100 «Архитектура».
Пособие содержит пояснения к выполнению контрольных работ по начертательной геометрии, варианты заданий, образцы выполнения заданий. Изучение начертательной геометрии необходимо для приобретения навыков и знаний, позволяющих студентам выполнять чертежи, решать проектные задачи ведущей дисциплины – «Архитектурное проектирование», а также для развития пространственного воображения. Общим для начертательной геометрии является метод построения изображений, называемый методом проецирования. В начертательной геометрии изучают теоретические основы этого метода, которые потом используются в архитектурном проектировании и рисовании.
КОНТРОЛЬНЫЕ РАБОТЫ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Правила оформления контрольных работ
Контрольные работы выполняется на листах чертежной бумаги формата А3 (297 х 420 мм) с помощью чертежных инструментов, с обводкой тушью и отмывкой плоскостей, теней. Эпюры в графическом отношении должны удовлетворять требованиям ГОСТов по оформлению чертежей.
Для качественного графического выполнения контрольных работ следует придерживаться следующих рекомендаций:
Линии чертежа должны быть следующей толщины:
видимых контуров 1,0мм – 0,8 мм;
невидимых контуров 0,5 - 0,4 мм;
осевых линий и линий вспомогательных построений 0,15-0,2 мм.
Все подписи на эпюрах выполнять архитектурным шрифтом высотой 10 мм, например:
Основную надпись расположить согласно данному образцу.
КОНТРОЛЬНАЯ РАБОТА 1
Контрольная работа 1 состоит из двух эпюров: эпюра 1 (на позиционные и метрические задачи), эпюра 2 (на пересечение многогранников).
Рис. 11. Построение высоты пирамиды
Рис. 12. Построение правильной пирамиды
Задача 3. Построить пересечение пирамиды и выреза здания.
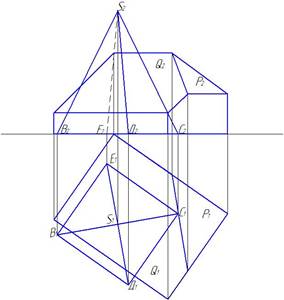
Располагаем пирамиду так, чтобы одна из сторон основания была параллельна стороне здания, а одна из точек основания пирамиды находилась на линии ската (рис. 13).
Рис. 13. Совмещение пирамиды и выреза здания
Теперь необходимо построить точки пересечения ребер пирамиды со скатом Q и точки пересечения линии карниза здания с гранями пирамиды ВSЕ и ДSС. Для того, чтобы найти точку пересечения линии карниза здания с гранью пирамиды ВSЕ, нужно задать через линию карниза секущую плоскость g (рис. 14).
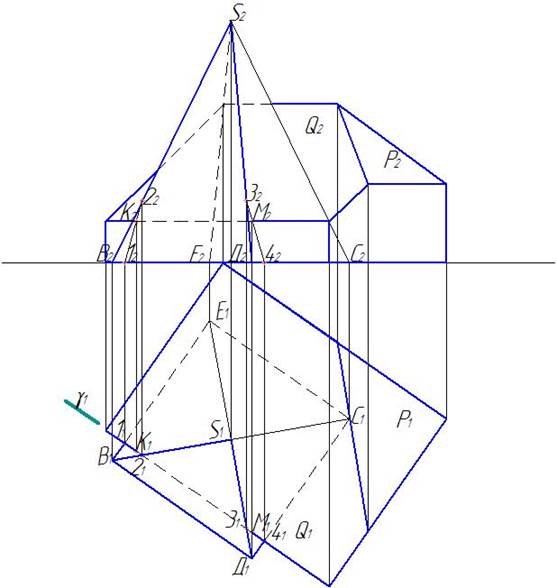
Рис. 14. Нахождение точек пересечения линии карниза здания с гранями пирамиды
Решение сводится к первой позиционной задаче – к нахождению точки пересечения прямой (в данном случае это линия карниза) и плоскости (сначала это грань пирамиды ВSЕ, а затем ДSС).
На горизонтальной плоскости проекций отмечаем точку 11 на стороне основания пирамиды ВЕ и точку 21 на ребре SB. На фронтальной плоскости проекций находим соответствующие этим точкам фронтальные проекции 12 и 22. Соединяем точки 12 и 22 прямой, которая пересечет линию карниза в точке К2. По проекционной линии находим горизонтальную проекцию этой точки – К1. Аналогичным образом находим точки М2 и М1.
Далее находим проекции точки пересечения ребра ЕS c плоскостью Q – скатом крыши здания (рис.15).
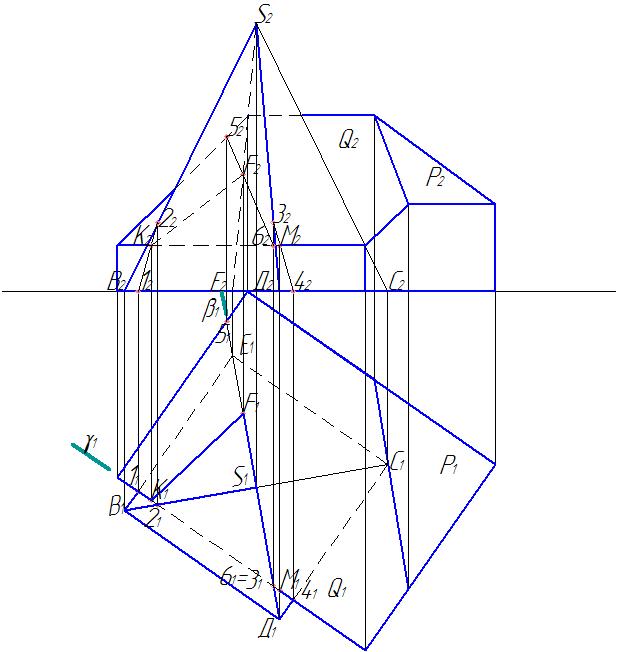
Рис. 15. Нахождение точки пересечения ребра пирамиды SЕ и ската крыши Q
И снова решаем первую позиционную задачу. Через ребро Е1S1 зададим проецирующую плоскость b1, найдем точки пересечения проекции этой плоскости со скатом Q1 . Это будут точки 51 и 61. Находим их фронтальные проекции 52 и 62. Соединяем их прямой линией и отмечаем точку F2 – точку пересечения этой линии с фронтальной проекцией ребра S2Е2. Находим горизонтальную проекцию этой точки – F1. Точки К1 и F1, К2 и F2 соединяем, учитывая видимость.
Таким же способом находим горизонтальную и фронтальную проекции точки пересечения ребра СS с плоскостью ската Q - это точки N2 и N1 (рис. 16).
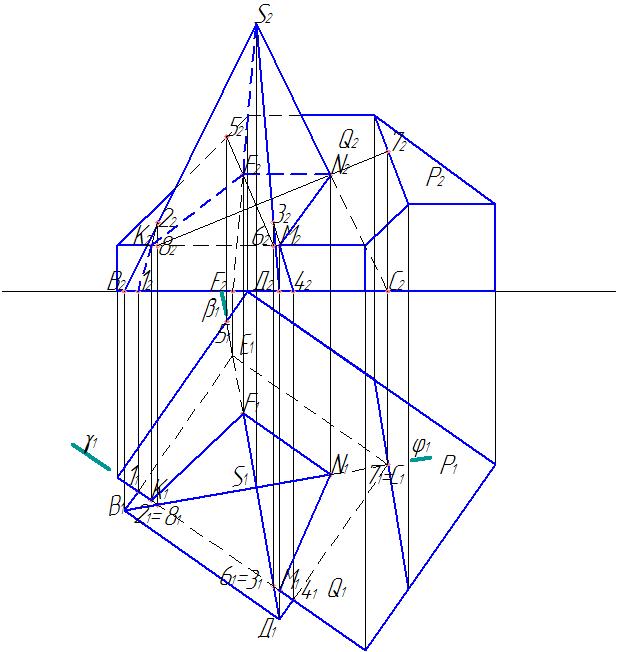
Рис. 16. Нахождение точки пересечения ребра пирамиды SC и ската крыши Q
Горизонтальные и фронтальные проекции точек К, F, N, М соединяем, учитывая видимость. Необходимо также соединить точку М2 с 42 и точку К2 с точкой 12. Это проекции врезки граней пирамиды и вертикальной стены выреза здания.
Задача 4. Построить следы плоскостей скатов кровли (Р и Q).
Строить следы начинаем с горизонтальной проекции ската Р. Линию раздела скатов 91 101 продолжаем до пересечения с осью Х, получаем точку А1 . На продолжении линии раздела скатов 92 102 находим фронтальную проекцию точки А2. Теперь продолжаем фронтальную проекцию 92 102 до пересечения с осью Х, где получим точку L2. По проекционной связи находим горизонтальную проекцию точки L1 (рис. 17)..
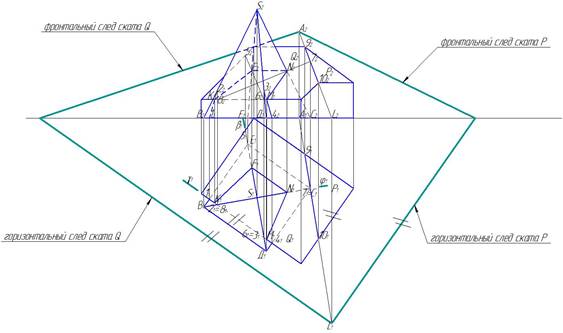
Рис. 17. Построение следов скатов Q и Р.
Горизонтальный след ската Р будет параллелен стороне этого ската, а горизонтальный след ската Q – параллелен стороне ската Q. Доводим горизонтальные следы до пересечения с осью Х, а затем эти точки соединяем с точкой А2. Следы построены.
Задача 5. Способом замены плоскостей проекций определить натуральную величину одного из скатов кровли.
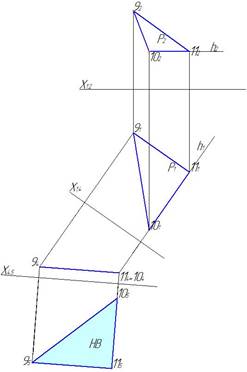
Лучше всего вынести проекции ската Р на свободное поле чертежа или на новом листе и решить задачу нахождения натуральной величины ската, сделав две замены плоскостей (рис.18). Сначала перпендикулярно горизонтали вводят плоскость П4 и плоскость Р1 превращают во фронтально-проецирующую плоскость, а затем к проекции 94 104 проводят параллельно новую горизонтальную плоскость П5.
Рис. 18. Нахождение натуральной величины плоскости Р
Начертательная геометрия
Учебно-методическое пособие
по выполнению контрольных работ
для студентов-бакалавров профиля подготовки
«Архитектурное проектирование» и «Проектирование городской среды».
Направление подготовки 270100 «Архитектура»
Астрахань – 2011
Учебно-методическое пособие рекомендовано для студентов бакалавров профиля подготовки «Архитектурное проектирование» и «Проектирование городской среды». Направление подготовки 270100 «Архитектура».
Содержит методические указания и задания к контрольным работам по начертательной геометрии, а также пояснения и примерные решения заданий, необходимые для понимания и самостоятельного выполнения контрольных работ. – Астрахань, 2011– с.
Утверждено на заседании кафедры НГиГ
Протокол № __ от ____ ________2011г.
Согласовано с УМО АИСИ
«____»__________20____
Рекомендовано к рассмотрению на методсовете направления «Строительство» АИСИ
Протокол №___ от «___»__________20_____
Утверждено на РИС АИСИ
Протокол №___ от «___»__________20_____
Составитель: Качуровская Наталья Михайловна, кандидат педагогических наук, доцент кафедры НГиГ
Рецензенты:
Козлова Ирина Алексеевна, кандидат технических наук, доцент кафедры «Начертательная геометрия» Астраханского государственного технического университета
Кокарев Александр Михайлович, кандидат технических наук, зав. кафедрой «Промышленное и гражданское строительство»
© Качуровская Н.М.
© ГАОУ АО ВПО «Астраханский инженерно-строительный институт»
СОДЕРЖАНИЕ
стр.
| Введение………………………………………………………… | |
| Контрольная работа №1……………........................................... Эпюр 1. Точка, прямая, плоскость................................................ | |
| Эпюр 2. Пересечение многогранных поверхностей (пример 1)..... |
ВВЕДЕНИЕ
Учебно-практическое пособие предназначено для студентов изучающих дисциплину «Начертательная геометрия», обучающихся по профилю подготовки «Архитектурное проектирование» и «Проектирование городской среды» направления подготовки 270100 «Архитектура».
Пособие содержит пояснения к выполнению контрольных работ по начертательной геометрии, варианты заданий, образцы выполнения заданий. Изучение начертательной геометрии необходимо для приобретения навыков и знаний, позволяющих студентам выполнять чертежи, решать проектные задачи ведущей дисциплины – «Архитектурное проектирование», а также для развития пространственного воображения. Общим для начертательной геометрии является метод построения изображений, называемый методом проецирования. В начертательной геометрии изучают теоретические основы этого метода, которые потом используются в архитектурном проектировании и рисовании.
КОНТРОЛЬНЫЕ РАБОТЫ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Правила оформления контрольных работ
Контрольные работы выполняется на листах чертежной бумаги формата А3 (297 х 420 мм) с помощью чертежных инструментов, с обводкой тушью и отмывкой плоскостей, теней. Эпюры в графическом отношении должны удовлетворять требованиям ГОСТов по оформлению чертежей.
Для качественного графического выполнения контрольных работ следует придерживаться следующих рекомендаций:
Линии чертежа должны быть следующей толщины:
видимых контуров 1,0мм – 0,8 мм;
невидимых контуров 0,5 - 0,4 мм;
осевых линий и линий вспомогательных построений 0,15-0,2 мм.
Все подписи на эпюрах выполнять архитектурным шрифтом высотой 10 мм, например:
Основную надпись расположить согласно данному образцу.
КОНТРОЛЬНАЯ РАБОТА 1
Контрольная работа 1 состоит из двух эпюров: эпюра 1 (на позиционные и метрические задачи), эпюра 2 (на пересечение многогранников).
cyberpedia.su
Учебно-практическое пособие предназначено для студентов-бакалавров изучающих дисциплину «Начертательная геометрия», обучающихся по заочной форме по профилям направления «Строительство». Пособие содержит пояснения к выполнению контрольных работ по начертательной геометрии, варианты заданий, образцы выполнения заданий. Выполнение заданий предусматривает использование учебников по начертательной геометрии.
Изучение начертательной геометрии необходимо для приобретения навыков и знаний, позволяющих составлять и читать технические чертежи, а также для развития пространственного воображения. Общим для начертательной геометрии является метод построения изображений, называемый методом проецирования. В начертательной геометрии изучают теоретические основы этого метода, которые потом используются в черчении и рисовании.
Правила оформления контрольных работ
Контрольные работы выполняется на листах чертежной бумаги формата А3 (297 х 420 мм) в карандаше с помощью чертежных инструментов. Эпюры в графическом отношении должны удовлетворять требованиям ГОСТов по оформлению чертежей.
Для качественного графического выполнения контрольных работ следует придерживаться следующих рекомендаций:
Линии чертежа должны быть следующей толщины:
видимых контуров 0,6 – 0,8 мм;
невидимых контуров 0,2 - 0,4 мм;
осевых линий и линий вспомогательных построений 0,15-0,2 мм.
Все подписи на эпюрах выполнять шрифтом 3,5мм и 5 мм.
Основную надпись выполнить согласно данному образцу:
Контрольная работа 1 состоит из двух эпюров: эпюра 1 (на позиционные и метрические задачи), эпюра 2 (на пересечение многогранника плоскостью) и шести задач для самостоятельной работы: 1, 2, 3, 4, 5, 6, расположенных на стр. 37.
С
одержание эпюра.
Даны плоскость треугольника АВС и прямая DE, требуется:
задача 1 – определить расстояние от точки D до плоскости, заданной треугольником АВС;
задача 2 – построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от неё на 50 мм.;
задача 3 – через прямую DE провести плоскость, перпендикулярную треугольнику АВС, построить линию пересечения этих двух плоскостей, определить видимость.
Указания к выполнению эпюра. Данные для выполнения эпюра взять из таблицы в соответствии с вариантом. Координаты точек даны в мм. Задачи 1 и 2 можно совместить на одном чертеже. Точку Е построить только для задачи 3.
Образец выполнения задания представлен на рисунке 9.
Задача 1
В первой задаче контрольной работы требуется найти расстояние от точки D до плоскости треугольника ABC. Кратчайшее расстояние от точки до плоскости есть перпендикуляр, опущенный из данной точки на эту плоскость.
Этап 1 (рис. 1). Для решения этой задачи необходимо, прежде всего, провести горизонталь (h3) из какой-нибудь вершины треугольника ABC на фронтальной плоскости проекций (П2) и фронталь (f1) – на горизонтальной плоскости проекций (П1) из любой вершины ΔАВС, удобной для этого построения. Обозначив точку пересечения фронтали со стороной ΔАВС на горизонтальной плоскости проекций точкой 11, нужно найти ее проекцию (по проекционной связи) на фронтальной проекции ΔАСВ, это будет точка 12.
Рис. 1 Этап 1 Рис. 2 Этап 2
Таким же образом находятся точки 22 и 21, используя горизонталь (h3). Из точки D2 опускаем ⊥ (перпендикуляр) на f2 (отрезок А212) и из точки D1 опускаем ⊥ на h2 (отрезок С1 21).
Этап 2 (рис. 2). Необходимо найти основание перпендикуляра как точку пересечения прямой DK и плоскости, заданной ΔАВС. Для этого продолжаем перпендикуляр из точки D2 (на фронтальной плоскости проекций) до пересечения со стороной А2С2 – обозначаем точку 42. Пересечение перпендикуляра со стороной А2В2 дает нам точку 32. Заключаем прямую 4232 во вспомогательную проецирующую плоскость β2, это действие дает нам возможность найти проекцию отрезка 4232 на горизонтальной плоскости проекций (П1) в плоскости ΔАВС – это отрезок 4131. Находим точку пересечения отрезка 4131 с перпендикуляром, опущенным из точки D1 и обозначаем ее К1. Используя проекционную связь, находим точку К2 на перпендикуляре, который опущен из точки D2. Таким образом, мы нашли точку пересечения перпендикуляра, опущенного из точки D на плоскость, заданную ΔАВС, на обеих проекциях.
Этап 3 (рис. 3). Следующий этап выполнения задания содержит в себе нахождение натуральной величины перпендикуляра DК.
Это действие можно проводить на любой из плоскостей проекций, мы выбираем горизонтальную плоскость и начинаем построение с восстановления перпендикуляра к отрезку D1К1 в точке D1 (пока произвольной длины). Переходим на фронтальную плоскость проекций и находим расстояние от точки К2 до D2 как разность их высот по отношению к оси Х. Найденное расстояние откладываем на восстановленном перпендикуляре к отрезку D1К1 в точке D1 на горизонтальной плоскости проекций. Отмечаем точку D0. Точку D0 соединяем с точкой К1. Отрезок D0К1 – является натуральной (истинной) величиной перпендикуляра DК к плоскости, заданной ΔАВС. Этот способ нахождения истинной величины расстояния от точки, лежащей вне плоскости, до плоскости называется способом прямоугольного треугольника.
Рис. 3 Этап 3 Рис. 4 Этап 4
Задача 2
Этап 4 (рис. 4). На этом этапе необходимо решить вторую задачу эпюра 1, т.е. построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от неё на 50 мм. Построение начинаем с того, что через любую вершину ΔАВС проводим линию параллельную перпендикуляру DК. На фронтальной плоскости (П2) эта линия будет // (параллельна) D2К2, а на горизонтальной плоскости (П1) - // D1К1. Отмечаем во фронтальной плоскости проекций (П2) на только что проведенной // перпендикуляру D2К2 линии через вершину С2 любую произвольную точку Р2. Находим ее проекцию на горизонтальной плоскости проекций (П1) на линии, проведенной через точку С1 параллельно перпендикуляру D1К1. Методом прямоугольного треугольника находим натуральную величину отрезка С2Р2. Для этого необходимо найти и измерить разность расстояний от точек С1 и Р1 до оси Х. На рис. 4 это расстояние обозначено буквой l. Теперь нужно возвратиться на фронтальную проекцию и провести перпендикуляр в точке С2 к отрезку С2Р2. На нем отложить отрезок l и конечную точку N2 соединить с точкой Р2. Полученный отрезок N2P2 и будет натуральной величиной отрезка С2Р2. Именно на отрезке N2P2 от точки N2 нужно отложить расстояние, равное 50 мм, и из конечной точки провести линию параллельную отрезку N2С2, которая пересечет отрезок С2Р2 в точке Т2 (бывают случаи, когда истинная величина отрезка С2Р2, т.е. отрезок N2С2, меньше, чем требуемое по условию задачи расстояние 50мм. Это не должно смущать студента, так как отрезок N2P2 можно продолжить за точку Р2, также как отрезок С2Р2).
Теперь, когда точка Т2, которая отстоит от плоскости ΔАВС на 50мм, найдена, нужно найти ее горизонтальную проекцию, используя проекционную связь. Точка Т1 будет располагаться на отрезке С1Р1. Далее необходимо задать плоскость, параллельную ΔАВС, используя свойство параллельности плоскостей, смысл, которого в следующем: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Возьмем две, пересекающиеся в точке С2, стороны С2В2 и С2А2 и через точку Т2 проведем прямые, одна из которых параллельна С2В2, а другая - С2А2. Ограничим угол В2С2А2 волнистой линией. Это будет плоскость, заданная двумя, пересекающимися в точке Т2, прямыми, параллельная ΔАВС. На горизонтальной плоскости проекций через точку Т1 проведем одну прямую, параллельную стороне С1В1, а другую прямую – параллельную С1А1. Полученный угол В1С1А1 ограничим волнистой линией. Таким образом, мы получили горизонтальную проекцию плоскости, параллельную ΔАВС, которая образована двумя пересекающимися прямыми.
Задача 3
В задаче 3 искомая плоскость, перпендикулярная к заданной, должна содержать в себе заданную прямую и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость. Точки пересечения заданной прямой и перпендикуляра определяют линию пересечения искомой и заданной плоскостей. Видимость плоскостей определяется при помощи конкурирующих точек скрещивающихся прямых, принадлежащих этим плоскостям.
Этап 5 (рис.5). Построения, выполняемые на этапе 5, повторяют построения, выполненные на этапах 1 и 2 и заключаются в построении перпендикуляров из точек D1 и D2 на проекции плоскости, заданной ΔАВС. Дело в том, что плоскость, которая должна пересечь ΔАВС, по условию задачи ей перпендикулярна, значит, одна из сторон новой плоскости, заданной скрещивающимися прямыми, должна являться перпендикуляром к ΔАВС. Точки К1 и К2 являются точками пересечения перпендикуляров, опущенных из точек D1 и D2 на горизонтальную и фронтальную плоскости ΔАВС. Эти точки являются началами отрезков, по которым будет проходить пересечение двух плоскостей. Но для построения плоскости необходимо ввести в наш чертеж точки Е1 и Е2.
Рис.5. Этап 5 Рис. 6. Этап 6
Этап 6 (рис.6). На горизонтальной проекции через прямую D1 Е1 задаем секущую плоскость и отмечаем точки пересечения D1 Е1 с ΔА1В1С1 - 51 и 61. Находим их соответствующие проекции на фронтальной плоскости – 52 и 62. Точки 52 и 62 соединяем между собой и продолжаем этот отрезок до пересечения с прямой Е2D2. Получили точку F2.
Этап 7 (рис.7). Соединяем точки F2 и К2 на фронтальной плоскости проекций, а также точки F1 и К1 на горизонтальной плоскости проекций. Отрезки F2 К2 и F1К1 – являются линиями пересечения заданной плоскости ΔАВС и искомой, перпендикулярной заданной.
Этап 8 (рис.8). На последнем этапе необходимо определить видимость пересечения двух плоскостей. Это можно определить, используя метод конкурирующих точек скрещивающихся прямых, которым принадлежат эти точки.
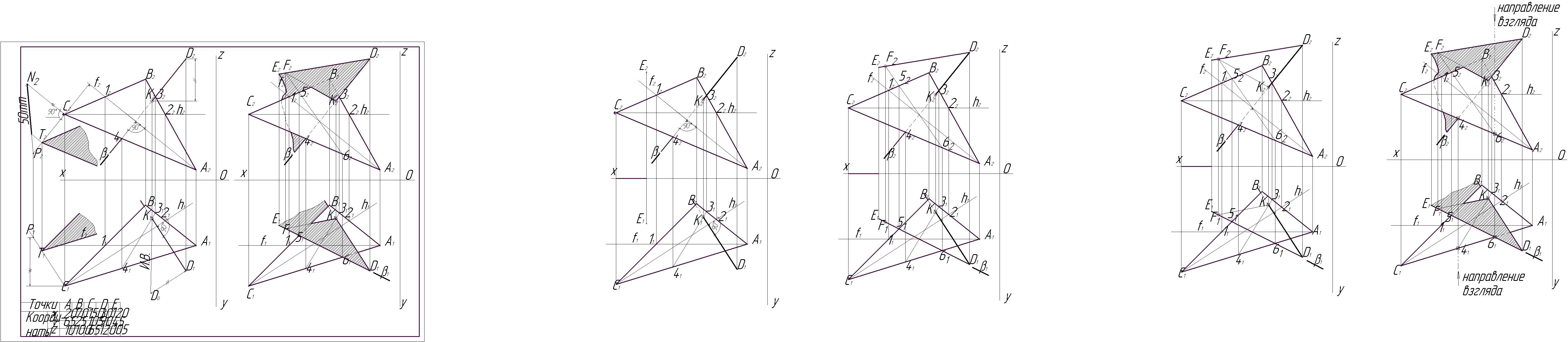
Рис.7. Этап 7 Рис. 8 Этап 8
Возьмем точку 61, в которой скрещиваются прямые С1А1 и Е1D1, и подымем проекционную связь на фронтальную плоскость проекций. По этой проекционной связи проследим сверху вниз расположение прямых С2А2 и Е2D2. Нас интересует, какая из этих прямых встретится на нашем пути (сверху вниз) раньше. Первой мы встречаем прямую Е2D2, а затем прямую С2А2. Из этого можно сделать вывод, что на горизонтальной проекции из двух рассматриваемых скрещивающихся прямых выше лежит прямая Е1D1. Это значит, что в этой плоскости проекций плоскость, заданная пересекающимися прямыми Е1D1 и К1D1,находится выше плоскости, заданной ΔАВС, значит, в этом месте она будет видимой до линии пересечения F1К1, а ΔАВС – невидимым.
Чтобы определить видимость пересекающихся плоскостей на фронтальной плоскости проекций, возьмем точку 42. В этой точке скрещиваются прямые С2А2 и D242. Опустим проекционную связь из этой точки на горизонтальную проекцию. И проследим, какая из прямых С1А1 и D141 встретится нам раньше, если смотреть на них снизу вверх. Как видно из чертежа, первой встречается С1А1, а затем D141. Это говорит о том, что на фронтальной проекции (с которой мы начинали свое исследование) ΔАВС, которому принадлежит прямая С1А1, будет видимым, плоскость, заданная пересекающимися прямыми Е1D1 и К1D1, – невидимой. Для более наглядного изображения нужно заштриховать одну из пересекающихся плоскостей и показать невидимые стороны плоскостей пунктирной линией.
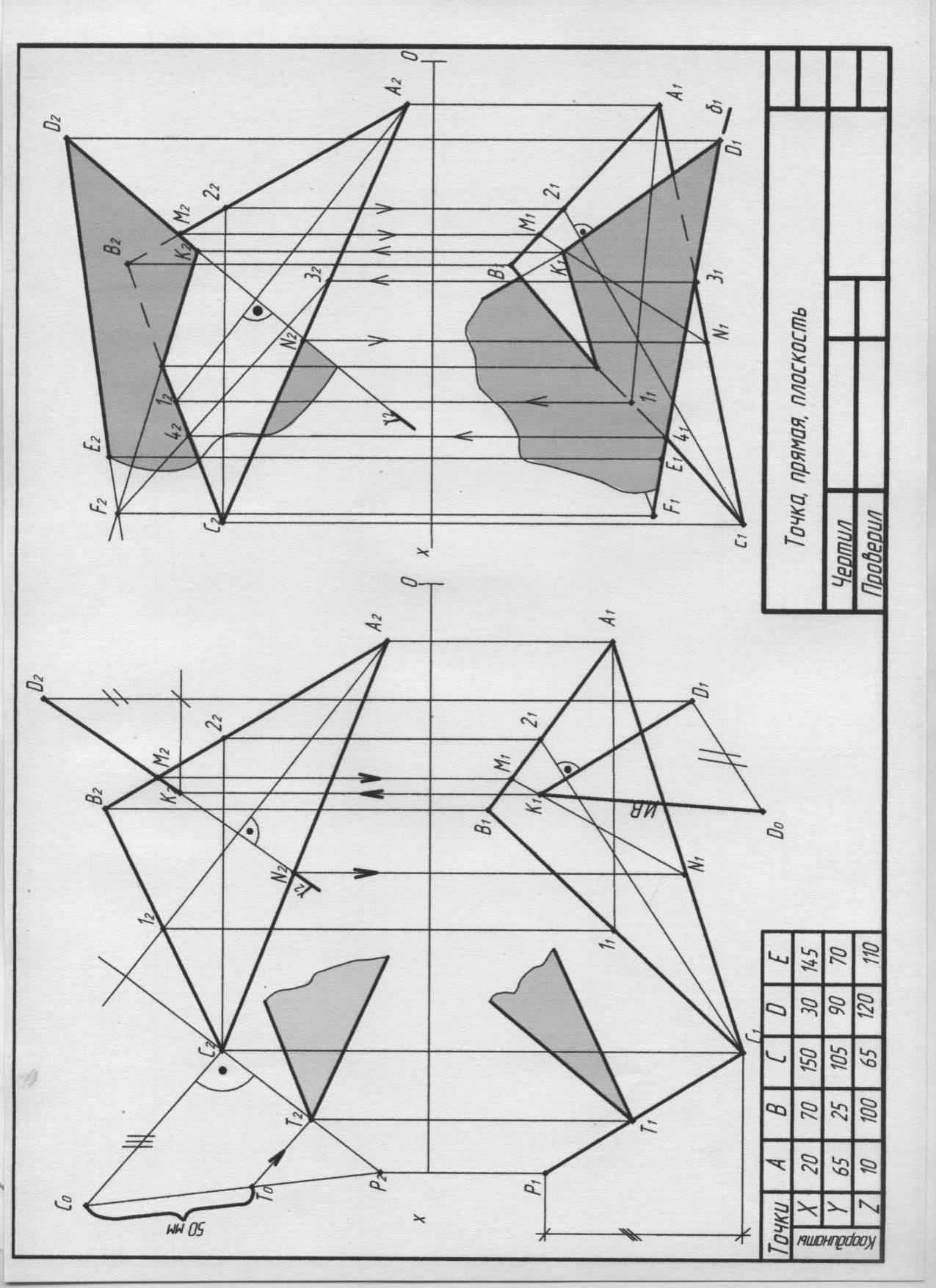
Рис.9. Пример выполнения эпюра №1
studfiles.net
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ» Технологический институт Кафедра
1 СПбГАСУ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Сборник заданий для практических занятий Направление подготовки: 270100 «Архитектура» Студент...........................................гр.............. Санкт-Петербург
Инженерная графика Кривальцевич Татьяна Владимировна Задания К лекции «Пересечение геометрических тел плоскостями. Построение разверток» Омск-2010 Требования к выполнению заданий: 1. Задание выполнить
Министерство общего и профессионального образования Российской Федерации СЕВЕРО-ЗАПАДНЫЙ ЗАОЧНЫЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ КАФЕДРА ИНЖЕНЕРНОЙ ГРАФИКИ НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Задания на контрольную работу
Л.Д. Письменко СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ Ульяновск 2001 Министерство образования РФ Ульяновский государственный технический университет Л.Д. Письменко СПОСОБЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ Методические
ПРАВИЛА ОФОРМЛЕНИЯ ЧЕРТЕЖЕЙ Основные правила оформления чертежей. Система стандартов. Форматы. Рамка и основная надпись чертежа. Линии чертежа. Шрифты чертежные. Оформление титульного листа. Нанесение
Б. М. Маврин, Е. И. Балаев СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА Практикум Самара 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ. 4 1. ПОСТРОЕНИЕ ИСХОДНЫХ ДАННЫХ.... 5 2. ПОСТРОЕНИЕ ВИНТОВОЙ ЛИНИИ НА ПОВЕРХНОСТЯХ ВРАЩЕНИЯ.. 5 3. ПОСТРОЕНИЕ КАРКАСА ЛИНЕЙЧАТОЙ ПОВЕРХНОСТИ КОНОИДА. 8 4. ОПРЕДЕЛЕНИЕ ВИДИМОЙ ЧАСТИ
Министерство образования и науки Российской Федерации Государственное образовательное учреждение высшего профессионального образования ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Б. М. Маврин, Е. И. Балаев ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ Практикум Самара 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ
Министерство образования и науки Самарской области государственное автономное учреждение среднего профессионального образования Самарский колледж транспорта и коммуникаций (ГАОУ СПО СКТК) Методические
КИНЕМАТИЧЕСКАЯ СХЕМА План 1. Правила выполнения схем 1.1. Общие требования к выполнению схем 1.2. Условные графические обозначения элементов 1.3. Позиционные обозначения элементов 1.4. Перечень элементов
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ.. 4 1. ОБЩИЙ АЛГОРИТМ РЕШЕНИЯ ЭПЮРА 2. 5 2. ПОСТРОЕНИЕ СЛЕДОВ ПЛОСКОСТИ..5 3. СОВМЕЩЕНИЕ ПЛОСКОСТИ С ПЛОСКОСТЬЮ ПРОЕКЦИЙ 13 4. ПОСТРОЕНИЕ ОСНОВАНИЯ МНОГОГРАННИК. 14 4.1. Построение
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕКИЙ УНИВЕРСИТЕТ (МАДИ) РАБОЧАЯ ТЕТРАДЬ ПО ЧЕРЧЕНИЮ Часть 2. Проекционное черчение Для студентов-иностранцев МОСКВА 2014 МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ
ОСНОВЫ МАШИНОСТРОИТЕЛЬНОГО ЧЕРЧЕНИЯ Проекционное черчение. Вопросы к заданиям 1 и 2 1. ГОСТ 2.301-68. Форматы. 1.1.Какие основные форматы листов установлены для чертежей? (обозначение, размеры сторон).
0 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕРСПЕКТИВА СХЕМАТИЗИРОВАННОГО
МИНОБРНАУКИ РОССИИ государственное образовательное учреждение высшего профессионального образования «Кузбасская государственная педагогическая академия» (КузГПА) Технолого-экономический факультет Кафедра
Б. М. Маврин, Е. И. Балаев ИЗОБРАЖЕНИЕ ТЕЛ ВРАЩЕНИЯ Практикум Самара 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ
Б. М. Маврин, В. И. Зырянова ГЕОМЕТРИЧЕСКИЕ ПО- СТРОЕНИЯ Практикум Самара 2003 3 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Министерство образования и науки Российской Федерации Вологодский государственный университет Кафедра начертательной геометрии и графики НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Методические указания и задания для самостоятельной
Федеральное агентство по образованию РФ СИБИРСКАЯ ГОСУДАРСТВЕННАЯ АВТОМОБИЛЬНО ДОРОЖНАЯ АКАДЕМИЯ Кафедра начертательной геометрии, инженерной и машинной графики Куликова О.М. СБОРНИК ЗАДАНИЙ ПО ИНЖЕНЕРНОЙ
Приложение 3. к программе Маляр строительный МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ (ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ СПЕЦИАЛЬНОЕ УЧЕБНО- ВОСПИТАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ДЛЯ ДЕТЕЙ И ПОДРОСТКОВ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Липецкий государственный университет» Факультет инженеров транспорта (наименование факультета) «УТВЕРЖДАЮ»
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Пермский государственный технический университет» Кафедра дизайна, графики и начертательной
docplayer.ru
Контрольная работа №1 по начертательной геометрии
Задача 1. Построить линию пересечения треугольников АВС и ЕДК и показать видимость их в проекциях. Определить натуральную величину треугольника АВС.
Данные для своего варианта взять из таблицы 1.1. Пример выполнения листа 1 приведен на рисунке 1.1.
Таблица 1.1 – Данные к задаче 1 (координаты, мм)
| хА | yA | zA | xB | yB | zB | xC | yC | zC | xD | yD | zD | xE | yE | zE | xK | yK | zK |
| 122 | 40 | 75 | 50 | 110 | 8 | 0 | 50 | 40 | 140 | 20 | 0 | 70 | 110 | 50 | 20 | 80 | 85 |
Рисунок 1.1. – Пример выполнения листа 1
Задача 2. Построить проекции пирамиды, основанием которой является треугольник АВС, а ребро SA определяет высоту h пирамиды.
Данные для своего варианта взять из таблицы 1.2. Пример выполнения листа 2 приведен на рисунке 1.2.
Таблица 1.2 – Данные к задаче 2 (координаты и размеры, мм)
| хА | yA | zA | xB | yB | zB | xC | yC | zC | h |
| 122 | 40 | 75 | 50 | 110 | 8 | 0 | 50 | 40 | 85 |
Задача 3. Построить линию пересечения пирамиды с прямой призмой.
Данные для своего варианта взять из таблицы 1.3. Пример выполнения задачи 3 приведен на рисунке 1.2.
Таблица 1.3 – Данные к задаче 3 (координаты и размеры, мм)
| хА | yA | zA | xB | yB | zB | xC | yC | zC | xD | yD | zD | xE | yE | zE | xK | yK | zK | xG | yG | zG | xU | yU | zU | h |
| 122 | 14 | 77 | 141 | 75 | 0 | 87 | 100 | 40 | 0 | 50 | 40 | 105 | 55 | 0 | 80 | 15 | 0 | 20 | 20 | 0 | 50 | 95 | 0 | 85 |
Задача 2 Задача 3
Рисунок 1.2. – Пример выполнения листа 2
Рисунок 1.3. – Пример выполнения листа 3
Задача 4. Построить развертки пересекающихся многогранников – прямой призмы с пирамидой. Показать на развертках линию их пересечения. Чтобы решить данную задачу, необходимо чертеж-задание для листа 3 получить, переведя на кальку формата А3 (297х420 мм) чертеж пересекающихся многогранников с листа 2 (задача 3). Пример выполнения листа 3 приведен на рисунке 1.3.
Задача 5. Построить линию пересечения конуса вращения плоскостью АВС общего положения. Данные для своего варианта взять из таблицы 1.4. Пример выполнения листа 4 дан на рисунке 1.4.
Таблица 1.4 – Данные к задаче 5 (координаты и размеры, мм)
| хK | yK | zK | хА | yA | zA | xB | yB | zB | xC | yC | zC | R | h |
| 85 | 70 | 0 | 48 | 26 | 68 | 16 | 48 | 68 | 90 | 142 | 8 | 42 | 95 |
Задача 6. Построить линию пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения – взаимно перпендикулярные проецирующие скрещивающиеся прямые.
Данные для своего варианта взять из таблицы 1.5. Пример выполнения данной задачи показан на рисунке 1.4.
Таблица 1.5 – Данные к задаче 6 (координаты и размеры, мм)
| хK | yK | zK | R | h | хE | yE | zE | R1 |
| 75 | 72 | 0 | 42 | 95 | 66 | 72 | 35 | 35 |
Задача 2 Задача 3
Рисунок 1.4. – Пример выполнения листа 4
Контрольная работа №2 по черчению
Задание по теме 1. Построить очертание кулачка. Данные для своего варианта взять из таблицы 2.1.Пример выполнения дан на рисунке 2.1.
Графическую работу выполнить карандашом на листе чертежной бумаги формата А3.
Таблица 2.1 – Данные к заданию по теме 1 (размеры, мм)
| R | R1 | R2 | R3 | a | b | d | d | h | t | x | y |
| 120 | 100 | 50 | 30 | 80 | 50 | 45 | 40 | 14 | 50,5 | 40 | 35 |
Рисунок 2.1. – Пример выполнения чертежа по теме 1
Задание по теме 2. Построить три вида детали по данному наглядному изображению в аксонометрической проекции. Данные для своего варианта взять из рисунка 2.2. Пример выполнения дан на рисунке 2.3
Графическую работу выполняют на листе чертежной бумаги формата А3 карандашом.
Рисунок 2.2. – Индивидуальное задание к чертежу по теме 2
Рисунок 2.3. – Пример выполнения чертежа по теме 2
Задание по теме 3. Построить три изображения и аксонометрическую проекцию предмета по его описанию. Предмет изобразить с двумя отверстиями – призматическим и цилиндрическим. Индивидуальные задания даны в таблицах 2.2. и 2.3. Пример выполнения графической работы дан на рисунке 2.4. Работу выполнить на листе чертежной бумаги формата А3 карандашом.
Таблица 2.2 – Данные к заданию по теме 3
| Внешняя форма предмета | Цилиндрическое отверстие |
| Шестиугольная правильная призма. Диаметр окружности, вписанной в шестиугольник основания, равен 80 мм. Две вершины основания лежат на вертикальной оси симметрии. Высота призмы 100 мм. | Сквозное отверстие диаметром 25 мм. Вертикально расположенная ось отверстия проходит через центр шестиугольника. |
Таблица 2.3 – Данные к заданию по теме 3 (размеры, мм)
| Размеры отверстия и расположение его от нижнего основания предмета (или центра сферы) | Форма призматического отверстия |
| a1=45 a2=35 b=50 z=25 |
|
Рисунок 2.4. – Пример выполнения чертежа по теме 3
Задание по теме 4. Построить третье изображение детали по двум данным, дать разрезы, построить натуральный вид наклонного сечения, а также наглядное изображение детали в аксонометрической проекции. Индивидуальное задание дано на рисунке 2.5. Пример выполнения работы дан на рисунках 2.6 и 2.7.
Рисунок 2.5. – Индивидуальное задание к чертежу по теме 4
Рисунок 2.6. – Пример выполнения чертежа по теме 4
Рисунок 2.7. – Пример выполнения чертежа по теме 4
Задание по теме 5. Вычертить: 1) болт, гайку, шайбу (и шплинт, если болт имеет отверстие под шплинт) по их действительным разрезам, которые следует взять из соответствующих стандартов; 2) упрощенное изображение этих деталей в сборе; 3) гнездо под резьбу, гнездо с резьбой, шпильку отдельно и шпильку в сборе с гайкой и шайбой (и шплинтом, если задана корончатая или прорезная гайка) по их действительным размерам, которые следует взять из соответствующих стандартов.
Варианты заданий даны в таблицах 2.4 и 2.5. Пример выполнения задания дан на рисунке 2.8.
Таблица 2.4 – Данные к заданию по теме 5 (размеры, мм)
| Резьба | Длина болта, мм | Исполнение | ГОСТ | ||||
| Болта | гайки | шайбы | болта | гайки | шайбы | ||
| М16 | 70 | 1 | 1 | - | 7805-70 | 5972-70 | 6402-70 |
| Резьба | Длина шпильки, мм | Исполнение | ГОСТ | ||||
| шпильки | гайки | шайбы | шпильки | гайки | шайбы | ||
| М20х1,5 | 60 | - | 2 | - | 22032-76 | 5918-73 | 6402-70 |
Рисунок 2.8. – Пример выполнения чертежа по теме 5
Задание по теме 6. Требуется составить спецификацию, выполнить эскизы всех деталей сборочной единицы (кроме стандартных изделий), выполнить сборочный чертеж. Деталь выбрать самостоятельно по месту работы или получить по указанию преподавателя на кафедре инженерной графики изделие (сборочную единицу), например, вентиль, пробковый кран, домкрат, тиски, масляный насос, форсунки двигателей, различные приспособления для обработки деталей на металлорежущих станках и др. изделия, состоящие из 7-ми деталей, не считая стандартных.
Задание по теме 7. Задание на деталирование чертежа общего вида выдается на кафедре инженерной графики во время установочной сессии.
gigabaza.ru
Контрольная работа
для студентов заочной формы обучения,
по дисциплине «Начертательная геометрия»
Общие требования к выполнению графических работ
Графические работы выполняются на листах чертѐжной бумаги формата А3
(420Χ297) карандашом (желательно Т, ТМ (Н, НВ) в тонких линиях и ТМ, (НВ, В) при обводке) с использованием чертѐжных инструментов. Все чертежи должны быть выполнены в масштабе 1:1 и иметь основную надпись по ГОСТ 2.104 – 68 форма 1 (185 х 55), заполненной шрифтом №7 и №3.5 по ГОСТ 2.304 –81,допускается использовать листы с основной надписью выполненной типографским способом. Чертежи должны быть выполнены технически грамотно, т.е. полностью соответствовать современным требованиям ГОСТов системы ЕСКД:
ГОСТ 2.301 –68Форматы.
ГОСТ 2.302 –68Масштабы.
ГОСТ 2.303 –68Линии.
ГОСТ 2.304 –81Шрифты чертѐжные.
ГОСТ 2.305 –68Изображения – виды, разрезы, сечения.
ГОСТ 2.306 –68Обозначения графические материалов и правила их нанесения на чертежах.
ГОСТ 2.307 –68Нанесение размеров и предельных отклонений. Шрифт размерных чисел и буквенных обозначений №5.
При выполнении заданий чѐтко соблюдать тип линий. Все линии вспомогательных построений сохранять.
Работы необходимо сшить и представить в виде «Альбома графических работ» с титульным листом (формат А3).
Состав задания
Задача 1. По заданным координатам (см. таблицы 1 и 8) построить проекции двух треугольников ABC и DEF. Найти линию пересечения двух треугольников и определить видимость сторон. Все вспомогательные линии построения необходимых точек сохранять. [1,2,3]
Задача 2. По двум проекциям гранного тела, построить третью проекцию.
Гранное тело имеет сквозное отверстие. Построить линию пересечения боковой поверхности со сквозным отверстием на трѐх проекциях. Все вспомогательные линии построения необходимых точек сохранять. Предусмотреть простые разрезы.
Поставить размеры. [4,5,7,9]
Задача 3. По двум проекциям тела вращения, построить третью проекцию. Тело вращения имеет сквозное отверстие. Построить линию пересечения боковой поверхности со сквозным отверстием на трѐх проекциях. Все вспомогательные линии построения необходимых точек сохранять. Предусмотреть простые разрезы.
Поставить размеры. [6,8,10]
Литература:
1 – Гордон В.О., Семенцов – Огневский М.А. Курс начертательной геометрии,
1988 --§26 с.70 рисунок 178.
2 – Чекмарѐв А.А. Начертательная геометрия и черчение, 1999 – §4,2…4,4
с.41…46 рисунки 4.8, 4.10, 4.11, 4.12, 4.13.
3 --Соломонов К.Н., Бусыгина Е.Б., Чиченѐва О.Н. Начертательная геометрия,
2004 --§3.6.2 с.47 рисунок 3.14.
4 – Гордон В.О., Семенцов – Огневский М.А. Курс начертательной геометрии,
1988 --§40 с.111,112 рисунок 268.
5 – Чекмарѐв А.А. Начертательная геометрия и черчение, 1999 – §12.8 с.181…185
рисунки 12.51 а,б 12.52 а,б,в,г.
6 – Чекмарѐв А.А. Начертательная геометрия и черчение, 1999 – §12.8 с.185…186
рисунки 12.53 а,в,г.
7 --Соломонов К.Н., Бусыгина Е.Б., Чиченѐва О.Н. Начертательная геометрия,
2004 --§5.2. с.71. рисунок 5.4, 5.5.
8 --Соломонов К.Н., Бусыгина Е.Б., Чиченѐва О.Н. Начертательная геометрия,
2004 --§7.6. с.112…116. рисунок 7.14 а,б.
9 – Брилинг Н.С. Черчение, 1989 --§12.2 с.159 рисунок 12.7.
10– Брилинг Н.С. Черчение, 1989 --§12.4 с.160…165 рисунок 12.15 а,б.
11– Миронов Е.Г., Миронова Р.С. и др. Сборник заданий по инженерной графике с примерами выполнения чертежей на компьютере 1988 – стр.116…119
12– Миронов Е.Г., Миронова Р.С. и др. Сборник заданий по инженерной графике с примерами выполнения чертежей на компьютере 1988 – стр.120…122
Варианты заданий к задаче 1
Таблица 1 – Координаты точек
Вари |
| XA |
| YA |
| ZA |
| XB |
| YB |
| ZB | XC | YC | ZC | XD | YD |
| ZD |
| XE |
| YE |
| ZE |
| XF | YF | ZF | |||||||||||||||||
анты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
1 |
| 130 |
| 40 |
| 60 |
| 90 | 90 | 90 |
| 20 |
| 30 |
| 20 |
| 70 |
| 20 |
|
| 95 |
| 0 |
|
| 100 |
| 60 | 140 | 65 |
| 25 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
2 |
| 125 |
| 90 |
| 10 |
| 0 | 85 | 50 |
| 55 |
| 20 |
| 80 |
| 120 |
| 60 |
|
| 50 |
| 20 |
| 30 |
| 70 | 65 | 105 |
| 15 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
3 |
| 135 |
| 45 |
| 50 |
| 80 | 80 | 115 |
| 20 |
| 10 |
| 40 |
| 120 |
| 0 |
|
| 95 |
| 65 |
| 85 |
| 20 | 25 | 45 |
| 85 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
4 |
| 0 |
| 55 |
| 40 |
| 50 | 110 | 0 |
| 120 |
| 40 |
| 75 |
| 10 |
| 80 |
|
| 60 |
| 80 |
| 20 |
| 90 | 110 | 80 |
| 5 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
5 |
| 20 |
| 12 |
| 90 |
| 85 | 80 | 23 |
| 135 |
| 50 |
| 85 |
| 70 |
| 85 |
|
| 110 |
| 0 |
|
| 35 |
| 20 | 120 | 0 |
| 52 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
| 0 |
| 50 |
| 85 |
| 50 | 105 | 25 |
| 115 |
| 8 |
| 75 |
| 110 |
| 65 |
|
| 55 |
| 55 |
|
| 0 |
| 115 | 15 | 70 |
| 40 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
7 |
| 115 |
| 90 |
| 10 |
| 52 | 25 | 80 |
| 0 |
| 80 |
| 45 |
| 65 |
| 105 |
| 80 |
| 130 |
| 20 |
| 35 | 10 | 50 |
| 0 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
8 |
| 120 |
| 40 |
| 75 |
| 5 | 50 | 0 |
| 0 |
| 55 |
| 40 |
| 125 |
| 20 |
|
| 55 |
| 20 |
| 10 |
| 40 | 75 | 110 |
| 110 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
9 |
| 15 |
| 10 |
| 90 |
| 85 | 80 | 25 |
| 130 |
| 50 |
| 80 |
| 75 |
| 85 |
|
| 110 |
| 0 |
|
| 30 |
| 15 | 120 | 0 |
| 50 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
10 |
| 120 |
| 10 |
| 88 |
| 52 | 80 | 25 |
| 0 |
| 50 |
| 83 |
| 70 |
| 85 |
|
| 110 |
| 135 |
| 35 |
| 20 | 15 | 0 |
| 53 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
11 |
| 20 |
| 50 |
| 10 |
| 83 | 120 | 80 |
| 135 |
| 58 |
| 50 |
| 68 |
| 30 |
|
| 85 |
| 0 |
|
| 120 |
| 35 | 120 | 90 |
| 0 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
12 |
| 135 |
| 50 |
| 80 |
| 85 | 80 | 25 |
| 20 |
| 10 |
| 90 |
| 110 |
| 80 |
|
| 5 |
|
| 80 |
| 20 |
| 90 | 10 | 80 |
| 60 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
13 |
| 135 |
| 80 |
| 50 |
| 83 | 25 | 80 |
| 20 |
| 90 |
| 10 |
| 68 |
| 110 |
| 85 |
| 125 |
| 55 |
| 25 | 0 | 90 |
| 10 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
14 |
| 50 |
| 80 |
| 25 |
| 120 | 8 | 85 |
| 0 |
| 50 |
| 80 |
| 70 |
| 85 |
|
| 110 |
| 135 |
| 35 |
| 20 | 15 | 0 |
| 52 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
| 0 |
| 50 |
| 80 |
| 50 | 80 | 25 |
| 120 |
| 10 |
| 88 |
| 135 |
| 35 |
|
| 20 |
| 18 |
|
| 0 |
| 53 | 70 | 85 |
| 110 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
16 |
| 115 |
| 8 |
| 75 |
| 50 | 105 | 23 |
| 0 |
| 50 |
| 85 |
| 35 |
| 50 |
|
| 55 |
| 80 |
| 85 |
| 105 | 100 | 0 |
| 45 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
17 |
| 130 |
| 50 |
| 80 |
| 85 | 80 | 25 |
| 15 |
| 10 |
| 90 |
| 0 |
| 30 |
|
| 15 |
| 75 |
| 85 |
| 110 | 120 | 0 |
| 50 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
18 |
| 0 |
| 80 |
| 45 |
| 50 | 25 | 80 |
| 115 |
| 90 |
| 9 |
| 10 |
| 50 |
|
| 0 |
|
| 65 |
| 105 |
| 80 | 130 | 20 |
| 35 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
19 |
| 25 |
| 50 |
| 20 |
| 65 | 115 | 130 |
| 145 |
| 20 |
| 55 |
| 85 |
| 130 |
| 0 |
|
| 165 |
| 115 |
| 20 | 35 | 0 |
| 148 | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
20 |
| 20 |
| 65 |
| 28 |
| 165 | 120 | 120 |
| 125 |
| 0 |
| 8 |
| 55 |
| 120 |
| 28 |
| 170 |
| 45 |
| 100 | 35 | 45 |
| 100 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Таблица 8 – Координаты точек | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
| Вари |
| XA |
| YA |
| ZA |
| XB |
| YB |
| ZB |
| XC |
| YC |
| ZC |
| XD |
| YD |
| ZD |
| XE |
| YE |
| ZE |
| XF |
| YF | ZF |
|
| ||||||||
| анты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
| 1 |
|
| 55 |
|
| 50 |
| 50 |
| 15 |
| 25 |
| 0 |
| 95 |
| 0 |
| 15 |
| 15 |
| 15 |
| 35 |
| 85 |
| 35 |
| 0 |
|
| 50 |
| 0 | 35 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
| 2 |
|
| 95 |
|
| 0 |
|
| 20 |
| 65 |
| 55 |
| 50 |
| 15 |
| 40 |
| 0 |
| 30 |
| 25 |
| 50 |
| 55 |
| 45 |
| 0 |
|
| 85 |
| 0 | 40 |
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
| 3 |
|
| 110 |
| 35 |
| 10 |
| 45 |
| 0 |
| 50 |
| 20 |
| 55 |
| 10 |
| 95 |
| 50 |
| 40 |
| 50 |
| 10 |
| 0 |
|
| 15 |
| 25 | 15 |
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
| 4 |
|
| 50 |
|
| 45 |
| 35 |
| 20 |
| 30 |
| 20 |
| 95 |
| 10 |
| 0 |
| 20 |
| 10 |
| 0 |
| 95 |
| 20 |
| 0 |
|
| 75 |
| 50 | 0 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
| 5 |
|
| 25 |
|
| 50 |
| 0 |
|
| 40 |
| 10 |
| 50 |
| 95 |
| 35 |
| 0 |
| 50 |
| 0 |
| 0 |
| 80 |
| 50 |
| 35 |
| 20 |
| 15 | 15 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
| 6 |
|
| 85 |
|
| 50 |
| 40 |
| 15 |
| 20 |
| 40 |
| 110 |
| 5 |
| 0 |
| 100 |
| 15 |
| 50 |
| 70 |
| 50 |
| 0 |
|
| 40 |
| 35 | 20 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
| 7 |
|
| 100 |
| 0 |
|
| 0 |
|
| 80 |
| 35 |
| 40 |
| 20 |
| 50 |
| 35 |
| 85 |
| 45 |
| 0 |
| 115 |
| 0 |
| 30 |
| 50 |
| 0 | 30 |
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 | 60 | 5 | 40 | 90 | 55 | 0 | 15 | 15 | 0 | 90 | 10 | 5 | 75 | 0 | 25 | 30 | 45 | 25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 | 10 | 15 | 0 | 80 | 55 | 50 | 90 | 5 | 0 | 55 | 45 | 0 | 100 | 10 | 35 | 70 | 10 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 | 15 | 15 | 20 | 70 | 50 | 50 | 100 | 0 | 0 | 95 | 45 | 0 | 60 | 0 | 45 | 20 | 0 | 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 | 115 | 20 | 0 | 10 | 55 | 0 | 35 | 5 | 45 | 65 | 15 | 0 | 95 | 55 | 50 | 60 | 45 | 50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 | 90 | 5 | 45 | 10 | 40 | 25 | 75 | 55 | 0 | 95 | 5 | 0 | 60 | 5 | 0 | 20 | 55 | 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 | 105 | 35 | 15 | 70 | 50 | 55 | 30 | 5 | 15 | 70 | 0 | 40 | 110 | 20 | 0 | 50 | 40 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 | 65 | 0 | 10 | 15 | 0 | 0 | 80 | 40 | 50 | 100 | 0 | 35 | 40 | 0 | 50 | 10 | 50 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 | 80 | 0 | 0 | 55 | 50 | 45 | 10 | 25 | 40 | 65 | 45 | 0 | 90 | 20 | 35 | 50 | 0 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 | 80 | 50 | 0 | 55 | 0 | 45 | 10 | 10 | 45 | 70 | 0 | 0 | 90 | 25 | 40 | 40 | 50 | 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 | 90 | 45 | 25 | 65 | 0 | 50 | 40 | 45 | 10 | 60 | 35 | 55 | 95 | 0 | 5 | 55 | 0 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 | 95 | 40 | 25 | 70 | 45 | 40 | 45 | 15 | 0 | 45 | 50 | 40 | 105 | 30 | 0 | 75 | 10 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 | 110 | 60 | 40 | 80 | 5 | 50 | 50 | 35 | 15 | 60 | 20 | 15 | 90 | 45 | 25 | 90 | 50 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 | 95 | 30 | 60 | 60 | 10 | 40 | 35 | 40 | 50 | 45 | 20 | 5 | 70 | 25 | 40 | 70 | 25 | 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 – Координаты точек
Вари | XA | YA | ZA | XB | YB | ZB | XC | YC | ZC | XD | YD | ZD | XE | YE | ZE | XF | YF | ZF |
анты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 | 56 | 50 | 50 | 15 | 25 | 0 | 95 | 0 | 15 | 15 | 15 | 35 | 85 | 35 | 0 | 50 | 0 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 | 95 | 0 | 20 | 65 | 55 | 50 | 15 | 40 | 0 | 30 | 25 | 50 | 55 | 45 | 0 | 85 | 0 | 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 | 110 | 35 | 10 | 45 | 0 | 50 | 20 | 55 | 10 | 95 | 50 | 40 | 50 | 10 | 0 | 15 | 20 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 | 50 | 45 | 35 | 20 | 30 | 20 | 95 | 10 | 0 | 20 | 10 | 0 | 95 | 20 | 0 | 75 | 50 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 | 25 | 50 | 0 | 40 | 10 | 50 | 95 | 35 | 0 | 50 | 0 | 0 | 80 | 50 | 35 | 20 | 15 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 | 85 | 50 | 40 | 15 | 20 | 40 | 110 | 5 | 0 | 110 | 15 | 50 | 70 | 50 | 0 | 40 | 35 | 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 | 95 | 0 | 0 | 80 | 35 | 40 | 20 | 50 | 35 | 85 | 45 | 0 | 115 | 0 | 30 | 50 | 0 | 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 | 60 | 5 | 40 | 90 | 55 | 0 | 15 | 15 | 0 | 90 | 10 | 5 | 75 | 0 | 25 | 30 | 45 | 25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 | 10 | 15 | 0 | 80 | 55 | 50 | 90 | 5 | 0 | 55 | 45 | 0 | 110 | 10 | 35 | 70 | 10 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 | 15 | 15 | 20 | 70 | 50 | 50 | 110 | 0 | 0 | 95 | 45 | 0 | 60 | 0 | 45 | 20 | 0 | 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 | 115 | 20 | 0 | 10 | 55 | 0 | 35 | 5 | 45 | 65 | 15 | 0 | 95 | 55 | 50 | 60 | 45 | 50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 | 90 | 5 | 45 | 10 | 40 | 35 | 75 | 55 | 0 | 95 | 5 | 0 | 60 | 5 | 0 | 20 | 55 | 45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 | 95 | 35 | 15 | 70 | 50 | 55 | 30 | 5 | 15 | 70 | 0 | 40 | 110 | 20 | 0 | 50 | 40 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 | 65 | 0 | 10 | 15 | 0 | 0 | 80 | 40 | 50 | 95 | 0 | 35 | 40 | 0 | 50 | 10 | 50 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 | 80 | 0 | 0 | 55 | 50 | 45 | 10 | 25 | 45 | 65 | 45 | 0 | 90 | 20 | 35 | 50 | 0 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 | 80 | 50 | 0 | 55 | 0 | 45 | 10 | 10 | 45 | 70 | 0 | 0 | 90 | 25 | 40 | 40 | 50 | 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 | 90 | 45 | 25 | 65 | 0 | 50 | 40 | 45 | 10 | 60 | 35 | 55 | 95 | 0 | 5 | 55 | 0 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 | 95 | 40 | 25 | 70 | 45 | 40 | 45 | 15 | 0 | 45 | 50 | 40 | 95 | 30 | 0 | 75 | 10 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 | 110 | 35 | 25 | 70 | 20 | 15 | 45 | 15 | 40 | 50 | 10 | 5 | 15 | 15 | 15 | 85 | 35 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 | 85 | 40 | 30 | 60 | 15 | 5 | 50 | 10 | 45 | 55 | 25 | 15 | 20 | 30 | 5 | 70 | 50 | 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 | 90 | 20 | 45 | 50 | 35 | 15 | 30 | 45 | 30 | 40 | 5 | 20 | 60 | 30 | 0 | 65 | 40 | 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 | 75 | 30 | 10 | 45 | 40 | 35 | 15 | 25 | 20 | 25 | 25 | 15 | 55 | 35 | 10 | 55 | 30 | 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 | 70 | 40 | 25 | 50 | 15 | 40 | 20 | 35 | 30 | 30 | 30 | 30 | 60 | 25 | 5 | 60 | 15 | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 | 110 | 60 | 40 | 80 | 5 | 50 | 50 | 35 | 15 | 60 | 20 | 15 | 90 | 45 | 25 | 90 | 50 | 35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 | 95 | 30 | 60 | 60 | 10 | 40 | 35 | 40 | 50 | 45 | 20 | 5 | 70 | 25 | 40 | 70 | 25 | 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 --Выбор вариантов
Вари |
|
|
| Задача №1 |
|
| Задача №2 |
| Задача №3 | ||||||
ант |
| (таблицы 1;8;2) | (стр.116…119)[11.] | (стр.120…122) [12.] | |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1…40 |
|
| 41…80 | 81…120 | 1…40 | 41…80 | 81…120 | 1…4 | 41…80 |
| 81…12 | |||
|
|
|
|
|
|
|
|
|
|
| 0 |
|
| 0 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 | Т.1 (1) |
|
| Т.1 (20) | Т.1 (19) | 1 | 18 | 2 | 2 | 1 | 18 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 | Т.1 (3) |
|
| Т.1 (18) | Т.1 (17) | 2 | 17 | 4 | 4 | 2 | 17 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 | Т.1 (5) |
|
| Т.1 (16) | Т.1 (15) | 3 | 16 | 6 | 6 | 3 | 16 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 | Т.1 (7) |
|
| Т.1 (14) | Т.1 (13) | 4 | 15 | 8 | 8 | 4 | 15 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 | Т.1 (9) |
|
| Т.1 (12) | Т.1 (11) | 5 | 14 | 10 | 10 | 5 | 14 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 | Т.1 (11) |
|
| Т.1 (10) | Т.1 (9) | 6 | 13 | 12 | 12 | 6 | 13 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 | Т.1 (13) |
|
| Т.1 (8) | Т.1 (7) | 7 | 12 | 14 | 14 | 7 | 12 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 | Т.1 (15) |
|
| Т.1 (6) | Т.1 (5) | 8 | 11 | 16 | 16 | 8 | 11 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 | Т.1 (17) |
|
| Т.1 (4) | Т.1 (3) | 9 | 10 | 18 | 18 | 9 | 10 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 | Т.1 (19) |
|
| Т.1 (2) | Т.1 (1) | 10 | 9 | 1 | 1 | 10 | 9 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 | Т.1 (2) |
|
| Т.1 (19) | Т.1 (20) | 11 | 8 | 3 | 3 | 11 | 8 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 | Т.1 (4) |
|
| Т.1 (17) | Т.1 (18) | 12 | 7 | 5 | 5 | 12 | 7 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 | Т.1 (6) |
|
| Т.1 (15) | Т.1 (16) | 13 | 6 | 7 | 7 | 13 | 6 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 | Т.1 (8) |
|
| Т.1 (13) | Т.1 (14) | 14 | 5 | 9 | 9 | 14 | 5 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 | Т.1 (10) |
|
| Т.1 (11) | Т.1 (12) | 15 | 4 | 11 | 11 | 15 | 4 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 | Т.1 (12) |
|
| Т.1 (9) | Т.1 (10) | 16 | 3 | 13 | 13 | 16 | 3 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 | Т.1 (14) |
|
| Т.1 (7) | Т.1 (8) | 17 | 2 | 15 | 15 | 17 | 2 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 | Т.1 (16) |
|
| Т.1 (5) | Т.1 (6) | 18 | 1 | 17 | 17 | 18 | 1 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 | Т.1 (18) |
|
| Т.1 (3) | Т.1 (4) | 10 | 17 | 4 | 4 | 10 | 17 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 | Т.1 (20) |
|
| Т.1 (1) | Т.1 (2) | 9 | 5 | 12 | 12 | 9 | 5 | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 | Т.8 (1) |
|
| Т.8 (20) | Т.8 (19) | 8 |
| 4 |
| 18 | 4 |
| 8 |
| 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 | Т.8 (3) |
|
| Т.8 (18) | Т.8 (17) | 7 |
| 6 |
| 17 | 6 |
| 7 |
| 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 | Т.8 (5) |
|
| Т.8 (16) | Т.8 (15) | 6 |
| 8 |
| 16 | 8 |
| 6 |
| 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 | Т.8 (7) | Т.8 (14) | Т.8 (13) | 5 | 10 | 15 | 10 | 5 | 15 |
|
|
|
|
|
|
|
|
|
|
25 | Т.8 (9) | Т.8 (12) | Т.8 (11) | 4 | 12 | 14 | 12 | 4 | 14 |
|
|
|
|
|
|
|
|
|
|
26 | Т.8 (11) | Т.8 (10) | Т.8 (9) | 3 | 14 | 13 | 14 | 3 | 13 |
|
|
|
|
|
|
|
|
|
|
27 | Т.8 (13) | Т.8 (8) | Т.8 (7) | 2 | 16 | 12 | 16 | 2 | 12 |
|
|
|
|
|
|
|
|
|
|
28 | Т.8 (15) | Т.8 (6) | Т.8 (5) | 1 | 18 | 11 | 18 | 1 | 11 |
|
|
|
|
|
|
|
|
|
|
29 | Т.8 (17) | Т.8 (4) | Т.8 (3) | 18 | 1 | 10 | 1 | 18 | 10 |
|
|
|
|
|
|
|
|
|
|
30 | Т.8 (19) | Т.8 (2) | Т.8 (1) | 17 | 3 | 9 | 3 | 17 | 9 |
|
|
|
|
|
|
|
|
|
|
31 | Т.8 (2) | Т.8 (19) | Т.8 (20) | 16 | 5 | 8 | 5 | 16 | 8 |
|
|
|
|
|
|
|
|
|
|
32 | Т.8 (4) | Т.8 (17) | Т.8 (18) | 15 | 7 | 7 | 7 | 15 | 7 |
|
|
|
|
|
|
|
|
|
|
33 | Т.8 (6) | Т.8 (15) | Т.8 (16) | 14 | 9 | 6 | 9 | 14 | 6 |
|
|
|
|
|
|
|
|
|
|
34 | Т.8 (8) | Т.8 (13) | Т.8 (14) | 13 | 11 | 5 | 11 | 13 | 5 |
|
|
|
|
|
|
|
|
|
|
35 | Т.8 (10) | Т.8 (11) | Т.8 (12) | 12 | 13 | 4 | 13 | 12 | 4 |
|
|
|
|
|
|
|
|
|
|
36 | Т.8 (12) | Т.8 (9) | Т.8 (10) | 11 | 15 | 3 | 15 | 11 | 3 |
|
|
|
|
|
|
|
|
|
|
37 | Т.8 (14) | Т.8 (7) | Т.8 (8) | 3 | 17 | 2 | 17 | 3 | 2 |
|
|
|
|
|
|
|
|
|
|
38 | Т.8 (16) | Т.8 (5) | Т.8 (6) | 7 | 4 | 1 | 4 | 7 | 1 |
|
|
|
|
|
|
|
|
|
|
39 | Т.8 (18) | Т.8 (3) | Т.8 (4) | 10 | 12 | 17 | 12 | 10 | 17 |
|
|
|
|
|
|
|
|
|
|
40 | Т.8 (19) | Т.8 (1) | Т.8 (2) | 15 | 4 | 5 | 4 | 15 | 5 |
|
|
|
|
|
|
|
|
|
|
Схема выбора варианта
Порядковый номер в зачѐтной книжке (две - три последние цифры) , по этому значению входим в таблицу 3 «Выбор варианта», в графу варианты и по горизонтали выбираем информацию из всех вертикальных граф таблицы.
Например: мой номер по зачѐтной книжке 68, в таблицу вхожу по варианту 68—
40 = 28;
для задачи №1 – вариант Т.8 …(6) – т.е. Таблица координат 8 , горизонтальная графа варианта 6 определяет восемнадцать координат для заданных двух треугольников.
Для задачи №2 – вариант выбираем согласно указанного варианта (по горизонтали) и согласно порядкового номера в зачѐтной книжке.
Для задачи №3 –вариантвыбираем согласно указанного варианта (по горизонтали) и согласно порядкового номера в зачѐтной книжке.
studfiles.net
