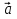, если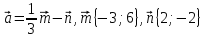 
Контрольная работа № 2 «Метод координат»
Вариант 1
1. Найдите координаты и длину вектора 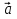, если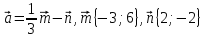
2.Напишите уравнение окружности с центром в точке Т(3;-2), проходящей через точку B(-2;0).
3.Треугольник MNK задан координатами своих вершин: M(-6;1), N(2;4), K(2;-2).
а) Докажите, что треугольник MNK – равнобедренный.
б) Найдите высоту, проведенную из вершины M.
4.Найдите координаты точки N,лежащей на оси абсцисс и равноудаленной от точек P(2;4) и K(5;-1).
5*. Докажите, что четырехугольник MNKP, заданный координатами своих вершин M(2;2), N(5;3), K(6;6), P(3;-5), является ромбом и вычислите его площадь.
Контрольная работа № 2 «Метод координат»
Вариант 2
1. Найдите координаты и длину вектора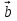 
, если 
.
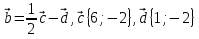2.Напишите уравнение окружности с центром в точке S(2;-1), проходящей через точку B(-3;2).
3.Треугольник FRT задан координатами своих вершин: F(2;-2), R(2;3), T(-2;1).
а) Докажите, что треугольник FRT – равнобедренный.
б) Найдите высоту, проведенную из вершины F.
4.Найдите координаты точки A,лежащей на оси ординат и равноудаленной от точек B(1;-3) и C(2;0).
5*. В равнобедренном треугольнике основание равно 10 см, а биссектриса, проведенная к основанию, равна 8 см. Найдите медиану, проведенную к боковой стороне.
Контрольная работа № 2 «Метод координат»
Вариант 3
1. Найдите координаты и длину вектора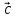 
, если 
.
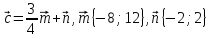2.Напишите уравнение окружности с центром в точке A(-3;2), проходящей через точку B(0;-2).
3.Треугольник FEC задан координатами своих вершин: F(-1;1), E(4;1), C(1;-3).
а) Докажите, что треугольник FEC – равнобедренный.
б) Найдите медианy, проведенную из вершины Е.
4.Найдите координаты точки N,лежащей на оси абсцисс и равноудаленной от точек P(-1;3) и K(0;2).
5*. В равнобедренном треугольнике основание равно 16 см, а высота, проведенная к основанию, равна 5 см. Найдите медиану, проведенную к боковой стороне.
Контрольная работа № 2 «Метод координат»
Вариант 4
1. Найдите координаты и длину вектора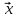 
, если 
.
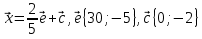2.Напишите уравнение окружности с центром в точке C(2;1), проходящей через точку D(5;5).
3.Треугольник CDE задан координатами своих вершин: C(2;2), D(6;5), E(5;-2).
а) Докажите, что треугольник CDE – равнобедренный.
б) Найдите биссектрису, проведенную из вершины C.
4.Найдите координаты точки Н, лежащей на оси ординат и равноудаленной от точек N(-2;-1) и K(4;1).
5*. Докажите, что четырехугольник PSQT, заданный координатами своих вершин P(3;0), S(-1;3), Q(-4;-1), T(0;-4), является квадратом и вычислите его площадь.
Ответы:
Вариант 1
1)
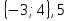
2)
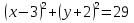
3б) 8
4) (1;0)
5) 8кв.ед.
Вариант 2
1)
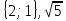
2)
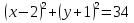
3б)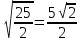 
4) (0;-1)
Вариант 3
1)
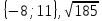
2)
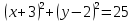
3б)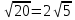 
4) (-3;0)
5) 
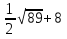кв.ед.
Вариант 4
1)
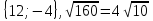
2)
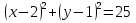
3б)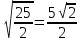
4) (0;3)
5) 25кв.ед.
infourok.ru
Вариант 1.
1. Концы отрезка АВ имеют координаты А(2; -2), В(-2; 2). Найдите координаты середины этого отрезка.
2. Даны точки А(2; 7), В(-2; 7).
а) Найдите координаты вектора ,
б) Найдите длину вектора .
3. Уравнение окружности имеет вид:
а) Постройте эту окружность;
б) Лежит ли точка А(-5; -3) на данной окружности? Ответ обоснуйте.
4* Даны точки М(-2; -1), N(-4; 3). Составьте уравнение окружности, для которой MN – диаметр окружности.
5* Найдите координаты точки пересечения прямых: -4х-14у+2=0 и 3х+6у+3=0.
6* Треугольник АВС задан координатами своих вершин: А(0;3), В(1; -4), С(5;2)
а) Напишите уравнение прямой АВ,
б) Напишите уравнение медианы АМ,
в) Найдите длину медианы АМ.
Вариант 2.
1. Концы отрезка СД имеют координаты С(-4; 3), Д(4; -3). Найдите координаты середины этого отрезка.
2. Даны точки С(-3; 5), В(3; -5).
а) Найдите координаты вектора ,
б) Найдите длину вектора .
3. Уравнение окружности имеет вид:
а) Постройте эту окружность;
б) Лежит ли точка А(-5; -5) на данной окружности? Ответ обоснуйте.
4* Даны точки А(2; 0), В(-2; 6). Составьте уравнение окружности, для которой АВ – диаметр окружности.
5* Найдите координаты точки пересечения прямых: х+2у+3=0 и 3х+5у+6=0.
6* Треугольник АВС задан координатами своих вершин: А(1;-4), В(5; 2), С(0;3)
а) Напишите уравнение прямой ВС,
б) Напишите уравнение медианы СМ,
в) Найдите длину медианы СМ.
контрольная работа "Метод координат", 9 классPDF / 176.66 Кб
xn--j1ahfl.xn--p1ai
Геометрия – 9. Контрольная работа «Метод координат» Вариант 1
1 часть
1. Дано: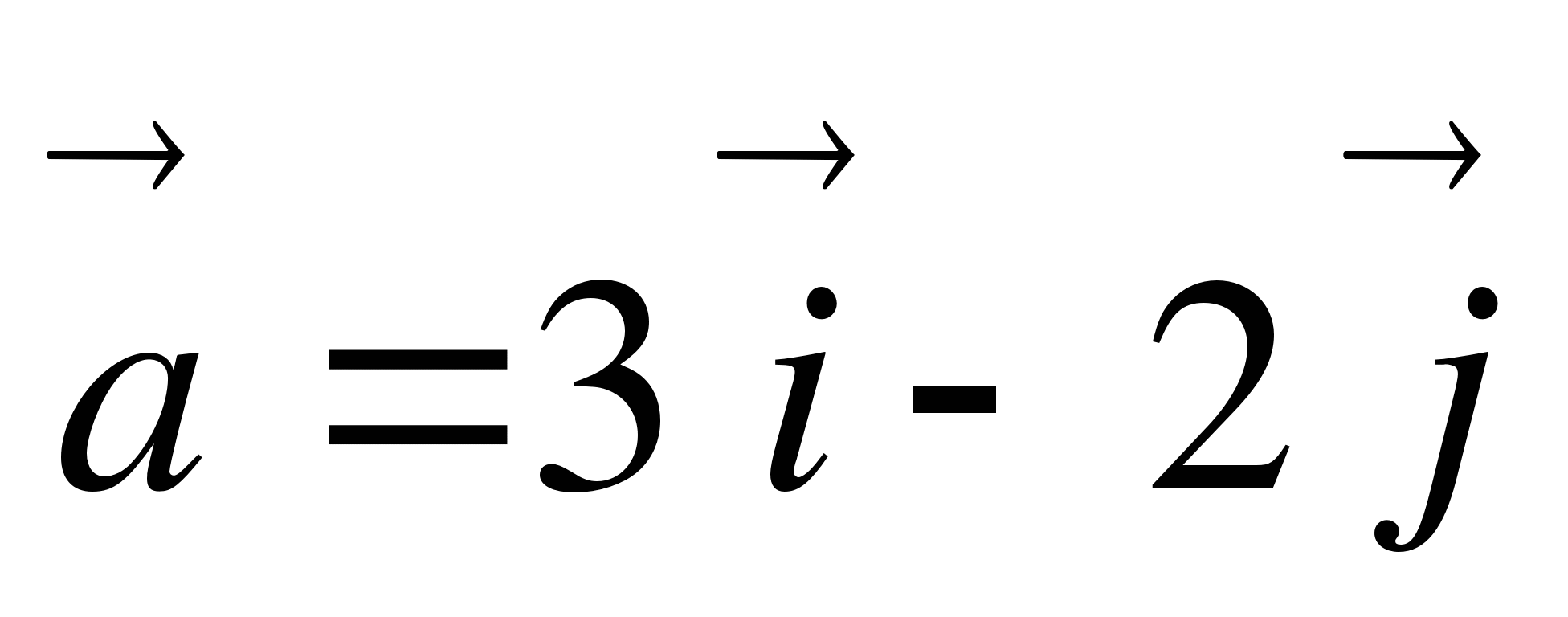 
. Найти: а) координаты вектора 
; б) длину вектора
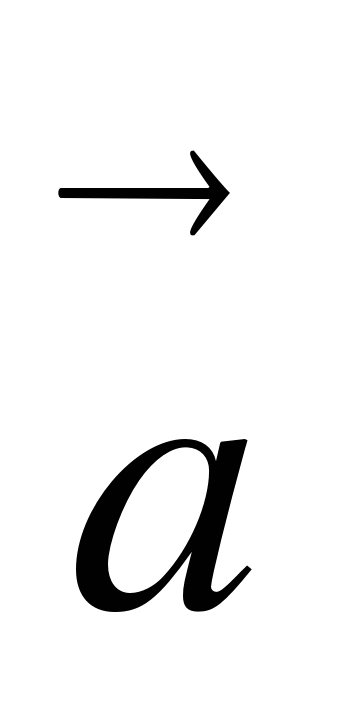
2. А(3; 4) и В(-2; 5). Найти: а) координаты вектора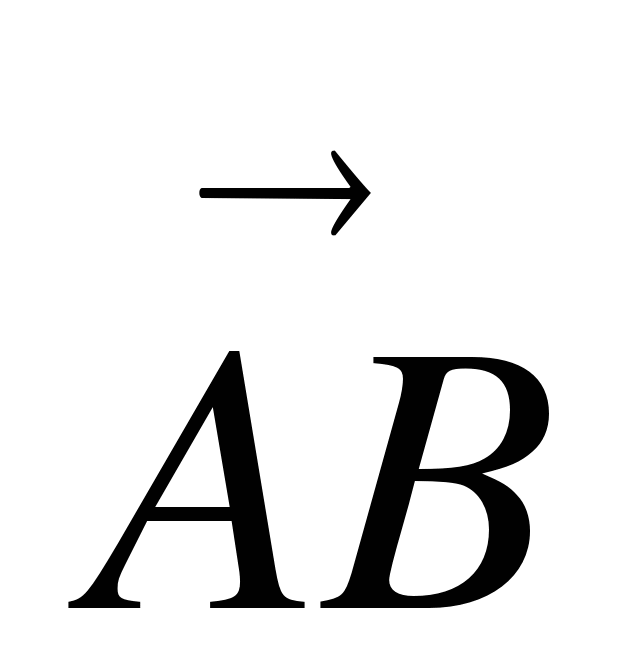 
; б) длину вектора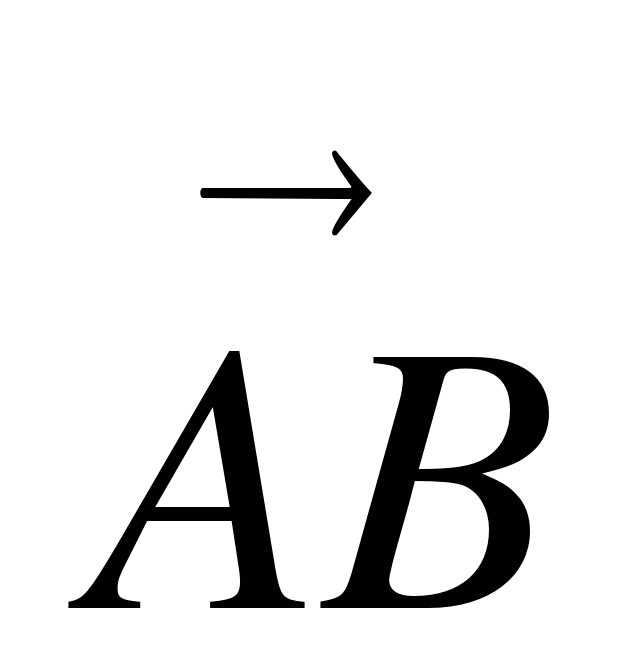 
3. АВ – диаметр окружности. Найдите координаты центра окружности, если
А(1; 4) и В(-3; 7)
4. Напишите уравнение окружности с центром в точке А(-2; 2) и радиусом 2
5. Принадлежит ли точка А(-4; 2) прямой 2х +у +2=0?
2 часть
6. Найдите координаты и длину вектора а, если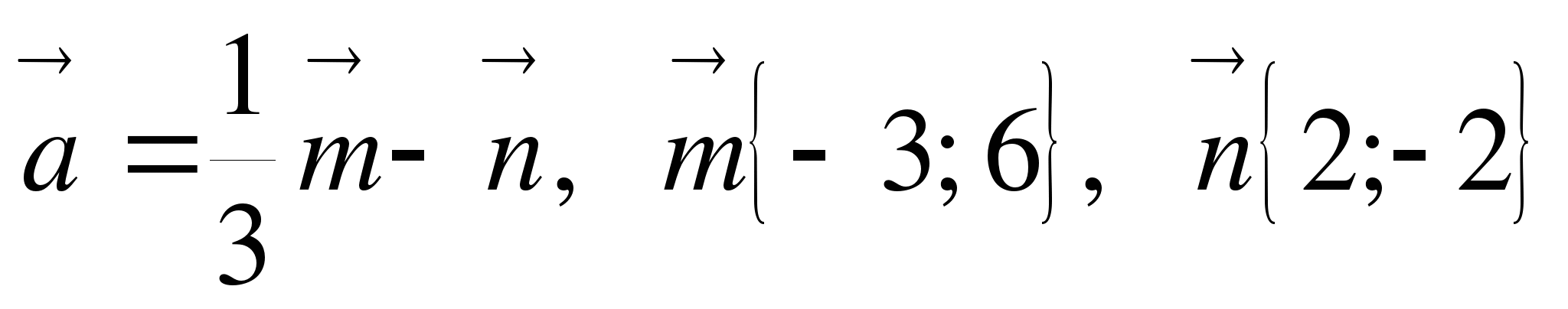 
7. Напишите уравнение окружности с центром в точке А(-3; 2), проходящей через точку В(1;-2)
8. Треугольник MNK задан координатами своих вершин: M(-6; 1), N(2; 4),
K(2; -2)
А) докажите, что треугольник MNK – равнобедренный
Б) найдите медиану, проведенную из вершины М
9. Напишите уравнение прямой, проходящей через точки А(0; -1) и С(-1,5; 0), проверьте лежит ли этой прямой точка В(3; -3)
Геометрия – 9. Контрольная работа «Метод координат» Вариант 2
1 часть
1. Дано: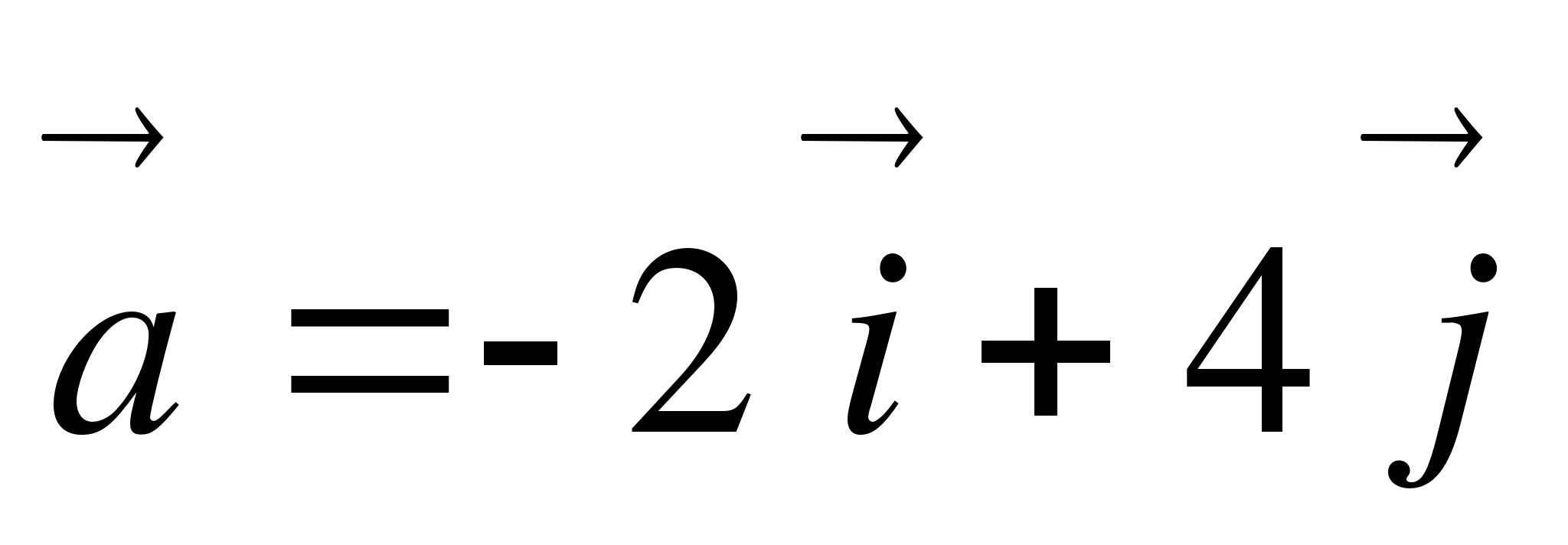 
. Найти: а) координаты вектора 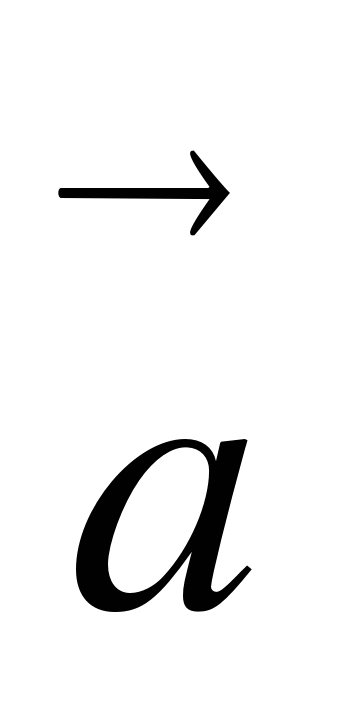; б) длину вектора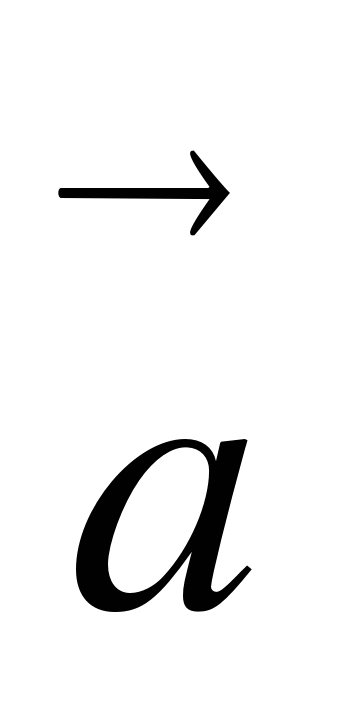
2. А(-2; 4) и В(1; -3). Найти: а) координаты вектора 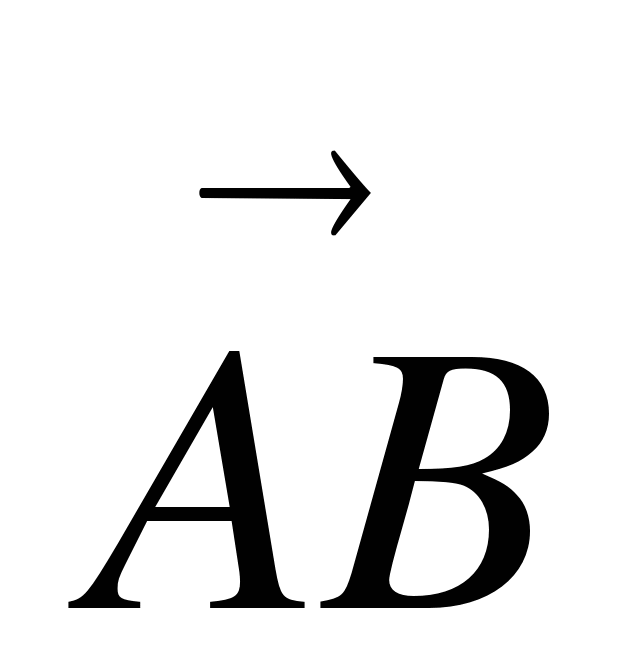; б) длину вектора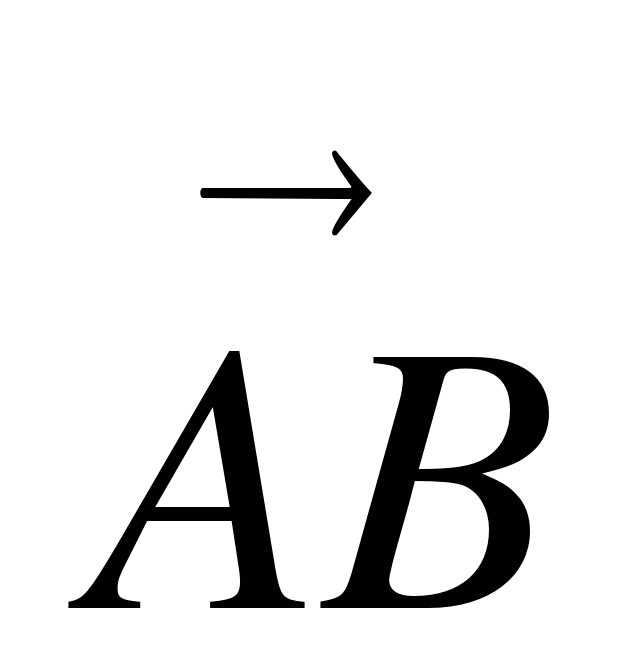
3. АВ – диаметр окружности. Найдите координаты центра окружности, если
А(-4; 1) и В(3; -7)
4. Напишите уравнение окружности с центром в точке А(3; -3) и радиусом 3
5. Принадлежит ли точка А(3; -5) прямой 2х +у –1=0?
2 часть
6
. Найдите координаты и длину вектора b, если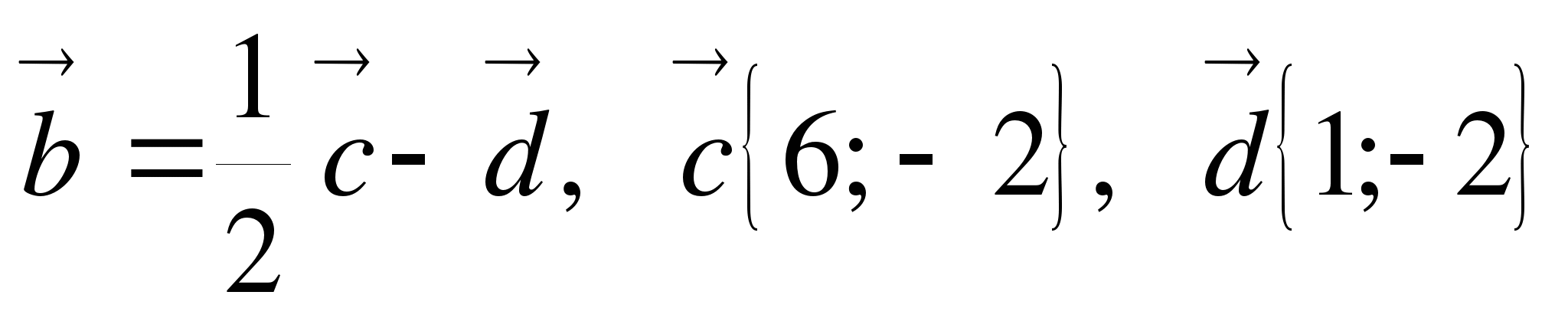 
7. Напишите уравнение окружности с центром в точке C(2; 1), проходящей через точку D(5;5)
8. Треугольник CDE задан координатами своих вершин: C(2; 2), D(6; 5),
E(5; -2)
А) докажите, что треугольник CDE – равнобедренный
Б) найдите медиану, проведенную из вершины C
9. Напишите уравнение прямой, проходящей через точки А(0; 1), и С(2; 0) проверьте лежит ли этой прямой точка В(-3; 2,5)
Геометрия – 9. Контрольная работа «Метод координат» Вариант 3
1 часть
1. Дано: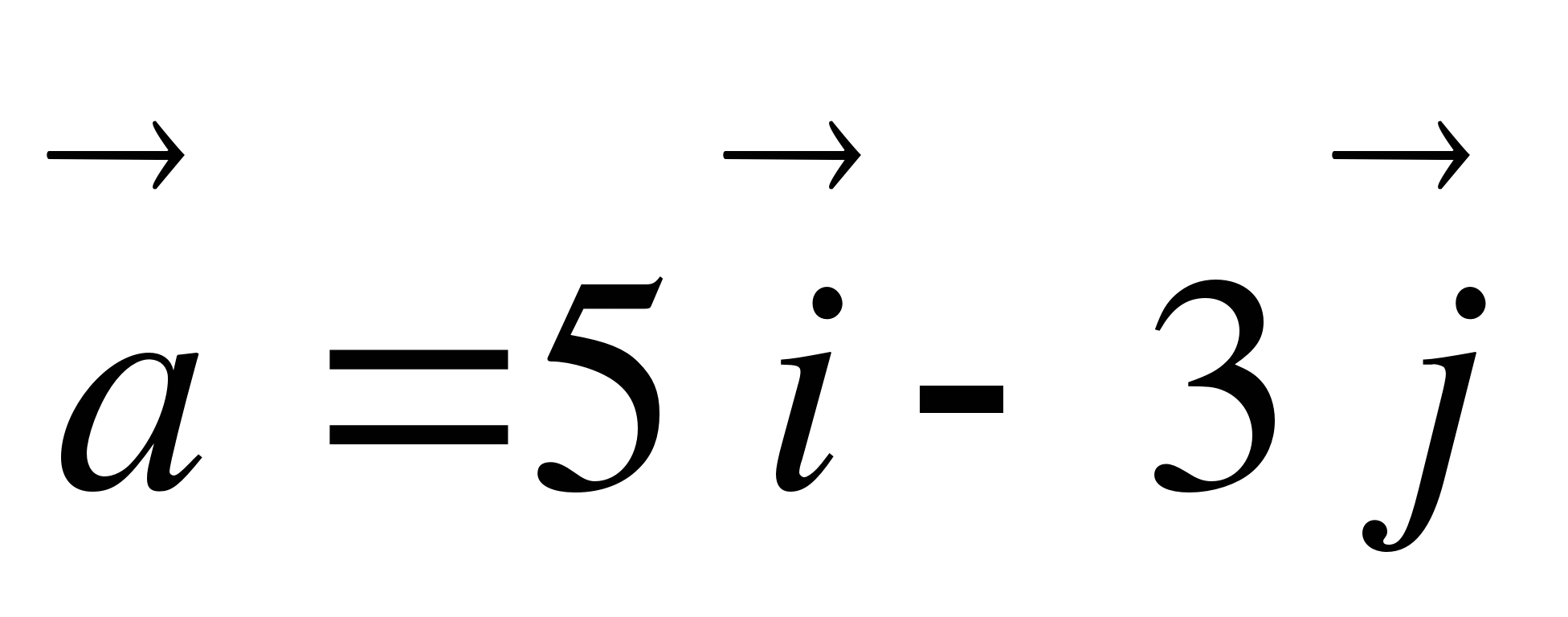 
. Найти: а) координаты вектора 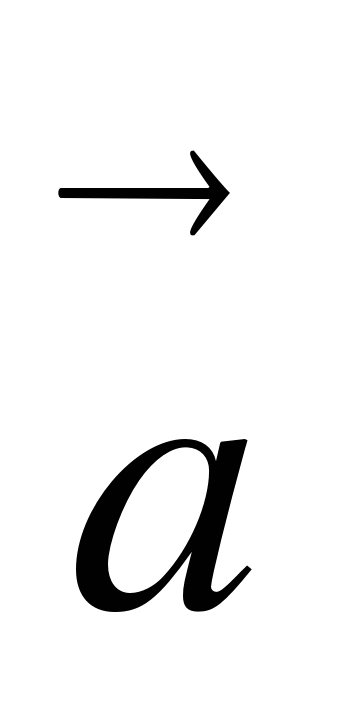; б) длину вектора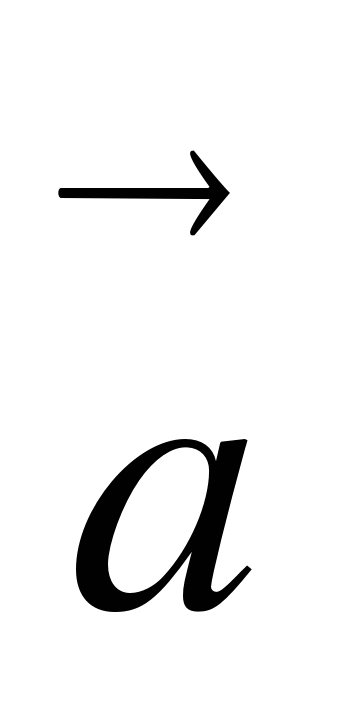
2. А(2;-5) и В(4; 3). Найти: а) координаты вектора 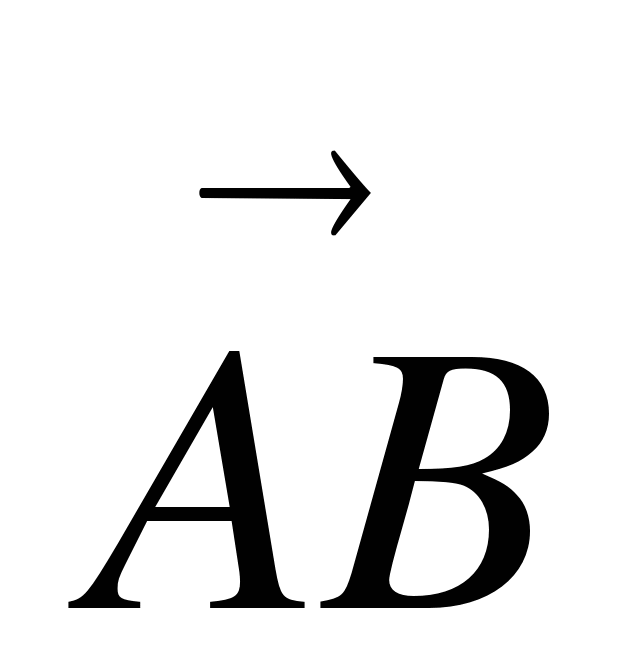; б) длину вектора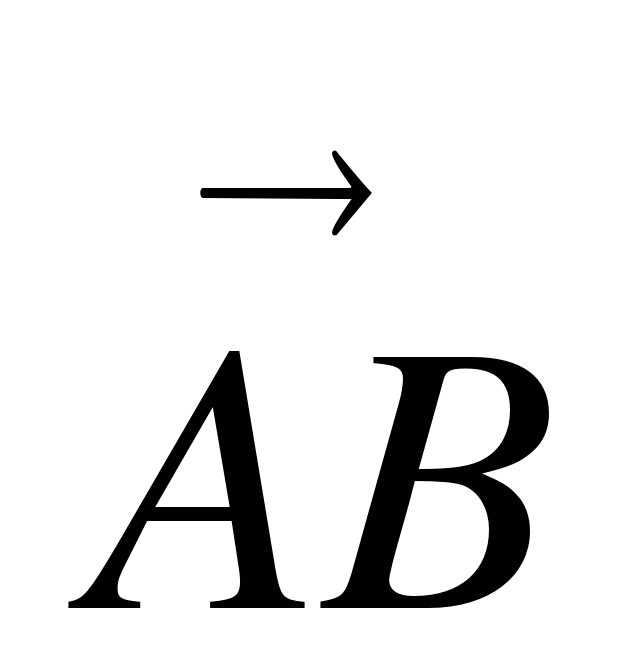
3. АВ – диаметр окружности. Найдите координаты центра окружности, если
А(-5; 7) и В(-1; 2)
4. Напишите уравнение окружности с центром в точке А(3; -2) и радиусом 3
5. Принадлежит ли точка А(3; -6) прямой 3х +2у +3=0?
2 часть
6. Найдите координаты и длину вектора а, если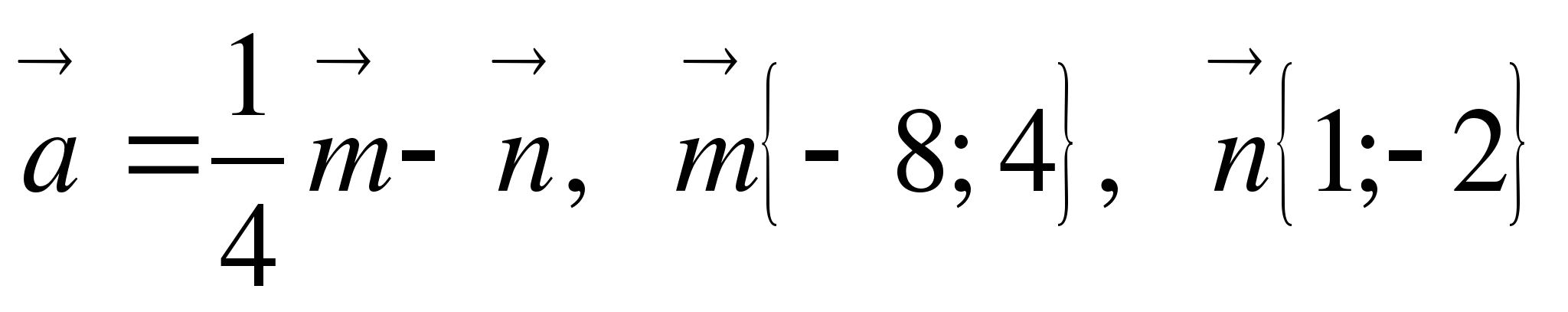 
7. Напишите уравнение окружности с центром в точке А(4;-3), проходящей через точку В(2;-1)
8. Треугольник MNK задан координатами своих вершин: M(1; 6), N(4; 2),
K(-3; 3)
А) докажите, что треугольник MNK – равнобедренный
Б) найдите медиану, проведенную из вершины М
9. Напишите уравнение прямой, проходящей через точки А(0; -1) и С(-1,5; 0), проверьте лежит ли этой прямой точка В(3; -3)
Геометрия – 9. Контрольная работа «Метод координат» Вариант 4
1 часть
1. Дано: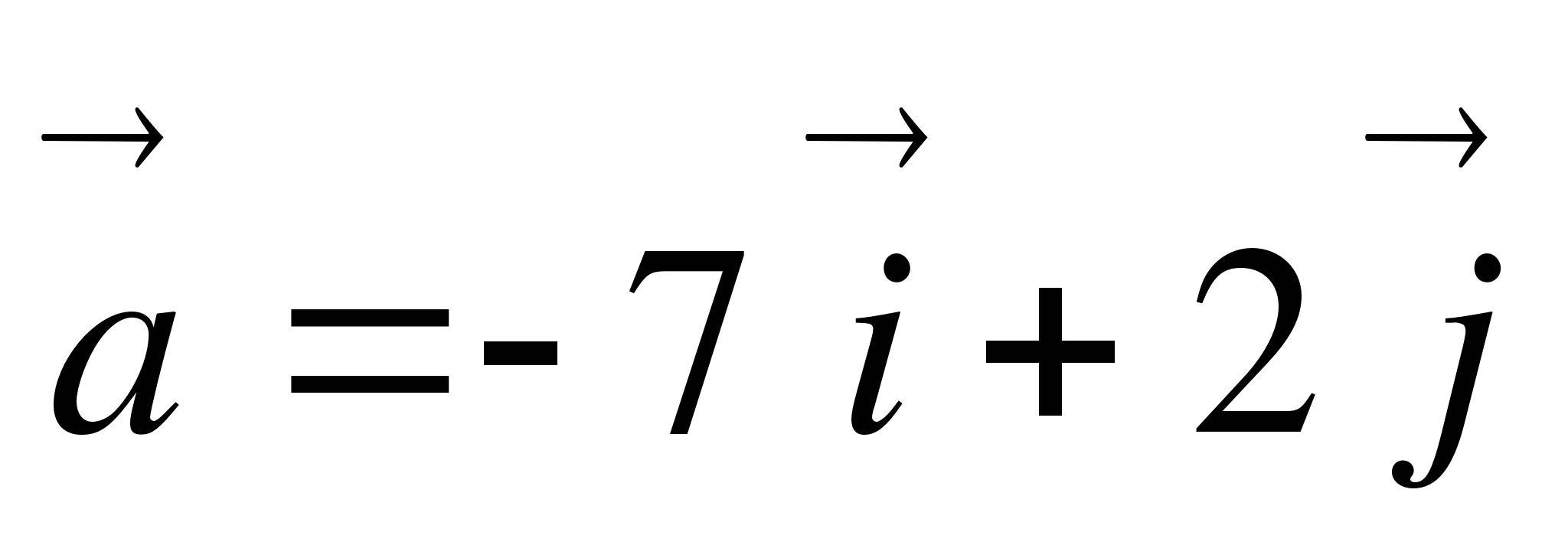 
. Найти: а) координаты вектора 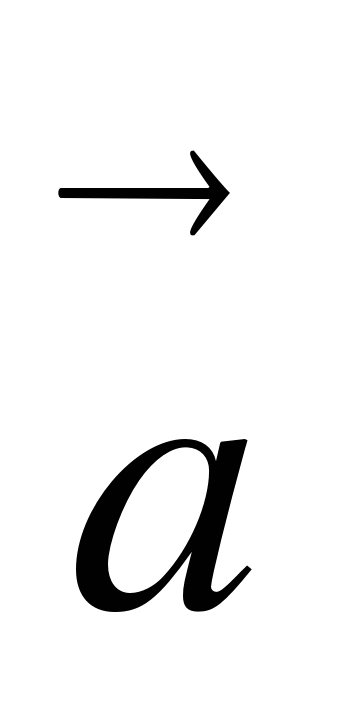; б) длину вектора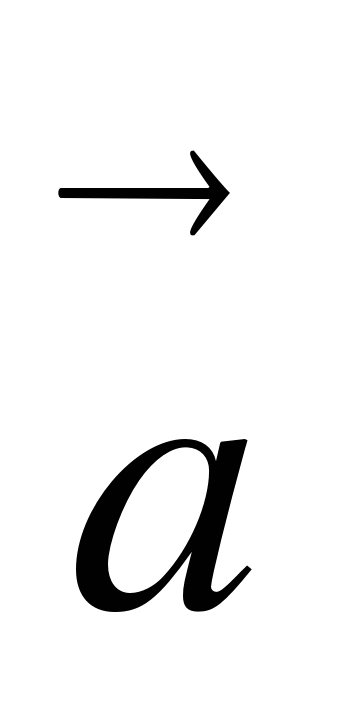
2. А(-3; 5) и В(7; -4). Найти: а) координаты вектора 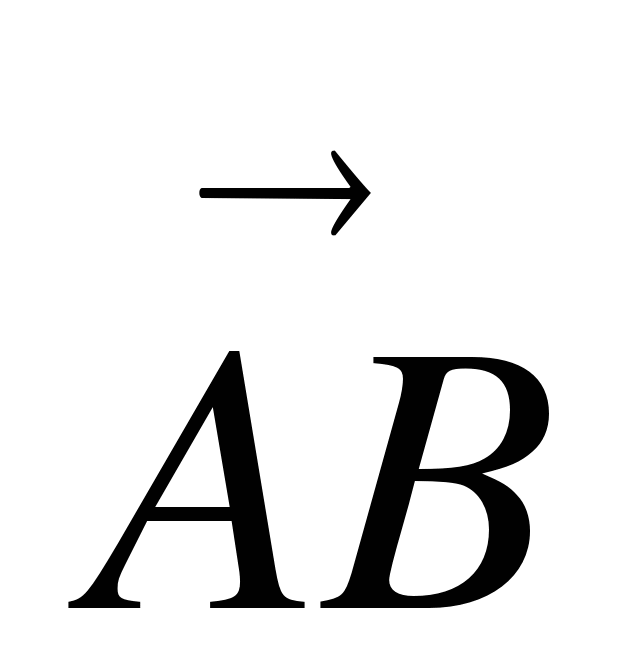; б) длину вектора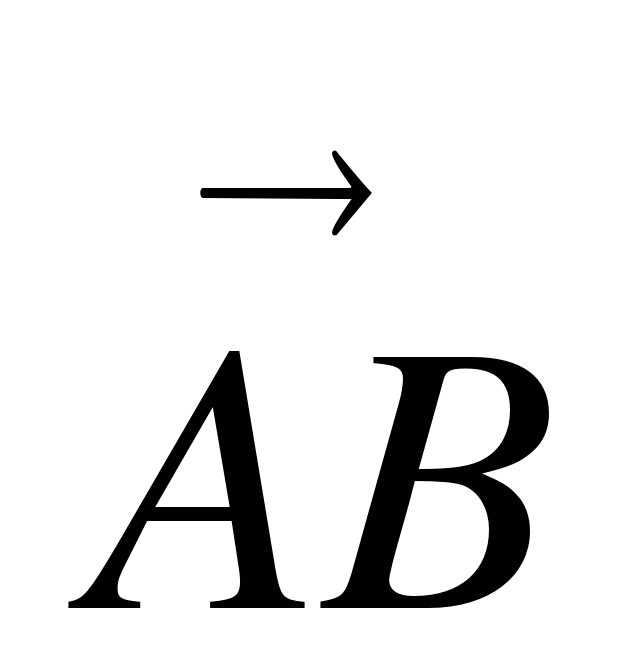
3. АВ – диаметр окружности. Найдите координаты центра окружности, если
А(8;3) и В(-3; 6)
4. Напишите уравнение окружности с центром в точке А(-4; 2) и радиусом 5
5. Принадлежит ли точка А(-4; 5) прямой 2х +3у –7=0?
2 часть
6. Найдите координаты и длину вектора b, если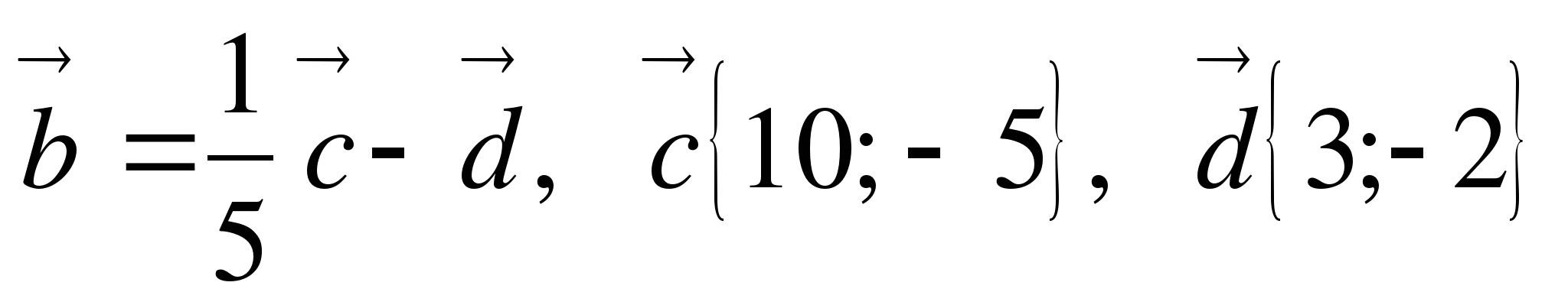 
7. Напишите уравнение окружности с центром в точке C(3; 4), проходящей через точку D(4;-3)
8. Треугольник CDE задан координатами своих вершин: C(2; 3), D(3; 5),
E(3; -1)
А) докажите, что треугольник CDE – равнобедренный
Б) найдите медиану, проведенную из вершины C
9. Напишите уравнение прямой, проходящей через точки А(0; 1), и С(2; 0) проверьте лежит ли этой прямой точка В(-3; 2,5)
infourok.ru
Контрольная работа по геометрии
по теме «Метод координат»
Вариант 1.
1. Найдите координаты вектора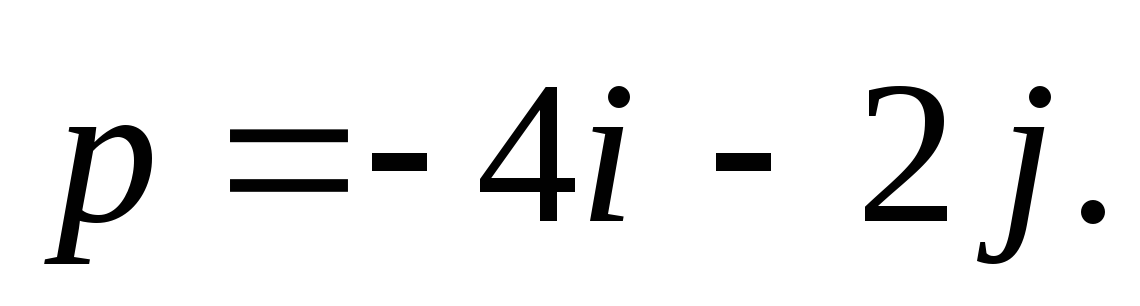 
(1 балл)
2. Запишите разложение вектора 
{7;-6} по координатным векторам 
и 
. (1 балл)
3. Концы отрезка PK имеют координаты P(-2;7), K(5;1). Точка А – середина отрезка PK. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками А(-6;3) и В(-3;7). (2 балла)
5. Найдите координаты вектора 
, если С (11;2), В(9; 5). (2 балла)
6. Найдите длину вектора 
{6;-8}. (2 балла)
7. Окружность задана уравнением (x-4)2+(y+3)2=8. Лежит ли точка А(-2;-5) на окружности? (2 балла)
8. Окружность задана уравнением (x+6)2+(y-3)2=25. Запишите уравнение прямой, параллельной оси Ох и проходящей через центр этой окружности. (2 балла)
9. Даны векторы 
{-1;3} и 
{4;2}. Найдите координаты вектора6- 0,5. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины А, если А(-3;2), В(-1;5), С(-1;-1). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
Контрольная работа по геометрии
по теме «Метод координат».
Вариант 2.
1. Найдите координаты вектора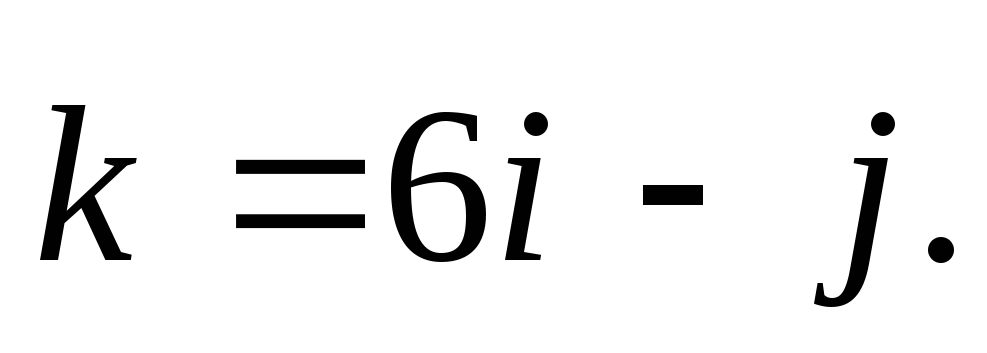 
(1 балл)
2. Запишите разложение вектора 
{-3;8} по координатным векторам и . (1 балл)
3. Концы отрезка ВС имеют координаты В(4;-9), С(-1;3). Точка А – середина отрезка ВС. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками М(7;-4) и К(1;4). (2 балла)
5. Найдите координаты вектора 
, если С (5;-2), Р(-3; 1). (2 балла)
6. Найдите длину вектора {12;-5}. (2 балла)
7. Окружность задана уравнением (x+1)2+(y-7)2=68. Лежит ли точка В(3;--1) на окружности? (2 балла)
8. Окружность задана уравнением (x+5)2+(y+4)2=9. Запишите уравнение прямой, параллельной оси Оy и проходящей через центр этой окружности. (2 балла)
9. Даны векторы {-10;5} и {3;-4}. Найдите координаты вектора 3+7. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины В, если А(-3;4), В(-1;-1), С(1;4). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
Контрольная работа по геометрии
по теме «Метод координат»
Вариант 3.
1. Найдите координаты вектора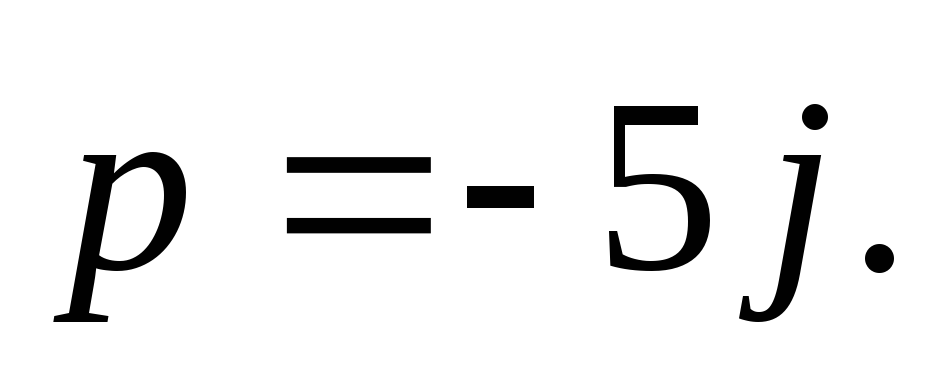 
(1 балл)
2. Запишите разложение вектора {-2;-4} по координатным векторам и . (1 балл)
3. Концы отрезка PK имеют координаты P(5;3), K(-4;7). Точка А – середина отрезка PK. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками А(2;-1) и В(10;5). (2 балла)
5. Найдите координаты вектора , если В (3;5), С(2; -1). (2 балла)
6. Найдите длину вектора {-5;8}. (2 балла)
7. Окружность задана уравнением (x+4)2+(y+3)2=5. Лежит ли точкаА(-2;-4) на окружности? (2 балла)
8. Окружность задана уравнением (x-13)2+(y-3)2=81. Запишите уравнение прямой, параллельной оси Ох и проходящей через центр этой окружности. (2 балла)
9. Даны векторы {-1;3} и {4;2}. Найдите координаты вектора3- 4. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины С, если А(-2;2), В(-2;-4), С(-5;-1). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
Контрольная работа по геометрии
по теме «Метод координат».
Вариант 4.
1. Найдите координаты вектора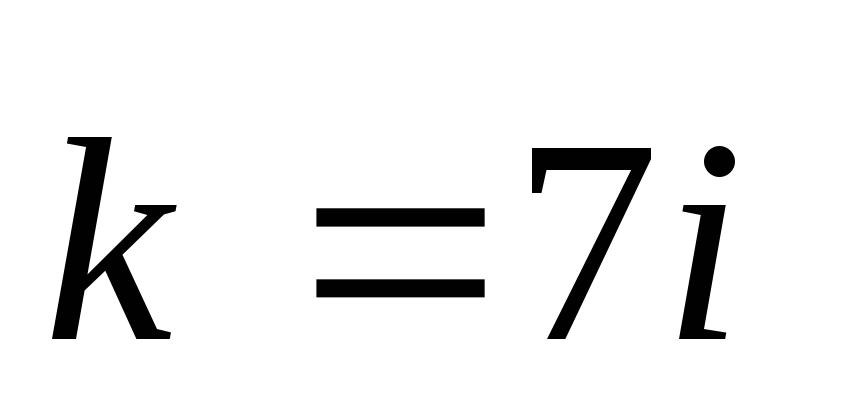 
(1 балл)
2. Запишите разложение вектора {4;-5} по координатным векторам и . (1 балл)
3. Концы отрезка ВС имеют координаты В(2;8), С(-6;-4). Точка А – середина отрезка ВС. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками М(-5;1) и К(-7;6). (2 балла)
5. Найдите координаты вектора , если С (4;0), Р(-2; 5). (2 балла)
6. Найдите длину вектора {8;-15}. (2 балла)
7. Окружность задана уравнением (x-1)2+(y-9)2=89. Лежит ли точка В(-4;1) на окружности? (2 балла)
8. Окружность задана уравнением (x+9)2+(y-4)2=36. Запишите уравнение прямой, параллельной оси Оy и проходящей через центр этой окружности. (2 балла)
9. Даны векторы {-1;5} и {3;-1}. Найдите координаты вектора 2-5. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины А, если А(1;7), В(-2;3), С(4;3). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
xn--j1ahfl.xn--p1ai
I вариант
В параллелограмме ABCD точка М является серединой стороны АВ, а точка N делит сторону CD в отношении 2 : 1, считая от точки С. Выразите векторы 
через векторы 
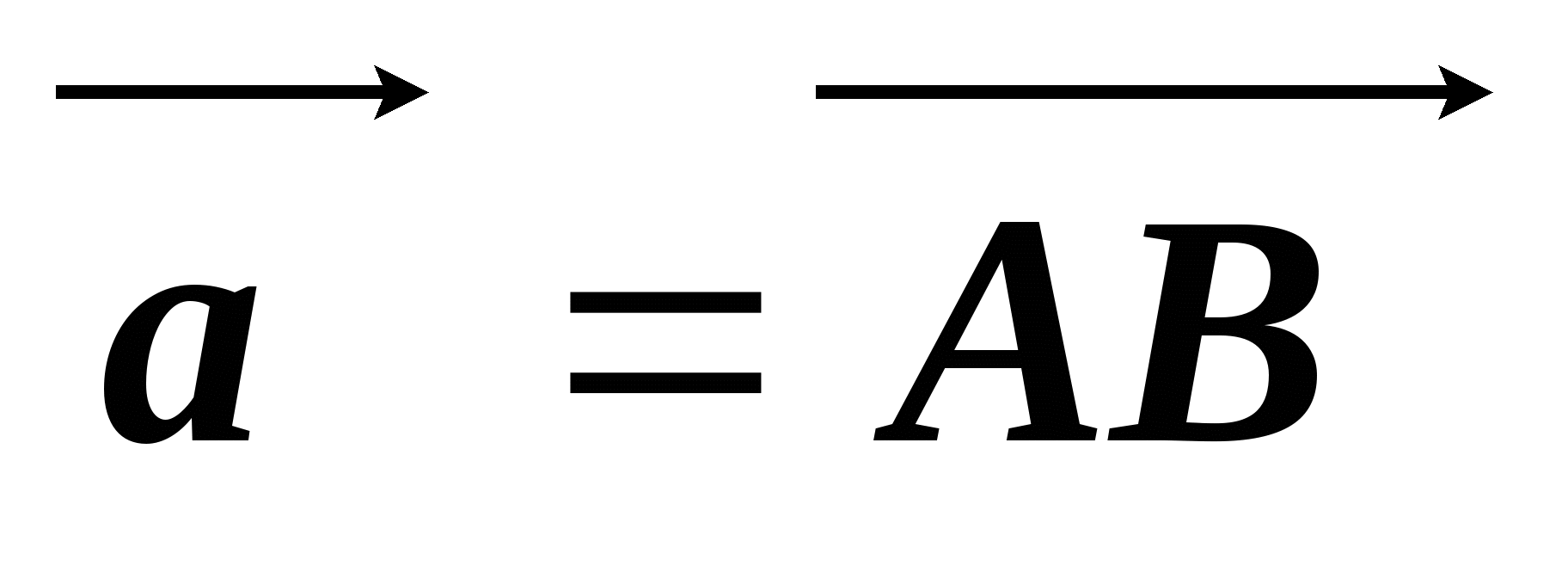и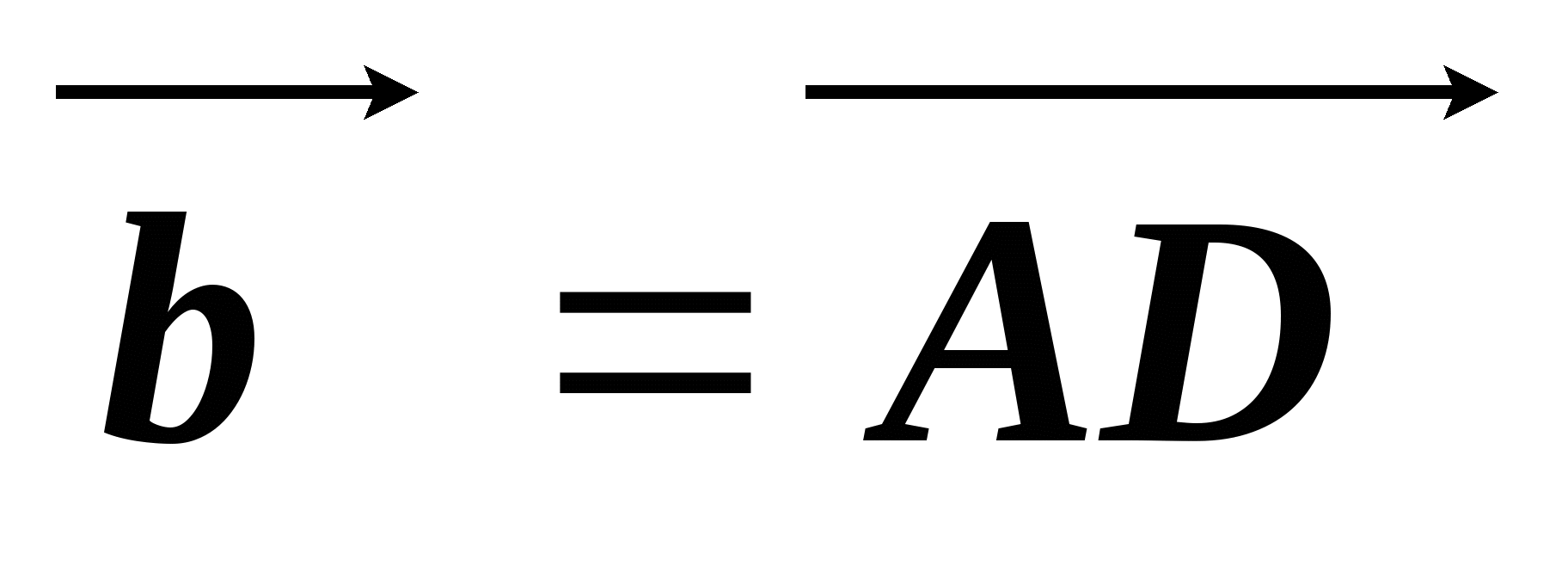 
.
Известно, что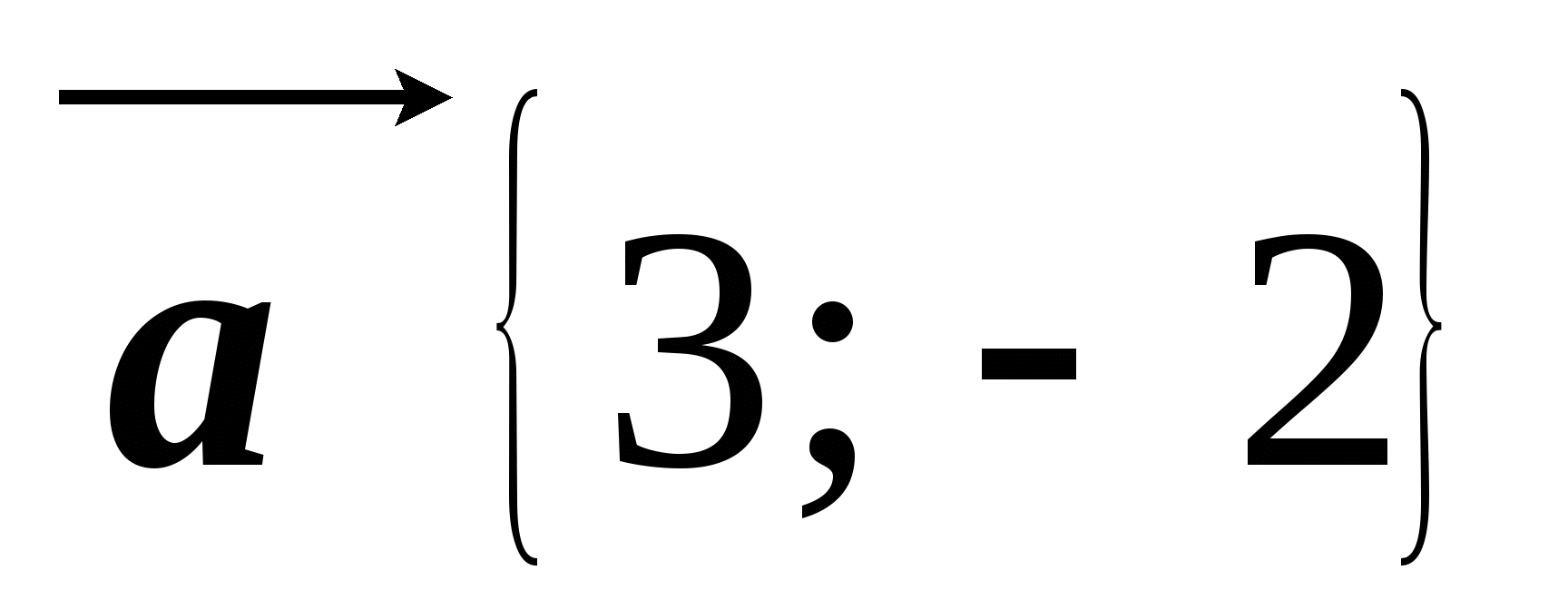 
, 
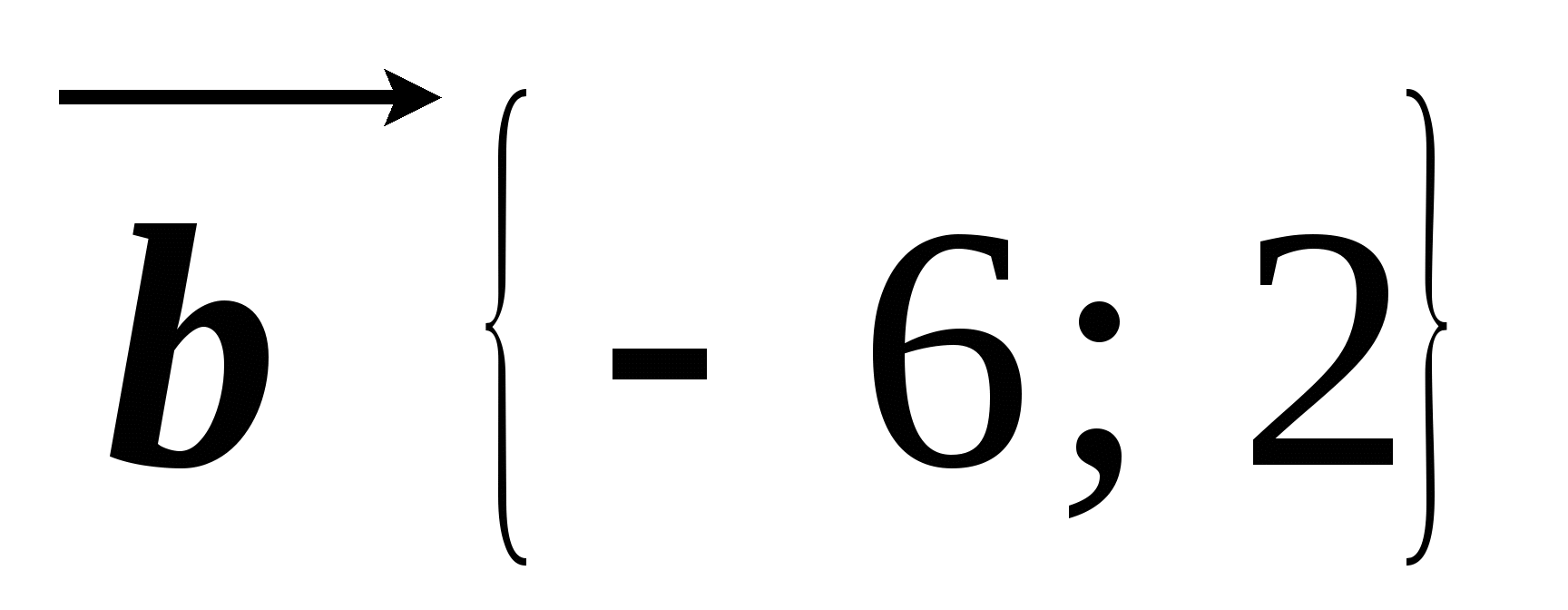. Найдите координаты вектора 
.
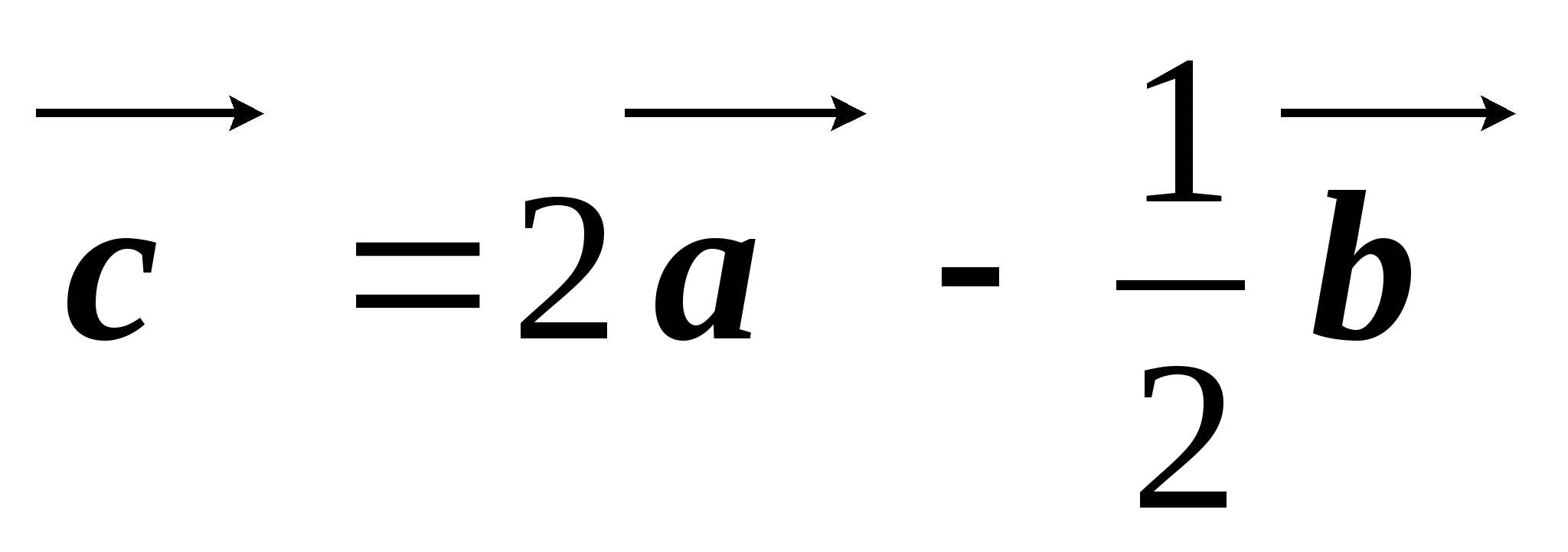Найдите координаты вектора 
и его длину, если M(-8; -2), N(4; -7)
Даны координаты вершин треугольника АВС: А(-6; 1), В(2; 4), С(2; -2).
а) Найдите длину медианы АD.
б) Докажите, что треугольник АВС – равнобедренный и найдите его площадь.
Постройте векторы 
и 
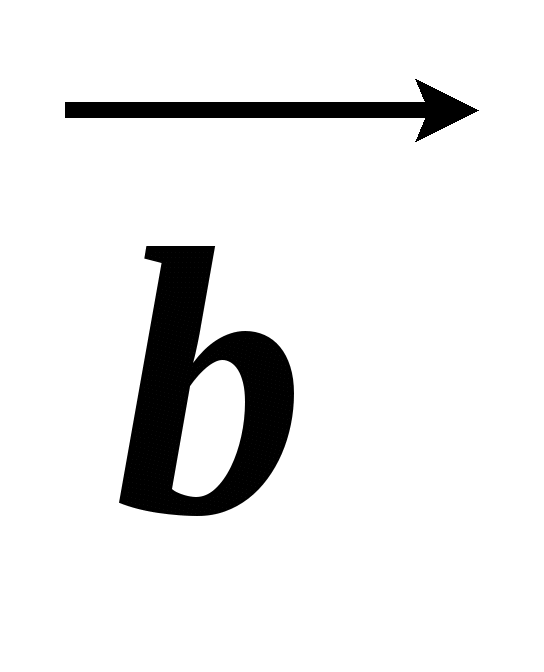, такие что 
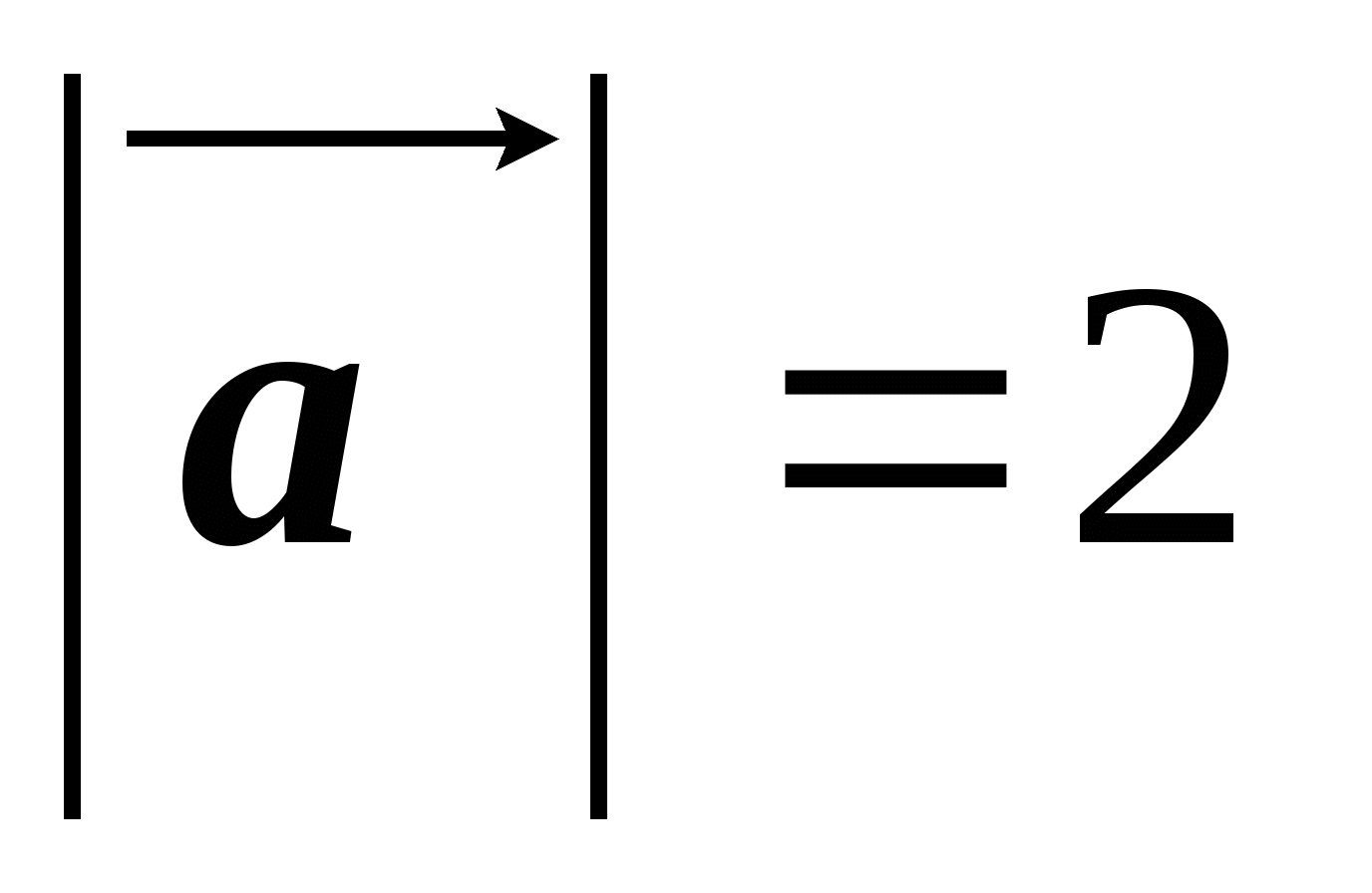см,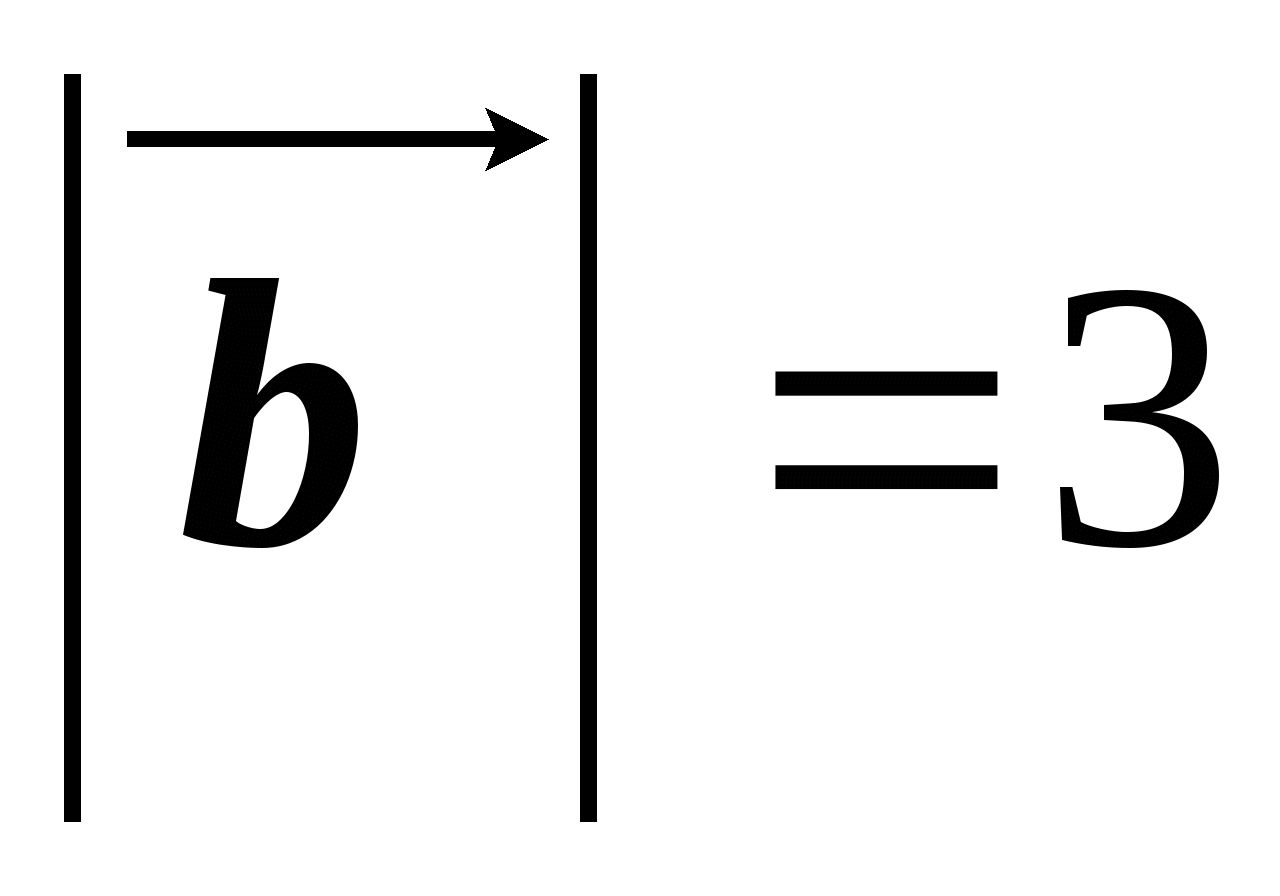 
см. Построить векторы
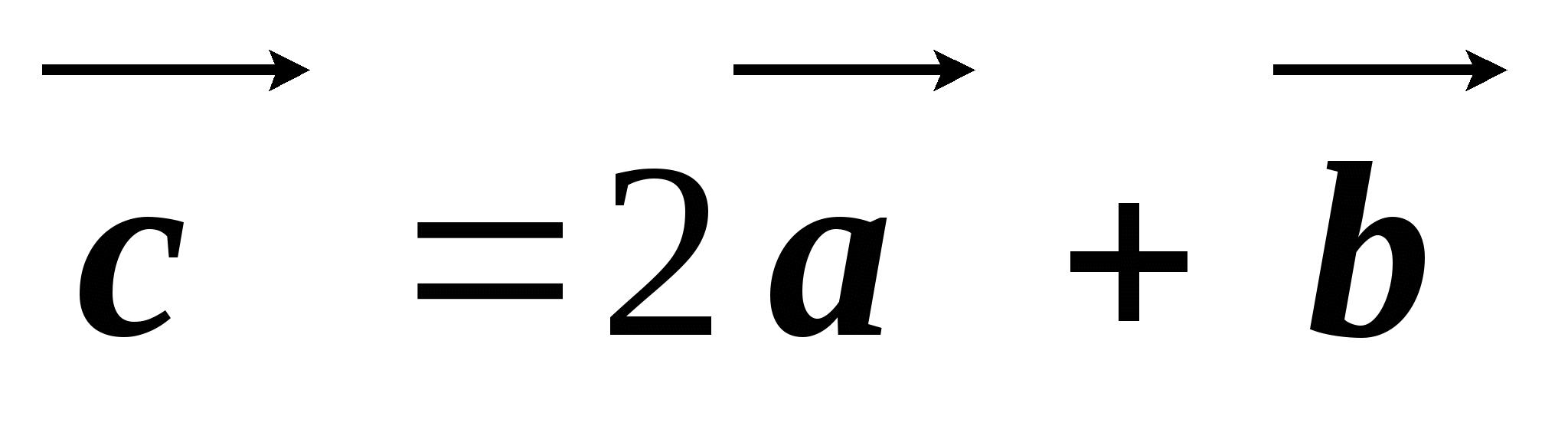и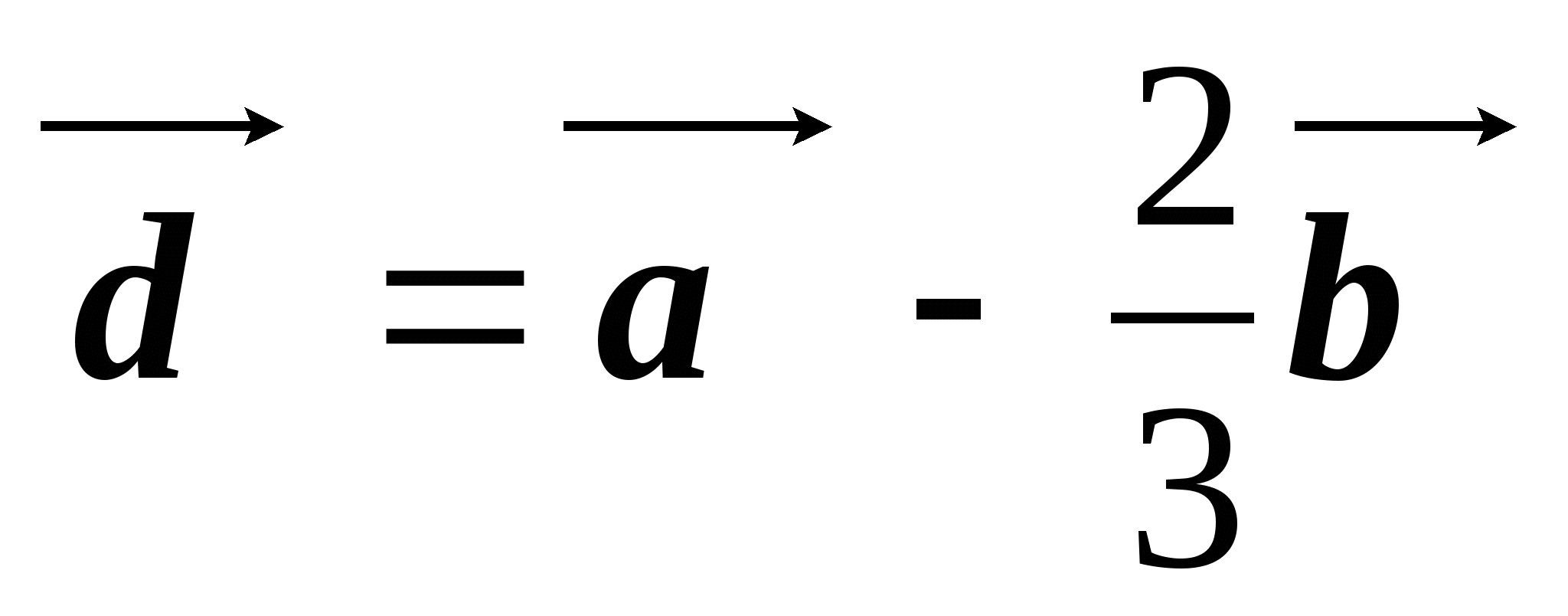 
II вариант
В параллелограмме ABCD точка К является серединой стороны АD, а точка P делит сторону BC в отношении 3 : 1, считая от точки B. Выразите векторы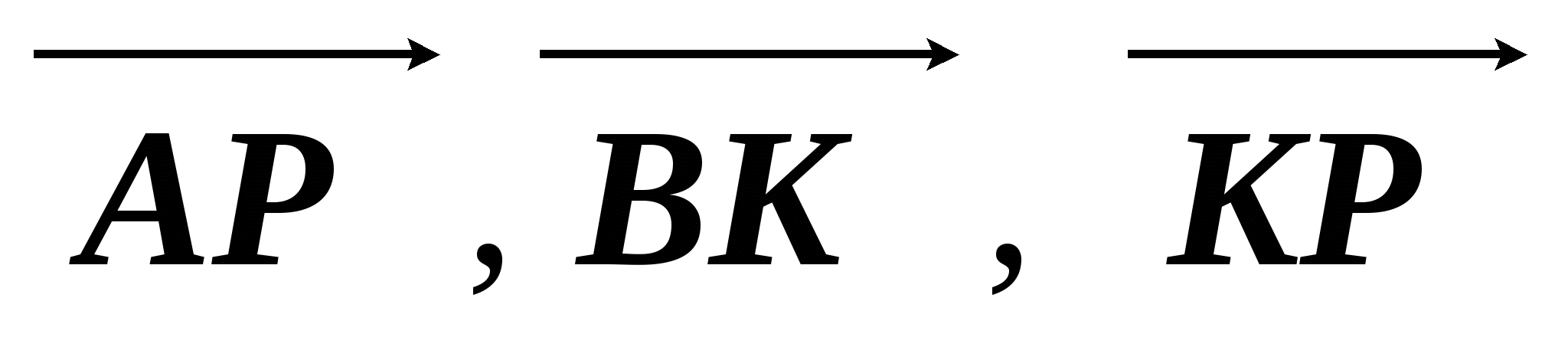 
через векторы 
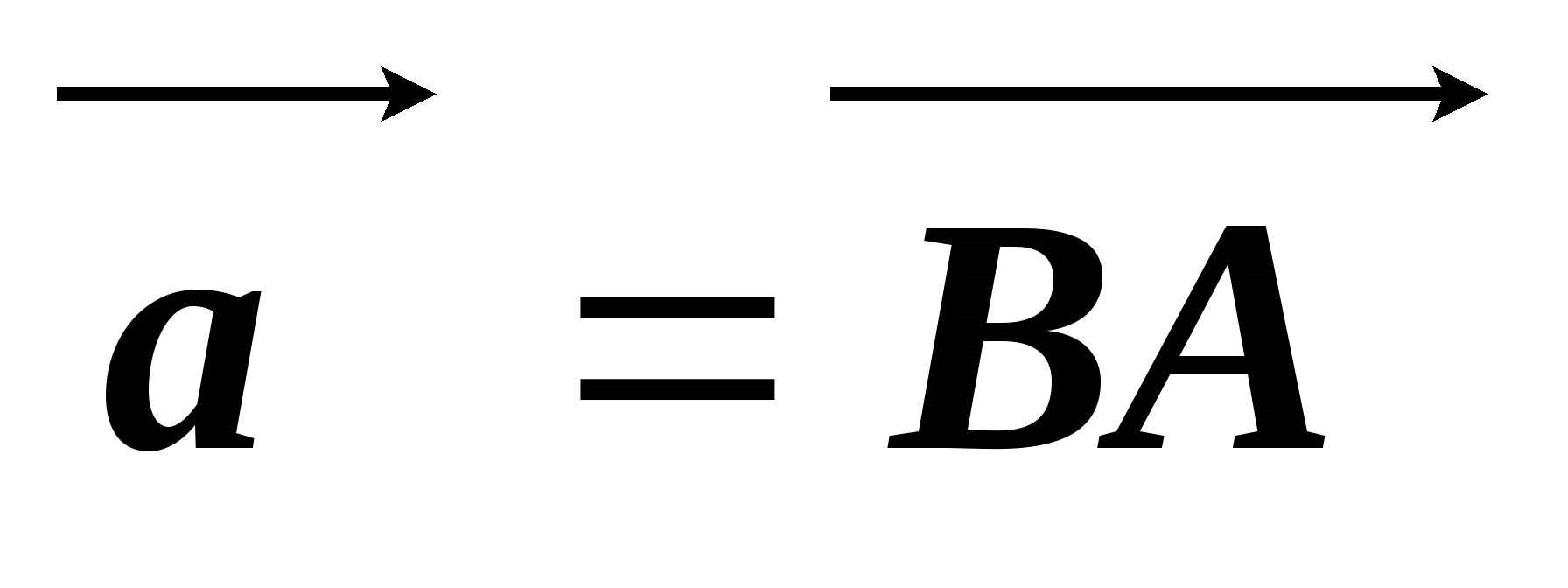и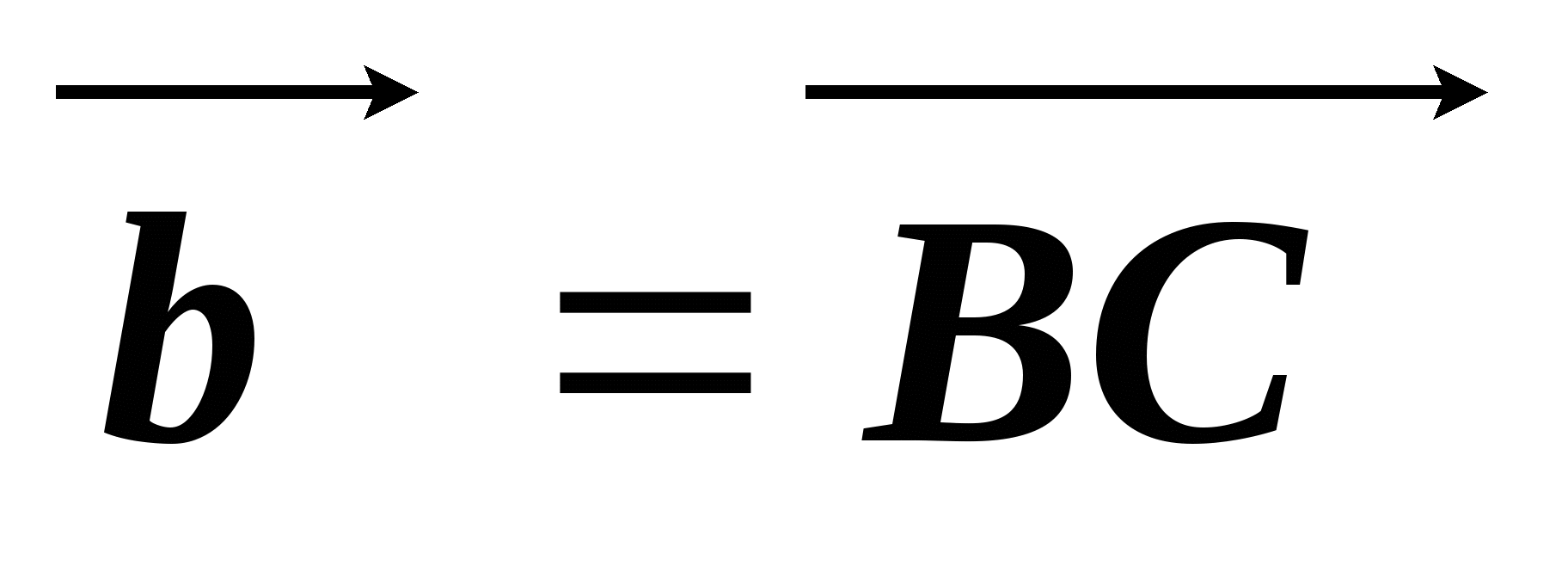 
.
Известно, что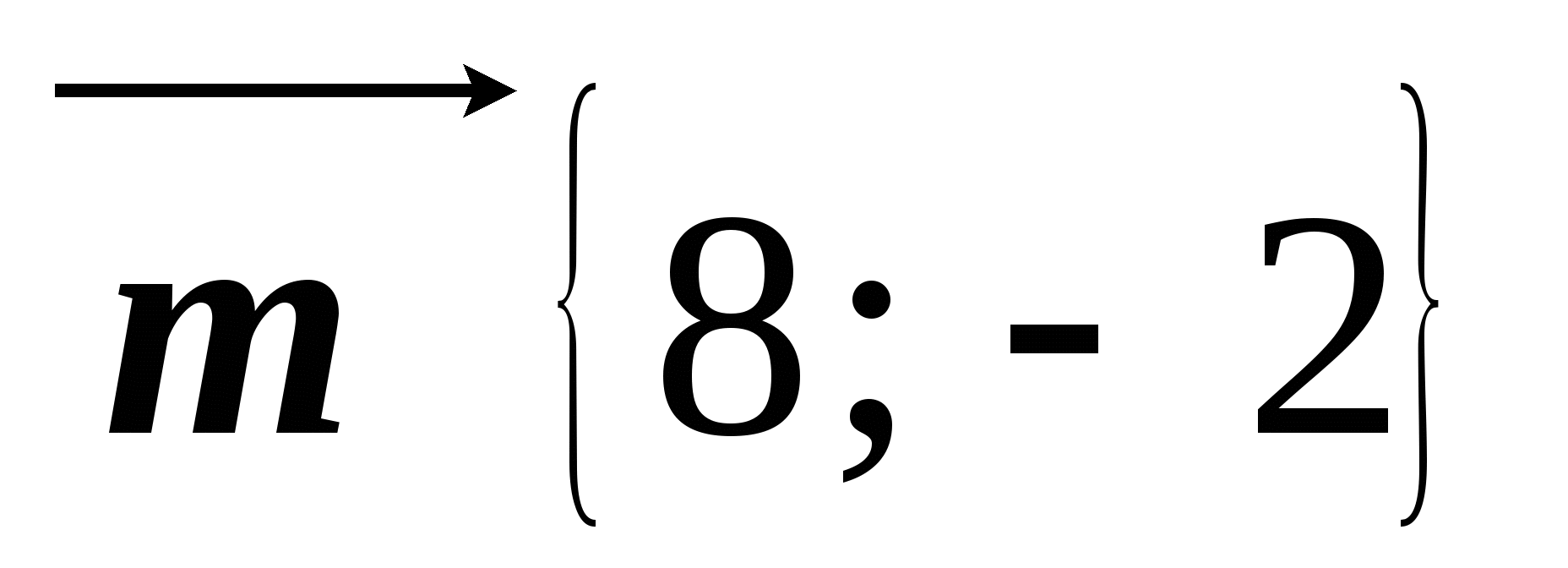 
, 
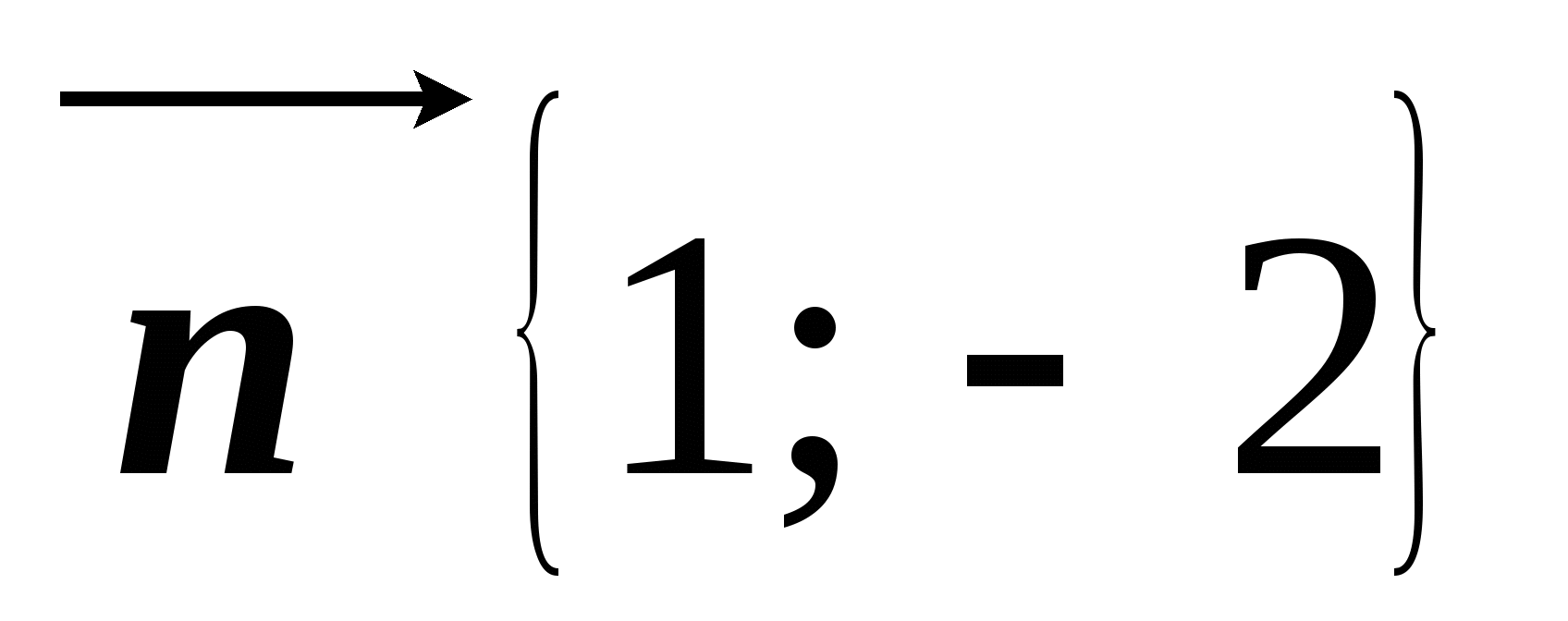. Найдите координаты вектора 
.
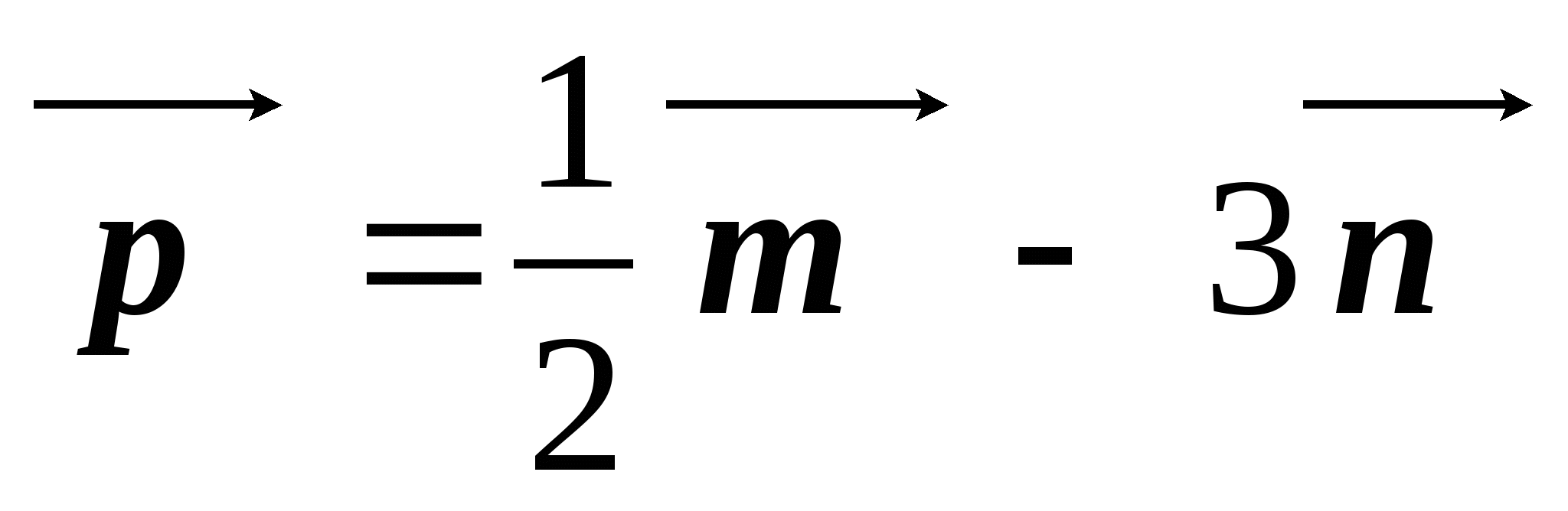Найдите координаты вектора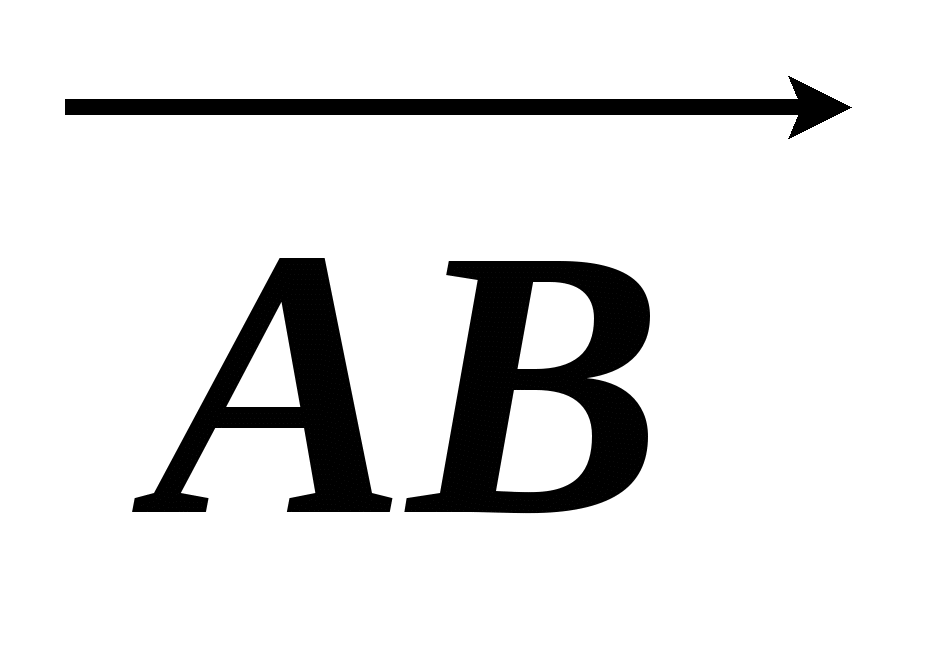 
и его длину, если A(-1; -3), B(-7; 5)
Даны координаты вершин треугольника MNK: M(-4; 1), N(0; 1), K(-2; 4)
а) Найдите длину медианы KP.
б) Докажите, что треугольник MNK – равнобедренный и найдите его площадь.
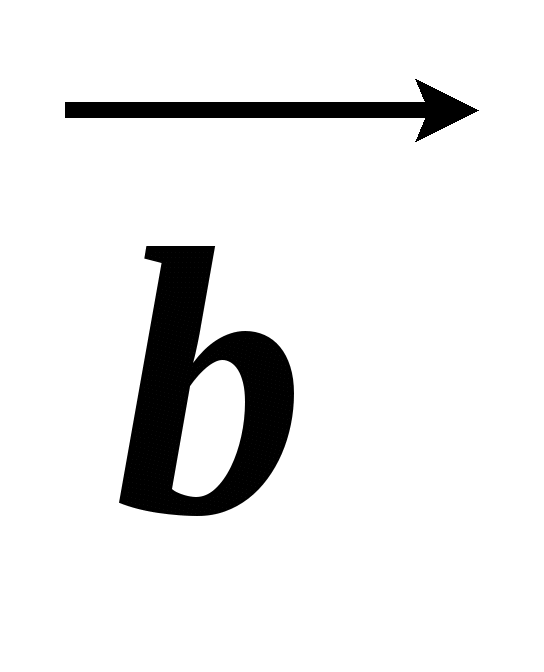Постройте векторы и , такие что 
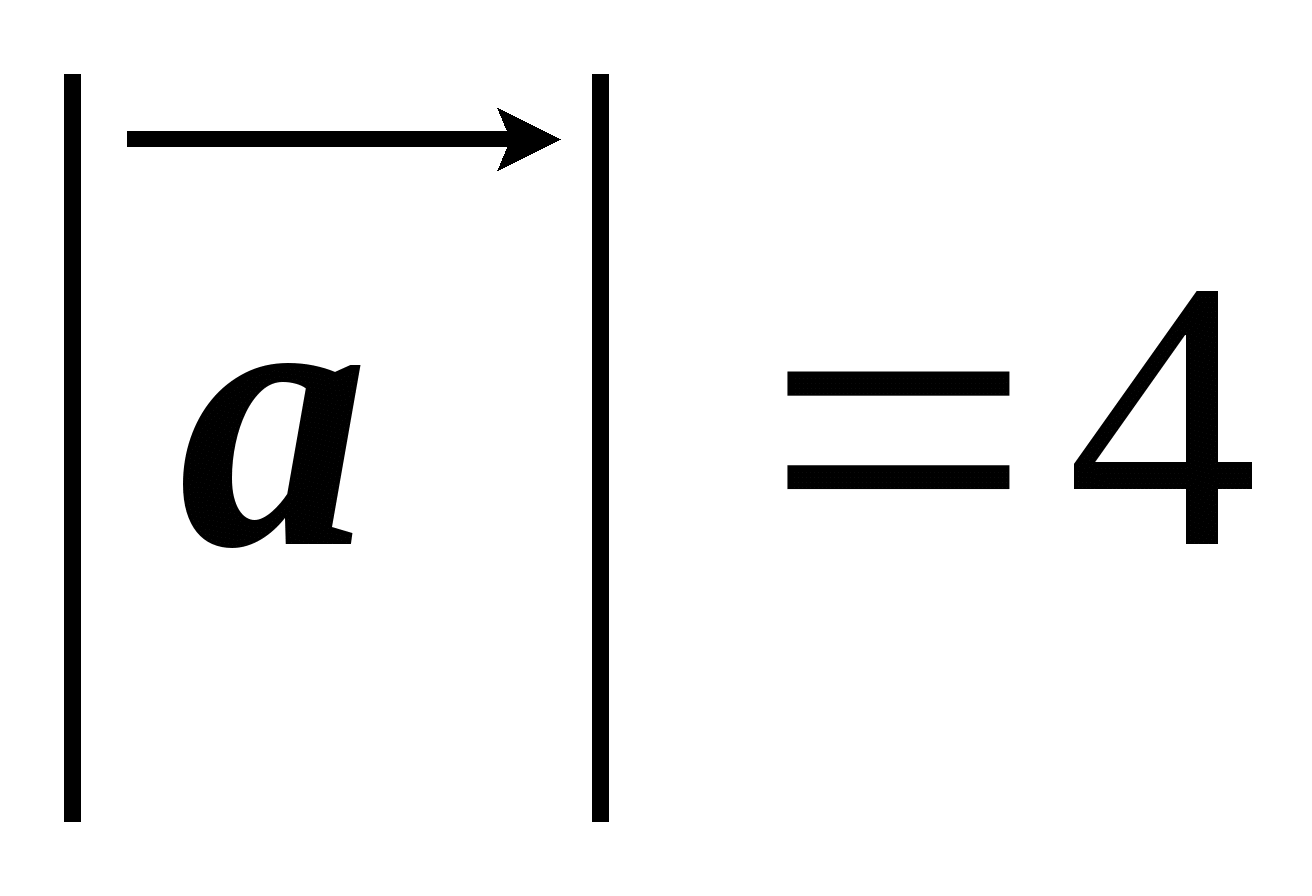см,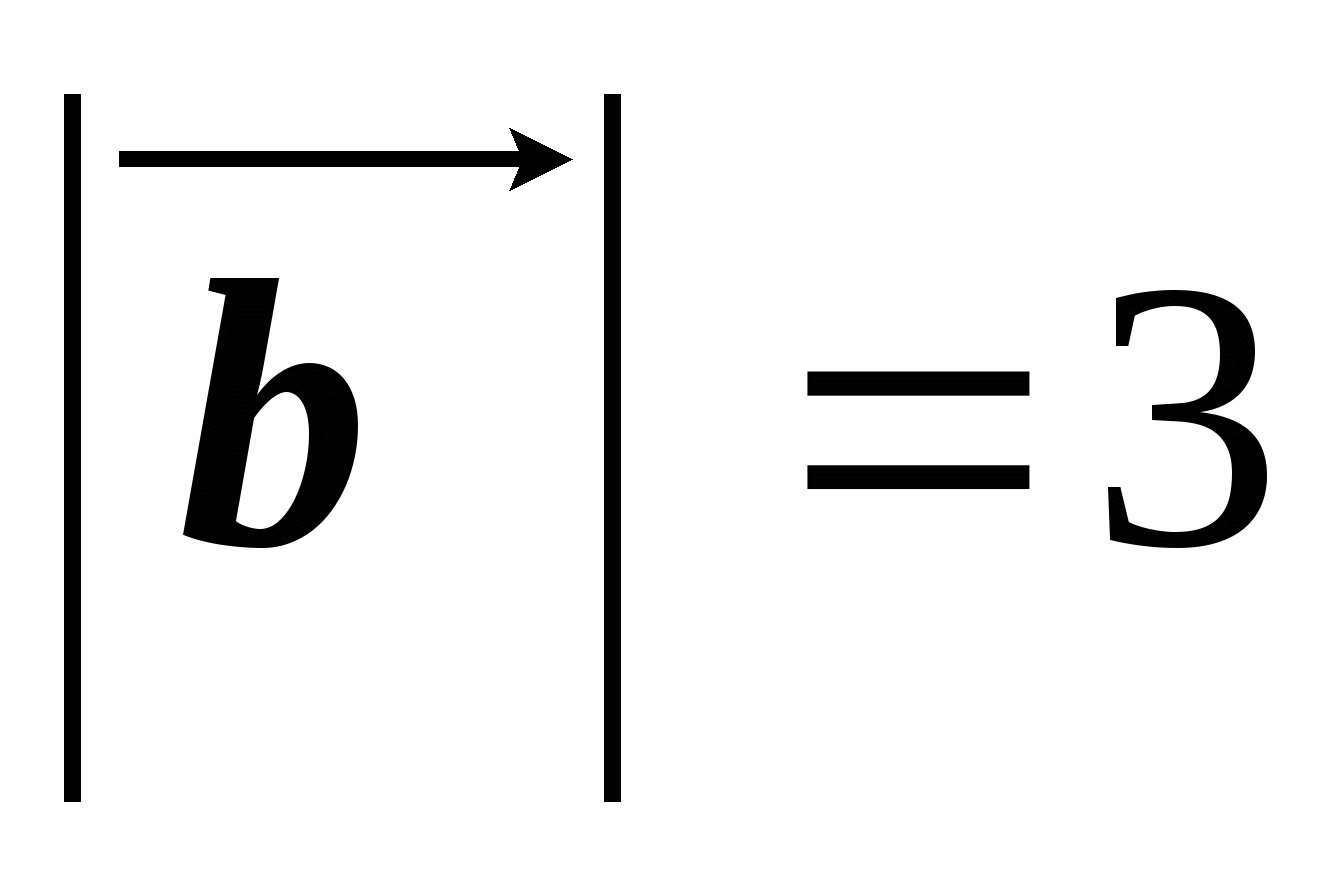 
см. Построить векторы
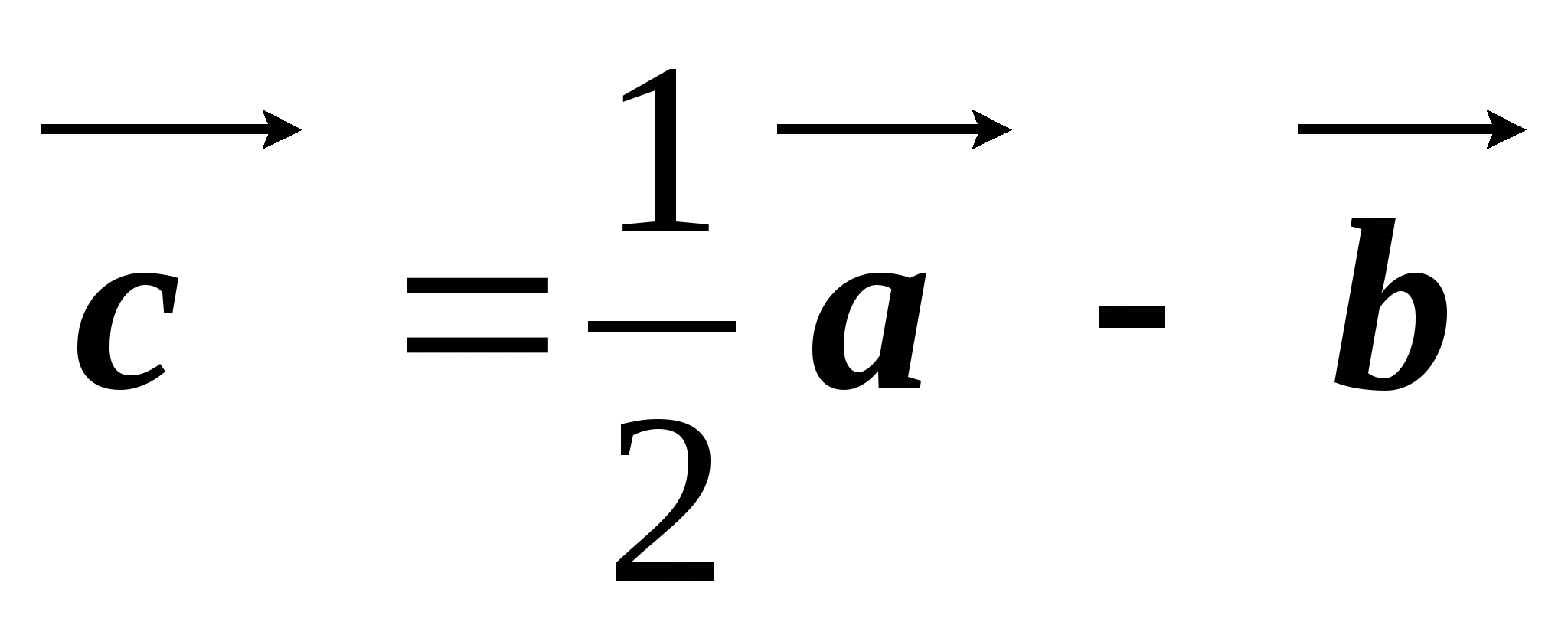и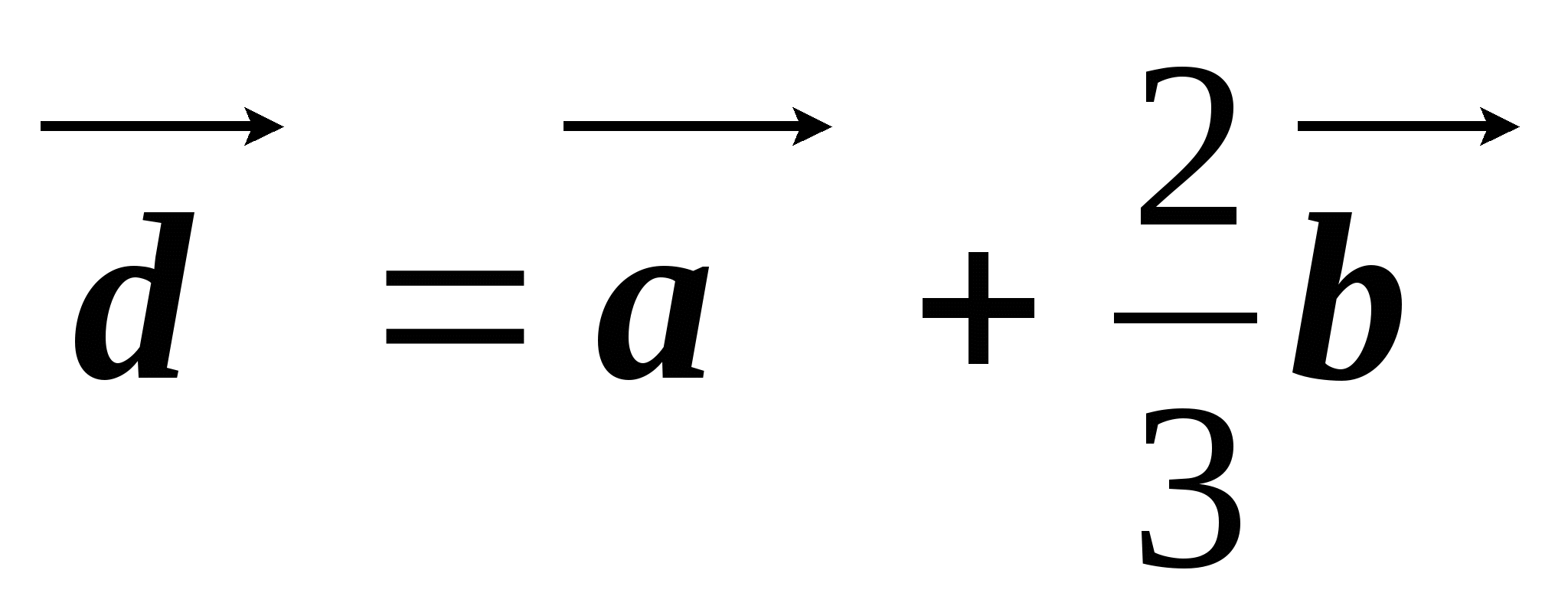 
III вариант
В параллелограмме ABCD точка М является серединой стороны CD, а точка N делит сторону AB в отношении 1 : 2, считая от точки A. Выразите векторы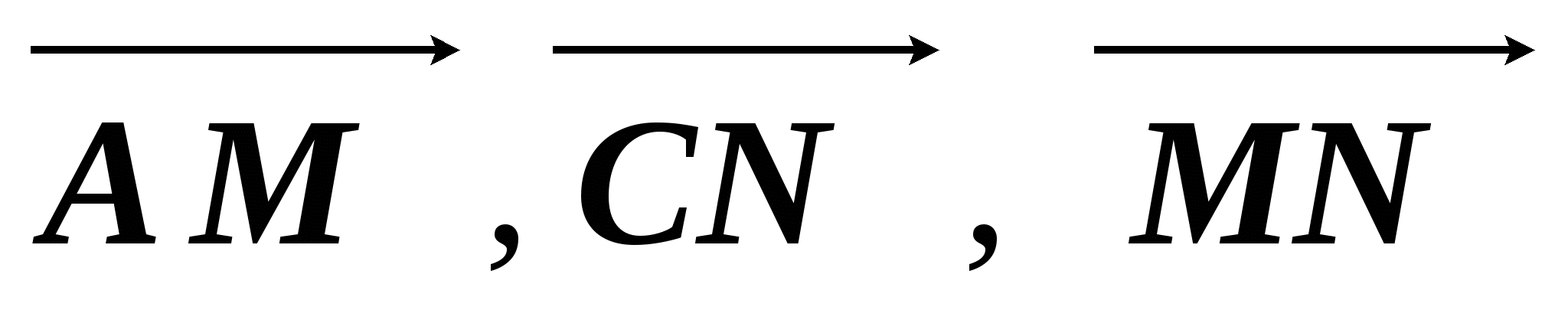 
через векторы 
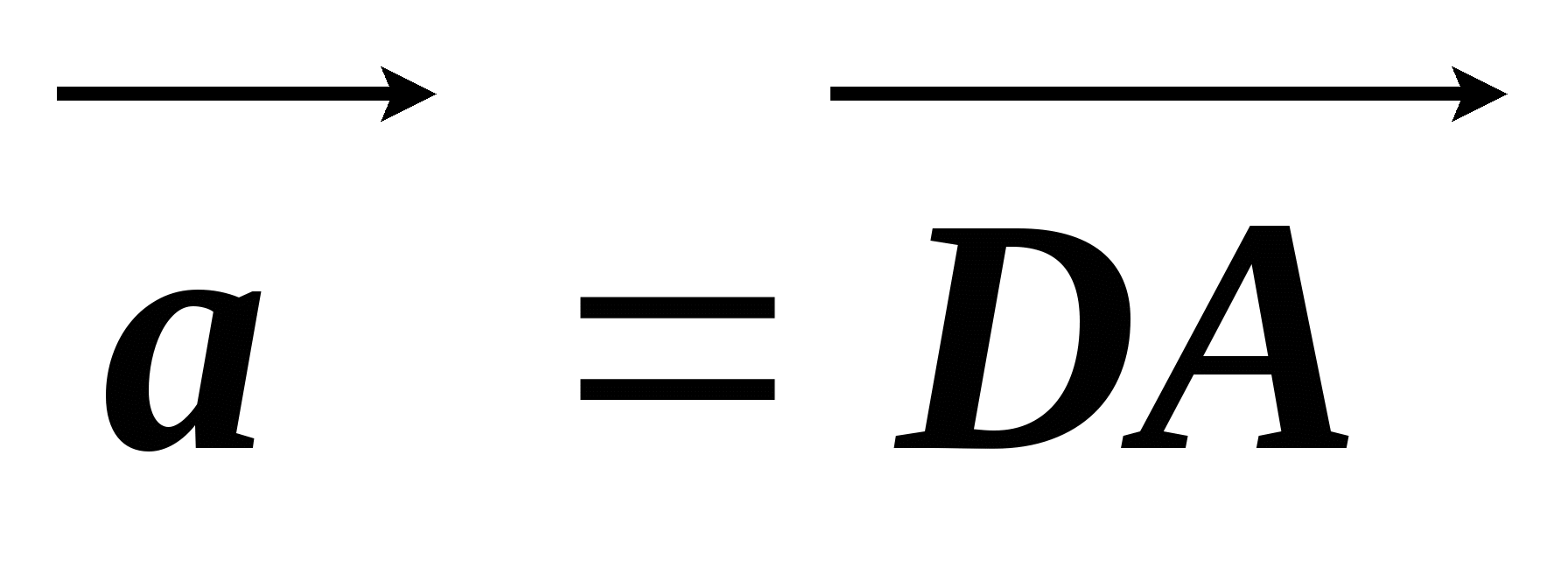и 
.
И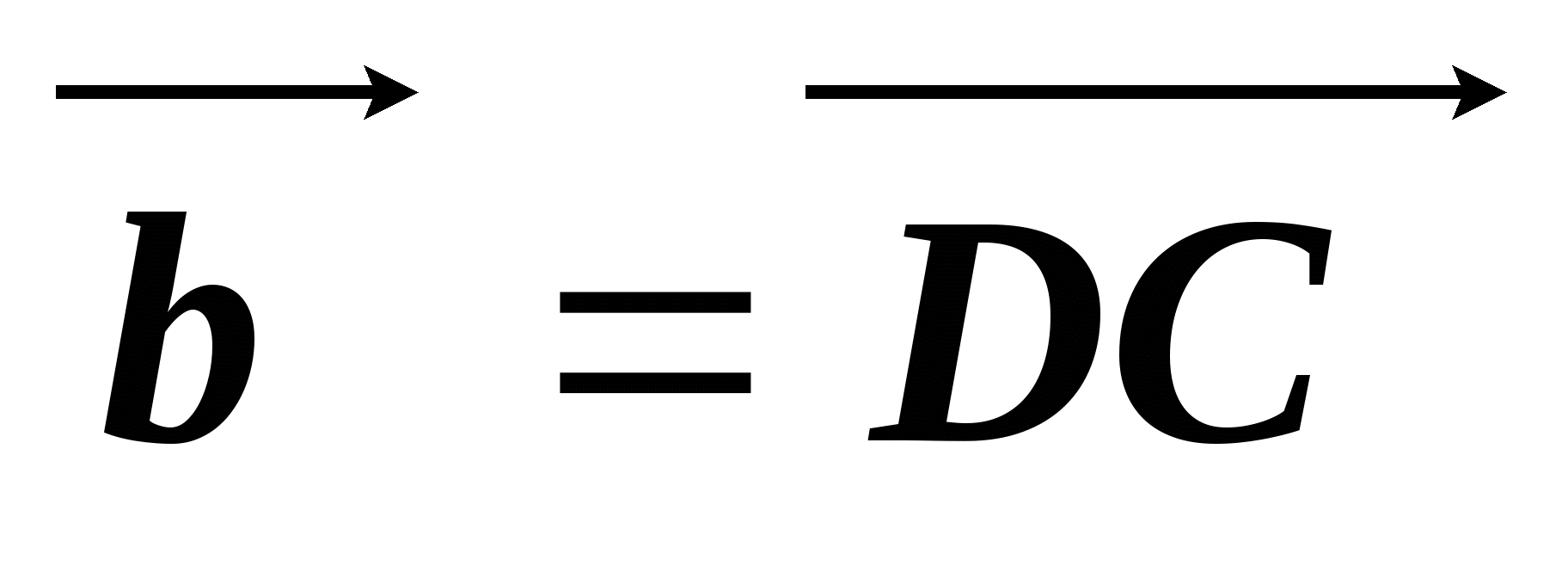звестно, что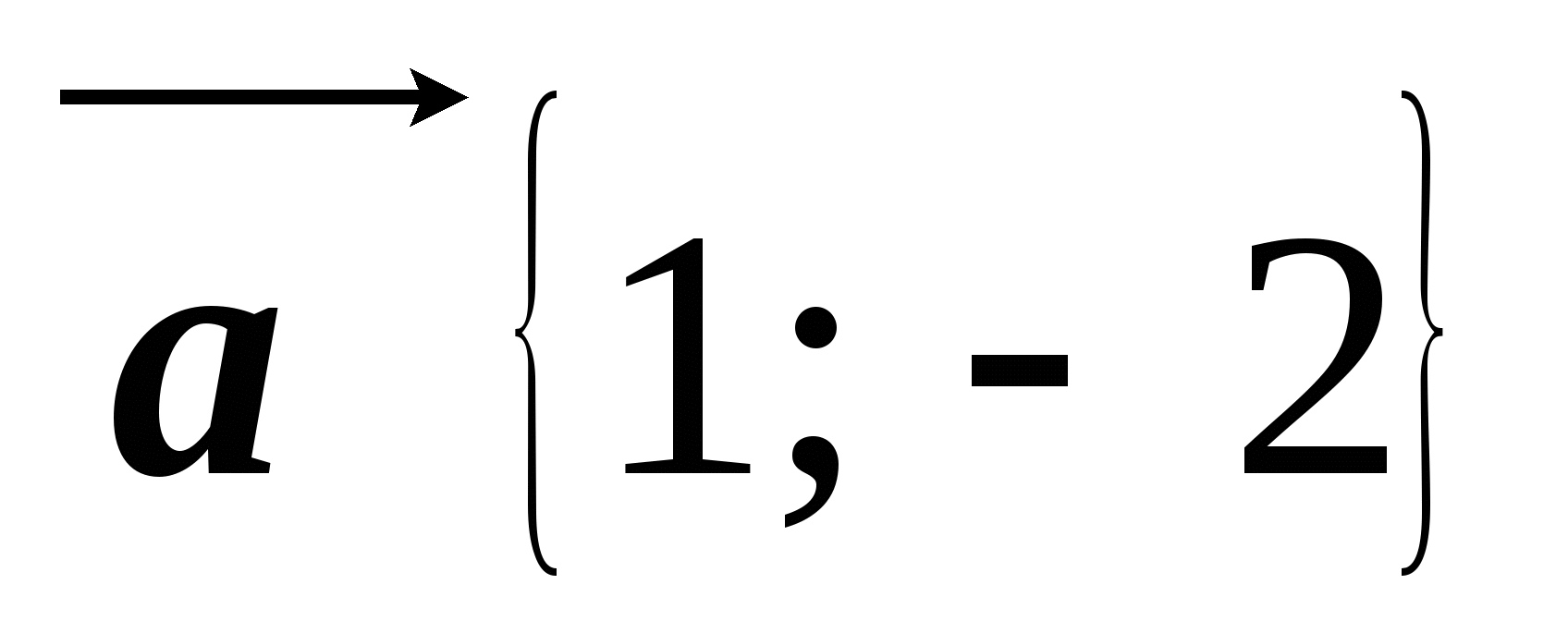 
, 
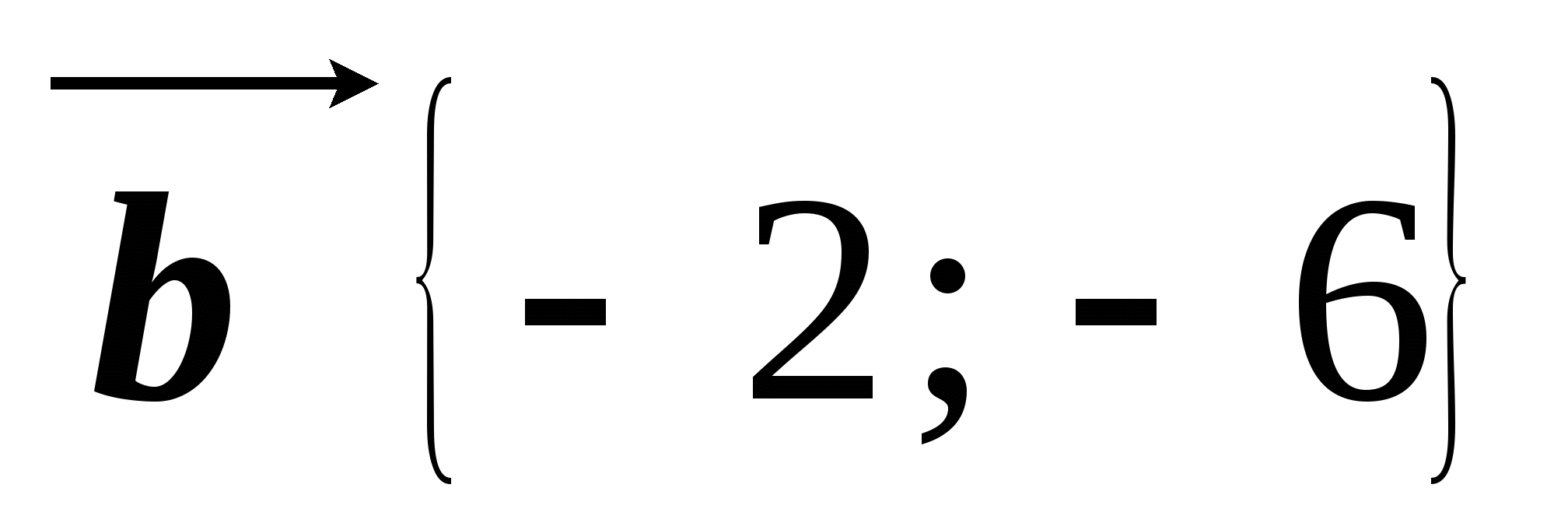. Найдите координаты вектора 
.
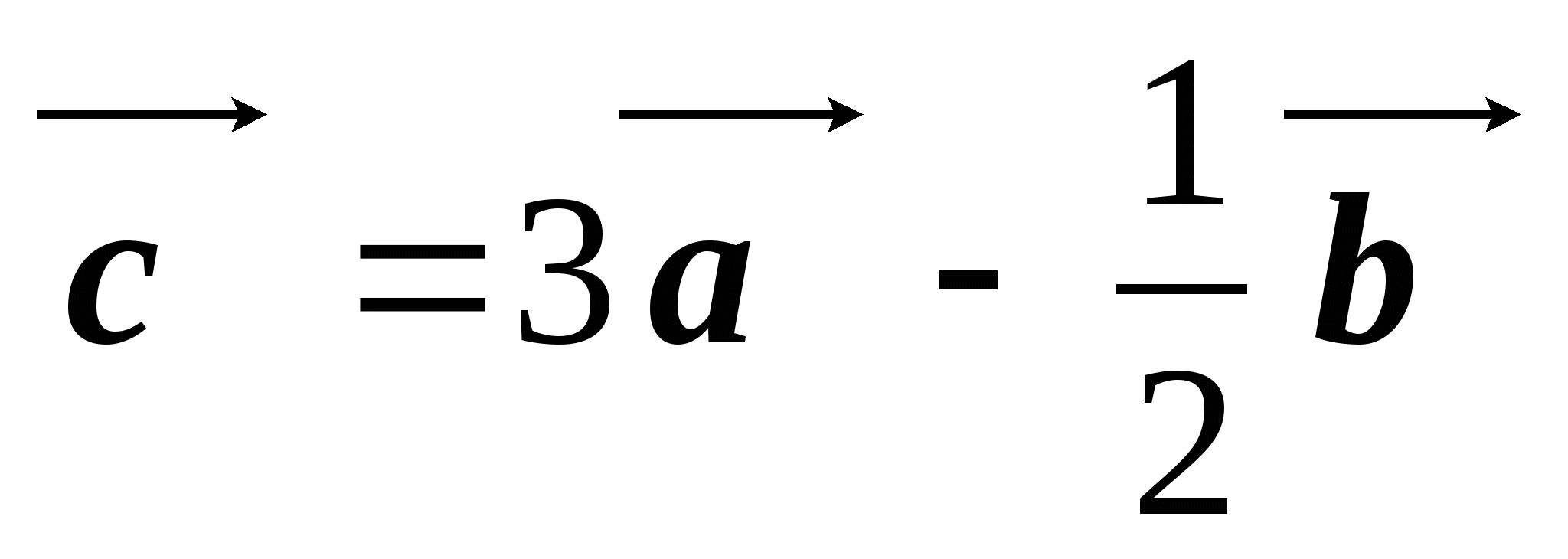Найдите координаты вектора и его длину, если M(-2; -3), N(-7; 9)
Даны координаты вершин треугольника АВС: А(0; -1), В(1; 2), С(2; -1).
а) Найдите длину медианы BD.
б) Докажите, что треугольник АВС – равнобедренный и найдите его площадь.
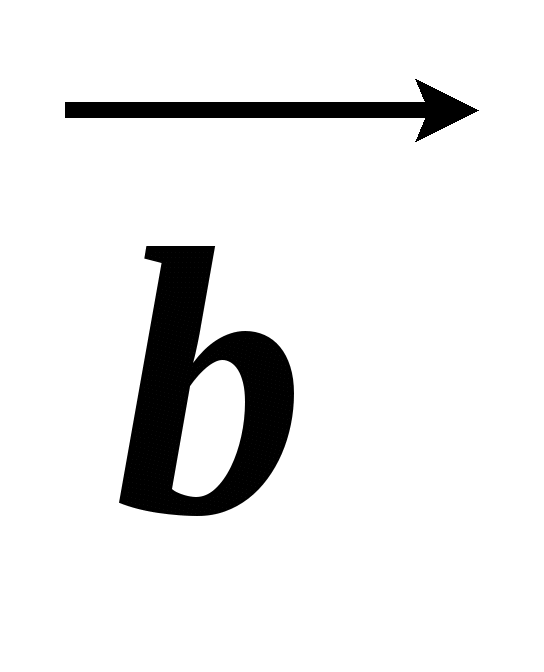Постройте векторы и , такие что 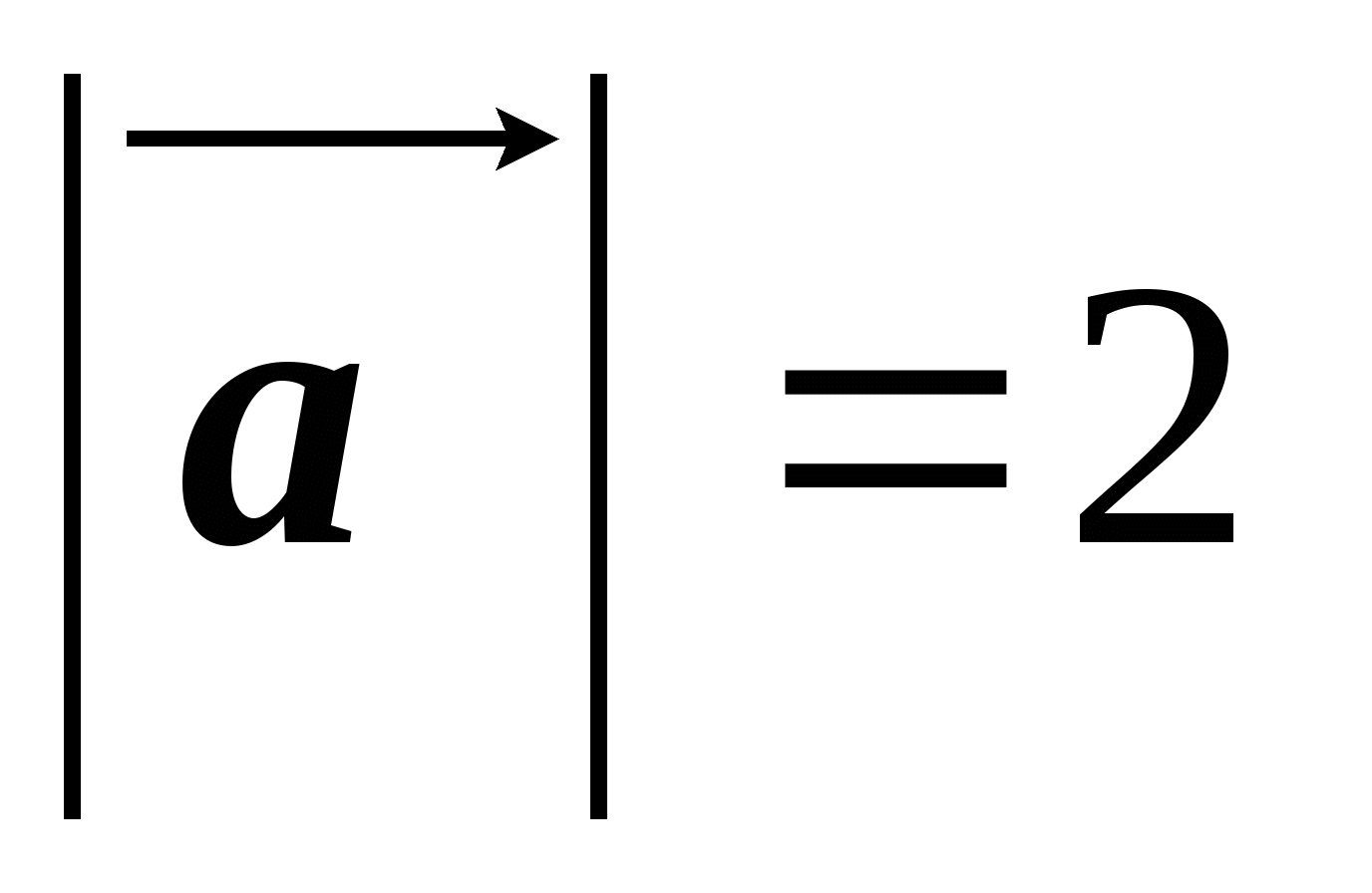см, 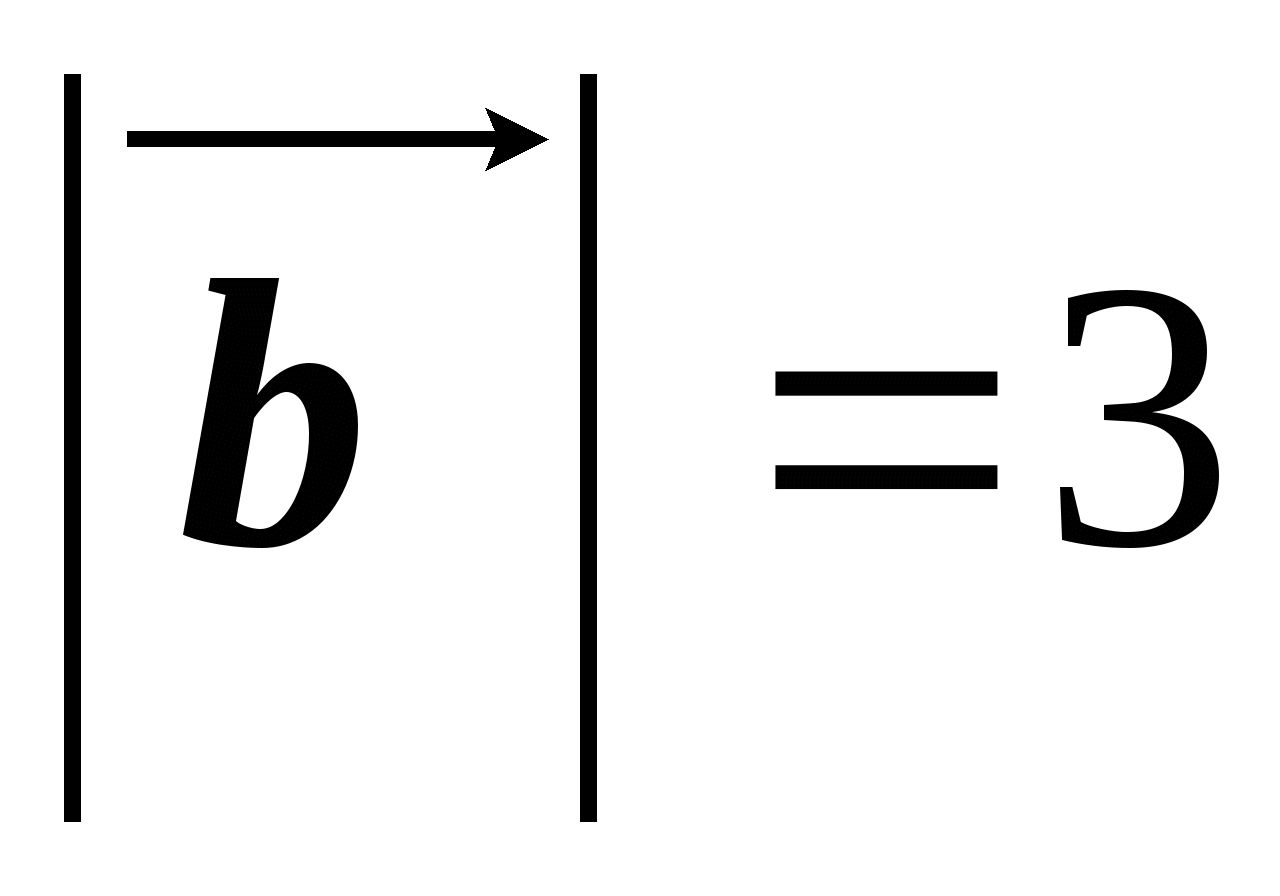см. Построить векторы
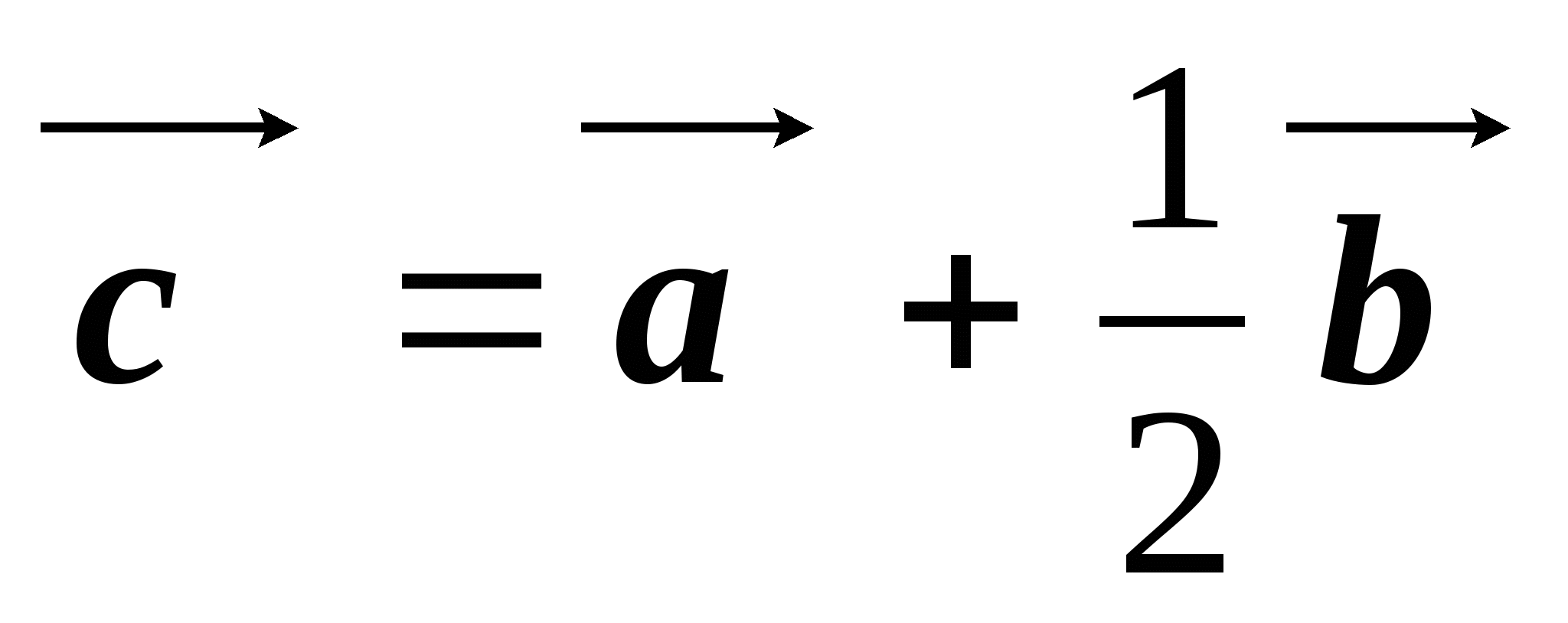и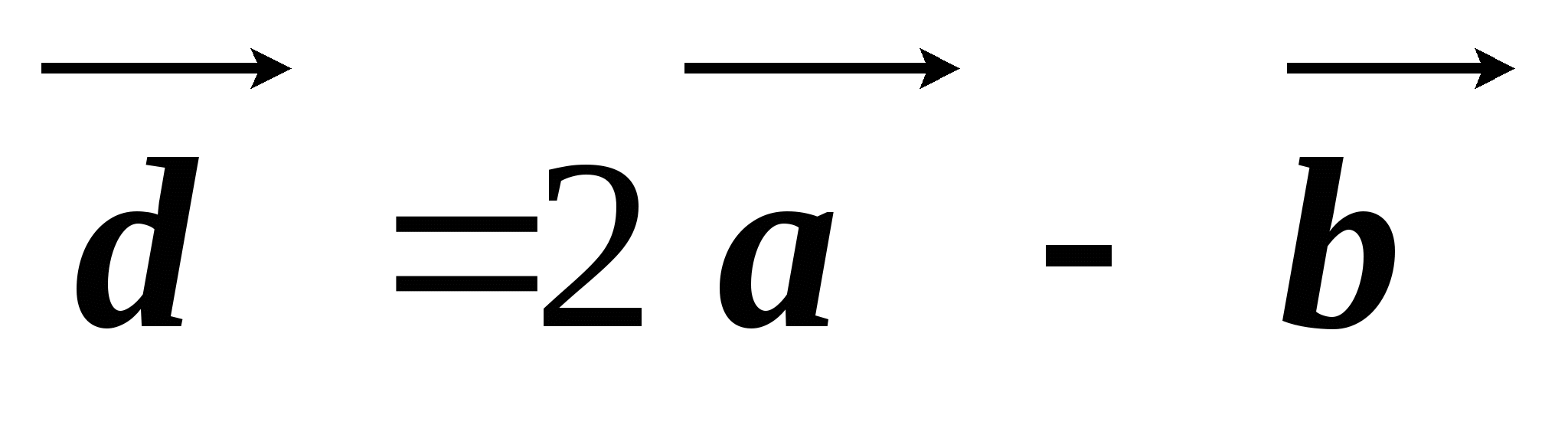 
IV вариант
В параллелограмме ABCD точка P является серединой стороны BC, а точка K делит сторону AD в отношении 1 : 3, считая от точки A. Выразите векторы 
через векторы 
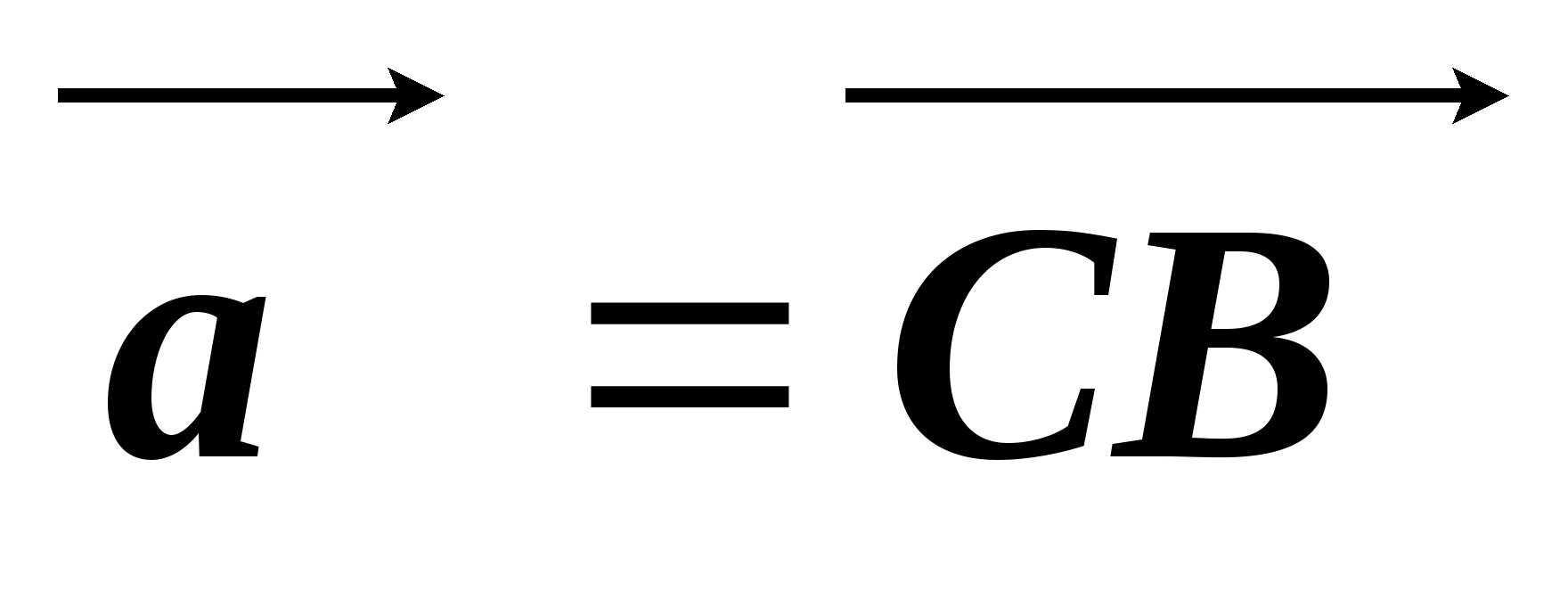и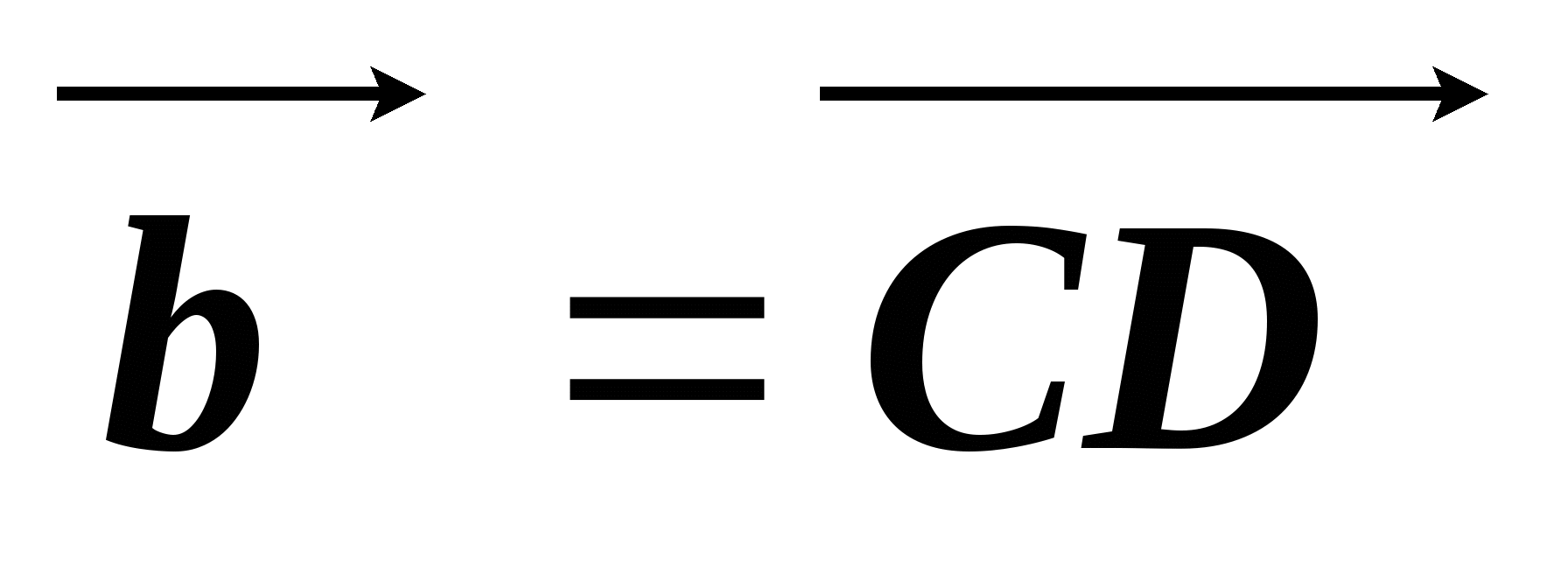 
.
Известно, что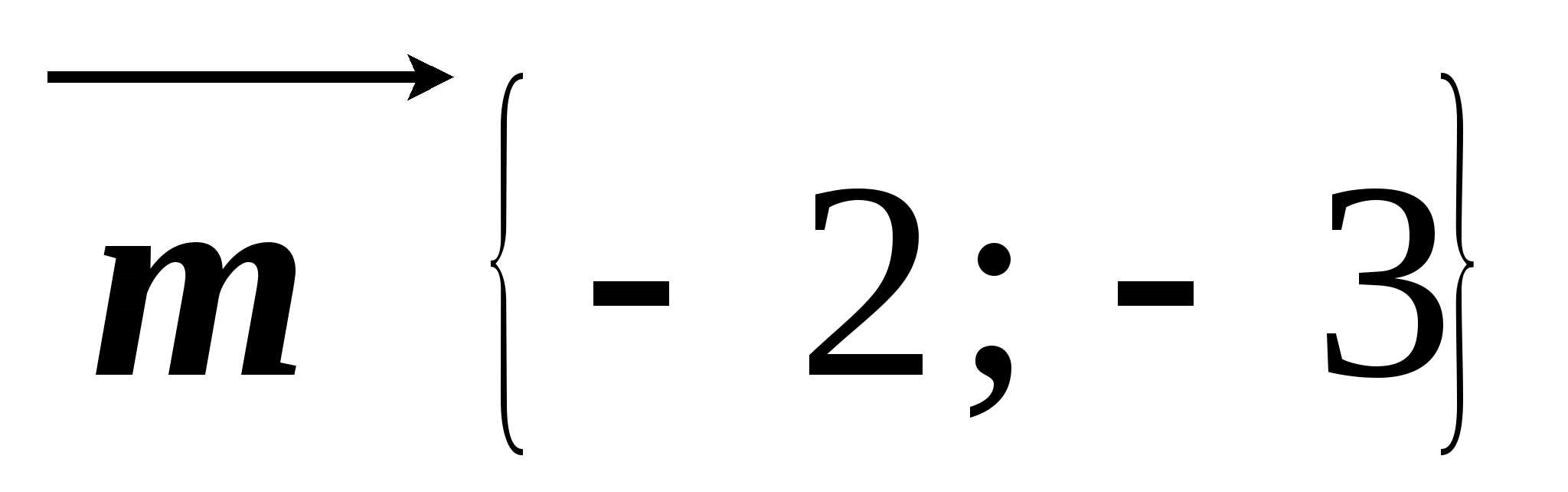 
, 
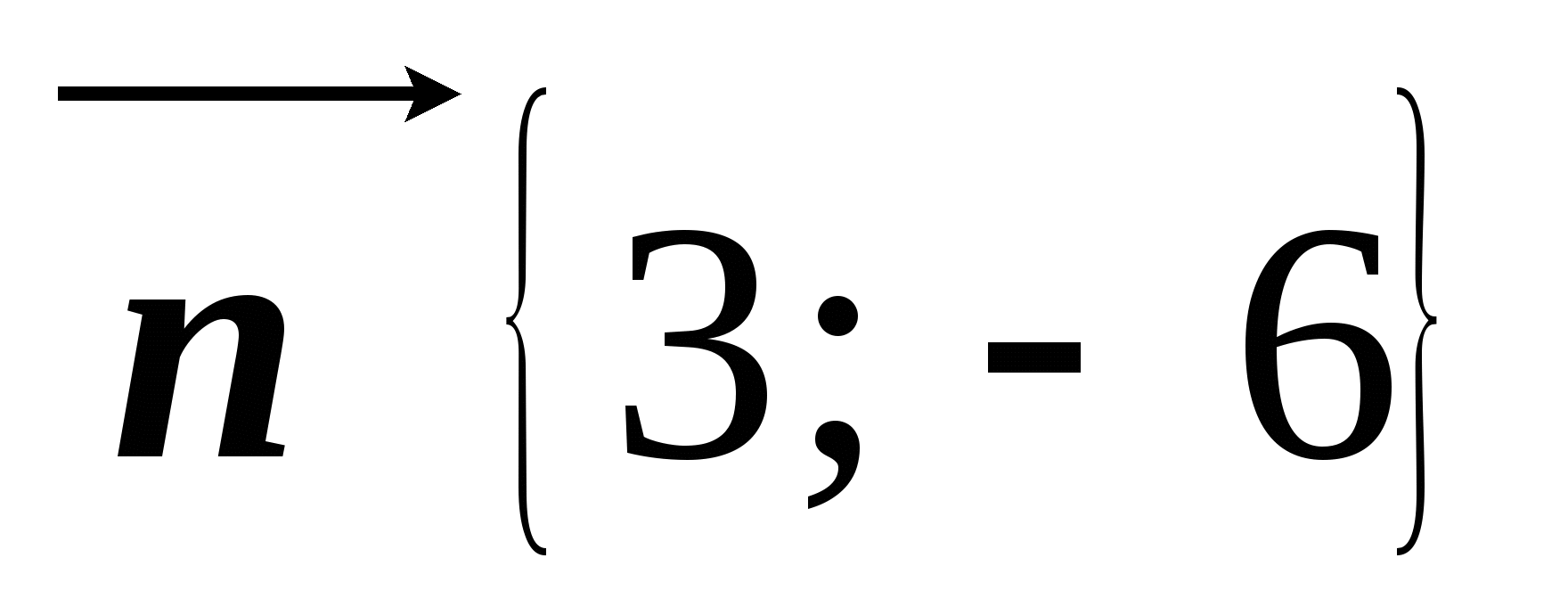. Найдите координаты вектора 
.
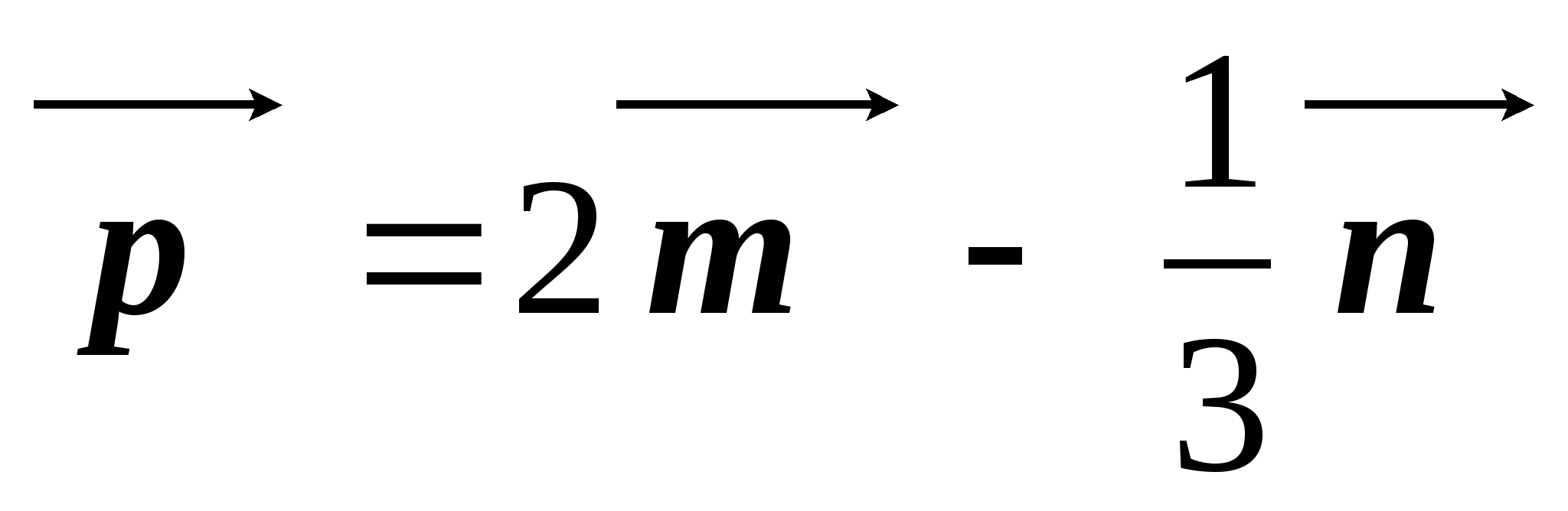Найдите координаты вектора 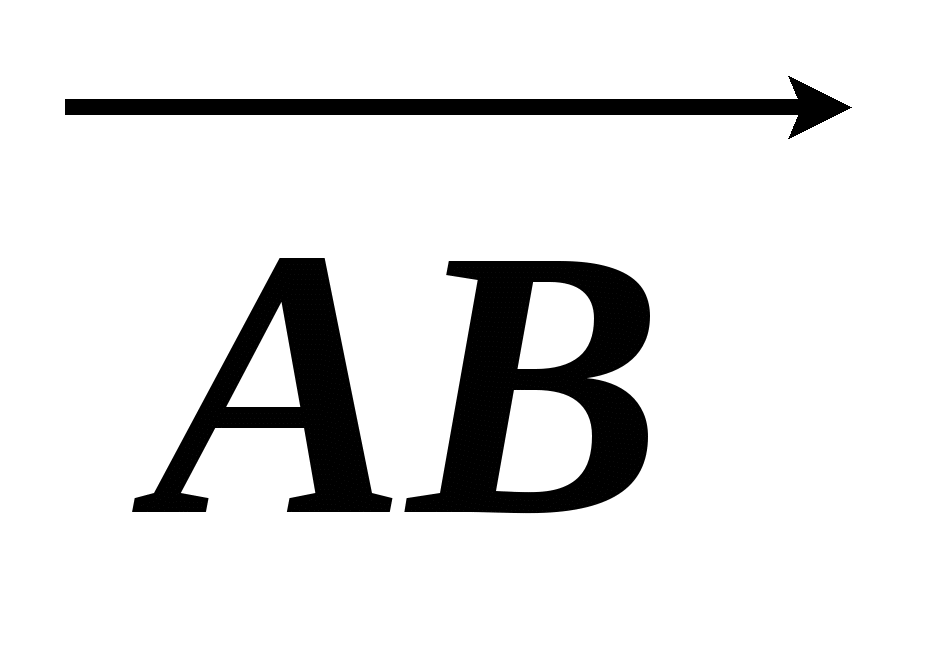и его длину, если A(8; 7), B(17; -5)
Даны координаты вершин треугольника MNK: M(-2; -1), N(3; 1), K(3; -3)
а) Найдите длину медианы MP.
б) Докажите, что треугольник MNK – равнобедренный и найдите его площадь.
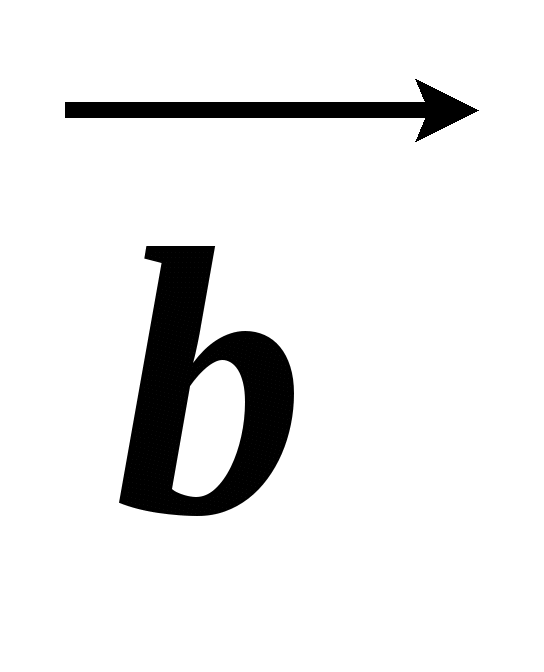Постройте векторы и , такие что 
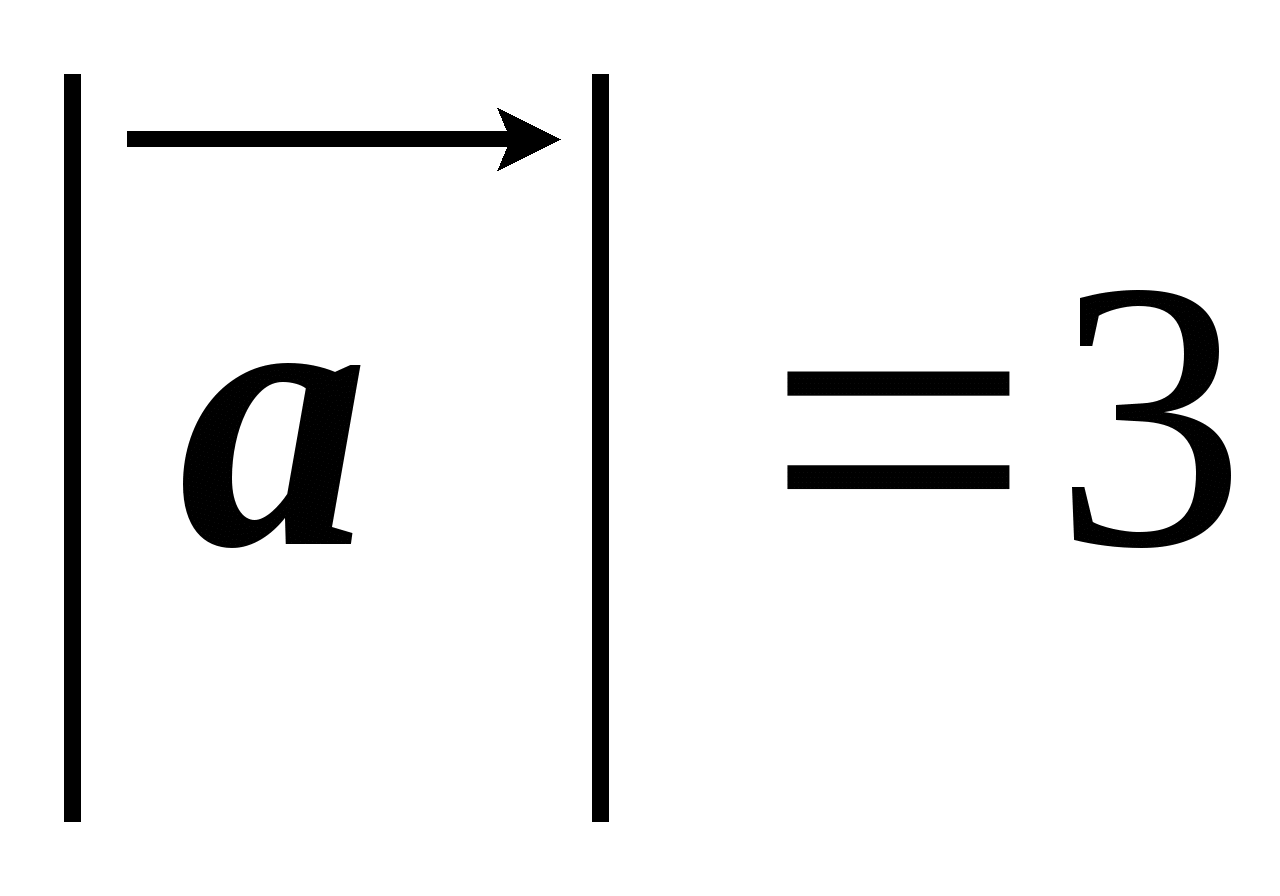см,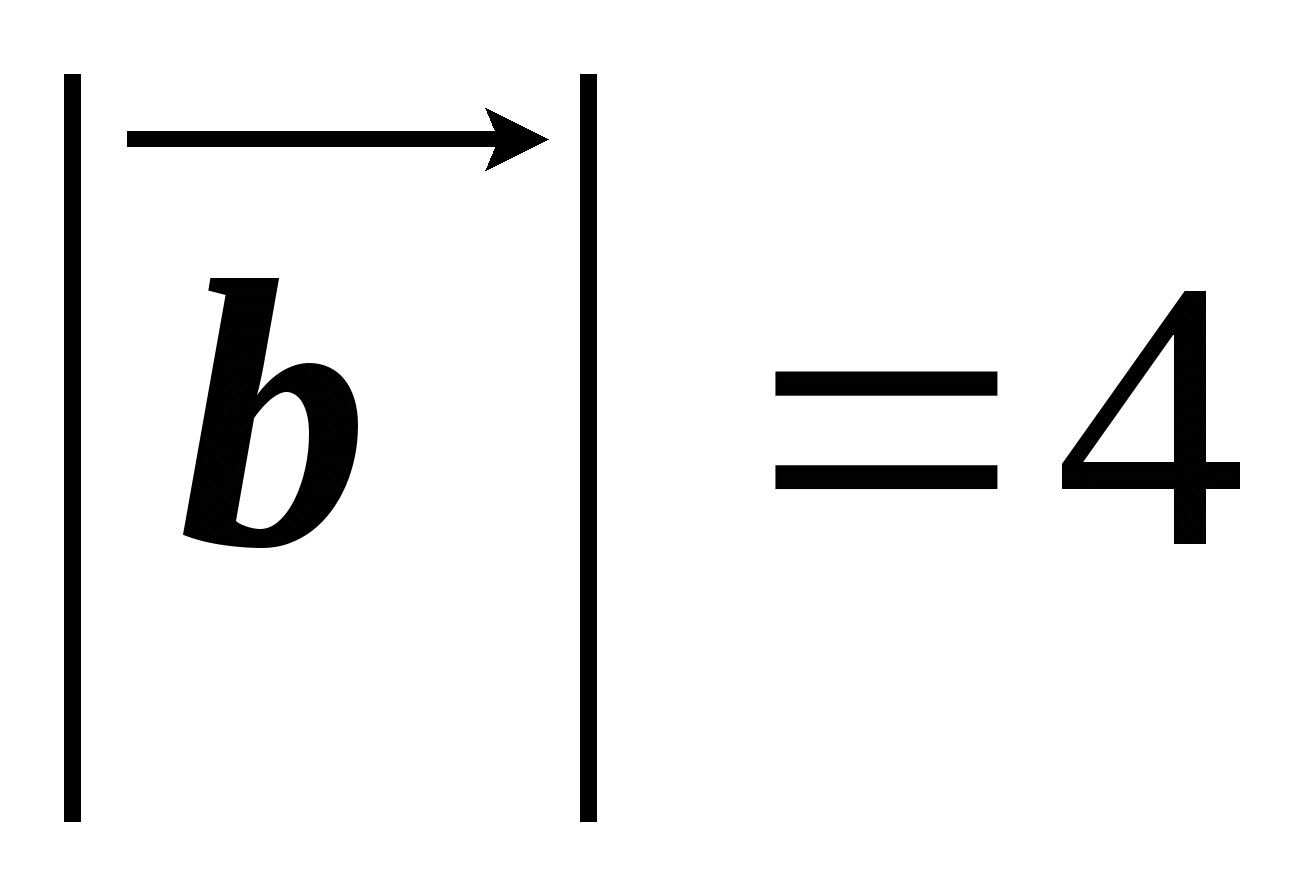 
см. Построить векторы
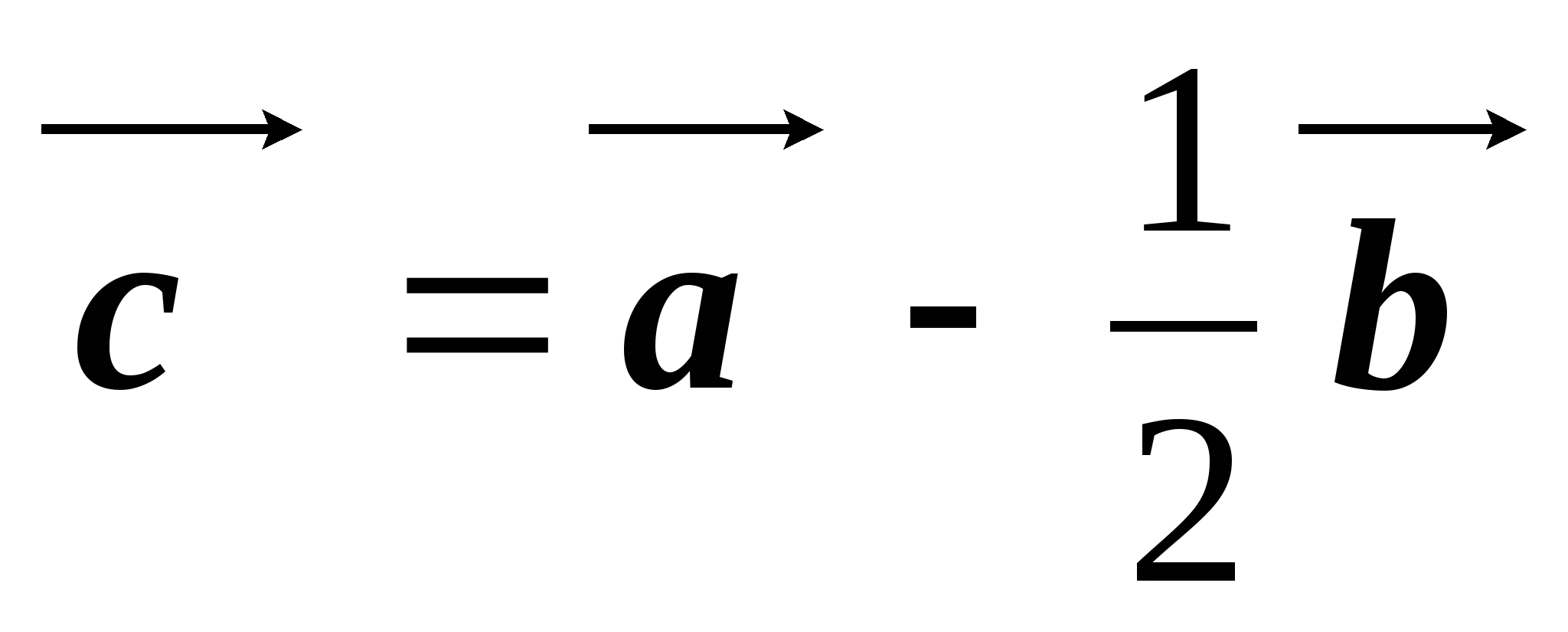и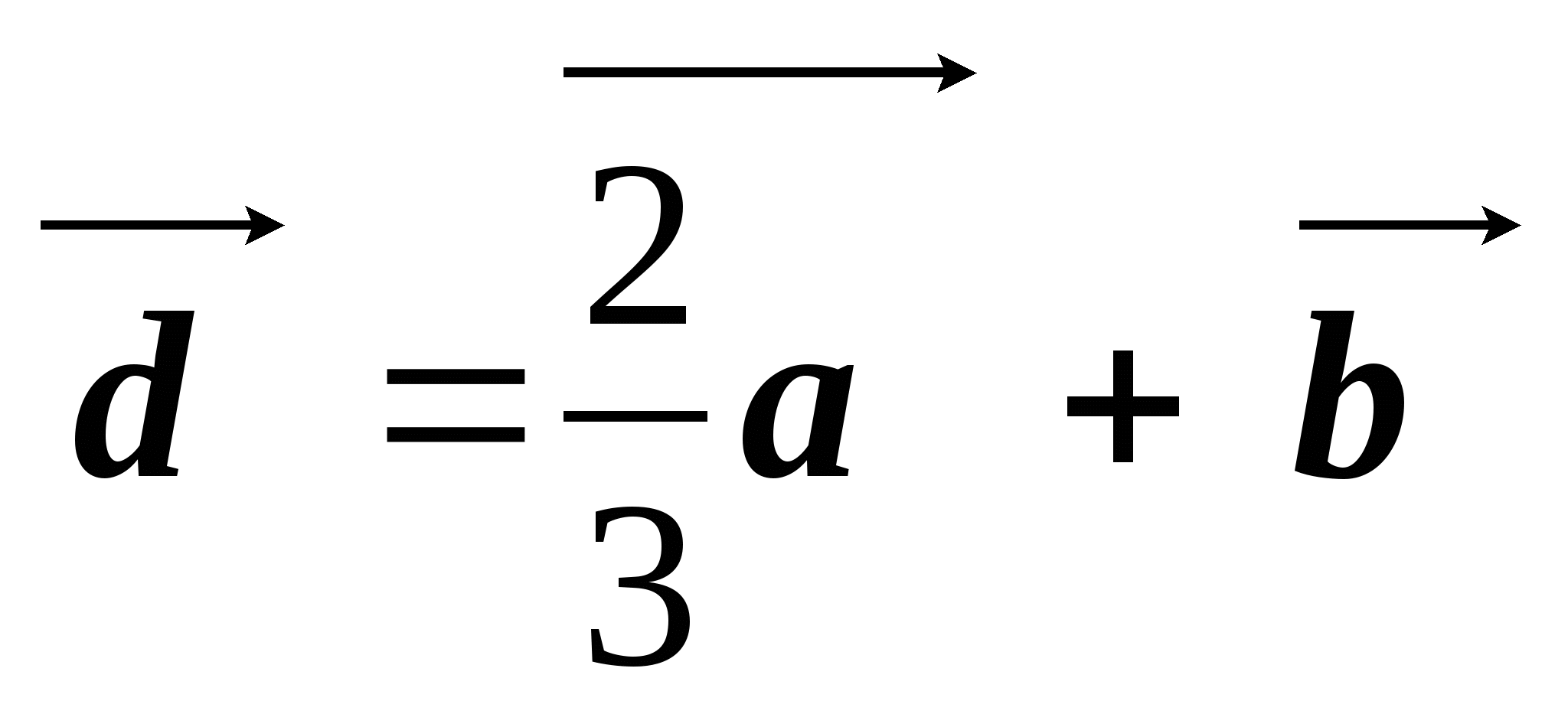 
infourok.ru
Контрольная работа «Метод координат»
9 класс, геометрия
Вариант 1
Концы отрезка АВ имеют координаты А(2; -2), В(-2; 2). Найдите координаты середины этого отрезка.
Напишите уравнение окружности с центром в точке Т(3;-2),R=4
А(0;3), В(1; -4). Напишите уравнение прямой АВ
4. Найдите координаты и длину вектора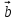 
, если 
.
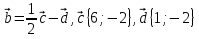5.Треугольник MNK задан координатами своих вершин: M(-6;1), N(2;4), K(2;-2).
а) Докажите, что треугольник MNK – равнобедренный.
б) Найдите высоту, проведенную из вершины M.
6. Найдите координаты точки пересечения прямых: -4х-14у+2=0 и 3х+6у+3=0.
7.Докажите, что четырехугольник MNKP, заданный координатами своих вершин M(2;2),N(5;3), K(6;6), P(3;-5), является ромбом и вычислите его площадь.
Вариант 2.
Концы отрезка СД имеют координаты С(-4; 3), Д(4; -3). Найдите координаты середины этого отрезка.
Напишите уравнение окружности с центром в точке S(2;-1) ,R=5
В(5; 2), С(0;3). Напишите уравнение прямой ВС.
4. Найдите координаты и длину вектора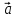 
, если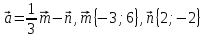 
5.Треугольник FRT задан координатами своих вершин: F(2;-2), R(2;3), T(-2;1).
а) Докажите, что треугольник FRT – равнобедренный.
б) Найдите высоту, проведенную из вершины F.
6. Найдите координаты точки пересечения прямых: х+2у+3=0 и 3х+5у+6=0.
7. Докажите, что четырехугольник PSQT, заданный координатами своих вершин P(3;0),S(-1;3), Q(-4;-1), T(0;-4), является квадратом и вычислите его площадь.
1. Найдите координаты и длину вектора 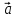, если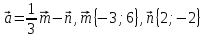
2.Напишите уравнение окружности с центром в точке Т(3;-2), проходящей через точкуB(-2;0).
3.Треугольник MNK задан координатами своих вершин: M(-6;1), N(2;4), K(2;-2).
а) Докажите, что треугольник MNK – равнобедренный.
б) Найдите высоту, проведенную из вершины M.
4.Найдите координаты точки N,лежащей на оси абсцисс и равноудаленной от точек P(2;4) иK(5;-1).
5*. Докажите, что четырехугольник MNKP, заданный координатами своих вершин M(2;2),N(5;3), K(6;6), P(3;-5), является ромбом и вычислите его площадь.
Контрольная работа № 2 «Метод координат»
Вариант 2
1. Найдите координаты и длину вектора 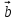, если .
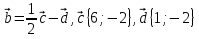2.Напишите уравнение окружности с центром в точке S(2;-1), проходящей через точкуB(-3;2).
3.Треугольник FRT задан координатами своих вершин: F(2;-2), R(2;3), T(-2;1).
а) Докажите, что треугольник FRT – равнобедренный.
б) Найдите высоту, проведенную из вершины F.
4.Найдите координаты точки A,лежащей на оси ординат и равноудаленной от точек B(1;-3) иC(2;0).
5*. В равнобедренном треугольнике основание равно 10 см, а биссектриса, проведенная к основанию, равна 8 см. Найдите медиану, проведенную к боковой стороне.
Контрольная работа № 2 «Метод координат»
Вариант 3
1. Найдите координаты и длину вектора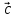 
, если 
.
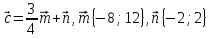2.Напишите уравнение окружности с центром в точке A(-3;2), проходящей через точкуB(0;-2).
3.Треугольник FEC задан координатами своих вершин: F(-1;1), E(4;1), C(1;-3).
а) Докажите, что треугольник FEC – равнобедренный.
б) Найдите медианy, проведенную из вершины Е.
4.Найдите координаты точки N,лежащей на оси абсцисс и равноудаленной от точек P(-1;3) иK(0;2).
5*. В равнобедренном треугольнике основание равно 16 см, а высота, проведенная к основанию, равна 5 см. Найдите медиану, проведенную к боковой стороне.
Контрольная работа № 2 «Метод координат»
Вариант 4
1. Найдите координаты и длину вектора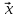 
, если 
.
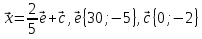2.Напишите уравнение окружности с центром в точке C(2;1), проходящей через точку D(5;5).
3.Треугольник CDE задан координатами своих вершин: C(2;2), D(6;5), E(5;-2).
а) Докажите, что треугольник CDE – равнобедренный.
б) Найдите биссектрису, проведенную из вершины C.
4.Найдите координаты точки Н, лежащей на оси ординат и равноудаленной от точек N(-2;-1) и K(4;1).
5*. Докажите, что четырехугольник PSQT, заданный координатами своих вершин P(3;0),S(-1;3), Q(-4;-1), T(0;-4), является квадратом и вычислите его площадь.
Ответы:
Вариант 1
1)
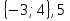
2)
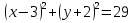
3б) 8
4) (1;0)
5) 8кв.ед.
Вариант 2
1)
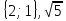
2)
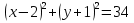
3б)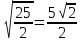 
4) (0;-1)
Вариант 3
1)
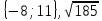
2)
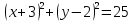
3б)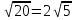 
4) (-3;0)
5) 
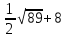кв.ед.
Вариант 4
1)
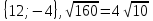
2)
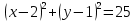
3б)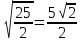
4) (0;3)
5) 25кв.ед.
Метод координат
Вариант 1
1. Даны точки А(-2; -2) и В(4; 6). Найдите координаты и длину векторов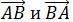 
. Решение
2. Даны векторы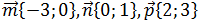 
. Найдите вектор 
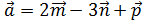и его длину. Решение
3. Напишите уравнение окружности с центром в точке А и радиусом 9, если точка А лежит на прямой y=-2x и её ордината равна 4. Решение
4. Напишите уравнение прямой, проходящей через точку (6; 0) и центр окружности, заданной уравнением x2 + (y - 2)2 = 9. Решение
5. Найдите значение x, при котором векторы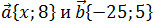 
коллинеарны.
Вариант 2
1. Даны точки А(-3; -1), В(1; -4) и С(6; 8). Найдите координаты и длину вектора 
Решение
2. Даны векторы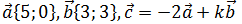 
Найдите значение k, если 
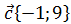Решение
3. Напишите уравнение окружности с диаметром АВ, если А(-2; 4) и В(-2; -2). Решение
4. Напишите уравнение прямой, проходящей через центр описанной окружности и вершину прямого угла треугольника АВС, если А(-3; 0), В(-3; 2), С(1; 0). Решение
5. Найдите значение x, при котором векторы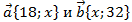 
коллинеарны. Решение
Вариант 1.
1. Концы отрезка АВ имеют координаты А(2; -2), В(-2; 2). Найдите координаты середины этого отрезка.
2. Даны точки А(2; 7), В(-2; 7).
а) Найдите координаты вектора ,
б) Найдите длину вектора .
3. Уравнение окружности имеет вид:
а) Постройте эту окружность;
б) Лежит ли точка А(-5; -3) на данной окружности? Ответ обоснуйте.
4* Даны точки М(-2; -1), N(-4; 3). Составьте уравнение окружности, для которой MN – диаметр окружности.
5* Найдите координаты точки пересечения прямых: -4х-14у+2=0 и 3х+6у+3=0.
6* Треугольник АВС задан координатами своих вершин: А(0;3), В(1; -4), С(5;2)
а) Напишите уравнение прямой АВ,
б) Напишите уравнение медианы АМ,
в) Найдите длину медианы АМ.
Вариант 2.
1. Концы отрезка СД имеют координаты С(-4; 3), Д(4; -3). Найдите координаты середины этого отрезка.
2. Даны точки С(-3; 5), В(3; -5).
а) Найдите координаты вектора ,
б) Найдите длину вектора .
3. Уравнение окружности имеет вид:
а) Постройте эту окружность;
б) Лежит ли точка А(-5; -5) на данной окружности? Ответ обоснуйте.
4* Даны точки А(2; 0), В(-2; 6). Составьте уравнение окружности, для которой АВ – диаметр окружности.
5* Найдите координаты точки пересечения прямых: х+2у+3=0 и 3х+5у+6=0.
6* Треугольник АВС задан координатами своих вершин: А(1;-4), В(5; 2), С(0;3)
а) Напишите уравнение прямой ВС,
б) Напишите уравнение медианы СМ,
в) Найдите длину медианы СМ.
infourok.ru
Контрольная работа по геометрии
по теме «Метод координат»
Вариант 1.
1. Найдите координаты вектора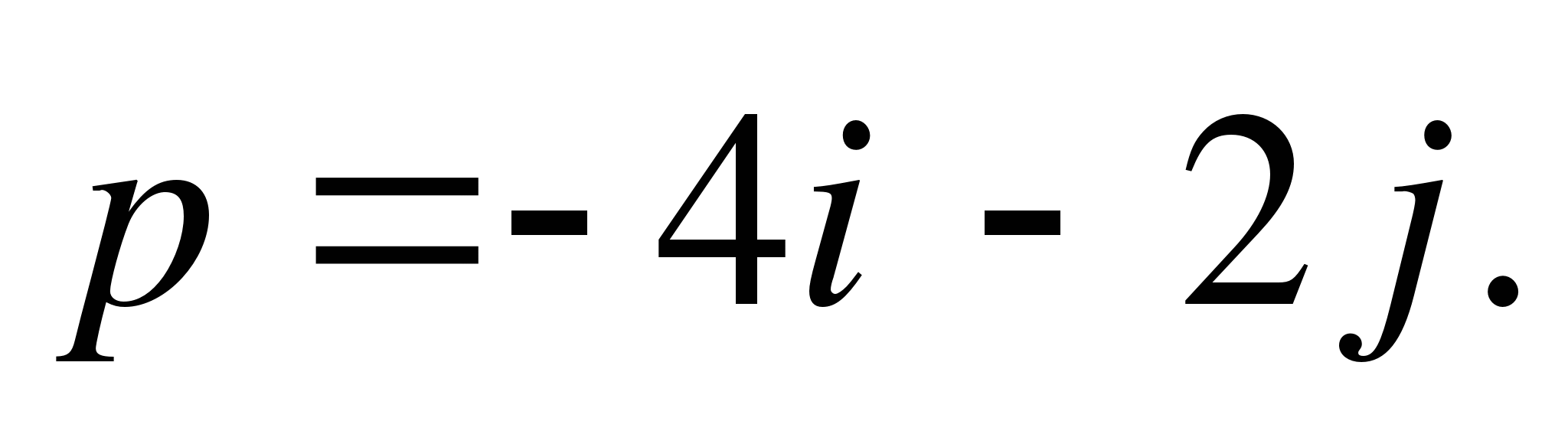 
(1 балл)
2. Запишите разложение вектора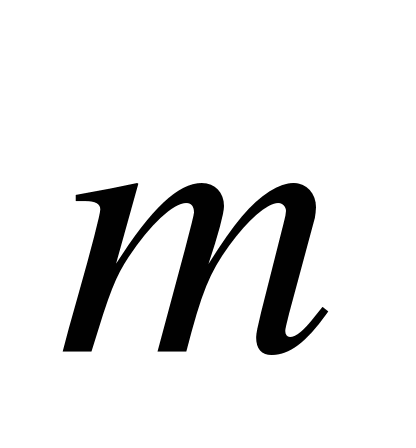 
{7;-6} по координатным векторам 
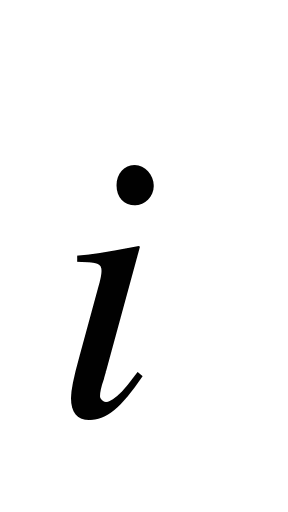и 
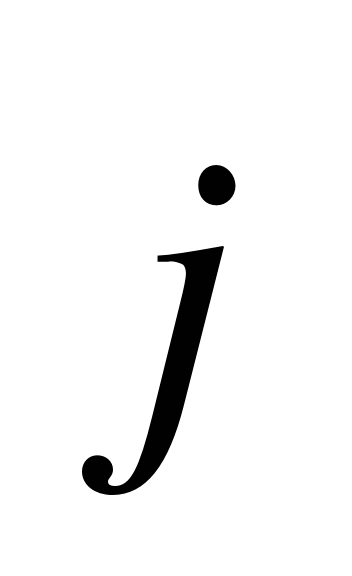. (1 балл)
3. Концы отрезка PK имеют координаты P(-2;7), K(5;1). Точка А – середина отрезка PK. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками А(-6;3) и В(-3;7). (2 балла)
5. Найдите координаты вектора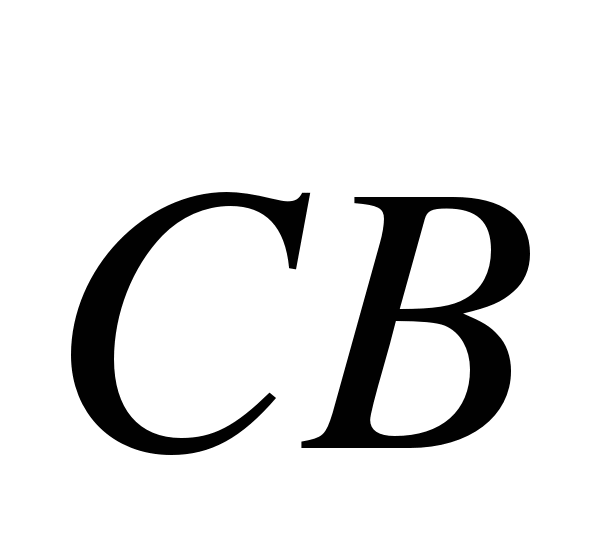 
, если С (11;2), В(9; 5). (2 балла)
6. Найдите длину вектора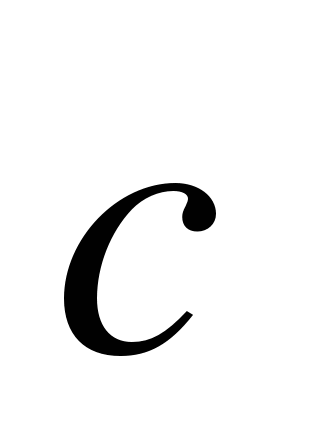 
{6;-8}. (2 балла)
7. Окружность задана уравнением (x-4)2+(y+3)2=8. Лежит ли точка А(-2;-5) на окружности? (2 балла)
8. Окружность задана уравнением (x+6)2+(y-3)2=25. Запишите уравнение прямой, параллельной оси Ох и проходящей через центр этой окружности. (2 балла)
9. Даны векторы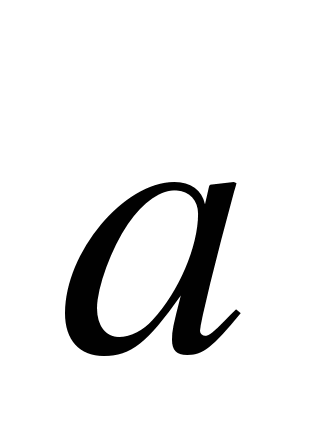 
{-1;3} и 
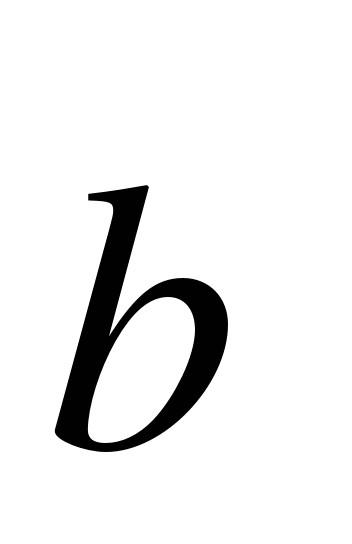{4;2}. Найдите координаты вектора6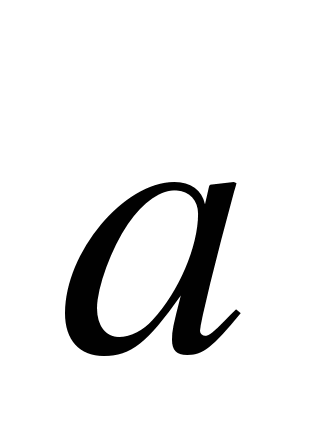- 0,5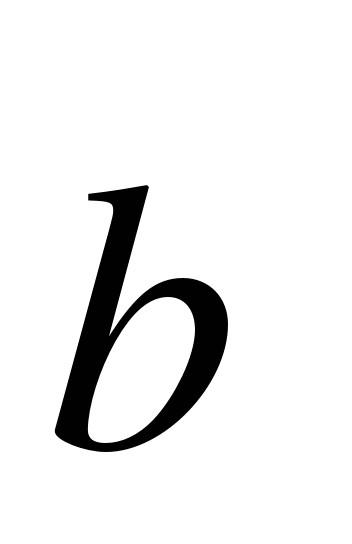. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины А, если А(-3;2), В(-1;5), С(-1;-1). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
Контрольная работа по геометрии
по теме «Метод координат»
Вариант 2.
1. Найдите координаты вектора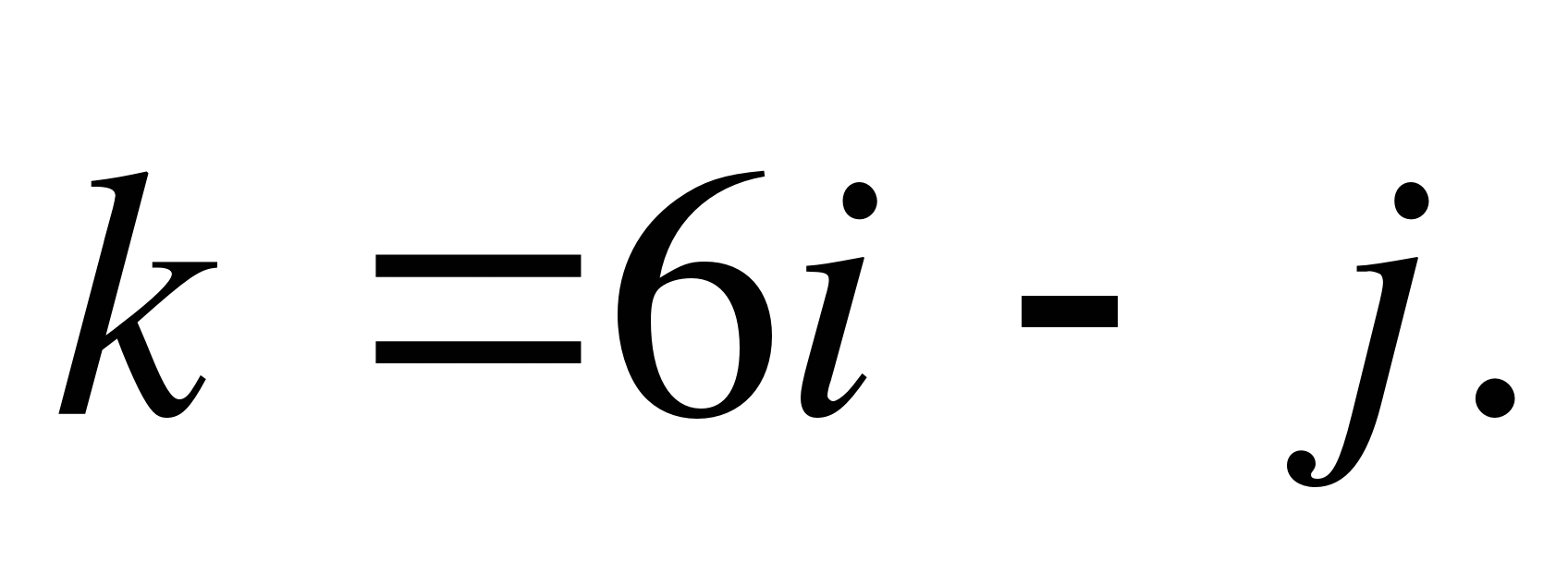 
(1 балл)
2. Запишите разложение вектора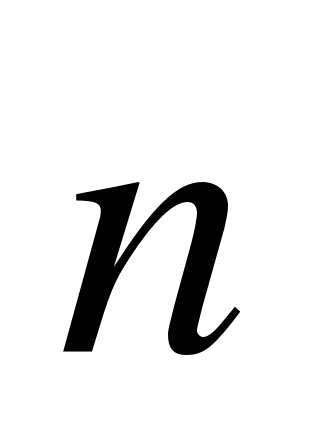 
{-3;8} по координатным векторам 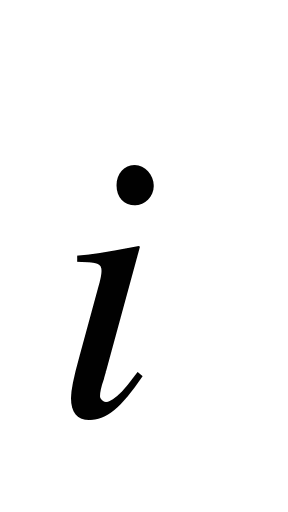и 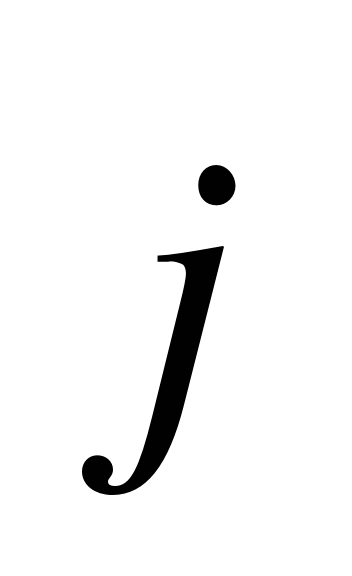. (1 балл)
3. Концы отрезка ВС имеют координаты В(4;-9), С(-1;3). Точка А – середина отрезка ВС. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками М(7;-4) и К(1;4). (2 балла)
5. Найдите координаты вектора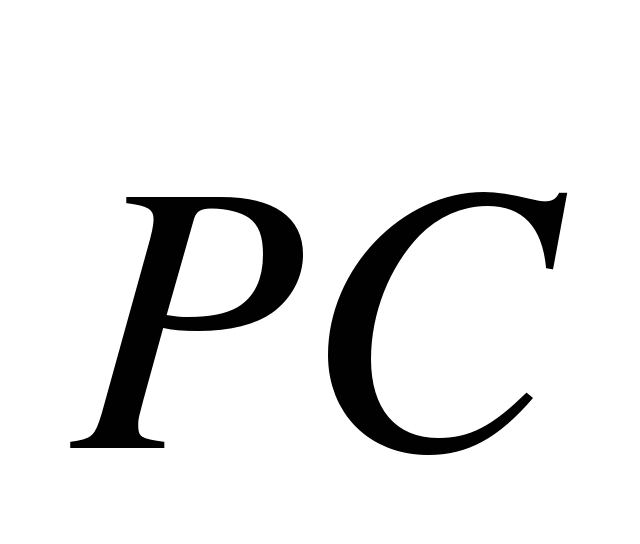 
, если С (5;-2), Р(-3; 1). (2 балла)
6. Найдите длину вектора 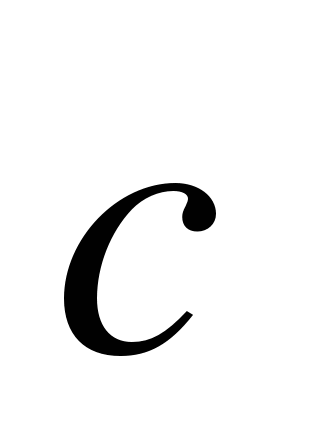{12;-5}. (2 балла)
7. Окружность задана уравнением (x+1)2+(y-7)2=68. Лежит ли точка В(3;--1) на окружности? (2 балла)
8. Окружность задана уравнением (x+5)2+(y+4)2=9. Запишите уравнение прямой, параллельной оси Оy и проходящей через центр этой окружности. (2 балла)
9. Даны векторы 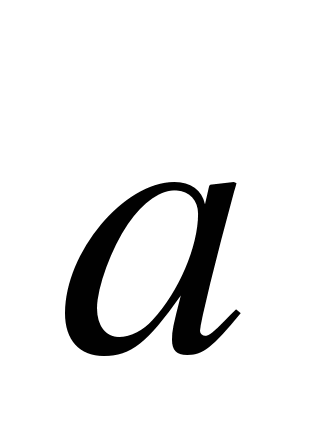{-10;5} и 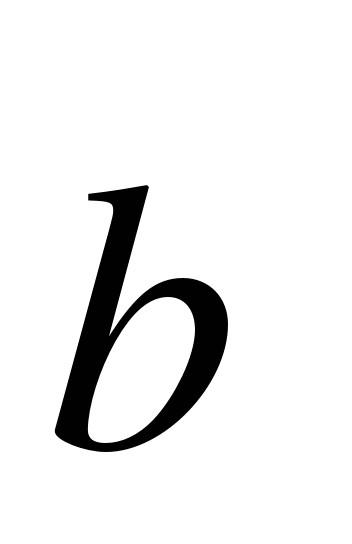{3;-4}. Найдите координаты вектора 3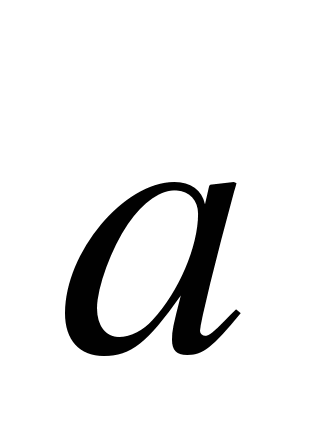+7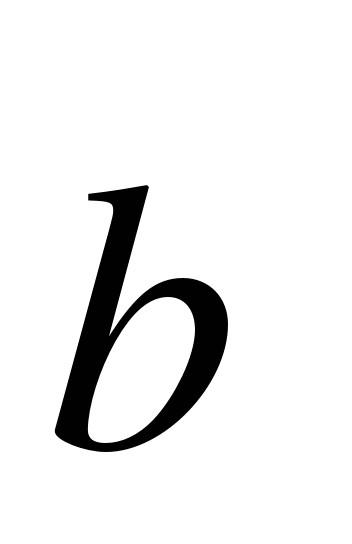. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины В, если А(-3;4), В(-1;-1), С(1;4). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
Контрольная работа по геометрии
по теме «Метод координат»
Вариант 3.
1. Найдите координаты вектора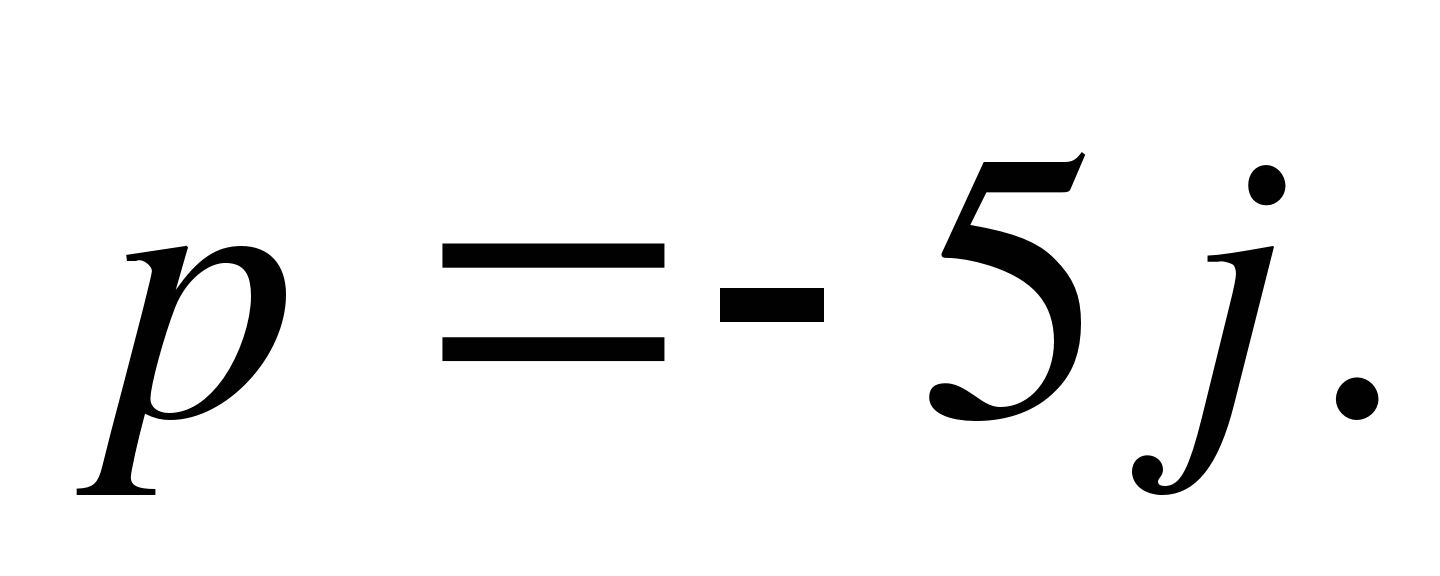 
(1 балл)
2. Запишите разложение вектора 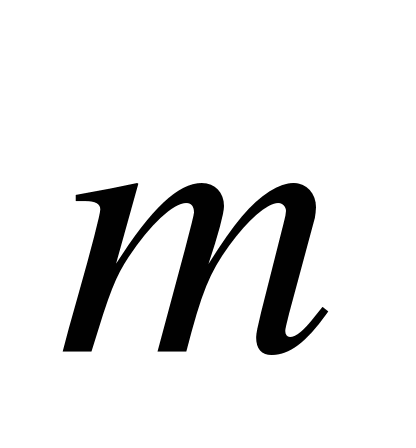{-2;-4} по координатным векторам 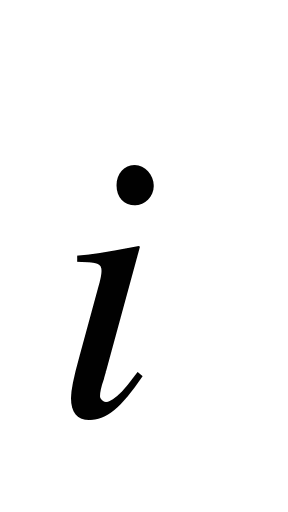и 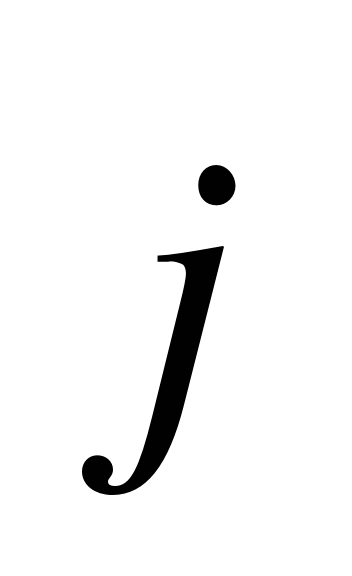. (1 балл)
3. Концы отрезка PK имеют координаты P(5;3), K(-4;7). Точка А – середина отрезка PK. Найдите координаты точки А. (2 балла)
4. Найдите расстояние между точками А(2;-1) и В(10;5). (2 балла)
5. Найдите координаты вектора 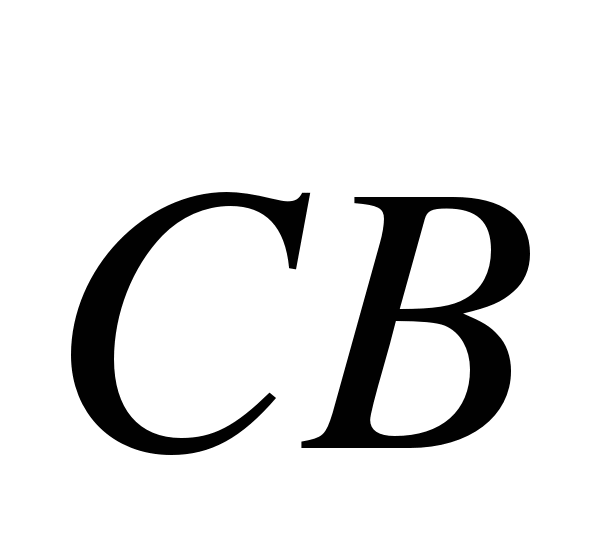, если В (3;5), С(2; -1). (2 балла)
6. Найдите длину вектора 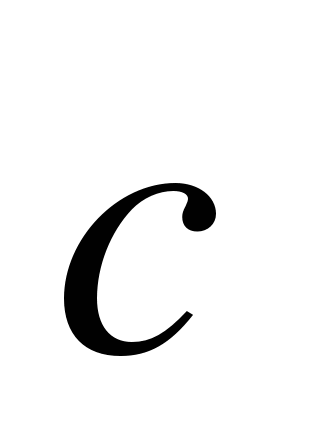{-5;8}. (2 балла)
7. Окружность задана уравнением (x+4)2+(y+3)2=5. Лежит ли точкаА(-2;-4) на окружности? (2 балла)
8. Окружность задана уравнением (x-13)2+(y-3)2=81. Запишите уравнение прямой, параллельной оси Ох и проходящей через центр этой окружности. (2 балла)
9. Даны векторы 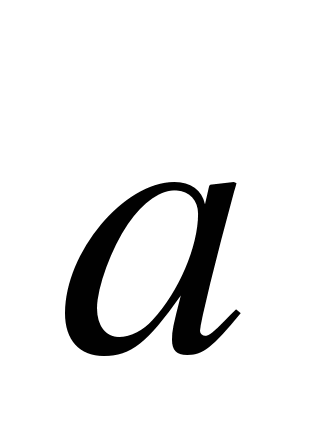{-1;3} и 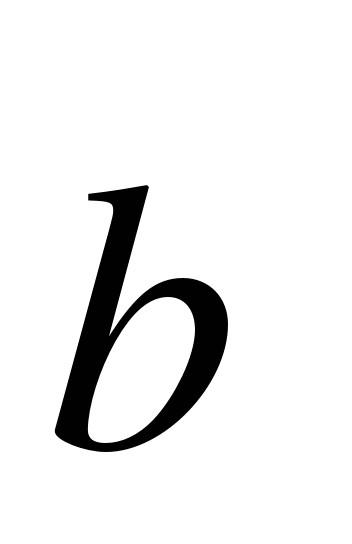{4;2}. Найдите координаты вектора3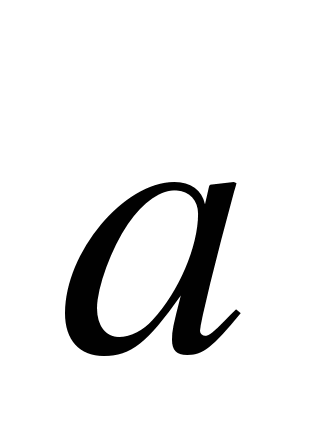- 4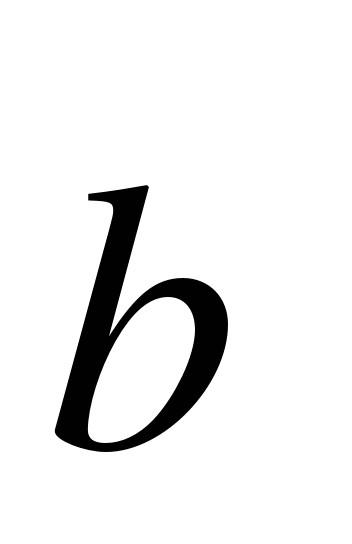. (3 балла)
10. Найдите высоту треугольника АВС, проведенную из вершины С, если А(-2;2), В(-2;-4), С(-5;-1). (6 баллов)
«5» - 20 - 23 балла
«4» - 15 - 19 баллов
«3» - 10 -14 баллов
«2» - менее 10 баллов
Контрольная работа по геометрии
по теме «Метод координат».
infourok.ru
