 1.2.
1.2. 
Федеральное государственное образовательное учреждение высшего профессионального образования
ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра «Прикладная математика»
А. В. Овчинников
Линейная алгебра
Учебно-методическийматериал для подготовки контрольных работ по темам
«Число и вектор Фробениуса», «Модель Леонтьева», «Линейное программирование», «Транспортная задача», «Разностные уравнения»
Для подготовки бакалавров направлений
080100.62 «Экономика» и 080500.62 «Менеджмент»
Москва 2010
Федеральное государственное образовательное учреждение высшего профессионального образования
ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра «Прикладная математика»
УТВЕРЖДАЮ
Ректор
__________М. А. Эскиндаров «______»____________2010 г.
А. В. Овчинников
Линейная алгебра
Учебно-методическийматериал для подготовки контрольных работ по темам
«Число и вектор Фробениуса», «Модель Леонтьева», «Линейное программирование», «Транспортная задача», «Разностные уравнения»
Рекомендовано Ученым Советом при факультете «Математические методы и анализ рисков» (протокол № 7 от 22 июня 2010 г.)
Одобрено кафедрой «Прикладная математика» (протокол № 12 от 19 мая 2010 г.)
УДК 519.6 (073) ББК 22.143
Г 65
Рецензент: В.М. Гончаренко, к.ф.-м.н.,доцент
А. В. Овчинников.
Линейная алгебра. Учебно-методическийматериал для подготовки контрольных работ по темам «Число и вектор Фробениуса», «Модель Леонтьева», «Линейное программирование», «Транспортная задача», «Разностные уравнения». – М: Финуниверситет, кафедра «Прикладная математика», 2010.
В данном издании представлено 30 вариантов контрольных работ по линейной алгебре для студентов первого курса по темам «Число и вектор Фробениуса. Модель Леонтьева. Линейное программирование. Транспортная задача. Разностные уравнения». Последний 30-йвариант приводится с подробными решениями.
УДК 519.6 (073) ББК 22.143
Г 65
Учебное издание
Алексей Витальевич Овчинников
Линейная алгебра. Учебно-методическийматериал для подготовки контрольных работы по темам «Число и вектор Фробениуса», «Модель Леонтьева», «Линейное программирование», «Транспортная задача», «Разностные уравнения».
Компьютерный набор, верстка: А. В. Овчинников
Формат 60х90/16. Гарнитура Times New Roman, Antiqua
Усл.п.л.0,6. Изд. № -2010.Тираж ___ экз.
Отпечатано в ФГОУ ВПО «Финансовый университет при Правительстве Российской Федерации»
©А. В. Овчинников, 2010
©ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010
Введение
Домашние контрольные работы по математике являются одной из основных форм текущего контроля самостоятельной работы студентов.
Виздании представлены материалы для двух домашних контрольных работ по второй части курса линейной алгебры, которая охватывает следующие темы: «Число и вектор Фробениуса», «Модель Леонтьева», «Линейное программирование», «Транспортная задача», «Разностные уравнения». В результате выполнения работы студенты, с одной стороны, демонстрируют умения и навыки, приобретенные в ходе лекций и практических занятий, и получают оценки, являющиеся существенной компонентой аттестации и баллов за работу в семестре.
Сдругой стороны, выполнение заданий домашней контрольной работы является важной частью подготовки к семестровому экзамену (зачету). Задания контрольной работы составлены так, чтобы охватить все основные типы задач по данным темам.
Сроки выполнения и сдачи домашних контрольных работ устанавливаются преподавателем. Оценки выставляются по итогам проверки письменных работ и собеседования (или аудиторной контрольной работы).
Внастоящем пособии представлено 30 вариантов домашних контрольных работ. К варианту № 30 приведены подробные решения, в которых продемонстрированы основные приемы и методы решения типовых задач.
Вцелях экономии места задачи сгруппированы не по вариантам, а по типам: сначала приведены 30 вариантов задачи № 1, затем — 30 вариантов задачи № 2 и т.д. Такая структура пособия объясняется тем, что у многих задач, приведенных в пособии, одинаковая текстовая часть, но различные числовые данные.
Правила оформления домашних контрольных работ
1.Работа должна быть выполняется аккуратно, разборчивым почерком, синей или черной ручкой на листах формата А4. Листы должны быть скреплены неразборным соединением (степлером, клеем и т.п.).
2.Работа снабжается титульным листом, на котором приводятся следующие данные: номер группы, фамилия студента, дата сдачи работы на проверку, ответы ко всем задачам в том же порядке, в котором задачи сформулированы (см. образец титульного листа на следующей странице). Если задача не решена, вместо ответа ставится прочерк.
3.Решения задач внутри работы должны быть приведены в той же последовательности, что их формулировки. Если в задаче предусмотрено несколько заданий, то они также должны быть решены в той последовательности, в которой сформулированы.
4.Перед решением указывается порядковый номер задачи, который необходимо выделить (маркером, рамкой и т.п). Условие переписывать не требуется. В конце решения приводится ответ по фор-
ме: «Ответ:. . . ».
5.Числовой ответ должен быть приведен в виде целого числа, или десятичной дроби с 4 знаками после запятой, или обыкновенной дроби, у которой и числитель, и знаменатель которой не превышают 9999. То же требование налагается на элементы матриц.
6.Неверное решение, решение задачи из другого варианта или задачи с измененным условием, отсутствие решения или выписанного на титульном листе ответа приводит к минимальной оценке задачи (0 баллов).
7.Отсутствие обоснования при верном решении влечет снижение оценки на 2 балла.

8.Неверный ответ (в том числе из-заошибок округления) при верном решении снижает оценку.
9.Оценка также снижается за небрежное оформление работы (зачеркнутый текст, вставки, неаккуратные чертежи и т.п).
Образец оформления титульного листа
Финансовый университет при Правительстве Российской Федерации
Кафедра «Прикладная математика» Линейная алгебра
Контрольная работа № 1
Выполнил студент группы ФК-1-1
Бесфамильный И. О.
Работа сдана 29 февраля 2007 г.
Ответы:
Задача № 1.
СЗ: λ1 = 2 ,λ2 = 4 ; СВ:xr1 = c1 (−9,1)T ,xr2 = c2 (−37,4)T , гдеc1 ,c2 ≠ 0 .
Задача № 2.
и так далее
Контрольная работа № 1
В состав контрольной работы № 1 входят четыре задачи по темам, изучаемым в первой половине семестра: число и вектор Фробениуса неотрицательной квадратной матрицы, модель Леонтьева, задача линейного программирования об оптимальном использовании ресурсов, а также задача о нахождении собственных значений и собственных векторов матрицы (задача № 1), цель которой — напомнить студентам соответствующие понятия, играющие важную роль
втеории Фробениуса.
1.СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ
МАТРИЦЫ
Найдите все собственные значения и собственные векторы данной матрицы.
1.1. | 47 |
|
| 88 | . |
| 19 |
|
| 24 | . | |||||||
20 | − | 37 | 1.11. −20 | −25 | ||||||||||||||
| − |
|
|
|
|
| . | 1.12. −36 | −43 | . | ||||||||
1.2. − |
| 3 | − |
| 40 | |||||||||||||
|
| 27 |
|
| 374 |
|
| 35 |
|
| 42 |
|
| |||||
1.3. | 77 |
| 456 | . | 39 |
| 144 | . | ||||||||||
12 | − | 71 | 1.13. | 8 | − | 29 | ||||||||||||
| − |
|
|
|
|
|
| − |
|
|
|
|
|
| ||||
1.4. | 52 |
| 204 | . | 1.14. | 43 |
|
| 78 | . | ||||||||
12 | − | 47 | 18 | − | 32 | |||||||||||||
| − |
|
|
| . | − |
|
|
|
|
|
| ||||||
1.5. |
| 3 |
|
| 14 | 1.15. −10 | − |
| 63 | |||||||||
| 23 |
| 114 |
|
|
|
| 59 |
|
| 372 |
| ||||||
| − |
| − |
|
|
| . | 1.16. − |
|
| − |
|
|
|
| |||
1.6. | 20 |
|
| 37 |
| 4 |
| 34 | ||||||||||
|
| 47 |
|
| 88 |
|
|
| 23 |
|
| 203 |
| |||||
| − |
|
| − |
|
|
| −7 |
|
|
|
|
|
| ||||
|
| 3 |
|
| 6 |
|
|
| 13 |
|
| |||||||
1.7. | 13 |
| 30 . |
| 1.17. | 2 | −8. |
| ||||||||||
| − |
| − |
|
|
|
| . | 1.18. − |
|
| −15 | . | |||||
1.8. − |
| 4 | − |
| 25 |
| 6 | |||||||||||
|
| 19 |
|
| 120 |
|
| 10 |
|
| 26 |
|
| |||||
1.9. −14 | −105 | . | 1.19. −8 | −15 | . | |||||||||||||
|
| 93 |
|
| 700 |
|
| 5 |
|
| 12 |
|
|
| ||||
1.10. | 30 |
| 100 | . | 1.20. | 19 |
|
| 16 | . | ||||||||
| 6 | − | 19 | 14 | − | 11 | ||||||||||||
| − |
|
|
|
|
| − |
|
|
|
|
|
| |||||
| 1.21. | 157 |
|
| 780 | . | |||
| − | 30 | − | 149 | |||||
|
|
|
|
|
|
| |||
| 27 |
|
| 66 |
| ||||
| 1.22. |
|
|
| . | ||||
| −7−16 |
| |||||||
| 1.23. |
| . | ||||||
| − | 41 | − | 315 | |||||
|
| 6 |
| 46 | |||||
|
|
|
|
|
|
|
|
| |
| 1.24. |
| 97 |
| 570 | . | |||
| −15 | −88 | |||||||
|
| . | |||||||
. | 1.25. − |
| 7 | − |
| 66 | |||
|
|
| 61 |
|
| 576 |
| ||
| 1.26. |
| 122 |
|
| 650 | |||
. | − |
| 25 | −133. | |||||
| 1.27. |
| 88 |
|
| 288 | . | ||
| −30 | − |
| 98 | |||||
| 1.28. |
| 97 |
|
| 735 | . | ||
| −14 | −106 | |||||||
| 1.29. |
| 95 |
|
| 204 | . | ||
| −48 | −103 | |||||||
| 1.30. | 76 |
| 666 | . | ||||
| − | 8 | − | 70 | |||||
|
|
|
|
|
|
| |||
7
2. ЧИСЛО И ВЕКТОРФРОБЕНИУСА
Найдите число Фробениуса и вектор Фробениуса матрицы A. При каких значенияхα матрицаαA продуктивна?
2.1. A = |
| 7 | 9 4 |
|
|
| 2.11. A = | 7 | 12 9 |
| 2.21. A = | 6 | 3 5 |
|
| |||||||
|
| 1 | 6 7 |
|
|
|
| 2 | 5 7 |
|
| 4 | 2 6 |
|
| |||||||
10 3 7 |
|
| 14 | 6 7 | 7 12 6 |
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
2.2. A = |
| 8 | 11 7 |
|
| 2.12. A = | 7 | 5 6 |
|
| 2.22. A = | 11 | 8 |
|
| 7 |
| |||||
|
| 2 | 6 8 |
|
|
| 4 | 3 7 |
|
|
| 5 | 6 11 |
| ||||||||
13 | 6 8 |
| 9 12 7 |
| 13 | 15 11 | ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
2.3. A = | 7 5 4 |
|
|
|
| 2.13. A = | 5 7 4 |
|
| 2.23. A = | 4 6 8 |
|
| |||||||||
| 3 4 7 |
|
|
|
|
| 1 4 5 |
|
|
| 3 1 4 |
|
| |||||||||
8 9 7 |
|
|
| 8 3 5 |
| 9 9 4 |
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
2.4. A = |
| 8 | 7 13 |
| 2.14. A = | 10 | 8 12 | 2.24. A = | 6 8 4 |
|
| |||||||||||
|
| 7 | 1 |
| 8 |
|
| 7 | 3 10 |
|
| 1 5 6 |
|
| ||||||||
14 | 21 |
| 8 | 15 | 21 10 | 9 3 6 |
| |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
2.5. A = |
| 4 | 8 10 |
|
| 2.15. A = | 10 | 8 |
| 4 |
| 2.25. A = | 7 | 6 9 |
| |||||||
|
| 3 | 1 |
| 4 |
|
|
| 3 | 7 10 |
|
| 5 | 2 7 |
| |||||||
11 | 9 |
| 4 |
| 11 | 9 10 | 11 | 15 7 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
2.6. A = | 10 | 5 |
| 9 |
| 2.16. A = | 6 | 3 7 |
|
| 2.26. A = | 5 | 7 10 |
| ||||||||
|
| 7 | 3 10 |
|
| 5 | 1 6 |
|
|
| 4 | 1 |
|
| 5 |
| ||||||
12 | 21 10 | 8 15 6 |
| 11 | 12 |
|
| 5 | ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
2.7. A = |
| 9 | 11 6 |
|
| 2.17. A = | 7 | 8 11 |
| 2.27. A = | 3 | 9 8 |
|
| ||||||||
|
| 2 | 7 9 |
|
|
| 5 | 2 |
|
| 7 |
|
| 1 | 2 3 |
|
| |||||
13 | 6 9 |
| 13 15 7 | 10 3 3 |
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
2.8. A = | 7 8 3 |
|
|
|
| 2.18. A = | 11 | 10 13 |
| 2.28. A = | 7 | 4 9 |
| |||||||||
| 1 6 7 |
|
|
|
|
| 7 | 4 11 |
|
| 6 | 1 7 |
| |||||||||
9 3 7 |
|
|
| 17 | 21 11 | 10 | 18 7 | |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
2.9. A = |
| 9 | 11 12 | 2.19. A = | 9 | 4 7 |
| 2.29. A = | 8 | 12 6 |
| |||||||||||
|
| 5 | 4 |
| 9 |
|
| 6 | 3 9 |
|
| 1 | 7 8 |
| ||||||||
16 | 15 |
| 9 | 10 | 18 9 | 13 | 3 8 | |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
2.10. A = | 12 | 9 11 |
| 2.20. A = | 7 | 5 8 |
| 2.30. A = | 10 | 9 |
|
| 7 |
| ||||||||
|
|
| 7 | 5 12 |
|
| 5 | 2 7 |
|
|
| 4 | 6 10 |
| ||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
| 16 21 12 |
|
| 10 | 15 7 |
|
| 13 | 12 10 |
| ||||||||||||
8
3. МОДЕЛЬЛЕОНТЬЕВА
Рассматривается двухотраслевая модель экономики. Задана балансовая таблица за прошедший год.
(1) Найдите валовой выпуск каждой отрасли в прошедшем году; запишите
вектор валового выпуска для прошедшего года. d
(2)Найдите матрицу Леонтьева A.
(3)Найдите матрицу полных затрат H.
(4)В следующем году конечное потребление продукции отрасли I увеличится на a %, а отрасли II — уменьшится наb %. Найдите конечное потреб-
ление продукции каждой отрасли в следующем году. Запишите вектор конечного потребления x для следующего года.
(5)Найдите валовой выпуск каждой отрасли в следующем году; запишите
вектор валового выпуска для прошедшего года. d
(6)На сколько процентов изменился валовой выпуск каждой отрасли в следующем году по сравнению с прошедшим?
(7)Известен вектор норм добавленной стоимости v в прошедшем году. Найдите равновесные цены продукции каждой отрасли в прошедшем году. Запишите вектор равновесных ценp.
Отрасли | Произв. потребление | Конечное |
|
|
| |
I |
|
| 2 | b = 30 %, | v = | 6 |
6 | 7 | |||||
производства | отрасль I | отрасль II | потребление | a = 20 %, |
| 4 |
|
|
|
|
|
|
|
II | 4 | 4 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Отрасли | Произв. потребление | Конечное |
|
|
| |
I |
|
| 5 | b = 40 %, | v = | 3 |
5 | 4 | |||||
производства | отрасль I | отрасль II | потребление | a = 20 %, |
| 7 |
|
|
|
|
|
|
|
II | 3 | 3 | 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Отрасли | Произв. потребление | Конечное |
|
|
| |
I |
|
| 1 | b = 70 %, | v = | 7 |
1 | 5 | |||||
производства | отрасль I | отрасль II | потребление | a = 50 %, |
| 1 |
|
|
|
|
|
|
|
II | 6 | 7 | 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Отрасли | Произв. потребление | Конечное |
|
|
| |
I |
|
| 3 | b = 60 %, | v = | 5 |
5 | 7 | |||||
производства | отрасль I | отрасль II | потребление | a = 40 %, |
| 3 |
|
|
|
|
|
|
|
II | 3 | 6 | 4 |
|
|
|
|
|
|
|
|
|
|
studfiles.net
по теме: «Решение и исследование систем линейных алгебраических уравнений»
Определение матрицы, ее размерности, порядка.
Виды матриц.
Действия над матрицами (сложение, умножение на число, транспонирование).
Определение согласованных матриц. Произведение матриц.
Основные свойства действий над матрицами.
Определители 1-го и 2-го порядка.
Определители 3-го порядка, правило треугольников (Саррюса).
Теорема Лапласа о разложении и псевдоразложении определителя.
Свойства определителей (без доказательства).
Определения минора и алгебраического дополнения элемента квадратной матрицы.
Определение решения системы уравнений и записать системы линейных алгебраических уравнений в общем виде.
Теорема Крамера (без доказательства), главный и вспомогательные определители системы л.а.у.
Определения совместности и несовместности, определенности и неопределенности системы уравнений.
Определения главной, расширенной, вырожденной, невырожденной матрицы.
Определение обратной матрицы к заданной. Теорема о существовании обратной матрицы (с доказательством).
Алгоритм нахождения обратной матрицы к заданной.
Запись системы в матричном виде, решение систем линейных алгебраических уравнений методом обратной матрицы.
Элементарные преобразования матриц, теорема об элементарных преобразованиях.
Суть метода Гаусса.
Определение линейной комбинации, линейной зависимости и независимости строк матрицы.
Определение ранга матрицы, его свойства, вычисление. Теорема о ранге матрицы.
Определение n-мерного пространства, базис пространства.
Какие системы называются однородными, неоднородными, равносильными?
Решение однородной системы линейных алгебраических уравнений, свойства решений. Фундаментальная система решений.
Теорема Кронекера – Капелли (с доказательством).
Решение неоднородной системы л.а.у.
Определение базисных и свободных переменных, понятие общего решения системы.
Определение частного и базисного решения системы л.а.у.
Применение метода Крамера для выражения базисных переменных через свободные.
Теорема об общем решении неоднородной системы л.а.у.
СПИСОК ЛИТЕРАТУРЫ.
Александров П.С. Курс аналитической геометрии и линейной алгебры. М., Наука 1979г.
Данко П.Е., Попов А.Г., Кожевникова Т.Я., «Высшая математика в упражнениях и задачах», М., Высшая школа, 1999г.
Долгов Н.М. Высшая математика. – К., Высшая школа, 1998.
Дубовик В.П., Юрик И.И. Высшая математика. - К., Высшая школа. 1993.
Ефимов Н.В. Краткий курс аналитической геометрии. – М., Высшая школа. 1978.
Зайцев И.Л. Высшая математика. – М., Высшая школа. 1991
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. Москва, Наука, 1999.
Лихолетов И.И. Высшая математика, теория вероятностей и математическая статистика. М., Высшая школа, 1976.
Пискунов Н.С., Дифференциальное и интегральное исчисления. Москва, Наука, 1978.
Письменный Д.Т. Конспект лекций по высшей математике. М., Айрис пресс, 2003.
Привалов И.И., Аналитическая геометрия. М., Наука 1966г.
Под редакцией Кремера Г.И. Высшая математика для экономистов. М., Банки и биржи. 1998 г.
Под редакцией Кручковича Г.И. Сборник задач по курсу высшей математики. М., Высшая школа, 1973 г.
Шипачев В.С. Высшая математика. – М., Высшая школа. 1990.
infourok.ru
Контрольные задания
по дисциплине «Линейная алгебра и
аналитическая геометрия» для студентов
направлений (специальностей):
- информатика и вычислительная техника;
- электроэнергетика и электротехника;
- управление в технических системах;
- экономика.
Задание №1.
Решите систему уравнений путем нахождения обратной матрицы.
 1.2.
1.2. 
1.3.  1.4.
1.4.
1.5.  1.6.
1.6.
1.7.  1.8.
1.8.
1.9.  1.10.
1.10.
Задание №2.
Даны векторы  и
и . Показать, что они образуют базис, и выразить вектор
. Показать, что они образуют базис, и выразить вектор через этот базис, решая соответствующую систему уравнений по правилу Крамера.
через этот базис, решая соответствующую систему уравнений по правилу Крамера.
2.1. 
2.2. 
2.3. 
2.4. 
2.5. 
2.6. 
2.7. 
2.8. 
2.9. 
2.10. 
Задание №3.
Решите систему методом Гаусса.
3.1.  3.2.
3.2.
3.3.  3.4.
3.4.
3.5.  3.6.
3.6.
3.7.  3.8.
3.8.
3.9.  3.10
3.10
Задание №4.
Найти собственные векторы и собственные значения линейного оператора, заданного в некотором базисе матрицей А.
4
 .1.
.1. 0 1 0 4.2. 1 -3 3
0 1 0 4.2. 1 -3 3
А= -3 4 0 А= -2 -6 13
-2 1 2 -1 -4 8
4
 .3.
.3. 4 -5 7 4.4. 5 6 3
4 -5 7 4.4. 5 6 3
А= 1 -4 9 А= -1 0 1
-4 0 5 1 2 -1
4
 .5.
.5. 4 -5 2 4.6. 2 -1 2
4 -5 2 4.6. 2 -1 2
А= 5 -7 3 А= 5 -3 3
6 -9 4 -1 0 -2

4 .7.
.7. 7 0 0 4.8. 3 1 0
7 0 0 4.8. 3 1 0
А= 10 -19 10 А= -4 -1 0
12 -24 13 4 -8 -2
4
 .9.
.9. 1 -3 4 4.10. 0 7 4
1 -3 4 4.10. 0 7 4
А= 4 -7 8 А= 0 1 0
6 -7 7 1 13 0
Задание №5.
Даны координаты вершин пирамиды ABCD.
Найти:
а) длину ребра AB;
б) угол между ребрами AB и AD;
в) угол между ребром AD и гранью ABC;
г) площадь грани ABC;
д) объем пирамиды;
е) уравнение прямой AB;
ж) уравнение плоскости ABD;
з) уравнение высоты, опущенной из вершины D на грань ABC.
5.1. A(4,2,5), B(0,7,2), C(0,2,7), D(1,5,0).
5.2. A(4,4,10), B(4,10,2), C(2,8,4), D(9,6,4).
5.3. A(4,6,5), B(6,9,4), C(2,10,10), D(7,5,9).
5.4. A(3,5,4), B(8,7,4), C(5,10,4), D(4,7,8).
5.5. A(10,6,6), B(-2,8,2), C(6,8,9), D(7,10,3).
5.6. A(1,8,2), B(5,2,6), C(5,7,4), D(4,10,9).
5.7. A(6,6,5), B(4,9,5), C(4,6,11), D(6,9,3).
5.8. A(7,2,2), B(5,7,7), C(5,3,1), D(2,3,7).
5.9. A(8,6,4), B(10,5,5), C(5,6,8), D(8,10,7).
5.10. A(7,7,3), B(6,5,8), C(3,5,8), D(8,4,1).
Задание №6.
Выяснить, какую линию задает уравнение второго порядка, приведя квадратичную форму к главным осям. Начертить эту линию в системе координат XОY.
6.1. 
6.2. 
6.3. 
6.4. 
6.5. 
6.6. 
6.7. 
6.8. 
6.9. 
6.10. 
Замечания.
В двойной нумерации, первое число означает номер задания, а второе- номер варианта. Например, 5.6. означает: задание №5 и вариант №6.
Номер варианта определяется последней цифрой в номере студбилета. Ноль соответствует 10-ому варианту
Выполнять в тетради в клетку.
Литература.
Курош А.Г. Курс высшей алгебры. М.: Наука, 2005.
Ильин В.А. Аналитическая геометрия. М.: Наука, 2003.
Проскуряков И.В. Сборник задач по линейной алгебре. М.: Лаборатория базовых знаний,2001.
Клетеник Д.В. Сборник задач по аналитической геометрии. СПб.: Специальная литература, 2003.
Баврин И.И., Матросов В.Л. Общий курс высшей математики. -М.: Просвещение, 2004.
Кожухов С.Ф. Системы линейных алгебраических уравнений. –Сургут, Изд-во СурГУ, 1999.
Кожухов С.Ф. Аналитическая геометрия. Прямая и плоскость. –Сургут, изд-во СурГУ, 2007.
studfiles.net
1. Дан определитель .
.
а) Запишите разложение данного определителя по четвёртому столбцу;
б) вычислите определитель, получив предварительно нули в какой – либо строке или столбце.
2. Решить систему уравнений методом обратной матрицы: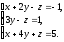
Значение  вычислить также методом Крамера.
вычислить также методом Крамера.
3. Исследовать систему на совместность и решить методом Гаусса
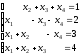
4. Дана система однородных линейных уравнений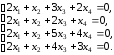
а) Докажите, что система имеет нетривиальные решения;
б) Найдите общее решение системы;
в) найдите фундаментальную систему решений.
5. При каких значениях параметра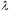 система линейных уравнений
система линейных уравнений
с расширенной матрицей  совместна?
совместна?
I.Даны четыре вектора: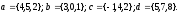
1.Доказать, что векторы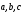 образуют базис и найти разложение вектора
образуют базис и найти разложение вектора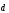 в этом базисе.
в этом базисе.
2. Найти косинус угла между векторами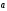 и
и .
.
3.Найти длину вектора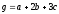 .
.
II.Даны четыре точки: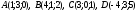 .
.
4.Найти объём пирамиды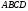 и длину высоты , опущенной из вершины
и длину высоты , опущенной из вершины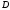 на грань
на грань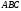 .
.
5.Найти проекцию вектора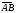 на ось вектора
на ось вектора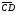 .
.
6.Найти координаты вектора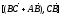 .
.
III.Параллелограмм построен на векторах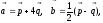 где
где  .
.
Определить: а) косинус тупого угла между диагоналями; б) длину высоты, опущенной на сторон
Контрольная работа по теме «Аналитическая геометрия»
1. Определить при каких значениях а прямая
(а+2)х + (а2 -9)у + 3а2 - 8а + 5 = 0 параллельна оси ОХ.
2. Составить уравнения прямых, параллельных прямой
3х - 4у - 10 = 0 и отстоящих от нее на расстояниеd=3
3. Даны вершины треугольника А(2,6), В(4,-2), С(-2,-6).
Составить уравнение высоты из вершины Аи уравнение медианы из вершиныС.
4. Привести к каноническому виду, назвать и построить
кривые: а) 16х2 + 25у2 + 32х - 100у - 284 = 0;
б) у2 - 4у - 20х + 24 = 0.
5. Из общих уравнений прямой : 2x + y – 3z – 9 = 0,
-2x + 3z + 4 = 0
получить канонические и параметрическое уравнения прямой.
6. Найти проекцию точки А(1,2,0) на плоскость
8x + 6y +8z – 25 = 0.
7. Построить тело, ограниченное поверхностями
х2 = z,
x + y = 2,
y ≥ 0, z ≥ 0.
I. Вычислить пределы
1. 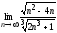 ; 2.
; 2.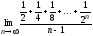 ;
;
3. 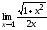 ; 4.
; 4.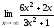 ;
;
5. 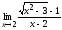 ; 6.
; 6.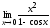 ;
;
7. 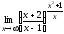 ; 8.
; 8.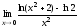 ;
;
9. 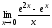 ; 10.
; 10.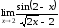 .
.
II. Определить порядок б. м. 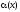 при
при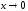 относительноx:
относительноx:
1. 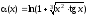 , 2.
, 2.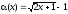 .
.
III. Найти точки разрыва функции, указать их характер. Построить график функции в окрестности точек разрыва:
1. 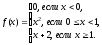 2.
2.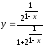 , 3.
, 3.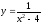 .
.
Контрольная работа
по теме «Дифференциальное исчисление функции одного переменного»
ВАРИАНТ №1
I. Найти производные следующих функций:
1. 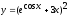 ; 2.
; 2.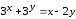 ; 3.
; 3.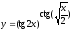 ;
;
II. Найти вторую производную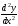 :
:
1. 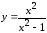 , 2.
, 2.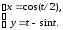 3.
3.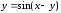
III. . Пользуясь правилом Лопиталя найти пределы:
1. 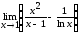 2.
2.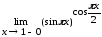
IVПровести полное исследование функции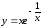 и построить её график
и построить её график
Контрольная работа
по теме «Дифференциальное исчисление ФНП»
ВАРИАНТ №1
I. Найти и построить область определения функции:
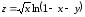 ;
;
Найти указанные производные
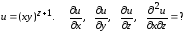
Проверить, удовлетворяет ли функция 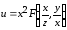 уравнению
уравнению 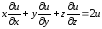 .
.
Составить уравнение нормали к поверхности 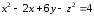 параллельно прямой
параллельно прямой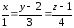 .
.
Найти наибольшее и наименьшее значение функции: 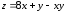 в замкнутой области, ограниченной линиями
в замкнутой области, ограниченной линиями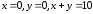 .
.
7.3 Промежуточный контроль.Данный вид контроля производится на основе баллов, полученных студентом при сдаче зачета или экзамена.
Образцы зачетных и экзаменационных материалов
ТПУ Экзамен Курс 1
Вариант 1
Сформулировать и доказать теорему Лагранжа.
Уравнения прямой в пространстве
Найдите пределы: а) 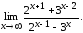 в)
в)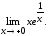
Найдите все частные производные первого порядка функции 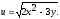
Определите точки перегиба и интервалы выпуклости и вогнутости функции 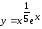 .
.
Дана система линейных уравнений 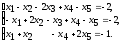 найдите общее решение системы;
найдите общее решение системы;
Составьте уравнение плоскости, которая проходит через точки 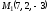 и
и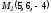 параллельно осиOx.
параллельно осиOx.
Приведите уравнение кривой к каноническому виду и постройте кривую
 .
.
8. Учебно-методическое и информационное обеспечение модуля дисциплины
8.1. Основная литература
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1976, 1980, 1984, …,2000 гг.
Ильин В.А., Позняк Э.Г. Линейная алгебра. М.: Наука, 1974.
Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1980,…,2003гг.
Проскуряков И.В. Сборник задач по линейной алгебре. М.: Физматгиз, 1966,…,1984гг
Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М.: Наука, 1982.
Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 1998.
Пискунов Н.С. Дифференциальное и интегральное исчисление (в 2-х томах) - М. Наука, Математический анализ:1967, 1978, 1985, 1986 гг.
Никольский С.М. Курс математического анализа (в 2-х томах).- М. Наука, 1975, 1983, 1990 гг..
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М. Наука, 1980,1984,1988 гг.
Кудрявцев Л.Д. Курс математического анализа (в 3-х томах).- М. Наука, 1970, 1981, 1988 гг.
Берман Г.Н. Сборник задач по курсу математического анализа. - М. Наука, 1972, 1975, 1977, 1985 гг.
Задачи и упражнения по математическому анализу (Под ред. Демидовича Б.П.) - М. Наука, 1972, 1978, 1990 гг.
studfiles.net
![Контрольная работа №1 и №2 по Линейной алгебре [17.02.15]](/800/600/http/studrb.ru/files/works_screen/2/36/34.png)
Вид работы: Контрольная работа
Тема: Контрольная работа №1 и №2 по Линейной алгебре
Дисциплина: Линейная алгебра
Скачивание: Бесплатно
Дата размещения: 17.02.15 в 12:12
1. Даны матрицы
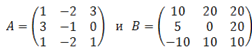
Найти ранг матрицы 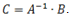
2. По формулам Крамера решить систему:
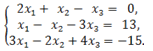
3. Решить систему линейных уравнений:
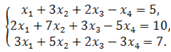
Найти какое-нибудь базисное решение.
4. Найти длину вектора 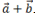 , если
, если 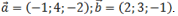
5. Даны четыре вектора:
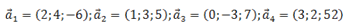
в некотором базисе. Показать, что векторы 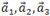 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 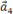 в этом базисе.
в этом базисе.
6. Найти собственные значения и собственные векторы линейного оператора  заданного матрицей
заданного матрицей 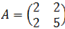
7. а) Методом Лагранжа привести квадратичную форму
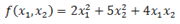
к каноническому виду (указать пример соответствующего преобразования координат).
б) По критерию Сильвестра исследовать на знакоопределенность квадратичную форму
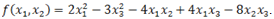
1. Даны уравнения двух сторон прямоугольника
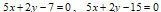
и уравнение его диагонали 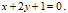
Составить уравнения остальных сторон и второй диагонали этого прямоугольника. Сделать чертеж.
2. Убедившись, что точка 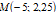 лежит на гиперболе
лежит на гиперболе 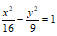 определить длины отрезков
определить длины отрезков 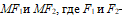 фокусы эллипса.
фокусы эллипса.
3. Центр окружности лежит на прямой x+y=0. Составить уравнение этой окружности, если она проходит через точки пересечения двух окружностей 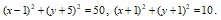
4. Найти расстояние от плоскости 2x+2y-z=15 до начала координат.
5. Найти угол между плоскостью 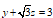 и линией пересечения плоскостей
и линией пересечения плоскостей 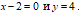
Не подходит Контрольная работа? Вы можете заказать у наших партнеров написание любой учебной работы на любую тему.
Заказать новую работу
+1
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Расскажите другим о работе:
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
studrb.ru