1. Закатилова Ирина Павловна
2.МОУ»Средняя школа №13» г.Кимры Тверской области
3.Учитель математики
Входная контрольная работа в 10 классе.
Вариант 1.
1.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
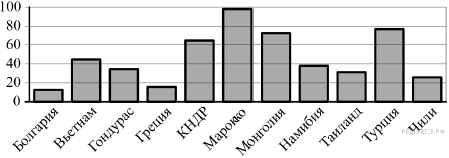
2.На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимала Греция?

3.Решите уравнение 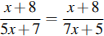 . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
4. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
5.Найдите значение выражения 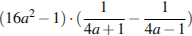
6.Решите на выбор одно из неравенств системы:
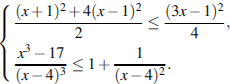
7.Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Решение.
Пусть  км/ч — скорость моторной лодки, тогда скорость лодки по течению равна
км/ч — скорость моторной лодки, тогда скорость лодки по течению равна  км/ч, а скорость лодки против течения равна
км/ч, а скорость лодки против течения равна  км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
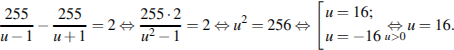
Ответ: 16.
Ответ: 16
Вариант 2
1.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
2.На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах.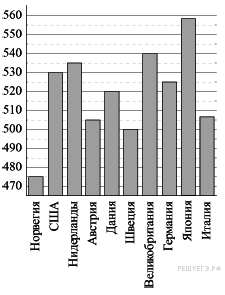
3.Решите уравнение 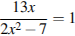 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
4. Решите уравнение 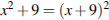
5.Найдите значение выражения 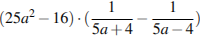
6. Решите на выбор одно из неравенств системы:
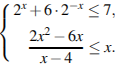
7.Решение.
Область определения уравнения задается соотношением 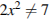 . На области определения имеем:
. На области определения имеем:
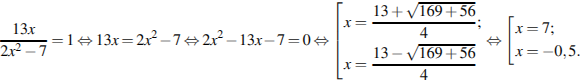
Оба найденный решения удовлетворяют условию 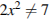 , меньший из них равен −0,5.
, меньший из них равен −0,5.
Ответ: −0,5.
Ответ: -0,5
Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Ответ: 12
Вариант 3.
1.Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
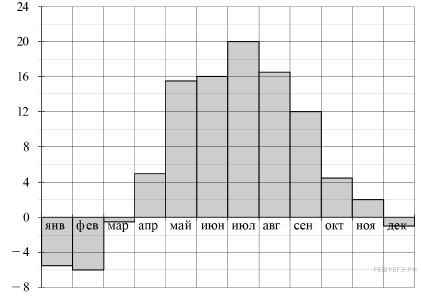
2.На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — средняя температура в градусах Цельсия. Определите по диаграмме наибольшую среднюю температуру в Минске в период с сентября по декабрь 2003 года. Ответ дайте в градусах Цельсия.
3.Найдите корень уравнения:  . Если уравнение имеет более одного корня, в ответе укажите больший из них.
. Если уравнение имеет более одного корня, в ответе укажите больший из них.
4.Решите уравнение 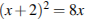
5.Найдите значение выражения 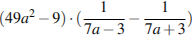
6. Решите на выбор одно из неравенств системы:

7.
Моторная лодка прошла против течения реки 84 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Вариант4 Решение.
Область допустимых значений: 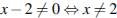 .
.
При 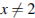 домножим на знаменатель:
домножим на знаменатель:
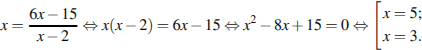
Оба корня лежат в ОДЗ. Больший из них равен 5.
Ответ: 5.
Ответ: 5
Решение.
Из диаграммы видно, что наибольшая среднемесячная температура в период с сентября по декабрь составляла 12 °C (см. рисунок).
Ответ: 12.
Ответ: 12
1.Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
2.На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия.
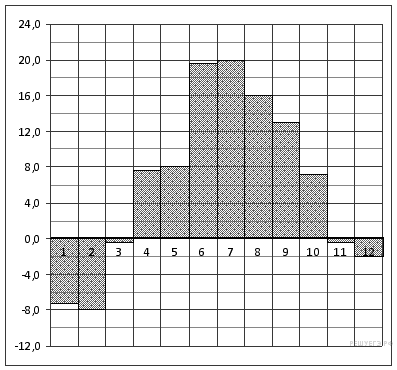
Решение.
Из графика видно, что было 5 месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия (см. рисунок).
Ответ: 5.
Ответ: 5
3. Решите уравнение 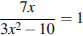 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней
4.Решите уравнение 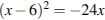 .
.
5. Найдите значение выражения 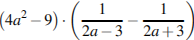
6. Решите на выбор одно из неравенств системы:
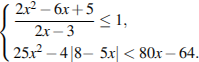
7.
Моторная лодка прошла против течения реки 140 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч. Ответ дайте в км/ч.
Решение.
Решим первое неравенство системы:

Решения:  или
или 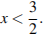
Решим второе неравенство системы:
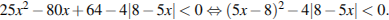
Сделаем замену 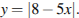 Тогда
Тогда 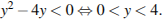
Вернемся к исходной переменной:
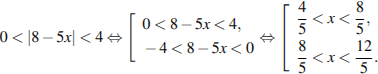
Вернемся к системе:
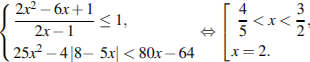
Ответ: 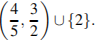
ответы
Решение.
Во время распродажи шампунь станет стоить 160 − 0,25  160 = 120 рублей. Разделим 1000 на 120:
160 = 120 рублей. Разделим 1000 на 120:
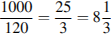 .
.
Значит, можно будет купить 8 флаконов шампуня.
Ответ: 8.
Ответ: 8
1
2
3
4
5
6
7
Вариант1
8
10
1
-7
-2
Решение 1 неравенства
Ответ:3
16
Вариант2
20
7
-0,5
-4
-8
Решение 2 системы
14
Вариант3
6
12
-3
2
6
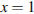 или
или 
4
Вариант4
34
5
-1
-6
6
 или
или 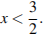
12
doc4web.ru
Входной контроль, 10 класс
1 вариант
Разложите на множители квадратный трехчлен: 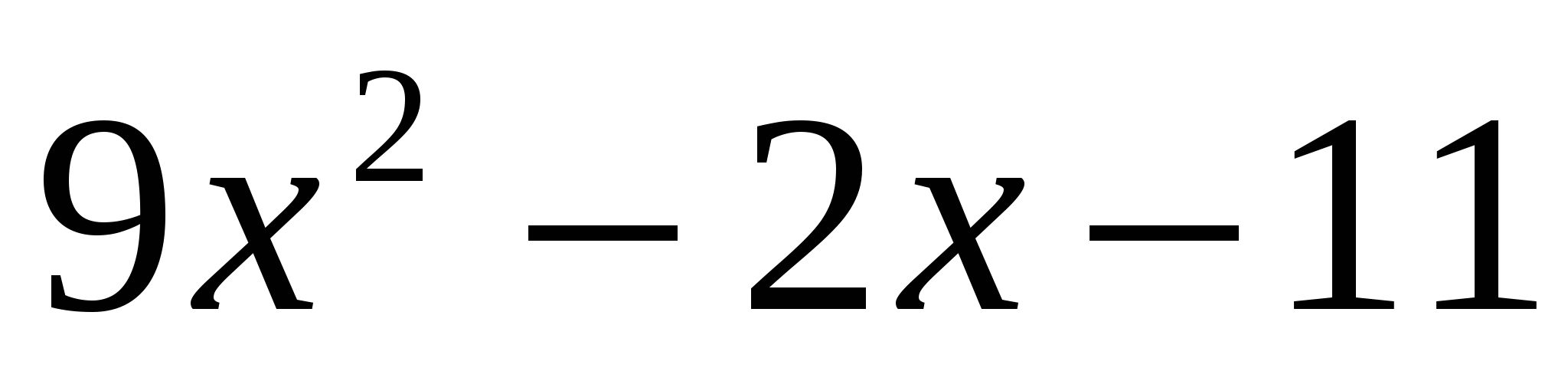 .
.
Постройте график функции 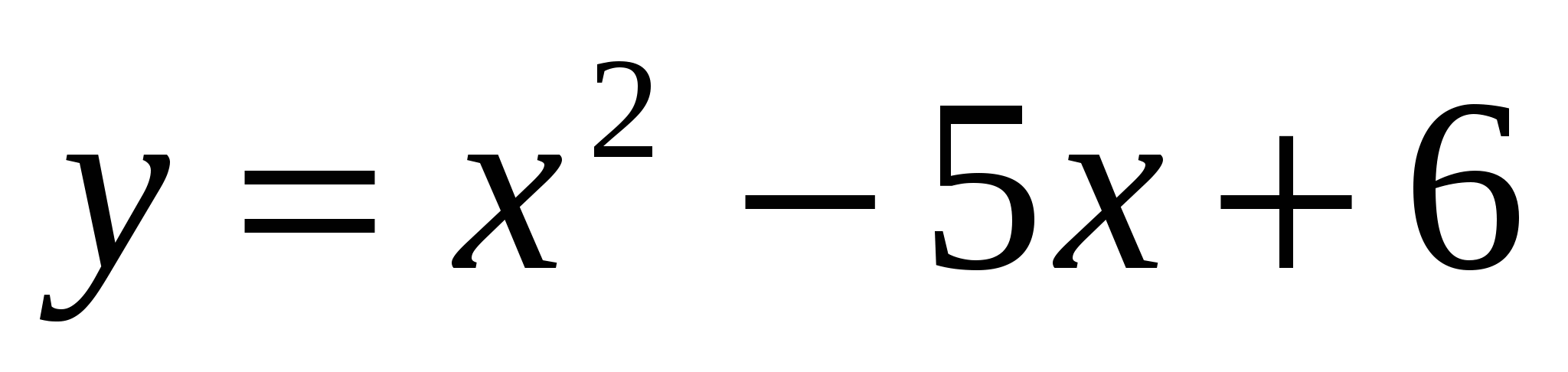 . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному 1,5;
. С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: 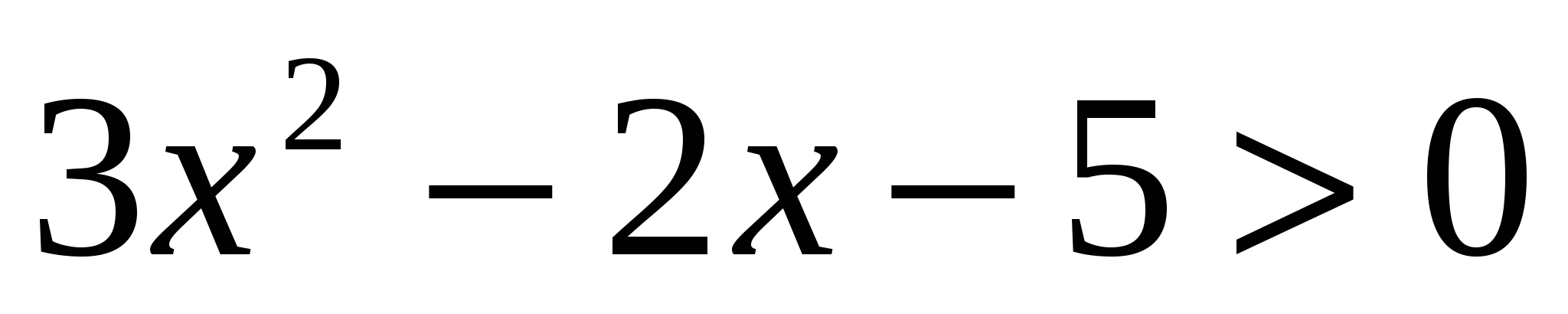 .
.
Решите систему уравнений: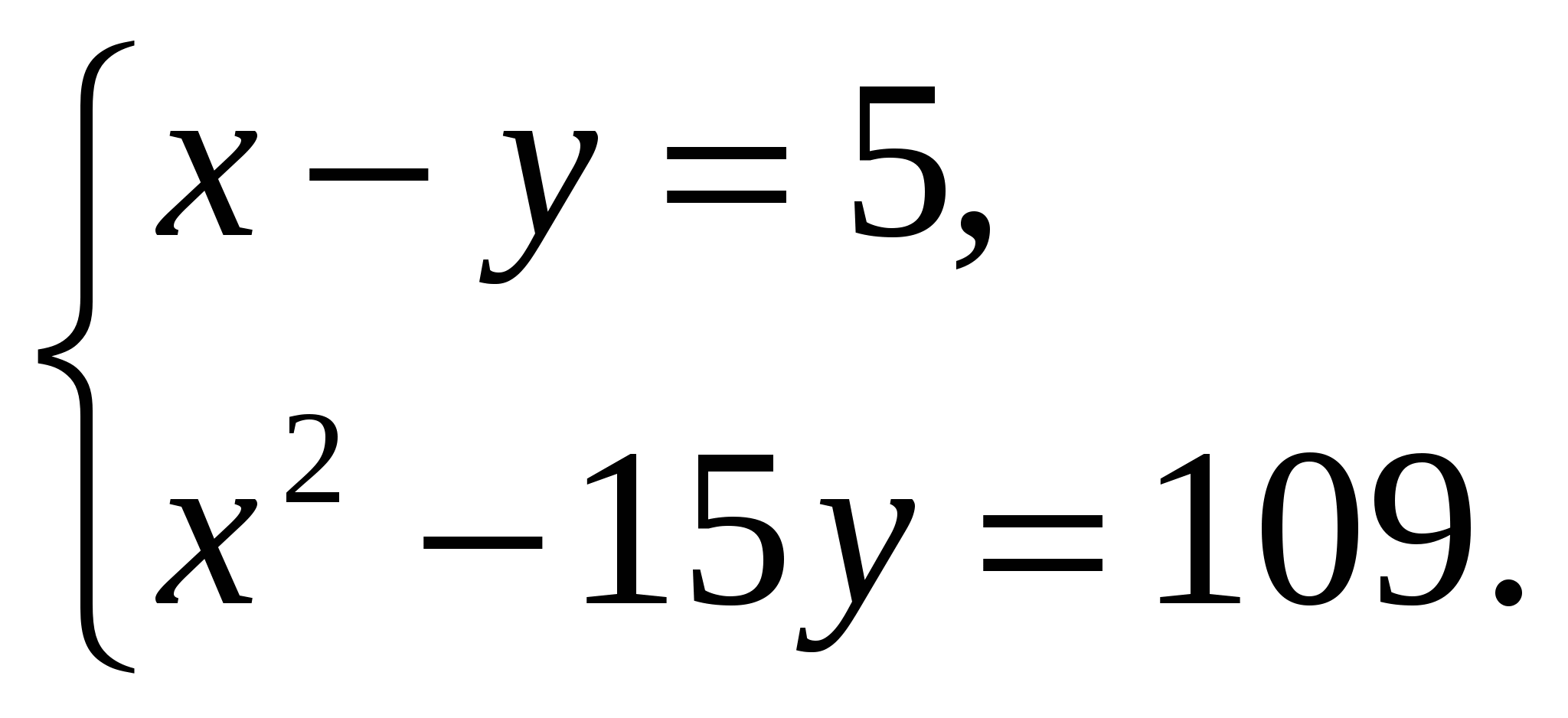
Упростите выражение: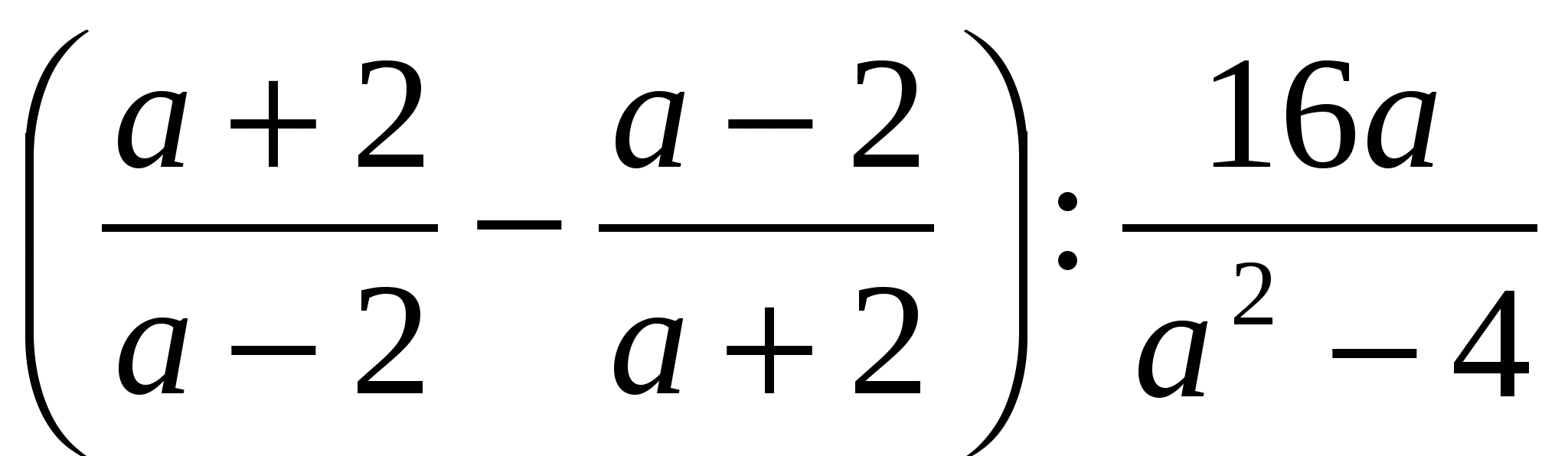 .
.
Решите уравнение:  .
.
Входной контроль, 10 класс
2 вариант
Разложите на множители квадратный трехчлен: 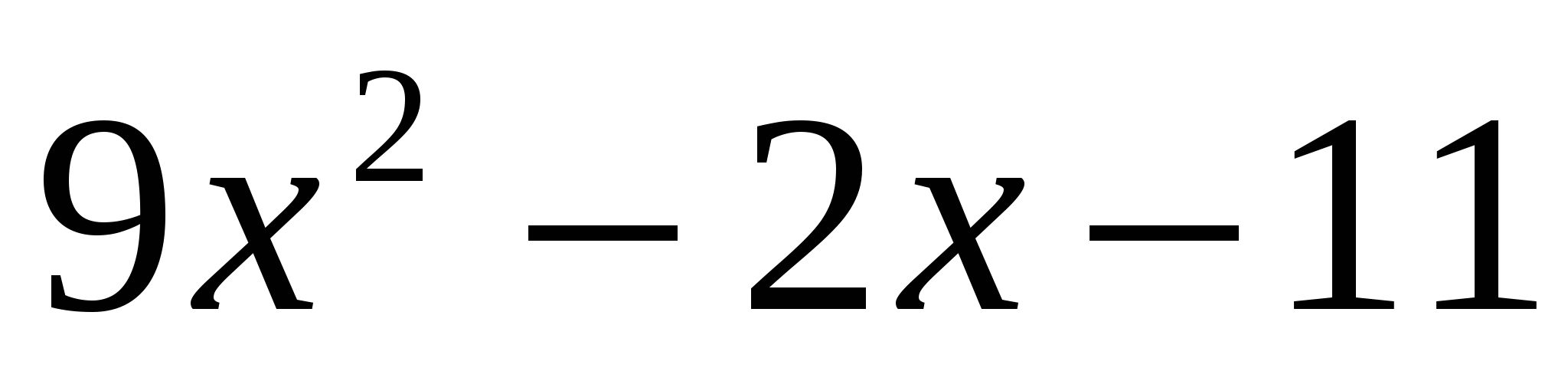 .
.
Постройте график функции  . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному -1,5;
. С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значения аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: 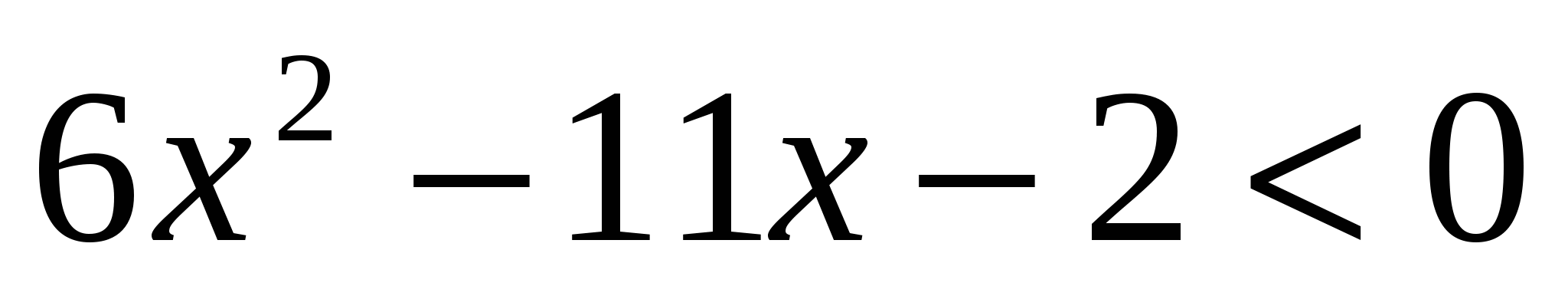 .
.
Решите систему уравнений: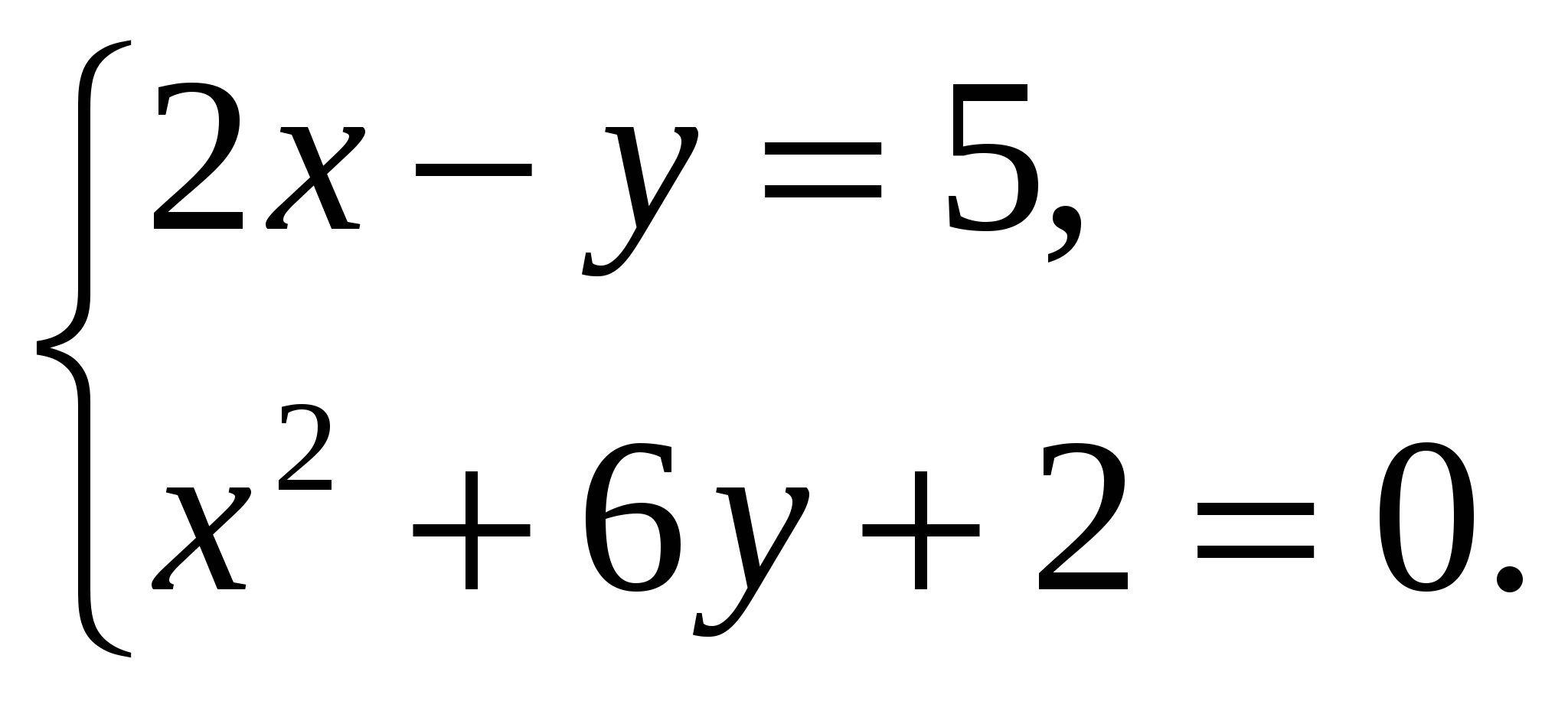
Упростите выражение: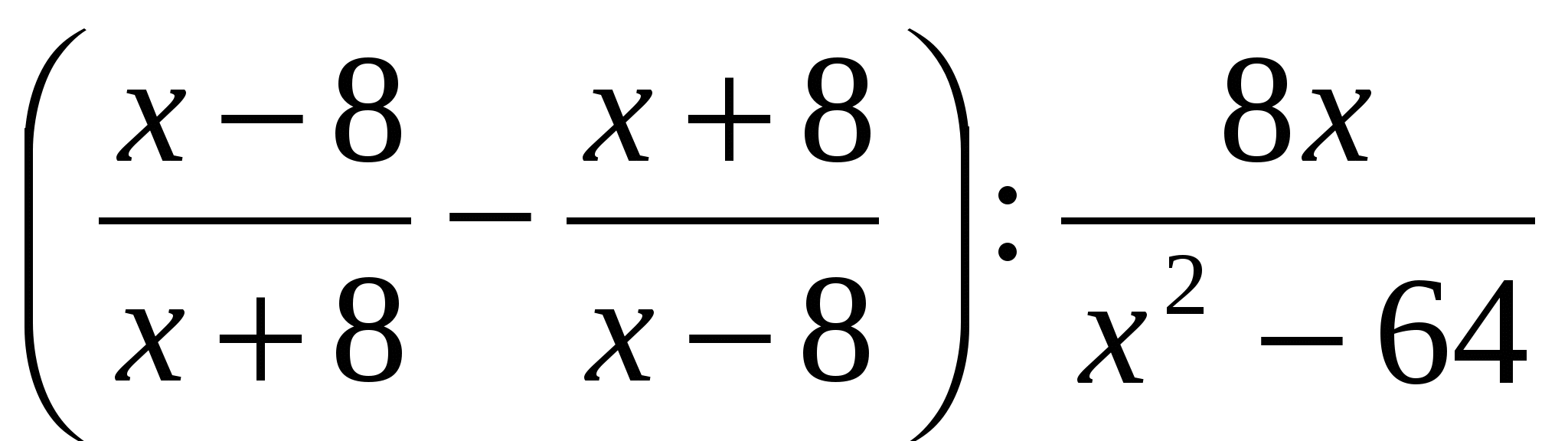 .
.
Решите уравнение: 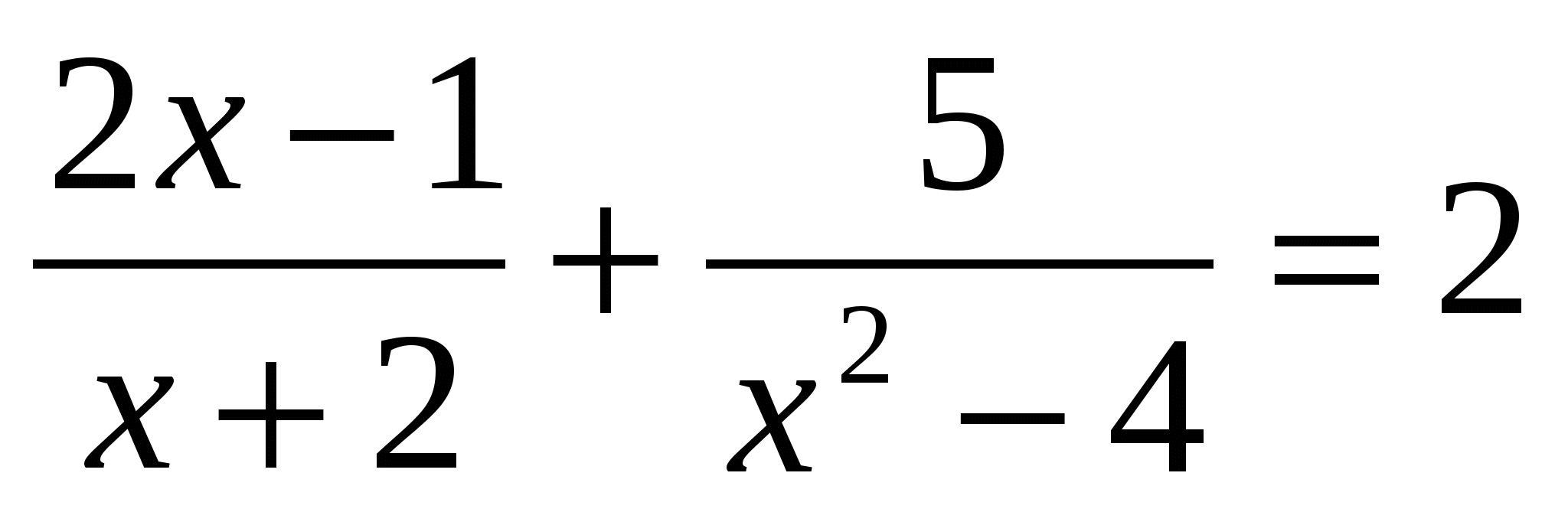 .
.
Входной контроль, 10 класс
вариант
Разложите на множители квадратный трехчлен: 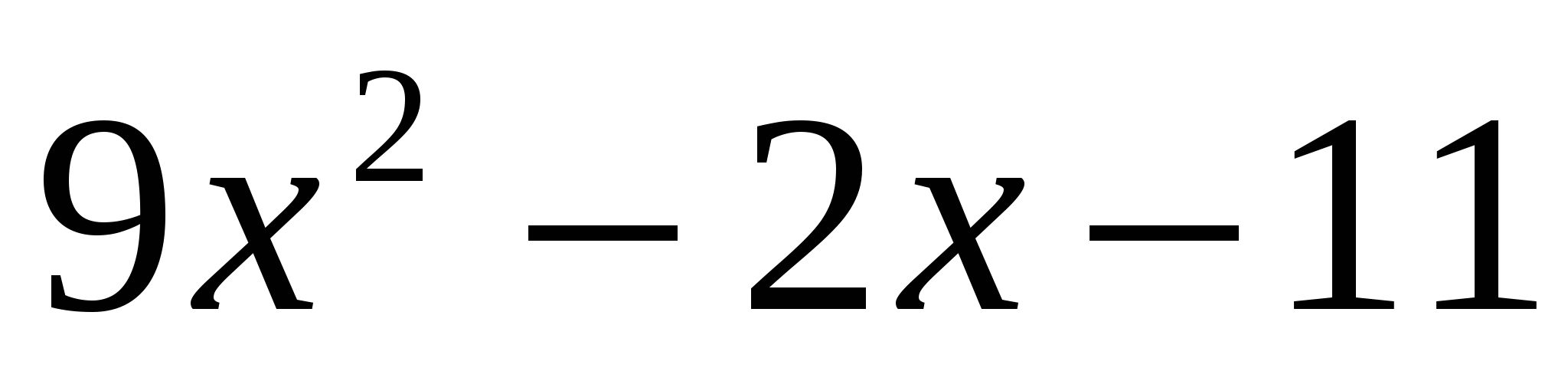 .
.
Постройте график функции 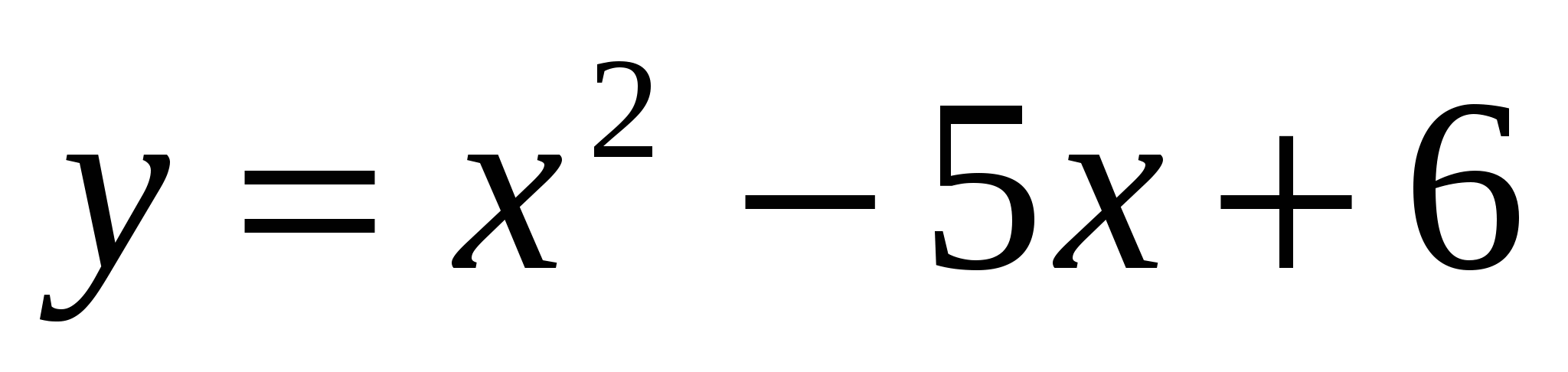 . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному 1,5;
. С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 5;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: 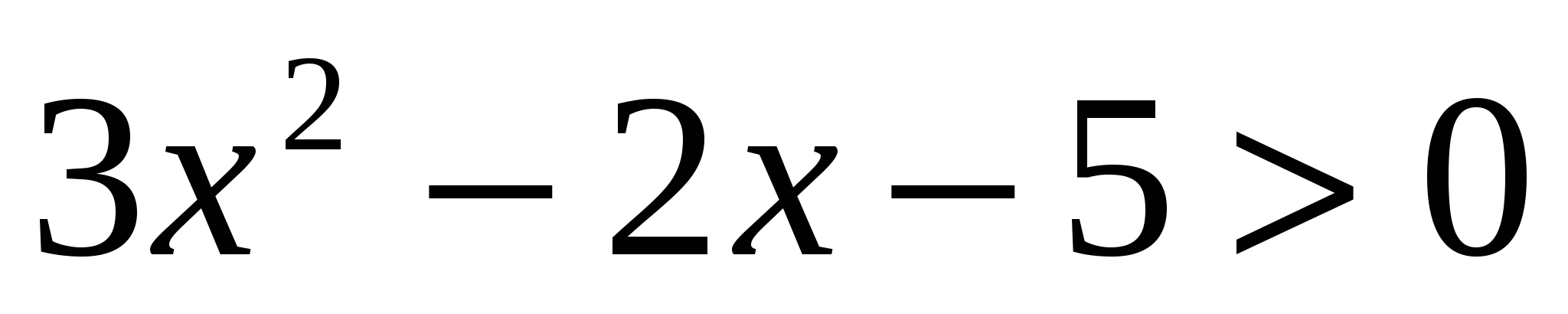 .
.
Решите систему уравнений: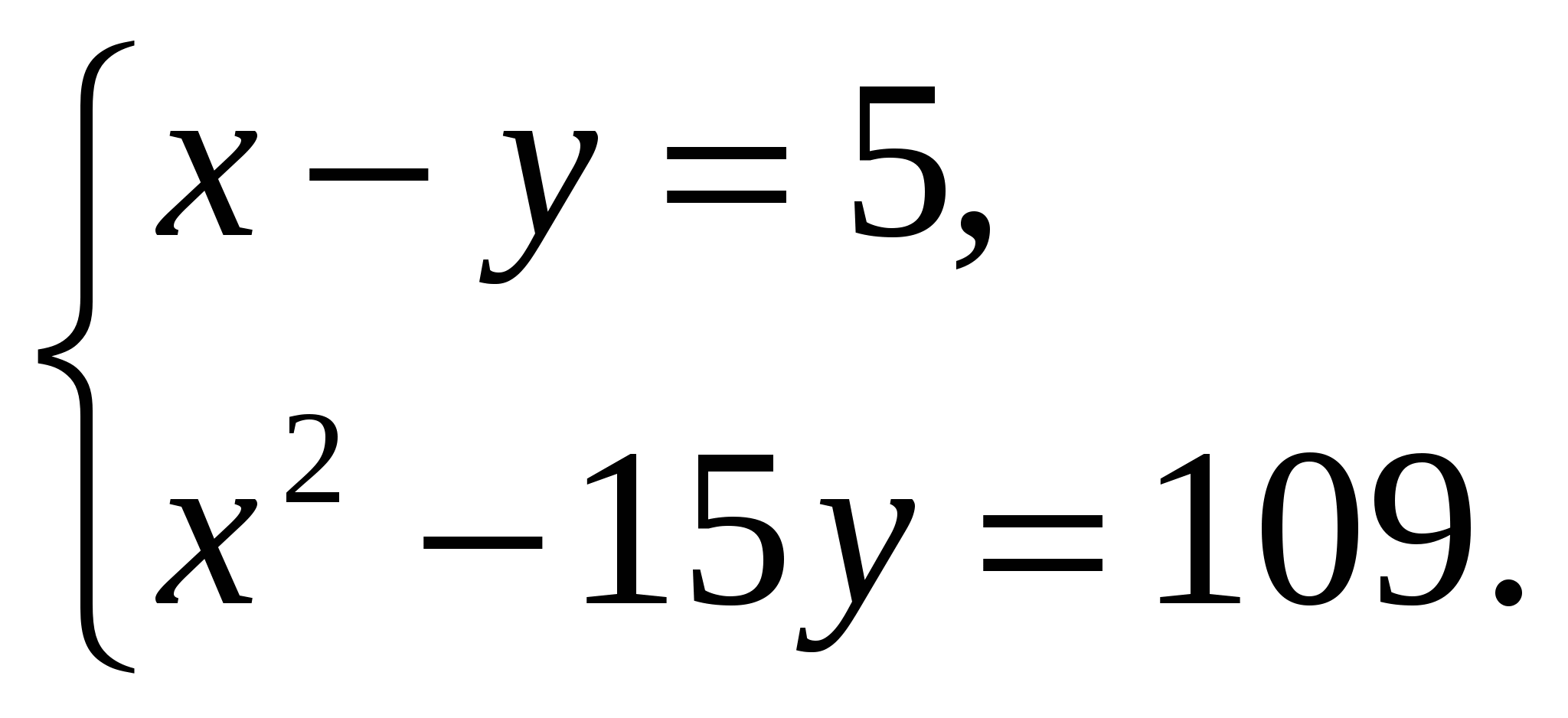
Упростите выражение: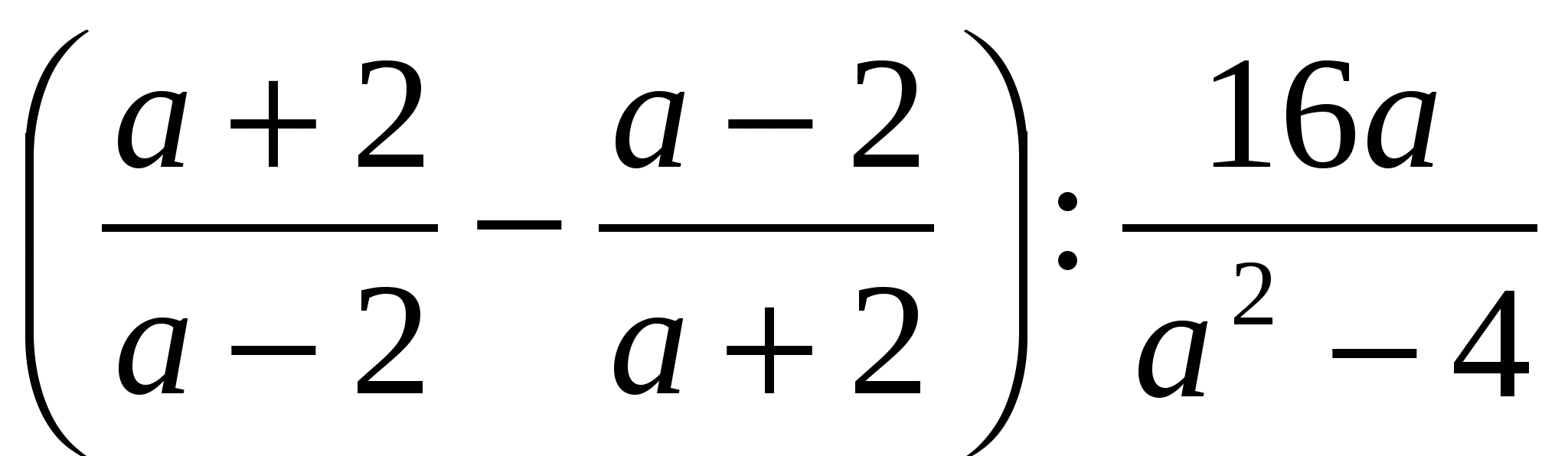 .
.
Решите уравнение:  .
.
Входной контроль, 10 класс
вариант
Разложите на множители квадратный трехчлен: 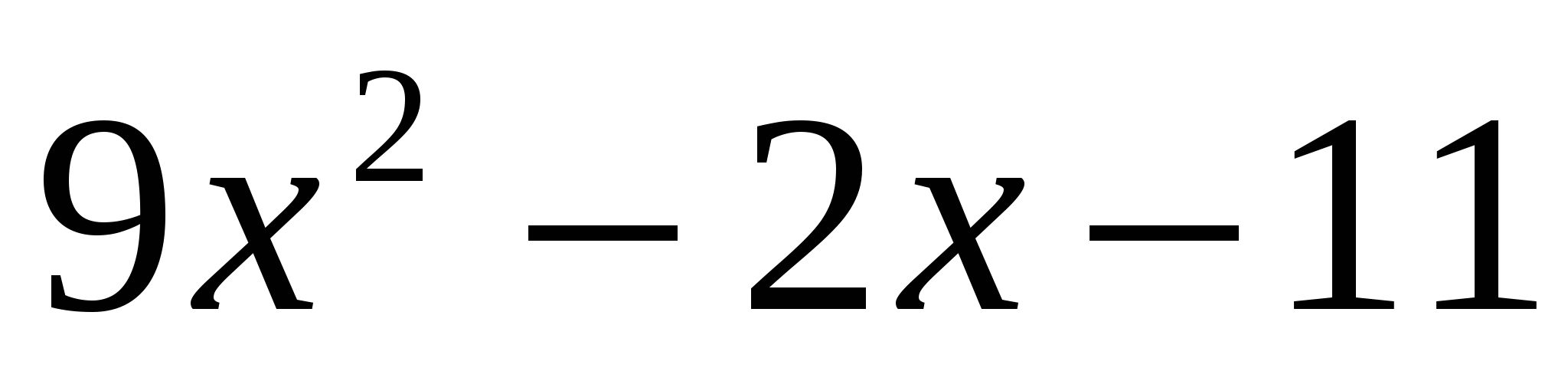 .
.
Постройте график функции  . С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному -1,5;
. С помощью графика функции найдите: а) значение функции, соответствующее значению аргумента, равному -1,5;
б) значения аргумента, при которых значение функции равно 3;
в) промежутки знакопостоянства функции;
г) промежутки возрастания и убывания функции;
д) область значений функции.
Решите неравенство: 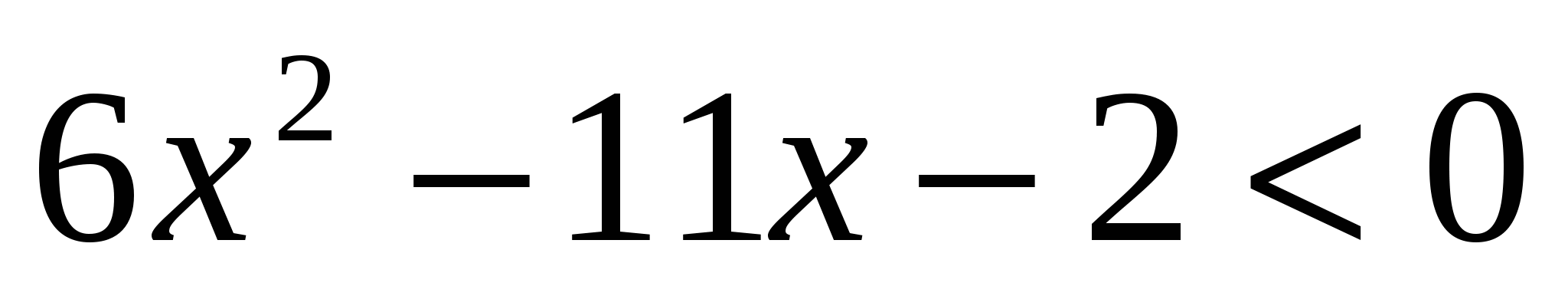 .
.
Решите систему уравнений: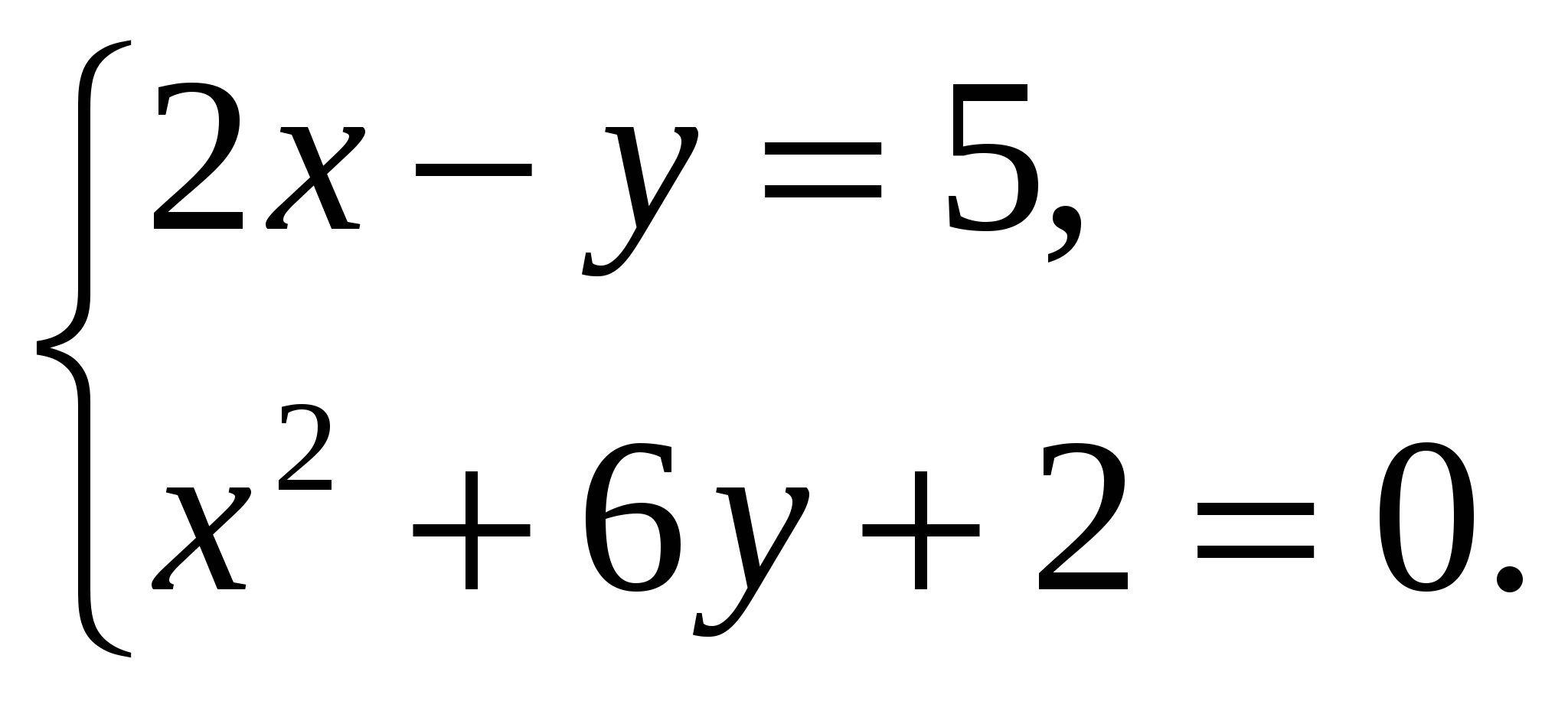
Упростите выражение: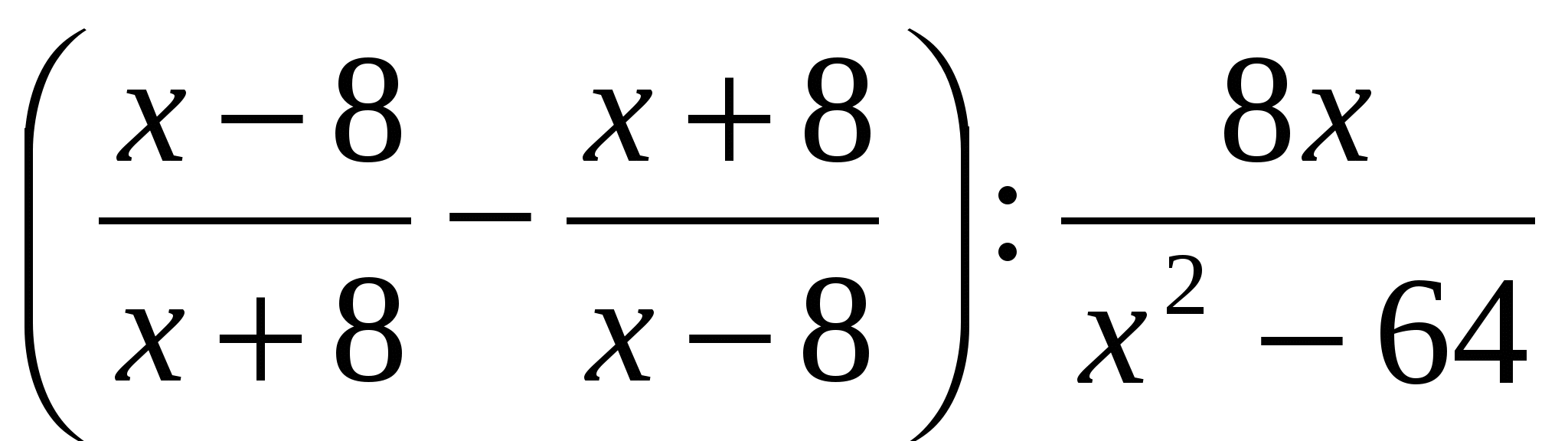 .
.
Решите уравнение: 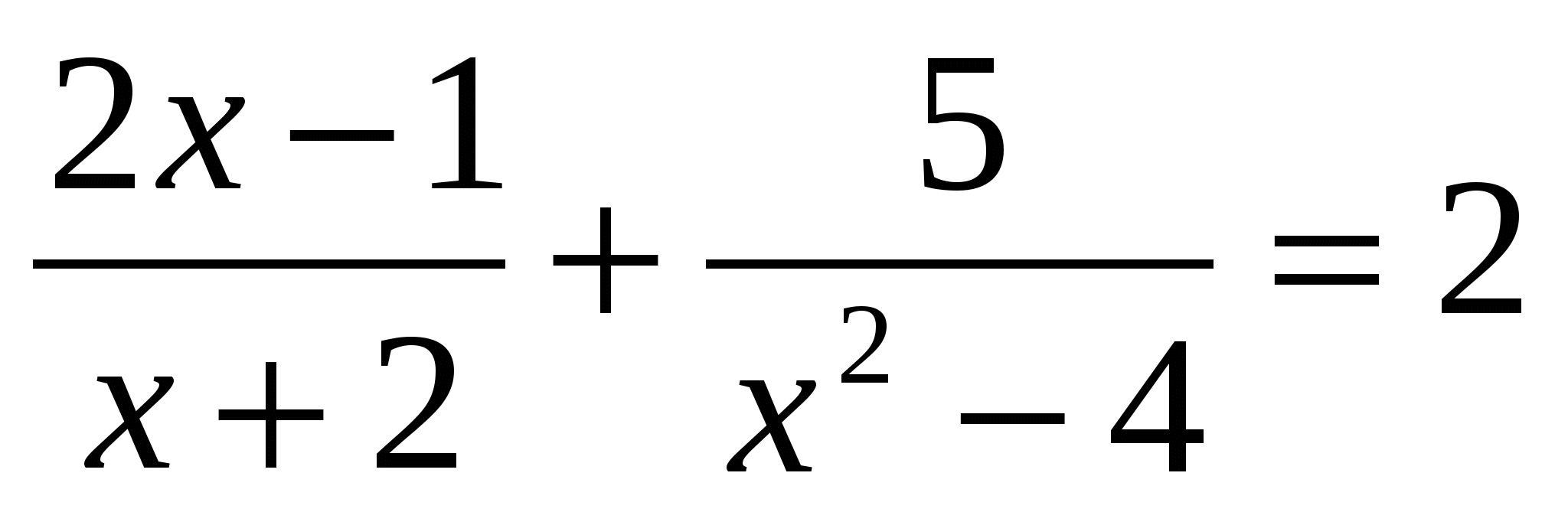 .
.
doc4web.ru
1. Закатилова Ирина Павловна
2.МОУ»Средняя школа №13» г.Кимры Тверской области
3.Учитель математики
Входная контрольная работа в 10 классе.
Вариант 1.
1.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
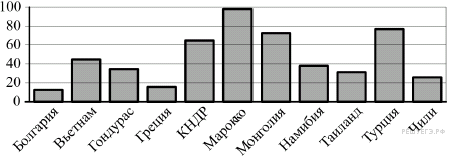
2.На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимала Греция?
3.Решите уравнение 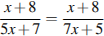 . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
4. Решите уравнение 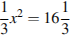 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
5.Найдите значение выражения 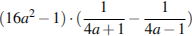
6.Решите на выбор одно из неравенств системы:
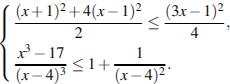
7.Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Решение.
Пусть  км/ч — скорость моторной лодки, тогда скорость лодки по течению равна
км/ч — скорость моторной лодки, тогда скорость лодки по течению равна  км/ч, а скорость лодки против течения равна
км/ч, а скорость лодки против течения равна  км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
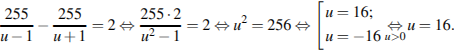
Ответ: 16.
Ответ: 16
Вариант 2
1.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
2.На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах.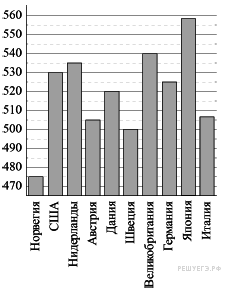
3.Решите уравнение 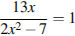 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
4. Решите уравнение 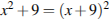
5.Найдите значение выражения 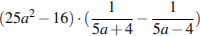
6. Решите на выбор одно из неравенств системы:
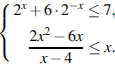
7.Решение.
Область определения уравнения задается соотношением 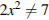 . На области определения имеем:
. На области определения имеем:
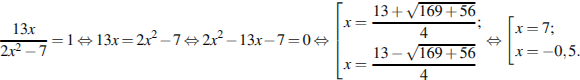
Оба найденный решения удовлетворяют условию 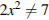 , меньший из них равен −0,5.
, меньший из них равен −0,5.
Ответ: −0,5.
Ответ: -0,5
Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Ответ: 12
Вариант 3.
1.Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
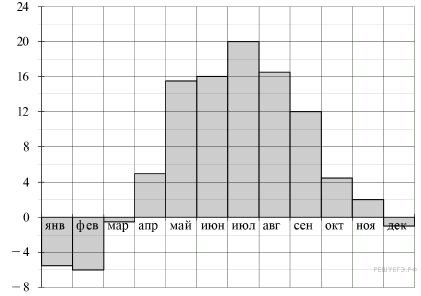
2.На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — средняя температура в градусах Цельсия. Определите по диаграмме наибольшую среднюю температуру в Минске в период с сентября по декабрь 2003 года. Ответ дайте в градусах Цельсия.
3.Найдите корень уравнения: 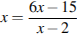 . Если уравнение имеет более одного корня, в ответе укажите больший из них.
. Если уравнение имеет более одного корня, в ответе укажите больший из них.
4.Решите уравнение 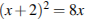
5.Найдите значение выражения 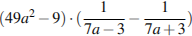
6. Решите на выбор одно из неравенств системы:
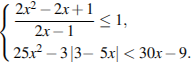
7.
Вариант4 Решение.
Область допустимых значений: 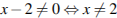 .
.
При 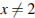 домножим на знаменатель:
домножим на знаменатель:
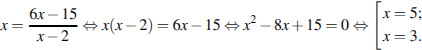
Оба корня лежат в ОДЗ. Больший из них равен 5.
Ответ: 5.
Ответ: 5
Решение.
Из диаграммы видно, что наибольшая среднемесячная температура в период с сентября по декабрь составляла 12 °C (см. рисунок).
Ответ: 12.
Ответ: 12
1.Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
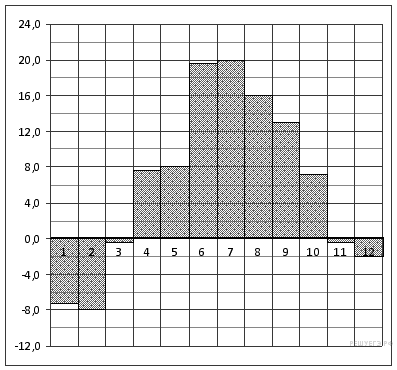
2.На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия.
Решение.
Из графика видно, что было 5 месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия (см. рисунок).
Ответ: 5.
Ответ: 5
3. Решите уравнение 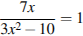 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней
4.Решите уравнение 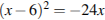 .
.
5. Найдите значение выражения 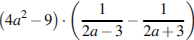
6. Решите на выбор одно из неравенств системы:
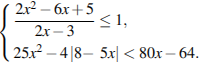
7.
Решение.
Решим первое неравенство системы:
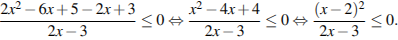
Решения:  или
или 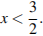
Решим второе неравенство системы:
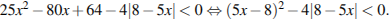
Сделаем замену 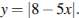 Тогда
Тогда 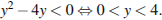
Вернемся к исходной переменной:
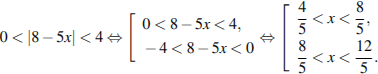
Вернемся к системе:
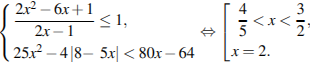
Ответ: 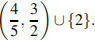
ответы
Решение.
Во время распродажи шампунь станет стоить 160 − 0,25  160 = 120 рублей. Разделим 1000 на 120:
160 = 120 рублей. Разделим 1000 на 120:
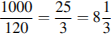 .
.
Значит, можно будет купить 8 флаконов шампуня.
Ответ: 8.
Ответ: 8
Решение 1 неравенстваОтвет:3
16
Вариант2
20
7
-0,5
-4
-8
Решение 2 системы
14
Вариант3
6
12
-3
2
6
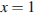 или
или 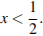
4
Вариант4
34
5
-1
-6
6
 или
или 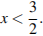
12
infourok.ru
Входная контрольная работа по информатике (10 класс)
Вариант I
Часть А
1. В кодировке КОИ-8 каждый символ кодируется одним байтом. Определите информационный объем сообщения из 20 символов в этой кодировке.
1) 20 бит 2) 80 бит 3) 160 бит 4) 320 бит
2. От разведчика была получена следующая шифрованная радиограмма, переданная с использованием азбуки Морзе:
– • – • – • • – – • – –
При передаче радиограммы было потеряно разбиение на буквы, но известно, что в радиограмме использовались только следующие буквы:
Т А У Ж Х
– • – • • – • • • – • • • •
Определите текст радиограммы. В ответе укажите, сколько букв было в исходной радиограмме.
1) 5 2) 6 3) 7 4) 12
3. Пользователь работал с каталогом Лето. Сначала он поднялся на один уровень вверх, затем спустился на один уровень вниз, потом ещё раз спустился на один уровень вниз. В результате он оказался в каталоге
C:\Фото\Экскурсии\Псков
Запишите полный путь каталога, с которым пользователь начинал работу.
1) C:\Лето
2) C:\Фото\Лето
3) C:\Фото\Тула\Лето
| A | B | C | D | E | |
| A | 3 | 5 | |||
| B | 3 | 1 | 6 | ||
| C | 5 | 1 | 4 | 1 | |
| D | 6 | 4 | 3 | ||
| E | 1 | 3 |
4. Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых приведена в таблице.
Определите длину кратчайшего пути между пунктами A и D (при условии, что передвигаться можно только по построенным дорогам).
1) 6 2) 7 3) 8 4) 9
5. Доступ к файлу karl.htm, находящемуся на сервере april.ru, осуществляется по протоколу http. Фрагменты адреса файла закодированы цифрами от 1 до 7. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.
1) http 2) karl 3) / 4) april 5) .htm 6) .ru 7) ://
6. Для какого из приведённых значений числа X истинно высказывание: НЕ (X ?
1) 5 2) 6 3) 7 4) 8
7. Ниже приведены фрагменты таблиц базы данных победителей городских предметных олимпиад:
|
|
Сколько дипломов I степени получили ученики 10-й школы?
1) 1 2) 2 3) 3 4) 4
Ч асть В
асть В
8. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
9. Сколько байт информации содержит сообщение объёмом
0,625 Кбайт? В ответе укажите одно число.
10. Дан фрагмент электронной таблицы:

Определите значение, записанное в ячейке C2. В ответе укажите одно число — искомое значение.
11. Скорость передачи данных через ADSL-соединение равна 64000 бит/c. Передача файла через это соединение заняла 16 секунд. Определите размер файла в килобайтах.
12. Сколько Кбайт информации содержит сообщение объемом 216бит? В ответе укажите одно число.
13. У исполнителя Конструктор две команды, которым присвоены номера:
1. приписать 2
2. разделить на 2
Первая из них приписывает к числу на экране справа цифру 2, вторая – делит его на 2. Составьте алгоритм получения из числа 14 числа 9, содержащий не более 5 команд. В ответе запишите только номера команд.
(Например, 22212 – это алгоритм:
разделить на 2
разделить на 2
разделить на 2
приписать 2
разделить на 2,
который преобразует число 8 в число 6.)
Если таких алгоритмов более одного, запишите любой из них.
14. В программе «:=» обозначает оператор присваивания, знаки «+», «–», «*» и «/» – соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики.
Определите значение переменной а после выполнения алгоритма:
a := 6
b := 2
b := a/2*b
a := 2*a+3*b
В ответе укажите одно целое число – значение переменной а.
15. Миша записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Мишина мама случайно постирала куртку вместе с запиской. После стирки Миша обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г:
| 17 | .44 | 4.144 | 9.13 |
| А | Б | В | Г |
Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
Входная контрольная работа по информатике (10 класс)
Вариант II
1. В одном из представлений кодировки Unicode на каждый символ отводится
два байта. Определите информационный объем слова из двадцати четырех
символов в этой кодировке.
1) 384 бита 2) 192 бита 3) 256 бит 4) 48 бит
2. От разведчика была получена следующая шифрованная радиограмма,
переданная с использованием азбуки Морзе:

При передаче радиограммы было потеряно разбиение на буквы, но известно,
что в радиограмме использовались только следующие буквы:

Определите текст радиограммы.
1) ГАИГАЧ 2) НАИГАН 3) НАИГАЧ 4) ГАИГАН
3. Пользователь работал с каталогом Логика. Сначала он поднялся на один уровень вверх, затем поднялся ещё на один уровень вверх, потом спустился на один уровень вниз. В результате он оказался в каталоге C:\Школа\Уроки\Химия.Запишите возможный полный путь каталога, с которым пользователь начинал работу.
1) C:\Школа\Уроки\Информатика\Логика
2) C:\Школа\Уроки\Логика
| A | B | C | D | E | F | |
| A | 1 | 5 | 15 | |||
| B | 1 | 2 | ||||
| C | 5 | 2 | 1 | |||
| D | 1 | 2 | 6 | |||
| E | 2 | 1 | ||||
| F | 15 | 6 | 1 |
4) C:\Школа\Информатика\Логика
4. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и F. Передвигаться можно только по дорогам, указанным в таблице.
7 2) 9 3) 11 4) 15
5. Доступ к файлу edu.txt, находящемуся на сервере htm.ru, осуществляется по протоколу http. Фрагменты адреса файла закодированы цифрами от 1 до 2. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.
1) htm 2) :// 3) / 4) http 5) .ru 6) .txt 7) edu
6. Для какого из приведённых значений числа X истинно высказывание: (X ?
1) 9 2) 8 3) 7 4) 6
7. Ниже приведены фрагменты таблиц базы данных победителей городских предметных олимпиад:
|
|
Сколько различных школ имеют победителей олимпиады по физике? Под победителями понимают дипломантов первой степени.
1) 1 2) 2 3) 3 4) 4
Часть В

8. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
9. Сколько байт информации занимает сообщение объемом
0,75 Кбайт. В ответе укажите одно число.
10. Дан фрагмент электронной таблицы:

Определите значение, записанное в ячейке C2. В ответе укажите одно число — искомое значение.
11. Максимальная скорость передачи данных по модемному протоколу V.34 составляет 24000 бит/c. Какое максимальное количество байт можно передать за 4 секунды по этому протоколу?
12. Сколько Мбайт информации содержит сообщение объемом 223 бит? В ответе укажите одно число.
13. У исполнителя Делитель две команды, которым присвоены номера:
1. раздели на 2
2. прибавь 1
Первая из них уменьшает число на экране в 2 раза, вторая увеличивает его на 1. Исполнитель работает только с натуральными числами. Составьте алгоритм получения из числа 23 числа 4, содержащий не более 5 команд. В ответе запишите только номера команд.
(Например, 11222 – это алгоритм:
раздели на 2
раздели на 2
прибавь 1
прибавь 1
прибавь 1,
который преобразует число 36 в 12).
Если таких алгоритмов более одного, то запишите любой из них.
14. В программе «:=» обозначает оператор присваивания, знаки «+», «–», «*» и «/» – соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики.
Определите значение переменной а после выполнения данного алгоритма:
a := 2
b := 5
b := 6+a*b
a := b/4*a
В ответе укажите одно целое число – значение переменной а.
15. Костя записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Костина мама случайно постирала куртку вместе с запиской. После стирки Костя обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г:
| .33 | 3.232 | 3.20 | 23 |
| А | Б | В | Г |
Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
kopilkaurokov.ru
1. Закатилова Ирина Павловна
2.МОУ»Средняя школа №13» г.Кимры Тверской области
3.Учитель математики
Входная контрольная работа в 10 классе.
Вариант 1.
1.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
2.На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимала Греция?

3.Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
4. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
5.Найдите значение выражения 
6.Решите на выбор одно из неравенств системы:

7.Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Решение.
Пусть  км/ч — скорость моторной лодки, тогда скорость лодки по течению равна
км/ч — скорость моторной лодки, тогда скорость лодки по течению равна  км/ч, а скорость лодки против течения равна
км/ч, а скорость лодки против течения равна  км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:

Ответ: 16.
Ответ: 16
Вариант 2
1.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
2.На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по математике в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл ниже, чем в Нидерландах.
3.Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
4. Решите уравнение 
5.Найдите значение выражения 
6. Решите на выбор одно из неравенств системы:

7.Решение.
Область определения уравнения задается соотношением  . На области определения имеем:
. На области определения имеем:

Оба найденный решения удовлетворяют условию  , меньший из них равен −0,5.
, меньший из них равен −0,5.
Ответ: −0,5.
Ответ: -0,5
Вариант 3.
1.Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
2.На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — средняя температура в градусах Цельсия. Определите по диаграмме наибольшую среднюю температуру в Минске в период с сентября по декабрь 2003 года. Ответ дайте в градусах Цельсия.

3.Найдите корень уравнения:  . Если уравнение имеет более одного корня, в ответе укажите больший из них.
. Если уравнение имеет более одного корня, в ответе укажите больший из них.
4.Решите уравнение 
5.Найдите значение выражения 
6. Решите на выбор одно из неравенств системы:

7.
Вариант4 Решение.
Область допустимых значений:  .
.
При  домножим на знаменатель:
домножим на знаменатель:

Оба корня лежат в ОДЗ. Больший из них равен 5.
Ответ: 5.
Ответ: 5
Решение.
Из диаграммы видно, что наибольшая среднемесячная температура в период с сентября по декабрь составляла 12 °C (см. рисунок).
Ответ: 12.
Ответ: 12
1.Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
2.На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия.

Решение.
Из графика видно, что было 5 месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия (см. рисунок).
Ответ: 5.
Ответ: 5
3. Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите меньший из корней
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней
4.Решите уравнение  .
.
5. Найдите значение выражения 
6. Решите на выбор одно из неравенств системы:

7.
Решение.
Решим первое неравенство системы:

Решения:  или
или 
Решим второе неравенство системы:

Сделаем замену  Тогда
Тогда 
Вернемся к исходной переменной:

Вернемся к системе:

Ответ: 
ответы
| Решение. Во время распродажи шампунь станет стоить 160 − 0,25
Значит, можно будет купить 8 флаконов шампуня.
Ответ: 8. Ответ: 8 | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Вариант1 | 8 | 10 | 1 | -7 | -2 | Решение 1 неравенства Ответ:3 | 16 |
| Вариант2 | 20 | 7 | -0,5 | -4 | -8 | Решение 2 системы | 14 |
| Вариант3 | 6 | 12 | -3 | 2 | 6 |
| 4 |
| Вариант4 | 34 | 5 | -1 | -6 | 6 |
| 12 |
globuss24.ru
1. Закатилова Ирина Павловна
2.МОУ»Средняя школа №13» г.Кимры Тверской области
3.Учитель математики
Входная контрольная работа в 10 классе.
Вариант 1.
1.Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
2.На диаграмме показано распределение выплавки цинка (в тысячах тонн) в 11 странах мира за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место - Болгария. Какое место занимала Греция?

3.Решите уравнение  . Если
уравнение имеет более одного корня, в ответе запишите
больший из корней.
. Если
уравнение имеет более одного корня, в ответе запишите
больший из корней.
4. Решите уравнение  . Если
уравнение имеет более одного корня, в ответе запишите
меньший из корней.
. Если
уравнение имеет более одного корня, в ответе запишите
меньший из корней.
5.Найдите значение выражения 
6.Решите на выбор одно из неравенств системы:

7.Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.Решение.
Пусть  км/ч -
скорость моторной лодки, тогда скорость лодки по течению
равна
км/ч -
скорость моторной лодки, тогда скорость лодки по течению
равна  км/ч, а
скорость лодки против течения равна
км/ч, а
скорость лодки против течения равна  км/ч.
На путь по течению лодка затратила на 2 часа меньше, отсюда
имеем:
км/ч.
На путь по течению лодка затратила на 2 часа меньше, отсюда
имеем:

Ответ: 16.
Ответ: 16
Вариант 2
1.Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
2.На диаграмме показан средний балл
участников 10 стран в тестировании учащихся 4-го класса,
по математике в 2007 году (по 1000-балльной шкале). По данным
диаграммы найдите число стран, в которых средний балл ниже,
чем в Нидерландах.
3.Решите уравнение  . Если
уравнение имеет более одного корня, в ответе запишите
меньший из корней.
. Если
уравнение имеет более одного корня, в ответе запишите
меньший из корней.
4. Решите уравнение 
5.Найдите значение выражения 
6. Решите на выбор одно из неравенств системы:

7.Решение.
Область определения уравнения задается
соотношением  . На области
определения имеем:
. На области
определения имеем:

Оба найденный решения удовлетворяют
условию  , меньший из
них равен −0,5.
, меньший из
них равен −0,5.
Ответ: −0,5.
Ответ: -0,5
Моторная лодка прошла против течения реки 143 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Ответ: 12
Вариант 3.
1.Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
2.На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали - средняя температура в градусах Цельсия. Определите по диаграмме наибольшую среднюю температуру в Минске в период с сентября по декабрь 2003 года. Ответ дайте в градусах Цельсия.

3.Найдите корень уравнения:  . Если
уравнение имеет более одного корня, в ответе укажите
больший из них.
. Если
уравнение имеет более одного корня, в ответе укажите
больший из них.
4.Решите уравнение 
5.Найдите значение выражения 
6. Решите на выбор одно из неравенств системы:

7.
Вариант4
Решение.
Область допустимых значений:  .
.
При  домножим на
знаменатель:
домножим на
знаменатель:

Оба корня лежат в ОДЗ. Больший из них равен 5.
Ответ: 5.
Ответ: 5
Решение.
Из диаграммы видно, что наибольшая среднемесячная температура в период с сентября по декабрь составляла 12 °C (см. рисунок).
Ответ: 12.
Ответ: 12
1.Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
2.На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия.

Решение.
Из графика видно, что было 5 месяцев, когда среднемесячная температура не превышала 4 градусов Цельсия (см. рисунок).
Ответ: 5.
Ответ: 5
3. Решите уравнение  . Если
уравнение имеет более одного корня, в ответе запишите
меньший из корней
. Если
уравнение имеет более одного корня, в ответе запишите
меньший из корней
4.Решите уравнение  .
.
5. Найдите значение выражения 
6. Решите на выбор одно из неравенств системы:

7.
Решение.
Решим первое неравенство системы:

Решения:  или
или 
Решим второе неравенство системы:

Сделаем замену  Тогда
Тогда

Вернемся к исходной переменной:

Вернемся к системе:

Ответ: 
ответы
Решение.
Во время распродажи шампунь станет стоить
160 − 0,25  160 = 120
рублей. Разделим 1000 на 120:
160 = 120
рублей. Разделим 1000 на 120:
 .
.
Значит, можно будет купить 8 флаконов шампуня.
Ответ: 8.
Ответ: 8
Решение 1 неравенства
Ответ:3
16
Вариант2
20
7
-0,5
-4
-8
Решение 2 системы
14
Вариант3
6
12
-3
2
6
 или
или 
4
Вариант4
34
5
-1
-6
6
 или
или 
12
botana.cc
Входная контрольная работа по русскому языку в 10 классе
Диктант с грамматическим заданием
1) Наступила тишина, слышно было только, как фыркали и жевали лошади да похрапывали спящие. 2) Где-то плакал чибис и изредка раздавался писк бекасов, прилетавших поглядеть, не уехали ли непрошеные гости.
3) Егорушка, задыхаясь от зноя, который особенно чувствовался после еды, побежал к осоке и отсюда оглядел местность. 4) Увидел он то же самое, что видел и до полудня: равнину, холмы, небо, лиловую даль. 5) Только холмы стояли поближе, да не было мельницы, которая осталась далеко позади. 6) От нечего делать Егорушка поймал в траве скрипача, поднёс его в кулаке к уху и долго слушал, как тот играл на своей скрипке. 7) Когда надоела музыка, он погнался за толпой жёлтых бабочек, прилетавших к осоке на водопой, и сам не заметил, как очутился опять возле брички.
8) Неожиданно послышалось тихое пение. 9) Песня, тихая, тягучая и заунывная, похожая на плач и едва уловимая слухом, слышалась то справа, то слева, то сверху, то из-под земли, точно над степью носился невидимый дух и пел. 10) Егорушка оглядывался по сторонам и не понимал, откуда эта странная песня. 11) Потом уже, когда он прислушался, ему стало казаться, что пела трава. 12) В своей песне она, полумёртвая, уже погибшая, без слов, но жалобно и искренне убеждала кого-то, что она ни в чём не виновата, что солнце выжигало её понапрасну; она уверяла, что ей страстно хочется жить, что она ещё молода и была бы красивой, если бы не зной и не засуха. 13) Вины не было, но она всё-таки просила у кого-то прощения и клялась, что ей невыносимо больно, грустно и жалко себя.
(По А.П.Чехову) (241 слово)
Грамматическое задание
1 вариант
Из предложений 1-3 выпишите слова, правописание приставки в которых зависит от последующего согласного.
Из предложений 3-7 выпишите слово с чередующейся гласной в корне, правописание которого является исключением из правила.
Из предложений 8-10 выпишите слово, в котором правописание Н или НН определяется правилом: «В наречии пишется столько Н, сколько и в слове, от которого оно образовано».
Из предложений 8-12 выпишите действительное причастие прошедшего времени.
Из предложения 13 выпишите союзы.
Среди предложений 1-5 найдите сложное предложение, одна из частей которого осложнена обособленным распространенным определением. Напишите номер этого предложения.
Среди предложений 8-10 найдите сложноподчиненное с придаточным изъяснительным. Напишите номер этого предложения.
Среди предложений 1-4 найдите сложное предложение с разными видами связи (бессоюзной и подчинительной). Напишите номер этого предложения.
2 вариант
Из предложений 8-11 выпишите слово, в котором правописание приставки зависит от ее значения – «неполнота действия».
Из предложений 8-12 выпишите слово с чередующейся гласной в корне.
Из предложений 1-5 выпишите слово, в котором правописание Н или НН определяется правилом: «В суффиксах отглагольных прилагательных пишется Н».
Из предложений 3-7 выпишите действительное причастие прошедшего времени.
Из предложения 12 выпишите неопределенное местоимение.
Среди предложений 1-5 найдите сложное предложение. Одна из частей которого осложнена обособленным обстоятельством. Напишите номер этого предложения.
Среди предложений 1-4 найдите сложноподчиненное с придаточным определительным. Напишите номер этого предложения.
Среди предложений 4-7 найдите сложноподчиненное с параллельным подчинением придаточных. Напишите номер этого предложения.
infourok.ru