«Омский летно-технический колледж гражданской авиации имени А.В. Ляпидевского» филиал Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Ульяновское высшее авиационное училище гражданской авиации (институт)»
(ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И))
КРАТКИЙ КУРС ЛЕКЦИЙ И
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине
«Математика»
Теория пределов
Омск - 2015
Рассмотрено
на заседании ЦМК ЕНДот «_____»__________20__г.
Протокол №_________
Разработал: Пищагина Е.С., преподаватель математики
Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика», тема «Теория пределов»/ Е.С. Пищагина - ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И), 2015. – 27 с.
Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика» предназначены для подготовки специалистов со средним профессиональном образованием. Включает теоретические сведения, примеры решения заданий, примерные варианты контрольных заданий. Типовые задачи даются с подробным решением. Рекомендуется я самостоятельной проработки. Основное назначение – помочь курсанту самостоятельно, без помощи педагога закрепить знания по теме «Теория пределов» и подготовиться к контрольной работе.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Краткий курс лекций и методические рекомендации по выполнению контрольной работы по естественно - научной дисциплине «Математика» предназначены для курсантов 1-го курса специальностей:
25.02.01 Техническая эксплуатация летательных аппаратов и двигателей;
25.02.03 Техническая эксплуатация электрифицированных и пилотажно-навигационных комплексов;
25.02.04 Летная эксплуатация летательных аппаратов.
Содержание раздела курса математики «Теория пределов» определяется федеральным государственным образовательным стандартом среднего профессионального образования (ФГОС СПО).
Пособие объединяет лекционный материал и примеры решения типовых задач, и может быть использовано для изучения и закрепления учебного материала.
Теория пределов.
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Итак, что же такое предел?
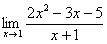
Любой предел состоит из трех частей:
1) Всем известного значка предела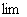 
.
2) Записи под значком предела, в данном случае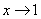 
. Запись читается «икс стремится к единице». Чаще всего – именно 
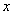, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (
).
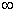3) Функции под знаком предела, в данном случае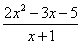 
.
Сама запись 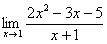читается так: «предел функции 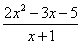при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала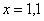 
, затем 
, 
, …, 
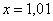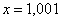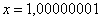, …. То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
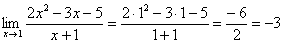
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
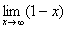
Разбираемся, что такое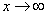 
? Это тот случай, когда 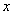неограниченно возрастает, то есть: сначала 
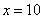, потом 
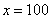, потом 
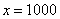, затем 
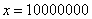и так далее до бесконечности.
А что в это время происходит с функцией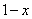 
? 
, 
, 
, …
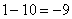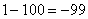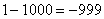Итак: если 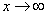, то функция 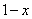стремится к минус бесконечности:
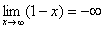
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию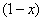 
бесконечность и получаем ответ.
Еще один пример с бесконечностью:
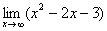
Опять начинаем увеличивать 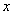до бесконечности, и смотрим на поведение функции: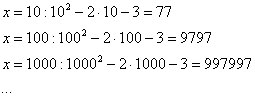
Вывод: при 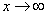функция 
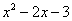неограниченно возрастает: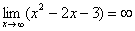
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
, 
, 
, 
, 
, 
, 
, 
, 
, 
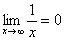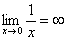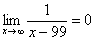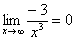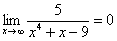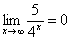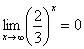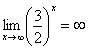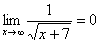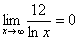Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если 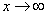, попробуйте построить последовательность 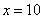, , 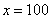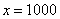. Если 
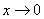, то 
, 
, 
.
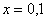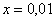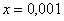Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: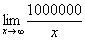 
, то все равно 
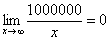, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как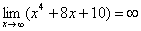 
, 
, 
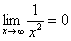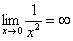и т.д.
Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!
На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.
Пределы с неопределенностью вида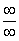 
и метод их решения
Сейчас мы рассмотрим группу пределов, когда 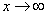, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример:
Вычислить предел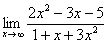 
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 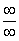. Можно было бы подумать, что 
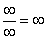, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим 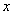в старшей степени:
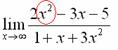Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим 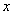в старшей степени:
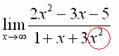Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 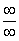необходимо разделить числитель и знаменатель на 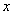в старшей степени.
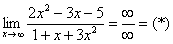Разделим числитель и знаменатель на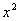 
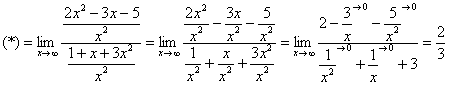
Вот оно как, ответ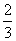 
, а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак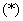 
, он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: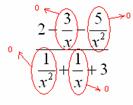
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 2
Найти предел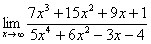 
Снова в числителе и знаменателе находим 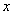в старшей степени:
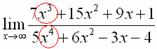Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.Согласно нашему алгоритму, для раскрытия неопределенности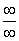 
делим числитель и знаменатель на 
.
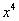Полное оформление задания может выглядеть так:
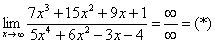
Разделим числитель и знаменатель на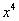
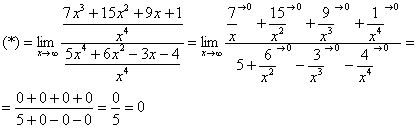
Пример 3
Найти предел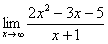 
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 (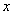 можно записать как 
)
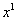Для раскрытия неопределенности 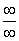необходимо разделить числитель и знаменатель на 
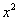. Чистовой вариант решения может выглядеть так:
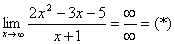
Разделим числитель и знаменатель на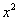
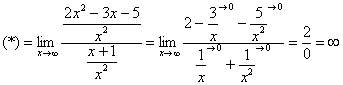
Под записью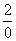 
подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида 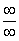у нас может получиться конечное число, ноль или бесконечность.
Пределы с неопределенностью вида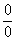 
и метод их решения
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с материалом о бесконечно малых функциях.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 4
Решить предел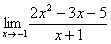 
Сначала попробуем подставить -1 в дробь:
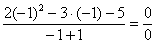В данном случае получена так называемая неопределенность 
.
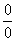Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 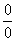, то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, то ознакомьтесь с методическим материалом «Горячие формулы школьного курса математики». Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
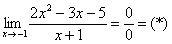
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
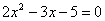Сначала находим дискриминант:
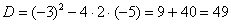И квадратный корень из него: 
.
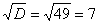В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни:
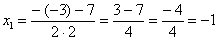
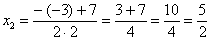
Таким образом:
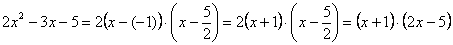
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель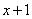 
уже является простейшим множителем, и упростить его никак нельзя.
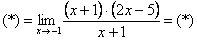
Очевидно, что можно сократить на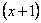 
:
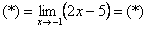
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
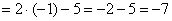
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
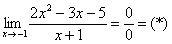
Разложим числитель на множители.
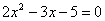
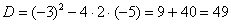
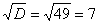
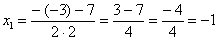
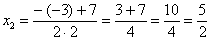
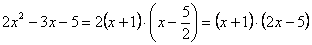
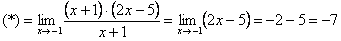
Пример 5
Вычислить предел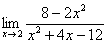 
Сначала «чистовой» вариант решения
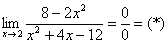
Разложим числитель и знаменатель на множители.
Числитель: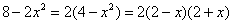 
Знаменатель: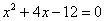
, 
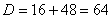
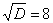
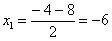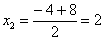
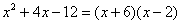
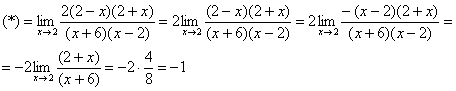
Что важного в данном примере?Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
! Важно
В ходе решения фрагмент типа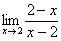 
встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
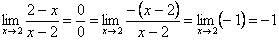, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида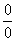
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел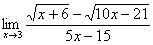 
Начинаем решать.
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
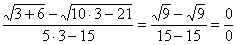
Получена неопределенность вида 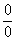, которую нужно устранять.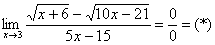
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 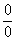используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем нашу нетленную формулу разности квадратов: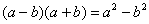 
И смотрим на наш предел: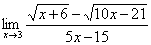 
Что можно сказать?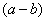 
у нас в числителе уже есть. Теперь для применения формулы осталось организовать 
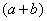(которое и называется сопряженным выражением).
Умножаем числитель на сопряженное выражение:
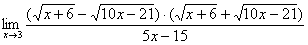
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, 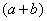мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на :
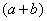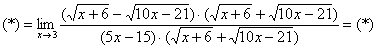
То есть, мы умножили числитель и знаменатель на сопряженное выражение.В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу :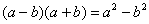
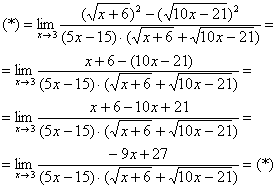
Неопределенность 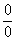не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
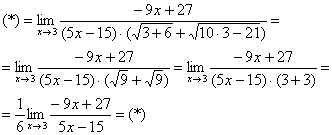
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
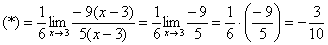
Готово.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
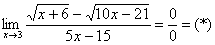
Умножим числитель и знаменатель на сопряженное выражение.
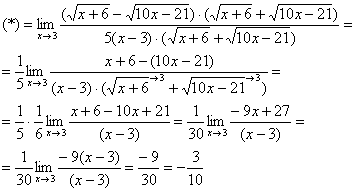
Пример 7
Найти предел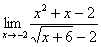 
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
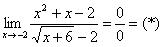
Разложим числитель на множители:
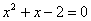
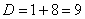
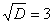
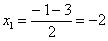
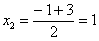
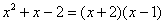
Умножим числитель и знаменатель на сопряженное выражение
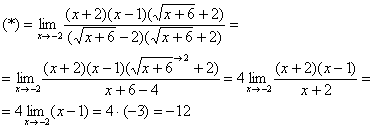
infourok.ru
«Омский летно-технический колледж гражданской авиации имени А.В. Ляпидевского» филиал Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Ульяновское высшее авиационное училище гражданской авиации (институт)»
(ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И))
КРАТКИЙ КУРС ЛЕКЦИЙ И
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине
«Математика»
Теория пределов
Омск - 2015
Рассмотрено
на заседании ЦМК ЕНДот «_____»__________20__г.
Протокол №_________
Разработал: Пищагина Е.С., преподаватель математики
Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика», тема «Теория пределов»/ Е.С. Пищагина - ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И), 2015. – 27 с.
Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика» предназначены для подготовки специалистов со средним профессиональном образованием. Включает теоретические сведения, примеры решения заданий, примерные варианты контрольных заданий. Типовые задачи даются с подробным решением. Рекомендуется я самостоятельной проработки. Основное назначение – помочь курсанту самостоятельно, без помощи педагога закрепить знания по теме «Теория пределов» и подготовиться к контрольной работе.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Краткий курс лекций и методические рекомендации по выполнению контрольной работы по естественно - научной дисциплине «Математика» предназначены для курсантов 1-го курса специальностей:
25.02.01 Техническая эксплуатация летательных аппаратов и двигателей;
25.02.03 Техническая эксплуатация электрифицированных и пилотажно-навигационных комплексов;
25.02.04 Летная эксплуатация летательных аппаратов.
Содержание раздела курса математики «Теория пределов» определяется федеральным государственным образовательным стандартом среднего профессионального образования (ФГОС СПО).
Пособие объединяет лекционный материал и примеры решения типовых задач, и может быть использовано для изучения и закрепления учебного материала.
Теория пределов.
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Итак, что же такое предел?
Любой предел состоит из трех частей:
1) Всем известного значка предела 
.
2) Записи под значком предела, в данном случае 
. Запись читается «икс стремится к единице». Чаще всего – именно 
, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (
).
3) Функции под знаком предела, в данном случае 
.
Сама запись читается так: «предел функции при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 
, затем 
, 
, …, 
, …. То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 
? Это тот случай, когда неограниченно возрастает, то есть: сначала 
, потом 
, потом 
, затем 
и так далее до бесконечности.
А что в это время происходит с функцией 
? 
, 
, 
, …
Итак: если , то функция стремится к минус бесконечности:
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.
Еще один пример с бесконечностью:
Опять начинаем увеличивать до бесконечности, и смотрим на поведение функции:
Вывод: при функция неограниченно возрастает:
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
,
,
,
,
,
,
,
,
,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность , , . Если , то
,
,
.
Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно
, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как ,
,
и т.д.
Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!
На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.
Пределы с неопределенностью вида и метод их решения
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример:
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что
, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на
в старшей степени.
Разделим числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 2
Найти предел Снова в числителе и знаменателе находим в старшей степени:
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на
.
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Пример 3
Найти предел
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
Для раскрытия неопределенности необходимо разделить числитель и знаменатель на
. Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность.
Пределы с неопределенностью вида и метод их решения
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с материалом о бесконечно малых функциях.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 4
Решить предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность
.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, то ознакомьтесь с методическим материалом «Горячие формулы школьного курса математики». Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
И квадратный корень из него: .
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни:
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.
Очевидно, что можно сократить на :
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители.
Пример 5
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель: Знаменатель:,
Что важного в данном примере?Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
! Важно
В ходе решения фрагмент типа встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел
Начинаем решать.
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида , которую нужно устранять.
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем нашу нетленную формулу разности квадратов: И смотрим на наш предел:
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать
(которое и называется сопряженным выражением).
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на
:
То есть, мы умножили числитель и знаменатель на сопряженное выражение.В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу :
Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
Готово.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Пример 7
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители:
Умножим числитель и знаменатель на сопряженное выражение
26
videouroki.net
Министерство образования, науки и молодежной политики
Краснодарского края
ГБПОУ КК «Колледж Ейский»
КРАТКИЙ КУРС ЛЕКЦИЙ И
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине
«Математика»
Теория пределов
Ейск – 2016
| Рассмотрено на заседании ПЦК математических и естественнонаучных дисциплин Протокол №___ от «___»___________2016г. Председатель ПЦК_________ Черных Л.С. | Рассмотрено ОМК ГБПОУ КК «Колледж Ейский» _________Е.Н.Литвинова Протокол №___ от «___»_______2016г. |
Краткий курс лекций и методические указания по выполнению контрольной работы по дисциплине «Математика» предназначены для подготовки специалистов со средним профессиональном образованием. Включает теоретические сведения, примеры решения заданий, примерные варианты контрольных заданий. Типовые задачи даются с подробным решением. Рекомендуется я самостоятельной проработки. Основное назначение – помочь студенту самостоятельно, без помощи педагога закрепить знания по теме «Теория пределов» и подготовиться к контрольной работе.
Разработчик:
ГБПОУ КК «Колледж Ейский» преподаватель Л.С.Черных
(место работы) (занимаемая должность) (инициалы, фамилия)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Краткий курс лекций и методические рекомендации по выполнению контрольной работы по естественно - научной дисциплине «Математика» предназначены для студентов 1-го курса.
Содержание раздела курса математики «Теория пределов» определяется федеральным государственным образовательным стандартом среднего профессионального образования (ФГОС СПО).
Пособие объединяет лекционный материал и примеры решения типовых задач, и может быть использовано для изучения и закрепления учебного материала.
Теория пределов.
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Итак, что же такое предел?
Любой предел состоит из трех частей:
1) Всем известного значка предела 
.
2) Записи под значком предела, в данном случае 
. Запись читается «икс стремится к единице». Чаще всего – именно 
, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (
).
3) Функции под знаком предела, в данном случае 
.
Сама запись читается так: «предел функции при икс стремящемся к единице».
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 
, затем 
, 
, …, 
, …. То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Готово.
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 
? Это тот случай, когда неограниченно возрастает, то есть: сначала 
, потом 
, потом 
, затем 
и так далее до бесконечности.
А что в это время происходит с функцией 
? 
, 
, 
, …
Итак: если , то функция стремится к минус бесконечности:
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию бесконечность и получаем ответ.
Еще один пример с бесконечностью:
Опять начинаем увеличивать до бесконечности, и смотрим на поведение функции:
Вывод: при функция неограниченно возрастает:
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
,
,
,
,
,
,
,
,
,
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность , , . Если , то
,
,
.
Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно
, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как ,
,
и т.д.
Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с очень интересными случаями, когда предела функции вообще не существует!
На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов.
Пределы с неопределенностью вида и метод их решения
Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены
Пример:
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что
, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим в старшей степени:Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим в старшей степени:Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на
в старшей степени.
Разделим числитель и знаменатель на
Вот оно как, ответ , а вовсе не бесконечность.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Пример 2
Найти предел Снова в числителе и знаменателе находим
в старшей степени:Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.Согласно нашему алгоритму, для раскрытия неопределенности делим числитель и знаменатель на
.
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Пример 3
Найти предел
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
Для раскрытия неопределенности необходимо разделить числитель и знаменатель на
. Чистовой вариант решения может выглядеть так:
Разделим числитель и знаменатель на
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.
Таким образом, при раскрытии неопределенности вида у нас может получиться конечное число, ноль или бесконечность.
Пределы с неопределенностью вида и метод их решения
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с материалом о бесконечно малых функциях.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Пример 4
Решить предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность
.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, то ознакомьтесь с методическим материалом «Горячие формулы школьного курса математики». Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
Сначала находим дискриминант:
И квадратный корень из него:
.
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни:
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель уже является простейшим множителем, и упростить его никак нельзя.
Очевидно, что можно сократить на :
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители.
Пример 5
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель: Знаменатель:
,
Что важного в данном примере?Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
! Важно
В ходе решения фрагмент типа встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Пример 6
Найти предел
Начинаем решать.
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида , которую нужно устранять.
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Вспоминаем нашу нетленную формулу разности квадратов: И смотрим на наш предел:
Что можно сказать? у нас в числителе уже есть. Теперь для применения формулы осталось организовать
(которое и называется сопряженным выражением).
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на
:
То есть, мы умножили числитель и знаменатель на сопряженное выражение.В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу :
Неопределенность не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
Готово.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Пример 7
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители:
Умножим числитель и знаменатель на сопряженное выражение
multiurok.ru
Указания по проведению
практической работы № ___1____
Задачи на вычисление пределов
(Название работы)
Специальность __080110, 080112, 080501__
_____________(___................. __)
(Подпись) (ФИО)
«_______» _________________200___г.
Цель работы:
1. Формировать умения и навыки вычисления пределов
2. Формировать умения и навыки самостоятельного умственного труда
3. Прививать умения и навыки работы со справочным материалом
4. Определить уровень остаточных знаний студентов по данной теме
Перечень справочной литературы :
1. Богомолов Н.В. «Практические занятия по математике», М: Высшая школа, 2004
2. Письменный Д. «Конспект лекций по высшей математике», ч.1., Москва, Айрис-Пресс, 2004
3. Шипачев В.С. «Задачник по высшей математике», М: Высшая школа, 2003
4. Выгодский М.Я. «Справочник по высшей математике», Росткнига, 2001
Краткие теоретические сведения:
Предел последовательности
Определение. Число 
называется
пределом последовательности 
, если
для любого положительно 
го
числа найдется такое натуральное число 
,
что при всех 
>
выполняется неравенство
Пишут: 
Графически это выглядит так:
n-
Т.е. элемент 
находится в 
- окрестности точки а. При
этом последовательности 
называется
сходящейся, в противном случае – расходящейся.
Основные свойства сходящихся последовательностей
1)Сходящаяся последовательность ограничена.
2)Пусть 
, 
, тогда а) 
б) 
в) 
3)Если 
и для всех 
выполняется неравенства 
, то 
.
4) Если 
и последовательность {уn} - ограниченная, то 
|
№1. Найти пределы: |
|
|
|
|
Бесконечно большие и бесконечно малые функции
Определение. Функция 
называется
бесконечно малой при 
, если 
Например: 1) 
при 
б. м. ф. т.к. 
2) 
при 
б. м. ф. т. к 
Определение. Функция 
называется
бесконечно большой при , если 
, 
или 
Например, 
есть б. б. Ф при 
; 
если
б. б. ф. при 
действительно 
и 
Теорема (о связи между функций, ее
приделом и бесконечно малой функцией). Если функция имеет придел, равный 
, то ее можно представить
как сумму числа и бесконечно
малой функции 
, т.е. если 
Теорема (обратная). Если функцию можно представить в виде
суммы числа А и б.м.ф. 
(x), то число А является пределом
функции, т.е если 
, то 
Например, требуется
вычислить 
. Представим числитель и
знаменатель в виде суммы числа и б.м.ф. 
Функции 
при есть б.м.ф. таким образом 
Основные теоремы о пределах
Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Теорема справедлива для алгебраической суммы любого конечного числа функций.
Теорема 2. Функция может иметь только один
предел при 
.
Теорема 3. Предел произведения двух функций равен произведению их пределов:
.
Следствие 1. Постоянный множитель можно выносить
за знак предела: 
Следствие 2. Предел степени с натуральным
показателем равен той же степени предела: 
.
Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.
Примеры:
1)
=
= 
=
=
=
=
=
2) 
=
=
3) 
Первый замечательный предел
Второй замечательный предел
или 
Примеры:
Вычислить:
1) 
.
2) 
.
3) 
4) 
=
=
=
№2. Найти пределы: 
№3. Найти пределы:
Порядок проведения работы:
1. Используя теоретические сведения выполнить предложенное преподавателем задание
2. Соответствующим образом оформить работу
|
Лист 1. Практическая работа по теме «Вычисление пределов» Выполнил:__________ (ФИО) группа:_____________ Проверил:__________ Оценка:____________ |
Лист 2. № примера Решение: Ответ: |
Оформление работы:
www.neuch.ru
1. Определения предела и непрерывности функции в точке. Свойства пределов.
Определение. Число А называется пределом функции у=f (x) в точке х0, если для всякого числа ε>0 существует такое число δ>0, что как только |x–x0| < 
( x ≠x0), то |f(x)–A| < ε Обозначение: 
. Определение. Функция у= f ( x ) называется непрерывной в точке х0, если 
. Из непрерывности основных элементарных функций и основных теорем о непрерывных функциях следует, что любая элементарная функция непрерывна во всякой точке, в которой она определена (при этом предполагается, конечно, что функция определена и в окрестности этой точки). 1. Предел постоянной равен самой постоянной, т.е. 
. 2. 
если 
и 
существуют. 3. 
, если и существуют. 4. 
если и существуют и 
.
Под знаком предела можно производить тождественные преобразования аналитического выражения, задающего функцию, не принимая во внимание поведение функции в предельной точке. Особый интерес приобретает случай преобразования аналитического выражения, задающего функцию f(х), в выражение, задающее функцию φ(х), непрерывную в самой точке х0 и совпадающую с f(х) в некоторой окрестности точки х0 без самой этой точки. Тогда очевидно, 
(1) Пример. Найти 
при: а) х 0=1; б) х 0=2; в) х 0 = ∞. Решение. а) 
, 
. Так как предел знаменателя отличен от нуля, можно применить теорему о пределе частного (свойство 4). Тогда 
. б) 
. Имеем неопределенность вида 
, следовательно, теорему о пределе частного применить нельзя. Но в окрестности точки х =2 имеем 4х2 – 9х + 2 ≠ 0 (при х ≠ 2), и поэтому дробь можно сократить на х – 2. Для этого разложим числитель и знаменатель на множители, воспользовавшись формулой ах2+bх+с= а(х–х1)(х–х2), где х1 и х2 – корни уравнения ах2 + bх + с = 0. Тогда 
в) 
. Имеем неопределенность вида 
. Чтобы найти предел, разделим числитель и знаменатель на х2, получим: 
Ответ: 
Пример. Найти 
. Решение. 
и 
. Имеем неопределенность вида 
, теорему о пределе частного применять нельзя. Преобразуем данное выражение, помножив числитель и знаменатель на выражение, сопряженное знаменателю, получим: 
= 
Ответ: 
.
2. Первый замечательный предел
Если угол х выражен в радианах, то 
. Первый замечательный предел можно применять в ряде случаев для раскрытия неопределенностей вида . Пример. Найти предел функции 
. Решение. Здесь неопределенность вида . Преобразуем данную функцию: 
. Обозначим 12х=U, причем 
т.е. при х => 0 и U => 0. Следовательно, 
. Аналогично, положив 3x=U , получим 
. Следовательно 
Ответ: 4. Пример. Найти 
. Имеем неопределенность вида 
. Решение. Обозначим arctg 6x = U, тогда 6х= tgU и при х => 0 имеем U => 0. Следовательно, 
. Ответ: 2.
3. Второй замечательный предел
Он имеет вид: 
, где е – иррациональное число, приблизительно равное 2,71828… . Логарифмы с основанием е называются натуральными и обозначаются logex =ln 1.0pt'>x. С помощью этого предела раскрывают так же неопределенность вида {1∞}. Пример . Найти 
. Здесь неопределенность вида {1∞}. Решение. Преобразуем выражение в скобках. 
. Обозначим 
, тогда 
, 
, 
, причем при n => ∞, имеем α => 0. Следовательно, 
Ответ: 
.
www.std72.ru
