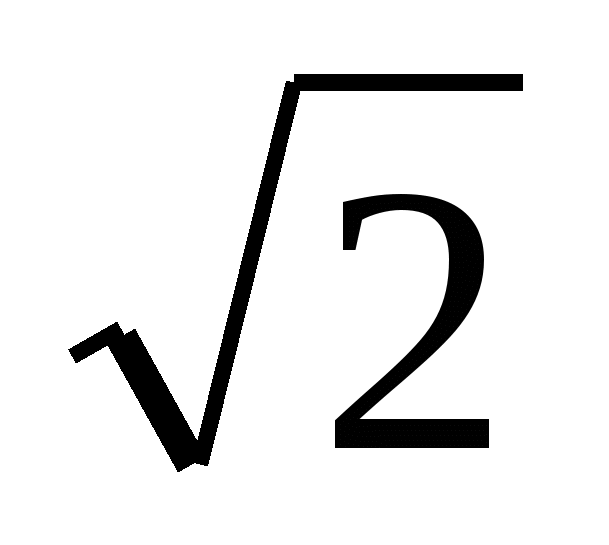 . Найдите диагональ грани куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
. Найдите диагональ грани куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.Главное управление образования Курганской области
Государственное бюджетное профессиональное образовательное учреждение
«Курганский технологический колледж
имени Героя Советского Союза Н.Я. Анфиногенова»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ЗАНЯТИЯ
по дисциплине
«Математика»
для специальности
09.02.02 «Компьютерные сети»
09.02.05 Прикладная информатика (по отраслям)
11.02.02 Техническое обслуживание и ремонт радиоэлектронной техники
(по отраслям)
21.02.05 «Земельно-имущественные отношения»
Автор: Гуржа Мария Александровна
ТЕХНОЛОГИЧЕСКАЯ КАРТА ЗАНЯТИЯ
Тема занятия: Решение задач по теме: «Призма. Параллелепипед. Куб»
Дисциплина: Математика
Специальность: 09.02.02 «Компьютерные сети»
Группа: 169
Специальность: 09.02.05 Прикладная информатика (по отраслям)
Группа: 163
Специальность: 11.02.02 Техническое обслуживание и ремонт радиоэлектронной техники (по отраслям)
Группа: 167
Специальность: 21.02.05 «Земельно-имущественные отношения»
Группа: 148, 149
Цели занятия:
1. Образовательная цель
Сформировать практические навыки студентов по расчету элементов многогранников класса призма
2. Воспитательная цель
Продолжить воспитание в студентах чувства долга и ответственности за выполняемую работу
3. Развивающая цель
Продолжить формирование у студентов анализировать информацию, выделять главное, систематизировать и обобщать
Тип занятия: урок закрепления нового материала
Оснащение:
1. Модели геометрических тел
2. Раздаточный материал
Ход занятия
Этап занятия
Деятельность преподавателя
Деятельность студентов
Продолжитель-
ность, мин.
1
2
3
4
1 Организацион-ный этап
- приветствие;
- фиксация готовности учащихся и кабинета
к учебному занятию;
- проверка посещаемости занятия;
- приветствие;
- готовность к занятию;
- участие в проверке посещаемости;
1 – 2
2 Подготови-тельный этап
- сообщение темы занятия;
- раскрытие цели занятия;
- обсуждение профессиональной и личной
значимости нового материала;
- постановка плана занятия;
- уяснение и запись темы занятия в тетрадь;
- уяснение образовательной цели занятия;
5 – 7
3 Этап закрепления материала
- консультирование обучающихся в
процессе решения практических задач;
- решение практических задач в
тетради и у доски;
50 – 60
4 Этап информи-рования о домаш-нем задании
- выдача информации о домашнем задании;
- запись домашнего задания;
2 – 3
5 Этап подведе-ния итогов занятия
- подведение итогов занятия
- осмысление студентами уровня освоения ими темы занятия
2 – 3
РАЗДАТОЧНЫЙ МАТЕРИАЛ
Задачи в раздаточном материале распределены по уровням сложности.
Задачи уровня «А» должны уметь решать все обучающиеся. Умение решать задачи уровня «А» соответствует оценке «удовлетворительно».
Задачи уровня «В» должны уметь решать все обучающиеся. Умение решать задачи уровня «В» соответствует оценке «хорошо».
Задачи уровня «С» должны уметь решать все обучающиеся. Умение решать задачи уровня «С» соответствует оценке «отлично».
Решение задач по теме «Призма. Параллелепипед. Куб»
А1. Ребро куба равно 3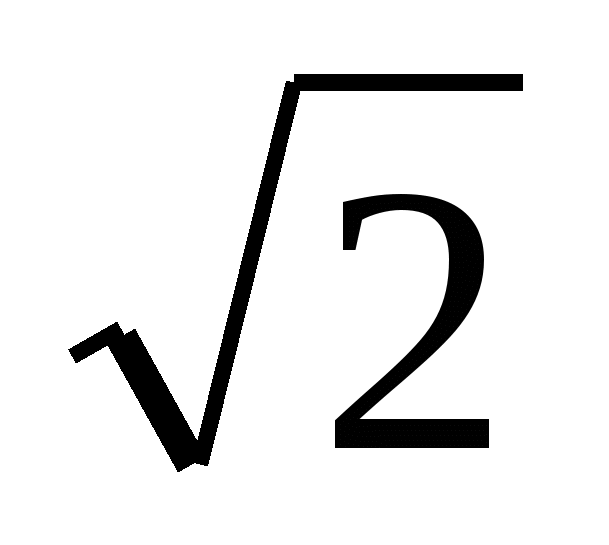 . Найдите диагональ грани куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
. Найдите диагональ грани куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
А2. Ребро куба равно 4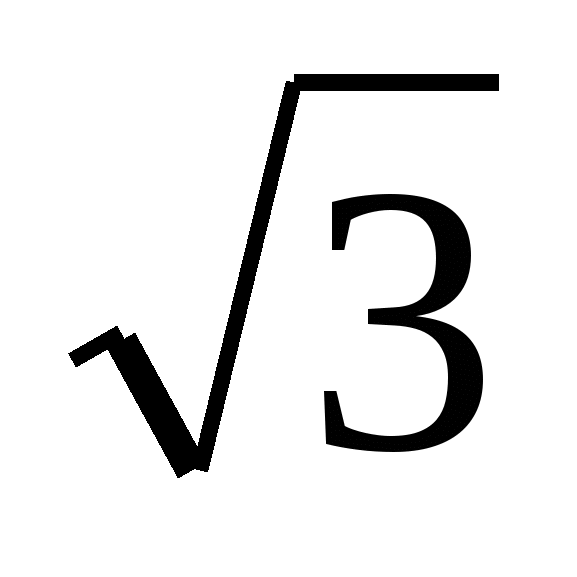 . Найдите диагональ грани куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
. Найдите диагональ грани куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
А3. Диагональ грани куба равна 2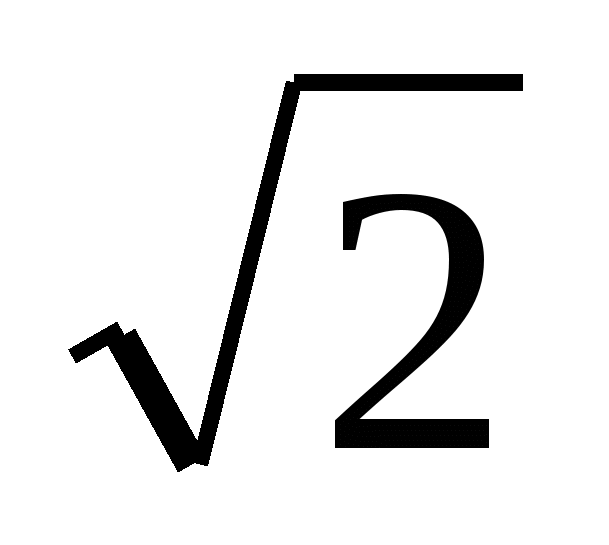 . Найдите ребро куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
. Найдите ребро куба, диагональ куба, площадь боковой поверхности и площадь полной поверхности куба.
А4. Диагональ куба равна 6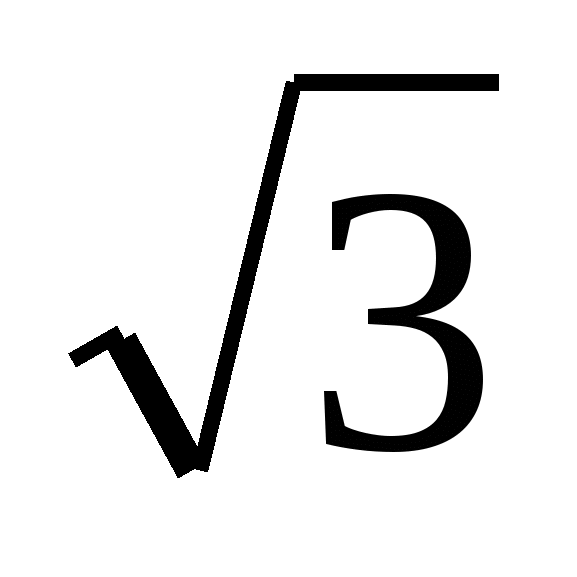 . Найдите ребро куба, диагональ грани куба, площадь боковой поверхности и площадь полной поверхности куба.
. Найдите ребро куба, диагональ грани куба, площадь боковой поверхности и площадь полной поверхности куба.
А5. У параллелепипеда три грани имеют площади 1м2, 2м2 и 3м2. Чему равна площадь полной поверхности параллелепипеда?
А6. В прямом параллелепипеде стороны оснований 6м и 8м образуют угол 300. Найдите площадь полной поверхности параллелепипеда, если его боковое ребро равно 5м.
А7. Вычислите диагонали прямоугольного параллелепипеда по трем его измерениям: а) 1м, 2м, 2м; б) 2см, 3см, 6см; в) 6дм, 6дм, 7дм.
Для каждого параллелепипеда вычислите площадь боковой поверхности и площадь полной поверхности.
А8. Вычислите площадь боковой поверхности и площадь полной поверхности прямоугольного параллелепипеда по трем его измерениям: 10см, 22см, 16см.
В1. Боковое ребро наклонной призмы равно 15см и наклонено к плоскости основания под углом 300. Найдите высоту призмы.
В2. Сколько диагоналей имеет n-угольная призма?
В3. В прямой треугольной призме все ребра равны. Площадь боковой поверхности составляет 12м2. Найдите высоту призмы.
В4. Боковая поверхность правильной четырехугольной призмы 32м2, а полная поверхность 40м2. Найдите высоту призмы.
В5. Расстояния между параллельными прямыми, содержащими боковые ребра наклонной призмы, равны 2см, 3см и 4см, а боковые ребра 5см. Найдите площадь боковой поверхности призмы.
В6. В правильной четырехугольной призме площадь основания 144см2, а высота 14 см. Найдите диагональ призмы.
С1. Диагонали трех граней прямоугольного параллелепипеда равны а, b, с. Найдите линейные размеры параллелепипеда.
С2. В прямой треугольной призме ABCА1B1C1 диагональ АВ1 равна 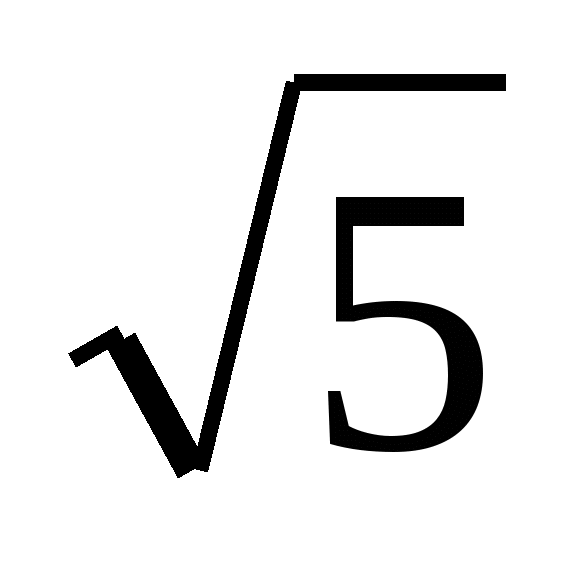 см, а высота равна 1см. Найдите площадь боковой поверхности призмы, если в ее основании лежит равносторонний треугольник АВС.
см, а высота равна 1см. Найдите площадь боковой поверхности призмы, если в ее основании лежит равносторонний треугольник АВС.
Правильные ответы
Номер задачи
Ответ
Номер задачи
Ответ
А1
dгр = 6
d =3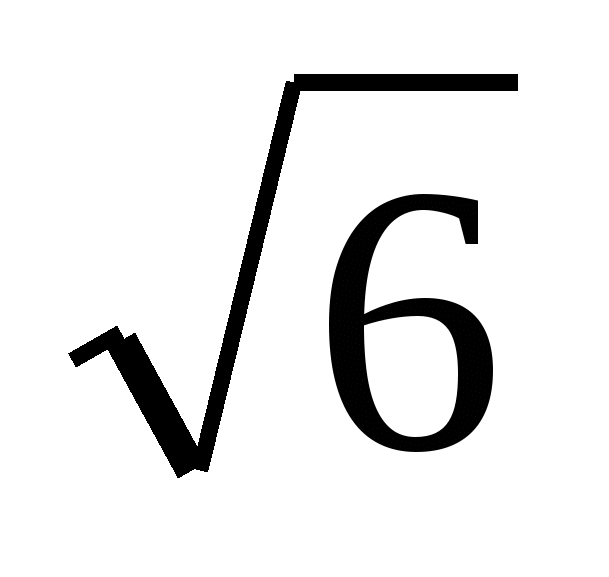
Sбок = 72
S = 108
В1
7,5см
А2
dгр = 4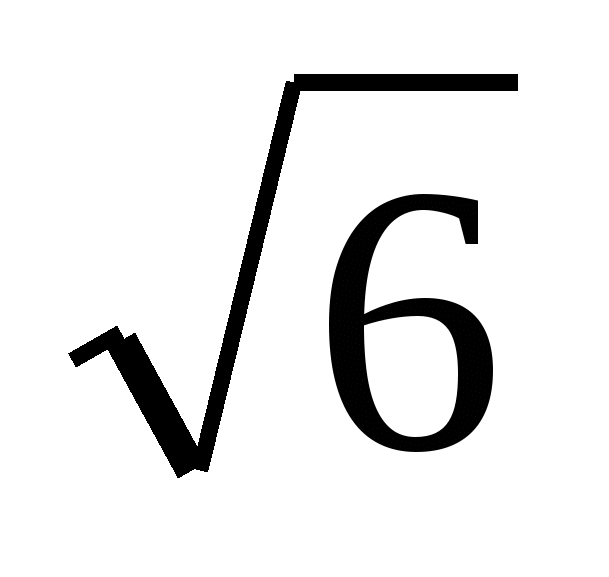
d = 12
Sбок = 192
S = 288
В2
n (n – 3)
А3
а = 2
d = 2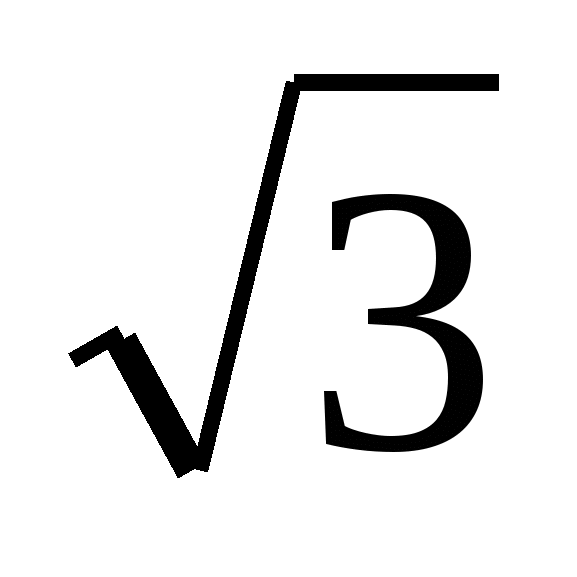
Sбок = 16
S = 24
В3
2м
А4
а = 6
dгр = 6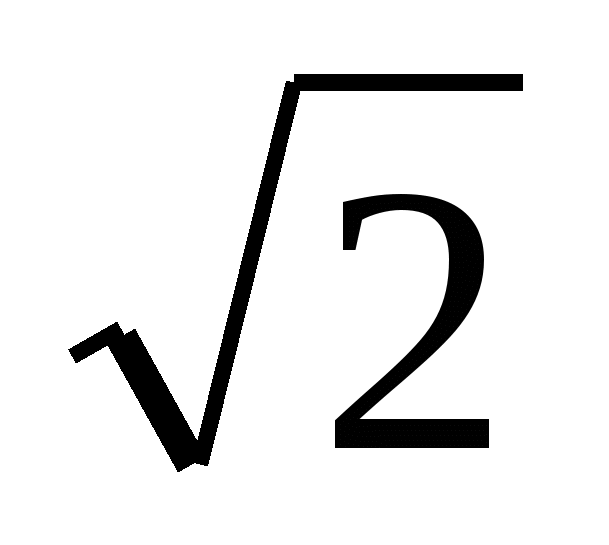
Sбок = 144
S = 216
В4
4м
А5
12м2
В5
45см2
А6
188м2
В6
22м
А7
а) d = 3м
Sбок = 12м2
S = 16м2
б) d = 7см
Sбок = 60см2
S = 72см2
в) d = 11дм
Sбок = 168дм2
S = 240дм2
С1
А8
Sбок = 1024см2
S = 1464см2
С2
6см2
Домашнее задание.
А9 (на оценку «удовлетворительно»).
В7 (на оценку «хорошо»). Площадь боковой поверхности правильной четырехугольной призмы равна 120м2. Найдите площадь ее основания, если длина бокового ребра 6м (Ответ: 25м2).
С3 (на оценку «отлично»). В прямом параллелепипеде стороны основания 3см и 5см, а одна из диагоналей основания 4см. Найдите большую диагональ параллелепипеда, зная, что меньшая диагональ образует с плоскостью основания угол в 600 (Ответ: 10см2).
infourok.ru
--PAGE_BREAK--
Призма.
Определение.Призма – многогранник, составленный из двух равных многоугольников A 1 A 2 … An
и B 1 B 2 … Bn, расположенных в параллельных плоскостях, и nпараллелограммов.
Два равных многоугольника, лежащие в параллельных плоскостях, называются основаниями призмы (A 1 A 2 … An
и B 1 B 2 … Bn ).
Остальные грани призмы, являющиеся параллелограммами, называются её боковыми гранями (AnA1B1Bn)
Рёбра, не лежащие в основании призмы, называются боковыми рёбрами (A1B1; A2B2… AnBn)
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы (h).
Диагональная плоскость– плоскость, проходящая через диагональ основания и боковое ребро призмы.
Диагональное сечение – фигура, полученная при пересечении диагональной плоскости с поверхностью призмы.
Перпендикулярное сечение– сечение призмы плоскостью, перпендикулярной её боковым рёбрам.
В призму можно вписать сферу тогда и только тогда, если в перпендикулярное сечение призмы можно вписать окружность, диаметр которой равен высоте призмы.
Если боковые рёбра призмы перпендикулярны к основаниям, то есть если основания служат нормальными сечениями боковой поверхности, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна её боковому ребру. Плоские углы основания являются плоскими углами двугранных углов между боковыми гранями.
Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные многоугольники.
В правильную призму можно вписать сферу тогда и только тогда, когда её высота равна диметру окружности, вписанной в основание.
Площадь боковой поверхности призмы– это сумма площадей всех её боковых граней.
S бок =Рп*/g/, где Рп – периметр перпендикулярного сечения, /g/ — длина бокового ребра
Площадь полной поверхности призмы– сумма площадей всех её граней
S полн =S бок +2 S осн
Объём призмы. Объёмомгеометрического тела называется величина части пространства, занимаемого этим телом.
Доп. справка:в геометрии принято:
· За единицу объёма принимают объём куба с ребром единичной длины.
· Равные тела имеют равные объёмы
· Объём объединения нескольких неперекрывающихся (т.е. не имеющих общих внутренних точек) тел равен сумме их объёмов
· Если одно тело содержит другое, то объём первого тела не меньше объёма второго
V=S осн *h
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
S бок = P осн *h
Частным случаем призмы является параллелепипед – призма, основанием которой служат параллелограммы.
Основные свойства параллелепипеда:
1. Противоположные грани параллелепипеда попарно равны и параллельны.
2. Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
3. сумма квадратов всех диагоналей параллелепипеда равна сумме квадратов всех его рёбер.
4. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Если все грани параллелепипеда являются прямоугольниками, то параллелепипед называется прямоугольным. В нём все диагонали равны между собой.
Если боковые рёбра параллелепипеда перпендикулярны основанию, то параллелепипед является прямым.
Куб также является частным случаем призмы.
Кубесть прямоугольный параллелепипед с равными рёбрами.
Объём параллелепипеда
V=S*h
Объём прямоугольного параллелепипеда
V=abc
Объём куба
V =a3
Диагональ прямоугольного параллелепипеда
d 2 = a 2 + b 2 + c 2 , где d – диагональ, a , b , c
– рёбра
Пирамида. продолжение --PAGE_BREAK--
www.ronl.ru

 Самостоятельная работа Вариант 1
Самостоятельная работа Вариант 1
Задание ЕГЭ Стереометрия Прямоугольный параллелепипед ,призма.
Найдите квадрат расстояния между вершинами 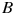 и
и  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 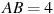 ,
, 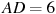 ,
, 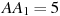 .
.
Найдите расстояние между вершинами 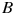 и
и  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 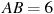 ,
, 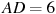 ,
, 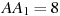 .
.
Найдите угол 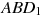 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 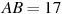 ,
, 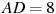 ,
, 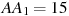 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Найдите угол 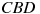 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 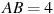 ,
, 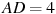 ,
, 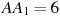 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Найдите угол 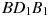 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 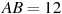 ,
, 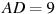 ,
, 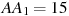 . Ответ дайте в градусах
. Ответ дайте в градусах
В правильной шестиугольной призме 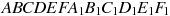 все ребра равны 23. Найдите угол
все ребра равны 23. Найдите угол 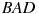 . Ответ дайте в градус
. Ответ дайте в градус
В правильной шестиугольной призме 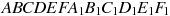 все ребра равны 48. Найдите расстояние между точками
все ребра равны 48. Найдите расстояние между точками 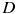 и
и  .
.
В правильной шестиугольной призме 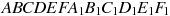 все ребра равны
все ребра равны 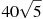 . Найдите расстояние между точками
. Найдите расстояние между точками  и
и  .
.
В правильной шестиугольной призме 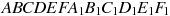 все ребра равны 31. Найдите тангенс угла
все ребра равны 31. Найдите тангенс угла 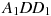 .
.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол 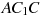 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Самостоятельная работа Вариант 2
Задание ЕГЭ Стереометрия Прямоугольный параллелепипед ,призма.
Найдите квадрат расстояния между вершинами 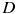 и
и  прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 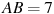 ,
, 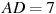 ,
,
Найдите расстояние между вершинами 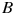 и
и 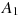 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 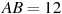 ,
, 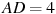 ,
, 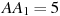 .
.
Найдите угол 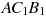 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 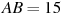 ,
, 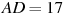 ,
, 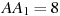 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Найдите угол 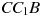 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 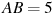 ,
, 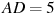 ,
, 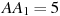 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Найдите угол 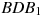 прямоугольного параллелепипеда, для которого
прямоугольного параллелепипеда, для которого 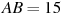 ,
, 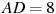 ,
, 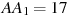 . Ответ дайте в градусах.
. Ответ дайте в градусах.
В правильной шестиугольной призме 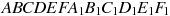 все ребра равны 38. Найдите расстояние между точками
все ребра равны 38. Найдите расстояние между точками  и
и  .
.
В правильной шестиугольной призме 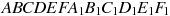 все ребра равны 41. Найдите расстояние между точками
все ребра равны 41. Найдите расстояние между точками  и
и  .
.
В правильной шестиугольной призме 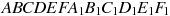 все ребра равны 38. Найдите расстояние между точками
все ребра равны 38. Найдите расстояние между точками  и
и  .
.
В правильной шестиугольной призме 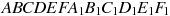 все ребра равны 45. Найдите тангенс угла
все ребра равны 45. Найдите тангенс угла 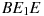 .
.
В правильной шестиугольной призме 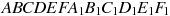 все ребра равны 6. Найдите угол
все ребра равны 6. Найдите угол 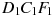 . Ответ дайте в градусах.
. Ответ дайте в градусах.
infourok.ru
№ 1. Площадь диагонального сечения куба равна  см2. Найдите площадь поверхности куба.
см2. Найдите площадь поверхности куба.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 2. Длины диагоналей трех граней прямоугольного параллелепипеда, имеющие общую вершину, равны  см,
см,  см и
см и  см. Найдите диагональ параллелепипеда.
см. Найдите диагональ параллелепипеда.
а)  см; б)
см; б)  см; в)
см; в)  см; г)
см; г)  см.
см.
№ 3. Стороны основания прямого параллелепипеда равны 1 см и 3 см, а синус угла между ними равен  . Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно
. Найдите угол, который образует большая диагональ параллелепипеда с основанием, если боковое ребро параллелепипеда равно  см.
см.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
№ 4. Площади двух диагональных сечений прямого параллелепипеда равны 48 см2 и 30 см2, а боковое ребро равно 6 см. Найдите площадь основания параллелепипеда, если оно является ромбом.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г)  см2.
см2.
№ 5. Сторона основания правильной шестиугольной призмы равна 4 см, а большая диагональ призмы образует с основанием угол, равный 600. Найдите площадь полной поверхности призмы.
а)  см2; б)
см2; б)  см2; в)
см2; в)  см2; г)
см2; г) см2.
№ 6. АВСА1В1C1 – наклонная треугольная призма. Двугранный угол при ребре АА1 равен 900. Расстояния от ребра АА1 до ребер ВВ1 и СС1 равны соответственно 4 см и 3 см. Найдите площадь боковой поверхности призмы, если её высота равна см и боковое ребро образует с основанием угол 600.
а) см2; б)
см2; в)
см2; г)
см2.
№ 7. АВСА1В1C1 – правильная треугольная призма. Через ребро А1В1 и точку М – середину АС - проведено сечение, площадь которого равна см2. Найдите высоту призмы, если сторона её основания равна 2 см.
а) см; б)
см; в)
см; г)
см.
№ 8. АВСDА1В1C1D1 – прямоугольный параллелепипед. Причем АВ = см, ВС =
см, ВВ1 =
см. Через точки А, В1 и С проведена плоскость. Найдите тангенс угла между плоскостями АВ1С и АВС.
а) ; б)
; в)
; г)
.
№ 1. Площадь поверхности куба равна см2. Найдите площадь диагонального сечения этого куба.
а) см2; б)
см2; в)
см2; г)
см2.
№ 2. Длины диагоналей трех граней прямоугольного параллелепипеда, имеющие общую вершину, равны см,
см и
см. Найдите диагональ параллелепипеда.
а) см; б)
см; в)
см; г)
см.
№ 3. Стороны основания прямого параллелепипеда равны 2 см и 4 см, а синус угла между ними равен . Найдите угол, который образует меньшая диагональ параллелепипеда с основанием, если её длина равна
см.
а) ; б)
 ; в)
; в) ; г)
 .
.
№ 4. Площади двух диагональных сечений прямого параллелепипеда равны 16 см2 и 27 см2. Основанием параллелепипеда является ромб, площадь которого равна 24 см2. Найдите длину бокового ребра параллелепипеда.
а) см; б)
см; в)
см; г)
см.
№ 5. Сторона основания правильной шестиугольной призмы равна 6 см, а большая диагональ призмы образует с основанием угол, равный 300. Найдите площадь полной поверхности призмы.
а) см2; б)
см2; в)
см2; г)
см2.
№ 6. АВСА1В1C1 – наклонная треугольная призма. Двугранный угол при ребре ВВ1 равен 600, а расстояния от ребра ВВ1 до ребер АА1 и СС1 равны соответственно 1 см и 2 см. Найдите площадь боковой поверхности призмы, если её высота равна см, а боковое ребро образует с основанием угол 300.
а) см2; б)
см2; в)
см2; г)
см2.
№ 7. МКРМ1K1P1 – правильная треугольная призма, сторона основания которой 4 см. Найдите площадь сечения призмы плоскостью, проходящей через точки Р, Е и F, где Е и F – середины ребер М1Р1 и К1Р1, а боковое ребро равно 3 см.
а) см2; б)
см2; в)
см2; г)
см2.
№ 8. АВСDА1В1C1D1 – прямоугольный параллелепипед, причем ВС = , СD =
, СС1 =
. Найдите тангенс угла между плоскостями ВС1D и АВС.
а) ; б)
; в)
; г)
.
multiurok.ru