ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
Вариант № 1.6
200 г.
Найти матрицу D = (C*A - B*A), если
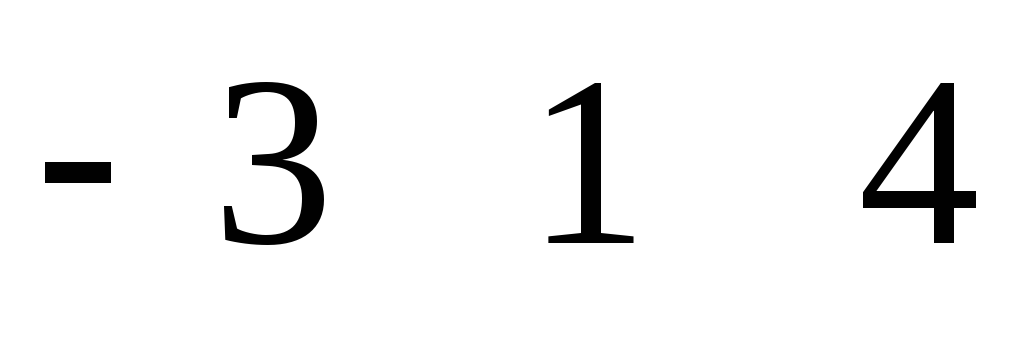
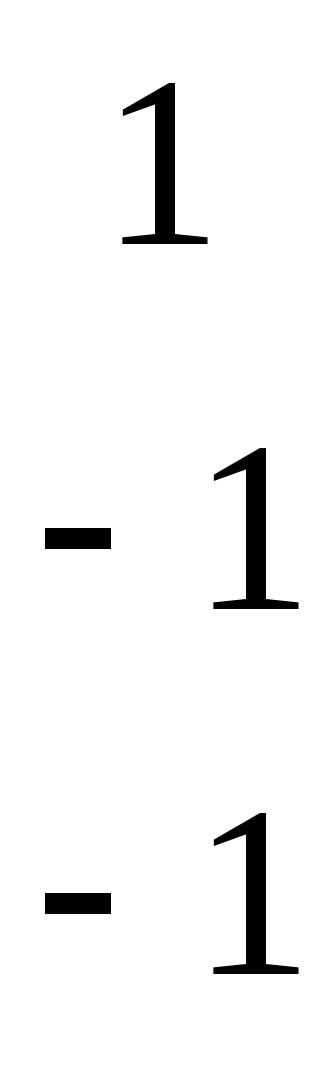
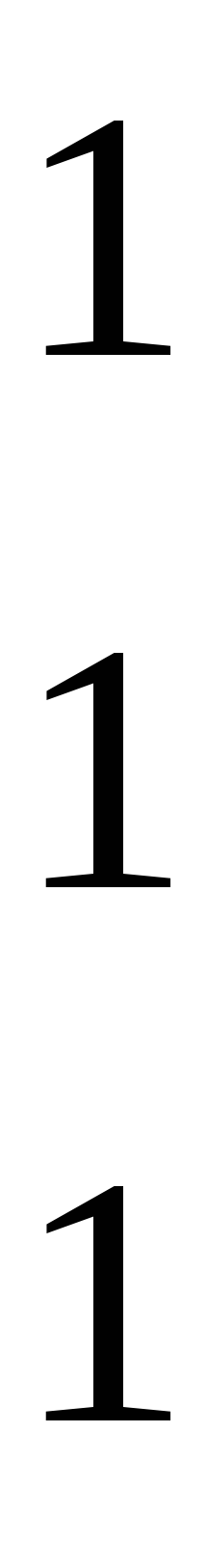
С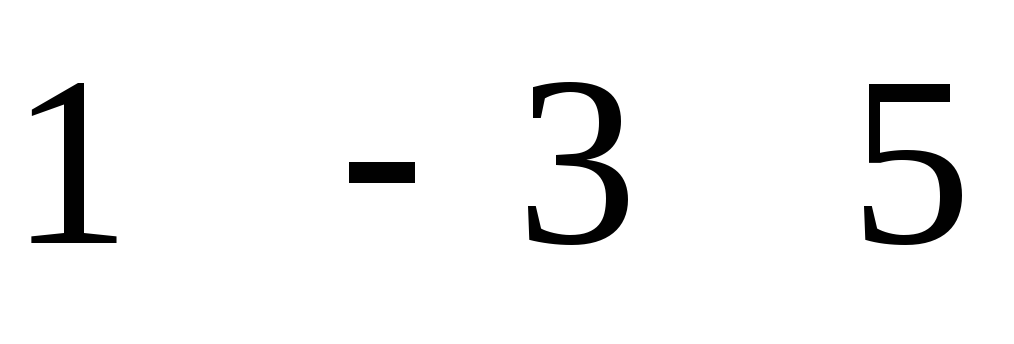
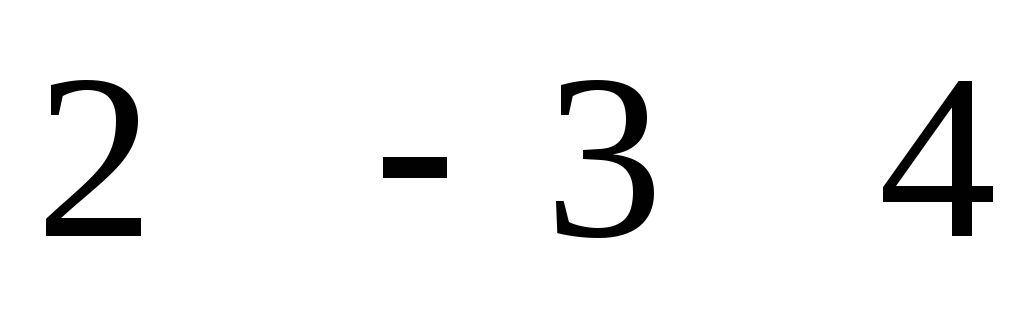= , B = , A = .
Решение: Используя правила умножения и сложения матриц находим:
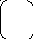
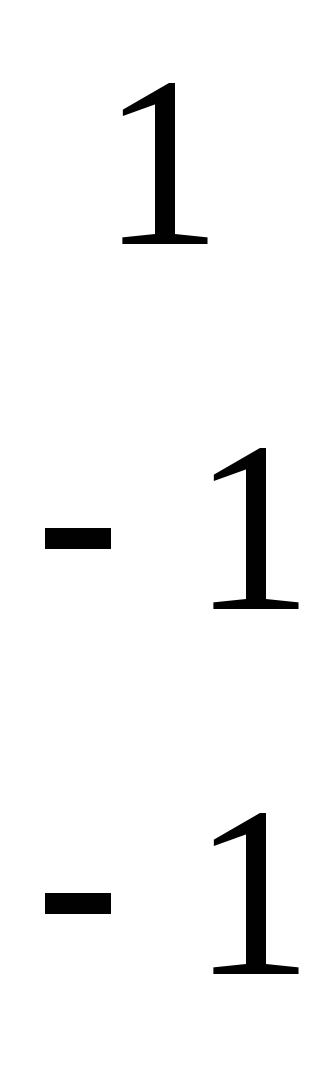
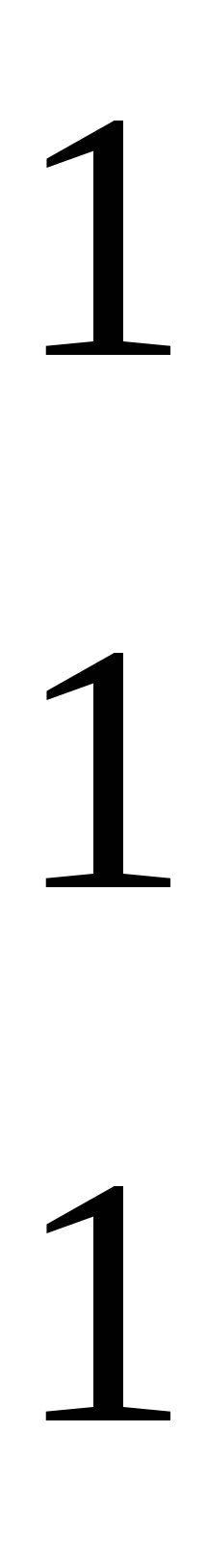
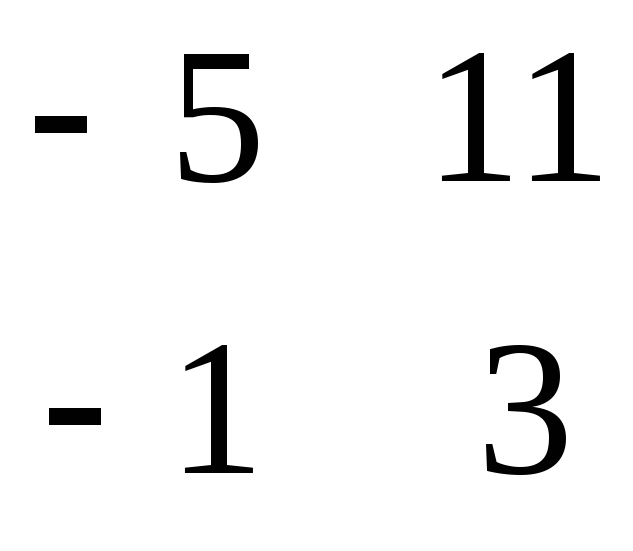
C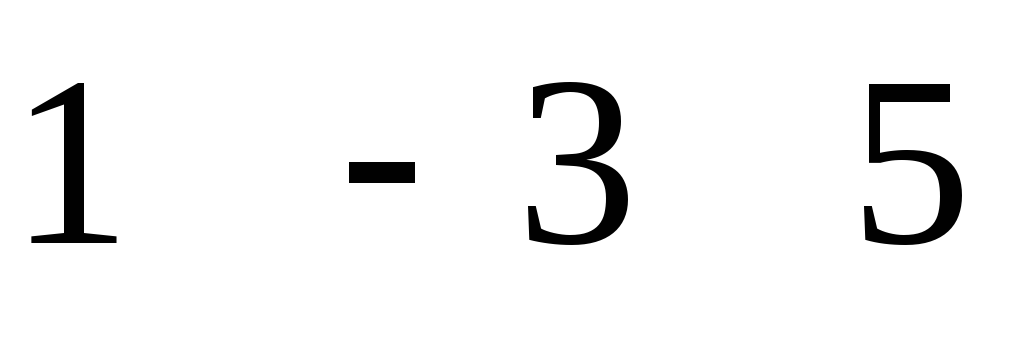
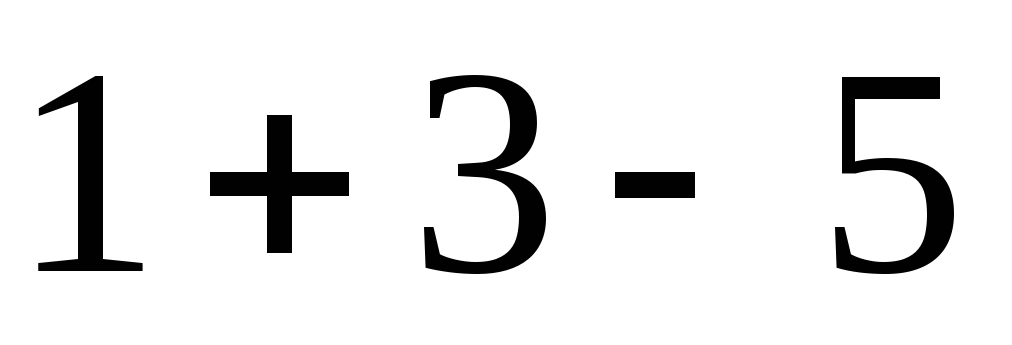
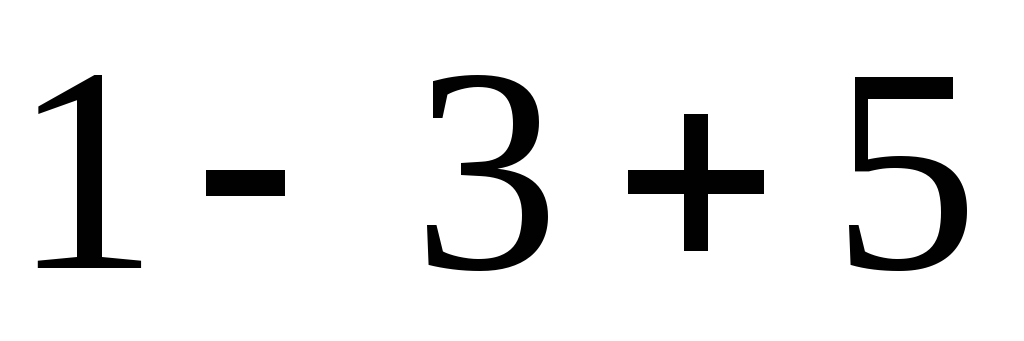*A = * = =
з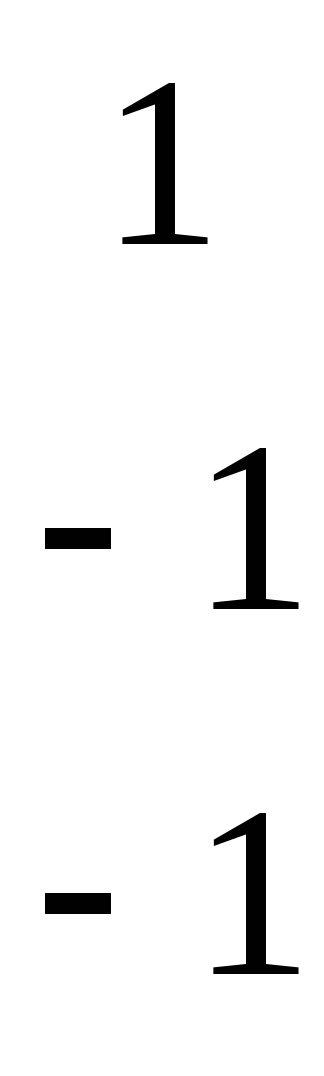
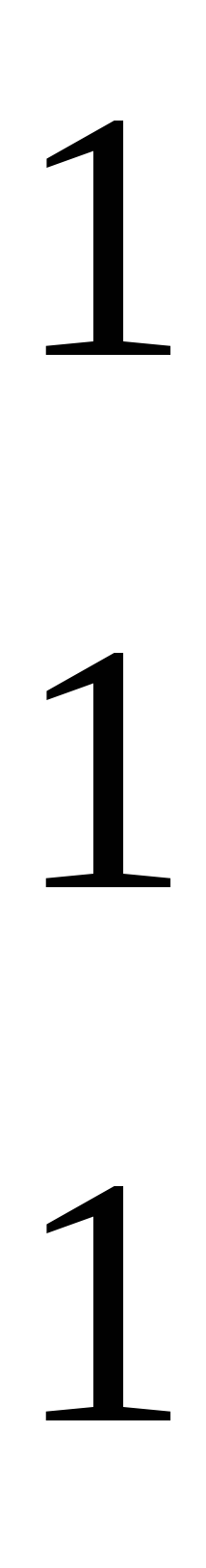
атем,
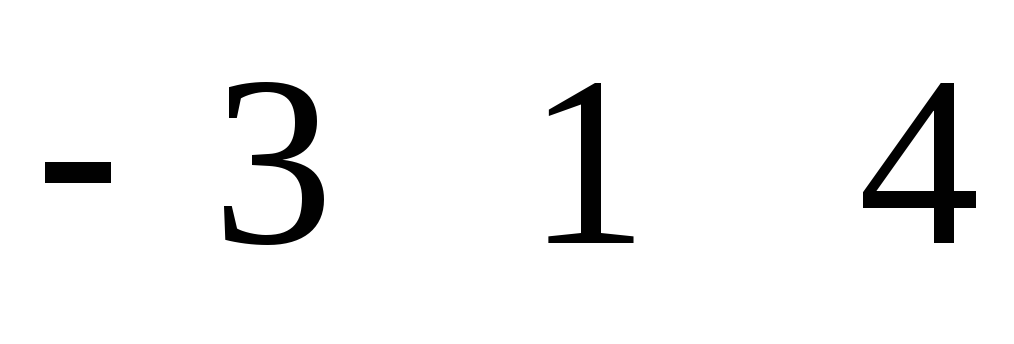
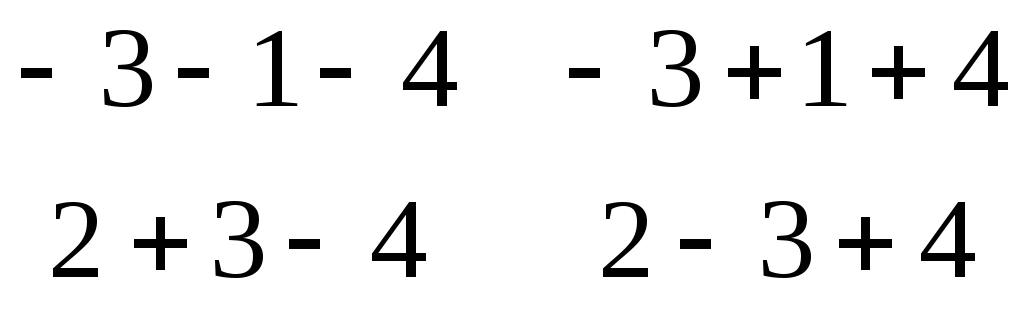
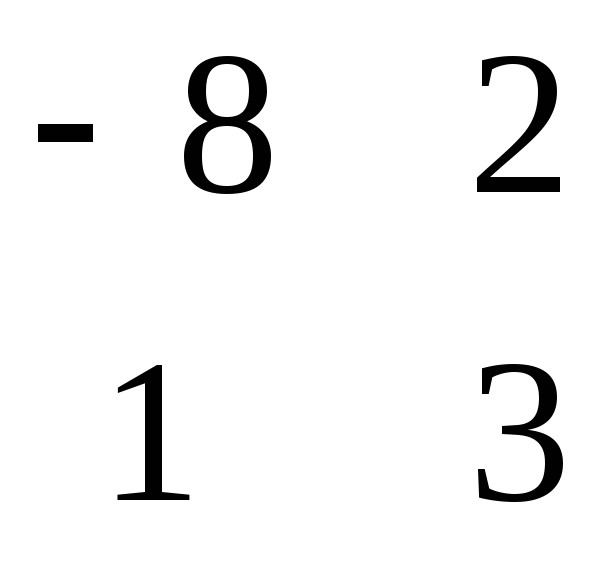
B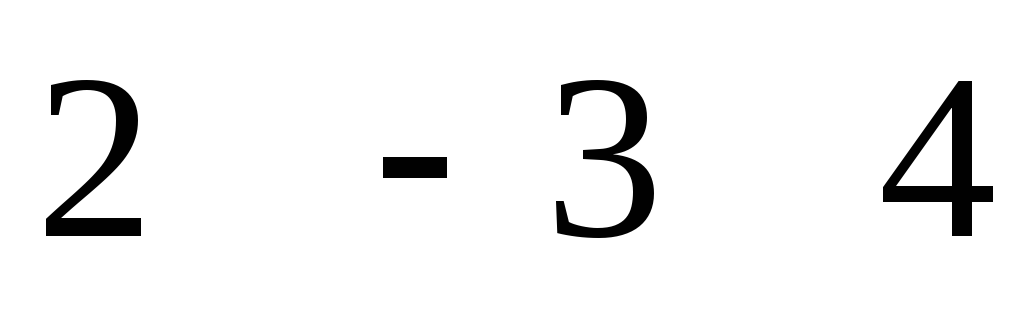
*A = * = =
Так, как матрицы C*A и B*A одного размера, то тогда находим матрицу D
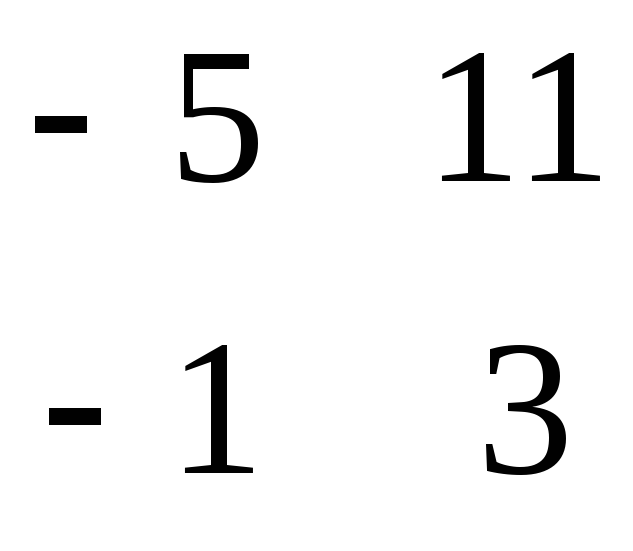
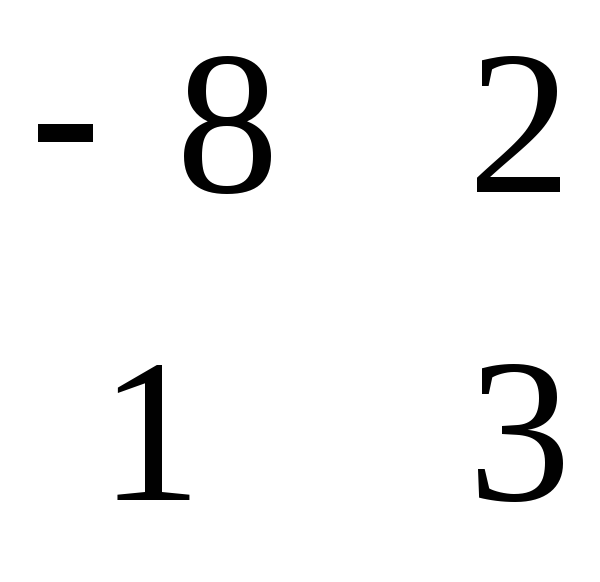
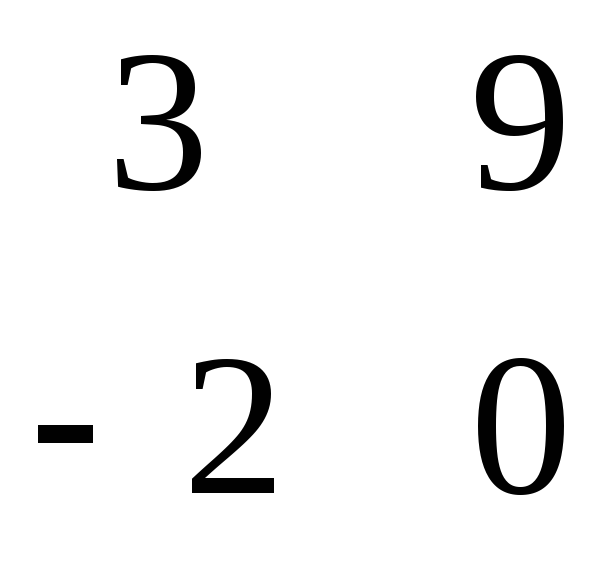
D = - =
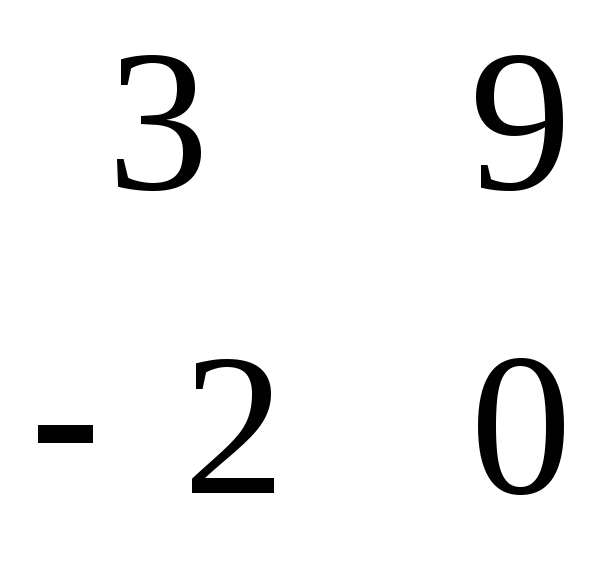
Ответ: D =
Вычислить определитель D, если
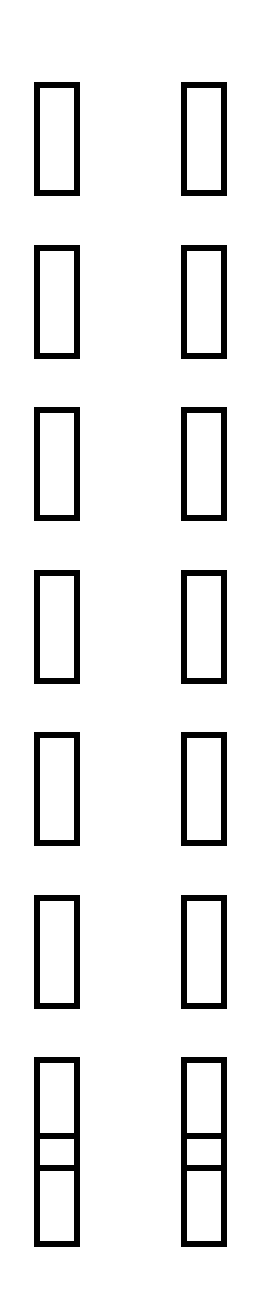
D =
Решение:
Пользуясь теоремой вычисление определителя можно свести к вычислению четырех определителей третьего порядка. Число этих определителей можно снизить до одного, получив, пользуясь свойствами определителя, в какой-либо строке или столбце три нулевых элемента. Получим нули в первом столбце. Для этого его третью строку умноженную на 1, вычтем из первой, затем эту же строку умноженную на 2, вычтем из второй, и умноженную на 4, вычтем из четвертой.
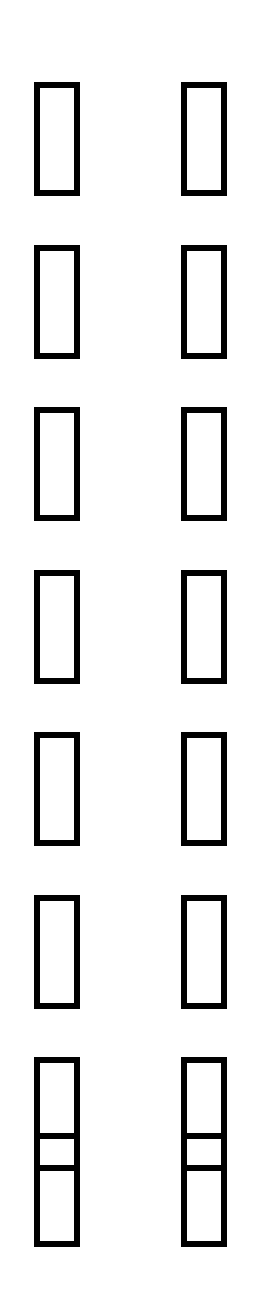
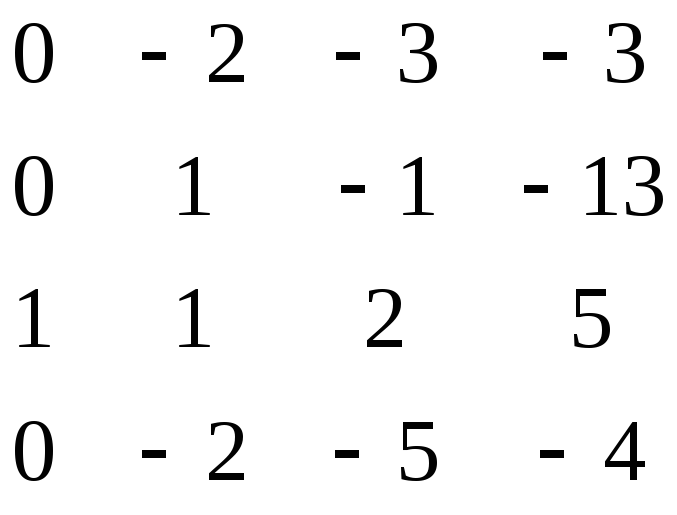
D=
Разлагая этот определитель по элементам первого столбца, получаем:
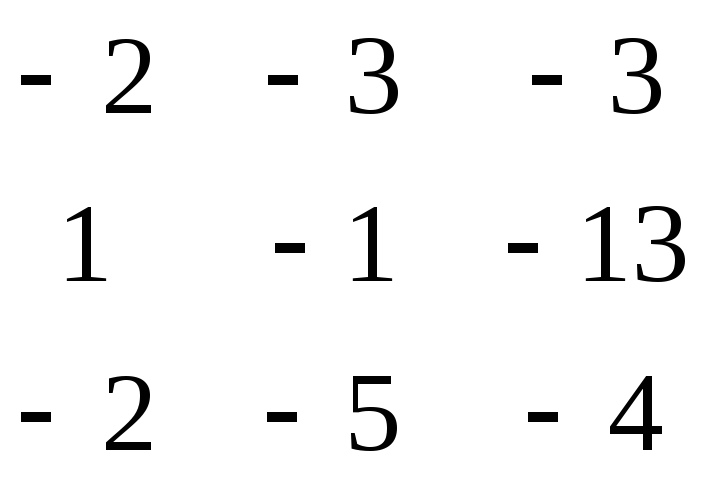
3+1
D= 1 * (-1) .
Т
еперь упрощаем определитель, получив нули в первом столбце:
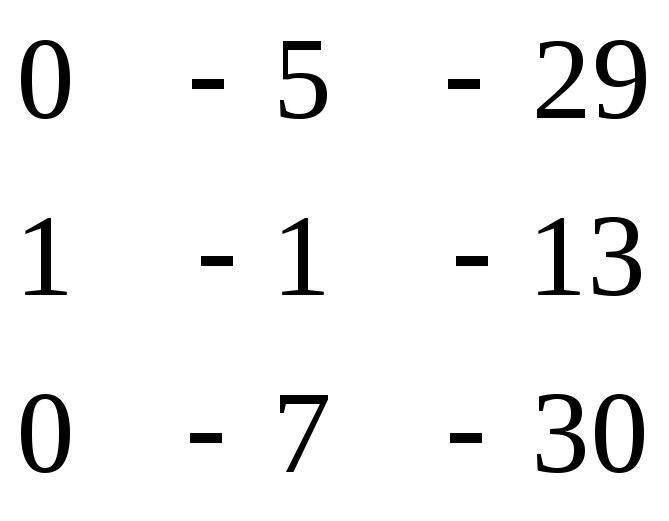
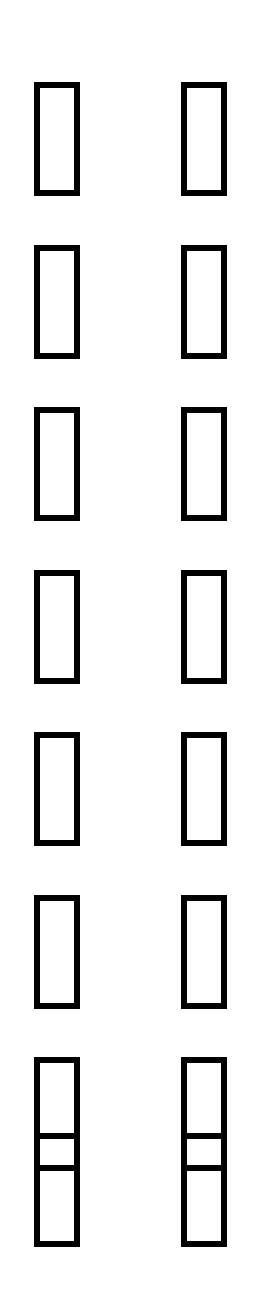
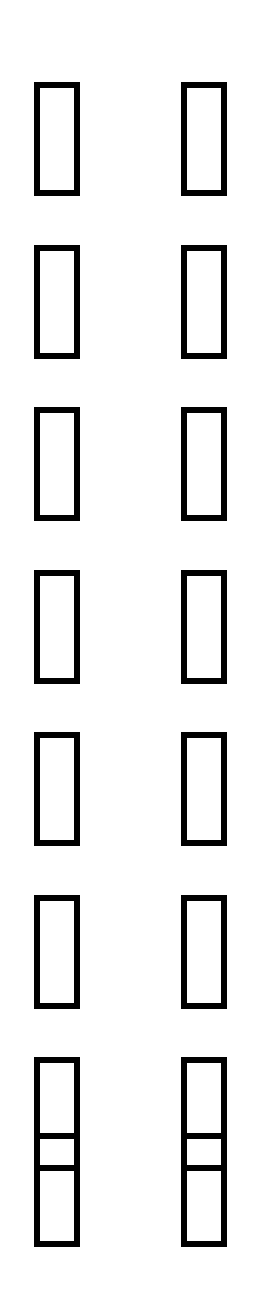
2+1
D = = 1* (-1) = - = - (150 – 203) = 53 (умножили
вторую строку на –2 и вычли ее из первой, а затем вычли из третьей). Затем вычисляем определитель по правилу определителя второго порядка.
Ответ: D = 53.
Р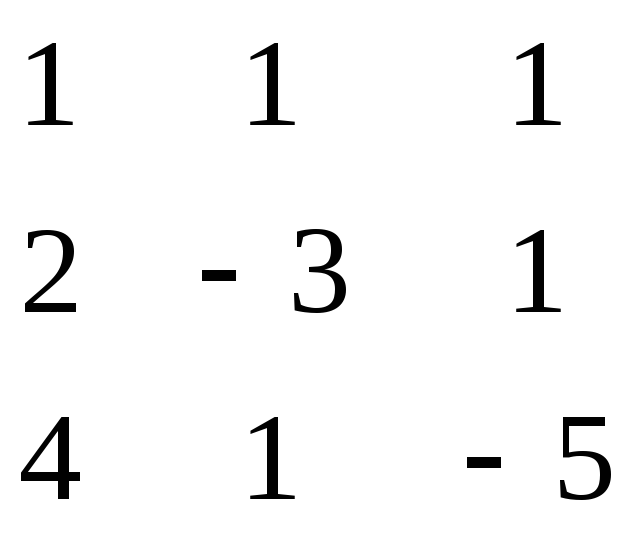
ешить матричное уравнение:
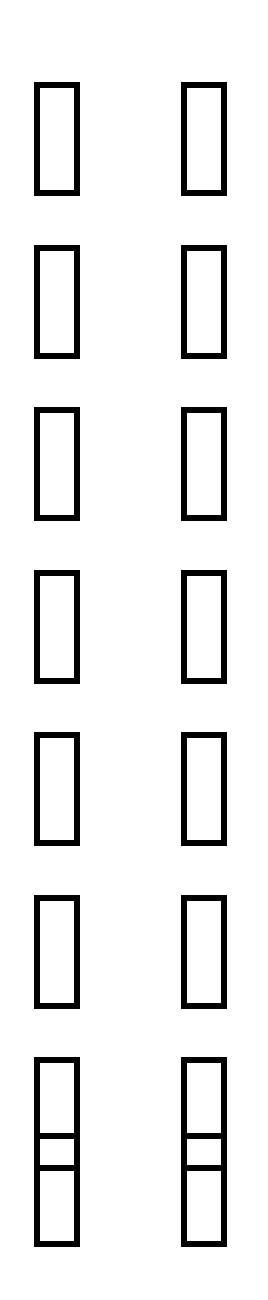
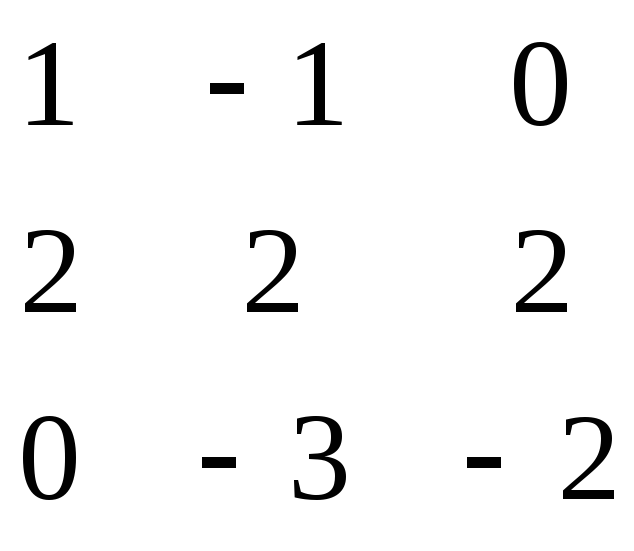
* Х = 42
Решение:
Обозначим
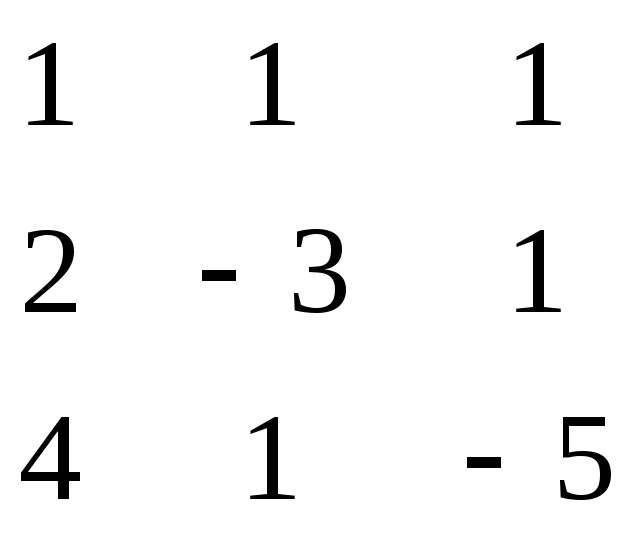
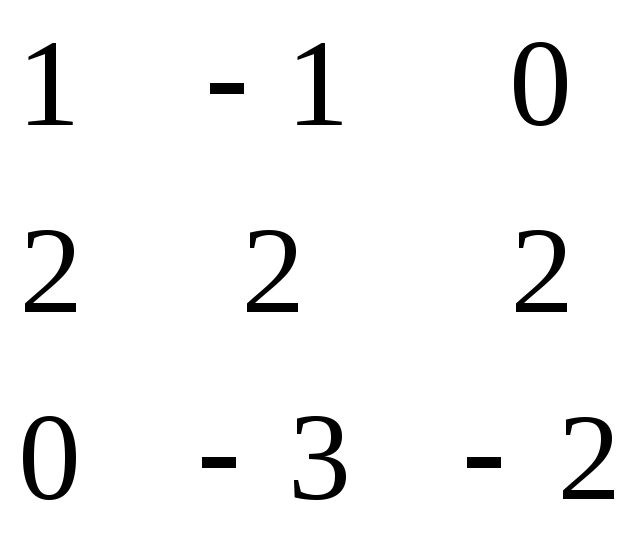
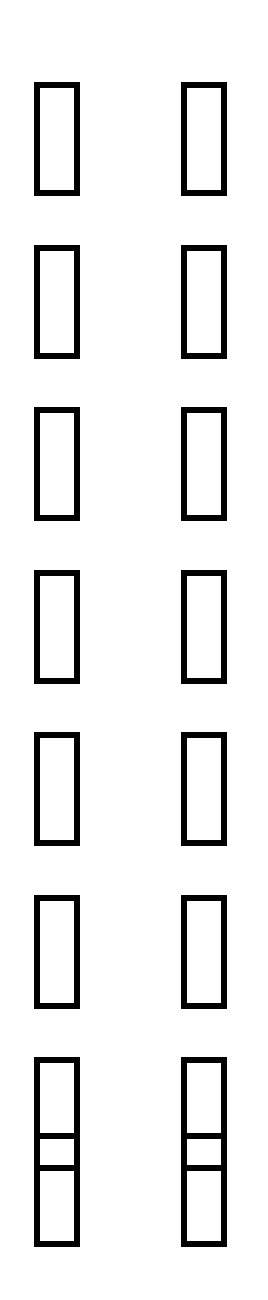
A= ;B=
Тогда данное уравнение можно записать в виде A*X = 42 * B. Так как
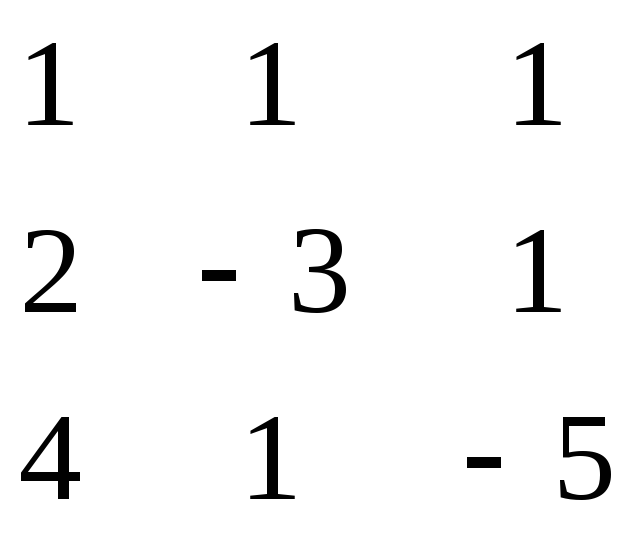
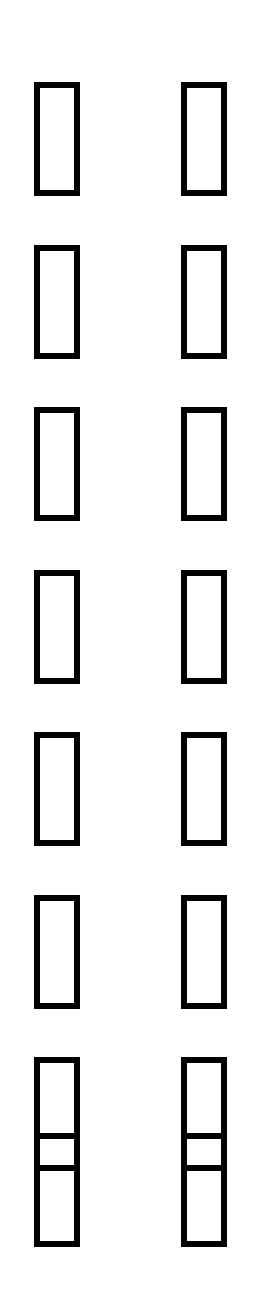
det A = = 15 + 4 + 2 + 12 + 10 – 1 = 42, то матрица А не вырождена, а
-1 -1 -1 -1
поэтому A *A*X = A *42*B, следовательно X = A * 42 B. Находим матрицу A .
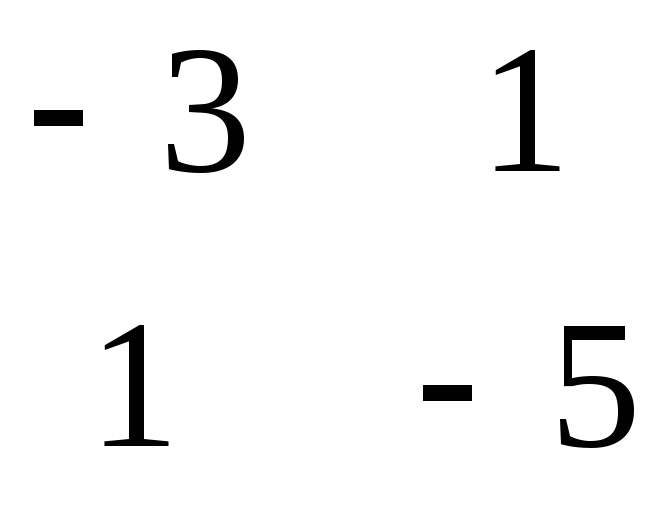
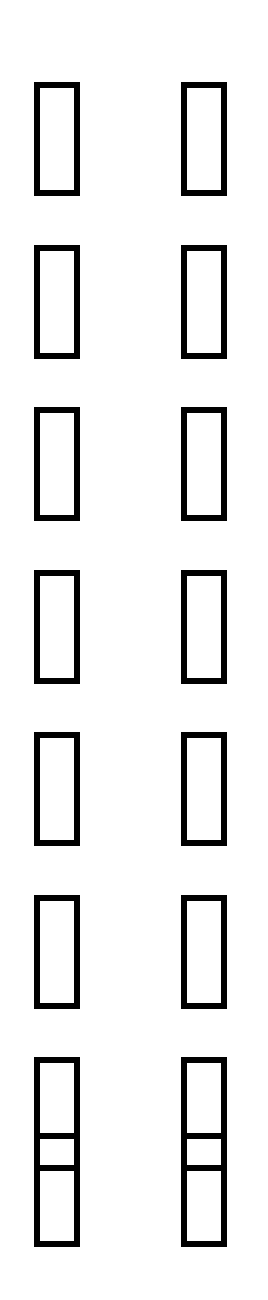
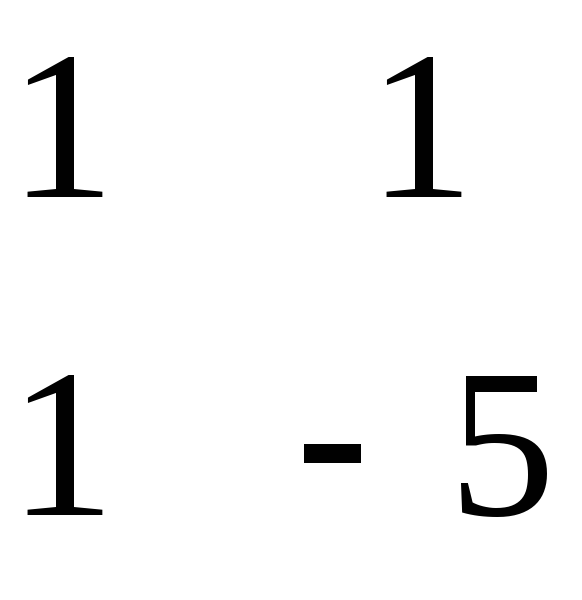
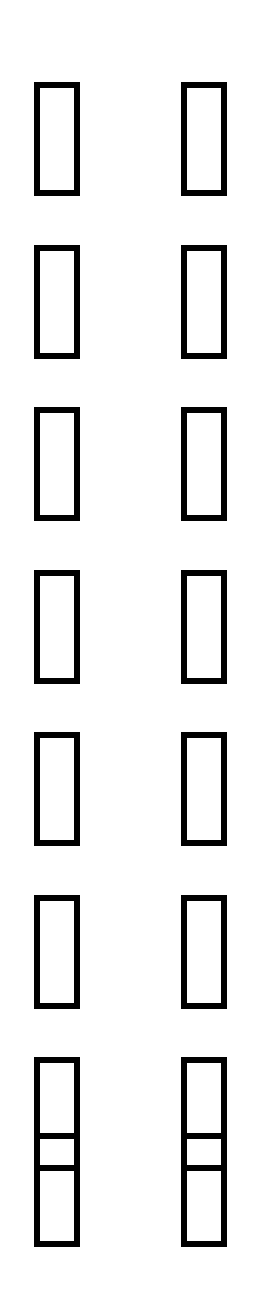
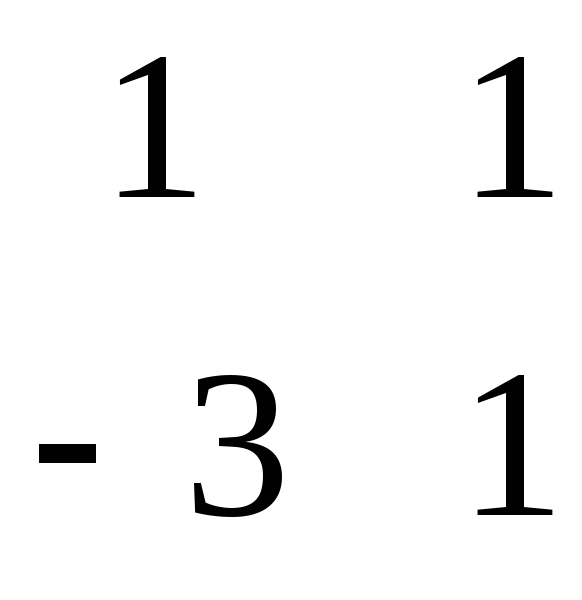
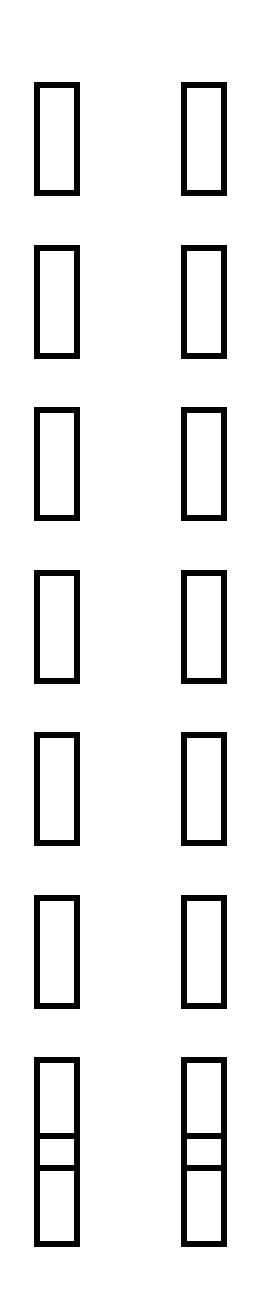
= = 14 = - = 6 = = 4
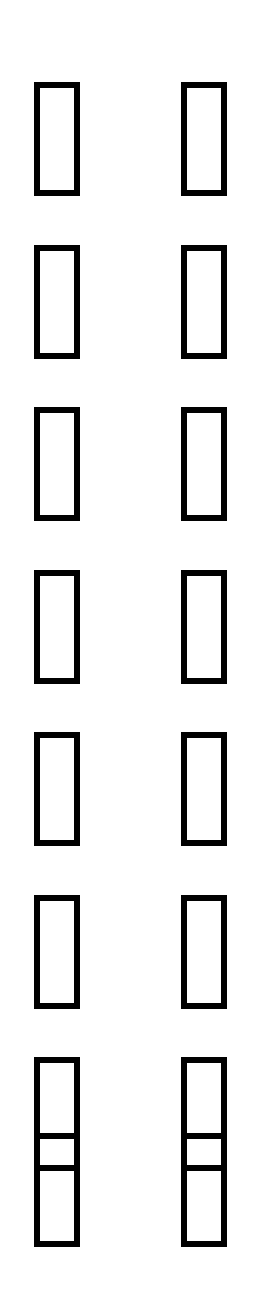
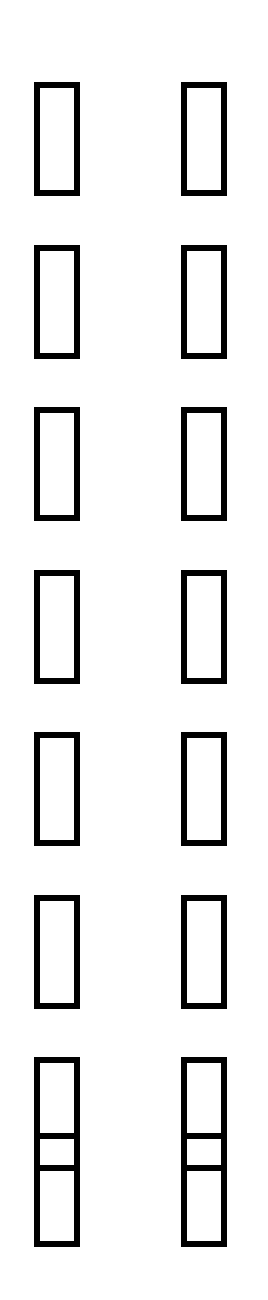
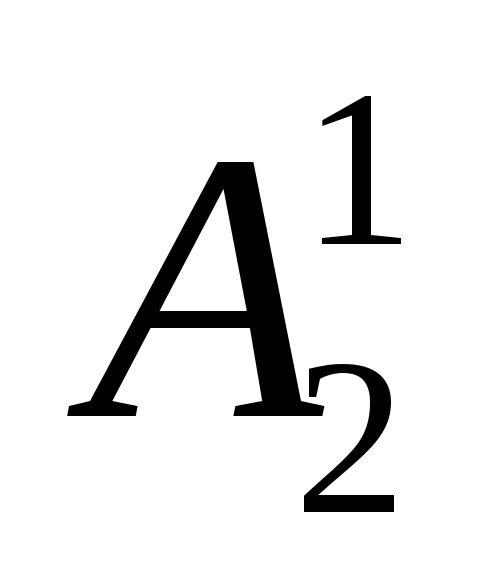
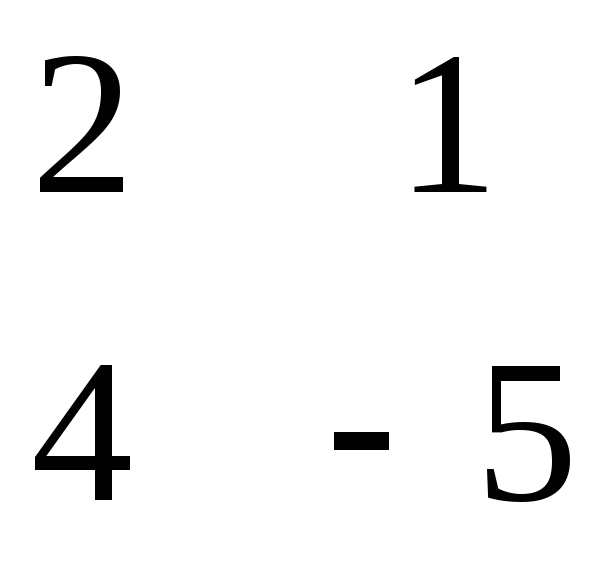
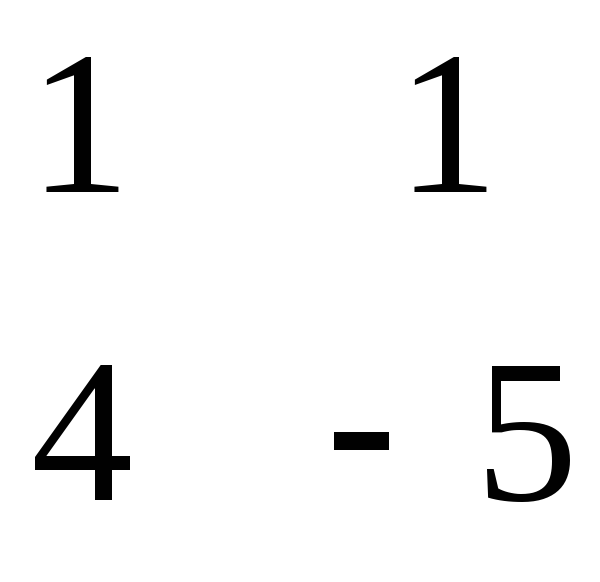
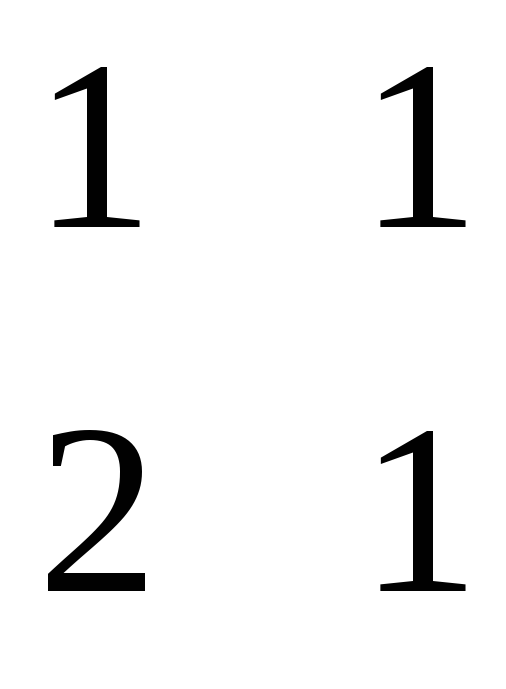
= - = 14 = = - 9 = - = 1
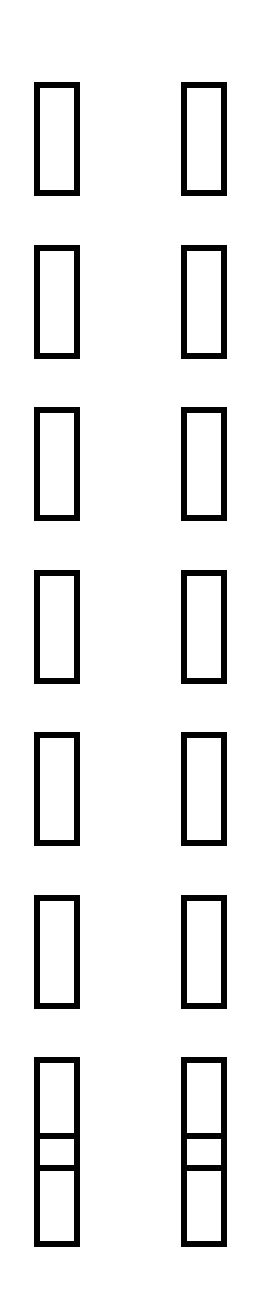
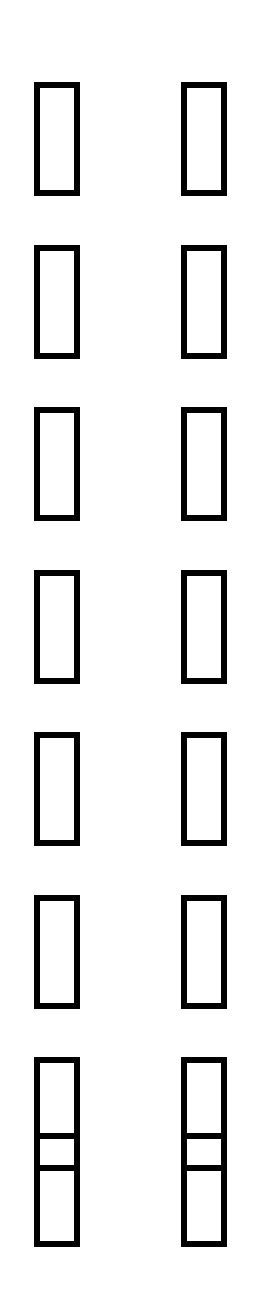
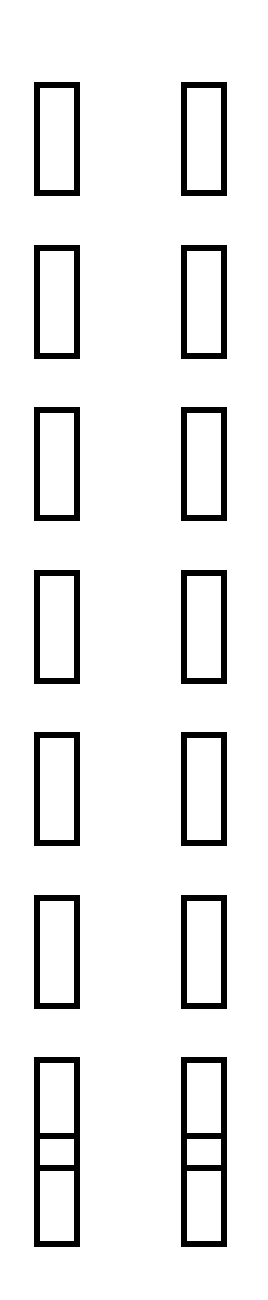
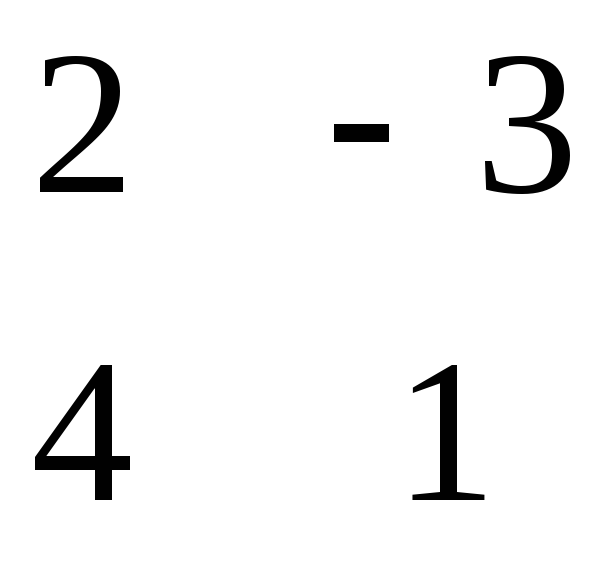
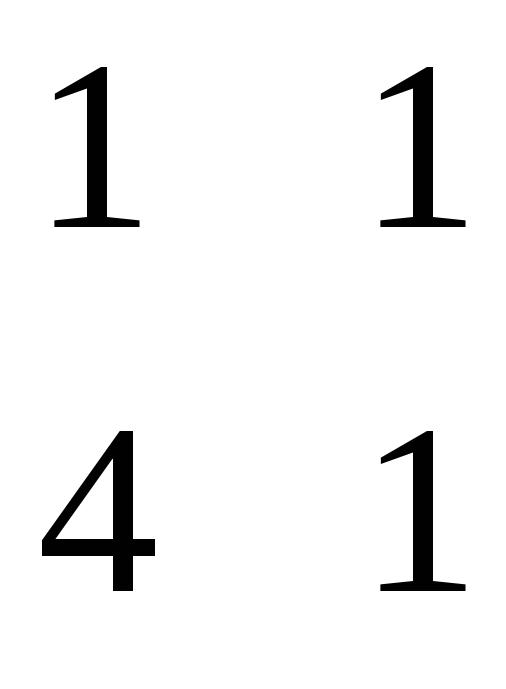
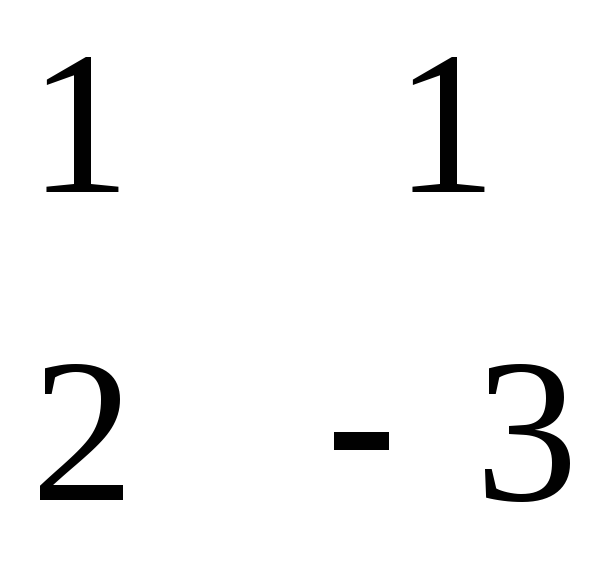
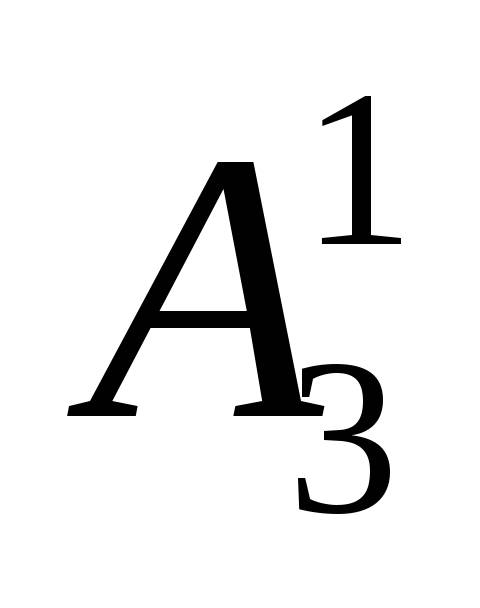
= = 14 = - = 3 = = - 5
Следовательно,
= ;
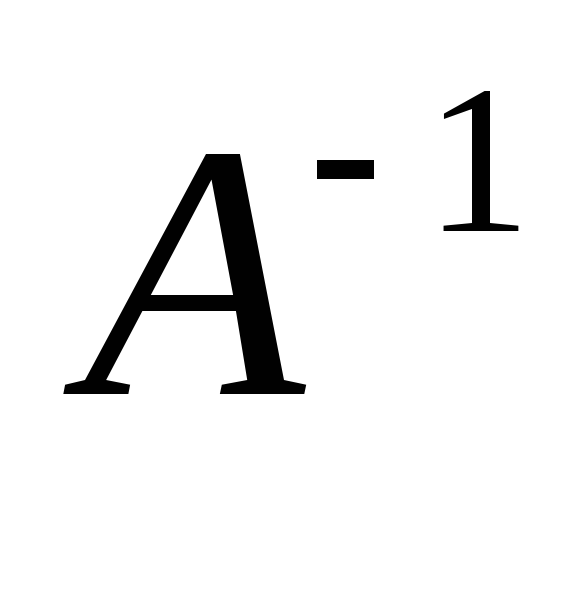
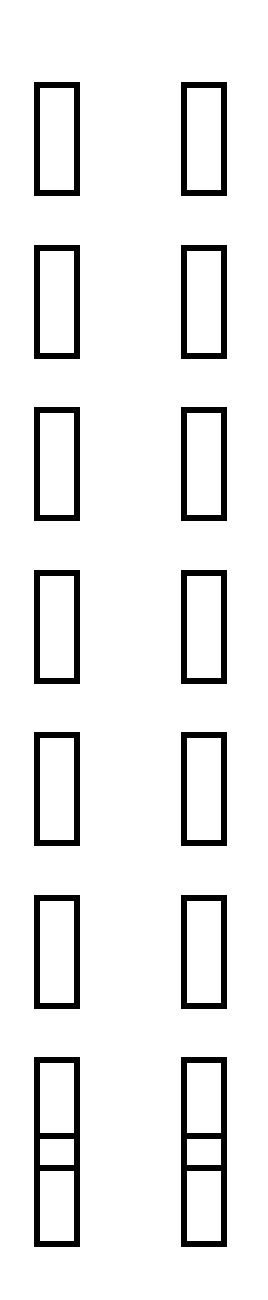
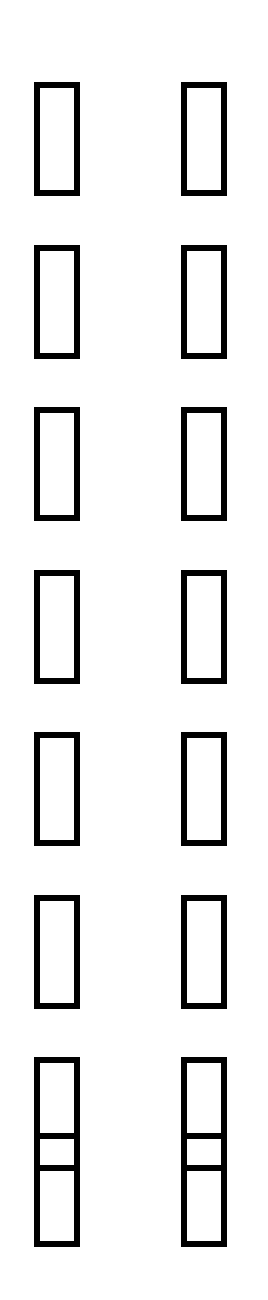
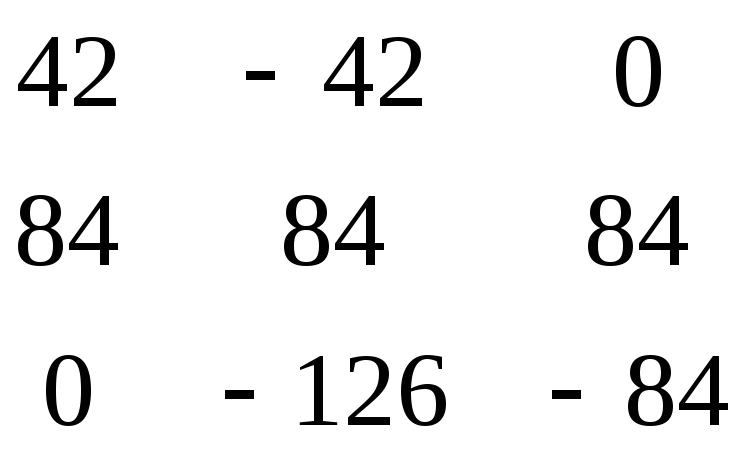
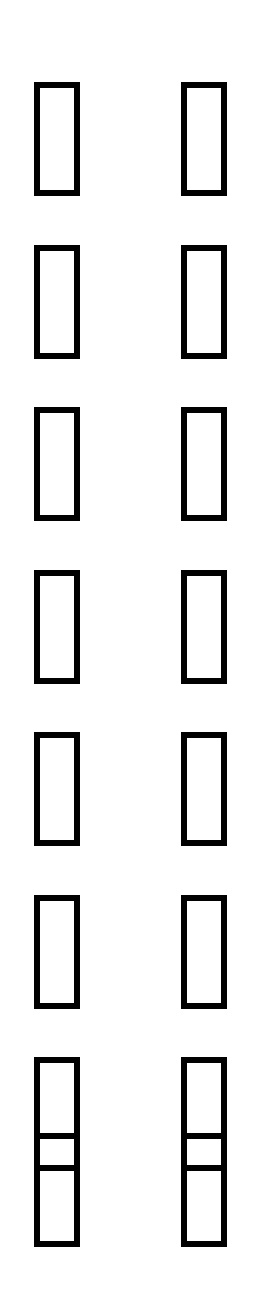
Х = * =
= = .
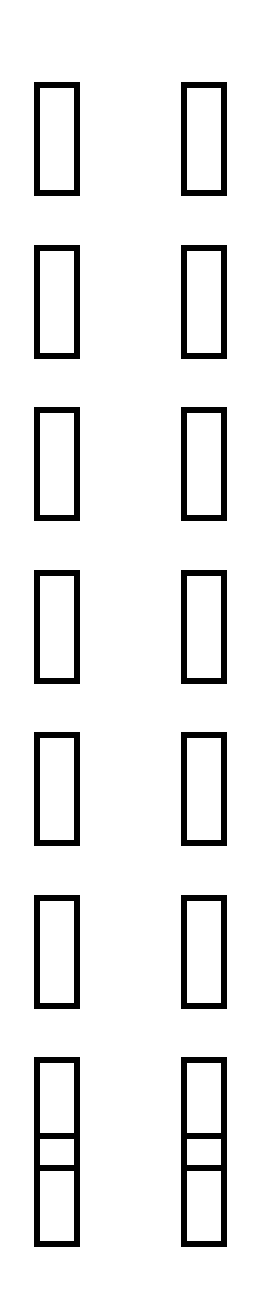
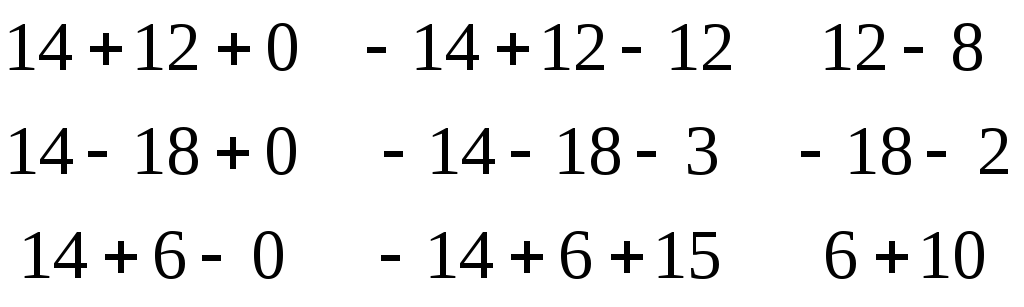
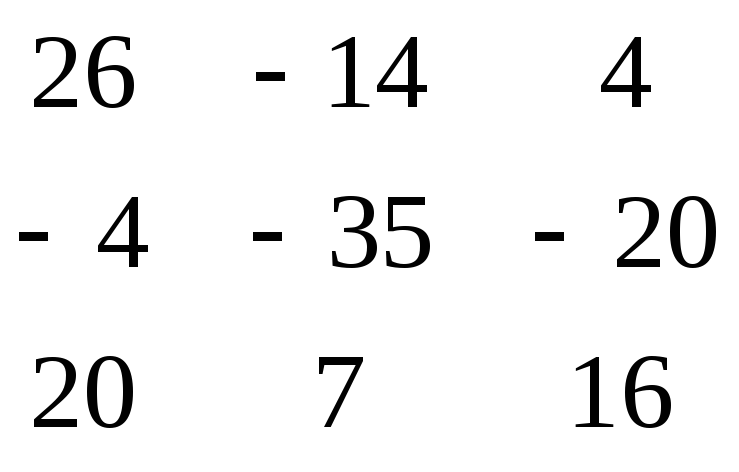
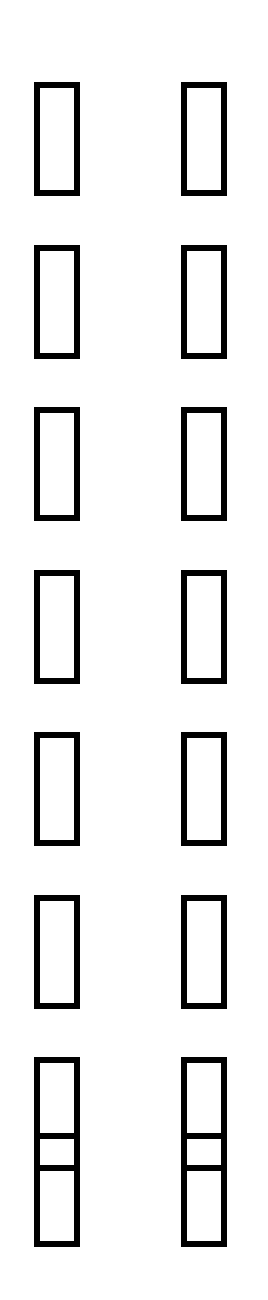
Проверка:
* = =
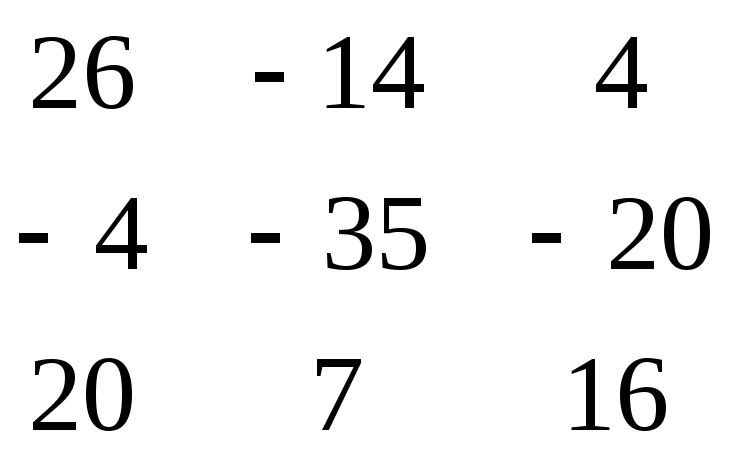
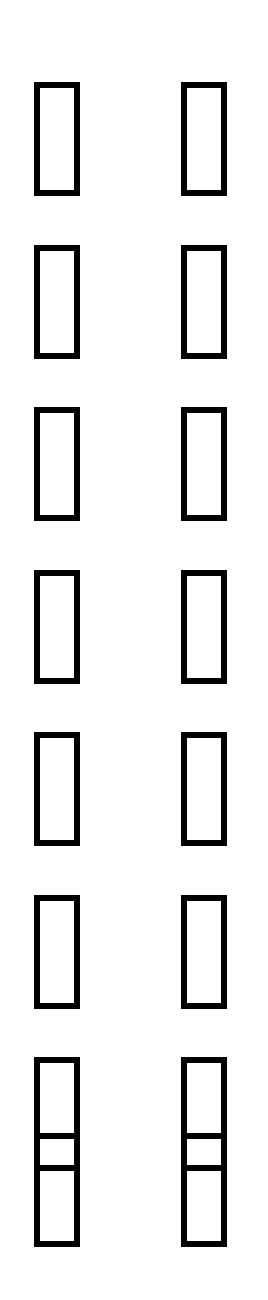
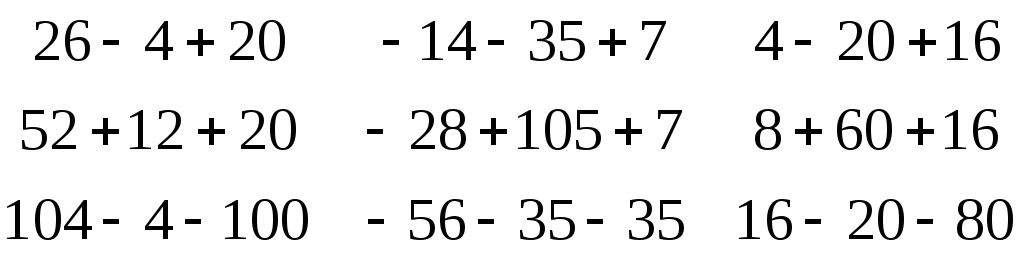
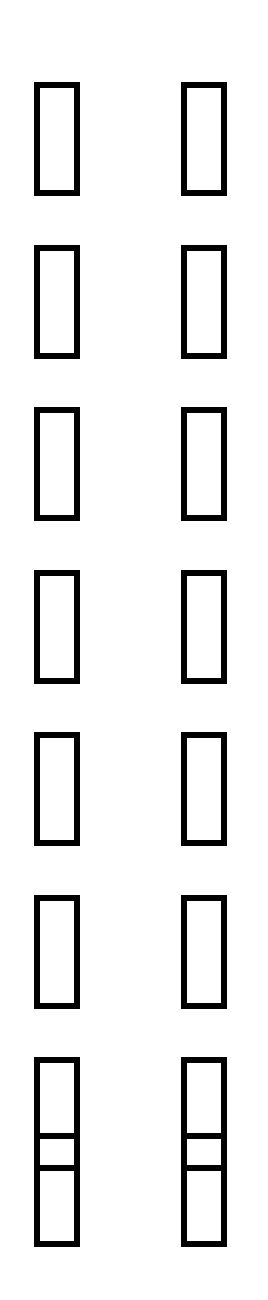
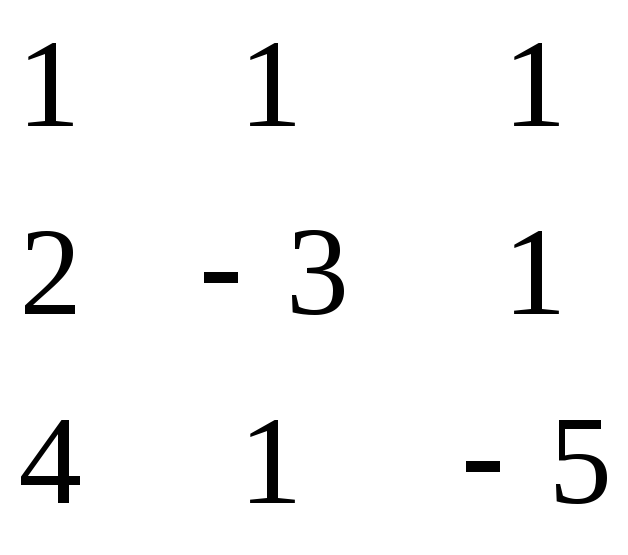
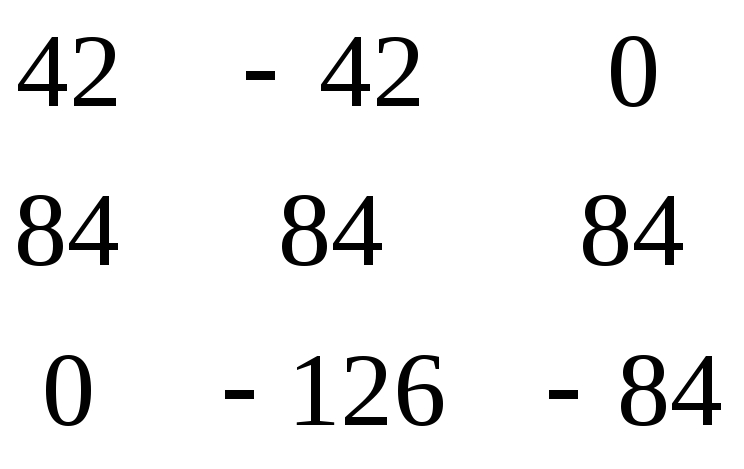
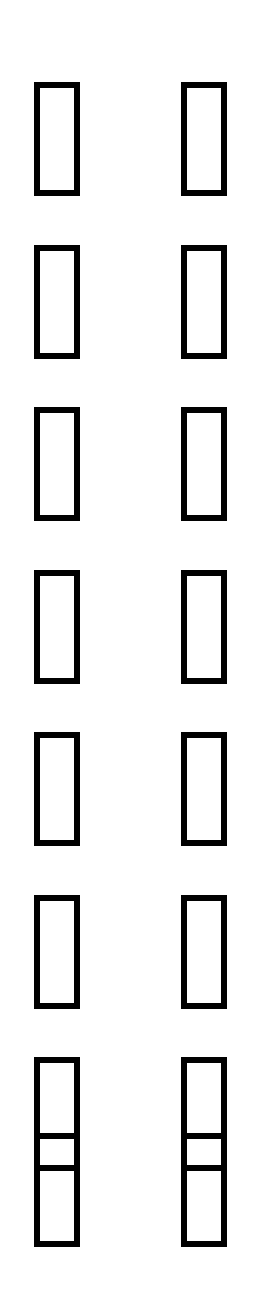
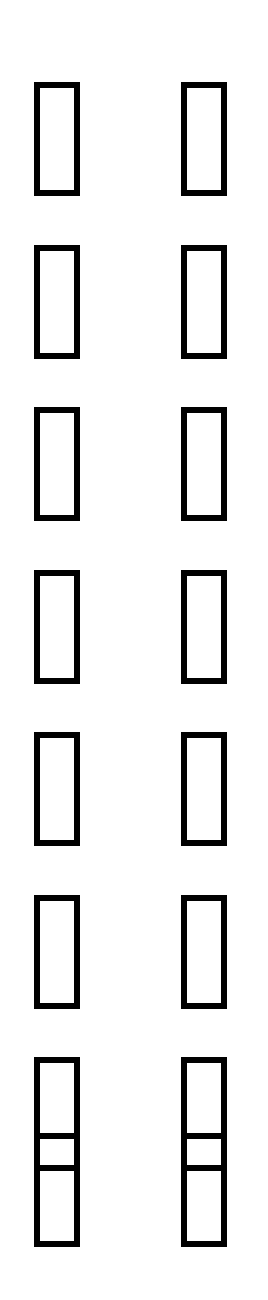
= = 42
Ответ: Следовательно, сделав проверку данного уравнения, можно сказать, что уравнение решено правильно, т.е
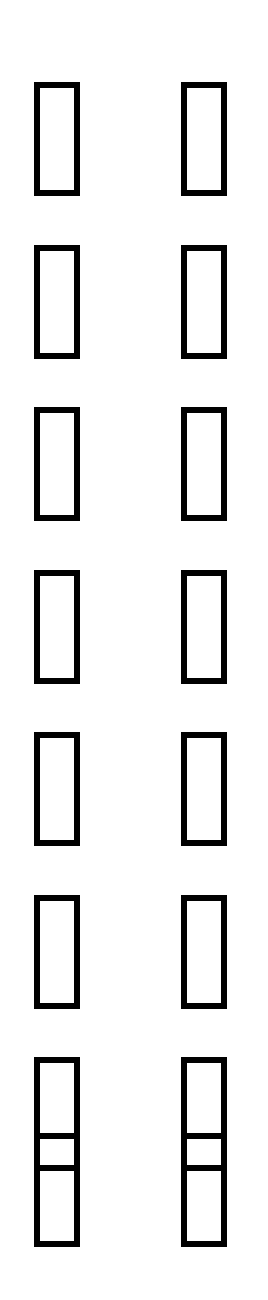
X =
studfiles.net
Контрольная работа натему:
«Матрицы, действия сними»
1. Историческаясправка
Понятие Матрица(в математике) было введено в работах У. Гамильтона и А. Кэли всередине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом(2-я половина 19 века и начало 20 века). И.А. Лаппо-Данилевский разработалтеорию аналитических функций от многих матричных аргументов и применил этутеорию к исследованию систем дифференциальных уравнений с аналитическимикоэффициентами. Матричные обозначения получили распространение в современнойматематике и её приложениях. Исчисление Матрица (в математике) развивается внаправлении построения эффективных алгоритмов для численного решения основныхзадач.
2. Раскрытиетемы
Понятие оматрице
Матрица –множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Дляобозначения матрицы используется надпись:
/>
aij, I – номер строки, j – номер столбца.
Элементыматрицы, стоящие на диагонали, идущие из верхнего левого угла называют главнойдиагональю, другую диагональ называют побочной.
/> пример 1.
Элементыглавной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
/> пример 2.
Есликоличество строк m матрицы не равно количеству столбцов n, то матрица называетсяпрямоугольной (пример 2).
Есликоличество столбцов матрицы совпадают с количеством строк, то матрица называетсяквадратной (пример 1).
Количествострок или столбцов в квадратной матрице называются ее порядком.
Если всеэлементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, томатрица называется диагональной (пример 3).
/>пример3
Если все числаглавной диагонали равны единице, то матрица называется единичной (пример 4).
/>пример 4
Если впрямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT = (2 3 5).пример 5.
Если n=1, то получаетсяматрица-столбец (пример 6).
/>пример 6.
Матрицы-строкиматрицы-столбцы называются векторами.
Свойстваматриц:
§ A + (B + C) = (A + B) + C
§ A + B = B + A
§ A(BC) = (AB) C
§ A (B + C) = AB + AC
§ (B + C) A = BA + CA
§ (AT) T= A
§ (A *B) T = BT * AT
Действия сматрицами
1. Сложениематриц
Матрицыодинакового размера можно складывать.
Суммой двухтаких матриц А и В называется матрица С, элементы которой равны суммесоответствующих элементов матриц А и В. Символически будем записывать так:А+В=С.
Пример.
/>
Легко видеть,что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулеваяматрица при сложении матриц выполняет роль обычного нуля при сложении чисел:А+0=А.
2. Вычитаниематриц.
Разностьюдвух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этогоопределения следует, что элементы матрицы С равны разности соответствующихэлементов матриц А и В.
Обозначаетсяразность матриц А и В так: С=А – В.
Пример.
/>
3.Умножение матриц
Рассмотримправило умножения двух квадратных матриц второго порядка.
/>
Произведениемматрицы А на матрицу В называется матрица С=АВ.
Правилаумножения прямоугольных матриц:
- Умножениематрицы А на матрицу В имеет смысл в том случае, когда число столбцов матрицы Асовпадает с числом строк в матрице В.
- Врезультате умножения двух прямоугольных матриц получается матрица, содержащая столькострок, сколько строк было в первой матрице и столько столбцов, сколько столбцовбыло во второй матрице.
/>
4. Умножениематрицы на число
При умноженииматрицы A на число a все числа, составляющиематрицу A, умножаются на числоa.Например, умножим матрицу /> начисло 2. Получим />, т.е. приумножении матрицы на число множитель «вносится» под знак матрицы.
5. Транспонированиематрицы
Транспонированнаяматрица – матрица AТ, полученная из исходной матрицы A заменой строкна столбцы.
Формально,транспонированная матрица для матрицы A размеров m*n – матрица AT размеров n*m, определённая как AT[i,j] = A [j, i].
Например,
/>
Свойстватранспонированных матриц
1. (AT)T = A
2.(A + B)T = AT + BT
3.(AB)T = BTAT
4.detA = detAT
Списоклитературы
1. Баврин, Матросов В.Л. Высшаяматематика: Учебник для студентов ВУЗов – М.: 2002.
2. Беллман Р. Введение втеорию матриц. – М.: Мир, 1969
3. Дж. Голуб, Ч. ВанЛоун Матричные вычисления. – М.: Мир, 1999.
www.ronl.ru
Контрольная работа на тему:
Матрицы, действия с ними
Понятие Матрица (в математике) было введено в работах У.Гамильтона и А.Кэли в середине 19 века. Основы теории созданы К.Вейерштрассом и Ф.Фробениусом (2-я половина 19 века и начало 20 века). И.А.Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление Матрица (в математике) развивается в направлении построения эффективных алгоритмов для численного решения основных задач.
Понятие о матрице
Матрица множество чисел, образующих прямоугольную таблицу, которая содержит m-строк и n-столбцов. Для обозначения матрицы используется надпись:
aij, I номер строки, j номер столбца.
Элементы матрицы, стоящие на диагонали, идущие из верхнего левого угла называют главной диагональю, другую диагональ называют побочной.
пример 1.
Элементы главной диагонали: 1,6,5. Побочной диагонали: 3,6,3. (пример 1)
пример 2.
Если количество строк m матрицы не равно количеству столбцов n, то матрица называется прямоугольной (пример 2).
Если количество столбцов матрицы совпадают с количеством строк, то матрица называется квадратной (пример 1).
Количество строк или столбцов в квадратной матрице называются ее порядком.
Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной (пример 3).
пример3
Если все числа главной диагонали равны единице, то матрица называется единичной (пример 4).
пример 4
Если в прямоугольной матрице m*n m=1, то получается матрица-строка (пример 5).
xT=(235). пример 5.
Если n=1, то получается матрица-столбец (пример 6).
пример 6.
Матрицы-строки матрицы-столбцы называются векторами.
Свойства матриц:
Действия с матрицами
Матрицы одинакового размера можно складывать.
Суммой двух таких матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В.Символически будем записывать так: А+В=С.
Пример.
Легко видеть, что сложение матриц подчиняется переместительному и сочетательному законам:
А+В=В+А
(А+В)+С=А+(В+С).
Нулевая матрица при сложении матриц выполняет роль обычного нуля при сложении чисел: А+0=А.
Разностью двух матриц А и В одинакового размера называется матрица С, такая, что
С+В=А
Из этого определения следует, что элементы матрицы С равны разности соответствующих элементов матриц А и В.
Обозначается разность матриц А и В так: С=А В.
Пример.
3. Умножение матриц
Рассмотрим правило умножения двух квадратных матриц второго порядка.
Произведением матрицы А на матрицу В называется матрица С=АВ.
Правила умножения прямоугольных матриц:
4. Умножение матрицы на число
При умножении матрицы A на число все числа, составляющие матрицу A, умножаются на число . Например, умножим матрицу на число 2. Получим , т.е. при умножении матрицы на число множитель вносится под знак матрицы.
Транспонированная матрица матрица AТ, полученная из исходной матрицы A заменой строк на столбцы.
Формально, транспонированная матрица для матрицы A размеров m*n матрица AT размеров n*m, определённая как AT[i, j] = A [j, i].
Например,
Свойства транспонированных матриц
1. (AT)T = A
2. (A + B)T = AT + BT
3. (AB)T = BTAT
4. detA = detAT
Список литературы
www.studsell.com
