по теме «Обыкновенные дифференциальные уравнения»
Определить тип дифференциального уравнения и найти его решение:
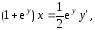
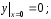
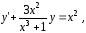
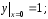
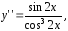
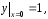
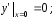
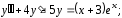
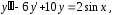
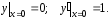
Важным теоретическим вопросом в теории дифференциальных уравнений является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и поэтому приходиться ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решений данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности (см. [2] и [4]).
Во всех вариантах контрольной работы дифференциальное уравнение первого порядка можно представить в виде разрешенном относительно первой производной:

где функция 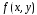 определена в некоторой области
определена в некоторой области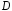 на плоскости
на плоскости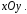
Множество точек 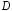 на плоскости называетсяобластью, если оно открыто и связно. Открытость
на плоскости называетсяобластью, если оно открыто и связно. Открытость 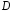 означает, что вместе с каждой своей точкой множество
означает, что вместе с каждой своей точкой множество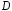 содержит и некоторый круг с центром в этой точке. Связность
содержит и некоторый круг с центром в этой точке. Связность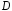 означает, что любые две точки
означает, что любые две точки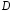 можно соединить ломаной, целиком содержащейся в
можно соединить ломаной, целиком содержащейся в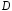 . В частности, плоскость
. В частности, плоскость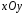 является областью.
является областью.
Для уравнения (1) справедлива следующая теорема.
Теорема Коши о существовании и единственности решения.
Пусть функция 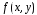 удовлетворяет двум условиям:
удовлетворяет двум условиям:
1) 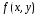 непрерывна в области
непрерывна в области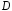 ;
;
2) имеет в 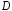 непрерывную частную производную
непрерывную частную производную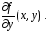
Тогда решение задачи Коши для уравнения (1) с начальными данными 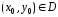 существует и единственно в том смысле, что существует единственная интегральная кривая уравнения (1), проходящая через точку
существует и единственно в том смысле, что существует единственная интегральная кривая уравнения (1), проходящая через точку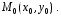
Задача нахождения решения уравнения (1), удовлетворяющего начальному условию
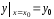 или, что то же самое,
или, что то же самое, 
называется задачей Коши.
В нашем примере
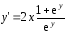 и функция
и функция 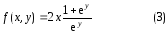
определена и непрерывна на всей плоскости 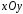 .
.
Вычислим частную производную 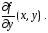 Для этого положим
Для этого положим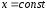 и будем рассматривать функцию
и будем рассматривать функцию
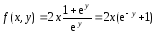
как функцию одной переменной 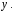 Применяя правила дифференцирования функции одной переменной, получим
Применяя правила дифференцирования функции одной переменной, получим
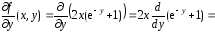
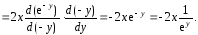
Здесь сначала постоянный множитель 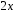 вынесли из под знака производной по переменной
вынесли из под знака производной по переменной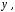 а затем применили правило дифференцирования сложной функции.
а затем применили правило дифференцирования сложной функции.
Таким образом, частная производная 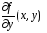 тоже определена и непрерывна на всей плоскости
тоже определена и непрерывна на всей плоскости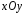 и, следовательно, теорема существования и единственности решения справедлива для уравнения (3) на всей плоскости.
и, следовательно, теорема существования и единственности решения справедлива для уравнения (3) на всей плоскости.
Анализ, проведенный выше, является основной частью решения задачи Коши, так как, используя программу типа Mathematiсa или зайдя на сайт www.wolframalpha.com (в режиме online и даже в пошаговой форме), Вы можете моментально получить решение.
Найдем общее решение дифференциального уравнения (3), не используя эти средства. Это уравнение с разделяющимися переменными (см. [2],[4] или[5]), так как оно имеет вид
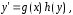
где правая часть есть произведение функции 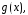 зависящей только от
зависящей только от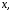 на функцию
на функцию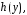 зависящую только от
зависящую только от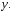
В нашем уравнении (3)
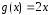 и
и 
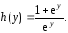
Эти функции определены и непрерывны при всех 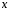 и
и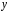 , причем
, причем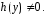
Заменим 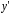 на
на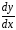 в уравнении (3):
в уравнении (3):
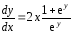
и разделим переменные, умножая обе части уравнения на выражение:

В результате получим уравнение


которое называется уравнением с разделенными переменными.
Считая 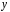 известной функцией от
известной функцией от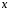 , равенство (4) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться на постоянное слагаемое.
, равенство (4) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться на постоянное слагаемое.
Интегрируя левую часть равенства (4) по 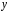 , а правую часть по
, а правую часть по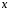 , получим
, получим
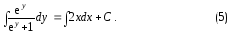
Интеграл 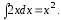
Интеграл 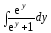 вычислим с помощью подстановки
вычислим с помощью подстановки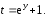
Учитывая, что 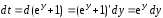 или
или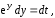
получаем
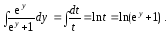
Подставляя полученные выражения в равенство (5), найдем общий интеграл уравнения (3)

В данном случае уравнение (6) можно разрешить относительно переменной 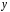 и получить общее решение дифференциального уравнения (3):
и получить общее решение дифференциального уравнения (3):
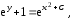
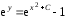 и
и 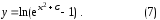
Общее решение (7) дифференциального уравнения (3) – это однопараметрическое семейство решений, существование и единственность которых гарантирует теорема существования и единственности. Оно включает в себя все решения любой задачи Коши.
Для нахождения искомого частного решения подставим в общее решение начальные значения 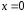 и
и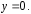 Получим
Получим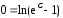 ,
,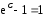 ,
,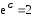 и
и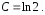
При таком выборе 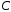 из общего решения (7) выделяется частное
из общего решения (7) выделяется частное

Ответ. Решением задачи Коши является функция 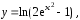 определенная на интервале
определенная на интервале
studfiles.net
Задача 1. Указать тип дифференциального уравнения и найти его общее решение.
| 1.1. | 1.2. |
| 1.3. | 1.4. |
| 1.5. | 1.6. |
| 1.7. | 1.8. |
| 1.9. | 1.10. |
| 1.11. | 1.12. |
| 1.13. | 1.14. |
| 1.15. | 1.16. |
| 1.17. | 1.18. |
| 1.19. | 1.20. |
| 1.21. | 1.22. |
| 1.23. | 1.24. |
| 1.25. | 1.26. |
| 1.27. | 1.28. |
| 1.29. | 1.30. |
Задача 2. Найти общее решение дифференциального уравнения.
| 2.1. | 2.2. |
| 2.3. | 2.4. |
| 2.5. | 2.6. |
| 2.7. | 2.8. |
| 2.9. | 2.10. |
| 2.11. | 2.12. |
| 2.13. | 2.14. |
| 2.15. | 2.16. |
| 2.17. | 2.18. |
| 2.19. | 2.20. |
| 2.21. | 2.22. |
| 2.23. | 2.24. |
| 2.25. | 2.26. |
| 2.27. | 2.28. |
| 2.29. | 2.30. |
Задача 3. Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
| 3.1. |
|
| 3.2. |
|
| 3.3. |
|
| 3.4. |
|
| 3.5. |
|
| 3.6. |
|
| 3.7. |
|
| 3.8. |
|
| 3.9. |
|
| 3.10. |
|
| 3.11. |
|
| 3.12. |
|
| 3.13. |
|
| 3.14. |
|
| 3.15. |
|
| 3.16. |
|
| 3.17. |
|
| 3.18. |
|
| 3.19. |
|
| 3.20. |
|
| 3.21. |
|
| 3.22. |
|
| 3.23. |
|
| 3.24. |
|
| 3.25. |
|
| 3.26. |
|
| 3.27. |
|
| 3.28. |
|
| 3.29. |
|
| 3.30. |
|
Задача 4. Найти общее решение системы дифференциальных уравнений.
| 4.1. | 4.2. |
| 4.3. | 4.4. |
| 4.5. | 4.6. |
| 4.7. | 4.8. |
| 4.9. | 4.10. |
| 4.11. | 4.12. |
| 4.13. | 4.14. |
| 4.15. | 4.16. |
| 4.17. | 4.18. |
| 4.19. | 4.20. |
| 4.21. | 4.22. |
| 4.23. | 4.24. |
| 4.25. | 4.26. |
| 4.27. | 4.28. |
| 4.29. | 4.30. |
1. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – М.: Айрис-пресс, 2004.
2. Бугров Я.С. Высшая математика. Дифференциальное и интегральное исчисление /
Я.С. Бугров. С.М. Никольский. – М.: Наука, 1984.
3. Бугров Я.С. Высшая математика. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров. С.М. Никольский. – М.: Наука, 1984.
4. Данко П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – 7изд., испр. – M.: ООО «Издательство Оникс»: ООО «Мир и Образование», 2008.
5. Задачи и упражнения по математическому анализу для ВТУЗов / под ред. А.В. Ефимова, В.П. Демидовича – М.: Наука, 1986.
6. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты. /
Л.А. Кузнецов – СПб.: Издательство «Лань», 2007.
7. Запорожец Г.И. Руководство к решению задач по математическому анализу: Учебное пособие. / Г.И Запорожец. - 5-е издание – СПб: Издательство «Лань», 2009.
8. Марон И.А. Дифференциальное и интегральное исчисление в примерах и задачах. Функции одной переменной / И.А. Марон – М.: Наука, 1970.
9. Рябушко А.П. Сборник индивидуальных заданий по высшей математике: Учебное пособие в 3 Ч. Ч2 / А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть. – Мн.: Высшая школа, 1991.
10. Кольчик И.В. Высшая математика: комплекс учебно-методических материалов. Ч. 2 / И.В, Кольчик. НГТУ. Нижний Новгород, 2007.
46
studfiles.net
Контрольная работа №5 Дифференциальные уравнения второго порядка с постоянными коэффициентами - страница №1/1
 Контрольная работа № 5
Контрольная работа № 5 Дифференциальные уравнения второго порядка с постоянными коэффициентами.
1.1. Однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
2. Найти частное решение

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

Найдем 

С учетом начальных условий получим систему:

Отсюда:

Тогда частное решение исходного уравнения примет вид:


Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

Найдем 

С учетом начальных условий получим систему:

Отсюда:

Тогда частное решение исходного уравнения примет вид:

5. Найти частное решение

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

Найдем 

С учетом начальных условий получим систему:

Отсюда:

Тогда частное решение исходного уравнения примет вид:


Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

Найдем 

С учетом начальных условий получим систему:

Отсюда:

Тогда частное решение исходного уравнения примет вид:

7. Найти частное решение

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

Найдем 

С учетом начальных условий получим систему:

Отсюда:

Тогда частное решение исходного уравнения примет вид:



Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

Найдем 

С учетом начальных условий получим систему:

Отсюда:

Тогда частное решение исходного уравнения примет вид:

1.2. Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
2. Найти частные решения, удовлетворяющие начальным условиям.

Искомое решение имеет вид:

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

 выберем в виде:
выберем в виде:

Находим производные:


И подставляем в левую часть уравнения:


Следовательно, общее решение неоднородного уравнения:

Найдем  :
:

И подставим в начальные условия:

Отсюда:

Тогда частное решение окончательно примет вид:


Искомое решение имеет вид:

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

 выберем в виде:
выберем в виде:

Находим производные:


И подставляем в левую часть уравнения:



Приравниваем коэффициенты при одинаковых степенях:


Следовательно, общее решение неоднородного уравнения:

Найдем  :
:

И подставим в начальные условия:


Отсюда:

Тогда частное решение окончательно примет вид:

5. Найти частные решения, удовлетворяющие начальным условиям.

Искомое решение имеет вид:

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

 выберем в виде:
выберем в виде:

Находим производные:


И подставляем в левую часть уравнения:


Следовательно, общее решение неоднородного уравнения:

Найдем  :
:

И подставим в начальные условия:

Отсюда:

Тогда частное решение окончательно примет вид:


Искомое решение имеет вид:

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

 выберем в виде:
выберем в виде:

Находим производные:


И подставляем в левую часть уравнения:



Приравниваем коэффициенты при одинаковых степенях:


Следовательно, общее решение неоднородного уравнения:

Найдем  :
:

И подставим в начальные условия:

Отсюда:

Тогда частное решение окончательно примет вид:

7. Найти частные решения, удовлетворяющие начальным условиям.

Искомое решение имеет вид:

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

 выберем в виде:
выберем в виде:

Находим производные:


И подставляем в левую часть уравнения:


Следовательно, общее решение неоднородного уравнения:

Найдем  :
:

И подставим в начальные условия:

Отсюда:

Тогда частное решение окончательно примет вид:


Искомое решение имеет вид:

Составим характеристическое уравнение:

Его корни равны:

Следовательно, общее решение имеет вид:

 выберем в виде:
выберем в виде:

Находим производные:


И подставляем в левую часть уравнения:



Приравниваем коэффициенты при одинаковых степенях:


Следовательно, общее решение неоднородного уравнения:

Найдем  :
:

И подставим в начальные условия:

Отсюда:

Тогда частное решение окончательно примет вид:

Контрольная работа № 6
Ряды, их применение.
Раздел 1. Числовые ряды.
2. Выписать три первых члена и исследовать сходимость числовых рядов:





Используем признак Даламбера:

Т.к. предел меньше единицы, то ряд сходится.





Применим интегральный признак Коши:

Т.к. интеграл существует, то ряд сходится.
5. Выписать три первых члена и исследовать сходимость числовых рядов:





Используем признак Даламбера:

Т.к. предел меньше единицы, то ряд сходится.





Применим интегральный признак Коши:

Т.к. интеграл не существует, то ряд расходится.
7. Выписать три первых члена и исследовать сходимость числовых рядов:





Используем признак Даламбера:

Т.к. предел меньше единицы, то ряд сходится.





Применим интегральный признак Коши:

Т.к. интеграл существует, то ряд сходится.
Раздел 2. Степенные ряды.
2. Найти область сходимости и проверить сходимость на границах интервала:



Находим R:

Значит область сходимости

Проверим сходимость на правой границе интервала:

Значит, границы включаются в область сходимости




Находим R:

Значит область сходимости

Проверим сходимость на правой границе интервала:

Значит, границы включаются в область сходимости

5. Найти область сходимости и проверить сходимость на границах интервала:



Находим R:

Значит область сходимости

Проверим сходимость на правой границе интервала:

Значит, границы включаются в область сходимости




Находим R:

Значит область сходимости

Проверим сходимость на правой границе интервала:

Значит, границы включаются в область сходимости

7. Найти область сходимости и проверить сходимость на границах интервала:



Находим R:

Значит область сходимости

Проверим сходимость на правой границе интервала:

Значит, границы включаются в область сходимости




Находим R:

Значит область сходимости

Проверим сходимость на правой границе интервала:

Значит, границы включаются в область сходимости

Раздел 3. Приложение степенных рядов.
3.1. Приближенное вычисление определенных интегралов.
2. Вычислить определенный интеграл с точностью до 0,001

5. Вычислить определенный интеграл с точностью до 0,001

7. Вычислить определенный интеграл с точностью до 0,001

3.2. Интегрирование дифференциальных уравнений с помощью рядов.
2. Найти три первых значащих члена разложения в степенной ряд решения дифференциального уравнения с заданным начальным условием:

Решение ищем в виде:

Необходимо найти 3 члена ряда отличных от нуля.
Из начального условия следует 
Подставляем начальное условие в правую часть исходного уравнения:

Продифференцируем решение в виде ряда:

И так как 
Продифференцируем левую и правую часть исходного уравнения:


С другой стороны,

Сравнивая значения 
Таким образом, искомое решение в виде ряда имеет вид:

5. Найти три первых значащих члена разложения в степенной ряд решения дифференциального уравнения с заданным начальным условием:

Решение ищем в виде:

Необходимо найти 3 члена ряда отличных от нуля.
Из начального условия следует 
Подставляем начальное условие в правую часть исходного уравнения:

Продифференцируем решение в виде ряда:

И так как 
Продифференцируем левую и правую часть исходного уравнения:


С другой стороны,

Сравнивая значения 

7. Найти три первых значащих члена разложения в степенной ряд решения дифференциального уравнения с заданным начальным условием:

Решение ищем в виде:

Необходимо найти 3 члена ряда отличных от нуля.
Из начального условия следует 
Подставляем начальное условие в правую часть исходного уравнения:

Продифференцируем решение в виде ряда:

И так как 
Продифференцируем левую и правую часть исходного уравнения:


С другой стороны,

Сравнивая значения 
Таким образом, искомое решение в виде ряда имеет вид:

davaiknam.ru