Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона») Литература. Контрольная работа бином ньютона
Бином Ньютона — методическая рекомендация. Алгебра, 11 класс.
|
1.
|
Определение разложения степени бинома
|
1 вид - рецептивный
|
среднее
|
4 Б.
|
Определение разложения степени бинома.
|
|
2.
|
Слагаемое в разложении степени бинома
|
2 вид - интерпретация
|
среднее
|
3 Б.
|
Вычисление требуемого слагаемого в разложении степени бинома.
|
|
3.
|
Сумма/разность слагаемых в разложении
|
2 вид - интерпретация
|
среднее
|
4 Б.
|
Вычисление суммы или разности слагаемых в разложении степени бинома.
|
|
4.
|
Слагаемое, содержащее данную переменную, в разложении степени бинома
|
2 вид - интерпретация
|
среднее
|
4 Б.
|
Определение слагаемого, содержащего данную переменную, в разложении степени бинома.
|
|
5.
|
Вычисление значения бинома
|
2 вид - интерпретация
|
среднее
|
4 Б.
|
Использование биноминальной формулы Ньютона для вычисления значения бинома, представленного в виде разложения степени бинома.
|
|
6.
|
Число рациональных слагаемых
|
3 вид - анализ
|
среднее
|
2 Б.
|
Задано разложение бинома Ньютона
|
|
7.
|
Алгебраическая сумма коэффициентов многочлена
|
3 вид - анализ
|
сложное
|
3 Б.
|
Заданы коэффициенты бинома Ньютона
|
|
8.
|
Слагаемое, не содержащее х
|
3 вид - анализ
|
сложное
|
3 Б.
|
Слагаемое содержит корень, вычисление размещения.
|
|
9.
|
Наибольшее слагаемое в разложении бинома Ньютона
|
3 вид - анализ
|
сложное
|
4 Б.
|
Бином содержит квадратный корень
|
www.yaklass.ru
Бином Ньютона, формула и пример решения по алгебре в 11 классе
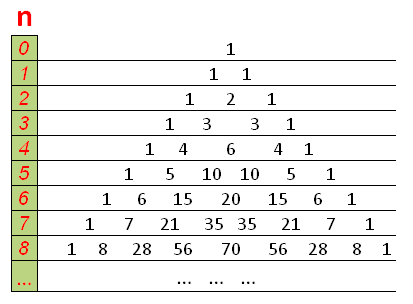
Ребята, на прошлом уроке мы с вами изучали перестановки и размещения. Сегодня мы остановимся на одном из самых замечательных применением формулы перестановок. Числа $C_n^{k}$ имеют очень красивую и знаменитую запись, которая имеет большое значение. Такая запись называется треугольником Паскаля: 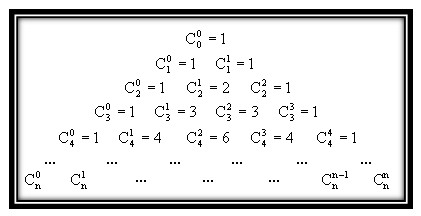 Правило записи треугольника легко запомнить. Каждое число в треугольнике паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте распишем несколько строк:
Правило записи треугольника легко запомнить. Каждое число в треугольнике паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте распишем несколько строк: 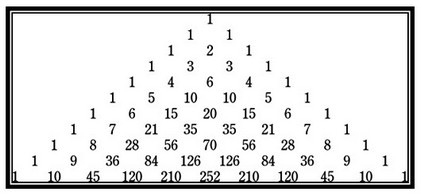 Математически свойство подсчета числа сочетаний без повторений можно записать еще вот так:
Математически свойство подсчета числа сочетаний без повторений можно записать еще вот так: 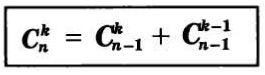 Как оказалось треугольника Паскаля находит свое применение и в другой математической задаче. Давайте вспомним несколько правил возведения в квадрат суммы. Самое первое правило, которое мы с вами выучили, это квадрат суммы: $(a+b)^2=a^2+2ab+b^2$. Довольно таки легко найти выражение и для следующей степени, используя правила перемножения многочленов: $(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$. Проделаем эту же операцию и для четвертой степени: $(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.
Как оказалось треугольника Паскаля находит свое применение и в другой математической задаче. Давайте вспомним несколько правил возведения в квадрат суммы. Самое первое правило, которое мы с вами выучили, это квадрат суммы: $(a+b)^2=a^2+2ab+b^2$. Довольно таки легко найти выражение и для следующей степени, используя правила перемножения многочленов: $(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$. Проделаем эту же операцию и для четвертой степени: $(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.Выпишем для наглядности все наши формулы:$(a+b)^1=a+b$.$(a+b)^2=a^2+2ab+b^2$.$(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$.$(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.
Давайте проведем небольшой анализ полученных формул.
Обратить внимание: показатель степени в левой части равен сумме показателей степеней в правой части для любого слагаемого.
Для четвертой степени, очевидно, что слева показатель равен 4. В правой части показатель степени при первом слагаемом равен для а четырем, для b нулю и в сумме равен 4.
Для второго слагаемого сумма показателей равна $3+1=4$, для следующего - $2+2=4$ и так до самого конца сумма показателей равна 4.
Ребята, посмотрите внимательно на коэффициенты в правой части. Что он вам напоминает? Правильно, коэффициенты образуют треугольник Паскаля.
Эти два замечательных свойства, замеченных выше, позволяют вычислять сумму двух одночленов в n-ой степени:$(a+b)^n=C_n^{0}a^n+C_n^{1}a^{n-1}b+C_n^{2}a^{n-2}b^2+C_n^{3}a^{n-3}b^3+...+C_n^{k}a^{n-k}b^k+...+C_n^{n-1}ab^{n-1}+C_n^{n}b^n$.
Давайте попробуем доказать нашу формулу:Рассмотрим слагаемое, стоящее на месте под номером $k+1$. По написанной выше формуле получаем, вот такое слагаемое: $C_n^{k}a^{n-k}b^k$.Нам нужно доказать, что коэффициент при данном одночлене как раз и равен $C_n^{k}$.Для того, чтобы двучлен возвести в n-ую степень нам нужно этот двучлен умножить на себя n раз, то есть: 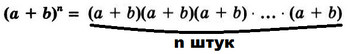 Чтобы получить требуемое слагаемое надо выбрать k штук множителей для b. Тогда получается $n-k$ множителей для а. В каком порядке будем выбирать данные множители не важно. Эта задача есть ни что иное как: число сочетаний из n элементов по k без повторений или $C_n^{k}$. Наша формула доказана.
Чтобы получить требуемое слагаемое надо выбрать k штук множителей для b. Тогда получается $n-k$ множителей для а. В каком порядке будем выбирать данные множители не важно. Эта задача есть ни что иное как: число сочетаний из n элементов по k без повторений или $C_n^{k}$. Наша формула доказана.
Полученная нами формула называется "Бином Ньютона".
$(a+b)^n=C_n^{0}a^n+C_n^{1}a^{n-1}b+C_n^{2}a^{n-2}b^2+C_n^{3}a^{n-3}b^3+...+C_n^{k}a^{n-k}b^k+...+C_n^{n-1}ab^{n-1}+C_n^{n}b^n$.
Коэффициенты, стоящие перед слагаемыми, это биномиальные коэффициенты.
Пример. Раскрыть скобки: а) $(y+1)^7$; б) $(z^2-3t)^5$.Решение. Применим нашу формулу:$а(y+1)^7=C_7^{0}y^7+C_7^{1}*y^6*1+C_7^{2}*y^5*1^2+C_7^{3}*y^4*1^3+C_7^{4}*y^3*1^4+$$+C_7^{5}*y^2*1^5+C_7^{6}*y*1^6+C_7^{7}*1^7$.
Вычислим все коэффициенты:$C_7^{0}=1$; $C_7^{1}=7$; $C_7^2=\frac{7!}{2!5!}=21$; $C_7^3=35$; $C_7^4=35$; $C_7^5=21$; $C_7^6=7$; $C_7^7=1$.
В итоге получаем: $(y+1)^7=y^7+7*y^6+21*y^5+35*y^4+35*y^3+21*y^2+7*y+1$.
б) $(z^2-3t)^5=C_5^{0}*(z^2)^5+C_5^{1}*(z^2 )^4*(-3t)^1+C_5^{2}*(z^2)^3*(-3t)^2+$$C_5^{3}*(z^2 )^2*(-3t)^3+C_5^{4}*(z^2)^1*(-3t)^4+C_5^{5}*(z^2)^0*(-3t)^5=$$z^{10}+5*z^8*(-3t)+10*z^6*(9t^2)+10*z^4*(-27t^3)+5*z^2*(81t^4)-243t^5=$$z^{10}-15z^8 t+90z^6t^2-270z^4t^3+405z^2t^4-243t^5$.
В конце урока обратим вниманием на еще одно удивительное свойство.Рассмотрим двучлен: $(x+1)^n$.Используя Бином Ньютона получим: При $х=1$ получаем: $(x+1)^n=C_n^{0}x^n+C_n^{1}x^{n-1}+C_n^{2}x^{n-2}+C_n^{3}x^{n-3}+...+C_n^{n-2}x^{2}+C_n^{n-1}x+C_n^{n}$.При $х=1$ получаем: $2^n=C_n^{0}+C_n^{1}+C_n^{2}+C_n^{3}+...+C_n^{n-2}+C_n^{n-1}+C_n^{n}$.
Задачи для самостоятельного решения
Избавтесь от скобок: а) $(x+2)^6$; б) $(3x+2y)^4$; в) $(2z-2t)^8$; г) $(x-4y)^5$.mathematics-tests.com
Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона») Литература
id_016
Курьякова Татьяна Сергеевна
учитель математики МОУ «СОШ №36», г. Ангарск
Бином Ньютона – одна из тем, рассмотрение которых способствует глубинному пониманию учащимися на только комбинаторных понятий, но и формул сокращенного умножения. В данной статье представлен один из вариантов лекции для старшеклассников по теме «Бином Ньютона».
Тема: «Бином Ньютона»
План лекции 1. Понятие бинома Ньютона
2. Свойства бинома и биномиальных коэффициентов
3. Типовые задачи по теме «Бином Ньютона»
4. Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона»)
Литература
1. Сборник конкурсных задач по математике для поступающих во втузы / Под ред. М.И.Сканави: Учеб. пособие. Санкт-Петербург, 1995. – с.84.
2. Супрун В.П. Избранные задачи повышенной сложности по математике. Мн.: Полымя, 1998. – 108с.
– 1 –
Понятие бинома Ньютона
Биномом Ньютона называют разложение вида:

Но, строго говоря, всю формулу нельзя назвать биномом, так как «бином» переводится как «двучлен». Кроме того, формула разложения была известна еще до Ньютона, Исаак Ньютон распространил это разложение на случай n
Цель изучения бинома Ньютона – упрощение вычислительных действий.
Компоненты формулы «бином Ньютона»:
правая часть формулы – разложение бинома;

 – биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
– биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Например, четвертая строчка треугольника как раз наглядно демонстрирует биномиальные коэффициенты для бинома четвертой степени:

Альтернатива треугольнику Паскаля:
перемножить почленно четыре скобки:
 ;
;
вспомнить разложение бинома Ньютона четвертой степени:

где Т – член разложения;  – порядковый номер члена разложения.
– порядковый номер члена разложения.
– 2 –
Свойства бинома и биномиальных коэффициентов

Число всех членов разложения на единицу больше показателя степени бинома, то есть равно 
Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома, то есть n
Доказательство
Рассмотрим  -й член разложения:
-й член разложения: 
Сумма показателей степеней a и b: 
Ч.т.д.
Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой:  (правило симметрии)
(правило симметрии)
Сумма биномиальных коэффициентов всех членов разложения равна 
Доказательство

Пусть  , тогда:
, тогда:
Тогда: 

Ч.т.д.
Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна 

Правило Паскаля: 
Доказательство – самостоятельно
Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби 

Доказательство – самостоятельно
– 3 –
Типовые задачи по теме «Бином Ньютона»
К типовым (стандартным) заданиям по данной теме можно отнести задачи на вычисление, среди которых:
Найти член (номер члена) разложения бинома
Вывести бином по известным членам разложения (по известной сумме)
Вычислить сумму биномиальных коэффициентов разложения бинома
и другие.
Продемонстрируем на примерах (их решение несложное, поэтому большинство предлагаем решить самостоятельно).
Пример 1
Разложить по формуле бином 
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на знакочередование!
Пример 2
Найти шестой член разложения 
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на знак!
Лучше начинать рассуждения со следующего: 
Пример 3
Найдите два средних члена разложения 
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на то, что эти члены равноотстоят от конца, поэтому их биномиальные коэффициенты будут равны.
НЕ ЗАБУДЬТЕ в процессе решения проводить преобразования степеней с одинаковыми основаниями (то есть упрощать).
Пример 4
В биномиальном разложении  найти член разложения, не содержащий х
найти член разложения, не содержащий х
Решение

Так как в разложении мы ищем член не содержащий х, то 
Тогда 
Ответ: 
– 4 –
Задачи, сводящиеся к использованию формулы бинома Ньютона
(нестандартные задачи по теме «Бином Ньютона»)
К нестандартным заданиям по данной теме можно отнести такие, в которых нет явного намека на необходимость использования бинома. Однако в итоге, решение сводится к нему и выглядит очень интересным.
Пример 5
Доказать, что для любых  и для любых
и для любых  верно неравенство Бернулли:
верно неравенство Бернулли:

Доказательство
Пусть 
Так как  , то
, то 
Переформулируем требование: Доказать, что  , где
, где 

Так как  , значит в разложении как минимум три члена разложения, тогда:
, значит в разложении как минимум три члена разложения, тогда:

Это означает, что 
Ч.т.д.
Пример 6
Доказать, что 
Доказательство – самостоятельно
(Подсказка: используйте неравенство Бернулли)
Пример 7
Доказать, что при любом натуральном n число  делится на 9
делится на 9
Доказательство
1 способ:


Ч.т.д.
2 способ:
Начнем рассматривать бином в общем виде:

Тогда 
Ч.т.д.
Пример 8
Решить уравнение 
Решение
Осуществим замену: 
Тогда уравнение перепишем: 
Применим формулу бинома к левой части уравнения:

В итоге 
Ответ: 

Дополнительные задания для самостоятельного выполнения
Найти номер члена разложения бинома  , не содержащего х.
, не содержащего х.
Найти пятый член разложения бинома  .
.
Найти сумму биномиальных коэффициентов членов, стоящих на нечетных местах в разложении бинома  , если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.
, если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.
Найти седьмой член разложения бинома  , если биномиальный коэффициент третьего члена равен 36.
, если биномиальный коэффициент третьего члена равен 36.
Сколько членов разложения бинома  являются целыми числами?
являются целыми числами?
Вычислить сумму  .
.
Найти алгебраическую сумму коэффициентов многочлена относительно х, получаемого в разложении бинома  .
.
Сумма нечетных биномиальных коэффициентов разложения  равна 512. Найти слагаемое, не содержащее х.
равна 512. Найти слагаемое, не содержащее х.
При каких значениях х четвертое слагаемое разложения  больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых?
При каком значении х четвертое слагаемое разложения  в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1?
в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1?
В какую наибольшую степень следует возвести бином  чтобы отношение четвертого слагаемого разложения к третьему было равно
чтобы отношение четвертого слагаемого разложения к третьему было равно  ?
?
gigabaza.ru
Электронный конспект для проведения урока+самостоятельная работа по теме "Формула бинома Ньютона"


 Формула бинома Ньютона
Формула бинома Ньютона
Возведение выражения (a + b) в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
(a + b)n = an + C1n an - 1 b + C2n an - 2 b2 +...+Ckn an - k bk +... + Cn - 1n abn - 1 + Cnnbn
Если k-й элемент разложения степени бинома обозначать через ТK , то
Тк = 
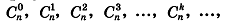
 - биноминальные коэффициенты
- биноминальные коэффициенты
Примеры:
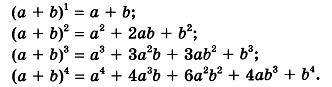
Примеры
№1
Разложите на множители:
(a + b)5 = ?
(a + b)n = an + C1n an - 1 b + C2n an - 2 b2 +...+Ckn an - k bk +... + Cn - 1n abn - 1 + Cnnbn
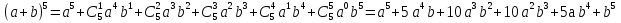
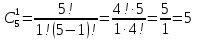
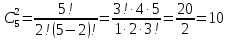
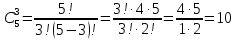
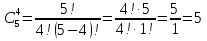
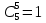
№ 2
Раскрыть скобки:
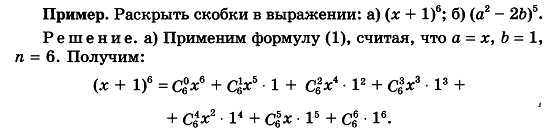
(a + b)n = an + C1n an - 1 b + C2n an - 2 b2 +...+Ckn an - k bk +... + Cn - 1n abn - 1 + Cnnbn
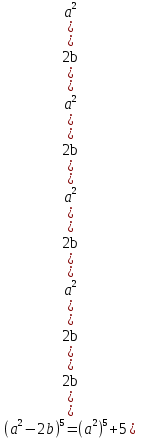 ………
………
Треугольник Паскаля
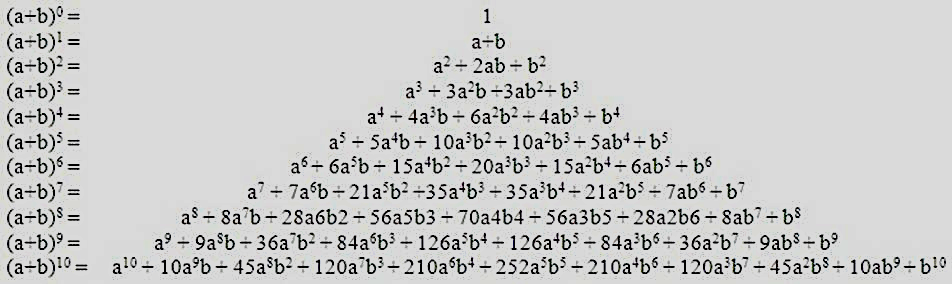
№ 3
Найдите коэффициент при 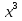 :
:
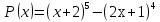
Решение:
Р(х) = …….+ 10х3∙22 +…..-(4∙(2х)3∙11)…..= …+40х3 …-(4∙8х3)+…= …+ 40х3…..- 32х3
Ответ: 40; -32
Подсчет биноминальных коэффициентов. Самостоятельная работа
№ 1
Вычислить:
а) C52; б) C83; г) C76; д) C104; e) C65
№ 2
Раскройте скобки в выражении:
А) 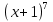 В)
В) 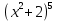
Б) 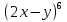 Г)
Г) 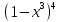
№ 3
Вычислить по формуле бинома Ньютона:
а) (√5 — √2 )4; б) (√6 + √2 )4; в) (√6 — √2)5; г) (√10 — √2)5.
№ 4
Найдите коэффициент при первой степени переменной x:
А) 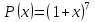
Б) 
№ 5
Найдите коэффициент при 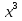 :
:
А) 
Б)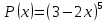
Внеаудиторная самостоятельная работа. Решение задачи по теме «Бином Ньютона».
№ 1
Возведите в четвертую степень выражение (х + 2у)
№ 2
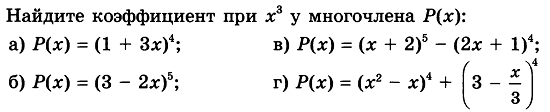
infourok.ru
2.1.9. Сочетания с повторениями
Задача. Найти количество сочетаний с повторениями изnпредметов поr.
сочетаний с повторениями изnпредметов поr.
Рассмотрим вывод формулы на примере с фотографиями (см. 2.1.2). Имеется nтипов предметов ( негатива). Нужно составить набор изr предметов (
негатива). Нужно составить набор изr предметов ( фотографий). Наборы различаются своим составом, а не порядком элементов. Например, разными будут наборы состава
фотографий). Наборы различаются своим составом, а не порядком элементов. Например, разными будут наборы состава и
и – один содержит три фотографии с первого негатива и по одной со второго и с третьего, а другой – одну с первого и четыре с третьего. Разложим эти наборы на столе, разделяя фотографии разного типа карандашами. Карандашей нам понадобится
– один содержит три фотографии с первого негатива и по одной со второго и с третьего, а другой – одну с первого и четыре с третьего. Разложим эти наборы на столе, разделяя фотографии разного типа карандашами. Карандашей нам понадобится , а фотографий
, а фотографий . Мы будем получать различные сочетания с повторениями, переставляя между собой эти
. Мы будем получать различные сочетания с повторениями, переставляя между собой эти предметов, т.е.
предметов, т.е. - число сочетаний с повторениями изnпредметов поrравно числу перестановок с повторениями длины
- число сочетаний с повторениями изnпредметов поrравно числу перестановок с повторениями длины состава
состава . В нашем примере
. В нашем примере

Иначе формулу сочетаний с повторениями можно записать


1.5.10. Решение задач 2,3 контрольной работы № 2
При решении задач комбинаторики рекомендуем выбирать нужную формулу, пользуясь блок-диаграммой (рис. 2.1).
Задача 3. В профком избрано 9 человек. Из них надо выбрать председателя, его заместителя и казначея. Сколькими способами это можно сделать?
Решение. Составим список в порядке: председатель, заместитель, казначей. Выбираем трех из 9 человек, т.е. . Порядок важен? Да, выбираем правую часть блок-диаграммы (рис. 2.1). Следующий вопрос: выбираем всеnэлементов? Нет. Повторения есть? Нет. Следовательно, наша выборка – размещение без повторений и количество таких выборок
. Порядок важен? Да, выбираем правую часть блок-диаграммы (рис. 2.1). Следующий вопрос: выбираем всеnэлементов? Нет. Повторения есть? Нет. Следовательно, наша выборка – размещение без повторений и количество таких выборок

Задача 2. Сколькими способами 40 человек можно рассадить в три автобуса, если способы различаются только количеством человек в каждом автобусе?
Решение. Выстроим 40 человек в очередь и выдадим каждому билет с номером автобуса. Получим выборку, например, такую: .В этой выборке 40 элементов (
.В этой выборке 40 элементов ( ), а значений – номеров автобусов – три (
), а значений – номеров автобусов – три ( ). Порядок важен? Чтобы ответить на этот вопрос, поменяем местами двух человек в очереди и посмотрим, изменилась ли выборка. Выборка не изменилась, т.к. количество людей в каждом автобусе осталось прежним. Порядок не важен, поэтому выбираем левую часть блок-диаграммы (рис. 2.1). Повторения есть? Да, в нашей выборке номер автобуса может встречаться несколько раз. Следовательно, выборка является сочетанием с повторениями из
). Порядок важен? Чтобы ответить на этот вопрос, поменяем местами двух человек в очереди и посмотрим, изменилась ли выборка. Выборка не изменилась, т.к. количество людей в каждом автобусе осталось прежним. Порядок не важен, поэтому выбираем левую часть блок-диаграммы (рис. 2.1). Повторения есть? Да, в нашей выборке номер автобуса может встречаться несколько раз. Следовательно, выборка является сочетанием с повторениями из по
по элементов:
элементов:

2.1.11. Бином Ньютона
В школе изучают формулы сокращенного умножения:

Бином Ньютона позволяет продолжить этот ряд формул. Раскроем скобки в следующем выражении:

Общий член суммы будет иметь вид  Чему равен коэффициентC? Он равен количеству способов, которыми можно получить слагаемое
Чему равен коэффициентC? Он равен количеству способов, которыми можно получить слагаемое (т.е. количеству способов, которыми можно выбратьkскобок с множителемa, а из остальных
(т.е. количеству способов, которыми можно выбратьkскобок с множителемa, а из остальных скобок взять множительb). Например, если
скобок взять множительb). Например, если то слагаемое
то слагаемое можем получить, выбрав множительaиз первой и пятой скобки. Каков тип выборки? Порядок перечисления не важен (выбираем сначала первую, затем пятую скобки, или, наоборот, сначала пятую, затем первую – безразлично), повторяющихся элементов (одинаковых номеров скобок) в выборке нет. Это сочетание без повторений. Количество таких выборок равно
можем получить, выбрав множительaиз первой и пятой скобки. Каков тип выборки? Порядок перечисления не важен (выбираем сначала первую, затем пятую скобки, или, наоборот, сначала пятую, затем первую – безразлично), повторяющихся элементов (одинаковых номеров скобок) в выборке нет. Это сочетание без повторений. Количество таких выборок равно

Таким образом, формула бинома для произвольного натурального nимеет вид:

или
 .
.
Пример. При получим формулу
получим формулу

т.к. 
Проверьте правильность формулы, перемножив  на
на .
.
Строгое доказательство формулы бинома Ньютона проводится методом математической индукции.
studfiles.net
ГЛАВА 2. БИНОМ НЬЮТОНА Свойства сочетаний. Бином Ньютона.
Авторы работы: Луцков Никита, 7ж класс
 Авторы работы: Луцков Никита, 7ж класс Sir Isaac Newton «Немало ещё людей, которые знают о Ньютоне лишь то, что связано с рассказом о яблоке.» С. И. Вавилов Без имени Ньютона нет физики, а для Ньютона
Авторы работы: Луцков Никита, 7ж класс Sir Isaac Newton «Немало ещё людей, которые знают о Ньютоне лишь то, что связано с рассказом о яблоке.» С. И. Вавилов Без имени Ньютона нет физики, а для Ньютона
Подробнее 3x x 2 + x = 0.
 4.. Метод замены переменной при решении алгебраических уравнений. В предыдущем пункте метод замены переменной был использован для разложения многочлена на множители. Данный метод широко применяется для
4.. Метод замены переменной при решении алгебраических уравнений. В предыдущем пункте метод замены переменной был использован для разложения многочлена на множители. Данный метод широко применяется для
Подробнее Qui genus humanum ingenio superavit
 Исаак Ньютон Qui genus humanum ingenio superavit Выполнила: ученица 9 класса «Б» Разумом он превосходил род человеческий гимназии 1517 Зюзюкова Мария Не знаю, как меня воспринимает мир, но сам себе я кажусь
Исаак Ньютон Qui genus humanum ingenio superavit Выполнила: ученица 9 класса «Б» Разумом он превосходил род человеческий гимназии 1517 Зюзюкова Мария Не знаю, как меня воспринимает мир, но сам себе я кажусь
Подробнее Тема 29 «Геометрическая прогрессия»
 Тема 29 «Геометрическая прогрессия» Последовательность чисел, каждый следующий член которой равен предыдущему, умноженному на одно и то же число, называется геометрической прогрессией. Это число называется
Тема 29 «Геометрическая прогрессия» Последовательность чисел, каждый следующий член которой равен предыдущему, умноженному на одно и то же число, называется геометрической прогрессией. Это число называется
Подробнее Примеры и комментарии
 72 Глава2 Многочлены Примеры и комментарии Алгоритмы А-01 Запись многочлена в стандартном виде А-02 Действия над многочленами А-03 Устные преобразования А-04 Формулы сокращенного умножения А-05 Бином Ньютона
72 Глава2 Многочлены Примеры и комментарии Алгоритмы А-01 Запись многочлена в стандартном виде А-02 Действия над многочленами А-03 Устные преобразования А-04 Формулы сокращенного умножения А-05 Бином Ньютона
Подробнее Алгебраические уравнения
 Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами
Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами
Подробнее Презентация (по физике)
 Презентация (по физике) Исаак Ньютон ( 04.01.1643 года - 31.03.1727 года ) Великобритания Выдающийся английский учѐный, заложивший основы современного естествознания, создатель классической физики, член
Презентация (по физике) Исаак Ньютон ( 04.01.1643 года - 31.03.1727 года ) Великобритания Выдающийся английский учѐный, заложивший основы современного естествознания, создатель классической физики, член
Подробнее РЯДЫ. Методические указания
 Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Подробнее Математика 8 класс Многочлены
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
Подробнее Глава 3. Определители
 Глава Определители Перестановки Q Рассмотрим множество первых натуральных чисел которое обозначим как Определение Перестановкой P множества элементов из Q назовем любое расположение этих элементов в некотором
Глава Определители Перестановки Q Рассмотрим множество первых натуральных чисел которое обозначим как Определение Перестановкой P множества элементов из Q назовем любое расположение этих элементов в некотором
Подробнее Пояснительная записка
 1 Пояснительная записка Рабочая программа элективного курса «МИР, МАТЕМАТИКА, МАТЕМАТИКИ» Для10-11 классов, составлена в соответствии с программой А.Н. Землякова «Элективные курсы в профильном обучении.
1 Пояснительная записка Рабочая программа элективного курса «МИР, МАТЕМАТИКА, МАТЕМАТИКИ» Для10-11 классов, составлена в соответствии с программой А.Н. Землякова «Элективные курсы в профильном обучении.
Подробнее Лекция 2: перечслительная комбинаторика
 Лекция 2: перечслительная комбинаторика Дискретная математика, ВШЭ, факультет компьютерных наук (Осень 2014 весна 2015) Задачи перечислительной кмбинаторики имеют типовой вид: «сколько способов сделать
Лекция 2: перечслительная комбинаторика Дискретная математика, ВШЭ, факультет компьютерных наук (Осень 2014 весна 2015) Задачи перечислительной кмбинаторики имеют типовой вид: «сколько способов сделать
Подробнее ОГЛАВЛЕНИЕ. Предисловие... 3
 ОГЛАВЛЕНИЕ Предисловие............................................ 3 Часть 1. Лекции......................................... 4 1. Определение и простейшие свойства чисел Фибоначчи.... 4 2. Биномиальные
ОГЛАВЛЕНИЕ Предисловие............................................ 3 Часть 1. Лекции......................................... 4 1. Определение и простейшие свойства чисел Фибоначчи.... 4 2. Биномиальные
Подробнее «Последняя загадка Пьера Ферма-2»
 «Последняя загадка Пьера Ферма-» Некоторое время назад я опубликовал работу «Последняя загадка Пьера Ферма» в которой записал доказательство Большой теоремы Ферма (http://wbabi.et/mitkovsky/mitkovsky6.pdf,
«Последняя загадка Пьера Ферма-» Некоторое время назад я опубликовал работу «Последняя загадка Пьера Ферма» в которой записал доказательство Большой теоремы Ферма (http://wbabi.et/mitkovsky/mitkovsky6.pdf,
Подробнее Делимость. Общие свойства
 И. В. Яковлев Материалы по математике MathUs.ru Содержание Делимость. Общие свойства 1 Всероссийская олимпиада школьников по математике................ 1 2 Московская математическая олимпиада........................
И. В. Яковлев Материалы по математике MathUs.ru Содержание Делимость. Общие свойства 1 Всероссийская олимпиада школьников по математике................ 1 2 Московская математическая олимпиада........................
Подробнее S = {1, 1, 1, } (1) N = (N раз). (2)
 7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у
7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у
Подробнее 1. Определители. a11 a12. a21 a22
 . Определители. Определитель второго порядка Пусть задана таблица четырех чисел, расположенных в две строки и в два столбца 2 () 2 22 Элементы а, а 2 образуют первую строку, элементы а 2, а 22 образуют
. Определители. Определитель второго порядка Пусть задана таблица четырех чисел, расположенных в две строки и в два столбца 2 () 2 22 Элементы а, а 2 образуют первую строку, элементы а 2, а 22 образуют
Подробнее ЭЛЕМЕНТЫ КОМБИНАТОРИКИ.
 ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. Правило произведения. Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то всего существует n m различных пар
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. Правило произведения. Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то всего существует n m различных пар
Подробнее УДК Елизаров Е.Б. Россия, г. Владикавказ
 УДК 511.11 Елизаров Е.Б. Россия, г. Владикавказ 1 Аннотация: Статья посвящена вечной теореме П.Ферма с простой постановкой задачи, но сложным решением, как это обычно бывает в теории чисел. Мне удалось
УДК 511.11 Елизаров Е.Б. Россия, г. Владикавказ 1 Аннотация: Статья посвящена вечной теореме П.Ферма с простой постановкой задачи, но сложным решением, как это обычно бывает в теории чисел. Мне удалось
Подробнее Глава 1 ВВЕДЕНИЕ В АЛГЕБРУ
 Глава ВВЕДЕНИЕ В АЛГЕБРУ.. КВАДРАТНЫЙ ТРЕХЧЛЕН... Вавилонская задача о нахождении двух чисел по их сумме и произведению. Одна из древнейших задач алгебры была предложена в Вавилоне, где была распространена
Глава ВВЕДЕНИЕ В АЛГЕБРУ.. КВАДРАТНЫЙ ТРЕХЧЛЕН... Вавилонская задача о нахождении двух чисел по их сумме и произведению. Одна из древнейших задач алгебры была предложена в Вавилоне, где была распространена
Подробнее ПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,..., n в строчку одно за другим.
 ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
Подробнее 1.3. Распределение молекул газа в сосуде.
 .3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания поведения одноатомного газа в сосуде. Рассмотрим распределение
.3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания поведения одноатомного газа в сосуде. Рассмотрим распределение
Подробнее 1.3. Распределение молекул газа в сосуде.
 .3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания одноатомного газа в сосуде. Рассмотрим распределение
.3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания одноатомного газа в сосуде. Рассмотрим распределение
Подробнее 3. Определители высших порядков
 Определители высших порядков Понятие определителя п-го порядка и его основные свойства Понятие определителя п-го порядка вводится на основе изучения структуры определителей -го и -го порядков Так например
Определители высших порядков Понятие определителя п-го порядка и его основные свойства Понятие определителя п-го порядка вводится на основе изучения структуры определителей -го и -го порядков Так например
Подробнее Рабочая программа по алгебре класс
 Рабочая программа по алгебре 10-11 класс Рабочую программу составили Кулуева В.И. Год разработки программы: 2015 год ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данная рабочая программа по математике для 10-11 классов (профильный
Рабочая программа по алгебре 10-11 класс Рабочую программу составили Кулуева В.И. Год разработки программы: 2015 год ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данная рабочая программа по математике для 10-11 классов (профильный
Подробнее Глава 1. Начала линейной алгебры
 Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
Подробнее ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ КРИВЫХ
 Лекция 4 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ КРИВЫХ Тема: Элементарная кривая Касательная Длина кривой План лекции Понятие и способы задания элементарной кривой Вектор-функция одного переменного Касательная к кривой
Лекция 4 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ КРИВЫХ Тема: Элементарная кривая Касательная Длина кривой План лекции Понятие и способы задания элементарной кривой Вектор-функция одного переменного Касательная к кривой
Подробнее ОГЛАВЛЕНИЕ. Предисловие... 5
 ОГЛАВЛЕНИЕ Предисловие............................................. 5 Глава первая Арифметика и алгебра..................................... 6 1.1. Числа и действия с ними.............................
ОГЛАВЛЕНИЕ Предисловие............................................. 5 Глава первая Арифметика и алгебра..................................... 6 1.1. Числа и действия с ними.............................
Подробнее Тема 1-8: Комплексные числа
 Тема 1-8: Комплексные числа А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр)
Тема 1-8: Комплексные числа А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр)
Подробнее Гл.1. Степенные ряды., постоянные, называемые коэффициентами ряда. Иногда рассматривают степенной ряд более
 Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
Подробнее Тема 3: Определители
 Тема 3: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало
Тема 3: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало
Подробнее Пояснительная записка
 1 Пояснительная записка Рабочая программа по курсу алгебры и начал математического анализа 10-11 классов составлена в соответствии с программой «Алгебра и начала математического анализа 10-11 классы» автора
1 Пояснительная записка Рабочая программа по курсу алгебры и начал математического анализа 10-11 классов составлена в соответствии с программой «Алгебра и начала математического анализа 10-11 классы» автора
Подробнее docplayer.ru
К самостоятельной работе №4 10 алгебра Рациональные выражения. Формулы бинома Ньютона, суммы и разности степеней. (п 1 2)
К самостоятельной работе № 4 10 алгебраРациональные выражения. Формулы бинома Ньютона, суммы и разности степеней. (п.2.1-2.2)
- Упростите выражение: а)

б)  в)
в) 
г) 
- Напишите разложение по формуле бинома Ньютона
 .
. - Найдите в разложении по формуле бинома Ньютона
 средний член.
средний член. - Сократите дробь: а)
 б)
б) 
Ответы:
- а)
 ; б)
; б)  в)
в)  ; г)
; г) 


- а)

б) 
К контрольной работе № 1 10 алгебра
Действительные числа. Рациональные выражения (п.1.1-2.5)
- Вычислите:
а) ; б)
; б)  ; в)
; в)  .
.- Сколько мелодий можно сыграть из пяти различных нот?
- Сколько мелодий можно сыграть из четырех различных нот, выбранных без повторения из семи заданных различных нот?
- Сколько можно сыграть аккордов из четырех нот, выбранных из семи заданных различных нот?
- Докажите, что для любого действительного числа
 справедливо неравенство
справедливо неравенство 
- Упростите выражение: а)

б)  в)
в) 
г) 
- Напишите разложение по формуле бинома Ньютона
 .
. - Сократите дробь: а)
 б)
б) 
- Решите уравнение:

- Решите неравенства: а)
 б)
б) 
- С помощью схемы Горнера разделите многочлен
 на многочлен
на многочлен  , укажите неполное частное
, укажите неполное частное  и остаток
и остаток  , если
, если  , а
, а  .
.
Ответы:- а) 40320; б) 60; в) 10.
- 120.
- 840.
- 35.
- а)
 ; б)
; б)  в)
в)  ; г)
; г) 

- а)

б) 
- а) -0,6; 3.
- а)
 ; б)
; б)  .
.  ,
, 
К самостоятельной работе № 5 10 алгебра
Рациональные уравнения. Системы рациональных уравнений (п.2.6-2.7)
- Решите уравнения:
а)  ; б)
; б) 
- Решите систему уравнений:

Ответы:
- а)
 б) 0.
б) 0. 

К самостоятельной работе № 6 10 алгебра
Метод интервалов решения неравенств. Рациональные неравенства.
Нестрогие неравенства. (п.2.8-2.10)
- Решите неравенства:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;
и)  к)
к)  л)
л)  .
.
Ответы:
- а)
 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  е) 16; ж)
е) 16; ж) ; з)
; з) ; и)
; и) ; к)
; к) ; л)
; л)
К контрольной работе № 2 10 алгебра
Рациональные уравнения и неравенства и их системы (п.2.6-2.11)
- Решите уравнение: а)
 ; б)
; б)  .
. - Решите систему уравнений:

- Решите неравенства: а)
 б)
б)  в)
в) 
г) 
- Решите систему неравенств: а)
 б)
б) 
Ответы:
- а) 3; б) -3; -1; 2.


- а)
 ; б)
; б)  ; в )
; в )  г)
г) 
- а)
 б)
б) 
lib2.podelise.ru
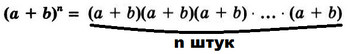 Чтобы получить требуемое слагаемое надо выбрать k штук множителей для b. Тогда получается $n-k$ множителей для а. В каком порядке будем выбирать данные множители не важно. Эта задача есть ни что иное как: число сочетаний из n элементов по k без повторений или $C_n^{k}$. Наша формула доказана.
Чтобы получить требуемое слагаемое надо выбрать k штук множителей для b. Тогда получается $n-k$ множителей для а. В каком порядке будем выбирать данные множители не важно. Эта задача есть ни что иное как: число сочетаний из n элементов по k без повторений или $C_n^{k}$. Наша формула доказана. Правило записи треугольника легко запомнить. Каждое число в треугольнике паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте распишем несколько строк:
Правило записи треугольника легко запомнить. Каждое число в треугольнике паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте распишем несколько строк:  Математически свойство подсчета числа сочетаний без повторений можно записать еще вот так:
Математически свойство подсчета числа сочетаний без повторений можно записать еще вот так: 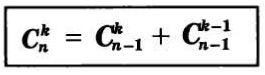 Как оказалось треугольника Паскаля находит свое применение и в другой математической задаче. Давайте вспомним несколько правил возведения в квадрат суммы. Самое первое правило, которое мы с вами выучили, это квадрат суммы: $(a+b)^2=a^2+2ab+b^2$. Довольно таки легко найти выражение и для следующей степени, используя правила перемножения многочленов: $(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$. Проделаем эту же операцию и для четвертой степени: $(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.
Как оказалось треугольника Паскаля находит свое применение и в другой математической задаче. Давайте вспомним несколько правил возведения в квадрат суммы. Самое первое правило, которое мы с вами выучили, это квадрат суммы: $(a+b)^2=a^2+2ab+b^2$. Довольно таки легко найти выражение и для следующей степени, используя правила перемножения многочленов: $(a+b)^3=(a^2+2ab+b^2)(a+b)=a^3+3a^2b+3ab^2+b^3$. Проделаем эту же операцию и для четвертой степени: $(a+b)^4=(a^3+3a^2b+3ab^2+b^3)(a+b)=a^4+4a^3b+6a^2b^2+4ab^3+b^4$.

 – биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
– биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
 ;
;
 – порядковый номер члена разложения.
– порядковый номер члена разложения.



 (правило симметрии)
(правило симметрии)

 , тогда:
, тогда: 










 найти член разложения, не содержащий х
найти член разложения, не содержащий х



 и для любых
и для любых  верно неравенство Бернулли:
верно неравенство Бернулли:


 , где
, где 

 , значит в разложении как минимум три члена разложения, тогда:
, значит в разложении как минимум три члена разложения, тогда:

 делится на 9
делится на 9










 , не содержащего х.
, не содержащего х. .
. , если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.
, если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена. , если биномиальный коэффициент третьего члена равен 36.
, если биномиальный коэффициент третьего члена равен 36. являются целыми числами?
являются целыми числами? .
. .
. равна 512. Найти слагаемое, не содержащее х.
равна 512. Найти слагаемое, не содержащее х. больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых? в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1?
в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1? чтобы отношение четвертого слагаемого разложения к третьему было равно
чтобы отношение четвертого слагаемого разложения к третьему было равно  ?
?

 Формула бинома Ньютона
Формула бинома Ньютона
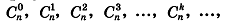
 - биноминальные коэффициенты
- биноминальные коэффициенты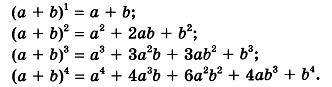
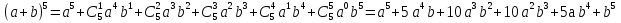
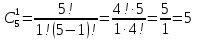
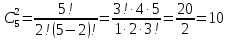
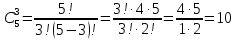
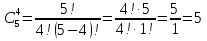
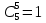
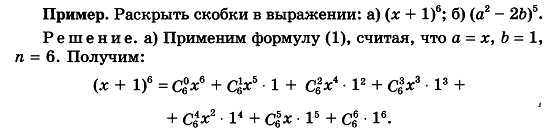
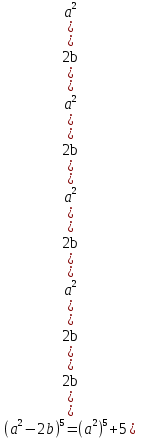 ………
………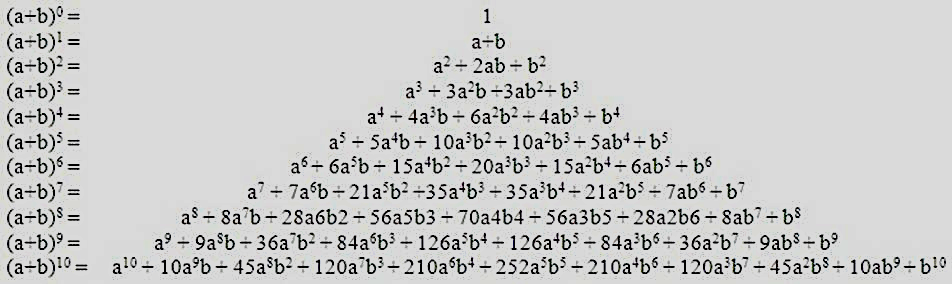

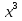 :
: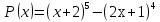
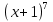 В)
В) 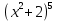
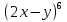 Г)
Г) 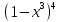
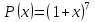


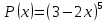
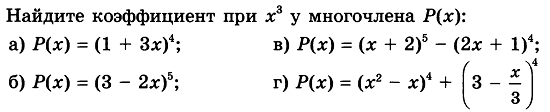
 сочетаний с повторениями изnпредметов поr.
сочетаний с повторениями изnпредметов поr. негатива). Нужно составить набор изr предметов (
негатива). Нужно составить набор изr предметов ( фотографий). Наборы различаются своим составом, а не порядком элементов. Например, разными будут наборы состава
фотографий). Наборы различаются своим составом, а не порядком элементов. Например, разными будут наборы состава и
и – один содержит три фотографии с первого негатива и по одной со второго и с третьего, а другой – одну с первого и четыре с третьего. Разложим эти наборы на столе, разделяя фотографии разного типа карандашами. Карандашей нам понадобится
– один содержит три фотографии с первого негатива и по одной со второго и с третьего, а другой – одну с первого и четыре с третьего. Разложим эти наборы на столе, разделяя фотографии разного типа карандашами. Карандашей нам понадобится , а фотографий
, а фотографий . Мы будем получать различные сочетания с повторениями, переставляя между собой эти
. Мы будем получать различные сочетания с повторениями, переставляя между собой эти предметов, т.е.
предметов, т.е. - число сочетаний с повторениями изnпредметов поrравно числу перестановок с повторениями длины
- число сочетаний с повторениями изnпредметов поrравно числу перестановок с повторениями длины состава
состава . В нашем примере
. В нашем примере


 . Порядок важен? Да, выбираем правую часть блок-диаграммы (рис. 2.1). Следующий вопрос: выбираем всеnэлементов? Нет. Повторения есть? Нет. Следовательно, наша выборка – размещение без повторений и количество таких выборок
. Порядок важен? Да, выбираем правую часть блок-диаграммы (рис. 2.1). Следующий вопрос: выбираем всеnэлементов? Нет. Повторения есть? Нет. Следовательно, наша выборка – размещение без повторений и количество таких выборок
 .В этой выборке 40 элементов (
.В этой выборке 40 элементов ( ), а значений – номеров автобусов – три (
), а значений – номеров автобусов – три ( ). Порядок важен? Чтобы ответить на этот вопрос, поменяем местами двух человек в очереди и посмотрим, изменилась ли выборка. Выборка не изменилась, т.к. количество людей в каждом автобусе осталось прежним. Порядок не важен, поэтому выбираем левую часть блок-диаграммы (рис. 2.1). Повторения есть? Да, в нашей выборке номер автобуса может встречаться несколько раз. Следовательно, выборка является сочетанием с повторениями из
). Порядок важен? Чтобы ответить на этот вопрос, поменяем местами двух человек в очереди и посмотрим, изменилась ли выборка. Выборка не изменилась, т.к. количество людей в каждом автобусе осталось прежним. Порядок не важен, поэтому выбираем левую часть блок-диаграммы (рис. 2.1). Повторения есть? Да, в нашей выборке номер автобуса может встречаться несколько раз. Следовательно, выборка является сочетанием с повторениями из по
по элементов:
элементов:


 Чему равен коэффициентC? Он равен количеству способов, которыми можно получить слагаемое
Чему равен коэффициентC? Он равен количеству способов, которыми можно получить слагаемое (т.е. количеству способов, которыми можно выбратьkскобок с множителемa, а из остальных
(т.е. количеству способов, которыми можно выбратьkскобок с множителемa, а из остальных скобок взять множительb). Например, если
скобок взять множительb). Например, если то слагаемое
то слагаемое можем получить, выбрав множительaиз первой и пятой скобки. Каков тип выборки? Порядок перечисления не важен (выбираем сначала первую, затем пятую скобки, или, наоборот, сначала пятую, затем первую – безразлично), повторяющихся элементов (одинаковых номеров скобок) в выборке нет. Это сочетание без повторений. Количество таких выборок равно
можем получить, выбрав множительaиз первой и пятой скобки. Каков тип выборки? Порядок перечисления не важен (выбираем сначала первую, затем пятую скобки, или, наоборот, сначала пятую, затем первую – безразлично), повторяющихся элементов (одинаковых номеров скобок) в выборке нет. Это сочетание без повторений. Количество таких выборок равно

 .
. получим формулу
получим формулу

 на
на .
. Авторы работы: Луцков Никита, 7ж класс Sir Isaac Newton «Немало ещё людей, которые знают о Ньютоне лишь то, что связано с рассказом о яблоке.» С. И. Вавилов Без имени Ньютона нет физики, а для Ньютона
Авторы работы: Луцков Никита, 7ж класс Sir Isaac Newton «Немало ещё людей, которые знают о Ньютоне лишь то, что связано с рассказом о яблоке.» С. И. Вавилов Без имени Ньютона нет физики, а для Ньютона  4.. Метод замены переменной при решении алгебраических уравнений. В предыдущем пункте метод замены переменной был использован для разложения многочлена на множители. Данный метод широко применяется для
4.. Метод замены переменной при решении алгебраических уравнений. В предыдущем пункте метод замены переменной был использован для разложения многочлена на множители. Данный метод широко применяется для  Исаак Ньютон Qui genus humanum ingenio superavit Выполнила: ученица 9 класса «Б» Разумом он превосходил род человеческий гимназии 1517 Зюзюкова Мария Не знаю, как меня воспринимает мир, но сам себе я кажусь
Исаак Ньютон Qui genus humanum ingenio superavit Выполнила: ученица 9 класса «Б» Разумом он превосходил род человеческий гимназии 1517 Зюзюкова Мария Не знаю, как меня воспринимает мир, но сам себе я кажусь  Тема 29 «Геометрическая прогрессия» Последовательность чисел, каждый следующий член которой равен предыдущему, умноженному на одно и то же число, называется геометрической прогрессией. Это число называется
Тема 29 «Геометрическая прогрессия» Последовательность чисел, каждый следующий член которой равен предыдущему, умноженному на одно и то же число, называется геометрической прогрессией. Это число называется  72 Глава2 Многочлены Примеры и комментарии Алгоритмы А-01 Запись многочлена в стандартном виде А-02 Действия над многочленами А-03 Устные преобразования А-04 Формулы сокращенного умножения А-05 Бином Ньютона
72 Глава2 Многочлены Примеры и комментарии Алгоритмы А-01 Запись многочлена в стандартном виде А-02 Действия над многочленами А-03 Устные преобразования А-04 Формулы сокращенного умножения А-05 Бином Ньютона  Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами
Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0,,, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0,,, коэффициентами  Презентация (по физике) Исаак Ньютон ( 04.01.1643 года - 31.03.1727 года ) Великобритания Выдающийся английский учѐный, заложивший основы современного естествознания, создатель классической физики, член
Презентация (по физике) Исаак Ньютон ( 04.01.1643 года - 31.03.1727 года ) Великобритания Выдающийся английский учѐный, заложивший основы современного естествознания, создатель классической физики, член  Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
Металлургический факультет Кафедра высшей математики РЯДЫ Методические указания Новокузнецк 5 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования  МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными  Глава Определители Перестановки Q Рассмотрим множество первых натуральных чисел которое обозначим как Определение Перестановкой P множества элементов из Q назовем любое расположение этих элементов в некотором
Глава Определители Перестановки Q Рассмотрим множество первых натуральных чисел которое обозначим как Определение Перестановкой P множества элементов из Q назовем любое расположение этих элементов в некотором  1 Пояснительная записка Рабочая программа элективного курса «МИР, МАТЕМАТИКА, МАТЕМАТИКИ» Для10-11 классов, составлена в соответствии с программой А.Н. Землякова «Элективные курсы в профильном обучении.
1 Пояснительная записка Рабочая программа элективного курса «МИР, МАТЕМАТИКА, МАТЕМАТИКИ» Для10-11 классов, составлена в соответствии с программой А.Н. Землякова «Элективные курсы в профильном обучении.  Лекция 2: перечслительная комбинаторика Дискретная математика, ВШЭ, факультет компьютерных наук (Осень 2014 весна 2015) Задачи перечислительной кмбинаторики имеют типовой вид: «сколько способов сделать
Лекция 2: перечслительная комбинаторика Дискретная математика, ВШЭ, факультет компьютерных наук (Осень 2014 весна 2015) Задачи перечислительной кмбинаторики имеют типовой вид: «сколько способов сделать  ОГЛАВЛЕНИЕ Предисловие............................................ 3 Часть 1. Лекции......................................... 4 1. Определение и простейшие свойства чисел Фибоначчи.... 4 2. Биномиальные
ОГЛАВЛЕНИЕ Предисловие............................................ 3 Часть 1. Лекции......................................... 4 1. Определение и простейшие свойства чисел Фибоначчи.... 4 2. Биномиальные  «Последняя загадка Пьера Ферма-» Некоторое время назад я опубликовал работу «Последняя загадка Пьера Ферма» в которой записал доказательство Большой теоремы Ферма (http://wbabi.et/mitkovsky/mitkovsky6.pdf,
«Последняя загадка Пьера Ферма-» Некоторое время назад я опубликовал работу «Последняя загадка Пьера Ферма» в которой записал доказательство Большой теоремы Ферма (http://wbabi.et/mitkovsky/mitkovsky6.pdf,  И. В. Яковлев Материалы по математике MathUs.ru Содержание Делимость. Общие свойства 1 Всероссийская олимпиада школьников по математике................ 1 2 Московская математическая олимпиада........................
И. В. Яковлев Материалы по математике MathUs.ru Содержание Делимость. Общие свойства 1 Всероссийская олимпиада школьников по математике................ 1 2 Московская математическая олимпиада........................  7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у
7.5. Новое геометрическое определение числа Что такое число? «Ливийский» период моей жизни, который продолжался с февраля 1995 по август 1997 г., был своеобразным и сознательным «заточением», кода я у  . Определители. Определитель второго порядка Пусть задана таблица четырех чисел, расположенных в две строки и в два столбца 2 () 2 22 Элементы а, а 2 образуют первую строку, элементы а 2, а 22 образуют
. Определители. Определитель второго порядка Пусть задана таблица четырех чисел, расположенных в две строки и в два столбца 2 () 2 22 Элементы а, а 2 образуют первую строку, элементы а 2, а 22 образуют  ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. Правило произведения. Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то всего существует n m различных пар
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. Правило произведения. Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то всего существует n m различных пар  УДК 511.11 Елизаров Е.Б. Россия, г. Владикавказ 1 Аннотация: Статья посвящена вечной теореме П.Ферма с простой постановкой задачи, но сложным решением, как это обычно бывает в теории чисел. Мне удалось
УДК 511.11 Елизаров Е.Б. Россия, г. Владикавказ 1 Аннотация: Статья посвящена вечной теореме П.Ферма с простой постановкой задачи, но сложным решением, как это обычно бывает в теории чисел. Мне удалось  Глава ВВЕДЕНИЕ В АЛГЕБРУ.. КВАДРАТНЫЙ ТРЕХЧЛЕН... Вавилонская задача о нахождении двух чисел по их сумме и произведению. Одна из древнейших задач алгебры была предложена в Вавилоне, где была распространена
Глава ВВЕДЕНИЕ В АЛГЕБРУ.. КВАДРАТНЫЙ ТРЕХЧЛЕН... Вавилонская задача о нахождении двух чисел по их сумме и произведению. Одна из древнейших задач алгебры была предложена в Вавилоне, где была распространена  ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще  .3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания поведения одноатомного газа в сосуде. Рассмотрим распределение
.3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания поведения одноатомного газа в сосуде. Рассмотрим распределение  .3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания одноатомного газа в сосуде. Рассмотрим распределение
.3. Распределение молекул газа в сосуде..3.. Распределение молекул между двумя половинками сосуда. Применим элементы теории вероятности для описания одноатомного газа в сосуде. Рассмотрим распределение  Определители высших порядков Понятие определителя п-го порядка и его основные свойства Понятие определителя п-го порядка вводится на основе изучения структуры определителей -го и -го порядков Так например
Определители высших порядков Понятие определителя п-го порядка и его основные свойства Понятие определителя п-го порядка вводится на основе изучения структуры определителей -го и -го порядков Так например  Рабочая программа по алгебре 10-11 класс Рабочую программу составили Кулуева В.И. Год разработки программы: 2015 год ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данная рабочая программа по математике для 10-11 классов (профильный
Рабочая программа по алгебре 10-11 класс Рабочую программу составили Кулуева В.И. Год разработки программы: 2015 год ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данная рабочая программа по математике для 10-11 классов (профильный  Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные  Лекция 4 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ КРИВЫХ Тема: Элементарная кривая Касательная Длина кривой План лекции Понятие и способы задания элементарной кривой Вектор-функция одного переменного Касательная к кривой
Лекция 4 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ КРИВЫХ Тема: Элементарная кривая Касательная Длина кривой План лекции Понятие и способы задания элементарной кривой Вектор-функция одного переменного Касательная к кривой  ОГЛАВЛЕНИЕ Предисловие............................................. 5 Глава первая Арифметика и алгебра..................................... 6 1.1. Числа и действия с ними.............................
ОГЛАВЛЕНИЕ Предисловие............................................. 5 Глава первая Арифметика и алгебра..................................... 6 1.1. Числа и действия с ними.............................  Тема 1-8: Комплексные числа А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр)
Тема 1-8: Комплексные числа А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр)  Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где
Гл Степенные ряды a a a Ряд вида a a a a a () называется степенным, где,,,, a, постоянные, называемые коэффициентами ряда Иногда рассматривают степенной ряд более общего вида: a a( a) a( a) a( a) (), где  Тема 3: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало
Тема 3: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало  1 Пояснительная записка Рабочая программа по курсу алгебры и начал математического анализа 10-11 классов составлена в соответствии с программой «Алгебра и начала математического анализа 10-11 классы» автора
1 Пояснительная записка Рабочая программа по курсу алгебры и начал математического анализа 10-11 классов составлена в соответствии с программой «Алгебра и начала математического анализа 10-11 классы» автора 
 в)
в) 

 .
. средний член.
средний член. б)
б) 
 ; б)
; б)  в)
в)  ; г)
; г) 




 ; б)
; б)  ; в)
; в)  .
. справедливо неравенство
справедливо неравенство 
 .
.
 б)
б) 
 на многочлен
на многочлен  , укажите неполное частное
, укажите неполное частное  и остаток
и остаток  , если
, если  , а
, а  .
. 
 ; б)
; б)  .
. ,
, 
 ; б)
; б) 

 б) 0.
б) 0.

 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ;
;  к)
к)  л)
л)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  е) 16; ж)
е) 16; ж) ; з)
; з) ; и)
; и) ; к)
; к) ; л)
; л)
 ; б)
; б)  .
. б)
б)  в)
в) 

 б)
б) 
 ; б)
; б)  ; в )
; в )  г)
г) 
 б)
б)