Главная » Контрольная » Контрольная по геометрии 8

Контрольные работы по геометрии 8 класс учебник Атанасян. Контрольная по геометрии 8


Контрольные работы по геометрии 8 класс учебник Атанасян

КОНТРОЛЬНАЯ РАБОТА № 1

Цель: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. Диагонали прямоугольника АВСD пересекаются в точке О. Найдите угол между диагоналями, если hello_html_m23d40380.gifАВО = 30°.

2. В параллелограмме KМNP проведена биссектриса угла МKР, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник KМЕ равнобедренный.

б) Найдите сторону KР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.

Вариант II

1. Диагонали ромба KМNP пересекаются в точке О. Найдите углы треугольника KОМ, если угол МNP равен 80°.

2. На стороне ВС параллелограмма АВСD взята точка М так, что АВ = ВМ.

а) Докажите, что АМ – биссектриса угла ВАD.

б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см.

Вариант III

(для более подготовленных учащихся)

1. Через вершину с прямоугольника АВСD проведена прямая, параллельная диагонали ВD и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N. Найдите периметр четырехугольника АСМN, если диагональ ВD равна 8 см.

2. Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке М, лежащей на стороне ВС. Луч DМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСD, если АN = 10 см.

КОНТРОЛЬНАЯ РАБОТА № 2

Цель: проверить знания, умения и навыки учащихся решать задачи по теме «Площадь. Теорема Пифагора».

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.

2. Площадь прямоугольной трапеции равна 120 см2, а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.

3. На стороне АС данного треугольника АВС постройте точку D так, чтобы площадь треугольника АВD составила одну треть площади треугольника АВС.

Вариант II

1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см2.

2. Найдите площадь трапеции АВСD с основаниями АD и ВС, если АВ = 12 см, ВС = 14 см, АD = 30 см, hello_html_m23d40380.gifВ = 150°.

3. На продолжении стороны KN данного треугольника KМN постройте точку Р так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KМN.

Вариант III(для более подготовленных учащихся)

1. Стороны параллелограмма равны 12 см и 8 см, а угол между высотами, проведенными из вершины тупого угла, равен 30°. Найдите площадь параллелограмма.

2. Середина М боковой стороны CD трапеции АВСD соединена отрезками с вершинами А и В. Докажите, что площадь треугольника АВМ в два раза меньше площади данной трапеции.

3. Точки А1, В1, С1 лежат соответственно на сторонах ВС, АС, АВ треугольника АВС, причем АВ1 = hello_html_1deb4a3a.gifAC, CA1 = hello_html_1deb4a3a.gifCB, BC1 = hello_html_1deb4a3a.gifBA. Найдите площадь треугольника А1В1С1, если площадь треугольника АВС равна 27

КОНТРОЛЬНАЯ РАБОТА № 3

Цели: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Ход урока

I. Краткий анализ самостоятельной работы и ее результаты.

II. Организация учащихся на выполнение работы.

III. Выполнение работы по вариантам.

Вариант I

1. На рисунке 1 АВ || СD. а) Докажите, что АО : ОС = ВО : ОD. б) Найдите АВ, если ОD = 15 см, ОВ = 9 см, СD = 25 см.

2. Найдите отношение площадей треугольников АВС и KMN, если АВ = 8 см, ВС = 12 см, АС = 16 см, KM = 10 cм, MN = 15 см, NK = 20 см.

Вариант II

1. На рисунке 2 MN || АС. а) Докажите, что АВ · BN = CВ · BM. б) Найдите MN, если AM = 6 см, ВM = 8 см, АС = 21 см.

2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см и АВ = 12 cм, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.

Вариант III(для более подготовленных учащихся)

1. Докажите, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения диагоналей трапеции и точку пересечения продолжения боковых сторон.

2. Даны отрезок АВ и параллельная ему прямая а. Воспользовавшись утверждением, доказанным в задаче 1, разделите отрезок АВ пополам при помощи одной линейки.

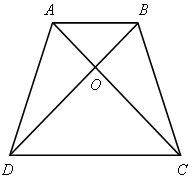
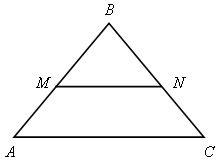
hello_html_m5f7d3db9.pnghello_html_14dcd2e1.png

Рис. 1 Рис. 2

Контрольная работа № 4

Цель: проверить знания и умения учащихся в решении задач и применении изученного материала.

Ход урока

I. Организация учащихся на выполнения работы.

II. Выполнение работы по вариантам.

Вариант I

1. В прямоугольном треугольнике АВС hello_html_m23d40380.gifА = 90°, АВ = 20 см; высота АD = 12 см. Найдите АС и cos C.

2. Диагональ ВD параллелограмма АВСD перпендикулярна к стороне АD. Найдите площадь параллелограмма АВСD, если АВ = 12 см,hello_html_m23d40380.gifА = 41°.

Вариант II

1. Высота ВD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DС, равный 18 см. Найдите АВ и соs A.

2. Диагональ АС прямоугольника АВСD равна 3 см и составляет со стороной АD угол 37°. Найдите площадь прямоугольника АВСD.

Вариант III(для более подготовленных учащихся)

1. Диагональ АС равнобедренной трапеции АВСD перпендикулярна к боковой стороне СD. Найдите площадь трапеции, если ее основания равны 10 см и 8 см.

2. Найдите отношение высот BN и AM равнобедренного треугольника АВС, в котором угол при основании ВС равен α.

КОНТРОЛЬНАЯ РАБОТА № 5

Цель: выяснить степень усвоения учащимися изученного материала.

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы.

Вариант I

1. Через точку А окружности проведены диаметр АС и две хорды АВ и АD, равные радиусу этой окружности. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Основание равнобедренного треугольника равно 18 см, а боковая сторона равна 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант II

1. Отрезок ВD – диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырехугольника АВСD и градусные меры дуг АВ, ВС, СD, АD.

2. Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант III(для более подготовленных учащихся)

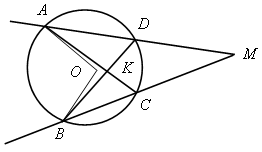
hello_html_21af4dd1.png

1. МА и МВ – секущие, АС и ВД – хорды окружности с центром О. Докажите, что hello_html_m23d40380.gifАОВ = hello_html_m23d40380.gifАKВ + hello_html_m23d40380.gifАМВ.

2. Площадь равнобедренной трапеции АВСD с основаниями ВС и АD, описанной около окружности с центром О и радиусом 3 см, равна 60 см2. Найдите радиус окружности, описанной около треугольника ОСD.

infourok.ru

Контрольные работы по геометрии 8 класс

Контрольная работа №1 по теме «Четырехугольники»

Вариант 1

  1. Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол между диагоналями, если ∠ АВО=30⁰.

  2. В параллелограмме КМNР проведена биссектриса угла МКР, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник КМЕ равнобедренный.

б) Найдите сторону КР, если МЕ=10 см, а периметр параллелограмма равен 52 см.

Вариант 2

  1. Диагонали ромба КМNР пересекаются в точке О. Найдите углы треугольника КОМ, если ∠ MNР=80⁰.

  2. На стороне ВС параллелограмма АВСД взята точка М так, что АВ=ВМ.

а) Докажите, что АМ- биссектриса угла ВАД.

б) Найдите периметр параллелограмма, если СД=8 см, СМ=4 см.

Вариант 3

  1. Через вершину С прямоугольника АВСД проведена прямая, параллельная диагонали ВД и пересекающая прямую АВ в точке М . Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС в точке N . Найдите периметр четырехугольника АСМN, если диагональ ВД равна 8 см.

  2. Биссектрисы углов А и Д параллелограмма АВСД пересекаются в точке М, лежащей на стороне ВС. Луч ДМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСД, если АN=10см.

Контрольная работа №2 по теме «Площадь»

Вариант 1

  1. Сторона треугольника равна 5 см, а высота , проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.

  2. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника.

  3. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.

4∗. В прямоугольной трапеции АВСК большая боковая сторона равна

3√2 см, угол К равен 45⁰, а высота СН делит основание АК пополам.

Найдите площадь трапеции.

Вариант 2

  1. Сторона треугольника равна 12 см, а высота , проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника.

  2. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника.

  3. Диагонали ромба равны 10 и 12 см. Найдите площадь и периметр ромба.

4∗. В прямоугольной трапеции АВСД большая боковая сторона равна

8 см, угол А равен 60⁰, а высота ВН делит основание АД пополам.

Найдите площадь трапеции.

Контрольная работа №3 по теме «Подобные треугольники»

Вариант 1

  1. Дано : ∠А=∠В, СО=4, ДО=6, АО=5.

Найти: а) ОВ; б) АС:ВД; в) S АОС: S ВОD.

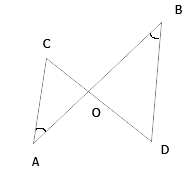
hello_html_m4a536240.png

Рис.1

  1. В треугольнике АВС АВ=4 см, ВС=1 см, АС=6 см, а в треугольнике МNК MK= 8 cм, MN=12 см, KN= 14 см. Найдите углы треугольника MNK, если ∠А= 80⁰, ∠В= 60⁰.

  2. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК ∥ АС, ВМ:АМ=1:4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.

4∗. В трапеции АВСД (АД и ВС- основания) диагонали пересекаются в точке О, АД=12 см, ВС=4 см. Найдите площадь треугольника ВОС, если площадь треугольника АОД равна 45 см².

Вариант 2

  1. Дано : РЕ=NK, MP=8, MN=12, ME=6.

Найти: а) МК; б) РЕ:NK; в) S МРЕ: S МКN.

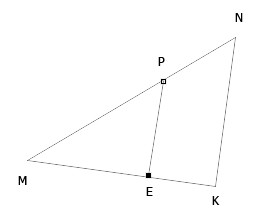
hello_html_m4bc2adcd.png

Рис.1

  1. В треугольнике АВС АВ=12 см, ВС=18 см, ∠В= 70⁰, а в треугольнике МNК MN=6 см, NК= 9 см, ∠N= 70⁰. Найдите сторону АC и угол С треугольника АВС, если МК=7 см, ∠К= 60⁰.

  2. Отрезки АВ и СД пересекаются в точке О так, что ∠АОС=∠ВДО, АО : ОВ=2:3. Найдите периметр треугольника АСО, если периметр треугольника ВОД равен 21 см.

4∗. В трапеции АВСД (АД и ВС- основания) диагонали пересекаются в точке О, площадь треугольника АОД равна 32 см², треугольника ВОС 8 см². Найдите меньшее основание трапеции, если большее из них равно 10 см.

Контрольная работа №4 по теме «Подобные треугольники»

Вариант 1

1. В прямоугольном треугольнике АВС ∠А=90⁰, АВ=20 см; высота АД=12 см. Найдите АС и cos∠C.

2. Диагональ ВД параллелограмма АВСД перпендикулярна стороне АД. Найдите площадь параллелограмма АВСД, если АВ=12 см, ∠А=41⁰.

Вариант 2

1. Высота ВД прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок ДС, равный 18 см. Найдите АВ и cos∠А.

2. Диагональ АС прямоугольника АВСД равна 3 см и составляет со стороной АД угол 37⁰. Найдите площадь прямоугольника АВСД.

Вариант 3 (для более подготовленных учащихся)

  1. Диагональ АС равнобедренной трапеции АВСД перпендикулярна боковой стороне СД. Найдите площадь трапеции, если её основания равны 10 см и 8 см.

  2. Найдите отношение высот ВN и АМ равнобедренного треугольника АВС, в котором угол при основании ВС равен ɑ.

Контрольная работа №5 по теме «Окружность»

Вариант 1

1. Через точку А окружности проведены диаметр АС и две хорды АВ и АД, равные радиусу этой окружности. Найдите углы четырехугольника АВСД и градусные меры дуг АВ, ВС, СД, АД.

2. Основание равнобедренного треугольника равно 18 см, а боковая сторона 15 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант 2

1. Отрезок ВД- диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна ему. Найдите углы четырехугольника АВСД и градусные меры дуг АВ, ВС, СД, АД.

2. Высота, проведенная к основанию равнобедренного треугольника , равна 9 см, а само основание равно 24 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.

Вариант 3 (для более подготовленных учащихся)

  1. МА и МВ- секущие, Аси ВД- хорды окружности с центром О . Докажите, что ∠АОВ=∠АКВ+∠АМВ

  2. Площадь равнобедренной трапеции АВСД с основаниями ВС и АД, описанной около окружности с центром О и радиусом 3 см, равна 60 см². Найдите радиус окружности, описанной около треугольника ОСД.

infourok.ru

Контрольные работы по геометрии 8 класс по учебнику «Геометрия 7 – 9»; авт. Л.С. Атанасян и другие.

Контрольные работы по геометрии 8 класс

на 1час и 2 часа в неделю в соответствии с учебным

планом и адаптированными программами ШНО

по учебнику «Геометрия 7 – 9»;

авт. Л.С. Атанасян и другие.

КОНТРОЛЬНАЯ РАБОТА № 1

по геометрии, 8 класс.

I вариант

  1. Один из углов параллелограмма равен 70˚. Найти остальные углы.

  1. Диагонали прямоугольника пересекаются в точке О, OD=15 см. Найти длину диагонали АС.

  1. Чему равен угол между диагональю и стороной квадрата?

  1. Периметр ромба ABCD равен 40 см. Угол В равен 60˚. Диагонали ромба пересекаются в точке О. Найти длину отрезка ОС.

II вариант

  1. Один из углов параллелограмма равен 100˚. Найти остальные углы.

  1. Диагонали прямоугольника ABCD пересекаются в точке О. Диагональ BD равна 16 см. Найти длину отрезка АО.

  1. Периметр квадрата равен 80 см. Найти длину стороны квадрата.

  1. В прямоугольной трапеции ABCD большее основание AD равно 25 см и образует с боковой стороной, равной 20 см угол в 60˚. Найти длину меньшего основания ВС.

по геометрии, 8 класс

I вариант

  1. Найти площадь параллелограмма, если одна из его сторон равна 10 см, а высота, проведенная к данной стороне равна 7 см.

  1. Найти площадь прямоугольника со сторонами 6 см и 8 см.

  1. В равнобедренном треугольнике основание равно 8 см, боковая сторона равна 5 см. Найти площадь этого треугольника.

  1. Найти площадь прямоугольной трапеции ABCD если меньшее основание АВ=2 см, большее основание DC=10 см, боковая сторона ВС=8 см, угол С равен 30˚.

II вариант

  1. Найти площадь параллелограмма, если одна из его сторон равна 20 см, а высота, проведенная к данной стороне равна 12 см.

  1. Найти площадь прямоугольного треугольника, если его катеты равны 4 см

и 3 см.

  1. В равнобедренном треугольнике боковая сторона равна 10 см,

биссектриса, проведенная к основанию равна 8 см. Найти площадь этого

треугольника.

4. Найти площадь прямоугольной трапеции, если её меньшее основание равно

6 см, высота равна 8 см, а острый угол равен 45˚.

по геометрии, 8 класс

на 2 часа в неделю или

(отмечено *) самостоятельная работа на 1 час в неделю

I вариант

  1. * В равнобедренном треугольнике угол при вершине равен 20˚, а в другом равнобедренном треугольнике угол при основании равен 80˚. Подобны ли эти треугольники?

  1. * В треугольнике АВС hello_html_m462ac668.gifС=90˚, М – середина АС; N – середина ВС; MN=6 см. Найти длину гипотенузы треугольника АВС.

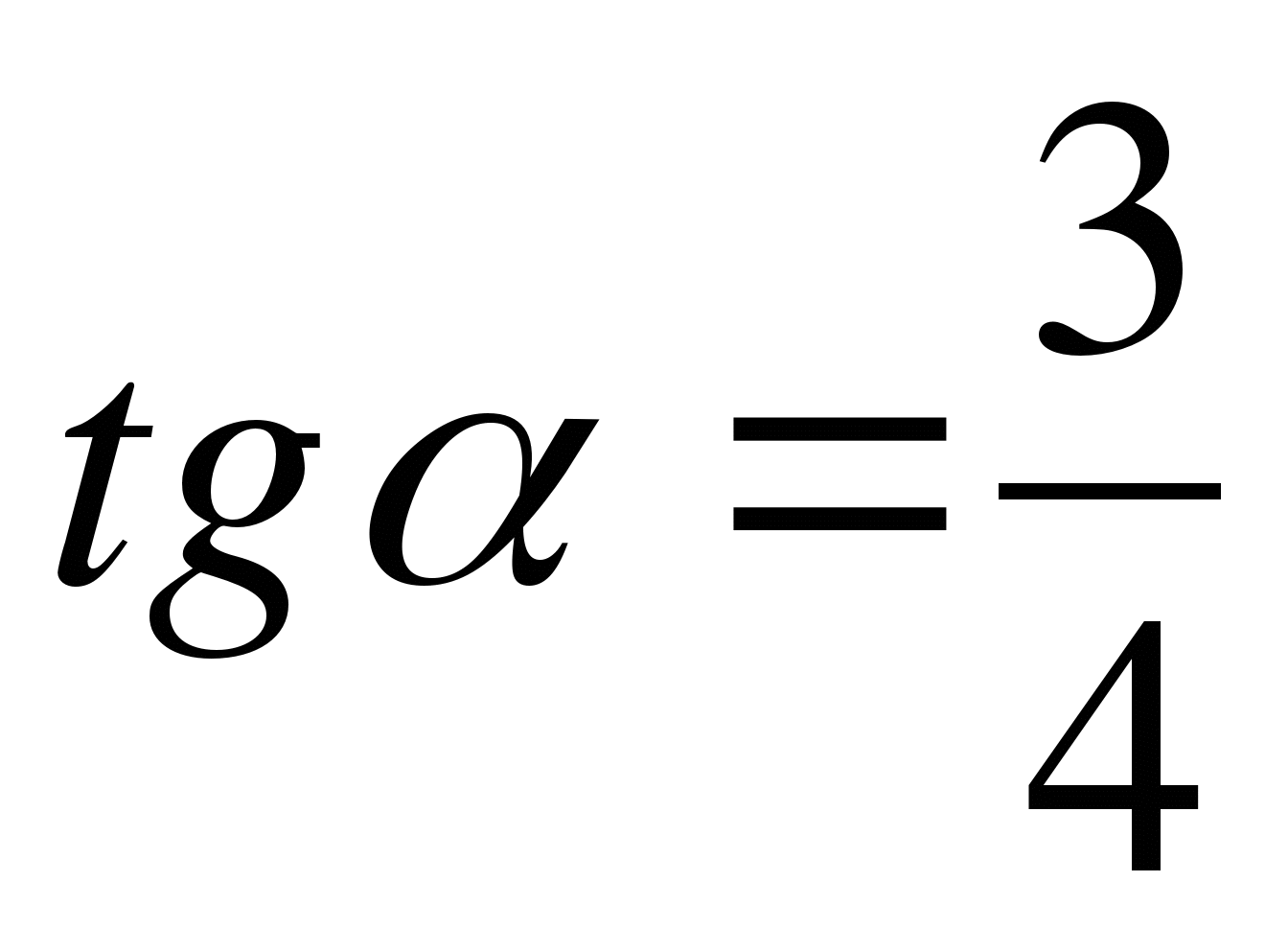  2. Построить угол hello_html_7c662469.gif, если hello_html_m642cb071.gif.

  1. Диагонали трапеции ABCD c большим основанием AD пересекаются в точке О. Найти длину меньшего основания ВС, если ОС=4 см, ОА=10 см, AD=25 см.

II вариант

  1. * В равнобедренном треугольнике угол при основании равен 50˚, а в другом равнобедренном треугольнике угол при вершине равен 80˚. Подобны ли эти треугольники?

  1. * В прямоугольнике АВСD точка М – середина стороны АВ, N – середина стороны ВС. Длина отрезка MN=5см. Найти длину диагоналей прямоугольника.

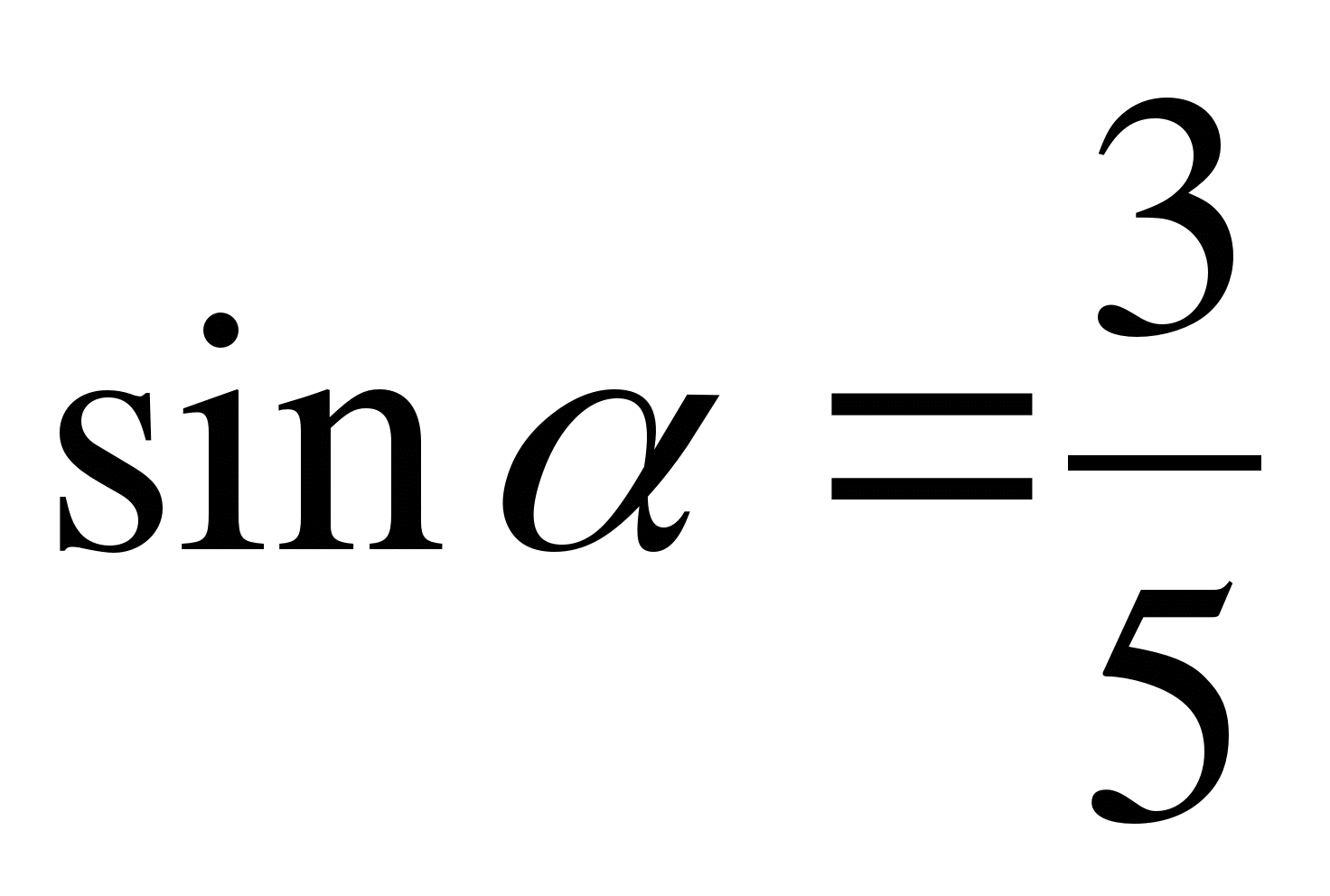  2. Построить угол hello_html_7c662469.gif, если hello_html_2e05f03b.gif.

  1. Боковые стороны трапеции АВ и CD продолжены до пересечения в точке М. Найти меньшее основание ВС, если большее основание AD=10 см, CD=12 см, DM=20 см.

по геометрии, 8 класс

на 2 часа в неделю.

I вариант

  1. К окружности с центром О проведена касательная в точке А, и на ней отмечена точка В. Угол АОВ равен 50˚. Определите величину угла АВО.

  1. Вершины треугольника MNK, вписанного в окружность, делят её на дуги, длины которых относятся как 1 : 2 : 3. Определите углы треугольника MNK.

  1. Прямоугольный треугольник с катетами 8 см и 6 см вписан в окружность. Найдите длину её радиуса.

  1. Около равностороннего треугольника АВС описана окружность, радиус которой равен 10 см. Найти радиус окружности, вписанной в этот треугольник.

II вариант

  1. К окружности с центром О проведена касательная в точке А, и на ней отмечена точка В. Угол АОВ равен 50˚. Определите величину угла АВО.

  1. Точки А, В и С окружности делят её на дуги, длины которых относятся как

2 : 3 : 4. Определить углы треугольника АВС.

  1. Прямоугольный треугольник, один катет которого равен 6 см, вписан в окружность радиусом 5 см. Найдите длину остальных сторон треугольника.

  1. В равносторонний треугольник ВСD вписана окружность, радиус которой равен 6 см. Найти радиус окружности, описанной около этого треугольника.

по геометрии, 8 класс.

I вариант

  1. Периметр прямоугольника равен 56 см. Одна его сторона равна 16 см. Вычислите длину диагонали прямоугольника.

  1. В параллелограмме ABCD hello_html_m462ac668.gifА=60˚, сторона АВ=10 см, а сторона ВС=15 см. Найдите площадь параллелограма ABCD.

  1. Прямая АВ, параллельная стороне DK треугольника DEK пересекает сторону DE в точке А и сторону EK в точке В; EB=8 см, BK=4 см, DK=6 см. Найти длину отрезка АВ.

  1. Описать окружность около прямоугольного треугольника АВС.

II вариант

  1. Периметр прямоугольника равен 34 см. Одна из его сторон равна 12 см. Найдите длину диагонали прямоугольника.

  1. В параллелограмме PMKN hello_html_m462ac668.gifМ=60˚, сторона РМ=12 см, сторона МК=11 см. Найдите площадь параллелограмма PMKN.

  1. Прямая DK, параллельная стороне AC треугольника ABC пересекает сторону AB в точке D и сторону BC в точке K; BD=8см, AD=2 см, DK=4 см. Найти длину отрезка АC.

  1. Описать окружность около равностороннего треугольника DEK.

Итоговый зачёт по геометрии за 8 класс.

1). Дать определение параллелограмма, ромба, прямоугольника,

квадрата, трапеции.

2). Какие свойства прямоугольника, параллелограмма, ромба

вы знаете?

3).

Дано: ABCD – ромб,

 A = 1200.

Найти:  BDC .

4). Записать формулы площадей параллелограмма, треугольника,

трапеции.

5).

Найти площадь прямоугольной трапеции ABCD.

6). Сформулировать теорему Пифагора.

7). Является ли треугольник прямоугольным, если его стороны

равны 9 см, 12 см и 15 см ?

8).

Найти AC.

9). Сформулируйте три признака подобия треугольников.

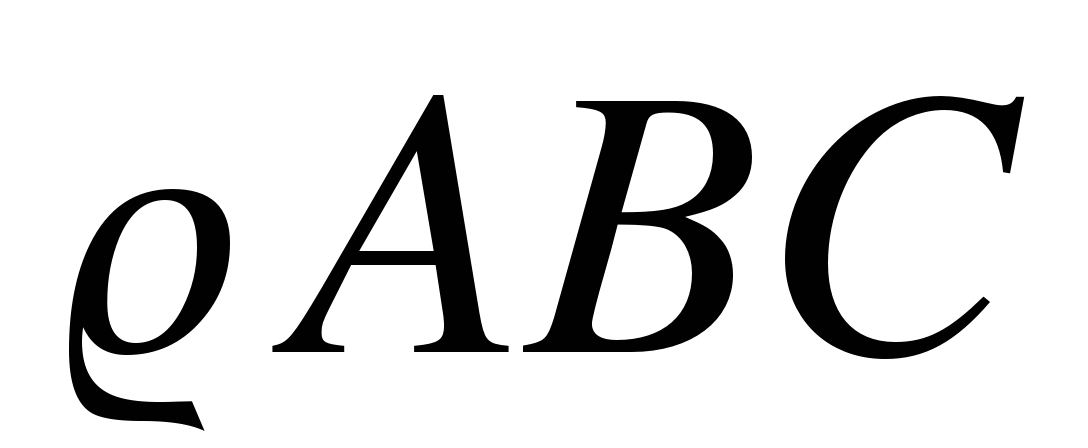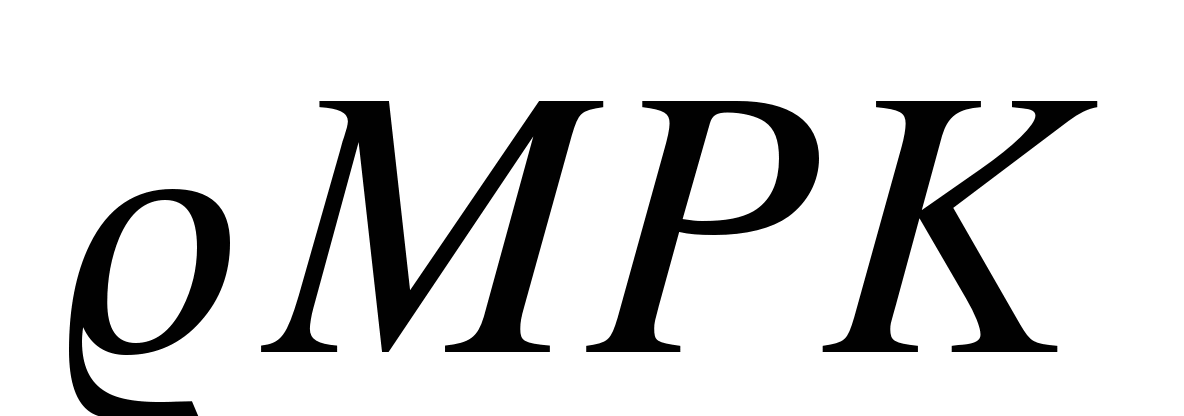10). Подобны ли hello_html_60c24a3d.gif и hello_html_509a1727.gif?

11). Дайте определение средней линии треугольника.

12).

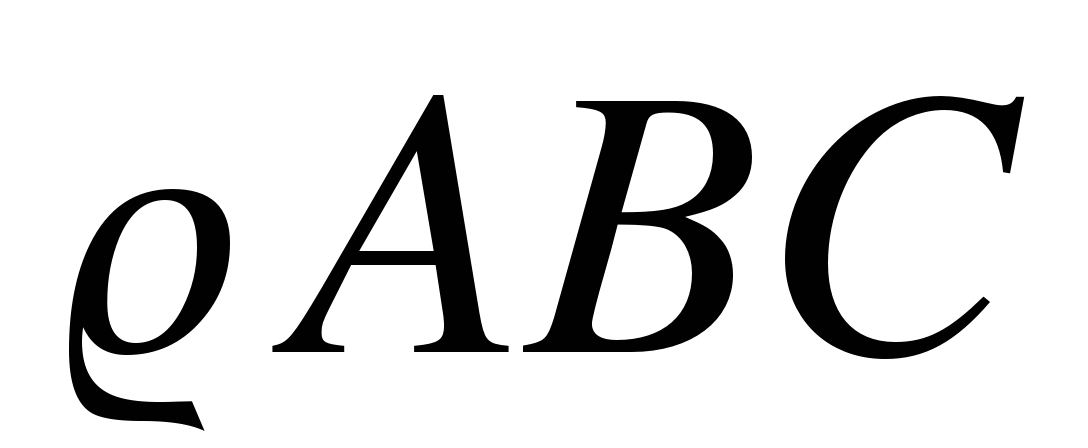Дано: hello_html_60c24a3d.gif,

BM = MA, BN = NC,

AC = 10,  A = 600

Найти: MN и  BMN.

13).

Найти: sin  и tg  .

14).

Найти  ABC, если величина

дуги ALC равна 1000.

15).

Дано: MA и AN - касательные,

 MAO = 400.

Найти:  AON.

16).

infourok.ru

Контрольные работы по геометрии ( 8 класс) страница 2

8 класс

Контрольная работа № 4

Вариант 1.

  1. Сформулируйте определение синуса острого угла в прямоугольном треугольнике.

  2. В прямоугольном треугольнике АВС (hello_html_m462ac668.gifС=90º) гипотенуза АВ=10 см, coshello_html_m462ac668.gifB=0,6. Найдите длину катета ВС.

  3. Найдите гипотенузу, катет и острый угол прямоугольного треугольника по катету а=12 см и противолежащему ему углу α=42º.

  4. Найдите углы параллелограмма КМНО, если сторона МН=18 м, высота МР=9 м, МО=15 м.

Вариант 2.

  1. Сформулируйте определение косинуса острого угла в прямоугольном треугольнике.

  2. В прямоугольном треугольнике АВС (hello_html_m462ac668.gifС=90º) гипотенуза АВ=8 см, sinhello_html_m462ac668.gifA=0,4. Найдите длину катета ВС.

  3. В прямоугольном треугольнике катет а=8 см и прилежащий к нему угол α=54º. Найдите второй катет, гипотенузу и острый угол.

  4. Найдите углы трапеции МРКС, если ее основания равны 12 м и 26 м, сторона РМ=10 м, высота РН=8 м.

8 класс

Контрольная работа № 5

Вариант 1.

  1. Дана окружность 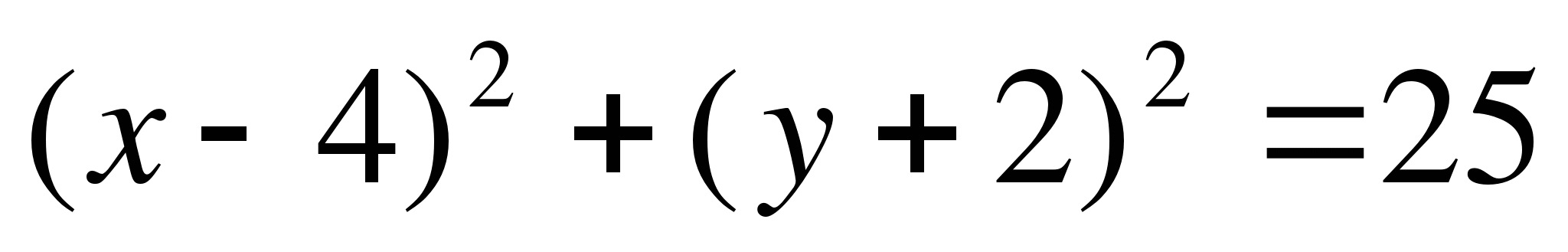hello_html_m2dbf5a1d.gif:

а) Чему равны радиусы окружности и координаты ее центра?

б) Докажите, что точки А и В лежат на окружности, если А(0;1) В(1;2).

  1. Вычислите длину хорды АВ из задачи № 1.

  2. Пользуясь таблицами, вычислите cos164º.

  3. В треугольнике АВС: А(2;-3), В(-2;3), С(6;-3) проведена средняя линия В1С1(параллельно ВС). Составьте ее уравнение.

Вариант 2.

  1. Дана окружность 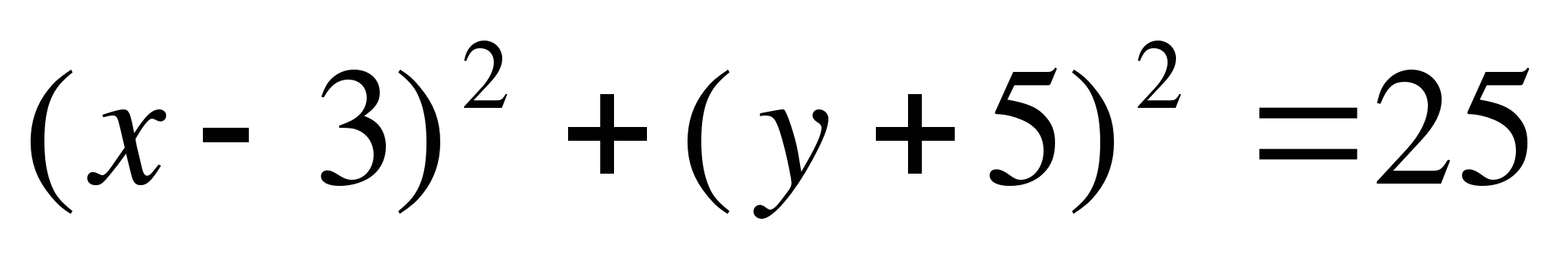hello_html_5e5db593.gif:

а) Чему равны радиусы окружности и координаты ее центра?

б) Докажите, что точки А и В лежат на окружности, если А(7;-2) В(0;-1).

  1. Вычислите длину хорды АВ из задачи № 1.

  2. Пользуясь таблицами, вычислите tg125º.

  3. В треугольнике АВС: А(-6;4), В(1;2), С(4;0) проведена медиана BD. Составьте уравнение прямой, содержащей эту медиану.

8 класс

Контрольная работа № 6

Вариант 1.

  1. Найдите координаты вектора АВ, если А(0;4), В(5;-8).

  2. Постройте вектор 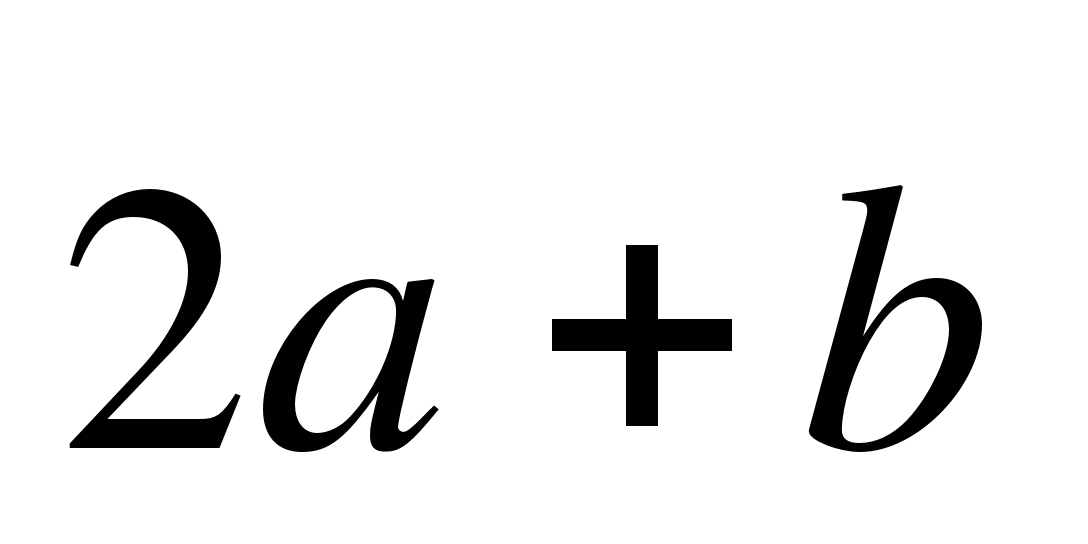hello_html_2a2ceef1.gif:

hello_html_294f7200.gifhello_html_34e00415.gif

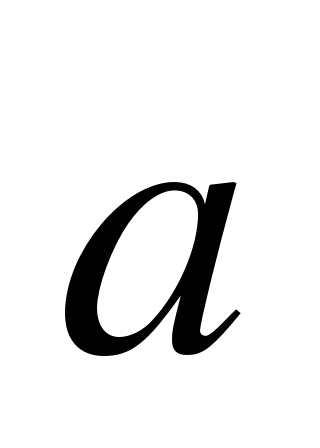
hello_html_m4e7aa322.gif

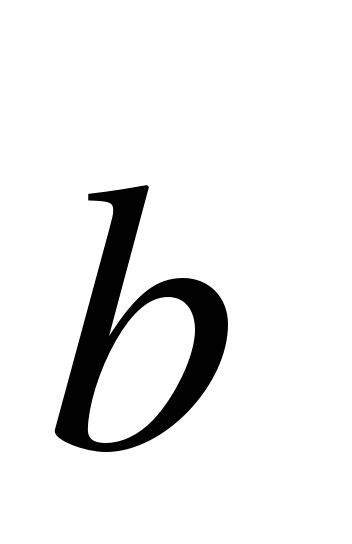
hello_html_76669928.gif

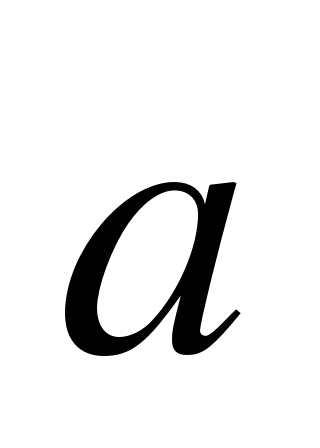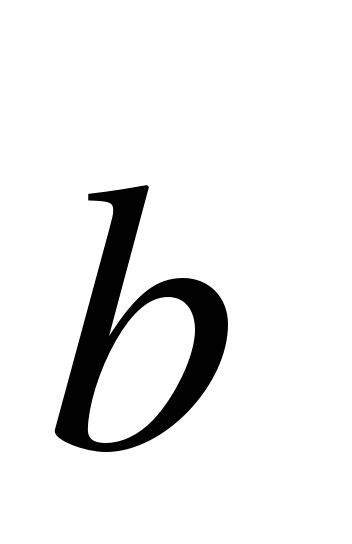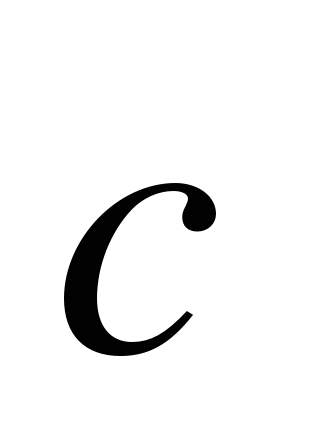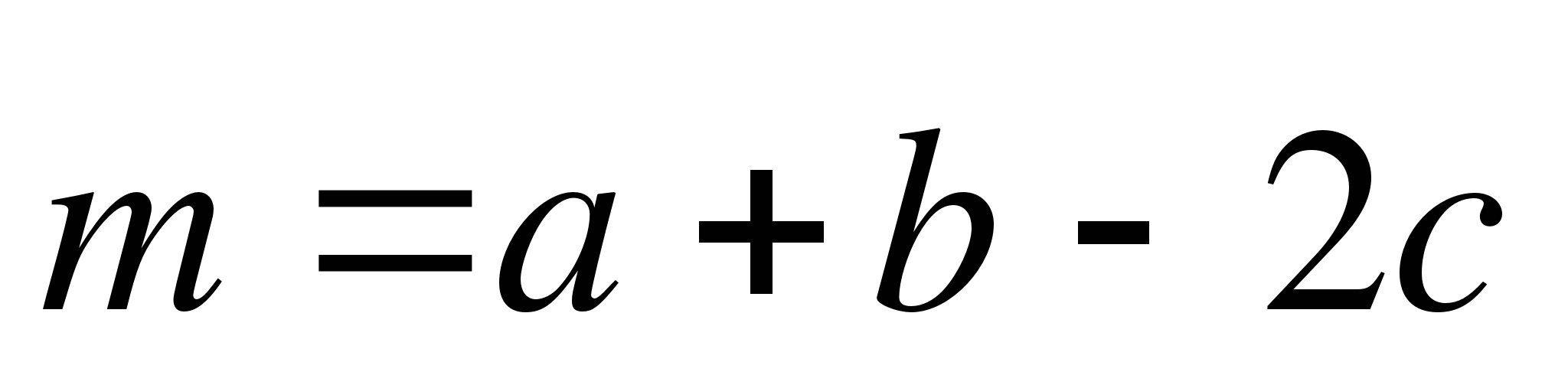  1. Даны векторы hello_html_m4e7aa322.gif(3;-2), hello_html_76669928.gif(4;0), hello_html_m5d09a471.gif(-3;-1). Найдите абсолютную величину вектора hello_html_5db629e7.gif.

  2. Даны четыре точки А(2;2), В(4;6), С(0;8), D(-2;4). Докажите с помощью векторов, что ABCD – прямоугольник.

Вариант 2.

  1. Найдите координаты вектора АВ, если А(-6;0), В(4;5).

  2. Постройте вектор 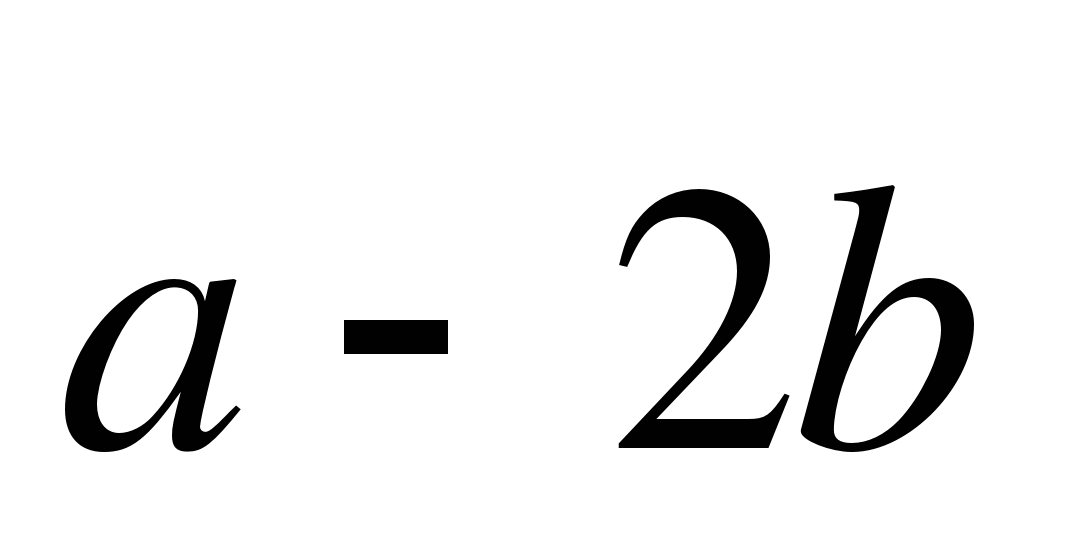hello_html_m54e2bc79.gif:

hello_html_294f7200.gifhello_html_34e00415.gif

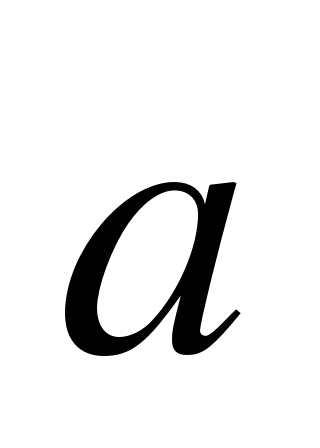
hello_html_m4e7aa322.gif

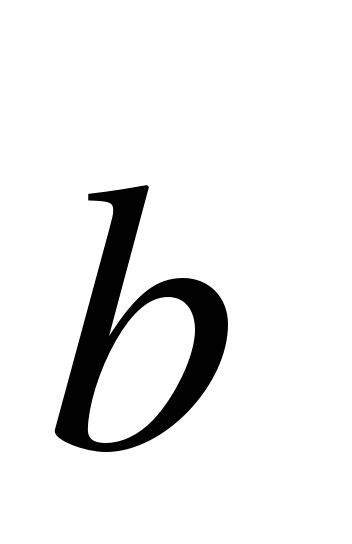
hello_html_76669928.gif

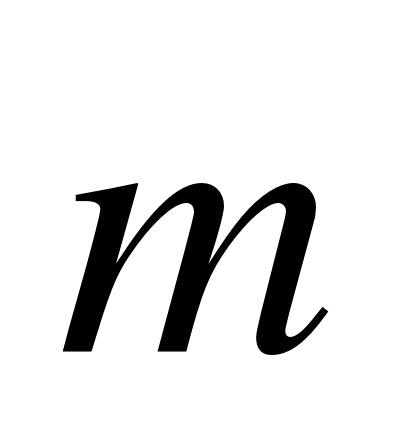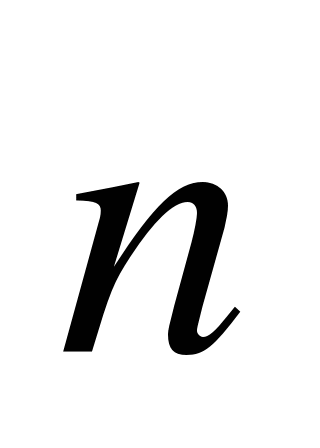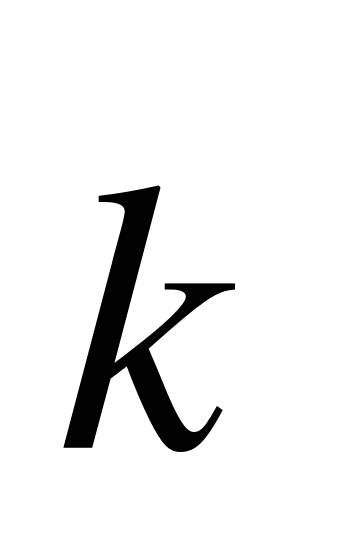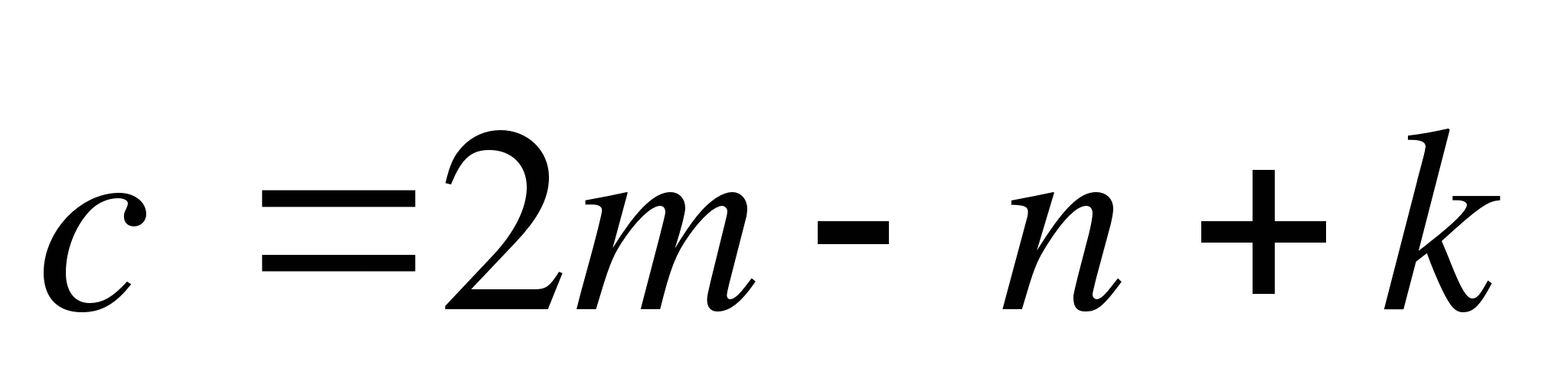  1. Даны векторы hello_html_m1bcc6f90.gif(-2;4), hello_html_m264c6e1.gif(0;3), hello_html_3fcce5ba.gif(1;-5). Найдите абсолютную величину вектора hello_html_m518a5225.gif.

  2. Даны четыре точки А(-1;5), В(1;9), С(3;5), D(1;1). Докажите с помощью векторов, что ABCD – ромб.

infourok.ru

Смотрите также