ГДЗ по геометрии 9 класс Б.Г. Зив Контрольные работы / К-5. Варианты / 2. Контрольная 9 класс геометрия
Сборник контрольных работ по геометрии, (9 класс)
СБОРНИК
КОНТРОЛЬНЫХ РАБОР ПО ГЕОМЕТРИИ
9 класс
Пояснительная записка
Контрольные работы содержат задания на воспроизведение (40%), применение (40%) и интеграцию (20%) предметных знаний. Тематические контрольные работы включают критерии оценивания, позволяющие отследить уровень усвоения учащимися стандартов данной темы. Содержательная матрица дает возможность учителю провести качественный анализ контрольной работы и спланировать коррекционную работу индивидуально для каждого ученика.
Предложение содержательной матрицы и критериев оценивания дает возможность учащимся планировать свою учебную деятельность для достижения более качественных результатов и впоследствии ее коррекцию.
.
Контрольная работа №1 9 класс.
Тема: «Векторы на плоскости».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач скалярное произведение векторов и его свойства, условия перпендикулярности и коллинеарности векторов,
находить координаты вектора и его абсолютную величину, выполнять действия с векторами;
- умение оформлять решение задачи.
| I вариант. |
| 1.Даны точки А(-2;4) и В(5;1).Найдите координаты вектора  и его абсолютную величину. 2. Дан параллелограмм АВСD. О- точка пересечения диагоналей. Найдите векторы 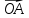 - -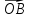 , ,  +2 +2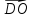 , ,  + +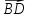 + +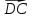
3.Даны векторы  (2;0), (2;0),  (1;2), (1;2),  (-3;m). Найдите значение m, при котором векторы (-3;m). Найдите значение m, при котором векторы А) и и  -2 -2 перпендикулярны. перпендикулярны. В) + + 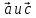 коллинеарны коллинеарны 4. Даны точки А(-1;4) и В(3;1), С(3;4). Найдите угол между векторами 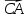 и и 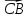 . . 5. Вычислите 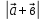 , если , если  =5, =5,  =8, а угол между векторами =8, а угол между векторами  и и  равен 600. равен 600. |
| II вариант. |
| 1. Даны точки А(3;-1) и В(1;4).Найдите координаты вектора АВ и его абсолютную величину. 2. Дан параллелограмм АВСD. О- точка пересечения диагоналей. Найдите векторы  - - 2 2 + +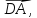  + + + +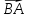
3. Даны векторы  (2;0), (2;0),  (1;2), (1;2),  (-3;m). Найдите значение m, при котором векторы (-3;m). Найдите значение m, при котором векторы А) и и 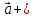 2 2 перпендикулярны. перпендикулярны. В) векторы  - - 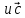 коллинеарны. коллинеарны. 4. Даны точки А(2;-1) и В(2;3), С(-1;-1). Найдите угол между векторами 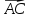 и и  5. Вычислите 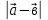 , если , если  =3, =3,  =4, а угол между векторами =4, а угол между векторами  и и  равен 600 равен 600 |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Координаты вектора и его абсолютная величина. | №1, | | | 20 % |
| Действия с векторами. Геометрический смысл. | №2 | | | 20% |
| Условия перпендикулярности и коллинеарности векторов. | | №3 | | 20% |
| Скалярное произведение и его свойства. | | №4 | №5 | 40 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Координаты вектора и его абсолютная величина. | Формула нахождения координат вектора. | 1 балл | 3 балла |
| Формула абсолютной величины. | 1 балл |
| Вычисления. | 1 балл |
| 2 | Действия с векто-рами. Геометричес-кий смысл. | Правило треугольника. | 1 балл | 3 балла |
| Правило параллелограмма. | 1 балл |
| Правило многоугольника. | 1 балл |
| 3 | Условия перпенди-кулярности и кол-линеарности векторов. | Условие коллинеарности векторов и вычисление . | 2 балла | 5 баллов |
| Условие перпендикулярности векторов и вычисления. | 2 балла |
| Оформление решения задачи. | 1 балл |
| 4 | Нахождение косинуса угла между векторами. | Нахождение координат вектора. | 1 балл | 5 баллов |
| Знание формулы нахождения косинуса угла между векторами. | 1 балл |
| Нахождение абсолютной величины. | 1 балл |
| Вычисление по формуле. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 5 | Скалярное произведение и его свойства. | Скалярный квадрат. | 2 балла | 5 баллов |
| ФСУ. | 1 балл |
| Вычисление. | 1 балл |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №2 9 класс.
Тема: «Преобразования плоскости».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач свойств симметрии относительно точки и прямой, параллельного переноса;
- знание и умение применять при решении задач свойств подобия;
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Найдите координаты точек симметричных данным А(-2;-1), В(1;3) и С(2;0) относительно: А)оси Ох в) оси Оу С) начала координат 2. При параллельном переносе точка А(3;-1) переходит в точку А1(5,-4). В какую точку в результате данного переноса перейдет точка В(-7;0) 3.Стороны треугольника равны 6см, 7см и 8см. Найдите периметр подобного ему треугольника, периметр которого равен 84см. 4. Дано: АВ=24см, ВС=16см, МВ=15см,NC=6cм , MN=20см. Доказать:  МВN МВN  АВС. Найти АС. АВС. Найти АС. А С 5. Найдите две стороны треугольника, если их сумма равна 91см, а биссектриса угла между ними делит третью сторону в отношении 5:8. |
| II вариант. |
| 1. Найдите координаты точек симметричных данным А(0;-1), В(1;-3) и С(-2;5) относительно: А)оси Ох в) оси Оу С) начала координат 2. При параллельном переносе точка А(-3;-4) переходит в точку А1(7,3). В какую точку в результате данного переноса перейдет точка В(0;5) 3. Стороны треугольника относятся как 2:5:6. Найдите периметр подобного ему треугольника, периметр которого равен 39см. 4. Дано: АО=15см, ВО=8см, АС=27см,DO=10cм , BC=16см. Доказать:  AOD AOD  COB. Найти АD. COB. Найти АD. 5. Найдите две стороны треугольника, если их разность равна 28см, а биссектриса угла между ними делит третью сторону на отрезки 43см и 29см. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Симметрия относительно точки и прямой. | №1, | | | 20 % |
| Параллельный перенос. | №2 | | | 20% |
| Подобие треугольников. | | №3,№4 | | 40% |
| Подобие треугольников. Свойство биссектрисы. | | | №5 | 20 % |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Симметрия относительно точки и прямой. | Симметрия относительно оси Ох. | 1 балл | 3 балла |
| Симметрия относительно оси Оу. | 1 балл |
| Симметрия относительно начала координат. | 1 балл |
| 2 | Параллельный перенос. | Формула, задающая параллельный перенос. | 1 балл | 3 балла |
| Вычисление вектора параллельного переноса. | 1 балл |
| Нахождение точки В 1. | 1 балл |
| 3 | Подобие треугольников. | Запись сторон подобного треугольника. | 1 балл | 5 баллов |
| Составление уравнения. | 1 балл |
| Вычисление коэффициента подобия. | 1 балл |
| Нахождение сторон подобного треугольника. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Подобие треугольников. | Применение признака подобия для доказательства. | 2 балла | 5 баллов |
| Нахождение стороны. | 2 балла |
| Оформление решения задачи. | 1 балл |
| 5 | Подобие треугольников. Свойство биссектрисы. | Знание свойства биссектрисы. | 1 балл | 5 баллов |
| Выполнение чертежа по условию задачи. | 1 балл |
| Введение неизвестного и составление уравнения. | 2 балла |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №6 9 класс.
Тема: «Многоугольники».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач пропорциональность отрезков хорд и секущих, формулы, связывающие стороны, периметр, площадь и радиусы вписанной и описанной окружностей связи величины центрального и вписанного углов
- умение выполнять чертеж по условию задачи;
- умение оформлять решение задачи..
| I вариант. |
| 1. По данным рисунка найдите угол х (О- центр окружности. 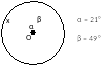
2. Дано: AB=0.7 см, ВЕ=0.5 см, СЕ=0.4 см. Найти: DE, DC 3.Внутренний угол правильного многоугольника в 3 раза больше внешнего угла. Найдите сторону многоугольника, если периметр равен 96 см. 4.Сторона правильного треугольника, описанного около окружности, равна 12 см. Найдите сторону правильного шестиугольника, вписанного в данную окружность. см. Найдите сторону правильного шестиугольника, вписанного в данную окружность. 5.Сторона правильного вписанного многоугольника стягивает в окружности радиуса 6 см дугу длиной 3 см. Найдите периметр многоугольника. см. Найдите периметр многоугольника.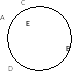 |
| II вариант. |
| 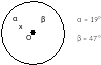
1. По данным рисунка найдите угол х (О- центр окружности. 2. Дано: СD=0.8 см, DЕ=0.2 см, AЕ=0.24 см Найти: BE, AB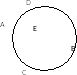 3.Сторона правильного многоугольника равна 5 см, а его внутренний угол на 108о больше внешнего угла. Найдите периметр многоугольника. 4.Сторона правильного шестиугольника, вписанного в окружность, равна 8см. Найдите сторону квадрата описанного около данной окружность. 5. Точки касания двух соседних сторон описанного многоугольника ограничивают в окружности радиуса 6см дугу длиной 4 см. Найдите периметр многоугольника. см. Найдите периметр многоугольника. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Центральные и вписанные углы. | №1 | | | 20% |
| Пропорциональность отрезков хорд и секущих | №2 | | | 20% |
| Правильные многоугольники | | №3, №4 | №5 | 60% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Центральные и вписанные углы. | Знание связи величины цент-рального и вписанного углов. | 1 балл | 4 балла |
| Умение применять. | 1 балл |
| Нахождение угла. | 1 балл |
| Сопутствующие пояснения. | 1 балл |
| 2 | Пропорциональность отрезков хорд и секущих. | Знание формулы. | 1 балл | 3 балла |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Правильные многоугольники. | Составление уравнения по условию. | 1 балл | 5 баллов |
| Знание формулы нахождения уг-ла правильного многоугольника. | 1 балл |
| Определение числа сторон многоугольника. | 1 балл |
| Нахождение периметра | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Формулы, связы-вающие стороны, периметр, площадь и радиусы вписан-ной и описанной окружностей. | Нахождение радиуса окружности. | 2 балла | 5 баллов |
| Нахождение стороны многоугольника. | 2 балла |
| Вычисления и оформление решения задачи. | 1 балл |
| 5 | Правильные многоугольники. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Определение количества сторон. | 2 балла |
| Вычисления. | 1 балл |
| Нахождение периметра. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №4 9 класс.
Тема: «Решение треугольников».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач теоремы синусов и косинусов, решать задачи на нахождение неизвестных элементов в треугольнке;
- умение оформлять решение задачи.
| I вариант. |
| 1.В треугольнике АВС  =350, =350,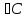 =250. Укажите наибольшую сторону треугольника. Ответ объясните. =250. Укажите наибольшую сторону треугольника. Ответ объясните. 2. Две стороны треугольника равны 3см и 8см, а угол между ними равен 600. Найдите периметр треугольника. 3. Решите треугольник АВС, если =750, =750, =450, АВ=2 =450, АВ=2 см. см. 4. Диагонали параллелограмма равны 12см и 20см, а угол между ними равен 600. Найдите стороны параллелограмма. 5. В прямоугольном треугольнике один из углов равен α, а катет, прилежащий к данному углу, равен а. Найдите биссектрису прямого угла. |
| II вариант. |
| 1. В треугольнике АВС ⦟В=550, ⦟А=1100. Укажите наименьшую сторону треугольника. Ответ объясните. 2. Две стороны треугольника равны 3см и 5см, а угол между ними равен 1200. Найдите периметр треугольника. 3. Решите треугольник АВС, если ⦟В=300, ⦟С=1050, АС=4см. 4. Стороны параллелограмма равны 10см и 16см, а угол между ними равен 600. Найдите диагонали параллелограмма. 5. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен β. Найдите биссектрису второго острого угла. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Теорема синусов | №1, | | №5 | 40% |
| Теорема косинусов | №2 | №4 | | 40% |
| Решение треугольника | | №3 | | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Теорема синусов. | Нахождение угла треугольника. | 1 балл | 3 балла |
| Знание следствия из теоремы синусов. | 1 балл |
| Запись ответа. | 1 балл |
| 2 | Теорема косинусов. | Знание теоремы косинусов. | 1 балл | 4 балла |
| Умение находить периметр. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Решение треугольника. | Нахождение угла треугольника. | 1 балл | 5 баллов |
| Применение теоремы синусов. | 2 балла |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Теорема косинусов. | Определение неизвестных элементов. | 1 балл | 5 баллов |
| Нахождение катета. | 1 балл |
| Нахождение острых углов. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 5 | Теорема синусов. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Применение определения биссектрисы. | 1 балл |
| Нахождение угла. | 1 балл |
| Нахождение биссектрисы. | 1 балл |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-20 баллов – «4»
21-22 балла – «5»
Контрольная работа №5 9 класс.
Тема: «Длина окружности и площадь круга».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач формулы площадей круга и его частей, длин окружности и дуги;
- умение оформлять решение задачи.
| I вариант. |
| 1. Длина окружности равна 8π. Вычислить площадь круга, ограниченного данной окружностью. 2. Градусная мера дуги окружности с радиусом 6см равна 300. Вычислите площадь кругового сектора, соответствующего этой дуге. 3.Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 720, а радиус окружности равен 6см. 4. Найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72 см2. см2. 5.Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 4см, а градусная мера дуги равна 600. |
| II вариант. |
| 1. Площадь круга равна 324π. Вычислите длину окружности, ограничивающую данный круг. 2. Градусная мера дуги окружности с радиусом 4см равна 450. Вычислите площадь кругового сектора, соответствующего этой дуге. 3. Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 360, а радиус окружности равен 12см. 4. Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 см2. 5. Найдите площадь фигуры, ограниченной дугой окружности и стягивающей ее хордой, если длина хорды равна 2см, а диаметр окружности равен 4см. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Площадь круга и его частей. Длина дуги. Длина окружности. | №1,№2 | №3, №4 | №5 | 100% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Площадь круга. Длина окружности. | Знание формулы длины окружности. | 1 балл | 3 балла |
| Знание формулы площади круга. | 1 балл |
| Вычисления. | 1 балл |
| 2 | Площадь кругового сектора. | Знание формулы. | 1 балл | 3 балла |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 3 | Длина дуги окружности. | Выполнение чертежа по условию задачи. | 1 балл | 4 балла |
| Знание формулы. | 1 балл |
| Вычисления. | 1 балл |
| Оформление решения задачи. | 1 балл |
| 4 | Площадь круга. Длина окружности. | Выполнение чертежа по условию задачи. | 1 балл | 6 баллов |
| Знание формул площадей фигур. | 1 балл |
| Нахождение стороны правильного многоугольника. | 1 балл |
| Нахождение радиуса. | 1 балл |
| Вычисления длины окружности (площади круга). | 1 балл |
| Оформление решения задачи. | 1 балл |
| 5 | Площадь сегмента. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Нахождение радиуса окружности (угла дуги). | 1 балл |
| Нахождение площади сектора. | 1 балл |
| Нахождение площади треугольника. | 1 балл |
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-14 баллов – «3»
15-19 балов – «4»
20-21 балл – «5»
xn--j1ahfl.xn--p1ai
Контрольные работы по геометрии 9 класс
| Вариант I часть. (1 балл) 1.Определите по рисунку вид движения. 1. Центральная симметрия. 2. Осевая симметрия. 3. Поворот . 4. Параллельный перенос. 2.Треугольник имеет центр симметрии. Определите вид треугольника. 1. Разносторонний. 2.Равносторонний 3. Равнобедренный 4.Такого треугольника нет. 3. Не обладает центром симметрии четырёхуголь-ник, изображённый на рисунке под буквой: 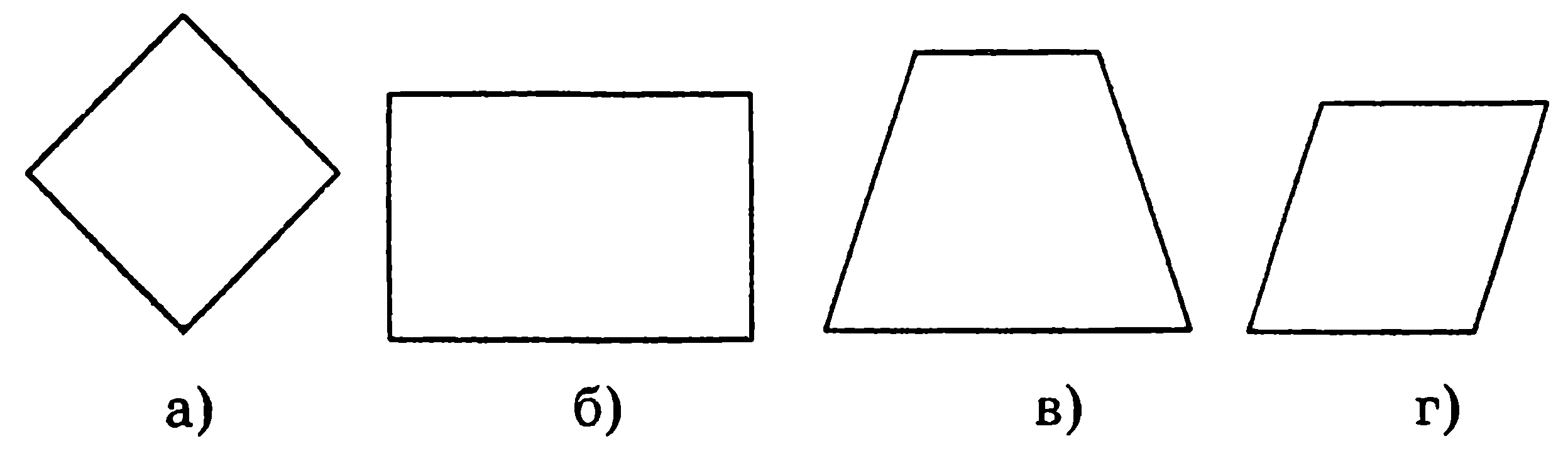
4. Не имеет оси симметрии фигура, изображенная на рисунке под буквой: 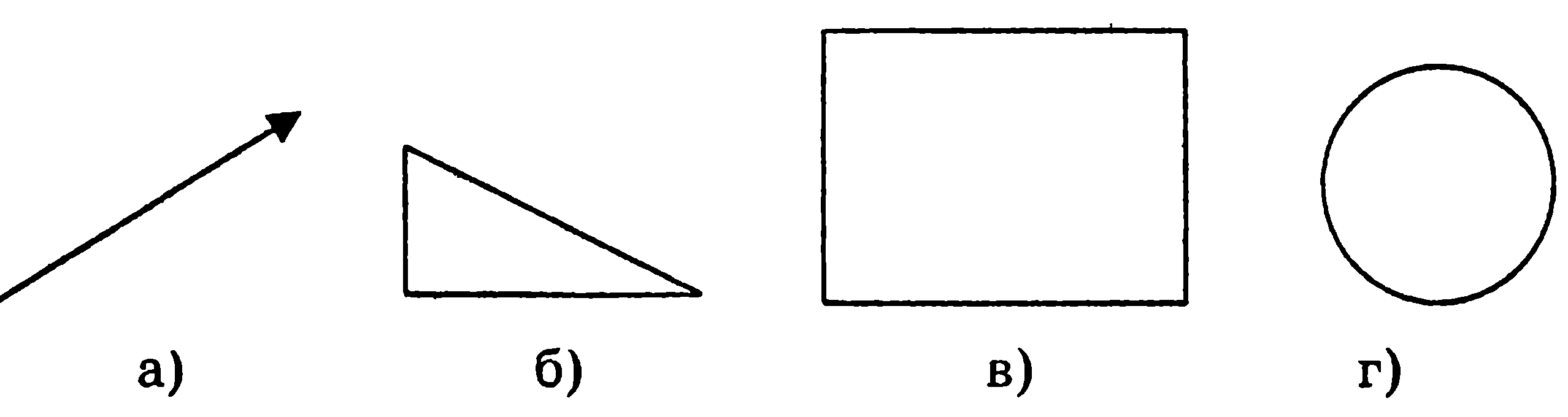
5. Многоугольник, изображённый на рис.4, перей-дёт сам в себя при повороте вокруг точки О на угол: 1) 600; 2) 900; 3) 1200; 4) 1500. 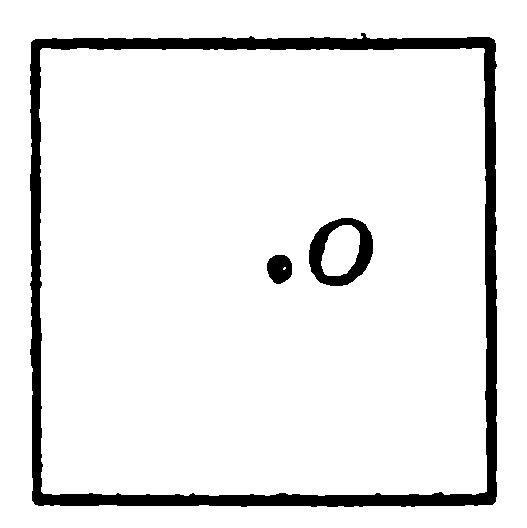 рис.4 рис.4
6.При параллельном переносе на 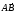 точка D прямоугольника ABCD переходит в точку … точка D прямоугольника ABCD переходит в точку … 7. При центральной симметрии точки А и В переходят соответственно в А1 и В1. При этом АВ=8см. Тогда А1В1= 8. Точка А имеет координаты: х = 3; у = – 4.Тогда точка В, симметричная точке А относительно оси абсцисс (х), будет иметь координаты … | II часть. (приведите полное решение) (2 б) 9. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону АВ. 10. При центральной симметрии относительно вершины С треугольника АВС вершина А переходит в точку М, а вершина В- в точку N. Найдите 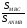 
Оформление работы. I часть 1. 5. 2. 6. 3. 7. 4. 8. 5» 11 - 12 баллов. «4» 8 – 10 баллов ( должно быть выполнено одно из заданий второй части). «3» 6 – 7 баллов. «2» менее 6 баллов. |
Вариант
1.Определите по рисунку вид движения.

1. Центральная симметрия. 2. Осевая симметрия.
3. Поворот . 4. Параллельный перенос.
2.Треугольник имеет ровно одну ось симметрии. Определите вид треугольника.
1. Разносторонний. 2.Равносторонний
3. Равнобедренный 4.Такого треугольника нет.
3. Не имеет центра симметрии фигура, изображенная на рисунке под буквой:
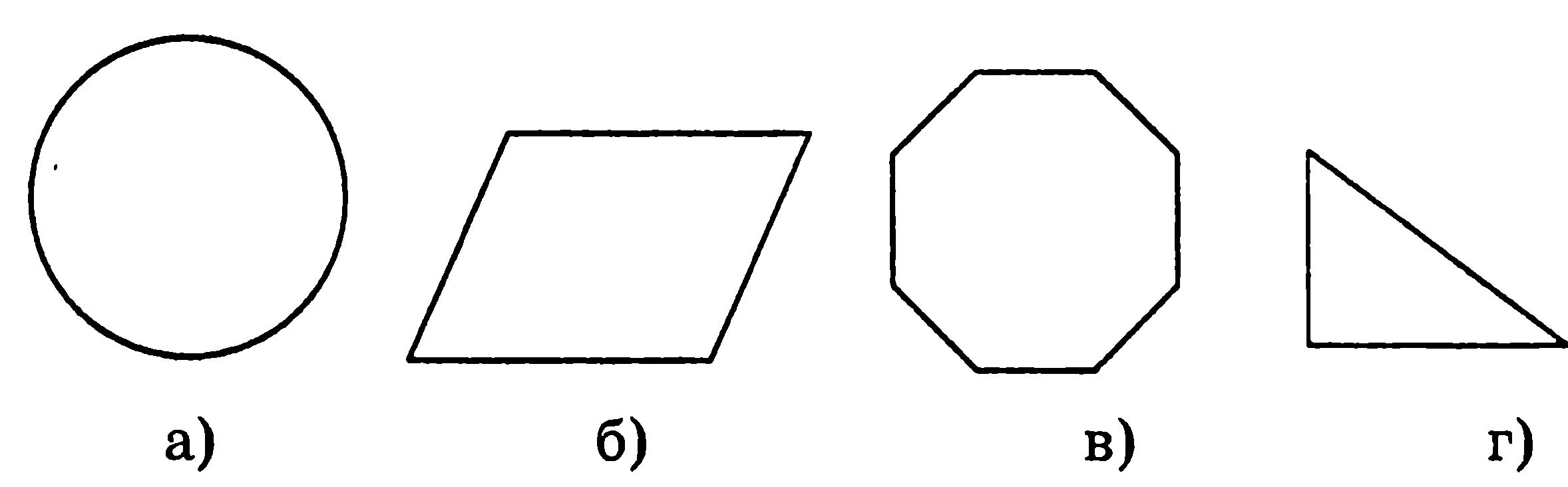
4. Не обладает осью симметрии четырёхугольник, изображённый на рисунке под буквой:
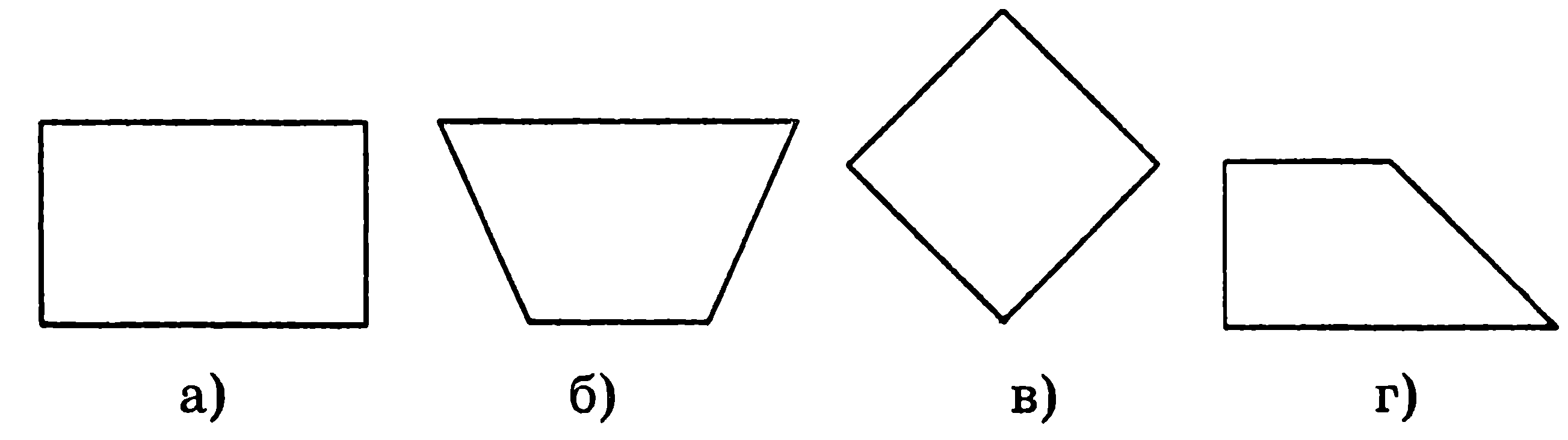
5. Многоугольник, изображённый на рис.4, перей-дёт сам в себя при повороте вокруг точки О (центр фигуры) на угол: 1) 600; 2) 450; 3) 1210; 4) 750.
 рис.4
рис.4
6.При параллельном переносе на 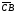 точка D ромба ABCD переходит в точку …
точка D ромба ABCD переходит в точку …
7. При центральной симметрии точки M и N переходят соответственно в M1 и N1. При этом MN=6см. Тогда M1N1=
8. Точка А имеет координаты: х = –5; у = 2.Тогда точка В, симметричная точке А относительно оси ординат (у), будет иметь координаты …
II часть. (приведите полное решение) (2 б)
9.Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны CD.
10. При центральной симметрии относительно вершины О треугольника NOС вершина C переходит в точку М, а вершина N- в точку D. Найдите 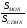
Оформление работы.
I часть
1. 5.
2. 6.
3. 7.
4. 8.
5» 11 - 12 баллов.
«4» 8 – 10 баллов ( должно быть выполнено одно из заданий второй части).
«3» 6 – 7 баллов.
«2» менее 6 баллов.
Вариант
1.Определите по рисунку вид движения.

1. Центральная симметрия. 2. Осевая симметрия.
3. Поворот . 4. Параллельный перенос.
2.Треугольник имеет ровно две оси симметрии. Определите вид треугольника.
1. Разносторонний. 2.Равносторонний
3. Равнобедренный 4.Такого треугольника нет.
3. Имеет центр симметрии фигура, изображённая на рисунке под буквой:
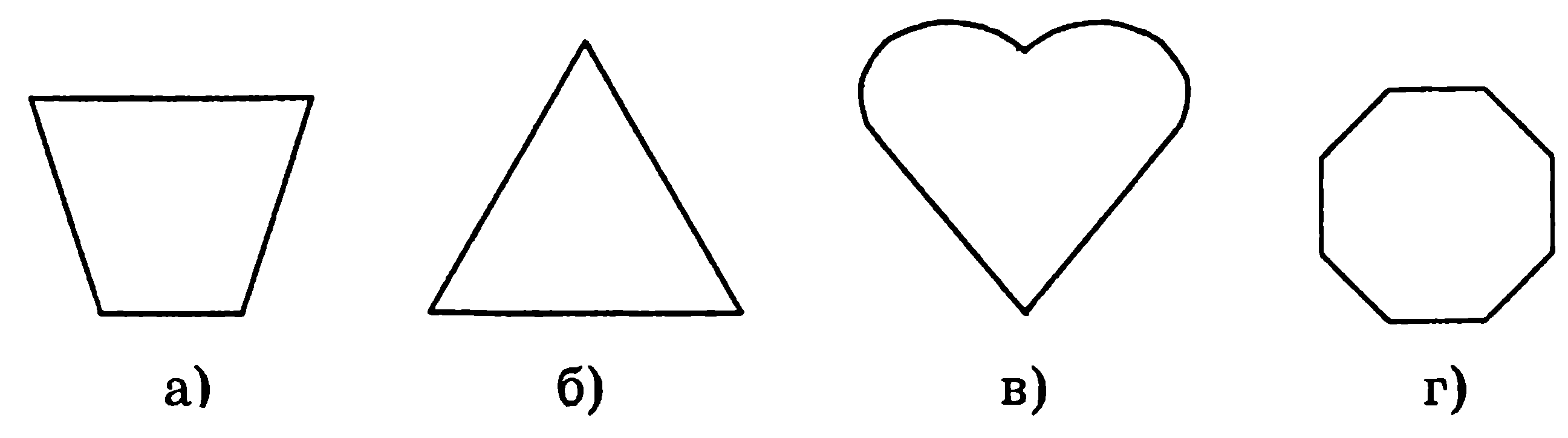
4. Не имеет оси симметрии фигура, изображенная на рисунке под буквой:
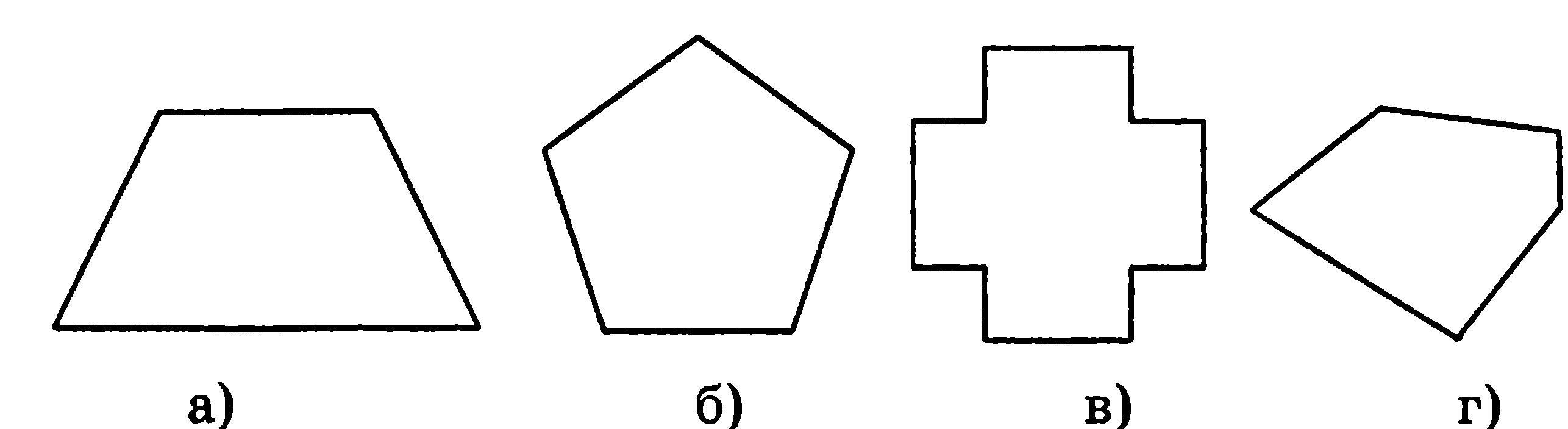
5. Многоугольник, изображённый на рис.4, перей-дёт сам в себя при повороте вокруг точки О (центр фигуры) на угол: 1) 600; 2) 450; 3) 1510; 4) 900.
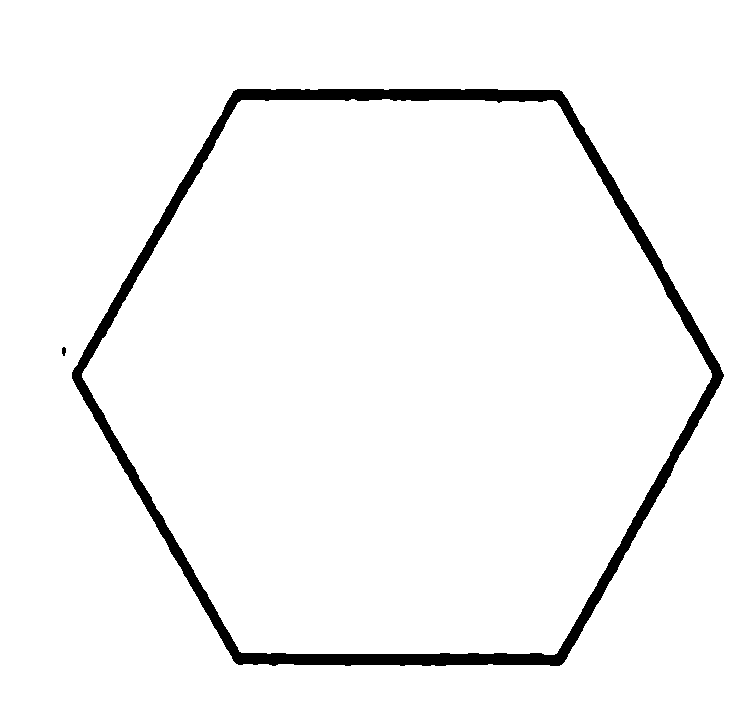 рис.4
рис.4
6.При параллельном переносе на 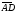 точка B прямоугольника ABCD переходит в точку …
точка B прямоугольника ABCD переходит в точку …
7. При центральной симметрии точки C и В переходят соответственно в C1 и В1. При этом CВ=10см. Тогда C1В1=
8. Точка А имеет координаты: х = – 2; у =5 .Тогда точка В, симметричная точке А относительно оси абсцисс (х), будет иметь координаты …
II часть. (приведите полное решение) (2 б)
9. Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую сторону СD.
10. При центральной симметрии относительно вершины С треугольника NСM вершина N переходит в точку B, а вершина M- в точку A. Найдите 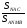

Оформление работы.
I часть
1. 5.
2. 6.
3. 7.
4. 8.
5» 11 - 12 баллов.
«4» 8 – 10 баллов ( должно быть выполнено одно из заданий второй части).
«3» 6 – 7 баллов.
«2» менее 6 баллов.
Вариант
1.Определите по рисунку вид движения.

1. Центральная симметрия. 2. Осевая симметрия.
3. Поворот . 4. Параллельный перенос.
2.Треугольник имеет три оси симметрии. Определите вид треугольника.
1. Разносторонний. 2.Равносторонний
3. Равнобедренный 4.Такого треугольника нет.
3. Не имеет центра симметрии фигура, изображенная на рисунке под буквой:
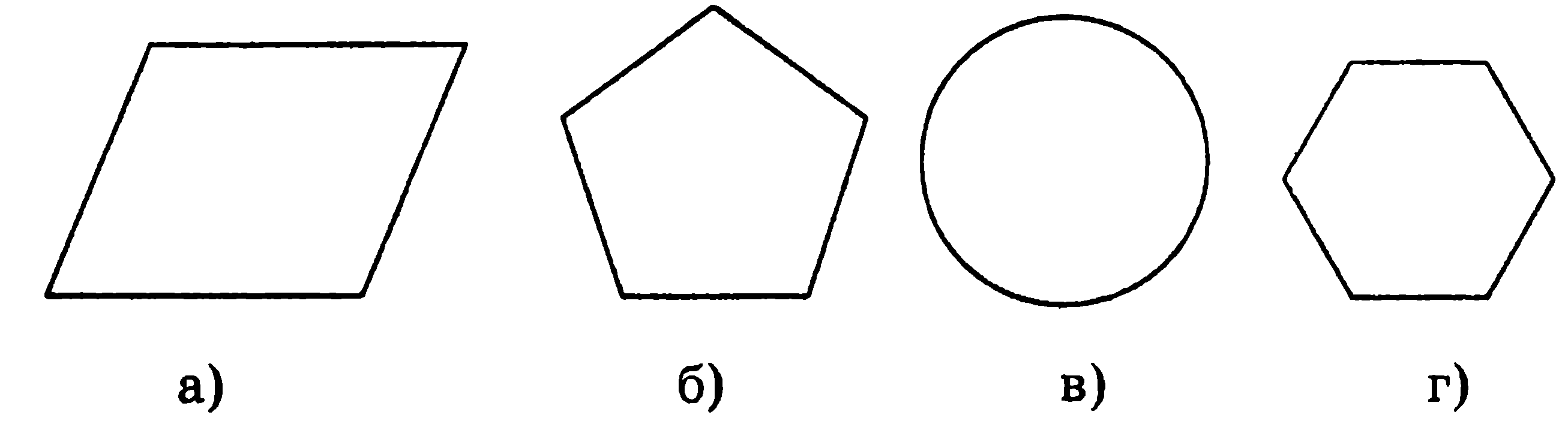
4. Не обладает осью симметрии четырёхугольник, изображённый на рисунке под буквой:
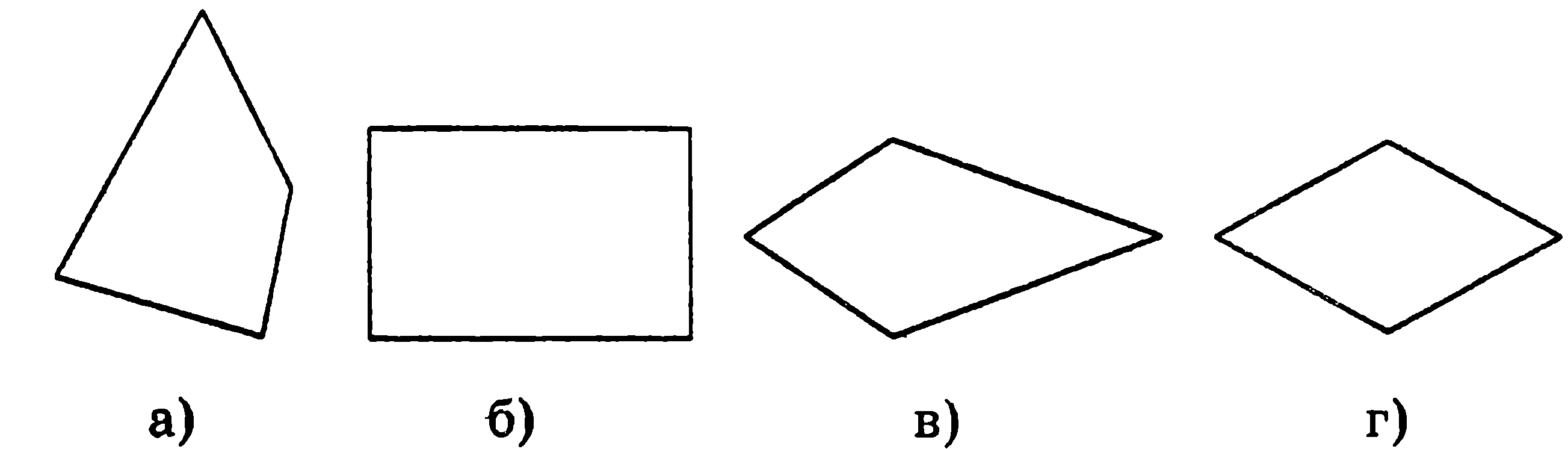
5. Многоугольник, изображённый на рис.4, перей-дёт сам в себя при повороте вокруг точки О на угол: 1) 600; 2) 900; 3) 1200; 4) 450.
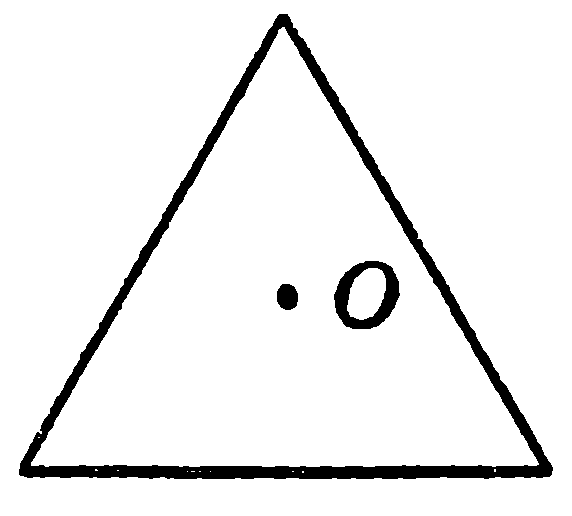 рис4.
рис4.
6.При параллельном переносе на 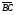 точка А ромба ABCD переходит в точку …
точка А ромба ABCD переходит в точку …
7. При центральной симметрии точки А и К переходят соответственно в А1 и К1. При этом
АК= 7см. Тогда А1К1=
8. Точка С имеет координаты: х = 6; у = – 9.Тогда точка В, симметричная точке С относительно оси ординат (у), будет иметь координаты …
II часть. (приведите полное решение) (2 б)
9.Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны АВ.
10. При центральной симметрии относительно вершины О треугольника DOM вершина M переходит в точку C, а вершина D- в точку N. Найдите 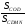

Оформление работы.
I часть
1. 5.
2. 6.
3. 7.
4. 8.
5» 11 - 12 баллов.
«4» 8 – 10 баллов ( должно быть выполнено одно из заданий второй части).
«3» 6 – 7 баллов.
«2» менее 6 баллов.
infourok.ru
ГДЗ по геометрии для 9 класса Б.Г. Зив
К—5 Вариант 2 1. 1) Начертите параллелограмм ABCD и отметьте на стороне ВС произвольную точку М. Постройте образ этого параллелограмма при переносе на вектор AM. 2) Начертите произвольный треугольник ABC и постройте его образ при повороте вокруг центра С на 60° против часовой стрелки. Чему будет равен угол между АВ и АХВХ, если АВ АХВХ? 2. Дан угол АОВ, ОС — биссектриса этого угла, М е OA и К е ОВ, причем ОМ = ОК. Докажите, что точки М и К симметричны относительно прямой ОС. 3. Даны две точки А(-5; 3) и В(3; 5). Докажите, что точка В может быть получена из точки А поворотом вокруг начала координат на 90° по часовой стрелке. Рис. 60 4*. Постройте треугольник, равный данному, так, чтобы основание его принадлежало данной прямой а, а вершина — данной прямой b (рис. 60). 85
Решебник / Контрольные работы / К-5. Варианты / 2




resheba.com
Контрольные работы по геометрии (9 класс)
Контрольная работа № 1
по геометрии 9 класс
вариант 1
1). Начертите два неколлинеарных вектора  и
и 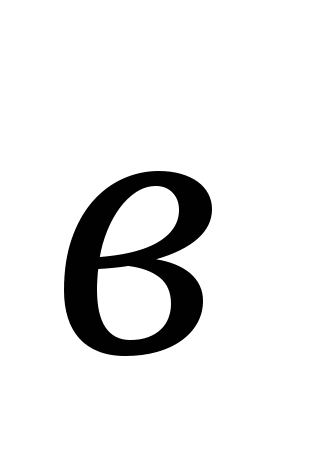 . Постройте векторы, равные:
. Постройте векторы, равные:
а). 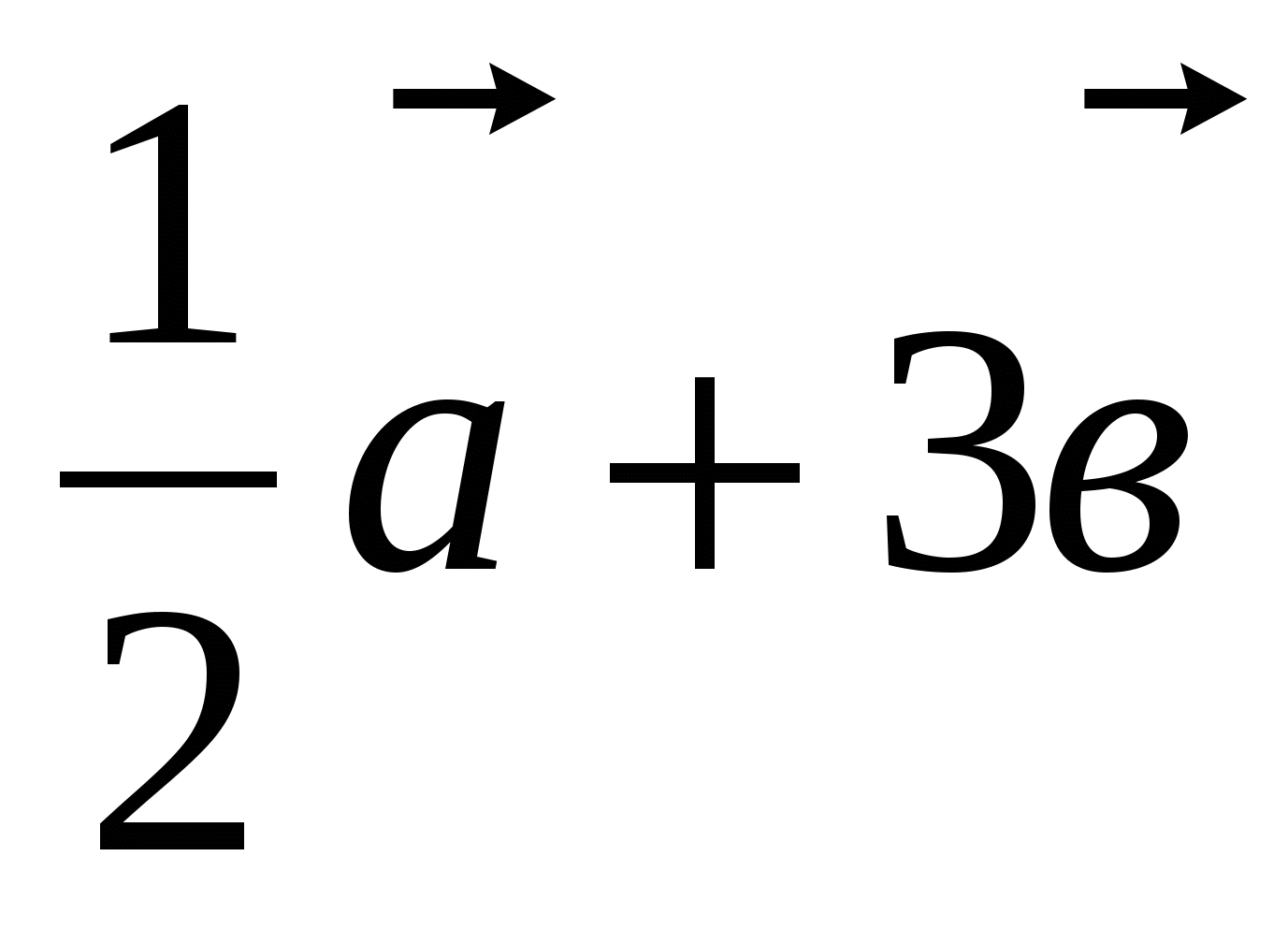 ; б).
; б). 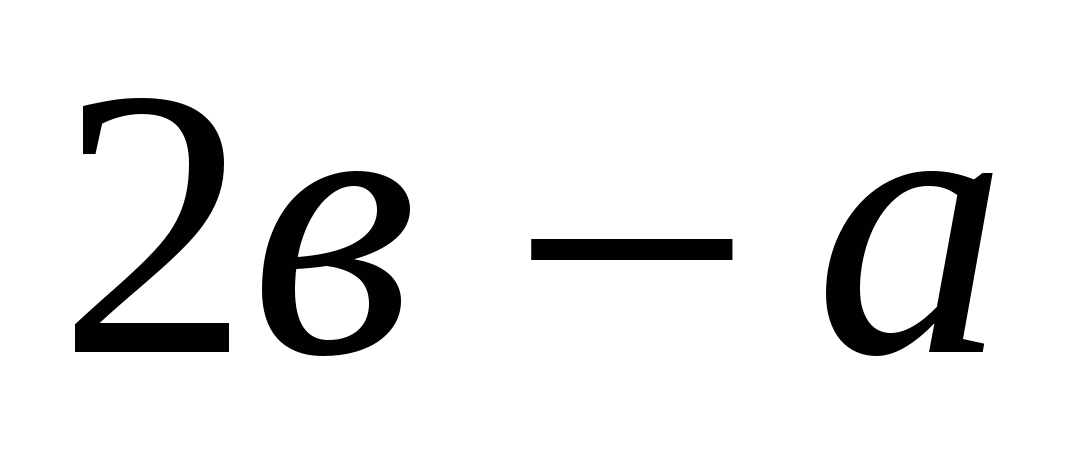
2). На стороне ВС ромба АВСD лежит точка К такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы 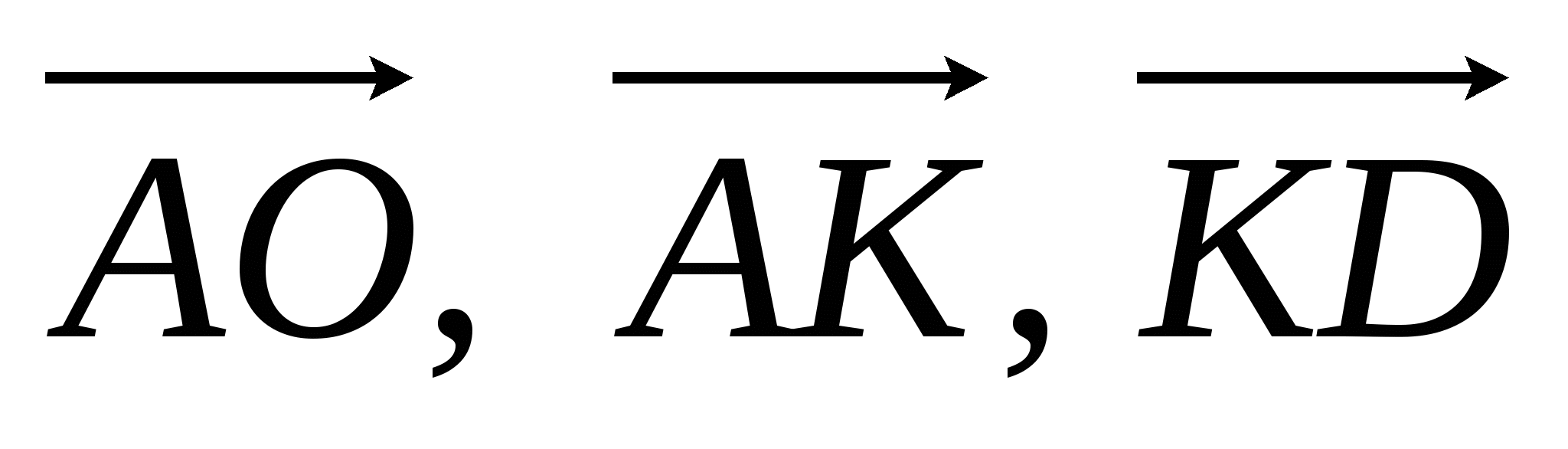 через векторы
через векторы 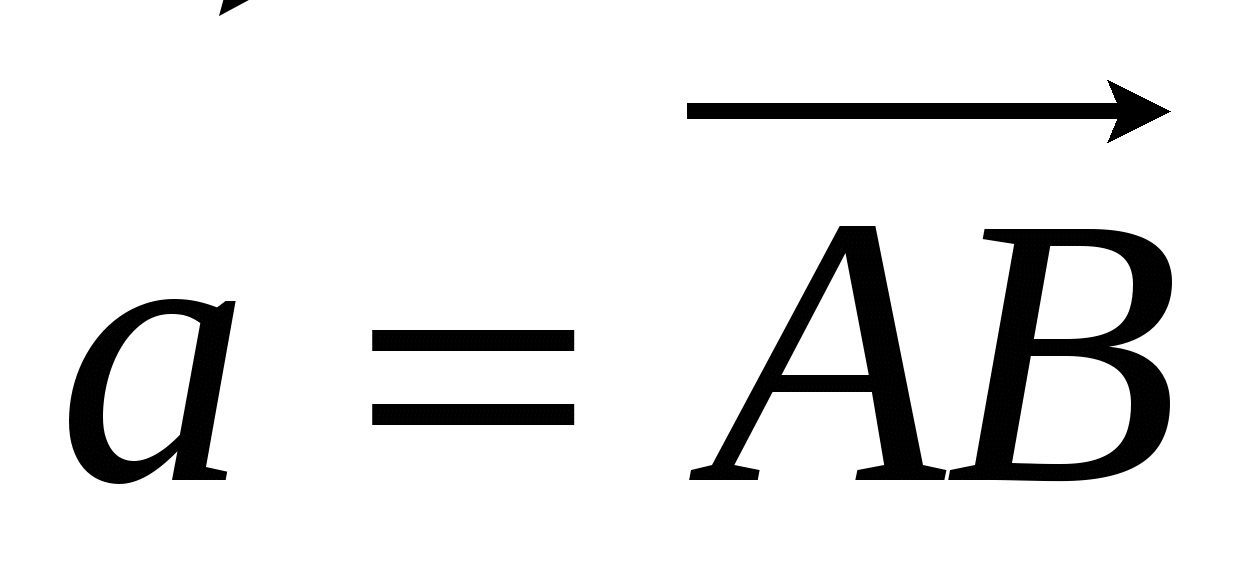 и
и 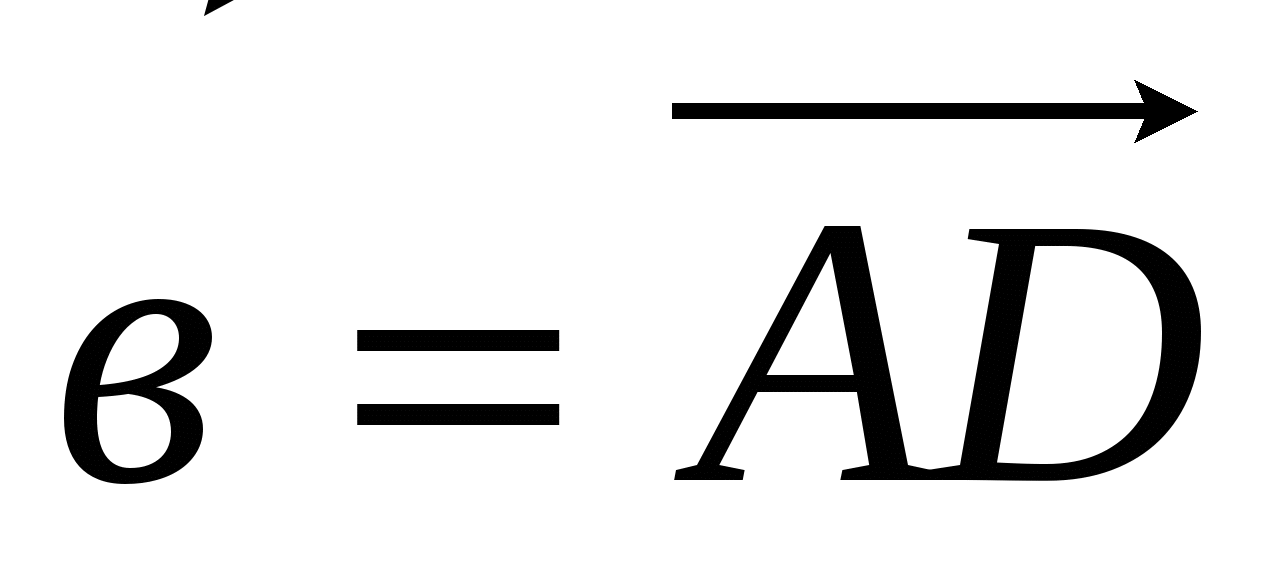 .
.
3). В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.
4). * В треугольнике АВС О – точка пересечения медиан. Выразите вектор 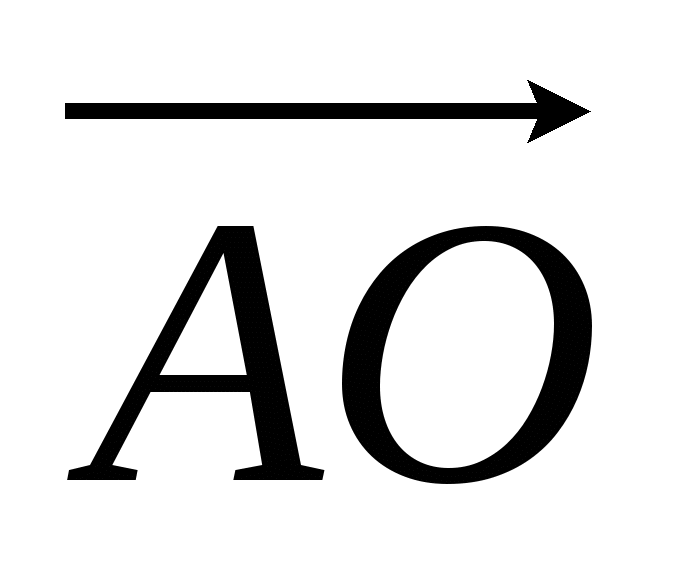 через векторы
через векторы 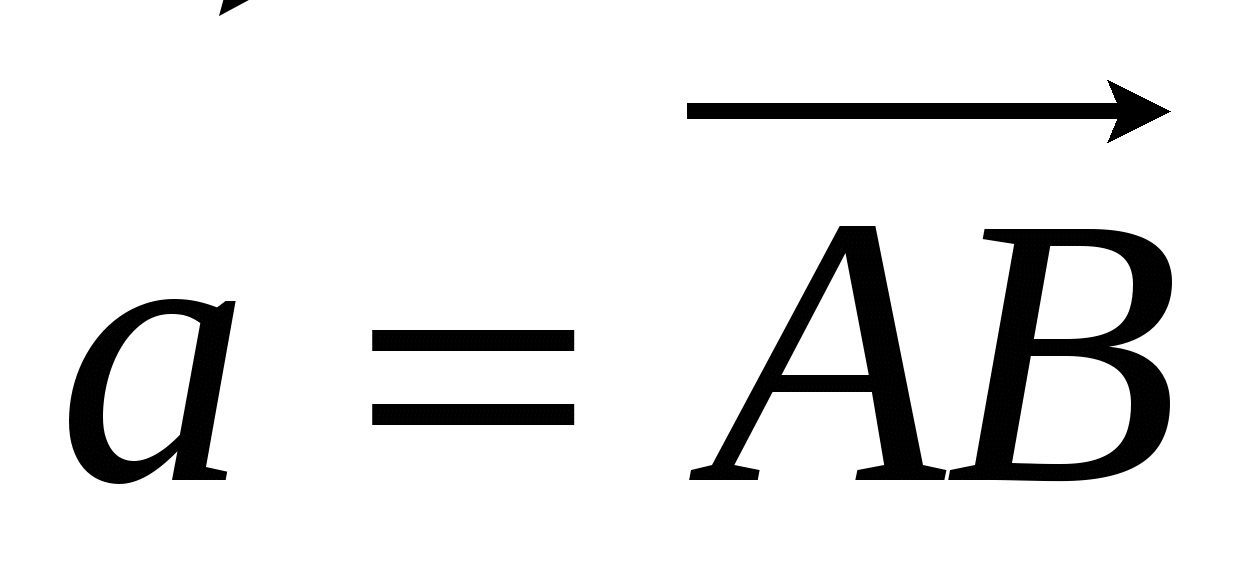 и
и 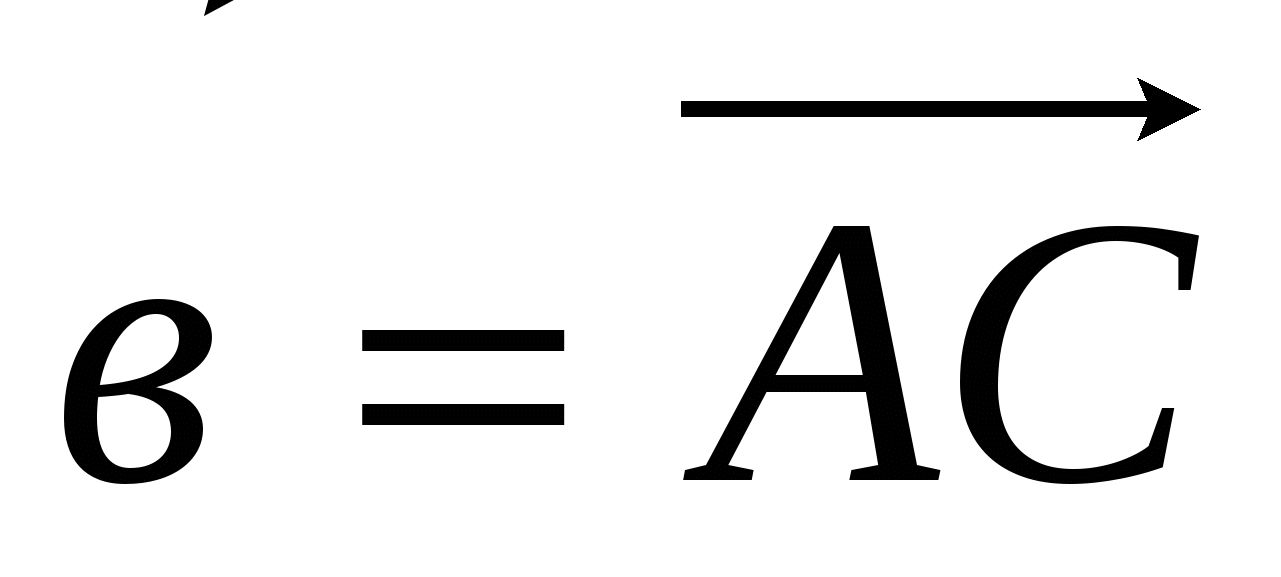 .
.
Контрольная работа № 1
по геометрии 9 класс
вариант 2
1). Начертите два неколлинеарных вектора 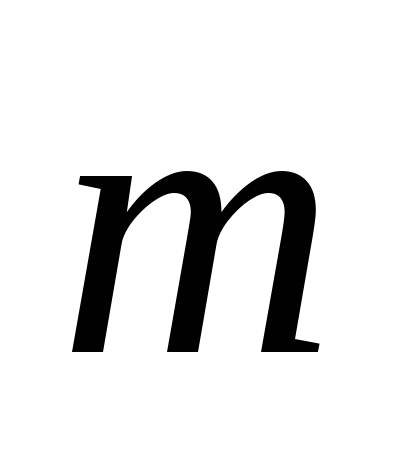 и
и 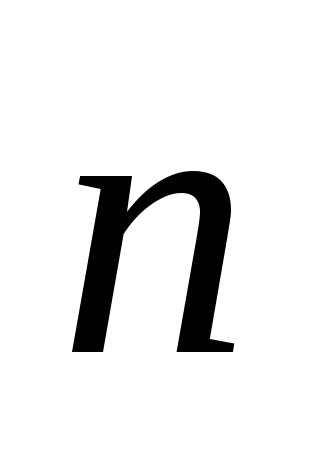 . Постройте векторы, равные:
. Постройте векторы, равные:
а). 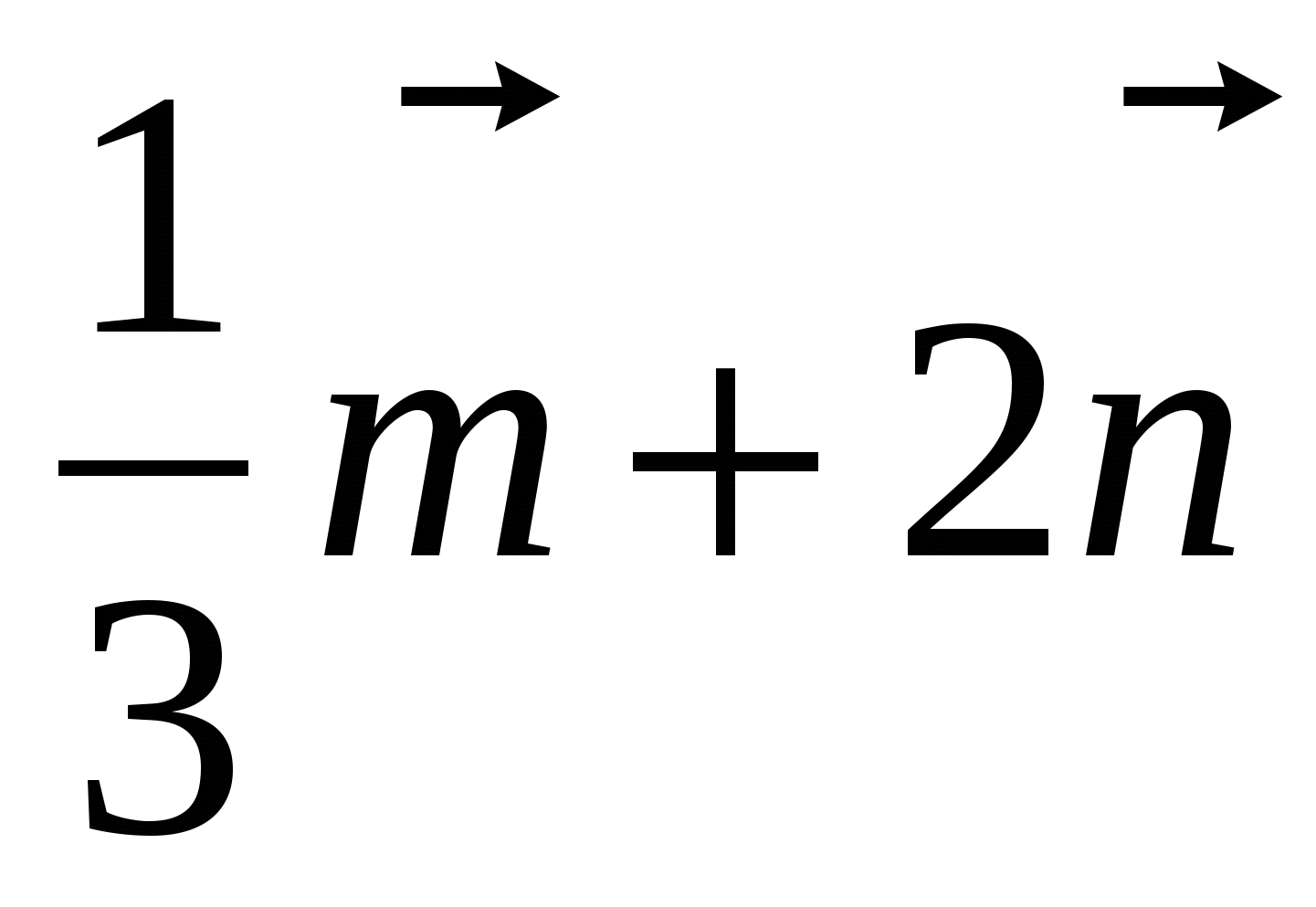 ; б).
; б). 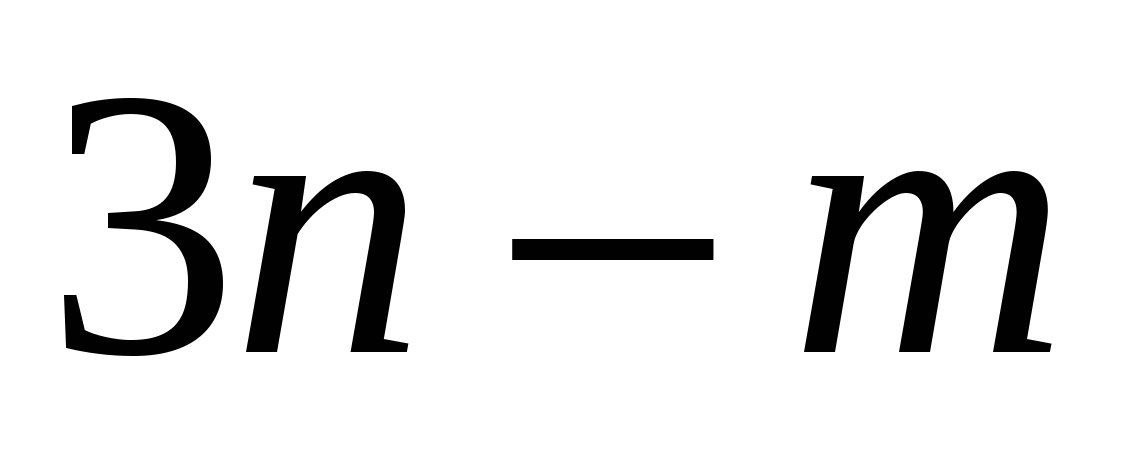
2). На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы 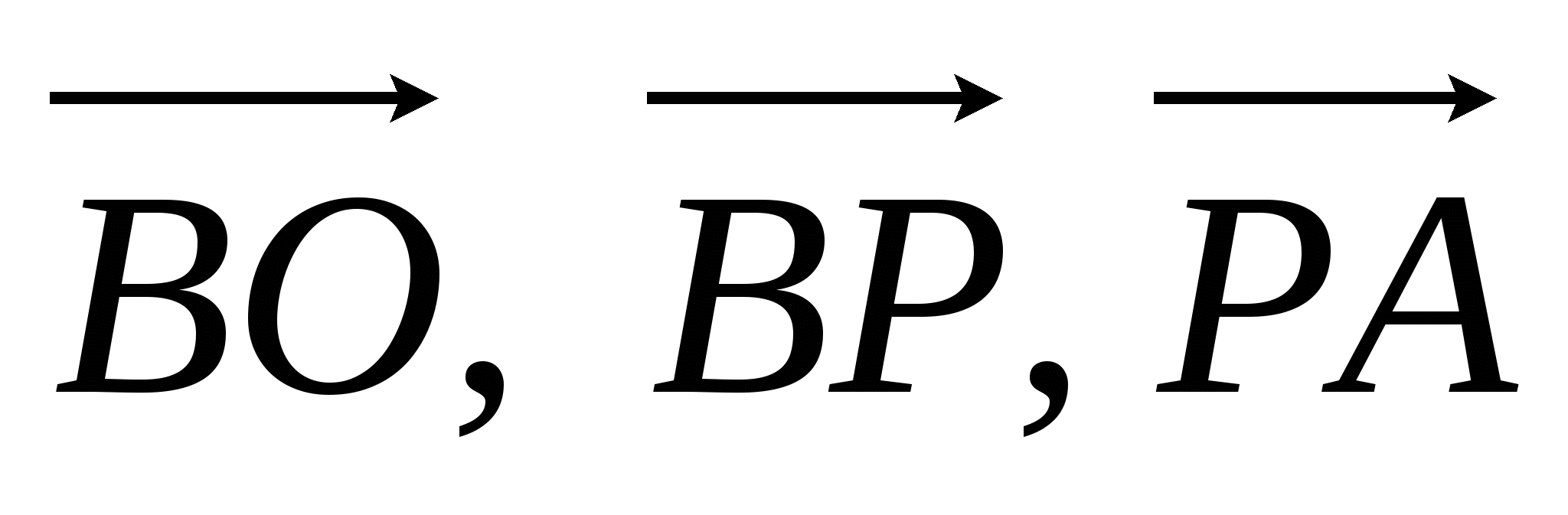 через векторы
через векторы 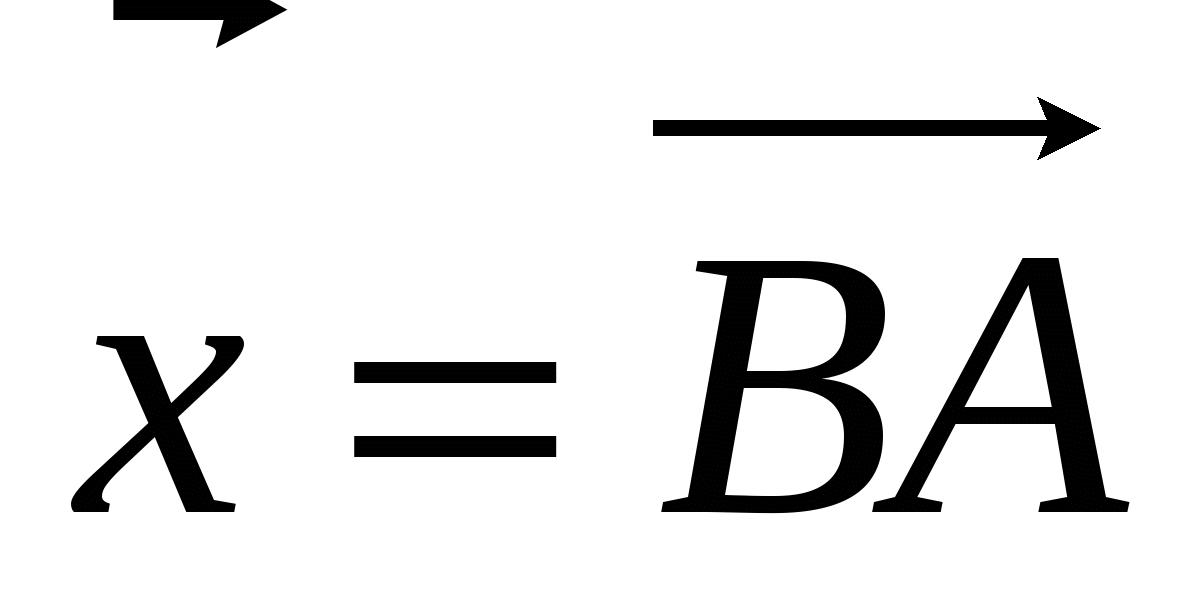 и
и 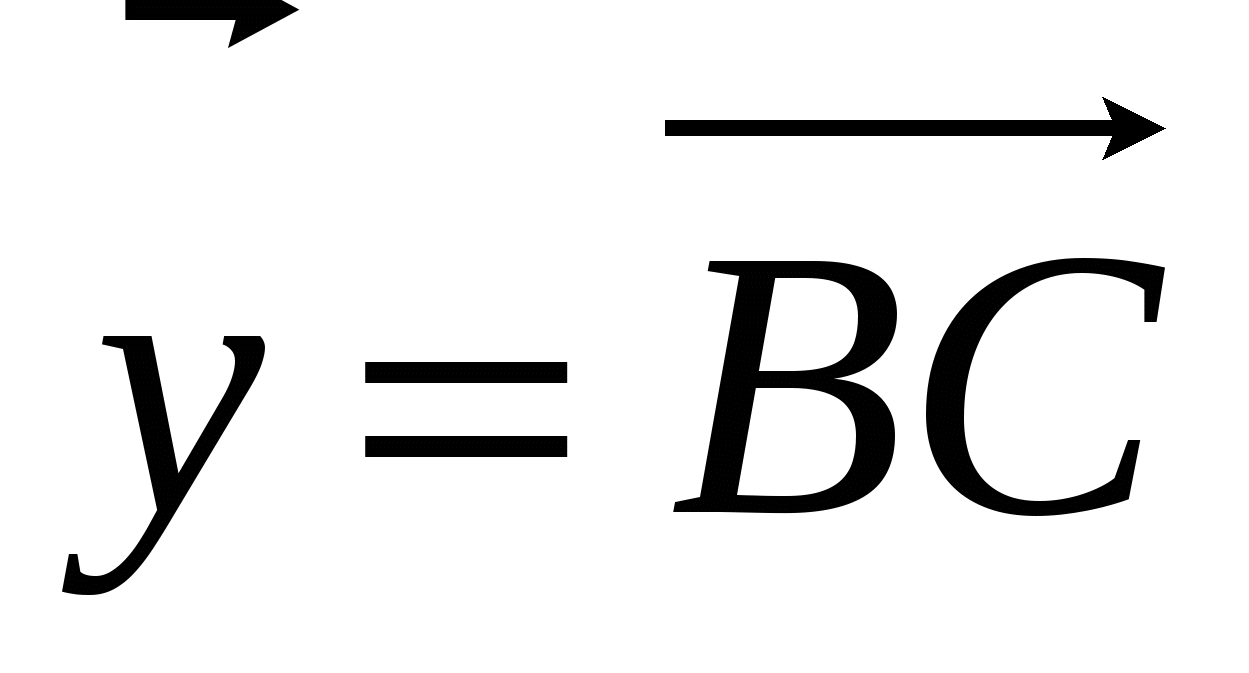 .
.
3). В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.
4). * В треугольнике МNK О – точка пересечения медиан, 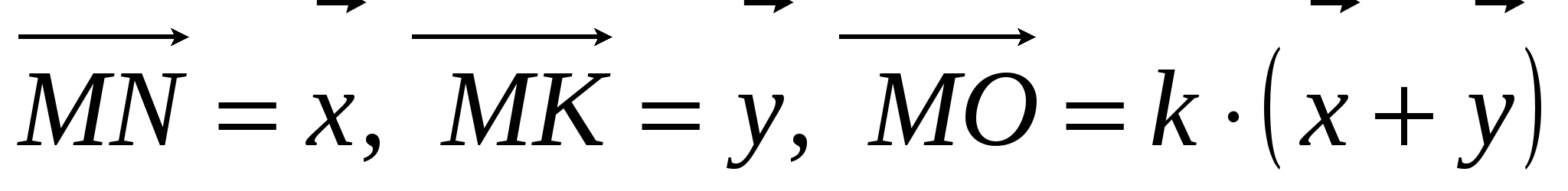 . Найдите число k.
. Найдите число k. Контрольная работа № 2
по геометрии 9 класс
вариант 1
1). Найдите координаты и длину вектора  , если
, если 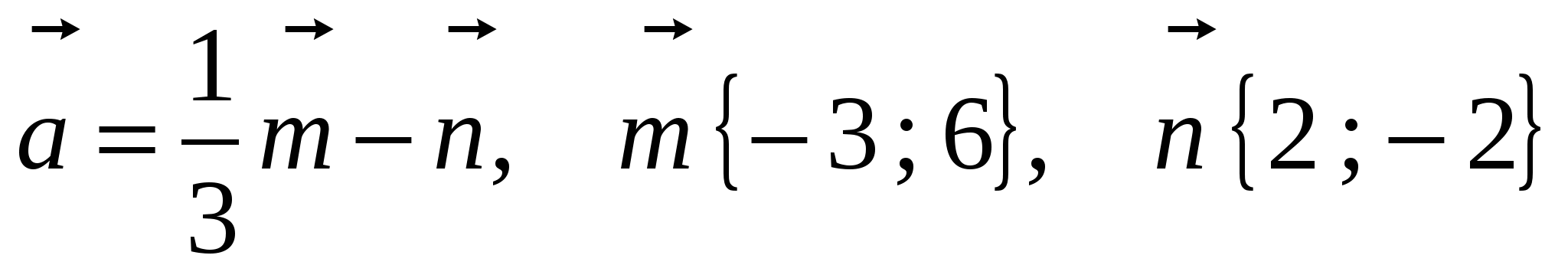 .
.
2). Напишите уравнение окружности с центром в точке А (- 3;2), проходящей через точку В (0; - 2).
3). Треугольник МNK задан координатами своих вершин: М ( - 6; 1 ), N (2; 4 ), К ( 2; - 2 ).
а). Докажите, что Δ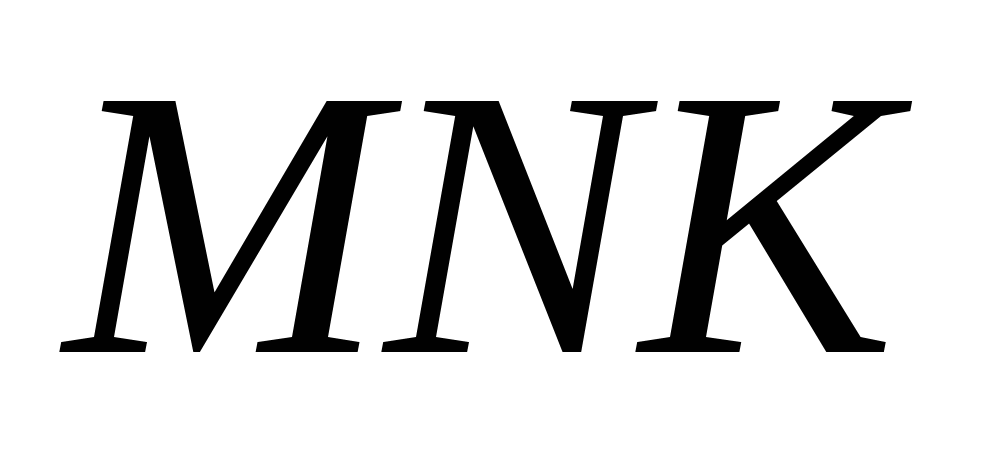 - равнобедренный;
- равнобедренный;
б). Найдите высоту, проведённую из вершины М.
4). * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( - 1; 3 ) и К( 0; 2
Контрольная работа № 2
по геометрии 9 класс
вариант 2
1). Найдите координаты и длину вектора 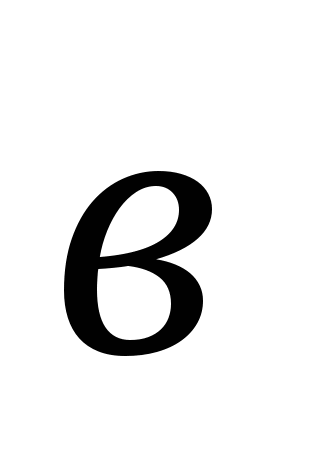 , если
, если  .
.
2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).
3). Треугольник СDЕ задан координатами своих вершин: С ( 2; 2 ), D (6; 5 ), Е ( 5; - 2 ).
а). Докажите, что Δ - равнобедренный;
- равнобедренный;
б). Найдите биссектрису, проведённую из вершины С.
4). * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; - 3 ) и С( 2; 0 ).
Контрольная работа № 3
по геометрии 9 класс
вариант 1
1). В треугольнике АВС 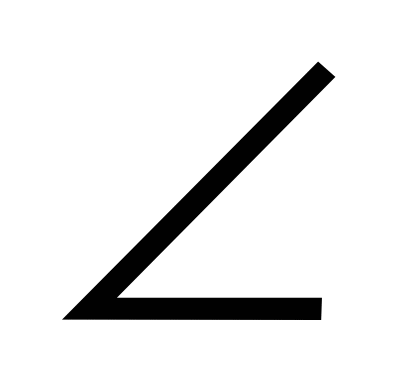 А = 450,
А = 450,
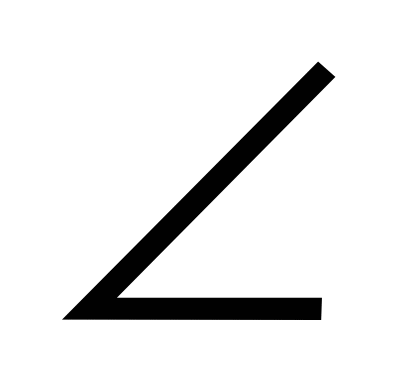 В = 600, ВС =
В = 600, ВС = 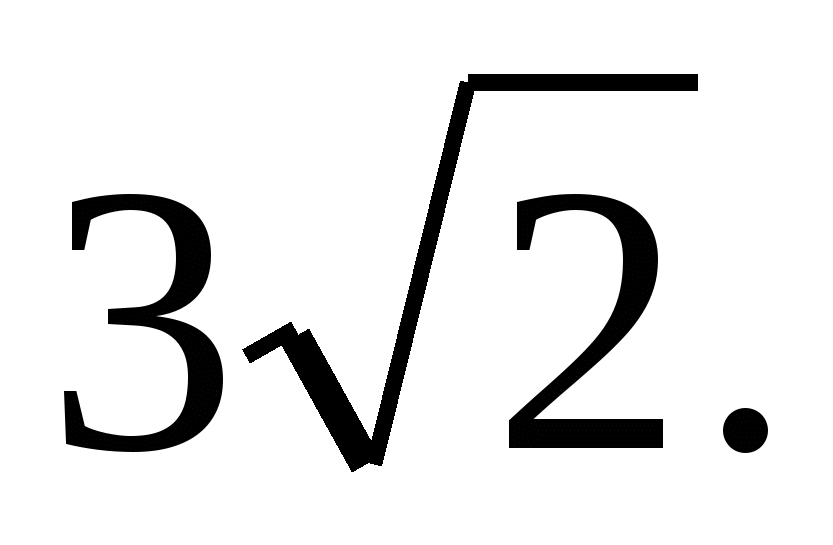 Найдите АС.
Найдите АС.
2). Две стороны треугольника равны
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ΔАВС АВ = ВС, 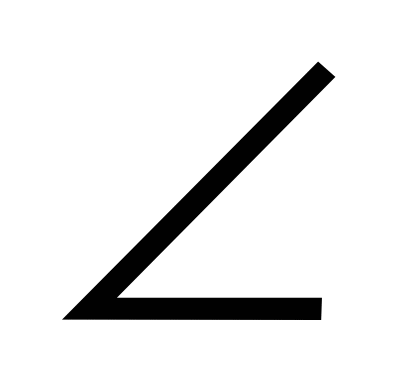 САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
Контрольная работа № 3
по геометрии 9 класс
вариант 2
1). В треугольнике СDE 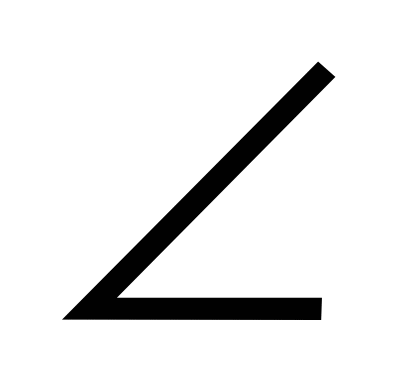 С = 300,
С = 300,
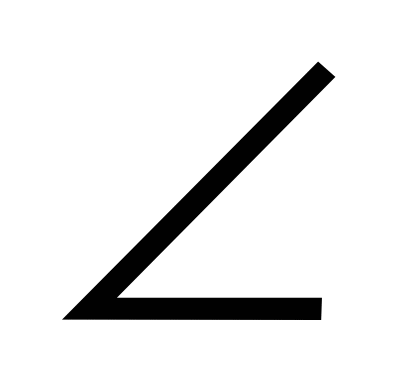 D = 450, СЕ =
D = 450, СЕ =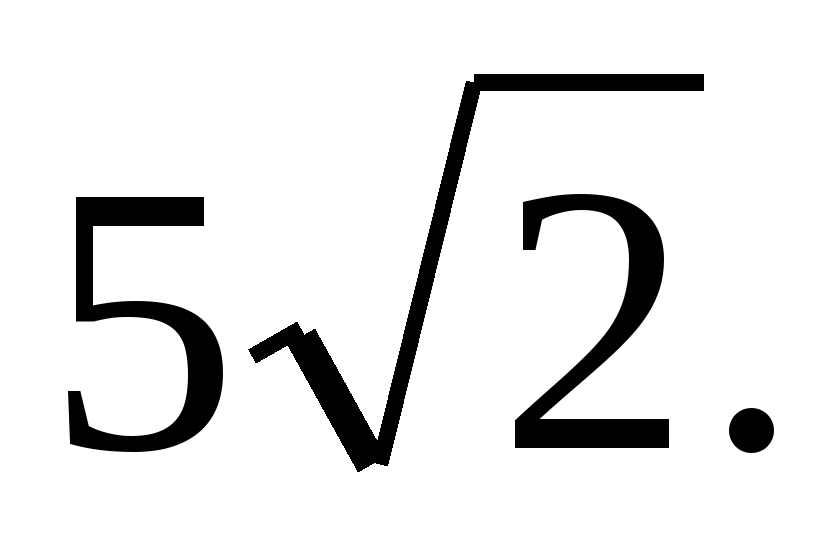 Найдите DE.
Найдите DE.
2). Две стороны треугольника равны
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ромбе АВСD АК – биссектриса угла САВ, 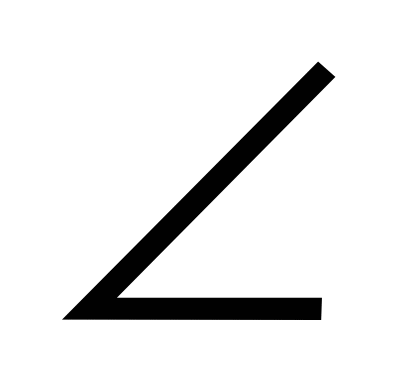 ВАD = 600, ВК = 12 см. Найдите площадь ромба.
ВАD = 600, ВК = 12 см. Найдите площадь ромба. Контрольная работа № 4
по геометрии 9 класс
вариант 1
1). Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 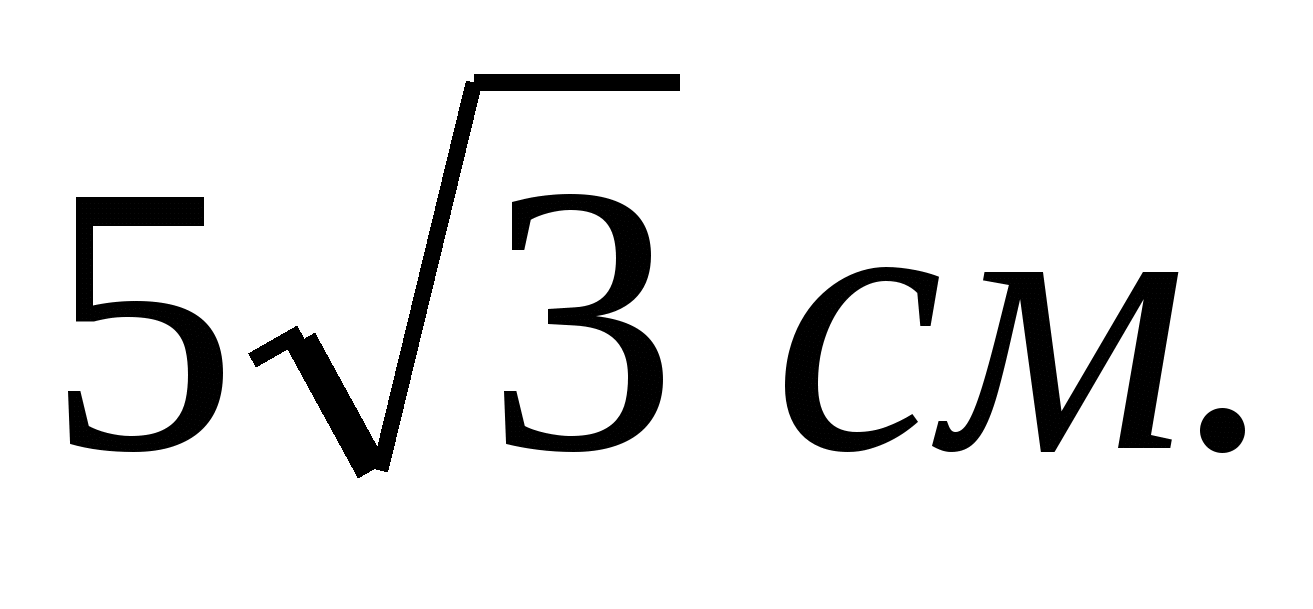
2). Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора?
3). Периметр правильного треугольника, вписанного в окружность, равен 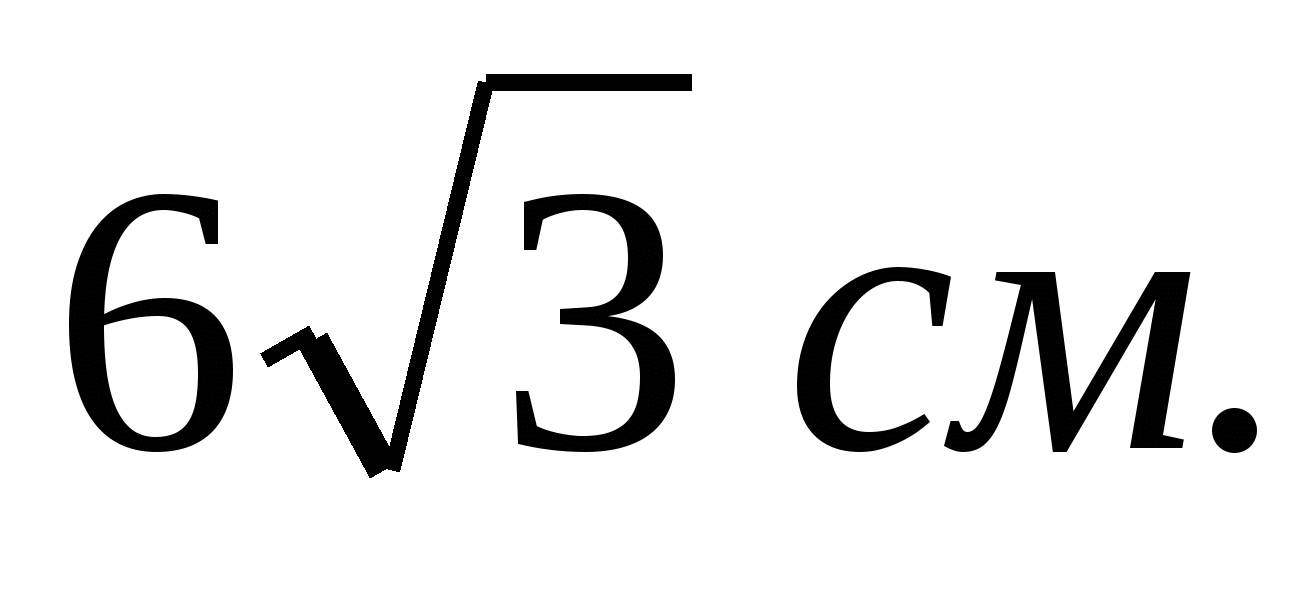 Найдите периметр правильного шестиугольника, описанного около той же окружности.
Найдите периметр правильного шестиугольника, описанного около той же окружности.
Контрольная работа № 4
по геометрии 9 класс
вариант 2
1). Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.
2). Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора?
3). Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.
Контрольная работа № 5
по геометрии 9 класс
вариант 1
1). Начертите ромб АВСD. Постройте образ этого ромба:
а). при симметрии относительно точки С;
б). при симметрии относительно прямой АВ;
в). При параллельном переносе на вектор 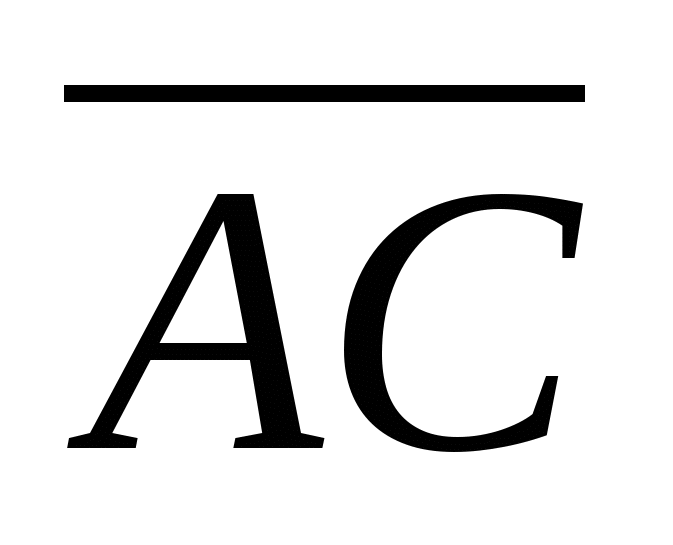 ;
;
г). При повороте вокруг точки D на 600 по часовой стрелке.
2). Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.
3). * Начертите два параллельных отрезка, длины которых равны. начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.
Контрольная работа № 5
по геометрии 9 класс
вариант 2
1). Начертите параллелограмм АВСD. Постройте образ этого параллелограмма:
а). при симметрии относительно точки D;
б). при симметрии относительно прямой CD;
в). При параллельном переносе на вектор 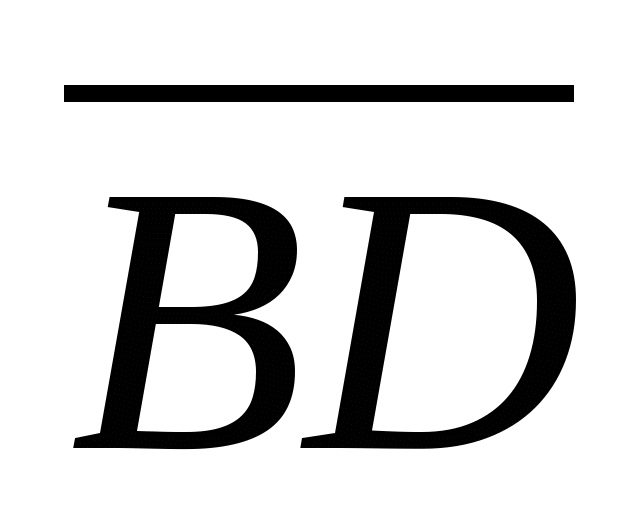 ;
;
г). При повороте вокруг точки А на 450 против часовой стрелки.
2). Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.
3).* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.
infourok.ru
Контрольные работы по геометрии для 9 класса
|
Контрольная работа № 1
|
|
1 вариант.
1). Начертите два неколлинеарных вектора и . Постройте векторы, равные:
а). ; б).
2). На стороне ВС ромба АВСD лежит точка К такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы через векторы и .
3). В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.
4). * В треугольнике АВС О – точка пересечения медиан. Выразите вектор через векторы и .
|
2 вариант
1). Начертите два неколлинеарных вектора и . Постройте векторы, равные:
а). ; б).
2). На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы через векторы и .
3). В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.
4). * В треугольнике МNK О – точка пересечения медиан, . Найдите число k.
|
|
Контрольная работа № 2
|
|
1 вариант.
1). Найдите координаты и длину вектора , если .
2). Напишите уравнение окружности с центром в точке А (- 3;2), проходящей через точку В (0; - 2).
3). Треугольник МNK задан координатами своих вершин: М ( - 6; 1 ), N (2; 4 ), К ( 2; - 2 ).
а). Докажите, что Δ - равнобедренный;
б). Найдите высоту, проведённую из вершины М.
4). * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( - 1; 3 ) и К( 0; 2 ).
|
2 вариант.
1). Найдите координаты и длину вектора , если .
2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).
3). Треугольник СDЕ задан координатами своих вершин: С ( 2; 2 ), D (6; 5 ), Е ( 5; - 2 ).
а). Докажите, что Δ - равнобедренный;
б). Найдите биссектрису, проведённую из вершины С.
4). * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; - 3 ) и С( 2; 0 ).
|
|
Контрольная работа № 3
|
|
1 вариант
1). В треугольнике АВС А = 450,
В = 600, ВС = Найдите АС.
2). Две стороны треугольника равны
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ΔАВС АВ = ВС, САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
|
2 вариант
1). В треугольнике СDE С = 300,
D = 450, СЕ = Найдите DE.
2). Две стороны треугольника равны
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ромбе АВСD АК – биссектриса угла САВ, ВАD = 600, ВК = 12 см. Найдите площадь ромба.
|
|
Контрольная работа № 4
|
|
1 вариант
1). Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна
2). Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора?
3). Периметр правильного треугольника, вписанного в окружность, равен Найдите периметр правильного шестиугольника, описанного около той же окружности.
|
2 вариант
1). Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.
2). Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора?
3). Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.
|
|
Контрольная работа № 5
|
|
1 вариант
1). Начертите ромб АВСD. Постройте образ этого ромба:
а). при симметрии относительно точки С;
б). при симметрии относительно прямой АВ;
в). При параллельном переносе на вектор ;
г). При повороте вокруг точки D на 600 по часовой стрелке.
2). Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.
3). * Начертите два параллельных отрезка, длины которых равны. начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.
|
2 вариант
1). Начертите параллелограмм АВСD. Постройте образ этого параллелограмма:
а). при симметрии относительно точки D;
б). при симметрии относительно прямой CD;
в). При параллельном переносе на вектор ;
г). При повороте вокруг точки А на 450 против часовой стрелки.
2). Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.
3).* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.
|
uchkopilka.ru
Контрольные работы по геометрии в 9 классе по учебнику атанасян л.с.
Контрольные работы
по геометрии
в 9 классе
по учебнику атанасян л.с.
Контрольная работа №1.
Вариант 1.
Начертите два неколлинеарных вектора  и
и  . Постройте векторы, равные:
. Постройте векторы, равные:
а)  +3
+3 ; б) 2
; б) 2 -
- .
.
2. На стороне ВС ромба ABCD лежит точка К так, что ВК=КС, О – точка пересечения диагоналей. Выразите векторы  ,
,  ,
,  через векторы
через векторы  =
= и
и  =
= .
.
В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.
4*. В треугольнике АВС О – точка пересечения медиан. Выразите вектор  через векторы
через векторы  =
=
 =
= .
.
Контрольная работа №1.
Вариант 2.
Начертите два неколлинеарных вектора  и
и  . Постройте векторы, равные:
. Постройте векторы, равные:
а)  +
+ ; б) 3
; б) 3 -
- .
.
2. На стороне СD квадрата ABCD лежит точка P так, что CP=PD, О – точка пересечения диагоналей. Выразите векторы  ,
,  ,
,  через векторы
через векторы  =
= и
и  =
= .
.
3.В равнобедренной трапеции один из углов равен 60°, боковая сторона равна 8 см, а меньшее основание
7 см. Найдите среднюю линию трапеции.
4*. В треугольнике MNK О – точка пересечения медиан,  =
=
 =
= ,
,  =k·(
=k·( +
+ ).
).
Контрольная работа №2.
Вариант 1.
Найдите координаты и длину вектора , если
, если
 = -
= - +
+ ,
,  ,
,  .
.
Даны координаты вершин треугольника АВС : А(-6;1), В(2;4), С(2;-2). Докажите, что треугольник АВС равнобедренный, и найдите высоту треугольника, проведённую из вершины А.
Окружность задана уравнением  +
+ =9. Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат.
=9. Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат.
Контрольная работа №2.
Вариант 2.
Найдите координаты и длину вектора , если
, если
 =
=  ,
,  ,
,  .
.
Даны координаты вершин четырёхугольника АВСD :
А(-6;1), В(0;5), С(6;-4)? D(0;-8). Докажите, что АВСD - прямоугольник, и найдите координаты точки пересечения его диагоналей.
Окружность задана уравнением  +
+ =16. Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.
=16. Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.
Контрольная работа №3.
Вариант 1.
Найдите угол между лучом ОА и положительной полуосью Ох, если А (-1;3).
Решите треугольник АВС, если см.
Найдите косинус угла М треугольника KLM, если
К (1;7), L(-2;4), M (2;0).
Контрольная работа №3.
Вариант 2.
Найдите угол между лучом ОВ и положительной полуосью Ох, если В (3;3).
Решите треугольник ВСD, если D=60°,
ВС= см.
см.
Найдите косинус угла A треугольника ABC, если
A (3;9), B(0;6), C (4;2).
Контрольная работа №4 .
Вариант 1.
Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.
Найдите площадь круга, если площадь вписанного в ограничивающую его окружность квадрата равна 72 .
.
Найдите длину дуги окружности радиуса 3 см, если её градусная мера равна 150°.
Контрольная работа №4 .
Вариант 2.
Периметр правильного шестиугольника, вписанного в окружность, равен 48 см. Найдите сторону квадрата, вписанного в ту же окружность.
Найдите длину окружности, если площадь вписанного в неё правильного шестиугольника равна 72 .
.
Найдите площадь кругового сектора, если градусная мера его дуги равна 120°, а радиус круга равен 12 см.
Контрольная работа №5.
Вариант 1.
Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно прямой, содержащей боковую
сторону АВ.
2. Две окружности с центрами  и
и  , радиусы которых равны, пересекаются в точках M и N. Через точку М проведена прямая, параллельная
, радиусы которых равны, пересекаются в точках M и N. Через точку М проведена прямая, параллельная 
 и пересекающая окружность с центром
и пересекающая окружность с центром  в точке D. Используя параллельный перенос, докажите, что четырёхугольник
в точке D. Используя параллельный перенос, докажите, что четырёхугольник  MD
MD является параллелограммом.
является параллелограммом.
Контрольная работа №5.
Вариант 2.
Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой
стороны CD.
Дан шестиугольник  . Его стороны
. Его стороны  и
и  ,
,  и
и  ,
,  и
и  попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали
попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали  ,
,  ,
,  данного шестиугольника пересекаются в одной точке.
данного шестиугольника пересекаются в одной точке.
Итоговая контрольная работа.
Вариант 1.
Часть 1.
1.Какое утверждение относительно треугольника со сторонами 5,9,15 верно?
а) треугольник остроугольный;
б) треугольник тупоугольный;
в) треугольник прямоугольный;
г) такого треугольника не существует.
2.Если одна из сторон треугольника на 3 см меньше другой, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:
а) 25 см; б) 40 см; в) 32 см; г) 20 см.
3.Если один из углов ромба равен 60°, а диагональ, проведённая из вершины этого угла, равна4 см, то периметр ромба равен:
см, то периметр ромба равен:
а) 16 см; б) 8 см; в) 12 см; г) 24 см.
4.Величина одного из углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника.
а) 84°; б) 92°; в) 80°; г) 87°.
5.В треугольнике АВС сторона а=7, сторона b=8, сторона с=5. Вычислите угол А.
а) 120°; б) 45°; в) 30°; г) 60°.
Часть 2.
1.В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.
2.В треугольнике ВСЕ .
3.Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3 ,
,
4.Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если её средняя линия равна 5.
5.Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС соответственно в точках Е и D. Найдите величину угла АВС (в градусах), если известно, что АЕ=1, ВD=3.
Итоговая контрольная работа.
Вариант 2.
Часть 1.
1.Какое утверждение относительно треугольника со сторонами 12,9,15 верно?
а) треугольник остроугольный;
б) треугольник тупоугольный;
в) треугольник прямоугольный;
г) такого треугольника не существует.
2.Если сходственные стороны подобных треугольников равны 2 см и 5 см, площадь первого треугольника равна 8  , то площадь второго треугольника равна:
, то площадь второго треугольника равна:
а) 5 ; б) 40
; б) 40  в) 60
в) 60  ; г) 20
; г) 20 .
.
3.Если в равнобедренном треугольнике длина основания равна 12 см, а его периметр равен 32 см , то радиус окружности, вписанной в треугольник, равен::
а) 4 см; б) 3 см; в) 6 см; г) 5 см.
4.В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найдите катеты треугольника.
а)12 см и 16 см; б)7 см и 11 см; в) 10 см и 13 см; г) 8 см и 15 см.
5.Стороны прямоугольника равны a и k. Найдите радиус окружности, описанной около этого прямоугольника.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Часть 2.
1.Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается стороны ВС в точке К, причём СК:ВК=5:8. Найдите площадь треугольника, если его периметр равен 72.
2.Около треугольника АВС описана окружность. Медиана треугольника АМ продлена до пересечения с окружностью в точке К. Найдите сторону АС, если АМ=18, МК=8, ВК=10.
3.Найдите основание равнобедренного треугольника , если угол при основании равен 30°, а взятая внутри треугольника точка находится на одинаковом расстоянии, равном 3, от боковых сторон и на расстоянии 2 от основания.
от основания.
4.Пусть М – точка пересечения диагоналей выпуклого четырёхугольника ABCD, в котором стороны АВ, АD, и ВС равны между собой. Найдите угол СМD (в градусах), если известно, что DМ=МС, а угол САВ не равен углу DBA.
5.На боковой стороне ВС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите квадрат расстояния от вершины А до центра окружности, если АD= , а угол АВС равен 120°.
, а угол АВС равен 120°.
multiurok.ru
контрольные работы по геометрии 9 класс по учебнику А.В. Погорелова
Контрольные работы Г-9 по Бурмистрову
Контрольная работа №1 «Подобие фигур» вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СД)
Контрольная работа № 1 «Подобие фигур» вариант 2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа №2 «Углы, вписанные в окружность» вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см
Контрольная работа №2 «Углы, вписанные в окружность» вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №3 «Решение треугольников» 1 вариант.
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5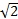 см и 3 см.
см и 3 см.
Сторона параллелограммам равна 2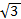 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3 «Решение треугольников» 2 вариант.
В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4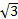 см и 7 см.
см и 7 см.
Найдите углы равнобокой трапеции, в которой боковая сторона равна 2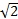 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
*Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №4 «Многоугольники» вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4 «Многоугольники» вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №5 «Площади многоугольников» вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5 «Площади многоугольников» вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45 . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №6 «Площадь круга и его частей» вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6 «Площадь круга и его частей» вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
Контрольная работа № 1
«Подобие фигур»
вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)
Контрольная работа № 1
«Подобие фигур»
вариант -2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа №1
«Подобие фигур»
вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)
Контрольная работа № 1
«Подобие фигур»
вариант -2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа № 1
«Подобие фигур»
вариант-1
№1. Через точку В стороны РК треугольника КРТ проведена прямая, параллельная стороне ТК и пересекающая сторону РТ в точке А. Вычислите длину отрезка АВ, если КТ=52см, АТ=12см, АР=36см
№2. Через вершину тупого угла В параллелограмма АВСD проведена высота ВК к стороне АD, АВ=9см, АК=6см, DК=2см
а) вычислите длину проекции стороны ВС на прямую СD.
в) подобны ли треугольники DВК и DВС ( М-проекция точки В на сторону СD)
Контрольная работа № 1
«Подобие фигур»
вариант -2
а) вычислите длины отрезков ВО и ОD.
в) подобны ли треугольники АОD и DОС, если АВ=5см, СD=10см? (ответ объясните).
Контрольная работа №2
«Углы, вписанные в окружность»
вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см
Контрольная работа №2 «Углы, вписанные в окружность»
вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №2
«Углы, вписанные в окружность»
вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см
Контрольная работа №2 «Углы, вписанные в окружность»
вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №2
«Углы, вписанные в окружность»
вариант-1
№1. Точки А и В делят окружность на дуги, градусные меры которых пропорциональны числам 6 и 9. Через точку А проведен диаметр АС. Вычислите градусные меры углов треугольника АВС.
№2. Хорды КМ и ТР окружности пересекаются в точке А. Вычислите:
а) градусную меру тупого угла, образованного этими хордами, если точки К, М, Т, Р делят окружность на дуги, градусные меры которых пропорциональны числам 2,3,6 и 9.
в) длину отрезка ТА, если АР на 7см больше ТА, КА=4,5см, МА=4см.
Контрольная работа №2 «Углы, вписанные в окружность»
вариант-2
№1. Точки С и D делят окружность на дуги, градусные меры которых пропорциональны числам 5 и 7. Через точку D проведен диаметр DК. Вычислите градусные меры углов треугольника СDК.
№2. Хорды АВ и КМ окружности пересекаются в точке Р. Вычислите:
а) градусную меру острого угла, образованного этими хордами, если точки А, В, К, М делят окружность на дуги, градусные меры которых пропорциональны числам 10, 4, 2, и 8.
в) длину отрезка КР, если РМ на 13см меньше КР, ВР=12см, АВ=19,5см.
Контрольная работа №3
«Решение треугольников»
вариант-1
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5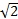 см и 3 см.
см и 3 см.
Сторона параллелограммам равна 2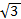 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3
«Решение треугольников»
вариант-2
В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4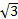 см и 7 см.
см и 7 см.
Найдите углы равнобокой трапеции, в которой боковая сторона равна 2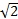 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
*Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №3
«Решение треугольников»
вариант-1
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5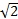 см и 3 см.
см и 3 см.
Сторона параллелограммам равна 2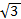 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3
«Решение треугольников»
вариант-2
В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4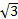 см и 7 см.
см и 7 см.
Найдите углы равнобокой трапеции, в которой боковая сторона равна 2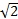 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
4* Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №3
«Решение треугольников»
вариант-1
.
В треугольнике АВС сторона АВ равна 11 см, угол ВАС=45⁰, угол АСВ=30⁰. Найдите сторону ВС.
Найдите сторону треугольника, лежащую против угла в 135⁰, если две другие стороны равны 5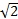 см и 3 см.
см и 3 см.
Сторона параллелограммам равна 2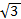 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
*Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.
Контрольная работа №3
«Решение треугольников»
вариант-2
. В треугольнике СЕD сторона СЕ равна 13 см, угол ЕDC=45⁰, угол DСЕ=60⁰. Найдите сторону ЕD.
Найдите сторону треугольника, лежащую против угла в 150⁰, если две другие стороны равны 4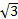 см и 7 см.
см и 7 см.
Найдите углы равнобокой трапеции, в которой боковая сторона равна 2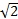 см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
см, а диагональ, равная 4 см, образует с основанием угол в 30⁰.
4* Диагональ параллелограмма делит его угол на два угла равные 45⁰ и 30⁰. Найдите отношение сторон параллелограмма.
Контрольная работа №4
«Многоугольники»
вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4
«Многоугольники»
вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №4
«Многоугольники»
вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4
«Многоугольники»
вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №4
«Многоугольники»
вариант-1
№1. Сумма углов правильного выпуклого многоугольника равна 1620º .Найдите число сторон этого многоугольника.
№2. Около правильного треугольника со стороной 5см описана окружность. Найдите
а) радиус описанной окружности;
в) сторону правильного шестиугольника, вписанного в эту окружность.
№3. Около правильного треугольника АВС описана окружность. Длина дуги АВ равна 2π см.
Найдите: а) радиус данной окружности; в) длину одной из медиан треугольника АВС.
Контрольная работа №4
«Многоугольники»
вариант-2
№1. Сумма углов правильного выпуклого многоугольника равна 1980º .Найдите число сторон этого многоугольника.
№2. В правильный четырехугольник со стороной 4см вписана окружность. Найдите
а) радиус окружности;
в) сторону правильного треугольника, описанного около данной окружности.
№3. Диаметры окружности АС и ВD пересекаются под углом 90º . Длина дуги ВС равна 4π см.
Найдите: а) радиус данной окружности; в) длины хорд с концами в точках А, В, С, D.
Контрольная работа №5
«Площади многоугольников»
вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5
«Площади многоугольников»
вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм
.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №5
«Площади многоугольников»
вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5
«Площади многоугольников»
вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм
.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №5
«Площади многоугольников»
вариант-1
№1. Найдите площадь треугольника со сторонами 4см, 13см и 15см.
№2. Стороны параллелограмма равны 4см и 6см. Меньшая его высота равна 3см. Вычислите вторую высоту параллелограмма.
№3. В равнобокой трапеции, один из углов которой равен 45º , большее основание равно 70см, а высота равна 10см. Вычислите площадь трапеции.
Контрольная работа №5
«Площади многоугольников»
вариант-2
№1. Найдите площадь треугольника со сторонами 8дм, 29дм, и 35дм
.
№2. Большая сторона параллелограмма 5см, высоты параллелограмма равны 2см и 2,5см. Вычислите вторую сторону параллелограмма.
№3. Боковая сторона трапеции, равная 40см, образует с большим её основанием угол в 45º . Вычислите площадь трапеции, если основания её равны 24см и 60см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников
пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников
пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-1
№1. Найдите площадь круга, диаметр которого 6см.
№2. Площади двух подобных многоугольников
пропорциональны числам 9 и 10. Периметр одного из них на 10см больше периметра другого. Вычислите периметры многоугольников.
№3. Вычислите площадь сектора, соответствующего центральному углу 45º , если радиус круга 4см.
№4. Вычислите площадь круга, вписанного в треугольник, стороны которого равны 10см, 24см, и 26см.
Контрольная работа №6
«Площадь круга и его частей»
вариант-2
№1. Найдите площадь круга, диаметр которого 8см.
№2. Площади двух подобных многоугольников пропорциональны числам 3 и 5. Сумма их площадей равна 510см. Вычислите периметры многоугольников
№3. Вычислите площадь сектора, соответствующего центральному углу 40º , если радиус круга 6см.
№4. Вычислите площадь круга, описанного около треугольника, стороны которого равны 20см, 21см, и 29см.
infourok.ru

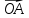 -
-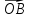 ,
,  +2
+2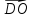 ,
,  +
+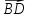 +
+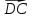
 (2;0),
(2;0),  (1;2),
(1;2),  (-3;m). Найдите значение m, при котором векторы
(-3;m). Найдите значение m, при котором векторы  и
и  -2
-2 перпендикулярны.
перпендикулярны. +
+ 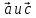 коллинеарны
коллинеарны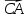 и
и 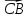 .
.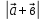 , если
, если  =5,
=5,  =8, а угол между векторами
=8, а угол между векторами  и
и  равен 600.
равен 600. -
- 2
2 +
+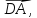
 +
+ +
+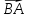
 (2;0),
(2;0),  (1;2),
(1;2),  (-3;m). Найдите значение m, при котором векторы
(-3;m). Найдите значение m, при котором векторы  и
и 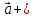 2
2 перпендикулярны.
перпендикулярны. -
-
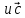 коллинеарны.
коллинеарны.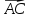 и
и 
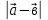 , если
, если  =3,
=3,  =4, а угол между векторами
=4, а угол между векторами  и
и  равен 600
равен 600 МВN
МВN  АВС. Найти АС.
АВС. Найти АС.


 см. Найдите сторону правильного шестиугольника, вписанного в данную окружность.
см. Найдите сторону правильного шестиугольника, вписанного в данную окружность. см. Найдите периметр многоугольника.
см. Найдите периметр многоугольника.


 =350,
=350,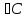 =250. Укажите наибольшую сторону треугольника. Ответ объясните.
=250. Укажите наибольшую сторону треугольника. Ответ объясните. =450, АВ=2
=450, АВ=2


 рис.4
рис.4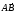 точка D прямоугольника ABCD переходит в точку …
точка D прямоугольника ABCD переходит в точку …




 рис.4
рис.4 точка D ромба ABCD переходит в точку …
точка D ромба ABCD переходит в точку …



 рис.4
рис.4 точка B прямоугольника ABCD переходит в точку …
точка B прямоугольника ABCD переходит в точку …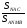



 рис4.
рис4. точка А ромба ABCD переходит в точку …
точка А ромба ABCD переходит в точку …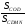




 и
и 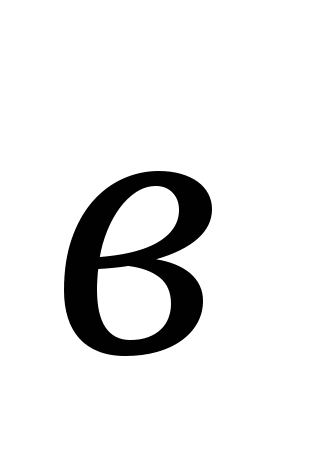 . Постройте векторы, равные:
. Постройте векторы, равные: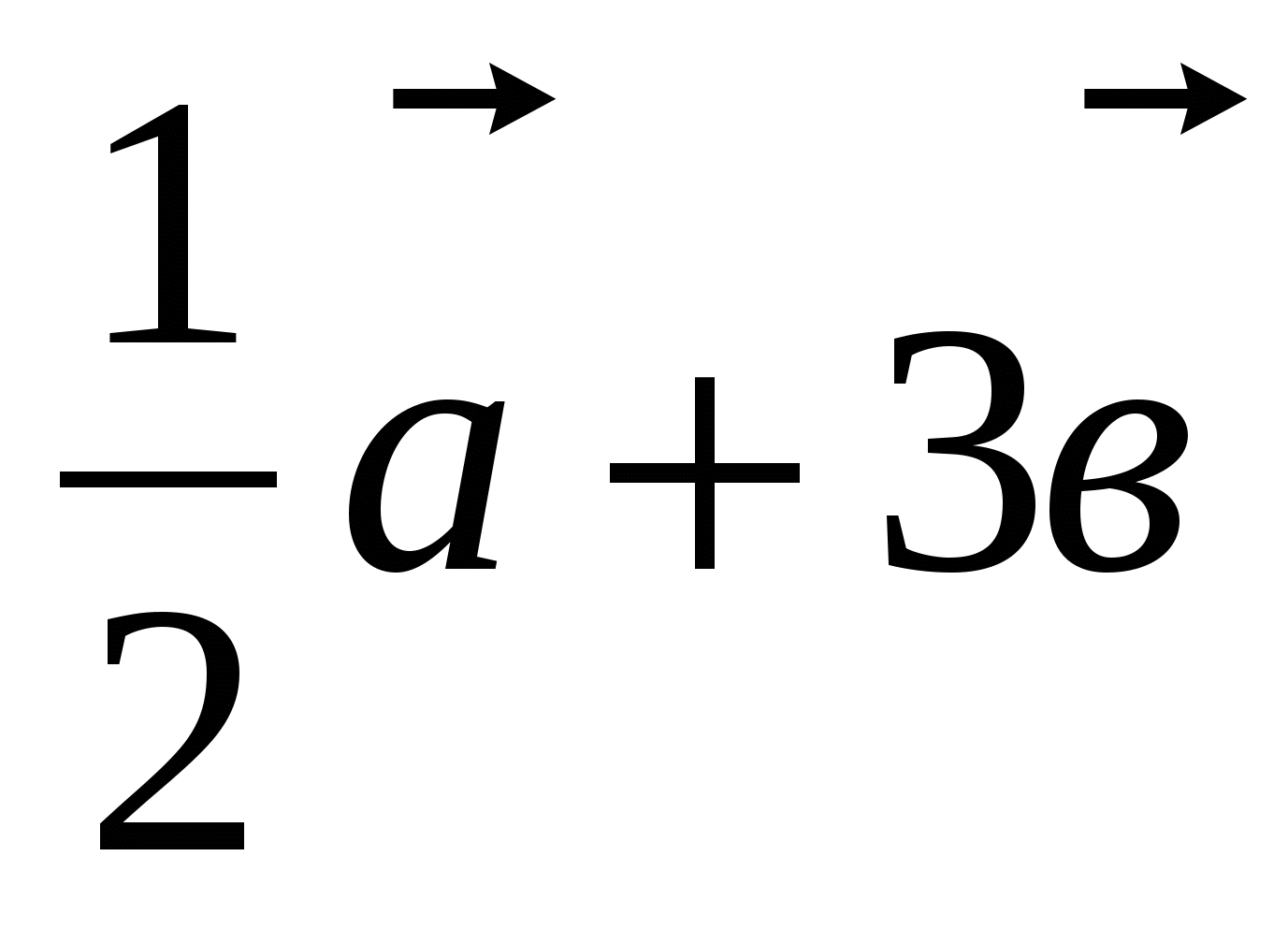 ; б).
; б). 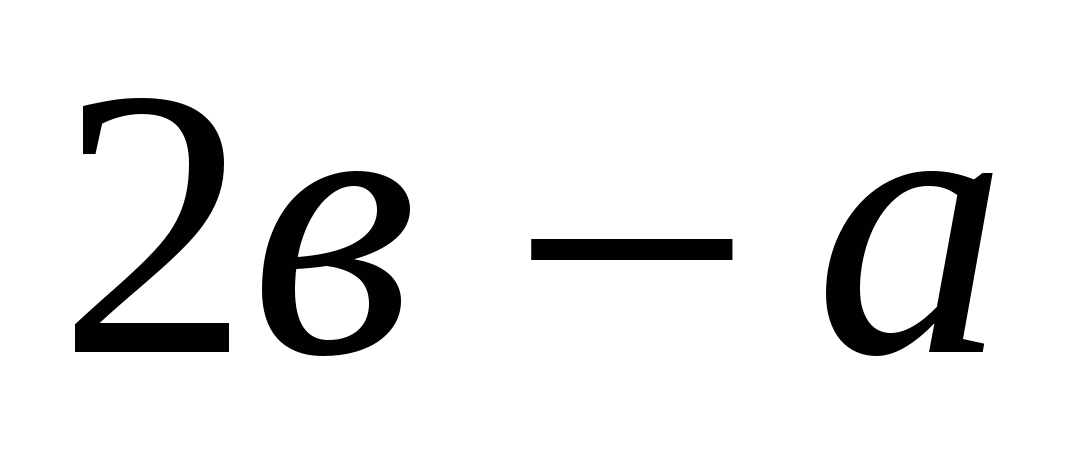
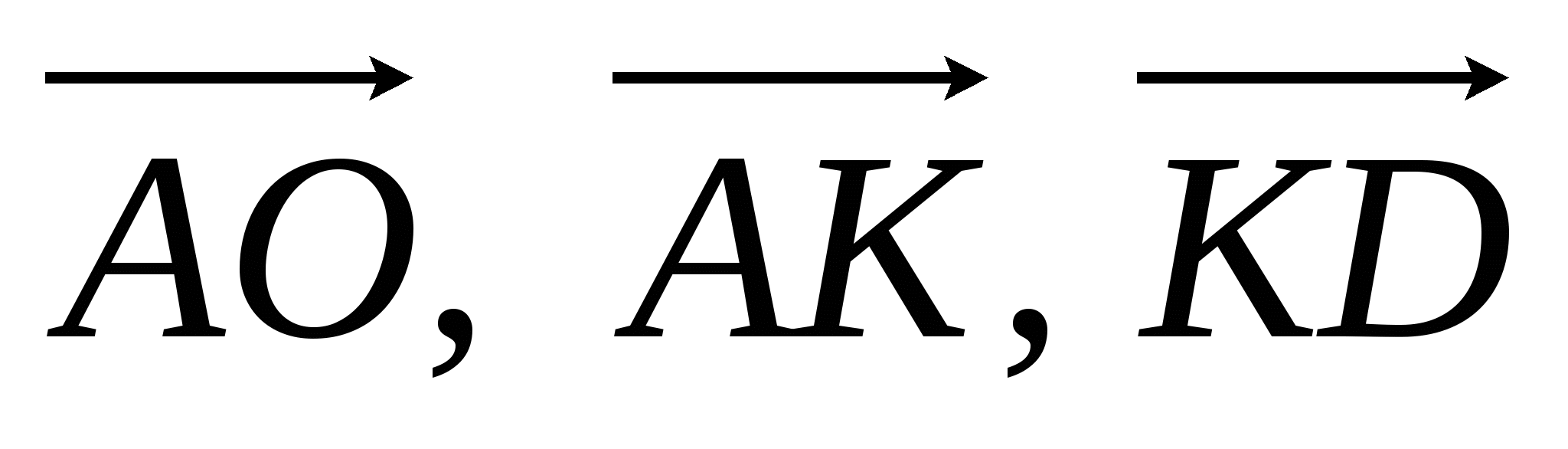 через векторы
через векторы 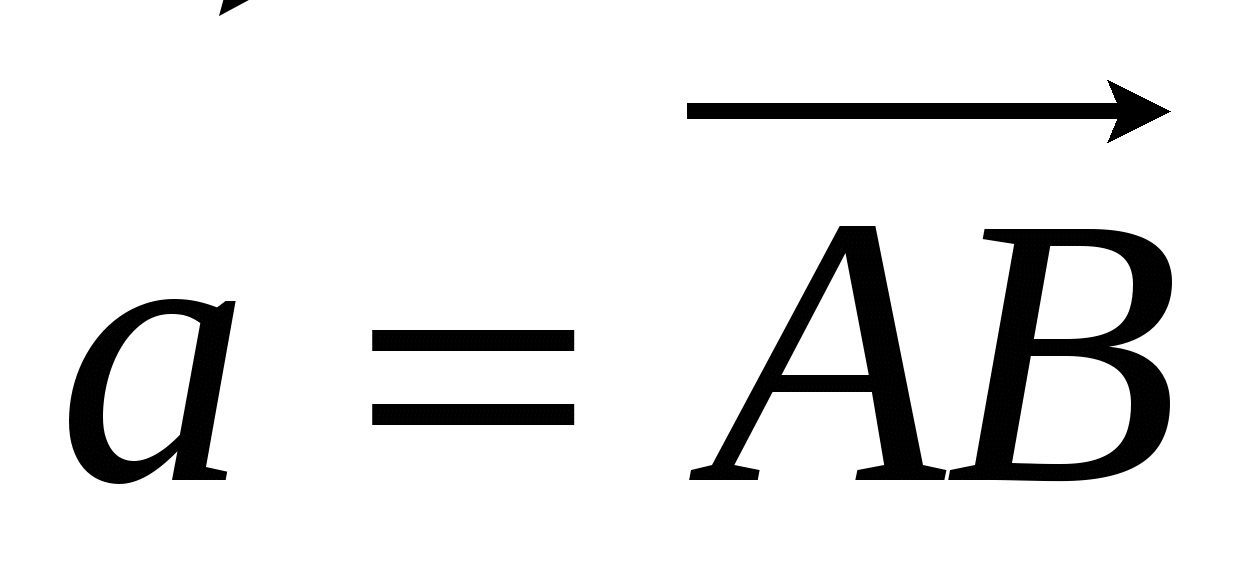 и
и 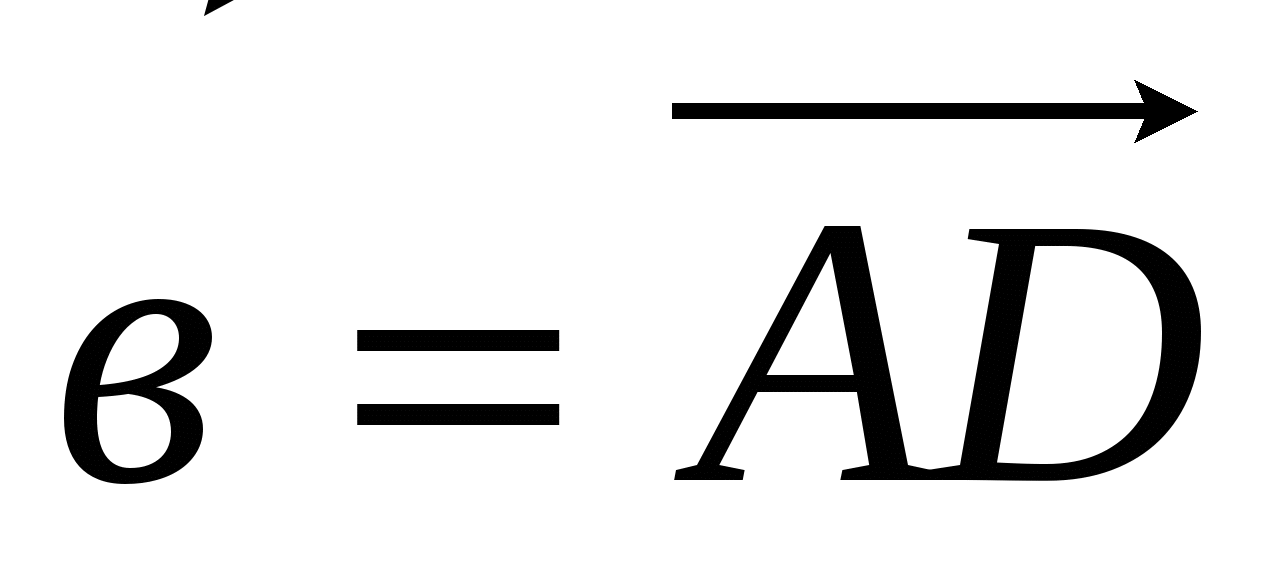 .
.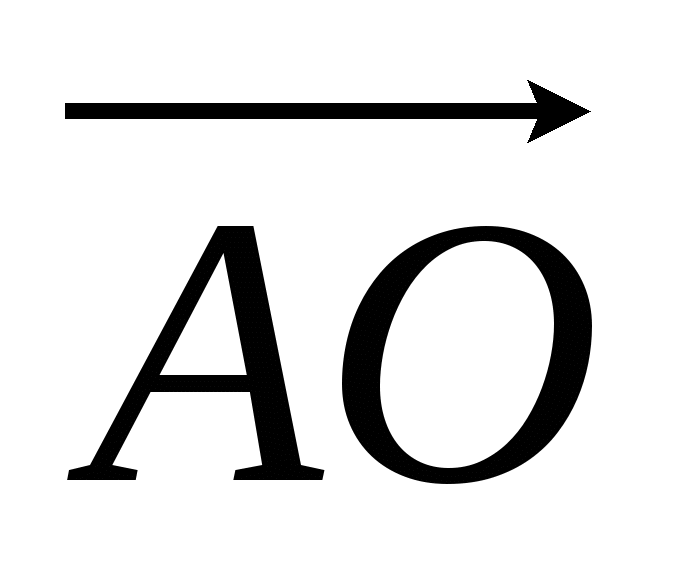 через векторы
через векторы 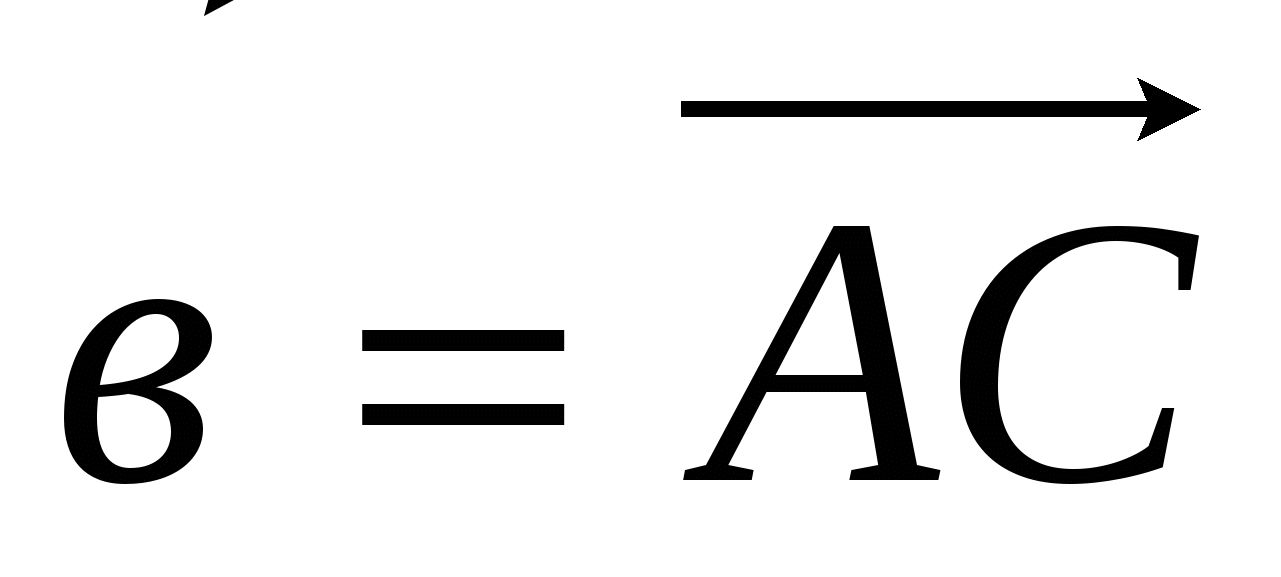 .
.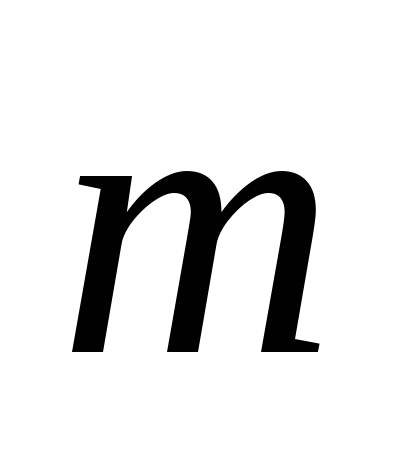 и
и 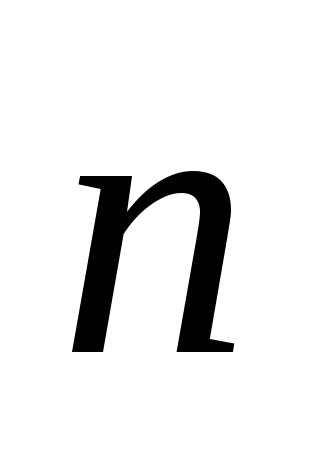 . Постройте векторы, равные:
. Постройте векторы, равные: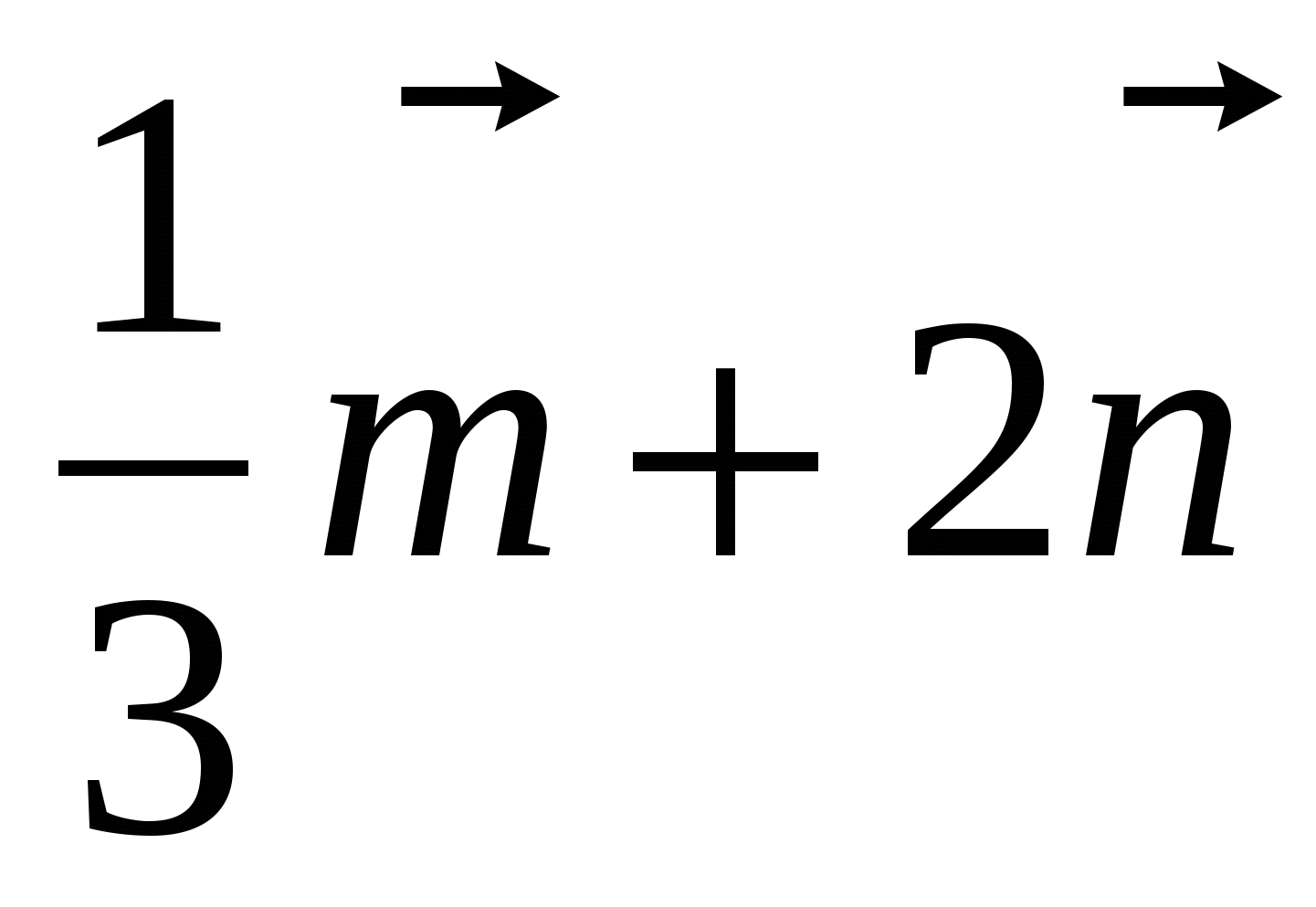 ; б).
; б). 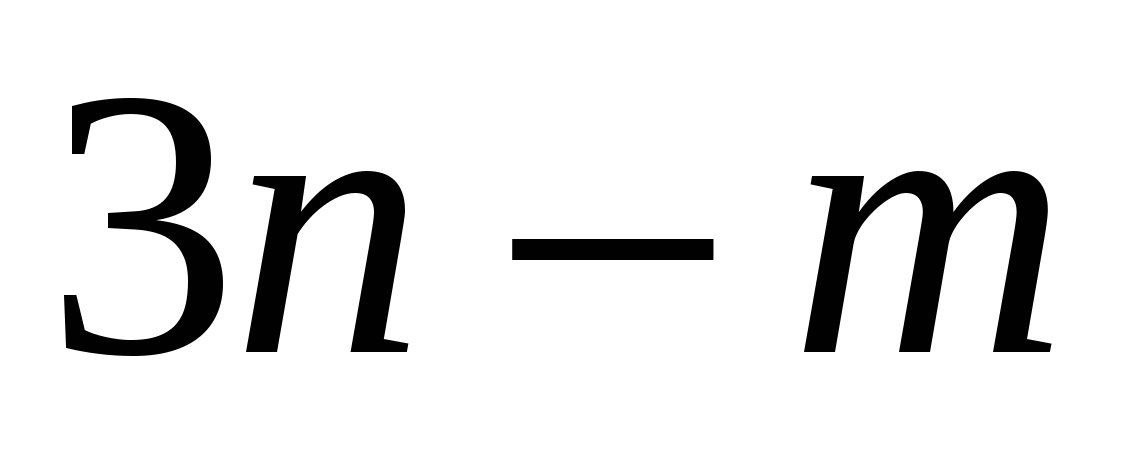
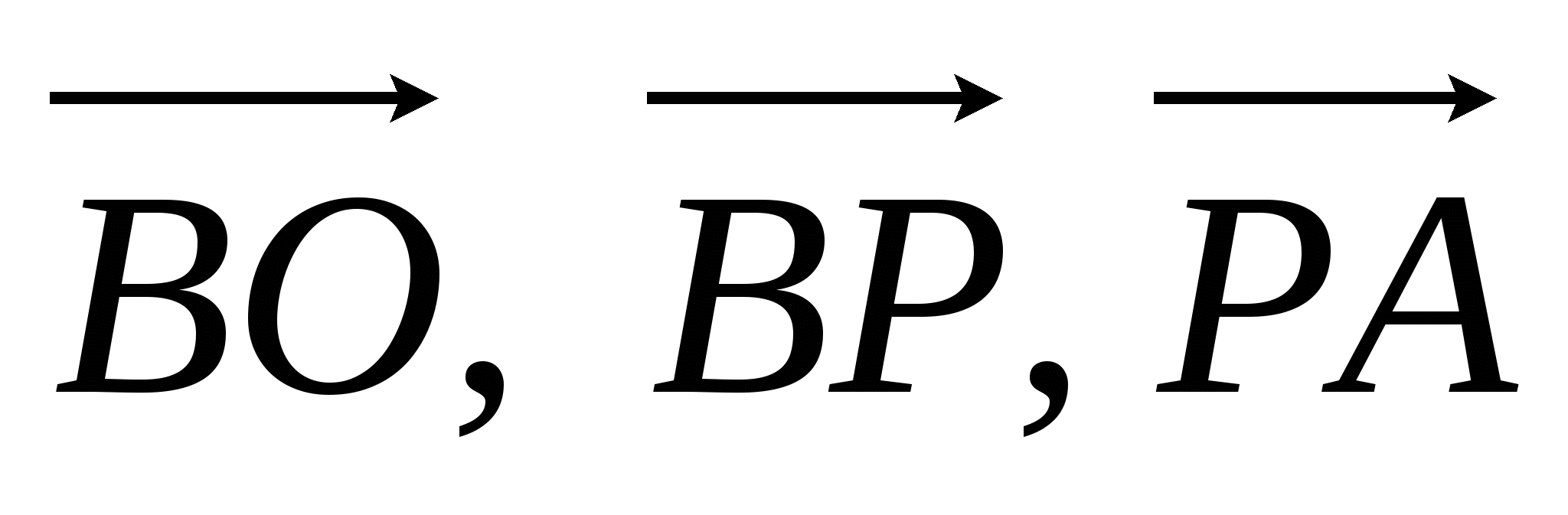 через векторы
через векторы 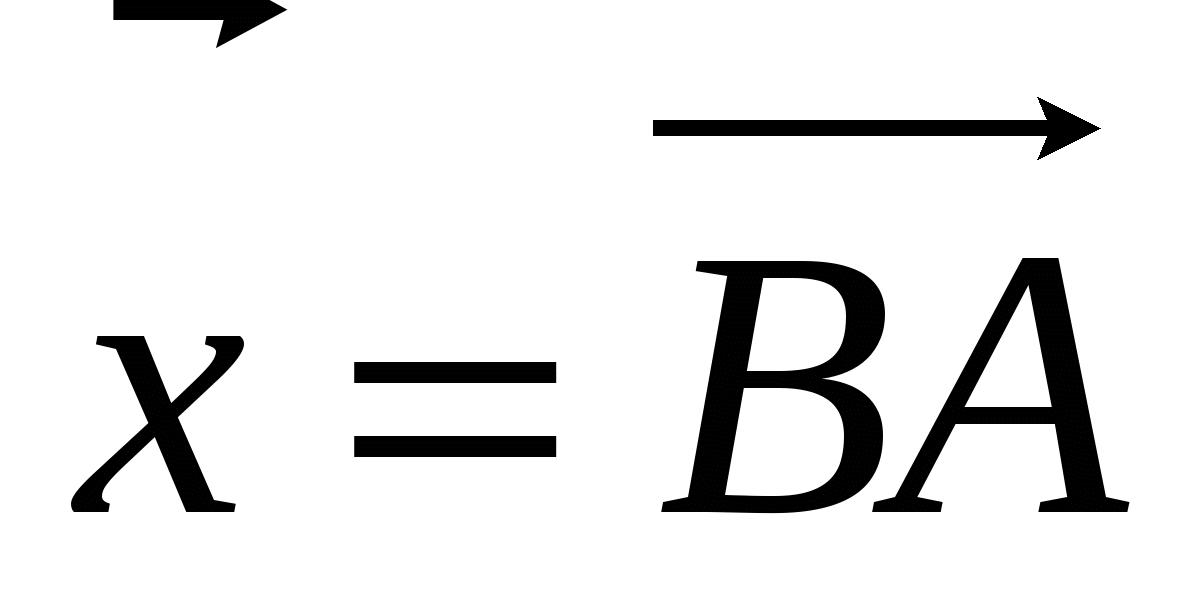 и
и 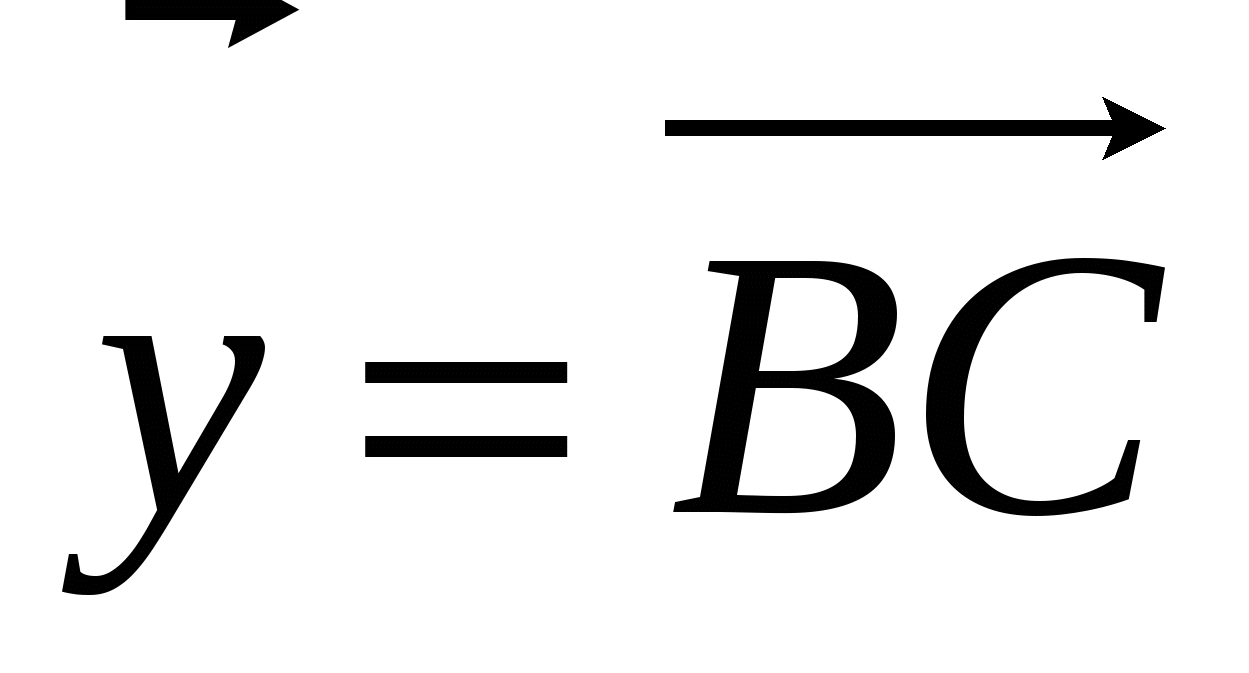 .
.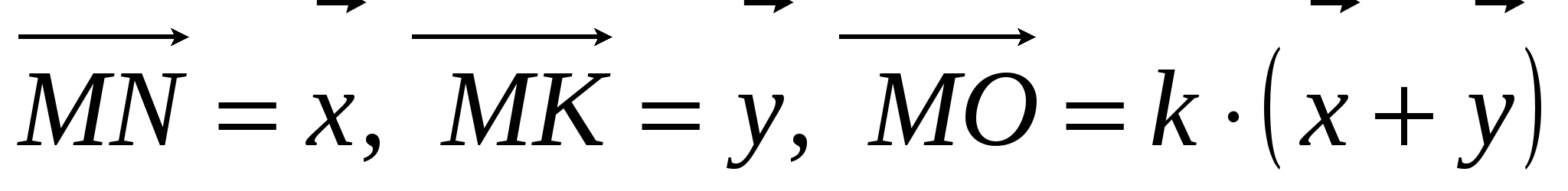 . Найдите число k.
. Найдите число k. 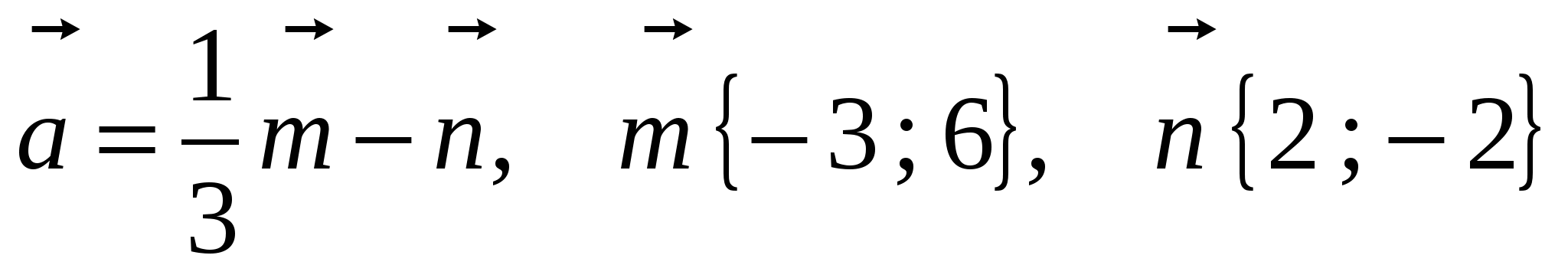 .
.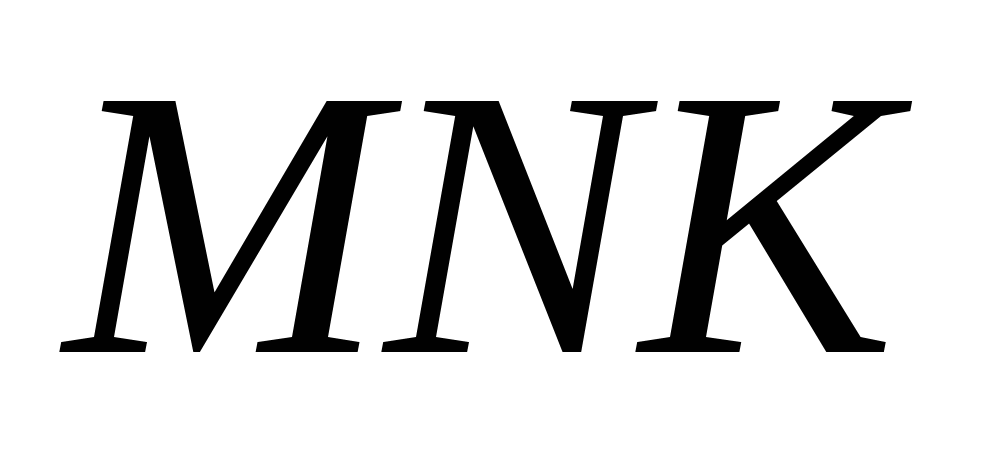 - равнобедренный;
- равнобедренный;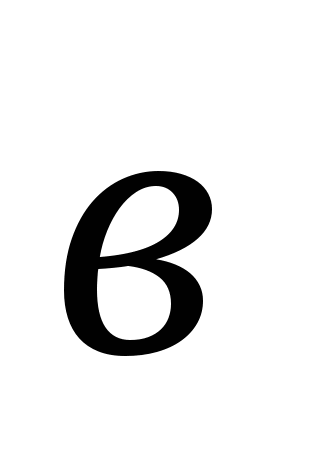 , если
, если 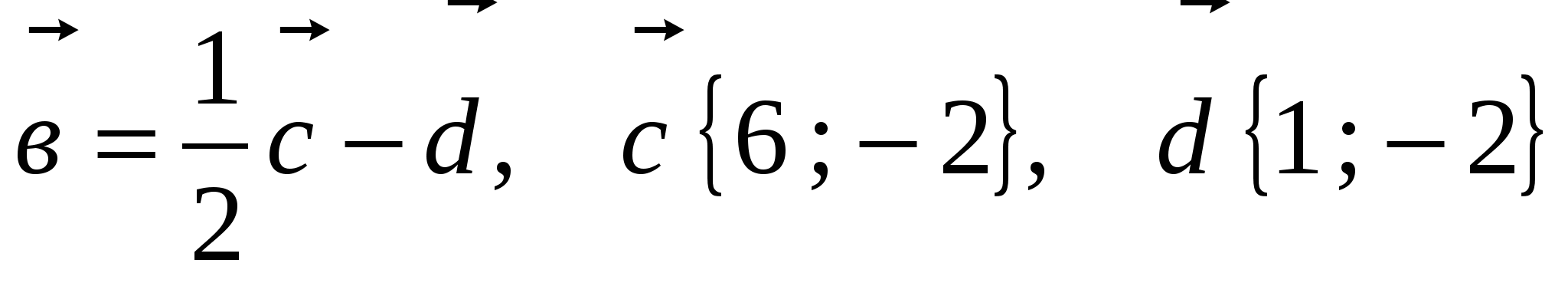 .
. - равнобедренный;
- равнобедренный;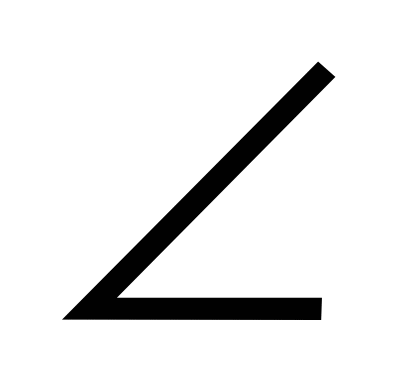 А = 450,
А = 450, 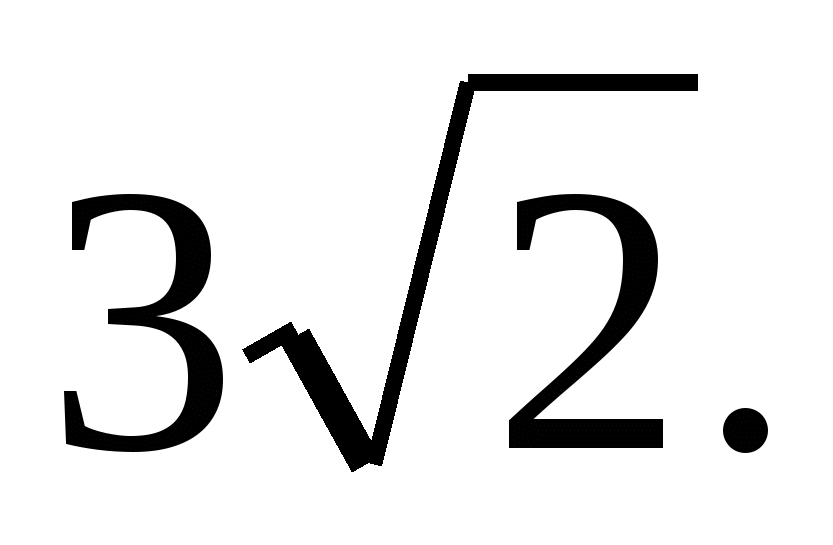 Найдите АС.
Найдите АС.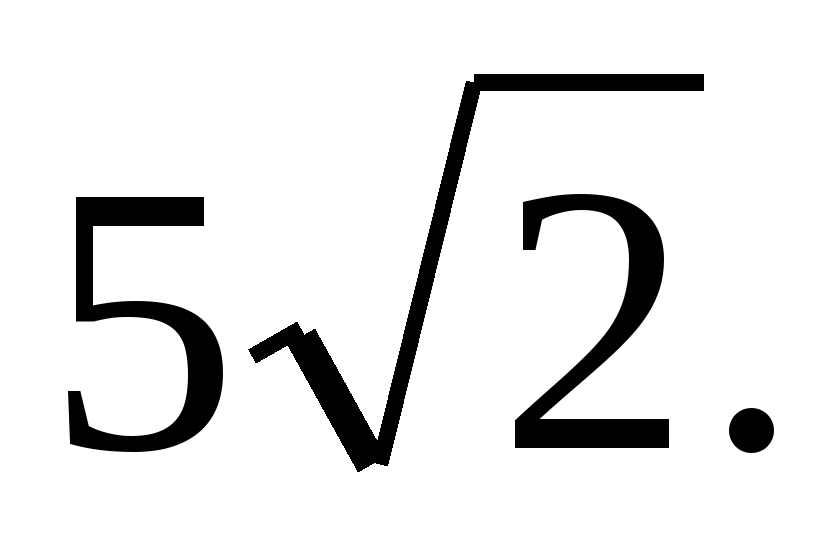 Найдите DE.
Найдите DE.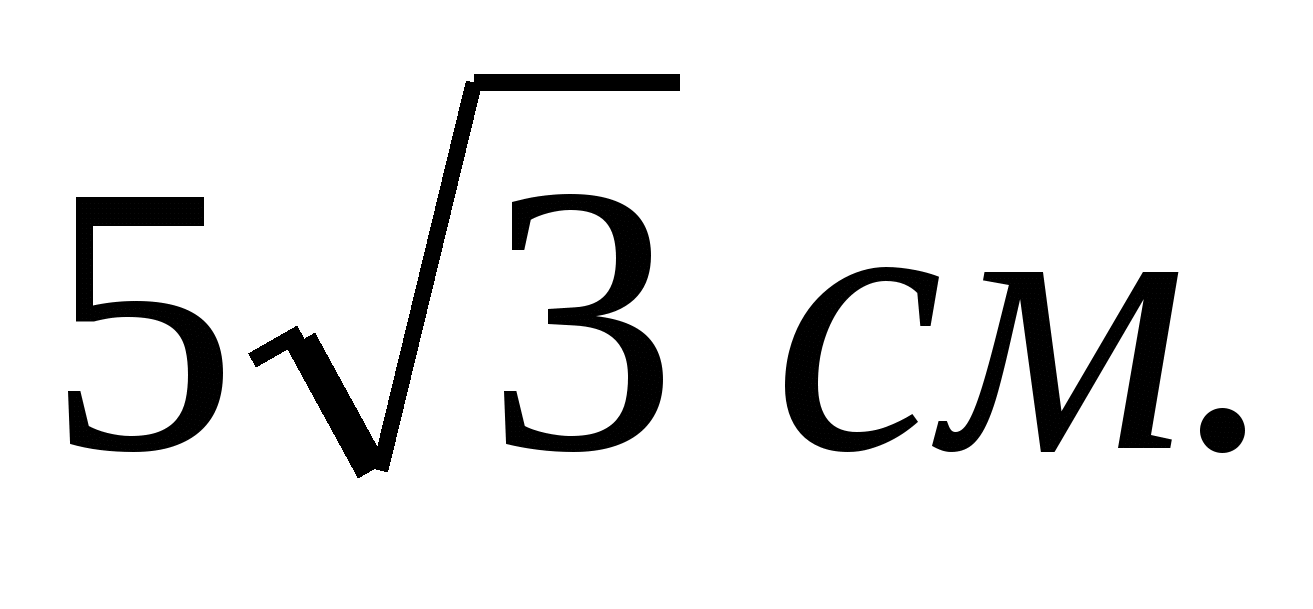
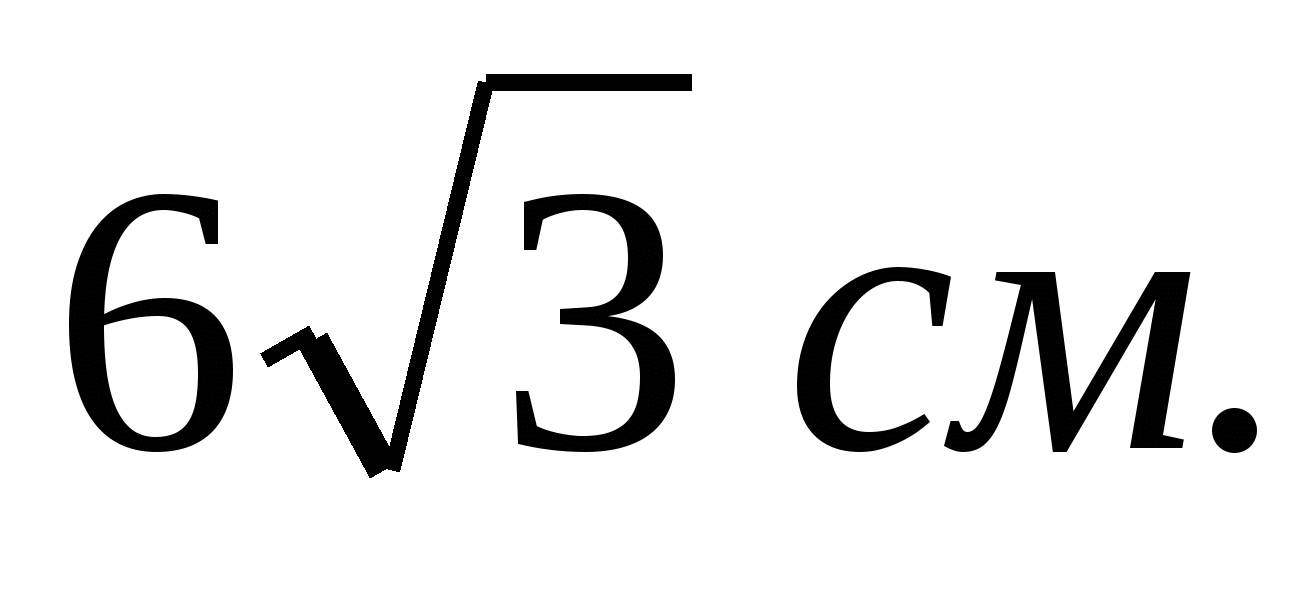 Найдите периметр правильного шестиугольника, описанного около той же окружности.
Найдите периметр правильного шестиугольника, описанного около той же окружности.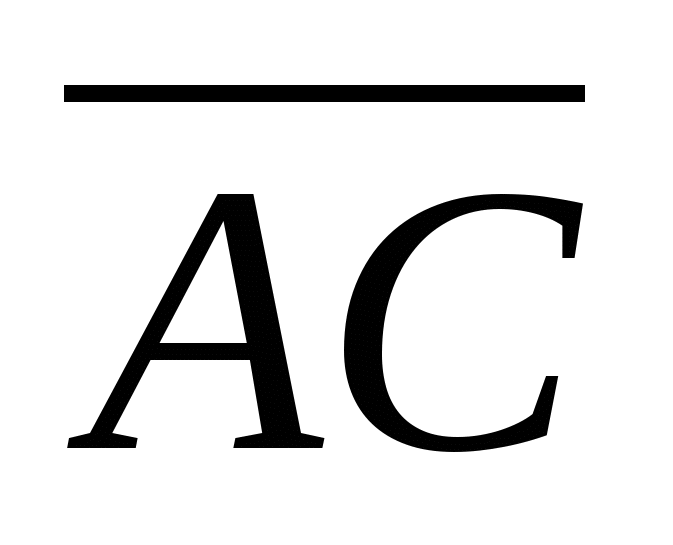 ;
;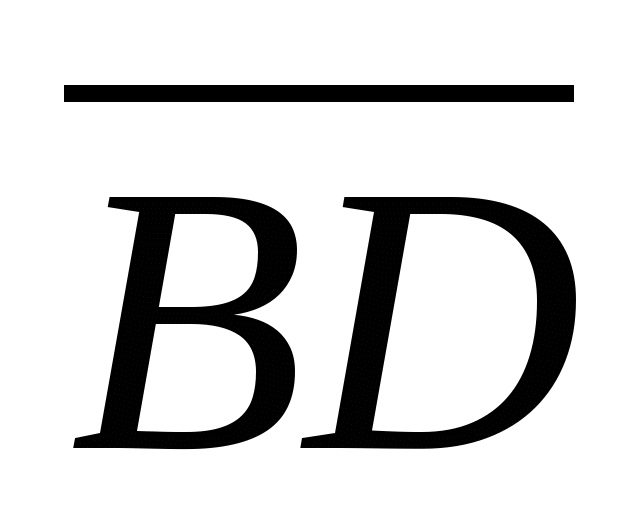 ;
; и
и  . Постройте векторы, равные:
. Постройте векторы, равные:  +3
+3 ,
,  ,
,  через векторы
через векторы  и
и  .
.
 .
. и
и  . Постройте векторы, равные:
. Постройте векторы, равные:  +
+ ; б) 3
; б) 3 ,
, 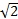 см и 3 см.
см и 3 см.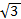 см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.
см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30⁰, равна 6 см.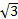 см и 7 см.
см и 7 см.



