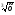 ; б) f(х)=
; б) f(х)=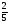
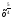
Контрольная работа : «Степенная функция и ее свойства»
Вариант1
1)Постройте схематически график функции у=х-4
а) Найдите область определения функции; б) Исследуйте на четность функцию; в)Определите промежутки знакопостоянства функции; г)Определите промежутки возрастания и убывания функции.
2)Найдите производную функции f(х):
а) f(х)=х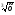 ; б) f(х)=
; б) f(х)=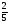
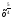
3) Найдите общий вид первообразных для функции f(х):
а) f(х)=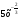 ; б) f(х)=
; б) f(х)=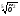

4)Вычислите: а)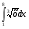 ; б)
; б)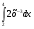
5) Составьте уравнение касательной к графику функции f(х)=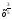 в точке х0=-1
в точке х0=-1
6) Найдите площадь фигуры, ограниченной линиями у=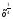 , у=1, х=16
, у=1, х=16
Вариант2
1)Постройте схематически график функции у=х-3
а) Найдите область определения функции; б) Исследуйте на четность функцию; в)Определите промежутки знакопостоянства функции; г)Определите промежутки возрастания и убывания функции.
2)Найдите производную функции f(х):
а) f(х)=х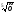 ; б) f(х)=
; б) f(х)=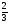
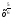
3) Найдите общий вид первообразных для функции f(х):
а) f(х)=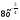 ; б) f(х)=
; б) f(х)=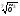

4)Вычислите: а)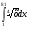 ; б)
; б)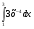
5) Составьте уравнение касательной к графику функции f(х)=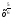 в точке х0=1
в точке х0=1
6) Найдите площадь фигуры, ограниченной линиями у=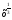 , у=1, х=8
, у=1, х=8
Контрольная работа : «Степенная функция и ее свойства»
Вариант1
1)Постройте схематически график функции у=х-4
а) Найдите область определения функции; б) Исследуйте на четность функцию; в)Определите промежутки знакопостоянства функции; г)Определите промежутки возрастания и убывания функции.
2)Найдите производную функции f(х):
а) f(х)=х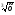 ; б) f(х)=
; б) f(х)=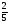
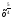
3) Найдите общий вид первообразных для функции f(х):
а) f(х)=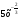 ; б) f(х)=
; б) f(х)=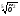

4)Вычислите: а)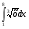 ; б)
; б)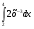
5) Составьте уравнение касательной к графику функции f(х)=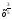 в точке х0=-1
в точке х0=-1
6) Найдите площадь фигуры, ограниченной линиями у=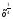 , у=1, х=16
, у=1, х=16
Контрольная работа : «Степенная функция и ее свойства»
Вариант1
1)Постройте схематически график функции у=х-4
а) Найдите область определения функции; б) Исследуйте на четность функцию; в)Определите промежутки знакопостоянства функции; г)Определите промежутки возрастания и убывания функции.
2)Найдите производную функции f(х):
а) f(х)=х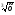 ; б) f(х)=
; б) f(х)=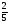
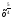
3) Найдите общий вид первообразных для функции f(х):
а) f(х)=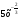 ; б) f(х)=
; б) f(х)=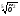

4)Вычислите: а)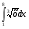 ; б)
; б)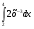
5) Составьте уравнение касательной к графику функции f(х)=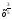 в точке х0=-1
в точке х0=-1
6) Найдите площадь фигуры, ограниченной линиями у=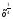 , у=1, х=16
, у=1, х=16
Вариант2
1)Постройте схематически график функции у=х-3
а) Найдите область определения функции; б) Исследуйте на четность функцию; в)Определите промежутки знакопостоянства функции; г)Определите промежутки возрастания и убывания функции.
2)Найдите производную функции f(х):
а) f(х)=х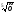 ; б) f(х)=
; б) f(х)=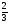
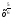
3) Найдите общий вид первообразных для функции f(х):
а) f(х)=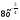 ; б) f(х)=
; б) f(х)=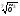

4)Вычислите: а)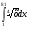 ; б)
; б)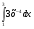
5) Составьте уравнение касательной к графику функции f(х)=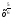 в точке х0=1
в точке х0=1
6) Найдите площадь фигуры, ограниченной линиями у=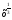 , у=1, х=8
, у=1, х=8
Контрольная работа : «Степенная функция и ее свойства»
Вариант2
1)Постройте схематически график функции у=х-3
а) Найдите область определения функции; б) Исследуйте на четность функцию; в)Определите промежутки знакопостоянства функции; г)Определите промежутки возрастания и убывания функции.
2)Найдите производную функции f(х):
а) f(х)=х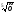 ; б) f(х)=
; б) f(х)=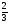
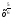
3) Найдите общий вид первообразных для функции f(х):
а) f(х)=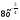 ; б) f(х)=
; б) f(х)=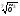

4)Вычислите: а)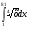 ; б)
; б)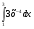
5) Составьте уравнение касательной к графику функции f(х)=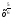 в точке х0=1
в точке х0=1
6) Найдите площадь фигуры, ограниченной линиями у=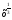 , у=1, х=8
, у=1, х=8
infourok.ru
Вариант 1
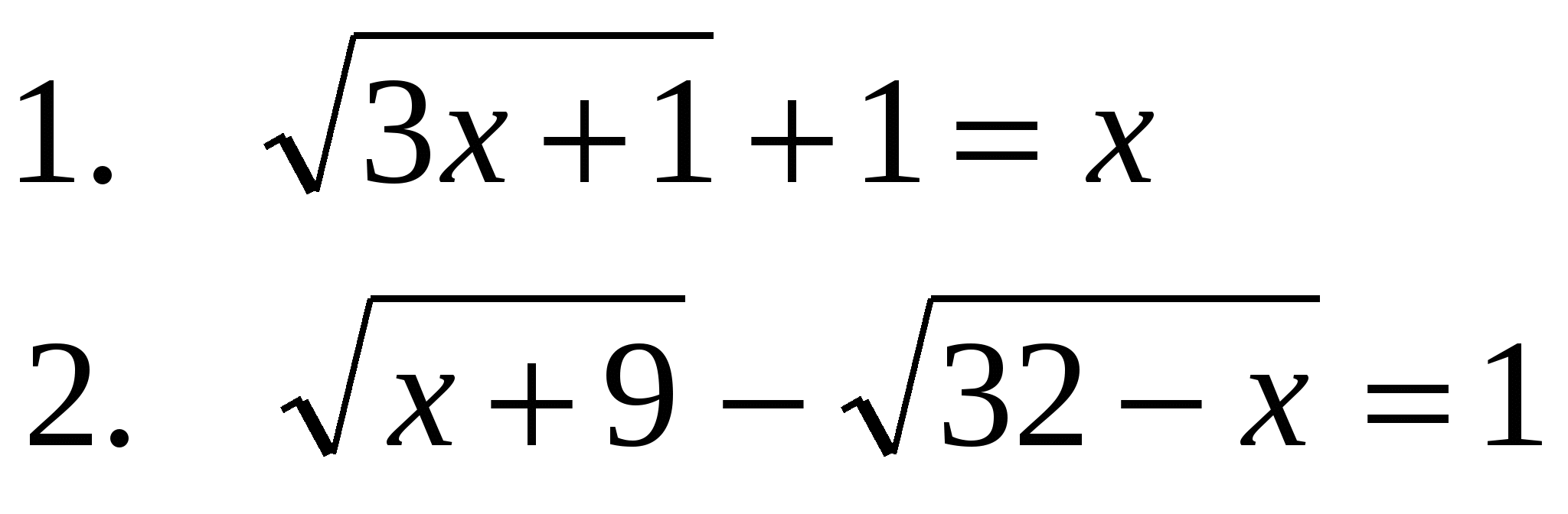
3. 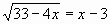
Вариант 2
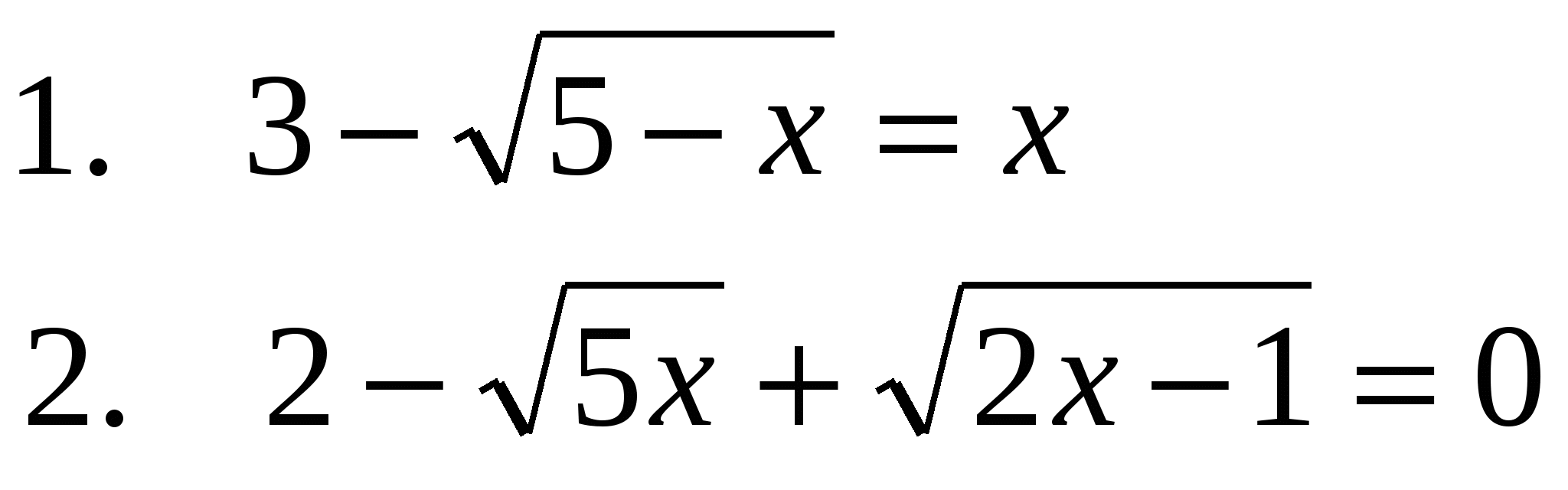
3. 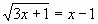
Вариант 3
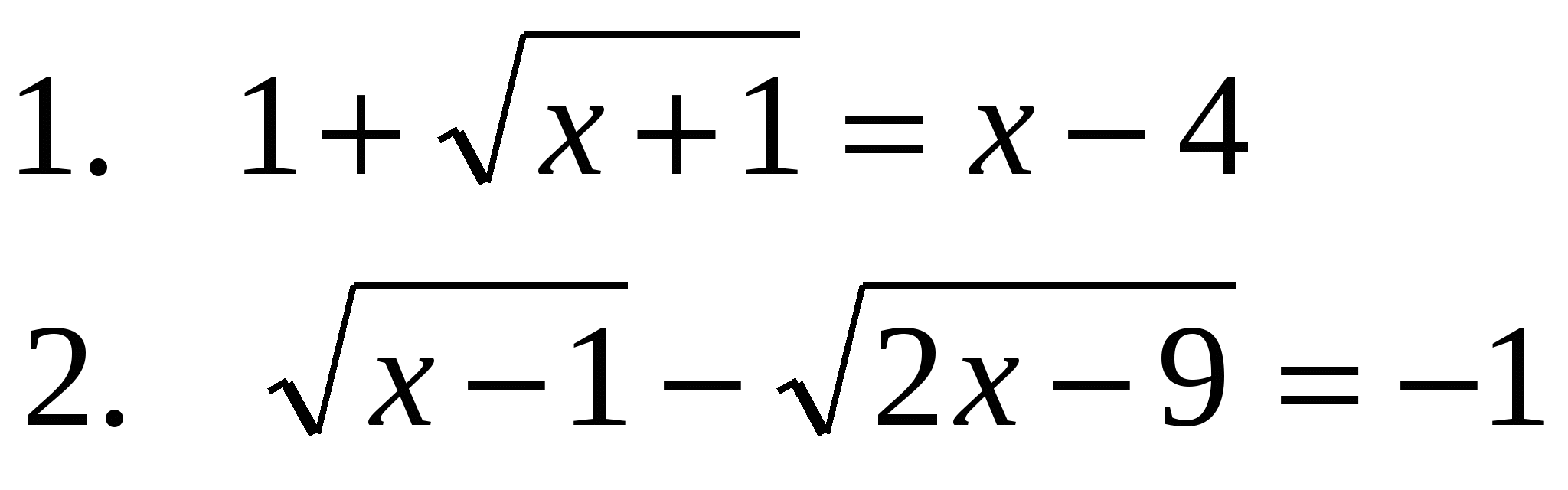
3. 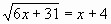
Вариант 4
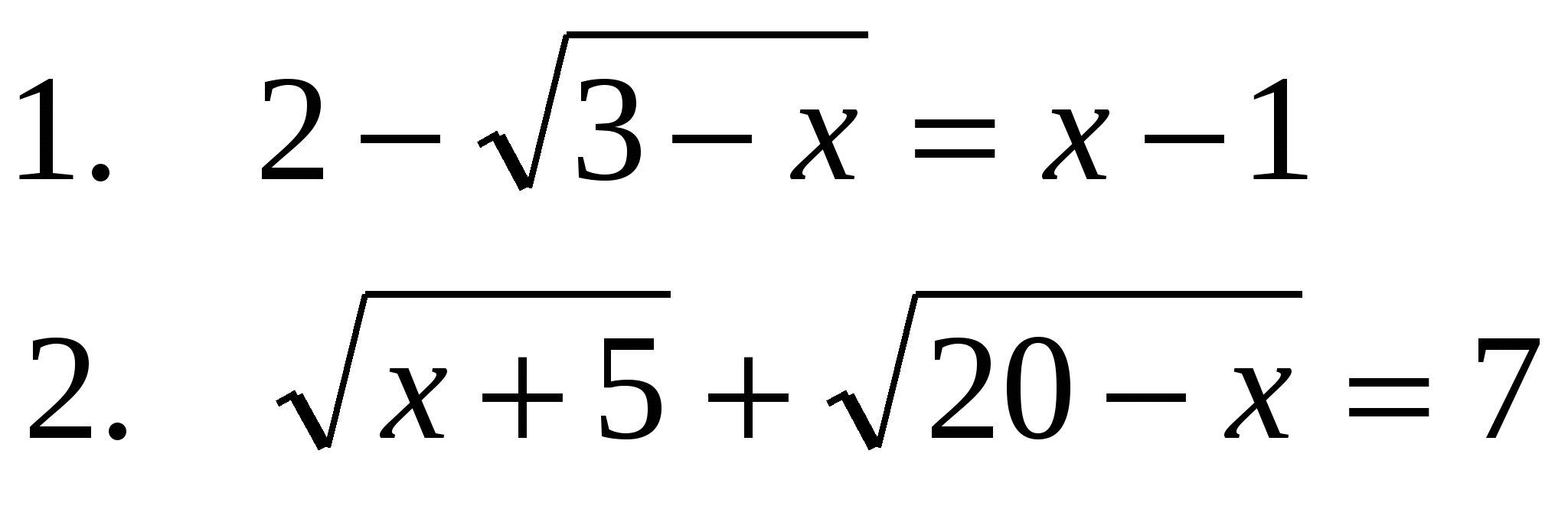
3. 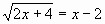
Вариант 5
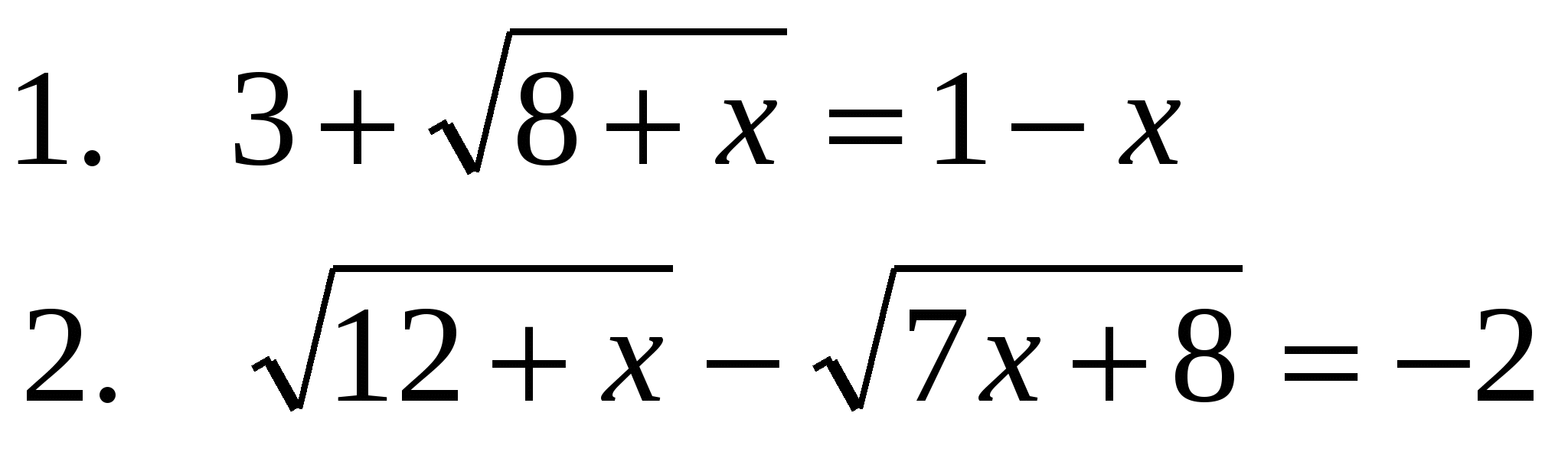
3. 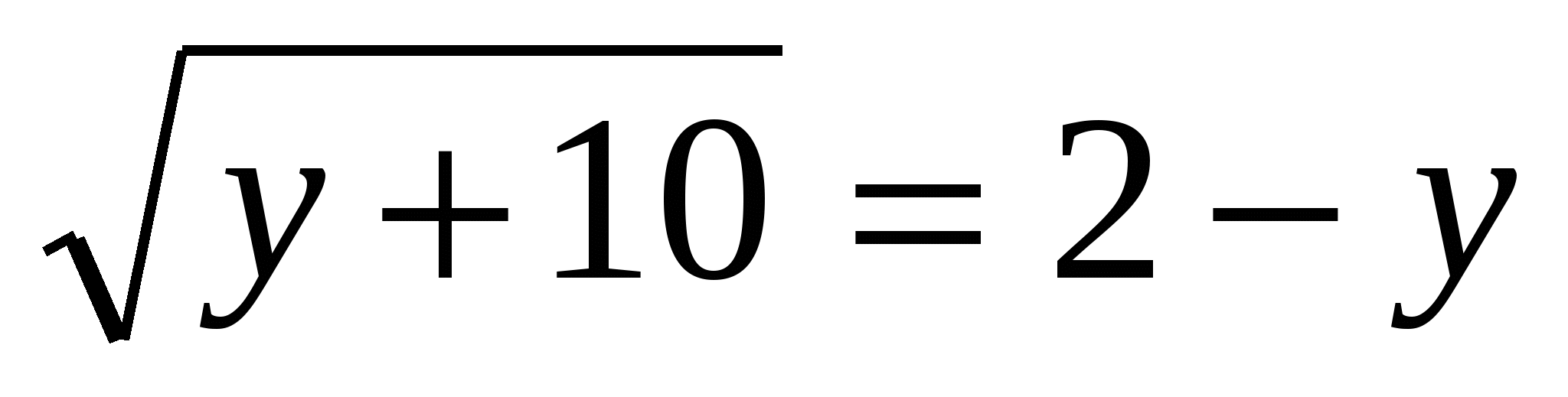
Вариант 6
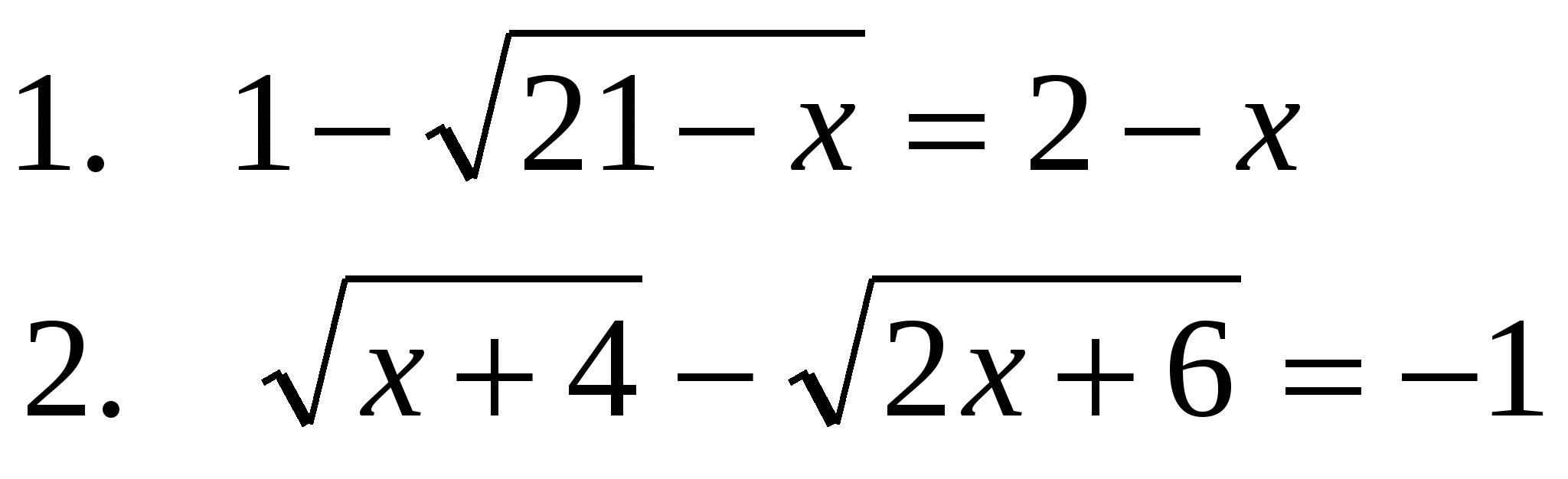
3. 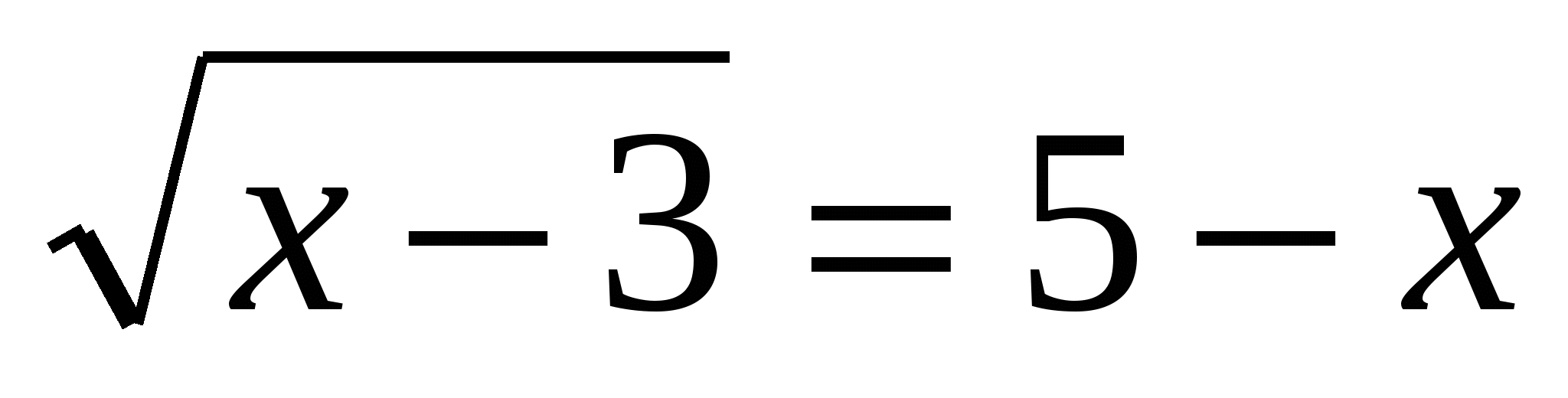
Вариант 7
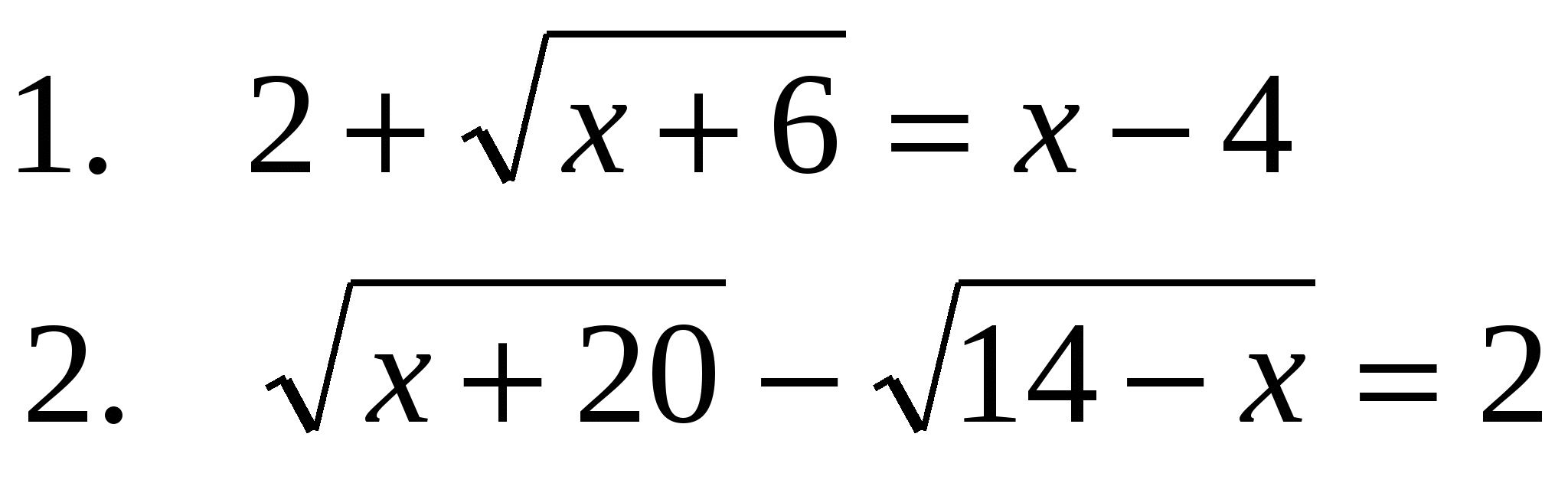
3. 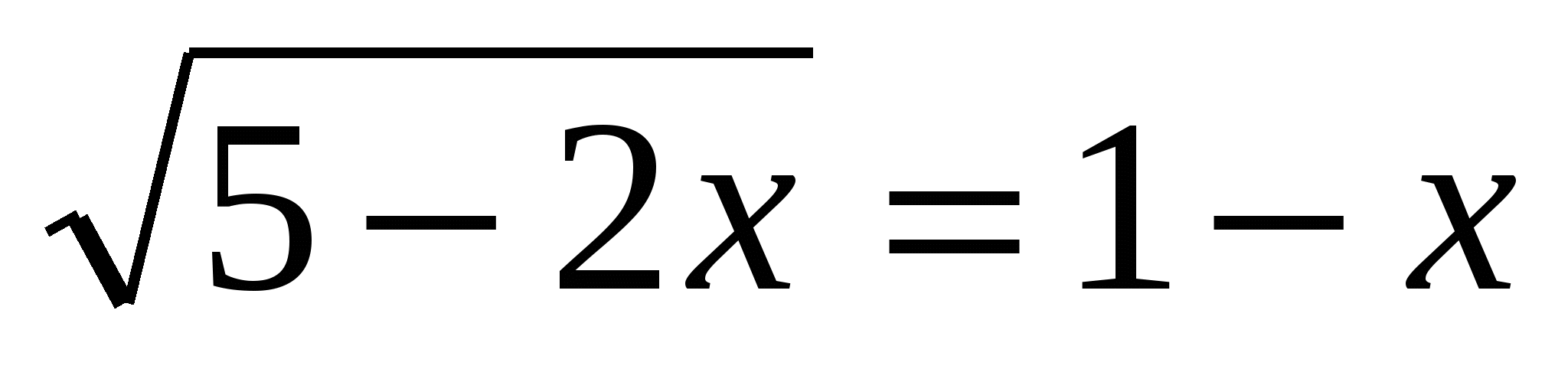
Вариант 8
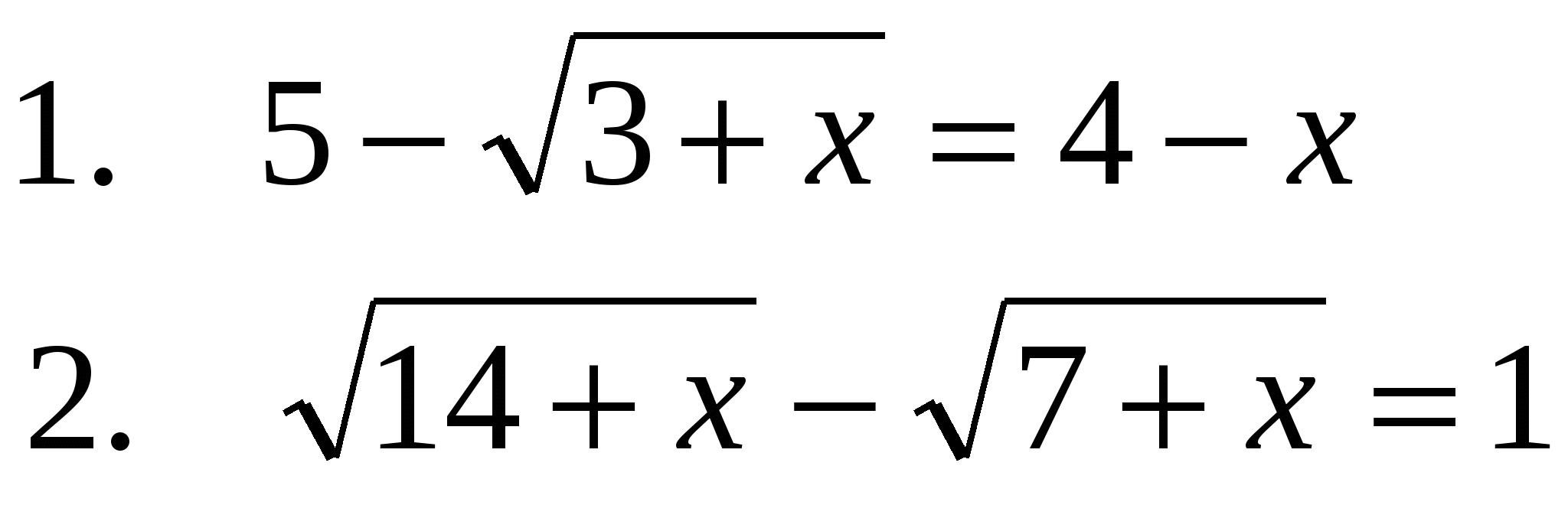
3. 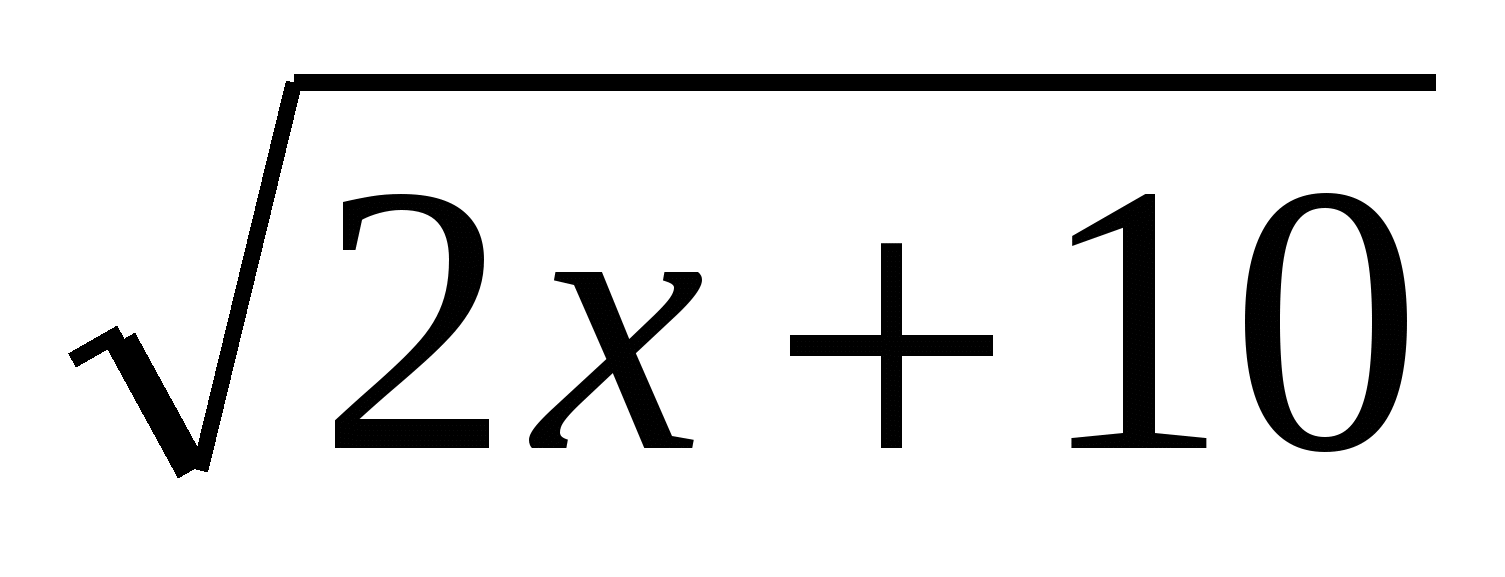 =х+1
=х+1
Вариант 9
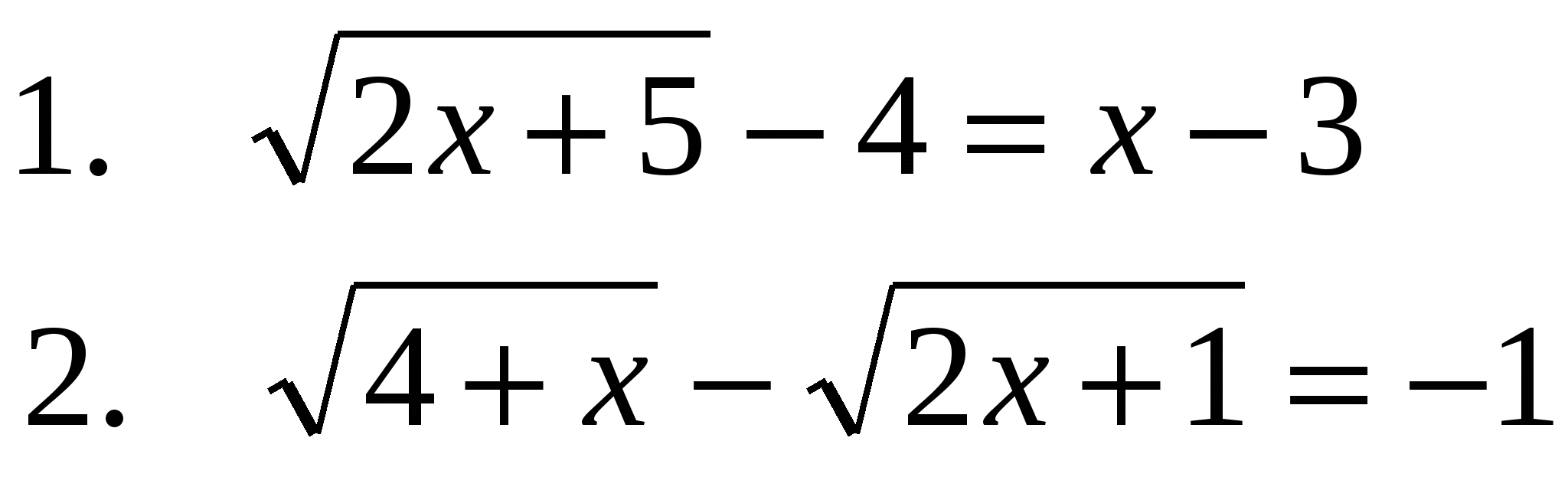
3. 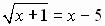
Вариант 10
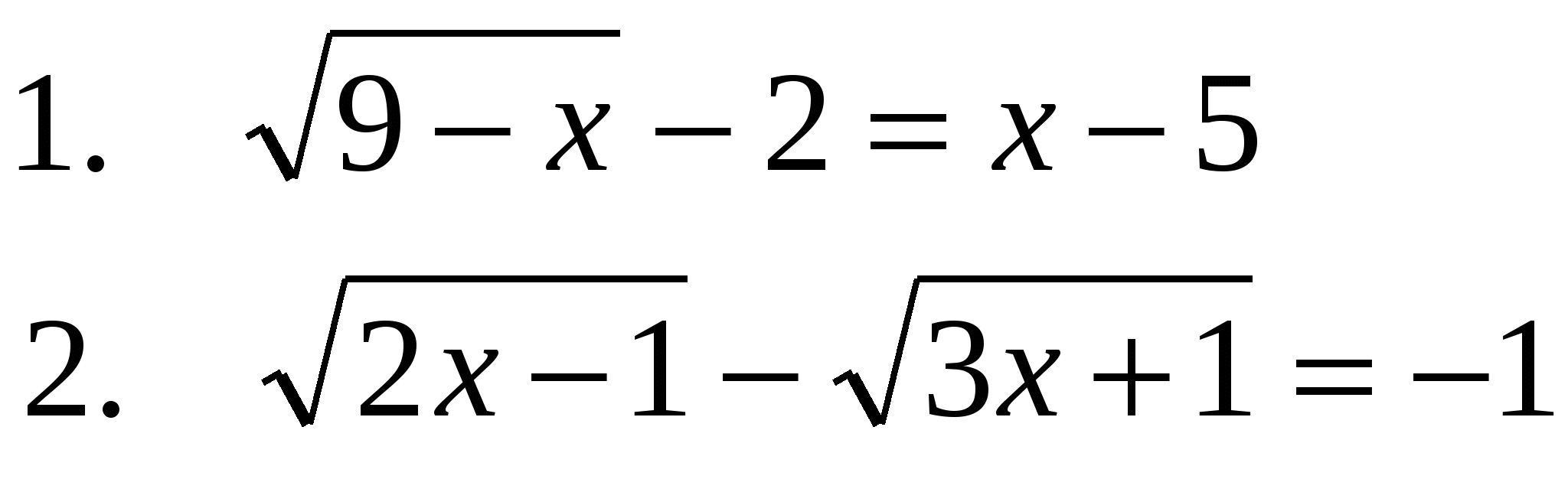
3. 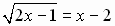
Вариант 10
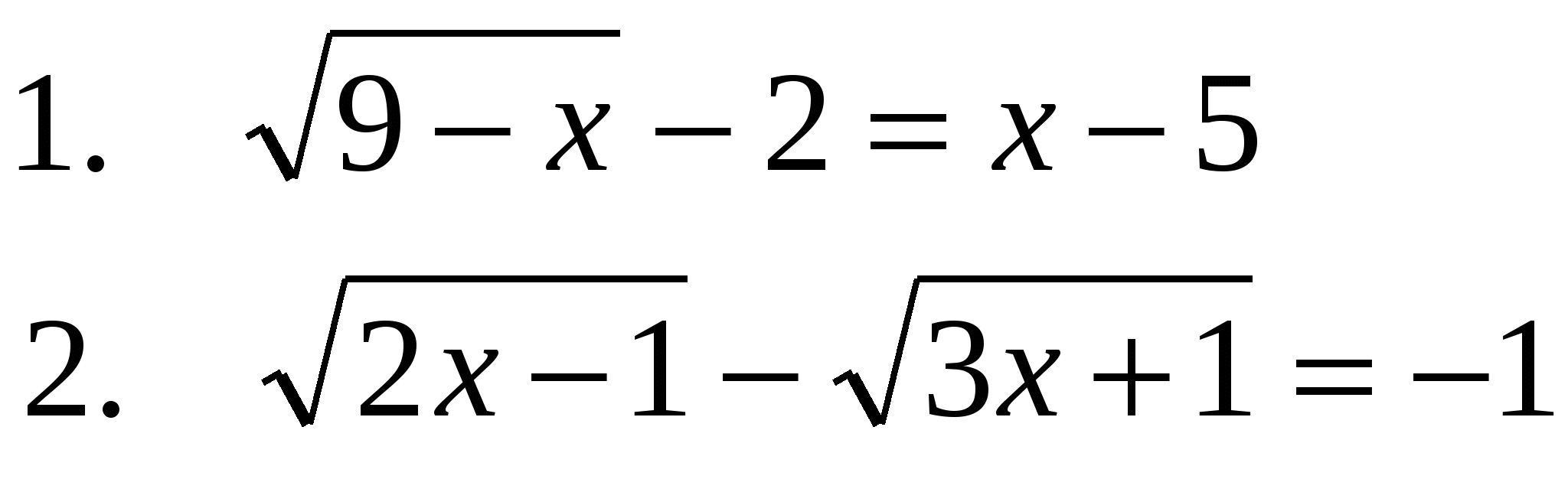
3. 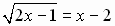
11вВариант 1
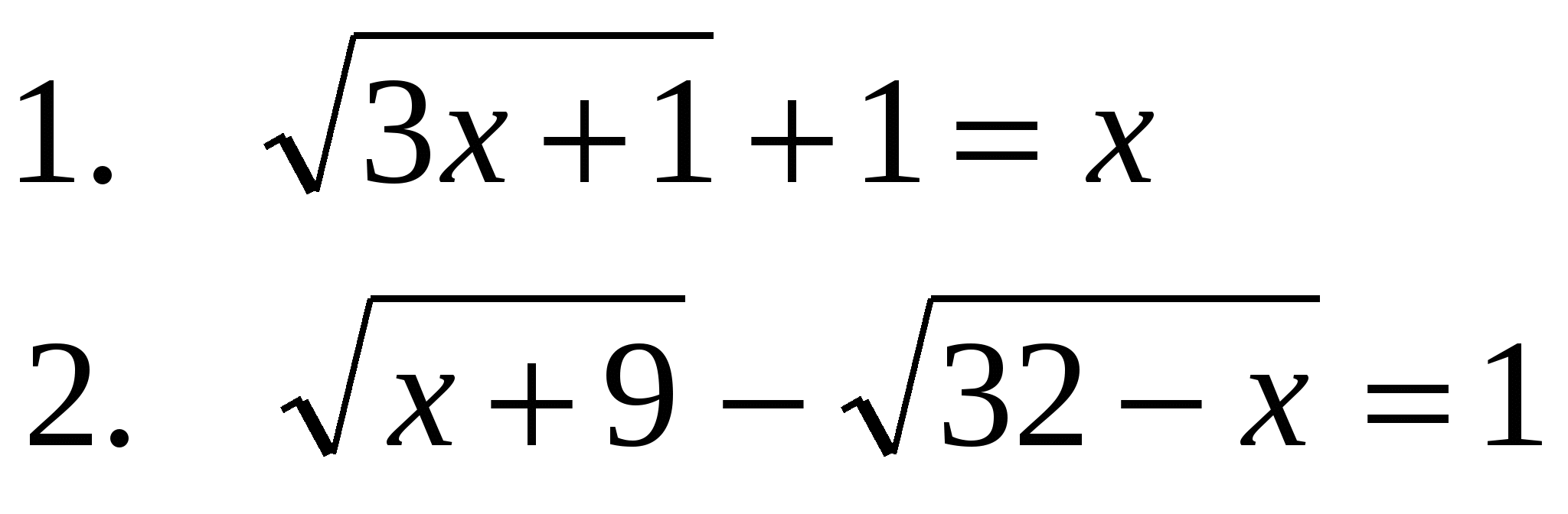
3. 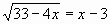
Вариант 2
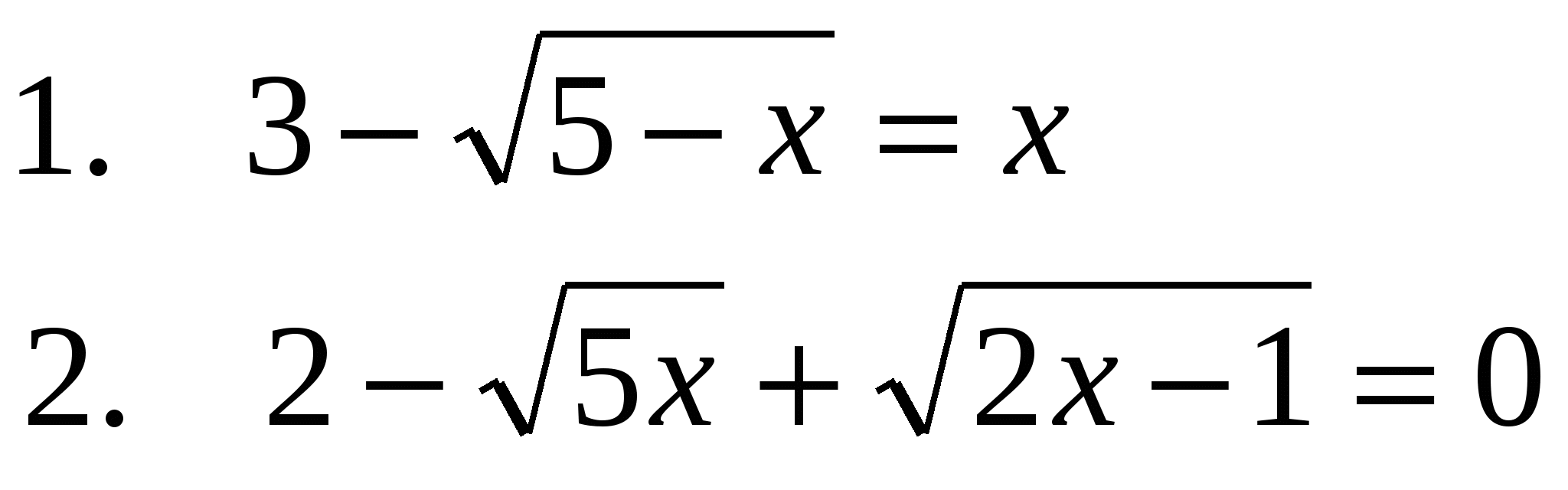
3. 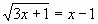
Вариант 3
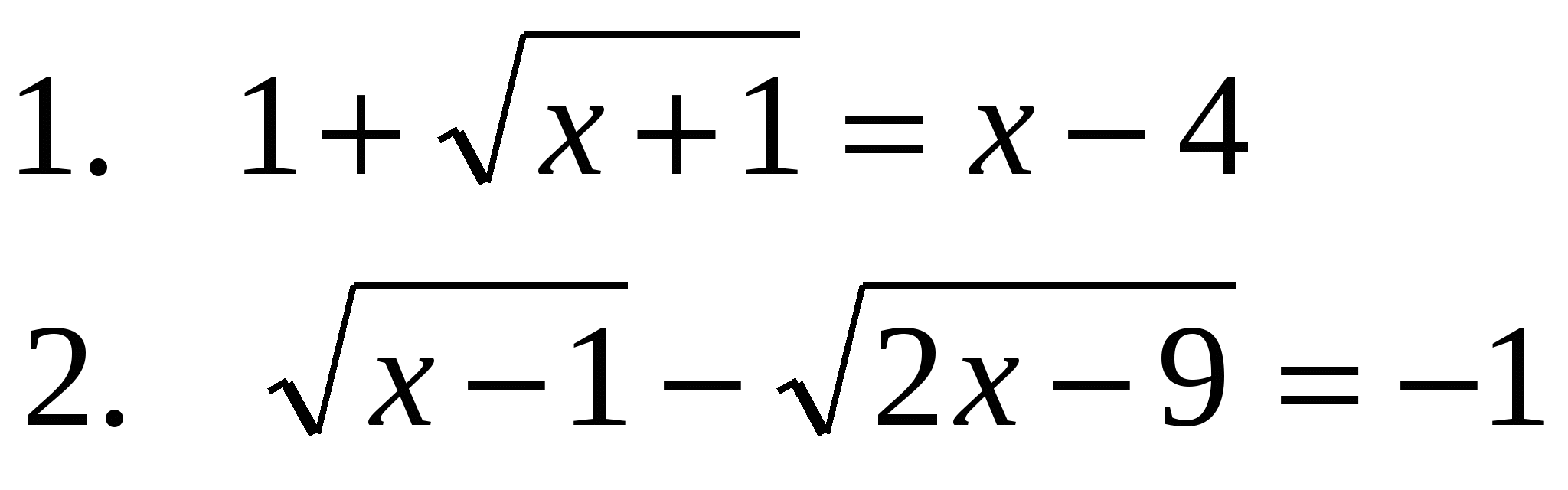
3. 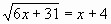
Вариант 4
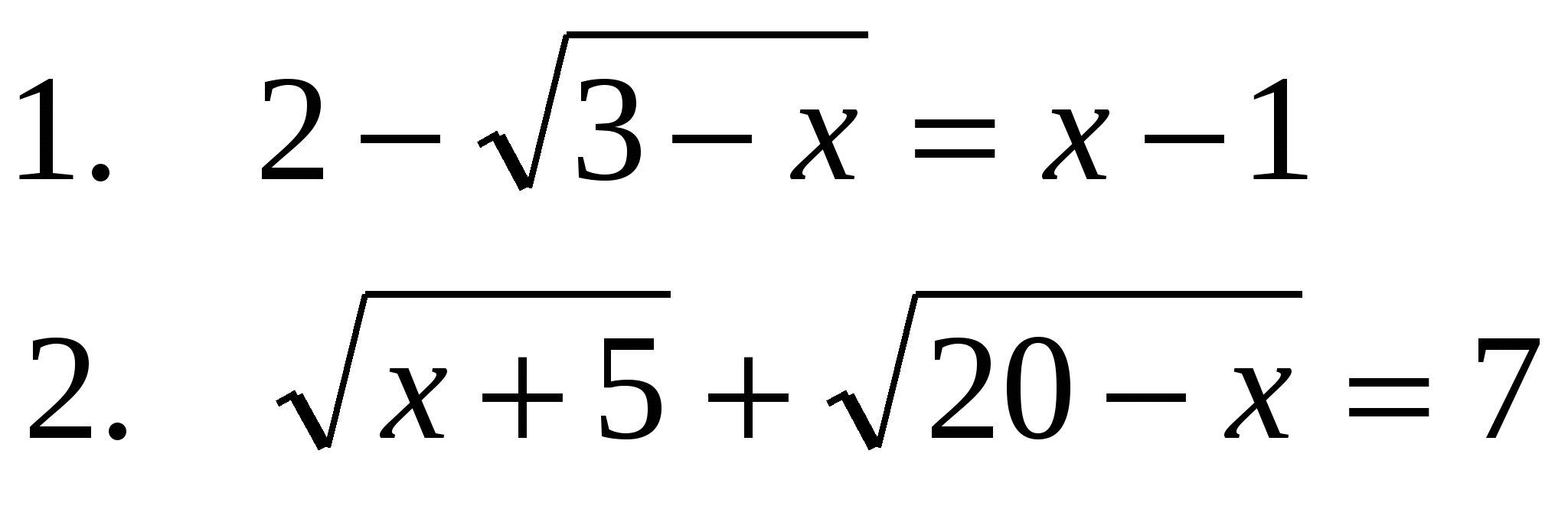
3. 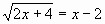
Вариант 5
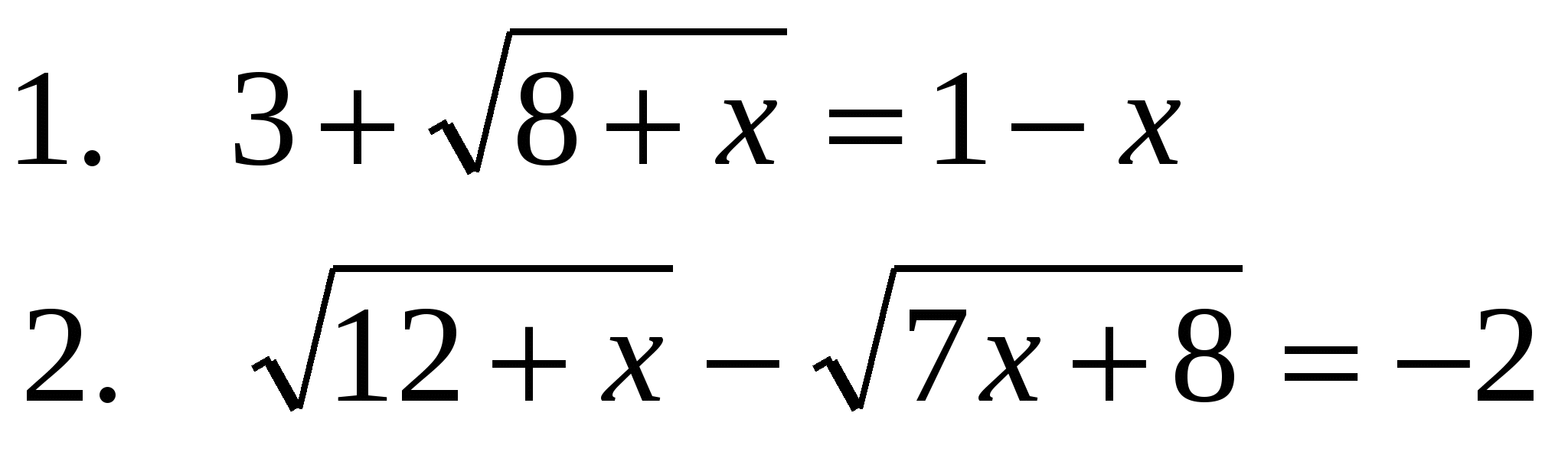
3. 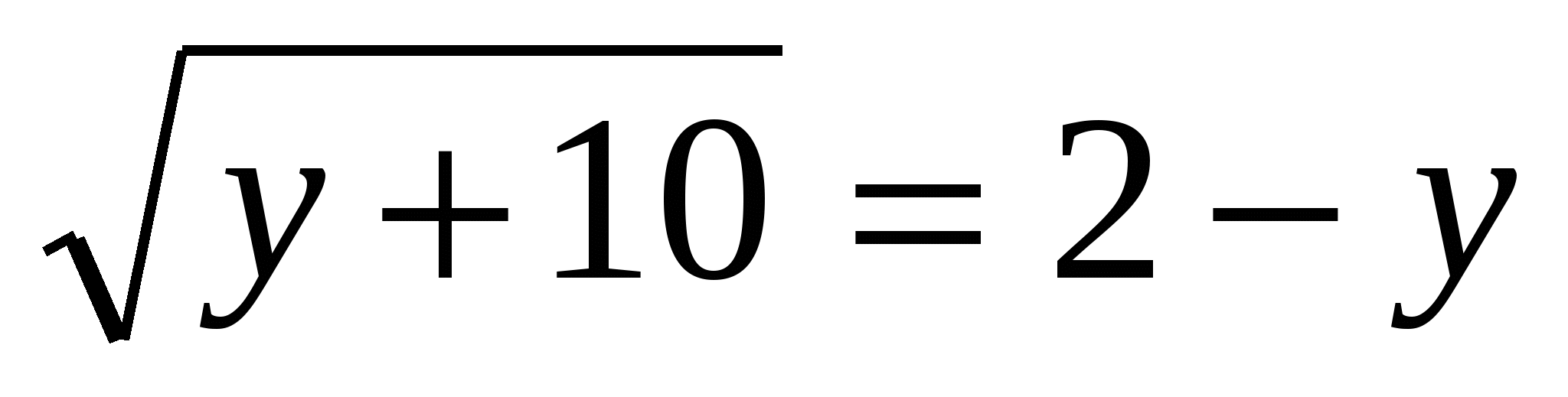
Вариант 6
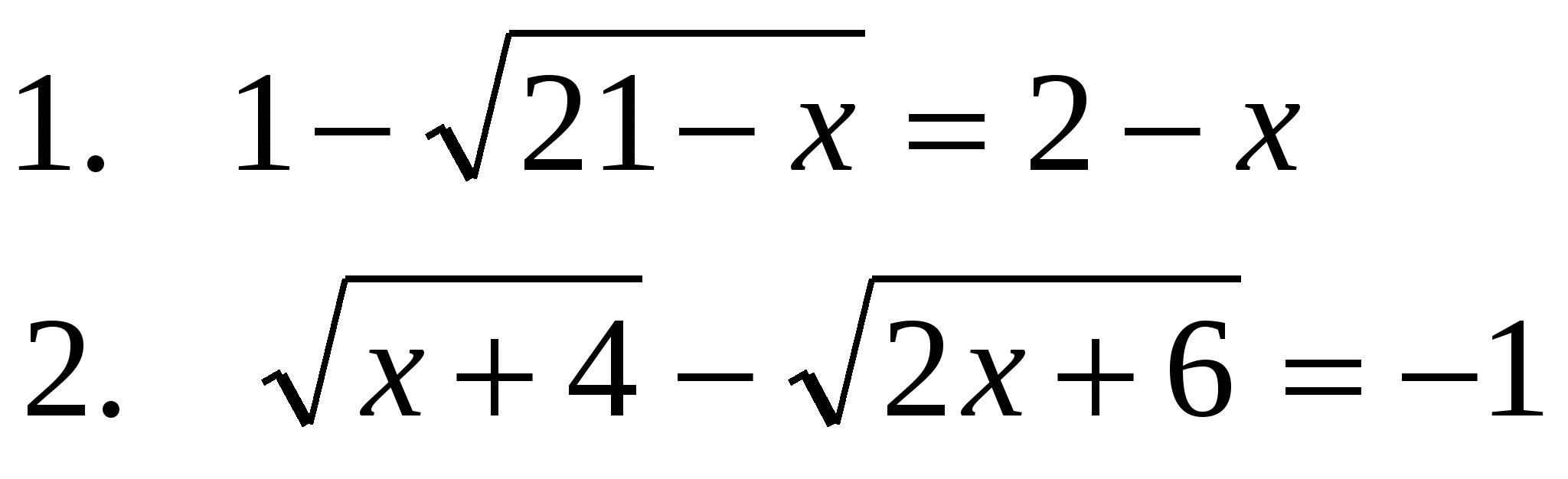
3. 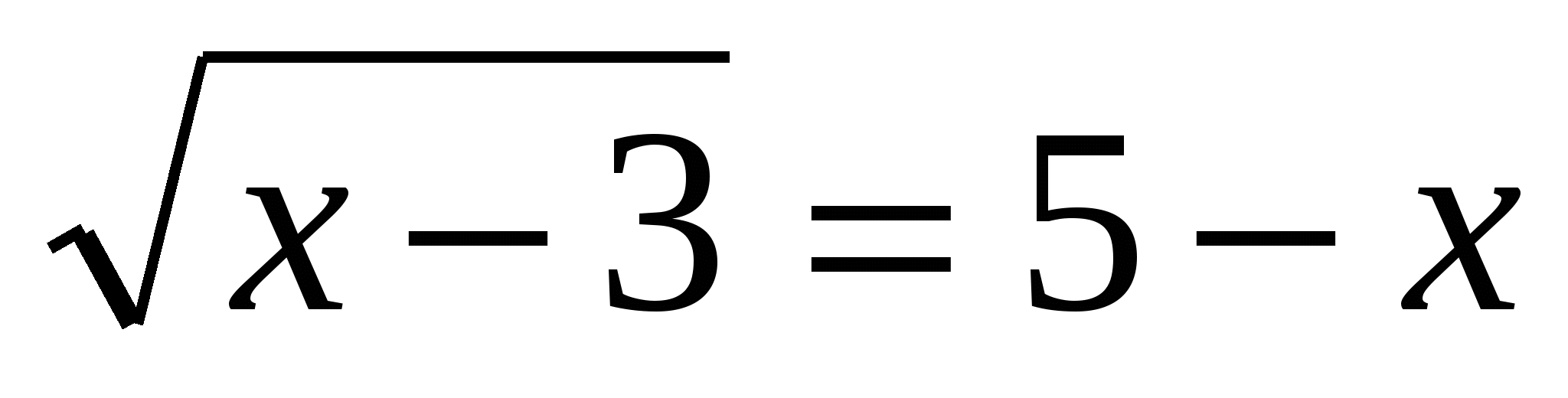
Вариант 7
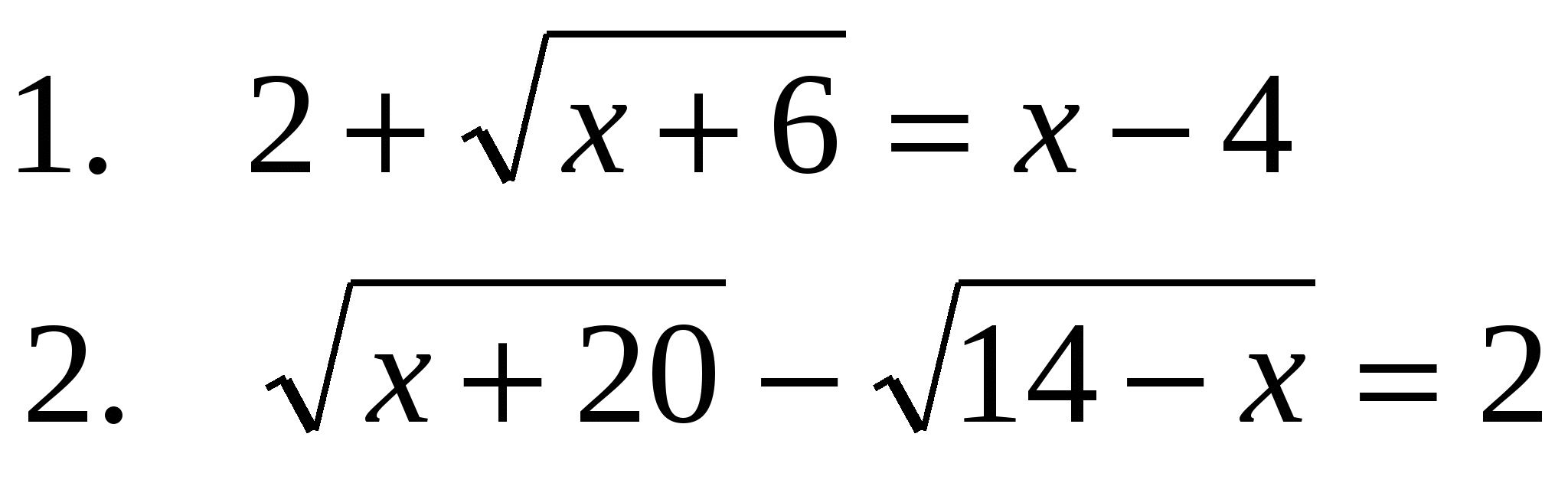
3. 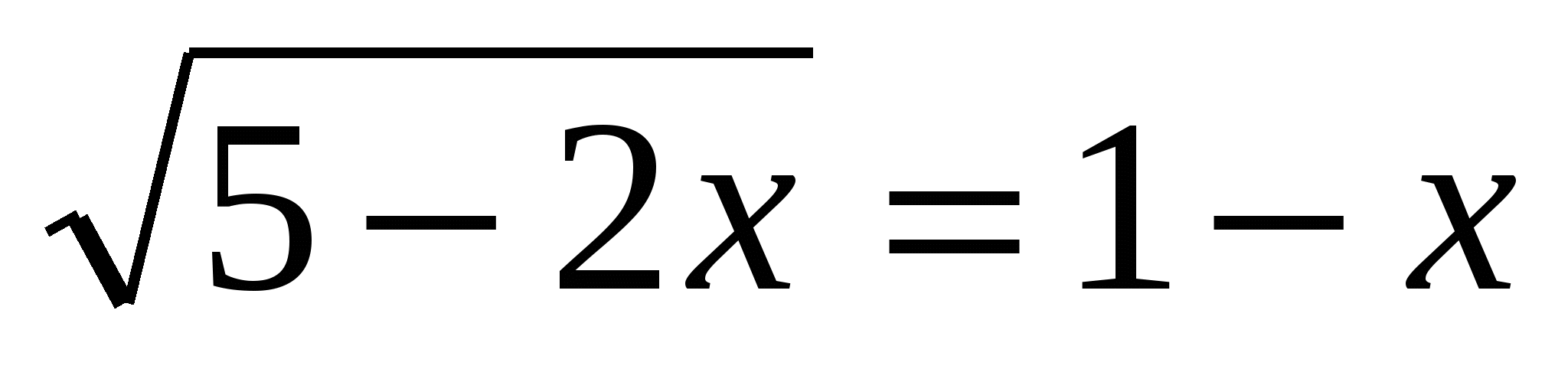
Вариант 8
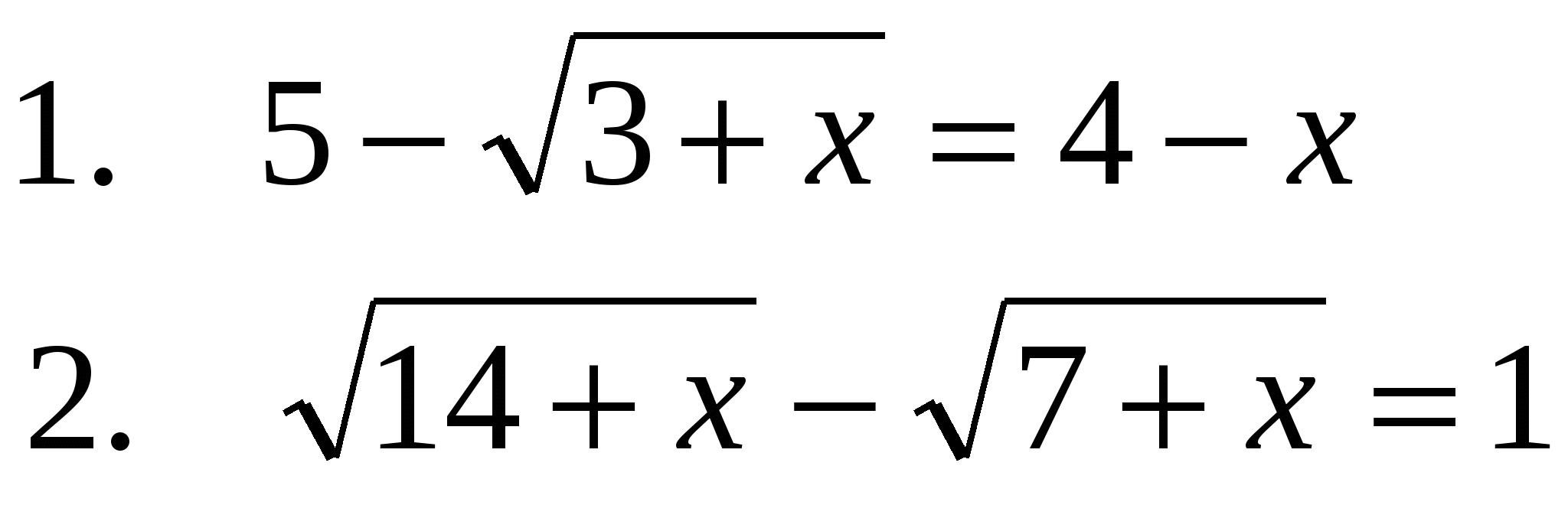
3. 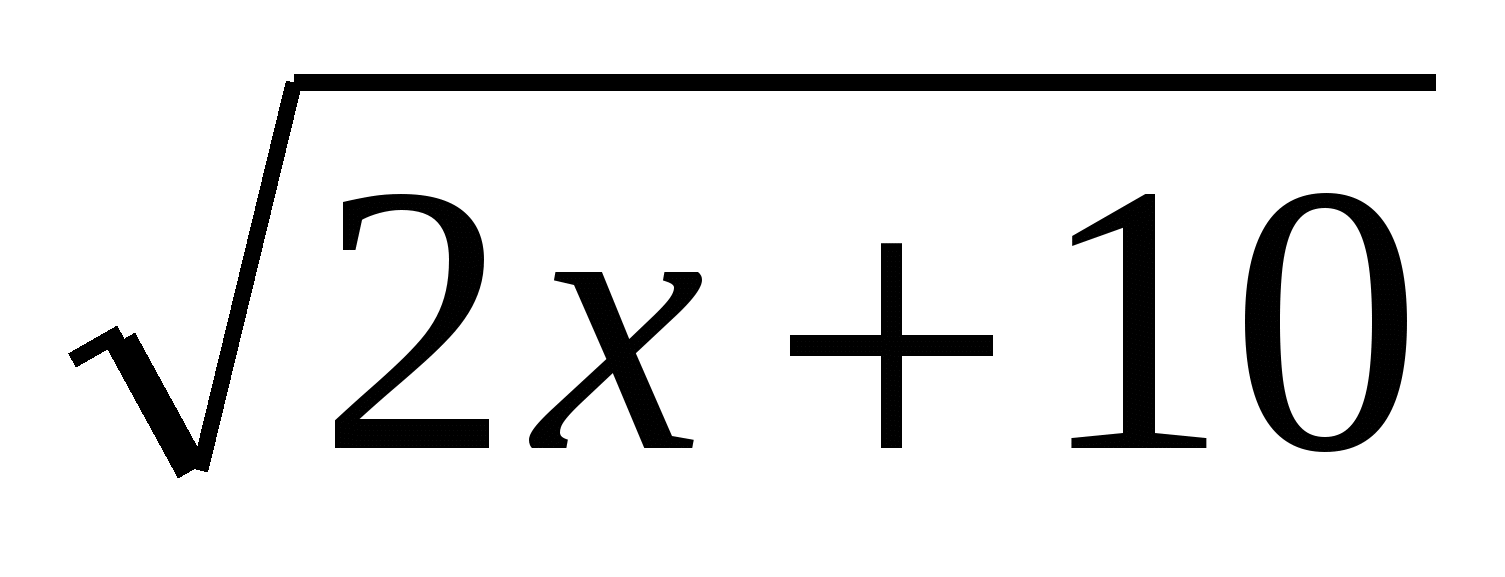 =х+1
=х+1
Вариант 9
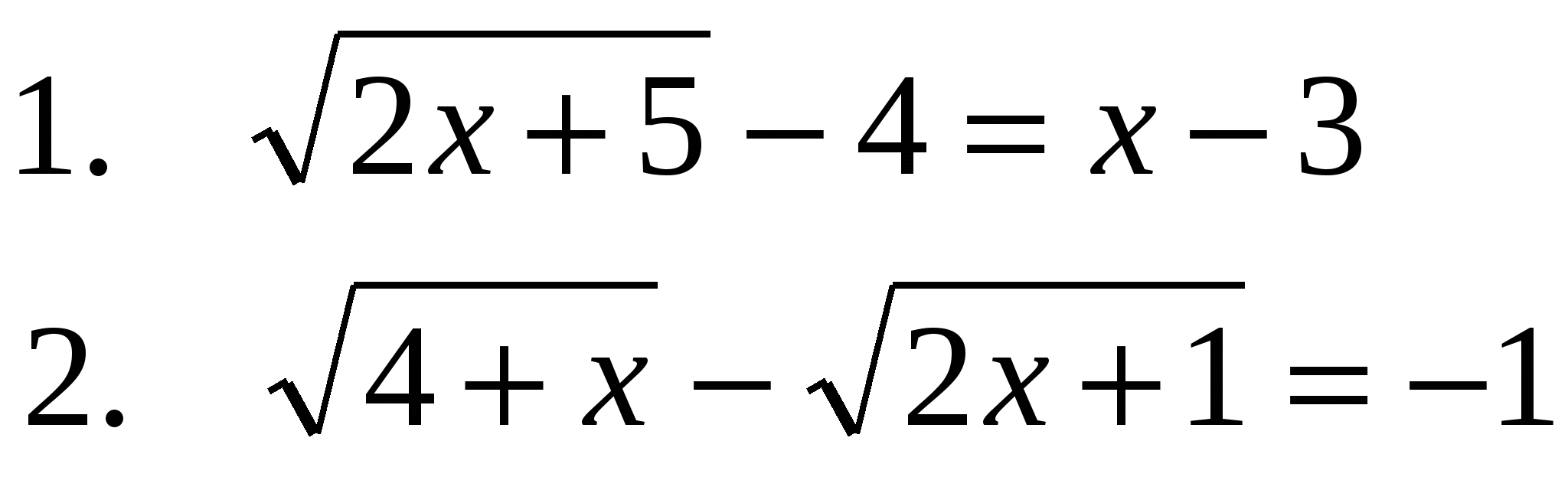
3. 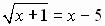
1в. 1. 5 2.16 3.6 2в. 1. 1, 2. 5, 3.5. 3в. 1.8, 2.17, 3. 3. 4в. 1.2;3, 2.4;11, 3. 6. 5в. 1.-4, 2. 4, 3. -1
6в. 1. 5, 2. 5, 3. 4, 7в. 1. 10, 2. 5, 3. -2. 8в. 1.1, 2. 2,3. 3. 9в. 1. 2, 2. 12, 3. 8. 10в. 1. 5,2. 5, 3. 5.
infourok.ru
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ.
Вариант 1.
1. Решить уравнение:
а) 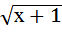 = 3; б) х =
= 3; б) х = 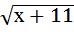 + 1; в)
+ 1; в) 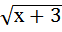 =
= 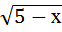 ;
;
г) 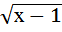 = х – 3; д)
= х – 3; д)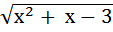 =
= 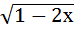 .
.
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ.
Вариант 2.
1. Решить уравнение:
а) 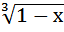 = 2; б) х –
= 2; б) х – 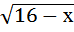 =10; в)
=10; в) 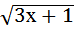 =
= 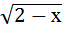 ;
;
г) 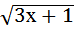 = х – 1; д)
= х – 1; д)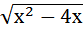 =
= 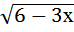 .
.
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ.
Вариант 3.
1. Решить уравнение:
а) 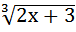 = 1; б) х =
= 1; б) х = 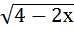 + 2; в)
+ 2; в) 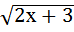 =
= 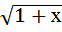 ;
;
г) 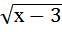 = х – 9; д)
= х – 9; д)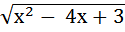 =
= 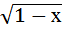 .
.
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ.
Вариант 4.
1. Решить уравнение:
а) 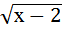 = 5; б) х =
= 5; б) х = 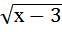 + 9; в)
+ 9; в) 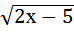 =
= 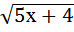 ;
;
г) 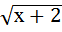 = 3х – 4; д)
= 3х – 4; д) 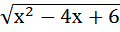 = х + 4
= х + 4
infourok.ru
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 1
1. Решите уравнение:
аº)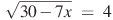 бº)
бº) 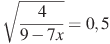 вº)
вº)
2º. Найдите корень уравнения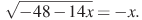 Если уравнение имеет более одного корня, укажите меньший из них.
Если уравнение имеет более одного корня, укажите меньший из них.
3. Решите систему уравнений
4. Решите неравенство: 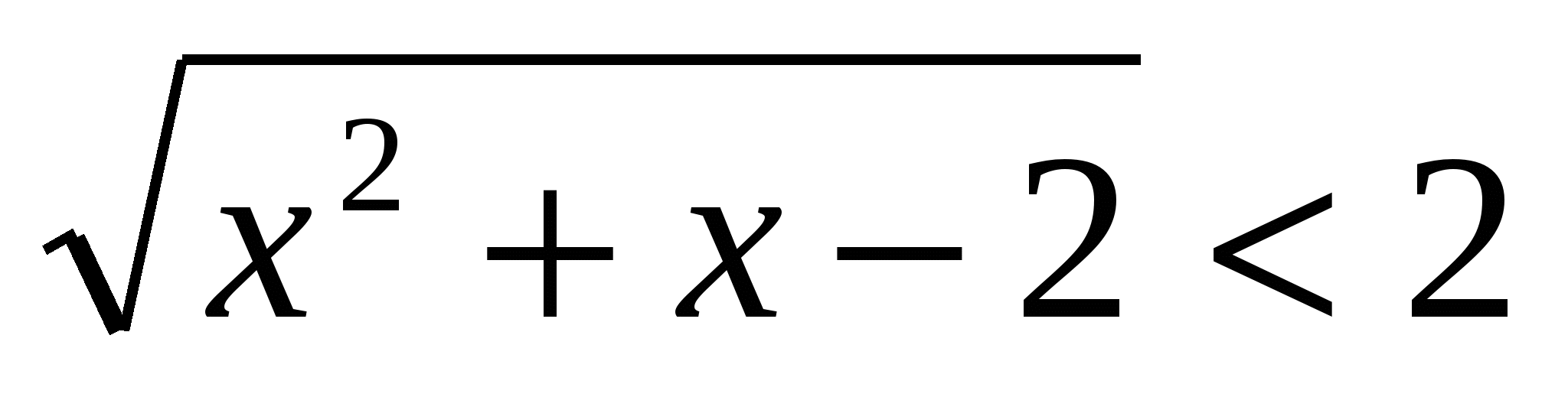 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 2
1. Решите уравнение:
аº) 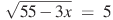 бº)
бº) 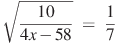 вº) г) .
вº) г) .
2º. Найдите корень уравнения . Если уравнение имеет более одного корня, укажите больший из них.
. Если уравнение имеет более одного корня, укажите больший из них.
3. Решите систему уравнений
4. Решите неравенство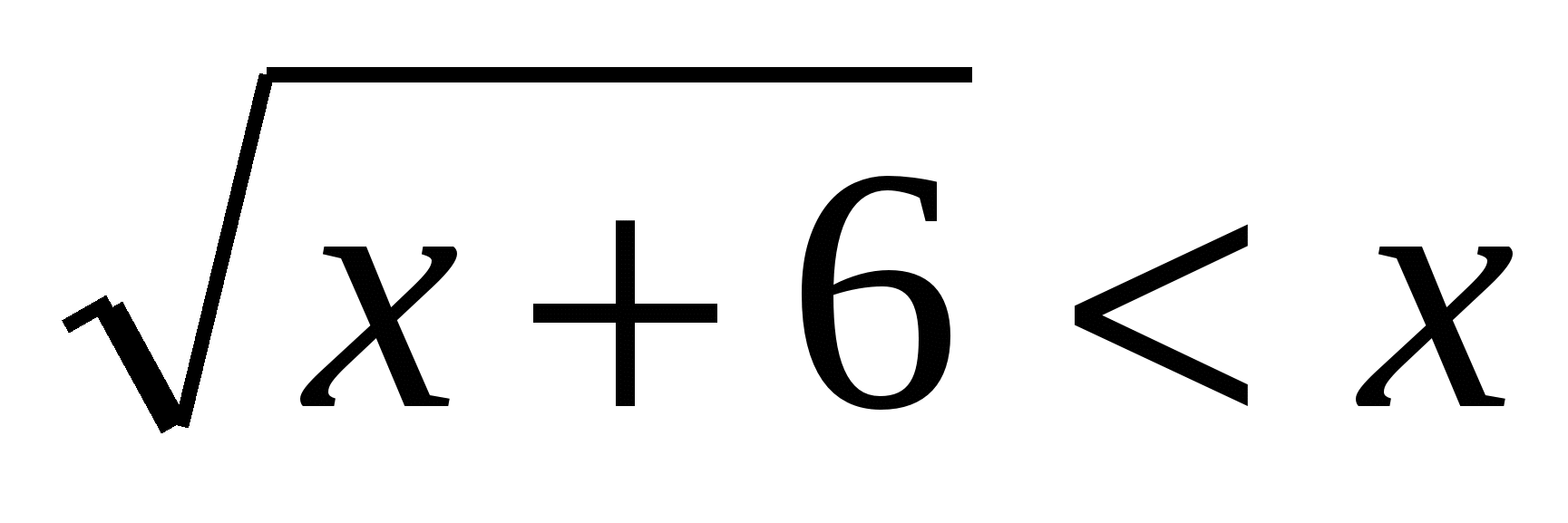 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 3
1.Решите уравнение:
аº)  бº)
бº) 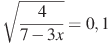
вº) г)
2º. Найдите корень уравнения. Если уравнение имеет более одного корня, укажите меньший из них.
3. Решите систему уравнений
4. Решите неравенство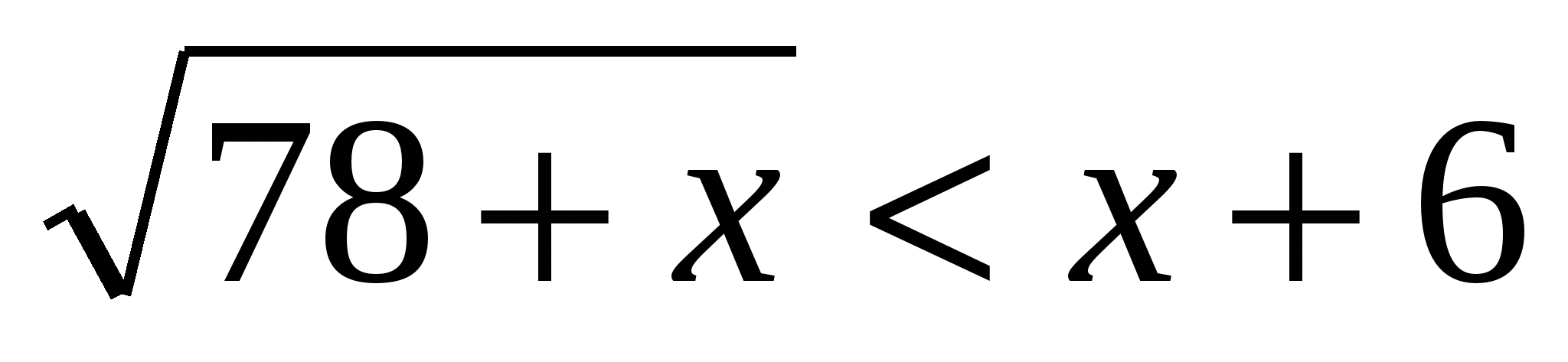 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 4
1.Решите уравнение:
аº)  бº)
бº) 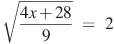 ; вº) г)
; вº) г)
2º. Найдите корень уравнения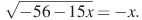 Если уравнение имеет более одного корня, укажите больший из них.
Если уравнение имеет более одного корня, укажите больший из них.
3. Решите систему уравнений
4. Решите неравенство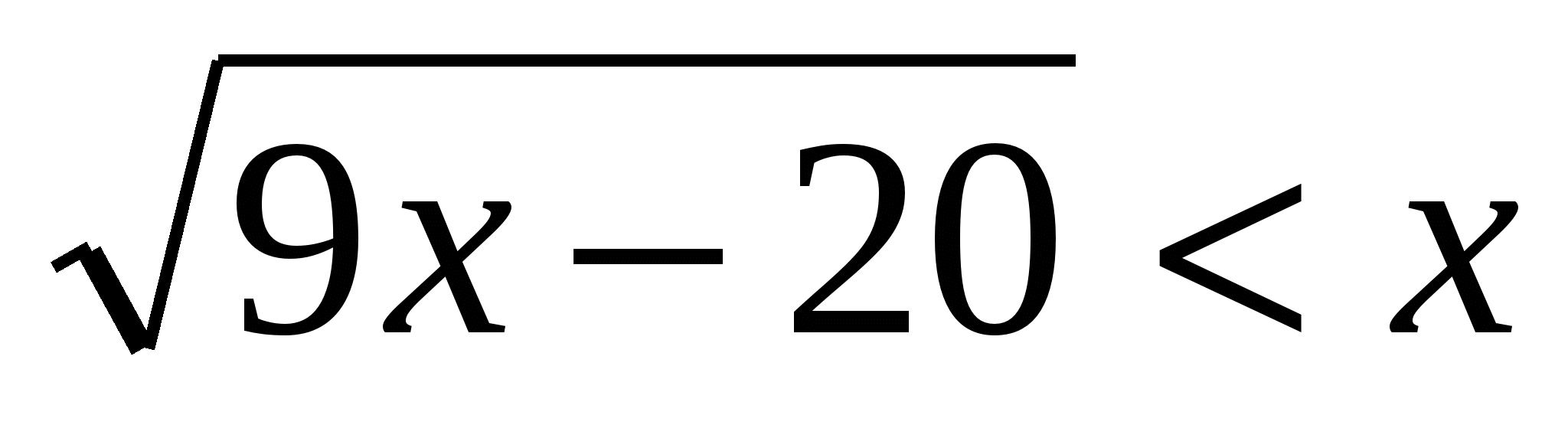 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 5
1. Решите уравнение:
аº)  бº)
бº) 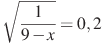 вº)
вº)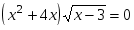
г).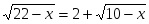
2º. Найдите корень уравнения . Если уравнение имеет более одного корня, укажите меньший из них.
. Если уравнение имеет более одного корня, укажите меньший из них.
3. Решите систему уравнений
4. Решите неравенство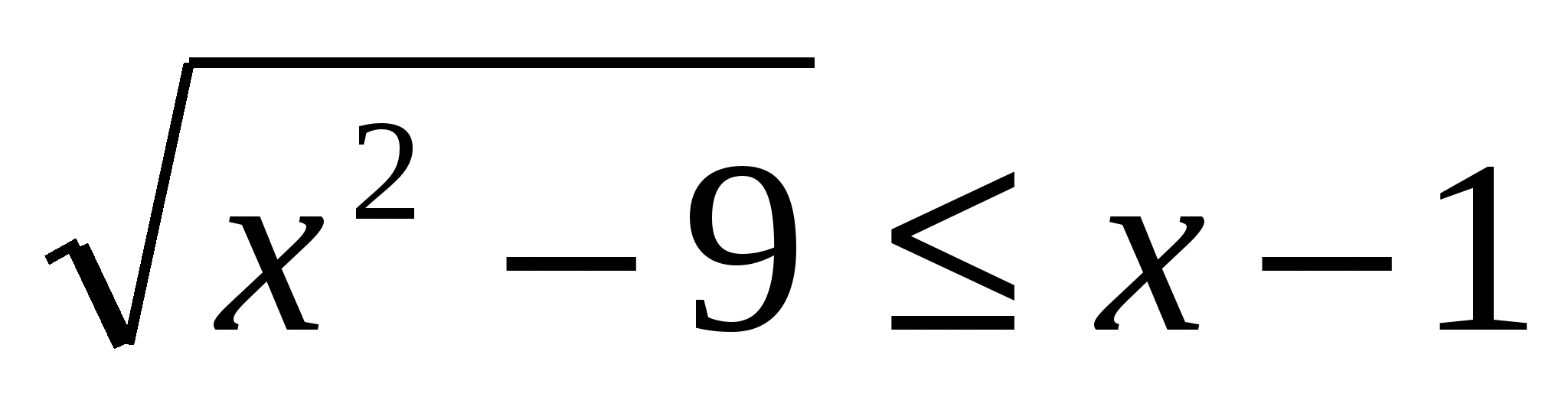 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 6
Решите уравнение:
аº) 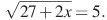 бº)
бº) 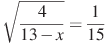 вº)
вº)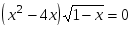 г)
г) 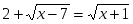
2º. Найдите корень уравнения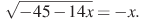 Если уравнение имеет более одного корня, укажите меньший из них.
Если уравнение имеет более одного корня, укажите меньший из них.
3. Решите систему уравнений
4. Решите неравенство: 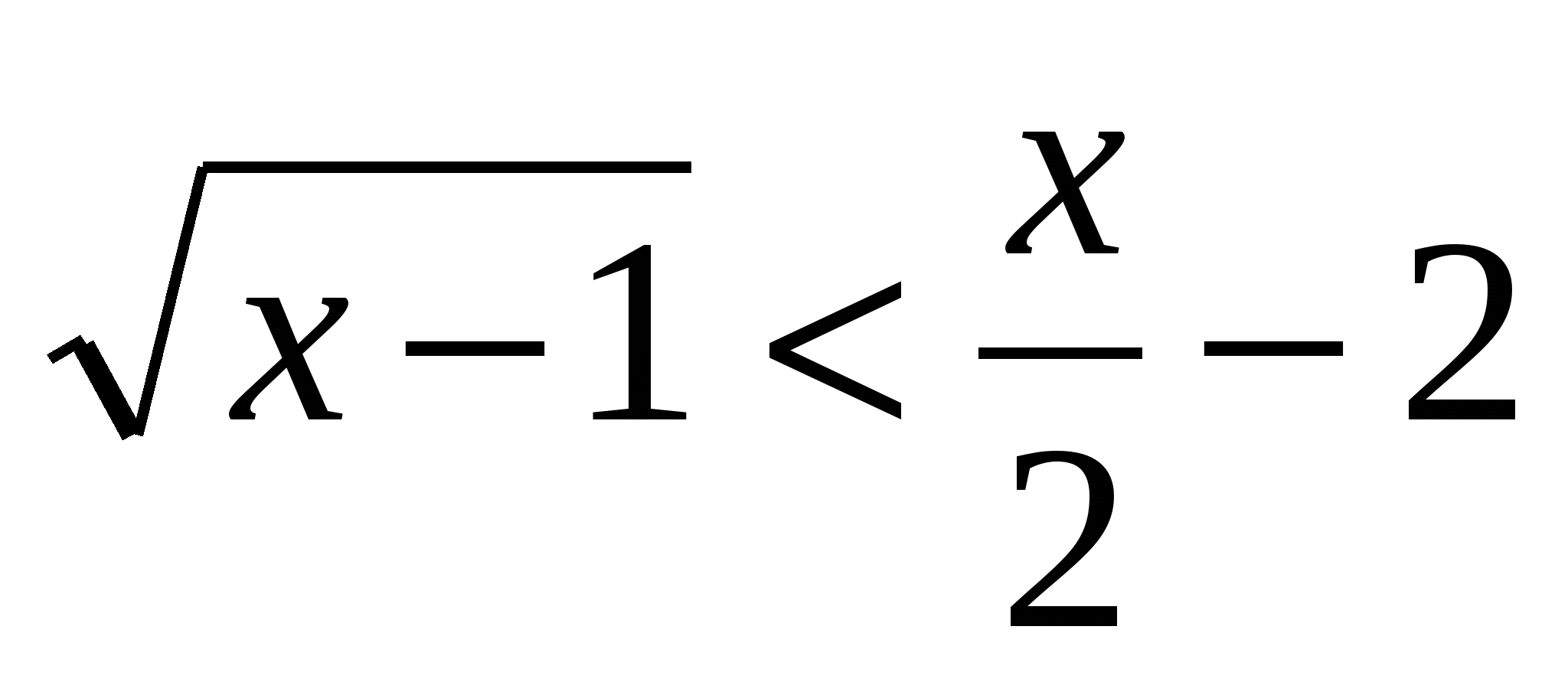 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 7
Решите уравнение:
аº) 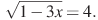 бº)
бº) 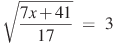 вº)
вº) 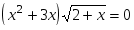
г)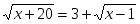 .
.
2º. Найдите корень уравнения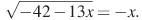 . Если уравнение имеет более одного корня, укажите больший из них.
. Если уравнение имеет более одного корня, укажите больший из них.
3. Решите систему уравнений
4. Решите неравенство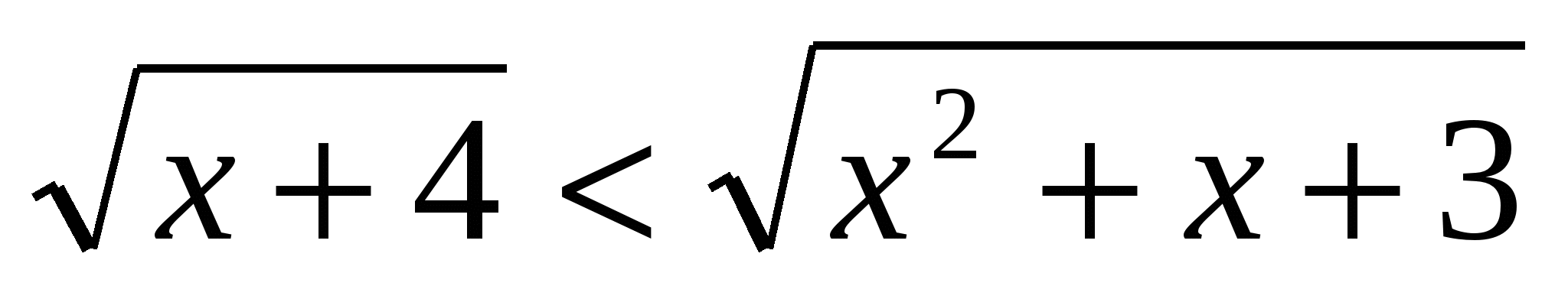 .
.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 8
1.Решите уравнение:
аº) 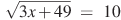 бº)
бº) 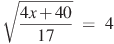 вº)
вº) 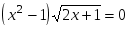
г)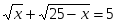
2º. Найдите корень уравнения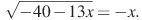 . Если уравнение имеет более одного корня, укажите меньший из них.
. Если уравнение имеет более одного корня, укажите меньший из них.
3. Решите систему уравнений
4. Решите неравенство.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 9
1.Решите уравнение:
аº)  бº)
бº) 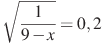 вº)
вº)
г) 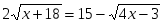
2º. Найдите корень уравнения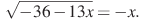 . Если уравнение имеет более одного корня, укажите больший из них.
. Если уравнение имеет более одного корня, укажите больший из них.
3. Решите систему уравнений
4. Решите неравенство.
Контрольная работа по теме «Корень n-ой степени, иррациональные уравнения и неравенства». 11 класс
Вариант 10
Решите уравнение:
аº) 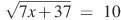 бº)
бº) 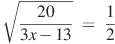 вº)
вº)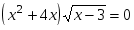
г).
2º. Найдите корень уравнения Если уравнение имеет более одного корня, укажите меньший из них.
Если уравнение имеет более одного корня, укажите меньший из них.
3. Решите систему уравнений
4. Решите неравенство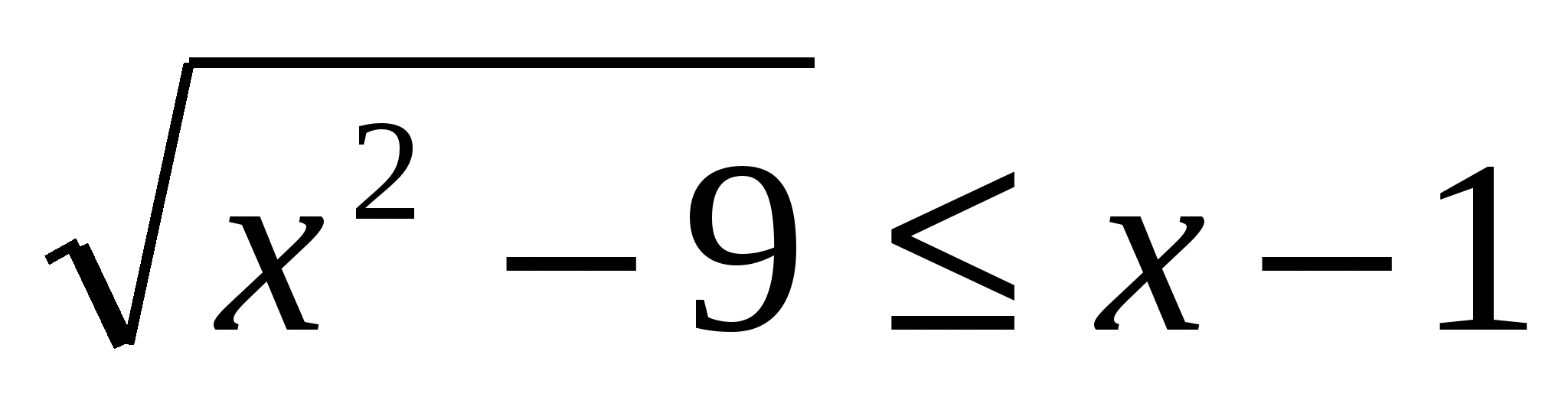 .
.
Работа рассчитана на 1 час.
Критерии оценивания:
«3» - верно решены задания 1а, 1б, 1в и 2
«4» - верно решены все задания 1, задание 2 и одно из заданий 3 или 4
«5» - все решено верно
Ответы
infourok.ru
Действия над векторами
Задача 1. Решите уравнение + = 5 Решение. Пусть = (х - 1; 1), = (5 - х; 2) + = (4; 3) ¦ + ¦= 5. Исходя из + ? ¦ + ¦ имеем ^^: = > 0 х = . Ответ: Задача 2. Решить уравнение х + = 2 Решение: ОДЗ: - 1 ? х ? 3. Рассмотрим векторы = (; ) и (х; 1)...
Действия над векторами
Задача 1. Решить систему уравнений х + у = 2 х2 + у2 = 4 Решение. ОДЗ: у ? 1 и х ? 1. Введем векторы = (х, у), = (; ). Левая часть первого уравнения системы является скалярным произведением векторов и . Определим длины этих векторов и их произведения. ¦¦=...
Дифференциальные уравнения в частных производных
Определение. Функция , имеющая непрерывные частные второго порядка в области и удовлетворяющая внутри уравнению Лапласа, называется гармонической функцией [15, c.78]: ...
Интегрирование иррациональных функций
...
Иррациональные уравнения
Существуют иррациональные уравнения, которые считаются для школьников обычных образовательных школ задачами повышенной трудности. Для решения таких уравнений лучше применять не традиционные методы, а приемы...
Математическое моделирование и численные методы в решении технических задач
...
Применение тригонометрической подстановки для решения алгебраических задач
...
Производная и ее применение для решения прикладных задач
Пример 1. Решение Переписав данное уравнение в виде , заметим, что его корнями являются абсциссы точек пересечения или касания графиков функций и . Для выяснения взаимного расположения графиков этих функций найдем их точки экстремумов...
Решение иррациональных уравнений
Если знаменатель дроби содержит иррациональное выражение, то часто целесообразно избавиться от последнего...
Уравнения, содержащие параметр
уравнение параметр неизвестное модуль 1. Знакомство с параметрами Для начала, стоило бы пояснить, что собой представляют уравнения с параметрами, которым посвящена моя работа. Итак, если уравнение (или неравенство), кроме неизвестных...
Функциональные уравнения на оси и полуоси
Теорема 2.1. Если функция f(t), заданная для всех значений t Q удовлетворяет уравнению f (x + у) = f (x) + f (y), (2.1) тождественно относительно х и у, то она имеет вид f(t) = Ct. Где C -- постоянное число. Доказательство: >Прежде всего...
Функциональные уравнения на оси и полуоси
Следующей задачей будет нахождение всех заданных на Q функций f(x), удовлетворяющих условию: f(x+y)=f(x)•f(y), (2.10) каковы бы ни были значения х и у. Уравнение (2.10) выражает общеизвестное правило умножения степеней: Теорема 2.2. Если функция f(t)...
Функциональные уравнения на оси и полуоси
Функциональное уравнение f(xy) = f(x)+f(y). (2.20) Есть запись логарифмирования произведения: Теорема 2.3. Если функция f(t), заданная для всех положительных значений tQ, притом не сводящаяся к нулю, удовлетворяет уравнению (2...
Функциональные уравнения на оси и полуоси
Наконец, рассмотрим функциональное уравнение f(x•y) = f(x) • f(y). (2.33) (при рациональных положительных x и y), это ничто иное, как правило возведения в степень произведения двух чисел: , Теорема 2.4. Если функция f(t)...
Функциональные уравнения на оси и полуоси
Найти все непрерывные в промежутке (-?, +?) функции f(x), удовлетворяющие условию: f(x+y)=f(x)+f(y), (3.1) каковы бы ни были значения х и у. Легко видеть, что линейные однородные функции вида f(x)=c•x (c=const) (3.2) удовлетворяют этому уравнению: с(x+y)=cx+cy...
math.bobrodobro.ru
Тест по теме «Решение иррациональных уравнений».
Пояснительная записка.
Тесты являются одной из самых популярных форм контроля знаний учащихся. Они обеспечивают простоту проверки ответов студентов и позволяют выявить пробелы в их знаниях. Тесты - это достаточно краткие испытания и предназначены для того, чтобы оценить успешность овладения конкретными знаниями, как отдельных разделов программы, так и всего курса в целом (итоговые тесты). Грамотно составленные тесты являются объективными показателями обученности студентов.
Тестовые задания по теме «Решение иррациональных уравнений», приведённые ниже, предназначены для проверки уровня знаний, умений и навыков студентов первого курса медицинского техникума по данной теме и могут помочь выпускникам при подготовке к ЕГЭ. При решении заданий данного теста необходимо хорошо знать и уметь применять на практике основные алгоритмы решения иррациональных уравнений. Структура заданий в этом тесте из четырёх вариантов основана на одной из традиционных форм теста, представляющей собой наличие четырёх предполагаемых ответов к каждому из десяти неравенств.
Тест «Решение иррациональных уравнений»
Вариант 1
1. Найдите корни уравнения  .
.
1. 2 2. -6 3. 14 4. корней нет
2. Решите уравнение  .
.
1. -3 2. 4 3. 9 4. корней нет
3. Найдите корни уравнения  .
.
1. 0;10 2. 0;-9 3. 0 4. корней нет
4. Решите уравнение 
1. -3 2. 3 3. 0;3 4. корней нет
5. Найдите корни уравнения 
1. 5 2. -3;5 3. -5;3 4. корней нет
6. Решите уравнение 3
1. 0;-1 2. 0;-1 3. -1 4. корней нет
7. Найдите корни уравнения 
1. 8 2.  3.
3.  4. -8
4. -8
8. Решите уравнение 
1. -2 2. -2;-1 3. -1 4. 
9. Найдите корни уравнения 
1. -10; 2. -10;10 3.
2. -10;10 3.  4. -10;
4. -10; 
10. Решите уравнение 
1. -16;-2;0 2. -16 3. 0;-2 4. -16;-2
Тест «Решение иррациональных уравнений»
Вариант 2
1. Найдите корни уравнения  .
.
1. 5 2. 96 3. -6 4. корней нет
2. Решите уравнение  .
.
1. 1,5 2. 4 3. 2. 4. корней нет
3. Найдите корни уравнения  .
.
1. 0 2. 0;9 3. 9 4. корней нет
4. Решите уравнение 
1. -3 2. 3 3. 1 4. корней нет
5. Найдите корни уравнения 
1. 5 2. -3;5 3. -5;3 4. корней нет
6. Решите уравнение 
1. 0;3 2. 0;-3 3. корней нет 4. 3
7. Найдите корни уравнения 
1. 15 2.  3.
3.  4. корней нет
4. корней нет
8. Решите уравнение 
1. 36 2. 24; 36 3. 24 4. 
9. Найдите корни уравнения 
1. 11;  2. 11;-11 3. -11 4. -11;
2. 11;-11 3. -11 4. -11;
10. Решите уравнение 
1. -7 2. 0 3. -7;0 4. корней нет
Тест «Решение иррациональных уравнений»
Вариант 3
1. Найдите корни уравнения  .
.
1.  2. -5 3. 5 4. корней нет
2. -5 3. 5 4. корней нет
2. Решите уравнение  .
.
1.  2.
2.  3. 9 4. корней нет
3. 9 4. корней нет
3. Найдите корни уравнения  .
.
1. 0;-7 2. 0; -13 3. 0 4. корней нет
4. Решите уравнение 
1. -3 2. 3 3.-3;3 4. корней нет
5. Найдите корни уравнения 
1. 5 2. -3;5 3. -5;3 4. корней нет
6. Решите уравнение 5
1. 0,2 2.-0,2 3. -0,1 4. корней нет
7. Найдите корни уравнения 
1. 19 2.  3.
3.  4. -19
4. -19
8. Решите уравнение 
1. -10 2. -10;-9 3. -9 4. 
9. Найдите корни уравнения 
1. -12; 2. -12;12 3.
2. -12;12 3.  4. -12;
4. -12; 
10. Решите уравнение 
1. -15;-2;0 2. -15 3. 0;-2 4. -15;-2
Тест «Решение иррациональных уравнений»
Вариант 4
1. Найдите корни уравнения  .
.
1. 2.
2.  3. 2 4. корней нет
3. 2 4. корней нет
2. Решите уравнение  .
.
1. 0,5 2. 4 3. -2. 4. корней нет
3. Найдите корни уравнения  .
.
1. 0 2. 0;21 3. 21 4. корней нет
4. Решите уравнение 
1. -1 2. 0 3. 1 4. корней нет
5. Найдите корни уравнения 
1. 8 2. -3;8 3. -8;3 4. -3
6. Решите уравнение 
1. -6 2. 3;-6 3. корней нет 4. 3
7. Найдите корни уравнения 
1. 90 2.  3.
3.  4. корней нет
4. корней нет
8. Решите уравнение 
1. 87 2. 27; 87 3. 27 4. 
9. Найдите корни уравнения 
1. 14;  2. 14;-14;
2. 14;-14;  3. -14 4. -14;
3. -14 4. -14; 
10. Решите уравнение 
1. -13 2. -3 3. -13;-3 4. корней нет
Ответы к тестам
Вариант 1
Вариант 2
Вариант 3
Вариант 4
№ пп
№ ответа
№ пп
№ ответа
№ пп
№ ответа
№ пп
№ ответа
1.
3
1.
2
1.
3
1.
3
2.
4
2.
4
2.
4
2.
4
3.
2
3.
3
3.
3
3.
3
4.
2
4.
2
4.
2
4.
1
5.
2
5.
2
5.
3
5.
2
6.
3
6.
4
6.
1
6.
3
7.
3
7.
3
7.
3
7.
3
8.
3
8.
1
8.
3
8.
1
9.
4
9.
4
9.
4
9.
4
10.
1
10.
1
10.
1
10.
3
www.metod-kopilka.ru
ВАРИАНТ I
Решите уравнение:
а) б)
б)  в)
в)  г)
г) 
2. Определите, при каких значениях х
функция  принимает
значение, равное 2.
принимает
значение, равное 2.
3. Решите системы уравнений:
а)  б)
б) 
4. Решите неравенства:
а)  >0 б)
>0 б)
 в)
в)  >-4
>-4
5. Упростите выражение и найдите его значение при а=3:

_________________________________________________________________________________
ВАРИАНТ II
Решите уравнение:
а) б)
б)  в)
в)  г)
г) 
2. Определите, при каких значениях х
функция  принимает
значение, равное 3.
принимает
значение, равное 3.
3. Решите системы уравнений:
а)  б)
б) 
4. Решите неравенства:
а)  <0 б)
<0 б)
 в)
в)  >-2
>-2
5. Упростите выражение и найдите его значение при а=3:

_________________________________________________________________________________
ВАРИАНТ III
Решите уравнение:
а) б)
б)  в)
в) 
г) 
2. Найдите абсциссу точки пересечения графиков
функций  и
и 
3. Решите системы уравнений:
а)  б)
б) 
4. Решите неравенства:
а)  б)
б)  >1 в)
>1 в)
 <2
<2
5. Упростите выражение и найдите его значение при а=0,8:

ВАРИАНТ IV
Решите уравнение:
а) б)
б)  в)
в)  г)
г) 
2. Найдите абсциссу точки пересечения графиков
функций  и
и 
3. Решите системы уравнений:
а)  б)
б) 
4. Решите неравенства:
а)  б)
б)  <1 в)
<1 в)
 >4
>4
5. Упростите выражение и найдите его значение при а=0,8:

_________________________________________________________________________________
ВАРИАНТ V
Решите уравнение:
а) б)
б) 
в)  г)
г) 
2. Найдите точки пересечения графиков функций
 и
и 
3. Решите системы уравнений:
а)  б)
б) 
4. Решите неравенства:
а)  б)
б)  >
> в)
в) 
5. Упростите выражение и найдите его значение при а=6:
 _________________________________________________________________________________
_________________________________________________________________________________
ВАРИАНТ VI
Решите уравнение:
а) б)
б) 
в)  г)
г) 
2. Найдите точки пересечения графиков функций
 и
и 
3. Решите системы уравнений:
а)  б)
б) 
4. Решите неравенства:
а)  б)
б)  <
< в)
в) 
5. Упростите выражение и найдите его значение при а=6:

botana.cc