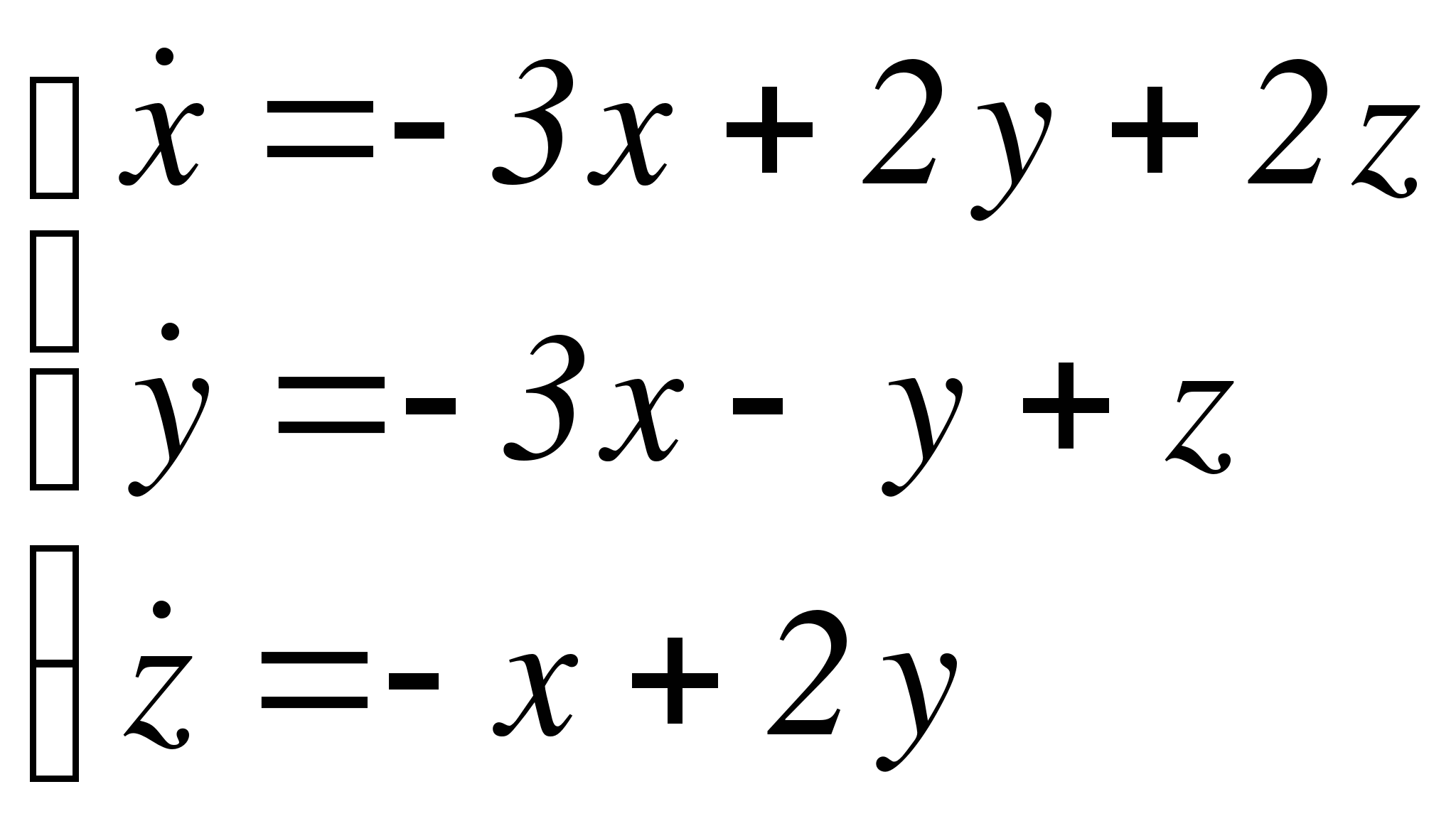
Задача 10. Найти общее решение уравнения .
Решение.
Уравнение не содержащее явно искомой функции.
Обозначим , где – новая неизвестная функция.
Тогда
Будем иметь:
Разделяем переменные и интегрируем:
– общее решение дифференциального уравнения.
Ответ.–общее решение дифференциального уравнения
Задача 11. Найти решение задачи Коши , .
Решение.
Уравнение не содержащее явно независимую переменную х.
Обозначим , где – новая неизвестная функция.
Тогда
Будем иметь:
Подставим в полученное решение условия задачи Коши.
Подставим в полученное решение условия задачи Коши.
- частное решение дифференциального уравнения.
Ответ.- частное решение дифференциального уравнения
Задача 12. Найти частное решение линейного неоднородного уравнения методом неопределенных коэффициентов, используя замену .
Решение.
Характеристическое уравнение соответствующего однородного уравнения:
Правая часть исходного уравнения имеет вид: , где и многочлен третьей степени (m=3).
Проверим, является ли корнем характеристического уравнения:
.
Следовательно, частное решение линейного неоднородного уравнения методом неопределенных коэффициентов будет иметь вид:
Вычислим производные:
Подставим полученные данные в уравнение:
Частное решение имеет вид:
Ответ.- частное решение дифференциального уравнения
Задача 13. Найти частное решение линейного неоднородного уравнения методом неопределенных коэффициентов, используя замену .
Решение.
Характеристическое уравнение соответствующего однородного уравнения:
Правая часть исходного уравнения имеет вид: , где и ,многочлен первой степени (m=1).
Проверим, является ли корнем характеристического уравнения:
.
Проверим, является ли корнем характеристического уравнения:
.
Таким образом, является корнем характеристического уравнения первой степени.
Следовательно, частное решение линейного неоднородного уравнения методом неопределенных коэффициентов будет иметь вид:
Вычислим производные:
Подставим полученные данные в уравнение:
Получим
Частное решение имеет вид:
Ответ. - частное решение дифференциального уравнения
Задача 14. Найти общее решение линейного неоднородного уравнения методом неопределенных коэффициентов, используя принцип суперпозиции.
Решение.
Характеристическое уравнение соответствующего однородного уравнения:
Общее решение соответствующего однородного уравнения имеет вид:
Правая часть исходного уравнения имеет вид: , где ,
В первой функции является корнем характеристического уравнения кратности 1, поэтому соответствующее частное решение имеет вид:
Во второй функции . Число не является корнем характеристического уравнения 1, поэтому соответствующее частное решение имеет вид:
Таким образом, частное решение исходного уравнения имеет вид:
Вычислим производные:
Подставим полученные данные в уравнение:
Получим
Частное решение имеет вид: .
Общее решение линейного неоднородного уравнения имеет вид:
Ответ. - общее решение линейного неоднородного уравнения
Задача 15. Найти общее решение линейного уравнения методом вариации произвольных постоянных.
infourok.ru
Контрольная работа
Задача 1. Найти общее решение линейной однородной системы
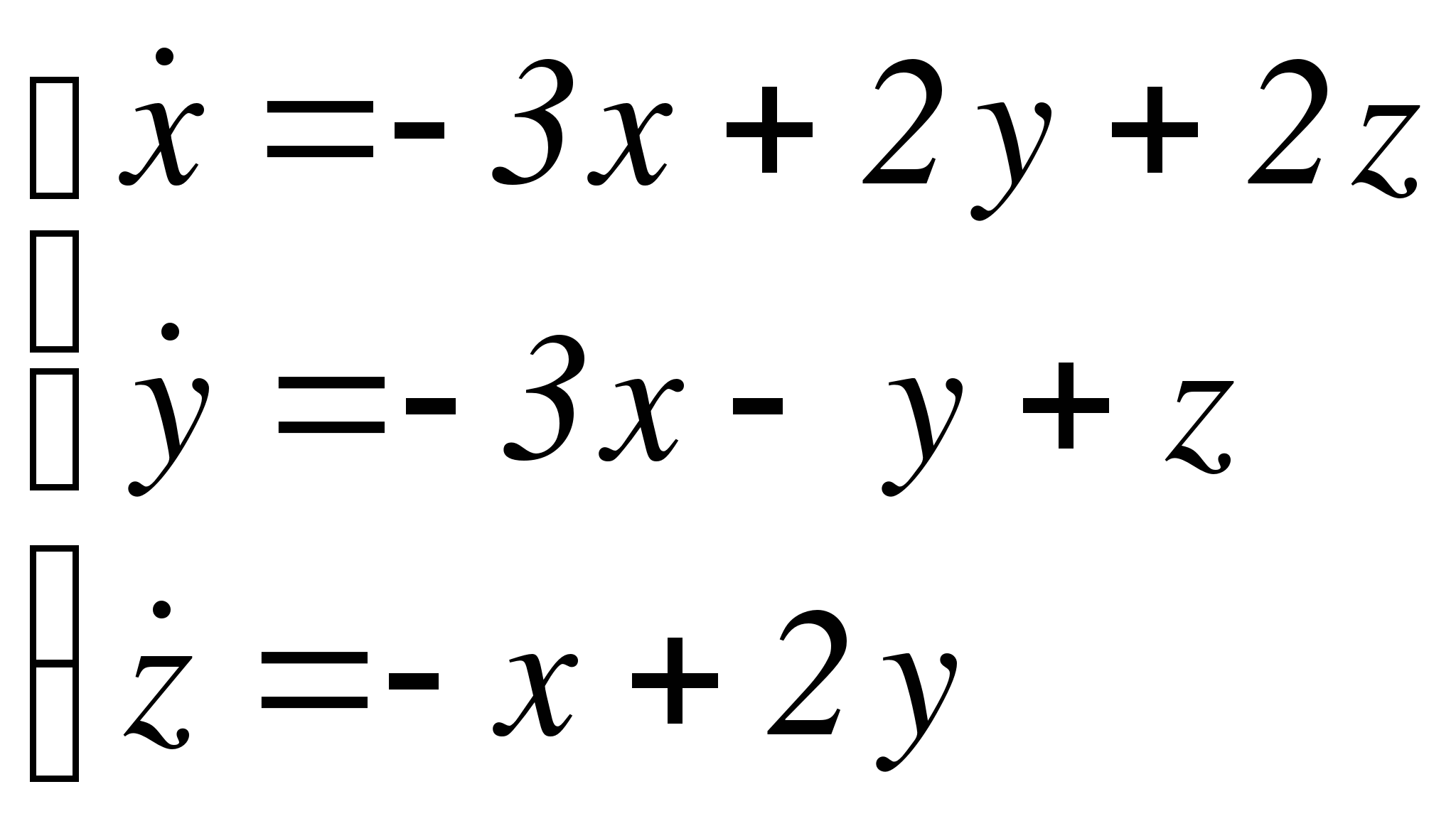
Решение.
Составляем характеристическое уравнение заданной системы:
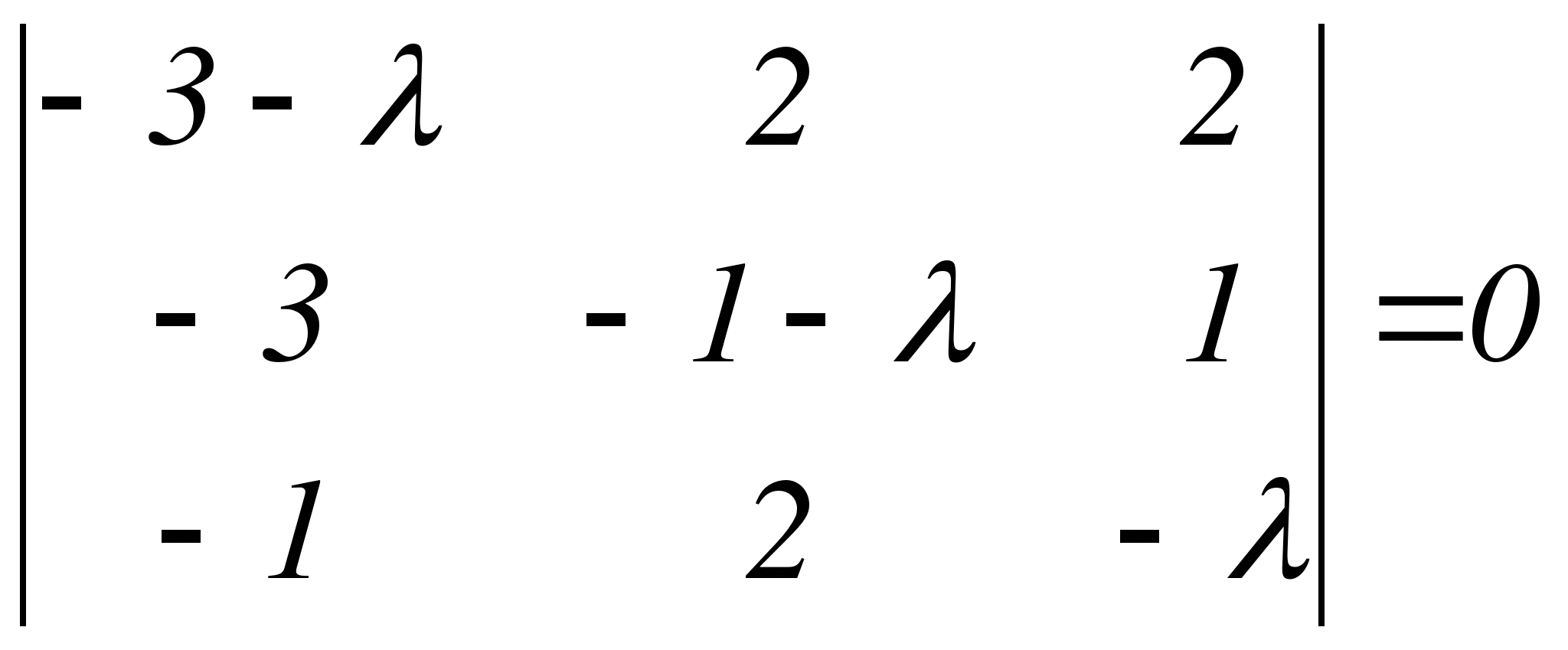
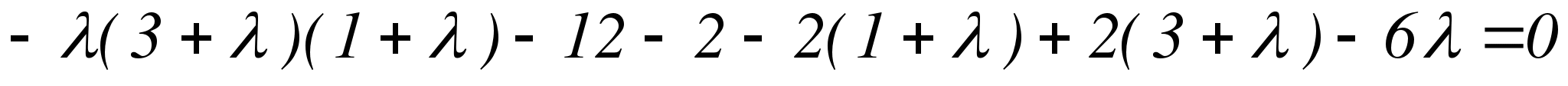
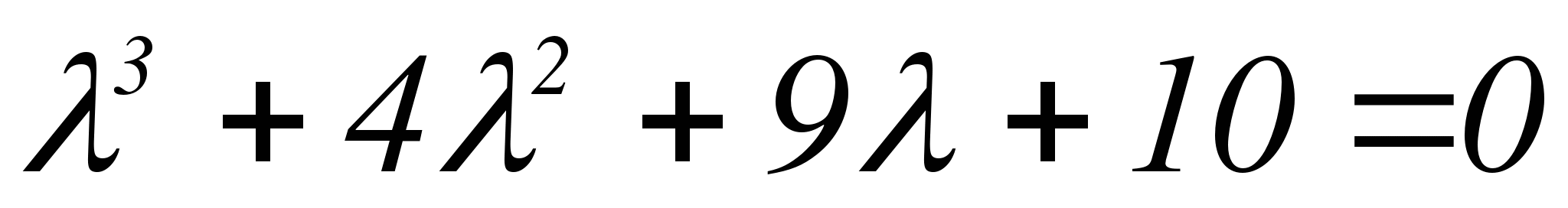
Подбором найдем действительный корень 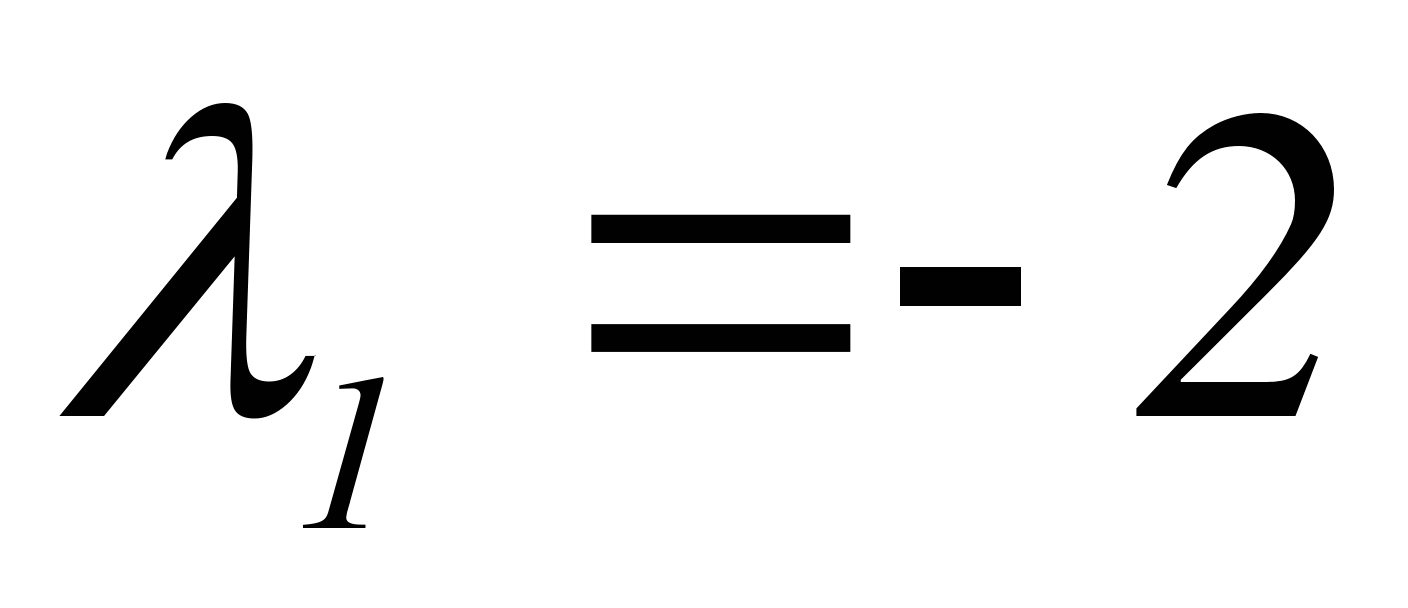
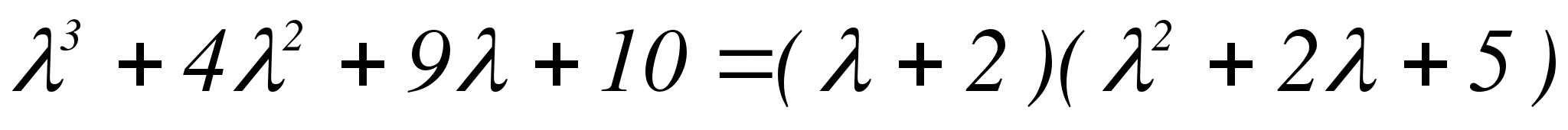
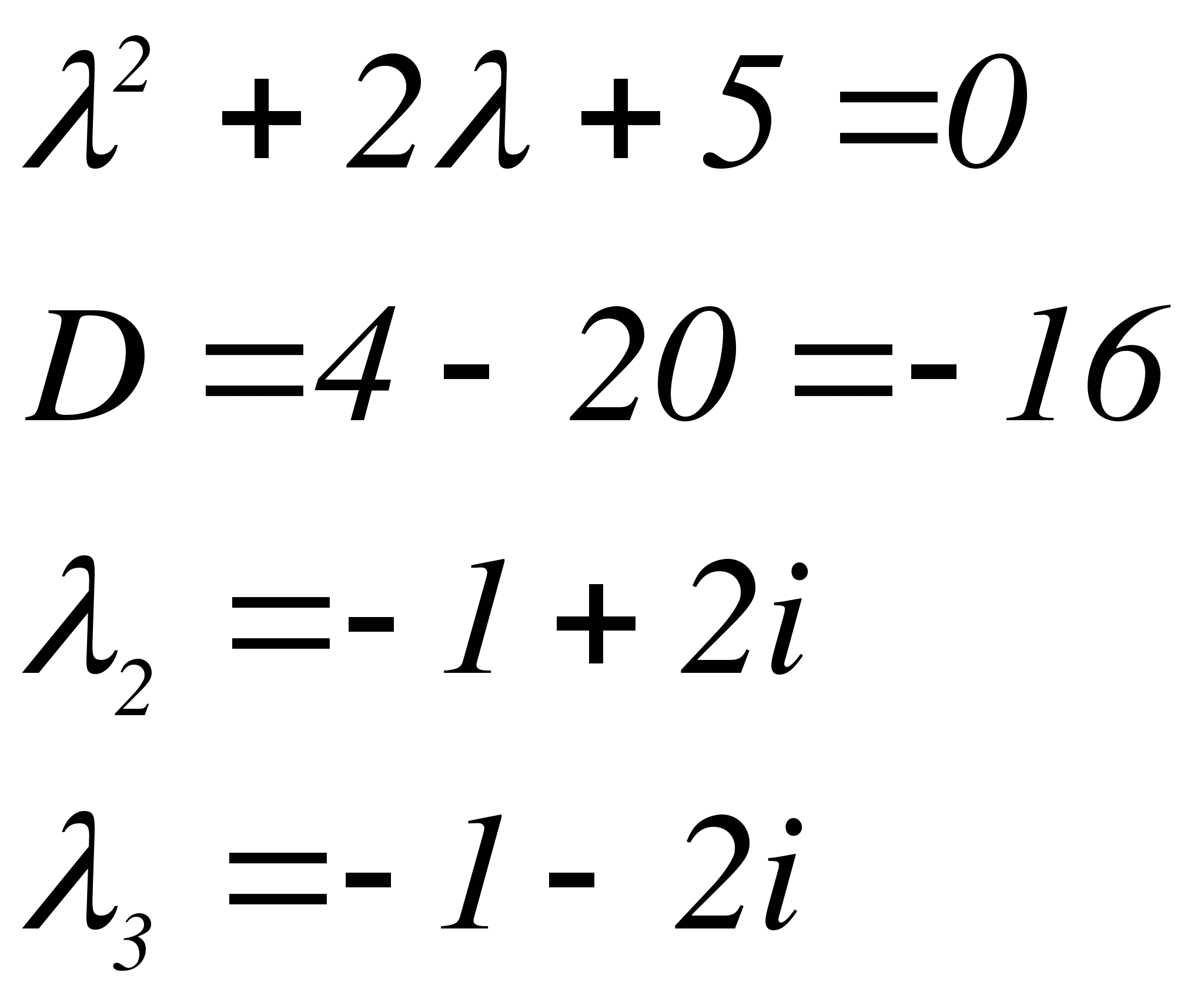
Строим 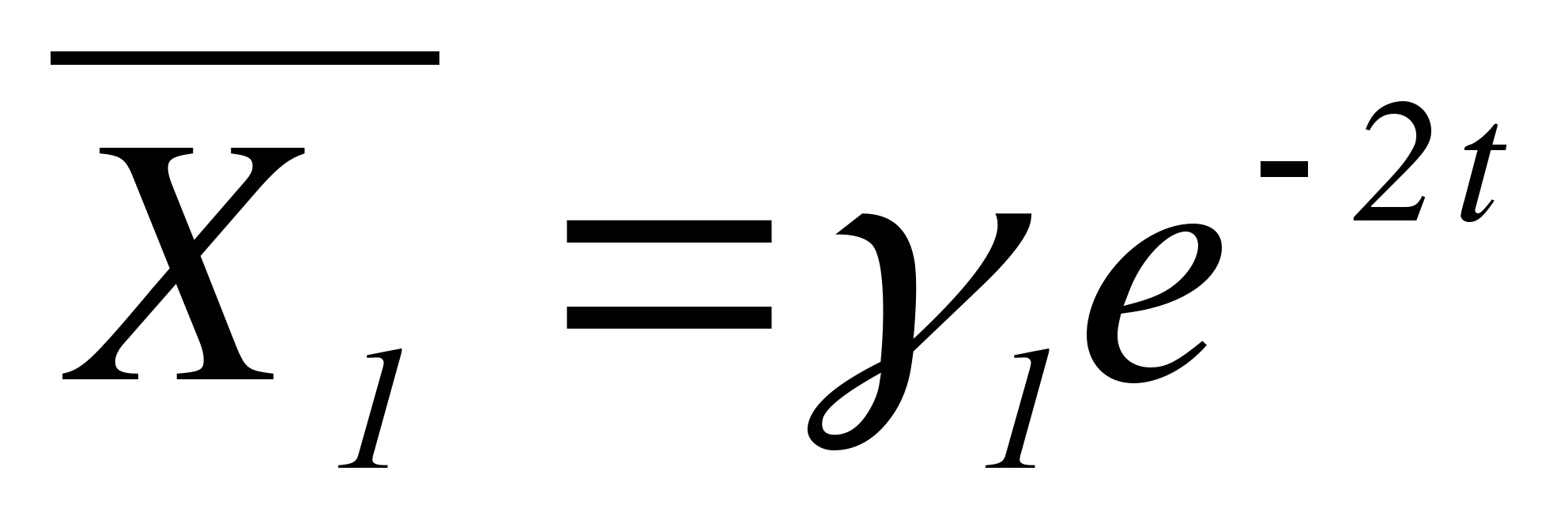 , где
, где 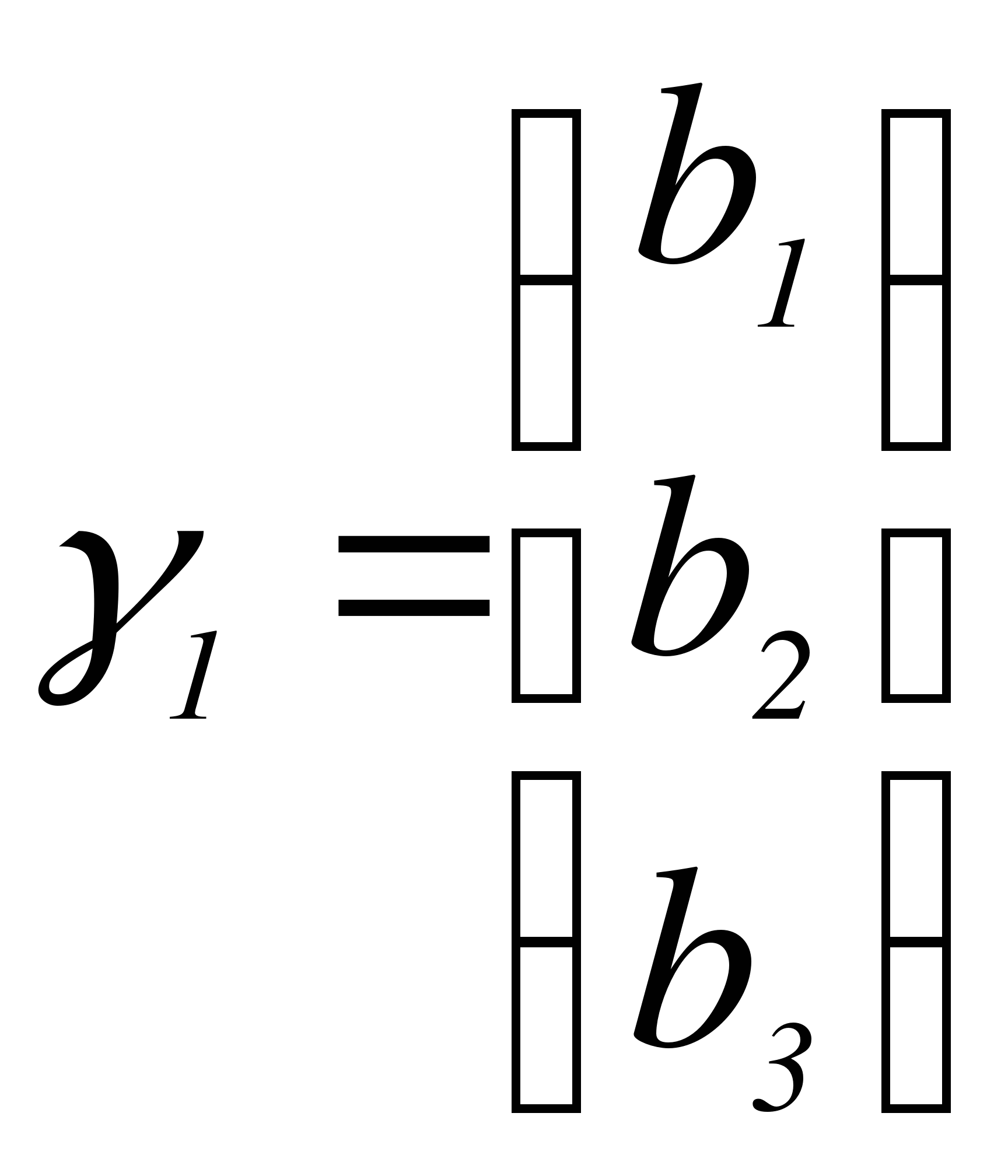 - собственный вектор матрицы А, соответствующий
- собственный вектор матрицы А, соответствующий 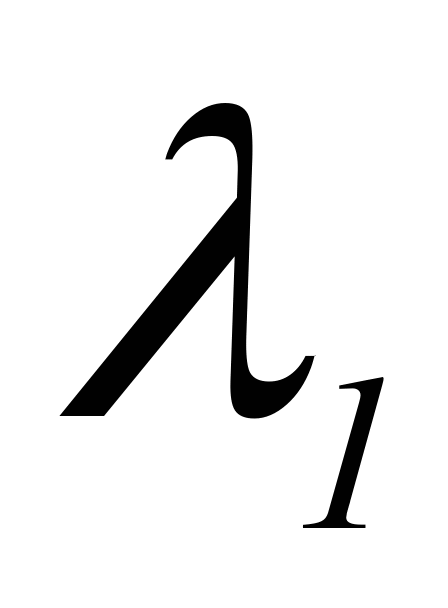 , т.е
, т.е 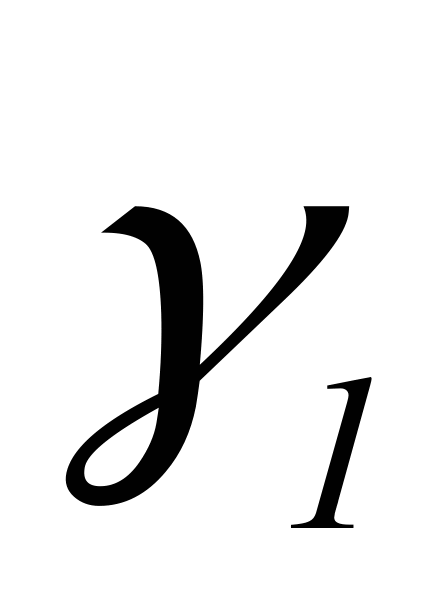 удовлетворяет системе
удовлетворяет системе 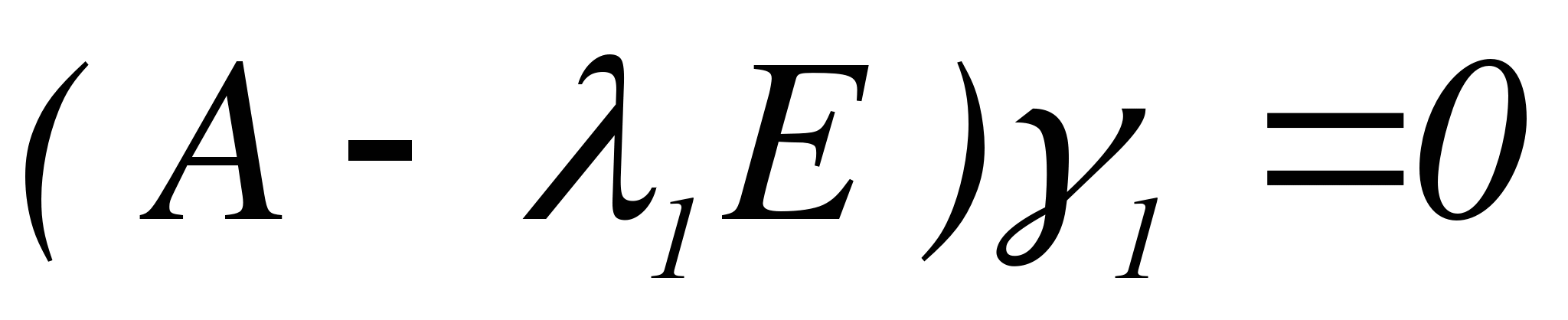 .
.
Тогда
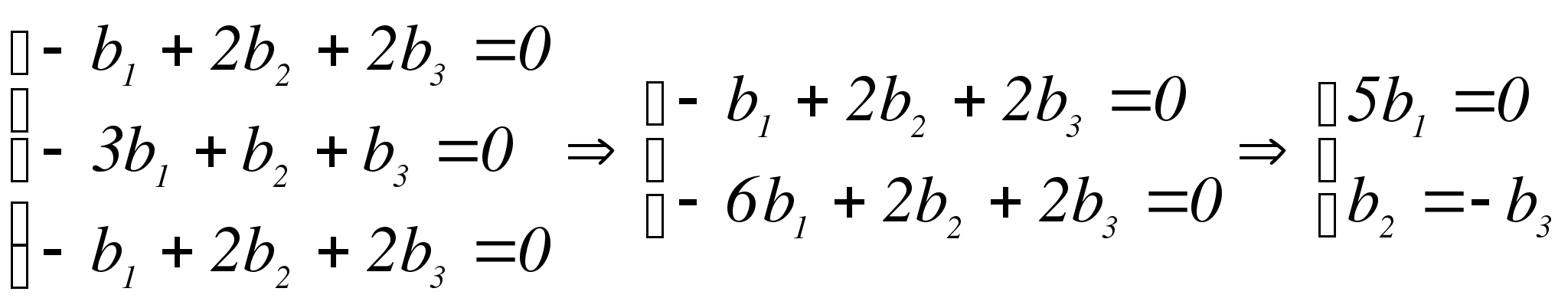
За 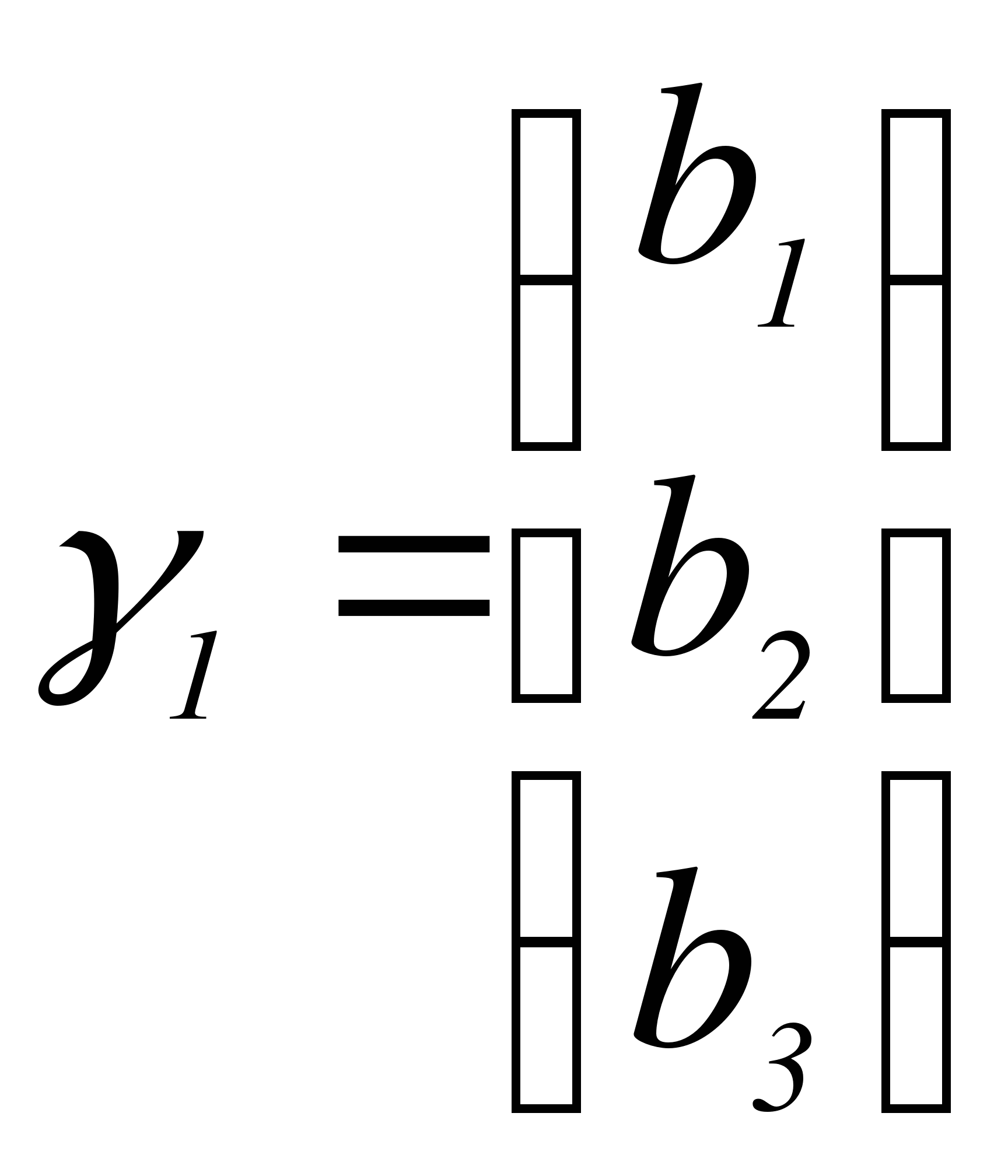 возьмем
возьмем 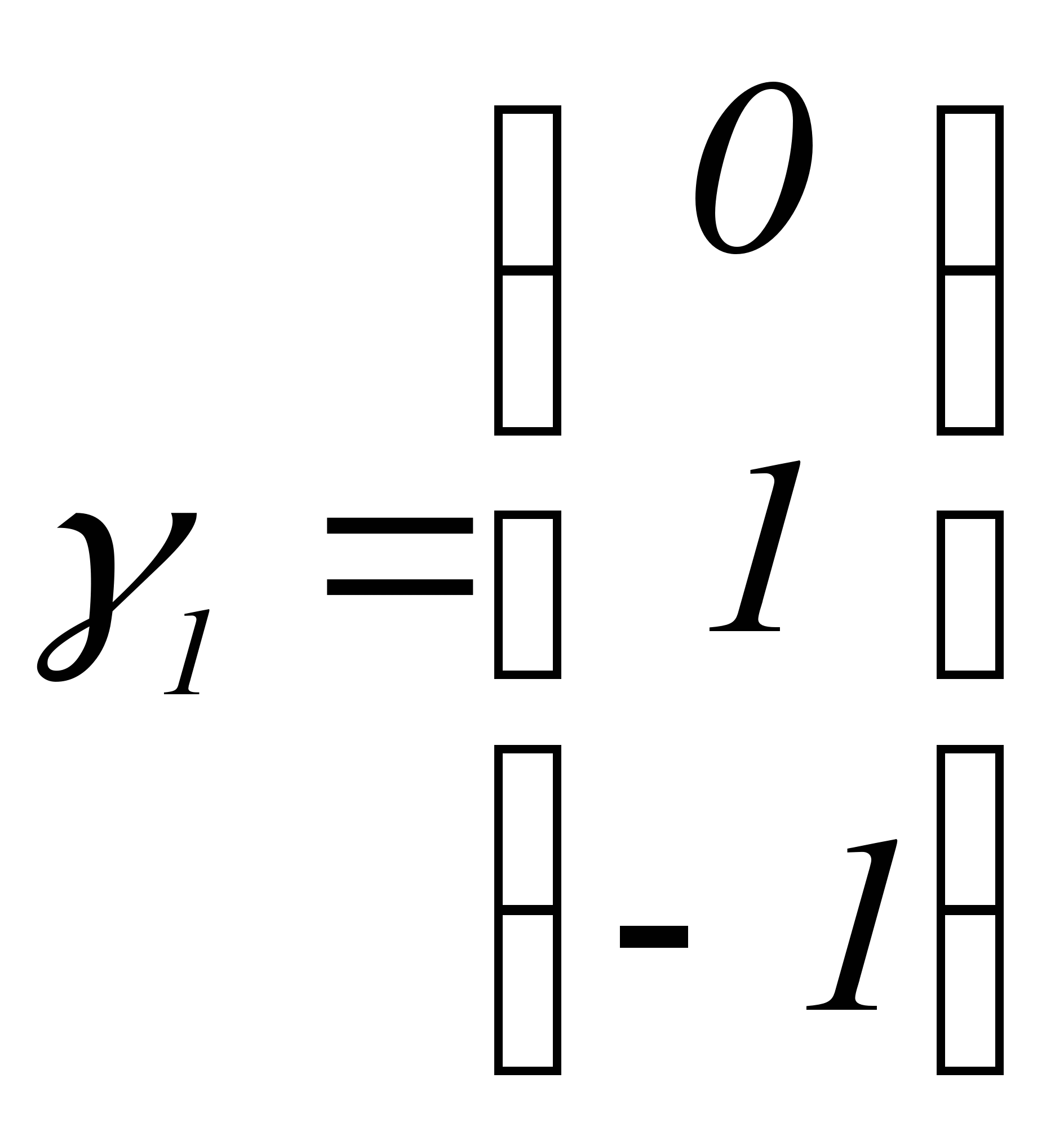 .
. 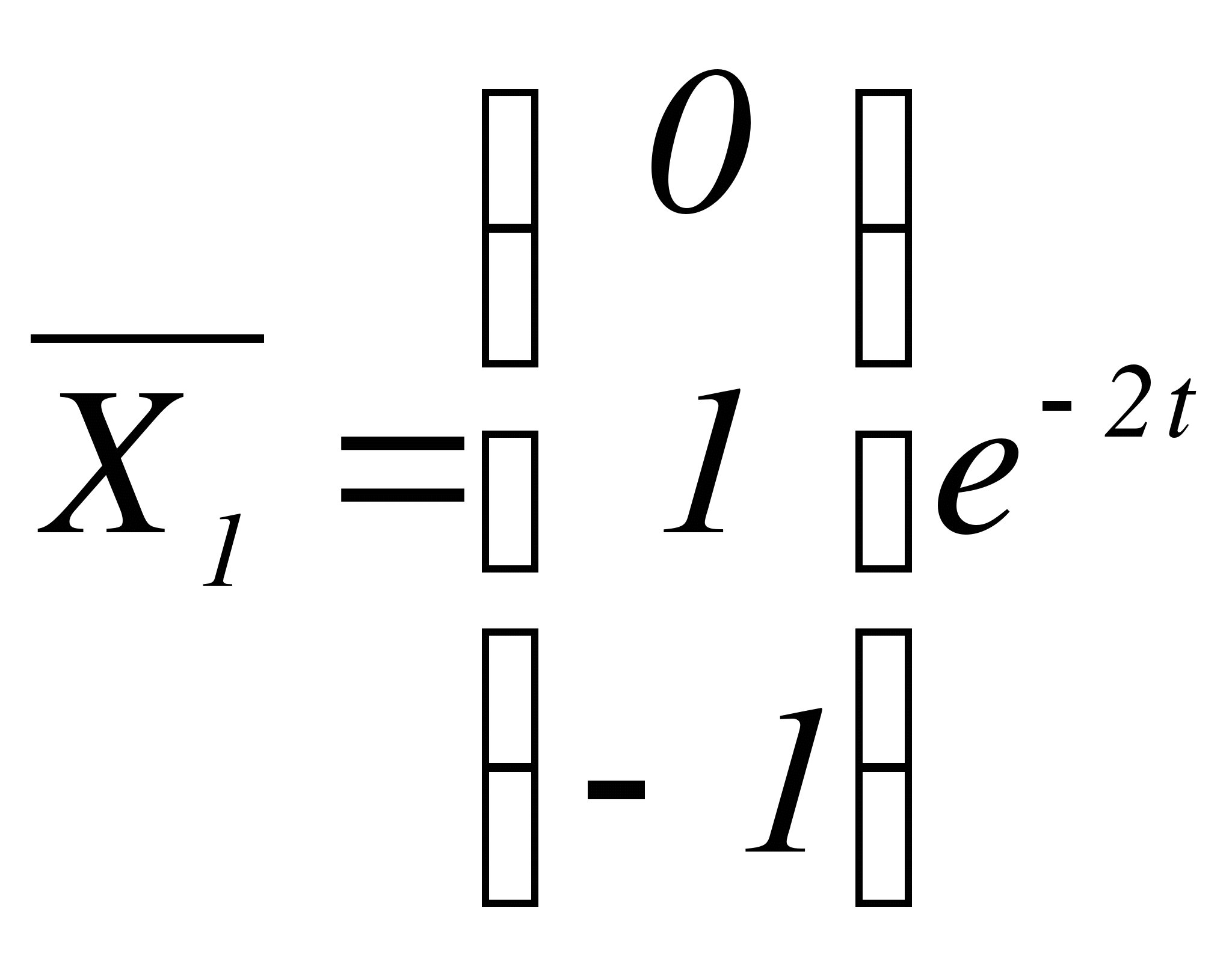
Строим 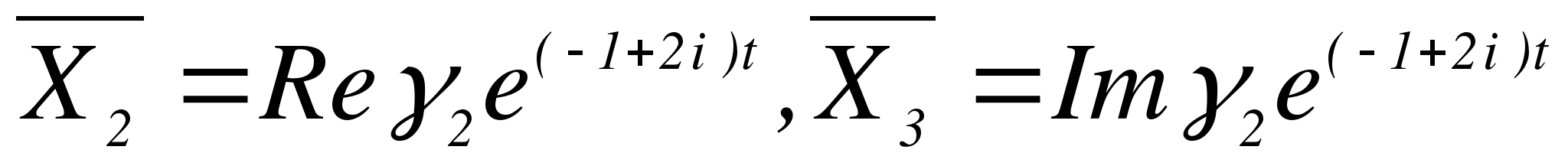 , где
, где 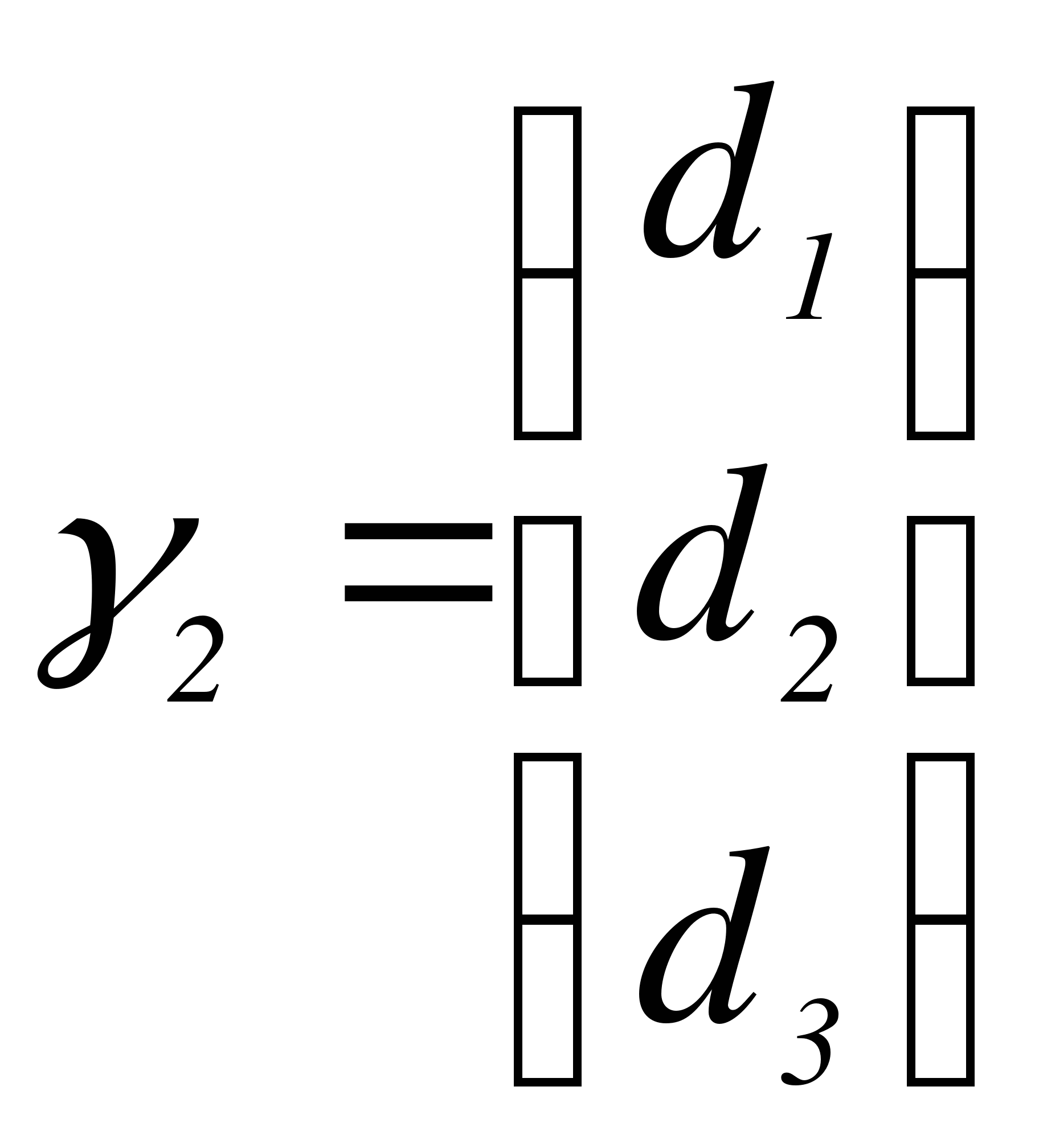 - собственный вектор матрицы А, соответствующий
- собственный вектор матрицы А, соответствующий 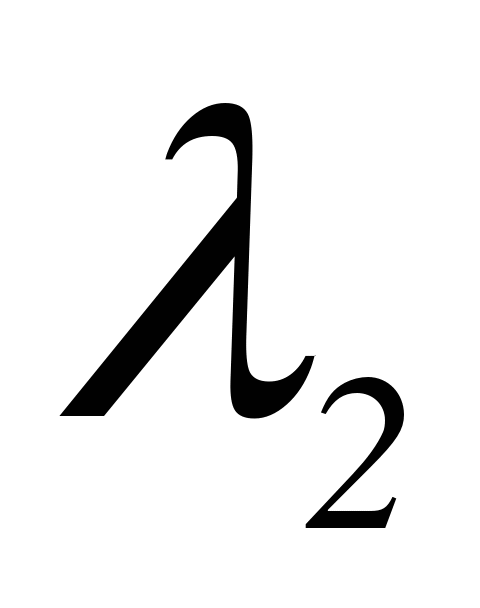 , т.е
, т.е 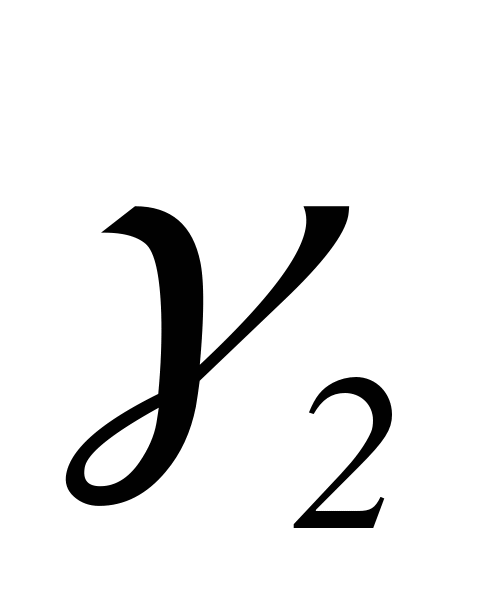 удовлетворяет системе
удовлетворяет системе 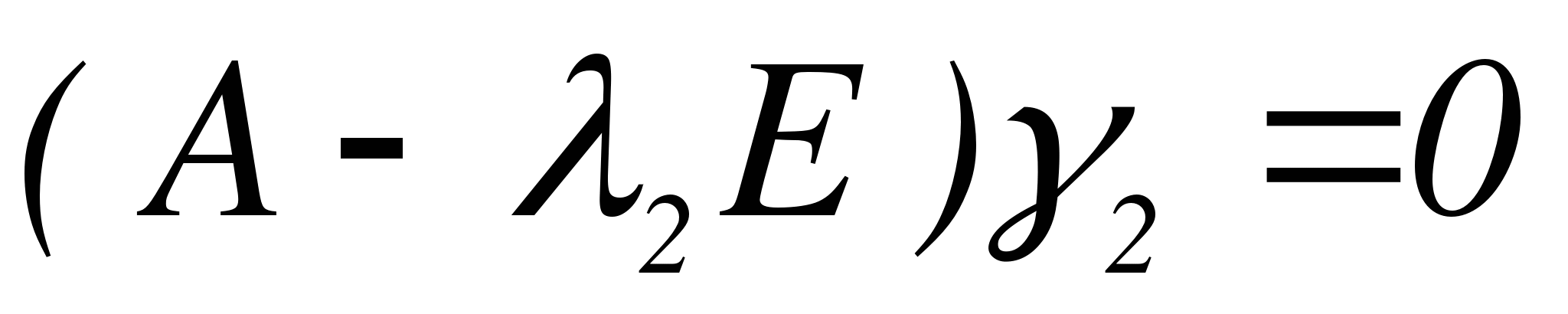 .
.
Тогда
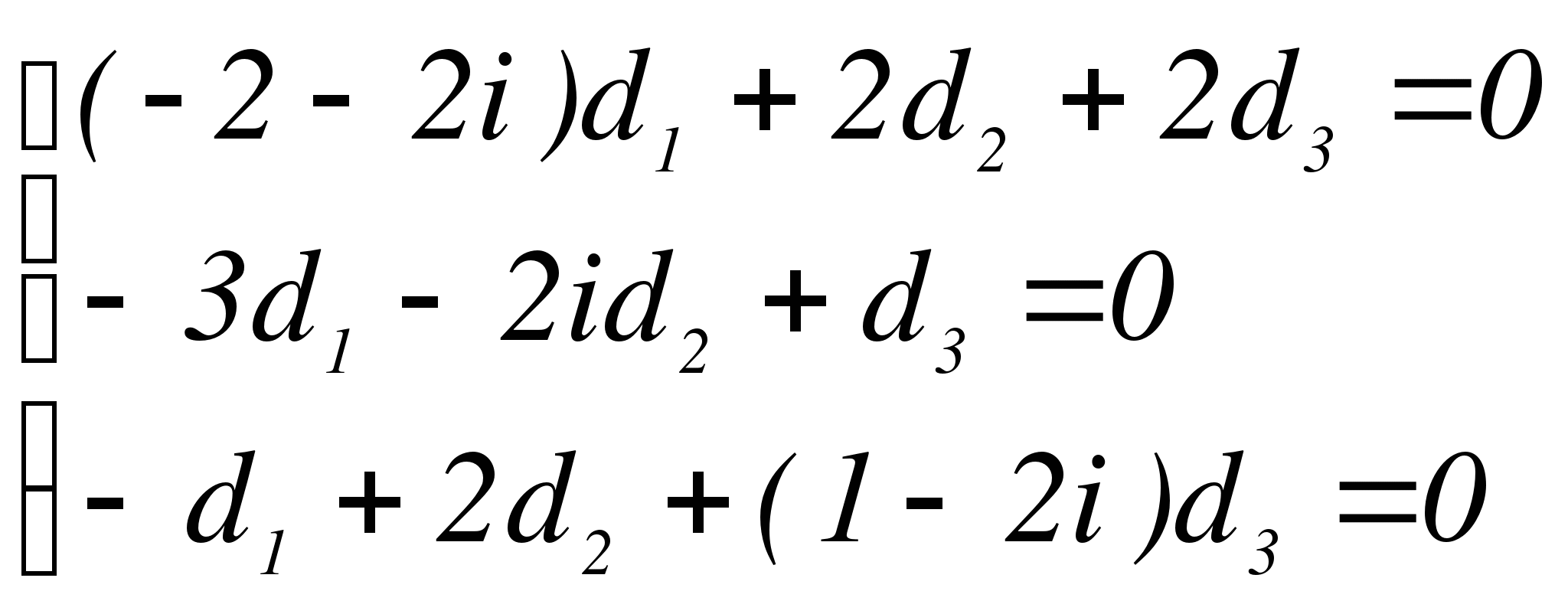
Первое уравнение сократим на 2. Затем ко второму уравнению прибавим первое, умноженное на 2i, а от третьего уравнения отнимем первое, умноженное на 2.
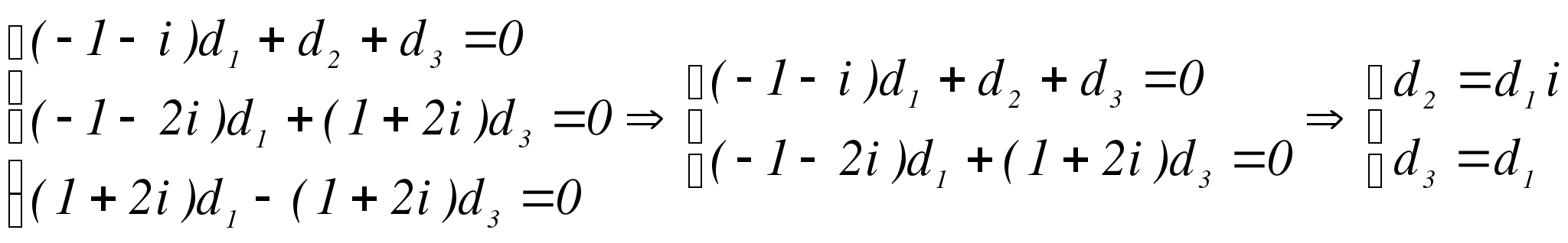
За 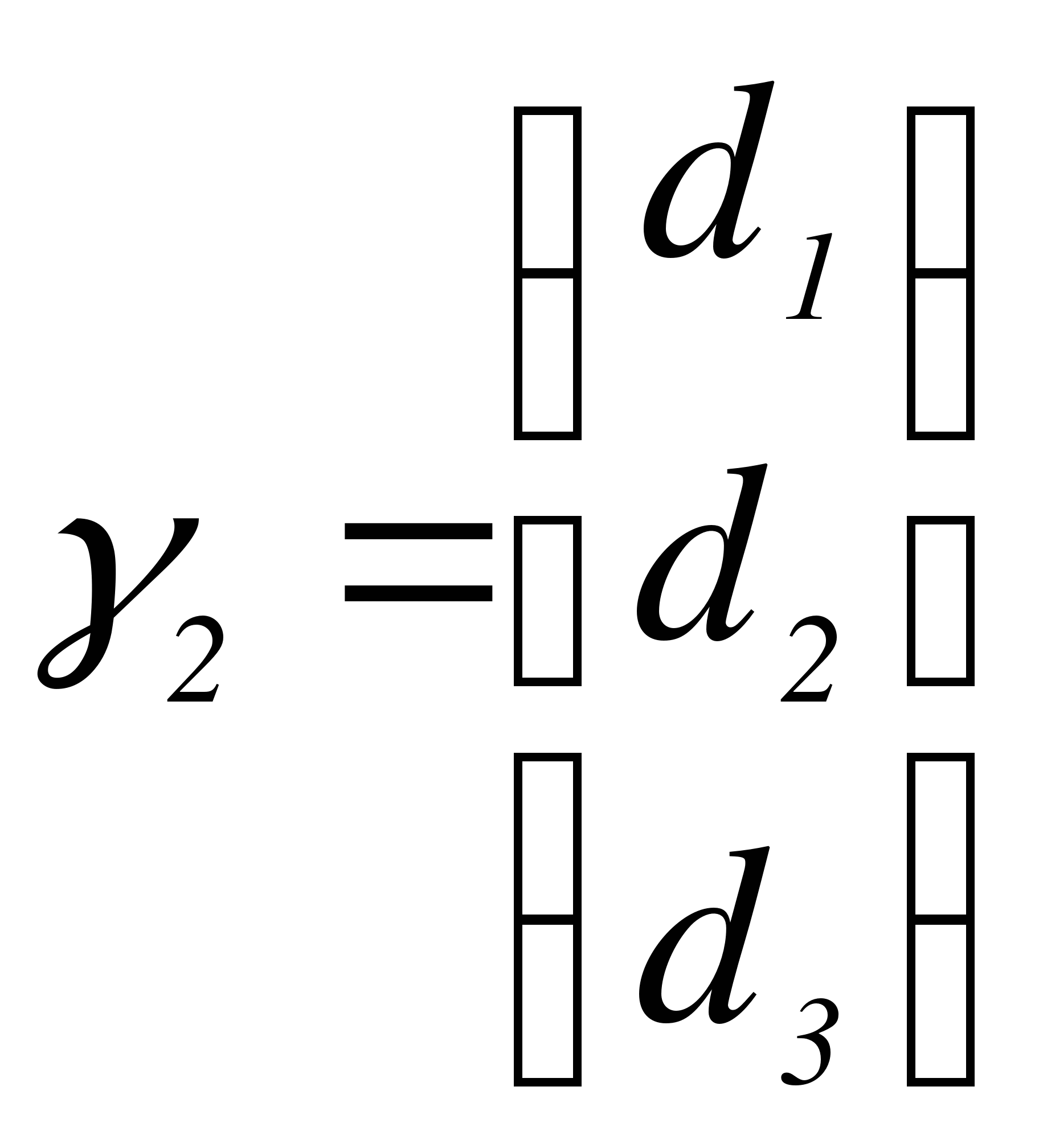 возьмем
возьмем 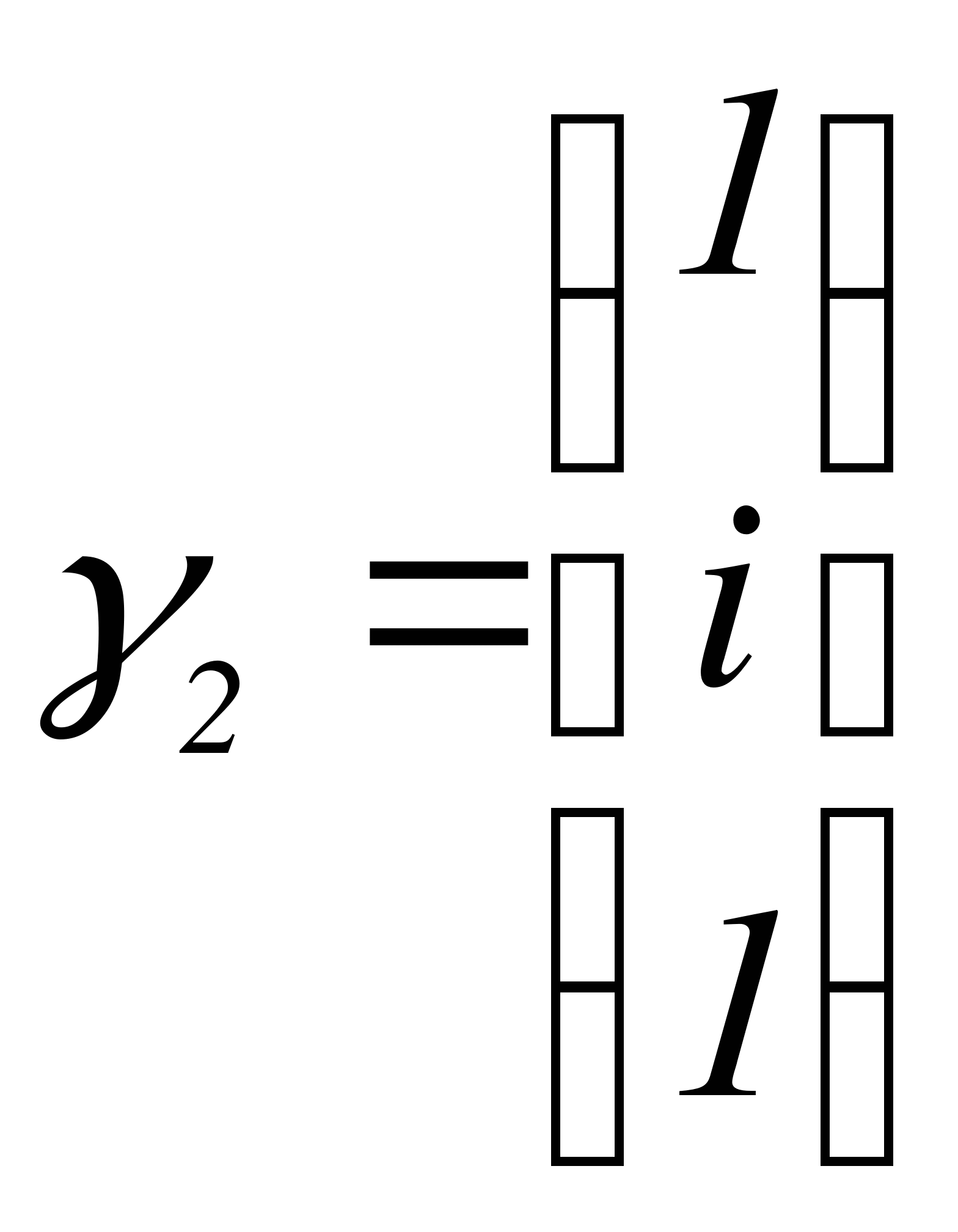
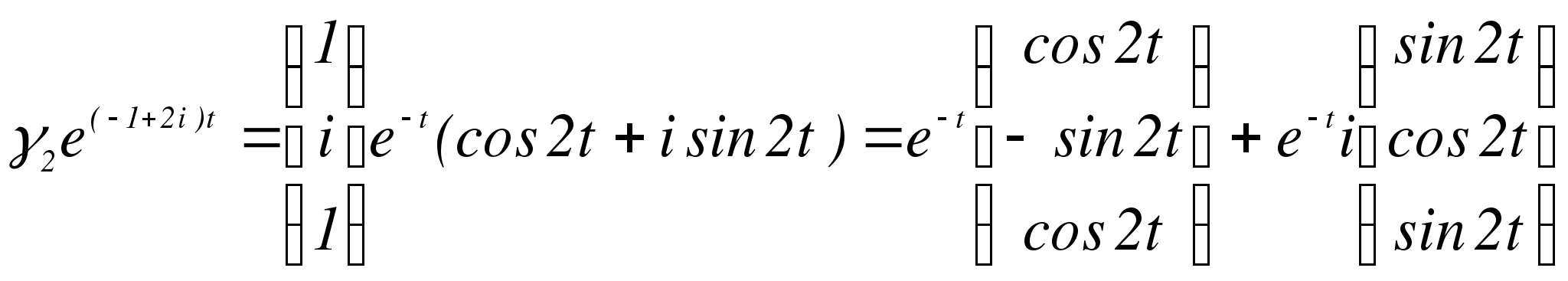
Следовательно, 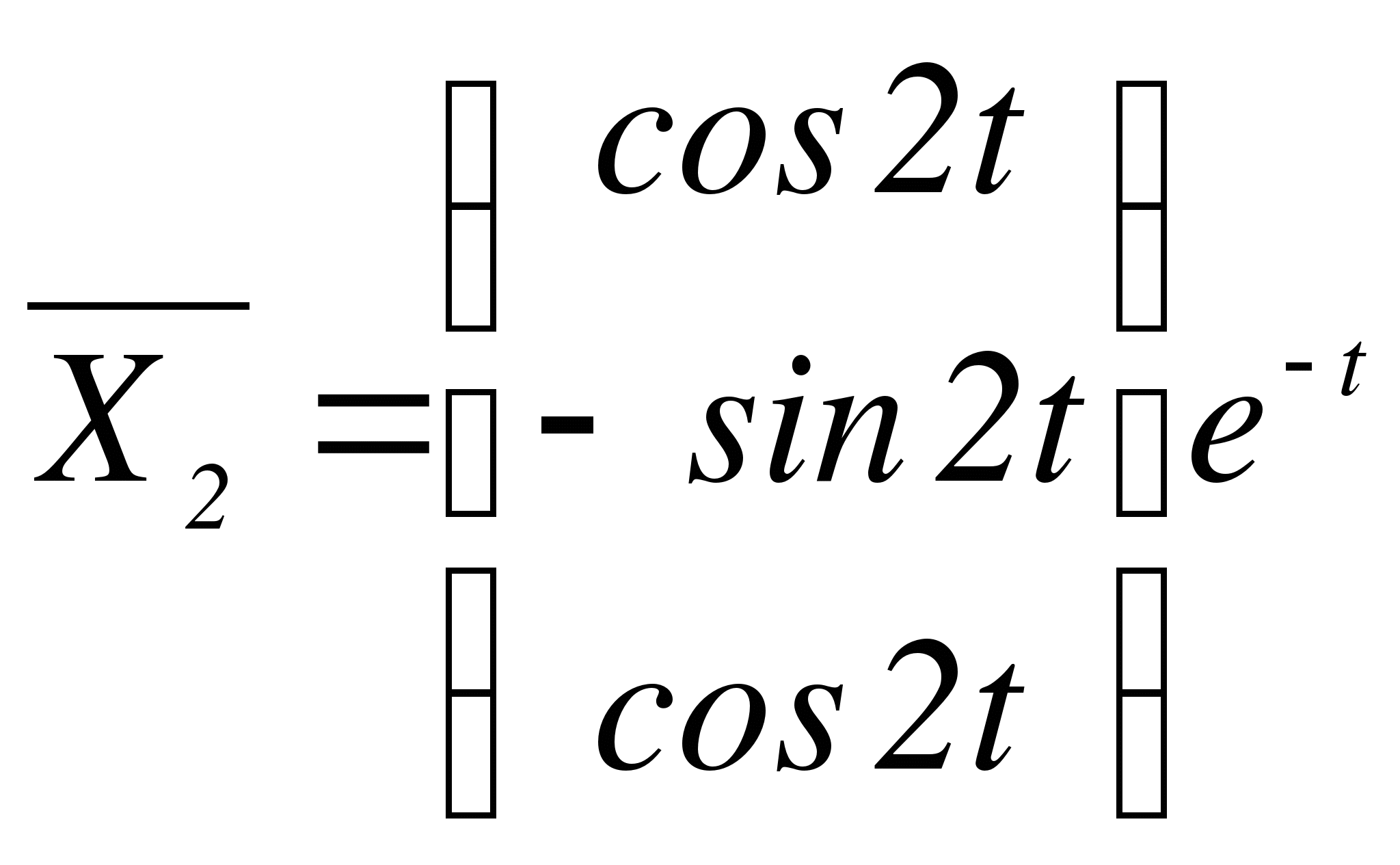 ,
, 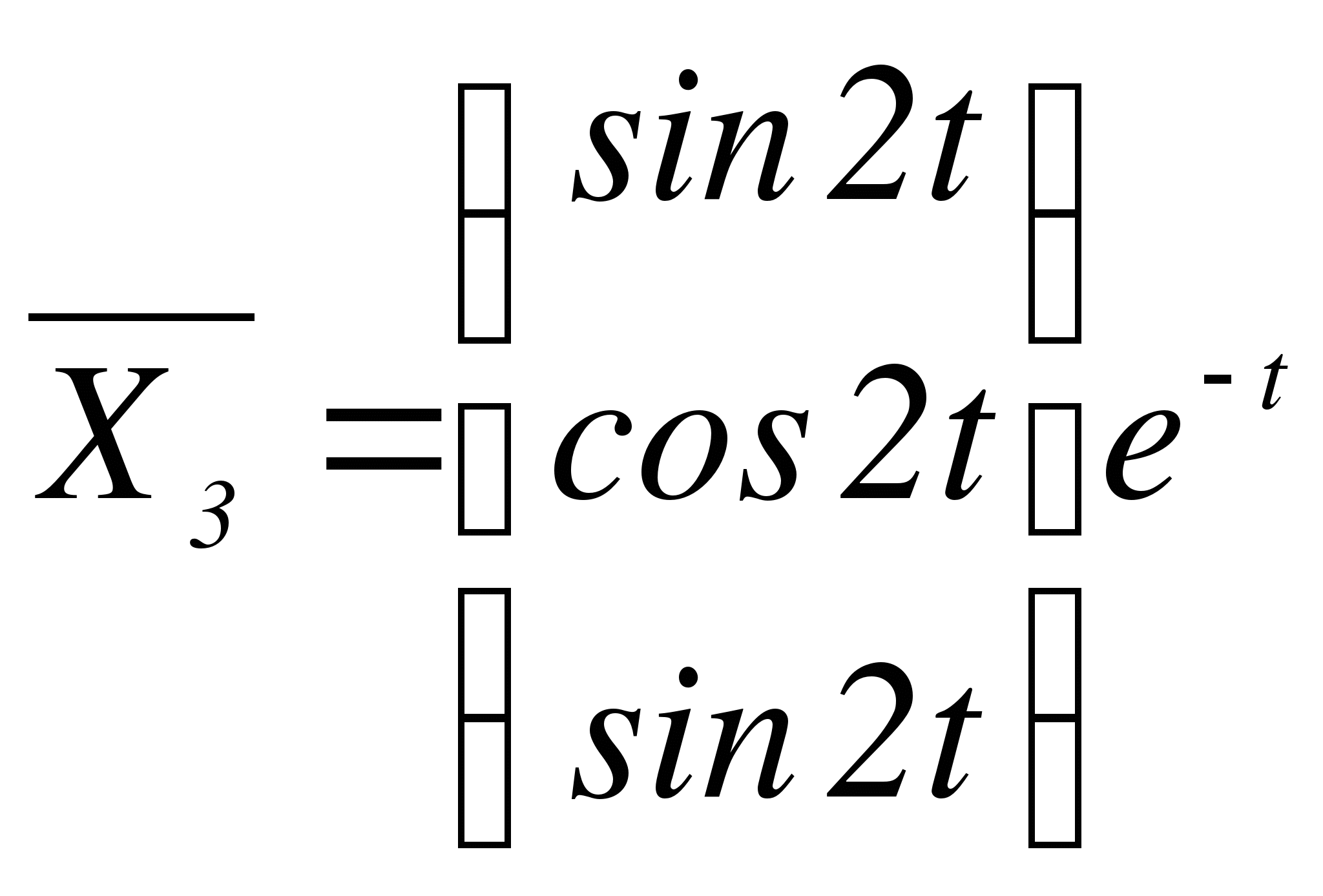
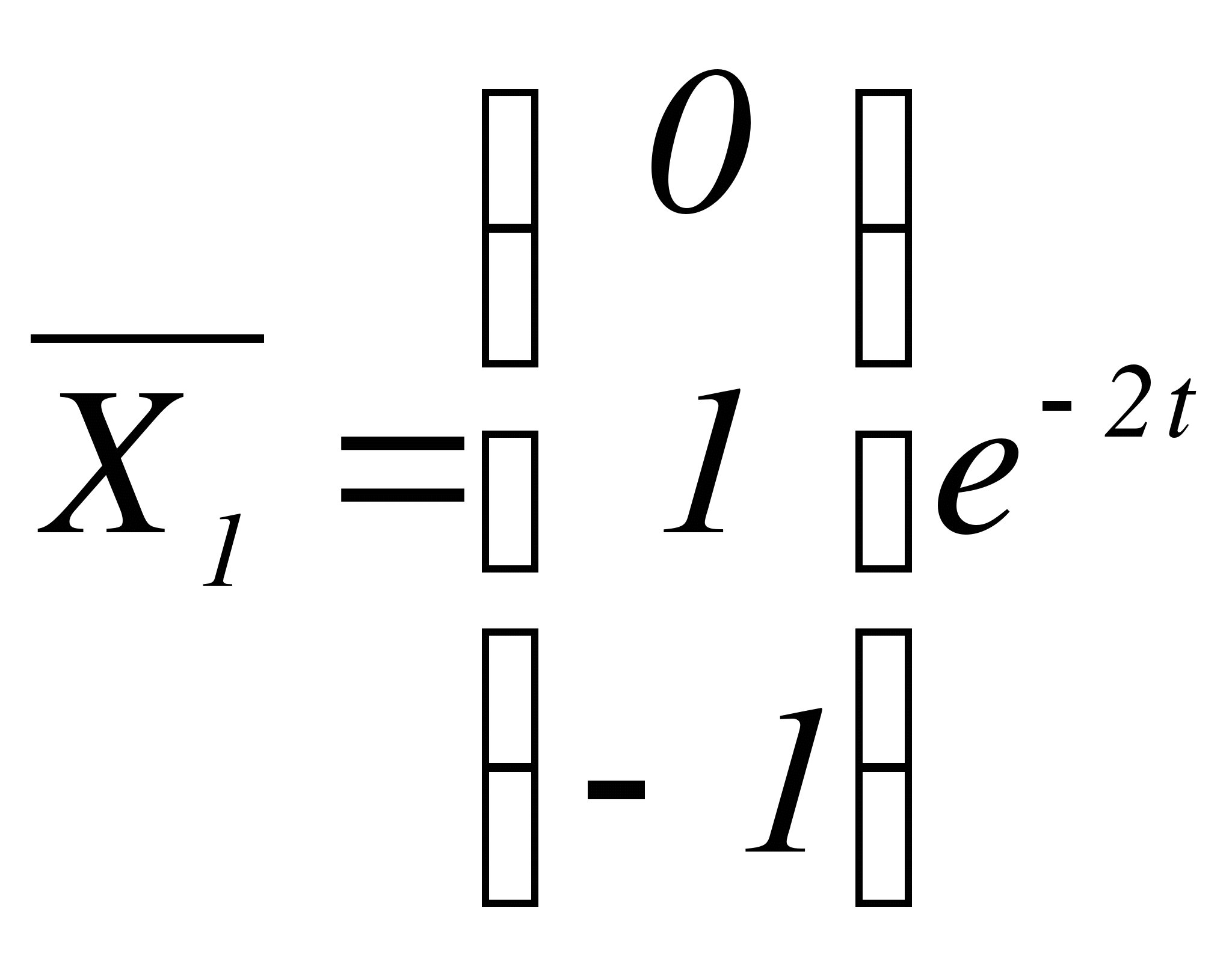 ,
, 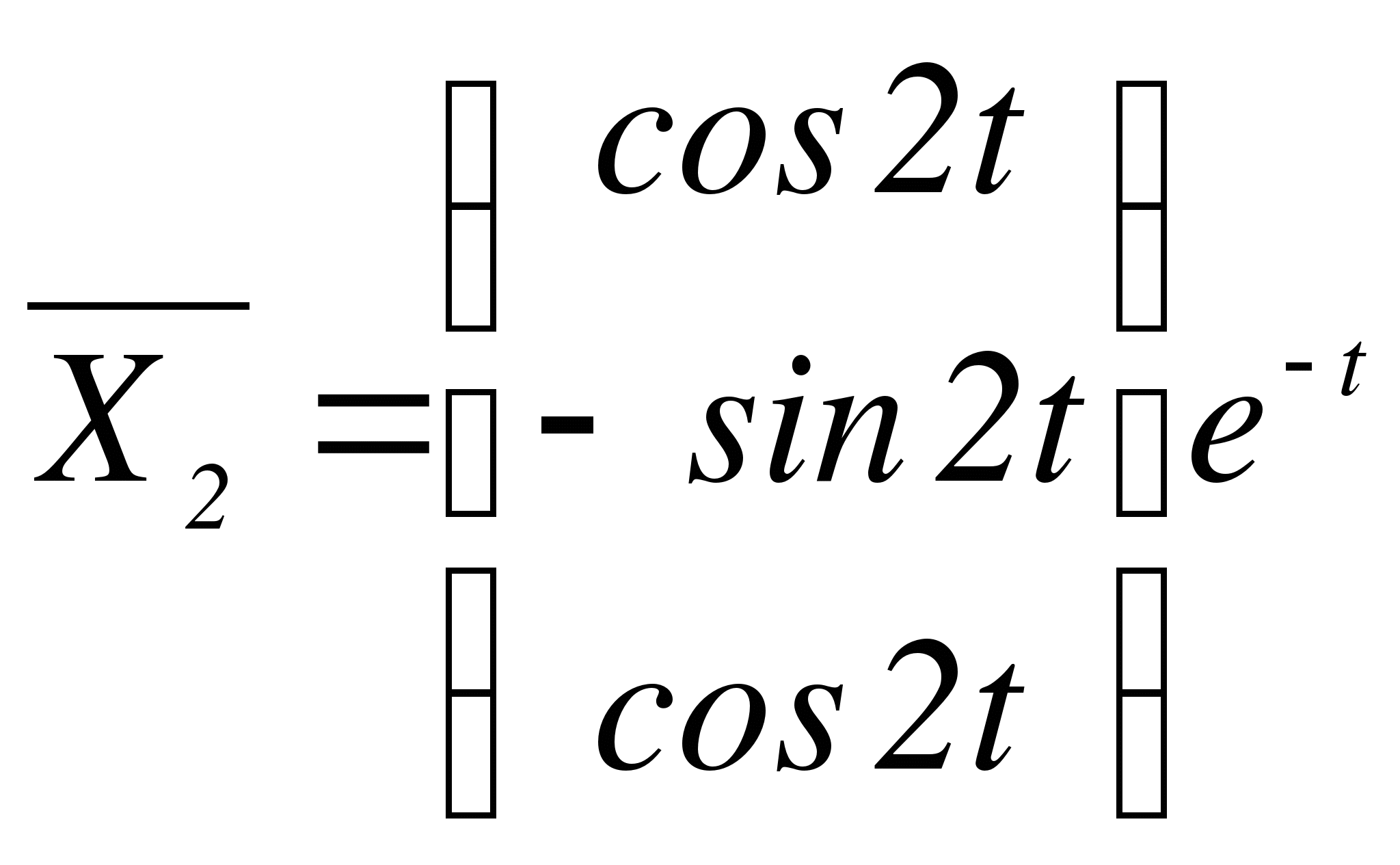 ,
, 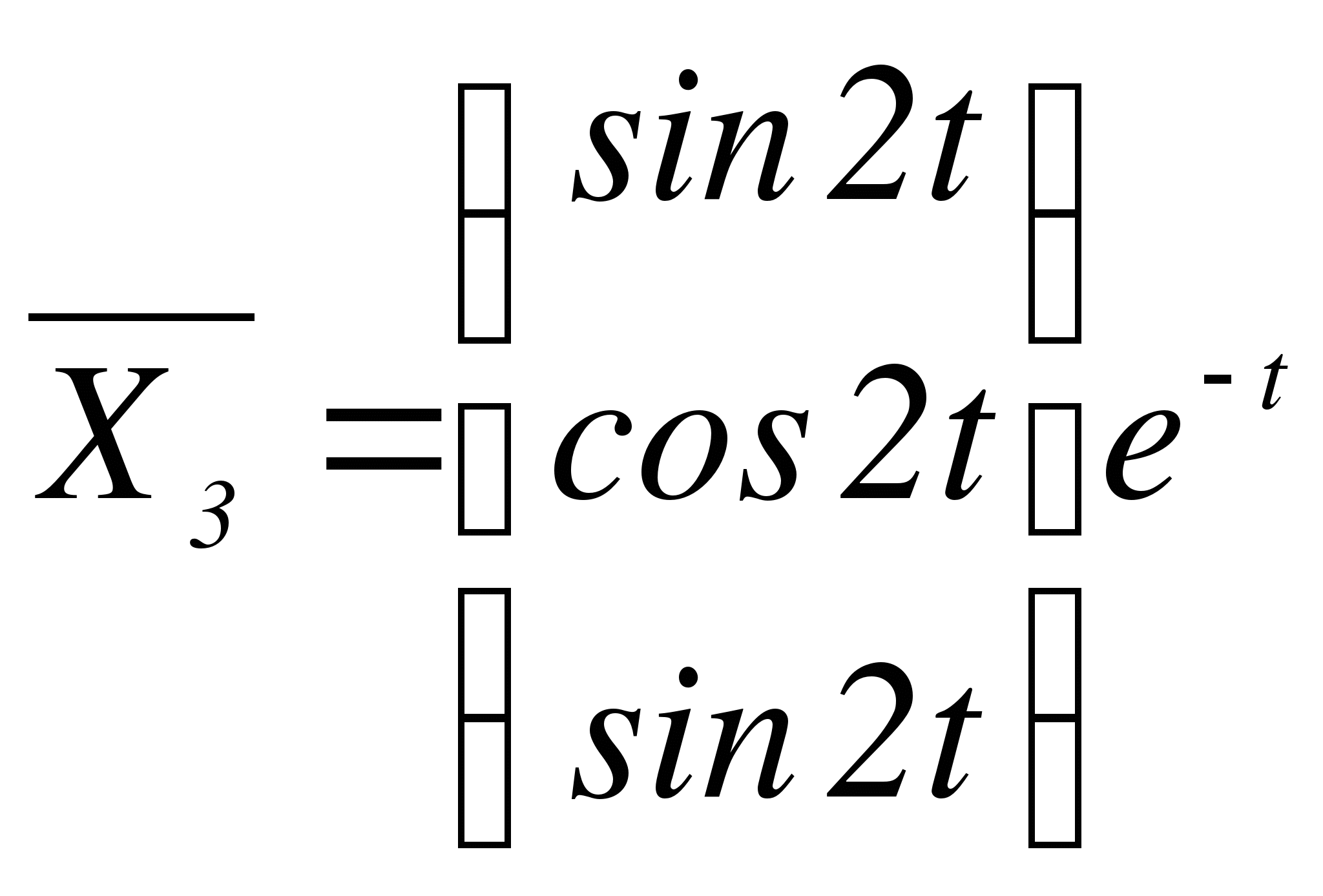 - фундаментальная система решений. Запишем общее решение исходной системы:
- фундаментальная система решений. Запишем общее решение исходной системы:
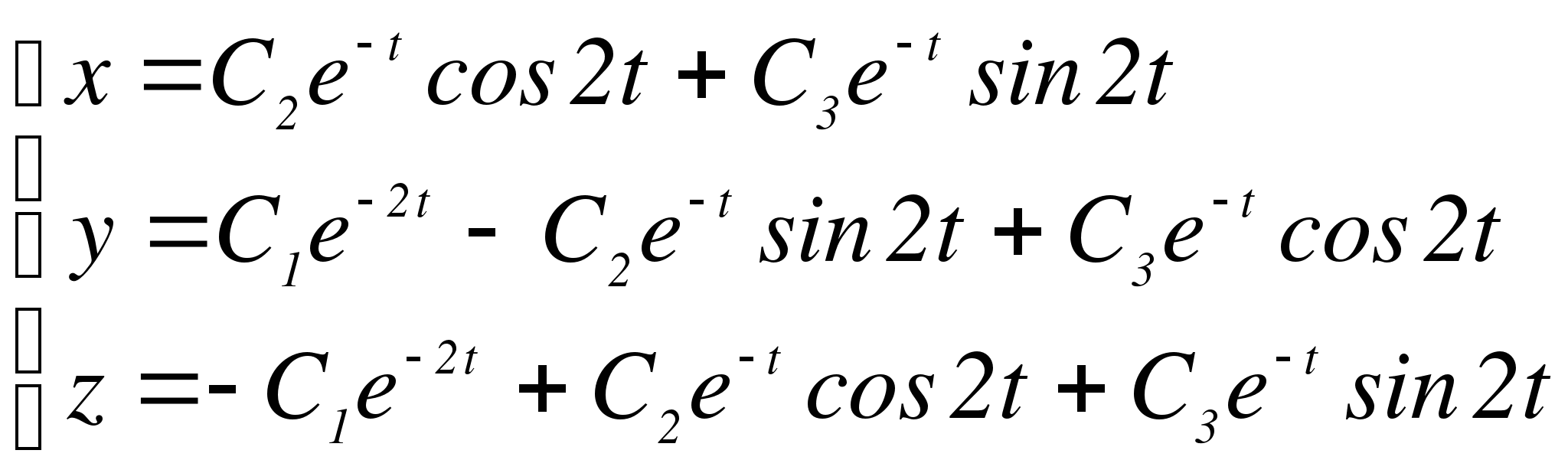
Ответ. 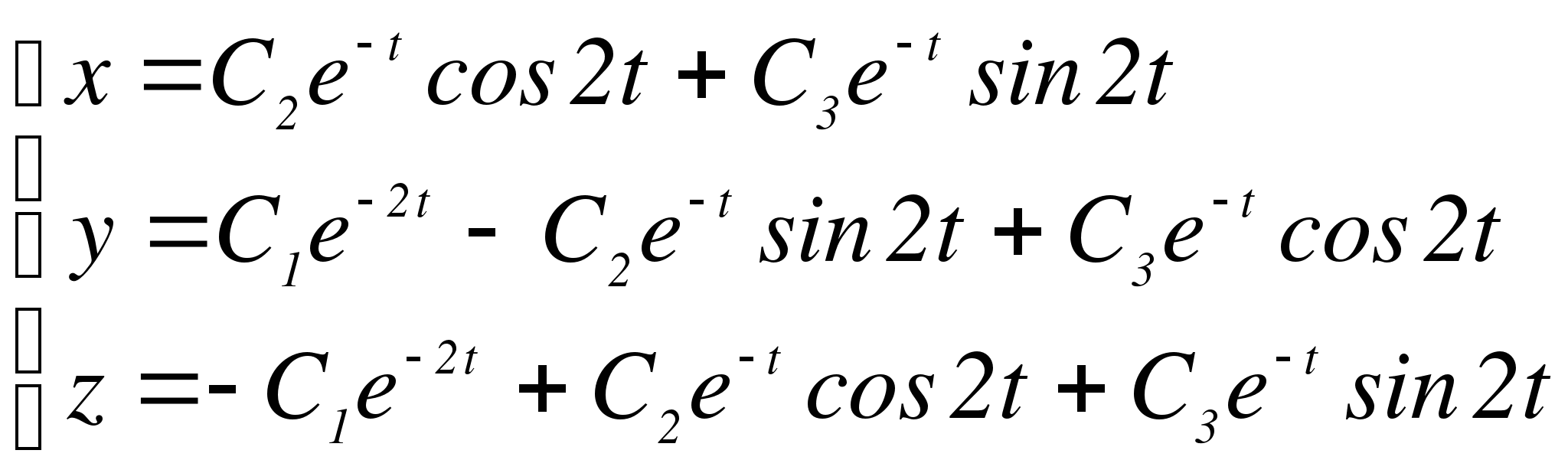 - общее решение линейной однородной системы
- общее решение линейной однородной системы
Задача 2. Найти общее решение линейной неоднородной системы методом неопределенных коэффициентов
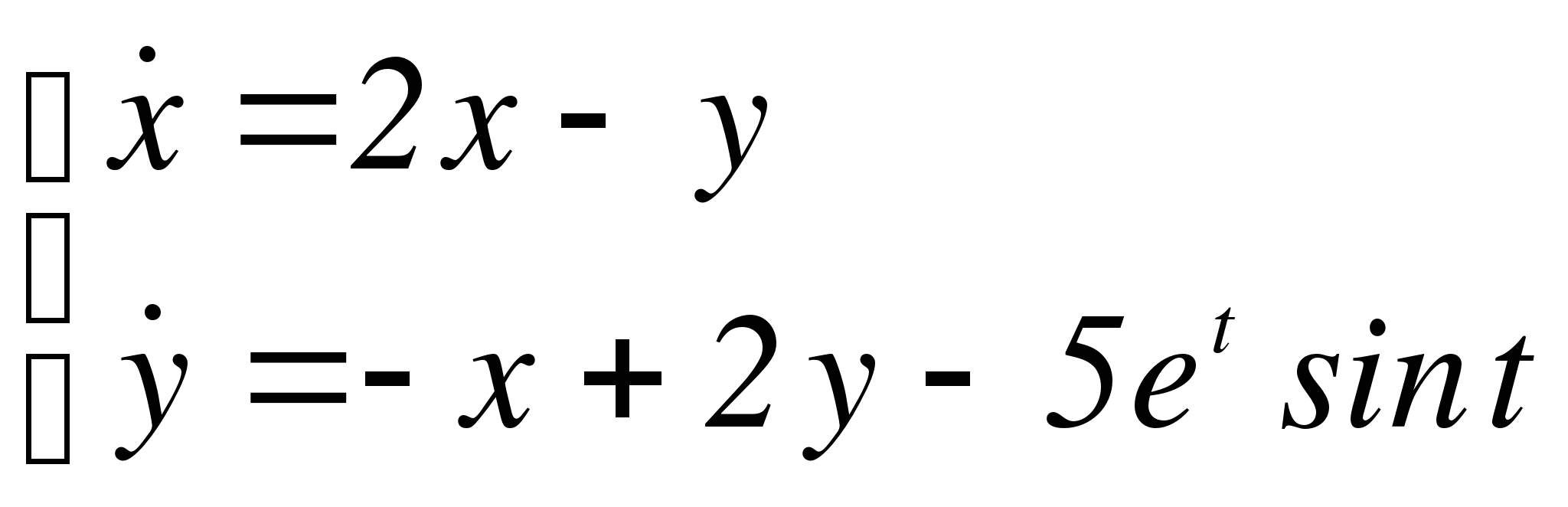
Решение.
Составляем характеристическое уравнение заданной системы:
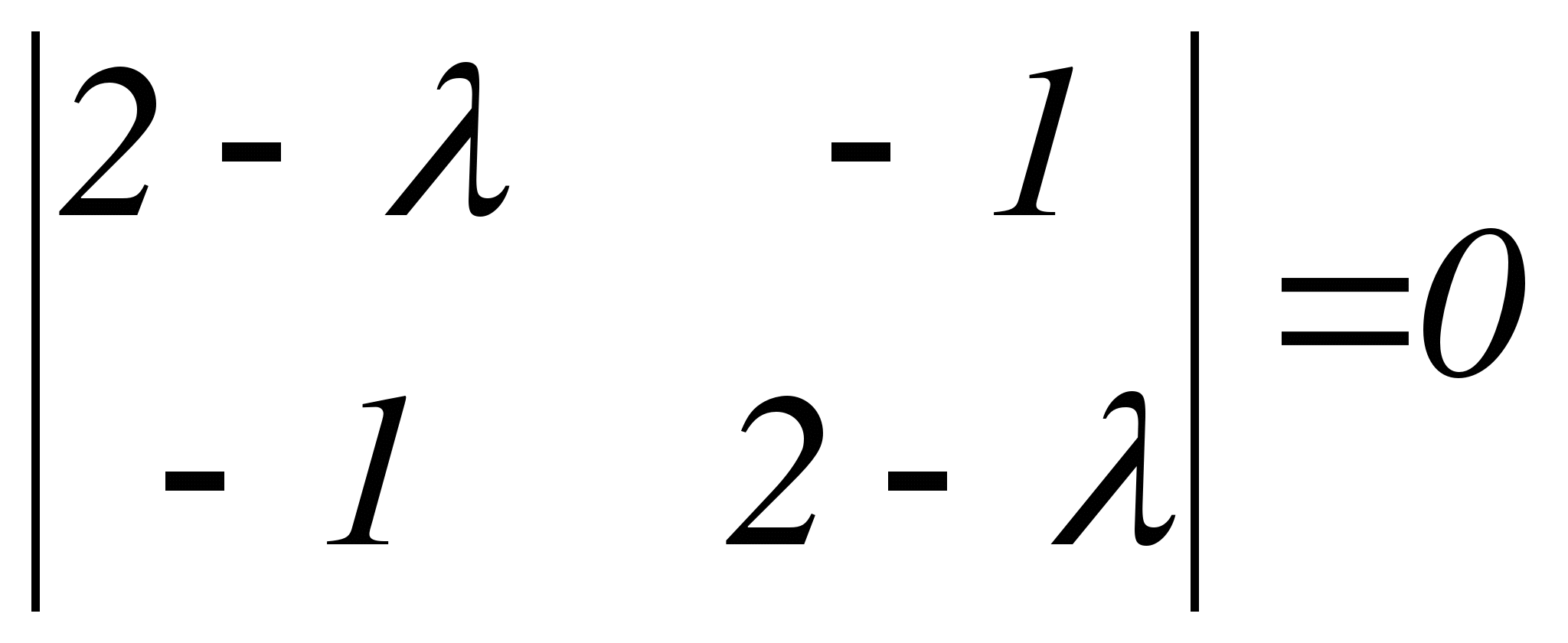
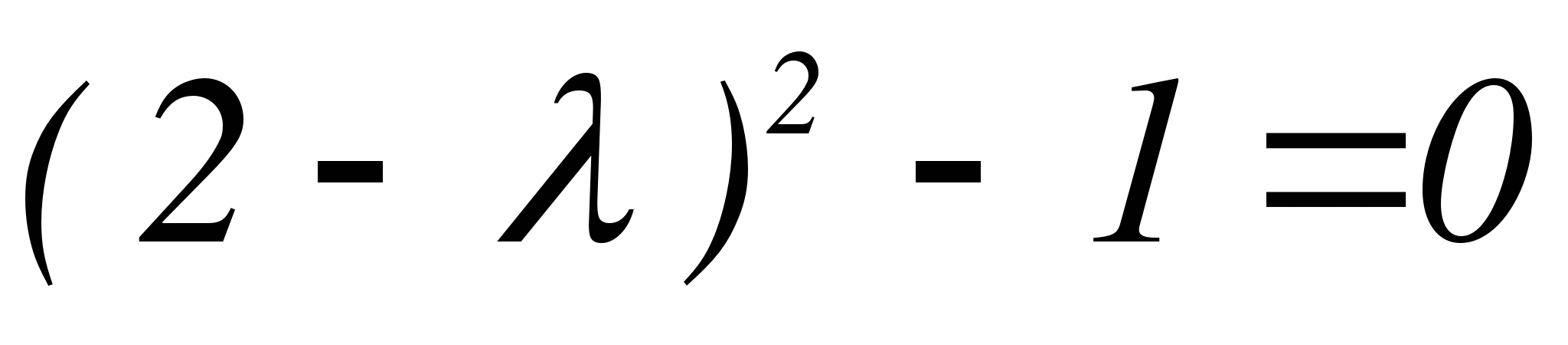
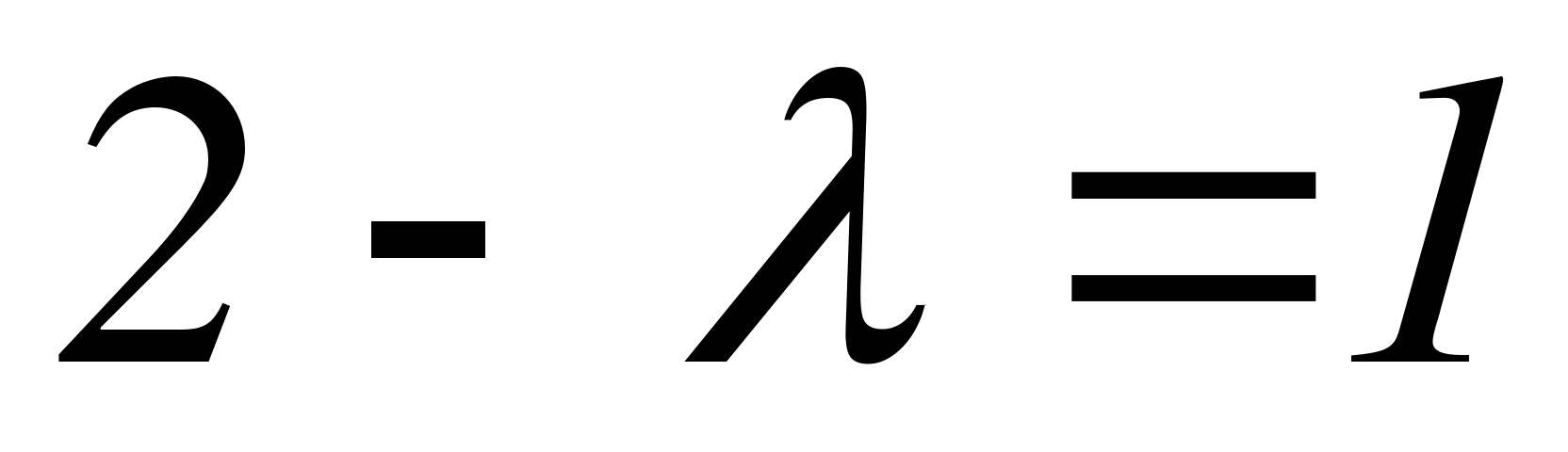 или
или 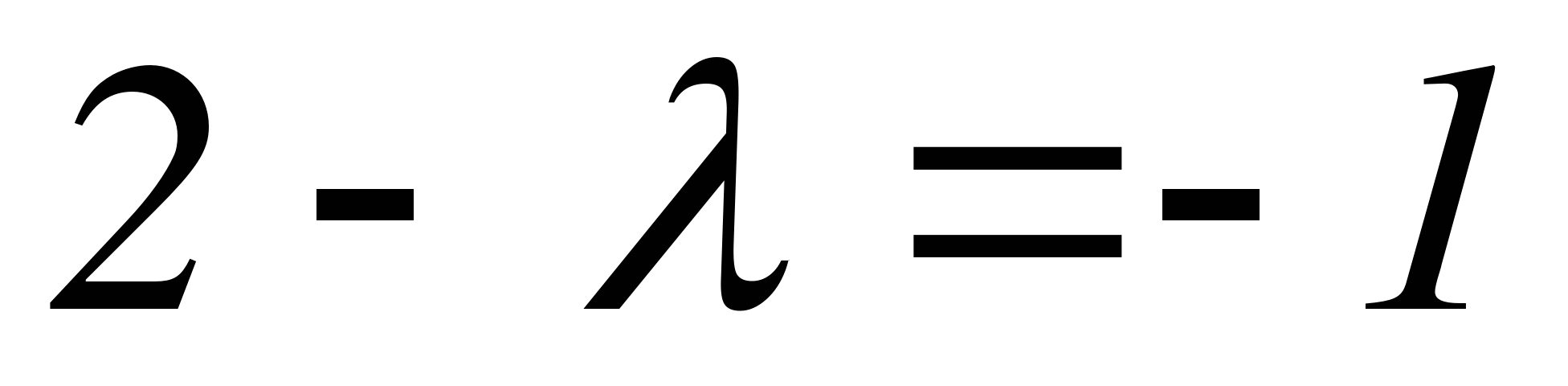
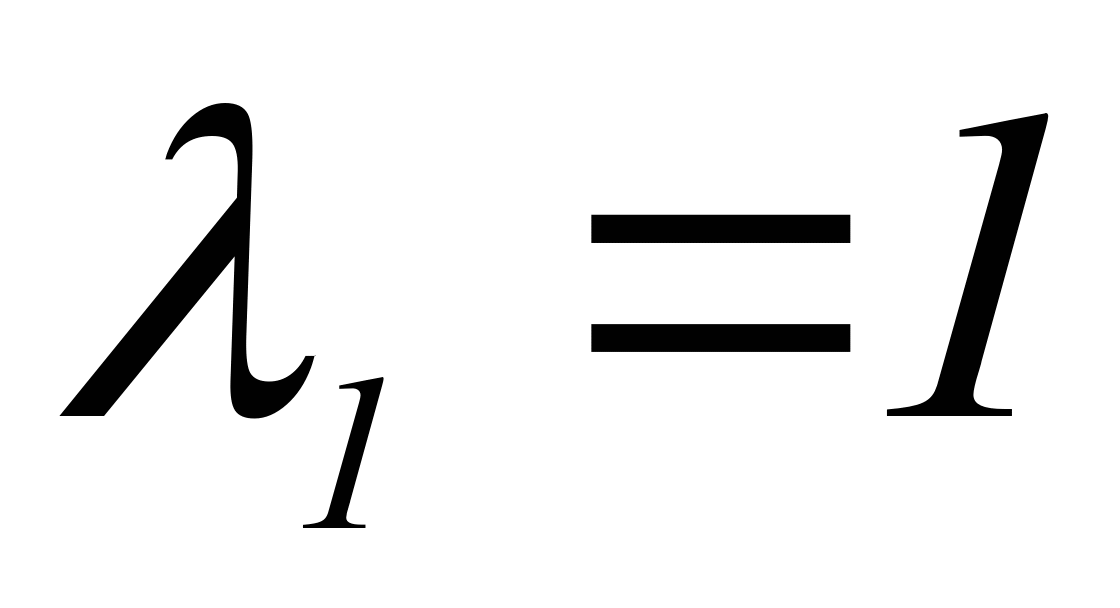 ,
, 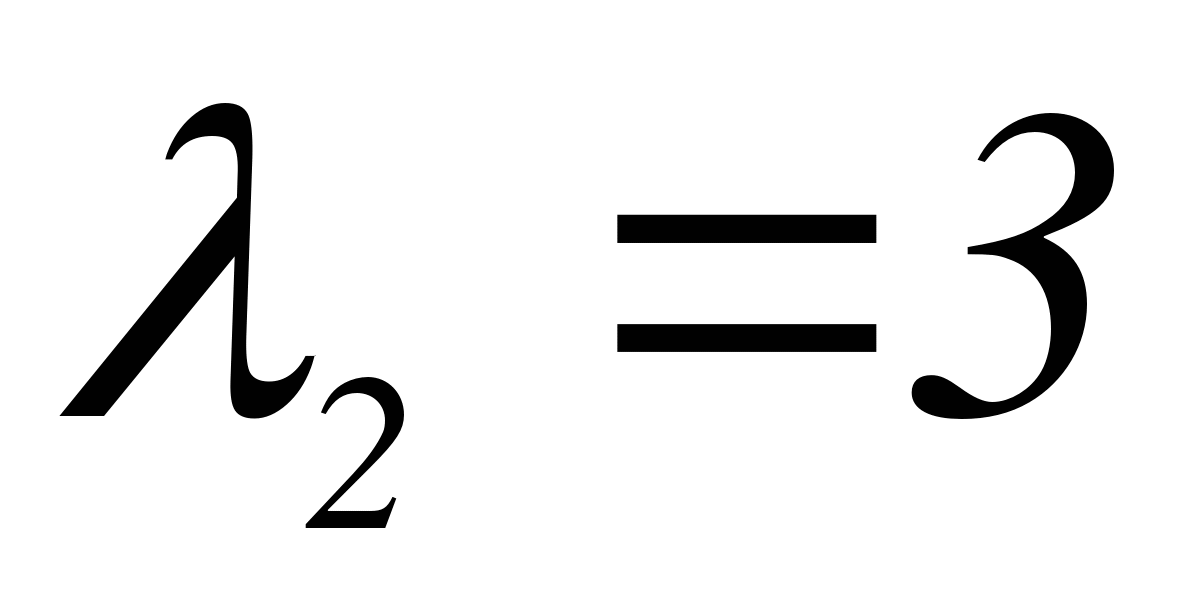
Строим 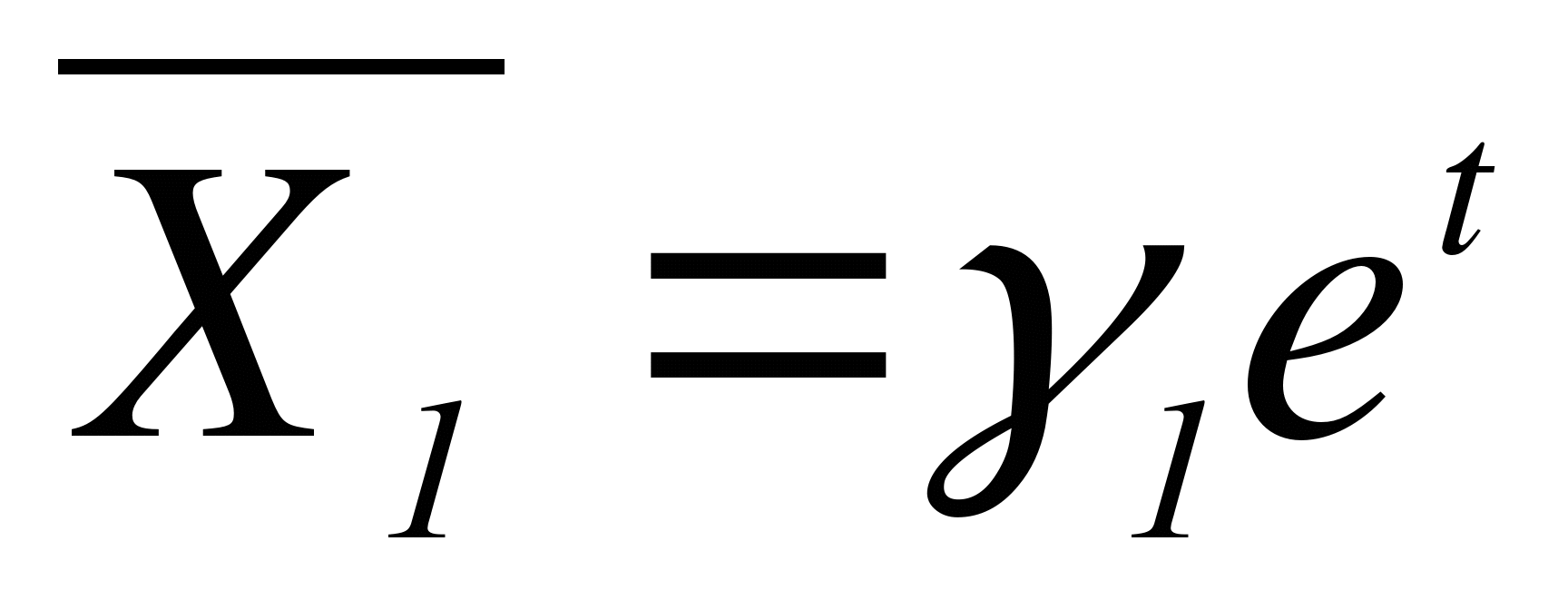 , где
, где 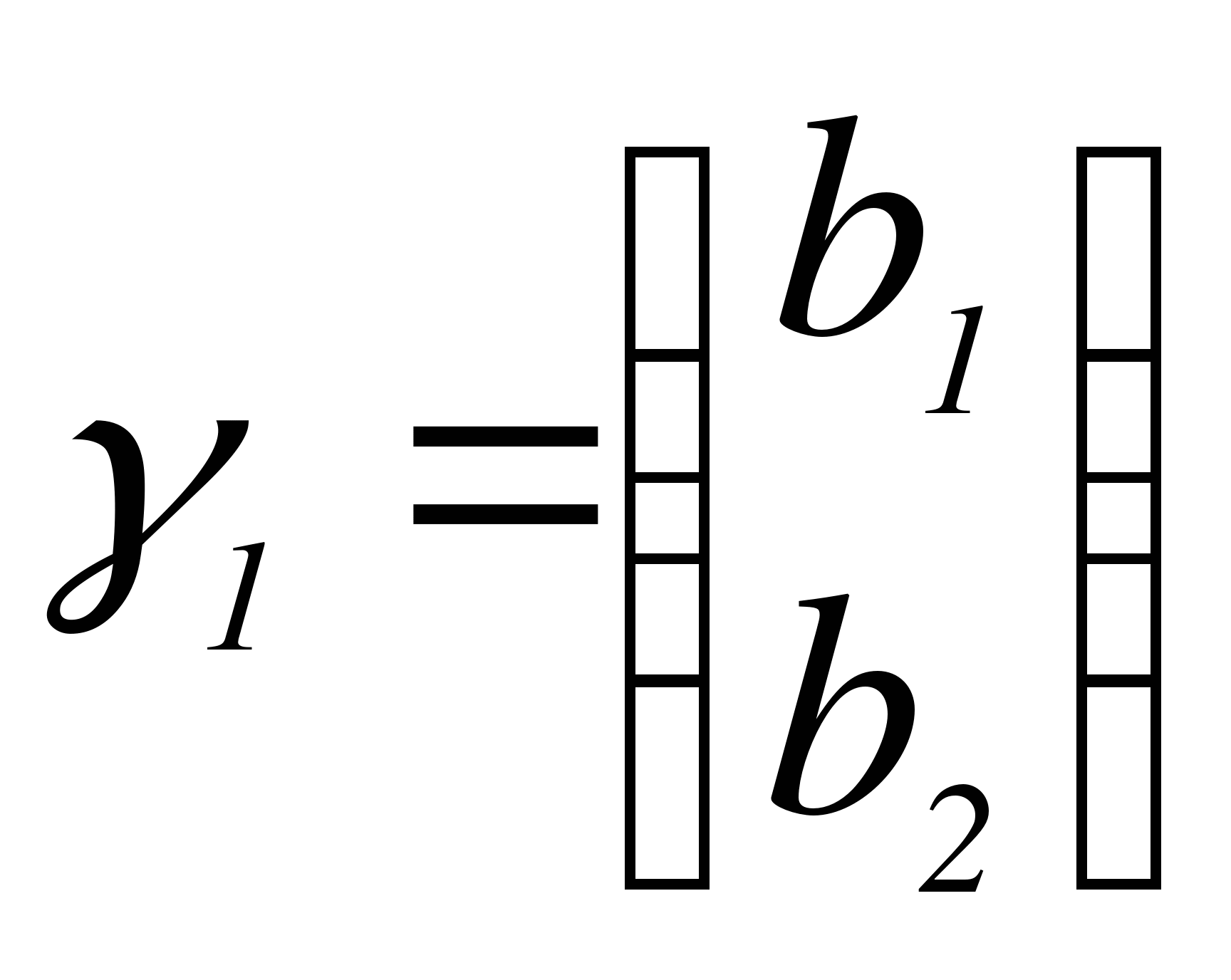 - собственный вектор матрицы А, соответствующий
- собственный вектор матрицы А, соответствующий 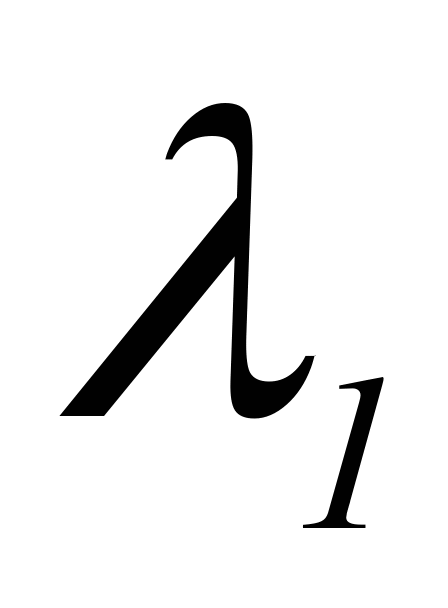 , т.е
, т.е 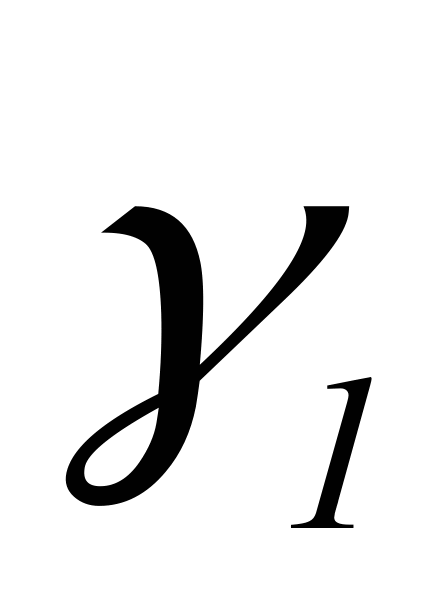 удовлетворяет системе
удовлетворяет системе 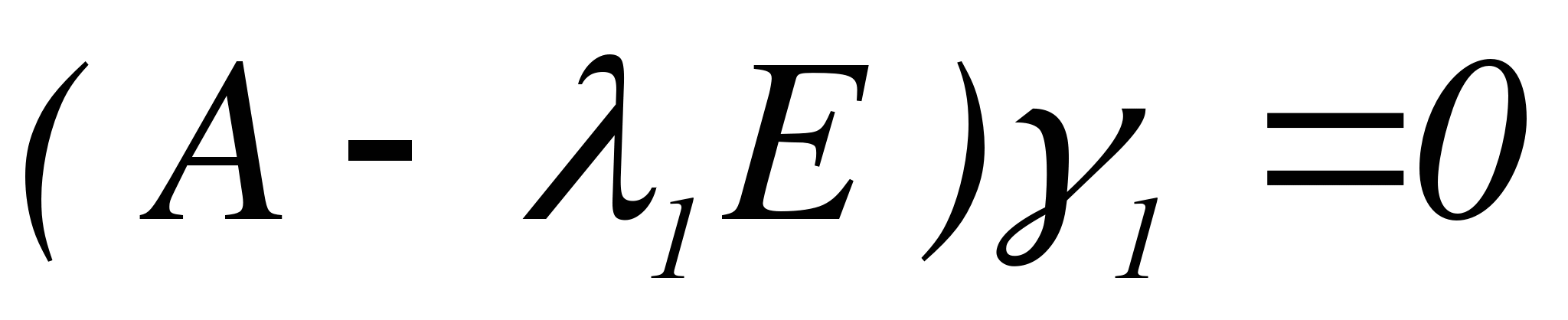 .
.
Тогда
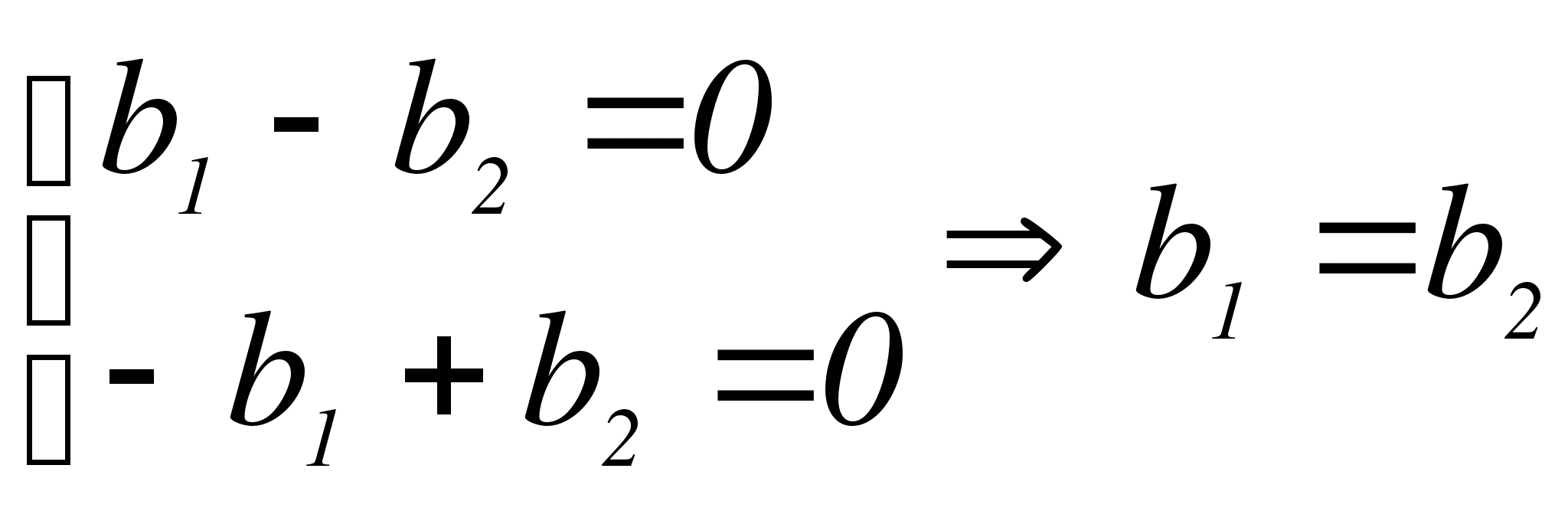
За 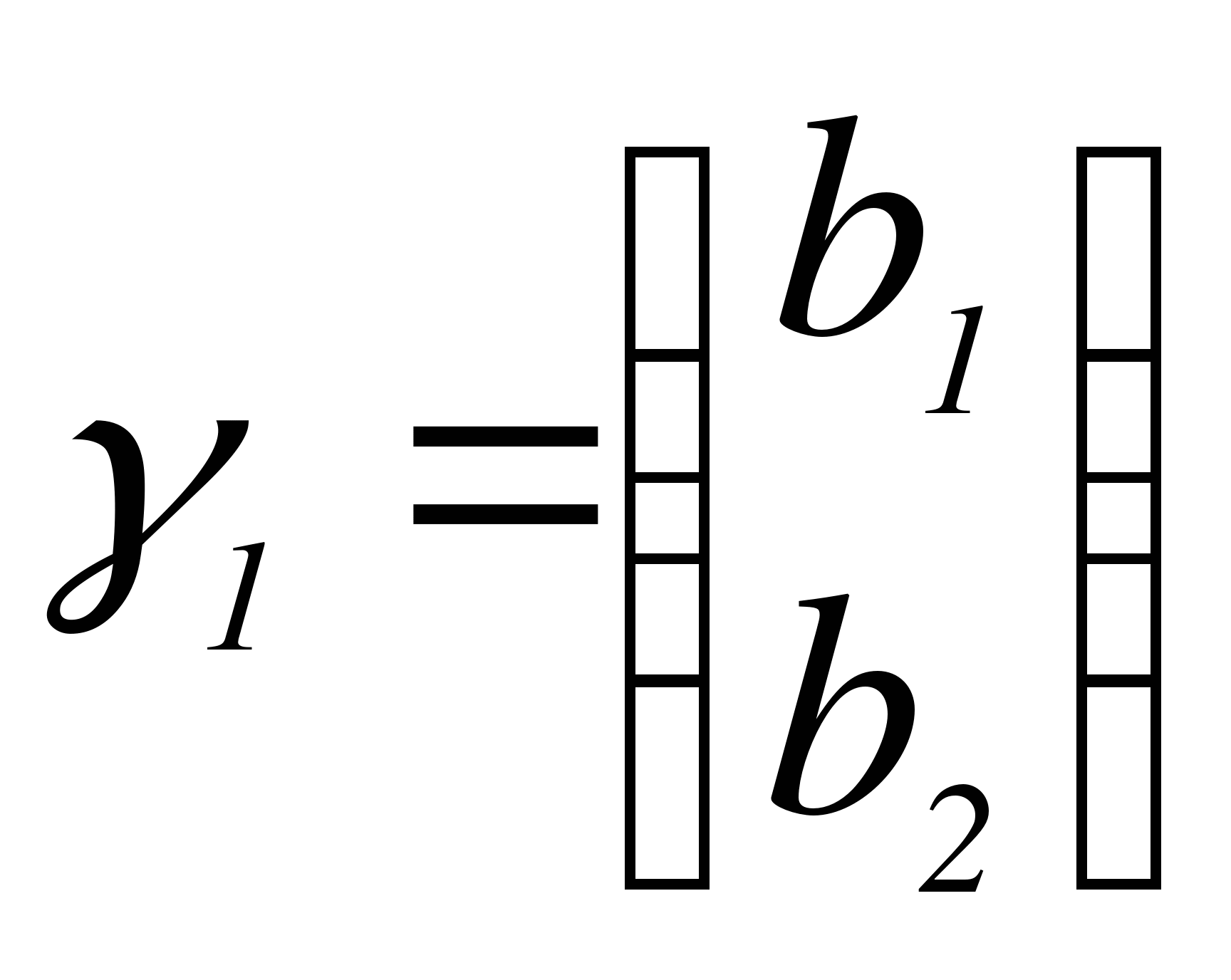 возьмем
возьмем 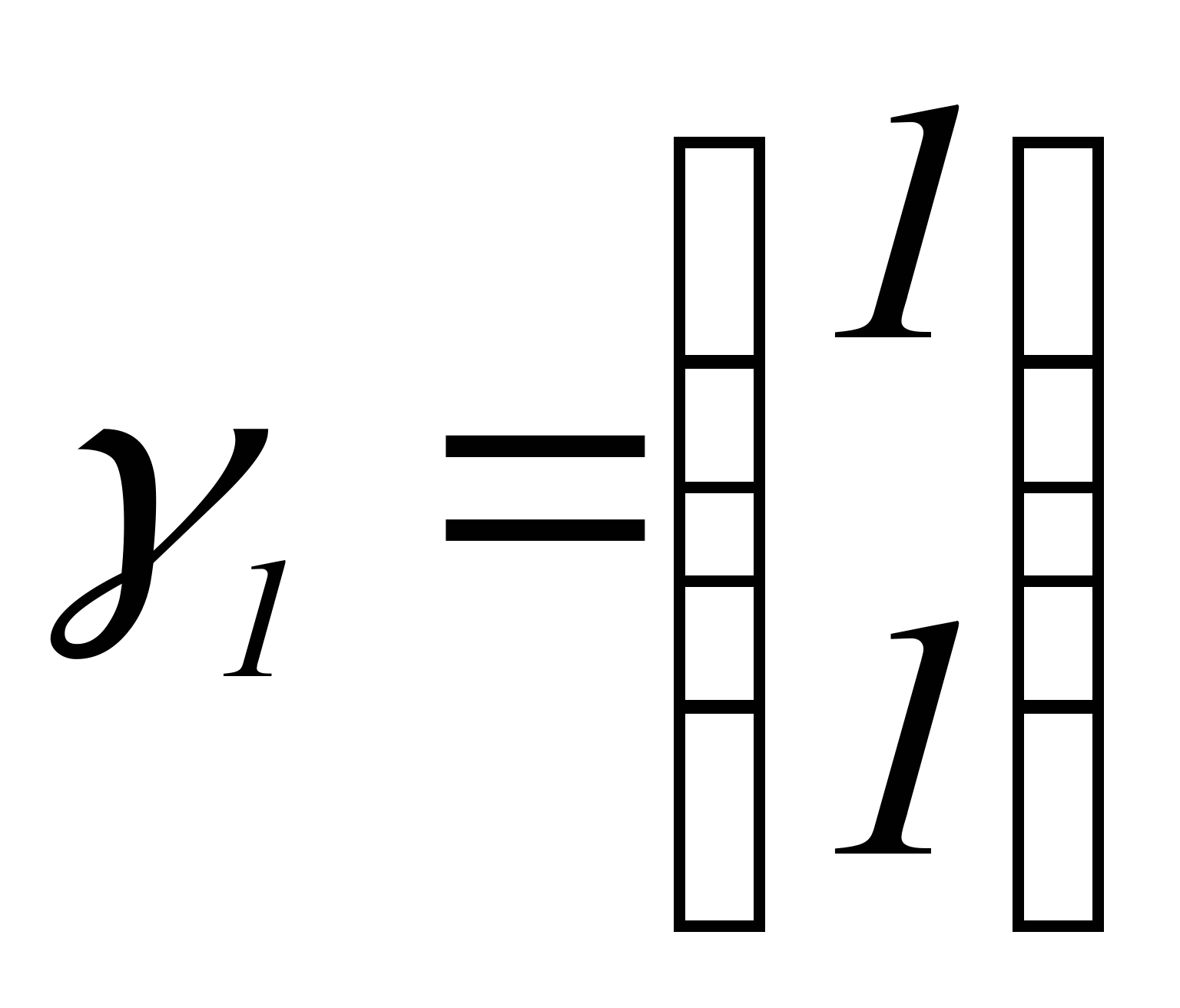 .
. 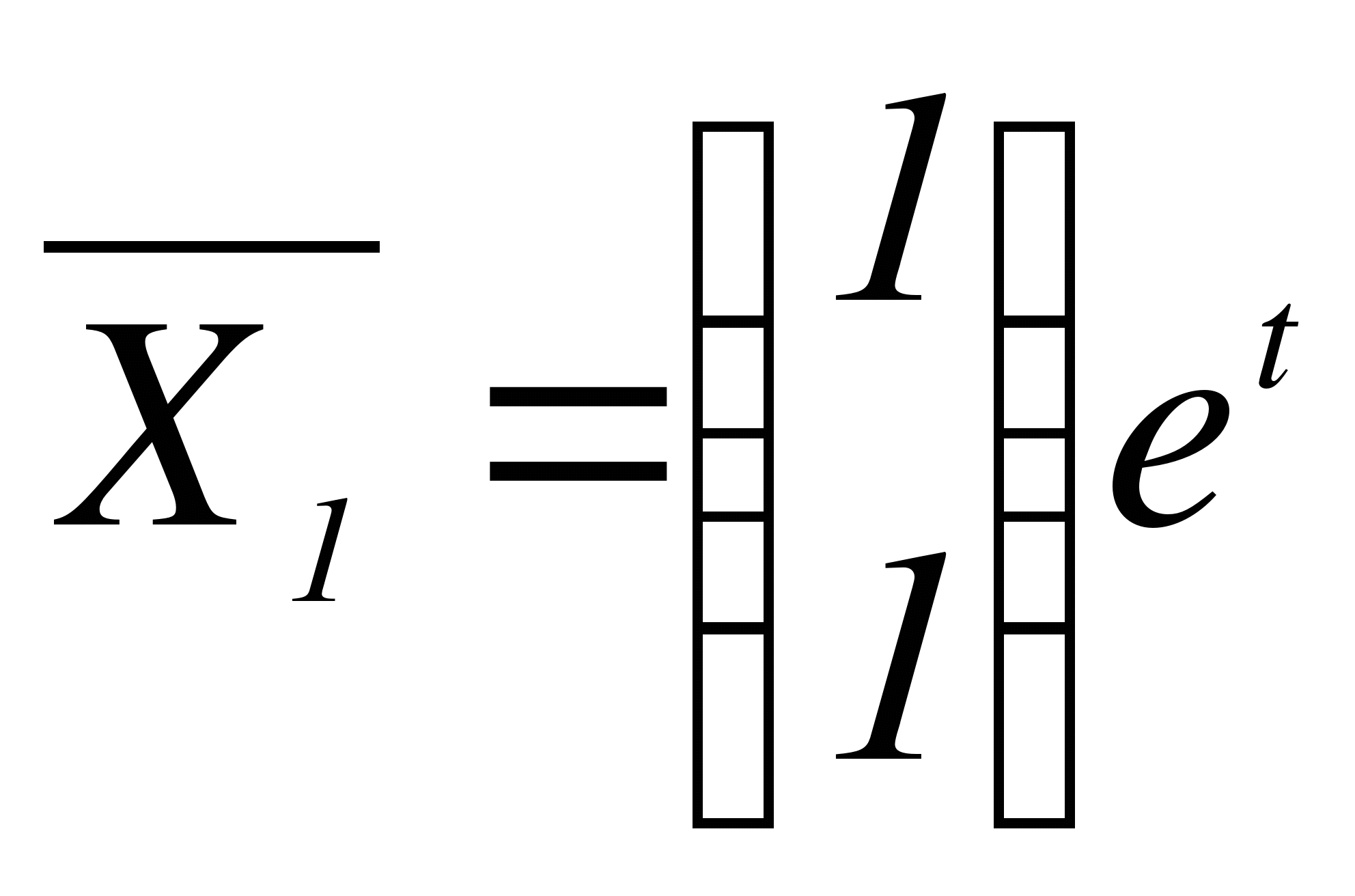
Строим 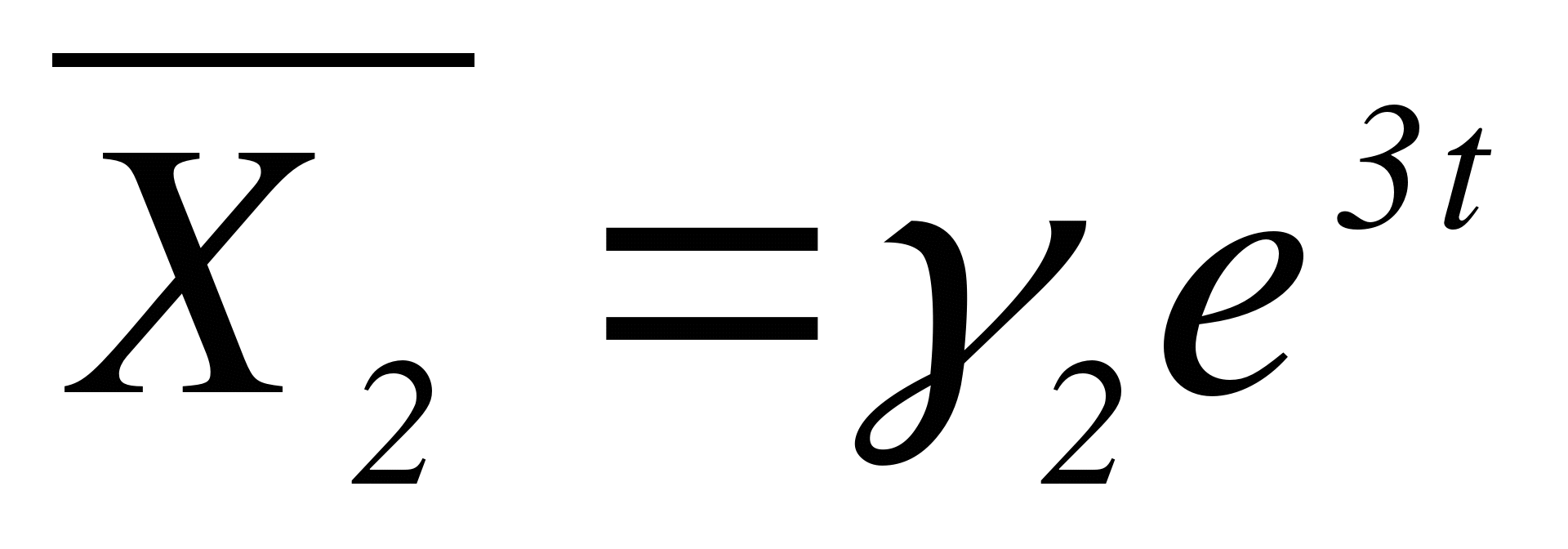 , где
, где 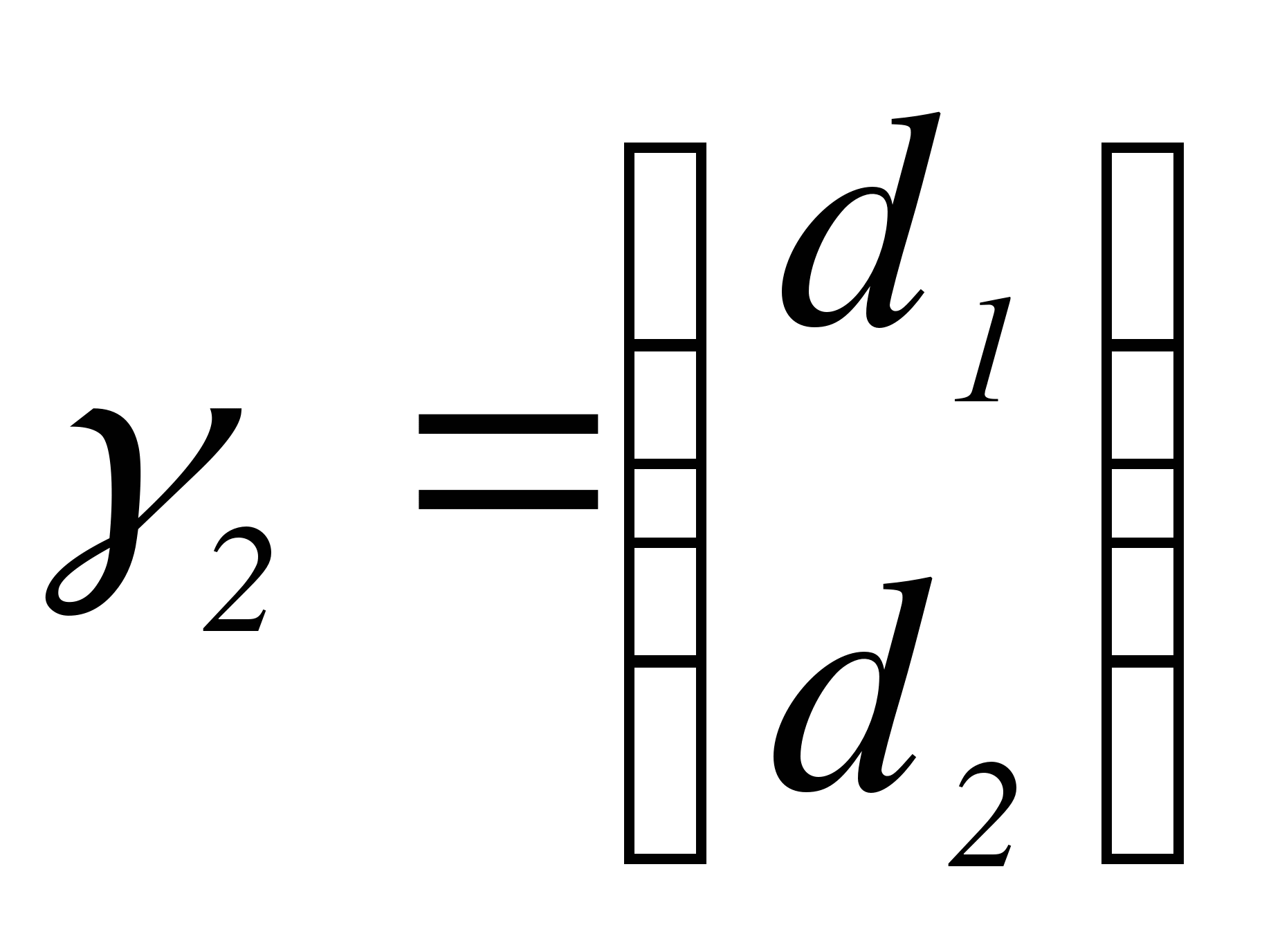 - собственный вектор матрицы А, соответствующий
- собственный вектор матрицы А, соответствующий 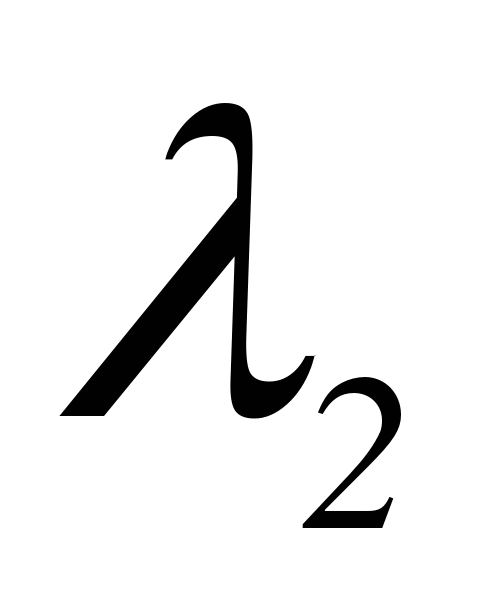 , т.е
, т.е 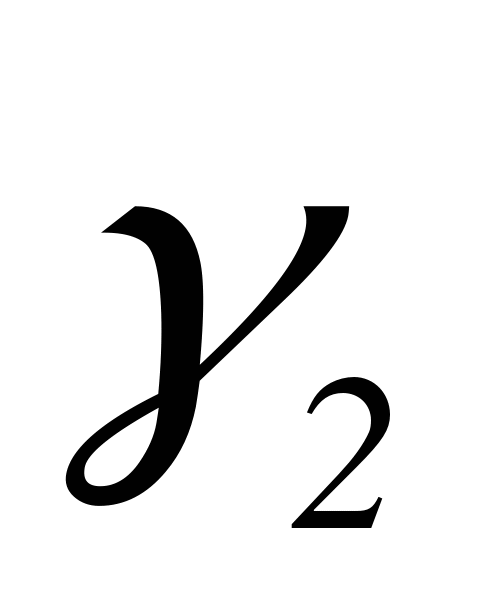 удовлетворяет системе
удовлетворяет системе 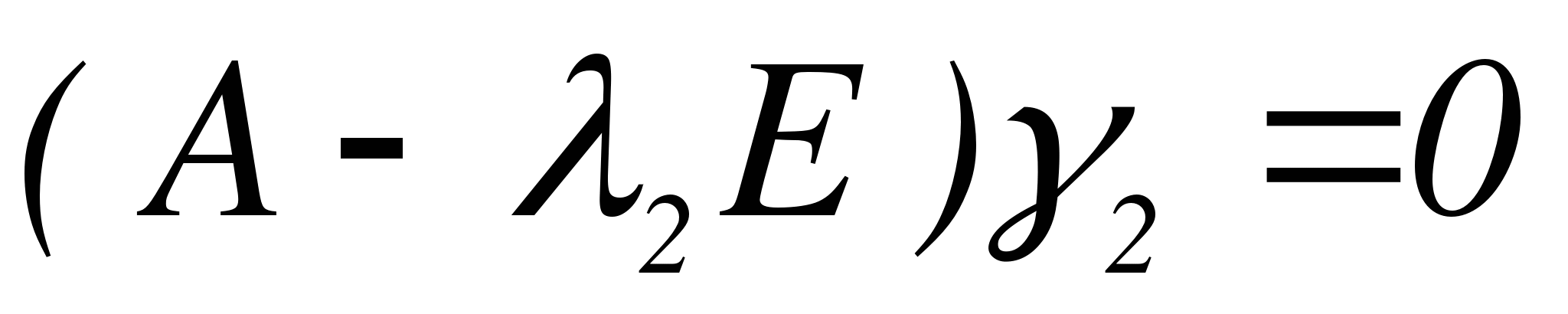 .
.
Тогда
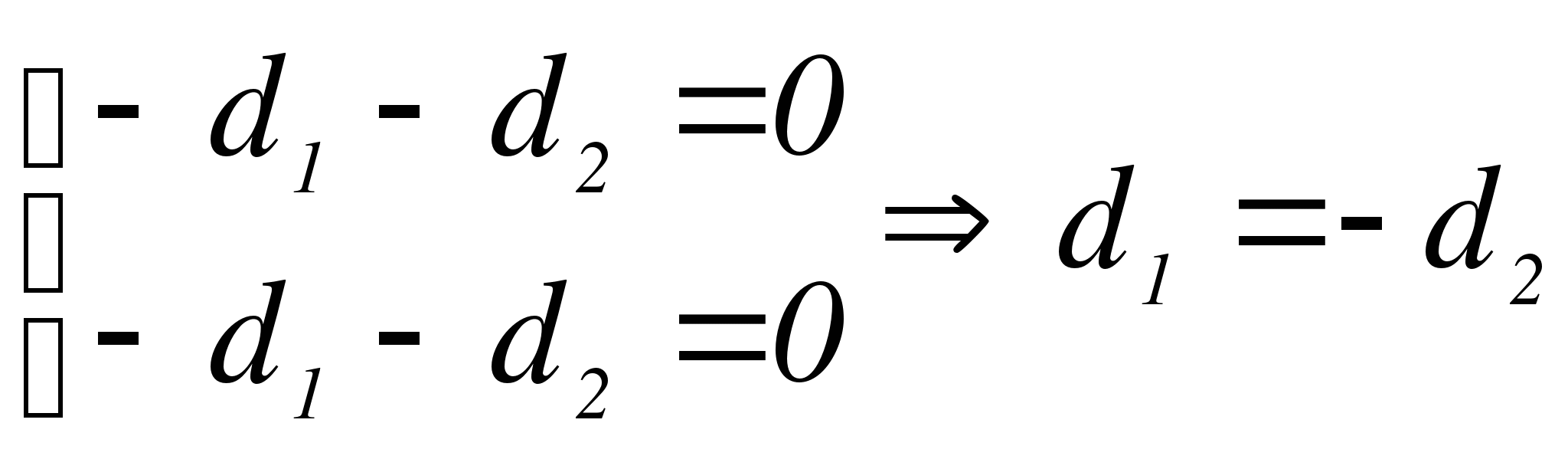
За 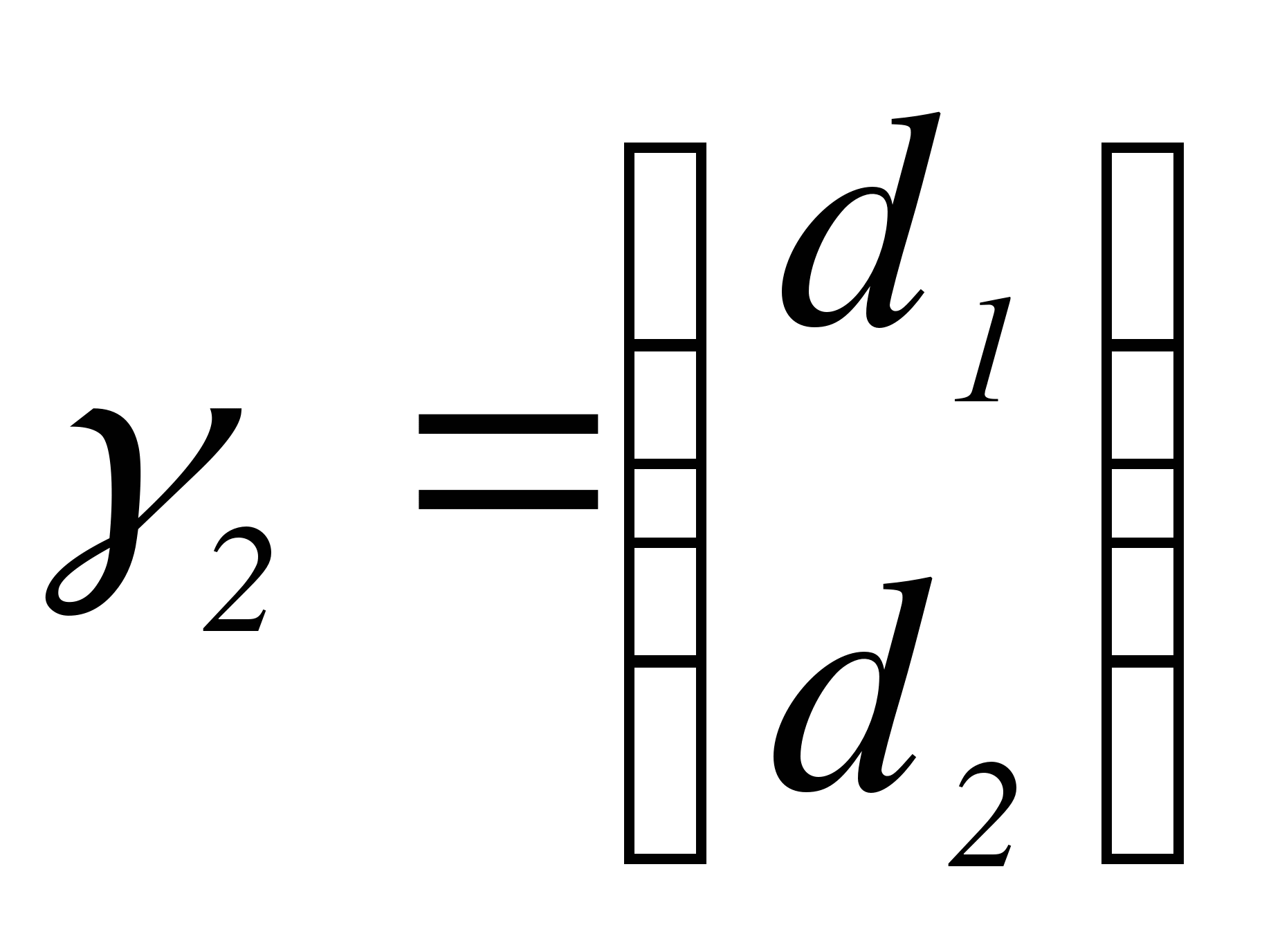 возьмем
возьмем 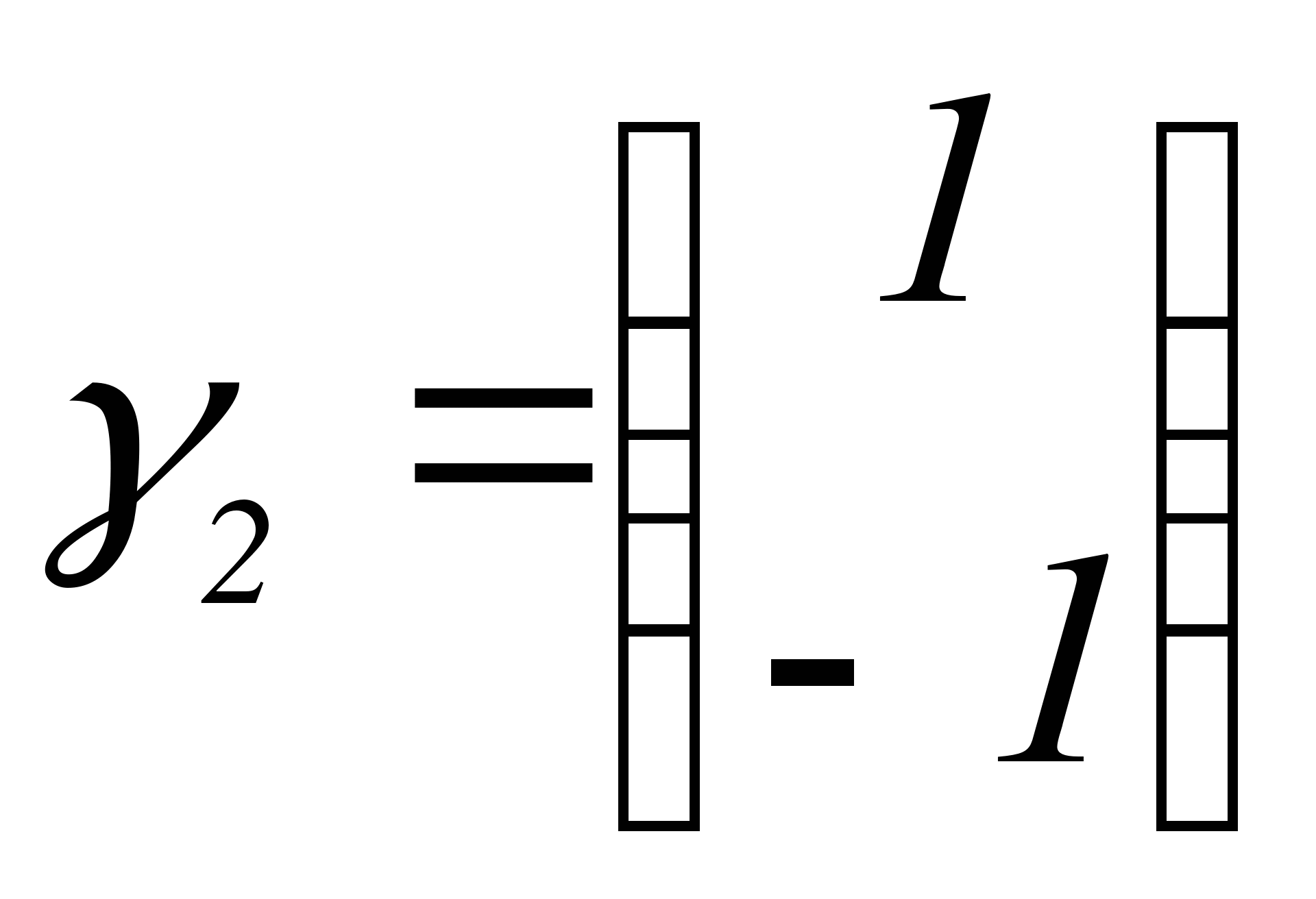 .
. 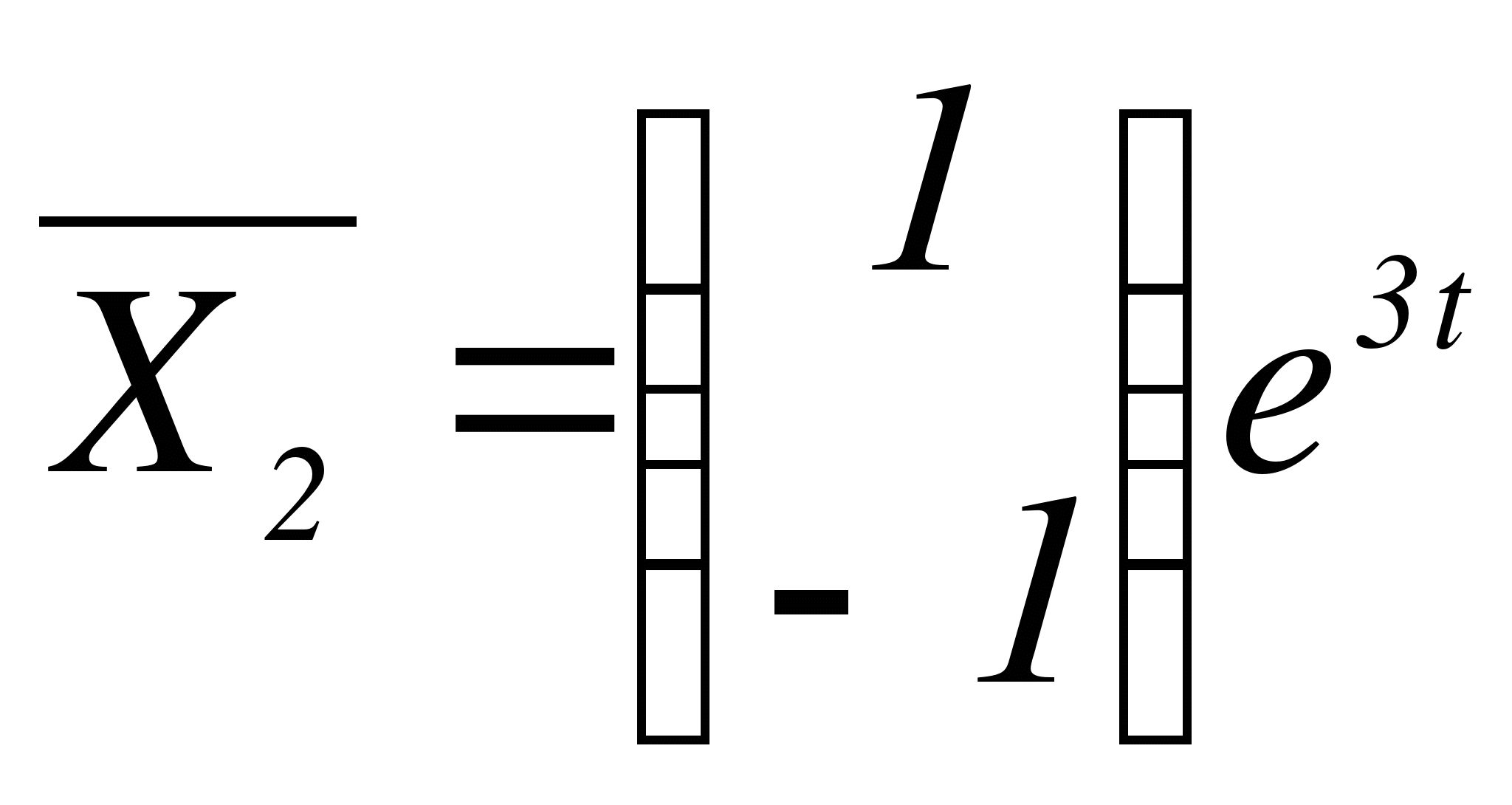
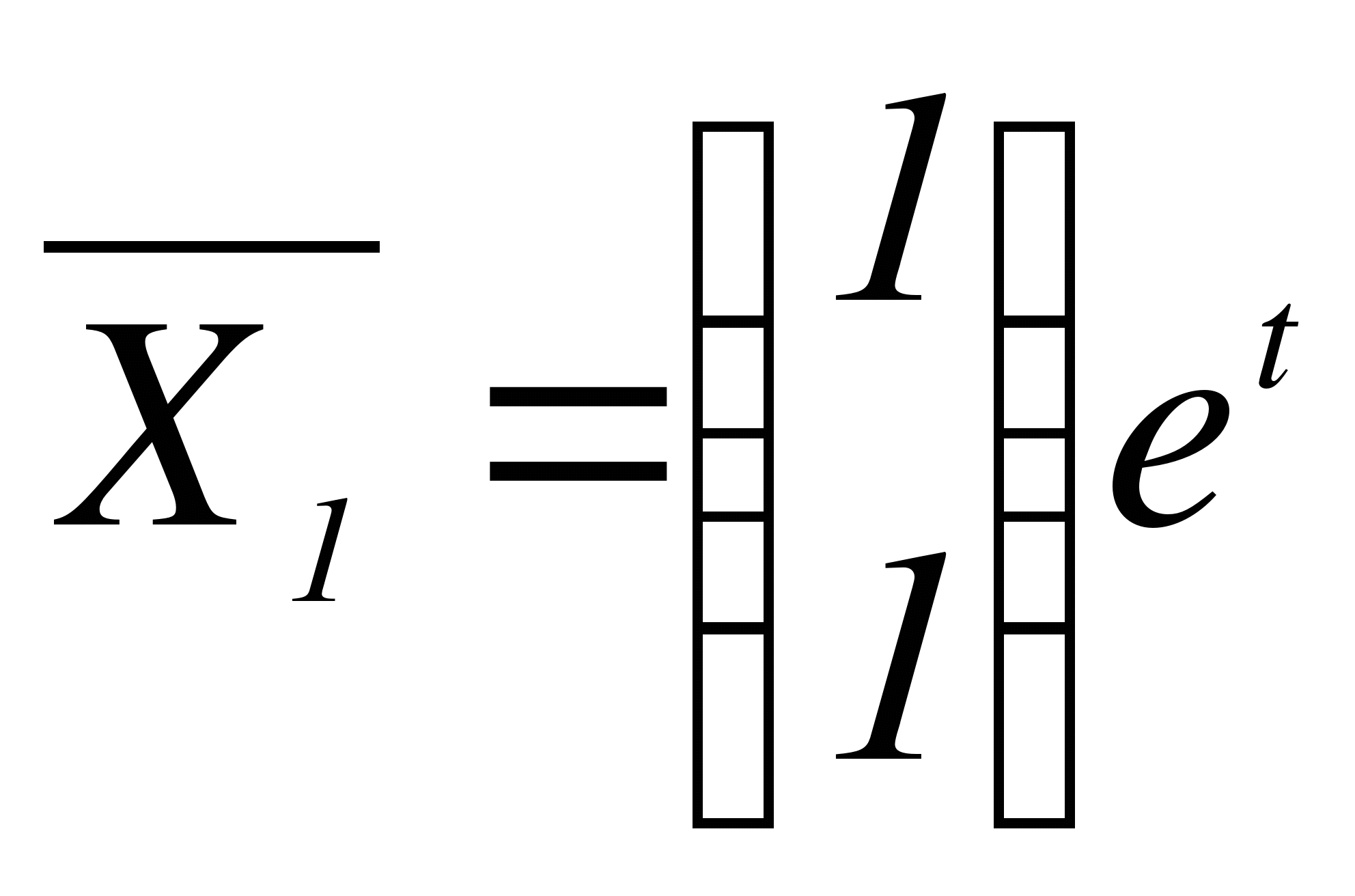 ,
, 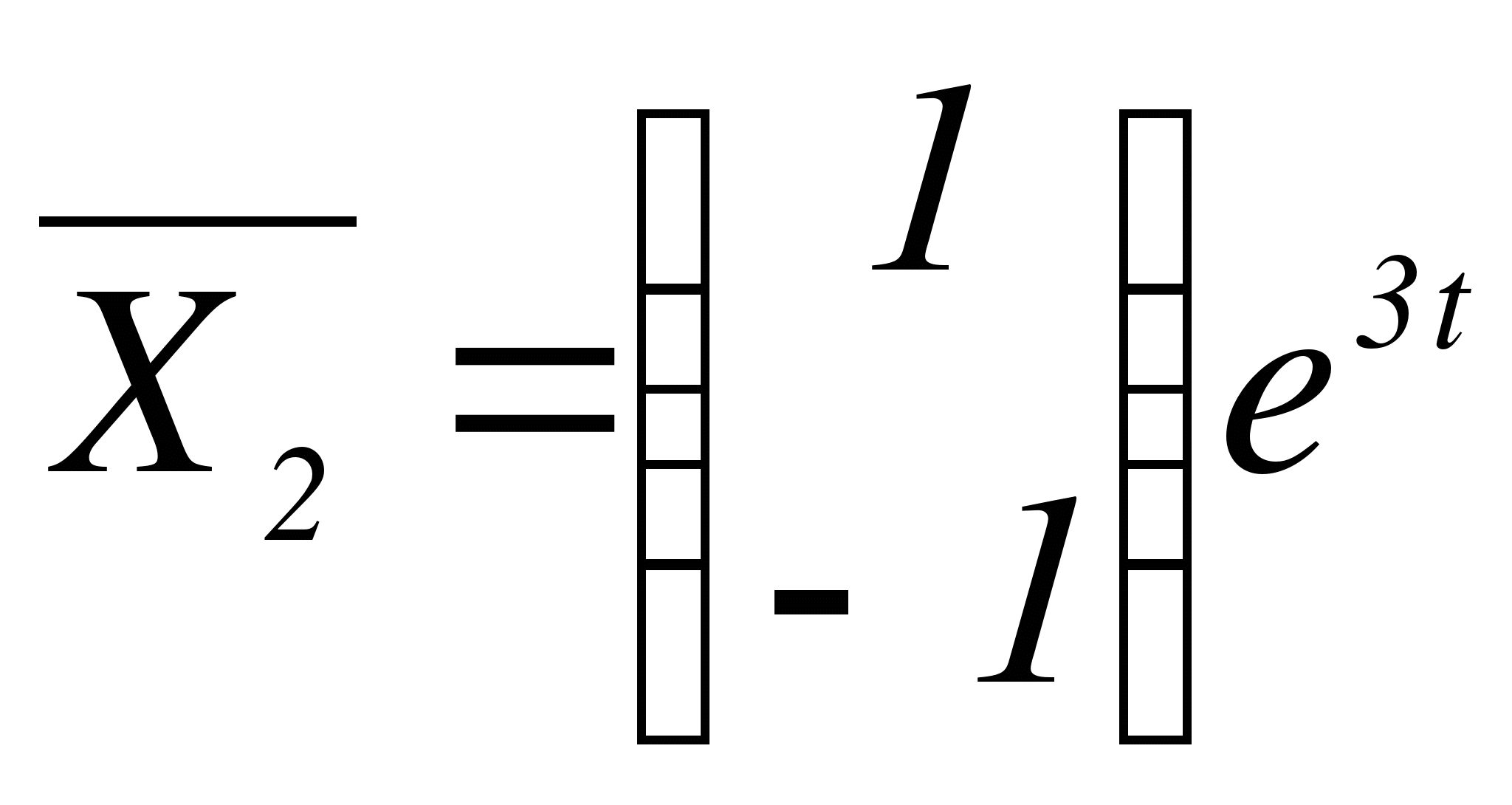 - фундаментальная система решений. Запишем общее решение однородной системы:
- фундаментальная система решений. Запишем общее решение однородной системы: 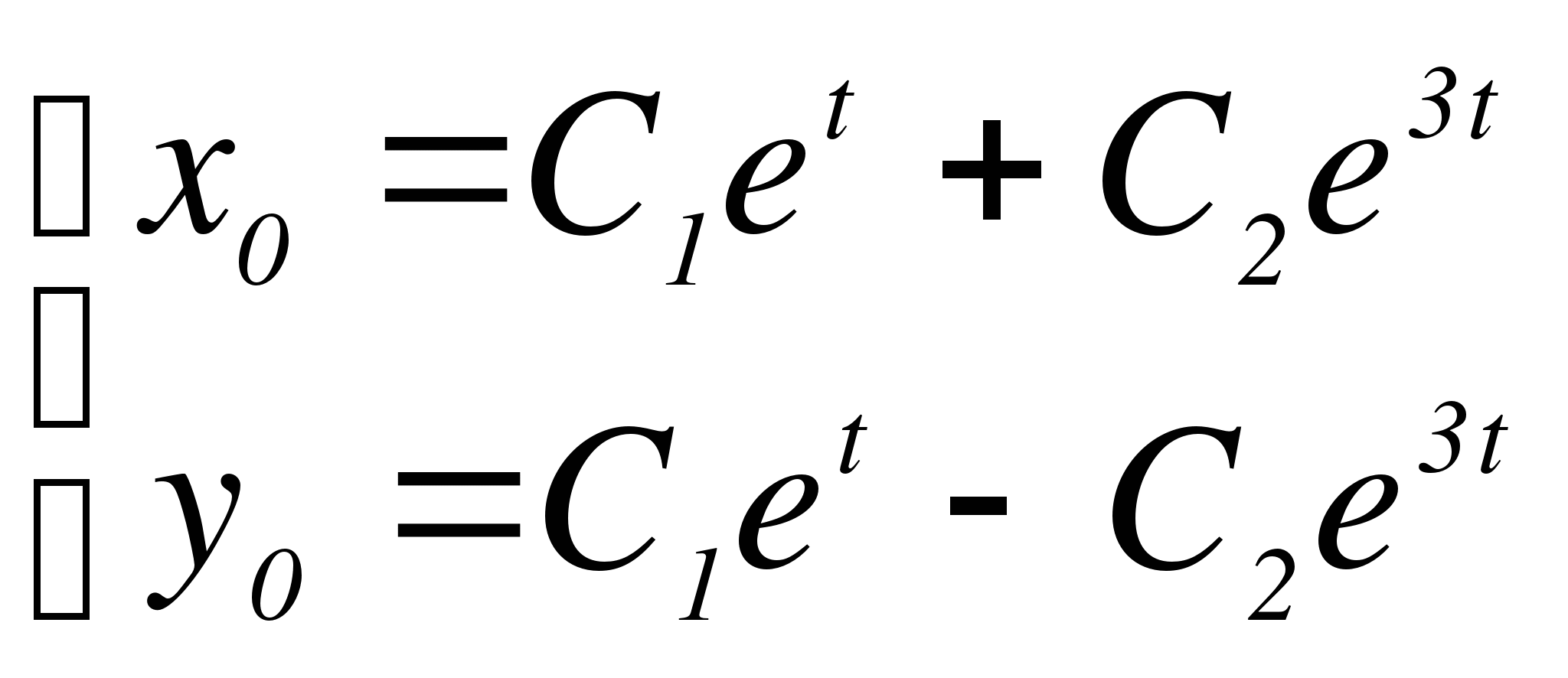
Теперь найдем частное решение.
Правая часть имеет вид квазимногочлена 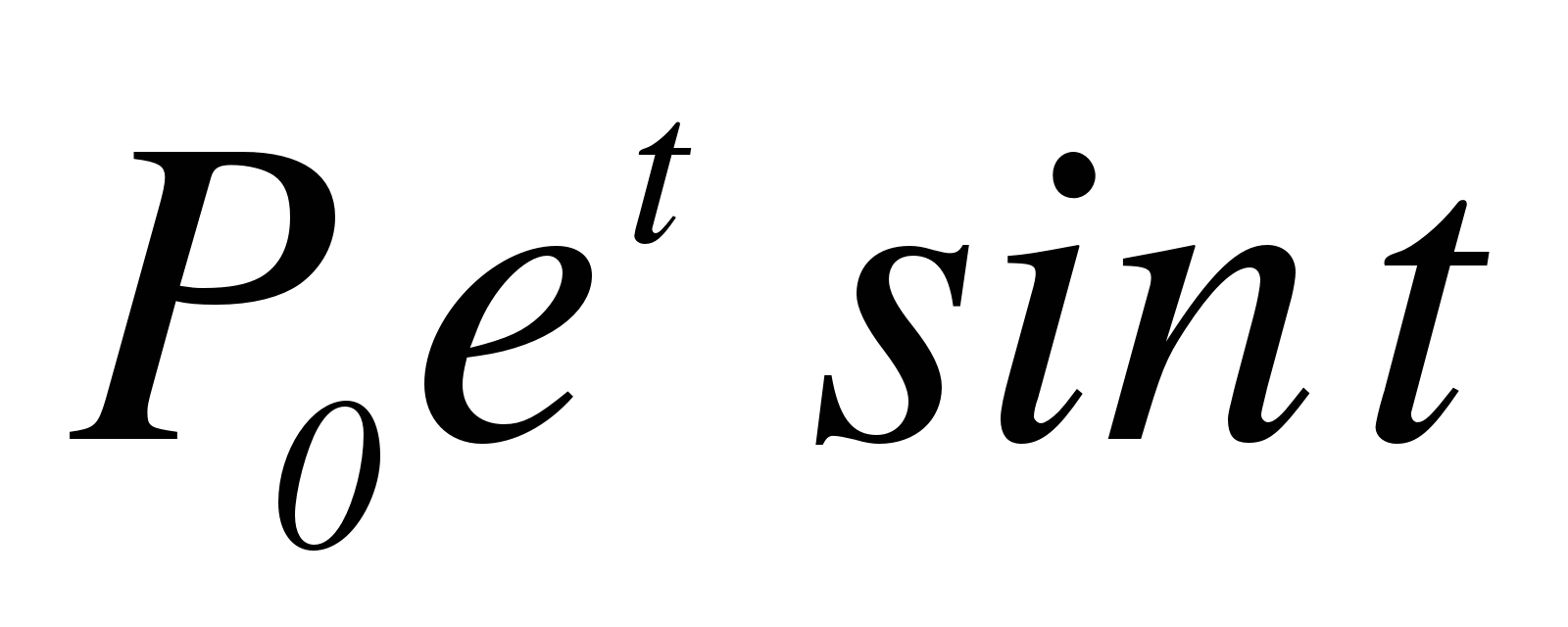
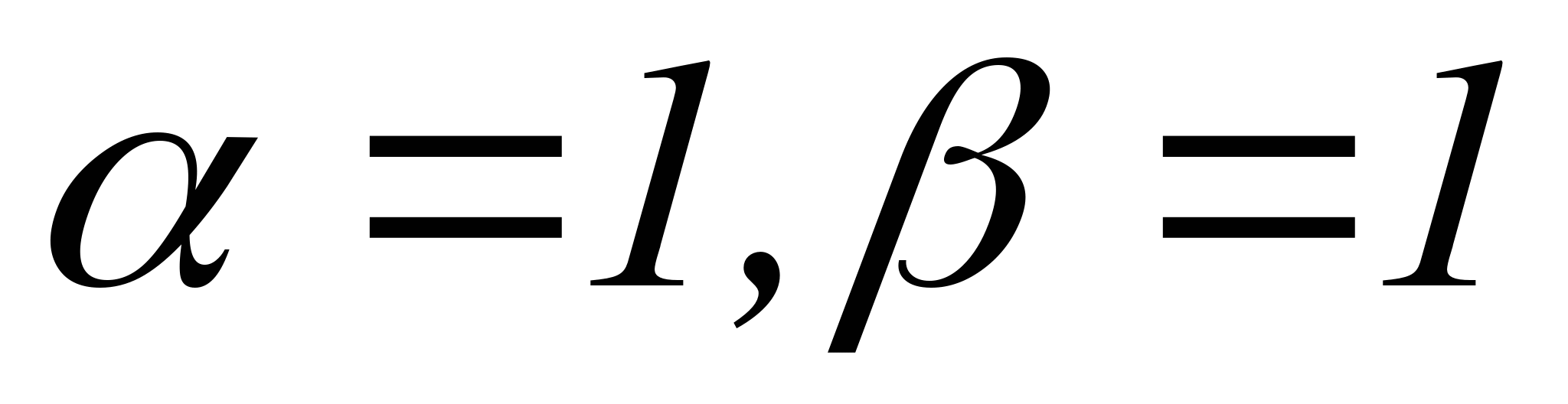 . Поскольку
. Поскольку 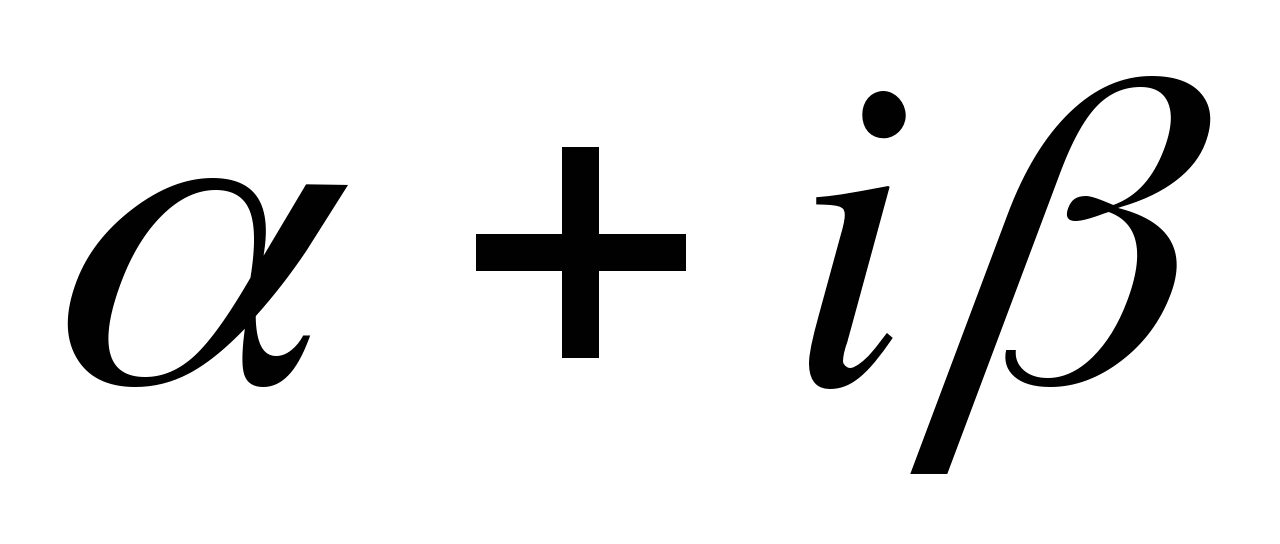 не совпадает ни с одним из собственных значений, то частное решение будем искать в виде, аналогичном f(t), т.е. полагаем
не совпадает ни с одним из собственных значений, то частное решение будем искать в виде, аналогичном f(t), т.е. полагаем
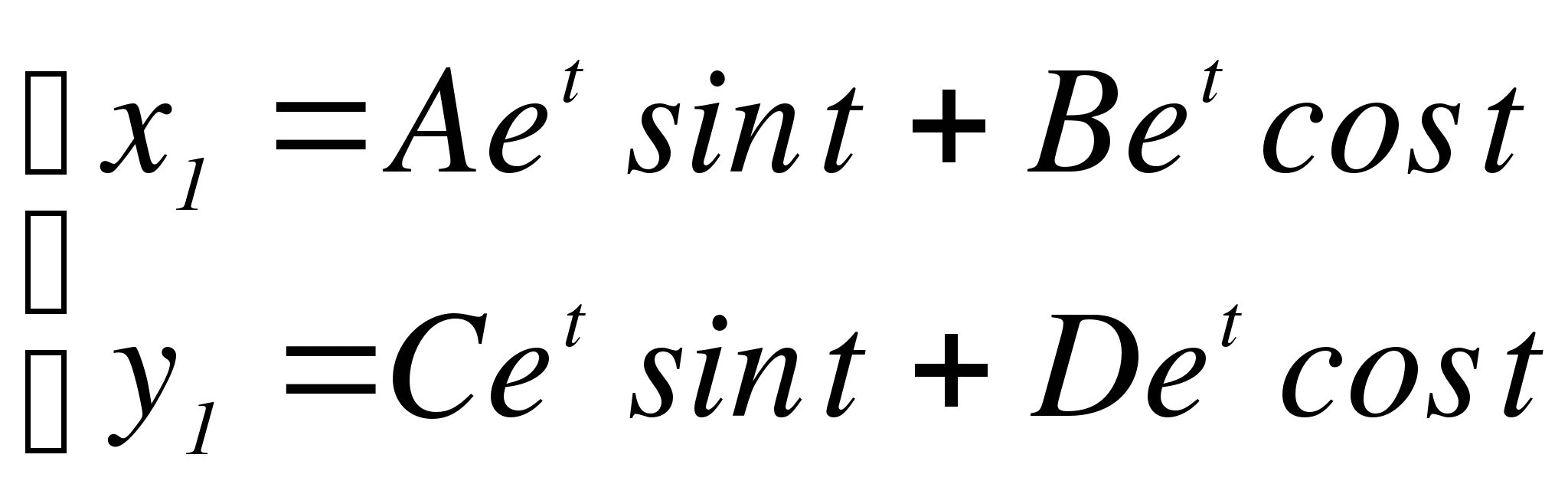
Неизвестные A, B, C, D найдем методом неопределенных коэффициентов.
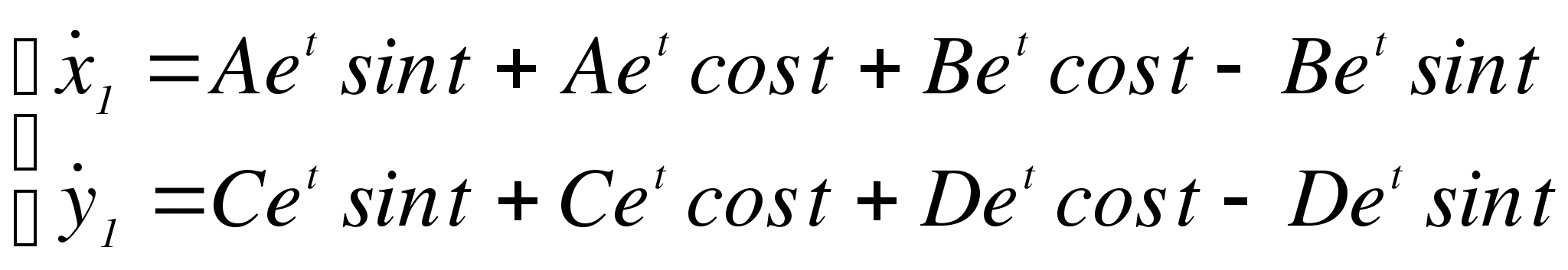
Подставляем в исходное неоднородное уравнение:
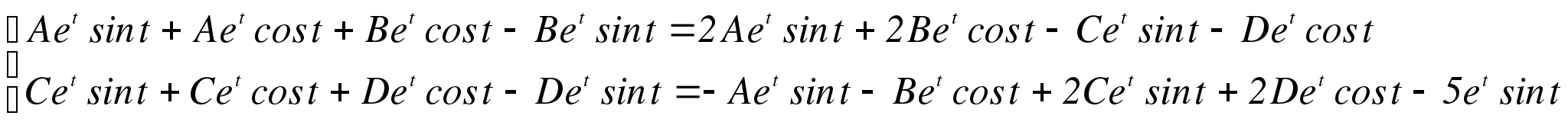
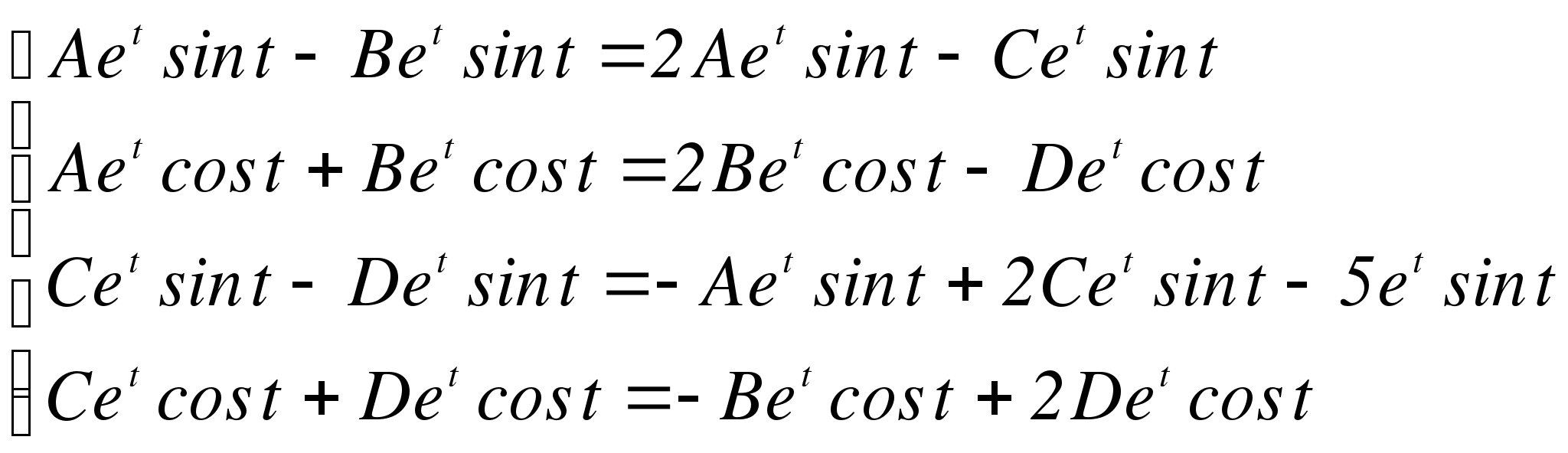
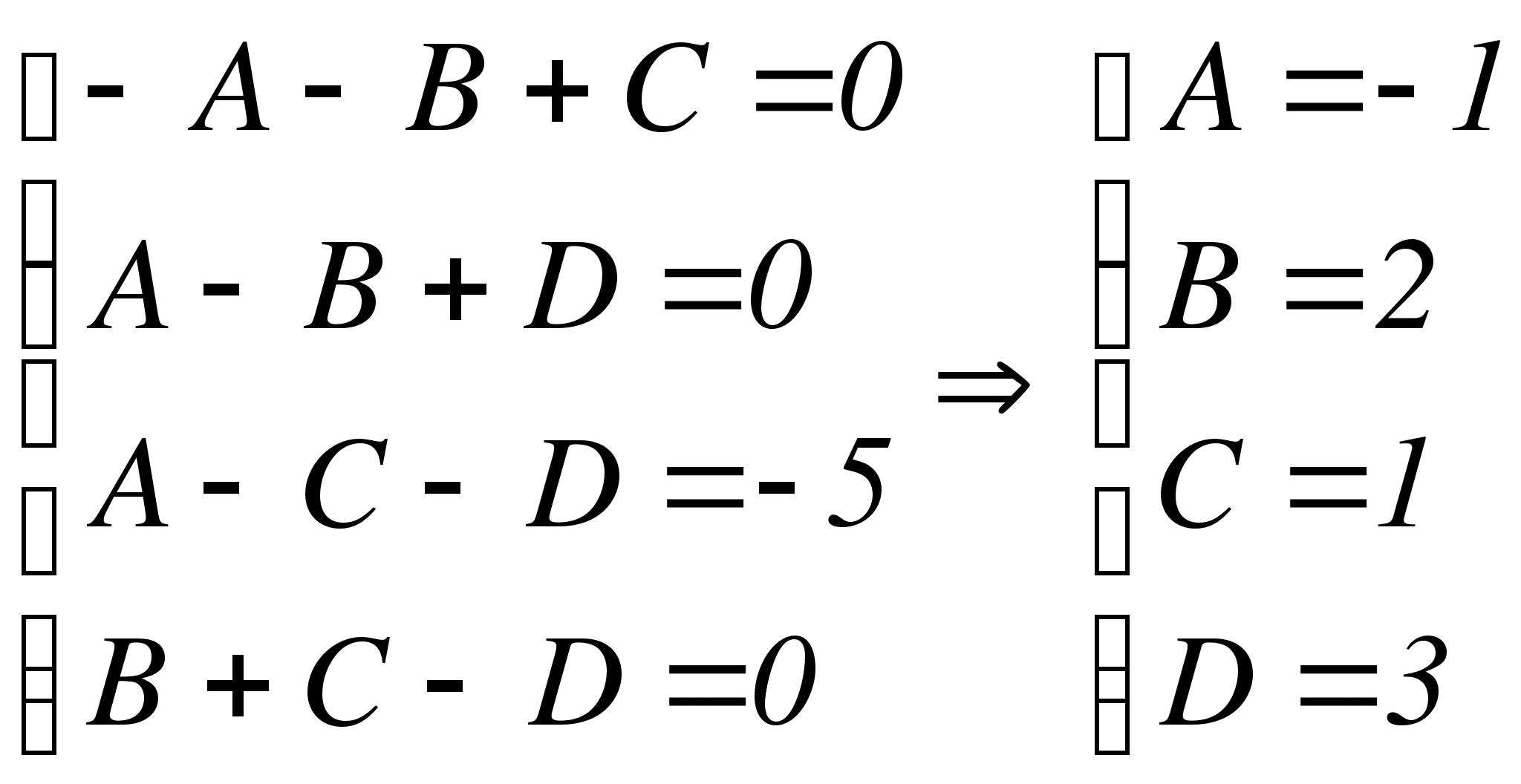
Частное решение имеет вид:
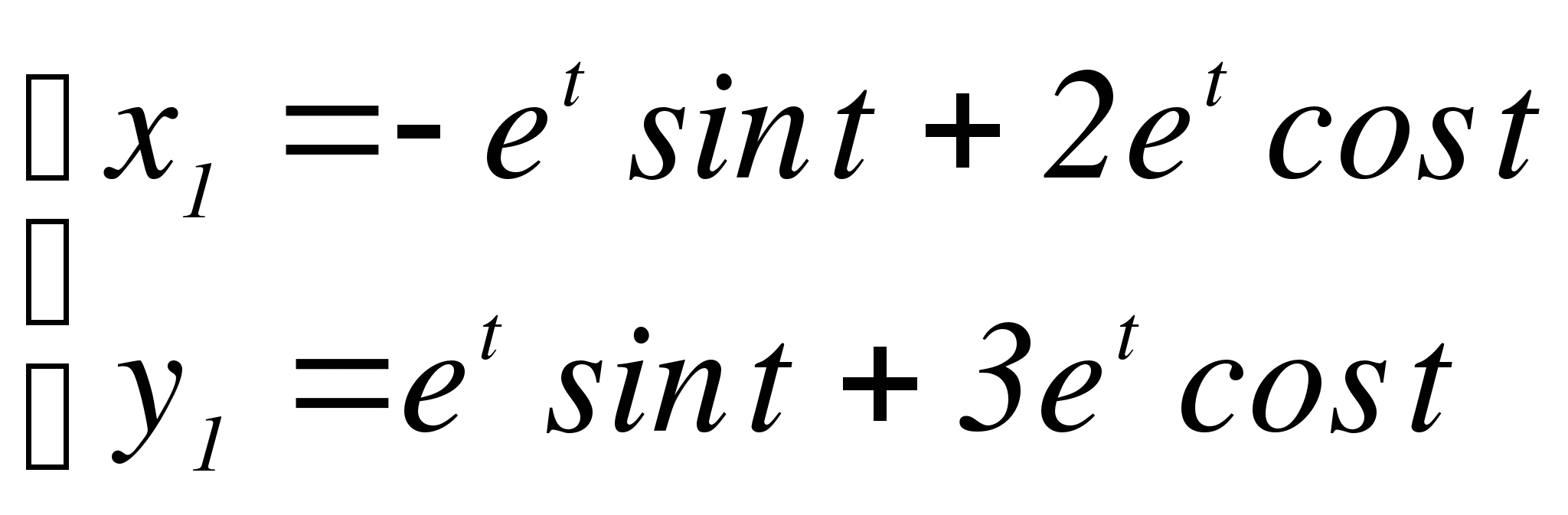
Тогда общее решение исходной неоднородной системы будет:
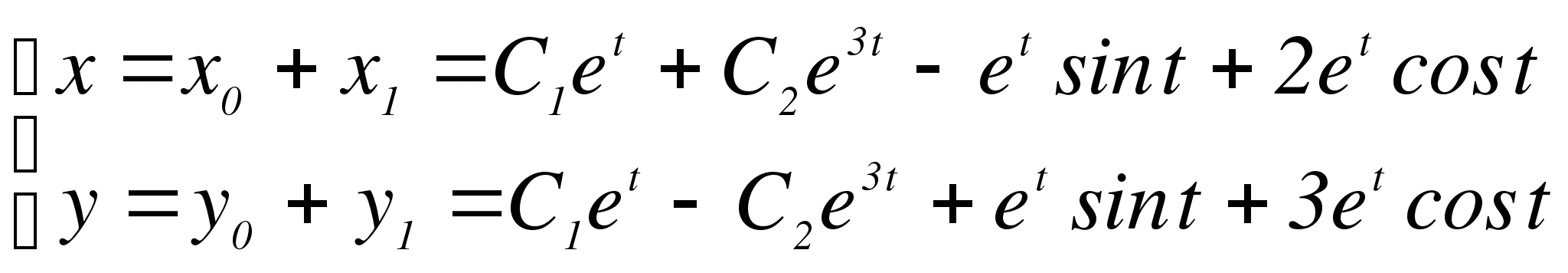
Ответ. 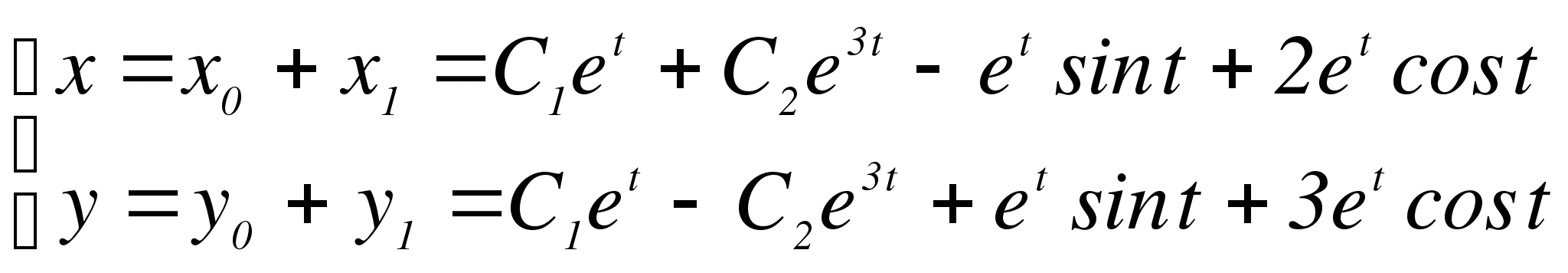 - общее решение линейной неоднородной системы
- общее решение линейной неоднородной системы
Задача 3. Найти общее решение линейной неоднородной системы методом вариации произвольных постоянных
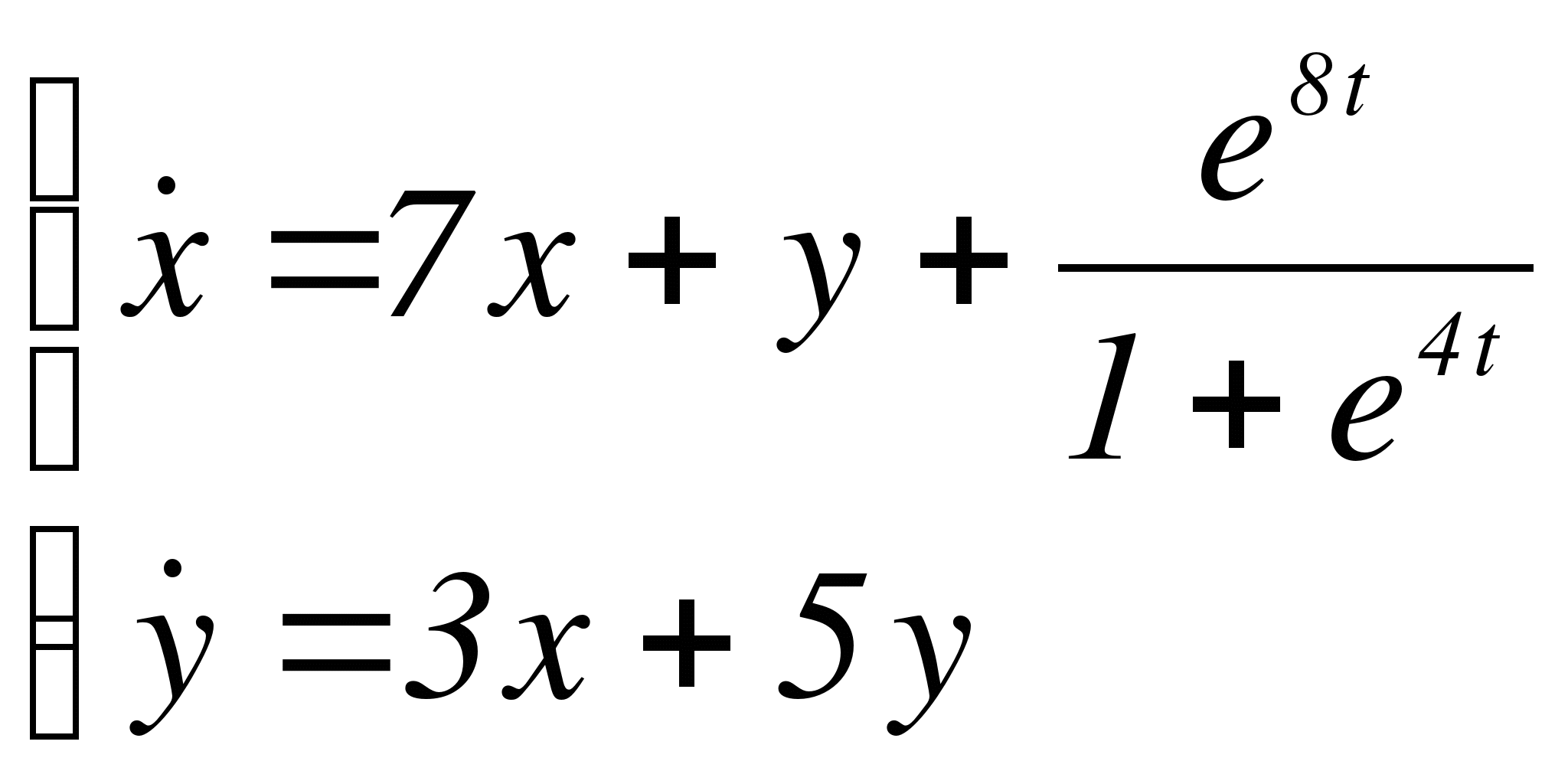
Решение.
Составляем характеристическое уравнение заданной системы:
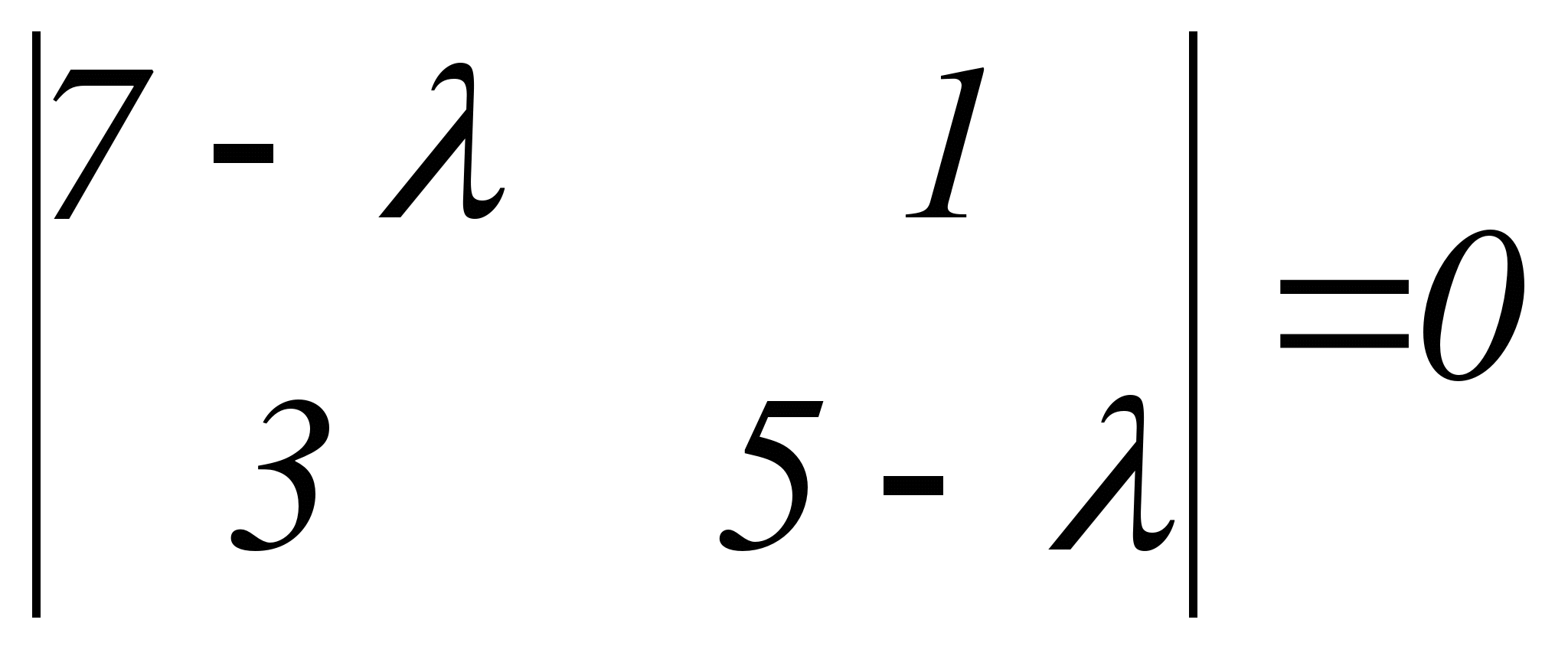
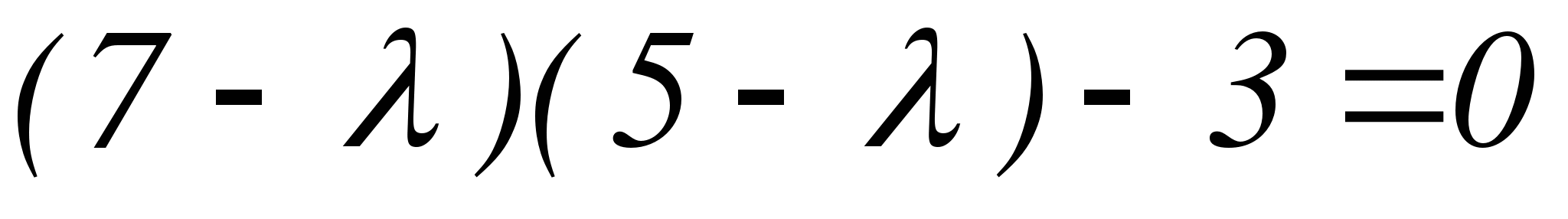
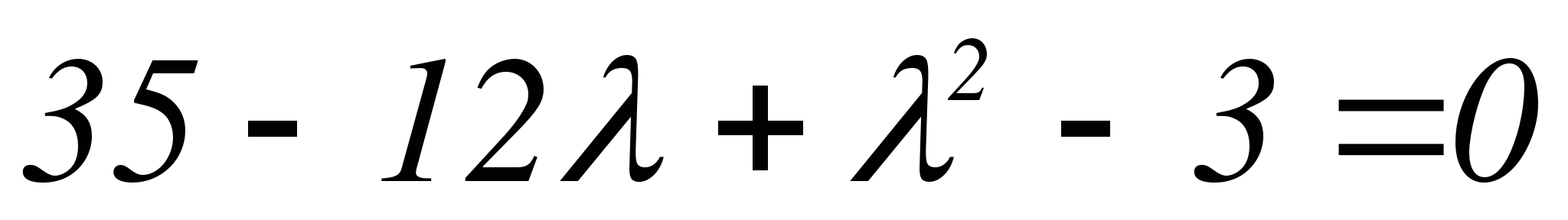
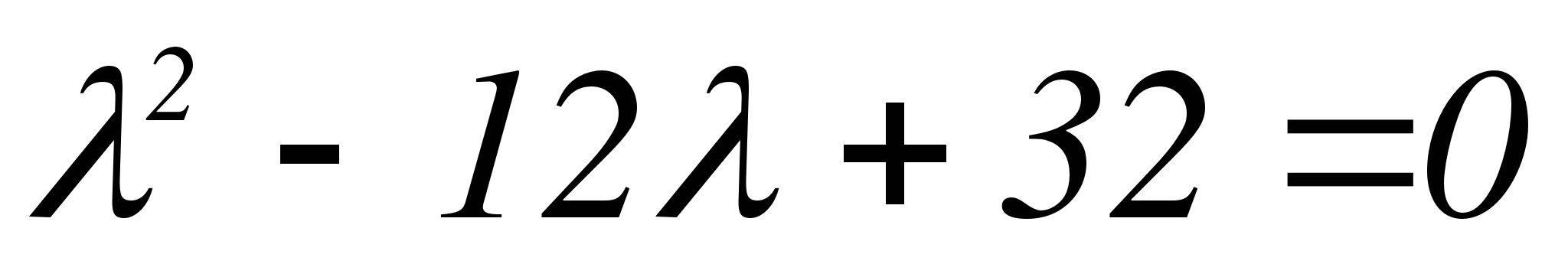
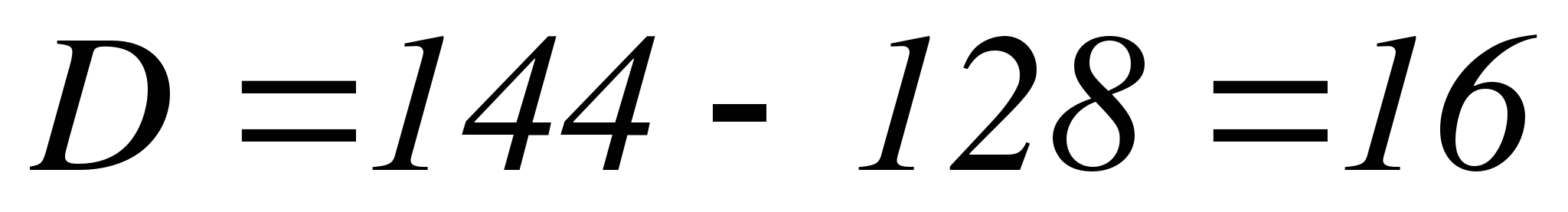
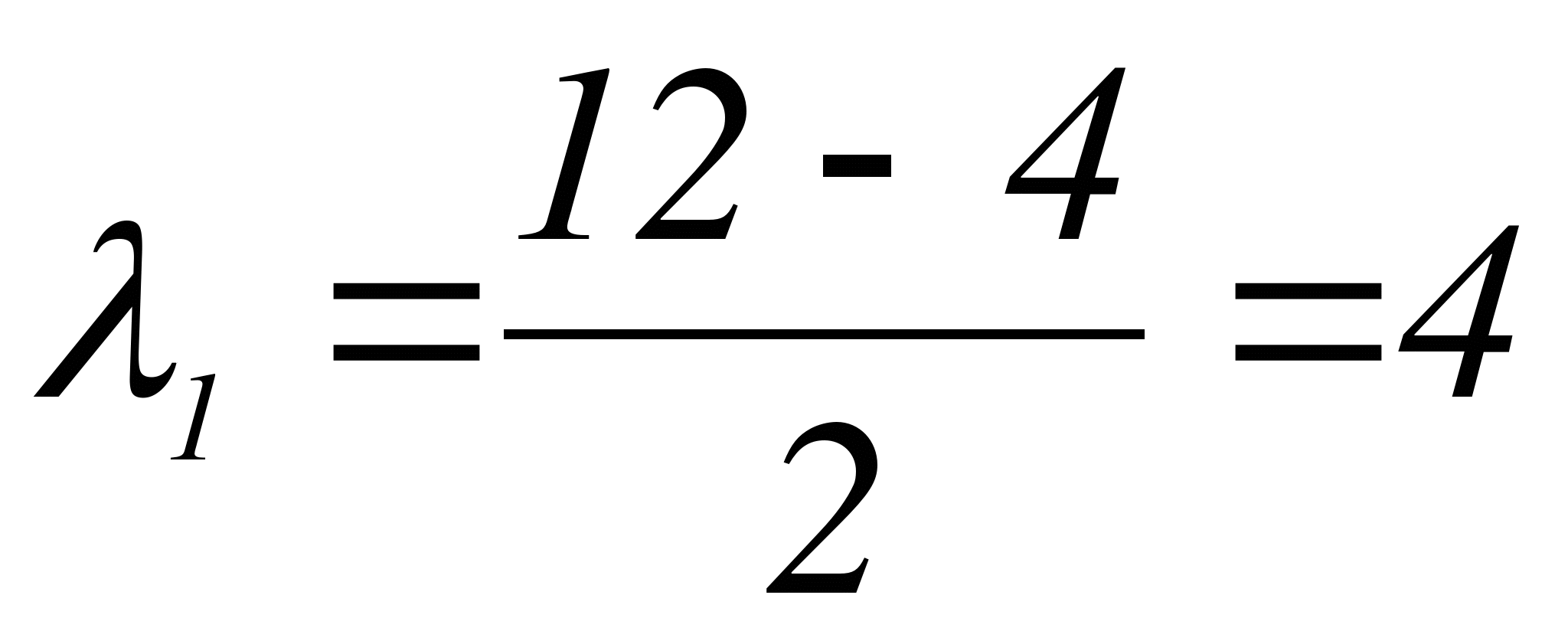 ,
, 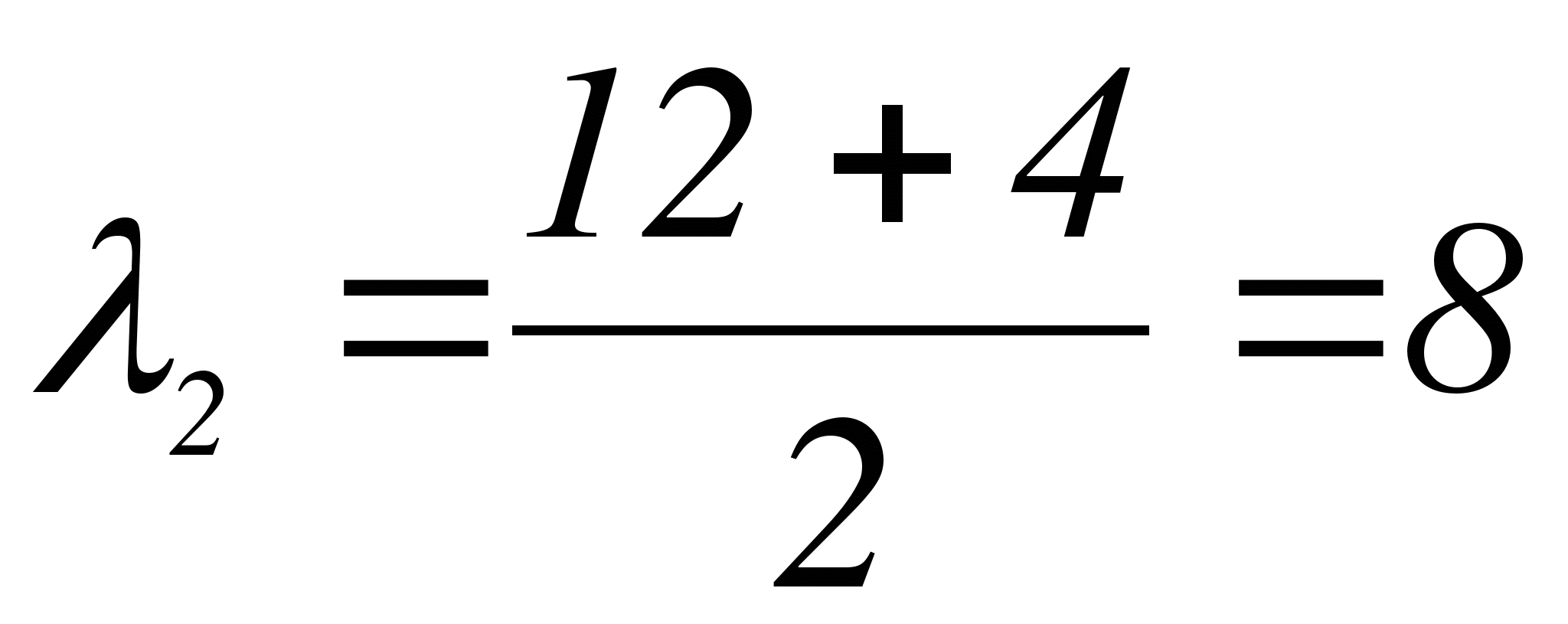
Строим 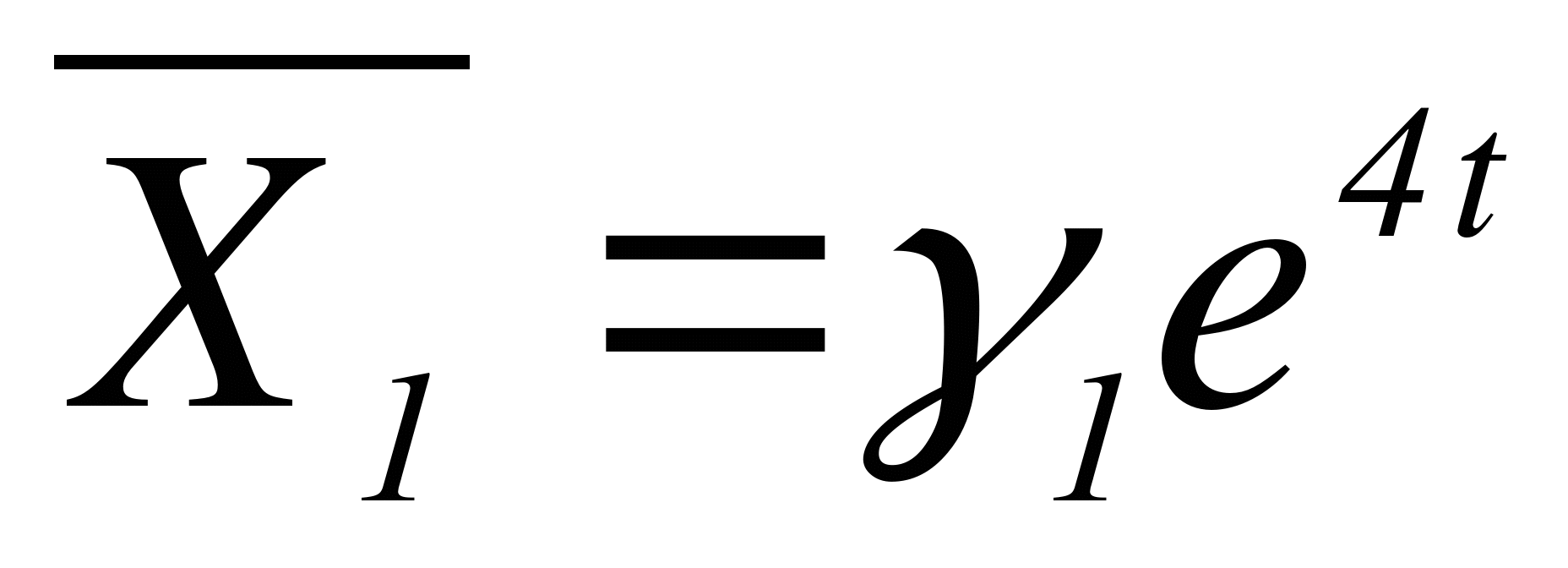 , где
, где 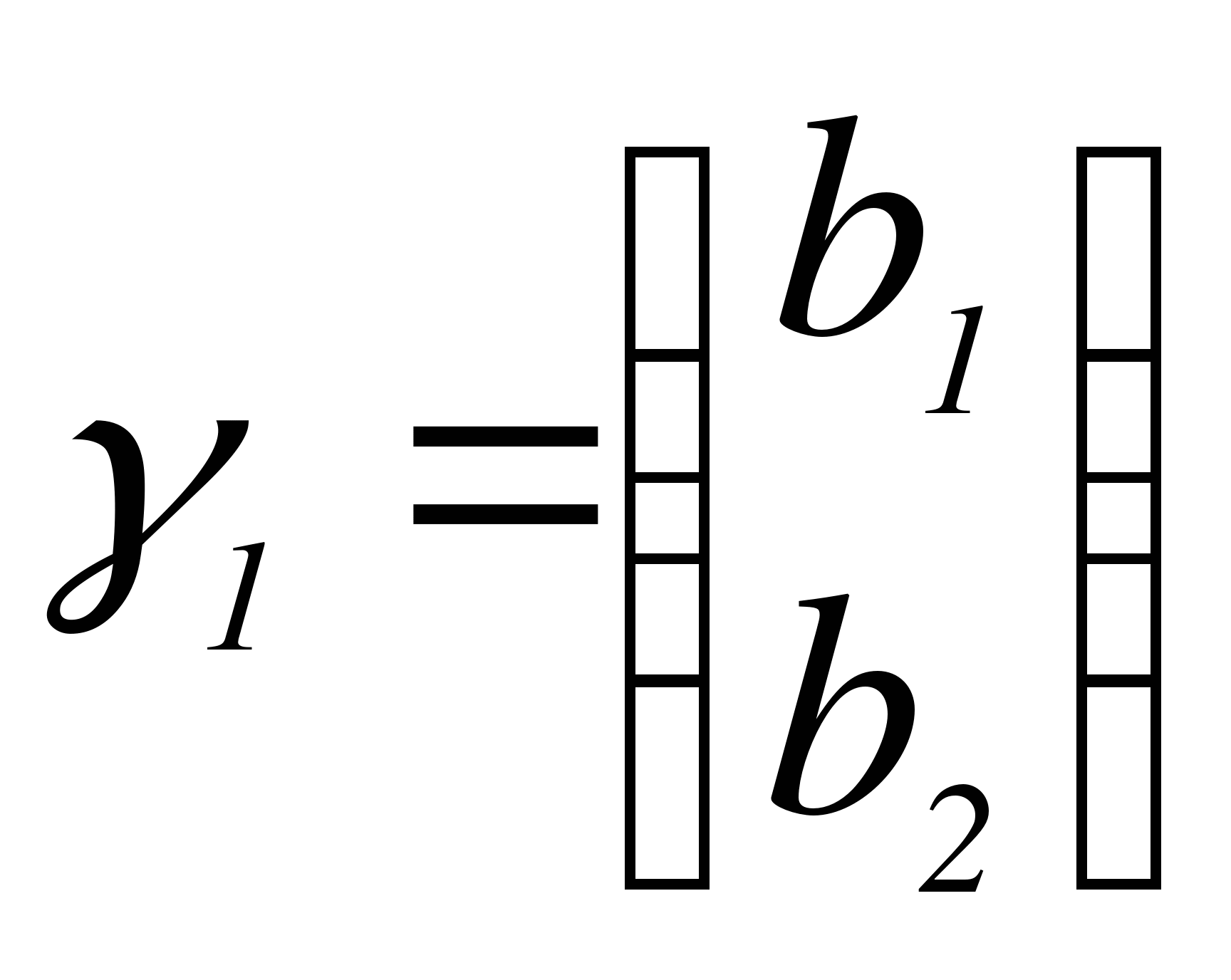 - собственный вектор матрицы А, соответствующий
- собственный вектор матрицы А, соответствующий 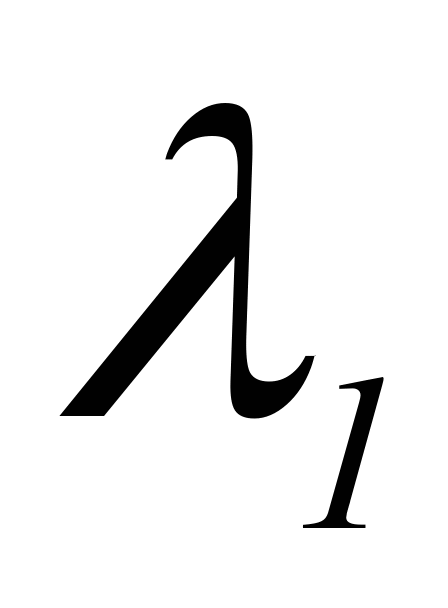 , т.е
, т.е 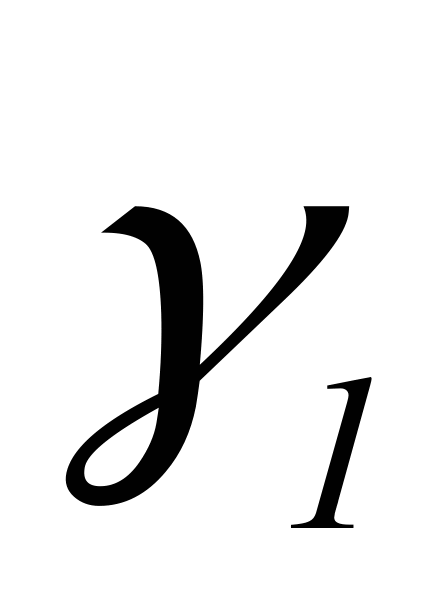 удовлетворяет системе
удовлетворяет системе 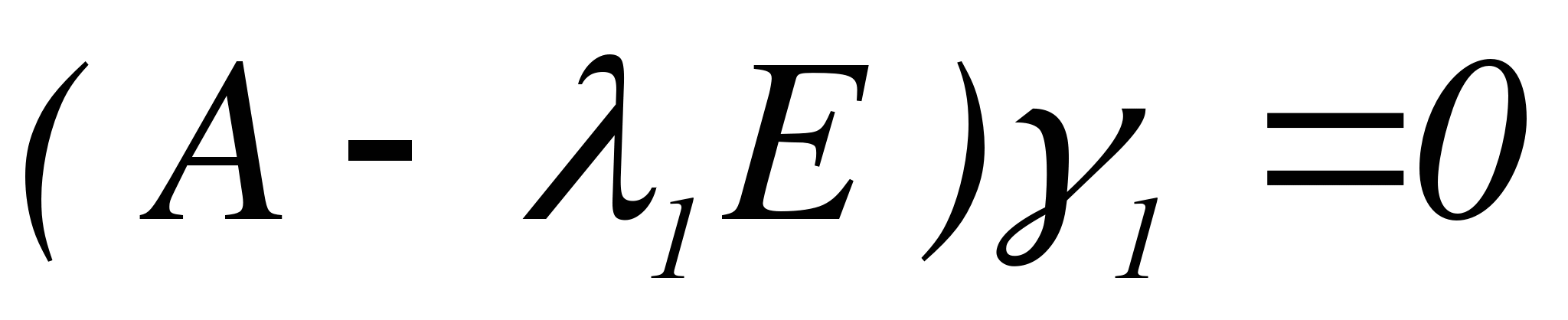 .
.
Тогда
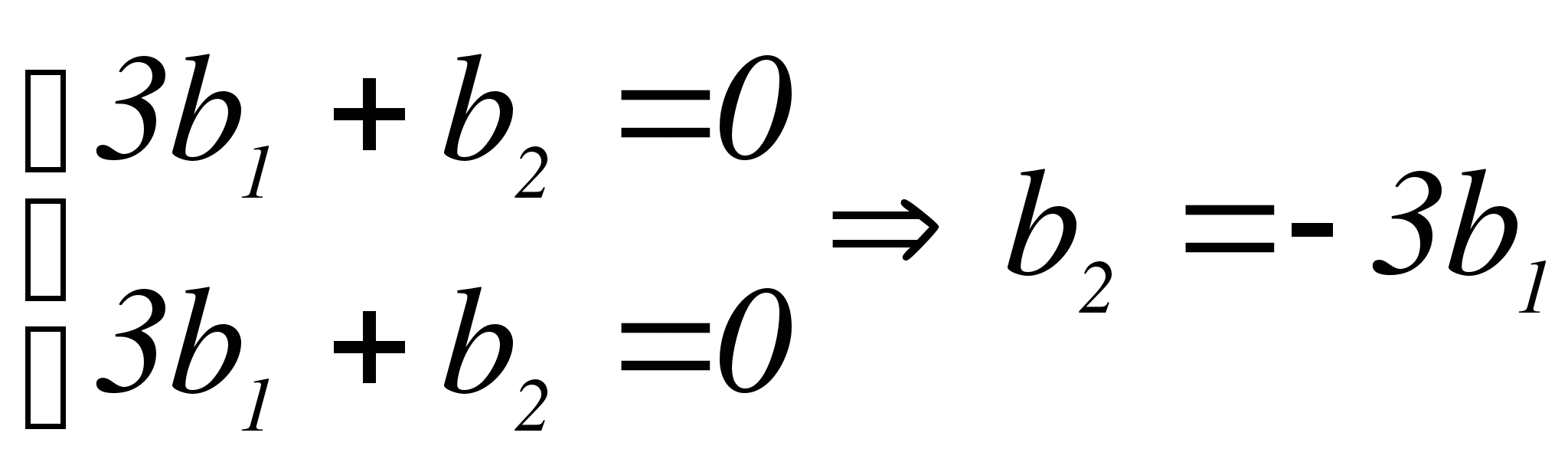
За 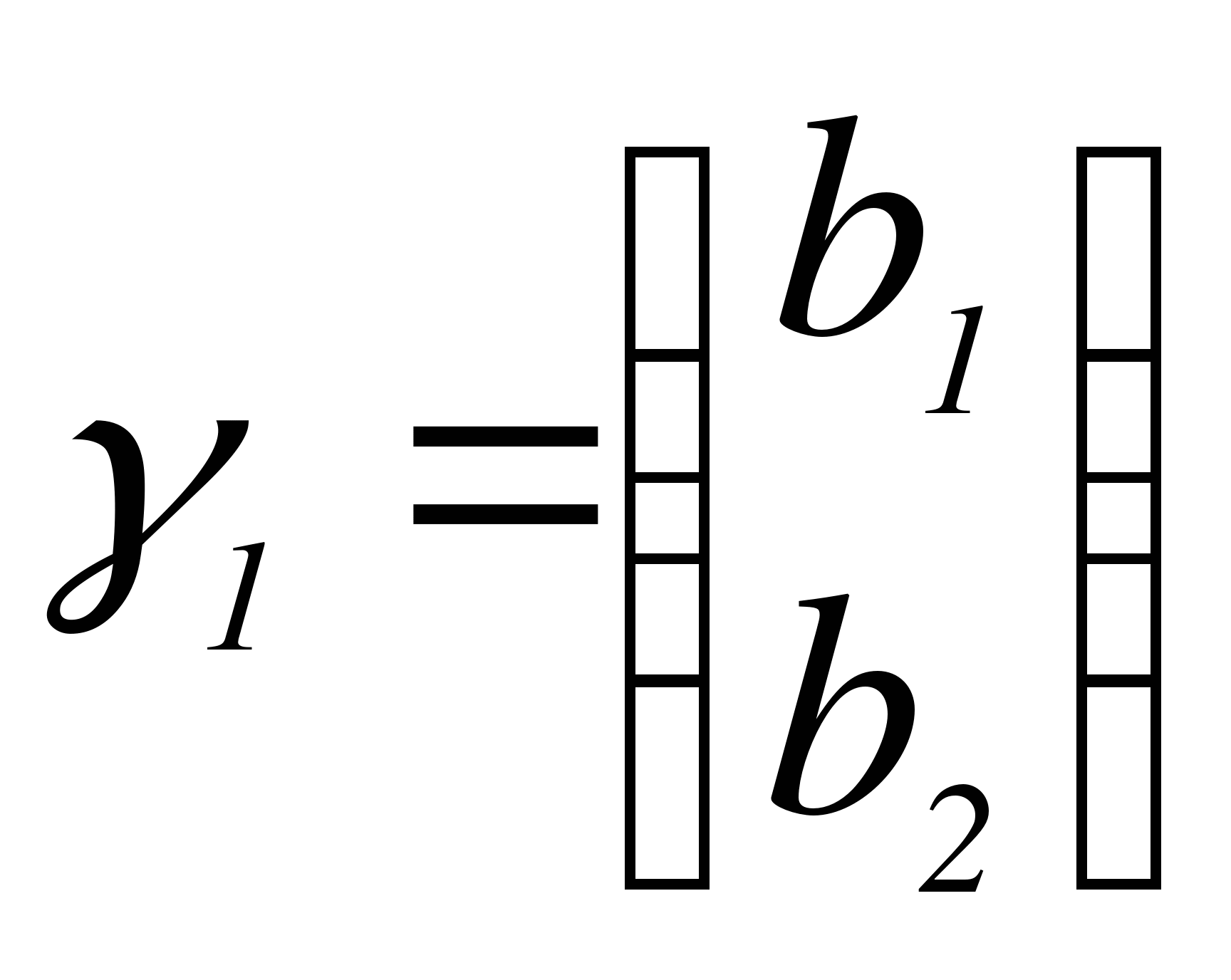 возьмем
возьмем 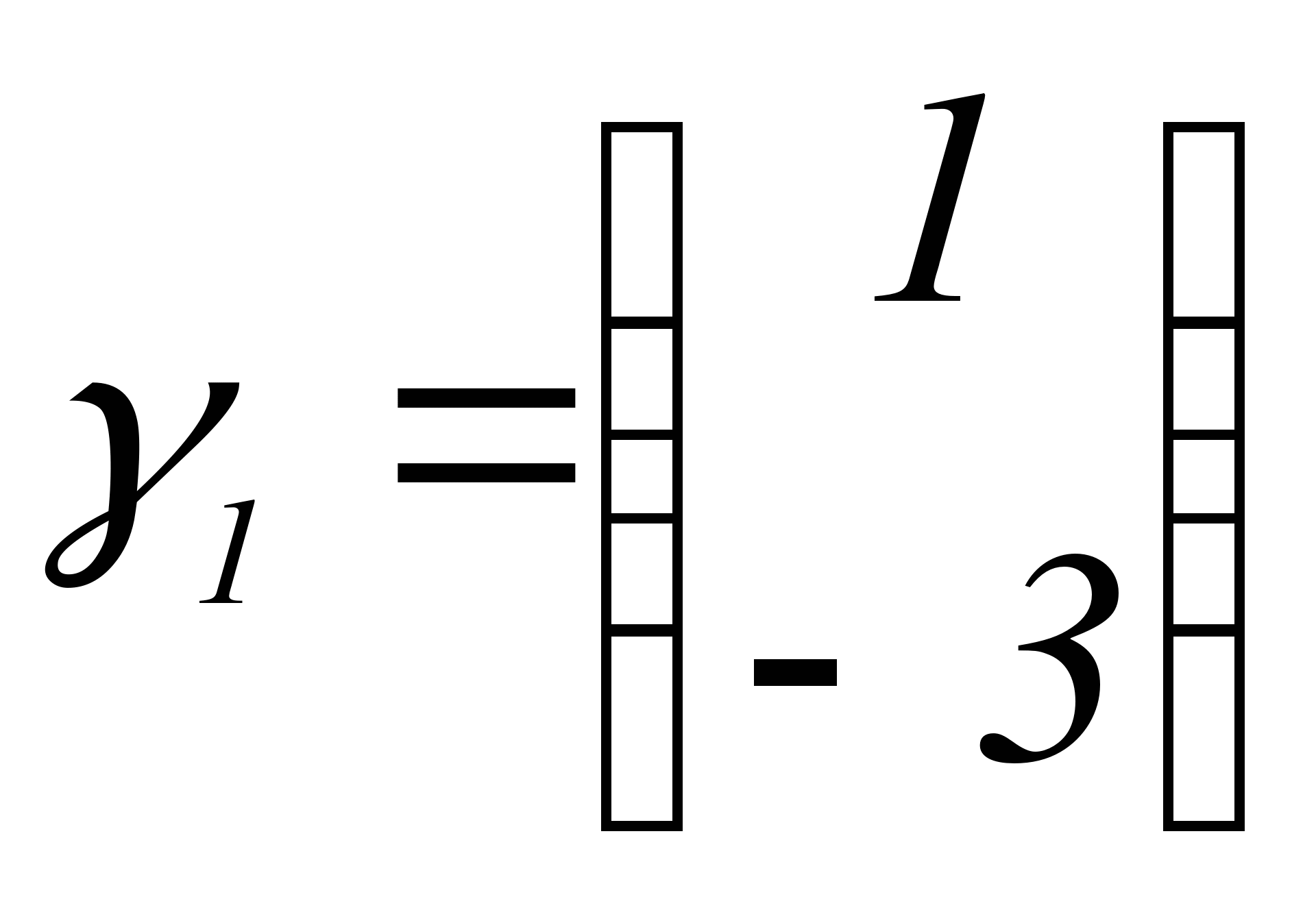 .
. 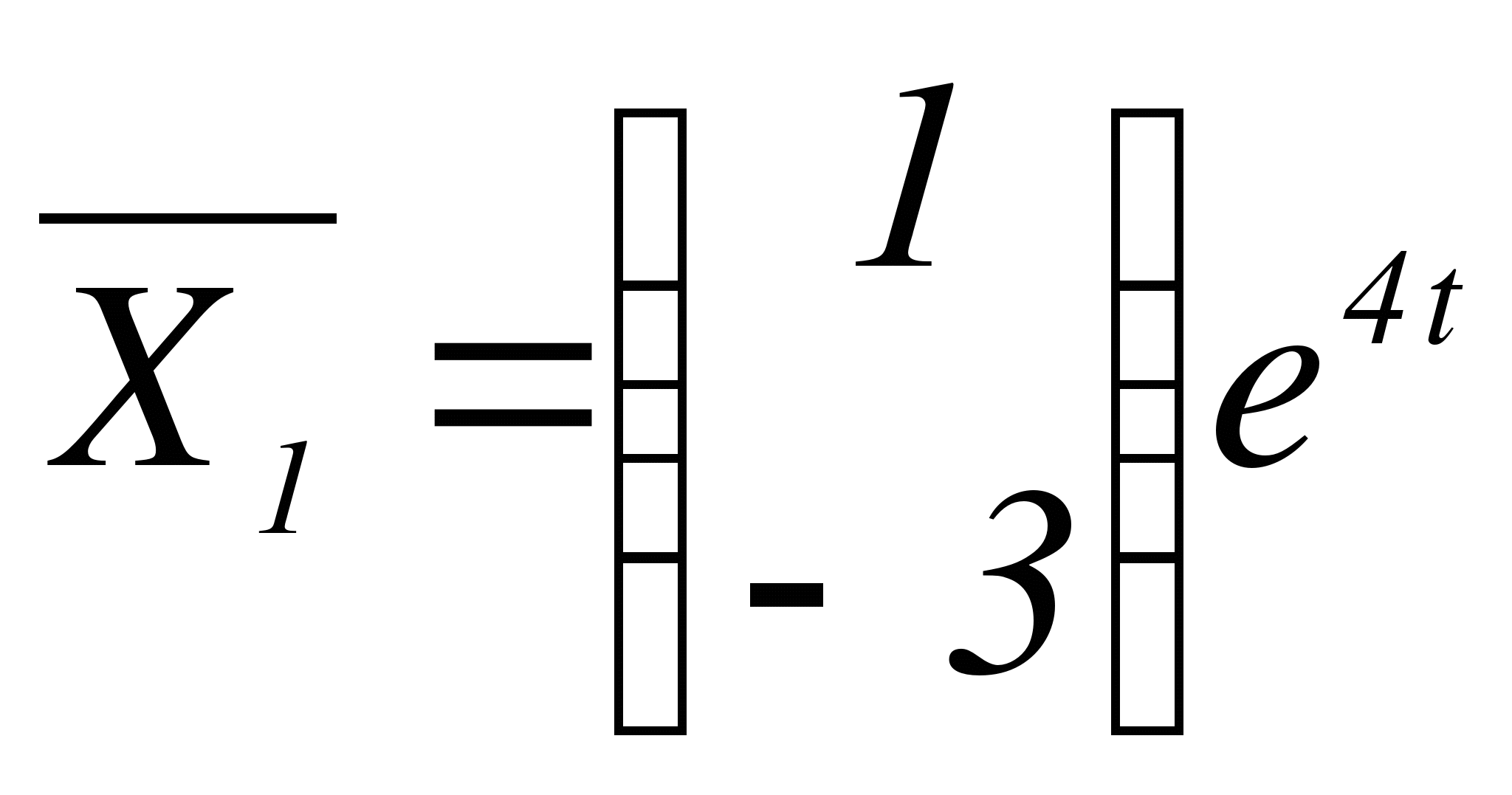
Строим 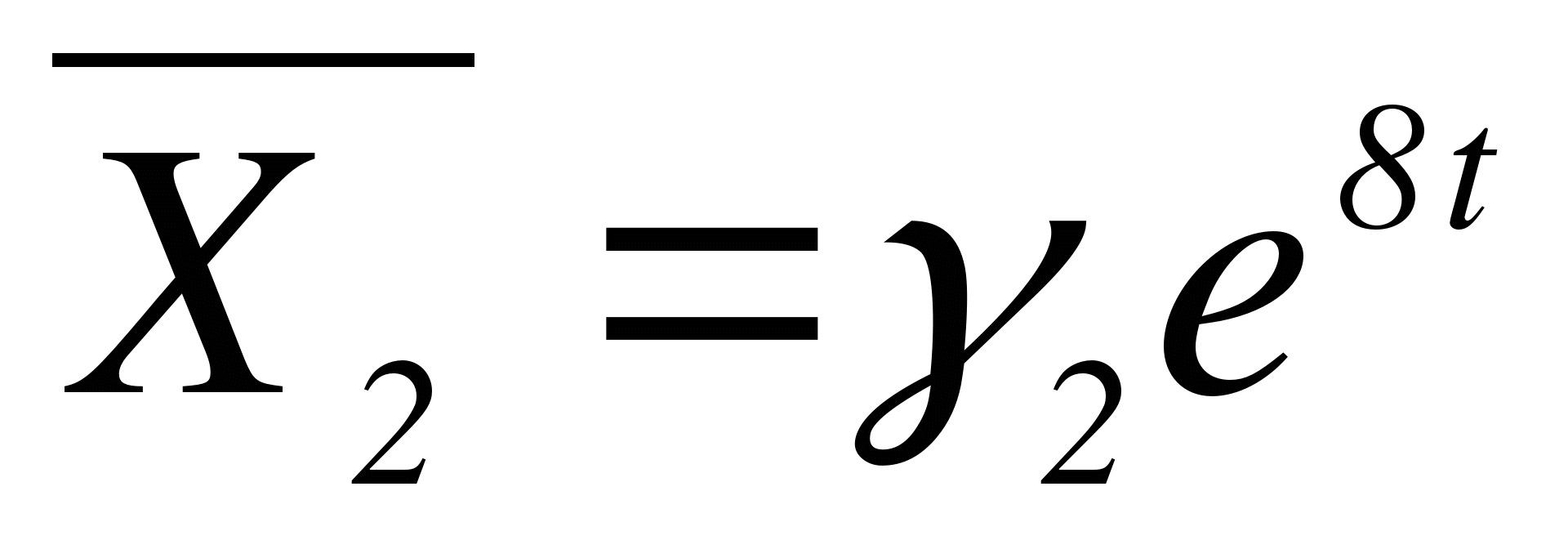 , где
, где 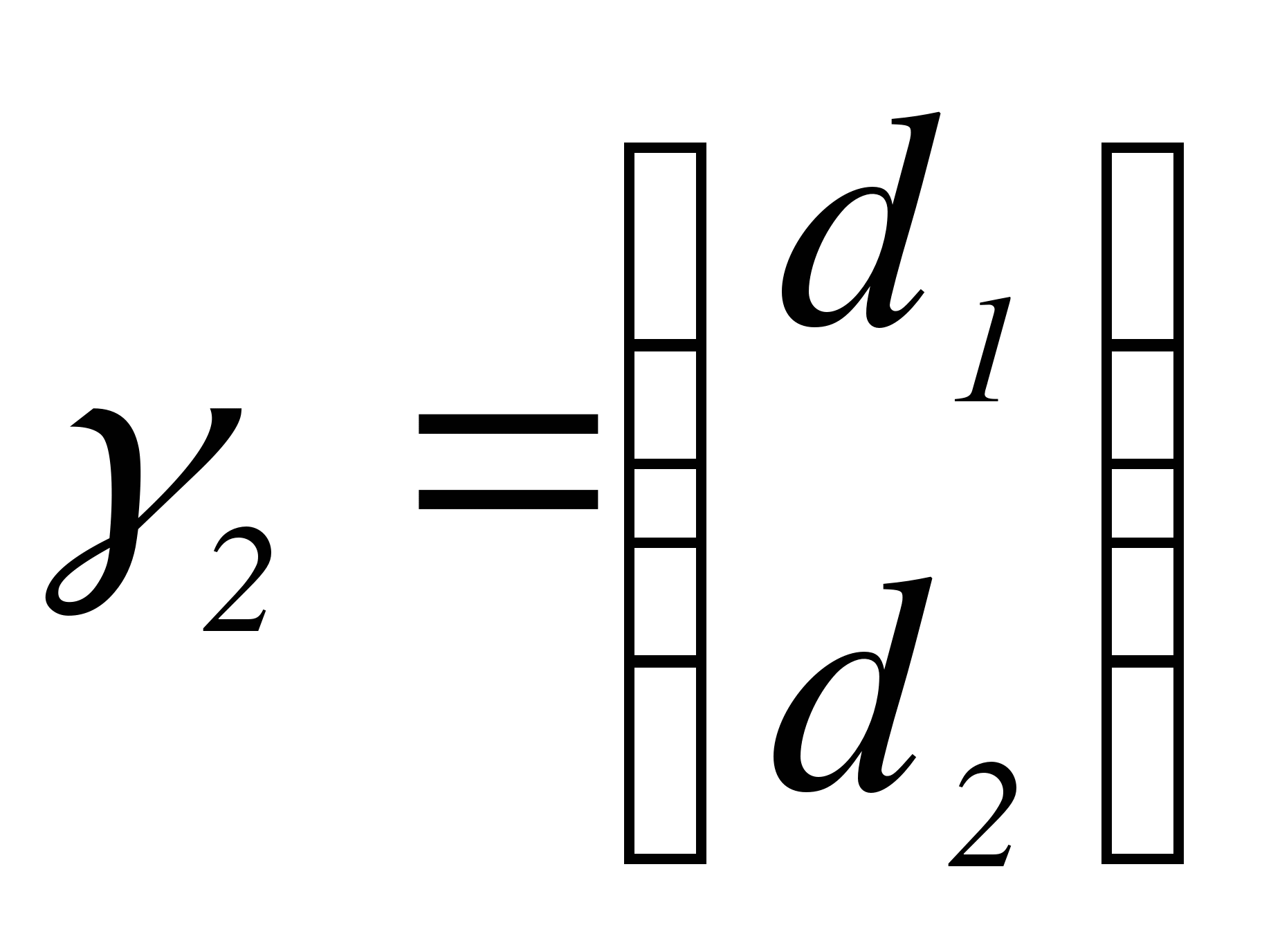 - собственный вектор матрицы А, соответствующий
- собственный вектор матрицы А, соответствующий 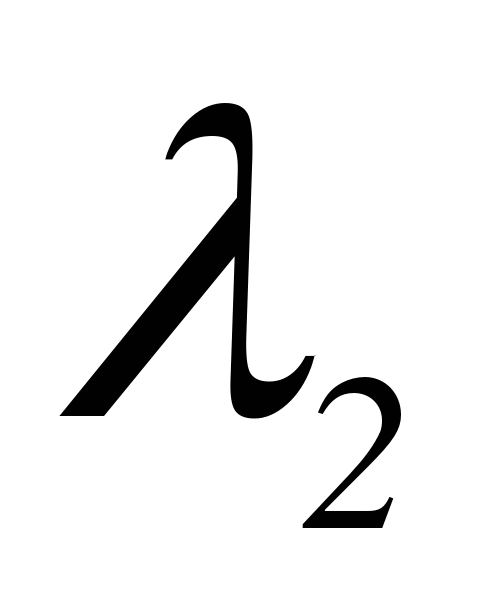 , т.е
, т.е 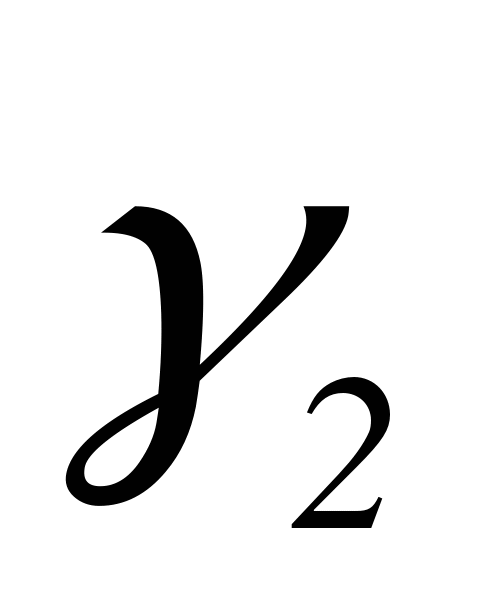 удовлетворяет системе
удовлетворяет системе 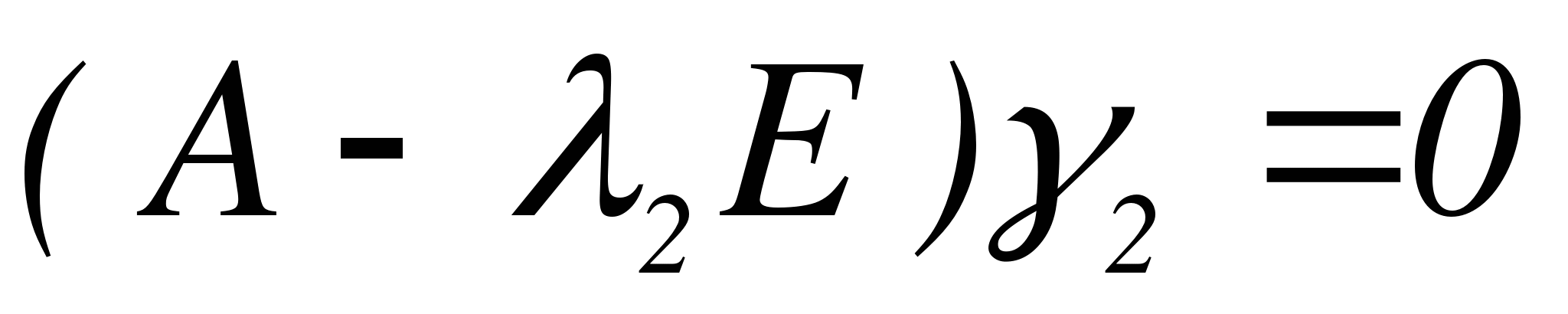 .
.
Тогда
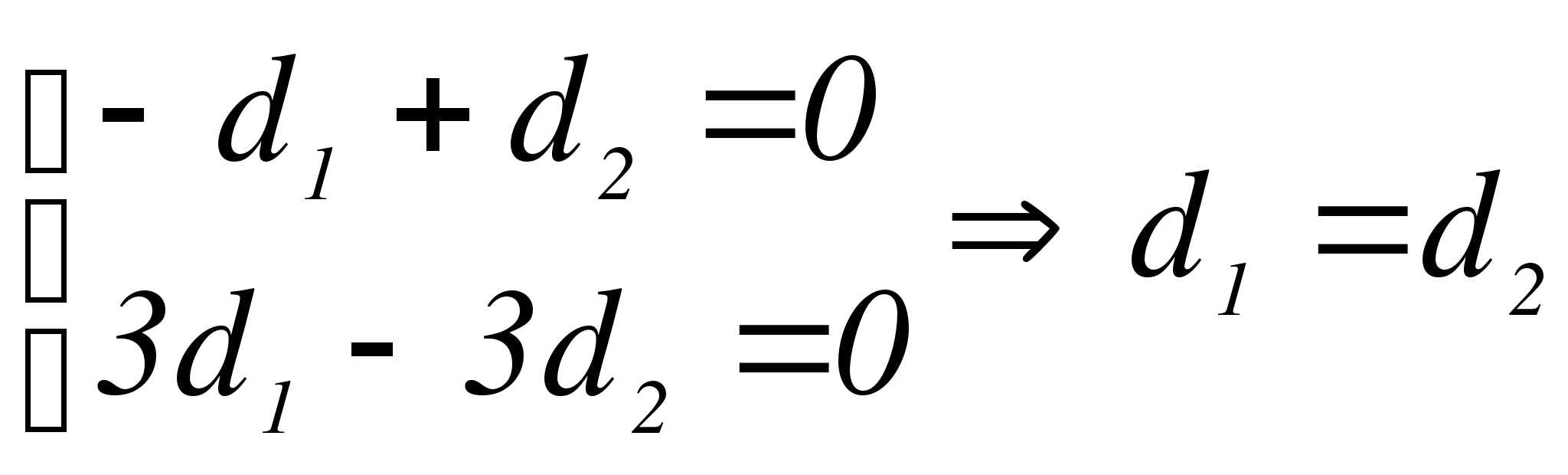
За 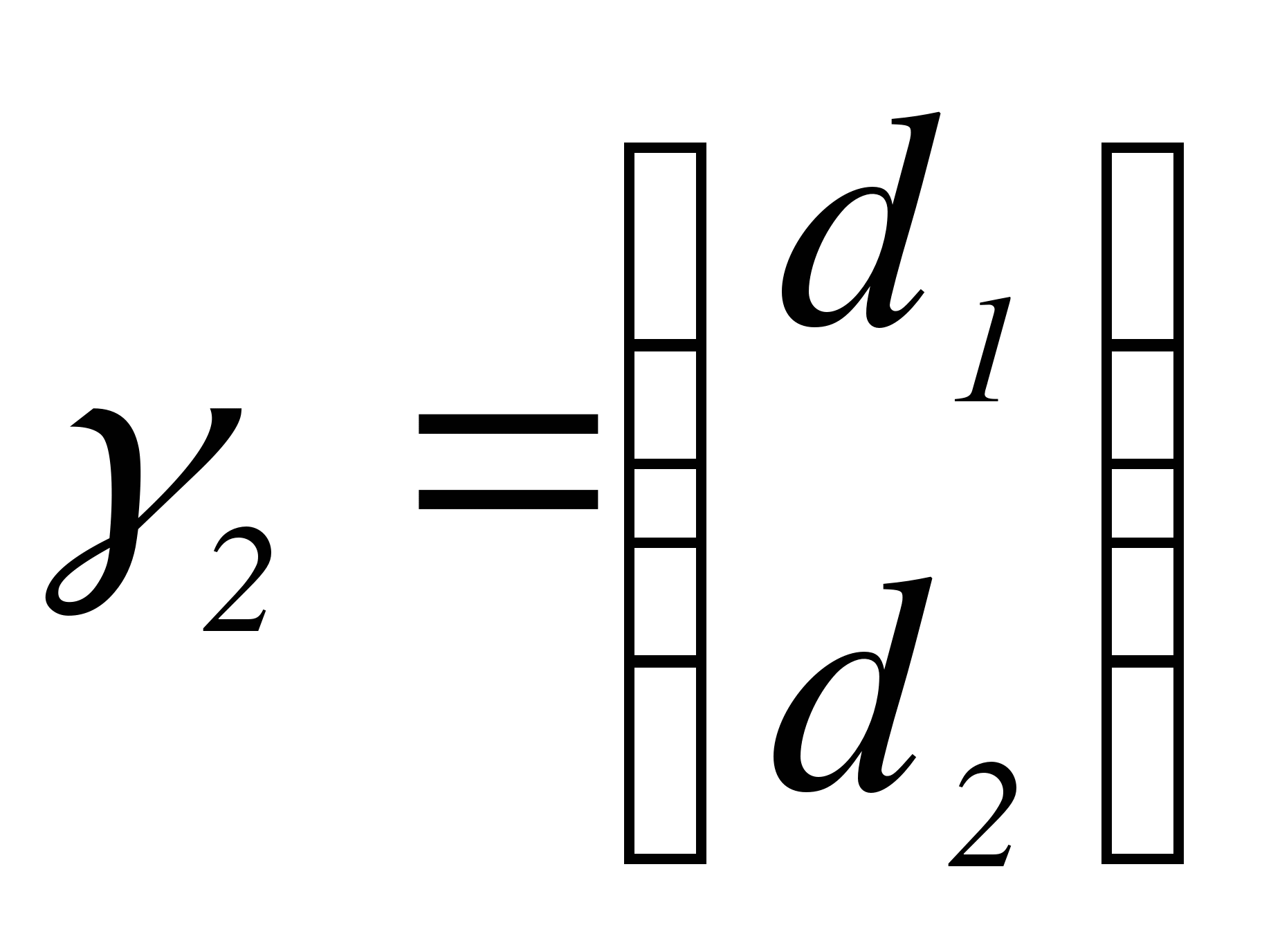 возьмем
возьмем 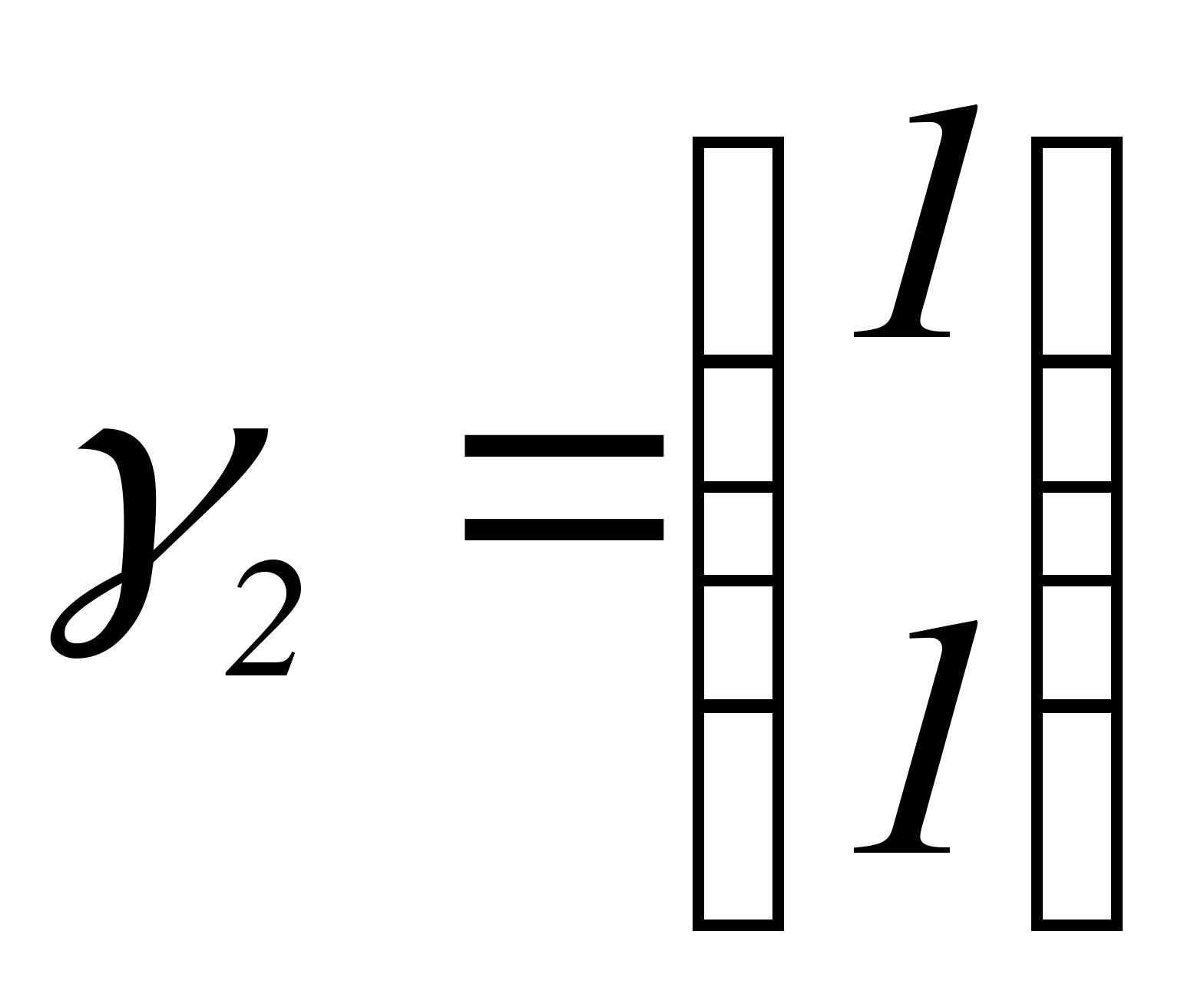 .
. 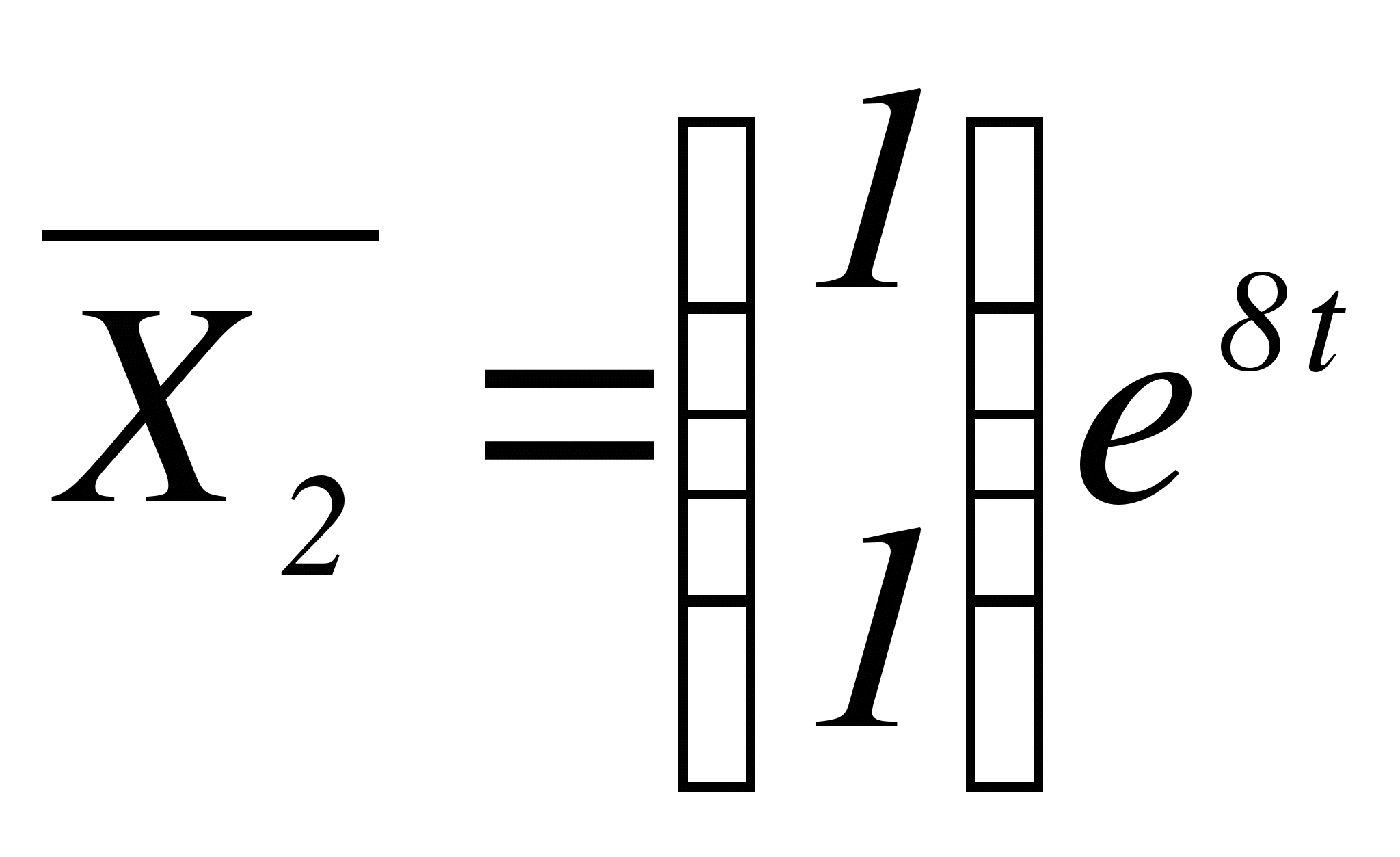
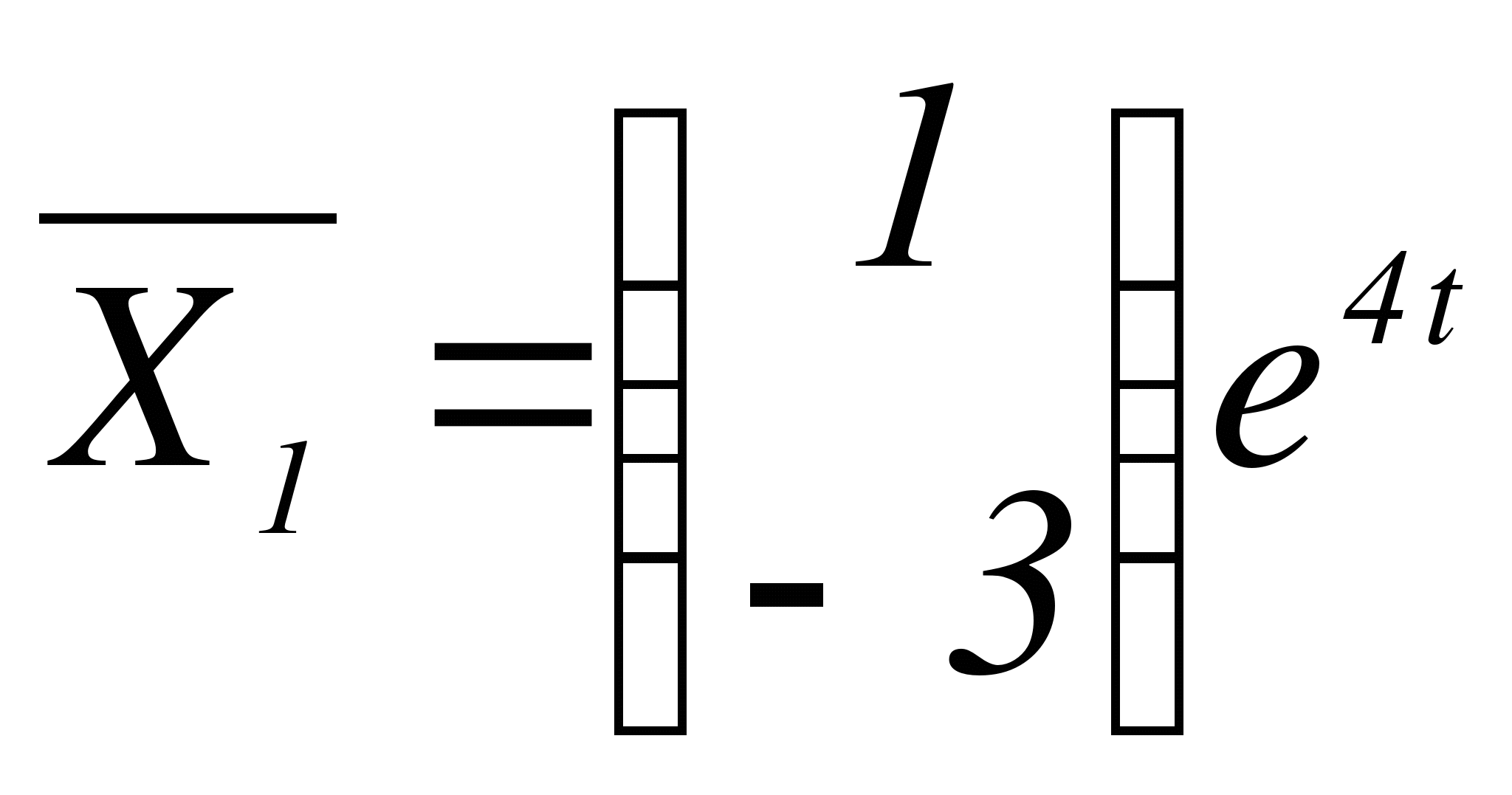 ,
, 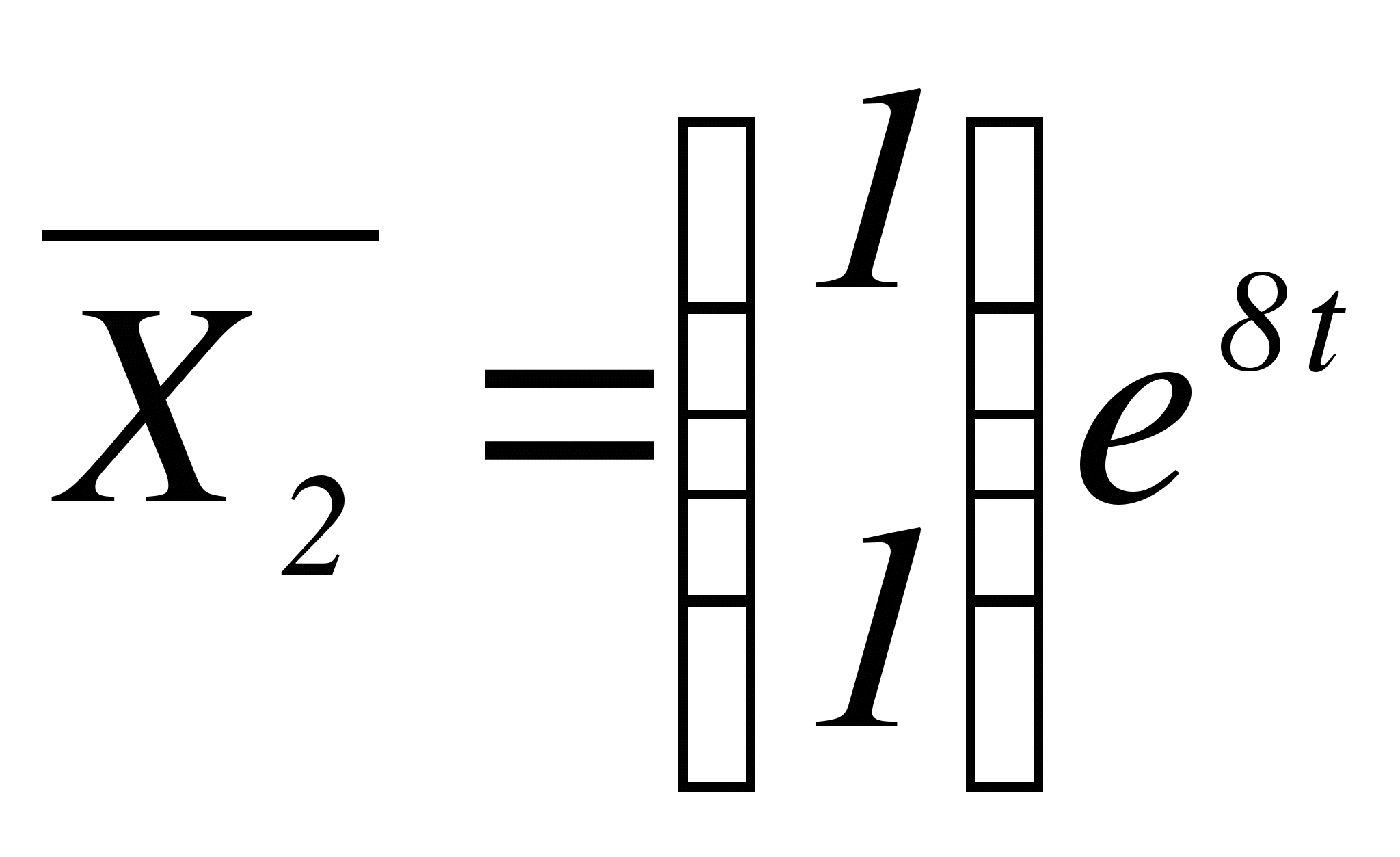 - фундаментальная система решений. Запишем общее решение однородной системы:
- фундаментальная система решений. Запишем общее решение однородной системы: 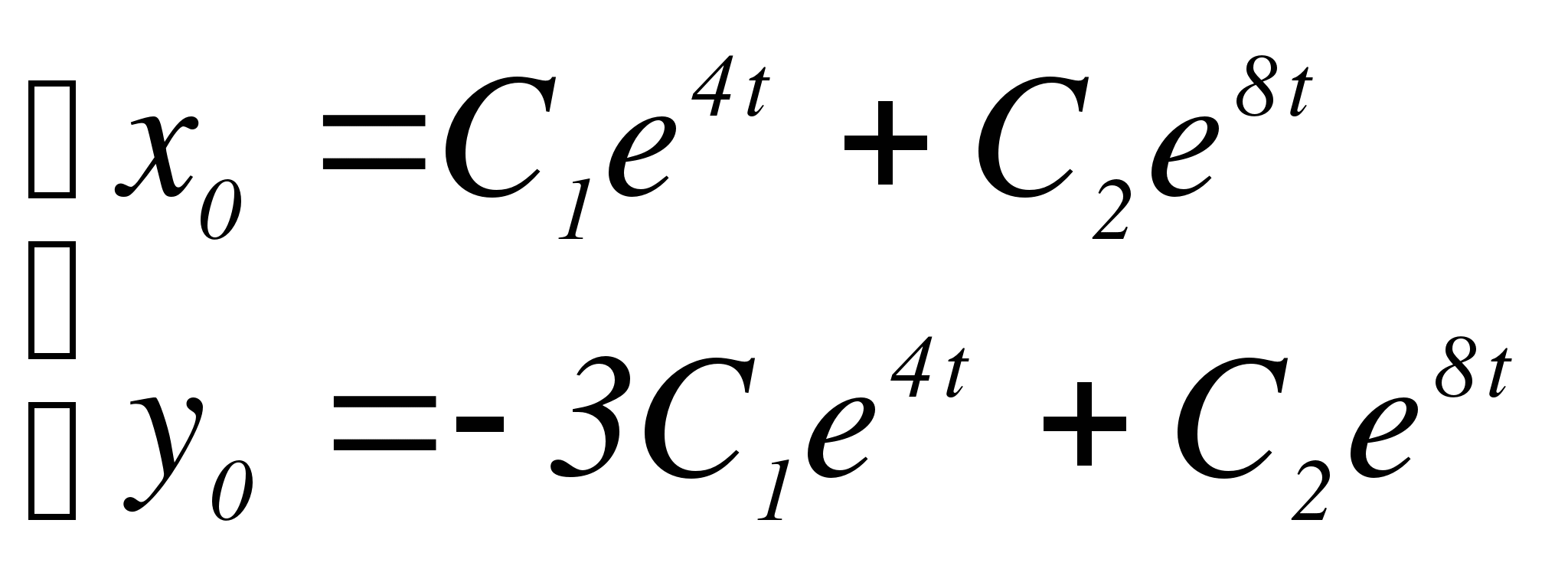
В соответствии с методом вариации постоянных, будем считать, что C1, C2 являются функциями переменной t:
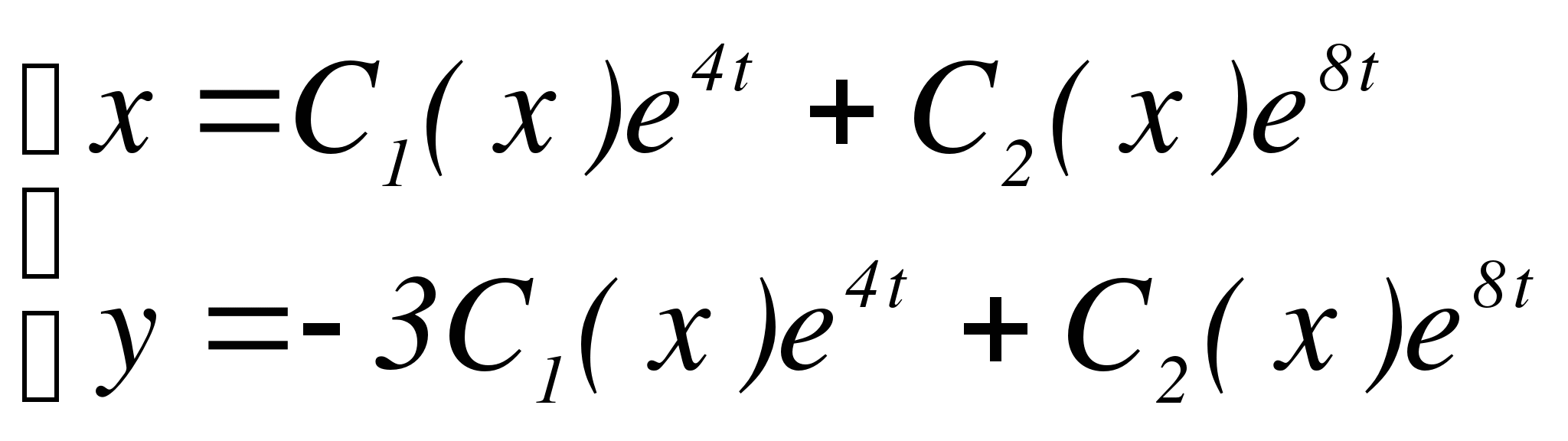
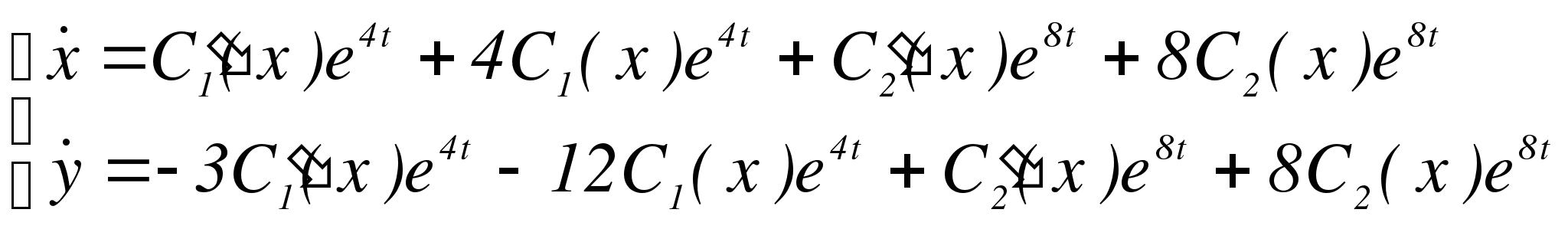
Подставим в систему:
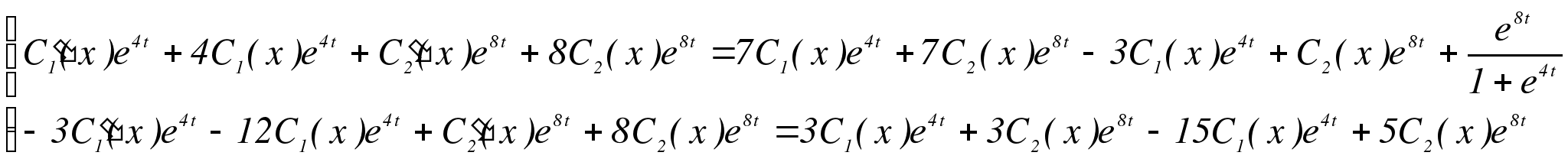
Получим:
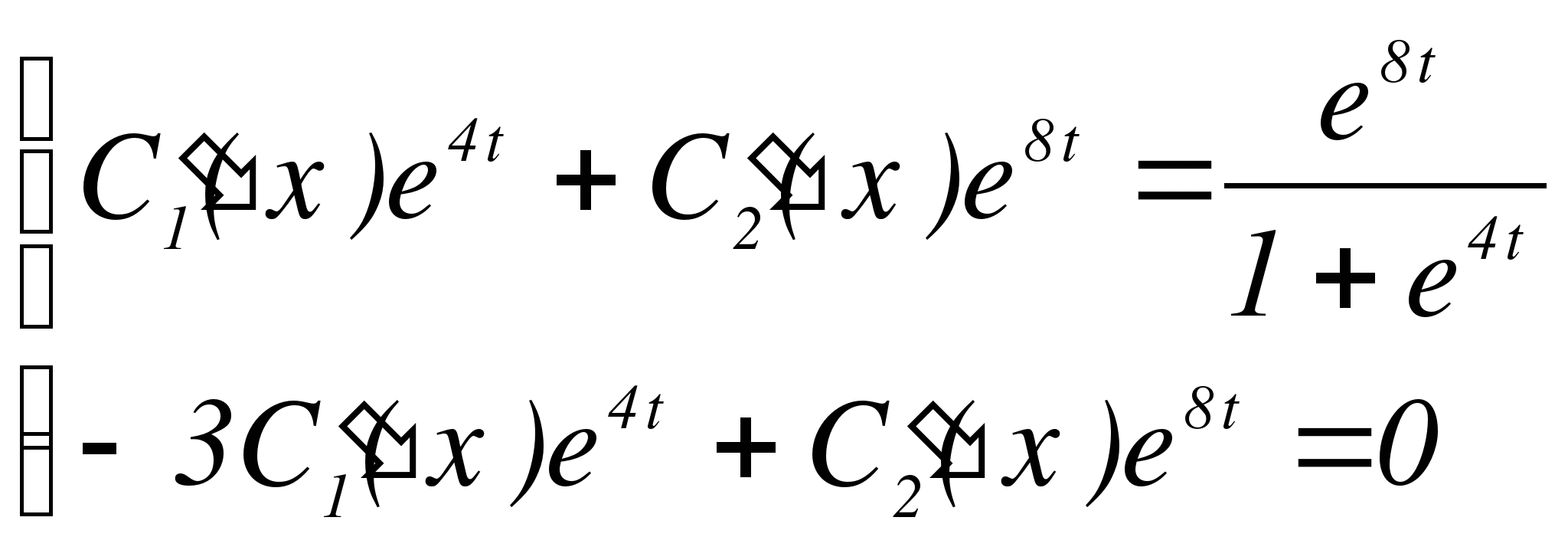
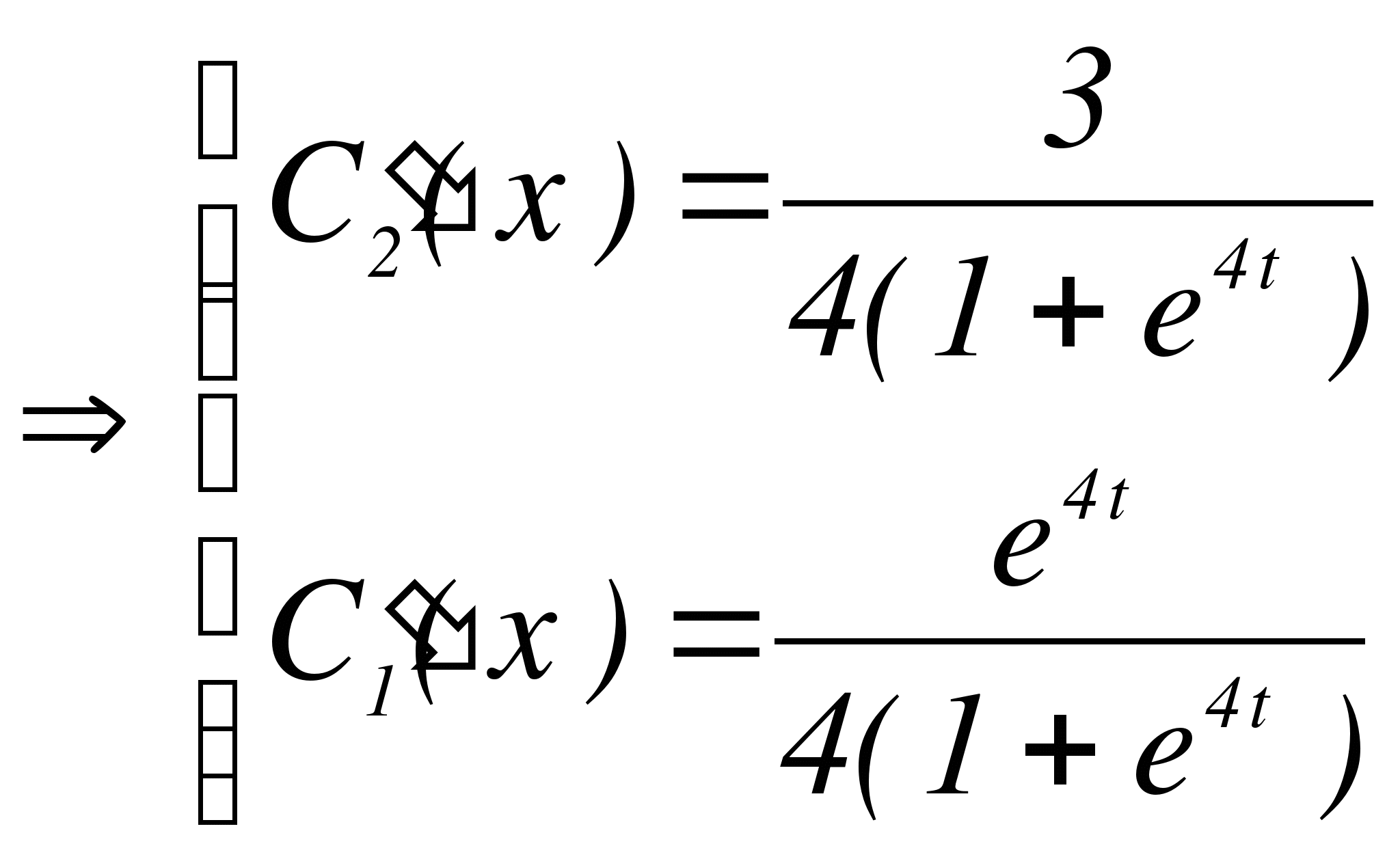
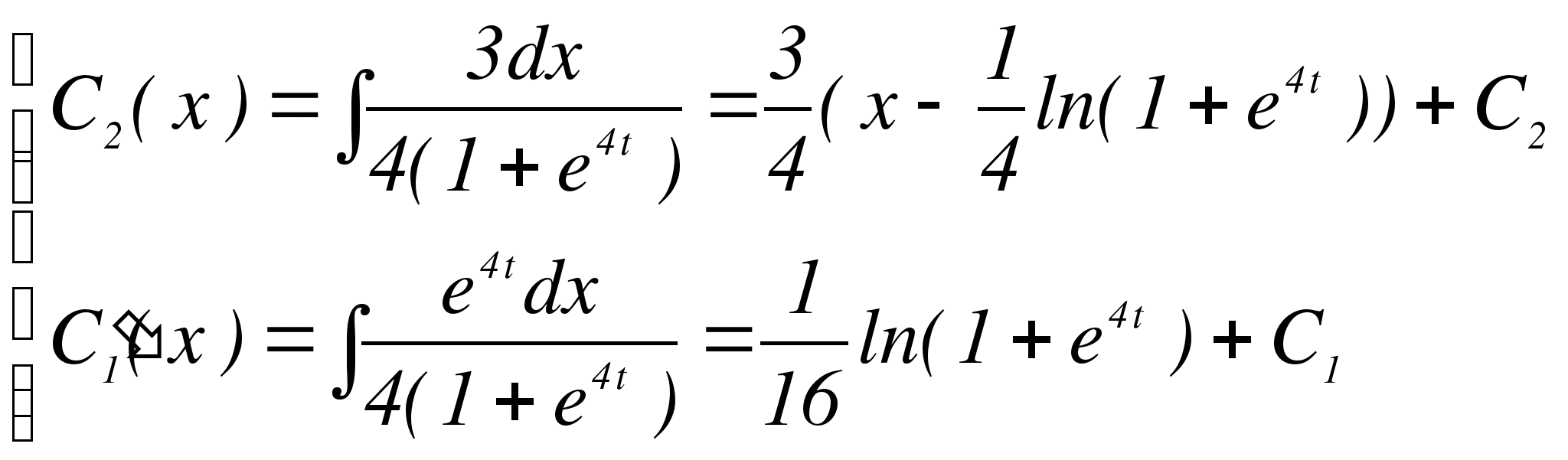
Тогда общее решение исходной неоднородной системы будет:
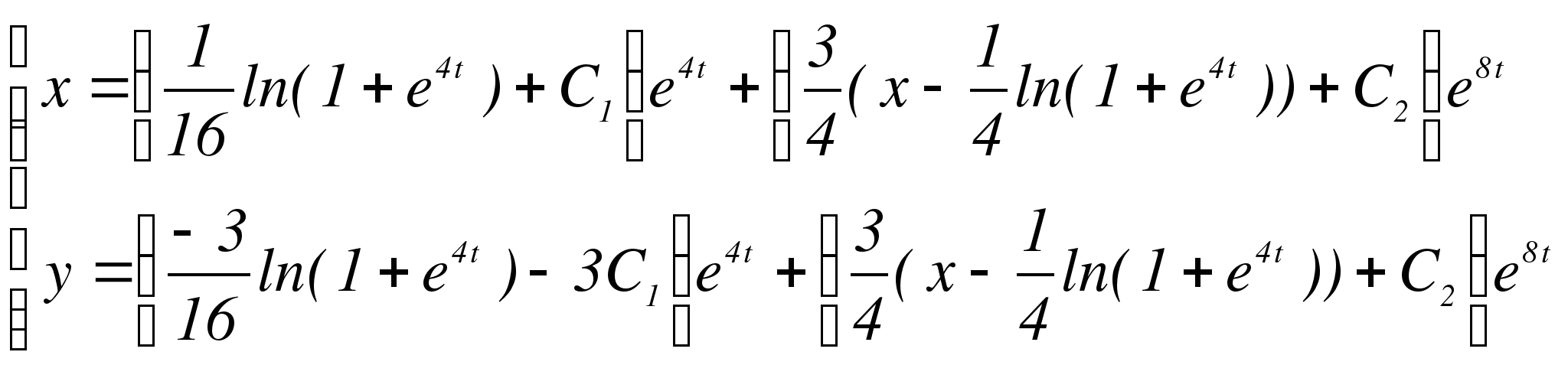
Ответ. 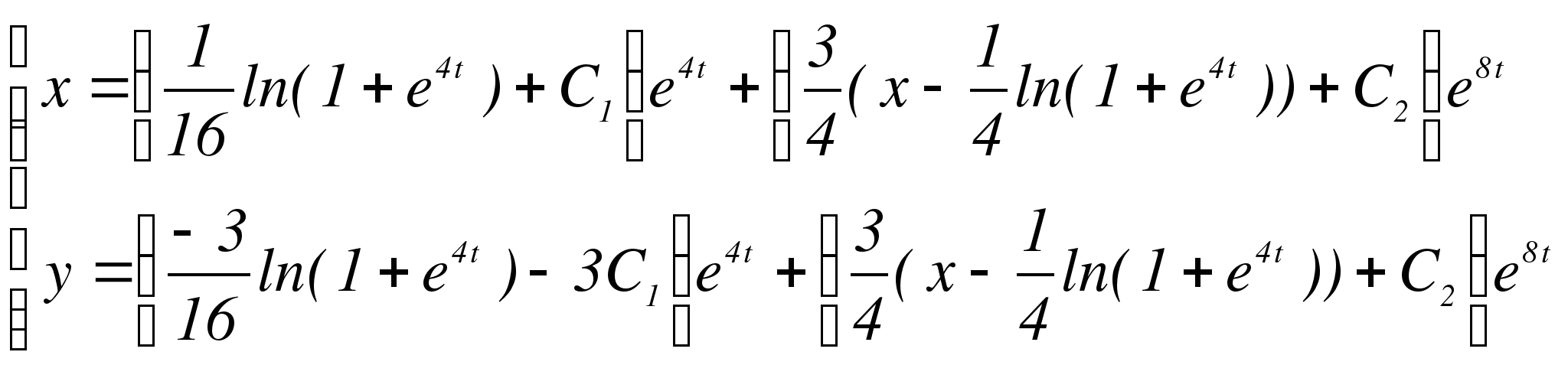 - общее решение линейной неоднородной системы
- общее решение линейной неоднородной системы
infourok.ru
5.1-5.30. Найдите общее решение дифференциальных уравнений
| 5.1. | a) b) c) | 5.2. | a) b) c) |
| 5.3. | a) b) c) | 5.4. | a) b) c) |
| 5.5. | a) b) c) | 5.6. | a) b) c) |
| 5.7. | a) b) c) | 5.8. | a) b) c) |
| 5.9. | a) b) c) | 5.10. | a) b) c) |
| 5.11. | a) b) c) | 5.12. | a) b) c) |
| 5.13. | a) b) c) | 5.14. | a) b) c) |
| 5.15. | a) b) c) | 5.16. | a) b) c) |
| 5.17. | a) b) c) | 5.18. | a) b) c) |
| 5.19. | a) b) c) | 5.20. | a) b) c) |
| 5.21. | a) b) c) | 5.22. | a) b) c) |
| 5.23. | a) b) c) | 5.24. | a) b) c) |
| 5.25. | a) b) c) | 5.26. | a) b) c) |
| 5.27. | a) b) c) | 5.28. | a) b) c) |
| 5.29. | a) b) c) | 5.30. | a) b) c) |
6.1-6.30. Найдите общее решение однородных дифференциальных уравнений.
| 6.1 | a) b) c) | 6.2. | a) b) c) |
| 6.3. | a) b) c) | 6.4. | a) b) c) |
| 6.5. | a) b) c) | 6.6. | a) b) c) |
| 6.7. | a) b) c) | 6.8. | a) b) c) |
| 6.9. | a) b) c) | 6.10. | a) b) c) |
| 6.11. | a) b) c) | 6.12. | a) b) c) |
| 6.13. | a) b) c) | 6.14. | a) b) c) |
| 6.15. | a) b) c) | 6.16. | a) b) c) |
| 6.17. | a) b) c) | 6.18. | a) b) c) |
| 6.19. | a) b) c) | 6.20. | a) b) c) |
| 6.21. | a) b) c) | 6.22. | a) b) c) |
| 6.23. | a) b) c) | 6.24. | a) b) c) |
| 6.25. | a) b) c) | 6.26. | a) b) c) |
| 6.27. | a) b) c) | 6.28. | a) b) c) |
| 6.29. | a) b) c) | 6.30. | a) b) c) |
7.1-7.30. Железнодорожная платформа массы m, выведенная из положения равновесия, совершает колебания в вертикальной плоскости под действием вынуждающей силы 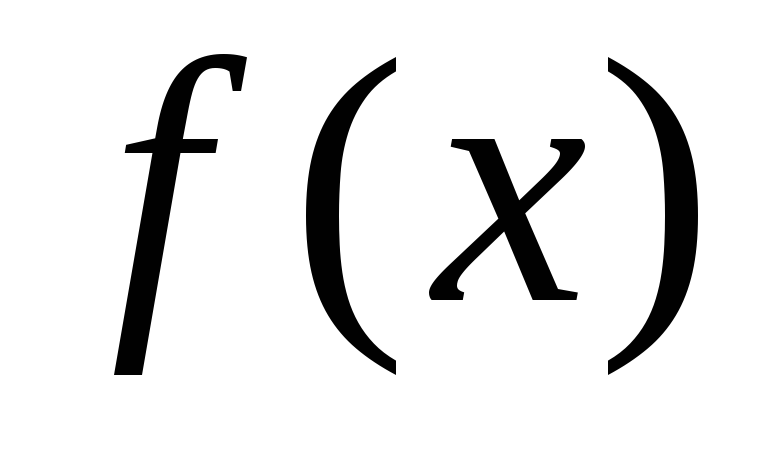 , гдех — время. Найдите зависимость отклонения платформы от положения равновесия
, гдех — время. Найдите зависимость отклонения платформы от положения равновесия 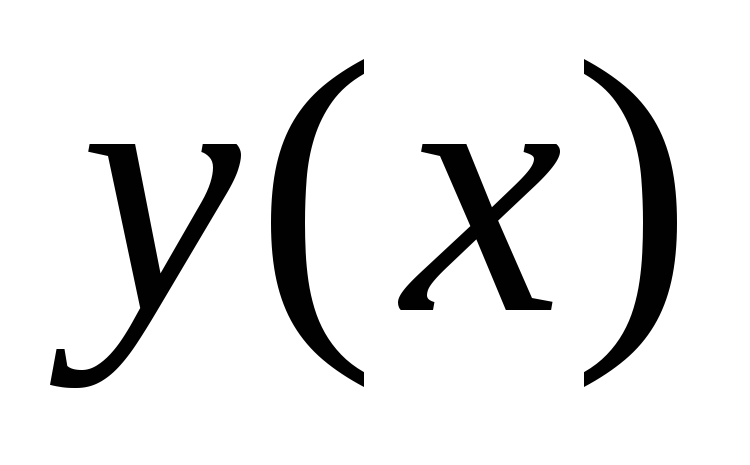 от времени, если сопротивление среды пропорционально скорости, с коэффициентом пропорциональности
от времени, если сопротивление среды пропорционально скорости, с коэффициентом пропорциональности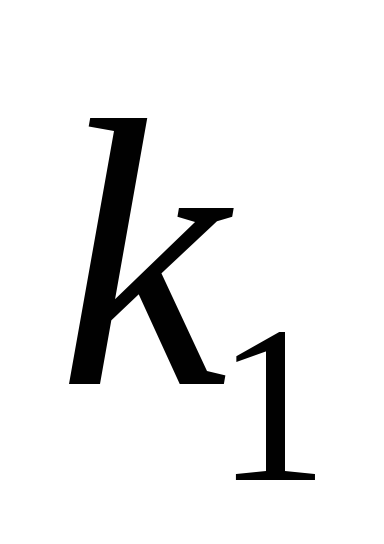 , а восстанавливающая сила рессоры, стремящаяся вернуть платформу в положение равновесия, пропорциональна величине отклонения, с коэффициентом пропорциональности
, а восстанавливающая сила рессоры, стремящаяся вернуть платформу в положение равновесия, пропорциональна величине отклонения, с коэффициентом пропорциональности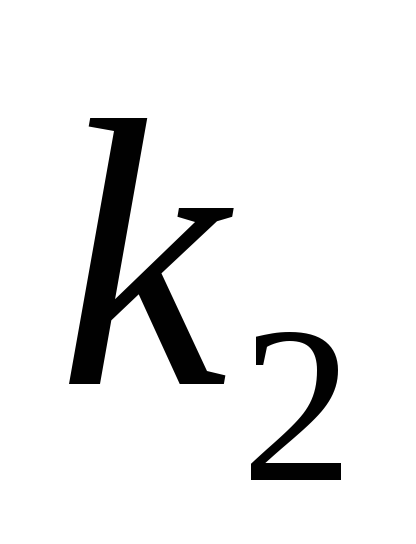 . Считается, что в момент времени
. Считается, что в момент времени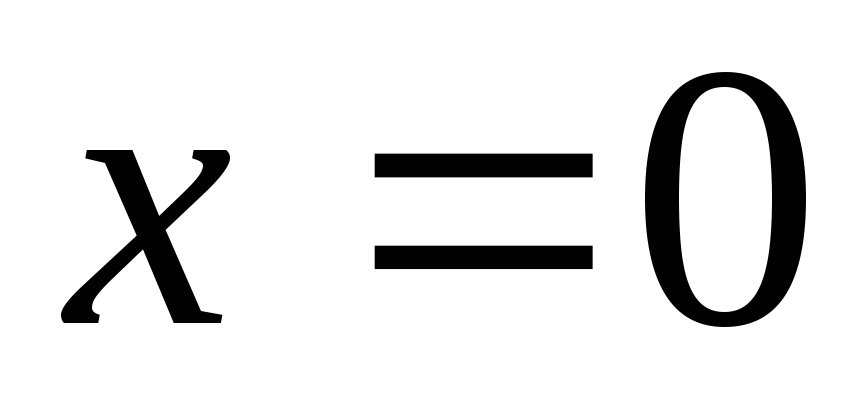 ,
,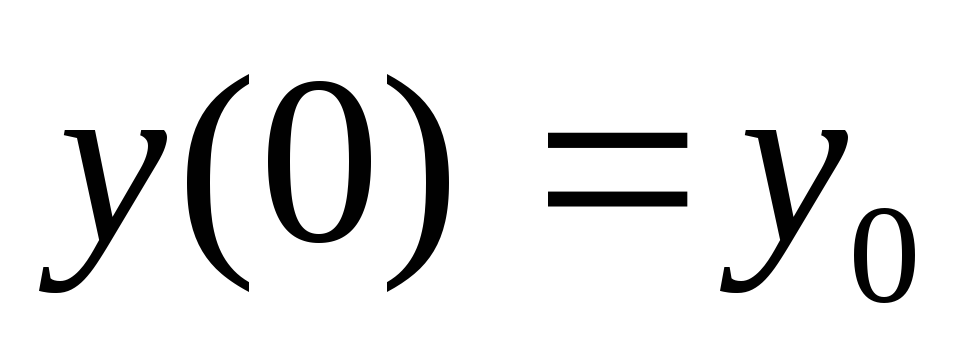 ,
,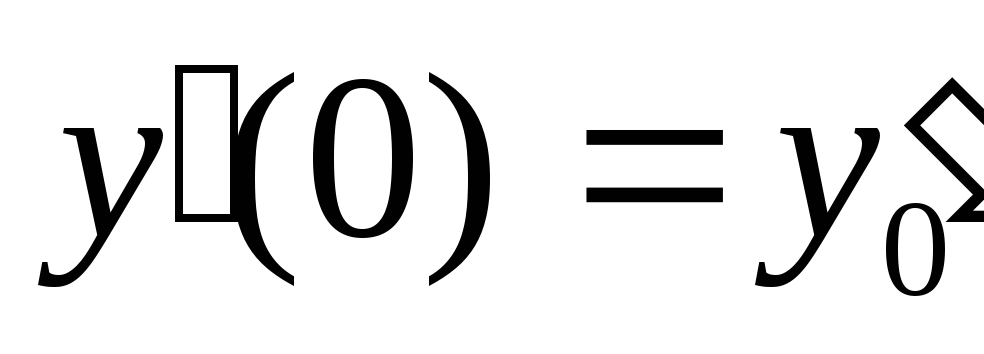 .
.
| № | m |
|
|
|
|
|
| 7.1 | 1 | -2 | 2 |
|
|
|
| 7.2 | 1 | -6 | 9 |
|
|
|
| 7.3 | 1 | -1 | 0 |
|
|
|
| 7.4 | 1 | 2 | -3 |
|
|
|
| 7.5. | 1 | 4 | 5 |
|
|
|
| 7.6. | 1 | 0 | -4 |
|
|
|
| 7.7. | 1 | 2 | 1 |
|
|
|
| 7.8. | 1 | -3 | -4 |
|
|
|
| 7.9. | 1 | 0 | -9 |
|
|
|
| 7.10. | 1 | 5 | 0 |
|
|
|
| 7.11. | 1 | -2 | 1 |
|
|
|
| 7.12. | 1 | 0 | 4 |
|
|
|
| 7.13. | 1 | 6 | -16 |
|
|
|
| № | m |
|
|
|
|
|
| 7.14. | 1 | 3 | 0 |
|
|
|
| 7.15. | 1 | -3 | 4 |
|
|
|
| 7.16. | 1 | -6 | 13 |
|
|
|
| 7.17. | 1 | 4 | 20 |
|
|
|
| 7.18. | 1 | 1 | 0 |
|
|
|
| 7.19. | 1 | 0 | -16 |
|
|
|
| 7.20. | 1 | -4 | 5 |
|
|
|
| 7.21. | 1 | 5 | -6 |
|
|
|
| 7.22. | 1 | 3 | -4 |
|
|
|
| 7.23. | 1 | 9 | 0 |
|
|
|
| 7.24. | 1 | 0 | 1 |
|
|
|
| 7.25. | 1 | 7 | -8 |
|
|
|
| 7.26. | 1 | -6 | 5 |
|
|
|
| 7.27. | 1 | -25 | 0 |
|
|
|
| 7.28. | 1 | 0 | 16 |
|
|
|
| 7.29. | 1 | -5 | 4 |
|
|
|
| 7.30. | 1 | 0 | 4 |
|
|
|
8.1-8.30. Дана система дифференциальных уравнений
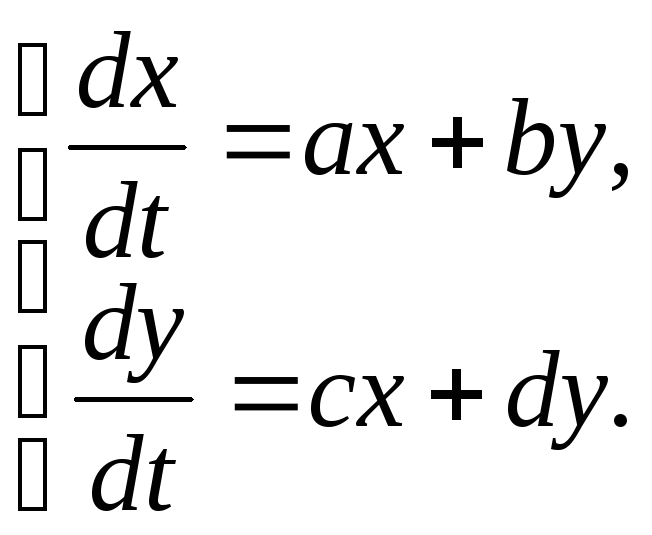
С помощью характеристического уравнения найти ее общее решение.
| № | a | b | c | d | № | a | b | c | d |
| 8.1. | -1 | 5 | 1 | 3 | 8.2. | -2 | 1 | -3 | 2 |
| 8.3. | 6 | 3 | -8 | -5 | 8.4. | 2 | 1 | -6 | 3 |
| 8.5. | 2 | 5 | 1 | 2 | 8.6. | 6 | -1 | 3 | 2 |
| 8.7. | -7 | 5 | 4 | -8 | 8.8. | -1 | 2 | -3 | 4 |
| 8.9. | -1 | 1 | 2 | -2 | 8.10. | -1 | -2 | 3 | 4 |
| 8.11. | -1 | -2 | 1 | 4 | 8.12. | -2 | 1 | 4 | 1 |
| 8.13. | 3 | -2 | 1 | 0 | 8.14. | 4 | 2 | 4 | 6 |
| 8.15. | -5 | -8 | -3 | -3 | 8.16. | 8 | -3 | 2 | 1 |
| 8.17. | -4 | 2 | 4 | -2 | 8.18. | 3 | 1 | 1 | 3 |
| 8.19. | -3 | 6 | 2 | 8 | 8.20. | 2 | 3 | 5 | 4 |
| 8.21. | 2 | 1 | 3 | 4 | 8.22. | 1 | 2 | 3 | 6 |
| 8.23. | 1 | -1 | -4 | 1 | 8.24. | 5 | 4 | 4 | 5 |
| 8.25. | -1 | 8 | 1 | 1 | 8.26. | 1 | -2 | -4 | 3 |
| 8.27. | -2 | -3 | -1 | 0 | 8.28. | 1 | -2 | -1 | 0 |
| 8.29. | 1 | -1 | -4 | 4 | 8.30. | 3 | -2 | 2 | 8 |
studfiles.net
Московский авиационный институт
(государственный технический университет)
Филиал «Восход»
Кафедра МиПОИС
Курсовая работа
по курсу: Дифференциальные уравнения
Студент гр. ДА 2-40
Воронцов О. В.
Байконур 2005 г.
1. Теоретическая часть
Дифференциальные уравнения, приводящиеся к однородным
Дифференциальные уравнения, которые приводятся к однородным, имеют вид:
/>
Возможны три случая:
Когда C1=C2 =0
/>
Когда
/>
/>
/>
Когда
/>
Вводятся новые переменные u и υ так, чтобы правая часть исходного уравнения в этих переменных была однородной функцией нулевого порядка. А именно, делается замена x=u+h, y= υ+k и подбираются постоянные h и k таким образом, чтобы в правой части исходного уравнения после подстановки пропали свободные члены. При подстановке x=u+h, y= υ+k в дробь приравниваются нулю свободные члены числителя и знаменателя, то есть записываются два равенства:
/>
Определитель данной системы линейных алгебраических уравнений: />, не равен нулю по условию, поэтому система имеет единственное решение, то есть существует единственная пара чисел h и k, такая что при подстановке x=u+h, y= υ+k правая часть исходного уравнения принимает вид />, а само уравнение: />. Полученное уравнение является однородным
2. Практическая часть
Задача 1. Найти общий интеграл дифференциального уравнения:
/>
Решение:
/>
– дифференциальное уравнение с разделяющимися переменными
Разделим переменные:
/>
/>
Проинтегрируем выражение:
/>
/>
/>
Ответ: />
Задача 2. Найти общий интеграл дифференциального уравнения:
/>
Решение:
/>
/>
/>
/>
Следовательно, исходное уравнение является однородным.
Пусть
/>
Произведём замену в исходном уравнении:
/>
/>— дифференциальное уравнение с разделяющимися переменными
Разделим переменные:
/>
Проинтегрируем а затем пропотенцируем выражение:
/>
/>
Но />/>
/>
/>
Ответ: />
Задача 3. Найти общий интеграл: />
Решение:
/>— дифференциальное уравнение, приводящееся к однородному
/>
Введём новые элементы:
/>,
где h и k должны удовлетворять уравнениям:
/>откуда />
Таким образом:
/>откуда />
Подставляя это в исходное уравнение, получим
/>
Или
--PAGE_BREAK--/>
Сделаем подстановку:
/>
/>
/>
/>
/>-
дифференциальное уравнение с разделяющимися переменными
/>
Упростим левую часть выражения
/>
1+z=A(z-1)+Bz
Z1: 1=A+B A=-1
z: 1=-A B=2
Проинтегрируем уравнение (**)
/>
/>
ln|z|–2ln|z–1|=ln|U|+C
/>
Пропотенцируем и подставим значение z в выражение
/>
Упрощая данное выражение, получим:
/>
/>
Ответ: />
Задача 4. Найти решение задачи Коши:/>/>
Решение:
/>– линейное уравнение
Воспользуемся методом Бернулли:
/>
/>
/>
a) />
Разделим переменные:
/>
/>
Проинтегрируем а затем пропотенцируем данное выражение:
/>
/>
/>
/>
б) />
Разделяя переменные, подставляя значение υ и интегрируя выражение получим:
/>
/>
/>
/>
/>
Следовательно:
/>
Найдём значение С2
y|п/4=1/2
/>
/>
Ответ: />
Задача 5. Решить задачу Коши: />
Решение:
/>
/>
/>
/>— линейное уравнение
Воспользуемся методом интегрирующего множителя:
/>
/>
/>
Ответ: />
Задача 6. Найти решение задачи Коши: />, y(0)=1
Решение:
/>— уравнение Бернулли
Подёлим данное уравнение на (:y2):
/>
Произведём замену и подставим её в исходное уравнение:
z=y-1/>
Следовательно:
/>
/>— линейное уравнение
Воспользуемся методом Бернулли:
/>
/>
/>
продолжение --PAGE_BREAK--/>
/>
Откуда:
/>
Найдём значение С2
/>
Следовательно:/>
Ответ: />
Задача 7. Найти общий интеграл дифференциального уравнения:
/>
Решение:
/>
— дифференциальное уравнение в полных дифференциалах
/>
/>
Следовательно, левая часть уравнения является полным дифференциалом некоторой функции />
/>(*)
Интегрируем по x первое из уравнений (*), при этом считаем, что С является функцией от y:
/>
Дифференцируя полученное, имеем:
/>
Но />
Откуда:
/>
/>
/>
Следовательно:
/>
Ответ:
/>
Задача 8. Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку М.
/>
Решение:
Чтобы решить данное дифференциальное уравнение необходимо построить семейство изоклин, показать на них угол наклона касательных и построить интегральные кривые таким образом, чтобы они пересекали изоклины под соответствующим углом:
/>
Откуда />
/>
В результате получим следующий график:
/>
Задача 9. Найти линию, проходящую через точку Ми обладающую тем свойством, что в любой точке М нормальный вектор />с концом на оси ординат имеет длину равную а и образует угол с положительным направлением оси ординат. М(6;4), a=10
Решение:
/>
/>
/>
/>
/>
/>
/>
/>
Подставляя значения функции в точке Mнайдём значение С:
/>
/>
Ответ: />
Задача 10. Найти общее решение дифференциального уравнения:
/>
Решение:
/>— дифференциальное уравнение третьего порядка
Пусть />
Подставив в исходное уравнение, получим:
/>
/>
Проинтегрируем и поделим на х данное выражение:
/>
Следовательно: />
Разделяя переменные и вновь интегрируя, получим:
/>
Повторяем процедуру в третий раз и получаем искомое выражение для y
/>
/>
/>
Ответ: />
Задача 11. Найти общее решение дифференциального уравнения:
/>
Решение:
Данное уравнение не содержит х в явном виде
Предположим, что /> откуда />
Тогда исходное уравнение будет выглядеть так:
/>
Разделим переменные и проинтегрируем выражение:
/>
/>
продолжение --PAGE_BREAK--Но/>. Тогда />
/>
Однако: />. Поэтому разделим переменные и проинтегрируем выражение:
/>
/>
Выясним значение С2:
/>
Следовательно: />
Ответ: />
Задача 12. Найти общее решение дифференциального уравнения:
/>
Решение:
/>— НЛДУ четвёртого порядка
Решение будет записано в виде:
/>/>
Запишем однородное линейное дифференциальное уравнение (ОЛДУ):
/>
Составим и решим для ОЛДУ характеристическое уравнение:
k4-3k3+3k2-k=0
k1=0
k3-3k2+3k-1=0
k2=1
по методу Горнера:
1 -3 3 -1
1 1 -2 1 0
k3-2k2+1=0
k3,4=1
Общее решение будет равно:
/>
Найдём частное решение:
/>
/>
/>
/>
6A-2Ax-B=2x
/>
/>
Откуда: />
Ответ: />
Задача 13. Найти общее решение дифференциального уравнения:
/>
Решение:
/>— НЛДУ с постоянными коэффициентами
Составим ОЛДУ и решим соответствующее характеристическое уравнение
/>
/>
/>
Решение НЛДУ запишется в виде:/>
Общее решение:/>
Найдём частное решение дифференциального уравнения:
/>
/>
Подставим найдённое в исходное уравнение и выразим коэффициенты
/>
/>
/>=> />
Частное решение: />
Решение дифференциального уравнения:
/>
Ответ: />
Задача 14. Найти общее решение дифференциального уравнения
/>
Решение:
/>— НЛДУ с постоянными коэффициентами
/>/>
Общее решение
/>
Найдём частное решение: />
/>
/>
Подставим найдённое в исходное уравнение и выразим неизвестные коэффициенты:
/>
/>
/>
Частное решение уравнения:
/>
/>=/>/>
Ответ:/>=/>/>
продолжение --PAGE_BREAK--Задача 15. Найти общее решение дифференциального уравнения: />
Решение:
По определению гиперболического синуса:
/>
Найдём общее решение
/>
/>
/>
Найдём частное решение:
/>
/>/>
/>
Подставив в исходные уравнения, найдём значения коэффициентов:
/>
/>
/>
/>
Ответ: />
Задача 16. Решить задачу Коши:
/>, />, />
Решение:
/>— НЛДУ
Общее решение запишем в виде/>
/>
Запишем ОЛДУ и найдём корни его характеристического уравнения:
/>
/>
/>
Общее решение имеет вид: />
Найдём решение частное:
/>,
где С1 и С2– решения системы дифференциальных уравнений
/>
/>
/>
/>
По теореме Крамера:
/>
/>
Интегрируя выражения, получим:
/>
/>
/>
/>
/>
Следовательно, решение будет выглядеть так:
/>
Найдём значения С1 и С2
/>
/>
/>
/>
/>
Ответ: />
Задача 17. Решить систему дифференциальных уравнений
/>
Решение:
Составим матрицу системы:
/>
Составим характеристическое уравнение det(A-λE)=0, то есть:
/>
/>
/>
/>
/>
/>
/>
/>
Найдём собственные векторы
1) />
/>
/>
/>
/>
/>
2) />
/>
/>
/>
/>
/>
/>
Запишем общее решение системы уравнений
/>
/>
/>
/>
/>
Отсюда получаем:
/>
Ответ: />
Задача 18. Найти кривые, у которых точка пересечения любых касательных с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.
Решение:
/>
/>
Но />
/>
/>=> />
Разделим переменные:
/>
Проинтегрируем и пропотенцируем выражение:
/>
/>
Ответ: />
www.ronl.ru
Примерный вариант заданий
1. Вычислить определитель

2. Найти обратную матрицу и выполнить проверку, умножив ее на исходную.
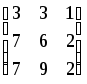
3. Найти ранг матрицы.

4. Решить систему уравнений методом Крамера.
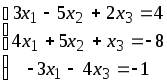
5. Решить систему методом Гаусса.
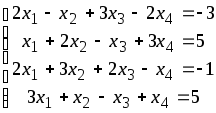
Контрольная работа № 2
Примерный вариант заданий
1.Найти пределы, не используя правило Лопиталя
а) 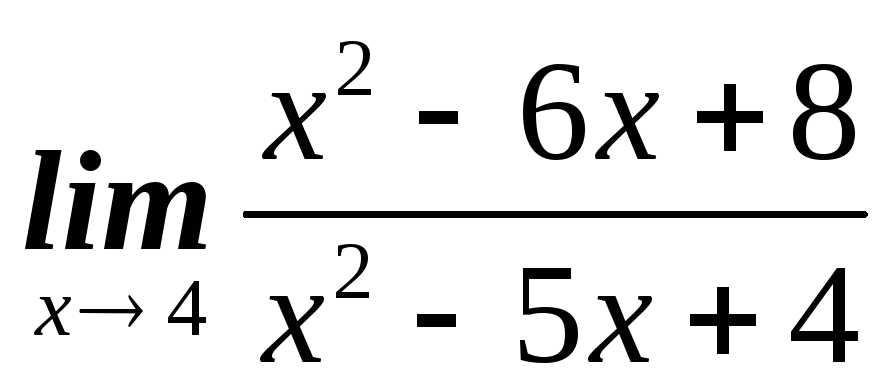 б)
б)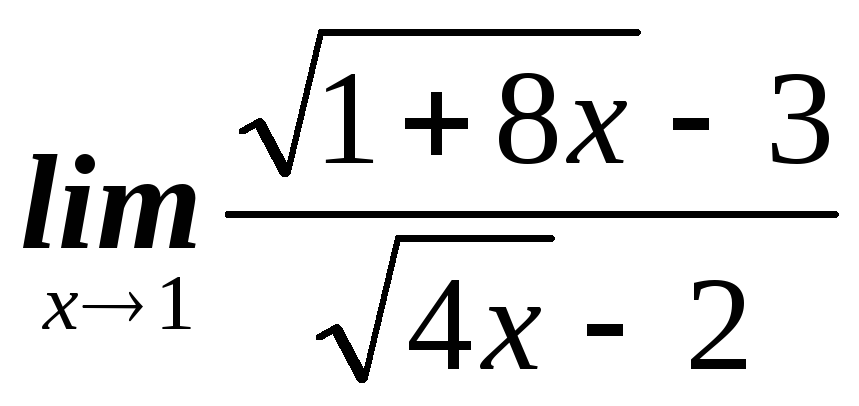
в) 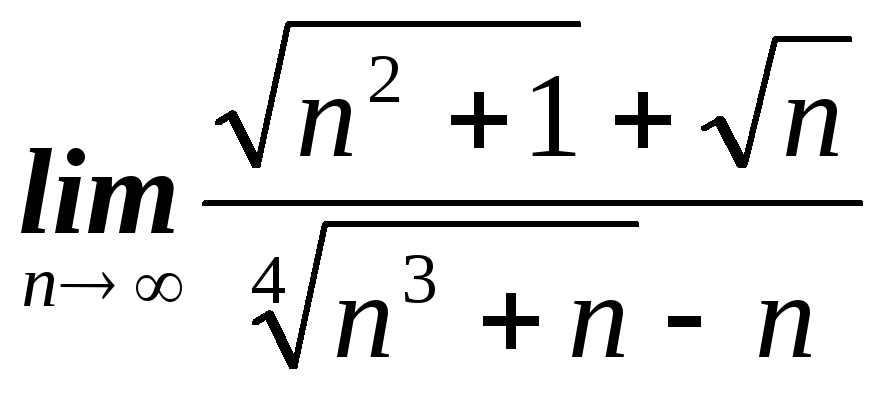
г) 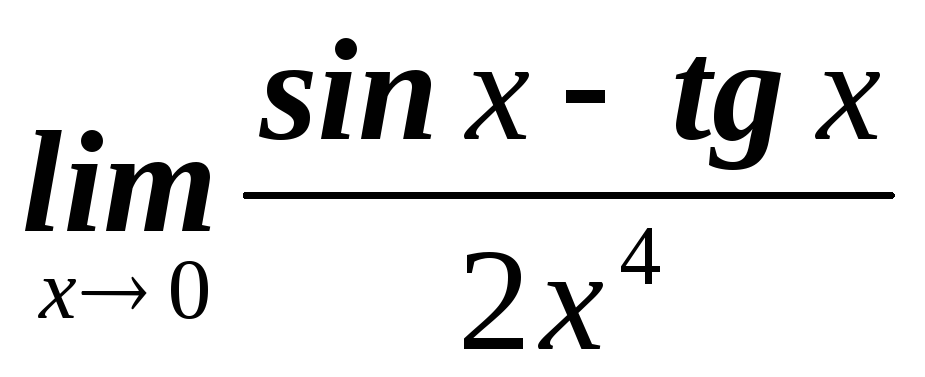 д)
д)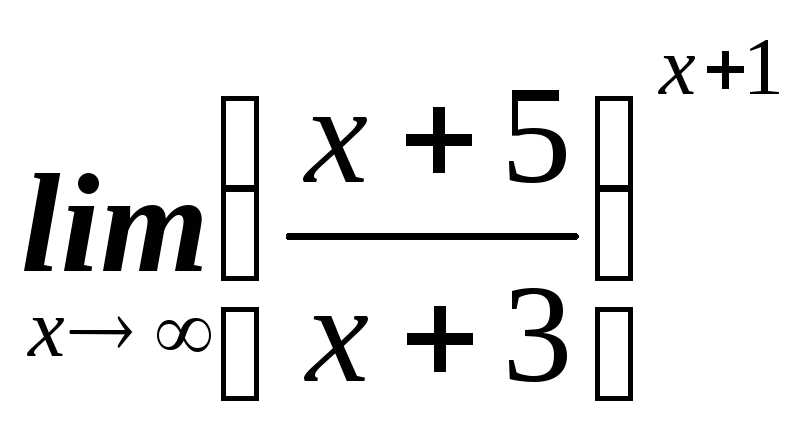
2.Найти пределы по правилу Лопиталя
а) 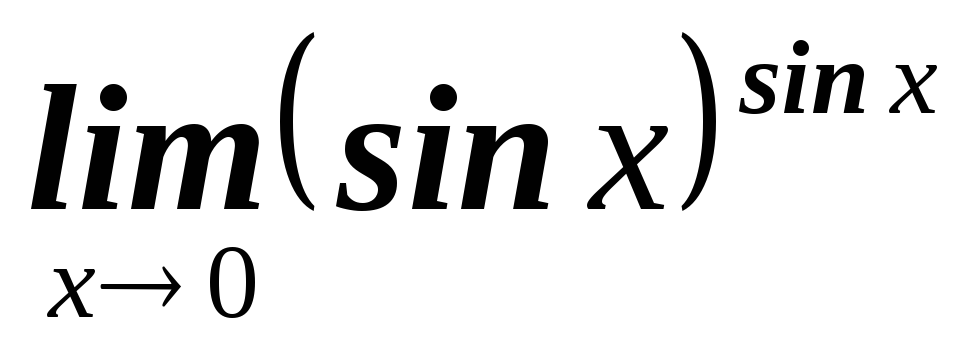 б)
б)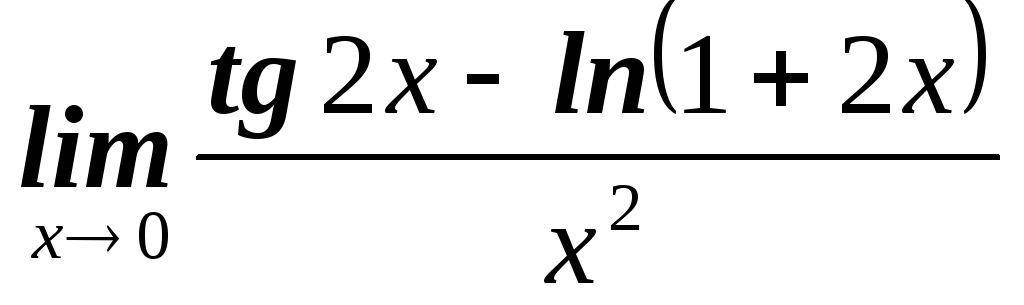
3.Найти производные функций
а) 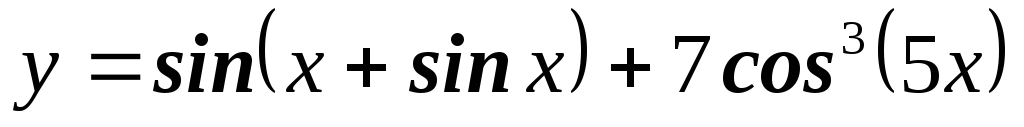
б) 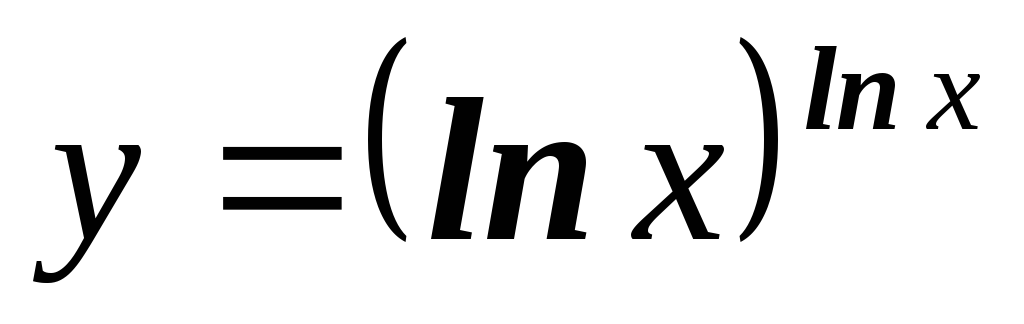
в) 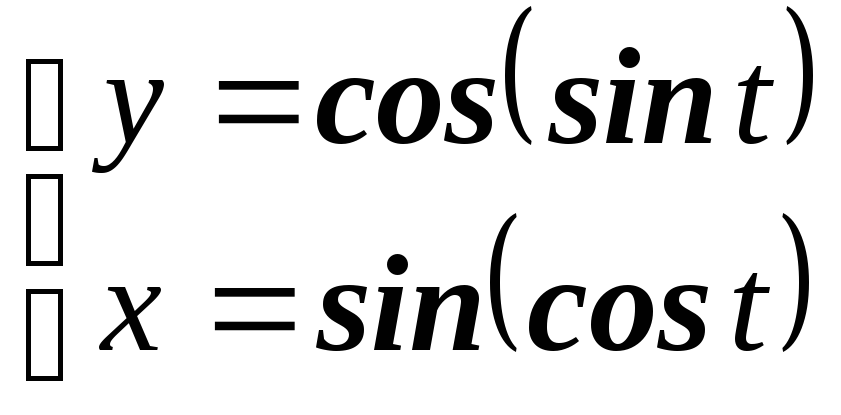
4.Найти вторую производную функции
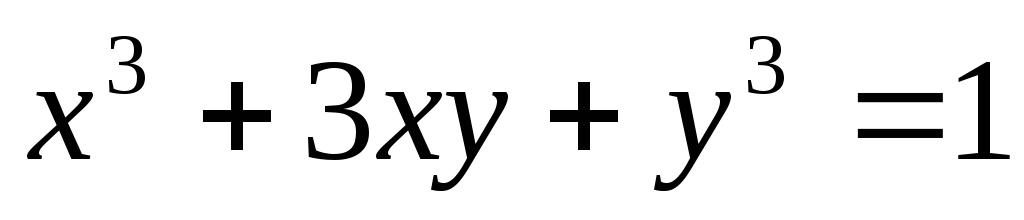
Примерный вариант билета для зачета
1. Вычислить определитель
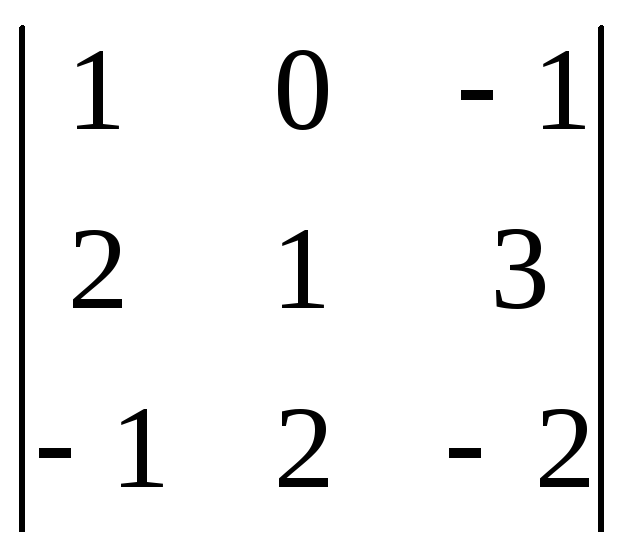
2. Решить систему уравнений методом Гаусса.
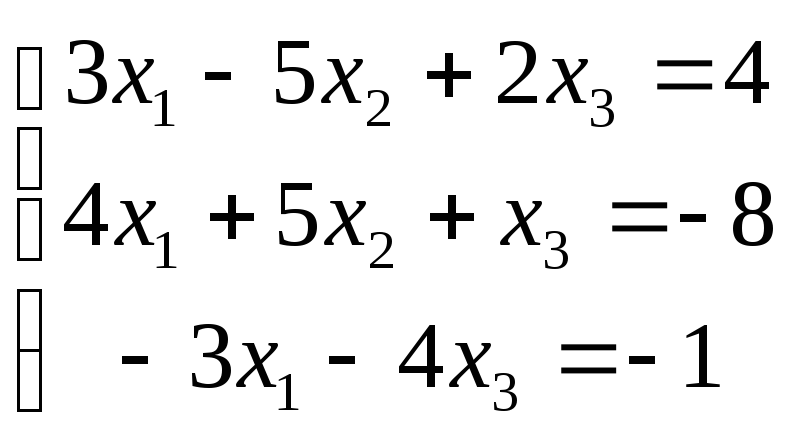
3. Найти пределы
а) 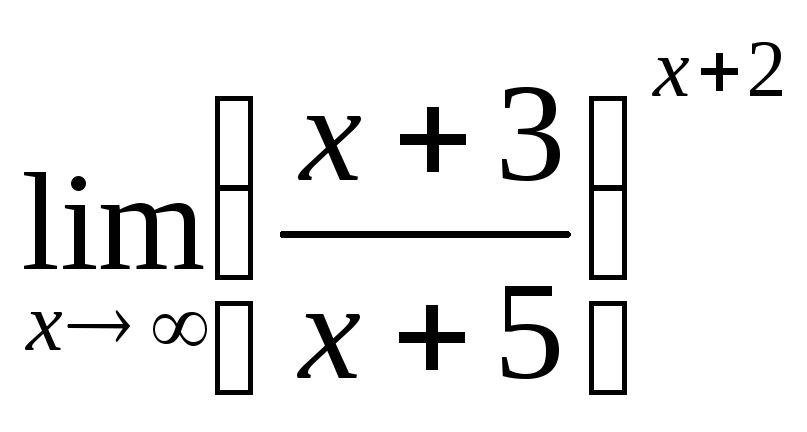 б)
б)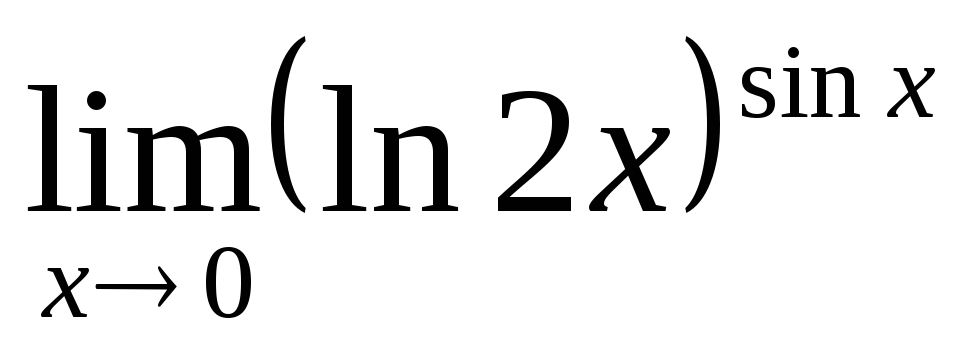
4. Найти производные функций
а) 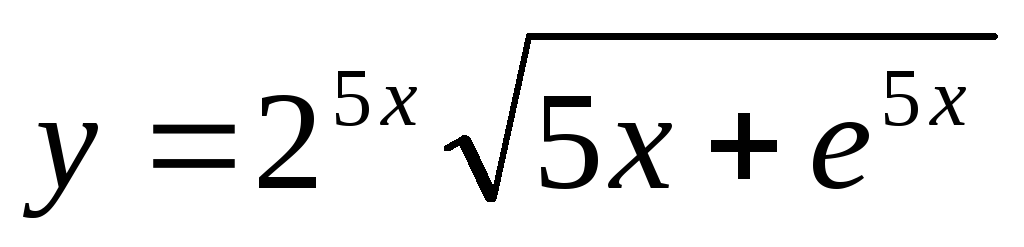
б) 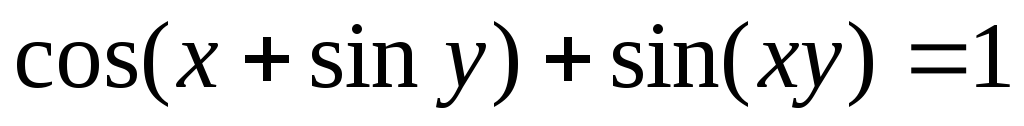
5. Найти
а) 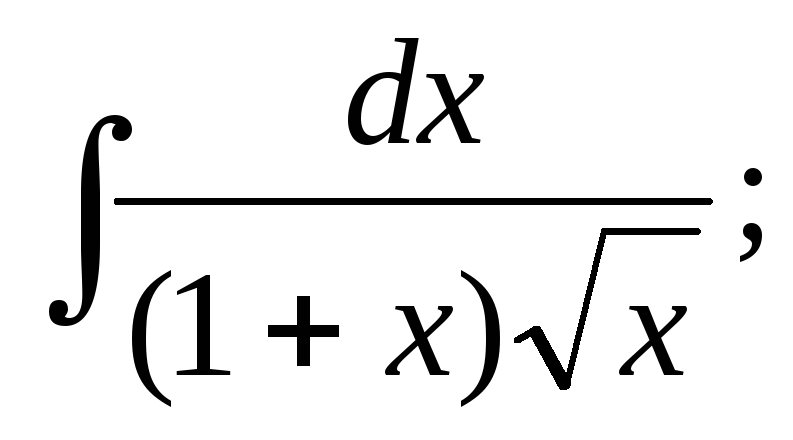 б)
б) 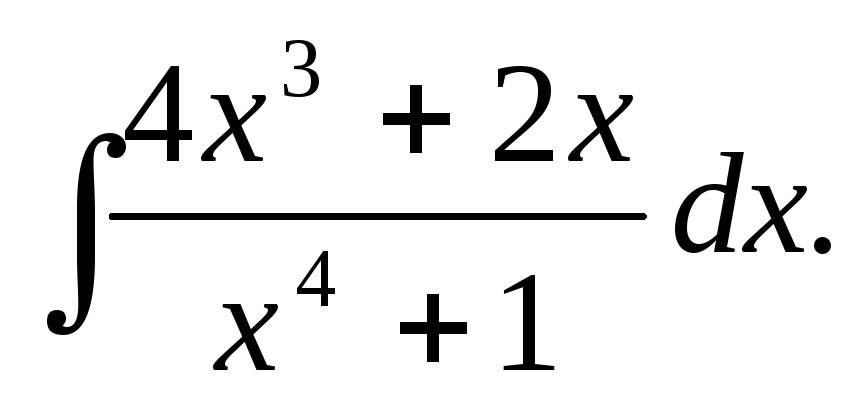
IIсеместр
Содержание лекций
Тема 18. Функции нескольких переменных. Предел и непрерывность. Частные производные. Дифференциал.
Определение функции нескольких переменных. Область определения и область значений функции двух и более переменных. Частные значения аргументов и частное значение функции. Поверхность в пространстве как график функции двух переменных. Предел и непрерывность функции в точке. Полное и частные приращения функции нескольких переменных. Частные производные, их механический смысл. Частные производные высших порядков. Дифференцируемость и полный дифференциал функции нескольких переменных. Достаточное условие дифференцируемости. Частные производные высших порядков. Приложение полного дифференциала в приближенных вычислениях.
Экстремум функции двух переменных. Определение точки максимума (минимума). Необходимое условие экстремума. Достаточное условие экстремума. Наибольшее и наименьшее значения функции двух переменных в замкнутой области.
Условный экстремум. Метод множителей Лагранжа. Функции нескольких переменных в экономической теории.
Определение дифференциального уравнения. Порядок дифференциального уравнения. Решение дифференциального уравнения. Общее и частное решение. Общий вид дифференциального уравнения первого порядка. Другие представления дифференциального уравнения первого порядка. Геометрический смысл общего и частного решений. Общий интеграл. Начальные условия для нахождения частного решения дифференциального уравнения первого порядка и их геометрический смысл (задача Коши). Дифференциальные уравнения с разделяющимися переменными и их решение. Дифференциальные уравнения первого порядка, разрешенные относительно производной, с правой частью – однородной функцией нулевого порядка.
Линейные неоднородные дифференциальные уравнения 1 – го порядка. Метод Бернулли. Метод Лагранжа вариации произвольной постоянной. Структура общего решения.
Общее и частное решения дифференциального уравнения второго порядка. Линейные однородные дифференциальные уравнения второго порядка. Однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение. Фундаментальная система решений. Общее решение. Линейные неоднородные дифференциальные уравнения второго порядка. Нахождение общего решения и частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и специальной правой частью уравнения.
studfiles.net